The Distribution Coefficients of Major and Minor Elements in Coral Skeletons Under Variable Calcium Seawater Concentrations

Coral skeletons are one of the best archives for past ocean seawater (SW) chemistry and isotopes. However, the distribution coefficients of major and minor elements in coral skeletons are not well determined. In this study, we launched an experiment to determine the distribution coefficients of multiple elements in corals’ skeletons by changing Ca concentrations in SW (Ca_SW). Two scleractinian corals, Pocillopora damicornis and Acropora cervicornis were cultured in modified Gulf of Eilat water (Red-Sea) with Ca_SW of approximately 10, 15, 20, and 25 mM. After almost three months, the newly grown skeletons were analyzed for the following elements: Li, Na, Mg, K, Sr, and Ba. Their ratios to Ca in the coral skeleton (El/Ca_coral) increased linearly with El/Ca_SW (with R² values above 0.98), crossing the origin and thus indicating constant distribution coefficient for each element over the experimental range of El/Ca_SW. The values of D_El were in good agreement with values reported for corals collected in natural seawater. However, differences were observed between the two species, and both were slightly deviating from inorganic aragonite D values. These deviations are well explained by Rayleigh fractionation process in the calcifying fluid (assuming it is mainly seawater). This was observed both for elements with D > 1 (Ba and Sr) and D < 1 (Li, Mg, Na, and K). P. damicornis showed open system behavior (∼20% of its Ca utilized) while A. cervicornis showed more closed calcifying reservoir (∼50% of its Ca utilized). The finding that the distribution coefficients of the six minor and trace elements are constant for a given species, should help in the reconstruction of past seawater chemistry based on multielement measurements in fossil corals. In particular, Na/Ca_coral can be used to reconstruct past ocean Ca concentrations and with El/Ca_coral ratios for other elements, their concentrations for the Cenozoic can be reconstructed.

Introduction

The changes in the elemental composition in Scleractinian corals skeletons, provide important archive and proxies for reconstructing ancient seawater (SW) chemistry. It is recognized, that the uptake and partition of elements that coprecipitate with CaCO₃ of coral skeleton, changes in response to biotic and abiotic factors e.g., temperature (Beck et al., 1992; Mitsuguchi et al., 1996; Cohen et al., 2001; Gaetani and Cohen, 2006; Gaetani et al., 2011), calcification rates (Livingston and Thompson, 1971; Mitsuguchi et al., 2003), and particularly SW chemistry (Goreau, 1959; Swart, 1981; Shen and Boyle, 1987, 1988; Lough and Barnes, 1990; Fallon et al., 2002; Alibert et al., 2003; Giri et al., 2018). Thus coral skeletons provide an important archive on long-term changes in SW chemistry (e.g., Gothmann et al., 2015), together with fluid inclusions in marine evaporites (Hardie, 1996; Horita et al., 2002). The majority of previous coral trace element studies have concentrated on Sr/Ca, Mg/Ca, and Ba/Ca that have long residence time (1–10 Ma) and are part of the conservative elements that show a constant ratio in SW. Therefore, changes in their ratios were ascribed mainly to abiotic factors e.g., Sr/Ca and Mg/Ca for sea surface temperature (Beck et al., 1992; McCulloch et al., 1994; Cohen et al., 2001; Marshall and McCulloch, 2002; Fallon et al., 2003), Ba/Ca for SW barium, oceanic upwelling and rivers runoff (Lea et al., 1989; Sinclair, 2005; LaVigne et al., 2011, 2016). On longer time scales (>10 Ma) these elemental ratios depend on SW chemistry that has changed over the phanerozoic (Ries, 2004; Gothmann et al., 2015 and references therein). Contrary to Sr/Ca, Mg/Ca, and Ba/Ca the ratios of Li/Ca, K/Ca and Na/Ca in coral skeletons received much less attention (Amiel et al., 1973; Mitsuguchi et al., 2010; Mitsuguchi and Kawakami, 2012; Rollion-Bard and Blamart, 2015; Yoshimura et al., 2017; Marchitto et al., 2018) even though they are the major or minor elements in SW and have measurable abundances in the skeletons. Combining both Li/Ca and Mg/Ca increased the significance of Mg/Li as a paleothermometer in corals (Hathorne et al., 2013b; Montagna et al., 2014; D’Olivo et al., 2018; Marchitto et al., 2018; Cuny-Guirriec et al., 2019). Recently a new palaeoceanographic proxy for reconstructing Ca concentration in ancient SW was introduced based on Na/Ca in foraminiferal calcitic shells (Hauzer et al., 2018). It was shown that the partition of Na into foraminifera shells is primarily related to the SW Na/Ca ratio, with no resolvable temperature sensitivity. In view of this novel potential proxy in foraminifera, and the measurements of Na/Ca in recent and fossil coral skeletons (e.g., Bar-Matthews et al., 1993; Mitsuguchi et al., 2010; Gothmann et al., 2015; Yoshimura et al., 2017), in the present study, we investigated the effect of elevated Ca_SW concentration on the partition of Li, Na, Mg, K, Sr, and Ba into the skeletons of the hermatypic corals Pocillopora damicornis and Acropora cervicornis.

Materials and Methods

Laboratory Culturing

Pocillopora damicornis and Acropora cervicornis mother colonies (raised for 8 years at Red Sea Fish Ltd. aquaculture facility) were cultured in the laboratory for 1 month before the experiment. The corals were held in 500 L recirculated system, running with filtered (1 μm polystyrene filter) Gulf of Eilat SW (salinity 40.65 ‰ diluted to a salinity of 35 ‰). Once a week, 10% of the system water was renewed to sustain chemical stability. The system was illuminated by LED lights (Reef Led 90, Red Sea) providing irradiance of 350 μmol photons m^–2 s^–1 for a light dark cycle of 12:12 h. Two experiments (labeled as exp1 and exp2) were conducted for 80 and 87 days, respectively. Each experiment included four groups, cultured in different calcium concentrations (Ca_SW) of ∼ 10, 15, 20, and 25 mM (Table 1). In the first experiment, each group included five P. damicornis fragments (∼ 1 cm in length; mean wet weight 187 ± 11 mg fragment^–1) and five A. cervicornis (∼ 1 cm in length; mean wet weight 205 ± 12 mg fragment^–1). In the second experiment, each group included ten P. damicornis fragments obtained from different mother colony than those of the first experiment (∼ 1 cm in length; mean wet weight 201 ± 25 mg fragment^–1) (Table 1). Each fragment, after weighing, was glued with ethyl cyanoacrylate glue (Scotch super glue gel, 3M United States) to the center of a microscope glass slide (Figure 1A). The slides were wet weighed again in order to subtract the cyanoacrylate and primary fragment weight, to assess the new skeleton growth at the end of the experiment. Each group was placed in an individual 75 L aquarium system, running with modified Gulf of Eilat SW (S = 35 ‰, Ca_SW ∼10.3 mM). Corals were fed weakly with liquid coral food (Reef Energy, Red Sea) and the water of each aquarium was circulated through a foam fractioner to remove excess DOC and aerate intensively the water. The first group was set as a control, and the Ca_SW level in each experimental group was modified using CaCl₂ anhydrous powder (99.99% trace metal basis, Sigma Aldrich) to a final concentration of approximately 15, 20 and 25 mM (Table 1). The carbonate chemistry was not modified, except for the dilution of alkalinity and DIC proportionally to the salinity and exchange with air CO₂. During the experiments, the aquaria were tightly covered with transparent plastic foil to minimize evaporation and the salinity was monitored daily with conductivity meter (WTW, multi 3620 IDS, Tetracon 325C conductivity probe, K = 0.475 cm^–1). The salinity of the aquaria was slightly elevated by the addition of CaCl₂ (Table 1). All other experimental conditions were kept approximately the same. O₂ and pH were measured weekly using WTW multi 3620 IDS (WTW optical IDS dissolved oxygen FDO 925; WTW IDS pH- electrodes Sentix 940, calibrated with Radiometer NBS certified buffers and the values are reported using the NBS scale). Note that the system was essentially open to the atmosphere (with aeration) and this kept the O₂ and pH relatively constant (Table 1). Total alkalinity (A_T) measurements were done weekly using an automatic potentiometric Gran titration beyond the second endpoint (Schneider and Erez, 2006) of roughly 5 g SW sample accurately weighed. The acid used was 0.025M HCl (ACS reagent 37%, Sigma Aldrich), and the titrator used was Metrohm 848 Titrino plus (Metrohm, Switzerland) with a precision of 0.008 mmol/Kg. Standard seawater reference solution (Scripps Institution of Oceanography, batch 173) was used to calibrate the A_T measurements. Using CO2SYS (Pierrot et al., 2006) we calculated the relevant carbonate chemistry parameters, including Ω_aragonite taking into account the Ca concentrations and the salinity changes caused by the addition of anhydrous CaCl₂. The data is summarized in the Supplementary Table 1.

TABLE 1

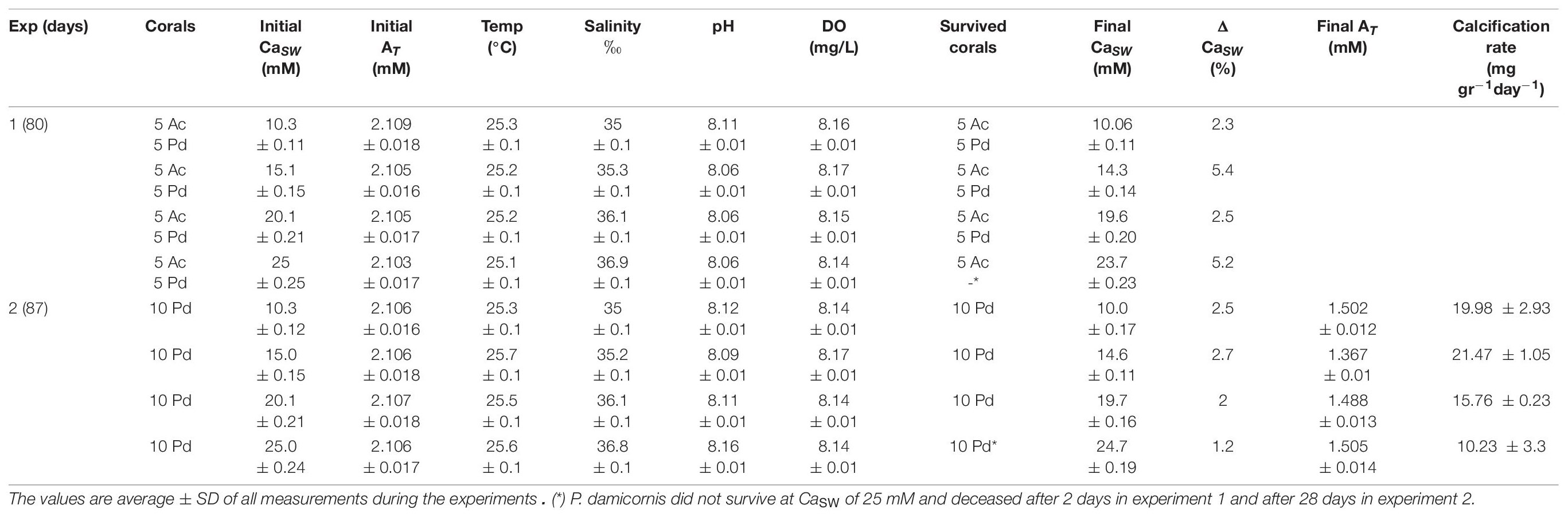
Table 1. Variable Ca_SW experimental conditions for coral culture (Ac is Acropora cervicornis; Pd is Pocillopora damicornis).

FIGURE 1

Figure 1. (A) P. damicornis fragment glued to a microscope slide. (B) New skeleton grew horizontally under the experimental conditions (white arrow).

Calcification Rates Measurements

Once a week, water samples were taken from each aquarium for elemental analysis and alkalinity measurement (in experiment 2 only). Calcification rates were calculated from the difference in A_T measured at the beginning and the end of the experiment. Calcification rates were calculated according to the calcification equation (Schneider and Erez, 2006) and reported in units of μmol CaCO₃ gr^–1 day^–1 :

$$Calcification\left(\mathrm{\mu }molCaC{O}_{3}g{r}^{-1}da{y}^{-1}\right)=\frac{\frac{\mathrm{△}{A}_T}{2}\times \left(V_{chamber}-V_{coral}\right)\times 1.0264}{T\times CWW}(1)$$

Where V_chamber (L), is the volume of the experimental chamber and V_coral (L) is the displacement volume of the coral, T is time in days and C_WW is the live coral wet weight (mg). Since culturing aquarium is ∼ 20,000 times larger than the coral fragments, the fragments volume is negligible.

Sample Preparation

At the end of the experiment (80 and 87 days), the slides were cleaned from any residual algae or bio-film with fine brush, without disturbing the newly grown horizontal section of the skeleton. After cleaning, the slides were wet weighed again and the tissue was removed with an airbrush and collected for further analysis. The slides with the remaining skeletons were treated with 5% NaOCl solution (Reagent grade 4.99%, Sigma Aldrich) for 8 h. to remove any residual organic tissue. Thereafter, the slides were thoroughly rinsed with DDW (18.18 MΩ cm) and finally moved to sonication bath containing DDW for 5 min. Finally, the slides were left for further 12 h. in DDW to remove residual SW and NaOCl solution from its cavities. After drying the slides in the oven (70°C for 24 h) the newly grown flat skeleton (Figure 1B) was carefully removed from the glass with a scalpel and spatula under a binocular. Part of the collected skeleton fragments were weighed, crushed and homogenized with a mortar and pestle. Roughly 50 mg of the homogenized skeleton powder (accurately weighed), was then dissolved in 10 ml 5% HNO₃ (≥ 99.999 Trace metal basis, Sigma Aldrich) for elemental analysis.

Elemental Analysis SW and Skeleton

Trace elements concentrations in the newly grown skeleton and the SW were analyzed by ICP-OES (Spectro Arcos II, Ametek Germany) for major and minor elements (Li, Na, Mg, K, Ca, Sr, and Ba). All samples were measured in duplicates without any further dilution using specific methods developed for enriched Na and enriched Ca matrixes. SW Elemental concentrations were determined from calibration curves validated by external standards (OSIL IAPSO standard P139, United Kingdom and High Purity Standards SW reference, United States) and by an internal Sc standard, once every 5 samples. Coral skeleton’s elemental analysis was determined from calibration curves generated from 5 multi element standard solutions containing 2000 mg/L Ca as matrix to match the CaCO₃ samples (Custom blends, High Purity Standards, United States). The Standard solutions minor and trace elements ranges included the average concentration of the elements in coral skeletons as described in the literature (Table 2). Complete analytical conditions including wavelengths, interferences, standard deviations and errors, as well as ICP-OES parameters are summarized in the Supplementary Table 2. The standard errors of the ratios to Ca in the SW and corals were Li/Ca = 0.927%, Na/Ca = 1.01%, Mg/Ca = 1.01%, K/Ca = 1.03%, Sr/Ca = 0.906%, Ba/Ca = 1.19% calculated from the duplicates.

TABLE 2

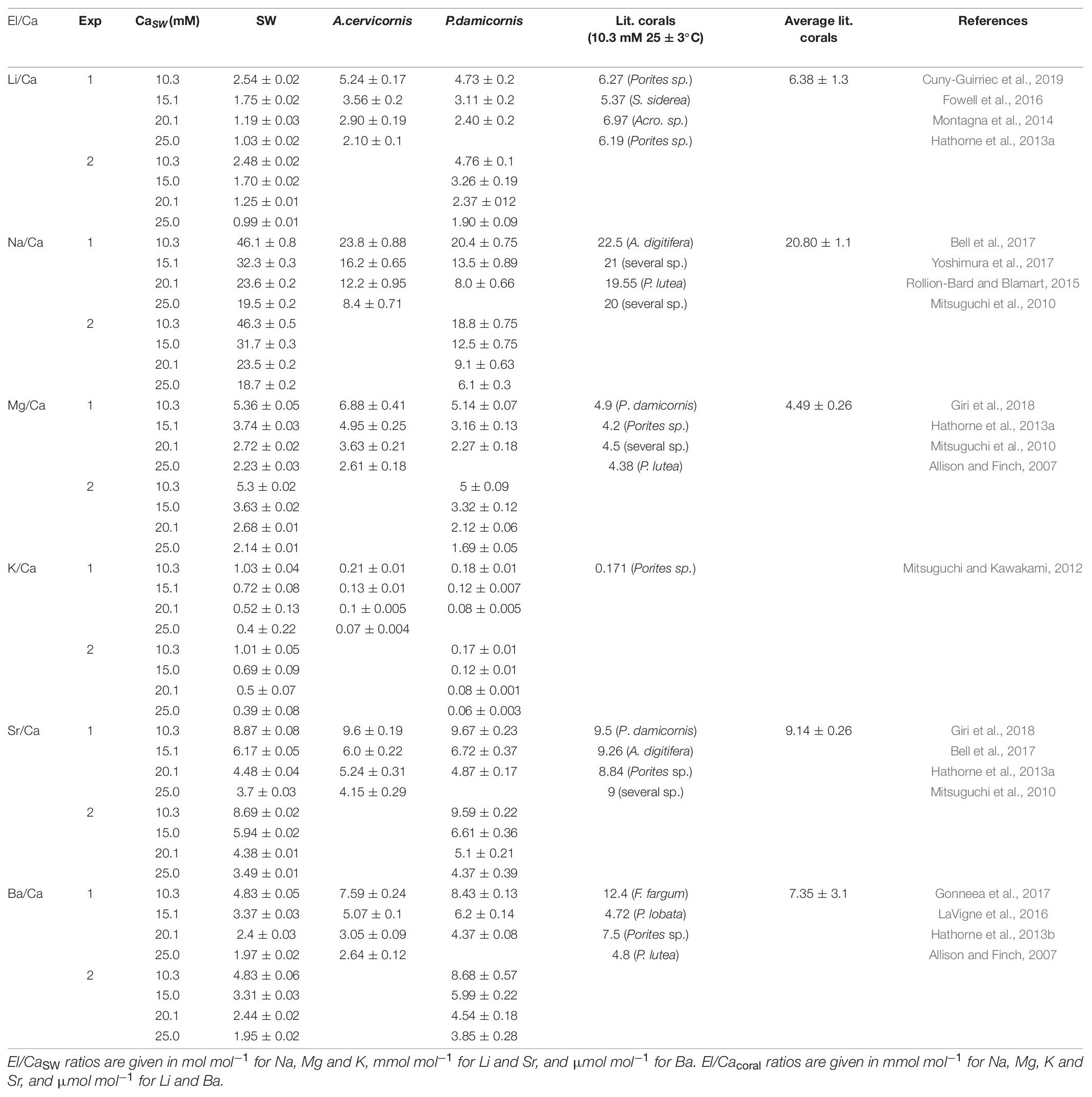
Table 2. El/Ca ratios in SW, new skeleton precipitated under the experimental conditions and the comparison to reported ratios in the literature.

Statistical Analysis

The influence of changing Ca_SW on the partition of elements in the coral skeleton was determined by linear correlation using Pearson correlation coefficients (r). P-Values below 0.05 were considered statistically significant unless otherwise noted. The variance in calcification rates and the variance in D_El between the two coral species and literature inorganic aragonite were determined by one-way ANOVA (Tukey-Kramer). Statistical analyses were performed using Origin Pro software for Windows (Version 2017, OriginLab, Inc.).

Results

Calcification Rate

Total growth and calcification rates were measured only in experiment 2 and were estimated by cumulative alkalinity depletion and by the change in the total coral fragments weight. Both methods were well correlated (R² = 0.989; p < 0.01) for P. damicornis fragments that were grown in Ca_SW of 10.3, 15.0, and 20.1 Mm (Table 1 and Figure 2). Based on the weekly A_T measurements, the corals calcification rates were quite uniform throughout the experiment despite the decrease in A_T (Supplementary Table 1 and Supplementary Figure 1). The average calcification rates were significantly different between the Ca groups with highest daily CaCO₃ addition at Ca_SW of 15.0 mM (21.47 ± 1.05 mg gr^–1 day^–1), followed by 10.3 mM (19.98 ± 2.93 mg gr^–1 day^–1), 20.1 mM (15.76 ± 0.23 mg gr^–1 day^–1) and the lowest CaCO₃ addition was observed at 25.0 mM (10.23 ± 3.3 mg gr^–1 day^–1) (Figure 2). Further to the low calcification rates, at Ca_SW of 25.0 mM corals fragments did not survive beyond the 28th day into the experiment. Note, however, that alkalinity depletion in this high calcium experiment was 5 times greater than the weight increase caused by inorganic precipitation of CaCO₃ in the aquarium. CO2SYS calculations showed that Ω_aragonite has changed during the experiment as A_T decreased. While this could have affected the values we report, we have no way to separate the effects of Ω_aragonite on the results using our sampling method. Therefore, our results represent an average of the Ω_aragonite for the entire experiment.

FIGURE 2

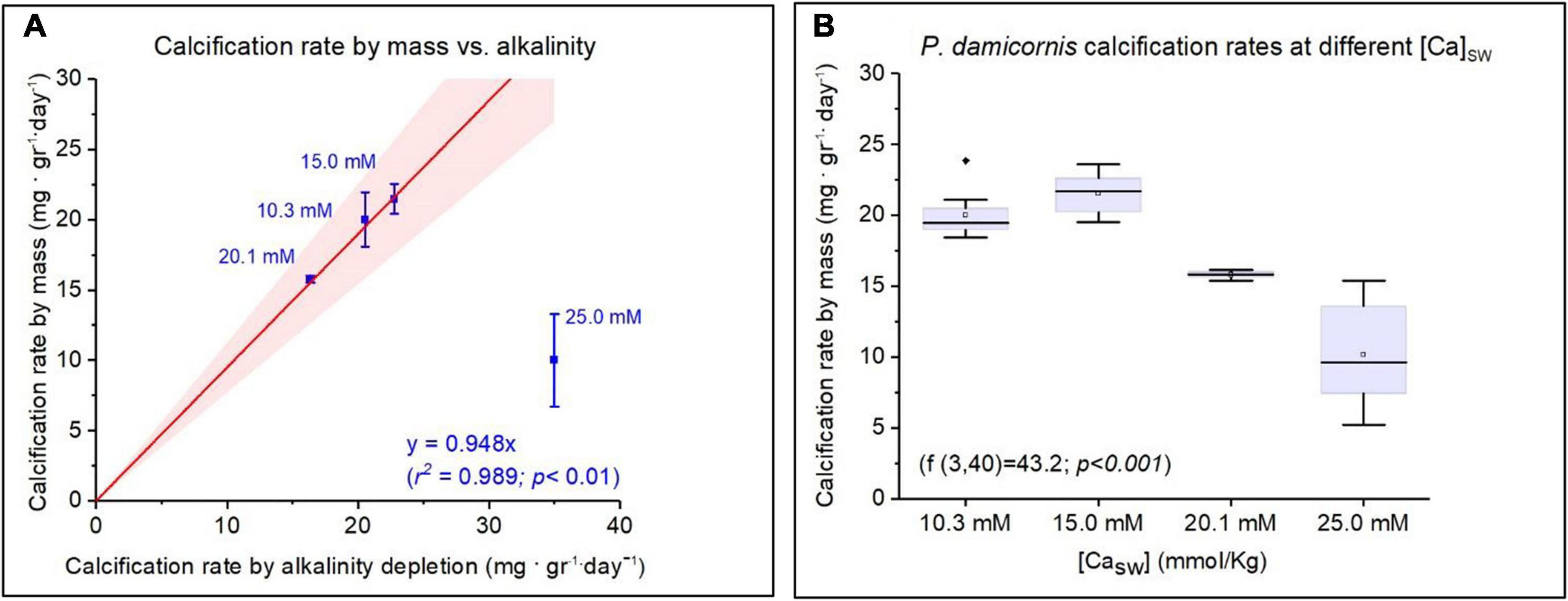
Figure 2. Calcification rates of Pocillopora damicornis under variable Ca_SW. (A) Calcification rate measured by mass addition compared to alkalinity depletion. Corals cultured under Ca_SW of 25 mM are excluded from the regression due to mortality on 28th day. (B) The Mean, median, and deviations of growth rate as a function of Ca_SW with maximum values showed at 15 mM (21.5 ± 1.05 mg. gr^–1. day^–1).

Skeleton Chemistry and Distribution Coefficients

Corals skeletal El/Ca (El/Ca_Coral) of the cultured groups and the culturing SW El/Ca (El/Ca_SW), are presented in Table 2 and Figure 3. The distribution coefficients for these elements (D_El) are the slopes of the linear regressions in Figure 3. These experimental values are compared to published natural and experimental coral values and to inorganic experimental values, are shown in Table 3. The natural coral D_El were normalized for 25 ± 2°C as both Sr and Mg are influenced by temperature. All conservative elements (Li, Na, Mg, K, Sr, and Ba) in the coral skeleton (El/Ca_coral) were positively correlated with Ca_SW for both species (Figure 3). The regression curves are linear, cross the origin and are highly significant with R² values of 0.99–0.98 (ρ values lower than 0.01 or 0.001; Figure 3). The distribution coefficients (D_El) are therefore constant and equal to the slope of El/Ca_coral and El/Ca_SW line. It is significant that the two separate experiments gave very close values for P. damicornis. which could be fitted with one linear equation. For both coral species, the obtained D_El values for Li, Mg, Na and K were lower than 1, in the range of 10^–4 to 10^–3, while for Sr and Ba, D_El values were higher than 1 (Table 3). D_El values between the two species shows significant difference (ρ > 0.05) between A. cervicornis and P. damicornis, with higher values for A. cervicornis for most elements excluding Ba and Sr (Figure 3). The significant difference between species is seen also for literature values (see values and references in Table 3). Coral D_El values show similar values for most elements as determined from inorganic experiments, excluding Li that shows D_inorganic > D_Coral and K that shows D_inorganic < D_Coral (Figure 4). These small but significant differences between the inorganic D_El values and the corals in our and other experiments may well be explained using Rayleigh fractionation model (see discussion).

FIGURE 3

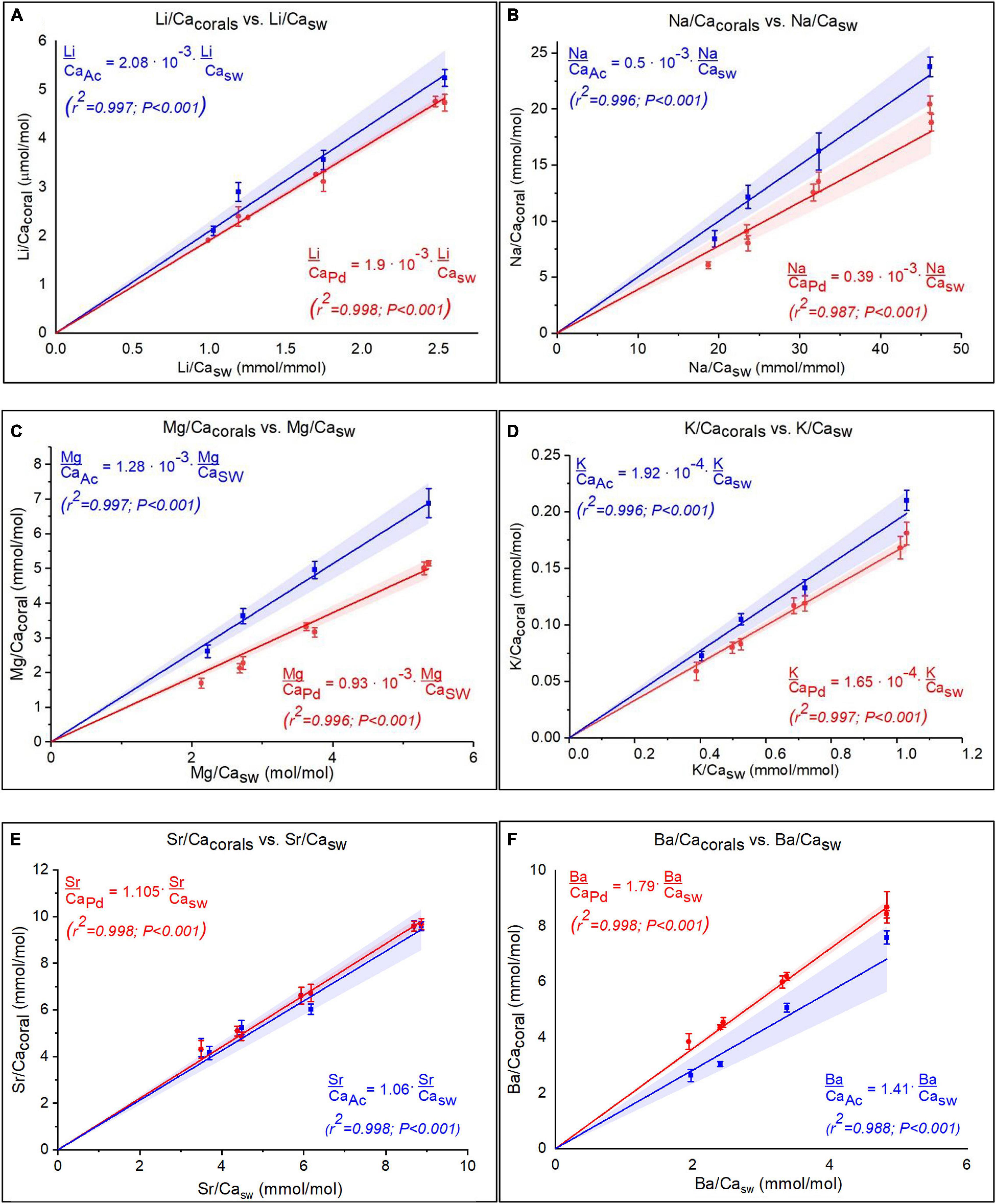
Figure 3. (A–F) El/Ca_coral as function of El/Ca_SW under variable Ca_SW for both species, for six elements (Pocillopora damicornis in red and Acropora cervicornis in blue). The regressions show linear positive correlations for all elements. Note that for P. damicornis data for two separate experiment are shown with slight differences that are within the error on the replicates. The linear regressions that cross the origin imply constant distribtion coefficient for all elements. The shaded area is the 95% confident bands.

TABLE 3

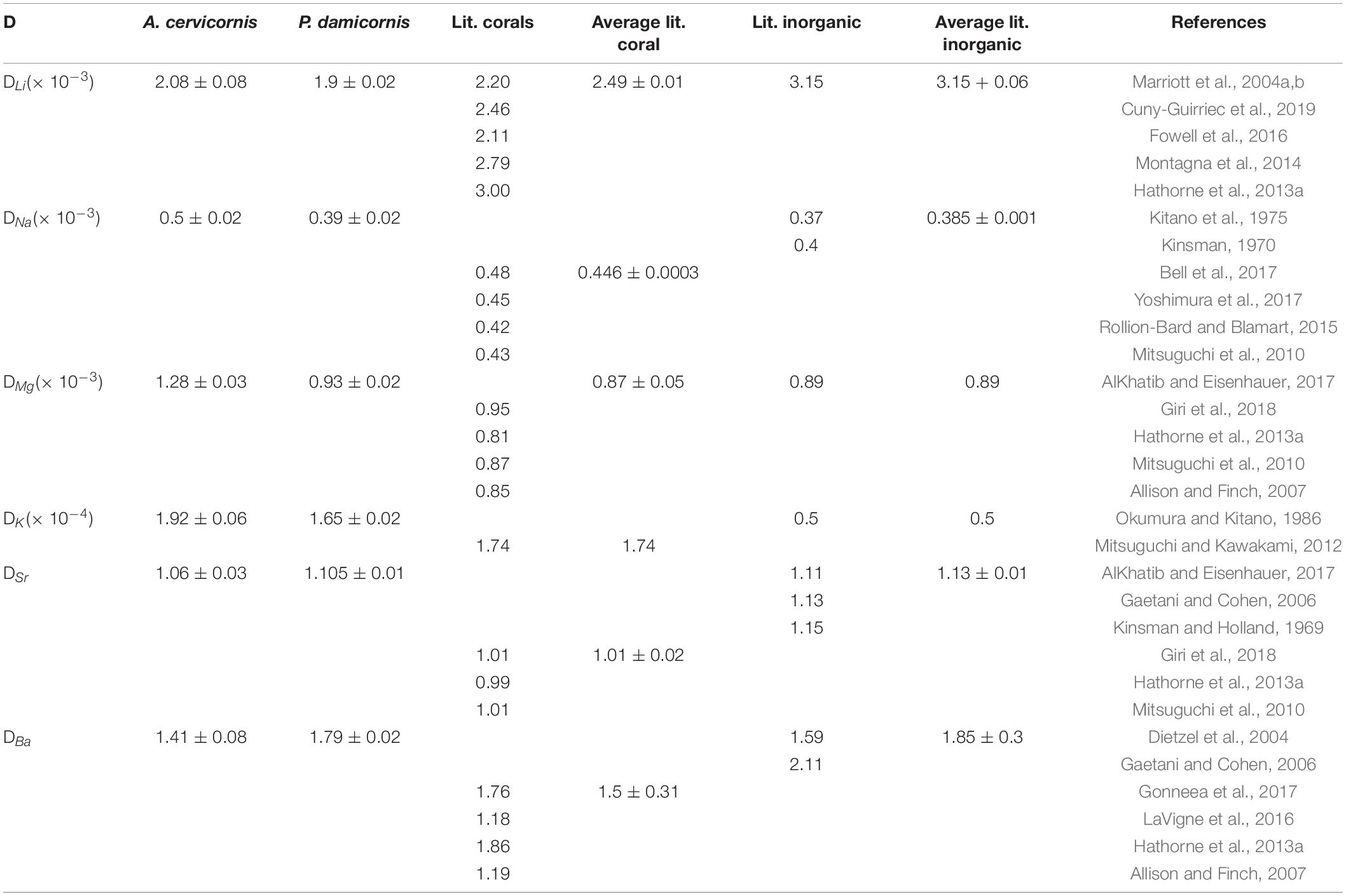
Table 3. D_El values for experimental corals compared to various coral species (field collected and experimental normalized to 25 ± 3°C) and inorganic studies.

FIGURE 4

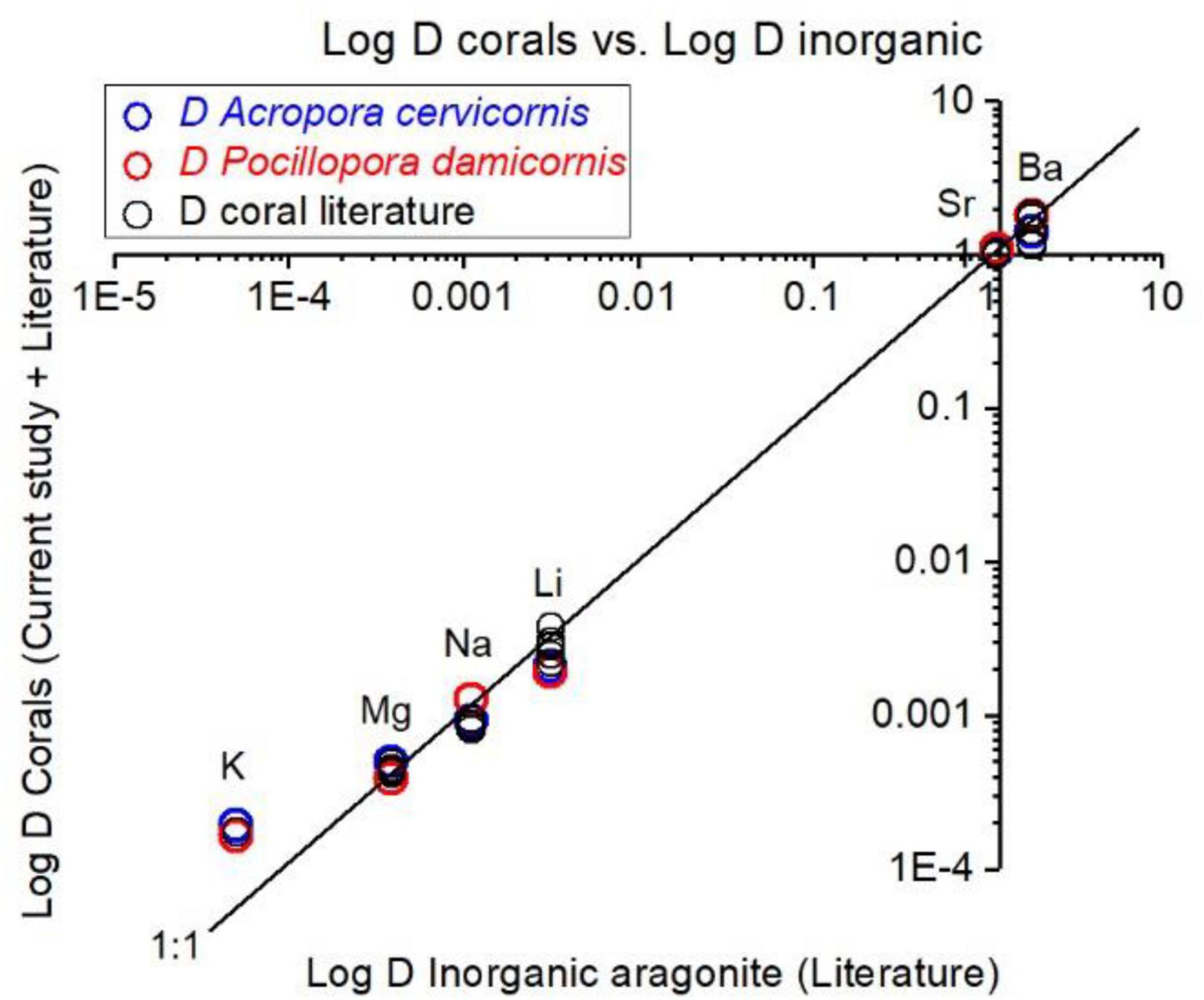
Figure 4. Experimental D_El values and literature values for corals, compared inorganic D_El of aragonite. Our coral D_El values agree well with literature coral values. For Ba, Sr, Mg, and Na the coral values are close to inorganic D values. For Li, inorganic D is higher than values in our experiments and for most of field collected corals (25°C). For K, inorganic D value is significantly lower than all corals. Suggested explanations for these discrepancies are explained in the section “Discussion.”

Discussion

Ca_SW Influence on Calcification Rates

A few studies have investigated the effect of Ca_SW on corals calcification rates (Yamazato, 1966; Chalker, 1976; Swart, 1979). They found that calcification rates increased with Ca_SW but Giri et al. (2018) did not observe such effect. This study demonstrates that calcification in P. damicornis increased up to 15 mM, but further increase to 20.1 and 25 mM decreased the calcification (Figure 2). Furthermore, it seems that the highest Ca_SW concentration caused severe stress that led to mortality of all corals after 28 days (experiment 2). In experiment 1 all the P. damicornis fragments deceased after 2 days in 25 mM Ca but A. cervicornis fragments survived at that concentration but the growth rates were not measured and visual observation of the horizontal growth was minimal. The inhibitory effect of high Ca_SW (> 15 mM) on calcification was documented also for A. cervicornis, A. formosa and A.squamosa (Chalker, 1976; Swart, 1979). Similar observations were made on the foraminifer O. ammonoides (Hauzer et al., 2018). Our experiment suggests that calcification rates do not influence coral D_El for Li, Na, Mg, K, Sr, and Ba.

The Effect of El/Ca_SW on El/Ca_coral

It is well documented that alkaline earth metals (Mg, Sr, and Ba) coprecipitate into corals skeletons as cations substituting for Ca (Livingston and Thompson, 1971; Amiel et al., 1973; Howard and Brown, 1984; Shen and Boyle, 1987, 1988; Sholkovitz and Shen, 1995; McCulloch et al., 2003). Alkali elements (Na, K, and Li) in coral skeletons were also measured (Mitsuguchi et al., 2010; Mitsuguchi and Kawakami, 2012; Hathorne et al., 2013a, b; Rollion-Bard and Blamart, 2015; Yoshimura et al., 2017). However, except for the early work of Swart (1979; 1981 for Sr, Mg, and Na) and the recent work of Giri et al. (2018 for Sr and Mg), we present here the most comprehensive experimental study to determine D values for Li, Na, Mg, K, Sr, and Ba in coral skeleton by changing El/Ca_SW. This experiment was carried out on two species, P. damicornis and A. cervicornis, over a large range of Ca_SW (10.3–25 mM). El/Ca_coral and El/Ca_SW in the control group (10.3 mM), were similar to those from field collected corals (Table 2) except for Li/Ca_coral where our values (∼ 5 μmol mol^–1) were lower than average field data (6.38 ± 1.3 μmol mol^–1). The source of this discrepancy is not clear but part of it may be related to the analytical procedure of the skeleton. It is also possible that this may be temperature related response of the two species used in this experiment (Montagna et al., 2014; D’Olivo et al., 2018; Cuny-Guirriec et al., 2019). For all elements we observe highly significant positive correlation between El/Ca_coral and El/Ca_SW under increased Ca_SW (Table 2 and Figure 3). These results agree with previous study showing such correlations under variable Ca_SW (Giri et al., 2018). The pioneering work of Swart (1981) who cultured four species under four variable Ca_SW and measured Sr, Mg, and Na in their skeletons agrees with our results, mainly for Sr (given the use of EPMA for the skeletal analysis with low sensitivity for concentrations lower than 1%). In inorganic precipitation experiments for aragonite, the El/Ca ratio increased for the alkali ions Li, Na, and K, with increasing their concentrations relative to Ca in the parent solution (Kitano et al., 1975; Okumura and Kitano, 1986). These results agree with our data for both species (Table 2 and Figure 3). However, the actual concentrations in the aragonite were similar to the coral values only for Na while for Li the inorganic values were higher, and for K, they were lower. Given that the inorganic experiments were not done in seawater and that kinetic effects are also possible there is a general agreement between the corals and the inorganic experiments.

D_El Values

For all the elements measured in this study (Li, Na, Mg, K, Sr, and Ba) we observe significant linear regression between El/Ca_coral and El/ Ca_SW going through the origin (Figure 3) suggesting constant distribution coefficients in their aragonitic skeletons. Although D_El values varied between P. damicornis and A. cervicornis, the values are in close proximity to those calculated from field values for various coral species and laboratory inorganic experiments (Figures 3, 4 and Table 3). While D_El for Na, Mg, Sr, and Ba were consistent with the average D_El of inorganic aragonite, D_Li for both species were significantly lower than the inorganic ones while D_K was significantly higher. Note, however, that all our experiments were done at constant temperature of 25.4 ± 0.2°C while natural corals are exposed to ∼ 10°C variability in their natural environment and D_Sr and D_Mg are temperature sensitive. For our corals, D_Ba was 1.79 ± 0.02 and 1.41 ± 0.08 for P. damicornis and A. cervicornis, respectively. D_Ba for Favia fargum was determined experimentally by Gonneea et al. (2017) by changing Ba/Ca_SW over a range of 7.3 to 43.9 μmole mole^–1 and temperatures of 22.4 to 27.7°C. Their average D_Ba was 1. 75 ± 0.14 over all the experimental range (temperature and Ba/Ca) and 1.76 ± 0.18 in the temperature experiment at Ba/Ca_SW closest to our experimental value. Yamazaki et al. (2021) measured D_Ba for initial settled polyps of A. gutatus as a function of Ba concentration and light intensity. Their D_Ba values were higher than all previous values ranging from 1.3 to 7.5 with higher values at lower light levels. In the latter paper, however (their Figure 1 and Table 1) the reported D_Ba values cannot be considered as distribution coefficients, because the linear plots of El/Ca_Coral vs El/Ca_SW have significant intercept with the Y axis. Surprisingly, if we combine all the data of this experiment and force the linear regression through the origin, we get a single D_Ba value of 1.91 ± 0.18 with R² of 0.88. This value is close to those reported in previous studies (Table 3). The behavior of the distribution coefficient between species relative to the inorganic ones and relative to each other may be well explained using a Rayleigh fractionation model as we show below.

Rayleigh Fractionation

Several geochemical models have been suggested to explain the elemental and isotopic composition of biogenic skeletal carbonates, based on thermodynamic and kinetic principles. These models in combination with biological calcification mechanisms can eventually be used to explain the chemical and isotopic composition of marine calcifyers in order to use them as environmental proxies (McConnaughey, 1989; Elderfield et al., 1996; Cohen et al., 2001; Gaetani and Cohen, 2006; Sinclair et al., 2006; Gagnon et al., 2007, 2012). The geochemical and biological models demonstrate that in corals, calcification proceeds from a calcifying fluid within semi-closed privileged space below the calicoblastic epithelium, often defined as the Extra Cellular Fluid (ECF). The major component of this fluid is SW that is supplied to the ECF by either paracellular pathways (Tambutte et al., 2012; Venn et al., 2020) or by another as yet unknown mechanism. Throughout calcification, some elements with D_El > 1 (e.g., Ba and Sr) are depleted in the ECF relative to Ca and these elements may be enriched in the skeleton. Other elements with D_El < 1 (e.g., Mg, Na, K, and Li) are enriched in the ECF while CaCO₃ is precipitated because more Ca is consumed relative to these elements. As a result, the apparent distribution coefficients measured in corals for these elements should be higher than their inorganic ones. This process can be described by a Rayleigh fractionation process, that explains the biogenic distribution coefficients of these elements in coral skeleton. This model was first introduced by Elderfield et al. (1996) to explain the variability of trace elements in foraminifera, and afterward was readily used also for corals (Gaetani and Cohen, 2006; Gagnon et al., 2007; Gaetani et al., 2011; Sinclair, 2015; Giri et al., 2018). The Rayleigh model was widely used to explain Ca and Sr isotopes in corals (Raddatz et al., 2013; Inoue et al., 2015; Gothmann et al., 2016). The use of Rayleigh model to explain the distribution coefficients of all elements in our study is very well justified, mainly because we measured experimentally the D values for two elements with D > 1 (Ba and Sr) and four elements with D < 1 (Li, Na, Mg, and K). In Figure 5 we show the expected Rayleigh functions for all six elements based on their inorganic D_El values (Table 3), as a function of f- the fraction of Ca utilized from the closed calcifying reservoir (as fully explained by Elderfield et al., 1996), where:

FIGURE 5

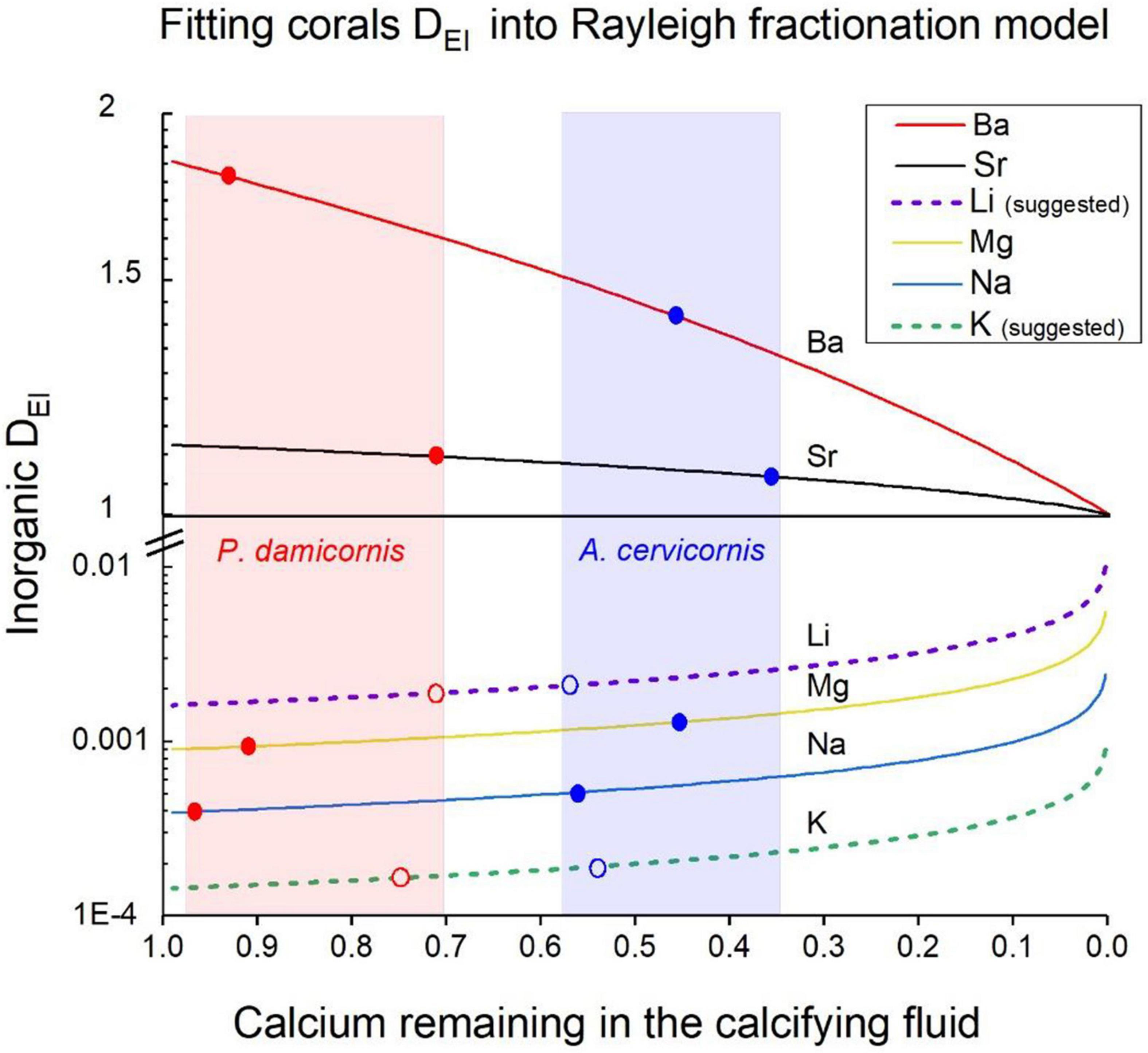
Figure 5. Fitting corals D_El values into a Rayleigh model for the calcifying fluid. Inorganic D_El values for aragonite precipitating from SW are the starting points of the curves on the Y axis. The solid and dotted lines show the evolution of coral D_El precipitating from a closed reservoir (the ECF) for all elements. As Ca is depleted from the ECF elements with D > 1 decrease relative to Ca while elements with D < 1 increase their concentration relative to Ca and D_El change accordingly. The Ca depletion is given by the f values (f = Cainitial/Cafinal). The blue dots are the D_El values for A. cervicornis and the red ones for P. damicornis. The shaded areas in light blue and red show the range of f values for these corals, respectively. Note that for Li and K we used D_El values marked with open dots as explained in the text.

$$D_{Coral}=(1-f^{Dinorg.})/\left(1-f\right)(2)$$

Next, we fitted our measured D_Coral values into Rayleigh fractionation curves for the two species (P. damicornis and A. cervicornis) as shown (Figure 5). Based on this model we conclude that P. damicornis behaves as relatively open system with f values between 0. 98 and 0.7 and for A. cervicornis f values range between 0.58 and 0.35 i.e., behaving as a half-open system for the various elements (Figure 5). For both species we marked the f ranges in light blue and red shades (Figure 5). As discussed above, D_El values of corals in experimental studies and many field studies show values that are very similar to our two species (normalized to 25°C). Unfortunately, the inorganic experimental D_El values show relatively wide range either similar to the corals or larger (e.g., Sr, Mg, Table 3 and Figure 4). For the Rayleigh model we used inorganic average values for Na, Sr and Ba (Table 3) for Mg we used the values of AlKhatib and Eisenhauer (2017). For two elements (Li and K) the reported inorganic D value fall out or the Rayleigh model shown in Figure 5: For Li the inorganic D value of 3.15 × 10 ^–3 (Marriott et al., 2004a, b) is significantly higher than both corals (2.08 × 10 ^–3 and 1.9 × 10 ^–3) and all the field corals (Figures 3, 4). But D_Li of Okumura and Kitano (1986) is 0.27 x10^–3 and the average D_Li of both inorganic experiments is 1.7 × 10^–3, a value that fits well our Rayleigh calculations (see below). Inorganic D_K is 0.5 × 10^–4 (Okumura and Kitano, 1986) a factor of 3 lower than the coral’s values (1.65 × 10 ^–4, 1.92 × 10 ^–4) yielding f values that are close to 1 for both species. We propose two possibilities to resolve the discrepancy in Li and K between the reported inorganic values and our Rayleigh model: The first is that D inorganic values for Li and K are inaccurate and should be modified. If we try to fit both species into their Rayleigh Ca utilization ranges, we need to assume D_Li to be 0.16 × 10^–3 instead of 0.315 × 10^–3 (Marriott et al., 2004b) i.e., a factor of 2 lower. We note that our Li/Ca_coral values (∼5 μmol mol^–1) are lower compared with average literature field corals (6.38 μmol mol^–1) as we discussed above (Table 3). Even if we take this field corals average it will require a lower inorganic D_Li (∼ 0.28 × 10^–3) to explain the field coral values. For potassium the inorganic D_K value needs to be 1.43 × 10^–4 instead of 0.5 × 10^–4 i.e., 3 times higher than reported (Okumura and Kitano, 1986) in order to fit our Rayleigh model (Open markers in Figure 5). A second possibility is that the corals concentrate K and reduce Li in the ECF. This explanation opens wide possibilities that cannot be resolved without further experiments dedicated to this specific question. For the present study, we chose the first possibility and suggest that more experimental work is needed to determine accurately D_Li and D_K in inorganic experiments. If we use the D_El values proposed above, we get a good fit to the Rayleigh model for both species (Figure 5) as well as for all the other elements (Na, Mg, Sr, and Ba). The use of the Rayleigh model to explain the various D_El for the two species strongly support the hypothesis that SW is the main source for ions at the ECF (Gaetani and Cohen, 2006; Gagnon et al., 2007; Gothmann et al., 2016; Giri et al., 2018). While these studies do not specifically spell this out, their use of the Rayleigh models, like ours, starts from SW composition at the ECF. Most of the Ca ions needed for calcification is available directly from SW as Ca_SW = 10.3 mM, and similarly part of the DIC (DIC_SW = 2 mM, see discussion on modification of DIC below). Bulk transport of SW is also the source for all the other trace and minor elements found in the skeleton, as can be concluded from their fit to the Rayleigh model. Obviously, the SW in the ECF is replenished once it is depleted of Ca and CO₃ during the calcification process. More evidence for SW at the ECF is discussed in relation to the calcification process is given below.

Implications for Calcification Mechanisms in Corals

We propose that the fluid in the ECF is essentially SW that arrives to the privileged calcifying space below the calicoblastic epithelium, probably by paracellular pathways (Tambutte et al., 2012). One of the main supports for bulk SW transport to the ECF is coming from observations on Calcein labeling of coral skeletons (Braun and Erez, 2004; Erez and Braun, 2007; Tambutte et al., 2012). Calcein, is a membrane-impermeable fluorescent dye and its presence in large parts of the ECF indicates the presence of SW. The newly precipitated coral aragonite crystals that grow in the flat coral preparation (e.g., Raz-Bahat et al., 2006) are homogeneously labeled with Calcein and provide an evidence that bulk SW is actually the calcifying fluid (e.g., Ohno et al., 2017; Venn et al., 2020). Further support of SW at the ECF is coming from the experiment of Gagnon et al. (2012) that studied the short-term incorporation of isotopes of Ca, Sr, Ba, and Tb into coral skeleton. The measurements using nanoSIMS showed that SW bulk transport is the main source of Ca (and all the other elements) in the ECF. Other pathways that can bring SW to the ECF such as mega-pinocytosis or SW vacuoles as seen in foraminifera (Bentov et al., 2009), or other leaky pathways are also possible. These may include tissue retraction between polyps as seen at the start of polyp bailout (e.g., Domart-Coulon et al., 2004), or through skeleton exposure due to physical or biological tissue damage (e.g., parrotfish injuries, worms, and mollusks burrowing). There are three major modifications of the SW at the ECF which are: (1) an increase in pH (e.g., Al-Horani et al., 2003; Venn et al., 2011; Gagnon, 2013). (2) Accumulation of DIC as a result of CO₂ diffusion and/or bicarbonate transport (e.g., McCulloch et al., 2012, 2017; Sevilgen et al., 2019). (3) Release of organic macromolecules (perhaps including proteins) that serve as an organic matrix which directs the growth patterns, texture, and crystallography of the skeleton (Allemand et al., 1998; Tambutté et al., 2011). Based on our Rayleigh model P. damicornis is more open system i.e., it utilized lower fraction of its Ca (∼ 20 %) while A. cervicornis behaves as a semi-closed system that utilizes higher fraction of Ca from its ECF (∼50%). Both strategies may influence the calcification rates: A. cervicornis may invest more energy in elevating the pH and DIC and therefore can utilize higher fraction of the SW Ca (Figure 5). P. damicornis on the other hand, exchanges its SW at the ECF faster and its pH and DIC elevations may therefore be lower. This may explain the difference in their calcification rates suggesting that the closed system strategy of A. cervicornis is more efficient. Based on the growth of P. damicornis in the second experiment, and the total growth in the first experiment we can estimate that A. cervicornis grew at least twice faster than P. damicornis (see Supplementary Table 3).

Independent evidence for our Rayleigh calcification model comes from B/Ca and δ¹¹B in laboratory and field studies. δ¹¹B is used to calculate the pH and B/Ca to calculate the CO₃ concentration at the ECF. These two parameters of the carbonate system allow calculation of the DIC in the calcifying fluid (Allison et al., 2014; DeCarlo et al., 2017, 2018). In addition, DeCarlo et al. (2017) suggested that Raman spectra of the skeleton correlate well with Ω_aragonite and this allows to calculate the Ca at the ECF. Similar approach was used by Ross et al. (2019) where the authors compared skeleton derived chemistry at the ECF for different species collected in several locations in Australia. In both studies, the data on Acropora species and P. damicornis, support our results i.e., Acropora calcifies faster than P. damicornis. Furthermore, their estimated DIC and Ω_aragonite yielded higher values for Acropora compared to Pocillopora which may explain Acropora’s faster calcification rate. In both papers mentioned above, the Ca estimates at the ECF for the Acropora species is lower than those of P. damicornis in agreement with our f values suggesting higher Ca utilization for Acropora. The geochemical ECF estimates represent longer time averages (days, weeks or months) and may show steady state chemical compositions of the ECF. There is good agreement of these values with the previous short-term microelectrode and fluorescent dyes experiments, that represent short term values of pH, DIC, and Ca (e.g., Al-Horani et al., 2003; Venn et al., 2011; Sevilgen et al., 2019 and references therein). Both types of studies support each other, and biological direct observation increase the confidence of the calcification mechanisms that are proposed based on geochemical data. The most significant process in the calcification mechanism is that the ECF is essentially seawater that is modified by the coral mainly to increase its pH, DIC, and Ω_aragonite. High Ω_aragonite values are needed to start precipitation of the skeleton, but during the precipitation process Ca, CO₃, DIC, and pH are all decreasing until calcification stops. The dynamics of these processes may be controlled by the diurnal cycle as light enhanced calcification is well documented in hermatypic corals (e.g., Cohen et al., 2016 and references therein).

Implications for Paleoceanographic Reconstructions

Corals are successfully applied as paleoceanography recorders mainly for paleotemperature based on δ¹⁸O, Sr/Ca, and Mg/Ca (e.g., Smith et al., 1979; Beck et al., 1992; Mitsuguchi et al., 1996; Felis et al., 2004; D’Olivo et al., 2018 and references therein). Reconstructions of ocean chemistry based on corals is scarce (Bender, 1973; Ries et al., 2006), but recently, the study of Gothmann et al. (2015), showed the high potential for such reconstructions over the past 200 Ma. Our findings strengthen the confidence of these paleo-studies have important implications for past ocean chemistry reconstruction. One of the main hurdles of proxies used in coral was the “vital effects” i.e., the deviation of coral skeletons from expected thermodynamic values of aragonite precipitation from seawater (e.g., McConnaughey, 1989; Adkins et al., 2003; Gagnon et al., 2007; Gothmann et al., 2016). In this study we show that seawater is the initial calcifying fluid at the ECF and fractionation of trace elements in the skeleton is constant for each species following a Rayleigh process from a semi-closed ECF reservoir. D_coral values are therefore constant (i.e., intercept 0 in the El/Ca plots) for each of the two species we studied (Figure 3). We propose that the closure of the ECF is mainly in order to modify its carbonate chemistry i.e., elevation of pH, DIC and Ω_aragonite and this closure is the main cause for Rayleigh process that we observe in coral skeletons trace elements.

Reconstruction of past seawater chemistry based on coral skeletons may be more reliable by measuring elements with D > 1 (Ba and Sr) and D < 1 (Na and Mg) and compare it to inorganic values. This may help to remove the vital effects related to the Rayleigh process. The most important ratio in these reconstructions is Na/Ca_skeleton as proposed by Hauzer et al. (2018) and Houedec et al. (2021) for foraminifera during the Cenozoic. This follows from the assumption that Na concentration is constant over the last 50–100 Ma and Ca_SW may be calculated from Na/Ca_coral. Na concentration in coral skeletons is relatively high (e.g., Mitsuguchi et al., 2010; the present study) and since Kawabata et al. (2021), suggested that Na substitutes Ca in the lattice of aragonite based on K-edge X-ray absorption near edge structure (XANES) measurements, the Na/Ca_coral may indeed be used as a proxy for Ca_SW. Once we know the past Ca, with information on temperature, it is also possible to calculate Sr, Mg, K, Li, and other elements that have shorter residence times (Mg ∼14 Ma; K ∼ 7 Ma; Sr ∼ 6 Ma; Li and Ca ∼ 1Ma; Pilson, 2013). Thus, despite the complex biological processes involved in the calcification of corals, their skeletons provide a unique and reliable archive for paleoceanoraphic reconstructions.

Summary

In this study two scleractinian corals species, Pocillopora damicornis and Acropora cervicornis were cultured under variable seawater calcium (Ca_SW) ranging from ∼10 to 25 mM. The results demonstrate that the incorporation of the conservative elements Li, Na, Mg, K, Sr and Ba into the coral’s skeletons, is directly related to the El/Ca_SW ratio. The significant linear regression between El/Ca_coral and El/Ca_SW, going through the origin, suggests constant distribution coefficients (D_coral) for each element. For both coral species, D_El values for Na, Mg, Sr, and Ba were in close proximity to the inorganic D_El values, however, D_Li were slightly lower and D_K higher than the inorganic values. Rayleigh fractionation model explains well the variation in D_El between the two species and the inorganic D_El yielding the following conclusions:

SW is the main source for ions at the ECF, which shows precipitation from a semiclosed reservoir, that can be modeled using Rayleigh fractionation process.

Different coral species demonstrate different strategies with respect to their Ca utilization from the ECF. P. damicornis behaves like relatively open system while A. cervicornis is a half-open system, that may be more efficient as it shows higher calcification rate.

For Li and K the published inorganic D_El values are inconsistent with the Rayleigh model based on the coral D_El. We propose that D_Li and D_K may be inaccurate and suggest hypothesized alternative values, however, this needs direct experimental study.

Finally, this study shows that coral skeletal trace elements may serve as highly reliable archive for paleoceanographic reconstructions. Na/Ca_coral may be used to calculate past Ca_SW for the Cenozoic (as Na_SW was probably constant). Other elemental concentrations may thus be calculated based on their skeletal values and D_El values of this paper.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JE designed and directed the study, and edited the manuscript. SR performed the growth experiments, ICP-OES analyses, processing and analyzing the data, and wrote the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

This study was funded by Israel Science Foundation # 790/16 to JE.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Yair Rosenthal and David Evans for initiating the idea that Na in biogenic carbonates may serve as a proxy for past SW calcium. We also thank Yigal Erel for reviewing this manuscript, Adam Levi, Hagar Hauzer, and Itzhak Geva for lab assistance, and the two reviewers for improving the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.657176/full#supplementary-material

References

Adkins, J. F., Boyle, E. A., Curry, W. B., and Lutringer, A. (2003). Stable isotopes in deep-sea corals and a new mechanism for “vital effects”. Geochimica et Cosmochimica Acta 67, 1129–1143. doi: 10.1016/S0016-7037(02)01203-6

CrossRef Full Text | Google Scholar

Al-Horani, F. A., Al-Moghrabi, S. M., and De Beer, D. (2003). The Mechanism of Calcification and Its Relation to Photosynthesis and Respiration in the Scleractinian Coral Galaxea fascicularis. Marine Biology 142, 419–426. doi: 10.1007/s00227-002-0981-8

CrossRef Full Text | Google Scholar

Alibert, C., Kinsley, l, Fallon, S. J., McCulloch, M. T., Berkelmans, R., and McAllister, F. (2003). Source of Trace Element Variability in Great Barrier Reef Corals Affected by the Burdekin Flood Plumes. Geochimica et Cosmochimica Acta 67, 231–246. doi: 10.1016/S0016-7037(02)01055-4

CrossRef Full Text | Google Scholar

AlKhatib, M., and Eisenhauer, A. (2017). Calcium and Strontium Isotope Fractionation during Precipitation from Aqueous Solutions as a Function of Temperature and Reaction Rate. II. Aragonite. Geochimica et Cosmochimica Acta 209, 320–342. doi: 10.1016/j.gca.2017.04.012

CrossRef Full Text | Google Scholar

Allemand, D., Tambutte, E., Girard, J. P., and Jaubert, J. (1998). Organic Matrix Synthesis in the Scleractinian Coral Stylophora Pistillata: Role in Biomineralization and Potential Target of the Organotin Tributyltin. The Journal of Experimental Biology 201, 2001–2009. doi: 10.1007/s13398-014-0173-7.2

CrossRef Full Text | Google Scholar

Allison, N., and Finch, A. A. (2007). High Temporal Resolution Mg/Ca and Ba/Ca Records in Modern Porites Lobata Corals. Geochemistry, Geophysics Geosystems 8, 1477. doi: 10.1029/2006GC001477

CrossRef Full Text | Google Scholar

Allison, N., Cohen, I., Finch, A. A., Erez, J., and Tudhope, A. W. (2014). Corals concentrate dissolved inorganic carbon to facilitate calcification. Nature Communications 5, 5741.

Google Scholar

Amiel, A. J., Miller, D. S., and Fridman, G. M. (1973). Distribution and Nature of Incorporation of Trace Elements in Modern Aragonitic Corals. Sedimentology 20, 47–64. doi: 10.1111/j.1365-3091.1973.tb01606.x

CrossRef Full Text | Google Scholar

Bar-Matthews, M., Wasserburg, G. J., and Chen, J. H. (1993). Diagenesis of fossil coral skeletons: Correlation between trace elements, textures, and 234U / 238U”. Geochim. Cosmochim. Acta 57, 257.

Google Scholar

Beck, J. W., Edwards, R. L., Ito, E., Taylor, F. W., Recy, J., Rougerie, F., et al. (1992). Sea-Surface Temperature from Coral Skeletal Strontium/Calcium Ratios. Science 257, 644–647. doi: 10.1126/science.257.5070.644

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, T., Nishida, K., Ishikawa, K., Suzuki, A., Nakamura, T., Sakai, K., et al. (2017). Temperature-Controlled Culture Experiments with Primary Polyps of Coral Acropora Digitifera: Calcification Rate Variations and Skeletal Sr/Ca, Mg/Ca, and Na/Ca Ratios. Palaeogeography, Palaeoclimatology, Palaeoecology 484, 129–135. doi: 10.1016/j.palaeo.2017.03.016

CrossRef Full Text | Google Scholar

Bender, M. L. (1973). Helium-uranium dating of corals. Gear chitn Cosmochim. Acta 37, 1229–1247.

Google Scholar

Bentov, S., Brownlee, C., and Erez, J. (2009). The role of seawater endocytosis in the biomineralization process in calcareous foraminifera. Proc. Natl. Acad. Sci. U.S.A. 106, 21500–21504. doi: 10.1073/pnas.0906636106

PubMed Abstract | CrossRef Full Text | Google Scholar

Braun, A., and Erez, J. (2004). Preliminary observations on sea water utilization during calcification in scleractinian corals. Eos. Trans. AGU 85, 14B–14B.

Google Scholar

Chalker, B. E. (1976). Calcium Transport during Skeletogenesis in Hermatypic Corals. Comparative Biochemistry and Physiology – Part A: Physiology 54, 455–459. doi: 10.1016/0300-9629(76)90049-9

CrossRef Full Text | Google Scholar

Cohen, A. L., Layne, G. D., Hart, S., and Lobel, P. S. (2001). Implications for the Paleotemperature Proxy A. Paleoceanography 16, 20–26.

Google Scholar

Cohen, I., Dubinsky, Z., and Erez, J. (2016). Light Enhanced Calcification in Hermatypic Corals: New Insights from Light Spectral Responses. Frontiers in Marine Science 2:122. doi: 10.3389/fmars.2015.00122

CrossRef Full Text | Google Scholar

Cuny-Guirriec, K., Douville, E., Reynaud, S., Allemand, D., Bordier, L., Canesi, M., et al. (2019). Coral Li/Mg Thermometry: Caveats and Constraints. Chemical Geology 523, 162–178. doi: 10.1016/j.chemgeo.2019.03.038

CrossRef Full Text | Google Scholar

D’Olivo, J. P., Sinclair, D. J., Rankenburg, K., and McCulloch, M. T. (2018). A Universal Multi-Trace Element Calibration for Reconstructing Sea Surface Temperatures from Long-Lived Porites Corals: Removing ‘Vital-Effects.’. Geochimica et Cosmochimica Acta 239, 109–135. doi: 10.1016/j.gca.2018.07.035

CrossRef Full Text | Google Scholar

DeCarlo, T. M., Comeau, S., Cornwall, C. E., and Mcculloch, M. T. (2018). Coral resistance to ocean acidification linked to increased calcium at the site of calcification. Proc. R. Soc. B 285, 20180564. doi: 10.1098/rspb.2018.0564

PubMed Abstract | CrossRef Full Text | Google Scholar

DeCarlo, T. M., D’Olivo, J. P., Foster, T., Holcomb, M., Becker, T., and McCulloch, M. T. (2017). Coral calcifying fluid aragonite saturation states derived from Raman spectroscopy. Biogeosciences 14, 5253–5269. doi: 10.5194/bg-14-5253-2017

CrossRef Full Text | Google Scholar

Dietzel, M., Gussone, N., and Eisenhauer, A. (2004). Co-Precipitation of Sr²⁺ and Ba²⁺ with Aragonite by Membrane Diffusion of CO₂ between 10 and 50 j C. Chemical Geology 203, 139–151. doi: 10.1016/j.chemgeo.2003.09.008

CrossRef Full Text | Google Scholar

Domart-Coulon, I., Tambutté, S., Tambutté, E., and Allemand, D. (2004). Short term viability of soft tissue detached from the skeleton of reef-building corals. J. Exp. Mar. Biol. Ecol. 309, 199–217.

Google Scholar

Elderfield, H., Bertram, C. J., and Erez, J. (1996). A Biomineralization Model for the Incorporation of Trace Elements into Foraminiferal Calcium Carbonate. Earth and Planetary Science Letters. 142, 409–423.

Google Scholar

Erez, J., and Braun, A. (2007). Calcification in hermatypic corals is based on direct seawater supply to the biomineralisation site. Geochim. Cosmochim. Acta 71, SA260.

Google Scholar

Fallon, S. J., McCulloch, M. T., and Alibert, C. (2003). Examining Water Temperature Proxies in Porites Corals from the Great Barrier Reef: A Cross-Shelf Comparison. Coral Reefs 22, 389–404. doi: 10.1007/s00338-003-0322-5

CrossRef Full Text | Google Scholar

Fallon, S. J., White, J. C., and McCulloch, M. T. (2002). Porites Corals as Recorders of Mining and Environmental Impacts: Misima Island, Papua New Guinea. Geochimica et Cosmochimica Acta 66, 45–62.

Google Scholar

Felis, T., Lohmann, G., and Kuhnert, H. (2004). Increased seasonality in Middle East temperatures during the last interglacial period. Nature 429, 164–168. doi: 10.1038/nature02546

PubMed Abstract | CrossRef Full Text | Google Scholar

Fowell, S. E., Sandford, K., Stewart, J. A., Castillo, K. D., Ries, J. B., and Foster, G. L. (2016). Intrareef variations in Li/Mg and Sr/Ca sea surface temperature proxies in the Caribbean reef-building coral Siderastrea siderea. Paleoceanography 31, 1315–1329.

Google Scholar

Gaetani, G. A., and Cohen, A. L. (2006). Element Partitioning during Precipitation of Aragonite from SW: A Framework for Understanding Paleoproxies. Geochimica et Cosmochimica Acta 70, 4617–4634. doi: 10.1016/j.gca.2006.07.008

CrossRef Full Text | Google Scholar

Gaetani, G. A., Cohen, A. L., Zhengrong, W., and Crusius, J. (2011). Rayleigh-Based, Multi-Element Coral Thermometry: A Biomineralization Approach to Developing Climate Proxies. Geochimica et Cosmochimica Acta 75, 1920–1932. doi: 10.1016/j.gca.2011.01.010

CrossRef Full Text | Google Scholar

Gagnon, A. C. (2013). Coral Calcification Feels the Acid. PNAS 110, 1567–1568. doi: 10.1073/pnas.1221308110

PubMed Abstract | CrossRef Full Text | Google Scholar

Gagnon, A. C., Adkins, J. F., and Erez, J. (2012). Seawater Transport during Coral Biomineralization. Earth and Planetary Science Letters 329–330, 150–161. doi: 10.1016/j.epsl.2012.03.005

CrossRef Full Text | Google Scholar

Gagnon, A. C., Adkins, J. F., Fernandez, D. P., and Robinson, L. F. (2007). Sr/Ca and Mg/Ca Vital Effects Correlated with Skeletal Architecture in a Scleractinian Deep-Sea Coral and the Role of Rayleigh Fractionation. Earth and Planetary Science Letters 261, 280–295. doi: 10.1016/j.epsl.2007.07.013

CrossRef Full Text | Google Scholar

Giri, S. J., Swart, P. K., and Devlin, Q. B. (2018). The Effect of Changing SW Ca and Mg Concentrations upon the Distribution Coefficients of Mg and Sr in the Skeletons of the Scleractinian Coral Pocillopora Damicornis. Geochimica et Cosmochimica Acta 222, 535–549. doi: 10.1016/j.gca.2017.11.011

CrossRef Full Text | Google Scholar

Gonneea, M. E., Cohen, A. L., DeCarlo, T. M., and Charette, M. A. (2017). Relationship between Water and Aragonite Barium Concentrations in Aquaria Reared Juvenile Corals. Geochimica et Cosmochimica Acta 209, 123–134. doi: 10.1016/j.gca.2017.04.006

CrossRef Full Text | Google Scholar

Goreau, T. F. (1959). The Physiology of Skeleton Formation in Corals. I. a Method for Measuring the Rate of Calcium Deposition By Corals Under Different Conditions. The Biological Bulletin 116, 59–75. doi: 10.2307/1539156

CrossRef Full Text | Google Scholar

Gothmann, A. M., Bender, M. L., Blättler, C. L., Swart, P. K., Giri, S. J., Adkins, J. F., et al. (2016). Calcium Isotopes in Scleractinian Fossil Corals since the Mesozoic: Implications for Vital Effects and Biomineralization through Time. Earth and Planetary Science Letters 444, 205–214. doi: 10.1016/j.epsl.2016.03.012

CrossRef Full Text | Google Scholar

Gothmann, A. M., Stolarski, J., Adkins, J. F., Schoene, B., Dennis, K. J., Schrag, D. P., et al. (2015). Fossil Corals as an Archive of Secular Variations in SW Chemistry since the Mesozoic. Geochimica et Cosmochimica Acta 160, 188–208. doi: 10.1016/j.gca.2015.03.018

CrossRef Full Text | Google Scholar

Hardie, L. A. (1996). Secular Variation in SW Chemistry: An Explanation for the Coupled Secular Variation in the Mineralogies of Marine Limestones and Potash Evaporites over the Past 600 m.Y. Geology 24, 279–283. doi: 10.1130/0091-76131996024<0279:SVISCA<2.3.CO

CrossRef Full Text | Google Scholar

Hathorne, E. C., Gagnon, A., Felis, T., Adkins, J., Asami, R., Boer, W., et al. (2013a). Interlaboratory study for coral Sr/Ca and other element/Ca ratio measurements. Geochemistry, Geophysics. Geosystems 14, 3730–3750. doi: 10.1002/ggge.20230

CrossRef Full Text | Google Scholar

Hathorne, E. C., Thomas, F., Atsushi, S., Hodaka, K., and Cabioch, G. (2013b). Lithium in the Aragonite Skeletons of Massive Porites Corals: A New Tool to Reconstruct Tropical Sea Surface Temperatures. Paleoceanography 28, 143–152. doi: 10.1029/2012PA002311

CrossRef Full Text | Google Scholar

Hauzer, H., Evans, D., Müller, W., Rosenthal, Y., and Erez, J. (2018). Calibration of Na Partitioning in the Calcitic Foraminifer Operculina Ammonoides under Variable Ca Concentration: Toward Reconstructing Past SW Composition. Earth and Planetary Science Letters 497, 80–91. doi: 10.1016/j.epsl.2018.06.004

CrossRef Full Text | Google Scholar

Horita, J., Zimmermann, H., and Holland, H. D. (2002). Chemical Evolution of SW during the Phanerozoic. Geochimica et Cosmochimica Acta 66, 3733–3756. doi: 10.1016/S0016-7037(01)00884-5

CrossRef Full Text | Google Scholar

Houedec, S. L., Erez, J., and Rosenthal, Y. (2021). Testing the influence of changing seawater Ca concentration on Elements/Ca ratios in planktic foraminifera: A culture experiment. Geochemistry, Geophysics, Geosystems 22, e2020GC009496. doi: 10.1029/2020GC009496

CrossRef Full Text | Google Scholar

Howard, L. S., and Brown, B. E. (1984). Heavy metals and reef corals. Oceanogr. Mar. Biol. Ann. Rev. 22, 195–210.

Google Scholar

Inoue, M., Gussone, N., Koga, Y., Iwase, A., Suzuki, A., Sakai, K., et al. (2015). Controlling Factors of Ca Isotope Fractionation in Scleractinian Corals Evaluated by Temperature, PH and Light Controlled Culture Experiments. Geochimica et Cosmochimica Acta 167, 80–92. doi: 10.1016/j.gca.2015.06.009

CrossRef Full Text | Google Scholar

Kawabata, T., Takeda, Y., Hori, M., Kandori, K., and Yaji, T. (2021). Partitioning of sodium into calcium carbonates synthesized at 10–40 °C: Influence of organic ligands and temperature. Chemical Geology 559, 119904. doi: 10.1016/j.chemgeo.2020.119904

CrossRef Full Text | Google Scholar

Kinsman, D. J. J. (1970). Trace cations in aragonite. Abstr. Geol. Soc. Am. 2, 596–597.

Google Scholar

Kinsman, J. J., and Holland, H. D. (1969). The Co-Precipitation of Cations with CaCO3 - IV. The Co-Precipitation of Sr2+ with Aragonite between 16” and 96°C. Geochimica et Cosmochimica Acta 33, 1–17. doi: 10.1016/0016-7037(69)90089-1

CrossRef Full Text | Google Scholar

Kitano, Y., Okumura, M., and Idogaki, M. (1975). Incorporation of Sodium, Chloride and Sulfate with Calcium Carbonate. Geochemical Journal 9, 75–84. doi: 10.2343/geochemj.9.75

CrossRef Full Text | Google Scholar

LaVigne, M., Grottoli, A. G., Palardy, J. E., and Sherrell, R. M. (2016). Multi-Colony Calibrations of Coral Ba/Ca with a Contemporaneous in Situ SW Barium Record. Geochimica et Cosmochimica Acta 179, 203–216. doi: 10.1016/j.gca.2015.12.038

CrossRef Full Text | Google Scholar

LaVigne, M., Hill, T. M., Spero, H. M., and Guilderson, T. P. (2011). Bamboo Coral Ba/Ca: Calibration of a New Deep Ocean Refractory Nutrient Proxy. Earth and Planetary Science Letters 312, 506–515. doi: 10.1016/j.epsl.2011.10.013

CrossRef Full Text | Google Scholar

Lea, D. W., Shen, G. T., and Boyle, E. A. (1989). Coralline barium records temporal variability in equatorial Pacific up- welling. Nature 340, 373–376.

Google Scholar

Livingston, H. D., and Thompson, G. (1971). Trace Elements Concentration in Some Modern Corals. Limnology and Oceanography 16, 786–796.

Google Scholar

Lough, J. M., and Barnes, D. J. (1990). Possible Relationships between Environmental Variables and Skeletal Density in a Coral Colony from the Central Great Barrier Reef. J. Exp. Mar. Biol. Ecol. 134, 221–241.

Google Scholar

Marchitto, T. M., Bryan, S. P., Doss, W., McCulloch, M. T., and Montagna, P. (2018). A Simple Biomineralization Model to Explain Li, Mg, and Sr Incorporation into Aragonitic Foraminifera and Corals. Earth and Planetary Science Letters 481, 20–29. doi: 10.1016/j.epsl.2017.10.022

CrossRef Full Text | Google Scholar

Marriott, C. S., Henderson, G. M., Belshaw, N. S., and Tudhope, A. L. (2004a). Temperature Dependence of d 7 Li, d 44 Ca and Li / Ca during Growth of Calcium Carbonate. Earth and Planetary Science Letters 222, 615–624. doi: 10.1016/j.epsl.2004.02.031

CrossRef Full Text | Google Scholar

Marriott, C. S., Henderson, G. M., Crompton, R., Staubwasser, M., and Shaw, S. (2004b). Effect of Mineralogy, Salinity, and Temperature on Li/Ca and Li Isotope Composition of Calcium Carbonate. Chemical Geology 212, 5–15. doi: 10.1016/j.chemgeo.2004.08.002

CrossRef Full Text | Google Scholar

Marshall, J. F., and McCulloch, M. T. (2002). An Assessment of the Sr/Ca Ratio in Shallow Water Hermatypic Corals as a Proxy for Sea Surface Temperature. Geochimica et Cosmochimica Acta 66, 3263–3280. doi: 10.1016/S0016-7037(02)00926-2

CrossRef Full Text | Google Scholar

McConnaughey, T. (1989). C-13 and O-18 Isotopic Disequilibrium in Biological Carbonates. 1. Patterns. Geochimica et Cosmochimica Acta 53, 151–162.

Google Scholar

McCulloch, M. T., D’Olivo, J. P., Falter, J., Holcomb, M., and Trotter, J. A. (2017). Coral calcification in a changing World: the interactive dynamics of pH and DIC up-regulation. Nature Communications 8, 686.

Google Scholar

McCulloch, M. T., Fallon, S., Wyndham, T., Hendy, E., Lough, J., and Barnes, D. (2003). Coral record of increased sediment flux to the inner Great Barrier Reef since European settlement. Nature 421, 727–730.

Google Scholar

McCulloch, M. T., Falter, J., Trotter, J., and Montagna, P. (2012). Coral resilience to ocean acidification and global warming through pH up- regulation. Nature Climate Change 2, 623–627.

Google Scholar

McCulloch, M. T., Gagan, G. K., Mortimer, G. E., Chivas, A. R., and Isdale, P. J. (1994). A High-Resolution Sr/Ca and δO ¹⁸ Coral Record from the Great Barrier Reef, Australia, and the 1982-1983 El Nino. Geochimica et Cosmochimica Acta 58, 2747–2754.

Google Scholar

Mitsuguchi, T., and Kawakami, T. (2012). Potassium and Other Minor Elements in Porites Corals: Implications for Skeletal Geochemistry and Paleoenvironmental Reconstruction. Coral Reefs 31, 671–681. doi: 10.1007/s00338-012-0902-3

CrossRef Full Text | Google Scholar

Mitsuguchi, T., Matsumoto, E., Abe, O., Uchida, T., and Isdale, P. J. (1996). Mg/Ca Thermometry in Coral Skeletons. Science 274, 961–963. doi: 10.1126/science.274.5289.961

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitsuguchi, T., Matsumoto, E., and Uchida, T. (2003). Mg/Ca and Sr/Ca Ratios of Porites Coral Skeleton: Evaluation of the Effect of Skeletal Growth Rate. Coral Reefs 22, 381–388. doi: 10.1007/s00338-003-0326-1

CrossRef Full Text | Google Scholar

Mitsuguchi, T., Uchida, T., and Matsumoto, E. (2010). Na / Ca Variability in Coral Skeletons. Geochemical Journal 44, 261–273.

Google Scholar

Montagna, P., McCulloch, M., Douville, E., López Correa, M., Trotter, J., Rodolfo-Metalpa, R., et al. (2014). Li/Mg Systematics in Scleractinian Corals: Calibration of the Thermometer. Geochimica et Cosmochimica Acta 132, 288–310. doi: 10.1016/j.gca.2014.02.005

CrossRef Full Text | Google Scholar

Ohno, Y., Iguchi, A., Shinzato, C., Inoue, M., Suzuki, A., Sakai, K., et al. (2017). An aposymbiotic primary coral polyp counteracts acidification by active pH regulation. Sci. Rep. 7, 40324.

Google Scholar

Okumura, M., and Kitano, Y. (1986). Coprecipitation of Alkali Metal Ions with Calcium Carbonate. Geochimica et Cosmochimica Acta 50, 49–58. doi: 10.1016/0016-7037(86)90047-5

CrossRef Full Text | Google Scholar

Pierrot, D., Lewis, E., and Wallace, D. (2006). MS Excel program developed for CO2 system calculations: ORNL/CDIAC-105a. Oak Ridge, TN: Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy.

Google Scholar

Pilson, M. E. Q. (2013). An Introduction to the Chemistry of the Sea, 2 Edn. Cambridge: Cambridge university press.

Google Scholar

Raddatz, J., Liebetrau, V., Rüggeberg, A., Hathorne, E., Krabbenhöft, A., Eisenhauer, A., et al. (2013). Stable Sr-Isotope, Sr/Ca, Mg/Ca, Li/Ca and Mg/Li Ratios in the Scleractinian Cold-Water Coral Lophelia Pertusa. Chemical Geology 352, 143–152. doi: 10.1016/j.chemgeo.2013.06.013

CrossRef Full Text | Google Scholar

Raz-Bahat, M., Erez, J., and Rinkevich, B. (2006). In vivo light-microscopic documentation for primary calcification processes in the hermatypic coral Stylophora pistillata. Cell. Tissue Res. 325, 361–368.

Google Scholar

Ries, J. B. (2004). Effect of Ambient Mg/Ca Ratio on Mg Fractionation in Calcareous Marine Invertebrates: A Record of the Oceanic Mg/Ca Ratio over the Phanerozoic. Geology 32, 981–984. doi: 10.1130/G20851.1

CrossRef Full Text | Google Scholar

Ries, J. B., Stanley, S. M., and Hardie, L. A. (2006). Scleractinian corals produce calcite, and grow more slowly, in artificial Cretaceous seawater. Geology 34, 525–528. doi: 10.1130/G22600.1

CrossRef Full Text | Google Scholar

Rollion-Bard, C., and Blamart, D. (2015). Possible Controls on Li, Na, and Mg Incorporation into Aragonite Coral Skeletons. Chemical Geology 396, 98–111. doi: 10.1016/j.chemgeo.2014.12.011

CrossRef Full Text | Google Scholar

Ross, C. L., DeCarlo, T. M., and McCulloch, M. T. (2019). Environmental and Physiochemical Controls on Coral Calcification along a Latitudinal Temperature Gradient in Western Australia. Global Change Biology 25, 431–447. doi: 10.1111/gcb.14488

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, K., and Erez, J. (2006). The Effect of Carbonate Chemistry on Calcification and Photosynthesis in the Hermatypic Coral Acropora Eurystoma. Limnology and Oceanography 51, 1284–1293. doi: 10.4319/lo.2006.51.3.1284

CrossRef Full Text | Google Scholar

Sevilgen, D. S., Venn, A. A., Hu, M. Y., Tambutté, E., De Beer, D., Planas-Bielsa, V., et al. (2019). Full in Vivo Characterization of Carbonate Chemistry at the Site of Calcification in Corals. Science Advances 5, 7447. doi: 10.1126/sciadv.aau7447

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, G. T., and Boyle, E. A. (1987). Lead in Corals: Reconstruction of Historical Industrial Fluxes to the Surface Ocean. Earth and Planetary Science Letters 82, 289–304. doi: 10.1016/0012-821X(87)90203-2

CrossRef Full Text | Google Scholar

Shen, G. T., and Boyle, E. A. (1988). Determination of Lead, Cadmium and Other Trace Metals in Annually-Banded Corals. Chemical Geology 67, 47–62. doi: 10.1016/0009-2541(88)90005-8

CrossRef Full Text | Google Scholar

Sholkovitz, E., and Shen, G. T. (1995). The Incorporation of Rare Earth Elements in Modern Coral. Geochimica et Cosmochimica Acta 59, 2749–2756. doi: 10.1016/0016-7037(95)00170-5

CrossRef Full Text | Google Scholar

Sinclair, D. J. (2005). Non-river flood barium signals in the skeletons of corals from coastal Queensland. Australia. Earth Planet. Sci. Lett. 237, 354–369.

Google Scholar

Sinclair, D. J. (2015). RBME Coral Temperature Reconstruction: An Evaluation, Modifications, and Recommendations. Geochimica et Cosmochimica Acta 154, 66–80. doi: 10.1016/j.gca.2015.01.006

CrossRef Full Text | Google Scholar

Sinclair, D. J., Williams, B., and Risk, M. (2006). A Biological Origin for Climate Signals in Corals - Trace Element ‘Vital Effects’ Are Ubiquitous in Scleractinian Coral Skeletons. Geophysical Research Letters 33, 183. doi: 10.1029/2006GL027183

CrossRef Full Text | Google Scholar

Smith, S. V., Buddemeier, R. W., Redalje, R. C., and Houck, J. E. (1979). Strontium-Calcium Thermometry in Coral Skeletons. Science 204, 404–407. doi: 10.1126/science.204.4391.404

PubMed Abstract | CrossRef Full Text | Google Scholar

Swart, P. K. (1979). Effect of seawater calcium concentrations on the growth and skeletal composition of a scleractinian coral – Acropora squamosa. J. Sediment. Petrol. 49, 951–954.

Google Scholar

Swart, P. K. (1981). The Strontium, Magnesium and Sodium Composition of Recent Scleractinian Coral Skeletons as Standards for Palaeoenvironmental Analysis. Palaeogeography, Palaeoclimatology, Palaeoecology 34, 115–136. doi: 10.1016/0031-0182(81)90060-2

CrossRef Full Text | Google Scholar

Tambutte, E., Tambutte, S., Segonds, N., Zoccola, D., Venn, A., Erez, J., et al. (2012). Calcein Labelling and Electrophysiology: Insights on Coral Tissue Permeability and Calcification. Proceedings of the Royal Society B: Biological Sciences 279, 19–27. doi: 10.1098/rspb.2011.0733

PubMed Abstract | CrossRef Full Text | Google Scholar

Tambutté, S., Holcomb, M., Ferrier-Pagès, C., Reynaud, S., Tambutté, E., Zoccola, D., et al. (2011). Coral Biomineralization: From the Gene to the Environment. Journal of Experimental Marine Biology and Ecology 408, 58–78. doi: 10.1016/j.jembe.2011.07.026

CrossRef Full Text | Google Scholar

Venn, A. A., Bernardet, C., Chabenat, A., Tambutté, E., and Tambutté, S. (2020). Paracellular Transport to the Coral Calcifying Medium: Effects of Environmental Parameters. The Journal of Experimental Biology 223, 227074. doi: 10.1242/jeb.227074

CrossRef Full Text | Google Scholar

Venn, A., Tambutté, E., Holcomb, M., Allemand, D., and Tambutté, S. (2011). Live Tissue Imaging Shows Reef Corals Elevate PH under Their Calcifying Tissue Relative to Seawater. PLoS ONE 6:20013. doi: 10.1371/journal.pone.0020013

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamazaki, T., Yano, M., Harii, S., and Watanabe, T. (2021). Effects of light on the Ba/Ca ratios in coral skeletons. Chemical Geology 559, 119911. doi: 10.1016/j.chemgeo.2020.119911

CrossRef Full Text | Google Scholar

Yamazato, K. (1966). Calcification in a Solitary Coral, Fungia Scutaria Lamarck in Relation to Environmental Factors. PhD Thesis. Honolulu, HI: University of Hawaii.

Google Scholar

Yoshimura, T., Tamenori, Y., Suzuki, A., Kawahata, H., Iwasaki, N., Hasegawa, H., et al. (2017). Altervalent Substitution of Sodium for Calcium in Biogenic Calcite and Aragonite. Geochimica et Cosmochimica Acta 202, 21–38. doi: 10.1016/j.gca.2016.12.003

CrossRef Full Text | Google Scholar