Magnitude Estimation for Earthquake Early Warning Using a Deep Convolutional Neural Network

Magnitude estimation is a vital task within earthquake early warning (EEW) systems (EEWSs). To improve the magnitude determination accuracy after P-wave arrival, we introduce an advanced magnitude prediction model that uses a deep convolutional neural network for earthquake magnitude estimation (DCNN-M). In this paper, we use the inland strong-motion data obtained from the Japan Kyoshin Network (K-NET) to calculate the input parameters of the DCNN-M model. The DCNN-M model uses 12 parameters extracted from 3 s of seismic data recorded after P-wave arrival as the input, four convolutional layers, four pooling layers, four batch normalization layers, three fully connected layers, the Adam optimizer, and an output. Our results show that the standard deviation of the magnitude estimation error of the DCNN-M model is 0.31, which is significantly less than the values of 1.56 and 0.42 for the τ_c method and P_d method, respectively. In addition, the magnitude prediction error of the DCNN-M model is not affected by variations in the epicentral distance. The DCNN-M model has considerable potential application in EEWSs in Japan.

Introduction

Earthquake early warning (EEW) systems (EEWSs) depend on stations located near the earthquake source area to monitor earthquakes and obtain location, ground shaking, and magnitude information using data from the first few seconds after P-wave arrival. They then send EEW information to the target sites before destructive seismic waves arrive (Allen and Kanamori, 2003). Over the past few decades, EEWSs have been shown to be an effective earthquake hazard mitigation approach and have been applied in many regions around the world, such as Japan (Hoshiba et al., 2008), Mexico (Aranda et al., 1995), Taiwan (Wu and Teng, 2002; Chen et al., 2015), California (Allen et al., 2009a), southern Italy (Zollo et al., 2009; Colombelli et al., 2020), and Iran (Heidari et al., 2012).

Magnitude estimation is an essential EEW task. Reliable EEW information and estimates of damage areas both rely on accurate magnitude determination. EEWSs estimate earthquake magnitudes based on the initial few seconds after P-wave arrival (Allen et al., 2009b). The final earthquake magnitude may be determined by the initial rupture rather than the overall earthquake rupture process (Olson and Allen, 2005; Wu and Zhao, 2006). The existing magnitude estimation methodologies mainly establish the regression functions between the parameter extracted from the initial several seconds after P-wave arrival and the catalog magnitudes (CMs) to predict the earthquake magnitudes. The τ_c method, which establishes the empirical relationship between the average period (τ_c) and the CMs, was proposed by Kanamori (2005) and has been demonstrated to have a relationship with the magnitude that is acceptable for EEWSs (Wu and Kanamori, 2008; Yamada and Mori, 2009). Wu and Zhao (2006) proposed the P_d method, which establishes an empirical correlation between the peak amplitude of displacement during the first 3 s after P-wave arrival and the CMs and was applied to predict magnitudes in southern California. The P_d method provides robust magnitude estimation, and it is feasible to use the peak amplitude of displacement during the first several seconds after P-wave arrival to predict magnitudes for EEWSs (Zollo et al., 2006; Tsang et al., 2007; Lin et al., 2011). The squared velocity integral (IV2), which was proposed by Festa et al. (2008), is related to the early radiated energy and can be used to determine earthquake magnitudes.

However, since a single parameter might provide little magnitude information regardless of whether it is governed by the frequency, amplitude, or energy, the accuracy of EEW magnitude estimation still needs to be improved. More accurate magnitude estimation will lead to more effective hazard mitigation. With the development of artificial intelligence, some researchers have combined magnitude estimation and support vector machines (SVMs) and indicated that artificial intelligence has excellent potential for use in EEW magnitude estimation applications (Reddy and Nair, 2013; Ochoa et al., 2017). In this study, we developed an advanced magnitude prediction model by using a deep convolutional neural network for magnitude estimation (DCNN-M). Following the analyses by Kanamori (2005), Wu and Kanamori (2005), and Wu and Zhao (2006), we also used the 3-s time window after P-wave arrival for DCNN-M model estimation. We used 12 magnitude estimation parameters from P-wave arrival for EEW related to the frequency, amplitude, and energy as input, which make the DCNN-M model interpretable, and trained the DCNN-M model using the training dataset. Then, the test dataset was used to test the DCNN-M model performance, and DCNN-M model magnitude estimates were compared to the τ_c method and P_d method results. Furthermore, as a test, we used the DCNN-M model to predict 31 additional earthquake events and obtained reliable magnitude estimates. We show that the DCNN-M model is robust enough to predict magnitudes in Japan and that it has considerable potential for application to EEWSs.

Data and Processing

In this study, we used strong-motion data from October 2007 through October 2017, which were obtained from the Kyoshin Network (K-NET) stations of the National Research Institute for Earth Science and Disaster Prevention (NIED) in Japan¹ (Aoi et al., 2011). The sampling rate of the strong-motion data was 100 Hz. We selected inland earthquakes from the K-NET catalog with magnitudes within the 3 ≤ M_JMA ≤ 8 range and focal depths shallower than 10 km. We had no epicentral distance requirements for the strong-motion data.

There were 1,836 inland earthquakes (Figure 1A) characterized by 19,263 three-component seismograms recorded by the K-NET stations (Figure 1B). The data were composed mainly of events within 3 ≤ M_JMA ≤ 6.9 but included three M_JMA7 and M_JMA7.4 events (see Supplementary Table 1). The P-wave arrival was determined automatically using the short-term averaging/long-term averaging algorithm (Allen, 1978). Acceleration records were integrated once and twice to obtain velocity and displacement seismograms, respectively. Then, the displacement seismograms were processed by using a Butterworth filter with a high-pass frequency of 0.075 Hz to remove low-frequency drift (Wu and Zhao, 2006). Moreover, selected seismic records were randomly divided into two datasets: a training dataset (15,410 three-component seismic records), which accounted for 80% of the strong-motion data, was used to train the DCNN-M model, and a test dataset (3,853 three-component seismic records), which accounted for 20% of the strong-motion data, was used to assess the DCNN-M model performance after training (Figure 2).

FIGURE 1

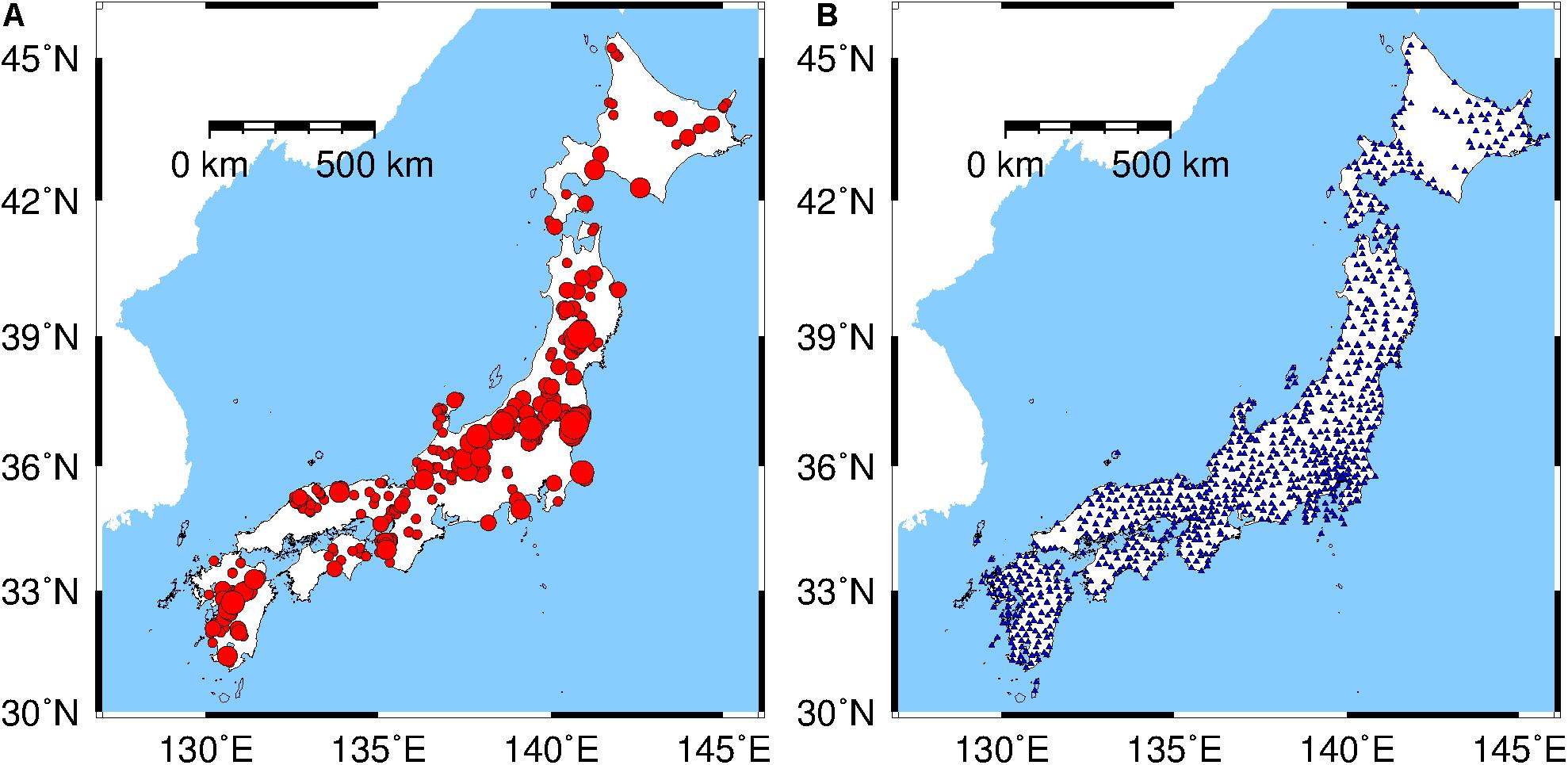
Figure 1. (A) The epicenter locations of the 1,836 inland earthquakes used in this paper. Solid red circles of different sizes indicate magnitudes within the range of 3 ≤ M_JMA ≤ 7.4. (B) The distribution of the stations (solid blue triangles) that recorded the strong-motion data used in this paper.

FIGURE 2

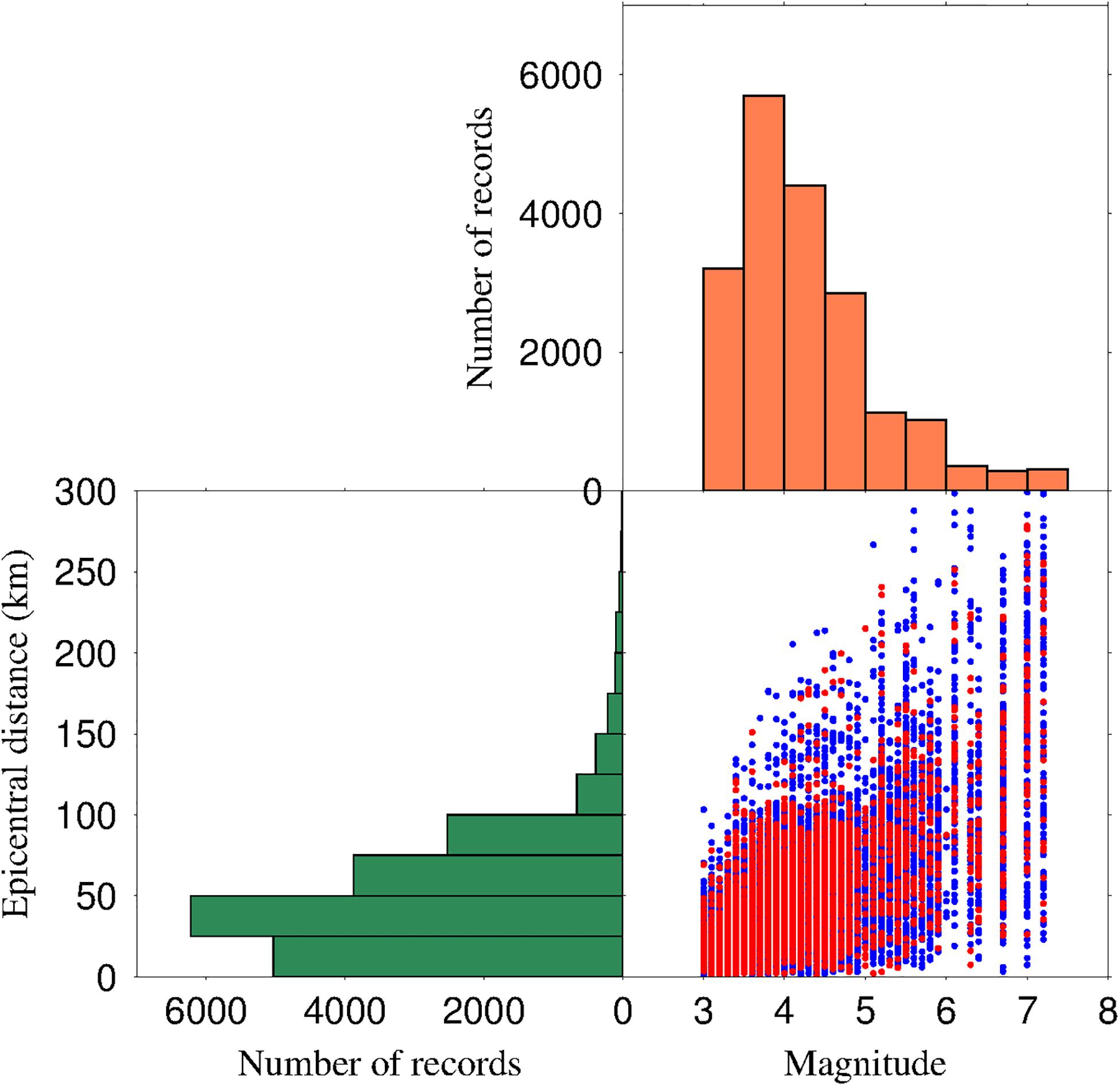
Figure 2. The distribution of the epicentral distance and magnitude records. A histogram for the number of selected seismic records with the magnitude is shown at the top. An interval of 0.5 is used for each magnitude bin. A histogram of the number of selected seismic records with the epicentral distance is shown at the bottom left. An interval of 25 km is used for each epicentral distance bin. The distribution between the magnitude and epicentral distance is shown at the bottom right. Solid blue circles indicate the training dataset used to train the DCNN-M model. Solid red circles indicate the test dataset used to test the DCNN-M model performance.

The Input Parameters

The P-wave parameters used to predict magnitude mainly include three categories for EEW: parameters related to amplitude, frequency and energy. Since a single parameter provides little earthquake magnitude information, multiple parameters might provide more information useful in magnitude prediction; thus, for EEW, 12 magnitude estimation parameters of the P-wave arrival related to the frequency, amplitude, and energy are selected as inputs to the DCNN-M model to make the DCNN-M model interpretable. It is important that these 12 P-wave parameters are correlated with magnitude in this paper. In this study, these P-wave parameters are introduced in the following paragraphs. Following the analysis of Kanamori (2005), Wu and Kanamori (2005), Wu and Zhao (2006), we also used the 3-s time window after P-wave arrival for DCNN-M model magnitude estimation. Furthermore, we corrected the parameters related to amplitude, energy and derivative parameters for the distance effect by normalizing them to a reference distance of 10 km (Zollo et al., 2006).

First, P-wave parameters related to amplitude include peak displacement (P_d), peak velocity (P_v), and peak acceleration (P_a), which provide information on the earthquake size and these amplitude-related parameters have relationships with the magnitude (Wu and Kanamori, 2005; Wu and Zhao, 2006). The single data points for the P-wave parameters related to amplitude as a function of magnitude are shown in Supplementary Figure 1. In addition, these parameters are defined as:

$$P_d=\underset{0\le t\le T}{\max }\left|d_{ud}\left(t\right)\right|(1)$$

$$P_v=\underset{0\le t\le T}{\max }\left|v_{ud}\left(t\right)\right|(2)$$

$$P_a=\underset{0\le t\le T}{\max }\left|a_{ud}\left(t\right)\right|(3)$$

where d_ud(t), v_ud(t), and a_ud(t) are the vertical components of the displacement, velocity, and acceleration time histories of the strong-motion data, respectively. Zero is the P-wave arrival time, and T is the length of the P-wave time window. In this paper, the linear relationship between the amplitude parameters, the magnitude and the hypocentral distance is shown in Supplementary Table 3, and the linear relationship between the amplitude parameters after normalization to a reference distance of 10 km and magnitude is shown in Supplementary Table 4.

Next, the P-wave parameters related to frequency include the average period (τ_c), product parameter (TP), and peak ratio (T_va). The average period has been proven to have an acceptable relationship with the magnitude (Kanamori, 2005) and it can be calculated as:

$$r=\frac{{\int }_0^T{v}_{ud}^2\left(t\right)\mathit{d}t}{{\int }_0^T{d}_{ud}^2\left(t\right)\mathit{d}t}(4)$$

$${\mathrm{\tau }}_c=\frac{2\mathrm{\pi }}{\sqrt{r}}(5)$$

The correlation of TP and magnitude was proposed by Huang et al. (2015), which has correlations with τ_c and P_d, and TP is defined as:

$$TP={\mathrm{\tau }}_c\times P_d(6)$$

where τ_c is the average period and P_d is the peak displacement. The peak ratio reflects the frequency components of the ground motion and has a correlation with magnitude (Böse, 2006; Ma, 2008), which has correlations with P_v and P_a, and it can be calculated as:

$$T_{va}=2\mathrm{\pi }\left(P_v/P_a\right)(7)$$

where P_v and P_a are the peak velocity and peak acceleration, respectively. The single data points for the P-wave parameters related to frequency as a function of magnitude are shown in Supplementary Figure 2. In this paper, the linear relationship between the frequency parameters and the magnitude is shown in Supplementary Table 5.

Finally, P-wave parameters related to the power of earthquakes include the P-wave index value (PI_v) (Nakamura, 2003), velocity squared integral (IV2) (Festa et al., 2008) and cumulative absolute velocity (CAV) (Reed and Kassawara, 1988; Böse, 2006). The single data points for the P-wave parameters related to energy as a function of magnitude are shown in Supplementary Figure 3. In addition, these parameters are calculated as:

$$P{I}_v=\underset{0\le t\le T}{\max }\text{log}\left|a_{ud}\left(t\right)\cdot v_{ud}\left(t\right)\right|(8)$$

$$IV2={\int }_0^T{v}_{ud}^2\left(t\right)\mathit{d}t(9)$$

$$CAV={\int }_0^T\left|a_3\left(t\right)\right|\mathit{d}t(10)$$

$$a_3\left(t\right)=\sqrt{a_{ud}^2\left(t\right)+a_{ew}^2\left(t\right)+a_{ns}^2\left(t\right)}(11)$$

where a₃(t) is the total acceleration of the three components. In this paper, the linear relationship between the energy parameters, the magnitude and the hypocentral distance is shown in Supplementary Table 6, and the linear relationship between the energy parameters after normalization to a reference distance of 10 km and magnitude is shown in Supplementary Table 7. Because, CAV considers the influence of both the amplitude and the duration of motion, we proposed three derivative parameters according to the CAV. They are cumulative vertical absolute displacement(cvad), cumulative vertical absolute velocity(cvav) and cumulative vertical absolute acceleration(cvaa). The single data points for the derivative parameters as a function of magnitude are shown in Supplementary Figure 4. These parameters are calculated as:

$$cvad=\underset{0\le t\le T}{sum}\left(\left|d_{ud}\left(t\right)\right|\right)(12)$$

$$cvav=\underset{0\le t\le T}{sum}\left(\left|v_{ud}\left(t\right)\right|\right)(13)$$

$$cvaa=\underset{0\le t\le T}{sum}\left(\left|a_{ud}\left(t\right)\right|\right)(14)$$

In this paper, the linear relationship between the derivative parameters, the magnitude and the hypocentral distance is shown in Supplementary Table 8, and the linear relationship between the derivative parameters after normalization to a reference distance of 10 km and magnitude is shown in Supplementary Table 9.

To prevent numerical problems caused by large variations between the ranges of the parameters and to improve the training efficiency of the model, these parameters are linearly scaled to [−1, 1] as the input of the deep convolutional neural network (Tezcan and Cheng, 2012). When scaled to [−1, 1], every parameter becomes:

$$x_{\text{norm}}=\frac{2x-\left(x_{\text{max}}+x_{\text{min}}\right)}{x_{\text{max}}-x_{\text{min}}}(15)$$

where x_norm is the original P-wave parameter and x_max and x_min are the maximum and minimum values of every P-wave parameter extracted from the strong-motion data in this study, respectively.

The DCNN-M Model

Earthquake early warning magnitudes are usually predicted via the empirical relationship between a single parameter extracted from the seismic data collected during the first few seconds after P-wave arrival and CMs. Since a single parameter provides little earthquake magnitude information, multiple parameters might provide more information useful in magnitude prediction. In addition, to make the model interpretable, for EEW, we used 12 magnitude estimation parameters related to the amplitude, frequency, and energy following the P-wave arrival (see Supplementary Text 1) as the inputs of the DCNN-M model.

The DCNN-M model was constructed based on a deep convolutional neural network and was used to predict magnitudes for EEW. The architecture of the DCNN-M model comprised 12 parameters extracted from the 3 s period after P-wave arrival as inputs, four convolutional layers, four batch normalization layers, four pooling layers, three fully connected layers, and an output (Figure 3). The output was the predicted magnitude (PM). The four convolutional layers had 124, 150, 190, and 250 filters. In each convolutional layer, the kernel size of the filter was 4, the stride was 2, the padding type was “same,” and the initialization was “TruncatedNormal.” A batch normalization layer followed each convolutional layer. The batch normalization layers made the setting of the hyperparameters freer, the network convergence speed faster, and the performance better (Ioffe and Szegedy, 2015). A pooling layer followed each batch normalization layer; we used max pooling, each max pooling size was 2, each stride was 2, and each padding type was “same.” The final pooling layer was flattened and then fed to the first fully connected layer. The three fully connected layers had 250, 125, and 60 neurons.

FIGURE 3

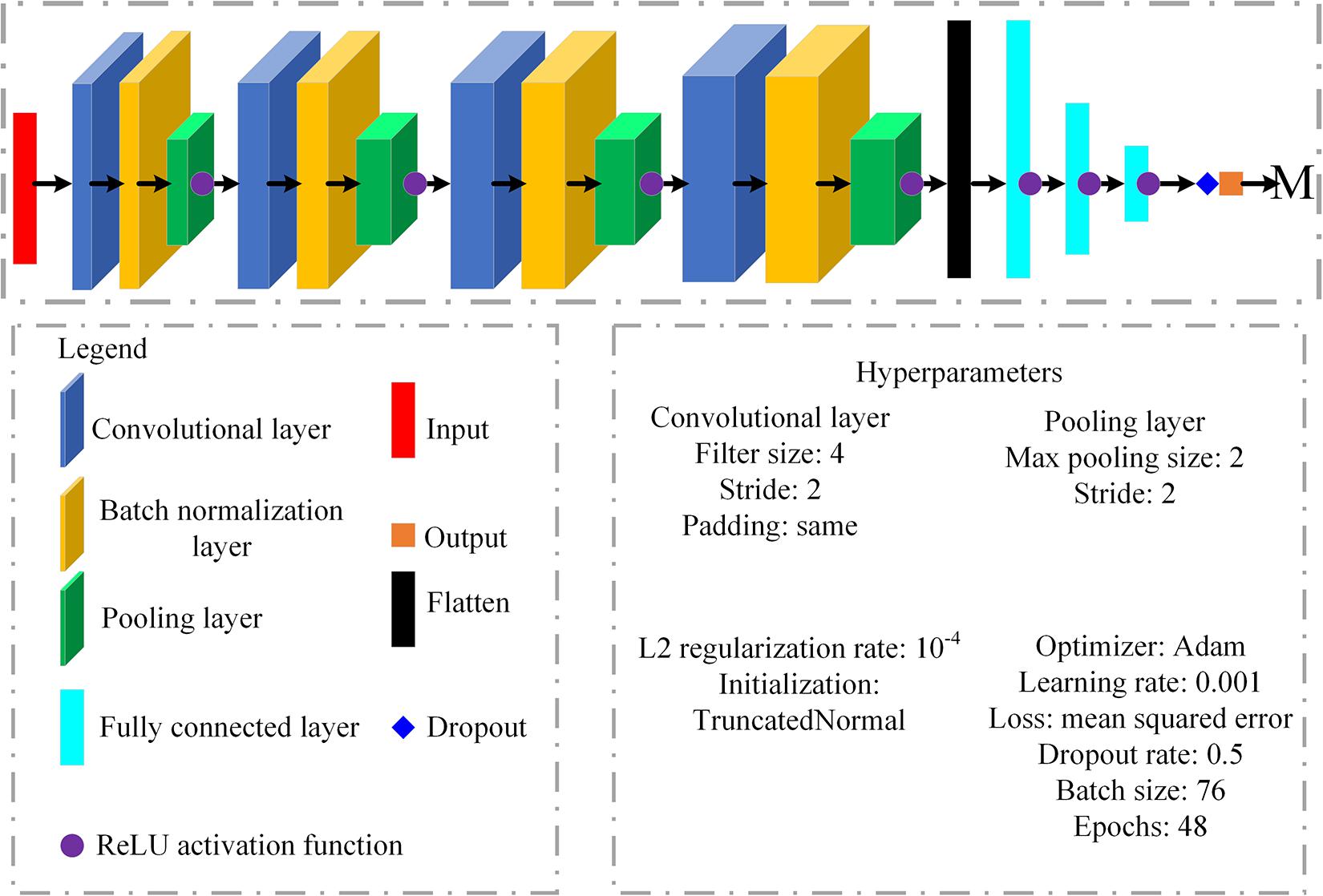
Figure 3. The architecture of the DCNN-M model. Twelve parameters related to the frequency, amplitude, and energy extracted from the 3-s period after P-wave arrival are used as the inputs of the DCNN-M model. The hyperparameters of the DCNN-M model include the filter size, stride, padding, initialization, optimizer, learning rate, regularization, and dropout, etc.

To prevent overfitting and ensure better generalizability, we applied L2 regularization with a regularization rate of 10^–4 to the convolutional layers and dropout with a dropout rate of 0.5 following the last fully connected layer (Srivastava et al., 2014; Jozinović et al., 2020). Moreover, the rectified linear unit (ReLU) activation function (Nair and Hinton, 2010) followed each pooling layer and fully connected layer. Because larger batch sizes lead to worse generalization performance (Keskar et al., 2016), we used 76 batch sizes and 48 epochs based on a tradeoff between efficiency and generalizability. We used a training dataset to train the DCNN-M model based on the Adam optimizer with a learning rate of 0.001 by optimizing a loss function defined as the mean squared error of the output (Kingma and Ba, 2014). In this study, the DCNN-M model was programmed using TensorFlow GPU 2.3 and trained using the training dataset, requiring approximately 1.5 min on an Nvidia Quadro T1000 GPU with 12 GB memory.

Results

In this study, the difference between the PM and CM is defined as the error (ω). The error (ω) and the standard deviation (σ) of the errors are expressed as:

$$\mathrm{\omega }=\text{PM}-\text{CM}(16)$$

$$\mathrm{\sigma }=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left({\mathrm{\omega }}_i-\varpi \right)}^2}(17)$$

where N is the number of records and ϖ is the mean of the errors.

Figure 4 depicts magnitude estimation for the training dataset (Figure 4A) and the test dataset (Figure 4B) based on the DCNN-M model. The PMs approximate the CMs in the training and test datasets. The standard deviations of the magnitude estimation errors are 0.31 for both the training and test datasets. This finding indicates excellent generalization performance and an absence of overfitting within the DCNN-M model.

FIGURE 4

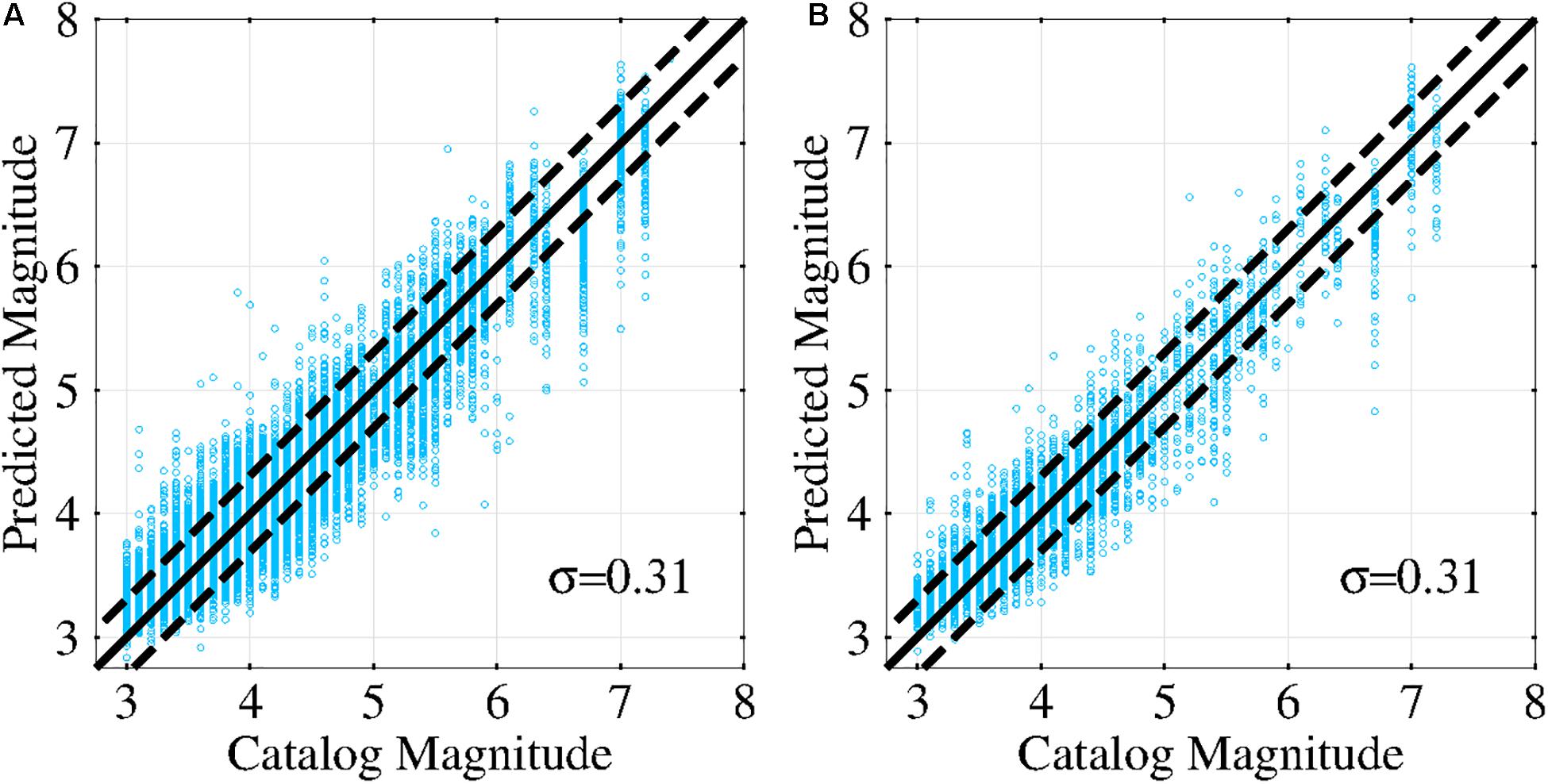
Figure 4. Correlations between the predicted and catalog magnitudes. (A) Magnitude estimation for the training dataset used to train the DCNN-M model. (B) The magnitude estimation of the test dataset used to test the DCNN-M model performance. When a data point is on the solid black 45° line, the predicted magnitude is equal to the catalog magnitude. The two black dashed lines indicate the range of one standard deviation of error.

The τ_c method and P_d method are widely used in the study of EEWS magnitude prediction (Kanamori, 2005; Wu and Kanamori, 2005; Wu and Zhao, 2006; Zollo et al., 2006; Colombelli et al., 2014). To evaluate the performance of the DCNN-M model, the τ_c method and P_d method were used to predict the magnitudes, and the results were compared.

For the same test dataset and the 3-s time window after P-wave arrival, Figures 5A–C show the τ_c method, P_d method, and DCNN-M model estimation results, respectively. The magnitude estimates of the τ_c method and P_d method are obtained based on Supplementary Tables 4, 5, respectively. The relationships used for magnitude estimation by the τ_c method and P_d method are given by:

FIGURE 5

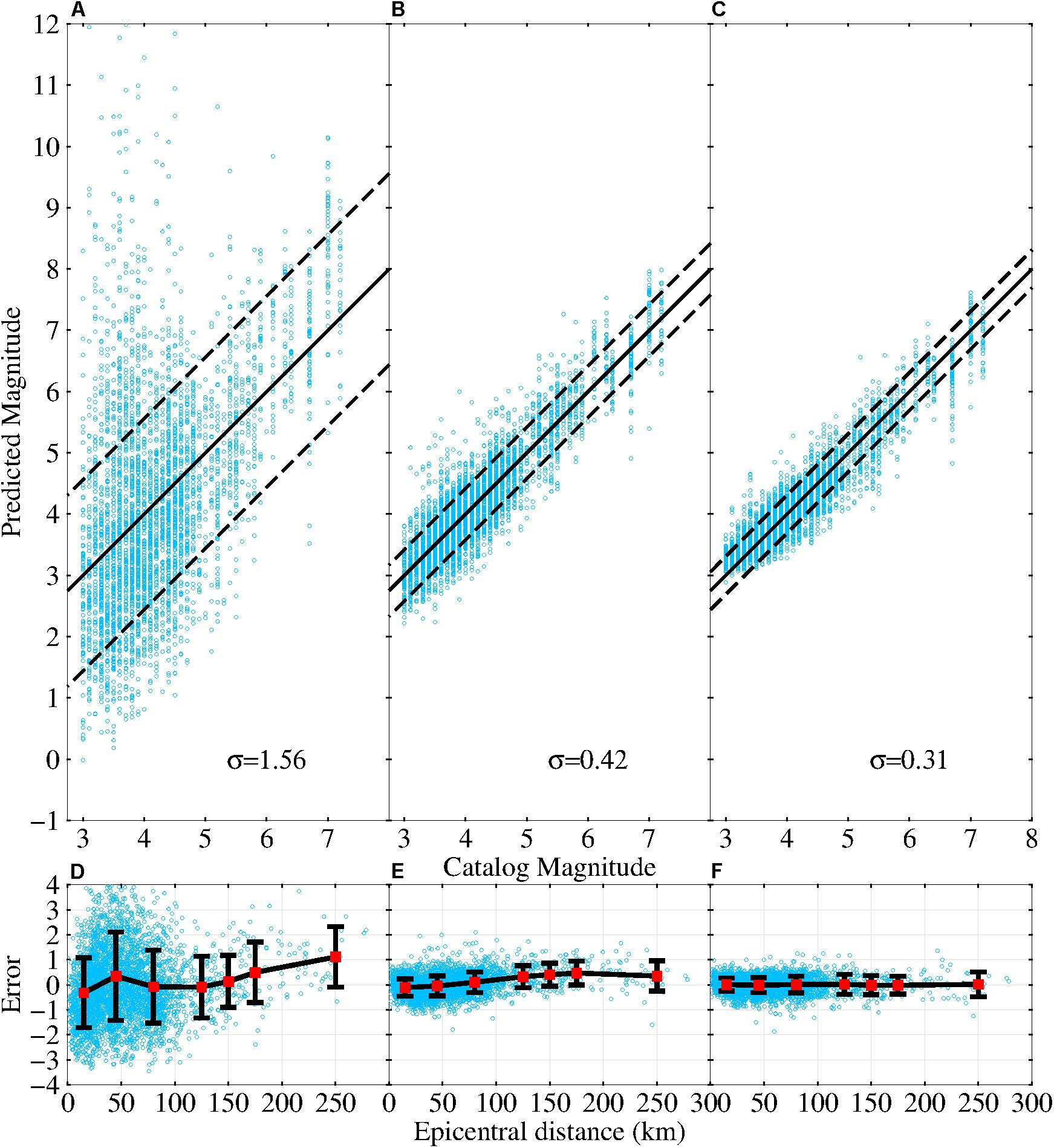
Figure 5. Catalog magnitudes versus predicted magnitudes produced using the test dataset by (A) the τ_c method, (B) the P_d method, and (C) the DCNN-M model. On the solid black 45° line, the predicted magnitude is equal to the catalog magnitude. The two black dashed lines indicate the locations of one standard deviation of error. The relationship between the epicentral distance and the error in the predicted magnitude for (D) the τ_c method, (E) the P_d method, and (F) the DCNN-M model. The epicentral distance is divided into seven sections: (0 km, 30 km), (30 km, 60 km), (60 km, 100 km), (100 km, 150 km), (125 km, 175 km), (150 km, 200 km), and (200 km, 200+ km). The position of the solid red square represents the mean of the errors within an epicentral distance. The length of the black bar shows the standard deviation of the magnitude estimation errors within an epicentral distance, which reflects the discreteness of the errors.

$$\text{log}\left({\mathrm{\tau }}_c\right)=-1.07\left(\pm 0.02\right)+0.19(\pm 0.01)M(18)$$

$$\text{log}\left(P_d^{10\text{km}}\right)=-4.84\left(\pm 0.02\right)+0.78(\pm 0.01)M(19)$$

Compared to the DCNN-M model results, the magnitude estimation results from the τ_c method and P_d method exhibit considerable scatter. The standard deviations of the magnitude estimation error are 1.56, 0.42, and 0.31 for the τ_c method, P_d method, and DCNN-M model, respectively. There is obvious magnitude overestimation (M_JMA ≤ 5) from the τ_c method and P_d method, but this issue is improved considerably in the DCNN-M model results. The magnitudes predicted by the DCNN-M model are closer to the vs. than those from the τ_c method and P_d method.

Furthermore, the variation in the magnitude estimation error with the epicentral distance is presented in Figure 5 for the τ_c method (Figure 5D), P_d method (Figure 5E), and DCNN-M model (Figure 5F). It can be observed from the distribution of circles that the τ_c method and P_d method exhibit larger errors than the DCNN-M model. In addition, the magnitude estimation errors from the τ_c method and P_d method have larger discreteness (black bars) than those from the DCNN-M model, and the means (red squares) of the magnitude estimation errors from the τ_c method and P_d method clearly vary with increasing epicentral distance. This phenomenon is especially true for the τ_c method. The mean (red square) of the DCNN-M model magnitude estimation errors is nearly zero, and the DCNN-M model magnitude estimation errors are not affected by the epicentral distance.

For a given test dataset, Table 1 compares the distribution of the magnitude estimation absolute errors for the τ_c method, P_d method, and DCNN-M model. As shown in Table 1, the absolute magnitude estimation errors of the DCNN-M model are concentrated mainly in the range of 0.6 magnitude units of approximately 2σ, and the results for the DCNN-M model are nearly 60 and 10% greater than those of the τ_c method and P_d method, respectively, in the range of 0.6 magnitude units. Moreover, for the absolute magnitude estimation errors greater than 1.2 magnitude units, the percentage of DCNN-M model results is nearly zero and is much less than those from the τ_c method and P_d method. These analyses also indicate that the DCNN-M model is more accurate than the τ_c method and P_d method and has considerable EEW application potential.

TABLE 1

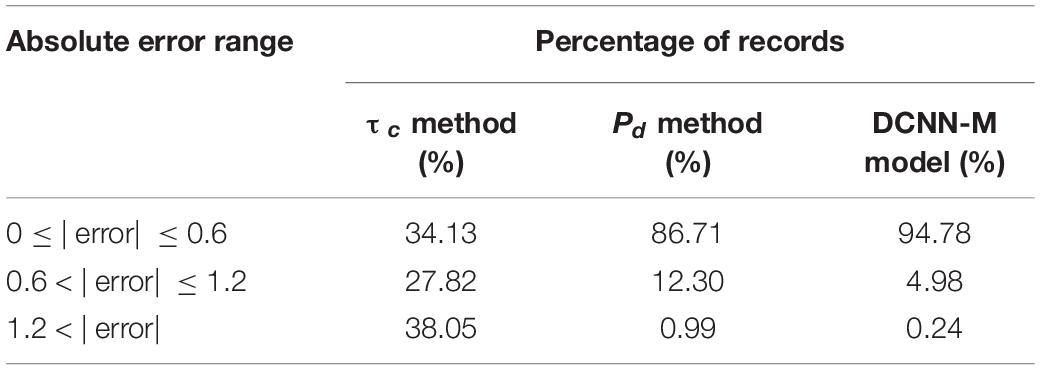
Table 1. The distribution of the magnitude estimation errors for the τ_c method, P_d method, and DCNN-M model.

Offline Application of the DCNN-M Model

To test the robustness of the DCNN-M model in analyzing new earthquake events, we tested the magnitude prediction of 31 additional events. These events were not included in the training and test datasets. These events (see Supplementary Table 2) occurred mainly between April 2018 and December 2019. Due to the small number of large earthquakes with M_JMA ≥ 6 in this time period, we also selected seven earthquakes with M_JMA ≥ 6 that occurred before October 2007. The distribution of stations and epicenters for the 31 events and the magnitude prediction for these events are shown in Figures 6A,B, respectively. The solid red circle shows the mean estimated magnitude of the DCNN-M model for an earthquake event. The PMs of these events are quite similar to the CMs, and nearly all of the PMs are within the standard deviation (0.31) of the errors for the DCNN-M model. In addition, the standard deviation of the errors for these events is 0.21. Moreover, reliable results without obvious magnitude overestimation and underestimation are obtained for events with M_JMA ≤ 7.2.

FIGURE 6

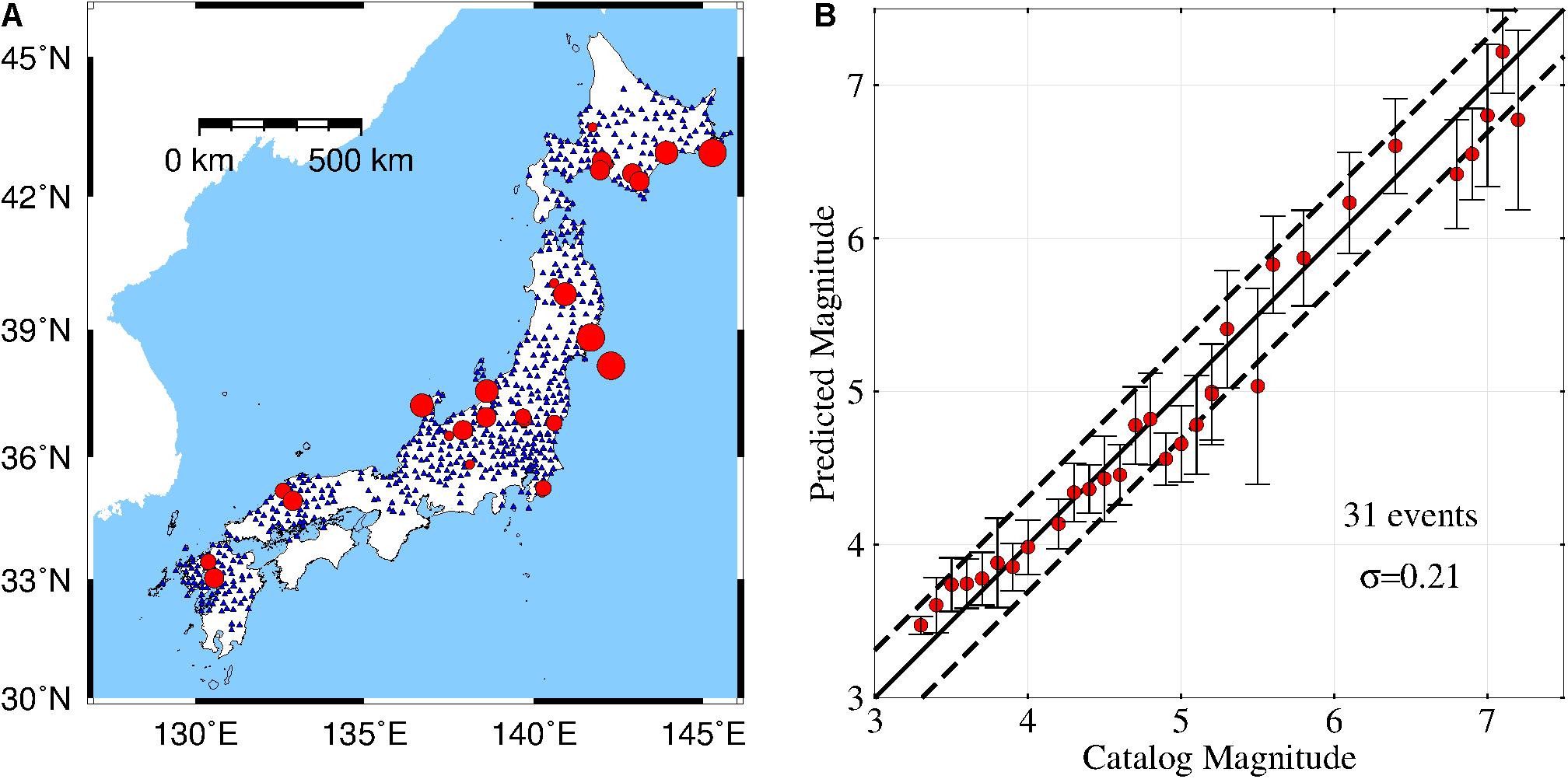
Figure 6. (A) The distribution of the epicenter locations and stations for 31 additional earthquakes. The solid red circles of different sizes represent magnitudes of 3 ≤ M_JMA ≤ 7.2. The solid blue triangles represent stations that recorded the 31 events. (B) Magnitudes determined using the DCNN-M model versus the catalog magnitudes for the 31 additional events. On the solid black 45° line, the predicted magnitude is equal to the catalog magnitude. The two black dashed lines indicate the locations (0.31) of the one standard deviation of errors for the DCNN-M model. The solid red circles show the mean of the estimated magnitudes of the DCNN-M model for the earthquake events. The length of the black bar shows the standard deviation of the magnitude estimation errors for each event.

Discussion and Conclusion

For the past several decades, EEW magnitudes have been determined by establishing regression functions between a single P-wave parameter and the CMs. The τ_c method and P_d method have been widely used in the study of EEW magnitude estimation (Kanamori, 2005; Wu and Kanamori, 2005; Wu and Zhao, 2006; Zollo et al., 2006; Colombelli et al., 2014). Since a single parameter might provide little magnitude information, we introduce an advanced magnitude prediction model named DCNN-M in this paper. DCNN-M uses a deep convolutional neural network to perform magnitude estimation. We used a training dataset to train the DCNN-M model and 12 parameters extracted from the initial 3 s of the P-wave record as inputs to the DCNN-M model. These parameters are related to the frequency, amplitude, and energy, which make the DCNN-M model interpretable. Additionally, although many of these input parameters might not be independent of each other, they are not completely the same, and more parameters might provide more information about the magnitude. In addition, a test dataset was used to test the DCNN-M model performance. The results were compared to those from the τ_c method and P_d method. As a further test, we used the DCNN-M model to predict 31 additional events.

In this study, we used 1,836 inland earthquakes from the K-NET catalog with magnitudes in the 3 ≤ M_JMA ≤ 7.2 range and focal depths shallower than 10 km. To use more accurate P-wave arrival information, first, we use the short-term averaging/long-term averaging algorithm (Allen, 1978) to determine the P-wave arrival automatically. Then compared with the P-wave arrival determined manually, the records that have a larger difference between the P-wave arrival determined automatically and the P-wave arrival determined manually are discarded. For the test dataset, DCNN-M magnitude estimation provided smaller errors and no obvious overall magnitude underestimation or overestimation relative to the τ_c method and P_d method. In principle, the DCNN-M model can be extended to earthquakes in other regions. We plan to test it with strong-motion data from China because most earthquakes in China are inland earthquakes with focal depths shallower than 10 km (Song et al., 2018). In this study, the problem of the possible underestimation of large earthquakes did not appear in the dataset of earthquakes with magnitudes in the 3 ≤ M_JMA ≤ 7.2 range. The problem of underestimation of large earthquakes (M_JMA ≥ 7.5) remains to be studied. Extending the training dataset magnitude range or the time window after P-wave arrival may solve problems related to larger (M_JMA ≥ 7.5) earthquakes (Colombelli et al., 2012; Chen et al., 2017).

The DCNN-M model trained using the training dataset could provide ideal test dataset magnitude estimation results. The standard deviations of the magnitude estimation errors of the training and test datasets were both 0.31. This finding indicates that the DCNN-M model provided good generalizability with no overfitting. Our results show that the magnitudes predicted by the DCNN-M model, which provided a standard deviation of 0.31 based on the 3-s time window after P-wave arrival, exhibited better agreement with the CMs than the magnitudes predicted using the τ_c method and P_d method, which provided standard deviations of 1.56 and 0.42, respectively. In addition, the magnitude estimates from the τ_c method provided considerable scatter and overestimation at M_JMA ≤ 5. These phenomena are consistent with the results of Carranza et al. (2015). In contrast, the PMs from the DCNN-M model significantly approximate the CMs. The τ_c parameter is used as an input to the DCNN-M model, but there is no significant overestimation at M_JMA ≤ 5. The reason may be that the DCNN-M model training reduces the influence of τ_c on the model magnitude, and the correlation between the frequency content of the τ_c parameter and magnitude is learned. The magnitude estimates from the DCNN-M model were not affected by the epicentral distance, unlike those of the τ_c method and P_d method. For the same test dataset, the absolute magnitude estimation errors of the DCNN-M model are mainly concentrated in the range of 0.6 magnitude units at approximately 2σ, and the percentage of the magnitude estimation error is 94.78% greater than those of the τ_c method and P_d method. This finding means that the DCNN-M model has better magnitude determination performance than the τ_c method and P_d method, and the probability that the magnitude estimation error is in the range of 0.6 magnitude units is 94.78%. Furthermore, we obtained reliable magnitude estimates without obvious magnitude overestimation and underestimation for 31 additional events using the DCNN-M model. These results indicate that the DCNN-M model has considerable EEW magnitude estimation application potential in Japan.

In Japan, magnitude is measured with the magnitude scale M_JMA; hence, the magnitude scale M_JMA is used as the target predicted by the DCNN-M model for the area of Japan in this paper. For different magnitude scales and user requirement, we could use the conversion relationship between different magnitude scales or use a different magnitude scale (likely M_w) as the target predicted by the DCNN-M model. Different magnitude scales might influence our results. We mainly propose a new magnitude model (DCNN-M) for magnitude determination in this paper for EEW. In the next step we will deeply study the influence of different magnitude scales on the DCNN-M model.

Importantly in this study, we corrected the parameters related to amplitude, energy and derivative parameters for the distance effect by normalizing them to a reference distance of 10 km (Zollo et al., 2006). In our application, based on real-time earthquake locations provided by an EEWS, the magnitude estimation of the DCNN-M model is determined. The method used to determine real-time earthquake locations is similar to that of Zollo et al. (2010), which was developed by Satriano et al. (2008). Moreover, it also provides the possibility to detect earthquake locations based on the deep learning method (Perol et al., 2018; Zhang et al., 2019, 2020) and has potential for future application in EEW.

However, the DCNN-M model hyperparameters, the size of the training dataset and the input parameters are also important in magnitude estimation. The hyperparameters include the number of layers, number of filters, dropout rate, optimizer, learning rate, batch size, and stride. In this paper, we tried several times to debug each hyperparameter of the DCNN-M model manually to identify those hyperparameters that might not be optimal. However, the comparison of the DCNN-M model magnitude estimates with those produced via the τ_c method and P_d method indicated that the DCNN-M model has considerable potential for EEW applications and provides robust magnitude estimation. In this study, we use 12 parameters extracted from the initial 3 s of the P-wave record as inputs to the DCNN-M model, and we may find that more parameters with magnitude information could be used as the input of the DCNN-M model in the future. To improve the performance of the DCNN-M model with regard to the magnitude estimation accuracy, the DCNN-M model hyperparameters and the input parameters need to be optimized, and the amount of strong-motion data still needs to be expanded (Perol et al., 2018). The DCNN-M model will be more effective at avoiding false EEW alarms than the τ_c method and P_d method.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JZ implemented and applied the method and wrote the related text. JS contributed to designing the methodology and revised the manuscript. SL and YW provided important suggestions for the interpretation of the results. All authors contributed to the redaction and final revision of the manuscript.

Funding

This research was financially supported by the National Key Research and Development Program of China (2018YFC1504003) and its provincial funding, the National Natural Science Foundation of China (51408564 and U1534202), and the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (2016A03).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the National Research Institute for Earth Science and Disaster Prevention (NIED), Japan, for providing the K-NET station strong-motion data. We are also grateful for the GMT software used by Wessel and Smith (1988).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.653226/full#supplementary-material

Footnotes

1. ^ http://www.kyoshin.bosai.go.jp/

References

Allen, R. M., Brown, H., Hellweg, M., Khainovski, O., Lombard, P., and Neuhauser, D. (2009a). Real–time earthquake detection and hazard assessment by ElarmS across California. Geophys. Res. Lett 36:L00B08. doi: 10.1029/2008gl036766

CrossRef Full Text | Google Scholar

Allen, R. M., Gasparini, P., Kamigaichi, O., and Böse, M. (2009b). The status of earthquake early warning around the world: an introductory overview. Seismol. Res. Lett. 80, 682–693. doi: 10.1785/gssrl.80.5.682

CrossRef Full Text | Google Scholar

Allen, R. M., and Kanamori, H. (2003). The potential for earthquake early warning in Southern California. Science 300, 786–789. doi: 10.1126/science.1080912

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, R. V. (1978). Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 68, 1521–1532. doi: 10.1007/BF02247958

CrossRef Full Text | Google Scholar

Aoi, S., Kunugi, T., Nakamura, H., and Fujiwara, H. (2011). Deployment of New Strong Motion Seismographs of K–NET and KiK–net. Berlin: Springer Netherlands Press.

Google Scholar

Aranda, J. M. E., Jiménez, A., Ibarrola, G., Alcantar, F., Aguilar, A., Inostroza, M., et al. (1995). Mexico city seismic alert system. Seismol. Res. Lett. 66, 42–53. doi: 10.1785/gssrl.66.6.42

CrossRef Full Text | Google Scholar

Böse, M. (2006). Earthquake Early Warning for Istanbul Using Artificial Neural Networks [Ph.D. thesis]. Karlsruhe: University of Karlsruhe.

Google Scholar

Carranza, M., Buforn, E., and Zollo, A. (2015). Testing the earthquake early–warning parameter correlations in the Southern Iberian Peninsula. Pure Appl. Geophys. 172, 2435–2448. doi: 10.1007/s00024-015-1061-6

CrossRef Full Text | Google Scholar

Chen, D. Y., Hsiao, N. C., and Wu, Y. M. (2015). The earthworm based earthquake alarm reporting system in Taiwan. Bull. Seismol. Soc. Am. 105, 568–579. doi: 10.1785/0120140147

CrossRef Full Text | Google Scholar

Chen, D. Y., Wu, Y. M., and Chin, T. L. (2017). An empirical evolutionary magnitude estimation for early warning of earthquakes. J. Asian. Earth Sci. 135, 190–197. doi: 10.1016/j.jseaes.2016.12.028

CrossRef Full Text | Google Scholar

Colombelli, S., Carotenuto, F., Elia, L., and Zollo, A. (2020). Design and implementation of a mobile device app for network–based earthquake early warning systems (EEWSs): application to the PRESTo EEWS in southern Italy. Nat. Hazards Earth Syst. Sci. 20, 921–931. doi: 10.5194/nhess-20-921-2020

CrossRef Full Text | Google Scholar

Colombelli, S., Zollo, A., Festa, G., and Kanamori, H. (2012). Early magnitude and potential damage zone estimates for the great Mw 9 Tohoku–Oki earthquake. Geophys. Res. Lett. 39:L22306. doi: 10.1029/2012gl053923

CrossRef Full Text | Google Scholar

Colombelli, S., Zollo, A., Festa, G., and Picozzi, M. (2014). Evidence for a difference in rupture initiation between small and large earthquakes. Nat. Comm. 5:3958. doi: 10.1038/ncomms4958

PubMed Abstract | CrossRef Full Text | Google Scholar

Festa, G., Zollo, A., and Lancieri, M. (2008). Earthquake magnitude estimation from early radiated energy. Geophys. Res. Lett. 35:L22307. doi: 10.1029/2008gl035576

CrossRef Full Text | Google Scholar

Heidari, R., Shomali, Z. H., and Ghayamghamian, M. R. (2012). Magnitude–scaling relations using period parameters τc and τpmax, for Tehran region. Iran. Geophys. J. Int. 192, 275–284. doi: 10.1093/gji/ggs012

CrossRef Full Text | Google Scholar

Hoshiba, M., Kamigaichi, O., Saito, M., Tsukada, S., and Hamada, N. (2008). Earthquake early warning starts nationwide in Japan. Eos. Trans. Am. Geophys. Union 89, 73–74. doi: 10.1029/2008EO080001

CrossRef Full Text | Google Scholar

Huang, P. L., Lin, T. L., and Wu, Y. M. (2015). Application of τc^∗Pd in earthquake early warning. Geophys. Res. Lett. 42, 1403–1410. doi: 10.1002/2014gl063020

CrossRef Full Text | Google Scholar

Ioffe, S., and Szegedy, C. (2015). Batch normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift arXiv [Preprint]. Available online at http://arxiv.org/abs/1502.03167 (accessed September 2020).

Google Scholar

Jozinović, D., Lomax, A., Štajduhar, I., and Michelini, A. (2020). Rapid prediction of earthquake ground shaking intensity using raw waveform data and a convolutional neural network. Geophys. J. Int. 222, 1379–1389. doi: 10.1093/gji/ggaa233

CrossRef Full Text | Google Scholar

Kanamori, H. (2005). Real–time seismology and earthquake damage mitigation. Annu. Rev. Earth Planet Sci. 33, 195–214. doi: 10.1146/annurev.earth.33.092203.122626

CrossRef Full Text | Google Scholar

Keskar, N. S., Mudigere, D., Nocedal, J., Smelyanskiy, M., and Tang, P. T. P. (2016). On Large–Batch Training for Deep Learning: Generalization Gap and Sharp Minima arXiv [Preprint]. Available online at: http://arxiv.org/abs/1609.04836 (accessed September 2020).

Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: A Method for Stochastic Optimization arXiv [Preprint]. available online at: http://arxiv.org/abs/1412.6980 (accessed November 2020).

Google Scholar

Lin, T. L., Wu, Y. M., and Chen, D. Y. (2011). Magnitude estimation using initial P–wave amplitude and its spatial distribution in earthquake early warning in Taiwan. Geophys. Res. Lett. 38:L09303. doi: 10.1029/2011gl047461

CrossRef Full Text | Google Scholar

Ma, Q. (2008). Study and Application on Earthquake Early Warning [Ph.D. thesis]. Harbin: Institute of engineering mechanics.

Google Scholar

Nair, V., and Hinton, G. E. (2010). “Rectified linear units improve restricted boltzmann machines,” in Proceedings of the 27th International Conference on International Conference on Machine Learning (ICML-10) (Haifa: Omnipress).

Google Scholar

Nakamura, Y. (2003). “A new concept for the earthquake vulnerability estimation and its application to the early warning system,” in Early Warning Systems for Natural Disaster Reduction, eds J. Zschau and A. Küppers (Berlin: Springer-Verlag).

Google Scholar

Ochoa, L. H., Niño, L. F., and Vargas, C. A. (2017). Fast magnitude determination using a single seismological station record implementing machine learning techniques. Geod. Geodyn. 9, 34–41. doi: 10.1016/j.geog.2017.03.010

CrossRef Full Text | Google Scholar

Olson, E. L., and Allen, R. M. (2005). The deterministic nature of earthquake rupture. Nature 438, 212–215. doi: 10.1038/nature04214

PubMed Abstract | CrossRef Full Text | Google Scholar

Perol, T., Gharbi, M., and Denolle, M. (2018). Convolutional neural network for earthquake detection and location. Sci. Adv. 4, 1–8. doi: 10.1126/sciadv.1700578

PubMed Abstract | CrossRef Full Text | Google Scholar

Reddy, R., and Nair, R. R. (2013). The efficacy of support vector machines (SVM) in robust determination of earthquake early warning magnitudes in central Japan. J. Earth Syst. Sci. 122, 1423–1434. doi: 10.1007/s12040-013-0346-3

CrossRef Full Text | Google Scholar

Reed, J. W., and Kassawara, R. P. (1988). A criterion for determining exceedance of the operating basis earthquake. Nucl. Eng. Des. 123, 387–396. doi: 10.1016/0029-5493(90)90259-z

CrossRef Full Text | Google Scholar

Satriano, C., Lomax, A., and Zollo, A. (2008). Real-time evolutionary earthquake location for seismic early warning. Bull. seism. Soc. Am. 98, 1482–1494. doi: 10.1785/0120060159

CrossRef Full Text | Google Scholar

Song, J. D., Jiao, C. C., Li, S. Y., and Hou, B. R. (2018). Prediction method of first–level earthquake warning for high speed railway based on two–parameter threshold of seismic P–wave. China Railw. Sci. 39, 138–144. (in Chinese),Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958.

Google Scholar

Tezcan, J., and Cheng, Q. (2012). Support vector regression for estimating earthquake response spectra. B Earthq. Eng. 10, 1205–1219. doi: 10.1007/s10518-012-9350-2

CrossRef Full Text | Google Scholar

Tsang, L. L. H., Allen, R. M., and Wurman, G. (2007). Magnitude scaling relations from P–waves in southern California. Geophys. Res. Lett. 34:L19304. doi: 10.1029/2007gl031077

CrossRef Full Text | Google Scholar

Wu, Y. M., and Kanamori, H. (2005). Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of P waves. Bull. Seismol. Soc. Am. 95, 1181–1185. doi: 10.1785/0120040193

CrossRef Full Text | Google Scholar

Wu, Y. M., and Kanamori, H. (2008). Development of an earthquake early warning system using real–time strong motion signals. Sensors Basel 8, 1–9. doi: 10.3390/s8010001

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y. M., and Teng, T. L. (2002). A virtual subnetwork approach to earthquake early warning. Bull. Seismol. Soc. Am. 92, 2008–2018. doi: 10.1785/0120010217

CrossRef Full Text | Google Scholar

Wu, Y. M., and Zhao, L. (2006). Magnitude estimation using the first three seconds P–wave amplitude in earthquake early warning. Geophys. Res. Lett. 33:L16312. doi: 10.1029/2006gl026871

CrossRef Full Text | Google Scholar

Yamada, M., and Mori, J. (2009). Using τc to estimate magnitude for earthquake early warning and effects of near–field terms. J. Geophys. Res. 114:B05301. doi: 10.1029/2008jb006080

CrossRef Full Text | Google Scholar

Zhang, M., Ellsworth, W. L., and Beroza, G. C. (2019). Rapid earthquake association and location. Seismol. Res. Lett. 90, 2276–2284. doi: 10.1785/0220190052

CrossRef Full Text | Google Scholar

Zhang, X., Zhang, J., Yuan, C., Liu, S., Chen, Z., and Li, W. (2020). Locating induced earthquakes with a network of seismic stations in Oklahoma via a deep learning method. Sci. Rep. 10:1941. doi: 10.1038/s41598-020-58908-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Zollo, A., Iannaccone, G., Lancieri, M., Cantore, L., Convertito, V., Emolo, A., et al. (2009). Earthquake early warning system in southern Italy: Methodologies and performance evaluation. Geophys. Res. Lett. 36:L00B07. doi: 10.1029/2008GL036689

CrossRef Full Text | Google Scholar

Zollo, A., Lancieri, M., and Nielsen, S. (2006). Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records. Geophys. Res. Lett. 33:L23312. doi: 10.1029/2006gl027795

CrossRef Full Text | Google Scholar

Zollo, A., Ortensia, A., Maria, L., Wu, Y. M., and Kanamori, H. (2010). A threshold-based earthquake early warning using dense accelerometer networks. Geophys J Int 183, 963–974. doi: 10.1111/j.1365-246X.2010.04765.x

CrossRef Full Text | Google Scholar