The Carbon-Sulfur Link in the Remineralization of Organic Carbon in Surface Sediments

Here we present the carbon isotopic composition of dissolved inorganic carbon (DIC) and the sulfur isotopic composition of sulfate, along with changes in sulfate concentrations, of the pore fluid collected from a series of sediment cores located along a depth transect on the Iberian Margin. We use these data to explore the coupling of microbial sulfate reduction (MSR) to organic carbon oxidation in the uppermost (up to nine meters) sediment. We argue that the combined use of the carbon and sulfur isotopic composition, of DIC and sulfate respectively, in sedimentary pore fluids, viewed through a δ¹³C_DIC vs. δ³⁴S_SO4 cross plot, reveals significant insight into the nature of carbon-sulfur coupling in marine sedimentary pore fluids on continental margins. Our data show systemic changes in the carbon and sulfur isotopic composition of DIC and sulfate (respectively) where, at all sites, the carbon isotopic composition of the DIC decreases before the sulfur isotopic composition of sulfate increases. We compare our results to global data and show that this behavior persists over a range of sediment types, locations and water depths. We use a reactive-transport model to show how changes in the amount of DIC in seawater, the carbon isotopic composition of organic matter, the amount of organic carbon oxidation by early diagenetic reactions, and the presence and source of methane influence the carbon and sulfur isotopic composition of sedimentary pore fluids and the shape of the δ¹³C_DIC vs. δ³⁴S_SO4 cross plot. The δ¹³C of the DIC released during sulfate reduction and sulfate-driven anaerobic oxidation of methane is a major control on the minimum δ¹³C_DIC value in the δ¹³C_DIC vs. δ³⁴S_SO4 cross plot, with the δ¹³C of the organic carbon being important during both MSR and combined sulfate reduction, sulfate-driven AOM and methanogenesis.

Introduction

Organic carbon oxidation in marine sediments is a key process in the global carbon and oxygen cycles as it mitigates the burial of reduced forms of carbon (Froelich et al., 1979; Berner, 1989; Kump and Arthur, 1999; Diester-Haass et al., 2009; Kump et al., 2011). When oxygen is present, this organic carbon remineralization is dominated by aerobic respiration. However, the depth of penetration of oxygen in marine sediments is limited, particularly on the continental shelf where the delivery of organic carbon is high (Froelich et al., 1979; Tromp et al., 1995; D’Hondt et al., 2015). In the absence of oxygen, anaerobic remineralization of organic carbon continues for many hundreds of meters below the sediment-water interface provided there are suitable alternative electron acceptors present (Froelich et al., 1979; Kasten et al., 2003). This anaerobic remineralization of organic carbon is important because when these electron acceptors are depleted, any remaining organically-derived material may be converted into methane through methanogenesis (Claypool and Kaplan, 1974; Whiticar and Faber, 1986; Whiticar, 1999; Sivan et al., 2007). Thus, exploring the controls on the remineralization of organic carbon is vital to resolving the carbon budget in dynamic sedimentary systems along continental margins.

The study of the subsurface anaerobic oxidation of organic carbon, which in the modern ocean is dominated by microbial sulfate reduction (MSR), is often achieved through the analysis of the chemistry of pore fluids, the fluids trapped between the grains of sediment on the ocean floor (Froelich et al., 1979; Berner, 1980; Kasten et al., 2003). These pore fluids chemically evolve from seawater as a function of the chemical reactions occurring below the seafloor and the rate of transport via diffusion of solutes and advection of fluids through the sediments (Berner, 1978; Froelich et al., 1979; Boudreau, 1997). Many studies have attempted to quantify the rate of anaerobic remineralization of organic carbon through numerical modeling of the concentration gradients within pore fluids using the diffusion coefficient of an ion of interest, the sediment porosity and the rate at which the concentration changes with depth (Berner, 1980; Boudreau, 1997; Sivan et al., 2007; Arndt et al., 2009; Wehrmann et al., 2011). One of the challenges of this approach is that the majority of the existing pore fluid data comes from the International Ocean Drilling Programs where the top meter of sediment is disturbed or not sampled. This top meter, sometimes called the sedimentary boundary layer, is often the most dynamic part of the sediment column and is the portion of sediment that is in direct contact with the overlying ocean (Sayles, 1979, 1981; Sun et al., 2016). Far fewer studies have been able to analyze the geochemistry of both the boundary layer and the underlying sediment to understand how processes that are happening in the uppermost sediment may—or may not—link to the better-studied processes occurring deeper within the sediment pile. Previous studies into carbonate recrystallization at ODP Sites, for example, have often failed to capture a significant proportion of the change in the calcium isotope ratio of pore fluids due to the lack of sampling resolution in the uppermost part of the sediment (Fantle and DePaolo, 2007; Fantle, 2015).

An important class of geochemical measurements that offers insight into the subsurface remineralization of organic carbon is the light stable isotope ratios in various dissolved ions in the sediment pore fluid. Organic carbon that reaches the sediment-water interface is enriched in the lighter ¹²C isotope relative to seawater DIC and when this organic carbon is oxidized, the carbon isotopic composition of the dissolved inorganic carbon (DIC) in the pore fluid is lowered, reflecting the addition of ¹²C-enriched DIC to the pore fluid (McCorkle et al., 1985; Meister et al., 2019). When organic carbon is converted into methane, the lighter ¹²C isotope preferentially ends up in the methane, producing methane with a very low δ¹³C and leaving the residual DIC enriched in the heavier ¹³C isotope. In the case of MSR, ³²S is preferentially reduced, leaving the ³⁴S behind; therefore, as sulfate concentrations are depleted in sedimentary pore fluids, the sulfur isotopic composition of the remaining sulfate increases (Berner, 1989; Canfield et al., 1993; Kasten and Jørgensen, 2000). Ultimately, the ³²S ends up in the product sulfide, and, when iron is present, possibly in the mineralized form, pyrite (Berner, 1989; Algeo et al., 2015). Oxygen isotopes in sulfate are also fractionated in a similar fashion to sulfur isotopes, where the lighter ¹⁶O is preferentially reduced leaving the heavy ¹⁸O behind (Brunner et al., 2005; Turchyn et al., 2006). Oxygen isotopes in sulfate are affected by an additional isotope equilibrium process with water, which may lead to the oxygen isotopic composition of the sulfate increasing faster than would be predicted for a unidirectional, kinetic isotope effect alone (Wortmann et al., 2007). The relative increase in the sulfur and oxygen isotopic composition of sulfate during MSR has been shown to relate to the rate of MSR (Wortmann et al., 2007; Antler et al., 2013, 2014). In this case, a fast increase in δ¹⁸O of sulfate relative to its δ³⁴S suggests there is a high rate of back-reaction and equilibration of oxygen isotopes in intermediate-valence-state-sulfur species with water, and thus a slower overall rate of MSR (Antler et al., 2013, 2014). Two other processes impact the sulfur isotope fractionation observed in sediments, the disproportionation of external sulfur intermediates and microbial sulfide oxidation, and the observed sulfur isotopic composition of sulfate may be due to a combination of all three processes (Jørgensen et al., 2019b; Pellerin et al., 2019). It is, in general, not possible to differentiate between sulfate reduction and sulfur disproportionation with only ³⁴S and ³²S measurements, although the measurement of other sulfur isotopes (such as ³³S) provides greater insight into the oxidative sulfur cycle (Johnston et al., 2005; Bradley et al., 2016; Jørgensen et al., 2019b).

Both the carbon and sulfur isotopic composition of sedimentary pore fluid DIC and sulfate, respectively, have been used, independently, to resolve questions in the deep biosphere and with the sedimentary oxidation or mineralization of carbon. In particular, the carbon isotopic composition of pore fluid DIC has been utilized to investigate the depth distribution of methane production (methanogenesis) and methane oxidation (methanotrophy) in sediments (Sivan et al., 2007; Meister et al., 2019). Similarly, the sulfur isotopic composition of pore fluid sulfate measured in sedimentary pore fluids has been used to explore the depth distribution of MSR and its coupling to methane oxidation (Jørgensen and Kasten, 2006; Wortmann et al., 2007; Sela-Adler et al., 2017; Jørgensen et al., 2019a). These studies have helped elucidate the redox changes to carbon and sulfur within sedimentary systems, but many questions remain. For example, there is still uncertainty about the proportion of sulfate that is consumed through anaerobic oxidation of methane (AOM) vs. through organic-matter driven MSR when both processes are occurring (Sivan et al., 2007; Egger et al., 2018). Understanding precisely how carbon and sulfur are coupled within marine sediments may be better achieved by directly comparing measurements of δ¹³C_DIC and δ³⁴S_SO4. This would have implications for our understanding of the cycling of carbon, particularly in the uppermost part of the sediment. MSR generates more DIC per mole of electron acceptor reduced than the microbial metal reduction processes such as iron and manganese reduction which should dominate in the uppermost sediment as they are energetically more favorable electron acceptors (Froelich et al., 1979). When MSR does occur in the uppermost sediment, this influences our understanding of the sources and sinks of alkalinity and DIC (Sayles, 1979, 1981).

In 2013, a site survey cruise (JC089) aboard the RRS James Cook took a series of surface multicores and longer piston cores along a depth transect on the southwestern Iberian Margin (Hodell et al., 2014). A Megacorer was used to collect multi-cores for pore fluid chemical analyses at each site, with emphasis on high-resolution (cm-scale) pore fluid geochemistry in the upper meter of sediment. Station JC089-06 is at the same location as IODP Site U1385 where deeper cores were recovered to 155.9 mbsf during IODP Leg 339 in December 2011–January 2012.

In this paper we present high resolution pore fluid geochemical and isotopic composition from the cores recovered on Cruise JC089 (Table 1). Specifically, we use the sulfur and oxygen isotopic composition of sulfate, along with changes in the concentration of sulfate, and the carbon isotopic composition of DIC to explore the oxidation of organic carbon along the Iberian continental margin, from shallow water depths (628 mbsl) to the abyssal plain (4,672 mbsl). The data are evaluated using a reactive transport model to constrain the underlying processes governing the oxidation of organic carbon and how they manifest as changes in shallow pore fluids. We propose that using δ¹³C_DIC vs. δ³⁴S_SO4 cross plot reveals significant information about the nature of carbon-sulfur coupling in marine sedimentary pore fluids on continental margins.

TABLE 1

Table 1. Sampling locations, method of coring and water depth.

Materials and Methods

Analytical Methods

Interstitial waters were extracted from up to three multi-cores at each station, using Rhizon samplers spaced at 1 cm intervals through sealed ports in the multicores. Rhizons and syringes were acid cleaned using 3 M HCl followed by 1.5 M HNO₃ and an overnight soak in high purity deionized water. Pore fluids were extracted from sub-cores of box cores at three sites and from piston cores collected at six sites on board ship. Piston cores were sampled using Rhizon samplers spaced at 20 cm intervals, while the sub-cores of box cores were sampled using Rhizon samplers spaced at 1 cm intervals. In situ micro-sensor oxygen concentration measurements were performed shipboard and calibrated using oxygen solubilities at the measured salinities and temperature according to the Unisense Gas tables (Garcia and Gordon, 1992; Skinner et al., 2019). A two-point calibration was performed using oxygen concentrations from the overlying water and in the anoxic part of the sediment. Alkalinity was measured on board (not presented here).

One milliliter aliquots of the pore fluid collected during cruise JC089 were separated from samples taken at five mega core sites (Sites 4, 5, 6, 9, and 11) and two of the piston cores (Sites 5 and 11). To the pore fluid aliquot, 1 mL of barium chloride solution was added to precipitate the aqueous sulfate as barite (BaSO₄). This barite was subsequently cleaned with 6 N HCl and three times with deionized water before being dried down to be weighed for isotope analysis. Sulfur isotope ratios in this barite were analyzed through combustion in a Flash Element Analyzer (Flash EA) coupled by continuous flow to a Delta Advantage mass spectrometer at the University of Cambridge in the Godwin Laboratory for Paleoclimate Research. Samples were run in sets of ∼20 bracketed by NBS 127 (δ³⁴S = 21.1‰) and are reported relative to the international standard VCDT. The 1σ standard deviation of the bracketing standards is used as the standard deviation for the samples in a particular run, although blind duplicates were also run at the end of each column to check the measured δ³⁴S value. The analytical precision on these runs was 0.2‰.

Oxygen isotope ratios in sulfate were analyzed through pyrolysis in a Temperature Conversion Element Analyzer (TC/EA) coupled by continuous helium flow to a Delta Advantage mass spectrometer. Barite for oxygen isotope analysis was run in triplicate and the average and standard deviation of the triplicate analyses are presented. Samples were bracketed by NBS 127 (δ¹⁸O_SO4 = 8.6‰) and an internal standard to correct for measurement drift and analytical error. The analytical precision on these runs was usually better than 0.5‰.

Carbon isotope ratios in the DIC were analyzed using a ThermoScientific GasBench II equipped with a CTC Analytics CombiPAL autosampler coupled to a Thermo Finnigan Delta V Mass Spectrometer. Three or four drops of orthophosphoric acid (100%) were preloaded into a reaction vial, which was capped, sealed and the headspace flushed with Helium gas. Approximately 1.5 ml of sample water was injected into the vial through the butyl rubber septa using a syringe and left to react for 1 h. The sample tubes were transferred to the GasBench and CTC CombiPal Autosampler and the resulting CO₂ in the head space analyzed using a Thermo Delta V Mass Spectrometer. A series of standards and reference samples distributed throughout the run were used to calibrate to the international standard VPDB. Results have a reproducibility of better than ± 0.1‰.

Sulfate concentrations were measured using ion chromatography on a Thermo Scientific Dionex ICS 5000+ HPIC, with an IonPac AS18 column using potassium hydroxide (31 mM KOH) as the eluent. Samples were diluted 10-fold in ultrapure MilliQ water and calibrated using 2.5–15% IAPSO standard seawater also diluted in ultrapure MilliQ water. Standard calibrations were run at the beginning and end of each measurement run, as well as a smaller subset of standards that were measured every 20 samples to calculate reproducibility and assess any drift in the measured concentrations. The error on repeated measurements of the standard was <2% for all ions.

Modeling Methods

Sulfate Reduction in CrunchTope

To explore the relative changes in pore fluid δ¹³C_DIC and δ³⁴S_SO4, we utilize the multi-component numerical reactive transport software CrunchTope (Druhan et al., 2013, 2014; Steefel et al., 2015). We use CrunchTope to simulate contemporaneous advection, diffusion and chemical reactions over a 10 m pore fluid column with a coexisting solid phase with a seawater Dirichlet upper boundary condition, and a Neumann or dC/dx = 0 lower boundary condition. The porosity is fixed at 0.8, with a constant sediment burial modeled using equal burial and fluid flow rate terms of 11 cm/year, approximately equal to the average burial rate at Site 6—IODP Site U1385 (Hodell et al., 2013). The diffusivity was calculated from a molecular diffusion coefficient of 9.19 × 10^–6 cm²/s and the porosity of the sediment column (Huber et al., 2017) and was the same for all species. The system is run from the initial conditions listed in Supplementary Table 1 and allowed to run until the fluid concentrations and isotopic composition are no longer changing with time, which is assumed to be steady state. CrunchTope is open-source software, and the input and database files for our model can be found within the Supplementary Material, along with the initial conditions (Supplementary Table 1) and equilibrium constants used (Supplementary Table 2). The goal is to use this isotope-enabled reactive transport model to explore the contemporaneous evolution of δ¹³C_DIC and δ³⁴S_SO4 in surface sediments undergoing MSR.

Microbial sulfate reduction is modeled with formaldehyde (CH₂O) representing the bulk composition of organic matter (Meister, 2013, 2014; Meister et al., 2019):

$$2\mathrm{C}{\mathrm{H}}_2\text{O}+{\text{SO}}_4^{2-}+2{\text{H}}^{+}\to 2{\text{CO}}_{2_{(\mathrm{aq})}}+{\text{H}}_2{\text{S}}_{(\mathrm{aq})}+2{\text{H}}_2\text{O}(1)$$

Microbial sulfate reduction is modeled as a catabolic Monod Biomass reaction, using a dual-Monod equation relating the growth rate (r; mol/kg H₂O/year) to the abundance of electron donor/acceptor (Hubbard et al., 2014), which in this case are formaldehyde (CH₂O) and sulfate (SO₄^2–):

$$r=\mathrm{\mu }\frac{[eDonor]}{\left[eDonor\right]K_{eDonor}}\frac{[eAcceptor]}{[eAcceptor]K_{eAcceptor}}(2)$$

Where μ (mol/kg H₂O/year) is the maximum specific growth rate of the microorganism, [eX] is the concentration of the electron donor/acceptor and K (mol/kg H₂O) is the half-saturation constant of the electron donor/acceptor. In order to track two isotope systems (carbon and sulfur) during sulfate reduction, each isotopologue is written as a separate aqueous kinetic reaction (Table 2), with the relative difference in the rate constants (μ) controlling the isotopic fractionation. The sulfur isotope fractionation during sulfate reduction is varied within the different model runs discussed below, while there is assumed to be no partitioning of carbon isotopes during sulfate reduction following experimental work (Londry and Des Marais, 2003).

TABLE 2

Table 2. The isotopologue-specific aqueous reactions required to track the carbon and sulfur isotopic composition of DIC and sulfate (respectively) during sulfate reduction.

The modeling of a second isotope system (δ¹³C) exerts a minor effect on the relative isotope fractionation displayed by the first isotope system (δ³⁴S), as the rate of each of the aqueous reactions is controlled by a Monod biomass equation which is sensitive to the limiting concentrations of both organic carbon and sulfate. This is verified by modeling just the sulfur isotopic composition, without tracking the carbon isotope composition in the pore fluid, then both the sulfur and carbon isotopic composition with the same initial concentrations of organic carbon and sulfate (Figure 1A). This shows that by modeling just one isotope system vs. two isotope systems, the impact on the resulting relative isotope fractionation for both carbon and sulfur isotope ratios in the pore fluid is nearly identical. As the rate for each of the individual aqueous reactions is controlled by the concentrations of the isotopologues of organic carbon and sulfate within the pore fluid, the minor-minor isotope reaction (Table 2, D) will proceed exceptionally slowly. However, our modeling shows that it is essential this reaction is included (Figure 1B) as without the minor-minor reaction the modeled pore fluids differ in their isotopic evolution. Additionally, if the minor-minor reaction were not included two reactions would consume ¹²C, whereas only one reaction would consume ¹³C. In order to model no carbon isotope fractionation during sulfate reduction, as detailed above, we must therefore include all of the isotopologue reactions. It is possible that adding a third or fourth isotope system following the same approach would eventually remove the need for tracking the most minor-minor isotope reactions, as their impact on the modeled isotope composition decreases significantly with each additional isotope system.

FIGURE 1

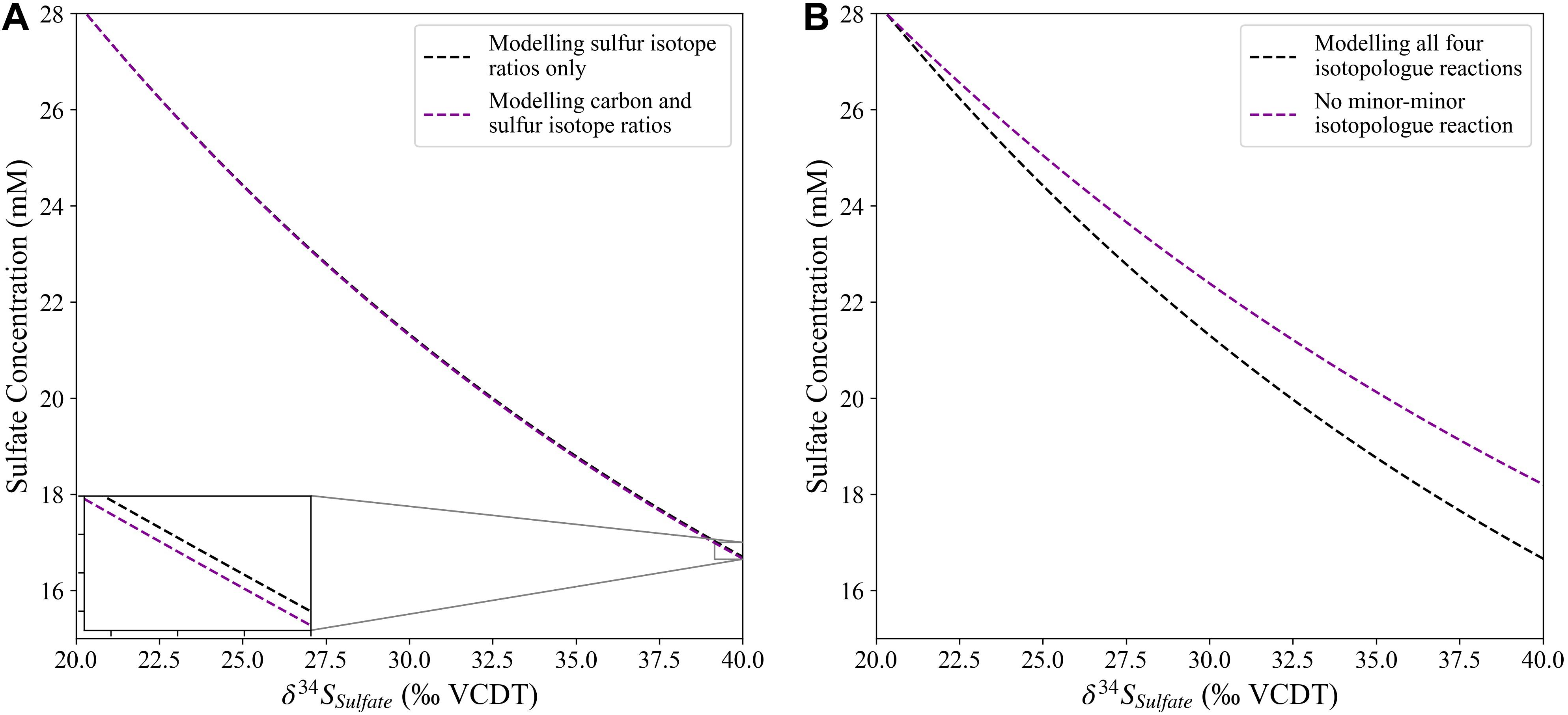
Figure 1. Panel (A) shows the minimal impact that simultaneously modeling the carbon and sulfur isotope systems in CrunchTope has on the sulfur isotopic composition of sulfate during microbial sulfate reduction. Panel (B) displays the importance of modeling all combinations of the isotope specific aqueous reactions including the minor-minor isotopologue reaction.

Aerobic Respiration in CrunchTope

The aerobic respiration of formaldehyde is also modeled using the dual Monod equation described above with the following stoichiometry:

$${\text{CH}}_2\text{O}+{\text{O}}_2\to {\text{CO}}_{2_{(aq)}}+{\text{H}}_2\text{O}(3)$$

Methanogenesis and Methanotrophy in CrunchTope

In order to investigate the impact that methanogenesis and methanotrophy can have on the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4, we add both reactions into the CrunchTope model described above. The controls on the δ¹³C of the DIC during methanogenesis and methanotrophy have recently been comprehensively reviewed by Meister et al. (2019). Methane production can be modeled with an initial breakdown of complex organic molecules generating hydrogen (Equation 4), which is then consumed during hydrogenotrophic methanogenesis (Equation 5; Claypool and Kaplan, 1974).

$$2{\text{CH}}_2\text{O}+2{\text{H}}_2\text{O}\to 2{\text{CO}}_{2_{(aq)}}+4{\text{H}}_{2_{(aq)}}(4)$$

$$2{\text{CO}}_{2_{(aq)}}+4{\text{H}}_{2_{(aq)}}\to {\text{CH}}_{4(aq)}+{\text{CO}}_{2_{(aq)}}+2{\text{H}}_2\text{O}(5)$$

Here, the formation of methane enriched in ¹²C from CO₂ (Equation 5) drives the residual DIC pool to become enriched in ¹³C. Hydrogenotrophic methanogenesis has been suggested to account for the majority of microbial methanogenesis in marine sediments, with acetoclastic methanogenesis dominating in freshwater environments (Claypool and Kaplan, 1974; Martens and Berner, 1974; Barnes and Goldberg, 1976; Whiticar and Faber, 1986; Whiticar, 1999; Sivan et al., 2007). The two stages of methanogenesis (Equations 4, 5) are also modeled using Monod equations, with the initial stage of methanogenesis requiring a single Monod equation and the final stage of methanogenesis a dual Monod equation.

The carbon isotope fractionation associated with hydrogenotrophic methanogenesis is >55‰ (Whiticar, 1999), and is significantly larger than the carbon isotope fractionation during the initial oxidation of organic matter, which is thought to be relatively insignificant (Meister et al., 2019). As CO_{2_(aq)} is found as both a product and a reactant in hydrogenotrophic methanogenesis (Equation 5), it is important to consider the effect that carbon isotope equilibrium during carbonate speciation can have on the carbon isotope composition of the various DIC species (Zhang et al., 1995). Carbon isotope equilibrium among the DIC species has recently been demonstrated in CrunchTope (Druhan et al., 2020) and we take the same modeling approach in this study.

Methanotrophy is modeled as sulfate-driven anaerobic oxidation of methane (AOM; Equation 6):

$${\text{CH}}_4+{\text{SO}}_4^{2-}+2{\text{H}}^{+}\to {\text{CO}}_{2_{(aq)}}+{\text{H}}_2{\text{S}}_{(aq)}+2{\text{H}}_2\text{O}(6)$$

Previous studies have shown that during the anaerobic oxidation of methane there is a substantial carbon isotope fractionation between −38 and −12% (Holler et al., 2009), where the residual methane is enriched in ¹³C. In the natural environment, this increase in δ¹³C of methane during methane oxidation hasn’t been readily observed, which has been suggested to be due to carbon isotope exchange between methane and CO_{2_(aq)} during AOM (Horita, 2001; Yoshinaga et al., 2014; Meister et al., 2019). This is implemented into CrunchTope as an equilibrium exchange reaction with an equilibrium fractionation factor of α_eq = 0.93 (Equation 7; Horita, 2001; Meister et al., 2019).

$${}^{12}\text{CO}_{2_{(aq)}}{+}^{13}{\text{CH}}_{4(aq)}{\leftrightarrow }^{12}{\text{CH}}_{4(aq)}{+}^{13}{\text{CO}}_{2_{(aq)}}(7)$$

The reaction scheme stoichiometry and rate constants of the model are given in Table 3.

TABLE 3

Table 3. The isotopologue-specific aqueous reactions required to track the carbon and sulfur isotopic composition of DIC and sulfate (respectively) during AOM and methanogenesis.

Results

At all five studied sites, the pore fluid sulfate concentrations decrease with depth while the pore fluid sulfate δ³⁴S and δ¹⁸O values increase with depth (Figure 2). We note that pore fluid δ³⁴S_SO4 and δ¹⁸O_SO4 increase fastest with sediment depth at Site 9 (2,323 mbsl) and slowest at the deepest water site, Site 5 (4,672 mbsl). However, the change in the sulfur and oxygen isotopic composition of sulfate as a function of the change in the sulfate concentrations is nearly identical at all sites (Figure 3). Over the five sites there is a similar increase in δ³⁴S_SO4 vs. δ¹⁸O_SO4; as mentioned above this slope has been linked to the overall cell-specific rate of MSR, suggesting a similar rate in sediments across the Iberian margin. It appears that the oxygen isotopic composition of sulfate may increase slightly faster than the sulfur isotopic composition of sulfate at Site 11 (Figure 4A). At one of the sites with piston core data (Site 9; 2,323 mbsl) we note that the cross plot of δ³⁴S_SO4 vs. δ¹⁸O_SO4 (Figure 4A) comes out of the apparent linear phase, where the sulfur and oxygen isotopic compositions covary, and into the equilibration phase, where δ¹⁸O_SO4 has reset through oxygen isotope equilibrium with water intracellularly and does not change further as the δ³⁴S_SO4 values continue to increase (Antler et al., 2014; Antler and Pellerin, 2018; Fotherby et al., 2021).

FIGURE 2

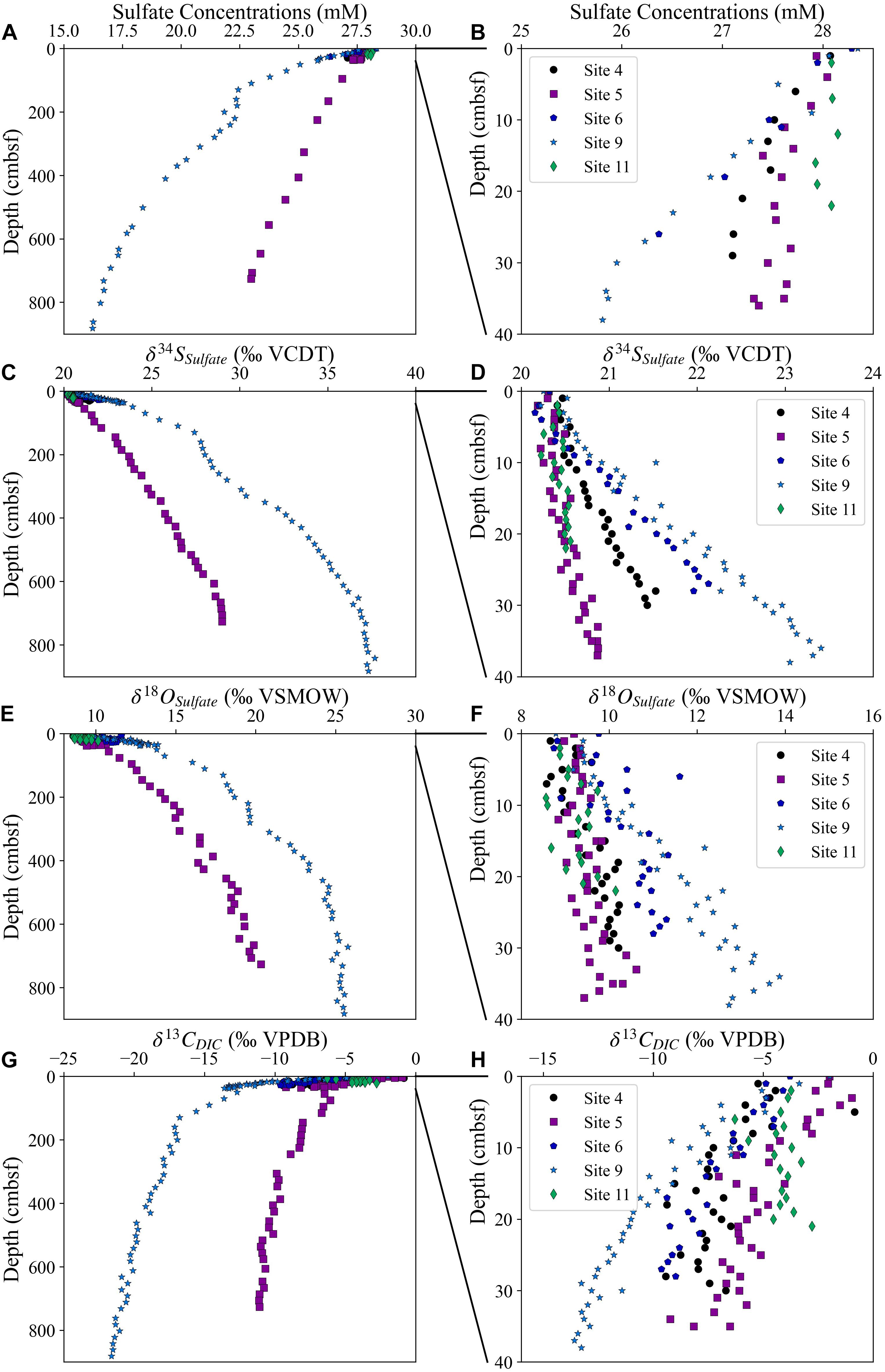
Figure 2. The sulfate concentrations from two piston and three multi cores (A,B), sulfur and oxygen isotopic composition of sulfate (C–F) and carbon isotopic composition of the DIC (G,H). Panels (A,C,E,G) display measurements over the entire depth range of the piston cores, whereas panels (B,D,F,H) display the same measurements over 40 cm below seafloor (cmbsf).

FIGURE 3

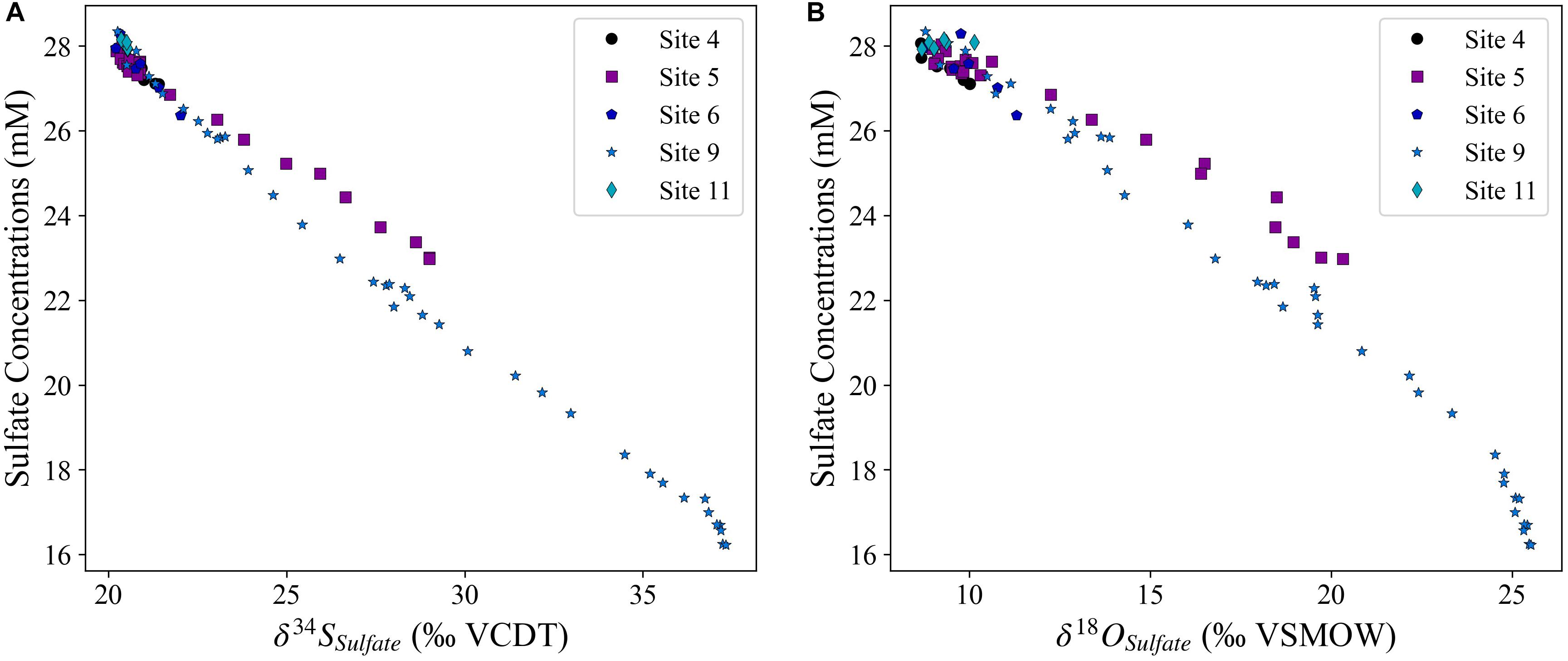
Figure 3. The increase in the sulfur (A) and oxygen (B) isotopic composition of sulfate as a function of the decrease in pore fluid sulfate concentrations.

FIGURE 4

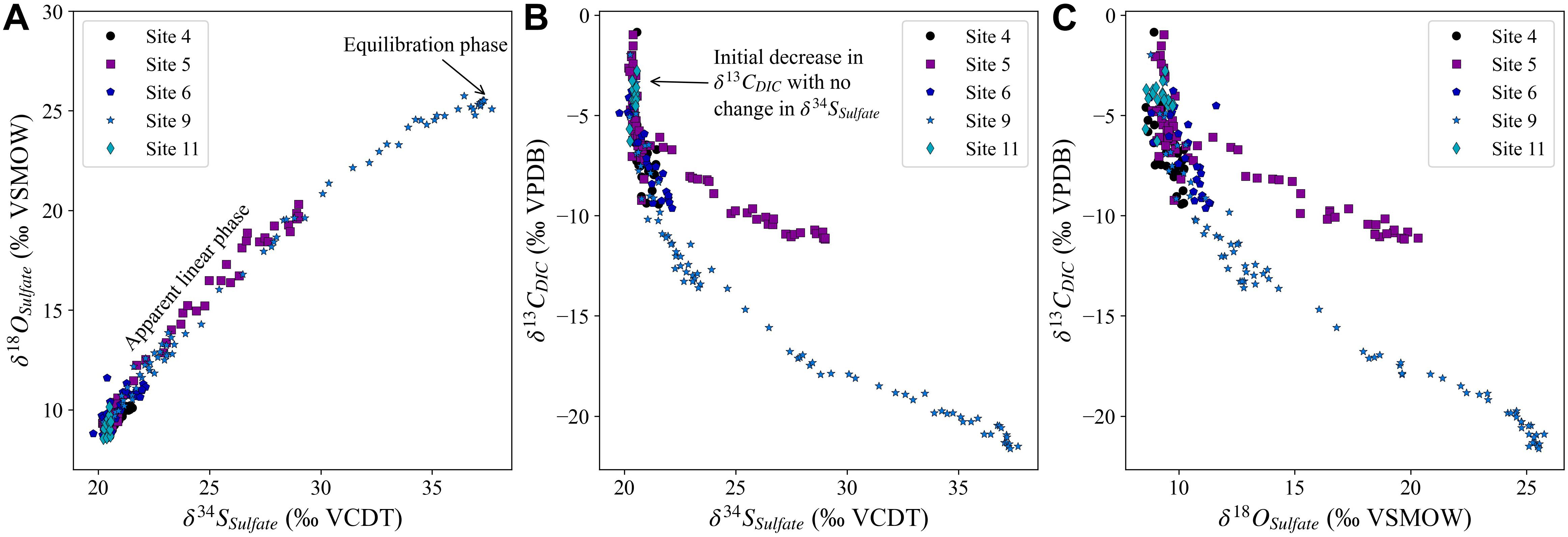
Figure 4. Panel (A) displays the relative change in the sulfur and oxygen isotopic composition of pore fluid sulfate at all five sites. The change in the sulfur (B) and oxygen (C) isotopic composition of sulfate vs. the change in the carbon isotopic composition of dissolved inorganic carbon.

The carbon isotope composition of the DIC decreases with depth as expected from the oxidation of organic carbon and the return of ¹²C-rich carbon to the DIC pool (Figures 2G,H). It has recently been shown that outgassing of CO₂-enriched pore fluids during Rhizon sampling can have a minor impact on measured δ¹³C_DIC, so measured δ¹³C_DIC may be slightly enriched in ¹³C relative to the original pore fluid values (Steiner et al., 2018). We note that when we plot δ¹³C_DIC vs. δ³⁴S_SO4 that δ¹³C_DIC decreases to −6‰ at all sites before there is an increase in δ³⁴S_SO4, and there is a similar trend displayed in δ¹³C_DIC vs. δ¹⁸O_SO4 (Figures 4B,C).

Discussion

Our data show a systematic correlation between the carbon isotopic composition of DIC and sulfur and oxygen isotopic composition in sulfate (Figure 4). We suggest that much of this relationship may be intrinsically linked to pore fluid MSR, as this is the major process which oxidizes organic carbon in modern marine sediment (Jørgensen et al., 2019b). The δ¹³C value of organic matter deposited in sediment varies between −20 and −30‰, enriched in the ¹²C isotope due to carbon isotope fractionation during photosynthesis (Hollander and McKenzie, 1991; Lehmann et al., 2002). During oxidation of organic matter, there is little carbon isotope fractionation (0–2‰; Londry and Des Marais, 2003). Therefore, during organic carbon oxidation δ¹³C_DIC will decrease toward that of the organic matter independent of the electron acceptor used during the microbial reaction. During MSR as δ¹³C_DIC trends toward the carbon isotopic composition of organic matter, δ³⁴S value of the residual sulfate will increase due to the distillation of the ³²S into the product sulfide. We initially hypothesize that the initial decrease in δ¹³C_DIC with a relatively small change in the sulfur isotopic composition of pore fluids sulfate could be due to the oxidation of organic carbon using electron acceptors other than sulfate, before the onset of MSR and the anticipated covariation between δ¹³C_DIC and δ³⁴S_SO4. Although there is a range of depositional conditions across the Iberian Margin, including varying sedimentary organic carbon content, the similarity of the correlation between δ¹³C_DIC and δ³⁴S_SO4 is remarkably consistent apart from at Site 5 (Figure 4B), demonstrating that the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4 allows resolution of fundamental processes without much of the added complications of length-scales.

Rayleigh Fractionation Subject to Transport

The two long piston cores, Site 5 and Site 9, have a large difference in the apparent sulfur isotope fractionation as evidenced by the change in δ³⁴S_SO4; often when using the change in the isotopic composition of pore fluid to resolve the sulfur isotope fractionation factor during MSR, Rayleigh distillation is used (Rudnicki et al., 2001; Breukelen and Prommer, 2008). When the apparent sulfur isotope fractionation is calculated using this simple closed-system Rayleigh fractionation approach, significantly different sulfur isotope fractionation factors are calculated for Site 5 and Site 9 (Figure 5A; Site 5 at −44.5‰ and Site 9 at −32‰). We compare this calculation using Rayleigh distillation with the sulfur isotope fractionation factors calculated using CrunchTope. The modeling approach described above is used, and the forward model of sulfate reduction as well as sediment burial and fluid transport accurately reproduce the measured sulfur isotope variations in both cores when the sulfate reduction rates are matched by controlling the sulfate reduction rate constant (μ_SR; mol/mol-CH₂O/year) and all other parameters are held constant. In order to fit the sulfate concentration profiles, the sulfate reduction rate constant (μ_SR) is lower at Site 5 (μ_SR = 4,200) than at Site 9 (μ_SR = 10,200). As Site 5 is located in much deeper water than Site 9 (4,672 mbsl relative to 2,323 mbsl), the difference in sulfate reduction rates is most likely due to the lower flux of organic carbon to the sediment in deeper water. The sulfur isotope fractionation (³⁴ε) is kept consistent for each model run (–45‰). With the higher sulfate reduction rate at Site 9, diffusion of seawater from the top of the column has a more significant impact on the apparent or observed sulfur isotope fractionation, whereas the lower rate of sulfate reduction at Site 5 lowers the impact that diffusion has on the apparent evolution of the sulfur isotopic composition of the pore fluid. Similarly, increasing the diffusion coefficient, or increasing the porosity of the system, will have the same directional impact as decreasing the rate of sulfate reduction, as the slope of the sulfate concentration-sulfur isotope plot is related to the balance of sulfate reduction and diffusion of sulfate within the pore fluid. Isotope-specific diffusion effects are not included for the different isotopologues during sulfate reduction as it has been previously shown that the impact of isotope-specific diffusion coefficients during microbially mediated sulfate reduction is considerably smaller than the error associated with the determination of the fractionation factor (Wortmann and Chernyavsky, 2011). The assumption of a consistent diffusion coefficient for ¹²C and ¹³C for both HCO₃^– and CO₃^2– has been previously used given the hydration of the molecules by a significant number of water molecules, which means the impact of ¹³C on the effective size of the molecule is very small (Zeebe et al., 1999).

FIGURE 5

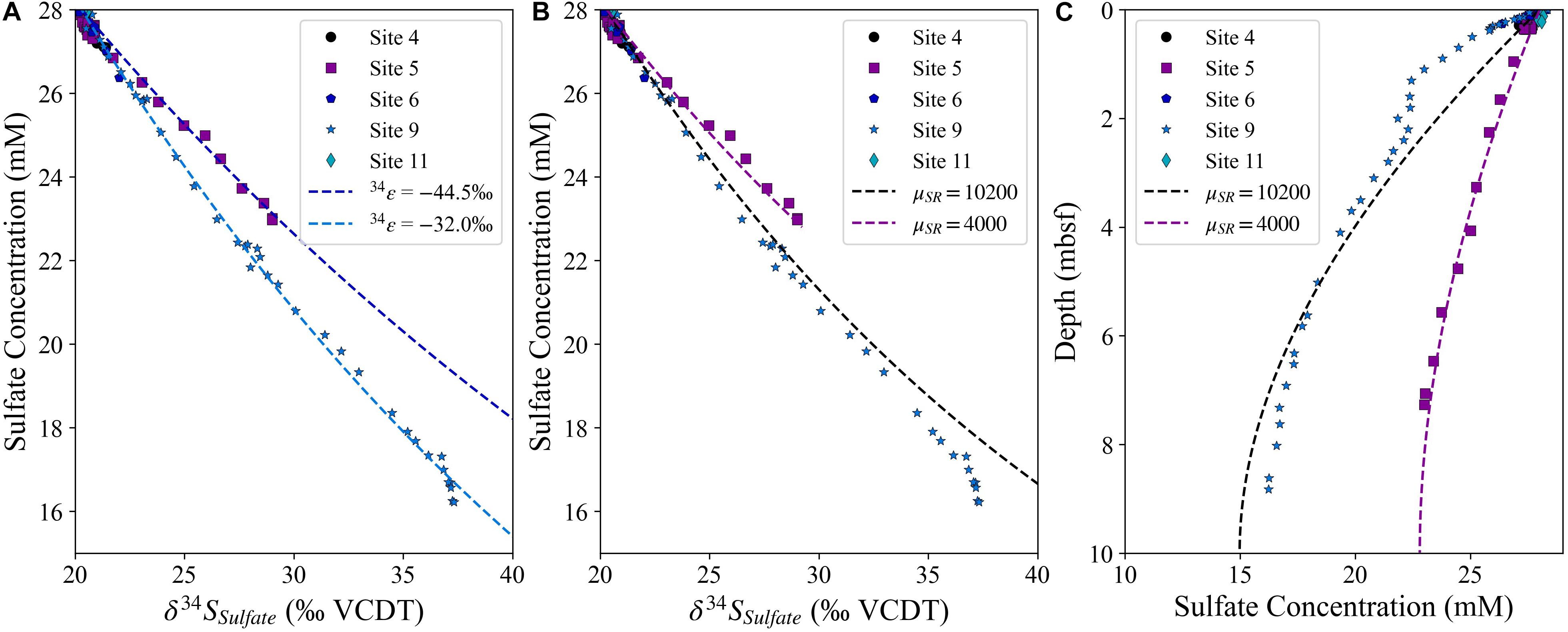
Figure 5. Panel (A) displays the change in sulfur isotopic composition of sulfate for modeled Rayleigh fractionation lines for ³⁴ε of –44.5 and –32‰ (dashed lines) compared to the measured data. Panels (B,C) display the change in sulfur isotopic composition of sulfate relative to the sulfate concentration and the sulfate concentrations relative to sediment depth, respectively using CrunchTope, with a constant ³⁴ε of –45‰.

The key finding is that the same sulfur isotope fractionation factor can explain the pore fluid sulfur isotope data when a full reactive transport model is used (Figure 5B). This demonstrates the limitations of modeling pore fluid data assuming closed-system Rayleigh fractionation, and highlights the importance of using reactive transport modeling, especially in the upper part of the sediment column where diffusive exchange with the overlying seawater is critically important. We also note that the sulfate concentration mismatch between the model and the data in the upper part of the sediment column (Figure 5C) suggests that the site may not be in steady state, which has previously been observed nearby at Site U1385 (Turchyn et al., 2016). However, when the sulfate concentration and δ³⁴S_SO4 profiles are compared in Figure 5B it can be seen that the sulfur isotope fractionation is similar throughout the sediment column.

Aerobic Respiration vs. Microbial Sulfate Reduction

Aerobic respiration, the breakdown of organic matter using dissolved oxygen as the electron acceptor, produces the largest free energy change of all of the oxidation reactions (Equation 3; Froelich et al., 1979). Aerobic respiration will persist in the water column and sediment as deep as oxygen can diffuse before it is fully depleted; therefore, in most continental margins, aerobic respiration will continue to, at, and below the sediment-water interface. As aerobic respiration involves release of the ¹²C-enriched organic carbon, but does not impact δ³⁴S_SO4, the relative evolution of the sulfur and carbon cross plot (Figure 4B) may be flagging the dynamics of aerobic respiration before the onset of MSR. To evaluate this effect, we compare a model of sulfate reduction (with no aerobic respiration—black line) to a model with both sulfate reduction and aerobic respiration (colored lines—viewed in a cross plot of δ¹³C_DIC vs. δ³⁴S_SO4; Figure 6). Our results suggest that the addition of aerobic respiration to a sediment column should cause a small, but noticeable, shift in the carbon isotopic composition of the DIC before the change in δ³⁴S_SO4 at the onset of MSR (Figure 6A). Changing the rate of aerobic respiration to reproduce the differences in the dissolved oxygen concentration profiles observed at these five sites (Figure 6B) has no significant impact on the evolution in the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4, with all five colored lines appearing identical (Figure 6A). We note that δ¹³C_DIC varies before δ³⁴S_SO4 even when there is no aerobic respiration, only MSR, due to the low initial concentration of DIC in seawater (∼2.5 mM) relative to the initial concentration of sulfate in seawater (28 mM). This means that small additions of DIC with a lower δ¹³C value (–20‰ vs. ∼0‰ in seawater) have a larger immediate observed geochemical effect than the removal of sulfate through MSR even with the large sulfur isotope fractionation. Furthermore, during MSR there is the release of two mole of DIC during the reduction of one mole of sulfate (Equation 1). The combination of these two factors causes a rapid decrease in δ¹³C_DIC relative to the slower increase in δ³⁴S_SO4, the shape of which can be further augmented by the release of ¹²C-enriched DIC during aerobic respiration.

FIGURE 6

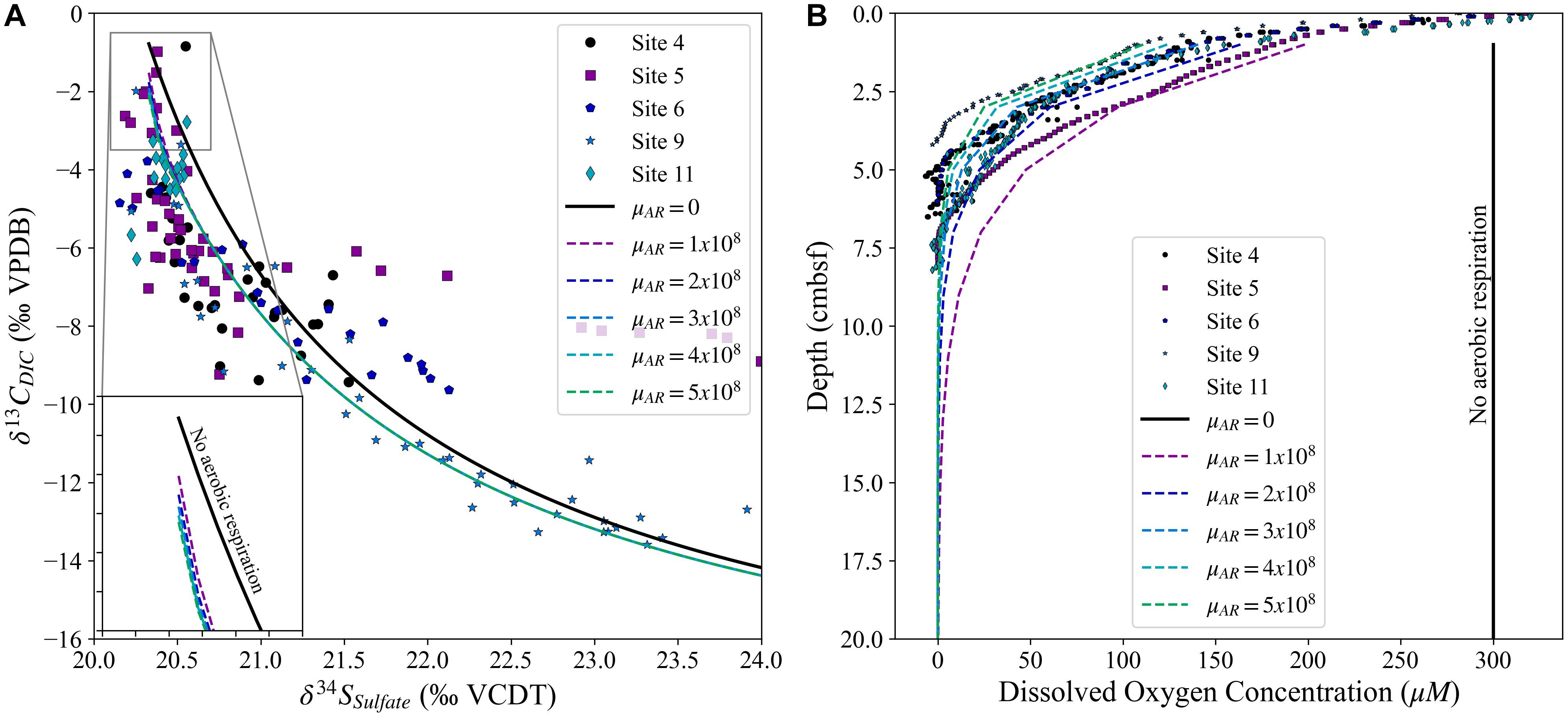
Figure 6. Panel (A) displays the change in sulfur isotopic composition of sulfate vs. the change in carbon isotopic composition of the DIC, while panel (B) displays the measured dissolved oxygen concentrations over the upper 20 cm of the five sites. In both panels the lines represent model runs for varying rates of aerobic respiration, with a constant rate of sulfate reduction, ranging from no aerobic respiration (black solid line) to aerobic respiration depleting the oxygen in the upper 5 cmbsf (green dashed line).

In some of the sites studied, however, there is a slightly larger initial decrease in δ¹³C_DIC relative to the increase in δ³⁴S_SO4 than predicted by the model that just includes aerobic respiration and MSR (Figure 6A). This hints that the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4 may contain additional information, allowing us to explore other chemical reactions such as iron or manganese reduction that in theory should occur before MSR. We explore the deviation from the model (Figure 6A) by performing a sensitivity analysis, varying δ¹³C_OrgC, initial (DIC), and the sulfur isotope fractionation factor to investigate how these variables cause deviations in the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4 in a sedimentary system where aerobic respiration and MSR are occurring (Figure 7). Our model suggests that changes in all three variables alter the sulfur/carbon isotope cross plot in similar, but slightly different, ways. Increasing the sulfur isotope fractionation factor or the boundary layer concentration of DIC produces a slower change in δ¹³C_DIC relative to δ³⁴S_SO4 (Figures 7C–F). However, this does not imply that our data suggest that there are different sulfur isotope fractionation factors among these sites, as a higher or lower sulfur isotope fractionation factor needs to also be consistent with the change in the pore fluid sulfate concentration (Figure 7F). We note that a change in the δ¹³C value of the organic carbon impacts the minimum carbon isotope composition of the pore fluid DIC as δ¹³C_DIC approaches the δ¹³C value of the organic carbon.

FIGURE 7

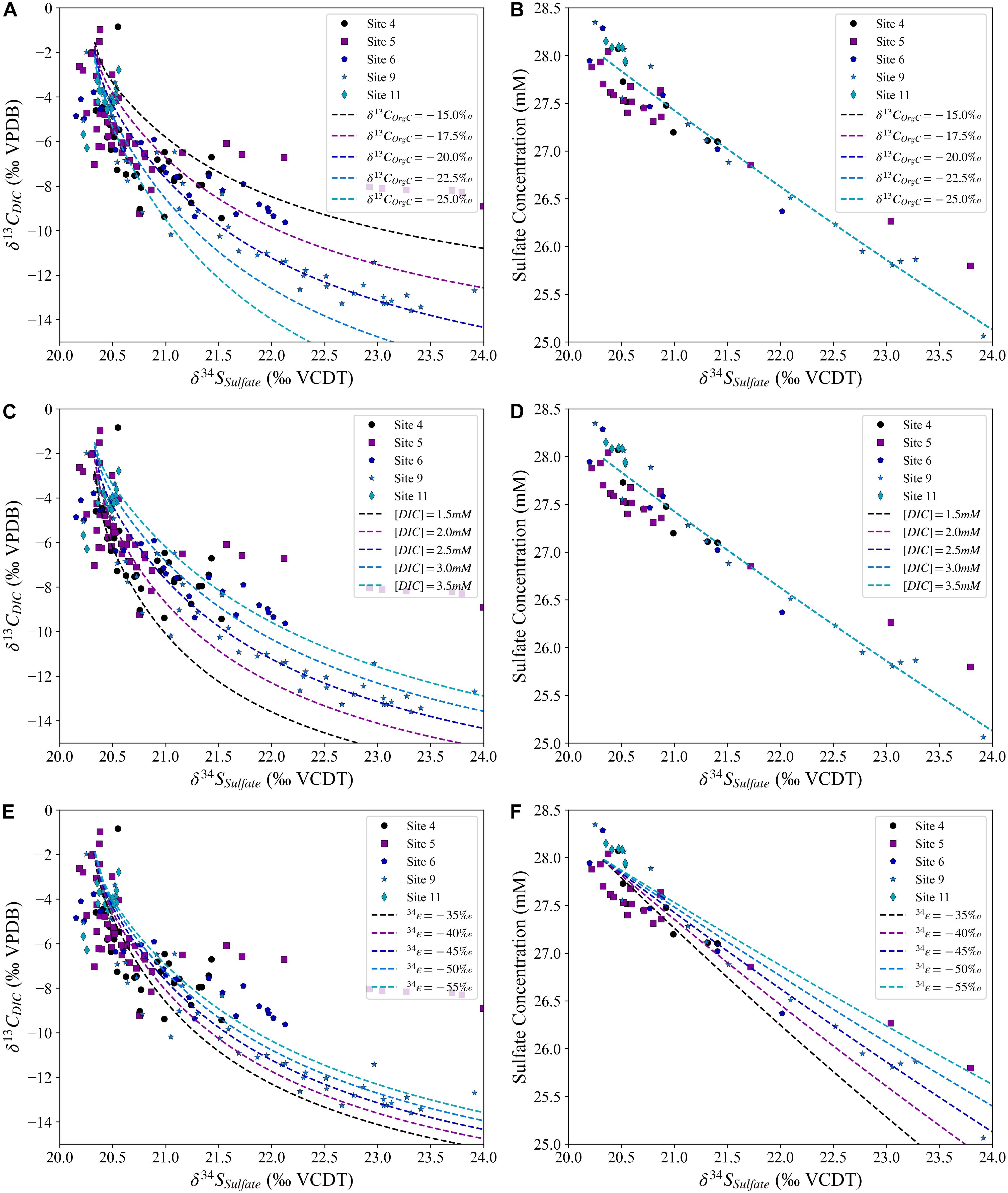
Figure 7. The sulfur and carbon isotopic composition for the model with varying carbon isotope composition of the organic carbon [δ¹³C_OrgC; (A,B)], initial dissolved inorganic carbon concentrations [(DIC); (C,D)] and sulfur isotope fractionation during sulfate reduction [³⁴ε; (E,F)] compared with the measured pore fluid values for the five sites. In panels (B,D) all five simulations are plotted; the lines are identical.

The Impact of Anaerobic Oxidation of Methane and Methanogenesis on the Sulfur/Carbon Cross Plot

We combine data from a wider compilation of sediment cores where both sulfur and carbon isotope compositions for pore fluids have been reported (Figure 8; Sivan et al., 2007; Antler et al., 2013, 2014, 2015; Rubin-Blum et al., 2014). Consistent with the sites from JC089, this global compilation shows rapidly decreasing δ¹³C_DIC before a significant increase in δ³⁴S_SO4 is seen. The range in the minimum δ¹³C_DIC value observed in the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4 can be matched by modeling a range of δ¹³C_OrgC values from −60 to −5‰. The site with the least-negative minimum in δ¹³C_DIC is ODP Site 1086, which is located off the coast of South Africa (Diester-Haass et al., 2004). The sediment at ODP Site 1086 is carbonate-rich with low organic carbon content, which causes a very low rate of sulfate reduction, with sulfate concentration reaching zero around 180 mbsf (Bradbury and Turchyn, 2018). The recrystallization of carbonate minerals, which is occurring at this site (Bradbury and Turchyn, 2018), releases carbon from the calcium carbonate with a δ¹³C value of approximately 0‰, which also will raise the minimum δ¹³C_DIC value. The overprinting of the isotopic signature of the microbial oxidation of organic carbon with carbonate recrystallization is only apparent in locations with very low rates of organic carbon burial and MSR such as ODP Site 1086 and Site 5 from the JC089 cruise.

FIGURE 8

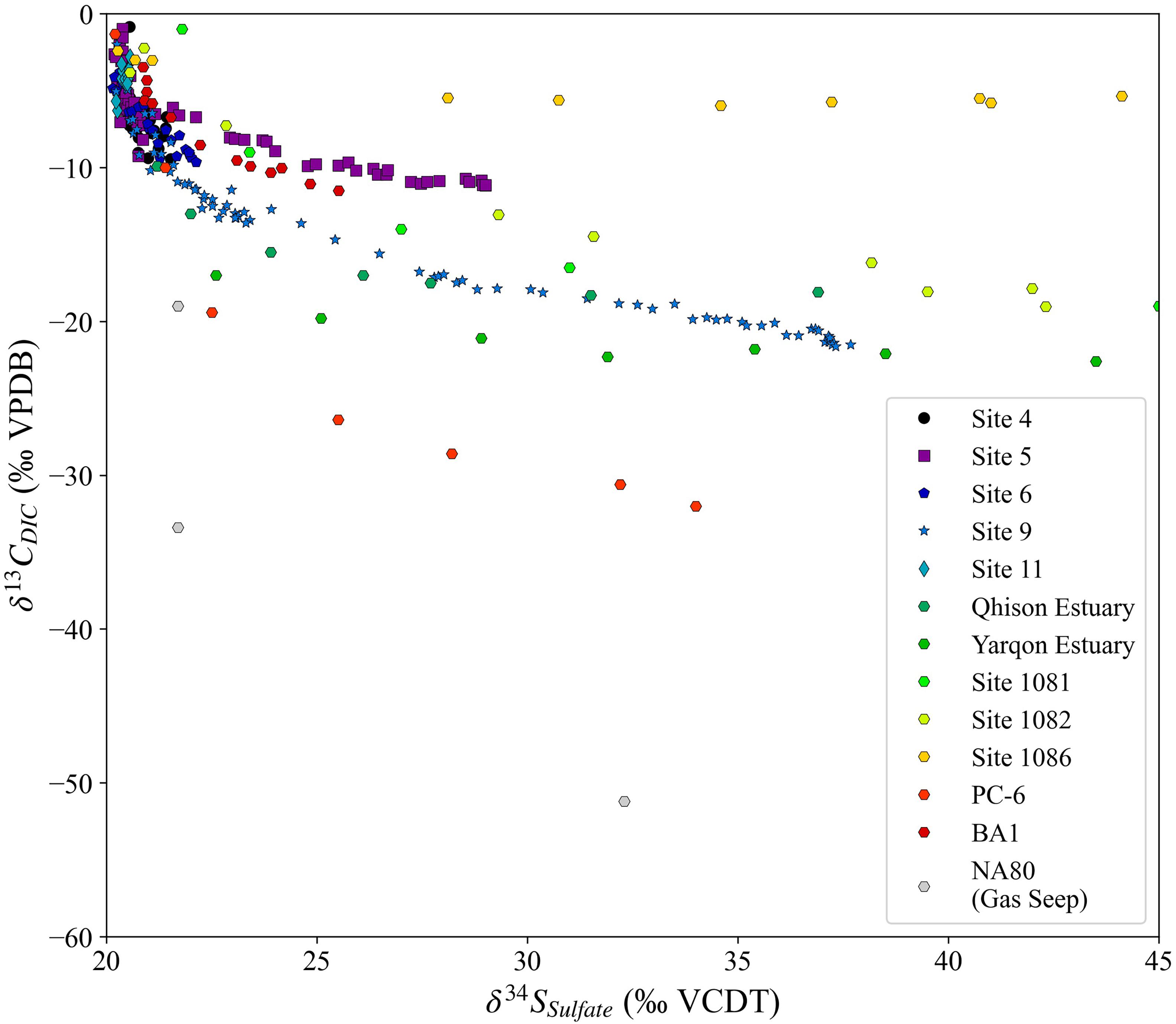
Figure 8. The sulfur and carbon isotopic composition for the sites in this paper with a wider range of sites from the literature (Sivan et al., 2007; Antler et al., 2013, 2014, 2015; Rubin-Blum et al., 2014).

While the carbon isotope composition of organic carbon may vary between −20‰ and −30‰ depending on the type of organic carbon being respired, it is exceptionally unlikely to become as low as −60‰ as needed to explain some of the lowest data in Figure 8 (Meyers, 1994; Galimov, 2006). In order to explain the lowest δ¹³C_DIC values, methane oxidation needs to be invoked. Here we consider the impact on the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4 of the presence of methane at some depth within the sediment column. At several of the sites shown in Figure 8, there is methane below the sampled section—for example at IODP Site U1385, which drilled deeper into these sediments at Site 6, there is an upward flux of methane (Turchyn et al., 2016). Below these shallowmost sediments, sulfate concentrations in the pore fluid could be decreasing to a sulfate-methane transition zone, a sharp interval where sulfate concentrations go to zero and methane, supplied by diffusion from sediments below, is oxidized via the anaerobic oxidation of methane coupled to MSR (sulfate-driven AOM). Sulfate-driven AOM will have a similar impact on δ³⁴S_SO4 as organic-matter driven MSR, but dramatically change δ¹³C_DIC. When methane is oxidized in the sulfate-methane transition zone through sulfate-driven AOM, it returns its ¹²C-enriched CO_{2_(aq)} back to the pore fluid (Whiticar and Faber, 1986; Whiticar, 1999; Sivan et al., 2007; Meister et al., 2019). A pore fluid profile of δ¹³C_DIC where methanogenesis and methanotrophy are both occurring will contain a rapid decrease from the sediment-water interface to the depth of methanotrophy where δ¹³C_DIC can be as low as −35‰ (Bradbury and Turchyn, 2019; Meister et al., 2019). Below the zone of methanotrophy, in the zone of methanogenesis, δ¹³C_DIC increases rapidly and can reach as high as +10 to +20‰ (Bradbury and Turchyn, 2019; Meister et al., 2019).

When MSR, sulfate-driven AOM and methanogenesis are combined, our model shows that the net effect of all three processes causes the minimum δ¹³C_DIC value to approach δ¹³C_OrgC, similar to previous studies (Meister et al., 2019). When the sulfate-methane transition zone (SMTZ) gets close to the sediment-water interface, however, the minimum δ¹³C_DIC value is no longer as negative, due to the diffusion of ¹³C-enriched DIC from the zone of methanogenesis and the overlying seawater and the loss of the ¹²C-enriched methane into seawater. In order for δ¹³C_DIC to be significantly lower than δ¹³C_OrgC, the methane must be diffusing from a deeper zone, or a different source, which leads to the release of ¹²C-enriched DIC into the pore fluid without the local effects of methanogenesis on δ¹³C_DIC. This effect is displayed by creating a simulation with methane being pumped in from the base of the column with a δ¹³C value of −75‰. In order to minimize the impact of pumping methane-enriched fluid in at the base of the column on fluid flow during sediment burial, a fluid containing 10 mM of methane was pumped in. Two different rates were tested (3E-6 and 6E-6 kg H₂O/s) and we verified that such low values had no impact on the velocity profile of fluid flow given sediment burial rates but allowed methane to diffuse up through the column. We can visualize the impact that the flux of methane from the base of the column has compared to higher rates of methanogenesis in Figure 9. When there is no methanogenesis and the highest flux of methane, the minimum in δ¹³C_DIC reaches −55‰, with a corresponding δ³⁴S_SO4 of around 42‰. If there is no methanogenesis or methane flux, the δ³⁴S_SO4 value increases to the maximum δ³⁴S_SO4 possible during sulfate reduction, as the minimum in δ¹³C_DIC will occur at the base of the sulfate reduction zone. Finally, if there is both methanogenesis and a flux of methane from below, the minimum δ¹³C_DIC value becomes less negative with an increasing rate of methanogenesis while the corresponding δ³⁴S_SO4 value becomes less positive (Figure 9).

FIGURE 9

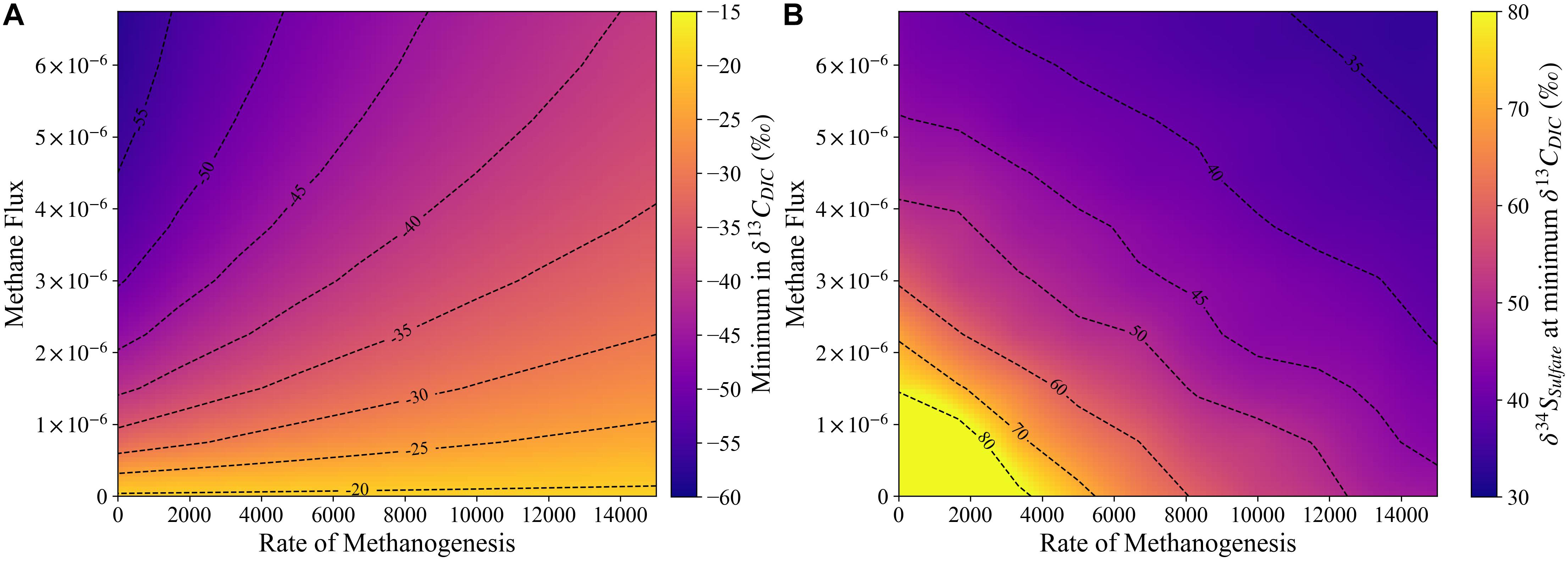
Figure 9. Contour plots displaying the impact of the rate of methanogenesis and methane flux on the minimum δ¹³C value (A) and the associated δ³⁴S value (B).

Summary—How to Interpret a Sulfur/Carbon Isotope Cross Plot

We propose that the cross plot of δ¹³C_DIC vs. δ³⁴S_SO4 holds significant information about the nature of carbon-sulfur coupling in marine sedimentary pore fluids on continental margins. The major controls on the initial decrease in δ¹³C_DIC relative to δ³⁴S are related to the early microbial diagenetic reactions as well as to the amount and δ¹³C of seawater DIC, which can be visualized in the upper left of the sulfur/carbon isotope cross plot, with lower DIC and greater intensity or number of early diagenetic reactions causing a larger decrease in δ¹³C_DIC before δ³⁴S_SO4 increases. The carbon isotopic composition of the DIC released from the oxidation of organic matter is a major control on the minimum δ¹³C_DIC value in the sulfur/carbon isotope cross plot, with δ¹³C of the organic carbon being important during both MSR and combined sulfate reduction, sulfate-driven AOM and methanogenesis. When MSR, sulfate-driven AOM and methanogenesis are occurring in the sediment column the minimum δ¹³C_DIC value is variable, but the overall trend will generally fit within the shaded area in Figure 10. In order for the minimum δ¹³C_DIC value to be below the shaded area, sulfate-driven AOM must occur with a source of methane external to the measured sedimentary pore fluids, with the relative amount of methane coming from in situ methanogenesis vs. an external flux of methane (as well as δ¹³C_CH4) controlling the absolute minimum δ¹³C_DIC value and associated δ³⁴S_SO4. Finally, in order for the minimum δ¹³C_DIC value to be significantly higher than the δ¹³C_OrgC there must be the release of carbon within the sedimentary system which is not enriched in ¹²C. We suggest this is occurring at Site 5 and ODP Site 1086, where carbon released during carbonate recrystallization causes the minimum δ¹³C_DIC value to be around −5‰ (Figure 10).

FIGURE 10

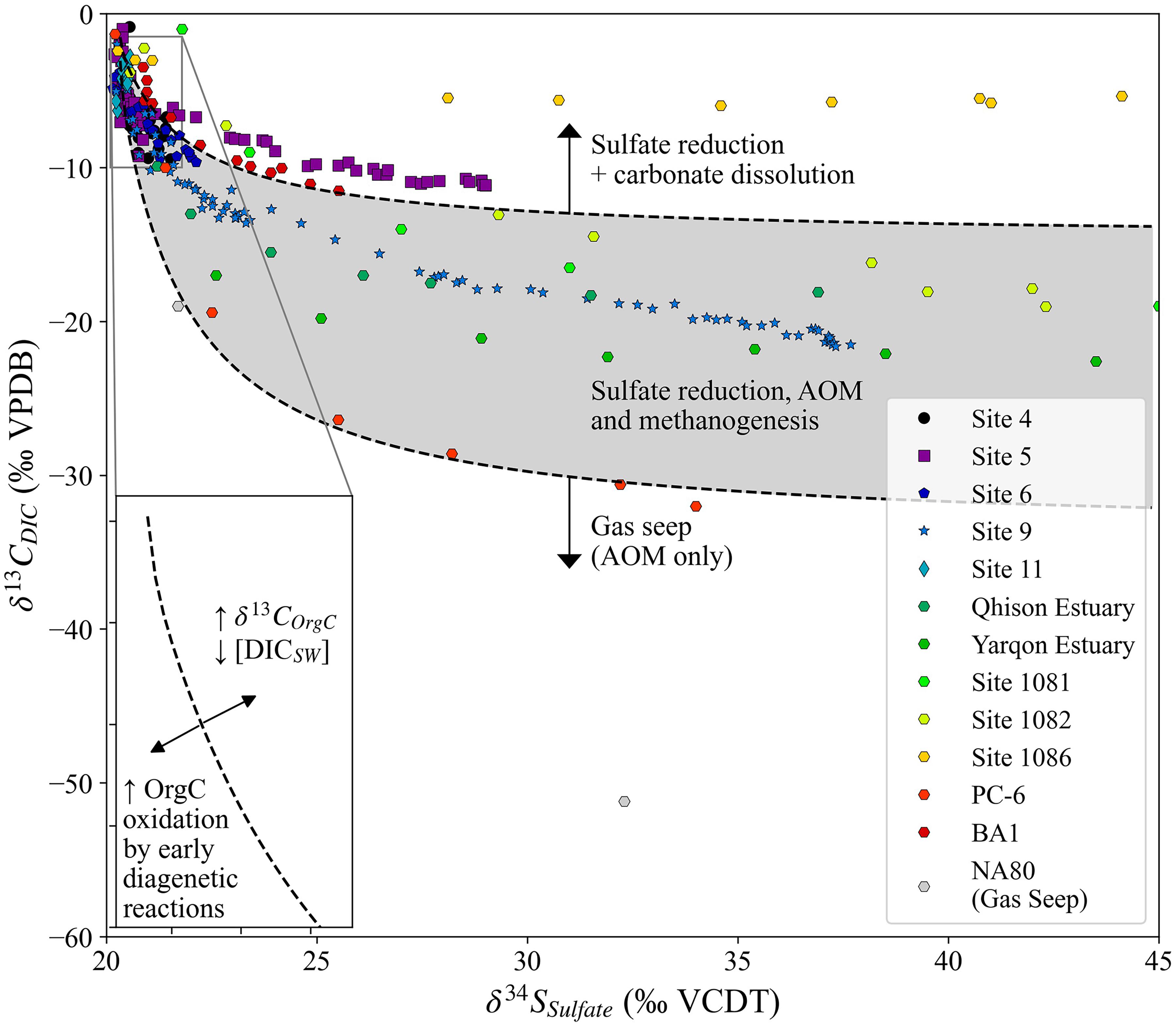
Figure 10. The sulfur and carbon isotopic composition of sulfate and DIC, respectively, for the sites in this paper and a range of literature sites (Sivan et al., 2007; Antler et al., 2013, 2014, 2015; Rubin-Blum et al., 2014). The isotopic compositions of the sites are overlaid by a schematic of the main controls on the sulfur/carbon isotope cross plot and the inset axis contains a schematic for the major controls on the upper left part of the profiles.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

AT, HB, and GA contributed to the conception and design of this study. AB produced the dataset with help from MG, GA, DS, AT, and DH. HB designed and implemented the model in collaboration with AF and JD. HB and AT wrote the manuscript with input from all co-authors.

Funding

This work was supported by NERC NE/R013519/1 to HB, ERC 307582 StG (CARBONSINK) to AT and NERC grant NE/J00653X/1 to DH.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors GA.

Acknowledgments

We would like to thank all the participants of cruise JC089 on board the R/V James Cook for recovering the Iberian Margin core material and pore fluids used in this study. We would also like to thank the editor LW and the two reviewers whose comments greatly strengthened this manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.652960/full#supplementary-material

References

Algeo, T. J., Luo, G. M., Song, H. Y., Lyons, T. W., and Canfield, D. E. (2015). Reconstruction of secular variation in seawater sulfate concentrations. Biogeosciences 12, 2131–2151. doi: 10.5194/bg-12-2131-2015

CrossRef Full Text | Google Scholar

Antler, G., and Pellerin, A. (2018). A critical look at the combined use of sulfur and oxygen isotopes to study microbial metabolisms in methane-rich environments. Front. Microbiol. 9:519. doi: 10.3389/fmicb.2018.00519

PubMed Abstract | CrossRef Full Text | Google Scholar

Antler, G., Turchyn, A. V., Herut, B., Davies, A., Rennie, V. C. F., and Sivan, O. (2014). Sulfur and oxygen isotope tracing of sulfate driven anaerobic methane oxidation in estuarine sediments. Estuar. Coastal Shelf Sci. 142, 4–11. doi: 10.1016/j.ecss.2014.03.001

CrossRef Full Text | Google Scholar

Antler, G., Turchyn, A. V., Herut, B., and Sivan, O. (2015). A unique isotopic fingerprint of sulfate-driven anaerobic oxidation of methane. Geology 43, 619–622. doi: 10.1130/G36688.1

CrossRef Full Text | Google Scholar

Antler, G., Turchyn, A. V., Rennie, V., Herut, B., and Sivan, O. (2013). Coupled sulfur and oxygen isotope insight into bacterial sulfate reduction in the natural environment. Geochim. Cosmochim. Acta 118, 98–117. doi: 10.1016/j.gca.2013.05.005

CrossRef Full Text | Google Scholar

Arndt, S., Hetzel, A., and Brumsack, H.-J. (2009). Evolution of organic matter degradation in Cretaceous black shales inferred from authigenic barite: a reaction-transport model. Geochim. Cosmochim. Acta 73, 2000–2022. doi: 10.1016/j.gca.2009.01.018

CrossRef Full Text | Google Scholar

Barnes, R. O., and Goldberg, E. D. (1976). Methane production and consumption in anoxic marine sediments. Geology 4, 297–300. doi: 10.1130/0091-761319764<297:MPACIA<2.0.CO;2

CrossRef Full Text | Google Scholar

Berner, R. A. (1978). Sulfate reduction and the rate of deposition of marine sediments. Earth Planet. Sci. Lett. 37, 492–498. doi: 10.1016/0012-821X(78)90065-1

CrossRef Full Text | Google Scholar

Berner, R. A. (1980). Early Diagenesis: A Theoretical Approach. Princeton, NJ: Princeton University Press.

Google Scholar

Berner, R. A. (1989). Biogeochemical cycles of carbon and sulfur and their effect on atmospheric oxygen over phanerozoic time. Glob. Planet. Change 1, 97–122. doi: 10.1016/0921-8181(89)90018-0

CrossRef Full Text | Google Scholar

Boudreau, B. P. (1997). Diagenetic Models and their Implementation: Modelling Transport and Reactions in Aquatic Sediments. Berlin: Springer.

Google Scholar

Bradbury, H. J., and Turchyn, A. V. (2018). Calcium isotope fractionation in sedimentary pore fluids from ODP Leg 175: resolving carbonate recrystallization. Geochim. Cosmochim. Acta 236, 121–139. doi: 10.1016/j.gca.2018.01.040

CrossRef Full Text | Google Scholar

Bradbury, H. J., and Turchyn, A. V. (2019). Reevaluating the carbon sink due to sedimentary carbonate formation in modern marine sediments. Earth Planet. Sci. Lett. 519, 40–49. doi: 10.1016/j.epsl.2019.04.044

CrossRef Full Text | Google Scholar

Bradley, A. S., Leavitt, W. D., Schmidt, M., Knoll, A. H., Girguis, P. R., and Johnston, D. T. (2016). Patterns of sulfur isotope fractionation during microbial sulfate reduction. Geobiology 14, 91–101. doi: 10.1111/gbi.12149

PubMed Abstract | CrossRef Full Text | Google Scholar

Breukelen, B. M. V., and Prommer, H. (2008). Beyond the rayleigh equation: reactive transport modeling of isotope fractionation effects to improve quantification of biodegradation. Environ. Sci. Technol. 42, 2457–2463. doi: 10.1021/es071981j

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunner, B., Bernasconi, S. M., Kleikemper, J., and Schroth, M. H. (2005). A model for oxygen and sulfur isotope fractionation in sulfate during bacterial sulfate reduction processes. Geochim. Cosmochim. Acta 69, 4773–4785. doi: 10.1016/j.gca.2005.04.017

CrossRef Full Text | Google Scholar

Canfield, D. E., Jørgensen, B. B., Fossing, H., Glud, R., Gundersen, J., Ramsing, N. B., et al. (1993). Pathways of organic carbon oxidation in three continental margin sediments. Mar. Geol. 113, 27–40. doi: 10.1016/0025-3227(93)90147-N

CrossRef Full Text | Google Scholar

Claypool, G. E., and Kaplan, I. R. (1974). “The origin and distribution of methane in marine sediments,” in Natural Gases in Marine Sediments Marine Science, ed. I. Kaplan (Boston, MA: Springer), 99–139. doi: 10.1007/978-1-4684-2757-8_8

CrossRef Full Text | Google Scholar

D’Hondt, S., Inagaki, F., Zarikian, C. A., Abrams, L. J., Dubois, N., Engelhardt, T., et al. (2015). Presence of oxygen and aerobic communities from sea floor to basement in deep-sea sediments. Nat. Geosci. 8, 299–304. doi: 10.1038/ngeo2387

CrossRef Full Text | Google Scholar

Diester-Haass, L., Billups, K., Gröcke, D. R., François, L., Lefebvre, V., and Emeis, K. C. (2009). Mid-Mmiocene paleoproductivity in the Atlantic Ocean and implications for the global carbon cycle. Paleoceanography 24:A1209. doi: 10.1029/2008PA001605

CrossRef Full Text | Google Scholar

Diester-Haass, L., Meyers, P. A., and Bickert, T. (2004). Carbonate crash and biogenic bloom in the late miocene: evidence from ODP Sites 1085, 1086, and 1087 in the Cape Basin, southeast Atlantic Ocean. Paleoceanography 19:A1007. doi: 10.1029/2003PA000933

CrossRef Full Text | Google Scholar

Druhan, J. L., Guillon, S., Lincker, M., and Arora, B. (2020). Stable and radioactive carbon isotope partitioning in soils and saturated systems: a reactive transport modeling benchmark study. Comput. Geosci. 1–11. doi: 10.1007/s10596-020-09937-6

CrossRef Full Text | Google Scholar

Druhan, J. L., Steefel, C. I., Conrad, M. E., and DePaolo, D. J. (2014). A large column analog experiment of stable isotope variations during reactive transport: I. A comprehensive model of sulfur cycling and δ34S fractionation. Geochim. Cosmochim. Acta 124, 366–393. doi: 10.1016/j.gca.2013.08.037

CrossRef Full Text | Google Scholar

Druhan, J. L., Steefel, C. I., Williams, K. H., and DePaolo, D. J. (2013). Calcium isotope fractionation in groundwater: molecular scale processes influencing field scale behavior. Geochim. Cosmochim. Acta 119, 93–116. doi: 10.1016/j.gca.2013.05.022

CrossRef Full Text | Google Scholar

Egger, M., Riedinger, N., Mogollón, J. M., and Jørgensen, B. B. (2018). Global diffusive fluxes of methane in marine sediments. Nat. Geosci. 11, 421–425. doi: 10.1038/s41561-018-0122-8

CrossRef Full Text | Google Scholar

Fantle, M. S. (2015). Calcium isotopic evidence for rapid recrystallization of bulk marine carbonates and implications for geochemical proxies. Geochim. Cosmochim. Acta 148, 378–401. doi: 10.1016/j.gca.2014.10.005

CrossRef Full Text | Google Scholar

Fantle, M. S., and DePaolo, D. J. (2007). Ca isotopes in carbonate sediment and pore fluid from ODP Site 807A: the Ca2+(aq)–calcite equilibrium fractionation factor and calcite recrystallization rates in Pleistocene sediments. Geochim. Cosmochim. Acta 71, 2524–2546. doi: 10.1016/j.gca.2007.03.006

CrossRef Full Text | Google Scholar

Fotherby, A., Bradbury, H. J., Antler, G., Sun, X., Druhan, J. L., and Turchyn, A. V. (2021). Modelling the effects of non-steady state transport dynamics on the sulfur and oxygen isotope composition of sulfate in sedimentary pore fluids. Front. Earth Sci. 8:587085. doi: 10.3389/feart.2020.587085

CrossRef Full Text | Google Scholar

Froelich, P. N., Klinkhammer, G. P., Bender, M. L., Luedtke, N. A., Heath, G. R., Cullen, D., et al. (1979). Early oxidation of organic matter in pelagic sediments of the eastern equatorial Atlantic: suboxic diagenesis. Geochim. Cosmochim. Acta 43, 1075–1090. doi: 10.1016/0016-7037(79)90095-4

CrossRef Full Text | Google Scholar

Galimov, E. M. (2006). Isotope organic geochemistry. Org. Geochem. 37, 1200–1262. doi: 10.1016/j.orggeochem.2006.04.009

CrossRef Full Text | Google Scholar

Garcia, H. E., and Gordon, L. I. (1992). Oxygen solubility in seawater: better fitting equations. Limnol. Oceanogr. 37, 1307–1312. doi: 10.4319/lo.1992.37.6.1307

CrossRef Full Text | Google Scholar

Hodell, D. A., Elderfield, H., Greaves, M., McCave, I. N., Skinner, L., Thomas, A., et al. (2014). The JC089 Scientific Party, JC089 Cruise Report—IODP Site Survey of the Shackleton Sites, SW Iberian Margin. Liverpool: British ocean data Centre.

Google Scholar

Hodell, D. A., Lourens, L., Stow, D. A. V., Hernández-Molina, J., and Alvarez Zarikian, C. A. (2013). The “Shackleton Site” (IODP Site U1385) on the iberian margin. Sci. Drill. 16, 13–19. doi: 10.5194/sd-16-13-2013

CrossRef Full Text | Google Scholar

Hollander, D. J., and McKenzie, J. A. (1991). CO2 control on carbon-isotope fractionation during aqueous photosynthesis: a paleo-pCO2 barometer. Geology 19, 929–932. doi: 10.1130/0091-76131991019<0929:CCOCIF<2.3.CO;2

CrossRef Full Text | Google Scholar

Holler, T., Wegener, G., Knittel, K., Boetius, A., Brunner, B., Kuypers, M. M. M., et al. (2009). Substantial 13C/12C and D/H fractionation during anaerobic oxidation of methane by marine consortia enriched in vitro. Environ. Microbiol. Rep. 1, 370–376. doi: 10.1111/j.1758-2229.2009.00074.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Horita, J. (2001). Carbon isotope exchange in the system CO2-CH4 at elevated temperatures. Geochim. Cosmochim. Acta 65, 1907–1919. doi: 10.1016/S0016-7037(01)00570-1

CrossRef Full Text | Google Scholar

Hubbard, C. G., Cheng, Y., Engelbrekston, A., Druhan, J. L., Li, L., Ajo-Franklin, J. B., et al. (2014). Isotopic insights into microbial sulfur cycling in oil reservoirs. Front. Microbiol. 5:480. doi: 10.3389/fmicb.2014.00480

PubMed Abstract | CrossRef Full Text | Google Scholar

Huber, C., Druhan, J. L., and Fantle, M. S. (2017). Perspectives on geochemical proxies: The impact of model and parameter selection on the quantification of carbonate recrystallization rates. Geochim. Cosmochim. Acta 217, 171–192. doi: 10.1016/j.gca.2017.08.023

CrossRef Full Text | Google Scholar

Johnston, D. T., Farquhar, J., Wing, B. A., Kaufman, A. J., Canfield, D. E., and Habicht, K. S. (2005). Multiple sulfur isotope fractionations in biological systems: a case study with sulfate reducers and sulfur disproportionators. Am. J. Sci. 305, 645–660. doi: 10.2475/ajs.305.6-8.645

PubMed Abstract | CrossRef Full Text | Google Scholar

Jørgensen, B. B., Beulig, F., Egger, M., Petro, C., Scholze, C., and Røy, H. (2019a). Organoclastic sulfate reduction in the sulfate-methane transition of marine sediments. Geochim. Cosmochim. Acta 254, 231–245. doi: 10.1016/j.gca.2019.03.016

CrossRef Full Text | Google Scholar

Jørgensen, B. B., Findlay, A. J., and Pellerin, A. (2019b). The biogeochemical sulfur cycle of marine sediments. Front. Microbiol. 10:849. doi: 10.3389/fmicb.2019.00849

PubMed Abstract | CrossRef Full Text | Google Scholar

Jørgensen, B. B., and Kasten, S. (2006). “Sulfur cycling and methane oxidation,” in Marine Geochemistry, eds H. D. Schulz and M. Zabel (Berlin: Springer Berlin Heidelberg), 271–309. doi: 10.1007/3-540-32144-6_8

CrossRef Full Text | Google Scholar

Kasten, S., and Jørgensen, B. B. (2000). “Sulfate reduction in marine sediments,” in Marine Geochemistry, eds H. D. Schulz and M. Zabel (Berlin: Springer), 263–281. doi: 10.1007/978-3-662-04242-7_8

CrossRef Full Text | Google Scholar

Kasten, S., Zabel, M., Heuer, V. B., and Hensen, C. (2003). “Processes and signals of non-steady-state diagenesis in deep-sea sediments and their pore waters,” in The South Atlantic in the Late Quaternary: Reconstruction of Material Budgets and Current Systems, eds G. Wefer, S. Mulitza, and V. Ratmeyer (Berlin: Springer), 431–459. doi: 10.1007/978-3-642-18917-3_20

CrossRef Full Text | Google Scholar

Kump, L. R., and Arthur, M. A. (1999). Interpreting carbon-isotope excursions: carbonates and organic matter. Chem. Geol. 161, 181–198. doi: 10.1016/S0009-2541(99)00086-8

CrossRef Full Text | Google Scholar

Kump, L. R., Junium, C., Arthur, M. A., Brasier, A., Fallick, A., Melezhik, V., et al. (2011). Isotopic evidence for massive oxidation of organic matter following the great oxidation event. Science 334, 1694–1696. doi: 10.1126/science.1213999

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, M. F., Bernasconi, S. M., Barbieri, A., and McKenzie, J. A. (2002). Preservation of organic matter and alteration of its carbon and nitrogen isotope composition during simulated and in situ early sedimentary diagenesis. Geochim. Cosmochim. Acta 66, 3573–3584. doi: 10.1016/S0016-7037(02)00968-7

CrossRef Full Text | Google Scholar

Londry, K. L., and Des Marais, D. J. (2003). Stable carbon isotope fractionation by sulfate-reducing bacteria. Appl. Environ. Microbiol. 69, 2942–2949. doi: 10.1128/AEM.69.5.2942-2949.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Martens, C. S., and Berner, R. A. (1974). Methane production in the interstitial waters of sulfate-depleted marine sediments. Science 185, 1167–1169. doi: 10.1126/science.185.4157.1167

PubMed Abstract | CrossRef Full Text | Google Scholar

McCorkle, D. C., Emerson, S. R., and Quay, P. D. (1985). Stable carbon isotopes in marine porewaters. Earth Planet. Sci. Lett. 74, 13–26. doi: 10.1016/0012-821X(85)90162-1

CrossRef Full Text | Google Scholar

Meister, P. (2013). Two opposing effects of sulfate reduction on carbonate precipitation in normal marine, hypersaline, and alkaline environments. Geology 41, 499–502. doi: 10.1130/G34185.1

CrossRef Full Text | Google Scholar

Meister, P. (2014). Two opposing effects of sulfate reduction on carbonate precipitation in normal marine, hypersaline, and alkaline environments: REPLY. Geology 42:e315. doi: 10.1130/G35240Y.1

CrossRef Full Text | Google Scholar

Meister, P., Liu, B., Khalili, A., Böttcher, M. E., and Jørgensen, B. B. (2019). Factors controlling the carbon isotope composition of dissolved inorganic carbon and methane in marine porewater: an evaluation by reaction-transport modelling. J. Mar. Syst. 200:103227. doi: 10.1016/j.jmarsys.2019.103227

CrossRef Full Text | Google Scholar

Meyers, P. A. (1994). Preservation of elemental and isotopic source identification of sedimentary organic matter. Chem. Geol. 114, 289–302. doi: 10.1016/0009-2541(94)90059-0

CrossRef Full Text | Google Scholar

Pellerin, A., Antler, G., Holm, S. A., Findlay, A. J., Crockford, P. W., Turchyn, A. V., et al. (2019). Large sulfur isotope fractionation by bacterial sulfide oxidation. Sci. Adv. 5:eaaw1480. doi: 10.1126/sciadv.aaw1480

PubMed Abstract | CrossRef Full Text | Google Scholar

Rubin-Blum, M., Antler, G., Turchyn, A. V., Tsadok, R., Goodman-Tchernov, B. N., Shemesh, E., et al. (2014). Hydrocarbon-related microbial processes in the deep sediments of the Eastern Mediterranean Levantine Basin. FEMS Microbiol. Ecol. 87, 780–796. doi: 10.1111/1574-6941.12264

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudnicki, M. D., Elderfield, H., and Spiro, B. (2001). Fractionation of sulfur isotopes during bacterial sulfate reduction in deep ocean sediments at elevated temperatures. Geochim. Cosmochim. Acta 65, 777–789. doi: 10.1016/S0016-7037(00)00579-2

CrossRef Full Text | Google Scholar

Sayles, F. L. (1979). The composition and diagenesis of interstitial solutions—I. Fluxes across the seawater-sediment interface in the Atlantic Ocean. Geochim. Cosmochim. Acta 43, 527–545. doi: 10.1016/0016-7037(79)90163-7

CrossRef Full Text | Google Scholar

Sayles, F. L. (1981). The composition and diagenesis of interstitial solutions—II. Fluxes and diagenesis at the water-sediment interface in the high latitude North and South Atlantic. Geochim. Cosmochim. Acta 45, 1061–1086. doi: 10.1016/0016-7037(81)90132-0

CrossRef Full Text | Google Scholar

Sela-Adler, M., Ronen, Z., Herut, B., Antler, G., Vigderovich, H., Eckert, W., et al. (2017). Co-existence of methanogenesis and sulfate reduction with common substrates in sulfate-rich estuarine sediments. Front. Microbiol. 8:766. doi: 10.3389/fmicb.2017.00766

PubMed Abstract | CrossRef Full Text | Google Scholar

Sivan, O., Schrag, D. P., and Murray, R. W. (2007). Rates of methanogenesis and methanotrophy in deep-sea sediments. Geobiology 5, 141–151. doi: 10.1111/j.1472-4669.2007.00098.x

CrossRef Full Text | Google Scholar

Skinner, L. C., Sadekov, A., Brandon, M., Greaves, M., Plancherel, Y., de la Fuente, M., et al. (2019). Rare earth elements in early-diagenetic foraminifer ‘coatings’: pore-water controls and potential palaeoceanographic applications. Geochim. Cosmochim. Acta 245, 118–132. doi: 10.1016/j.gca.2018.10.027

CrossRef Full Text | Google Scholar

Steefel, C. I., Appelo, C. A. J., Arora, B., Jacques, D., Kalbacher, T., Kolditz, O., et al. (2015). Reactive transport codes for subsurface environmental simulation. Comput. Geosci. 19, 445–478. doi: 10.1007/s10596-014-9443-x

CrossRef Full Text | Google Scholar

Steiner, Z., Lazar, B., Erez, J., and Turchyn, A. V. (2018). Comparing Rhizon samplers and centrifugation for pore-water separation in studies of the marine carbonate system in sediments. Limnol. Oceanogr. Methods 16, 828–839. doi: 10.1002/lom3.10286

CrossRef Full Text | Google Scholar

Sun, X., Higgins, J., and Turchyn, A. V. (2016). Diffusive cation fluxes in deep-sea sediments and insight into the global geochemical cycles of calcium, magnesium, sodium and potassium. Mar. Geol. 373, 64–77. doi: 10.1016/j.margeo.2015.12.011

CrossRef Full Text | Google Scholar

Tromp, T. K., Van Cappellen, P., and Key, R. M. (1995). A global model for the early diagenesis of organic carbon and organic phosphorus in marine sediments. Geochim. Cosmochim. Acta 59, 1259–1284. doi: 10.1016/0016-7037(95)00042-X

CrossRef Full Text | Google Scholar

Turchyn, A. V., Antler, G., Byrne, D., Miller, M., and Hodell, D. A. (2016). Microbial sulfur metabolism evidenced from pore fluid isotope geochemistry at Site U1385. Glob. Planet. Change 141, 82–90. doi: 10.1016/j.gloplacha.2016.03.004

CrossRef Full Text | Google Scholar

Turchyn, A. V., Sivan, O., and Schrag, D. P. (2006). Oxygen isotopic composition of sulfate in deep sea pore fluid: evidence for rapid sulfur cycling. Geobiology 4, 191–201. doi: 10.1111/j.1472-4669.2006.00079.x

CrossRef Full Text | Google Scholar

Wehrmann, L. M., Risgaard-Petersen, N., Schrum, H. N., Walsh, E. A., Huh, Y., Ikehara, M., et al. (2011). Coupled organic and inorganic carbon cycling in the deep subseafloor sediment of the northeastern Bering Sea Slope (IODP Exp. 323). Chem. Geol. 284, 251–261. doi: 10.1016/j.chemgeo.2011.03.002

CrossRef Full Text | Google Scholar

Whiticar, M. J. (1999). Carbon and hydrogen isotope systematics of bacterial formation and oxidation of methane. Chem. Geol. 161, 291–314. doi: 10.1016/S0009-2541(99)00092-3

CrossRef Full Text | Google Scholar

Whiticar, M. J., and Faber, E. (1986). Methane oxidation in sediment and water column environments—isotope evidence. Org. Geochem. 10, 759–768. doi: 10.1016/S0146-6380(86)80013-4

CrossRef Full Text | Google Scholar

Wortmann, U. G., Chernyavsky, B., Bernasconi, S. M., Brunner, B., Böttcher, M. E., and Swart, P. K. (2007). Oxygen isotope biogeochemistry of pore water sulfate in the deep biosphere: dominance of isotope exchange reactions with ambient water during microbial sulfate reduction (ODP Site 1130). Geochim. Cosmochim. Acta 71, 4221–4232. doi: 10.1016/j.gca.2007.06.033

CrossRef Full Text | Google Scholar

Wortmann, U. G., and Chernyavsky, B. M. (2011). The significance of isotope specific diffusion coefficients for reaction-transport models of sulfate reduction in marine sediments. Geochim. Cosmochim. Acta 75, 3046–3056. doi: 10.1016/j.gca.2011.03.007

CrossRef Full Text | Google Scholar

Yoshinaga, M. Y., Holler, T., Goldhammer, T., Wegener, G., Pohlman, J. W., Brunner, B., et al. (2014). Carbon isotope equilibration during sulphate-limited anaerobic oxidation of methane. Nat. Geosci. 7, 190–194. doi: 10.1038/ngeo2069

CrossRef Full Text | Google Scholar

Zeebe, R. E., Bijma, J., and Wolf-Gladrow, D. A. (1999). A diffusion-reaction model of carbon isotope fractionation in foraminifera. Mar. Chem. 64, 199–227. doi: 10.1016/S0304-4203(98)00075-9

CrossRef Full Text | Google Scholar

Zhang, J., Quay, P. D., and Wilbur, D. O. (1995). Carbon isotope fractionation during gas-water exchange and dissolution of CO2. Geochim. Cosmochim. Acta 59, 107–114. doi: 10.1016/0016-7037(95)91550-D

CrossRef Full Text | Google Scholar