Late Cenozoic Denudation and Topographic Evolution History of the Lhasa River Drainage in Southern Tibetan Plateau: Insights From Inverse Thermal History Modeling

The interaction of surface erosion (e.g., fluvial incision) and tectonic uplift shapes the landform in the Tibetan Plateau. The Lhasa River flows toward the southwest across the central Gangdese Mountains in the southern Tibetan Plateau, characterized by a low-relief and high-elevation landscape. However, the evolution of low-relief topography and the establishment of the Lhasa River remain highly under debate. Here, we collected thermochronological ages reported in the Lhasa River drainage, using a 3D thermokinematic model to invert both late Cenozoic denudation and relief history of the Lhasa River drainage. Our results show that the Lhasa River drainage underwent four-phase denudation history, including two-stage rapid denudation at ∼25–16 Ma (with a rate of ∼0.42 km/Ma) and ∼16–12 Ma (with a rate of ∼0.72 km/Ma). In the latest Oligocene–early Miocene, uplift of the Gangdese Mountains triggered the rapid denudation and the formation of the current main drainage of the Lhasa River. In the middle Miocene, the second stage of the rapid denudation and the high relief were associated with intense incision of the Lhasa River, which is probably due to the enhanced Asian summer monsoon precipitation. This later rapid episode was consistent with the records of regional main drainage systems. After ∼12 Ma, the denudation rate decreases rapidly, and the relief of topography in the central Gangdese region was gradually subdued. This indicates that the fluvial erosion resulting from Asian monsoon precipitation increase significantly impacts on the topographic evolution in the central Gangdese region.

Introduction

The landscape evolution of the orogenic belt results from the complex interaction between tectonic uplift and surface erosion (e.g., fluvial incision). However, surface erosion is also influenced by tectonic forcing and climatic change on the different temporal scales (Davis et al., 1983; England and Molnar, 1990; Whipple et al., 2000; Schildgen et al., 2009; Whipple, 2009). For example, the tectonic uplift creates a topographic gradient that increases fluvial incision and triggers landslides (Ahnert, 1970; Wilson and Fowler, 2011; Wang et al., 2012; Tian et al., 2015). An intensified monsoon precipitation or increased amplitudes of glacial–interglacial climatic fluctuations could also enhance fluvial incision (Zhang et al., 2001; Pan et al., 2003; Clift et al., 2008; Wang et al., 2012, 2015; Nie et al., 2018), which may in turn have an impact on tectonic activity (Zeitler et al., 2001; Whipple, 2009). Thus, how tectonics, climate, and surface erosion are coupled to control the evolution of topography is a fundamental question.

The Tibetan Plateau, created by the India–Asia collision since the Cenozoic (Molnar et al., 2010), is a natural laboratory for examining the coupling of tectonics, climate, and erosion in shaping the landscape. Previous studies have important findings in the Himalayas (Beaumont et al., 2001; Bookhagen et al., 2005; Clift et al., 2008; Zhang et al., 2012) and the southern and southeastern Tibetan Plateau (Lang and Huntington, 2014; Liu-Zeng et al., 2018; Nie et al., 2018; Shen et al., 2019). However, these studies have not reached a consensus about the mechanism of the landscape evolution in some regions, such as the Gangdese region, a low-relief and high-elevation landscape in the southern Tibetan Plateau (Figure 1). In the Gangdese region, quantitative inversion of thermochronological ages of Gangdese batholith suggests a rapid exhumation stage from the Oligocene to the Miocene or ∼22–18 Ma due to the activity of the Gangdese Thrust system (Copeland et al., 1995; Yin et al., 1999; Dai et al., 2013). In contrast, other thermochronology studies suggest that the rapid denudation since ∼23 or 20–10 Ma was linked to regional river incision or the intensification of the Asian monsoon (Li et al., 2016; Ge et al., 2017). Tremblay et al. (2015) indicated that a rapid exhumation stage at ∼12 Ma has been interpreted as river incision in the Gangdese region. Thus, distinguishing the effects of regional tectonic, the fluvial incision, and intensification of the Asian monsoon on the landscape evolution of the central Gangdese region since the early Miocene remains the major ramifications.

FIGURE 1

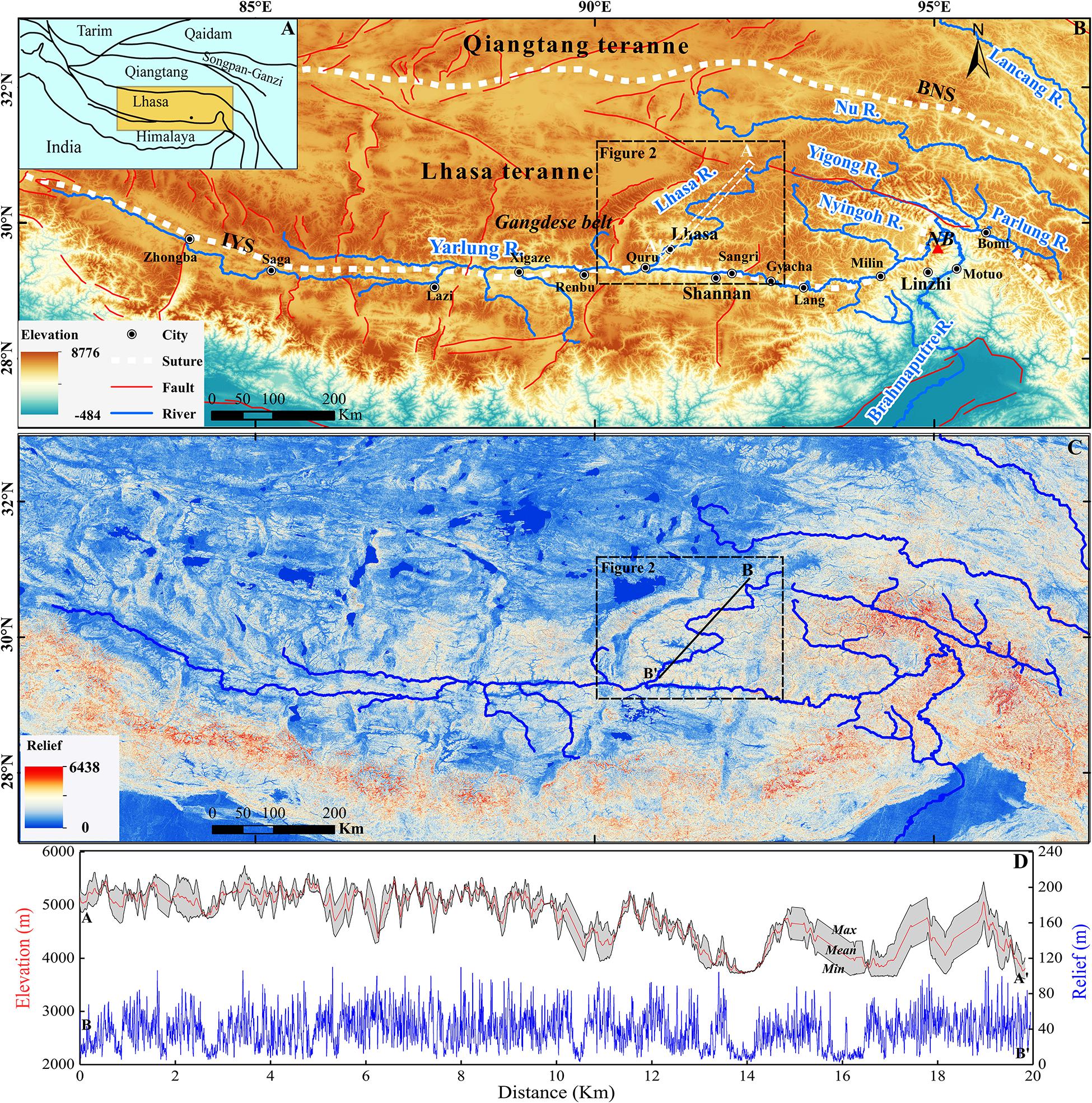
Figure 1. Tectonic frame and regional topography of the southern Tibetan Plateau. (A) Five different east–west-trending terranes in the Tibetan Plateau. Orange rectangular shows the extent of (B). (B) The main faults and rivers and the topography of the southern Tibetan Plateau. The black box shows the extent of Figure 2. White dashed box indicates the locations of elevation swath profiles in (D). IYS, Indus-Yarlung suture zone; BNS, Bangong-Nujiang suture zone; NB: Namche Barwa. (C) Topographic relief of the southern Tibetan Plateau. The black line indicates the locations of the relief profile in (D). (D) Relief and elevation swath profiles across the Lhasa River drainage.

The Lhasa River is one of the large rivers that cross the central Gangdese Mountains in southeastern Tibetan Plateau. The formation of the Lhasa River and its incision could influence on the evolution of low-relief landscape on the central Gangdese Mountains. However, the time of significant incision of the Lhasa River remains highly debated. One view indicates that the Lhasa River probably formed and incised before 80 Ma based on the age of sediment accumulation near Lhasa River outlet (Laskowski et al., 2019). The study of the evolution of the Yarlung River into which Lhasa flows suggests that the current Lhasa River possibly formed at 26–19 Ma (Wang et al., 2013; Li et al., 2017). Based on the numerical simulations and the inversion of thermochronological ages, Tremblay et al. (2015) believe that the current river in the southern Tibetan Plateau formed at ∼12–11 Ma. Thus, the timing of the Lhasa River initial flowing across the central Gangdese which could affect the landform evolution in this area is still unclear.

Low-temperature thermochronology may be able to provide information to solve this problem by carefully quantifying rates and transition time of denudation of the Lhasa River drainage. However, previous studies in the Lhasa River drainage have only considered one-dimension cooling, neglecting potential effects of temporally varying topography and laterally varying denudation (Braun, 2002; Gallagher et al., 2005a, b; Luszczak et al., 2018). A numerical simulation method for inverse thermal history modeling, three-dimensional (3D) thermal kinematic model Pecube (Braun, 2002, 2003; Braun et al., 2012) coupled with the neighborhood algorithm (Sambridge, 2010a, b), has considered these limiting factors of one-dimension cooling. This method has been successfully applied to the inversion of denudation and topographic evolution in orogenic regions (Braun et al., 2012; Wang et al., 2016; McDannell et al., 2018; Shen et al., 2019; Yang et al., 2019). Here, we used this 3D thermokinematic modeling approach to invert both denudation and topographic evolution history in the Lhasa River drainage using low-temperature thermochronologic data from the Lhasa River Valley. The aims of this work are (i) to constrain the timing of the establishment of the modern Lhasa River and the evolution history of relatively low-relief topography in the southern Tibetan Plateau and (ii) to distinguish the respective roles that tectonics and climate played on the topographic evolution through numerical modeling of both thermal and relief histories in a drainage, using the Lhasa River drainage in the southern Tibetan Plateau as a case.

Regional Setting

The Cenozoic India–Asia collision created the high-elevation topography of the Tibetan Plateau, consisting of five different east–west-trending terranes, namely the Himalaya, Lhasa, Qiangtang, Songpan-Ganze, and Qaidam from south to north (Yin and Harrison, 2000; Figure 1A). The Lhasa terrane, located in the southern Tibetan Plateau, is bounded by the Bangong-Nujiang suture to the north and by the Indus-Yarlung suture to the south (Li et al., 2016). The Lhasa River headwaters originate in the eastern portion of the Lhasa terrane. The main trunk of the Lhasa River drains to the southwest across the Gangdese Mountains and merges into the east-flowing Yarlung River, forming a so-called barbed junction (Figure 1B). Our study area is located in the Lhasa River drainage within the Lhasa terrane (Figure 1B).

The extensive and widely exposed Late Triassic–Eocene Gangdese batholith intruded into the Paleozoic–Mesozoic sedimentary units in the study area (Ji et al., 2009; Zhu et al., 2011), which should record the later crustal thermal history. In the southern and central Lhasa River drainage, the Gangdese region exposes the lower Jurassic volcano-sedimentary sequence of the Yeba Group (Zhu et al., 2011), the lower Cretaceous volcanic rocks of the Sangri Group, and the Cretaceous–Tertiary volcanic rocks of the Linzizong Group (Mo et al., 2008; Figure 2). The widely distributed Paleozoic sedimentary strata in the Lhasa River drainage consist of Ordovician and Carboniferous to Cretaceous clastic sediments (Wei et al., 2014), and the middle–late Jurassic deposits mainly distribute on the upper reaches of Lhasa River. However, the Paleocene–Eocene sedimentary rocks in the Lhasa River drainage are limited or apparently absent (Yin and Harrison, 2000). The Quaternary sediments expose along the lower reaches of the Lhasa River and the Rift valley (Figure 2).

FIGURE 2

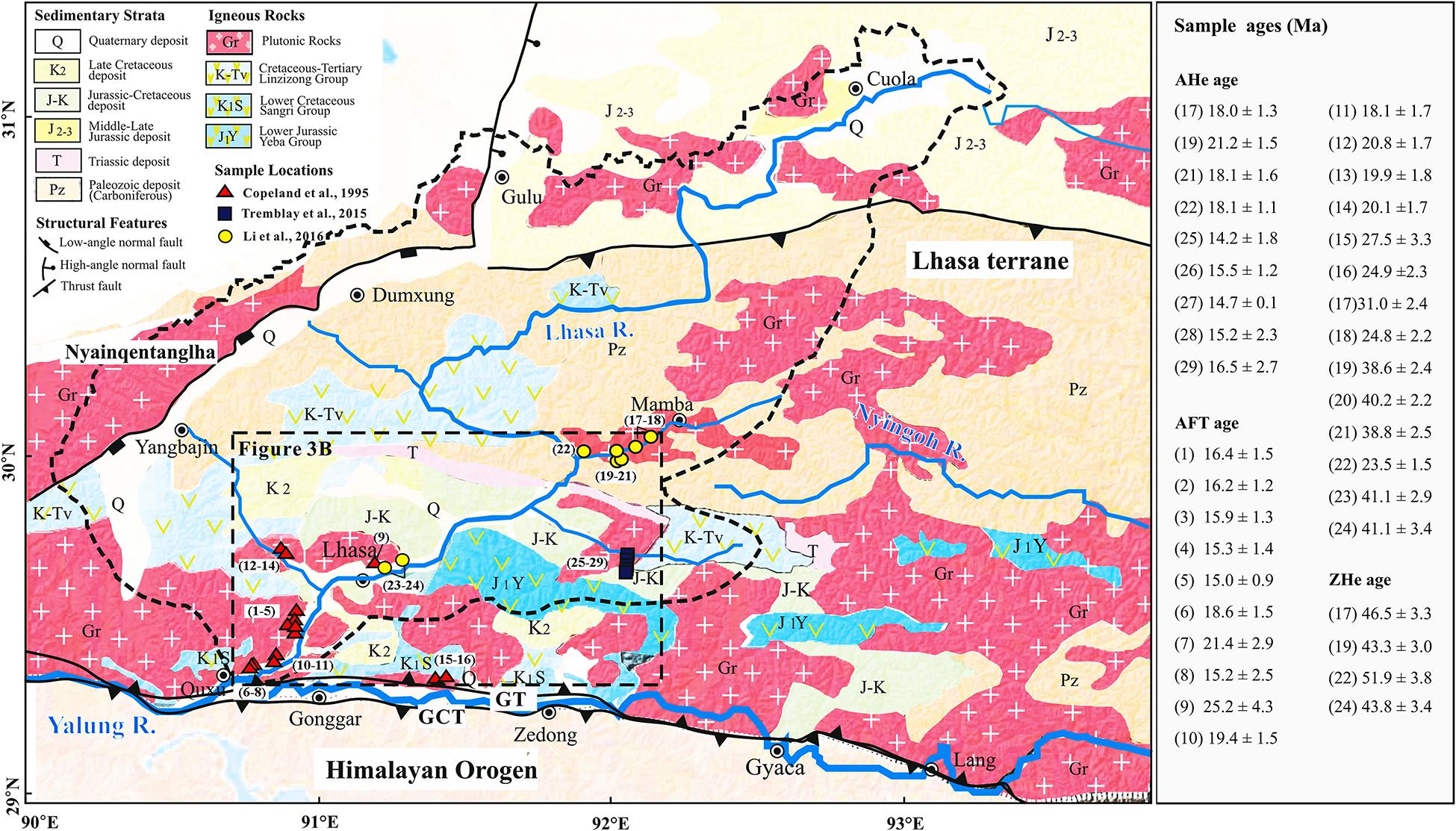
Figure 2. Simplified geologic map and locations of the collected thermochronological data of the Lhasa River drainage in the southern Tibet Plateau [modified from Zhang et al. (2012)]. The black box shows the extent of Figure 3B. GT, Gangdese Thrust; GCT, Great Counter Thrust. The number in the black box represents the position of the compiled sample.

The main faults in the study area since the Cenozoic include the Gangdese Thrust (GT), the Great Counter Thrust (GCT), and the north–south-trending normal fault (Figure 2). The north-dipping Gangdese Thrust activated between ∼30 and 23 Ma and has an estimated 50–60 km of shortening along the Indus-Yarlung Zangpo suture zone (Yin et al., 1999; Wei et al., 2014). The south-dipping Great Counter Thrust belt juxtaposed the passive continental margin sediments of northern India over the Indus-Yarlung ophiolites (Yin et al., 1999; Li Y. L. et al., 2015). The isotopic dating of Gangdese batholith in southern Tibetan Plateau constrains that the activity of GCT was between ∼25 and 10 Ma (Yin et al., 1999; Harrison et al., 2000). The north–south-trending Yangbajing-Yardong graben system developed during the late Miocene, which reflects the E–W extensional regime in the Tibetan Plateau (Harrison et al., 1992; Li Y. L. et al., 2015).

The climate in the Lhasa River drainage is substantially influenced by the South Asian summer monsoon (Figure 1). Global monsoon systems are generally considered to be associated with seasonal changes in the land–sea thermal contrast and the shift of Intertropical Convergence Zone (Gadgil, 2003; Wang et al., 2017). During the boreal summer when the sensible heating of the Asian continent by solar insolation is at a maximum, the Intertropical Convergence Zone is located over the Indian continent, where the SE trade winds in the Southern Hemisphere change direction to NE after crossing the equator (Wang et al., 2017). The SE trade winds bring air masses carrying abundant moisture from the Bay of Bengal to the north and northwest (Bookhagen et al., 2005). When these vortexes encounter the frontal terrain of the Himalaya, they were released to produce a large amount of topographic precipitation, and only a small part of the water vapor can be transported further to high-altitude areas on the Tibetan Plateau through the valleys of the Himalayan transverse river (Bookhagen and Burbank, 2010). The precipitation of modern Lhasa River drainage do not exceed 500 mm (Bookhagen and Burbank, 2010).

Analysis Methods

Data and Age–Elevation Relationship

In order to constrain the timing of rapid denudation of the Lhasa River, the published thermochronological ages in Lhasa River valley were compiled (Figure 2). This low-temperature thermochronological dataset includes 9 apatite (U-Th)/He (AHe) ages, 24 apatite fission-track (AFT) ages, and 4 zircon (U-Th)/He (ZHe) ages (Copeland et al., 1995; Tremblay et al., 2015; Li et al., 2016; Figure 2 and Supplementary Table 1). Five AHe ages ranging from 14.2 ± 1.8 to 16.5 ± 2.7 Ma are from the middle reaches and along a 1.2-km elevation transect in the eastern tributary of the Lhasa River (Tremblay et al., 2015), and four AHe ages ranging from 18.0 ± 1.3 to 21.2 ± 1.5 Ma are from the eastern tributary valley of the Lhasa River (Li et al., 2016; Figure 2 and Supplementary Table 1). AFT ages, ranging between 15.0 ± 0.9 and 41.1 ± 3.4 Ma, are mainly from the middle and lower reaches of the Lhasa River valley, but two are from the Yarlung River valley (Figure 2 and Supplementary Table 1). ZHe ages, ranging between 43 ± 3.0 and 51.9 ± 3.8 Ma, are from the valley-wall transects in the middle and lower reaches of the Lhasa River (Li et al., 2016; Figure 2 and Supplementary Table 1). However, six ZHe ages from the tributary of Lhasa River reported in Tremblay et al. (2015) are much younger than the ZHe and AFT and AHe ages in the region reported in Copeland et al. (1995) and Li et al. (2016). This is probably caused by the locally structural/thermal effect. In order to avoid the uncertainty, these data are not selected. All thermochronological ages, at elevation between 3,600 and 5,478 m, were collected from Mesozoic and Early Cenozoic Gangdese batholith granites.

In order to provide first-order estimates of the denudation parameters in Pecube, the age–elevation relationship (AER) was plotted from thermochronological data from river valleys. Here, we assume that the Lhasa River drainage underwent the history of uniform denudation in space, and then the variable slopes of the different AERs can be interpreted as reflecting a change in the denudation rate of this region (Gallagher et al., 2005a, b; Beek et al., 2010). The ZHe data suggest a relatively rapid denudation rate of 0.09 km/Ma between ∼47 and ∼43 Ma, but a lower rate of 0.01 km/Ma between ∼43 and ∼15 Ma from the AFT data (Figure 3A). The steeper age–elevation relationship from AHe data implies an increase in regional denudation rates to ∼0.289 km/Ma from ∼23 to ∼16 Ma and ∼0.331 km/Ma between ∼16 and ∼12 Ma (Figure 3A). Varying denudation rates are also suggested by the AFT data, which indicates a rapid denudation phase at around ∼23 Ma. These data were used to set the possible variation range of the parameters in the modeling (see details in the following).

FIGURE 3

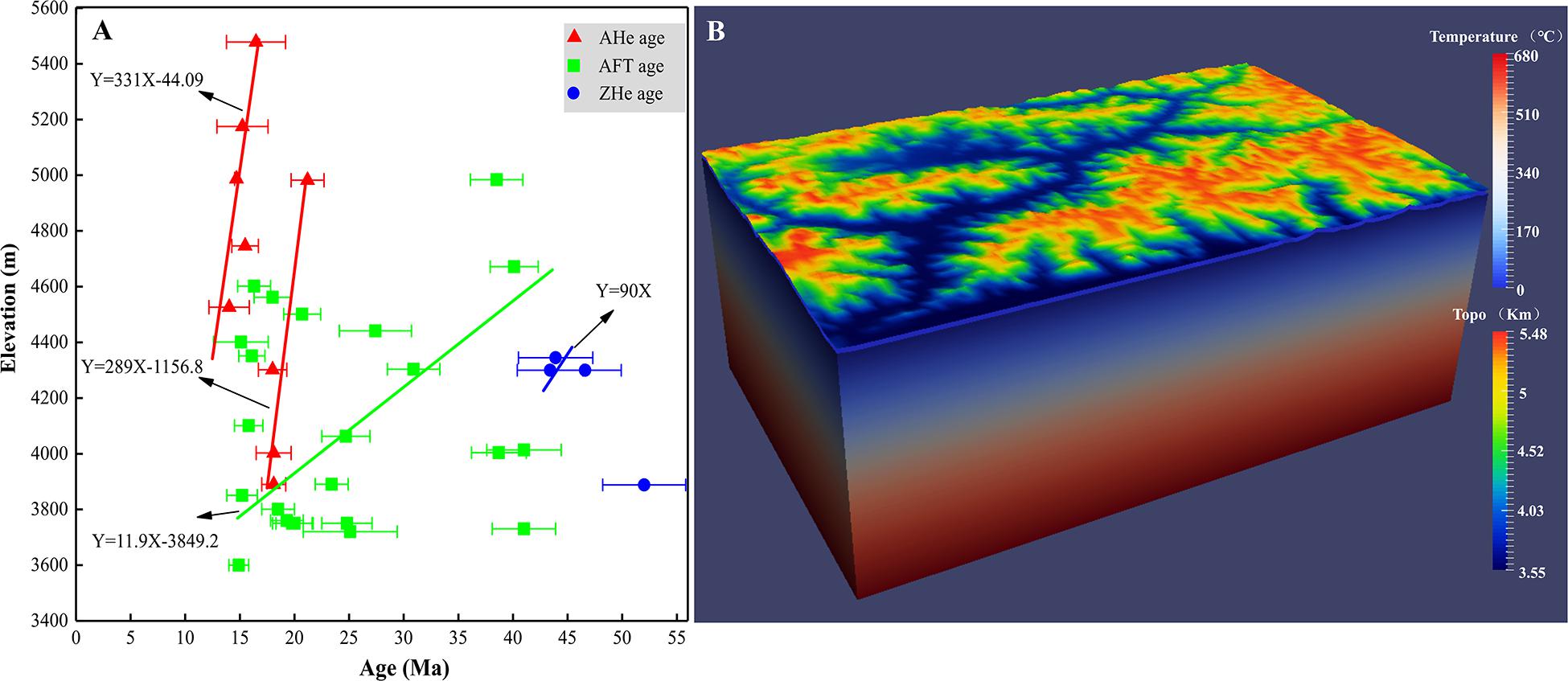
Figure 3. (A) Denudation rates estimated from the age–elevation relationship from the Lhasa River drainage according to least-square fitting. (B) Model setup for the 3D thermokinematic model (parameters are given in Table 2). The model calculates the evolving thermal field of a 50-km-thick crustal block using a combination of geothermal, rock denudation, and landscape evolution parameters.

In fact, the estimation from the AER is simply one-dimensional, which possibly under- or overestimates the denudation rate (Braun et al., 2012), because of neglecting the possible effects of temporally varying topography on underlying isotherms, and/or neglecting possible effects of relief development. Moreover, the internal consistency between the different datasets and their inferred interpretation has not been assessed. Thus, we will analyze these data using Pecube (Braun et al., 2012) to more quantitatively infer the denudation and relief history of Lhasa River drainage.

Thermokinematic Modeling

Pecube is a finite-element thermokinematic modeling that solves the 3D heat transport equation (Braun, 2003):

$\mathrm{\rho }c\left(\frac{\partial T}{\partial t}+\mathrm{\nu }\frac{\partial T}{\partial z}\right)=\frac{\partial }{\partial x}k\frac{\partial T}{\partial x}+\frac{\partial }{\partial y}k\frac{\partial T}{\partial y}+\frac{\partial }{\partial z}k\frac{\partial T}{\partial z}+H(1)$

where T(x,y,z,t) is the temperature (°C), ρ is the rock density (kg/m³), c is the heat capacity (J/kg/K), v is the vertical velocity of the rock particle relative to the base of the crust (km/Ma), k denotes conductivity (W/m/k), and H is the radioactive heat production (W/m³). In a crustal block, the thermal properties such as rock conductivity, heat capacity, density, and heat production were assumed to remain constant through time, and then Eq. (1) was solved to reflect a crustal block undergoing lateral and vertical rock particle transport, denudation, and surface change. The surface change is incorporated here using the relief factor R, defined as the ratio between the relief amplitude (Δh_i) when rocks passed through the closure isotherms and the modern-day relief amplitude (Δh₀) (Valla et al., 2010):

$R=\frac{\mathrm{\Delta }{h}_i}{\mathrm{\Delta }{h}_0}(2)$

when R = 0, the initial topography is a plateau at the maximum present-day elevation; when R = 1, the paleo-relief was the same as the modern topography; for R < 1, the paleo-relief is lower than today, while for R > 1, the paleo-relief is higher than today.

During a Pecube model inversion, a two-step neighborhood algorithm was used (Sambridge, 2010a, b). The first step involves an iterative search in the multidimensional parameter space in order to find sets of input parameters that minimize the misfit between observed and predicted data. The misfit was calculated as

$m=\frac{1}{n}\sqrt{\sum _{i=1}^n\frac{{\left(p_i-o_i\right)}^2}{{\mathrm{\sigma }}_i^2}}(3)$

where m is the misfit value; n is the number observed data; and for each data point i, is the age predicted by Pecube; o_i and σ_i are the observed age and its error, respectively. The second step of the neighborhood algorithm is an appraisal of the search results to define statistical limits on the ranges of input parameters that provide a good fit to the observed age data (Sambridge, 2010b), and Bayesian inference is used to produce posterior probability density functions (PPDFs) for each individual parameter using a likelihood function L,

$L=\exp \left(-\frac{n}{2}\sqrt{\sum _{i=1}^n\frac{{\left(p_i-o_i\right)}^2}{{\mathrm{\sigma }}_i^2}}\right)(4)$

The appraisal yields 1D and 2D PPDFs for the model parameters that are presented for each set of model parameters in Table 1.

TABLE 1

Table 1. Values of parameters of input and inversion results.

The input thermokinematic parameters used in Pecube are listed inTable 2. We set a 50-km depth model, and thebasal temperature of the model is a free parameter ranging between500 and 1,000°C, which is equivalent to an initialgeothermal gradient of ∼10–20°C/km. The initialgeothermal gradient in the Lhasa River drainage should be lower thanthe present-day (∼20–30°C/km), because the late Cenozoic denudation should have increased the thermal gradient to the current values (Ehlers, 2005). The starting time of the model was set as 41 Ma, as the reported oldest thermochronological age in the main trunk of the Lhasa River valley is ∼41 Ma. Cenozoic faults are absent within the selected simulation area (Figure 2); thus, the faults are not considered in our model. The geometry of the surface topography was extracted from 90-m resolution DEMs (Figure 3B).

TABLE 2

Table 2. Thermokinematic and elastic parameters used in this study.

In order to obtain a more robust and detailed view of the denudation rate, transition time, and topographical relief in the Lhasa River drainage, two scenarios were modeled as the “denudation scenario” and the “relief scenario.” Here, we defined the “denudation scenario” as a steady evolution of topography scenario considering only spatially and temporally varying rock denudation rates, without considering the complex evolution of topography, and the initial topography changes linearly through time to modern. Based on previous studies for the denudation history in the Gangdese region, we have known apparently more than two-stage denudation history since 41 Ma in the Lhasa River drainage (Li et al., 2016). Thus, the assumption of three-phase, four-phase, and five-phase denudation history in the “denudation scenario” since 41 Ma was tested, respectively.

The inverted parameters are preliminarily set based on the AER, including the slope of AHe and AFT ages with uncertainty (Figure 3A). The parameters of the three-phase denudation history include (1) first and second transition time (T1, 30–10 Ma, and T2, 20–10 Ma, the reference basis for boundary setting shown in Supplementary Table 2); (2) denudation rates of the first, second, and third phase (E1 = 0–1.5 km/Ma, E2 = E3 = 0–2 km/Ma, referring from the slope of AHe and AFT in AER); and 3) initial relief (R, 0–2). The parameters of the four-phase denudation history include (1) first, second, and third transition time (T1, 30–20 Ma; T2, 25–15 Ma; and T3, 15–10 Ma); (2) denudation rates of the first, second, third, and fourth phase (E1 = 0–1.5 km/Ma; E2 = E3 = E4 = 0–2 km/Ma); and (3) initial relief (R, 0–2). For the five-phase denudation history, the parameters include (1) first, second, third, and fourth transition time (T1, 40–30 Ma; T2, 30–20 Ma; T3, 25–15 Ma; and T4, 15–10 Ma); (2) denudation rates of the first, second, third, fourth, and fifth phase (E1 = E2 = 0–1.5 km/Ma; E3 = E4 = E5 = 0–2 km/Ma); and (3) initial relief (R, 0–2).

The incision of the Lhasa River will affect the topographical relief. We also define a “relief scenario” to consider not only spatially and temporally varying rock denudation rates, but also the multistage evolution of topography due to the impact of the fluvial incision. The detailed parameters of this scenario were set according to the results of the “denudation scenario,” including four-phase denudation and topographic evolution history (Table 1, see section “denudation Scenario” for details). Inverted parameters of this scenario include the following: (1) the first, second, and third transition time set as 24.6, 15.5, and 12.3 Ma, respectively, according to the simulation result of the four-stage denudation in the “denudation scenario”; (2) the range of denudation rates of the first, second, third, and fourth phase, which are the same as four-phase denudation history in the “denudation scenario”; and (3) topographic relief of the initial, first, second, and third transition time (R = R1 = 0–1.5, R2 = R3 = 0–2). The input parameters of the modeling under different denudation stages and different scenarios are shown in Table 1.

Modeling Results

Denudation Scenario

The results for best fitting of the three-phase denudation are shown in Table 1. We found the slow denudation at a rate of 0.29 km/Ma from 41 to 16 Ma, the rapid denudation at a rate of 1.75 km/Ma between 16 and 12 Ma, and a slow rate of 0.18 km/Ma since ∼12 Ma (Table 1 and Supplementary Figure 1). However, a rapid phase of denudation since ∼23 Ma reported by Li et al. (2016) is not reproduced in this modeling. For the inversion of five-phase denudation history, the denudation rates of best fitting of the first phase (a rate of 0.09 km/Ma from ∼41 to 31.5 Ma) and second phase (a rate of 0.02 km/Ma from ∼31.5 to 23.8 Ma) are not more than 0.1 km/Ma (Table 1 and Supplementary Figure 2), which can be considered as a slow denudation phase. Moreover, the minimum misfit value of the forward result for the three-phase and five-phase denudation history is 0.74 and 0.40, respectively, which is higher than the four-phase denudation history (0.35) (Table 1). Therefore, the assumption of four-phase denudation is much more possible for the Lhasa River drainage since 41 Ma.

The results for the inversion of four-phase denudation are shown in Figure 4. The best-fitting model shows that the transition time of four-phase denudation is 24.6, 15.5, and 12.3 Ma, respectively. The slow denudation phases are the episode between ∼40 and 24.6 Ma with a rate of 0.07 km/Ma and the episode of ∼12 Ma to the present with a rate of 0.08 km/Ma. The rapid denudation rates were the second and third phases that were 0.39 km/Ma from 24.6 to 15.5 Ma and 1.22 km/Ma from 15.5 to 12.3 Ma. Note that 1.22 km/Ma from 15.5 to 12.3 Ma from the modeled denudation rate was higher. The age of the best-fit forward model in this scenario is also basically close to the observed age, except that ZHe is slightly younger (Figure 5A).

FIGURE 4

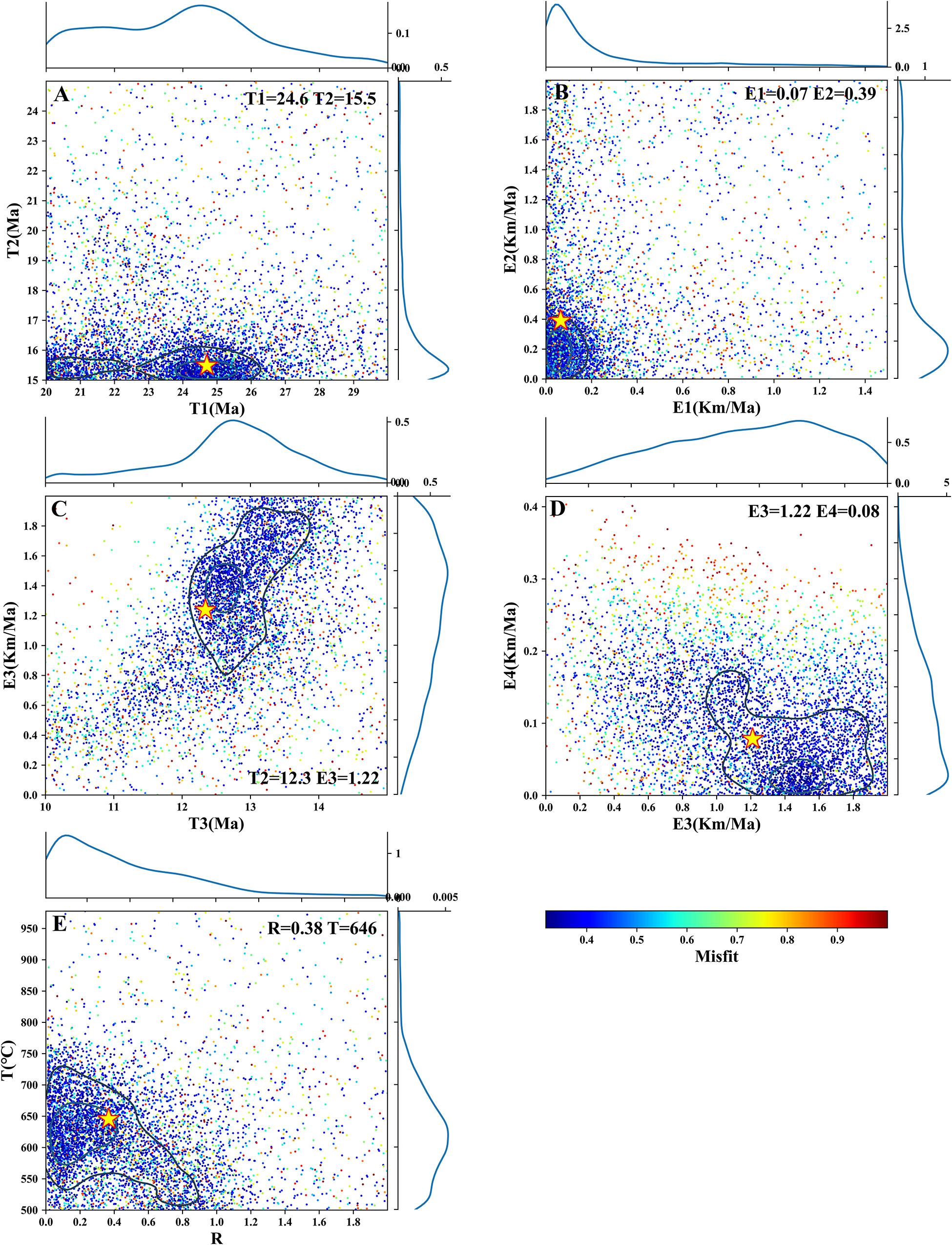
Figure 4. Scatterplots of Pecube inversion misfits for the four-stage denudation scenario model of the Lhasa River drainage. Colored dots represent individual forward-model runs plotted in 2D projections of the parameter space with color corresponding to misfit values. Posterior probability density functions for parameter values are plotted along the axes. The best-fit solution is represented by a yellow star with 2σ (black) and 1σ (light blue) confidence contours. (A–D) Transition time and denudation rate during the four stage (transition time T1, T2, and T3; denudation rate E1, E2, E3, and E4); (E) basal temperature T and relief factor of initial topography R.

FIGURE 5

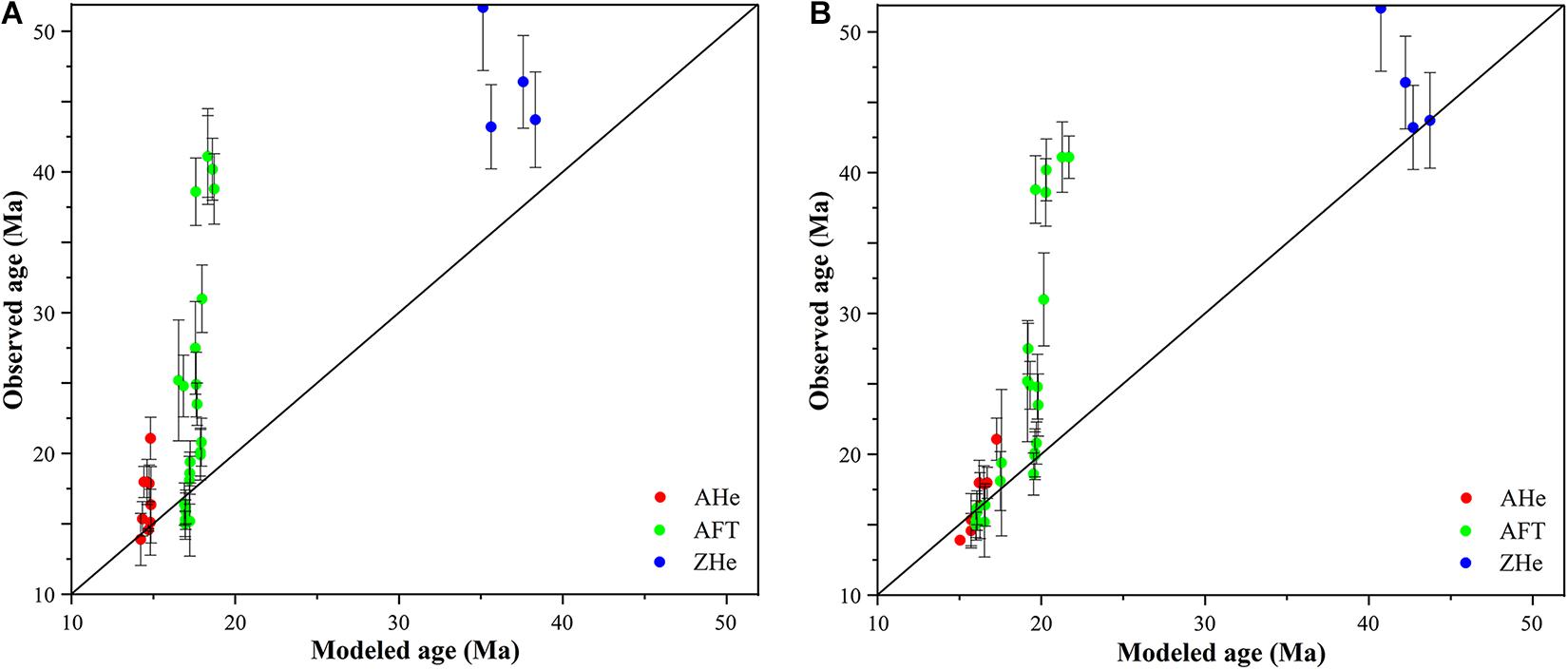
Figure 5. Comparison of observed and predicted thermochronological data for the best-fit parameters. (A) Comparison of observed and predicted thermochronological data under the “denudation scenario” with four-stage denudation. (B) Comparison of observed and predicted thermochronological data under the “relief scenario.”

Relief Scenario

The incision of the Lhasa River valley leads to rapid denudation and changes in topographic relief. However, the simulation of the denudation scenario only inverted the initial relief. Therefore, we set the topography scenario with three additional relief parameters to invert the change of denudation rates and the evolution of topographic relief under the four-phase denudation (Table 1). The best-fitting model shows that the denudation rate of the four phases was 0.09, 0.42, 0.72, and 0.16 km/Ma, respectively (Figure 6). The denudation rate of the third stage in the relief scenario was lower than that of the denudation scenario, and the denudation rate in the other stages is close to the denudation scenario. The best fitting of the relief factor was 0.49 at 41 Ma, 0.85 at 24.6 Ma, 0.82 at 15.5 Ma, and 1.58 at 12.3 Ma, respectively. The relief factors at 41 and 25 Ma are not well converging and their errors are relatively large (Figures 6, 7), but the obvious changes in the relief after ∼25 Ma have been well constrained (Figure 6). All ages of forwarding simulation under the relief scenario are basically consistent with the observed ages (Figure 5B).

FIGURE 6

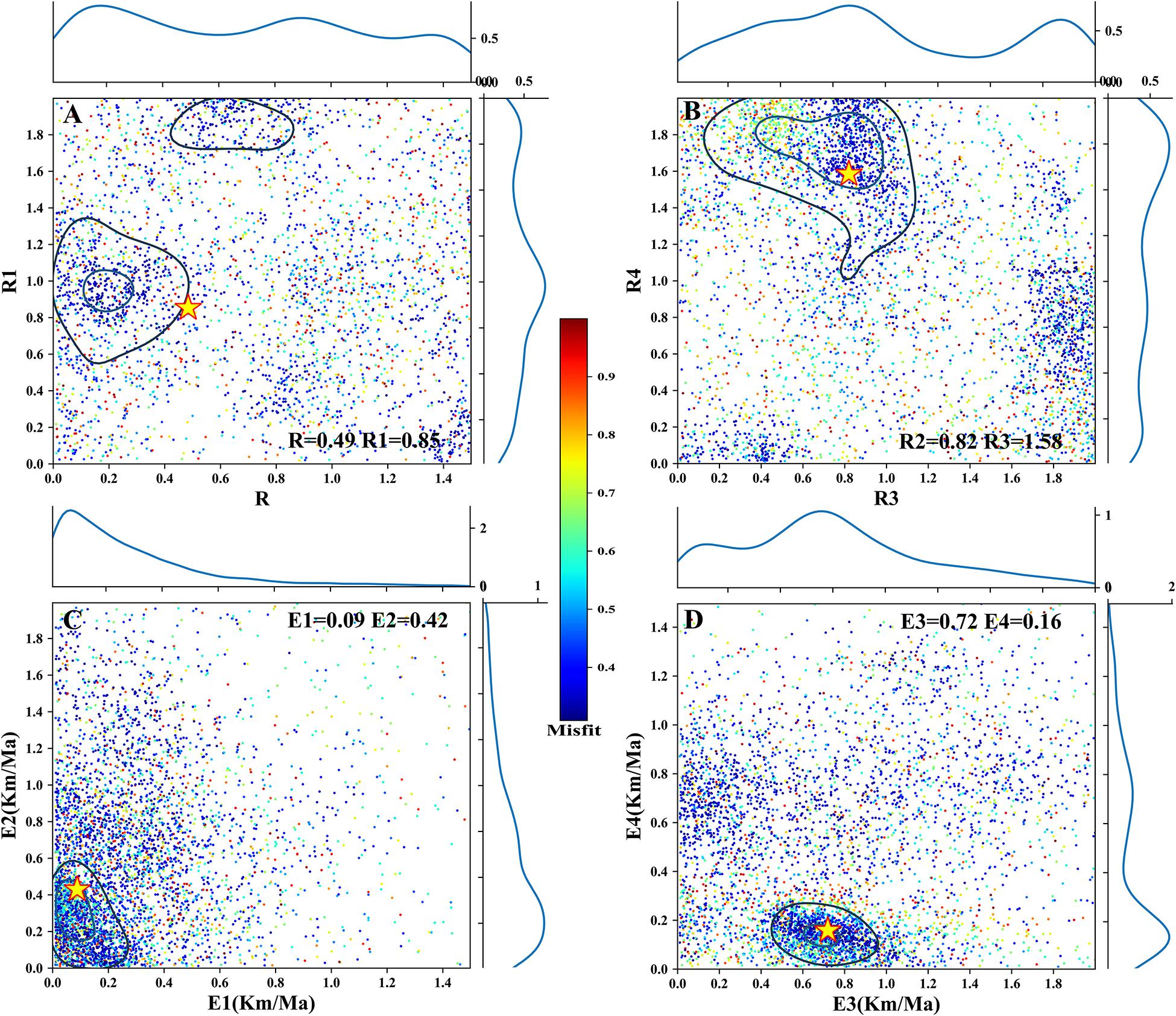
Figure 6. Scatterplots of Pecube inversion misfits for the relief scenario model of the Lhasa River drainage. Colored dots represent individual forward-model runs plotted in 2D projections of the parameter space with colors corresponding to misfit values. Posterior probability density functions for parameter values are plotted along the axes. The best-fit solution is represented by a yellow star with 2σ (black) and 1σ (light blue) confidence contours. (A–D) Relief factor and denudation rate during the four stage (relief factor R, R1, R2, and R3; denudation rate E1, E2, E3, and E4).

FIGURE 7

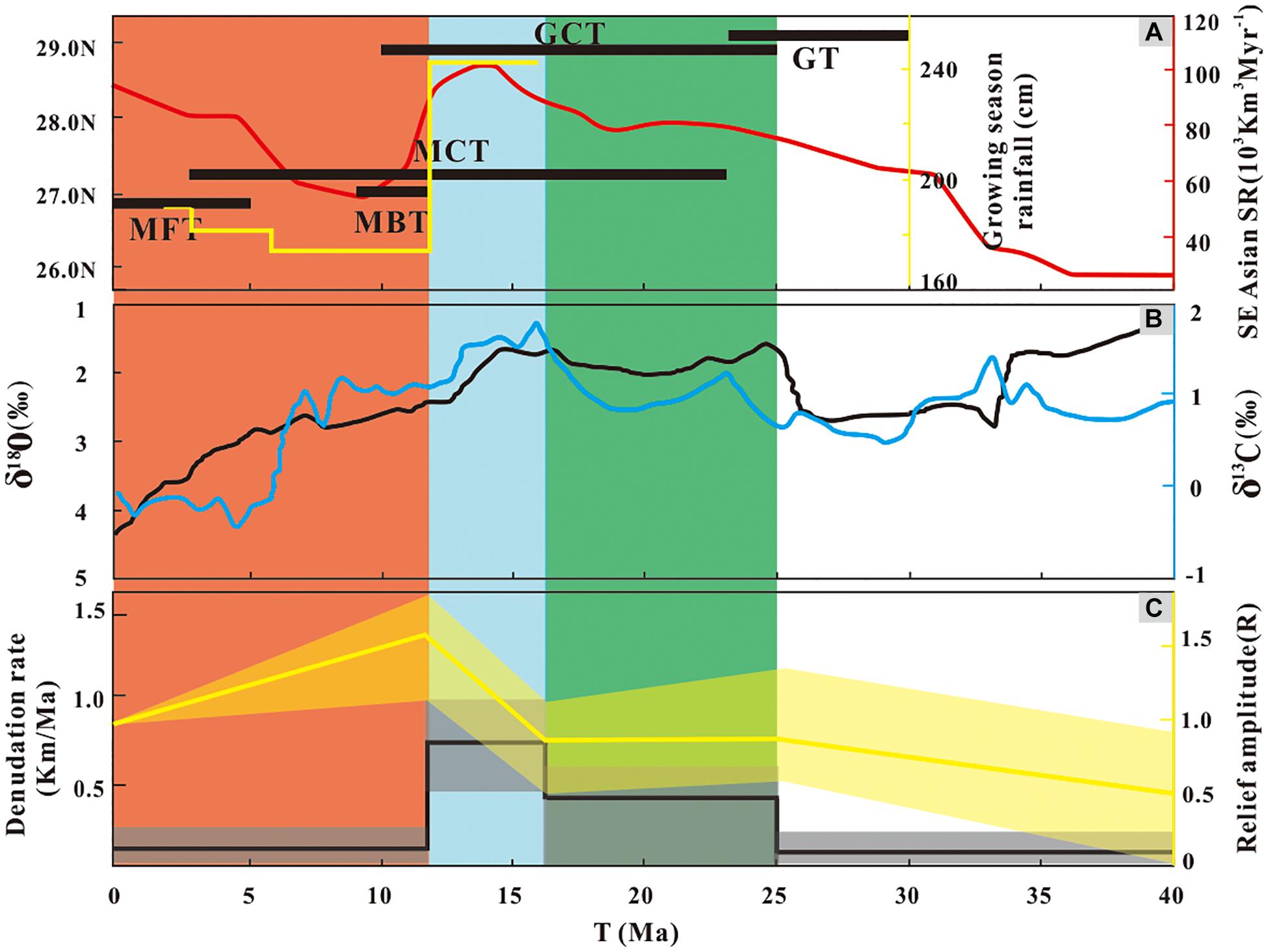
Figure 7. A comparison of the geologic events in south Tibet and Himalaya, the Asian summer monsoon, and the denudation rate and relief history of the Lhasa River drainage since ∼40 Ma. (A) The black horizontal lines represent the main deformation events for tectonic units of southern Tibet and Himalaya (Li Y. L. et al., 2015). MCT, Main Central thrust; MBT, Main Boundary thrust; MFT, Main Frontal thrust. The yellow line represents that growing season precipitation modeled from CLAMP (Climate-Leaf Analysis Multivariate Program) for the eastern Himalayan Siwalik fossil leaf assemblages (Khan et al., 2019). The red line represents the Southeastern Asian offshore sedimentary accumulation rate (SR) (Clift, 2006). (B) The benthic oxygen and carbon isotope record is represented by black and blue lines, respectively (Zachos et al., 2001). (C) Continuous black and yellow lines represent the best-fit denudation rate and relief of the Lhasa River drainage, respectively. The shaded line represents 1σ uncertainty on these estimates.

Discussion

The Timing of Establishment of the Modern Lhasa River

In this study, we found that the thermochronological ages in the main trunk are 41–14 Ma according to published thermochronological ages. The denudation history result of the modeling shows that rapid denudation started at ∼25 Ma (Table 1 and Figure 4). The establishment of rivers will definitely cause rapid denudation of the valley. Of course, other factors such as increased tectonic uplift and rainfall and related discharge could also lead to the enhancement of river incision and rapid denudation. However, we suggest that the rapid denudation of the Lhasa River valley before 25 Ma may be also recorded by thermochronological data if the modern Lhasa River exists before 25 Ma. In fact, we only found that the rapid denudation of the Lhasa River valley started at ∼25 Ma, probably suggesting that the modern Lhasa River in its modern extent did not exist prior to 25 Ma. In addition, the paleoaltimetric studies (e.g., carbon and oxygen stable isotopes) suggest that the northern portion of the Lhasa terrane where the Lhasa River originates was uplifted to near-modern elevations since around 25–23 Ma or much earlier (Rowley and Currie, 2006; DeCelles et al., 2007; Tian et al., 2013; Ding et al., 2014). If the Lhasa River did not start to develop at ∼25 Ma, the rapid denudation might imply that the northern Lhasa terrane must have the rapid rock uplift, and thus, it can maintain the current elevation. However, the northern Lhasa terrane did not undergo rapid rock uplift since the late Oligocene (Hetzel et al., 2011; Li et al., 2016), which suggested that this rapid denudation episode is most likely associated with the initial incision of the upper reaches of the Lhasa River.

In addition, the main trunk of the Lhasa River drains to the southwest across the Gangdese Mountains and merges into the Yarlung River (Figure 1B). Gangdese conglomerates are exposed discontinuously along the Yarlung River, and the depositional age of the Gangdese conglomerates is 26–23 Ma in the Xigaze forearc basin near the Lhasa River outlet (Wang et al., 2013; Carrapa et al., 2014). Paleocurrent measurements and provenance data indicate that the initial detritus of the Gangdese conglomerates were entirely derived from the north (mainly from the Gangdese arc) (Wang et al., 2013; Li et al., 2017), suggesting that the southward-draining relatively large rivers existed in the Gangdese region at least before ∼23 Ma, and a large amount of material from the Gangdese arc can be transported southward. Furthermore, Laskowski et al. (2019) proposed that the paleo-Lhasa River may form since the Late Cretaceous based on the sedimentary provenance analysis. However, Li et al. (2018) summarized the incision history of modern tributaries of the Yarlung River and showed that tributaries on the north side of the Yarlung River (originating from the Lhasa terrane, including the Lhasa River) have only recorded progressively northward cooling episodes since the early Miocene. This could also verify the result of thermal history modeling. The southward-draining paleo-Lhasa River proposed by Laskowski et al. (2019) probably did not follow the current Lhasa River channel. In summary, according to these thermochronological, sedimentological, and paleoaltimetric evidence, the modern Lhasa River was probably established during the latest Oligocene–earliest Miocene.

Forcing for the Late Cenozoic Denudation and Topographic Evolution of Lhasa River Drainage

The Latest Oligocene–Early Miocene

Our best-fit model shows that the Lhasa River drainage underwent a rapid denudation from 24.6 to 15.5 Ma (with a rate of 0.42 km/Ma) (Figure 7C). The onset of rapid denudation occurred slightly earlier compared with the previous reported rapid exhumation timing (∼23 or 20–10 Ma) (Li et al., 2016; Ge et al., 2017). The topographic relief did not change significantly with the increase of denudation during this stage (Figure 7C), suggesting a possible overall uplift in a large area including the Lhasa River drainage during this phase. The Gangdese Thrust is a north-dipping fault developed at the southern margin of the Lhasa River drainage (Figure 2), and it was active during late Oligocene–early Miocene (Yin et al., 1994; Li G. W. et al., 2015). Thus, the rapid denudation and relatively stable relief in this stage are most likely associated with the activity of the Gangdese Thrust (Figure 7A).

Moreover, we also compared the denudation rate with climate change (Figure 7B) and found that the rapid denudation in this stage also corresponds to the intensification of the Asian monsoon. Recent studies have shown that climatic change (precipitation or glacier development) determines the denudation of a large-scale area (Montgomery et al., 2001; Clift et al., 2008), but the orogenic tectonics could only trigger the erosion of the relatively local region (Beaumont et al., 2001; Luszczak et al., 2018; Yang et al., 2019; Shen et al., 2019). Based on this hypothesis, we have summarized the cooling history of five large rivers in the southeastern Tibetan Plateau from ∼40 Ma to the present to identify the possible effect of climate on the denudation (Figure 8). This result suggests that not all rivers on the southeastern Tibetan Plateau underwent a rapid cooling at this period (Figure 8B), indicating that the rapid denudation at this stage is not dominated by climate, which further validates our viewpoint.

FIGURE 8

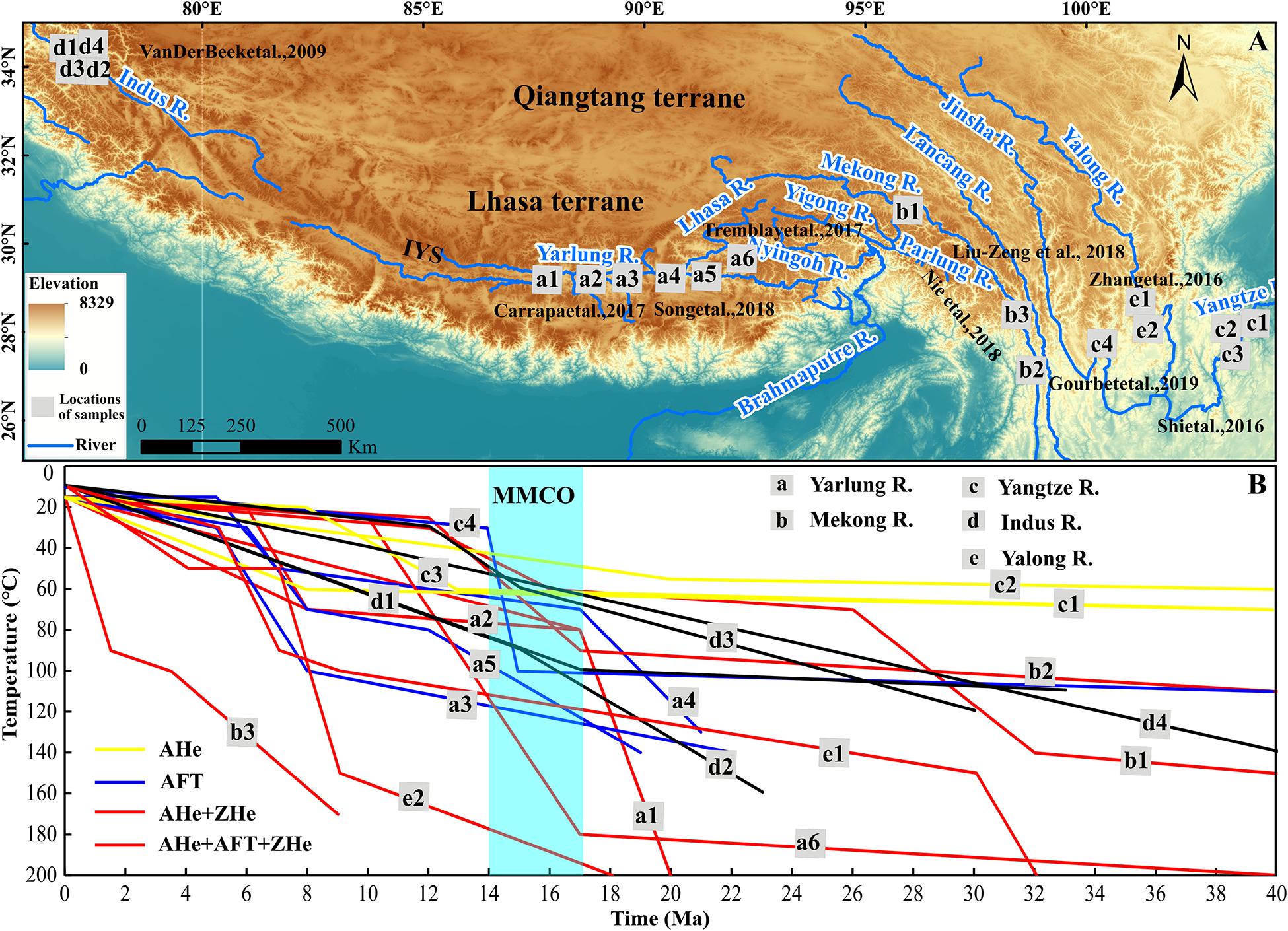
Figure 8. Cooling history of large rivers in the southern Tibet Plateau retrieved by Hefty (Ketcham, 2005) or QtQt (Gallagher, 2012). (A) Sampling sites of the river detrital or bedrock low-temperature thermochronology in the southern Tibetan Plateau. The letters a, b, c, d, and e represent the study sites of the Yarlung River, Mekong River, Yangtze River, Indus River, and Yalong River, respectively. (B) 2D thermal history modeling (Hefty or QtQt) results of thermochronological ages from the large rivers in the southern Tibetan Plateau (data from van der Beek et al., 2009; Tremblay et al., 2015; Shi et al., 2016; Zhang et al., 2016; Carrapa et al., 2017; Nie et al., 2018; Song et al., 2018; Liu-Zeng et al., 2018; Gourbet et al., 2019). MMCO, middle Miocene climate optimum.

The Gangdese Thrust leads to the further uplift of the Gangdese Mountains, which could cut off the external paleodrainage from north to south in the southern Tibetan Plateau (Zhang et al., 2012; Han et al., 2019). At the same time, the southward paleodrainage in the southern Gangdese Mountains also rapidly incised in response to the uplift of the Gangdese Mountains, leading to the formation of the initial Lhasa River. In the early Miocene, the development of the GCT system caused the uplift of the southern terranes (the Xigaze forearc basin, YTSZ, and Tethyan Himalaya) that might block the originally southward paleoflows (Wang et al., 2013; Li et al., 2018). The westward-flowing paleo-Yarlung River initiated at ∼22 Ma (Wang et al., 2013) and captured the initial paleo-Lhasa River, possibly leading to the formation of the so-called barbed junction with southwestward-flowing tributaries (modern Lhasa River) of the Yarlung River (Figure 2). Theoretically, the formation of the modern Lhasa River will definitely lead to an increase in topographic relief, but the result of our simulation suggests that the topographic relief did not change significantly with the increase of denudation during this stage (Figure 7). This is probably related to the overall uplift of the central Gangdese Mountains during this phase due to the development of the GT and GCT (Figure 7A).

The Middle Miocene

Although previous studies have generally estimated a rapid denudation stage of the Gangdese region at ∼23–0 or 20–10 Ma (Dai et al., 2013; Li et al., 2016; Ge et al., 2017), our modeling shows that a period of intense denudation existed at ∼15.5–12.3 Ma (with a rate of 0.72 km/Ma) (Figure 7C). The topographic relief in Lhasa River drainage also increased significantly (Figure 7C). An important climate event, the middle Miocene climate optimum (MMCO, ∼17–14 Ma) happened, which is characterized by the warmest climate and highest atmospheric CO₂ concentrations during this period (Zachos et al., 2001; Tripati et al., 2009). The MMCO corresponds to a phase of enhanced East and South Asian summer monsoon precipitation with large amplitude variability as recorded by offshore Southeastern Asian sediment accumulation rates (Clift, 2006; Yang et al., 2020). Meanwhile, the activity of the south-dipping GCT caused uplift and denudation of the Xigaze forearc basin, YTSZ, and Tethyan Himalaya in the southernmost Lhasa terrane (Wang et al., 2013; Li Y. L. et al., 2015). However, the middle reach of the Lhasa River is close to the central Lhasa terrane, and the tectonic activity of GCT should have a little impact on the denudation of the Lhasa River. Thus, we suggest that the intense denudation in this stage is more likely to be related to the large increasing Asian summer monsoon precipitation.

Furthermore, the cooling history of five large rivers in the southeastern Tibetan Plateau also underwent rapid cooling at this stage (Figure 8B), and this spatially large-scale synchronous rapid denudation including in the Lhasa River drainage should be dominated by climate (Montgomery et al., 2001; Clift et al., 2008). This is consistent with the fast incision of the Lhasa River, which leads to the topographic relief to increase rapidly (R3 = 1.6), which resulted in a relatively high-relief landscape (Figure 7C).

After ∼12 Ma

The denudation rate and relief in the Lhasa River drainage significant decreased after ∼12 Ma. The geological evidence suggested that the Himalaya experienced significant rock uplift since the late Miocene (Figure 7, e.g., MBT and MFT); thus, the orographic barrier to precipitation in the southern Tibetan Plateau would have strengthened (Tremblay et al., 2015), but the Lhasa River valley could be the only access for moisture penetration to the north and the precipitation decreased here. Therefore, the denudation rate significantly decreased. Another possibility was that a stationary knickzone results from coupling between focused rock uplift and rapidly fluvial incision within the Namche Barwa Syntaxis during the late Miocene (Lang and Huntington, 2014; Zeitler et al., 2014), creating a high-elevation base level for the drainage network upstream which inhabited the incision of the upper reaches of the Yarlung River. The decreasing of incision and low transport capacity in the upper Lhasa River might have led to the accumulation of the Lhasa River and reduced the topographic relief.

Conclusion

Based on a set of thermochronological ages reported in the Lhasa River valley, we have used a 3D thermokinematic model to carefully quantify rates and transition time of denudation under different scenarios. Two-stage rapid denudation rates at ∼25–16 Ma (with a rate of 0.42 km/Ma) and ∼16–12 Ma (with a rate of 0.72 km/Ma) are revealed. Furthermore, the results of the drainage denudation history were combined with the data of topographic evolution to distinguish the tectonic and climate controls on geomorphic evolution of the Lhasa River drainage. The rapid denudation of the first phase (∼25–16 Ma) could be caused by the activity of the Gangdese Thrust, which led to the overall uplift of the Gangdese Mountains. This might result in the reorganization of southward paleodrainage in the southern Tibetan Plateau, and the modern Lhasa River started to develop. The second stage of the fast denudation and high relief which correspond to a ubiquitous increase of fluvial incision in the southern Tibetan Plateau should be related to enhanced Asian summer monsoon precipitation during the middle Miocene. After that, the denudation rate decreased rapidly due to the uplift of the Himalayas barrier to precipitation, and a low-relief landscape gradually developed in the Gangdese region.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

DC built the 3D model and wrote the first draft of the text. XW and GL guided the overarching research direction and advised on the interdisciplinary context. WZ advised on the geology. HL advised on the climatology. All authors contributed to the revision of the text.

Funding

This research is supported by the Second Tibetan Plateau Scientific Expedition Program (STEP) (2019QZKK0205; 2019QZKK2304), the National Natural Science Foundation of China (41971005), and the National Key Research and Development Program (grant number 2016YFA0600500).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thanks to Yang Yu, Qiang Su, and Zhengchen Li for their suggestions in writing. Jean Braun is thanked for providing the Pecube code. We also thank the reviewers RJ and JD for their helpful suggestions to improve the manuscript and editor GR for professional editorial handling.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.636459/full#supplementary-material

References

Ahnert, F. (1970). Functional relationships between denudation, relief, and uplift in large mid-latitude drainage basins. Am. J. Sci. 268, 243–263. doi: 10.2475/ajs.268.3.243

PubMed Abstract | CrossRef Full Text | Google Scholar

Beaumont, C., Jamieson, R. A., Nguyen, M. H., and Lee, B. (2001). Himalayan tectonics explained by extrusion of a low-viscosity crustal channel coupled to focused surface denudation. Nature 414, 738–742. doi: 10.1038/414738a

PubMed Abstract | CrossRef Full Text | Google Scholar

Beek, P. A. V. D., Valla, P. G., Herman, F., Braun, J., Persano, C., Dobson, K. J., et al. (2010). Inversion of thermochronological age-elevation profiles to extract independent estimates of denudation and relief history - I: theory and conceptual model. Earth Planet. Sci. Lett. 296, 9–22. doi: 10.1016/j.epsl.2010.04.032

CrossRef Full Text | Google Scholar

Bookhagen, B., and Burbank, D. W. (2010). Toward a complete Himalayan hydrological budget: spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge. J. Geophys. Res. Earth Surf. 115:F03019. doi: 10.1029/2009JF001426

CrossRef Full Text | Google Scholar

Bookhagen, B., Thiede, R. C., and Strecker, M. R. (2005). Late Quaternary intensified monsoon phases control landscape evolution in the northwest Himalaya. Geology 33, 149–152. doi: 10.1130/G20982.1

CrossRef Full Text | Google Scholar

Braun, J. (2002). Quantifying the effect of recent relief changes on age–elevation relationships. Earth Planet. Sci. Lett. 200, 331–343. doi: 10.1016/S0012-821X(02)00638-6

CrossRef Full Text | Google Scholar

Braun, J. (2003). Pecube: a new finite-element code to solve the 3D heat transport equation including the effects of a time-varying, finite amplitude surface topography. Comput. Geosci. 29, 787–794. doi: 10.1016/S0098-3004(03)00052-9

CrossRef Full Text | Google Scholar

Braun, J., van der Beek, P., Valla, P., Robert, X., Herman, F., and Glotzbach, C. (2012). Quantifying rates of landscape evolution and tectonic processes by thermochronology and numerical modeling of crustal heat transport using PECUBE. Tectonophysics 524, 1–28. doi: 10.1016/j.tecto.2011.12.035

CrossRef Full Text | Google Scholar

Carrapa, B., Mohd, F., Kapp, P. A., Decelles, P. G., and Gehrels, G. (2017). Tectonic and erosional history of southern tibet recorded by detrital chronological signatures along the yarlung river drainage. Geol. Soc. Am. Bull. 129, 570–581. doi: 10.1130/B31587.1

CrossRef Full Text | Google Scholar

Carrapa, B., Orme, D. A., Decelles, P. G., Kapp, P., Cosca, M. A., and Waldrip, R. (2014). Miocene burial and exhumation of the India-Asia collision zone in southern Tibet: response to slab dynamics and erosion. Geology 42, 443–446. doi: 10.1130/G35350.1

CrossRef Full Text | Google Scholar

Clift, P. D. (2006). Controls on the erosion of Cenozoic Asia and the flux of clastic sediment to the ocean. Earth Planet. Sci. Lett. 241, 571–580. doi: 10.1016/j.epsl.2005.11.028

CrossRef Full Text | Google Scholar

Clift, P. D., Hodges, K. V., Heslop, D., Hannigan, R., Van Long, H., and Calves, G. (2008). Correlation of Himalayan exhumation rates and Asian monsoon intensity. Nat. Geosci. 1, 875–880. doi: 10.1038/ngeo351

CrossRef Full Text | Google Scholar

Copeland, P., Harrison, T. M., Pan, Y., Kidd, W. S. F., Roden, M., and Zhang, Y. (1995). Thermal evolution of the Gangdese batholith, southern Tibet: a history of episodic unroofing. Tectonics 14, 223–236. doi: 10.1029/94TC01676

CrossRef Full Text | Google Scholar

Dai, J. G., Wang, C. S., Hourigan, J., Li, Z. J., and Zhuang, G. S. (2013). Exhumation history of the Gangdese batholith, Southern Tibetan Plateau: evidence from Apatite and Zircon (U-Th)/He thermochronology. J. Geol. 121, 155–172. doi: 10.1086/669250

CrossRef Full Text | Google Scholar

Davis, D., Suppe, J., and Dahlen, F. A. (1983). Mechanics of fold-and-thrust belts and accretionary wedges. J. Geophys. Res. 88, 1153–1172. doi: 10.1029/JB088iB02p01153

CrossRef Full Text | Google Scholar

DeCelles, P. G., Quade, J., Kapp, P., Fan, M. J., Dettman, D. L., and Ding, L. (2007). High and dry in central Tibet during the Late Oligocene. Earth Planet. Sci. Lett. 253, 389–401. doi: 10.1016/j.epsl.2006.11.001

CrossRef Full Text | Google Scholar

Ding, L., Xu, Q., Yue, Y. H., Wang, H. Q., Cai, F. L., and Li, S. (2014). The andean-type gangdese mountains: paleoelevation record from the paleocene-eocene linzhou basin. Earth Planet. Sci. Lett. 392, 250–264. doi: 10.1016/j.epsl.2014.01.045

CrossRef Full Text | Google Scholar

Ehlers, T. A. (2005). Crustal thermal processes and the interpretation of thermochronometer data. Low Temp. Thermochronol. 58, 315–350. doi: 10.2138/rmg.2005.58.12

CrossRef Full Text | Google Scholar

England, P., and Molnar, P. (1990). Surface uplift, uplift of rocks, and exhumation of rocks. Geology 18, 1173–1177.

Google Scholar

Gadgil, S. (2003). The Indian monsoon and its variability. Annu. Rev. Earth Planet. Sci. 31, 429–467. doi: 10.1146/annurev.earth.31.100901.141251

CrossRef Full Text | Google Scholar

Gallagher, K. (2012). Transdimensional inverse thermal history modeling for quantitative thermochronology. J. Geophys. Res. Solid Earth 117:B02408. doi: 10.1029/2011JB008825

CrossRef Full Text | Google Scholar

Gallagher, K., Stephenson, J., Brown, R., Holmes, C., and Ballester, P. (2005a). Exploiting 3D spatial sampling in inverse modeling of thermochronological data. Low Temp. Thermochronol. 58, 375–387. doi: 10.2138/rmg.2005.58.14

CrossRef Full Text | Google Scholar

Gallagher, K., Stephenson, J., Brown, R., Holmes, C., and Fitzgerald, P. (2005b). Low temperature thermochronology and modeling strategies for multiple samples 1: vertical profiles. Earth Planet. Lett. 237, 193–208. doi: 10.1016/j.epsl.2005.06.025

CrossRef Full Text | Google Scholar

Ge, Y. K., Dai, J. G., Wang, C. S., Li, Y. L., Xu, G. Q., and Danisik, M. (2017). Cenozoic thermo-tectonic evolution of the Gangdese batholith constrained by low-temperature thermochronology. Gondwana Res. 41, 451–462. doi: 10.1016/j.gr.2016.05.006

CrossRef Full Text | Google Scholar

Gourbet, L., Yang, R., Fellin, M. G., Paquette, J. L., Willett, S. D., Gong, J. F., et al. (2019). Evolution of the yangtze river network, southeastern tibet: insights from thermochronology and sedimentology. Lithosphere 12, 3–18. doi: 10.1130/L1104.1

CrossRef Full Text | Google Scholar

Han, Z. P., Sinclair, H. D., Li, Y. L., Wang, C. S., Tao, Z., and Qian, X. Y. (2019). Internal drainage has sustained low-relief tibetan landscapes since the early miocene. Geophys. Res. Lett. 46, 8741–8752. doi: 10.1029/2019GL083019

CrossRef Full Text | Google Scholar

Harrison, T. M., Copeland, P., Kidd, W. S. F., and Yin, A. (1992). Raising Tibet. Science 255, 1663–1670. doi: 10.1126/science.255.5052.1663

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrison, T. M., Yin, A., Grove, M., Lovera, O. M., Ryerson, F. J., and Zhou, X. H. (2000). The Zedong Window: a record of superposed Tertiary convergence in southeastern Tibet. J. Geophys. Res. Solid Earth 105, 19211–19230. doi: 10.1029/2000JB900078

CrossRef Full Text | Google Scholar

Hetzel, R., Dunkl, I., Haider, V., Strobl, M., von Eynatten, H., Ding, L., et al. (2011). Peneplain formation in southern Tibet predates the India-Asia collision and plateau uplift. Geology 39, 983–986. doi: 10.1130/g34504y.1

CrossRef Full Text | Google Scholar

Ji, W. Q., Wu, F. Y., Chung, S. L., Li, J. X., and Liu, C. Z. (2009). Zircon U-Pb geochronology and Hf isotopic constraints on petrogenesis of the Gangdese batholith, southern Tibet. Chem. Geol. 262, 229–245. doi: 10.1016/j.chemgeo.2009.01.020

CrossRef Full Text | Google Scholar

Ketcham, R. A. (2005). Forward and inverse modeling of low-temperature thermochronometry data. Rev. Mineral. Geochem. 58, 275–314. doi: 10.2138/rmg.2005.58.11

CrossRef Full Text | Google Scholar

Khan, M. A., Bera, M., Spicer, R. A., Spicer, T. E. V., and Bera, S. (2019). Palaeoclimatic estimates for a latest Miocene-Pliocene flora from the Siwalik Group of Bhutan: Evidence for the development of the South Asian Monsoon in the eastern Himalaya. Palaeogeogr. Palaeoclimatol. Palaeoecol. 514, 326–335. doi: 10.1016/j.palaeo.2018.10.019

CrossRef Full Text | Google Scholar

Lang, K. A., and Huntington, K. W. (2014). Antecedence of the Yarlung-Siang-Brahmaputra River, eastern Himalaya. Earth Planet. Sci. Lett. 397, 145–158. doi: 10.1016/j.epsl.2014.04.026

CrossRef Full Text | Google Scholar

Laskowski, A. K., Orme, D. A., Cai, F. L., and Ding, L. (2019). The Ancestral Lhasa River: a late cretaceous trans-arc river that drained the proto-Tibetan Plateau. Geology 47, 1029–1033. doi: 10.1130/G46823.1

CrossRef Full Text | Google Scholar

Li, G. W., Kohn, B., Sandiford, M., Ma, Z. L., and Xu, Z. Q. (2018). Post-collisional exhumation of the Indus-Yarlung suture zone and Northern Tethyan Himalaya, Saga, SW Tibet. Gondwana Res. 64, 1–10.

Google Scholar

Li, G. W., Kohn, B., Sandiford, M., Xu, Z. Q., Tian, Y. T., and Seiler, C. (2016). Synorogenic morphotectonic evolution of the Gangdese batholith, South Tibet: Insights from low-temperature thermochronology. Geochem. Geophys. Geosyst. 17, 101–112. doi: 10.1002/2015GC006047

CrossRef Full Text | Google Scholar

Li, G. W., Tian, Y. T., Kohn, B. P., Sandiford, M., Xu, Z. Q., and Cai, Z. H. (2015). Cenozoic low temperature cooling history of the Northern Tethyan Himalaya in Zedang, SE Tibet and its implications. Tectonophysics 643, 80–93. doi: 10.1016/j.tecto.2014.12.014

CrossRef Full Text | Google Scholar

Li, S., Ding, L., Xu, Q., Wang, H. Q., Yue, Y. H., and Baral, U. (2017). The evolution of Yarlung Tsangpo River: constraints from the age and provenance of the Gangdese Conglomerates, southern Tibet. Gondwana Res. 41, 249–266. doi: 10.1016/j.gr.2015.05.010

CrossRef Full Text | Google Scholar

Li, Y. L., Wang, C. S., Dai, J. G., Xu, G. Q., Hou, Y. L., and Li, X. H. (2015). Propagation of the deformation and growth of the Tibetan-Himalayan orogen: a review. Earth Sci. Rev. 143, 36–61. doi: 10.1016/j.earscirev.2015.01.001

CrossRef Full Text | Google Scholar

Liu-Zeng, J., Zhang, J. Y., McPhillips, D., Reiners, P., Wei, W., and Pik, R. (2018). Multiple episodes of fast exhumation since Cretaceous in southeast Tibet, revealed by low-temperature thermochronology. Earth Planet. Sci. Lett. 490, 62–76. doi: 10.1016/j.epsl.2018.03.011

CrossRef Full Text | Google Scholar

Luszczak, K., Persano, C., Braun, J., and Stuart, F. M. (2018). How local crustal thermal properties influence the amount of denudation derived from low-temperature thermochronometry. Geology 46, E439–E439. doi: 10.1130/G39036.1

CrossRef Full Text | Google Scholar

McDannell, K. T., Zeitler, P. K., and Idleman, B. D. (2018). Relict topography within the Hangay mountains in Central Mongolia: quantifying long-term exhumation and relief change in an old landscape. Tectonics 37, 2531–2558. doi: 10.17605/OSF.IO/BPHYS

PubMed Abstract | CrossRef Full Text | Google Scholar

Mo, X. X., Niu, Y. L., Dong, G. C., Zhao, Z. D., Hou, Z. Q., Zhou, S., et al. (2008). Contribution of syncollisional felsic magmatism to continental crust growth: a case study of the Paleogene Linzizong volcanic Succession in southern Tibet. Chem. Geol. 250, 49–67. doi: 10.1016/j.chemgeo.2008.02.003

CrossRef Full Text | Google Scholar

Molnar, P., Boos, W. R., and Battisti, D. S. (2010). Orographic controls on climate and paleoclimate of Asia: thermal and mechanical roles for the Tibetan Plateau. Annu. Rev. Earth Planet. 38, 77–102. doi: 10.1146/annurev-earth-040809-152456

CrossRef Full Text | Google Scholar

Montgomery, D. R., Balco, G., and Willett, S. D. (2001). Climate, tectonics, and the morphology of the Andes. Geology 29, 579–582. doi: 10.1130/0091-761320010292.0.CO;2

CrossRef Full Text | Google Scholar

Naito, N., Ageta, Y., Iwata, S., Matsuda, Y., Suzuki, R., Karma, et al. (2006). Glacier shrinkages and climate conditions around Jichu Dramo Glacier in the Bhutan Himalayas from 1998 to 2003. Bull. Glaciol. Res. 23, 51–61. doi: 10.1007/s11407-999-0013-0

CrossRef Full Text | Google Scholar

Nie, J. S., Ruetenik, G., Gallagher, K., Hoke, G., Garzione, C. N., and Wang, W. T. (2018). Rapid incision of the Mekong River in the middle Miocene linked to monsoonal precipitation. Nat. Geosci. 11, 944–948. doi: 10.1038/s41561-018-0244-z

CrossRef Full Text | Google Scholar

Pan, B. T., Burbank, D., Wang, Y. X., Wu, G. J., Li, J. J., and Guan, Q. Y. (2003). A 900 ky record of strath terrace formation during glacial-interglacial transitions in northwest China. Geology 31, 957–960. doi: 10.1130/G19685.1

CrossRef Full Text | Google Scholar

Rowley, D. B., and Currie, B. S. (2006). Palaeo-altimetry of the late Eocene to Miocene Lunpola basin, central Tibet. Nature 439, 677–681. doi: 10.1038/nature04506

PubMed Abstract | CrossRef Full Text | Google Scholar

Sambridge, M. (2010a). Geophysical inversion with a neighbourhood algorithm—I. Searching a parameter space. Geophys. J. R. Astron. Soc. 138, 479–494. doi: 10.1046/j.1365-246X.1999.00876.x

CrossRef Full Text | Google Scholar

Sambridge, M. (2010b). Geophysical inversion with a neighbourhood algorithm–II. Appraising the ensemble. Transl. World Ssmol. 138, 727–746. doi: 10.1046/j.1365-246x.1999.00900.x

CrossRef Full Text | Google Scholar

Schildgen, T. F., Ehlers, T. A., Whipp, D. M., van Soest, M. C., Whipple, K. X., and Hodges, K. V. (2009). Quantifying canyon incision and Andean Plateau surface uplift, southwest Peru: a thermochronometer and numerical modeling approach. J. Geophys. Res. Earth Surf. 114:F04014. doi: 10.1029/2009JF001305

CrossRef Full Text | Google Scholar

Shen, X. M., Tian, Y. T., Zhang, G. H., Zhang, S. M., Carter, A., and Kohn, B. (2019). Late miocene hinterland crustal shortening in the longmen shan thrust belt, the eastern margin of the Tibetan Plateau. J. Geophys. Res. Solid Earth 124, 11972–11991. doi: 10.1029/2019JB018358

CrossRef Full Text | Google Scholar

Shi, H. C., Shi, X. B., Glasmacher, U. A., Yang, X. Q., and Stockli, D. F. (2016). The evolution of eastern Sichuan basin, Yangtze block since Cretaceous: constraints from low temperature thermochronology. J. Asian Earth Sci. 116, 208–221. doi: 10.1016/j.jseaes.2015.11.008

CrossRef Full Text | Google Scholar

Song, S. Y., Cao, D. Y., Zhang, Q. C., Wang, A. M., and Peng, Y. W. (2018). Apatite fission track evidence for Miocene denudation history in the Gangdese conglomerate belt and Yarlung Tsangpo River: Implications for the evolution of Southern Tibet. J. Asian Earth Sci. 160, 159–167. doi: 10.1016/j.jseaes.2018.04.021

CrossRef Full Text | Google Scholar

Tian, Y. T., Kohn, B. P., Gleadow, A. J. W., and Hu, S. B. (2013). Peneplain formation in southern Tibet predates the India-Asia collision and plateau uplift Comment. Geology 41, E295–E296. doi: 10.1130/G33617C.1

CrossRef Full Text | Google Scholar

Tian, Y. T., Kohn, B. P., Hu, S. B., and Gleadow, A. J. W. (2015). Synchronous fluvial response to surface uplift in the eastern Tibetan Plateau: implications for crustal dynamics. Geophys. Res. Lett. 42, 29–35. doi: 10.1002/2014GL062383

CrossRef Full Text | Google Scholar

Tremblay, M. M., Fox, M., Schmidt, J. L., Tripathy-Lang, A., Wielicki, M. M., Harrison, T. M., et al. (2015). Erosion in southern Tibet shut down at similar to 10 Ma due to enhanced rock uplift within the Himalaya. Proc. Natl. Acad. Sci. U.S.A. 112, 12030–12035. doi: 10.1073/pnas.1515652112

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripati, A. K., Roberts, C. D., and Eagle, R. A. (2009). Coupling of CO2 and ice sheet stability over major climate transitions of the last 20 million years. Science 326, 1394–1397. doi: 10.1126/science.1178296

PubMed Abstract | CrossRef Full Text | Google Scholar

Valla, P. G., Herman, F., van der Beek, P. A., and Braun, J. (2010). Inversion of thermochronological age-elevation profiles to extract independent estimates of denudation and relief history - I: Theory and conceptual model. Earth Planet. Sci. Lett. 295, 511–522. doi: 10.1016/j.epsl.2010.04.032

CrossRef Full Text | Google Scholar

van der Beek, P., Van Melle, J., Guillot, S., Pecher, A., Reiners, P. W., Nicolescu, S., et al. (2009). Eocene Tibetan plateau remnants preserved in the northwest Himalaya. Nat. Geosci. 2, 364–368. doi: 10.1038/ngeo503

CrossRef Full Text | Google Scholar

Wang, F., Feng, H., Shi, W., Zhang, W., Wu, L., Yang, L., et al. (2016). Relief history and denudation evolution of the northern Tibet margin: constraints from 40Ar/39Ar and (U–Th)/He dating and implications for far-field effect of rising plateau. Tectonophysics 675, 196–208. doi: 10.1016/j.tecto.2016.03.001

CrossRef Full Text | Google Scholar

Wang, J. G., Hu, X. M., Garzanti, E., and Wu, F. Y. (2013). Upper oligocene-lower miocene gangrinboche conglomerate in the Xigaze area, Southern Tibet: implications for Himalayan Uplift and Paleo-Yarlung-Zangbo initiation. J. Geol. 121, 425–444.

Google Scholar

Wang, P. X., Wang, B., Cheng, H., Fasullo, J., Guo, Z. T., Kiefer, T., et al. (2017). The global monsoon across time scales: mechanisms and outstanding issues. Earth Sci. Rev. 174, 84–121.

Google Scholar

Wang, X. Y., Lu, H. Y., Vandenberghe, J., Zheng, S. H., and van Balen, R. (2012). Late Miocene uplift of the NE Tibetan Plateau inferred from basin filling, planation and fluvial terraces in the Huang Shui catchment. Glob. Planet. Change 88-89, 10–19. doi: 10.1016/j.gloplacha.2012.02.009

CrossRef Full Text | Google Scholar

Wang, X. Y., Vandenberghe, J., Yi, S. W., Van Balen, R., and Lu, H. Y. (2015). Climate-dependent fluvial architecture and processes on a suborbital timescale in areas of rapid tectonic uplift: an example from the NE Tibetan Plateau. Glob. Planet. Change 133, 318–329. doi: 10.1016/j.gloplacha.2015.09.009

CrossRef Full Text | Google Scholar

Wei, L. G., Sandiford, M., Liu, X. H., Xu, Z. Q., Wei, L. J., and Li, H. Q. (2014). Provenance of Late Triassic sediments in central Lhasa terrane, Tibet and its implication. Gondwana Res. 25, 1680–1689. doi: 10.1016/j.gr.2013.06.019

CrossRef Full Text | Google Scholar

Whipp, D. M. Jr., Ehlers, T. A., Blythe, A. E., Huntington, K. W., Hodges, K. V., and Burbank, D. W. (2007). Plio-Quaternary exhumation history of the central Nepalese Himalaya: 2. Thermokinematic and thermochronometer age prediction model. Tectonics 26:TC3003. doi: 10.1029/2006TC001991

CrossRef Full Text | Google Scholar

Whipple, K. X. (2009). The influence of climate on the tectonic evolution of mountain belts (vol 2, pg 97, 2009). Nat. Geosci. 2, 730–730. doi: 10.1038/ngeo413

CrossRef Full Text | Google Scholar

Whipple, K. X., Hancock, G. S., and Anderson, R. S. (2000). River incision into bedrock: Mechanics and relative efficacy of plucking, abrasion, and cavitation. Geol. Soc. Am. Bull. 112, 490–503. doi: 10.1130/0016-760620001122.0.CO;2

CrossRef Full Text | Google Scholar

Wilson, C. J. L., and Fowler, A. P. (2011). Denudational response to surface uplift in east Tibet: evidence from apatite fission-track thermochronology. Geol. Soc. Am. Bull. 123, 1966–1987. doi: 10.1130/B30331.1

CrossRef Full Text | Google Scholar

Yang, R., Herman, F., and Fellin, M. G. (2019). Exhumation and topographic evolution of the Namche Barwa Syntaxis, eastern Himalaya. Tectonophysics 722, 43–52. doi: 10.1016/j.tecto.2017.10.026

CrossRef Full Text | Google Scholar

Yang, X. P., Groeneveld, J., Jian, Z. M., Steinke, S., and Giosan, L. (2020). Middle miocene intensification of South Asian Monsoonal Rainfall. Paleoceanogr. Paleoclimatol. 35, 1–18. doi: 10.1029/2020PA003853

CrossRef Full Text | Google Scholar

Yin, A., and Harrison, T. M. (2000). Geologic evolution of the Himalayan-Tibetan orogen. Annu. Rev. Earth Planet. Sci. 28, 211–280. doi: 10.1146/annurev.earth.28.1.211

CrossRef Full Text | Google Scholar

Yin, A., Harrison, T. M., Murphy, M. A., Grove, M., Nie, S., and Ryerson, F. J. (1999). Tertiary deformation history of southeastern and southwestern Tibet during the Indo-Asian collision. Geol. Soc. Am. Bull. 111, 1644–1664. doi: 10.1130/0016-760619991112.3.CO;2

CrossRef Full Text | Google Scholar

Yin, A., Harrison, T. M., Ryerson, F. J., Chen, W. J., Kidd, W. S. F., and Copeland, P. (1994). Tertiary structural evolution of the Gangdese Thrust System, Southeastern Tibet. J. Geophys. Res. Solid Earth 99, 18175–18201. doi: 10.1029/94JB00504

CrossRef Full Text | Google Scholar

Zachos, J., Pagani, M., Sloan, L., Thomas, E., and Billups, K. (2001). Trends, rhythms, and aberrations in global climate 65 Ma to present. Science 292, 686–693. doi: 10.1126/science.1059412

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeitler, P. K., Meltzer, A. S., Brown, L., Kidd, W. S. F., Lim, C., and Enkelmann, E. (2014). “Tectonics and topographic evolution of Namche Barwa and the easternmost Lhasa block, Tibet,” in Toward an Improved Understanding of Uplift Mechanisms and the Elevation History of the Tibetan Plateau, eds J. Nie, B. K. Horton, and G. D. Hoke (Boulder, CO: Geological Society of America), 23–58. doi: 10.1130/2014.2507(02

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeitler, P. K., Meltzer, A. S., Koons, P. O., Craw, D., Hallet, B., Chamberlain, C. P., et al. (2001). Erosion, Himalayan geodynamics, and the geomorphology of metamorphism. GSA Today 11, 4–9. doi: 10.1130/1052-517320010112.0.CO;2

CrossRef Full Text | Google Scholar

Zhang, H. P., Oskin, M. E., Liu-Zeng, J., Zhang, P. Z., Reiners, P. W., and Xiao, P. (2016). Pulsed exhumation of interior eastern Tibet: implications for relief generation mechanisms and the origin of high-elevation planation surfaces. Earth Planet. Sci. Lett. 449, 176–185. doi: 10.1016/j.epsl.2016.05.048

CrossRef Full Text | Google Scholar

Zhang, J. Y., Yin, A., Liu, W. C., Wu, F. Y., Lin, D., and Grove, M. (2012). Coupled U-Pb dating and Hf isotopic analysis of detrital zircon of modern river sand from the Yalu River (Yarlung Tsangpo) drainage system in southern Tibet: constraints on the transport processes and evolution of Himalayan rivers. Geol. Soc. Am. Bull. 124, 1449–1473. doi: 10.1130/B30592.1

CrossRef Full Text | Google Scholar

Zhang, P. Z., Peter, M., and William, R. W. (2001). Increased sedimentation rates and grain sizes 2–4 Myr ago due to the influence of climate change on erosion rates. Nature 410, 891–897. doi: 10.1038/35073504

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, D. C., Zhao, Z. D., Niu, Y. L., Mo, X. X., Chung, S. L., and Hou, Z. Q. (2011). The Lhasa Terrane: record of a microcontinent and its histories of drift and growth. Earth Planet. Sci. Lett. 301, 241–255. doi: 10.1016/j.epsl.2010.11.005

CrossRef Full Text | Google Scholar