- 1Institute of Risk Analysis, Prediction and Management (Risks-X), Academy for Advanced Interdisciplinary Studies, Southern University of Science and Technology (SUSTech), Shenzhen, China
- 2Department of Earth and Space Sciences, Southern University of Science and Technology (SUSTech), Shenzhen, China
The study of induced seismicity at sites of fluid injection is paramount to assess the seismic response of the earth’s crust and to mitigate the potential seismic risk. However statistical analysis is limited to events above the completeness magnitude
Introduction
The evaluation of the completeness magnitude
The present study aims at filling this gap by an in-depth analysis of the magnitude frequency distribution (MFD) at multiple sites. To the best of our knowledge, this is the first study dedicated to completeness magnitude analysis in the induced seismicity context. We will test different
The BMC method has been successfully applied in various regions of the world, but so far only in the context of natural seismicity: Taiwan (Mignan et al., 2011), Mainland China (Mignan et al., 2013), Switzerland (Kraft et al., 2013), Lesser Antilles arc (Vorobieva et al., 2013), California (Tormann et al., 2014), Greece (Mignan and Chouliaras, 2014), Iceland (Panzera et al., 2017), South Africa (Brandt, 2019) and Venezuela (Vásquez and Bravo de Guenni, n.d.)1. It becomes urgent to apply it to induced seismicity, which requires a reformulation of the model. Based on the new parameterization and additional information on incomplete (so-called censored) data, we will discuss how such information could improve induced seismicity data mining, or in other words, how it could improve knowledge on the underground feedback activation and the management of the associated risk.
Materials and Methods
Induced Seismicity Data
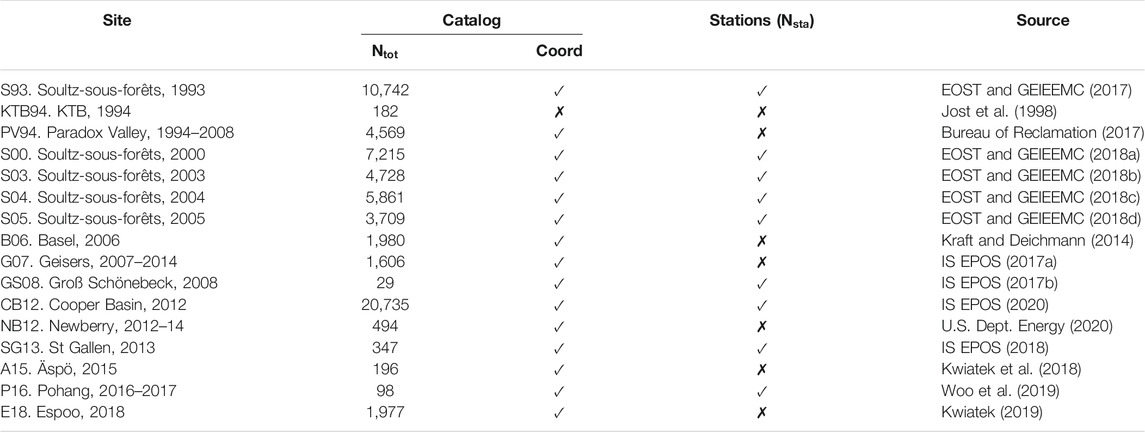
We consider 16 underground stimulations by deep fluid injection (Table 1), all of which are publicly available and often available from dedicated data portals (e.g., EOST and GEIE EMC, IS EPOS): the Soultz-sous-Forêts stimulations at the GPK1 well in 1993 [S93] (Cornet et al., 1997), GPK2 well in 2000 [S00] (Cuenot et al., 2008), GPK3 well in 2003 [S03] (Calò and Dorbath, 2013) and GPK4 well in both 2004 [S04] and 2005 [S05] (Charléty et al., 2007), the KTB deep drilling site [KTB94] (Jost et al., 1998), the Paradox Valley continuous injection from 1994 to 2008 [PV94] (Ake et al., 2005), the 2006 Basel 1 well stimulation [B06] (Häring et al., 2008; Kraft and Deichmann, 2014), the 2007–2014 Geysers [G07] Prati-9 and Prati-29 well injections (Kwiatek et al., 2015), the 2008 Groß Schönebeck injection [GS07] (Kwiatek et al., 2010), the Cooper Basin Habanero 4 well stimulation of 2012 [CB12] (Baisch et al., 2015). the Newberry Volcano EGS demonstration 2012 stimulation and 2014 restimulation [NB12] (Cladouhos et al., 2013; Cladouhos et al., 2015), the 2013 St Gallen reservoir simulation [SG13] (Diehl et al., 2017), the 2015 Äspö Hard Rock Laboratory experiment [A15] (Kwiatek et al., 2018), the 2016–2017 Pohang stimulation experiment [P16] (Woo et al., 2019), and the 2018 Espoo stimulation [E18] near Helsinki (Kwiatek, 2019). Most stimulations considered took place at EGS sites.
Depending on the parameters provided (see Table 1), different completeness analysis levels are achievable. When earthquake coordinates are not included, the study is limited to the bulk MFD analysis (Woessner and Wiemer, 2005; Mignan and Woessner, 2012) and to the application of the Asymmetric Laplace distribution (Mignan, 2019); when earthquake coordinates are included, observed completeness magnitude
Since this study is solely dedicated to seismicity completeness, data such as total volume injected, flow rate profile, or injection/post-injection windows are not considered (only mentioned in the discussion, Discussion and Perspectives on Data Mining). For statistical analyses related to the fluid injection process at different sites, the reader can refer to, e.g., Dinske and Shapiro (2013), van der Elst et al. (2016), Mignan et al. (2017) or Bentz et al. (2020).
Standard Magnitude Frequency Distribution Analysis
The bulk magnitude frequency distribution (MFD) of an earthquake catalog can be described by a probability density function that takes the form:
where
We should have the condition
Various methods have been proposed to estimate
Spatial heterogeneities in
Local MFDs of cells
with mode
Asymmetric Laplace Mixture Model
The sum of local “angular” MFDs of different
with
Any MFD shape can be fitted by the flexible ALMM based on the Expectation-Maximization (EM) algorithm (Dempster et al., 1977). The initial parameter values are estimated by applying
with
At each EM iteration
The maximization step (M-step) then updates the component parameters. The best number of components
Bayesian Magnitude of Completeness Mapping Method
The last method to be tested in the present study is the Bayesian Magnitude of Completeness (BMC) method that consists in using Bayesian inference to estimate
Following Bayes' Theorem, we obtain the posterior completeness magnitude
where
Results
Results of a Standard
We first apply the standard methods of
Figure 1 shows the cumulative bulk MFD for the 16 fluid injections and the matching
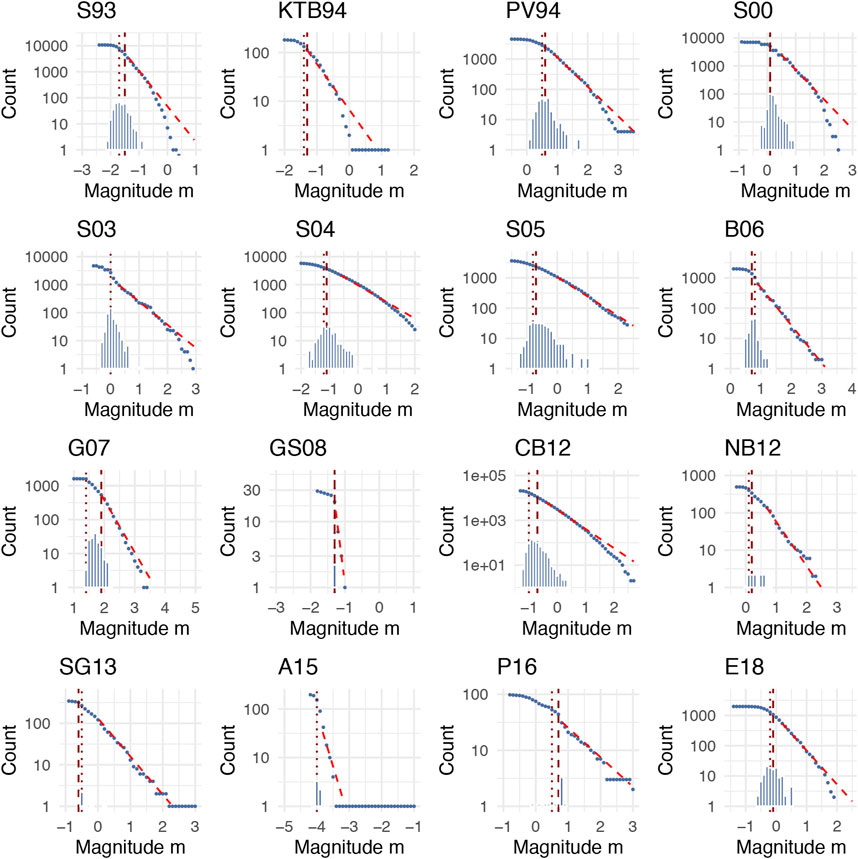
FIGURE 1. Cumulative magnitude frequency distribution (MFD) of 16 underground stimulations. The histogram shows the
Figure 2 shows
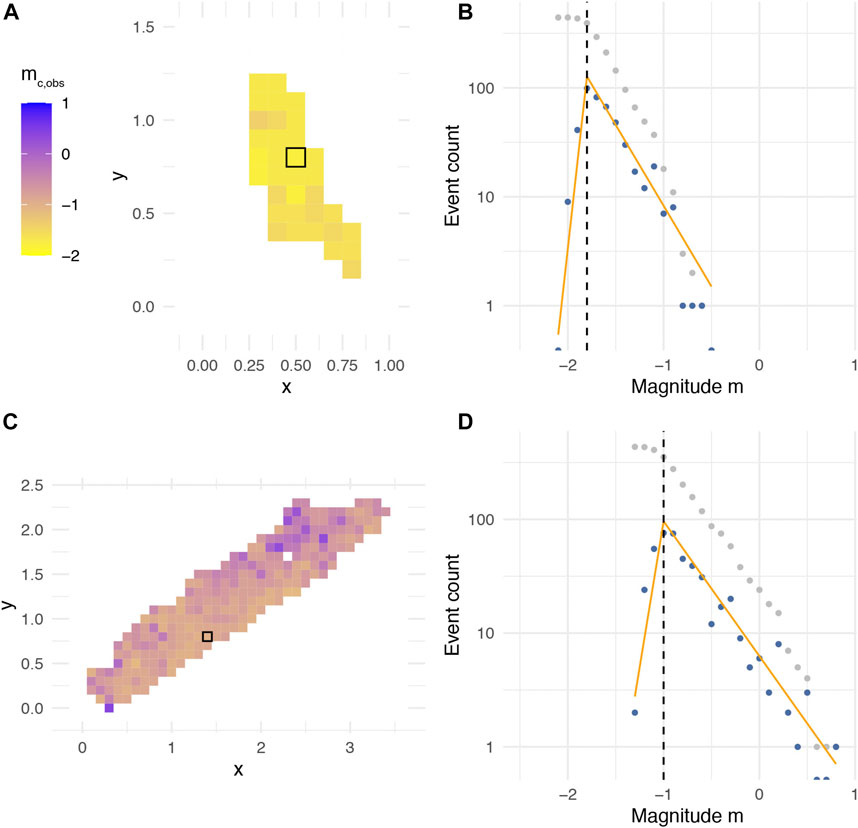
FIGURE 2. Examples of 100 m-resolution
This so-called standard
Asymmetric Laplace Mixture Model Fits
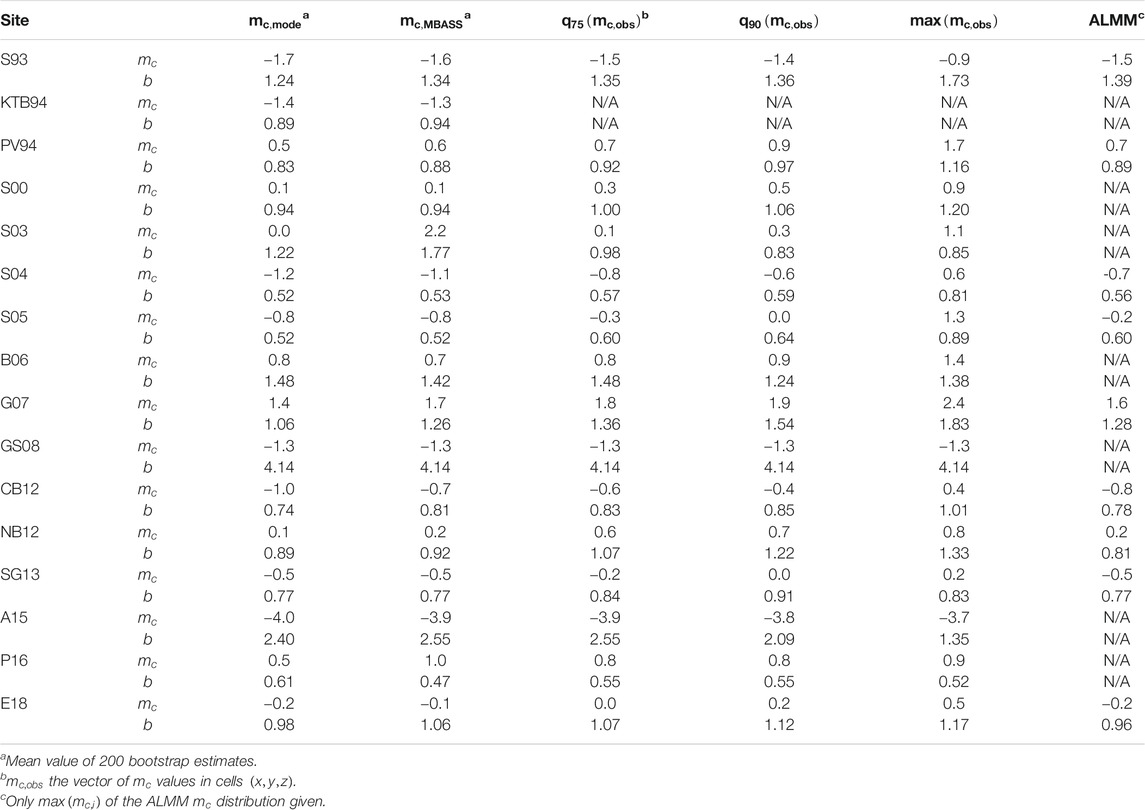
We then apply the ALMM to the 16 magnitude vectors but only get reasonable fits for 9 of them. We find that the ALMM requires
Figure 3 shows the 9 ALMM fits (for S93, PV94, S04, S05, G07, CB12, NB12, SG13 and E18). Parameters
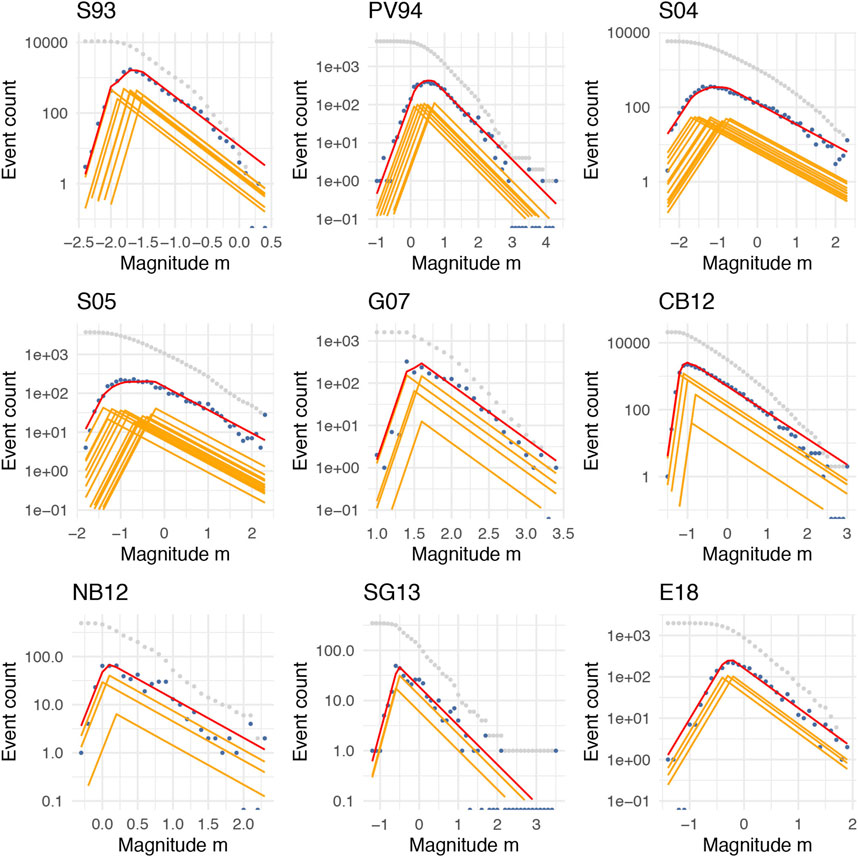
FIGURE 3. Non-cumulative MFD (in blue) of 9 underground stimulations for which an Asymmetric Laplace Mixture Model (ALMM) fit is available, shown in red, with the mixture components shown in orange. See Table 2 for some values.
The ALMM is highly sensible to abnormal fluctuations in the non-cumulative MFD, which are often not visible from the cumulative MFD. In the case of Soultz-sous-Fôrets, the S00 non-cumulative MFD shows significant drops in the number of events inconsistent with any model monotonously increasing up to
Bayesian Magnitude of Completeness Prior and Posterior
We define a BMC prior model for induced seismicity by combining the relation between
Figure 4 represents the BMC prior derived from 7 datasets: S93, S04, S05, GS08, CB12, SG13, and P16. The model, represented by the solid curve, is defined as
with distance
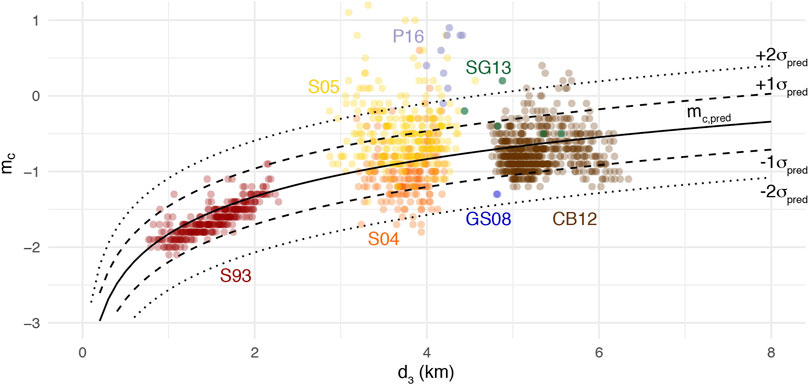
FIGURE 4. Prior model
Two datasets, S00 and S03, were not included in this analysis as event declaration depended in those cases on two triggering conditions from both the downhole and surface networks (EOST and GEIEEMC, 2018a; EOST and GEIEEMC, 2018b), which is likely inconsistent with the simple
We then combine the

FIGURE 5. Observed
Discussion and Perspectives on Data Mining
We reviewed some standard approaches to estimate the completeness magnitude
The present study could help refine future seismic hazard analyses, since the parameter
We first showed the impact of
While
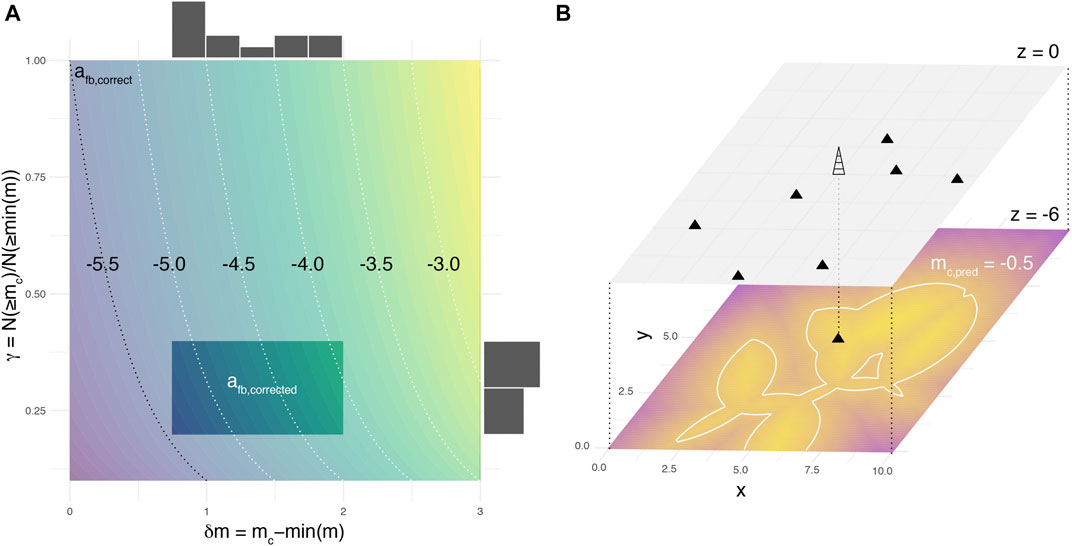
FIGURE 6. Induced seismicity data mining potential from completeness analysis. (A) Estimating the underground feedback parameter
Finally, if the BMC method allows defining robust
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here See Table 1 and reference list.
Author Contributions
AM did all the research and writing.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
Vásquez, R., and Bravo de Guenni, L. n. d. Bayesian estimation of the spatial variation of the completeness magnitude for the Venezuelan seismic catalogue. Available at: https://www.statistics.gov.hk/wsc/CPS204-P47-S.pdf. (Accessed Aug 2014)
References
Ake, J., Mahrer, K., O’Connell, D., and Block, L. (2005). Deep-injection and closely monitored induced seismicity at Paradox Valley, Colorado. Bull. Seismol. Soc. Am. 95, 664–683. doi:10.1785/0120040072
Aki, K. (1965). Maximum likelihood estimate of b in the formula Log N = a-bM and its confidence limits. Bull. Earthq. Res. Inst. Univ. Tokyo 43, 237–239.
Amorèse, D. (2007). Applying a change-point detection method on frequency-magnitude distributions. Bull. Seismol. Soc. Am. 97 (1), 742–751. doi:10.1785/0120060181
Baisch, S., Rothert, E., Stang, H., Vörös, R., Koch, C., and McMahon, A. (2015). Continued geothermal reservoir stimulation experiments in the Cooper Basin (Australia). Bull. Seismol. Soc. Am. 105, 198–209. doi:10.1785/0120140208
Bentz, S., Kwiatek, G., Martínez-Garzón, P., Bohnhoff, M., and Dresen, G. (2020). Seismic moment evolution during hydraulic stimulations. Geophys. Res. Lett. 47, e2019GL086185. doi:10.1029/2019gl086185
Brandt, M. B. C. (2019). Performance of the South African national seismograph network from october 2012 to february 2017: spatially varying magnitude completeness. S. Afr. J. Geol. 122, 57–68. doi:10.25131/sajg.122.0004
Broccardo, M., Mignan, A., Grigoli, F., Karvounis, D., and Rinaldi, A. P (2020). Induced seismicity risk analysis of the hydraulic stimulation of a geothermal well on Geldinganes, Iceland. Nat. Hazards Earth Syst. Sci. 20 (1573-1), 593. doi:10.5194/nhess-20-1573-2020
Broccardo, M., Mignan, A., Wiemer, S., Stojadinovic, B., and Giardini, D. (2017). Hierarchical bayesian modeling of fluid-induced seismicity. Geophys. Res. Lett. 44 (11), 357–411. doi:10.1002/2017gl075251
Bureau of Reclamation (2017). Paradox Valley earthquake catalogue. Available at: https://www.usbr.gov/uc/wcao/progact/paradox/RI.html. (Accessed June 2017)
Calò, M., and Dorbath, C. (2013). Different behaviours of the seismic velocity field at Soultz-sous-Fôrets revealed by 4-D seismic tomography: case study of GPK3 and GPK2 injection tests. Geophys. J. Int. 194 (1), 119–121. doi:10.1093/gji/ggt153
Charléty, J., Cuenot, N., Dorbath, L., Dorbath, C., Haessler, H., and Frogneux, M. (2007). Large earthquakes during hydraulic stimulations at the geothermal site of Soultz-sous-Forêts. Int. J. Rock Mech. Mining Sci. 44 (1), 105–111. doi:10.1016/j.ijrmms.2007.06.003
Cladouhos, T. T., Petty, S., Nordin, Y., Moore, M., Grasso, K., and Uddenberg, M. (2013). “Microseismic monitoring of Newberry Volcano EGS demonstration,” in Proc. 38th workshop geotherm. Reservoir. Engineering, February 11-13, 2013 (Stanford, CA: Stanford University).
Cladouhos, T. T., Petty, S., Swyer, M., Uddenberg, M., and Nordin, Y. (2015). “Results from Newberry Volcano EGS demonstration,” in Proc. 40th workshop geotherm. Reserv. Eng, January 26–28, 2015 (Stanford, CA: Stanford University).
Cornet, F. H., Helm, J., Poitrenaud, H., and Etchecopar, A. (1997). Seismic and aseismic slips induced by large-scale fluid injections. Pure Appl. Geophys. 150, 563–583. doi:10.1007/s000240050093
Cuenot, N., Dorbath, C., and Dorbath, L. (2008). Analysis of the microseismicity induced by fluid injections at the EGS site of soultz-sous-forêts (alsace, France): implications for the characterization of the geothermal reservoir properties. Pure Appl. Geophys. 165, 797–828. doi:10.1007/s00024-008-0335-7
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977). Maximum likelihood from incomplete data via theEMAlgorithm. J. R. Stat. Soc. Ser. B 39, 1–22. doi:10.1111/j.2517-6161.1977.tb01600.x
Diehl, T., Kraft, T., Kissling, E., and Wiemer, S. (2017). The induced earthquake sequence related to the St. Gallen deep geothermal project (Switzerland): fault reactivation and fluid interactions imaged by microseismicity. J. Geophys. Res. Solid Earth 122 (7), 272–277. doi:10.1002/2017jb014473
Dinske, C., and Shapiro, S. A. (2013). Seismotectonic state of reservoirs inferred from magnitude distributions of fluid-induced seismicity. J. Seismol. 17, 13–25. doi:10.1007/s10950-012-9292-9
EOST and GEIEEMS (2017). Episode: 1993 stimulation soultz-sous-forêts [collection]. EOST CDGP 107, 2247–2257. doi:10.25566/SSFS1993
EOST and GEIEEMS (2018a). Episode: 2000 stimulation soultz-sous-forêts [collection]. EOST CDGP [Epub ahead of print]. doi:10.25577/SSFS2000
EOST and GEIEEMS (2018b). Episode: 2003 stimulation soultz-sous-forêts [collection]. EOST CDGP [Epub ahead of print]. doi:10.25577/SSFS2003
EOST and GEIEEMS (2018c). Episode: 2004 stimulation soultz-sous-forêts [collection]. EOST CDGP [Epub ahead of print]. doi:10.25577/SSFS2004
EOST and GEIEEMS (2018d). Episode: 2005 stimulation soultz-sous-forêts [collection]. EOST CDGP [Epub ahead of print]. doi:10.25577/SSFS2005
Gutenberg, B., and Richter, C. F. (1944). Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 34, 184–188.
Häring, M. O., Schanz, U., Ladner, F., and Dyer, B. C. (2008). Characterisation of the Basel 1 enhanced geothermal system. Geothermics 37, 469–495. doi:10.1016/j.geothermics.2008.06.002
IS EPOS (2017a). Episode: THE geysers Prati 9 and Prati 29 cluster. Available at: https://tcs.ah-epos.eu/#episode. (Accessed November 2020)
IS EPOS (2017b). Episode: gross schoenebeck. Available at: https://tcs.ah-epos.eu/#episode. (Accessed November 2020)
IS EPOS (2018). Episode THE GEYSERS Prati 9 and Prati 29 cluster. Available at: https://tcs.ah-epos.eu/#episode. (Accessed November 2020)
IS EPOS (2020). Episode: cooper BASIN. Available at: https://tcs.ah-epos.eu/#episode. (Accessed November 2020)
Jost, M. L., Büsselberg, T., Jost, Ö., and Harjes, H. P. (1998). Source parameters of injection-induced microearthquakes at 9 km depth at the KTB deep drilling site, Germany. Bull. Seismol. Soc. Am. 88, 815–832.
Kamer, Y., and Hiemer, S. (2015). Data-driven spatial b value estimation with applications to California seismicity: to b or not to b. J. Geophys. Res. Solid Earth 120 (5), 191–195. doi:10.1002/2014jb011510
Kijko, A., and Smit, A. (2017). Estimation of the frequency-magnitude gutenberg-richterb‐value without making assumptions on levels of completeness. Seismol. Res. Lett. 88, 311–318. doi:10.1785/0220160177
Kraft, T., and Deichmann, N. (2014). High-precision relocation and focal mechanism of the injection-induced seismicity at the Basel EGS. Geothermics 52, 59–73. doi:10.1016/j.geothermics.2014.05.014
Kraft, T., Mignan, A., and Giardini, D. (2013). Optimization of a large-scale microseismic monitoring network in northern Switzerland. Geophys. J. Int. 195, 474–490. doi:10.1093/gji/ggt225
Kwiatek, G., Bohnhoff, M., Dresen, G., Schulze, A., Schulte, T., and Zimmermann, G. (2010). Microseismicity induced during fluid-injection: a case study from the geothermal site at Groß Schönebeck, North German Basin. Acta Geophys. 58, 995–1020. doi:10.2478/s11600-010-0032-7
Kwiatek, G. (2019). Controlling fluid-induced seismicity during a 6.1-km-deep geothermal stimulation in Finland. Sci. Adv. 5, eaav7224. doi:10.1126/sciadv.aav7224
Kwiatek, G., Martínez-Garzón, P., Dresen, G., Bohnhoff, M., Sone, H., and Hartline, C. (2015). Effects of long-term fluid injection on induced seismicity parameters and maximum magnitude in northwestern part of the Geysers geothermal field. J. Geophys. Res. Solid Earth 120 (7), 101–107. doi:10.1002/2015jb012362
Kwiatek, G., Martínez-Garzón, P., Plenkers, K., Leonhardt, M., Zang, A., and von Specht, S. (2018). Insights into complex subdecimeter fracturing processes occurring during a water injection experiment at depth in Äspö Hard Rock Laboratory, Sweden. J. Geophys. Res. Solid Earth 123, 6616–6635. doi:10.1029/2017JB014715
MacQueen, J. (1967). “Some methods for classification and analysis of multivariate observations,” in Proc. 5th berkeley symposium on mathematics, statistics and probability Editors M. L. M. Le Cam and J. Neyman (Univ. California Press), vol. 5.1, 281–297.
Martinsson, J., and Jonsson, A. (2018). A new model for the distribution of observable earthquake magnitudes and applications to $b$ -value estimation. IEEE Geosci. Rem. Sens. Lett. 15, 833–837. doi:10.1109/lgrs.2018.2812770
Mignan, A., Broccardo, M., Wiemer, S., and Giardini, D. (2017). Induced seismicity closed-form traffic light system for actuarial decision-making during deep fluid injections. Sci. Rep. 7, 13607. doi:10.1038/s41598-017-13585-9
Mignan, A., and Chen, C.-C. (2016). The spatial scale of detected seismicity. Pure Appl. Geophys. 173, 117–124. doi:10.1007/s00024-015-1133-7
Mignan, A., and Chouliaras, G. (2014). Fifty years of seismic network performance in Greece (1964-2013): spatiotemporal evolution of the completeness magnitude. Seismol. Res. Lett. 85, 657–667. doi:10.1785/0220130209
Mignan, A. (2012). Functional shape of the earthquake frequency-magnitude distribution and completeness magnitude. J. Geophys. Res. 117, B08302. doi:10.1029/2012jb009347
Mignan, A. (2019). Generalized earthquake frequency-magnitude distribution described by asymmetric Laplace mixture modelling. Geophys. J. Int. 219 (1), 348–351. doi:10.1093/gji/ggz373
Mignan, A., Jiang, C., Zechar, J. D., Wiemer, S., Wu, Z., and Huang, Z. (2013). Completeness of the Mainland China earthquake catalog and implications for the setup of the China earthquake forecast testing center. Bull. Seismol. Soc. Am. 103, 845–859. doi:10.1785/0120120052
Mignan, A., Landtwing, D., Kästli, P., Mena, B., and Wiemer, S. (2015). Induced seismicity risk analysis of the 2006 Basel, Switzerland, Enhanced Geothermal System project: influence of uncertainties on risk mitigation. Geothermics 53, 133–146. doi:10.1016/j.geothermics.2014.05.007
Mignan, A., Karvounis, D., Broccardo, M., Wiemer, S., and Giardini, D. (2019). Including seismic risk mitigation measures into the Levelized Cost of Electricity in enhanced geothermal systems for optimal siting. Appl. Energ. 238, 831–850. doi:10.1016/j.apenergy.2019.01.109
Mignan, A. (2016). Static behaviour of induced seismicity. Nonlin. Process. Geophys. 23, 107–113. doi:10.5194/npg-23-107-2016
Mignan, A., Werner, M. J., Wiemer, S., Chen, C. C., and Wu, Y. M. (2011). Bayesian estimation of the spatially varying completeness magnitude of earthquake catalogs. Bull. Seismol. Soc. Am. 101, 1371–1385. doi:10.1785/0120100223
Mignan, A., and Woessner, J. (2012). Estimating the magnitude of completeness for earthquake catalogs. Available at: http://www.corssa.org: Community Online Resource for Statistical Seismicity Analysis. (Accessed November 2020)
Ogata, Y., and Katsura, K. (1993). Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues. Geophys. J. Int. 113, 727–738. doi:10.1111/j.1365-246x.1993.tb04663.x
Panzera, F., Mignan, A., and Vogfjörð, K. S. (2017). Spatiotemporal evolution of the completeness magnitude of the Icelandic earthquake catalogue from 1991 to 2013. J. Seismol. 21, 615–630. doi:10.1007/s10950-016-9623-3
Ringdal, F. (1975). On the estimation of seismic detection thresholds. Bull. Seismol. Soc. Am. 65 (1), 631.
Sasaki, S. (1998). Characteristics of microseismic events induced during hydraulic fracturing experiments at the Hijiori hot dry rock geothermal energy site, Yamagata, Japan. Tectonophysics 289, 171–188. doi:10.1016/s0040-1951(97)00314-4
Tormann, T., Wiemer, S., and Mignan, A. (2014). Systematic survey of high-resolution b value imaging along Californian faults: inference on asperities. J. Geophys. Res. Solid Earth 119 (2), 029–32. doi:10.1002/2013jb010867
U.S. Department of Energy (2020). Newberry. Available at: http://fracture.lbl.gov/cgi-bin/Web_CatalogSearch.py. (Accessed November 2020)
van der Elst, N. J., Page, M. T., Weiser, D. A., Goebel, T. H. W., and Hosseini, S. M. (2016). Induced earthquake magnitudes are as large as (statistically) expected. J. Geophys. Res. Solid Earth 121 (4), 575–584. doi:10.1002/2016jb012818
Villiger, L., Gischig, V. S., Doetsch, J., Krietsch, H., and Dutler, N. O. (2020). Influence of reservoir geology on seismic response during decameter-scale hydraulic stimulations in crystalline rock. Solid Earth 11, 627–655. doi:10.5194/se-11-627-2020
Vorobieva, I., Narteau, C., Shebalin, P., Beauducel, F., Nercessian, A., and Clouard, V. (2013). Multiscale mapping of completeness magnitude of earthquake catalogs. Bull. Seismol. Soc. Am. 103 (2), 188–192. doi:10.1785/0120120132
Wiemer, S., and Wyss, M. (2000). Minimum magnitude of completeness in earthquake catalogs: examples from Alaska, the western United States, and Japan. Bull. Seismol. Soc. Am. 90, 859–869. doi:10.1785/0119990114
Woessner, J., and Wiemer, S. (2005). Assessing the quality of earthquake catalogues: estimating the magnitude of completeness and its uncertainty. Bull. Seismol. Soc. Am. 95, 684–698. doi:10.1785/0120040007
Keywords: enhanced geothermal system, earthquake detection, earthquake monitoring, completeness magnitude, magnitude frequency distribution, bayesian inference, mixture modeling
Citation: Mignan A (2021) Induced Seismicity Completeness Analysis for Improved Data Mining. Front. Earth Sci. 9:635193. doi: 10.3389/feart.2021.635193
Received: 30 November 2020; Accepted: 10 February 2021;
Published: 29 March 2021.
Edited by:
Rebecca M. Harrington, Ruhr University Bochum, GermanyReviewed by:
Qi Yao, China Earthquake Networks Center, ChinaJoern Lauterjung, German Research Centre for Geosciences, Germany
Copyright © 2021 Mignan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arnaud Mignan, bWlnbmFuYUBzdXN0ZWNoLmVkdS5jbg==
 Arnaud Mignan
Arnaud Mignan