- 1Department of Soil and Water Conservation, Changjiang River Scientific Research Institute (CRSRI), Wuhan, China
- 2Research Center on Mountain Torrent and Geologic Disaster Prevention, Ministry of Water Resources, Wuhan, China
The initial of debris flow can be classified into two types based on their triggering positions, that is, debris flow from slope and debris flow from gully or channel. For the former, great progress has been achieved on the mechanisms of soil failure and liquefaction. The framework established by a series of theories or laws, such as the Mohr–Coulomb criteria, the unsaturated soil mechanics, and the critical state of soil mass, has been used widely in industry and research. However, the details and discrimination basis for the transformation process from landslide into debris flow still need to be further clarified. Relatively, debris flow from gully or channel is more complex due to its various mass sources and the diversity of processes. Nevertheless, through a great number of case studies and experimental statistics, people have gradually recognized the influential rule and critical condition of factors from landform, hydrology, and other aspects on debris flow initiation. Furthermore, based on the theories of granular flow, continuum mechanics, and rheological law, some typical event-based scenarios can also be reproduced by different single-/two-phase depth integral/average numerical models. However, some key knowledge on mechanism and application level is still insufficient, such as the erosion and entrainment mechanism of materials from different sources, the boundary tractions and materials exchange, as well as the selection of prediction indicators. Three current discriminated methodologies for debris flow initiation, that is, the safety factor method, the rainfall indicator method, and the comprehensive assessment method, were summarized in this article. Considering the technical limitation of each methodology, it is believed that the establishment or improvement of a unified, stable, and open-access database system for event registration and query, as well as the development of large-scale and high-precision rainfall monitoring, is still regarded as the important aspect of debris flow prevention in the future. In addition, as an economic and efficiency means for obtaining information on potential threats and real-time hazard messages, the multielement method for debris flow is recommended as a long-term reference.
Introduction
The term “debris flow” is a cage name for the torrent that occurs in mountainous areas and carries a large amount of sediment, stones, and other debris materials. In order to define the object more clearly, researchers and corresponding institutions worldwide have defined the debris flow in different ways. For example, the United States Geological Survey (USGS) regarded debris flow as a kind of rapid landslide (Brabb et al., 1999). Qian and Wang (1984) indicated that debris flow was a two-phase solid–liquid mixed flow filled with clay and boulders occurring in valleys and slopes. Furthermore, the energy of debris flow mainly came from the properties of solid particles themselves, such as gravity, the discrete force from particles colliding, or the buoyant force produced by high volume mud. Iverson (1997b) pointed out that both forces from solid and fluid had great influence on debris flow movement, which was also the point to distinguish debris flow from some similar processes, such as rock fall and hyperconcentrated flow. Some other scholars like King (1999) and Shu et al. (2018) believed that debris flow was a mixture of loose mud, sand, soil, rock, water, and air flowing down the slope under gravity, in which at least 50% of the solid material must be loose sand or large particles. Overall, although these concepts have different interpretations, the basic consensus of debris flow can still be reached, that is, two essential characteristics of debris flow processes: first, the mass in motion has at least the state of solid–liquid phase or pseudomono phase; second, the movement of mass depends on both solid and fluid forces. The discussion of debris flows later in this article will be based on this fundamental concept.
Due to the characteristics of sudden outburst and high energy density, debris flows often cause huge disasters. Monitoring and early warning is an essential method of disaster prevention and mitigation. However, being a worldwide problem, for now, there is no mature, reliable, and widely applicable debris flow monitoring and early warning plan for promotion. One reason for this is the relatively poor understanding of the process mechanism of debris flow; the other might be related to the complexity of debris flow development environment and the limitations of different monitoring means. In recent years, with the increase of extreme weather and geological events, large-scale debris flow disasters occurred more frequently. Based on these accumulated cases, new or improved algorithms, theories, and equipment were constantly integrated and innovated. However, literature reviews in almost the same period mainly focused on the movement mechanism of debris flow or some other subdivided fields (Iverson and Ouyang, 2015; Cui et al., 2016; Hürlimann et al., 2019; Yu et al., 2020), lacking comprehensive summary of relevant theories and technologies.
Accordingly, this article attempts to systematically organize and summarize the existing research progress on theory and application, to provide further reference on debris flow prevention, especially on the fundamental ideas and corresponding developmental direction in the future. Considering that the cognition and prediction of debris flow initiation is more practical for prolonging the leading time and improving the alarm system performance (Hürlimann et al., 2019), this article focuses on two aspects, that is, the initiation mechanism of debris flow and related discrimination or prediction methods.
Initiation Mechanism of Debris Flow
The formation of debris flow is not only barely affected by the external environmental determinants such as rainfall, snow melting, human activities, and geological landform but also related to the properties of loose materials like particle grading, soil dispersion, and water content. Thus, analyzing the coupling critical relationships between these factors is the key to reveal mechanism of debris flow initiation.
Currently, there is no universal standard for the classification of debris flow initiation. Some scholars classified debris flow according to the way it is induced, that is, by shallow landslide and by runoff (Tang and Zhang, 2008). Others such as Wang (2001) divided debris flow into three types: the first type was that the landslide materials rushed into flow and mixed with water to form debris flow; the second type was debris flow formed by the hydraulic erosion of sediment on the channel or gully bed; and the third type was debris flow formed by the entrainment of deposits from bank collapse. Furthermore, the second type usually developed stony debris flow, which was mainly due to the rich pebbles and gravels on the river bed in mountainous areas, while the first and third types were prone to develop viscous debris flow due to the wider grain grading.
Based on the fundamental concept stated above, debris flow is presumably regarded as the product of solid–liquid phases coupling. Therefore, even the debris flow occurred in river channel can hardly be technically recognized as a totally hydraulic-dominated process since it is difficult to cut off the connection completely between the gully or channel deposits and the gravity process such as landslides and collapses. Moreover, the debris flow just formed by sediment from river bed scouring is not typical in most events. In fact, this type is more likely to be reproduced by a solid model in a laboratory environment. Hence, the above classification has limitations on description to a certain extent. Herein, for defining the type more concretely and intuitively, the debris flow initiation is classified into slope initiation and gully or channel initiation based on the triggering position (Figure 1). They are different in driving force, material source, and conditions of underlying surface, and they are all important units to promote the process of disaster chain.
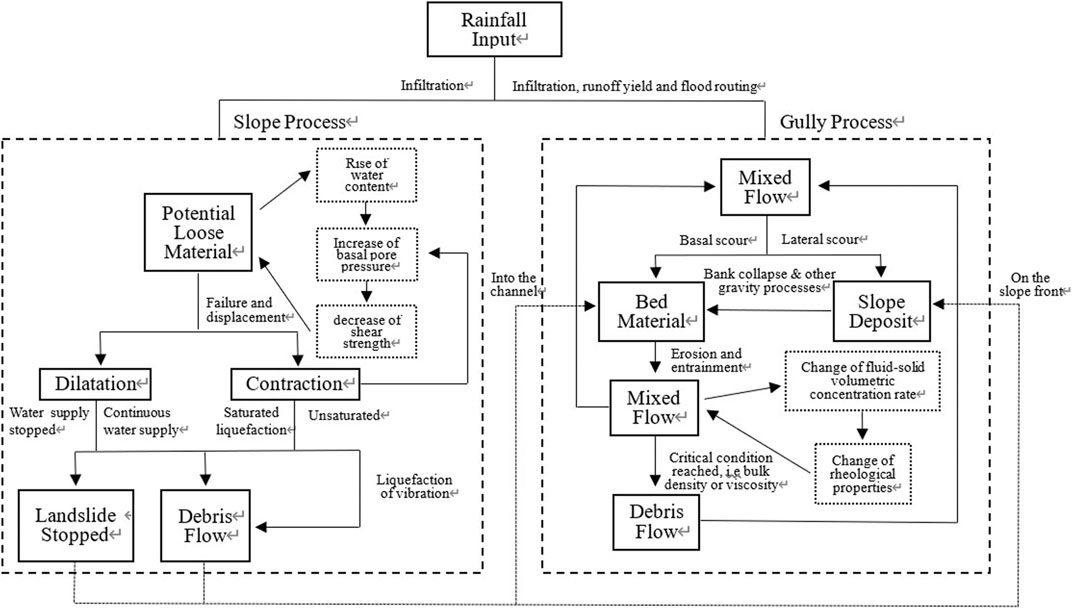
FIGURE 1. Difference and connection between the general initial types of debris flow from slope and gully.
Debris Flow Starting from Slope (Slope Debris Flow)
This phenomenon denotes a kind of debris flow process formed and moving on a slope, including small-scale gullies and so-called colluvium deposits in hollow region (CDHs from Zhang et al., 2020). It is usually driven by external forces such as continuous rainfall, rainstorm, melted ice, and snow. A large number of experiments and witness evidences have shown that slope debris flow generally begins with the process chain of softening, cracking, creep of the loose material, as well as footslope failure. After that, the slope failure proceeds into local collapse and liquefaction under continuous shear stress. Subsequently, the processes can be extended to the surrounding areas, and eventually lead to the overall initiation of debris flow (Morton and Cambell, 1974; Gabet and Mudd, 2006; Li et al., 2010; Zhou et al., 2017; Liao et al., 2017; Pan et al., 2017; Qiao et al., 2018; Li et al., 2019). Some other reports also indicated that slope materials could be transformed into debris flow directly without collapse or slide processes (Williams and Guy, 1973; Iverson, 1997b; Hu et al., 2015; Chen, 2016).
Generally, it is believed that the initiation of debris flow is mainly determined by water supply, landform, physical properties of potential loose materials, and corresponding stress states. Takahashi (1978), Takahashi (2007) calculated that the critical slope for debris flow occurring was only about 14.5° based on mechanical equilibrium. Many event-based cases also showed that in some areas, rainfall intensity of 10 mm/h or even lower could trigger landslides and debris flows (Wang et al., 1997; Cannon et al., 2008; Guzzetti et al., 2008; Zhou and Tang, 2013). Therefore, it seems that for most slope debris flows, precipitation and slope can hardly be the bottleneck or restricting factors for initiation. The initial mechanism is mainly related to internal properties and corresponding stress state of slope materials.
Grain composition and porosity of loose materials are two crucial properties that affect the initiation of debris flow. Grain composition determines porosity and permeability of soil layer to some extent. According to Cui (1991), the content of fine particles less than 1 mm was a useful indicator to reflect the structure and strength of loose materials, and it had a negative correlation with the critical slope of debris flow initiation. This was because the quantity increase of fine content could significantly reduce the porosity of soil, thereby decreasing the permeability coefficient or hydraulic conductivity of soil layer (Chen et al., 2006; Zhou et al., 2012; Yang et al., 2016). That means lower intensity of rainfall can also exceed the critical point for soil saturation and cause a series of chain reactions, such as increase in pore water pressure and reduction in effective stress (Wang et al., 1997; Gao et al., 2011). In recent years, some scholars have also proved that higher volume of fine particles did not necessarily cause initiation of debris flow. Rather, once a critical point was reached, erosion occurred (Zhou et al., 2017). In addition, the content of clay or sand can also contribute to the efficiency of debris flow initiation. Sandy soil has higher water permeability, which helps to reach the critical point more quickly (Gabet and Mudd, 2006).
According to the critical state theory of soil mass (Casagrande, 1936), under the action of continuous shear stress, soil mass can reach a critical porosity through dilation or contraction, regardless of its original state being compacted or loose. If the original state of soil is loose, high porosity may lead to massive positive pore pressure in the process of contraction, and the probability of debris flow initiation will increase sharply (Hutchinson, 1986; Fleming et al., 1989; Gabet and Mudd, 2006). In fact, during the whole process of soil deformation, continuous dilation and contraction may occur frequently, resulting in dynamic change of soil porosity, which in turn will affect water content and pore pressure of the soil. Therefore, the importance of porosity is more reflected in its water storage and pressure conduction, as well as the resulting changes in soil stress state.
The effective stress and cohesion determine the shear strength of soil mass based on Mohr–Coulomb criterion. This criterion can also be used to interpret the processes of slope instability and debris flow initiation. The limit equilibrium or safety factor method based on this criterion has been used widely in the field of engineering consultation. By further introducing the theory of unsaturated soil mechanics (Fredlund et al., 1978), Qi and Huang (2003) added the influences of pore water pressure and pore air pressure to the traditional formula of shear strength and proposed a discriminant formula to judge whether the loose material was started or not (Table 1, Formula 1). The basic idea of this formula is that with the continuous rainfall input, matrix suction of loose material decreases significantly with the increase of water content, resulting in reduction of shear strength. When the loose material is saturated and the shear strength is less than the tangential stress produced by flow and gravity, debris flow will occur.

TABLE 1. Some typical formulas on initial discrimination of debris flow and entrainment/erosion rate.
Although the probability of slope material liquefaction and transformation into debris flow increases sharply after saturated, soil saturation is not a necessary condition for the development of debris flow (Iverson and Vallance, 2001; Chen et al., 2006). Thus, the applicability of above theories has limitations to some extent. Besides, there is no further analysis on the liquefaction mechanism and the transformation process from solid to fluid. In view of this, some researchers put forward the so-called slurry making theory and soft base effect of landslide transforming into debris flow based on case investigation and ring shear test (Chen, 1992; Zhang et al., 2009). However, physical description had not been described in details. Iverson of USGS had made a more beneficial exploration on this issue.
Based on theoretical derivation and large-scale solid model experiments, two liquefaction mechanisms of landslide transforming into debris flow were proposed by Iverson et al. (1997a); Iverson (1997b); Iverson and Vallance (2001). One was that for the soil mass with negligible cohesion, liquefaction occurred when the pore water pressure increased to the value of total normal stress, that is, the effective stress dropped to 0. The other was that for the cohesive soil mass, in addition to maintaining a high level of pore water pressure, it was necessary to reduce the cohesive force by vibration before liquefaction. The increase of pore water pressure, mainly caused by soil contraction and continuous water supply, was the main cause for landslide transforming into debris flow. While the vibration of soil mass was mainly realized by earthquake or movement on a rough slope, that is, converting kinetic energy into heat energy of soil particles. Combined with the Coulomb grain flow equation (Iverson, 1997b), the author realized the mathematical simulation of the whole process of landslide debris flow and reproduced the initial processes under the two liquefaction mechanisms in solid model experiments (Iverson et al., 1997a).
Iverson’s work indicated the critical influence of pore water pressure on the formation of landslide debris flow in different mechanisms and soil types on mathematical and physical level and strongly promoted the application of relevant indicators in debris flow prediction and early warning research. Additionally, the work provided a more systematic, coherent, and dialectical understanding of the connections among the Mohr–Coulomb criterion, the unsaturated soil mechanics theory, the critical state theory of soil mass, and the vibration of liquefaction. However, some process details, especially the issues on soil liquefaction, are still needed to be addressed, such as how to establish the mathematical relationship between vibration energy and soil cohesion, the relationships between different soil properties and liquefaction vibration, and the corresponding critical phenomena. If these issues cannot be discussed sufficiently, it is difficult to break through the framework of safety factor method on slope debris flow initiation.
Debris Flow Starting from Gully or Channel (Gully Debris Flow)
This phenomenon means that the initiation and movement of debris flow mainly occur on the gully or channel bed. It can be formed by the erosion of bed basal materials or by the entrainment of bank collapse materials caused by continuous lateral erosion. Compared with slope debris flow, gully debris flow has more diversity in material sources and development forms. Besides, the development environment of gully debris flows usually presents lower requirement on channel gradient because of the dramatic influence from water flow, that is, the initiation of gully debris flow is more sensitive to the channel gradient. Therefore, the traditional research on the initiation of gully debris flow mainly focuses on the relationships among discharge, channel gradient, and the grain composition of loose materials.
Being the most direct triggering factor of gully debris flow, the influence of discharge is the first concern. It is generally believed that the critical discharge for gully debris flow always increases with the increase of particle size (Table 1, Formula 2). However, some studies have pointed out that the potential energy provided by channel slope should also be considered. If the channel slope is very small and the particle size is large enough concurrently, it can only develop bed load movement even if the discharge is very large (Wang, 2001). Based on a great number of experiments, Wang (2001) established the empirical relationship between the critical slope and the median diameter of loose materials in the process of debris flow formed by flow scouring (Table 1, Formula 3). By laying nearly homogeneous gravel layer in the flume with gradient from 12 to 20°, Gregoretti and Fontana (2008) carried out an experiment and summarized the rule of critical discharge of gully debris flow initiation under different particle size and slope conditions (Table 1, Formula 4). The outcome was used to estimate the critical discharges of erosion-induced debris flow events in 6 catchments in Dolomites of Italy. The author believed that the formula was competent for general sensitivity analysis.
In addition to the process research represented by the above achievements, that is, summarizing empirical or semiempirical relationships through solid model experiments, researchers also tried to further expand their knowledge from mechanical or energy level (Table 1, Formula 5, 6).
Takahashi (1978) constructed a model for critical slope calculation of gully debris flow from the perspective of mechanical equilibrium based on Bagnold’s theory of granular flow. The model assumed a scenario that in an infinite gully slope, the loose material reached the state of saturation after being soaked by flow water, and then failure and debris flow occurred due to the excess shear stress. Blijenberg (2007) provided the safety factor version of the model and applied it to the Alps in southern France. It was found that the results of the model were too conservative, that is, even in cases where only extreme rainstorms could induce debris flows, the cases would still be considered unsafe. The author believed that one of the important reasons for this was that the loose materials in the channel were difficult to reach the state of saturation under the flow scouring, which had also been confirmed by some recent experimental studies (Pan et al., 2017; Li et al., 2019). On one hand, the flow at the beginning would take away the fine particles to form enough pores in loose materials; on the other hand, the water carrying a large amount of sand and stone was likely to bypass these pores and flow through the surface of loose materials directly during the flood process.
Besides, Wang (2001) pointed out that the loose materials in Takahashi’s model might be washed away by water flow before failure; thus, the critical slope obtained from this model was overestimated to some extent. Iverson and Ouyang (2015) also believed that such models based on granular flow theory were not suitable for gully debris flows because these debris flow processes were far away from equilibrium, commonly.
Gully debris flow may present wave-like discontinuous characteristic due to the erosion and entrainment of loose materials (Iverson and Ouyang, 2015). The eroded materials continuously concentrated to the front and provided energy through particle collision, so that the front could move in the channel with gentle or even reverse slope (Wang, 2001; Lyu et al., 2017; Gregoretti et al., 2018). Therefore, erosion and entrainment are an important mechanism for gully debris flow development. Case analyses and experimental studies showed that most of the erosion and entrainment occurred at the stage of front passing (Haas and Woerkom, 2016; McArdell, 2016). The scouring depth of riverbed usually increased with the increase of channel gradient, flow depth, discharge, basal shear stress, front water content, and particle size (Theule et al., 2015; Haas and Woerkom, 2016; Vázquez et al., 2016; Frank et al., 2017).
Furthermore, theoretical analysis indicated that when the density of mixed layer was distinctive with that of riverbed layer, the changes of eroded material volume and pore water pressure during the entrainment process might affect entrainment rate as a feedback effect (Iverson, 2005). Compared with the undisturbed bed material, the eroded material was more likely to be entrained by runoff due to the decrease of cohesion (McGuire et al., 2017). Some researchers believed that when the debris flow passed through the riverbed, it would rapidly infiltrate and saturate the bed material with a certain thickness, that is, forming a moist layer. Consequently, the layer would be eroded completely when the safety factor was less than 1 (Huang and Tang, 2017).
Before being transformed into debris flow, the riverbed materials must undergo complex mechanisms such as material exchange, energy transfer, and rheology during the processes of erosion, deposition, and entrainment, among which the problems of erosion and entrainment have aroused widespread concern in the academic community. However, although the physical senses of these two phenomena are different (Iverson and Ouyang, 2015), they are generally considered to be uniform when calculating the erosion or entrainment rate.
Many studies have established the relationship between the entrainment rate and the process of hyperconcentrated flow transforming into debris flow by using numerical models. Based on the specific rheological law and continuum theory, these models were usually presented in the form of single-/two-phase depth-average/integral model coupling the formula of entrainment rate (Stancanelli et al., 2015; McGuire et al., 2017; Mergili et al., 2017; Vagnon et al., 2018; Gregoretti et al., 2018, 2019; Liu and He, 2020; Zhou et al., 2019). Among these entrainment formulas, there were not only empirical formulas established by the parameters of sediment concentration and slope gradient before and after scouring (Table 1, Formula 7; Takahashi, 1978; Frank et al., 2017) but also mechanism or semi-mechanism formulas based on the physical relationships among riverbed morphology, velocity, and basal shear stress (Table 1, Formula 8, 9). The motion state of mixed flow in these models was basically determined by the volumetric proportion of solid and liquid factions, for example, the empirical threshold value from the apparent viscosity or the volumetric sediment concentration (McGuire et al., 2017; Bout et al., 2018; Liu and He, 2020).
The above numerical simulation originated from depth-average/integral model coupling entrainment rate formula could restore the evolution characteristics of some typical debris flow events to some extent, especially the characteristic of rheology and the amplification effect. However, there are yet some problems to be solved in theory (Iverson and Ouyang, 2015; Garres-Díaz et al., 2020).
The first one is the conservation of momentum of the mixture fluid after entraining new loose material, that is, whether the energy of the debris front is increased or decreased after the loose material is absorbed, which needs to be further analyzed in different scenarios. The second one is the changes of volume and excess pore water pressure of entraining front caused by the density difference between mixture fluid and loose material, as well as the corresponding feedback effects on erosion, deposition, and rheological processes, which call for more experimental and simulation studies. The third one is that the existing entrainment rate formulas rarely considered the material supplement caused by lateral erosion and bank collapse, which may play a greater role in the formation of debris flow (Lyu et al., 2017).
In addition, although the existing technology of numerical simulation can provide some support for the estimation of critical rainfall or discharge, its calculation time is too long to meet the requirements of monitoring and early warning in terms of timeliness. This technology is more suitable for scenario analysis and risk or hazard assessment. Therefore, the relatively simple discrimination method for debris flow initiation has gradually become a research hotspot. For instance, Berti and Simoni (2005) established a runoff yield model for initial area of debris flow in Dolomites area of Italy based on kinematic wave equation. It was found that the critical discharge for the initiation of loose materials was so small that the interval of threshold values between the generation of surface runoff and the debris flow initiation could be ignored. Hence, the author believed that the study and simulation of runoff generation process was an alternative and relatively convenient way to identify the initiation of debris flow.
Shu et al. (2017) proposed a discriminant for particle initiation of nonhomogeneous debris flow by using the Shields number based on sediment movement mechanics, that is, when the ratio of flow shear stress to critical particle starting stress was larger than 1, the particle initiation occurred. This idea was similar to Berti’s and Simoni’s hypothesis and was supported by Tillery and Rengers (2020). However, since the initiation of sediment particles or the formation of surface runoff is not a sufficient condition for debris flow initiation, there are limitations to use these methods for discrimination.
Taking the bulk density >1,300 kg/m3 as the basis of gully debris flow formation, Dang et al. (2014) and Wang et al. (2018) built another type of discrimination indicator based on the same formula framework by using the parameters such as flow power and dimensionless shear stress. However, the threshold of these indicators would change with the variation of volumetric solid concentration. Thus, a range of tests are needed to calibrate the parameters before being applicated. Moreover, the relevant monitoring indicators are not easy to accurately measure when disasters occur, so it is difficult to promote.
In a word, although people have gained some knowledge on the initiation of gully debris flow, there is still room for further development and improvement in terms of erosion or entrainment mechanism of loose materials from different sources, the boundary tractions and materials exchange, and the construction and application of rapid discrimination method.
Discrimination Methods for Debris Flow Initiation
The discrimination or prediction methods here refer to a series of key elements monitoring and initial node determination of debris flow in the potential formation area, that is, material source area, which can provide important reference for early warning of debris flow disasters. For now, there were many means of test for debris flow monitoring and early warning worldwide, such as the research using geophone, seismometer, and other seismic monitoring facilities based on the change of ground amplitude, frequency, or energy of the event (Palau et al., 2017; Walter et al., 2017; Lai et al., 2018; Coviello et al., 2019). Some of them could even distinguish debris flow from flood flow (Schimmel et al., 2018). However, compared with the initial discrimination, these methods are usually more sensitive to the process of debris flow movement. Moreover, due to the issues of noise discrimination, use cost, deployment, and installation, it is difficult to promote on a large scale.
In addition, considering the role of local convective weather in mountainous areas on debris flow prediction, some studies have also tried to use the cloud-to-ground lightning flash data and the convective available potential energy (CAPE) to establish correlation (Turkington et al., 2016; Underwood et al., 2016). However, due to the scale conversion and other reasons, for now, it was difficult to support the high reliability local initial prediction.
According to the current engineering practice, three basic discrimination methodologies for debris flow initiation can be summarized in general, that is, the safety factor method, the rainfall indicator method, and the comprehensive assessment method. The former refers to the models established based on the principle of mechanical equilibrium, and its representative achievements have been introduced in the previous sections (Takahashi, 1978; Iverson and Vallance, 2001; Qi and Huang, 2003; Blijenberg, 2007; Dang et al., 2014; Shu et al., 2018; Wang et al., 2018). This section mainly combs and summarizes the ideas and contents of the latter two methodologies and does not involve the hardware and technology of sensors and network communication.
Rainfall Indicator Method
The rainfall is an indispensable condition of external force for most debris flow events. Due to the relatively lower technical threshold and system maintenance cost, it is the most popular method in the world to use rainfall index for debris flow monitoring and early warning (Table 2), and its representative method is the power law equation (I-D method) proposed by Caine (1980)
where I is the critical rainfall intensity per unit time, which can be the peak intensity (Cannon et al., 2008) or the average intensity (Brunetti et al., 2010); D is the rainfall duration; and α and β are the empirical calibration parameters, respectively.

TABLE 2. Some typical discrimination formulas of debris flow occurrence based on the rainfall indicator method.
The method assumes that there is a nonlinear relationship between the critical rainfall intensity and the rainfall duration, and the former decreases with the increase of the latter. In practice, two strategies of the method, that is, the upper limit method and the lower limit method are used commonly. The former takes the maximum rainfall intensity that cannot cause debris flow events at a specific time and space as the critical point, while the latter takes the minimum rainfall intensity that can induce debris flow events as the point (Guzzetti et al., 2008). Obviously, the lower limit method is more conservative and prone to false alarm, while the upper limit method is loose and prone to fail alarm. If any interval value is taken as the critical point, it mainly depends on the empirical judgment and has strong subjectivity.
In conjunction with USGS, the National Oceanic and Atmospheric Administration (NOAA) started the work of monitoring and early warning for wildfire-induced debris flow in mountainous areas of Southern California since 2005 (Restrepo et al., 2008). A determination method of critical rainfall intensity based on the I-D idea was proposed during the project. The method, providing a path for the objective selection of the I-D curve, used receiver operating characteristic curve (ROC) to find the equilibrium solution under the conditions of minimum false/fail alarm rate and maximum accuracy rate based on the outputs from the upper limit method and the lower limit method (Staley et al., 2013). Besides, as an empirical statistical method, the same purpose, that is, objectively setting the critical point, can also be realized by using trial and error or multi-objective optimization algorithms (Wu et al., 2018; Yan et al., 2020).
The traditional I-D method requires high spatial and temporal resolution on historical data, which is not in line with the reality that most mountainous areas lack or do not have data at all. What is more, it does not consider the impact of antecedent rainfall accumulation. Although this can be compensated partly by constructing I-D curves under different antecedent rainfall scenarios, the efficiency and convenience will decline. Therefore, scholars from different regions are constantly trying to develop or improve relevant methods. For example, Glade et al. (2000) proposed an initial discriminant for landslide by improving the antecedent precipitation index model (Bruce and Clark, 1966) in New Zealand (Table 2, Formula 1); a debris flow prediction model in Jiangjia gully in China was put forward by the Institute of Mountain Hazards and Environment, CAS, 2000 based on long-term observation and water balance principle (Table 2, Formula 2). These discrimination methods based on rainfall intensity–antecedent effective rainfall, that is, I-A method, have also been applied in many early warning cases of flash floods and debris flows (Clark et al., 2014; Deng et al., 2018), and it is especially suitable for those watersheds with better vegetation coverage and greater water storage potential. However, some findings reported that the early warning effect of I-D method was better than that of I-A method for the watersheds with sandy soil (Abancó et al., 2016), and the minimum duration of rainfall triggering debris flow should even be upgraded to the key indicator (Pastorello et al., 2020).
In view of the lack of data in mountainous areas, the conventional method is to use the data of nearby stations for analogy or interpolation. However, recent studies have shown that these methods were easy to overestimate or underestimate the rainfall threshold to some extent (Marra et al., 2016; Destro et al., 2017; Marra et al., 2017), especially for the convective weather events with small watershed scale. Even if the data of adjacent basins were used, they might lead to calculation errors. Fortunately, radar rainfall measurement could improve this situation to a certain extent (Abancó et al., 2016).
In addition, there are two indirect solutions: 1) according to the determined contour maps of maximum rainstorm and their coefficients of variation, the design rainstorms with different frequencies can be calculated, and then, the results consistent with the frequency of historical disaster events can be taken as the regional critical rainfall. This idea has been widely used in the field of prediction and early warning of regional flash floods and debris flows (Liang and Yao, 2008; Duan, 2009). 2) The threshold of the key index for debris flow initiation can be obtained by using various mechanism or semi-mechanism models (Huang and Tang, 2017; Bout et al., 2018; Zhou et al., 2019; Liu et al., 2020), and then, the critical rainfall value can be deduced according to the threshold. For example, Pan et al. (2018) first obtained the critical flow depth for debris flow based on Takahashi’s model and then deduced the rainfall threshold by using the water balance equation of stored-full runoff; Zhang et al. (2019) used the safety factor method and the excess infiltration–saturation runoff model to obtain the bulk density of mixed flow and then established the I-D curve according to whether the density reached the critical condition of debris flow formation. Although there is no requirement for historical data in this kind of scheme, the process model used here usually has certain theoretical assumptions. Therefore, the mechanism of runoff generation and the types of debris flow, that is, stony debris flow, viscous debris flow, or other types, should be clarified before its application. Besides, the scheme also needs to ensure the reliability of some key parameters such as the gully morphology and the infiltration rate, thus the workload in early stage is generally large.
Comprehensive Assessment Method
There are a number of factors that affect the initiation of debris flow, and solely relying on rainfall indicators for discrimination and early warning will have many limitations. Especially for some small watersheds where environment changes rapidly, the comprehensive assessment method can achieve twice the result with half the effort. According to the number of elements considered and the difference of estimation means, the comprehensive assessment method can be roughly divided into the multielement method and the key-element method. The former has the similar technical process with the natural hazard assessment, but it emphasizes more on the input of dynamic factors, data fusion, and rapid response. The latter is more associated with hydraulic and soil mechanic tests or field observation, and the indices of investigation are more concentrated.
It should be noted that the boundaries of this classification are not always clear. Many methods integrate the advantages of each idea. For example, the US Flash Flood Guidance (FFG) system not only considered the results from hydrological forecast, which could be regarded as the combination of key-element method and rainfall indicator method, but also referred to the level of Flash Flood Potential Index (FFPI) of each watershed based on the multielement method (Clark et al., 2014). The similar examples also appeared in the works of Posner and Georgakakos (2015) and Berenguer et al. (2015).
Multielement Method
Typical examples of the multielement method are the susceptibility assessment of wildfire-induced debris flows in western United States, and the works from Kung et al. (2012), Yu et al. (2013), Yu et al. (2014), Yu et al. (2015) in Taiwan and Western China, respectively. In recent years, the frequent occurrence of postfire debris flow in California has been fully concerned by the academia. Due to the frequent disturbance of wildfire on underlying surface, empirical relationships between the threshold value obtained by the rainfall indicator method and the events presented great uncertainty. Therefore, many studies have built the multielement indices system from rainfall, landform, vegetation, soil erodibility, disaster damage, and other aspects. The logistic regression, decision tree, naive Bayes, and other machine learning algorithms were used to establish the classification model for debris flow initiation discrimination. The results showed that the accuracy of related models, that is, area under the ROC curve (AUC), could reach over 0.7 (Kern et al., 2017; Staley et al., 2017; Addison et al., 2019; Cui et al., 2019).
Taking 181 slopes above 15 degrees in Nantou County of Taiwan as samples, Kung et al. (2012) divided the impact factors into the real-time factors such as rainfall, vegetation, and material source characteristic and the non–real-time factors such as slope length and lithology. Subsequently, a set of discrimination systems for debris flow initiation were established based on comparative analysis among the multiple regression, the multivariate analysis, and the backpropagation method. The results showed that the discrimination model based on backpropagation method had the highest accuracy, and the contributions of relevant indicators were ranked as NDVI, effective infrared band, effective rainfall intensity, and accumulated rainfall.
Yu et al. (2013), Yu et al. (2014), and Yu et al. (2015) further developed 1 h and 10 min rainfall forecast models by improving the indices of landform, geology, and precipitation in the formation model for debris flow in Chenyulan watershed of Taiwan (Table 1, Formula 10). It is reported that the models have been verified by using the historical data in Yunnan, Guizhou, Sichuan, Gansu, and other areas of China. However, the application site was limited to the source area, which hindered the promotion of these models to some extent.
The theoretical framework of this kind of method is relatively simple, and the elements considered are more comprehensive than the key-element method. Especially with the support of machine learning and big data analysis, the reliability of the results is further improved. Currently, it is a powerful tool for understanding potential threats and grasping real-time hazard information in time. However, there are still some subjective effects in the establishment of index system, algorithm, and weight design of this method. In particular, the selection of some sensitive indicators will show great differences due to different regions and algorithms. For instance, the vegetation element is an important index in both postfire debris flow models and Kung’s model, but it is not considered in Yu’s models at all. Furthermore, due to the needs of macro analysis and rapid response, the multielement method has higher requirements for the convenience of data acquisition. Therefore, the real-time data usually come from rainfall stations and remote sensing monitoring, while the index data that are relatively hard to collect, such as particle size, pore water pressure, and dry density of loose materials, are rarely considered. The more targeted key-element method can better make up for these deficiencies.
Key-Element Method
The key-element method mainly focuses on the key physical properties related to the initiation of debris flow, such as dry density, water content, and pore pressure. The data of this method are usually collected from field test/observation, large-scale solid model experiment, and geotechnical test. On this basis, the coupling critical relationships among these indicators to debris flow initiation are explored by means of statistics, hydrometeorological or dynamic analysis methods. Formulas 2–5 in Table 1 are the representative results of this kind of method. Besides, the three-dimensional coupling curved surfaces proposed by Cui (1991) and Qiao et al. (2018) also belong to this method (Figure 2).
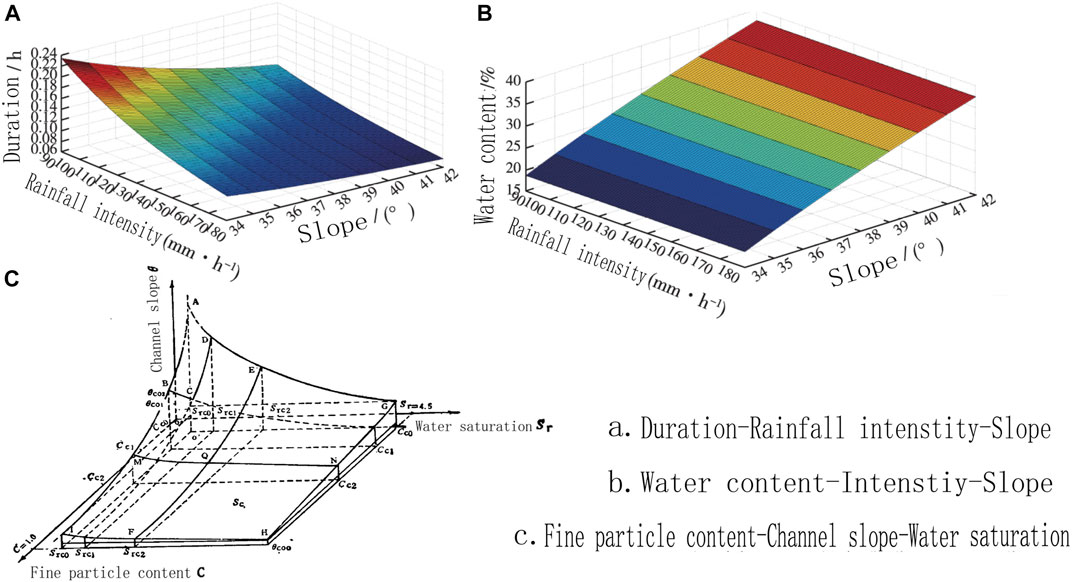
FIGURE 2. Typical 3-dimensional discrimination models based on the key-element method ((A), (B)Qiao et al., 2018; (C)Cui, 1991).
Generally, it is necessary to monitor the state of material sources when using the key-element method. Some data of indices, such as the critical void ratio and the effective stress, can be tested by pre-sampling. The soil moisture can also be calculated by a mathematical model (Posner and Georgakakos, 2015), but other indices need to be monitored in real time. Due to the high cost of monitoring and the difficulty of facility deployment for debris flows, the type and number of monitoring indicators are usually strictly controlled. For instance, the pore water pressure is widely accepted as a key indicator of debris flow development. However, Qiao et al. (2018) found that the indicator only showed strong response under extreme conditions such as rainstorm and steep slope, and it presented great volatility and randomness during the experimental process. Accordingly, they believed that the pore water pressure was not an ideal indicator for debris flow initiation and eliminated it in the model.
In addition, the accumulation of loose material caused by earthquake and wildfire will be reconsolidated due to vegetation restoration and natural compaction of soil, which could increase the rainfall threshold significantly (Guo et al., 2016). Therefore, it is necessary to resample and recalibrate the model periodically when using this method.
Conclusion and Prospect
The research on initial mechanism of debris flow is the basis of related disaster prevention and mitigation, which is of great significance to improve the performance of debris flow monitoring and early warning. In this article, by summarizing recent research progress of debris flow initiation mechanism and related discrimination or prediction methods, it is found that great findings have been made in the process mechanisms of slope and channel. Furthermore, the discrimination formulas derived from a series of theories, including the Mohr–Coulomb criterion, the unsaturated soil mechanics theory, the critical state theory of soil mass, the continuum theory, the granular flow theory, and the rheological law, have also been used widely in the field of prediction and early warning. However, there are still some problems to be solved in the process mechanism details and the optimization of prediction and early warning scheme.
For future research and preventive practice, the following issues are worthy of attention:
The transformation mechanism of landslide into debris flow, especially the vibration liquefaction and its application need to be further explored. Is there a critical phenomenon in the process of vibration liquefaction? What elements can be developed into monitoring and early warning indicators? How to determine the relevant threshold? If these questions cannot be answered effectively, it is difficult to break through the framework of safety factor method.
The erosion or entrainment of mixed flow has an important influence on transformation of flash floods into different types of debris flows. Future research can be further expanded and improved in the following issues: the erosion or entrainment modes of loose materials from different sources, the boundary tractions and materials exchange during the process of entrainment and deposition, as well as the rapid identification of different types of debris flow initiation and the selection of corresponding key indicators.
Currently, empirical analysis combined with the machine learning technology has obvious effect on improving the prediction accuracy of debris flow. To meet the needs of big data analysis, the establishment or improvement of a unified, stable, and open access database system for event registration and query, as well as the development of large-scale and high-precision rainfall monitoring are still regarded as the important aspects of debris flow prevention in the future, which is also applicable to the prevention of flash floods.
The multielement method from the comprehensive assessment method is a powerful tool for understanding potential threats and grasping real-time hazard information in time, and the results can also be used as a strong basis for the implementation of the rainfall indicator method and the key-element method. It should be popularized in debris flow disaster-prone areas to make it a long-term reference for local government and residents.
Author Contributions
The first author finished the overall literature investigate and paper writing work, the second author was responsible for the literature investigate and consulting work of slope debris flow, and the third author undertook the literature investigate and chart modification on gully debris flow.
Funding
This research has been sponsored by the National Key R&D Program of China (Grant No. 2018YFC1505201), and the Special Fund of Chinese Central Government for Basic Scientific Research Operations in Commonweal Research Institutes (No. CKSF2019497/TB).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abancó, C., Hürlimann, M., Moya, J., and Berenguer, M. (2016). Critical rainfall conditions for the initiation of torrential flows. Results from the Rebaixader catchment (Central Pyrenees). J. Hydrol. 541, 218–229. doi:10.1016/j.jhydrol.2016.01.019
Addison, P., Oommen, T., and Sha, Q. (2019). Assessment of post-wildfire debris flow occurrence using classifier tree. Geomatics, Nat. Haz. Risk 10 (1), 505–518. doi:10.1080/19475705.2018.1530306
Berenguer, M., Sempere-Torres, D., and Hürlimann, M. (2015). Debris-flow forecasting at regional scale by combining susceptibility mapping and radar rainfall. Nat. Hazards Earth Syst. Sci. 15, 587–602. doi:10.5194/nhess-15-587-2015
Berti, M., Bernard, M., Gregoretti, C., and Simoni, A. (2020). Physical interpretation of rainfall thresholds for runoff generated debris flows. J. Geophys. Res. Earth Surf. 125 (6), e2019JF005513. doi:10.1029/2019JF005513
Berti, M., and Simoni, A. (2005). Experimental evidences and numerical modelling of debris flow initiated by channel runoff. Landslides 2 (3), 171–182. doi:10.1007/s10346-005-0062-4
Blijenberg, H. M. (2007). Application of physical modelling of debris flow triggering to field conditions: limitations posed by boundary conditions. Eng. Geol. 91 (1), 25–33. doi:10.1016/j.enggeo.2006.12.010
Bout, B., Lombardo, L., van Westen, C. J., and Jetten, V. G. (2018). Integration of two-phase solid fluid equations in a catchment model for flashfloods, debris flows and shallow slope failures. Environ. Model. Softw. 105, 1–16. doi:10.1016/j.envsoft.2018.03.017
Brabb, E. E., Colgan, J. P., and Best, A. T. C. (1999). The purpose of the present map is to show where debris flows have occurred in the United States and where these slope movements might be expected in the future. Available at: https://pubs.usgs.gov/mf/1999/2329/ (Accessed December 01, 2016).
Bruce, J. P., and Clark, R. H. (1966). Introduction to hydrometeorology. Oxford, United Kingdom: Pergamon Press, 317.
Brunetti, M. T., Peruccacci, S., Rossi, M., Luciani, S., Valigi, D., and Guzzetti, F. (2010). Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 10 (3), 447–458. doi:10.5194/nhess-10-447-2010
Caine, N. (1980). The rainfall intensity: duration control of shallow landslides and debris flows. Geogr. Ann. Ser. A, Phys. Geogr. 62 (1-2), 23–27. doi:10.1080/04353676.1980.11879996
Cannon, S. H., Gartner, J. E., Wilson, R. C., Bowers, J. C., and Laber, J. L. (2008). Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California. Geomorphology 96 (3), 250–269. doi:10.1016/j.geomorph.2007.03.019
Casagrande, A. (1936). Characteristics of cohesionless soils affecting the stability of slopes and earth fills. J. Boston Soc. Civil Eng. 23 (1), 13–32.
Chen, C.-Y. (2016). Landslide and debris flow initiated characteristics after typhoon Morakot in Taiwan. Landslides 13 (1), 153–164. doi:10.1007/s10346-015-0654-6
Chen, X. Q., Cui, P., Feng, Z. L., Chen, J. C., and Li, Y. (2006). Artificial rainfall experimental study on landslide translation to debris flow. Chin. J. Rock Mech. Eng. 25 (1), 106–116.
Chen, Z. S. (1992). Motion transformation of high-locality landslide. Mountain Res. 10 (4), 225–228.
Clark, R. A., Gourley, J. J., Flamig, Z. L., Hong, Y., and Clark, E. (2014). CONUS-wide evaluation of national weather service flash flood guidance products. Weather Forecast. 29 (2), 377–392. doi:10.1175/waf-d-12-00124.1
Coviello, V., Arattano, M., Comiti, F., Macconi, P., and Marchi, L. (2019). Seismic characterization of debris flows: insights into energy radiation and implications for warning. J. Geophys. Res. Earth Surf. 124 (6), 1440–1463. doi:10.1029/2018jf004683
Cui, P. (1991). Experimental study on starting conditions and mechanism of debris flow. Chin. Sci. Bull. 36 (21), 1650–1652.
Cui, P., Gao, K. C., and Wei, F. Q. (2005). The forecasting of debris flow. Bull. Chin. Acad. Sci. 20 (5), 17–23. doi:10.16418/j.issn.1000-3045.2005.05.006
Cui, P., Tang, J. B., and Lin, Z. P. (2016). Research progress of resistance character of debris-flow. Adv. Eng. Sci. 48 (3), 1–11. doi:10.15961/j.jsuese.2016.03.001
Cui, Y. F., Cheng, D, Q., and Chan, D. (2019). Investigation of post-fire debris flows in Montecito. ISPRS Int. J. Geo-inf 8 (1), 18. doi:10.3390/ijgi8010005
Dang, C., Chu, N. N., and Ding, Y. (2014). The critical condition for the formation of debris flow induced by glacial lake outburst flood. J. Glaciology Geocryology 36 (5), 1176–1183.
Deng, M., Chen, N., and Ding, H. (2018). Rainfall characteristics and thresholds for periglacial debris flows in the Parlung Zangbo Basin, southeast Tibetan Plateau. J. Earth Syst. Sci. 127 (11). doi:10.1007/s12040-017-0913-0
Destro, E., Marra, F., Nikolopoulos, E. I., Zoccatelli, D., Creutin, J. D., and Borga, M. (2017). Spatial estimation of debris flows-triggering rainfall and its dependence on rainfall return period. Geomorphology 278, 269–279. doi:10.1016/j.geomorph.2016.11.019
Duan, S. R. (2009). Analysis of computation results of critical rainfall causing flood disasters in representative small basins. Water Resour. Plann. Des. 2, 20–22.
Egashira, S., Honda, N., and Itoh, T. (2001). Experimental study on the entrainment of bed material into debris flow. Phys. Chem. Earth, C: Solar, Terrestrial Planet. Sci. 26, 645–650. doi:10.1016/s1464-1917(01)00062-9
Fleming, R. W., Ellen, S. D., and Algus, M. A. (1989). Transformation of dilative and contractive landslide debris into debris flows—an example from marin County, California. Eng. Geology 27 (1-4), 201–223. doi:10.1016/0013-7952(89)90034-3
Frank, F., McArdell, B. W., Oggier, N., Baer, P., Christen, M., and Vieli, A. (2017). Debris-flow modeling at Meretschibach and Bondasca catchments, Switzerland: sensitivity testing of field-data-based entrainment model. Nat. Hazards Earth Syst. Sci. 17, 801–815. doi:10.5194/nhess-17-801-2017
Fredlund, D. G., Morgenstern, N. R., and Widger, R. A. (1978). The shear strength of unsaturated soils. Can. Geotech. J. 15, 313–321. doi:10.1139/t78-029
Gabet, E. J., and Mudd, S. M. (2006). The mobilization of debris flows from shallow landslides. Geomorphology 74 (1-4), 207–218. doi:10.1016/j.geomorph.2005.08.013
Gao, B., Zhou, J., and Zhang, J. (2011). Macro-meso analysis of water-soil interaction mechanism of debris flow starting process. Chin. J. Rock Mech. Eng. 30 (12), 2567–2573.
Garres-Díaz, J., Bouchut, F., Fernández-Nieto, E. D., Mangeney, A., and Narbona-Reina, G. (2020). Multilayer models for shallow two-phase debris flows with dilatancy effects. J. Comput. Phys. 419, 109699. doi:10.1016/j.jcp.2020.109699
Glade, T., Crozier, M., and Smith, P. (2000). Applying probability determination to refine landslide-triggering rainfall thresholds using an empirical “antecedent daily rainfall model”. Pure Appl. Geophys. 157 (6–8), 1059–1079. doi:10.1007/s000240050017
Gregoretti, C., Degetto, M., Bernard, M., and Boreggio, M. (2018). The debris flow occurred at Ru secco creek, Venetian Dolomites, on 4 august 2015: analysis of the phenomenon, its characteristics and reproduction by models. Front. Earth Sci. 6, 80. doi:10.3389/feart.2018.00080
Gregoretti, C., and Fontana, G. D. (2008). The triggering of debris flow due to channel-bed failure in some alpine headwater basins of the Dolomites: analyses of critical runoff. Hydrol. Process. 22 (13), 2248–2263. doi:10.1002/hyp.6821
Gregoretti, C., Stancanelli, L. M., Bernard, M., Boreggio, M., Degetto, M., and Lanzoni, S. (2019). Relevance of erosion processes when modelling in-channel gravel debris flows for efficient hazard assessment. J. Hydrol. 568, 575–591. doi:10.1016/j.jhydrol.2018.10.001
Gregoretti, C. (2000). The initiation of debris flow at high slopes: experimental results. J. Hydraulic Res. 38, 83–88. doi:10.1080/00221680009498343
Guo, X., Cui, P., Li, Y., Ma, L., Ge, Y., and Mahoney, W. B. (2016). Intensity-duration threshold of rainfall-triggered debris flows in the Wenchuan Earthquake affected area, China. Geomorphology 253, 208–216. doi:10.1016/j.geomorph.2015.10.009
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P. (2007). Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 98, 239–267. doi:10.1007/s00703-007-0262-7
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P. (2008). The rainfall intensity-duration control of shallow landslides and debris flows: an update. Landslides 5 (1), 3–17. doi:10.1007/s10346-007-0112-1
Haas, T., and Woerkom, T. (2016). Bed scour by debris flows: experimental investigation of effects of debris flow composition. Earth. Surf. Process. Landf. 41 (13), 195–1966. doi:10.1002/esp.3963
Hu, W., Xu, Q., Wang, G. H., van Asch, T. W. J., and Hicher, P.-Y. (2015). Sensitivity of the initiation of debris flow to initial soil moisture. Landslides 12 (6), 1139–1145. doi:10.1007/s10346-014-0529-2
Huang, X., and Tang, C. (2017). Quantitative analysis of dynamic features for entrainment-outburst-induced catastrophic debris flows in Wenchuan earthquake area. J. Eng. Geol. 25 (6), 1491–1500. doi:10.13544/j.cnki.jeg.2017.06.012
Hürlimann, M., Coviello, V., Bel, C., Guo, X., Berti, M., Graf, C., et al. (2019). Debris-flow monitoring and warning: review and examples. Earth-Science Rev. 199, 102981. doi:10.1016/j.earscirev.2019.102981
Hutchinson, J. N. (1986). A sliding-consolidation model for flow slides. Can. Geotech. J. 23 (2), 115–126. doi:10.1139/t86-021
Institute of Mountain Hazards and Environment, CAS (2000). Debris flows in China. Beijng, China: The Commercial Press.
Iverson, R. M., and Ouyang, C. (2015). Entrainment of bed material by Earth surface mass flows: review and reformulation of depth integrated theory. Rev. Geophys. 53 (1), 27–58. doi:10.1002/2013rg000447
Iverson, R. M. (2005). Regulation of landslide motion by dilatancy and pore pressure feedback. J. Geophys. Res. 110 (F2). doi:10.1029/2004JF000268
Iverson, R. M., Reid, M. E., and LaHusen, R. G. (1997a). Debris-flow mobilization from landslides. Annu. Rev. Earth Planet. Sci. 25 (1), 85–138. doi:10.1146/annurev.earth.25.1.85
Iverson, R. M. (1997b). The physics of debris flows. Rev. Geophys. 35 (3), 245–296. doi:10.1029/97rg00426
Iverson, R. M., and Vallance, J. W. (2001). New views of granular mass flows. Geol 29 (2), 115–118. doi:10.1130/0091-7613(2001)029<0115:nvogmf>2.0.co;2
Kern, A. N., Addison, P., Oommen, T., Salazar, S. E., and Coffman, R. A. (2017). Machine learning based predictive modeling of debris flow probability following wildfire in the intermountain Western United States. Math. Geosci. 49 (6), 717–735. doi:10.1007/s11004-017-9681-2
King, H. M. (1999). What is a debris flow? Available at: https://geology.com/articles/debris-flow/ (Accessed July 11, 1999).
Kung, H. Y., Chen, C. H., and Ku, H. H. (2012). Designing intelligent disaster prediction models and systems for debris-flow disasters in Taiwan. Expert Syst. Appl. 39 (5), 5838–5856. doi:10.1016/j.eswa.2011.11.083
Lai, V. H., Tsai, V. C., Lamb, M. P., Ulizio, T. P., and Beer, A. R. (2018). The seismic signature of debris flows: flow mechanics and early warning at Montecito, California. Geophys. Res. Lett. 45, 5528–5535. doi:10.1029/2018gl077683
Li, C., Zhu, W. H., Lu, X. B., et al. (2010). Studied on landslide translating into debris-flow under rainfall. China Civil Eng. J. 43 (s1), 499–505. doi:10.15951/j.tmgcxb.2010.s1.008
Li, W., Wei, X. L., Song, X. Y., et al. (2019). Experimental study on scouring and initiation of debris flow with continuous increase of waterflow. Highw. Eng. 44 (4), 54–62. doi:10.19782/j.cnki.1674-0610.2019.04.010
Liang, G. M., and Yao, L. K. (2008). Study on determining the critical rainfall of rainstorm debris flow. Subgrade Eng. 6, 3–5.
Liao, L. P., Zhu, Y. Y., Yang, Z. Q., et al. (2017). The mechanical property of gravel soil in seismic area and its critical state in initiating debris flow. Mountain Res. 35 (4), 506–516. doi:10.16089/j.cnki.1008-2786.000248
Liu, W., and He, S. (2020). Comprehensive modelling of runoff-generated debris flow from formation to propagation in a catchment. Landslides 17 (7), 1529–1544. doi:10.1007/s10346-020-01383-w
Liu, X., Wang, F., Nawnit, K., Lv, X., and Wang, S. (2020). Experimental study on debris flow initiation. Bull. Eng. Geol. Environ. 79, 1565–1580. doi:10.1007/s10064-019-01618-8
Lyu, L., Wang, Z., Cui, P., and Xu, M. (2017). The role of bank erosion on the initiation and motion of gully debris flows. Geomorphology 285, 137–151. doi:10.1016/j.geomorph.2017.02.008
Marra, F., Destro, E., Nikolopoulos, E. I., Zoccatelli, D., Creutin, J. D., Guzzetti, F., et al. (2017). Impact of rainfall spatial aggregation on the identification of debris flow occurrence thresholds. Hydrol. Earth Syst. Sci. 21 (9), 4525–4532. doi:10.5194/hess-21-4525-2017
Marra, F., Nikolopoulos, E. I., Creutin, J. D., and Borga, M. (2016). Space-time organization of debris flows-triggering rainfall and its effect on the identification of the rainfall threshold relationship. J. Hydrol. 541, 246–255. doi:10.1016/j.jhydrol.2015.10.010
McArdell, B. W. (2016). Field measurements of forces in debris flows at the illgraben: implications for channel-bed erosion. IJECE 9, 194–198. doi:10.13101/ijece.9.194
McGuire, L. A., Rengers, F. K., Kean, J. W., and Staley, D. M. (2017). Debris flow initiation by runoff in a recently burned basin: is grain-by-grain sediment bulking or en masse failure to blame? Geophys. Res. Lett. 44 (14), 7310–7319. doi:10.1002/2017gl074243
Melo, R., Van Asch, T., and Zêzere, J. L. (2018). Debris flow run-out simulation and analysis using a dynamic model. Nat. Hazards Earth Syst. Sci. 18 (2), 555–570. doi:10.5194/nhess-18-555-2018
Mergili, M., Fischer, J.-T., Krenn, J., and Pudasaini, S. P. (2017). r.avaflow v1, an advanced open-source computational framework for the propagation and interaction of two-phase mass flows. Geosci. Model. Dev. 10 (2), 553–569. doi:10.5194/gmd-10-553-2017
Morton, D. M., and Campbell, R. H. (1974). Spring mudflows at wrightwood, southern California. Q. J. Eng. Geology. Hydrogeology 7 (4), 377–384. doi:10.1144/gsl.qjeg.1974.007.04.09
Palau, R. M., Hürlimann, M., Pinyol, J., Moya, J., Victoriano, A., Génova, M., et al. (2017). Recent debris flows in the Portainé catchment (Eastern Pyrenees, Spain): analysis of monitoring and field data focussing on the 2015 event. Landslides 14, 1161–1170. doi:10.1007/s10346-017-0832-9
Pan, H.-L., Jiang, Y.-J., Wang, J., and Ou, G.-Q. (2018). Rainfall threshold calculation for debris flow early warning in areas with scarcity of data. Nat. Hazards Earth Syst. Sci. 18 (5), 1395–1409. doi:10.5194/nhess-18-1395-2018
Pan, L., Wei, X. L., Zhang, Y. F., et al. (2017). Influence of initial water content on glacial debris flow triggering process. J. Soil Water Conservation 31 (6), 116–122.
Pastorello, R., D’Agostino, V., and Hürlimann, M. (2020). Debris flow triggering characterization through a comparative analysis among different mountain catchments. CATENA 186, 104348. doi:10.1016/j.catena.2019.104348
Posner, A. J., and Georgakakos, K. P. (2015). Soil moisture and precipitation thresholds for real-time landslide prediction in El Salvador. Landslides 12, 1179–1196. doi:10.1007/s10346-015-0618-x
Qi, G. Q., and Huang, R. Q. (2003). Study on formation mechanism of debris flow based on unsaturated soil mechanics theory. Chin. J. Geol. Hazard Control. 14 (3), 12–15.
Qian, N., and Wang, Z. Y. (1984). Preliminary study on the movement mechanism of debris flow. Acta Geographica Sinica 51 (1), 33–43.
Qiao, J. P., Li, M. L., Yang, Z. J., et al. (2018). Warning model study of debris flow slope source starting based on experimental method. Adv. Water Sci. 29 (1), 64–72. doi:10.14042/j.cnki.32.1309.2018.01.008
Restrepo, P., Jorgensen, D. P., Cannon, S. H., Costa, J., Laber, J., Major, J., et al. (2008). Joint NOAA/NWS/USGS prototype debris flow warning system for recently burned areas in southern California. Bull. Am. Meteorol. Soc. 89 (12), 1845–1852. doi:10.1175/2008bams2416.1
Schimmel, A., Hübl, J., McArdell, B., and Walter, F. (2018). Automatic identification of alpine mass movements by a combination of seismic and infrasound sensors. Sensors 18 (5), 1658. doi:10.3390/s18051658
Shu, A. P., Zhang, X., Duan, G. S., et al. (2017). Distinguish relations for the critical initiation of non-homogeneous debris flow. J. Hydraulic Eng. 48 (7), 757–764. doi:10.13243/j.cnki.slxb.20170109
Shu, A., Tian, L., Wang, S., Rubinato, M., Zhu, F., Wang, M., et al. (2018). Hydrodynamic characteristics of the formation processes for non-homogeneous debris-flow. Water 10 (4), 452. doi:10.3390/w10040452
Staley, D. M., Kean, J. W., Cannon, S. H., Schmidt, K. M., and Laber, J. L. (2013). Objective definition of rainfall intensity-duration thresholds for the initiation of post-fire debris flows in southern California. Landslides 10 (5), 547–562. doi:10.1007/s10346-012-0341-9
Staley, D. M., Negri, J. A., Kean, J. W., Laber, J. L., Tillery, A. C., and Youberg, A. M. (2017). Prediction of spatially explicit rainfall intensity-duration thresholds for post-fire debris-flow generation in the western United States. Geomorphology 278, 149–162. doi:10.1016/j.geomorph.2016.10.019
Stancanelli, L. M., Lanzoni, S., and Foti, E. (2015). Propagation and deposition of stony debris flows at channel confluences. Water Resour. Res. 51, 5100–5116. doi:10.1002/2015wr017116
Takahashi, T. (2009). A review of Japanese debris flow research. IJECE 2 (1), 1–14. doi:10.13101/ijece.2.1
Takahashi, T. (2007). Debris flow mechanics, prediction and countermeasures. London, United Kingdom: Taylor and Francis Group, 108.
Takahashi, T. (1978). Mechanical characteristics of debris flow. J. Hydraulic Division, ASCE 104 (HY8), 1153–1169. doi:10.1061/jyceaj.0005046
Tang, C., and Zhang, S. C. (2008). Study progress and expectation for initiation mechanism and prediction of hydraulic-driven debris flows. Adv. Earth Sci. 23 (8), 787–793.
Theule, J. I., Liébault, F., Laigle, D., Loye, A., and Jaboyedoff, M. (2015). Channel scour and fill by debris flows and bedload transport. Geomorphology 243, 92–105. doi:10.1016/j.geomorph.2015.05.003
Tillery, A. C., and Rengers, F. K. (2020). Controls on debris flow initiation on burned and unburned hillslopes during an exceptional rainstorm in southern New Mexico, USA. Earth Surf. Process. Landforms 45 (4), 1051–1066. doi:10.1002/esp.4761
Turkington, T., Remaître, A., Ettema, J., Hussin, H., and Van Westen, C. (2016). Assessing debris flow activity in a changing climate. Climatic Change 137, 293–305. doi:10.1007/s10584-016-1657-6
Underwood, S. J., Schultz, M. D., Berti, M., Gregoretti, C., Simoni, A., Mote, T. L., et al. (2016). Atmospheric circulation patterns, cloud-to-ground lightning, and locally intense convective rainfall associated with debris flow initiation in the Dolomite Alps of northeastern Italy. Nat. Hazards Earth Syst. Sci. 16, 509–528. doi:10.5194/nhess-16-509-2016
Vagnon, F., Pirulli, M., Yague, A., and Pastor, M. (2019). Comparison of two depth-averaged numerical models for debris flow runout estimation. Can. Geotech. J. 56, 89. doi:10.1139/cgj-2017-0455
Van Asch, T. W. J., Tang, C., Alkema, D., Zhu, J., and Zhou, W. (2014). An integrated model to assess critical rainfall thresholds for run-out distances of debris flows. Nat. Hazards 70 (1), 299–311. doi:10.1007/s11069-013-0810-z
Vázquez, R., Capra, L., and Coviello, V. (2016). Factors controlling erosion/deposition phenomena related to lahars at Volcán de Colima, Mexico. Nat. Hazards Earth Syst. Sci. 16, 1881–1895. doi:10.5194/nhess-16-1881-2016
Walter, F., Burtin, A., McArdell, B. W., Hovius, N., Weder, B., and Turowski, J. M. (2017). Testing seismic amplitude source location for fast debris-flow detection at Illgraben, Switzerland. Nat. Hazards Earth Syst. Sci. 17, 939–955. doi:10.5194/nhess-17-939-2017
Wang, T., Chen, N. S., Deng, M. F., et al. (2018). Study on the critical hydraulic condition of debris flow in scoured channel. J. Sediment Res. 43 (1), 38–43. doi:10.16239/j.cnki.0468-155x.2018.01.007
Wang, Y. Y., Zou, R. Y., and Liu, X. F. (1997). Interrelated research ofrelationship between debris flow’s trigger and permeational coefficient. J. Soil Water Conservation 4, 77–83.
Wang, Z. Y. (2001). Experimental study on debris flow head and the energy theory. J. Hydraulic Eng. 3, 18–26.
Williams, G. P., and Guy, H. P. (1973). Erosional and depositional aspects of hurricane Camille in Virginia. Fairbanks, AK: US Geological Survey, 804.
Wu, M. H., Wang, J. P., and Chen, I. C. (2018). Optimization approach for determining rainfall duration-intensity thresholds for debris flow forecasting. Bull. Eng. Geology. Environ. 78 (2), 1–7. doi:10.1007/s10064-018-1314-6
Yan, Y., Zhang, Y., Hu, W., Guo, X.-J., Ma, C., Wang, Z.-A., et al. (2020). A multiobjective evolutionary optimization method based critical rainfall thresholds for debris flows initiation. J. Mt. Sci. 17, 1860–1873. doi:10.1007/s11629-019-5812-1
Yang, J. B., Chen, X. C., Wang, H., Tian, X. P., and Jia, L. R. (2016). An experimental study of relationship between fine grain content and permeability coefficient of debris flow deposits. Rock Soil Mech. 37 (11), 3184–3190. doi:10.16285/j.rsm.2016.11.018
Yu, B., Li, L., Wu, Y., and Chu, S. (2013). A formation model for debris flows in the Chenyulan River Watershed, TaiwanTaiwan. Nat. Hazards 68 (2), 745–762. doi:10.1007/s11069-013-0646-6
Yu, B., Zhu, Y., Wang, T., Chen, Y., and Zhu, Y. (2014). Prediction model for occurrence of debris flows in channels with runoff initiation mechanism. J. Eng. Geology. 22 (3), 450–455. doi:10.13544/j.cnki.jeg.2014.03.014
Yu, B., Zhu, Y., Wang, T., and Zhu, Y. B. (2015). Research on the 10-minute rainfall prediction model for debris flows. Adv. Water Sci. 26 (3), 347–355. doi:10.3390/w10111536
Yu, G.-A., Yao, W., Huang, H. Q., and Liu, Z. (2020). Debris flows originating in the mountain cryosphere under a changing climate: a review. Prog. Phys. Geogr. Earth Environ., 0309133320961705. doi:10.1177/0309133320961705
Zhang, M., Hu, R. L., Yin, Y. P., and Cui, F. P. (2009). Study of transform mechanism of landslide-debris flow with ring shear test. Chin. J. Rock Mech. Eng. 29 (4), 822–832.
Zhang, S. J., Xu, C. X., Wei, F. Q., Hu, K. H., Xu, H., Zhao, L. Q., et al. (2019). A physics-based model to derive rainfall intensity-duration threshold for debris flow. Geomorphology 351, 106930. doi:10.1016/j.geomorph.2019.106930
Zhang, Y., Chen, N., Liu, M., Wang, T., Deng, M., Wu, K., et al. (2020). Debris flows originating from colluvium deposits in hollow regions during a heavy storm process in Taining, southeastern China. Landslides 17, 335–347. doi:10.1007/s10346-019-01272-x
Zhou, J., Chen, C., Du, Q., and Zhang, J. (2017). Centrifugal model tests on the influence of fine contents on the debris flow initiation process. J. Hunan University(Natural Sciences) 44 (9), 165–173. doi:10.16339/j.cnki.hdxbzkb.2017.09.021
Zhou, S. Y., Gao, L., and Zhang, L. M. (2019). Predicting debris-flow clusters under extreme rainstorms: a case study on Hong Kong Island. Bull. Eng. Geol. Environ. 78, 5775–5790. doi:10.1007/s10064-019-01504-3
Zhou, W., and Tang, C. (2013). Rainfall thresholds for debris flows occurrence in the Wenchuan earthquake area. Adv. Water Sci. 24 (6), 786–793. doi:10.14042/j.cnki.32.1309.2013.06.013
Keywords: initial mechanism, research progress, slope and channel processes, discrimination method, debris flow disasters
Citation: Du J, Fan Z-j, Xu W-t and Dong L-y (2021) Research Progress of Initial Mechanism on Debris Flow and Related Discrimination Methods: A Review. Front. Earth Sci. 9:629567. doi: 10.3389/feart.2021.629567
Received: 16 November 2020; Accepted: 15 February 2021;
Published: 07 May 2021.
Edited by:
Biswajeet Pradhan, University of Technology Sydney, AustraliaReviewed by:
Md Nazmul Azim Beg, Tulane University, United StatesJun Niu, China Agricultural University, China
Copyright © 2021 Du, Fan, Xu and Dong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jun Du, ZHhqeDIwMDZAMTI2LmNvbQ==
 Jun Du
Jun Du Zhong-jie Fan1,2
Zhong-jie Fan1,2