Effect of Ocean Fluid Changes on Pressure on the Seafloor: Ocean Assimilation Data Analysis on Warm-Core Rings off the Southeastern Coast of Hokkaido, Japan on an Interannual Timescale

The relationship between sea surface height (SSH) and seawater density anomalies, which affects the pressure on the seafloor (PSF) anomalies off the southeastern coast of Hokkaido, Japan, was analyzed using the eddy-resolving spatial resolution ocean assimilation data of the JCOPE2M for the period 2001–2018. On an interannual (i.e., year-to-year) timescale, positive SSH anomalies of nearly 0.1 m appeared off the southeastern coast of Hokkaido, Japan, in 2007, associated with a warm-core ring (WCR), while stronger SSH anomalies (∼0.2 m) related to a stronger WCR occurred in 2016. The results show that the effects of such positive SSH anomalies on the PSF are almost canceled out by the effects of negative seawater density anomalies from the seafloor to the sea surface (SEP; steric effect on PSF) due to oceanic baroclinic structures related to the WCRs, especially in offshore regions with bottom depths greater than 1000 m. This means that oceanic isostasy is well established in deep offshore regions, compared with shallow coastal regions. To further verify the strength of the oceanic isostasy, oceanic isostasy anomalies (OIAs), which represent the barotropic component of SSH anomalies, are introduced and analyzed in this study. OIAs are defined as the sum of the SSH anomalies and SEP anomalies. Our results indicate that the effect of oceanic fluid changes due to SSH and seawater density anomalies (i.e., OIAs) on PSF changes cannot be neglected on an interannual timescale, although the amplitudes of the OIAs are nearly 10% of those of the SSH anomalies in the offshore regions. Therefore, to better estimate the interannual-scale PSF anomalies due to crustal deformation related to slow earthquakes including afterslips, long-term slow slip events, or plate convergence, the OIAs should be removed from the PSF anomalies.

1 Introduction

Along the eastern coast of Japan, ocean trenches such as the Japan Trench and Kuril Trench are found (Figure 1A). Along the slopes of trenches, megathrust earthquakes often occur, such as the 2011 Pacific Coast of Tohoku Earthquake. It has been reported that slow slip events (SSEs) frequently occur in these regions (Shelly et al., 2007; Obara and Kato, 2016; Uchida et al., 2016; Araki et al., 2017). Recently, Nishikawa et al. (2019) pointed out that SSEs play a role in limiting the occurrence of megathrust earthquakes. Therefore, better monitoring of SSEs is useful to understand the mechanism of the occurrence of megathrust earthquakes and improve the prediction of megathrust earthquakes.

FIGURE 1

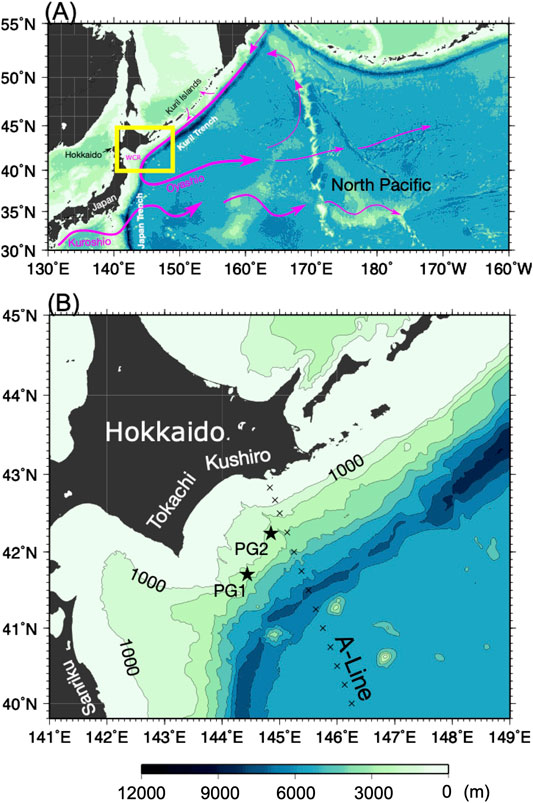
FIGURE 1. (A) Map of the western North Pacific. Sea surface currents (Kuroshio and Oyashio) are schematically shown by purple arrows. (B) Map for the analysis area off Tokachi and Kushiro (off the southeastern coast of Hokkaido) marked by a yellow square in (A) with bottom topography. Contour interval is 1000 m. On the contour of 1000 m depth, a contour label is shown. The ocean bottom pressure gauges (PG1 and PG2) are marked by black stars and the CTD stations at A-line by black crosses.

In contrast to conventional earthquakes, slow earthquakes including SSEs (e.g., Ide et al., 2007) do not emit seismic waves. A useful tool for monitoring slow earthquakes is the ocean bottom pressure gauge. Itoh et al. (2019) reported that crustal deformation caused by the afterslip of the 2003 Tokachi-oki earthquake occurred for 7.5 years from 2003 to 2011, using inland Global Positioning System (GPS) data in Hokkaido, Japan, and pressure on the seafloor (PSF; see Table 1 for the abbreviations and corresponding full names and units of the variables used in this study) data obtained off the southeastern coast of Hokkaido, Japan. They showed that the crustal deformation increased by approximately 2 × 10^–1 m (i.e., 2 × 10^–1 dbar) from 2003 to 2011. Thus, a precision of 1 × 10^–2 dbar of the PSF data is required to identify such changes. In this study, we focus on the oceanic fluid changes off the southeastern coast of Hokkaido, Japan, which can affect the PSF changes in this region, and briefly discuss their relationships after the occurrence of the 2003 Tokachi-oki earthquake. As described in Section 2.3, the observed PSF data used in this study are of sufficient precision to evaluate this relationship.

TABLE 1

TABLE 1. Abbreviations, their full names or explanation, units, and corresponding equations and figures of the variables used in this study.

Observed PSF data include both the pressure changes due to crustal deformation as well as those due to oceanic fluid changes (Ariyoshi et al., 2016). The area off the east coast of Japan facing the North Pacific is one of the most active areas of ocean fluid variations in the global oceans owing to the very strong Kuroshio (e.g., Nitani, 1972; Kawabe, 2005; Nagano et al., 2018, 2019) and Oyashio currents (e.g., Kono, 1997; Joyce and Dunworth-Baker, 2003; Ito et al., 2004; Kuroda et al., 2015), and numerous oceanic mesoscale eddies (e.g., Tai and White, 1990; Qiu et al., 1991; Ichikawa and Imawaki, 1994; Aoki et al., 1995; Ebuchi and Hanawa, 2000; Sugimoto et al., 2017). Thus, the oceanic fluid changes related to such phenomena can affect the PSF in the areas around the Japan Trench and Kuril Trench. Therefore, to more accurately estimate the crustal deformations related to the SSEs and other slow crustal deformations such as plate motions by use of the PSF, PSF changes caused by the oceanic fluid variabilities should be removed from the PSF data.

In our previous study (Hasegawa et al., 2019), we investigated the effect of oceanic fluid change on the PSF change off the southeastern coast of Hokkaido, Japan, using observational data, as an interdisciplinary study with solid Earth science and fluid Earth science. In the previous study, we analyzed PSF data obtained by the ocean bottom pressure gauges at the PG1 and PG2 stations (Figure 1B) that were recorded by the Long-Term Deep Sea Floor Observatory off Kushiro-Tokachi in the Kuril Trench deployed by the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) (Kawaguchi et al., 2000), repeated observations of conductivity-temperature-depth (CTD) data along the A-line (Figure 1B) by the Fisheries Research Agency, and altimetric sea surface height (SSH) data provided by the Archiving, Validation and Interpretation of Satellite Oceanographic data (AVISO). We focused on the effect of oceanic fluid changes related to substantially baroclinic anticyclonic eddies, called warm-core rings (WCRs), which are of the similar kind to oceanic mesoscale eddies observed along the east coast of Japan and other regions of the world (e.g., Tomosada, 1986; Itoh and Sugimoto, 2002), on PSF changes on an interannual (i.e., year-to-year) timescale.

The impact of the WCRs on the PSF in 2007–2008 and 2012–2013 was studied by Hasegawa et al. (2019). It was found that the WCRs with large positive SSH anomalies lead to retreats of the Oyashio Current after El Niño events (e.g., Trenberth, 1997; Hasegawa and Hanawa, 2003a; McPhaden et al., 2006). Hasegawa et al. (2019) also showed that although the large positive SSH anomalies due to the WCR appeared at PG2 in 2007 (i.e., the seawater volume above PG2 was larger than usual), the effect of positive SSH anomalies on the PSF change was canceled out by the effect of the negative seawater density anomalies due to the WCR (i.e., the density of seawater was reduced due to the WCR compared to the usual value), which resulted in very small changes in the PSF. Therefore, to better understand the effects of oceanic fluid changes on the PSF, a more comprehensive description of the relationship between SSH anomalies and seawater density anomalies on an interannual timescale is required.

The observational CTD data used in Hasegawa et al. (2019) do not cover the wide areas off the southeastern coast of Hokkaido, Japan, because of the limited number of in-situ observations obtained using such instrument. Instead, analyses using numerical models are useful, as demonstrated by Inazu et al. (2012) and Muramoto et al. (2019). These studies investigated the effect of oceanic fluid changes on PSF on a timescale of 2–20 days. They used a non-linear, single-layer barotropic ocean model, which is very useful for simulating oceanic barotropic variations on timescale of 2–20 days (Inazu et al., 2012). In addition to such a short timescale, interannual-timescale variations have also been found in crustal deformations related to long-term SSEs (e.g., Hirose and Obara, 2005; Ide et al., 2007; Uchida et al., 2016; Nakata et al., 2017; Kobayashi and Tsuyuki, 2019), afterslip (e.g., Miyazaki et al., 2004; Ide et al., 2007; Itoh et al., 2019), silent earthquakes (e.g., Franco et al., 2005; Ide et al., 2007), and plate convergence (e.g., Miyashita, 1987; DeMets et al., 1990). While the non-linear, one-layer barotropic ocean model is effective for the shorter timescale of 2–20 days, it is less effective for representing baroclinic ocean changes on timescales longer than 20 days (Inazu et al., 2012). To analyze the oceanic fluid variations on the interannual timescale related to the WCRs, continuously stratified ocean models accounting for both barotropic and baroclinic components are more suitable.

Our final goal is to quantitatively estimate the effects of SSH and seawater density anomalies on PSF anomalies related to the slow earthquakes (e.g., Ide et al., 2007) on an interannual timescale. To reach this aim, as the next step of our previous observational study (Hasegawa et al., 2019), the purpose of this study is to investigate the relationship between SSH and seawater density anomalies over the entire area off the southeastern coast of Hokkaido, Japan, with a special reference to WCRs, using the ocean assimilation data of the eddy-resolving ocean assimilation data (JCOPE2M; Miyazawa et al., 2017; 2019). The JCOPE2M estimates the optimal solution by using observational data and a continuously stratified numerical ocean model. In this study, we used SSH data and vertical profiles of temperature and salinity from the seafloor to the sea surface of the JCOPE2M to explore the relationship between SSH and oceanic density anomalies on an interannual timescale. In addition, we briefly discuss the effect of the ocean fluid changes estimated from the JCOPE2M assimilation data on changes in PSF observed by the ocean bottom pressure gauges at PG1 and PG2 on an interannual timescale. The analysis method used in this study for the SSH anomalies and vertical profiles of temperature and salinity of the JCOPE2M is applicable to observational data, i.e., altimetric SSH data, temperature and salinity vertical profiles obtained by shipboard-CTD, Argo profiling floats (Argo Science Team, 1998; Argo Science Team, 2001), eXpendable Conductivity Temperature Depth profilers (XCTDs), moorings, etc., not only in the region off the southeastern coast of Hokkaido, Japan, but also in other places where both interannual-scale crustal deformations caused by slow earthquakes and oceanic fluid variations exist.

The remainder of this article is organized as follows. In Section 2, the assimilation data of the JCOPE2M, observed altimetric SSH data, and observed PSF data used in this study are described. In Section 3, the relationship between the SSH and seawater density anomalies on an interannual timescale is investigated with a special reference to the WCRs. Discussions are given in Section 4, and concluding remarks are presented in Section 5.

2 Data

2.1 Ocean Assimilation Data

The assimilation data analyzed in this study were obtained from a reanalysis experiment of the eddy-resolving spatial resolution ocean assimilation model developed by JAMSTEC (JCOPE2M; Miyazawa et al., 2017; Miyazawa et al., 2019). JCOPE2M is based on the Princeton Ocean Model, which adopts the vertical discretization of sigma coordinates (Mellor et al., 2002). The model domain is the western North Pacific (10.5°N to 62°N, 108°E to 180°E). The horizontal resolution is 1/12° in both zonal and meridional directions, and the model has 46 vertical levels from the ocean bottom to the sea surface. It is forced by surface wind stress and heat and salt fluxes derived from the NCEP/NCAR reanalysis data (Kalnay et al., 1996). The experimental period is January 1993 to the present. The multiscale 3D-VAR assimilation scheme is used in the JCOPE2M. Observation data of the SSH anomaly, sea surface temperature, and vertical profile data of temperature and salinity are assimilated in the JCOPE2M. SSH data provided by the JCOPE2M do not include the atmospheric pressure change effect (i.e., the IB component; Ponte and Gaspar, 1999). In this study, we used the outputs of the SSH data and vertical profiles of temperature and salinity from the JCOPE2M reanalysis experiment.

We analyzed monthly SSH anomalies and other variables on an interannual timescale in this study. The analysis period for the JCOPE2M outputs from January 2001 to December 2018 was chosen to cover the analysis period of the observed PSF data at PG1 and PG2. The monthly anomalies were calculated as follows. First, daily vertical profiles of the potential density of seawater from the seafloor to the sea surface at each grid point were calculated using the daily outputs of vertical profiles of the temperature and salinity from January 1, 2001, to December 31, 2018. Subsequently, monthly averaged vertical profiles of the potential density were calculated from the daily vertical profiles of the potential density at each grid point from January 2001 to December 2018. Additionally, monthly SSH data were also calculated using the daily outputs of the SSH data at each grid point for the same period. Subsequently, the monthly climatologies (i.e., long-term average) of these variables were calculated by averaging the monthly variables for the individual calendar months from January 2001 to December 2018. Thereafter, the monthly anomalies of these variables were calculated by subtracting the monthly climatologies from the monthly averaged data. A 15-months running mean filter was adopted for the monthly anomalies to highlight the interannual-scale variations of these variables.

2.2 Altimetric Sea Surface Height (SSH) Data

To evaluate the SSH anomalies of the JCOPE2M, satellite altimeter data (i.e., observed altimetric SSH data) provided by AVISO were used in this study. Daily SSH anomalies of the 1/4° × 1/4° gridded delayed-time updated mapped data (DT-SLA-H) (AVISO, 2008) from January 1, 2001, to December 31, 2018, were analyzed. Monthly SSH anomalies from January 2001 to December 2018 were calculated in the same way as the JCOPE2M SSH anomalies. A 15-months running mean filter was also adopted for the altimetric SSH data.

2.3 Pressure on the Seafloor (PSF) Data

The PSF data obtained by the ocean bottom pressure gauges at PG1 and PG2 on the Long-Term Deep Sea Floor Observatory off Kushiro–Tokachi in the Kuril Trench (Kawaguchi et al., 2000) were used to discuss the PSF anomalies and effect of oceanic fluid changes on the PSF. The locations of PG1 (41.7040° N, 144.4375° E) and PG2 (42.2365° N, 144.8454° E) are shown as black stars in Figure 1B. The PSF gauges were deployed at depths of 2218 m and 2210 m for PG1 and PG2, respectively (also see the website of the Submarine Cable Data Center of JAMSTEC, http://www.jamstec.go.jp/scdc/top_e.html, for detailed information and data usage). The ocean bottom pressure gauges of this system are digiquartz pressure transducers (Model 2813 E) manufactured by Hewlett-Packard. The accuracy and resolution of the sensors were 7 × 10^–2 dbar and 5 × 10^–3 dbar, respectively. The original data were observed at a sampling rate of 8 kHz.

The PSF data for PG1 and PG2 were analyzed in our previous study (Hasegawa et al., 2019) from 2003 to 2014. In this study, we extended the data length, and PSF data from October 8, 2003, to December 31, 2018, were used. The raw data were averaged to hourly data. Subsequently, the daily mean data were calculated after removing tides from the hourly data by using the tide-eliminating filter proposed by Thompson (1983). Then, the sensor drift components were removed from the detided daily mean data by exponential and linear functions as done in our previous study (Hasegawa et al., 2019). In this study, the data length for calculating the drift component was from October 13, 2003, to December 26, 2018, which is extended compared to that of Hasegawa et al. (2019). The parameters used to estimate the sensor drift in this study are shown in Table 2, and are slightly changed from those used in Hasegawa et al. (2019). After the drift component was removed from the daily PSF data, monthly averaged PSF data were obtained from the residual daily data. The PSF monthly climatologies were calculated for the period from January 2004 to December 2018. Then, the monthly PSF anomalies from January 2004 to December 2018 were calculated by subtracting the monthly climatologies from the monthly PSF data. Afterward, a 15-months running mean filter was adopted for the monthly PSF anomalies to highlight the interannual-scale variations such as SSH anomalies.

TABLE 2

TABLE 2. Regression coefficients A (dbar), B (d⁻¹), C (dbar d⁻¹), and D (dbar) for the exponential and linear functions to estimate the sensor drift component (p_d) of the detided daily PSF data at PG1 and PG2. p_d is represented by the equation; p_d = A exp (B t) + C t + D, where t is the time (days). These parameters were calculated for the period from October 13, 2003, to December 26, 2018.

As described in Section 1, based on previous studies (Uchida et al., 2016; Itoh et al., 2019) a precision of 1 × 10^–2 dbar of the PSF data is required for analysis on interannual-scale PSF anomalies in this study. Assuming a Gaussian error distribution, the random errors of the 15-months running mean filtered PSF anomalies were estimated to be approximately 1.5 × 10^–6 dbar. This is much smaller than the required precision for PSF and the amplitudes of the 15-months running mean filtered PSF anomalies at PG1 and PG2 (approximately 1 × 10^–2 dbar), as shown in Section 4.1.

3 Results

3.1 Positive Peaks of SSH Anomalies at PG1 and PG2

First, we detected the periods in which SSH anomalies showed positive peaks of during the analysis period at PG1 and PG2, respectively. As shown in previous studies (e.g., Hasegawa et al., 2019), the WCRs were accompanied by positive SSH anomalies around PG1 and PG2. Black thick solid lines in Figures 2A,B show the timeseries of SSH anomalies from the JCOPE2M data at the grid point closest to PG1 (41.625° N, 144.375° E) and PG2 (42.125°N, 144.875° E), respectively. It is shown that the SSH anomalies of the JCOPE2M at both PG1 and PG2 show positive SSH anomalies (approximately 5 × 10^–2) in the year 2007, which is consistent with our previous study using observed altimetric SSH data (Hasegawa et al., 2019). Additionally, much stronger positive peaks (approximately 1.5 × 10^–1) were found in the year 2016, both at PG1 and PG2. These two positive SSH anomalies were also observed in the observed altimetric SSH (AVISO-SSH) anomalies (red thick solid lines in Figures 2A,B).

FIGURE 2

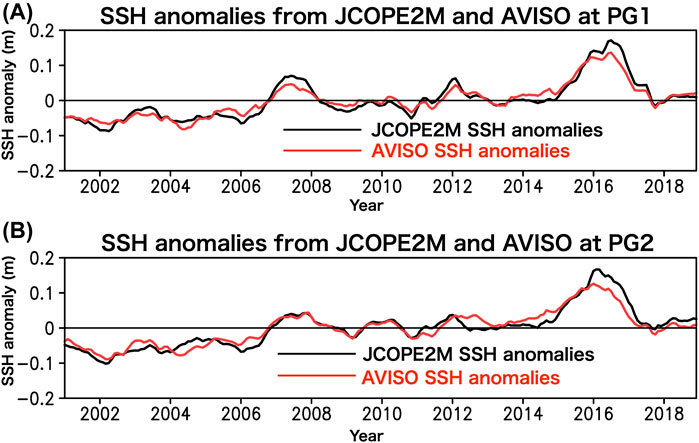
FIGURE 2. (A) Timeseries of the JCOPE2M SSH anomalies (black thick solid line) and the observe altimetric AVISO-SSH anomalies (red thick solid line) at PG1 (indeed, the closest grid point to the location of PG1, i.e., 41.625° N, 144.375° E). The unit is m. (B) Same as (A) but at PG2 (indeed, the closest grid point to the location of PG2, i.e., 42.125° N, 144.875° E).

The standard deviations calculated during August 2001–May 2018 (i.e., both the start and end periods of the 15-months running mean filter, in which the data cannot be adequately filtered by the running mean filter, were eliminated from the original analysis period) of the JCOPE2M-SSH and AVISO-SSH anomalies at PG1 (PG2) were approximately 5.5 × 10^–2 (5.6 × 10^–2) m and 4.9 × 10^–2 (3.9 × 10^–2) m, respectively. Thus, the difference in the standard deviation between the JCOPE2M and AVISO-SSH anomalies at PG1 (PG2) is approximately 6.0 × 10^–3 (1.7 × 10^–2) m for this period.

Therefore, the gross features of the JCOPE2M SSH data represent the strong positive SSH anomalies at these locations. In the following subsections, we focus on oceanic fluid changes in the years 2007 and 2016 as case studies.

3.2 SSH and Seawater Density Anomalies Related to the WCRs in 2007 and 2016

Figure 3A shows the spatial pattern of the yearly averaged SSH anomalies in 2007. As shown in Figure 3A, a WCR existed in this period around PG1 and PG2. This WCR shows a relatively large positive SSH anomaly of approximately 0.1 m around its center. In 2016 (Figure 3B), a much stronger WCR was distributed over a wide area off the southeastern coast of Hokkaido, Japan, including the locations of PG1 and PG2, with large positive SSH anomalies of approximately 0.2 m around its center. Since a 1-m increase in SSH can lead to a nearly 1-dbar increase in the PSF, the SSH anomalies had the potential to increase the PSF by nearly 0.1 dbar and 0.2 dbar around the center of these WCRs in 2007 and 2016, respectively.

FIGURE 3

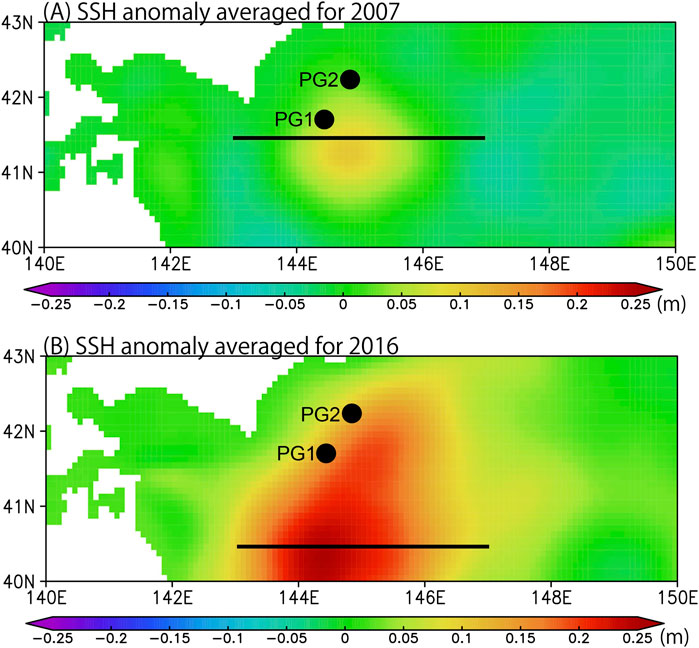
FIGURE 3. (A) Spatial distribution of the yearly averaged SSH anomaly for the year 2007. The unit is m. The black horizontal line along 41.5° N denotes the longitude range for the longitude-depth diagram of σ_θ in Figure 4A. Black circles denote the location of PG1 and PG2. (B) Same as (A) but for the year 2016. The black horizontal line along 40.5° N denotes the longitude range for the longitude-depth diagram of σ_θ in Figure 4B.

Subsequently, we investigated the vertical profiles of seawater density related to the WCRs in the two cases. Figure 4A shows the depth-longitude diagram of the yearly averaged σ_θ (σ_θ is defined as follows: σ_θ = ρ – 1000 [kg/m³], where ρ [kg/m³] is the potential density of seawater) and the yearly averaged σ_θ anomaly along a horizontal line at 41.5° N from 143° E to 147° E, which is across the center of the WCR, in 2007 (Figure 3A). As shown in Figure 4A, relatively large negative σ_θ anomalies appear centered at 145° E, where the center of the WCR is located (Figure 3A), from the sea surface to a depth of approximately 900 m. Along the line, associated with the negative σ_θ anomalies, the isopycnal depths shown by black contours in Figure 4A display a slightly downward lens-like shape, showing the oceanic baroclinic structure due to the WCR. It is expected that such a negative anomaly of σ_θ generates a low seawater mass in the WCR area, when compared with the normal condition, resulting in a reduction of the PSF in this area. For the year 2016, in which much stronger positive SSH anomalies appeared (Figure 3B), negative σ_θ anomalies and downward lens-like shape (i.e., the oceanic baroclinic structure) were also much stronger than those in 2007 (Figure 4B). Thus, it is suggested that the effect of the positive SSH anomalies on the PSF can be canceled out by the effect of the negative seawater density anomalies on the PSF in both 2007 and 2016.

FIGURE 4

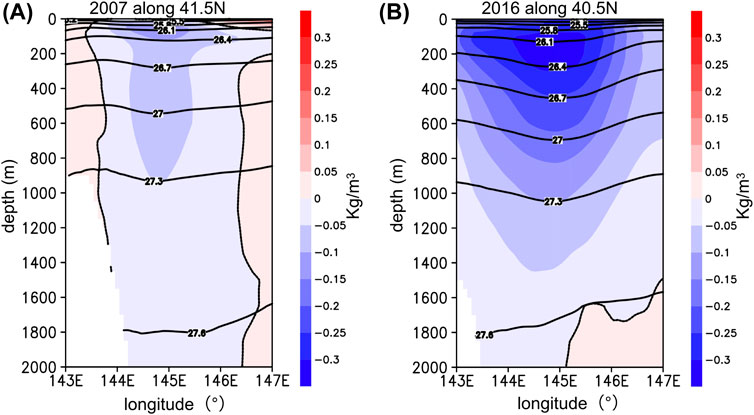
FIGURE 4. (A) Longitude-depth diagram of the yearly averaged σ_θ (contour) and σ_θ anomaly (shaded color) for the year 2007, along the 41.5° N-horizontal line from 143° E to 147° E which is indicated by the black line in Figure 3A. The unit is kg/m³. (B) Same as (A) but for the year 2016 along 40.5° N-horizontal line from 143° E to 147° E which is indicated by the black line in Figure 3B.

To evaluate the effect of seawater density anomalies on the PSF quantitatively and compare it with that of the SSH anomalies, we introduced a “steric effect on pressure on the seafloor” (hereafter SEP). The SEP was calculated at each grid point using daily vertical profiles of potential temperature and salinity from the ocean bottom to the sea surface of the JCOPE2M assimilation data. The SEP between the seafloor and the sea surface along the vertical pressure axis is defined as

$SEP=-\frac{1}{g}{\displaystyle \underset{p1}{\overset{p2}{\int }}\delta \text{d}p},(1)$

where g = 9.81 m/s² is the gravitational acceleration; p is the pressure (Pa); p1 is the pressure at the sea surface, that is, p1 is fixed to 0 Pa; p2 is the pressure close to the seafloor (if the ocean bottom depth is H m, p2 is set to H × 10⁴ Pa); and δ is the specific volume anomaly (m³/kg). The SEP has a unit of m in this definition. The definition of the SEP is similar to that of the steric height and geopotential distance anomaly, which are widely used in physical oceanography (see Supplementary Material 1). In this study, the monthly averaged SEP anomaly was calculated from the daily SEP, and a 15-months running mean filter was adopted for the monthly SEP anomaly. If the seawater density increases (decreases) from the mean value, that is, the seawater density anomaly is positive (negative), the vertically integrated δ will decrease (increase) from the mean value. This leads to a negatively smaller (larger) SEP value compared to the mean value, that is, a positive (negative) SEP anomaly. The positive (negative) SEP anomaly leads to an increase (decrease) in the PSF from the mean value. For example, an SEP anomaly of +1 m can lead to a +1 dbar (i.e., +1 × 10⁴ Pa) PSF anomaly. Figure 5A shows the spatial pattern of the yearly averaged SEP anomaly in 2007. The SEP anomaly pattern is very similar to that of the SSH anomaly (black contours in Figure 5A; also see Figure 3A), but with opposite anomaly signs. In 2016, the spatial pattern of the SEP anomaly (Figure 5B) was also similar to that of the SSH anomaly (black contours in Figure 5B; also see Figure 3B) with opposite anomaly signs. Thus, in both cases, the effects of positive SSH anomalies related to WCRs on the PSF were partly canceled out by the negative SEP anomalies due to the negative seawater density anomalies of the WCRs.

FIGURE 5

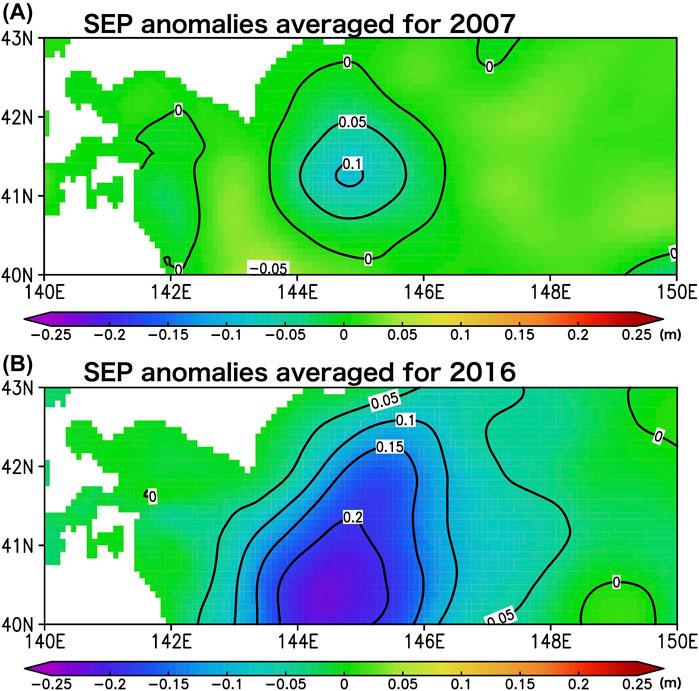
FIGURE 5. (A) Spatial distribution of the yearly averaged SEP anomaly for the year 2007 (color shades). The yearly averaged SSH anomalies for the year 2007 are shown by black contours. The unit is m. (B) Same as (A) but for the year 2016.

3.3 Introduction of Ocean Isostasy Anomaly (OIA)

To evaluate the total effect of the SSH anomaly and seawater density anomalies on the PSF anomaly, we introduced a variable called the ocean isostasy anomaly (OIA) in this study. The OIA is defined as,

$OIA=SSHanomaly+SEPanomaly.(2)$

The OIA represents the component of the SSH anomaly associated with the vertically uniform fluid motion with the same velocity as the bottom current, called the barotropic component in this study (see Supplementary Material 1). If the value of OIA is zero, it implies that the effect of the SSH anomaly on the PSF anomaly is perfectly canceled out by the SEP anomaly; that is, ocean isostasy is perfectly established when the OIA is zero. In this case, the total effect of the SSH and seawater density anomalies does not change the PSF. If the value of OIA is +1 m, that is, ocean isostasy is not perfectly established, the total effect of the SSH and seawater density anomalies will change the PSF anomaly by nearly +1 dbar.

Figure 6A shows the spatial pattern of the yearly averaged OIA in 2007. A relatively large positive OIA of approximately +0.025 m appeared around 41°N, 145°E during this period. In 2016, a relatively large OIA of approximately +0.025 m appeared at 40.5°N, 144.5°E (Figure 6B). Large positive anomalies were also found along the coast of Sanriku (around 40.5° N, 141.5° E; see Figure 1B for the location of Sanriku). It is also shown that relatively large negative OIAs of approximately −0.025 m appeared east of the positive OIA areas in 2007 and 2016. It is expected that strong negative SEP anomalies around the WCR area in 2016 (Figure 5B), related to the strong negative seawater density anomalies (Figure 4B), can effectively cancel out the strong positive SSH anomalies (black contours in Figure 5B represent SSH anomalies; also see Figure 3B). Due to such canceling effects of the SEP anomalies, the amplitudes of the OIA in 2016 were similar to those in 2007 (Figure 6), although the positive SSH anomalies were stronger in 2016 than in 2007 (black contours in Figures 5A,B; also see Figures 3A,B). As shown in Figures 3, 6, the amplitudes of the OIAs are nearly 10% of those of the SSH anomalies in large areas off the southeastern coast of Hokkaido, Japan.

FIGURE 6

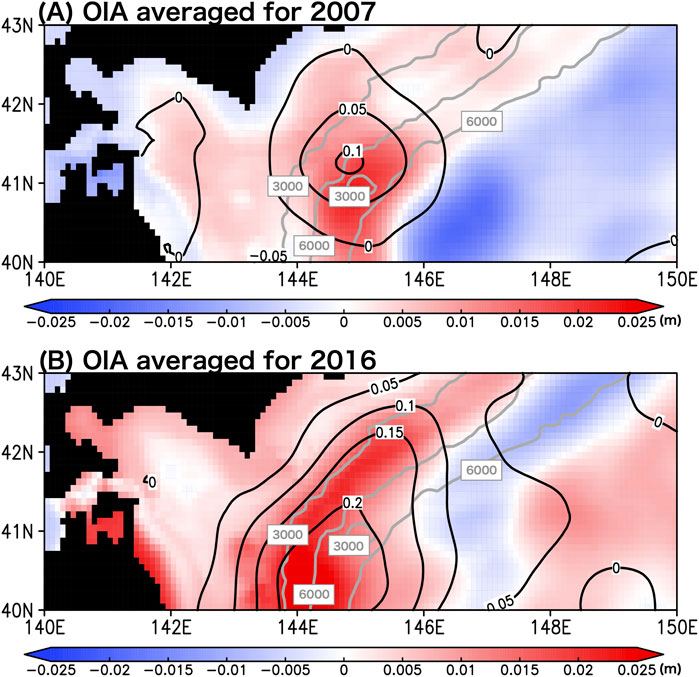
FIGURE 6. (A) Spatial distribution of the yearly averaged OIA for the year 2007 (shaded color). The yearly averaged SSH anomalies for the year 2007 are shown by black contours. The unit is m. The bottom depths of 3000 and 6000 m are shown by the gray solid contours. (B) Same as (A) but for the year 2016.

Here, we discuss the relationship between OIAs and SSH anomalies related to the WCRs. The OIAs exhibited non-homogeneous patterns in the WCR area, indicated by relatively large positive SSH anomaly regions (black contours in Figures 6A,B; also see Figures 3A,B), in both 2007 and 2016. In 2007, a relatively large positive OIAs appeared around 40.5°N, 145°E in the southern part of the WCR (Figure 6A), while, in most parts of the WCR region, the OIA values were positive but small. In 2016, a large positive OIA existed within a large part of the WCR area, as illustrated by the strong positive SSH anomalies exceeding 0.15 m (Figure 6B). However, at the eastern limb of the WCR centered at 41°N, 145.5°E, the positive OIA values were less than those in the other areas of the WCR. Large OIAs were found to be localized at the regions of water depths greater than 3000 m (see Figure 1B), where ocean isostasy was not perfectly established or the barotropic flow component remained in the WCR structure, as observed by Owens and Warren (2001). In the other small-OIA areas, ocean isostasy was thought to be established more completely.

3.4 Regression and Correlation Relationships Between SSH and SEP Anomalies

In the previous subsections, case studies focusing on the WCRs that occurred in 2007 and 2016 were conducted. In this subsection, we explore both the regression and correlation relationships between SSH and SEP anomalies over a long period, from August 2001 to May 2018. Figure 7A shows the spatial pattern of regression coefficients between SSH and SEP anomalies calculated for the period from August 2001 to May 2018. The regression coefficients represent the ratio of SEP anomalies to SSH anomalies. Figure 7A shows that large negative regression coefficients of nearly −0.9 are distributed in the offshore regions with bottom depths greater than 1000 m. This result implies that nearly 90% of the effect of the SSH anomaly on the PSF anomaly is canceled out by the SEP anomaly (i.e., seawater density anomaly) in those regions. In other words, the amplitudes of the OIAs are nearly 10% of those of the SSH anomalies due to the canceling effect of the seawater density anomalies in those regions. That is, the barotropic component of the SSH anomalies are nearly 10% of the total SSH anomalies in the offshore region on an interannual timescale, in general, supporting the results shown in Figures 3–6. In contrast to the offshore region, negative regression coefficients are small in coastal regions with bottom depths less than 1000 m, that is, shallower than the main pycnocline in the region. Thus, ocean isostasy is better established in the deep offshore region with bottom depths greater than 1000 m rather than in the shallow coastal areas with bottom depths less than 1000 m.

FIGURE 7

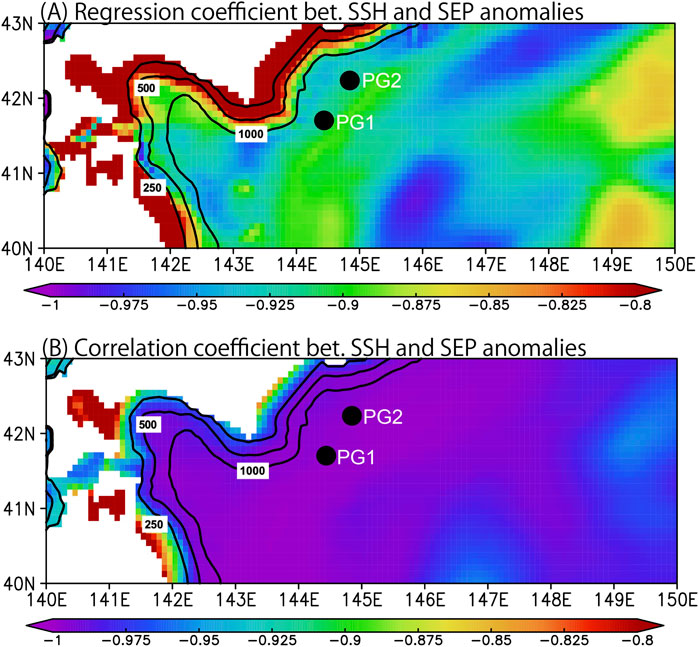
FIGURE 7. (A) Spatial distribution of the regression coefficient between SSH and SEP anomalies. The period for the calculation of the regression coefficient is from August 2001 to May 2018. That is, both the start and end periods of the 15-months running mean filter, in which the data cannot be adequately filtered by the running mean filter, were eliminated from the original analysis period. Black solid lines show contours of bottom depths of 250, 500, and 1000 m. Black circles denote the locations of PG1 and PG2. (B) Same as (A) but for the correlation coefficient.

Figure 7B shows the spatial pattern of correlation coefficients between the SSH and SEP anomalies during the analysis period. Large negative correlation coefficients of approximately −0.95 appeared in offshore areas and small negative values in coastal areas (Figure 7B), similar to the regression coefficients (Figure 7A). This means that the SSH and SEP anomalies are negatively in-phase in offshore regions. For example, in Figure 8A, scatter plots between SSH and SEP anomalies at PG1, which located in the offshore region (see Figure 7B and Figure 1B for the location of PG1), show clear negative correlation and regression relationships. The negative correlation and regression relationships between SSH and SEP anomalies are also shown by the timeseries of SSH and SEP anomalies at PG1 (black and red solid lines in Figure 8B). The correlation and regression coefficients are −0.9983 and −0.9167, respectively at PG1. Such negative correlation and regression relationships indicate that the effect of the SSH anomaly on the PSF is almost canceled out by the seawater density anomaly (i.e., SEP anomaly). As a result, the amplitude of the OIA (green solid line in Figure 8B) is much smaller than those of the SSH and SEP anomalies, which is in line with the results shown in Figures 3–6. At PG2, similar result is obtained (not shown here) and the correlation and regression coefficients are −0.9980 and −0.9153, respectively.

FIGURE 8

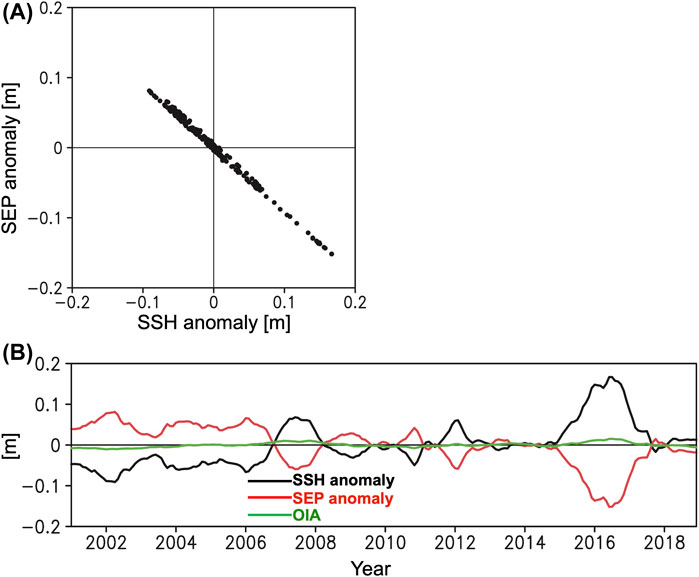
FIGURE 8. (A) Scatter plots between SSH and SEP anomalies at the closest grid point to PG1 for the period from January 2001 to December 2018. The unit is m. (B) Timeseries of the SSH anomaly (black thick solid line), SEP anomaly (red thick solid line), and OIA (green thick solid line) at PG1. The unit is m.

4 Discussions

4.1 Comparison Between the OIA and Observed PSF Anomalies at PG1 and PG2

In this subsection, we compare the OIA with the observed PSF anomalies at PG1 and PG2. Figures 9A,B show the OIAs from the JCOPE2M (gray solid line) and observed PSF anomalies (black solid line) at PG1 and PG2, respectively. During the analysis period, the OIAs range from approximately −1 × 10^–2 to +1 × 10^–2 m for PG1 and PG2. Although the PSF anomalies are nearly +5 × 10^–2 dbar in 2007 at PG1 (Figure 9A), the PSF anomalies at PG1 and PG2 ranged from -2 × 10^–2 to +2 × 10^–2 dbar for almost the entire period except for 2007 (Figures 9A,B).

FIGURE 9

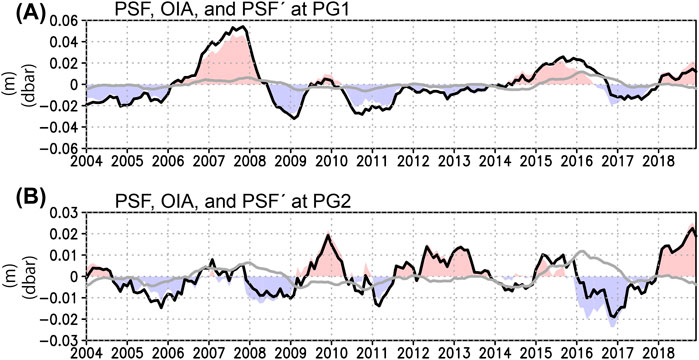
FIGURE 9. (A) Timeseries of OIA (in m; gray solid line), PSF anomalies (in dbar; black solid line), PSF anomalies after the OIAs were subtracted from the original PSF anomalies (PSF′) at PG1 (color shades of red and blue colors). A 1-m change in OIA is almost equal to 1-dbar change in PSF. Here, we assumed that a 1-m change in OIA is perfectly equal to 1-dbar change in PSF for calculating PSF′. OIAs were re-calculated using monthly climatologies from January 2004 to December 2018, to match the data length of the PSF at PG1 and PG2. (B) Same as (A) but for PG2.

The standard deviations of the OIAs and PSF anomalies were calculated from August 2004 to May 2018 at PG1 and PG2. At PG1, the standard deviations of the OIAs and PSF anomalies were 5.0 × 10^–3 m and 1.9 × 10^–2 dbar, respectively. At PG2, the standard deviations of the OIAs and PSF anomalies were 3.9 × 10^–3 m and 8.6 × 10^–3 dbar, respectively. As described in Section 3.3, a +1-m change in OIA will change the PSF anomaly by nearly +1 dbar. Thus, the standard deviations of the OIAs account for approximately 26 and 45% of those of the PSF anomalies, at PG1 and PG2, respectively. Therefore, it can be said that although the amplitude of the OIAs is approximately 10% of the SSH anomalies as described in the previous subsections, the amplitudes of the OIAs are not much less than those of the PSF anomalies at PG1 and PG2.

To discuss the effect of the OIAs on PSF anomalies at PG1 and PG2 after the 2003 Tokachi-oki earthquake, we calculated the PSF anomalies after the removal of the OIAs from the original PSF anomalies (hereafter PSF′) as follows,

$PS{F}^{\prime }=PSF-OIA.(3)$

The timeseries of PSF′ at PG1 and PG2 are shown as color shades of red and blue in Figures 9A,B, respectively. After the 2003 Tokachi-oki earthquake, both the PSF and PSF′ anomalies showed increasing tendencies from 2004 to 2007 at PG1 (Figure 9A). The PSF anomalies at PG1 increased from nearly −2.0 × 10^–2 to +5.0 × 10^–2 dbar during this period. On the other hand, positive values of PSF′ around 2007 were nearly +3.0 × 10^–2 to 4.5 × 10^–2 dbar in 2007, weaker than those of PSF around 2007 by approximately 1.0 × 10^–2 dbar, due to the positive OIAs in this period (Figure 9A). During 2004–2005, negative values of PSF′ at PG1 were almost the same as those of PSF, since the OIAs were nearly zero during this period (Figure 9A). As a result, the increasing tendency of PSF′ from 2004 to 2007 was weak compared with that of PSF. At PG2, relatively large positive values of PSF (nearly +5.0 × 10^–3 dbar) appeared around 2007, while PSF′ showed nearly zero due to positive OIAs in this period (Figure 9B). As a result, at PG2, PSF′ showed an increasing tendency from the late 2005 to mid-2006, although an increasing tendency of PSF is found from the late 2005 to early 2007.

As described in Section 3.1, the standard deviation from the JCOPE2M SSH anomalies is greater by approximately 6.0 × 10^–3 (1.7 × 10^–2) m than that from the AVISO-SSH anomalies at PG1 (PG2). The amplitudes of the OIAs at PG1 and PG2 were nearly 10% of those of the SSH anomalies, due to the canceling effect of the seawater density (i.e., SEP) against the effect of the SSH anomalies on the PSF changes on an interannual timescale, as described in Section 3.4. When it is assumed that the difference in the standard deviation between the JCOPE2M and AVISO SSH anomalies (hereafter, SDdif) is perfectly equivalent to the errors in the SSH anomalies of the JCOPE2M, the errors in the OIA can be estimated to be approximately 10% of the SDdif (see Supplementary Material 2). In this case, the OIA errors (PSF′ errors) at PG1 and PG2 are estimated to be approximately ±6.0 × 10^–4 and ±1.7 × 10^–3 m (dbar), respectively. Thus, there is a possibility that the OIA (PSF′) would be overestimated or underestimated by approximately 6.0 × 10^–4 m (dbar) at PG1 and by approximately 1.7 × 10^–3 m (dbar) at PG2, respectively. The error in PSF′ at PG1 (approximately ±6.0 × 10^–4 dbar) is less than one tenth of the differences in the amplitude between PSF and PSF′ (i.e., amplitude of the OIA) around the year 2007 at PG1, as described above. At PG2, the error in PSF′ (approximately ±1.7 × 10^–3 dbar) is approximately one third of the differences in amplitude between PSF and PSF′ around 2007, also as described above. Therefore, the difference in SSH anomalies between the JCOPE2M assimilation data and the AVISO observational data could not strongly affect the result for the year 2007 in Figure 9, especially at PG1. Additionally, it should be noted that observational errors were included in the observational AVISO-SSH data. The data assimilation could reduce the observational errors by use of the numerical ocean model simulation, if the numerical ocean model simulation adequately reproduced the real oceanic variations. Thus, the SDdif might not perfectly represent the error of the JCOPE2M SSH data; there is a possibility that the SDdif partly reflects the improvement in the SSH data accuracy by the JCOPE2M assimilation. Therefore, the error of the OIA (PSF′) would be less than the values estimated above. In future, improvement of data accuracies of both the assimilation data and the observed SSH data would provide more accurate estimations for the SSH, OIA and PSF′.

This result does not disprove the existence of the crustal deformations due to the afterslip related to the 2003 Tokachi-oki earthquake showing PSF increases of approximately 2.0 × 10^–1 m from 2003 to 2011 (Itoh et al., 2019) and the periodic SSE with an amplitude of approximately 5.0 × 10^–2 m (Uchida et al., 2016) around PG1 and PG2. It can be argued that subtracting OIAs from PSF anomalies on an interannual timescale would be useful to estimate interannual-scale PSF changes related to the slow earthquakes more precisely. In future, further studies focusing on the comparison between OIAs and PSF anomalies will be conducted.

In 2016, the OIAs showed an increasing tendency, while the PSF anomalies showed a decreasing tendency both at PG1 and PG2 (Figures 9A,B). The reason for this difference in tendency between the OIAs and PSF is unclear. It might be due to i) errors of temperature and salinity of the JCOPE2M assimilation data, associated with the ocean fluid structures in the 2016 WCR, ii) a remaining sensor drift component of the ocean bottom pressure gauges that was not removed by the linear and exponential functions used in this study (see Section 2.3), and iii) unknown interannual-scale seismic activities during this period. To explore the reason for this difference is beyond the scope of this study. In Section 4.5, the factors that are not considered in the JCOPE2M are described.

The results of the present study suggest that the OIAs should be estimated and compared with the PSF anomalies not only along the southeastern coast of Hokkaido, Japan, but also in other regions where oceanic currents and/or oceanic mesoscale eddies are dominant on an interannual timescale. These include areas such as the Dense Ocean floor Network system for Earthquakes and Tsunamis (DONET1 and DONET2) including the Kuroshio area, the Seafloor Observation Network for Earthquakes and Tsunamis along the Japan Trench (S-net) including the Kuroshio-Oyashio Confluence region, the Nankai Trough Seafloor Observation Network for Earthquakes and Tsunamis (N-net) including Kuroshio area, and other areas showing strong seismic activity and strong oceanic fluid variations in the world (e.g., Ariyoshi et al., 2016). If the amplitudes of OIA cannot be neglected, compared to PSF anomalies in such areas, the OIAs should be removed from the PSF anomalies to better detect the PSF changes due to crustal deformation related to SSEs and other slow crustal movements on an interannual timescale.

4.2 OIA Proxy

To calculate the OIAs, SSH and SEP anomalies are needed, as shown in Eq. (2). SSH anomalies can be calculated using the altimetric SSH anomaly data obtained from the AVISO website or other similar public institutions, instead of the SSH anomalies of the ocean assimilation data. The SEP is calculated using the vertical profile of the potential density from the seafloor to the sea surface, as shown in Eq. (1). To create the vertical profile of potential density, vertical profiles of the temperature and salinity data from the sea floor to the sea surface are required. Such data can be obtained from CTD observations by research vessels, XCTDs, mooring buoys, Argo floats, etc., as well as the ocean assimilation data and outputs of continuously stratified ocean numerical model hindcast simulations. Therefore, the analysis method used in this study, using the SSH anomalies and vertical profiles of temperature and salinity of the JCOPE2M, can be applied to such observational data and outputs of continuously stratified ocean numerical models. If vertical profiles of temperature and salinity data from the sea floor to the sea surface are not available for the analysis period, the SEP cannot be calculated directly. In this case, we can approximately estimate the OIA indirectly from the regression coefficient between the SSH and SEP anomalies, calculated using the data observed during a period before (or after) the analysis period in the analysis area. In this study, the estimated OIA using such a method is called the “proxy of OIA” (POIA). The POIA is calculated as follows: Using the regression coefficient between the SSH and SEP anomalies, the SEP anomaly is estimated as

$SEPanomaly=RC\times SSHanomaly,(4)$

where, RC is the regression coefficient between the SSH and SEP anomalies (i.e., RC is the ratio of the SEP anomaly to the SSH anomaly), as shown in Figure 7A. From Eqs. (2) and (4), POIA is calculated as

$POIA=\left(1+RC\right)\times SSHanomaly.(5)$

If RC is -0.9, as seen in the offshore area off the southeastern coast of Hokkaido as described in Section 3.4, POIA can simply be estimated from Eq. (5) as follows:

$POIA=0.1\times SSHanomaly.(6)$

To demonstrate the POIA method using Eq. (5), POIA was calculated by use of the regression coefficient between the SSH and SEP anomalies from the JCOPE2M (Figure 7A), and the observed altimetric SSH anomaly (AVISO SSH anomaly) at each grid point on an interannual timescale (Figure 10). Figure 10A shows the spatial pattern of the POIA averaged for the year 2007. It is shown in Figure 10A that the positive POIAs distributed in the WCR area with the positive SSH anomalies centered at 41.5°N, 145°E. It is also shown in Figure 10A that negative POIAs distributed along the coast of Sanriku and south of Hokkaido, Japan. Such spatial pattern of the POIA in 2007 is similar to that of the OIA in 2007 (Figure 6A). However, the POIAs in the south part of the WCR area show negative values (Figure 10A), while the OIAs in this area show positive values (Figure 6A). In the year 2016, both the POIAs (Figure 10B) and OIAs (Figure 6B) show relatively strong positive values in the WCR area and the areas along the coast of Sanriku and south of Hokkaido, Japan. However, positive POIA distributed around 41°N, 147°E and around 42.5°N, 148°E (Figure 10B), while the OIAs in these areas displayed negative values in 2016 (Figure 6B). Along the south coast of Hokkaido, the positive values of the POIA (Figure 10B) is stronger by approximately 0.01 m than those of the OIA (Figure 6B). It is also shown that the amplitudes of POIA (Figure 10A) near the center of the WCR (around 41.5°N, 145°E) were smaller by approximately 0.005 m than those of OIA (Figure 6A). The differences in the spatial pattern and the amplitudes between the POIA and OIA would be caused by the error in the observed altimetric SSH anomalies used in calculation of the POIA, and that in the assimilation data used in the calculations for the OIA and for the regression coefficient between SSH and SEP anomalies. It should be also noted that the effective spatial resolution at midlatitude of the observed altimetric SSH data is estimated to be approximately 200 km (Ballarotta et al., 2019), although the horizontal grid interval of the AVISO-SSH dataset is 1/4° × 1/4° (i.e., approximately 25 km × 25 km in midlatitude). Therefore, the differences in the spatial pattern and in the amplitudes between the POIA and OIA include the error due to the low spatial resolution of the AVIOS-SSH data compared to the 1/12° × 1/12° spatial resolution of the JCOPE2M assimilation data. To evaluate quantitatively each error is beyond the scope of this study. The result in this study suggests that the POIA method could be more useful in the areas near the center of the WCRs and along the coast of the Sanriku and south of Hokkaido compared to the other areas in the analysis area, while there is a difference of approximately 0.005–0.01 m in amplitude between the POIA and OIA. It can be said that the next-generation of the observed SSH anomalies could provide more accurate POIA in the future.

FIGURE 10

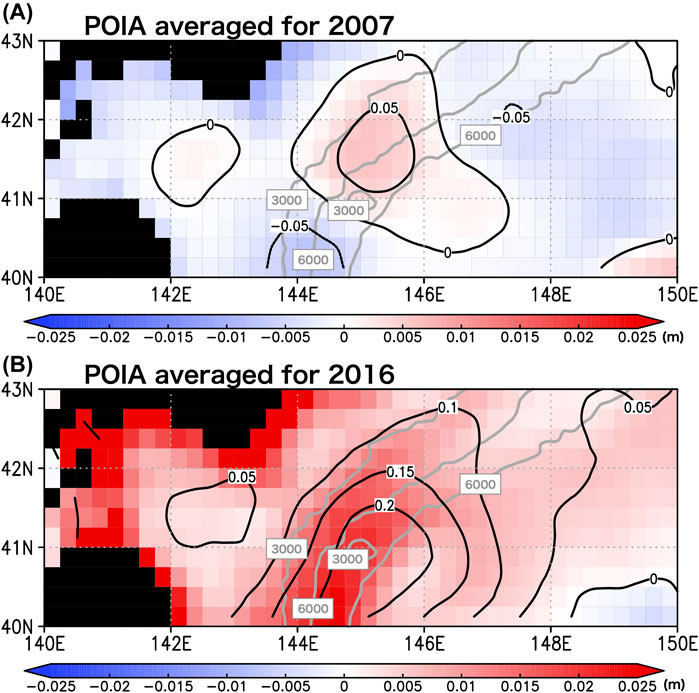
FIGURE 10. (A) Spatial distribution of the yearly averaged POIA that were calculated by use of the regression coefficient between the SSH and SEP anomalies from the JCOPE2M (Figure 7A), and the observed altimetric SSH anomalies (AVISO SSH anomalies) at each grid point on an interannual timescale for the year 2007 (shaded color). The yearly averaged the AVISO SSH anomalies for the year 2007 are shown by black contours. The unit is m. The bottom depths of 3000 and 6000 m are shown by the gray solid contours. To make the POIA, the regression coefficient between SSH and SEP anomalies from the JCOPE2M with the 1/12° × 1/12° grid were re-gridded to match the spatial grid point of the AVISO SSH anomalies with the 1/4° × 1/4° grid by use of a spatial averaging of the regression coefficient using a 0.1° spatial window centered at each grid point of the AVISO SSH anomalies. (B) Same as (A) but for the year 2016.

Note that the definition of POIA requires that the regression relationship between SSH and SEP does not change significantly from the period in which the RC is calculated for the analysis period. For the area off the southeastern coast of Hokkaido, Japan, the regression coefficient on an interannual timescale does not seem to change significantly in the analysis period as shown in Figures 8A,B. However, there are oceanic variations longer than interannual timescales, namely, longer than the timescale of the El Niño–Southern Oscillation (ENSO), such as quasi-decadal ENSO-like variations (e.g., Luo and Yamagata, 2001; Hasegawa and Hanawa, 2003b; White et al., 2003; Hasegawa et al., 2007a, 2013), interdecadal or multidecadal variations (e.g., Tanimoto et al., 1993; Mantua et al., 1997; Minobe, 1999; Hasegawa et al., 2007b), and climate regime shifts (e.g., Nitta and Yamada, 1989; Trenberth, 1990; Yasunaka and Hanawa, 2003) in the global ocean. Thus, when the POIA is used, it is suitable to consider a possible long-term change in the regression relationship between the SSH and SEP anomalies. It should also be noted that this method should be adopted in regions where the SSH and SEP anomalies are negatively in-phase; that is, the regions in which the correlation coefficient between the SSH and SEP anomalies is negatively high. For example, Eq. (5) can be applied to the deep offshore area off the southeastern coast of Hokkaido, Japan, where the correlation coefficients between the SSH and SEP anomalies are negatively high (nearly −0.95), as shown in Figure 7B.

4.3 Increasing Trend of SSH Anomaly at PG1 and PG2

Figure 2 shows an increasing trend in the SSH anomalies of both the JCOPE2M and observational data for the analysis period. As shown in Figure 8, the positive trend of the SSH anomalies at PG1 is almost canceled by the negative SEP anomalies (i.e., negative seawater density anomalies). In addition, Figure 9 shows that the OIAs do not show strong linear trends. Thus, it can be said that linear OIA trends could be neglected on an interannual timescale in this region. Moreover, it could be speculated that if the increasing trend of the SSH anomalies in this area is generated by global warming, global warming could also cause a warming trend of the seawater. Thus, the increasing trend of SSH could be, at least partly, canceled out by the decreasing trend of seawater density (i.e., decreasing trend of SEP) due to the warming trend of seawater. To explore the linear trends and their relationship to the global warming will be further investigated in future works.

4.4 Relationship Between the Strong WCR in 2016 and the Preceding Strongest El Niño

Hasegawa et al. (2019) indicated a possible relationship between ENSO and WCRs off the southeastern coast of Hokkaido, Japan, using observational data from 2003 to 2014. They showed that positive SSH anomalies related to WCRs appeared in this region approximately 30 months after the onset of El Niño events. Thus, it is suggested that the preceding El Niño events could be used as prediction indicators for WCRs in this region. In this study, as shown in Figures 2, 3, very large positive SSH anomalies related to the strong WCR appeared in this region in 2016. It has been reported that the tropical Pacific showed the pre-condition for an El Niño event in 2014, followed by a very strong El Niño event from 2015 to 2016 (Hu and Fedorov, 2017). This El Niño event is the strongest event during the observational record. It can be speculated that the strong El Niño event leads to the strong WCR with the strong SSH anomalies off the southeastern coast of Hokkaido, Japan, in 2016. In future work, the generation mechanism of strong WCRs by strong El Niño events will be further investigated to improve the prediction skill of WCRs with a lead time longer than one year.

4.5 Factors Not Considered in the JCOPE2M

Several factors were not adequately considered in the JCOPE2M. First, the ocean model used in the JCOPE2M assimilation scheme does not include a sea ice model. Therefore, the oceanic volume changes due to sea ice change were not directly calculated in the ocean model of the JCOPE2M. The lack of such seawater volume changes could lead to uncertainties in the SSH anomalies of the JCOPE2M. Nevertheless, the changes in seawater temperature and salinity due to sea ice changes were included in the observational temperature and salinity data (CTD data) that were assimilated into the JCOPE2M. Thus, temperature and salinity data of the JCOPE2M contained the effect of sea ice changes to some degree. It would be useful to include a sea ice model in the ocean model to produce more accurate assimilation data in the future. Secondly, in the JCOPE2M, basin-wide and seasonal cycle steric effects are removed from SSH anomalies in order to effectively represent oceanic mesoscale eddies (Kagimoto et al., 2008). Thus, when seasonal cycle changes of SSH and OIA are investigated, this point should be considered. In the present study, as described in Section 2, seasonal cycle changes (i.e., monthly climatologies) of SSH data and other variables were removed from the anomalies to focus on the interannual-scale variations. The JCOPE2M does not include a tide model in its ocean model. The lack of a tide model in the JCOPE2M is favorable for this study, as we did not intend to analyze the oceanic fluid changes due to tides, as described in Section 2. Such factors may be considered in the future assimilation systems depending on the analysis target and purpose.

4.6 Future Interdisciplinary Studies

In this study, it was shown that ocean isostasy is better established in the offshore regions with ocean bottom depths greater than 1000 m. It can be speculated that the ocean bottom shape along with the bottom depth might also affect the ocean current and ocean structure that can affect ocean isostasy. In future, collaboration with theoretical studies of ocean fluid dynamics focusing on the bottom depth and shape (e.g., Uehara and Miyake, 1999; Kubokawa, 2008; Miyama et al., 2018) will be conducted to further explore the relationship between ocean bottom depth/bottom shape and degree of ocean isostasy.

In this study, we focused on ocean fluid changes due to the WCRs found off the southeastern coast of Hokkaido, Japan. It has been reported that the WCRs also play an important role in marine biogeochemical changes and fisheries resources changes (e.g., Imanaga and Hirano, 1984; Chiang and Taniguchi, 2000; Kaeriyama et al., 2013). In addition, recently Sugimoto et al. (2017) pointed out that the warm sea surface temperatures of the WCRs off Sanriku, Japan, have an impact on the local atmospheric changes in the region. The WCRs off the southeastern coast of Hokkaido, Japan, may have a similar impact on atmospheric changes. Thus, interdisciplinary studies focusing on the WCRs among seismology, physical oceanography, marine biogeochemistry, fisheries science, atmospheric science, etc. may lead to new approaches of science activities, including the promotion of joint use of various data, collaboration on in-situ observations in this area, and developing of ocean and atmosphere assimilation models including such new data. Additionally, such interdisciplinary studies would be conducted in the future, not only for the area off the southeastern coast of Hokkaido, Japan, but also for the coastal areas of Sanriku (i.e., areas including the S-net) along which WCRs propagate northward to the southeastern coast of Hokkaido, Japan, the Kuroshio area (i.e., areas including the N-net and DONET1/DONET2), and other areas in the world where seismic activity is strong, and oceanic currents and mesoscale eddies are dominant.

5 Concluding Remarks

In this study, we explored the relationship between the SSH and sea water density anomalies (i.e., SEP anomalies), with a special reference to the WCRs off the southeastern coast of Hokkaido, Japan, on an interannual (i.e., year-to-year) timescale from January 2001 to December 2018, using eddy-resolving ocean assimilation data of the JCOPE2M based on a continuously stratified numerical model. We show that positive SSH anomalies with amplitudes in the order of 0.1 m appeared off the southeastern coast of Hokkaido, Japan, in the years 2007 and 2016 in association with WCRs. During this period, negative SEP anomalies with amplitudes similar to those of the SSH anomalies but with opposite signs, related to the oceanic baroclinic structures of WCRs with negative seawater density anomalies, also appeared in this region. We further show that nearly 90% of the effect of the positive SSH anomalies on the PSF anomalies are canceled out by negative SEP anomalies (i.e., negative seawater density anomalies), especially in offshore regions with ocean bottom depths deeper than 1000 m. The results of this study support our previous observational study (Hasegawa et al., 2019) that showed that the PSF anomalies are nearly zero when large positive SSH anomalies and oceanic baroclinic structures with negative seawater density anomalies due to a WCR appeared at PG2 in 2007.

To evaluate the total effect of the SSH and seawater density (i.e., SEP) anomalies on the PSF anomalies, the OIA was introduced in this study. The results show that the amplitudes of OIAs are nearly 10% of those of SSH anomalies, ranging from −0.025 m to +0.025 m in 2007 and 2016. This is because nearly 90% of the effect of SSH anomalies on the PSF is canceled out by the seawater density anomalies in deep offshore areas with water depths greater than 1000 m. Thus, it can be said that ocean isostasy is better established in deep offshore regions than in shallow coastal regions.

The results of this study suggest that the effect of OIAs, that is, ocean fluid changes, on PSF anomalies cannot be neglected on an interannual timescale in the areas off the southeastern coast of Hokkaido, Japan. In past studies, ocean barotropic effects on PSF were explored using a non-linear, single-layer barotropic ocean model on a shorter timescale (Inazu et al., 2012; Muramoto et al., 2019). Based on the case studies concerning the WCRs off the southeastern coast of Hokkaido, Japan, including the Kuril Trench, the results of the present study suggest that the effect of the OIA changes on PSF anomalies on an interannual timescale should be taken into consideration as well as the shorter-timescale barotropic changes. Moreover, the results indicate that the effect of OIA changes should be estimated when PSF anomalies due to crustal deformation related to slow earthquakes, including long-term SSEs, are explored on an interannual timescale. Accordingly, if an OIA change is not negligible, compared with the PSF anomaly change, the OIA should be removed from the PSF change to better evaluate the PSF anomaly change due to crustal deformations, not only in the region off the southeast coast of Hokkaido, Japan, but also in other regions.

Data Availability Statement

The JCOPE2M assimilation data were provided by the Application Laboratory of JAMSTEC. The data can be distributed to any interested person. To use the JCOPE2M assimilation data, it is required to contact the member of the Application Laboratory via email (jcope@jamstec.go.jp). For details of the usage of the JCOPE2M assimilation data, please see the website of the Application Laboratory of JAMSTEC (http://www.jamstec.go.jp/jcope/htdocs/e/distribution/index.html). The altimetric SSH data were provided by AVISO. The AVISO SSH data is available for download from the FTP website of the Copernicus Marine and Environment Monitoring Service (CMEMS). PSF data at PG 1 and PG 2 were obtained as a part of the JAMSTEC observational project of the “Long-Term Deep Sea Floor Observatory off Kushiro -Tokachi in the Kuril Trench”. The PSF data is available on the JAMSTEC website for this project (http://www.jamstec.go.jp/scdc/top_e.html).

Author Contributions

TH calculated monthly anomalies of the assimilation data from the daily data, analyzed them, made figures, and wrote this manuscript. TH also calculated the observed monthly PSF anomalies at PG1 and PG2 from the hourly data and analyzed the observed altimetric SSH data. AN calculated the coefficients used for the removal of sensor drift of PSF at PG1 and PG2, gave important comments about the definitions of SEP and OIA, barotropic and baroclinic component of the WCRs, variabilities of Kuroshio, Oyashio, and WCRs, and made a prototype of Fig 1. KA gave important comments about the OIA, the afterslip related to the 2003 Tokachi-oki earthquake, SSEs, other crustal deformations on an interannual timescale. TM conducted an initial check of the SSH and seawater density vertical profiles of JCOPE2M in the analysis region and confirmed that JCOPE2M suitably reproduces the ocean structures related to WCRs. TM also provided the important comments about the factors not considered by the JCOPE2M. TM and KA also gave important comments concerning the idea of POIA. HM made hourly PSF data from the raw data at PG1 and PG2 and performed their initial checks and provided important comments about the data procedure for making the hourly PSF data at PG 1and PG2 and the increasing trends of SSH anomalies at PG1 and PG2. RI checked and provided the raw PSF data for PG1 and PG2. MW gave important comments about the marine biogeochemical studies related to the WCRs off the southeastern coast of Hokkaido, Japan. All coauthors collaborated with the corresponding author (TH) in the construction of the manuscript and approved the final manuscript.

Funding

This work was partly supported by the Japan Society for the Promotion of Science (JSPS), Grant-in-Aid for Scientific Research (KAKENHI) Grant Nos. JP15H02835, JP15H04228, JP17K05660, JP17K19093, JP18H03726, JP19H02411, JP20H04349, JP20H2236, and JP20K04072.

Conflict of Interest

The authors declare that this study was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The satellite altimeter data were provided by AVISO. The authors wish to express their sincere thanks to Ruochao Zhang for help with the FTP of the JCOPE2M assimilation data. The authors would also like to thank Youichi Tanimoto, Atsushi Kubokawa, Takeshi Horinouchi, Kay I. Ohshima, Kimio Hanawa, Yosuke Fujii, Masanori Konda, Kazuyuki Uehara, Yoshimi Kawai, Fumiaki Kobashi, Shusaku Sugimoto, Toshio Suga, Takane Hori, members of the Faculty of Environmental Earth Science/Graduate School of Environmental Science at Hokkaido University, members of the Physical Oceanography Laboratory at Tohoku University, and members of the Research Institute for Maine Geodynamics at JAMSTEC for their helpful discussions, suggestions, comments, support, and encouragements. The authors would also like to thank Editage (www.editage.com) for English language editing. The authors are deeply grateful to the editor, Dr Laura Wallace (University of Texas), and two reviewers for their constructive comments during the review process.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.600930/full#supplementary-material.

References

Aoki, S., Imawaki, S., and Ichikawa, K. (1995). Baroclinic disturbances propagating westward in the Kuroshio Extension region as seen by a satellite altimeter and radiometers. J. Geophys. Res. 100, 839–855. doi:10.1029/94JC02255

CrossRef Full Text | Google Scholar

Araki, E., Saffer, D. M., Kopf, A. J., Wallace, L. M., Kimura, T., Machida, Y., et al. IODP (2017). Expedition 365 shipboard scientist. Science 356, 1157–1160. doi:10.1126/science.aan3120

PubMed Abstract | CrossRef Full Text | Google Scholar

Argo Science Team, (1998). On the design and implementation of Argo: an initial plan for a global array of profiling floats. GODAE report. 5, Melbourne, VIC: GODAE Internal Project Office.

CrossRef Full Text | Google Scholar

Argo Science Team, (2001). “Argo: the global array of profiling floats,” in Observing the oceans in the 21st century. Editors C. J. Koblinsky, and N. R. Smith (Melbourne: GODAE Project Office, Bureau of Meteorology), 248–258.

CrossRef Full Text | Google Scholar

Ariyoshi, K., Matsumoto, H., Inoue, T., Nagano, A., Hasegawa, T., Kido, M., et al. (2016). “Extraction of crustal deformations and oceanic fluctuations from ocean bottom pressures,” in OCEANS 2016 MTS/IEEE Monterey, San Francisco, CA, September 19–22, 2016, 1–5.

CrossRef Full Text | Google Scholar

AVISO (2008). Technical Reports. SSALTO/DUACS user handbook: (M)SLA and (M)ADT near-real time and delayed time products. CLS, ramonville st agnes. Available at: https://icdc.cen.uni-hamburg.de/fileadmin/user_upload/icdc_Dokumente/AVISO/hdbk_duacs.pdf (Accessed October 3, 2008).

CrossRef Full Text | Google Scholar

Ballarotta, M., Ubelmann, C., Pujol, M.-I., Taburet, G., Fournier, F., Legeais, J.-F., et al. (2019). On the resolutions of ocean altimetry maps. Ocean Sci. 15, 1091–1109. doi:10.5194/os-15-1091-2019

CrossRef Full Text | Google Scholar

Chiang, K.-P., and Taniguchi, A. (2000). Distribution and modification of diatom assemblages in and around a warm core ring in the western North pacific Frontal zone east of Hokkaido. J. Plankton Res. 22, 2061–2074. doi:10.1093/plankt/22.11.2061

CrossRef Full Text | Google Scholar

DeMets, C., Gordon, R., Argus, D., and Stein, S. (1990). Current plate motion. Geophys. J. Int. 101, 425–478. doi:10.1111/j.1365-246X.1990.tb06579.x

CrossRef Full Text | Google Scholar

Ebuchi, N., and Hanawa, K. (2000). Mesoscale eddies observed by TOLEX-ADCP and TOPEX/POSEIDON altimeter in the Kuroshio recirculation region south of Japan. J. Oceanogr. 56, 43–57. doi:10.1023/A:1011110507628

CrossRef Full Text | Google Scholar

Franco, S., Kostoglodov, V., Larson, K., Manea, V., Manea, M., and Santiago, J. (2005). Propagation of the 2001–2002 silent earthquake and interplate coupling in the Oaxaca subduction zone, Mexico, Earth Planet. Sp. 57, 973–985. doi:10.1186/BF03351876

CrossRef Full Text | Google Scholar

Hasegawa, T., Ando, K., Ueki, I., Mizuno, K., and Hosoda, S. (2013). Upper-ocean salinity variability in the tropical Pacific: case study for quasidecadal shift during the 2000s using TRITON buoys and Argo floats. J. Clim. 26, 8126–8138. doi:10.1175/JCLI-D-12-00187.1

CrossRef Full Text | Google Scholar

Hasegawa, T., and Hanawa, K. (2003a). Heat content variability related to ENSO events in the Pacific. J. Phys. Oceanogr. 33, 407–421. doi:10.1175/1520-0485(2003)033<0407:HCVRTE>2.0.CO;2

CrossRef Full Text | Google Scholar

Hasegawa, T., and Hanawa, K. (2003b). Decadal-scale variability of upper ocean heat content in the tropical Pacific. Geophys. Res. Lett. 30, 1272. doi:10.1029/2002GL016843

CrossRef Full Text | Google Scholar

Hasegawa, T., Nagano, A., Matsumoto, H., Ariyoshi, K., and Wakita, M. (2019). El Niño-related sea surface elevation and ocean bottom pressure enhancement associated with the retreat of the Oyashio southeast of Hokkaido, Japan. Mar. Geophys. Res. 40, 505–512. doi:10.1007/s11001-019-09392-8

CrossRef Full Text | Google Scholar

Hasegawa, T., Yasuda, T., and Hanawa, K. (2007a). Generation mechanism of quasidecadal variability of upper ocean heat content in the equatorial Pacific Ocean. J. Geophys. Res. 112, C08012. doi:10.1029/2006JC003755

CrossRef Full Text | Google Scholar

Hasegawa, T., Yasuda, T., and Hanawa, H. (2007b). Multidecadal variability of the upper ocean heat content anomaly field in the North Pacific and its relationship to the Aleutian Low and the Kuroshio transport. Pap. Meteor. Geophys. 58, 155–166. doi:10.2467/mripapers.58.155

CrossRef Full Text | Google Scholar

Hirose, H., and Obara, K. (2005). Repeating short- and long-term slow slip events with deep tremor activity around the Bungo channel region, southwest Japan. Earth Planet. Sp. 57, 961–972. doi:10.1186/BF03351875

CrossRef Full Text | Google Scholar

Hu, S., and Fedorov, A. V. (2017). The extreme El Niño of 2015–2016 and the end of global warming hiatus. Geophys. Res. Lett. 44, 3816–3824. doi:10.1002/2017GL072908

CrossRef Full Text | Google Scholar

Ichikawa, K., and Imawaki, S. (1994). Life history of a cyclonic ring detached from the Kuroshio Extension as seen by the Geosat altimeter. J. Geophys. Res. 99, 15953–15966. doi:10.1029/94JC01139

CrossRef Full Text | Google Scholar

Ide, S., Beroza, G., Shelly, D., and Uchide, T. (2007). A scaling law for slow earthquakes. Nature 447, 76–79. doi:10.1038/nature05780

PubMed Abstract | CrossRef Full Text | Google Scholar

Imanaga, D., and Hirano, T. (1984). Horizontal distribution of the Japanese sardine in relation to oceanic front at the purse seine fishing grounds southeast of Hokkaido. Null. Jap. Soc. Sci. Fish. 50, 577–589.

CrossRef Full Text | Google Scholar

Inazu, D., Hino, R., and Fujimoto, H. (2012). A global barotropic ocean model driven by synoptic atmospheric disturbances for detecting seafloor vertical displacements from in situ ocean bottom pressure measurements. Mar. Geophys. Res. 33, 127–148. doi:10.1007/s11001-012-9151-7

CrossRef Full Text | Google Scholar

Ito, S., Uehara, K., Miyao, T., Miyake, H., Yasuda, I., Watanabe, T., et al. (2004). Characteristics of SSH anomaly based on TOPEX/POSEIDON altimetry and in situ measured velocity and transport of Oyashio on OICE. J. Oceanogr. 60, 425–438. doi:10.1023/B:JOCE.0000038059.54334.6b

CrossRef Full Text | Google Scholar

Itoh, S., and Sugimoto, T. (2002). Behavior of warm-core rings in a double-gyre wind-driven ocean circulation model. J. Oceanogr. 58:651–660. doi:10.1023/A:1022838205678

CrossRef Full Text | Google Scholar

Itoh, Y., Nishimura, T., Ariyoshi, K., and Matsumoto, H. (2019). Interplate slip following the 2003 Takashi-oki earthquake from ocean bottom pressure gauge and land GNSS data. J. Geophys. Res. 124, 4205–4230. doi:10.1029/2018JB016328

CrossRef Full Text | Google Scholar

Joyce, T. M., and Dunworth‐Baker, J. (2003). Long‐term hydrographic variability in the northwest pacific ocean. Geophys. Res. Lett. 30, 1043. doi:10.1029/2002GL015225

CrossRef Full Text | Google Scholar

Kaeriyama, H., Ambe, D., Shimizu, Y., Fujimoto, K., Ono, T., Yonezaki, S., et al. (2013). Direct observation of 134Cs and 137Cs in surface seawater in the western and central North Pacific after the Fukushima Dai-ichu nuclear power plant accident. Biogeosciences 10, 4287–4295. doi:10.5194/bg-10-4287-2013

CrossRef Full Text | Google Scholar

Kagimoto, T., Miyazawa, Y., Guo, X., and Kawajiri, H. (2008). “High resolution Kuroshio forecast system: description and its applications,” in High resolution numerical modelling of the atmosphere and ocean. Editors K. Hamilton, and W. Ohfuchi (New York, NY: Springer).

CrossRef Full Text | Google Scholar

Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., and Gandin, L. (1996). The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–471. doi:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2

CrossRef Full Text | Google Scholar

Kawabe, M. (2005). Variations of the Kuroshio in the southern region of Japan—condition for large meander of the Kuroshio. J. Oceanogr. 61, 529–537. doi:10.1007/s10872-005-0060-0

CrossRef Full Text | Google Scholar

Kawaguchi, K., Hirata, K., Mikada, H., Kaiho, Y., and Iwase, R. (2000). “An expendable deep seafloor monitoring system for earthquake and tsunami observation network,” in OCEANS 2000 MTS/IEEE Conference and Exhibition, San Francisco, CA, September 11–14, 2000, 3, 1719–1722.

CrossRef Full Text | Google Scholar

Kobayashi, A., and Tsuyuki, T. (2019). Long-term slow slip event detected beneath the Shima Peninsula, central Japan, from GNSS data. Earth Planet. Sp. 71, 60. doi:10.1186/s40623-019-1037-3

CrossRef Full Text | Google Scholar

Kono, T. (1997). Modification of the Oyashio water in the Hokkaido and Tohoku areas. Deep Sea Res. 44, 669–688. doi:10.1016/S0967-0637(96)00108-2

CrossRef Full Text | Google Scholar

Kubokawa, A. (2008). Quasigeostrophic planetary waves in a two-layer ocean with one-dimensional periodic bottom topography. Geophys. Astrophys. Fluid Dyn. 102, 119–137. doi:10.1080/03091920701614334

CrossRef Full Text | Google Scholar

Kuroda, H., Wagawa, T., Shimizu, Y., Ito, S.-I., Kakehi, S., and Okunishi, T. (2015). Interdecadal decrease of the Oyashio transport on the continental slope off the southeastern coast of Hokkaido, Japan. J. Geophys. Res. 120, 2504–2522. doi:10.1002/2014JC10402

CrossRef Full Text | Google Scholar

Luo, J., and Yamagata, T. (2001). Long-term El niño-southern oscillation (ENSO)-like variation with special emphasis on the south pacific. J. Geophys. Res. 106, 22211–22227. doi:10.1029/2000JC000471

CrossRef Full Text | Google Scholar

Mantua, N. J., Hare, S. R., Zhang, Y., and Wallace, J. M., and Francis, R. C. (1997). A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Amer. Meteor. Soc. 78, 1069–1079. doi:10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2

CrossRef Full Text | Google Scholar

McPhaden, M. J., Zebiak, S. E., and Glantz, M. H. (2006). ENSO as an integrating concept in earth science. Science 314, 1740–1745. doi:10.1126/science.1132588

PubMed Abstract | CrossRef Full Text | Google Scholar

Mellor, G. L., Hakkinen, S., Ezer, T., and Patchen, R. (2002). “A generalization of a sigma coordinate ocean model and an inter comparison of model vertical grids,” in Ocean forecasting: conceptual basis and applications. Editors N. Pinardi, and J. D. Woods (New York: Springer), 55–72.

CrossRef Full Text | Google Scholar

Minobe, S. (1999). Resonance in bidecadal and pentadecadal climate oscillations over the North Pacific: role in climate regime shifts. Geophys. Res. Lett. 26, 855–858. doi:10.1029/1999GL900119

CrossRef Full Text | Google Scholar

Miyama, T., Mitsudera, H., Nishigaki, H., and Furue, R. (2018). Dynamics of a quasi-stationary jet along the subarctic front in the North pacific ocean (the western isoguchi jet): an ideal two-layer model. J. Phys. Oceanogr. 48, 807–830. doi:10.1175/jpo-d-17-0086.1

CrossRef Full Text | Google Scholar

Miyashita, K. (1987). A model of plate convergence in southwest Japan, inferred from leveling data associated with the 1946 Nanaimo Earthquake. J. Phys. Earth. 35, 449–467. doi:10.4294/jpe1952.35.449

CrossRef Full Text | Google Scholar

Miyazaki, S., Segall, P., Fukuda, J., and Kato, T. (2004). Space time distribution of afterslip following the 2003 Takashi-oki earthquake: implications for variations in fault zone frictional properties. Geophys. Res. Lett. 31, L06623, doi:10.10129/2003GL019410

CrossRef Full Text | Google Scholar

Miyazawa, Y., Kuwano-Yoshida, A., Doi, T., Nishikawa, H., Narazaki, T., Fukuoka, T., et al. (2019). Temperature profiling measurements by sea turtles improve ocean state estimation in the Kuroshio-Oyashio Confluence region. Ocean Dyn. 69, 267–282. doi:10.1007/s10236-018-1238-5

CrossRef Full Text | Google Scholar

Miyazawa, Y., Varlamov, S. M., Miyama, T., Guo, X., Kiyomatsu, K., Kachi, M., et al. (2017). Assimilation of high-resolution sea surface temperature data into an operational nowcast/forecast system around Japan using a multi-scale three-dimensional variational scheme. Ocean Dyn. 67, 713–728. doi:10.1007/s10236-017-1056-1

CrossRef Full Text | Google Scholar

Muramoto, T., Ito, Y., Inazu, D., Wallace, L. M., Hino, R., Suzuki, S., et al. (2019). Seafloor crustal deformation on ocean bottom pressure records with nontidal variability corrections: Application to Hikurangi margin, New Zealand. Geophys. Res. Lett. 46, 303–310. doi:10.1029/2018GL080830

CrossRef Full Text | Google Scholar

Nagano, A., Hasegawa, T., Matsumoto, H., and Ariyoshi, K. (2018). Bottom pressure change associated with the 2004–2005 large meander of the Kuroshio south of Japan. Ocean Dyn. 68, 847–865. doi:10.1007/s10236-018-1169-1

CrossRef Full Text | Google Scholar

Nagano, A., Yamashita, Y., Hasegawa, T., Ariyoshi, K., Matsumoto, H., and Shinohara, M. (2019). Characteristics of an atypical large-meander path of the Kuroshio current south of Japan formed in September 2017. Mar. Geophys. Res. 40, 525–539. doi:10.1007/s11001-018-9372-5

CrossRef Full Text | Google Scholar

Nakata, R., Hino, H., Kuwatani, T., Yoshioka, S., Okada, M., and Hori, T. (2017). Discontinuous boundaries of slow slip events beneath the Bungo Channel, southwest Japan. Sci. Rep. 7, 6129. doi:10.1038/s41598-017-06185-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishikawa, T., Matsuzawa, T., Ohta, K., Uchida, N., Nishimura, T., and Ide, S. (2019). The slow earthquake spectrum in the Japan Trench illuminated by the S-net seafloor observatories. Science 365, 808–813. doi:10.1126/science.aax5618

PubMed Abstract | CrossRef Full Text | Google Scholar

Nitani, H. (1972). “Beginning of the Kuroshio,” in Kuroshio-its physical aspects. Editors H. Stommel, and K. Yoshida (Tokyo: University of Tokyo Press), 129–163.

CrossRef Full Text | Google Scholar

Nitta, T., and Yamada, S. (1989). Recent warming of tropical sea surface temperature and its relationship to the Northern Hemisphere circulation. J. Meteorol. Soc. Jpn. 67, 375–383. doi:10.2151/jmsj1965.67.3_375

CrossRef Full Text | Google Scholar

Obara, K., and Kato, A. (2016). Connecting slow earthquakes to huge earthquakes. Science 353, 253–257. doi:10.1126/science.aaf1512

PubMed Abstract | CrossRef Full Text | Google Scholar

Owens, W. B., and Warren, B. A. (2001). Deep circulation in the northwest corner of the Pacific Ocean. Deep Sea Res. 48, 959–993. doi:10.1016/S0967-0637(00)00076-5

CrossRef Full Text | Google Scholar

Ponte, R. M., and Gaspar, P. (1999). Regional analysis of the inverted barometer effect over the global ocean using TOPEX/POSEIDON data and model results. J. Geophys. Res. 104, 15587–15601. doi:10.1029/1999JC900113

CrossRef Full Text | Google Scholar

Qiu, B., Kelly, K., and Joyce, T. (1991). Mean flow and variability of the Kuroshio Extension from the Geosat altimetry data. J. Geophys. Res. 96, 18491–18507. doi:10.1029/91JC01834

CrossRef Full Text | Google Scholar

Shelly, D., Beroza, G., and Ide, S. (2007). Non-volcanic tremor and low-frequency earthquake swarms. Nature 446, 305–307. doi:10.1038/nature05666

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugimoto, S., Aono, K., and Fukui, S. (2017). Local atmospheric response to warm mesoscale ocean eddies in the Kuroshio-Oyashio Confluence region. Sci. Rep. 7, 11871, doi:10.1038/s41598-017-12206-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Tai, C.-K. and White, W. B. (1990). Eddy variability in the Kuroshio Extension as revealed by Geosat Altimetry: energy propagation away from the Jet, Reynolds stress, and seasonal cycle. J. Phys. Oceanogr. 20, 1761–1777. doi:10.1175/1520-0485(1990)020<1761:EVITKE>2.0.CO;2

CrossRef Full Text | Google Scholar

Tanimoto, Y., Iwasaka, N., Hanawa, K., and Toba, Y. (1993). Characteristic variations of sea surface temperature with multiple time scales in the North Pacific. J. Clim. 6, 1153–1160. doi:10.1175/1520-0442(1993)006<1153:CVOSST>2.0.CO;2

CrossRef Full Text | Google Scholar

Thompson, R. (1983). Low-pass filters to suppress inertial and tidal frequencies. J. Phys. Oceanogr. 13, 1077–1083. doi:10.1175/1520-0485(1983)013<1077:LPFTSI>2.0.CO;2

CrossRef Full Text | Google Scholar

Tomosada, A. (1986). Generation and decay of Kuroshio warm-core rings. Deep Sea Res. 33, 1475–1486. doi:10.1016/0198-0149(86)90063-4

CrossRef Full Text | Google Scholar

Trenberth, K. E. (1990). Recent observed interdecadal climate changes in the Northern Hemisphere. Bull. Amer. Meteor. Soc. 71, 988–933. doi:10.1175/1520-0477(1990)071<0988:ROICCI>2.0.CO;2

CrossRef Full Text | Google Scholar

Trenberth, K. E. (1997). The definition of El Niño. Bull. Amer. Meteor. Soc. 78, 2771–2778. doi:10.1175/1520-0477(1997)078<2771:TDOENO>2.0.CO;2

CrossRef Full Text | Google Scholar

Uchida, N., Iinuma, T., Nadeau, R. M., Bürgmann, R., and Hino, R. (2016). Periodic slow slip triggers megathrust zone earthquakes in northeastern Japan. Science 351, 488–492.doi:10.1126/science.aad3108

PubMed Abstract | CrossRef Full Text | Google Scholar

Uehara, K., and Miyake, H. (1999). Deep flows on the slope inshore of the kuril–kamchatka trench southeast off cape erimo, Hokkaido. J. Oceanogr. 55, 559–573. doi:10.1023/A:1007828517317

CrossRef Full Text | Google Scholar

White, W. B., Tourre, Y. M., Barlow, M., and Dettinger, M. (2003). A delayed action oscillator shared by biennial, interannual, and decadal signals in the Pacific basin. J. Geophys. Res. 108, 1–18. doi:10.1029/2002JC001490

CrossRef Full Text | Google Scholar

Yasunaka, S., and Hanawa, K. (2003). Regime shifts in the Northern Hemisphere SST field: revisited in relation to tropical variations, J. Meteorol. Soc. Jpn. 81, 415–424. doi:10.2151/jmsj.81.415

CrossRef Full Text | Google Scholar