Stable Strontium Isotopic Compositions of River Water, Groundwater and Sediments From the Ganges–Brahmaputra–Meghna River System in Bangladesh

Introduction

Chemical weathering of continental rocks plays a vital role in determining ocean chemistry and the global climate. The ⁸⁷Sr/⁸⁶Sr ratio in continental runoff is important for understanding isotopic mass balances in the oceanic Sr cycle (Vance et al., 2009; Peucker-Ehrenbrink et al., 2010). Analyses of stable (δ⁸⁸Sr) and radiogenic (⁸⁷Sr/⁸⁶Sr) strontium isotope ratios are used to identify differences in the lithological and weathering controls on the Sr isotopic composition of water and sediment (e.g., Halicz et al., 2008).

Values of δ⁸⁸Sr in the world’s major rivers range from 0.13 to 0.57‰ (Krabbenhöft et al., 2010; Pearce et al., 2015) and are affected primarily by bedrock lithology (e.g., Stevenson et al., 2018). The large seasonal variations of δ⁸⁸Sr (>0.5‰) in river water of the Xijiang River in China have been attributed to the different isotope signatures of silicate and carbonate rocks (Wei et al., 2013). Some recent studies have shown that the upper limit of δ⁸⁸Sr of river waters exceeds the bulk δ⁸⁸Sr values of local bedrocks, an indication that minerals with high δ⁸⁸Sr values have been preferentially dissolved (Chao et al., 2015; Andrews and Jacobson, 2018). The preferential incorporation of ⁸⁶Sr into secondary clay and calcite is an important influence on the Sr isotopic budget in river systems; fractionation of ⁸⁸Sr/⁸⁶Sr, but not ⁸⁷Sr/⁸⁶Sr, accompanies secondary mineral precipitation (Halicz et al., 2008; Chao et al., 2013; Stevenson et al., 2016; AlKhatib and Eisenhauer, 2017; Liu et al., 2017; Shalev et al., 2017) as well as plant uptake in soil (de Souza et al., 2010; Andrews et al., 2016). However, the δ⁸⁸Sr signature behaves conservatively during water mass mixing and stream transport (Andrews et al., 2016; Andrews and Jacobson, 2017). It is still uncertain to what degree the variation of δ⁸⁸Sr values in large multi-lithology river systems can be attributed to solute sources, water–sediment interactions, or secondary mineral formation.

The discharge volume of the Ganges–Brahmaputra river system is the second-largest of the world’s rivers, as well as the second-highest sediment flux (Millman and Syvitski, 1992), and the chemical flux and isotopic variations of its waters are therefore important determinants of the oceanic isotopic mass balance (Bickle et al., 2018; Tipper et al., 2006). The Ganges and Brahmaputra rivers arise on the Himalayan–Tibetan Plateau (Figure 1), where active physical erosion and chemical weathering are associated with glacier flow, landslides, and monsoonal rainfall. These two Himalayan rivers show large seasonal variations in their discharge and chemical composition (Webster et al., 2010). Previous studies have reported that dolomite and silicate detritus strongly influence the highly radiogenic ⁸⁷Sr/⁸⁶Sr signatures (>0.8) of rivers draining the Himalayan orogen and its floodplain, and the metamorphic carbonates have taken on the highly radiogenic signal from the silicates (e.g., Jacobson et al., 2002; Bickle et al., 2003; Oliver et al., 2003). Secondary minerals also play important roles in riverine chemistry; for instance, river waters can lose a significant fraction of Ca (up to 70% in the Ganges; Bickle et al., 2018) to precipitation of secondary calcite in floodplain sediments. Calculations of weathering fluxes are complicated by the extent of element uptake by secondary minerals, especially in a floodplain. Eroded Himalayan materials show a progressive formation of secondary clay during their transport from the high mountains to the Ganges floodplain (Lupker et al., 2012). In contrast, the Meghna River and its tributaries drain only the Bengal Plain, where eroded Himalayan material may be more fully weathered in this low-relief environment. The mass of Ca derived from silicate and carbonate weathering can be calculated based on mass balance calculation using ⁸⁷Sr/⁸⁶Sr (e.g., Jacobson et al., 2002; Bickle et al., 2018). Strontium is one of the most important elements in weathering studies to disentangle silicate from carbonate weathering fluxes from primary sources and loss of elements to secondary minerals. Characterization of detrital mineralogy and seasonal hydrology is useful for apportioning the release of Sr by carbonate or silicate weathering; however, it is uncertain how much the formation of clay and carbonate minerals in the plain affects the spatial and temporal variation of δ⁸⁸Sr values.

FIGURE 1

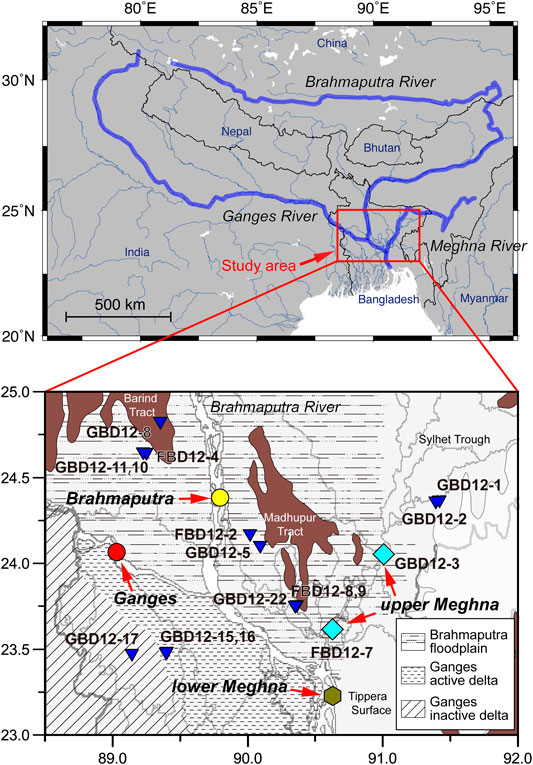
FIGURE 1. Location map showing courses of the Ganges, Brahmaputra, and Meghna Rivers and our sampling area in Bangladesh (red square). The detailed map shows locations of sampling points of the Ganges (red), Brahmaputra (yellow), Meghna Rivers (light blue), the lower Meghna River, below its confluence with the Ganges–Brahmaputra river system (orange), and groundwater (blue) and patterns on the map represent geomorphic features of the Bengal Plain in Bangladesh. The brown areas are the major Pleistocene terraces.

The global flux of Sr in groundwater is estimated to be a few tens of percent of the total continental Sr flux (Beck et al., 2013), making it the second-largest input of Sr to the ocean after riverine flux. The highly radiogenic ⁸⁷Sr/⁸⁶Sr of groundwater in the Bengal Plain potentially influences the global oceanic ⁸⁷Sr/⁸⁶Sr ratio (Basu et al., 2001), and the local flow cells of shallow groundwater provide a flux of Sr into downstream rivers (Harvey, 2002). The δ⁸⁸Sr value of groundwater is less well constrained than that of river waters (Neymark et al., 2014; Andrews and Jacobson, 2017; Shalev et al., 2017). Floodplains play an important role in the downstream evolution of river water chemistry and contribute a significant fraction of the total chemical fluxes to the ocean (Pogge von Strandmann et al., 2017; Bickle et al., 2018). The sediment load in floodplains consists of incompletely weathered material derived from rapid denudation of high mountains by vigorous physical erosion (i.e., a weathering-limited regime). Therefore, continued weathering of Himalayan-derived sediment during its transport through the Gangetic floodplain (Lupker et al., 2012) makes a dominant contribution to the alkalinity flux from the Ganges River (Bickle et al., 2018). However, the extent of water–sediment interactions and their influence on Sr isotope systematics in groundwater, where water residence times are long, remain unknown for the millennial time scale of a steady-state weathering regime. Our objective in sampling groundwater in the Bengal Plain in Bangladesh was to resolve whether weathering at shallow and deeper sediment depths differs in the contribution of primary mineral dissolution, secondary mineral formation, and adsorption/desorption processes.

In this study, we investigated Sr isotopic variations of river water from the Ganges, Brahmaputra, and Meghna rivers in Bangladesh in the dry and wet seasons. The exchangeable, carbonate and silicate fractions of the bedload sediment were analyzed to precisely apportion Sr sources. We also measured variations of the stable isotope composition of Sr in groundwater to identify the factors governing the solute chemistry of groundwater in the Bengal Plain.

Materials and Methods

Study Area and Samples

The Ganges and Brahmaputra rivers originate in the high Himalayas, join together in Bangladesh, and empty into the Bay of Bengal through a complex distributary system on the Bengal Plain, in Bangladesh and the neighboring West Bengal province of India (Figure 1). The Ganges River flows from the Gangotri glacier in the western Himalayas, accepts the flow of several large rivers within India, and in Bangladesh is joined by the Brahmaputra and Meghna rivers. The mean annual discharge of the Ganges River above its confluence with the Brahmaputra River is 1.1 × 10⁴ m³ s⁻¹, and maximum flood discharges reach 5.5 × 10⁴ m³ s⁻¹ during the rainy season (Webster et al., 2010). The Brahmaputra River flows east across the Tibetan Plateau, then southwest into eastern India and south to Bangladesh. The mean annual discharge of the Brahmaputra River near its mouth is 2.0 × 10⁴ m³ s⁻¹, and maximum flood discharges reach 6.4 × 10⁴ m³ s⁻¹ during the rainy season (Webster et al., 2010). The Meghna River arises in the low hills of eastern India and joins a distributary of the Ganges–Brahmaputra system in Bangladesh to form a much larger stream, referred to here as the lower Meghna River (Figure 1). The upper Meghna River is small compared to the Ganges and Brahmaputra rivers, with an average annual discharge of 0.35 × 10⁴ m³ s⁻¹ (Parua, 2010).

The Ganges and Brahmaputra rivers flow across many different rock types. Their headwaters drain metamorphic rocks (high-grade schist, gneiss, quartzite, and metamorphosed carbonate rocks), felsic intrusives, and sandstone, shale, and limestone of Paleozoic and Mesozoic age (e.g., Heroy et al., 2003). In contrast, their middle and lower reaches traverse widespread Pleistocene Himalayan alluvium. The Meghna River flows only across lowland deposits of Himalayan alluvium in Bangladesh.

Sampling in Bangladesh was undertaken during the dry season (16–23 February) and wet season (22–25 September) of 2012. Samples of midstream surface waters were collected at three locations in the Ganges–Brahmaputra river system above and below their confluence and single locations in an upper tributary of the Meghna River (the Kushiyara River), the main stream of the upper Meghna River, and the lower Meghna River (Figure 1; Tables 1, 2). Bedload sediment samples were collected during dry lowstand periods in January 2011 to access the midstream surface bedload. The samples were taken in a sealable plastic bag and dried in an oven at 60°C. Groundwater samples were taken from 14 wells on the Bengal Plain (Figure 1; Table 1). Before groundwater sampling, each well was pumped for a while to obtain stable temperature and electrical conductivity, as similar to other papers (e.g., Paul et al., 2010).

TABLE 1

TABLE 1. Sampling information and analytical results for river water and groundwater samples.

TABLE 2

TABLE 2. Sampling information and analytical results for bedload sediment samples.

Analytical Methods

Water samples were passed through acetate membrane filters (0.45 µm pore size) and acidified with ultrapure HNO₃ (Tamapure-AA-100, Tama Chemicals, Japan). Ionic concentration, pH, and total alkalinity data were previously reported by Manaka et al. (2017) and Manaka et al. (2019). Water temperature and pH were measured by 826 pH Mobile Meter (Metrohm, Herisau) immediately at the sampling site. Total alkalinity was measured by Gran titration with 0.05 mol kg⁻¹ HCl (ABU91, Radiometer). pCO₂ and HCO₃⁻ concentrations were then calculated from the pH and total alkalinity values using the carbonate equilibrium calculation program CO₂calc (Robbins et al., 2010). The major cation and anion concentrations were measured by ion chromatography (Dionex ICS-2000 and DX-500) at the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) and the National Institute of Advanced Industrial Science and Technology. The Sr concentrations were determined by inductively coupled plasma mass spectrometry (PerkinElmer ELAN-DRC II) at JAMSTEC. The uncertainties in elemental concentrations estimated from repeat analysis of the laboratory standard solution during the measurements were generally better than 5%.

A sequential leaching and digestion procedure was used to isolate different Sr-bearing phases in the sediment samples (Moore et al., 2013; Andrews et al., 2016). Subsamples of the <2 mm fraction weighing 1.0 g were reacted with 10 ml of 1 M ammonium chloride (NH₄Cl, adjusted to pH 8) and then with 4 M acetic acid to leach out exchangeable and carbonate fractions, respectively. The acetic acid leaching was repeated three times to ensure complete recovery of carbonate fractions. Each leachate was centrifuged and the supernatants were passed through 0.45 µm PTFE syringe filters. The remaining silicate fractions were digested in a 1:1 mixture of HF and HNO₃. Strontium was recovered from the samples by using a Sr-Spec resin (Eichrom resin).

Stable and radiogenic Sr isotopic compositions were analyzed simultaneously by double-spike thermal ionization mass spectrometry (Wakaki et al., 2017) by using a TRITON TIMS (Thermo Scientific, Germany) at Kochi Core Center, Japan. The stable Sr isotope composition was analyzed by the double-spike technique using the ⁸⁴Sr/⁸⁶Sr, ⁸⁷Sr/⁸⁶Sr, and ⁸⁸Sr/⁸⁶Sr ratios of the unspiked and spiked samples and expressed as per mil (‰) deviations relative to the NIST SRM-987 reference material expressed as:

${\mathrm{\delta }}^{88}\text{Sr }=\text{ {}{(}^{88}{\text{Sr/}}^{86}\text{Sr}){}_{\text{sample}}/{{(}^{88}{\text{Sr/}}^{86}\text{Sr})}_{\text{NBS}-\text{987}}-1\text{}}\text{ ×}1\text{,}000(1)$

An aliquot of the sample solution was spiked with an ⁸⁴Sr-⁸⁶Sr double spike. The ⁸⁷Sr/⁸⁶Sr ratio of the unspiked sample was measured on an unspiked aliquot by a conventional internal normalization technique using ⁸⁶Sr/⁸⁸Sr = 0.1194 and the exponential law. The NIST SRM-987 reference is typically measured eight times during every analytical session, Faraday cup gain was measured and corrected every day, and potential systematic bias in the ⁸⁷Sr/⁸⁶Sr ratio caused by the aging effect of the Faraday cup detectors was further corrected to ⁸⁷Sr/⁸⁶Sr_SRM-987 = 0.710248 for each session. The average values of uncorrected ⁸⁷Sr/⁸⁶Sr_SRM-987, which are used for this secondary correction, ranged from 0.710246 to 0.710264 during this study. Repeated analysis of seawater reference materials with this method gives ⁸⁷Sr/⁸⁶Sr of 0.7091719 ± 0.0000044 (2SD, n = 34). The external error was estimated as 2SD repeatability of multiple analyses of SRM-987 during each analytical session (Wakaki et al., 2017). Typical SE internal and 2SD external errors of δ⁸⁸Sr values were 0.006‰ and 0.020‰, respectively. Repeat analyses of an in-house Sr stable isotopic reference reagent Wako-9999 (Wakaki et al., 2017) gave δ⁸⁸Sr = 0.322 ± 0.025 (2SD, n = 45). δ⁸⁸Sr of rock standards were 0.297 ± 0.030‰ (n = 4) for JB-2, 0.295 ± 0.029‰ (n = 1) for BIR-1, and 0.249 ± 0.027‰ (n = 1) for BHVO-2 (Table 1). δ⁸⁸Sr of seawater analyzed by our method was 0.407 ± 0.012‰ (2SD, n = 11, Wakaki et al., 2017), which is consistent with an average value of 0.392 ± 0.025‰ for seawater samples from the Atlantic, Pacific, Indian, and Southern Oceans (Wakaki et al., 2017).

Hydrogen (δD) and oxygen (δ¹⁸O) isotope ratios of the water samples were determined by a cavity ring-down spectrometer (Picarro L2120-i, Picarro Inc., USA), and calibrated with the VSMOW2 and SLAP2 standards. Isotopic data are given in per mil relative to Vienna Standard Mean Ocean Water (V-SMOW). The 2SD precision for δ¹⁸O and δD analysis were ±0.05‰ and ±1.0‰, respectively. The accuracy was checked by three laboratory standards DOW (δ¹⁸O = −0.09‰, δD = −0.27‰), SLW2 (δ¹⁸O = −10.82‰, δD = −70.80‰), and ICE2 (δ¹⁸O = −14.51‰, δD = −106.3‰), and these were consistent with the reported values of DOW (δ¹⁸O = −0.075‰, δD = 0.593‰), SLW2 (δ¹⁸O = −10.82‰, δD = −71.00‰), and ICE2 (δ¹⁸O = −14.51‰, δD = −105.8‰).

Results and Discussion

Water and Solute Sources of River Water and Groundwater

Hydrogen and Oxygen Isotopic Compositions of River Water and Groundwater

The δD and δ¹⁸O values we measured for river water from the Ganges, Brahmaputra, and Meghna rivers are listed in Table 1. The variations in these measurements reflect strong orographic, altitude, and evaporative effects. The deviation of δD and δ¹⁸O from the global meteoric water line is expressed as the deuterium excess (d-excess = δD − 8*δ¹⁸O; Dansgaard, 1964), which is negatively correlated with relative humidity (i.e., greater kinetic fractionation during evaporation lowers d-excess for surface water and raises d-excess for water vapor).

The rivers in the Ganges floodplain, precipitation, and the Nepalese rivers of the Ganges headwaters have been shown to have d-excess values of 5.5 ± 0.6‰, 8.8 ± 1.0‰, and 12.3 ± 0.8‰, respectively (Bickle et al., 2018). Water of the Ganges main stem in Bangladesh had an average d-excess value of 9.0‰ in our measurements (Table 1), a value between those of the floodplain and mountain rivers. In contrast, the average d-excess was greatest for the Brahmaputra River samples (12.9‰) and within the range of the Nepalese rivers. The difference in d-excess between the two Himalayan rivers indicates that the Brahmaputra River carries water and solutes derived predominantly from mountain rivers and the Ganges River is strongly affected by discharge from the floodplain. This is consistent with the greater contribution of upstream precipitation and snow/glacial melts from the high-elevation mountains to the annual discharge in the Brahmaputra River (Immerzeel et al., 2010).

The d-excess of the upper Meghna River, which drains only the Bengal Plain, showed large seasonal differences (5.6‰ for low water and 9.2‰ for high water; Table 1). The lower value indicates that the kinetic fractionation during evaporation occurs. The d-excess of Bengal Plain groundwater allows estimates of its sources and the degree of evapotranspiration. Aggarwal et al. (2000) identified four types of groundwater in Bangladesh (types I–IV with increasing depth) on the basis of their distinct δD, δ¹⁸O, and ³H values and ¹⁴C activity. They reported that, in general, type I (δ¹⁸O = –5.5 to –3.5‰) and II (δ¹⁸O = –7‰) groundwaters (depths down to 70–100 m) are recharged regularly and have residence times of tens to 100 years. For type III groundwater (δ¹⁸O = –6‰, depths of 100–300 m), residence times are about 3,000 years. They also reported that type IV groundwater (δ¹⁸O = –3‰, depths >300 m) was recharged soon after the last glacial maximum and that both type III and IV groundwaters are isolated from surface waters (types I and II) and do not receive recharge from local rain and floodwaters. Type II groundwater, found mainly in the nearshore area with high salinity, was not identified in our samples.

In shallow type I groundwater, the large scatter in d-excess values of our samples (Figure 2) is inherited from isotopic variations in the recharging waters in the plain, which have undergone significant evaporative loss resulting in lower d-excess, and from mixing with river water with high d-excess during widespread flooding. We found that d-excess converged with increasing depth to a narrow range at depths below 70 m. Both ⁸⁷Sr/⁸⁶Sr ratios and δ⁸⁸Sr values of groundwater samples showed a similar trend, with a large scatter at shallow depths and convergence with increasing depths (Figure 2). The chemical properties of groundwaters at depths from 70 to 240 m appear to converge to those of type III. This is consistent with a groundwater classification based on well depths rather than δ¹⁸O. The difference of δ¹⁸O values for type III between our and reference data may be a reflection of the small sample sizes, as Aggarwal et al. (2000) and this study combined measured only about 20 samples of type III and type IV waters. It should be noted that the average d-excess at depths below 240 m has a characteristic high value of 9.6‰, indicating a relatively small evaporative loss. This would reflect past climatic conditions of higher humidity or lower temperature (Uemura et al., 2008) on the floodplain or in the regions where moisture originated. These differences in hydrologic conditions, especially the residence time, are closely linked to the extent of interactions between dissolved cations and sediments, as discussed in Changes in Sr Isotope Ratios and Water–Sediment Reaction Time with Groundwater Depth.

FIGURE 2

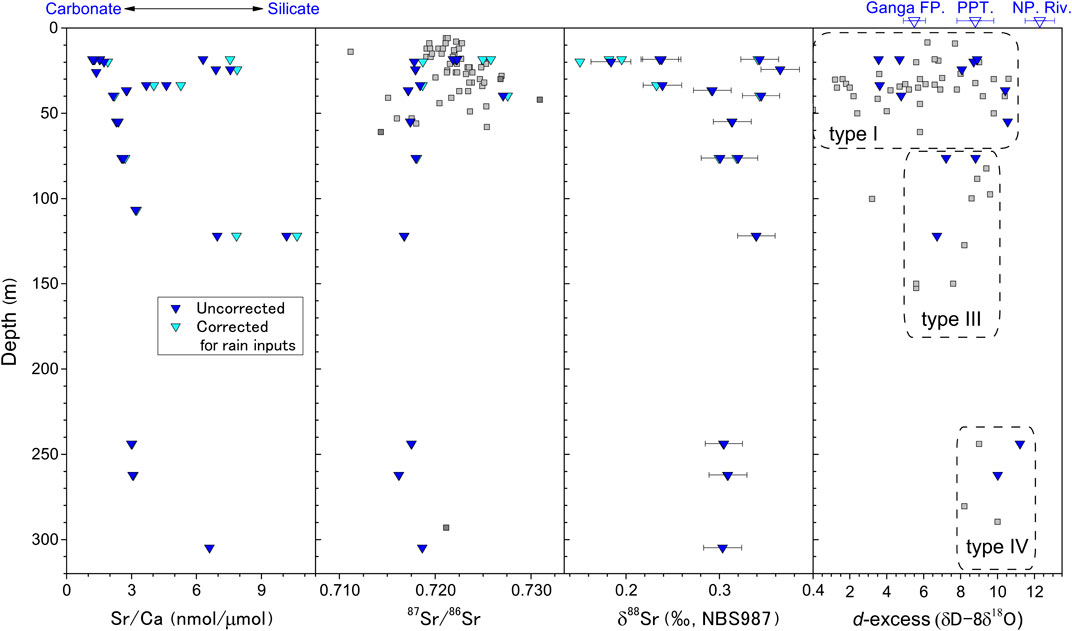
FIGURE 2. Depth profiles of Sr/Ca, ⁸⁷Sr/⁸⁶Sr, δ⁸⁸Sr, and d-excess in groundwater samples from Bangladesh. Sr data are corrected (light blue) and uncorrected (blue) for atmospheric contributions. Error bars indicate 2SD values. Grey squares are data from Paul et al. (2010). The d-excess values for the Ganges floodplain rivers (Ganga FP.), precipitation (PPT.), and the Nepalese rivers (NP. Riv.) are from Bickle et al. (2018).

Contributions of Atmospheric, Silicate and Carbonate Sources to Water Chemistry

The concentrations of Sr in our river water and groundwater samples are presented in Table 1, along with major cation and anion data reported by Manaka et al. (2015), Manaka et al. (2017), and Manaka et al. (2019). The water samples from the Ganges and Brahmaputra rivers had greater total dissolved solids, and higher Ca and Mg concentrations than those from the upper Meghna River (Figure 3). Most element concentrations were higher in the dry season than in the wet season (Table 1), likely because of the dilution of river waters during the wet season.

FIGURE 3

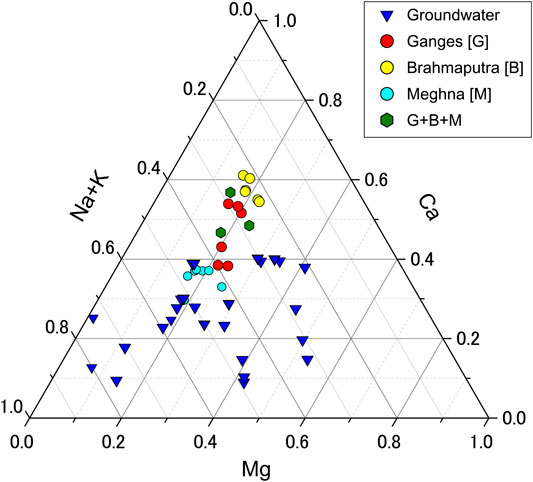
FIGURE 3. Ternary diagram of major cation compositions of river water and groundwater samples with previously published values. “G+B+M” indicates the sample from the lower Meghna River, below its confluence with the Ganges–Brahmaputra river system. Cation and anion concentrations are from Manaka et al. (2015), Manaka et al. (2017), and Manaka et al. (2019).

The Sr/Ca and Sr isotopic values of river water and groundwater have been corrected for the atmospheric contribution on the basis of the molar ratio of Sr to Cl of rainwater (e.g., Andrews et al., 2016), assuming that Cl in river water is derived predominantly from salts sourced from seawater, aerosols, and evaporitic rocks (see details in Supplementary Information). The corrections for stations in the Meghna River were less than −0.00028 for ⁸⁷Sr/⁸⁶Sr and less than +0.006‰ for δ⁸⁸Sr. Corrections for the groundwater samples, shown in Figure 2, were less than −0.00047 for ⁸⁷Sr/⁸⁶Sr and less than +0.006‰ for δ⁸⁸Sr, except for three shallow samples with large (13.7–25.5%) atmospheric Sr inputs, which had ⁸⁷Sr/⁸⁶Sr differences of 0.00090–0.00351 and δ⁸⁸Sr differences of 0.033–0.054‰. The impacts of atmospheric inputs on δ⁸⁸Sr are generally small relative to the analytical reproducibility of ±0.025‰.

An important question is whether the extent to which the weathering of carbonate and silicate rocks and the loss of Sr to secondary minerals and clays could account for the riverine δ⁸⁸Sr composition. To estimate the relative contributions of silicate and carbonate weathering to Sr isotope systematics, we relied on the Sr/Ca ratios of the bedload and reference data (Bickle et al., 2018; Jacobson et al., 2002). In the bedload samples from the Ganges and Brahmaputra rivers, the carbonate fractions had similar Sr/Ca ratios, 0.56 and 0.77 mmol/mol, respectively, and nearly identical δ⁸⁸Sr (Table 2). The Sr/Ca ratio for the Ganges River samples is close to the average value (0.544 ± 0.061 mmol/mol) of acetic acid leaches of Ganges River bedload sediment collected upstream, from Rajshahi in the Ganges floodplain (Galy et al., 1999a) and Rishikesh (Bickle et al., 2018). The Sr/Ca ratios in the carbonate fraction of Himalayan glacial soil, at the earliest stage of pedogenesis of Himalayan metamorphic rocks, range from 0.47 to 0.82 mmol/mol (Jacobson et al., 2002). The similarity of these carbonate Sr/Ca values suggests that the carbonates of the Ganges and Brahmaputra river bedload in Bangladesh are primarily derived from Himalayan carbonate source rocks. The higher carbonate Sr/Ca in the Brahmaputra River and upper Meghna River (1.34 mmol/mol) reflects the relative abundance of dolomite over calcite, as dolomite is more resistant to carbonate weathering and yields less Ca (Bickle et al., 2018). The Mg/Ca ratios of the carbonate leachates are 0.09 mol/mol for the Ganges and 0.81 mol/mol for the Brahmaputra River bedload samples (Table 2), consistent with there being more dolomite. Besides, the carbonate fractions of the Ganges, Brahmaputra, and Meghna rivers have closely similar δ⁸⁸Sr values regardless of the variation in their ⁸⁷Sr/⁸⁶Sr, Sr/Ca, and Mg/Ca ratios, which reflect the relative abundances of dolomite and calcite. Therefore, the different sources of carbonate Sr have a similar δ⁸⁸Sr value, thus the carbonate fractions indicate a well-defined δ⁸⁸Sr source, independent of carbonate mineralogy.

The catchment of the Ganges River is composed mainly of weathered sedimentary and volcanic rocks with high clay content, whereas that of the Brahmaputra River is composed predominantly of less-weathered, coarser sediments (e.g., Coleman, 1969). The silicate fraction of the Brahmaputra bedload has a Sr/Ca ratio of 69.67 mmol/mol, about twice those of the Ganges and upper Meghna rivers (27.76 and 38.27 mmol/mol, respectively), most likely due to incongruent dissolution (e.g., a significant depletion of plagioclase in the samples) or sorting effects of silicate materials (Lupker et al., 2012; Bickle et al., 2018). The laboratory leaching experiment of shale suggested that preferential dissolution of ⁸⁸Sr-enriched minerals occurs at an early stage of weathering, corresponding to the dissolution order of feldspar, chlorite, and then illite (Chao et al., 2015). It is important to note that δ⁸⁸Sr in the silicate fractions of our bedload samples (0.351–0.516‰) are all higher than the average of igneous rocks, 0.30 ± 0.02‰ (Moynier et al., 2010; Charlier et al., 2012; Amsellem et al., 2018). This cannot be explained by preferential leaching of ⁸⁸Sr-enriched phases from silicate rocks (Chao et al., 2015) or clay formation that results in lower δ⁸⁸Sr values of sediments (Stevenson et al., 2016). Therefore, the higher δ⁸⁸Sr and Sr/Ca of the silicate fractions can be attributed to hydrodynamic sorting of different minerals having unique δ⁸⁸Sr values (Lupker et al., 2012; Andrews and Jacobson, 2017; Andrews and Jacobson, 2018). Sediment hydrodynamic sorting results in coarse-grained and quartz-rich fractions for floodplain deposits, and the transported load gets enriched in clay and phyllosilicate (Lupker et al., 2012). Moreover, during sediment transit from the Himalayan front to the Bengal Plain, sediments become depleted in mobile components such as Na, K, and carbonates, and K-feldspar dissolution likely represents K release (Lupker et al., 2012). Although the mineral specific data of δ⁸⁸Sr is still limited, K-feldspar (0.455‰) can account for the high δ⁸⁸Sr values, but chlorite (0.317‰) on the contrary has a similar value to the average of igneous rocks (Andrews and Jacobson, 2018).

To address the problem of sediment heterogeneity, we used the Sr/Ca ratios for the silicate (3.22 mmol/mol) and carbonate (0.544 mmol/mol) sources of the Ganges River floodplain to calculate the fraction of carbonate- (F_carb) and silicate-derived Sr (F_sil = 1 − F_carb) attributing to solute sources (Table 1). The end-member values are estimated based on mass balance calculations using the mean solute chemistry and Sr isotopic compositions of the Ganges River (Bickle et al., 2018). Although all river waters plot within the range of binary mixing between silicate and carbonate sources, some groundwater samples had rain-corrected Sr/Ca ratios (Sr/Ca*) higher than the silicate value of 3.22 mmol/mol, suggesting that sediment heterogeneity is apparent at local scales.

The average Sr contribution from carbonate calculated from the element concentration data of Manaka et al. (2017) was similar in the Ganges (52%) and Brahmaputra (49%) river samples, but the range was wider for the Ganges River samples (39–62%) than for the Brahmaputra River samples (45–56%) (Supplementary Table S1). The rain-corrected Sr/Ca ratio of all river waters (Table 1) was higher in the dry season than in the wet season, probably due to precipitation of secondary calcite; Ganges River water, in particular, was extremely supersaturated with respect to calcite (Ω_calcite = 12.5; Table 1, Supplementary Information). This seasonal difference was greatest in the Ganges River (Sr/Ca* was 2.01 in the dry season and 1.57 in the wet season) and smaller in the Brahmaputra (1.96 and 1.71) and upper Meghna rivers (2.51 and 2.31). The loss of Ca due to secondary calcite precipitation in waters of the Ganges River and its floodplain tributaries best explains the changes in the share of Sr contributed by carbonates for the Ganges River samples, and the initial share should be greater, comparable to the values of ∼65% calculated by deconvolution of the chemical and isotopic inputs to the Ganges River (Bickle et al., 2018). Secondary mineral formation dominantly occurs in low-altitude plains, where long water–rock interaction times favor the progress of chemical reactions toward equilibrium (Pogge von Strandmann et al., 2017). For the Brahmaputra River, the smaller seasonal variation in Sr/Ca indicates a smaller amount of secondary calcite precipitation, probably related to a smaller water input from floodplain discharges as expected from the high d-excess in the Brahmaputra River, similar to that of the Nepalese rivers.

In contrast to the similarities between the Himalayan rivers, the river water and groundwater of the Bengal Plain clearly differ in chemistry. The upper Meghna River, above its confluence with the Ganges, was characterized by a share of Sr contributed by carbonates that was ∼30% lower than those of the Ganges and Brahmaputra rivers (Table 1). The groundwater samples were generally more enriched in Na and K and had higher total dissolved solids than the surface waters, but they varied widely in composition and displayed no spatial trends (Figure 2). These characteristics likely reflect local heterogeneities in mineral compositions and different degrees of chemical interaction between groundwater and sediment. Moreover, the chemical and isotopic compositions of the groundwater are also a consequence of the secondary mineral controls as discussed in Sr Isotope Ratios and Water–Sediment Reaction Time with Groundwater Depth. Our evidence suggests that the latter is a critical control on Sr isotope systematics in a floodplain, the result of longer water–rock interaction in deep groundwater leading to more congruent weathering.

Radiogenic and Stable Strontium Isotopes

Mixing Trend of ⁸⁷Sr/⁸⁶Sr Between Himalayan and Floodplain Waters

The highest ⁸⁷Sr/⁸⁶Sr ratios were observed in the waters of the Ganges River; they were lower in the Brahmaputra River and still lower in the upper Meghna River. We also discerned seasonal variations of ⁸⁷Sr/⁸⁶Sr in river water from the Ganges (dry season ∼0.727, wet season ∼0.725; Table 1) and Brahmaputra (dry season ∼0.720, wet season ∼0.718), but not the upper Meghna River (∼0.716). The mean ⁸⁷Sr/⁸⁶Sr ratios for all groundwater samples were about 0.722 and 0.715 in the dry and wet seasons, respectively. Among the world’s largest rivers, those that drain the Himalayas have the highest ⁸⁷Sr/⁸⁶Sr ratios (Figure 4A), reflecting the influence of dolomite and mica from Paleoproterozoic rocks of the Lesser Himalayan sequence (e.g., Galy et al., 1999b; Bickle et al., 2003; Oliver et al., 2003) and the fact that progressively smaller amounts of radiogenic Sr are added to river water from the lowland deposits in their lower reaches. The river waters at the upstream Siwalik Hills have ⁸⁷Sr/⁸⁶Sr ratios of 0.72–0.74 (Quade et al., 1997; Galy et al., 1999b). Our data for the Ganges River are similar to previously published values, and they confirm that the river and groundwater samples in the Bengal Plain are less radiogenic.

FIGURE 4

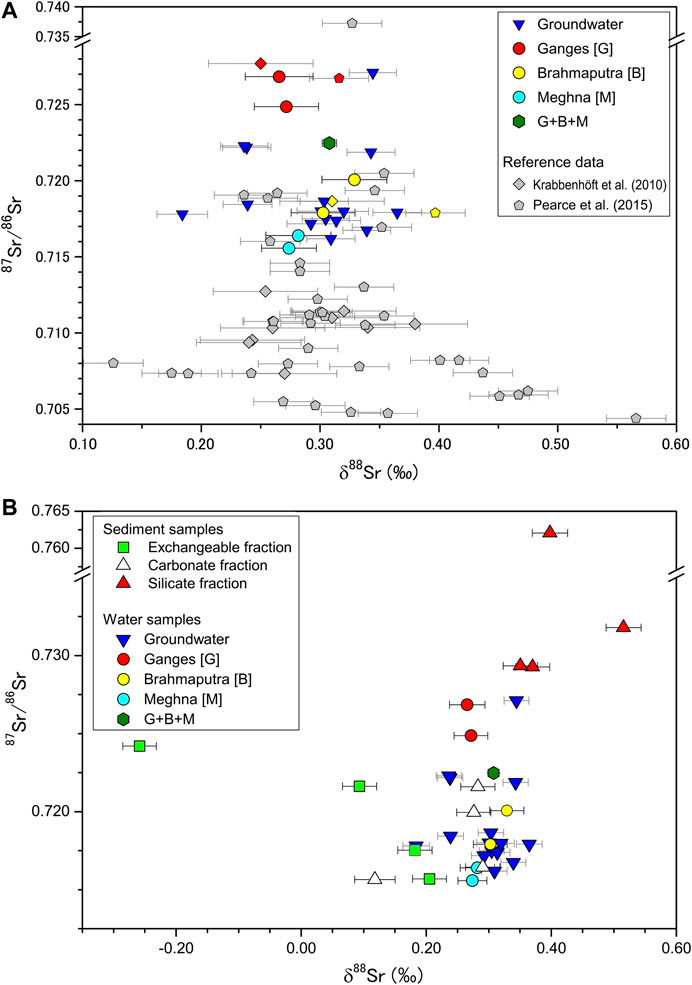
FIGURE 4. (A) δ⁸⁸Sr vs. ⁸⁷Sr/⁸⁶Sr for river water and groundwater samples in Bangladesh. Data for the world’s largest rivers reported by Krabbenhöft et al. (2010) and Pearce et al. (2015) are also shown. “G+B+M” indicates the sample from the lower Meghna River, below its confluence with the Ganges–Brahmaputra river system. Bars represent a 2SD error. The internal errors of δ⁸⁸Sr measurements are comparable to long-term external reproducibility (see also Analytical Methods), therefore the reference data are plotted with the long-term reproducibility of each laboratory: 0.025‰ (n = 33) from Pearce et al. (2015) and 0.044‰ (n = ∼90) from Krabbenhöft et al. (2009). (B) δ⁸⁸Sr vs. ⁸⁷Sr/⁸⁶Sr showing values for exchangeable, carbonate, and silicate phases of the sediment samples. Values for river water and groundwater from (A) are also shown.

To define ⁸⁷Sr/⁸⁶Sr end-member sediment sources for the Ganges–Brahmaputra–Meghna drainage basin within Bangladesh, we used our data and previously published data to construct plots of ⁸⁷Sr/⁸⁶Sr vs. 1/Sr for river water and groundwater in the basin.

Considering only our river water samples and those of Manaka et al. (2017), which were taken from the Bengal Plain during the same field surveys, we identified specific end-member mixing trends for each of the Ganges, Brahmaputra, and Meghna rivers (Figure 5B). A similar mixing trend was evident in δ⁸⁸Sr, as discussed in the following section. The highest ⁸⁷Sr/⁸⁶Sr ratios were from the Ganges River samples, which showed a mixing-trend intercept of 0.7335. This end-member ⁸⁷Sr/⁸⁶Sr ratio is close to that of the mean output flux from the Himalayas (Bickle et al., 2018) and lies between those of the carbonate and silicate fractions in the bedload sample from the Ganges River (Figure 6A). The ⁸⁷Sr/⁸⁶Sr value for the Brahmaputra River sample was distinctly lower (Figure 5B), suggesting that the extremely high ⁸⁷Sr/⁸⁶Sr components of Himalayan rocks made a smaller contribution compared to the Ganges River. The intercept value for the end-member mixing trend of Meghna River water was 0.7150 (Figure 5B). This low ⁸⁷Sr/⁸⁶Sr ratio, together with the larger Na and K contributions from upper Meghna River water, suggests that the lower Meghna River waters contain a larger component of silicate-derived Sr from less radiogenic floodplain sediments.

FIGURE 5

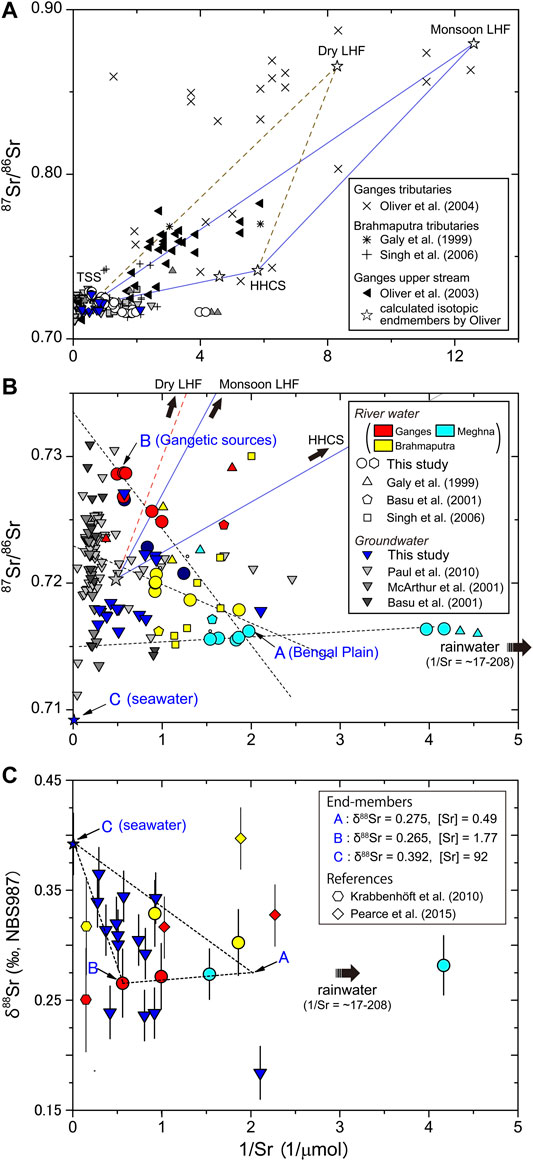
FIGURE 5. ⁸⁷Sr/⁸⁶Sr vs. 1/Sr. (A) River water from Himalayan tributaries of the Ganges and Brahmaputra rivers from previously published analyses (Galy et al., 1999; Basu et al., 2001; McArthur et al., 2001; Singh et al., 2006; Paul et al., 2010); also shown are isotopic end-members for the Tibetan Sedimentary Series (TSS), High Himalayan Crystalline Series (HHCS), and Lesser Himalaya formations (LHF) determined by Oliver et al. (2003). (B) Detail of (A) showing river water and groundwater samples from this study and previously published analyses in Bangladesh. The green hexagons are data for the lower Meghna River downstream of its confluence with the Ganges–Brahmaputra river system. The red (and dotted) lines show the mixing trends we identified in our samples for the Ganges, Brahmaputra, and Meghna river waters. The ratio of ⁸⁷Sr/⁸⁶Sr to 1/Sr for modern seawater is also plotted. (C) δ⁸⁸Sr vs. 1/Sr of river water and groundwater samples of the Bengal Plain from this study, Krabbenhöft et al. (2010), and Pearce et al. (2015). The dashed lines show the mixing trends between end-members A, B, and C (see text for details).

FIGURE 6

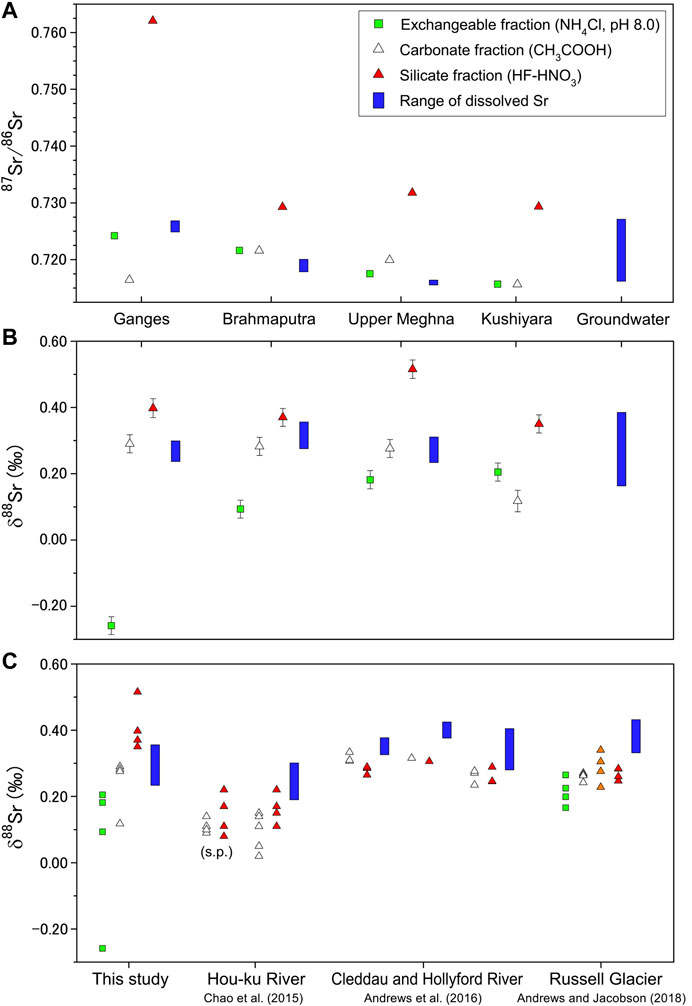
FIGURE 6. (A)⁸⁷Sr/⁸⁶Sr and (B) δ⁸⁸Sr for river sediment samples in Bangladesh along with the ranges of dissolved Sr of river water and groundwater samples. (C) Compilation of δ⁸⁸Sr values from sequential leaching of riverine bedload and suspended particles (s.p.) of this study, the Hou-ku River in Taiwan (Chao et al., 2015), the Cleddau and Hollyford rivers in New Zealand (Andrews et al., 2016) and subglacial discharge of the Russell Glacier in Greenland (Andrews and Jacobson, 2018). Orange triangle represents 1M HNO₃ leachate.

The data in ⁸⁷Sr/⁸⁶Sr–1/Sr space can be described by a mixture of three (or more) components (Figure 5B). We selected three end-members to represent the isotopic and elemental compositions of the intersection points of end-member mixing trends for the combined Ganges, Brahmaputra, and Meghna rivers (end-member A), the Ganges River (end-member B), and seawater (end-member C, which derived from atmospheric inputs and or salt leaching from soils, Aggarwal et al., 2000). End member A probably represents the average chemical weathering inputs from the Bengal Plain. Corresponding end-member values of δ⁸⁸Sr were selected in δ⁸⁸Sr–1/Sr space (Figure 5C), as discussed in Source-Rock and Fractionation Controls on δ⁸⁸Sr. The processes that disturb the mixing of these sources include atmospheric deposition, with ⁸⁷Sr/⁸⁶Sr of 0.712 and 1/Sr > 17 (Galy et al., 1999b), and significant loss of Sr to secondary minerals. These processes did not affect most of the ⁸⁷Sr/⁸⁶Sr and δ⁸⁸Sr data from the Bengal Plain, which thus could be confidently ascribed to a mixture of Sr derived from the three end-members.

The Sr-isotope data for groundwater from the Bengal Plain lie largely within the range of the combined data of this study and Manaka et al. (2017) for the waters of the Ganges–Brahmaputra–Meghna river system (Figure 5B). Generally speaking, the groundwater samples had ⁸⁷Sr/⁸⁶Sr values between those of the Himalayan rivers and the upper Meghna River (0.715578–0.716401), which drains only the Bengal Plain. This may reflect a smaller influence from highly radiogenic Sr in dolomite and silicate minerals such as K-feldspar and mica (Supplementary Figure S1). The aquifers in Bangladesh differ considerably in their host lithology, and groundwater quality varies both laterally and with depth (UNDP, 1982). The high Na and K contents of our groundwater samples (Figure 3) suggest that their major cation compositions have been influenced more strongly by silicate weathering than by carbonate weathering.

Source-Rock and Fractionation Controls on δ⁸⁸Sr

The mean δ⁸⁸Sr values of the Ganges and Brahmaputra rivers are almost identical to those previously reported by Krabbenhöft et al. (2010), but slightly lower than those reported by Pearce et al. (2015) (Figure 5C). The data of Krabbenhöft et al. (2010) are obtained from nearly the same location for the Ganges River, and 102 km upstream for the Brahmaputra River compared to our sampling sites. The localities for both the Ganges and Brahmaputra River samples of Pearce et al. (2015) are close to their confluence point (Rajbari and Aricha, according to the information of Burke et al., 2018). Differences between δ⁸⁸Sr values reported in various studies of particular rivers, presented by Pearce et al. (2015), maybe a result of differences in relative fractions of chemical weathering inputs derived from the high mountains, floodplain, and southern tributaries (Bickle et al., 2018). The variations of δ⁸⁸Sr among our samples collected in dry and wet seasons were within the analytical error, thus the relative inputs from the distinct Sr sources were effectively the same at a given sampling site regardless of season, suggesting δ⁸⁸Sr is insensitive to monsoon weathering. Calcium and carbonate ion concentrations reported in Manaka et al. (2019) show that Ω_calcite values are notably higher during the dry season, especially for the Ganges river (12.5), whereas the δ⁸⁸Sr values appear to have been unaffected by calcite precipitation, which increases δ⁸⁸Sr values. Here we wish to address the sensitivity of δ⁸⁸Sr to the extent of calcite precipitation using a closed/semi-closed type fractionation. Assuming the seasonal difference in Sr/Ca* (2.01 for the dry and 1.57 for the wet seasons) is solely caused by secondary calcite precipitation, about 30% of Ca is lost in the dry season of the Ganges floodplain. A part of dissolved Sr in the water co-precipitates with calcite and their relationship is expressed as Rayleigh fractionation (Bickle et al., 2018):

${\left[\text{Sr}\right]}_{\text{w }}={\left[\text{Sr}\right]}_0\text{ × }\gamma {\text{K}}_{\text{d}}(2)$

where [Sr]_w and [Sr]₀ are the Sr concentrations in the measured water and that prior to secondary calcite precipitation, γ is the fraction of Ca remaining after precipitation, and the K_d value of 0.05 (Bickle et al., 2018) is the Sr/Ca molar partitioning coefficient for secondary calcite. Eq. (2) gives the loss of Sr to secondary calcite is about 1.8%. Then, we estimated an impact of secondary calcite precipitation on the δ⁸⁸Sr values of the Ganges river water using a closed system isotope fractionation:

${\mathrm{\delta }}^{88}{\text{Sr}}_{\text{w }}={\mathrm{\delta }}^{88}{\text{Sr}}_{\text{0 }}+1000\left(\mathrm{\alpha }-1\right)\text{ln}\left({\text{f}}_{\text{W}}^{\text{Sr}}\right)(3)$

${\text{f}}_{\text{w}}^{\text{Sr}}={\left[\text{Sr}\right]}_{\mathrm{w}}/{\left[\text{Sr}\right]}_0(4)$

where δ⁸⁸Sr_w and δ⁸⁸Sr₀ are the Sr isotopic composition of river waters and their initial values; α is the fractionation factor between the dissolved Sr and calcite; ${\text{f}}_{\text{w}}^{\text{Sr}}$ is the fraction of Sr remaining in the water. The calcite-fluid fractionation factor of −0.11‰ for the K_d value of 0.05 (Al Khatib and Eisenhauer, 2017, the calculated α value of 0.99989) was used for the calculation. As a result, an increase of riverine δ⁸⁸Sr of 0.002‰ should occur for secondary calcite precipitation. This value is subtle and 14-fold less than that of the 2SD repeatability of our analysis (Wakaki et al., 2017, ±0.025, n = 45). Therefore, the impact of Sr co-precipitation with secondary calcite is considered to be negligible.

The two Himalayan rivers have clearly different chemical compositions (Figures 3, 4). The δ⁸⁸Sr of Ganges River water (0.269‰) is lower than that of the Brahmaputra River (0.316‰), reflecting the character of the solutes and sediments transported by the two rivers. The higher δ⁸⁸Sr for the Brahmaputra River is consistent with Krabbenhöft et al. (2010) and Pearce et al. (2015) (Figures 4A, 5C).

The three different Sr-bearing phases in bedload samples have a 0.8‰ range of isotopic variation whereas river water and groundwater vary by only 0.2‰ (Figures 4B, 6). In our leaching experiments, the δ⁸⁸Sr values increased systematically from the exchangeable to the carbonate to the silicate fraction, with the exception of the carbonate fraction of the Kushiyara River, where is close to GBD12-3 in Figure 1, bedload (Figure 6). The Ganges and Brahmaputra river bedload had nearly identical δ⁸⁸Sr values of ∼0.29‰ for carbonate and ∼0.38‰ for silicate. The carbonates contributed 53.3% of the Sr in the Ganges River bedload but only 1.3% of the Sr in the Brahmaputra River bedload (Table 2). These are consistent with that δ⁸⁸Sr values for the Brahmaputra River are more strongly affected by high Himalayan silicate sources.

The sediments carried by the Ganges River are more strongly weathered and have higher clay content than the sediments of the Brahmaputra River (Khan et al., 2019; Coleman, 1969). In the Bengal Plain the δ⁸⁸Sr values of exchangeable fractions in bedload samples were 0.07–0.53‰ lower than those of the corresponding river waters (Figure 6B), a difference that reflects isotopic fractionation related to secondary processes such as adsorption, chelation, and ion exchange by which clay minerals preferentially incorporate ⁸⁶Sr. In the Ganges River, the Sr/Ca molar partitioning factors for exchangeable fraction and river water (D_Sr/Ca) as well as the δ⁸⁸Sr values are markedly lower (0.46, −0.258‰) than those for the Brahmaputra (0.87, 0.093‰) and Meghna (0.77, 0.182‰) Rivers. Khan et al. (2019) showed that the clay mineral assemblage in the Ganges-Brahmaputra-Meghna river system consists of illite, smectite, kaolinite, and chlorite: the Ganges sediments are more enriched in smectite formed in the lowland floodplain, and the Brahmaputra sediments are rich in illite. Moreover, the distribution patterns of the clay mineral assemblages of the Brahmaputra and Meghna rivers are similar (Khan et al., 2019). It is therefore plausible that the clay mineralogy is linked to the δ⁸⁸Sr and D_Sr/Ca values of exchangeable fractions. Both smectite and illite are 2:1 layer type clays, but their chemical properties are different (e.g., Missana et al., 2008). Isomorphic cation substitution in smectite takes place in the tetrahedral and octahedral sheets. On the contrary, substitution in illite takes place predominantly in the tetrahedral sheets, and consequently, illite presents lower cation exchange capacity than smectite because cations only at the external surfaces are exchangeable. In addition, smectite is expanding clay that hosts water in interlayer sites, resulting in expansion of interlayer spacing, whereas illite has no swelling interlayers. A difference of the substitution sites and structural changes associated with cation substitution and hydration state may result in magnitudes of Sr isotopic fractionation and the exchangeable fractions and ambient waters. Stevenson et al. (2016) suggested that the ⁸⁸Sr enrichment in dissolved Sr is a consequence of preferential uptake of ⁸⁶Sr by secondary minerals. A greater degree of Sr incorporation by clay minerals leads residual waters to be isotopically heavier than the source materials. A previous study of the Russell Glacier in western Greenland reported that suspended sediment δ⁸⁸Sr values were identical to the bedload sediment and found no evidence for an isotopically light clay reservoir (Andrews and Jacobson, 2018). No significant contribution of clay adsorption to δ⁸⁸Sr values has also been reported in a sedimentary watershed in southwestern Taiwan (Chao et al., 2015). Although the exchangeable fractions show preferential uptake of ⁸⁶Sr, we also did not find a lower δ⁸⁸Sr reservoir in the silicate fraction of the bedload sediments. Although the Ganges River particularly has a greater abundance of clay minerals in its catchment and the greater extent of ⁸⁶Sr uptake by the exchangeable fraction, the Ganges river water has the lower δ⁸⁸Sr values relative to its bedload carbonate and silicate fractions (Table 2). There is, therefore, little evidence that clay minerals exert an influence on the δ⁸⁸Sr of the Ganges river water.

The total chemical weathering flux of the Ganges–Brahmaputra–Meghna rivers has a δ⁸⁸Sr value of 0.308‰ (sample GBD12-04, Table 1), nearly the same as those of the carbonate fraction of bedload (∼0.29‰) and silicate rocks of all types (0.30 ± 0.02‰) (Amsellem et al., 2018; Charlier et al., 2012; Moynier et al., 2010). A plot of δ⁸⁸Sr vs. Sr/Ca for water samples and sequential leaching of riverine bedload can be a good indicator to differentiate primary and secondary Sr sources (Figure 7). The rivers lie on the mixing line between the Sr/Ca ratios of silicate and carbonate sources of the Ganges River floodplain (Bickle et al., 2018) with estimated δ⁸⁸Sr values of the average of igneous rocks (0.30‰, Amsellem et al., 2018; Charlier et al., 2012; Moynier et al., 2010), and the average of carbonate fraction of the bedload sediments from the Ganges, Brahmaputra, and upper Meghna rivers (0.283‰, this study). It is likely that the δ⁸⁸Sr values of these rivers represent an average δ⁸⁸Sr composition for all of the catchments in this large drainage area and their various rock types (i.e., close to the mean values of bulk carbonate and silicate rocks), with little influence from secondary carbonate and clay minerals. Therefore, the extent of Sr loss or addition by secondary processes does not have a great influence on Sr budget during the transport processes. This inference supports the reliability of using Sr/Ca and ⁸⁷Sr/⁸⁶Sr ratios to estimate inputs of solutes derived from carbonates and silicates (Bickle et al., 2018).

FIGURE 7

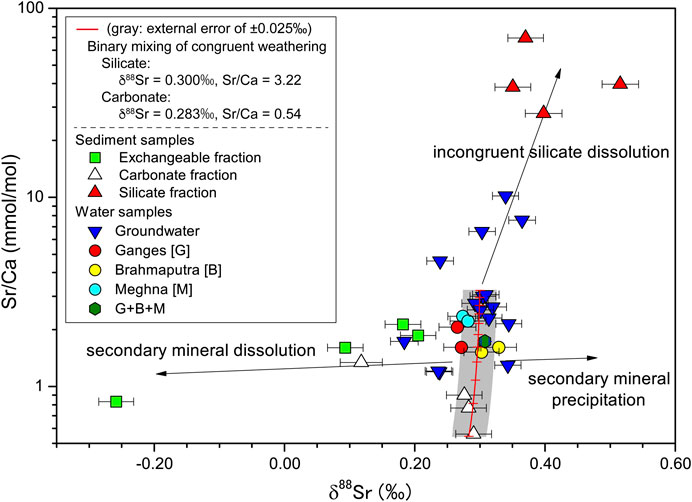
FIGURE 7. δ⁸⁸Sr vs. Sr/Ca for water samples and for exchangeable, carbonate, and silicate phases of the sediment samples. “G+B+M” indicates the sample from the lower Meghna River, below its confluence with the Ganges–Brahmaputra river system. Red line shows the binary mixing between a congruent dissolution of silicate and carbonate rocks with increment lines of 10% step in the fraction of carbonate- (F_carb) and silicate-derived Sr (F_sil = 1−F_carb). The end-member values are estimated based on mass balance calculations using the mean solute chemistry and Sr isotopic compositions of the Ganges River (3.22 mmol/mol for silicate and 0.544 mmol/mol for carbonate, Bickle et al., 2018), the average of igneous rocks (0.30‰, Amsellem et al., 2018; Charlier et al., 2012; Moynier et al., 2010), and the average of carbonate fraction of the bedload sediments from the Ganges, Brahmaputra, and upper Meghna Rivers (0.28‰, this study). Gray area represents a typical external 2SD error of δ⁸⁸Sr values.

Changes in Sr Isotope Ratios and Water–Sediment Reaction Time with Groundwater Depth

The objective of sampling groundwater in the Bengal Plain was to resolve the significance of longer water–sediment interaction times on Sr isotopic heterogeneity in a weathering system with high denudation rates and widespread floodplains. The residence times range from tens of years for shallow (0–70 m) type I groundwater to several thousand years or longer for deep type III and type IV groundwater (Aggarwal et al., 2000). The Sr concentrations of our groundwater samples ranged from 0.47 to 3.55 μmol/kg (Table 1), and the average concentration was about four times higher than concentrations in water samples from the upper Meghna River (samples GBD12-3 and FBD12-7). The ⁸⁷Sr/⁸⁶Sr ratios of our groundwater samples ranged from 0.716189 to 0.727104 (Figure 2; Table 1). Compared to the river water, the chemical properties of groundwaters strongly reflected the contributions of silicate sources (Figure 3) with widely varying ⁸⁷Sr/⁸⁶Sr ratios and most closely corresponded to the silicate fractions of bedload samples (Figure 6A). Moreover, ⁸⁷Sr/⁸⁶Sr ratios and other chemical parameters varied greatly in shallow type I groundwater, then converged with depth to a narrow range of about 0.717 for type III and type IV groundwater (Figure 2).

The depth profile of δ⁸⁸Sr (Figure 2) also showed it to vary widely in the shallow groundwater, but it was more uniform (∼0.31‰) at depths greater than 70 m. As with the Himalayan rivers, δ⁸⁸Sr of deep groundwater appears to be close to the values of the carbonate fraction and the bulk silicate Earth. Such a relationship implies that the deep groundwater reaches a steady-state and silicate weathering is more congruent (in which the water chemistry approximates the rock chemistry, less secondary mineral formation, and less incongruent dissolution of silicate minerals occurred in the deeper groundwater). The residence time of type III and IV groundwaters suggests that the time required for their isotopic equilibration is on the order of thousands of years. These results imply that the δ⁸⁸Sr composition of deep groundwater is also in a steady-state with respect to both stable and radiogenic Sr isotopes. Obviously, more isotope data for the deep groundwater samples are still in need of further constraint. Lithium isotope ratios (δ⁷Li) are a tracer of silicate weathering processes, even in catchments dominated by carbonate rocks (e.g., Kısakűrek et al., 2005). If δ⁷Li values of waters are close to those of silicate rocks with an average of 0.6 ± 0.6‰ (Sauzéat et al., 2015), weathering is interpreted as congruent, while high δ⁷Li implies greater secondary mineral formation (Pogge von Strandmann et al., 2017). The average δ⁷Li values in the deep groundwater in the Bengal Basin (12.2‰ for type III and 8.7‰ for type IV) are several ‰ lower than those at shallow depths (<50 m, 16.1‰ for type I) (Bagard et al., 2015; Manaka et al., 2017). Moreover, δ⁷Li values of older groundwaters are closer to those of primary silicate rocks. Although δ⁸⁸Sr values would not reflect solely the silicate weathering, as we will discuss later, the depth changes in δ⁸⁸Sr and δ⁷Li suggest more congruent silicate weathering, therefore less influence of secondary minerals.

On the other hand, shallow groundwater samples had δ⁸⁸Sr values both higher and lower than those of deep groundwater. We infer that this variability is caused by the kinetically limited dissolution of minerals, such that weathering proceeds in a non-steady-state and weathering-limited regime at a time scale of tens to 100 years. Figure 7 shows that some shallow groundwaters plotted outliers from the mixing trend for the rivers likely reflect interaction with the ⁸⁸Sr-enriched phases from silicate fractions and the carbonate/exchangeable fraction with a low δ⁸⁸Sr value (Figure 7). Chao et al. (2015) and Andrews and Jacobson (2018) have shown that the preferential dissolution of ⁸⁸Sr-enriched phases occurs early during silicate weathering of sedimentary and metamorphic rocks. The preferential dissolution of ⁸⁸Sr-enriched minerals can account for the increases in δ⁸⁸Sr and Sr/Ca for some shallow groundwater similar to that the high Sr/Ca ratios of the silicate fractions of bedload are caused by incongruent dissolution and/or sorting effects of silicate materials (discussed in Contributions of Atmospheric, Silicate and Carbonate Sources to Water Chemistry).

Precipitation of secondary calcite likely plays a role in driving the dissolved load to higher δ⁸⁸Sr values (Liu et al., 2017); however, because all but one of the Ω_calcite values of the groundwater samples were less than 1.0 (Table 1), precipitation of calcite is unlikely in the Bengal Plain. Moreover, their δ⁸⁸Sr values are relatively insensitive to the amounts of the Sr loss to secondary carbonate, as similar to that of the floodplain. Instead, preferential dissolution of ⁸⁸Sr-depleted carbonate appeared to have lowered δ⁸⁸Sr values. Groundwater sample GBD12-8 from the Barind Tract, a Pleistocene terrace in northwestern Bangladesh, had a δ⁸⁸Sr value of 0.184‰ (rain-corrected value of δ⁸⁸Sr* = 0.151‰), by far the lowest value we measured. The ⁸⁷Sr/⁸⁶Sr ratio for this sample was similar to those of the other groundwater samples, but the Sr/Na ratio was notably lower, indicating a source with a low Sr concentration. Among the parameters we studied, Sr/Na showed noteworthy correlations with HCO₃/Na (r = 0.80) and Ca/Na (r = 0.56), implying active dissolution of carbonates. K (likely related to clay minerals), Cl, and SO₄ (derived from salts) concentrations appeared to be unrelated to δ⁸⁸Sr and Sr concentrations. The carbonate fraction in the bedload of the Kushiyara River, an upper tributary of the Meghna River, had a very low δ⁸⁸Sr value of 0.118‰ (Table 2). This carbonate is considered to be a local secondary carbonate because compared to the exchangeable fraction, this fraction has a low Mg/Ca, almost identical ⁸⁷Sr/⁸⁶Sr, and lower δ⁸⁸Sr, indicating secondary precipitation from ambient waters. Its δ⁸⁸Sr value is also consistent with observations indicating a local influence from isotopically distinct carbonates in a plot of δ⁸⁸Sr vs. Sr/Ca (Figure 7). Overall, three-component mixing (Figure 5B,C) and dissolution kinetics of minerals can account for differences in δ⁸⁸Sr in the shallow groundwater. Isotopic fractionation does occur during secondary mineral formation but does not have resolvable impacts on the δ⁸⁸Sr values particularly for water samples. Therefore, it is not necessarily required to explain most of the riverine and groundwater variations. The δ⁸⁸Sr values can be used to elucidate primary and secondary Sr sources as well as congruent and incongruent silicate weathering especially for groundwater samples, and thus can be applied to local weathering processes in the floodplain.

Finally, we determined that the concentration-weighted mean of δ⁸⁸Sr for all of our groundwater samples was 0.309‰, which is the same as that of the water of the lower Meghna River below its confluence with the Ganges–Brahmaputra river system (0.308‰; see GBD 12-4 mean in Table 1). These results indicate that the δ⁸⁸Sr compositions of the groundwater and river fluxes are much the same. Weathering in the low-altitude plains makes an important contribution to the oceanic δ⁸⁸Sr budget via surface and submarine groundwater discharges, and the mean weathering output from the Bengal Plain has Sr isotope characteristics similar to those of the Ganges–Brahmaputra river system. The δ⁸⁸Sr compositions of groundwater Sr flux need to be more carefully assessed by considering hydrological models, but the marine Sr isotope budget can be going to be simplified.

Summary

We investigated δ⁸⁸Sr and ⁸⁷Sr/⁸⁶Sr ratios in river waters at five locations, bedload sediments at four locations (in three types of Sr-bearing fractions), and groundwater in 14 wells in the Ganges–Brahmaputra–Meghna drainage basin in Bangladesh. Water samples collected at the same locations during February and September 2012 (dry and wet seasons, respectively) showed no significant seasonal differences in δ⁸⁸Sr. Both ⁸⁷Sr/⁸⁶Sr and δ⁸⁸Sr of these waters are primarily controlled by three-component mixing of Sr from the Bengal floodplain and the Himalayan rivers. Some shallow groundwater samples are isotopically distinct from the river waters due to sediment heterogeneity and dissolution kinetics of minerals. Both the radiogenic and stable Sr isotope compositions of our groundwater samples down to 70 m depth were scattered, but the δ⁸⁸Sr values of groundwater samples converged to about 0.31‰ at greater depths, a value close to those of the carbonate fraction and the bulk silicate Earth. This finding implies that longer residence times favor a supply-limited regime and congruent dissolution of both carbonate and silicate minerals. The concentration-weighted mean δ⁸⁸Sr of our groundwater samples (0.309‰) was effectively identical to that of water from the lower Meghna River (0.308‰) downstream of its confluence with the Ganges–Brahmaputra river system. Although the contribution of groundwater to the flux of Sr to the Bay of Bengal varies in magnitude according to the calculation method used, our results support our hypothesis that the groundwater and river discharge to the Bay of Bengal have similar δ⁸⁸Sr compositions.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

TY, HK, SW, and NO contributed to conception of the study. Samples were collected by TY, HK, TM, AS, and ZH. TY, SW, and TI performed the isotopic analysis. TY wrote the first draft of the manuscript with input from NO, TI, and SW. SW wrote the analytical sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was undertaken with the support of Japan Society for the Promotion of Science (JSPS) to TY (no. 16H05883, 19K21908) and to SW (no. 18K03814) to H.K. (no. 22224009).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Kazuya Nagaishi and Tatsuya Kawai of Marine Work Japan; Daisuke Araoka and the laboratory staff at the University of Tokyo; Akihiko Inamura of AIST; and Nahid Nowsher, Sabbir Ahamed, and Mostafa Tarek of Jashore University of Science and Technology for their support during the survey sampling and analysis. The constructive and insightful suggestions of the reviewers greatly improved the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.592062/full#supplementary-material.

References

Aggarwal, P. K., Basu, A. R., Poreda, R. J., Kulkarni, K., Froehlich, K., Tarafdar, S., et al. (2000). TC project BGD/8/016. A report on isotope hydrology of groundwater in Bangladesh: implications for characterization and mitigation of arsenic in groundwater. Vienna, Austria: International atomic energy agency, 5.

Google Scholar

AlKhatib, M., and Eisenhauer, A. (2017). Calcium and strontium isotope fractionation in aqueous solutions as a function of temperature and reaction rate; I. Calcite. Geochem. Cosmochim. Acta. 209, 296–319. doi:10.1016/j.gca.2016.09.035

CrossRef Full Text | Google Scholar

Amsellem, E., Moynier, F., Day, J. M. D., Moreira, M., Puchtel, I. S., and Teng, F.-Z. (2018). The stable strontium isotopic composition of ocean island basalts, mid-ocean ridge basalts, and komatiites. Chem. Geol. 483, 595–602. doi:10.1016/j.chemgeo.2018.03.030

CrossRef Full Text | Google Scholar

Andrews, M. G., and Jacobson, A. D. (2018). Controls on the solute geochemistry of subglacial discharge from the Russell Glacier, Greenland Ice Sheet determined by radiogenic and stable Sr isotope ratios. Geochem. Cosmochim. Acta. 239, 312–329. doi:10.1016/j.gca.2018.08.004

CrossRef Full Text | Google Scholar

Andrews, M. G., Jacobson, A. D., Lehn, G. O., Horton, T. W., and Craw, D. (2016). Radiogenic and stable Sr isotope ratios (⁸⁷Sr/⁸⁶Sr, δ^88/86Sr) as tracers of riverine cation sources and biogeochemical cycling in the Milford Sound region of Fiordland, New Zealand. Geochem. Cosmochim. Acta. 173, 284–303. doi:10.1016/j.gca.2015.10.005

CrossRef Full Text | Google Scholar

Andrews, M. G., and Jacobson, A. D. (2017). The radiogenic and stable Sr isotope geochemistry of basalt weathering in Iceland: role of hydrothermal calcite and implications for long-term climate regulation. Geochem. Cosmochim. Acta. 215, 247–262. doi:10.1016/j.gca.2017.08.012

CrossRef Full Text | Google Scholar

Bagard, M.-L., West, A. J., Newman, K., and Basu, A. R. (2015). Lithium isotope fractionation in the Ganges-Brahmaputra floodplain and implications for groundwater impact on seawater isotopic composition. Earth Planet Sci. Lett. 432, 404–414. doi:10.1016/j.epsl.2015.08.036

CrossRef Full Text | Google Scholar

Basu, A. R., Jacobsen, S. B., Poreda, R. J., Dowling, C. B., and Aggarwal, P. K. (2001). Large groundwater strontium flux to the oceans from the Bengal Basin and the marine strontium isotope record. Science 293, 1470–1473. doi:10.1126/science.1060524

PubMed Abstract | CrossRef Full Text | Google Scholar

Beck, A. J., Charette, M. A., Cochran, J. K., Gonneea, M. E., and Peucker-Ehrenbrink, B. (2013). Dissolved strontium in the subterranean estuary - implications for the marine strontium isotope budget. Geochem. Cosmochim. Acta. 117, 33–52. doi:10.1016/j.gca.2013.03.021

CrossRef Full Text | Google Scholar

Bickle, M. J., Bunbury, J., Chapman, H. J., Harris, N. B. W., Fairchild, I. J., and Ahmad, T. (2003). Fluxes of Sr into the headwaters of the Ganges. Geochem. Cosmochim. Acta. 67, 2567–2584. doi:10.1016/s0016-7037(03)00029-2

CrossRef Full Text | Google Scholar

Bickle, M. J., Chapman, H. J., Tipper, E., Galy, A., De La Rocha, C. L., and Ahmad, T. (2018). Chemical weathering outputs from the flood plain of the Ganga. Geochem. Cosmochim. Acta. 225, 146–175. doi:10.1016/j.gca.2018.01.003

CrossRef Full Text | Google Scholar

Burke, A., Present, T. M., Paris, G., Rae, E. C. M., Sandilands, B. H., Gaillardet, J., et al. (2018). Sulfur isotopes in rivers: insights into global weathering budgets, pyrite oxidation, and the modern sulfur cycle. Earth Planet Sci. Lett. 496, 168–177. doi:10.1016/j.epsl.2018.05.022

CrossRef Full Text | Google Scholar

Chao, H.-C., You, C.-F., Liu, H.-C., and Chung, C.-H. (2015). Evidence for stable Sr isotope fractionation by silicate weathering in a small sedimentary watershed in southwestern Taiwan. Geochem. Cosmochim. Acta. 165, 324–341. doi:10.1016/j.gca.2015.06.006

CrossRef Full Text | Google Scholar

Chao, H.-C., You, C.-F., Liu, H.-C., and Chung, C.-H. (2013). The origin and migration of mud volcano fluids in Taiwan: evidence from hydrogen, oxygen, and strontium isotopic compositions. Geochem. Cosmochim. Acta. 114, 29–51. doi:10.1016/j.gca.2013.03.035

CrossRef Full Text | Google Scholar

Charlier, B. L. A., Nowell, G. M., Parkinson, I. J., Kelley, S. P., Pearson, D. G., and Burton, K. W. (2012). High temperature strontium stable isotope behaviour in the early solar system and planetary bodies. Earth Planet Sci. Lett. 329-330, 31–40. doi:10.1016/j.epsl.2012.02.008

CrossRef Full Text | Google Scholar

Coleman, J. M. (1969). Brahmaputra river: channel processes and sedimentation. Sediment. Geol. 3, 129–239. doi:10.1016/0037-0738(69)90010-4

CrossRef Full Text | Google Scholar

Dansgaard, W. (1964). Stable isotopes in precipitation. Tellus 16, 436–468. doi:10.3402/tellusa.v16i4.8993

CrossRef Full Text | Google Scholar

de Souza, G. F., Reynolds, B. C., Kiczka, M., and Bourdon, B. (2010). Evidence for mass-dependent isotopic fractionation of strontium in a glaciated granitic watershed. Geochem. Cosmochim. Acta. 74, 2596–2614. doi:10.1016/j.gca.2010.02.012

CrossRef Full Text | Google Scholar

Galy, A., France-Lanord, C., and Derry, L. A. (1999). The strontium isotopic budget of Himalayan rivers in Nepal and Bangladesh. Geochem. Cosmochim. Acta. 63, 1905–1925. doi:10.1016/s0016-7037(99)00081-2

CrossRef Full Text | Google Scholar

Galy, A., and France-Lanord, C. (1999). Weathering processes in the Ganges-Brahmaputra basin and the riverine alkalinity budget. Chem. Geol. 159, 31–60. doi:10.1016/s0009-2541(99)00033-9

CrossRef Full Text | Google Scholar

Halicz, L., Segal, I., Fruchter, N., Stein, M., and Lazar, B. (2008). Strontium stable isotopes fractionate in the soil environments? Earth Planet Sci. Lett. 272, 406–411. doi:10.1016/j.epsl.2008.05.005

CrossRef Full Text | Google Scholar

Harvey, C. F. (2002). Groundwater flow in the Ganges delta. Science 296, 1563. doi:10.1126/science.296.5573.1563a

PubMed Abstract | CrossRef Full Text | Google Scholar

Heroy, D. C., Kuehl, S. A., and Goodbred, S. L. (2003). Mineralogy of the Ganges and Brahmaputra rivers: implications for river switching and late quaternary climate change. Sediment. Geol. 155, 343–359. doi:10.1016/s0037-0738(02)00186-0

CrossRef Full Text | Google Scholar

Immerzeel, W. W., Van Beek, L. P., and Bierkens, M. F. (2010). Climate change will affect the Asian water towers. Science 328, 1382–1385. doi:10.1126/science.1183188

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacobson, A. D., Blum, J. D., and Walter, L. M. (2002). Reconciling the elemental and Sr isotope composition of Himalayan weathering fluxes: insights from the carbonate geochemistry of stream waters. Geochem. Cosmochim. Acta. 66, 3417–3429. doi:10.1016/s0016-7037(02)00951-1

CrossRef Full Text | Google Scholar

Kısakűrek, B., James, R. H., and Harris, N. B. W. (2005). Li and δ⁷Li in Himalayan rivers: proxies for silicate weathering? Earth Planet Sci. Lett. 237, 387–401. doi:10.1016/j.epsl.2005.07.019

CrossRef Full Text | Google Scholar

Khan, M. H. R., Liu, J., Liu, S., Seddique, A. A., Cao, L., and Rahman, A. (2019). Clay mineral compositions in surface sediments of the Ganges-Brahmaputra-Meghna river system of Bengal Basin, Bangladesh. Mar. Geol. 412, 27–36. doi:10.1016/j.margeo.2019.03.007

CrossRef Full Text | Google Scholar

Krabbenhöft, A., Eisenhauer, A., Böhm, F., Vollstaedt, H., Fietzke, J., Liebetrau, V., et al. (2010). Constraining the marine strontium budget with natural strontium isotope fractionations (⁸⁷Sr/⁸⁶Sr∗, δ^88/86Sr) of carbonates, hydrothermal solutions and river waters. Geochem. Cosmochim. Acta. 74, 4097–4109. doi:10.1016/j.gca.2010.04.009

CrossRef Full Text | Google Scholar

Krabbenhöft, A., Fietzke, J., Eisenhauer, A., Liebetrau, V., Böhm, F., and Vollstaedt, H. (2009). Determination of radiogenic and stable strontium isotope ratios (⁸⁷Sr/⁸⁶Sr; δ⁸⁸/⁸⁶Sr) by thermal ionization mass spectrometry applying an ⁸⁷Sr/⁸⁴Sr double spike. J. Anal. At. Spectrom. 24, 1267–1271. doi:10.1039/b906292k

CrossRef Full Text | Google Scholar

Liu, H.-C., You, C.-F., Zhou, H., Huang, K.-F., Chung, C.-H., Huang, W.-J., et al. (2017). Effect of calcite precipitation on stable strontium isotopic compositions: insights from riverine and pool waters in a karst cave. Chem. Geol. 456, 85–97. doi:10.1016/j.chemgeo.2017.03.008

CrossRef Full Text | Google Scholar

Lupker, M., France-Lanord, C., Galy, V., Lavé, J., Gaillardet, J., Gajurel, A. P., et al. (2012). Predominant floodplain over mountain weathering of Himalayan sediments (Ganga basin). Geochem. Cosmochim. Acta. 84, 410–432. doi:10.1016/j.gca.2012.02.001

CrossRef Full Text | Google Scholar

Manaka, T., Araoka, D., Yoshimura, T., Hossain, H. M. Z., Nishio, Y., Suzuki, A., et al. (2017). Downstream and seasonal changes of lithium isotope ratios in the Ganges‐Brahmaputra river system. Geochem. Geophys. Geosyst. 18, 3003–3015. doi:10.1002/2016gc006738

CrossRef Full Text | Google Scholar

Manaka, T., Hossain, H. M. Z., Yoshimura, T., Suzuki, A., and Kawahata, H. (2019). Monthly changes in pCO₂ in the Ganges River: implications for carbon release from soil to the atmosphere via inland waters. J. Agric. Meteorol. 75, 47–55. doi:10.2480/agrmet.d-18-00007

CrossRef Full Text | Google Scholar

Manaka, T., Ushie, H., Araoka, D., Otani, S., Inamura, A., Suzuki, A., et al. (2015). Spatial and seasonal variation in surface water pCO₂ in the Ganges, Brahmaputra, and Meghna rivers on the Indian subcontinent. Aquat. Geochem. 21, 437–458. doi:10.1007/s10498-015-9262-2

CrossRef Full Text | Google Scholar

McArthur, J. M., Ravenscroft, P., Safiulla, S., and Thirlwall, M. F. (2001). Arsenic in groundwater: testing pollution mechanisms for sedimentary aquifers in Bangladesh. Water Resour. Res. 37, 109–117. doi:10.1029/2000wr900270

CrossRef Full Text | Google Scholar

Milliman, J. D., and Syvitski, J. P. M. (1992). Geomorphic/tectonic control of sediment discharge to the ocean: the importance of small mountainous rivers. J. Geol. 100, 525–544. doi:10.1086/629606

CrossRef Full Text | Google Scholar

Missana, T., Garcia-Gutierrez, M., and Alonso, M. (2008). Sorption of strontium onto illite/smectite mixed clays. Phys. Chem. Earth 33, S156–S162. doi:10.1016/j.pce.2008.10.020

CrossRef Full Text | Google Scholar

Moore, J., Jacobson, A. D., Holmden, C., and Craw, D. (2013). Tracking the relationship between mountain uplift, silicate weathering, and long-term CO₂ consumption with Ca isotopes: southern Alps, New Zealand. Chem. Geol. 341, 110–127. doi:10.1016/j.chemgeo.2013.01.005

CrossRef Full Text | Google Scholar

Moynier, F., Agranier, A., Hezel, D. C., and Bouvier, A. (2010). Sr stable isotope composition of Earth, the Moon, Mars, Vesta and meteorites. Earth Planet Sci. Lett. 300, 359–366. doi:10.1016/j.epsl.2010.10.017

CrossRef Full Text | Google Scholar

Neymark, L. A., Premo, W. R., Mel'nikov, N. N., and Emsbo, P. (2014). Precise determination of δ⁸⁸Sr in rocks, minerals, and waters by double-spike TIMS: a powerful tool in the study of geological, hydrological and biological processes. J. Anal. Atomic Spectrom. 29, 65–75. doi:10.1039/c3ja50310k

CrossRef Full Text | Google Scholar

Oliver, L., Harris, N., Bickle, M., Chapman, H., Dise, N., and Horstwood, M. (2003). Silicate weathering rates decoupled from the ⁸⁷Sr/⁸⁶Sr ratio of the dissolved load during Himalayan erosion. Chem. Geol. 201, 119–139. doi:10.1016/s0009-2541(03)00236-5

CrossRef Full Text | Google Scholar

Parua, P. K. The Ganga: water use in the Indian subcontinent. Berlin, Germany: Springer Science & Business Media (2010).

Paul, M., Reisberg, L., Vigier, N., Zheng, Y., Ahmed, K. M., Charlet, L., et al. (2010). Dissolved osmium in Bengal plain groundwater: implications for the marine Os budget. Geochem. Cosmochim. Acta. 74, 3432–3448. doi:10.1016/j.gca.2010.02.034

CrossRef Full Text | Google Scholar

Pearce, C. R., Parkinson, I. J., Gaillardet, J., Charlier, B. L. A., Mokadem, F., and Burton, K. W. (2015). Reassessing the stable (δ^88/86Sr) and radiogenic (⁸⁷Sr/⁸⁶Sr) strontium isotopic composition of marine inputs. Geochem. Cosmochim. Acta. 157, 125–146. doi:10.1016/j.gca.2015.02.029

CrossRef Full Text | Google Scholar

Peucker-Ehrenbrink, B., Miller, M. W., Arsouze, T., and Jeandel, C. (2010). Continental bedrock and riverine fluxes of strontium and neodymium isotopes to the oceans. G-cubed 11, Q03016. doi:10.1029/2009gc002869

CrossRef Full Text | Google Scholar

Pogge von Strandmann, P., Frings, P. J., and Murphy, M. J. (2017). Lithium isotope behaviour during weathering in the Ganges alluvial plain. Geochem. Cosmochim. Acta. 198, 17–31. doi:10.1016/j.gca.2016.11.017

CrossRef Full Text | Google Scholar

Quade, J., Roe, L., DeCelles, P. G., and Ojha, T. P. (1997). The late Neogene ⁸⁷Sr/⁸⁶Sr record of lowland Himalayan rivers. Science 276, 1828–1831. doi:10.1126/science.276.5320.1828

CrossRef Full Text | Google Scholar

Robbins, L. L., Hansen, M. E., Kleypas, J. A., and Meylan, S. C. (2010). U.S. Geological Survey Open-File Report 2010-1280. CO₂calc: a user-friendly seawater carbon calculator for windows, mac OS X, and iOS (iPhone). Available at:https://pubs.er.usgs.gov/publication/ofr20101280, 1–17.

Google Scholar

Sauzéat, L., Rudnick, R. L., Chauvel, C., Garçon, M., and Tang, M. (2015). New perspectives on the Li isotopic composition of the upper continental crust and its weathering signature. Earth Planet Sci. Lett. 428, 181–192. doi:10.1016/j.epsl.2015.07.032

CrossRef Full Text | Google Scholar

Shalev, N., Gavrieli, I., Halicz, L., Sandler, A., Stein, M., and Lazar, B. (2017). Enrichment of ⁸⁸Sr in continental waters due to calcium carbonate precipitation. Earth Planet Sci. Lett. 459, 381–393. doi:10.1016/j.epsl.2016.11.042

CrossRef Full Text | Google Scholar

Singh, S. K., Kumar, A., and France-Lanord, C. (2006). Sr and ⁸⁷Sr/⁸⁶Sr in waters and sediments of the Brahmaputra river system: silicate weathering, CO₂ consumption and Sr flux. Chem. Geol. 234, 308–320.

CrossRef Full Text | Google Scholar

Stevenson, E. I., Aciego, S. M., Chutcharavan, P., Parkinson, I. J., Burton, K. W., Blakowski, M. A., et al. (2016). Insights into combined radiogenic and stable strontium isotopes as tracers for weathering processes in subglacial environments. Chem. Geol. 429, 33–43. doi:10.1016/j.chemgeo.2016.03.008

CrossRef Full Text | Google Scholar

Stevenson, R., Pearce, C. R., Rosa, E., Hélie, J. F., and Hillaire-Marcel, C. (2018). Weathering processes, catchment geology and river management impacts on radiogenic (⁸⁷Sr/⁸⁶Sr) and stable (δ^88/86Sr) strontium isotope compositions of Canadian boreal rivers. Chem. Geol. 486, 50–60. doi:10.1016/j.chemgeo.2018.03.039

CrossRef Full Text | Google Scholar

Tipper, E., Galy, A., and Bickle, M. (2006). Riverine evidence for a fractionated reservoir of Ca and Mg on the continents: implications for the oceanic Ca cycle. Earth Planet Sci. Lett. 247, 267–279. doi:10.1016/j.epsl.2006.04.033

CrossRef Full Text | Google Scholar

Uemura, R., Matsui, Y., Yoshimura, K., Motoyama, H., and Yoshida, N. (2008). Evidence of deuterium excess in water vapor as an indicator of ocean surface conditions. J. Geophys. Res.: Atmospheres 113, D19114. doi:10.1029/2008jd010209

CrossRef Full Text | Google Scholar

UNDP (1982). Groundwater survey, the hydrogeological condition of Bangladesh. UNDP Technical Report, DP/UN/BGD-74-009/1.

Vance, D., Teagle, D. A., and Foster, G. L. (2009). Variable Quaternary chemical weathering fluxes and imbalances in marine geochemical budgets. Nature 458, 493–496. doi:10.1038/nature07828

PubMed Abstract | CrossRef Full Text | Google Scholar

Wakaki, S., Obata, H., Tazoe, H., and Ishikawa, T. (2017). Precise and accurate analysis of deep and surface seawater Sr stable isotopic composition by double-spike thermal ionization mass spectrometry. Geochem. J. 51, 227–239. doi:10.2343/geochemj.2.0461

CrossRef Full Text | Google Scholar

Webster, P. J., Jian, J., Hopson, T. M., Hoyos, C. D., Agudelo, P. A., Chang, H.-R., et al. (2010). Extended-range probabilistic forecasts of Ganges and Brahmaputra floods in Bangladesh. Bull. Am. Meteorol. Soc. 91, 1493–1514. doi:10.1175/2010bams2911.1

CrossRef Full Text | Google Scholar

Wei, G., Ma, J., Liu, Y., Xie, L., Lu, W., Deng, W., et al. (2013). Seasonal changes in the radiogenic and stable strontium isotopic composition of Xijiang River water: implications for chemical weathering. Chem. Geol. 343, 67–75. doi:10.1016/j.chemgeo.2013.02.004

CrossRef Full Text | Google Scholar