Electric Mode Excitation in the Atmosphere by Magnetospheric Impulses and ULF Waves

Variations of vertical atmospheric electric field E_z have been attributed mainly to meteorological processes. On the other hand, the theory of electromagnetic waves in the atmosphere, between the bottom ionosphere and earth’s surface, predicts two modes, magnetic H (TE) and electric E (TH) modes, where the E-mode has a vertical electric field component, E_z. Past attempts to find signatures of ULF (periods from fractions to tens of minutes) disturbances in E_z gave contradictory results. Recently, study of ULF disturbances of atmospheric electric field became feasible thanks to project GLOCAEM, which united stations with 1 sec measurements of potential gradient. These data enable us to address the long-standing problem of the coupling between atmospheric electricity and space weather disturbances at ULF time scales. Also, we have reexamined results of earlier balloon-born electric field and ground magnetic field measurements in Antarctica. Transmission of storm sudden commencement (SSC) impulses to lower latitudes was often interpreted as excitation of the electric TH₀ mode, instantly propagating along the ionosphere–ground waveguide. According to this theoretical estimate, even a weak magnetic signature of the E-mode ∼1 nT must be accompanied by a burst of E_z well exceeding the atmospheric potential gradient. We have examined simultaneous records of magnetometers and electric field-mills during >50 SSC events in 2007–2019 in search for signatures of E-mode. However, the observed E_z disturbance never exceeded background fluctuations ∼10 V/m, much less than expected for the TH₀ mode. We constructed a model of the electromagnetic ULF response to an oscillating magnetospheric field-aligned current incident onto the realistic ionosphere and atmosphere. The model is based on numerical solution of the full-wave equations in the atmospheric-ionospheric collisional plasma, using parameters that were reconstructed using the IRI model. We have calculated the vertical and horizontal distributions of magnetic and electric fields of both H- and E-modes excited by magnetospheric field-aligned currents. The model predicts that the excitation rate of the E-mode by magnetospheric disturbances is low, so only a weak E_z response with a magnitude of ∼several V/m will be produced by ∼100 nT geomagnetic disturbance. However, at balloon heights (∼30 km), electric field of the E-mode becomes dominating. Predicted amplitudes of horizontal electric field in the atmosphere induced by Pc5 pulsations and travelling convection vortices, about tens of mV/m, are in good agreement with balloon electric field and ground magnetometer observations.

Introduction: Are There Ultra-Low-Frequency Signatures in Atmospheric Electric Field?

The mutual fertilization of two geophysical disciplines—space physics and atmospheric electricity, has been rather low so far. This neglect is related to the fact that variations of the atmospheric electric field are commonly considered to be totally influenced by local meteorological processes. As a result, the magnetospheric community and atmospheric electricity community practically do not interact. In particular, in studies of waves and transients in the ultra-low-frequency (ULF) band (from mHz to Hz), the impact of magnetospheric disturbances on gradient of atmospheric potential (i.e., vertical electric field E_z) was commonly neglected, besides a few studies mentioned below.

Electromagnetic waves in the atmosphere, between the conductive layers of the bottom ionosphere and earth’s surface, can be decomposed into the magnetic H-mode (TE or THM mode) and electric E-mode (TH or TEM mode). Each mode has a specific partial impedance characterizing its interaction with the earth’s crust (Berdichevsky et al., 1971). The H-mode carries a vertical magnetic field disturbance, B_z, while the E-mode carries a vertical electric field disturbance, E_z. Upon modeling of magnetospheric MHD wave (Alfven (Hughes and Southwood, 1976) and fast compressional (Hamieri and Kivelson, 1991) modes) interaction with the ionosphere-atmosphere-ground system, the contribution of the E-mode is commonly neglected, so the ground response is believed to be produced by the H-mode only (Alperovich and Fedorov, 2007).

The E-modes are effectively excited in the ELF-VLF bands (e.g., Schumann resonances and sferics) by lightning electric discharges. Does the E-mode contribute also in the electromagnetic field of ULF waves? So far, there is no definitive answer to this question.

Apart from space physics applications, this problem is of key importance for magnetotelluric sounding (MTS) fundamentals. On the assumption that the incident ULF field is composed of a superposition of partial E- and H-modes, a new method of MTS, directional analysis, was developed by Chetaev (1970). This method is based on the premise that the spatial structure of ULF pulsations above a high-resistive crust does not meet the plane wave approximation and should be modeled as a horizontally propagating inhomogeneous plane wave with a complex wave vector (Dmitriev, 1970; Chetaev, 1985). According to this concept, the electric mode carrying a large vertical electric field/current in the air is a part of a primary wave. In this regard, verification of possible occurrences of E_z in the atmosphere in the ULF range is of fundamental importance for adequate MTS.

Attempts to detect ULF signatures in atmospheric E_z field have given contradictory results. Multicomponent magnetic and telluric observations provided seemingly promising results on the existence of the E-mode (Vinogradov, 1960; Savin et al., 1991). However, these studies used measurements of vertical telluric field in boreholes. Therefore, it is not clear whether the ULF signature in E_z was indeed caused by an incident partial E-mode, or by mode conversion owing to crust conductivity inhomogeneities. Direct measurements of the vertical electric field in the atmosphere seemingly indicated the possibility of the E-mode existence in the Pc3 (Chetaev et al., 1975) and Pc1 (Chetaev et al., 1977) frequency bands.

On the other hand, Anisimov et al. (1993) found no systematic pulsations in atmospheric E_z field coherent with geomagnetic Pc3 pulsations at middle latitude. Rare events with quasiperiodic variations of E_z were possibly the result of advection by wind of spatially inhomogeneous aero electric structures. At high latitude, the coherence between E_z fluctuations and simultaneous geomagnetic pulsations was low, though they both sometimes demonstrated periodic variations in the same period range 5–30 min (Kleimenova et al., 1996).

The problem is further complicated by the sporadic occurrence on the ground of periodic long-lasting variations of E_z owing to small-scale meteorological processes in the ULF band. Upon the upward transmission, the near-surface electric field noise attenuates exponentially and becomes negligible at the typical balloon heights (∼30 km). The electric field as observed by balloon platform is actually a local ohmic response to current, because a balloon is drifting with the wind, so space charge structures are not moving past balloon. Therefore, the balloon experiments are more promising than the ground observations for the study of magnetospheric effects in atmospheric electric field.

The ideal observational conditions in Antarctica (more than 30% days at the surface and >90% of the days at balloon altitude match the “fair weather” condition) enabled Bering et al. (1987) to address the long-standing problem of coupling between atmospheric electricity and space weather disturbances at ULF time scales using the coordinated balloon-born electric and ground magnetic observations. Several electric and magnetic field events were recorded during the 1985–86 Balloon Campaign at South Pole Station (Bering et al., 1988, Bering et al., 1990, Bering et al., 1995; Lin et al., 1995). However, no detailed theoretical analysis of these events was performed, so in Simultaneous Geomagnetic and Ez Variations During Storm Sudden Commencement Events, we will reexamine the results of the early balloon campaigns.

Another remaining controversy is related to the possibility of excitation of the electric TH_o mode (fundamental mode of the atmosphere–ground waveguide) by a magnetic storm sudden commencement (SSC). Kikuchi and Araki (1979) interpreted the propagation of SSC impulse from polar to low latitudes as “instantaneous” propagation of electromagnetic disturbance in TH₀ mode in the ionosphere-ground waveguide. This E-mode should carry a significant E_z disturbance, which can be detected by a sensor with a sufficient sampling rate (Yumoto et al., 1997). However, this predicted feature of SSC impulse was never validated.

In contrast to ubiquity of geomagnetic high-sampling observations, until recently there was no regular monitoring of the atmospheric electric field with a high time resolution. The previously mentioned results on occurrence of ULF pulsations in E_z field near the earth’s surface were obtained from short-term observational campaigns, and these data were mostly lost completely, so the results cannot be verified. Recently, the study of short-period disturbances of the atmospheric electric field became feasible thanks to the project GLOCAEM (GLObal Coordination of Atmospheric Electricity Measurements), which united the high-resolution (up to 1 sec) measurements of potential gradient worldwide (Nicoll et al., 2019). The GloCAEM atmospheric electricity database for potential gradient measurements provided insights into a number of meteorological processes. Here, this database is used to examine the influence of geomagnetic disturbances on atmospheric electric field and to resolve a controversy about the possibility of the E-mode excitation by SSC. Also, we reexamine the results of coordinated balloon-born electric and ground magnetic observations in Antarctica.

To interpret the results of the SSC observations and earlier balloon experiments in Antarctica, we have developed a numerical model of electromagnetic ULF response to the incidence of oscillating magnetospheric field-aligned currents onto a realistic ionosphere–atmosphere system.

Database of Geomagnetic and Atmospheric Measurements

To examine the impact of an interplanetary shock on the atmospheric electric field E_z as well, we used the list of observed SSC provided by International Index Service (http://isgi.unistra.fr and http://www.obsebre.es). The occurrence of IP shocks can also be seen in the plasma pressure p from the 1 min OMNI database (https://omniweb.gsfc.nasa.gov). We have examined all SSC events during the period 2007–2019.

As a source of information on disturbances of atmospheric electric field, we used the data provided by the project GloCAEM (GloCAEM.wordpress.com), which provides a portal to freely access potential gradient data from 17 sites worldwide. From available long-term 1 sec observations of atmospheric potential gradient (E_z), we have chosen data from the following sites:

-Reading (United Kingdom) 2011–2019, geographical coordinates 51.44°N, 0.94°W

-Hermon (Israel) 2015–2017, geographical coordinates 33°18′ N, 35°47′E

- CAS2 (Argentina) 2016–2019, geographical coordinates 31.80°S, 69.29°W

Available 1 sec data from some stations (e.g., Nycenk and Tripura) are low-quality, with too much interference, and have been omitted.

For magnetic field variations, we use the 1 min data from the INTERMAGNET array (https://intermagnet.github.io) from the following stations: near-equatorial stations MBO and AAE; midlatitude European stations ESK, LER, BFE, and CLF in the same region as atmospheric electricity sites. An SSC is a global phenomenon of a planetary scale, thus very close colocation of magnetometer and electric field sensor is not a crucial necessity. The map with location of selected stations is shown in Figure 1.

FIGURE 1

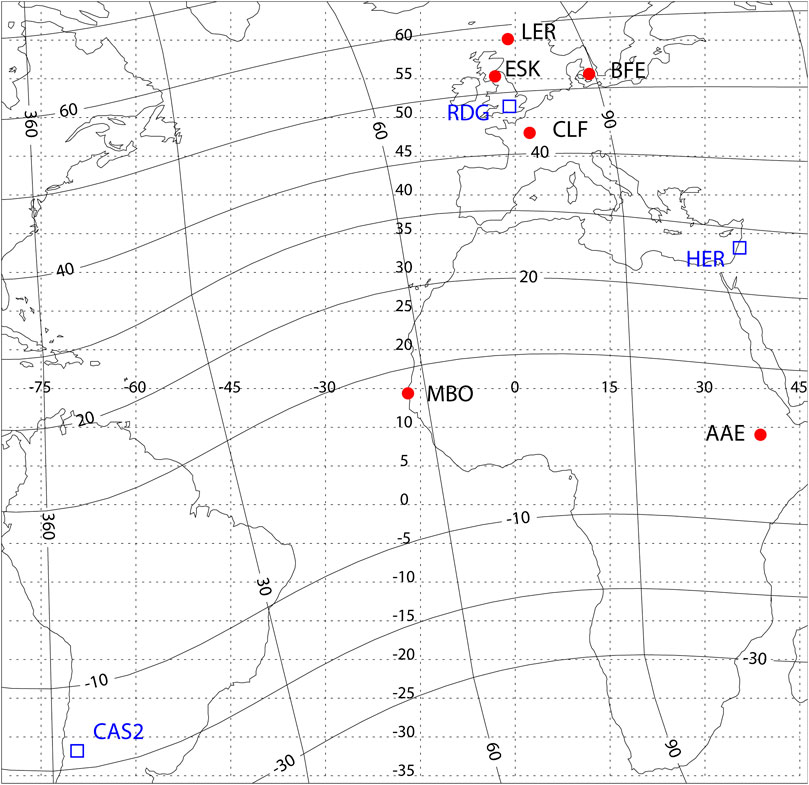
FIGURE 1. The map with location of selected atmospheric electricity stations (blue empty squares) and magnetometers (red dots). Solid lines denote geomagnetic coordinates, and dotted lines correspond to geographic coordinates.

An ideal place for monitoring the fine characteristics of atmospheric electricity is the Antarctic plateau, because of the lack of anthropogenic influences, weak and stable winds, and lack of low-altitude clouds. A large database of 10 sec atmospheric E_z and J_z observations with high-sensitive field-mill and current collector has been collected at South Pole, Vostok, and Concordia stations (Byrne et al., 1991; Few et al., 1992; Burns at al., 1998). With the use of these data, relationships between variations of the atmospheric electricity and IMF parameters (Frank-Kamenetsky et al., 1999), and the ionospheric electric potential (Corney et al., 2003) were found. The Antarctic atmospheric electricity data are available via website (http://globalcircuit.phys.uh.edu). From available 10 sec magnetometer data from South Pole observatory and atmospheric electric field and current measurements during the period 1991–1993, we have analyzed 18 SSC events.

The balloon experimenters have stored their data and made them available online (https://uh.edu/research/spg/data.html). Payloads at an altitude of ∼32 km carried 3-axis double probe electric field detectors and provided 15-s averaged 3-axis electric field data. We have re-analyzed the results of the 1985–86 Balloon Campaign at South Pole Station (Bering et al., 1987; Bering et al., 1995).

Estimate of E_z Perturbations Accompanying Storm Sudden Commencement Events

Among a large variety of MHD disturbances in the near-earth environment, special attention has been paid to the study of SSC’s caused by interaction of an interplanetary shock with the magnetosphere (Araki, 1977). The impulsive impact of a shock can bring a significant amount of energy and momentum into the magnetosphere in a very short time (Curto et al., 2007). Despite the seeming simplicity of such impact, the complexity of geomagnetic and plasma phenomena stimulated by an interplanetary shock turns out to be surprisingly large (Pilipenko et al., 2018). SSC transmission from high to low latitudes was often associated with the electric mode in the ionosphere–ground waveguide, instantly propagating along the earth’s surface (Kikuchi and Araki, 1979). Among possible electric modes in the atmospheric waveguide, the fundamental TH₀ mode without a cutoff frequency is excited most effectively by a magnetospheric Alfven wave. Distinctive features of TH₀ mode are the propagation velocity just somewhat less than the light speed, and weak attenuation, which is due to the geometrical factor, not due to dissipation in the ionosphere (Kikuchi, 2014). Therefore, it seems that the TH₀ mode may contribute to geomagnetic response far from the MHD disturbance incident on the ionosphere (Kikuchi and Hashimoto, 2016). This notion about the TH₀ mode has been applied to interpret prompt SSC transmission from auroral to low latitudes (Kikuchi, 1986; Chi et al., 2001).

However, in the original papers on the TH_o mode, the excitation rate of this mode by magnetospheric sources was not considered. Simple scaling shows that a vertical current J_z penetrating into the atmosphere resulting from the magnetospheric field-aligned current $J_Z^{\left(M\right)}$ with a transverse scale L is determined by the ratio between the resistance of the ionospheric E-layer (which is inversely proportional to the height-integrated Pedersen conductance Σ_P) and the resistance of the atmospheric column between the ground and height of the ionospheric conductive layer:

$J_Z/J_Z^{\left(M\right)}\simeq {\left(L/L_{\ast }\right)}^2.(1)$

In the atmosphere with exponential height-increasing conductivity ${\sigma }_A\left(z\right)={\sigma }_0\exp \left(z/\alpha \right)$ and negligible displacement current $\omega \ll {\sigma }_0/{\epsilon }_0$ (that is for frequencies less than ∼1 Hz), the parameter $L_{\ast }$ is $L_{\ast }=\sqrt{{\Sigma }_P/\left({\sigma }_0\alpha \right)}$. For typical values Σ_P = 20 S, Σ₀ = 2*10⁻¹⁴ S/m, and α = 10 km $L_{\ast }$∼10⁴ km. This simple estimate shows that a somewhat significant part of the magnetospheric current would penetrate to the low-conductive atmosphere only for extremely large-scale disturbances. Thus, SSC seems to be a very promising source of E-mode excitation, because the scale of an SSC-associated source is the distance between the dawn and dusk ionospheric vortices, which is about several thousand km.

Let us estimate the expected magnitude of the vertical electric component E_z of the TH₀ mode. From the subsystem of Maxwell’s equations for the E-mode, one can obtain the relationship between the components E_z and B_y of a wave propagating with the horizontal wave vector $k\equiv k_x$:

$\frac{E_z}{B_y}\simeq \frac{kc}{k_0{\epsilon }_A}.(2)$

Here, the dielectric permittivity is ${\epsilon }_A=1+i{\sigma }_A/{\epsilon }_0\omega$, and k₀ = ω/c is the vacuum wave number. Assuming that $k\simeq R_E^{-1}$, Eq. 2 yields in the case $\omega \ll {\sigma }_0/{\epsilon }_0$:

$\frac{E_z}{B_y}\simeq \frac{i}{\mu {\sigma }_0{R}_E}.(3)$

From the relationship (Eq. 3), it follows that a TH₀ mode with magnetic component B_y∼1 nT in the atmosphere with σ₀ = 10⁻¹³ S/m must be accompanied by a spike of atmospheric electric field E_z at the earth’s surface with amplitude ∼10³ V/m. Thus, even a weak magnetic signature of the E-mode must be accompanied by a burst of E_z exceeding the atmospheric potential gradient. More rigorous treatment of the problem of magnetospheric field-aligned current interaction with the multilayered ionosphere-atmosphere-ground system will be provided in Modeling of E-Mode Excitation by Magnetospheric FAC.

Simultaneous Geomagnetic and E_z Variations During Storm Sudden Commencement Events

We compare the above theoretical estimate with simultaneous observations of the atmospheric E_z field and geomagnetic variations (X-component). We have identified >50 events with simultaneous variations of E_z and ΔX. We examine the time intervals in the ±10 min vicinity of SSC events. The plots in Figure 2 present examples, showing vertical electric field E_z (mV/m) from available stations and magnetic field ΔX (nT) component from selected stations. The data on the solar wind dynamic pressure has too many missing values for these events and are not shown. The moment of each SSC is marked by vertical lines in Figure 2.

FIGURE 2

FIGURE 2. Four events with seemingly bursts of E_z during SSC. Upper panels show variations of the atmospheric potential gradient, E_z, and bottom panel shows magnetograms (X component) from magnetometers in the same LT sector.

In a majority of the events, no response of E_z on SSC was seen. The lack of E_z response imposes a limit on a possible amplitude of an expected electric mode—it is at least less than sensor sensitivity and background noise level. In none of >50 SSC events during 2007–2019 recorded by magnetometers and atmospheric electricity stations from the GLOCAEM array or Antarctica was a similar disturbance noticed.

However, in some events, a burst of E_z during an SSC can be seen. Figure 2 presents several promising events. Let us exclude for a moment the possibility that the geomagnetic and E_z disturbances were just mere coincidences. In any case, the amplitudes of E_z disturbance occurring simultaneously with SSC do not exceed ∼10 V/m. A similar negative result was obtained using E_z and J_z observations at the South Pole station (not shown). Therefore, SSC cannot be exciting or associated with the TH₀ mode.

Modeling of E-Mode Excitation by Magnetospheric FAC

Basic features of electric field transmission from the ionosphere into the near-earth atmosphere in the DC approximation (when the time scale is larger than the relaxation time τ > ε₀/σ₀ ∼ 20 min) can be understood in a simple 1D model (Park, 1976). This model predicts that a potential difference Φ between the ionosphere and ground supports E_z varying with altitude z as follows:

$E_z\left(z\right)=\Phi {\Sigma }_A/{\sigma }_A\left(z\right).$

Here, Σ_A is the total conductance of the atmospheric column ${\Sigma }_A^{-1}={\displaystyle \int {\sigma }_A^{-1}}\left(z\right)dz$. Typical values are ${\Sigma }_A\simeq {10}^{-17}{\text{S/m}}^2$, σ₀ ∼ 10⁻¹⁴ S/m, and Φ ∼ 250 kV. This relationship shows that a modification of the atmospheric conductivity profile ${\sigma }_{\mathrm{A}}\left(\mathrm{z}\right)$ by precipitation of high-energy solar particles (Kokorowski et al., 2006) or emanation of radioactive gas (Harrison et al., 2010) can modify $E_z(z)$ structure.

Penetration of nonsteady field, e.g., in the ULF band, is different and seldom studied. We have elaborated a model of the electromagnetic ULF response to an incidence of oscillating magnetospheric azimuthally symmetric FAC field-aligned current onto the realistic ionosphere and atmosphere. A similar multilayer model of the ionosphere-atmosphere-ground system has been used to examine the transmission of Pc1 waves through the ionosphere to the ground (Fedorov et al., 2018). The geomagnetic field B₀ at high latitudes may be assumed to be vertical. The problem is azimuthally symmetric, so a cylindrical coordinate system $\left\{z,\rho ,\varphi \right\}$ is used, with ρ = 0 in the axis of the current tube.

The model is based on a numerical solution of the full-wave equations in the realistic ionosphere. At the ground-atmosphere interface, the impedance boundary condition is imposed $E_{\varphi }/B_{\rho }=E_{\rho }/B_{\varphi }=Z_g/\mu$, where Z_g is the surface impedance. The ground conductivity is assumed to be σ_g = 10⁻⁴ S/m. The parameters of the ionospheric collisional plasma were reconstructed using the IRI model (http://irimodel.org). The IRI parameters were chosen to correspond to day 2009, 06/21, 02 UT (premidnight) at auroral latitude (geographic latitude 56.5^° and latitude 280.8^°). According to the IRI model, the ionospheric conductances would be Σ_P = 0.95 S and Σ_H = 1.40 S.

The vertical profile of atmospheric conductivity is modeled by exponential dependence ${\sigma }_A\left(z\right)={\sigma }_0\text{exp}\left(\text{z}/\alpha \right)$ that merges the IRI-predicted conductivity at z = 80 km. The choice of a more realistic conductivity profile will not change the results noticeably. The complex atmospheric conductivity that includes displacement current is given by $\sigma \left(z\right)={\sigma }_A\left(z\right)-i\epsilon {\epsilon }_0\omega$ (where ${\epsilon }_0$ is the vacuum permittivity). Figure 3 shows the altitude dependence of the absolute magnitude of the complex conductivity (black line). The magnitude of the displacement current for frequencies from 2 mHz to 1 Hz is denoted by vertical lines. Evidently, at low altitudes, $\sigma \left(\mathrm{z}\right)$ is determined by the displacement current, while at higher z, it is determined by the conductivity current. The height where $\omega {\epsilon }_0\epsilon ={\sigma }_A\left(z\right)$ is denoted z = z* (ω).

FIGURE 3

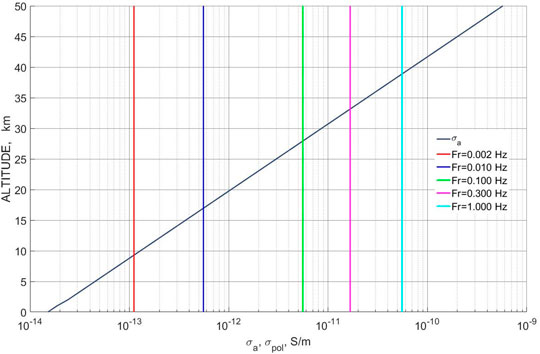
FIGURE 3. The altitude dependence of the absolute magnitude of the atmospheric conductivity |σ_A (z)| (black line). The magnitude of the displacement current $\epsilon {\epsilon }_0\omega$ for frequencies from 2 mHz to 1 Hz is denoted by vertical lines.

We have calculated both the vertical and horizontal distributions of magnetic and electric field components, including the vertical electric field in the atmosphere. The 6-component electromagnetic field is excited by an incident Alfven wave (that is, oscillatory field-aligned current) with horizontal radius R = 350 km. The amplitudes of all field components are normalized in such a way as to have the unit magnetic disturbance on the ground B_ρ (z = 0) = 1 nT for all frequencies in the region of spatial maximum ρ = ρ_max. The magnetic mode in the atmosphere is excited by ionospheric Hall currents. These eddy currents produce a magnetic response in the atmosphere in the radial direction, that is, in the B_ρ component. The electric mode in the atmosphere is associated with vertical current. This current produces a magnetic disturbance in the azimuthal direction, that is, in the B_ϕ component. Thus, B_ρ and E_ϕ components are associated with H-mode, while B_ϕ and E_ρ components are associated with the E-mode.

The radial distribution of the amplitudes of the magnetic components on the ground for various frequencies is shown in Figure 4. The maximum of B_ρ (ρ) is reached at ${\rho }_{\text{max}}=R/\sqrt{2} \simeq 280$ km (Figure 4, upper panel). The distribution of B_ϕ (ρ) component is rather similar (Figure 4, middle panel). This component is associated with the E-mode in the atmosphere, and it is about four orders of magnitude weaker than the radial component, associated with the H-mode. The occurrence of the vertical magnetic component B_z is due to inhomogeneity of an initial field, and its magnitude is determined by the ratio between the skin-depth and horizontal wave scale (Pilipenko et al., 1998). In contrast to horizontal components, the vertical component B_z(ρ) has spatial maximum beneath the current center ρ = 0 (Figure 4, bottom panel).

FIGURE 4

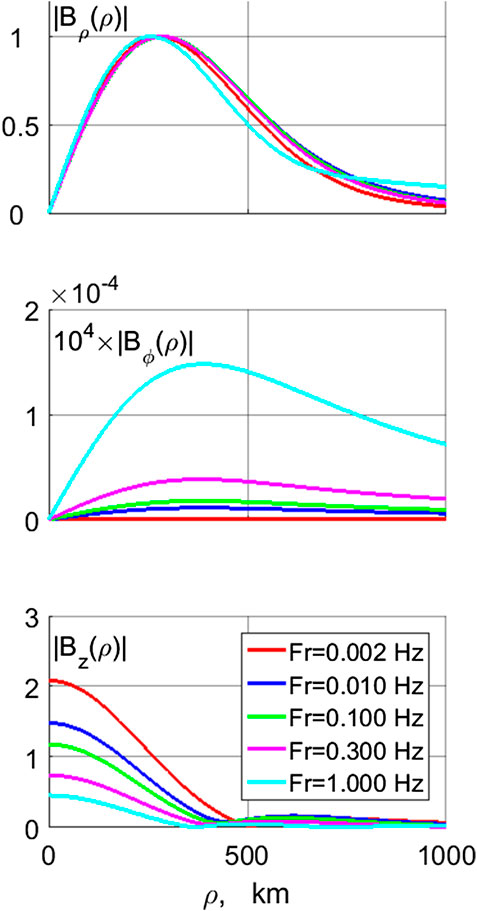
FIGURE 4. The radial distribution of the magnetic component amplitudes (in nT), from top to bottom - B_ρ (ρ), B_ϕ (ρ), and B_z (ρ), on the ground for various frequencies.

The radial distribution of the electric component amplitudes on the ground for various frequencies is shown in Figure 5. The electric field of the H-mode is revealed in the E_ϕ component, whereas the E-mode has E_ρ and E_z components. The distribution of horizontal electric components is similar to that of horizontal magnetic components (Figure 5, upper and middle panels). However, the vertical electric component E_z, associated with the E-mode, has maximum beneath the source at ρ = 0 (Figure 5, bottom panel). Amplitude of E_ρ component, ∼3 10⁻⁵ mV/m, is about four orders of magnitude less than amplitude of E_ϕ component, ∼0.2 mV/m. As expected for the electric field structure near the surface of a conductor, the normal to the surface electric field component E_z, ∼80 mV/m is much larger than the transverse component.

FIGURE 5

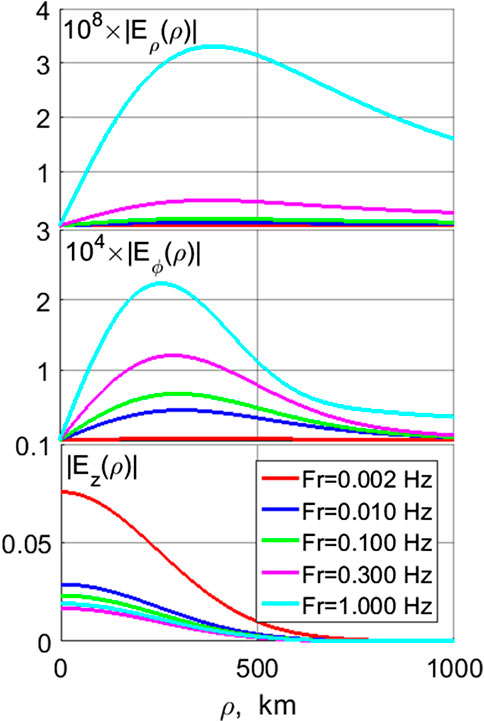
FIGURE 5. The radial distribution on the ground of the electric component amplitudes, E_ρ (ρ), E_ϕ (ρ), and E_z (ρ) (in V/m), for various frequencies (shown in legend).

The altitude profile of the horizontal magnetic components at the distance ρ_max is presented in Figure 6. The steep variation at z∼90 km is related to a π/2 rotation of the polarization ellipse in the Е-layer. The B_ρ component is nearly the same at all altitudes in the atmosphere. The B_ϕ component is many orders of magnitude less than the B_ρ component. The vertical magnetic component B_z is comparable in amplitude with the B_ρ component and just weakly increases with altitude.

FIGURE 6

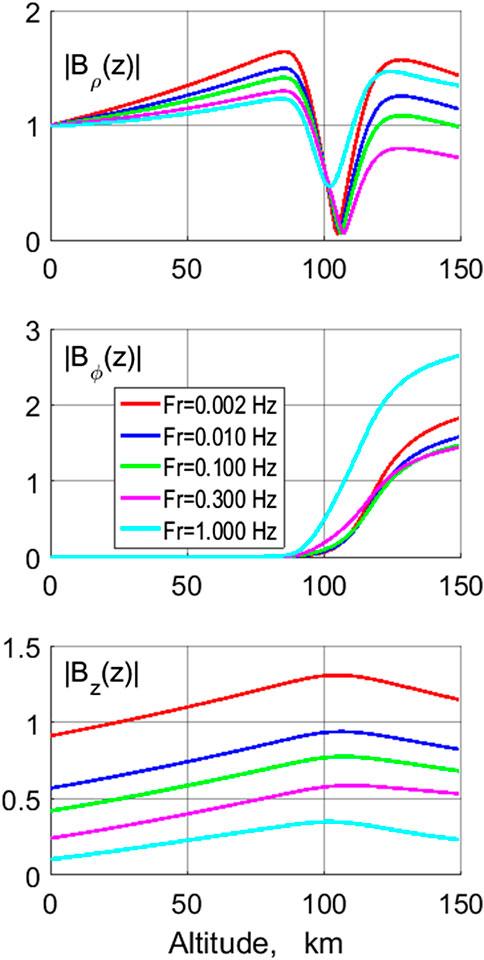
FIGURE 6. The altitudinal profiles of the horizontal magnetic components (in nT) B_ρ (z), B_ϕ (z) at ρ = ρ_max and the vertical component $B_z\left(z\right)$ at ρ = 0.

The altitude profiles of the horizontal electric field components at ρ_max and vertical component E_z (z) at ρ = 0 are presented in Figure 7. The E_ϕ (z) component only weakly depends on altitude for low frequencies, but for higher frequencies, it grows with altitude up to the E-layer, as expected from Faraday’s law ${\partial }_z{E}_{\varphi }=i\omega B_{\rho }$. The altitude dependence of the E_ρ (z) component changes drastically at height z = z*, where the Ohmic current equals the displacement current. This component is nearly constant in the more conductive upper atmosphere (z > z*), but it drops in the less conductive lower atmosphere (z < z*). For the vertical electric component, the modeling results can be understood, remembering that the altitude distribution of E_z (z) is proportional to the total complex conductivity Σ (z). The E_z perturbation at higher altitudes, z > z*, decays exponentially $E_z\left(z\right)\propto {\sigma }_A{\left(z\right)}^{-1}$, whereas at lower altitudes, z < z*, E_z (z) is nearly constant. In the ionosphere (>80 km), the E_z component vanishes owing to the high field-aligned conductivity of the ionospheric plasma.

FIGURE 7

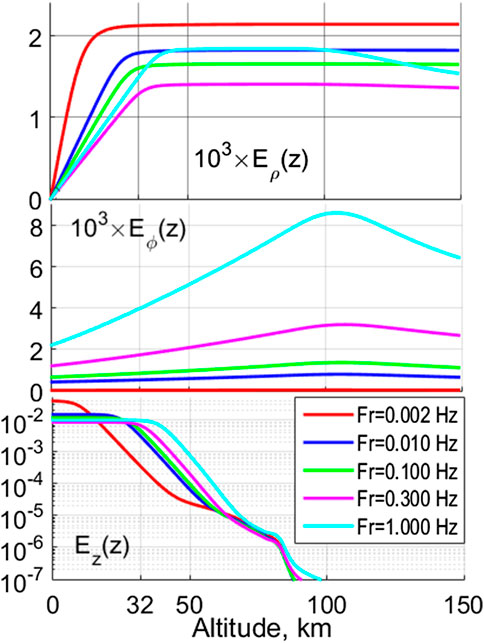
FIGURE 7. The altitudinal profiles of the horizontal electric components E_ρ (z), E_ϕ (z) at ρ = ρ_max and the vertical component $E_z\left(z\right)$ at ρ = 0.

The relative magnitude of the atmospheric electric field disturbances owing to magnetospheric ULF variations may be seen in Figure 8. This figure compares the altitude structure of all three electric field components. At the ground, the horizontal components drop to very low magnitudes prescribed by the boundary impedance relationship. On the ground, the electric field of H-mode is dominating, E_ρ << E_ϕ. However, because E_ρ increases fast until z ∼ z*, at the balloon height (∼30 km), the electric field of the E-mode becomes much larger, E_ρ >> E_ϕ.

FIGURE 8

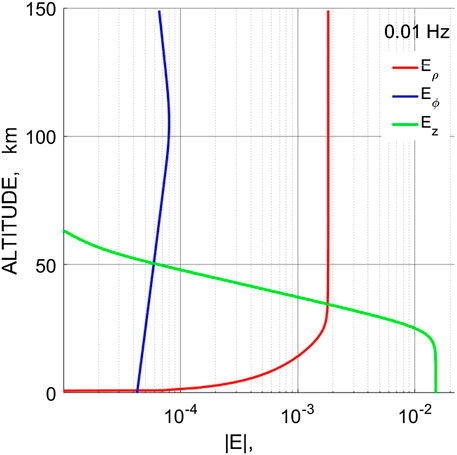
FIGURE 8. The altitudinal structure of all three electric field components E_ρ (z), E_ϕ (z), and E_z (z) (in V/m).

This behavior can be comprehended from the following consideration. At the earth’s surface, electric E^(g) and magnetic B^(g) components of the E-mode are about five orders of magnitude less than those of the H-mode. Magnetic components of both modes slowly vary with altitude: B_ϕ is practically constant till ∼40 km and B_ρ increases about 1.5 times only till 80 km. The behavior of electric components is more complicated. From Faraday’s law, it follows that the electric field of the H-mode varies with altitude as $E_{\varphi }\left(z\right)\cong E_{\varphi }^{\left(g\right)}-i\omega z{B}_{\rho }^{\left(g\right)}\approx E_{\varphi }^{\left(g\right)}$. So, this electric field component is nearly constant throughout the atmosphere. The electric field of the E-mode strongly varies with altitude $E_{\rho }\left(z\right)\cong E_{\rho }^{\left(g\right)}-i(k^2/k_0) zc{B}_{\varphi }^{\left(g\right)}\approx -i(k^2/k_0) zc{B}_{\varphi }^{\left(g\right)}$. As a result, the ratio of electric fields of both modes varies with altitude as $\left|E_{\rho }\left(z\right)/E_{\varphi }\left(z\right)\right|=(k^{2}zc/k_0)|B_{\varphi }^{\left(g\right)}/E_{\varphi }^{\left(g\right)}|$. Therefore, starting from ground values $B_{\varphi }^{\left(g\right)}=1.1\ast {10}^{-6}nT, E_{\varphi }^{\left(g\right)}=2.5\ast {10}^{-6}V/m$, for k = 10⁻³ 1/km, and T = 500 s, this ratio will grow linearly with altitude as $\left|E_{\rho }\left(z\right)/E_{\varphi }\left(z\right)\right|=3.2z \left(\text{km}\right)$. Thus, at balloon heights, electric field of the E-mode becomes much larger than that of the H-mode, whereas, on the other hand, the magnetic field of the E-mode (B_ϕ) is much less than that of the H-mode (B_ρ) in the entire atmosphere (up to the E-layer).

Observations of E_z Perturbations During Travelling Convection Vortice and Pc3-5 Events in Antarctica

Responses of the atmospheric electric field associated with impulsive and wave magnetospheric disturbances were observed during the balloon campaigns. The reported events include travelling convection vortices (TCVs) and Pc5 pulsations.

TCVs in the high latitude ionosphere are revealed on the ground as magnetic impulsive events with duration ∼5–10 min. These localized daytime disturbances are thought to be responses to transients in the solar wind or magnetosheath. A survey of the campaign data looked for unipolar magnetic pulses above background in the vertical component B_Z on the ground and electric field perturbations ≥10 mV/m at balloon altitude (Lin et al., 1995). From total of 112 events found, electric field responses were observed for 90% of the events with the average E_z amplitude ∼15 mV/m.

For example, the TCV event on January 3, 1986, was recorded by both the South Pole magnetometer and the balloon electric field sensor (Bering et al., 1990). This TCV was estimated to have a radius ∼350 km and moved antisunward along the oval at a speed of ∼4 km/s. The magnetometer observed a unipolar impulse in the magnetic vertical B_z component of ∼80 nT and a bipolar impulse in the horizontal B_x component of ∼100 nT. The accompanying atmospheric electric field pulse was less than 10 mV/m in the E_z component (at the noise level), and ∼40 mV/m in the eastward E_y and ∼25 mV/m in the poleward E_x components. In another event on Jan. 14, 1986, the TCV impulse amplitudes were ∼20 nT in the horizontal magnetic and ∼15 mV/m in the electric fields. The spike in the vertical E_z field reached ∼40 mV/m.

As an example of Pc5 pulsations, the event on July 9, 1975, may be presented (Maclennan et al., 1978). During this event coincident magnetic field, transverse electric field and electron precipitation fluctuations with 5 min period were measured around ∼06 LT by ground magnetometer and balloon-borne double-probe and scintillation counter. The balloon reached a ceiling altitude of ∼35 km. The experiment recorded magnetic variations with a peak-to-peak amplitude in the B_x component of ∼6 nT and in the B_y component of ∼8 nT, which were coherent with horizontal electric field variations with peak-to-peak amplitudes in the N-S component E_x of ∼20 mV/m and in the E-W component E_y of ∼15 mV/m.

Thus, the normalized transverse electric field response to TCV magnetic pulses is $E_{\perp }/B_{\perp }$ ∼ (0.4–0.8) (mV/m)/nT and to Pc5 waves is $E_{\perp }/B_{\perp }$ ∼ 2.5 (mV/m)/nT. The normalized response of vertical electric field to TCV magnetic pulses is $E_Z/B_{\perp }$ ∼ 2 (mV/m)/nT.

The expected model magnitude of an atmospheric electric field disturbance may be estimated from Figure 5 for a 1 nT magnetic disturbance. The horizontal electric field disturbance at typical balloon altitude (32 km) is about 1.5 mV/m, depending on frequency. Thus, for a typical ground magnetic amplitude (20 nT), the balloon measurements should reveal an E perturbation of about 30 mV/m. This value is in a good agreement with the results of balloon observations discussed above (e.g., Bering et al., 1990). At the same time, the inductive electric field produced by the H-mode E_ϕ at balloon height would be ∼1 mV/m only.

Amplitudes of the vertical and horizontal components become comparable at an altitude of ∼30 km. For the ground magnetic disturbance with B = 1 nT and f ∼ 10 mHz, the predicted vertical electric field disturbance is ∼0.02 V/m. Thus, for intense ULF disturbances of the geomagnetic field ∼100 nT, the disturbance of the ground level atmospheric field must be ∼2 V/m. This value is small, and it can be detected by modern electric field sensors only under extremely quiet weather conditions.

Apparent Impedances of H- and E-Modes

Simultaneous measurements of the wave electric and magnetic components gives one the possibility to determine the apparent wave impedance in order to obtain additional information about the wave mode. This method was applied by Pilipenko et al. (2012) to the radar-measured electric field and ground geomagnetic field of Pc5 waves and by Bering et al. (1998) to the analysis of coordinated balloon-born electric and ground magnetometer measurements. More importantly, a preliminary knowledge of the atmosphere–ionosphere impedance gives one the possibility to estimate the wave electric field amplitude in the ionosphere from ground magnetometer observations.

Here, we first provide simple analytical estimates and then support them with numerical modeling. For the H-mode excited by a toroidal Alfvenic-type magnetospheric disturbance, the ratio between the dominant components of the electric field in the ionosphere, E_x, and ground magnetic response, B_x, follows from the thin ionosphere theory (Pilipenko et al., 2012):

$\frac{E_x}{B_x}=\frac{1}{\mu {\Sigma }_H\sin I}\text{or}\frac{E_x\left[\text{mV/m}\right]}{B_x\left[\text{nT}\right]}\simeq \frac{0.8}{{\Sigma }_H\left[\text{S}\right]}\text{.}(4)$

For the E-mode, the relationship between electric field in the ionosphere and ground magnetic disturbance was derived by Hughes, (1974). Here, we present a similar relationship for a wave infinite in the E-W direction (k_y = 0) and localized in N-S direction ($k\equiv k_{\text{x}}$). The ratio between the meridional electric field E_x and the azimuthal component of the magnetic field B_y on the ground is given by

$\frac{E_x\left(z\right)}{B_y}=-i\frac{k^2{c}^2\alpha }{\omega }\ln \left({\mathrm{e}}^{-z/\alpha }+i\frac{{\sigma }_0}{\omega {\epsilon }_0}\right).(5)$

This ratio is altitude-dependent and does not depend on the ionospheric conductivity. At altitudes $z>z_{\ast }$, the ratio coincides with the equation from Hughes, (1974) (transformed into SI units):

$\frac{E_x\left(z\right)}{B_y}=-i\frac{k^2{c}^2\alpha }{\omega }\text{ln}\left(-i\frac{\omega {\epsilon }_0}{{\sigma }_0}\right).(6)$

Liu and Berkey, (1994) and Yizengaw et al. (2018) used the relationship between ionospheric electric field and magnetic field fluctuations from Hughes, (1974) to estimate the amplitude of the ionospheric electric field fluctuations driven by geomagnetic pulsations. However, the relationships they have used were incorrect choices. Moreover, it is wrong to model ULF pulsations as an E-mode.

The numerically calculated apparent impedances for both electric (E) and magnetic (H) modes (that is, the ratio E (z = 120 km)/B (z = 0) is shown in Figure 9. For the H-mode, the ratio E_ρ/B_ρ ∼ 0.6 (mV/m)/nT. This value is very close to the theoretical estimate (4) for Σ_H∼1.4 S. For the E-mode, the ratio E_ρ/B_ϕ is frequency dependent, slowly decreasing from ∼10² (V/m)/nT at f ∼ 3 mHz to ∼10 (V/m)/nT at f ∼ 1 Hz. Therefore, the E-mode impedance is at least four to five orders of magnitude larger that the impedance of the H-mode. Interpretation of ULF waves as E-mode would provide unrealistically high magnitudes of the wave electric field in the ionosphere.

FIGURE 9

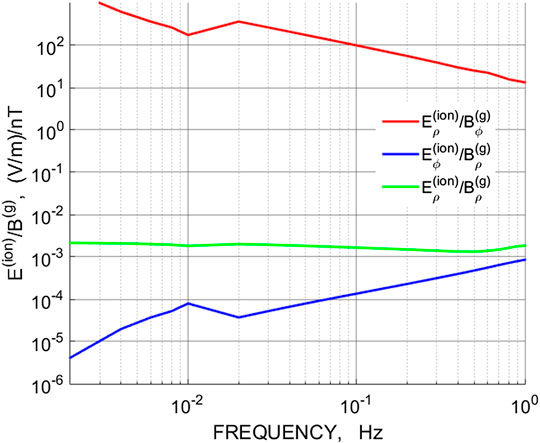
FIGURE 9. The frequency dependence of the apparent impedances (that is E (f)/B (f) amplitude ratios) for magnetic and electric modes.

An attempt to compare Pc1-3 pulsations using the South Pole search-coil magnetometer and balloon E-field data was made by Bering et al. (1998). While magnetic component was clearly observed as narrow-band emissions with power spectral densities (PSDs) $P_f^{\left(B\right)}$ ∼ 0.1 (nT)²/Hz in Pc1 band and ∼9 (nT)²/Hz in Pc3 band, the balloon-borne detector observed broadband emission without prominent features in the electric field spectra. During these events, the noise power spectral densities (PSDs) in the Pc1 and Pc3 bands were P_f ∼ 2 10³ and ∼4 10² (mV/m)²/Hz, correspondingly. According to the modeling results, E/B ∼ 2 (mV/m)/nT at f = 0.01–0.3 Hz (Figure 7), so at balloon heights, the PSD of the electric component could be $P_f^{\left(E\right)}=P_f^{\left(B\right)}{\left(E/B\right)}^2$ ∼0.4 (mV/m)²/Hz in the Pc1 band and ∼30 (mV/m)²/Hz in Pc3 band. Thus, the PSD of theoretically possible electric components of geomagnetic Pc1 and Pc3 pulsations was below the noise level.

Discussion

The conclusion in Estimate of E_zPerturbations Accompanying Storm Sudden Commencement Events about the occurrence of large E_z in the ULF electric mode was made earlier in Zybin et al. (1974) from other considerations. The ULF field in the atmosphere can be locally approximated as an inhomogeneous plane wave with a horizontal wave vector k. In this approximation, the vertical component E_z in the field of Pc3-5 pulsations must appear. The expected magnitude of E_z must be coupled with magnetic component magnitude as follows: $E_z=\left(k/\omega {\epsilon }_o\right)B_{\perp }$. For the commonly observed horizonal velocity of Pc3-5 pulsations ω/k ∼ 20 km/s, pulsations with a magnetic component amplitude B_⊥ = 1 nT should be accompanied by disturbances of E_z ∼60 V/m. To put it another way, the E_z component in the air can be estimated from the continuity of vertical current at the interface earth’s crust—air $E_z^{\left(air\right)}=\left({\sigma }_g/\omega {\epsilon }_o\right)E_z^{\left(ground\right)}$. According to this estimate, the amplitude components of E_z in the air should be a few tens of V/m according to borehole observations of J_z for σ_g ∼ 10⁻⁴ S/m and ω∼0.01 s⁻¹.

Our search for an E_z signature in disturbances from magnetospheric sources has given negative results. Even for the most promising source—large-scale intense SSC impulses, observations show that the excitation of the E-mode is negligible. Therefore, the assumption of the directional analysis (Chetaev et al., 1975; Chetaev et al., 1977; Chetaev, 1985) on the occurrence of the E-mode in the incident ULF wave field is not supported by observations. Nonetheless, the mathematical formalism developed in the frameworks of the directional analysis may be applied for MTS in the ELF band (e.g., Schumann resonance).

Our numerical modeling has resulted in a rather paradoxical conclusion. Excitation of the E-mode by magnetospheric sources is very weak, and this mode practically does not contribute into the ULF wave magnetic field. The E-mode contribution into the horizontal telluric field produced by ULF pulsations is also negligible. However, in the atmosphere, at the balloon heights, the electric field of this mode becomes dominant. Thus, an adequate interpretation of coordinated balloon-ground observations of Pc5 waves and TCVs is possible only with account of multimode structure of ULF disturbance in the atmosphere comprising both H- and E-modes. The important aspect of this problem is the polarization structure of H- and E-modes (Nenovski, 1999). The pertinent theoretical modeling and comparison with data from coordinated balloon-ground observations will be considered elsewhere.

At the same time, periodic fluctuations of the atmospheric electric field E_z in the ULF range that are not associated with geomagnetic disturbances are quite common. These fluctuations may confuse and mislead a researcher upon a search of simultaneous geomagnetic and atmospheric electricity pulsations. Periodic fluctuations of the atmospheric potential gradient and vertical atmospheric current J_z in the range of Pc4-5 frequencies were observed by Yerg and Johnson, (1974) and in the Pc1 and Pc3 bands by Anisimov et al. (1984). These fluctuations were not coherent with geomagnetic pulsations, so authors suggested that they may be caused by nonmagnetospheric sources, e.g., infrasound emissions from distant meteorological sources. Pc5 pulsations of atmospheric electric field were observed near local midnight under very clear weather by balloon campaign (altitude ∼32 km) (Liao et al., 1994). Both transverse and vertical electric field components of pulsations had amplitudes of 20–30 mV/m, but no similar signal was observed in magnetometer or riometer data. Narrow-band wave packets in the Pc1 band in both horizontal and vertical components of the atmospheric electric field without a ground magnetic response were detected during the 1985–86 South Pole Balloon Campaign (Bering and Benbrook, 1995). The driving mechanisms of such “electrostatic” ULF pulsations are very speculative and have not been established.

The model implicitly assumes that a single cylindrical FAC is spread along the ionosphere out to infinity. In realistic magnetosphere–ionosphere disturbances, coupled incident and return FACs of opposite polarity are formed at various distances from each other, from about ten thousand km in SSC events to few hundred km in TCV or Pc5 events. If the geometry of the magnetosphere–ionosphere current system is known, the modeled electromagnetic fields due to each isolated FAC are to be summed up.

We have considered a simple geometry with the plane ionosphere and ground and vertical geomagnetic field B₀. This assumption is well justified for the consideration of local structure of electromagnetic disturbance at distances less than 10³ km from an incident FAC. At larger distances upon propagation to low latitudes, additional factors become noticeable: ionosphere/ground curvature, inclination of geomagnetic field, and lateral inhomogeneity of ionospheric parameters. However, the magnetic field decreases with distance as ∼r⁻², so at large distances, the response would be too weak to observe. Probably, there is no need to advance theory to interpret very weak signatures at large distances from a source.

Conclusion

We have addressed the long-standing problem of coupling between atmospheric electricity and space weather disturbances at ULF time scales (from fractions minutes to tens of mins). The generation of ULF impulses and noises by atmospheric electric discharges is a more or less well-known aspect of the problem (see Pilipenko, 2012). The inverse aspect, the influence of magnetospheric magnetic disturbances on the atmospheric electric field is much less studied.

The GloCAEM atmospheric electricity field-mill measurements with 1 sec cadence have been used to examine the influence of geomagnetic SSC disturbances on atmospheric electricity. The predicted mechanism of SSC transmission by the electric-type TH₀ mode along the earth–ionosphere waveguide was not confirmed. Observations with field-mills and current collectors in Antarctica also have not found any signature of the E-mode accompanying SSC magnetic pulses. Therefore, the model of prompt transmission of disturbances from auroral latitudes to low latitudes by the atmospheric TH₀ mode is not supported by observations and should be rejected.

We have advanced the theory of ULF disturbance transmission though the ionosphere and atmosphere to the ground by considering the possible role of the electric mode. The constructed model of electromagnetic ULF response to an incidence of oscillating magnetospheric field-aligned current onto the realistic ionosphere is based on a numerical solution of the full-wave equations in the atmospheric-ionospheric collisional plasma whose parameters were reconstructed using the IRI model and a realistic vertical profile of atmospheric conductivity. The modeling strictly proved that excitation of the electric mode is weak and its contribution into the field of ULF waves on the ground is very small. In a most favorable situation, only a weak E_z disturbance with a magnitude of ∼several V/m could be produced by a large-scale intense (∼100 nT) geomagnetic disturbance. At the same time, the predicted amplitudes of electric field at balloon heights, ∼few tens of mV/m, induced by Pc5 pulsations and travelling convection vortices are in good agreement with coordinated balloon—ground magnetometer observations. Therefore, E-mode excitation by magnetospheric ULF disturbances cannot be completely ignored, because an adequate interpretation of balloon observations is possible only on the basis of a model comprising both H- and E-modes.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: http://www.wdcb.ru/arctic_antarctic/antarctic_magn_3.ru.html.

Author Contributions

VP performed theoretical analysis, EF did numerical modeling, VM-B analyzed data, and EB provided observational data.

Funding

This study was supported by the grants PLR-1744828 (VP) from the U.S. National Science Foundation and 20-05-00787 (EF, VM-B) from the Russian Fund for Basic Research. Details of the GloCAEM project are here https://drive.google.com/open?id=1l7VI98q4FfX5AoOEi5Y_kr-HL-58jp9E.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alperovich, L. S., and Fedorov, E. N. (2007). “Hydromagnetic waves in the magnetosphere and the ionosphere,”in Astrophysics and space science library (Berlin, Germany: Springer Science & Business Media), Vol. 353, 418.

CrossRef Full Text | Google Scholar

Anisimov, S. V., Rusakov, N. N., and Troitskaya, V. A. (1984). Short-period variations of the vertical electric current in the air. J. Geomagn. Geoelectr. 36, 229–238. doi:10.5636/jgg.36.229

CrossRef Full Text | Google Scholar

Anisimov, S. V., Kurneva, N. A., and Pilipenko, V. A. (1993). Input of electric mode into the field of Pc3-4 pulsations. Geomagn. Aeron. 33 (3), 35–41.

CrossRef Full Text | Google Scholar

Araki, T. (1977). Global structure of geomagnetic sudden commencements, Planet. Space Sci. 25, 373–384. doi:10.1016/0032-0633(77)90053-8

CrossRef Full Text | Google Scholar

Berdichevsky, M. N., Van’jan, L. L., and Dmitriev, V. I. (1971). Concerning the possibility to neglect vertical currents during magnetotelluric sounding. Izv. AN SSSR, Fizika Zemli, N5, 69–78.

CrossRef Full Text | Google Scholar

Bering, E. A., and Benbrook, J. R. (1995). Intense 2.3‐Hz electric field pulsations in the stratosphere at high auroral latitude. J. Geophys. Res. Space Phys. 100, 7791–7806. doi:10.1029/94JA02680

CrossRef Full Text | Google Scholar

Bering, E. A., Benbrook, J. R., Howard, J. M., Oró, D. M., Stansbery, E. G., Theall, J. R., et al. (1987). The 1985-86 South Pole balloon campaign. Memoirs of the National Institute of Polar Research 48, 313–317.

CrossRef Full Text | Google Scholar

Bering, E. A., Benbrook, J. R., Byrne, G. J., Liao, B., Theall, J. R., Lanzerotti, L. J., et al. (1988). Impulsive electric and magnetic field perturbations observed over South Pole: flux transfer events? Geophys. Res. Lett. 15, 1545–1548. doi:10.1029/GL015i013p01545

CrossRef Full Text | Google Scholar

Bering, E. A., Lanzerotti, L. J., Benbrook, J. R., Lin, Z.‐M., Maclennan, C. G., Wolfe, A., et al. (1990). Solar wind properties observed during high-latitude impulsive perturbation events. Geophys. Res. Lett. 17, 579–582. doi:10.1029/GL017i005p00579

CrossRef Full Text | Google Scholar

Bering, E. A., Benbrook, J. R., Liao, B., Theall, J. R., Lanzerotti, L. J., and MacLennan, C. G. (1995). Balloon measurements above the South pole: study of the ionospheric transmission of ULF waves. J. Geophys. Res. 100, 7807–7820. doi:10.1029/94JA02810

CrossRef Full Text | Google Scholar

Bering, E. A., Benbrook, J. R., Engebretson, M. J., and Arnoldy, R. L. (1998). Simultaneous electric and magnetic field observations of Pc1–2 and Pc3 pulsations. J. Geophys. Res.: Space Physics 103, 6741–6761. doi:10.1029/97JA03327

CrossRef Full Text | Google Scholar

Burns, G. B., Frank-Kamenetsky, A. V., Troshichev, O. A., Bering, E. A., and Papitashvili, V. O. (1998). The geoelectric field: a link between the troposphere and the ionosphere. Ann. Glaciol. 27, 651–654. doi:10.3189/1998AoG27-1-651-654

CrossRef Full Text | Google Scholar

Byrne, G. J., Bering, E. A., Few, A. A., and Morris, G. A. (1991). Measurements of atmospheric conduction currents and electric fields at the South pole. Antarct. J. U. S. 26, 291–294.

CrossRef Full Text | Google Scholar

Chetaev, D. N. (1970). About structure of geomagnetic pulsation field and magnetotelluric soundings. Solid Earth Phy. 2, 52–56.

CrossRef Full Text | Google Scholar

Chetaev, D. N. (1985). Directional analysis of magnetotelluric observations. Moscow: Nauka, 228.[in Russian]

CrossRef Full Text | Google Scholar

Chetaev, D. N., Fedorov, E. N., Krylov, S. M., Lependin, V. P., Morghounov, V. A., Troitskaya, V. A., et al. (1975). On the vertical electric component of the geomagnetic pulsation field. Planet. Space Sci. 23, 311–314. doi:10.1016/0032-0633(75)90136-1

CrossRef Full Text | Google Scholar

Chetaev, D. N., Chernysheva, S. P., Morghounov, V. A., Sheftel, V. A., and Zemliankin, G. A. (1977). On the pulsations of Ez(air) in the frequency range of Pc1. Planet. Space Sci 26, 507–508. doi:10.1016/0032-0633(78)90071-5

CrossRef Full Text | Google Scholar

Chi, P. J., Russell, C. T., Raeder, J., Zesta, E., Yumoto, K., Kawano, H., et al. (2001). Propagation of the preliminary reverse impulse of sudden commencements to low latitudes. J. Geophys. Res. 106, 18857–18864. doi:10.1029/2001JA900071

CrossRef Full Text | Google Scholar

Corney, R. G., Burns, G. B., Michael, K., Frank-Kamenetsky, A. V., Troshichev, O. A., Bering, E. A., et al. (2003). The influence of polar-cap convection on the geoelectric field at Vostok, Antarctica. J. Atmos. Sol. Terr. Phys. 65, 345–354. doi:10.1016/S1364-6826(02)00225-0

CrossRef Full Text | Google Scholar

Curto, J. J., Araki, T., and Alberca, L. F. (2007). Evolution of the concept of Sudden storm commencements and their operative identification. Earth Planets Space 59, i–xii. doi:10.1186/BF03352059

CrossRef Full Text | Google Scholar

Dmitriev, V. I. (1970). Impedance of a stratified media for an inhomogeneous plane wave. Izv. AN SSSR. Fizika Zemli N7, 63–69.

CrossRef Full Text | Google Scholar

Fedorov, E. N., Pilipenko, V. A., Engebretson, M. J., and Hartinger, M. D. (2018). Transmission of a magnetospheric Pc1 wave beam through the ionosphere to the ground. J. Geophys. Res. B: Space Phys. 123, 3965–3982. doi:10.1029/2018JA0253381–18

CrossRef Full Text | Google Scholar

Few, A. A., Morris, G. A., Bering, E. A., Benbrook, J. R., Chadwick, R., and Byrne, G. J. (1992). Surface observations of global atmospheric electric phenomena at Amundsen-Scott South Pole Station. Antarct. J. U. S. 27, 307–309.

CrossRef Full Text | Google Scholar

Frank-Kamenetsky, A. V., Burns, G. B., Troshichev, O. A., Papitashvili, V. O., Bering, E. A., and French, W. J. R. (1999). The geoelectric field at Vostok, Antarctica: it’s relation to the interplanetary magnetic field and the polar cap potential difference. J. Atmos. Sol. Terr. Phys. 61, 1347–1356. doi:10.1016/S1364-6826(99)00089-9

CrossRef Full Text | Google Scholar

Hameiri, E., and Kivelson, M. G. (1991). Magnetospheric waves and the atmosphere-ionosphere layer. J. Geophys. Res. 96, 21125–21134.

CrossRef Full Text | Google Scholar

Harrison, R. G., Aplin, K. L., and Rycroft, M. J. (2010). Atmospheric electricity coupling between earthquake regions and the ionosphere. J. Atmos. Sol. Terr. Phys. 72, 376–381. doi:10.1016/j.jastp.2009.12.004

CrossRef Full Text | Google Scholar

Hughes, W. J., and Southwood, D. J. (1976). The screening of micropulsation signals by the atmosphere and ionosphere. J. Geophys. Res. 81, 3234–3240. doi:10.1029/JA081i019p03234

CrossRef Full Text | Google Scholar

Hughes, W. J. (1974). The effect of the atmosphere and ionosphere on long period magnetospheric micropulsations. Planet. Space Sci 22, 1157–1172. doi:10.1016/0032-0633(74)90001-4

CrossRef Full Text | Google Scholar

Kikuchi, T. (1986). Evidence of transmission of polar electric field to the low latitude at times of geomagnetic sudden commencement. J. Geophys. Res. 91, 3101–3105. doi:10.1029/JA091iA03p03101

CrossRef Full Text | Google Scholar

Kikuchi, T. (2014). Transmission line model for the near-instantaneous transmission of the ionospheric electric field and currents to the equator. J. Geophys. Res. 119, 1131–1156. doi:10.1002/2013JA019515

CrossRef Full Text | Google Scholar

Kikuchi, T., and Araki, T. (1979). Transient response of uniform ionosphere and preliminary reverse impulse of geomagnetic storm sudden commencement. J. Atmos. Terr. Phys. 41, 917–925. doi:10.1016/0021-9169(79)90093-X

CrossRef Full Text | Google Scholar

Kikuchi, T., and Hashimoto, K. K. (2016). Transmission of the electric fields to the low latitude ionosphere in the magnetosphere-ionosphere current circuit. Geoscience Letters 3, 1–11. doi:10.1186/s40562-016-0035-6

CrossRef Full Text | Google Scholar

Kleimenova, N. G., Nikiforova, N. N., Kozyreva, O. V., and Michnowsky, S. (1996). Long-period geomagnetic pulsations and fluctuations of the atmospheric electric field intensity at the polar cap latitudes. Geomagn. Aeron. 35 (N4), 469–477.

CrossRef Full Text | Google Scholar

Kokorowski, M., Sample, J. G., Holzworth, R. H., Bering, E. A., Bale, S. D., Blake, J. B., et al. (2006). Rapid fluctuations of stratospheric electric field following a solar energetic particle event. Geophys. Res. Lett. 33, L20105. doi:10.1029/2006GL027718

CrossRef Full Text | Google Scholar

Liao, B., Benbrook, J. R., Bering, E. A., Byrne, G. J., Theall, J. R., Lanzerotti, L. J., et al. (1994). Balloon observations of nightside Pc5 quasi‐electrostatic waves above the South Pole. J. Geophys. Res.: Space Physics 99, 3879–3891. doi:10.1029/93JA02753

CrossRef Full Text | Google Scholar

Lin, Z. M., Bering, E. A., Benbrook, J. R., Liao, B., Lanzerotti, L. J., Maclennan, C. G., et al. (1995). Statistical studies of impulsive events at high latitudes. J. Geophys. Res.: Space Physics 100, 7553–7566. doi:10.1029/94JA01655

CrossRef Full Text | Google Scholar

Liu, J. Y., and Berkey, F. T. (1994). Phase relationships between total electron content variations, Doppler velocity oscillations and geomagnetic pulsations. J. Geophys. Res. 99, 17539–17545. doi:10.1029/94JA00869

CrossRef Full Text | Google Scholar

Maclennan, C. G., Lanzerotti, L. J., Hasegawa, A., Bering, E. A., Benbrook, J. R., Sheldon, W. R., et al. (1978). On the relationship of ∼3 mHz (Pc5) electric, magnetic, and particle variations. Geophys. Res. Lett. 5, 403–406. doi:10.1029/GL005i005p00403

CrossRef Full Text | Google Scholar

Nenovski, P. (1999). Asymmetry in the electric and magnetic field polarization of geomagnetic pulsations. J. Atmos. Sol. Terr. Phys. 61, 1007–1015. doi:10.1016/S1364-6826(99)00048-6

CrossRef Full Text | Google Scholar

Nicoll, K. A., Harrison, R. G., Barta, V., Bor, J., Brugge, R., et al. (2019). Towards a global network for atmospheric electric field monitoring. J. Atmos. Sol. Terr. Phys. 184, 18–29. doi:10.1016/j.jastp.2019.01.003

CrossRef Full Text | Google Scholar

Park, C. G. (1976). Downward mapping of high-latitude ionospheric electric fields to the ground. J. Geophys. Res. 81, 168–174. doi:10.1029/JA081i001p00168

CrossRef Full Text | Google Scholar

Pilipenko, V. A. (2012). Impulsive coupling between the atmosphere and ionosphere/magnetosphere. Space Sci. Rev. 168, 533–550. doi:10.1007/s11214-011-9859-8

CrossRef Full Text | Google Scholar

Pilipenko, V., Vellante, M., Anisimov, S., De Lauretis, M., Fedorov, E., and Villante, U. (1998). Multi-component ground-based observation of ULF waves: goals and methods. Ann. Geofisc. 41, 63–77. doi:10.4401/ag-3794

CrossRef Full Text | Google Scholar

Pilipenko, V., Belakhovsky, V., Kozlovsky, A., Fedorov, E., and Kauristie, K. (2012). Determination of the wave mode contribution into the ULF pulsations from combined radar and magnetometer data: method of apparent impedance. J. Atmos. Sol. Terr. Phys. 77, 85–95. doi:10.1016/j.jastp.2011.11.013

CrossRef Full Text | Google Scholar

Pilipenko, V. A., Bravo, M., Romanova, N. V., Kozyreva, O. V., Samsonov, S. N., and Sakharov, Y. A. (2018). Geomagnetic and ionospheric responses to the interplanetary shock wave of March 17, 2015. Izvestiya Phys. Solid Earth 54 (N5), 721–740. doi:10.1134/S1069351318050129

CrossRef Full Text | Google Scholar

Savin, M. G., Nikiforov, V. M., and Kharakhinov, V. M. (1991). About anomalies of vertical electric component of telluric field at Northern Sakhalin. Izv. AN SSSR. Fizika Zemli N2, 100–108.

CrossRef Full Text | Google Scholar

Vinogradov, I. A. (1960). New experimental data on vertical component of short-period oscillations of telluric current field. Geol. and Geophys. В6, 100–105.

PubMed Abstract | CrossRef Full Text | Google Scholar

Yerg, D. G., and Johnson, K. R. (1974). Short‐period fluctuations in the fair‐weather electric field. J. Geophys. Res. 79, 2177–2184. doi:10.1029/JC079i015p02177

CrossRef Full Text | Google Scholar

Yizengaw, E., Zesta, E., Moldwin, M. B., Magoun, M., Tripathi, N. K., Surussavadee, C., et al. (2018). ULF wave‐associated density irregularities and scintillation at the equator. Geophys. Res. Lett. 45, 5290–5298. doi:10.1029/2018GL078163

CrossRef Full Text | Google Scholar

Yumoto, K., Pilipenko, V., Fedorov, E., Kurneva, N., and De Lauretis, M. (1997). Magnetospheric ULF wave phenomena stimulated by SSC. J. Geomagn. Geoelectr. 49, 1179–1195. doi:10.5636/jgg.49.1179

CrossRef Full Text | Google Scholar

Zybin, K. Yu., Krylov, S. M., Lependin, V. P., Morgunov, V. А., Troitskaya, V. А., and Chetaev, D. N. (1974). About vertical electric component of the geomagnetic pulsation field. Doklady AN SSSR 218 (4), 828–829.

CrossRef Full Text | Google Scholar