Prediction of the Variability of Changes in the Intensity and Frequency of Climate Change Reinforced Multi-Day Extreme Precipitation in the North-Central Vietnam Using General Circulation Models and Generalized Extreme Value Distribution Method

Introduction

Extreme precipitation (EP) is the major cause of floods, erosion and landslides, which result in severe damages to agriculture and infrastructures. It has been reported that during the past century, there has been a significant increase in extreme precipitation events; and more notably, in many regions, especially mid-latitude regions, increases in annual heavy precipitation events were disproportionate compared to changes in mean values (IPCC, 2013). For instance, in the United States, the frequency of extreme precipitation events since the 1920s/1930s was found to sizably increase (Kunkel, 2003). In Germany, an analysis of precipitation observed during 1901–2000 shows that climate was getting more extreme in the winter during this period (Tromel and Schonwiese, 2007). A similar finding was reported by Zolina et al. (2008), and that a positive linear trend in heavy precipitation was found not only for winter but also for spring and autumn since 1950. Significant increases in Evapotranspiration (ET) were also observed in different regions of China in the second half of the 20th century, including its western part, the middle and lower Yangtze River basin, and its southeast coastal part (Zhao et al., 2014).

Although observations have shown significant increases in extreme precipitation and it is widely acknowledged that extreme climate events in general and ET in particular potentially produce greater impacts on the society and environment than a shift in average values (IPCC, 2007), less attention has been paid to their future changes, especially at regional and local scales. This may be due to the lack of an effective method. To date, General Circulation Model (GCM) is still the most common tool for the simulation and prediction of climate change in large scales. However, because the spatial resolution of GCMs is generally low so that it is not appropriate to directly use their output for local scale, especially for extreme precipitation because extreme precipitation is a much localized phenomenon (Ye and Li, 2011). In order to overcome the shortcoming of coarse spatial resolution of GCMs, the downscaling approaches, including dynamical downscaling and statistical downscaling have been introduced and have become widely used in research (IPCC, 2001). The dynamic method refers to the use of Regional Climate Models which utilize large scale and lateral boundary conditions of GCMs to generate finer spatial resolution outputs; while in the statistical method, a statistical relationship between the observations of large scale variables and that of a local variable is used for the calculation of the local variable in the future from the GCM output (Trzaska and Schnarr, 2014). The use of downscaling in climate research became widespread in the early 1990s (Wilby and Wigley, 1997). In Europe during the 1990s, the Dutch Meteorological institute (KNMI) and the Danish Meteorological institute (DMI) built the Regional Atmospheric Climate Model (RACMO) based on the High Resolution Limited Area Model (HIRLAM). Another related regional climate model called HIRHAM established in 1992 (Christensen et al., 1996), which was based on a subset of the regional HIRLAM and global ECHAM models (Roeckner et al., 2003), combining the dynamics of the former with the parameterization schemes of the latter. Other regional models include Weather Research and Forecasting (WRF) and the HadRCM3 at the United Kingdom. Hadley Centre, and RCA from the Swedish Rossby Centre. In North America, the North American Regional Climate Change Assessment Program (NARCCAP) was established with the efforts to produce high-resolution climate change simulations for the North American region, and in 2004, it launched experiment 0.0 and 0.1 to compare (among other things) temperature and precipitation from the models with observations. In Asia, the Regional Climate Model Intercomparison Project (RMIP) (Fu et al., 2005) was established to examine and compare different climatological drivers to those of its American and European counterparts. The drivers in question included the Asian monsoon and the effect of the Tibetan Plateau on the large-scale flows crossing the Eurasian continent. In recent years, numerous studies applied downscaling was conducted (such as Rummukainen, 2010; Maraun et al., 2010; Gutiérrez et al., 2013; Trzaska and Schnarr, 2014). For extremes, most of the past work on extremes and their dependency on climate change has involved RCMs or empirical-statistical downscaling (ESD), using some index representing extremes (e.g., STARDEX). ESD-based approaches can involve a number of different methods and may be set up to estimate parameters of the probability distribution function describing the local climate. However, some methods may not be well suited for downscaling extremes because they are unable to prescribe values outside the historical sample on which it is trained. According to Deser et al. (2012), from an analytics perspective, it will become possible to derive better information about extreme events, especially if ensembles of GCMs increase in size, their resolution is improved, the range of natural variability is better represented, and improved tools use the latest statistical methods, and hence attribute probabilities. In short, although downscaling methods are able to provide outputs which can be used for a local scale, they require either extensive computational power or a huge number of observations.

The present study predicts changes in future multi-day extreme precipitation using both the result of climate models through the application of Simple Climate Model so-called pattern scaling method and the trend of historical extreme precipitation using Generalized Extreme Value (GEV) distribution. Pattern scaling method was first introduced by Santer et al. (1990) with the assumption that the local response of a climate variable is linearly related to the global mean temperature change, with the geographical pattern of change independent of the forcing. Spatial features of the externally forced change, standardized by global average temperature warming, were estimated on the basis of 2xCO2 equilibrium simulations by mixed-layer ocean GCMs. These patterns were assumed to remain stable also during a transient simulation where the main external forcing is an increase in well-mixed greenhouse gases. These common features explain a large portion of the variability of the externally forced changes in temperature and precipitation over time and across scenarios within a given model. Pattern scaling has been widely used, its application therefore has a rich literature. Ruosteenoja et al. (2007), Watterson (2008), Giorgi (2008), Harris et al. (2010), Cabre et al. (2010), and Watterson and Whetton (2011) used pattern scaling to produce regional climate change projections, and Dessai et al. (2005) and Fowler et al. (2007) used pattern scaling for impact studies. Although limitations of this method have been found, such as it was less accurate for strongly mitigated stabilization scenarios (May, 2012) or it needs to be modified if future scenarios include significant changes over time in the strength of regional sources of pollution (May, 2008), many model experiments have shown that precipitation patterns scale linearly with global average temperature to a good degree of accuracy (Neelin et al., 2006; Shiogama et al., 2010), and that pattern scaling method is accurately applicable for climate change projection in general and precipitation projection in particular. Meanwhile, GEV distribution is a continuous probability distribution evolved within extreme value theory and is used as an approximation to model the maxima of long or finite sequences of random variables. The use of GEV distribution in extreme precipitation analysis and prediction is well documented. For instance, Rahmani et al. (2014) used GEV (Weibull type) distribution to calculate the extreme precipitation frequency in Kansas and the adjacent states in the United States. Xia et al. (2012) and Du et al. (2014) used (GEV) and Generalized Pareto distribution (GPD) to study the historical extreme precipitation frequency and its spatio-temporal variations in Haihe and Huaihe river basins of China. Benyahya et al. (2014) compared GEV with other four probability distributions (Generalized Logistic, Weibull, Gamma, and Lognormal) to identify the appropriate methods providing the most accurate seasonal maximum precipitation in southern Quebec of Canada. Rahman et al. (2013) investigated the suitability of GEV and other different probability distributions based on large Australian annual maximum flood datasets. In the Netherlands, most previous studies applied the GEV model to climatological statistics to describe the monthly and annual distribution of precipitation maxima (such as Buishand et al., 2009; https://www.sciencedirect.com/science/article/pii/S2212094716300433, Hanel and Buishand, 2010; Overeem and Buishand, 2012). It was found that the monthly variation generated by the GEV distribution model contains information about return levels (Rust et al., 2009). Previous studies have shown that GEV distribution is appropriate for extreme precipitation prediction, especially for the greatest values. According to Kharin et al. (2007) because it is impossible to collect observations for future climate conditions, using the GEV is a step to verify if a particular climate model can be used to assess potential effects of climate change on future extreme weather events.

In Vietnam, extreme precipitation is a serious concern due to its direct and indirect effects (through flooding, erosion and landslides) on agriculture, socio-economic activities and human life. Efforts have been made in analysis and prediction of extreme precipitation locally and nationally. Ho et al. (2011) studied extreme climatic events, including hot days, cold nights and heavy rainfall days in seven climatic sub-regions in Vietnam, based on historical observed data (1961–2007) and climate projections of the International Center for Theoretical Physics regional climate model version 3 (RegCM3). Extremes of each sub-region detected from the simulation of RegCM3 for the baseline period 1980–1999 were applied to the projection in the years 2001–2050, based on the IPCC SRES A1B and A2 scenarios, to reveal the changing trend of extremes in the future. The RegCM3 projections indicate that, the rainy season heavy rainfall events tend to decrease for allsub-regions except for two, in northwest and south-central Vietnam. Strong opposite projected changes in precipitation extremes over the southern half of Vietnam seem to be linked to changes in southwesterly air flow from the Bay of Bengal and the number of strong tropical cyclones coming from the South China Sea and the NW Pacific. Raghavan et al. (2017) applied a systematic ensemble high resolution climate modeling to study extreme precipitation over Vietnam using the PRECIS model developed by the Hadley Center in United Kingdom. The PRECIS model simulations were conducted at a horizontal resolution of 25 km for the baseline period 1961–1990 and a future climate period 2061–2090 under scenario A1B. The annual cycles and seasonal averages of precipitation over different sub-regions of Vietnam show the ability of the model in reproducing the observed peak and magnitude of monthly rainfall. The climate extremes of precipitation were also fairly well captured. Projections of future climate show both increases and decreases in the mean climate over different regions of Vietnam. The analyses of future extreme rainfall using the STARDEX precipitation indices show an increase in 90th percentile precipitation (P90p) over the northern provinces (15–25%) and central highland (5–10%) and over southern Vietnam (up to 5%). The total number of wet days (Prcp) indicates a decrease of about 5–10% all over Vietnam. Consequently, an increase in the wet day rainfall intensity (SDII), is likely inferring that the projected rainfall would be much more severe and intense which have the potential to cause flooding in some regions. Risks due to extreme drought also exist in other regions where the number of wet days decreases. In addition, the maximum 5 days consecutive rainfall (R5d) increases by 20–25% over northern Vietnam but decreases in a similar range over the central and southern Vietnam. Nam et al. (2015) assessed the near future (2,026–2,035) changes in extreme rainfall over Vietnam using projections by four high resolution multi-model belonging to the Coupled Model Intercomparison Project phase five, as compared to the baseline period (1979–2003). Results (ensemble mean) show that the highest precipitation amount in 3-day period and total precipitation on very wet days will greatly increase in the near future climate with larger increases in the northwest and southwest. Meanwhile, the highest precipitation amounts in one-and consecutive 5-day tend to be slightly increasing.

The application of GEV distribution and pattern scaling method in the present study for the North Central Region of Vietnam is a new method applied in Vietnam, and its result is expected to present another outlook of the future precipitation extreme in the studied region.

Materials and Methods

The Study Area and Data

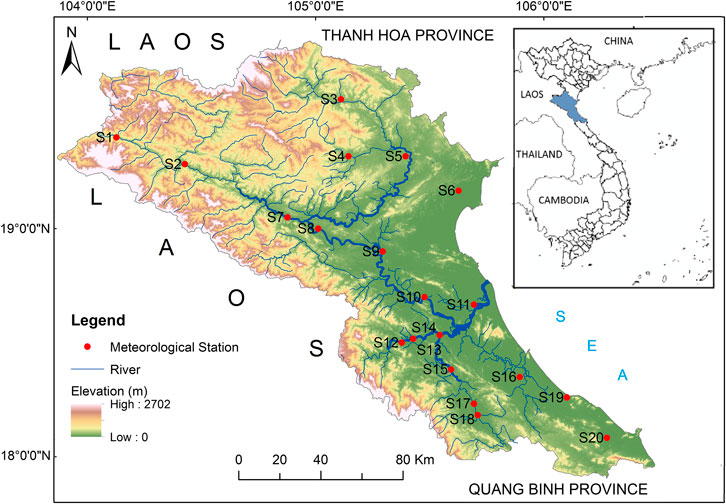
The area selected for this study is the Lower Ca River Basin (LCRB) (17^o50'N-20^o50'N, 103^o14'E-106^o10'E), which is one of the largest river basins in Vietnam. The LCRB is situated in the North Central Region with a basin area of 17,730 km², covering the entire Provinces of Nghe An and Ha Tinh and a part of Nhu Xuan District of Thanh Hoa Province. The North Central Region in general and the LCRB in particular is well-known as a hotspot of flooding in Vietnam due to high frequency and severity of floods in the region. Geographic location of the LCRB is shown in Figure 1.

FIGURE 1

FIGURE 1. Geographic location of the LCRB and meteorological stations in the basin.

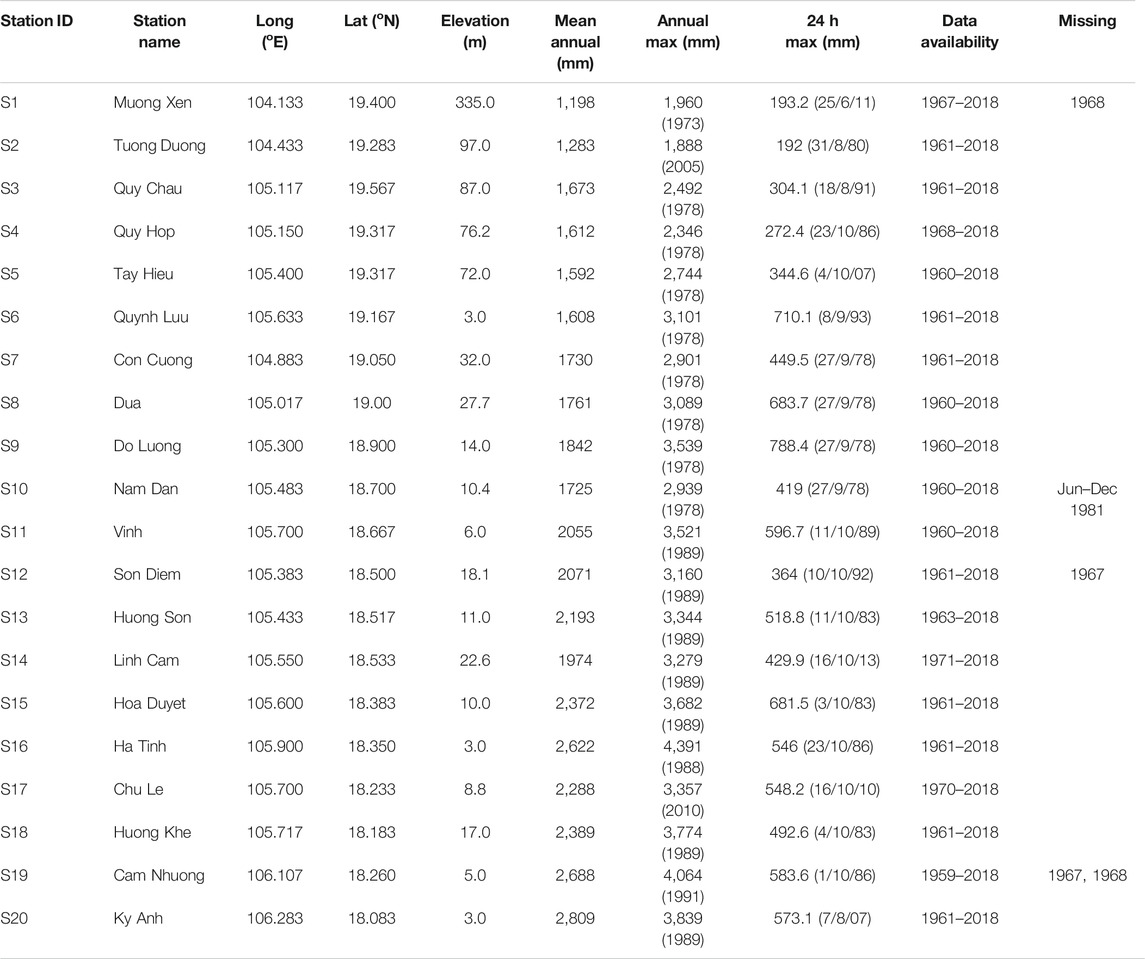
Located in a tropical monsoon region, climate of the LCRB is characterized by two distinct seasons: rainy season (May to October) and dry season (November to April of the next year). The rainy season is hot and humid with temperature up to more than 42°C and humidity up to 95% around June and July, while the dry season is cold and dry with the lowest temperature dropping to 0^oC around January. Precipitation in the LCRB is abundant, but is seasonally and spatially uneven distributed (Giang et al., 2014; OECD, 2020). According to data of 20 gauges recorded from the 1960s to date, annual precipitation in the basin was mostly more than 1,000 mm, and exceeded 4,000 mm in some wet years. Mean annual precipitation for the observation period (mostly 1960–2018) varies from 1,200 mm to 2,800 mm depending on the weather station, with an average of approximately 2,000 mm. Precipitation was found to have an increasing trend from north-west to south-east direction, with all of 10 gauges in the North of Vinh (S11) having mean annual precipitation below 2,000 mm and eight of nine gauges in the South of Vinh having mean annual precipitation above 2,000 mm (Except for S14, which has mean annual precipitation of 1,974 mm) (Table 1). During the observation period, there were some very wet years, of which historic extreme precipitations and historic floods were recorded; they are 1978, 1988, 1989, 1991, and 2010. The highest annual precipitation in the basin was 4,391 mm (in 1988 at S16) and the highest daily precipitation was 788.4 mm, recorded on September 27, 1978 at S9. Although the basin receives a high amount of precipitation annually, more than 80% of precipitation is in the wet season, and 80% of this amount fall in the flood months which typically lasts from August to October. This seasonal uneven distribution of precipitation is the main factor causing annual floods and droughts in the basin.

TABLE 1

TABLE 1. List of meteorological stations used in this study.

An analysis of historical rainfall and flood data shows that in the study area, on average, the number of days from it starts raining till floods reach the peak level is 5 days. The present study therefore calculated the change of the maximum consecutive 5-days precipitation, which is defined as five-day extreme precipitation in this study.

In this study, twenty long-term historical observation stations in the LCRB with daily data mostly date back to more than 50 years were employed. The observed daily station data was firstly aggregated for every five consecutive days to construct a five days total precipitation time series and five-days maximum total precipitation was analyzed. The volume resolution of 24-h precipitation is 0.1 mm and there is missing data at three stations: S10 (missing June- December, 1981), S12 (missing 1967) and S19 (missing 1967 and 1968).

Methods

The present study applied Generalized Extreme Value (GEV) distribution for extreme precipitation analysis. GEV distribution is a continuous probability distribution evolved within extreme value theory and is used as an approximation to model the maxima of long or finite sequences of random variables. It is parameterized with the three parameters: Shape parameter (γ), location parameter (μ) and scale parameter (σ), and is presented by the following functions:

${\mathit{F}}_{\mathit{\sigma ,\gamma ,\mu }}\left(\mathit{x}\right)\mathit{=}\mathit{exp}\left[\mathrm{-}{\left(\mathit{1+\gamma }\frac{\mathit{x-\mu }}{\mathit{\sigma }}\right)}^{\mathit{-1/\gamma }}\right]\mathit{ with 1+\gamma }\left(\frac{\mathit{x-\mu }}{\mathit{\sigma }}\right)\mathit{ >0, \gamma }\ne \mathit{0 }(1)$

and

$\mathit{ }{\mathit{F}}_{\mathit{\sigma ,\gamma ,\mu }}\left(\mathit{x}\right)\mathit{=exp}\left(\mathrm{-}{\mathit{e}}^{\mathrm{-}\frac{\mathit{x-\mu }}{\mathit{\sigma }}}\right)\mathit{ with \gamma =0}(2)$

where μ ∈ R and σ > 0. The shape parameter γ determines the type of GEV distribution. There are three types of distribution called Fréchet, Gumbel, and Weibull corresponding to γ < 0, γ = 0, and γ > 0, respectively.

The three parameters of GEV distribution (i.e. σ, μ, and γ) can be estimated by different approaches depending on the object investigated. In hydrology and climatology, an approach known as Probability Weighted Moments (PWM) (Greenwood et al., 1979; Landwehr et al., 1979; Hosking et al., 1985) is widely used. Thus, in this study, GEV function parameters for the GCM baseline and future periods were estimated using the PWM method for each GCM grid (x,y). The change of extreme precipitation in a future period compared to the baseline period corresponding to a specific return period (the estimated time interval between precipitation events of a similar intensity) T is determined as:

$\mathit{\Delta }{\mathit{P}}_{\mathit{TFR}\left(\mathit{xy}\right)\mathit{ }}\mathit{=}{\mathit{P}}_{\mathit{TFR}\left(\mathit{xy}\right)}\mathrm{-}\mathit{ }{\mathit{P}}_{\mathit{T}\left(\mathit{xy}\right)}(3)$

Where P_T(xy) is baseline extreme precipitation value for the grid (xy) attainted from applying GEV function to GCM simulation for the baseline period. In IPCC AR5, the baseline period is 1986–2005, centered by 1995 (Collins et al., 2013). P_TFR(xy) is projected precipitation value for the future year F under Representative Concentration Pathway R for the same grid. The future year F is the central year of a projected period (20 years in principle).

As global warming is driven by increased radiative forcing, the Pattern Scaling method applied in this study can be described as: for a given P_T, its anomaly ΔP^*_T in future year (F) under Representative Concentration Pathway R for grid (x,y) can be derived as:

$\Delta {\mathit{P}}_{\mathit{TFR}\left(\mathit{xy}\right)}^{\mathit{*}}\mathit{=}\Delta {\mathit{C}}_{\mathit{F}}\cdot {\mathit{P}}_{\mathit{T}\left(\mathit{xy}\right)}^{\mathit{\text{'}}}(4)$

where ΔC_F is the difference between annual global mean temperature in future year F and that of the baseline period derived from applying the Model for the Assessment of Greenhouse-gas Induced Climate Change (MAGICC) (Wigley, 2008); and ΔP'_T(xy) is the change rate of P_T at grid (x,y) in response to that change of annual global mean temperature.

Pattern scaling method assumes that, for a given GCM, ΔP'_T(xy) can be obtained from any simulation run of that GCM. Practically, however, such a homogeneous result seldom happens for given available GCM data. This may be due to the GCM simulation period of 20 years is not long enough to obtain ΔP'_T(xy) with sufficient statistical significance. Another possible reason would be that the change rate of precipitation P_T does not have a linear relationship with the annual global temperature change in nature. In fact, in order to obtain more accurate predictions of future climate, deeper studies of the relationships between the change rate of climate variables and the global mean temperature changes are in need. However, such further studies require extensive experiments with purposely designed input and outputs of GCM simulation, which cannot be obtained by current technologies. Nevertheless, according to Ruosteenoja et al. (2007), error of pattern-scaling method in constructing regional climate projections for extreme events seems to be not very large. Thus, if pattern scaling method is applied for calculating ΔP'_T(xy) for a given GCM, in order to reduce the effects of the GCM internal variability from different RCPs and time periods when calculating ΔP'_T(xy), it is desirable to take into the calculation all available GCM outputs. Mitchell (2003) and Ruosteenoja et al. (2007) recommended a least squares regression method as follows:

$\Delta {\mathit{P}}_{\mathit{T}\left(\mathit{xy}\right)}^{\mathit{\text{'}}}=\frac{{\displaystyle \sum _{\mathit{F}=1}^{\mathit{m}}{\displaystyle \sum _{\mathit{R}=1}^{\mathit{n}}\Delta {\mathit{C}}_{\mathit{FR }}\cdot \Delta {\mathit{P}}_{\mathit{TFR}\left(\mathit{xy}\right)}}}}{{\displaystyle \sum _{\mathit{F}=1}^{\mathit{m}}{\displaystyle \sum _{\mathit{R}=1}^{\mathit{n}}{\left(\Delta {\mathit{C}}_{\mathit{FR}}\right)}^2}}}(5)$

where m is the number of simulation periods from a GCM and n is the number of Representative Concentration Pathway. For a given baseline extreme precipitation value P_T, a spatial ΔP'_T was calculated by applying Eq. 5 to each GCM grid (x,y). After that, ΔP^*_T can be determined from Eq. 4 with a given ΔC_F, and the future extreme precipitation value for grid (xy) can be determined by the following equation:

${\mathit{P}}_{\mathit{TFR}\left(\mathit{xy}\right)}=\mathit{ }{\mathit{P}}_{\mathit{OT}\left(\mathit{xy}\right)}+\mathit{ }\Delta {\mathit{P}}_{\mathit{TFR}\left(\mathit{xy}\right)}^{\mathit{*}}(6)$

where P_OT(xy) is the observed extreme value with return period T.

To establish the GEV function for a future year F, ΔP_T(xy) was calculated for seven different return period (i.e., 2, 5, 10, 20, 50, and 100 years) based on Eq. 6. Then, the Levenberg-Marquardt algorithm developed by Press et al. (1997) was applied to fit the seven extreme values to GEV function in order to calculate the GEV function parameters. It should be noted that although the same GEV function parameters were applied to all selected GCMs, the change pattern of extreme precipitation for the same region (or more precisely for the same GCM grid) may vary among GCM simulations due to inter-model uncertainty. To quantify the widest possible range of uncertainties, large ensembles of GCM predictions are needed. The quantified uncertainty range is helpful information for proposing proper countermeasure for tackling future climate change impact.

In the present study, fourteen GCMs from the Coupled Model Intercomparison Project phase five (CMIP5) archive (which is also the data source for IPCC AR5 climate change projections) were employed. The selection of GCMs was principally based on the spatial resolution of the GCMs. In each GCM family, only one GCM with highest resolution was selected. In the case there were two or more GCMs with the same resolution, the latest GCM was selected. A list of GCMs employed is presented in Table 2.

TABLE 2

TABLE 2. List of GCMs used in this study.

Results and Discussion

Change in the Intensity of Extreme Precipitation Events

To investigate the spatial variation of change of extreme precipitation, ensemble median of all fourteen GCMs listed in Table 1 was carried out for all twenty local stations in the studied basin. Employing multiple ensemble members helps to reduce bias prediction of each single member GCM. Results reveal increases in precipitation extremes in the future time periods (2050, 2070, and 2090) relative to the baseline scenario (1986–2005) under all the three RCP pathways, but with a divergent pattern depending on the RCP and the return period (Figure 2). Among the three scenarios, extreme precipitation increases the most under RCP8.5, followed by RCP6.0 and increases the least under RCP2.6 for all return periods. Both RCP6.0 and RCP8.5 show an upward trend throughout the projection period but the increment is steadier under the higher RCP. The low RCP2.6 pathway shows a downward trend in the increase of the extreme precipitation from 2050 forward. The trend is steady from 2050 to 2070 but becoming almost balance at around 1.0% from 2070 to 2090. Overall, it can be seen that the predictions of the three RCP pathways diverge with time, with smaller differences in 2050 and largest differences in 2090. The projections discussed above correspond with the characteristics of the RCP pathways, which show similar levels of greenhouse gas emission in early 21st century, and then the emission becomes to diverge: RCP8.5 drives a sharp increase overtime, RCP6.0 drives a moderate increase till the end of the 21st century while RCP2.6 drives a moderate increase till halfway through the century, peaks around 2050 and declines thereafter. The correspondence between predicted future mean monthly/annual temperature and precipitation to emission scenarios has been reported by a number of studies applying Special Report on Emissions Scenarios (SRES) scenarios (IPCC, 2000) for different regions in the world such as United States (Liu et al., 2012), Spain (Ribalaygua et al., 2013), and Southeast Asia (Giang et al., 2014). For RCP pathways, because these scenarios were very recently adopted by the IPCC (Collins et al., 2013), little research applying them for extreme climates in general and extreme precipitation in particular has been published. However, the characteristic of extreme precipitation change under RCP scenarios may vary. Ahn et al. (2016) found that future extreme precipitation over South Korea, neither the mean value nor frequency had a significant trend such as temperature response to radiative forcing under RCP4.5 and RCP8.5. In contrast, findings of Saeed et al. (2013) show that future extreme precipitation over the greater Congo region in Africa could change prominently, led by RCP8.5, then RCP4.5 and then RCP2.6. Similar behavior was found by Janssen (2013) for precipitation in the United States under RCP4.5 and RCP8.5: the higher the RCP, the more prominent change is expected for both intensity and frequency. These findings point to the fact that a region may differ from another in the sensitivity to the radiative forcing which varies in the RCPs, as indicated in Shindell et al. (2012). To our knowledge, however, no research has been published for multi-day extreme precipitation, which is focused in the present study.

FIGURE 2

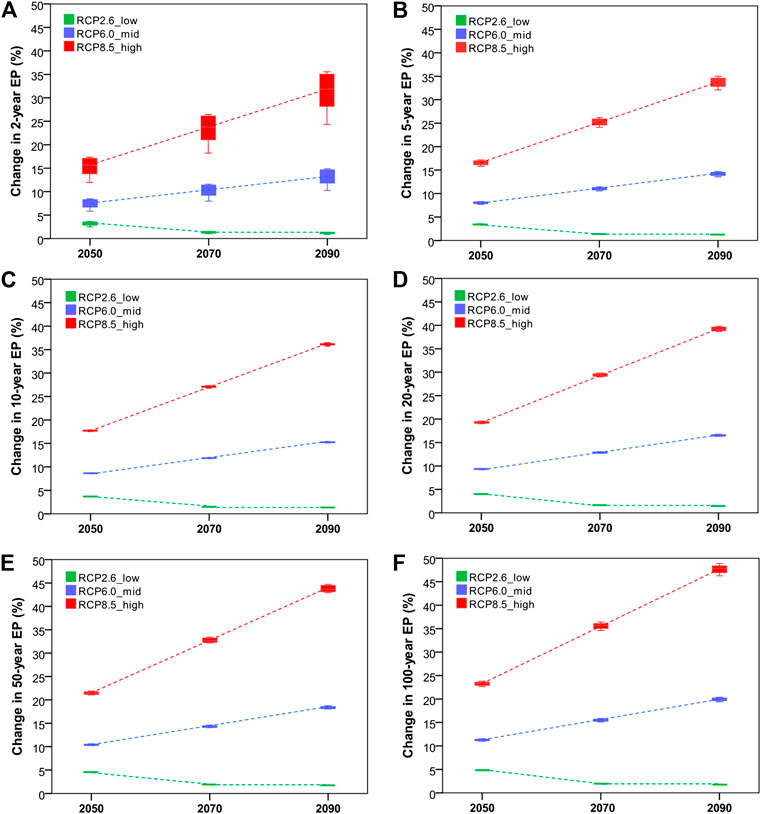
FIGURE 2. Spatial variability of change in future 5-day extreme precipitation under the ensemble scenario corresponding to different return periods: T = 2 years (A), T = 5 years (B), T = 10 years (C), T = 20 years (D), T = 50 years (E), and T = 100 years (F). Figure presents data of 20 stations.

It is noticeable that spatial variability of extreme precipitation also consistent with the temporal change: The variability increases with time under RCP8.5 and RCP6.0 but decreases with time under RCP2.6, although the variability under RCP2.6 is very small. In addition, the higher the RCP, the greater the spatial variability it produces. For instance, the increase of the total 5-days precipitation with T = 2 ranges between 11.96 and 17.35% (standard deviation S_td = 1.72%) in 2050, 18.21–26.47% (S_td = 2.65%) in 2070, and 24.32–35.55% (S_td = 3.59%) in 2090 under RCP8.5. Under RCP6.0 it ranges between 5.82 and 8.46% (S_td = 0.84%) in 2050, 7.99–11.59% (S_td = 1.15%) in 2070, and 10.25–14.87 (S_td = 1.47%) in 2090, meanwhile under RCP2.6 it ranges between 2.49–3.63% (S_td = 0.36%), 1.02–1.49% (S_td = 0.15%), and 0.92–1.34% (S_td = 0.15) in 2050, 2070, and 2090, respectively.

Interestingly, comparison among the return periods, it is clear that spatial variability of smaller extremes (closer to the lower tail) and greater extremes (closer to the upper tail) is greater than medium extremes. More specifically, the variability starts highest for T = 2, but then reduces for T = 5, and reduces more for T = 10. However, after T = 10 it starts to rise for T = 20, rise more for T = 50, and then more so for T = 100. This characteristic occurs under all the three pathways, although under RCP2.6, the difference among the return periods is very small. This characteristic can be explained by the characteristic of GEV distribution. When fitting data to GEV distribution, the uncertainty is often largest at its tails, in other words, medium extremes are usually most fitted to the distribution while small extremes and large extremes are often lie farther from the GEV curve. This leads to variability in GEV values among local datasets.

Most noticeable in Figure 2 is that extreme precipitation in the LCRB with a return period of two years has large spatial variability, especially in the end of the 21st century under the highest RCP pathway (range between 24.32 and 35.55%); despite the moderate basin size. Review from literature shows that large spatial variability in the change of precipitation at local scale driven by a warmer climate was also abundantly reported. For instance, research by Mahmood et al. (2015) for the Jhelum river basin of Pakistan and India, which has similar basin size as the LCRB in the present study, reveals that precipitation change in the studied basin spatially varies from a decrease of 12% to an increase of 12% in the 2050s, and from a decrease of 11% to an increase of 16% in the 2080s under SRES scenario A2. Research by Keuser (2012) for Milwaukee County of the United State (3,082 km²) and 24 km buffer around it shows that spatial variation of precipitation increases relative to the current climate is likely to be large, ranging from 15.8 to 39.6% in 2050s and from 21.3 to 46% in 2080s, also under SRES scenario A2. Note that both studies used downscaled GCMs output together with trends in observed precipitation for the predictions, which is similar to the method used in the present study. According to Ye and Li (2011) and Li et al. (2011), precipitation in general and extreme precipitation in particular is a much localized phenomenon and not always strongly influenced by large-scale dynamics. This means that although a large-scale GCM gives homogenous prediction for future precipitation change for the region within its particular grid, more detailed approach such as downscaling or pattern scaling may result in large spatial variability of the precipitation change. Spatial distribution of 5-days extreme precipitations for different return periods and their increase in 2070 under the highest RCP (RCP8.5) compared to the baseline period is shown in Figure 3.

FIGURE 3

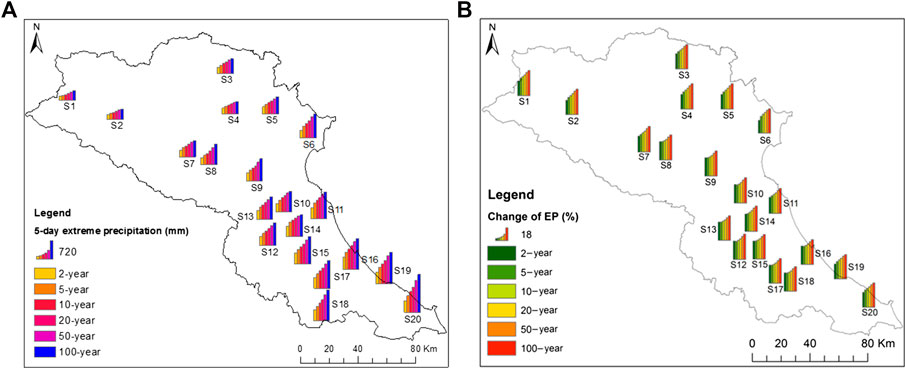
FIGURE 3. Spatial variability of baseline 5-days extreme precipitation (A) and its change in 2070 according to RCP8.5 scenario (B).

Comparison among the predictions of the employed GCMs for 2050, 2070, and 2090 under the three pathways is presented in Figure 4 wherein data for Vinh (S11), which is considered as the most central station in the LCRB, is shown. Prediction of the selected GCMs is very divergent, but can be divided into two groups:

FIGURE 4

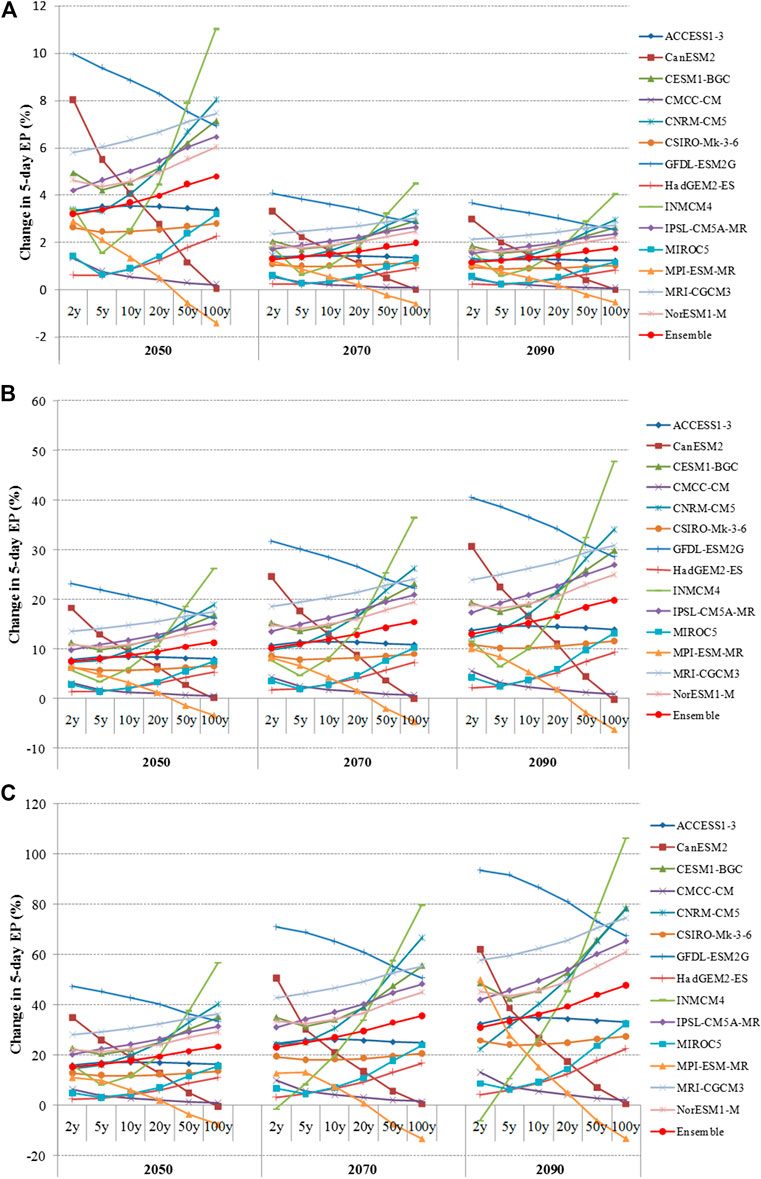
FIGURE 4. Change in 5-day extreme precipitation under 14GCMs and their ensemble at Vinh Station corresponding to RCP2.6 (A), RCP6.0 (B), and RCP8.5 (C).

- Five GCMs including ACCESS1-3, CanESM2, CMCC-CM, GFDL-ESM2G, and MPI-ESM-MR predict greater increases to smaller extremes and smaller increases to greater extremes. This is represented by downward lines in Figure 4 with CanESM2 being the steepest, representing the most typical for this tendency. For example, this model predicts that under RCP8.5 in 2070 5-days extreme precipitation increases 50.60% for T = 2, 30.27% for T = 5, 20.87% for T = 10, 13.48% for T = 20, 5.51% for T = 50, and 0.39% for T = 100 compared to the baseline period. This rate then decreases from 62.18% (T = 2) to 0.37% (T = 100) in 2090. More noticeably among this group is that the downward line of MPI-ESM-MR passes through the X-axis after the return period T = 20, meaning that the change of extreme precipitation relative to the baseline period turns from an increase for T = 2, 5, 10, and 20 to a decrease for T = 50 and T = 100. In general, prediction of this model shows that by the end of 21st century 5-days extreme precipitation is expected to change from +2.89 to −1.40% under RCP2.6, from +10.04 to −6.26% under RCP6.0, and from +50.09 to −13.24% under RCP8.5.

- The other nine GCMs including CESM1-BGC, CNRM-CM5, CSIRO-Mk-three to six, HadGEM2-ES, INMCM4, IPSL-CM5A-MR, MIROC5, MRI-CGCM3, and NorESM1-M predict smaller increases to smaller extremes and greater increases to greater extremes. This is represented by the upward lines in Figure 4. Among these models, INMCM4 shows the most dramatically upward trend toward more extreme precipitation, except for a short down from T = 2 to T = 5 for all three future time periods under RCP2.6 and RCP6.0 and for 2050 under RCP8.5. The largest range of 5-days extreme precipitation change relative to the baseline period according to this model is in 2090 under RCP8.5 when it rises from a decrease of 5.93% for T = 2 to an increase of 106.28% for T = 100.

Prediction of the ensemble median of the 14 selected GCMs is in line with the later group: smaller increases for smaller extremes and greater increases for greater extremes. Under this ensemble scenario, in mid-21st century, 5-days extreme precipitation at S11 with return period ranging from T = 2 years to T = 100 years is expected to rise between 3.19% (T = 2 years) and 4.81% (T = 100 years) under RCP2.6, between 7.43 and 11.28% under RCP6.0, and between 15.19 and 23.28% under RCP8.5. Meanwhile, by the end of the 21st century, it would rise between 1.17 and 1.78%, 13.03–19.93%, and 30.90–47.90% under RCP2.6, RCP6.0 and RCP8.5 respectively.

Considering the prediction of each individual GCM relative to the three RCPs, it is obvious that the magnitude of change produced by each individual GCM under RCP2.6 is smaller than RCP6.0, and smaller still than RCP8.5. The change under RCP2.6 becomes smaller while the change under RCP6.0 and RCP8.5 becomes greater toward the end of this century. These behaviors of prediction are consistent with the characteristics of RCP pathways as discussed earlier in this paper. An overview of the predictions of the employed GCMs for 20 monitoring stations in the study area under the three pathways is presented in Figure 5.

FIGURE 5

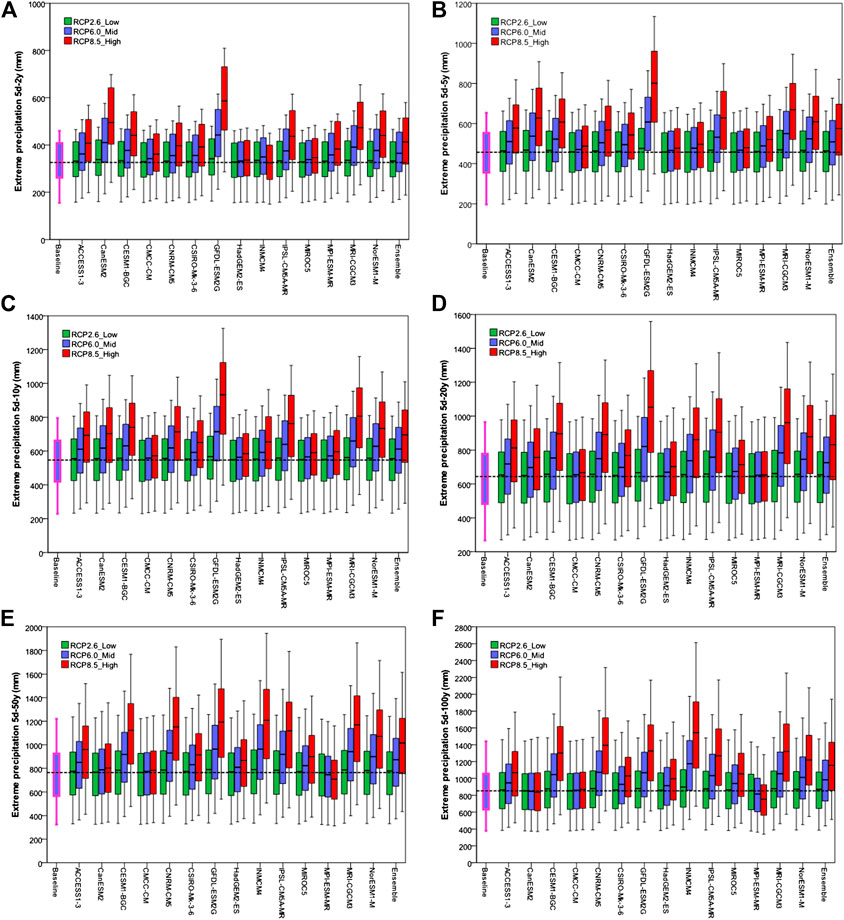
FIGURE 5. Variation of projected 5-day extreme precipitation under 14GCMs and their ensemble in 2070 corresponding to different return periods: T = 2 years (A), T = 5 years (B), T = 10 years (C), T = 20 years (D), T = 50 years (E), and T = 100 years (F). Figure presents data of 20 monitoring stations

Change in the Frequency of Extreme Precipitation Events

Frequency of extreme precipitation, represented by its return period provides important information for assessing its impact to the environment and society as well as for decision making. For instance, a return period of T-years represents an extreme precipitation event that has a 1/T probability of occurring in any given year. Stationary climate assumes that the frequency of extreme climates does not change over time (Klein et al., 2009). However, according to IPCC (2007), the frequency of extreme climates in general and extreme precipitations in particular has been changing and more so in the future. In this study, we examined the changes in the frequency of future extreme precipitations which presently have return periods of 2, 5, 10, 20, 50 and 100 years.

Figure 6 presents the change for five-days extreme precipitation at Vinh (S11) in 2050, 2070, 2090 relative to the baseline period. It can be seen that for all return levels, extreme precipitation is likely to be more frequent (as their return periods shorten) in the future, except for a few cases wherein it remains unchanged or becomes less frequent. In general, the uncertainty in the frequency is smallest for present return levels with T = 2 years and largest for present return levels with T = 100 years in all three RCPs. The uncertainty also increases consistently with the order of the RCPs (RCP8.5 > RCP6.0 > RCP2.6) and increases with time.

FIGURE 6

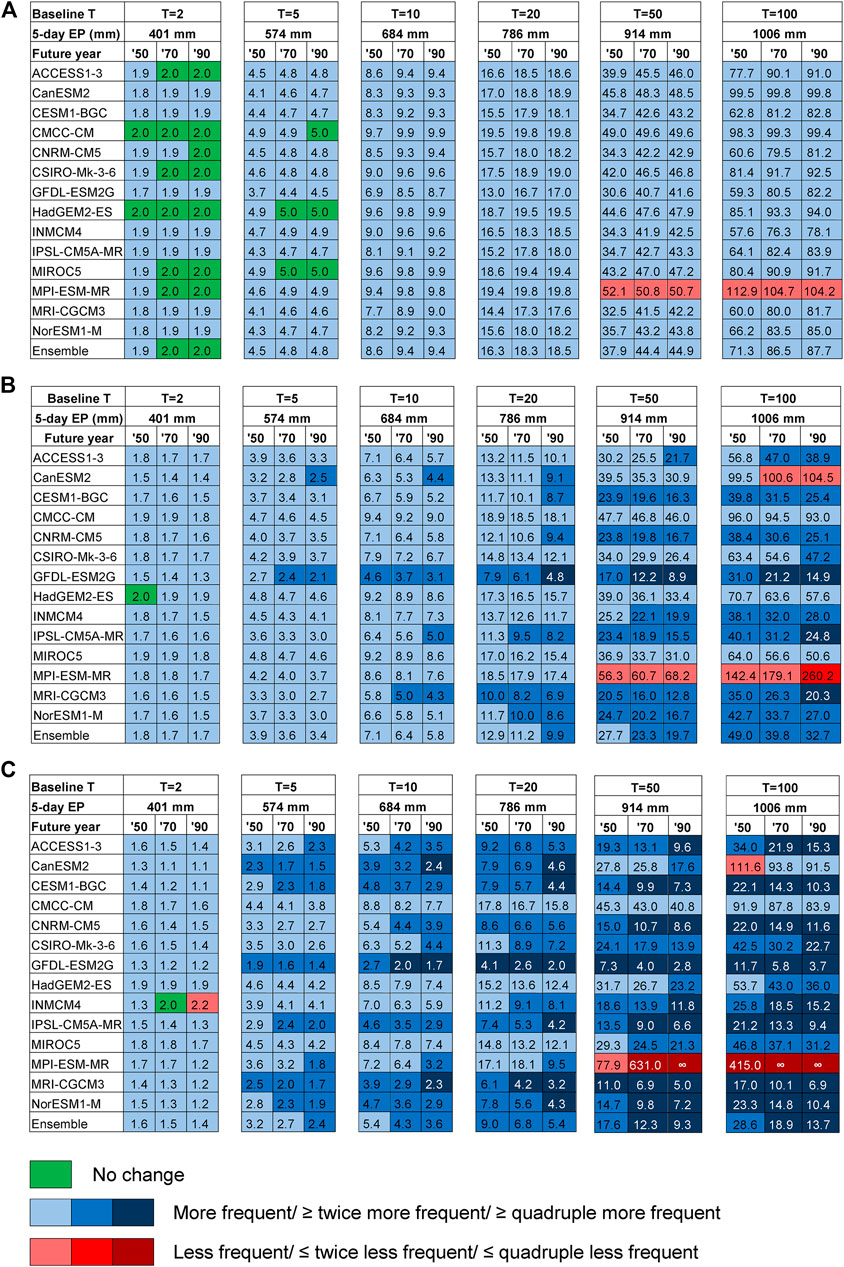
FIGURE 6. Change in frequency of extreme precipitation according to RCP 2.6 (A), RCP 6.0 (B), and RCP 8.5 (C). Number in each block presents the future return period of current return level.

Specifically, under RCP2.6 extreme precipitation is projected to remain unchanged in frequency in many cases for T = 2 years, but only in 7 cases for T = 5 years (in 2090 under CMCC-CM, and in 2070 and 2090 under HadGEM2-ES and MIROC5), and in no cases for the other greater return periods. The frequency is also projected to decrease but only in six cases (for return level with current return period T = 50 and T = 100 years in 2050, 2070, and 2090. All are under MPI-ESM-MR). The other majority of cases show an increase in frequency. However, it should be noted that all of the increases or decreases in frequency under RCP2.6 are within twice less frequent to twice more frequent.

Under RCP6.0, only one case exhibits an unchanged frequency, meanwhile many cases exhibit double frequency (twice more frequent) or beyond and a few cases exhibit quadruple frequency or beyond. In comparison with RCP2.6, the decrease in frequency was also projected for larger extremes (with current return period T = 50 and T = 100 years), but for eight cases under CanESM2 and MPI-ESM-MR in which one case show a double decrease in frequency (return level with current return period T = 100 in 2090 under MPI-ESM-MR).

Under RCP8.5, many cases show a double (or more) increase in frequency, even for lower return levels, meanwhile the number of cases with a quadruple (or more) increase has become more dominant in larger return levels. The number of cases which show a balance frequency and a decreased frequency remains the same compared with RCP6.0 although they are not exactly the same cases. Most noticeable among the cases with decreased frequency is that three of these cases are likely not to happen in the future as their predicted frequency is infinitive. These cases include the return levels with current return period T = 50 in 2090 and T = 100 in 2070 and 2090, all are under MPI-ESM-MR.

Conclusion and Recommendation

This study investigated the variability in the intensity and frequency of future multi-day extreme precipitation using pattern scaling method coupled with Generalized Extreme Value Analysis with the case study of the LCRB in the Northcentral Vietnam of Vietnam. The results exhibit different uncertainties following the characteristics of RCP scenarios and depending on each GCM employed. In general, the uncertainty in both intensity and frequency is in line with the order of the RCP scenarios and increase with time. In the future, multi-day precipitation is likely to become more extreme and more frequent in most cases. The increase in extreme precipitation found in this study was in line with findings of previous studies on climate change in Vietnam including the Northcentral region, however, the pattern of change was different due to the difference in methodologies and the GCMs used. It is also valuable to note that the present study provided more details of the pattern of changes in both intensity and frequency of extreme precipitation. The shortening of return periods for extreme precipitation events and greater intensity of such events has potential consequences for the increase in flood magnitude and frequency, which could ultimately produce large impacts on the environment and society. Therefore, planning and decision making of durable infrastructure along with flood mitigation strategies to cope with such events are recommended.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

PQG performed the design of study, data collection and analysis, model simulation, and manuscript writing and edition. People whole gave comments and advice for the improvement of the manuscript have been acknowledged in the Acknowledgment section.

Funding

This research was supported by Japan Society for the Promotion of Science (JSPS).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author wishes to thank Vietnam Institute of Meteorology-Hydrology and Climate Change, Hydro-Meteorological Data Center for providing data for this research. Appreciation is also given to researchers at The University of Tokyo, Vietnam National University of Agriculture, and Ha Long University for their useful comments and suggestions for the improvement of the article.

References

Ahn, J. B., Jo, S., Suh, M. S., Cha, D. H., Lee, D. K., Hong, S. Y., et al. (2016). Changes of precipitation extremes over South Korea projected by the 5 RCMs under RCP scenarios. Asia Pac. J. Atmos. Sci. 52, 223–236. doi:10.1007/s13143-016-0021-0

CrossRef Full Text | Google Scholar

Benyahya, L., Gachon, P., St-Hilaire, A., and Laprise, R. (2014). Frequency analysis of seasonal extreme precipitation in Southern Quebec (Canada): an evaluation of regional climate model simulation with respect to two gridded datasets. Nord. Hydrol. Res. 45 (1), 115–133. doi:10.2166/nh.2013.066

CrossRef Full Text | Google Scholar

Buishand, T. A., Jilderda, R., and Wijngaard, J. B. (2009). Regionale verschillen in extreme neerslag. Available at:https://edepot.wur.nl/191834https://edepot.wur.nl/191834.

Google Scholar

Cabre, M. F., Solman, S. A., and Nunez, M. N. (2010). Creating regional climate change scenarios over Southern South America for the 2020’s and 2050’s using the pattern scaling technique: validity and limitations. Clim. Change 98 (3–4), 449–469. doi:10.1007/s10584-009-9737-5

CrossRef Full Text | Google Scholar

Christensen, J. H., Christensen, O. B., Lopez, P., van Meijgaard, , and Botzet, M. (1996). Research Report, 96–4. The HIRHAM4 regional atmospheric climate model. Danish Meteorological Institute.

Google Scholar

Collins, M., Knutti, R., Arblaster, J., Dufresne, J. L., Fichefet, T., Friedlingstein, P., et al. (2013). “Long-term climate change: projections, commitments and irreversibility,” in Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment Report of the intergovernmental panel on climate change. Editors T. F. Stocker, D. Qin, G. K. Plattner, M. Tignor, S. K. Allen, J. Boschunget al. (Cambridge, United Kingdom and New York, NY: Cambridge University Press), 1029–1136.

Google Scholar

Collins, W. J., Bellouin, N., Doutriaux-Boucher, M., Gedney, N., Halloran, P., Hinton, T., et al. (2011). Development and evaluation of an Earth-System modelHadGEM2. Geosci. Model Dev. (GMD). 4, 1051–1075. doi:10.5194/gmdd-4-997-2011

CrossRef Full Text | Google Scholar

Deser, C., Knutti, R., Solomon, S., and Phillips, A. S. (2012). Communication of the role of natural variability in future North American climate. Nat. Clim. Change (11), 775–779. doi:10.1038/NCLIMATE1562

CrossRef Full Text | Google Scholar

Dessai, S., Lu, X. F., and Hulme, M. (2005). Limited sensitivity analysis of regional climate change probabilities for the21^st century. J. Geophys. Res. Atmos. 110 (D19), D19108. doi:10.1029/2005JD005919

CrossRef Full Text | Google Scholar

Dix, M., Vohralik, P., Bi, D., Rashid, H., Marsland, S., O’Farrell, S., et al. (2013). The Access coupled model: documentation of core CMIP5 simulations and initial results. Aust. Meteorol. Oceanogr. J. 63, 83–99. doi:10.22499/2.6301.004

CrossRef Full Text | Google Scholar

Du, H., Xia, J., Zeng, S., She, D., and Liu, J. (2014). Variations and statistical probability characteristic analysis of extreme precipitation events under climate change in Haihe River Basin, China. Hydrol. Process 28 (3), 913–925. doi:10.1002/hyp.9606

CrossRef Full Text | Google Scholar

Dufresne, J. L., Foujols, M. A., Denvil, S., Caubel, A., Marti, O., Olivier, A., et al. (2013). Climate change projections using the IPSL-CM5 Earth system model: from CMIP3 to CMIP5. Clim. Dynam. 40, 2123–2165. doi:10.1007/s00382-012-1636-1

CrossRef Full Text | Google Scholar

Dunne, J. P., John, J. G., Adcroft, A. J., Griffies, S. M., Hallberg, R. W., Shevliakova, E., et al. (2012). GFDL’s ESM2 Global coupled climate-carbon earth system models. part I: physical formulation and baseline simulation characteristics. J. Clim. 25, 6646–6665. doi:10.1175/JCLI-D-11-00560.1

CrossRef Full Text | Google Scholar

Fogli, P. G., Manzini, E., Vichi, M., Alessandri, A., Patara, L., Gualdi, S., et al. (2009). INGV-CMCC carbon (ICC): a carbon cycle earth system model. CMCC Res. Pap.-Euro-Mediterranean Center Clim. Change, 31. Available at: https://www.cmcc.it/wp-content/uploads/2012/05/rp0061-ns-04-2009.pdf. doi:10.2139/SSRN.1517282

CrossRef Full Text | Google Scholar

Fowler, H. J., Blenkinsop, S., and Tebaldi, C. (2007). Linking climate change modelling to impacts studies: recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 27 (12), 1547–1578. doi:10.1002/joc.1556

CrossRef Full Text | Google Scholar

Fu, C., Wang, S., Xiong, Z., Gutowski, W. J., Lee, D.-K., McGregor, J. L., et al. (2005). Regional climate model intercomparison project for Asia. Bull. Am. Meteorol. Soc. 86, 257–266. doi:10.1175/BAMS-86-2-257

CrossRef Full Text | Google Scholar

Giang, P. Q., Toshiki, K., Sakata, M., Kunikane, S., and Vinh, T. Q. (2014). Modelling climate change impacts on the seasonality of water resources in the upper Ca river watershed in Southeast Asia. Sci. World J. 2014, 279135. doi:10.1155/2014/279135

CrossRef Full Text | Google Scholar

Giorgi, F. (2008). A simple equation for regional climate change and associated uncertainty. J. Clim. 21 (7), 1589–1604. doi:10.1175/2007jcli1763.1

CrossRef Full Text | Google Scholar

Greenwood, J. A., Landwehr, J. M., Matalas, N. C., and Wallis, J. R. (1979). Probability-weighted moments: definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 15, 1049–1054. doi:10.1029/WR015i005p01049

CrossRef Full Text | Google Scholar

Gutiérrez, J. M., San-Martín, D., Brands, S., Manzanas, R., and Herrera, S. (2013). Reassessing statistical downscaling techniques for their robust application under climate change conditions. J. Clim. 26 (1), 171–188. doi:10.1175/JCLI-D-11-00687.1

CrossRef Full Text | Google Scholar

Hanel, M., and Buishand, T. A. (2010). On the value of hourly precipitation extremes in regional climate model simulations. J. Hydrol. 393, 265–273. doi:10.1016/j.jhydrol.2010.08.024

CrossRef Full Text | Google Scholar

Harris, G. R., Collins, M., Sexton, D. M. H., Murphy, J. M., and Booth, B. B. B. (2010). Probabilistic projections for 21st century European climate. Nat. Hazards Earth Syst. Sci. 10 (9), 2009–2020. doi:10.5194/nhess-10-2009-2010

CrossRef Full Text | Google Scholar

Ho, T. M. H., Phan, V. T., Le, N. Q., and Nguyen, Q. T. (2011). Extreme climatic events over Vietnam from observational data and RegCM3 projections. Clim. Res. 49 (2), 87–100. doi:10.3354/cr01021

CrossRef Full Text | Google Scholar

Hosking, J. R. M., Wallis, J. R., and Wood, E. F. (1985). Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 27, 251–261. doi:10.2307/1269706

CrossRef Full Text | Google Scholar

IPCC (2000). Special Report on emissions scenarios: a special report of working group III of the intergovernmental panel on climate change. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

IPCC (2001). IPCC climate change 2001: impact, Adaptation and Vulnerability.Contribution of working group II to the third assessment report of the intergovernmental panel on climate change. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

IPCC (2007). Climate change 2007: synthesis report. Contribution of working groups I, II and III to the fourth assessment report of the intergovernmental panel on climate change. Geneva, Switzerland: IPCC, 104.

Google Scholar

IPCC (2013). “Climate Change 2013: the physical science basis,” in The working group I contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Editors T. F. Stocker, D. Qin, G. K. Plattner, M. Tignor, S. K. Allen, J. Boschunget al. (Cambridge, United Kingdom and New York, NY: Cambridge University Press), 1535.

Google Scholar

Iversen, T., Bentsen, M., Bethke, I., Debernard, J. B., Kirkevåg, A., Seland, O., et al. (2013). The Norwegian Earth system model, NorESM1–M. Part 2: climate response and scenario projections. Geosci. Model Dev. 6, 1–27. doi:10.5194/gmd-6-389-2013

CrossRef Full Text | Google Scholar

Janssen, E. (2013). Trends and projections of extreme precipitation over the contiguous United States. Master’s thesis. Urbana (IL): University of Illinois at Urbana-Champaign.

Google Scholar

Keuser, A. P. M. (2012). Decadal changes and future projections of precipitation in the metropolitan area of Milwaukee. Master’s thesis. Milwaukee (WI): The University of Wisconsin-Milwaukee.

Google Scholar

Kharin, V. V., Zhang, X., and Hegerl, G. C. (2007). Changes in temperature and precipitation extremes in the IPCC ensenble of global coupled model simulations. J. Clim. 20, 1419–1444. doi:10.1175/JCLI4066.1

CrossRef Full Text | Google Scholar

Klein, T., Zwiers, F. W., and Zhang, X. (2009). “Guidelines on Analysis of extremes in a changing climate in support of informed decisionsfor adaptation,” in World meteorological organization collection(s) and series. (Geneva, Switzerland: World Meteorological Organization), Vol 1500, 56.

Google Scholar

Kunkel, K. E. (2003). North American trends in extreme precipitation. Nat. Hazards 29, 291–305. doi:10.1023/A:1023694115864

CrossRef Full Text | Google Scholar

Landwehr, J., Matalas, N., and Wallis, J. (1979). Probability weighted moments comparedwith some traditional techniques in estimating gumbel parameters and quantiles. Water Resour. Res. 15, 1055–1064. doi:10.1029/WR015i005p01055

CrossRef Full Text | Google Scholar

Li, F., Collins, W. D., Wehner, M. F., Williamson, D. L., and Olson, J. G. (2001). Response of precipitation extremes to idealized global warming in an aqua-planet climate model: towards a robust projection across different horizontal resolutions. Tellus 63A, 876–883. doi:10.1111/j.1600-0870.2011.00543.x

CrossRef Full Text | Google Scholar

Liu, L., Hong, Y., Hocker, J. E., Shafer, M. A., Carter, L. M., Gourley, J. J., et al. (2012). Analyzing projected changes and trends of temperature and precipitation in the southern USA from 16 downscaled global climate models. Theor. Appl. Climatol. 109, 345–360. doi:10.1007/s00704-011-0567-9

CrossRef Full Text | Google Scholar

Long, M. C., Lindsay, K., Peacock, S., Moore, J. K., and Doney, S. C. (2013). Twentieth century oceanic carbon uptake and storage in CESM1(BGC). J. Clim. 26, 6775–6800. doi:10.1175/JCLI-D-12-00184.1

CrossRef Full Text | Google Scholar

Mahmood, R., Babel, S. M., and Shaofeng, J. (2015). Assessment of temporal and spatial changes of future climate in theJhelum river basin, Pakistan and India. Weather Clim. Extremes. 10, 40–55. doi:10.1016/j.wace.2015.07.002

CrossRef Full Text | Google Scholar

Maraun, D., Wetterhall, F., Ireson, A. M., Chandler, R. E., Kendon, E. J., Widmann, M., et al. (2010). Precipitation downscaling under climate change: recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 48 (3), 219. doi:10.1029/2009RG000314

CrossRef Full Text | Google Scholar

May, W. (2008). Climatic changes associated with a global“2 °C-stabilization”scenario simulated by the ECHAM5/MPI-OM coupled climate model. Clim. Dynam. 31 (2–3), 283–313. doi:10.1007/s00382-007-0352-8

CrossRef Full Text | Google Scholar

May, W. (2012). Assessing the strength of regional changes in near-surface climate associated with a globalwarming of 2°C. Clim. Change. 110 (3–4), 619–644. doi:10.1007/s10584-011-0076-y

CrossRef Full Text | Google Scholar

Mitchell, T. D. (2003). Pattern scaling: an examination of the accuracy of the technique for describing future climates. Clim. Change. 60, 217–242. doi:10.1023/A:1026035305597

CrossRef Full Text | Google Scholar

Nam, D. H., Dung, N. Q., Duong, P. C., Mai, D. T., and Thuan, D. H. (2015). “Near future changes in extreme rainfall over Vietnam projected by CMIP5 high resolution climate models,” in Vietnam-Japan Workshop on Estuaries, Coasts and Rivers 2015, Hoi An, Vietnam, September 7–8, 2015.

Google Scholar

Neelin, J. D., Münnich, M., Su, H., Meyerson, J. E., and Holloway, C. E. (2006). Tropical drying trends in global warming models and observations. Proc. Natl. Acad. Sci. USA. 103 (16), 6110–6115. doi:10.1073/pnas.0601798103

PubMed Abstract | CrossRef Full Text | Google Scholar

OECD (2020). “Multi-dimensional review of Viet Nam towards an integrated, transparent and sustainable economy,” in OECD Development Pathways. (Paris, France: OECD Publishing). doi:10.1787/367b58c-en

CrossRef Full Text | Google Scholar

Overeem, A., and Buishand, A. (2012). Statistiek van extreme gebiedsneerslag in Nederland (RPRT). KNMI. Available at: https://library.wur.nl/WebQuery/wurpubs/427690.

Google Scholar

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (1997). Numerical recipes in C. New York, NY: Cambridge University Press.

Google Scholar

Raghavan, S. V., Vu, M. T., and Liong, S. Y. (2017). Ensemble climate projections of mean and extreme rainfall over Vietnam. Global Planet. Change 148, 96–104. doi:10.1016/j.gloplacha.2016.12.003

CrossRef Full Text | Google Scholar

Rahman, A. S., Rahman, A., Zaman, M. A., Haddad, M., Ahsan, A., and Imteaz, M. A. (2013). A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 69 (3), 1803–1813. doi:10.1007/s11069-013-0775-y

CrossRef Full Text | Google Scholar

Rahmani, V., Hutchinson, S. L., Hutchinson, J. M. S., Aavudai, A., et al. (2014). Extreme daily rainfall event distribution patterns in Kansas. J. Hydrol. Eng. 19 (4), 707–716. doi:10.1061/(ASCE)HE.1943-5584.0000839

PubMed Abstract | CrossRef Full Text | Google Scholar

Ribalaygua, J., Pino, M. R., Pórtoles, J., Roldán, E., Gaitán, E., Chinarro, D., et al. (2013). Climate change scenarios for temperature and precipitation in Aragón (Spain). Sci. Total Environ. 463-464, 1015–1030. doi:10.1016/j.scitotenv.2013.06.089

PubMed Abstract | CrossRef Full Text | Google Scholar

Roeckner, E., Bäuml, G., Bonaventura, L., Brokopf, R., Esch, M., Giorgetta, M., et al. (2003). Report No.: 349. The atmospheric general circulation model ECHAM 5. PART I: model description. Hamburg, Germany: Max Planck Institute for Meteorology.

CrossRef Full Text | Google Scholar

Rotstayn, L. D., Jeffrey, S. J., Collier, M. A., Dravitzki, S. M., Hirst, A. C., Syktus, J. I., et al. (2012). Aerosol- and greenhouse gas-induced changes in summer rainfall and circulation in the Australasian region: a study using single-forcing climate simulations. Atmos. Chem. Phys. 12, 6377–6404. doi:10.5194/acp-12-6377-2012

CrossRef Full Text | Google Scholar

Rummukainen, M. (2010). State-of-the-art with regional climate models. Wiley Interdiscip. Rev. Clim. Change 1 (1), 82–96. doi:10.1002/wcc.8

CrossRef Full Text | Google Scholar

Ruosteenoja, K., Tuomenvirta, H., and Jylhä, K. (2007). GCM-based regional temperature and precipitation change estimates for Europe under four SRES scenarios applying a super-ensemble pattern-scaling method. Clim. Change 81, 193–208. doi:10.1007/s10584-006-9222-3

CrossRef Full Text | Google Scholar

Rust, H. W., Maraun, D., and Osborn, T. J. (2009). Modelling seasonality in extreme precipitation: a UK case study. Eur. Phys. J. Spec. Top. 174, 99–111. doi:10.1140/epjst/e2009-01093-7

CrossRef Full Text | Google Scholar

Saeed, F., Haensler, A., Weber, T., Hagemann, S., and Jacob, D. (2013). Representation of extreme precipitation events leading to opposite climate change signals over the Congo basin. Atmosphere 4, 254–271. doi:10.3390/atmos4030254

CrossRef Full Text | Google Scholar

Santer, B. D., Wigley, T. M. L., Schlesinger, M. E., and Mitchell, J. F. B. (1990). Report No.: 47. Developing climate scenarios from equilibrium GCM results. Available at: https://pure.mpg.de/rest/items/item_2566446/component/file_2566445/content

Google Scholar

Shindell, D. T., Voulgarakis, A., Faluvegi, G., and Milly, G. (2012). Precipitation response to regional radiative forcing. Atmos. Chem. Phys. 12, 6969–6982. doi:10.5194/acp-12-6969-2012

CrossRef Full Text | Google Scholar

Shiogama, H., Hanasaki, N., Masutomi, Y., Nagashima, T., Ogura, T., Takahashi, K., et al. (2010). Emission scenario dependencies in climate change assessments of the hydrological cycle. Clim. Change 99 (1–2), 321–329. 10.1007/s10584-009-9765-1

CrossRef Full Text | Google Scholar

Stevens, B., Giorgetta, M., Esch, M., Mauritsen, T., Crueger, T., Rast, S., et al. (2013). Atmospheric component of the MPI-M Earth system model: ECHAM6. J. Adv. Model. Earth Syst. 5, 146–172. doi:10.1002/jame.20015

CrossRef Full Text | Google Scholar

Tromel, S., and Schonwiese, C. D. (2007). Probability change of extreme precipitation observed from 1901 to 2000 in Germany. Theor. Appl. Climatol. 87, 29–39. doi:10.1007/s00704-005-0230-4

CrossRef Full Text | Google Scholar

Trzaska, S., and Schnarr, E. (2014). A review of downscaling methods for climate change projections. Burlington, Vermont: United States Agency for International Development Tetra Tech ARD.

Google Scholar

Voldoire, A., Sanchez-Gomez, E., Salas y Mélia, D., Decharme, B., Cassou, C., Sénési, S., et al. (2013). The CNRM-CM5.1 global climate model: description and basic evaluation. Clim. Dynam. 40, 2091–2121. doi:10.1007/s00382-011-1259-y

CrossRef Full Text | Google Scholar

Volodin, E. M., Dianskii, N. A., and Gusev, A. V. (2010). Simulating present-day climate with the INMCM4.0 coupled model of the atmospheric and oceanic general circulations. Izvestiya Atmos. Ocean. Phys. 46, 414–431. doi:10.1134/S000143381004002X

CrossRef Full Text | Google Scholar

Von Salzen, K., Scinocca, J. F., McFarlane, N. A., Li, J., Cole, J. N. S., Plummer, D., et al. (2013). The Canadian fourth generation atmospheric global climate model (CanAM4). Part I: representation of physical processes. Atmos. Ocean. 51, 104–125. doi:10.1080/07055900.2012.755610

CrossRef Full Text | Google Scholar

Watanabe, M., Suzuki, T., O’ishi, R., Komuro, Y., Watanabe, S., Emori, S., et al. (2010). Improved climate simulation by MIROC5: mean states, variability, and climate sensitivity. J. Clim. 23, 6312–6335. doi:10.1175/2010JCLI3679.1

CrossRef Full Text | Google Scholar

Watterson, I. G. (2008). Calculation of probability density functions for temperature and precipitation change under global warming. J. Geophys. Res. Atmos. 113 (D12), D12106. doi:10.1029/2007JD009254

CrossRef Full Text | Google Scholar

Watterson, I. G., and Whetton, P. H. (2011). Joint PDFs for Australian climate in future decades and an idealized application to wheat crop yield. Aust. Meteorol. Oceanogr. J. 61, 221–223. doi:10.22499/2.6104.003

CrossRef Full Text | Google Scholar

Wigley, T. M. L. (2008). MAGICC/SCENGEN 5.3: user manual version 2. Available at: http://www.cgd.ucar.edu/cas/wigley/magicc/UserMan5.3.v2.pdf (Accessed February 10, 2020).

Google Scholar

Wilby, R. L., and Wigley, T. M. L. (1997). Downscaling general circulation model output: a review of methods and limitations. Prog. Phys. Geogr. 21, 530–548. doi:10.1177/030913339702100403

CrossRef Full Text | Google Scholar

Xia, J., Du, H., Zeng, S., She, D., Zhang, Y., Yan, Z., et al. (2012). Temporal and spatial variations and statistical models of extreme runoff in Huaihe River Basin during 1956–2010. J. Geogr. Sci. 22 (6), 1045–1060. doi:10.1007/s11442-012-0982-6

CrossRef Full Text | Google Scholar

Ye, W., and Li, Y. (2011). “A method of applying daily GCM outputs in assessing climate change impact on multiple day extreme precipitation for Brisbane River catchment.” in 19th International Congress on Modelling and Simulation, Perth, Australia, December, 12–16, 2011

Google Scholar

Yukimoto, S., Yoshimura, H., Hosaka, M., Sakami, T., Tsujino, H., Hirabara, M., et al. (2011). Meteorological research institute-earth system model v1(MRI-ESM1)-model description. Ibaraki, Japan: Technical Report of MRI, 88.

Google Scholar

Zhao, Y., Zou, X., Cao, L., and Xu, X. (2014). Changes in precipitation extremes over the Pearl River Basin, Southern China, during 1960–2012. Quat. Int. 333, 26–39. doi:10.1016/j.quaint.2014.03.060

CrossRef Full Text | Google Scholar

Zolina, O., Simmer, C., Kapala, A., Bachner, S., Gulev, S., and Maechel, H. (2008). Seasonally dependent changes of precipitation extremes over Germany since 1950 from a very dense observational network. J. Geophys. Res. Atmos. 113, D06110. doi:10.1029/2007JD008393

CrossRef Full Text | Google Scholar