Triple Oxygen Isotope Measurements by Multi-Collector Secondary Ion Mass Spectrometry

Secondary ion mass spectrometry (SIMS) is a powerful technique for in situ triple oxygen isotope measurements that has been used for more than 30 years. Since pioneering works performed on small-radius ion microprobes in the mid-80s, tremendous progress has been made in terms of analytical precision, spatial resolution and analysis duration. In this respect, the emergence in the mid-90s of the large-radius ion microprobe equipped with a multi-collector system (MC-SIMS) was a game changer. Further developments achieved on CAMECA MC-SIMS since then (e.g., stability of the electronics, enhanced transmission of secondary ions, automatic centering of the secondary ion beam, enhanced control of the magnetic field, 10¹²Ω resistor for the Faraday cup amplifiers) allow nowadays to routinely measure oxygen isotopic ratios (¹⁸O/¹⁶O and ¹⁷O/¹⁶O) in various matrices with a precision (internal error and reproducibility) better than 0.5‰ (2σ), a spatial resolution smaller than 10 µm and in a few minutes per analysis. This paper focuses on the application of the MC-SIMS technique to the in situ monitoring of mass-independent triple oxygen isotope variations.

Introduction

Being third in terms of abundance in the Solar System (Lodders, 2003), oxygen is of upmost importance as it plays a critical role in most biological and geological processes. In planetary science, oxygen isotopes are powerful proxies that are nowadays commonly used to decipher the formation of terrestrial and extra-terrestrial rocks. Pioneering works on oxygen isotope (¹⁸O/¹⁶O ratio) measurements in rocks date back to the 1930s (e.g., Cohn and Urey, 1938) before flourishing from the 1960s (e.g., Clayton and Epstein, 1961; O’Neil and Clayton, 1964). At that time, it was considered superfluous to measure the least abundant stable isotope of oxygen (¹⁷O), as isotopes for light elements (H, C, N, O, S) had been theorized to vary mass-dependently (Urey, 1947). Therefore, until recently almost all terrestrial oxygen isotope studies were limited to ¹⁸O/¹⁶O measurements. In the early 2000s, with the advent of laser fluorination techniques, the measurement of ¹⁷O opened new fields of exploration in the area of physical chemistry, terrestrial biogenic and atmospheric evolution, paleoclimatology as well as present day atmospheric sciences (Bindeman et al., 2007; Rumble et al., 2007; Landais et al., 2008; Luz and Barkan, 2010; Pack and Herwartz, 2014). Except for atmospheric components, such as O₃, CO₂, H₂O₂, which display mass-independent fractionation (MIF) due to photochemical processes (Thiemens, 2006), all terrestrial samples plot on a straight line with a slope of ∼1/2 in a plot of δ¹⁷O versus δ¹⁸O, the so-called Terrestrial Fractionation Line–TFL (Sharp et al., 2018). However, small mass-dependent deviations from the TFL (<0.2‰) that are helpful for deciphering formation processes can be observed in terrestrial samples (Sharp et al., 2018). The situation is different for extra-terrestrial samples since the remarkable discovery in 1973 of mass-independent oxygen isotopic variation in high-temperature condensates from primitive meteorites (Clayton et al., 1973; Clayton, 2008). Since then, triple oxygen isotope analyses have been performed in numerous types of extra-terrestrial material, such as primitive and differentiated meteorites (e.g., Clayton and Mayeda, 1984; Clayton and Mayeda, 1999; Greenwood et al., 2012), lunar samples from Apollo missions (e.g., Hashizume and Chaussidon, 2005; Ireland et al., 2014; Young et al., 2016) or solar wind from the Genesis mission (McKeegan et al., 2011), using either laser fluorination and gas-source mass spectrometry for bulk analysis or secondary ion mass spectrometry (SIMS) for in situ analysis.

The history of oxygen isotope measurements in natural samples by SIMS started more than 30 years ago with the arrival of the first generation of small-radius magnetic-sector ion microprobes (CAMECA IMS 3f) in Earth sciences laboratories. For the first time, an in situ technique enabled isotopic measurements of small or chemically/isotopically zoned samples to be performed at few micron-scale levels. Initially, oxygen isotope measurements performed by small-radius ion microprobes were subject to several issues, for instance instabilities due to charge build-up during analyses of electrically insulating samples (e.g., silicates or oxides), low count rates, isobaric interferences (namely ¹⁶OH on ¹⁷O) or variable and unconstrained instrumental mass fractionations (IMF), leading to poor precision (at a few permil level on ¹⁸O/¹⁶O ratios) and poor accuracy. As a consequence, earlier studies were limited to extra-terrestrial material with large isotopic variations (e.g., McKeegan, 1987; Lorin et al., 1990; Yurimoto et al., 1994) while terrestrial samples were ruled out due to their smaller range of variations. Subsequently, thanks to important technical developments such as the use of a normal-incidence electron gun to compensate sample charging effects, the energy filtering of secondary ions to efficiently remove the ¹⁶OH interference or the improvement of the electron multiplier (EM) detectors, the precision has significantly improved to reach the permil level on ¹⁸O/¹⁶O ratios (Valley and Graham, 1991; Hervig, 1992; Hervig et al., 1992; Riciputi and Paterson, 1994; Eiler et al., 1997). In order to improve the accuracy of a measurement, a precise control of the IMF, which corresponds to the difference between the true isotopic composition of a sample and the value measured with the ion microprobe, is needed. The IMF depends on the physics of the mass spectrometer, the analytical settings and the mineralogy of the sample. Because the latter effect cannot be predicted by any physical model, it has to be calibrated empirically with appropriate standards that match the chemistry and the mineralogy of samples (Shimizu and Hart, 1982; Benninghoven et al., 1987; Eiler et al., 1997). Despite these advances, the quality of the analysis remained severely limited by the physics of small-radius ion microprobes that did not allow sufficient instrumental transmission of secondary ions at high mass resolving power (MRP), mandatory to resolve ¹⁷O from ¹⁶OH (MRP ≈ 5 000), nor simultaneous measurements of the three oxygen isotopes. A breakthrough for oxygen isotope measurements by SIMS arose with the development in the mid-1990s of the first large-radius ion microprobe equipped with a multi-collector system (CAMECA IMS 1270). CAMECA later developed the IMS 1280, 1280-HR and 1300-HR³ series wheras ASI proposed the SHRIMP IIe, SI, IV and V developed at the Australian National University. Especially developed for Earth and planetary sciences, these multi-collector SIMS (MC-SIMS) instruments overcome the weaknesses listed above as they allow efficient transmission at high MRP and the simultaneous measurement of the three oxygen isotopes.

The current article aims to first describe the different classical settings used for triple oxygen isotope measurements by MC-SIMS before emphasizing recent technical and analytical developments. Finally, recent examples of application in planetary sciences will be shown.

Analytical Approaches and Results

A very distinctive characteristic of oxygen isotopes is the large difference of abundances between the major (¹⁶O = 99.762%) and minor (¹⁷O = 0.038%, ¹⁸O = 0.200%) isotopes. As a consequence and independently of the instrument settings, the factor of ∼2,500 between ¹⁶O and ¹⁷O abundances requires an ion detection system with a wide dynamic range. Classically, large-radius ion microprobes are equipped with a set of electron multipliers (EMs) and Faraday cups (FCs) that cover different counting ranges.

Secondary ions entering the FC detector produce a current which is converted into a voltage by a high impedance preamplifier and is counted after passing through a voltage/frequency converter. FC preamplifier boards can be set with 10¹⁰Ω, 10¹¹Ω and 10¹²Ω resistors allowing maximum count rates of ∼ 6 × 10⁹ cps, ∼ 6 × 10⁸ cps and ∼ 6 × 10⁷ cps, respectively. Preamplifier boards of SHRIMP instruments can also be equipped with a capacitor instead of a resistor allowing FCs to work in charge mode instead of current mode (Ireland et al., 2014). Although appearing to be a promising instrument for high precision triple oxygen isotope measurements (see abstracts by Bridges and Ireland, 2015; Loiselle et al., 2019), no high precision triple oxygen data using a large-radius SHRIMP instrument has been published to our knowledge. Therefore, hereafter we will mostly discuss settings and results obtained with CAMECA instruments. The internal error of an analysis performed on a FC is limited by the shot noise and Johnson-Nyquist (JN) noise (e.g. Wieser and Schwieters, 2005; Ickert and Stern, 2013; Koornneef et al., 2013; Ireland et al., 2014). Shot noise has a Poisson distribution and basically expresses the relationship between count rate and measurement precision, i.e., 1/√N with N the number of counts. JN noise corresponds to the blackbody radiation in a resistor due to thermal agitation of electrons and is expressed as ΔV = √4∙k_B∙R∙T∙(1/t) where ΔV is the one sigma standard deviation (1SD) noise (in volts), k_B is the Boltzmann constant, R is the resistor value in ohm, T is the temperature in Kelvin and t the integration time in seconds. From the latter equation it is clear that 1) if the resistor value is increased by a factor of 10 (e.g., 10¹²Ω instead of 10¹¹Ω), the signal to noise ratio is theoretically ∼ three times higher at a given intensity, i.e., 10/√10, and 2) increasing the counting time allows to reduce the JN noise. For a given analytical condition (count rate, counting time, amplifier's resistor), the sum (in a quadratic way) of shot noise and JN noise indicates the best achievable internal precision. Raw signals obtained with a FC are corrected from the gain and the background electrical noise of the FC detector. The former is very stable and is commonly calibrated at the beginning of an analytical session while the latter can be measured during the pre-analysis surface sputtering in multicollection mode (see details below). JN noise dictates the theoretical level of precision at which the background can be measured. Therefore, for a given counting time the precision is expected to be better for a 10¹²Ω resistor compared to a 10¹¹Ω or a 10¹⁰Ω. Long-term stability (24 h) of backgrounds measured every 5 min for 90 s on FCs (similar to usual analytical conditions, see below for details) equipped with 10¹⁰Ω, 10¹¹Ω, and 10¹²Ω resistors are shown on Figure 1. The reproducibility (1SD) for the 10¹⁰Ω, 10¹¹Ω and 10¹²Ω resistors backgrounds are 2,600 cps (Fig. 1A), 600 cps (Fig. 1B) and 150 cps (Fig. 1C) respectively. These values are 2–3 times higher than the level of precision predicted by the JN noise equation for the same integration time, i.e. 1SD = 850 cps, 270 cps and 90 cps for a 10¹⁰Ω, 10¹¹Ω, and 10¹²Ω resistor respectively. This is explained by the fact that preamplifier boards are sensitive to thermal variations and even a small variation of the room temperature, for instance 1°C variation over 24 h is enough for the FC backgrounds to shift significantly, as illustrated by the gray arrows on Figure 1. Such low frequency thermal drift is not an issue for the external reproducibility of standards since the background is measured between each sample.

FIGURE 1

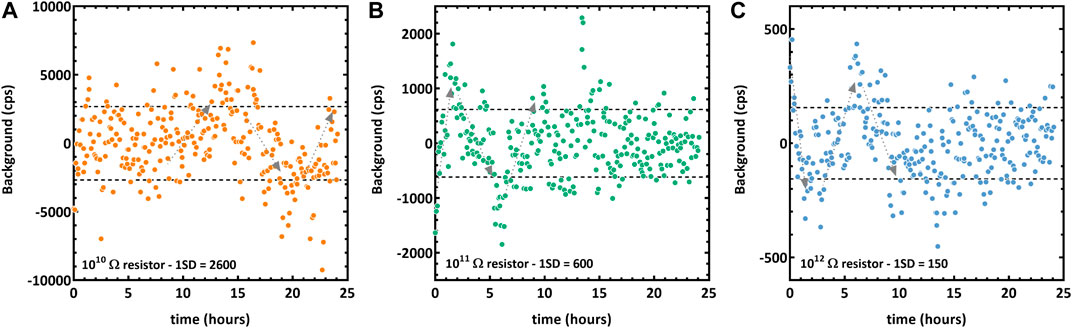
FIGURE 1. Long-term stability of L′2, H1 (multicollection) and FC2 (monocollection) FCs backgrounds equipped with 10¹⁰Ω, 10¹¹Ω, and 10¹²Ω preamplifiers, respectively. Backgrounds are measured for 90 s every 5 min. Dotted lines correspond to the standard deviation (1SD): ∼2,600 cps on L′2, ∼600 cps on H1 and ∼150 cps on FC2. Dotted gray arrows display thermal drifts of FC preamplifiers due to small room temperature variations.

The EM detector is appropriate for the measurement of low count rates, below 10⁶ cps. When a secondary ion hits the first dynode an amplified stream of secondary electrons is emitted through successive dynode stages with an overall gain of about 10⁸ that depends on the first dynode ion/electron conversion efficiency and other dynodes amplification efficiency. The charge pulse produced by the last dynode is then converted into a voltage pulse whose amplitude varies with the EM gain and is randomly distributed according to a Pulse Height Amplitude (PHA) distribution curve. It is well known that the EM gain drops with time, proportionally to the incident ion rate. This so-called EM aging effect can be controlled by monitoring the drift of the PHA curve towards low voltages and is compensated by increasing the EM high voltage (Schuhmacher et al., 2004). An illustration of the EM aging effect is shown on Figure 2B. The EM is also subject to the dead-time effect that occurs when two or more ions impact the first dynode within a sufficiently short time interval to be counted as a single ion (typically a few tens of nanoseconds). Even if the EM dead-time effect obeys a well known mathematical law, the accuracy of the dead-time correction is crucial as it can contribute significantly to the uncertainty on isotopic ratios once count rates exceed 10⁵ cps (e.g., Ireland et al., 2014). Even if the theoretical precision attainable with an EM, predicted by the counting statistics (shot noise), is better than 0.1‰ for count rates above 10⁶ cps, in practice it is affected by the EM aging and dead-time effects. As a consequence, count rates lower than ∼ 2 × 10⁵ cps are preferred to avoid fast time-dependent drift of the EM gain and significant dead-time correction that limits the isotopic ratio data precision.

FIGURE 2

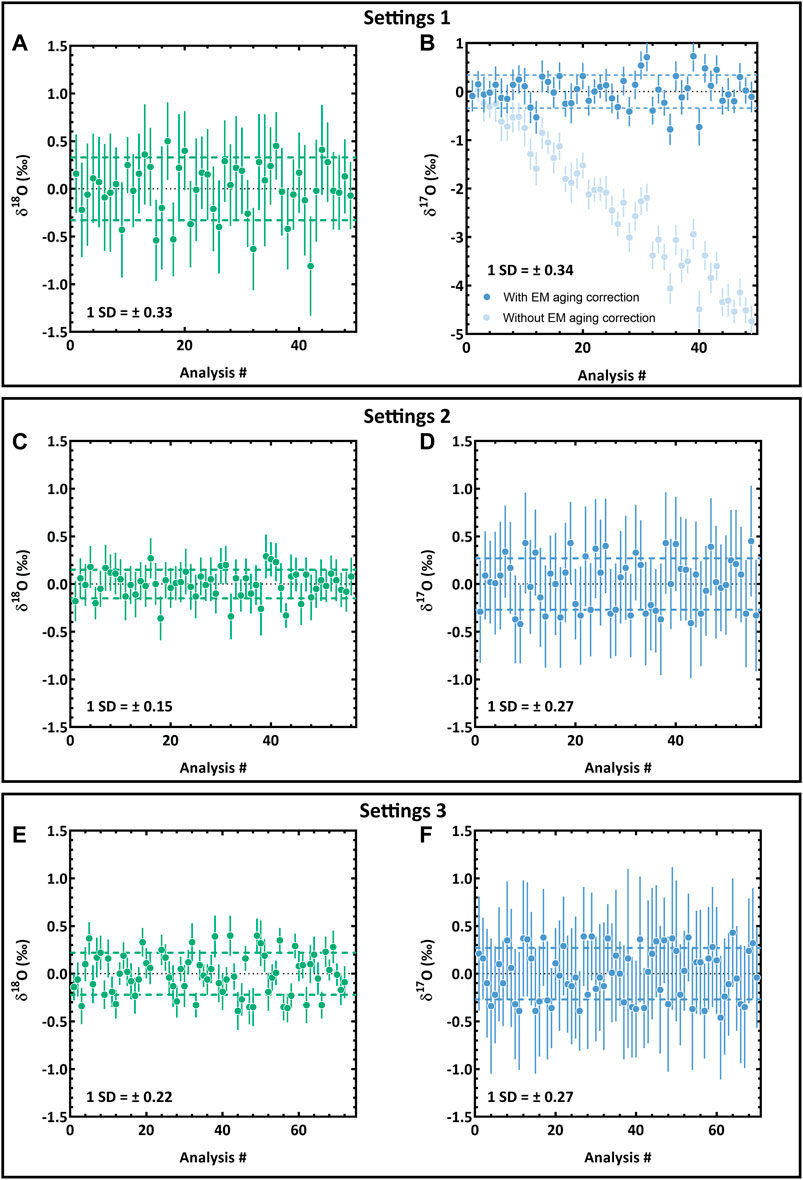
FIGURE 2. Reproducibility of δ¹⁸O (A, C and E); and δ¹⁷O (B, D and F) measurements in San Carlos olivine standard for the three different SIMS analytical settings (see text for details). Error bars are ±2SE (standard error). Dotted lines corresponds to the external reproducibility (±1SD).

The general settings for triple oxygen isotope analysis by CAMECA MC-SIMS are given hereafter. Samples are sputtered with a primary Cs⁺ beam accelerated at 10 kV and set in Gaussian mode (primary beam size controlled by the primary column lenses and gaussian primary intensity distribution). The Gaussian mode is usually preferred to the Kohler illumination mode (primary beam size controlled by the primary aperture size and homogeneous primary intensity distribution) as it allows a smaller primary beam for a given primary intensity and a more stable beam shape. A raster is usually applied to the Gaussian primary beam (from 5 × 5 μm² to 20 × 20 μm²) to ensure flat-bottomed pits. Charge build-up on the sample surface of insulating materials (most minerals and rocks) is neutralized by a normal-incident electron gun (NEG) beam. The electron beam (∼125 μm diameter) is centered on the analyzed area and works in auto-compensation mode, thanks to an excess of electrons above the sample surface and impact energy close to 0 eV. Negative secondary ^{16, 17,18}O⁻ ions are accelerated at 10 kV and analyzed in multicollection mode using an axial collector of the monocollection for ¹⁷O⁻ and two off-axis collectors of the multicollection for ¹⁶O⁻ and ¹⁸O⁻. By adjusting the entrance (∼90–110 µm) and axial exit (∼180–210 µm) slits widths, the axial MRP is set at ∼ 6,000–7,000 in order to remove the ¹⁶OH⁻ interference on ¹⁷O⁻, whereas the multicollection MRP is set at ∼ 2,500 (slit #1–500 µm) which is generally (at the exception of H₂O-rich minerals or glasses) sufficient to resolve the ¹⁷OH⁻ interference on ¹⁸O⁻. The transfer optics settings are usually set at 40–100 µm (corresponding to a field magnification from ∼200 to ∼80) to insure an efficient instrumental transmission and to fill in the field aperture set at 1,500–3,000 µm. The purpose of the transfer optic lenses, apertures and slits is to insure a maximum transmission of secondary ions for a given mass resolution while minimizing secondary beam aberrations before entering the double-focusing mass spectrometer. The energy slit is closed at 30–40 eV in order to remove high-energy secondary ions and therefore to minimize chromatic secondary aberrations. Gains of the FC detectors are inter-calibrated at the beginning of each analytical session. Usually, automatic secondary beam centering in the transfer optics and mass calibration controls are implemented in the analysis routine. It is noteworthy that on instruments equipped with an optional NMR (nuclear magnetic resonance) teslameter, allowing long-term magnetic field regulation, no mass calibration control is needed during analysis. Measurements typically consist of a 60–90 s pre-analysis sputtering to clean the sample surface and attain stable count rates on detectors, during which noise backgrounds of the FC detectors are measured, followed by automatic beam centering and mass calibration controls (if needed), and 30 to 50 cycles of 4 or 5 s integration time for data acquisition. A measurement typically takes 7–10 min. Isotopic ratios are expressed in the delta notation (in ‰) and normalized to the Vienna Standard Mean Ocean Water (VSMOW) composition:

${\mathrm{\delta }}^{\text{x}}\text{O}=\left[\left({}^{\text{x}}\text{O}/{}^{16}\text{O}\right)/{\left({}^{\text{x}}\text{O}/{}^{16}\text{O}\right)}_{\text{VSMOW}}-1\right]\times 1\text{,}000\text{,}\text{with}\text{x}=17\text{or}18$

Data presented in the following illustrate the pros and cons of different settings used for triple oxygen isotope measurements. Results have been obtained in multicollection mode with a MRP at 7,000, a 100 µm transfer optics settings, a field aperture opened at 1,500 for settings 1 and 3 and 2,500 for the settings 2, 90 s of pre-analysis sputtering and 30 cycles of 5 s integration time.

Until recently, two different settings were mainly used to perform high precision triple oxygen isotopes analysis by MC-SIMS, ¹⁷O⁻ being measured on an axial detector either on an EM or on a 10¹¹Ω FC with advantages for each settings (Table 1, e.g., Aleon et al., 2002; Krot et al., 2006; Chaussidon et al., 2008; Valley and Kita, 2009; Kita et al., 2010; Libourel and Chaussidon, 2011). In the first case (settings 1 in the following), a small primary beam diameter can be used (<10 µm), allowing analysis of small targets, e.g. zoned minerals smaller than 50 µm that are quite common for instance in primitive meteorites. However, even if the count rate for ¹⁷O⁻ is kept at ∼2 × 10⁵ cps or below, a careful monitoring of the drift due to EM aging effect is needed and EM high voltage adjustment must be done regularly, limiting the internal error on δ¹⁷O at ∼ 0.3‰ (2SE; Figure 2B e.g., Chaussidon et al., 2008). For these conditions the count rate for ¹⁸O⁻, measured on a 10¹¹Ω FC, is ∼1 × 10⁶ cps, generating a larger internal error on δ¹⁸O, typically 0.5‰ (2SE; Table 1). As a consequence, the long-term external reproducibility on the standard (San Carlos olivine - SCOl) is relatively poor, i.e. ±0.33 (1SD) on δ¹⁸O and ±0.34 (1SD) on δ¹⁷O (Figure 2A,B). In the second case (settings 2), the primary current needs to be increased in order to reach ∼1 × 10⁶ cps for ¹⁷O⁻ measured on the axial 10¹¹Ω FC, but to the detriment of the spatial resolution because of the larger beam diameter, ∼ 20 µm typically (Table 1). Internal errors on δ¹⁷O and δ¹⁸O are typically 0.5‰ and 0.2‰, respectively, (Table 1; Figure 2C,D). Results show that the long-term external reproducibility on SCOl with settings 2 is better than with settings 1, i.e. ± 0.15 (1SD) on δ¹⁸O and ±0.27 (1SD) on δ¹⁷O (Table 1; Figure 2C,D, Kita et al., 2010; Schrader et al., 2014; Tenner et al., 2015; Vacher et al., 2016, Vacher et al., 2017, Vacher et al., 2018; Marrocchi et al., 2018, Marrocchi et al., 2019). However settings 2 are not appropriate when only small sample areas are available. Occasionally, for very small samples, specific settings were developed in order to achieve a spatial resolution better than 3 µm yet to the detriment of the precision due to lower ¹⁷O⁻ and ¹⁸O⁻ intensities that are measured on EMs (e.g., Nakamura et al., 2008).

TABLE 1

TABLE 1. Primary beam parameters, counting times, multicollection configurations, typical counts rates and uncertainties observed for the three different MC-SIMS settings.

The development during the last decade of FC preamplifier boards equipped with 10¹²Ω resistor (and even 10¹³Ω resistor for thermal ionization mass spectrometry instruments) allows to reduce the JN noise contribution and therefore extends the lower-range use of FC detectors (e.g., Makishima and Nakamura, 2010; Wielandt and Bizzarro, 2011; Koornneef et al., 2013, 2014). The adaptation of 10¹²Ω amplifier boards for large-radius ion microprobes was first done on SHRIMP instruments (Ireland et al., 2014) and more recently on CAMECA instruments (Siron et al., 2021, this paper). The use of a 10¹²Ω preamplifier board on the axial collector opens a third path for triple oxygen isotope measurements by combining the advantages and mitigating the inconveniences of settings 1 and 2 (see settings 3, Table 1, Siron et al., 2021). Data presented here have been acquired with a FC preamplifier board equipped with a 10¹²Ω resistor developed through the collaboration between the CAMECA's R&D team and the CRPG ion probe team. As shown on Figure 1, count rates as low as 3 × 10⁵ cps for ¹⁷O⁻ can be measured while keeping an internal precision better than ∼0.5‰ (2SE; Table 1). For settings 3 a small primary beam size can be used (<10 µm) and still achieve reproducibility similar to settings 2 (Table 1, Figure 2E,F). The striking advantage of the 10¹²Ω FC compared to the 10¹¹Ω FC is illustrated in Figure 3 showing that 0.2‰ (2SE) precision level can be reached for count rates as low as ∼ 6 × 10⁵ cps with a 10¹²Ω FC, whereas count rates >3 × 10⁶ cps are required for a 10¹¹Ω FC in order to reach the same precision level (Table 2, Figure 3). There is an excellent agreement between measured internal errors and expected errors determined from the combination of shot noise and JN noise, as a function of the count rates on 10¹¹Ω FC and 10¹²Ω FC (Figure 3, Table 2). One possible inconvenience of the 10¹²Ω FC may come from the longer settling time compared to 10¹¹Ω FC (Koornneef et al., 2013; Ireland et al., 2014). The CAMECA 10¹²Ω preamplifier board design has been optimized in order to reduce the settling time; it was measured at ∼ 5 s for a precision at 0.1‰ level, which is similar to 10¹¹Ω preamplifier boards. To be noted that for multicollection measurements, this settling time has little influence on the analysis duration as it only applies at the beginning of data acquisition.

FIGURE 3

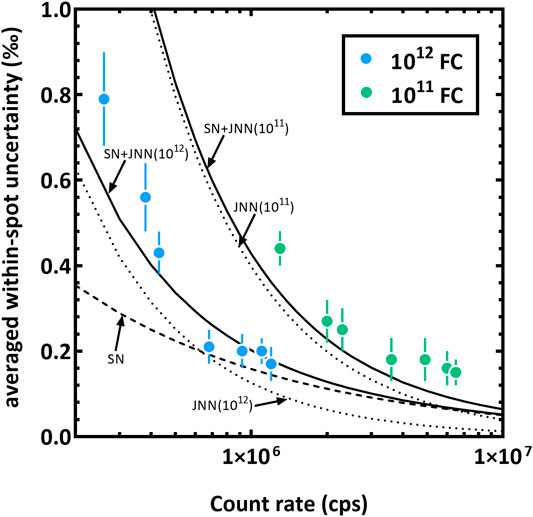
FIGURE 3. Typical standard error (2SE) obtained for oxygen isotope measurements on FCs equipped with 10¹¹Ω or 10¹²Ω preamplifiers as a function of the count rate (in cps). Similar low standard errors are reached for count rates higher than ∼5 × 10⁵ cps for the 10¹²Ω preamplifier and for count rates higher than ∼2.5 × 10⁶ cps for the 10¹¹Ω amplifier. Shot noise (SN, dashed lines), Johnson-Nyquist noise (JNN, dotted lines) and SN + JNN (thick lines) theoretical variations are also shown (see text for details). Each data point is the average of five analyses (the error bars are ±1SD).

TABLE 2

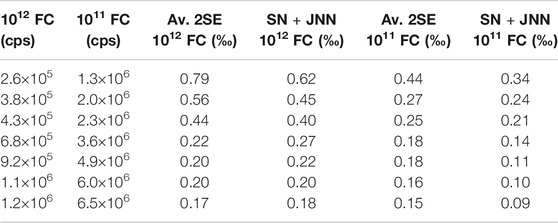
TABLE 2. Average standard errors (2SE, internal errors) observed for 10¹²Ω FC and 10¹¹Ω FC detectors for different count rates and a 150 s total counting time. Expected shot noise (SN) plus Johnson-Nyquist noise (JNN) for 10¹²Ω and 10¹¹Ω amplifiers are also given (2σ).

Practical Application

Studying the triple oxygen isotopic composition of extra-terrestrial materials is of upmost importance as it allows to constrain their origin and their conditions of formation, and therefore deciphering the formation of our Solar System (e.g., Yurimoto et al., 2008; Tenner et al., 2018; Greenwood and Anand, 2020). Although less precise than fluorination (<0.1‰ on δ¹⁷O and δ¹⁸O; e.g., Greenwood and Anand, 2020), the MC-SIMS (<0.5‰) in situ technique is particularly suitable for the study of isotopically heterogeneous and/or small samples that require both high precision and high spatial resolution. MC-SIMS is perfectly designed and has long been used for the study of three-oxygen isotopic compositions of primitive meteorite components, i.e., Ca, Al-rich inclusions (CAIs), ameboid olivine aggregates (AOAs), chondrules or matrix components that usually contain minerals much smaller than 100 µm (e.g., Aleon et al., 2002; Chaussidon et al., 2008; Kita et al., 2010; Tenner et al., 2015; Vacher et al., 2016; Vacher et al., 2017; Kawasaki et al., 2017; Marrocchi et al., 2018, Marrocchi et al., 2019; Aléon et al., 2018; Krot et al., 2019; Vacher et al., 2019; Piralla et al., 2020). It is worth noting that these studies have been done using either settings 1 or settings 2, limiting either the spatial resolution or the analytical precision (Table 1). As shown here and in a recent paper by Siron et al. (2021),10¹²Ω FC detectors give access to a new analytical protocol (settings 3) providing both improved lateral resolution and reproducibility. MC-SIMS instruments equipped with 10¹²Ω FC detectors currently represent the state-of-the-art of the technology for in situ measurements of triple oxygen isotopes.

Chondrules are igneous, submillimeter-sized silicate spheroids with a relatively simple mineralogy (i.e., olivine, low-Ca pyroxene, and glassy mesostasis ± Fe-Ni metal beads) and the main high-temperature component of primitive meteorites. They have been known for a very long time, but despite being apparently quite simple objects their mechanisms of formation remain a subject of controversy among cosmochemists (see for instance reviews by Connolly and Jones, 2016; Jones et al., 2018). Recently, complex textures and chemical zoning, at the scale of a few to a few tens of microns, have been revealed in chondrule silicates (particularly olivine grains), indicating a rather complex history of formation (Libourel and Portail, 2018; Marrocchi et al., 2018, Marrocchi et al., 2019). Those complex features in olivine grains go along with large isotopic variations of oxygen isotopes and silicon isotopes that reveal the coexistence of relict olivine inherited from condensates (AOAs-like material) with olivine crystallized in-situ in interaction with the nebular gas (Marrocchi et al., 2018, Marrocchi et al., 2019; Villeneuve et al., 2020). Figure 4 shows an example of a chondrule with small (<50 µm) olivine grains that yield complex chemical zonings similar to those described by Libourel and Portail (2018) and Marrocchi et al., 2018, Marrocchi et al., 2019. With the use of the 10¹²Ω FC detector, it is now possible to properly characterize mass-independent variations of oxygen isotopes within zoned olivine grains in chondrules at a fine scale (<10 µm) while keeping a precision better than 0.5‰ on δ¹⁷O and δ¹⁸O (2σ).

FIGURE 4

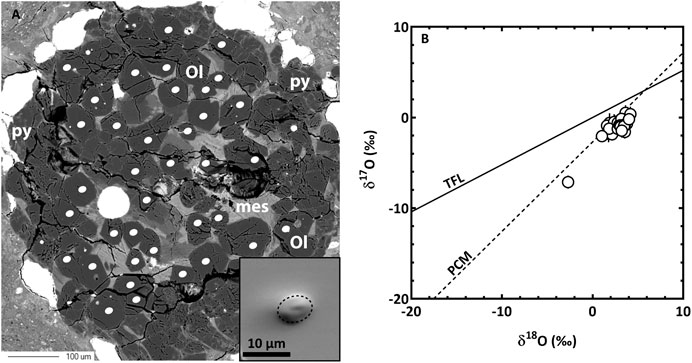
FIGURE 4. (A) Backscattered electron image of a type I POP chondrule from the primitive meteorite Renazzo. An example of the beam shape obtained with settings 3 is shown in the inset on the lower right of the image. (B) Three-oxygen isotopes diagram of 34 analyses in the olivine grains of the chondrule. Typical uncertainties for δ¹⁸O and δ¹⁷O are 0.3–0.4‰ and 0.4–0.6‰ respectively (2σ). TFL stands for the Terrestrial Fractionation Line (slope ∼0.52) and PCM for the Primitive Chondrules Minerals line (slope ∼1; Ushikubo et al., 2012). The data with the ¹⁶O-rich composition corresponds to a relict olivine grain while the other data are host olivine grains that crystalized in the melt and equilibrated with the surrounding gas during chondrule formation. Ol = olivine, py = pyroxene, mes = mesostatis.

Conclusion

SIMS is the sole technique that allows in situ measurements of oxygen isotopes with a lateral resolution of less than 10 µm. Since the first attempts of using small-radius ion microprobes during the mid-80s, tremendous technical and analytical advances have been made. MC-SIMS instruments allowed overcoming the weaknesses of the small-radius ion microprobes in terms of stability, mass resolution, instrumental collection efficiency and transmission. A major breakthrough arose in the mid-90s with the development of a multicollector system on the CAMECA large-radius ion microprobe. Since then, further developments were implemented that enhance data precision and accuracy, such as the more stable electronics, the automatic secondary beam centering, the NMR control of the magnetic field, among others. More recently, latest generations of large-radius ion microprobes (CAMECA IMS 1280, 1280-HR, 1300-HR³ and ASI SHRIMP IIe, SI, IV, V) were equipped with 10¹²Ω resistor FC preamplifier boards. Data presented here show that CAMECA MC-SIMS equipped with 10¹² Ω FCs are now able to provide triple oxygen isotopic measurements in various kind of matrices (silicates, glasses, oxides and carbonates) with a precision (internal error and reproducibility) better than 0.5‰ on δ¹⁷O and δ¹⁸O (2σ), a beam size smaller than 10 μm, and in less than 10 min per analysis. Therefore, state-of-the-art MC-SIMS is currently the most suitable technique for studying triple oxygen isotopic variations in heterogeneous samples that require both high precision and high spatial resolution, such as primitive meteorites.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The CRPG ion probe team is grateful to the Europlanet research infrastructure that provided funds for the development of the 10¹² Ω resistor FC preamplifiers for CRPG SIMS instruments.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Two of the co-authors are members of a commercial company (CAMECA-AMETEK). However, non of researcher from CRPG have any commercial interest with CAMECA-AMETEK. Technical improvements presented in the manuscript result from a collaboration between engineers from CAMECA and scientists from CRPG on instruments installed at CRPG.

Acknowledgments

We thank the two reviewers and associated editor for constructive comments that improved the quality of the manuscript. This is CRPG contribution #2744.

References

Aleon, J., Krot, A. N., and McKeegan, K. D. (2002). Calcium-aluminum-rich inclusions and amoeboid olivine aggregates from the CR carbonaceous chondrites. Meteoritics Planet Sci. 37, 1729–1755. doi:10.1111/j.1945-5100.2002.tb01160.x

CrossRef Full Text | Google Scholar

Aléon, J., Marin-Carbonne, J., McKeegan, K. D., and El Goresy, A. (2018). O, Mg, and Si isotope distributions in the complex ultrarefractory CAI Efremovka 101.1: assimilation of ultrarefractory, FUN, and regular CAI precursors. Geochim. Cosmochim. Acta 232, 48–81. doi:10.1016/j.gca.2018.04.001

CrossRef Full Text | Google Scholar

Benninghoven, A., Rudenauer, F. G., and Werner, H. W. (1987). Secondary ion mass spectrometry: basic concepts, instrumental aspects, applications and trends. New York, NY: John Wiley and Sons, 435.

Bindeman, I. N., Eiler, J. M., Wing, B. A., and Farquhar, J. (2007). Rare sulfur and triple oxygen isotope geochemistry of volcanogenic sulfate aerosols. Geochim. Cosmochim. Acta 71, 2326–2343. doi:10.1016/j.gca.2007.01.026

CrossRef Full Text | Google Scholar

Bridges, J. C., and Ireland, T. R. (2015). Oxygen isotope analyses by SHRIMP of chondrules in highly unequilibrated LL3 chondrites. 46^th Lunar Planet. Sci. Conf. LPI contribution No. 1832, 1674.

Chaussidon, M., Libourel, G., and Krot, A. N. (2008). Oxygen isotopic constraints on the origin of magnesian chondrules and on the gaseous reservoirs in the early solar system. Geochim. Cosmochim. Acta 72, 1924–1938. doi:10.1016/j.gca.2008.01.015

CrossRef Full Text | Google Scholar

Clayton, R. N., and Epstein, S. (1961). The use of oxygen isotopes in high-temperature geological thermometry. J. Geol. 69, 447–452. doi:10.1086/626760

CrossRef Full Text | Google Scholar

Clayton, R. N., Grossman, L., and Mayeda, T. K. (1973). A component of primitive nuclear composition in carbonaceous meteorites. Science 182, 485–488. doi:10.1126/science.182.4111.485

CrossRef Full Text | Google Scholar

Clayton, R. N., and Mayeda, T. K. (1999). Oxygen isotope studies of carbonaceous chondrites. Geochim. Cosmochim. Acta 63, 2089–2104. doi:10.1016/S0016-7037(99)00090-3

CrossRef Full Text | Google Scholar

Clayton, R. N., and Mayeda, T. K. (1984). The oxygen isotope record in Murchison and other carbonaceous chondrites. Earth Planet Sci. Lett. 67, 151–161. doi:10.1016/0012-821X(84)90110-9

CrossRef Full Text | Google Scholar

Clayton, R. N. (2008). Oxygen isotopes in the early solar system–A historical perspective. Rev. Mineral. Geochem. 68, 5–14. doi:10.2138/rmg.2008.68.2

CrossRef Full Text | Google Scholar

Cohn, M., and Urey, H. C. (1938). Oxygen exchange reactions of organic compounds and water. J. Am. Chem. Soc. 60, 679–687. doi:10.1021/ja01270a052

CrossRef Full Text | Google Scholar

Connolly, H. C., and Jones, R. H. (2016). Chondrules: the canonical and noncanonical views. J. Geophys. Res. Planets 121, 1885–1899. doi:10.1002/2016JE005113

CrossRef Full Text | Google Scholar

Eiler, J. M., Graham, C., and Valley, J. W. (1997). SIMS analysis of oxygen isotopes : matrix effects in complex minerals and glasses. Chem. Geol. 138, 221–244. doi:10.1016/S0009-2541(97)00015-6

CrossRef Full Text | Google Scholar

Greenwood, R. C., and Anand, M. (2020). What is the oxygen isotope composition of venus? The scientific case for sample return from earth’s “sister” planet. Space Sci. Rev. 216, 52. doi:10.1007/s11214-020-00669-8

CrossRef Full Text | Google Scholar

Greenwood, R. C., Franchi, I. A., Gibson, J. M., and Benedix, G. K. (2012). Oxygen isotope variation in primitive achondrites: the influence of primordial, asteroidal and terrestrial processes. Geochim. Cosmochim. Acta 94, 146–163. doi:10.1016/j.gca.2012.06.025

CrossRef Full Text | Google Scholar

Hashizume, K., and Chaussidon, M. (2005). A non-terrestrial 16O-rich isotopic composition for the protosolar nebula. Nature 434, 619–622. doi:10.1038/nature03432

CrossRef Full Text | Google Scholar

Hervig, R. L. (1992). Oxygen isotope analysis using extreme energy filtering. Chem. Geol. Isot. Geosci. Sect. 101, 185–186. doi:10.1016/0009-2541(92)90216-R

CrossRef Full Text | Google Scholar

Hervig, R. L., Williams, P., Thomas, R. M., Schauer, S. N., and Steele, I. M. (1992). Microanalysis of oxygen isotopes in insulators by secondary ion mass spectrometry. Int. J. Mass Spectrom. Ion Process. 120, 45–63. doi:10.1016/0168-1176(92)80051-2

CrossRef Full Text | Google Scholar

Ickert, R. B., and Stern, R. A. (2013). Matrix corrections and error analysis in high-precision SIMS 18O/16O measurements of Ca-Mg-Fe garnet. Geostand. Geoanal. Res. 37, 429–448. doi:10.1111/j.1751-908X.2013.00222.x

CrossRef Full Text | Google Scholar

Ireland, T. R., Schram, N., Holden, P., Lanc, P., Ávila, J., Armstrong, R., et al. (2014). Charge-mode electrometer measurements of S-isotopic compositions on SHRIMP-SI. Int. J. Mass Spectrom. 359, 26–37. doi:10.1016/j.ijms.2013.12.020

CrossRef Full Text | Google Scholar

Jones, R. H., Villeneuve, J., and Libourel, G. (2018). “Thermal Histories of chondrules,” in Chondrules. Cambridge, United Kingdom: Cambridge University Press, 57–90.

Kawasaki, N., Itoh, S., Sakamoto, N., and Yurimoto, H. (2017). Chronological study of oxygen isotope composition for the solar protoplanetary disk recorded in a fluffy Type A CAI from Vigarano. Geochim. Cosmochim. Acta 201, 83–102. doi:10.1016/j.gca.2015.12.031

CrossRef Full Text | Google Scholar

Kita, N. T., Nagahara, H., Tachibana, S., Tomomura, S., Spicuzza, M. J., Fournelle, J. H., et al. (2010). High precision SIMS oxygen three isotope study of chondrules in LL3 chondrites: role of ambient gas during chondrule formation. Geocheim. Cosmochim. Acta 74, 6610–6635. doi:10.1016/j.gca.2010.08.011

CrossRef Full Text | Google Scholar

Koornneef, J. M., Bouman, C., Schwieters, J. B., and Davies, G. R. (2014). Measurement of small ion beams by thermal ionisation mass spectrometry using new 1013Ohm resistors. Anal. Chim. Acta 819, 49–55. doi:10.1016/j.aca.2014.02.007

CrossRef Full Text | Google Scholar

Koornneef, J. M., Bouman, C., Schwieters, J. B., and Davies, G. R. (2013). Use of 1012 ohm current amplifiers in Sr and Nd isotope analyses by TIMS for application to sub-nanogram samples. J. Anal. At. Spectrom. 28, 749–754. doi:10.1039/c3ja30326h

CrossRef Full Text | Google Scholar

Krot, A. N., Ma, C., Nagashima, K., Davis, A. M., Beckett, J. R., Simon, S. B., et al. (2019). Mineralogy, petrography, and oxygen isotopic compositions of ultrarefractory inclusions from carbonaceous chondrites. Geochemistry 79, 125519. doi:10.1016/J.CHEMER.2019.07.001

CrossRef Full Text | Google Scholar

Krot, A. N., Yurimoto, H., McKeegan, K. D., Leshin, L. A., Chaussidon, M., Libourel, G., et al. (2006). Oxygen isotopic compositions of chondrules: implications for evolution of oxygen isotopic reservoirs in the inner solar nebula. Chemie der Erde–Geochemistry 66, 249–276. doi:10.1016/j.chemer.2006.07.002

CrossRef Full Text | Google Scholar

Landais, A., Barkan, E., and Luz, B. (2008). Record of δ 18 O and 17 O-excess in ice from Vostok Antarctica during the last 150,000 years. Geophys. Res. Lett. 35, L02709. doi:10.1029/2007GL032096

CrossRef Full Text | Google Scholar

Libourel, G., and Chaussidon, M. (2011). Oxygen isotopic constraints on the origin of Mg-rich olivines from chondritic meteorites. Earth Planet Sci. Lett. 301, 9–21. doi:10.1016/j.epsl.2010.11.009

CrossRef Full Text | Google Scholar

Libourel, G., and Portail, M. (2018). Chondrules as direct thermochemical sensors of solar protoplanetary disk gas. Sci. Adv. 4, eaar3321. doi:10.1126/sciadv.aar3321

CrossRef Full Text | Google Scholar

Lodders, K. (2003). Solar system Abundances and condensation temperatures of the elements. Astrophys. J. 591, 1220–1247. doi:10.1086/375492 | Google Scholar

CrossRef Full Text | Google Scholar

Loiselle, L., Holden, P., Avila, J. N., Lanc, P., Bridges, J. C., MacArthur, J. L., et al. (2019). The O isotope composition of martian meteorites unsing SHRIMP SI: evidence of multiple reservoirs in silicate minerals of the regolith breccia northwest africa 8114, 50th Lunar Planet. Sci. Conf. LPI Contribution No. 2132, id.2648.

Lorin, J. C., Slodzian, R., Dennebouy, R., and Chaintreau, M. (1990). “SIMS measurement of oxygen isotope ratios in meteorites and primitive solar matter,” in Secondary ion mass spectrometry, SIMS VII. Editors A. Benninghoven, C. A. Evans, K. D. McKeegan, S.H. A, and H. W. Werner (Chichester, United Kingdom: John Wiley), 377–380.

Luz, B., and Barkan, E. (2010). Variations of 17O/16O and 18O/16O in meteoric waters. Geochim. Cosmochim. Acta 74, 6276–6286. doi:10.1016/j.gca.2010.08.016

CrossRef Full Text | Google Scholar

Makishima, A., and Nakamura, E. (2010). Precise isotopic determination of Hf and Pb at sub-nano gram levels by MC-ICP-MS employing a newly designed sample cone and a pre-amplifier with a 1012 ohm register. J. Anal. At. Spectrom. 25, 1712. doi:10.1039/c0ja00015a

CrossRef Full Text | Google Scholar

Marrocchi, Y., Euverte, R., Villeneuve, J., Batanova, V., Welsch, B., Ferrière, L., et al. (2019). Formation of CV chondrules by recycling of amoeboid olivine aggregate-like precursors. Geochim. Cosmochim. Acta 247, 121–141. doi:10.1016/j.gca.2018.12.038

CrossRef Full Text | Google Scholar

Marrocchi, Y., Villeneuve, J., Batanova, V., Piani, L., and Jacquet, E. (2018). Oxygen isotopic diversity of chondrule precursors and the nebular origin of chondrules. Earth Planet Sci. Lett. 496, 132–141. doi:10.1016/j.epsl.2018.05.042

CrossRef Full Text | Google Scholar

McKeegan, K. D., Kallio, A. P. A., Heber, V. S., Jarzebinski, G., Mao, P. H., Coath, C. D., et al. (2011). The oxygen isotopic composition of the sun inferred from captured solar wind. Science 332, 1528–1532. doi:10.1126/science.1204636

CrossRef Full Text | Google Scholar

McKeegan, K. D. (1987). Oxygen isotopes in refractory stratospheric dust particles: proof of extraterrestrial origin. Science 237, 1468–1471. doi:10.1126/science.237.4821.1468

CrossRef Full Text | Google Scholar

Nakamura, T., Noguchi, T., Tsuchiyama, A., Ushikubo, T., Kita, N. T., Valley, J. W., et al. (2008). Chondrulelike objects in short-period comet 81P/wild 2. Science 321, 1664–1667. doi:10.1126/science.1160995

CrossRef Full Text | Google Scholar

O’Neil, J. R., and Clayton, R. N. (1964). “Oxygen isotope geothermometry,” in In Isotopic and cosmic chemistry. Editors H. Craig, S. L. Miller, and G. J. Wasserburg (Amsterdam, NL: North-Holland), 157–168.

Pack, A., and Herwartz, D. (2014). The triple oxygen isotope composition of the Earth mantle and understanding D17O in terrestrial rocks and minerals. Earth Planet Sci. Lett. 390, 138–145. doi:10.1016/j.epsl.2014.01.017

CrossRef Full Text | Google Scholar

Piralla, M., Marrocchi, Y., Verdier-Paoletti, M. J., Vacher, L. G., Villeneuve, J., Piani, L., et al. (2020). Primordial water and dust of the Solar System: insights from in situ oxygen measurements of CI chondrites. Geochim. Cosmochim. Acta 269, 451–464. doi:10.1016/j.gca.2019.10.041

CrossRef Full Text | Google Scholar

Riciputi, L. R., and Paterson, B. A. (1994). High spatial resolution measurement of O isotope ratios in silicates and carbonates by ion microprobe. Am. Mineral. 79, 1227–1230.

Rumble, D., Miller, M. F., Franchi, I. A., and Greenwood, R. C. (2007). Oxygen three-isotope fractionation lines in terrestrial silicate minerals: an inter-laboratory comparison of hydrothermal quartz and eclogitic garnet. Geochim. Cosmochim. Acta 71, 3592–3600. doi:10.1016/j.gca.2007.05.011

CrossRef Full Text | Google Scholar

Schrader, D. L., Nagashima, K., Krot, A. N., Ogliore, R. C., and Hellebrand, E. (2014). Variations in the O-isotope composition of gas during the formation of chondrules from the CR chondrites. Geochim. Cosmochim. Acta 132, 50–74. doi:10.1016/j.gca.2014.01.034

CrossRef Full Text | Google Scholar

Schuhmacher, M., Fernandes, F., and De Chambost, E. (2004). Achieving high reproducibility isotope ratios with the Cameca IMS 1270 in the multicollection mode. Appl. Surf. Sci. 231–232, 878–882. doi:10.1016/j.apsusc.2004.03.157

CrossRef Full Text | Google Scholar

Sharp, Z. D., Wostbrock, J. A. G., and Pack, A. (2018). Mass-dependent triple oxygen isotope variations in terrestrial materials. Geochemical Perspect. Lett. 7, 27–31. doi:10.7185/geochemlet.1815

CrossRef Full Text | Google Scholar

Shimizu, N., and Hart, S. R. (1982). Applications of the ion microprobe to geochemistry and cosmochemistry. Annu. Rev. Earth Planet Sci. 10, 483–526. doi:10.1146/annurev.ea.10.050182.002411

CrossRef Full Text | Google Scholar

Siron, G., Fukuda, K., Kimura, M., and Kita, N. T. (2021). New constraints from 26Al-26Mg chronology of anorthite bearing chondrules in unequilibrated ordinary chondrites. Geochim. Cosmochim. Acta 293, 103–126. doi:10.1016/j.gca.2020.10.025

CrossRef Full Text | Google Scholar

Tenner, T. J., Nakashima, D., Ushikubo, T., Kita, N. T., and Weisberg, M. K. (2015). Oxygen isotope ratios of FeO-poor chondrules in CR3 chondrites: influence of dust enrichment and H2O during chondrule formation. Geochim. Cosmochim. Acta 148, 228–250. doi:10.1016/j.gca.2014.09.025

CrossRef Full Text | Google Scholar

Tenner, T. J., Ushikubo, T., Nakashima, D., Schrader, D. L., Weisberg, M. K., Kimura, M., et al. (2018). “Oxygen isotope characteristics of chondrules from recent studies by secondary ion mass spectrometry,” in Chondrules. Cambridge, United Kingdom: Cambridge University Press, 196–246.

Thiemens, M. H. (2006). History and applications OF mass-independent isotope effects. Annu. Rev. Earth Planet Sci. 34, 217–262. doi:10.1146/annurev.earth.34.031405.125026

CrossRef Full Text | Google Scholar

Urey, H. C. (1947). The thermodynamic properties of isotopic substances. J. Chem. Soc. 1947, 562–581. doi:10.1039/jr9470000562

CrossRef Full Text | Google Scholar

Ushikubo, T., Kimura, M., Kita, N. T., and Valley, J. W. (2012). Primordial oxygen isotope reservoirs of the solar nebula recorded in chondrules in Acfer 094 carbonaceous chondrite. Geochim. Cosmochim. Acta 90, 242–264. doi:10.1016/j.gca.2012.05.010

CrossRef Full Text | Google Scholar

Vacher, L. G., Marrocchi, Y., Verdier-Paoletti, M. J., Villeneuve, J., and Gounelle, M. (2016). Inward radial mixing of interstellar water ices in the solar protoplanetary disk. Astrophys. J. Lett. 827, L1. doi:10.3847/2041-8205/827/1/L1

CrossRef Full Text | Google Scholar

Vacher, L. G., Marrocchi, Y., Villeneuve, J., Verdier-Paoletti, M. J., and Gounelle, M. (2017). Petrographic and C and O isotopic characteristics of the earliest stages of aqueous alteration of CM chondrites. Geochim. Cosmochim. Acta 213, 271–290. doi:10.1016/j.gca.2017.06.049

CrossRef Full Text | Google Scholar

Vacher, L. G., Marrocchi, Y., Villeneuve, L., Verdier-Paoletti, M. J., and Gounelle, M. (2018). Collisional and alteration history of the CM parent body. Geochim. Cosmochim. Acta 239, 213–234. doi:10.1016/j.gca.2018.08.006

CrossRef Full Text | Google Scholar

Vacher, L. G., Piralla, M., Gounelle, M., Bizzarro, M., and Marrocchi, Y. (2019). Thermal evolution of hydrated asteroids inferred from oxygen isotopes. Astrophys. J. 882, L20. doi:10.3847/2041-8213/ab3bd0

CrossRef Full Text | Google Scholar

Valley, J. W., and Graham, C. M. (1991). Ion microprobe analysis of oxygen isotope ratios in granulite facies magnetites: diffusive exchange as a guide to cooling history. Contrib. Mineral. Petrol. 109, 38–52. doi:10.1007/BF00687199

CrossRef Full Text | Google Scholar

Valley, J. W., and Kita, N. T. (2009). In-situ oxygen isotope geochemistry by ion microprobe. Mineral. Assoc. Canada Short Course 41, 19–63. doi:10.1111/ggr.12232

CrossRef Full Text | Google Scholar

Villeneuve, J., Marrocchi, Y., and Jacquet, E. (2020). Silicon isotopic compositions of chondrule silicates in carbonaceous chondrites and the formation of primordial solids in the accretion disk. Earth Planet Sci. Lett. 542, 116318. doi:10.1016/j.epsl.2020.116318

CrossRef Full Text | Google Scholar

Wielandt, D., and Bizzarro, M. (2011). A TIMS-based method for the high precision measurements of the three-isotope potassium composition of small samples. J. Anal. At. Spectrom. 26, 366–377. doi:10.1039/c0ja00067a

CrossRef Full Text | Google Scholar

Wieser, M. E., and Schwieters, J. B. (2005). The development of multiple collector mass spectrometry for isotope ratio measurements. Int. J. Mass Spectrom. 242, 97–115. doi:10.1016/j.ijms.2004.11.029

CrossRef Full Text | Google Scholar

Young, E. D., Kohl, I. E., Warren, P. H., Rubie, D. C., Jacobson, S. A., and Morbidelli, A. (2016). Oxygen isotopic evidence for vigorous mixing during the Moon-forming giant impact. Science 351, 493–496. doi:10.1126/science.aad0525

CrossRef Full Text | Google Scholar

Yurimoto, H., Krot, A. N., Choi, B.-G., Aléon, J., Kunihiro, T., and Brearley, A. J. (2008). Oxygen isotopes of chondritic components. Rev. Mineral. Geochem. 68, 141–186. doi:10.2138/rmg.2008.68.8

CrossRef Full Text | Google Scholar

Yurimoto, H., Nagasawa, H., Mori, Y., and Matsubaya, O. (1994). Micro-distribution of oxygen isotopes in a refractory inclusion from the Allende meteorite. Earth Planet Sci. Lett. 128, 47–53. doi:10.1016/0012-821X(94)90025-6

CrossRef Full Text | Google Scholar