On the Long Range Clustering of Global Seismicity and its Correlation With Solar Activity: A New Perspective for Earthquake Forecasting

Large earthquakes occurring worldwide have long been recognized to be non Poisson distributed, so involving some large scale correlation mechanism, which could be internal or external to the Earth. We have recently demonstrated this observation can be explained by the correlation of global seismicity with solar activity. We inferred such a clear correlation, highly statistically significant, analyzing the ISI-GEM catalog 1996–2016, as compared to the Solar and Heliospheric Observatory satellite data, reporting proton density and proton velocity in the same period. However, some questions could arise that the internal correlation of global seismicity could be mainly due to local earthquake clustering, which is a well-recognized process depending on physical mechanisms of local stress transfer. We then apply, to the ISI-GEM catalog, a simple and appropriate de-clustering procedure, meant to recognize and eliminate local clustering. As a result, we again obtain a non poissonian, internally correlated catalog, which shows the same, high level correlation with the proton density linked to solar activity. We can hence confirm that global seismicity contains a long-range correlation, not linked to local clustering processes, which is clearly linked to solar activity. Once we explain in some details the proposed mechanism for such correlation, we also give insight on how such mechanism could be used, in a near future, to help in earthquake forecasting.

Introduction

Worldwide seismicity does not follow a Poisson distribution (e.g., Corral, 2005), but the character and cause of such internal correlation has not been explained till now. Recently, Marchitelli et al. (2020) found a clear correlation between the global seismicity and the proton density associated to the solar activity. This finding represents the first evidence allowing to propose an explanation for the internal correlation among worldwide earthquakes: it can be due to a triggering effect from high proton density. A mechanism has been proposed for such a triggering effect, in terms of an inverse piezoelectric effect, which would produce strain/stress pulses in the quartz crystals, abundant on large faults, as a response to huge current discharges from the ionosphere.

However, the character and properties of the internal correlation observed in global seismicity have never been analyzed before: it is not clear, for instance, if it only depends from local clustering, which could only be due to the very trivial and well known physical mechanisms of stress redistribution (Stein et al., 1992; Troise et al., 1998). In this case, any correlation found with large scale events (like the solar activity) would obviously be meaningless.

In this paper, after recalling the main results of Marchitelli et al. (2020), we first analyze the global earthquake catalog (ISI-GEM, from 1964 to 2016), by applying to it the most appropriate and “neutral” de-clustering able to eliminate local clustering. After such de-clustering procedure, we demonstrate the presence, in the catalog, of a long range internal correlation, which still correlates, at a very high statistical significance, with proton density generated by solar activity.

Once demonstrated the robustness, against any possible bias due to other local stress interaction effects, of the correlation between global seismicity and solar activity, we discuss more the proposed physical mechanism for the triggering effect.

Finally, we discuss how the new evidence could be, in future, used to improve earthquake forecast.

Internal Correlation of Global Seismicity

By interpreting the internal correlation of global seismic catalogs, an important concern would be to investigate the role played by local, short-range clustering, which mainly depends from well recognized physical mechanisms of stress interaction (Stein et al., 1992; Troise et al., 1998). Such an investigation is important, and at our knowledge never afforded, because it can enlighten if the internal correlation in the global catalog is due, besides to short range clustering, also to some long-range clustering which would be much more interesting to explain, with respect to such trivial effects of local stress interaction. Although it is almost impossible to distinguish, among such effects of stress interaction, foreshocks, main events, aftershocks and background seismicity (e.g., Bak et al., 2002), all of these effects have a common, well grounded physically, property to act only within relatively short distances (comparable to the fault size: see Wells and Coppersmith, 1994). As a consequence, in order to eliminate, from the earthquake catalog, such short-range effects, an appropriate de-clustering method should consider, as correlated events, all couples which occur within a given distance (on the order of the largest fault size between the two events) and within a suitable time window.

So, in order to obtain a declustered catalog we used the ISC-GEM catalog (Storchak et al., 2013; Storchak et al., 2015; Di Giacomo et al., 2018) that is complete from M ≥ 6.0 for shallow events (depth up to 60 km) from early fifties. Epicentral locations however improve dramatically since 1964. We used therefore the time interval 1964–2016. In order to de-cluster it, we considered all the event pairs that were comprised in a time window of 6 months and that were spaced less than twice the fault length of the larger of the two events, according to the formula for a generic earthquake according to Wells and Coppersmith (1994). We anyway considered a minimum epicentral distance of 160 km, that is that any two events spaced less then 160 km within a time interval were anyway considered correlated, not depending from the fault size. If a pair satisfied this criteria, we discarded the smaller. Even discarded events were considered however as able to trigger other events. In this way we ended up with about 60% of the original earthquakes.

We used two data sets both based on the ISC-GEM catalog (Storchak et al., 2013).

The first data set, we applied such a de-clustering procedure, is relative to the shallow (depth < 60 km) M ≥ 8.00 events that occurred since 1905. There are 83 of them. We manually de-clustered it so to discard even events, located within the mentined distance, occurring to within 3 years from another one. We remained with 76 events. Both data sets are available as Supplementary Material.

The second data set is relative to the shallow (depth < 60 km) M ≥ 6.00 events that occurred since 1964. The choice of 1964 as lower bound is due to the fact that epicentral location quality dramatically increases starting from that date.

Once the new de-clustered catalog was obtained, we checked it for poissonianity. Then, we applied the algorithm devised by Harabaglia (2020) to verify poissonianity. This algorithm states that

$$

λ(Δt_i) = −log[SP(Δt_i)]/Δt_i

where SP(Δt_i) is the Survival Probability Function at the Δt_i timing interval. If the data set where truly poissonian, SP(Δt) = exp (−μΔt) (where μ is the average value of Δt), so that λ should be constant over the entire Δt_i data set. This approach is even more powerful than that devised by Vecchio et al. (2008).

Figure 1 shows λ for the de-clustered data set with M > 8. Inter-event times are normalized to the average value of about 536.5 days. As far as the first six points are concerned, they refer to earthquake pairs that occurs at distances between 2,375 and 14,091 km with mean of 6,993 km and median of 6,479 km: hardly aftershocks. This is tantamount to say that long range (both temporally and spatially) internal correlation do exist.

FIGURE 1

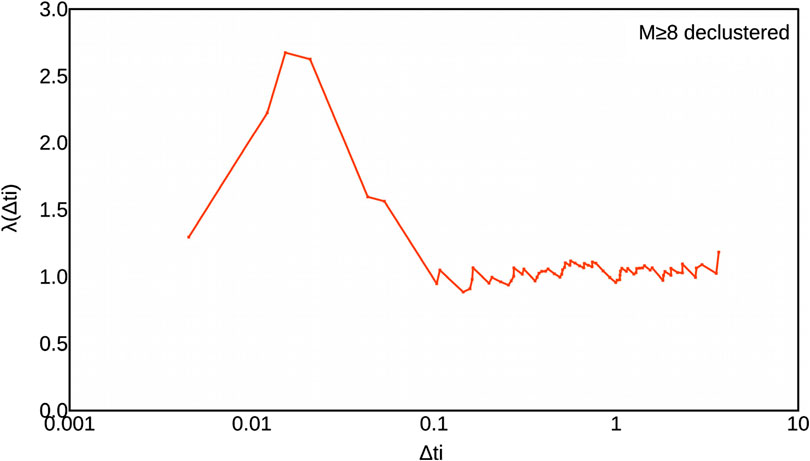
FIGURE 1. Poisson’s test according to Harabaglia (2020), for the declustered M ≥ 8, depth≤60 km worldwide ISC-GEM catalog in the period 1904–2016. The catalog is normalized. Perfect poissonianity would be represented by an horizontal line.

In Figure 2A we show for each earthquake its relation, in terms of Δt vs. Δd, with every single event that follows it, up to the end of the catalog; that is, we show over 14 × 106 pairs of data. The left side of Figure 2A is the most interesting. The lower left corner is the area of foreshocks and aftershocks. The upper left corner represents the non poissonian distribution that will survive any de-clustering process. Figure 2B is the equivalent of Figure 1 for the shallow (depth < 60 km) M ≥ 6.00 data set after de-clustering according to the method used in appendix. It is obvious that for Δt_i of 20.000 s or less the non poissonianity is evident. In Figure 2C we show the Survival Probability Functions both in terms of Δt and Δd, relatively to the declustered M ≥ 6.00 data set. It is clearly visible that Δt_i spans over more orders of magnitude with respect to Δd_i. This means that events are more clustered in time than in space, so that a kind of long range interaction, which is not destroyed by the local de-clustering, exists in the catalog. The obvious consequence of this finding is that a global process is affecting the seismicity.

FIGURE 2

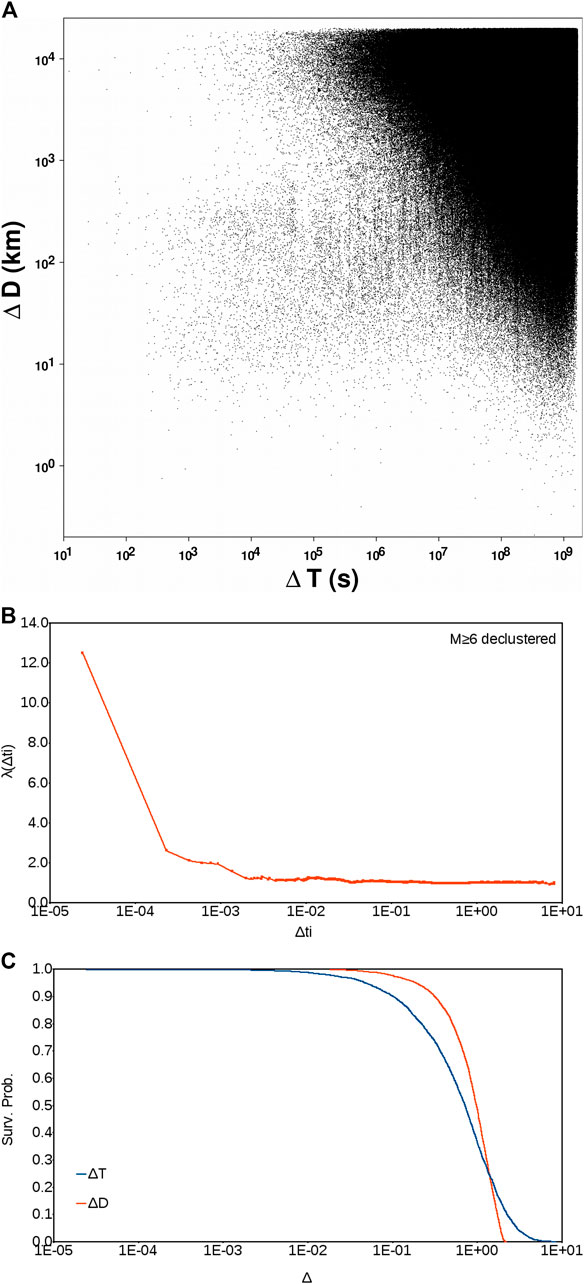
FIGURE 2. (A) M ≥ 6, depth≤60 km, worldwide ISC-GEM catalog in the period 1964–2016. Each point represents ∆T vs. ∆D of every event with respect to all other earthquakes that occurred after it. There are over 14 × 10⁶ pairs. (B) Poisson’s test as in Figure 1) but relative to the declustered M ≥ 6, depth ≤ 60 km worldwide ISC-GEM catalog in the period 1964–2016. (C) Survival Probability functions both in time (blue) and in space (red) for the data set of (B). Both temporal and spatial functions are normalized.

Analyzing the Correlation With Solar Activity

Once we stated the de-clustered seismic catalogs still are non poissonian, so evidencing a long range correlation among the worldwide earthquakes we want to specify its origin. Marchitelli et al. (2020) showed that the whole worldwide seismic catalog ISC-GEM, with threshold magnitude M > 5.6, is clearly correlated with the proton density as recorded by the SOHO (Solar and Helioscopic Observatory) satellite, at a confidence level as high as 99.999%. Here, we want to check if also the ISC-GEM catalog, de-clustered as explained in the former paragraph, is still correlated with the proton density. We have to consider the period 1996–2016, in order to compare it with the SOHO proton density data; so, we can use the whole ISC-GEM catalog (with earthquakes of any depth) down to the magnitude threshold of completeness M = 5.6. Using such a catalog, which is exactly the same used by Marchitelli et al. (2020) for our computations, will make easier the comparison with previous results.

We then apply the de-clustering method previously described to this catalog. Such a de-clustered catalog has only 3,241 events, instead of 6,612 of the original one analyzed by Marchitelli et al. (2020).

We used the conceptual Molchan (1990) method, as modified and adapted by Marchitelli et al. (2020) to test the correlation with the SOHO proton density catalog. We recall here the method. The procedure has been adapted from the concept of the Molchan diagram (Molchan, 1990). We start considering a time window whose length in days is 0.01 of the total catalog: 0.01 × 6,774 = 67.74, rounded to 68 days. We than consider all the parts of length 68 days in the catalog, by sliding progressively the 68 days windows of 1 day each step, until the 68th day corresponds to the ending day of the catalog. In this way, we obtain 6,774 − 68 = 6,706 time windows. For each time window, we compute if the Event Relative Rate R, for earthquakes occurring within 24 h from the end of a density peak, is higher or lower than the average number of events per day computed from the whole catalog (1,322/6,774 = 0.196 events/day): if it is higher, the prediction outcome is positive, otherwise it is negative. In case there is, in a given time window, no day occurring after the end of a density peak, that window is excluded from the count. On the Y axis, we indicated the fraction of the sliding time windows with a prediction failure. Then, we repeat the same procedure and computation for time windows progressively larger, from a fraction 0.01 to 1 of the total catalog time duration; for each fractional length of the sliding window, indicated on the X axis, we report on the Y axis the fraction of prediction failures. For a totally random outcome, the fraction of prediction failures is around 0.5; a number significantly smaller indicates a significant correlation, whereas a number significantly higher would indicate a significant anti-correlation.

In Figure 3A we show the results obtained, by the modified Molchan method applied to the de-clustered catalog, with the best fitting threshold of 16 counts cm⁻³ for the proton density. We want to stress that such a best fitting threshold is only slightly larger than the best one used for the original (non de-clustered) catalog in Marchitelli et al. (2020). However, how it can be seen from Figure 3B, which reports the values of the modified Molchan integral (fraction of prediction failures), the best fitting value of 16 counts cm⁻³ is another, almost equivalent, best fitting value also for the original catalog. We see that total fraction of failures amounts to 10% for the de-clustered catalog (it is 5.5% for the original catalog), so indicating the correlation is highly significant. In the next chapter, we will discuss anyway in more detail the results obtained, with different threshold values, for the original and the de-clustered catalog.

FIGURE 3

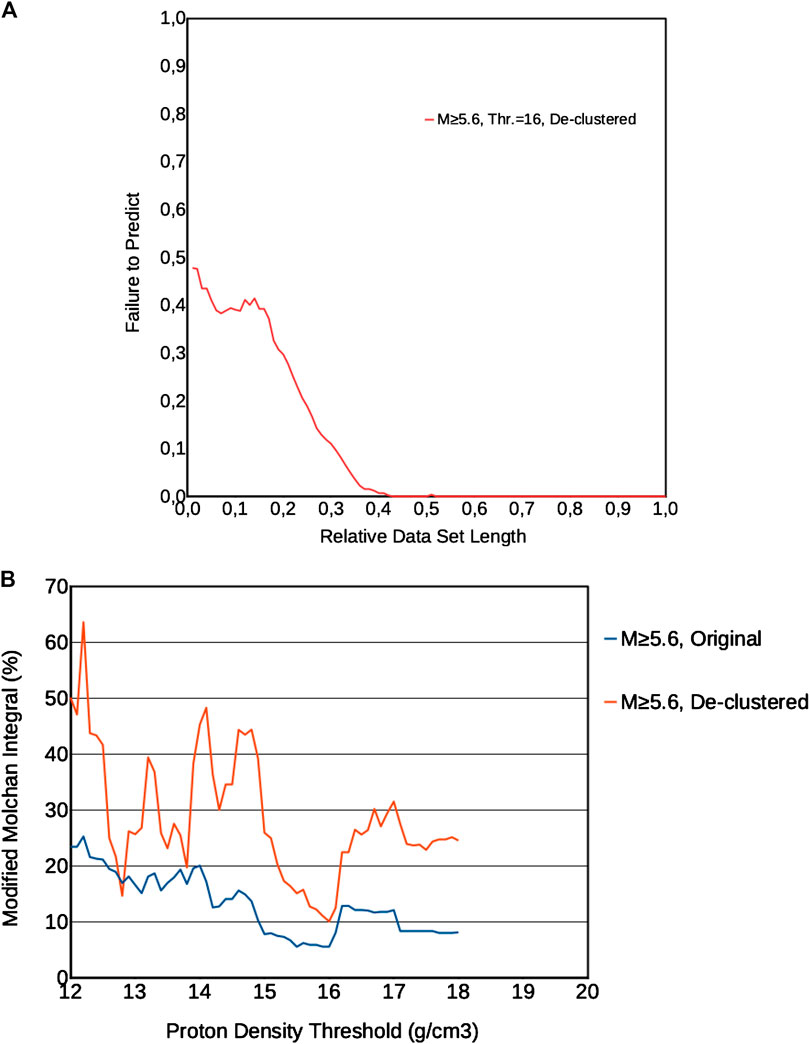
FIGURE 3. (A) modified Molchan method, defined as in Marchitelli et al. (2020), applied to the de-clustered catalog with magnitude M > 5.6. (B) Values of the Molchan integrals (total fraction of prediction failure) for all the tested values of proton density threshold, for the original catalog with M > 5.6 (blue line) and for the de-clustered catalog with M > 5.6.

FIGURE 4

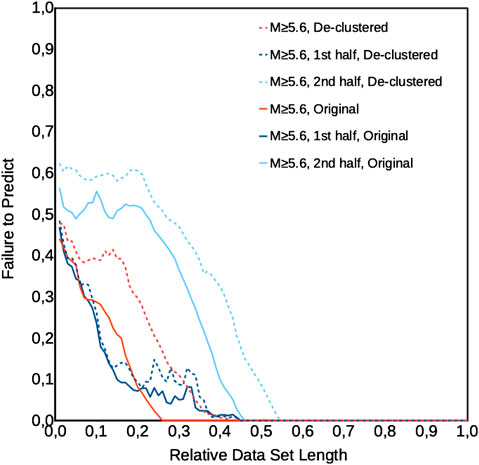
FIGURE 4. Modified Molchan diagrams (Marchitelli et al., 2020) applied to the whole original catalog, first half (1996–2006) and second half (2006–2016), and to the corresponding de-clustered catalogs. Diagrams for the original catalog and its partitions are marked by continuous lines (colors are indicated in the figure); diagrams for the corresponding de-clustered catalogs are indicated by dashed lines (colors indicated in figure).

We have then demonstrated that also cutting from the catalog the local clustering, a long-range internal correlation remains, which is still significantly correlated with proton density due to solar activity.

Discussion and Conclusions

Although the non poissonian character of worldwide earthquake catalogs was a well recognized effect since more than half a century, we demonstrate here, for the first time in a clear way, that internal correlation among worldwide earthquakes is dominated by a long range clustering effect. Such effect is well distinct from local clustering, which is due to local stress interaction among the faults.

Once such long range effect has been identified, we have shown that correlation between solar activity and earthquakes still holds even for de-clustered data sets, after removing the local clustering effects. This means that the long range internal correlation of the worldwide catalog, which has not a simple physical explanation, is certainly linked with proton density modulated by solar activity. We could also speculate if the short range clustering, which is generally interpreted in terms of local stress interaction, would also be affected by proton density. In principle, there would be no reason to neglect interaction with solar activity at all scales. In fact, the correlation inferred by Marchitelli et al. (2020) for the whole, not de-clustered catalog, i.e., including the local clustering, appears to be even more significant than the results obtained with the de-clustered catalog. Even the test with the modified Molchan-like method (Molchan, 1990; Marchitelli et al., 2020) indicates a total failure integral, for the de-clustered catalog, of 10%, compared with 5% obtained with the original catalog. This confirms that the proton density effect on seismicity is significant at all scales, and also adds to the common, local stress interaction effects, in order to increase short range clustering. It is important to stress that we hypothesize the influence of high proton density just represents a triggering effect, which adds up to the tectonic loading, which is by far the most important factor for earthquake generation. Such a triggering effect, able to anticipate earthquakes on faults already close to tectonic loading (De Natale et al., 2011) would obviously act at any scale (because there is no reason to believe the contrary), so being able to affect the foreshock-mainshock-aftershock sequences also at local scale.

However, besides we were able, by using an appropriate de-clustering technique, to isolate and put in evidence the long range internal correlation of the worldwide earthquake catalog, we are anyway convinced (and the results obtained here, even more clear using the whole catalog, represent a further confirmation) that any statistical analysis to infer the properties of an earthquake sequence should avoid de-clustering procedures. As an example, it is quite obvious that the generation mechanism in case of multiple events is still poorly understood. For instance in Italy, in 2016, we had 3 M > 6 events spaced apart few tenths of kilometers. The first occurred on August 24th, the second on October 26th and the third on October 30th. The latter being also the largest. Does it means that stress transfer induced the three events in sequence or does it imply that a larger slow process, such as that envisaged by Michel et al. (2019), was in place? In fact slow earthquakes have been recognized at least since Jordan (1991) and Ihmlé et al. (1993) but only recently it has been hypothesized that they could last for months (Michel et al., 2019). Moreover, Harabaglia (2020) showed that an event occurrence probability strongly depends on the timing interval of the two events that preceeded it. This dependence holds even at long timing intervals. Such an effect is so strong, that it can explain large Italian earthquakes (M > 6) where the occurrence rate is on the order of a few tenths per century.

The main reason however we are against declustering is that it certainly adds a high degree of subjectivity. There is in fact no commonly accepted method: declustering therefore would make any statistical finding about the catalog weaker.

We proceed now to discuss how our results correlate with the well known main cycles of solar activity. Some researchers had previously claimed the existence of some correlation between earthquake occurrence and the main period of solar activity, lasting 11 years (e.g., Mazzarella and Palumbo, 1989). Since our data catalogs last only 21 years, less than twice the period of 11 years, we could not see anyway such eventual periods. However, since in our hypothesis the influence of proton density is only a trigger, which can destabilize faults already close to a critical loading, what we should note in periods of low solar activity is just a decrease of correlation with seismicity. Marchitelli et al. (2020), applying their modified Molchan method to the original catalog (non declustered) noted in fact that, for the second half of the catalog (2006–2016), corresponding to considerably lower solar activity, the correlation with worldwide seismicity was less marked. Here, we show in detail the different results obtained, for the original and the de-clustered catalogs, in the whole period and in the two half periods (1996–2005 and 2006–2016) characterized by very different levels of solar activity.

Figure 1 shows the modified Molchan diagrams for the original and the de-clustered whole catalogs, as well as the same diagrams applied to the first and second halves of the original and of the de-clustered catalogs. We used, for such figure, a common value for the proton density threshold of 16.0 counts cm⁻³, which appears to be a closely best fitting value for all the catalogs (the value of 15.5 counts cm⁻³ used by Marchitelli et al. for the original catalog gives an almost equivalent total prediction failure: 0.054 instead of 0.055). The total prediction failures for the original catalog are 0.05 for both the total catalog and the first half; whereas it is 0.17 for the second part, in the period of considerably lower solar activity. For the de-clustered catalog, the total prediction failure is 0.10 for the total catalog, 0.07 for the first half and 0.23 for the second half. These results confirm the observation that, in periods of lower solar activity, the correlation between proton density and global earthquakes is lower.

Once the correlation between solar activity (proton density) and worldwide seismicity is assessed, as we demonstrate, beyond any reasonable doubt, what remains is to describe the mechanism producing such a correlation.

Marchitelli et al. (2020) postulated a mechanism of interaction involving electric discharges, caused by high electric potentials induced by large proton density. However, also magnetic effects (i.e., Duma and Ruzhin, 2003), should be considered, which could be even more effective for deep earthquakes. We anyway prefer the electric hypothesis since it would allow for a more extensive involvement of this rupture mechanism. We think that the charged particles interact with the magnetosphere and through a Coulomb effect they alter the electric circuit, which constantly crosses the entire planet. Since Quartz crystals are by far the most common elements in the crust, any increment of potential can cause the Quartz dilatation/contraction (depending from the current polarity) and favor the rupture nucleation. An inverse piezoelectric rupture nucleation could in fact occur even in absence of anomalous solar activity since electric currents flow throughout the entire planet constantly, as proven by the constant existence of lightning. This explanation could even allow for a feed-back mechanism. Recently, Martinelli et al. (2020a); Martinelli et al. (2020b) conducted a series of laboratory tests on Quartz crystals. In particular Martinelli et al. (2020b) showed that stressed Quartz crystals emit radiowaves. This means that nearby crystals could be in turn deformed and this could lead to a catastrophic process. Any alteration of the electric potential: external, due to the solar activity, or internal, caused by electric currents that flow through the crust, could add to this process.

Once the most appropriate mechanism will be precisely assessed for the solar-earthquake interactions, is could likely represent a powerful element to help in earthquake forecast. Actually, a large number of methods devoted to earthquake forecast have been implemented: an extensive review can be found, for example, in Martinelli (2020), as far as geofluid precursors are concerned. Among the most promising methods, anyway, there is the “pattern recognition” approach (Rotwain and Novikova, 1999; Kossobokov et al., 2002; Peresan et al., 2005). These pattern recognition algorithms, as well as any algorithm for probabilistic earthquake forecast, can in future include proton density as a key element. In addition, if the mechanism of proton density-earthquake interaction could be, in a near future, deeply understood, it could be used for short term forecasting (about 1 day in advance) in a more efficient way and in a completely different way, just detecting the preparatory processes we discussed above.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://www.isc.ac.uk/iscgem/ http://umtof.umd.edu/pm/crn/.

Author Contributions

PH elaborated statistical programs and analyses; VM worked the original idea; GN and CT wrote the core of the paper; all authors participated to the data analysis and interpretation, and contributed to write the final version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We gratefully acknowledge Paolo Plescia and Alexey Lyubushin, who reviewed the paper and greatly helped to improve it. This work has been partially supported by the project OT4CLIMA, funded by the Italian Ministry of Education, University and Research (D.D. 2261 del 6.9.2018, PON R&I 2014-2020 and FSC).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.595209/full#supplementary-material

References

Bak, P., Christensen, K., Danon, L., and Scanlon, T. (2002). Unified scaling law for earthquakes. Phys. Rev. Lett. 88, 178501–178504. doi:10.1103/PhysRevLett.88.178501

CrossRef Full Text | Google Scholar

Corral, A. (2005). Time-decreasing hazard and increasing time until the next earthquake. Phys. Rev. E 71, 017101. doi:10.1103/physreve.71.017101

CrossRef Full Text | Google Scholar

De Natale, G., Crippa, B., Troise, C., and Pingue, F. (2011). Abruzzo, Italy, earthquakes of April 2009: heterogeneous fault-slip models and stress transfer from accurate inversion of ENVISAT-InSAR data. Bull. Seismol. Soc. Am. 101 (5), 2340–2354. doi:10.1785/0120100220

CrossRef Full Text | Google Scholar

Di Giacomo, D., Engdahl, E. R., and Storchak, D. A. (2018). The ISC-GEM earthquake catalogue (1904-2014): status after the extension project. Earth Syst. Sci. Data. 10, 1877–1899. doi:10.5194/essd-10-1877-2018

CrossRef Full Text | Google Scholar

Duma, G., and Ruzhin, Y. (2003). Diurnal changes of earthquake activity and geomagnetic Sq-variations. Nat. Hazards Earth Syst. Sci. 3, 171–177. doi:10.5194/nhess-3-171-2003

CrossRef Full Text | Google Scholar

Harabaglia, P. (2020). Non-Poissonian earthquake occurrence probability through empirical survival functions. Appl. Sci. 10 838. doi:10.3390/app10030838

CrossRef Full Text | Google Scholar

Ihmlé, P. F., Harabaglia, P., and Jordan, T. H. (1993). Teleseismic detection of a slow precursor to the great 1989 macquarie ridge earthquake. Science 261 (5118), 177–183. doi:10.1126/science.261.5118.177

CrossRef Full Text | Google Scholar

Jordan, T. H. (1991). Far-field detection of slow precursors to fast seismic ruptures. Geophys. Res. Lett. 18 (11), 2019–2022. doi:10.1029/91GL02414

CrossRef Full Text | Google Scholar

Kossobokov, V. G., Romashkova, L. L., Panza, G. F., and Peresan, A. (2002). Stabilizing intermediate-term medium-range earthquake predictions. J Seismol Earthq Eng. 8, 11–19.

Google Scholar

Marchitelli, V., Harabaglia, P., Troise, C., and De Natale, G. (2020). On the correlation between solar activity and large earthquakes worldwide. Sci. Rep. 10, 11495. doi:10.1038/s41598-020-67860-3

CrossRef Full Text | Google Scholar

Martinelli, G. (2020). Previous, current, and future trends in research into earthquake precursors in geofluids. Geosciences 10, 189. doi:10.3390/geosciences10050189

CrossRef Full Text | Google Scholar

Martinelli, G., Plescia, P., and Tempesta, E. (2020a). “Pre-Earthquake” micro-structural effects induced by shear stress on α-quartz in laboratory experiments. Geosciences 10, 155. doi:10.3390/geosciences10050155

CrossRef Full Text | Google Scholar

Martinelli, G., Plescia, P., and Tempesta, E. (2020b). Electromagnetic emissions from quartz subjected to shear stress: spectral signatures and geophysical implications. Geosciences 10, 140. doi:10.3390/geosciences10040140

CrossRef Full Text | Google Scholar

Mazzarella, A., and Palumbo, A. (1989). Does the solar cycle modulate seismic and volcanic activity?. J. Volcanol. Geoth. Res. 39 (1), 89–93. doi:10.1016/0377-0273(89)90023-1

CrossRef Full Text | Google Scholar

Michel, S., Gualandi, A., and Avouac, J.-P. (2019). Similar scaling laws for earthquakes and Cascadia slow-slip events. Nature 574, 522–526. doi:10.1038/s41586-019-1673-6

CrossRef Full Text | Google Scholar

Molchan, G. M. (1990). Strategies in strong earthquake prediction. Phys. Earth Planet. In. 61, 84–98. doi:10.1016/0031-9201(90)90097-H

CrossRef Full Text | Google Scholar

Peresan, A., Kossobokov, V., Romashkova, L., and Panza, G. (2005). Intermediate-term middle-range earthquake predictions in Italy: a review. Earth Sci. Rev. 69 (1–2), 97–132. doi:10.1016/j.earscirev.2004.07.005

CrossRef Full Text | Google Scholar

Rotwain, I., and Novikova, O. (1999). Performance of the earthquake prediction algorithm CN in 22 regions of the world. Phys. Earth Planet. In. 111, 207–213. doi:10.1016/s0031-9201(98)00161-7

CrossRef Full Text | Google Scholar

Stein, R. S., King, G. C. P., and Lin, J. (1992). Change in failure stress on the southern san andreas fault system caused by the 1992 magnitude = 7.4 landers earthquake. Science 258, 1328–1332. doi:10.1126/science.258.5086.1328

CrossRef Full Text | Google Scholar

Storchak, D. A., Di Giacomo, D., Bondár, I., Engdahl, E. R., Harris, J., Lee, W. H. K., et al. (2013). Public release of the ISC-GEM global instrumental earthquake catalogue (1900-2009). Seismol Res. Lett. 84, 810–815. doi:10.1785/0220130034

CrossRef Full Text | Google Scholar

Storchak, D. A., Di Giacomo, D., Engdahl, E. R., Harris, J., Bondár, I., Lee, W. H. K., et al. (2015). The ISC-GEM global instrumental earthquake catalogue (1900-2009): introduction. Phys. Earth Planet. In. 239, 48–63. doi:10.1016/j.pepi.2014.06.009

CrossRef Full Text | Google Scholar

Troise, C., De Natale, G., Pingue, F., and Petrazzuoli, S. M. (1998). Evidence for static stress interaction among earthquakes in the south-central Apennines (Italy). Geophys. J. Int. 134, 809–817. doi:10.1046/j.1365-246x.1998.00610.x

CrossRef Full Text | Google Scholar

Vecchio, A., Carbone, V., Sorriso-Valvo, L., De Rose, C., Guerra, I., and Harabaglia, P. (2008). Statistical properties of earthquakes clustering. Nonlin. Processes Geophys. 15, 333–338. doi:10.5194/npg-15-333-2008

CrossRef Full Text | Google Scholar

Wells, D., and Coppersmith, K. (1994). New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 84, 974–1002.

Google Scholar