- Department of Earth Sciences, University of Hawai‘i at Mānoa, Honolulu, HI, United States
Our current knowledge of the genesis, ascent, storage, and eruption of mafic magmas is intimately linked with olivine, its primary crystal cargo. Recent claims that phenocryst-size crystals can grow rapidly and non-concentrically are challenging our perception of what olivine zoning represents (e.g., controlled by growth and/or diffusion), and whether accurate magma crystallization and diffusion timescales can be retrieved. A series of cooling experiments using a dry basalt was carried out in order to quantify the kinetics of olivine growth as a function of the degree of undercooling, and to characterize morphological changes occurring with time. After a 24 h equilibration step at 1290°C (10°C above the olivine liquidus), experiments were rapidly cooled to final temperatures Tf = 1270, 1255, 1240, or 1220°C (imposing undercoolings of −ΔT = 10, 25, 40, and 60°C, respectively). Growth rates estimated via 3D microtomography renderings of experimental crystals attain 10–7 m/s, and are found to be almost an order of magnitude higher than those calculated using 2D sections of the same experiments. We show that mm-sized crystals similar to those found in natural Kīlauea samples can be produced after a few hours under moderate undercooling conditions (25–60°C). Growth rates decrease faintly with time, accompanying transitions between skeletal/hopper and more polyhedral morphologies. Growth rates generally increase until −ΔT = 40°C, and decrease slightly at −ΔT = 60°C as rates of nucleation likely increase. The −ΔT = 40°C vicinity may therefore represent a thermal “sweet spot” for the formation of phenocrysts in dry basalt. Olivine overgrowths on crystals that survived initial dissolution grow slower than homogeneously nucleated crystals, illustrating how new and old crystals in natural magmas likely respond differently to a thermal perturbation. We suggest that the main growth direction of natural olivine (a- or c-axis) may be a sensitive function of undercooling and the presence of a pre-existing growth substrate. Olivine grows faster along the a-axis under moderate to high undercooling conditions, while preferred development along the c-axis likely occurs under lower undercooling conditions and/or as rims grow around existing crystals. The early history of skeletal olivine crystals is controlled by diffusion in the melt (diffusion-controlled growth regime), while their long-term compositional zoning history is mainly controlled by diffusive re-equilibration.
Introduction: Overview of Olivine Growth Rates and Morphology
Olivine is a widespread mineral in ultramafic to intermediate volcanic and igneous rocks (e.g., basalt to andesite, shoshonite, komatiite, boninite, peridotite, or gabbro) representative of various tectonic settings (Pearce and Cann, 1973). In primitive ocean island basalt, for instance, olivine is the only crystallizing phase and thus the main record for a number of given magmatic processes (fractionation, magma mixing, magma degassing, magma transport). Olivine is also common in extraterrestrial rocks like on the Moon. In fact, the early history of lunar rocks is inferred from the kinetics of solidification of the “magma ocean,” where olivine was the first crystallizing phase (e.g., Isaacson et al., 2011). Olivine is also a primary phase in Martian basalt, and its composition yields key insights on the evolution of volcanism on Mars (e.g., Ody et al., 2013). For petrologists working on mafic magmas in terrestrial or extraterrestrial rocks, comparing experimental and natural olivine morphologies is crucial in order to retrieve the disequilibrium conditions and cooling history during a magmatic event (First and Hammer, 2016).
The crystallization kinetics of olivine can provide quantitative information about timescales of magma storage and differentiation. The crystal size distribution (CSD) method, where measured crystal dimensions are linked to duration based on available growth rate estimates (e.g., Vinet and Higgins, 2010), is one example. Growth rates are usually assumed to be lower in deep reservoirs where magmas crystallize close to equilibrium, and higher during magma ascent and rapid cooling (Armienti et al., 1994). Knowledge of growth rates is also crucial to characterize the competition between growth and diffusion kinetics under variable magma temperature conditions. Applications of geospeedometry generally require crystallization to be much faster than diffusion, meaning that growth-induced compositional zoning can be effectively discarded from diffusion models and timescale extraction (Costa et al., 2008). Quantification of olivine growth rates is therefore needed to discriminate between chemical zoning resulting from growth vs. diffusion (Shea et al., 2015b). Diffusion modeling is rapidly becoming a central theme for petrological interpretations based on olivine compositions (Lynn et al., 2017), and verifying underlying assumption about growth rates is now imperative. Improving the accuracy of growth rate and morphological development models for olivine could also provide valuable information about the rate of entrapment of olivine-hosted melt inclusions and their fidelity in preserving original melt compositions (Faure et al., 2003, 2007). If growth is fast compared to diffusive re-equilibration of elements in the surrounding melt, boundary layers can form and compromise the interpretation of melt inclusion compositions (Faure and Schiano, 2005). Timescales for the formation of the boundary layers therefore also require robust estimates of growth rates.
Much of our knowledge of the morphological development, reaction rates, thermodynamics of crystallization in silicate melts comes from early experimental work on lunar basalt (e.g., Lofgren et al., 1974; Walker et al., 1976). Donaldson (1976) focused on the crystallization of olivine in lunar and other basaltic–picritic–peridotitic rocks, showing that its morphology depends primarily on the degree of undercooling (i.e., ΔT = Tliq−T; the time-independent thermodynamic driving force expressed as the difference between the olivine liquidus and the temperature considered). Four growth morphologies are usually associated with different growth conditions (Donaldson, 1976): polyhedral, tabular, skeletal/hopper, and dendritic by order of increasing growth rate. At relatively low −ΔT (∼10–40°C), olivine is well-faceted (“polyhedral”) morphologies, whereas crystals grown at higher −ΔT (∼40–150°C) exhibit hopper cavities and/or skeletal to dendritic branching (Donaldson, 1976). Although transitions between different morphologies are poorly constrained and may depend on melt composition, polyhedral, tabular, and hopper morphologies are typically representative of low undercooling (−ΔT < 60°C) and dendrites are formed at −ΔT > 60°C (Faure et al., 2003). Thus, undercooling controls olivine growth rate, and thereby the final crystal morphology (Faure et al., 2003). The formation of hopper olivine, a morphology prone to entrapment of melt inclusions, has been notably associated with preferential faster growth along the a-axis direction (e.g., Faure et al., 2003).
Because olivine phenocrysts usually exhibit polyhedral morphologies in magmas, they are canonically viewed as having grown slowly at low degrees of undercooling and in a concentric “tree-ring” fashion (e.g., Clark et al., 1986). Thus, studies using olivine to interpret magmatic processes have largely assumed near-equilibrium conditions for phenocryst crystallization and element partitioning (Pearce, 1984). The assumption that polyhedral olivine grows slowly under near-equilibrium conditions has been contested by Welsch et al. (2014), who showed that even large polyhedral olivine phenocrysts can preserve morphological remnants (e.g., stepped hopper cavities) of an early rapid growth. They hypothesized that olivine initially grows rapidly, forming a skeletal olivine framework that is progressively infilled as undercooling and growth rates decrease. Experimental studies have also demonstrated that mineral growth rates also depend on the delay in nucleation (cf. Hammer, 2008 and references therein). The delay in nucleation increases with lower undercooling or lower olivine content (Donaldson, 1979), and nucleation controls growth rate by forcing distribution of the crystalizing mass around few or numerous crystals – i.e., lower nucleation density corresponding to higher growth rate (e.g., Swanson, 1977).
Despite being one of the most studied minerals, the growth rate of olivine is poorly constrained. Early estimates of growth rates relevant to the development of skeletal crystals based on a diffusion-limited aggregation model (Fowler et al., 1989), diffusion coefficients measurements (Donaldson, 1975), or apparent size distribution density (Armienti et al., 1991) all hovered around ∼10–9 m/s. A more thorough, systematic quantification of growth rates as a function of undercooling was carried out by Jambon et al. (1992), who crystallized olivine within feldspar melt inclusions in a tholeiite basalt. Despite the clever experimental setup designed to avoid olivine crystallization on melt inclusion walls, the small size of olivine crystals formed (≤50 μm), coupled with difficulties in estimating the dimensions of complex 3D skeletal crystals in a 2D section, imply substantial uncertainty in the growth-rate data. Their results showed that lower growth rates (10–10–10–9 m/s) yielded polyhedral crystals at −ΔT = 15–35°C, whereas higher growth rates (∼10–8–10–7 m/s) produce skeletal morphologies at −ΔT = 56–150°C. Melt inclusion migration experiments performed at very low undercoolings also yielded very slow olivine growth rates around 10–9 m/s (Schiano et al., 2006). These two studies are currently the only available sources for olivine growth-rate vs. undercooling data for natural magma compositions.
Growth-rate experiments addressing the complexities of 3D morphologies in a natural basalt using new imaging techniques are thus urgently needed. In order to quantify the preferred interfacial direction of growth, the evolution of these 3D morphologies need to be considered as a function of undercooling. This study focuses on the effects of undercooling and time on olivine growth rate, after a small-to-moderate temperature perturbation (10–60°C), using a 3D quantitative approach. The 3D textural attributes of olivine yield new insights on the undercooling required for phenocryst crystallization, their growth rates, the origin of skeletal olivine in mafic rocks, the evolution of olivine morphologies and its framework as a function of undercooling and time. We also discuss the implications of these results for discriminating growth vs. diffusion induced zoning.
Materials and Methods
Experimental Protocol
A natural parental Kīlauea tholeiitic composition (see Supplementary Table B for chemical composition) was used as starting material for our crystallization experiments, partly because Hawaiian basalts have played a central role in our understanding of the formation and evolution of mafic magmas (Garcia, 2015). This composition also has the advantage of replicating complexities that exist in natural systems (e.g., all major, minor, and trace elements present), while avoiding the effects of crystallization of other mineral phases (e.g., Clague et al., 1995; Garcia and Hulsebosch, 1995; Herzberg, 2011). Phase equilibria of Hawaiian tholeiitic magmas show that olivine is the only crystallizing phase for >100°C below the liquidus (Wright, 1971), which is also consistent with MELTS models at 1-atm and a range of fO2 (Figure 1A). Oxygen fugacity conditions are relatively well constrained for Kīlauea magmas within ∼1 order of magnitude in log(fO2) (Rhodes and Vollinger, 2005; Helz et al., 2017). The low viscosity of tholeiitic basalts also has the benefit of reducing kinetic delays for melting and crystallization. The starting material consists in glassy, weakly olivine-phyric (<4 vol.%) pyroclasts from the 1820 CE eruption at Kīlauea with a relatively primitive bulk composition (11.4 wt.% MgO, with an equilibrium olivine composition Fo85.5) (Garcia et al., 2003). Olivine crystals >500 μm were removed from the starting powder in order to reduce variations in starting composition induced by the presence of large phenocrysts between different experiments. One olivine phenocryst “seed” (∼0.5–1 mm) from the 1820 CE powder with typical core composition Fo87–89 (Lynn et al., 2017) was added to every experiment to test for the potential effect of overgrowth on calculated olivine growth rates. Each experiment consists in two duplicate ∼5 mm diameter beads of starting material glued with polyvinyl alcohol around rhenium wire loops. Using rhenium largely circumvents problems of Fe, Ni, and Co loss to precious metals (e.g., Borisov and Jones, 1999; Filiberto et al., 2010). EDS analyses of rhenium wires after experimental runs yield barely detectable (<0.1 wt.%) Fe, Ni, or Co. Having a duplicate for each experiment meant that one could be used for 3D measurements, while the other could be sectioned and (1) analyzed for glass compositions, and (2) measured for 2D growth rates (see below). The two Re wires holding the charges were attached to a hanger so as to be side-by-side, and then hung on a 0.38 mm “zap” platinum wire, within in a 1-atm CO2 – H2 gas-mixing furnace with fO2 control. One-atmosphere experiments are appropriate for the study of Hawaiian tholeiite magmas, which typically crystallize at low pressure (0.05–0.2 GPa; Wright and Klein, 2014) and are H2O-poor (∼0.1–0.5 wt.%; Wallace and Anderson, 1998). The olivine liquidus temperature (Tliq = 1280 ± 3°C) was defined by carrying out equilibrium experiments (see Supplementary Material for details), and tallies well with the value predicted by MELTS (1282°C) for this composition.
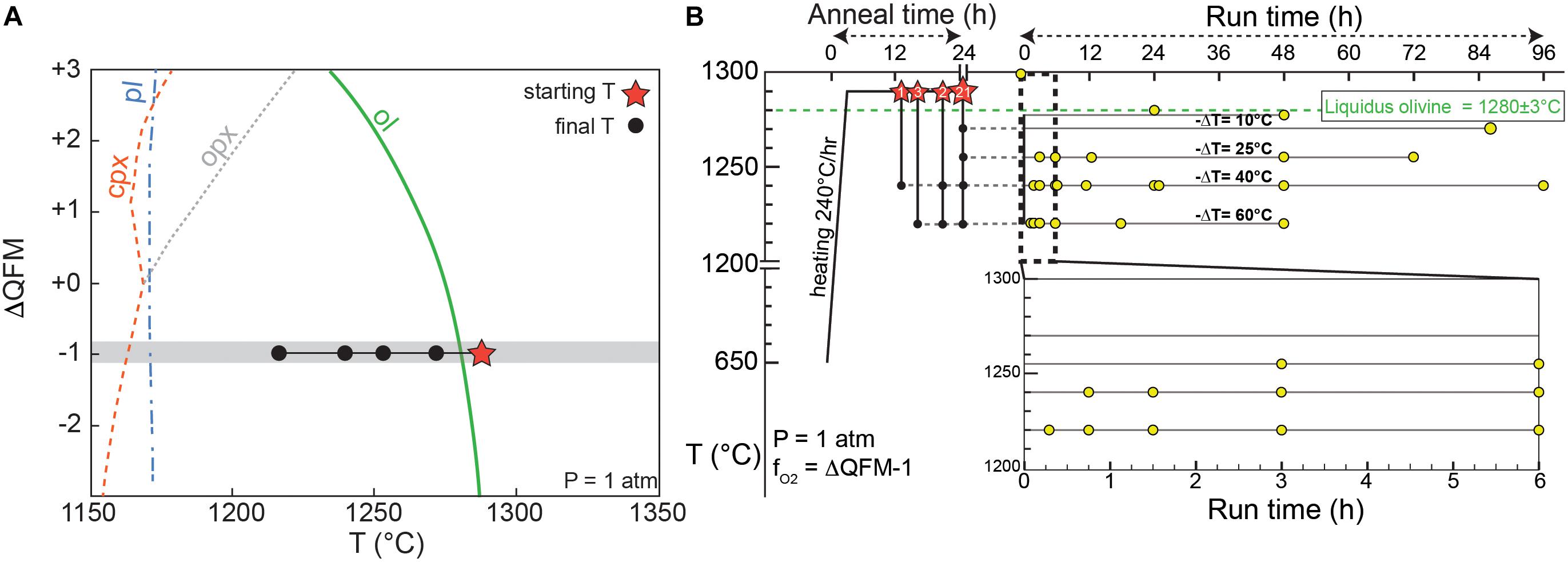
Figure 1. (A) Temperature-fO2 phase equilibria diagram calculated from MELTS using the Kīlauea 1820CE bulk composition at 1 atm (modified from Shea et al., 2019). Gray region shows the range in fO2 imposed in the experiments. (B) Proposed experimental strategy, with initial superliquidus anneal periods (red stars over the olivine-in curve, numbers indicate the number of experiments for each anneal time). Anneals were followed by rapid cooling to final conditions (black circles) at T = 1220, 1240, 1255, or 1270°C, and left for dwell times 20 min – 4 days. Yellow dots are experimental quenches at given T–t conditions (27 runs total).
The starting material was annealed for ∼24 h at Ti = 1290°C, about 10°C above the olivine liquidus (Figure 1B) to ensure dissolution of any finely crushed residual olivine and formation of pure melt plus the added larger olivine seed. After annealing, samples were cooled in a 2–4 min single step to the final temperature Tf = 1270, 1255, 1240, or 1220°C (imposing −ΔT = 10, 25, 40, and 60°C respectively, Figure 1B) for isothermal experiments. This range in undercooling was chosen to (1) promote a range in olivine growth rates (Jambon et al., 1992; Faure et al., 2003), and (2) be applicable to common processes such as magma mixing, where a somewhat abrupt change in temperature might occur between a recharge and a resident magma (e.g., Lynn et al., 2017). In this sense, our experiments are well-suited for the quantification of growth rate and for scenarios of rapid temperature changes, but are not meant to reproduce more continuous cooling conditions occurring in natural magma. Run durations between 20 min and 4 days were selected to resolve the early stages of growth and the beginning of crystal maturation. An additional experiment (Ti = 1290°C, Tf = 1220°C) was quenched at the end of the 4 min-long rapid cooling step and lacked newly formed olivine entirely. Mg X-ray maps acquired within a sample quenched after 24 h at the initial conditions (1290°C) confirmed the absence of localized magnesium heterogeneities that could influence subsequent growth of olivine (see Supplementary Figure S2).
It should be noted that aside from differences in experimental volumes and techniques used to estimate growth rates, the experimental strategy employed herein differs from that of Jambon et al. (1992) in one major respect: they used closed melt inclusions as experimental vessels for olivine crystallization in order to isolate the process of growth from that of nucleation, while our olivine is allowed to grow “freely” in a much larger volume of melt. This strategy allowed them to explore growth even at high degrees of undercooling (−ΔT = 150°C), a region where nucleation rates could otherwise have an important effect in on crystal sizes (e.g., Waters and Lange, 2013). In our experiments, both nucleation and growth contribute to producing the final crystal population, with the disadvantage that separating the two becomes difficult, but with the key advantage of being directly applicable to natural crystallizing magmas where nucleation is uninhibited.
Analytical Methods
Major and minor element composition (Si, Ti, Al, Fe, Mn, Mg, Ca, Na, K, P) of the experimental glasses were determined using a JEOL JXA-8500F Hyperprobe with five wavelength-dispersive spectrometers at the University of Hawai‘i. Glasses were analyzed using an accelerating voltage of 15 kV, a probe current of 10–20 nA, with a defocused 10–15 μm beam. Peak counting time was 40 s for each element. A99 basalt glass (USNM 113498/1) and VG2 was used for Si, Al, Fe, Mg, Ca, K-Orthoclase (OR-1) for K, Sphene glass for Ti, Durango F-Apatite for P, and Verma Garnet for Mn. Relative precision (2σ) based on repeat analysis of standards is better than 1% for Si, Ti, Al, Fe, Mg, Ca, 1.5% for Mn, about 4% for Na, 20% for K, and 40% for P. Accuracy is <1% for Si, Al, Mg, Ca, Na, K, about 2% for Ti, Fe, P, and 5% for Mn.
Textural Analyses
Measuring the dimensions of crystals on a 2D section is problematic due to intersection effects. Sectioning even a single crystal of a given size and morphology can cause substantial variability in section dimensions (Shea et al., 2015a). As a result, tracking the transient growth of crystals with potentially complex morphologies in 2D likely leads to significant added uncertainty. To circumvent these issues, a full, high-resolution 3D textural characterization was performed at the X-ray UTCT facility hosted at the University of Texas. For each experiment, 2D growth rates were also estimated from measured exposed crystal areas and compared with 3D measurements.
Three-dimensional analyses on seven experimental charges embedded in resin were performed using a Xradia microXCT Scanner. The samples were rotated and imaged between a standard cone-beam micro-CT (Feldkamp et al., 1984; Turbell, 2001) and a X-ray detector. The detector-sample distance was fixed at 35.5 mm for all scans, yielding a voxel size of 3.43 μm. The analytical challenge consisted in resolving the low density contrast between olivine and surrounding glass. A relatively low mean X-ray energy of 70 kV helped distinguish the glass from the crystals. Reconstruction parameters were optimized to reduce beam-hardening artifacts (see Supplementary Table C). The duration of one individual scan varies from 3 to 9 h depending on the resolution and the magnification. After the post-reconstruction phase, the contrast of all slices was improved using the ImageJ software. All image stacks combined were then imported in AvizoTM for manual segmentation and volume rendering. Minor smoothing was applied to minimize jagged edges. Comparison of 3D images of skeletal crystals with a 2D section from the same crystal allowed us to quickly establish and verify clear connections between crystals that appear disconnected on a 2D section. Most olivine crystals (i.e., those that appeared through at least a few slices and therefore with sizes >10–20 μm) were well resolved in the 3D renderings. Higher resolution BSE images collected using the microprobe helped confirm that the 3D renderings were not missing large populations of small crystals. Growth rates were calculated in three ways: “2D” and “3D” growth rates were obtained by dividing the dimension of the longest of the three axes (a, b, or c) by the experimental time. “Chemically”-calculated growth rates were determined from mass-balance using initial and final glass MgO contents (with the initial MgO content equal to 11.35 wt.% and the final glass composition corresponding to the composition at the end of the experiment; the fraction of olivine and the growth rates are then derived from the difference of magnesium content; see Supplementary Material for details). In essence, these values provide theoretical maximum attainable growth rates.
Results and Interpretations
Textural and Morphological Characteristics
Olivine is the only crystallizing phase in the experimental charges. The total olivine content estimated by mass-balance calculation shows that olivine crystallization occurs as a two-step process, with a high crystallization rate phase followed by a low crystallization rate “plateau” where additional crystallization is minimal (Figure 2 and calculations available in the Supplementary Material). This evolution is typical of a rapid response to disequilibrium, and slower attainment of an equilibrium state (Avrami, 1939; Johnson and Mehl, 1939; Kirkpatrick, 1981). A near equilibrium crystal content is reached after ∼3 h for a −ΔT = 60°C, ∼6 h for a −ΔT = 40°C, and ∼12 h for a −ΔT = 25°C, consistent with an undercooling dependence of crystallization rates. Higher degrees of undercooling result in higher crystal content, reflecting a larger disequilibrium. The rapid increase in crystallization rates is well observed at −ΔT = 60 and 40°C, but becomes slightly delayed at 25°C, and significantly delayed at 10°C. Run products contain phenocryst-size olivine with various two-dimensional morphologies. Single crystals are randomly oriented in all runs. Olivine from the −ΔT = 60°C and −ΔT = 40°C series generally exhibit skeletal crystals (Figures 3C–H) and the −ΔT = 25°C series reflects a transition between hopper/skeletal and polyhedral habits (Figures 3A,B). True dendritic crystals – defined here as a branch-like habit with no apparent overall faceted form – are not produced in any of the runs. Short runs at high undercooling reflecting the initiation of growth (Figures 3C–G) show more acicular and smaller crystals. Longer experiments (>6 h, Figures 4A,D) display a high density of >1 mm crystals (see variation of the crystal size in Table 1), with the appearance of growth sub-units or “buds” (e.g., Welsch et al., 2013) (Figure 4A). Short experiments with −ΔT = 40–60°C (Figures 4B,C,E) grow preferentially along the a-axis direction. The lack of preferential growth with small undercooling (e.g., −ΔT = 25°C runs, Figures 3A,B) suggests that growth along a preferential direction increases with the undercooling. Primary olivine branches form rapidly (<0.5 h for −ΔT = 40–60°C) after reaching the final temperature (Figure 3G), and an outer, faceted shell forms after a few minutes to a few hours depending on the degree of undercooling (Figures 3C–G). After typically a few hours, skeletal olivine (Figures 3D–H) display secondary branches that often track the outer shell interfacial directions, and which connect the primary branches. These secondary branches progressively fill the crystals and lead to partial or complete entrapment of open and closed hour-glass inclusions (Figures 3D,E).
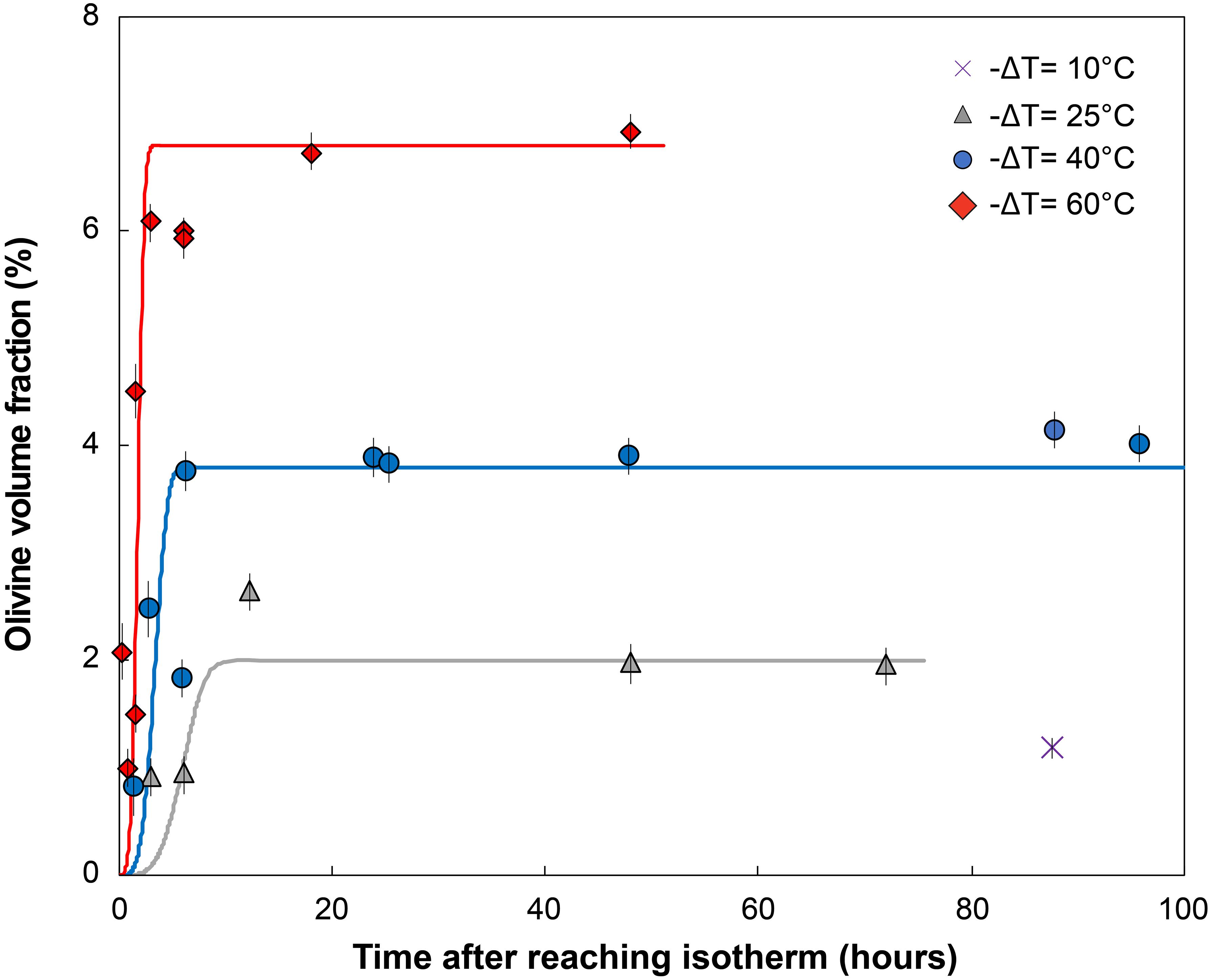
Figure 2. Percentage of olivine crystallized vs. time after reaching the final isotherm (hours). Olivine volume fraction is obtained by mass-balance from the MgO content measured in the glass before and after crystallization (see Supplementary Material for details). Each point represents the average of three to eight electron microprobe spots per experiment, typically five to six spots. Error bars show the 2σ variation in the analysis. Global trends for each temperature were calculated from the Avrami equation φx = 1 – exp(–kvIG3t4) with φx the crystal volume fraction, I the crystal nucleation rate, G the crystal growth rate, t the time, and assuming a volumetric factor kv = 4π/3 for spherical crystals. No attempt was made to utilize growth or nucleation rates from the experiments to calculate these curves. Instead, parameters (see Supplementary Table E) were chosen to best fit the data, to provide first-order predictions of the topology of crystallization rates.
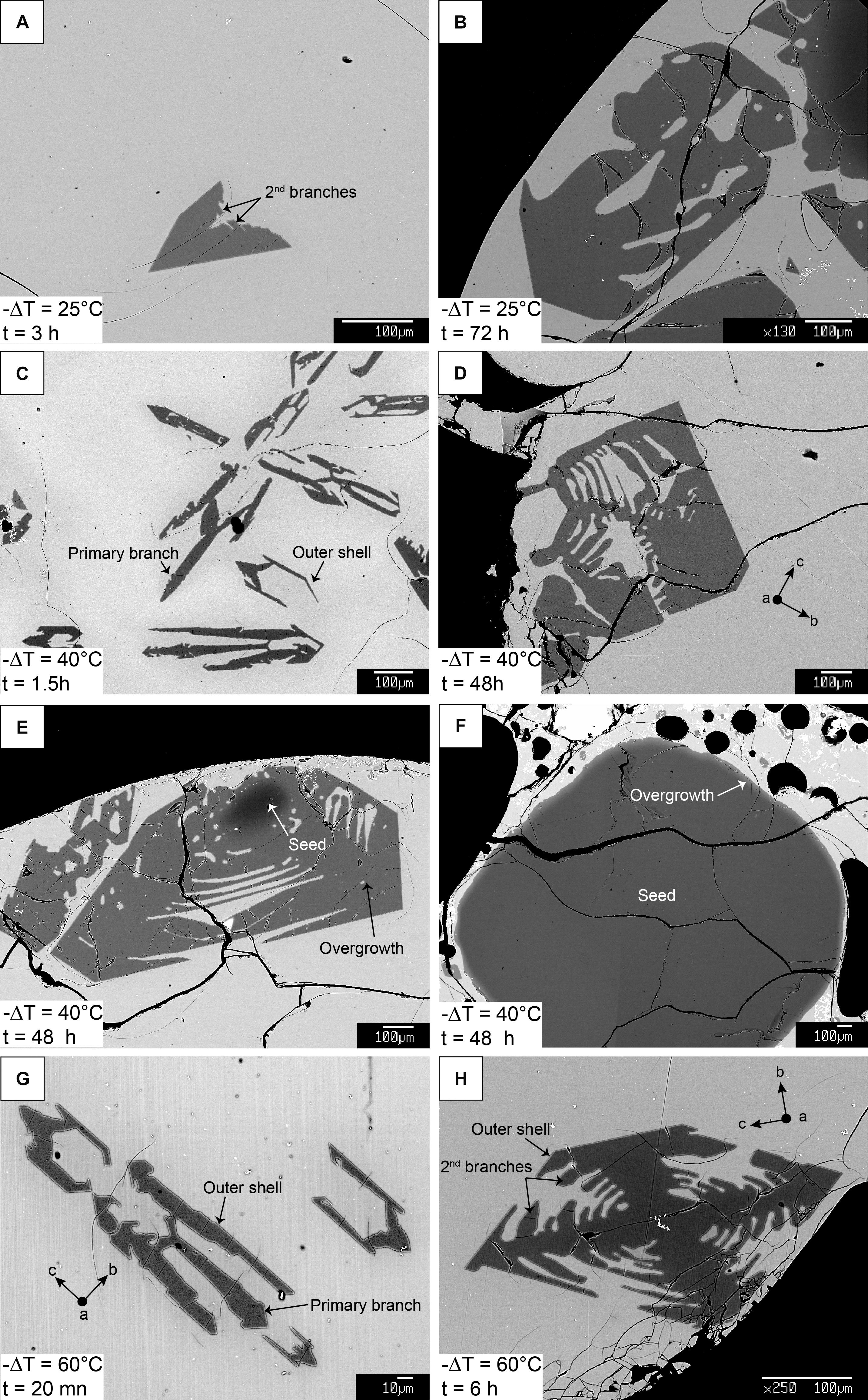
Figure 3. BSE images of experimental olivine at different times and temperatures showing processes of growth and ripening. Panels (A,C,G) and (B,D,H) display shorter and longer experimental durations for each undercooling, respectively. Sections elongated along the c-axis in panels (C,D,G,H) are commonly observed in 2D. However, 3D scans reveal that true elongation is most often along the a-axis, illustrating how sectioning effects can influence measured growth rates. Panels (E) and (F) are examples of two overgrown seeds in the same charge at –ΔT = 40°C, 48 h, showing how seed size has a strong influence on growth rate and morphology along a given direction.

Figure 4. Volume rendering of experimental olivine at different times and temperatures. (A) Crystals from an experiment at −ΔT = 60°C, 18 h; (B) Experiment at −ΔT = 60°C, 6 h; (C) Experiment at −ΔT = 60°C, 3 h; (D) Experiment at −ΔT = 40°C, 6.5 h; (E) Experiment at −ΔT = 40°C, 1.5 h; (F,G) Microscope and secondary electron image showing hourglass melt inclusions (m.i.) and the well-faceted morphology of a crystal from the 1820CE eruption of Kīlauea volcano that is also elongated along the a-axis.
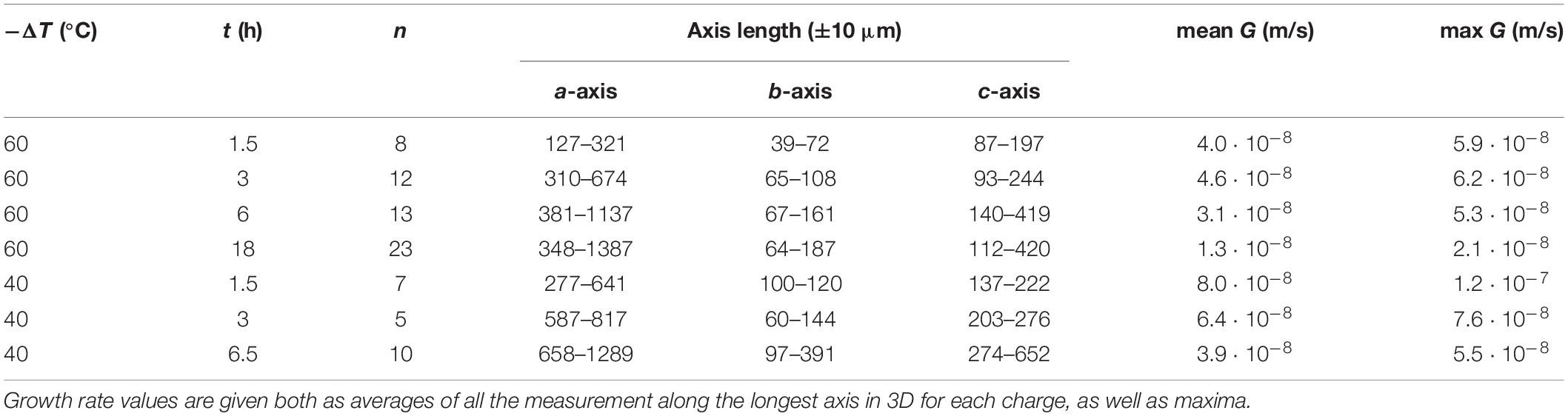
Table 1. Average length of experimental crystals measured in 3D (n = number of crystals measured) along the three crystallographic axes a, b, and c.
Growth Rates
Growth rates are first presented by examining crystal sizes obtained from 3D μCT renderings of the −ΔT = 40–60°C runs. Measurements of the olivine were performed considering the edges of the crystals, and not with the maximum elongation of the primary branches. The error associated with this assumption reaches 10% for the fastest calculated growth rates, but is <5% for the lowest calculated growth rates. The maximum crystal size, observed systematically along the a-axis, increases slightly with time for all runs, although there is significant overlap between the different runs (Figure 5B). Values range between 120 μm for short runs (e.g., 1.5 h at −ΔT = 60°C) and 1400 μm for the longest run analyzed (18 h at −ΔT = 60°C). In −ΔT = 60°C runs, olivine crystals display a linear increase in the average a-/b-axis ratio during the first 6 h (Figure 5B) from a/b = 4 after 1.5 h to 7 after 6 h (Figure 5A). Then, the subsequent decrease of the a-/b-axis ratio can be interpreted by maturation of crystals through growth along the b-axis. A more gradual increase of the a-/b-axis ratio is observed for −ΔT = 40°C runs. The a-/b-axis ratio increases with time (3–6 for t = 1.5 h runs and between 2 and 15 for t = 18 h runs). This ratio is more variable for the −ΔT = 60°C runs compared to the −ΔT = 40°C runs. The same general trend is observed for the a-/c-axis ratio, with less departure from the main positive trend (c.f. Supplementary Table D). The highest values of the a-/b-axis ratio correspond to early skeletal crystals which are growing under high disequilibrium conditions with the melt. Smaller crystals that likely nucleated later during the run and larger, more mature crystals both have lower a-/c-axis and a-/b-axis ratios, likely reflecting a lower degree of undercooling.
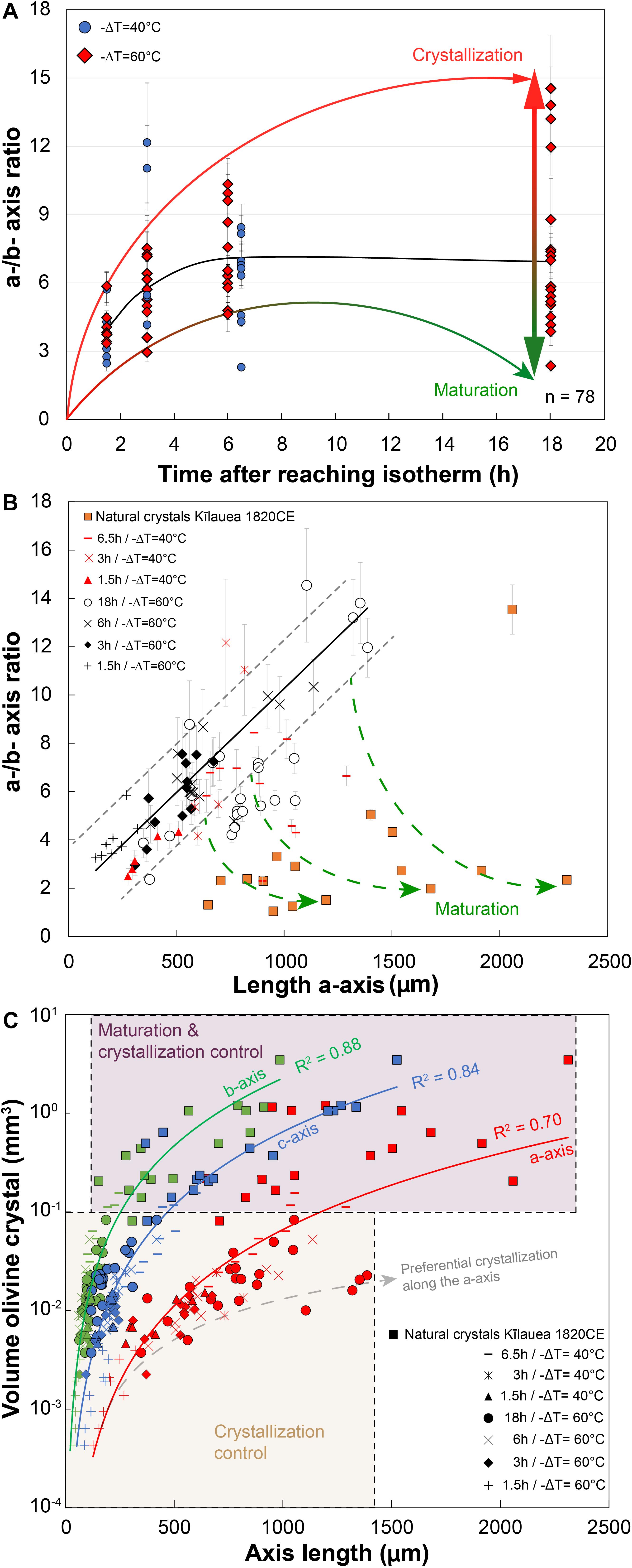
Figure 5. 3D measurements of the a- and b-axis dimensions of experimental olivine for 40 and 60°C of undercooling, illustrating processes of crystal growth and maturation. (A) a-/b-axis ratio vs. time after reaching isotherm; number of crystals n = 78. (B) a-/b-axis ratio vs. length of the a-axis for different run durations with 40 and 60°C undercooling. Experimental olivine is compared to natural olivine of different sizes from the 1820CE Kīlauea eruption. Natural macrocrysts were photographed with a stereomicroscope in the three directions for axis length measurements. Green arrows extrapolate this ratio that could be interpreted as an evolution of the degree of maturation along the b-axis, typically occurring after a few hours and for crystals longer than 700 microns. A roughly similar linear trend in (B) marks the main trajectory of growth before significant maturation occurs. Error bars: gray lines correspond to the standard deviation and the measurement error on each axis was estimated at 10 microns for experimental charges. (C) Volume of experimental and natural olivine (in log unit) vs. length of the a-, b-, and c-axis. The maturation along the b- and c-axis reduces the crystallization along the a-axis and explains the lower best fit residual for the a-axis (R2 = 0.7).
Maturation along the b-axis starts after 6.5 h and 18 h for a −ΔT = 40 and 60°C, respectively (Figure 5B), meaning that lowering of the degree of undercooling or disequilibrium has a key role for maturation. A similar evolution is observed along the c-axis (c.f. Supplementary Table D). Maturation along the b-axis is faster close to the liquidus temperature. The consequence is that the volume of trapped glass inclusions globally increases with undercooling, and is also proportional to the size of the crystals (inclusions vary from 10–4 mm3 for a 400-μm olivine to 5 × 10–3 mm3 for a 1100-μm olivine crystal). The olivine maturation process is more obvious when the crystal size exceeds 700 μm. Compared to experimental runs at −ΔT = 40–60°C, most of the natural olivine crystals (skeletal, polyhedral, and budded crystals) from the 1820CE eruption of Kīlauea volcano have lower a-/b-axis ratios between 0.5 and 5. Extrapolation of our growth model to these natural crystals would indicate protracted maturation over timescales greater than 18 h.
The calculated volume of all experimental and natural olivine follows the same power law when considering the three axes independently (Figure 5C). The volume of olivine crystals increases with time, with values barely attaining the range measured for natural olivine (0.1–4 mm3) for the longest runs (6.5 h at −ΔT = 40°C or 18 h at −ΔT = 60°C). Crystal >0.1 mm3 are especially scattered around these main trends for the a-axis. The threshold at 0.1 mm3 marked the transition from a crystallization regime during the first hours to a crystallization and maturation regime.
Growth rates, estimated from 3D renderings and MgO content of experimental charges, slowly decrease with time, with the shortest run time associated with the highest values around 10–7 m/s (Figure 6). Longest experiments thus yield the lowest values for growth rates. This temporal decrease in growth rate may be in part associated with integration of size data over longer experimental durations (e.g., Hammer, 2008; Brugger and Hammer, 2010). This integration effect may be deconvoluted by computing the growth rate as the change in crystal size between two successive experiments with different durations (i.e., rather than integrating the final size over the total duration) (see Supplementary Table B). Both calculation methods display a decrease in growth rate with time, though the effect of time integration becomes important after 3 h.
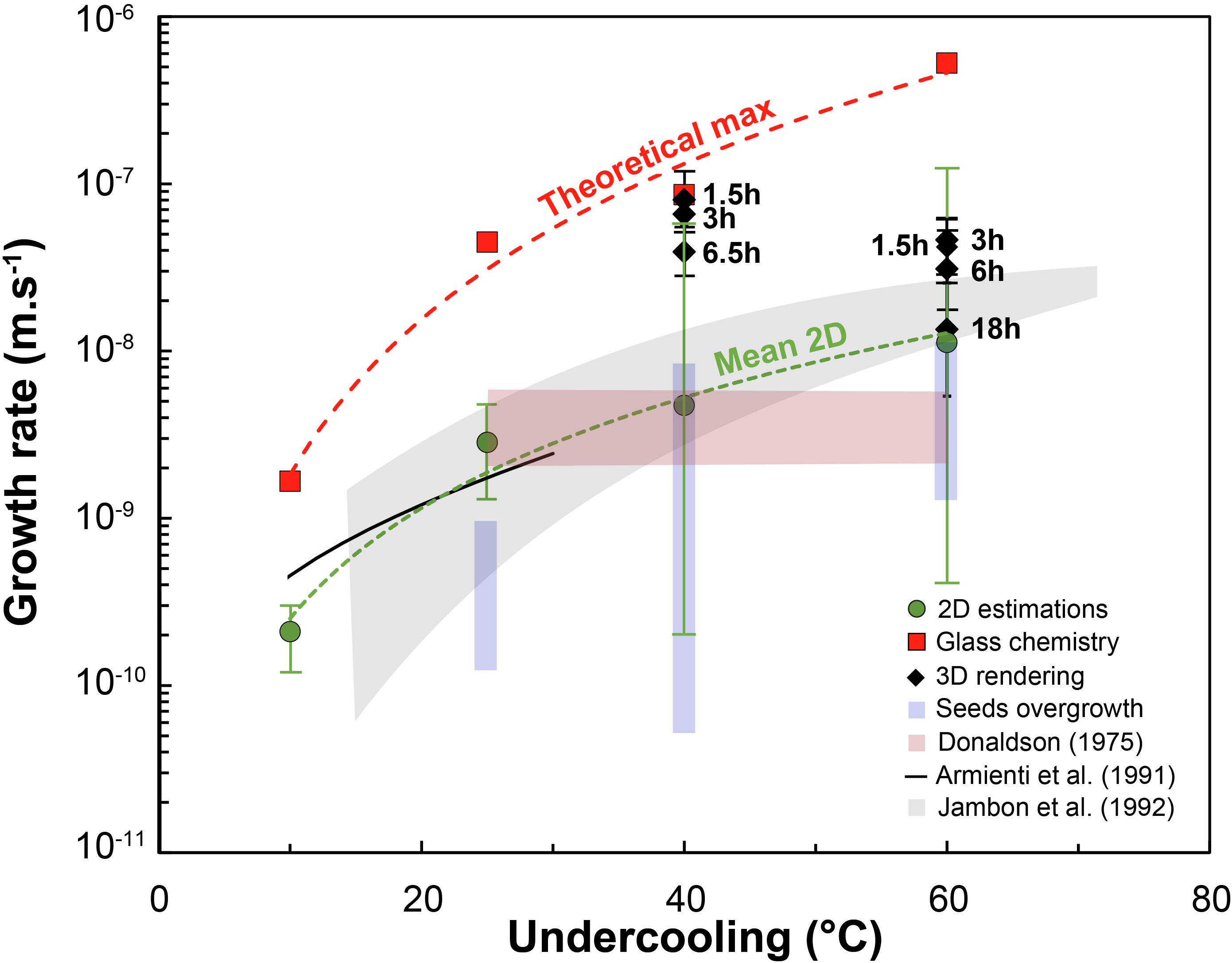
Figure 6. Growth rate (m/s) vs. undercooling (°C). 2D estimates from this and other studies (e.g., Armienti et al., 1991; Jambon et al., 1992) are compared with 3D data along with values calculated from mass-balance. The latter are obtained by calculating the dimensions of a single crystal representing all the crystallized mass within an experiment, and are thus theoretical maxima. Error bars for the 3D data coincide with the minimum and maximum calculated growth rate for crystals of different sizes.
Two dimensional estimations of growth rates are consistent with previous values from Jambon et al. (1992). Both 3D measurements and MgO chemistry-obtained growth rates are within the same order of magnitude ∼10–8–10–7 m/s for a −ΔT = 40–60°C (Figure 6). The 3D values are one order of magnitude higher than those from Jambon et al. (1992) for −ΔT = 40°C runs, and within the same order of magnitude for −ΔT = 60°C. The major difference in the present dataset is the decrease of growth rate with undercooling from 40 to 60°C undercooling. This decrease is likely due to the transition from growth-controlled crystallization to nucleation-controlled crystallization. This competition between nucleation and growth rates is inferred to commonly lead to fewer, larger crystals at low undercooling and numerous smaller crystals at high undercooling (e.g., Waters and Lange, 2013). The trade-off between how a crystallizing mass is distributed around fewer or more numerous crystals is well known and described by the Avrami equation (1939). Nucleation rate calculated from this equation using the 3D-measured growth rates and crystal fractions is about 105 olivine/m3 at −ΔT = 40°C and 106 olivine/m3 at −ΔT = 60°C, consistent with a shift toward undercooling values where nucleation becomes influential.
In some experiments it was possible to measure the 2D size of overgrown crystal seeds. Compared to 2D data from crystals that nucleated homogeneously in the charge, seed overgrowths generally yield lower growth rates. Values hover around 10–10–10–9 m/s at −ΔT = 25°C, 10–10–10–8 m/s at −ΔT = 40°C and 10–9–10–8 m/s at −ΔT = 60°C, about one order of magnitude lower at −ΔT = 25°C, and comparable to newly formed crystals at −ΔT = 40–60°C.
Discussion
The results presented above provide us with important constraints on growth rate of olivine as a function of time and undercooling. They highlight the relatively rapid growth kinetics of olivine in dry tholeiitic basalt, the comparatively slower process of maturing to larger phenocrysts, and importance of considering 3D morphology for growth rate calculations. The next sections examine the implications of these results in the context of (1) natural phenocryst growth, (2) growth mechanisms and element partitioning, and (3) the link between the presence of skeletal crystals in basalt magma and magma mixing processes. Subsequently, (4) a new development model for olivine is proposed, (5) the controversy surrounding the competition between growth and diffusion and its influence on compositional zoning is discussed in light of newly obtained growth rates, and (6) the applicability of the results to other basalts.
Growth of Olivine Phenocrysts in Natural Magmas
Our experiments show that phenocryst-size olivine frameworks can be formed in 1–2 h. Previous growth rate estimates (Donaldson, 1975; Armienti et al., 1991; Jambon et al., 1992; Wallace and Anderson, 1998; Ni et al., 2014) implied formation of mm-sized olivine crystals would take at least tens of days (Wallace and Anderson, 1998) or even tens of years (Mangan, 1990). The morphology of experimental crystals matches that of natural crystals (e.g., the 1820CE Kīlauea olivine), with a tendency to be elongate along the a-axis and contain large hourglass inclusions. Crystal buds observed in natural olivine (e.g., Welsch et al., 2013) also form in the longer experimental charges. The broad range in crystal sizes in longer experiments may be related to differences in the timing of nucleation (smaller crystals nucleate later), and/or controlled by the competition of crystals for olivine component from the melt (crystals able to grow quicker were less impeded by other crystals). The crystal size-experimental duration relationships indicate that for undercoolings between 25 and 60°C, the induction time for crystallization is <3 h (<20 min for a −ΔT = 60°C). Such small induction times imply that there is no significant barrier to crystal nucleation at the beginning of our experiments. This rapid nucleation process for moderate-to-high undercooling likely diminishes greatly after the first generation of olivine forms. Also, at equal analytical resolution, the 40 and 60°C undercooling experiments have notable differences in the number density of crystals, with the 60°C runs showing more individuals. The notable decrease in 3D-derived growth rates from −ΔT = 40–60°C is associated with an increasing influence of nucleation on how the crystallizing mass is distributed. The undercooling region around 40°C can therefore be regarded as a sweet-spot for the formation of phenocrysts: growth rates are near their maxima, while nucleation rates are still low. The limited number of undercooling values examined herein precludes a precise resolution of this region, and future experiments are needed to fully demonstrate the decreasing trend in growth rates at high ΔT.
Knowledge of the pre-eruptive history of the magma and the control over the presence or absence of nuclei at the beginning of the experiments is essential to make an analogy between experiments and natural mafic rocks (Faure et al., 2003). Natural basaltic rocks usually display large variation of olivine textures with skeletal and more mature olivine cargo (e.g., Milman-Barris et al., 2008), where both olivine dissolution and crystallization processes may be involved. Like pre-existing olivine in a magma chamber, seeds introduced in the experiments can undergo dissolution and rim growth, therefore allowing the influence of pre-existing substrate on growth rates. Growth rate values obtained for overgrowth rims are much lower compared to those of crystals that nucleated homogeneously in the charge (Figure 6), suggesting that the presence of a pre-existing surface is an important parameter for growth kinetics. The crystallizing mass is distributed around a larger surface during rim overgrowth, resulting in lower values of growth rates. Seed overgrowth often occurs more isotropically, lacking the strong preferential growth direction observed in homogeneously nucleated crystals. Compared to newly formed crystals, rims are by definition exposed to a greater surface area of melt, meaning that olivine-forming components are more readily available and less easily locally depleted. At medium undercooling, the growth of primary branches is hence less favored for overgrown olivine than for olivine grown after homogeneous nucleation. Extrapolation of these results to natural magma reservoir systems suggests that old crystallized olivine subject to thermal and chemical disequilibrium do not grow at the same rates as new olivine crystals. The same thermal history in a magmatic chamber can thus lead to a large variation of growth rates for old and new cargo undergoing homogeneous nucleation or rim overgrowth. This variation could explain the low calculated growth rates based on bulk olivine cargo with crystal population density data (Armienti et al., 1991).
Growth Mechanisms and Consequences for Element Partitioning in Olivine
The transition from polyhedral to skeletal olivine was explained by Faure et al. (2007) as an excess of chemical supersaturation at olivine corners associated with stronger local disequilibrium (Berg, 1938), thereby promoting preferential growth along diagonal branches. Protuberances on crystal corners pierce through the regions that are least depleted in olivine-forming components (boundary layers) to create elongated crystals (Hammer, 2008). The increase in disequilibrium at moderate undercooling has been associated with the development of a layer-spreading nucleation mechanism (Faure et al., 2007). For medium undercooling values investigated in our experiments (25–60°C), spiral growth and layer-by-layer growth are often cited as dominant mechanisms for interface reaction (Ni et al., 2014). The hopper/skeletal morphologies instead suggest that the growth rate was primarily limited by chemical diffusion (Ni et al., 2014) with the formation of chemical gradients at crystal–liquid interfaces (Figure 7 and Faure and Schiano, 2005).

Figure 7. Chemical maps of magnesium (A) and iron (B) of a skeletal olivine that crystallized in 20 min, subject to 60°C of undercooling. The presence of wide boundary layers at the crystal–liquid interface suggests that crystallization occurred under the diffusion-controlled growth regime.
Under the diffusion-controlled growth regime, the high growth rates extracted from our experiments also bear important consequences for element partitioning in olivine. Elements that are either highly compatible (Mg, Ni) or incompatible (Al, P) in olivine will be rapidly depleted or enriched in boundary layers (Figures 7,8, Milman-Barris et al., 2008; Shea et al., 2015b), causing depletion or enrichment in the crystal compared to equilibrium concentrations (Lasaga, 1982; Watson and Müller, 2009). In one experiment, the presence of boundary layers in Mg during diffusion-controlled growth caused the Kd to attain fairly low values 0.27–0.28 (equilibrium Kd values range between 0.3 and 0.345, Roeder and Emslie, 1970; Matzen et al., 2011) mostly due to lowering of the Mg partition coefficient DMg (Figure 8). Rapid growth may therefore impact our ability to discern equilibrium vs. disequilibrium in a basalt assemblage. Shea et al. (2015b) and Watson et al. (2015) calculated that growth rates approaching 10–7 m/s were needed to explain two- to threefold enrichments of trace elements like P or Al. A major issue with the boundary layer model as proposed previously was that high undercoolings that may be difficult to achieve in natural systems (e.g., −ΔT = 110°C) were needed to raise growth rates to levels that induced enough enrichment in these elements (Jambon et al., 1992). The present results show that growth rates estimated from 3D can attain these values without necessitating extreme undercooling conditions. A companion paper based on the same experiments (Shea et al., 2019) fully explores the consequences of rapid growth for P and Al, and shows that the boundary layer enrichment model works for certain elements like Al but not for P. Regardless of the peculiar behavior of P, the concentration of other elements is clearly affected by disequilibrium caused by rapid growth, which may even affect Fe–Mg contents in olivine (Figure 7). Our results relax the requirement for unrealistically large undercooling and may pave to way to better understanding the extent to which olivine major and trace element compositions can be controlled by disequilibrium processes.
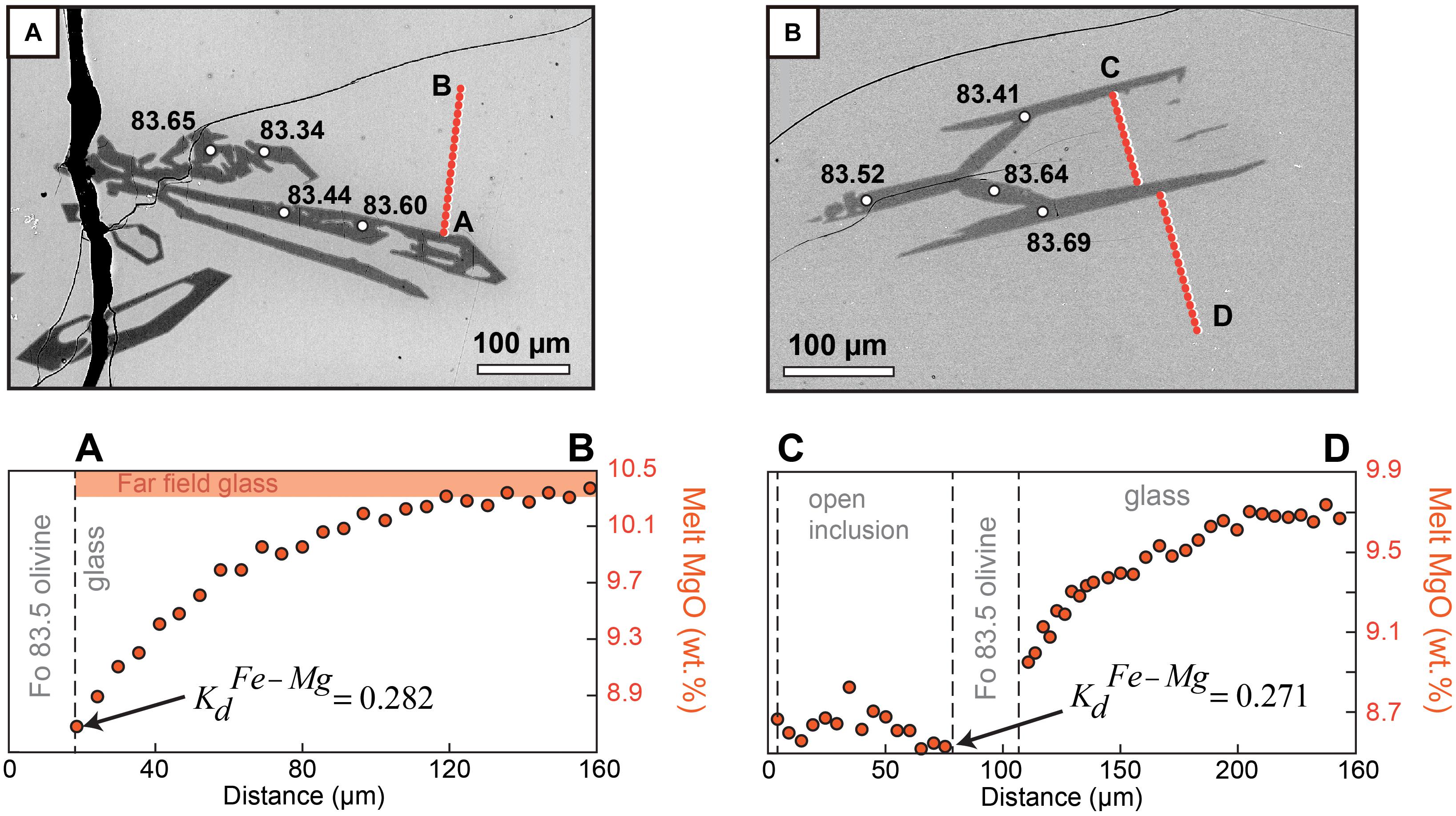
Figure 8. Influence of rapid olivine growth on Fe–Mg partitioning in a run performed at –ΔT = 60°C and 1.5 h dwell time at the final conditions. Transects A–B and C–D show the presence of boundary layers in Mg during diffusion-controlled growth (change of 1–2 wt.% between far field and interface) around two different crystals from the same charge. Values on the backscatter electron images give Fo content measured at different locations. Both (A) and (B) are around Fo83.5. Equilibrium Kd values range between 0.3 and 0.345 (Roeder and Emslie, 1970; Matzen et al., 2011). Rapid growth appears to cause the Kd to decrease to 0.27–0.28 mostly due to the lower Mg partition coefficient DMg (by contrast DFe does not vary significantly since boundary layers in Fe are much more subtle).
Origin of Skeletal Crystals
Previous experimental studies focusing on the formation of spinifex and dendritic olivine have shown that preferential elongation of olivine occurs either at low cooling rate of 1–5°C/h under a thermal gradient (spinifex, Faure et al., 2006) or at high cooling rates of 1639–2182°C/h (dendritic, Faure et al., 2007). The formation of dendritic olivine has also been explained as a competition mechanism between the growth of dendrites and the growth of the parental hopper crystals (Faure et al., 2003). Skeletal olivine morphologies with “stair-like” hopper cavities and elongated open glass inclusions parallel to the (010) and (021) faces form at moderate–high cooling rates (Faure et al., 2007) but the major parameter controlling the morphology is the undercooling (Faure et al., 2003). The formation of glass inclusions in phenocryst-sized skeletal olivine is experimentally enhanced by applying several cooling–heating cycles (Faure and Schiano, 2005). These results suggested that glass inclusions in natural olivine could form during cycles of magma convection (Colin et al., 2012). However, experiments from Ni et al. (2014) produced skeletal olivine in basaltic melt under static conditions, suggesting that convection is not essential to form these crystals. Here, we propose that the transition between skeletal to hopper crystals is directly related to the decrease of the undercooling with time, which can occur isothermally. The formation of natural hopper-to-skeletal phenocrysts such as those from Kīlauea (Shea et al., 2015b and this study) does not necessitate thermal convection but can result from sudden undercooling of 25–60°C and a maturation phase exceeding 18 h. This magnitude of undercooling can result from magma recharge and mixing, where the exact degrees of thermal and chemical (i.e., constitutional) undercooling depend on the temperature and chemical differences between mixing end-members (e.g., Lynn et al., 2017). Skeletal and hopper olivine elongated along the a-axis are frequently found in active effusive volcanoes like Stromboli (Metrich et al., 2010), Etna (Spilliaert et al., 2006), Piton de la fournaise (Welsch et al., 2013), mid-oceanic ridge pillow basalt (Colin et al., 2012), and Kīlauea (Figures 4F,G), where mixing processes are inferred to be common (Viccaro et al., 2006; Corsaro et al., 2009; Vinet and Higgins, 2010; Pioli et al., 2014; Shizimu et al., 2015; Lynn et al., 2017; Petrone et al., 2018; Sundermeyer et al., 2018). These observations support that mixing between cooler degassed magma with a hotter undegassed magma can promote rapid hopper/skeletal olivine crystallization and glass inclusion entrapment (Wallace and Anderson, 1998).
Updated Model for the Development of Skeletal Crystals
Based on observations of olivine morphology in natural samples from La Reunion, Welsch et al. (2013, 2014) proposed that the development of skeletal olivine involves the rapid propagation of primary branches along the [101] direction, leading to elongation of crystal units along the c-axis. The dominance of olivine elongated along the a-axis over crystals elongated along b or c-axis in our experiments suggests that faster growth along the b and c-axis may occur under different thermal histories, where thermal and/or compositional disequilibrium are lower or less abrupt. The decrease in growth rate along the a-axis with respect to other axes (Figure 5B) with decreasing undercooling agrees well with this scenario. Despite important differences in the direction of the main growth axes, our experiments agree with the inferred direction of primary branches proposed by Welsch et al. (2014) along the a–c plane. The rapid formation of an outer shell (a few minutes at −ΔT = 60°C) connected to these primary branches leads to entrapment of glass inclusions (Figure 3D). These large glass inclusions are then variably segmented by secondary branches originating from the primary structure without necessitating thermal fluctuations. The final stage is the complete isolation, along (010) and (021) faces, of round glass inclusions. The development of the primary branches seems closely linked to the growth of the (010) and (021) faces and the hexagonal shape of the cavities with the macro-steps described inside the crystal track the different secondary branches (Figures 9A,B). The propensity for olivine to readily develop this outer shell compared to other phases such as feldspar or pyroxene may partly explain why glass inclusions are abundant in olivine.
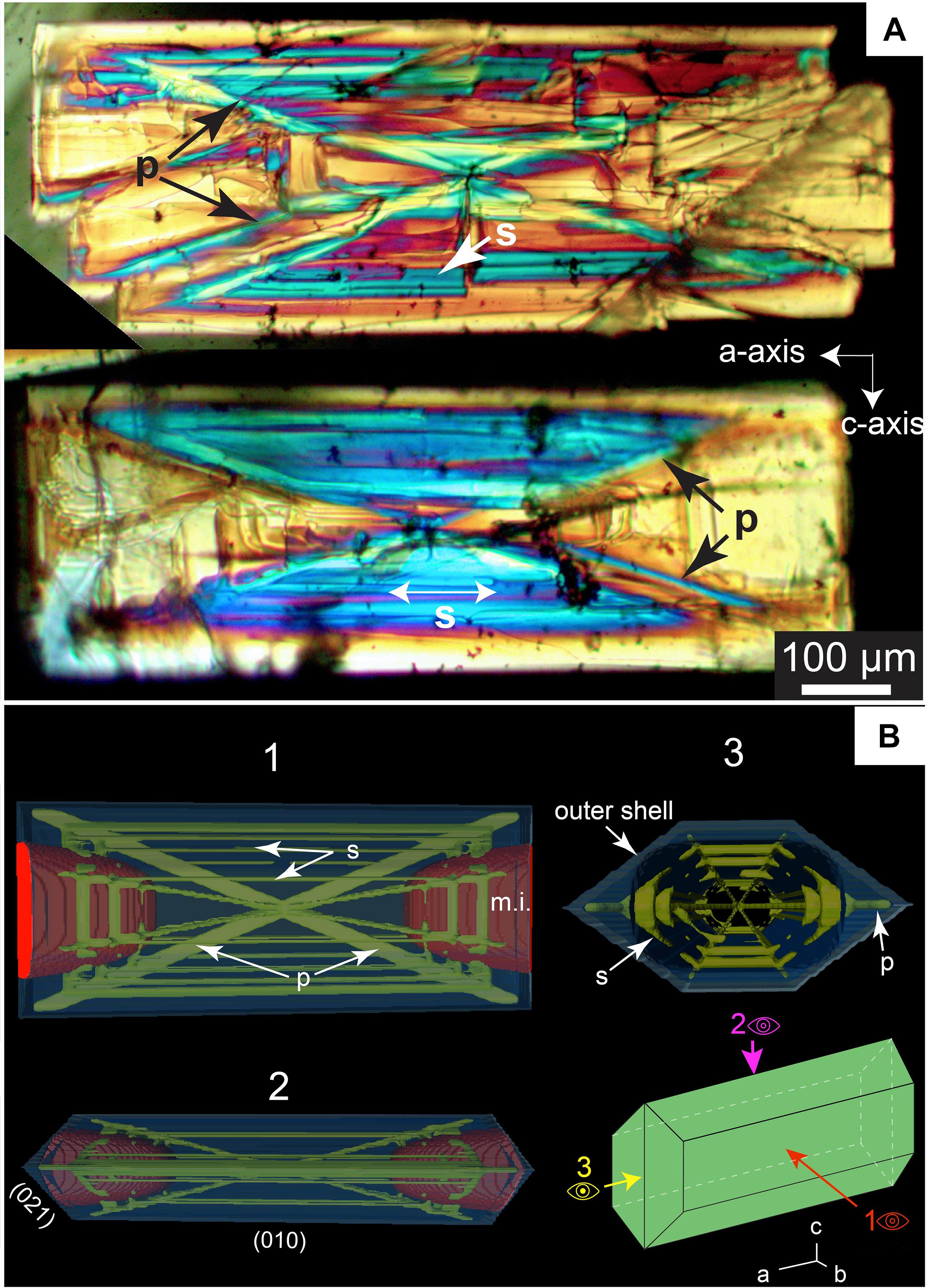
Figure 9. (A) Cross-polarized photograph of two skeletal olivine crystals elongated along the a-axis that crystallized in 45 min with 60°C of undercooling. The variation in the birefringence is associated here with variations in thickness; Primary (“p”) and secondary branches (blue regions, symbol “s” in the figure) are thicker than hourglass hopper cavities regions (in yellow, “m.i.” for melt inclusion in the figure). (B) 3D model of a skeletal crystal elongated along the a-axis with hour-glass inclusions representative of experimental crystals. The primary and secondary branches are distinguished from the outer shell. In this view, the outer shell traps the glass inclusions and the primary and secondary branches segment the melt pockets. The crystal infills and grows further along the b-axis during the maturation process.
Implications for Chemical Zoning in Olivine: Growth vs. Diffusion
The accuracy of timescales retrieved from diffusion modeling of chemical zoning patterns measured in natural crystals depends partly on the assumption that gradual compositional changes were not continuously acquired during crystal growth (Costa et al., 2008). Rapid growth is therefore an essential tenet of successful geospeedometry applications in the context of magmatic processes. This assumption can be tested rigorously by examining Fe–Mg isotopes in zoned olivine (e.g., Oeser et al., 2015) or by focusing on skeletal crystals that preserve multi-stage magma mixing histories (Shea et al., 2015b). In the latter study, it was proposed that if olivine crystallization commonly occurred through formation of initial diagonal branches, then any concentric zoning pattern would be the result of diffusion, not growth. The kinetic competition between growth and diffusion is therefore critical in resolving the issues of growth vs. diffusion-induced chemical zoning. Our results can be placed in this context by comparing the distances traveled during olivine growth with distances of element transport in olivine (Fe–Mg, Dohmen and Chakraborty, 2007; Li, Dohmen et al., 2010; Figure 10). Li is one of the fastest diffusing elements in olivine, and provides us with an upper limit for competing with growth rates. The calculations show that growth proceeds at a much faster pace than diffusion of Fe–Mg and Li on timescales of minutes to hours. Growth-induced zoning could occur during this period if the fraction of olivine crystallizing is significant enough to change the melt composition substantially. In the experiments, the low overall fractions crystallized (<10 vol.%) mean that little to no zoning in Fe–Mg occurs (e.g., Figure 7). Once growth rates slow down, diffusion progressively becomes an efficient mechanism to transport elements from rim toward the inside of a crystal. Thus, growth is likely to occur as rapid pulses during thermal and/or compositional perturbations (e.g., magma mixing), while diffusion should be responsible for most gradual compositional changes observed in erupted mineral cargo.
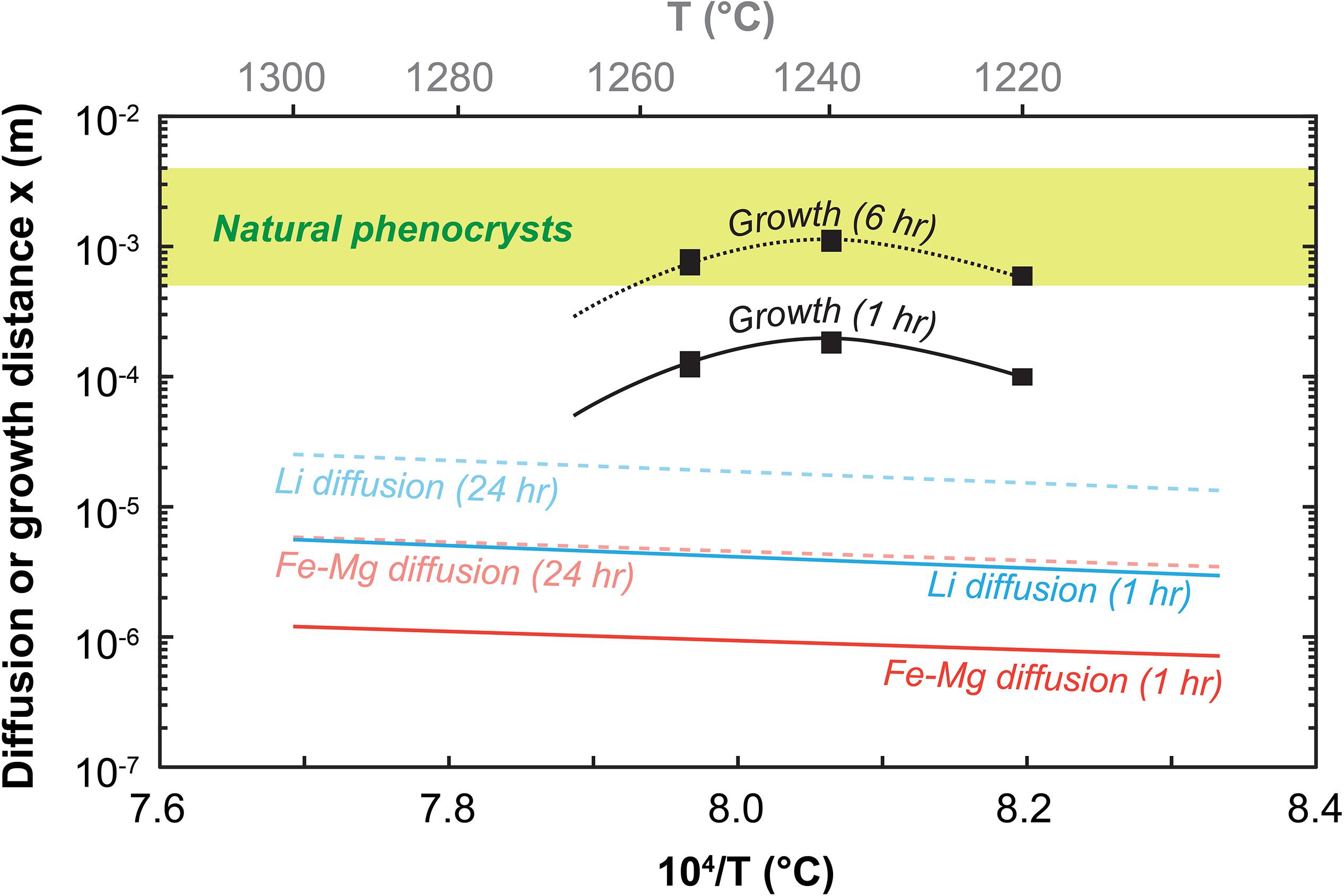
Figure 10. The early competition between growth and diffusion in olivine as a function of temperature. Distances attained after 1–6 h of olivine growth and 1–24 h of diffusion of Li and Fe–Mg are calculated as x = Gt with G the growth rate and x = , respectively [diffusivities from Dohmen and Chakraborty (2007) and Dohmen et al. (2010), see Supplementary Material for details, average and maximum growth rates are from this study and are bound by the black rectangular symbol thickness]. This comparison shows that the early history of an olivine – and therefore its chemical make-up – is dominated by growth. Diffusion is inefficient at these short timescales even for faster elements like Li. After ∼3–6 h, growth slows down (cf. Figure 6), near final crystal sizes are reached, and diffusion gradually becomes the dominant mechanism to induce or modify compositional zoning in olivine.
Applicability of Growth-Rate Results to Other Basalts
The growth rate data derived from the present study are most directly applicable to Kīlauea tholeiitic magmas, which are H2O-poor (<1 wt.%, e.g., Gerlach, 1986; Wallace and Anderson, 1998; Tuohy et al., 2016). This section addresses how the results may or may not be extrapolated to other basalt types (mid-ocean ridge basalt MORB, large igneous provinces LIP, wet arc basalt, komatiites).
Development of skeletal olivine morphologies likely occurs under the diffusion-controlled growth regime (e.g., Hammer, 2008; also see the section “Growth Mechanisms and Consequences for Element Partitioning in Olivine”). In this regime, diffusion of the main crystal-forming elements in the melt (Mg, Fe, and Si) toward the olivine interface controls the transition from polyhedral to skeletal growth. Since partitioning of Si and Fe between olivine and melt is not very far from unity, and they do not get depleted or enriched significantly in the boundary layer, growth rates may largely be determined by the mobility of Mg in the melt (e.g., Donaldson, 1975). Extrapolation of the present relationships between undercooling and growth regime to other basalt types will thus depend on whether Mg diffusivities are comparable. MORB, LIP, and Komatiite magmas are also H2O-poor; hence, Mg diffusivities depend mostly on temperature. Although their temperatures differ in the mantle, MORB and LIP are on average comparable to near surface Kīlauea basalt temperatures in the shallow crust (1100–1250°C, Fisk, 1984; Ho and Cashman, 1997; Thordarson and Self, 1998; Helz et al., 2014). Our growth rate results are therefore expected to apply there as well. On the other hand, Mg diffusion is likely much faster in hotter Komatiite melts (Green et al., 1975), meaning that the formation of boundary layers may require additional undercooling than the range applied for the Kīlauea basalt. Finally, element diffusivities in the melt also depend on water content. In wet arc basalts, addition of H2O in melts increases element diffusivity, meaning that diffusion-controlled growth and thus skeletal branching of olivine may be harder to achieve. While H2O-rich arc basalts tend to be colder than dry tholeiites, the effect of temperature on the magnesium diffusivity is apparently smaller than the effect of water [see Zhang et al. (2010) for a summary]. For instance, DMg = 7.3 × 10–12 m2/s at 1200°C for a dry basalt while DMg = 4.5 × 10–11 m2/s for the same basalt at 1050°C with 6 wt.% H2O (Zhang et al., 2010), suggesting that the addition of H2O is not compensated by a decrease in temperature. Nonetheless, skeletal olivine can be found in arc basalt, where additional undercooling may also incur due to decompression-induced degassing (e.g., Kuritani, 1999). Additional experiments are therefore required to test whether the degrees of undercooling required to initiate the diffusion-controlled growth regime and drive rapid growth are indeed higher in hydrous arc basalt, as would be predicted by these first order element diffusivity considerations.
Conclusion
Phenocryst-size olivine can form in a magma chamber a few hours after a thermal disequilibrium that can be readily induced by common magma mixing processes. Our experiments performed under low-to-moderate undercooling conditions (10–60°C) prove that it is possible to form skeletal and hopper olivine under isothermal conditions after an initial perturbation. Local thermal gradients or magma convection are not sine qua non-conditions for the development and maturing of phenocrystic olivine. Our results show that olivine growth is marked by the rapid development (a few hours) of an outer shell that enables the confinement of glass inclusions. Polyhedral olivine produced at lower undercooling (10 and 25°C) support the notion that relaxation of undercooling with time drives the transition between different crystal morphologies. 3D renderings of experimental charges showed that the development of olivine is a two-step process with preferential crystallization along the a-axis followed by maturation along the other axes. Natural olivine with low a-/b-ratios <5 presumably results from a protracted maturation period along the b-axis. Importantly, the order of magnitude difference between 2D and 3D growth rates illustrates the significance of considering the real complexities of olivine morphologies.
For moderate undercooling between 25 and 60°C, growth rates calculated for seed overgrowths (rims) are one order of magnitude lower than homogeneously nucleated crystals. The same thermal history in a magmatic chamber can lead to a large variation of growth rates for old and new cargo undergoing homogeneous nucleation and/or growth on existing crystals. The widespread occurrence of both olivine archetypes (elongated along c or a) in natural samples may therefore be associated with (1) their formation under a wide range of undercooling conditions and/or (2) the coexistence of both newly grown olivine (elongated along a) and olivine formed by multiple growth events where overgrowth rims are less prone to skeletal branching and elongation along a. Finally, the decrease in growth rate with undercooling at 60°C illustrates the importance of considering both nucleation and growth in yielding final crystal populations in magmas, where moderate undercooling (−ΔT = 40°C) may result in larger phenocrysts than high undercooling conditions.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
AM and TS carried out the experiments and microprobe analyses. AM led the writing of the manuscript and performed the 3D volume processing. Both authors contributed to the interpretations.
Funding
This work was supported by a National Science Foundation (NSF) grant to TS (EAR 1725321).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Jessica Maisano at the NSF-supported UTCT facility for assistance with the microtomography scans, and Emily First for help in the experimental lab. They also thank the reviewers and editor for the numerous insightful and constructive comments, which helped improve the original version of the manuscript significantly. The timeliness of the editorial and review process was greatly appreciated. This is SOEST contribution number 10842.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00300/full#supplementary-material
References
Armienti, P., Innocenti, F., Pareschi, M. T., Pompilio, M., and Rocchi, S. (1991). Crystal population density in not stationary volcanic systems: estimate of olivine growth rate in basalts of Lanzarote (Canary Islands). Mineral. Petrol. 44, 181–196. doi: 10.1007/BF01166962
Armienti, P., Pareschi, M. T., Innocenti, F., and Pompilio, M. (1994). Effects of magma storage and ascent on the kinetics of crystal growth. Contrib. Mineral. Petrol. 115, 402–414. doi: 10.1007/BF00320974
Avrami, M. (1939). Kinetics of phase change. I general theory. J. Chem. Phys. 7, 1103–1112. doi: 10.1063/1.1750380
Berg, W. F. (1938). Crystal growth from solutions. Proc. R. Soc. A 164, 79–95. doi: 10.1098/rspa.1939.0006
Borisov, A., and Jones, J. H. (1999). An evaluation of Re, as an alternative to Pt, for the 1 bar loop technique: an experimental study at 1400°C. Am. Mineral. 84, 1528–1534. doi: 10.2138/am-1999-1006
Brugger, C. R., and Hammer, J. E. (2010). Crystallization kinetics in continuous decompression experiments: implications for interpreting natural magma ascent processes. J. Petrol. 51, 1941–1965. doi: 10.1093/petrology/egq044
Clague, D. A., Moore, J. G., Dixon, J. E., and Friesen, W. B. (1995). Petrology of Submarine Lavas from Kilauea’s Puna Ridge, Hawaii. J. Petrol. 36, 299–349. doi: 10.1093/petrology/36.2.299
Clark, A. H., Pearce, T. H., Roeder, P. L., and Wolfson, I. (1986). Oscillatory zoning and other microstructures in magmatic olivine and augite: Nomarski interference contrast observations on etched polished surface. Am. Mineral. 71, 734–741.
Colin, A., Faure, F., and Burnard, P. (2012). Timescales of convection in magma chambers below the Mid-Atlantic ridge from melt inclusions investigations. Contrib. Mineral. Petrol. 164, 677–691. doi: 10.1007/s00410-012-0764-2
Corsaro, R. A., Civetta, L., Di Renzo, V., and Miraglia, L. (2009). Petrology of lavas from the 2004–2005 flank eruption of Mt. Etna, Italy: inferences on the dynamics of magma in the shallow plumbing system. Bull. Volcanol. 71, 781–793. doi: 10.1007/s00445-009-0264-z
Costa, F., Dohmen, R., and Chakraborty, S. (2008). “Timescales of magmatic processes from modeling the zoning patterns of crystals,” in Minerals, Inclusions and Volcanic Processes. RiMG 69, eds K. D. Putirka, and I. I. I. F. J. Tepley, (Chantilly, VA: Mineralogical Society of America), 545–594. doi: 10.2138/rmg.2008.69.14
Dohmen, R., and Chakraborty, S. (2007). Fe–Mg diffusion in olivine II: point defect chemistry, change of diffusion mechanisms and a model for calculation of diffusion coefficients in natural olivine. Phys. Chem. Mineral. 34, 409–430. doi: 10.1007/s00269-007-0158-6
Dohmen, R., Kasemann, S. A., Coogan, L., and Chakraborty, S. (2010). Diffusion of Li in olivine. Part I: experimental observations and a multi species diffusion model. Geochim. Cosmochim. Acta 74, 274–292. doi: 10.1016/j.gca.2009.10.016
Donaldson, C. H. (1975). Calculated diffusion coefficients and the growth rate of olivine in a basalt magma. Lithos 8, 163–174. doi: 10.1016/0024-4937(75)90023-7
Donaldson, C. H. (1976). An experimental investigation of olivine morphology. Contrib. Mineral. Petrol. 57, 187–213. doi: 10.1007/bf00405225
Donaldson, C. H. (1979). An experimental investigation of the delay in nucleation of olivine in mafic magmas. Contrib. Mineral. Petrol. 69, 21–32. doi: 10.1007/BF00375191
Faure, F., Arndt, N., and Libourel, G. (2006). Formation of spinifex texture in komatiites: an experimental study. J. Petrol. 47, 1591–1610. doi: 10.1093/petrology/egl021
Faure, F., and Schiano, P. (2005). Experimental investigation of equilibration conditions during forsterite growth and melt inclusion formation. Earth Planet Sci. Lett. 236, 882–898. doi: 10.1016/j.epsl.2005.04.050
Faure, F., Schiano, P., Trolliard, G., Nicollet, C., and Soulestin, B. (2007). Textural evolution of polyhedral olivine experiencing rapid cooling rates. Contrib. Mineral. Petrol. 153, 405–416. doi: 10.1007/s00410-006-0154-8
Faure, F., Trolliard, G., Nicollet, C., and Montel, J.-M. (2003). A developmental model of olivine morphology as a function of the cooling rate and the degree of undercooling. Contrib. Mineral. Petrol. 145, 251–263. doi: 10.1007/s00410-003-0449-y
Feldkamp, L. A., Davis, L. C., and Kress, J. W. (1984). Practical cone-beam algorithm. J Opt. Soc. Am. A 1, 612–619. doi: 10.1364/JOSAA.1.000612
Filiberto, J., Musselwhite, D. S., Gross, J., Burgess, K., Le, L., and Treiman, A. H. (2010). Experimental petrology, crystallization history, and parental magma characteristics of olivine-phyric shergottite NWA 1068: implications for the petrogenesis of “enriched” olivine-phyric shergottites. Meteorit. Planet. Sci. 45, 1258–1270. doi: 10.1111/j.1945-5100.2010.01080.x
First, E., and Hammer, J. E. (2016). Igneous cooling history of olivine-phyric shergottite Yamato 980459 constrained by dynamic crystallization experiments. Meteorit. Planet. Sci. 51, 1233–1255. doi: 10.1111/maps.12659
Fisk, M. R. (1984). Depths and temperatures of mid-ocean-ridge magma chambers and the composition of their source magmas. Geol. Soc. Lond. Spec. Pub. 13, 17–23. doi: 10.1144/gsl.sp.1984.013.01.02
Fowler, A. D., Stanley, H. E., and Daccord, G. (1989). Disequilibrium silicate mineral textures: fractal and non-fractal features. Nature 341, 134–138. doi: 10.1038/341134a0
Garcia, M. O. (2015). “How and why Hawaiian volcanism has become pivotal to our understanding of volcanoes from their source to the surface,” in Hawaiian Volcanoes: From Source to Surface, Geophysical Monograph, First Edn, eds R. Carey, V. Cayol, M. Poland, and D. Weis, (Washington, DC: American Geophysical Union), 208. doi: 10.1002/9781118872079.ch1
Garcia, M. O., and Hulsebosch, T. P. (1995). “Olivine-rich submarine basalts from the southwest rift zone of Mauna Loa volcano: implications for magmatic processes and geochemical evolution,” in Mauna Loa Revealed: Structure, Composition, History, and Hazards Geophysical Monograph, Vol. 92, eds J. M. Rhodes, and J. P. Lockwood, (Washington, DC: American Geophysical Union), 219–239. doi: 10.1029/GM092p0219
Garcia, M. O., Pietruszka, A. J., and Rhodes, J. M. (2003). A petrologic perspective of kõlauea volcano’s summit magma reservoir. J. Petrol. 44, 2313–2339. doi: 10.1093/petrology/egg079
Gerlach, T. M. (1986). Exsolution of H2O, CO2, and S during eruptive episodes at Kilauea volcano, Hawaii. J. Geophys. Res. 91, 12177–12185. doi: 10.1029/JB091iB12p12177
Green, D. H., Nicholls, I. A., Viljoen, M., and Viljoen, R. (1975). Experimental demonstration of the existence of peridotitic liquids in earliest archean magmatism. Geology 3, 11–14. doi: 10.1130/0091-761319753<11:edoteo>2.0.co;2
Hammer, J. E. (2008). Experimental studies of the kinetics and energetics of magma crystallization. Rev. Mineral Geochem. 69, 9–59. doi: 10.2138/rmg.2008.69.2
Helz, R. T., Clague, D. A., Sisson, T. W., and Thornber, C. R. (2014). “Petrologic insights intobasaltic volcanism at historically active Hawaiian volcanoes,” in Characteristics of Hawaiian Volcanoes, USGS Professional Paper 1801, Chap. 6, eds M. P. Poland, T. J. Takahashi, and C. M. Landowski, (Reston, VA: U.S. Geological Survey), 1–55. doi: 10.3133/pp1801
Helz, R. T., Cottrell, E., Brounce, M. N., and Kelley, K. A. (2017). Olivine-melt relationships and syneruptive redox variations in the 1959 eruption of Kīlauea Volcano as revealed by XANES. J. Volcanol. Geotherm. Res. 33, 1–14. doi: 10.1016/j.jvolgeores.2016.12.006
Herzberg, C. (2011). Basalts as temperature probes of Earth’s mantle. Geology 39, 1179–1180. doi: 10.1130/focus122011.1
Ho, A. M., and Cashman, K. V. (1997). Temperature constraints on the Ginkgo flow of the Columbia River Basalt group. Geology 25, 403–406.
Isaacson, P. J., Pieters, C. M., Besse, S., Clark, R. N., Head, J. W., Klima, R. L., et al. (2011). Remote compositional analysis of lunar olivine-rich lithologies with moon mineralogy mapper (M3) spectra. J. Geophys. Res. Atmos. 116:E00G11. doi: 10.1029/2010JE003731
Jambon, A., Lussiez, P., Clocchiatti, R., Weisz, J., and Hernandez, J. (1992). Olivine growth rates in a tholeiitic basalt; an experimental study of melt inclusions in plagioclase. Chem. Geol. 96, 277–287. doi: 10.1016/0009-2541(92)90059-E
Johnson, W. A., and Mehl, R. F. (1939). Reaction kinetics in processes of nucleation and growth. Trans. Am. Inst. Mining Metall. Petrol. Eng. 195:416.
Kirkpatrick, R. J. (1981). Kinetics of crystallization in igneous rocks. Mineral. Soc. Am. 8, 321–398. doi: 10.1515/9781501508233-012
Kuritani, T. (1999). Phenocryst crystallization during ascent of alkali basalt magma at Rishiri Volcano, northern Japan. J. Volcanol. Geotherm. Res. 88, 77–97. doi: 10.1016/s0377-0273(98)00105-x
Lasaga, A. C. (1982). Toward a master equation in crystal growth. Am. J. Sci. 282, 1264–1288. doi: 10.2475/ajs.282.8.1264
Lofgren, G. E., Donaldson, C. H., Williams, R. J., Mullins, O., and Usselman, T. M. (1974). Experimentally produced textures and mineral chemistry of Apollo 15 quartz normative basalts. Lunar Planet. Sci. Conf. 5, 549–568.
Lynn, K. J., Shea, T., and Garcia, M. O. (2017). Nickel variability in Hawaiian olivine: evaluating the relative contributions from mantle and crustal processes. Am. Mineral 102, 507–518. doi: 10.2138/am-2017-5763
Mangan, M. T. (1990). Crystal size distribution systematics and the determination of magma storage times: the 1959 eruption of Kilauea volcano, Hawaii. J. Volcanol. Geotherm. Res. 44, 295–302. doi: 10.1016/0377-0273(90)90023-9
Matzen, A. K., Baker, M. B., Beckett, J. R., and Stolper, E. M. (2011). Fe–Mg partitioning between olivine and high-magnesian melts and the nature of Hawaiian parental liquids. J. Petrol. 52, 1243–1263. doi: 10.1093/petrology/egq089
Metrich, N., Bertagnini, A., and Di Muro, A. (2010). Conditions of magma storage, degassing and ascent at Stromboli: new insights into the volcano plumbing system with inferences on the eruptive dynamics. J. Petrol. 51, 603–626. doi: 10.1093/petrology/egp083
Milman-Barris, M. S., Beckett, J. R., Baker, M. B., Hofmann, A. E., Morgan, Z., Crowley, M. R., et al. (2008). Zoning of phosphorus in igneous olivine. Contrib. Mineral. Petrol. 155, 739–765. doi: 10.1007/s00410-007-0268-7
Ni, H., Keppler, H., Walte, N., Schiavi, F., Chen, Y., Masotta, M., et al. (2014). In situ observation of crystal growth in a basalt melt and the development of crystal size distribution in igneous rocks. Contrib. Mineral. Petrol. 167:1003. doi: 10.1007/s00410-014-1003-9
Ody, A., Poulet, F., Bibring, J. P., Loizeau, D., Carter, J., Gondet, B., et al. (2013). Global investigation of olivine on Mars: insights into crust and mantle compositions. J. Geophys. Res. Planets 118, 234–262. doi: 10.1029/2012JE004149
Oeser, M., Dohmen, R., Horn, I., Schuth, S., and Weyer, S. (2015). Processes and time scales of magmatic evolution as revealed by Fe-Mg chemical and isotopic zoning in natural olivines. Geochim. Cosmochim. Acta 154, 130–150. doi: 10.1016/j.gca.2015.01.025
Pearce, J. A., and Cann, J. R. (1973). Tectonic setting of basic volcanic rocks determined using trace element analyses. Earth Planet Sci. Lett. 19, 290–300. doi: 10.1016/0012-821X(73)90129-5
Pearce, T. H. (1984). The analysis of zoning in magmatic crystals with emphasis on olivine. Contrib. Mineral. Petrol. 86, 149–154. doi: 10.1007/BF00381841
Petrone, C. M., Braschi, E., Francalanci, L., Casalini, M., and Tommasini, S. (2018). Rapid mixing and short storage timescale in the magma dynamics of a steady-state volcano. Earth Planet. Sci. Lett. 492, 206–221. doi: 10.1016/j.epsl.2018.03.055
Pioli, L., Pistolesi, M., and Rosi, M. (2014). Transient explosions at open-vent volcanoes: the case of Stromboli (Italy). Geology 42, 863–866. doi: 10.1130/G35844.1
Rhodes, J. M., and Vollinger, M. J. (2005). Ferric/ferrous ratios in 1984 Mauna Loa lavas: a contribution to understanding the oxidation state of Hawaiian magmas. Contrib. Mineral. Petrol. 149, 666–674. doi: 10.1007/s00410-005-0662-y
Roeder, P. L., and Emslie, R. F. (1970). Olivine-liquid equilibrium. Contrib. Mineral. Petrol. 29, 275–289. doi: 10.1007/bf00371276
Schiano, P., Provost, A., Clocchiatti, R., and Faure, F. (2006). Transcrystalline melt migration and earth’s mantle. Science 314, 970–974. doi: 10.1126/science.1132485
Shea, T., Costa, F., Krimer, D., and Hammer, J. E. (2015a). Accuracy of timescales retrieved from diffusion modeling in olivine: a 3D perspective. Am. Mineral. 100, 2026–2042. doi: 10.2138/am-2015-5163
Shea, T., Hammer, J. E., Hellebrand, E., Mourey, A. J., Costa, F., First, E., et al. (2019). Phosphorus and aluminum zoning in olivine: contrasting behavior of two nominally incompatible trace elements. Contrib. Mineral. Petrol. 174:85. doi: 10.1007/s00410-019-1618-y
Shea, T., Lynn, K. J., and Garcia, M. O. (2015b). Cracking the olivine zoning code: distinguishing between crystal growth and diffusion. Geology 43, 935–938. doi: 10.1130/G37082.1
Shizimu, K., Saal, A. E., Myers, C. E., Nagel, A. N., Hauri, E. H., Forsyth, D. W., et al. (2015). Two-component mantle melting-mixing model for the generation of mid-ocean ridge basalts: implications for the volatile content of the Pacific upper mantle. Geochim. Cosmochim. Acta 176, 44–80. doi: 10.1016/j.gca.2015.10.033
Spilliaert, N., Allard, P., Metrich, N., and Sobolev, A. V. (2006). Melt inclusion record of the conditions of ascent, degassing, and extrusion of volatile-rich alkali basalt during the powerful 2002 flank eruption of Mount Etna (Italy). J. Geophys. Res. 111:B04203. doi: 10.1029/2005JB003934
Sundermeyer, C., Di Muro, A., Techmer, K., Gordeychik, B., and Wörner, G. (2018). “Heritage and residence of olivines based on Fe-Mg diffusion from the August-November 2015 eruption at Piton de la Fournaise, La Réunion,” in Proceedings of the EGU General Assembly 2018, Vienna, 6194.
Swanson, S. E. (1977). Relation of nucleation and crystal-growth rate to the development of granitic textures. Am. Mineral. 62, 966–978.
Thordarson, T., and Self, S. (1998). The Roza Member, Columbia river basalt group: a gigantic pahoehoe lava flow field formed by endogenous processes? J. Geophys. Res. Solid Earth 103, 27411–27445. doi: 10.1029/98jb01355
Tuohy, R. M., Wallace, P. J., Loewen, M. W., Swanson, D. A., and Kent, A. J. R. (2016). Magma transport and olivine crystallization depths in Kilauea’s East Rift Zone inferred from experimentally rehomogenized melt inclusions. Geochim. Cosmochim. Acta 185, 232–250. doi: 10.1016/j.gca.2016.04.020
Turbell, H. (2001). Cone-beam Reconstruction Using Filtered Backprojection, Ph.D. thesis, Linköping University, Linköping.
Viccaro, M., Ferlito, C., Cortesogno, L., Cristofolini, R., and Gaggero, L. (2006). Magma mixing during the 2001 event at Mount Etna (Italy): effects on the eruptive dynamics. J. Volcanol. Geotherm. Res. 149, 139–159. doi: 10.1016/j.jvolgeores.2005.06.004
Vinet, N., and Higgins, M. D. (2010). Magma solidification processes beneath Kilauea volcano, Hawaii: a quantitative textural and geochemical study of the 1969-1974 Mauna Ulu lavas. J. Petrol. 51, 1297–1332. doi: 10.1093/petrology/egq020
Walker, D., Kirkpatrick, R. J., Longhi, J., and Hays, J. F. (1976). Crystallization history of lunar picritic basalt Sample 12002; phase-equilibria and cooling-rate studies. Geol. Soc. Am. Bull. 87, 646–656.
Wallace, P. J., and Anderson, A. T. Jr. (1998). Effects of eruption and lava drainback on the H2O contents of basaltic magmas at Kilauea Volcano. Bull. Volcanol. 59, 327–344. doi: 10.1007/s004450050195
Waters, L. E., and Lange, R. A. (2013). Crystal-poor, multiply saturated rhyolites (obsidians) from the Cascade and Mexican arcs: evidence of degassing induced crystallization of phenocrysts. Contrib. Mineral. Petrol. 166, 731–754. doi: 10.1007/s00410-013-0919-9
Watson, E. B., Cherniak, D. J., and Holycross, M. E. (2015). Diffusion of phosphorus in olivine and molten basalt. Am. Mineral. 100, 2053–2065. doi: 10.2138/am-2015-5416
Watson, E. B., and Müller, T. (2009). Non-equilibrium isotopic and elemental fractionation during diffusion-controlled crystal growth under static and dynamic conditions. Chem. Geol. 267, 111–124. doi: 10.1016/j.chemgeo.2008.10.036
Welsch, B., Faure, F., Famin, V., Baronnet, A., and Bachelery, P. (2013). Dendritic crystallization: a single process for all the textures of olivine in basalts? J. Petrol. 54, 539–574. doi: 10.1093/petrology/egs077
Welsch, B., Hammer, J., and Hellebrand, E. (2014). Phosphorus zoning reveals dendritic architecture of olivine. Geology 42, 867–870. doi: 10.1130/G35691.1
Wright, T. L. (1971). Chemistry of Kilauea and Mauna Loa lavas in space and time. U.S. Geological Survey Professional Paper 735. Washington, DC: United States Government Printing Office, 40. doi: 10.3133/pp735
Wright, T. L., and Klein, F. W. (2014). Two hundred years of magma transport and storage at Kīlauea Volcano, Hawai’i, 1790-2008. USGS Professional Paper 1806. Washington, DC: United States Department of the Interior, doi: 10.3133/pp1806
Keywords: olivine, growth rates, 3D morphology, diffusion, basalt
Citation: Mourey AJ and Shea T (2019) Forming Olivine Phenocrysts in Basalt: A 3D Characterization of Growth Rates in Laboratory Experiments. Front. Earth Sci. 7:300. doi: 10.3389/feart.2019.00300
Received: 24 July 2019; Accepted: 31 October 2019;
Published: 15 November 2019.
Edited by:
Teresa Ubide, The University of Queensland, AustraliaReviewed by:
Philipp Ruprecht, University of Nevada, Reno, United StatesTakeshi Kuritani, Hokkaido University, Japan
Silvio Mollo, Sapienza University of Rome, Italy
Copyright © 2019 Mourey and Shea. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adrien J. Mourey, YW1vdXJleUBoYXdhaWkuZWR1
 Adrien J. Mourey
Adrien J. Mourey Thomas Shea
Thomas Shea