Barbara Tripoli
Michael Manga
Jerome Mayeux1- 1Department of Earth and Planetary Science, University of California, Berkeley, Berkeley, CA, United States
- 2Advanced Light Source, Lawrence Berkeley National Laboratory, Berkeley, CA, United States
Crystals and bubbles nucleate and grow in a magma that experiences a range of temperatures, pressures and strain-rates. We have a good conceptual and sometimes quantitative understanding of how crystallization and bubble nucleation are controlled by decompression and cooling. Here we explore the effect of strain-rate on the crystallization kinetics of magmas. In order to understand the interaction between deformation and crystallization, samples of basalt were deformed during their crystallization. We made measurements at subliquidus conditions (1160°C) and deformed samples in compression at strain-rates varying from 0 to 2 × 10–4 s–1 for a total strain of 0.31. We simultaneously imaged the samples using X-ray micro-tomography. Without deformation, no crystallization was observed over the course of a 260 min experiment. Once deformation was applied, crystallization initiated. Deformation increased the nucleation rate, increased crystal growth rates, and decreased the incubation time. Increasing the strain-rate, however, does not show a discernable effect of crystallization kinetics. We hypothesize that deformation may have an effect on the parameters that govern the crystallization kinetics of magmas, such as activation energy and diffusion by changing chemical potentials.
Introduction
Considerable effort has been devoted to studying magma rheology in order to understand the transport of magma into and through the Earth’s crust and the eruptions of volcanoes. From magma reservoirs to Earth’s surface, magmatic liquids are subject to various deformation processes including shearing, extension and compression. The response of magma to this deformation is a function of intensive parameters (e.g., melt composition, crystal and bubble fraction) and extensive conditions (temperature, pressure) and has been widely studied (e.g., Shaw et al., 1968; Spera et al., 1988; Pinkerton and Stevenson, 1992; Caricchi et al., 2007; Cordonnier et al., 2009; Pistone et al., 2012). On the way to the surface, magmatic liquids also undergo textural and structural changes generated by depressurization, cooling and changes in oxygen fugacity leading to disequilibrium rheology (e.g., Giordano et al., 2007; Kolzenburg et al., 2016, 2017,2018a,b,c; Vetere et al., 2019) and crystallization (e.g., Arzilli and Carroll, 2013; Vetere et al., 2013, 2015). Crystals and bubbles thus nucleate and grow in a magma that experiences a range of temperatures, pressures and strain-rates.
We have a good conceptual and sometimes quantitative understanding of how crystallization and bubble nucleation are controlled by decompression and cooling. Since all magmas have deformed during their ascent, understanding if and why deformation affects their crystallization are relevant for relating observations in natural samples to those from laboratory experiments that only vary pressure, temperature and composition. The effect of deformation on the crystallization kinetics of basaltic magma has been studied experimentally at high strain-rates and strains (Kouchi et al., 1986; Vona and Romano, 2013; Kolzenburg et al., 2018b). Shear-enhanced crystallization can in some cases have a large effect on the evolution of rheology and hence magma and lava flow (e.g., Kolzenburg et al., 2018b).
Although flow-enhanced nucleation in polymer melts has been well-documented experimentally and probed with molecular simulations (e.g., Nicholson and Rutledge, 2019 for a recent review), fewer studies have been performed on silicate melts. Kouchi et al. (1986) deformed basaltic melts in torsion at a constant sub-liquidus temperature. By comparing the obtained microstructure with an undeformed sample, they noticed that the crystal nucleation rate is higher and that the nucleation incubation time is shorter in deformation experiments. The crystalline phases are small and acicular in all dynamic experiments performed at low undercooling, which is in contrast to the theory of the dependence of crystal morphologies upon undercooling (Lofgren, 1974; Kirkpatrick et al., 1979). Instead, we expect euhedral crystals at low undercooling and acicular crystals at high undercooling (e.g., Shea and Hammer, 2013; Pontesilli et al., 2019).
An increase in crystal growth rate was also observed in concentric cylinder experiments by Vona and Romano (2013) in basaltic melts, by Chevrel et al. (2015) in andesitic melts, and by Campagnola et al. (2016) in tephriphonolitic melts. The authors of these studies explained their results by the thinning of the diffusion boundary layer around the growing crystals. The induced flow in the silicate liquid facilitates the transport of elements close to the liquid/crystal interface and thus favors crystal growth by supplying to the crystal surface fresh liquid that has not been depleted of components compatible in crystalline phases. In these three studies, however, the samples were deformed using a concentric cylinder apparatus which promotes highly efficient advection. The role of other parameters influencing the crystallization kinetics, such as the activation energy, are thus difficult to assess.
Here we first review the equations governing the nucleation and growth rates of crystals in melts and their incubation time. Then we present new results on the crystallization kinetics of spinel and Fe-Ti oxides in basaltic melts undergoing deformation by unconfined uniaxial compression. The influence of strain-rate on crystal nucleation and growth is characterized in situ using X-ray micro-tomography.
Crystal Nucleation and Growth
The steady state nucleation rate J of crystals in melt follows an Arrhenius equation and its simplified form is:
where T is the temperature, KB is the Boltzmann constant, A is the pre-exponential term and E is the energy term. Although the equations used for calculating A and E differ in different studies, the parameters included in these equations are similar. The pre-exponential term A represents the transport of atoms to the crystal nuclei and includes the frequency of attachment attempts and the concentration of atoms in the vicinity of the nuclei (e.g., Hammer, 2008). Other studies include as well in the pre-exponential term A the energy at the interface between the nuclei and the melt σint (e.g., Fokin et al., 2006). The energy term E generally includes the activation energy necessary for the incorporation of atoms in the nuclei, the bulk free energy decrease driving crystallization, and the interfacial free energy between nuclei and the melt.
If the nucleus forms spontaneously in the melt, i.e., homogeneous nucleation, it needs to reach a certain critical size to grow further. Otherwise, it becomes unstable and collapses (e.g., Swanson, 1977). The time needed for these stable nuclei to form is called the incubation time and is calculated using (Fokin et al., 2007):
where ΔGv is the thermodynamic driving force for crystallization, a is a size parameter, D is the diffusion coefficient and σint is the interfacial energy between nuclei and melt.
The growth rate of crystals in silicate melts is limited by two main processes: the migration efficiency of compatible elements through the melt and their attachment efficiency to the crystal surface (Loomis, 1981). If the attachment rate is slower than the transport of elements in the melt, the growth rate G of crystals is “interface-controlled” and the equation takes a form similar to the nucleation rate:
As for the nucleation rate, the pre-exponential term B represents the transport of atoms across the crystal-melt interface and includes the frequency of attachment attempts, the thickness of the molecular layer, and the fraction of sites available for attachment on the crystal surface (Kirkpatrick, 1975). If the migration of elements is slower than the attachment rate, the growth rate of crystals is “diffusion-controlled” and scales as:
where t is time and k is a constant (Müller-Krumbhaar, 1975).
Materials and Methods
In order to study the effects of deformation on the crystallization of magmas, we used a high temperature deformation apparatus developed at the Advanced Light Source, Lawrence Berkeley National Laboratory (Figure 1). This hot cell has been designed to image samples using X-ray micro-tomography during mechanical loading (maximum force of 2.2 kN) at temperatures up to 2300°C (Haboub et al., 2014). Six infrared halogen lamps are symmetrically arranged to focus light, and thus heat, in the central part of the chamber, where samples are held between two water-cooled grippers. The combination of the focused heat and the cooling system produces a hot zone on the sample of approximately 8 mm length, with the central 5 mm having a constant temperature. As the heat absorption of the sample depends on the sample’s surface properties, temperature calibration for different applied lamp currents was performed by placing a K-type thermocouple in the middle of the hot zone of our selected basaltic samples. Our experiments complement direct observations of crystallization in basalt made using 4D X-ray microtomography (Polacci et al., 2018) and imaged optically in a moissanite cell (Schiavi et al., 2009; Ni et al., 2014) by documenting the effects of deformation.
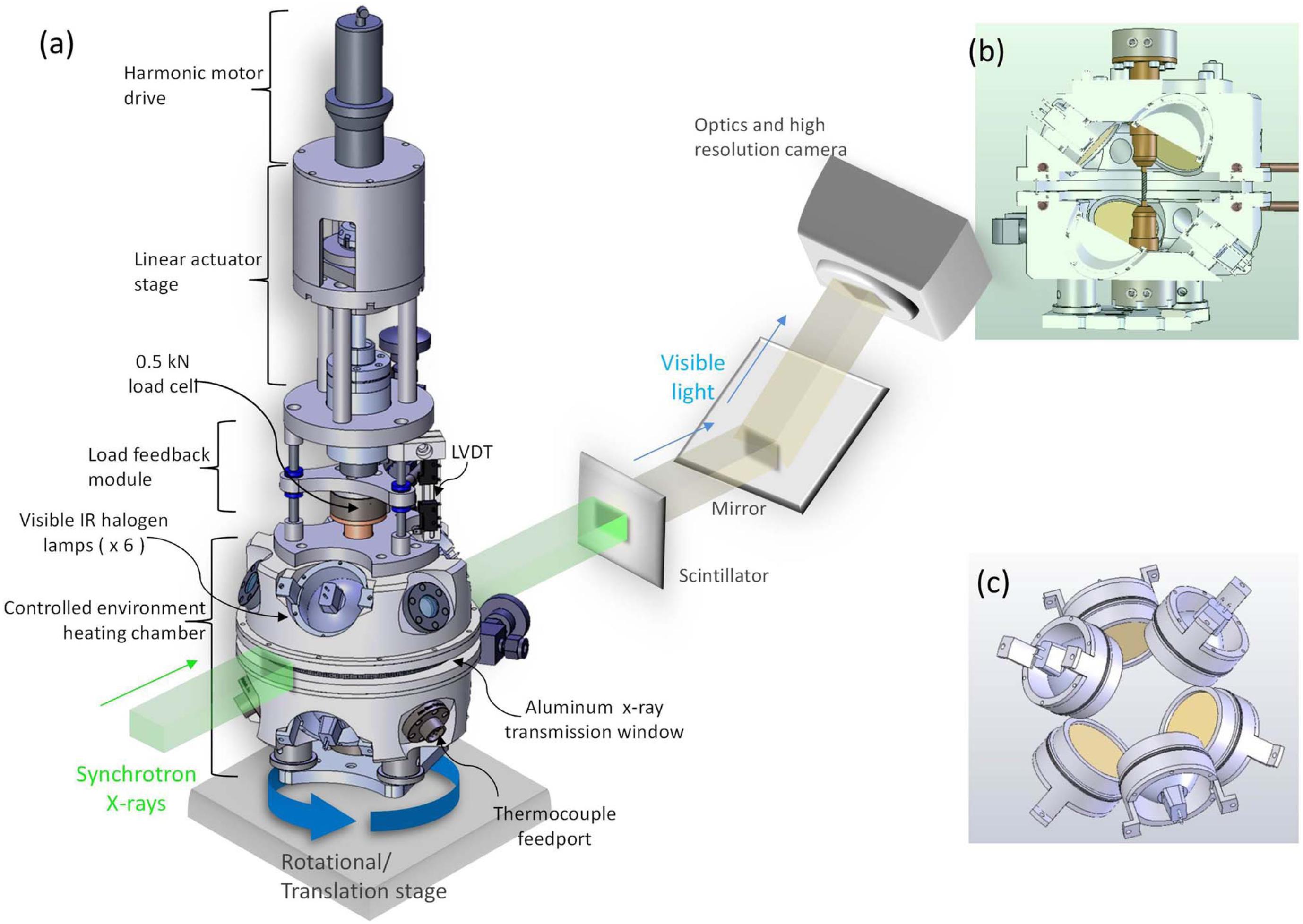
Figure 1. Drawing showing the deformation apparatus developed by Haboub et al. (2014). (a) Complete view of the apparatus placed on a rotation and translation stage for X-ray micro-tomography. (b) Cross section through the heating chamber. Diameter of the cylindrical X-ray transmission window in a (and shown in b) is 15 cm. (c) View of six halogen lamps positioned around the heating chamber. Reprinted from Haboub et al. (2014), with the permission of AIP Publishing.
The sample selected for this study is the mid-Miocene Lovejoy basalt, the product of a large flood eruption in Northern California (Garrison et al., 2008). Its homogeneous composition and nearly aphyric texture favor the in situ melting of its microlites of plagioclase, olivine, pyroxene and iron oxides (Figure 2B). Five cylindrical cores of 30 mm length and 3.42 mm diameter were drilled and their extremities were cut perpendicular to the long axis and polished. As a first step, we melted the central part of the cored samples in the hot cell. The temperature was first increased up to 1000°C at a rate of 200°C/min, then from 1000 to 1250°C at a rate of 4°C/min, and finally held for 30 min at 1250°C. We selected this method to remove crystals for two main reasons: (1) Drilling a long and thin core in glass as well as obtaining a large amount of basaltic glass free of crystals are difficult to achieve; (2) Longer times at 1250°C were not possible as the melt would flow downward under the influence of gravity and separate from the upper part of the sample (Figure 2A). These times should be long enough for at least local chemical heterogeneity to be removed. Following the 30 min at 1250°C, the sample was rapidly quenched by powering down the lamps. After this first step, the melted zone measured 8 mm in length and contained a volume fraction of 0.02 (± 0.01) of spinel and less than 0.01 of iron oxides. No quenched microlites were observed in Secondary Electron Microscopy images (Figure 2C).
Figure 2. (A) Cores of the Lovejoy basalt before (on the left) and after (in the middle) the melting phase at 1250°C. The core on the right is an example of a melt separating from the top part due to its lower viscosity at higher temperature. (B) SEM images of the Lovejoy basalt before the melting phase. (C) SEM images of the Lovejoy basalt showing the structure of the zone melted at 1250°C. Cpx: clinopyroxene; Grd: groundmass; Plag: plagioclase; Ol: olivine.
During the second step, these melted samples of basalt were deformed during their crystallization. We selected a temperature of 1160°C in order to image the crystallization of spinel and oxides, minerals that we could reliably image because their density is higher than the melt. Indeed, at temperatures lower than 1160°C, the crystallizing phase, i.e., plagioclase, is not readily distinguishable from the melt due to its similar density (e.g., Arzilli et al., 2015). Using the high temperature deformation apparatus, we deformed four samples in compression at four different strain-rates: 2 × 10–5, 6 × 10–5, 1 × 10–4, and 2 × 10–4 s–1. After every 500 μm of displacement, we quenched the samples to room temperature by powering off the lamps, which permitted a cooling rate reaching 50°C/s between the investigated temperature (1160°C) and the glass transition (678°C). We then imaged the cores using X-ray micro-tomography (XRT) (see Supplementary Material S.A. for details). We used monochromatic X-rays with energies of 33 kev and a voxel linear dimension of 1.28 microns. As the time required to scan the sample was about 15 min, we decided to not image the sample at high temperature as any bubbles move upward and additional crystallization may occur during the scans – any motion of a few pixels creates image artifacts. After each scan, the sample was reheated rapidly by switching the lamps back on with heating rates reaching approximately 50°C/s. This cycle, involving a sequence of heating, deforming, quenching and scanning the sample, was repeated five times until the total strain reached 0.31. This total strain corresponds to the ratio of the five applied deformations (total of 2.5 mm) to the hot zone length (8 mm). Experiments at higher strains were not performed in order to avoid the accumulation of stress located near the interface between the melted and the unmelted parts of the sample (Mogi, 2007). Although a load cell records the applied stress (Figure 1), the viscosity of our samples is so low that instrument noise prevents us from measuring rheology on these samples. In order to characterize the crystallization at static conditions, one sample was held at 1160°C without applying any deformation. This sample was quenched for XRT imaging every 52 min, which corresponds to the time elapsed during one deformation step at the lowest strain rate. The total duration at 1160°C was 260 min.
The obtained XRT images were first segmented for spinels, Fe-Ti oxides and melt using the Fiji plugin Trainable Weka Segmentation (Arganda-Carreras et al., 2017). We then used the volume obtained from these XRT images for measuring the number densities and the volume fractions of Fe-Ti oxides and spinels using the Fiji plugin Particle Analyzer within BoneJ (Doube et al., 2010).
After the experiments, samples were cut horizontally through the hot zone and embedded in epoxy for chemical analyses. The composition of the minerals and their surrounding melts, i.e., within 25 μm distance, were measured using a Scanning Electron Microscope (SEM) located in the Department of Earth Sciences, at ETH Zurich (Switzerland). In order to determine the stable mineral assemblage at these P-T conditions, we repeated the same temperature sequence on the sample of basalt in a high temperature furnace and kept the sample at 1160°C without deforming it for 65 h, corresponding to an amount of time significantly long to more closely reach equilibrium. After quenching, this sample was then imaged using X-ray microtomography. The measurement parameters of energy beam, resolution and exposure time, as well as the image processing, were kept the same as during the deformation experiments. These results were then compared to the mineral assemblage estimated by thermodynamic calculations using MELTS (Gualda et al., 2012) at a temperature of 1160°C and atmospheric pressure and fO2 (see Table 1 and Supplementary Material S.B. for more details).
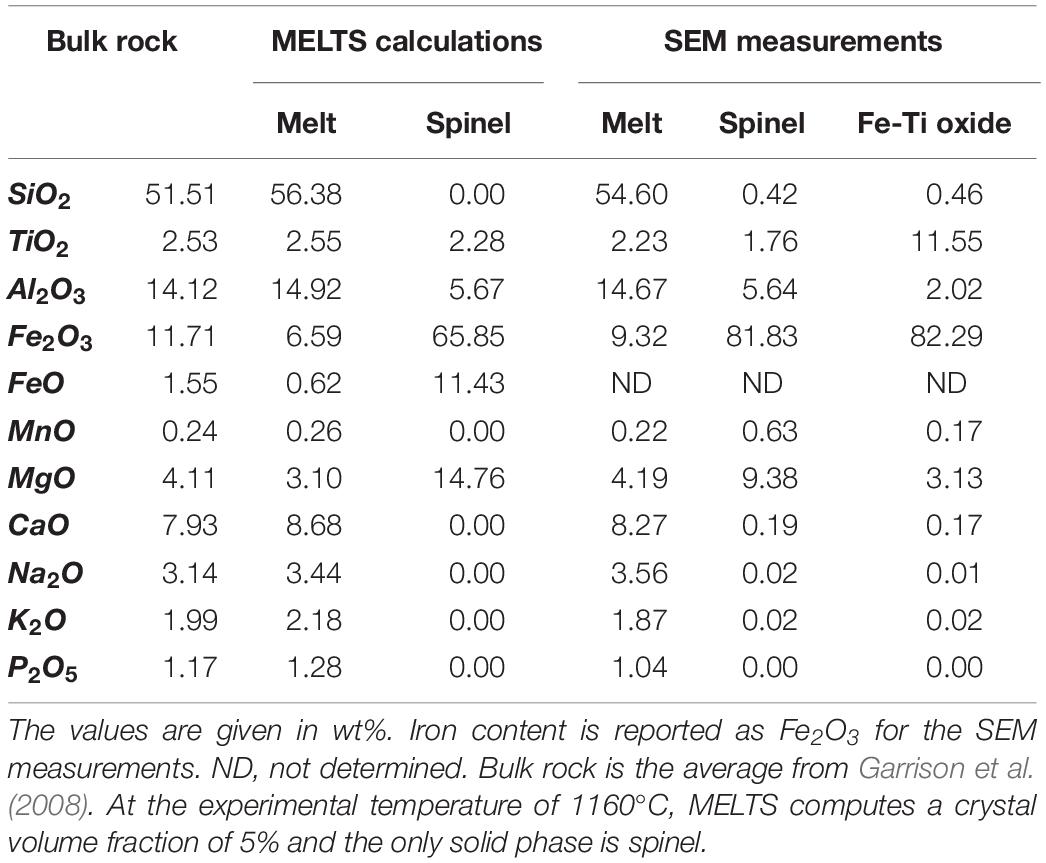
Table 1. Composition of the crystals and the residual melt of the Lovejoy basalt modeled by MELTS (Gualda et al., 2012) and measured by Secondary Electron Microprobe (SEM).
The main advantage of the micro-tomography experiments is that the imaging is non-destructive and hence we can document the progression of nucleation and crystal growth on the same samples in a device that also allows us to apply deformation. Further the crystals are characterized in three dimensions. There are also disadvantages. First, the spatial resolution of the microtomography is lower than SEM or Transmission Electron Microscopy images, and nucleation by definition begins at small scales. Second, because the density of the dominant mineral, plagioclase is so similar to the melt, we are only able to document the first phases that crystallize at the highest temperatures, limiting the temperatures and crystallizing phases we could explore. Third, the finite time available for imaging and the requirement that the sample not flow too fast under the influence of gravity, further limit the range of compositions and temperatures that we could consider.
Results
Under static conditions there was no additional crystallization during the 260 min experiment. The spinel and iron oxide fractions and number densities remain constant throughout the experiment. By increasing the strain-rate up to 1.0 × 10–4 s–1, within 50 min crystallization occurs on preexisting surfaces, such as bubbles and crystals, as noted by Pleše et al. (2018), and in the melt, where no preexisting surfaces were visible. Number densities and volume fractions of both crystal phases increase rapidly after 50 min (Figure 3 and Table 2). After 50 min of deformation, spinel number density stays constant and amounts to 17 (± 1) × 103 mm–3. Their volume fraction reaches a constant value of 0.08 (± 0.01) after 150 min (slightly larger than the MELTS equilibrium value of 0.05). The Fe-Ti oxide number density continuously increases up to 6 (± 1) × 103 mm–3 and their volume fraction reaches a constant value of 0.016 (± 0.002) after 50 min.
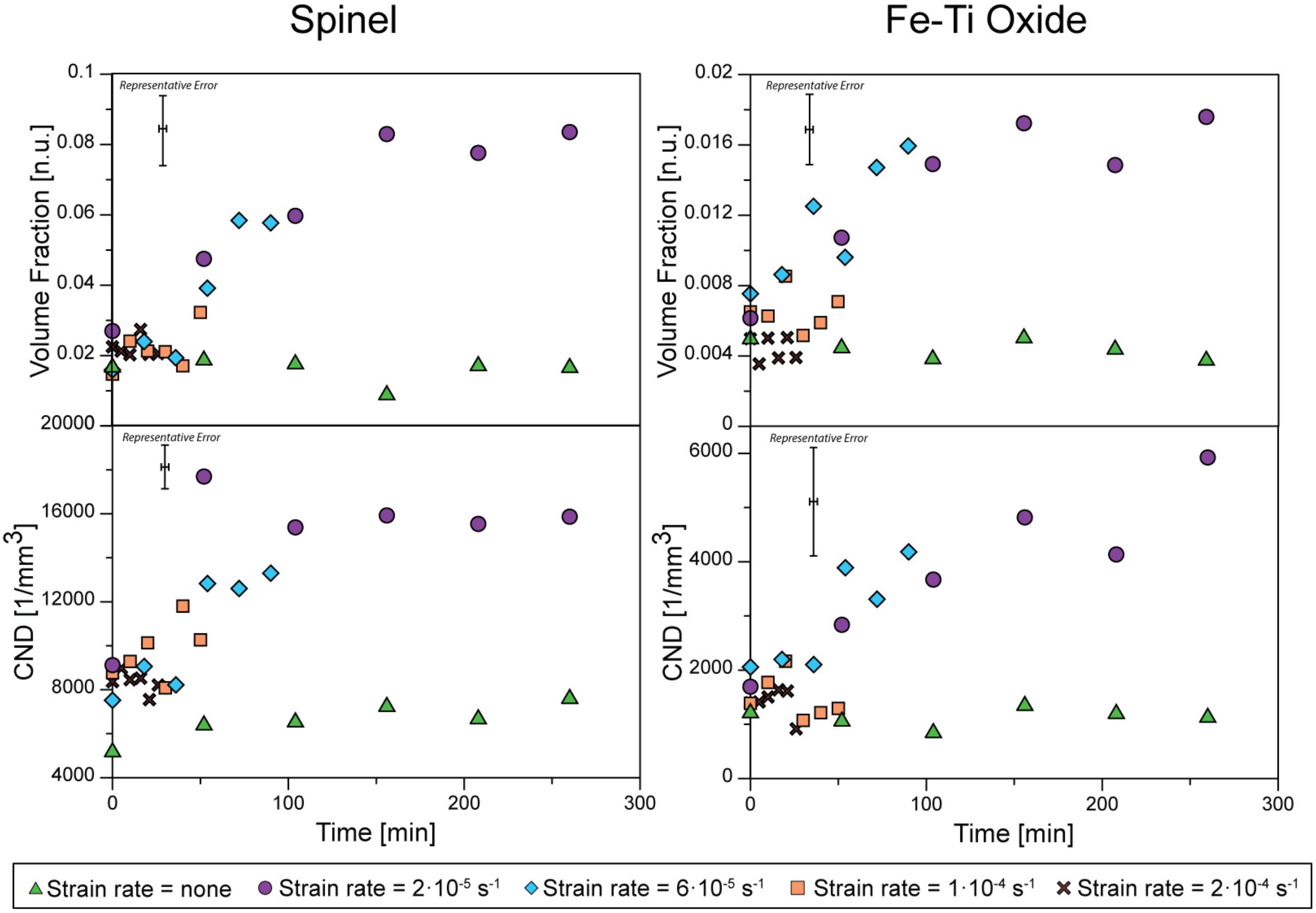
Figure 3. Microstructure evolution of the spinel (on the left) and Fe-Ti oxide (on the right) determined using the XRT images. The volume fraction and the crystal number density (CND) are plotted for each strain rate applied during the experiments.
Table 2. Summary of the experiments.
In our experiments, varying the strain-rate during deformation has no clear effect. Indeed, the increase in number densities and volume fractions of the lower strain-rate experiments are similar, i.e., the measured values for different strain-rates are within the error bars during crystallization (Figure 3). All dynamic experiments with a duration over 50 min have newly formed crystals. At the highest strain-rate (2.0 × 10–4 s–1), no additional crystallization is observed after reaching the highest crystallinity. However, as the total strain applied in all experiments was kept constant (0.31), the experimental time for the sample deformed at 2.0 × 10–4 s–1 was only 26 min and thus did not reach the 50 min required for crystallization under deformation in the other experiments.
The sample left for 65 h at 1160°C contains a spinel volume fraction of 0.05 and no iron oxide. Thermodynamic calculations using MELTS predicts the same fraction of spinel (Supplementary Material), i.e., 0.05, having a composition similar to the one measured by SEM (Table 1), and no iron oxide. We can thus assume that the thermodynamic equilibrium assemblage for this basalt at 1160°C and atmospheric pressure and fO2 is composed uniquely of spinel at a volume fraction of about 0.05. As this spinel fraction is higher than the spinel fraction in the undeformed sample, we can also assume that the incubation time under static conditions is longer than 260 min.
The newly formed spinels are recognized from older ones by their shape. The spinels grown during deformation are platy (white crystals in Figure 4A) whereas those already present have a vermiform structure (colored crystals in Figure 4A). The spinels grown during the 65 h static experiment have more commonly an octahedral shape.
Figure 4. Images displaying features associated with the spinels. (A) 3D reconstruction, performed using Dragonfly software, of newly formed spinel (in white) and already present spinel (in red) in the sample deformed at 2 × 10–5 s–1 at t = 260 min. The different colors represent the aspect ratio of the crystals and are used here only for visualization purposes. (B) Elongated spinel crystals nucleated during deformation [white crystals in panel (C)] and vermicular spinel crystals already present [colored crystals in panel (C)] grew during deformation and have an aureole of microlite-free melt visible in SEM images.
Secondary Electron Microscopy on the recovered samples reveals some features not observable during X-ray imaging. During the second step of the experiments, iron-rich microlites with a diameter of less than 1 μm (are assumed to) form in the melt during quenching (e.g., Zhou et al., 2000). The resolution of 1.28 μm prevents us from recognizing these features during the X-ray imaging. Interestingly, we observe in the deformed samples the presence of a microlite-free zone around the crystals (Figure 5) in addition to the depletion of iron around newly formed crystals.
Figure 5. SEM images of the samples recovered after the deformation experiment. Elongated spinel crystals nucleated during deformation or vermicular spinels grown during deformation have an aureole of microlite-free melt visible in SEM images. (A) Phenocrysts of spinels in the sample deformed at 2 × 10–5 s–1 and its groundmass (B). (C) Phenocrysts of spinels in the sample deformed at 6 × 10–5 s–1 and its groundmass (D). (E) Phenocrysts of spinels in the sample deformed at 1 × 10–5 s–1 and its groundmass (F). (G) Phenocrysts of spinels in the sample deformed at 2 × 10–4 s–1. (H) Phenocrysts of spinels in the undeformed sample. In panels (G,H), no aureole of microlite-free melt is visible.
Discussion
Our experiments were performed over time scales comparable to the incubation time, allowing us to document the effects of deformation on incubation, nucleation rates, and crystal growth. Our results show that deformation has an effect on the crystallization kinetics of magmas by (1) increasing the nucleation rate (variation in CND), (2) increasing the growth rate (variation in crystal fraction) and (3) decreasing the incubation time (corresponding to 50 min under dynamic conditions and more than 260 min under static conditions). Our experiments confirm that deformation affects crystallization in basaltic melts, not just for large strains and strain-rates where advection is important (Kouchi et al., 1986; Vona and Romano, 2013; Kolzenburg et al., 2018b).
Each parameter used in the nucleation and growth models (Eq. 1–4) is assessed to understand the potential origins of the observed variations.
Possible Origins of Deformation-Induced Crystallization
During our crystallization experiments, the temperature is held constant. The difference in nucleation rate between the deformed and undeformed samples must thus be linked to A and/or E. Previous studies proposed that A increases during deformation because there is a higher flow of elements to the crystal-melt interface (Kouchi et al., 1986; Vona and Romano, 2013; Kolzenburg et al., 2018b). In this case, deformation favors chemical homogenization of the melt. However, our deformed samples display a zone around the newly formed crystals which is depleted in iron, i.e., a zone that is free of quenched microlites (Figure 4). As the undeformed sample did not further crystallize during the experiment and does not present any aureole of microlite-free melt around its crystals, we interpreted this feature as the diffusion boundary layer depleted in iron. Kouchi et al. (1986) observed that the thickness of the boundary layer decreased with increasing deformation rate. This discrepancy between our and their observations might be linked to the experimental method employed. Previous studies considered much larger strain-rates and strains (Kouchi et al., 1986; Vona and Romano, 2013; Kolzenburg et al., 2018b) which would increase the advection efficiency. In our compression experiments, the concentration of reactant atoms is not increased by deformation.
Another possibility involves a variation in the energy state of the system. Minimization of the Gibbs free energy can be used to establish phase equilibria at fixed temperature and pressure using changes in state functions of a system, such as enthalpy and entropy, and/or intensive properties, such as chemical potentials and activities (Ghiorso and Sack, 1995). Since the local description of chemical equilibrium at an interface can be modified by stresses
where μ is the chemical potential, F is the Helmholtz free energy, σn is the normal stress across the interface and V is the molar volume, variations in stress may also change properties such as diffusion and mineralogy that are influenced by chemical potential (e.g., Wheeler, 2017).
The rate of a chemical reaction is influenced by the concentration of the reactant molecule and the activation energy, i.e., the minimum energy required to start a chemical reaction. For crystallization, the activation energy is better defined as the energy barrier that must be overcome to produce a stable crystal nucleus. Molecules commonly absorb thermal energy to overcome this barrier. In the case of crystallization from melt, this energy is used to rearrange, break and/or build bonds in the chains of silica tetrahedra present in the melt (Kirkpatrick, 1983) and when the less energetic, more stable crystal nucleus is formed, energy is released in the form of latent heat of crystallization.
Stress may help molecules overcome the activation energy. Indeed, the activation strain model states that the activation energy can be decomposed into the energy associated with the structural deformation undergone by the reactant molecules, i.e., strain energy, and the energy resulting from the bonding of these molecules, i.e., interaction energy (Van Zeist and Bickelhaupt, 2010; Fernández and Bickelhaupt, 2014). An applied stress during melt deformation may thus bring strain energy into the system and helps to distort and/or disrupt chains of silica tetrahedra that ultimately favor the formation of crystal nuclei. A decrease in activation energy during deformation-induced crystallization has been observed in various type of material such as polymers (Sun et al., 1984; Chien and Weiss, 1988; Kumaraswamy et al., 1999; Xu et al., 2011), metal alloys (Lee et al., 2006; Wang et al., 2015), oil and butter (Yang et al., 2011), and metals (e.g., Donovan and Stobbs, 1981; Chen et al., 1994) and might explain impact-induced vesiculation of magmas (Rothery et al., 2007; Carey et al., 2012).
The activation energy is present in the energy term of Eqs. (1) and (3) and thus influences nucleation and growth rates. However, we observed as well a decrease in incubation time for crystallization in our experiments. Variations in the normal stress on interfaces produced by deformation give rise to gradients in chemical potential (Eq. 5), and can promote diffusion (Eqs. 2, 4), in turn increasing both the nucleation rates and decreasing the incubation time. The diffusion coefficient can be calculated using the Arrhenius relation , where E is the activation energy for diffusion and D0 is the diffusion coefficient at high temperature where KBT >> E (Zhang, 2010). The crystallizing phases in our experiments contain Fe, Mg, Ti and Al (Table 1) and their activation energy for diffusion in basaltic melts are 264 ± 17 kJ/mol (Lowry et al., 1982), 240 ± 20 (Chen and Zhang, 2009), 255 ± 86 and 313 ± 26 kJ/mol [determined by Zhang (2010) from data produced by Chen and Zhang (2009)], respectively. Burkhard (2005) determined the activation energy for the nucleation and the growth of Fe-Ti oxides in basaltic melt and their values, i.e., 292 and 343 (± 7) kJ/mol, respectively, are particularly close to the activation energy for diffusion. We may thus assume that strain energy provided during deformation was sufficient to promote a higher diffusivity of elements by the same mechanism presented before, i.e., distortion and/or breaking of chains of silica tetrahedra.
Variation in the Mineral Assemblage
Our studies, combined with previous studies, show that deformation increases nucleation and growth rates and reduces the incubation time of crystals in silicate melts. In addition, we observed the growth of Fe-Ti oxides that did not disappear during the melting phase of the sample preparation as well as the nucleation of new crystals of the same composition. These Fe-Ti oxides are not present in the sample left 65 h at 1160°C and are not predicted by thermodynamic modeling using MELTS. This suggests that deformation might also promote the formation of metastable phases that leads to kinetic-controlled crystallization, rather than only the thermodynamically favored phases (e.g., Woodward and Baer, 1944; Cölfen and Mann, 2003). In this case, the activation energy for the nucleation of the metastable phase needs to be lower than the activation energy of the stable phase. As no Fe-Ti oxides crystallized in the undeformed samples, deformation may be the external factor lowering activation energy for crystallization of metastable and stable phases by changing the chemical potential of the various interfaces present (Eq. 5). Our experiments, however, do not document an effect of the metastable phases on stable phases.
Implications for Natural Samples
The texture (mineralogy, crystal shape and number density) of erupted magmas are commonly used to infer ascent dynamics by comparing natural samples with those created experimentally (e.g., Castro and Dingwell, 2009; Brugger and Hammer, 2010; Riker et al., 2015 for some examples). Our findings that deformation changes the mineralogy, growth rate, and number density imply that an additional variable may need to be considered when connecting lab studies and natural samples. In some cases, the deformation-enhanced growth and nucleation of crystals (here over several 10 s of minutes) may be negligible compared to those produced by the large changes in pressure that accompany rapid ascent. However, in lava flows where pressure changes are small, deformation may play a relatively greater role in promoting crystallization and natural strain-rates are typically much larger than those we considered. For the basalt we considered, for example, in 260 min the static sample did not change crystallinity but does approach a different steady value of about 10% after several 10 s of minutes in the presence of deformation. Our experimental apparatus and imaging constraints limited the range of strain-rates, temperatures and compositions we could study. Further experimental and theoretical analyses may lead to a better quantification of the role of deformation and thus identify when and how deformation affects the interpretation of natural samples.
Conclusion
Deformation enhances the crystallization kinetics in magmas. Based on X-ray images collected during the experiments, we observed that the nucleation and growth rates of spinels and Fe-Ti oxides increase when deformation is applied to a basaltic melt. A decrease in the incubation time is also observed during deformation. These changes in the crystallization kinetics upon deformation do not depend on the strain rate, at least for the temperatures and range of strain rates investigated. We suggest that the applied stress helps the system to overcome the activation energy involved in crystallization kinetics and in diffusion of elements by changing chemical potentials. Models might be tested in the future by exploring a broader range of temperatures, achieving greater spatial resolution in the imaging, finding approaches to image low absorption contrast minerals, and considering a longer spectrum of time scales.
Data Availability Statement
All datasets for the plots in this paper are included in the manuscript.
Author Contributions
BT conceived the study and acquired, analyzed, and interpreted the data. MM acquired and interpreted the data. JM acquired and analyzed the data. HB acquired the data.
Funding
The authors acknowledge the financial support of the Swiss National Science Foundation (grant P2EZP2_162226) with additional support from the US NSF EAR 1615203.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Dilworth Parkinson and Kristen Fauria for their instructions and recommendations for tomography analyses at the Advanced Light Source and Eric Reusser and Lukas Martin for their help using the SEM at ETHZ. We also thank the ALS for providing many days of beamtime between 2016 and 2017 for performing these experiments. We also thank the two reviewers for thorough reviews and identifying ways to clarify the presentation and interpretation. The raw images and automated reconstructions acquired using the X-ray tomography are stored by the United States Department of Energy at spot.nersc.gov.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00250/full#supplementary-material
References
Arganda-Carreras, I., Kaynig, V., Rueden, C., Eliceiri, K. W., Schindelin, J., Cardona, A., et al. (2017). Trainable Weka segmentation: a machine learning tool for microscopy pixel classification. Bioinformatics 33, 2424–2426. doi: 10.1093/bioinformatics/btx180
Arzilli, F., and Carroll, M. R. (2013). Crystallization kinetics of alkali feldspars in cooling and decompression-induced crystallization experiments in trachytic melt. Contrib. Mineral. Petrol. 166, 1011–1027. doi: 10.1007/s00410-013-0906-1
Arzilli, F., Mancini, L., Voltolini, M., Cicconi, M. R., Mohammadi, S., Giuli, G., et al. (2015). Near-liquidus growth of feldspar spherulites in trachytic melts: 3D morphologies and implications in crystallization mechanisms. Lithos 216-217, 93–105. doi: 10.1016/j.lithos.2014.12.003
Brugger, C. R., and Hammer, J. E. (2010). Crystallization kinetics in continuous decompression experiments: implications for interpreting natural magma ascent processes. J. Petrol. 51, 1941–1965. doi: 10.1093/petrology/egq044
Burkhard, D. J. (2005). Nucleation and growth rates of pyroxene, plagioclase, and Fe-Ti oxides in basalt under atmospheric conditions. Eur. J. Mineral. 17, 675–685.
Campagnola, S., Vona, A., Romano, C., and Giordano, G. (2016). Crystallization kinetics and rheology of leucite-bearing tephriphonolite magmas from the Colli Albani volcano (Italy). Chem. Geol. 424, 12–29. doi: 10.1016/j.chemgeo.2016.01.012
Carey, R. J., Manga, M., Degruyter, W., Swanson, D., Houghton, B., Orr, T., et al. (2012). External triggered renewed bubble nucleation in basaltic magma: the October 12 2008 eruption at Halema‘uma‘u Overlook vent, Kilauea, Hawai‘I, USA. J. Geophys. Res. 117:B11202. doi: 10.1029/2012JB009496
Caricchi, L., Burlini, L., Ulmer, P., Gerya, T., Vassalli, M., and Papale, P. (2007). Non-newtonian rheology of crystal-bearing magmas and implications for magma ascent dynamics. Earth Planet. Sci. Lett. 264, 402–419. doi: 10.1016/j.epsl.2007.09.032
Castro, J. M., and Dingwell, D. B. (2009). Rapid ascent of rhyolitic magma at Chaiten volcano. Chile. Nature 461, 780–783. doi: 10.1038/nature08458
Chen, H., He, Y., Shiflet, G. J., and Poon, S. J. (1994). Deformation-induced nanocrystal formation in shear bands of amorphous alloys. Nature 367, 541–543. doi: 10.1038/367541a0
Chen, Y., and Zhang, Y. (2009). Clinopyroxene dissolution in basaltic melt. Geochim. Cosmochim. Acta 73, 5730–5747. doi: 10.1016/j.gca.2009.06.016
Chevrel, M. O., Cimarelli, C., deBiasi, L., Hanson, J. B., Lavallée, Y., Arzilli, F., et al. (2015). Viscosity measurements of crystallizing andesite from Tungurahua volcano (Ecuador). Geochem. Geophys. Geosyst. 16, 870–889. doi: 10.1002/2014gc005661
Chien, M. C., and Weiss, R. (1988). Strain-induced crystallization behavior of poly (ether ether ketone)(PEEK). Polym. Eng. Sci. 28, 6–12. doi: 10.1002/pen.760280103
Cölfen, H., and Mann, S. (2003). Higher-order organization by mesoscale self-assembly and transformation of hybrid nanostructures. Angew. Chem. Int. Ed. 42, 2350–2365. doi: 10.1002/anie.200200562
Cordonnier, B., Hess, K.-U., Lavallee, Y., and Dingwell, D. (2009). Rheological properties of dome lavas: case study of Unzen volcano. Earth Planet. Sci. Lett. 279, 263–272. doi: 10.1016/j.epsl.2009.01.014
Donovan, P., and Stobbs, W. (1981). The structure of shear bands in metallic glasses. Acta Metallurgica 29, 1419–1436. doi: 10.1016/0001-6160(81)90177-2
Doube, M., Kłosowski, M. M., Arganda-Carreras, I., Cordelières, F. P., Dougherty, R. P., Jackson, J. S., et al. (2010). BoneJ: free and extensible bone image analysis in ImageJ. Bone 47, 1076–1079. doi: 10.1016/j.bone.2010.08.023
Fernández, I., and Bickelhaupt, F. M. (2014). The activation strain model and molecular orbital theory: understanding and designing chemical reactions. Chem. Soc. Rev. 43, 4953–4967. doi: 10.1039/c4cs00055b
Fokin, V. M., Schmelzer, J. W., Nascimento, M. L., and Zanotto, E. D. (2007). Diffusion coefficients for crystal nucleation and growth in deeply undercooled glass-forming liquids. J. Chem. Phys. 126:234507. doi: 10.1063/1.2746502
Fokin, V. M., Zanotto, E. D., Yuritsyn, N. S., and Schmelzer, J. W. (2006). Homogeneous crystal nucleation in silicate glasses: a 40 years perspective. J. Non Cryst. Solids 352, 2681–2714. doi: 10.1016/j.jnoncrysol.2006.02.074
Garrison, N. J., Busby, C. J., Gans, P. B., Putirka, K., and Wagner, D. L. (2008). A mantle plume beneath California? The mid-Miocene Lovejoy flood basalt, northern California. Geol. Soc. Am. Spec. Pap. 438, 551–572. doi: 10.1130/2008.2438(20)
Ghiorso, M. S., and Sack, R. O. (1995). Chemical mass transfer in magmatic processes IV. A revised and internally consistent thermodynamic model for the interpolation and extrapolation of liquid-solid equilibria in magmatic systems at elevated temperatures and pressures. Contrib. Mineral. Petrol. 119, 197–212. doi: 10.1007/s004100050036
Giordano, D., Polacci, M., Longo, A., Papale, P., Dingwell, D. B., Boschi, E., et al. (2007). Thermo-rheological magma control on the impact of highly fluid lava flows at Mt. Nyiragongo. Geophys. Res. Lett. 34: L06301.
Gualda, G. A., Ghiorso, M. S., Lemons, R. V., and Carley, T. L. (2012). Rhyolite-MELTS: a modified calibration of MELTS optimized for silica-rich, fluid-bearing magmatic systems. J. Petrol. 53, 875–890. doi: 10.1093/petrology/egr080
Haboub, A., Bale, H. A., Nasiatka, J. R., Cox, B. N., Marshall, D. B., Ritchie, R. O., et al. (2014). Tensile testing of materials at high temperatures above 1700°C with in situ synchrotron X-ray micro-tomography. Rev. Sci. Instrum. 85:083702. doi: 10.1063/1.4892437
Hammer, J. E. (2008). Experimental studies of the kinetics and energetics of magma crystallization. Rev. Mineral. Geochem. 69, 9–59. doi: 10.2138/rmg.2008.69.2
Kirkpatrick, R. J., Klein, L., Uhlmann, D., and Hays, J. F. (1979). Rates and processes of crystal growth in the system anorthite-albite. J. Geophys. Res. Solid Earth 84, 3671–3676. doi: 10.1029/jb084ib07p03671
Kolzenburg, S., Di Genova, D., Giordano, D., Hess, K. U., and Dingwell, D. B. (2018a). The effect of oxygen fugacity on the rheological evolution of crystallizing basaltic melts. Earth Planet. Sci. Lett. 487, 21–32. doi: 10.1016/j.epsl.2018.01.023
Kolzenburg, S., Giodano, D., Hess, K. U., and Dingwell, D. B. (2018b). Shear rate-dependent disequilibrium rheology and dynamics of basalt solidification. Geophys. Res. Lett. 45, 6466–6475. doi: 10.1029/2018gl077799
Kolzenburg, S., Giordano, D., Di Muro, A., and Dingwell, D. (2018c). Equilibrium viscosity and disequilibrium rheology of a high magnesium basalt from piton De La Fournaise volcano, La Reunion, Indian Ocean, France. Ann. Geophys. 61:18.
Kolzenburg, S., Giordano, D., Cimarelli, C., and Dingwell, D. B. (2016). In Situ thermal characterization of cooling/crystallizing lavas during rheology measurements and implications for lava flow emplacement. Geochim. Cosmochim. Acta 195, 244–258. doi: 10.1016/j.gca.2016.09.022
Kolzenburg, S., Giordano, D., Thordarson, T., Höskuldsson, A., and Dingwell, D. B. (2017). The rheological evolution of the 2014/2015 eruption at Holuhraun, central Iceland. Bull. Volcanol. 79:45.
Kouchi, A., Tsuchiyama, A., and Sunagawa, I. (1986). Effect of stirring on crystallization kinetics of basalt: texture and element partitioning. Contrib. Mineral. Petrol. 93, 429–438. doi: 10.1007/bf00371713
Kumaraswamy, G., Issaian, A. M., and Kornfield, J. A. (1999). Shear-enhanced crystallization in isotactic polypropylene. 1. Correspondence between in situ rheo-optics and ex situ structure determination. Macromolecules 32, 7537–7547. doi: 10.1021/ma990772j
Lee, S.-W., Huh, M.-Y., Chae, S.-W., and Lee, J.-C. (2006). Mechanism of the deformation-induced nanocrystallization in a Cu-based bulk amorphous alloy under uniaxial compression. Scripta Materialia 54, 1439–1444. doi: 10.1016/j.scriptamat.2006.01.002
Lofgren, G. (1974). An experimental study of plagioclase crystal morphology; isothermal crystallization. Am. J. Sci. 274, 243–273. doi: 10.2475/ajs.274.3.243
Loomis, T. P. (1981). An investigation of disequilibrium growth processes of plagioclase in the system anorthite-albite-water by methods of numerical simulation. Contrib. Mineral. Petrol. 76, 196–205. doi: 10.1007/bf00371959
Lowry, R. K., Henderson, P., and Nolan, J. (1982). Tracer diffusion of some alkali, alkaline-earth and transition element ions in a basaltic and an andesitic melt, and the implications concerning melt structure. Contrib. Mineral. Petrol. 80, 254–261. doi: 10.1007/bf00371355
Müller-Krumbhaar, H. (1975). Diffusion theory for crystal growth at arbitrary solute concentration. J. Chem. Phys. 63, 5131–5138. doi: 10.1063/1.431321
Nicholson, D. A., and Rutledge, G. C. (2019). An assessment of models for flow-enhanced nucleation in an n-alkane melt by molecular simulation. J. Rheol. 63, 465–475. doi: 10.1122/1.5091945
Ni, H., Keppler, H., Walte, N., Schiavi, F., Chen, Y., Masotta, M., and Li, Z. (2014). In situ observation of crystal growth in a basalt melt and the development of crystal size distribution in igneous rocks. Contrib. Mineral. Petrol. 167:1003. doi: 10.1007/s00410-014-1003-9
Pinkerton, H., and Stevenson, R. J. (1992). Methods of determining the rheological properties of magmas at sub-liquidus temperatures. J. Volcanol. Geotherm. Res. 53, 47–66. doi: 10.1016/0377-0273(92)90073-m
Pistone, M., Caricchi, L., Ulmer, P., Burlini, L., Ardia, P., Reusser, E., et al. (2012). Deformation experiments of bubble-and crystal-bearing magmas: rheological and microstructural analysis. J. Geophys. Res. Solid Earth 117, 1–39.
Pleše, P., Higgins, M., Mancini, L., Lanzafame, G., Brun, F., Fife, J., et al. (2018). Dynamic observations of vesiculation reveal the role of silicate crystals in bubble nucleation and growth in andesitic magmas. Lithos 296, 532–546. doi: 10.1016/j.lithos.2017.11.024
Pontesilli, A., Masotta, M., Nazzari, M., Mollo, S., Armienti, P., Scarlato, P., et al. (2019). Crystallization kinetics of clinopyroxene and titanomagnetite growing from a trachybasaltic melt: new insights from isothermal time-series experiments. Chem. Geol. 510, 113–129. doi: 10.1016/j.chemgeo.2019.02.015
Polacci, M., Arzilli, F., La Spina, G., Le Gall, N., Cai, B., Hartley, M. E., et al. (2018). Crystallisation in basaltic magmas revealed via in situ 4D synchrotron X-ray microtomography. Sci. Rep. 8:8377. doi: 10.1038/s41598-018-26644-6
Riker, J. M., Cashman, K. V., Rust, A. C., and Blundy, J. D. (2015). Experimental constraints on plagioclase crystallization during H2O- and H2O-CO2- saturated magma decompression. J. Petrol. 56, 1967–1998. doi: 10.1093/petrology/egv059
Rothery, D. A., Sumner, J. M., Spieler, O., and Dingwell, D. B. (2007). Impact vesiculation – A new trigger for volcanic bubble growth and degassing. eEarth Discuss. 2, 151–167. doi: 10.5194/eed-2-151-2007
Schiavi, F., Walte, N., and Keppler, H. (2009). First in situ observation of crystallization processes in a basaltic-andesitic melt with the moissanite cell. Geology, 37, 963–966. doi: 10.1130/g30087a.1
Shaw, H., Wright, T., Peck, D., and Okamura, R. (1968). The viscosity of basaltic magma; an analysis of field measurements in Makaopuhi lava lake, Hawaii. Am. J. Sci. 266, 225–264.
Shea, T., and Hammer, J. E. (2013). Kinetics of cooling-and decompression-induced crystallization in hydrous mafic-intermediate magmas. J. Volcanol. Geothermal Res. 260, 127–145. doi: 10.1016/j.jvolgeores.2013.04.018
Spera, F. J., Borgia, A., Strimple, J., and Feigenson, M. (1988). Rheology of melts and magmatic suspensions: 1. Design and calibration of concentric cylinder viscometer with application to rhyolitic magma. J. Geophys. Res. Solid Earth 93, 10273–10294. doi: 10.1029/jb093ib09p10273
Sun, T., Pereira, J., and Porter, R. S. (1984). Crystallization kinetics for poly (ethylene terephthalate) oriented by solid-state coextrusion. J. Polym. Sci. Part B Polym. Phys. 22, 1163–1171. doi: 10.1002/pol.1984.180220702
Swanson, S. (1977). Relation of nucleation and crystal-growth rate to the development of granitic textures. Am. Mineral. 62, 966–978.
Van Zeist, W.-J., and Bickelhaupt, F. M. (2010). The activation strain model of chemical reactivity. Organ. Biomol. Chem. 8, 3118–3127.
Vetere, F., Iezzi, G., Behrens, H., Cavallo, A., Misiti, V., Dietrich, M., et al. (2013). Intrinsic solidification behaviour of basaltic to rhyolitic melts: a cooling rate experimental study. Chem. Geol. 354, 233–242. doi: 10.1016/j.chemgeo.2013.06.007
Vetere, F., Iezzi, G., Behrens, H., Holtz, F., Ventura, G., Misiti, V., et al. (2015). Glass forming ability and crystallisation behaviour of sub-alkaline silicate melts. Earth Sci. Rev. 150, 25–44. doi: 10.1016/j.earscirev.2015.07.001
Vetere, F., Murri, M., Alvaro, M., Domeneghetti, M. C., Rossi, S., Pisello, A., et al. (2019). Viscosity of pyroxenite melt and its evolution during cooling. J. Geophys. Res. Planets 124, 1451–1469.
Vona, A., and Romano, C. (2013). The effects of undercooling and deformation rates on the crystallization kinetics of Stromboli and Etna basalts. Contrib. Mineral. Petrol. 166, 491–509. doi: 10.1007/s00410-013-0887-0
Wang, Y., Yu, M., Qiao, Q., You, F., Li, C., Xu, Z., et al. (2015). Effect of plastic deformation on the crystal structure and crystallization activation energy of Ni-WP alloy coating. J. Mater. Eng. Perform. 24, 2653–2657. doi: 10.1007/s11665-015-1551-9
Wheeler, J. (2017). The effects of stress on reactions in the Earth: sometimes rather mean, usually normal, always important. J. Metamorphic Petrol. 36, 439–461. doi: 10.1111/jmg.12299
Woodward, R., and Baer, H. (1944). Studies on Diene-addition reactions. II. 1 The reaction of 6, 6-pentamethylenefulvene with maleic anhydride. J. Am. Chem. Soc. 66, 645–649. doi: 10.1021/ja01232a042
Xu, J.-Z., Chen, C., Wang, Y., Tang, H., Li, Z.-M., and Hsiao, B. S. (2011). Graphene nanosheets and shear flow induced crystallization in isotactic polypropylene nanocomposites. Macromolecules 44, 2808–2818. doi: 10.1021/ma1028104
Yang, D., Hrymak, A. N., and Kamal, M. R. (2011). Crystal morphology of hydrogenated castor oil in the crystallization of oil-in-water emulsions: part II. Effect of shear. Ind. Eng. Chem. Res. 50, 11594–11600. doi: 10.1021/ie1025997
Zhang, Y. (2010). Diffusion in minerals and melts: theoretical background. Rev. Mineral. Geochem. 72, 5–59. doi: 10.2138/rmg.2010.72.2
Keywords: deformation, crystallization, X-ray micro-tomography, activation energy, diffusion, chemical potential
Citation: Tripoli B, Manga M, Mayeux J and Barnard H (2019) The Effects of Deformation on the Early Crystallization Kinetics of Basaltic Magmas. Front. Earth Sci. 7:250. doi: 10.3389/feart.2019.00250
Received: 11 June 2019; Accepted: 05 September 2019;
Published: 27 September 2019.
Edited by:
Fabio Arzilli, The University of Manchester, United KingdomReviewed by:
Matteo Masotta, University of Pisa, ItalyStephan Kolzenburg, Ludwig Maximilian University of Munich, Germany
Copyright © 2019 Tripoli, Manga, Mayeux and Barnard. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Barbara Tripoli, YmFyYmFyYS50cmlwb2xpMDE2MzBAZ21haWwuY29t; Michael Manga, bWFuZ2FAc2Vpc21vLmJlcmtlbGV5LmVkdQ==
†ORCID: Barbara Tripoli, http://orcid.org/0000-0002-1663-3991; Michael Manga, http://orcid.org/0000-0003-3286-4682