- Department of Earth and Environmental Sciences, Tulane University, New Orleans, LA, United States
When deltas dock at continental margins they construct thick stratigraphic intervals and activate continental slope sediment routing systems (SRS). Given their thickness, these deposits have the capacity to store detailed paleo-environmental records. Several competing theories describe how SRS comprised of linked deltas-continental slopes respond to sea level cycles of varying magnitude and periodicity. I explore this in a physical experiment where the topography of a coupled delta-slope system was monitored at high resolution. This allows development of process-based theory for the response of SRS to external forcings at the land-ocean interface. Connection between these environments was promoted with input conditions that generated plunging hyperpycnal flows at river mouths. The experiment had three stages, which included: (1) a delta-slope system aggrading with no sea level cycles, (2) a system responding to low magnitude and high frequency sea level cycles, and (3) a system responding to a high magnitude and long period cycle. All stages shared an identical background pseudo-subsidence rate. Here the magnitudes and periods of sea level cycles are discussed relative to key autogenic scales. I find that, on average, sediment transport to the marine is promoted during lowstand conditions in all stages. However, the scale of the sea level cycles with respect to emergent autogenic scales controls the predictability of this response, with greater stochasticity and thus lower predictability for the response to smaller and shorter sea level cycles. Analysis of two SRS suggests that predictable responses can require sea level cycle amplitudes greater than 50 m and periods longer than 200 kyrs, but will vary with system size.
Introduction
Sediment routing systems, which transport sediment from sources to sinks, consist of linked segments within which the dominant morphodynamic processes remain fairly constant (Allen, 2008; Sømme et al., 2009b; Allen, 2017). The coupling of these segments occur at important Earth-surface boundaries which fundamentally alter the method, rate, and variability of sediment transport. Here I explore the coupling of sediment transport segments that occur at the shoreline, with a specific focus on deltas and their down system environments. In particular, I explore how the magnitude and period of sea level cycles influence the extraction of mass to deposition across the delta-slope transition.
The influence of sea level, or relative sea level (RSL) change in regions with substantial vertical Earth-surface motion due to tectonics, on sediment transport and stratigraphy is not a new question. It has been explored since the time of Gilbert (1890) and ramped up with the advent and examination of hydrocarbon exploration derived seismic surveys, which motivated the development of sequence stratigraphic methods and interpretations (Vail et al., 1977; Van Wagoner et al., 1990; Catuneanu et al., 2009). While the largely qualitative, observational, and conceptual approaches underpinning sequence stratigraphy continue to teach us about continental margin stratigraphy, the approaches championed by the source to sink movement require quantitative data for theory development garnered from field observations and numerical and physical experiments.
In today’s icehouse highstand conditions many deltas are separated from the shelf-edge by wide continental shelves (Sweet and Blum, 2016). With these conditions transport of sediment to the deep marine, and in particular coarse sediment, is limited. Icehouse conditions refer to time periods in Earth history when the waxing and waning of continental scale ice sheets result in high amplitude (≥ 100 m) sea level fluctuations, while greenhouse refers to periods with no continental-scale glaciers and thus small-magnitude Milankovitch-forced RSL cycles from the thermal expansion contraction of water. Efficient transport of sediment to the deep marine is currently limited to rivers that link to submarine canyons or fjords (Xu et al., 2004; Vendettuoli et al., 2019). However, analysis of continental margin stratigraphy exposed in outcrop and reflection seismic data suggest that shelf-edge deltas efficiently fed slope systems during recent icehouse lowstand conditions as well as greenhouse periods (Porębski and Steel, 2003; Straub et al., 2012; Sylvester et al., 2012). Here, I present a detailed set of measurements derived from a physical laboratory experiment on the role of RSL in the partitioning of sediment between dominantly terrestrial vs. dominantly marine settings at shelf-edge deltas. In particular, I focus on (A) the sea level cycle characteristics necessary to induce stratigraphic signatures that can clearly be linked to paleo sea level change and (B) the timing and magnitude of sediment delivery to regions past a shelf-edge.
Motivating this experimental study are a suite of results from numerical experiments that explore the impact of RSL variations on sediment dispersal across the shelf-edge during icehouse vs. greenhouse Earth conditions (Harris et al., 2016, 2018). The numerical model used in these studies, Dionisos, simulates sediment transport at basinal length-scales and geological time-scales based off diffusive transport of sediment (Granjeon, 1999). This diffusive algorithm adequately replicates depositional patterns over long spatial and temporal scales. However, over shorter length and time scales morphodyamic processes resulting from the coupling of topography, flow, and sediment transport produce rich stochastic behavior that is not well described by diffusion (Kim et al., 2014; Paola, 2016; Hajek and Straub, 2017). Some of this stochasticity arises due to internal processes within sediment routing systems, for example dune and channel migration and avulsions which are commonly called autogenic processes.
Even with a diffusive description of sediment transport, these models make several predictions that challenge conventional wisdom about the role of RSL change in sediment delivery to the continental slope and beyond due to emergent model autogenic dynamics. These dynamics result from lateral gradients in deposition, which aid occasional channel formation and compensational stacking of lobes. Specifically, I highlight the following results: (1) Harris et al. (2016) found a trivially small difference in cumulative deepwater sand delivery between a model of continental margin evolution with a eustatic history derived from a field compilation and a second model with no eustatic variations. While peak delivery of sand to the deep marine did occur during short periods of sea level fall in the variable eustacy model, similar episodes of sand delivery occur in the constant eustacy model when transport systems occasionally reached and became temporarily locked at the shelf-edge. (2) The delivery of sand to the deep marine is not well correlated to rate or amplitude of sea level fall, which holds regardless of the diffusion coefficients used in the models (Harris et al., 2018).
Motivated by these numerical observations, I conducted a physical experiment to examine the coupling of deltas to the continental slope. Specifically I focus on systems with rivers that spawn hyperpycnal flows downstream of the shoreline. While the diffusion scheme used in Dionisos likely produces muted autogenic dynamics over time scales of delta lobe growth and abandonment, physical experiments are known for self-organization and complex stochastic behavior (Paola et al., 2009).
This work is also motivated and informed by theory which predicts threshold characteristics of sea level cycles necessary to produce geomorphic and stratigraphic signals which can confidently be distinguished from autogenic processes and products (Li et al., 2016; Yu et al., 2017). This theory was recently tested in a set of deltaic experiments, but these experiments lacked a slope downstream of the shoreline and the collection of high resolution bathymetry, both of which are present in this study.
Materials and Methods
To study the influence of RSL on the partitioning of sediment between dominantly terrestrial vs. marine environments, I conducted a physical laboratory experiment in the Deepwater Basin housed in the Tulane University Sediment Dynamics and Stratigraphy Laboratory. The basin is 6 m long, 4 m wide, and 2.2 m deep (Figure 1A). Sea level is controlled through a weir, which is in hydraulic communication with the basin. The weir is on a computer-controlled vertical slide that allows for sub-millimeter-scale elevation control of sea level. The sea level elevation was monitored and logged once a minute with a transducer to ensure that it matched target elevations.
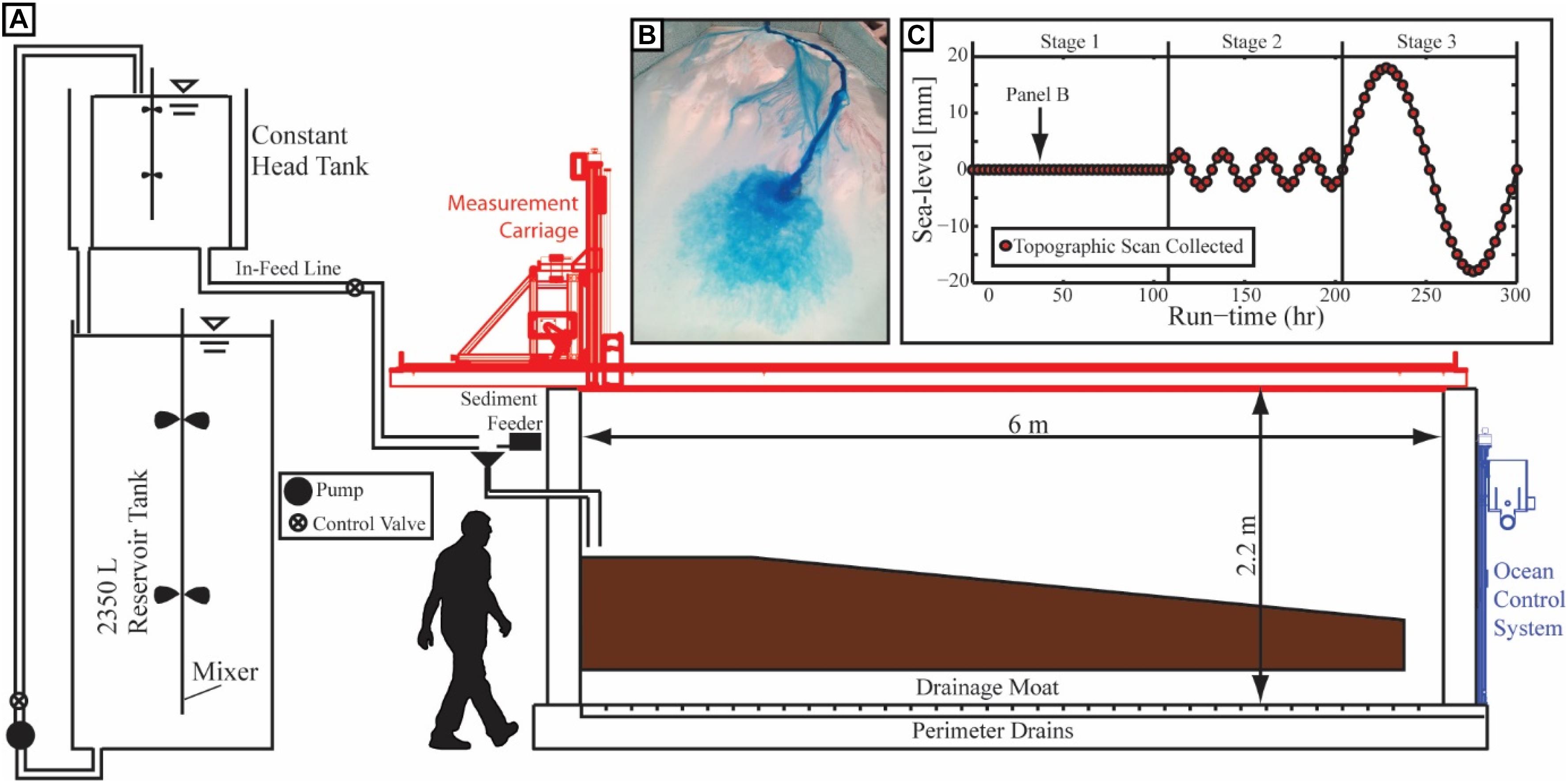
Figure 1. Schematic diagram of the experimental facility and experimental conditions. (A) Dip view of the facility and initial topographic form with important basin dimensions noted. A saline mixture was pumped from a reservoir tank to a constant head tank before mixing with sediment in a funnel and then entering the basin. (B) Characteristic perspective photo of experimental surface with input flow dyed for visualization. (C) Time series of sea-level, minus the long term drift imposed for pseudo-subsidence and referenced to sea level at the start of stage 1 with time of topographic scans noted with red filled circles.
The initial basin topography was characterized in dip by a 1.2 m long flat shelf which connected to a 3.8 m long segment with a 10% slope. Initial topography did not vary in the strike direction. While steeper than typical continental margins, the 10% slope was implemented to match other experimental studies which used distorted Froude scaling to show that increasing the slope for laboratory systems helps better replicate field scale processes (Cantelli et al., 2011).
The input flow to the basin was designed to help facilitate transport of sediment to the deep marine by hyperpycnal flows. Flow was introduced via a constant head tank as a mixture of water and dissolved salt, which gave it a 2% excess density relative to the fresh water of the basin ocean. To keep the density contrast between the input flow and ocean, a system was implemented to extract dense flow at the base of the basin and replace it with fresh water from above at a rate equal to 11 times the saline input. The salinity of our river input and ocean might seem counterintuitive given that deltas constructed at land-ocean interfaces have fresh water in their rivers, which empty into saline oceans. However, this choice was made to promote hyperpycnal plunging of flows in the marine and thus promote transport of sediment to the continental slope. Similar to previous studies, the salt introduced can be thought of as the washload component of a system, which bypasses the region of study (Straub et al., 2008; Hamilton et al., 2017). Once every 3 h the experiment was paused and fresh water was cycled into the basin until no salinity could be detected. The input hydrograph was also designed to include floods to facilitate pumping of sediment to the deep marine. Base flow to the experiment was 1.54 × 10-4 m3/s. Floods were two-times the base flow and occurred for a continuous 6 min during each run-hour. The ratio of time at base flow to flood was set to mimic seasonal floods on large river deltas. The length of the flood-base flow cycle is set so that a large number of cycles occurred in the time necessary to aggrade, on average, a single channel depth everywhere on the delta top, which has been shown to be an important timescale of autogenic activity (Wang et al., 2011).
Supply of sediment to the basin was controlled through a computer interface. During base flow conditions the sediment delivery rate was 3.53 × 10-4 kg/s and the ratio of sediment to water delivery rate was kept constant for base flow and flood conditions at a volumetric ratio of 1:1000. The input sediment mixture was designed to mimic earlier experimental work (Hoyal and Sheets, 2009; Li et al., 2016) with particle diameters ranging from 1 to 1000 μm with a mean of 67 μm and was dominantly white quartz. One quarter of the coarsest 23.5% of the sediment distribution was commercially dyed red to aid visualization of stratigraphic architecture. A small amount of commercially available polymer (New Drill Plus, distributed by Baker Hughes Inc.) was added to the sediment mixture to enhance sediment cohesion, which aids formation of channels in experiments. I used this sediment mixture as earlier experimental studies found that its fine grain sizes are transported in suspension through the self-organized deep and relatively stable channels and resulted in pumping of substantial volumes of sediment to the marine (Straub et al., 2015). The combination of the saline input flow, fresh water receiving basin, and suspended sediment resulted in continuous plunging of hyperpycnal flows at river mouths which traversed down the basin slope as turbid underflows (Figure 1B).
The experiment included a 120 h build out stage in which sea level was kept constant. The main phase of the experiment followed when I imposed a constant rate of sea level rise ( = 0.25 mm/h), meant to simulate a constant long term subsidence rate. This pseudo-subsidence resulted in a terrestrial accommodation production rate that matched the average percentage of the volumetric sediment input rate trapped in the terrestrial, determined from earlier experimental work (Straub et al., 2015). As such, long term sea level rise induced a long term deposition rate on the delta-top, that matched . This allowed the mean location of the shoreline to remain constant, with superimposed variations due to autogenic processes and sea level cycles. The main phase of the experiment included three stages: (1) no sea level cycles, (2) small amplitude and short period sea level cycles, and (3) a large amplitude and long period sea level cycle (Figure 1C). Stage 1 was 108 h and produced slightly more than two channel depths of stratigraphy over the entire delta-top (maximum autogenic channel depths were ∼12 mm deep).
Following Li et al. (2016), I scale the magnitude and period of sea level cycles in stages 2 and 3 to critical autogenic space and time scales. The magnitude of sea level cycles, MRSL, (i.e., difference in elevation from cycle peak to trough) is compared to the maximum autogenic channel depth, Hc:
While the period of a sea level cycle, TRSL, is compared to the average time necessary to deposit one channel depth of stratigraphy over the entire delta-top, which utilizes the long term delta-top deposition rate, , as:
Which allows:
Stage 2 included four sequential sea level cycles characterized by H∗ = 0.5 and T∗ = 0.5, and thus were small in comparison to the autogenic scales. Stage 3 included one sea level cycle characterized by H∗ = 2 and T∗ = 2, and thus was large in comparison to the autogenic scales. Ideally I would run a larger number of sea level cycles for all stages, to allow exploration of statistical variability to forcings. However, results from a similar set of experiments on sea level forcing response of deltas, with no down system slope, indicate a quick adjustment of the deltas to their cycle forcing parameters (Yu et al., 2017).
It is worth noting that Tc does not equal the time scale of avulsion, TA, as initially defined by Mohrig et al. (2000). TA is defined as the depth of a system’s channels divided by the in-channel, local aggradation rate, measured over one avulsion cycle. The aggradation rate used in the formulation of Tc is the long term or geological rate (i.e., measured over long enough timescales that rates are temporally persistent; Jerolmack and Sadler, 2007). Typically, Tc is several orders of magnitude greater than TA. As such, Tc does not relate to the average periodicity of any one surface process, but rather estimates the time necessary for even dispersal of sediment across a basin resulting from the full suite of autogenic processes (Wang et al., 2011).
The input current was dyed twice an hour with blue food coloring to aid visualization of morphodynamics. This was done for 1 min of each flood and then 30 min later for 1 min of base flow conditions. Aerial images of the experimental surface were collected at the very end of each dye pulse. Maps of the entire experimental surface were collected every 3 h of run-time with a 1 Khz long range displacement laser connected to a data logger and housed on a measurement carriage capable of movement in all three Cartesian directions. Sequential topographic maps were collected on a common grid with a horizontal grid spacing of 5 mm in the down-basin and cross-basin directions. This produced maps with a vertical resolution of 0.25 mm. For stratigraphic analysis, the topographic maps were used to construct synthetic stratigraphy by stacking all topographic scans and clipping for erosion. Following the completion of the experimental run, the deposit was sectioned along three primarily dip oriented transects and imaged with a digital camera for stratigraphic characterization.
Results
General System Dynamics
I start with a general description of the system dynamics prior to the quantitative analysis of mass partitioning from source to sink. Pseudo-subsidence was turned on at the start of stage 1 with one major river channel located on the river-left side of the basin. This channel and its delta lobe protruded well past the shelf-slope break and remained fixed in position for approximately 70 h before the first large scale lobe avulsion (Figures 2, 3). This time-scale of stability is significantly longer than the compensation time-scale for the stage and longer than any time between avulsions in a previous deltaic experiment that used a very similar setup to that discussed here, but without a coupled slope system (Straub et al., 2015; Li et al., 2017). This might point to enhanced stability of terrestrial channels when their tips reach a shelf-edge, as quantified in previous experiments (Kim et al., 2013). This was followed by several smaller scale avulsion events. As the system reorganized, the long term pseudo-subsidence resulted in drowning of old delta lobes and the construction of a shelf environment. I characterize the shelf in our experiment to be low sloping (S = 0.05 m/m) marine environments that were constructed in terrestrial settings, but later drowned due to the local RSL history.
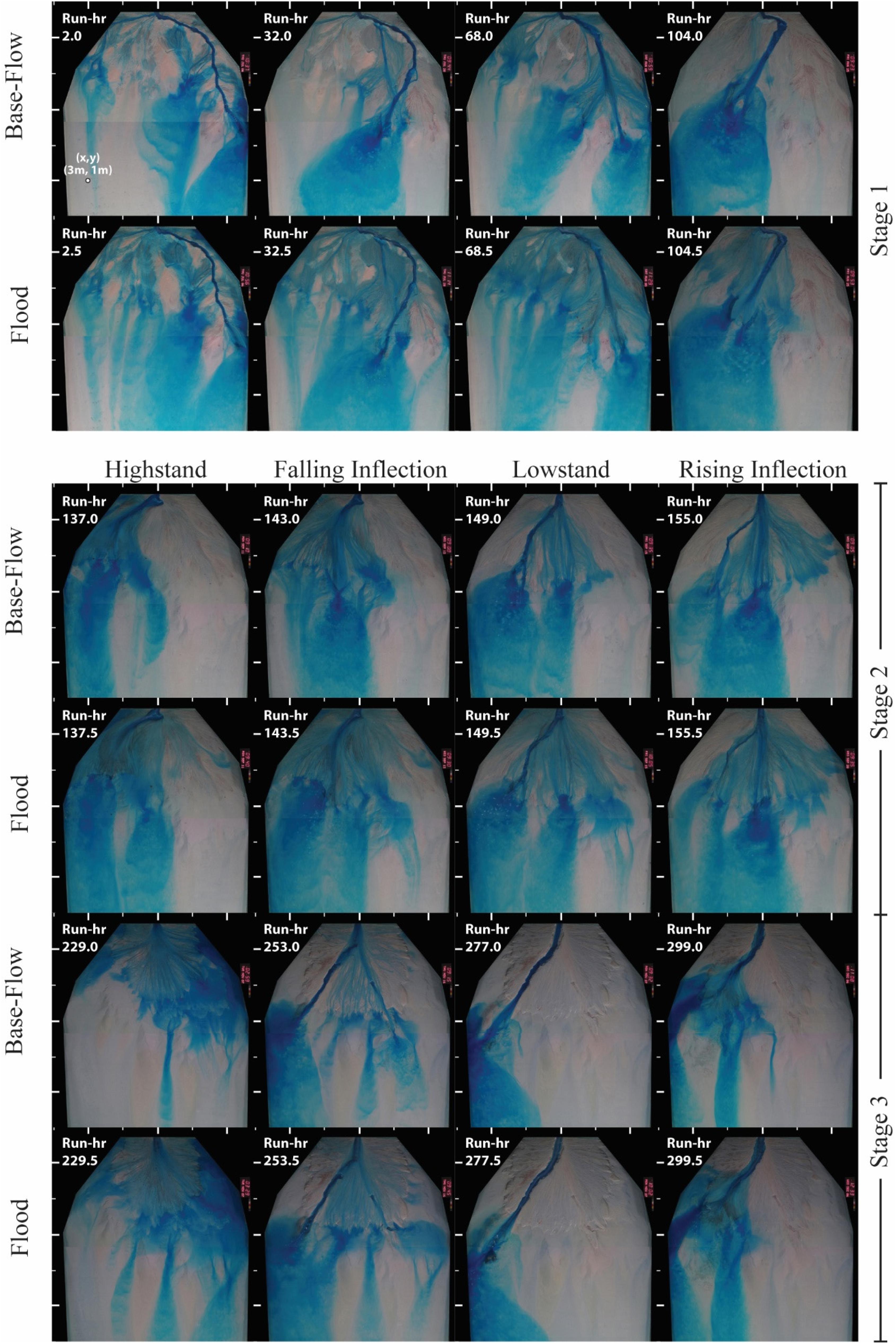
Figure 2. Overhead images of the three experimental stages. Images display transport system at key time periods in sea level cycles (stages 2 and 3), or for key periods in an autogenic channel cycle (stage 1). Photos from base flow conditions and then succeeding flood are shown. Images were taken after 1 full minute of dye release into the basin. Major tick marks on images borders have a 1 m spacing and a reference location is noted in the upper left photo with distances from the proximal basin wall (x) and from the river right basin wall (y).
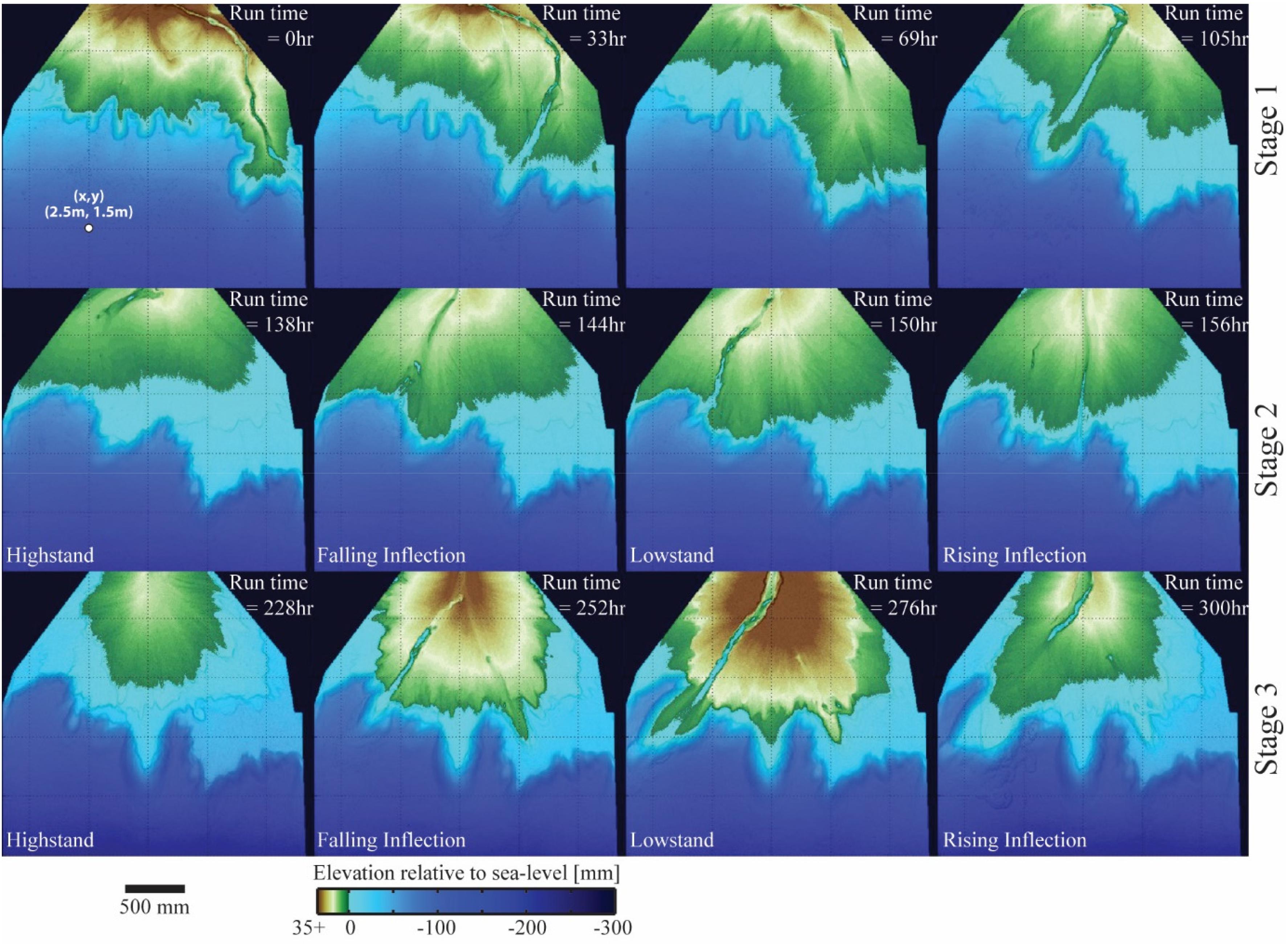
Figure 3. Topographic maps of the three experimental stages. Maps display transport system at key time periods in sea level cycles (stages 2 and 3), or for key periods in an autogenic channel cycle (stage 1). Line spacing of grid over topographic maps is 0.5 m and a reference location is noted in the upper left map with distances from the proximal basin wall (x) and from the river right basin wall (y).
During stage 1, input flow and sediment was routed to the shoreline through a mixture of channelized and overbanking flow. Coarse sediment was largely confined to the channels while overbanking flow resulted in substantial fine grained deposition on the delta-top. Deposition at the shoreline was dominated by coarse grained delta lobes. Sediment that bypassed the delta foresets in turbid underflows was almost exclusively fine grained. These underflows were sheet-like and lacked any detectable channelization. Underflows traversed the entire length of the basin and plunged into the distal basin moat, but lacked much suspended sediment at this point. The only significant difference between base and flood flow conditions was the amount of terrestrial overbanking flow, which was noticeably higher during flood events.
The small magnitude and short period RSL cycles of stage 2 drove reorganization of channel networks, most of which occurred during highstand conditions when the terrestrial system shrunk in size and the shelf system expanded. However, this was not always the case. Between the second and third RSL cycles a single channel formed down the center of the basin during rising sea level conditions. This channel remained in place during the highstand, pumping high sediment volumes to the marine, and continued to remain open through the succeeding lowstand. Similar to stage 1, a significant amount of the input flow left the terrestrial channels to the overbank during both base and flood flow during the entirety of all stage 2 sea level cycles (Figures 2, 3).
The single RSL cycle of stage 3 produced clear geomorphic responses (Figures 2, 3). Initial rising and then highstand sea level conditions drove a rapid shoreline transgression and wide scale expansion of the experimental shelf. As our experimental setup did not include waves, no large scale erosional ravinement surface formed on the shelf during transgression. During highstand the delta-top system had high lateral mobility and relatively little channelization. During falling sea level conditions channelization occurred that eventually collapsed into a single erosional corridor on the river right side of the basin. This channel was deep and wide enough to contain all flow during base and flood flow conditions. As such, this channel acted as a conveyor belt, transporting all of the input flow and sediment to the marine and the terrestrial overbank was starved of sediment. While the size of the shelf decreased during falling and lowstand conditions, it did not completely disappear as sediment transport and deposition to the marine was laterally constricted to the river right side of the basin.
Stratigraphic Architecture
The surface dynamics discussed above resulted in a stratigraphic package with delta-top deposits that averaged roughly 0.07 m in thickness, shelf-edge delta foresets in excess of 0.15 m thick and slope deposits that tapered from roughly 0.03 m down to 0.005 m thick. Panels of the preserved strata were generated by vertically slicing the final deposit along three dominantly dip panels. I took advantage of the locations of the transport system during each stage of the experiment when selecting the location of the dip panels. These included: (1) a panel down the river left side of the basin that aligned with the longest lived autogenic channel path during stage 1, (2) a panel down the center of the basin that captured the strata deposited during several of the stage 2 cycles, and (3) a panel down the river right side of the basin that was aligned with the dominant flow path during stage 3 (Figure 4).
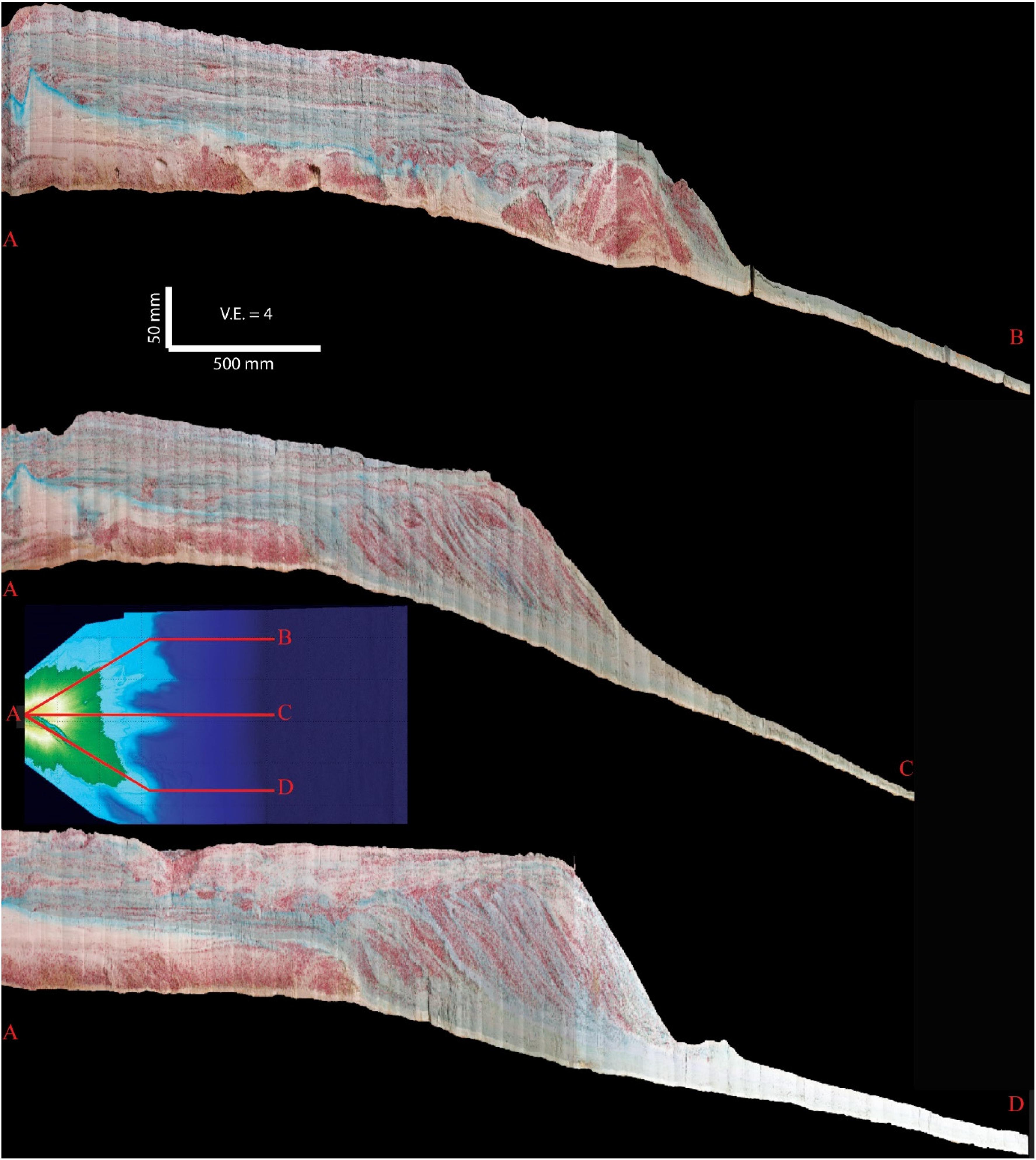
Figure 4. Images of preserved physical stratigraphy of the three experimental stages. Primary transport direction is from left to right. Blue staining is from food coloring used to dye input flow and is primarily present on the fine grained strata. Insert panel gives location of sections, which are displayed with a 4X vertical exaggeration.
Delta-top strata along the center and river left transects were similar in nature and included interbedded layers of red sand and white fine grained strata with occasional oblique channel cuts of similar depth. The delta-top strata along the river right transect included the large erosional channel fill from stage 3. The coarsest deposits in each transect were found in the shelf-edge foresets with fine grained strata constructing the down dip slope strata.
To complement the facies information contained within images of the physical stratigraphy, I construct volumes of synthetic stratigraphy by stacking DEMs of topography that are clipped to account for erosion in the topographic time-series (Figure 5). As I know the run-time associated with each map and the corresponding sea level, I can paint panels of synthetic strata by position within an RSL cycle. The complete spatial coverage of the basin allows me to extract these cross-sections along any path I wish. As sea level did not cycle in stage 1, I focus on a comparison of stage 2 and 3. I extract dip sections of synthetic stratigraphy along identical transects as our physical stratigraphy. The strata of the dip panel that ran down the middle of the basin shows that delta-top stratigraphy was constructed during both highstand and lowstand conditions of RSL during stage 2 and stage 3, but with a preference for deposition during highstand conditions. At least along this transect, a significant amount of the foreset strata was also deposited during highstand conditions, but with a cap on the foreset strata deposited during the subsequent lowstand.
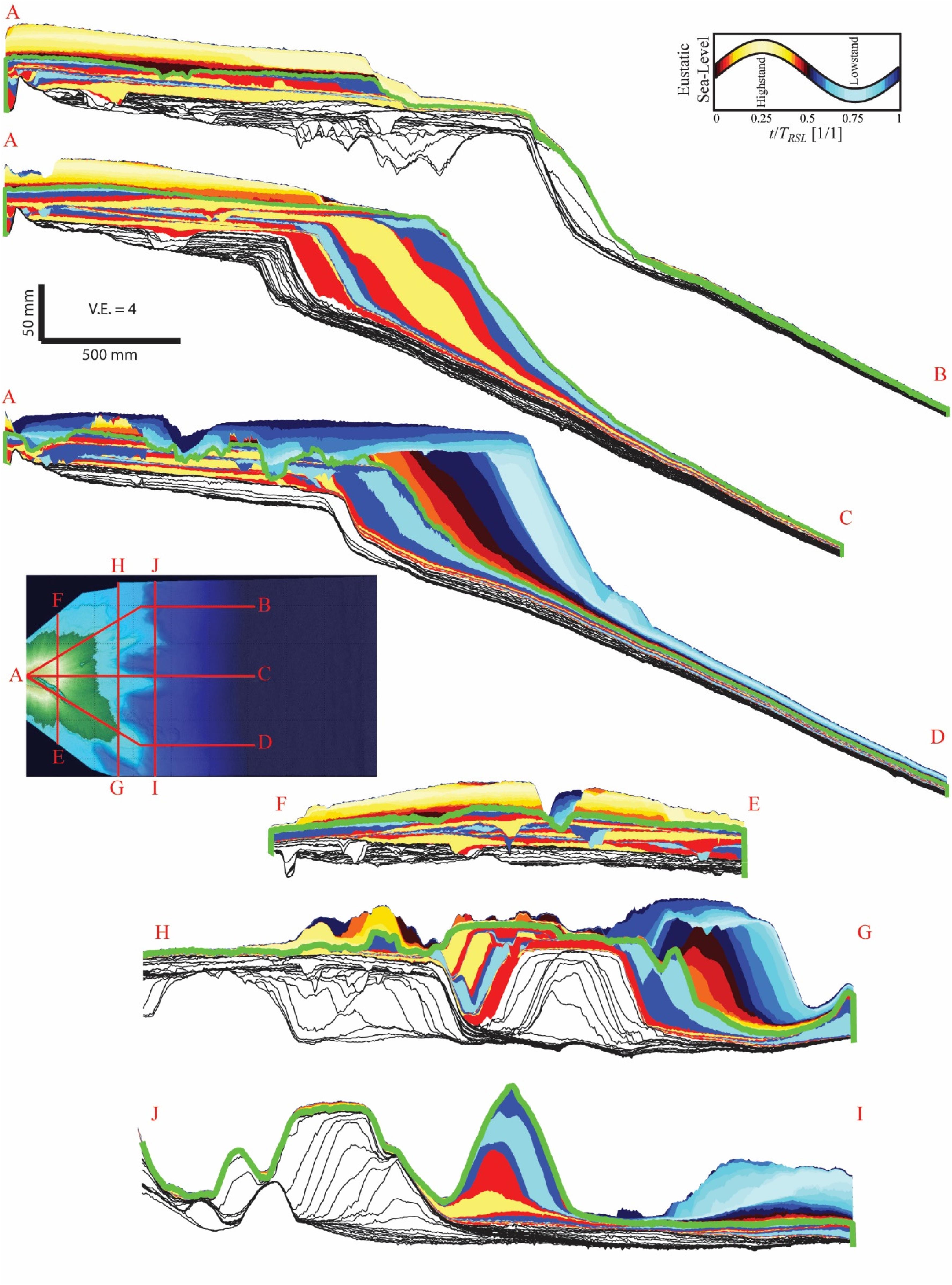
Figure 5. Panels of synthetic stratigraphy with deposits painted as a function of time of deposition within a sea level cycle. Stage 1 strata is displayed without coloring, but with preserved time horizons as black solid lines. Thick green lines denote break between stage 2 and 3 strata. Insert map details location of each transect; color bar details how synthetic stratigraphic color corresponds to time of deposition.
Synthetic strata analyzed down the river right side of the basin, following the path of the dominant erosional channel of stage 3, reveals that foreset construction began during highstand, but its growth accelerated as sea level fell to its lowstand position. Preserved delta-top strata along this transect was deposited during lowstand conditions as earlier highstand delta-top deposits were largely eroded and transported down-dip.
I also extracted panels of strata oriented in the strike direction. Here I compare three panels: one oriented half-way down the delta-top, one near the initial shelf-slope break, and one near the toe of the dominant shelf-edge delta foresets. I see a general decrease in preserved strata deposited in highstand conditions and an increase in preserved lowstand strata as you progress from source to sink.
Quantifying the Relationship Between RSL and Mass Extraction
The central goal of this study is to quantify the conditions necessary for RSL cycles to influence the depositional patterns of linked shelf-edge delta and slope systems. It is common to assume that sea level cycles influence the location of deposition, with deposition moving basinward as sea level falls and vice versa with sea level rise (Van Wagoner et al., 1990; Catuneanu et al., 2009). I explore this in the experimental strata by constructing a set of modified Wheeler diagrams (Wheeler, 1964). First, I construct these for individual dip and strike sections. The dip section comes from the basin bisect line (Figure 6A), while the strike section is from the location of the shelf-edge at the beginning of the experiment (Figure 6B). I generate a matrix populated with the preserved deposition rates from sequential pairs of topographic maps. I note that these are preserved deposition rates and are thus constructed after topographic clipping has occurred to account for post depositional erosion. This is done for each downstream location on the dip section and each cross-stream location on the strike section, with the distance between measurement locations equal to the 5 mm topographic grid. To facilitate comparison of our experiment to field systems, I normalize deposition rates by the imposed long-term pseudo-subsidence rate:
Where D(x or y) is the deposition rate at either a given downstream (x) or cross-stream (y) location.
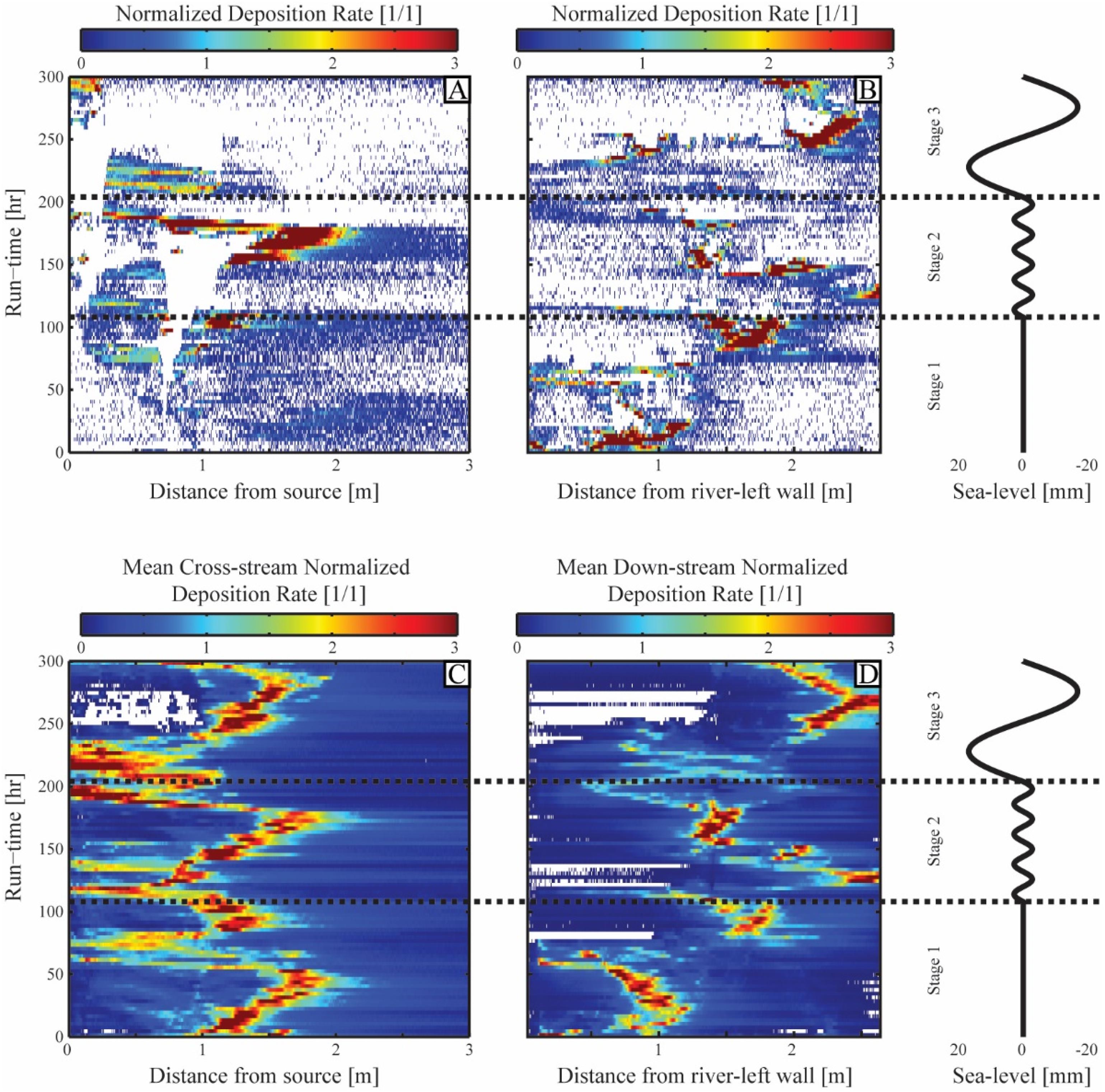
Figure 6. Modified Wheeler diagrams detailing how mean deposition rate varies both with distance from source, lateral position in basin and run time. (A) Wheeler diagram generated from a single dip section down the basin centerline (transect A–C in Figure 5). (B) Wheeler diagram generated from a single strike transect located at the location of the shelf-edge at the beginning of the experiment (transect G–H in Figure 5). (C) Mean dip oriented Wheeler diagram generated from the average of all dip transects in the topographic maps. (D) Mean strike oriented Wheeler diagram generated from the average of all strike transects in the topographic maps. White locations on Wheeler diagrams represent stratigraphic hiatuses. Black dashed lines demarcate stage breaks and experimental sea level history is shown to aid analysis of time-space information.
On these two-dimensional sections, I observe extreme variability in deposition rates in space and time, with a large number of stratigraphic hiatuses. Measured D∗ values peak at values in excess of 20 over delta foresets, but it is difficult to link depositional dynamics to the imposed sea level history in either dip or strike.
In an effort to decrease the “depositional noise” associated with looking at single dip or strike transects, I generated a second set of modified Wheeler diagrams. For this, an average dip-oriented Wheeler diagram was generated by averaging all dip oriented rows in the topographic dataset (n = 531) (Figure 6C). The same process was used to construct an average strike oriented diagram by averaging all strike oriented columns in the topographic dataset (n = 923) (Figure 6D).
I observe D∗ values ranging from 0 to 3 in the basin averaged Wheeler diagrams with highest values over delta foresets (Figure 6). Looking at the dip section, in stage 1 peak D∗ values initially move basinward, until making a rapid sourceward transition at the time of the first major avulsion. This is followed by smaller cycles of progradation then retrogradation of peak D∗ values. I observe no clear imprint of the stage 2 small amplitude and short period cycles in the Wheeler diagram. In comparison to the short period sea level cycles, a much longer period autogenic progradation and then retrogradational cycle is observed. The high magnitude and long period sea level cycle of stage 3, though, drove a clear response in the location of peak deposition rates. The initial rise in sea level toward highstand conditions drove peak D∗ values toward the sediment source, while falling sea level during this cycle drove a basinward shift in D∗. Stage 3 was also the only stage with a stratigraphic hiatus over the entire width of the proximal depositional system. This hiatus occurred during the falling portion of the stage 3 cycle as the terrestrial system entrenched through erosion and pushed sediment to the marine.
The basin averaged strike section again shows similar character in the first and second stages with zones of deposition shifting laterally to compensate for topographic lows. Stage 3, however, is characterized by deposition that remains on the river right side of the basin and a stratigraphic hiatus that spans most of the river left side of the basin during falling sea level. This stratigraphic hiatus is largely associated with inactivity rather than erosion, as the transport system was confined to the river right side of the basin at this time.
The modified Wheeler diagram presented above helps visualize movement of the peak depocenters in the experiment, but I am also interested in describing the cumulative extraction of mass to deposition as a function of distance from the sediment source and how this varies (1) between stages and (2) over the course of individual sea level cycles. This can be useful in identifying if sea level cycle characteristics promote the pumping of sediment to more distal locations and if the cumulative source to sink movement of the depocenter is in phase with imposed sea level cycles. To accomplish this I generate mass extraction curves as a function of downstream distance for each experimental stage. I use the Paola and Martin (2012) definition of mass extraction as the total sediment flux lost to deposition up to a distance of interest, x, from the source normalized by the input sediment flux to the basin, QS0:
Where B(x) is the width of the basin at location x. A tangible example of this transformation is χ(x) = 0.5, where half of the sediment input to the basin is deposited upstream of location x and half of the sediment is still in flux. χ(x) = 0.5 also represents the depositional midpoint of the basin (Paola and Martin, 2012).
I start the analysis of mass extraction by generating bulk χ(x) curves for each stage (Figure 7A). This is done with an isopach map generated by differencing topography at the end of each experimental stage from the topography at the start of the stage. The shape of the χ(x) curves is similar for the three stages with an initial slow growth of χ(x) over distances from the sediment source that were typically delta-top environments. Then a rapid growth in χ(x) is observed between 1 and 2 m from the basin entrance, which was typically delta foreset and upper slope. Finally, χ(x) slowly grows over 2–4 m from the source, which was always a marine slope environment. Using the DEM database, I also calculate the average distance from the basin entrance to the shoreline for each stage and post this on the χ(x) curves (Figure 7). This allows me to measure the mass portioning between dominantly terrestrial and dominantly marine settings in each stage. I find that in stage 1, 19% of the input mass was deposited in the terrestrial, while both stages 2 and 3 had 32% of the input mass deposited in the terrestrial. The biggest difference in the χ(x) curves of the three stages is the slow initial growth of χ(x) in stage 1 relative to stage 2 and 3. The distance from the entrance to the mean shoreline is near identical for all stages, but the sediment extracted inbound of the shoreline is less in stage 1 relative to stages 2 and 3. This is likely linked to the long lived and relatively stable channel that was present through much of stage 1, which efficiently pumped sediment to the marine.
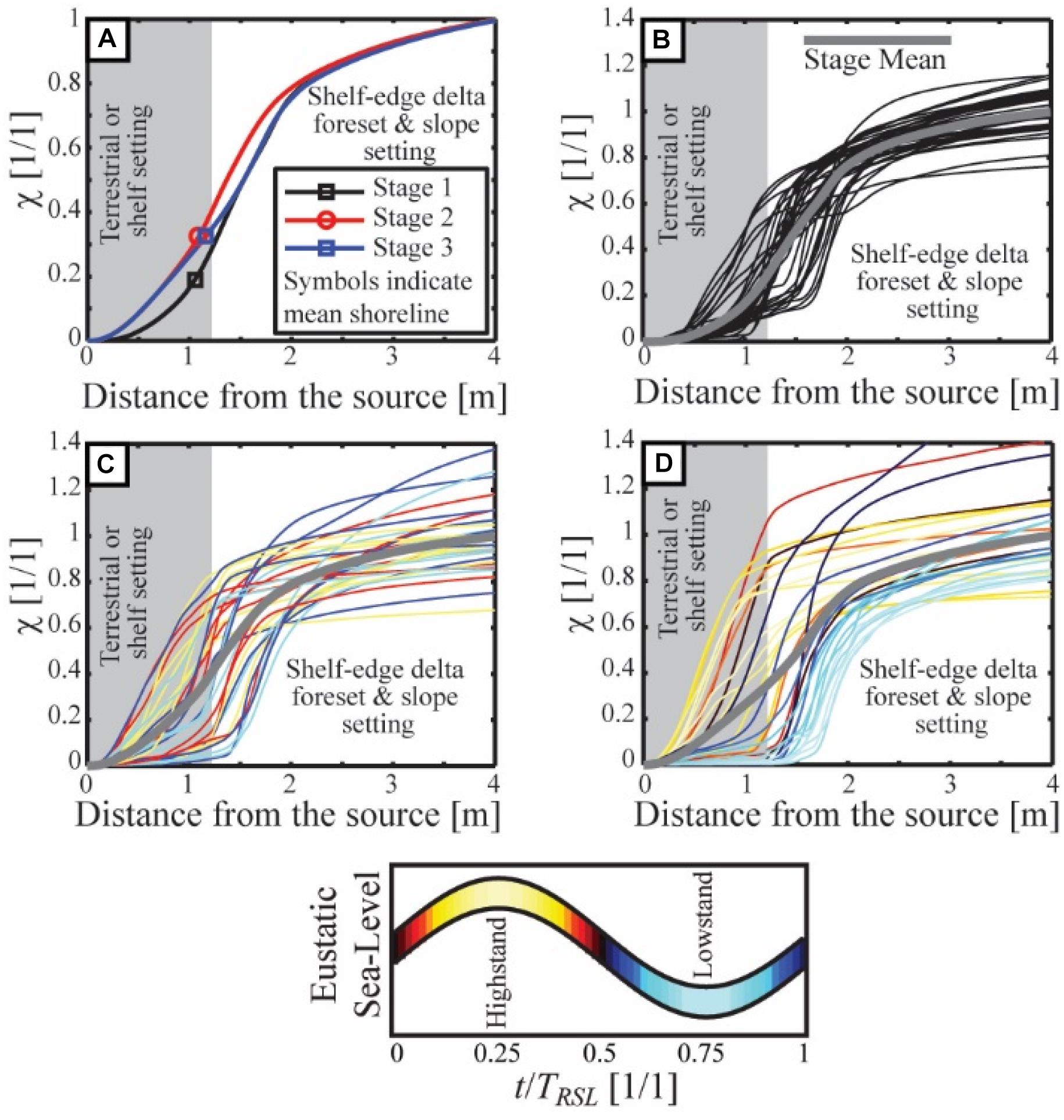
Figure 7. Relationship between distance from source and mass extraction for experimental deposit. (A) χ(x) curve for bulk stage deposits with position of mean shoreline noted for each stage. (B) χ(x) curves for each 3 h window between topographic scans in stage 1, thick solid gray line is the mean stage trend. (C,D) χ(x) curves for 3 h windows between topographic scans in stage 2 and 3, respectively. Color of curve corresponds to time of sample window with respect to a sea level cycle and solid gray lines show the mean stage trends.
Next I calculate χ(x) curves for each sequential set of DEMs, following the clipping process for post-depositional erosion. This serves two purposes: (1) to characterize the amount of variability in the location of mass extraction due to both autogenic and allogenic reorganization of channel networks and (2) to identify if position in a sea level cycle results in predictable changes in the mass extraction trend. Regarding point 2, minus autogenic dynamics I might expect that sea level would be correlated with the proximal-distal trend of mass extraction: lower sea level might result in proximal bypass and more distal mass extraction, relative to the mean χ(x) curve of a sea level cycle.
A comparison of stage 1 and 2 suggest a similar amount of variability in χ(x) curves around the mean trend (Figures 7B,C). χ sometimes exceeds a value of 1 in these curves due to erosion and redeposition of previously deposited sediment, which can result in a greater volume of sediment deposited and preserved in a given 3 h period than input to the basin during that same time. A greater spread around the mean is observed for the χ(x) curves of stage 3 (Figure 7D), suggesting an imprint of the forcing that exceeds the stochastic variability.
The position within a sea level cycle does not produce predictable shifts in χ(x) curves for the low magnitude, short period cycles of stage 2. While some periods of low sea level correspond to a basinward shift in the mass extraction trend, relative to the mean stage trend, other periods of low sea level are associated with enhanced proximal mass extraction relative to the mean trend (Figure 7C). In contrast, a clear and predictable response of χ(x) is seen in stage 3 with low RSL associated with more distal mass extraction and vice versa (Figure 7D).
Earlier in the description of the synthetic stratigraphic panels I noted a general trend of a reduction in preserved strata deposited in highstand conditions and an increase in preserved lowstand strata with movement from source to sink. My goal here is to quantify this trend. This is done with a calculation of a parameter, αD, first presented by Yu et al. (2017) which quantifies when, on average, during a sea level cycle deposition occurs, and how this changes as a function of mass extraction location. This metric is constructed as:
Where (χ) is the mean thickness of strata deposited during run hour i at a mass extraction location χ, ηSL, i is the sea level during run hour i and N is the total number of run hours analyzed. For strata deposited during a given RSL cycle, αD theoretically could take any value between -1 and 1. In descriptive terms, a value of -1 would represent a deposit at a mass extraction location of interest that was constructed only when sea level was at the trough of a cycle, while a value of 1 would represent deposits constructed only when sea level was at the peak of a cycle.
As no sea level cycles were present in stage 1, αD remains a constant value of 0 for all χ locations. In stages 2 and 3 αD is a positive value inbound of the mean stage shoreline suggesting a preference for highstand deposition (Figure 8). In both stages this preference increases with distance from the source until reaching peak values. However, the peak in αD is significantly higher in stage 3 compared to stage 2 indicating rapid deposition in proximal locations during highstand conditions for large magnitude sea level cycles. At more distal mass extraction locations this trend is reversed. Between χ locations of 0.6 – 0.8, I observe negative αD values in both stages, with the trend reaching lower values in stage 3 compared to stage 2. This indicates a preference for rapid marine deposition during lowstand conditions increases with the magnitude of a sea level cycle. Toward the end of the transport system, αD starts to rise back toward 0, suggesting a loss in preference for deposition as a function of location in a sea level cycle. However, it should be denoted that at these extremely distal locations the deposit thickness drops dramatically, likely making identification of this signal in field scale systems difficult.
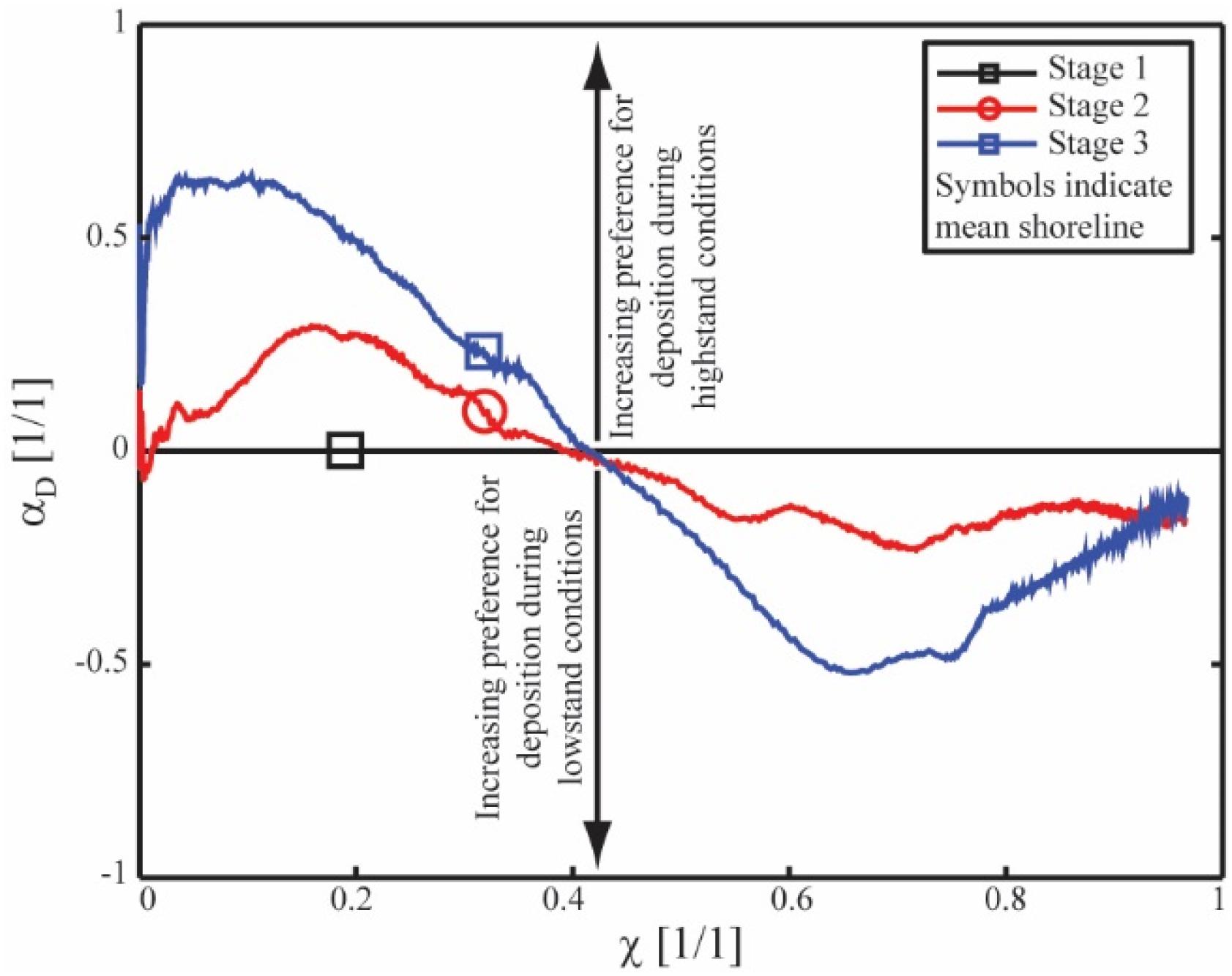
Figure 8. Data defining average position within a sea level cycle in which sediment is deposited as a function of distance from basin entrance. Symbols indicate position of mean shoreline for each stage.
Discussion
I start with a general summary of my experimental findings and a comparison to the observations from the numerical experiments of Harris et al. (2016, 2018). For this comparison I loosely upscale the experimental stages to field conditions using the emergent experimental autogenic scales. Here I provide a rough upscaling to a Mississippi River scale system by assuming similarity in morphodynamic response between experimental (denoted with e) and prototype (denoted with p) systems that share dimensionless ratios that compare autogenic and allogenic scales. I stress that, as with all stratigraphic experiments, this experiment is not a simulation of any one particular system as it is challenging to match many important dimensionless numbers that describe the flow and sediment transport fields when comparing lab to field systems. However some emergent geomorphic scales and the scale invariance of many processes allow some dynamics to be compared to field systems (Paola et al., 2009). As such, this comparison gives a rough feel for the time scales and responses that should be expected for field scale systems.
I start with upscaling the magnitude of the experimental sea level cycles:
Given that deep autogenic sections of the Mississippi River in its backwater reach are ∼50 m in depth (Nittrouer et al., 2012), the stage 2 and 3 sea level cycles scale to 25 and 100 m, respectively.
Next I upscale the duration or period of the experimental sea level cycles using the following relationship:
Using Equation 2 and a value for the Mississippi River reported from biostratigraphic dates ( = 0.26 m/kyr) (Straub et al., 2009) the stage 2 and 3 sea level cycles scale to 96 and 384 kyrs, respectively.
The scaling above, however, only holds for the autogenic scales of the Mississippi River Delta. If we apply Equations 7, 8 to compare our stages 2 and 3 to the Rhine River Delta, which has Hc and values of 7 m and 1.2 mm/yr respectively (Zagwijn, 1989; Hijma et al., 2009), we get significantly different scaling. For the Rhine Delta, my stage 2 and 3 sea level cycles scale to 3.5 and 14 m with durations of 2.9 and 11.7 kyrs, respectively. The comparison of the Mississippi and Rhine River Delta systems suggest the following. First, not all river deltas respond to a given sea level cycle in the same way. Larger systems, with their larger autogenic scales, will be less sensitive to sea level cycles compared to their smaller neighboring systems. This point has been highlighted in a number of recent studies (Li et al., 2016; Yu et al., 2017; Trower et al., 2018). Second, these results suggest that care should be taken in universally applying one set of rules to icehouse condition deltas and another to greenhouse condition deltas. For example, the response of larger deltas with autogenic scales similar to icehouse sea level cycles might be similar to the response of smaller systems to high frequency and low magnitude greenhouse scale sea level cycle, like those proposed for the Late Cretaceous and earlier Paleogene (Tibert and Leckie, 2004; Miller, 2009). Third, while some large systems in icehouse conditions might behave like smaller systems in greenhouse conditions, on average the autogenic scales of deltas will be larger, relative to the scales of imposed sea level cycles, during greenhouse conditions and thus on average less sensitive to those cycles. This will facilitate more continuous connections between terrestrial and slope conditions during these times, similar to what has been proposed from numerical modeling studies (Sømme et al., 2009a).
Linking Mass Partitioning Along Source to Sink Profiles to Sea Level Cycles
In our experiments the relationship between mass extraction and physical distance from basin entrance was near identical in the three experimental stages (Figure 7A). The stage that pumped the most sediment to the marine was the one that lacked any sea level cycles, however this difference was only 13%. This increase in pumping of sediment to the marine in stage 1 can be linked to the long lived and relatively stable channel present for more than half of this stage. This channel produced a delta lobe that protruded far past the initial shelf-slope break. This is in line with a previous experiment that observed a stabilization of channels that are able to pump their sediment into deep waters (Kim et al., 2013). While avulsions still occur after this shelf-edge docking, their frequency is thought to be reduced, thus facilitating sediment flux to the marine.
The similarity in the χ(x) mean trend of stage 2 and 3 is striking and supports the notion that partitioning of sediment along a source to sink transect is largely driven by the long term basin accommodation production trend. By long-term, I mean time scales important for generation of basin subsidence, which exceed most Milinkovic sea level cycle fluctuations. While the bulk mass extraction trends for individual stages are similar (Figure 7A), my analysis of the average position within a sea level cycle during which preserved strata was constructed (Figure 8) suggest a preference for terrestrial strata constructed during highstands and marine strata constructed during lowstands. This preference is muted in the low magnitude and short period cycles of stage 2 in comparison to the high magnitude and long period cycle of stage 3, but still present.
It is important to note that the preference for terrestrial deposition during highstands and marine deposition during lowstands, apparent in our αD analysis, is a time averaged result. Specifically, the signal present in the stage 2 deposit is the average result of the four cycles in this stage. Without excellent time control, this signal might be difficult to tease out from stratigraphic architecture constructed in marginal marine settings forced with small magnitude and short period sea level cycles. For example, the experimental transport system experiencing stage 2 scale sea level cycles did not always produce predictable products of the allogenic forcing. The variability in the short term mass extraction trends of stage 2 was similar to the variability in the mass extraction curves of the autogenic stage 1 (Figures 7B,C), which suggest that their stratigraphic architecture was also similar. In addition, lowstand conditions in stage 2 did not always force a basinward movement of the transport system. In contrast, the high magnitude and long period sea level cycle of stage 3 produced a predictable movement of the depocenter with position in a sea level cycles and the changes in the location of mass extraction during lowstand (or highstand) conditions exceeded the autogenic stochastic variability in depocenter location (Figure 7D).
I now return to the observations from numerical experiments detailed in the set of papers by Harris et al. (2016, 2018). An exact comparison of the numerical experiments of Harris et al. (2016, 2018) to our physical experiment is not possible due to experimental scaling parameters. In addition, the channel depths in the numerical experiments of Harris et al. are unknown, making estimation of H∗ and T∗ for their numerical experiments imprecise. However, many of their modeled sea level cycles are less than 30 m in magnitude and occur over less than 100 kyr in a domain with forcing conditions motivated by the passive margin of the northeast United States. This might suggest H∗ and T∗ values close to 1.
The physical experimental results support the finding of Harris et al. (2016, 2018) that only a small difference in sediment delivery exists between systems forced with constant vs. dynamic sea level histories. For systems experiencing sea level cycles that are small relative to their autogenic scales, the timing of sediment delivery to the marine does have a preference for lowstand conditions. Similar to the findings of Harris et al. (2016), I note that this response can be variable, and due to autogenic processes sometimes the opposite of those predicted by purely allogenic models. For example, the channel that formed between the second and third sea level cycles of stage 2 was able to keep sediment delivery to the marine high, even as sea level rose. This channel was similar to some of the autogenic stage 1 channels and its growth rate allowed it to continue to extend, even under long term shoreline transgression of the rest of the delta. However, the response to sea level cycles that are large in comparison to the system’s autogenic scales seem to be predictable and in line with long standing theory (Van Wagoner et al., 1990). Large drops in sea level correlate with pronounced basinward movement of the depocenter and increased sediment delivery to the marine. For a Mississippi scale system, this would mean sea level cycles with amplitudes in excess of 50 m and/or periods in excess of 200 kyrs. However, as previously mentioned, these scales will vary with the size of a system as autogenic time and space scales typically correlate with system size (Hajek and Straub, 2017). Thus smaller systems will more easily produce detectable responses in the delivery of sediment to the marine compared to a larger system exposed to the same sea level cycle (Li et al., 2016).
Pumping of Sediment Past Experimental Delta Foresets
A key point to highlight from the system described here is the difficulty in pumping sediment past delta foresets in physical experiments. The experimental design was crafted to promote pumping of sediment past shelf-edge delta fronts to continental slope settings. These conditions included frequent flood events and an input flow that had excess density relative to the receiving basin. Even with these design parameters ∼80% of the input sediment was stored in the delta top and foreset. In comparison, a detailed seismic analysis of a shelf-edge delta and linked submarine channels in the northeastern Gulf of Mexico found a 50:50 split between shelf and slope volumes (Sylvester et al., 2012). Clearly, more work is necessary to identify the experimental parameter space necessary to promote flux of high sediment volumes to the marine.
While the flux of sediment past delta foresets is not as high as some systems, I can still compare the resulting slope isopachs in the three stages. Stage 1 and 2 share similar slope deposits and volumes (Figures 9A,B) that were spread over the full width of the platform. In comparison, the high magnitude and long period sea level cycle of stage 3 produced a slope deposit that was more isolated in lateral extent, but with thicker deposits at distal locations compared with the other stages (Figure 9C).
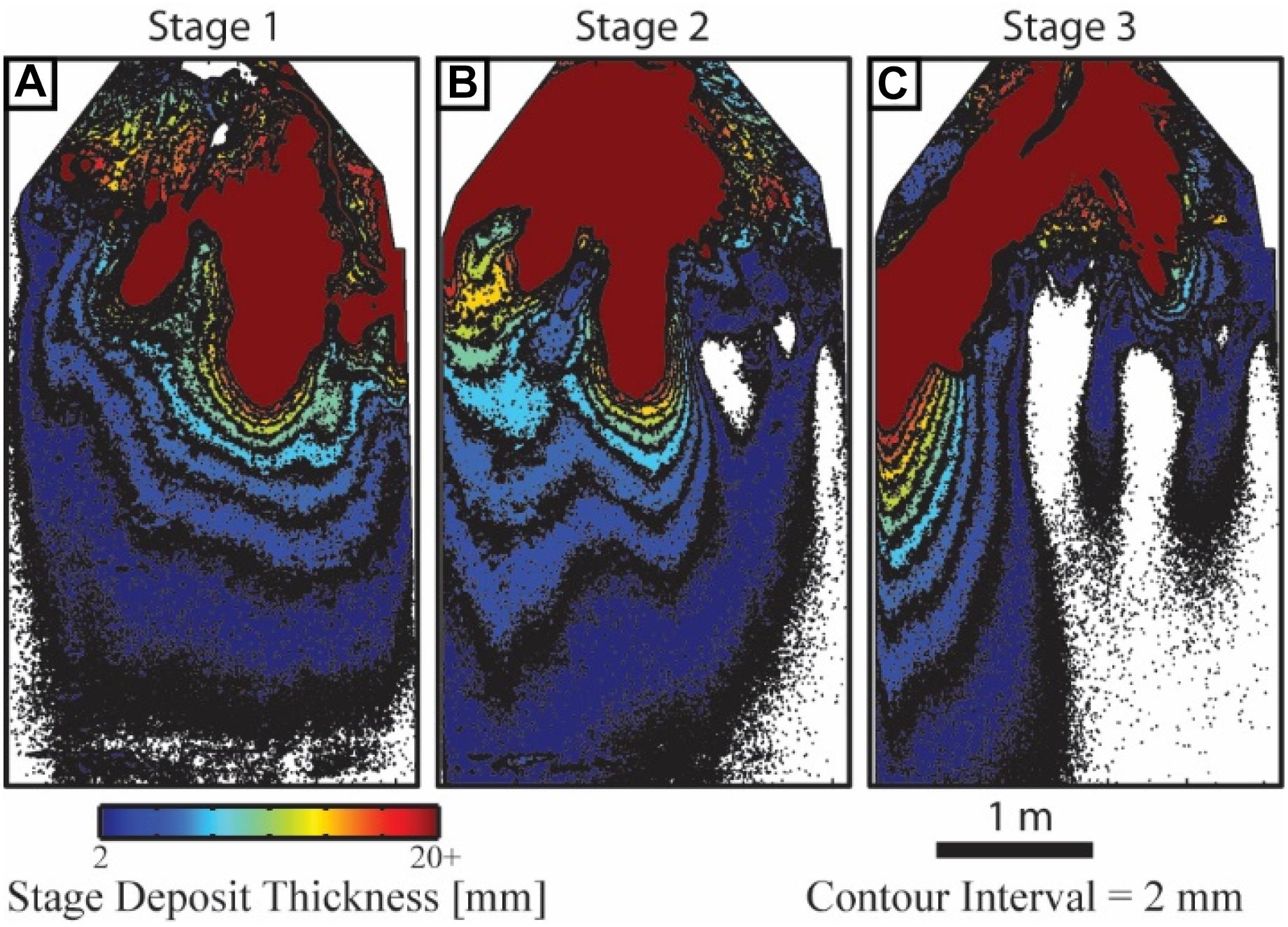
Figure 9. Maps highlighting deposit thickness trends on experimental slope for three experimental stages. Colorbar limits set to highlight slope deposit patterns with a 2 mm contours overlain.
Conclusion
The key results, which directly relate to the development of process-based theory for source-to-sink sediment routing systems, are twofold:
(1) Results from a physical experiment on linked shelf-edge delta and slope systems suggest that the scale of sea level cycles does not strongly influence the pumping of sediment to the marine, if one averages sediment delivery over a full cycle. This delivery of sediment to the marine is similar to systems with no sea level cycles, which due to long autogenic scales when deltas dock at shelf-edge, can actually have sustained rates of deepwater sediment delivery for long periods.
(2) While the magnitude and period of sea level cycles does not influence the long term delivery of sediment to the marine (i.e., a rate averaged over an entire RSL cycle), these parameters do influence the timing of deep marine sediment delivery. Sea level cycles with scales in excess of autogenic dynamic scales produce predictable responses during a sea level cycle with maximum delivery during ultimate lowstands. In contrast, sea level cycles with scales less than autogenic scales produce varied responses. On average marine sedimentation is delivered during lowstands for small cycles, but this response can sometimes be flipped, with high marine delivery during highstands. The handoff between predictable to stochastic response can be on the order of 50 m and 200 kyrs for large river systems.
Data Availability
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This study was supported in part by the National Science Foundation (EAR-1424312).
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I thank the past and present members of the Tulane Sediment Dynamics and Stratigraphy Laboratory, particularly Anjali Fernandes and Tushar Bishnoi, for the help in setting up the experimental initial conditions and for the help in cutting the final deposit. Finally, I thank the editors DH and Julie Fosdick for handling the submission, and the reviewers JB and KM for the reviews that helped to increase the clarity of the manuscript.
References
Allen, P. A. (2008). “Time scales of tectonic landscapes and their sediment routing systems”, in Landscape Evolution: Denudation, Climate and Tectonics Over Different Time and Space Scales Gallager, K., Jones, and Wainwright, J. London: Geological Society Of London
Allen, P. A. (2017). Sediment Routing Systems: The Fate of Sediment From Source to Sink, Cambridge: Cambridge University Press.
Cantelli, A., Pirmez, C., Johnson, S., and Parker, G. (2011). Morphodynamic and stratigraphic evolution of self-channelized subaqueous fans emplaced by turbidity currents. J. Sediment. Res. 81, 233–247. doi: 10.2110/jsr.2011.20
Catuneanu, O., Abreu, V., Bhattacharya, J. P., Blum, M. D., Dalrymple, R. W., Eriksson, P. G., et al. (2009). Towards the standardization of sequence stratigraphy. Earth Sci. Rev. 92, 1–33.
Gilbert, G. K. (1890). Lake Bonneville, U.S. Geologic Survey Monograph 1. Washington, D.C, U.S. Government Printing Office
Granjeon, D. (1999). Concepts and Applications of a 3-D Multiple Lithology, Diffusive Model in Stratigraphic Modeling. France: Special Publications of SEPM
Hajek, E. A., and Straub, K. M. (2017). Autogenic sedimentation in clastic stratigraphy. Ann. Rev. Earth Planet. Sci. 45, 681–709. doi: 10.1146/annurev-earth-063016-015935
Hamilton, P., Gaillot, G., Strom, K., Fedele, J., and Hoyal, D., (2017). linking hydraulic properties in supercritical submarine distributary channels to depositional-lobe geometryP. hamilton et al. linking hydraulic properties in submarine channels to depositional-lobe geometry. J. Sediment. Res. 87, 935–950. doi: 10.2110/jsr.2017.53
Harris, A. D., Covault, J. A., Madof, A. S., Sun, T., Sylvester, Z., and Granjeon, D. (2016). Three-dimensional numerical modeling of eustatic control on continental-margin sand distributionA. d. harris et al. numerical modeling of eustatic control on continental-margin sand distribution. J. Sediment. Res. 86, 1434–1443. doi: 10.2110/jsr.2016.85
Harris, A. D., Baumgardner, S. E., Sun, T., and Granjeon, D. (2018). A poor relationship between sea level and deep-water sand delivery. Sediment. Geol. 370, 42–51. doi: 10.1016/j.sedgeo.2018.04.002
Hijma, M. P., Cohen, K., Hoffmann, G., Van der Spek, A. J., and Stouthamer, E. (2009). From river valley to estuary: the evolution of the Rhine mouth in the early to middle Holocene (western Netherlands, Rhine-Meuse delta). Netherlands J. Geosci. 88, 13–53. doi: 10.1017/s0016774600000986
Hoyal, D. C. J. D., and Sheets, B. A. (2009). Morphodynamic evolution of experimental cohesive deltas. J. Geophys. Res. Earth Surf. 114:F02009
Jerolmack, D. J., and Sadler, P. (2007). Transience and persistence in the depositional record of continental margins. J. Geophys. Res. Earth Surf. 112:F03S13.
Kim, W., Petter, A., Straub, K., and Mohrig, D. (2014). “Investigating the autogenic process response to allogenic forcing: Experimental geomorphology and stratigraphy”: From Depositional Systems to Sedimentary Successions on the Norwegian Continental Margin, ed J. P. Wonham A. W. Martinius, Hoboken: John Wiley & Sons, Ltd, 127–138. doi: 10.1002/9781118920435.ch5
Kim, Y., Kim, W., Cheong, D., Muto, T., and Pyles, D. R. (2013). Piping coarse-grained sediment to a deep water fan through a shelf-edge delta bypass channel: tank experiments. J. Geophys. Res. Earth Surf. 118, 2279–2291. doi: 10.1002/2013jf002813
Li, Q., Yu, L., and Straub, K. M. (2016). Storage thresholds for relative sea-level signals in the stratigraphic record. Geology 44, 179–182. doi: 10.1130/g37484.1
Li, Q., Matthew Benson, W., Harlan, M., Robichaux, P., Sha, X., Xu, K., et al. (2017). Influence of sediment cohesion on deltaic morphodynamics and stratigraphy over basin-filling time scales. J. Geophy. Res. Earth Surf. 122, 1808–1826. doi: 10.1002/2017jf004216
Miller, K. G. (2009). Palaeoceanography: broken greenhouse windows. Nat. Geosci. 2:465. doi: 10.1038/ngeo563
Mohrig, D., Heller, P. L., Paola, C., and Lyons, W. J. (2000). Interpreting avulsion process from ancient alluvial sequences: Guadalope-Matarranya (northern Spain) and wasatch formation (western Colorado). Geol. Soc. Am. Bull. 112, 1787–1803.
Nittrouer, J. A., Shaw, J., Lamb, M. P., and Mohrig, D. (2012). Spatial and temporal trends for water-flow velocity and bed-material sediment transport in the lower mississippi river. Geol. Soc. Am. Bull. 124, 400–414. doi: 10.1130/b30497.1
Paola, C., Straub, K. M., Mohrig, D., and Reinhardt, L. (2009). The “unreasonable effectiveness” of stratigraphic and geomorphic experiments. Earth Sci. Rev. 97, 1–43. doi: 10.1016/j.earscirev.2009.05.003
Paola, C., and Martin, J. M. (2012). Mass-balance effects in depositional systems. J. Sediment. Res. 82, 435–450. doi: 10.1016/j.jenvrad.2016.07.028
Paola, C. (2016). A mind of their own: recent advances in autogenic dynamics in rivers and deltas. SEPM Spec. Publ. 106, 5–17. doi: 10.2110/sepmsp.106.04
Porębski, S. J., and Steel, R. J. (2003). Shelf-margin deltas: their stratigraphic significance and relation to deepwater sands. Earth Sci. Rev. 62, 283–326. doi: 10.1016/s0012-8252(02)00161-7
Sømme, T. O., Helland-Hansen, W., and Granjeon, D. (2009a). Impact of eustatic amplitude variations on shelf morphology, sediment dispersal, and sequence stratigraphic interpretation: Icehouse versus greenhouse systems. Geology 37, 587–590. doi: 10.1130/g25511a.1
Sømme, T. O., Helland-Hansen, W., Martinsen, O., and Thurmond, J. (2009b). Relationships between morphological and sedimentological parameters in source-to-sink systems: a basis for predicting semi-quantitative characteristics in subsurface systems. Basin Res. 21, 361–387. doi: 10.1111/j.1365-2117.2009.00397.x
Straub, K. M., Mohrig, D., McElroy, B., Buttles, J., and Pirmez, C. (2008). Interactions between turbidity currents and topography in aggrading sinuous submarine channels: a laboratory study. Geol. Soc. Am. Bull. 120, 368–385. doi: 10.1130/b25983.1
Straub, K. M., Paola, C., Mohrig, D., Wolinsky, M. A., and George, T. (2009). Compensational stacking of channelized sedimentary deposits. J. Sediment. Res. 79, 673–688. doi: 10.2110/jsr.2009.070
Straub, K. M., Mohrig, D., and Pirmez, C., (2012). Architecture of an aggradational tributary submarine-channel network on the continental slope offshore Brunei Darussalam, in Application Of Seismic Geomorphology Principles To Continental Slope And Base-Of-Slope Systems: Case Studies From Seafloor And Sub-Seafloor Analogues eds B. E., Prather M. E., Deptuck D., Mohrig, B., van Hoorn and R. B., Wynn Tulsa: Society for Sedimentary Geology
Straub, K. M., Li, Q., and Benson, W. M. (2015). influence of sediment cohesion on deltaic shoreline dynamics and bulk sediment retention: a laboratory study. Geophys. Res. Lett. 42, 9808–9815. doi: 10.1002/2015gl066131
Sweet, M. L., and Blum, M. D. (2016). Connections between fluvial to shallow marine environments and submarine canyons: implications for sediment transfer to deep water. J. Sediment. Res. 86, 1147–1162. doi: 10.2110/jsr.2016.64
Sylvester, Z., Deptuck, M., Prather, B., Pirmez, C., O’Byrne, C., Mohrig, D., et al. (2012). Seismic stratigraphy of a shelf-edge delta and linked submarine channels in the northeastern gulf of mexico: application of the principles of seismic geomorphology to continental-slope and base-of-slope systems: case studies from seafloor and near-seafloor analogues. SEPM Spec. Publ. 99, 31–59. doi: 10.2110/pec.12.99.0031
Tibert, N. E., and Leckie, R. M. (2004). High-resolution estuarine sea level cycles from the Late Cretaceous: Amplitude constraints using agglutinated foraminifera. J Foram. Res. 34, 130–143. doi: 10.2113/0340130
Trower, E. J., Ganti, V., Fischer, W. W., and Lamb, M. P. (2018). Erosional surfaces in the upper cretaceous castlegate sandstone (Utah, USA): sequence boundaries or autogenic scour from backwater hydrodynamics?. Geology 46, 707–710. doi: 10.1130/g40273.1
Vail, P. R., Mitchum, R. M., and Thompson, S., III. (1977). “Seismic stratigraphy and global changes of sea-level: Part 3. Relative changes of sea level from coastal onlap”, in Seismic Stratigraphy - Applications to Hydrocarbon Exploration ed C. E., Payton Tulsa AAPG Memoir 63–82.
Van Wagoner, J. C., Mitchum, R. M., Campion, K. M., and Rahmanian, V. D. (1990). Siliciclastic Sequence Stratigraphy in Well Logs, Cores, and Outcrops: Concepts for High-Resolution Correlation of Time and Facies: Tulsa: American Association of Petroleum Geologists:
Vendettuoli, D., Clare, M., Clarke, J. H., Vellinga, A., Hizzet, J., Hage, S., et al. (2019). Daily bathymetric surveys document how stratigraphy is built and its extreme incompleteness in submarine channels. Earth. Planet. Sci. Lett. 515, 231–247. doi: 10.1016/j.epsl.2019.03.033
Wang, Y., Straub, K. M., and Hajek, E. A. (2011). Scale-dependent compensational stacking: An estimate of autogenic time scales in channelized sedimentary deposits: Geology 39, 811–814. doi: 10.1130/g32068.1
Wheeler, H. E. (1964). Baselevel, lithosphere surface, and time-stratigraphy. Geol. Soc. Am. Bull. 75, 599–610.
Xu, J. P., Nobel, M. A., and Rosenfeld, L. K., (2004). In-situ measurments of velocity structure within turbidity currents. Geophys. Res. Lett. 31:L09311
Yu, L., Li, Q., and Straub, K. M. (2017). Scaling the response of deltas to relative-sea-level cycles by autogenic space and time scales: a laboratory study. J. Sediment. Res. 87, 817–837. doi: 10.2110/jsr.2017.46
Keywords: shelf-edge delta, autogenics, laboratory experiments, stratigraphy, sea level
Citation: Straub KM (2019) Morphodynamics and Stratigraphic Architecture of Shelf-Edge Deltas Subject to Constant vs. Dynamic Environmental Forcings: A Laboratory Study. Front. Earth Sci. 7:121. doi: 10.3389/feart.2019.00121
Received: 17 February 2019; Accepted: 07 May 2019;
Published: 28 May 2019.
Edited by:
David Mark Hodgson, University of Leeds, United KingdomReviewed by:
Janok Bhattacharya, McMaster University, CanadaKatherine Leigh Maier, National Institute of Water and Atmospheric Research (NIWA), New Zealand
Copyright © 2019 Straub. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kyle M. Straub, a21zdHJhdWJAdHVsYW5lLmVkdQ==
 Kyle M. Straub
Kyle M. Straub