What We Talk About When We Talk About Uncertainty. Toward a Unified, Data-Driven Framework for Uncertainty Characterization in Hydrogeology

A habit of basing convictions upon evidence and giving them only that degree of certainty which the evidence warrants, would, if it became general, cure most of the ills from which the world is suffering.

-Bertrand Russel

1. Introduction

Uncertainty is a central and unavoidable feature of decision problems that people face both in everyday life, as well as in virtually every field of science. Hydrogeology is no exception to that. In fact, the relevance of uncertainty to hydrogeology is particularly high, due to the high variability of many subsurface properties combined with a general scarcity of data. These factors have led to the development of stochastic hydrogeology where the subsurface properties are modeled as random variables (Gelhar, 1993; Rubin, 2003). Despite the wealth of research on stochastic modeling, a systematic investigation into the quantification of uncertainty and its impact on decision problems has remained limited. For example, Dagan (2002) noted that uncertainty “is a topic that has received little attention” and more recently, Kitanidis (2015) again pointed out that “it is somewhat surprising that this topic has not received more attention”. Instead, most discussions evolve around the specific topic of stochastic concepts, which is a closely related but ultimately an independent topic. For example, in a discussion forum, Zhang and Zhang (2004) solicited contributions discuss the perceived lack of applications that stochastic concepts have seen in hydrogeology. Of these contributions, only Ginn (2004) and Rubin (2004) discussed uncertainty briefly in the context of probability assessments. This lack may be explainable by the limited scope of that discussion forum, where only a fixed number of questions were to be answered by the contributors. However, more recently, Sanchez-Vila and Fernandez-Garcia (2016) organized a Special Issue that covered that same question but allowed for more space and personal involvement from the participants. While the topic of uncertainty was touched upon in all solicited contributions, none of them discussed its nature or aims. This neglect contrasts the closely related fields of hydrology (Mantovan and Todini, 2006; Vrugt et al., 2009; Clark et al., 2011) as well as geology (Wellmann and Regenauer-Lieb, 2012; Bond, 2015; de la Varga and Wellmann, 2016) which have and continue to have a broad and deep discussion about the nature, sources, aims and direction of uncertainty analysis. One of the main impediments for further progress in the field of uncertainty characterization, that has been identified, is the lack of a coherent terminology and framework (Montanari, 2007; Montanari et al., 2009).

A significant challenge for the establishment of a consistent framework of uncertainty analysis in hydrogeology is caused by the most prevalent workflow of inverse theory, or, inversion for short (Neuman, 2004; Tarantola, 2005; Carrera et al., 2005; Franssen Hendricks et al., 2009; Biegler et al., 2010; Menke, 2012; Linde et al., 2015; Zhdanov, 2015). This workflow, known as point estimation in inference, is based on a (regularized) data fitting or optimization approach which tries to identify a unique solution to the inverse problem. Typical examples in hydrogeology are goodness-of-fit criteria, i.e., the task of finding a single set of parameters such that the distance between predictions and observations is minimized (Indelman et al., 1996; Sánchez-Vila et al., 1999; Firmani et al., 2006; Schneider and Attinger, 2008; Riva et al., 2009; Copty et al., 2011; Pechstein et al., 2016; Zech et al., 2016). Even when point-estimators are not applied during calibration and a probabilistic sampling of the parameter distribution is advised instead, often the analysis is performed again, by deriving single solutions through, e.g., averaging (Neuman, 2014). There seems to be a deep distrust of the generally non-unique nature of scientific inference. Strangely, no rationale for this distrust is ever asked for nor provided.

Since this workflow of inversion was not designed to account for uncertainties in the inference, it consequently exhibits a number of problems from that perspective. First, aiming for a single best estimate neglects all other parameter sets that are possible but may be less plausible. Neglecting possible states can be problematic for inference alone (Good, 2009a). For uncertainty analysis, point estimation is even more problematic since the use of a single best estimate implies absolute certainty. Second, these studies usually use the observed data only, without any reference to available background data and are therefore liable to the base rate fallacy (Barhillel, 1980;Kahneman et al., 1982).

Responses to this have been mixed and often inconsistent (Nearing et al., 2016). Arguably, the most obvious concern is centered around the so-called problem of equifinality (Beven, 2006), i.e., the observation that many, often diverging, parameter sets may provide nearly identical goodness-of-fit values. One response to this insight has been the development and application of the generalized likelihood uncertainty estimation (GLUE) framework (Beven and Binley, 1992). Although often described as an (informal) Bayesian method, it has been strongly criticized in the literature (Mantovan and Todini, 2006; Stedinger et al., 2008). Another seminal response has been the development of the differential evolution adaptive metropolis framework (DREAM, Vrugt et al., 2009; Laloy and Vrugt, 2012; Laloy et al., 2013). Unlike GLUE, DREAM is a fully Bayesian inference method and uncertainty estimator and has seen many applications in hydrology since its publication. Although DREAM has seen applications in hydrogeology too (Mariethoz et al., 2010; Hansen et al., 2012; Shi et al., 2014; Xu et al., 2017; Laloy et al., 2016; Hayek et al., 2018), no universally accepted Bayesian framework for uncertainty analysis currently exists. A rising number of Bayesian inversion methods for inference have been published over the years (see e.g., Cardiff and Kitanidis, 2009; Rubin et al., 2010; Shi et al., 2014; Elsheikh et al., 2014; Saley et al., 2016), yet, the overall adoption of such methods has remained limited. This lackluster adoption rate can, e.g., be seen by the almost total absence of Bayesian methods in the aforementioned special issue on stochastic hydrogeology. Only Cirpka and Valocchi (2016) even care to mention this topic and only in the context of Bayesian model selection.

One problem that all the above-mentioned uncertainty frameworks share, is the lack of formalized prior derivation. Hydrogeology itself has only produced a small number of studies on this topic (Kitanidis, 2012; Li et al., 2017; Cucchi et al., 2019), which is sadly in line with the situation in many other fields. Since specifying the prior is the first step in any Bayesian analysis, high emphasis should be put on this step. However, coming up with universal and objective guidelines for every conceivable situation has proven to be elusive, so far (Earman, 1992; Scales and Tenorio, 2001). In fact, detractors of Bayesian inference are often criticizing the need to define a prior, claiming this step to be necessarily subjective and arbitrary (Kass and Wasserman, 1996; Ulrych et al., 2001; Kass, 2011). On the other hand, proponents of Bayesian inference cite the ability to include background knowledge in the form of prior probabilities as one of its major strengths (Jaynes, 1968).

To this date, the single most used inference framework in hydrogeology is arguably the Model-Independent Parameter Estimation and Uncertainty Analysis framework (PEST, Doherty, 2004). PEST itself constitutes a diverse set of optimization and estimation tools to calibrate a wide range of environmental models. The uncertainty framework allows users to estimate the predictive uncertainty of the model output using a somewhat inconsistent mixture of Bayesian and calibration techniques (Doherty, 2010). Such an eclectic approach to inference and uncertainty characterization may look intriguing. However, as Kitanidis (2015) pointed out, combining elements from two internally consistent systems is very risky.

In this manuscript, we will instead make the case for a single coherent data-driven framework for uncertainty characterization in hydrogeology. As we will argue below, this framework ought to be the Bayesian interpretation of probability, i.e., the system of probabilistic reasoning as developed by Ramsey (1931), Finetti (1975), Savage (1954), and others. When making this case, we will follow the reasoning of Pearl (1988b), who, while talking about Bayesian probability in the context of artificial intelligence, said the following:

Obviously, there are applications where strict adherence to the dictates of probability theory would be computationally infeasible, and their compromises will have to be made. Still, we find it more comfortable to compromise an ideal theory that is well-understood than to search for a surrogate theory, with only gut feeling for guidance. The merits of a theory-based approach are threefold:

1. The theory can be consulted to ensure that compromises are made only when necessary and that their damage is kept to a minimum.

2. When system performance does not match expectations, knowing which compromises were made helps identify the adjustments needed.

3. Compromised theories facilitate scientific communication; one need specifies only the compromise made, treating the rest of the theory as common knowledge.

To follow the advice of Pearl (1988b), we will start by describing such an ideal theory, outline the present challenges for its application and explain how to address them. In section 2, we will make the case for Bayesian probability by contrasting it to potential competitors. Next, in section 3, we will conceptualize the different forms of uncertainty using the Bayesian framework and identify the most relevant forms for hydrogeology. Finally in section 4, we will make a number of practical propositions by outlining what is currently missing, what compromises need to be made to make the Bayesian paradigm viable and what the relevant steps are that may help to reduce or even eliminate some of these compromises.

2. Reasoning With Uncertainty

A discussion about uncertainty should begin with a clear understanding of what is meant by this term. In a slightly ironic twist, the term uncertainty is far from being well-defined, both in everyday use as well as in the sciences. In fact, when scanning the hydrogeological literature, a wide range of, often conflicting, definitions, and conceptualizations are used (Hoffman and Hammonds, 1994; Hofer, 1996; Walker et al., 2003; Brown, 2004; Carrera et al., 2005; Refsgaard et al., 2007, 2012; Tartakovsky, 2013; Bond, 2015; Enemark et al., 2019). We will therefore start by providing an overview of different models that have been developed to conceptualize this term and facilitate both qualitative and quantitative reasoning. To avoid the often ad-hoc or gut driven nature of uncertainty analysis that is found in the literature, we will start by presenting frameworks that were developed in the field of epistemology, i.e., the field of philosophy concerned with the character of knowledge.

In general, uncertainty should be understood as a measure that describes the distance or gap between a current state of an agent and the one representing absolute certainty. The latter is formalized by the True and False statements found in classic logic, whereas the former extends this concept. Consequently, we will begin by describing models for such partial certainty as found in modern epistemic logic. As argued above, we will make the case for Bayesianism, i.e., the idea that certainty equals probability and vice versa. Only in the next step we will discuss a concept of uncertainty and make the case for the Kullback-Leibler divergence as the distance measure between current and absolute certainty.

2.1. Models for Reasoning With Certainty and the Case for Probabilities

In modern epistemology, certainty is defined over possible states of reality, collectively known as the set of possible worlds Ω (Halpern, 2003; Fagin et al., 2004). In Bayesianism, the equivalent term would be possibility space (Kruschke, 2010), whereas the equally labeled sample space Ω from probability theory may or may not have the same meaning depending on its interpretation (see below). This possibility space is now meant to contain, next to the true state of affairs, all other possibilities that are compatible with a given set of constraints and data available to an epistemic agent. Such an epistemic agent may be a human, but with the advent of artificial intelligence, computational agents have increasingly become the focus of modern research (Russell and Norvig, 2009). The epistemic state of such an agent is then defined by a function that assigns weights to each possible world ω. This function is known as a certainty or credence distribution.

Despite its relatively short history, the field of modern epistemology has already developed a number of different measures to describe that certainty distribution. These measures differ both mathematically as well as conceptually. The latter difference can best be understood by viewing these different measures as extensions of classical logic. In logic, a simple True or False relationship exists between a statement and the reality that this statement is trying to describe. In these extensions, discussed below, this simple relationship becomes more flexible and allows for different kinds of degrees of certainty (Darwiche and Pearl, 1997).

The most common approach is to conceptualize such a gradual degree of certainty as stemming from uncertain or incomplete knowledge. This means that, similar to classical logic, a given statement is objectively either true or false in reality. However, due to the agent's limited knowledge, she cannot fully determine its veracity and has to assign a limited certainty to it. This is known as a degree of belief and it is described by a number between 0 and 1, corresponding to False and True in classic logic. It can be shown that such degrees of belief follow the rules of probability theory, i.e., the certainty of an agent is to be described by a probability measure (Savage, 1954; Lindley, 1987). To illustrate this model; consider a statement about the mean conductivity of a given sample being above a given threshold, say, 10⁻³m/s. The certainty of this statement could then be ascertained if we would have access to a well-calibrated histogram of conductivity values of samples from the aquifer the sample was taken from.

An extension of this model is derived by the additional inclusion of uncertainty stemming from ignorance. Using the now (in)famous epistemology of the former US Secretary of Defense Donald Rumsfeld (2002), probability describes the known unknowns whereas ignorance is about the unknown unknowns. To illustrate this concept, let us consider a revised version of the above problem: Suppose that our knowledge base is now less certain such that the sample is only with 90% probability from the aforementioned aquifer, but with 10% probability of some unknown provenience. This leaves a 10% certainty gap in our reasoning system. The seminal work of Dempster (1968) demonstrated a way of handling this gap, whereas the later extensions of Shafer (1976) made this calculus into a full reasoning and inference system. The resulting reasoning framework is the Dempster-Shafer theory, evidence theory or theory of belief functions. Like in the example above, Dempster–Shafer theory is often praised for being able to combine evidence from different sources with different kinds of uncertainty attached to it. Its applicability has, however, been limited due to a number of criticisms (Pearl, 1988b,a, 1990). Note that other fields use similar concepts, with sometimes very different notations. In economy, for instance, uncertainties from lack of knowledge are called risk, whereas uncertainties from ignorance are called Knightian uncertainties or simply uncertainties (Knight, 1921). On the other hand, political science and decision theory often describe uncertainties as a lack of knowledge and ignorance, shallow, and deep uncertainty, respectively (Walker et al., 2013).

An alternative approach is to model uncertainty stemming from uncertain truth. This means that the veracity of a given statement may never be fully determined, even in cases of complete knowledge. Using the above example, this could be the case if the statement is altered such that conductivity of the sample is said to be large. Even if all relevant data on this sample are gathered, e.g., some laboratory testing may determine the conductivity being 10⁻³m/s, no definitive certainty can be determined. A statement that the conductivity of the sample is large given that the conductivity is 10⁻³m/s may be considered as sort-of-true. The point is that our limited degree of certainty is not caused by limited knowledge but by some vagueness or fuzziness in the statement itself. Measures that are able to describe such situations are confusingly called possibility measures, although no particular connection to above possibility space exists, and the related mathematical framework is, more appropriately, called fuzzy logic (Zadeh, 1978; Dubois and Prade, 1988). Reasoning systems that employ fuzzy logic have seen wide-ranging applications in engineering, modern logic, artificial intelligence systems etc., which testifies to their versatility and usefulness.

Despite the existence of these comparably sophisticated systems for reasoning under uncertainty, the simplest approach of probabilistic reasoning has seen a strong resurgence in the last decades with the introduction of Bayesian networks (Pearl, 1988b; Neapolitan, 1990). These networks are probabilistic graphical models that represent the, typically causal, relationship between different physical processes.

Using the above statements, we would assert that probabilistic reasoning is the most-suited framework for reasoning under uncertainty in hydrogeology. Probability represents a simple, yet very flexible tool that is able to capture most of the problems encountered in this field. Fuzzy logic, although often employed in engineering, does not offer much additional benefit since most evidence being used is numerical in nature and therefore has virtually no fuzziness associated with it. Contrary to that, Dempster-Shafer theory does offer relevant benefits as an uncertainty framework, which do however, need to be considered in context. The first benefit is simply due to the fact that many situations of subsurface analysis do include an element of deep uncertainty, in particular the topic of structural uncertainty. To address that, we will deal with this problem exhaustively below and describe a way how to turn this deep into shallow uncertainty. In this way we are making the topic of structural uncertainty fully amendable to probabilistic analysis. Second, as pointed out by Rubin et al. (2018), the Dempster-Shafer theory can be helpful in accounting for unknown unknowns that result from the interaction of hydrogeological problems with societal developments in general (Walker et al., 2013; Maier et al., 2016). This second benefit is very important but does not necessarily conflict with our notion of probability as a default system for uncertain reasoning. Since Dempster-Shafer theory is a full generalization of probability theory, it is easy to embed a fully probabilistic analysis within a larger framework. In addition to these benefits, the Dempster-Shafer theory has a number of drawbacks that make reasoning with it counter intuitive and hamper its applicability for real-world problems. In particular, it is not possible to employ it on top of existing techniques compared to probability theory or even fuzzy logic and its applicability to decision theory remains controversial. Although the number of applications in earth sciences is rising, it is still a niche theory with only few practical applications (Malpica et al., 2007). In summary, we propose to use probabilistic reasoning as the main tool of uncertainty analysis, while being aware of its limitations, and being prepared to account for other types of uncertainty by embedding probability measures within a larger analysis possibly using the Dempster-Shafer theory.

2.2. On the Interpretation of Probability

Owing to the seminal work of Kolmogorov (1933), modern probability theory is fully grounded in set theory and as such, it is as well founded and defined as any other field of mathematics (Kallenberg, 2002). Yet, unlike many other mathematical disciplines, there is no clear consensus about where to locate probability in real-world situations.

Roughly speaking, two different interpretations of probability can be distinguished; physical as well as epistemic probability (Figure 1). The first interpretation regards probability as an actual property of physical systems comparable to, e.g., mass, energy and momentum (Figure 1, upper right corner). This is best captured in its most widely applied form; frequentism, where the probability of an event is equated with the relative frequency of this event in an often-repeated random experiment (Neyman and Pearson, 1928, 1933). This definition has garnered wide support in the sciences, due to its clear and lucid formulation (von Mises, 1982). On the other side, the epistemic interpretation regards probability as an intrinsic property of epistemic agents (Figure 1, upper left corner). This means that, unlike mass, energy or momentum; probability is not a property of a physical system but of the epistemic state of an agent that is trying to reason about said system (Finetti, 1975; Savage, 1954;Jeffrey, 1992).

FIGURE 1

Figure 1. Illustration from Descartes (1662) visualizing the difference between physical objects (upper right corner) and their epistemic representations (upper left corner).

2.2.1. The Case for Bayesianism

The discussion about the best or most appropriate interpretation for any given situation is still ongoing and we do not want to uncritically favor any side. For our topic, however, the epistemic interpretation, called Bayesian interpretation, of probability seems to be the only appropriate one. The main rationales for its use shall be discussed in the following.

First, the epistemic interpretation is simply the more comprehensive interpretation of the two. In fact, it is a full generalization of the physical interpretation, since it is able to cover all cases described by the latter and then some. This is not the case for the frequentist interpretation since its application is constrained to cases where physical frequencies are available. This inclusiveness of Bayesianism is often obfuscated by calling it the subjective interpretation of probability, as opposed to the objective interpretation of frequentism. But such a characterization is misguided since epistemic probabilities can be subjective, objective and everything in between (Berger, 2006; Williamson, 2010).

Second, the concept of a long-running sequence of random experiments is ill defined in the context of hydrogeology. This is not to deny the relationship that relative frequencies of, say, conductivity values from other sites have on the characterization of a given site. As described above, most Bayesians would agree that such frequencies should always be used when available (Rubin, 1984). The difference to frequentism is not the importance of observed frequencies but the role they play in defining probability. Within the context of hydrogeological site characterization, we would argue that equating those frequencies with probability, and the use of frequentist methods therefore as well, is rather contrived (Renard, 2007).

Third, uncertainty is a property of knowledge and therefore fundamentally epistemic. This fact is often obfuscated by the practice of separating uncertainty into so called aleatoric and epistemic uncertainty, somewhat mimicking the above distinction between physical and epistemic probability (Hoffman and Hammonds, 1994; Helton and Burmaster, 1996; O'Hagan et al., 2006; Gong et al., 2013). Generally speaking, epistemic uncertainty is said to be reducible by collecting more data whereas aleatoric uncertainty is caused by intrinsic randomness which cannot be further reduced by data. Typically, the latter is illustrated by referring to activities like throwing a die or tossing a coin. The problem with such examples is that both these activities are demonstrably deterministic without any intrinsic randomness (Diaconis et al., 2007). It may be argued that the physical world itself exhibits pure randomness on the quantum level of reality. This notion, associated with the Copenhagen interpretation of quantum mechanics was dominant for the better part of the 20th century but has become marginalized more recently in favor of the Everett (Deutsch, 1999; Sebens and Carroll, 2016) and Bayesian (Schack et al., 2001; Fuchs and Schack, 2013) interpretations. Whatever the case may be, within the context of the macroscopic physical laws relevant to hydrogeophysics, these debates are completely immaterial. On the macroscopic level, the laws of classical physics exhibit no randomness, which can therefore not suddenly manifest in situations that are fully determined by these laws.

The last major reason, for why frequentism does not provide an adequate framework for uncertainty analysis concerns the nature of frequentist inference itself. Following Royall (1997), any statistical inference, as well as any other form of evidential assessment, can be thought of as addressing a series of three questions; (i) What does the evidence say?; (ii) What should I believe?; and (iii) What should I do? Uncertainty itself concerns the second question, i.e., the question of belief but frequentist inference actually does not address this question at all (see Table 1). To explain why, let us start at question (i); the question of evidence. Evidence is central to the field of inference but surprisingly difficult to pin down (Feldman and Conee, 1985; Achinstein, 2003; Dougherty, 2011). In general, the evidence of some observations are those aspects of it which justify or lend credence to a hypothesis under question. The most important theoretical advance for the quantification of this notion came in the form of the Likelihood Principle (LP, Barnard et al., 1962), stating that all the evidence of the data is contained in their likelihood. Although some criticism exists, the LP is broadly accepted in the field of epistemology, due to being derived from extremely simple axioms (Barnett, 1999; Good, 2009b; Bandyopadhyay and Forster, 2011; Grossman, 2011). This first step alone, therefore, puts some pressure on frequentist hypothesis testing since it does not meet this criterion. In contrast to that, frequentist estimation, like calibration, parameterization, regression etc.; does not necessarily conflict with this principle. Here, the problem comes in the second step, i.e., using the evidence to justify belief. Frequentism does not deal with belief but uses the evidence, or some proxy thereof, to jump directly to decisions. As outlined above, decisions are made by deriving point estimates, for instance by applying a significance criterion to a p-value or an optimality criterion to some estimation procedure (Table 1). Some optimality criteria can be derived on evidential grounds, like the Maximum Likelihood (ML) estimator. While ML estimators are widely used, many other estimators exist, which typically divert from ML by trying to reproduce only certain features of the data or contain some application-specific reasoning (Krause et al., 2005; Pushpalatha et al., 2012; Bennett et al., 2013; Moriasi et al., 2015). This work flow, which forms the blueprint of most inference techniques in hydrogeology, is in contrast to the principles of Bayesian inference. First, Bayesian inference meets the LP by using only the likelihood to assess the evidential support of the data. As mentioned above, adherence to the LP is not unique to Bayesianism, but a necessary prerequisite. The most important difference comes in the next step, when Bayesian inference uses Bayes' theorem to compute the belief that follows from the evidence. This step is simply a conclusion from the axioms of probability theory and a number of more recent studies have demonstrated how updating through Bayes' theorem does indeed maximize the epistemic accuracy of an agent (Greaves and Wallace, 2006; Leitgeb and Pettigrew, 2010; Easwaran, 2013). However, the application of Bayes' theorem requires the derivation of the prior probability, which is regularly criticized. We will deal with this question in more detail below and continue for now with the above schematic. Having determined the belief given the evidence concludes the inferential part of the statistical analysis. This, however, leaves open the last step of the analysis, which is to make an informed decision. In above terms, this can mean to decide which parameter θ to use or which hypothesis to accept. In Bayesianism, decision making is done by maximizing the expected utility. Like the two other steps, the decision making through maximizing the expected utility is derived from simple axioms making it the most well-subscribed paradigm in decision making. What is important for us is that this last step is independent of the other two and the specification of the utility function is therefore left to the decision maker. This clear separation of inference and decision makes Bayesianism so relevant to uncertainty analysis.

TABLE 1

Table 1. Comparison of the different concepts used in frequentism and Bayesianism.

Combined, reasons like this have led to the strong rise Bayesian methods have seen in many fields like physics (von Toussaint, 2011), biology (Huelsenbeck et al., 2001), environmental science (Clark, 2005), clinical research (Berry, 2006), genetics (Beaumont and Rannala, 2004), psychology (Wagenmakers, 2007), cognitive science (Clark, 2015), and many more. In addition, these reasons have made Bayesianism the leading paradigm in the field of philosophy of science (Howson and Urbach, 2005; Bandyopadhyay and Forster, 2011;Easwaran, 2011a).

2.3. Bayesian Uncertainty Analysis

Having established Bayesianism as the most appropriate framework for uncertainty analysis, we will quickly restate the basic properties of Bayesian inference and prediction. In addition to that, we will demonstrate how the Bayesian framework provides an axiomatically based definition of uncertainty and therefore allows a quantitative assessment of uncertainty reduction as provided by the inference.

2.3.1. Inference

Inference is defined as the process of characterizing a probability function using data. In Bayesian inference, this probability is defined over the possibility space Ω (Kruschke, 2010). As the name implies, Ω is supposed to contain all states that are possible for a given situation, i.e., states whose probability cannot be set a priori to zero. To avoid the curse of dimensionality, this space is typically approximated by a parsimonious parametric model, which is fully determined by the specification of its parameters θ. The initial certainty for these parameters θ, is the aforementioned prior p(θ). The likelihood of each parameter set θ is determined by the data generating process, which in hydrogeology is usually defined through partial differential equations. Combining prior and likelihood, Bayes' theorem can now be used to determine the probability conditioned on the data z called the posterior

$\begin{array}{ll}p(\theta |z)=\frac{p(z|\theta )}{p(z)}p(\theta ).& (1)\end{array}$

The only missing element in Equation (1) is the probability of the data p(z) often called the marginal likelihood or the evidence. However, for most scenarios, this probability is only a normalization constant. It can therefore be omitted and Equation (1) can be computed by normalizing p(z|θ)p(θ). This latter form is often used in the literature, since modern sampling methods are versions of the Markov-Chain-Monte-Carlo method, which guarantees this normalization by design.

Looking at this workflow, it becomes clear how Bayesian inference is the general probabilistic framework for the inverse problem with the likelihood being the Bayesian representation of the relevant forward problem.

2.3.2. Prediction

Using the conditioned, i.e., posterior, probability p(θ|z), the predictive probability for new unobserved data, i.e., predictions, z* is given by

$\begin{array}{ll}p(z^{\ast }|z)={\displaystyle {\int }_{\Theta }p}(z^{\ast }|\theta )p(\theta |z)\text{d}\theta .& (2)\end{array}$

Bayesian prediction of new data z* given the old data z is therefore achieved by marginalizing the posterior probability p(θ|z) times the predictive probability p(z*|θ) of the model as defined by θ.

This influence of the parameterized space of possible worlds Θ on both Bayesian inference and prediction also provides a formal description of two closely related epistemological problems in science; namely the Theory-ladenness of Science and the Duhem-Quine Hypothesis. The former roughly states that scientific inference is always affected by, usually implicitly held, beliefs of the investigator and is strongly associated with the works of Kuhn (1962) and Feyerabend (1975). The latter is more general and states that scientific inference is always under-determined by our observations and additional assumptions are needed to make sensible conclusions. Next to Duhem (1906) and Quine (1951), important contributions to the development of this notion came, e.g., from Van Fraassen (1980), Laudan (1990), and Stanford (2001). Note that the Bayesian framework does not solve this problem but does make the impact of Θ on the findings transparent. This means that all theoretical presuppositions are contained in the definition of Θ and only influence inference and prediction by virtue of its choice and through the aforementioned equations.

2.3.3. Uncertainty

In addition to properly describing the change of beliefs due to new evidence, Bayes' theorem provides a mathematically rigorous way to characterize the uncertainty represented in a probability distribution as well as the uncertainty reduction achieved during the inference. This is possible due to the intricate relationship between the concept of information in information theory and the way probabilities are updated in Bayesian inference (Ebrahimi et al., 2010). According to Shannon (1948), the information of a particular value of θ_i is given by I(θ_i) = −log₂(p(θ_i)), with log₂ being the logarithm of base 2. Due to this choice, information is usually measured in bits, with other bases simply leading to other units. To characterize the information content of a probability function of a discrete variable, Shannon (1948) introduced the expected value of information

$\begin{array}{ll}H={\displaystyle \int p(\theta )I(\theta )\text{d}\theta =-\int p(\theta ){log}_2(p(\theta ))\text{d}}\theta .& (3)\end{array}$

As recounted by Tribus and McIrvine (1971), Shannon initially called this quantity uncertainty but was unfortunately convinced by John von Neuman to use the term entropy instead. In addition, the Shannon entropy only describes the uncertainty with respect to a state of complete ignorance which is implicitly defined in his first and second axioms. Due to this limitation, the Shannon entropy is not suited for Bayesian inference, where updating from arbitrary priors to posteriors is possible. To that end, Equation (3) needs to be amended such that the uncertainty with respect to other degrees of certainty can be described. This extended concept is known as the Kullback-Leibler (KL) divergence (Kullback and Leibler, 1951) but should be more appropriately called relative entropy/uncertainty or information

$\begin{array}{ll}{D}_{\text{KL}}={\displaystyle \int p}(\theta ){\log }_2\left(\frac{p(\theta )}{q(\theta )}\right)\text{d}\theta .& (4)\end{array}$

Due to its positive sign, the KL divergence is the negative relative entropy of p with respect to q. It therefore belongs to the class of entropy measures meaning that uncertainty is the entropy of a probability function. Such measures have several advantages compared to, say, variance-based measures like Sobol indices that are often used in the literature (Ebrahimi et al., 2010). Compared to the Shannon entropy, this quantity is more fundamental in several ways. First, DKL can be easily extended to continuous as well as multidimensional variables. Second, DKL describes the uncertainty as expressed in one distribution with respect to another and therefore reduces to the Shannon entropy in the marginal case of a flat q. Finally, DKL connects the concept of information with the updating from the prior to the posterior in Bayesian inference. If p and q are identified with the posterior and prior distribution, respectively, then DKL is a measure for the information and therefore the uncertainty reduction achieved during the inference (Hou, 2005; Tang et al., 2016).

2.4. Challenges of Bayesianism

Although Bayesianism has become such a popular position in the sciences, it has also received its fair share of criticism (Gelman, 2008; Easwaran, 2011b). These criticisms often include rather formal issues like the problem of logical omniscience and the problem of old evidence (Garber, 1983). Others, however, are more relevant to its applicability and should therefore be discussed in the following. Looking at Equation (1), we see that Bayesian inference consists of determining three expression only. Next to the likelihood, which is also often used outside of Bayesian inference, two expressions are peculiar to it and therefore need to be looked at in detail.

First, let us look at the marginal likelihood in Equation (1), which poses the biggest computational problem. Since a direct computation of this expression generally involves multi-dimensional integrals, Bayesian inference was, for a long time, confined to a comparably small number of simple cases. Nowadays, Markov-Chain-Monte-Carlo (MCMC) methods are used (Gelfand and Smith, 1990; Tierney, 1994; Chib and Greenberg, 1995), which circumvent the computation of these often-intractable integrals by sampling directly from the non-normalized posterior. Implementations of MCMC samplers exist as either standalone versions (Lunn et al., 2009; Gelman et al., 2015; Depaoli et al., 2016) or they are implemented for popular languages like R (Martin et al., 2011; Lindgren and Rue, 2015; Denwood, 2016) and Python (Patil et al., 2010;Foreman-Mackey et al., 2013).

Second, let us turn to the prior in Equation (1), which is both a theoretical and computational problem. The theoretical problem, known as the problem of the priors (Osherson et al., 1993), is caused by the limited number of restrictions that Bayesianism puts on a reasoning system to be rational. Taken to the extreme, an agent would be free to believe anything as long as there is no contradiction to the axioms of probability (Romeijn, 2017). In reality, however, common sense dictates that a sound opinion is constrained by additional sources of evidence. Responses from Bayesians to this obvious clash have been mixed, with roughly two extreme camps existing; subjective Bayesianism and objective Bayesianism. Subjective Bayesians stick to the purely theoretical principles and try to mitigate the conflict through expert elicitation, i.e., the application of formal rules to elicit expert opinions on a given topic and turn them into prior distributions (O'Hagan et al., 2006; Albert et al., 2012). On the other end, we find objective Bayesians who claim that additional conditions on rational beliefs, in particular prior beliefs, are necessary. These additional conditions revolve around the principle of equivocation, which means that, if no evidence favors one possibility, a rational agent should initially equivocate between all possibilities (Williamson, 2010). A more sophisticated version of this idea is the Maximum Entropy (ME) method (Jaynes, 1957a,b), where non-flat priors are possible if some additional, often physically based, constraints or symmetry arguments make some possibilities less credible from the start. In practice, most statisticians, scientist and engineers strive for objectivity but use primarily tried-and-tested approaches, which strike a balance between objectivity and applicability. While the ME method has found some application in hydrogeology (Woodbury and Ulrych, 1993), most studies rely on using flat or extremely wide distributions over some parameter range derived from the literature (Woodbury and Ulrych, 1996, 2000; Marchant and Lark, 2007; Diggle and Ribeiro, 2007; Murakami et al., 2010; Laloy et al., 2013; Shi et al., 2014; Geiges et al., 2015; Mara et al., 2017; Hayek et al., 2018). Unfortunately, this procedure is not as harmless as often perceived, since neither are ranges particularly objective nor are flat priors necessarily uninformative (a property which is often used as a proxy for objectivity) (Gelman et al., 2017). In general, current use of objective and uninformative priors in hydrogeology is seriously lacking compared to the standards established in statistics. To give an example of the latter, let us consider so called reference priors. These priors are based on the idea to systematically minimize the impact on the inference. If properly done, the results would then be dominated by the data alone (Bernardo, 1997). Another example is the use of the data themselves to determine the best prior. This method is called empirical Bayes (Carlin and Louis, 2000; Malinverno and Briggs, 2004), since it uses only the empirically available data for the inference. These methods have been very successful in statistics due to their ease of application and apparent objectivity (Valakas and Modis, 2016) but have been heavily criticized on theoretical grounds. The main critique is that by using the data for both the likelihood and the prior, empirical priors–and to a lesser extend reference priors as well—use the data twice. This is a clear violation of the LP, which is generally seen as a necessary element of Bayesianism (Lindley, 1987; Good, 2009b).

A final point concerns Bayesian decision theory. Including this topic under challenges may seem strange given that the Bayesian framework enjoys the best integration with decision theory of any inferential framework. Beginning with the seminal works of von Neumann and Morgenstern (1944) and Savage (1954), Bayesianism has become the de-facto standard in modern decision theory (Berger, 1985; Jeffrey, 1992; Bernardo and Smith, 2000; Robert, 2001; Koehler and Harvey, 2004; Baron, 2004; Parmigiani and Inoue, 2009; Gilboa, 2009). It should consequently be one of its biggest assets. Alas, that is not what we see. Instead, very little effort has been devoted to connecting Bayesian inference with any of the established models from decision theory. To substantiate this pessimism, we simply refer here to the review of Tartakovsky (2013), who gives an excellent overview of this topic yet still fails to find more than a handful of studies, which apply Bayesian decision theory to hydrogeology. As explained above, this lack is of little consequence for the specific topic of uncertainty analysis. It is, however, clearly a challenge for Bayesian inference in general. Looking at Table 1, current practice means to only implement the first and second step out of all three. While not the focus of this manuscript, we opine that a full appreciation of the Bayesian framework will only become a reality once all its elements are common knowledge and regularly applied.

3. What Kind of Uncertainties are We Talking About

To organize the different forms and sources of uncertainties, a wide range of often conflicting notations is used in the literature (Hoffman and Hammonds, 1994; Hofer, 1996; Walker et al., 2003; Brown, 2004; Carrera et al., 2005; Refsgaard et al., 2007; Kwakkel et al., 2010; Biegler et al., 2010; Refsgaard et al., 2012; Guillaume et al., 2012; Tartakovsky, 2013; Caers et al., 2014; Bond, 2015; Enemark et al., 2019). In the following, we are going to describe and contextualize these notations using the formalism established above.

3.1. Understanding Uncertainties Using the Framework of Bayesianism

A common approach is to separate uncertainties into epistemic and aleatoric uncertainties (Kiureghian and Ditlevsen, 2009; Beven and Young, 2013; Bond, 2015). As already explained above, all uncertainties in Bayesianism are necessarily epistemic and aleatoric uncertainties simply do not exist in this framework. In our opinion, this distinction can make sense for practical applications because, due to often highly non-linear processes, reality always has a tipping point—sometimes sudden, sometimes more gradual—beyond which the additional collection of data becomes too costly to be reasonably entertained. Identifying such tipping points is important for any engineering task in order to estimate sensible directions for the additional data gathering. This notion is often implicitly confirmed by authors who otherwise seem to argue for the physical presence of aleatoric uncertainty within macroscopic phenomena. Fox and Ülkümen (2011) for example admit as much when saying "Aleatory uncertainty is attributed to outcomes that for practical purposes cannot be predicted and are therefore treated as stochastic". Another situation, where the use of aleatoric uncertainty seems justified, is in the presence of so-called statistical uncertainty (Beven and Young, 2013). This means that the statistical variation of a given population, say, the conductivity values of an aquifer, puts an “inherent” limit on how much the uncertainty can be reduced. From a Bayesian perspective, such reasoning is simply false. Kiureghian and Ditlevsen (2009), for instance, articulate this problem when stating that “The distinction between aleatory and epistemic uncertainties is determined by our modeling choices.” To illustrate this point and get at the root of this prevailing misunderstanding, let us look at the already used example of conductivity values of an aquifer. Using, e.g., the whole aquifer as the population, there is indeed an intrinsic limit of how much the uncertainty can be reduced through sheer data collection. It would, therefore, seem that this uncertainty fits the above definition of being aleatoric. However, as Kiureghian and Ditlevsen (2009) pointed out, there is no metaphysical reason to model the whole aquifer as a single statistical population. If enough data are collected, the aquifer can easily be split up into, say, its hydrofacies, each of which would now have a much-reduced statistical uncertainty. This process of fine graining our statistical model, depending on the amount of data, can be repeated ad infinitum, which shows that no statistical variation is ever intrinsic to reality but only determined by our model. The last class of examples, which are often used to demonstrate aleatoric uncertainty are actually cases of deep or Knightian uncertainty (Fox and Ülkümen, 2011; Beven and Young, 2013). Deep uncertainty is certainly an important and even dominant form of uncertainty in everyday situations. However, as explained above, it should be modeled by the Dempster-Shafer framework and treating it within a probabilistic context is necessarily error prone. In summary, aleatoric uncertainty, as used in the literature, is an inconsistent mixture of several distinct concepts, with varying levels of usefulness.

The second differentiation is to separate uncertainties into inferential and predictive uncertainties. Within Bayesianism, these uncertainties are simply defined via Equations (1) and (2), respectively. This means that the inferential uncertainty is the DKL of the posterior vs. the prior distribution, whereas the predictive uncertainty is given as the DKL of the predictive distribution with the data vs. without them.

Another important differentiation is to separate uncertainties into input and parametric uncertainties (Refsgaard et al., 2012; Tartakovsky, 2013). Within the context of Bayesianism, input uncertainty is simply the uncertainty that is passed down from receiving nodes in a Bayesian network. This means, the input uncertainty of a given node is the combined uncertainty of its parent nodes. On the other hand, parametric uncertainty is uncertainty in the parameters θ of the used parametric model and is therefore identical to the inferential uncertainty given by Equation (1).

The last concept to be discussed is the topic of structural and conceptual uncertainty. Both these terms are used in sometimes overlapping and sometimes conflicting ways (Refsgaard et al., 2012; Tartakovsky, 2013; Enemark et al., 2019). In general, it is not even clear whether these two terms do differ in meaningful ways. From a Bayesian perspective, both refer to the necessary approximation of the possibility space Ω by a lower-dimensional parametric subspace Θ. Since describing Ω, e.g., the conductivity field of a real-world aquifer, in full detail is both impossible, due to the scarcity of data, as well as numerically intractable, such approximations will always be necessary. From our perspective, it can be beneficial to use two different terms in order to distinguish between the uncertainty expressed between the different parametric models, called structural models in the following, and the uncertainty being expressed within any such given structural model. In the following, we will focus on the latter and use the term structural uncertainty to describe this category.

Having used the Bayesian framework to put the different forms of uncertainty into a proper context, we will finish this section by ranking these different forms according to their relevance for hydrogeological modeling. Since such a ranking is strongly dependent on the context, we will shortly discuss each form individually. First, parametric uncertainty is doubtless one of the dominant forms regardless of the situation. Bayesian inference is perfectly suited to handle it, provided that proper priors are provided. Structural uncertainty is also very important, due to the often-pronounced spatial pattern of many aquifers. Handling this form of uncertainty as well as structural modeling in general is comparably underdeveloped. Instead, structural uncertainty is often recast as a form of process uncertainty, in particular in the case of transport processes (Neuman and Tartakovsky, 2009). While such alternative process models may be important for pure modeling purposes, we are very skeptical about their use in uncertainty analysis. In addition to this, the parameters of such models are often pure convenience parameters and they are difficult or impossible to condition on point measurements. As mentioned above, conceptual uncertainty is not going to be the focus of this paper. Instead, we are going to describe in the following the range of structural models, which are used in hydrogeology and try to identify the most relevant paradigms. Finally, input uncertainty is technically not part of hydrogeology since the uncertainty is passed down from the parent nodes of the Bayesian network. This is quite apparent in case of groundwater recharge, where the input uncertainty is the accumulated uncertainty of the meteorological, land surface, and soil compartments of a complex hydrological model.

3.2. On the Role of the Structural Model

At this point, we have identified structural and parametric uncertainty as the most relevant categories of hydrogeological uncertainty. While in theory both are of similar importance, the way to handle them in practice is very different. Parametric uncertainty can be reduced by collecting more data and is primarily a question of data acquisition. On the other hand, structural uncertainty is connected to the model for the subsurface heterogeneity itself. It is therefore much harder to quantify, which has wide ranging ramifications for uncertainty analysis. To investigate this problem in more detail, we will first present and discuss the most common paradigms for generating subsurface structures.

The most famous of these paradigms is the Gaussian process (GP) model, also known as Multivariate Gaussian or a Gaussian random field (Rasmussen and Williams, 2006). In its basic form, a GP is a very parsimonious model and can therefore be applied in situations where only few data are available, as often the case in hydrogeology. In addition, a GP is hierarchical by nature and therefore scales well with the amount of data available, i.e., the dimensionality of Θ can be arbitrarily matched with the amount of data available for the inference (Gelfand and Schliep, 2016). However, employing a GP as the structural model for a conductivity field makes a number of strong assumptions about the properties and characteristics of the conductivity field, some of which have been strongly criticized (Gómez-Hernández and Wen, 1998; Zinn and Harvey, 2003; de Marsily et al., 2005; Linde et al., 2015). The most important of these criticisms concerns the inability of GPs to reproduce long-ranging high-conductivity structures, which are reported to exist in many real-world aquifers (Abelin et al., 1991; Zheng and Gorelick, 2003; Kerrou et al., 2008). As a result, using a GP as the structural model for an aquifer will lead to a failure to (i) detect the presence of such features as well as (ii) to predict certain behaviors of, say, break-through curves (Heße et al., 2015; Savoy et al., 2017).

To improve on some of the limitations of GPs, truncated pluri-Gaussian models have been developed (Le Loc'h and Galli, 1997; Galli et al., 1994; Emery, 2004; Armstrong et al., 2011). These methods can be seen as an extension of the Gaussian paradigm by embedding Gaussian SRFs within a larger hierarchical framework. Here, hierarchy means that the Gaussian SRFs are used to create a larger spatial structure. This larger structure is typically representing distinct hydrogeolocial units, like hydrofacies or lithofacies. Despite some success in recent years (Emery, 2007; Mariethoz et al., 2009; Serrano et al., 2014), their overall geological realism has remained limited, and alternative paradigms have continued to attract considerable attention.

Surface-based modeling is one of these other paradigms (Caumon et al., 2009), often implemented in terms of implicit surfaces (Calcagno et al., 2008; Chilés et al., 2004). Although not particularly suited for modeling intricate structures and low scale heterogeneity, this paradigm provides a realistic representation of the main geological structures and allows to integrate a good range of information, including geological data (contact points, surface orientations, faults) but also information coming from geophysical surveys.

Geological structures can also be represented as geometrical objects using object-based models (Koltermann and Gorelick, 1996). Object-based method are mainly based on geometrical considerations about the expected shapes.

Process-based methods on the other hand arguably provide the most realistic representation of real word structures (Koltermann and Gorelick, 1996). Software implementations of this paradigm are available both as commercial and academic releases, and for unconditional simulations the computational costs are acceptable. Nevertheless, as is the case for object-based methods, process-based methods have difficulty in honoring all the observed conditioning data, which puts some limit on their applicability.

The last, modeling paradigms discussed here are the multiple-point statistic (MPS) based techniques (Guardiano and Srivastava, 1993; Strebelle, 2002; Mariethoz and Caers, 2014). In contrast to geostatistical methods based on two-point statistics, these methods allow to reproduce more realistic structures, which better represent important features observed in real world aquifers like connectivity. Computational costs remain relatively high compared to other paradigms. Nevertheless, MPS simulation algorithms intrinsically honor all the observed conditioning data, and the flexibility of the technique allows for the incorporation of information coming from different sources, in a straightforward way.

Together, these paradigms form the basis of most of the models used for generating subsurface heterogeneity. In addition to the properties already mentioned, they also differ in how much they are amendable to a Bayesian framework (Table 2). The Gaussian paradigm is very well-suited, since most of its parameters are simple statistics of typical hydrogeological variables (e.g., conductivity, porosity, storativity etc.). Consequently, there exists a direct way to derive these parameters from real-world measurements. The truncated pluri-Gaussian paradigms scores lower in this regard since a crucial feature of this method is the derivation and application of the truncation rule. These rules usually ought to come from expert elicitation but little to no guidelines exist on how to formalize this process. The surface-based paradigm fares much better in this regard since the inference of subsurface structures is able to draw on observable features of the subsurface. In fact, the possibility to frame these paradigms within a Bayesian framework was already explored by Wellmann et al. (2018) and de la Varga et al. (2018). Next is the object-based paradigm, where quite often objects are drawn based on purely geometrical considerations. It is therefore not straightforward to use this paradigm in a Bayesian framework. Nevertheless, object-based methods can profit from the statistics about the morphological attributes of real-world geological objects (Gibling, 2006; Colombera et al., 2012). Process-based models, on the other hand, are built on a plausible physical model by mimicking the geological genesis of the subsurface. However, the parameter of these models are usually pure convenience parameters making the derivation of prior PDFs subjective. The last paradigm discussed above are MPS, which is not without problems from a Bayesian perspective. However, its overall aptitude is arguably higher than the two former paradigms. First of all, realizations of MPS models are easy to condition on point measurements, which is an important feature. Looking at the generating mechanism itself, we see that its parameters are simple convenient parameters that are not directly connected to physical principles. Despite this clear drawback, MPS realizations are based in training images, which means the method is based on observable features of the subsurface.

TABLE 2

Table 2. Overview of the different paradigms for sub-surface structure generation applied in hydrogeology.

In conclusion, we would argue that two of the above presented paradigms stand out as the most viable candidates for Bayesian uncertainty analysis. First, the Gaussian paradigm, which scores high on almost every metric except geological realism (see Table 2). While this is only one point of many, it is arguably the most important one. At the same time, GPs score so high on the other metrics, in particular its wide use, that it should not be excluded. Furthermore, GPs are good candidates for subdomain models within a larger hierarchical modeling framework and can consequently form an important component of a larger and more realistic framework. The second relevant paradigm is MPS, which, in some sense, can be placed on the other end of the spectrum of the paradigms presented here. This is to say that models based on MPS have a high degree of geological realism but suffer from a lack of ready-made software tools, that they are comparably unknown to practitioners and that they are computationally demanding. However, both paradigms have the ability to incorporate a variety of data sources and the generation of heterogeneous structures is based on observable characteristics of the subsurface. In addition, if the MPS framework is used to generate only the categorical SRF of the different hydrogeological units, it can be seamlessly integrated with the Gaussian paradigm. With these two candidate paradigms in mind, we will continue our discussion on Bayesian uncertainty analysis.

4. Toward a Data-Driven Uncertainty Characterization

As we have discussed earlier, Bayesianism is not free of practical and theoretical problems. Of these, the question of prior derivation was presented as the most pressing, with no universally accepted guideline for prior derivation existing in the literature. In this last part of the manuscript, we are going to lay out the current challenges and explain a possible solution by using data-driven priors.

4.1. Putting Prior Derivation on Solid Grounds

In this paper, we want to make the case for combining aspects of objective Bayesianism with frequentist reasoning (Rubin, 1984; Bayarri and Berger, 2004; Little, 2006). While we fully agree that objectivity is an important goal in any scientific or engineering enterprise, we do not think that this needs to be achieved by minimizing the impact of the prior as often argued. On the contrary! Priors can have both a strong impact on the analysis and being objective. This can be achieved if these priors are derived from well-defined empirical frequencies (see, e.g., Li et al., 2017 for a rare example for hydrogeology). Hydrogeological variables like conductivity and porosity are physical properties or can at least be soundly derived from them (Di Palma et al., 2017). As a result, their parametric and structural uncertainties can be calibrated against observed frequencies. This feature, that the parameters of stochastic hydrogeology relate to physical quantities, makes this mixture of Bayesian analysis and frequentist reasoning the natural choice for prior derivation. This notion has, e.g., been voiced by Gelman (2008) when saying that a hardcore Bayesian is someone “who would apply Bayesian methods to all problems” whereas a reasonable person “would apply Bayesian inference in situations where prior distributions have a physical basis or a plausible scientific model.”

Such basis should be a formalized knowledge base, i.e., a database DB = (_{Xi, Zi)i ≤ n}, containing all investigated and cataloged cases. In the field of hydrogeology, these cases should be identified with investigated and cataloged sites. Furthermore, n is the number of these sites, Z_i are the measurements of the target variable at each site i and $X_i=(X_i^1,\dots ,X_i^m)$ is a vector containing the m cataloged characteristics/features of each site. In hydrogeology, such characteristics may include latitude, longitude, climatic properties, rock type, environment type, physiographic properties etc.

4.1.1. Prior Derivation Using Machine Learning

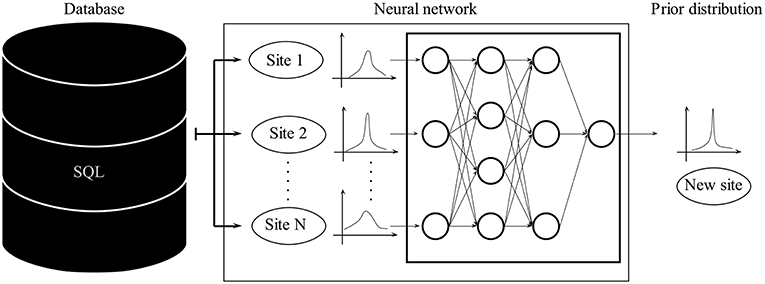
To derive prior distributions from an established database DB, a large variety of techniques can be used, including machine learning. Here, for brevity, we illustrate only a single example of these techniques, namely supervised feature learning (Figure 2). As described above, the used database DB contains, next to the measurements, the features associated with each site. Feature learning would allow to determine the most predictive features as well as the functional dependency for any give site. The result would be a function that maps the observable features of a site to the distribution of its conductivity values (or any other target variable). Common machine learning methods that can tackle such tasks include Random Forests (Breiman, 2001; Segal and Xiao, 2011), Gradient Boosting Trees (Elith et al., 2008), or Bayesian Additive Regression Trees (Chipman et al., 2010; Pratola et al., 2014; Kapelner and Bleich, 2016).

FIGURE 2

Figure 2. Schematic of prior derivation machine learning tools.

4.1.2. Prior Derivation Using Similarity-Weighted Frequencies

Machine learning tools like neural networks are well-established in data science. However, they can be extremely computationally expensive, need large amounts of data and the resulting models are notoriously hard to interpret.

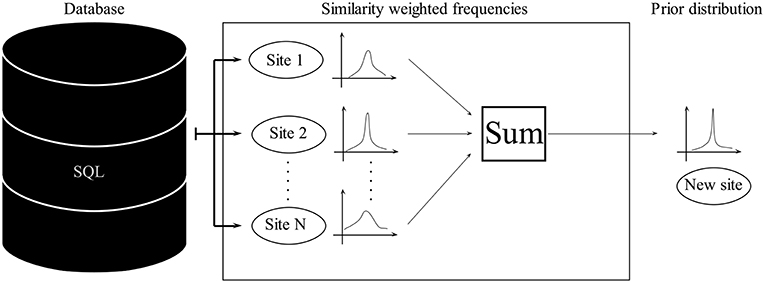
Recent developments in the field of epistemology have provided a sound mathematical procedure to formalize the intuitive notion about how different cases can be made amenable to frequentist reasoning and therefore provide the basis for combining aspects of frequentism and Bayesianism (Billot et al., 2005; Gilboa et al., 2006, 2010). The basic idea behind it can be easily illustrated (Figure 3). Given a similarity function s, more on this later, the probability of the target variable at a new site n+1 can be expressed as

$\begin{array}{ll}p(Z_{n+1}^s)=\frac{{\displaystyle {\sum }_{i\le n}s(X_i,X_{n+1})p(Z_i)}}{{\displaystyle {\sum }_{i\le n}s(X_i,X_{n+1})}}.& (5)\end{array}$

FIGURE 3

Figure 3. Schematic of prior derivation using similarity-weighted frequencies.

Since Equation (5) strongly depends on the specification of the similarity function s(Z_i, Z_j), Gilboa et al. (2010) propose a simple best fit approach to find such a function, as the s_opt(Z_i, Z_j) that best explains the given database. To handle the curse of dimensionality, a parametric model should be used. Following again Gilboa et al. (2010), we use an exponential model here for demonstration

$\begin{array}{ll}s(X_i,Y_j)=exp\left(-\sqrt{{\displaystyle \sum _{j\le m}}{w}_j{(x^j-x^{{}^{\prime }j})}^2}\right).& (6)\end{array}$

At this point, the task of finding the prior distribution for a target variable has first been transformed into finding s, and then—by virtue of a parametric model—transformed into finding the appropriate weights w = (w₁, …, w_m). Gilboa et al. (2010) propose a simple best-fit approach, i.e., finding w_opt such that the sum of squared errors between all elements in the database is minimized. The principle behind this similarity function and the way it is used to estimate probability is identical to kernel density estimation but extended to the feature space of our database. The choice of the name similarity function, instead of kernel, was motivated by Gilboa et al. (2010) to emphasize the epistemic nature of the procedure.

4.1.3. Prior Derivation Using Bayesian Hierarchical Modeling

Although the above procedure is axiomatically elegant, it is not without flaws. One problem is that the used database might be too small to contain a relevant number of observations. Basing the prior on such a database would lead to attribute a zero probability to structures that have not yet been cataloged. Another problem is the incorporation of data on different scales like summary statistics of certain sites.

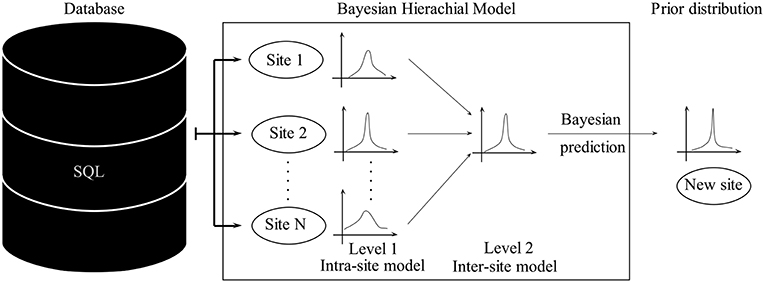
Such challenges can be handled by Bayesian hierarchical modeling, which provides a natural way to partially pool data from different sites by incorporating the structural dependencies between the data points. In hydrogeology, it is not immediately clear how data from different sites can be combined and jointly used for the inference. Hierarchical models facilitate a partial pooling by first assimilating data from each site independently and, in a next step, modeling each site as elements of a population of sites (Figure 4). Bayesian statistics is easy to adapt to such schemes by modeling the parameters of each site as being conditional on the statistics of the upper levels.

FIGURE 4

Figure 4. Schematic of prior derivation using a Bayesian hierarchical model.

One drawback of Bayesian hierarchical modeling, compared to a similarity weighted approach, is that the prior distribution of a new, as of yet, unexplored site, is simply a random sample from all possible sites and therefore has a comparably large uncertainty. Narrowing down the uncertainties could be done by narrowing down the number of used sited by restricting the analysis to similar sites, only. Yet, this would necessitate the existence of a huge database, which we currently do not have (Cucchi et al., 2019).

4.2. Hydrogeological Data Science in the Context of Bayesian Uncertainty Analysis

At this point, it should become clear that, irrespective of the details of the aforementioned approaches, the performance of data-driven methods is not only determined by the sophistication of the used method but is equally dependent on the amount and kind of data being used (Halevy et al., 2009). This means that a simple algorithm, having a lot of data, can easily outperform a highly complex one, with only a modest amount of data. Increasing the amount of available data is consequently of similar importance compared to the development of ever better algorithms.

In general, data generation in hydrogeology is quite costly compared to, say, hydrology, meteorology or land-surface modeling. To counter such challenges, much has been invested in the development and deployment of cost-effective methods for subsurface characterization. As a result, the total amount of data being collected every year is quite substantial. However, collecting these data and making them available to practitioners remains difficult. To demonstrate why this a problem, we can use, e.g., the schematic proposed by Rogati (2017). Using the well-known hierarchy of human motivation (Maslow, 1943), Rogati (2017) promotes a hierarchy of needs in data science. According to this schematic, hydrogeology has focused most of its effort only on the first level of this hierarchy, where she puts data collection, data storage and data transformation. However, already at the second level, where she puts routines, protocols and infrastructure for moving and storing the data, hydrogeology is comparably underdeveloped. Given that the hierarchy proposed by Rogati (2017) has 6 levels in total, we can confidently state that hydrogeology has a long way to go before having a viable ecosystem for modern data-driven analysis.

This is not to say that there have not been efforts to provide standardized procedures for sharing and storing data in hydrogeology (Boisvert and Brodaric, 2011; Brodaric et al., 2018; Wojda et al., 2010). However, these data collection initiatives focus almost exclusively on indirect measurements like hydraulic heads or are restricted to some specific measurement sites. In contrast, the efforts to collect direct hydrogeological measurements have been so far been rather modest. For example, the largest open-access databases on the topic of hydraulic conductivity is the World-Wide HYdrogeological Parameter DAtabase (WWHYPDA, Comunian and Renard, 2009), which contains a little bit over 20.000 measurements from approximately 50 different sites. This does only reflect a tiny fraction of the total amount of data that has been collected on this topic and is not even close to what anyone would label as big data. This situation means that the field of hydrogeology is currently seriously under equipped for the deployment of any data-driven method in general and the derivation of data-driven priors in particular.

Focusing on the topic of data-driven priors, we can state that only a minimum number of tools currently exists. The WWHYPDA provides a modicum of data on hydraulic conductivity, which can be used to determine parametric uncertainty for a given site (Cucchi et al., 2019). However, the amount of data for other variables (e.g., porosity) is much lower and currently not sufficient for use in a Bayesian context. Concerning structural uncertainty, the situation is even less promising. Since the measurements cataloged in the WWHYPDA do currently not contain spatial coordinates, it is not possible to determine simple two-point statistics like a variogram or covariance function. This means that even for a simple paradigm like Gaussian SRFs, there are no databases from which prior distributions for, say, the parameters of a variogram function can be derived. It should come as no surprise, that the situation for more complex structural models is no better. In this last portion of the paper, we would therefore like to present a list of challenges as well as possible solutions for the field of Bayesian uncertainty analysis.

4.2.1. Parametric Uncertainty

Currently, the amount of data contained in WWHYPDA barely allows one to tackle the challenges of parametric uncertainty. The modest amount of data represented in WWHYPDA is probably caused by the lack of user contributions and/or policies that encourage the systematic and central publication of hydrogeological measurements. Probably, the best way to quickly populate databases like WWHYPDA with a sufficient amount of data would be to incorporate data spread in regional/national repositories, but also strongly interact with boards of the main scientific journals and set up a tighter interaction between authors and open data collection initiatives.

4.2.2. Structural Uncertainty (Gaussian Process Paradigm)

A Gaussian process is the simplest paradigm that can be used to describe structural uncertainty, with spatial structures defined by two-point statistics through variograms or covariance functions.

To the best of the authors' knowledge, there is no widely available open-source database, which provides practitioners with a catalog of either estimated variogram functions or measurements that allows one to estimate them.

The abilities of the WWHYPDA could be expanded to that purpose with only a modest amount of effort. Compared to its current implementation, only the coordinates of the measurements need to be added as a feature.

4.2.3. Structural Uncertainty (Multiple-Point Statistics Paradigm)

In the text above, multiple-point statistics was identified as the overall most promising paradigm to realistically represent structural uncertainty. Some efforts have been made to share repositories of training images [see for example (2014), companion site of the book Mariethoz and Caers, 2014], in some cases focusing on some specific environments (Pushpalatha et al., 2008). In addition, other efforts were made to create database of analogs, with initiatives mainly sponsored by oil companies like the SafariDB (2019a), the Sedimentary Analogs Database and Research Consortium (2019b), the Fluvial Architecture Knowledge Transfer System (Colombera et al., 2012), CarbDB (Jung and Aigner, 2012), and WODAD (Kenter and Harris, 2006). In these cases, the access to the full functionalities of the database is very often restricted to the partner institution/companies. Therefore, when talking about open-access databases, the available resources are quite limited. In practice, a set of TIs that can even be remotely called representative of earths subsurface structures simply does not exists, and the efforts made by consortium sponsored or private companies are often governed by very restrictive access policies. As a result, the task of building up an open-access knowledge base for Bayesian structural uncertainty analysis, or any other data-driven modeling efforts, has to start from scratch. Within the scope of this manuscript, we can neither detail the specific architecture of such a knowledge base nor explain the necessary steps to create one. We will, however, try to formulate a set of desiderata that such a data base should meet.

First, the data base should contain a representative sample of the structures encountered in the subsurface. Such a desideratum may sound obvious w.r.t. any statistical analysis. It does, however, need special attention due to being somewhat vague and elusive. For example, particularly in the case of three-dimensional case studies, TIs could come from high-resolution reconstructions of aquifer analogs (Bayer et al., 2011; Comunian et al., 2011; Bayer et al., 2015), but also be the result of a more or less complex simulation with object-based or process-based methods. Therefore TIs, in particular within a Bayesian context, can represent very different entities depending on how they were created.

Second, to derive prior distributions, the most predictive features of the cataloged sites must be reported as well. This desideratum is again somewhat weak, since it is not a priori clear what features of a site are most predictive of its subsurface structure.

In case a database meeting these desiderata becomes successful, the algorithm for prior derivation has to be adapted to the specifics of the MPS paradigm. As already discussed above, recasting this paradigm in a Bayesian framework is not straightforward, since the parameters for generating random realizations are derived ad-hoc and cannot, in general, be exchanged between different workflows. So, instead of deriving prior distributions over some parameters, the prior distribution should be defined over the TIs themselves. In this framework, one could provide a given prior distribution to each TI, for example based on the ranking procedure proposed by Pérez et al. (2014) computed using a portion of the available data. Then, uncertainty could be assessed by distributing the number of realizations for each TI proportionally to the prior computed in the previous step.

Probably, embedding or strongly connecting a database of TIs within a structure like WWHYPDA, as argued by Comunian and Renard (2009), would improve its usefulness, because facies codes of categorical TIs could be directly linked to parameter distributions. Moreover, if included in the WWHYPDA structure, TIs could be also organized in a more efficient and flexible way within the provided catalog of hydrogeological environments.

5. Conclusions

In this manuscript, we made the case for a unified data-driven framework for hydrogeological uncertainty analysis. Following Pearl (1988b), we attempted this by first identifying the most suitable theory for such a framework, motivating its use, explaining its properties, identifying the current challenges, showing what kind of approximations needed to be made to make the framework viable, and finally detailing a road map to fill the gaps which currently exist.

As the ideal theory for such a unified framework, we have argued for Bayesianism. This was done by contrasting the Bayesian framework with its most relevant competitors. In the realm of uncertain reasoning, these competitors include fuzzy as well as Dempster-Shafer reasoning, whereas in the realm of probabilistic reasoning, the main competitor is the frequentist framework. While all of these frameworks have their merits, the Bayesian framework is the only one combining a sound epistemology with wide-spread use and application. We then explained the main features, as well as challenges, of this framework and how it relates to the specifics of the field of hydrogeology.

With this foundation, we proceeded to contextualize the different forms of uncertainty, used in the literature. Of these forms, we identified structural and parametric uncertainty as the two most relevant. Parametric uncertainty is mainly a question of data collection, data preparation, and data dissemination. In contrast, structural uncertainty is equally a conceptual challenge, i.e., the hydrogeological community is still lacking a paradigm for generating subsurface structures, which is widely accepted and used. To make this point, we reviewed the most common of these paradigms and discussed their most salient features. Special attention was put on their compatibility with a Bayesian framework. We tentatively identified two paradigms as the most relevant: Gaussian multivariate random fields as well as multiple-point statistics. While the Gaussian paradigm is mathematically elegant, it suffers from a lack of geological realism. On the other hand, the multiple-point statistics paradigm is very promising due to its conceptual clarity. To provide the data for the needed prior distribution, training images are the natural choice.

Finally, we make the point that the field of hydrogeology needs to increase its efforts in order to provide a large open-access databases with direct hydrogeological measurements. The examples given here are derived from specific applications, i.e., Bayesian uncertainty analysis, but the general point is independent of such concerns. As long as virtually all efforts are focused on the measurements themselves, we remain stuck on the first level of the hierarchy described by Rogati (2017). Without investing at least, a modicum of work into reaching the second level, all the advances of modern data science will remain restricted to extremely myopic and small data sets, at best, and completely out of reach, at worst. From our perspective, the reasons for the inability of our community to “move up” remains somewhat of a mystery. After all, managing and maintaining a database is easy compared to the sophisticated network of measurement operations that are managed worldwide, and a minor redirection of resources from Level 1 to Level 2 of the schematic depicted by Rogati (2017) would make a big difference. In fact, we can hardly think of a more impactful way of how to spend one's money when trying to improve hydrogeological data science. We therefore close this paper with a call for such an initiative.

Author Contributions

As the main author, FH has worked on every section of the article. AC's input was focused on the last portion of the manuscript dealing with the models for generating subsurface structures and the challenges of databases. SA provided overall guidance for the development of the main ideas presented here.

Funding

For the finalization of this manuscript. FH was financially supported by the Deutsche Forschungsgemeinschaft via grant HE 7028/2-1.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

(2014). Multiple-Point Geostatistics: Stochastic Modeling With Training Images. Companion site of the book by G. Mariethoz and J. K. Caers section “TRAINING IMAGE LIBRARY.” Available online at: http://www.trainingimages.org/training-images-library.html (Online; accessed March 26, 2019).

(2019a). SafariDB: The Geological Outcrop Database. Available online at: https://safaridb.com/ (Online; accessed March 26, 2019).

(2019b). The Sedimentary Analogs Database and Research Consortium. Available online at: http://sedimentaryanalogsdatabase.com/ (Online; accessed March 26, 2019).

Abelin, H., Birgersson, L., Moreno, L., Widén, H., Ågren, T., and Neretnieks, I. (1991). A large-scale flow and tracer experiment in granite: 2. results and interpretation. Water Resour. Res. 27, 3119–3135. doi: 10.1029/91WR01404

CrossRef Full Text | Google Scholar

Achinstein, P. (2003). The Book of Evidence. Oxford Studies in the Philosophy of Science. Oxford University Press.

Google Scholar

Albert, I., Donnet, S., Guihenneuc-Jouyaux, C., Low-Choy, S., Mengersen, K., and Rousseau, J. (2012). Combining expert opinions in prior elicitation. Bayesian Anal. 7, 503–531. doi: 10.1214/12-BA717

CrossRef Full Text | Google Scholar

Armstrong, M., Galli, A., Beucher, H., Loc'h, G., Renard, D., Doligez, B., et al. (2011). Plurigaussian Simulations in Geosciences. Berlin; Heidelberg: Springer.

Google Scholar

Bandyopadhyay, P. S., and Forster, M. R. (eds.) (2011). Philosophy of Statistics, Vol. 7 of Handbook of the Philosophy of Science. Amsterdam: Elsevier.

Barhillel, M. (1980). The base-rate fallacy in probability judgements. Acta Psychol. 44, 211–233. doi: 10.1016/0001-6918(80)90046-3

CrossRef Full Text | Google Scholar

Barnard, G. A., Jenkins, G. M., and Winsten, C. B. (1962). Likelihood inference and time series. J. R. Stat. Soc. Ser. A 125, 321–372.

Google Scholar

Barnett, V. (1999). Comparative Statistical Inference, 3rd Edn. Chichester: Wiley.

Google Scholar

Baron, J. (2004). “Chapter: Normative Models of Judgment and Decision Making,” in Blackwell Handbook of Judgment and Decision Making; Handbooks of Experimental Psychology, eds D. J. Koehler and N. Harvey (Malden, MA: Blackwell Publishing Ltd), 19–37.

Google Scholar

Bayarri, M. J., and Berger, J. O. (2004). The interplay of bayesian and frequentist analysis. Stat. Sci. 19, 58–80. doi: 10.1214/088342304000000116

CrossRef Full Text | Google Scholar

Bayer, P., Comunian, A., Höyng, D., and Mariethoz, G. (2015). High resolution multi-facies realizations of sedimentary reservoir and aquifer analogs. Sci. Data 2:150033. doi: 10.1038/sdata.2015.33

PubMed Abstract | CrossRef Full Text | Google Scholar

Bayer, P., Huggenberger, P., Renard, P., and Comunian, A. (2011). Three-dimensional high resolution fluvio-glacial aquifer analog: Part 1: Field study. J. Hydrol. 405, 1–9. doi: 10.1016/j.jhydrol.2011.03.038

CrossRef Full Text | Google Scholar

Beaumont, M., and Rannala, B. (2004). The Bayesian revolution in genetics. Nat. Rev. Genet. 5, 251–261. doi: 10.1038/nrg1318

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, N. D., Croke, B. F. W., Guariso, G., Guillaume, J. H. A., Hamilton, S. H., Jakeman, A. J., et al. (2013). Characterising performance of environmental models. Environ. Model. Softw. 40, 1–20. doi: 10.1016/j.envsoft.2012.09.011

CrossRef Full Text | Google Scholar

Berger, J. (2006). The case for objective bayesian analysis. Bayesian Anal. 1, 385–402. doi: 10.1214/06-BA115

CrossRef Full Text | Google Scholar

Berger, J. O. (1985). Statistical Decision Theory and Bayesian Analysis. Springer Series in Statistics. New York, NY; Berlin; Heidelberg; Tokyo: Springer.

Google Scholar

Bernardo, J., and Smith, A. (2000). Bayesian Theory (Wiley Series in Probability and Statistics). Chichester: Wiley.

Bernardo, J. M. (1997). Noninformative priors do not exist: a discussion. J. Stat. Plan. Inference 65, 159–189.

Google Scholar

Berry, D. (2006). Bayesian clinical trials. Nat. Rev. Drug Discov. 5, 27–36. doi: 10.1038/nrd1927

PubMed Abstract | CrossRef Full Text | Google Scholar

Beven, K. (2006). A manifesto for the equifinality thesis. J. Hydrol. 320, 18–36. doi: 10.1016/j.jhydrol.2005.07.007

CrossRef Full Text | Google Scholar

Beven, K. and Binley, A. (1992). The future of distributed models: model calibration and uncertainty prediction. Hydrol. Process. 6, 279–298. doi: 10.1002/hyp.3360060305

CrossRef Full Text | Google Scholar

Beven, K. and Young, P. (2013). A guide to good practice in modeling semantics for authors and referees. Water Resour. Res. 49, 5092–5098. doi: 10.1002/wrcr.20393

CrossRef Full Text | Google Scholar

Biegler, L., Biros, G., Ghattas, O., Heinkenschloss, M., Keyes, D., Mallick, B., et al. (eds.) (2010). Large-Scale Inverse Problems and Quantification of Uncertainty. Chichester: Wiley.

Google Scholar

Billot, A., Gilboa, I., Samet, D., and Schmeidler, D. (2005). Probabilities as similarity-weighted frequencies. Econometrica 7, 1125–1136. doi: 10.1111/j.1468-0262.2005.00611.x

CrossRef Full Text | Google Scholar

Boisvert, E., and Brodaric, B. (2011). Groundwater markup language (gwml)–enabling groundwater data interoperability in spatial data infrastructures. J. Hydroinformatics 14:93. doi: 10.2166/hydro.2011.172

CrossRef Full Text | Google Scholar

Bond, C. E. (2015). Uncertainty in structural interpretation: lessons to be learnt. J. Struct. Geol. 74(Suppl. C), 185–200. doi: 10.1016/j.jsg.2015.03.003

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. doi: 10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

Brodaric, B., Boisvert, E., Chery, L., Dahlhaus, P., Grellet, S., Kmoch, A., et al. (2018). Enabling global exchange of groundwater data: groundwaterml2 (gwml2). Hydrogeol. J. 26, 733–741. doi: 10.1007/s10040-018-1747-9

CrossRef Full Text | Google Scholar

Brown, J. D. (2004). Knowledge, uncertainty and physical geography: towards the development of methodologies for questioning belief. Trans. Inst. Br. Geogr. 29, 367–381. doi: 10.1111/j.0020-2754.2004.00342.x

CrossRef Full Text | Google Scholar

Caers, J., Park, K., and Scheidt, C. (2014). Modeling Uncertainty of Complex Earth Systems in Metric Space, 1–25. Berlin; Heidelberg: Springer.

Google Scholar

Calcagno, P., Chilés, J., Courrioux, G., and Guillen, A. (2008). Geological modelling from field data and geological knowledge: part i. modelling method coupling 3d potential-field interpolation and geological rules. Phys. Earth Planet. Inter. 171, 147–157. doi: 10.1016/j.pepi.2008.06.013

CrossRef Full Text | Google Scholar

Cardiff, M., and Kitanidis, P. K. (2009). Bayesian inversion for facies detection: an extensible level set framework. Water Resour. Res 45. doi: 10.1029/2008WR007675

CrossRef Full Text | Google Scholar

Carlin, B. P., and Louis, T. A. (2000). Bayes and Empirical Bayes Methods for Data Analysis, 2nd Edn. Number 69 in CRC Texts in Statistical Science. Boca Raton, FL; London; New York, NY; Washington, DC: Chapman & Hall.

Google Scholar

Carrera, J., Alcolea, A., Medina, A., Hidalgo, J., and Slooten, L. J. (2005). Inverse problem in hydrogeology. Hydrogeol. J. 13, 206–222. doi: 10.1007/s10040-004-0404-7

CrossRef Full Text | Google Scholar

Caumon, G., Collon-Drouaillet, P., Le Carlier de Veslud, C., Viseur, S., and Sausse, J. (2009). Surface-based 3d modeling of geological structures. Math. Geosci. 41, 927–945. doi: 10.1007/s11004-009-9244-2

CrossRef Full Text | Google Scholar

Chib, S., and Greenberg, E. (1995). Understanding the metropolis-hastings algorithm. Am. Stat. 49, 327–335. doi: 10.2307/2684568

CrossRef Full Text | Google Scholar

Chilés, J., Aug, C., Guillen, A., and Lees, T. (2004). “Modelling the geometry of geological units and its uncertainty in 3d from structural data: The potential-field method,” in Orebody Modelling and Strategic Mine Planning.

Google Scholar

Chipman, H. A., George, E. I., and McCulloch, R. E. (2010). BART: bayesian additive regression trees. Ann. Appl. Stat. 4, 266–298. doi: 10.1214/09-AOAS285

CrossRef Full Text | Google Scholar

Cirpka, O. A., and Valocchi, A. J. (2016). Debates-stochastic subsurface hydrology from theory to practice: Does stochastic subsurface hydrology help solving practical problems of contaminant hydrogeology? Water Resour. Res. 52, 9218–9227. doi: 10.1002/2016WR019087

CrossRef Full Text | Google Scholar

Clark, A. (2015). Surfing Uncertainty: Prediction, Action, and the Embodied Mind. Oxford: Oxford University Press.

Google Scholar

Clark, J. S. (2005). Why environmental scientists are becoming Bayesians. Ecol. Lett. 8, 2–14. doi: 10.1111/j.1461-0248.2004.00702.x

CrossRef Full Text | Google Scholar

Clark, M. P., Kavetski, D., and Fenicia, F. (2011). Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resour. Res. 47. doi: 10.1029/2010WR009827

CrossRef Full Text | Google Scholar

Colombera, L., Felletti, F., Mountney, N. P., and McCaffrey, W. D. (2012). A database approach for constraining stochastic simulations of the sedimentary heterogeneity of fluvial reservoirs. AAPG Bull. 96, 2143–2166. doi: 10.1306/04211211179

CrossRef Full Text | Google Scholar

Comunian, A., and Renard, P. (2009). Introducing wwhypda: a world-wide collaborative hydrogeological parameters database. Hydrogeol. J. 17, 481–489. doi: 10.1007/s10040-008-0387-x

CrossRef Full Text | Google Scholar

Comunian, A., Renard, P., Straubhaar, J., and Bayer, P. (2011). Three-dimensional high resolution fluvio-glacial aquifer analog - Part 2: geostatistical modeling. J. Hydrol. 405, 10–23. doi: 10.1016/j.jhydrol.2011.03.037

CrossRef Full Text | Google Scholar

Copty, N. K., Trinchero, P., and Sanchez-Vila, X. (2011). Inferring spatial distribution of the radially integrated transmissivity from pumping tests in heterogeneous confined aquifers. Water Resour. Res. 47. doi: 10.1029/2010WR009877

CrossRef Full Text | Google Scholar

Cucchi, K., HeSSe, F., Kawa, N., Wang, C., and Rubin, Y. (2019). Ex-situ priors: a Bayesian hierarchical framework for defining informative prior distributions in hydrogeology. Adv. Water Resour. 126, 65–78. doi: 10.1016/j.advwatres.2019.02.003

CrossRef Full Text | Google Scholar

Dagan, G. (2002). An overview of stochastic modeling of groundwater flow and transport: From theory to applications. Eos Trans. Am. Geophys. Union 83, 621–625. doi: 10.1029/2002EO000421

CrossRef Full Text | Google Scholar

Darwiche, A., and Pearl, J. (1997). On the logic of iterated belief revision. Artif. Intell. 89, 1–29. doi: 10.1016/S0004-3702(96)00038-0

CrossRef Full Text | Google Scholar

de la Varga, M., Schaaf, A., and Wellmann, F. (2018). Gempy 1.0: open-source stochastic geological modeling and inversion. Geosci. Model Dev. Discuss. 2018, 1–50. doi: 10.5194/gmd-2018-61

CrossRef Full Text

de la Varga, M., and Wellmann, J. F. (2016). Structural geologic modeling as an inference problem: a bayesian perspective. Interpretation 4, SM1–SM16. doi: 10.1190/INT-2015-0188.1

CrossRef Full Text | Google Scholar

de Marsily, G., Delay, F., Gonçalvès, J., Renard, P., Teles, V., and Violette, S. (2005). Dealing with spatial heterogeneity. Hydrogeol. J. 13, 161–183. doi: 10.1007/s10040-004-0432-3

CrossRef Full Text | Google Scholar

Dempster, A. P. (1968). A Generalization of Bayesian Inference. J. R. Stat. Soc. Ser. B Methodol. 30, 205–247.

Google Scholar

Denwood, M. J. (2016). runjags: an r package providing interface utilities, model templates, parallel computing methods and additional distributions for mcmc models in jags. J. Stat. Softw. 71, 1–25. doi: 10.18637/jss.v071.i09

CrossRef Full Text | Google Scholar

Depaoli, S., Clifton, J. P., and Cobb, P. R. (2016). Just another gibbs sampler (JAGS): flexible software for MCMC implementation. J. Educ. Behav. Stat. 41, 628–649. doi: 10.3102/1076998616664876

CrossRef Full Text | Google Scholar

Descartes, R. (1662). De Homine. Leffen & Moyardus.

Google Scholar

Deutsch, D. (1999). Quantum theory of probability and decisions. Proc. R. Soc. A Math. Phys. Eng. Sci. 455, 3129–3137. doi: 10.1098/rspa.1999.0443

CrossRef Full Text | Google Scholar

Di Palma, P. R., Guyennon, N., Heße, F., and Romano, E. (2017). Porous media flux sensitivity to pore-scale geostatistics: a bottom-up approach. Adv. Water Resour. 102(Suppl. C), 99–110. doi: 10.1016/j.advwatres.2017.02.002

CrossRef Full Text | Google Scholar

Diaconis, P., Holmes, S., and Montgomery, R. (2007). Dynamical bias in the coin toss. SIAM Rev. 49, 211–235. doi: 10.1137/S0036144504446436

CrossRef Full Text | Google Scholar

Diggle, P. J., and Ribeiro, P. J. (2007). Model-based Geostatistics, 1st Edn. New York, NY: Springer.

Doherty, J. (2004). PEST, Model Independent Parameter Estimation, User Manual, 5th Edn. Oxlex: Watermark Numerical Computing.

Doherty, J. (2010). Methodologies and Software for PEST-Based Model Predictive Uncertainty Analysis. Watermark Numerical Computing.

Dougherty, T. (ed.) (2011). Evidentialism and Its Discontents. Oxford: Oxford University Press.

Dubois, D. and Prade, H. (1988). Possibility Theory: An Approach to Computerized Processing of Uncertainty. New York, NY: Springer.

Google Scholar

Duhem, P. (1906). La Théorie Physique: Son Objet et sa Structure. Paris; Lyon: ENS Éditions.

Earman, J. (1992). Bayes or Bust. Cambridge, MA: MIT Press.

Google Scholar

Easwaran, K. (2011a). Bayesianism i: introduction and arguments in favor. Philos. Compass 6, 312–320. doi: 10.1111/j.1747-9991.2011.00399.x

CrossRef Full Text | Google Scholar

Easwaran, K. (2011b). Bayesianism ii: applications and criticisms. Philos. Compass 6, 321–332. doi: 10.1111/j.1747-9991.2011.00398.x

CrossRef Full Text | Google Scholar

Easwaran, K. (2013). Expected accuracy supports conditionalization-and conglomerability and reflection. Philos. Sci. 80, 119–142. doi: 10.1086/668879

CrossRef Full Text | Google Scholar

Ebrahimi, N., Soofi, E. S., and Soyer, R. (2010). Information measures in perspective. Int. Stat. Rev. 78, 383–412. doi: 10.1111/j.1751-5823.2010.00105.x

CrossRef Full Text | Google Scholar

Elith, J., Leathwick, J. R., and Hastie, T. (2008). A working guide to boosted regression trees. J. Anim. Ecol. 77, 802–813. doi: 10.1111/j.1365-2656.2008.01390.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Elsheikh, A. H., Wheeler, M. F., and Hoteit, I. (2014). Hybrid nested sampling algorithm for bayesian model selection applied to inverse subsurface flow problems. J. Comput. Phys. 258, 319–337. doi: 10.1016/j.jcp.2013.10.001

CrossRef Full Text | Google Scholar

Emery, X. (2004). Properties and limitations of sequential indicator simulation. Stochastic Environ. Res. Risk Assess. 18, 414–424. doi: 10.1007/s00477-004-0213-5

CrossRef Full Text | Google Scholar

Emery, X. (2007). Simulation of geological domains using the plurigaussian model: new developments and computer programs. Comput. Geosci. 33, 1189–1201. doi: 10.1016/j.cageo.2007.01.006

CrossRef Full Text | Google Scholar

Enemark, T., Peeters, L. J., Mallants, D., and Batelaan, O. (2019). Hydrogeological conceptual model building and testing: a review. J. Hydrol. 569, 310–329. doi: 10.1016/j.jhydrol.2018.12.007

CrossRef Full Text | Google Scholar

Fagin, R., Halpern, J. Y., Moses, Y., and Vardi, M. (2004). Reasoning About Knowledge. Cambridge, MA: A Bradford Book.

Feldman, R., and Conee, E. (1985). Evidentialism. Philos. Stud. 48, 15–34.

Google Scholar

Feyerabend, P. (1975). Against Method: Outline of an Anarchist Theory of Knowledge. London: New Left Books.

Finetti, B. D. (1975). Theory of Probability. A Critical Introductory Treatment. Chichester: Wiley.

Google Scholar

Firmani, G., Fiori, A., and Bellin, A. (2006). Three-dimensional numerical analysis of steady state pumping tests in heterogeneous confined aquifers. Water Resour. Res. 42. doi: 10.1029/2005WR004382

CrossRef Full Text | Google Scholar

Foreman-Mackey, D., Hogg, D. W., Lang, D., and Goodman, J. (2013). emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 125, 306–312. doi: 10.1086/670067

CrossRef Full Text | Google Scholar

Fox, C. R., and Ülkümen, G. (2011). “Chapter Distinguishing Two Dimensions of Uncertainty,” in Perspectives on Thinking, Judging, and Decision Making, 1st Edn, eds W. Brun, G. Keren, G. Kirkebøen and H. Montgomery (Oslo: Universitetsforlaget). 21–35.

Franssen Hendricks, H.-J., Alcolea, A., Riva, M., Bakr, M., van der Wiel, N., Stauffer, F., et al. (2009). A comparison of seven methods for the inverse modelling of groundwater flow. Application to the characterisation of well catchments. Adv. Water Resour. 32, 851–872. doi: 10.1016/j.advwatres.2009.02.011

CrossRef Full Text | Google Scholar

Fuchs, C. A., and Schack, R. (2013). Quantum-bayesian coherence. Rev. Mod. Phys. 85:1693. doi: 10.1103/RevModPhys.85.1693

CrossRef Full Text | Google Scholar

Galli, A., Beucher, H., Le Loc'h, G., Doligez, B., and Group, H. (1994). “The pros and cons of the truncated gaussian method,” in Geostatistical Simulations, eds. M. Armstrong and P. A. Dowd (Dordrecht: Springer), 217–233.

Google Scholar

Garber, D. (1983). “Old evidence and logical omniscience in bayesian confirmation theory,” in Testing Scientific Theories, Vol. 10 of Minnesota Studies in the Philosophy of Science, ed J. Earman (Minneapolis, MN: University of Minnesota), 99–131.

Google Scholar

Geiges, A., Rubin, Y., and Nowak, W. (2015). Interactive design of experiments: a priori global versus sequential optimization, revised under changing states of knowledge. Water Resour. Res. 51, 7915–7936. doi: 10.1002/2015WR017193

CrossRef Full Text

Gelfand, A. E., and Schliep, E. M. (2016). Spatial statistics and Gaussian processes: a beautiful marriage. Spatial Stat. 18, 86–104. doi: 10.1016/j.spasta.2016.03.006

CrossRef Full Text | Google Scholar

Gelfand, A. E., and Smith, A. F. M. (1990). Sampling-based approaches to calculating marginal densities. J. Am. Stat. Assoc. 85, 398–409.

Google Scholar

Gelhar, L. (1993). Stochastic Subsurface Hydrology. Engelwood cliffs, NJ: Prentice-Hall.

Google Scholar

Gelman, A. (2008). Objections to Bayesian statistics. Bayesian Anal. 3, 445–449. doi: 10.1214/08-BA318

CrossRef Full Text | Google Scholar

Gelman, A., Lee, D., and Guo, J. (2015). Stan: a probabilistic programming language for Bayesian inference and optimization. J. Educ. Behav. Stat. 40, 530–543. doi: 10.3102/1076998615606113

CrossRef Full Text | Google Scholar

Gelman, A., Simpson, D., and Betancourt, M. (2017). The prior can often only be understood in the context of the likelihood. Entropy 19:555. doi: 10.3390/e19100555

CrossRef Full Text | Google Scholar

Gibling, M. R. (2006). Width and thickness of fluvial channel bodies and valley fills in the geological record: A literature compilation and classification. J. Sediment. Res. 76, 731–770. doi: 10.2110/jsr.2006.060

CrossRef Full Text | Google Scholar

Gilboa, I. (2009). Theory of Decision Under Uncertainty. Cambridge: Cambridge University Press.

Google Scholar

Gilboa, I., Lieberman, O., and Schmeidler, D. (2006). Empirical similarity. Rev. Econ. Stat. 88, 433–444. doi: 10.1162/rest.88.3.433

CrossRef Full Text | Google Scholar

Gilboa, I., Lieberman, O., and Schmeidler, D. (2010). On the definition of objective probabilities by empirical similarity. Synthese 172, 79–95. doi: 10.1007/s11229-009-9473-4

CrossRef Full Text | Google Scholar

Ginn, T. R. (2004). On the application of stochastic approaches in hydrogeology. Stochast. Environ. Res. Risk Assess. 18, 282–284. doi: 10.1007/s00477-004-0199-z

CrossRef Full Text | Google Scholar

Gómez-Hernández, J. J., and Wen, X.-H. (1998). To be or not to be multi-Gaussian? A reflection on stochastic hydrogeology. Adv. Water Resour. 21, 47–61. doi: 10.1016/S0309-1708(96)00031-0

CrossRef Full Text | Google Scholar

Gong, W., Gupta, H. V., Yang, D., Sricharan, K., and Hero, A. O. (2013). Estimating epistemic and aleatory uncertainties during hydrologic modeling: an information theoretic approach. Water Resour. Res. 49, 2253–2273. doi: 10.1002/wrcr.20161

CrossRef Full Text | Google Scholar

Good, I. J. (2009a). "Chapter Rational decisions," in Good Thinking: The Foundations of Probability and Its Applications (Dover Books on Mathematics), 3–15.

Good, I. J. (2009b). Good Thinking: The Foundations of Probability and Its Applications. Minneapolis, MN: Dover Books on Mathematics.

Greaves, H. and Wallace, D. (2006). Justifying conditionalization: Conditionalization maximizes expected epistemic utility. Mind 115, 607–632. doi: 10.1093/mind/fzl607

CrossRef Full Text | Google Scholar

Grossman, J. (2011). “The likelihood principle,” in Philosophy of Statistics, Vol. 7 of Handbook of the Philosophy of Science, eds P. S. Bandyopadhyay and M. R. Forster (Amsterdam: North-Holland), 553–580.

Google Scholar

Guardiano, F. B., and Srivastava, R. M. (1993). “Multivariate geostatistics: Beyond bivariate moments,” in Geostatistics: Troia '92, Vol. 1, ed A. Soares, A (Dordrecht: Kluwer), 133–144.

Google Scholar

Guillaume, J. H. A., Qureshi, M. E., and Jakeman, A. J. (2012). A structured analysis of uncertainty surrounding modeled impacts of groundwater-extraction rules. Hydrogeol. J. 20, 915–932. doi: 10.1007/s10040-012-0864-0

CrossRef Full Text | Google Scholar

Halevy, A., Norvig, P., and Pereira, F. (2009). The unreasonable effectiveness of data. IEEE Intell. Syst. 24, 8–12. doi: 10.1109/MIS.2009.36

CrossRef Full Text | Google Scholar

Halpern, J. Y. (2003). Reasoning About Uncertainty. Cambridge MA; London: MIT Press.

Hansen, T. M., Cordua, K. S., and Mosegaard, K. (2012). Inverse problems with non-trivial priors: efficient solution through sequential gibbs sampling. Comput. Geosci. 16, 593–611. doi: 10.1007/s10596-011-9271-1

CrossRef Full Text | Google Scholar

Hayek, M., Younes, A., Zouali, J., Fajraoui, N., and Fahs, M. (2018). Analytical solution and Bayesian inference for interference pumping tests in fractal dual-porosity media. Comput. Geosci. 22, 413–421. doi: 10.1007/s10596-017-9701-9

CrossRef Full Text | Google Scholar

Helton, J. C., and Burmaster, D. E. (1996). Guest editorial: treatment of aleatory and epistemic uncertainty in performance assessments for complex systems. Reliabil. Eng. Syst. Saf. 54, 91–94. doi: 10.1016/S0951-8320(96)00066-X

CrossRef Full Text | Google Scholar

Heße, F., Savoy, H., Osorio-Murillo, C. A., Sege, J., Attinger, S., and Rubin, Y. (2015). Characterizing the impact of roughness and connectivity features of aquifer conductivity using bayesian inversion. J. Hydrol. 531(Pt 1), 73–87. doi: 10.1016/j.jhydrol.2015.09.067

CrossRef Full Text | Google Scholar

Hofer, E. (1996). When to separate uncertainties and when not to separate. Reliabil. Eng. Syst. Saf. 54, 113–118. doi: 10.1016/S0951-8320(96)00068-3.

CrossRef Full Text | Google Scholar

Hoffman, F. O., and Hammonds, J. S. (1994). Propagation of uncertainty in risk assessments: the need to distinguish between uncertainty due to lack of knowledge and uncertainty due to variability. Risk Anal. 14, 707–712. doi: 10.1111/j.1539-6924.1994.tb00281.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, T. Y. (2005). Multiscale Computation of Fluid Flow in Heterogeneous Media. Springer.

Google Scholar

Howson, C., and Urbach, P. (2005). Scientific Reasoning: The Bayesian Approach, 3rd Edn. Peru: Open Court.

Google Scholar

Huelsenbeck, J., Ronquist, F., Nielsen, R., and Bollback, J. (2001). Evolution - Bayesian inference of phylogeny and its impact on evolutionary biology. Science 294, 2310–2314. doi: 10.1126/science.1065889

CrossRef Full Text | Google Scholar

Indelman, P., Fiori, A., and Dagan, G. (1996). Steady flow toward wells in heterogeneous formations: mean head and equivalent conductivity. Water Resour. Res. 32, 1975–1983. doi: 10.1029/96WR00990

CrossRef Full Text | Google Scholar

Jaynes, E. T. (1957a). Information theory and statistical mechanics. Phys. Rev. 106, 620–630. doi: 10.1103/PhysRev.106.620

CrossRef Full Text | Google Scholar

Jaynes, E. T. (1957b). Information theory and statistical mechanics. ii. Phys. Rev. 108, 171–190. doi: 10.1103/PhysRev.108.171

CrossRef Full Text | Google Scholar

Jaynes, E. T. (1968). Prior probabilities. IEEE Trans. Syst. Sci. Cybern. 4, 227–241. doi: 10.1109/TSSC.1968.300117

CrossRef Full Text | Google Scholar

Jeffrey, R. (1992). Probability and the Art of Judgment. Cambridge Studies in Probability, Induction and Decision Theory. Cambridge, MA; London: Cambridge University Press.

Google Scholar

Jung, A. and Aigner, T. (2012). Carbonate geobodies: hierarchical classification and database - a new workflow for 3d reservoir modelling. J. Petrol. Geol. 35, 49–65. doi: 10.1111/j.1747-5457.2012.00518.x

CrossRef Full Text | Google Scholar

Kahneman, D., Slovic, P., and Tversky, A., (eds.) (1982). Judgment Under Uncertainty: Heuristics and Biases. Cambridge, MA; London: Cambridge University Press.

Google Scholar

Kallenberg, O. (2002). Foundations of Modern Probability. New York, NY: Springer.

Google Scholar

Kapelner, A., and Bleich, J. (2016). bartMachine: machine learning with Bayesian additive regression trees. J. Stat. Softw. 70, 1–40. doi: 10.18637/jss.v070.i04

CrossRef Full Text | Google Scholar

Kass, R. E. (2011). Statistical inference: the big picture. Stat. Sci. 26, 1–9. doi: 10.1214/10-STS337

PubMed Abstract | CrossRef Full Text | Google Scholar

Kass, R. E., and Wasserman, L. (1996). The selection of prior distributions by formal rules. J. Am. Stat. Assoc. 91, 1343–1370.

Google Scholar

Kenter, J. and Harris, P. (2006). “Web-based outcrop digital analog database (wodad): archiving carbonate platform margins,” in AAPG International Conference (Cambridge MA; London) 5–8.

Google Scholar

Kerrou, J., Renard, P., Franssen, H.-J. H., and Lunati, I. (2008). Issues in characterizing heterogeneity and connectivity in non-multigaussian media. Adv. Water Resour. 31, 147–159. doi: 10.1016/j.advwatres.2007.07.002

CrossRef Full Text | Google Scholar

Kitanidis, P. K. (2012). Generalized priors in bayesian inversion problems. Adv. Water Resour. 36, 3–10. doi: 10.1016/j.advwatres.2011.05.005

CrossRef Full Text | Google Scholar

Kitanidis, P. K. (2015). Persistent questions of heterogeneity, uncertainty, and scale in subsurface flow and transport. Water Resour. Res. 51, 5888–5904. doi: 10.1002/2015WR017639

CrossRef Full Text | Google Scholar

Kiureghian, A. D., and Ditlevsen, O. (2009). Aleatory or epistemic? does it matter? Struct. Saf. 31, 105–112. doi: 10.1016/j.strusafe.2008.06.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Knight, F. H. (1921). Risk, Uncertainty, and Profit. Boston, MA: Hart, Schaffner & Marx; Houghton Mifflin Co.

Google Scholar

Koehler, D. J. and Harvey, N. (eds.) (2004). Blackwell Handbook of Judgment and Decision Making. Malden, MA: Blackwell.

Google Scholar

Kolmogorov, A. N. (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung. Ergebnisse der Mathematik und ihrer Grenzgebiete. Berlin; Heidelberg; New York, NY: Springer.

Koltermann, C. E., and Gorelick, S. M. (1996). Heterogeneity in sedimentary deposits: a review of structure-imitating, process-imitating, and descriptive approaches. Water Resour. Res. 32, 2617–2658. doi: 10.1029/96WR00025

CrossRef Full Text | Google Scholar

Krause, P., Boyle, D. P., and Bäse, F. (2005). Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 5, 89–97. doi: 10.5194/adgeo-5-89-2005

CrossRef Full Text | Google Scholar

Kruschke, J. K. (2010). Doing Bayesian Data Analysis: A Tutorial with R and BUGS. Amsterdam: Academic Press.

Google Scholar

Kuhn, T. (1962). The Structure of Scientific Revolutions, 1st Edn. Chicago, IL: University of Chicago Press.

Kullback, S., and Leibler, R. A. (1951). On information and sufficiency. Ann. Math. Stat. 22, 79–86.

Google Scholar

Kwakkel, J., Walker, W., and Marchau, V. (2010). Classifying and communicating uncertainties in model-based policy analysis. Int. J. Technol. Policy Manage. 10, 299–315. doi: 10.1504/IJTPM.2010.036918

CrossRef Full Text | Google Scholar

Laloy, E., Linde, N., Jacques, D., and Mariethoz, G. (2016). Merging parallel tempering with sequential geostatistical resampling for improved posterior exploration of high-dimensional subsurface categorical fields. Adv. Water Resour. 90, 57–69. doi: 10.1016/j.advwatres.2016.02.008

CrossRef Full Text | Google Scholar

Laloy, E., Rogiers, B., Vrugt, J. A., Mallants, D., and Jacques, D. (2013). Efficient posterior exploration of a high-dimensional groundwater model from two-stage markov chain monte carlo simulation and polynomial chaos expansion. Water Resour. Res. 49, 2664–2682. doi: 10.1002/wrcr.20226

CrossRef Full Text | Google Scholar

Laloy, E., and Vrugt, J. A. (2012). High-dimensional posterior exploration of hydrologic models using multiple-try dream(zs) and high-performance computing. Water Resour. Res. 48. doi: 10.1029/2011WR010608

CrossRef Full Text | Google Scholar

Laudan, L. (1990). “Demystifying underdetermination,” in Scientific Theories, ed C. W. Savage (University of Minnesota Press), 267–97.

Google Scholar

Le Loc'h, G. and Galli, A. (1997). Truncated plurigaussian method: theoretical and practical points of view. Geostat. Wollongong 96, 211–222.

Google Scholar

Leitgeb, H., and Pettigrew, R. (2010). An objective justification of Bayesianism I: measuring inaccuracy. Philos. Sci. 77, 201–235. doi: 10.1086/651317

CrossRef Full Text | Google Scholar

Li, X., Li, Y., Chang, C.-F., Tan, B., Chen, Z., Sege, J., et al. (2017). Stochastic, goal-oriented rapid impact modeling of uncertainty and environmental impacts in poorly-sampled sites using ex-situ priors. Adv. Water Resour. 111, 174–191. doi: 10.1016/j.advwatres.2017.11.008

CrossRef Full Text | Google Scholar

Linde, N., Renard, P., Mukerji, T., and Caers, J. (2015). Geological realism in hydrogeological and geophysical inverse modeling: a review. Adv. Water Resour. 86(Pt A), 86–101. doi: 10.1016/j.advwatres.2015.09.019

CrossRef Full Text | Google Scholar

Lindgren, F., and Rue, H. (2015). Bayesian spatial modelling with R-INLA. J. Stat. Softw. 63, 1–25. doi: 10.18637/jss.v063.i19

CrossRef Full Text | Google Scholar

Lindley, D. V. (1987). The probability approach to the treatment of uncertainty in artificial intelligence and expert systems. Stat. Sci. 2, 17–24.

Google Scholar

Little, R. J. (2006). Calibrated Bayes: a Bayes/frequentist roadmap. Am. Stat. 60, 213–223. doi: 10.1198/000313006X117837

CrossRef Full Text | Google Scholar

Lunn, D., Spiegelhalter, D., Thomas, A., and Best, N. (2009). The bugs project: evolution, critique and future directions. Stat. Med. 28, 3049–3067. doi: 10.1002/sim.3680

CrossRef Full Text | Google Scholar

Maier, H., Guillaume, J., van Delden, H., Riddell, G., Haasnoot, M., and Kwakkel, J. (2016). An uncertain future, deep uncertainty, scenarios, robustness and adaptation: how do they fit together? Environ. Model. Softw. 81, 154–164. doi: 10.1016/j.envsoft.2016.03.014

CrossRef Full Text | Google Scholar

Malinverno, A., and Briggs, V. (2004). Expanded uncertainty quantification in inverse problems: hierarchical Bayes and empirical Bayes. Geophysics 69, 1005–1016. doi: 10.1190/1.1778243

CrossRef Full Text | Google Scholar

Malpica, J. A., Alonso, M. C., and Sanz, M. A. (2007). Dempster-Shafer Theory in geographic information systems: a survey. Expert Syst. Appl. 32, 47–55. doi: 10.1016/j.eswa.2005.11.011

CrossRef Full Text | Google Scholar

Mantovan, P., and Todini, E. (2006). Hydrological forecasting uncertainty assessment: incoherence of the GLUE methodology. J. Hydrol. 330, 368–381. doi: 10.1016/j.jhydrol.2006.04.046

CrossRef Full Text | Google Scholar

Mara, T. A., Fajraoui, N., Guadagnini, A., and Younes, A. (2017). Dimensionality reduction for efficient Bayesian estimation of groundwater flow in strongly heterogeneous aquifers. Stochast. Environ. Res. Risk Assess. 31, 2313–2326. doi: 10.1007/s00477-016-1344-1

CrossRef Full Text | Google Scholar

Marchant, B. P., and Lark, R. M. (2007). The Matérn variogram model: implications for uncertainty propagation and sampling in geostatistical surveys. Geoderma 140, 337–345. doi: 10.1016/j.geoderma.2007.04.016

CrossRef Full Text | Google Scholar

Mariethoz, G., and Caers, J. (2014). Multiple-point Geostatistics: Stochastic Modeling with Training Images, 376. Chichester: Wiley.

Google Scholar

Mariethoz, G., Renard, P., and Caers, J. (2010). Bayesian inverse problem and optimization with iterative spatial resampling. Water Resour. Res. 46. doi: 10.1029/2010WR009274

CrossRef Full Text | Google Scholar

Mariethoz, G., Renard, P., Cornaton, F., and Jaquet, O. (2009). Truncated plurigaussian simulations to characterize aquifer heterogeneity. Groundwater 47, 13–24. doi: 10.1111/j.1745-6584.2008.00489.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, A. D., Quinn, K. M., and Park, J. H. (2011). MCMCpack: Markov Chain Monte Carlo in R. J. Stat. Softw. 42, 1–21. doi: 10.18637/jss.v042.i09

CrossRef Full Text | Google Scholar

Maslow, A. H. (1943). A theory of human motivation. Psychol. Rev. 50, 370–396.

Google Scholar

Menke, W. (2012). Geophysical Data Analysis: Discrete Inverse Theory. Amsterdam: Academic Press.

Google Scholar

Montanari, A. (2007). What do we mean by “uncertainty”? the need for a consistent wording about uncertainty assessment in hydrology. Hydrol. Process. 21, 841–845. doi: 10.1002/hyp.6623

CrossRef Full Text | Google Scholar

Montanari, A., Shoemaker, C. A., and van de Giesen, N. (2009). Introduction to special section on uncertainty assessment in surface and subsurface hydrology: an overview of issues and challenges. Water Resour. Res. 45. doi: 10.1029/2009WR008471.W00B00

CrossRef Full Text | Google Scholar

Moriasi, D. N., Gitau, M. W., Pai, N., and Daggupati, P. (2015). Hydrologic and water quality model: performance measures and evaluation criteria. Trans. Asabe 58, 1763–1785. doi: 10.13031/trans.58.10715

CrossRef Full Text | Google Scholar

Murakami, H., Chen, X., Hahn, M. S., Liu, Y., Rockhold, M. L., Vermeul, V. R., et al. (2010). Bayesian approach for three-dimensional aquifer characterization at the Hanford 300 Area. Hydrol. Earth Syst. Sci. 14, 1989–2001. doi: 10.5194/hess-14-1989-2010

CrossRef Full Text | Google Scholar

Neapolitan, R. E. (1990). Probabilistic Reasoning in Expert Systems: Theory and Algorithms. New York, NY: John Wiley & Sons, Inc.

Google Scholar

Nearing, G. S., Tian, Y., Gupta, H. V., Clark, M. P., Harrison, K. W., and Weijs, S. V. (2016). A philosophical basis for hydrologic uncertainty. Hydrol. Sci. J. 61, 1666–1678. doi: 10.1080/02626667.2016.1183009

CrossRef Full Text | Google Scholar

Neuman, S. P. (2004). Stochastic groundwater models in practice. Stochast. Environ. Res. Risk Assess. 18, 268–270. doi: 10.1007/s00477-044-0192-6

CrossRef Full Text | Google Scholar

Neuman, S. P. (2014). The new potential for understanding groundwater contaminant transport. Groundwater 52, 653–U177. doi: 10.1111/gwat.12245

PubMed Abstract | CrossRef Full Text | Google Scholar

Neuman, S. P., and Tartakovsky, D. M. (2009). Perspective on theories of non-fickian transport in heterogeneous media. Adv. Water Resour. 32, 670–680. doi: 10.1016/j.advwatres.2008.08.005

CrossRef Full Text | Google Scholar

Neyman, J., and Pearson, E. S. (1928). On the use and interpretation of certain test criteria for purposes of statistical inference: Part i. Biometrika 20A, 175–240.

Google Scholar

Neyman, J., and Pearson, E. S. (1933). On the problem of the most efficient tests of statistical hypotheses. Philos. Trans. R. Soc. Lond. Ser. A 231, 289–337.

Google Scholar

O'Hagan, A., Buck, C. E., Daneshkhah, A., Eiser, J. R., Garthwaite, P. H., Jenkinson, D. J., et al. (2006). Uncertain Judgements: Eliciting Experts' Probabilities. Amsterdam: Wiley.

Google Scholar

Osherson, D., Shafir, E., and Smith, E. E. (1993). Ampliative inference: on choosing a probability distribution. Cognition 49, 189–210. doi: 10.1016/0010-0277(93)90004-F

PubMed Abstract | CrossRef Full Text | Google Scholar

Parmigiani, G. and Inoue, L. (eds.) (2009). Decision Theory: Principles and Approaches. Probability & Mathematical Statistics. Chichester: Wiley.

Google Scholar

Patil, A., Huard, D., and Fonnesbeck, C. J. (2010). PyMC: Bayesian stochastic modelling in Python. J. Stat. Softw. 35, 1–81. doi: 10.18637/jss.v035.i04

PubMed Abstract | CrossRef Full Text | Google Scholar

Pearl, J. (1988a). On probability intervals. Int. J. Approx. Reason. 2, 211–216.

Google Scholar

Pearl, J. (1988b). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. San Francisco, CA: Morgan Kaufmann.

Google Scholar

Pearl, J. (1990). Reasoning with belief functions: an analysis of compatibility. Int. J. Approx. Reason. 4, 363–389.

Google Scholar

Pechstein, A., Attinger, S., Krieg, R., and Copty, N. K. (2016). Estimating transmissivity from single-well pumping tests in heterogeneous aquifers. Water Resour. Res. 52, 495–510. doi: 10.1002/2015WR017845

CrossRef Full Text | Google Scholar

Pérez, C., Mariethoz, G., and Ortiz, J. M. (2014). Verifying the high-order consistency of training images with data for multiple-point geostatistics. Comput. Geosci. 70, 190–205. doi: 10.1016/j.cageo.2014.06.001

CrossRef Full Text | Google Scholar

Pratola, M. T., Chipman, H. A., Gattiker, J. R., Higdon, D. M., McCulloch, R., and Rust, W. N. (2014). Parallel Bayesian Additive Regression Trees. J. Comput. Graph. Stat. 23, 830–852. doi: 10.1080/10618600.2013.841584

CrossRef Full Text | Google Scholar

Pushpalatha, R., Perrin, C., Moine, N. L., and Andréassian, V. (2012). A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 420–421, 171–182. doi: 10.1016/j.jhydrol.2011.11.055

CrossRef Full Text | Google Scholar

Pyrcz, M., Boisvert, J., and Deutsch, C. (2008). A library of training images for fluvial and deepwater reservoirs and associated code. Comput. Geosci. 34, 542–560. doi: 10.1016/j.cageo.2007.05.015

CrossRef Full Text | Google Scholar

Quine, W. V. O. (1951). Two dogmas of empiricism. Philos. Rev. 60, 20–43.

Google Scholar

Ramsey, F. P. (1931). “Chapter Truth and Probability,” in Foundations of Mathematics and other Logical Essays, ed R.s B. Braithwaite (New York, NY: Harcourt, Brace and Company), 156–198.

Rasmussen, C. E. and Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. Cambridge MA; London: MIT Press.

Google Scholar

Refsgaard, J. C., Christensen, S., Sonnenborg, T. O., Seifert, D., Hojberg, A. L., and Troldborg, L. (2012). Review of strategies for handling geological uncertainty in groundwater flow and transport modeling. Adv. Water Resour. 36, 36–50. doi: 10.1016/j.advwatres.2011.04.006

CrossRef Full Text | Google Scholar

Refsgaard, J. C., van der Sluijs, J. P., Højberg, A. L., and Vanrolleghem, P. A. (2007). Uncertainty in the environmental modelling process–a framework and guidance. Environ. Model. Softw. 22, 1543–1556. doi: 10.1016/j.envsoft.2007.02.004

CrossRef Full Text | Google Scholar

Renard, P. (2007). Stochastic hydrogeology: What professionals really need? Ground Water 45, 531–541. doi: 10.1111/j.1745-6584.2007.00340.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Riva, M., Guadagnini, A., Neuman, S. P., Janetti, E. B., and Malama, B. (2009). Inverse analysis of stochastic moment equations for transient flow in randomly heterogeneous media. Adv. Water Resour. 32, 1495–1507. doi: 10.1016/j.advwatres.2009.07.003

CrossRef Full Text | Google Scholar

Robert, C. P. (2001). The Bayesian Choice. New York, NY: Springer.

PubMed Abstract | Google Scholar

Rogati, M. (2017). The AI Hierarchy of Needs.

Romeijn, J.-W. (2017). “Philosophy of statistics,” in The Stanford Encyclopedia of Philosophy, ed E. N. Zalta (Metaphysics Research Lab; Stanford University).

Google Scholar

Royall, R. (1997). Statistical Evidence: A Likelihood Paradigm. Monographs on Statistics & Applied Probability. Boca Raton, FL; London; New York, NY; Washington, DC: Chapman & Hall/CRC.

Google Scholar

Rubin, D. B. (1984). Bayesianly justifiable and relevant frequency calculations for the applied statistician. Ann. Stat. 12, 1151–1172.

Google Scholar

Rubin, Y. (2003). Applied Stochastic Hydrogeology. New York, NY: Oxford University Press.

Google Scholar

Rubin, Y. (2004). Stochastic hydrogeology - challenges and misconceptions. Stochast. Environ. Res. Risk Assess. 18, 280–281. doi: 10.1007/s00477-004-0193-5

CrossRef Full Text | Google Scholar

Rubin, Y., Chang, C.-F., Chen, J., Cucchi, K., Harken, B., Heße, F., et al. (2018). Stochastic hydrogeology's biggest hurdles analyzed and its big blind spot. Hydrol. Earth Syst. Sci. Discuss. 2018, 1–36. doi: 10.5194/hess-2018-290

CrossRef Full Text | Google Scholar

Rubin, Y., Chen, X., Murakami, H., and Hahn, M. (2010). A Bayesian approach for inverse modeling, data assimilation, and conditional simulation of spatial random fields. Water Resour. Res. 46. doi: 10.1029/2009WR008799

CrossRef Full Text | Google Scholar

Rumsfeld, D. H. (2002). DoD News Briefing - Secretary Rumsfeld and Gen. Myers. Online Transcript.

Russell, S., and Norvig, P. (2009). Artificial Intelligence: A Modern Approach, 3rd Edn. Englewood Cliffs, NJ: Pearson.

Saley, A. D., Jardani, A., Ahmed, A. S., Raphael, A., and Dupont, J. (2016). Hamiltonian monte carlo algorithm for the characterization of hydraulic conductivity from the heat tracing data. Adv. Water Resour. 97, 120–129. doi: 10.1016/j.advwatres.2016.09.004

CrossRef Full Text | Google Scholar

Sanchez-Vila, X., and Fernandez-Garcia, D. (2016). Debates-Stochastic subsurface hydrology from theory to practice: why stochastic modeling has not yet permeated into practitioners? Water Resour. Res. 52, 9246–9258. doi: 10.1002/2016WR019302

CrossRef Full Text | Google Scholar

Sánchez-Vila, X., Meier, P. M., and Carrera, J. (1999). Pumping tests in heterogeneous aquifers: an analytical study of what can be obtained from their interpretation using jacob's method. Water Resour. Res. 35, 943–952. doi: 10.1029/1999WR900007

CrossRef Full Text | Google Scholar

Savage, L. J. (1954). The Foundations of Statistics. New York, NY: Dover Publications.

Google Scholar

Savoy, H., Kalbacher, T., Dietrich, P., and Rubin, Y. (2017). Geological heterogeneity: goal-oriented simplification of structure and characterization needs. Adv. Water Resour. 109(Suppl. C), 1–13. doi: 10.1016/j.advwatres.2017.08.017

CrossRef Full Text | Google Scholar

Scales, J. A., and Tenorio, L. (2001). Prior information and uncertainty in inverse problems. Geophysics 66, 389–397. doi: 10.1190/1.1444930

CrossRef Full Text | Google Scholar

Schack, R., Brun, T. A., and Caves, C. M. (2001). Quantum Bayes rule. Phys. Rev. A 64. doi: 10.1103/PhysRevA.64.014305

CrossRef Full Text | Google Scholar

Schneider, C. L., and Attinger, S. (2008). Beyond Thiem: a new method for interpreting large scale pumping tests in heterogeneous aquifers. Water Resour. Res. 44. doi: 10.1029/2007WR005898

CrossRef Full Text | Google Scholar

Sebens, C. T., and Carroll, S. M. (2016). Self-locating uncertainty and the origin of probability in everettian quantum mechanics. Br. J. Philos. Sci. 67, 25–74. doi: 10.1093/bjps/axw004

CrossRef Full Text | Google Scholar

Segal, M. and Xiao, Y. (2011). Multivariate random forests. Wiley Interdiscipl. Rev. Data Min. Knowl. Discov. 1, 80–87. doi: 10.1002/widm.12

CrossRef Full Text | Google Scholar

Serrano, R. P., Guadagnini, L., Riva, M., Giudici, M., and Guadagnini, A. (2014). Impact of two geostatistical hydro-facies simulation strategies on head statistics under non-uniform groundwater flow. J. Hydrol. 508, 343–355.

Google Scholar

Shafer, G. (1976). A Mathematical Theory of Evidence. Princeton, NJ; London: Princeton University Press.

Google Scholar

Shannon, C. E. (1948). The mathematical theory of communication. Bell Syst. Techn. J. 27, 306–317.

Google Scholar

Shi, X., Ye, M., Curtis, G. P., Miller, G. L., Meyer, P. D., Kohler, M., et al. (2014). Assessment of parametric uncertainty for groundwater reactive transport modeling. Water Resour. Res. 50, 4416–4439. doi: 10.1002/2013WR013755

CrossRef Full Text | Google Scholar

Stanford, P. K. (2001). Refusing the devil's bargain: what kind of underdetermination should we take seriously? Philos. Sci. 68, S1–S12. doi: 10.1086/392893

CrossRef Full Text | Google Scholar

Stedinger, J. R., Vogel, R. M., Lee, S. U., and Batchelder, R. (2008). Appraisal of the generalized likelihood uncertainty estimation (glue) method. Water Resour. Res. 44. doi: 10.1029/2008WR006822

CrossRef Full Text | Google Scholar

Strebelle, S. (2002). Conditional simulation of complex geological structures using multiple-point statistics. Math. Geol. 34, 1–21. doi: 10.1023/A:1014009426274

CrossRef Full Text | Google Scholar

Tang, Y., Marshall, L., Sharma, A., and Smith, T. (2016). Tools for investigating the prior distribution in Bayesian hydrology. J. Hydrol. 538, 551–562. doi: 10.1016/j.jhydrol.2016.04.032

CrossRef Full Text | Google Scholar

Tarantola, A. (2005). Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia, PA: SIAM.

Google Scholar

Tartakovsky, D. M. (2013). Assessment and management of risk in subsurface hydrology: a review and perspective. Adv. Water Resour. 51, 247–260. doi: 10.1016/j.advwatres.2012.04.007

CrossRef Full Text | Google Scholar

Tierney, L. (1994). Markov-chains for exploring posterior distributions. Ann. Stat. 22, 1701–1728.

Google Scholar

Tribus, M., and McIrvine, E. C. (1971). Energy and information. Sci. Am. 224, 179–188.

Ulrych, T. J., Sacchi, M. D., and Woodbury, A. (2001). A Bayes tour of inversion: a tutorial. Geophysics 66:55. doi: 10.1190/1.1444923

CrossRef Full Text | Google Scholar

Valakas, G., and Modis, K. (2016). Using informative priors in facies inversion: the case of c-isr method. Adv. Water Resour. 94, 23–30. doi: 10.1016/j.advwatres.2016.04.019

CrossRef Full Text | Google Scholar

Van Fraassen, B. (1980). The Scientific Image. Oxford: Oxford University Press.

Google Scholar

von Mises, R. (1982). Probability, Statistics and Truth. New York, NY: Dover.

Google Scholar

von Neumann, J., and Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton, NJ; Oxford: Princeton University Press.

Google Scholar

von Toussaint, U. (2011). Bayesian inference in physics. Rev. Mod. Phys. 83, 943–999. doi: 10.1103/RevModPhys.83.943

CrossRef Full Text | Google Scholar

Vrugt, J., ter Braak, C., Gupta, H., and Robinson, B. (2009). Equifinality of formal (dream) and informal (glue) bayesian approaches in hydrologic modeling? Stochast. Environ. Res. Risk Assess. 23, 1011–1026. doi: 10.1007/s00477-008-0274-y

CrossRef Full Text | Google Scholar

Wagenmakers, E.-J. (2007). A practical solution to the pervasive problems of p values. Psychon. Bull. Rev. 14, 779–804. doi: 10.3758/BF03194105

PubMed Abstract | CrossRef Full Text | Google Scholar

Walker, W., Harremoës, P., Rotmans, J., van der Sluijs, J., van Asselt, M., Janssen, P., et al. (2003). Defining uncertainty: a conceptual basis for uncertainty management in model-based decision support. Integr. Assess. 4, 5–17. doi: 10.1076/iaij.4.1.5.16466

CrossRef Full Text | Google Scholar

Walker, W. E., Lempert, R. J., and Kwakkel, J. H. (2013). Deep Uncertainty, 395–402. Boston, MA: Springer.

Google Scholar

Wellmann, J. F., de la Varga, M., Murdie, R. E., Gessner, K., and Jessell, M. (2018). Uncertainty estimation for a geological model of the sandstone greenstone belt, western australia - insights from integrated geological and geophysical inversion in a bayesian inference framework. Geol. Soc. Lond. Spec. Publ. 453, 41–56. doi: 10.1144/SP453.12

CrossRef Full Text | Google Scholar

Wellmann, J. F., and Regenauer-Lieb, K. (2012). Uncertainties have a meaning: information entropy as a quality measure for 3-d geological models. Tectonophysics 526–529(Suppl. C), 207–216. doi: 10.1016/j.tecto.2011.05.001

CrossRef Full Text | Google Scholar

Williamson, J. (2010). In Defence of Objective Bayesianism. Oxford: Oxford University Press.

Google Scholar

Wojda, P., Brouyère, S., Derouane, J., and Dassargues, A. (2010). Hydrocube: an entity-relationship hydrogeological data model. Hydrogeol. J. 18, 1953–1962. doi: 10.1007/s10040-010-0653-6

CrossRef Full Text | Google Scholar

Woodbury, A. D., and Ulrych, T. J. (1993). Minimum relative entropy: forward probabilistic modeling. Water Resour. Res. 29.

Google Scholar

Woodbury, A. D., and Ulrych, T. J. (1996). Minimum relative entropy inversion: theory and application to recovering the release history of a groundwater contaminant. Water Resour. Res. 32, 2671–2681.

Google Scholar

Woodbury, A. D., and Ulrych, T. J. (2000). A full-bayesian approach to the groundwater inverse problem for steady state flow. Water Resour. Res. 36, 2081–2093. doi: 10.1029/2000WR900086

CrossRef Full Text | Google Scholar

Xu, T., Valocchi, A. J., Ye, M., and Liang, F. (2017). Quantifying model structural error: efficient Bayesian calibration of a regional groundwater flow model using surrogates and a data-driven error model. Water Resour. Res. 53, 4084–4105. doi: 10.1002/2016WR019831

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1978). Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1, 3–28.

Google Scholar

Zech, A., Müller, S., Mai, J., Heße, F., and Attinger, S. (2016). Extending Theis' solution: using transient pumping tests to estimate parameters of aquifer heterogeneity. Water Resour. Res. 52, 6156–6170. doi: 10.1002/2015WR018509

CrossRef Full Text | Google Scholar

Zhang, Y.-K., and Zhang, D. (2004). Forum: the state of stochastic hydrology. Stochast. Environ. Res. Risk Assess. 18, 265. doi: 10.1007/s00477-004-0190-8

CrossRef Full Text | Google Scholar

Zhdanov, M. S. (2015). Inverse Theory and Applications in Geophysics. Amsterdam: Elsevier Science.

Google Scholar

Zheng, C. and Gorelick, S. M. (2003). Analysis of solute transport in flow fields influenced by preferential flowpaths at the decimeter scale. Ground Water 41, 142–155. doi: 10.1111/j.1745-6584.2003.tb02578.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zinn, B., and Harvey, C. F. (2003). When good statistical models of aquifer heterogeneity go bad: a comparison of flow, dispersion, and mass transfer in connected and multivariate Gaussian hydraulic conductivity fields. Water Resour. Res. 39. doi: 10.1029/2001WR001146

CrossRef Full Text | Google Scholar