- 1Department of Physics, Institute for Marine and Atmospheric Research, Utrecht University, Utrecht, Netherlands
- 2Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, Netherlands
- 3Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, United States
- 4Norwegian Polar Institute, Fram Centre, Tromsø, Norway
Glaciers outside of the ice sheets are known to be important contributors to sea level rise. In this work, we provide an overview of changes in the mass of the world's glaciers, excluding those in Greenland and Antarctica, between 2002 and 2016, based on satellite gravimetry observations of the Gravity Recovery and Climate Experiment (GRACE). Glaciers lost mass at a rate of 199 ± 32 Gt yr−1 during this 14-yr period, equivalent to a cumulative sea level contribution of 8 mm. We present annual mass balances for 17 glacier regions, that show a qualitatively good agreement with published estimates from in situ observations. We find that annual mass balance varies considerably from year to year, which can in part be attributed to changes in the large-scale circulation of the atmosphere. These variations, combined with the relatively short observational record, hamper the detection of acceleration of glacier mass loss. Our study highlights the need for continued observations of the Earth's glacierized regions.
1. Introduction
Compared to the much larger ice sheets, glaciers tend to be located in more temperate environments with a majority of their surface experiencing ablation each year. This makes glaciers particularly sensitive to changes in climate and one of the most visible indicators of global warming. Even though their total potential contribution to sea level rise of about 324 ± 8 mm (Farinotti et al., 2019) is orders of magnitude lower than that of the ice sheets of Greenland and Antarctica, they have been the single largest mass contributor to sea level rise in the twentieth century, responsible for 0.5–0.6 mm yr−1 (IPCC, 2013). Model predictions indicate that glaciers will continue to play an important role in the coming decades, with a projected mass loss equivalent to 5–17 cm sea level rise by the end of the century (Huss and Hock, 2015; Marzeion et al., 2018). The impact of rising sea levels is global, but shrinking of these frozen freshwater compounds will also have profound local societal and environmental effects. Disappearance and degradation of habitat, and changes in water supply, for example, may strongly affect local communities (Huss et al., 2017; Wester et al., 2019). The release of freshwater into the ocean may not only disturb marine ecosystems (Slemmons et al., 2013), but future accumulation of glacial freshwater in key areas of deep convection also has the potential to interfere with the thermohaline circulation (Yang et al., 2016; Bamber et al., 2018).
Before the advent of satellite gravimetry and altimetry, estimates of global glacier mass change were based on analysis of non-continuous direct and geodetic mass-balance measurements of a few hundred glaciers. Most of these glaciers are small and located in maritime climate regions, with an uneven distribution between different types of glaciers. This, together with the fragmented records of in-situ mass balance, called for extrapolation of the data, with results varying between studies, depending on the statistical approach used. Kaser et al. (2006) reported an increase in glacier mass loss from 137 ± 68 Gt yr−1 for 1961–1990 to 353 ± 68 Gt yr−1 for 2001–2004, whereas Meier et al. (2007) estimated a 2006 mass loss of 402±95 Gt yr−1. Both these estimates were significantly lower than the 508 ± 72 Gt yr−1 mass loss for 2001–2005 put forward in Cogley (2009). It should be noted that all these estimates included mass losses from the peripheral glaciers to the Antarctic and Greenland ice sheets that are not included in this study.
Satellite platforms provide near-complete coverage at regular intervals of the Earth's cryosphere, which led to a leap forward in our understanding of the state of the cryosphere. Using GRACE observations, Jacob et al. (2012) estimated the mass loss of 148 ± 30 Gt yr−1 for 2003–2010, excluding the peripheral glaciers on Antarctica and Greenland. Combining GRACE, altimetry and in situ measurements, Gardner et al. (2013) showed that glaciers lost 215 ± 26 Gt yr−1 between 2003 and 2009, with the peripheral glaciers adding another 44 ± 12 Gt yr−1. This is about three times the contribution of the Antarctic ice sheet during that period, and similar to that of the Greenland Ice Sheet (Shepherd et al., 2012). Furthermore, subsampling the altimetry data in the regions around the locations of the in situ data used in Cogley (2009) showed that the local mass balance measurements are generally more negative than the regional mean, implying that in situ based estimates of regional glacier loss are likely biased too negative. Using a least-squares inversion based on sea-level fingerprints of regional mass anomalies, Rietbroek et al. (2016) reported an mean annual glacier mass deficit of 141 ± 26 Gt yr−1 for 2002-2014, but this estimate did not include some key contributors such as the southern part of the Canadian Arctic. Schrama et al. (2014), estimated a mass loss of 162 ± 10 Gt yr−1 between 2003 and 2013, based on GRACE observations, and Reager et al. (2016) estimated a mass loss of 253 Gt yr−1 for the period 2002–2014 using an updated methodology to Gardner et al. (2013). In all these studies, ice loss was particularly pronounced in the North Atlantic Arctic region but also in Alaska and more temperate, mid-latitude regions such as the High Mountain Asia and the Patagonian ice fields.
Motivated by completion of the GRACE mission in 2017, and recent improvements of the data quality, we present an update of the status of the world's glaciers. In contrast to earlier studies, we provide estimates of annual mass balances for all regions defined in the Randolph Glacier Inventory (RGI; RGI Consortium, 2017)-except for the peripheral glaciers of Greenland and Antarctica, which are too closely positioned to the ice sheet to be isolated by the ~350 km horizontal resolution of GRACE.
2. Data and Methods
Our analysis is based on monthly GRACE Stokes coefficients from the latest releases, from three different processing centers: CSR RL06 from the Center for Space Research (Bettadpur, 2018), JPL RL06 from the Jet Propulsion Laboratory (Yuan, 2018) and ITSG-Grace2018 from TU Graz Mayer-Gürr et al. (2018). These solutions use updated parameters and processing algorithms, and improved models to estimate background gravity signals, such as high-frequency ocean and atmosphere mass fluctuations. Compared to earlier releases, noise in the time series is reduced by 20–50%, with the highest reduction at lower latitudes, where groundtrack separation between passes is generally larger. Although the GRACE satellites were in operation until mid-2017, we only use data spanning April 2002 to August 2016. Stokes coefficients from later months are heavily affected by the loss of the accelerometer on the GRACE-B satellite in October 2016 and are too noisy to retrieve mass changes at scales typical for the glacier regions considered in this study (PO.DAAC, 2018). We use coefficients up to degree and order 60, and apply the common post-corrections to the Level-2 data: inclusion of the degree-1 coefficients—which are not observed by the twin satellites—using the estimates of Swenson et al. (2008); and replacement of the poorly constrained C20 coefficients by values obtained from satellite laser ranging (Cheng et al., 2013). Furthermore, we remove correlated noise in the GRACE data using an adaptation of the method of Wouters and Schrama (2007): we first fit a 3rd order polynomial to the monthly time series of all Stokes coefficients, for each degree and order individually, to preserve the long-term variability. Next, we apply an empirical orthogonal function decomposition to the residuals, and filter out noise by rejecting the modes that cannot be distinguished from a white-noise process with 95% confidence. We then restore the long-term variability using the fitted polynomial function from the first step, and apply a 150 km Gaussian smoothing to the resulting Stokes coefficients to reduce remaining noise. These coefficients are then converted to maps of equivalent water height anomalies, following (Wahr et al., 1998).
To retrieve the mass changes in the 17 RGI regions considered in this study, we define global 0.5° × 0.5° grid of mass concentrations (“mascons”), as in Gardner et al. (2013). These mascons are initially given a loading of one in cells where RGI 6.0 indicates a glacierized area of 100 km2 or more, and zero elsewhere (Figure 1). The resulting map is then converted to synthetic GRACE observations, by applying the same degree/order cut-off in the spherical domain and applying the same Gaussian smoothing. The mascon loadings within each of the RGI subregions are adjusted in an iterative process, first in coarse steps of ±100 Gt, until the spatial root-mean-square difference with the actual GRACE observations is minimized. Next, the step size is reduced and the iteration is re-initiated, and this process is repeated until changes in all basins are smaller than 0.1 Gt. A detailed description of the method can be found in Wouters et al. (2008) and Wouters (2010). The 100 km2 limit for the mascons is based on a trade-off between completeness and an acceptable range of uncertainty of the estimates; in cells with a smaller glacier coverage, the GRACE signal will be dominated by (non-ice) hydrological signals, which needs to be corrected for, as we will discuss later. Globally, the mascons cover approximately 90% of the total glacier area in RGI 6.0. As in Jacob et al. (2012) and Gardner et al. (2013), we also include mascons in Greenland and Antarctica, to remove signals from these ice sheets, and in the plains of the Indian subcontinent, where signals from extensive groundwater extraction may otherwise contaminate our glacier mass change estimates in the neighboring High Mountain Asia region (RGI regions 13–15).
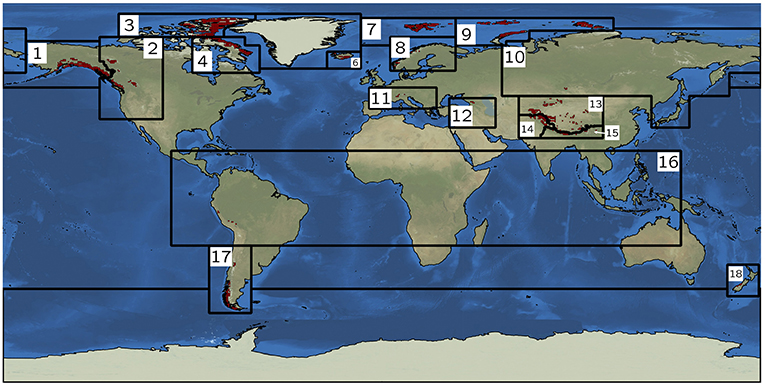
Figure 1. Outlines of the RGI 6.0 regions, and location of the mascons used to retrieve the glacier mass loss from the GRACE data. Region names: 1: Alaska, 2: Western Canada and US, 3: Arctic Canada North, 4: Arctic Canada South, 6: Iceland, 7: Svalbard, 8: Scandinavia, 9: Russian Arctic, 10: North Asia, 11: Central Europe, 12: Caucasus and Middle East, 13: Central Asia, 14: South Asia West, 15: South Asia East, 16: Low Latitudes, 17: Southern Andes, 18: New Zealand.
We derive three time series of mass change for each RGI region, one for each processing center. Each of these processing centers uses a slightly different approach and/or background models to estimate the Stokes coefficients, and it has been shown that using the ensemble mean of the solutions suppresses noise in the time series (Sasgen et al., 2007; Sakumura et al., 2014). We use the weighted mean of the three solutions, with the monthly uncertainties in the individual time series as weights. These uncertainties are based on the reported calibrated errors, propagated for each region and scaled in such a way that the mean of the monthly uncertainties for the mid-mission period (mid 2003–mid 2015) matches the noise level estimated using the empirical approach of Wahr et al. (2006). In this approach, the time series are high-pass filtered with a cut-off period of 4 months and the standard deviation of the remaining signal is considered to represent a more realistic, yet conservative estimate of the noise level. In contrast to Sasgen et al. (2007) and Sakumura et al. (2014), we do not use the mean of the CSR, JPL, and ITSG time series, as this may introduce spurious jumps in months where data is missing in one or more of the solutions. Instead, we first compute the time derivative of the mass anomalies—i.e., the difference between successive months—and then apply the weighted-averaging. The combined time series is then obtained from the running sum of the resulting weighted mass changes, as shown in Figure 2. Typically, noise in the time series (computed following the method of Wahr et al., 2006 discussed earlier) is 10–20% lower than the best individual solution. Depending on the region, the CSR, ITSG, and JPL solutions contribute 40–65, 15–45, and 10–30%, respectively, to the combination. Monthly errors of the combined time series are based on the weighted-average root-square sum of the errors in the individual time series, scaled to match the empirical mid-mission noise level.
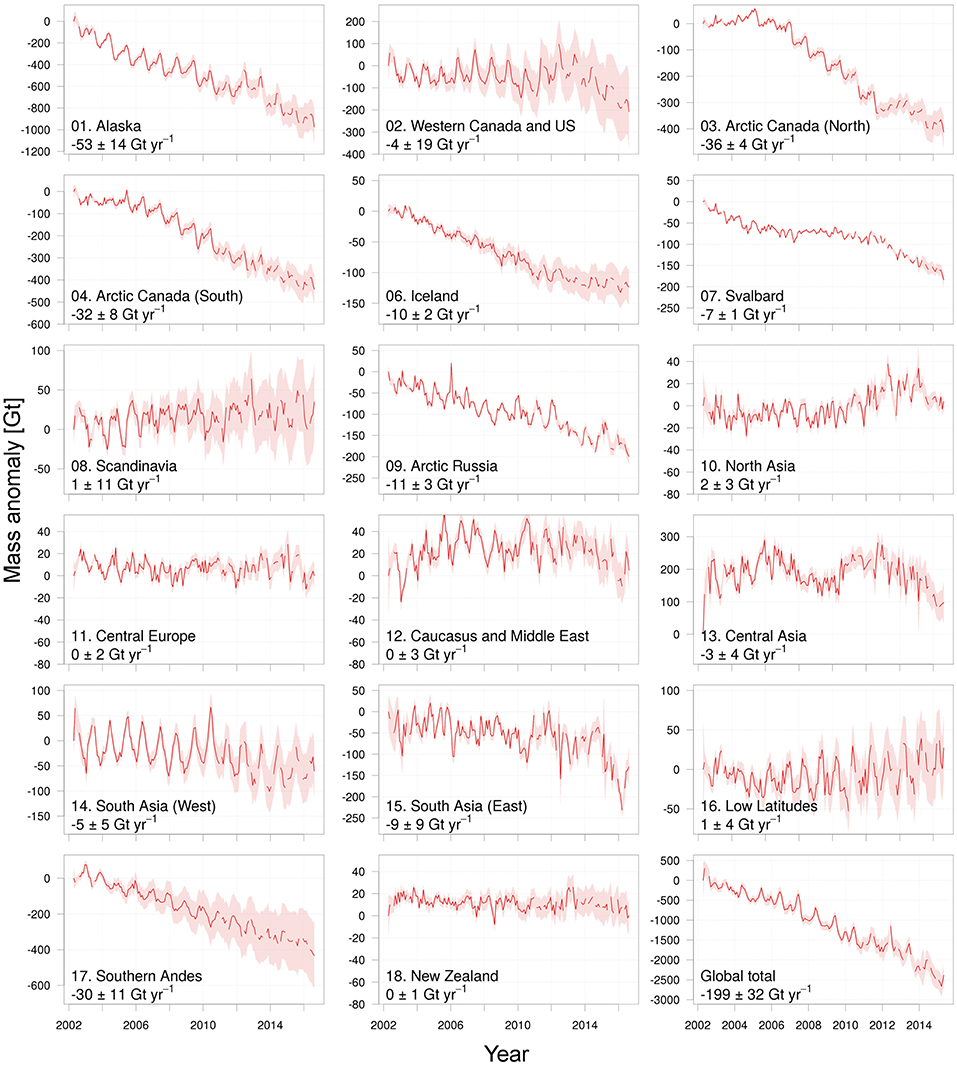
Figure 2. Time series of cumulative mass anomalies for all RGI regions, except for the peripherial glaciers of Greenland and Antarctica, which cannot be resolved by GRACE. Note the difference in range on the y-axis between the different subfigures. Uncertainties grow in time due to the cumulative effect of uncertainties in the GIA correction.
GRACE observes the integral mass change on and beneath the Earth's surface. Therefore, a number of corrections need to be applied to the data in order to isolate the glacier change signal. To account for glacial isostatic adjustment (GIA), the mass displacement in the Earth's interior in response to changes in ice mass loading since the Last Glacial Maximum, we use the model of Caron et al. (2018). This model combines vertical land rates from Global Navigation Satellite System stations and relative sea level curves in a Bayesian framework to estimate the geoid changes induced by GIA, together with an associated standard error. In the Russian Arctic (RGI region 09), we use the model of Root et al. (2015), which was specifically tailored for this region. To account for mass displacement in response to load changes since the Little Ice Age (LIA), which are not included in these GIA models, we use the LIA models of Larsen et al. (2005) for Alaska (RGI region 01), Jacob et al. (2012) High Mountain Asia (RGI region 13–15), and Ivins and James (2004) for the Southern Andes (RGI region 17). For Iceland (RGI region 06), we use the recent model of Sørensen et al. (2017). We note that our LIA correction is smaller than that reported in their study (3 vs. 5.5 Gt yr−1), due to the different method to retrieve the mass changes from the GRACE data. Uncertainties for the GIA correction are based on the standard errors derived from the probability density function reported in Caron et al. (2018), an ensemble of GIA solutions with varying ice loading history for the Russian Arctic (Root et al., 2015), and varying ice loading history and earth structure models for Iceland (Sørensen et al., 2017).
To correct for hydrological signals in the GRACE observations—that can be significant at mid- and low-latitudes— we subtract monthly mass changes derived from the Global Land Data Assimilation System Version 2.1 (GLDAS V2.1; Rodell et al., 2004; Beaudoing and Rodell, 2016) from the time series. Forced with model and observation-based data sets of atmospheric circulation, precipitation and short- and longwave radiation, GLDAS V2.1 simulates land surface parameters and fluxes at a 0.25 degree resolution from 2000 to present. Since the model shows unrealistically large variations in glacierized regions, we mask out grid points that are classified as ice in the native resolution of the models. Scanlon et al. (2018) demonstrated that long-term changes in land-storage vary considerably between different models, therefore, we include a second model to estimate the uncertainty in the hydrological correction. The PCRaster Global Water Balance 2 model (PCR-GLOBW 2; Sutanudjaja et al., 2018) provides changes in the water column at a resolution of 5 arcmin resolution and includes the effects of anthropogenic impacts, such as groundwater and surface water withdrawal, which is not included in GDLAS V2.1. PCR-GLOBW 2 data is currently available to December 2015. The uncertainty in the hydrological correction is taken as the difference between the models.
Hydrological models like GLDAS and PCR-GLOBW do not consider changes in water storage of hydropower reservoirs which are often located nearby glacierized areas. As an example of the potential impact of this on regional GRACE signals, we estimate a time series of mass anomalies for all hydropower reservoirs in Norway based on water level statistics published by the Norwegian Water Resources and Energy Directorate (http://vannmagasinfylling.nve.no, accessed 1 March 2019). The statistics are provided as weekly percentages of total storage capacity which we estimate to 71 Gt based on upscaling of known storage volumes for 85% of the total reservoir area. The resulting reservoir mass anomalies are shown in Figure S2 together with the GRACE signal for Scandinavia (RGI region 08).
High-frequency ocean mass signals are removed using ocean circulation models by the processing centers to avoid aliasing of these signals into the monthly Stokes coefficients. To assess the impact of this correction, we added back the removed signal and recomputed the time series. Differences are small in all regions, except for the Russian Arctic, where the model correction induces a long-term trend of –1.8 Gt yr−1. This is most likely related to unphysical model drift in shallow ocean regions (personal communication H. Dobslaw). Therefore, we add back the model correction, and include 50% of this correction in the uncertainties.
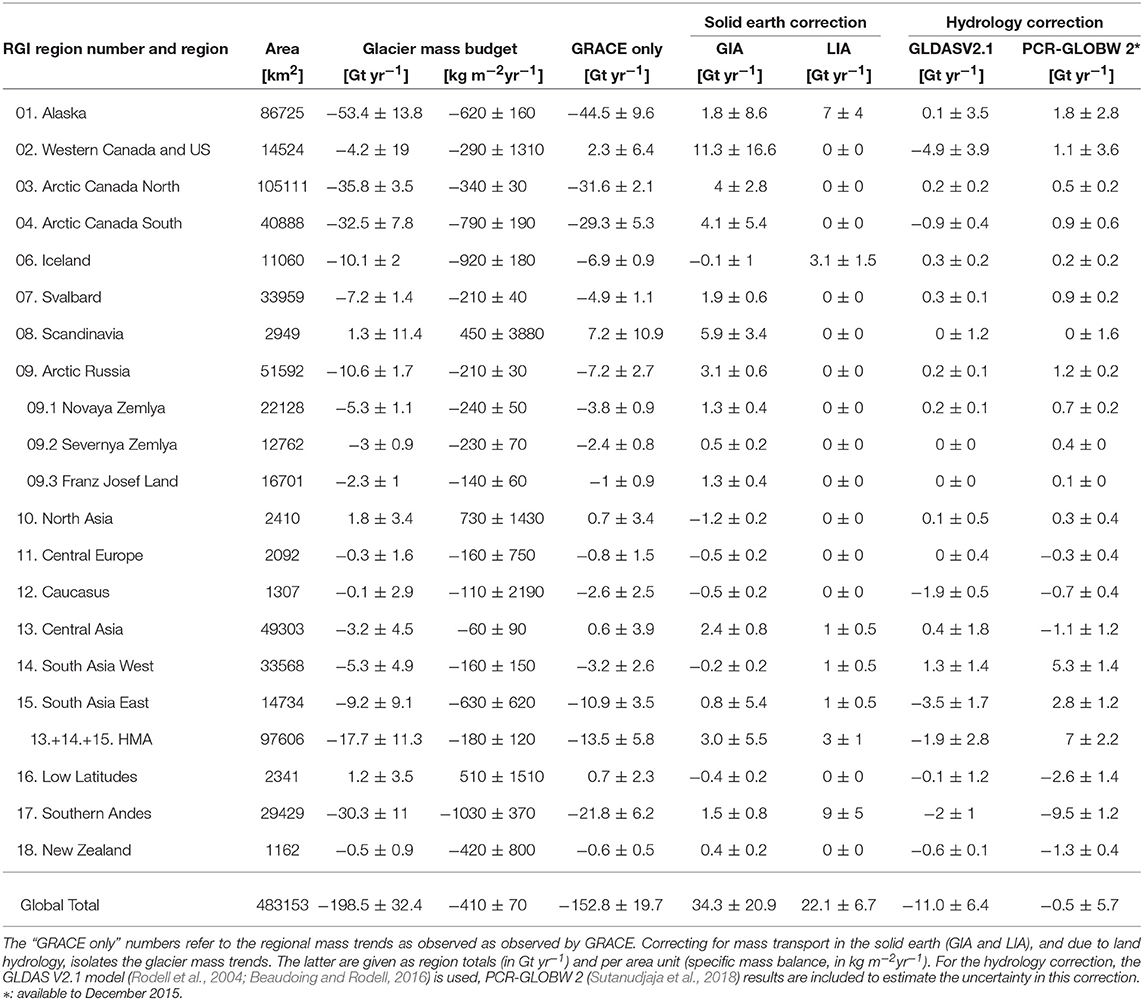
To estimate the long-term mass balance of each region we apply an error-weighted least square fit to the time series. We simultaneously fit a constant, a linear trend and seasonal and semi-seasonal harmonics. We do not attempt to estimate accelerations in the time series as the results are highly affected by interannual variability. For example, in Arctic Canada North (RGI region 03), an acceleration of –9 Gt yr−2 is found for the period April 2002–December 2012. Extending the record to include the years between 2013 and 2016 reduces the estimate of acceleration to –2 Gt yr−2, highlighting the sensitivity of the acceleration estimates to the chosen period. Trends for the full period from April 2002 to August 2016 are given in Table 1. Values for the 2006–2015 balance years (defined as October 2005 to September 2015 for regions in the Northern Hemisphere, and April 2005 to March 2015 for those in the Southern Hemisphere, are given in Table S1). The 2-sigma uncertainties account for the formal error of the fit, including propagation of the monthly errors, the uncertainties in the GIA, LIA, hydrology and ocean correction, and the exclusion of glacier areas smaller than 100 km2, by scaling the estimated trends by the ratio of the total area reported in RGI 6.0 and the mascon area.
To assess the impact of the processing methodology on the results, we compare our trends to independent results based on JPL mascons (JPL RL06Mv1; Watkins et al., 2015). In this approach, mass variations are estimated directly from the Level-1 GRACE data, in 4551 equal-area 3° spherical caps, distributed evenly over the Earth's surface. Because a-priori information, for example from geophysical models, can be easily incorporated in the inversion process, the JPL mascon solutions suffer less from the typical North-South striping observed in spherical harmonics solutions. Furthermore, a Coastline Resolution Improvement (CRI) filter is applied to the data, to reduce leakage from land signals into the ocean caused by the limited spatial resolution of GRACE. Trends were derived using the approach described in Reager et al. (2016) and are shown in Table S2.
Annual mass balances are computed as the difference between the mass anomalies for October 1 and September 30 of the previous year, for regions in the Northern Hemisphere. For example, for mass balance year 2005 we take the difference of October 1 2005 and September 30 2004, where the day values are obtained through spline interpolation of the monthly time series. For regions in the Southern Hemisphere (RGI regions 16-18: Low Latitudes, Southern Andes and New Zealand), we use April 1 and March 31. As can be seen in Figure 2, the GRACE time series contains gaps, especially in the later phase of the mission, when no data was collected during phases when the satellites were in eclipse, to lengthen the mission's lifetime. We fill these gaps using cubic spline interpolation on the time series, using the four data points left and right of the gaps (Grund, 1979). Such an interpolation introduces two types of errors: due to measurement noise in the available months, and due to the interpolation itself. To account for the first type of error, we repeated the spline interpolation 10 000 times, while adding random noise within one standard deviation of the estimated monthly noise level to the available data points. The standard deviation of the 10 000 realizations of the interpolated points is then taken as the one-sigma uncertainty for these months. The second uncertainty arises from the fact that the spline interpolation is a mathematical procedure which connects points without knowledge of the actual climatological conditions. For example, when interpolating a missing August month, it does not take into account that local temperatures, and hence melt rates, are generally higher than in September (in the Northern Hemisphere). We address this issue using the time series between July 2003 and December 2010, when no data outages occurred. We consecutively leave out 1 months, which we then fill using the spline interpolation, and compare the interpolated and observed value. The uncertainty of the second type is then computed as the median difference of all same months of the year (e.g., the uncertainty for a missing January month is based on the median difference of all January months between 2004 and 2010). We repeat these period leaving out 2 consecutive months, to determine the uncertainties for periods with a 2-month data outage. For climatological comparison between RGI regions, we divided the annual mass balances (in unit Gt yr−1) by their regional glacier areas to provide specific mass balances (in unit kg m−2yr−1) as shown in Figure 3 for the major RGI regions and in Figure S1 for the smaller RGI regions.
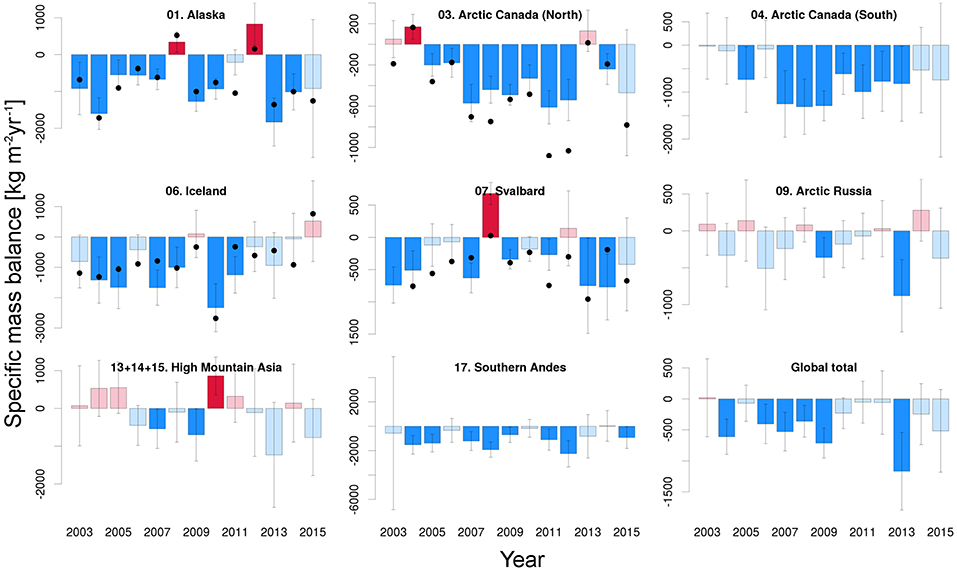
Figure 3. Annual specific mass balance for the larger RGI regions in kg m−2yr−1. Mass balance years run from October 1 to September 31 for regions in the Northern Hemisphere, and April 1 to March 31 for regions in the Southern Hemisphere. Note the difference in range on the Y-axis between the different subfigures. Values which are not significantly different from zero are plotted in pale colors. Black dots indicate the annual mass balance derived taking the mean mass balance from in-situ observations in the region, where available (see text for details, Figure S2 and Table S3 for station locations).
We compare our GRACE-based annual mass balances to measurements made in the field, based on glaciological mass balance records in the World Glacier Monitoring Service database Zemp et al. (2015); WGMS (2017). Despite the potential sampling biases in these records—as discussed in the introduction—such a comparison may provide qualitative insight into the robustness of the interannual variability captured by our GRACE analysis. A correlation analysis between GRACE and in-situ annual mass balances was carried out in regions where at least three in situ records were available, covering the full period of 2003 to 2015. An exception was made for Svalbard, where in 2003 only measurements along the western coast of Spitsbergen were available. Here, we use data from 2004 to 2015 instead, to include data from Etonbreen glacier basin of the Austfonna ice cap. To avoid biases due to geographical oversampling, we first average records located within 50 km of each other, and then calculate the regional mass balances by averaging all available records.
To further interpret the GRACE annual mass balances, we correlate the results to a number of climate indices: the Artic Oscillation (AO), the North Atlantic Oscillation (NAO), the Pacific Decadal Oscillation (PDO), NINO 1+2, 3, 3.4, and 4, and the Southern Oscillation index (SOI). All indices were obtained through climexp.knmi.nl. Correlation was performed using 4-month averages of the indices, at various lags ranging from October-January to June-September.
3. Results and Discussion
Collectively, the 17 RGI regions show an overall mass loss of 199 ± 32 Gt yr−1 during the period April 2002–August 2016. Our spherical harmonics solution is consistent with the JPL mascon solution for the same period (Table S2) and an earlier multi-method estimate of –215±35 Gt yr−1 for the period 2003–2009 (Gardner et al., 2013). An apparent acceleration of the mass loss is visible in the time series (Figure 2), with an estimated value of 7.8 ± 3.5 Gt yr−2. However, year-to-year inspection of the global specific mass balances (Figure 3) shows that this is largely the result of a temporary decrease in mass balance between 2005 and 2009, and the particularly negative mass balance of 2013, when the global specific mass balance reached a value of –1170 ± 620 kg m−2yr−1. Between 2010 and 2012, annual mass balances were less negative, and more recent years (2014–2015) were close to the long-term (2002–2016) average. The link between increasing air temperatures and glacier mass loss is well-established, but given the heterogeneous distribution across the continents, a strong correlation between deviations from the long-term average in global air temperatures and annual mass balance should not be expected. Indeed, we find this correlation to be insignificant (r = −0.18 with p = 0.56, where a negative correlation indicates a more negative mass balance linked to positive temperate anomalies). A significant correlation is found with the May-August NAO (r = −0.57;p = 0.04), but this is merely a representation of the large degree of regional variability in the Artic associated with this mode, as we will discuss below.
The largest net contributor to the global mass loss is Alaska (when considering the RGI Arctic Canada North and South regions as separate contributors), with an average mass loss of 53 ± 14 Gt yr−1, equivalent to a long-term specific mass balance of –620 ± 160 kg m−2yr−1. The most negative specific balance of –1830 ± 650 kg m−2yr−1 is observed in 2013, followed by 2004 (–1600 ± 430 kg m−2yr−1), whereas positive values are found in 2008 and 2012. Qualitatively, this is in agreement with mass balance estimates from in situ observations at individual glaciers in the region (Wolverine, Lemon Creek, Taku, and Gulkana), which show similar extremely negative and moderately positive mass balances in these years (Figure 3; r = 0.85;p < 0.01). We find that interannual variations in the mass balance are negatively correlated with the May-September PDO and May-August NAO, with correlation values of –0.56 (p = 0.05) and –0.77 (p < 0.01), respectively (Bitz and Battisti, 1999; Josberger et al., 2007; Arendt et al., 2009).
The total mass loss of the Southern Andes region (30 ± 11 Gt yr−1) is only about half that of Alaska, but relative to its glacier area, this region shows the most pronounced downwasting of all regions considered. Apart from 2013, the region consistently shows negative mass balances throughout the observation period, with an average of –1030 ± 370 kg m−2yr−1. Braun et al. (2019) estimated the 2000-2011/2015 mass loss in the region at 19 ± 0.6 Gt yr−1 by differencing digital elevation models derived from synthetic aperture radar interferometry. This is smaller than our estimate, but not inconsistent given the different time span and overlapping uncertainty range. Both the GRACE data and the results by Braun et al. (2019) show that nearly all of the regional mass loss can be attributed to the Patagonian Ice Fields.
Similar extreme negative mass balances are observed in Iceland, where glaciers lost on average 920 ± 180 kg m−2yr−1, or 10 ± 2 Gt yr−1 when integrated over the area, between 2003 and 2015. Icelandic glaciers are highly sensitive to changes in near-surface air temperature because of their area altitude distribution (Hock et al., 2009), and to aerosol radiative forcing following volcanic eruptions (e.g., Flanner et al., 2014). This is reflected in the high interannual variability we find in our GRACE-based annual mass balances, with changes of up to 2400 kg m−2yr−1 between consecutive years. Our annual mass balances are in good qualitative agreement with averaged in-situ observations from 8 glacier locations (r = 0.75; p < 0.01). Both types of records show a reduced mass loss since the extreme melt following the eruption of the Eyjafjallajökull in the warm summer of 2010 (Björnsson et al., 2013). Such a reduction of the mass loss was also evident in the altimetry-based estimate of Foresta et al. (2016), who reported a mass loss of 5.8 ± 0.7 Gt yr−1 for the period October 2010–September 2015, which compares well with the 4.8 ± 3 Gt yr−1 in this study (vs. 11 ± 2 Gt yr−1 in the preceding years).
Both the Northern and Southern regions of the Canadian Arctic showed extensive mass loss in the period 2006–2012, that can be attributed to increasing summer temperatures induced by a weak, westerly-positioned Arctic circumpolar vortex (Gardner et al., 2011, 2012). No significant increase in discharge (VanWychen et al., 2014), or decrease in precipitation has been reported (Noël et al., 2018). Near-zero mass balances are observed in the following two years, 2013 and 2014, when a positive NAO phase lead to advection of cool, wet air toward these regions (Box and Sharp, 2017). Indeed, we find a significant correlation between annual mass balance and May-August NAO in the Northern region (r = 0.77, p < 0.01), whereas the variations in the Southern region are better explained by the May-July AO (r = 0.63, p = 0.03). In the Northern region, the GRACE annual mass balances correlate well with those derived from four in situ records (r = 0.92; p < 0.01). No similar validation data is available for the Southern region.
In the eastern parts of the Arctic, the same atmospheric circulation patterns led to opposite glacier behavior in Svalbard and the Russian Arctic, with near zero or positive mass balance between 2004 and 2012, but large mass losses in 2013. Both regions experienced a comparable negative specific mass balance of –220 kg m−2yr−1 during the observational period, but given its larger area, the Russian Arctic showed a larger overall mass loss (7 ± 1 Gt yr−1 for Svalbard, vs. 11 ± 3 Gt yr−1 for the Russian Arctic). This is not significantly different from a previous estimate of 9.8 ± 1.9 Gt yr−1 for the 2003–2009 period, based on ICESat altimetry (Moholdt et al., 2012). Correlations have opposite signs to those found in the Canadian Arctic, with r = –0.64 (p = 0.02) and r = –0.58 (p = 0.04) for the correlation between summer NAO and annual mass balance in Svalbard and Arctic Russia, respectively. Increased mass losses on Svalbard since 2012 can partly be attributed to the surge of Basin-3 on Austfonna ice cap (Dunse et al., 2015), but most of the negative mass balance in 2013 is explained by increased surface melting (Lang et al., 2015). A reasonable correlation of r = 0.62 (p = 0.03) is found with local mass balance, where it should be kept in mind that 6 out of 7 of the measurement sites are located on the western coast of Spitsbergen. Out of the three main archipelagoes of the Russian Arctic, Novaya Zemlya (RGI subregion 09.1) accounted for about 50% of the total mass loss, although specific mass rates in Severnaya Zemlya were comparable. No in situ records are available from the Russian Arctic.
In the High Mountain Asia region (RGI regions 13-15; Central Asia, South Asia West and East), interannual variability in mass balance is large, due to variations in precipitation associated with changing atmospheric circulation (Yao et al., 2012). The total mass loss of 17.7±11.3 Gt yr−1 for 2002–2016 is in good agreement with Brun et al. (2017), who reported a mass loss of 16.3 ± 3.5 for a slightly longer period, 2000–2016. However, when looking at the individual regions, we only observe good agreement for South Asia West (5 Gt yr−1 mass loss in this study, vs. 6 Gt yr−1 in Brun et al. (2017)). These three regions are also where the spherical harmonics solution of this study deviates the most from the JPL mascons solution despite being similar for High Mountain Asia as a whole (Supplementary Table S2). Mass loss in Central Asia is underestimated (3 Gt yr−1 vs. 6 Gt yr−1), and overestimated in South Asia East (9 Gt yr−1 vs. 4 Gt yr−1). We find that annual mass balance in the Central Asia is positively correlated with all four Niño indices (November-February), with correlation values ranging from r = 0.64 (p = 0.02) for NINO4 to r = 0.83 (p < 0.01) for NINO1+2, most likely through modulation of the monsoon circulation (Shaman and Tziperman, 2005; Kumar et al., 2006).
Combined, the ten regions discussed above make up more than 99% of the total mass loss. In the remaining seven regions, where glacier areas are typically an order of magnitude smaller, no significant changes are observed, either because the glacial signal is too small to be distinguished from the background noise, or uncertainties in the GIA and hydrology corrections are large. For Scandinavia, comparison of the GRACE-derived and in situ annual mass balances reveals a good agreement in the year-to-year variability (r = 0.81; p < 0.01), but a too positive mean annual mass balance in the GRACE results, considering that all monitored glaciers have lost mass since year 2000 (Andreassen et al., 2016). The close resemblance between mass anomalies of GRACE and water storage variations in Norwegian hydropower reservoirs (Figure S3) shows that this can be an issue for several of the smaller glacier regions that have comparable reservoir areas in the vicinity, in particular Western Canada and US, and Central Europe (RGI regions 03 and 11). The uncorrected impact of reservoir storage variations can partly explain why the seasonal amplitudes in the time series of these regions (Figure 2) appear to be comparatively larger and shifted in time from an expected minimum glacier mass at the end of the summer melt season to an expected minimum reservoir storage at the end of the winter before onset of snowmelt runoff. This severely limits our ability to resolve seasonal and annual glacier mass changes in affected regions, but for long-term mass trends over the whole 14-year GRACE period, we expect the impact to be relatively small. Our derived glacier mass trends for Scandinavia and Central Europe are close to zero, whereas the time series for Western Canada and US (Figure 2) indicate small changes until 2012 and then a period of mass loss thereafter, consistent with Menounos et al. (2019) who reported an increase in mass loss from 2.9 ± 3.1 Gt yr−1 in 2000-2009 to 12.3 ±4.6 Gt yr−11 in 2009-2018 based on differencing of digital elevation models. No significant correlations were found between GRACE and in situ annual mass balances for Western Canada and US (r = 0.49; p = 0.09), and Central Europe (r = 0.55; p = 0.06). Other small RGI regions (North Asia, Caucasus, Low Latitudes and New Zealand) constitute only 1.5% of the global glacier area and are thus of minor importance in a sea level perspective despite clearly negative specific mass balances from in-situ records (Gardner et al., 2013).
4. Conclusions
In this study, we provide time series of glacier mass loss, together with annual estimates of specific mass balance, for all RGI regions, excluding the peripheral glaciers of Greenland and Antarctica. For the larger regions, these annual mass balances agree well with in situ observations and independent estimates from altimetry. Smaller regions are hampered by a low signal-to-noise ratio and uncertainties in the necessary corrections for GIA and hydrology. Improvement of these model corrections, including anthropogenic influences as demonstrated by our case study of Norwegian hydropower reservoirs, are a prerequisite to resolve the ongoing changes in these smaller regions. In High Mountain Asia, overall agreement was found with independent observations of mass loss, but less so when looking at the three distinct regions that make up High Mountain Asia. We associate this agreement at the regional scale but disagreement at the subregions as being caused by the coarse horizontal resolution of GRACE, which causes “signal leakage” between neighboring subregions. Until a leap forward is made to a finer spatial resolution of gravimetry missions, resolving small-scale mass change signals will have to rely on combination of GRACE observations with auxiliary data, either from climate models, or other remote sensing techniques (e.g., Sasgen et al., 2019).
Variations in regional mass loss are predominantly driven by local atmospheric circulation changes, particularly those that modify summer near-surface air temperatures. We find that annual mass balance, notably in the Northern Hemisphere, correlate well with climate indices such as the AO, PDO, ENSO, and, in particular, the NAO, leading to substantial interannual variability. This—combined with the relatively large uncertainties in the current GRACE observations in some regions—hampers the detection of a possible acceleration in the mass loss, which calls for continued and improved global observations of the Earth's glaciers and ice caps. Nevertheless, it is clear that during the GRACE-era, their overall mass balance was strongly negative. Since 2003, the world's glaciers have lost about 3000 Gt, equivalent to a sea level rise of 8 mm. The average mass loss rate of 199 ± 32 Gt yr−1 is only slightly smaller than that of Greenland, and about twice that of Antarctica for the same period (WCRP Global Sea Level Budget Group, 2018).
Author Contributions
BW designed and performed the GRACE data analysis, and wrote a first draft of the manuscript. AG carried out the analysis of the JPL mascon time series. GM examined the impact of hydropower water storage on the GRACE results in Scandinavia. All authors contributed to the analysis of the data and further writing of the manuscript.
Funding
BW was funded by NWO VIDI grant 016.Vidi.171.063. AG's efforts were supported by NASA's Cryosphere Science program.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Jason E. Box is acknowledged for his work on correlation of climate indices that inspired part of this study, and David N. Wiese for producing the JPL mascons and commenting on the GRACE analysis. We thank Bart Root and Alexander Jarosch for providing us with the GIA corrections for the Barentz region and Iceland, respectively, and Edwin H. Sutanudjaja for the PCR-GLOBWB v2 model data. We thank Geert Jan van Oldenborgh for making the climate indices available on climexp.knmi.nl.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00096/full#supplementary-material
References
Andreassen, L. M., Elvehøy, H., Kjøllmoen, B., and Engeset, R. V. (2016). Reanalysis of long-term series of glaciological and geodetic mass balance for 10 Norwegian glaciers. Cryosphere 10, 535–552. doi: 10.5194/tc-10-535-2016
Arendt, A., Walsh, J., and Harrison, W. (2009). Changes of Glaciers and Climate in Northwestern North America during the Late Twentieth Century. J. Clim. 22, 4117–4134. doi: 10.1175/2009JCLI2784.1
Bamber, J. L., Tedstone, A. J., King, M. D., Howat, I. M., Enderlin, E. M., van den Broeke, M. R., et al. (2018). Land ice freshwater budget of the Arctic and North Atlantic oceans: 1. Data, methods, and results. J. Geophys. Res. Oceans 123, 1827–1837. doi: 10.1002/2017JC013605
Beaudoing, H., and Rodell, M. (2016). GLDAS Noah Land Surface Model L4 Monthly 0.25 x 0.25 Degree V2.1. doi: 10.5067/SXAVCZFAQLNO
Bettadpur, S. V. (2018). UTCSR Level-2 Processing Standards Document for Product Release 06. Tech. Rep. GRACE 327-742, UTCSR, Austin, TX, 17.
Bitz, C. M., and Battisti, D. S. (1999). Interannual to decadal variability in climate and the glacier mass balance in Washington, Western Canada, and Alaska. J. Clim. 12, 3181–3196. doi: 10.1175/1520-0442(1999)012<3181:ITDVIC>2.0.CO;2
Björnsson, H., Pàlsson, F., Gudmundsson, S., Magnúúson, E., Adalgeirsdóttir, G., Jóhannesson, T., et al. (2013). Contribution of Icelandic ice caps to sea level rise: trends and variability since the Little Ice Age. Geophysical Research Letters 40, 1546–1550. doi: 10.1002/grl.50278
Box, J., and Sharp, M. (2017). “Chap. Changes to Arctic land ice,” in Snow, Water, Ice and Permafrost in the Arctic (SWIPA) (Oslo: Arctic Monitoring and Assessment Programme (AMAP), 137–168. Available online at: https://www.amap.no/documents/doc/snow-water-ice-and-permafrost-inthe-arctic-swipa-2017/1610
Braun, M. H., Malz, P., Sommer, C., Farías-Barahona, D., Sauter, T., Casassa, G., et al. (2019). Constraining glacier elevation and mass changes in South America. Nat. Clim. Change 9, 130–136. doi: 10.1038/s41558-018-0375-710.1038/s41558-018-0375-7
Brun, F., Berthier, E., Wagnon, P., Kääb, A., and Treichler, D. (2017). A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 10, 668. doi: 10.1038/ngeo2999
Caron, L., Ivins, E., Larour, E., Adhikari, S., Nilsson, J., and Blewitt, G. (2018). GIA model statistics for GRACE hydrology, cryosphere, and ocean science. Geophys. Res. Lett. 45, 2203–2212. doi: 10.1002/2017GL076644
Cheng, M., Tapley, B. D., and Ries, J. C. (2013). Deceleration in the earth's oblateness. J. Geophys. Res. 118, 740–747. doi: 10.1002/jgrb.50058
Cogley, J. G. (2009). Geodetic and direct mass-balance measurements: comparison and joint analysis. Ann. Glaciol. 50, 96–100. doi: 10.3189/172756409787769744
Dunse, T., Schellenberger, T., Hagen, J. O., Kääb, A., Schuler, T. V., and Reijmer, C. H. (2015). Glacier surge mechanisms promoted by a hydro-thermodynamic feedback to summer melt. Cryosphere 9, 197–215. doi: 10.5194/tc-9-197-2015
Farinotti, D., Huss, M., Fürst, J. J., Landmann, J., Machguth, H., Maussion, F., et al. (2019). A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 12, 168–173. doi: 10.1038/s41561-019-0300-3
Flanner, M. G., Gardner, A. S., Eckhardt, S., Stohl, A., and Perket, J. (2014). Aerosol radiative forcing from the 2010 eyjafjallajökull volcanic eruptions. J. Geophys. Res. Atmos. 119, 9481–9491. doi: 10.1002/2014JD021977
Foresta, L., Gourmelen, N., Pálsson, F., Nienow, P., Björnsson, H., and Shepherd, A. (2016). Surface elevation change and mass balance of Icelandic ice caps derived from swath mode CryoSat-2 altimetry. Geophys. Res. Lett. 43: 12, 138–145. doi: 10.1002/2016GL071485
Gardner, A., Moholdt, G., Arendt, A., and Wouters, B. (2012). Accelerated contributions of Canada's Baffin and Bylot Island glaciers to sea level rise over the past half century. The Cryosphere. 6, 1103–1125. doi: 10.5194/tc-6-1103-2012
Gardner, A. S., Moholdt, G., Cogley, J. G., Wouters, B., Arendt, A. A., Wahr, J., et al. (2013). A reconciled estimate of Glacier contributions to sea level rise: 2003 to 2009. Science 340, 852–857. doi: 10.1126/science.1234532
Gardner, A. S., Moholdt, G., Wouters, B., Wolken, G. J., Burgess, D. O., Sharp, M. J., et al. (2011). Sharply increased mass loss from glaciers and ice caps in the Canadian Arctic Archipelago. Nature 473, 357–360. doi: 10.1038/nature10089
Grund, F. (1979). Forsythe, G. E. / Malcolm, M. A. / Moler, C. B., Computer methods for mathematical computations. Englewood Cliffs, New Jersey 07632. Prentice Hall, Inc., 1977. XI, 259 S. ZAMM J. Appl. Math. Mech. 59, 141–142. doi: 10.1002/zamm.19790590235
Hock, R., de Woul, M., Radiá, V., and Dyurgerov, M. (2009). Mountain glaciers and ice caps around Antarctica make a large sea-level rise contribution. Geophys. Res. Lett. 36:L07501. doi: 10.1029/2008GL037020
Huss, M., Bookhagen, B., Huggel, C., Jacobsen, D., Bradley, R., Clague, J., et al. (2017). Toward mountains without permanent snow and ice. Earths Future 5, 418–435. doi: 10.1002/2016EF000514
Huss, M., and Hock, R. (2015). A new model for global glacier change and sea-level rise. Front. Earth Sci. 3:54. doi: 10.3389/feart.2015.00054
Ivins, E. R., and James, T. S. (2004). Bedrock response to Llanquihue Holocene and present-day glaciation in southernmost South America. Geophys. Res. Lett. 31:L24613. doi: 10.1029/2004GL021500
Jacob, T., Wahr, J., Pfeffer, W. T., and Swenson, S. (2012). Recent contributions of glaciers and ice caps to sea level rise. Nature 482, 514–518. doi: 10.1038/nature10847
Josberger, E. G., Bidlake, W. R., March, R. S., and Kennedy, B. W. (2007). Glacier mass-balance fluctuations in the Pacific Northwest and Alaska, USA. Ann. Glaciol. 46, 291–296. doi: 10.3189/172756407782871314
Kaser, G., Cogley, J. G., Dyurgerov, M. B., Meier, M. F., and Ohmura, A. (2006). Mass balance of glaciers and ice caps: consensus estimates for 1961-2004. Geophys. Res. Lett. 33, 19501. doi: 10.1029/2006GL027511
Kumar, K. K., Rajagopalan, B., Hoerling, M., Bates, G., and Cane, M. (2006). Unraveling the mystery of Indian monsoon failure during El Niño. Science 314, 115–119. doi: 10.1126/science.1131152
Lang, C., Fettweis, X., and Erpicum, M. (2015). Stable climate and surface mass balance in Svalbard over 1979-2013 despite the Arctic warming. The Cryosphere 9, 83-101. doi: 10.5194/tc-9-83-2015
Larsen, C. F., Motyka, R. J., Freymueller, J. T., Echelmeyer, K. A., and Ivins, E. R. (2005). Rapid viscoelastic uplift in southeast Alaska caused by post-Little Ice Age glacial retreat. Earth Planet. Sci. Lett. 237, 548–560. doi: 10.1016/j.epsl.2005.06.032
Marzeion, B., Kaser, G., Maussion, F., and Champollion, N. (2018). Limited influence of climate change mitigation on short-term glacier mass loss. Nat. Clim. Change 8, 305–308. doi: 10.1038/s41558-018-0093-1
Mayer-Gürr, T., Behzadpour, S., Ellmer, M., Kvas, A., Klinger, B., Strasser, S., et al. (2018). ITSG-Grace2018 - Daily and Static Gravity Field Solutions from GRACE. GFZ Data Services. doi: 10.5880/ICGEM.2018.003
Meier, M. F., Dyurgerov, M., Rick, U. K., O'Neel, S., Pfeffer, W. T., Anderson, R., et al. (2007). Glaciers dominate eustatic sea-level rise in the 21st century. Science 317, 1064–1067. doi: 10.1126/science.1143906
Menounos, B., Hugonnet, R., Shean, D., Gardner, A., Howat, I., Berthier, E., et al. (2019). Heterogeneous changes in Western North American glaciers linked to decadal variability in zonal wind strength. Geophys. Res. Lett. 46, 200–209. doi: 10.1029/2018GL080942
Moholdt, G., Wouters, B., and Gardner, A. S. (2012). Recent mass changes of glaciers in the Russian High Arctic. Geophys. Res. Lett. 39:L10502. doi: 10.1029/2012GL051466
Noël, B., Berg, W. J., Lhermitte, S., Wouters, B., Schaffer, N., and Broeke, M. R. (2018). Six decades of glacial mass loss in the Canadian Arctic Archipelago. J. Geophys. Res. Earth Surface 123, 1430–1449. doi: 10.1029/2017JF004304
PO.DAAC (2018). GRACE. 2001. GRACE ACC1B R3 Transplant Data. Ver. 3. PO.DAAC. Dataset (accessed October 13, 2018)
Reager, J. T., Gardner, A. S., Famiglietti, J. S., Wiese, D. N., Eicker, A., and Lo, M.-H. (2016). A decade of sea level rise slowed by climate-driven hydrology. Science 351, 699–703. doi: 10.1126/science.aad8386
RGI Consortium (2017). Randolph Glacier Inventory (RGI) - A Dataset of Global Glacier Outlines: Version 6.0. Tech. rep., Global Land Ice Measurements from Space, Boulder, CO, USA. doi: 10.7265/N5-RGI-60
Rietbroek, R., Brunnabend, S.-E., Kusche, J., Schröter, J., and Dahle, C. (2016). Revisiting the contemporary sea-level budget on global and regional scales. Proc. Natl. Acad. Sci. U.S.A.113, 1504–1509. doi: 10.1073/pnas.1519132113
Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C.-J., et al. (2004). The global land data assimilation system. Bull. Am. Meteorol. Soc. 85, 381–394. doi: 10.1175/BAMS-85-3-381
Root, B. C., Tarasov, L., and Wal, W. (2015). GRACE gravity observations constrain Weichselian ice thickness in the Barents Sea. Geophys. Res. Lett. 42, 3313–3320. doi: 10.1002/2015GL063769
Sakumura, C., Bettadpur, S., and Bruinsma, S. (2014). Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 41, 1389–1397. doi: 10.1002/2013GL058632
Sasgen, I., Konrad, H., Helm, V., and Grosfeld, K. (2019). High-resolution mass trends of the Antarctic ice sheet through a spectral combination of satellite gravimetry and radar altimetry observations. Remote Sens. 11:144. doi: 10.3390/rs11020144
Sasgen, I., Martinec, Z., and Fleming, K. (2007). Wiener optimal combination and evaluation of the Gravity Recovery and Climate Experiment (GRACE) gravity fields over Antarctica. J. Geophys. Res. Solid Earth 112:B04401. doi: 10.1029/2006JB004605
Scanlon, B. R., Zhang, Z., Save, H., Sun, A. Y., Müller Schmied, H., van Beek, L. P. H., et al. (2018). Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. U.S.A.115, E1080–E1089. doi: 10.1073/pnas.1704665115
Schrama, E. J. O., Wouters, B., and Rietbroek, R. (2014). A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from grace data. J. Geophys. Res. Solid Earth 119, 6048–6066. doi: 10.1002/2013JB010923
Shaman, J., and Tziperman, E. (2005). The effect of enso on tibetan plateau snow depth: a stationary wave teleconnection mechanism and implications for the south asian monsoons. J. Clim. 18, 2067–2079. doi: 10.1175/JCLI3391.1
Shepherd, A., Ivins, E. R., Geruo, A., Barletta, V. R., Bentley, M. J., Bettadpur, S., et al. (2012). A reconciled estimate of ice-sheet mass balance. Science 338, 1183–1189. doi: 10.1126/science.1228102
Slemmons, K., Saros, J., and Simon, K. (2013). The influence of glacial meltwater on alpine aquatic ecosystems: a review. Environ. Sci. Process. Impacts 15, 1794–1806. doi: 10.1039/c3em00243h
Sørensen, L. S., Jarosch, A. H., Aõalgeirsdóttir, G., Barletta, V. R., Forsberg, R., Pálsson, F., et al. (2017). The effect of signal leakage and glacial isostatic rebound on GRACE-derived ice mass changes in Iceland. Geophys. J. Int. 209, 226–233. doi: 10.1093/gji/ggx008
Sutanudjaja, E. H., van Beek, R., Wanders, N., Wada, Y., Bosmans, J. H. C., Drost, N., et al. (2018). PCR-GLOBWB 2: a 5 arcmin global hydrological and water resources model. Geosci. Model Dev. 11, 2429–2453. doi: 10.5194/gmd-11-2429-2018
Swenson, S., Chambers, D., and Wahr, J. (2008). Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 113:B08410. doi: 10.1029/2007JB005338
VanWychen, W., Burgess, D. O., Gray, L., Copland, L., Sharp, M., Dowdeswell, J. A., et al. (2014). Glacier velocities and dynamic ice discharge from the Queen Elizabeth Islands, Nunavut, Canada. Geophys. Res. Lett. 41, 484–490. doi: 10.1002/2013GL058558
Wahr, J., Molenaar, M., and Bryan, F. (1998). Time variability of the earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 103, 30305–30229.
Wahr, J., Swenson, S., and Velicogna, I. (2006). Accuracy of GRACE mass estimates. Geophys. Res. Lett. 33:L06401. doi: 10.1029/2005GL025305
Watkins, M. M., Wiese, D. N., Yuan, D., Boening, C., and Landerer, F. W. (2015). Improved methods for observing Earth's time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 120, 2648–2671. doi: 10.1002/2014JB011547
WCRP Global Sea Level Budget Group (2018). Global sea-level budget 1993-present. Earth Syst. Sci. Data 10, 1551–1590. doi: 10.5194/essd-10-1551-2018
Wester, P., Mishra, A., Mukherji, A., and Bhakta Shrestha, A. (2019). The Hindu Kush Himalaya Assessment Mountains, Climate Change, Sustainability and People: Mountains, Climate Change, Sustainability and People. Cham: Springer. doi: 10.1007/978-3-319-92288-1
WGMS (2017). Global Glacier Change Bulletin No. 2 (2014-2015). Zurich: CSU(WDS)/IUGG(IACS)/UNEP/UNESCO/WMO, World Glacier Monitoring Service. Publication based on database version: doi: 10.5904/wgms-fog-2017-10
Wouters, B. (2010). Identification and Modelling of Sea Level Change Contributors - On GRACE Satellite Gravity Data and Their Application to Climate Monitoring (Ph.D. thesis). Delft University of Technology. Available online at: https://ncgeo.nl/index.php/nl/publicaties/gele-serie/item/2580-pog-73-woutersidentification-and-modeling-of-sea-levelchange-contributors
Wouters, B., Chambers, D., and Schrama, E. (2008). GRACE observes small-scale mass loss in Greenland. Geophys. Res. Lett. 35:L20501. doi: 10.1029/2008GL034816
Wouters, B., and Schrama, E. J. O. (2007). Improved accuracy of GRACE gravity solutions through empirical orthogonal function filtering of spherical harmonics. Geophys. Res. Lett. 34:23711. doi: 10.1029/2007GL032098
Yang, Q., Dixon, T. H., Myers, P. G., Bonin, J., Chambers, D., and van den Broeke, M. R. (2016). Recent increases in Arctic freshwater flux affects Labrador Sea convection and Atlantic overturning circulation. Nat. Commun. 7:10525. doi: 10.1038/ncomms10525
Yao, T., Thompson, L., Yang, W., Yu, W., Gao, Y., Guo, X., et al. (2012). Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Change 2:663. doi: 10.1038/nclimate158010.1038/nclimate1580
Yuan, D.-N. (2018). JPL Level-2 Processing Standards Document For Level-2 Product Release 06. Tech. Rep. GRACE 327-745, JPL, Pasadena, CA, 17.
Keywords: GRACE, glaciers, ice caps, sea level, mass balance
Citation: Wouters B, Gardner AS and Moholdt G (2019) Global Glacier Mass Loss During the GRACE Satellite Mission (2002-2016). Front. Earth Sci. 7:96. doi: 10.3389/feart.2019.00096
Received: 15 October 2018; Accepted: 18 April 2019;
Published: 21 May 2019.
Edited by:
Matthias Holger Braun, University of Erlangen Nuremberg, GermanyReviewed by:
Roelof Rietbroek, University of Bonn, GermanyHorst Machguth, Université de Fribourg, Switzerland
Copyright © 2019 Wouters, Gardner and Moholdt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bert Wouters, Yi53b3V0ZXJzQHV1Lm5s
 Bert Wouters
Bert Wouters Alex S. Gardner
Alex S. Gardner Geir Moholdt
Geir Moholdt