Impact of Fjord Geometry on Grounding Line Stability

Åkesson, Henning; Nisancioglu, Kerim H.; Nick, Faezeh M.

doi:10.3389/feart.2018.00071

ORIGINAL RESEARCH article

Front. Earth Sci., 05 June 2018

Sec. Cryospheric Sciences

Volume 6 - 2018 | https://doi.org/10.3389/feart.2018.00071

Impact of Fjord Geometry on Grounding Line Stability

$\r\nHenning kesson*&#x;$ Henning Åkesson¹^*^†

Kerim H. Nisancioglu^1,2

Faezeh M. Nick³

¹Department of Earth Science, University of Bergen, Bjerknes Centre for Climate Research, Bergen, Norway
²Centre for Earth Evolution and Dynamics, University of Oslo, Oslo, Norway
³Department of Arctic Geology, University Centre in Svalbard, Longyearbyen, Norway

Recent and past retreat of marine-terminating glaciers are broadly consistent with observed ocean warming, yet responses vary significantly within regions experiencing similar ocean conditions. We assess how fjord geometry modulates glacier response to a regional ocean warming on decadal to millennial time scales, by using an idealized, numerical model of fast-flowing glaciers including a crevasse-depth calving criterion. Our simulations show that, given identical climate forcing, grounding line responses can differ by tens of kilometers due to variations in channel width. We identify fjord mouths and embayments as vulnerable geometries, showing that glaciers in these fjords are prone to rapid, irreversible retreat, independent of the presence of a fjord sill. This irreversible retreat has relevance for the potential future recovery of marine ice sheets, if the current anthropogenic warming is reduced, or reversed, as well as for the response of marine ice sheets to past climate states; including the warm Bølling-Allerød interstadial, the Younger Dryas cold reversal and the Little Ice Age.

1. Introduction

The dynamics of grounding lines (GL), the boundary between grounded ice and a floating ice shelf or the ocean, fundamentally control the stability of marine ice sheets and their associated sea level contributions. Studies of paleo-ice sheets, as well as model predictions, suggest that marine ice sheets are capable of rapidly discharging large amounts of ice into the ocean, contributing significantly to sea level rise (Dutton et al., 2015; DeConto and Pollard, 2016; Mengel et al., 2016). Marine terminating margins are highly dynamic and have been shown to respond non-linearly and asynchronously to climate forcing (Carr et al., 2013a, 2015). Predictions of future ice sheet evolution under climate warming therefore require an accurate understanding of grounding line dynamics (Durand and Pattyn, 2015).

This study uses a numerical model suitable for axially symmetric, fast-flowing glaciers to assess the effect of fjord geometry on grounding line stability on decadal and longer time scales. We focus particularly on the role of channel width and investigate whether grounding line migration is reversible for different types of synthetic fjord geometries.

Numerous feedbacks between climate forcing, ice dynamics and geometry make it challenging to predict the evolution of marine-terminating glaciers. Observations over the last two decades show that many of these glaciers are retreating in Greenland (Straneo and Heimbach, 2013; Jensen et al., 2016), Antarctica (Cook et al., 2016), Svalbard (Błaszczyk et al., 2009), Patagonia (Sakakibara and Sugiyama, 2014), and Alaska (McNabb and Hock, 2014), broadly consistent with warmer subsurface waters and warmer air temperatures. However, the dynamic evolution of each glacier is subject to both external and glacier-specific factors, the latter including the topographic setting. Observed changes of marine-terminating glaciers are therefore not straightforward to interpret, and recent changes are indeed highly heterogeneous in space (e.g., Moon and Joughin, 2008; Carr et al., 2013a; McNabb and Hock, 2014). Glaciers influenced by the same regional climate display different and sometimes opposite behavior (Howat et al., 2008). Similarly, reconstructions of marine-terminating glaciers in Greenland (Hughes et al., 2012) and Scandinavia (Mangerud et al., 2013; Stokes et al., 2014) show spatially variable and temporally asynchronous retreat histories. These lines of evidence suggest that regional climate forcing alone cannot fully explain the behavior of these glaciers, nor can a regional climate projection be used uncritically to predict future ice sheet evolution.

Grounding lines resting on retrograde bedrock slopes (deepening upstream) are inherently unstable (Weertman, 1974; Schoof, 2007; Gudmundsson et al., 2012), without additional buttressing. This situation implies that flux feedbacks at the grounding line trigger a self-sustained retreat, termed the marine ice sheet instability (MISI). This classic “one dimensional” theoretical framework offers insight into the stability of Antarctic or Laurentide ice streams flowing into ice shelves (Bougamont et al., 2003; Jamieson et al., 2014; Margold et al., 2015), as well as marine-terminating glaciers flowing through deep troughs into fjords in Greenland (Moon et al., 2012), Canada (Briner et al., 2009), Norway (Mangerud et al., 2013), Alaska (O'Neel et al., 2005), Svalbard (Błaszczyk et al., 2009), and Patagonia (Rott et al., 1998). In comparison, the impact of changes in fjord width, which is the focus of this study, has received little attention. Observational (Mercer, 1961; Warren and Glasser, 1992; Bougamont et al., 2003; Carr et al., 2013b, 2014) and model (Jamieson et al., 2012, 2014) evidence suggest that channel width influences retreat, yet these studies are often restricted to short time scales of a decade or two, or tied to a specific location.

Marine ice sheets evolve on a range of time scales, further complicating the interpretation of the history of their margins' positions. The relatively short observational record needs to be placed in context of the long-term history of natural variability and interaction with climate. For example, it is still unclear to what extent the widespread grounding line retreat observed along the margins of the West Antarctic Ice Sheet results from long-term natural forcing, or the recent anthropogenic warming (Bakker et al., 2017; Smith et al., 2017).

In contrast to grounding line retreat, the impact of fjord geometry on the mechanisms behind glacier advance remain largely understudied. An understanding of marine-terminating glacier retreat-advance cycles is relevant to several unsolved problems in glaciology and climate dynamics, including Heinrich events (Broecker et al., 1992; Álvarez-Solas et al., 2011; Bassis et al., 2017), oscillatory glacier behavior (Warren, 1994) and iceberg calving (e.g., Benn et al., 2007). The effect of bedrock slopes on ice stream and marine-terminating glacier variability has been investigated (Brown et al., 1982; Amundson, 2016; Robel et al., 2016; Schoof et al., 2017), as well as the effect of coupling ice and sediment dynamics (Brinkerhoff et al., 2017), but few studies have assessed the influence of fjord width in retreat-advance cycles.

This paper places the recent rapid changes of marine ice sheet margins, and their relationship with climate, in a long-term dynamical context. In particular, we assess the significance of bedrock sills, overdeepenings and variations in fjord width for the dynamic evolution of glaciers on decadal to millennial time scales. We use a dynamic flowline model on idealized glacier geometries, which is representative of a range of real-world marine-terminating glaciers, to investigate the geometric controls on grounding line stability. Based on a large ensemble of experiments we investigate whether hysteresis arises as a result of the presence of lateral bottlenecks and embayments in fjords. Further, we show that geometric information can be used to “predict” moraine positions, and identify contemporary glaciers particularly vulnerable to future warming.

2. Model Description

We use a dynamic, depth- and width-integrated numerical model (Vieli et al., 2001; Vieli and Payne, 2005; Nick et al., 2010, 2013) to simulate ice flow. Variants of this flowline model have previously been applied to Greenlandic and Antarctic outlet glaciers and ice streams (Nick et al., 2009, 2012, 2013; Vieli and Nick, 2011; Jamieson et al., 2014), as well as idealized glacier settings (Nick et al., 2010; Enderlin et al., 2013a,b; Amundson, 2016; Schoof et al., 2017). These studies, together with observational evidence of marine-terminating glacier change, have provided insights into glacier sensitivity to external forcing and site-specific factors. Yet most studies are restricted to time scales of less than a century. Here, we quantify the effects of fjord bathymetry, and fjord width, on grounding line stability and large-scale glacier behavior on decadal to millennial time scales.

2.1. Ice Flow Model

The ice flow model is detailed in previous work (Nick et al., 2009, 2010, 2013). Only the essentials are outlined here.

2.1.1. Continuity and Force Balance

We assume a straight, axially symmetric glacier along the central flowline. For a flowband of width W and thickness H, assuming vertical side walls, mass continuity (Van der Veen, 2013) is expressed by

\begin{array}{l} \frac{\partial H}{\partial t} = Ḃ - \frac{1}{W} \frac{\partial Q}{\partial x}, & (1) \end{array}

where t is time, x is the along-flow coordinate along the central flowline, Ḃ is the specific surface mass balance rate (m a⁻¹ ice eq.) and Q = UHW is the ice flux through a cross-section, with U being the depth- and width-averaged velocity.

Momentum balance between driving and resistive (longitudinal, basal, lateral) stresses gives

\begin{array}{l} ρ_{i} g H \frac{\partial h}{\partial x} = 2 \frac{\partial}{\partial x} (H ν \frac{\partial U}{\partial x}) - μ A_{s} {[(H - \frac{ρ_{w}}{ρ_{i}} D) U]}^{1 / m} \\ - \frac{2 H}{W} {(\frac{5 U}{λ A W})}^{1 / n}, & (2) \end{array}

where h is the surface elevation, ρ_w and ρ_i are densities of seawater and ice, respectively, D is the depth of the glacier base below sea level, n = 3 is Glen's flow law exponent and g is the gravitational acceleration.

Assuming that basal drag depends on sliding velocity, basal roughness and effective pressure, we use a non-linear sliding law with exponent m = 3 (Van der Veen and Whillans, 1996; Vieli and Payne, 2005). The transition from grounded to floating ice is handled by setting the friction parameter μ to zero once ice thickness is less than the flotation thickness, and to unity otherwise (Nick et al., 2010). Similar to Amundson (2016), we vary the sliding parameter A_s linearly with bed elevation, to represent changes in water availability from the ice divide to the grounding line. Values for A_s are similar to what is used for Greenlandic outlet glaciers by Nick et al. (2013). Basal friction is thus largest at the ice divide, approaches zero toward the grounding line, and equals zero for any floating ice shelf (if present). Note that A_s is fixed in time, as we do not change the surface climate in our simulations, and thus do not expect any change in basal water.

In Equation (2) ν is the depth-averaged effective viscosity, defined as

\begin{array}{l} ν = A^{- 1 / n} | \frac{\partial U}{\partial x} |^{(1 - n) / n} . & (3) \end{array}

The flow rate factor A influences both effective viscosity and lateral drag. We assume a spatiotemporally constant A = 1.68 × 10⁻²⁴ Pa⁻³ s⁻¹. This corresponds to ice temperatures of -2 °C (Cuffey and Paterson, 2010), and is representative for present-day marine-terminating glaciers in Alaska (Amundson et al., 2010) and southern Greenland (Thomsen and Thorning, 1992).

Lateral drag is parameterized by integrating horizontal shear stress over the channel width (Van der Veen, 2013). The softening factor λ is, for simplicity, kept equal to one, except in those sensitivity experiments assessing the effects of variations in the lateral drag (see section 3.3).

2.1.2. Climate Forcing and Boundary Conditions

To isolate geometric effects, surface mass balance is kept constant in time and is assumed to depend linearly on initial surface elevation, so that

\begin{array}{l} Ḃ (z) = max (Γ (z - z_{E L A}), min Ḃ), & (4) \end{array}

where $Γ = \frac{\partial Ḃ}{\partial z}$ is the vertical mass balance gradient. z_ELA represents the equilibrium line altitude (ELA), while min Ḃ represents surface mass balance at sea level and is prescribed as −1.2 m water equivalent (w.e.) a⁻¹ and Γ = 0.005 a⁻¹ (Van de Wal et al., 2005), roughly representative for Greenland outlet glaciers outside south Greenland.

If an ice shelf is present, we use a spatially invariant submarine melt rate between the grounding line and the calving front. Note that submarine melt at the vertical front of the ice shelf is not included, and we assume no basal melt for the grounded ice.

As boundary conditions, we prescribe an ice divide (x = 0) where the ice velocity is set to zero. At the calving front, the depth-integrated deviatoric stress $σ_{x x}^{'}$ is given by the balance between the depth-integrated longitudinal stress and the difference between hydrostatic and cryostatic pressure, so that

\begin{array}{l} σ_{x x}^{'} = \frac{1}{2} ρ_{i} g (H - \frac{ρ_{w}}{ρ_{i}} \frac{D^{2}}{H}) . & (5) \end{array}

Inserting Equation (5) into Glen's flow law (Glen, 1955) gives the velocity gradient (stretching rate) at the calving front as

\begin{array}{l} \frac{\partial U}{\partial x} = A {[\frac{ρ_{i} g}{4} (H - \frac{ρ_{w}}{ρ_{i}} \frac{D^{2}}{H})]}^{n} . & (6) \end{array}

To track the grounding line and calving front, the model employs a flotation criterion (Van der Veen and Whillans, 1996) on a moving grid (Vieli and Payne, 2005; Nick et al., 2010), with a spatial resolution of Δx = 300 m and time step of Δt = 0.001 a. We discuss the sensitivity of grounding line retreat to grid resolution in section 5.4.

2.2. Calving Model

We apply a crevasse-depth calving criterion, which links the terminus longitudinal stress gradient to the depth of surface and basal crevasses, and any water present in surface crevasses. Calving occurs when surface crevasses penetrate the entire glacier thickness, or when surface and basal crevasses meet. This criterion has been described at length previously by Benn et al. (2007) and Nick et al. (2010). A crevasse water depth of 100 m is used throughout our simulations; this value is comparable to what is used by Nick et al. (2010), for a glacier of similar dimensions. Since we focus on grounding line migration, we keep the crevasse water depth fixed throughout our simulations. We stress that the crevasse-depth criterion is not meant to represent how calving occurs, nor does the crevasse water depth necessarily have a literal physical meaning. Rather, the criterion provides a link between the stretching rate close to the terminus, and the mean rates of mass loss from iceberg calving. Note that given the way the crevasse water depth calving criterion is formulated (see section 2 of the paper by Nick et al., 2010 for details), the model is not designed for very small water depths, in particular not smaller than the crevasse water depth.

3. Experimental Setup

3.1. Fjord Geometries

To isolate the effect of topography, we conduct experiments with identical climate forcing on different idealized geometries. These geometries are representative of past and present marine-terminating glaciers in Greenland (e.g., Warren and Glasser, 1992; Moon et al., 2012), Alaska (e.g., McNabb and Hock, 2014), Svalbard (e.g., Błaszczyk et al., 2009), Patagonia (e.g., Rott et al., 1998), and past glaciers in Norway (e.g., Mangerud et al., 2013; Stokes et al., 2014), and Arctic Canada (Briner et al., 2009). Our control (CTRL) geometry consists of a bed sloping linearly toward the sea (Figure 1a), a wide upper part and a straight 5 km wide fjord channel (Figure 1b).

FIGURE 1

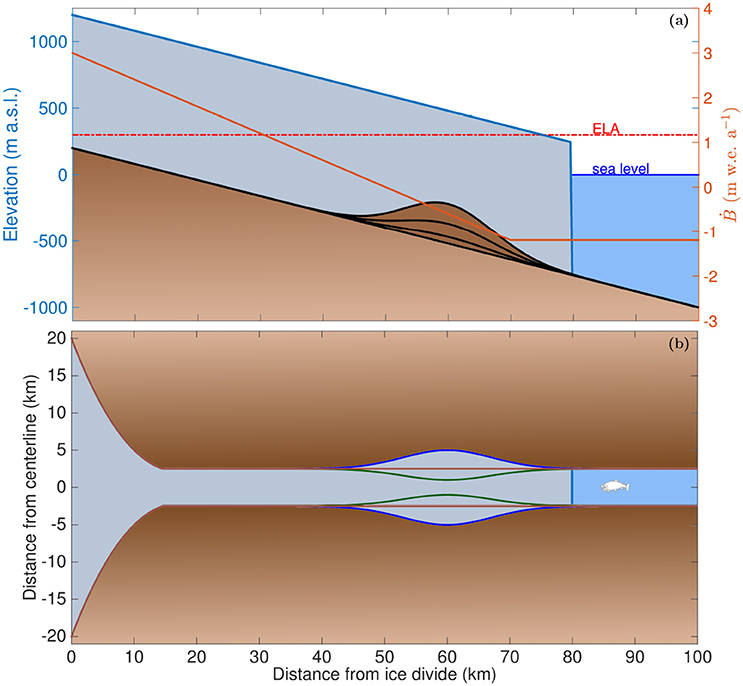
Figure 1. (a) Bedrock geometries, ELA, and the initial glacier geometry before spinup (left y-axis), and surface mass balance (SMB; right y-axis). (b) Plan view of control (CTRL), embayment (W10), and bottleneck (W3) channel geometries. Details are provided in Table 1.

We alter the control bed topography and width as summarized in Table 1. First, we add a Gaussian-shaped bedrock bump of varying amplitude (geometries B50, B150, and B300). Second, we assess how the presence of a basal pinning point combined with an embayment (B150W10) or a bottleneck (B150W3) influence the grounding line stability. Third, we perform experiments with an embayment (W10) and a narrow bottleneck (W3), on the smooth prograde CTRL bed. All the Gaussian bedrock bumps and channel width variations have a “radius” of 20 km, meaning they extend from 40 to 80 km along the flowline.

TABLE 1

Table 1. Fjord geometries used in the experiments.

3.2. Model Spinup and Retreat

For all geometries, we initialize the model with a 1,000 m thick block of ice with a calving front position L at x = 80 km (Figure 1). The initial glacier has a vertical calving face, meaning that the calving front L coincides with the grounding line position GL. When a floating tongue evolves in the experiments, L≠GL. The initial glacier surface is the same in the experiments with and without a fjord sill present. All the model glaciers are forced with a constant climate until they approach a steady-state. We require that dV/dt < 0.001 km³ a⁻¹, dL/dt < 0.1 m a⁻¹, and dGL/dt < 0.1 m a⁻¹, ensuring a stable surface topography, calving front, and grounding line. As climate forcing, we fix the ELA to 200 m above sea level (a.s.l.) and apply a submarine melt rate of 5 m a⁻¹. This forcing is purposely chosen such that all glaciers reach a stable position downstream of any imposed bedrock bumps, or fjord width variations. We keep the climate identical across all glacier geometries. Due to the different geometries, the steady-state grounding line positions vary between x ~ 95 − 105 km.

Once a stable state is reached, we strengthen the ocean forcing by tripling the submarine melt rate to 15 m a⁻¹, representing warmer subsurface waters along the glacier front. This could either be caused by increased advection of warm subsurface water from the shelf into the fjord, or by increased entrainment of warm subsurface water at the glacier front due to increased subglacial discharge caused by higher surface melt and runoff in a warming climate (Jenkins, 2011; Xu et al., 2013; Jackson et al., 2014). We run the simulations with this higher melt rate until the glaciers reach a new steady-state, or until they become land-terminating, whichever occurs first.

3.3. Lateral Weakening

To assess how fjord width controls grounding line behavior under different conditions of lateral drag, we conduct sensitivity experiments by changing the softening factor λ in Equation (2). Starting from the steady-state of the embayment geometry (W10) with λ = 1, we test the impact of lateral drag by varying the softening factor between a value of λ = 0.5 (increased later drag) and λ = 1.5 (reduced lateral drag). Changes are applied uniformly along the flowline, and we investigate the response as the submarine melt is increased from 5 to 15 m ⁻¹, as described above.

Reduced lateral drag (here represented by an increased softening factor λ) represents a situation with cryohydrologic warming at the glacier margins. This could be caused by increased surface runoff entering crevasses along the margins (Van Der Veen et al., 2011; Dunse et al., 2015), hydraulic weakening due to marginal ice with higher water content (Van Der Veen et al., 2011), or shear margin warming induced by thermomechanical feedbacks (Bondzio et al., 2017).

3.4. Hysteresis

We perform additional experiments to investigate whether a given fjord geometry can lead to asymmetric grounding line migration under warm to cold cycles in ocean forcing. If the system exhibits hysteresis, then more than one stable grounding line position is possible for a given ocean forcing. Equivalently, we would have hysteresis if a given grounding line position is not exclusively associated with a particular forcing, that is, the grounding line behavior depends on its past migration. We test fjord channels with wide (W10), straight (CTRL) and narrow (W3) sections combined with the seaward, linearly downsloping smooth bedrock, as well as the medium-sized bedrock bumps with (B150W10) and without (B150) a wide section.

Starting from an initial steady-state, we increase the submarine melt from 5 to 15 m a⁻¹ incrementally using 1 m a⁻¹ steps, and then decrease it back to 5 m a⁻¹ with the same steps. In addition to testing for asymmetric grounding line migration, we aim to quantify the ocean forcing required to cause grounding line retreat for the different geometries. A submarine melt rate of 15 m a⁻¹ is not high enough to cause retreat of the grounding line upstream of embayments/bottlenecks in all experiments. Therefore, we continue to increase the submarine melt rates until either the grounding line (i) retreats upstream of the embayment/bottleneck and stabilizes, or (ii) retreats up on land, in which case we stop the simulation. For experiments (i), we decrease the submarine melt rates back to 5 m a⁻¹. Each melt rate is applied for 5,000 years, with all simulations starting from the steady-state associated with the previous melt rate. The efficiency of the flowline model allows for these comprehensive hysteresis experiments, which would not have been computationally feasible with a higher-order model.

4. Results

4.1. Grounding Line Retreat

After applying the enhanced ocean forcing (15 m a⁻¹), all glaciers retreat (Figures 2, 3). The small bedrock bump (B50) does not alter the retreat of the grounding line significantly compared to the control run (not shown here). For the large bedrock bump (B150), with identical climate forcing, the grounding line stabilizes on top of the bump (Figure 2a). Grounding line velocity increases by 67% in the first 100 years, peaks at 430 m a⁻¹ after 670 years and then drops somewhat toward a steady-state velocity of ~400 m a⁻¹, finishing 250 % higher than the pre-retreat velocity. The maxima in the along-flow velocity profiles in Figure 2a results from a smaller flux gate area at the bedrock bump than up- and downstream. Mass conservation at the smaller cross-sectional area requires faster ice flow to maintain the same ice flux over the bump.

FIGURE 2

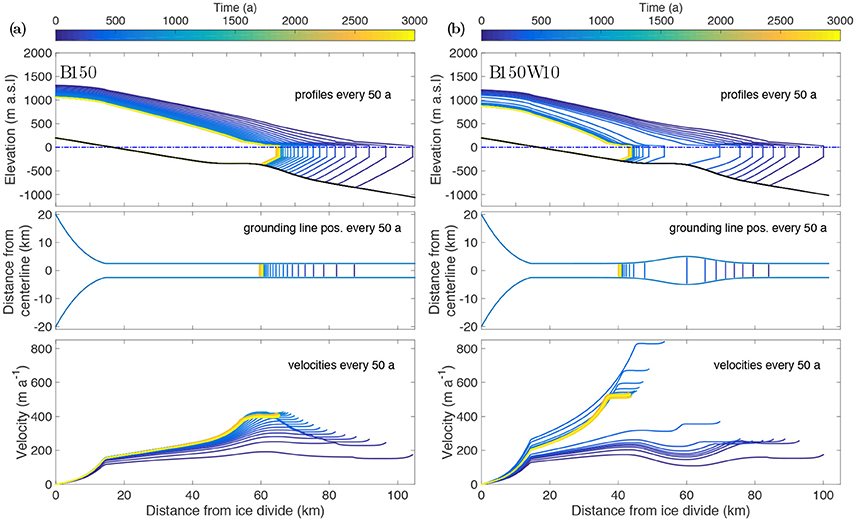
Figure 2. Different response to identical ocean forcing: glacier geometry, grounding line positions and velocities along the flowline for geometries with (a) 150 m bed bump (B150); and (b) 150 m bed bump coinciding with a 10 km wide embayment (B150W10).

FIGURE 3

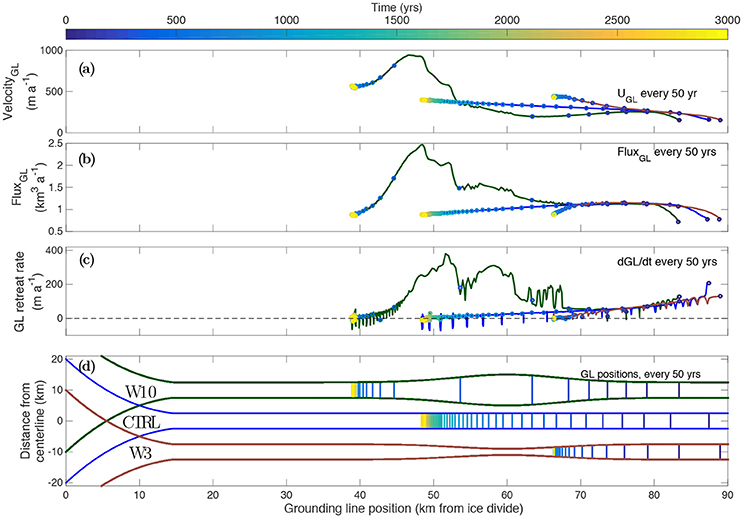
Figure 3. Non-linear, variable effects of channel width on grounding line (GL) retreat. (a) velocity (U_GL), (b) flux, and (c) retreat rate (dGL/dt), under a step tripling of submarine melt on a smooth prograde bed. Line colors represent the different channel geometries in (d): W10 – embayment (green); CTRL — straight (blue); W3 — narrow bottleneck (brown). The colored dots in (a–c), and the colored GL positions in (d), correspond with the time given in the colorbar, and are plotted every 50 years.

In experiment B150W10 we widen the fjord juxtaposed with the bedrock bump from experiment B150 (Figure 2b). This wide section, or embayment, is 10 km at its widest point, twice as wide as the rest of the fjord channel. The grounding line initially retreats at a steady pace of ~55 m a⁻¹ for the first 300 years. As the grounding line retreats up the bedrock bump and into the embayment, the glacier thins considerably. The ice shelf base flattens, implying that the grounding line retreats faster than the calving front. In contrast to experiment B150, the bedrock bump in B150W10 does not stop the retreat. The grounding line retreats past the bedrock bump and embayment within 150 years, this corresponds to an average retreat rate of ~140 m a⁻¹. Grounding line retreat out of the embayment is faster than the retreat into it, with a variable retreat rate peaking at 385 m a⁻¹.

In our second suite of experiments with a smooth prograde bed, we investigate the impact of an embayment (W10) and a bottleneck (W3), and compare these to the control geometry (CTRL). Velocity in the control run increases linearly with time, until the grounding line reaches a new steady-state position at x = 49 km (Figure 3a). The grounding line initially retreats at 120 m a⁻¹, a rate which decreases linearly with time. Conversely, the flux at the grounding line increases temporarily over the first 100–150 years, and then decreases to a similar value as the initial flux (Figure 3b).

The retreat in the fjord with an embayment (W10) is similar to that observed in the experiment combining an embayment with a bedrock bump (B150W10, Figure 2b). The grounding line retreats steadily toward the embayment, before accelerating to a peak rate of 400 m a⁻¹, with an average of about 160 m a⁻¹ through the wide section (Figure 3c). As the ice front passes through the embayment, ice velocity at the grounding line increases. The velocity does not peak at the widest point (x = 60 km), as may be expected, but instead further upstream, when the grounding line passes the section where the fjord narrows in again. At its peak, velocity at the grounding line is about five times higher than that at the initial state (Figure 3a). When the grounding line stabilizes upstream of the embayment, its velocity is lower than the peak velocities but still more than three times the initial values. The grounding line flux follows a similar pattern, peaking with three times more ice passing through than before the enhanced ocean melt is applied, before stabilizing at the pre-retreat flux.

For the bottleneck geometry (W3) velocity increases to about twice that of the CTRL experiment (Figure 3). This result reflects the choked flux gate, and thereby a higher required velocity to maintain the same flux. The 3 km narrow bottleneck prevents further retreat due to increased lateral drag (cf. Equation 2) stabilizing the grounding line at x = 67 km. Note that this stable position is not located at the narrowest point, but about half-way into the narrow section. At the new stable position, velocity at the grounding line is twice that of the initial velocity associated with a weaker ocean forcing (Figure 3a). However, this higher ice velocity occurs where the fjord is narrow and relatively shallow, giving a smaller flux gate. Therefore, the flux at the new stable position of the grounding line is similar to the flux at its initial position, before applying the enhanced submarine melt (Figure 3b).

In summary, the glaciers in the synthetic geometries first retreat in a similar pattern. However, the along-flow width changes facilitate an accelerated response to ocean forcing when the grounding line passes through embayments. We find that the grounding line responds linearly in the fjords without geometric variations, and non-linearly in the fjords with large cross-sectional geometric changes (Figures 3, 4). Fjord width plays a key role, but there is no simple relationship between grounding line retreat rate, or flux, and fjord width. We elaborate further on the impact of channel width in section 5.1.

FIGURE 4

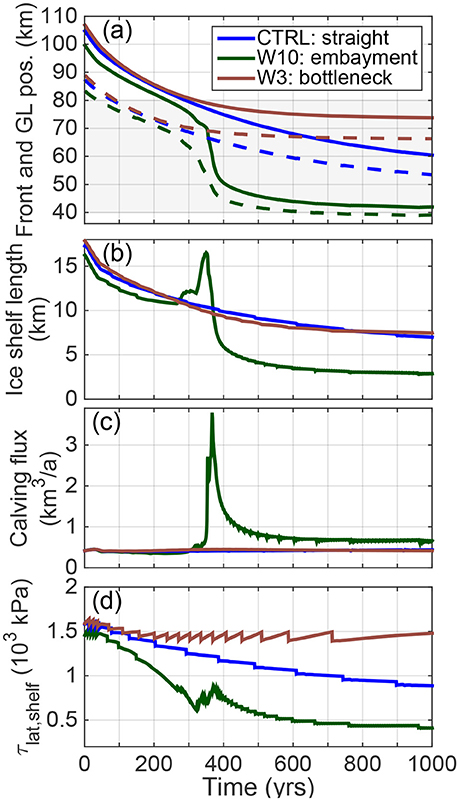
Figure 4. (a) Front (solid lines) and grounding line (dashed lines) evolution for geometries W10 (flat, embayment), CTRL (flat, straight), and W3 (flat, bottleneck), corresponding to the colors in Figure 3. All geometries have smooth, prograde beds. The extent of the embayment in W10 and the bottleneck in W3 is shown with gray shading; (b) ice shelf length; (c) calving flux; and (d) integrated lateral drag for any ice shelf present, i.e., $τ_{l a t, s h e l f} = \int_{G L}^{L} τ_{l a t} d x$ , where GL and L represent the grounding line and calving front positions, respectively. Only the first 1,000 years are shown to emphasize the details. Simulations continue for another 2,000 years to steady state.

4.2. Lateral Weakening

Perturbation experiments, using the W10 fjord geometry, show that different values for the lateral drag can change the timing of retreat by ±100 years (Figure 5). However, the pattern of retreat remains qualitatively unchanged, relative to the original experiments with λ = 1. With weaker ice (λ> 1, i.e., less lateral drag), retreat through the embayment occurs earlier and progresses faster (Figure 5a). Conversely, with increased lateral drag (λ < 1), retreat is delayed and prolonged. When the grounding line retreats through the embayment, the imposed softening results in differences in lateral drag on the order of ± 40–50% relative to the original experiments with λ = 1 (not shown here).

FIGURE 5

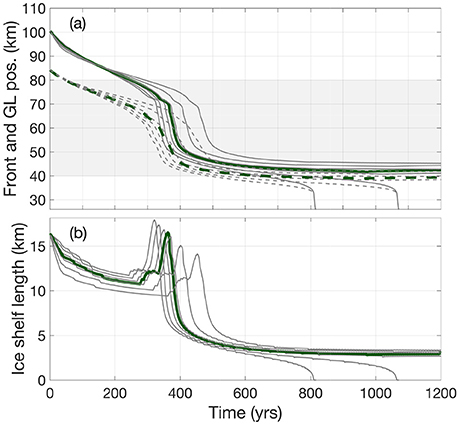
Figure 5. (a) Front (solid lines) and grounding line (dashed lines) evolution for different values of the softening factor λ ∈ [0.5, 1.5], using the W10 fjord geometry with an embayment on a smooth, prograde bed. Thicker lines represent simulations using the default value λ = 1. The extent of the embayment in W10 is shown with gray shading. (b) Ice shelf length for the experiments in (a). For clarity, only the first 1,200 years are shown. Simulations continue for another 1,800 years to steady state.

The amount of lateral drag impacts the ice shelf length (Figure 5b): when lateral drag is reduced due to softening by lateral shear (λ > 1), the simulated ice shelves are longer (and vice versa). Grounding line positions are affected by changes in lateral drag, as the ice shelves adapt to the imposed changes to the stress configuration in order to provide the same amount of buttressing.

4.3. Hysteresis

Our simulations show that all the geometries containing sills and/or bottlenecks (B50, B150, B300, W3, B150W10, B150W3) require strong ocean forcing for retreat to be triggered (Figure 6). For example, melt rates increasing from 7 to 8 m a⁻¹ in fjords without embayments only cause a retreat of a few kilometers. In stark contrast, an increase from 7 to 8 m a⁻¹ in experiments with embayments (W10 and B150W10) triggers a 30 km irreversible retreat. A similar dramatic retreat for geometries with stabilizing bottlenecks (W3, B150W3) and higher bedrock bumps (B150, B300) require melt rates 3 to 8 times higher. However, for some threshold ocean forcing, strikingly small changes in submarine melt induce large, irreversible grounding line retreat.

FIGURE 6

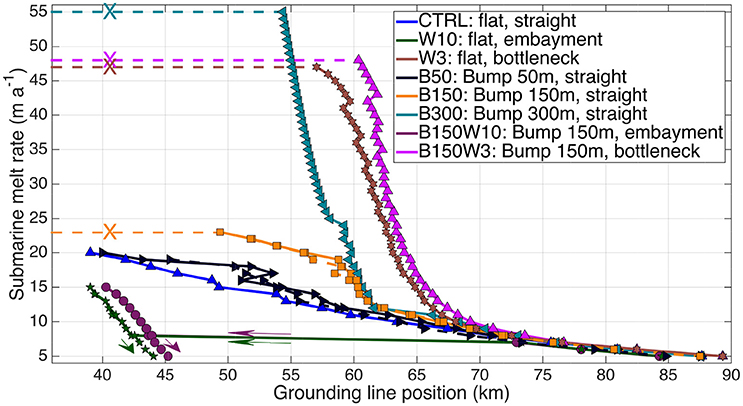
Figure 6. Effect of submarine melt on grounding line migration, for different fjord geometries. Submarine melt rates are increased incrementally from 5 m a⁻¹ using 1 m a⁻¹ steps. Each simulation of 5,000 years starts from the steady-state associated with the previous melt rate. For the geometries with a steady-state upstream of the bedrock bumps/width variations from x = 50–70 km, submarine melt rate is relaxed back to 5 m a⁻¹ in 1 m a⁻¹ steps. Crosses (X) on dashed lines for experiments B150, B300, B150W3, and W3 mean no possible marine-based steady-state positions for these geometries and corresponding melt rates.

We only find hysteresis for fjords with embayments. This occurs irrespective of the presence of a bedrock sill; the difference in grounding line position with (B150W10) and without (W10) the sill is only ~1.2 km (Figure 7). We discuss the implications of this behavior, and show real-world examples in section 5.2.

FIGURE 7

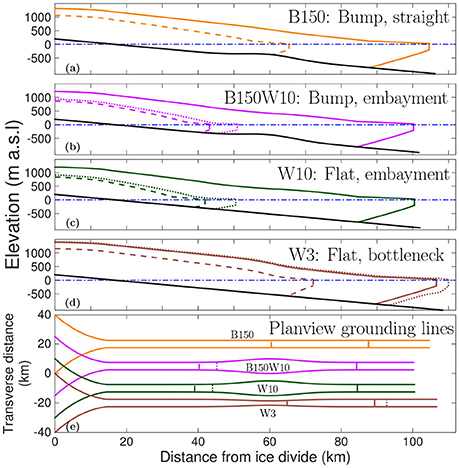
Figure 7. Hysteresis dependent on fjord geometry: profiles (a–d) and planview (e) of glacier geometries and grounding line positions at initial (submarine melt rate = 5 m a⁻¹, solid lines), retreated (15 m a⁻¹, dashed lines) and readvanced (5 m a⁻¹, dotted lines) positions. Colors and melt rates correspond to Figure 6. Note that for B150, the initial (solid) and readvanced (dotted) positions overlap.

5. Discussion

5.1. Impact of Fjord Width on Glacier Stability

We find that, despite identical climate forcing and bedrock topography, the grounding line retreat may differ by several tens of kilometers depending on the channel width geometry (Figure 3). This behavior confirms that the presence of embayments, bottlenecks, fjord mouths and wide fjord sections can strongly modulate the response of marine-terminating glaciers to external forcing.

In Figure 4 we also show that ice shelf evolution and its interplay with grounding line stability clearly depend on along-flow variations in channel width. Several studies have highlighted links between ice shelf length (or sidewall area), lateral drag, and grounding line stability (Little et al., 2009, 2012; Goldberg et al., 2012; Gudmundsson, 2013; Haseloff and Sergienko, 2017; Schoof et al., 2017), but none of these considered channels of spatially non-uniform width. As the glacier front enters the embayment in experiment W10, the floating tongue lengthens as the grounding line retreats faster than the calving front in the wide section (Figure 4b). As the ice shelf lengthens, the amount of buttressing temporarily increases (Figure 4d), due to a larger “sidewall area” for which lateral drag is present (Little et al., 2012; Schoof et al., 2017). After the initial lengthening, the shelf collapses (Figure 4b), shelf buttressing drops (Figure 4d), and calving rates abruptly increase, peaking at 800% higher than pre-shelf collapse (Figure 4c); this is followed by a rapid retreat of the grounding line through the embayment.

In addition to the ice shelf collapse, retreat of the grounding line into the embayment entails three important mechanisms: (i) The widening fjord, and initial shelf lengthening, expose a larger sub-shelf area to submarine melt, thinning the glacier faster from below. Since submarine melt rates are uniformly applied in our model, the cumulative submarine melt flux increases as the channel widens. This widening, and enhanced impact of submarine melt, accelerates the retreat of the glacier compared to similar experiments with expanding floating ice tongues in fjords with uniform channel width (Little et al., 2009; Goldberg et al., 2012). (ii) Lateral drag decreases with the widening fjord (cf. Equation 2), resulting in speedup, dynamic thinning and further retreat (Raymond, 1996). Note that the lateral drag is parameterized in our model. The implications of this is further discussed in section 5.4 below. (iii) Mass conservation requires thinning of the glacier in order to retain the same flux at the grounding line (O'Neel et al., 2005; Carr et al., 2014). These effects work efficiently in tandem, as illustrated by our modeled rapid retreat through the embayment in experiments B150W10 and W10 (Figures 2b, 3, respectively).

Note that the ratio between fjord width and ice thickness at the grounding line determines the impact of ice shelf changes and mechanisms (i)–(iii). We expect that these effects are diminished for narrow, thick glaciers with deep grounding lines, but significant for thinner glaciers closer to flotation. Experiment B150W10 exemplifies the combined effect of a shallow grounding line on a bedrock sill and a widening channel (Figure 2).

Studies of Antarctic ice streams (Jamieson et al., 2012, 2014) as well as outlet glaciers in Greenland (Warren and Glasser, 1992; Carr et al., 2013b, 2014; Steiger et al., 2017), Patagonia (Warren, 1993), and Alaska (O'Neel et al., 2005) have highlighted channel width as an important factor controlling retreat rates and stability. We build on these studies by showing the striking impact of fjord width on grounding line retreat in a systematic, synthetic framework, and on time scales longer than have been studied in the aforementioned studies. We find that the grounding line flux increases when the grounding line retreats from a wide fjord section into a narrow channel (Figure 3b), given that the preceding retreat of the grounding line is fast and associated with loss of a floating tongue (cf. experiment W10 in Figure 4). This simulated increase in grounding line flux in experiment W10 (with GL at around km 45–50) is a consequence of the concurrent increase in grounding line velocity (Figure 3a). Retreat into the narrow and shallow fjord means the cross-sectional area decreases, lateral drag increases, the surface upstream of the grounding line steepens, and the driving stress increases. As a result, the ice velocity at the grounding line increases, compensating for the narrow flux gate by increasing the flux through the grounding line. The implication is that ice sheet discharge into the ocean may accelerate at the upstream (narrow) ends of embayments.

For the experiment with a bottleneck (W3), surface steepening upstream of the grounding line results in driving stresses exceeding 250 kPa (not shown here). A high lateral drag of 150 kPa balances 60% of this driving stress, with basal drag providing ~30% and longitudinal stress ~10%. Our simulated stress magnitudes are similar to those estimated for Columbia Glacier in Alaska (O'Neel et al., 2005) and Helheim Glacier in Greenland (Howat et al., 2005). In contrast, our modeled drag is approximately half the drag estimated for the strong shear margins of Jakobshavn Isbræ in Greenland (Shapero et al., 2016; Bondzio et al., 2017). Our idealized geometries resemble those of Columbia and Helheim glaciers rather than Jakobshavn Isbræ. The latter also has a very weak bed, rendering a high lateral drag necessary. We emphasize that lateral drag in our model is parameterized and width-averaged. Comparisons with real-glacier stresses are therefore not straightforward, and future work with a model resolving two horizontal dimensions (2HD) may be needed to assess this effect.

5.2. Irreversible Retreat in Embayments

We find irreversible retreat in fjords with embayments, regardless of the presence of a sill (Figure 7). Sills co-located with wide mouths, or open bays are common in glaciated fjord landscapes such as Greenland, Norway, Alaska, Patagonia, Svalbard and Arctic Canada. Our findings suggest that these fjords are particularly vulnerable to ocean warming; due to their wide mouths allowing for high cumulative submarine melt fluxes, loss of lateral drag, thinning and retreat (see section 5.1). A real-world example is the rapid early Holocene retreat of Sam Ford Fjord outlet glacier in the Canadian Arctic, where irreversible retreat occurred from a sill located in a wide fjord mouth (Briner et al., 2009). This fjord is similar to our geometry, being 4–6 km wide (cf. our CTRL fjord width = 5 km), with its mouth widening to >10 km (cf. our W10 embayment width = 10 km), and narrowing as the bed deepens inland of the sill (cf. our B150W10).

Embayments are also common where a tributary glacier and the main trunk coalesce. For example, this situation is plausible for Jakobshavn Isbræ during the Little Ice Age, when a northern tributary may have become disconnected from the main channel, forming separate calving fronts and a wide open embayment (Steiger et al., 2017). A similar scenario holds true for Eqalorutsit Kangigdlit Sermia (EKS) in south Greenland, where the lower end of a formerly ice-filled valley now has become a wide embayment downstream of the present calving front (west-east oriented valley to the right in Figure 8b). A third example is the well-studied Columbia Glacier in Alaska, which after nearly two centuries of stability, began to retreat rapidly in the 1980s (Meier and Post, 1987). In the late 1990s, the glacier retreated into a narrow bottleneck (cf. our geometry W3), causing an intermittent stabilization for 6–8 years (Walter et al., 2010). However, continued surface thinning and calving enabled further retreat into an embayment (cf. our geometry W10). By 2011, Columbia Glacier had split into a western branch and a main trunk (Post et al., 2011), with the two newly formed termini located upstream of the embayment, as supported by our idealized simulations (cf. Figures 3, 8).

FIGURE 8

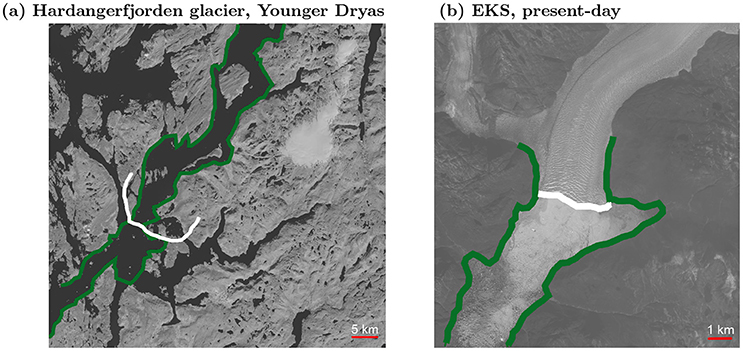
Figure 8. Influence of geometry in real-world glacier fjord systems. (a) Hardangerfjorden outlet glacier, Scandinavian Ice Sheet. The white line represents the Younger Dryas terminal moraine (Mangerud et al., 2013). (b) Eqalorutsit Kangigdlit Sermia (EKS), present-day Greenland. The glacier front is highlighted in white. Satellite imagery in (a,b) from Landsat 8, 2017, available from the U.S. Geological Survey (earthexplorer.usgs.gov). Green lines added to highlight fjord widths.

The hysteresis found here is also relevant for understanding the evolution of marine-terminating glaciers during past climate states, such as the Little Ice Age, the Younger Dryas cold reversal, or even Heinrich-events. There are several examples of embayments prohibiting advance in the literature; Hardangerfjorden in Norway (Mangerud et al., 2013, see Figure 8a) and EKS in Greenland (Warren and Glasser, 1992, see Figure 8b) are two examples. The Hardangerfjorden glacier retreated far inland during the warm Bølling-Allerød interstadial, and readvanced during the cold Younger Dryas to a position just upstream of an embayment. This behavior is analogous to our hysteresis found for widened fjords (e.g., W10 and W150W10 in Figure 7). EKS's Little Ice Age limit coincides with a 2 km narrow bottleneck, supporting our suggestion to use geometry to predict moraine locations (see section 5.3 below). This demonstrates that the long term history and the impact of fjord geometry should be accounted for when explaining retreat and advance of marine-terminating glaciers in response to past (or future) climate change.

Moreover, we simulate reversible grounding line migration for experiments with a bed bump. However, our simulations do not imply that channel width variation is a prerequisite for hysteresis. In experiments with bedrock bumps and bottlenecks (geometry B150, B300, B150W3, W3); Figure 7), no stable grounding line positions exist upstream of the bumps, and a complete (hysteresis) cycle of ocean forcing cannot be completed. Our experiments thus complement rather than contradict findings by Schoof (2007), who found hysteresis for retreat across an overdeepened bed.

5.3. Using Geometry to Predict Moraine Locations

Due to calving dynamics and the influence of geometry, marine-terminating glaciers are questionable climate indicators (Mann, 1986; Post et al., 2011). Despite the need to understand long-term marine-terminating glacier change and their non-trivial response to climate, only a handful of studies have combined geomorphology with numerical models (Jamieson et al., 2012, 2014; Lea et al., 2014). In particular, how fjord geometry influences the location of submerged terminal moraines is a fundamental, yet under-explored question. Moraines form by an advancing glacier, or during intermittent still-stands during retreat (Dowdeswell et al., 2016). Our results suggest that submarine moraines will form preferentially at the head of embayments (Figures 3, 9a), as noted by Mercer (1961) for Alaskan tidewater glaciers, and by Warren and Glasser (1992) for south Greenland glaciers. Analogously, narrow bottlenecks promote stability in our simulations (Figures 3, 9b). Moraines found in these configurations may bias their use as past climate indicators, since the geometric influence alters, and in some cases dominates, the response to external forcing. These concepts are simple yet have profound implications for our ability to correctly explain the observed evolution of marine-terminating glaciers, as well as predict their potential future retreat. We note that in our simulations, where the goal is to isolate the impact of fjord geometry on glacier behavior, we neglect sediment processes, which have been shown to influence grounding line migration (Brinkerhoff et al., 2017). Combining the knowledge gained on the impact of fjord width on glacier stabilization with a sedimentation model, is a priority for future work.

FIGURE 9

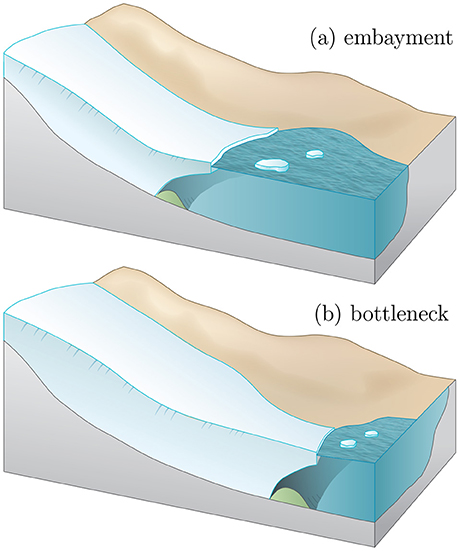
Figure 9. Geometry as a predictor of moraine positions (green bumps) and of future vulnerable glaciers, based on our experiments. (a) Grounding lines and moraines in troughs with embayments are expected to be just upstream of the wider section (cf. geometry W10). (b) Narrow bottlenecks promote stability and moraine formation (cf. geometry W3).

Stokes et al. (2014) reconstructed the retreat of eight neighboring glaciers in northern Norway, finding a heterogeneous response despite a similar regional climate forcing. Though retrograde slopes are more likely to induce rapid retreat (e.g., Schoof, 2007), Stokes et al. (2014) found a stronger correlation between retreat rate and fjord width, rather than with water depth, as is consistent with our results. However, they also found one or two examples of narrow 2–3 km wide troughs (cf. experiment W3 with a 3 km narrow bottleneck) hosting relatively fast glacier retreat that is likely explained by a deepening bed. The details of this retreat are however blurred by chronological constraints.

In addition to fjord width and basal topography, the size of the upstream catchment, as well as the mass throughput, are important factors in sustaining a stable grounding line (Payne and Dongelmans, 1997; Stokes et al., 2014; Amundson, 2016). As an example, a narrow fjord with a relatively small catchment area, a low mass throughput, and a deep grounding line, may be more prone to rapid retreat due to the lower ice flux to the grounding line. However, the effects of catchment area remain ambiguous, as illustrated for glaciers on Novaya Zemlya by Carr et al. (2014); who found no relationship between retreat and catchment size over a period of two decades. The impact of mass throughput is related to the ambient climate. We envisage that the higher surface melt experienced by glaciers in maritime regions, such as Norway, Alaska, southern and western Greenland, can influence basal sliding and affect the sensitivity of the grounding line to climate perturbations. The details of basal sliding have been highlighted as integral to grounding line stability (Tsai et al., 2015; Gagliardini et al., 2016; Gladstone et al., 2017) and will depend on basal hydrology, as well as the underlying geology. However, links between the surface climate, basal slip and grounding line migration remain largely speculative on decadal to millennial time scales.

Our experiments build on observational studies by quantifying transient and steady-state behavior under different trough widths. We find that unstable retreat can occur, not only on retrograde beds as found previously (e.g., Schoof, 2007), but also in fjord embayments, where fjord width increases upstream, i.e., in fjords with “retrograde width.”

The picture is complicated by the presence of ice shelf buttressing (e.g., Goldberg et al., 2009; Gudmundsson, 2013; Schoof et al., 2017). The tendency of ice shelves to form is expected to depend on the geometry. Few robust records of ice shelf presence exist (Jakobsson et al., 2011), though Stokes et al. (2014) anticipate that ice shelves have a tendency to form in narrow and/or shallow fjords, while wide and/or overdeepened fjords are less likely to form ice shelves. In general, we find that the ice shelf is longer in the fjord with a bottleneck (W3), compared to the fjord with an embayment (W10) (Figure 4b). However, the most prominent effect of geometry on floating ice, in our experiments, is the transient ice shelf lengthening during initial retreat into the embayment in experiment W10 (Figure 4b). As the grounding line retreats further into the embayment, this ice shelf rapidly collapses, as explained above. Ice shelf length has previously been pointed out as a key metric for grounding line stability, due to ice shelf buttressing and lateral drag (Alvarez-Solas et al., 2010; Goldberg et al., 2012; Schoof et al., 2017). Here we add to this knowledge by suggesting that ice shelf length, and thereby grounding line stability, may depend on along-flow variations in trough width.

Our finding that marine-terminating glaciers do not tend to readvance into downstream widening fjords (Figures 7b,c) is supported by studies of formerly glaciated fjords in northern Norway (Stokes et al., 2014). The well-studied Hardangerfjorden (Mangerud et al., 2013) and Lysefjorden (Briner et al., 2014) glaciers in southwestern Norway also confirm our findings of width-controlled moraine formation. These marine-terminating glaciers deposited prominent moraines during the Younger Dryas cold-reversal (c. 12.7 to 11.6 ka ago). For Hardangerfjorden, the stable position lies just upstream of a wide and relatively shallow area, as predicted by our simulations (c.f. Figures 7e, 8a), whereas Lysefjorden's moraine is located upstream of a wide section, in a narrow bottleneck (Briner et al., 2014).

We find that fast, irreversible retreat occurs through fjord embayments for synthetic geometries. The real-world examples discussed highlight that along-flow variations in fjord width can be an important control on grounding line stability. However, these examples are by no means exhaustive. Observations by a number of studies of real-world glaciers have emphasized that basal topography can also be an important control on grounding line stability (e.g., Alley et al., 2007; Joughin et al., 2010; Carr et al., 2015; Hill et al., 2017). We therefore stress that to determine the stability of individual, real-world glaciers; both basal topography and fjord width have to be assessed. Further, an accurate model representation of these glaciers likely requires future studies resolving ice flow in two horizontal dimensions (2HD), allowing for a more comprehensive assessment of the relative importance of basal and lateral fjord topography.

Figure 9 summarize our findings with respect to the “prediction” of moraine positions based on the fjord geometry. Our postulated relationship between geometry, glacier stability, and moraine positions highlights a new potential direction of research, but cannot be validated in the present study. These relationships should be assessed using a more sophisticated glacier model, ideally including a realistic ocean forcing. In addition, it would be beneficial to incorporate explicit erosion, sediment transport and deposition, and relate these factors to geometry and climate. However, the observational constraints of these processes remain poor and models therefore still remain highly parameterized (e.g., Alley, 1991; Oerlemans and Nick, 2006), though physically-based models using detailed observational data are emerging (Mugford and Dowdeswell, 2011; Love et al., 2016; Brinkerhoff et al., 2017).

5.4. Model Limitations

Models have limited value without real-world examples, and their parameters need to be constrained by observations. It can however be challenging to isolate geometric effects when studying inherently noisy glacier systems. Our idealized model framework allows for a dynamical interpretation of glacier behavior using model parameters commonly found in the literature (e.g., Nick et al., 2013).

Width-integrated models carry several assumptions. The first, most fundamental one, is that model glaciers are straight and axially symmetric around the central flowline. Real-world glaciers may have variable topography on either side of the fjord, though we expect such effects to be second order here. Secondly, ice thickness in the model is assumed to be laterally uniform. Thinner marginal ice would provide less lateral drag than the lateral drag calculated by our width-integrated model. Width variations in such a situation would therefore have a smaller impact than presented here, making our experiments upper end-members. However, our simulations with weakened margins and reduced lateral drag (section 4.2), show similar rapid retreat regardless of the degree of lateral softening (Figure 5). A third model assumption is the straight calving front oriented perpendicular to the glacier flowline. In a real-world setting, glaciers tend to flow faster at the center than along the margins, and the central part of the glacier is therefore likely to reach flotation earlier. This could lead to errors in the driving stress. However, this is not deemed critical in our experiments focusing on long time scales. Finally, width-averaged models neglect transverse velocity gradients and thus ignores transverse longitudinal stresses. These stresses may not be negligible for the large width variations in our experiments (especially in experiments W10 and B150W10), and we therefore expect our findings to be upper-bounds with respect to the importance of width variations.

Grounding line retreat in flowline-type models has been suggested to depend on parameter choices (Enderlin et al., 2013b), as well as the calving law employed (Haseloff and Sergienko, 2017; Schoof et al., 2017). The crevasse-water-depth criterion we use assumes that calving is a result of longitudinal stretching (Benn et al., 2007). This is likely suitable for glaciers with floating tongues (Joughin et al., 2008; Walter et al., 2010), such as the ones we simulate, but may be less so for tidewater glaciers where melt undercutting plays an important role (Rignot et al., 2015; Benn et al., 2017). An interesting extension of our study would be to quantify the effect of channel geometry under different calving laws.

While our model accounts for buttressing by channel walls, our representation of lateral drag is parameterized and may underestimate rates of grounding line retreat, as noted by Jamieson et al. (2014). Our model thus does not, by definition, resolve across-flow variations in stresses. Lateral resistive stresses are likely important for glaciers flowing in relatively narrow troughs such as those in Greenland, as well as for some Antarctic ice streams (Raymond, 1996). While our model does not resolve transverse stress gradients, our sensitivity experiments with varying lateral softening (section 4.2) suggest that lateral drag affects the timing and rate of retreat for a given geometry, though the simulated sequence of highly non-linear retreat remains unchanged (section 4.2).

Model investigations resolving lateral variations in shear stresses do exist (Gudmundsson, 2013; Pattyn et al., 2013), yet these studies do not include along-flow variations in channel width. Schoof et al. (2017) use an equivalent 1D model to study grounding line stability in a straight channel, and show that the form of the relationship between grounding line flux and basal geometry depends on the relative importance of lateral drag, provided by floating ice and basal drag just upstream of the grounding line. Our study supports the importance of ice shelf drag as a decisive factor for grounding line stability (sections 5.1 and 5.3), and demonstrates that significant additional grounding line retreat may occur if the width, and not only the basal topography of a fjord, varies along-flow.

Three-dimensional, higher-order studies have to date proved computationally impractical for sensitivity studies on long time-scales and are analytically cumbersome (Schoof et al., 2017). Most studies to date also neglect calving and focus solely on grounding line migration. Our study is an intermediate step toward such multi-physics studies of combined basal and lateral variations in topography. In a future study, we aim to include a higher-order representation of grounding line dynamics and buttressing, in order to test the results presented here on idealized fjord geometries as well as examples from fjord systems on Greenland and in Norway.

With regards to climate forcing, we deliberately focus solely on changing conditions at the ice-ocean boundary. The implementation of ocean forcing is highly idealized and should be complemented by future studies resolving physical processes at the ice-ocean interface. Moreover, warmer atmospheric conditions, resulting in changes to surface mass balance and subglacial discharge are likely coupled to oceanic changes and entrainment of warm water at the submarine margin; the relative importance of such effects demands future study. For simplicity, as in similar studies (Nick et al., 2013; Bassis et al., 2017), the surface mass balance-altitude feedback is left out and the surface mass balance profile is kept constant in time. We acknowledge that including the surface mass balance-altitude feedback may accelerate the simulated glacier response, and therefore we believe our simulated retreat rates to be conservative estimates.

Our findings are robust with respect to model resolution. For the complex geometries, the length of grounding line retreat varies by <5% (<2 km) between the grid size of 300 m we use, and a finer grid size of 100 m. For the CTRL geometry, the differences are 6%. The CTRL channel lacks geometric variations capable of pinning the grounding line to a specific location (cf. Figures 1, 3), which we believe explains the higher sensitivity to grid size for the latter.

5.5. Channel Width as a Future Predictor

Our simulations show that along-flow variations in channel width may alter the response of fjord glaciers to an ocean warming by tens of kilometers. Inevitably, these findings need to be placed in the context of the contemporary and future climate warming. The strong control of geometry means that present-day retreat cannot be interpreted without considering past changes. When explaining ongoing changes of marine ice sheet margins, our findings call for scrutiny of how geometry downstream of current grounding lines and calving fronts may have influenced the current state of the glaciers. The observed retreat may in fact be ongoing adjustments due to historic changes controlled by topography downstream. Similarly, studies should consider long-term past retreat in order to correctly predict future grounding line migration.

Channel width variations upstream of present-day grounding lines can also be used to identify glaciers particularly vulnerable to future warming and in need of more detailed assessment. Such first-order estimates could be based on remotely sensed data, or airborne field campaigns, substantially reducing the need to undertake complex ship and ground-based operations to map the fjord bathymetry and the glacier bed. As noted above, both the bed and channel width may significantly alter glacier evolution in response to climatic change, so any detailed studies of specific glaciers would need to study these geometric factors in tandem.

We find that retreat may be irreversible for grounding lines that have undergone retreat through fjord embayments, or wider channel sections. If anthropogenic greenhouse gases are reduced in the future, and thereby limit or even reverse climate warming, grounding lines that have retreated to a location upstream of embayments may not be able to readvance to their initial positions.

6. Conclusions

We have used a flowline model with synthetic geometries to assess the effect of ocean warming and fjord geometry, and in particular varying channel width, on grounding line stability.

We find that under identical ocean warming, variations of along-flow channel width render grounding line responses differing by several tens of kilometers. Modeled grounding line retreat rates through embayments increase three- to seven-fold in our simulations. Glacier velocities are higher post-retreat than pre-retreat, despite considerable mass loss and stabilized grounding lines. We highlight fjord mouths and embayments as particularly vulnerable configurations, in agreement with data from the paleo-record and present-day observations.

Our simulations also show that grounding line retreat through fjord embayments is likely to be rapid and irreversible, regardless of the presence of a fjord sill. Given a reversal of the imposed ocean warming, grounding lines, that have retreated through an embayment, will not readvance to their initial positions. This has implications for the potential of marine ice sheets and glaciers to recover from a prospective reversal of the current anthropogenic ocean warming. It is also relevant for understanding the behavior of marine terminating glaciers during past climate states, such as the Younger Dryas cold reversal, the Little Ice Age, as well as during Heinrich events.

Our findings imply that when interpreting reconstructions, present-day observations and future projections of marine terminating glaciers, the long-term history, as well as the impact of gjord geometry, must be considered carefully. As demonstrated with our ensemble of model experiments, geometrical constraints, such as embayments and narrow sections of fjords, decouple grounding line migration of glaciers from their contemporary climate, thereby challenging our interpretation of a possible link between glacier evolution and climate. By comparing our model results with observed, as well as reconstructed glacier frontal positions in fjords, we identify locations at the head of fjord embayments and downstream of narrow bottlenecks as particularly stable positions. These locations are hypothesized to be preferential for moraine formation and should be further investigated through field based studies.

Author Contributions

HÅ, KN, FN designed the research, HÅ performed the model runs with significant input from KN and FN, FN provided the glacier model, with modifications implemented by HÅ together with FN. HÅ created all figures except one, made by KN, and wrote the paper, with substantial contributions from the other authors. The model code is available from FN (faezeh.nick@gmail.com). The model output can be obtained upon request from the corresponding author.

Funding

This research has received funding from the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement 610055 as part of the ice2ice project. HÅ was supported by the Research Council of Norway (project no. 229788), as part of the project Eurasian Ice Sheet and Climate Interactions (EISCLIM). FN's work was funded by the ConocoPhillips Northern Area Program (CRIOS: Calving Rates and Impact on Sea Level). This research is also supported by the Research Council of Norway via the NOTUR project NN4659K Models of past ice and climate.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the free access to Landsat imagery from USGS (earthexplorer.usgs.gov). The authors wish to thank Basile de Fleurian and Nadine Steiger for thorough discussions, Mathieu Morlighem for feedback on an earlier version of the manuscript, and Eva Bjørseth for scientific illustrations. Thanks also to Felix Ng and the two reviewers who provided invaluable and constructive feedback during the review process, greatly improving the quality of our paper.

References

Alley, R. B. (1991). Sedimentary processes may cause fluctuations of tidewater glaciers. Ann. Glaciol. 15, 119–124. doi: 10.1017/S0260305500009630