A Snow Density Dataset for Improving Surface Boundary Conditions in Greenland Ice Sheet Firn Modeling

Fausto, Robert S.; Box, Jason E.; Vandecrux, Baptiste; van As, Dirk; Steffen, Konrad; MacFerrin, Michael J.; Machguth, Horst; Colgan, William; Koenig, Lora S.; McGrath, Daniel; Charalampidis, Charalampos; Braithwaite, Roger J.

doi:10.3389/feart.2018.00051

METHODS article

Front. Earth Sci., 07 May 2018

Sec. Cryospheric Sciences

Volume 6 - 2018 | https://doi.org/10.3389/feart.2018.00051

This article is part of the Research Topic Melt Water Retention Processes in Snow and Firn on Ice Sheets and Glaciers: Observations and Modeling View all 12 articles

A Snow Density Dataset for Improving Surface Boundary Conditions in Greenland Ice Sheet Firn Modeling

$\r\nRobert S. Fausto*$ Robert S. Fausto¹^*

Jason E. Box¹

Baptiste Vandecrux^1,2

Dirk van As¹

Konrad Steffen^3,4,5

Michael J. MacFerrin⁶

Horst Machguth^7,8

William Colgan^1,6

Lora S. Koenig⁹

Daniel McGrath¹⁰

Charalampos Charalampidis¹¹

Roger J. Braithwaite¹²

¹Geological Survey of Denmark and Greenland, Copenhagen, Denmark
²Arctic Technology Centre, Technical University of Denmark, Lyngby, Denmark
³Swiss Federal Research Institute WSL, Birmensdorf, Switzerland
⁴Swiss Federal Institute of Technology, Zurich, Switzerland
⁵Swiss Federal Institute of Technology, Lausanne, Switzerland
⁶Cooperative Institute for Research in Environmental Sciences, University of Colorado Boulder, Boulder, NV, United States
⁷Department of Geography, University of Zurich, Zurich, Switzerland
⁸Department of Geosciences, University of Fribourg, Fribourg, Switzerland
⁹National Snow and Ice Data Center, University of Colorado, Boulder, NV, United States
¹⁰Geosciences Department, Colorado State University, Fort Collins, CO, United States
¹¹Bavarian Academy of Sciences and Humanities, Munich, Germany
¹²University of Manchester, Manchester, United Kingdom

The surface snow density of glaciers and ice sheets is of fundamental importance in converting volume to mass in both altimetry and surface mass balance studies, yet it is often poorly constrained. Site-specific surface snow densities are typically derived from empirical relations based on temperature and wind speed. These parameterizations commonly calculate the average density of the top meter of snow, thereby systematically overestimating snow density at the actual surface. Therefore, constraining surface snow density to the top 0.1 m can improve boundary conditions in high-resolution firn-evolution modeling. We have compiled an extensive dataset of 200 point measurements of surface snow density from firn cores and snow pits on the Greenland ice sheet. We find that surface snow density within 0.1 m of the surface has an average value of 315 kg m⁻³ with a standard deviation of 44 kg m⁻³, and has an insignificant annual air temperature dependency. We demonstrate that two widely-used surface snow density parameterizations dependent on temperature systematically overestimate surface snow density over the Greenland ice sheet by 17–19%, and that using a constant density of 315 kg m⁻³ may give superior results when applied in surface mass budget modeling.

Introduction

The mass budget of the Greenland ice sheet has grown increasingly negative during the past two decades (e.g., Kjeldsen et al., 2015; Van den Broeke et al., 2016). There is a strong impetus to constrain critical processes in order to reduce uncertainties in mass balance estimates (e.g., Shepherd et al., 2012; IPCC, 2013; Khan et al., 2015). In particular, an improved understanding of ice-sheet-wide snow and firn properties can reduce uncertainties in: remotely-sensed or modeled ice sheet mass budget (e.g., Van den Broeke et al., 2016), identifying internal layers for calculating accumulation rates from combined radar and firn core surveys (Hawley et al., 2006, 2014; de la Peña et al., 2010; Miège et al., 2013; Karlsson et al., 2016; Koenig et al., 2016; Overly et al., 2016; Lewis et al., 2017), and quantifying meltwater retention (Harper et al., 2012; Humphrey et al., 2012; Machguth et al., 2016) and accumulation rates (López-Moreno et al., 2016; Schaller et al., 2016) from firn cores and snow pits. Improved estimates of surface snow density, which serves as an important boundary condition in firn densification modeling, can reduce uncertainties in mass budget studies (e.g., Sørensen et al., 2011; Csatho et al., 2014; Hurkmans et al., 2014; Morris and Wingham, 2014; Colgan et al., 2015) that convert remotely-sensed volume changes to mass changes based on either depth-density profile relations or surface snow density parameterizations. Ice sheet models that assess the surface mass budget, such as SICOPOLIS (Greve et al., 2011) or PISM (Aschwanden et al., 2012), are also limited by uncertainties in surface snow density. Fausto et al. (2009) found that the inclusion of firn densification in SICOPOLIS through a physical description of the retention capacity yields a 10% increase in the accuracy of the present-day surface mass budget.

Regional climate models calculate firn densification (e.g., Vionnet et al., 2012; Langen et al., 2015; Steger et al., 2017), but are limited by uncertainties in surface snow density feeding into their subsurface schemes. Some models use surface snow density parameterizations based on temperature to implicitly account for spatiotemporal variability (e.g., Reeh et al., 2005; Kuipers Munneke et al., 2015). Other models use parameterizations that depend on wind speed (e.g., Gallée et al., 2013) or a combination of air temperature and wind speed (e.g., Vionnet et al., 2012), while for instance Langen et al. (2015) used a constant surface snow density value.

The parameterizations based on temperatures rely on in-situ firn measurements with a coarse vertical resolution. For instance, Reeh et al. (2005) used a firn model to infer surface snow density from the 10-m firn temperature and depth-density profiles, while Kuipers Munneke et al. (2015) used the average density of the top meter of snow/firn, which would systematically overestimate surface snow density in regional climate model studies (Steger et al., 2017) if interpreted as the surface value. Most firn-evolution models operate at a centimeter-scale vertical resolution, requiring a surface snow density boundary condition derived at a resolution finer that 1 m. Using observational data sampled at high vertical resolution, one can derive the true surface value and avoid systematically overestimating surface snow density and consequently the density of the entire firn column. More accurate firn density-depth profiles yield improvements for mass budget studies of the Greenland ice sheet (e.g., Li and Zwally, 2011; Ligtenberg et al., 2011; Simonsen et al., 2013; Csatho et al., 2014; Overly et al., 2016; Steger et al., 2017).

The aim of this study is to present a spatially extensive density dataset for the Greenland ice sheet derived from 200 density-profile measurements, and to investigate the observed spatiotemporal variability for the top 0.1 m of snow/firn. In an application of this dataset, we quantify the performance of the observation-based temperature-dependent surface snow density parameterizations by Kuipers Munneke et al. (2015) and Reeh et al. (2005) that are often used as boundary conditions in surface mass budget studies of the Greenland ice sheet (e.g., Csatho et al., 2014; Steger et al., 2017).

Methods

Dataset

Our surface density dataset consists of 200 point observations, along with the geographic location, annual air temperature and annual accumulation rate for these locations. The oldest surface density data were collected by Benson (1962) in 1954 in Northwest Greenland at latitudes between 70° to 77° N (Appendix C). These measurements include annual accumulation rates and 10 m firn temperatures reported by Mock and Weeks (1965) (Appendix A). Data from both the percolation and ablation areas of the southern and western ice sheet sections near 61.3° N (Nordbo Gletscher) and 69.7° N (Paakitsoq), respectively, were collected by Braithwaite et al. (1982, 1994). Our dataset also includes data from the Program for Arctic Regional Climate Assessment (PARCA) (Mosley-Thompson et al., 2001; Thomas and Investigators, 2001). Further, the SUrface Mass balance and snow depth on sea ice working grouP (SUMuP) provided accumulation rates, snow depths and density values at various sites on the ice sheet (Koenig et al., 2013; Montgomery et al., 2018), including observations from a study of Greenland accumulation (Hawley et al., 2014) and firn aquifers (Forster et al., 2013; Koenig et al., 2014; Miège et al., 2016). We gathered annual air temperatures, accumulation rates, and density observations from snow pits and firn cores from the Greenland Climate Network (GC-Net) (Steffen et al., 1996), the Programme for Monitoring of the Greenland Ice Sheet (PROMICE) (Van As et al., 2016b), and the Arctic Circle Traverses (ACTs) (e.g., Machguth et al., 2016). Lastly, we also included observations by Schaller et al. (2016) from the NEEM to EGRIP traverse, and from the López-Moreno et al. (2016) Greenland circumnavigation. Accumulation rates in the database are not long-term averages, but represent the preceding year's snowfall. Figure 1 provides a map of all measurement locations. All data are available as Supplementary Material. Figure 2a illustrates that 28% of the observations were taken in the mid-1950s, only 2% were taken in the 1980s and 1990s, while 70% were obtained between 1999 and 2016. 94% of the measurements were gathered at elevations exceeding 1,000 m above sea level (Figure 2d).

FIGURE 1

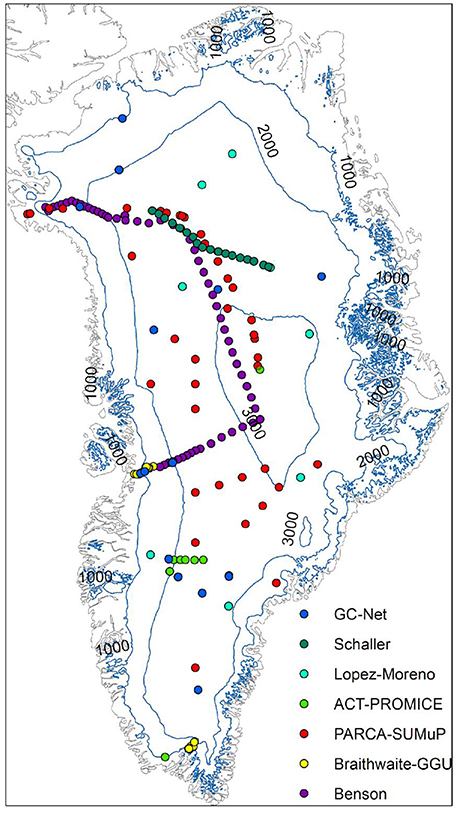
Figure 1. Locations of all surface snow density measurement locations in our dataset. Contours lines indicate elevations in meters above sea level.

FIGURE 2

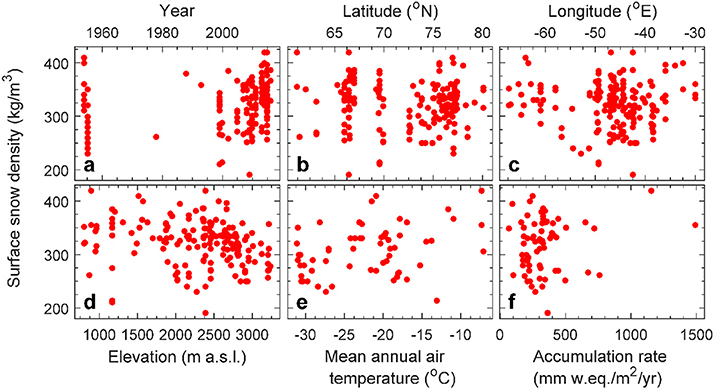
Figure 2. Density of the top 0.1 m of snow plotted against site- and campaign-specific parameters: (a) year, (b) latitude, (c) longitude, (d) elevation, (e) annual mean near-surface air temperature, and (f) accumulation rate.

Defining the surface layer as the upper 0.1 m of snow yields that in most cases the surface layer was deposited in multiple snowfall events, except for areas located at relatively low elevations in the south and southeast of the ice sheet, where individual precipitation events typically produce more than 0.1 m of snow (Burgess et al., 2010). Where possible, the annual air temperature was calculated as the average over the 365 days prior to the date for which the surface snow density was determined. Where air temperature measurements are not available, i.e., for the older data by Benson (1962) and Braithwaite et al. (1994), but firn-core temperatures were, we use 10 m firn temperature as annual air temperature following e.g., Reeh et al. (2005), Polashenski et al. (2014), and Kuipers Munneke et al. (2015). This is a fair approximation since 10 m firn temperatures reflect the conductive temperature wave propagation in places with little or no melt (Benson, 1962). Though valid for the earlier observations in our dataset, recent increases in ice sheet melt area have reduced the dry snow facies of the ice sheet (McGrath et al., 2013) and therefore the applicability of this methodology.

Commonly, snow/firn was sampled in snow pits using a fixed volume cutter at 0.05–0.1 m vertical resolution. These samples were weighed using a variety of scales. When density data were derived from a core, the snow was extracted from the core barrel and typically sub-sampled into 0.1 m sections before being weighed. Conger and McClung (2009) investigated measurement errors of several different density cutters and conclude that measurement accuracy was within 3–12%. They also conclude that the absolute measurement uncertainty is within 11% of true density. A discussion of density cutters by Proksch et al. (2016) reaches a similar uncertainty of 9%. For the data in our database, sampling uncertainty is not documented in any of the field campaigns, however it seems reasonable to assume that surface snow density is known within 10%. Typically, this measurement uncertainty is smaller than the spatial variability in surface snow density in the vicinity of the measurement location (e.g., Proksch et al., 2015). We argue that the point measurements in our dataset do not represent fresh snow, as the persistent katabatic winds in Greenland compact surface snow within days after snowfall (e.g., Liston et al., 2007).

Firn Model Initialization

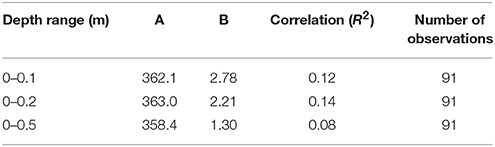
We test a surface snow density parameterization for the Greenland ice sheet that is dependent on temperature, similar to commonly used parameterizations by Kuipers Munneke et al. (2015) and Reeh et al. (2005). We assume a linear dependence of surface snow density (ρ) in kg m⁻³ on annual air temperature (T_a) in °C, in what we refer to as parameterization P1:

\begin{array}{rcl} ρ = A + B \cdot T_{a} & (1) \end{array}

We determine the fit coefficients by orthogonal linear regression to all available T_a values in our dataset, and find a best fit for A = 362.1 and B = 2.78 (Table 1) for the top 0.1 m of snow. Kuipers Munneke et al. (2015) determined the coefficients of Equation (1) using annual surface temperature T_s in °C simulated by RACMO2.3 and the average density of the uppermost 1 m of snow/firn, and found what we here refer to as parameterization P2:

\begin{array}{rcl} ρ_{KM 15} = 481 + 4.834 \cdot T_{s} & (2) \end{array}

Reeh et al. (2005) derived surface snow density as a function of the 10-m firn temperature (T_f) from the near-surface part of their depth-density profiles by determining the load at 5 m depth, as calculated by their model, so that it fits the corresponding load derived from the measured depth-density profiles (parameterization P3):

\begin{array}{rcl} ρ_{R 05} = 625 + 18.7 \cdot T_{f} + 0.293 \cdot T_{f}^{2} & (3) \end{array}

There is a ca. 40% overlap between our dataset and the data feeding into the Kuipers Munneke et al. (2015) and Reeh et al. (2005) parameterizations that stems from them also using the Benson (1962), Braithwaite et al. (1994), and PARCA (Mosley-Thompson et al., 2001) datasets.

TABLE 1

Table 1. Fit coefficients and statistics for parameterization P1 (Equation 1).

To highlight the importance of sampling depth ranges in producing an observationally-based boundary condition for firn models in Greenland, we also test P1 (Equation 1) using the average density of the top 0.2 and 0.5 m of snow/firn in our analysis (Table 1). We theorize that, by using density data obtained as close to the surface as possible, we avoid introducing a systematic bias due to compaction. Yet by focusing only on the top layer of snow/firn, we likely introduce more scatter in our results due to additional variability by single weather events. We investigate such considerations below.

Results

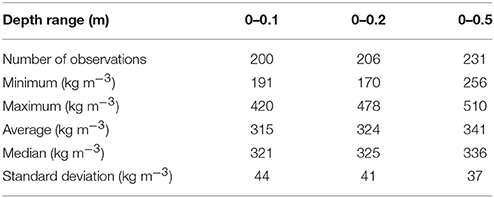
Surface snow density in our 200-value database ranges between 190 and 420 kg m⁻³, with an average of 315 kg m⁻³ and associated standard deviation of 44 kg m⁻³ (Figure 3, Table 2). Using the 10% measurement uncertainty range chosen in the methods section, we determine the average uncertainty to be ± 32 kg m⁻³. The measurement uncertainty is smaller than the 44 kg m⁻³ standard deviation, which demonstrates a significant natural variability in the top 0.1 m of snow most likely due to differences in precipitation events and influences from weather in general. Yet the variability in surface snow density could also depend on location or annual air temperature as investigated below.

FIGURE 3

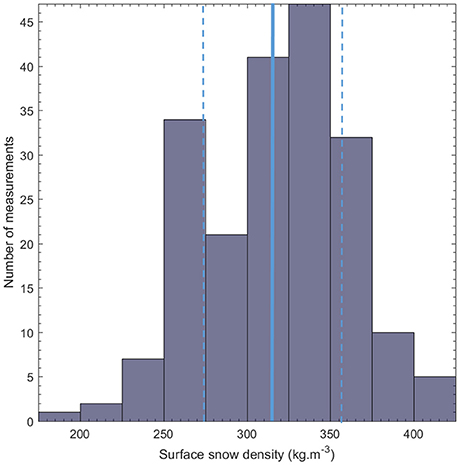
Figure 3. Number of surface snow density measurements over the Greenland ice sheet. Blue solid and dashed lines indicate the average and standard deviation of the dataset, respectively.

TABLE 2

Table 2. Surface snow density dataset metadata for three depth ranges.

There is no significant temporal trend in surface snow density (Figure 2a), indicating that the relatively large timespan over which measurements were collected does not introduce a bias. Figure 2 also illustrates that surface snow density is not significantly correlated with latitude, longitude, elevation, nor annual accumulation rate. Remarkably, also annual air temperature does not prove to be a strong predictor of surface snow density (Figure 2e). Even in a stepwise linear regression we find that no combination of variables in our database adequately predicts the surface snow density (results not presented). We quantify the poor predictive skill of annual air temperature in all three parameterizations in Table 3, showing root mean square error (RMSE) values for the top 0.1 m of snow to be 42–84 kg m⁻³, with mean biases of + 19% (P2) and +17% (P3). For the 0–0.1 m depth range, RMSE values for P2 and P3, are respectively a factor of 2.0 and 1.8 higher than those for our P1 parameterization (Table 3).

TABLE 3

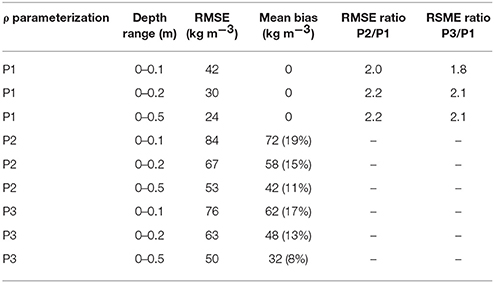
Table 3. Root-mean-square error (RMSE), mean bias and RMSE ratio values for parameterizations using annual mean air temperature: P1 (this study), P2 (Kuipers Munneke et al., 2015) and P3 (Reeh et al., 2005).

Average snow/firn density increases from 315 to 341 kg m⁻³ as the averaging depth range increases from 0.1 to 0.5 m (Table 2). Simultaneously, the standard deviation decreases indicative of a reduction in small-scale spatial variability (Table 2), i.e., differences in snow/firn density profiles are growing smaller due to compaction and as the relative influence of single weather events reduces. As a result of using larger depth ranges yielding larger average densities, the performance of parameterizations P2 and P3 increases judging from reducing RMSE values, but they still overestimate the average density of the top 0.5 m of snow/firn by 11% (P2) and 8% (P3) (Table 3). Even taking into account that T_a (Equation 1) typically exceeds T_s (Equation 2) by a few degrees does not make up for more than 10 kg m⁻³ of the P2 overestimate.

Figure 4 illustrates the dependence of surface snow density on annual air temperature for the top 0.1, 0.2, and 0.5 m of snow/firn, confirming that (1) air temperature is a poor predictor of surface snow density, (2) variability of surface snow density decreases with increasing depth range, (3) existing temperature-based parameterizations tend to overestimate surface snow density, (4) especially for snow density nearest the surface, and revealing that (5) the predictive skill of parameterizations P2 and P3 is poorest for annual temperatures exceeding −20°C. Consequently, we judge that using a single constant value to represent surface snow density on the Greenland ice sheet may be preferred over using a temperature-dependent parameterization.

FIGURE 4

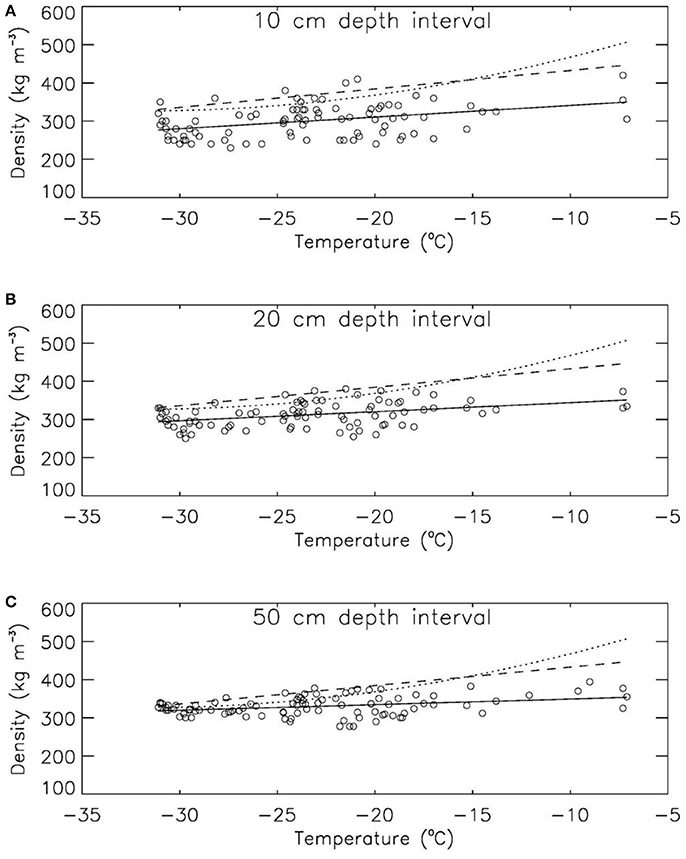
Figure 4. Orthogonal linear regression fits (solid lines) for temperature-dependent parameterization P1 (Table 1) for (A) depth range 0–0.1 m, (B) depth range 0–0.2 m, and (C) depth range 0–0.5 m. Circles represent our observational dataset. Parameterizations by Kuipers Munneke et al. (2015) and Reeh et al. (2005) are plotted as dashed and dotted lines, respectively.

Discussion

Depth Range

We use a smaller depth range to better represent surface snow density than previous studies. Assessing density closer to the surface is important for producing a more accurate upper boundary condition to be used in firn evolution models that would produce too high firn densities along the entire depth profile. Figure 4, Table 3 confirm that using relatively large depth ranges in determining a surface snow density parameterization results in overestimated values by Kuipers Munneke et al. (2015) and Reeh et al. (2005). Our smallest tested depth range of 0–0.1 m reveals larger natural variability, but would not introduce a considerable systematic bias in firn evolution modeling even if a vertical grid resolution finer than 0.1 m is used. In surface mass balance modeling, the choice of vertical resolution of the subsurface directly influences the calculation of key variables, such as the meltwater retention capacity of the snow/firn column. The more variable density in the top 0.1 m of snow compared to the top 0.2 m (factor of 1.4 more variable) or 0.5 m (1.8), is due to the influence of single precipitation events and subsequent weather forcing. We contend that this increased variability is preferable over the introduction of a systematic bias in surface mass balance modeling.

The top of the snowpack compacts rapidly after snowfall (e.g., Brun et al., 1997; Liston et al., 2007), as the crystal structure of freshly deposited snow breaks down within days due to wind and redistribution of drifting snow (e.g., Kotlyakov, 1961; Kojima, 1967; Pahaut, 1976). Surface snow densification by wind, which generally only influences the top 0.1 m, becomes insignificant after a few days (Brun et al., 1997). For most or all observations in our dataset, we can safely assume that wind compaction has occurred already. Therefore, our dataset and resulting products should not be used in models to prescribe or validate fresh snow densities (e.g., Vionnet et al., 2012), but rather to define the upper boundary condition (i.e., minimum density) in firn evolution models that do not calculate micro-scale snow physics and densification by wind, snow drift and redistribution.

In regions where large snowfall events occur, such as in south Greenland, density measurements of the top 0.1 m of snow may reflect the conditions during one snowfall event and subsequent weather-dependent densification prior to measurement. All of the snow-density measurements in our database were taken in spring and summer, meaning that our average and parameterization may be seasonally biased. Dibb and Fahnestock (2004) investigated the seasonality of the surface snow density at Summit in Greenland, and found a seasonal standard deviation of 30% in density in the top 0.03 m of snow as determined from 22 measurements during a two-year period. However, seasonal variation in the surface snow density is likely to increase with elevation (Brun et al., 1997) with standard deviation values lower than 30% in regions away from the three dome sites in Greenland where persistent katabatic winds and their influence on snow compaction do not occur (e.g., Noël et al., 2014). In general, katabatic winds are strongest in winter due to surface radiative cooling, and at lower elevations (below 2,000 m above sea level) due to larger surface slopes (e.g., Van As et al., 2013; Noël et al., 2014), resulting in wind-packing of fresh surface snow within days.

Temperature Dependence

Higher air temperatures result in higher snow and firn densities through increased compaction (Zwally and Li, 2002). It is therefore desirable to ensure that parameterizations of surface snow density remain appropriate even as the climate changes (e.g., Reeh et al., 2005; Morris and Wingham, 2014). Studies of Greenland accumulation rates and firn properties document a recent densification in the overall firn column and attribute it to climate warming (e.g., de la Peña et al., 2015; Charalampidis et al., 2016a; Machguth et al., 2016; Overly et al., 2016). If we assume that temperature-dependent densification processes are responsible for the transformation of freshly-fallen snow to the surface snow densities of our dataset, the inclusion of temperature as a variable in a parameterization (Equation 1) explicitly accounts for atmospheric warming. In this case, a parameterization is better capable of representing changing surface conditions due to climate variability. For instance, our temperature-dependent parameterization suggests that the observed 2.7°C warming at Summit over the period 1982–2011 (McGrath et al., 2013) had lead to a local surface snow density increase of 8 kg m⁻³. But even a large temperature increase of 10°C anywhere in Greenland would only cause a densification of 28 kg m⁻³ in the top 0.1 m of snow, which is smaller than the 32 kg m⁻³ measurement uncertainty and 44 kg m⁻³ standard deviation of the dataset (Table 2). For larger depth ranges the temperature sensitivity (B-values in P1, see Table 2) is considerably smaller and thus more insignificant given the measurement uncertainty and natural variability. The insignificant densification as a result of warming supports the notion that temperature is a poor predictor of the variability of surface snow density in the top 0.1, 0.2, and 0.5 m of snow/firn, and that using a constant value may be preferable in some applications.

Modeling Implications and Limitations

The choice of a surface snow density boundary condition influences calculations of available pore space by models simulating the surface mass budget of the Greenland ice sheet. Steger et al. (2017) discussed the limitations and inaccuracies of their Greenland ice sheet surface mass budget simulations by regional climate model RACMO2.3, and conclude that the Kuipers Munneke et al. (2015) parameterization systematically overestimates surface snow density, impacting pore space available for refreezing at depth. Langen et al. (2015) and Charalampidis et al. (2016b) applied a constant surface snow density value of 330 kg m⁻³ in regional climate model HIRHAM5, while Langen et al. (2017) applied a parameterization depending on latitude, longitude and elevation, derived from our dataset, in a new model version. The latter study found that the parameterization yields an ice-sheet-wide average of surface snow density that is 7% lower than using a constant density value of 330 kg m⁻³, signifying a higher meltwater retention capacity in the snow and firn. Langen et al. (2017) also documented that the firn density profiles simulated by HIRHAM5 using their parameterization satisfactorily resemble measured profiles. Yet based on our own findings we suspect that using a constant surface snow density value of 315 ± 32 kg m⁻³ as boundary condition, a value 5% lower than that used by Langen et al. (2015), should perform equally well in Greenland-wide surface mass budget simulations.

Using our dataset for the top 0.1 m of snow, as opposed to using those for larger depth ranges, comes at the cost of a higher variability (standard deviation in Table 2) due to a larger influence of meteorology-dependent processes like snow drift (Brun et al., 1997; Hörhold et al., 2011; Koenig et al., 2016). The larger variability could also stem from snowfall events depositing more than 0.1 m of snow. Layers below the top 0.1 m are not much influenced by wind compaction, snow drift and redistribution, and will primarily be subject to the less efficient densification through rounding or settling of snow grains from vapor fluxes in the subsurface layers (e.g., Albert and Shultz, 2002). Surface mass budget models using our constant value of 315 kg m⁻³ for the top 0.1 m of snow may therefore misrepresent relatively low-density layers below 0.1 m depth deposited during large snowfall events. Regions where snowfall may exceed 0.1 m in single events are typically located at lower elevations on the southern and southeastern parts of the ice sheet (e.g., Burgess et al., 2010).

Our dataset has sparse coverage in the northern and eastern sectors of the ice sheet, possibly introducing a spatial bias in our results. Figure 5 illustrates that the elevation distribution of our measurement locations broadly reflects the overall area-elevation distribution of the ice sheet as determined from the GIMP digital elevation model (Howat et al., 2014). Some lower elevation ranges (1,000–1,750 m above sea level) are relatively underrepresented in our dataset, while some higher elevation ranges are comparatively overrepresented. Our parameterization could benefit from acquiring additional measurements from elevations between 1,000 and 1,750 m above sea level, i.e., in the lower percolation area of the ice sheet (Benson, 1962). The lower percolation area is considered crucial for properly determining the surface mass budget, as firn properties influencing meltwater retention capacity vary substantially across the ice sheet (Van As et al., 2016a; Langen et al., 2017).

FIGURE 5

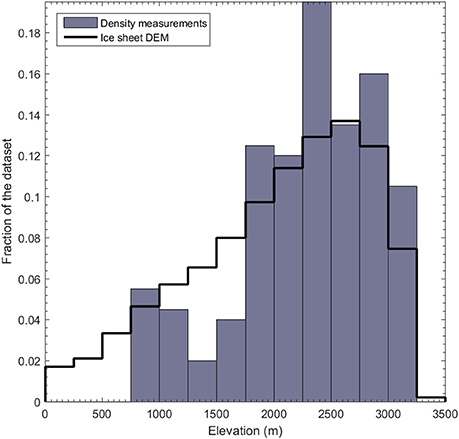
Figure 5. Elevation distribution of the surface snow density measurement locations compared to the area-elevation distribution of the entire Greenland ice sheet.

Conclusions

We constructed a dataset of surface snow density for the top 0.1, 0.2, and 0.5 m of snow/firn on the Greenland ice sheet based on 200 in situ measurements collected during the 1953–2016 timespan. We found that only the annual air temperature has a weak predictive skill of surface snow density in the construction of a temperature-dependent parameterization. Our parameterization yields surface snow densities of 32–72 kg m⁻³ (8–19%) lower than earlier parameterizations do, thus beyond the 32 kg m⁻³ measurement uncertainty range. Yet since the natural variability in surface snow density is found to be large with e.g., a 44 kg m⁻³ standard deviation for the top 0.1 m of snow, the temperature sensitivity of surface snow density is not found to be significant, indicating that an average surface snow density of 315 kg m⁻³ could be the preferred choice as a boundary condition for models calculating the surface mass budget of the Greenland ice sheet.

Author Contributions

RF conceived the study and wrote the manuscript; BV and RF did the statistical analysis. All authors contributed with field data and continuously discussed the results and developed the analysis further.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer, CM, declared a past collaboration with two of the authors, JB and LK, to the handling editor.

Acknowledgments

This work was supported by the Danish Research Council Grant FNU 4002-00234 and the Programme for Monitoring of the Greenland Ice Sheet (www.promice.dk). The author team would like to thank all the reviewers and scientific editor, T. Bartholomaus, for help and constructive criticism, which improved the manuscript significantly. We acknowledge J. T. M. Lenaerts for a collegial review and valuable comments. LK was supported by NASA Cryospheric Sciences program NASA Award NNX15AC62G.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2018.00051/full#supplementary-material

Data Sheet 1. Surface density dataset consists of point observations (0–10, 0–20, 0–50 cm), along with the geographic location, annual air temperature and annual accumulation rates.

References

Albert, M. R., and Shultz, E. F. (2002). Snow and firn properties and air-snow transport processes at Summit, Greenland. Atmos. Environ. 36, 2789–2797. doi: 10.1016/S1352-2310(02)00119-X