Corrigendum: Energetics of Slope Flows: Linear and Weakly Nonlinear Solutions of the Extended Prandtl Model

A corrigendum on
Energetics of Slope Flows: Linear and Weakly Nonlinear Solutions of the Extended Prandtl Model

by Güttler, I., Marinović, I., Večenaj, Ž., and Grisogono, B. (2016). Front. Earth Sci. 4:72. doi: 10.3389/feart.2016.00072

In the original article, there were mistakes in Figures 2, 4, 6 as published. The interaction term [last right-hand side term in Equation (3) of our published paper] was erroneously multiplied by the average heat conductivity constant. The corrected Figures 2A–C, Figures 4A–C, and Figure 6 appear below.

Figure 2: Correction of the original Figure 2, panels A-C. Only panel C is updated.

Figure 4: Correction of the original Figure 4, panels A-C. Only panel C is updated.

Figure 6: Correction of the original Figure 6. Panels from C to H are updated.

FIGURE 2

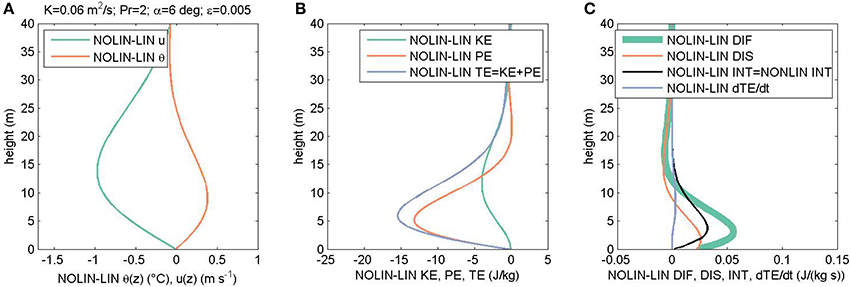
Figure 2. (A–C) Differences between nonlinear and linear (Figure 1) solutions of the (extended) Prandtl model (cf. Grisogono et al., 2015). Panels (D–F) of the original Figure 2 are unchanged.

FIGURE 4

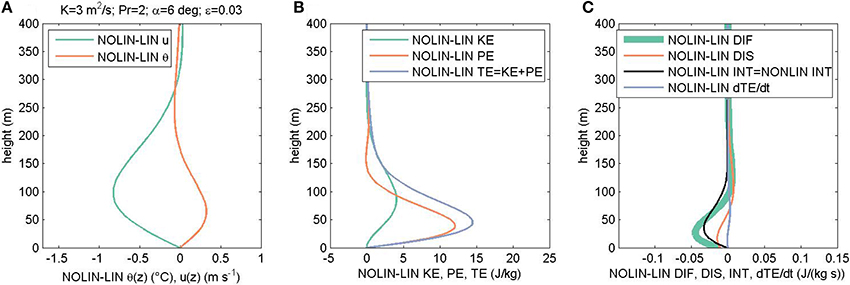
Figure 4. Same as Figure 2 but for anabatic flow.

FIGURE 6

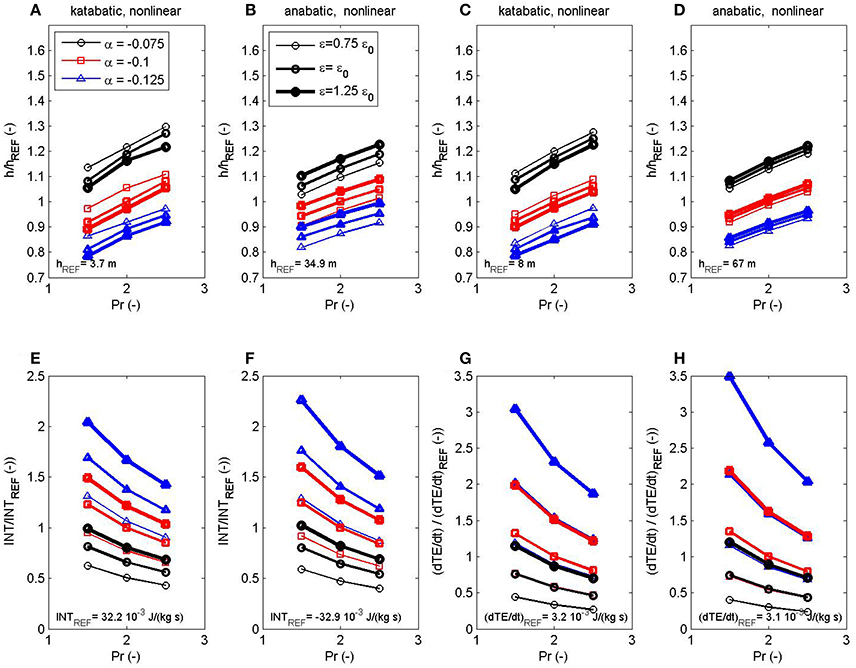
Figure 6. The height of the maximum of the interaction term INT (A,B), the height of the maximum of the storage term ∂TE/∂t (C,D), the maximum INT value (E,F), and the maximum ∂TE/∂t value (G,H) for katabatic (A,C,E,G) and anabatic (B,D,F,H) nonlinear cases. Selected measures are determined as functions of Prandtl number Pr (x axis), slope angle α (different color) and nonlinearity parameter ε (different line thickness). Values in panels are relative to the corresponding h_REF (A–D), INT_REF (E,F) and ∂TE/∂t_REF (G,H).

The same error that led to the correction of Figures 2, 4, 6 had an impact on the content of the paper. This error leads to five minor changes in several paragraphs:

(1) A correction has been made to Results, Katabatic flow, Nonlinear case, 1st paragraph. The following sentence (lines 11–12) is modified:

Its amplitude is comparable to the other two governing terms in the energy equation.

(2) A correction has been made to Results, Anabatic flow, Nonlinear case, 1st paragraph. The sentences spanning the last 9 lines of the paragraph have been modified as follows:

In contrast to katabatic flow, the TE diffusion DIF now departs from the dissipation DIS toward lower values (Figure 4C). Also, while in both katabatic and anabatic flow the amplitude of INT is comparable in magnitude to DIF and DIS, the sign of INT is now reversed, becoming negative in the case of anabatic flow.

(3) A correction has been made to Results, Energetics: Katabatic and Anabatic Flows, 5th paragraph. Here, several numerical estimates are now corrected and the following sentence (lines 9–11) is modified:

Also, INTmax varies from ~0.01 J/kg/s to ~ 0.07 J/kg/s in katabatic flow, while it is negative and varies from ~ −0.07 J/kg/s to ~ −0.01 J/kg/s in anabatic flow.

(4) A correction has been made to Results, Energetics: Katabatic and Anabatic Flows, 6th paragraph. Again, several numerical estimates are now corrected and the following two sentences (line 6–10 and 13–16) are modified:

For nonlinear katabatic flow, and based on the specific selection of model parameters, maximum values of ∂TE/ ∂t range from ~10⁻³ J/kg/s to ~0.01 J/kg/s at heights ranging from ~6 to ~10 m (Figures 6C,G).

For the nonlinear anabatic flow, maximum values of ∂TE/∂t range from ~10⁻³ J/kg/s to ~0.01 J/kg/s at heights ranging from ~55 to ~82 m (Figures 6D,H).

(5) A correction has been made to Discussion, 4th paragraph. The following sentence from the 2nd half of the paragraph (lines 27–31) is modified:

Also, imbalance among the energy terms in this nonlinear model may suggest that there is perhaps no real steady-state nonlinear slope flow; thus, excursions from pure steadiness could occur in nonlinear thermally driven flows.

The authors apologize for the computational error. Although the correction of this error had an impact in several places in the published paper, there are no changes in the scientific conclusions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Grisogono, B., Jurlina, T., Večenaj, Ž., and Güttler, I. (2015). Weakly nonlinear Prandtl model for simple slope flows. Q. J. R. Meteorol. Soc. 141, 883–892. doi: 10.1002/qj.2406

CrossRef Full Text | Google Scholar