- Osservatorio Vesuviano, Istituto Nazionale di Geofisica e Vulcanologia, Napoli, Italy
Many calderas show remarkable unrest, which often does not culminate in eruptions (non-eruptive unrest). In this context the interpretation of the geophysical data collected by the monitoring networks is difficult. When the unrest is eruptive, a vent opening process occurs, which leads to an eruption. In calderas, vent locations typically are scattered over a large area and monogenic cones form. The resulting pattern is characterized by a wide dispersion of eruptive vents, therefore, the location of the future vent is not easily predictable. We propose an interpretation of the deformation associated to unrest and vent pattern commonly observed at calderas, based on a physical model that simulates the intrusion and the expansion of a sill. The model can explain both the uplift and any subsequent subsidence through a single process. Considering that the stress mainly controls the vent opening process, we try to gain insight on the vent opening in calderas through the study of the stress field produced by the intrusion of an expanding sill. We find that the tensile stress in the rock above the sill is concentrated at the sill edge in a ring-shaped area with radius depending on the physical properties of magma and rock, the feeding rate and the magma cooling rate. This stress field is consistent with widely dispersed eruptive vents and monogenic cone formation, which are often observed in the calderas. However, considering the mechanical properties of the elastic plate and the rheology of magma, we show that remarkable deformations may be associated with low values of stress in the rock at the top of the intrusion, thereby resulting in non-eruptive unrest. Moreover, we have found that, under the assumption of isothermal conditions, the stress values decrease over time during the intrusion process. This result may explain why the long-term unrest, in general, do not culminate in an eruption. The proposed approach concerns a general process and is applicable to many calderas. In particular, we simulate the vertical displacement as occurred in the centre of Campi Flegrei caldera during the last decades, and we obtain good agreement with the data of a leveling benchmark near the center of the caldera.
1. Introduction
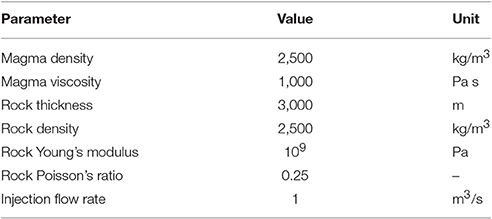
Calderas typically show strong ground deformation, with uplift episodes followed by subsidence, remarkable geothermal activity and seismicity mainly characterized by earthquake swarms. In volcanic environments the acceleration of ground deformation, degassing and seismicity, are generally interpreted as precursors of an eruption (Swanson et al., 1983; Voight, 1988; Voight and Cornelius, 1991; Newhall and Hoblitt, 2002; Marzocchi et al., 2008; Bell et al., 2011). However, in calderas the acceleration of these phenomena (ground deformation, degassing and seismicity) does not necessarily culminate in an eruption (Newhall and Dzurisin, 1988; Biggs et al., 2014; Acocella et al., 2015). Examples are the non-eruptive unrest at Campi Flegrei caldera (Italy) during 1968–1970 and 1982–1984 (Del Gaudio et al., 2010; D'Auria et al., 2011), Long Valley (California) during 1978–2000 (Hill, 2006), Rabaul (Papua New Guinea) in 1984 (McKee et al., 1984), Sierra Negra (Galápagos Islands, Ecuador) in 1996 (Chadwick et al., 2006), Yellowstone (USA) between 2004 and 2010 (Chang et al., 2010), Santorini (Greece) in 2011–2012 (Newman et al., 2012; Lagios et al., 2013), which were accompanied by significant variations in the monitoring parameters but were not followed by an eruption (Segall, 2013; Acocella et al., 2015). In particular, in the last decades, Campi Flegrei has shown a total uplift of more than 3 m (Bianchi et al., 1987), followed by subsidence (Del Gaudio et al., 2010), as shown in Figure 1. This behavior stimulated a long debate if the deformation is due to hydrothermal or magma migration (see e.g., Lundgren et al., 2001; Gottsmann et al., 2006; Trasatti et al., 2008).
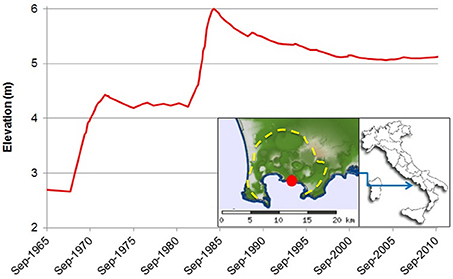
Figure 1. Uplift and subsidence at Campi Flegrei caldera (yellow dashed line in the inset) between 1965 and 2010, recorded at the benchmark 25 (red dot) of the leveling network of Campi Flegrei (modified after Del Gaudio et al., 2010). The main uplift episodes occurred in 1968-1972 and 1982–1985 periods. These two non-eruptive unrest led to the evacuation of the town of Pozzuoli.
Recently, new technology allowed an improvement in volcano monitoring and produced valuable data set of observations and geophysical measurements. This improvement of volcano monitoring allowed us to increase our knowledge upon the calderas behavior (Newhall and Dzurisin, 1988; Geyer and Martí, 2008; Sobradelo et al., 2010; Acocella et al., 2015). In particular, Acocella et al. (2015), in a review article, conclude that “where established, the root cause for unrest is always magmatic; while external earthquakes or hydrothermal processes may definitely enhance unrest, no unrest was of purely hydrothermal or tectonic origin; magma always appears as the crucial ingredient, though in most cases, magma may also induce changes in the hydrothermal system, supplying this with fluids and energy.”
Moreover, in many cases, the structure of the shallow plumbing system and the dynamic processes in calderas are consistent with the emplacement of sill-like magma intrusions (Okada, 1985; Amoruso et al., 2007; Onizawa et al., 2007; Jónsson, 2009; Chang et al., 2010; Woo and Kilburn, 2010; Chadwick et al., 2011; Maccaferri et al., 2011; Menand, 2011; Unglert et al., 2011; Bagnardi and Amelung, 2012; Manconi and Casu, 2012; Bagnardi et al., 2013; Corbi et al., 2015; D'Auria et al., 2015a; Richardson et al., 2015; Rivalta et al., 2015; Trasatti et al., 2015; Le Mével et al., 2016). Usually the intrusion of a sill is modeled as a pressure increase in a horizontal crack (e.g., Fialko et al., 2001; Woo and Kilburn, 2010) which causes deformations and ground uplift. Once the intrusion ends, the ground uplift should be permanent, but in calderas subsidence is often observed which is usually explained through other processes such as regional extension (Dvorak and Mastrolorenzo, 1991), regional earthquakes (Pritchard et al., 2013; Takada and Fukushima, 2013), magma degassing (Chiodini et al., 2003; Pritchard et al., 2013) or the compaction of porous material caused by a pressure drop within the hydrothermal system (Todesco et al., 2014). We have adopted an alternative model which is able to explain both uplift and subsidence in the framework of a single process of intrusion and spreading of a sill. The model is basically governed by the feeding rate, the rheology of magma and the mechanical properties of the rock above the intrusion (Bunger and Cruden, 2011; Michaut, 2011; Macedonio et al., 2014; Giudicepietro et al., 2016), However, we do not exclude that magma degassing can contribute to the deformation processes, especially in felsic calderas.
2. Overview of the Model
We assume that the sill intrudes at a certain depth beneath the caldera along a horizontal mechanical discontinuity, such as a bedding plane or a contact between two different stratigraphic units. Magma rises from a deeper zone and enters the sill through a feeding point with a given mass flow rate. The sill expands radially and its front moves away from the feeding point (see Figure 2). The radial expansion of the sill is caused by the radial gradient of magma pressure due to the bending of the rocks at the top of the intrusion and to the radial variation of the thickness of the sill (Bunger and Cruden, 2011; Michaut, 2011; Macedonio et al., 2014). The joint effect of these two components is obtained through the numerical solution of the equation for the elastic plate, coupled with equations for the dynamics of magma flow (Bunger and Cruden, 2011; Michaut, 2011; Macedonio et al., 2014). This can be expressed by the following equation which describes the radial expansion of the sill (Macedonio et al., 2014):
where h is the thickness of the sill, ρm is magma density, μ is the viscosity, q is the injection rate at the center of the sill, r is the radial coordinate and t is time. The term proportional to the gravity constant g accounts for the spreading due to the radial gradient of the thickness of the sill, whereas the term proportional to the flexural rigidity of the rock D accounts for the pressure gradient generated by the elastic deformation of the overlying rock. The flexural rigidity of the rock D is defined as:
where d, E, and ν are the thickness, the Young's modulus and the Poisson's ratio of the rock, respectively.
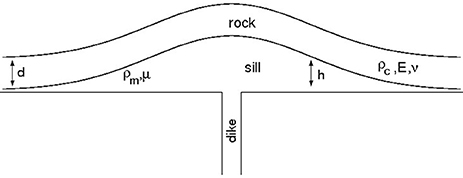
Figure 2. Sketch of the sill, h is the thickness of the sill which corresponds to the uplift at the surface (not to scale), and d is the thickness of the rock. The sill is not to scale, its real thickness is much smaller than its width.
In this model we do not include the effects of rock fracturing in the plate above the sill and we neglect the elasticity of the bedrock below the sill. Moreover, the model does not take into account the cooling of magma, so it must be considered as a limiting case with negligible cooling. When cooling is not negligible we expect a conductive cooling of magma occurring at the contact with the wall rocks. In these conditions the temperature is not constant and the viscosity varies with the temperature. The effect of magma cooling increases the viscosity over time, especially at the front of the sill, and thus hinders the lateral spreading of the intrusion and increases the thickness of the sill in the central part. This effect may be important to confine the expansion of the sill and in general of intrusive bodies, as shown for the laccolithes by Thorey and Michaut (2014, 2016). To conceptually assess the effect of cooling, we have implemented the possibility of a variable temperature, which decreases linearly with the distance from the feeding point. Table 1 shows the parameters necessary for our model and the values that we used for the simulation of a reference case (REF). These parameters are typical for calderas and are the same as used by Macedonio et al. (2014). Among the parameters, a major role is played by magma viscosity and rock Young's modulus. As shown by Giudicepietro et al. (2016), high magma viscosity produces larger stress values in the rock, while low viscosity leads to lower stresses and favors the radial spreading of the sill. High-rock Young's modulus gives high stress intensity, whereas low values of Young's modulus produce a reduction of the stress associated with the intrusive process (Giudicepietro et al., 2016). In this work we choose a Young's modulus of 109 Pa for the reference case (REF) and we increased it by factor of 10 for the mafic calderas and decrease it by a factor of 100 for the felsic calderas. Correspondingly, we used a typical magma viscosity of 1,000 Pa s for the reference case, 100 Pa s for the low silicic (mafic) magma, and 10,000 Pa s for the high silicic (felsic) magma (see Table 1). Moreover, to account for smooth variations of magma injection rate, instead of considering a box-like magma input (Macedonio et al., 2014), we considered an input characterized by a linear ramp, a steady state, and a linear decrease of the mass flow rate (see Figure 3).
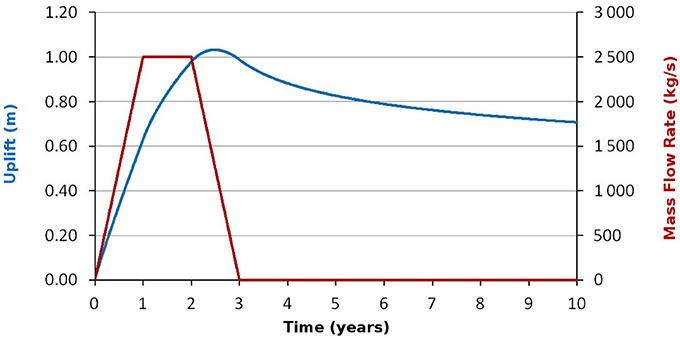
Figure 3. Plot of the uplift in meters (left axis) over time of the maximum uplift point (blue line) for the REF case (see Table 1). The red line represents the mass flow rate (right axis) of magma filling the sill.
3. Behavior Predicted by the Model
The model of spreading sill predicts that during the magma intrusion the elastic plate above the sill bends, producing a ground uplift (h in Figure 2), which has its maximum value at the center of the sill and decreases toward the sill front (Figure 2). Figure 3 shows the uplift in the center of the sill and the mass flow rate over time, used for the simulation. The mass flow rate is 2,500 kg/s (once reached its maximum value). The other parameters are reported in Table 1. Figure 3 shows that when magma feeding decreases, also the uplift velocity decreases too, until the uplift stops and a subsidence begins. In Figure 3 we can also note that when the feeding rate is constant, the uplift velocity (slope of the blue line) slightly decreases over time. This trend can be seen more clearly in Figure 4 that shows the result of a simulation with a longer period of magma feeding and different mass flow rate history. In case of low flexural rigidity of the elastic plate, the model predicts that, even if we assume a constant feeding rate of the sill over the entire duration of the numerical experiment (e.g., 10 years), the subsidence may appear anyway, as shown by Macedonio et al. (2014). If we simulate two magmatic input with the same mass flow rate, as shown in Figure 5, can see that second uplift is smaller than the first one. In Figure 6 two minor inputs of the same size follow a main magmatic input. Under this condition the minor inputs produce a small uplift that in real cases could be close to the detection limit of standard monitoring systems. The reason why the uplift is gradually smaller in the repeated magmatic input is that the radius of the sill increases over time and each new magmatic input produces a smaller bending of the elastic plate in the central part of the sill. The results of simulations described above are similar to trends observed in calderas. For example, the dynamics provided by the model can mimic the evolution of vertical deformation in the central area of Campi Flegrei, with a good approximation (Figure 7), using appropriate magmatic inputs. At the front of the sill the vertical displacement tends to zero. When the front of the sill moves radially its propagation generates the bending of new undeformed portions of the elastic plate, which causes a transient tilt of the surface and a peak of stress in the elastic plate. Figure 8 shows the vertical and radial deformations and the stress evolution at different times of the intrusion. Figures 9, 10 show the distribution of the radial (σrr) and tangential (σθθ) stresses associated to the deformation of the elastic plate (the other components of the stress associated to the intrusion of the sill, such as σrθ are null).
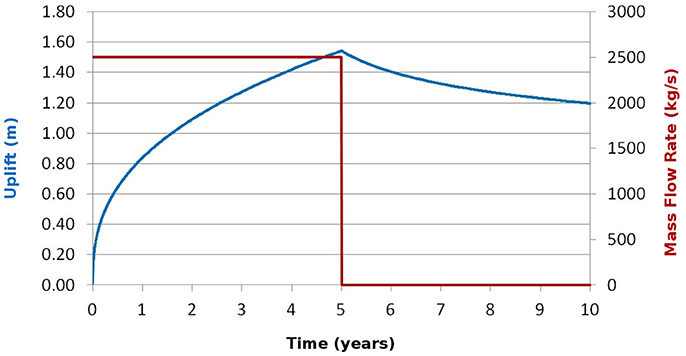
Figure 4. Plot of the uplift (blue line, left axis) over time of the center of the sill. The red line represents the mass flow rate (right axis) of magma filling the sill over time. Note that the rate of the uplift decreases even for a constant mass flow rate (2,500 kg/s).
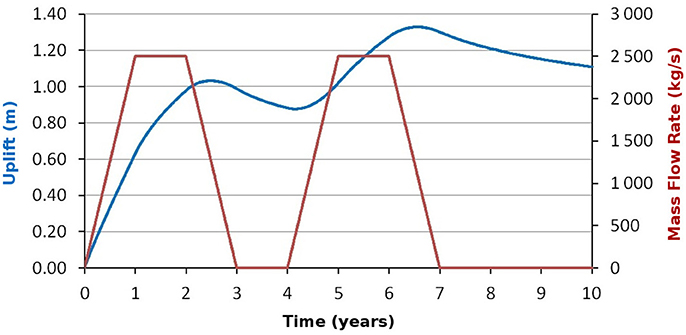
Figure 5. Simulation of two magma inputs. The blue line is the uplift (left axis) over time of the maximum uplift point (center of the sill). The red line represents the mass flow rate over time (right axis).
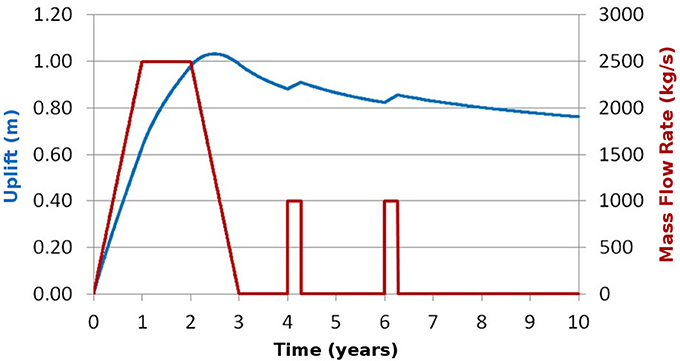
Figure 6. Simulation of the uplift in the maximum uplift point (blue line, left axis) for multiple magma inputs repeated in time. A main input is followed by two smaller magmatic inputs (red line, right axis).
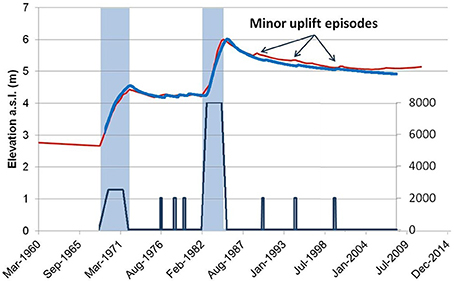
Figure 7. Comparison of the ground uplift (left axis) in the central area of the Campi Flegrei caldera (red line), measured at benchmark n.25 of the leveling network of Osservatorio Vesuviano - INGV (Del Gaudio et al., 2010) and the ground uplift obtained from a simulation (blue line), using the parameters in Table 1. The dark blue line is the mass flow rate in kg/s (right axis). The two light blue rectangles indicate the two major uplifts.
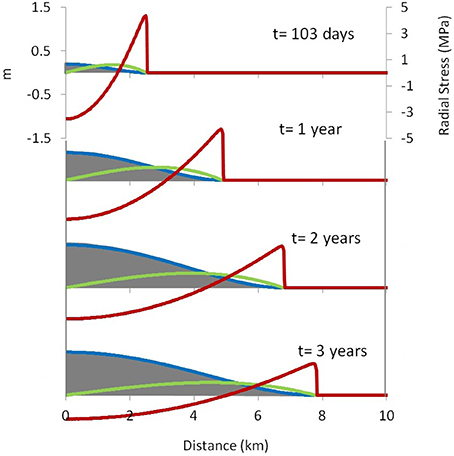
Figure 8. The sill thickness and stress at the bottom of the elastic plate obtained in the REF case simulation (Table 1; Figure 3). On the horizontal axis, the distance from the point of magma injection (km). The uplift (blue line) and the radial displacement (green line) at four different times (103 days, 1 year, 2 years, and 3 years) are shown (meters; left axis). The red lines represent the radial stress (MPa, right axis) at the base of the elastic plate (negative values for compression and positive values for traction).
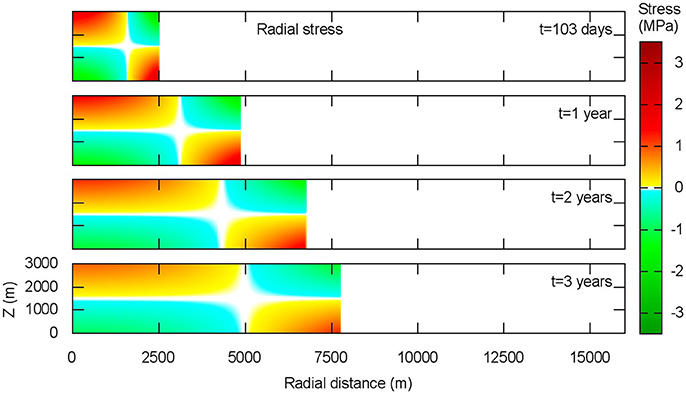
Figure 9. The distribution of the radial stress (σrr) in the elastic plate at four different times (103 days, 1 year, 2 years, and 3 years). Red indicates traction and green indicates compression.
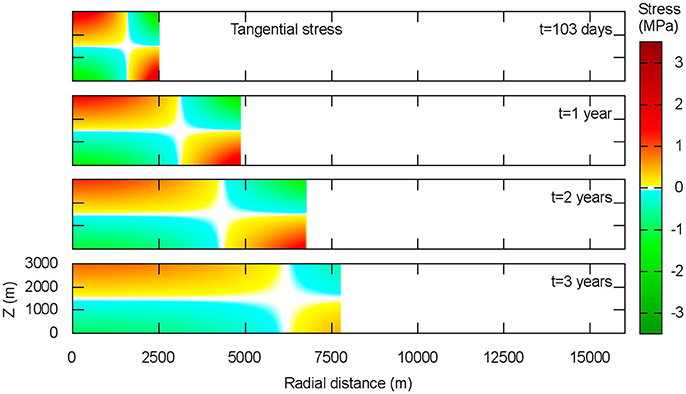
Figure 10. The distribution of the tangential stress (σθθ) in the elastic plate at four different times (103 days, 1 year, 2 years, and 3 years). Red indicates traction and green indicates compression.
Looking at the bottom of the plate, we notice that the stress is compressive at the center and tensile at the front of the sill. At the beginning of the intrusion, the stress in the elastic plate is relatively high and it is concentrated in the central part and at the front of the sill, where the plate bends. In a general case, after a given time (e.g., 103 days for the REF case) the stress starts to decrease over time, especially in the central part where the bending becomes smaller. This behavior changes if we consider a variable magma viscosity, as we will show later.
4. Role of Magma and Rock Properties
The spreading sill model shows that magma viscosity and the flexural rigidity of the rocks above the sill play an important role in modulating the ground deformation and the stress in the rock (Giudicepietro et al., 2016). The internal stress in the plate above the sill is an important factor because it may cause the rock failure and the consequent opening of eruptive vents. However, the stress in deep rocks cannot be easily measured, therefore it is usually unknown. We can only investigate the stress conditions through geophysical methods, e.g., we can retrieve the orientation of the stress tensor through the inversion of focal mechanisms of earthquakes (D'Auria et al., 2015a; Massa et al., 2016). Conversely, the ground deformation, that is considered as an indicator of stress in the rock, can be measured quite easily through various techniques. However its relationship with the stress depends on the mechanical properties of the rock body that forms the roof of the intrusion, which are often unknown. To investigate this aspect, we have carried out numerical experiments varying the rock Young's modulus and the magma viscosity to simulate the behavior of felsic and mafic calderas, following the traditional classification (Newhall and Dzurisin, 1988), also adopted by Acocella et al. (2015). It is known that the felsic calderas are usually characterized by magma with high viscosity and rocks with poorer mechanical characteristics (e.g., tuff or other pyroclastic rocks). Conversely, mafic calderas are characterized by low viscosity magma and rocks predominantly formed by lava flows, with stronger mechanical characteristics. So, following Giudicepietro et al. (2016), we perform two simulations characterized by higher magma viscosity and lower rock Young's modulus representative of the felsic calderas (Felsic) and lower magma viscosity and higher rock Young's modulus representative of the mafic calderas (Mafic). We use the same mass flow rate history of the reference case (REF) that is shown in Figure 3. The values of magma viscosity and rock Young's modulus are reported in Table 2. The results of these two simulations are compared with the REF case in Figure 11. This figure shows that under “Felsic” conditions we obtain stronger vertical deformation and lower values of stress in the rock above the sill. On the contrary, we obtain smaller vertical deformation and a larger value of stress for “Mafic” conditions.
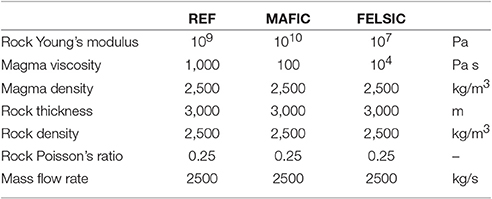
Table 2. Input parameters used for the simulations shown in Figure 11.
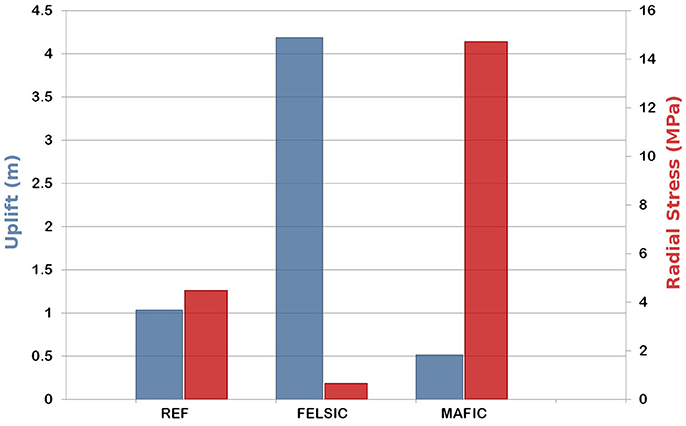
Figure 11. Maximum uplift (blue, left axis) and maximum stress (red, right axis) obtained in the simulations with high magma viscosity-low rock Young's modulus (FELSIC) and low magma viscosity-high rock Young's modulus (MAFIC) compared with the reference case (REF). For parameter setting see Table 2.
5. Effect of Magma Cooling
The cooling of magma during the intrusion of a sill is a complex process that depends on several variables such as the injection rate, the magma flow velocity, the duration of the intrusion, the thickness of the sill, the thermal conductivity of magma and rock and the temperature of the crustal environment. In order to obtain clues about the effect of cooling, that may occur during the intrusion of a sill, we consider a simulation with the same input parameters of the reference case (Table 1), in which the viscosity varies with magma temperature. We simplify the magma cooling process assuming a linear variation of the magma temperature with the distance between the sill front and the injection point. Moreover we assume that the magma temperature does not vary along the vertical direction. To estimate the viscosity variation with temperature, we use experimental data from Misiti et al. (2011), which refer to a latitic magma erupted at Campi Flegrei (Fondo Riccio eruption, about 9 ka B.P.). As a test we have arbitrarily chosen a radial temperature decrease of 33 K/km. The initial temperature is 1,230 K that corresponds to a viscosity of 1,000 Pa s, the same as the REF case. Figure 12, shows the temperature and viscosity variations with distance, assuming a water content of 3 wt% (that is consistent with the measurements of Cannatelli et al., 2007). In Figure 13 we can see that the numerical experiment with variable viscosity confines the deformation within a given radius beyond which there is almost no magma flow. In our experiment this radius is about 5.5 km, which is the order of magnitude of the radius of Campi Flegrei caldera. The effect of magma cooling produces a greater uplift of the central part of the elastic plate and highest stress values.
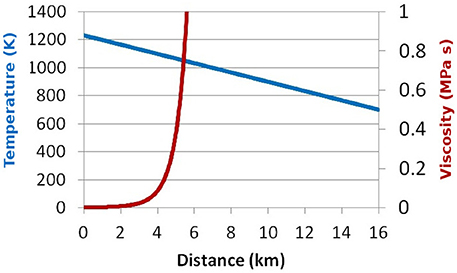
Figure 12. Viscosity of a latitic magma (red line, right axis) as a function of radial distance of the sill front from the point of magma injection, assuming a linear variation of magma temperature (blue line, left axis). The viscosity is calculated following Misiti et al. (2011).
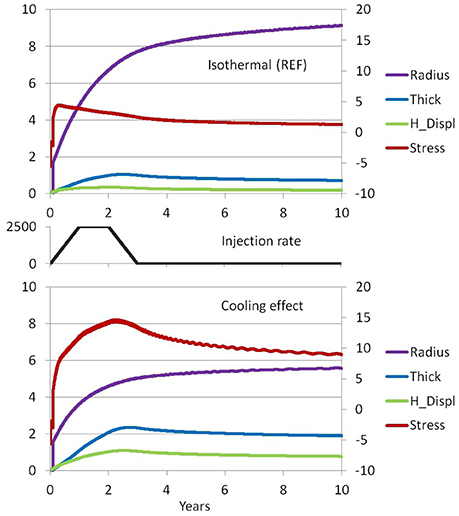
Figure 13. Comparison of results obtained with isothermal condition (top) and temperature dependent viscosity (bottom) using the same input parameters for simulating the intrusion of a sill. The red line is the maximum stress, located at the front of the sill, in MPa (right axis). The magenta line is the radius of the sill in km (left axis). The blue line is the maximum thickness of the sill, located at the center of the sill, in m (left axis). The green line is the maximum horizontal displacement (see Figure 8). In the middle plot, the magma injection rate in kg/s.
6. Implication of Sill Intrusion for Geothermal Activity
The sill spreading model is consistent with the development of a large geothermal system. Repeated intrusions of sills at shallow depth can provide a significant amount of heat and produce a large surface that can account for efficient heat transfer into the overlying rocks. Part of the heat can be transported by the gas that exsolves from magma and enters into the rock above the magma body. In general, when magma rises from a deeper source toward the surface, its pressure decreases and gas are released. Macedonio et al. (2014) estimated that, considering a magma of Campi Flegrei (Di Matteo et al., 2004), when 1 wt% of gas contained in magma exsolves, passing from 8 to 3 km of depth, the whole magma is subjected to an increase in volume of about 20%. In these conditions, the gas can accumulate at the top of the sill and may form a cap. If the rocks above the sill have a certain degree of permeability with respect to gas, the accumulation of gas at the top of the sill is temporary. In a given time, which depends on gas pressure and rock permeability, the gas can flow into the overlying rock following preferential pathways, such as fractured zones and pre-existing conduits, or through the porous medium. This degassing mode can increase the subsidence at the end of the intrusion, as it gradually decreases the volume in the region where the sill emplaced, and can power the geothermal system by supplying hot fluids (Chiodini et al., 2016). This mechanism is consistent with the dynamics of semi-plugged felsic calderas (Acocella et al., 2015), which are typically restless calderas with repeated non-eruptive unrest (e.g., Campi Flegrei).
7. Discussion
Our numerical experiments, based on the sill model proposed by Macedonio et al. (2014), show that the dynamics of unrest at calderas is consistent with the intrusion of sills at shallow depth. The proposed model can explain the subsidence that follows the uplift crises observed at calderas.
Considerations on the solubility of gas into magma, based on experimental studies (e.g., Di Matteo et al., 2004), suggest the possible separation of a gas phase inside the sill, therefore the emplacement of sills at shallow depth below the calderas is consistent with the formation of large geothermal systems, especially in semiplugged calderas (Acocella et al., 2015), where gas can gradually pass in overlying rocks, bringing with it considerable amount of heat. Repeated magmatic intrusions may induce changes in the hydrothermal system, supplying this with fluids and energy, which may affect deformation, seismicity as well as the geochemical parameters (Acocella et al., 2015). However, the relationship between the sill intrusion and the hydrothermal system is not included in the present model.
The sill intrusion model can mimic the deformation history at the center of Campi Flegrei over the last decades, as shown in Figure 7. The model was previously used to interpret GPS and InSAR data collected during the 2012–2013 volcanic unrest at Campi Flegrei (D'Auria et al., 2015b). D'Auria et al. (2015b) interpreted the ground deformation as the effect of the intrusion of a sill at shallow depth. The rock Young's modulus and the Poisson's ratio were assumed 5×109 Pa and 0.25, respectively. The model allowed the authors to estimate the volume (4.2×106 m3), the depth (about 3,100 m), and the viscosity of the intruded magma (about 30,000 Pa s) (D'Auria et al., 2015b). Maximum residual between InSar data and the model were of the order of 1 cm after a maximum uplift of about 30 cm.
In the simulations carried out in the present work, we neglected fracturing and we assumed a pure elastic behavior of the rocks. However, we investigated the role of the mechanical properties by varying the Young's module of the rock. Moreover, to account for different magma properties, we varied also the viscosity of magma for representing two types of calderas (as from Acocella et al., 2015): Felsic calderas, characterized by higher magma viscosity and lower rock Young's modulus, and Mafic calderas, characterized by lower magma viscosity and higher rock Young's modulus (see Figure 11). The Felsic and Mafic types considered here are not examples of natural calderas but they are prototypes for the numerical experiments. We adopted Young's modulus and viscosity values used in Macedonio et al. (2014) and in Giudicepietro et al. (2016), which are limit values chosen taking into account the experimental work of Hoek and Diederichs (2006), Heap et al. (2009, 2014). We chosen limit values for the rheological and mechanical parameters of the model to emphasize differences in system behavior under different conditions. Results show that the characteristics of the felsic calderas favor the occurrence of considerable ground deformations associated with lower stress values. These results are consistent with the observation that felsic calderas show remarkable deformation during non-eruptive unrest (Newhall and Dzurisin, 1988; Acocella et al., 2015).
Finally, we aim to evaluate the effect of magma cooling through simulations with variable temperature and viscosity. Taking into consideration the cooling of magma, we can see that the radius of the sill is smaller and the thickness in the central zone is greater than that of the isothermal case. Moreover, contrary to the isothermal condition, which allows a decrease of the stress over time, cooling favors the increase of the stress over time.
8. Conclusion
• We propose a model of expanding sill suitable for explaining the dynamic processes that are observed in many calderas. This result is in agreement with recent studies that highlight the important role of sill intrusions in the evolution of calderas and volcanic fields (Michaut and Jaupart, 2006; Rivalta, 2010; Corbi et al., 2015; Richardson et al., 2015; Di Vito et al., 2016; Le Mével et al., 2016; Papale et al., 2017).
• The rheological properties of magma and the mechanical properties of rock affect the stress field generated by the intrusion of the sill. This aspect is important because the evolution of the stress field affects the probability that unrest at calderas ends in eruption and controls the location of the future eruptive vents. The expanding sill model predicts that after a given time, about 100 days for our reference case (REF), the stress decreases over time. Therefore, in general, eruptions should be more likely in the early stages of unrest, as noticed by Newhall and Dzurisin (1988) and Acocella et al. (2015).
• In case of magma cooling, viscosity increases over time, especially at the front of the sill and inhibits the expansion of the sill that becomes thicker. The stress in the rock increases during magma intrusion, unlike in the case of negligible cooling (isothermal).
• The role of gas is important in modulating uplift and subsidence often observed in calderas and in transferring heat and fluids into the hydrothermal system above the sill.
Author Contributions
FG has made a substantial contribution to the conception and design of numerical experiments, in the frame of the general model proposed in the article. She make a substantial contribution in drafting the article. GM has made an important contribution in the physical aspects of fluid dynamics of magmas. MM has made an important contribution on the study of dynamic processes of active volcanic systems. The authors, working in close collaboration with each other, shared the interpretation of the results obtained from the numerical experiments carried out using the models described in the article.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a shared affiliation, though no other collaboration, with the authors and states that the process nevertheless met the standards of a fair and objective review.
Acknowledgments
Numerical simulations where performed at Osservatorio Vesuviano (INGV, Napoli) using the computing resources funded by the PON-MIUR “VULCAMED” project (PONa3_00278). The authors thank Novella Tedesco for her precious help with the English language improvements. The authors thank the Editors and the Reviewers who have helped us improve this article. This work benefited of the Agreement between Istituto Nazionale di Geofisica e Vulcanologia and the Italian Presidenza del Consiglio dei Ministri, Dipartimento della Protezione Civile (DPC). This paper does not necessarily represent DPC official opinion and Policies.
References
Acocella, V., Di Lorenzo, R., Newhall, C., and Scandone, R. (2015). An overview of recent (1988-2014) caldera unrest: knowledge and perpectives. Rev. Geophys. 53, 896–955. doi: 10.1002/2015rg000492
Amoruso, A., Crescentini, L., Linde, A. T., Sacks, I. S., Scarpa, R., and Romano, P. (2007). A horizontal crack in a layered structure satisfies deformation for the 2004–2006 uplift of Campi Flegrei. Geophys. Res. Lett. 34:L22313. doi: 10.1029/2007GL031644
Bagnardi, M., and Amelung, F. (2012). Space-geodetic evidence for multiple magma reservoirs and subvolcanic lateral intrusions at Fernandina Volcano, Galápagos Islands. J. Geophys. Res. 117:B10406. doi: 10.1029/2012JB009465
Bagnardi, M., Amelung, F., and Poland, M. P. (2013). A new model for the growth of basaltic shields based on deformation of Fernandina volcano, Galápagos Islands. Earth Planet. Sci. Lett. 377–378, 358–366. doi: 10.1016/j.epsl.2013.07.016
Bell, A. F., Greenhough, J., Heap, M. J., and Main, I. G. (2011). Challenges for forecasting based on accelerating rates of earthquakes at volcanoes and laboratory analogues. Geophys. J. Int. 185, 718–723. doi: 10.1111/j.1365-246X.2011.04982.x
Bianchi, R., Coradini, A., Federico, C., Giberti, G., Lanciano, P., Pozzi, J. P., et al. (1987). Modeling of surface deformation in volcanic areas: the 1970-1972 and 1982-1984 crises of Campi Flegrei, Italy. J. Geophys. Res. 92, 14139–14150. doi: 10.1029/JB092iB13p14139
Biggs, J., Ebmeier, S. K., Aspinall, W. P., Lu, Z., Pritchard, M. E., Sparks, R. S. J., et al. (2014). Global link between deformation and volcanic eruption quantified by satellite imagery. Nat. Commun. 5:3471. doi: 10.1038/ncomms4471
Bunger, A. P., and Cruden, A. R. (2011). Modeling the growth of laccoliths and large mafic sills: role of magma body forces. J. Geophys. Res. 116:B02203. doi: 10.1029/2010jb007648
Cannatelli, C., Lima, A., Bodnar, R. J., De Vivo, B., Webster, J. D., and Fedele, L. (2007). Geochemistry of melt inclusions from the Fondo Riccio and Minopoli 1 eruptions at Campi Flegrei (Italy). Chem. Geol. 237, 418–432. doi: 10.1016/j.chemgeo.2006.07.012
Chadwick, W. W. Jr., Geist, D. J., Jónsson, S., Poland, M., Johnson, D. J., and Meertens, C. M. (2006). A volcano bursting at the seams: inflation, faulting, and eruption at Sierra Negra volcano, Galápagos. Geology 34, 1025–1028. doi: 10.1130/G22826A.1
Chadwick, W. W. Jr., Jónsson, S., Geist, D. J., Poland, M., Johnson, D. J., Batt, S., et al. (2011). The May 2005 eruption of Fernandina volcano, Galápagos: the first circumferential dike intrusion observed by GPS and InSAR. Bull. Volcanol. 73, 679–697. doi: 10.1007/s00445-010-0433-0
Chang, W.-L., Smith, R. B., Farrell, J., and Puskas, C. M. (2010). An extraordinary episode of Yellowstone caldera uplift, 2004–2010, from GPS and InSAR observations. Geophys. Res. Lett. 37:L23302. doi: 10.1029/2010gl045451
Chiodini, G., Paonita, A., Aiuppa, A., Costa, A., Caliro, S., De Martino, P., et al. (2016). Magmas near the critical degassing pressure drive volcanic unrest towards a critical state. Nat. Commun. 7:13712. doi: 10.1038/ncomms13712
Chiodini, G., Todesco, M., Caliro, S., Del Gaudio, C., Macedonio, G., and Russo, M. (2003). Magma degassing as a trigger of bradyseismic events: the case of Phlegrean Fields (Italy). Geophys. Res. Lett. 30, 17–20. doi: 10.1029/2002GL016790
Corbi, F., Rivalta, E., Pinel, V., Maccaferri, F., Bagnardi, M., and Acocella, V. (2015). How caldera collapse shapes the shallow emplacement and transfer of magma in active volcanoes. Earth Planet. Sci. Lett. 431, 287–293. doi: 10.1016/j.epsl.2015.09.028
D'Auria, L., Giudicepietro, F., Aquino, I., Borriello, G., Del Gaudio, C., Lo Bascio, D., et al. (2011). Repeated fluid-transfer episodes as a mechanism for the recent dynamics of Campi Flegrei caldera (1989-2010). J. Geophys. Res. 116:B04313. doi: 10.1029/2010JB007837
D'Auria, L., Massa, B., Cristiano, E., Del Gaudio, C., Giudicepietro, F., Ricciardi, G., and Ricco, C. (2015a). Retrieving the stress field within the Campi Flegrei caldera (Southern Italy) through an integrated geodetical and seismological approach. Pure Appl. Geophys. 172, 3247–3263. doi: 10.1007/s00024-014-1004-7
D'Auria, L., Pepe, S., Castaldo, R., Giudicepietro, F., Macedonio, G., Ricciolino, P., et al. (2015b). Magma injection beneath the urban area of Naples: a new mechanism for the 2012–2013 volcanic unrest at Campi Flegrei caldera. Sci. Rep. 5:13100. doi: 10.1038/srep13100
Del Gaudio, C., Aquino, I., Ricciardi, G. P., Ricco, C., and Scandone, R. (2010). Unrest episodes at Campi Flegrei: a reconstruction of vertical ground movements during 1905–2009. J. Volcanol. Geotherm. Res. 195, 48–56. doi: 10.1016/j.jvolgeores.2010.05.014
Di Matteo, V., Carrol, M. R., Behrens, H., Vetere, F., and Brooker, R. A. (2004). Water solubility in trachytic melts. Chem. Geol. 213, 187–196. doi: 10.1016/j.chemgeo.2004.08.042
Di Vito, M. A., Acocella, V., Aiello, G., Barra, D., Battaglia, M., Carandente, A., et al. (2016). Magma transfer at Campi Flegrei caldera (Italy) before the 1538 AD eruption. Sci. Rep. 6:32245. doi: 10.1038/srep32245
Dvorak, J. J., and Mastrolorenzo, G. (1991). The mechanisms of recent vertical crustal movements in Campi Flegrei caldera, southern Italy. GSA Special Paper 263, 1–47. doi: 10.1130/SPE263-p1
Fialko, Y., Khazan, Y., and Simons, M. (2001). Deformation due to a pressurized horizontal circular crack in an elastic half-space, with applications to volcano geodesy. Geophys. J. Int. 146, 181–190. doi: 10.1046/j.1365-246X.2001.00452.x
Geyer, A., and Martí, J. (2008). The new worldwide collapse caldera database (CCDB): a tool for studying and understanding caldera processes. J. Volcanol. Geotherm. Res. 175, 334–354. doi: 10.1016/j.jvolgeores.2008.03.017
Giudicepietro, F., Macedonio, G., D'Auria, L., and Martini, M. (2016). Insight into vent opening probability in volcanic calderas in the light of a sill intrusion model. Pure Appl. Geophys. 173, 1703–1720. doi: 10.1007/s00024-015-1190-y
Gottsmann, J., Folch, A., and Rymer, H. (2006). Unrest at Campi Flegrei: a contribution to the magmatic versus hydrothermal debate from inverse and finite element modeling. J. Geophys. Res. 111:B07203. doi: 10.1029/2005JB003745
Heap, M. J., Baud, P., Meredith, P. G., Vinciguerra, S., and Reuschlé, T. (2014). The permeability and elastic moduli of tuff from Campi Flegrei, Italy: implications for ground deformation modelling. Solid Earth 25, 25–44. doi: 10.5194/se-5-25-2014
Heap, M. J., Vinciguerra, S., and Meredith, P. G. (2009). The evolution of elastic moduli with increasing crack damage during cyclic stressing of a basalt from Mt. Etna volcano. Tectonophysics 471, 153–160. doi: 10.1016/j.tecto.2008.10.004
Hill, D. (2006). “Unrest in Long Valley Caldera, California, 1978-2004,” in Mechanisms of Activity and Unrest at Large Calderas, vol. 269 of Special Publications, eds C. Troise, G. De Natale, and C. R. J. Kilburn (London: Geological Society), 1–24.
Hoek, E., and Diederichs, M. S. (2006). Empirical estimation of rock mass modulus. Int. J. Rock. Mech. Min. 43, 203–215. doi: 10.1016/j.ijrmms.2005.06.005
Jónsson, S. (2009). Stress interaction between magma accumulation and trapdoor faulting on Sierra Negra volcano, Galápagos. Tectonophysics 471, 36–44. doi: 10.1016/j.tecto.2008.08.005
Lagios, E., Sakkas, V., Novali, F., Bellotti, F., Ferretti, A., Vlachou, K., et al. (2013). SqueeSAR™ and GPS ground deformation monitoring of Santorini Volcano (1992-2012): tectonic implications. Tectonophysics 594, 38–59. doi: 10.1016/j.tecto.2013.03.012
Le Mével, H., Gregg, P. M., and Feigl, K. L. (2016). Magma injection into a long-lived reservoir to explain geodetically measured uplift: application to the 2007-2014 unrest episode at Laguna del Maule volcanic field, Chile. J. Geophys. Res. Solid Earth 121, 6092–6108. doi: 10.1002/2016JB013066
Lundgren, P., Usai, S., Sansosti, E., Lanari, R., Tesauro, M., Fornaro, G., et al. (2001). Modeling surface deformation observed with syntetic aperture radar interferometry at Campi Flegrei caldera. J. Geophys. Res. 106, 19355–19366. doi: 10.1029/2001JB000194
Maccaferri, F., Bonafede, M., and Rivalta, E. (2011). A quantitative study of the mechanisms governing dike propagation, dike arrest and sill formation. J. Volcanol. Geotherm. Res. 208, 39–50. doi: 10.1016/j.jvolgeores.2011.09.001
Macedonio, G., Giudicepietro, F., D'Auria, L., and Martini, M. (2014). Sill intrusion as a source mechanism of unrest at volcanic calderas. J. Geophys. Res. Solid Earth 119, 3986–4000. doi: 10.1002/2013JB010868
Manconi, A., and Casu, F. (2012). Joint analysis of displacement time series retrieved from SAR phase and amplitude: impact on the estimation of volcanic source parameters. Geophys. Res. Lett. 39:L14301. doi: 10.1029/2012GL052202
Marzocchi, W., Sandri, L., and Selva, J. (2008). BET_EF: a probabilistic tool for long- and short-term eruption forecasting. Bull. Volcanol. 70, 623–632. doi: 10.1007/s00445-007-0157-y
Massa, B., D'Auria, E., Cristiano, E., and De Matteo, A. (2016). Determining the stress field in active volcanoes using focal mechanisms. Front. Earth Sci. 4:103. doi: 10.3389/feart.2016.00103
McKee, C. O., Lowenstein, P. L., de Saint Ours, P., Talai, B., Itikarai, I., and Mori, J. J. (1984). Seismic and ground deformation crises at Rabaul Caldera: prelude to an eruption? Bull. Volcanol. 47, 397–411. doi: 10.1007/BF01961569
Menand, T. (2011). Physical controls and depth of emplacement of igneous bodies: a review. Tectonophysics 500, 11–19. doi: 10.1016/j.tecto.2009.10.016
Michaut, C. (2011). Dynamics of magmatic intrusions in the upper crust: theory and applications to laccoliths on Earth and the Moon. J. Geophys. Res. 116:B05205. doi: 10.1029/2010JB008108
Michaut, C., and Jaupart, C. (2006). Ultra-rapid formation of large volumes of evolved magma. Earth Planet. Sci. Lett. 250, 38–52. doi: 10.1016/j.epsl.2006.07.019
Misiti, V., Vetere, F., Freda, C., Scarlato, P., Behrens, H., Mangiacapra, A., et al. (2011). A general viscosity model of Campi Flegrei (Italy) melts. Chem. Geol. 290, 50–59. doi: 10.1016/j.chemgeo.2011.08.010
Newhall, C. G., and Dzurisin, D. (1988). Historical Unrest at Large calderas of the World. 1855, Pt.2. Department of the Interior, U.S. Geological Survey.
Newhall, C. G., and Hoblitt, R. P. (2002). Constructing event trees for volcanic crises. Bull. Volcanol. 64, 3–20. doi: 10.1007/s004450100173
Newman, A. V., Stiros, S., Feng, L., Psimoulis, P., Moschas, F., Saltogianni, V., et al. (2012). Recent geodetic unrest at Santorini Caldera, Greece. Geophys. Res. Lett. 39:L06309. doi: 10.1029/2012GL051286
Okada, Y. (1985). Surface deformation due to shear and tensile faults in a half-space. BSSA 75, 1135–1154.
Onizawa, S., Oshima, H., Aoyama, H., Mori, H. Y., Maekawa, T., Suzuki, A., et al. (2007). P-wave velocity structure of usu volcano: implication of structural controls on magma movements and eruption locations. J. Volcanol. Geotherm. Res. 160, 175–194. doi: 10.1016/j.jvolgeores.2006.10.005
Papale, P., Montagna, C. P., and Longo, A. (2017). Pressure evolution in shallow magma chambers upon buoyancy-driven replenishment. Geochem. Geophys. Geosyst. 18, 1214–1224. doi: 10.1002/2016GC006731
Pritchard, M. E., Jay, J. A., Aron, F., Henderson, S. T., and Lara, L. E. (2013). Subsidence at southern Andes volcanoes induced by the 2010 Maule, Chile earthquake. Nat. Geosci. 6, 632–636. doi: 10.1038/ngeo1855
Richardson, J. A., Connor, C. B., Wetmore, P. H., Connor, L. J., and Gallant, E. A. (2015). Role of sills in the development of volcanic fields: insights from lidar mapping surveys of the San Rafael Swell, Utah. Geology 43, 1023–1026. doi: 10.1130/G37094.1
Rivalta, E. (2010). Evidence that coupling to magma chambers controls the volume history and velocity of laterally propagating intrusions. J. Geophys. Res. 115:B07203. doi: 10.1029/2009JB006922
Rivalta, E., Taisne, B., Bunger, A. P., and Katz, R. F. (2015). A review of mechanical models of dike propagation: schools of thought, results and future directions. Tectonophysics 638, 1–42. doi: 10.1016/j.tecto.2014.10.003
Segall, P. (2013). “Volcano deformation and eruption forecasting,” in Remote Sensing of Volcanoes and Volcanic Processes: Integrating Observation and Modelling, vol. 380 of Special Publications, eds D. M. Pyle, T. A. Mather, and J. Biggs (London: Geological Society), 85–106.
Sobradelo, R., Geyer, A., and Martí, J. (2010). Statistical data analysis of the CCDB (Collapse Caldera Database): insights on the formation of caldera systems. J. Volcanol. Geotherm. Res. 198, 241–252. doi: 10.1016/j.jvolgeores.2010.09.003
Swanson, D. A., Casadevall, T. J., Dzurisin, D., Malone, S. D., Newall, C. G., and Weaver, C. S. (1983). Predicting eruptions at Mount St. Helens, June 1980 through December 1982. Science 221, 1369–1376. doi: 10.1126/science.221.4618.1369
Takada, Y., and Fukushima, Y. (2013). Volcanic subsidence triggered by the 2011 Tohoku earthquake in Japan. Nat. Geosci. 6, 637–641. doi: 10.1038/ngeo1857
Thorey, C., and Michaut, C. (2014). “Effect of a temperature-dependent viscosity on the spreading of laccoliths,” in AGU Fall Meeting Abstracts, vol. 1 (American Geophysical Union), 4751.
Thorey, C., and Michaut, C. (2016). Elastic-plated gravity currents with a temperature-dependent viscosity. J. Fluid Mech. 805, 88–117. doi: 10.1017/jfm.2016.538
Todesco, M., Costa, A., Comastri, A., Colleoni, F., Spada, G., and Quareni, F. (2014). Vertical ground displacement at Campi Flegrei (Italy) in the fifth century: rapid subsidence driven by pore pressure drop. Geophys. Res. Lett. 41, 1471–1478. doi: 10.1002/2013GL059083
Trasatti, E., Casu, F., Giunchi, C., Pepe, S., Solaro, G., Tagliaventi, S., et al. (2008). The 2004-2006 uplift episode at Campi Flegrei caldera (Italy): constraints from SBAS-DInSAR ENVISAT data and Bayesian source inference. Geophys. Res. Lett. 35:L07308. doi: 10.1029/2007GL033091
Trasatti, E., Polcari, M., Bonafede, M., and Stramondo, S. (2015). Geodetic constraints to the source mechanism of the 2011-2013 unrest at Campi Flegrei (Italy) caldera. Geophys. Res. Lett. 42, 3847–3854. doi: 10.1002/2015gl063621
Unglert, K., Savage, M. K., Fournier, N., Ohkura, T., and Abe, Y. (2011). Shear wave splitting, vp/vs, and GPS during a time of enhanced activity at Aso caldera, Kyushu. J. Geophys. Res. 116:B11203. doi: 10.1029/2011JB008520
Voight, B. (1988). A method for prediction of volcanic eruptions. Nature 332, 125–130. doi: 10.1038/332125a0
Voight, B., and Cornelius, R. R. (1991). Prospects for eruption prediction in near real-time. Nature 350, 695–698. doi: 10.1038/350695a0
Keywords: sill intrusion, caldera dynamics, unrest at calderas, volcanic process modeling, magma fluid dynamics, magmatic reservoir evolution
Citation: Giudicepietro F, Macedonio G and Martini M (2017) A Physical Model of Sill Expansion to Explain the Dynamics of Unrest at Calderas with Application to Campi Flegrei. Front. Earth Sci. 5:54. doi: 10.3389/feart.2017.00054
Received: 16 December 2016; Accepted: 09 June 2017;
Published: 04 July 2017.
Edited by:
Gilda Maria Currenti, Istituto Nazionale di Geofisica e Vulcanologia, ItalyCopyright © 2017 Giudicepietro, Macedonio and Martini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Flora Giudicepietro, ZmxvcmEuZ2l1ZGljZXBpZXRyb0Bpbmd2Lml0
 Flora Giudicepietro
Flora Giudicepietro Giovanni Macedonio
Giovanni Macedonio Marcello Martini
Marcello Martini