
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Earth Sci., 06 June 2017
Sec. Geochemistry
Volume 5 - 2017 | https://doi.org/10.3389/feart.2017.00043
This article is part of the Research TopicDeep Carbon in Earth: Early Career Scientist Contributions to the Deep Carbon ObservatoryView all 17 articles
Geo-fluids consisting of C-O-H volatiles are the main mode of transport of mass and energy throughout the lithosphere and are commonly found confined in pores, grain boundaries and fractures. The confinement of these fluids by porous media at the length scales of a few nanometers gives rise to numerous physical and chemical properties that deviate from the bulk behavior. Studying the structural and dynamical properties of these confined fluids at the length and time scales of nanometers and picoseconds, respectively forms an important component of understanding their behavior. To study confined fluids, non-destructive penetrative probes are needed. Nuclear magnetic resonance (NMR) by virtue of its ability to monitor longitudinal and transverse magnetization relaxations of spins, chemical shifts brought about by the chemical environment of a nucleus, and measuring diffusion coefficient provides a good opportunity to study dynamics and chemical structure at the molecular length and time scales. Another technique that gives insights into the dynamics and structure at these length and time scales is neutron scattering (NS). This is because the wavelength and energies of cold and thermal neutrons used in scattering experiments are in the same range as the spatial features and energies involved in the dynamical processes occurring at the molecular level. Molecular Dynamics (MD) simulations on the other hand help with the interpretation of the NMR and NS data. Simulations can also supplement the experiments by calculating quantities not easily accessible to experiments. Thus, using NMR, NS, and MD simulations in conjunction, a complete description of the molecular structure and dynamics of confined geo-fluids can be obtained. In the current review, our aim is to show how a synergistic use of these three techniques has helped shed light on the complex behavior of water, CO2, and low molecular weight hydrocarbons. After summarizing the theoretical backgrounds of the techniques, we will discuss some recent examples of the use of NMR, NS, and MD simulations to the study of confined fluids.
All over Earth's crust, fluids have a dominating role in transporting Earth's energy and mineral reserves (Liebscher and Heinrich, 2007). Fluids with volatile carbon, hydrogen and oxygen (C-H-O) species are found in the lithosphere in large proportions besides different electrolytes and silica (Cole et al., 2013). The effects of coupled reactive-transport processes seen in geological systems vary by the properties and reactivity of these crustal fluids over wide ranges of different parameters including temperature, pressure and fluid composition. The comparative strengths of complicated molecular scale interactions in geologic fluids, and the changes in those interactions with temperature, pressure, and fluid composition, are vital keys for the observed fluid properties. Complicated intermolecular interactions of C-H-O result in their distinctive thermophysical behaviors, such as large deviations in the volumetric properties from ideality, vapor-liquid equilibria, and critical phenomena.
A fundamental goal in geochemistry is to form a comprehensive and fundamental understanding of the thermophysical properties, structures, dynamics, and reactivity of complex geologic fluids and molecules (water and other C-H-O-N-S fluids, electrolytes, and organic-biological molecules) at different length scales. Hydrocarbons, such as methane and ethane, CO2, and aqueous solutions can fill the pores or fractures of numerous types of complex heterogeneous Earth materials present in the systems outlined above. This accessible porosity within the solids has a range of length scales (d as pore diameter or fracture aperture) including micro-, meso-, and macroporous regimes (d < 2.0 nm, 2.0 < d < 50 nm, and d > 50 nm, respectively, as defined by IUPAC). There are a number of factors determining the way fluids, and with them reactants and products of intrapore alterations move into and through these nano-environments, wet, and finally adsorb and react with the solid surfaces. Usually, the behaviors of confined fluids are affected by the size, shape, and topology of confinement and by the competition of liquid-liquid and liquid-matrix interactions upon getting closer to the surfaces (Cole et al., 2004; Vogel, 2010). Fundamental understanding requires detailed characterization of these confinement effects. There is a common consideration that the combined structure and behaviors of bulk fluids are varied by solid substrates, confinement between two mineral surfaces, or in narrow pores due to the interplay of the length scales of the fluid and the confinement length scale (Gelb et al., 1999).
Various interactions of guest molecules, such as alkanes, CO2, and water with the pore walls have long been an area of research. The continued research efforts cover not only experimental but also computational studies for a better understanding of the confined systems to explore new applications in various areas ranging from catalytic conversion to selective adsorption (Kärger et al., 2014). In attempting to analyze the nanoconfined fluid behavior, there are two important aspects: detailed characterization of the nanoporous host material and deviation of confined fluid behavior from that of the bulk. In the current review article, we will summarize different aspects of confinement effects on the fluid behavior. First, we will give a brief introduction on different nanoporous materials. Next, we describe three techniques that contribute significantly to our ability to probe fluid-solid interactions in nanoporous media or at surfaces: nuclear magnetic resonance (NMR) spectroscopy, neutron scattering (NS), and molecular dynamics (MD) simulations. Finally, we will provide some examples of contributions to a study of fluids in confined structures as studied by these techniques.
Nanoporous materials can be divided into three broad groups: natural Earth materials, modified natural materials, such as select clay minerals, and engineered synthetic proxies (see Table 1). These nanoporous materials provide substrates for studying confined fluid behaviors. However, these nanoporous materials have properties, such as pore diameter, pore volume, surface chemistry, etc. that can vary or might be tuned by various ways, such as synthetic conditions or even modifications. Because of their complexity, basic characterization of the nanoporous materials in detail is required.
Among the nanoporous materials, natural clays form an important subset of porous systems with tunable properties and relatively lower surface area with respect to that of synthetic nanoporous silica-type proxies. The layered structure of the clay minerals offers the opportunity to study the interaction between different types of fluids and substrates varying in chemical and physical properties (Gupta and Bhattacharyya, 2012). Clay minerals are able to intercalate chemical species into their interlayer spaces thereby changing the layer dimensions. The layered structure of clays can be manipulated by introducing stable pillars in the interlamellar region. This leads to stability of the pore structure in pillared clays which form an ideal proxy material to study two-dimensional confinement (Cool and Vasant, 1998, see Figure 1A). In particular, kaolinite and montmorillonite clays have been used to study fluid-solid interactions at surfaces or in the interlayers. Kaolinite structure is composed of a tetrahedral silica sheet interchanging with an octahedral alumina sheet forming the 1:1 clay mineral sheet (Brigatti et al., 2013; Ok et al., 2014). Montmorillonites, an important class of clays with both swelling and shrinking abilities, are 2:1 phyllosilicates where the perfect stoichiometry is given as [(Na, Ca)0.33(Al, Mg)2(Si4O10)(OH)2.nH2O]. Montmorillonites can enlarge and compress the interlayer space by swelling and shrinking where the major driving force is the uptake and release of H2O into and out of interlayers (Loring et al., 2014). In addition, acids can activate the clays so that clays are useful as solid catalysts (Breen and Moronta, 1999). It is important to note that depending on the geographical origin, clays differ in elemental composition, charge density, and locus of isomorphous substitution. For example, SWy-2 (Wyoming), STx-1 (Texas), and SAz-1 (Cheto, Arizona) bentonites have dioctahedral structure, while SWy-2 is aluminum rich, STx-1 has low iron content, and SAz-1 is magnesium rich (Breen and Moronta, 1999). These aforementioned unique properties of the clay minerals make them ideal natural nanosystems, to explore wetting, transport and reactivity of confined fluids.

Figure 1. Transmission electron microscope (TEM) images of some porous materials with well-ordered pore structures (A–C) or an irregular pore network (D). (A) Pillared clay with a layered structure leading to interlamellar porosity; (B) ZSM-5 zeolite with pores in the form of channels with diameter of 0.5 nm; (C) MCM–41 with pores in the form of channels of variable diameter; and (D) Silica aerogel with irregularly shaped mesopores.
In addition to the porous natural clay minerals, there are also synthetic or modified natural porous proxies available for use in the studies of confined fluids. Among the synthetic porous systems, zeolites, for example, are considered a class of inorganic microporous crystalline materials with wide applications in gas separation, catalysis, petrochemistry, magnetism, medicine, and microelectronics (Zones and Davis, 1996; Davis, 2002; Čejka et al., 2010; Meng and Xiao, 2014; Li et al., 2015). Zeolites are synthesized from silicate, aluminosilicates or kaolinites hydrothermally (Johnson and Arshad, 2014; Meng and Xiao, 2014). Zeolite framework consists of four connected frameworks of AlO4 and SiO4 tetrahedra, and these four frameworks are joined, by sharing oxygens (Johnson and Arshad, 2014). This gives rise to an intricate structure of connected porous networks. Further these networks give rise to various pore shapes like spherical sodalite cages found in Na-Y type zeolite or channel like pores as in ZSM-5 zeolites (Figure 1B).
Although the confined molecules may not always form ordered structure in a micropore, micropores can be organized in an ordered pattern utilizing the periodicity of a crystal. This establishes long-range regular arrangement of the molecules under confinement and collaborative molecular assembly in microporous matrix systems (Ueda et al., 2012). Such a candidate of porous system with well-defined pore structure and high crystallinity is isoreticular metal-organic frameworks (IRMOFs), a series of porous compounds with regular and homogeneous pores (Eddaoudi et al., 2001). Among the IRMOFs, [Zn4O(BDC)3]n (BDC = benzene-1,4-dicarboxylate) (IRMOF-1) is the prototype of a series of these compounds where zinc oxide and terephthalic acid moieties are three-dimensionally connected with each other establishing a porous framework resembling “a jungle gym” (Ueda et al., 2012).
One of the most utilized and investigated nanoporous matrix is mesoporous silica materials, a class of nanoporous materials with tunable pore sizes, large surface areas, and even controllable particle size and shapes (Asefa and Tao, 2012). These materials can exhibit uniform cylindrical pores in the form of channels as in MCM-41 (Figure 1C) or they can have irregularly shaped pore structure as in the case of silica aerogel (Figure 1D). These mesoporous materials have gained widespread interest due to their potential applications as supports for functional novel materials (Al-Othman, 2012). Because of their high surface areas, these materials might be used as hosts to confine fluids. In this regard, these materials are ideal model engineered proxies in studying fluid behavior under confinement, which has significance in different areas including physical chemistry and geochemistry.
These natural, synthetic, and originally natural but synthetically or thermally modified nanoporous matrix systems have been utilized as ideal models for studying various fluids ranging from methane, CO2 to H2O upon confining the fluids into the nanopores of these matrix systems. A summary of some of representative nanoporous materials is provided along with their properties in Table 1. In what follows, after introducing the NMR, NS, and MD simulation techniques, we discuss some examples of their use in the studies of molecular confinement in different pore types mentioned above. The intent is not to provide an exhaustive review of all such studies but rather present only a very few key examples.
Atomic nuclei are positively charged and have an intrinsic angular momentum. This gives rise to a magnetic dipole which is referred to as nuclear spin (James, 1998). A nuclear spin interacting with an external strong static magnetic field B0 undergoes precession with a frequency called the Larmor frequency ω0 around the field direction. Besides interaction with the external magnetic field, the spin experiences internal electric and magnetic fields so that the resonance frequency can be moved by a frequency ω relative to ω0 (Macomber, 1998). For conducting NMR measurements, radio frequency (rf) pulses are employed to control the magnetization of a nuclear spin ensemble.
Upon excitation of the spin ensemble, relaxation processes restore the equilibrium magnetization. The characteristic times describing the relaxation of the magnetization vector components parallel and perpendicular to the external magnetic field (B0) are defined as longitudinal (T1) and transverse (T2) magnetization relaxation times. T1 and T2 values of molecules depend on fluctuations of the NMR interactions (spin-lattice and spin-spin) that arise from molecular motion. Because of that, T1 and T2 measurements have become common and traditional methods to investigate molecular reorientation not only in pure bulk state but also in confined space (Abragam, 1961; Freedman and Heaton, 2004; Vogel, 2010; Walbrecker and Behroozmand, 2012). The T1 distributions reflect the complex composition of different systems, such as crude oils and the distribution of pore sizes in sedimentary rocks (Freedman and Heaton, 2004). For water-saturated rocks, the surface interaction is usually dominant and provides a mechanism for estimating pore-size distributions from T1 distributions (Allen et al., 1997). T2 decaying curves are also correlated to viscosity of different complex mixtures as in the case of crude oil (Freedman and Heaton, 2004). In addition, when samples of saturated porous media are measured, the amplitude of the T2 measurements is directly proportional to porosity, and the decay rate is related to the pore size and the fluid type and its viscosity in the pore space. Short T2 times generally indicate small pores with large surface-to-volume ratios and low permeability. Conversely, longer T2 times indicate larger pores with higher permeability (Anovitz and Cole, 2015). Table 2 summarizes some of the NMR techniques commonly employed for studying both nanoporous matrix systems and confined fluids relevant to geochemistry.
For NMR relaxation in liquid-dominated geologic systems, it is usually supposed that relaxation happens in the rapid diffusion regime (Behroozmand et al., 2014). In the case of rapid diffusion, the net observed relaxation rate for a single pore is as follows,
where 1/T1B is the relaxation rate of bulk water, S/V is the surface-area-to-volume of the pore (inversely proportional to the pore radius rpore), ρ1 is the longitudinal surface relaxivity (Brownstein and Tarr, 1979). Similar to 1/T1, the transverse relaxation rate 1/T2 is the rate at which protons dephase during the return process to equilibrium. The expression for 1/T2 in this way contains an additional term to explain internal magnetic field gradients G involved by diffusing protons:
Here, ρ2 is the transverse surface relaxivity, 1/T2B is the relaxation rate of bulk water, D is the self-diffusion coefficient of water, γ is the gyromagnetic ratio of the hydrogen nucleus, and tE is the echo time, a timing parameter of the measurement. Relaxation in geologic systems with insignificant magnetic susceptibility is governed by surface relaxation, where the expression for 1/T2 becomes (Grunewald and Knight, 2009):
Compared to diffusion, NMR longitudinal relaxation time (T1) is more sensitive, and gives insight into more localized movements of confined molecules, such as translation and rotation on a time scale comparable to the reciprocal of the NMR angular frequency (approximately 1 ns) (Slichter, 1990; Corsaro et al., 2013). Longitudinal relaxation itself is an energy driven process, and is a measure of the dipolar interactions of the spins with the local environments (Corsaro et al., 2013). There are various molecular motions including dipole-dipole interactions, spin-rotation interactions, scalar-coupling, chemical shift anisotropy, and possible interaction due to presence of some paramagnetic substances in natural systems that contribute to T1 in liquids (Inlow et al., 1975). It was also argued by Kleinberg et al. (1994) that nucleus-electron interactions rather than pore dimensions govern the proton relaxation rate of pore-confined fluids in natural systems. In attempting to characterize the porous silica glass, for instance, D'Orazio and co-workers have focused on different degrees of filling the porous material with distilled water by both diffusion NMR and NMR relaxation measurements. Both longitudinal (T1) and transverse (T2) relaxation measurements revealed linear behavior with respect to the degree of fluid filling down to monolayer coverage. This was explained by the homogeneity of pore space leading to equal distribution of water (Bhattacharja et al., 1989; D'Orazio et al., 1990a,b). It is also well-known that nanoporous silica, for example, is heterogeneous with surface –OH groups as revealed by solid-state magic angle spinning (MAS) cross-polarization (CP) 29Si NMR (Sindorf and Maciel, 1983).
Nuclear magnetic resonance (NMR) provides a non-invasive method of probing the geometry of porous media (Callaghan et al., 1991; Cotts, 1991; Vogt et al., 2002; Sen, 2004). NMR spectroscopy aids in the description and classification of the structures and assembly of the porous spaces over various nanometer scales, and hence contributes to a better description of how fluids are confined into the nanopores and how the fluid molecules move in the confined state within the pores (Packer, 2003). Thus, by measuring the limitation inflicted on the diffusive and relaxation activities by boundaries where particles reside, information directly related to the characteristics of the pore space is obtained (Packer, 2003; Song, 2007; Kittler et al., 2014).
Another NMR technique of interest is the pulsed field gradient (PFG) NMR. The PFG method measures translational diffusion, which is a random (stochastic) movement of molecules due to internal kinetic energy. Translational diffusion is the most basic type of transport seen in both natural and industrial systems (Hawlicka, 1995; Price, 1997). Due to heterogeneities in magnetic susceptibility of samples, such as porous materials, internal gradients will be induced, and the measured diffusion coefficient will be shorter than the real diffusion coefficient (Cotts, 1989). In order to overcome this problem, stimulated echo (STE) PFG sequence is utilized. PFGSTE sequence is considered as a three-90° pulse sequence consisting of three intervals: prepare, the store, and the read intervals (Tanner, 1970; Sørland et al., 1997). PFGSTE is a well-established NMR method, and has been utilized for measuring diffusivity in porous media. Moreover, the echo signal measured in PFGSTE is proportional to the self-intermediate scattering function (Callaghan, 1991), which, as we shall see later is accessible in a NS experiment and can be calculated from MD simulations. Thus, the measured signal in PFGSTE provides a link between NMR and NS experiments. However, as the length and time scales accessible with the two techniques are different, they can be used to obtain complementary information. The interested reader should refer to the literature work for a detailed explanation of the technique (Tanner, 1970; Sørland et al., 1997).
It is also possible to employ MAS NMR for narrowing line-widths of NMR spectra, which could become broader due to inhomogeneity in heterogeneous systems consisting of confined fluid and nanoporous matrices. MAS NMR also helps with eliminating anisotropic contributions in NMR spectra, and extracting more information about the heterogeneous systems. In liquids, molecules reorient themselves rapidly. In solution NMR, rapid tumbling of the molecules average out molecular orientation dependent anisotropic interactions to zero on the NMR time scale yielding sharply defined spectral lines. In “true solids,” there is no such motion, and solid-state NMR, instead, gives broader spectral lines that limit most information of interest. In order to achieve similar information for a solid like we observe for liquid samples, mechanical spinning of the solid sample about an axis making a certain angle with the direction of the external magnetic field can lead to a dramatic reduction of the NMR linewidth. Mechanical rotation at any angle by itself is not sufficient enough due to the molecular orientation dependence of the form (3cos2θ-1)/2, which is known as the second order Legendre polynomial, and where θ is the angle that describes the orientation of the spin interaction tensor by reference to the static magnetic field. When the angle is equal to 54.74 degrees, that is the sample is spun at the “magic angle” from where the name of the technique implies, it becomes possible to remove the effects of chemical shift anisotropy, both homonuclear and heteronuclear coupling effects and to narrow lines from quadrupolar nuclei (Schmidt-Rohr and Spiess, 1994; Duer, 2004).
In addition to studying confined behavior of gas molecules by NMR spectroscopy, there are also contributions on fluid behavior in liquid state under confinement. PFG NMR spectroscopy, which is sometimes described as Pulsed Gradient Spin Echo (PGSE) or Diffusion Ordered SpectroscopY (DOSY) (Galvosas et al., 2001), has become a preferred technique for exploring the behavior of confined molecules in porous systems and has been commonly employed in scientific efforts on zeolites (Vasenkov et al., 2001) and Mobil Catalyst Material (MCM-41) based mesoporous silica systems (Stallmach et al., 2000). DOSY NMR determines diffusion coefficient based on the following equation:
where I is the observed signal intensity for the gradient power g, I0 is signal intensity for zero gradient power g, D is diffusion coefficient, γ is gyromagnetic ratio of the observed nuclei, δ is duration of PFG, and Δ is diffusion time (Kuchel et al., 2012).
By proper insertion of pulsed magnetic field gradients of duration δ, intensity g, and observation time t in the defocusing and refocusing period of the NMR pulse sequence, the monitored spin-echo becomes dependent on the translational motion of the molecules that move the nuclear spin under examination (Stallmach et al., 2000, 2001). Vogt et al. (2002) studied diffusion of water and hexadecane in medium and coarse sands from glacial sand deposits in central Germany. Due to the limitation of the diffusion path at the pore/grain interface, the measured diffusion coefficient in the confined area/volume of the pores depends on the observation time t. Using the “short-time diffusion” model, surface-to-volume (S/V) ratios were extracted from diffusion measurements, and it was found that the S/V ratios were independent of fluid and were in agreement with known geometrical properties of the sand grains. Simultaneous measurements of longitudinal magnetic relaxation (T1) revealed dependence of T1 on chemical properties of the fluid/grain interface, which did not help with quantification of geometrical characteristics of the pore/grain interface in the uncombined deposits.
However, heterogeneity limits performing diffusion NMR experiments of mixtures within porous materials (Pampel et al., 2005; Fernandez et al., 2008). In these heterogeneous porous matrices, T2 decays due to not only a continuous dipolar interaction between the spins under investigation but also differences in the interior magnetic fields. These effects, including the limitation in the mobility of the guest molecules, broaden the NMR signal and this yields reduced resolution in the NMR spectra (Pampel et al., 2005; Fernandez et al., 2008). Applying PFG and MAS techniques on the same probe solves this problem (Nivarthi et al., 1994; Pampel et al., 2003; Gaede and Gawrisch, 2004). MAS PFG NMR allowed, for instance, investigating complex formation in an acetone-alkane mixture, which is restricted to nanoporous host systems (Fernandez et al., 2008) and molecular diffusion in zeolites (Pampel et al., 2005). A more interesting MAS probe without FG was designed to investigate the evolution of adsorption of fluids on nanoporous solids (Xu et al., 2007). The results obtained by this method showed clearly the viability of a new technique for conducting in situ solid-state NMR investigations of adsorption processes into nanoporous host systems and possible subsequent reactions.
One of the NMR relaxometry techniques applied for studying confined fluids is fast field-cycling (FFC). FFC NMR relaxometry is the method of choice for gaining insight into the frequency dependence of relaxation rates. Because of that it is also considered as nuclear magnetic relaxation dispersion (NMRD). The advantage of the longitudinal relaxation rate (1/T1) as a function of large frequency ranges is to isolate the typical NMR dispersion properties related to various processes of molecular dynamical behaviors (Kimmich and Anoardo, 2004; Steele et al., 2015). Fluid dynamics at the solid interface, transport in confined medium (filtration, imbibition, and conduction) (Korb, 2006), and phase transitions in confinement (Diakova et al., 2012) are some examples probed by FFC NMR technique. For the details of the FFC NMR applications on confined fluids, the interested reader could refer to the review articles by Steele et al. (2015) and Kimmich and Anoardo (2004).
Thermal and cold neutrons, because of their characteristic wavelength being of the order of interatomic spacing in a crystal and their energy matching that of elementary excitations at molecular level, offer an ideal opportunity to study the structure and dynamics of materials with the help of NS (Bacon, 1975). Moreover, because the scattering of neutrons depends on interaction with the nucleus, rather than from the electron cloud in an atom, the NS cross sections are independent of the atomic number of the scatterer. This makes the study of lighter elements, in particular hydrogen, possible unlike in X-ray scattering where the scattering due to light elements is mostly obscured by heavier elements present in the sample. Moreover, because the NS cross sections are dependent on the nature of the nucleus, isotopic contributions in a NS experiment can be distinguished. All these properties make neutrons an ideal tool to probe the structure and dynamics in solids and liquids.
Neutron beams used to interrogate samples can be obtained from the nuclear chain reactions taking place in a nuclear reactor, after moderating them to lose energy by about six orders of magnitude to a few millielectron volts (meV)1. Another high flux source of neutrons is a spallation source where a highly energetic proton beam strips off neutrons from a target material. Several countries run reactor based and spallation based neutron sources with user programs that cater to the study of materials. Spallation sources are present in USA, UK, Japan, Switzerland and Sweden (upcoming), whereas reactor based sources are present in USA, Canada, France, Germany, Hungary, India, Indonesia, South Korea, Japan, and Australia2. The concept of a NS experiment is shown in the schematic below (see Figure 2).
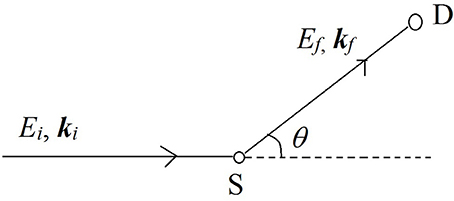
Figure 2. A simple schematic of a neutron scattering experiment. A beam of neutrons with energy Ei and momentum ħki is scattered by the sample (S) and after exchanging some energy and momentum with the sample, the beam is detected by the detector (D) with a final energy Ef and momentum ħkf. The scattering event deflects the path of the neutron beam by an angle θ which defines the wavevector transfer in the scattering event.
Neutrons with a well-defined energy and momentum vector from the source are scattered by the material sample (S) and are detected by the detector (D). The difference in energy (E = Ei-Ef) and momentum (ℏQ = ℏki-ℏkf) of the neutrons before and after the scattering event is recorded using a variety of methods3. These differences in energy and wave-vector encode the information about the structure and dynamics of molecules in the scattering sample. The reader is referred to literature overviews by Bacon (1975), Bée (1988), and Vogel and Priesmeyer (2006) for further technical details on the methods of recording the energy and momentum transfers.
In general, what is measured with the detector is the double differential cross section, which can be defined as the probability that a neutron with incident energy Ei is scattered in a direction Ω within a solid angle dΩ after an exchange of energy within the range ℏω = E and ℏ(ω+dω). Further, it can be shown that this double differential cross section is proportional to a quantity, called scattering law S(Q,ω) which is a property of the scattering sample alone. The scattering law is related to the van Hove correlation function G(r,t), which gives the probability of finding a particle at a position r, given that some other or the same particle was at origin at time t = 0. The van Hove correlation function thus contains the complete information on the structure and dynamics of molecules in a sample. Fourier transforming the van Hove correlation function in space converts it into a function in the reciprocal space, called the intermediate scattering function I(Q,t). Taking another Fourier transform in time gives the scattering law. As we shall see later, the intermediate scattering function can be calculated directly from the trajectories obtained in an MD simulation and thus serves a link between the experiments and simulations.
Depending on whether the neutrons detected after a scattering event are discriminated for their energies or not, the scattering experiment can be used to obtain information about dynamics or structure, respectively, in the sample. Further, the inelastic scattering experiments, in which energy discrimination is made for the scattered neutrons, can be used to study either stochastic or periodic motions of the molecules in the sample. The stochastic motion can be studied using a small exchange of energy between the neutrons and the sample leading to a broadening of the elastic line (E = 0 in the spectrum) on either side. In practice, the elastic line has a finite width (resolution) due to the characteristics of the instrument. The stochastic molecular motion in the sample causes a further broadening of the elastic line over resolution, which is called quasielastic broadening (see Figure 3). A scattering technique, which focuses on this broadening to study stochastic molecular motions, is called quasielastic neutron scattering (QENS). Examples of stochastic motion include diffusion and random rotational jumps that make up the rotational motion. Periodic motions on the other hand include the vibrational stretching, bending of molecules. These motions give rise to a definite non-zero energy exchange between the neutrons and the molecules in the sample and lead to non-zero energy peaks in the spectrum. The scattering experiments designed to study these non-zero energy (inelastic) peaks are called inelastic neutron scattering (INS) experiments. A cartoon schematic depicting these differences is shown in Figure 3. Neutron spin echo (NSE) is another technique, which directly measures the difference in the energies of the neutrons before and after the scattering event instead of measuring them separately. Measuring the energy transfer directly improves the energy resolution dramatically. As it is used to measure stochastic motions, NSE is considered equivalent to QENS but with improved resolution and thus an ability to study much slower molecular motion. Further, as this technique measures the intermediate scattering function instead of scattering law, the interpretation of experimental data is more straightforward. A detailed discussion of NSE as a tool to study molecular motion can be found in Richter et al. (2005).
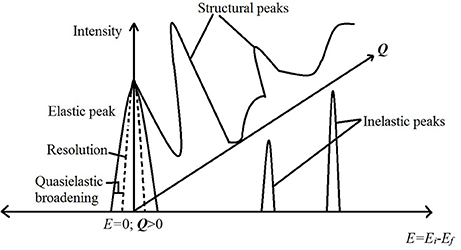
Figure 3. A cartoon schematic depicting the information obtained from a neutron scattering experiment. The horizontal axis is the energy transfer while the vertical direction depicts intensity of scattered neutrons. The third dimension going into the page is the Q axis. Peaks on the Q axis are obtained by not discriminating the scattered neutrons in energy (i.e., integrating all energies) and are structural peaks revealing information about the structure in the sample. The peak at E = 0 is the elastic peak. A broadening of this elastic peak contains information on the stochastic motion of molecules and is measured in quasielastic neutron scattering (QENS). The peaks at non-zero energies are due to periodic motion of molecules in the sample and are measured in an inelastic neutron scattering (INS) experiment.
With a variety of instruments available, a typical NS experiment may cover a range of length scales from a few angstrom (diffraction) to a few microns (small angle neutron scattering; low Q region of the Q axis in Figure 3). The time range covered ranges between a few hundreds of femtosecond (high energy inelastic) to a few microseconds (QENS with NSE instruments). We do not include examples of neutron diffraction experiments here due to limitations of space.
With the advent of economical computers, large numerical calculations have become possible. This has given rise to a large number of studies using numerical calculations for a deterministic system at small as well as large length scales. These numerical calculations can be used to model a variety of systems from quarks to galaxies and covering a variety of fields from physics to cognitive psychology and social sciences. One particular method of simulation pertinent to the study of matter at molecular level is the classical MD simulation. In a classical MD simulation, Newton's equations of motion for a system made up of molecules representing the material of interest are solved numerically to obtain the trajectories of the constituent molecules. A plethora of algorithms are available to solve these equations of motion. A detailed discussion of these algorithms and their advantages can be found elsewhere (Hoover, 1986; Allen and Tildesley, 1987; Frenkel and Smit, 2001). For a conservative system made up of a large number of molecules, the equation of motion can be written as
where Ui is the total potential energy of molecule i due to all other molecules. Once this potential energy is determined for a system, the equation can be solved numerically to yield trajectories (i.e., ri as a function of time). Thus, two important inputs for the simulation are the starting positions [ri(0)] of molecules comprising the system and the potential energy (Ui) of interaction of the molecules (called Force Field). The starting positions are usually defined on a regular lattice, which, takes on a more random structure as the simulation progresses. The force field is normally determined by empirical fitting of properties calculated from the simulations with their experimentally determined values. For example, Martin and Siepmann (1998) have obtained force field for alkanes by fitting the experimental data for critical temperatures and saturated liquid densities with simulated values. Similarly, a variety of force fields have been derived for water which include simple point charge (SPC) by Berendsen et al. (1987), TIP3P by Jorgensen et al. (1983) and their extensions. Guillot (2002) has compiled a list of various force fields available for modeling water. Once the starting positions have been set and the force field chosen, the equations of motions are solved numerically by choosing a time step of simulation. This is the shortest unit of time simulated by the program and is chosen in such a way that it is short enough to capture molecular processes of interest and long enough to result in a meaningful time length of simulation. Usually a time step of 1 femtosecond (fs) is used to simulate molecular processes like diffusion. After the execution of the simulation, positions of all constituent molecules at all times—trajectories [ri(t)]—are obtained. These trajectories can then be used to calculate various thermodynamic quantities of interest. For example, the diffusion coefficient can be obtained by calculating the mean squared displacement (MSD) of the constituent atoms from the trajectories and studying its evolution in time. Another important quantity that can be calculated from the trajectories is the intermediate scattering function defined in the previous section. This quantity can serve as a link between the simulations and NS experiments (Gautam, 2017) and can be calculated from the simulation trajectories using the expression.
where angular brackets denote an average over different time origins and molecules and the bar indicates an average over different Q vectors with the same magnitude. Another quantity that can serve as the link between experiments and the simulations is the orientational correlation functions (OCF) defined as,
Here, u is a unit vector attached to the molecule and Pl[x] is the Legendre polynomial of the order l with argument x. The l = 1 component of OCF is the dipole correlation function and can be measured directly in a dielectric spectroscopy experiment. It can also be obtained from IR spectrum. The OCF with l = 2 can be measured in light scattering and NMR experiments.
In the following sections, some examples of the use of the above mentioned three techniques in investigating the behaviors of C-O-H based confined fluids are provided.
Methane (CH4) is one of the most interesting and important molecule of energy relevance whose behavior under nanoporous confinement has been studied by NMR spectroscopy (Ok et al., 2017). Koskela et al. (1996) and Koskela et al. (1998) studied the behavior of methane confined into silicoaluminophosphate (SAPO) and aluminophsopahte (AlPO) molecular sieves, respectively, by both static and MAS 13C and 13C-{1H} NMR spectroscopy at variable temperatures. The silicoaluminophosphate molecular sieves (SAPO-n) have intracrystalline pore volumes (H2O) from 0.18 to 0.48 cm3/g and adsorption pore diameters from 0.3 to 0.8 nm, covering the scale of pore volumes and pore sizes known in zeolites and in silica and aluminophosphate molecular sieves (Lok et al., 1984; Table 1). When CH4 was confined into SAPO-11 molecular sieve, there was reduction in CH4 symmetry. This was attributed to the interactions with both the charge-compensating protons and the channel walls. However, upon confining CH4 into AlPO4-11 molecular sieves, there were three different signals of 13C-enriched methane observed. The existence of three 13C NMR signals of methane was attributed to the dispersal of methane gas in four different reservoirs (Jameson et al., 1997). There were “free gas” reservoirs (I) and the adsorbed molecules existing in the inner region of the crystallites (IV) gas molecules. The rest of the nonadsorbed molecules are able to move between the crystallites (reservoir II), some of which might be adsorbed inside the channels, but close to the crystallite surface (reservoir III). If the exchange is rapid relative to the NMR time scale, a lifetime-weighted average of shielding in the two reservoirs is detected leading to the central resonance in the 13C NMR spectrum.
An example of an agreement between the NMR and QENS (spin echo) results is provided by a study of diffusion of methane in zeolites. While Caro et al. (1975) used PFG-NMR, Cohen de Lara et al. (1983) utilized spin echo QENS to obtain the diffusion coefficient of methane in A-type zeolites. A diffusion coefficient of 6 × 10−6 cm2/s was obtained from the QENS data. Jobic et al. (1989) studied translational dynamics of methane in NaZSM-5 by combining NMR and QENS methods. With both techniques, the intracrystallline self-diffusion coefficients for methane at temperatures in the range 200–250 K were found to be within 10−5–10−4 cm2/s. The activation energy of methane self-diffusion was determined to be 4–5 kJmol−1 by applying both of the techniques.
Another example of the use of QENS to study confined methane is a comparative study of methane in AlPO4-5 and ZSM-48 channels. The channel diameters of AlPO4-5 and ZSM-48 are 0.8 and 0.5 nm, respectively. Thus, ZSM-48 imposes a stricter geometrical confinement on the adsorbed molecules. In the QENS study, it was observed that in AlPO4-5 methane molecules exhibit ordinary one dimensional diffusion. However, in ZSM-48 while a similar diffusion process was observed at lower loadings, at moderate loadings of methane, single-file diffusion of the adsorbent molecules was found in the channel pores where the molecules are forced to move in a single file in absence of enough space for a molecule to overtake other molecules (Jobic et al., 1997). This was the first instance of use of QENS to observe single-file diffusion of confined molecules which is a result of a strict geometrical confinement.
Among different aspects of research on natural gas, a significant focus is on capture and storage mechanisms that largely depend on hydrate-forming conditions. Most of methane on Earth is found trapped inside hydrates. The total methane content in the hydrates ranges between 2 × 103 and 4 × 106 gigatons and could be larger than the methane content from all other sources put together (Kvenvolden, 1988). Methane hydrates thus are a good potential energy resource. At the same time, they are a potential greenhouse gas threat as release into the atmosphere could accelerate global warming. Dissociation of oceanic methane hydrates has been attributed to the carbon isotope excursion at the end of Paleocene (Dickens et al., 1995). A comprehensive review of clathrate hydrates of natural gases can be found in Sloan (2003) and Sloan and Koh (2007). Here we describe a few example studies of methane clathrates using NMR, NS, and MD simulations.
The NMR technique provides insight into both qualitative and quantitative hydrate properties including structure forms, cage occupancies, and guest constituent compositions (Ripmeester and Ratcliffe, 1988; Seo and Lee, 2003). There have been several reports on NMR investigation of methane hydrate decomposition (Dec et al., 2007; Gupta et al., 2007). For example, Seo and Lee (2003) found by acquiring 13C NMR spectra of pure methane, mixed methane+tetrahydrafuran(THF), and mixed methane+neohexane hydrates that methane molecules might be existing only in a fraction of 512 cages in the mixture with THF due to the existence of water-soluble THF preventing complete filling of methane molecules into small cages. One of the most important conclusions was that it was not possible to encase methane molecules at all in the 51264 cages of structure II. Methane and ethane gas mixtures form two common gas hydrate structures—structure I (sI) and structure II (sII) depending on the gas-phase composition, temperature and pressure as shown in Figure 4 (Subramanian et al., 2000; Dec et al., 2007).
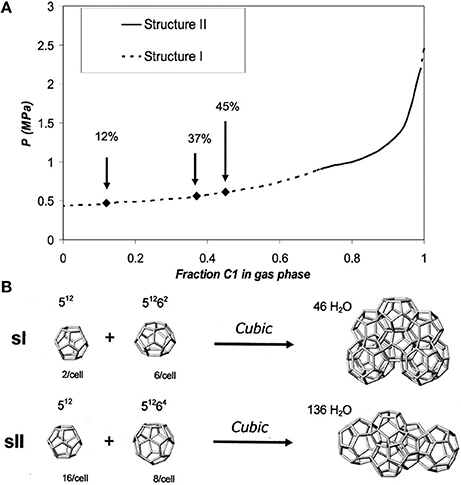
Figure 4. (A) Pressure vs. methane gas phase composition for the methane + ethane + water system at 272 K. Arrows indicate methane gas phase compositions used by Dec et al. (2007). (B) Polyhedral cages and partial unit cells of sI and sII clathrate hydrates. Reprinted with permission from Dec et al. (2007), Copyright 2007 American Chemical Society.
Using neutron diffraction, Tulk et al. (2012) studied cage occupancies in the high pressure structure H methane hydrate. The results from this experiment provided data for refinement of intermolecular potential parameters for the water-methane interactions in clathrate structures.
Recently, Casco et al. have used NS to study the growth of synthetic methane hydrates in nanoporous carbon material. The inelastic NS spectra from confined synthetic methane hydrates matched with the spectra of methane hydrates from the Pacific sea floor. The confinement of synthetic hydrates was found to result in faster growth kinetics. The synthetic hydrate formation in nanopores is thus less demanding than the formation of natural hydrates and occurs with the same stoichiometry as that found in nature (Casco et al., 2015). Myshakin et al. (2009) studied methane hydrate decomposition using MD simulation and found a dependence of the decomposition rate on the hydration number. Further, the rate of the cage destruction indicated that it occurs via an activated mechanism.
The behavior of CH4 and CO2 at certain temperature-pressure conditions can also produce interesting molecular interactions. Methane-CO2 replacement in natural gas hydrates was studied by 13C NMR spectroscopy (Lee et al., 2013). It was shown by MD simulations that the substitution of CH4 by CO2 in sI hydrate cages has a negative free energy (Dornan et al., 2007). This indicated spontaneous replacement of CH4 by CO2 from sI hydrates, causing the release of CH4. 13C NMR was used to monitor the release of CH4 and sequestration of CO2 (Lee et al., 2013). In addition, the CO2 composition in the hydrate phase and the chemical formula of the mixed gas hydrate after replacement can be easily approximated from the information on the ratio of the 13C MAS NMR resonance lines of CH4 in large and small cages. Contributions on the behavior of confined fluids include adsorption equilibrium of CO2 and CH4 into different confined systems, such as shale. Duan et al. (2016) studied the adsorption equilibrium isotherm data of CO2 and CH4 at 278, 298, and 318 K on rock samples from southeastern Sichuan Basin of China with a total organic carbon (TOC) of 2.58 wt%, inorganic components of quartz and orthoclase, and a wide pore size distribution. They demonstrated that the adsorption capacity of CO2 is higher than that of CH4 on shale. These results suggest a possible path forward for enhancing CH4 recovery and securing CO2 storage by injecting CO2 into shale reservoir rocks. A fundamental understanding of competitive sorption of CO2 and CH4 under nanoconfinement can be explored by high-pressure MAS NMR spectroscopy. For example, Qian et al. (2011) investigated dry reformation of methane with CO2 over 1.0 wt% Rhodium (Rh)/SBA-15 catalyst by both 13C and 1H MAS NMR measurements. It was possible by 13C MAS NMR to track the 13C-labeled reactants, such as CH3O* and CH2O* species during the carbon exchange reaction between CH4 and CO2 dry reforming reaction.
Water transport through the terrestrial subsurface forms an important component of global water cycle. The interaction of water with subsurface minerals affects a variety of geochemical phenomena including ion adsorption and exchange, mobility of contaminants, weathering, hydrothermal alteration, soil moisture and flow of CO2 (Brown, 2001; Wang et al., 2006). Layered clays form a major family of minerals. Structural water plays an important role in the stability of the structure in clays. This has resulted in a large number of studies of water confined in clays. Swenson et al. (2000) reported a QENS study on the dynamics of water in the vermiculite clays. This study employed orienting the clay sample in two perpendicular directions to study motion along the platelets forming the pore space in the clays and perpendicular to it. No significant water motion was detected in the direction perpendicular to the platelets thus implying a two-dimensional motion of water along the planes of the platelets. The diffusion of this confined water was found to be only slightly reduced compared to the bulk. This study was further extended using neutron spin echo to study the slower component of water dynamics (Swenson et al., 2001). It was found that the intermediate scattering functions exhibited a stretched exponential behavior typical of a non-Arrhenius fragile liquid. This is because the confined water experiences very different environments inside the clay at different points. This gives rise to a broad distribution of the time scales of motion. Malikova et al. (2006) used a combination of QENS experiments using both time of flight and spin echo instruments and MD simulations to study water confined in clays. They found that the time of flight measurements overestimate the water dynamics. An analysis of the elastic incoherent structure factor (EISF) using the simulation data, helped interpret the QENS data. Porion et al. (2007) used a combination of NMR and multiscale modeling consisting of Monte Carlo and MD simulations and Brownian dynamics calculations to study the structure and dynamics of water in dense clay sediments. MD simulations were also used to interpret the NSE data on water dynamics in hectorite clays and resulted in good agreement (Marry et al., 2011). QENS and MD simulations studies were combined by Michot et al. (2007) to understand water dynamics in Na saponite clays. Two rotational motions with different time scales of the confined water molecules were found. The faster of these was found to be independent of the adsorbed amount of water, whereas the slower one was found to slow down further for lower adsorption of water. A similar slowing down of water translational motion with lower loading was found in the case of hydrotalcite (Mitra et al., 2007). Chakrabarty et al. (2006) studied the effect of intercalation on the dynamics of water in saponite clays. It was found that the diffusion of water in the intercalated clay is enhanced. Bordallo et al. (2008) also studied the effect of cations on the dynamics of water in the interlayer spaces. They found that the Na+ cations facilitate the mobility of water. Further, they found that due to the quasielastic contribution from the magnetic fluctuations caused by Fe3+ ions, water diffusion was overestimated.
The behavior of water in engineered nanoporous materials has also been of great interest in the chemistry and materials sciences arenas. For example, Liu et al. (2014) have investigated diffusion of water by PFG NMR inside multiwalled (MW) and single walled (SW) carbon nanotubes (CNT), an important model system in the field nanofluidics and for carbonaceous materials in rocks. The diffusivity of water in double-walled carbon nanotubes (DWNTs) with an average inner diameter of 2.3 ± 0.3 nm was twice that in multiwalled carbon nanotubes (MWNTs) with an average inner diameter of 6.7 ± 0.8 nm in the temperature range of 263–223 K. Moreover, the effective self-diffusion coefficient in DWNTs is an order of magnitude higher than that reported for mesoporous silica materials, such as MCM-41 with a similar pore size. The faster diffusivity of water in CNTs was attributed to the ordered hydrogen bonds formed between water molecules within the channels of CNTs and the weak interaction between water and the CNT walls. In combined NS and MD simulation study, Kolesnikov et al. (2004) found that water inside a SWNT at 273 K exists in two different populations—one made up of a cylindrical shell concentric with the nanotube and the other making a one-dimensional chain. The confined water in this system exhibited anomalously soft dynamics. Single particle dynamics of water in both SWNT and DWNT have also been studied using QENS (Mamontov et al., 2006). Water in the nanotubes with an inner diameter of 1.4 nm was found to exhibit a fragile to strong transition at 218 K. This transition was not observed up to above 200 K for the 1.6 nm tubes. In an independent MD simulation study (Hummer et al., 2001), it was concluded that the one-dimnensional chain of water confined in a carbon nanotube showed concerted pulse-like motion. This concerted rapid motion along the tube axis results from tight hydrogen bonding network.
A large number of NMR approaches ranging from static solid-state, high-resolution MAS to PFG NMR have been used to interrogate the behaviors of small molecules in porous silica materials exhibiting either a narrow pore-size distribution with periodic structures as in MCM-41 or wider confinement pore sizes with non-periodic structures, such as in silica controlled pore glasses (CPG). Hence, for molecules with lower molecular weights, such as H2O, the confinement dimensions investigated range from a few to a few hundred molecular diameters (Vogel, 2010).
D'Orazio et al. (1990b) conducted both longitudinal (T1) and transverse (T2) magnetization relaxation measurements on water in unsaturated silica pore glass. NMR relaxation measurements along with diffusion coefficient determinations of confined water in porous media helped achieve a better understanding of the dynamics of fluids in random geometries. For a loading larger than the first adsorbed monolayer, the two component fluid-solid system was homogeneous at least over a few micrometers. A linear correlation between the relaxation times and the fraction of the occupied pore volume was seen, which demonstrated that the interaction responsible for the relaxation was confined to the first monolayer. Whereas, when there was less amount of confined fluid than the corresponding monolayer of fluid on the surface of the solid, the relaxation rates increased above the values predicted by assuming no evolution of the molecular interaction during drying. It was concluded that rotational and translational degrees of freedom were correlated, indicating that an adsorbed water molecule was allowed to rotate only during a jump to a neighboring site and that, most probably; one of the O-H bonds rotates in the plane of the surface.
In addition to studying confined water behavior in random geometries with non-periodic structures, water behavior under confinement has also been explored in ordered (i.e., pores aligned in a single orientation) mesoporous silicas, such as MCM-41 with a 2–6 nm pore diameter, and SBA-15 with a 5–10 nm pore diameter (Grünberg et al., 2004; Buntkowsky et al., 2007). Grünberg et al. (2004) employed both 1H MAS and static solid-state NMR spectroscopy in order to study the adsorption of H2O in MCM-41 and SBA-15. Various differences have been observed in water behavior in confined state depending on the type of porous silica. It was found that some of the H2O molecules were strongly bound to the surface of SBA-15, and these water molecules could be removed by only heating. Stronger bounded H2O molecules were observed in the case of SBA-15 structure but not in MCM-41. At higher filling ratios, in MCM-41 there was a bimodal-line distribution of chemical shifts of the H2O molecules, where one signal was at the position of inner bulk H2O, while the second peak was at the position of H2O molecules in fast exchange with surface–SiOH groups. For SBA-15, Grünberg et al. observed only one signal continuously changing chemical shift. This outcome resulted from different filling mechanisms of the pores of MCM-41 and SBA-15. In the case of MCM-41 with a smaller pore diameter, low water loading led to the wetting of the surfaces, with subsequent higher water loadings producing more complete pore filling in the direction of the pore axis. However, because of its larger pore diameter, the filling of the pores in SBA-15 occurs radially from the pore surface to the pore center. In addition, PFG NMR results on confined water in MCM-41 demonstrated the anisotropy of the intra-particle diffusion. The components of the obtained axisymmetric diffusion tensor are assigned to diffusion parallel and perpendicular to the channel axis of the hexagonally arranged MCM-41 channel system (Stallmach et al., 2000).
Small angle neutron scattering (SANS) has been used to study the density variation of one-dimensional water trapped inside MCM-41-S channels of diameter 1.9 and 1.5 nm (Liu et al., 2008). The water inside the pore could be kept in a liquid state up to 160 K. The density of this 1-D confined water was approximately 8% higher than that of the bulk water. Using QENS it was found that diffusion of water confined in MCM-41-S was suppressed with respect to that in the bulk by a factor of about two (Takahara et al., 1999, 2005). Further, this suppression of diffusivity was found to be stronger for stronger confinement (i.e., smaller pore sizes). A much slower component of this confined water was further studied using neutron spin echo and the result on suppression of diffusivity was found consistent for slow dynamics too (Yoshida et al., 2008). Using MD simulations, Gallo et al. (2010) showed that water forms a double layered structure inside MCM-41 channels. Further, the intermediate scattering functions calculated from the MD data showed stretched exponential behavior consistent with the experimental data obtained in the QENS and NSE measurements mentioned above.
Tsukahara et al. (2007) used NMR to study confined water in synthetic quartz glass containing confined (300–4,000 nm) spaces fabricated by electron-beam lithography and plasma etching. They compared the relative magnitude of the water-surface interaction, via the 1H 1/T1 values, for water in a confining medium with unmodified hydrophilic surface decorated with -OH groups vs. that with a modified hydrophobic surface having -CH3 groups. The interaction of H2O with -CH3 was weaker than with the -OH groups, but the confinement effect in the hydrophobic case appeared to be dominant over that in the hydrophilic case as a function of the pore size. This was explained by suggesting that the highly directional hydrogen bonding networks along with hydrophobic hydration surrounding the -CH3 groups promoted the formation of coupled H2O molecules.
Diffusion of H2O in a seal rock was studied by low-field NMR method (Fluery et al., 2009). Utilizing a MARAN 23.7 MHz from Oxford Instruments, both relaxation and diffusion experiments were conducted. Determination of continuous T2 relaxation time distributions on two samples showed groups with three different pore sizes. Moreover, in diffusion measurements, the magnetization carried by molecules was followed, not the direct displacements of the molecules. Therefore, the lifetime of magnetization must be long enough. Because of that D2O sample with 99.5% purity was used where no signal of D2O was recorded, and rather a 1H water concentration decreasing as a function of time was measured by simply recording the magnetization as a function of time. Because diffusion of CO2 in bulk water (2 × 10−9 m2s−1 at 25°C) is very close to the self-diffusion of water (2.3 × 10−9 m2s−1) at the same temperature, these authors suggested the mobility of H in the sample could be viewed as a proxy for the upper limit of mobility of CO2 in a porous matrices.
A recent MD simulation study by Chiavazzo et al. (2014) attempted to generalize the behavior of water under confinement by using a universal law to predict the diffusion coefficient of water under confinement with a single parameter of the ratio of volumes of confined and total water in the pore. They simulated water in 58 different environments including nanopores, nanoparticles proteins and carbon nanotubes to obtain the diffusion coefficients of water at 300 K (see Figure 5). The diffusion coefficient of water in all these cases tend to fall on a single universal equation
where D is the diffusion coefficient, the subscripts C and B stand for the confined and bulk components, respectively and the parameter θ is the ratio of the volumes of water that feels the interactions with the interface and the total volume accessible to water in the pore. In a recent study, Osti et al. (2016) have applied this universal scaling law to several NS studies on the dynamics of confined water. Thus, a combination of NMR, NS, and MD simulation has not only contributed to studies of water in different confining media, but also has tried to systematically universalize the behavior of confined water.
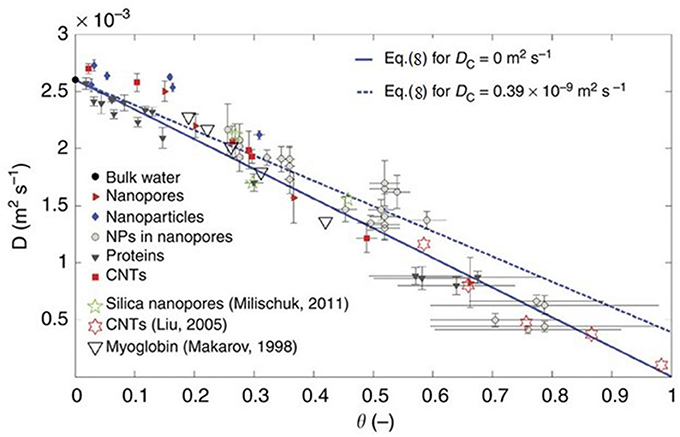
Figure 5. Self-diffusion coefficient of water in different systems as a function of scaling parameter θ. Reproduced from Chiavazzo et al. (2014).
Low molecular weight hydrocarbons other than methane confined in several different host structures have also been studied extensively. Apart from the obvious application based interests, these have attracted attention because of the peculiar counter intuitive observations. For example, in an MD simulation study, Yashonath and Santikary (1994) observed a maximum in the translational diffusion coefficient of model molecules as a function of molecular size in Na-Y and Na-A type zeolites. This was termed as levitation effect, where the adsorbed molecule gets levitated for a particular size as a result of a cancellation of the interactions it experiences from the opposite walls of the host. This resulted in a systematic study of a large number of low molecular weight hydrocarbons in various zeolites. A study of the intermediate scattering functions of these systems for smaller model molecules and model molecules exhibiting the diffusion maxima showed a marked difference between their behaviors (Ghorai and Yashonath, 2005). In terms of real molecules, several QENS experiments and MD simulation studies have been undertaken to study acetylene (Mitra et al., 2004; Gautam et al., 2006), ethane (Jobic et al., 1992; Chong et al., 2005), propane (Sayeed et al., 2003), propylene (Sharma et al., 2009, 2010), butane (Jobic et al., 1993), butadiene (Gautam et al., 2007, 2008), and pentane (Jobic et al., 2009) in different zeolites. In addition to a focus on the translational diffusion, rotational motion of these molecules in zeolites has also been studied exclusively (Jobic et al., 1992; Mukhopadhyay et al., 2004; Gautam et al., 2010, 2016). One particular system of interest here is ethane in AlPO4-5. For this system, NMR and QENS experiments reported conflicting features. While NMR measurements predicted presence of a single-file diffusion (Gupta et al., 1995), no such feature was observed in the QENS experiment (Jobic et al., 1997). To resolve this conflict, MD simulations on the system were carried out that indicated an absence of single-file diffusion in defect free AlPO4-5 (Demontis et al., 2001).
PFG NMR was also utilized for investigating fluid behavior upon confining the fluid into zeolites (Gratz et al., 2009; Freude et al., 2013). Gratz et al. (2009) studied diffusional behavior of some hydrocarbons, such as propane and propylene adsorbed in NaX zeolites by PFG NMR. In Diffusion EXchange SpectroscopY (DEXSY) spectral mapping, there were on diagonal and off-diagonal peaks where the former belonged to the adsorbed phase and the latter were fingerprints of molecules migrating from exterior regions of the zeolite crystals into the crystallites and vice versa (Figure 6). The most interesting result was observed on the confined mixtures of hydrocarbons after the mixtures were adsorbed into the zeolites. The diffusion coefficients of the hydrocarbons in the mixture deviated only negligibly from those of the single constituent system, which emphasizes that the governing interactions happen between the adsorbed molecules and the zeolite hosts.
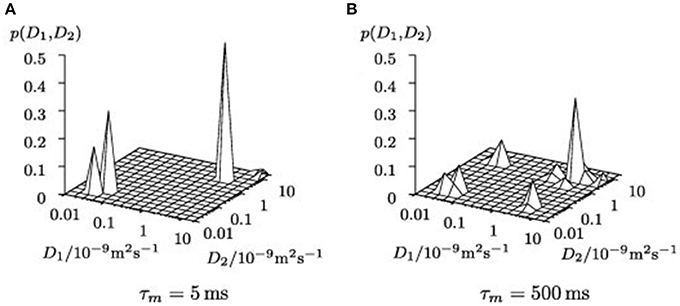
Figure 6. Uncorrected 2D inverse Laplace transformed NMR signal maps of DEXSY experiments for different mixing times τm (A) τm = 5 ms, (B) τm = 500 ms. Reprinted from Gratz et al. (2009), Copyright 2009 with permission from Elsevier.
Because zeolites exhibit a variety of pore structures, it is possible to study the influence of pore geometry on the dynamic behaviors of the confined fluid. Zeolites ZSM-5 and 5A were used for the comparison of dynamics of n-hexane (Stepanov et al., 2003) by combining 2H NMR and neutron scattering. ZSM-5 is a zeolite having straight channels interconnected by zig-zag channels, each consisting of ten-membered oxygen rings (Kokotailo et al., 1978). The porous volume of zeolite 5A consists of a cubic array of α-cages (approximate diameter of 11.2 Å), interconnected through eight-membered oxygen windows of free effective diameter 4.4 Å. Each α-cage has access to six similar neighbor α-cages (Adams and Haselden, 1984). The differences in the structures of the zeolites were reflected in the dynamics of confined n-hexane. In ZSM-5, the molecule sits in the channels segments and the energy barrier between two sites is small. Whereas, in 5A zeolite, the n-hexane molecule spends a longer time in the α-cages before moving to the adjacent cage. The 2H NMR spectra indicated that the more confined adsorption geometry of n-hexane in the ZSM-5 structure, in the form of anisotropic motions, whereas isotropically reorienting molecules were evidenced in the α-cages of 5A zeolite. The diffusion coefficient of n-hexane, obtained by NS measurements at 300 K, was more than four orders of magnitude larger in ZSM-5 compared with 5A zeolite.
In another study to probe the effect of pore structure on the rotational motion of confined fluid, MD simulations of ethane in ZSM-5 were carried out (Gautam et al., 2016). As mentioned above, ZSM-5 has three different types of pores—straight channels, zig-zag channels and the intersections of these two types of channels—the last imposing the most relaxed confinement. It was found that the rotational motion of ethane in ZSM-5 was hindered. The extent of this hindrance was found to be greatest in the zig-zag channels and least in the intersections, thus indicating the importance of pore geometry. Further, the rotational motion was found to get enhanced at higher loadings, in agreement with the experimental QENS study carried out on this system earlier (Jobic et al., 1992). We note here, that this enhancement of rotational motion at higher loading (or correspondingly, higher pressure) is consistent with an enhancement of translational diffusion at higher pressures observed for methane in carbon aerogel (Chathoth et al., 2010) and propane in silica aerogel (Gautam et al., 2015).
Bär et al. (1999) compared hydrogen self-diffusion in zeolites by PFG NMR and QENS. In this study large zeolite crystallites, such as NaX with diameters ≥30 and 100 μm and NaA with diameter ≥15 μm were utilized. The short (T2) times and the low spin density, put a limitation on the accuracy of the PFG NMR diffusivities. However, the PFG NMR results were in satisfactory agreement with the evidence obtained by QENS measurements. The unexpected low diffusivity of hydrogen in silicalite was explained as a result of the effect of the pentasil chains confining a significant portion of the hydrogen molecules.
Due to an increased concern over the rise in atmospheric CO2 levels, CO2 sequestration efforts have seen a dramatic increase over the past few years. This has resulted in studies on migration of CO2 through porous networks. For example, Bowers et al. (2014) studied incorporation of supercritical CO2 in smectite by in situ 13C and 23Na MAS NMR. They observed that there was line broadening in the 13CO2 resonance at 90°C and 50 bar CO2 pressure for Na-hectorite, consistent with CO2 pressure in the interlayers. They also acquired 23Na NMR spectra for the base Na-hectorite and 13C and 23Na NMR spectra for a composite of the Na-hectorite and Suwannee River humic acid. The 13C NMR spectra indicated a progressive increase in the width of the 13CO2 resonance from a supercritical CO2 blank to the Na-hectorite to the composite showing progressively increasing interaction of the CO2 and solids. The interested reader could refer to a recent review article by Kirkpatrick et al. (2015) on combined efforts of NMR and computational molecular modeling efforts on mineral surfaces and interlayer filling by H2O, cations, anions, CO2, and natural organic matter (NOM).
A number of studies have focused on how the presence of CO2 has impacted the dynamics of confined hydrocarbons. The fact that CO2 has a very small NS cross section compared to hydrocarbons makes it invisible in presence of hydrocarbons and thereby facilitates studying the effect of CO2 on their dynamics. For example, Salles et al. (2013) have used QENS and MD simulations to study the effect of CO2 on the dynamics of methane in metal organic framework type solids which are porous materials with pores about 1 nm in diameter. QENS has also been used by Chathoth et al. (2012), Patankar et al. (2016), and Gautam et al. (2015) to study the effect of CO2 on the dynamics of methane, ethane and propane confined in mesoporous carbon aerogel, silica pore glass and silica aerogel, respectively. In all three studies, CO2 was found to enhance the diffusion of the confined hydrocarbon. In case of ethane in CPG, the quasielastic broadening in the QENS spectra was modeled as a sum of two Lorentzian functions which indicated presence of two different populations of molecules moving at two different time scales. These two populations represent ethane molecules that occupied the central regions of the pore which has a mean diameter of 7.5 nm and those that were close to the pore walls. A similar decomposition of two populations of ethane molecules could be observed for ethane molecules when CO2 was added. However, the diffusion coefficients obtained by modeling of the QENS data in the latter case were higher for either population, indicating that CO2 enhances the diffusion of ethane in CPG (Figure 7). Independent MD simulation studies have also confirmed that CO2 enhances the diffusion of confined hydrocarbon. Le et al. (2015, 2016) have shown that presence of CO2 enhances the diffusivity of n-butane and n-octane in silica slit nanopores, by replacing the hydrocarbons from the pore walls thereby making them free to move through the pore network.
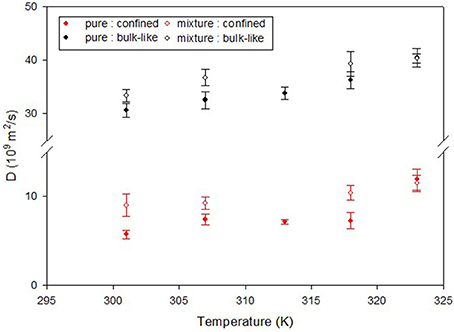
Figure 7. Diffusion coefficient of ethane in CPG silica with 7.5 nm pores obtained from a QENS study. Two populations of ethane molecules were found that contributed to the quasielastic width—a bulk like population (black symbols) and another population that exhibited reduced mobility due to confinement (red symbols). The effect of CO2 can be seen as an enhancement of the diffusivity of ethane in presence of CO2 (open symbols) compared to that in the absence of CO2 (solid symbols). Reprinted with permission from Patankar et al. (2016), Copyright 2016 American Chemical Society.
Exploring the behavior of C-O-H fluids confined in micro- and mesoporous systems provides a foundation for quantifying geologically relevant systems where mass and energy transport occur. Confinement of these fluids in porous systems gives rise to rich behavior that results from an interplay of geometrical restriction imposed by different pore sizes, the interaction between the porous material and the fluid, and the nature of the confined fluid itself. While in relatively large mesopores, the fluid motion might occur at different time scales as a function of location in the pore, for example, existence of a bulk-like and confined components of motion in a mesoporous material, a stricter geometrical confinement can lead to a severely constrained motion, like single file molecular diffusion. Within a given porous material, time scales of motion of confined fluids can exhibit interesting dependencies on the molecular size and concentration of the confining fluid, for example levitation effect observed in the case of confined hydrocarbons. Anomalous pressure dependence has also been seen on the dynamics of gases confined in mesoporous media. Water, as a confined fluid, exhibits even richer behavior due to the effects of hydrogen bonding. A concerted motion of water molecules can result from the hydrogen bonding network. All these effects lead to a wide variety of length and time scales relevant to the study of confined fluids and as such, require versatile tools for a thorough study of behavior of geologically relevant confined fluids. Further, the techniques that probe the behavior of confined fluids at the molecular level depend heavily on the interpretation of the measured data and as such can be prone to subjective bias. Therefore, if possible it is advantageous to look at each problem from different perspectives. This is possible by using a combination of different techniques to understand the phenomena of interest. Nuclear magnetic resonance (NMR) and NS are two such techniques that can provide complimentary information on confined fluids. A synergistic use of these techniques has been successful in revealing important structural and dynamical information on fluid-substrate interactions. Further, MD simulations, which provide information in real space and time coordinates, can underpin the interpretation of the experimental data. MD simulations have been used to resolve conflicting results derived from NMR and NS. Thus, a combination of NMR, NS, and MD simulations provides a powerful “tool kit” to contribute toward a more complete understanding of confined important fluids of geological relevance.
In the current report, after a short introduction to the importance of confinement effect on fluids having significance in mass and energy transport of earth, we summarized which nano- and mesoporous matrix systems have been utilized for investigating confined fluid behavior. Further, we provide examples of how NMR, NS, and MD approaches have been employed for studying behavior of confined fluids as a function of temperatures, pressure, confinement size, confinement dimensionality, to name a few. These examples have highlighted unusual behavior of confined fluids, including anomalous pressure or loading dependences and effects of variable pore structures. We have also discussed how MD simulation studies on water in a variety of confined spaces have helped systemize its immensely complex behavior by proposing a universal scaling law for diffusion of confined water. With ever-growing enhancement of computing power, in near future it should be possible to use MD simulations to study systems with confinement sizes larger than a few nanometers without coarse graining that is currently necessary. Similar advancements in NS and NMR instrumentation might extend the energy and time scales accessible at present. We believe that a combination of NMR, NS, and MD simulations will provide otherwise unobtainable structural and dynamical information about model confined fluid systems where fluids are confined into porous engineered proxies. Such an approach will continue contributing to understand these systems at geological conditions relevant for Earth's surface, its subsurface and the surfaces of other planets deep into the interior.
All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors (SG and DC) would like to acknowledge the support provided by the US Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences, Geosciences Program under grant DESC0006878. SO would like to thank the Sloan Foundation-funded Deep Carbon Observatory for support of the NMR effort.
1. ^1 meV energy corresponds to 8.067 cm−1
2. ^A list of neutron sources around the world with user programs can be found at http://idb.neutron-eu.net/neutron-centres.html or http://www.ncnr.nist.gov/nsources.html
3. ^ħ = h/2π is the reduced Planck constant.
Adams, J. M., and Haselden, D. A. (1984). The structure of dehydrated zeolite 5A (Si/Al = 1.02) by neutron profile refinement. J. Solid State Chem. 51, 83–90. doi: 10.1016/0022-4596(84)90318-9
Allen, D., Crary, S., Freedman, B., Andreani, M., Klopf, W., Badry, R., et al. (1997). How to use borehole nuclear magnetic resonance. Schlumberger. Oilfield Rev. 9, 34–57.
Allen, M. P., and Tildesley, D. J. (1987). Computer Simulation of Liquids. Oxford: Oxford University Press.
Al-Othman, Z. A. (2012). A review: fundamental aspects of silicate mesoporous materials. Materials 5, 2874–2902. doi: 10.3390/ma5122874
Anovitz, L. M., and Cole, D. R. (2015). Characterization and analysis of porosity and pore structures. Rev. Mineral. Geochem. 80, 61–164. doi: 10.2138/rmg.2015.80.04
Asefa, T., and Tao, Z. (2012). Mesoporous silica and organosilica materials—Review of their synthesis and organic functionalization. Can. J. Chem. 90, 1015–1031. doi: 10.1139/v2012-094
Bär, N. K., Ernst, H., Jobic, H., and Kärger, J. (1999). Combined quasi-elastic neutron scattering and NMR study of hydrogen diffusion in zeolites. Magn. Reson. Chem. 37, S79–S83. doi: 10.1002/(sici)1097-458x(199912)37:13<s79::aid-mrc545>3.0.co;2-0
Behroozmand, A. A., Keating, K., and Auken, E. (2014). A review of the principles and applications of the NMR technique for near-surface characterization. Surv. Geophys. 36, 27–85. doi: 10.1007/s10712-014-9304-0
Berendsen, H. J. C., Grigera, J. R., and Straatsma, T. P. (1987). The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271. doi: 10.1021/j100308a038
Bhattacharja, S., D'Orazio, F., Tarczon, J. C., and Halperin, W. P. (1989). Internal structure of porous silica: a model system for characterization by nuclear magnetic resonance. J. Am. Ceram. Soc. 72, 2126–2130. doi: 10.1111/j.1151-2916.1989.tb06043.x
Bordallo, H. N., Aldridge, L. P., Churchman, G. J., Gates, W. P., Telling, M. T. F., Kiefer, K., et al. (2008). Quasielastic neutron scattering studies on clay interlayer space highlighting the effect of the cation in confined water dynamics. J. Phys. Chem. C 112, 13982–13991. doi: 10.1021/jp803274j
Bowers, G. M., Hoyt, D. W., Burton, S. D., Ferguson, B. O., Varga, T., and Kirkpatrick, R. J. (2014). In situ 13C and 23Na magic angle spinning NMR investigation of supercritical CO2 incorporation in smectite–Natural organic matter composites. J. Phys. Chem. C 118, 3564–3573. doi: 10.1021/jp410535d
Breen, C., and Moronta, A. (1999). Influence of layer charge on the catalytic activity of mildly acid-activated Tetramethylammonium-exchanged Bentonites. J. Phys. Chem. B 103, 5675–5680. doi: 10.1021/jp9901646
Brigatti, M. F., Galan, E., and Theng, B. K. (2013). “Structure and mineralogy of clay minerals, Chapter 2,” in Handbook of Clay Science, Vol. 5A, eds F. Bergaya and G., Lagaly (Amsterdam: Elsevier), 21–81.
Brown, G. E. Jr. (2001). How minerals react with water. Science 294, 67–70. doi: 10.1126/science.1063544
Brownstein, K. R., and Tarr, C. E. (1979). Importance of classical diffusion in NMR studies of water in biological cells. Phys. Rev. A 19, 2446–2453. doi: 10.1103/PhysRevA.19.2446
Buntkowsky, G., Breitzke, H., Adamczyk, A., Roelofs, F., Emmler, T., Gedat, E., et al. (2007). Structural and dynamical properties of guest molecules confined in mesoporous silica materials revealed by NMR. Phys. Chem. Chem. Phys. 9, 4843–4853. doi: 10.1039/b707322d
Callaghan, P. T. (1991). Principles of Nuclear Magnetic Resonance Microscopy. Oxford: Clarendon Press.
Callaghan, P. T., Coy, A., MacGowan, D., Packer, K. J., and Zelaya, F. O. (1991). Diffraction-like effects in NMR diffusion studies of fluids in porous solids. Nature 351, 467–469. doi: 10.1038/351467a0
Caro, J., Karger, J., Pfeifer, H., and Schollner, R. (1975). Zur Selbstdiffusion von Methan in 5A-Zeolithen. Z. Phys. Chem. 256, 698–704.
Casco, M. E., Albero, J. S., Ramirez-Cuesta, A. J., Rey, F., Jorda, J. L., Bansode, A., et al. (2015). Methane hydrate formation in confined nanospace can surpass nature. Nat. Comm. 6, 6432. doi: 10.1038/ncomms7432
Čejka, J., Corma, A., and Zones, S. (2010). Zeolites and Catalysis: Synthesis Reactions and Applications. Weinheim: Wiley.
Chakrabarty, D., Gautam, S., Mitra, S., Gil, A., Vicente, M. A., and Mukhopadhyay, R. (2006). Dynamics of adsorbed water in saponite clay: neutron scattering study. Chem. Phys. Lett. 426, 296–300. doi: 10.1016/j.cplett.2006.05.131
Chathoth, S. M., He, L., Mamontov, E., and Melnichenko, Y. B. (2012). Effect of carbon dioxide and nitrogen on the diffusivity of methane confined in nano-porous carbon aerogel. Micropor. Mesopos. Mat. 148, 101−106. doi: 10.1016/j.micromeso.2011.07.019
Chathoth, S. M., Mamontov, E., Melnichenko, Y. B., and Zamponi, M. (2010). Diffusion and adsorption of methane confined in nano-porous carbon aerogel: a combined quasi-elastic and small-angle neutron scattering study. Micropor. Mesopos. Mat. 132, 148−153. doi: 10.1016/j.micromeso.2010.02.012
Chiavazzo, E., Fasano, M., Asinari, P., and Decuzzi, P. (2014). Scaling behavior for the water transport in nanoconfined geometries. Nat. Comm. 5, 3565. doi: 10.1038/ncomms4565
Chong, S. S., Jobic, H., Plazanet, M., and Sholl, D. S. (2005). Concentration dependence of transport diffusion of ethane in silicalite: a comparison between neutron scattering experiments and atomically detailed simulations. Chem. Phys. Lett. 408, 157–161. doi: 10.1016/j.cplett.2005.04.023
Cohen de Lara, E., Kahn, R., and Mezei, F. (1983). Determination of the intracrystalline diffusion coefficient of methane in A zeolites by means of neutron spin-echo experiments. J. Chem. Soc. Faraday Trans. 1 79, 1911–1920. doi: 10.1039/f19837901911
Cole, D. R., Gruszkiewicz, M. S., Simonson, J. M., Chialvo, A. A., and Melnichenko, Y. B. (2004). “Influence of nanoscale porosity on fluid behavior,” in Water-Rock Interaction, Vol. 1, eds R. Wanty and R. Seal (Rotterdam: A Balkema Publishers), 735–739.
Cole, D. R., Ok, S., Striolo, A., and Phan, A. (2013). “Hydrocarbon behavior at nanoscale interfaces,” in Carbon in Earth, Reviews in Mineralogy and Geochemistry, Vol. 75, eds R. M. Hazen, A. P. Jones, and J. A. Baross (Chantilly, VA: Mineralogical Society of America), 495–545.
Cool, P., and Vasant, E. F. (1998). “Pillared Clays: Preparation, Characterization and Applications,” in Molecular Sieves–Science and Technology. 1. Synthesis, eds H. G. Karge and J. Weitkamp (Berlin;Heidelberg: Springer), 265–288.
Corsaro, C., Maisano, R., Mallamace, D., and Dugo, G. (2013). 1H NMR study of water/methanol solutions as a function of temperature and concentration. Physica A 392, 596–601. doi: 10.1016/j.physa.2012.11.008
Cotts, R. M. (1989). Pulsed field gradient stimulated echo methods for improved NMR diffusion measurements in heterogeneous systems. J. Magn. Reson. 83, 252–266. doi: 10.1016/0022-2364(89)90189-3
Davis, M. E. (2002). Ordered porous materials for emerging applications. Nature 417, 813–821. doi: 10.1038/nature00785
Dec, S. F., Bowler, K. E., Stadterman, L. L., Koh, C. A., and Sloan, E. D. Jr. (2007). NMR study of methane+ethane structure I hydrate decomposition. J. Phys. Chem. A 111, 4297–4303. doi: 10.1021/jp070442y
Demontis, P., Gonzalez, J. G., Suffritti, G. B., and Tilocca, A. (2001). Statics and dynamics of ethane molecules in AlPO4-5: A molecular dynamics simulation study. J. Am. Chem. Soc. 123, 5069–5074. doi: 10.1021/ja003940s
Diakova, G., Korb, J. P., and Bryant, R. G. (2012). The magnetic field dependence of water T1 in tissues. Magn. Reson. Med. 68, 272–277. doi: 10.1002/mrm.23229
Dickens, G. R., O'Neil, J. R., Rea, D. K., and Owen, R. M. (1995). Dissociation of oceanic methane hydrate as a cause of the carbon isotope excursion at the end of Paleocene. Paleoocean 10, 965–971. doi: 10.1029/95PA02087
D'Orazio, F., Bhattacharja, S., Halperin, W. P., and Gerhardt, R. (1990a). Fluid transport in partially filled porous sol-gel silica glass. Phys. Rev. B 42, 6503–6508. doi: 10.1103/PhysRevB.42.6503
D'Orazio, F., Bhattacharja, S., Halperin, W. P., Eguchi, K., and Mizusaki, T. (1990b). Molecular diffusion and nuclear-magnetic-resonance relaxation of water in unsaturated porous silica glass. Phys. Rev. B 42, 9810–9818. doi: 10.1103/PhysRevB.42.9810
Dornan, P., Alavi, S., and Woo, T. K. (2007). Free energies of carbon dioxide sequestration and methane recovery in clathrate hydrates. J. Chem. Phys. 127, 124510-1–124510-8. doi: 10.1063/1.2769634
Duan, S., Gu, M., Du, X., and Xian, X. (2016). Adsorption equilibrium of CO2 and CH4 and their mixture on Sichuan basin shale. Energy Fuels 30, 2248–2256. doi: 10.1021/acs.energyfuels.5b02088
Eddaoudi, M., Moler, D. B., Li, H., Chen, B., Reineke, T. M., O'Keeffe, M., et al. (2001). Modular chemistry:secondary building units as a basis for the design of highly porous and robust metal−organic carboxylate frameworks. Acc. Chem. Res. 34, 319–330. doi: 10.1021/ar000034b
Fernandez, M., Pampel, A., Takahashi, R., Sato, S., Freude, D., and Kärger, J. (2008). Revealing complex formation in acetone-n-alkanes mixtures by MAS PFG NMR diffusion measurement in nanoporous hosts. Phys. Chem. Chem. Phys. 10, 4165–4171. doi: 10.1039/b802929f
Fluery, M., Berne, P., and Bachaud, P. (2009). Diffusion of dissolved CO2 in caprock. Energy Procedia 1, 3461–3468. doi: 10.1016/j.egypro.2009.02.137
Freedman, R., and Heaton, N. (2004). Fluid characterization using nuclear magnetic resonance logging. Petrophysics 45, 241–250. Available online at: http://cat.inist.fr/?aModele=afficheN&cpsidt=15792357
Frenkel, D., and Smit, B. (2001). Understanding Molecular Simulations: From Algorithms to Applications. San Diego, CA: Academic Press.
Freude, D., Beckert, S., Stallmach, F., Kurzhals, R., Taschner, D., Toufar, H., et al. (2013). Ion and water mobility in hydrated Li-LSX zeolite studied by 1H, 6Li and 7Li NMR spectroscopy and diffusometry. Micropor. Mesopos. Mat. 172, 174–181. doi: 10.1016/j.micromeso.2013.01.011
Gaede, H. C., and Gawrisch, K. (2004). Multi-dimensional pulsed field gradient magic angle spinning NMR experiments on membranes. Magn. Reson. Chem. 42, 115–122. doi: 10.1002/mrc.1329
Gallo, P., Roovere, M., and Chen, S.-H. (2010). Anomalous dynamics of water confined in MCM-41 at different hydrations. J. Phys. 22:284102. doi: 10.1088/0953-8984/22/28/284102
Galvosas, P., Stallmch, F., Seiffert, G., Kärger, J., Kaess, U., and Majer, G. (2001). Generation and application of ultra-high-intensity magnetic field gradient pulses for NMR spectroscopy. J. Magn. Reson. 151, 260–268. doi: 10.1006/jmre.2001.2381
Gautam, S. (2017). “Use of quasielastic neutron scattering and molecular dynamics simulation to study molecular dynamics under confinement,” in Horizons in World Physics, Vol. 290, ed A. Reimer (New York, NY: Nova Science Publishers), 25–44.
Gautam, S., Liu, T., Patankar, S., Tomasko, D., and Cole, D. (2016). Location dependent orientational structure and dynamics of ethane in ZSM5. Chem. Phys. Lett. 648, 130–136. doi: 10.1016/j.cplett.2016.02.021
Gautam, S., Liu, T., Rother, G., Jalarvo, N., Mamontov, E., Welch, S., et al. (2015). Dynamics of propane in nanoporous silica aerogel: a quasielastic neutron scattering study. J. Phys. Chem. C 119, 18188–18195. doi: 10.1021/acs.jpcc.5b03444
Gautam, S., Mitra, S., Chaplot, S. L., and Mukhopadhyay, R. (2008). Dynamics of 1,3-butadiene adsorbed in Na-Y zeolite: a molecular dynamics simulation studies. Phys. Rev. E 77:061201. doi: 10.1103/physreve.77.061201
Gautam, S., Mitra, S., Mukhopadhyay, R., and Chaplot, S. L. (2006). Diffusion of acetylene inside Na-Y zeolite: molecular dynamics simulation studies. Phys. Rev. E 74:041202. doi: 10.1103/PhysRevE.74.041202
Gautam, S., Mitra, S., Sayeed, A., Yashonath, S., Chaplot, S. L., and Mukhopadhyay, R. (2007). Diffusion of 1,3-butadiene in Na-Y zeolite: neutron scattering study. Chem. Phys. Lett. 442, 311–315. doi: 10.1016/j.cplett.2007.05.109
Gautam, S., Sharma, V. K., Mitra, S., Chaplot, S. L., and Mukhopadhyay, R. (2010). Rotational dynamics of propylene in ZSM-5 zeolitic frameworks. Chem. Phys. Lett. 501, 345–350. doi: 10.1016/j.cplett.2010.11.080
Gelb, L. D., Gubbins, K. E., Radhakrishnan, R., and Sliwinska-Bartkowiak, M. (1999). Phase separation in confined systems. Rep. Prog. Phys. 62, 1573–1659. doi: 10.1088/0034-4885/62/12/201
Ghorai, P. K., and Yashonath, S. (2005). Levitation effect: distinguishing anomalous from linear regime of guests sorbed in zeolites through the decay of intermediate scattering function and wavevector dependence of self-diffusivity. J. Phys. Chem. B 109, 3979–3983. doi: 10.1021/jp046121t
Gratz, M., Wehring, M., Galvosas, P., and Stallmach, F. (2009). Multidimensional NMR diffusion studies in microporous materials. Micropor. Mesopos. Mat. 125, 30–34. doi: 10.1016/j.micromeso.2009.02.014
Grünberg, B., Emmler, T., Gedat, E., Shenderovich, I., Findenegg, G. H., Limbach, H.-H., et al. (2004). Hydrogen bonding of water confined in mesoporous silica MCM-41 and SBA-15 studied by 1H solid-state NMR. Chem. Eur. J. 10, 5689–5696. doi: 10.1002/chem.200400351
Grunewald, E., and Knight, R. (2009). A laboratory study of NMR relaxation times and pore coupling in heterogeneous media. Geophysics 74, 215–221. doi: 10.1190/1.3223712
Guillot, B. (2002). A reappraisal of what we have learnt during three decades of computer simulations on water. J. Mol. Liq. 101, 219–260. doi: 10.1016/S0167-7322(02)00094-6
Gupta, A., Dec, S. F., Koh, C. A., and Sloan, E. D. (2007). NMR investigation of methane hydrate dissociation. J. Phys. Chem. C 111, 2341–2346. doi: 10.1021/jp066536+
Gupta, S. S., and Bhattacharyya, K. G. (2012). Adsorption of heavy metals on kaolinite and montmorillonite: a review. Phys. Chem. Chem. Phys. 14, 6698–6723. doi: 10.1039/c2cp40093f
Gupta, V., Nivarthi, S. S., McCormick, A. V., and Davis, H. T. (1995). Evidence of single-file diffusion of ethane in the molecular sieve AlPO4-5. Chem. Phys. Lett. 247, 596–600. doi: 10.1016/S0009-2614(95)01246-X
Hawlicka, E. (1995). Self-diffusion in multicomponent liquid systems. Chem. Soc. Rev. 34, 13743–13750. doi: 10.1039/cs9952400367
Hummer, G., Rasaiah, J. C., and Noworyta, J. P. (2001). Water conduction through the hydrophobic channel of a carbon nanotube. Nature 414, 188–190. doi: 10.1038/35102535
Inlow, R. O., Joesten, M. D., and Van Wazer, J. R. (1975). Spin-lattice relaxation and hydrogen bonding in methanol-solvent mixtures. J. Phys. Chem. 79, 2307–2312. doi: 10.1021/j100588a016
James, T. L. (1998). Fundamentals of NMR. Nuclear Magnetic Resonance. Bethesda, MD: Biophysical Society.
Jameson, C. J., Jameson, A. K., Gerald, I. I. R. E., and Lim, H.-M. (1997). Anisotropic Xe chemical shifts in zeolites. The role of intra-and intercrystallite diffusion. J. Phys. Chem. B 42, 8418–8437. doi: 10.1021/jp971013a
Jobic, H., Bée, M., and Caro, J. (1993). “Translational mobility of n-butane and n-hexane in ZSM-5 measured by quasielastic neutron scattering,” in Proceedings of the Ninth International Zeolite Conference, Vol. II, eds R. Von Ballmos, J. B. Higgins, and M. M. J. Treacy (Montreal, QC: Butterworth Heinemann), 121–128.
Jobic, H., Bée, M., Caro, J., Bülow, M., and Kärger, J. (1989). Molecular self-diffusion of methane in zeolite ZSM-5 by quasi-elastic neutron scattering and nuclear magnetic resonance pulsed field gradient technique. J. Chem. Soc. Faraday Trans. 1 85, 4201–4209. doi: 10.1039/f19898504201
Jobic, H., Bée, M., and Kearly, G. J. (1992). Dynamics of ethane and propane in zeolite ZSM-5 studied by quasielastic neutron scattering. Zeolites 12, 146–151. doi: 10.1016/0144-2449(92)90075-Z
Jobic, H., Borah, B. J., and Yashonath, S. (2009). Neutron scattering and molecular dynamics evidence for levitation effect in nanopores. J. Phys. Chem. B 113, 12635–12638. doi: 10.1021/jp907453a
Jobic, H., Hahn, K., Karger, J., Bée, M., Tuel, A., Noack, M., et al. (1997). Unidirectional and single file diffusion of molecules in one dimensional channel systems. A quasielastic neutron scattering study. J. Phys. Chem. B 101, 5834–5841. doi: 10.1021/jp970773i
Johnson, E. B. G., and Arshad, S. E. (2014). Hydrothermally synthesized zeolites based on kaolinite: a review. Appl. Clay Sci. 97–98, 215–221. doi: 10.1016/j.clay.2014.06.005
Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W., and Klein, M. L. (1983). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. doi: 10.1063/1.445869
Kärger, J., Binder, T., Chmelik, C., Hibbe, F., Krautscheid, H., Krishna, R., et al. (2014). Microimaging of transient guest profiles to monitor mass transfer in nanoporous materials. Nat. Mater. 13, 333–343. doi: 10.1038/nmat3917
Kimmich, R., and Anoardo, E. (2004). Field-cycling NMR relaxometry. Prog. Nuc. Magn. Reson. Spect. 44, 257–320. doi: 10.1016/j.pnmrs.2004.03.002
Kirkpatrick, R. J., Kalinichev, A. G., Bowers, G. M., Yazaydin, A. O., Krishnan, M., Saharay, M., et al. (2015). NMR and computational molecular modeling studies of mineral surfaces and interlayer galleries: a review. Am. Mineral. 100, 1341–1354. doi: 10.2138/am-2015-5141
Kittler, W. C., Obruchkov, S., Galvosas, P., and Hunter, M. W. (2014). Pulsed second order field NMR for real time PGSE and single-shot surface to volume ratio measurements. J. Magn. Reson. 247, 42–49. doi: 10.1016/j.jmr.2014.08.005
Kleinberg, R. L., Kenyon, W. E., and Mitra, P. P. (1994). Mechanism of NMR relaxation of fluids in rock. J. Magn. Res. Ser. A 108, 206–214. doi: 10.1006/jmra.1994.1112
Kokotailo, G. T., Lawton, S. L., Olson, D. H., and Meier, W. M. (1978). Structure of synthetic zeolite ZSM-5. Nature 272, 437–438. doi: 10.1038/272437a0
Kolesnikov, A. I., Zanotti, J. M., Loong, C. K., Thiyagarajan, P., Moravsky, A. P., Loutfy, R. O., et al. (2004). Anomalously soft dynamics of water in a nanotube: a revelation of nanoscale confinement. Phys. Rev. Lett. 93:035503. doi: 10.1103/PhysRevLett.93.035503
Korb, J.-P. (2006). “Surface diffusion of liquids in disordered nanoporres and materials: a field cycling relaxometry approach,” in Fluid Transport Nanoporous Materials, eds W. C. Connor, and J. Fraissard (Dordrecht: Springer), 415–437.
Koskela, T., Yhlihautala, M., Vaara, J., and Jokisaari, J. (1996). 13C NMR spectroscopy of methane adsorbed in SAPO-11 molecular sieve. Chem. Phys. Lett. 261, 425–430. doi: 10.1016/0009-2614(96)00996-7
Koskela, T., Ylihautala, M., Jokisaari, J., and Vaara, J. (1998). 13C NMR of methane in an AlPO4-11 molecular sieve: exchange effects and shielding anisotropy. Phys. Rev. B 58, 14833–14836. doi: 10.1103/PhysRevB.58.14833
Kuchel, P. W., Pages, G., Nagashima, K., and Chuang, K. H. (2012). Stesjkal-tanner equation derived in full. Concepts Magn. Reson. A 40A, 205–214. doi: 10.1002/cmr.a.21241
Kvenvolden, K. A. (1988). Methane hydrate–a major reservoir of carbon in the shallow geosphere? Chem. Geol. 71, 41–51. doi: 10.1016/0009-2541(88)90104-0
Langmi, H. W., Ren, J., North, B., Mathe, M., and Bessarabov, D. (2014). Hydrogen storage in metal-organic frameworks: a review. Electrochim. Acta 128, 368–392. doi: 10.1016/j.electacta.2013.10.190
Le, T., Ogbe, S., Striolo, A., and Cole, D. R. (2016). N-octane diffusivity enhancement via carbon dioxide in silica slit nanopores–a molecular dynamics simulation study. Mole. Simu. 42, 745–752. doi: 10.1080/08927022.2015.1089991
Le, T., Striolo, A., and Cole, D. R. (2015). CO2-C4H10 mixtures simulated in silica slit pores: relation between structure and dynamics. J. Phys. Chem. C 119, 15274–15284. doi: 10.1021/acs.jpcc.5b03160
Lee, S., Park, S., Lee, Y., and Seo, Y. (2013). Thermodynamic and 13C NMR spectroscopic verification of methane-carbon dioxide replacement in natural gas hydrates. Chem. Eng. J. 225, 636–640. doi: 10.1016/j.cej.2013.03.117
Li, J., Corma, A., and Yu, J. (2015). Synthesis of new zeolite structures. Chem. Soc. Rev. 44, 7112–7127. doi: 10.1039/C5CS00023H
Liebscher, A., and Heinrich, C. A. (eds.). (2007). Fluid-Fluid Interactions. Reviews in Mineralogy and Geochemistry. Chantilly, VA: Mineralogical Society of America.
Liu, D., Zhang, Y., Liu, Y., Wu, J., Chen, C.-C., Mou, C.-Y., et al. (2008). Density measurement of 1-D confined water by small angle neutron scattering method: pore size and hydration level dependencies. J. Phys. Chem. B 112, 4309–4312. doi: 10.1021/jp710331k
Liu, X., Pan, X., Zhang, S., Han, X., and Bao, X. (2014). Diffusion of water inside carbon nanotubes studied by pulsed field gradient NMR spectroscopy. Langmuir 30, 8036–8045. doi: 10.1021/la500913r
Lok, B. M., Messina, C. A., Patton, R. L., Gajek, R. T., Cannan, T. R., and Flanigen, E. M. (1984). Silicoaluminophosphate molecular sieves: another new class of microporous crystalline inorganic solids. J. Am. Chem. Soc. 106, 6092–6093. doi: 10.1021/ja00332a063
Loring, J. S., Ilton, E. S., Chen, J., Thompson, C. J., Martin, P. F., Benezeth, P., et al. (2014). In situ study of CO2 and H2O partitioning between Na−montmorillonite and variably wet supercritical carbon dioxide. Langmuir 30, 6120–6128. doi: 10.1021/la500682t
Macomber, R. S. (1998). A Complete Introduction to Modern NMR Spectroscopy. New York, NY: John Wiley & Sons.
Malikova, N., Cadene, A., Marry, V., Dubois, E., and Turq, P. (2006). Diffusion in water in clays on the microscopic scale: modelling and experiment. J. Phys. Chem. B 110, 3206–3214. doi: 10.1021/jp056954z
Mamontov, E., Burnham, C. J., Chen, S.-H., Moravsky, A. P., Loong, C.-K., de Souza, N. R., et al. (2006). Dynamics of water confined in single- and double-walled carbon nanotubes. J. Chem. Phys. 124:194703. doi: 10.1063/1.2194020
Marry, V., Dubois, E., Malikova, N., Durand-Vidal, S., Longeville, S., and Breu, J. (2011). Water dynamics in hectorite clays: influence of temperature studied by coupling neutron spin echo experiments and molecular dynamics. Environ. Sci. Technol. 45, 2850–2855. doi: 10.1021/es1031932
Martin, M. G., and Siepmann, J. I. (1998). Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 102, 2569–2577. doi: 10.1021/jp972543+
Meng, X., and Xiao, F.-S. (2014). Green routes for synthesis of zeolites. Chem. Rev. 114, 1521−1543. doi: 10.1021/cr4001513
Michot, L. J., Delville, A., Humbert, B., Plazanet, M., and Levitz, P. (2007). Diffusion of water in a synthetic clay with tetrahedral charges by combined neutron time of flight measurements and molecular dynamics simulations. J. Phys. Chem. C 111, 9818–9831. doi: 10.1021/jp0690446
Mitra, S., Pramanik, A., Chakrabarty, D., Juranyi, F., Gautam, S., and Mukhopadhyay, R. (2007). Diffusion of water adsorbed in hydrotalcite: neutron scattering study. J. Phys. 92:012167. doi: 10.1088/1742-6596/92/1/012167
Mitra, S., Sumitra, S., Umarji, A. M., Mukhopadhyay, R., Yashonath, S., and Chaplot, S. L. (2004). Acetylene diffusion in Na-Y zeolite. Pramana J. Phys. 63, 449–453. doi: 10.1007/BF02705014
Mukhopadhyay, R., Sayeed, A., Mitra, S., Kumar, A. V., Rao, M. N., Yashonath, S., et al. (2004). Rotational dynamics of propane in Na-Y zeolite: a molecular dynamics and quasielastic neutron scattering study. Phys. Rev. E 66:061201. doi: 10.1103/PhysRevE.66.061201
Myshakin, E. M., Jiang, H., Warzinski, R. P., and Jordon, K. D. (2009). Molecular dynamics simulation of methane hydrate decomposition. J. Phys. Chem. A 113, 1913–1921. doi: 10.1021/jp807208z
Nivarthi, S. S. S., McCormick, A. V., and Davis, H. T. (1994). Diffusion anisotropy in molecular sieves: a Fourier transform PFG NMR study of methane in A1PO4-5. Chem. Phys. Lett. 229, 297–301. doi: 10.1016/0009-2614(94)01059-5
Ok, S., Hoyt, D. W., Andersen, A., Sheets, J., Welch, S. A., Cole, D. R., et al. (2017). Surface interactions and confinement of methane: a high pressure magic angle spinning NMR and computational chemistry study. Langmuir 33, 1359–1367. doi: 10.1021/acs.langmuir.6b03590
Ok, S., Sadaf, S., and Walder, L. (2014). Basic characterization and investigation of a fluorinated terpolymer in pure state and in mixtures with kaolinite at solid interphases of thin films prepared by facile solution cast and nonsolvent methods. High Perform. Polym. 26, 779–789. doi: 10.1177/0954008314529601
Osti, N., Cote, A., Mamontov, E., Ramirez-Cuesta, A., Wesolowski, D. J., and Diallo, S. O. (2016). Characteristic features of water dynamics in restricted geometries investigated with quasi-elastic neutron scattering. Chem. Phys. 465–466, 1–8. doi: 10.1016/j.chemphys.2015.11.008
Packer, K. J. (2003). Magnetic resonance in porous media: forty years on. Magn. Reson. Imaging 21, 163–168. doi: 10.1016/S0730-725X(03)00120-6
Pampel, A., Fernandez, M., Freude, D., and Kärger, J. (2005). New options for measuring molecular diffusion in zeolites by MAS PFG NMR. Chem. Phys. Lett. 407, 53–57. doi: 10.1016/j.cplett.2005.03.062
Pampel, A., Kärger, J., and Michel, D. (2003). Lateral diffusion of a transmembrane peptide in lipid bilayers studied by pulsed field gradient NMR in combination with magic angle sample spinning. Chem. Phys. Lett. 379, 555–561. doi: 10.1016/j.cplett.2003.08.093
Patankar, S., Gautam, S., Rother, G., Podlesnyak, A., Ehlers, G., Liu, T., et al. (2016). Role of confinement on adsorption and dynamics of ethane and an ethane-CO2 mixture in mesoporous CPG silica. J. Phys. Chem. C 120, 4843–4853. doi: 10.1021/acs.jpcc.5b09984
Porion, P., Michot, L. J., Faugere, A. M., and Delville, A. (2007). Structural and dynamical properties of the water molecules confined in dense clay sediments: a study combining 2H NMR spectroscopy and multiscale molecular modeling. J. Phys. Chem. C 111, 5441–5453. doi: 10.1021/jp067907p
Price, W. S. (1997). Pulsed-field gradient nuclear magnetic resonance as a tool for studying translational diffusion: part 1. Basic theory. Concepts Magn. Reson. 9, 299–366. doi: 10.1002/(SICI)1099-0534(1997)9:5<299::AID-CMR2>3.0.CO;2-U
Qian, L., Ren, Y., Wang, Y., Yue, B., and He, H. (2011). Controlled atmosphere 13C and 1H MAS NMR study of reforming route of methane with carbon dioxide over Rh/SBA-15. Appl. Catal. A 401, 114–118. doi: 10.1016/j.apcata.2011.05.004
Richter, D., Monkenbusch, M., Arbe, A., and Colmenero, J. (2005). Neutron Spin Echo in Polymer Systems. Berlin; Heidelberg: Springer.
Ripmeester, J. A., and Ratcliffe, C. I. (1988). Low-temperature cross-polarization/magic angle spinning 13C NMR of solid methane hydrates: structure, cage occupancy, and hydration number. J. Phys. Chem. 92, 337–339. doi: 10.1021/j100313a018
Salles, F., Jobic, H., Devic, T., Guillerm, V., Serre, C., Koza, M. M., et al. (2013). Diffusion of binary CO2/CH4 mixtures in the MIL-47(V) and MIL-53(Cr) metal−organic framework type solids: a combination of neutron scattering measurements and molecular dynamics simulations. J. Phys. Chem. C 117, 11275−11284. doi: 10.1021/jp403225t
Sayeed, A., Mitra, S., Kumar, A. V. A., Mukhopadhyay, R., Yashonath, S., and Chaplot, S. L. (2003). Diffusion of propane in zeolite Na-Y: a molecular dynamics and quasielastic neutron scattering study. J. Phys. Chem. B 107, 527–533. doi: 10.1021/jp025576k
Schmidt-Rohr, K., and Spiess, W. H. (1994). Multidimensional Solid-State NMR and Polymers. London: Academic Press.
Sen, P. N. (2004). Time-dependent diffusion coefficient as a probe of geometry. Concepts Magn. Reson. A 23, 1–21. doi: 10.1002/cmr.a.20017
Seo, Y.-T., and Lee, H. (2003). 13C NMR analysis and gas uptake measurements of pure and mixed gas hydrates: development of natural gas transport and storage method using gas hydrate. Korean J. Chem. Eng. 20, 1085–1091. doi: 10.1007/BF02706941
Sharma, V. K., Gautam, S., Mitra, S., and Mukhopadhyay, R. (2010). Dynamics of propylene adsorbed in Na-Y and Na-ZSM5 zeolites: a QENS and MD simulation study. Z. Phys. Chem. 224, 133–152. doi: 10.1524/zpch.2010.6096
Sharma, V. K., Gautam, S., Mitra, S., Rao, M. N., Tripathi, A. K., Chaplot, S. L., et al. (2009). Dynamics of adsorbed hydrocarbon in nanoporous zeolite framework. J. Phys. Chem. B 113, 8066–8072. doi: 10.1021/jp9014405
Sindorf, D. W., and Maciel, G. E. (1983). Silicon-29 NMR study of dehydrated/rehydrated silica gel using cross polarization and magic-angle spinning. J. Am. Chem. Soc. 105, 1487–1493. doi: 10.1021/ja00344a012
Slichter, C. P. (1990). Principles of Magnetic Resonance. New York, NY: Springer Series in Solid State Science.
Sloan, E. D. Jr. (2003). Fundamental principles and applications of natural gas hydrates. Nature 426, 353–359. doi: 10.1038/nature02135
Sloan, E. D. Jr., and Koh, C. (2007). Clathrate Hydrates of Natural Gases. Boca Raton FL: CRC press.
Song, Y.-Q. (2007). Novel NMR techniques for porous media research. Cement Concrete Res. 37, 325–328. doi: 10.1016/j.cemconres.2006.02.013
Sørland, G. H., Hafskjold, B., and Herstadt, O. (1997). A stimulated-echo method for diffusion measurements in heterogeneous media using pulsed field gradients. J. Magn. Reson. 124, 172–176. doi: 10.1006/jmre.1996.1029
Stallmach, F., Graser, A., Kärger, J., Krause, C., Jeschke, M., Oberhagemann, U., et al. (2001). Pulsed field gradient NMR studies of diffusion in MCM-41 mesoporous solids. Micropor. Mesopos. Mat. 44, 745–753. doi: 10.1016/S1387-1811(01)00256-6
Stallmach, F., Kärger, J., Krause, C., Jeschke, M., and Oberhagemann, U. (2000). Evidence of anisotropic self-diffusion of guest molecules in nanoporous materials of MCM-41 type. J. Am. Chem. Soc. 122, 9237–9242. doi: 10.1021/ja001106x
Stallmach, F., Pusch, A.-K., Splith, T., Horch, C., and Merker, S. (2015). NMR relaxation and diffusion studies of methane and carbon dioxide in nanoporous ZIF-8 and ZSM-58. Micropor. Mesopos. Mat. 205, 36–39. doi: 10.1016/j.micromeso.2014.08.034
Steele, R. M., Korb, J. P., Ferrante, G., and Bubici, S. (2015). New applications and perspectives of fast field cycling NMR relaxometry. Magn. Reson. Chem. 54, 502–509. doi: 10.1002/mrc.4220
Stepanov, A. G., Shegai, T. O., Luzgin, and Jobic, H. (2003). Comparison of the dynamics of n-hexane in ZSM-5 and 5A zeolite structures. Eur. Phys. J. E Soft Matter 12, 57–61. doi: 10.1140/epje/i2003-10037-3
Subramanian, S., Kini, R. A., Dec, S. F., and Sloan, E. D. Jr. (2000). Evidence of structure II hydrate formation from methane+ethane mixtures. Chem. Eng. Sci. 55, 1981–1999. doi: 10.1016/S0009-2509(99)00389-9
Swenson, J., Bergman, R., and Howells, W. S. (2000). Quasielastic neutron scattering study of 2-dimensional water in a vermiculite clay. J. Chem. Phys. 113, 2873–2879. doi: 10.1063/1.1305870
Swenson, J., Bergman, R., and Longeville, S. (2001). A neutron spin echo study of confined water. J. Chem. Phys. 115, 11299–11305. doi: 10.1063/1.1420728
Takahara, S., Nakano, M., Kittaka, S., Kuroda, Y., Mori, T., Hamano, H., et al. (1999). Neutron scattering study on dynamics of water molecules in MCM-41. J. Phys. Chem. B 103, 5814–5819. doi: 10.1021/jp984136j
Takahara, S., Sumiyama, S., Kittaka, S., Yamaguchi, T., and Bellissent-Funel, M. C. (2005). Neutron scattering study on dynamics of water molecules in MCM-41. 2. Determination of translational diffusion coefficient. J. Phys. Chem. B 109, 11231–11239. doi: 10.1007/s10450-005-5971-y
Tanner, J. E. (1970). Use of the stimulated echo in NMR diffusion studies. J. Chem. Phys. 52, 2523–2526. doi: 10.1063/1.1673336
Tsukahara, T., Hibara, A., Ikeda, Y., and Kitamori, T. (2007). NMR study of water molecules confined in extended nanospaces. Angew. Chem. Int. Ed. 46, 1180–1183. doi: 10.1002/anie.200604502
Tulk, C. A., Klug, D. D., dos Santos, A. M., Karotis, G., Guthrie, M., Molaison, J. J., et al. (2012). Cage occupancies in the high pressure structure H methane hydrate: a neutron diffraction study. J. Chem. Phys. 136, 054502. doi: 10.1063/1.3679875
Ueda, T., Kurokawa, K., Kawamura, Y., Miyakubo, K., and Eguchi, T. (2012). 1H NMR study of molecular motion of benzene and n-decane confined in the nanocavities of metal-organic frameworks. J. Phys. Chem. C 116, 1012–1019. doi: 10.1021/jp209746n
Vasenkov, S., Bohlmann, W., Galvosas, P., Geier, O., Liu, H., and Kärger, J. (2001). PFG NMR study of diffusion in MFI-type zeolites: evidence of the existence of intracrystalline transport barriers. J. Phys. Chem. B 105, 5922–5927. doi: 10.1021/jp003899f
Vogel, M. (2010). NMR studies on simple liquids in confinement. Eur. Phys. J. Special Topics 189, 47–64. doi: 10.1140/epjst/e2010-01309-9
Vogel, S. C., and Priesmeyer, H.-G. (2006). “Neutron Production, Neutron Facilities and Neutron Instrumentation,” in Neutron Scattering in Earth Sciences, Reviews in Mineralogy and Geochemistry, Vol. 63, ed H.-R. Wenk (Chantilly: Mineralogical Society of America), 27–58.
Vogt, C., Galvosas, P., Klitzschm, N., and Stallmach, F. (2002). Self-diffusion studies of pore fluids in unconsolidated sediments by PFG NMR. J. Appl. Geophys. 50, 455–467. doi: 10.1016/S0926-9851(02)00195-7
Walbrecker, J. O., and Behroozmand, A. A. (2012). Surface-NMR measurements of the longitudinal relaxation time T1 in a homogenenous sand aquifer in Skive, Denmark. J. Appl. Geophys. 87, 46–52. doi: 10.1016/j.jappgeo.2012.08.009
Wang, J., Kalinichev, A. G., and Kirkpatrick, R. J. (2006). Effects of substrate structure, dynamics and energetics of water at mineral interfaces: a molecular dynamics modeling study. Geochim. Cosmo. Acta 70, 562–582. doi: 10.1016/j.gca.2005.10.006
Wilson, S. T., Lok, B. M., Messina, C. A., Cannan, T. R., and Flanigen, E. M. (1982). Aluminophosphate Molecular sieves: a new class of microporous crystalline inorganic solids. J. Am. Chem. Soc. 104, 1146–1147. doi: 10.1021/ja00368a062
Xu, M., Harris, K. D., Thomas, J. M., and Vaughan, D. E. (2007). Probing the evolution of adsorption on nanoporous solids by in situ solid-state NMR spectroscopy. Chem. Phys. Chem. 8, 1311–1313. doi: 10.1002/cphc.200700218
Yashonath, S., and Santikary, P. (1994). Diffusion of sorbates in zeolites Y and A: novel dependence on sorbate size and strength of sorbate-zeolite interaction. J. Phys. Chem. 98, 6368–6376. doi: 10.1021/j100076a022
Yoshida, K., Yamaguchi, T., Kittaka, S., Bellissent-Funel, M. C., and Fouquet, P. (2008). Thermodynamic, structural, and dynamic properties of supercooled water confined in mesoporous MCM-41 studied with calorimetric, neutron diffraction, and neutron spin-echo measurements. J. Chem. Phys. 129, 054702 doi: 10.1063/1.2961029
Keywords: confined fluids, porous materials, diffusion, nuclear magnetic resonance, neutron scattering, MD simulations, relaxation
Citation: Gautam SS, Ok S and Cole DR (2017) Structure and Dynamics of Confined C-O-H Fluids Relevant to the Subsurface: Application of Magnetic Resonance, Neutron Scattering, and Molecular Dynamics Simulations. Front. Earth Sci. 5:43. doi: 10.3389/feart.2017.00043
Received: 14 January 2017; Accepted: 19 May 2017;
Published: 06 June 2017.
Edited by:
Alysia Danielle Cox, Montana Tech of the University of Montana, United StatesReviewed by:
Dennis D. Klug, National Research Council Canada (NRC-CNRC), CanadaCopyright © 2017 Gautam, Ok and Cole. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Siddharth S. Gautam, Z2F1dGFtLjI1QG9zdS5lZHU=
†Present Address: Salim Ok, Petroleum Research Center, Kuwait Institute for Scientific Research, Safat, Kuwait
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.