Convective Boundary Layer Heights Over Mountainous Terrain—A Review of Concepts

Mountainous terrain exerts an important influence on the Earth's atmosphere and affects atmospheric transport and mixing at a wide range of temporal and spatial scales. The vertical scale of this transport and mixing is determined by the height of the atmospheric boundary layer, which is therefore an important parameter in air pollution studies, weather forecasting, climate modeling, and many other applications. It is recognized that the spatio-temporal structure of the daytime convective boundary layer (CBL) height is strongly modified and more complex in hilly and mountainous terrain compared to flat terrain. While the CBL over flat terrain is mostly dominated by turbulent convection, advection from multi-scale thermally driven flows plays an important role for the CBL evolution over mountainous terrain. However, detailed observations of the CBL structure and understanding of the underlying processes are still limited. Characteristics of CBL heights in mountainous terrain are reviewed for dry, convective conditions. CBLs in valleys and basins, where hazardous accumulation of pollutants is of particular concern, are relatively well-understood compared to CBLs over slopes, ridges, or mountain peaks. Interests in the initiation of shallow and deep convection, and of budgets and long-range transport of air pollutants and trace gases, have triggered some recent studies on terrain induced exchange processes between the CBL and the overlying atmosphere. These studies have helped to gain more insight into CBL structure over complex mountainous terrain, but also show that the universal definition of CBL height over mountains remains an unresolved issue. The review summarizes the progress that has been made in documenting and understanding spatio-temporal behavior of CBL heights in mountainous terrain and concludes with a discussion of open research questions and opportunities for future research.

Introduction

The effect of mountains on the Earth's atmosphere has long been recognized and studied (Atkinson, 1981; Barry, 1992; Whiteman, 2000; Chow et al., 2013). Almost 50% of the Earth's land surface is covered by hilly and mountainous terrain (Meybeck et al., 2001) and the effect of mountains on weather and climate is oftentimes felt far away from the mountains.

Mountains exert an influence on the atmosphere in two basic ways that can be described as passive and active effects (Geiger, 1961). Passive effects involve momentum exchange between the surface and the atmosphere and occur when a flow is modified by the presence of mountains. Examples include flow blocking, flow channeling, and lee waves. There are many review articles on the passive effects when air flows over or around mountains (e.g., Queney, 1948; Smith, 1979; Wood, 2000; Jackson et al., 2013; Richner and Hächler, 2013). Active effects involve thermal and radiative energy exchange processes and occur when the terrain interacts with the diurnal heating and cooling cycle. Examples include thermally driven wind systems generated by horizontal temperature and pressure differences. These effects are most pronounced in cloudless conditions and weak synoptic pressure gradients. Several review articles exist on thermally driven wind systems in mountainous terrain (Whiteman, 1990; Zardi and Whiteman, 2013). At any moment, passive and active effects play an important role in determining the dynamical and thermodynamical atmospheric structure, with their individual roles depending on factors such as wind speed, cloud cover, and atmospheric stability. The current review paper focuses on the height of the atmospheric boundary layer during daytime, dry, convective conditions when active effects are dominant.

The atmospheric boundary layer is usually defined as the atmospheric layer that interacts directly with the Earth's surface on a time scale of a few hours or less (e.g., Stull, 1988). During daytime convective conditions, the atmospheric boundary layer is also called the convective boundary layer (CBL). Knowledge of CBL height and structure is useful or required in many applications such as air-quality studies, aerial spraying- and fire weather operations, regional climatology investigations, and weather forecasting.

In flat, homogeneous terrain, the CBL has been investigated intensively (e.g., Stull, 1988). The CBL grows by upward sensible heat flux at the surface and downward sensible heat flux (entrainment) at the top of the CBL. The convergence of the sensible heat flux causes the CBL to warm and grow in depth. The CBL growth rate is affected primarily by the characteristics of the surface-based temperature inversion at sunrise, the strength of the elevated temperature inversion, the free-atmospheric stability, and by the upward sensible heat flux at the surface. Subsidence at the top of the CBL will slow its growth rate.

Over mountainous terrain, the atmospheric structure becomes much more complicated. Transport and mixing processes such as those related to mountain waves (Smith et al., 2007), rotors (Doyle and Durran, 2007), and thermally-driven wind systems (Zardi and Whiteman, 2013) may affect CBL variability. One of the first attempts at describing the thermal structure of the CBL over mountainous terrain was made by Ekhart (1948). Ekhart analyzed radiosonde data and found that, compared to flat terrain, the diurnal amplitude of temperature in mountainous regions not only increases toward the surface, but is also significant at higher elevations. Ekhart concluded that the atmosphere above the mountain ridges is very different and independent from the valley atmosphere. Based on analyses of the diurnal temperature range and the winds at various locations, Ekhart makes a distinction between four different mountain atmospheres (Figure 1): the slope atmosphere with a depth of at most a couple of 100 m; a valley atmosphere, characterized by along valley flows; a large-scale mountain atmosphere which is influenced by the active (thermal) and passive (dynamical) effects of the entire mountain range; and the free atmosphere which is the unperturbed atmosphere at great horizontal and vertical distance from the mountain chain. Our major objectives of this review paper are to highlight some important aspects of CBL structure in mountainous terrain, to provide an overview of the current concepts, and to identify fruitful areas of future research.

FIGURE 1

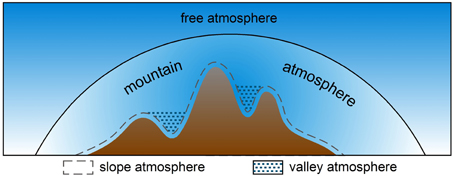
Figure 1. Structure of the lower atmosphere over a mountain. The solid line indicates the boundary between the free atmosphere and the atmosphere influenced by the mountain. The dashed line indicates the top of the slope atmosphere, while the hatched pattern indicates the valley atmosphere (after Ekhart, 1948).

The structure of this review paper will follow Ekhart's notion of a slope, valley, and mountain atmosphere with each of the “atmospheres” discussed separately. After defining CBL height and its determination, we will discuss the CBL height over slopes, valleys, basins, mountain tops and plateaus, and entire mountain ranges. Current notions concerning exchange processes between the CBL and the free atmosphere in mountainous terrain are also reviewed. We will conclude this review paper with a discussion of possible areas for future research.

Definition and Determination of CBL Heights

One of the challenges of describing the spatio-temporal variability of the CBL height is the lack of consensus regarding its definition and determination. This is especially true for complex, mountainous terrain. While the term CBL is used throughout this review, other terms are used in the literature such as convective mixed layer or simply mixed or mixing layer (AMS, 2000). The term “mixing layer” is also used for the nocturnal boundary layer with high levels of shear-generated turbulence. In the CBL, convectively generated turbulence dominates over shear generated turbulence to produce vigorous mixing which tends to make the potential temperature, moisture, tracer concentrations, and momentum independent of height in a major portion of the CBL.

At the top of the CBL, there is usually an increase in potential temperature and wind speed and a sharp decrease in humidity and pollutant concentration (Figure 2). A layer in which potential temperature increases with height or in which the temperature lapse rate is less than the dry adiabatic lapse rate is considered a stable layer. Such a layer could be surface-based or elevated. The top of the CBL is often defined as the base of an elevated stable layer. This criterion is used as the working definition in many of the examples provided in this paper. It should be recognized however, that other definitions exist that are using either air pollution (Maughan et al., 1982; Baxter, 1991; Myrick et al., 1994; Seibert et al., 2000) or turbulence parameters (Holzworth, 1972; Norton and Hoidale, 1976; Deardorff et al., 1980; Cai and Steyn, 1993; Vogelezang and Holtslag, 1996; Beyrich, 1997; Adler and Kalthoff, 2014; Dai et al., 2014) to indicate the CBL top. For example, Seibert et al. (2000) define the CBL top as “the height of the layer adjacent to the ground over which pollutants or any constituents emitted within this layer or entrained into it become vertically dispersed by convection or mechanical turbulence within a time scale of about an hour.” They note that this definition corresponds to the top of the entrainment zone; a zone at the top of the CBL that is not well-mixed and where turbulence intensity weakens. In their definition, the CBL top is therefore not necessarily located at the base of an elevated stable layer.

FIGURE 2

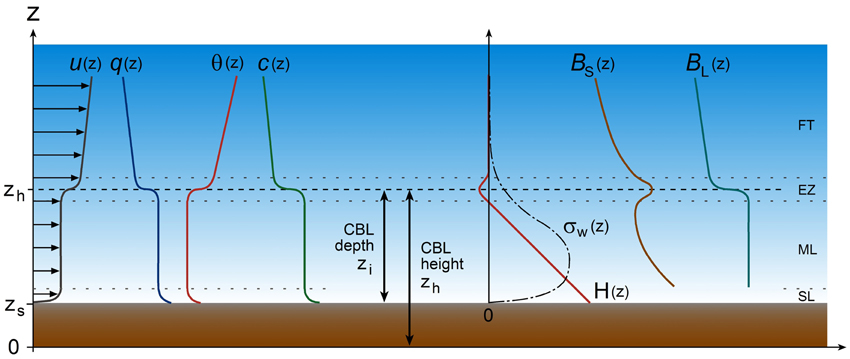
Figure 2. Idealized vertical structure of the lower troposphere under daytime convective conditions over flat and homogeneous terrain, subdivided into the surface layer (SL), the mixed layer (ML), the entrainment zone (EZ), and the free troposphere (FT). The vertical profiles represent wind velocity u(z), specific humidity q(z), potential temperature θ(z), air pollutant concentration c(z), vertical turbulent sensible heat flux H(z), standard deviation of turbulent vertical velocity fluctuations σ_w(z), and backscatter signal intensities B_S(z) from a sodar and B_L(z) from a lidar. z_s is the terrain height while z_i and z_h are the depth and the height of the CBL, respectively.

Conventionally, CBL heights have been determined most frequently from vertical temperature profiles. In recent years, the development and availability of remote sensors such as sodars (sound detection and ranging) and lidars (light detection and ranging) have provided alternatives to this conventional method and have enabled the documentation of the daily variation of the CBL height at large temporal and spatial resolution. Sodars detect temperature fluctuations (turbulence), winds, and wind shear, while lidars detect vertical aerosol distribution. Particularly, downward looking airborne lidars have proven useful for the investigation of the spatial variability of CBL heights (e.g., Melfi et al., 1985; Kiemle et al., 1995; Hayden et al., 1997; Hägeli et al., 2000; De Wekker et al., 2004). An elevated maximum in the return signal from sodar emitted acoustic waves is caused by sharp vertical changes in turbulence and temperature stratification and usually indicates the height of the CBL top. The CBL top is also characterized by a vertical gradient in aerosol concentrations that can be determined by a sharp change in the range corrected return signal from lidar emitted laser pulses (Figure 2). An overview of the determination of CBL heights from remote sensing is given by Emeis et al. (2008). Several studies over flat terrain have shown a good correspondence between estimates of the CBL height from lidar and temperature profiles (Coulter, 1979; Van Pul et al., 1994; Marsik et al., 1995; Hayden et al., 1997; Hennemuth and Lammert, 2006) with maximum differences on the order of a few hundred meters in deep afternoon CBLs. Figure 2 provides a visual summary of the various methods discussed above to estimate the CBL top over flat and homogeneous terrain. Over mountainous terrain, several issues arise with the comparability of the various methods. For example, presence of upper-level turbulence induced by thermally driven flows can make the turbulence-based methods impractical or inapplicable (De Wekker, 2008; Catalano and Moeng, 2010). Also, mountain venting processes can cause aerosols and humidity to be transported above the CBL top (De Wekker et al., 2004; Steyn et al., 2013; Adler and Kalthoff, 2014). We will further discuss these processes and the implications for determining CBL heights over mountainous terrain in Section “Vertical Transport and Mixing Between the CBL and the Free Troposphere”.

We are making a distinction between CBL depth and CBL height. In applications where the volume of air in which e.g., pollutants are mixed is considered, or for scaling arguments, it is important to use CBL depth z_i (or thickness) which is the height of the CBL top above ground level (AGL). On the other hand, for investigating the extent to which the CBL follows the terrain, it is appropriate to use the CBL height z_h, which is the height of the CBL top above mean sea level (MSL). If the terrain elevation z_s is known, CBL height and CBL depth can be easily converted (Figure 2).

CBL Height in Mountainous Terrain

While the focus of this review is on the thermal structure of the CBL in mountainous terrain, the accompanying flow structure is of critical importance for the investigation of CBL heights. Flows that interact with CBL heights over hilly and mountainous terrain are often thermally driven and occur at a wide range of spatial and temporal scales (Whiteman, 1990; Zardi and Whiteman, 2013). Diurnal winds in valleys generally blow up the valley during daytime and down the valley during nighttime, termed upvalley and downvalley flows, respectively. Similarly, flows blowing up the slope during daytime and down the slope during nighttime are termed upslope and downslope flows, respectively. Large-scale thermally driven wind systems in mountainous areas are also known as mountain-plain wind systems and have been given various names for basin and plateau topographies. The mountain-plain wind system with near surface winds directed from a plain toward a plateau has been called a plain-to-plateau wind (Mannouji, 1982). Similarly, a mountain-plain wind system carrying air from the plains over a mountain range into a basin has been called a plain-to-basin wind (Kimura and Kuwagata, 1993). The importance of these thermally driven wind systems for CBL heights over mountainous terrain will be demonstrated throughout the next sections that consecutively discuss CBL heights over slopes, valleys, basins and plateaus, and entire mountain ranges. Many of the reviewed observational studies that have contributed to recent understanding of CBL heights in mountainous terrain did not employ vertical soundings of turbulence parameters. Conceptual diagrams of CBL top behavior shown for these terrain settings therefore use the base of the elevated stable layer (or ‘capping inversion’) as commonly available criterion for CBL height detection.

Slope CBL

In the spectrum of atmospheres present over mountainous terrain, the slope atmosphere constitutes the smallest spatial scales (Figure 1). However, many of the CBL structures observed over mountainous terrain originate in the slope CBL which therefore, deserves much attention. The most striking feature of the CBL over slopes during daytime fair weather conditions is the development of thermally induced upslope winds. These upslope flows interact with turbulent convection and affect CBL heights, not only over slope locations but also over adjacent plain, valley, basin, plateau, and ridge locations. The importance of the slope atmosphere in affecting other parts of the mountain atmosphere makes the slope CBL an appropriate starting point in this review paper. To this end, we consider an idealized time-height cross section of the various wind systems at a particular location over a slope on a fair weather day (Figure 3). Vertical potential temperature profiles at selected times of the day are also shown to illustrate boundary layer structure evolution. Note that these profiles are idealized, with, for example, the presence of an elevated stable layer at ridge height limiting slope CBL growth to greater heights. Just before sunrise, the near surface airflow over slopes is typically down-valley (in draining valleys), but stagnant conditions could also occur (in pooling valleys or enclosed basins). Downslope flows typically become weaker during the course of the night and are often imperceptible just before sunrise (e.g., Whiteman, 1990). The importance of these nighttime downslope winds for daytime CBL development arises because of the associated overnight accumulation of cold air in valleys and basins. The strong stability in these cold air pools leads to rather slow CBL growth rates over valley and basin floors and lower sidewalls after sunrise. In contrast, only shallow and weak inversions are usually found over upper slopes and mountain tops at sunrise, since most of the cold air forming during the night drained to lower terrain. In Figure 3, we assume that toward the end of the night (t₁ in Figure 3) the surface based inversion over the valley center or the adjacent plain exceeds the height of the slope location. If the valley inversion top were below the slope location, downslope winds would still be present at the surface and the average stability up to the ridge height h_r would be much smaller.

FIGURE 3

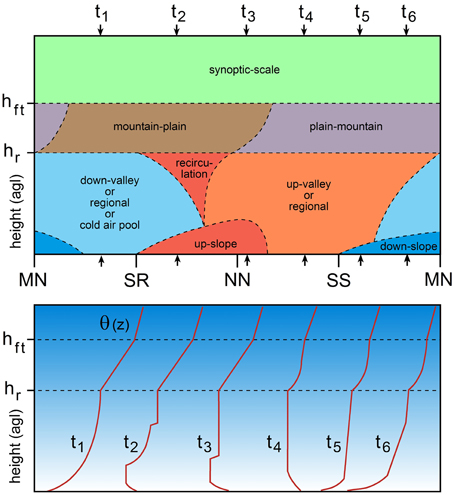
Figure 3. Diurnal boundary layer structure over a slope. Upper panel: time-height section of airflow regimes over a slope during fair weather conditions. h_r and h_ft are the height of surrounding ridges and the base height of the free troposphere, respectively. Ticks on the time axis indicate midnight (MN), sunrise (SR), noon (NN), and sunset (SS). Lower panel: vertical profiles of potential temperature θ(z) over the slope at selected times t₁ to t₆ marked in the upper panel by small arrows.

After sunrise an upslope wind layer develops over insolated slopes with a return circulation toward the valley center aloft (t₂ in Figure 3). After erosion of the nocturnal valley inversion layer, up-valley winds or other regional wind systems become dominant in the neutrally or weakly stably stratified layer between the upslope wind layer and ridge top. For the common situation with a stably stratified ambient atmosphere, upslope wind conditions are associated with an along-slope gradient in potential temperature in the slope wind layer. The upslope winds are therefore characterized by cold air advection which often leads to the phenomenon of undercutting (Kossmann et al., 1998), also known from cold air advection associated with other thermally induced wind systems such as sea breezes (e.g., Blumenthal et al., 1978; McElroy and Smith, 1991; Lu and Turco, 1994). The cold air advection counteracts heating due to the turbulent and radiative heat flux convergences over the slopes. This negative feedback mechanism limits the intensity of the daytime slope wind circulation (Prandtl, 1942) and represents a possible reason for non-stationary upslope flow behavior (Vergeiner and Dreiseitl, 1987; Hunt et al., 2003; Bastin and Drobinski, 2005). The along-slope advection of cold air (t₃ in Figure 3) leads to the formation of a stable layer near the top of the slope wind layer (Kossmann et al., 1998). Consequently, the CBL depth over slopes often coincides with the depth of the slope wind layer (e.g., Segal et al., 1987; Ye et al., 1987; Kuwagata and Kondo, 1989), similar to how the internal boundary layer depth in coastal areas coincides with the depth of the sea-breeze layer (Johnson and O'Brien, 1973; Mizzi and Pielke, 1984; Physick et al., 1989). Non-stationary upslope flows, in their turn, result in highly variable CBL depths over slopes, with the possible occurrence of sudden jumps to higher or lower values (Kossmann et al., 1998).

During the course of the afternoon, slope flows become less well-defined and are often overpowered by the up-valley or regional winds due to downward turbulent momentum transfer (t₄ in Figure 3). Vigorous mixing induced by thermals originating at the surface can also make horizontal temperature gradients and resulting advective transport less important than turbulence-induced convective transport. This convective mixing results in a deepening of the CBL over the slopes similar to flat terrain.

After sunset, surface cooling leads to the formation of downslope winds in the developing surface inversion layer, while up-valley and/or regional winds still prevail aloft in a residual layer (t₅ in Figure 3). Later, up-valley winds will cease and may be replaced by down-valley winds (t₆ in Figure 3). The mountain atmosphere above ridge height is characterized by the presence of a large scale, diurnally reversing mountain-plain wind system which is often masked by strong synoptic flows and therefore may be too weak to be observed. In the presence of significant heating of the elevated terrain, the atmosphere at ridge top height becomes destabilized during the day (t₄–t₆ in Figure 3) as was already observed by Ekhart (1948).

Observations and models have shown many different scenarios for the behavior of thermal and dynamical structures over sloping surfaces (Figure 4). The classical daytime slope flow regime in valleys by Wagner (1932) is shown in Figure 4A, where the upslope flows detach from the slope without preference to any particular along-slope location. This leads to a more or less continuous detrainment from the slope flow layer and compensating subsidence over the valley center. This conceptual model was extended by Vergeiner (1982). Based on energetic considerations he concluded that upslope winds prefer to detach from the slope at elevations where particularly strong inversions are present in the valley atmosphere (Figure 4B). This process favors the existence of two or more stacked slope wind circulations and associated entrainment and detrainment to and from the slope wind layer. A recent modeling study by Wagner et al. (2014) showed that in deeper valleys, stacked slope wind circulations are more likely to occur. Furthermore, in laboratory experiments, Princevac and Fernando (2008) show that the upslope flow is forced to detach from the slope as the flow approaches an extremely strong inversion (Figure 4C). In a conceptual model of valley inversion breakup by Whiteman (1982), the upslope winds vent into a neutral or weakly stratified layer above the valley inversion built up during the previous night (Figure 4D). This means that slope flow detachment in this conceptual model occurs at elevations above the (subsiding) valley inversion. Reuten et al. (2005) provide observational evidence that scenarios where the return circulation penetrates into the inversion capping the upslope wind layer, might be typical only for cases with shallow CBLs in the valley or over the adjacent plain. Later in the day, when the CBL in the valley or over the plain exceeds a critical height (about half the height of the nearby ridges), the return circulation occurs within the turbulent valley/slope CBL (Figure 4E). In these situations, turbulent vertical momentum transfer within the CBL mixes the upslope wind layer with the return circulation aloft, possibly weakening or destroying the organized slope wind circulation. An upslope flow re-circulation contained within the CBL has also been found in numerical model simulations (e.g., Demko and Geerts, 2010). Another type of CBL behavior observed over a slope is described by Kossmann et al. (1998) for cases with a terrain following CBL top or residual layer top (Figure 4F). In such situations with near- neutral stratification above the slope flow layer, any weakening of the along-slope cold air advection due to disturbances in the upslope flow can lead to turbulent erosion of the inversion above the slope wind layer. This results in a sudden increase of CBL height from the top of the slope wind layer to the top of the near-neutral layer. Re-intensification of the upslope winds might then re-establish an inversion above the slope wind layer due to undercutting. During the course of the day, these mechanisms can lead to significant oscillations in CBL depth above slopes and in the associated vertical convergence of turbulent sensible heat fluxes (Kossmann et al., 1998). In summary, a wide range of different slope flow regimes exists that interact in various ways with the CBL height. Investigation of these interactions and the relevant processes is difficult, due in large part to the presence of ambient synoptically-driven flows which mask the weak return flows.

FIGURE 4

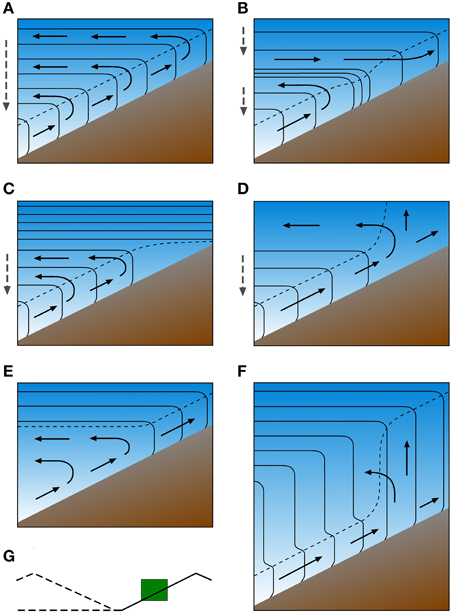
Figure 4. Conceptual models of slope wind circulation and CBL structure over a slope on a fair weather day. The green box in (G) on the lower left shows the location of the depicted cross section over a slope facing a valley or a plain. Thin solid and dashed lines represent isentropes and the top of the turbulent CBL, respectively. Solid and dashed arrows indicate the airflow and the compensating subsidence over the valley center or over the plain. (A) Slope wind circulation with homogeneously stratified atmosphere over the valley center or plain. (B) Two staggered slope wind circulations separated by a strongly stratified layer. (C) Slope wind circulation limited to lower slope due to strongly stratified layer aloft. (D) Slope wind venting into neutrally stratified layer aloft. (E) Recirculation of slope winds within the turbulent CBL. (F) Jump in CBL depth due to erosion of the inversion above the upslope wind layer and a deep neutrally stratified layer aloft.

The characteristics of the upslope flow circulation have strong implications for the dispersion of air pollutants. Return flows within the turbulent CBL cause trapping of pollutants within the valley (Reuten et al., 2005). On the other hand, air pollutants transported by return circulations above the turbulent CBL can be re-entrained into the valley CBL due to subsidence over the valley (Whiteman and McKee, 1978), or vented into the free troposphere (see Section “Summary and Directions for Future Research”). Subsidence induced by the return flow can also result in a decrease of the CBL depth near a mountain base (Section “Mountain Range CBL”) and affects CBL development in valleys as illustrated in the next section.

Valley CBL

CBL evolution can be notably different from valley to valley depending on the relative importance of surface heating, subsidence, and other processes in valley atmospheres. A schematic illustration of vertical potential temperature profiles at four consecutive times (t0–t3) observed over valley floors under a variety of conditions is shown in Figure 5. Note that these profiles are idealized with the assumption that nighttime cooling takes place up to ridge height while a neutrally stratified layer capped by an inversion is present above the valley atmosphere. Three basic patterns of CBL development in valleys have been observed in which the patterns are dominated by either surface heating (type 1, Figure 5B), subsidence heating (type 2; Figure 5C), or horizontal heat transfer from the heated slope surface (type 3; Figure 5D). The first two patterns are based on simultaneous observations of the wind- and temperature structure in various deep Colorado valleys primarily during the morning transition period (Whiteman, 1982; Whiteman and McKee, 1982). In type 1, CBL growth is similar to that over flat terrain while in type 2 the CBL height remains at a rather constant level until the top of the early morning temperature inversion descends to the top of the underlying CBL. The rate of subsidence of the temperature inversion over the valley center is determined by the rate of withdrawal of air mass from the valley by upslope flows (e.g., as indicated in Figure 4D). The subsiding valley inversion contributes locally to the heating of the valley atmosphere (Brehm and Freytag, 1982; Whiteman, 1982; Kuwagata and Kimura, 1995) and thus has an important impact on valley CBL evolution. Type 2 typically occurs in valleys during winter time or in situations with small surface sensible heat fluxes at the valley floor when the stability in the valley atmosphere remains weakly stable throughout the day. Many of the valleys studied by Whiteman (1982) showed a CBL evolution that resembled a combination of the type 1 and type 2 patterns.

FIGURE 5

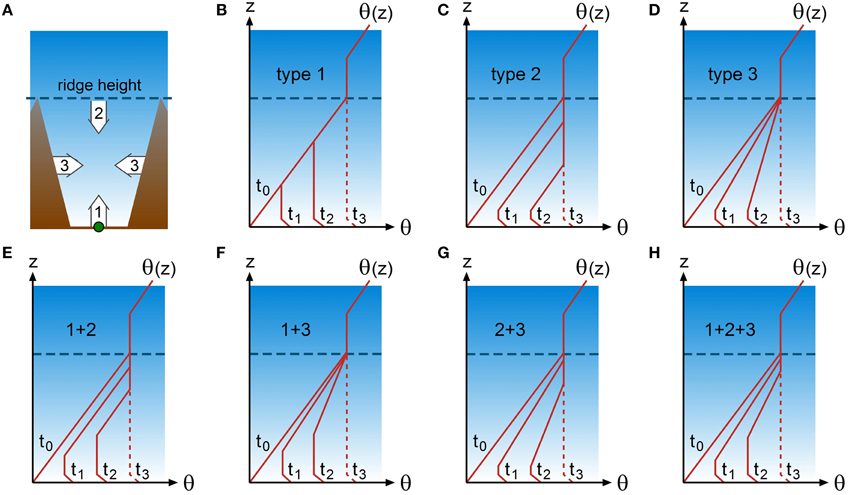
Figure 5. Conceptual models of CBL development in the center of a valley. The location of the idealized vertical profiles of potential temperature θ(z) at times t₀–t₃ is shown by the green dot in (A). (B–D) in the top row show three basic types of CBL development, while (E–H) in the bottom row show four combinations (mixed types) of the three basic types. The main direction of heat supply and erosion of the valley inversion for the three basic types are illustrated by numbered arrows in (A): arrow 1: turbulent heat flux from the valley floor (type 1); arrow 2: subsiding valley inversion (type 2); and arrow 3: heating from valley side walls by slope wind recirculation (type 3). The dashed line at t₃ indicates that a well-mixed potential temperature profile throughout the entire valley atmosphere does not necessarily occur.

Upslope flows play a different role in the daytime heating of the boundary layer over valleys compared to the heating of the slope atmosphere. While upslope flows indirectly enhance local heating of the atmosphere in the valley center by subsidence, these flows also counteract daytime heating over slopes as a result of along-slope cold air advection (see previous section). However, both cold air advection and subsidence heating tend to counteract CBL growth. Type 3 (Figure 5D) illustrates a situation with surface heating but without subsidence. This pattern without a deep CBL reaching ridge height is often observed in Alpine valleys (e.g., Freytag, 1985; Furger et al., 2000; Rotach et al., 2004) and valleys in the Andes mountains (Kalthoff et al., 2002; Khodayar et al., 2008). Note that a well-mixed potential temperature profile throughout the entire valley atmosphere, as indicated by the dashed lines at t₃ in Figure 5, does not necessarily occur, especially if surface heating is weak. The absence of well-mixed potential temperature profiles in the valley atmosphere has been attributed to heat transfer from the valley sidewall surfaces to the valley atmosphere (De Wekker, 2002; Serafin and Zardi, 2010a) and to strong along-valley advection of cold air, due to e.g., a lake or coast near the valley entrance (Bischoff-Gauss et al., 2008; Khodayar et al., 2008; Laiti et al., 2014). Model simulations by Wagner et al. (2014, 2015) show that, compared to wide reference valleys, daytime along-valley cold air advection is stronger for deeper valleys, for valleys narrowing in the up-valley direction, and for valleys with a strongly inclined valley floor. During the calm period in the morning transition phase between the erosion of down-valley winds in the remaining elevated valley inversion and the onset of up-valley winds (with associated cold air advection), a relatively deep valley CBL can develop for a short period of time (Eigenmann et al., 2009).

Horizontal transport and mixing processes away from the slope surface were already hypothesized by Wagner (1932) and evidence of these processes can be seen, for example, in recent observations and simulations of aerosol transport in the Inn Valley (Gohm et al., 2009; Lehner and Gohm, 2010). Horizontal heat transfer from the slope to the valley center can weaken or strengthen stability in the valley inversion, depending on the along-slope variations of the slope wind re-circulation intensity, of the heat supply provided by valley sidewall heating, and of the valley air volume with height (De Wekker et al., 2005; Schmidli, 2013). Observations and model results indicate that the amount of sensible heat available for heating the slope boundary layer generally increases with elevation up to the snow line (Brehm, 1986; Mannstein, 1989; Wenzel et al., 1997; De Wekker et al., 1998; Noppel and Fiedler, 2002) which can be attributed to decreasing soil moisture availability with elevation. Although the diabatic heating from the slopes increases with elevation, the volume of air to be heated in a horizontal layer of the valley atmosphere also increases with elevation. This volume or topographic amplification factor (TAF) effect depends on the area height distribution of the valley sidewalls (Steinacker, 1984; Müller and Whiteman, 1988; Liechti and Neininger, 1994) and can contribute to a decreasing heating rate with increasing elevation in the valley atmosphere. Recent model studies confirm the influence of the volume effect, but also find that the magnitude of the heating rate of the valley atmosphere strongly depends on along-valley cold air advection and slope wind induced export of heat from the valley to heights above ridge level (Schmidli and Rotunno, 2010; Schmidli, 2013; Leukauf et al., 2015).

Type 1 CBL development in valleys is characterized by a steady growth in CBL depth during erosion of the valley inversion, while types 2 and 3 exhibit a slow growth in the initial phase, followed by a sudden increase in CBL depth at the time when erosion of the inversion is completed (t₃ in Figure 5). In many cases however, the three basic processes described above act simultaneously and over a range of spatial and temporal scales which can lead to any of the other patterns sketched in Figures 5E–H. In the absence of surface heat flux observations and multiple soundings in time and/or space, it is difficult to isolate the underlying processes of importance in a certain situation. The actual time from t₀ to t₃ in Figure 5 can be highly variably as well, depending on the atmospheric situation, valley surface characteristics, and season. In dry and broad valleys, t₃ in type 1 may be reached in a couple of hours while in deep valleys with abundance of vegetation and moisture, the vertical temperature structure may remain relatively stationary with a change from t₀ to t₁ that takes most of the day.

In contrast to the temporal evolution of CBLs in valleys, the spatial structure of CBL height and the associated wind and temperature fields along and across a valley have not been given much attention. In many studies, such as those where mass budgets are calculated, it is assumed that temperature- and wind structure is horizontally homogeneous across the valley and that the along-valley atmospheric structure is simple, with monotonically increasing/decreasing or constant flows along the valley (Freytag, 1987). Hewson and Gill (1944) presented temperature data on a cross section of the Columbia Valley near Trail, BC. Their aircraft observations showed that cross-valley differences in temperature of about 3–4°C can occur on a constant height surface due to unequal heating of the slopes. Similar observations were made by Hennemuth (1985) in a deep Swiss valley. Depending on the orientation of the valley, an asymmetric removal of temperature inversions in a high mountain valley can occur as observed by Kelly (1988). One would expect non-horizontal CBL heights across the valley in these situations (Figure 6A).

FIGURE 6

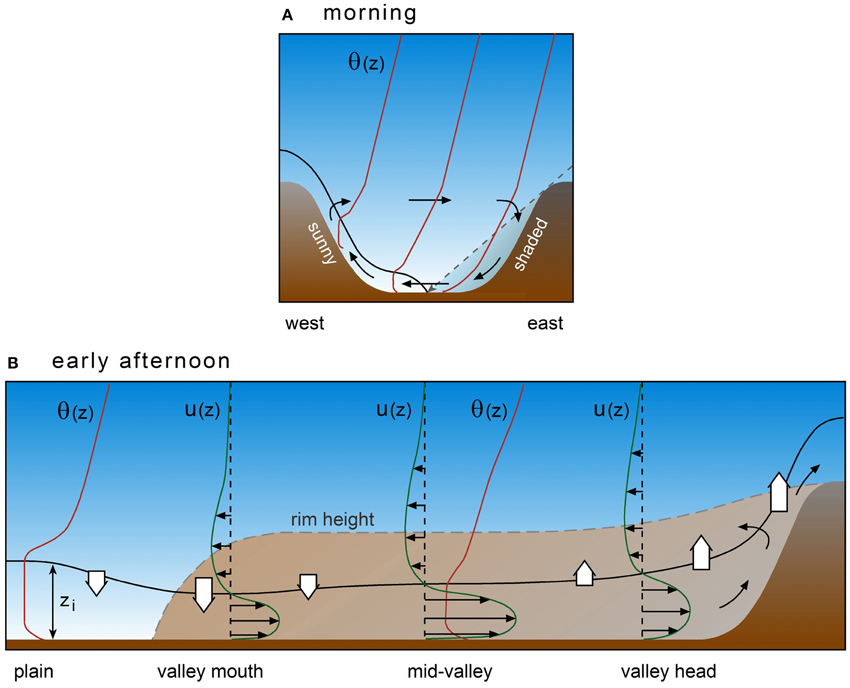
Figure 6. Vertical cross sections of thermal wind circulation and CBL structure in a valley for (A) a cross valley section during the morning transition and (B) an along valley section around noon or mid-afternoon. The solid black line indicates CBL depth z_i. Thin solid vectors indicate airflow components in the cross section direction. Red solid lines indicate vertical profiles of potential temperature θ(z). The dashed line in (A) indicates a sun ray which separates the sunny and shaded parts of the valley. Green lines in (B) indicate vertical profiles of the horizontal along-valley wind component with the horizontal black vectors depicting the direction of the flow. Curved black vectors and vertically pointing white arrows indicate subsidence or lifting at the CBL top caused by horizontal divergence or convergence of the along-valley airflow.

Along-valley CBL height structure is affected by areas of horizontal flow divergence or convergence and resulting compensating vertical motions along the valley. Freytag (1987) concluded from valley air mass budgets that compensating lifting and subsidence are strongest at the valley head and the valley mouth, respectively. Bianco et al. (2011) indeed found deeper valley CBLs near the valley head associated with deceleration of the thermally driven up-valley winds (Figure 6B). They hypothesized that these deeper CBLs were caused by lifting due to the convergence in the horizontal wind field in the valley, as was already observed by Freytag (1987). Similarly, compensating subsidence as a result of divergence at the valley mouth represents a mechanism for shallower CBLs at the valley mouth than at the valley head. Model simulations by Rampanelli et al. (2004) show that CBLs can be significantly deeper over the plain than in the valley where along-valley cold air advection counteracts CBL growth (Figure 6B). Spatial variability in cold air advection and varying heating rates along the valley as a result of the complex flow pattern also cause irregularities in CBL heights along the valley (De Wekker, 2002; Weigel et al., 2006). In other situations however, observed afternoon CBL heights are horizontally homogeneous along and across the valley despite the presence of complex and asymmetric flow patterns (Kuwagata and Kimura, 1995, 1997; De Wekker et al., 2005).

Not only thermally driven flows but also dynamically driven flows can have an effect on CBL heights in a valley. For example accelerating/decelerating flows related to the varying intensity of channeled synoptic winds along a valley may be associated with decreasing/increasing CBL heights in along-valley direction due to effects of air mass conservation (Frank, 1997). In valleys with a curved valley axis, flows can cause asymmetric CBL heights across the valley (Weigel and Rotach, 2004). Also, channeling effects in these curved valleys can induce along-valley confluence or diffluence with along-valley differences in vertical motions that can enhance or suppress CBL growth (Kossmann and Sturman, 2003). Mountain waves traveling across the valley can also modulate the CBL height in valleys (Worthington, 2002).

Basin and Plateau CBLs

Basins and plateaus are common land forms in many parts of the world, influencing atmospheric motions that extend in scale from the local scale to thousands of kilometers. CBL development shows some degree of similarity in basins, valleys and over plateaus. The similarity with plateaus holds in particular for basins with an elevated basin floor and justifies a simultaneous discussion of basin and plateau CBLs.

Basins are concave land forms that, in contrast to valleys, are characterized by no or only a small number of low lying exits to surrounding terrain. Hence, upvalley flows are suppressed or non-existent in basins. The distinction between basins and valleys, however, can be somewhat arbitrary and there are basins where the low lying exits appear as side valleys where up and down valley flows are observed.

Any of the valley CBL development patterns (Figure 5) can also occur in basin atmospheres. In the absence of nighttime downvalley flows however, the early morning stability of the near-surface air layer in basins may be enhanced compared to valleys. Cold air drainage from the surrounding slopes accumulates and stagnates in the basin (Wolyn and McKee, 1989; Whiteman et al., 2001). These cold air pools can delay CBL growth in basins compared to valleys. During daytime, the basin atmosphere warms up more than the surrounding plains due to the TAF effect. This basin warming can promote a plain-to-basin flow in the afternoon which crosses the mountain ridges and saddles surrounding the basin (Kimura and Kuwagata, 1993; Doran and Zhong, 1994; De Wekker et al., 1998; Regmi et al., 2003). The cold air advection associated with these thermally driven flows can have a large impact on the heat balance of the basin's atmosphere (Whiteman et al., 2000; Kossmann et al., 2002) and has been hypothesized to reduce or level off CBL growth in the afternoon (Muñoz and Undurraga, 2010). Especially in situations when basin CBLs are deep and extend above the surrounding ridges (Figure 7A), a sudden reduction in CBL height on the basin-side slope can occur after the onset of the plain-to-basin wind in the late afternoon (Figure 7B). The air quality in large cities that are situated in basin-like environments may be affected considerably by the plain-to-basin winds and their effect on thermal structure and CBL heights (Fast and Zhong, 1998; Kitada and Regmi, 2003; de Foy et al., 2005, 2006; Panday et al., 2009).

FIGURE 7

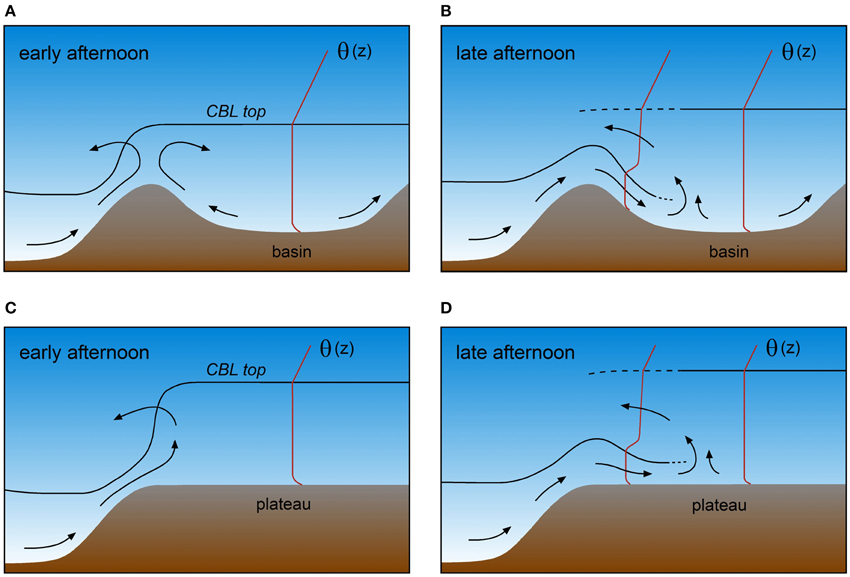
Figure 7. CBL evolution in the afternoon over a mountain basin (A,B) and over a plateau (C,D). Airflow and vertical profiles of potential temperature θ are shown by arrows and red lines, respectively. The intrusion of cold air in the late afternoon leads to shallower CBLs over both basins and plateaus.

While plain-to-basin winds can potentially affect CBL heights in basins, CBL heights themselves could play a role in the initiation of these winds. Kimura and Kuwagata (1993) concluded from their observations and numerical modeling that plain-to-basin winds do not occur when the CBL height over the plains is lower than the mountain height. In contrast, De Wekker et al. (1998) showed that the CBL over the plains does not necessarily have to grow above the mountain height to generate plain-to-basin winds. The ratio of the CBL height over the plains to the mountain height may affect the plain-to-basin wind by modifying the horizontal temperature gradient above mountain height, but this ratio is not a critical factor for the development of the plain-to-basin wind. Even if the CBL height over the plains is lower than the mountain height, air can still be transported from the plains to the basin atmosphere.

The processes described above occur for basins with floors ranging in height between the surrounding plains height and the height of the surrounding ridges. As the basin floor becomes more elevated compared to the surrounding plains height, the elevated heating source (Hafner et al., 1987; Kuwagata and Sumioka, 1991) increases the horizontal temperature gradient between the plains and the basin, and plain-to-basin winds are expected to occur earlier. For basins, upslope winds over the inner slopes of the basin sidewalls counteract the regional-scale plain-to-basin winds (Figure 7A). With increasing basin floor height, the topography approaches that of a plateau and the plain-to-basin wind becomes a plain-to-plateau wind. It is sometimes difficult to distinguish between elevated basins and plateaus. While some geographical regions are denoted as “plateau” they should probably be classified meteorologically as elevated broad valleys or basins. Studies such as those by Yang et al. (2004) over the Tibetan Plateau in Asia or by Egger et al. (2005) over the Altiplano of South America may therefore not necessarily be representative of “pure” plateau CBLs. On the other hand, the Mexico “basin” may be classified meteorologically as an elevated basin or even as a plateau (Bossert, 1997; Whiteman et al., 2000). Surface heating over plateaus is able to generate a relatively uniform CBL that extends over the elevated flat terrain. An observational study by Chen et al. (2013) confirms the occurrence of particularly deep CBLs over a large and high plateau (the Tibetan Plateau). For a distinct plateau CBL to develop, the horizontal scale of the plateau needs to be much larger than the typical CBL height. Plateau-like topographic features such as mesas and buttes may be too small to form their own CBLs as expected for large plateaus.

While observational studies of CBL development over well-defined plateaus are sparse, several numerical model studies have investigated the daytime evolution of CBLs over idealized plateaus (Mannouji, 1982; Gaertner et al., 1993; Bossert and Cotton, 1994; Zängl and Gonzalez Chico, 2006; Zawar-Reza and Sturman, 2006). These studies show that plateau CBLs often develop to a significantly greater depth than over the surrounding plains. Deep CBLs over plateaus represent an elevated heat source and are promoted by various effects such as the lower air density at higher elevations (higher heating rate of the air for a given heat flux convergence); weaker initial temperature stratification in the morning (cold air drains along the slopes away from the plateau surface toward the adjacent plains); meso-scale lifting caused by flow convergence of upslope winds developing over the slopes around the plateau; and sparse vegetation on high plateaus (high Bowen ratio).

The daytime evolution of plateau CBLs and the formation of a plain-to-plateau circulation are associated with the formation of a heat low over the plateau. The interaction of the heat low and the plateau-induced thermal circulation is important for the development of moist convection and strongly influences the onset of the summer monsoon over the Tibetan Plateau (Yanai et al., 1992). Model results by Zängl and Gonzalez Chico (2006) suggest that, despite the strong pressure gradients related to the presence of the heat low over the plateau, upslope winds entering the plateau (“inflow”) only slowly propagate over the plateau (Figure 7C). During daytime, the organized structure of the upslope winds arriving on the plateau may be destroyed by strong turbulence over the plateaus, causing no or very slow propagation of the inflow. The combination of greater CBL depths and the higher terrain elevation over plateaus leads to strong horizontal temperature gradients and spatial variability in CBL height between the plateau and the surrounding plains (Figure 7C). The CBL height variability depends on factors such as the CBL height over the plains relative to plateau height, and the strength of the upslope flows and the plain-plateau circulation (Zängl and Gonzalez Chico, 2006). In the late afternoon when turbulent boundary layer convection weakens, the upslope winds turn into a density current which quickly propagates over the plateau (Figure 7D) and possibly collides with density currents generated at the opposing end of the plateau. Similar transitions from thermally driven winds under convective conditions to density currents in the nocturnal stable boundary layer have been observed in other topographic settings (Taylor et al., 2005).

Mountain Range CBL

While attempts have been made to describe the CBL height over valleys, slopes, basins, and plateaus individually, many observations show the integrative effect of the various processes responsible for the CBL height over any of these landscape features. The resulting CBL behavior over a mountain range can vary considerably in space and time. An intriguing question that is difficult to answer relates to the extent to which the CBL height follows the terrain. This question is important, for example, for air pollution transport over mountain ridges and for designing research aircraft flight strategies where mean and turbulence measurements are needed within the CBL.

A conceptual model based on observations of diurnal CBL behavior over an extended mountainous area with multiple ridges and valleys is shown in Figure 8. In the night and early morning before sunrise, cold air accumulates in the valleys resulting in an atmospheric stability in the valleys that is larger than over the mountain ridges (Figure 8A). After sunrise, the larger stability in the valleys leads to a slower growth of the CBL in the valleys than over the mountain ridges (Figure 8B). After the valley inversion breaks up, the CBL develops faster in the valleys than over the mountain ridges. Thus, in the early afternoon, the CBL top more or less follows the underlying terrain (Figure 8C). If the CBL in the valleys keeps growing faster there than over the mountain ridges, the top of the CBL eventually becomes level (Figure 8D). Under certain conditions, (almost) terrain following CBL tops as in Figure 8C will be the final status of CBL development before the onset of the evening transition with its stable boundary layer formation. The development of level CBL tops as in Figure 8D is more likely on long summer days with weak early morning stratification, and strong surface heating.

FIGURE 8

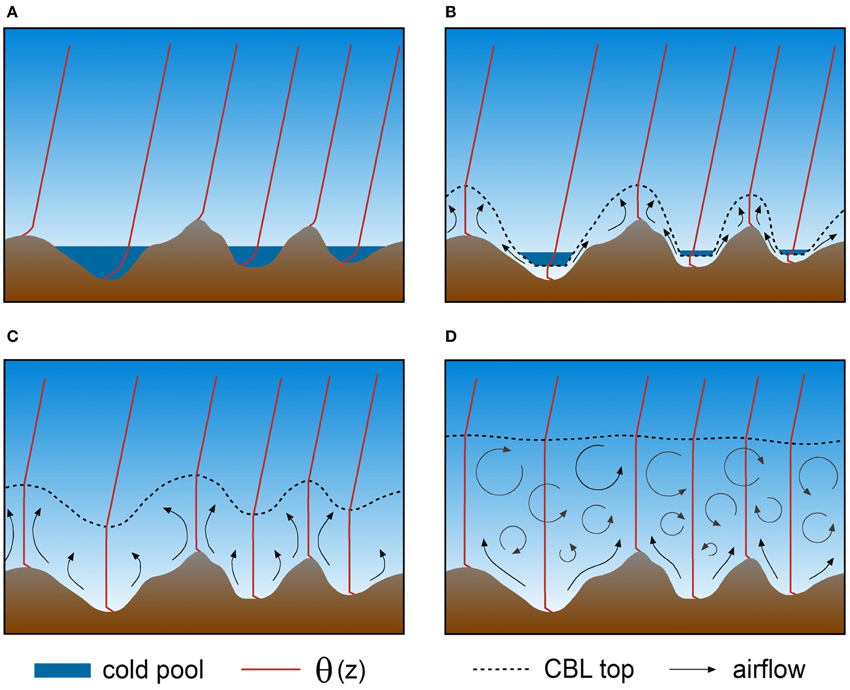
Figure 8. Conceptual model of the CBL development over mountainous terrain on a fair weather day (A) before sunrise, (B) in the early morning, (C) at noon, and (D) in the late afternoon. Dark blue shading indicates strongly stable stratification in nocturnal cold air pools. Arrows indicate thermal circulation and turbulent mixing. The dashed lines indicate the top of the turbulent CBL. Vertical profiles of potential temperature θ are shown in red at several locations along the cross section (after Fiedler et al., 1987).

Studies that have alluded to the question of terrain-following vs. level CBL heights found the general pattern of CBL behavior described above from theoretical and numerical investigations (Stull, 1992; Walko et al., 1992; De Wekker et al., 1997; Gopalakrishnan et al., 2000; De Wekker, 2002; Tian and Parker, 2002; Tian et al., 2003; Catalano and Moeng, 2010) and from observations (Lenschow et al., 1979; Banta, 1982, 1984; Fiedler et al., 1987; Dayan et al., 1988; De Wekker, 1995; Binder, 1997; Kalthoff et al., 1998; Kossmann et al., 1998). In the observational studies, CBL heights were derived mostly from in-situ aircraft and radiosonde measurements during intensive measurement campaigns. Climatological analyses using radiosonde data have also been performed (Dayan et al., 1988; Liu and Liang, 2010) and show a variety of CBL height behaviors, from terrain-following to more level CBL heights.

While the studies mentioned above used vertical profiles of thermodynamic variables to determine CBL heights, other studies have used airborne backscatter lidar to derive information on CBL height variability over mountain ranges. From these lidar observations, Nyeki et al. (2000) and De Wekker et al. (2004) concluded that aerosol layer (AL) heights did not follow the underlying topography. However, while AL heights were initially equated with CBL heights, numerical simulations by De Wekker et al. (2004) showed large differences between CBL and AL heights over a large region in the Swiss Alps. In contrast to AL heights, CBL heights tended to follow the terrain but differences between AL and CBL heights became smaller in the course of the day. Differences in AL and CBL heights have been explained by the presence of orographically induced transport and mixing processes between the turbulent CBL and the overlying atmosphere which will be discussed in the next Section.

Closely related to the question of terrain-following vs. level CBL heights is how the CBL evolves over individual mountain tops and ridges and their direct surroundings. Various advective effects illustrated in Figure 9 are known to influence CBL heights in these terrain locations. As was pointed out in the conceptual model (Figure 8), a relatively deep CBL can exist over the mountain top early in the day because cold air forming during nighttime drains to lower terrain which results in shallower and weaker surface-based temperature inversions at sunrise over mountain ridges and peaks than over surrounding valleys or plains. Such “bulging” CBLs over mountain tops and ridges have been observed in several field studies that were mostly performed to investigate dry convection over mountain tops and ridges preceding moist convection later in the day (e.g., Braham and Draginis, 1960; Fosberg, 1967, 1969; Raymond and Wilkening, 1980, 1982; Demko and Geerts, 2010). Many of these studies do not explicitly address variability of CBL heights but from their published data, some information about CBL heights can be derived. In general, the studies show that the bulging of the CBL over the highest elevations is caused by heating of the slopes and ridgetops and a resulting “convection core”. Lifting generated by upslope winds can enhance this bulging CBL height behavior (Figure 9A), while background winds forcing the convective core to move downwind of isolated mountain tops can also cause a wavelike pattern of the CBL height (Fosberg, 1969). Banta (1982) and Kirshbaum (2011) observed and modeled a lee side convergence zone induced by upslope flows on the leeside of the mountains. These convergence zones can result in an increased spatial variability of CBL height with increased heights at the convergence zones. While convective cores appear to be attached to terrain features, Banta (1982) speculated the transient (non-stationary and short-lived) nature of these increased CBL heights at the convergence zones. Transient CBL height features associated with thermal activity over mountains and sinking air motions adjacent to them, have also been found in the form of relatively low CBL heights (depressed CBL heights) near mountain bases (Figure 9B; De Wekker, 2008; Serafin and Zardi, 2010b).

FIGURE 9

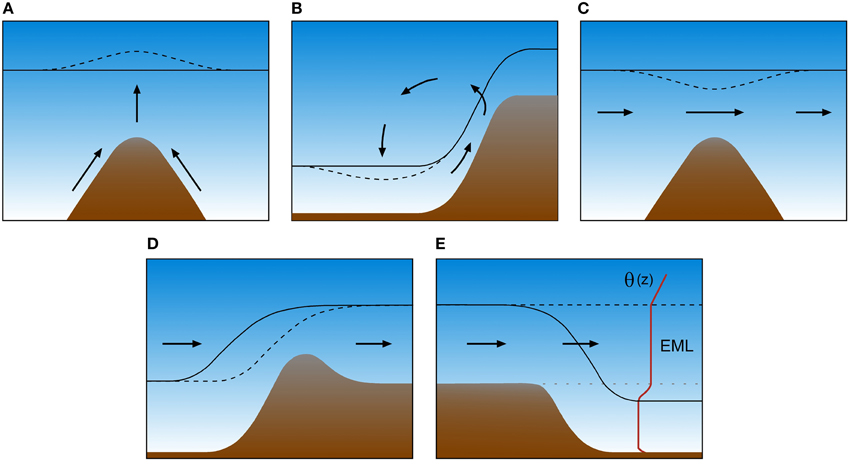
Figure 9. Schematic illustration of advective effects on CBL structure over mountainous terrain. (A) Lifted CBL top over a ridge due to convergence of upslope winds, (B) depressed CBL at a mountain base due to subsiding return circulation of a slope wind system, (C) lowered CBL top over a ridge due to Bernoulli effect, (D) depressed CBL over a ridge due to horizontal advection of a tilted CBL top, and (E) formation of an elevated mixed layer (EML) over a valley due to horizontal advection of a CBL formed over high windward terrain. The solid and dashed black lines indicate the top of the CBL before and after considering the advective effect. Arrows illustrate the airflow.

Other observations indicate a CBL over the mountain top that is thinner than the CBL over adjacent regions, indicating a CBL that does not follow the terrain but is rather level. Asimakopoulos et al. (1980, 1994) used data from sodar measurements and radiosonde measurements on a 1000 m high isolated mountain top location to show that there is minimal or no effect of the orography on the height of the CBL in some situations (i.e., a level CBL top) while in other situations the capping inversion over the mountain top decreases in height. They argued that during convective conditions with CBL heights exceeding the mountain height and with moderate wind speeds, a decrease in CBL height can be explained by a speed-up of the winds over the mountain top due to the Bernoulli effect (Figure 9C). Relatively shallow CBLs can also exist over mountain tops because of the exposure of mountain tops to cold air advection due to upslope winds and because of the advection of a capping inversion by the mean horizontal wind (Figure 9D; Kossmann et al., 1998). Furthermore, shallow mountain top CBLs are favored by the small terrain surface area at mountain top height, which is limiting the total surface heat flux available for CBL growth at the mountain top (De Wekker, 1995).

Over mountain ranges in dry climates such as over the continental mountainous terrain in western North America, deep and level afternoon CBLs exceeding 2–3 km in depth are frequently present (Cramer and Lynott, 1961; Holzworth, 1964; Cramer, 1972; Norton and Hoidale, 1976; Raymond and Wilkening, 1980). Occasionally, the warm air produced in these deep CBLs above a mountain range can be advected off the mountains into the surrounding atmosphere. These advected CBLs can sometimes be detected over the adjacent plains (Figure 9E) where they form elevated mixed or residual layers that can affect air quality (Steinbacher et al., 2004) and the development of afternoon thunderstorms (Arritt et al., 1992; Stensrud, 1993).

In summary, a range of spatial CBL top behaviors is observed which can be organized in four distinct patterns (Figure 10): bulging CBL heights over mountain tops and ridges and suppressed CBL growth in valleys, also referred to as hyper terrain following (Figure 10A), terrain-following (Figure 10B) and level (Figure 10C) CBL heights, and lower CBL heights over mountain tops and ridges than over adjacent terrain, also referred to as contra terrain following (Figure 10D).

FIGURE 10

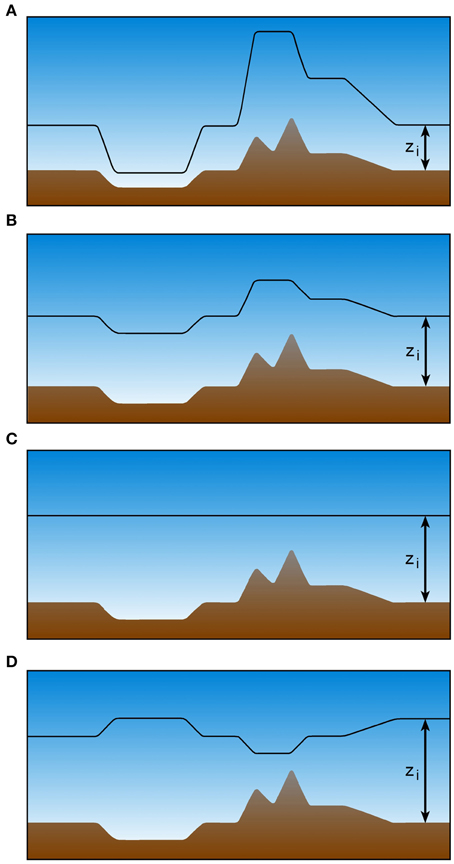
Figure 10. Schematic illustration of four types of CBL top behavior. (A) Hyper terrain following, (B) terrain following, (C) level, (D) contra-terrain following (after Stull, 1992). The solid black line indicates CBL depth z_i.

General conclusions regarding circumstances under which different behaviors occur have seldom been made, but factors such as atmospheric stability, synoptic wind speed, and vertical and horizontal scales of the orography are found to be important. A theoretical study on factors determining the spatial behavior of the CBL top was conducted by Stull (1992). In this study, an equation for the tendency of the CBL top to become more horizontal in the course of the day was derived by applying the mass conservation equation for a CBL over hilly terrain. Advection, entrainment and friction were found to make the CBL follow the terrain while gravitational forces tend to make the top of the CBL more level. Stull's theory shows further that deeper CBLs are less terrain following than shallower ones and that the mixed layer top is less level over orographical features that have a larger horizontal extent. These latter implications of the theory are generally corroborated by the observations mentioned earlier and were also quantified by Kalthoff et al. (1998) using a scale analysis.

The role of advection in making the CBL height more or less terrain following is not entirely clear but its potential importance is recognized (e.g., Kossmann et al., 1998). Figure 9 showed that there is a strong interaction between the flows that are responsible for the horizontal advection and the CBL height. For example, the shallow CBL depth over a mountain ridge illustrated in Figure 9D is caused by advective effects and will tend to make the CBL height more level (De Wekker, 1995; Kossmann et al., 1998). However, Stull (1992) assumes isentropic flows which makes the top of the CBL follow the orography more closely with increasing wind speed. Stull's (1992) theoretical model excludes effects of thermally driven circulations and therefore is unable to describe the under-cutting by thermal circulations that was shown previously (Section “Slope CBL”) to play an important role in CBL height behavior over slopes.

De Wekker (1995) and Binder (1997) proposed the use of an effective sensible heat flux for use in growth rate models that implicitly takes into account the effects of advection, orography shape and other effects that influence CBL growth over mountain ridges. The magnitude of the calculated effective sensible heat flux that would lead to comparable CBL growth over homogeneous terrain, was only about 20% of the sensible heat flux observed at the surface but the relative contributions of individual effects were unclear.

Even though several studies have now investigated meteorological and terrain effects on CBL growth over mountain ridges, conclusive and general statements are still difficult to make.

Vertical Transport and Mixing between the CBL and the Free Troposphere

Understanding vertical transport and mixing of air pollution between the CBL and the free troposphere (FT) and the effects of these processes on air quality represent a major application of the knowledge gained in more basic studies of CBL behavior over mountainous terrain. Addressing vertical transport and mixing is also important with respect to the determination of CBL height by lidar measurements that rely on the presence of air pollution, or more specifically, aerosols that scatter the radiation emitted by a laser. Aerosols are only a subset of air pollutants but the physical transport and mixing processes acting on them are the same as on other air pollutants.

The diurnal boundary layer cycle over flat terrain has two ways of vertically transporting air pollutants in the atmosphere—pollutants are mixed upward by convection through a deepening CBL during daytime, while pollutants in the residual layer (the elevated remnant of the previous day's CBL) are entrained downward into the growing CBL. It is frequently assumed that constituents within the CBL are well-mixed and capped by an inversion. The inversion acts as a lid and limits the transport of constituents to the atmosphere above. As pointed out in Section “Definition and Determination of CBL Heights,” these characteristics are often used to define the top of the CBL. There is increasing observational support now that pollutants emitted within the CBL over complex terrain are often transported upward into atmospheric layers above the CBL. In other words, they cannot be considered to be confined within the turbulent CBL. This vertical transport of air pollutants from the CBL to the free atmosphere often manifests itself as elevated aerosol layers (e.g., Wakimoto and McElroy, 1986; McKendry et al., 1997; Tyson and D'Abreton, 1998; Carnuth and Trickl, 2000; McKendry and Lundgren, 2000; Millan et al., 2002; Nyeki et al., 2002; Frioud et al., 2003; Emeis et al., 2007) and/or a deepening of the surface-based aerosol layer, transforming into a residual layer after sunset (De Wekker et al., 2004; Henne et al., 2004).

Some of the hypothesized mechanisms that transport air pollutants between the CBL and the FT in mountainous terrain are summarized in a conceptual diagram in Figure 11. Rotach et al. (2015) also discusses some of these mechanisms in some more detail. Figure 11 highlights the generation of multi-layer temperature and air pollution profiles and also the close connection of spatial CBL and AL structure with vertical transport and mixing mechanisms. The dotted line depicts the AL height which can be considered the maximum vertical extent of aerosol transport while the dashed line depicts the CBL height, defined as the base of a capping inversion that limits the depth of penetrative convection. While AL and CBL heights are approximately equal over flat terrain, mountainous terrain exerts a profound influence on aerosol distribution in the atmosphere: mixing and transport processes are often enhanced compared to those over flat and horizontally homogeneous terrain and the equality of AL and CBL heights breaks down. CBL heights are considerably lower than AL heights, show more spatial variability, and tend to follow the terrain more than AL heights, although the extent to which the CBL height follows the terrain decreases during the day (De Wekker et al., 2004). De Wekker et al. (2004) pointed out that simultaneous measurements of atmospheric temperature structure and AL height are rarely available and that conclusions about mixing processes and CBL/AL correspondence are mostly based on modeling results.

FIGURE 11

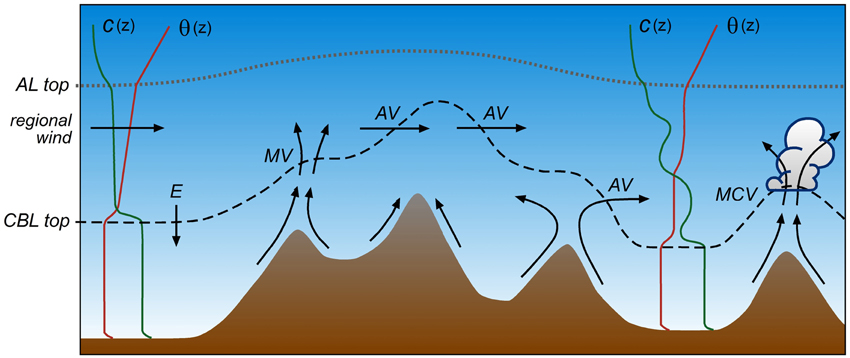
Figure 11. Schematic illustration of mountain induced exchange processes between the convective boundary layer and the overlying atmosphere. E, entrainment; AV, advective venting; MV, mountain venting; and MCV, mountain-cloud venting. Vectors indicate airflow while c(z) and θ(z) indicate vertical profiles of pollutant concentration and potential temperature, respectively. The dotted and dashed line indicate the top of the aerosol layer (AL) and the CBL, respectively (after Kossmann et al., 1999; De Wekker, 2002; De Wekker et al., 2004).

If CBL heights follow the terrain and ambient winds or slope flow re-circulations are quasi-horizontal, advective venting can occur, a process that has been quantified for case studies in the Black Forest region in Germany during the TRACT (Transport of Air pollutants over Complex Terrain) field study (Kossmann et al., 1999) and for climatological periods over the Alps (Henne et al., 2005). Transport by slope flows is one of the mechanisms by which heat and mass can be transported from the CBL to the FT in mountainous terrain (Wakimoto and McElroy, 1986; Lu and Turco, 1994; Fast and Zhong, 1998; Lugauer et al., 1998; Kossmann et al., 1999; Fiedler et al., 2000; Sasaki et al., 2004; Gohm et al., 2009; Harnisch et al., 2009; Langford et al., 2010). The slope flow mechanism has been given several names including “chimney effect” (Lu and Turco, 1994) and mountain venting (Kossmann et al., 1999; De Wekker et al., 2004; Henne et al., 2005). This effect can be particularly strong when slope flows converge over a mountain summit or when there is an additional sea breeze flow in coastal terrain (McKendry et al., 1997). Compensating lifting and CBL to FT transport are also triggered by along-valley flow convergence (Kossmann and Sturman, 2003; Henne et al., 2004; Weigel et al., 2007), or by terrain-associated convergence zones on the lee sides of isolated mountains or mountain ranges (Edinger and Helvey, 1961). Regional scale plain-to-mountain winds combine with these slope and valley flow mechanisms to lead to a transport of boundary layer air to the FT over the entire mountain range (Henne et al., 2005; Lang et al., 2015), a mechanism that has been termed “alpine pumping” (Lugauer and Winkler, 2005). Vertical transport and mixing by urban heat island–induced circulations is an additional process that can play an important role in the venting of pollutants in urbanized valleys (Rendón et al., 2014, 2015).

Mountain cloud venting (MCV) is a particularly effective CBL-FT exchange process induced by the initiation of moist convection in hilly and mountainous terrain (Kalthoff et al., 2013). MCV originates from cloud venting, a process that has been studied extensively over flat terrain (Ching et al., 1988; Cotton et al., 1995). During the summer, cumulus convection occurs almost daily over the mountain ranges of the interior western United States (e.g., Banta and Schaaf, 1987). Moist convection typically develops in a deep CBL, capped by a weakly stably layer, and under weak winds. Several studies have been conducted in the last decade that focus on convection initiation and associated vertical exchange processes. These studies include VERTIKATOR (Vertical Exchange and Orography, Barthlott et al., 2006; Hasel, 2006) and COPS (Convective and Orographical Induced precipitation Study) in the Black Forest in southwestern Germany (Kottmeier et al., 2008; Wulfmeyer et al., 2008), CUPIDO (Cumulus Photogrammetric, in-situ and Doppler Observations) in the southwestern US (Damiani et al., 2008; Geerts et al., 2008; Demko and Geerts, 2010), BLLAST (Boundary-Layer Late Afternoon and Turbulence) in southern France (Lothon et al., 2014), and as part of HyMeX (Hydrological cycle in the Mediterranean eXperiment; Drobinski et al., 2014) on the island of Corsica (Adler and Kalthoff, 2014). Thermally driven wind systems are important for the initiation of convective clouds and therefore of MCV, because slope winds often generate convergence zones over the mountain ridges, which are therefore favored areas for the onset of convection (Orville, 1965; Raymond and Wilkening, 1980; Holroyd, 1982; Klitch et al., 1985; Toth and Johnson, 1985; Pielke and Segal, 1986; Tripoli and Cotton, 1989; Tian and Parker, 2002; Stein, 2004; Barthlott et al., 2006; Kottmeier et al., 2008). Forecasting of local convection in mountainous terrain and thus of MCV processes is extremely challenging and relies on an accurate simulation of CBL growth and structure prior to moist convection onset. Even numerical weather prediction models that have sufficient resolution to resolve the thermally driven circulations have difficulties simulating the surface fluxes and CBL growth over complex terrain and accurately predicting the timing and intensity of moist convection (e.g., Trentmann et al., 2009).

The various venting processes described above and in Figure 11 are closely related to CBL top levelness illustrated in Figure 10. Mountain (cloud) venting processes that act predominantly in the vertical direction would tend to make the CBL top less level, while advective venting processes can make the CBL top more level.

Summary and Directions for Future Research

This review discussed current knowledge of CBL heights in mountainous terrain. Much progress has been made in understanding CBL heights from observational, numerical, theoretical, and laboratory studies. A major barrier to improving our present understanding arises from the multitude of processes acting simultaneously over a range of spatial and temporal scales. These difficulties often hamper a thorough explanation of all the observed and modeled features of CBLs in mountainous terrain and cause difficulties in isolating the effect of individual factors on CBL height. In situ and remote sensing observations are crucial for advancing our knowledge of boundary layers in mountainous terrain. Remote sensors such as lidars and sodars have been very helpful in identifying the multilayered structure and in continuously observing the spatiotemporal structure of the mountain atmosphere. These measurements have helped alleviate the limitations of sporadic radiosonde profiles in a spatially varying CBL. However, there are also challenges related to the use of different measured variables for the determination of CBL height. Thermodynamic measurements have traditionally been used in CBL height determination based on the importance of surface based convection in turbulent mixing and transport. Remote sensing measurements frequently observe the integrated result of different mixing and transport mechanisms (not limited to surface based convection) and have added insight but also complexity to understanding CBL heights over complex terrain such as those related to advective effects from thermally driven flows. In particular the use of lidar-derived AL heights as a proxy for CBL heights always needs to be assessed for individual cases. There is observational and numerical evidence that lidar-derived AL heights frequently exceed CBL heights over mountainous terrain. This consideration is becoming more important as an increasing number of ground-based ceilometer and lidar networks and space-borne lidar measurements are used to extract information about CBL heights at regional and larger scales. To reduce the level of uncertainty and ambiguity of CBL height observations, multiple instruments at several strategically chosen locations across a mountain range with a variety of in-situ and remote sensors need to be deployed.

From the basic concepts and understanding of the separate slope, valley, and mountain atmospheres, including basins and plateaus, we arrived at a general understanding of boundary layer structure over mountainous terrain. Complex terrain wind systems and CBL evolution are closely connected. Examples include the lowering of the CBL top due to subsiding motions that compensate for upslope flows on the sidewalls and the undercutting of the CBL due to cold air advection from upslope and upvalley flows, producing internal boundary layers and multilayered thermal structures. Boundary layer evolution in valleys is relatively well-understood compared to the evolution over slopes, plateaus, and ridges. Several approaches have been developed to describe the CBL height quantitatively, and in particular the reduced growth in valley boundary layers in the morning hours. These models could be extended to situations with cross-valley flow due to asymmetric heating in the morning, non-homogeneous conditions in the along-valley direction, and the presence of tributary valleys. Boundary layers over slopes and ridges have received less attention than boundary layers over valleys and are complicated by additional advective effects related to thermally driven flows and their interaction with synoptic flows. Some initial approaches have been developed to quantify the leveling of the CBL height over mountainous terrain that need to be tested and further expanded. It is generally observed that CBLs become more level in the late afternoon and during the evening transition period. Models describing these observations can help, for example, to explain the spatio-temporal variability of air quality measurements at mountain top locations and to determine the spatial representativeness of these measurements. While meteorological and chemical measurements are often made at mountain top locations, CBL heights over mountain tops are rarely studied. It is often assumed that the mountain top does not develop a CBL and free tropospheric background air is sampled. While this may be true for mountain tops at elevations high above the adjacent valley or plains CBL, this assumption is not valid when the valley or plains CBL exceeds the mountain top height (Lugauer et al., 1998; De Wekker et al., 2009; Ketterer et al., 2014; Lee et al., 2015).

Daytime thermally driven flows have historically received less attention than their nighttime counterparts, particularly for the case of upslope flows (Atkinson, 1981; Whiteman, 2000; Zardi and Whiteman, 2013). This is partly due to observational limitations; the deep daytime boundary layer requires the utilization of sounding systems with large vertical range making it more difficult to sample the daytime than the nighttime mountain boundary layer. Furthermore, vigorous mixing within the CBL and coupling with larger-scale synoptic flows make it difficult to study the effects of or even observe the presence of upslope flows. Many potentially important effects of upslope flow on CBL height behavior remain unexplored, including the importance of along-slope cold air advection.

The spatial distribution and patchiness of the vegetation and surface cover in hilly and mountainous terrain can have a strong impact on CBL evolution and its thermodynamic structure. Changes of the surface energy budget resulting from heterogeneous land cover directly influence the surface turbulent fluxes of moisture, momentum and heat, which act as the link between the atmosphere and the underlying soil-vegetation system. No studies have been performed to investigate the combined impact of land cover heterogeneity and orography on CBL heights. Knowledge is also limited on the effects of the geographical location (mid-latitude, tropical, etc), season, and scale of the terrain features (shallow vs. deep valleys, gentle vs. steep slopes, etc) on CBL heights. Numerical simulations can be helpful in these situations to correctly distinguish between orography and other effects on the variability of observed CBL heights.

CBL height behavior is closely coupled to vertical transport and mixing processes in mountainous terrain (Rotach et al., 2015) and the transport of pollutants over regional and even global spatial scales (Steyn et al., 2013). It is the spatial CBL height variability that promotes venting processes (e.g., via slope wind recirculation) between the turbulent boundary layer and the overlying atmosphere. Studies suggest that it is useful for mountainous terrain to distinguish between the height of the turbulent CBL and the height to which pollutants (released from the surface) can reach. Over flat terrain, these heights are identical but over mountainous terrain the thermally driven flows can contribute to the transport of pollutants across the CBL top (Section “Vertical Transport and Mixing Between the CBL and the Free Troposphere”) which challenges the traditional concept of a “mixing height” over mountainous terrain. De Wekker et al. (2004) suggested that because pollutants are transported and/or mixed in mountainous areas to the AL height, the AL height is a more relevant parameter for air pollution studies than the CBL height in mountainous terrain and may be more closely identified with the commonly used term “mixing height” (Seibert et al., 2000). One may also refer to the layer that is influenced by mountain-induced circulations and venting processes, and therefore more relevant to exchange studies, as the mountain CBL (De Wekker, 2002; Adler and Kalthoff, 2014; Adler et al., 2015). Such a mountain CBL would be similar to the conceptual model of a “mountain atmosphere” that Ekhart (1948) introduced (Figure 1). Whether layers above the base of the inversion (capping the highly turbulent layer above the surface) should be considered part of the CBL when influenced by thermally driven flows will depend on the application of the CBL height data. For example, the layer above the inversion base should not be considered part of the CBL in cases where CBL height data are needed to parameterize turbulent boundary layer fluxes. In contrast, the layer influenced by thermally driven flows above the inversion base should be considered part of the CBL when CBL height data are used to determine the possible effects of (valley) boundary layer air on background air pollution monitoring at mountain tops or in exchange studies. In recent years several projects have been initiated to study the effects of thermally-driven flows on exchange processes between the atmospheric boundary layer and the overlying free atmosphere (Section “Vertical Transport and Mixing Between the CBL and the Free Troposphere”).

CBL heights and closely related vertical transport and mixing processes have more recently gained attention in explaining the uncertainty in estimating air pollution and greenhouse gas budgets (e.g., Sun and de Wekker, 2011; Rotach et al., 2014). The global transport models that are used for carbon budget estimates, for example, are too coarse to take into account vertical exchange processes due to spatial heterogeneity in CBL height over complex terrain. More research is needed to parameterize these effects in these coarse models and their impact on the greenhouse gas budgets.

While it is acknowledged that there is a relationship between convection initiation and CBL height behavior over complex terrain, details of this relationship remain unclear. For example, do shallow CBLs over ridges decrease or increase the likelihood of moist convection? Are terrain-following or level CBL tops more favorable for the occurrence of moist convection? How important is the advection of mountain CBLs over the adjacent plains for the generation of severe weather? What is the relationship between the height of the dry (cloud free) CBL top and the lifting condensation level? Answering these questions requires collaborative field experiments that collect data on both dry CBLs and moist convection processes.

The investigation of CBL heights over mountainous terrain can benefit from recent technological advances in measurement techniques including the use of mobile vertical sounding systems (such as from airborne downward looking Doppler lidars, car-borne upward-looking Doppler lidars, and unmanned aerial systems). Networks of ceilometers and aerosol lidars that have been set up to monitor cloud ceiling and aerosol structure, and satellite-based measurements using lidar and radio occultation can provide regional to global coverage of CBL heights and provide opportunities to investigate the effect of mountain regions on these larger scales. Cup anemometers traditionally used in operational surface station networks are increasingly replaced by ultra-sonic anemometers-thermometers. This will make measurements of variances (turbulence intensities) and covariances (e.g., surface sensible heat flux) from which CBL height estimates can be made, more commonly available in coming years.

Numerical simulations at fine (micro- to mesoscale) resolutions will continue to be important for investigating processes underlying specific CBL height behavior and parameterizing these processes in global models at coarse resolutions. Systematic simulations of CBL development over idealized terrain features can also be used to investigate, for example, the separate effects of orography and land use on CBL height behavior. Also, future land-use changes in mountainous terrain due to reforestation, deforestation, urbanization, melting glaciers, shifting treelines, changing vegetation/precipitation patterns, and other anthropogenic and natural activities can have profound impacts on CBL dynamics and closely related air pollution transport processes in many parts of the world. Small-scale laboratory studies can play a role in identifying and quantifying processes which are not well-represented by numerical models due to simplifications or inappropriate parameterizations.

CBL height investigations over mountainous terrain remain important and challenging despite recent progress. The combination of different scientific approaches, such as observational studies, numerical or physical modeling studies, and theoretical studies will continue to close existing gaps in understanding of the relevant processes. New instrumental and computational techniques combined with new generations of scientists will likely lead to new findings that question some of the established views, and to revisions of existing conceptual models of CBL structure in mountainous terrain that were reviewed in this paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was funded by NSF award ATM-1151445, Office of Naval Research award N00014-11-1-0709, and by NOAA award NA13OAR4310065. We would like to thank Dave Whiteman, Mathias Rotach, Norbert Kalthoff, Bianca Adler, Frank Beyrich, and Charles Chemel for providing comments and suggestions that improved the manuscript.

References

Adler, B., and Kalthoff, N. (2014). Multi-scale transport processes observed in the boundary layer over a mountainous island. Bound. Layer Meteorol. 153, 515–537. doi: 10.1007/s10546-014-9957-8

CrossRef Full Text | Google Scholar

Adler, B., Kalthoff, N., Kohler, M., Handwerker, J., Wieser, A., Corsmeier, U., et al. (2015). The variability of water vapour and pre-convective conditions over the mountainous island of Corsica. Q. J. R. Meteorol. Soc. doi: 10.1002/qj.2545. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Arritt, R. W., Wilczak, J. M., and Young, G. S. (1992). Observations and numerical modelling of an elevated mixed layer. Mon. Weather Rev. 120, 2869–2880.

Google Scholar

AMS (2000). Glossary of Meteorology, American Meteorological Society. Available online at: http://glossary.ametsoc.org

Asimakopoulos, D. N., Deligiorgi, D. G., and Lalas, D. P. (1980). Acoustic sounder observations of the atmospheric boundary Layer from the top of a steep mountain. J. Appl. Meteorol. 19, 109–112.

Google Scholar

Asimakopoulos, D. N., Helmis, C. G., and Deligiorgi, D. G. (1994). Climatological evaluation of sodar recordings over complex terrain. Int. J. Remote Sens. 15, 383–392. doi: 10.1080/01431169408954082

CrossRef Full Text | Google Scholar

Atkinson, B. W. (1981). Meso-scale Atmospheric Circulations. London: Academic Press.

Google Scholar

Banta, R. M., and Schaaf, C. B. (1987). Thunderstorm genesis zones in the Colorado Rocky Mountains as determined by traceback of geosynchronous satellite images. Mon. Weather Rev. 115, 463–476.

Google Scholar

Banta, R. M. (1982). An Observational and Numerical Study of Mountain Boundary-layer Flow. Atmospheric Science Paper No. 350. Colorado State University.

Google Scholar

Banta, R. M. (1984). Daytime boundary-layer evolution over mountainous terrain: Part I. observations of dry circulations. Mon. Weather Rev. 112, 340–356.

Google Scholar

Barry, R. G. (1992). Mountain Weather and Climate, 2nd Edn. London: Routledge.

Google Scholar

Barthlott, C., Corsmeier, U., Meißner, C., Braun, F., and Kottmeier, C. (2006). The influence of mesoscale circulation systems on triggering convective cells over complex terrain. Atmos. Res. 81, 150–175. doi: 10.1016/j.atmosres.2005.11.010

CrossRef Full Text | Google Scholar

Bastin, S., and Drobinski, P. (2005). Temperature and wind velocity oscillations along a gentle slope during sea breeze events. Bound. Layer Meteorol. 114, 573–594. doi: 10.1007/s10546-004-1237-6

CrossRef Full Text | Google Scholar

Baxter, R. A. (1991). Determination of mixing heights from data collected during the 1985 SCCCAMP field program. J. Appl. Meteorol. 30, 598–606.

Google Scholar

Beyrich, F. (1997). Mixing height estimation from sodar data - a critical discussion. Atmos. Environ. 31, 3941–3953. doi: 10.1016/S1352-2310(97)00231-8

CrossRef Full Text | Google Scholar

Bianco, L., Djalalova, I. V., King, C. W., and Wilczak, J. M. (2011). Diurnal evolution and annual variability of boundary–layer height and its correlation to other meteorological variables in California's Central Valley. Bound. Layer Meteorol. 140, 491–511. doi: 10.1007/s10546-011-9622-4

CrossRef Full Text | Google Scholar

Binder, H.-J. (1997). Tageszeitlich und Räumliche Entwicklung der Konvektiven Grenzschicht über Stark Gegliedertem Gelände. Dissertation, Faculty of Physics, University of Karlsruhe.

Bischoff-Gauss, I., Kalthoff, N., Khodayar, S., Fiebig-Wittmaack, M., and Montecinos, S. (2008). Model simulations of the boundary-layer evolution over an arid andes valley. Bound. Layer Meteorol. 128, 357–379. doi: 10.1007/s10546-008-9293-y

CrossRef Full Text | Google Scholar

Blumenthal, D. L., White, W. H., and Smith, T. B. (1978). Anatomy of a Los Angeles smog episode: pollutant transport in the daytime sea breeze regime. Atmos. Environ. 12, 893–907. doi: 10.1016/0004-6981(78)90028-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bossert, J. E. (1997). An investigation of flow regimes affecting the Mexico City region. J. Appl. Meteor. 36, 119–140. doi: 10.1175/1520-0450(1997)036<0119:AIOFRA>2.0.CO;2

CrossRef Full Text | Google Scholar

Bossert, J. E., and Cotton, W. R. (1994). Regional-scale flows in mountainous terrain. Part II: simplified numerical experiments. Mon. Weather Rev. 122, 1472–1489.

Google Scholar

Braham, R. R., and Draginis, H. (1960). Roots of orographic cumuli. J. Meteorol. 17, 214–226.

Google Scholar

Brehm, M., and Freytag, C. (1982). Erosion of night-time thermal circulation in an Alpine valley. Arch. Meteorol. Geoph. Biokl. B31, 331–352. doi: 10.1007/BF02263439

CrossRef Full Text | Google Scholar

Brehm, M. (1986). Experimentelle und Numerische Untersuchungen der Hangwindschicht und Ihrer Rolle bei der Erwärmung von Tälern. Wiss. Mitt. Meteor Inst. München.

Cai, X.–M., and Steyn, D. G. (1993). Mesoscale Meteorological Modelling Study of the Lower Fraser Valley, B.C., Canada from July 17 to 20, 1985. Department of Geography Occasional Paper No. 40. University of British Columbia, Vancouver, BC.

Carnuth, W., and Trickl, T. (2000). Transport studies with the IFU three wavelength aerosol lidar during the VOTALP Mesolcina experiment. Atmos. Environ. 34, 1425–1434. doi: 10.1016/S1352-2310(99)00423-9

CrossRef Full Text | Google Scholar

Catalano, F., and Moeng, C.-H. (2010). Large-eddy simulation of the daytime boundary layer in an idealized valley using the weather research and forecasting numerical model. Bound. Layer Meteorol. 137, 49–75. doi: 10.1007/s10546-010-9518-8

CrossRef Full Text | Google Scholar

Chen, X., Añel, J. A., Su, Z., de la Torre, L., Kelder, H., van Peet, J., et al. (2013). The deep atmospheric boundary layer and its significance to the stratosphere and troposphere exchange over the Tibetan Plateau. PLoS ONE 8:e56909. doi: 10.1371/journal.pone.0056909

PubMed Abstract | CrossRef Full Text | Google Scholar

Ching, J. K. S., Shipley, S. T., and Browell, E. V. (1988). Evidence for cloud venting of mixed layer ozone and aerosols. Atmos. Environ. 22, 225–242. doi: 10.1016/0004-6981(88)90030-3

CrossRef Full Text | Google Scholar

Chow, F. K., De Wekker, S. F. J., and Snyder, B., Eds. (2013). Mountain Weather Research and Forecasting. Recent Progress and Current Challenges. Berlin: Springer.

Google Scholar

Cotton, W. R., Alexander, G. D., Hertenstein, R., Walko, R. L., McAnelly, R. L., and Nicholls, M. (1995). Cloud venting - A review and some new global annual estimates. Earth Sci. Rev. 39, 169–206. doi: 10.1016/0012-8252(95)00007-0

CrossRef Full Text | Google Scholar

Coulter, R. L. (1979). A comparison of three methods for measuring mixing-layer height. J. Appl. Meteorol. 8, 1495–1499.

Google Scholar

Cramer, O. P., and Lynott, R. E. (1961). Cross-section analysis in the study of windflow over mountainous terrain. Bull. Am. Meteorol. Soc. 42, 693–702.

Cramer, O. P. (1972). Potential temperature analysis for mountainous terrain. J. Appl. Meteorol. 11, 44–50.

Google Scholar

Dai, C., Wang, Q., Gao, J.-Z., and Zhou, M. (2014). Determining boundary-layer height from aircraft measurements. Bound. Layer Meteor. 152, 277–302. doi: 10.1007/s10546-014-9929-z

CrossRef Full Text | Google Scholar

Damiani, R., Zehnder, J., Geerts, B., Demko, J., Haimov, S., Petti, J., et al. (2008). Cumulus photogrammetric, In-situ and doppler observations: the CuPIDO 2006 experiment. Bull. Am. Meteorol. Soc. 89, 57–73. doi: 10.1175/BAMS-89-1-57

CrossRef Full Text | Google Scholar

Dayan, U., Shenhav, R., and Graber, M. (1988). The spatial and temporal behavior of the mixed layer in Israel. J. Appl. Meteorol. 27, 1382–1394.

Google Scholar

de Foy, B., Caetano, E., Magana, V., Zitacuaro, A., Cardenas, B., Retama, A., et al. (2005). Mexico City basin wind circulation during the MCMA-2003 field campaign. Atmos. Chem. Phys. 5, 2267–2288. doi: 10.5194/acp-5-2267-2005

CrossRef Full Text | Google Scholar

de Foy, B., Clappier, A., Molina, L. T., and Molina, M. J. (2006). Distinct wind convergence patterns in the Mexico City basin due to the interaction of the gap winds with the synoptic flow. Atmos. Chem. Phys. 6, 1249–1265. doi: 10.5194/acp-6-1249-2006

CrossRef Full Text | Google Scholar

De Wekker, S. F. J., Ameen, A., Song, G., Stephens, B. B., Hallar, A. G., and McCubbin, I. (2009). A preliminary investigation of boundary layer effects on daytime atmospheric CO2 concentrations at a mountaintop location in the Rocky Mountains. Acta Geophys. 57, 904–922. doi: 10.2478/s11600-009-0033-6

CrossRef Full Text | Google Scholar

De Wekker, S. F. J., Kossmann, M., and Fiedler, F. (1997). “Observations of daytime mixed layer heights over mountainous terrain during the TRACT field campaign,” 12th AMS Symposium on Boundary Layers and Turbulence, 28 July – 1 August 1997, Vancouver, BC.

De Wekker, S. F. J., Steyn, D. G., Fast, J. D., Rotach, M. W., and Zhong, S. (2005). The performance of RAMS in representing the convective boundary layer structure in a very steep valley. Environ. Fluid Mech. 5, 35–62. doi: 10.1007/s10652-005-8396-y

CrossRef Full Text | Google Scholar

De Wekker, S. F. J., Steyn, D. G., and Nyeki, S. (2004). A comparison of aerosol-layer and convective boundary-layer structure over a mountain range during STAAARTE'97. Bound. Layer Meteorol. 113, 249–271. doi: 10.1023/B:BOUN.0000039371.41823.37

CrossRef Full Text | Google Scholar

De Wekker, S. F. J., Zhong, S., Fast, J. D., and Whiteman, C. D. (1998). A numerical study of the thermally driven plain-to-basin wind over idealized basin topographies. J. Appl. Meteorol. 37, 606–622. doi: 10.1175/1520-0450(1998)037<0606:ANSOTT>2.0.CO;2

CrossRef Full Text | Google Scholar

De Wekker, S. F. J. (1995). The Behaviour of the Convective Boundary Layer Height Over Orographically Complex Terrain. MS thesis University of Karlsruhe, Agricultural University, Germany/Wageningen.

De Wekker, S. F. J. (2002). Structure and Morphology of the Convective Boundary Layer in Mountainous Terrain. Ph.D. dissertation, University British Columbia, British Columbia, BC.

De Wekker, S. F. J. (2008). Observational and numerical evidence of depressed convective boundary layer heights near a mountain base. J. Appl. Meteorol. Clim. 47, 1017–1026. doi: 10.1175/2007JAMC1651.1

CrossRef Full Text | Google Scholar

Deardorff, J. W., Willis, G. E., and Stockton, B. H. (1980). Laboratory studies of the entrainment zone of a convectively mixed layer. J. Fluid Mech. 100, 41–64. doi: 10.1017/S0022112080001000

CrossRef Full Text | Google Scholar

Demko, J. C., and Geerts, B. (2010). A numerical study of the evolving convective boundary layer and orographic circulation around the Santa Catalina Mountains in Arizona. Part I: circulation without deep convection. Mon. Weather Rev. 138, 1902–1922. doi: 10.1175/2009MWR3098.1

CrossRef Full Text | Google Scholar

Doran, J. C., and Zhong, S. (1994). Regional drainage flows in the Pacific Northwest. Mon. Weather Rev. 122, 1158–1167.

Google Scholar

Doyle, J. D., and Durran, D. R. (2007). Rotor and sub-rotor dynamics in the lee of three dimensional terrain. J. Atmos. Sci. 64, 4202–4221. doi: 10.1175/2007JAS2352.1

CrossRef Full Text | Google Scholar

Drobinski, P., Ducrocq, V., Alpert, P., Anagnostou, E., Béranger, K., Borga, M., et al. (2014). HyMeX, a 10-year multidisciplinary program on the Mediterranean water cycle. Bull. Am. Meteorol. Soc. 95, 1063–1082. doi: 10.1175/BAMS-D-12-00242.1

CrossRef Full Text | Google Scholar

Edinger, J., and Helvey, R. (1961). The San Fernando convergence zone. Bull. Am. Meteorol. Soc. 42, 626–635.

Egger, J., Blacutt, L., Ghezzi, F., Heinrich, R., Kolb, P., Lämmlein, S., et al. (2005). Diurnal circulation of the Bolivian Altiplano. Part I: observations. Mon. Weather Rev. 133, 911–924. doi: 10.1175/MWR2894.1

CrossRef Full Text | Google Scholar

Eigenmann, R., Metzger, S., and Foken, T. (2009). Generation of free convection due to changes of the local circulation system. Atmos. Chem. Phys. 9, 8587–8600. doi: 10.5194/acp-9-8587-2009

CrossRef Full Text | Google Scholar

Ekhart, E. (1948). De la structure thermique de l'atmosphere dans la montagne [On the thermal structure of the mountain atmosphere]. La Meteorologie 4, 3–26. [English translation: Whiteman, C.D., and Dreiseitl, E. (1984). Alpine Meteorology: Translations of Classic Contributions by A.Wagner, E. Ekhart and F. Defant. PNL-5141/ASCOT-84-3. Pacific Northwest Laboratory, Richland, Washington, 121 pp, Available online at: http://www.osti.gov/bridge/product.biblio.jsp?osti_id=6665518]

Emeis, S., Jahn, C., Münkel, C., Münsterer, C., and Schäfer, K. (2007). Multiple atmospheric layering and mixing-layer height in the Inn valley observed by remote sensing. Meteorol. Z. 16, 415–424. doi: 10.1127/0941-2948/2007/0203

CrossRef Full Text | Google Scholar

Emeis, S., Schäfer, K., and Münkel, C. (2008). Surface-based remote sensing of the mixing-layer height—A review. Meteorol. Z. 17, 621–630. doi: 10.1127/0941-2948/2008/0312

CrossRef Full Text | Google Scholar

Fast, J. D., and Zhong, S. (1998). Meteorological factors associated with inhomogeneous ozone concentrations within the Mexico City basin. J. Geophys. Res. D103, 18927–18946. doi: 10.1029/98JD01725

CrossRef Full Text | Google Scholar

Fiedler, F., Adrian, G., and Hugelmann, C.-P. (1987). Beobachtete Phänomene während des Tulla-Experimentes, 3rd PEF Statuskolloquium 10.-12.3.1987, Bd. 2. Karlsruhe: KfK-PEF 12.

Fiedler, F., Bischoff-Gauß, I., Kalthoff, N., and Adrian, G. (2000). Modeling of the transport of a tracer in the Freiburg-Schauinsland area. J. Geophys. Res. D105, 1599–1610. doi: 10.1029/1999JD900911

CrossRef Full Text | Google Scholar

Fosberg, M. A. (1967). Numerical analysis of convective motions over a mountain ridge. J. Appl. Meteorol. 6, 889–904.

Google Scholar

Fosberg, M. A. (1969). Airflow over a heated coastal mountain. J. Appl. Meteorol. 8, 436–442.

Google Scholar

Frank, H. P. (1997). “Simulation of the convective mixed layer over Athens,” in Proceedings EURASAP Workshop on the Determination of the Mixing Height – Progress and Problems (Roskilde: Riso National Laboratory), 145–148. Report Riso-R-997(EN).

Freytag, C. (1985). MERKUR-results: aspects of the temperature field and the energy budget in a large Alpine valley during mountain and valley wind. Contrib. Atmos. Phys. 58, 458–476.

Google Scholar

Freytag, C. (1987). Results from the MERKUR experiment: mass budget and vertical motions in a large valley during mountain and valley wind. Meteorol. Atmos. Phys. 37, 129–140. doi: 10.1007/BF01040843

CrossRef Full Text | Google Scholar

Frioud, M., Mitev, V., Matthey, R., Haberli, C. H., Richner, H., Werner, R., et al. (2003). Elevated aerosol stratification above the Rhine Valley under strong anticyclonic conditions. Atmos. Environ. 37, 1785–1797. doi: 10.1016/S1352-2310(03)00049-9

CrossRef Full Text | Google Scholar

Furger, M., Dommen, J., Graber, W. K., Poggio, L., Prévôt, A., Emeis, S., et al. (2000). The VOTALP Mesolcina Valley Campaign 1996 – concept, background, and some highlights. Atmos. Environ. 34, 1395–1412. doi: 10.1016/S1352-2310(99)00377-5

CrossRef Full Text | Google Scholar

Gaertner, M. A., Fernandez, C., and Castro, M. (1993). A two-dimensional simulation of the Iberian summer thermal low. Mon. Weather Rev. 121, 2740–2756.

Google Scholar

Geerts, B., Miao, Q., and Demko, J. C. (2008). Pressure perturbations and upslope flow over a heated, isolated mountain. Mon. Weather Rev. 136, 4272–4288. doi: 10.1175/2008MWR2546.1

CrossRef Full Text | Google Scholar

Geiger, R. (1961). Das Klima der bodennahen Luftschicht. 4th Edn. Braunschweig: Vieweg Verlag.

Gohm, A., Harnisch, F., Vergeiner, J., Obleitner, F., Schnitzhofer, R., Hansel, A., et al. (2009). Air pollution transport in an alpine valley: results from airborne and ground-based observations. Bound. Layer Meteorol. 131, 441–463. doi: 10.1007/s10546-009-9371-9

CrossRef Full Text | Google Scholar

Gopalakrishnan, S. G., Baidya Roy, S., and Avissar, R. (2000). An evaluation of the scale at which topographical features affect the convective boundary layer using large eddy simulations. J. Atmos. Sci. 57, 334–351.

Google Scholar

Hafner, T. A., Reinhard, M. E., Weisel, E. L., and Fimpel, H. P. (1987). Boundary layer aspects and elevated heat source effects of the Alps. Meteorol. Atmos. Phys. 31, 61–73. doi: 10.1007/BF01045140

CrossRef Full Text | Google Scholar

Hägeli, P., Steyn, D. G., and Strawbridge, K. B. (2000). Spatial and temporal variability of mixed-layer depth and entrainment zone thickness. Bound. Layer Meteorol. 97, 47–71. doi: 10.1023/A:1002790424133

CrossRef Full Text | Google Scholar

Harnisch, F., Gohm, A., Fix, A., Schnitzhofer, R., Hansel, A., and Neininger, B. (2009). Spatial distribution of aerosols in the Inn Valley atmosphere during wintertime. Meteorol. Atmos. Phys. 103, 215–228. doi: 10.1007/s00703-008-0318-3

CrossRef Full Text | Google Scholar

Hasel, M. (2006). Strukturmerkmale und Modelldarstellung der Konvektion über Mittelgebirgen. Dissertation, Faculty of Physics, University of Karlsruhe.

Hayden, K. L., Anlauf, K. G., Hoff, R. M., Strapp, W. J., Bottenheim, J. W., Wiebe, H. A., et al. (1997). The vertical chemical and meteorological structure of the boundary layer in the Lower Fraser Valley during Pacific'93. Atmos. Environ. 31, 2089–2106. doi: 10.1016/S1352-2310(96)00300-7

CrossRef Full Text | Google Scholar

Henne, S., Furger, M., Nyeki, S., Steinbacher, M., Neininger, B., de Wekker, S. F. J., et al. (2004). Quantification of topographic venting of boundary layer air to the free troposphere. Atmos. Chem. Phys. 4, 497–509. doi: 10.5194/acp-4-497-2004

CrossRef Full Text | Google Scholar

Henne, S., Furger, M., and Prévôt, A. S. H. (2005). Climatology of mountain venting induced moisture layers in the lee of the Alps. J. Appl. Meteorol. 44, 620–633. doi: 10.1175/JAM2217.1

CrossRef Full Text | Google Scholar

Hennemuth, B., and Lammert, A. (2006). Determination of the atmospheric boundary layer height from radiosonde and lidar backscatter. Bound. Layer Meteorol. 120, 181–200. doi: 10.1007/s10546-005-9035-3

CrossRef Full Text | Google Scholar

Hennemuth, B. (1985). Temperature field and energy budget in a small Alpine valley. Contrib. Atmos. Phys. 58, 545–559.

Google Scholar

Hewson, E. W., and Gill, G. C. (1944). Meteorological Investigations in the Columbia River Valley near Trail, B.C. United States Department of Interior, Bureau of Mines, Bulletin.

Holroyd, E. W. (1982). Some observations on the mountain-generated cumulonimbus rainfall on the Northern Great Plains. J. Appl. Meteorol. 21, 560–565

Google Scholar

Holzworth, G. C. (1964). Estimates of mean maximum mixing depths in the contiguous U.S. Mon. Weather Rev. 92, 235–242.

Google Scholar

Holzworth, G. C. (1972). Mixing Heights, Wind Speeds, and Potential for Urban Air Pollution Throughout the Contiguous United States. North Carolina, NC: Environmental Protection Agency; Office of Air Programs Publication AP-101; Research Triangle Park.

Google Scholar

Hunt, J. C. R., Fernando, H. J. S., and Princevac, M. (2003). Unsteady thermally driven flows on gentle slopes. J. Atmos. Sci. 60, 2169–2182.

Google Scholar

Jackson, P. L., Mayr, G., and Vosper, S. (2013). “Dynamically-driven winds,” in Mountain Weather Research and Forecasting: Recent Progress and Current Challenges, eds F. Chow, S. F. J. De Wekker, and B. Synder (New York, NY: Springer), 121–218.

Google Scholar

Johnson, A. Jr., and O'Brien, J. J. (1973). A study of an Oregon sea breeze event. J. Appl. Meteorol. 12, 1267–1283

Google Scholar

Kalthoff, N., Binder, H.-J., Kossmann, M., Vögtlin, R., Corsmeier, U., Fiedler, F., et al. (1998). Temporal evolution and spatial variation of the boundary layer over complex terrain. Atmos. Environ. 32, 1179–1194. doi: 10.1016/S1352-2310(97)00193-3

CrossRef Full Text | Google Scholar

Kalthoff, N., Bischoff-Gauß, I., Fiebig-Wittmaack, M., Fiedler, F., Thürauf, J., Novoa, E., et al. (2002). Mesoscale wind regimes in Chile at 30 S. J. Appl. Meteorol. 41, 953–970. doi: 10.1175/1520-0450(2002)041<0953:MWRICA>2.0.CO;2

CrossRef Full Text | Google Scholar

Kalthoff, N., Träumner, K., Adler, B., Späth, S., Behrendt, A., Wieser, A., et al. (2013). Dry and moist convection in the boundary layer over the Black Forest - a combined analysis of in situ and remote sensing data. Meteorol. Z. 22, 445–461. doi: 10.1127/0941-2948/2013/0417

CrossRef Full Text | Google Scholar

Kelly, R. D. (1988). Asymmetric removal of temperature inversions in a high mountain valley. J. Appl. Meteorol. 27, 664–673.

Google Scholar

Ketterer, C., Zieger, P., Bukowiecki, N., Collaud Coen, M., Maier, O., Ruffieux, D., et al. (2014). Investigation of the planetary boundary layer in the Swiss Alps using remote sensing and in situ measurements. Bound. Layer Meteorol. 151, 317–334. doi: 10.1007/s10546-013-9897-8

CrossRef Full Text | Google Scholar

Khodayar, S., Kalthoff, N., Fiebig-Wittmaack, M., and Kohler, M. (2008). Evolution of the atmospheric boundary layer structure of an arid Andes valley. Meteorol. Atmos. Phys. 99, 181–198. doi: 10.1007/s00703-007-0274-3

CrossRef Full Text | Google Scholar

Kiemle, C., Kästner, M., and Ehret, G. (1995). The convective boundary layer structure from lidar and radiosonde measurements during the EFEDA'91 campaign. J. Atmos. Ocean. Technol. 12, 771–782.

Google Scholar

Kimura, F., and Kuwagata, T. (1993). Thermally induced wind passing from plain to basin over a mountain range. J. Appl. Meteorol. 32, 1538–1547

Google Scholar

Kirshbaum, D. J. (2011). Cloud-resolving simulations of deep convection over a heated mountain. J. Atmos. Sci. 68, 361–378. doi: 10.1175/2010JAS3642.1

CrossRef Full Text | Google Scholar

Kitada, T., and Regmi, R. P. (2003). Dynamics of air pollution transport in late wintertime over Kathmandu Valley, Nepal, as revealed with numerical simulation. J. Appl. Meteorol. 42, 1770–1798.

Google Scholar

Klitch, M. A., Weaver, J. F., Kelly, F. P., and Vonder Haar, T. H. (1985). Convective cloud climatologies constructed from satellite imagery. Mon. Weather Rev. 113, 326–337.

Google Scholar

Kossmann, M., Corsmeier, U., De Wekker, S. F. J., Fiedler, F., Vögtlin, R., Kalthoff, N., et al. (1999). Observations of handover processes between the atmospheric boundary layer and the free troposphere over mountainous terrain. Contrib. Atmos. Phys. 72, 329–350.

Google Scholar

Kossmann, M., and Sturman, A. P. (2003). Pressure-driven channeling effects in bent valleys. J. Appl. Meteorol. 42, 151–158. doi: 10.1175/1520-0450(2003)042<0151:PDCEIB>2.0.CO;2

CrossRef Full Text | Google Scholar

Kossmann, M., Sturman, A. P., Zawar-Reza, P., McGowan, H. A., Oliphant, A. J., Owens, I. F., et al. (2002). Analysis of the wind field and heat budget in an alpine lake basin during summertime fair weather conditions. Meteorol. Atmos. Phys. 81, 27–52. doi: 10.1007/s007030200029

CrossRef Full Text | Google Scholar

Kossmann, M., Vögtlin, R., Corsmeier, U., Vogel, B., Fiedler, F., Binder, H.-J., et al. (1998). Aspects of the convective boundary layer structure over complex terrain. Atmos. Environ. 32, 1323–1348. doi: 10.1016/S1352-2310(97)00271-9

CrossRef Full Text | Google Scholar

Kottmeier, C., Kalthoff, N., Barthlott, C., Corsmeier, U., Van Baelen, J., Behrendt, A., et al. (2008). Mechanisms initiating deep convection over complex terrain during COPS. Meteorol. Z. 17, 931–948. doi: 10.1127/0941-2948/2008/0348

CrossRef Full Text | Google Scholar

Kuwagata, T., and Kimura, F. (1995). Daytime boundary layer evolution in a deep valley. Part I: observations in the Ina Valley. J. Appl. Meteorol. 34, 1082–1091.

Google Scholar

Kuwagata, T., and Kimura, F. (1997). Daytime boundary layer evolution in a deep valley. Part II: numerical simulation of the cross-valley circulation. J. Appl. Meteorol. 36, 883–895.

Google Scholar

Kuwagata, T., and Kondo, J. (1989). Observation and modeling of thermally induced upslope flow. Bound. Layer Meteorol. 49, 265–293. doi: 10.1007/BF00120973

CrossRef Full Text | Google Scholar

Kuwagata, T., and Sumioka, M. (1991). The daytime heating process over complex terrain in central Japan under fair and calm weather conditions. Part III: daytime thermal low and nocturnal thermal high. J. Meteorol. Soc. Japan 69, 91–103.

Google Scholar

Laiti, L., Zardi, D., de Franceschi, M., Rampanelli, G., and Giovannini, L. (2014). Analysis of the diurnal development of a lake-valley circulation in the Alps based on airborne and surface measurements. Atmos. Chem. Phys. 14, 9771–9786. doi: 10.5194/acp-14-9771-2014

CrossRef Full Text | Google Scholar

Lang, M. N., Gohm, A., and Wagner, J. S. (2015). The impact of embedded valleys on daytime pollution transport over a mountain range, Atmos. Chem. Phys. 15, 11981–11998. doi: 10.5194/acp-15-11981-2015

CrossRef Full Text | Google Scholar

Langford, A. O., Senff, C. J., Alvarez, R. J., Banta, R. M., and Hardesty, R. M. (2010). Long-range transport of ozone from the Los Angeles Basin: a case study. Geophys. Res. Lett. 37. doi: 10.1029/2010GL042507

CrossRef Full Text | Google Scholar

Lee, T. R., De Wekker, S. F. J., Pal, S., Andrews, A., and Kofler, J. (2015). Meteorological controls on the diurnal variability of carbon monoxide mixing ratio at a mountaintop monitoring site in the Appalachian Mountains. Tellus B 67:25659. doi: 10.3402/tellusb.v67.25659

CrossRef Full Text | Google Scholar

Lehner, M., and Gohm, A. (2010). Idealised simulations of daytime pollution transport in a steep valley and its sensitivity to thermal stratification and surface albedo. Bound. Layer Meteorol. 134, 327–351. doi: 10.1007/s10546-009-9442-y

CrossRef Full Text | Google Scholar

Lenschow, D. H., Stankov, B. B., and Mahrt, L. (1979). The rapid morning boundary-layer transition. J. Atmos. Sci. 36, 2108–2124.

Google Scholar

Leukauf, D., Gohm, A., Rotach, M., and Wagner, J. S. (2015). The impact of temperature inversion breakup on the exchange of heat and mass in an idealized valley: sensitivity to radiative forcing. J. Appl. Meteorol. Climatol. 54, 2199–2216. doi: 10.1175/JAMC-D-15-0091.1

CrossRef Full Text | Google Scholar

Liechti, O., and Neininger, B. (1994). ALPTHERM: a PC-based model for atmospheric convection over complex topography. Tech. Soaring 18, 73–78.

Google Scholar

Liu, S., and Liang, X.-Z. (2010). Observed diurnal cycle climatology of planetary boundary layer height. J. Clim. 23, 5790–5809. doi: 10.1175/2010JCLI3552.1

CrossRef Full Text | Google Scholar

Lothon, M., Lohou, F., Pino, D., Couvreux, F., Pardyjak, E. R., Reuder, J., et al. (2014). The BLLAST field experiment: boundary-layer late afternoon and turbulence. Atmos. Chem. Phys. 14, 10931–10960. doi: 10.5194/acpd-14-10789-2014

CrossRef Full Text | Google Scholar

Lu, R., and Turco, R. P. (1994). Air pollutant transport in a coastal environment. Part I: two-dimensional simulations of sea-breeze and mountain effects. J. Atmos. Sci. 51, 2285–2308.

Google Scholar

Lugauer, M., Baltensperger, U., Furger, M., Gäggeler, H. W., Jost, D. T., Schwikowski, M., et al. (1998). Aerosol transport to the high Alpine sites Jungfraujoch (3454 m asl) and Colle Gnifetti (4452 m asl). Tellus B 50, 76–92.

Google Scholar

Lugauer, M., and Winkler, P. (2005). Thermal circulation in South Bavaria – climatology and synoptic aspects. Meteorol. Z. 14, 15–30. doi: 10.1127/0941-2948/2005/0014-0015

CrossRef Full Text | Google Scholar

Mannouji, N. (1982). A numerical experiment on the mountain and valley winds. J. Meteorol. Soc. Japan 60, 1085–1105.

Mannstein, H. (1989). Die radiometrisch bestimmte Oberflächentemperatur im Gebirge und die Ermittlung des Stroms fühlbarer Wärme. Dissertation, University of Munich.

Marsik, F. J., Fischer, K. W., McDonald, T. D., and Samson, P. J. (1995). Comparison of methods for estimating mixing height used during the 1992 Atlanta Field Intensive. J. Appl. Meteorol. 34, 1802–1814.

Google Scholar

Maughan, R. A., Spanton, A. M., and Williams, M. L. (1982). An analysis of the frequency distribution of sodar derived mixing heights classified by atmospheric stability. Atmos. Environ. 16, 1209–1218. doi: 10.1016/0004-6981(82)90209-8

CrossRef Full Text | Google Scholar

McElroy, J. L., and Smith, T. B. (1991). Lidar descriptions of mixing-layer thickness characteristics in a complex terrain/coastal environment. J. Appl. Meteorol. 30, 585–597.

Google Scholar

McKendry, I. G., and Lundgren, J. (2000). Tropospheric layering of ozone in regions of urbanized complex and/or coastal terrain: a review. Prog. Phys. Geogr. 24, 329–354. doi: 10.1177/030913330002400302

PubMed Abstract | CrossRef Full Text | Google Scholar

McKendry, I. G., Steyn, D. G., Lundgren, J., Hoff, R. M., Strapp, W., Anlauf, K., et al. (1997). Elevated ozone layers and vertical down-mixing over the Lower Fraser Valley. Atmos. Environ. 31, 2135–2146. doi: 10.1016/S1352-2310(96)00127-6

CrossRef Full Text | Google Scholar

Melfi, S. H., Spinhirne, J. D., Chou, S.-H., and Palm, S. P. (1985). Lidar observation of vertically organized convection in the planetary boundary layer over the ocean. J. Clim. Appl. Meteorol. 24, 806–821.

Google Scholar

Meybeck, M., Green, P., and Vörösmarty, C. J. (2001). A new typology for mountains and other relief classes: an application to global continental water resources and population distribution. Mt. Res. Dev. 21, 34–45. doi: 10.1659/0276-4741(2001)021[0034:antfma]2.0.co;2

CrossRef Full Text | Google Scholar

Millan, M. M., Sanz, M. J., Salvador, R., and Mantilla, E. (2002). Atmospheric dynamics and ozone cycles related to nitrogen deposition in the western Mediterranean. Environ. Pollut. 10, 167–186. doi: 10.1016/S0269-7491(01)00311-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Mizzi, A. P., and Pielke, R. A. (1984). A numerical study of the mesoscale atmospheric circulation observed during a coastal upwelling event on 23 August 1972. Part I: sensitivity studies. Mon. Weather Rev. 112, 76–90.

Google Scholar

Müller, H., and Whiteman, C. D. (1988). Breakup of a nocturnal temperature inversion in the Dischma Valley during DISKUS. J. Appl. Meteorol. 27, 188–194.

Google Scholar

Muñoz, R. C., and Undurraga, A. A. (2010). Daytime mixed layer over the Santiago Basin: description of two years of observations with a lidar ceilometer. J. Appl. Meteorol. Climatol. 49, 1728–1741. doi: 10.1175/2010JAMC2347.1

CrossRef Full Text

Myrick, R. H., Sakiyama, S. K., Angle, P. R., and Sandhu, A. S. (1994). Seasonal mixing heights and inversions at Edmonton, Alberta. Atmos. Environ. 28A, 723–729. doi: 10.1016/1352-2310(94)90049-3

CrossRef Full Text | Google Scholar

Noppel, H., and Fiedler, F. (2002). Mesoscale heat transport over complex terrain by slope winds – A conceptual model and numerical simulations. Bound. Layer Meteorol. 104, 73–97. doi: 10.1023/A:1015556228119

CrossRef Full Text | Google Scholar

Norton, C. L., and Hoidale, G. B. (1976). The diurnal variation of mixing height by season over White Sands missile range, New Mexico. Mon. Weather Rev. 104, 1317–1320.

Google Scholar

Nyeki, S., Eleftheriadis, K., Baltensperger, U., Colbeck, I., Fiebig, M., Fix, A., et al. (2002). Airborne lidar and in-situ aerosol observations of an elevated layer, leeward of the European Alps and Apennines. Geophys. Res. Lett. 29, 1852. doi: 10.1029/2002GL014897

CrossRef Full Text | Google Scholar

Nyeki, S., Kalberer, M., Colbeck, I., De Wekker, S. F. J., Furger, M., Gäggeler, H. W., et al. (2000). Convective boundary layer evolution to 4 km asl over high-alpine terrain: airborne lidar observations in the Alps. Geophys. Res. Lett. 27, 689–692. doi: 10.1029/1999GL010928

CrossRef Full Text | Google Scholar

Orville, H. D. (1965). A numerical study of the initiation of cumulus clouds over mountainous terrain. J. Atmos. Sci. 22, 684–699.

Google Scholar

Panday, A. K., Prinn, R. G., and Schär, C. (2009). Diurnal cycle of air pollution in the Kathmandu Valley, Nepal: 2. Modeling results. J. Geophys. Res. 114, D21308. doi: 10.1029/2008jd009808

CrossRef Full Text | Google Scholar

Physick, W. L., Abbs, D. J., and Pielke, R. A. (1989). Formulation of the thermal internal boundary layer in a mesoscale model. Bound. Layer Meteorol. 49, 99–111. doi: 10.1007/BF00116407

CrossRef Full Text | Google Scholar

Pielke, R. A., and Segal, M. (1986). “Mesoscale circulations forced by differential terrain heating,” in Mesoscale Meteorology and Forecasting, ed P. Ray (Boston, MA: American Meteorological Society), 516–548.

Google Scholar

Prandtl, L. (1942). Führer durch die Strömungslehre. Braunschweig: Vieweg-Verlag.

Princevac, M., and Fernando, H. J. S. (2008). Morning breakup of cold pools in complex terrain. J. Fluid Mech. 616, 99–109. doi: 10.1017/S0022112008004199

CrossRef Full Text | Google Scholar

Queney, P. (1948). The problem of air flow over mountains: a summary of theoretical results. Bull. Am. Meteorol. Soc. 29, 16–26.

Google Scholar

Rampanelli, G., Zardi, D., and Rotunno, R. (2004). Mechanisms of up-valley winds. J. Atmos. Sci. 61, 3097–3111. doi: 10.1175/JAS-3354.1

CrossRef Full Text | Google Scholar

Raymond, D. J., and Wilkening, M. (1980). Mountain-induced convection under fair weather conditions. J. Atmos. Sci. 37, 2693–2700.

Google Scholar

Raymond, D. J., and Wilkening, M. H. (1982). Flow and mixing in New Mexico mountain cumuli. J. Atmos. Sci. 39, 2211–2228.

Google Scholar

Regmi, R. P., Kitada, T., and Kurata, G. (2003). Numerical simulation of late wintertime local flows in Kathmandu Valley, Nepal: implication for air pollution transport. J. Appl. Meteorol. 42, 389–403. doi: 10.1175/1520-0450(2003)042<0389:NSOLWL>2.0.CO;2

CrossRef Full Text | Google Scholar

Rendón, A. M., Salazar, J. F., Palacio, C. A., and Wirth, V. (2015). Temperature inversion breakup with impacts on air quality in urban valleys influenced by topographic shading. J. Appl. Meteorol. Climatol. 54, 302–321. doi: 10.1175/JAMC-D-14-0111.1

CrossRef Full Text | Google Scholar

Rendón, A. M., Salazar, J. F., Palacio, C. A., Wirth, V., and Brötz, B. (2014). Effects of urbanization on the temperature inversion breakup in a mountain valley with implications for air quality. J. Appl. Meteorol. Climatol. 53, 840–858. doi: 10.1175/JAMC-D-13-0165.1

CrossRef Full Text | Google Scholar

Reuten, C., Steyn, D. G., Strawbridge, K. B., and Bovis, P. (2005). Observations of the relationship between the upslope flows and the convective boundary layer in steep terrain. Bound. Layer Meteorol. 116, 37–61. doi: 10.1007/s10546-004-7299-7

CrossRef Full Text | Google Scholar

Richner, H., and Hächler, P. (2013). “Understanding and forecasting alpine foehn,” Mountain Weather Research and Forecasting: Recent Progress and Current Challenges, eds F. Chow, S. F. J. De Wekker, and B. Synder (New York, NY: Springer), 219–260.

Google Scholar

Rotach, M. W., Calanca, P., Vogt, R., Steyn, D. G., Graziani, G., Andretta, M., et al. (2004). The turbulence structure and exchange processes in an Alpine valley: the Riviera project. Bull. Am. Soc. 85, 1367–1385. doi: 10.1175/BAMS-85-9-1367

CrossRef Full Text

Rotach, M. W., Gohm, A., Lang, N., Leukauf, D., Stiperski, I., and Wagner, S. (2015). On the vertical exchange of heat, mass and momentum over complex, mountainous terrain. Front. Earth Sci. 3:76. doi: 10.3389/feart.2015.00076

CrossRef Full Text | Google Scholar

Rotach, M. W., Wohlfahrt, G., Hansel, A., Reif, M., Wagner, J., and Gohm, A. (2014). The world is not flat: implications for the global carbon balance. Bull. Am. Meteorol. Soc. 95, 1021–1028. doi: 10.1175/BAMS-D-13-00109.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sasaki, T., Wu, P., Mori, S., Hamada, J.-I., Tauhid, Y. I., Yamanaka, M. D., et al. (2004). Vertical moisture transport above the mixed layer around the mountains in western Sumatra. Geophys. Res. Lett. 31, L08106. doi: 10.1029/2004GL019730

CrossRef Full Text | Google Scholar

Schmidli, J., and Rotunno, R. (2010). Mechanisms of along-valley winds and heat exchange over mountainous terrain. J. Atmos. Sci. 67, 3033–3047. doi: 10.1175/2010JAS3473.1

CrossRef Full Text | Google Scholar

Schmidli, J. (2013). Daytime heat transfer processes over mountainous terrain. J. Atmos. Sci. 70, 4041–4066. doi: 10.1175/JAS-D-13-083.1

CrossRef Full Text | Google Scholar

Segal, M., Ookuchi, Y., and Pielke, R. A. (1987). On the effect of steep slope orientation on the intensity of daytime upslope flow. J. Atmos. Sci. 44, 3587–3592.

Google Scholar

Seibert, P., Beyrich, F., Gryning, S.-E., Joffre, S., Rasmussen, A., and Tercier, P. (2000). Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 34, 1001–1027. doi: 10.1016/S1352-2310(99)00349-0

CrossRef Full Text | Google Scholar

Serafin, S., and Zardi, D. (2010a). Structure of the atmospheric boundary layer in the vicinity of a developing upslope flow system: a numerical model study. J. Atmos. Sci. 67, 1171–1185. doi: 10.1175/2009JAS3231.1

CrossRef Full Text | Google Scholar

Serafin, S., and Zardi, D. (2010b). Daytime heat transfer processes related to slope flows and turbulent convection in an idealized mountain valley. J. Atmos. Sci. 67, 3739–3756. doi: 10.1175/2010JAS3428.1

CrossRef Full Text | Google Scholar

Smith, R. B., Doyle, J. D., Jiang, Q., and Smith, S. A. (2007). Alpine gravity waves: lessons from MAP regarding mountain waves generation and braking. Q. J. R. Meteorol. Soc. 133, 917–936. doi: 10.1002/qj.103

CrossRef Full Text | Google Scholar

Smith, R. B. (1979). The influence of mountains on the atmosphere. Adv. Geophys. 21, 87–230. doi: 10.1016/S0065-2687(08)60262-9

CrossRef Full Text | Google Scholar

Stein, J. (2004). Exploration of some convective regimes over the Alpine orography. Q. J. R. Meteorol. Soc. 130, 418–502. doi: 10.1256/qj.02.220

CrossRef Full Text | Google Scholar

Steinacker, R. (1984). Area-height distribution of a valley and its relation to the valley wind. Contrib. Atmos. Phys. 57, 64–71.

Google Scholar

Steinbacher, M., Henne, S., Dommen, J., Wiesen, P., and Prevot, A. S. (2004). Nocturnal trans-alpine transport of ozone and its effects on air quality on the Swiss Plateau. Atmos. Environ. 36, 4539–4550. doi: 10.1016/j.atmosenv.2004.05.008

CrossRef Full Text | Google Scholar

Stensrud, D. J. (1993). Elevated residual layers and their influence on surface boundary-layer evolution. J. Atmos. Sci. 50, 2284–2293.

Google Scholar

Steyn, D. G., De Wekker, S. F. J., Kossmann, M., and Martilli, A. (2013). “Boundary Layers and Air Quality in Mountainous Terrain,” in Chapter 5 Mountain Weather Research and Forecasting, Recent Progress and Current Challenges, eds F. K.Chow, S. F. J. De Wekker, and B. Snyder (Berlin: Springer), 261–290.

Google Scholar

Stull, R. B. (1988). An Introduction to Boundary Layer Meteorology. Dordrecht: Kluwer Academic Publishers.

Google Scholar

Stull, R. B. (1992). “A theory for mixed-layer-top levelness over irregular topography,” in Proceedings of the 10th AMS Symposium on Turbulence and Diffusion (Portland).

Google Scholar

Sun, J., and de Wekker, S. F. J. (2011). “Atmospheric carbon dioxide transport over complex terrain,” in Mountain Ecosystems: Dynamics, Management and Conservation, ed K. E. Richards (New York, NY: Nova Science Publishers), 101–121.

Google Scholar

Taylor, J. R., Kossmann, M., Low, D. J., and Zawar-Reza, P. (2005). Summertime easterly surges in southeastern Australia: a case study of thermally forced flow. Aust. Meteorol. Mag. 54, 213–223.

Google Scholar

Tian, W., and Parker, D. J. (2002). Two-dimensional simulation of orographic effects on mesoscale boundary-layer convection. Q. J. R. Meteorol. Soc. 128, 1929–1952. doi: 10.1256/003590002320603476

CrossRef Full Text | Google Scholar

Tian, W., Parker, D. J., and Kilburn, C. A. D. (2003). Observations and numerical simulation of atmospheric cellular convection over mesoscale topography. Mon. Weather Rev. 131, 222–235. doi: 10.1175/1520-0493(2003)131<0222:OANSOA>2.0.CO;2

CrossRef Full Text | Google Scholar

Toth, J., and Johnson, R. H. (1985). Summer surface flow characteristics over northeast Colorado. Mon. Weather Rev. 113, 1779–1800.

Google Scholar

Trentmann, J., Keil, C., Salzmann, M., Barthlott, C., Bauer, H.-S., Schwitalla, T., et al. (2009). Multi-model simulations of a convective situation in mountainous terrain. Meteorol. Atmos. Phys. 103, 95–103. doi: 10.1007/s00703-008-0323-6

CrossRef Full Text | Google Scholar

Tripoli, G. J., and Cotton, W. R. (1989). Numerical study of an observed orogenic mesoscale convective system: Part 1. Simulated genesis and comparison with observations. Mon. Weather Rev. 117, 272–304.

Google Scholar

Tyson, P. D., and D'Abreton, P. C. (1998). Transport and recirculation of aerosols off southern Africa - Macroscale plume structure. Atmos. Environ. 32, 1511–1524.

Google Scholar

Van Pul, W. A. J., Holtslag, A. A. M., and Swart, D. P. J. (1994). A comparison of ABL heights inferred routinely from lidar and radiosondes at noontime. Bound. Layer Meteorol. 68, 173–191. doi: 10.1007/BF00712670

CrossRef Full Text | Google Scholar

Vergeiner, I., and Dreiseitl, E. (1987). Valley winds and slope winds – observations and elementary thoughts. Meteorol. Atmos. Phys. 36, 264–286. doi: 10.1007/BF01045154

CrossRef Full Text | Google Scholar

Vergeiner, I. (1982). Eine energetische Théorie der Hangwinde. 17 Internationale Tagung fiir Alpine Météorologie, Berchtesgaden. Ann. Meteor. 19, 189–191.

Vogelezang, D. H. P., and Holtslag, A. A. M. (1996). Evaluation and model impacts of alternative boundary-layer height formulations. Bound. Layer Meteorol. 81, 245–269. doi: 10.1007/BF02430331

CrossRef Full Text | Google Scholar

Wagner, A. (1932). Neue Theorie des Berg- und talwindes [New theory of the mountain and valley wind]. Meteorol. Z. 49, 329–341.

Wagner, J. S., Gohm, A., and Rotach, M. W. (2014). The impact of valley geometry on daytime thermally driven flows and vertical transport processes. Q. J. R. Meteorol. Soc. 141, 1780–1794. doi: 10.1002/qj.2481

CrossRef Full Text | Google Scholar

Wagner, J. S., Gohm, A., and Rotach, M. W. (2015). Influence of along-valley terrain heterogeneity on exchange processes over idealized valleys. Atmos. Chem. Phys. Discuss. 15, 415–451. doi: 10.5194/acpd-15-415-2015

CrossRef Full Text | Google Scholar

Wakimoto, R. M., and McElroy, J. L. (1986). Lidar observations of elevated pollution layers over Los Angeles. J. Clim. Appl. Meteorol. 25, 1583–1599.

Google Scholar

Walko, R. L., Cotton, W. R., and Pielke, R. A. (1992). Large eddy simulation of the effects of hilly terrain on the convective boundary layer. Bound. Layer Meteorol. 58, 133–150. doi: 10.1007/BF00120755

CrossRef Full Text | Google Scholar

Weigel, A. P., Chow, F. K., and Rotach, M. (2007). The effect of mountainous topography on moisture exchange between the “surface” and the free atmosphere. Bound. Layer Meteorol. 125, 227–244. doi: 10.1007/s10546-006-9120-2

CrossRef Full Text | Google Scholar

Weigel, A. P., Chow, F. K., Rotach, M. W., Street, R. L., and Xue, M. (2006). High-resolution large-eddy simulations of flow in a steep Alpine valley. Part II: Flow structure and heat budgets. J. Appl. Meteorol. Clim. 45, 87–107. doi: 10.1175/JAM2323.1

CrossRef Full Text | Google Scholar

Weigel, A. P., and Rotach, M. W. (2004). Flow structure and turbulence characteristics of the daytime atmosphere in a steep and narrow Alpine valley. Q. J. R. Meteorol. Soc. 130, 2605–2627. doi: 10.1256/qj.03.214

CrossRef Full Text | Google Scholar

Wenzel, A., Kalthoff, N., and Fiedler, F. (1997). On the variation of the energy-balance components with orography in the Upper Rhine Valley. Theor. Appl. Climatol. 57, 1–9. doi: 10.1007/BF00867973

CrossRef Full Text | Google Scholar

Whiteman, C., Zhong, S., Bian, X., Fast, J., and Doran, J. C. (2000). Boundary layer evolution and regional-scale diurnal circulations over the Mexican plateau. J. Geophys. Res. D105, 10081–10102. doi: 10.1029/2000JD900039

CrossRef Full Text | Google Scholar

Whiteman, C. D., and McKee, T. B. (1978). Air pollution implications of inversion descent in a mountain valley. Atmos. Environ. 12, 2151–2158. doi: 10.1016/0004-6981(78)90170-1

CrossRef Full Text | Google Scholar

Whiteman, C. D., and McKee, T. B. (1982). Breakup of temperature inversions in deep mountain valleys: Part II. thermodynamic model. J. Appl. Meteorol. 21, 290–302.

Google Scholar

Whiteman, C. D., Zhong, S., Shaw, W. J., Hubbe, J. M., Bian, X., and Mittelstadt, J. (2001). Cold pools in the Columbia Basin. Weather Forecast. 16, 432–447. doi: 10.1175/1520-0434(2001)016<0432:CPITCB>2.0.CO;2

CrossRef Full Text | Google Scholar

Whiteman, C. D. (1982). Breakup of temperature inversions in deep mountain valleys. Part I: observations. J. Appl. Meteorol. 21, 270–289.

Google Scholar

Whiteman, C. D. (1990). “Observations of thermally developed wind systems in mountainous terrain,” in Atmospheric Processes Over Complex Terrain. Meteorological Monographs, Vol. 23, ed W. Blumen (Boston, MA: American Meteorological Society), 5–42.

Google Scholar

Whiteman, C. D. (2000). Mountain Meteorology - Fundamentals and Applications. New York, NY: Oxford University Press.

Google Scholar

Wolyn, P. G., and McKee, T. B. (1989). Deep stable layers in the intermountain western United States. Mon. Weather Rev. 117, 461–472.

Google Scholar

Wood, N. (2000). Wind flow over complex terrain: a historical perspective and the prospect for large-eddy modelling. Bound. Layer Meteorol. 96, 11–32. doi: 10.1023/A:1002017732694

CrossRef Full Text | Google Scholar

Worthington, R. M. (2002). Mountain waves launched by convective activity within the boundary layer above mountains. Bound. Layer Meteorol. 103, 469–491. doi: 10.1023/A:1014965029602

CrossRef Full Text | Google Scholar

Wulfmeyer, V., Behrendt, A., Bauer, H.-S., Kottmeier, C., Corsmeier, U., Blyth, A., et al. (2008). The convective and orographically-induced precipitation study: a research and development project of the World Weather Research Program for improving quantitative precipitation forecasting in low-mountain regions. Bull. Am. Meteorol. Soc. 89, 1477–1486. doi: 10.1175/2008BAMS2367.1

CrossRef Full Text | Google Scholar

Yanai, M., Li, C., and Song, Z. (1992). Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon. J. Meteorol. Soc. Japan 70, 319–351.

Google Scholar

Yang, K., Koike, T., Fujii, H., Tamura, T., Xu, X., Bian, L., et al. (2004). The daytime evolution of the atmospheric boundary layer and convection over the Tibetan Plateau: observations and simulations. J. Meteorol. Soc. Japan 82, 1777–1792. doi: 10.2151/jmsj.82.1777

CrossRef Full Text | Google Scholar

Ye, Z. J., Segal, M., and Pielke, R. A. (1987). Effects of atmospheric thermal stability and slope steepness on the development of daytime thermally induced upslope flow. J. Atmos. Sci. 44, 3341–3354.

Google Scholar

Zängl, G., and Gonzalez Chico, S. (2006). The thermal circulation of a grand plateau: sensitivity to the height, width, and shape of the plateau. Mon. Weather Rev. 134, 2581–2600. doi: 10.1175/MWR3207.1

CrossRef Full Text | Google Scholar

Zardi, D., and Whiteman, C. D. (2013). “Diurnal mountain wind systems,” in Mountain Weather Research and Forecasting: Recent Progress and Current Challenges, eds F. Chow, S. F. J. De Wekker, and B. Synder (New York, NY: Springer), 35–119.

Google Scholar

Zawar-Reza, P., and Sturman, A. P. (2006). Two-dimensional numerical analysis of a thermally generated mesoscale wind system observed in the Mackenzie Basin, New Zealand. Aust. Meteorol. Mag. 55, 19–34.

Google Scholar