- 1Institute of Atmospheric and Cryospheric Sciences, University of Innsbruck, Innsbruck, Austria
- 2Zentralanstalt für Meteorologie und Geodynamik, Vienna, Austria
- 3Institut für Physik der Atmosphäre, Deutsches Zentrum für Luft und Raumfahrt, Oberpfaffenhofen, Germany
The role of the atmospheric boundary layer (ABL) in the atmosphere-climate system is the exchange of heat, mass, and momentum between “the earth's surface” and the atmosphere. Traditionally, it is understood that turbulent transport is responsible for this exchange and hence the understanding and physical description of the turbulence structure of the boundary layer is key to assess the effectiveness of earth-atmosphere exchange (EAE). This understanding is rooted in the (implicit) assumption of a scale separation or spectral gap between turbulence and mean atmospheric motions, which in turn leads to the assumption of a horizontally homogeneous and flat (HHF) surface as a reference, for which both physical understanding and model parameterizations have successfully been developed over the years. Over mountainous terrain, however, the ABL is generically inhomogeneous due to both thermal (radiative) and dynamic forcing. This inhomogeneity leads to meso-scale and even sub-meso-scale flows such as slope and valley winds or wake effects. It is argued here that these (sub)meso-scale motions can significantly contribute to the vertical structure of the boundary layer and hence vertical exchange of heat and mass between the surface and the atmosphere. If model grid resolution is not high enough the latter will have to be parameterized (in a similar fashion as gravity wave drag (GWD) parameterizations take into account the momentum transport due to gravity waves in large-scale models). In this contribution we summarize the available evidence of the contribution of (sub)meso-scale motions to vertical exchange in mountainous terrain from observational and numerical modeling studies. In particular, a number of recent simulation studies using idealized topography will be summarized and put into perspective—so as to identify possible limitations and areas of necessary future research.
Introduction
According to Stull (1988) the Atmospheric Boundary Layer (ABL) is defined “as that part of the troposphere that is directly influenced by the presence of the earth's surface, and responds to surface forcing with a timescale of about an hour or less.” Stull adds that “These forcings include frictional drag, evaporation and transpiration, heat transfer, pollutant emission, and terrain induced flow modification.” Due to these surface forcings (mainly friction and heat exchange) ABL flows are generally turbulent, and hence turbulent transport plays an important role and determines to a large extent the exchange efficiency of energy, mass, and momentum between the surface and the atmosphere. One may, therefore, also define, the ABL as that atmospheric layer through which the earth-atmosphere exchange (EAE) is effectuated. The so-called “boundary layer approximation” assumes—mostly for the purpose of ABL parameterizations in numerical models—that turbulent transport exceeds that associated with the mean flow, especially in the vertical direction. Hence a “single column” (vertical) approach is usually employed in ABL parameterizations for models with grid-scales larger than typical ABL heights (order 1 km). For horizontally homogeneous and flat (HHF) surfaces this indeed covers the entire vertical exchange so that at the time when numerical atmospheric modeling emerged—with large-scale, low-resolution models where topography is smoothed and horizontal gradients are correspondingly small—successful one-dimensional ABL parameterizations were developed. These are formulated based on similarity theory using the properties of different “scaling regimes” (e.g., Holtslag and Nieuwstadt, 1986).
Since the world is not flat (Rotach et al., 2014) and—maybe with the exception of the oceans—not generally horizontally homogeneous, the efficiency of the exchange between the “surface” and the “free atmosphere” is not controlled by vertical turbulent transport in the ABL alone. The effect of horizontal inhomogeneity on the ABL structure and thus EAE has been studied using the concept of “internal boundary layers” (Garratt, 1990; Savelyev and Taylor, 2005) and its consequences on “vertical” transport. However, little research has been done concerning the impact of non-flat surfaces on the earth-atmosphere exchange (EAE). As “non-flat” intrinsically means horizontally inhomogeneous (Rotach and Zardi, 2007), i.e., “non-HHF,” the purpose of this paper is to summarize current understanding concerning net exchange of energy, mass, and momentum between the topographically shaped surface on the one hand and the atmosphere on the other hand in the presence of substantial topography. By “substantial” we mean that the influencing topography is characterized by length scales which are on the same order or even larger than the ABL height of the hypothetical “undisturbed far upstream” boundary layer. We note that this exceeds what is usually denoted as EAE, i.e., the turbulent fluxes at the surface. Rather, this corresponds to identifying the entire ABL in mountainous terrain as the “agent” of EAE and requires identification of (sub-) meso-scale processes contributing to this exchange (Section Exchange Processes Over Complex, Mountainous Topography). In Section Observed Evidence for Earth-Atmosphere Exchange Over Mountainous Terrain we review the sparse evidence for EAE over mountainous terrain based on real-terrain atmospheric studies (both experimental and modeling) and in Section Idealized-Terrain Numerical Simulations we focus on results from high-resolution numerical modeling using idealized terrain. Finally, in Section Outlook we identify the critical gaps in knowledge concerning EAE over mountainous terrain thereby suggesting future research directions.
Exchange Processes Over Complex, Mountainous Topography
Exchange processes can generally be identified as having dynamic or thermodynamic origin, even if the dynamically forced processes also depend on the thermodynamic state (background stratification) of the atmosphere.
Dynamically Forced Exchange Processes Over Mountainous Terrain
Under the condition of a stably stratified background flow, topography (variability in surface elevation) can produce gravity waves at all scales (Baines, 1995; Nappo, 2002), which transport energy and momentum, in a direction normal to the phase propagation (Holton and Hakim, 2013). In numerical models, the effect of subgrid-scale topography in extracting momentum from the mean flow has long been recognized at global (hemispheric) scales (Palmer et al., 1986) and corresponding “gravity-wave drag parameterizations” have been developed and implemented. Nevertheless, for stable background flow Lott and Miller (1997) noted that the linear gravity wave response may not be sufficient to fully cover the effect of sub-grid scale topography on the momentum budget, and therefore proposed to add some “low level drag” below the level of blocked flow (which depends on the stratification and flow conditions). Their work demonstrates that such low level drag can be of equal magnitude as the gravity-wave drag alone. Applying the sum of the two contributions as “orographic drag parameterization” compares favorably to direct drag measurements as performed during PYREX (Bougeault et al., 1993) and also improves model predictions (using the ECMWF model at T103 and T206 resolution at the time) of mean flow characteristics.
Even under neutral conditions, the state of the ABL is modified due to topography. Based on the work of Jackson and Hunt (1975), Hunt et al. (1988a) have developed a linearized theoretical framework for the boundary layer structure over low topography (with a vertical extension of the boundary layer being much smaller than the half-width of the hill so as to allow for linearization) that has later been extended to stratified flows (Hunt et al., 1988b) and is comprehensively summarized by Belcher and Hunt (1998). This framework allows estimation of the additional drag a “hilly” surface exerts on the flow (Belcher et al., 1993), thus giving rise to an additional impact of sub-grid scale topography on the flow. Essentially a “wavy surface” will transport more momentum toward the surface than the boundary layer parameterization alone will determine, and thus slows down the flow. The need for an additional parameterization at least for global NWP and climate models has been recognized and introduced into model parameterizations (e.g., Wood and Mason, 1993; Wood et al., 2001). However, the extent to which sub-meso scale terrain variability may contribute to momentum exchange in high-resolution NWP models remains to be investigated. Belcher and Hunt (1998) further note that over low hills modification of mean flow and turbulence structure in the boundary layer (Raupach et al., 1992) also affect the exchange of mass and energy, but to a lesser extent than momentum transfer is affected.
Thermally Forced Exchange Processes Over Mountainous Terrain
Exchange between earth and atmosphere is associated with flows induced by differential heating in relation to topography, occurring at a range of horizontal scales due to varying slope angles and exposition. Thermally forced flows, driven by radiative heating have a clear daily cycle and occur preferentially during clear-sky conditions with weak synoptic forcing. Under overcast conditions spatial variability of diabatic heating is essentially zero even in complex topography (Matzinger et al., 2003) and if the synoptic forcing is considerable it may easily mask the thermal flow. Mechanisms and examples have been discussed extensively in the literature—most recently in a comprehensive review by Zardi and Whiteman (2013) that updates Whiteman (2000). We therefore concentrate on the vertical exchange associated with these flows (see Sections Observed Evidence For Earth-Atmosphere Exchange Over Mountainous Terrain and Idealized-Terrain Numerical Simulations) and very briefly characterize their properties relevant for this.
At the meso-α scale (conventionally taken to range up to some 200 km; Orlanski, 1975) a mountain range, or isolated mountain, is often associated with a thermal low, thus causing flow toward the topography during the day. Different names have been coined for this phenomenon depending on location and application. Figure 1 seeks to summarize these flows graphically.
- Plain-to-mountain flow (Kleinschmidt, 1922; De Wekker et al., 1998; Weissmann et al., 2005) is the classical, idealized situation where the difference in temperature between equal heights over the plain and over the mountain leads to the establishment of a thermally driven flow. In Figure 1, this would typically be flow normal to the mountain or the mountain range. These flows can transport air pollutants from major cities in the plain, or moisture from the humid boundary layer over the plain into the mountains (or vice versa). A plain situated at the entrance of a major valley running normal to the mountain range, can result in plain-to-mountain flow being the driver for the valley wind system (see below, meso-β scale). Viewed as part of a mountain-plain circulation (Weissmann et al., 2005) a plain-to-mountain flow is, in both concept and simulations, associated with a return flow either within (e.g., Demko et al., 2009) or above (dashed arrows in Figure 1) the boundary layer. Return flows are, of course, difficult to experimentally document since they are often masked by (even weak) synoptic flow (Weissmann et al., 2005).
- Mountain venting (Kossmann et al., 1999; De Wekker et al., 2004; Henne et al., 2005) refers to the vertical exchange associated with the plain-to-mountain flow or mountain-plain circulation. While the mechanism for this vertical exchange has sometimes been attributed to boundary layer growth beyond the top of the mountains (e.g., Nyeki et al., 2000), real-terrain (De Wekker et al., 2004) and idealized (e.g., Wagner et al., 2015b) simulations indicate that the exchange is not the result of a uniform mixing process (i.e., “boundary layer growth”) but preferably occurs through the slope flows (meso-γ scale, see below), i.e., through organized vertical motions (Kossmann et al., 1999). De Wekker and Kossmann (this volume) discuss in more detail the difference between the boundary layer height and the “mixing height.” Kossmann et al. (1999) further distinguish two different venting types, what they call “mountain venting” and “advective venting.” Both are (thermo-)dynamically driven meso-scale flows that export boundary layer to the free atmosphere, the former by vertically crossing the ABL top and the latter if the meso-scale flow crosses an inclined ABL top (e.g., over a slope).
- Alpine pumping: this expression has specifically been introduced (Lugauer and Winkler, 2005) for the mountain-plain circulation in the alpine foreland north of the Alps and in relation to the development of convection.
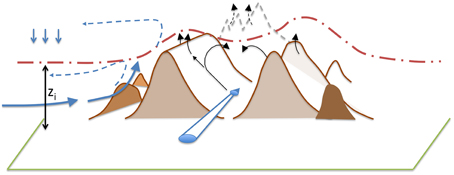
Figure 1. Conceptual sketch of thermally driven flows in mountainous terrain. “zi” denotes the Mixed layer height (red dash-dotted line) over the adjacent plain. Blue arrows, plain-to- mountain circulation and valley wind circulation; black arrows, slope-flow and mountain venting. Situation during daytime.
At the meso-β scale (20–200 km), temperature and hence pressure differences between “valley” and “plain” (see Figure 1) give rise to a valley wind system directed up-valley during the day and down-valley during the night. There has been some debate in the literature concerning the origin of the elevated daytime (reduced nighttime) temperature in a valley as compared to the reference plain. We refer to the discussion of results from (idealized) numerical simulations (Section Idealized-Terrain Numerical Simulations) to address this question. The valley wind system contributes in two ways to vertical exchange. Firstly, if the valley narrows up-valley the “geometric effect” leads to a net export (import) of mass for up-valley (down-valley) flows during daytime (nighttime) and hence exchange of trace constituents such as moisture or pollutants (Weigel et al., 2007). Secondly, turbulent transport through a lid separating the valley air from the “free tropospheric air”—or more generally through the valley boundary layer top (see De Wekker and Kossmann, this volume)—constitutes another possible mechanism for EAE in mountainous terrain. Again, when understood as a circulation pattern arising from a locally baroclinic circulation in along–valley direction, the valley wind system is associated with a return flow aloft. Similar to the plain-to-mountain scale this return flow is evident from idealized numerical simulations (e.g., Rampanelli et al., 2004) but hard to document experimentally, even if some evidence seems to be available (see Zardi and Whiteman, 2013 and references therein).
At the meso-γ scale (2–20 km) the difference between the near-surface temperature above a slope and that at some horizontal distance from the slope leads to a pressure gradient toward (away from) the slope and hence the establishment of an up-slope (down-slope) flow during the day (night). For these flows to establish, physically a sloped terrain is sufficient and models such as the classical Prandtl model (Prandtl, 1942, 1952), extended over the years to include e.g., rotational effects (Stiperski et al., 2007), weak non-linearity (Grisogono et al., 2015) or temporal variations in the forcing (Zardi and Serafin, 2015) have been devised for their description. In mountainous terrain, slopes are often associated with some symmetry in a valley so that a locally baroclinic stratification across the valley leads to a slope-flow circulation (see Figure 1). In numerical simulations (when employing over idealized terrain) this circulation is usually symmetric while in reality this is not necessarily the case (e.g., Weigel and Rotach, 2004; Gohm et al., 2009; see also below, Figure 5). Both, isolated slope flows (in Figure 1 this might refer to the “outer slope” of a mountain range or to the slope of an isolated mountain) and cross-valley circulations are associated with transport of mass and energy in the slope-wind layer (generally: the boundary layer on the slope) and thus contribute to EAE over mountainous terrain. Its efficiency depends on slope (valley) geometry and atmospheric forcing conditions as will be discussed in more detail in Section Idealized-Terrain Numerical Simulations.
At the micro-scale, comprising terrain features with horizontal scales < 2 km, EAE is mostly, or perhaps exclusively affected under (very) stable conditions through so-called sub-meso motions. According to Mahrt (2014) very stable conditions are particularly likely to occur “in basins, local depressions and valleys with weak down-valley slopes.” Under these conditions of strong stability the well-known theoretical similarity framework for turbulent exchange no longer holds (i.e., the flow is not fully turbulent) and exchange processes occur through complicated and hitherto poorly understood interactions between intermittent turbulence, wave activity, small-scale (submeso) organized motions, and a wealth of other features. Relatively little is known at present concerning these flows, nothing to say about their interaction or exchange efficiency. Mahrt (2014) provides a number of emerging research topics and requirements in order to better understand and formally treat these situations.
Observed Evidence for Earth-atmosphere Exchange Over Mountainous Terrain
Evidence for EAE over mountainous terrain may arise from large observational campaigns such as the Mesoscale Alpine Programme (MAP; Bougeault et al., 2001), and/or through real-terrain numerical modeling. In this section we summarize such evidence separately for momentum, energy and mass.
Momentum Exchange
For momentum transport over topography due to both gravity waves and modified boundary layer structure (Belcher and Hunt, 1998) indirect evidence can be sought by comparing near-surface wind climatologies from large-scale numerical models with those from observational networks. This is used to confirm that the “westerly bias” (too strong and too westerly surface winds, especially in the winter NH) has been correctly alleviated by the use of a gravity wave drag (GWD) parameterization (e.g., Palmer et al., 1986; Lott and Miller, 1997). It should be noted, however, that this “westerly bias” is not the only model deficiency for which remedy is sought by introducing a GWD parameterization in a global atmospheric model, and also that mountains are not the only source of gravity waves (see Kim et al., 2013). Kim et al. (2013) also discuss the difficulty of reliably measuring momentum flux (and even more so, its divergence) in order to directly compare a GWD parameterization with observations. Again, as some sort of indirect evidence, high-resolution meso-scale numerical modeling of a particular case study (e.g., Doyle and Shapiro, 2000) can—when successfully validated against observations—be used to diagnose momentum transport and thus evaluate a parameterization.
Milton and Wilson (1996) analyzed the momentum budget of the Unified Model of the UK MetOffice. For the GWD parameterization used at that time, the largest deviations in momentum were found in the lower troposphere (boundary layer) over major mountain ranges. Besides improving the GWD parameterization Milton and Wilson (1996) introduced another parameterization for orographic drag (form drag due to sub-grid scale orography) thus substantially reducing the inconsistency in the momentum balance and the “westerly bias” in mid latitudes by up to 2 ms−1.
Parameterizations of orographic drag are often based on introducing an additional contribution to the roughness length due to subgrid-scale orography, yielding a so-called “effective roughness length” (Taylor et al., 1989; Wood and Mason, 1993). Good correspondence of observed effective roughness lengths with those parameterized (e.g., Wood and Mason, 1993) using the additional drag as a source for momentum transport is another means of indirect evidence for the importance of this process.
The observational study of Turnipseed et al. (2004) identifies gravity waves as the main drivers for the exchange of momentum and energy in stable boundary layers. Up to 50% of the total scalar variance can be accounted for by low frequency waves. They also point to the rare, but significant, influence of meso-scale gravity waves on boundary layer characteristics. Over moderate terrain, Medeiros and Fitzjarrald (2014) attribute the missing drag to averaging over their non-homogeneous terrain. Focusing on the small-scale end of the gravity wave spectrum, Sun et al. (2015) give a detailed review of the wave-turbulence interaction in the stable boundary layer.
Energy (Heat) Exchange
The introduction of GWD parameterizations in numerical models provides an improved distribution of global temperatures (e.g., Kim et al., 2013—even if this effect is the result of an adjustment process to the thermal wind balance) and hence indirect evidence for modified energy exchange due to processes related to topography. Still, it is quite difficult to experimentally assess the effect of thermally forced meso-scale circulations (as described in Section Thermally Forced Exchange Processes Over Mountainous Terrain) for a real-terrain case study or a regional climatology over mountainous terrain. For heat exchange, therefore, there is little direct experimental evidence available—and only very limited indirect evidence. The difficulty with measuring the effect of energy exchange between the surface and the atmosphere in complex terrain may be best illustrated by the results of Kossmann et al. (1999). While clearly documenting the exchange of, e.g., NO2 through mountain venting, the attribution to exchange of, e.g., moisture (nothing to say about sensible heat) turned out to be difficult due to complicated interaction between different processes and comparably small vertical gradients. A rare example of indirect evidence for vertical heat exchange may be the study of Weigel and Rotach (2004) in the Riviera Valley in southern Switzerland (Rotach et al., 2004). On several days with weak synoptic forcing (“pure” thermally driven flow) a Mixed Layer initially started to develop in the morning but—despite continuing surface forcing—the valley atmosphere re-stabilized during the early afternoon. This re-stabilization was attributed to a “secondary circulation” in addition to the primary symmetric valley wind circulation, transporting potentially warmer air from aloft into the valley and thus heating it from above. This hypothesized circulation was attributed to valley curvature and later (Weigel et al., 2006) supported by high-resolution numerical simulations. Indeed the modeled valley atmosphere—corresponding to the observations—was characterized by a single circulation pattern transporting heat down the primarily heated eastern slope thus leading to re-stabilization in the (early) afternoon.
While the impact of topographically-modified boundary layer structure on momentum transport—even if restricted to small slopes due to linearization (Belcher and Hunt, 1998)—has been, at least indirectly, experimentally confirmed (see Section Momentum Exchange), its role in scalar exchange has, to the knowledge of the authors, not been demonstrated in the field. Some findings according to linear theory are discussed in Raupach and Finnigan (1997) and extended to the non-linear regime by conducting “preliminary” (as the authors denote it) wind tunnel experiments. Results indicate that surface fluxes (sensible and latent heat, as well as their sum, i.e., available energy) exhibit significant spatial and temporal differences between flat and complex terrain, but when regionally averaged (using a simple slab model for the convective boundary layer) this difference vanishes. Whether this is due to the highly idealized setting, the symmetry of the topography used, or the total insignificance of heat transport due to complex topography remains to be clarified.
Mass Exchange
The most intuitive examples of mass exchange are related to cloud formation over an isolated mountain due to mountain venting (note that since we are interested in un-resolved subgrid-scale exchange processes we are not referring here to orographic precipitation, (e.g., Rotunno and Houze, 2007), where the large-scale synoptic flow impinges on a mountain (ridge) and gives rise to cloud formation and precipitation). Geerts et al. (2008) present some 2 months of data around Santa Catalina Mountains (with a diameter of about 30 km) to document the plain-to-mountain flow (convergence) due to the frequent development of a heat low over the topography that is associated with moist boundary layer air being transported to the mountain, and cloud (thunderstorm) formation over the peak. Further experimental (Demko et al., 2009) and modeling (Demko and Geerts, 2010) evidence from the same mountains reveals that—at least over this very mountain range—the convergent flow is solenoidal and largely confined to the convective boundary layer.
Henne et al. (2004) used different kinds of airborne and surface-based instrumentation, in combination with interpolation schemes and transport modeling to estimate EAE for a relatively small, steep and convergent valley (Leventina Valley) in southern Switzerland. For their 3 example days in summer, experiencing fair weather, and thermally forced conditions, their rough estimates of the mass fluxes in and out of the valley atmosphere indicated that the “valley boundary layer air” was replaced about three times per day, thus giving rise to pollutant exchange (either export of in-valley emissions or vice versa). In a subsequent study in similar weather conditions Henne et al. (2005) used different surface networks (including meso-net and soundings) to attribute enhanced moisture content in an elevated layer in the lee of the Alps (2500–3500 m above sea level, respective lee side, depending on flow conditions) to study mountain venting. Its efficiency was estimated as 30% of the boundary layer air being exchanged per hour during daytime. This lee side upper level moisture excess was detectable even when averaged over the entire summer season (JJA).
Similarly, using moisture as a tracer, Weigel et al. (2007) modeled the various contributions of exchange processes to the moisture exchange in and out of the Riviera Valley in southern Switzerland, again for a few fair weather days in summer. Results from this non-hydrostatic modeling, run at 350 m horizontal grid spacing, were previously subject to rigorous validation (Chow et al., 2006; Weigel et al., 2006) so that we treat the simulation results from this real-case study as “observation.” Comparison of EAE with the valley resolved or completely unresolved in the model indicates that contributions of individual exchange processes vary widely in time, and the cumulated daytime exchange was underestimated by a factor of about three when the valley was not resolved at all.
Mass exchange related to a possibly super-critical flow pattern (Zangl et al., 2001) was hypothesized to contribute to the extraordinarily strong valley wind in one of the deepest valleys on Earth, the Kali Kandaki Valley in Nepal (Egger et al., 2000). Even if the numerical simulations of Zangl et al. (2001) suggested a strong impact of humidity and hence moisture exchange, this could not be substantiated in a second field campaign (Egger et al., 2002).
All these examples concerning moisture exchange over complex topography are limited to a few usually fair weather, weak synoptic forcing days at a particular location. For these conditions they demonstrate the potential of primarily (valley) geometry and thermally driven flows to substantially contribute to mass (and hence moisture) exchange between the mountainous surface and the free atmosphere. To what degree other flow conditions and topographic landforms (e.g., basins) contribute to such exchange will have to be subject of further research.
CO2 is another potential tracer for mass exchange, but the low resolution of global CO2 inversion models is insufficient to resolve the impact of meso-scale (thermal) circulations on CO2 exchange processes (Pérez-Landa et al., 2007). A combination of high-resolution numerical modeling and experimental data from a 2-week campaign in the coastal region of Valencia (E) influenced by profound topography, was used by Pérez-Landa et al. (2007) to assess the impact of non-resolved meso-scale circulations. While encountering a number of difficulties—e.g., the “correct” attribution of source (sink) strength, timing and localization to the “tracer” (CO2)—as usual in a study with pioneering character such as this one, the authors could clearly demonstrate the importance of thermal circulations (dominantly sea breeze in their case, but in combination with topographic forcing) on the regional budget of CO2. Similarly concerned with the quality of CO2 budget modeling using coarse-grid inversion technique, Pillai et al. (2011) present evidence for the impact of thermally driven circulations on the flux-tower site “Ochsenkopf” situated in the “Fichtelgebirge,” a moderately high—some 500 m elevation with respect to surroundings—pre-alpine region in southern Germany. By demonstrating that “the effects of meso-scale transport such as mountain-valley circulations and mountain-wave activities on atmospheric CO2 distributions are reproduced remarkably well in the high-resolution models” they indirectly confirm the importance of these exchange processes in mountains terrain. Sun et al. (2010), in a multi-scale and multi-disciplinary study using a wealth of different observational and modeling techniques, investigated the processes influencing the regional CO2 budget over the Rocky Mountains (CO). Within the mountain boundary layer, CO2 was found to be transported effectively by drainage (night-time) and up-slope flows thereby largely affecting the local net ecosystem exchange at one of the rare (Rotach et al., 2014) mountainous “flux tower sites.” At a regional scale, they quite successfully and for the first time applied the “regional budget” approach to assess the flux tower's representativeness for larger scale fluxes of CO2. As an overall conclusion they state that even if the distribution of CO2 over mountains terrain, and hence the exchange processes contributing to it, is complicated, it is “predictable” if sufficient high-resolution information and modeling capacity is available. Using the same database, Sun and De Wekker (2011) investigated two detailed case studies through which they demonstrated the interplay between slope flow and convective boundary layer mixing on the slope of the Rocky Mountains. Even some experimental evidence for the return flow aloft (see Figure 1) could be observed.
Exchange of aerosols is a readily observable example for the exchange of mass in mountainous terrain. Nyeki et al. (2000) have documented elevated aerosol layers—reaching over the tops of the Alps, i.e., up to some 4200 m a.s.l. (above sea level, see Figure 2)—and attributed this to the growth of the convective boundary layer up to this level. More recently, simulations of De Wekker et al. (2004) have shown that the height of the “aerosol layer” does not correspond to the “mixed layer” (or convective boundary layer) height (see discussion in Section Thermally Forced Exchange Processes Over Mountainous Terrain). Similar conclusions had already been drawn by De Wekker (2002), based on simulations of the Riviera Valley (Rotach et al., 2004) with the meteorological part of the simulations validated using observations (De Wekker et al., 2005), but the aerosols (particles) artificially being introduced into the domain. However, the elevated aerosol concentrations as in Figure 2 can be taken as experimental evidence for (i) the efficiency of mass exchange over truly complex topography and (ii) the fact that different processes, i.e., turbulent exchange within the mountain boundary layer and meso-scale processes (mountain venting), are co-responsible for the total EAE over mountainous terrain. The relative importance of these (and geometrical, i.e., terrain related) processes, to EAE is likely dependent on several external factors and cannot be determined experimentally. The next section on idealized modeling will address some of these questions.
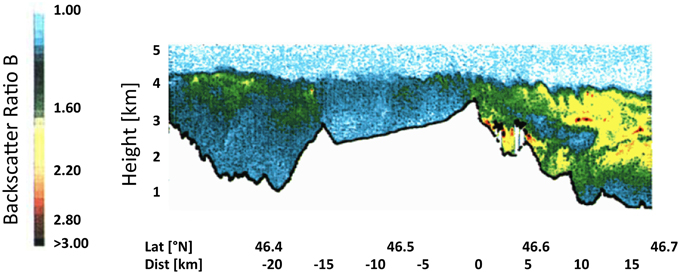
Figure 2. Backscatter ratio as measured with airborne lidar over a transect across the Alps on July 30 1997, 16.20 LST (reproduced with permission from Nyeki et al., 2000). The highest visible peak (at horizontal distance 0) is Jungfraujoch. The Rhone Valley at approximately −20 km.
A particular form of mass exchange over a mountainous area occurs over the western Tibetan Plateau where the ABL can grow in late winter very high (up to 5000 m a.s.l., e.g., Chen et al., 2013). Together with the surface elevation of some 4000 m above sea level this means that the boundary layer top can reach the neighborhood of the tropopause. While the reasons for these deep boundary layers are under debate (Chen et al., under review and references therein) it is clear that what is usually termed stratosphere-troposphere exchange under such conditions results in exchange of mass (e.g., ozone) from the stratosphere directly into the near-surface region thus potentially having profound implications on atmospheric chemistry (e.g., Škerlak et al., 2014).
Idealized-terrain Numerical Simulations
Most of the work dedicated to the derivation of parameterizations for orographic drag or boundary layer modification over low hills is based on idealized simulations in concert with the respective theoretical framework (e.g., Smith, 1979, 2007; Teixeira, 2014). Since the results of these simulations are already widely employed in large-scale numerical models and comprehensive reviews are available (e.g., Kim et al., 2013) we only briefly refer here to more recent efforts based on idealized modeling to assess the interaction of gravity waves with boundary layer processes.
Most of the research effort studying the interaction between boundary layers and gravity waves in recent years focused on the influence of the boundary layer in modifying meso-scale mountain wave characteristics (e.g., Jiang et al., 2006, 2008; Smith, 2007; Jiang and Doyle, 2008; Stiperski and Grubišič, 2011). The majority of these studies used 2D idealized terrain profiles. The theoretical framework of Smith (2007) and idealized simulations of Jiang et al. (2006, 2008) and Jiang and Doyle (2008) have shown that mountain waves are absorbed within the boundary layer, thus the wave drag and wave momentum flux above the boundary layer are reduced and wave patterns shifted upstream. Boundary layer height, stability and non-hydrostacity were found to be among the most important parameters. The convective boundary layer was found to be most effective in reducing wave amplitude and drag (Jiang and Doyle, 2008). The effect is less pronounced for narrow mountains and very non-linear flow (e.g., high mountains) where the boundary layer height is small compared to flow depth. Vosper and Brown (2007) noted the significant reduction in total drag due to small-scale hills. On the other hand, Steeneveld et al. (2008, 2009), investigating the effect of small-scale terrain on the stable boundary layer characteristics, found that drag caused by small-scale gravity waves can be on the same order as the turbulent drag and accounts for the missing drag in standard drag parameterizations.
In a recent investigation Kirshbaum (2013) studied the dynamic response of an idealized heated mountain (i.e., a “mountainlike heat source”) using a linearized scaling of the Boussinesq set of equations in a two-layer approach. Three different regimes are identified exhibiting distinctly different patterns with respect to vertical exchange between the lower (boundary) layer and the troposphere (upper layer). Among these regimes, the one representing a convective boundary layer flow under weak wind forcing produced the strongest and most localized updrafts and thus vertical exchange. Clearly, simulations of this kind are constrained by the necessity to restrict the slope angles (linearization) but they provide insight in the theoretical understanding of what has been termed plain-to-mountain flows in Section Thermally Forced Exchange Processes Over Mountainous Terrain.
Over the last decade or so a number of modeling studies were performed using idealized terrain (and idealized atmospheric conditions, too) to study exchange processes due to thermally driven flows over complex terrain (Noppel and Fiedler, 2002; Rampanelli et al., 2004; Catalano and Cenedese, 2010; Catalano and Moeng, 2010; Schmidli and Rotunno, 2010, 2012; Serafin and Zardi, 2010a,b, 2011; Schmidli, 2013; Wagner et al., 2014, 2015a,b; Lang et al., 2015; Leukauf et al., 2015). Results clearly demonstrate that energy and mass is exchanged as the result of thermally driven (turbulent) flows (meso-scale circulations) due to the presence of topography. They may be summarized as follows.
Heating Mechanism of a Valley
Most often, the Topographic Amplification Factor (TAF; Steinacker, 1984; based on Wagner, 1932) or so-called valley volume effect is employed in order to explain the elevated (reduced) temperature in a valley, as compared to a neighboring plain, leading to the thermally forced valley flow. Based on the argument that a smaller air volume is heated (cooled) by the same amount of solar heating (cooling) than over the plain the TAF is not dependent on (mean) vertical motions. Rather it considers the valley as a closed system without net fluxes at its top. This seems to be at odds with the apparent vertical motions associated with the cross-valley circulation (meso-γ scale; see also the black arrows in Figure 1) and hence the argument (e.g., Rampanelli et al., 2004; Serafin and Zardi, 2010b, 2011) that the excess valley daytime-heating be predominantly due to subsidence heating in the middle of the valley thus bringing high-potential temperature air from the free atmosphere aloft down into the valley. Schmidli (2013), in a comprehensive budgeting study showed that indeed the vertical contribution to the advection term in the heat budget equation can locally be positive (i.e., downward, thus heating the valley from above). This is the case in the center of the valley and for elevated levels. However, other components of the advection term (most prominently the along-slope component), which form the cross-valley circulation together with the subsidence in the center of the valley, lead to substantial cooling. Consequently, if the heat budget for the bulk of the valley is considered, Schmidli (2013) demonstrated that the net effect of the cross-valley circulation (subsidence in the middle of the valley plus slope flow advection) is to cool the bulk valley volume. When averaged over the entire valley depth the contribution of subsidence is negligible. Hence, the excess heating according to the TAF actually constitutes an upper limit for the heat exchange into (out of) a valley that is somewhat reduced by the cross-valley circulation. Overall, idealized simulations show that the cross-valley circulation contributes to energy exchange between the valley and the free troposphere. Subsidence heating—while locally being relevant as a heat source in the center of the valley (Schmidli, 2013) is not the dominant factor of the enhanced daily temperature amplitude in valleys (as compared to a reference plain).
Exchange is Dependent on Geometry
Most numerical idealized-terrain simulations use one pre-defined terrain configuration that corresponds to an “average valley” (often straight, and symmetric with respect to the valley axis, often 1500 or 2000 m deep, using a trapezoid or cosine-type cross-valley shape and usually uniform in surface characteristics and, if three-dimensional at all, then without along-valley slope). Wagner et al. (2015a) systematically varied the height-to-width ratio and length of an idealized (straight) valley attached to a plain to study the impact on EAE efficiency. While relatively low (and/or wide) valleys exhibit the “classical” picture of a single slope-flow circulation ranging up to higher-than-ridge top around noon (Figure 3), relatively steeper and narrower valleys exhibit stronger slope flows giving rise to the formation of two vertically stacked circulation cells within the valley. Serafin and Zardi (2010b) similarly found a stronger cross-valley circulation in the narrower valley (of their two configurations) and two stacked circulation cells can be distinguished (even if they are not explicitly discussed). However, the development of the associated plain-to-mountain flow is also dependent on the height-to-width ratio of the valley system. These mean flow conditions have a profound impact on the vertical exchange associated with the valley and slope flow circulations. Comparing EAE for the different valley-plain systems to that of a plain alone suggests a mass exchange (as based on numerical tracer release experiments) that is three to four times more efficient over the mountain-plain system. Introducing further inhomogeneity in the valley simulation, Wagner et al. (2015b) found that both, along-valley slope as well as narrowing, substantially increase the strength of the valley wind system. Associated with this, narrowing of the valley cross-section enhances the vertical exchange of mass (as measured with a released tracer at different positions) by a factor between 1.8 and 2.8 while introducing an along-valley slope increases vertical exchange by a factor of about 1.2. Clearly, these numbers are dependent on the detailed choices concerning topography (e.g., introducing along-valley slope) and original set-up (e.g., type of cross-section) and idealization. Still, they give a rough estimate of how important geometrical aspects can be on the exchange over complex mountainous terrain.
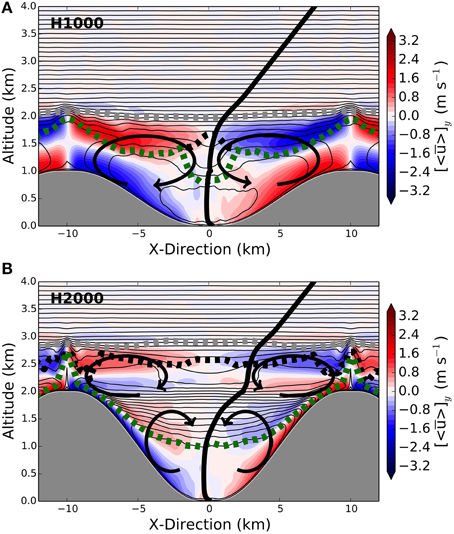
Figure 3. Effect of height-to-width ratio on the thermally forced cross-valley circulation. Potential temperature (thin contour lines), cross-valley wind speed (color shading), and three different boundary layer heights are shown for a 1000 m (A) and 2000 m (B) deep valley with identical forcing and after 6 h of simulation. See Wagner et al. (2015a) for the definition of the boundary layer heights and the simulations. The bold black line denotes the valley-mean potential temperature profile.
Lang et al. (2015) have extended the geometry as used by all the above studies where “the valley” is usually made up by two parallel ridges of equal heights (but slightly different cross-sections in the different studies). They have embedded a valley with variable depth into a “mountain range” (Figure 4). Releasing a passive tracer at different near-surface locations they studied mass transfer to the free atmosphere influenced by the combined effect of plain-to-mountain flow and slope circulations. For a deep embedded valley the slope wind regime was found to establish within large parts of the valley while an elevated (less deep) valley allowed the plain-to-mountain flow to descend into the valley thus replacing the opposing slope flow on the upwind side of the valley. Comparing the “aerosol layer depth” (i.e., the height up to which the aerosol mixes) with the different estimates of CBL depth (Figures 4B,D) indicates the fraction of tracer that has been mixed up by processes other than turbulent mixing. Overall, a more than three-fold enhancement of tracer EAE was found for the various mountain ridge topographies when compared to the reference plain simulation (for comparison, in the example of Figure 4 the difference between the deep and the shallower valley amounts to some 20%).
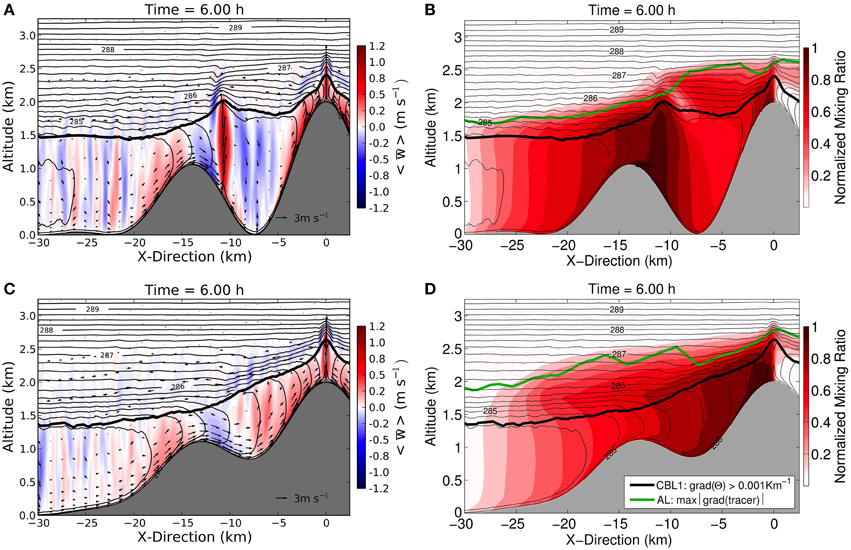
Figure 4. Flow and temperature fields, (A) and (C) and tracer concentration, (B) and (D) from high-resolution numerical simulations of a deep embedded valley (upper row) and a shallower embedded valley (lower row) in a mountain range. Thin solid lines: potential, temperature, arrows x-z wind vector, color shading vertical velocity, (A) and (C), and tracer mixing ratio, (B) and (D). The black bold solid line corresponds to the Convective Boundary Layer height (diagnosed from first height where the gradient of potential temperature exceeds 0.001 km−1 when searching from the below), green line: “aerosol layer height” (diagnosed from maximum gradient in mixing ratio). The tracer is released across the entire mountain range at the lowest eight grid points (about 110 m from ground) at constant rate. Figure reassembled from different figures in Lang et al. (2015). See this paper for details of the simulations.
Schmidli and Rotunno (2012) did not change the geometry of the valley itself, but its surrounding (periodic valleys, vs. one isolated valley on a plain vs. valley in an elevated plateau). They found considerable differences in the strength of the valley wind system that could be attributed to the upper-level pressure distribution and advective momentum transport between the valley and its surroundings while direct impact of the surroundings on the valley heat budget was relatively minor. All the idealized studies cited above were conducted with zero synoptic pressure difference (purely thermally driven flows), indicating a potential limitation of idealized simulations carried out so far. Even a minor along-valley pressure gradient at upper levels will likely influence the valley wind system through momentum exchange between the valley and the atmosphere and hence the efficiency of the EAE in truly complex terrain through the geometric factors discussed above. The degree to which this will be effective, however, will require some additional research even if real-terrain simulations (e.g., Zangl, 2009) seem to indicate that valley flow characteristics are quite robust features.
Exchange is Dependent on Atmospheric Forcing
Similar to valley geometry other factors like the spatial distribution of surface properties such as roughness length and soil moisture, and the strength of the solar forcing (i.e., season, latitude) can be expected to modify topographic flows and EAE in mountainous terrain. In the simulations discussed above, net radiation at the surface forces the thermal valley flow either through an assumed spatially homogeneous but time-dependent surface heat flux (e.g., Rampanelli et al., 2004; Wagner et al., 2015a,b) or temperature (Catalano and Cenedese, 2010), or through a full surface exchange scheme (e.g., Serafin and Zardi, 2010a,b, 2011; Schmidli and Rotunno, 2010, 2012). The latter set-up then corresponds to placing an east-west running valley to the equator and choosing an equinox so as to ensure symmetry along the valley axis. Clearly, in a real valley (at least off the equator) solar forcing (net radiation) is largely different in timing and magnitude at different positions within a valley (e.g., Matzinger et al., 2003), leading to a correspondingly similar spatial spatio-temporal variability of surface heat fluxes (Rotach et al., 2008). Figure 5 shows the impact of the spatial variability of solar forcing on the instantaneous flow and stratification. As can be seen, the actual flow structure deviates from symmetric with potentially important consequences on pollutant redistribution within a valley (e.g., Gohm et al., 2009). However, when it comes to the overall exchange characteristics between the valley and the atmosphere, for example the total mass exchanged over daytime, or the estimated impact on the valley heat budget, results are quite insensitive to those asymmetries.
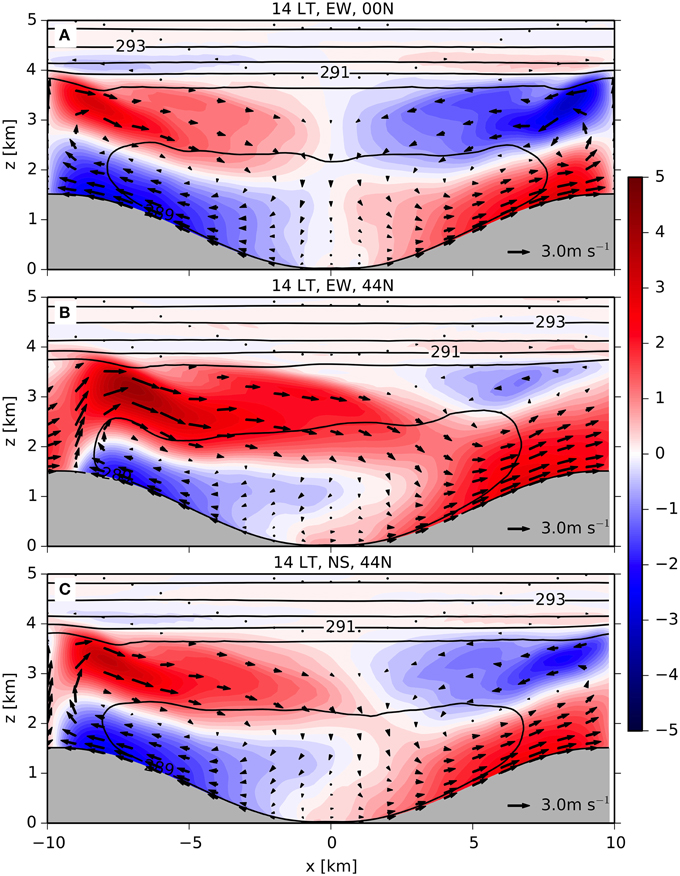
Figure 5. Flow and temperature fields from high-resolution simulation of a 1.5 km deep symmetric valley, (A) at the equator, east-west orientation; (B) at 44°N, east-west orientation; and (C) at 44°N, north-south orientation. Solid lines are isentropes, arrows xz-wind vectors, the color code for the x-component of the wind [ms−1]. The panels show the situation on the second day of the simulation, 2 pm local time. The solar forcing in all three panels corresponds to the case of 550 Wm−2 amplitude (roughly 240 Wm−2 amplitude in surface heat flux) of Leukauf et al. (2015). For details of the simulations see Leukauf et al. (2015) or Wagner et al. (2015a,b).
The studies cited above all used dry or low soil moisture conditions—in order to avoid the additional “complication” of cloud formation—and some medium time-dependent surface heat flux (200–300 W m−2 amplitude) as a thermal forcing. Leukauf et al. (2015) systematically varied this forcing by using a maximum short-wave net radiation in a parameterization of the daily cycle between 150 and 850 W m−2 (corresponding to surface heat flux with amplitudes of 5–450 W m−2). While their analysis was basically motivated by studying the break-up of the nighttime cold pool, it additionally provides insight into the efficiency of EAE over their idealized valley system. Not surprisingly, the complete break up of the cold pool required a minimum net short-wave forcing (an amplitude of 450 W m−2 for the given geometry). Similarly, the energy and mass exchange between the valley and the atmosphere was found to be strongly dependent on this fact. While a surprisingly consistent factor of “about three” had previously been reported for the number of times the “valley atmosphere was exchanged” over a convective day (Henne et al., 2004 from observations; Weigel et al., 2007 for real valley simulations; Wagner et al., 2015a; Lang et al., 2015 for idealized geometry simulations), this figure reduces to some 30% (i.e., a factor of 1.3) for a net short wave forcing just not strong enough to entirely break up the cold pool (400 W m−2 amplitude in solar forcing). For the strongest solar forcing, on the other hand, more than five times the valley atmosphere is exported during the daytime period. Bearing in mind that this study again used a symmetric valley configuration the geometry-related amplifications (such as for sloping valley axis, narrowing valley, etc.) as discussed above will similarly modify these numbers.
Overall, idealized simulations have tremendously advanced our understanding of the impact of gravity waves under conditions of stable stratification, as well as purely thermally driven valley-atmosphere exchange processes. Despite this, the degree of idealization is substantial, and imposes some limitations on the applicability of the findings. Idealized studies of mass-fluxes over topography for dynamically forced flows are awaiting their realization. Similarly, we are not aware of idealized simulations concerned with the interaction of the purely thermally driven flows with an overlying (possibly only weak) synoptic flow. As far as surface properties are concerned, real-terrain simulations have shown soil moisture (e.g., Chow et al., 2006; Szintai et al., 2010) to modify the flow characteristics but there seems to be no systematic idealized study to put these results into context and estimate the impact on EAE. Processes related to moisture in the atmosphere such as cloud formation (or even precipitation) will certainly have an impact of valley-atmosphere exchange that will have to be investigated using idealized modeling.
Outlook
Topography as a particular form of surface condition to the atmospheric flow is apparently responsible for various processes leading to modifications of EAE when compared to the pure boundary layer turbulent transport over flat terrain. In this contribution we have attempted to identify these processes and give examples from observational studies and numerical simulations using real and idealized atmospheric and terrain-conditions. Today's modeling capabilities appear to be advanced enough to capture these processes, or at least allow for an estimate of their exchange efficiency, provided that the model's spatial resolution is sufficiently high. Wagner et al. (2014) concluded that the grid scale needs to be some 10–20 times smaller than the relevant topographic scale in order to properly resolve these processes. Many numerical models for global numerical weather prediction (NWP) or climate scenario simulations, however, still have grid spacing far from this requirement and this is likely to remain so for the decades to come even if computing power continues to increase at its present pace. Thus, these models would need parameterizations to cover EAE due to unresolved (sub-grid scale) topography. While such parameterizations are in operation for momentum exchange due to gravity wave and orographic drag for some time now (and of course still have room for improvement, see Kim et al., 2013 and Teixeira, 2014), they are still missing for energy and mass exchange. Most likely, their (missing) impact is somewhere “buried” in tuned parameters of the boundary layer and surface exchange schemes—thus giving rise to acceptable verification scores for the mean flow variables at large scales. While this was sufficient (and important) to reproduce the large-scale dynamical fields for many years and has led to an impressive improvement of forecast quality over the last decades (Bauer et al., 2015), even large-scale atmospheric models progressively extend their scope. Most notably, many NWP and climate models are being developed into Earth-System simulators (e.g., Palmer, 2012; Flato et al., 2013) thus adding—among others—atmospheric constituents (beyond water vapor) as prognostic variables. This evidently makes it necessary to also capture processes relevant for mass exchange from and to the surface, and this also over mountainous terrain. One may debate whether taking into account unresolved processes should be achieved by increasing resolution ad infinitum or by more rigorously moving to ensemble approaches (Palmer, 2012)—but they should be taken into account.
We have, in the previous sections, pointed to a number of missing pieces required on the way of establishing an extended boundary layer parameterization for topography and it seems that the community is still some distance from proposing a blueprint for such an endeavor. Still, a number of potentially useful future research directions can be summarized as follows.
➢ First of all, our understanding of the boundary layer structure and associated processes of turbulent transport over mountainous terrain is still very limited (Rotach and Zardi, 2007). Thus, in order to establish a better assessment of the relative importance of turbulent exchange vs. meso-scale transport the former must be understood in much more depth. Recent efforts in which numerical modeling and observations are combined for limited (e.g., Fernando et al., 2015) or extended (e.g., Stiperski et al., 2012) periods of time go in this direction.
➢ Sensitivity studies for idealized simulations need to be extended. Notably, the community seems to agree on an initial background stability (of 0.003 Km−1) and often only the 2nd day is analyzed in order to minimize effects of initialization. While this is certainly sufficient for the boundary layer processes themselves, the growth of the boundary layer is known to be sensitive to overlying stability (e.g., Chen et al., under review), which in these idealized configurations will be given by the initial stratification.
➢ Other interesting sensitivities for idealized simulations would include further geometrical effects such as curvature (Weigel and Rotach, 2004), asymmetry of ridge top height (as initiated in Lang et al., 2015) or introduction of side valleys; and surface properties such as characteristic distribution of soil moisture or surface parameters.
➢ The rigorous budgeting approach of Schmidli (2013) should be applied to real-terrain simulations in order to assess the degree to which results can be transferred. Most likely this would require inclusion of background flow (such as in Zangl, 2009) even if weak. This would also allow, or even necessitate investigation of the interaction between purely thermally driven flows (as currently in the idealized simulations) and dynamically forced flows.
➢ Systematic observations in order to evaluate the numerical models in complex terrain are required. When assessing the extent to which turbulent exchange and meso-scale circulations contribute to total exchange in very high-resolution simulations, the former is rarely “verified.” This requires the ability to reliably measure near-surface turbulence in mountainous terrain (see e.g., Stiperski and Rotach, 2015) and, probably even more so, the assessment of turbulence profiles in such terrain (e.g., Adler and Kalthoff, 2014).
➢ Verifying actual exchange processes often suffers from the fact that a one-to-one attribution is hampered by the abundance of the investigated tracer sources (most obvious for heat, but similar for water vapor or CO2). Tracers which are more specific for one particular surface type would be better suited to establishing unique relations between elevated or non-zero concentrations aloft and the corresponding surface sources so as to demonstrate the efficiency of the hypothesized exchange processes. While such tracers are easily implemented in a numerical model they first need to be identified (which surface type exclusively emits which marker substance?) and second the measurement of their concentration and turbulent exchange must be possible. Suitable strategies should be worked out in order to overcome this difficulty.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Guest Associate Editor Peter Sheridan declares that, despite having collaborated with author Ivana Stiperski, the review process was handled objectively.
References
Adler, B., and Kalthoff, N. (2014). Multi-scale transport processes observed in the boundary layer over a mountainous island. Boundary Layer Meteorol. 153, 515–537. doi: 10.1007/s10546-014-9957-8
Baines, P. G. (1995). Topographic Effects in Stratified Flows. Cambridge, UK: Cambridge Univ. Press.
Bauer, P., Thorpe, A., and Brunet, G. (2015). The quiet revolution of numerical weather prediction. Nature 525, 47–35. doi: 10.1038/nature14956
Belcher, S. E., and Hunt, J. R. C. (1998). Turbulent flows over hills and waves. Ann. Rev. Fluid Mech. 30, 507–538. doi: 10.1146/annurev.fluid.30.1.507
Belcher, S. E., Newley, T. M. J., and Hunt, J. C. R. (1993). The drag on an undulating surface due to the flow of a turbulent boundary layer. J. Fluid Mech. 249, 557–596. doi: 10.1017/S0022112093001296
Bougeault, P., Binder, P., Buzzi, A., Dirks, R., Houze, R., Kuettner, J., et al. (2001). The MAP special observing period. Bull. Amer. Meteorol. Soc. 82, 433–462. doi: 10.1175/1520-0477(2001)082<0433:TMSOP>2.3.CO;2
Bougeault, P., Jansa, A., Attie, J. L., Beau, I., Benech, B., Benoit, R., et al. (1993). The atmospheric momentum budget over a major mountain range: first results of the PYREX field program. Ann. Geophys. 11, 395–341.
Catalano, F., and Cenedese, A. (2010). High-resolution numerical modeling of thermally driven slope winds in a valley with strong capping. J. Appl. Meteorol. Climatol. 49, 1859–1880. doi: 10.1175/2010JAMC2385.1
Catalano, F., and Moeng, C. (2010). Large-eddy simulation of the daytime boundary layer in an idealized valley using the weather research and forecasting numerical model. Boundary Layer Meteorol. 137, 49–75. doi: 10.1007/s10546-010-9518-8
Chen, X., Añel, J. A., Su, Z., de la Torre, L., Kelder, H., van Peet, J., et al. (2013). The deep atmospheric boundary layer and its significance to the stratosphere and troposphere exchange over the Tibetan Plateau. PLoS ONE 8:e56909. doi: 10.1371/journal.pone.0056909
Chow, F. K., Weigel, A. P., Street, R. L., Rotach, M. W., and Xue, M. (2006). High-resolution large-eddy simulations of flow in a steep Alpine valley. Part I: methodology, verification, and sensitivity studies. J. Appl. Meteorol. Climatol. 45, 63–86. doi: 10.1175/JAM2322.1
Demko, J., and Geerts, B. (2010). A numerical study of evolving convective boundary layer and oro- graphic circulation around the Santa Catalina Mountains in Arizona. Part I: circulation without deep convection. Mon. Wea. Rev. 138, 1902–1922. doi: 10.1175/2009MWR3098.1
Demko, J., Geerts, B., and Miao, Q. (2009). Boundary layer transport and cumulus development over a heated mountain: an observational study. Mon. Wea. Rev. 137, 447–468. doi: 10.1175/2008MWR2467.1
De Wekker, S. F. J. (2002). Structure and Morphology of the Convective Boundary Ayer Over Mountainous Terrain. Ph.D. thesis, Univ British Columbia.
De Wekker, S. F. J., Steyn, D. G., Fast, J. D., Rotach, M. W., and Zhong, S. (2005). The performance of RAMS in representing the convective boundary layer structure in a very steep valley. Environ. Fluid Mech. 5, 35–62. doi: 10.1007/s10652-005-8396-y
De Wekker, S. F. J., Steyn, D. G., and Nyeki, S. (2004). A comparison of aerosol layer- and convective boundary layer structure over a mountain range during STAAARTE'97. Boundary Layer Meteor. 113, 249–271. doi: 10.1023/B:BOUN.0000039371.41823.37
De Wekker, S. F. J., Zhong, S., Fast, J. D., and Whiteman, C. D. (1998). A numerical study of the thermally driven plain-to-basin wind over idealized basin topographies. J. Appl. Meteor. 37, 606–622
Doyle, J. D., and Shapiro, M. A. (2000). A multi-scale simulation of an extreme downslope wind-storm over Norway. Meteorol. Atmos. Phys. 74, 83–101. doi: 10.1007/s007030070027
Egger, J., Bajrachaya, S., Egger, U., Heinrich, R., Reuder, J., Shakya, P., et al. (2000). Diurnal winds in the Himalayan Kali Gandaki valley. Part I: observations. Mon. Wea. Rev. 128, 1106–1122. doi: 10.1175/1520-0493(2000)128<1106:DWITHK>2.0.CO;2
Egger, J., Bajrachaya, S., Heinrich, R., Kolb, P., Lammlein, S., Mech, M., et al. (2002). Diurnal winds in the Himalayan Kali Gandaki valley. Part III: remotely piloted aircraft soundings. Mon. Wea. Rev. 130, 2042–2058. doi: 10.1175/1520-0493(2002)130<2042:DWITHK>2.0.CO;2
Fernando, H., Pardyjak, E., Di Sabatino, S., Chow, F., De Wekker, S., Hoch, S., et al. (2015). The MATERHORN – unraveling the intricacies of mountain weather. Bull. Am. Meteor. Soc. doi: 10.1175/bams-d-13-00131.1. [Epub ahead of print].
Flato, G., Marotzke, J., Abiodun, B., Braconnot, P., Chou, S. C., Collins, W., et al. (2013). “Evaluation of climate models,” in Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, P. M. Midgley (Cambridge; New York, NY: Cambridge University Press).
Garratt, J. R. (1990). The internal boundary layer – a review. Boundary Layer Meteorol. 50, 171–203. doi: 10.1007/BF00120524
Geerts, B., Miao, Q., and Demko, J. (2008). Pressure perturbations and upslope flow over a heated, isolated mountain. Mon. Wea. Rev. 136, 4272–4288. doi: 10.1175/2008MWR2546.1
Gohm, A., Harnisch, F., Vergeiner, J., Obleitner, F., Schnitzhofer, R., Hansel, A., et al. (2009). Air pollution transport in an alpine valley: results from airborne and ground-based observations. Boundary Layer Meteorol. 131, 441–463. doi: 10.1007/s10546-009-9371-9
Grisogono, B., Jurlina, T., Vecenaj, Z., and Guttler, I. (2015). Weakly nonlinear Prandtl model for simple slope flows. Q. J. R. Meteorol Soc. 141, 883–892. doi: 10.1002/qj.2406
Henne, S., Furger, M., Nyeki, S., Steinbacher, M., Neininger, B., De Wekker, S. F. J., et al. (2004). Quantification of topographic venting of boundary layer air to the free troposphere. Atmos. Chem. Phys. 4, 497–509. doi: 10.5194/acp-4-497-2004
Henne, S., Furger, M., and Prévôt, A. S. H. (2005). Climatology of mountain venting induced moisture layers in the lee of the Alps. J. Appl. Meteorol. 44, 620–633. doi: 10.1175/JAM2217.1
Holton, J. R., and Hakim, G. J. (2013). An Introduction to Dynamic Meteorology. Waltham, MA; Oxford, UK: Academic Press.
Holtslag, A. A. M., and Nieuwstadt, F. T. M. (1986). Scaling the atmospheric boundary layer. Boundary Layer Meteorol. 36, 201–209. doi: 10.1007/BF00117468
Hunt, J. R. C., Leibovich, S., and Richards, K. J. (1988a). Turbulent shear flows over low hills. Q. J. R. Meteorol. Soc. 114, 1435–1470.
Hunt, J. R. C., Richards, K. J., and Brighton, P. W. M. (1988b). Stratified flows over low hills. Q. J. R. Meteorol. Soc. 114, 859–868.
Jackson, P. S., and Hunt, J. R. C. (1975). Turbulent wind low over a low hill. Q. J. R. Meteorol. Soc. 101, 929–955. doi: 10.1002/qj.49710143015
Jiang, Q., and Doyle, J. D. (2008). On the diurnal variation of mountain waves. J. Atmos. Sci. 65, 1360–1377. doi: 10.1175/2007JAS2460.1
Jiang, Q., Doyle, J. D., and Smith, R. B. (2006). Interaction between trapped waves and boundary layers. J. Atmos. Sci. 63, 617–633. doi: 10.1175/JAS3640.1
Jiang, Q., Smith, R. B., and Doyle, J. D. (2008). Impact of the atmospheric boundary layer on mountain waves. J. Atmos. Sci. 65, 592–608. doi: 10.1175/2007JAS2376.1
Kim, Y.-J., Eckermann, S. D., and Chun, H.-Y. (2013). An overview of the past, present and future of gravity− wave drag parametrization for numerical climate and weather prediction models. Atmos. Ocean 41, 65–98. doi: 10.3137/ao.410105
Kirshbaum, D. J. (2013). On thermally forced circulations over heated terrain. J. Atmos. Sci. 70, 1690–1709. doi: 10.1175/JAS-D-12-0199.1
Kleinschmidt, E. (1922). Der taegliche Gang des Windes in der freien Atmosphaere und auf Berggipfeln (The diurnal course of the wind in the free atmosphere and on mountain tops). Beitr. Phys. Atmos. 10, 1–15.
Kossmann, M., Corsmeier, U., De Wekker, S. F. J., Fiedler, F., Voegtlin, S., Kalthoff, N., et al. (1999). Observations of handover processes between the atmospheric boundary layer and the free troposphere over mountainous terrain. Contrib. Atmos. Phys. 72, 329–350.
Lang, M. N., Gohm, A., and Wagner, J. S. (2015). The impact of embedded valleys on daytime pollution transport over a mountain range, Atmos. Chem. Phys. Discuss. 15, 14315–14356. doi: 10.5194/acpd-15-14315-2015
Leukauf, D., Gohm, A., Rotach, M. W., and Wagner, J. S. (2015). The impact of the temperature inversion breakup on the exchange of heat and mass in an idealized valley: sensitivity to the radiative forcing. J. Appl. Meteorol. Climatol. 54, 2199–2216. doi: 10.1175/jamc-d-15-0091.1
Lott, F., and Miller, M. J. (1997). A new subgrid-scale orographic drag parametrization: its formulation and testing. Q. J. R. Meteorol. Soc. 123, 101–127. doi: 10.1002/qj.49712353704
Lugauer, M., and Winkler, P. (2005). Thermal circulation in South Bavaria - climatology and synoptic aspects. Meteor. Z. 14, 15–30. doi: 10.1127/0941-2948/2005/0014-0015
Mahrt, L. (2014). Stably stratified atmospheric boundary layers. Ann. Rev. Fluid Mech. 46, 23–45. doi: 10.1146/annurev-fluid-010313-141354
Matzinger, N., Andretta, M., van Gorsel, E., Vogt, R., Ohmura, A., and Rotach, M. W. (2003). Surface radiation budget in an Alpine valley. Q. J. R. Meteorol. Soc. 129, 877–895. doi: 10.1256/qj.02.44
Medeiros, L. E., and Fitzjarrald, D. E. (2014). Stable boundary layer in complex terrain. Part I: linking fluxes and intermittency to an average stability index. J. Appl. Meteorol. Cimatol. 53, 2196–2215. doi: 10.1175/JAMC-D-13-0345.1
Milton, S. F., and Wilson, C. A. (1996). Impact of parameterised subgrid-scale orographic forcing on systematic errors in a global NWP model. Mon. Wea. Rev. 124, 2023–2045.
Noppel, H., and Fiedler, F. (2002). Mesoscale heat transport over complex terrainby slope winds. A conceptual model and numerical simulations. Boundary Layer Meteorol. 104, 73–97. doi: 10.1023/A:1015556228119
Nyeki, S., Kalberer, M., Colbeck, I., De Wekker, S. F. J., Furger, M., Gäggeler, H. W., et al. (2000). Convective boundary layer evolution to 4 km ASL over high-alpine terrain: airborne lidar observations in the Alps. Geophys. Res. Lett. 27, 689–692. doi: 10.1029/1999GL010928
Orlanski, I. (1975). A rational subdivision of scales for atmospheric processes. Bull. Am. Meteorol. Soc. 56, 527–530.
Palmer, T. N. (2012). Towards the probabilistic earth-system simulator: a vision for the future of climate and weather prediction. Q. J. R. Meteorol. Soc. 138, 841–861. doi: 10.1002/qj.1923
Palmer, T. N., Shutts, G. J., and Swinbank, R. (1986). Alleviation of a systematic westerly bias in general circulation and numerical weather prediction models through an orographic gravity wave drag parameterization. Q. J. R. Meteorol. Soc. 112, 1001–1039. doi: 10.1002/qj.49711247406
Pérez-Landa, G., Ciais, P., Sanz, M. J., Giol, B., Miglietta, F., Palau, J. L., et al. (2007). Mesoscale circulations over complex terrain in the Valencia coastal region, Spain—Part 2: modeling CO2 transport using idealized surface fluxes. Atmos. Chem. Phys. 7, 1851–1868. doi: 10.5194/acp-7-1851-2007
Pillai, D., Gerbig, C., Ahmadov, R., Rodenbeck, C., Kretschmer, R., Koch, T., et al. (2011). High-resolution simulations of atmospheric CO2 over complex terrain - representing the Ochsenkopf mountain tall tower. Atmos. Chem. Phys. 11, 7445–7464. doi: 10.5194/acp-11-7445-2011
Rampanelli, G., Zardi, D., and Rotunno, R. (2004). Mechanisms of up-valley winds. J. Atmos. Sci. 61, 3097–3111. doi: 10.1175/JAS-3354.1
Raupach, M. R., and Finnigan, J. J. (1997). The influence of topography on meteorological variables and surface-atmosphere interactions. J. Hydrol. 190, 182–213. doi: 10.1016/S0022-1694(96)03127-7
Raupach, M. R., Weng, W. S., Carruthers, D. J., and Hunt, J. C. R. (1992). Temperature and humidity fields and fluxes over low hills. Q. J. R. Meteorol. Soc. 118, 191–225. doi: 10.1002/qj.49711850403
Rotach, M. W., Andretta, M., Calanca, P., Weigel, A. P., and Weiss, A. (2008). Boundary layer characteristics and turbulent exchange mechanisms in highly complex terrain. Acta Geophysicae 56, 194–219. doi: 10.2478/s11600-007-0043-1
Rotach, M. W., Calanca, P., Graziani, G., Gurtz, J., Steyn, D. G., Vogt, R., et al. (2004). Turbulence structure and exchange processes in an Alpine Valley: the Riviera project. Bull. Am. Meteorol. Soc. 85, 1367–1385. doi: 10.1175/BAMS-85-9-1367
Rotach, M. W., Wohlfahrt, G., Hansel, A., Reif, M., Wagner, J., and Gohm, A. (2014). The world is not flat - implications for the global carbon balance. Bull. Am. Meteor. Soc. 95, 1021–1028. doi: 10.1175/BAMS-D-13-00109.1
Rotach, M. W., and Zardi, D. (2007). On the boundary layer structure over highly complex terrain: key findings from MAP. Q. J. R. Meteorol. Soc. 133, 937–948. doi: 10.1002/qj.71
Rotunno, R., and Houze, R. (2007). Lessons on orographic precipitation from the Mesoscale Alpine Programme. Q. J. R. Meteorol. Soc. 133, 811–830. doi: 10.1002/qj.67
Savelyev, S. A., and Taylor, P. A. (2005). Internal boundary layers: I. Height formulae for neutral and diabatic flows. Boundary Layer Meteorol. 115, 1–25. doi: 10.1007/s10546-004-2122-z
Schmidli, J. (2013). Daytime heat transfer processes over mountainous terrain. J. Atmos. Sci. 70, 4041–4066. doi: 10.1175/JAS-D-13-083.1
Schmidli, J., and Rotunno, R. (2010). Mechanisms of along-valley winds and heat exchange over mountainous terrain. J. Atmos. Sci. 67, 3033–3047. doi: 10.1175/2010JAS3473.1
Schmidli, J., and Rotunno, R. (2012). Influence of the valley surroundings on valley wind dynamics. J. Atmos. Sci. 69, 561–579. doi: 10.1175/JAS-D-11-0129.1
Serafin, S., and Zardi, D. (2010a). Structure of the atmospheric boundary layer in the vicinity of a developing upslope flow system: a numerical model study. J. Atmos. Sci. 67, 1171–1185. doi: 10.1175/2009JAS3231.1
Serafin, S., and Zardi, D. (2010b). Daytime heat transfer processes related to slope flows and turbulent convection in an idealized mountain valley. J. Atmos. Sci. 67, 3739–3756. doi: 10.1175/2010JAS3428.1
Serafin, S., and Zardi, D. (2011). Daytime development of the boundary layer over a plain and in a valley under fair weather conditions: a comparison by means of idealized numerical simulations. J. Atmos. Sci. 68, 2128–2141. doi: 10.1175/2011JAS3610.1
Škerlak, B., Sprenger, M, and Wernli, H. (2014). A global climatology of stratosphere-troposphere exchange using the ERA-Interim dataset from 1979 to 2011. Atmos. Chem. Phys. 14, 913–917. doi: 10.5194/acp-14-913-2014
Smith, R. B. (1979). The influence of mountains on the atmosphere. Adv. Geophys. 33, 87–230. doi: 10.1016/S0065-2687(08)60262-9
Smith, R. B. (2007). Interacting mountain waves and boundary layers. J. Atmos. Sci. 64, 594–607. doi: 10.1175/JAS3836.1
Steeneveld, G. J., Holtslag, A. A. M., Nappo, C. J., van de Wiel, B. J. H., and Mahrt, L. (2008). Exploring the role of small-scale terrain drag on stable boundary layers over land. J. Appl. Meteorol. Climatol. 47, 2518–2530. doi: 10.1175/2008JAMC1816.1
Steeneveld, G. J., Nappo, C. J., and Holtslag, A. A. M. (2009). Estimation of orographically induced wave drag in the stable boundary layer during CASES99. Acta Geophys. 57, 857–881. doi: 10.2478/s11600-009-0028-3
Steinacker, R. (1984). Area-height distribution of a valley and its relation to the valley wind. Contrib. Atmos. Phys. 57, 64–71.
Stiperski, I., and Grubišič, V. (2011). Trapped lee wave interference in the presence of surface friction. J. Atmos. Sci. 68, 918–936. doi: 10.1175/2010JAS3495.1
Stiperski, I., Kavčič, I., Grisogono, B., and Durran, D. R. (2007). Including Coriolis effects in the Prandtl model for katabatic flow. Q. J. R. Meteorol. Soc. 133, 101–106. doi: 10.1002/qj.19
Stiperski, I., and Rotach, M. W. (2015). On the measurement of turbulent fluxes over complex mountainous topography. Boundary Layer Meteorol. doi: 10.1007/s10546-015-0103-z. [Epub ahead of print].
Stiperski, I., Rotach, M. W., and Gohm, A. (2012). Boundary layer measurements in complex terrain: innsbruck-box, session AS2.1, Air-Land Interactions. Geophys. Res. Abstr. 2012, EGU2012-8863.
Stull, R. B. (1988). An Introduction to Boundary Layer Meteorology. Dordrecht: Kluwer. doi: 10.1007/978-94-009-3027-8
Sun, J., and De Wekker, S. F. J. (2011). “Atmospheric carbon dioxide transport over complex terrain,” in Mountain Ecosystems: Dynamics, Management and Conservation, ed K. E. Richards (New York, NY: Nova Science Publishers), 101–121.
Sun, J., Nappo, C. J., Mahrt, L., Belušić, D., Grisogono, B., Stauffer, D. R., et al. (2015). Review of wave-turbulence interactions in the stable atmospheric boundary layer. Rev. Geophys. 53. doi: 10.1002/2015rg000487
Sun, J., Oncley, S. P., Burns, S. P., Stephens, B. B., Lenschow, D. H., Campos, T., et al. (2010). A multiscale and multidisciplinary investigation of ecosystem–atmosphere CO2 exchange over the Rocky Mountains of Colorado. Bull. Am. Meteor. Soc. 91, 209–230. doi: 10.1175/2009BAMS2733.1
Szintai, B., Kaufmann, P., and Rotach, M. W. (2010). Simulation of pollutant transport in complex terrain with a numerical weather prediction-particle dispersion model combination. Boundary Layer Meteorol. 137, 373–396. doi: 10.1007/s10546-010-9541-9
Taylor, P. A., Sykes, R. I., and Mason, P. J. (1989). On parameterisation of drag over small-scale topography in neutrally-stratified boundarylayer flow. Boundary Layer Meteorol. 48, 409–422. doi: 10.1007/BF00123062
Teixeira, M. A. C. (2014). The physics of orographic gravity wave drag. Front. Phys. 2:43. doi: 10.3389/fphy.2014.00043
Turnipseed, A. A., Anderson, D. E., Burns, S. P., Blanken, P. D., and Monson, R. K. (2004). Airflows and turbulent flux measurements in mountainous terrain: Part 2: mesoscale effects. Agric. Forest Meteorol. 125, 187–205. doi: 10.1016/j.agrformet.2004.04.007
Vosper, S. B., and Brown, A. R. (2007). Numerical simulations of sheltering in valleys: the formation of nighttime cold-air pools. Boundary Layer Meteorol. 127, 429–448. doi: 10.1007/s10546-008-9272-3
Wagner, A. (1932). Neue theorie der berg- und talwinde [New theory of mountain and valley winds]. Meteorol. Z. 49, 329–341.
Wagner, J. S., Gohm, A., and Rotach, M. W. (2014). The impact of horizontal model grid resolution on the boundary layer structure over an idealized valley. Mon. Wea. Rev. 142, 3446–3465. doi: 10.1175/MWR-D-14-00002.1
Wagner, J. S., Gohm, A., and Rotach, M. W. (2015b). Influence of along-valley terrain heterogeneity on exchange processes over idealized valleys. Atmos. Chem. Phys. 15, 6589–6603; 15, 415–451.
Wagner, J. S., Gohm, A., and Rotach, M. W. (2015a). The impact of valley geometry on daytime thermally driven flows and vertical transport processes. Q. J. R. Meteorol. Soc. doi: 10.1002/qj.2481. [Epub ahead of print].
Weigel, A. P., Chow, F. K., and Rotach, M. W. (2007). The effect of mountainous topography on moisture exchange between the “surface” and the free atmosphere. Boundary Layer Meteorol. 125, 227–244. doi: 10.1007/s10546-006-9120-2
Weigel, A. P., Chow, F. K., Rotach, M. W., Street, R. L., and Xue, M. (2006). High-resolution large-eddy simulations of flow in a steep Alpine valley. Part II: flow structure and heat budgets. J. Appl. Meteorol. Clim. 45, 87–107. doi: 10.1175/JAM2323.1
Weigel, A. P., and Rotach, M. W. (2004). Flow structure and turbulence characteristics of the daytime atmosphere in a steep and narrow Alpine valley. Q. J. R. Meteorol. Soc. 130, 2605–2627. doi: 10.1256/qj.03.214
Weissmann, M., Braun, F., Gantner, L., Mayr, G., Rham, S., and Reitebuch, O. (2005). The alpine mountain plaincirculation: airborne doppler lidar measurements and numerical simulations. Mon. Wea. Rev. 133, 3095–3109. doi: 10.1175/MWR3012.1
Whiteman, C. D. (2000). Mountain Meteorology: Fundamentals and Applications. New York, NY: Oxford University Press.
Wood, N., Brown, A. R., and Hewer, F. E. (2001). Parameterizing the effects of orography on the boundary layer: an alternative to effective roughness lengths. Q. J. R. Meteorol. Soc. 127, 759–777. doi: 10.1002/qj.49712757303
Wood, N., and Mason, P. J. (1993). The pressure force induced by neutral turbulent flow over hills. Q. J. R. Meteorol. Soc. 119, 1233–1267. doi: 10.1002/qj.49711951402
Zangl, G. (2009). The impact of weak synoptic forcing on the valley-wind circulation in the Alpine Inn Valley. Meteorol. Atmos. Phys. 105, 37–53. doi: 10.1007/s00703-009-0030-y
Zangl, G., Egger, J., and Wirth, V. (2001). Diurnal winds in the Himalayan Kali Gandaki valley. Part II: modeling. Mon. Wea. Rev. 129, 1062–1078. doi: 10.1175/1520-0493(2001)129<1062:DWITHK>2.0.CO;2
Keywords: mountain meteorology, boundary layers, horizontal inhomogeneity, thermally driven flows, gravity waves
Citation: Rotach MW, Gohm A, Lang MN, Leukauf D, Stiperski I and Wagner JS (2015) On the Vertical Exchange of Heat, Mass, and Momentum Over Complex, Mountainous Terrain. Front. Earth Sci. 3:76. doi: 10.3389/feart.2015.00076
Received: 29 August 2015; Accepted: 17 November 2015;
Published: 21 December 2015.
Edited by:
Peter F. Sheridan, Met Office, UKReviewed by:
Moacyr Cunha De Araujo, Universidade Federal de Pernambuco, BrazilKe Wei, Institute of Atmospheric Physics, Chinese Academy of Sciences, China
Copyright © 2015 Rotach, Gohm, Lang, Leukauf, Stiperski and Wagner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mathias W. Rotach, bWF0aGlhcy5yb3RhY2hAdWliay5hYy5hdA==
 Mathias W. Rotach
Mathias W. Rotach Alexander Gohm
Alexander Gohm Moritz N. Lang
Moritz N. Lang Daniel Leukauf
Daniel Leukauf Ivana Stiperski1
Ivana Stiperski1 Johannes S. Wagner
Johannes S. Wagner