
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Dev. Psychol., 23 September 2024
Sec. Cognitive Development
Volume 2 - 2024 | https://doi.org/10.3389/fdpys.2024.1441395
This article is part of the Research TopicAdvances in Metacognition and ReflectionView all 10 articles
Introduction: Cognitive reflection is the ability and disposition to reflect on one's own thinking, allowing a person to identify and correct judgments grounded in intuition rather than logic. Cognitive reflection strongly predicts school-aged children's understanding of counterintuitive science concepts. Here, we asked whether children's cognitive reflection similarly predicts a domain-general scientific skill: the interpretation of covariation data.
Method: Five- to 12-year-olds (N = 74) completed a children's Cognitive Reflection Test (CRT-D) and measures of executive functioning. They also interpreted covariation data presented in 2 x 2 contingency tables.
Results and discussion: CRT-D performance predicted children's overall accuracy and the strategies they used to evaluate the contingency tables, even after adjusting for their age, set-shifting ability, inhibitory control, and working memory. Thus, the relationship between cognitive reflection and statistical reasoning emerges early in development. These findings suggest cognitive reflection is broadly involved in children's scientific thinking, supporting domain-general data-interpretation skills in addition to domain-specific conceptual knowledge.
Human reasoning and decision-making are often characterized by the coexistence and interaction of fast intuitive processes and more costly deliberative analytic processes (Kahneman, 2011). The Cognitive Reflection Test (CRT; Frederick, 2005) and its variants (e.g., verbal CRT, Sirota et al., 2021) are the most widely used measures of individual differences in analytic vs. intuitive thinking in adults. CRTs are designed to measure the ability and disposition to override an intuitive incorrect response and engage in deliberative reflection to generate a correct alternative response. Consider the famous bat-and-ball item: “A bat and a ball cost $1.10 in total. The bat costs $1 more than ball. How much does the ball cost?” A majority of adults provide the intuitively cued response of 10 cents, failing to realize that the bat itself would then cost $1.10. Adults who provide the correct answer of 5 cents are thought to have engaged in analytic reflection, detecting and inhibiting the incorrect intuitive response that first came to mind and effortfully generating a correct response in its place (see also Bago and De Neys, 2019).
Adult performance on the CRT is widely known as an excellent predictor of rational thinking on heuristics-and-biases tasks and normative thinking dispositions (e.g., Frederick, 2005; Toplak et al., 2011). More broadly, adults with greater cognitive reflection tend to prioritize analysis over intuition across many domains. For example, they demonstrate greater conceptual understanding of science (e.g., astronomy and thermodynamics; Shtulman and McCallum, 2014) and are more likely to endorse contested scientific beliefs (e.g., evolution, climate change, and vaccination; Gervais, 2015; Pennycook et al., 2023). They are also better at rejecting empirically unjustifiable claims, including fake news (Pennycook and Rand, 2019), conspiracy theories (Swami et al., 2014), paranormal beliefs (Pennycook et al., 2012), and social stereotypes (Blanchar and Sparkman, 2020).
Recent studies using a verbal CRT for elementary-school-aged children, the Cognitive Reflection Test–Developmental Version (CRT-D), have found cognitive reflection to be a similarly powerful predictor of children's thinking and reasoning (Shtulman and Young, 2023). Performance on the CRT-D predicts rational thinking on heuristics-and-biases tasks and normative thinking dispositions in children from the U.S. (Young et al., 2018) as well as China (Gong et al., 2021). Furthermore, the CRT-D predicts children's understanding of counterintuitive concepts in biology, physics, and mathematics, as well as their ability to learn from instruction targeting these concepts (Young and Shtulman, 2020a,b; Young et al., 2022).
The above evidence suggests cognitive reflection supports the development of domain-specific scientific knowledge. However, domain-general scientific skills and practices (e.g., data interpretation, experimentation, and argumentation) are also fundamental to the development of scientific thinking (Zimmerman, 2007; Shtulman and Walker, 2020; NGSS Lead States, 2013). The present study investigates whether cognitive reflection predicts children's successful interpretations of covariation data.
Interpreting covariation data is a critical skill, as both children and adults need to draw conclusions from and update beliefs in response to data encountered in their everyday lives. By the end of the preschool years, children are able to interpret and revise their beliefs based on simple patterns of covariation data (Koerber et al., 2005; Schulz et al., 2007). However, many children and adults have great difficulty interpreting more complex patterns of covariation. When presented with covariation data in a 2 x 2 contingency table like the one shown in Figure 1, children and adults commonly generate inaccurate judgments and use non-optimal strategies that often neglect parts of the data (Shaklee and Mims, 1981; Shaklee and Paszek, 1985; Saffran et al., 2019; Osterhaus et al., 2019). For example, Saffran et al. (2016) found that 2nd and 4th graders justified their covariation judgments by mentioning only two-cells of a contingency table (e.g., A and B, but not C and D) on ~33% of trials, and mentioned the normative comparison of ratios (i.e., conditional probabilities) on only ~3% of trials.
Prior research has not directly examined whether cognitive reflection predicts children's interpretations of covariation data presented in 2 x 2 contingency tables. However, cognitive reflection does predict reasoning on several related tasks. In adults, cognitive reflection is positively associated with accurate interpretations of covariation data that are presented sequentially (e.g., Saltor et al., 2023). Stanovich, Toplak, and colleagues have also found that cognitive reflection predicts adolescent and adult performance on composite measures of scientific thinking that include items on covariation detection in 2 x 2 contingency tables, though they do not report correlations with covariation items specifically (Stanovich et al., 2016; Toplak and Stanovich, 2024).
Obersteiner et al. (2015) have suggested children's invalid strategy use on 2 x 2 contingency tables arises from two common intuitive biases: base-rate bias (i.e., ignoring the base rate at which some effect occurs) and whole number bias (i.e., focusing on whole number components of fractions rather than the overall ratios). Children with greater cognitive reflection are less likely to exhibit both of these biases. For example, CRT-D performance predicts normative reasoning on base-rate sensitivity and denominator neglect/ratio bias tasks (e.g., Gong et al., 2021; Young and Shtulman, 2020a). Furthermore, middle school students' CRT-D performance positively predicts their mature number sense, including perceiving fractions as numbers (rather than separate numerators and denominators) and rich conceptual understandings of rational and whole numbers (Kirkland et al., 2024).
Finally, considering multiple hypotheses and focusing on disconfirmation (rather than confirmation) are both thought to improve correct interpretation of contingency tables (e.g., Osterhaus et al., 2019). Cognitive reflection facilitates children's reasoning about possibilities (Shtulman et al., 2023), and might similarly facilitate children's reasoning about multiple hypotheses. Additionally, adults who rely on counterexamples to solve reasoning problems tend to have higher CRT scores and more accurate covariation judgments (Béghin and Markovits, 2022; Thompson and Markovits, 2021). These multiple lines of evidence suggest children who exhibit greater cognitive reflection should be more successful in interpreting covariation data than those who exhibit less.
In this study we measured school-aged children's performance on the CRT-D and explicit judgments of covariation data presented in 2 x 2 contingency tables. We adopted our stimuli and procedure from Saffran et al. (2016). That is, we presented data in a grounded context (i.e., plant foods and plant growth) using symmetrical tables that compared two potential causes rather than the presence and absence of one candidate cause (i.e., Food A vs. Food B, rather than Food A vs. No Food). Both contextual grounding and symmetry of variables support children's and adults' successful interpretations of covariation data (Osterhaus et al., 2019; Saffran et al., 2016). We considered children's covariation judgment accuracy and strategy use. Prior research has usually examined children's and adults' strategies for interpreting covariation data by eliciting verbal explanations and justifications (e.g., Saffran et al., 2016, 2019) or by evaluating patterns of correct responding across items (e.g., Shaklee and Paszek, 1985; Osterhaus et al., 2019). We used patterns of responding, including specific errors, to assess children's strategies.
We also measured children's executive functions, including set-shifting, inhibitory control, and working memory. Inhibitory control processes have been hypothesized to support children's covariation judgments (e.g., reducing base-rate and whole number biases; Obersteiner et al., 2015). Similarly, limited working memory capacity might contribute to children's use of strategies that neglect parts of a data table (Saffran et al., 2019). However, prior research has not directly examined children's executive functions and their evaluations of 2 x 2 contingency tables. Measuring executive functions also allowed us to further examine the predictive utility of cognitive reflection. Research with children and adults suggests the predictive strength of cognitive reflection is largely independent of executive functions (e.g., Toplak et al., 2011; Young and Shtulman, 2020a), but this may not be the case for interpreting covariation data. Thus, we asked whether the CRT-D is a useful predictor of covariation judgment accuracy and strategy use after adjusting for children's age and executive functions.
Our participants were 74 children in kindergarten through 6th grade. Their mean age was 7 years and 5 months, and they were approximately balanced for gender (42 female, 32 male). Children were recruited from public playgrounds in Southern California. The present data is a subset of 86 children reported on in Gorman (1986) investigation of fake news detection. Eight children from this larger dataset did not complete the covariation judgment task and were excluded from the present analyses. Additionally, four children who had not yet entered kindergarten were excluded, as the covariation judgment task we used has not been used with preschoolers in prior research.
Children completed the 9 item CRT-D (Young and Shtulman, 2020a) as a measure of cognitive reflection. The test consists of brainteasers designed to elicit intuitive, yet incorrect, responses that children can correct upon further reflection. An example item is “If you're running a race and you pass the person in second place, what place are you in?” The lure response is first, but the correct answer is second, as you have not passed the person in first. We used the number of correct responses as children's score, with higher scores indicating greater cognitive reflection.
Children completed two verbal fluency tasks as measures of endogenous set-shifting (Munakata et al., 2012). They named as many animals as they could in 1 min and as many foods as they could in 1 min (without repetition). To be successful, children had to recognize the need to switch subcategories when they had exhausted exemplars from the current subcategory (e.g., breakfast foods) and also decide what new subcategory to switch to (e.g., desserts, fruits, or snacks) without external cues. Children's responses were audio-recorded and transcribed. Children's performance on the animal and food tasks were similar (MeanAnimal = 12.6, SDAnimal = 5.5 vs. MeanFood = 11.9, SDFood = 5.6) and highly correlated, r(38) = 0.73. We used the mean number of items across the animal and food tasks as children's verbal fluency score. In cases where we did not have data for both verbal fluency tasks (e.g., due to recording errors or attrition), we scored their performance on a single verbal fluency task.
Children completed the tablet-based Flanker Test from the NIH Toolbox Cognition Battery (Zelazo et al., 2013; iPad Version 1.11). The test measures both attention and inhibitory control, requiring children to indicate the left-right orientation of a middle stimulus while inhibiting attention to four flanking stimuli. Scoring of the Toolbox Flanker is based on both accuracy and reaction time (Zelazo et al., 2013). We used uncorrected standardized scores (Mean = 100, SD = 15), which reflect overall level of performance relative to the entire NIH Toolbox normative sample, regardless of age or other demographic factors. Higher scores indicate better performance.
Children completed a backward digit span task that required maintenance and manipulation of items in working memory (Alloway et al., 2009). The experimenter read a sequence of numbers at a pace of one per second. Children were then asked to repeat the numbers in reverse order. Children were given a practice trial of 3 digits and then test trials starting at 2 digits, increasing by 1 digit after every 2 trials. The task ended when children failed both trials of a given length or at the conclusion of the 8-digit trials. We used the highest span with at least one correct trial as children's score (Alloway et al., 2009). Scores could range from 1 to 8 (a score of 1 was assigned if children failed both 2-digit trials).
We used six 2 × 2 contingency table items from Saffran et al. (2016). Items were presented in the context of a story about scientists developing different plant foods to improve plant growth. The rows of the tables were labeled with illustrations indicating “Food A” and “Food B,” the two levels of the independent variable. The columns of the tables were labeled with illustrations indicating the “plant is growing” and the “plant is dying,” the two levels of the dependent variable. Cell frequencies were depicted with illustrations and numbers. Figure 2 shows an example item as presented to children and the cell frequencies of the six items. The normative strategy for solving such problems is to compare conditional probabilities. In this strategy, also called comparison of ratios, a solver compares the proportion of cases with growing plants that received Food A to the proportion of cases with growing plants that received Food B [e.g., A/(A+B) vs. C/(C+D)].
As described in Saffran et al. (2016), items were designed with a number of characteristics in mind. There were two items depicting no relationship (Items 3 and 6), two items favoring Food A (Items 2 and 4), and two items favoring Food B (Items 1 and 5). For the majority of items, attention to only the first row (A vs. B strategy) or only the first column (A vs. C strategy) would yield incorrect judgments. The structure of relationships between cell values also varied across items. Three items included the same cell value twice (Items 1, 3, 6), one item had cell values that were simple multiples (Item 6), and other items had less salient relationships (e.g., 16 is about half of 30 in Item 4). Finally, the difference between the cells in the two rows and the cells in the two columns was the same for Items 3 and 5, but not the other items.
Children completed the study on-site with the consent of their guardians. Trained research assistants worked one-on-one with the children to complete the tasks at tables adjacent to the playgrounds. Depending on the measure, research assistants either read the items aloud or displayed them on an iPad, and the children responded verbally or via touch screen. Children completed the tasks in the following order: animal verbal fluency, Flanker, CRT-D, covariation judgment (described below), backward digit span, food verbal fluency. Children also completed a short (<5 min) fake news detection activity between the CRT-D and covariation judgment tasks; the results for this activity are presented in Gorman (1986) and will not be considered here. Most children completed the entire study session in 20–25 min.
The procedure and script of our covariation task closely followed the symmetrical condition of Experiment 1 in Saffran et al. (2016). A researcher first introduced the covariation judgment task by providing a grounded context with the following story:
In this game you are going to think about some scientists that are trying to invent foods that help plants grow. Each scientist has invented two different plant foods and wants to figure out if one food is better for helping plants grow, or if there is no difference between the foods. So each scientist did an experiment. The scientists gave one of their foods to one set of plants, and then gave their other food to a different set of plants. After a few weeks, the scientists checked to see if the plants grew well or died.
After the introduction, the researcher explained the structure of a sample table that contained no data:
Each scientist wrote down what they saw in a table like this. This row will show the plants that got food A (researcher pointed across 1st row). This row will show the plants that got food B (researcher pointed across 2nd row). This column will show the plants that grew well (researcher pointed down 1st column). This column will show the plants that died (researcher pointed down 2nd column).
The researcher then asked two comprehension questions to make sure children understood the meaning and structure of the table (“Before we move on, can you show me which box will have plants that got food A and are growing? Can you show me which box will have plants that got food B and are dying?). Children who failed these questions received a second explanation of the sample table and answered the comprehension questions again. After passing the comprehension questions, children were presented with the six contingency tables one at a time in random order. For each table children were asked to make a judgment about which plant food was better based on the results of the scientist's experiment (e.g., “Here are the results of the first scientist. Is food A or food B better for plants or is there no difference?”). Children's six judgments were scored for accuracy (e.g., responding Food B for Item 1). The McDonald's ω total of the measure was 0.77 (Zinbarg et al., 2005).
We coded children's response patterns across the items for the use of six strategies observed in prior studies (see Saffran et al., 2016). Strategies relying on all four cells of the tables included the normative comparison of ratios strategy [e.g., A/(A+B) vs. C/(C+D)] and the comparison of differences strategy [e.g., (A-C) vs. (B-D)]. Strategies relying on just two cells of the tables included A vs. B, C vs. D, A vs. C, and B vs. D. Table 1 shows the expected response patterns of these strategies across the 6 items.
We coded children's strategy use according to the following scheme. First, we coded children as using a given strategy if their response patterns exactly matched the expected pattern generated by that strategy across all six items. Seventeen children met this criterion. Next, we coded the remaining children as using a given strategy if their response patterns matched the expected pattern generated by that strategy on five of six items. Twenty-one additional children matched a strategy on five of six items. Previous studies have employed similar, less stringent criteria when coding children's strategies for interpreting 2 x 2 contingency tables (e.g., Shaklee and Paszek, 1985), allowing for noise or distraction. Finally, we coded the 36 children whose response patterns did not match any strategy on at least five items as using other/mixed strategies.
A potential concern with coding matches on five of six items is the possibility of ties (i.e., matching more than one strategy). The probability of matching more than one strategy on five of six items is 0.0069 (see Supplementary material). Thus, the opportunity for ties, given the coding scheme and strategy particulars, was quite low. Three children did have response patterns that matched two strategies on five of six items (see Table 1). Two children matched on the comparison of ratios and comparison of differences strategies (both 4-cell strategies). One child matched on C vs. D and B vs. D (both 2-cell strategies).
In the following strategy use analyses, we compared children in terms of the larger 4-cell, 2-cell, and mixed/other strategy categories. We classified the two children matching on comparison of ratios and comparison of differences in the larger 4-cell strategy category and the child that matched on C vs. D and B vs. D in the larger 2-cell strategy category.
Table 2 presents summary statistics of and bivariate Pearson correlations among our variables of interest. As can be seen in Table 2, our primary data set contained missing verbal fluency, Flanker, and backward digit span data for a number of children. Three children were missing verbal fluency data due to audio-recording failures. Thirty-one children were missing Flanker data due to experimenter or software errors. Eleven children were missing backward digit span data due to drop out or parent interruption. One possible reason for data loss was our setting (playgrounds), which may have introduced additional distractions and interruptions compared to more typical lab settings. Overall, 36 of 74 children provided incomplete data, resulting in missing values for 10.1% of the primary data set. We ran a Hawkins test for data missing completely at random (MCAR) with the R package MissMech (Jamshidian et al., 2014), which revealed insufficient evidence to reject the assumption that data were MCAR (p = 0.499). To increase statistical power, reduce bias, and account for the uncertainty induced by these missing data, we generated 50 imputed data sets via predictive mean matching using the R package mice (van Buuren and Groothuis-Oudshoorn, 2011; for multiple imputation details, see: https://osf.io/t37hn/). We used these multiply imputed data for all following inferential analyses.
We fit a Bayesian multilevel logistic regression model to examine the predictive utility of cognitive reflection, along with age and executive functions, for children's judgment accuracy (for an analogous Frequentist analysis, see the Supplementary material). We modeled children's judgment accuracy as repeated binomial trials (i.e., correct vs. incorrect across the 6 covariation items) with CRT-D, age, verbal fluency, Flanker, and backward digit span as predictors. The model also included by-participant random intercepts. Predictor variables were scaled to mean = 0 and SD = 1. We used weakly informative priors for all regression parameters, including Normal (μ = 0, σ = 2.5) for beta coefficients. We used the brm_multiple() function from the R package brms to fit the model to each of the 50 imputed data sets and produce a final pooled model by combining the posterior distributions from each imputed fit (Bürkner, 2017). We report median posterior point-estimates and 89% Credible Intervals (CrI) from this pooled model distribution. Graphical posterior predictive checks, Rhat values, and effective posterior sample size (ESS) values were satisfactory (Muth et al., 2018).
Finally, we used projective predictive variable selection (via the R package projpred; Piironen et al., 2023) to examine the importance of model predictors for out-of-sample predictive performance (i.e., how well a model should predict a new child's judgment accuracy). This method uses posterior information from a reference model to find smaller candidate models whose predictive distributions closely match the reference predictive distribution (Piironen and Vehtari, 2017). The method begins with a forward search through the model space, starting from an empty model (intercept-only), and at each step adding the variable that minimizes the predictive discrepancy to the reference model. Next, Bayesian leave-one-out cross-validation (Vehtari et al., 2017) and a decision criterion are used to determine the final size of the submodel. We selected the smallest submodel within 1 standard error of the predictive performance of the reference model, using expected log pointwise predictive density (elpd) as the measure of predictive performance. This approach allowed us to assess the relative importance of the CRT–D as a predictor in comparison to other measured variables. As an example, if projective predictive variable selection suggested a model with age, CRT-D, and Flanker as predictors, we could conclude that age is the most important predictor, followed by CRT-D and then Flanker. Further, we could conclude that any variables not selected add no additional predictive information. For further details on the models and projective predictive variable selection, see: https://osf.io/t37hn/.
Figure 3A shows the relationship between CRT-D and children's judgment accuracy. A 1 SD increase in CRT-D predicted a 1.65 increase in the odds of a correct judgment, 89% CrI [1.23, 2.22]. Figure 3B and Supplementary Table 1 display the parameter estimates from the model. Children's age also predicted judgment accuracy. A 1 SD increase in age predicted a 1.48 increase in the odds of a correct judgment, 89% CI [1.02, 2.18]. Projective predictive variable selection suggested a submodel with CRT-D and no other predictors. The model with CRT-D as the only predictor had similar out-of-sample predictive performance to the full model, Δ elpd = 0.64, SE = 2.59. Overall, these results indicate that CRT-D performance predicted children's correct interpretations of covariation data over and above their age and executive functions. Furthermore, CRT-D performance is the single best predictor of children's covariation judgement accuracy among the measured variables.
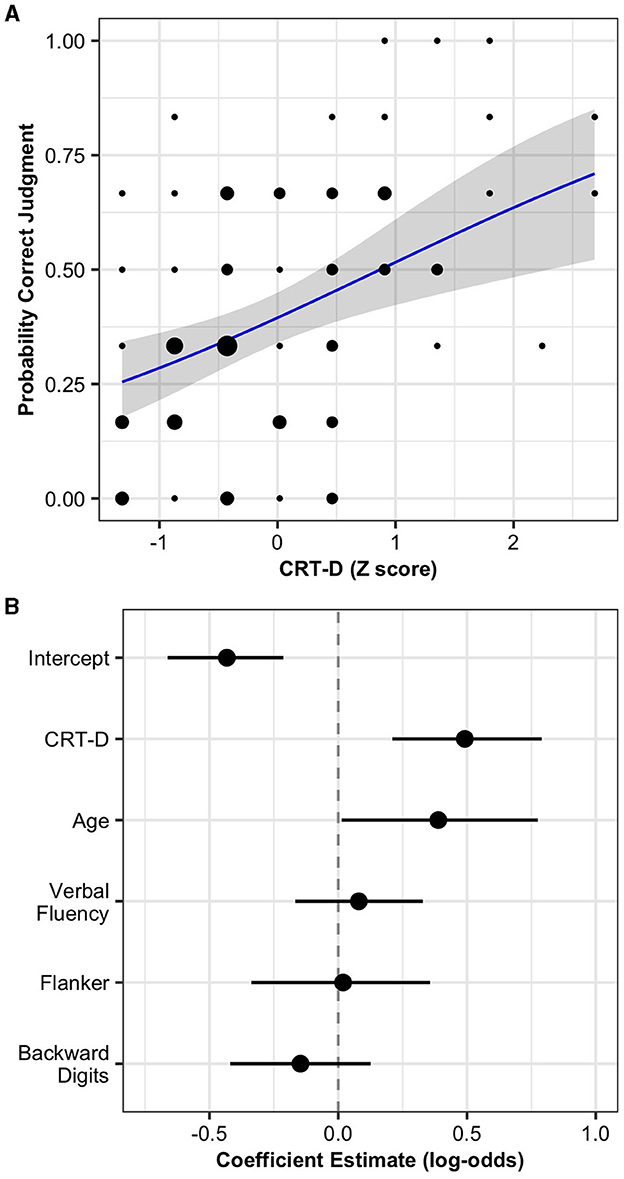
Figure 3. (A) Estimated probability of correct covariation judgment by CRT-D score. Ribbons represent 89% Credible Intervals. Points represent children's raw percent of correct judgments with size proportional to number of children. (B) Accuracy model coefficient estimates with 89% Credible Intervals.
Children's verbal fluency, Flanker, and backward digit span did not predict judgment accuracy in the model that included CRT-D. These measures also did not predict judgment accuracy when considered independently and modeled as single predictors (see Supplementary Figure 1).
Table 3 summarizes children's coded strategy use, including mean judgment accuracies by strategy group. Consistent with previous research using the same materials (Saffran et al., 2016, 2019), more children used a two-cell strategy than a four-cell strategy, with A vs. C being the most common. Similarly, descriptive results show that overall judgment accuracy was weakly connected to strategy categories. For example, children that used a two-cell C vs. D or B vs. D strategy judged more items correctly than children that used a two-cell A vs. B or A vs. C strategies, and children that used a more sophisticated four-cell comparison of differences strategy.
We fit a Bayesian multinomial logistic regression model to examine the relationships between cognitive reflection, age, and executive functions on children's strategy use (for an analogous Frequentist analysis, see Supplementary material). We modeled children's strategy use with two-cell strategies as the reference category and CRT-D, age, verbal fluency, Flanker, and backward digit span as predictors. Similar to our accuracy model, we used scaled predicter variables (mean = 0, SD = 1) and weakly informative priors [e.g., Normal (μ = 0, σ = 2.5) for beta coefficients]. We generated a pooled model from fits to the 50 imputed data sets and performed projective predictive variable selection. Graphical posterior predictive checks, Rhat values, and ESS values were satisfactory. For details, see: https://osf.io/t37hn/.
Figure 4A shows the relationships between CRT-D and children's strategy use. A 1 SD increase in CRT-D predicted an 8.02 increase in the odds of using a four-cell strategy over a two-cell strategy, 89% CrI [3.12, 22.03]. Additionally, a 1 SD increase in CRT-D predicted a 2.29 increase in the odds of using a mixed/other strategy over a two-cell strategy, 89% CrI [1.06, 5.06]. Figure 4B and Supplementary Table 4 display the parameter estimates from the strategy use model. Projective predictive variable selection suggested a submodel with CRT-D and no other predictors. The model with CRT-D as the only predictor had similar out-of-sample predictive performance to the full model, Δ elpd =0.59, SE = 3.74. Overall, these results indicate that CRT-D performance predicted children's strategy use over and above their age and executive functions. Furthermore, CRT-D performance is the single best predictor of children's strategy use among the variables measured.
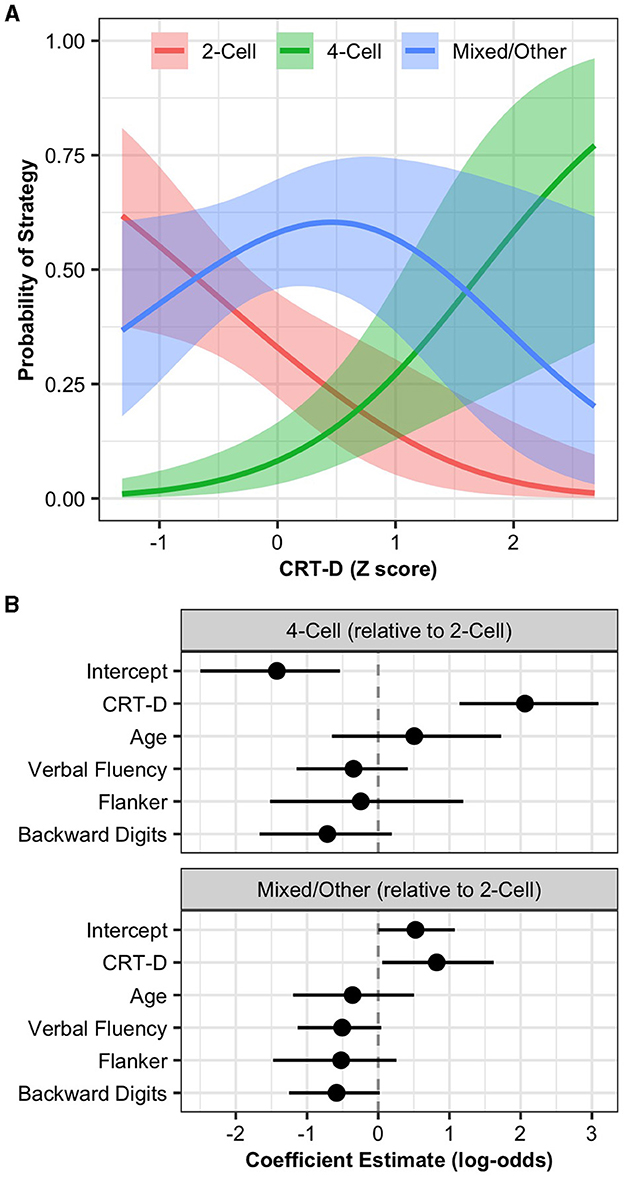
Figure 4. (A) Estimated strategy probabilities by CRT-D score. Ribbons represent 89% Credible Intervals. (B) Strategy use model coefficient estimates with 89% Credible Intervals.
Children's age, verbal fluency, Flanker, and backward digit span did not predict strategy use in the model that included CRT-D. When considered independently and modeled as single predictors (see Supplementary Figure 2), only children's age predicted using a four-cell strategy over a two-cell strategy, OR = 2.28, 89% CrI = [1.27, 4.26]. However, children's age (OR = 0.58, 89% CrI = [0.35, 0.95]), Flanker (OR = 0.52, 89% CrI = [0.28, 0.90]), and backward digit span (OR = 0.60, 89% CrI = [0.37, 0.94]) independently predicted using a mixed/other strategy relative to a two-cell strategy. These effects suggest that with increasing age, inhibitory control, and working memory, children were more likely to use a two-cell strategy over a mixed/other strategy. In contrast, children with greater cognitive reflection were more likely to use a mixed/other strategy over a two-cell strategy (i.e., in the combined model).
The present study examined whether cognitive reflection predicts school-aged children's interpretations of covariation data. In line with prior research, a majority of children in the present study had difficulty interpreting covariation data presented in 2 x 2 contingency tables and used sub-optimal strategies that neglected parts of the data (e.g., Shaklee and Mims, 1981; Shaklee and Paszek, 1985; Saffran et al., 2016). However, we found children with greater CRT-D scores generated more accurate judgments and were more likely to use sophisticated four-cell strategies than children with lower CRT-D scores. Cognitive reflection predicted correct interpretations and strategy use even after adjusting for children's age, set-shifting, inhibitory control, and working memory. Moreover, if we wanted to predict a new school-aged child's accuracy or strategy use in the present task, their CRT-D score is the first and only measure we should collect. Age and the executive functioning measures did not provide any additional out-of-sample predictive value.
Our findings are consistent with prior research demonstrating cognitive reflection predicts covariation judgment accuracy in adolescents and adults (e.g., Saltor et al., 2023; Stanovich et al., 2016; Toplak and Stanovich, 2024). Why does cognitive reflection facilitate children's correct interpretations of covariation data? One possibility is that cognitive reflection helps children override intuitive base-rate and whole number biases (e.g., Young and Shtulman, 2020a; Gong et al., 2021; Kirkland et al., 2024), which are thought to drive inadequate strategies on 2 x 2 contingency tables (Obersteiner et al., 2015). Similarly, overall mathematical ability supports successful interpretations of covariation data in adults (Osterhaus et al., 2019). Children's cognitive reflection is positively associated with greater math ability in several domains, including understanding the equal sign (Young and Shtulman, 2020a), mature number sense (Kirkland et al., 2024), and use of the distributive property (Clerjuste et al., 2024). It may be that more reflective children in the present study were more likely to have the requisite mathematical skills to correctly judge 2 x 2 contingency tables, even after adjusting for age. Future research should directly measure children's base-rate bias, whole number bias, and general mathematical ability to better understand the relationship between cognitive reflection and interpretations of covariation data.
Another explanation is that cognitive reflection facilitates children's modal cognition and greater consideration of possibilities (Shtulman et al., 2023, 2024). Children with greater cognitive reflection may have approached the data tables by entertaining multiple hypotheses (e.g., Food A is better vs. Food B is better vs. Food A and B are similar), thereby increasing their focus on disconfirming hypotheses and considering more data cells (Ackerman and Thompson, 2017; Osterhaus et al., 2019). In contrast, less reflective children may have focused on confirmatory testing of fewer hypotheses (e.g., Food A is better, so compare A vs. C). Similarly, adults with greater cognitive reflection are more likely to rely on counterexamples when solving reasoning problems (Thompson and Markovits, 2021). A greater consideration of counterexamples may have led children to focus on disconfirmation in the present study. Future studies are needed to investigate the role of cognitive reflection in children's hypothesis testing. Comparing more and less reflective children in open-ended experimentation or causal learning tasks would be a fruitful approach to exploring how cognitive reflection influences children's navigation of hypothesis spaces and their strategies for testing those hypotheses.
Children with greater cognitive reflection likely had a metacognitive advantage in the present task. Xu et al.'s (2022) Meta-Reasoning framework suggests metacognitive monitoring and control are integral to our reasoning and problem-solving processes. In adults, the CRT has been used to study several meta-reasoning processes. For example, more reflective adults have superior conflict detection (i.e., sensitivity to conflict between intuitive judgments and logical principles; Šrol and De Neys, 2021), better meta-reasoning discrimination (i.e., deciding whether an answer is likely correct and should be reported or withheld; Strudwicke et al., 2023), and are less likely to overestimate their performance relative to less reflective individuals (Mata et al., 2013). Xu et al. (2022) argue that failure on the CRT is essentially a metacognitive failure associated with the Feeling of Rightness. Individuals with a strong Feeling of Rightness are less likely to reconsider, change, or spend additional time thinking about an initial intuitive response. In contrast, a weak Feeling of Rightness should trigger deliberation and a greater probability of changing answers.
Although the present study was not designed to examine children's meta-reasoning, children's use of mixed/other strategies may be an indicator of meta-reasoning. In particular, children's age, inhibitory control, and working memory predicted an increased use of two-cell strategies over mixed/other strategies. However, cognitive reflection predicted greater use of mixed/other strategies relative to two-cell strategies. One interpretation of these puzzling results is that more reflective children were more metacognitively aware of the inadequacy of their strategies across items and attempted to compensate by using multiple strategies throughout the task (as opposed to using multiple strategies by happenstance, as children with lower executive function skills may have done). To test this possibility, future studies should employee methods from the meta-reasoning and problem-solving literatures, such as eliciting confidence ratings and verbal justifications of strategies. If children's meta-reasoning is indexed by cognitive reflection, we should expect children with greater CRT-D scores to show a stronger correspondence between confidence ratings and strategy variability.
Executive functions did not support children's interpretations of 2 x 2 contingency tables in the present task. Set-shifting, inhibitory control, and working memory (measured via verbal fluency, Flanker, and backward digit span tasks, respectively) did not predict judgment accuracy or strategy-use after adjusting for cognitive reflection. When considered in isolation, both inhibitory control and working memory predicted increased use of two-cell strategies (relative to mixed/other strategies). These results are surprising given prior suggestions that inhibitory control and working memory might support the use of four-cell strategies (Obersteiner et al., 2015; Saffran et al., 2019). To our knowledge, prior research has not directly measured children's executive functions and judgments of 2 x 2 contingency tables. It is an open question whether these results would generalize to different measures of executive functions (e.g., visuospatial working memory rather than verbal working memory) or older samples with more requisite math knowledge to execute four-cell strategies.
Additionally, while cognitive reflection draws on executive function skills (e.g., inhibiting an intuitive response, shifting to an alternative response, and holding the question and possible responses in mind), it also requires the metacognitive ability to engage, coordinate, and sustain these skills on one's own (Simonovic et al., 2023; Shtulman and Young, 2023). Thus, the pattern of cognitive reflection predicting reasoning above and beyond executive functioning in children and adults (e.g., Young and Shtulman, 2020a; Shtulman et al., 2023; Toplak et al., 2011) may be the rule rather than the exception.
This study suggests that cognitive reflection may be broadly involved in children's scientific thinking. Prior research has shown that cognitive reflection supports children's domain-specific scientific knowledge (Young and Shtulman, 2020a,b). The present data highlight that cognitive reflection similarly supports children's data interpretation, a domain-general scientific skill. Further research might explore the role of cognitive reflection in children's evidence and data evaluation in other contexts, including interpretation of ambiguous, disconfirming, or confounded data (Cook et al., 2011; Schulz and Bonawitz, 2007; Theobald et al., 2024). Future work should also explore the role of cognitive reflection in other scientific skills and practices. Given children's performance in the present task, we might expect cognitive reflection to support hypothesis testing, falsification, and experimentation skills more generally.
Furthermore, given influential social models of rationality, we might expect cognitive reflection to support reasoning from disagreement (Young et al., 2012; Langenhoff et al., 2023), collaboration (Shtulman and Young, 2021), and argumentation (Mercier and Sperber, 2011). Research has already begun to explore some of these avenues. For example, Nissel and Woolley (2024) demonstrated that cognitive reflection predicted children's preference for arguments supported by statistical visualizations over anecdotal evidence. We anticipate cognitive reflection will be implicated in many domain-general scientific skills and practices.
Our findings have potential implications for education. Prior studies suggest more reflective children tend to learn more from instruction on counterintuitive science and mathematics concepts (Young and Shtulman, 2020b; Young et al., 2022). Children with greater cognitive reflection might similarly learn more from instruction on how to evaluate 2 x 2 contingency tables and other statistical reasoning topics, where performance is often undermined by inaccurate intuitions. If so, children's CRT-D performance might be used to target children who are ready for instruction or in need of additional or alternative instruction. Recent research has also found modest success in enhancing adult cognitive reflection via intervention (e.g., Isler and Yilmaz, 2023; Simonovic et al., 2023). It remains an open question whether children's cognitive reflection can be substantively improved via targeted instruction and training. Success in enhancing children's cognitive reflection might yield downstream effects, such as improving interpretation of 2 x 2 contingency tables and facilitating science learning more broadly.
To conclude, we have shown that cognitive reflection is a strong and unique predictor of elementary-school-aged children's correct interpretation of covariation data and the strategies they use to evaluate the 2 x 2 contingency tables. Indeed, the CRT-D was the single best out-of-sample predictor of children's judgment accuracy and strategy use, outperforming age, set-shifting, inhibitory control, and working memory. These data highlight cognitive reflection as a critical variable in children's data-interpretation skills and contribute to a growing literature demonstrating that cognitive reflection is broadly involved in children's developing scientific thinking.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: Open Science Framework, https://osf.io/t37hn/.
The studies involving humans were approved by Occidental College's Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.
AY: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Supervision, Visualization, Writing – original draft, Writing – review & editing. AS: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the James S. McDonnell Foundation through an Understanding Human Cognition Scholar Award to Andrew Shtulman.
We would like to thank Kidspace Children's Museum, Julieta Alas, Connor Allison, Taleen Berberian, Yukimi Hiroshima, Ellen McDermott, Phoebe Patterson, Khetsi Pratt, and Emma Ragan for their assistance with data collection. We also extend our gratitude to Andrea Saffran and Martha Alibali for sharing their materials and engaging in helpful discussions about their task.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fdpys.2024.1441395/full#supplementary-material
Ackerman, R., and Thompson, V. A. (2017). Meta-reasoning: monitoring and control of thinking and reasoning. Trends Cogn. Sci. 21, 607–617. doi: 10.1016/j.tics.2017.05.004
Alloway, T. P., Gathercole, S. E., Kirkwood, H., and Elliott, J. (2009). The cognitive and behavioral characteristics of children with low working memory. Child Dev. 80, 606–621. doi: 10.1111/j.1467-8624.2009.01282.x
Bago, B., and De Neys, W. (2019). The smart System 1: evidence for the intuitive nature of correct responding on the bat-and-ball problem. Think. Reason. 25, 257–299. doi: 10.1080/13546783.2018.1507949
Béghin, G., and Markovits, H. (2022). Reasoning strategies and prior knowledge effects in contingency learning. Mem. Cogn. 50, 1269–1283. doi: 10.3758/s13421-022-01319-w
Blanchar, J. C., and Sparkman, D. J. (2020). Individual differences in miserly thinking predict endorsement of racial/ethnic stereotypes. Soc. Cogn. 38, 405–421. doi: 10.1521/soco.2020.38.5.405
Bürkner, P. C. (2017). brms: an R package for Bayesian multilevel models using Stan. J. Statist. Softw. 80, 1–28. doi: 10.18637/jss.v080.i01
Clerjuste, S. N., Guang, C., Miller-Cotto, D., and McNeil, N. M. (2024). Unpacking the challenges and predictors of elementary-middle school students' use of the distributive property. J. Exp. Child Psychol. 244:105922. doi: 10.1016/j.jecp.2024.105922
Cook, C., Goodman, N. D., and Schulz, L. E. (2011). Where science starts: spontaneous experiments in preschoolers' exploratory play. Cognition 120, 341–349. doi: 10.1016/j.cognition.2011.03.003
Frederick, S. (2005). Cognitive reflection and decision making. J. Econ. Perspect. 19, 25–42. doi: 10.1257/089533005775196732
Gervais, W. M. (2015). Override the controversy: analytic thinking predicts endorsement of evolution. Cognition 142, 312–321. doi: 10.1016/j.cognition.2015.05.011
Gong, T., Young, A. G., and Shtulman, A. (2021). The development of cognitive reflection in China. Cogn. Sci. 45:e12966. doi: 10.1111/cogs.12966
Gorman, M. E. (1986). How the possibility of error affects falsification on a task that models scientific problem solving. Br. J. Psychol. 77, 85–96. doi: 10.1111/j.2044-8295.1986.tb01984.x
Isler, O., and Yilmaz, O. (2023). How to activate intuitive and reflective thinking in behavior research? A comprehensive examination of experimental techniques. Behav. Res. Methods 55, 3679–3698. doi: 10.3758/s13428-022-01984-4
Jamshidian, M., Jalal, S., and Jansen, C. (2014). MissMech: an R Package for testing homoscedasticity, multivariate normality, and missing completely at random (MCAR). J. Statist. Softw. 56, 1–31. doi: 10.18637/jss.v056.i06
Kirkland, P. K., Guang, C., Cheng, Y., and McNeil, N. M. (2024). Mature number sense predicts middle school students' mathematics achievement. J. Educ. Psychol. 2024:880. doi: 10.1037/edu0000880
Koerber, S., Sodian, B., Thoermer, C., and Nett, U. (2005). Scientific reasoning in young children: preschoolers' ability to evaluate covariation evidence. Swiss J. Psychol. 64, 141–152. doi: 10.1024/1421-0185.64.3.141
Langenhoff, A. F., Engelmann, J. M., and Srinivasan, M. (2023). Children's developing ability to adjust their beliefs reasonably in light of disagreement. Child Dev. 94, 44–59. doi: 10.1111/cdev.13838
Mata, A., Ferreira, M. B., and Sherman, S. J. (2013). The metacognitive advantage of deliberative thinkers: a dual-process perspective on overconfidence. J. Personal. Soc. Psychol. 105:353. doi: 10.1037/a0033640
Mercier, H., and Sperber, D. (2011). Why do humans reason? Arguments for an argumentative theory. Behav. Brain Sci. 34, 57–74. doi: 10.1017/S0140525X10000968
Munakata, Y., Snyder, H. R., and Chatham, C. H. (2012). Developing cognitive control. Curr. Direct. Psychol. Sci. 21, 71–77. doi: 10.1177/0963721412436807
Muth, C., Oravecz, Z., and Gabry, J. (2018). User-friendly Bayesian regression modeling: a tutorial with rstanarm and shinystan. Quantit. Methods Psychol. 14, 99–119. doi: 10.20982/tqmp.14.2.p.099
NGSS Lead States (2013). Next Generation Science Standards: For States, By States. Washington, DC: The National Academies Press.
Nissel, J., and Woolley, J. D. (2024). Anecdata: children's and adults' evaluation of anecdotal and statistical evidence. Front. Dev. Psychol. 2:1324704. doi: 10.3389/fdpys.2024.1324704
Obersteiner, A., Bernhard, M., and Reiss, K. (2015). Primary school children's strategies in solving contingency table problems: the role of intuition and inhibition. ZDM 47, 825–836. doi: 10.1007/s11858-015-0681-8
Osterhaus, C., Magee, J., Saffran, A., and Alibali, M. W. (2019). Supporting successful interpretations of covariation data: beneficial effects of variable symmetry and problem context. Quart. J. Exp. Psychol. 72, 994–1004. doi: 10.1177/1747021818775909
Pennycook, G., Bago, B., and McPhetres, J. (2023). Science beliefs, political ideology, and cognitive sophistication. J. Exp. Psychol. 152, 80–97. doi: 10.1037/xge0001267
Pennycook, G., Cheyne, J. A., Seli, P., Koehler, D. J., and Fugelsang, J. A. (2012). Analytic cognitive style predicts religious and paranormal belief. Cognition 123, 335–346. doi: 10.1016/j.cognition.2012.03.003
Pennycook, G., and Rand, D. G. (2019). Lazy, not biased: susceptibility to partisan fake news is better explained by lack of reasoning than by motivated reasoning. Cognition 188, 39–50. doi: 10.1016/j.cognition.2018.06.011
Piironen, J., Paasiniemi, M., Catalina, A., Weber, F., and Vehtari, A. (2023). projpred: Projection Predictive Feature Selection. R Package Version 2.8.0. Available at: https://mc-stan.org/projpred/
Piironen, J., and Vehtari, A. (2017). Comparison of Bayesian predictive methods for model selection. Statist. Comput. 27, 711–735. doi: 10.1007/s11222-016-9649-y
Saffran, A., Barchfeld, P., Alibali, M. W., Reiss, K., and Sodian, B. (2019). Children's interpretations of covariation data: explanations reveal understanding of relevant comparisons. Learn. Instr. 59, 13–20. doi: 10.1016/j.learninstruc.2018.09.003
Saffran, A., Barchfeld, P., Sodian, B., and Alibali, M. W. (2016). Children's and adults' interpretation of covariation data: does symmetry of variables matter? Dev. Psychol. 52:1530. doi: 10.1037/dev0000203
Saltor, J., Barberia, I., and Rodr?guez- Ferreiro, J. (2023). Thinking disposition, thinking style, and susceptibility to causal illusion predict fake news discriminability. Appl. Cogn. Psychol. 37, 360–368. doi: 10.1002/acp.4008
Schulz, L. E., and Bonawitz, E. B. (2007). Serious fun: preschoolers engage in more exploratory play when evidence is confounded. Dev. Psychol. 43, 1045–1050. doi: 10.1037/0012-1649.43.4.1045
Schulz, L. E., Bonawitz, E. B., and Griffiths, T. L. (2007). Can being scared cause tummy aches? Naive theories, ambiguous evidence, and preschoolers' causal inferences. Dev. Psychol. 43, 1124–1139. doi: 10.1037/0012-1649.43.5.1124
Shaklee, H., and Mims, M. (1981). Development of rule use in judgments of covariation between events. Child Dev. 1981, 317–325. doi: 10.2307/1129245
Shaklee, H., and Paszek, D. (1985). Covariation judgment: systematic rule use in middle childhood. Child Dev. 1985, 1229–1240. doi: 10.2307/1130238
Shtulman, A., Goulding, B., and Friedman, O. (2024). Improbable but possible: training children to accept the possibility of unusual events. Dev. Psychol. 60, 17–27. doi: 10.1037/dev0001670
Shtulman, A., Harrington, C., Hetzel, C., Kim, J., Palumbo, C., and Rountree-Shtulman, T. (2023). Could it? Should it? Cognitive reflection facilitates children's reasoning about possibility and permissibility. J. Exp. Child Psychol. 235:105727. doi: 10.1016/j.jecp.2023.105727
Shtulman, A., and McCallum, K. (2014). “Cognitive reflection predicts science understanding,” in Proceedings of the 36th Annual Conference of the Cognitive Science Society, eds. P. Bello, M. Guarini, M. McShane, and B. Scassellati (Austin, TX: Cognitive Science Society), 2937–2942.
Shtulman, A., and Walker, C. (2020). Developing an understanding of science. Ann. Rev. Dev. Psychol. 2, 111–132. doi: 10.1146/annurev-devpsych-060320-092346
Shtulman, A., and Young, A. G. (2021). Learning evolution by collaboration. BioScience 71, 1091–1102. doi: 10.1093/biosci/biab089
Shtulman, A., and Young, A. G. (2023). The development of cognitive reflection. Child Dev. Perspect. 17, 59–66. doi: 10.1111/cdep.12476
Simonovic, B., Vione, K., Stupple, E., and Doherty, A. (2023). It is not what you think it is how you think: a critical thinking intervention enhances argumentation, analytic thinking and metacognitive sensitivity. Think. Skills Creat. 49:101362. doi: 10.1016/j.tsc.2023.101362
Sirota, M., Dewberry, C., Juanchich, M., Valuš, L., and Marshall, A. C. (2021). Measuring cognitive reflection without maths: development and validation of the verbal cognitive reflection test. J. Behav. Decision Mak. 34, 322–343. doi: 10.1002/bdm.2213
Šrol, J., and De Neys, W. (2021). Predicting individual differences in conflict detection and bias susceptibility during reasoning. Think. Reason. 27, 38–68. doi: 10.1080/13546783.2019.1708793
Stanovich, K. E., West, R. F., and Toplak, M. E. (2016). The Rationality Quotient: Toward a Test of Rational Thinking. Cambridge, MA: MIT Press.
Strudwicke, H. W., Bodner, G. E., Williamson, P., and Arnold, M. M. (2023). Open-minded and reflective thinking predicts reasoning and meta-reasoning: evidence from a ratio-bias conflict task. Think. Reason. 2023, 1–27. doi: 10.1080/13546783.2023.2259548
Swami, V., Voracek, M., Stieger, S., Tran, U. S., and Furnham, A. (2014). Analytic thinking reduces belief in conspiracy theories. Cognition 133, 572–585. doi: 10.1016/j.cognition.2014.08.006
Theobald, M., Colantonio, J., Bascandziev, I., Bonawitz, E., and Brod, G. (2024). Do reflection prompts promote children's conflict monitoring and revision of misconceptions? Child Dev. 95, e253–e269. doi: 10.1111/cdev.14081
Thompson, V. A., and Markovits, H. (2021). Reasoning strategy vs. cognitive capacity as predictors of individual differences in reasoning performance. Cognition 217:104866. doi: 10.1016/j.cognition.2021.104866
Toplak, M. E., and Stanovich, K. E. (2024). Measuring rational thinking in adolescents: the assessment of rational thinking for youth (ART-Y). J. Behav. Decision Mak. 37:e2381. doi: 10.1002/bdm.2381
Toplak, M. E., West, R. F., and Stanovich, K. E. (2011). The Cognitive Reflection Test as a predictor of performance on heuristics-and-biases tasks. Mem. Cogn. 39, 1275–1289. doi: 10.3758/s13421-011-0104-1
van Buuren, S., and Groothuis-Oudshoorn, K. (2011). mice: multivariate imputation by chained equations in R. J. Statist. Softw. 45, 1–67. doi: 10.18637/jss.v045.i03
Vehtari, A., Gelman, A., and Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statist. Comput. 27, 1413–1432. doi: 10.1007/s11222-016-9696-4
Xu, S., Shtulman, A., and Young, A. G. (2022). “Can children detect fake news?,” in Proceedings of the 44th Annual Meeting of the Cognitive Science Society, eds. J. Culbertson, A. Perfors, H. Rabagliati, and V. Ramenzoni (Toronto, ON: Cognitive Science Society), 2988–2993.
Young, A. G., Alibali, M. W., and Kalish, C. W. (2012). Disagreement and causal learning: others' hypotheses affect children's evaluations of evidence. Developmental Psychology 48, 1242. doi: 10.1037/a0027540
Young, A. G., Powers, A., Pilgrim, L., and Shtulman, A. (2018). “Developing a cognitive reflection test for school-age children,” in Proceedings of the 40th Annual Conference of the Cognitive Science Society, eds. T. T. Rogers, M. Rau, X. Zhu, and C. W. Kalish (Austin, TX: Cognitive Science Society), 1232–1237.
Young, A. G., Rodriguez-Cruz, J., Castaneda, J., Villacres, M., Macksey, S., and Church, R. B. (2022). “Individual differences in children's mathematics learning from instructional gestures [Conference presentation abstract],” in 2022 Meeting of the Cognitive Development Society. Madison, WI. Available at: https://cogdevsoc.org/wp-content/uploads/2022/04/CDS2022AbstractBook.pdf (accessed May 1, 2024).
Young, A. G., and Shtulman, A. (2020a). Children's cognitive reflection predicts conceptual understanding in science and mathematics. Psychol. Sci. 31, 1396–1408. doi: 10.1177/0956797620954449
Young, A. G., and Shtulman, A. (2020b). How children's cognitive reflection shapes their science understanding. Front. Psychol. 11:532088. doi: 10.3389/fpsyg.2020.01247
Zelazo, P. D., Anderson, J. E., Richler, J., Wallner-Allen, K., Beaumont, J. L., and Weintraub, S. (2013). NIH Toolbox Cognition Battery (CB): measuring executive function and attention. Monogr. Soc. Res. Child Dev. 78, 16–33. doi: 10.1111/mono.12032
Zimmerman, C. (2007). The development of scientific thinking skills in elementary and middle school. Dev. Rev. 27, 172–223. doi: 10.1016/j.dr.2006.12.001
Keywords: cognitive reflection, scientific thinking, evidence evaluation, statistical reasoning, data interpretation, development
Citation: Young AG and Shtulman A (2024) Children's cognitive reflection predicts successful interpretations of covariation data. Front. Dev. Psychol. 2:1441395. doi: 10.3389/fdpys.2024.1441395
Received: 31 May 2024; Accepted: 30 August 2024;
Published: 23 September 2024.
Edited by:
Igor Bascandziev, Harvard University, United StatesReviewed by:
Maria Theobald, University of Trier, GermanyCopyright © 2024 Young and Shtulman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrew G. Young, YXlvdW5nMjBAbmVpdS5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.