Languages for Computer Music

Specialized languages for computer music have long been an important area of research in this community. Computer music languages have enabled composers who are not software engineers to nevertheless use computers effectively. While powerful general-purpose programming languages can be used for music tasks, experience has shown that time plays a special role in music computation, and languages that embrace musical time are especially expressive for many musical tasks. Time is expressed in procedural languages through schedulers and abstractions of beats, duration and tempo. Functional languages have been extended with temporal semantics, and object-oriented languages are often used to model stream-based computation of audio. This article considers models of computation that are especially important for music programming, how these models are supported in programming languages, and how this leads to expressive and efficient programs. Concrete examples are drawn from some of the most widely used music programming languages.

Introduction

Music presents a rich set of design goals and criteria for written expression. Traditional music notation evolved to denote musical compositions that were more-or-less fixed in form. While not exactly a programming language, music notation contains control structures such as repeats and optional endings that are analogous to modern programming languages (Jin and Dannenberg, 2013).

Traditional music notation and theory about musical time developed in the thirteenth century, while the comparable use of graphs to plot time-based phenomena in science did not occur until the sixteenth century (Crosby, 1997). Perhaps music can also motivate revolutionary thinking in computer science. Certainly, music is unlike many conventional applications of computers. Music exists over time, while in conventional computation, faster is always better. Music often includes many voices singing in harmony or counterpoint, while conventional computer architectures and programming languages are sequential, and parallelism is often considered to be a special case. Music making is often a collaborative process, while computation is often viewed as discrete operations where input is provided at the beginning and output occurs at the end. Perhaps music will help to expand thinking about computer languages in general.

Before embarking on a broad discussion of languages for computer music, it will be useful to survey the landscape. To begin, the timeline in Figure 1 shows a number of computer music languages and their date of introduction or development. A number of these will be used throughout this article to illustrate different trends and concepts.

FIGURE 1

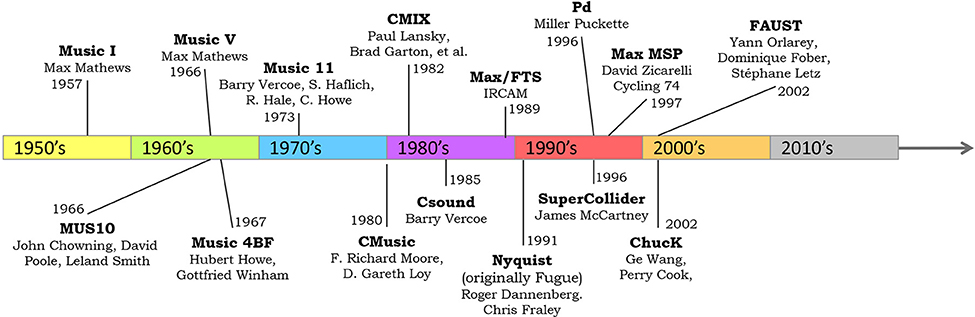
Figure 1. A timeline of representative and historically significant computer music languages. The selection here includes only languages that support digital audio signal generation and processing.

In the next paragraphs, we will introduce some of the dimensions of programming languages including their syntax, semantics, implementation issues, and resources for their users. These will be useful in the following sections where we will describe what makes music special and different (section Why Is Music Different), models of musical time (section Models of Time and Scheduling), models for sound synthesis and audio signal processing (section Models for Sound Synthesis), and examples (section Some Examples). Section Conclusions presents conclusions.

Syntax

Syntax refers to the surface level of notation. Most computer music languages are text-based languages with a syntax similar to other programming languages; for example, one might write x + y to add two variables, f(x,y) to evaluate a function with 2 arguments, or if (c) then f(x,y) to perform a conditional operation.

Graphical syntax has been especially popular in computer music. Figure 2 illustrates simple expressions in this form, and we will discuss graphical music programming languages later. Whether the syntax is text-based or graphical, music languages have to deal with timing, concurrency and signals, so perhaps even more important than syntax is the program behavior or semantics.

FIGURE 2

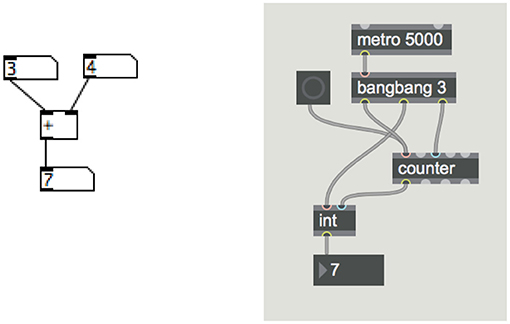
Figure 2. Graphical syntax examples. At left, a Pd program to add 3 + 4. At right, a Max program to show the number of button presses in the previous 5 s.

Semantics

Semantics refers to the “meaning” or the interpretation of text or graphical notation in a programming language. Semantically, many programming languages are quite similar. They deal with numbers, text strings, arrays, and aggregates in ways that are very much a reflection of the underlying hardware, which includes a large memory addressable by integers and a central processing unit that sequentially reads, writes, and performs arithmetic on data.

Since music computation often includes parallel behaviors, carefully timed output, signal processing and the need to respond to real-time input, we often find new and interesting semantics in music languages. Music languages include special data types such as signals and scores, explicit specifications for temporal aspects of program behavior and provisions for real-time scheduling and interaction.

Run-Time Systems

Semantics at the language design level often relate to the “run-time system” at the implementation level. The term “run-time system” describes the organization of computation and a collection of libraries, functions, and resources available to the running program. In short, the run-time system describes the “target” of the compiler or interpreter. A program is evaluated (“run”) by translating it into to a lower-level language expressed in terms of the run-time system.

Run-time systems for computer music, like music language semantics, are often driven by the special requirements of musical systems. In systems with audio signal processing, special attention must be paid both to efficiency and to the need for synchronous sample-by-sample processing. Concurrency in music often motivates special run-time support such as threads, processes, functional programming, lazy evaluation, or other approaches. The importance of time in music leads to scheduling support and the association of explicit timing with computation or musical events.

Libraries

Most musicians are not primarily software developers. Their main interest is not to develop new software, but to explore musical ideas. Ready-made modules often facilitate exploration or even inspire new musical directions; thus, libraries of reusable program modules are important for most computer musicians. This sometimes inhibits the adoption of new languages, which do not emerge with a mature set of ready-made capabilities and examples. One trend in computer music software is “plug-in” architectures, allowing libraries (especially audio effects and software synthesizers) to be used by multiple languages and software systems.

Programming Environment

Another important factor for most computer musicians is the programming environment. In earlier days of computing, programs were prepared with a simple text editor, compiled with a translator, and executed by the operating system. Modern language development is typically more integrated, with language-specific editors to check syntax and offer documentation, background compilation to detect semantic errors, and the ability to tie run-time errors directly to locations in the program text. Some programming languages support “on-the-fly” programming (or “live coding”) where programs can be modified during program execution. Some music programming environments include graphical time-based or score-like representations in addition to text (Lindemann, 1990; Assayag et al., 1999; Yi, 2017).

Community and Resources

Like other programming languages, computer music languages often enjoy communities of users who author tutorials, help answer questions online, post example code and maintain open source implementations. While a vibrant community may have little to do with the technical merits of a computer music language, the existence of a helpful community has a large impact on the attractiveness of a language to typical users.

Why Is Music Different

We have mentioned a number of dimensions in which computer music languages differ from “ordinary” general purpose programming languages. This section will focus on some of these differences, and in particular, the importance of time in music programming.

Music Happens in Time

While difficult to define precisely, a key characteristic of music is the presentation of sound in some form of temporal organization. Thus, time features prominently in music representations and music programming languages.

Programming Languages Traditionally Focus on Getting Answers Fast

Traditional computer languages and computer science theory are largely concerned with computing answers as soon as possible. Algorithms are often described as a sequence of steps. We design algorithms to minimize the number of steps, design languages to express those steps efficiently, and design hardware to perform those steps as fast as possible. Key measures of quality in traditional computer science theory are time complexity (how long will a program run?) and space complexity (how much memory is required?).

Music Demands Producing “Answers” at the Right Time

While computing answers quickly is important, in music the “answer” itself is situated in time. In real-time music systems, the timing of musical events is as important as their content. Computer music languages deal with time in different ways:

• An event-based, implicitly timed approach views computation as arising from input events such as a key pressed on a musical keyboard. Programs describe what to do when an input event arrives, and the response is as fast as possible; thus, timing is implicitly determined by the times of events.

• Explicit “out-of-time” systems do not run in real time and instead keep track of musical time as part of the computation. For example, an automatic composition system might generate a musical score as quickly as possible, but it must keep track of the logical progression of time in the music and pass this time along into the program output, which is some kind of musical score representation or perhaps an audio file.

• Precisely timed systems adapt the explicit “out-of-time” approach to a real-time, or “in-time” system. The idea is to maintain an accurate accounting of the “ideal” time of each output event so that even if real computation lags behind now and then, cumulative error can be eliminated. This approach is widely used and is particularly useful when there are multiple processes that need to be musically synchronized.

• Sample-synchronous computation is required for audio signal processing. Here, time is effectively quantized into sample periods (typically 44,100 samples per second, the sample rate used by CD Audio). Computation proceeds strictly sample-by-sample in a largely deterministic fashion. In practice, operating systems cannot schedule and run a computation for every sample (e.g., every 22 μs), so samples are computed slightly ahead of time in batches of around 1 to 20 ms of audio. Thus, while computation logically proceeds synchronously sample-by-sample, the process must actually compute faster than and slightly ahead of real time to avoid any interruptions in the flow of samples to the output.

Music Timing Is Rich (Tempo, Synchronization, Meter)

Musical time is typically measured in beats rather than seconds. Beats nominally occur at a steady tempo, that is, so many beats per second, but in actual music performance, tempo can vary or even pause, and beats can be displaced. Beats are often organized into measures and phrases, creating a hierarchical time structure. Furthermore, performers may not adhere strictly to tempo and beats, choosing rather to introduce expressive timing variations. All of these aspects of musical time can be modeled computationally, and some languages have specific facilities to represent hierarchical time and tempo structures.

For example, Nyquist evaluates expressions within an environment that maps from “logical time” (e.g., beats) to “physical time” (seconds). This mapping can express local tempo as slope (derivative), and mappings can be nested to represent hierarchical structures such as a swing feel (local perturbations of time) within an overall increasing tempo.

Events, Gestures, and Sound

Musical computation takes place at different levels of granularity. A musical “event” usually refers to a macro-scale behavior that has a beginning, duration, and end time. Conventional musical notes can be considered events, but so can the performance of an entire movement of a sonata, for example. Events are often represented by the invocation of functions in programming languages.

“Gestures” in the computer music community usually refer to a continuous function of time, typically a time sequence of sensor values. Examples include pitch-bend information from a MIDI keyboard, accelerometer data from a dancer, and the X-Y path of a mouse. Gestural computations require concurrent processing over time and there may be special language support for this.

“Sound” refers to sequences of audio samples. Because audio sample periods are in the range of microseconds while the (worst case) response time of computers to events is often multiple milliseconds, audio processing usually requires special organization, buffers, and scheduling, and this has a great impact on computer music languages, as we will see in the next section.

The need to process events, gestures, and sounds is one of the main motivations for computer music languages. Often, computer music languages borrow most of their designs from conventional programming languages, and it is these time-based concepts that drive the differences.

Data Flow and Synchronous Behavior

Many computer music languages enable audio processing. Music audio is often large, e.g., a 20-min composition in 8 channels of floating point samples takes ~1.7 gigabytes of storage. To deal with such large sizes and also to enable real-time control, audio is usually computed incrementally by “streaming” the audio samples through a graph of generators and operators.

Figure 3 illustrates a simple example that mixes two incoming channels, delays them, filters them, and pans the result to two output channels. The computation expressed by this graph is synchronous, meaning that for each computational step, a node accepts a sample from each input (on the left) and generates a sample for each output (on the right). Samples must never be ignored (dropped) or duplicated. This style of processing is sometimes called “data flow” and is quite different from processing in more common procedural and object-oriented languages. The need to support this type of synchronous signal processing has had a strong influence on computer music language design, as we shall see.

FIGURE 3

Figure 3. An audio computation graph.

A Good Music Programming Language Should Be a Good Language

There are many languages designed specifically to describe musical scores and event sequences. In particular, languages such as ABC (Walshaw, 2017) for encoding music notation are common. See also Adagio (Dannenberg, 1998), Guido (Hoos et al., 1998), MUSIC-XML (Good, 2001), and Lillypond (Nienhuys and Nieuwenhuizen, 2003). In spite of the success of these examples, music is not so restricted and well-defined that it does not need the power of general-purpose programming languages. In particular, traditional music compositions rely on notation to communicate a fixed sequence of notes and rhythms, whereas modern computer music composition and performance emphasizes dynamic computation of notes and rhythms, and in general, sound events. This requires a more powerful and expressive language.

To illustrate this point, consider one of the earliest programming languages for music, Music V, which included a specialized “score” language to invoke sound synthesis events (e.g., “notes”) along a timeline, and an “orchestra” language that described the signal processing to occur within each sound event. Since the score language simply presented a static list of events, their times, and parameters, Music V was not a very general language in terms of computation. However, users soon developed more general “score generating languages” as front-ends to overcome limitations of Music V. This is evidence that music programming languages should be flexible to allow any computation to be expressed.

Music Is Not One Thing

Just as there are many styles of music, there are many ways to approach music computationally. Some languages attempt to focus on just one aspect of computation, e.g., Faust (Orlarey et al., 2009) is a language for describing audio signal processing algorithms, but it mostly leaves instantiation and control of these algorithms to other languages and systems. Other languages, such as Nyquist (Dannenberg, 1997b) and Open Music (Bouche et al., 2017), strive to be more general, with facilities for scores, automated music composition, control, signal analysis, and sound synthesis. The variety of musical problems and language design goals makes the study and design of computer music languages all the more interesting.

Flexibility to Compose Solutions Is More Important Than Ready-Made Capabilities

It is difficult to define a general language that cleanly addresses many types of problems. Languages attempting to support many different tasks often have several “sub-languages” to handle different programming requirements. For example, Music V has separate score and orchestra languages, and Max MSP has a similar syntax but different semantics and scheduling for control, audio signals, and image processing. In general, ready-made “solutions” within programming languages and systems tend to be overly specific and ultimately limiting. Therefore, more general languages with the flexibility to create new solutions for the problems at hand are more broadly useful. Within these languages, specific solutions are often developed as sharable packages and libraries.

Models of Time and Scheduling

Time is essential to music, and musicians have sophisticated abstractions of time. In this section, we will consider some of the abstractions and how these are reflected in programming languages.

Logical Time Systems

The most important time concept for computer music systems is the idea of logical time. Logical time is also a key concept for computer simulations that model behaviors and the progress of time. A simulation must keep track of simulated time even though simulations may run faster or slower than real time. Similarly, music systems can keep track of simulated, or logical time, computing the precise, ideal time at which events should occur. When a real-time system falls behind (the logical time is less than real time), the system can compute the next event earlier to catch up, and if logical time is greater than real time, the system can wait. Thus, systems based on precise logical times can avoid accumulating timing errors.

For example, Nyquist has operators to control when computations take place within a logical time system. To create a musical notes at times 0.5 and 3, one could write:

   sim(pluck(c4) @ 0.5, pluck(d4) @ 3)

Nyquist instantiates the pluck function at logical times 0.5 and 3, and the resulting sounds are combined by sim. In practice, Nyquist runs ahead of real time, keeping samples in a playback buffer, and output timing is accurate to within a sample period.

Tempo and Time Deformation

In addition to logical time, music systems often model tempo and beats, which essentially “warp” or “deform” musical time relative to real time. FORMULA (Anderson and Kuivila, 1990) was an early system with elaborate mechanisms for tempo and time deformation. In FORMULA, tempo changes are precisely scheduled events, and tempo can be hierarchical. For example, one process can regulate tempo, and another process, operating within the prescribed tempo framework, can implement a temporary speeding up and slowing down, or rubato.

In Nyquist, tempo changes are represented by mappings from one time system to another. These mappings can be combined through function composition to create nested structures such as tempo and rubato. These mappings can be specified using continuous functions, represented as sequences of samples just like audio (Dannenberg, 1997a).

Non-preemptive Threads in Formula and ChucK

One way to express concurrency and precise logical timing is to use threads or co-routines. Threads allow multiple computations to proceed concurrently rather than sequentially. Precise timing is obtained by introducing “sleep” or “wait” functions that pause computation of one thread, perhaps allowing other threads to run. In conventional programs, calling a “sleep” function would result in an approximately timed pause; then the thread would be scheduled to resume at the next opportunity. This of course can lead to the accumulation of small timing errors that can be critical for music applications.

A solution used in many computer music languages is to keep track of logical time within each thread. When the thread “sleeps,” its logical time is advanced by a precise amount. The thread with the lowest logical time always runs next until another “sleep” is made to advance its logical time. In this scheme, threads do not preempt other threads because, logically, time does not advance until a thread sleeps.

In FORMULA, “threads” are called processes, and “sleeping” is achieved by calling time_advance(delay), which indicates quite directly that logical time is manipulated. The decision to actually suspend computation depends on the relationship between logical time and real time. If logical time is greater, the process should suspend until real time catches up. If logical time is less, the process is behind schedule and should continue to compute as fast as possible until it catches up to real time.

In ChucK, threads are called “shreds” and the “sleep” operation is denoted by the “ChucK” operator (“ = >”). For example, advancing time by 500 ms is performed by the command

   500::ms = > now;

In many cases, it is not sufficient to wait to run threads until real time meets their logical time. Output is often audio, and audio samples must be computed ahead of real time in order to be transferred to digital-to-analog converters. Therefore, some form of “time advance” is used, where threads are scheduled to keep their logical time a certain time interval ahead of real time. Thus, output is computed slightly early, and there is time to transfer output to device driver buffers ahead of deadlines.

Models for Sound Synthesis

As mentioned earlier, sound and signal computation is synchronous and often expressed as a graph where nodes represent computations and edges represent the flow of audio samples (Bernardini and Rocchesso, 1998). In some cases, the computational nodes have parameters such as filter frequencies, delay times, scale factors, etc., that can be updated, resulting in a hybrid that combines synchronous data-flow computation with asynchronous parameter updates.

In MaxMSP and Pd, audio computation graphs are described graphically. Figure 4 illustrates a simple program in Pd that generates a sinusoid tone, with a slider to adjust the frequency parameter.

FIGURE 4

Figure 4. Audio signal graph expressed in Pd.

Functional Programming

Another approach to representing audio signal graphs is functional programming languages. In the functional approach, audio computation is viewed as functions applied to (infinite) streams of samples. For example, in Nyquist, one can write the command

   play lp(buzz(15, C4, lfo(6) * 5),

           env(1, 0, 1, 900, 900, 1)) ~ 3

The function buzz generates a tone with 15 harmonics, a pitch of C4, and frequency variation determined by the function lfo, which creates a vibrato-like signal that is scaled using “* 5.” The buzz signal is passed through a low-pass filter (lp) with a cutoff frequency determined by a time-varying “envelope” function specified by the env function. The entire expression is evaluated in the context of the “~ 3” operation, which means to “stretch” time computations by a factor of 3, resulting in a 3-s-long sound (This is an example of creating a logical time system that is “stretched” relative to real time).

This example shows how functional notation can be used to describe audio computation graphs. Strictly speaking, nested functions alone describe tree structures, but by introducing variables, one can describe any acyclic graph structure where nodes are functions and edges are sounds or other values.

In conventional programming languages, sub-expressions are evaluated first, then functions are applied (this is called applicative-order evaluation). This could be a problem if sounds are very long (large) or if sounds are derived from real-time input. Nyquist solves this problem through lazy evaluation, where sounds are represented by run-time structures that will eventually compute samples, but not until they are needed.

In lazy evaluation systems, function arguments (i.e., sub-expressions) are not evaluated before passing them to functions (outer expressions). For example, we could construct a list containing f (1), f (2), …, f (N) without ever applying function f. Later, if the program selects the 3rd element of the list for output, the evaluator would need to evaluate f (3). When expressions are evaluated on demand, it is possible to express infinite sequences, yet evaluate them incrementally with finite memory. This approach is taken by Nyquist, which uses lazy evaluation to implement a built-in data type called SOUND, and Faust, which allows signal processing to be expressed as the computation of infinite sequences of numbers.

Because the run-time behavior of signal processing functions is quite sophisticated, few computer music languages have any way to define fundamentally new signal processing functions. Instead, the language provides a set of “primitive” functions such as oscillators, filters, and control signal generators (examples are buzz, lp, and lfo, respectively) that can be composed into more interesting functions. This is one shortcoming of most computer music languages. Even with hundreds of signal processing primitives, there are always new ideas, and new primitives must be implemented in another language (typically in the lower-level languages C or C++, but we will see exceptions such as Faust).

Objects and Updates

Functional programming, especially for real-time systems, is not very popular. Another way to model audio computation graphs is with objects and object-oriented programming. In this approach, we do not view sounds as “values” and we do not rely on the language and runtime system to implement them efficiently using lazy evaluation. Instead, we can use a somewhat less abstract approach that exposes the underlying implementation. Instead of sounds as values, we represent sounds as “objects”—a programming structure that packages a collection of operations or “methods” with a collection of data values.

In the “sound-as-object” approach, we can still write programs that look more-or-less like functional programming, e.g., buzz(15, c4, lfo(6) * 5), only now, buzz, lfo and “*” return objects that are linked together forming an audio computation graph. To “play” the graph, one typically “pulls” samples from the root node by calling its compute method. This method may recursively call compute methods on other nodes. For example the compute method of buzz will call that of “*,” which will call that of lfo. Each object will use returned samples to compute and return its own samples.

By replacing sounds with objects that compute sounds, we can achieve a functional programming style without the complications of lazy evaluation and garbage collection used by Nyquist (Dannenberg, 1997c). This sound-as-object approach is common, but not quite as powerful as the sound-as-values approach. For example, in Nyquist one can write:

   set x = osc(c4)

   play seq(cue(x), cue(x) @ 2)

which will have the effect of playing x at both time 0 and time 2 (the “@” operator is another logical time system constructor that shifts logical time of the expression on the left relative to the logical time system in effect). If x is a reference to an object, and if the object is used to generate a sound at time 0, the samples will no longer exist at time 2. In contrast, Nyquist saves the samples comprising x at least long enough to access them again 2 s later as required by this expression.

While objects might be a limitation in this example, objects have the advantage in real-time systems that they can be modified or updated to change their behavior. Consider the vibrato function lfo(6) from previous paragraphs. If lfo(6) is a value, it is wholly defined by this expression. On the other hand, if lfo(6) creates an object, one can imagine that, at some later time, the program could send a “set_frequency” message to the object to change the rate of vibrato.

Thus, the object-oriented approach provides an intuitive way to mix synchronous sample-by-sample computations with asynchronous real-time event processing. Amatriain (2005) goes further to propose a general model for interactive audio and music processing where the fundamental building blocks are objects with:

• other signal-generating objects as inputs,

• event-like inputs that invoke object methods (functions),

• signals as outputs, and

• event-like outputs, providing a way for the object to send notifications about the signal

Figure 5 illustrates this object model, and, of course, the model is recursive in that a signal-processing object can be composed from the combination of other signal-processing objects. The CLAM system (Amatriain et al., 2006) used this model within a C++ language framework.

FIGURE 5

Figure 5. Amatriain's object model of signal computation.

Block Computation

Music audio computation speed can be a significant problem, especially for real-time systems. One way to make computation more efficient is to compute samples in vectors or blocks. Audio computation requires the program to follow links to objects, call functions, and load coefficients into registers. All of this overhead can take as much time as the arithmetic operations on samples. With block computation, we compute block-by-block instead of sample-by-sample. Thus, much of the computational overhead can be amortized over multiple samples. While this is a seemingly small detail, it can result in a factor of two speedup.

Unfortunately, block computation creates a number of headaches for language designers that have yet to be resolved. The main problem with block computation is that logical computation times are quantized into larger steps than would be the case for individual samples, which typically have a period of 22 μs. In contrast, blocks of 64 samples (a common choice) have periods of 1.4 ms. There are signal-processing situations where 1.4 ms is simply not precise enough. A simple example is this: suppose that an amplitude envelope is composed of linear segments that can change slope at each block boundary. This means that the rise time of a sudden onset can be 0, 1.4, or 2.8 ms, but nothing in between. We are sensitive to the sound quality of these different rise times.

Some languages, such as Csound (Lazzarini et al., 2016), allow the user to specify the block size so that smaller blocks can be used when it matters, but using smaller blocks to solve one particular problem will result in less efficient computation everywhere. Max/MSP allows different parts of the audio computation to use different block sizes. Music V uses a variable block size. In Music V, a central scheduler keeps track of the logical time of the next event, which might begin a note or other signal processing operation. If the next logical time is far enough in the future, a full sized block is computed. If the next logical time is a few samples in the future, then the audio computation graph is traversed to compute just the next few samples. This allows the graph to be updated with sample-accurate timing.

Another way to save computation is to compute some signals at a lower control rate. Many signals are used to control amplitude, frequency, filter cutoffs, and other parameters that change relatively slowly. Typically, these control signals can outnumber audio signals, so control rate computation can save a substantial amount of computation. This affects language design because signal-processing primitives may come in two types: audio rate and control rate. Often, the control rate is set to the block rate so that a control signal has just one sample per block while audio signals have many samples (e.g., 8 to 64) per block.

Some Examples

Now that we have explored some issues and design elements that influence computer music programming languages, it is time to look at some specific languages. There is not space for complete descriptions, so this section aims to convey the flavor and unique characteristics found in a selection of examples.

Music N

The earliest computer music languages were created by Max Mathews at Bell Labs starting in 1957. A series of languages named MUSIC I, MUSIC II, etc. inspired similar languages including MUSIC 360 for the IBM 360, MUSIC 4BF implemented in FORTRAN, MUSIC 11 for the PDP-11, and Csound implemented in the C programming language. Because the underlying semantics are so similar, these programs are often referred to as “Music N.”

The most characteristic aspect of Music N is the separation of the “score” and “orchestra” languages, so Music N is really two languages that work together. The score language is essentially an unstructured list of events. Each event has a starting time, duration, an instrument, and a list of parameters to be interpreted by the instrument. The following example shows a few notes from a Music V score (Mathews et al., 1969):

   NOT 0 1 .50 125 8.45 ;

   NOT .75 1 .17 250 8.45 ;

   NOT 1.00 1 .50 500 8.45 ;

Each line plays one note. The first note (line 1) starts at time 0, uses instrument #1, has a duration of 0.5 s, and has two more parameters for amplitude and pitch control.

The orchestra language defines instrument #1 as follows:

   INS 0 1 ;

   OSC P5 P6 B2 F2 P30 ;

   OUT B2 B1 ;

   END ;

The idea is that for each note in the score, an instance of an instrument is created. An instance consists of data for each of the signal processing “objects” OSC and OUT. These objects take parameters from the score using “P” variables (e.g., the amplitude and pitch are denoted by P5 and P6, which take the 5^th and 6^th fields from the note in the score).

While its syntax is primitive due to 1960's era computing capabilities, Music V paved the way for many future languages. One big idea in Music V is that instruments are created with a time and duration that applies to all of their signal-processing elements. This idea was extended in Nyquist so that every function call takes place within an environment that specifies time, duration (or stretch factor), and other parameters. Although Music V instruments describe sequential steps (e.g., OSC before OUT in this example), there are clear data-dependent connections (OSC outputs to buffer B2, which is read by OUT), and in a modern language like Nyquist, merely by allowing nested expressions, one can write something like play(osc(c4)), indicating data dependencies and data flow in a functional style.

Thus, Music N made several contributions and innovations. First is the idea that one can create virtual “instruments” by combining various signal processing elements that generate, filter, mix, and process streams of digital audio samples. In Music V, these elements (such as OSC and OUT in the example) are called “unit generators.” Nearly all software synthesizers use this concept. Second, Music V introduced the idea that virtual instruments can be invoked somewhat like functions in sequential programming languages, but instances of instruments can exist over time and in parallel, computing a block of samples at each time step. Third, Music V introduced the essential ingredient of time into computer music languages. When instruments are invoked, they are given a starting time and duration, which affect not only the instrument but also all of the unit generators activated inside the instrument.

It should be mentioned that the “modern” Music N language is Csound, which has progressed far beyond the early Music V. In particular, Csound supports a much more modern expression syntax, many more unit generators, some procedural programming, and provisions for real-time control.

Nyquist, mentioned earlier, is also a descendent of Music V. If one considers a Music V score to denote the sum of the results of many timed function calls, and Music V orchestras as functions that return sounds, defined in terms of unit generators and other functions, then much of the semantics of Music V can be expressed in a functional programming style. This is more powerful than Music N because it unifies the ideas of score and orchestra, allowing “instruments” to contain scores and sequences, scores to be hierarchically composed of sub-scores, and instruments to contain sub-instruments.

Max/MSP and Pd

In contrast to Music N, Max/MSP (Puckette, 2002) and its open-source twin Pd (Puckett, 1996) are visual programming languages, but they at least share the idea of “unit generators.” Sound synthesis is accomplished by “drawing” unit generators and “connecting” them together with virtual wires, creating data flow graphs as we saw in Figure 4.

Max/MSP does not normally structure data-flow graphs into “instruments,” make instances of graphs, or attach time and duration to graphs. These are limitations, but Max/MSP has the nice property that there is a one-to-one correspondence between the visual interface and the underlying unit generators.

Timing, sequencing and control in Max/MSP is accomplished by sending “update” messages to unit generators. For example, the “patch” in Figure 6 contains a mixture of signal-processing unit generators and message-passing objects. The dashed lines represent signals and the solid lines represent connections for message passing. This patch uses sfplay~ to play a sound file. The output of sfplay~ is passed through *~, which multiplies the signal by another value to implement a volume control, and the audio output is represented by dac~. To control the patch, there is no score. Instead, when “1” is sent to sfplay~, it plays to the end of the file (the user simply “drags and drops” the desired file from the computer's file browser). The user can click on the message box containing “1” to send that message. Similarly, the user can control volume by dragging the cursor up or down on the number box containing “0.72.” Changes are sent as messages to *~, which updates its internal scale factor to the new number.

FIGURE 6

Figure 6. A simple “patch” in Max/MSP to play a sound file with volume control.

SuperCollider

SuperCollider (McCartney, 2002) is primarily a real-time interactive computer music language, having roughly the same goals as Max/MSP. However, SuperCollider is text-based and emphasizes (1) more flexible control structures, (2) treating objects as data and (3) support for functional programming. For the most part, SuperCollider is organized around object classes. The class UGen represents unit generators, class Synth represents a collection of unit generators that produce audio output, and class Stream represents a sequence of values, which are often parameters for sound events (e.g., notes).

SuperCollider separates control from synthesis, using two processes communicating by messages. One reason for this is to insulate the time-critical signal processing operations in the synthesis engine, scsynth, from less predictable control computations in the composition language, sclang.

SuperCollider illustrates some of the trade-offs faced by language designers. Earlier versions of SuperCollider had a more tightly coupled control and synthesis systems, allowing control processing to be activated directly and synchronously by audio events. Also, audio processing algorithms, or instruments, could be designed algorithmically at the time of instrument instantiation. In the latest version, instrument specifications can be computed algorithmically, but instruments must be prepared and compiled in advance of their use. This makes it faster to instantiate instruments, but creates a stronger separation between control and synthesis aspects of programs.

Figure 7 contains a very short SuperCollider program to play a sequence of chords transposed by a random amount. In this program, the SynthDef describes an instrument named sawSynth, which consists of three sawtooth oscillators (Saw, parameterized by an array of 3 frequencies, returns three oscillators, which are reduced to stereo by Splay). The sound is then low-pass filtered by LPF, which is controlled by a slowly varying cutoff frequency generated by LFNoise2. The ar() and kr() methods denote audio rate and control rate versions of unit generators, where lower-frequency control-rate processing is used for efficiency. The instrument is compiled and loaded into the synthesizer engine.

FIGURE 7

Figure 7. A simple SuperCollider composition and synthesis program, based on examples by Bruno Ruviaro (http://sccode.org/1-54H).

The Pbind expression constructs messages using patterns Pseq, Prand, and Pkey to generate parameter values for the synthesizer and to control the duration of each event. For example, Pseq alternately selects the array [50, 53, 55, 57], generating one chord, and another array [53, 56, 58, 60], offset by a random integer from 0 to 10 (using Pwhite). The result of each pattern generator is of type Stream, which represents an infinite sequence of values. In this case, playing the stream generates an infinite sequence of events representing chords, and sends the events to be played by the synthesizer.

ChucK

ChucK (Wang et al., 2015) is an open source project that originally focused on “live coding,” or writing and modifying code in real time as a music performance practice. ChucK terminology uses many plays on words; for example, ChucK refers to precise timing (described earlier) as “strongly timed,” which is a reference to a class of conventional languages that are “strongly typed.”

ChucK uses a construct called a “shred” (similar to and rhymes with the conventional term “thread,” and possibly a reference to “shredding” or virtuosic lead electric guitar playing.) A shred is the basic module of ChucK, providing a thread and some local variables whose lifetimes are that of the thread. In Figure 8, the first line creates a data flow graph using the unit generators SinOsc, ADSR, and dac. The “ChucK” operator (=>) forms the connections. Notice how this syntax not only establishes connections, but also names the unit generators (s and e, short for for “sinusoid” and “envelope”). This ability to reference unit generators and update them corresponds to Amatriain's “Objects and Updates” model, as we will see in the code.

FIGURE 8

Figure 8. ChucK example code. (based on http://chuck.cs.princeton.edu/doc/examples/basic/adsr.ck).

One might expect a different syntax, e.g., dac(SinOsc(ADSR)), which would allow unit generators (such as mixers and multipliers) to accept multiple inputs and parameters. In ChucK, additional parameters are set in various ways using additional statements. You can see e.set(…) used to set envelope parameters, and 0.5 = > s.gain used to set the oscillator gain.

After initializing variables, values, and connections, a typical ChucK shred enters a while loop that describes a repeating sequential behavior. Here, we see e.keyOn() and e.keyOff(), used to start and stop the envelope, and 800::ms = > now, used to pause the shred for 800 ms of logical time. During the pause, the unit generators continue to run and generate audio.

In ChucK, unit generators compute one sample at a time, which is less efficient than block-at-a-time computation, but it allows the thread to awaken and update unit generators with sample-period accuracy. This allows for some very interesting control and synthesis strategies that interleave “standard” unit generators with custom control changes.

Faust

While most computer music languages provide some way to express “notes” or sound events that instantiate an audio flow graph (or, in Max/MSP, send messages to audio objects that already exist), Faust (Orlarey et al., 2009) is designed purely to express audio signal computation. Faust also differs from most other languages because it does not rely on a limited set of built-in unit generators. Instead, Faust programs operate at the audio sample level and can express unit generators. In fact, Faust can output code that compiles into unit generators for a variety of languages such as Csound, described earlier.

Rather than inter-connecting pre-compiled unit-generators at run time like many other languages, Faust produces code in the C++ programming language (also other languages such as Java, Javascript, and WebAssembly) that must then be compiled. This compilation avoids much of the overhead of passing data between unit-generators, allowing the primitive elements of Faust to be very simple operators such as add, multiply, and delay. These operations apply to individual samples.

Although Faust is text-based, it uses an unusual syntax to encode block diagrams as an alternative to more conventional functional notation. In functional notation, we write f (input1, input2) to denote the output of f with inputs input1 and input2, but in Faust, we write input1, input2: f as if signals are flowing left-to-right. The comma (,) denotes “parallel composition,” which is to say that input1 and input2 are fed in parallel to f. The colon (:) denotes “sequential composition”: data flows from input1, input2 into f. Other composition operators describe feedback loops, splitting (fan-out) and summing (fan-in).

Figure 9 contains an example of a Faust program to generate a sine tone with frequency and amplitude controls (Orlarey, 2015). Here, we see a mixture of functional notation, “block diagram” notation, and infix notation. Typically, a sine tone computation would be built into a language, because at best, it would be very, inefficient to describe this computation in terms of available operations. Because Faust works at the sample level and writes code for an optimizing compiler, it is practical to describe oscillators, filters, and many signal processing algorithms. In fact, this is the main goal of Faust.

FIGURE 9

Figure 9. A program in Faust to generate a sine tone.

In Figure 9, the second line describes the phase computation. The third line simply scales the phase by 2π and computes the sine. In functional notation, we would say osc(f) = sin(2π · phasor(f)). The phasor function should therefore return a signal where samples increase step-by-step from 0 to 1, then wrap around (using the modulus function fmod) to 0. In a procedural programming language, we might define a variable phase and assign new values to it, e.g.,

   phase = fmod(phase + increment, 1);

But Faust is a functional language with no variables or assignment operators, so the algorithm is expressed using feedback denoted by “~_.” This says to take a copy of the output and feed it back into the input. Thus, the previous sample of phase is combined with f/ma.SR, and these two signals are added (by “+”) and become the first argument to fmod.

The last definition, of process, illustrates that graphical user interface elements can be considered signal generators. Here, a slider labeled “freq” controls the amount by which phase is incremented as a way to change the oscillator frequency, and “level” controls a scale factor of the samples output by osc.

Faust is specialized to describe audio signal processing algorithms. For example, it would be difficult to use Faust to compose a melody. Nevertheless, Faust has become quite popular for creating unit generators and signal processing plug-ins that can be used in other languages and systems. There are substantial libraries of Faust functions, Faust is able to generate ready-to-use modules for a number of different systems, and Faust helps developers avoid many low-level details of programming directly in C or C++.

Conclusions

Computer music languages offer a fascinating collection of techniques and ideas. Computer music languages differ from other languages in that they must deal with time, complex concurrent behaviors, and audio signals. All of these concepts are fairly intuitive as they relate to music, but they can be very tricky to program in conventional programming languages. Because music making is more a creative process than an engineering discipline, it is important for languages to support rapid prototyping and experimentation, which also leads to specialized notations, syntax and semantics.

Computer Music Language Challenges

We have seen a number of design issues and some solutions, but there are many challenges for future language designers. We saw how Music N described music synthesis in two languages: the score language, which specifies timing and parameters for synthesis computations, and the orchestra language, which describes the synthesis computations as a graph of interconnected unit generators. In practice, there is a third language needed to describe the internal processing of each unit generator. Nyquist showed a way to unify the score and orchestra languages into a mostly-functional programming language, but it would be even better if Nyquist could define new unit generators as well. Chronic (Brandt, 2000, 2002) was one approach to bridging this gap, but it required special conventions for expressing signal processing algorithms, almost as if using a separate language. Faust (Orlarey et al., 2004, 2009) and Kronos (Norilo, 2015) offer very clean notations for describing unit generators, but neither includes a flexible or powerful notation for events, scores, dynamic instantiation of concurrent behaviors or time-based scheduling.

The functional programming approach seems natural for signal processing because it is a good match to synchronous data flow or stream-processing behaviors that we see inside unit generators. Functional programming is also natural for the expression of interconnected graphs of unit generators. However, it is also natural to view unit generators as stateful objects that operate on signals synchronously while allowing asynchronous updates to parameters such as volume, frequency, and resonance. It is the nature of music that things change. If “change” could always be expressed as a signal, perhaps music representations would be simpler, but in practice, “change” often arises from discrete events, for example key presses on a musical keyboard. Intuitively, these are state changes, so an important challenge in music language design is providing “natural” functional descriptions of signal flow while at the same time enabling the expression of state changes, discrete events, and their interaction with signals.

A third challenge is to facilitate the inspection and understanding of complex real-time music programs. Max/MSP, with its visual representation of computation graphs, makes it easy to insert probes and visualizations of messages and signals; thus, it ranks highly in terms of transparency. However, Max/MSP does not encourage abstraction in the form of functions, classes, multiple concurrent instances of behaviors, or recursion, and even iteration can be awkward to design and observe. Gibber (Roberts et al., 2015), a live-coding language, takes the innovative approach of animating the source code to indicate when statements are evaluating. Even the font sizes of expressions can be modulated in real time to reflect the amplitude of the signal they are generating. This kind of dynamic display of programs draws attention to active code and helps to associate sounds with the expressions that gave rise to them. In Aura (Danenberg, 2004), one can design instruments from unit generators with a visual editor (inspired by Max) as well as with code. The visual instrument editor automatically generates a graphical control panel for the instrument so that the user can test the instrument interactively, either before incorporating the instrument into a composition, or after that when questions arise. The general challenge for language designers is to provide useful inspection and debugging facilities, especially for real-time music performances involving timed, concurrent behaviors.

Language Development Is Active

Although computer music language development began in the 1950's, there is quite a lot of activity today. If anything, fast computing hardware has opened new capabilities, created more demand for creative music software, and encouraged more development. Faster computers also facilitate software development. Ambitious language development projects can be accomplished faster than ever before. On the other hand, users have become accustomed to advanced programming environments with automatic command completion, pop-up hints, reference materials, syntax-directed editing and other conveniences, and this adds to the burdens of language development. Failure to provide these amenities makes new languages more difficult to learn and use.

Wide Range of Users, Wide Range of Needs

Another factor that keeps music language development lively is the many different disciplines and needs of users. Music applications range from theoretical music analysis to live coding. Other applications include generating and controlling MIDI data (an interface designed for and universally used by commercial synthesizers), algorithmic composition, and music typesetting. Applications we have already discussed include music signal processing and event-based real-time systems. Each application area motivates different language organizations and semantics. To some extent, different levels of technical expertise—from beginner to professional software developer—also place emphasis on different aspects of music programming. For all these reasons, we can expect that music language design and development will remain active and interesting for the foreseeable future.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer, GF, and handling editor declared their shared affiliation at the time of the review.

References

Amatriain, X. (2005). An Object-Oriented Metamodel for Digital Signal Processing. Ph.D. Thesis, Universitat Pompeu Fabra, Barcelona.

Amatriain, X., Arumi, P., and Garcia, D. (2006). “CLAM: a framework for efficient and rapid development of cross-platform audio applications,” in Proceedings of ACM Multimedia (New York, NY: ACM), 951–954.

Google Scholar

Anderson, D. P., and Kuivila, R. (1990). “A system for computer music performance,” in ACM Transactionas on Computer Systems (New York, NY: ACM), 56–82.

Google Scholar

Assayag, G., Rueda, C., Laurson, M., Agon, C., and Delerue, O. (1999). Computer assisted composition at Ircam: patchWork & OpenMusic. Comput. Music J. 23, 59–72.

Google Scholar

Bernardini, N., and Rocchesso, D. (1998). “Making sounds with numbers: a tutorial on music software dedicated to digital audio,” in Proceedings of COST G-6 DAFX (Barcelona).

Google Scholar

Bouche, D., Nika, J., Chechile, A., and Bresson, J. (2017). Computer-aided composition of musical processes. J. N. Music Res. 46, 3–14. doi: 10.1080/09298215.2016.123013

CrossRef Full Text | Google Scholar

Brandt, E. (2000). “Temporal type constructors for computer music programing,” in Proceedings of the 2000 International Computer Music Conference (San Francisco, CA: International Computer Music Association), 328–331.

Brandt, E. (2002). Temporal Type Constructors for Computer Music Programming. Ph.D. Thesis, School of Computer Science, Carnegie Mellon University Pittsburgh. Available online at: https://www.cs.cmu.edu/~music/chronic/.

Crosby, A. (1997). The Measure of Reality: Quantification and Western Society, 1250-1600. Cambridge: Cambridge University Press.

Google Scholar

Danenberg, R. B. (2004). “Combining visual and textual representations for flexible interactive signal processing,” in The ICMC 2004 Proceedings (San Francisco, CA: International Computer Music Association).

Google Scholar

Dannenberg, R. B. (1997a). Abstract time warping of compound events and signals. Comput. Music J. 21, 61–70.

Google Scholar

Dannenberg, R. B. (1997b). Machine tongues XIX: nyquist, a language for composition and sound synthesis. Comput. Music J. 21, 50–60.

Google Scholar

Dannenberg, R. B. (1997c). the implementation of nyquist, a sound synthesis language. Comput. Music J. 21, 71–82.

Google Scholar

Dannenberg, R. B. (1998). The CMU MIDI Toolkit. Manual, Carnegie Mellon University, Carnegie Mellon University, Pittsburgh. Available online at: http://www.cs.cmu.edu/~music/cmt/cmtman.txt.

Good, M. (2001). “MusicXML for notation and analysis,” in The Virtual Score: Representation, Retrieval, Restoration, eds W. B. Hewlett and E. Selfridge-Field (Cambridge: MIT Press), 113–124.

Google Scholar

Hoos, H., Hamel, K., Renz, K., and Kilian, J. (1998). “The GUIDO music notation format - a novel approach for adequately representing score-level music,” Proceedings of the International Computer Music Conference (San Francisco, CA: International Computer Music Association), 451–454.

Google Scholar

Jin, Z., and Dannenberg, R. B. (2013). “Formal semantics for music control flow,” in Proceedings of the 2013 International Computer Music Conference (San Francisco, CA: International Computer Music Association), 85–92.

Google Scholar

Lazzarini, V., Yi, S., Ffitch, J., Heintz, J., Brandtsegg, Ø., and McCurdy, I. (2016). Csound: A Sound and Music Computing System. Cham: Springer.

Google Scholar

Lindemann, E. (1990). “ANIMAL - A rapid prototyping environment for computer music systems,” in Proceedings of the International Computer Music Conference (San Francisco, CA: International Computer Music Association), 241–244.

Google Scholar

Mathews, M. V., Miller, J. E., Moore, F. R., Pierce, J. R., and Risset, J. C. (1969). The Technology of Computer Music. Cambridge, MA: MIT Press.

Google Scholar

McCartney, J. (2002). Rethinking the computer music language: supercollider. Comput. Music J. 26, 61–68. doi: 10.1162/014892602320991383

CrossRef Full Text | Google Scholar

Nienhuys, H-W., and Nieuwenhuizen, J. (2003). “Lilypond, a system for automated music engraving,” in Proceedings of the XIV Colloquium on Musical Informatics (XIV CIM 2003) (Firenza: Tempo Reale), 1–6.

Google Scholar

Norilo, V. (2015). Kronos: a declarative metaprogramming language for digital signal processing. Comput. Music J. 39, 30–48. doi: 10.1162/COMJ_a_00330

CrossRef Full Text | Google Scholar

Orlarey, Y. (2015). A Sine Oscillator. Available online at: http://faust.grame.fr/examples/2015/09/30/oscillator.html (accessed Jan 26, 2018).

Orlarey, Y., Fober, D., and Letz, S. (2004). Syntactical and semantical aspects of faust. Soft Comput. 8, 623–632. doi: 10.1007/s00500-004-0388-1

CrossRef Full Text | Google Scholar

Orlarey, Y., Fober, D., and Letz, S. (2009). FAUST: An Efficient Functional Approach to DSP Programming. New Computational Paradigms for Computer Music. Paris: Editions Delatour.

Google Scholar

Puckett, M. (1996). “Pure data,” in Proceedings, International Computer Music Conference (San Francisco, CA: International Computer Music Association), 224–227.

Puckette, M. (2002). Max at Seventeen. Comput. Music J. 26, 31–43. doi: 10.1162/014892602320991356

CrossRef Full Text | Google Scholar

Roberts, C., Wakefield, G., Wright, M., and Kuchera-Morin, J. (2015). Designing musical instruments for the browser. Comput. Music J. 39, 27–40. doi: 10.1162/COMJ_a_00283

CrossRef Full Text | Google Scholar

Walshaw, C. (2017). Available online at: abcnotation.com (Accessed January 29, 2018).

Wang, G., Cook, P. R., and Salazar, S. (2015). ChucK: a strongly timed computer music language. Comput. Music J. 39, 10–29. doi: 10.1162/COMJ_a_00324

CrossRef Full Text | Google Scholar

Yi, S. (2017). Blue - a Music Composition Environment for Csound. Available online at: http://blue.kunstmusik.com/ (Accessed January 29, 2018).