Andrew J. Goodwin1,2*
Danny Eytan1,3
William Dixon1Sebastian D. Goodfellow1,4Zakary Doherty5
Robert W. Greer1
Alistair McEwan2Mark Tracy6,7Peter C. Laussen8Azadeh Assadi1,9
Mjaye Mazwi1,10- 1Department of Critical Care Medicine, The Hospital for Sick Children, Toronto, ON, Canada
- 2School of Biomedical Engineering, University of Sydney, Sydney, NSW, Australia
- 3Department of Medicine, Technion - Israel Institute of Technology, Haifa, Israel
- 4Department of Civil and Mineral Engineering, University of Toronto, Toronto, ON, Canada
- 5Research Fellow, School of Rural Health, Monash University, Melbourne, VIC, Australia
- 6Neonatal Intensive Care Unit, Westmead Hospital, Sydney, NSW, Australia
- 7Department of Paediatrics and Child Health, The University of Sydney, Sydney, NSW, Australia
- 8Department of Anesthesia, Boston Children's Hospital, Boston, MA, United States
- 9Department of Engineering and Applied Sciences, Institute of Biomedical Engineering, University of Toronto, Toronto, ON, Canada
- 10Department of Paediatrics, University of Toronto, Toronto, ON, Canada
A firm concept of time is essential for establishing causality in a clinical setting. Review of critical incidents and generation of study hypotheses require a robust understanding of the sequence of events but conducting such work can be problematic when timestamps are recorded by independent and unsynchronized clocks. Most clinical models implicitly assume that timestamps have been measured accurately and precisely, but this custom will need to be re-evaluated if our algorithms and models are to make meaningful use of higher frequency physiological data sources. In this narrative review we explore factors that can result in timestamps being erroneously recorded in a clinical setting, with particular focus on systems that may be present in a critical care unit. We discuss how clocks, medical devices, data storage systems, algorithmic effects, human factors, and other external systems may affect the accuracy and precision of recorded timestamps. The concept of temporal uncertainty is introduced, and a holistic approach to timing accuracy, precision, and uncertainty is proposed. This quantitative approach to modeling temporal uncertainty provides a basis to achieve enhanced model generalizability and improved analytical outcomes.
“A man with a watch knows what time it is. A man with two watches is never sure.” – Segal's Law
1. Introduction
Time is an essential concept in both clinical research and the practice of medicine in general (1–6). This is especially true in areas of practice such as critical care where large amounts of data are being collected, and where accurate and consistently recorded times are essential for the creation of a defensible medical record (7–9). A clear sense of the temporal relationship between an exposure or treatment and the subsequent patient condition is the means by which clinicians generate differential diagnoses and determine the efficacy of treatments (10–13). The significance of time in medical decision-making is underscored by the field's reliance on time series data as a means of determining patient trajectories in longitudinal monitoring (14), for example while following the progression of septic shock (15) or monitoring glucose levels in diabetic patients (16). Recent research focusing on clinical time series data has also demonstrated that actionable information may be embodied in the timestamps alone. i.e., the sequence and timing of the data collection process contains information above and beyond the physiological values that are being measured and recorded (17, 18).
Although identification of causal relationships, review of critical incidents, and generation of study hypotheses all require a robust understanding of the sequence of events (19), conducting such work in a clinical setting can be problematic when timestamps are recorded by independent and unsynchronized clocks (20–23). Additionally, the process of transferring timestamps into clinical and research databases may be adversely impacted by a multitude of random errors (24). These errors affect the measurement of time, thereby creating a situation where the timestamps stored in clinical databases may not necessarily represent the true time that an event occurred.
Measurement errors in general will typically occur early in the modeling process. These errors introduce bias and uncertainty that will propagate through downstream analysis (25–27), confounding the process of research and discovery of new phenomena (28–31). While quantification of uncertainty and analysis of measurement errors are ubiquitous concepts in fields such as physics and engineering (32–35) such techniques remain relatively uncommon in the medical literature (36) making it difficult for readers to judge the robustness of clinical research (37–39).
The temporal component of physiological measurements is important, and therefore should also be considered when assessing the impact of measurement errors (40), yet this process has been constrained by the fact that medicine has been relatively slow to embrace a robust approach to the measurement of time (41–43). To address this problem, we need to establish a formal and principled discipline around identification of timing errors and quantification of temporal uncertainty (44–46).
1.1. Motivation and overview
Our research group is embedded in critical care, a dynamic environment in which the patient condition can change rapidly, and where such changes are associated with significant modification of risk. Since 2016 we have been continuously recording high frequency physiological data streams in the critical care unit at The Hospital for Sick Children in Toronto, Ontario and have amassed a database of over one million patient-hours of data, comprising more than four trillion unique physiological measurements (47). Each observation in this database has been assigned a millisecond precision timestamp by at least two separate clocks, providing an ideal substrate for exploring the behavior of timekeeping systems in the critical care environment (48). As part of our efforts to develop robust physiological models and clinical decision support systems we have concluded it was prudent to explore potential biases and uncertainties around all sources of information used in these models, with an initial focus on the measurement of time (49, 50).
In order to achieve this goal, we began by identifying all timekeeping devices and by noting potential sources of timing error in an attempt to establish a preliminary understanding of their individual and collective impact (51). During this process we considered erroneous timepieces (Section 2), delays due to algorithmic effects (Section 3), human factors (Section 4), and random errors introduced by software and other systems (Section 5).
Building on this foundation we adopted a holistic approach to the measurement of accuracy, precision and uncertainty that could be consistently applied across a wide range of timepieces, data sources, and time scales. We then explored mechanisms by which the accuracy and precision of timestamps in our databases could be improved, either through retrospective correction of systematic errors, or prospectively via modification of our data collection procedures and systems (Section 6). Finally, after identifying and correcting systematic timing errors, we quantified any residual temporal uncertainty and incorporated this information as a core component of our physiological modeling and machine learning projects (Section 7).
This narrative review provides a broad overview of the issues we considered during this process, bringing together concepts from metrology, statistics, biomedical engineering, and numerical analysis to introduce the concept of temporal uncertainty in a clinical setting.
1.2. Temporal resolution, accuracy, and precision
All measurements are subject to errors (35), including measurements of time (40, 52). We consider the true time and our erroneous measurement of time to be two different variables (53), and we define accuracy to be the difference between these two values (see Figure 1). For our purposes we adopted Coordinated Universal Time (UTC) as the underlying, yet unobserved, source of truth (54–56). Where possible we used a relatively accurate and precise master clock as a close approximation of UTC as described in Section 6.1.
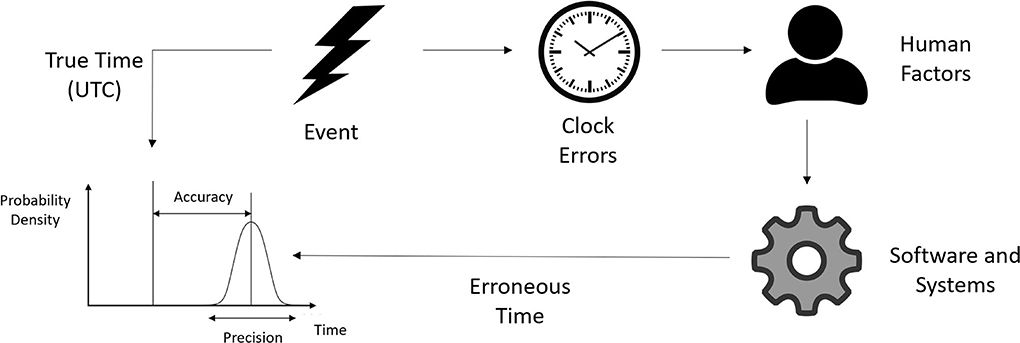
Figure 1. Times recorded in clinical databases may not represent the true time the event occurred. The precision and accuracy of a recorded time may be affected by several different factors.
We define the resolution of a timepiece as its ability to display or discern a precise moment, with lower resolution timepieces being less capable of describing the exact time an event occurred (57). Precision is related to resolution but is usually used to describe uncertainty that results from a random process. Modeling uncertainty due to precision and resolution is discussed in detail in Section 7.1. The terms precision and resolution will be used interchangeably throughout this review.
It is important to note that timing errors and uncertainties not only relate to the accuracy and precision of discrete times, but also to the accuracy and precision of the rate at which measured times drift away from true time, i.e., we also need to measure the quality of our timestamps as a function of time (see Section 2.2).
1.3. Temporal uncertainty
As an illustration of the utility of temporal uncertainty, consider as an example the situation where someone says “I'll meet you at the store in twenty minutes” and how that statement feels different from someone saying “I'll meet you at the store in nineteen minutes”. The presence of a rounded number in the former statement conveys a sense of indeterminacy about the time period, whereas “nineteen minutes” may be understood by a human listener as being somewhat more precise. Computer algorithms however are unable to understand this kind of implied precision and will assume that all recorded times are equally precise unless more information is explicitly provided. Our goal with this work is to quantify the uncertainty associated with measurements of time, and to make this information explicitly available to our models as an additional property of each temporal measurement.
Uncertainties in general may be classified as either epistemic or aleatoric, where epistemic uncertainties may be modeled and reduced, and aleatoric uncertainties may be characterized but not reduced (58, 59). It is useful to keep these distinctions in mind since our goal in this work is to identify, model, and correct epistemic temporal uncertainties, and to represent any remaining aleatoric temporal uncertainty as a probability density function. Techniques that can be used to model temporal uncertainty are discussed in Section 7.
Aleatoric uncertainties may be further categorized into homoscedastic uncertainty, where the variance of the errors remains constant for all recorded times, and heteroscedastic uncertainty, where some measurements of time in the same dataset are noisier than others (60). Situations that result in heteroscedastic temporal uncertainties are discussed in Section 7.2.
2. Erroneous timepieces in a clinical environment
Complex clinical environments may contain multiple devices that are all capable of recording timestamped data. If these devices are not synchronized it can be difficult to know which clock (if any) was the source of truth when retrospectively analyzing data. In this section we summarize the work of other groups who have observed inaccurate clocks in a clinical setting, and we describe the mechanisms that result in erroneous measurement of time.
2.1. Inaccurate clocks
Medical devices such as ventilators, cardiac monitors, regional saturation monitors, and renal replacement therapy devices may all individually use different approaches to how they manage and report time (61). Some devices may use a proprietary time synchronization system, while others may keep time independently, requiring manual programming to ensure that the displayed time is accurate (22, 62, 63). As a result of this variability, a single event observed by different medical devices may be recorded with different timestamps. Similarly, the elapsed time between two related events may be erroneously measured if different devices are used to record each event.
The accuracy of clocks in clinical settings has been documented by many researchers, including one study by Goldman who examined over 1700 clocks and over 1300 medical devices at four different hospitals (64). This investigation found that inaccurate timekeeping was pervasive and concluded that significant cost savings and improvements to patient safety could be gained if more rigorous approaches to timekeeping were adopted. Other groups have also published evidence of clinical timekeeping issues (4, 62, 65–76), and the potential hazards associated with unsynchronized clocks in medical devices was considered to be so serious by the Pennsylvania Patient Safety Authority that they issued an advisory warning about the problem in 2012 (77).
Figure 2 gives a schematic overview of the accuracy and resolution of various sources of time that may be found in a typical intensive care environment. The data shown in this figure are conceptual estimates only and have been generated by collating information from the research cited in Sections 2–5. Note that each axis has a logarithmic scale that spans eight orders of magnitude. Elongated ellipses are used to indicate that the precision or accuracy of a particular timepiece may be more variable along one of the axes. The position of a device shown in this figure indicates its approximate precision and accuracy before any of the timekeeping improvements described in Section 6 have been implemented.
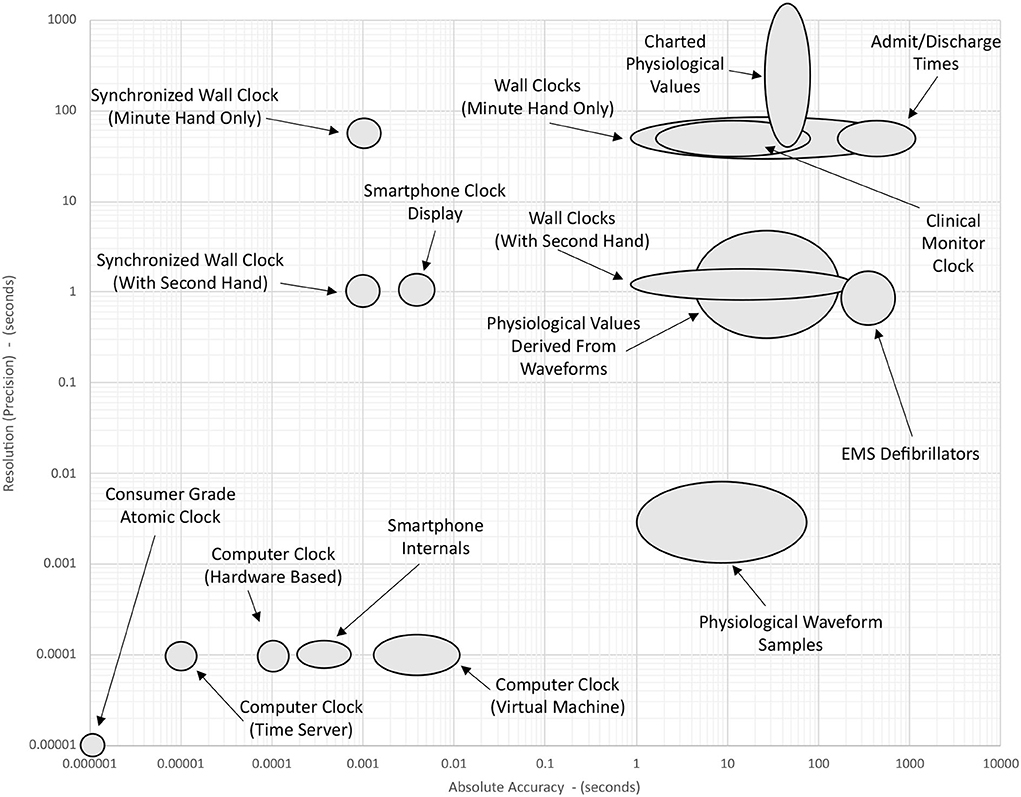
Figure 2. Approximate accuracy and resolution of different time sources in the ICU. Positions of the ellipses are determined by the summation of factors discussed in the literature cited in Sections 1–4. The position of a device shown in this figure indicates its approximate precision and accuracy before any of the timekeeping improvements described in Section 6 have been implemented.
2.2. Clock drift
Drift is defined as the gradual change in the magnitude of the measurement error over time (78). In the case of timing errors, drift results from a situation where a timepiece does not run at exactly the same rate as an accurate reference clock. The units of clock drift are seconds (of error) per second which is often stated as parts per million (ppm).
The drift rate of clocks and other timekeeping systems can be experimentally measured and systematically corrected. For example, Singh et al. measured the drift rate between clocks in a video camera and in the server housing the Electronic Medical Record (EMR) as part of a study examining the physical manipulation of neonates (79). In this situation, the two timepieces were found to have a relative drift rate of around 140ppm (around 0.5 s per hour).
Even within a seemingly homogeneous system, crystal oscillators and microelectromechanical oscillators may exhibit some variance in frequency (80, 81). The oscillation frequencies of these components may be affected by environmental factors such as variations in temperature or the flexible power management provided by modern microprocessors (82). Vilhar and Depolli encountered this phenomenon when they attempted to synthesize a 12-lead electrocardiogram (ECG) using multiple identical wireless sensors, each of which were observed to have a slightly different sample rate (83). Minor variations in the ECG sample rates of each sensor made it difficult to precisely synchronize the data streams during later analysis (84). Uncertain and variable delays over the wireless network also confounded the problem in this case.
2.3. Inaccurate and imprecise sample rates
Precise timing and synchronization of signals requires that the sample rates of sensors are precisely specified, yet medical device manufacturers' advertised sample rates may be inaccurate and should not be relied upon (85–87). These devices typically contain a crystal or microelectromechanical oscillator that generates a very stable resonance frequency which can be used to measure the passage of time. Although the sample rates of these components are often known by the manufacturer to five or more significant figures (80) they may be colloquially reported in documentation and marketing material using more rounded values (88).
For example, Jarchi and Casson found that PPG and motion data recorded using a Shimmer 3 GSR+ unit (Shimmer Sensing, Dublin, Ireland) (89) had a true sample rate of 255.69 Hz despite being marketed as having a sample rate of 256 Hz (90). Similarly, Vollmer et al. measured the true sample frequency of five different wearable biomedical sensors and found that their sample rates differed from the manufacturers stated sample rate by up to 290ppm (87).
Signals with imprecisely defined sample frequencies can become problematic if they are subsequently used for timekeeping purposes (84, 91). This kind of error is especially impactful in digital storage systems that use inferred time (see Section 2.4).
2.4. Inferred time
Physiological waveforms and other high frequency signals are often stored in a format that does not explicitly define the time for each individual sample, but instead relies on the sample rate to infer time. For example, the Waveform Database (WFDB) file format used by Physionet (92) calculates the time as a function of the sample frequency and the number of samples that have elapsed since the start of the file (93). Similarly, the Critical Care Data Exchange Format (94) supports inferred time for the storage of waveform data among several other options (95). Time series data that relies on inferred timestamps may be susceptible to drift as a result of imprecisely defined sample rates, and uncertainty associated with this imprecision will be cumulative. This concept is discussed in more detail in Section 7.1.
3. Algorithmic effects
A typical pre-processing pipeline for time series data may involve multiple computational steps (96, 97), each of which has the potential to impact timestamps in some way. These algorithms may either be applied to the data within a medical device, or may be the result of external data processing, or both (98). In this section, we discuss various algorithms that may be applied to physiological time series data and how these algorithms can introduce delays into the timestamps.
3.1. Moving averages and temporal abstraction
Multimodal medical time series will often comprise one or more irregularly sampled data streams (99–101). These data may be subsequently altered by parameterization or regularization of time, generating a periodic sequence that is smoother, more continuous, and therefore more amenable to analysis (102–104). Care must be taken however when calculating a moving average as several methods are available, each of which may affect the timing of the resultant data in different ways (105).
The Philips X2 multi-module, for instance, calculates the heart rate during normal rhythm by taking the average from the last twelve R-R intervals (106). Similarly, pulse oximetry is typically calculated as a moving average, introducing a delay with a magnitude related to the size of the averaging window (107–109).
3.2. Pre-processing of physiological waveforms
High-frequency physiological waveforms may be subject to a wide variety of smoothing, filtering, and buffering processes, each of which can introduce delays of different magnitudes. When two signals experience a different delay before being timestamped then they may appear to be out of phase when subsequently analyzed. Offsets of this kind are mentioned in the documentation for the MIMIC-II database, which informs users that the signals are not suitable for inter-waveform analysis (110). Sukiennik et al. overcame this problem by quantifying and correcting the delay between ECG and Arterial Blood Pressure (ABP) waveforms before calculating a cross correlation of the two signals (111). Variable delays were also documented in a different context by Bracco and Backman who observed that the display of the ABP waveform on a patient monitor was delayed by 900 ms, whereas the display of the photoplethysmography (PPG) waveform on the same monitor was delayed by 1,400 ms (112).
Adding complexity to this issue is the fact that the magnitude of the delay on an individual signal may not be constant with respect to time (113). Several groups have recently explored this phenomenon in PPG waveforms where the delay was observed to follow a characteristic saw-tooth pattern over time (114, 115).
3.3. Variables derived from physiological waveforms
Although physiological waveforms are potentially a rich source of insight into patient condition, they are cumbersome and typically not stored permanently in the EMR (11, 47). Instead, lower frequency derivative values are generated that describe the trend in behavior of the underlying signal (116). Classic examples of this include the calculation of Heart Rate (HR) from R-peaks in a patient's ECG (117) and derivation of diastolic and systolic blood pressures from the peaks and troughs of the ABP waveform (118). Algorithms that derive such features from physiological waveforms often introduce a delay in the availability of the derivative value, and the magnitude of the delays between derived variables may differ (119–121).
4. Human factors
Clinical time series data can incorporate events that were not automatically recorded by clinical monitors (122, 123). This aspect of the data collection process may be impacted by the biases, fallibility, and unpredictability of the person recording the data. Examples of such information include the timing and dosage of therapeutic drugs, times of blood sample extraction, or any other form of data relying on handwritten notes. This section describes how these human factors can introduce errors into the measurement of time.
4.1. Access to multiple sources of time
Multiple timepieces may be within view at any given moment, each of which may be displaying a different time (124). Researchers or clinicians will sometimes randomly select which of these timepieces to use when making an observation. This effect was demonstrated by Ferguson et al. who found significant variability in timepiece preferences among clinicians during emergencies, with 50% of respondents relying on wall clocks, and 46% electing to use personal timepieces (22). Observations made using randomly selected timepieces will contain a mix of errors stemming from the accuracy of the available clocks. Even in a well-synchronized system the intrinsic resolution of each available timepiece may differ, resulting in a mix of aleatoric uncertainties of different magnitudes being associated with the measurements. This concept is discussed in more detail in Section 7.1 and is illustrated in Figure 3.
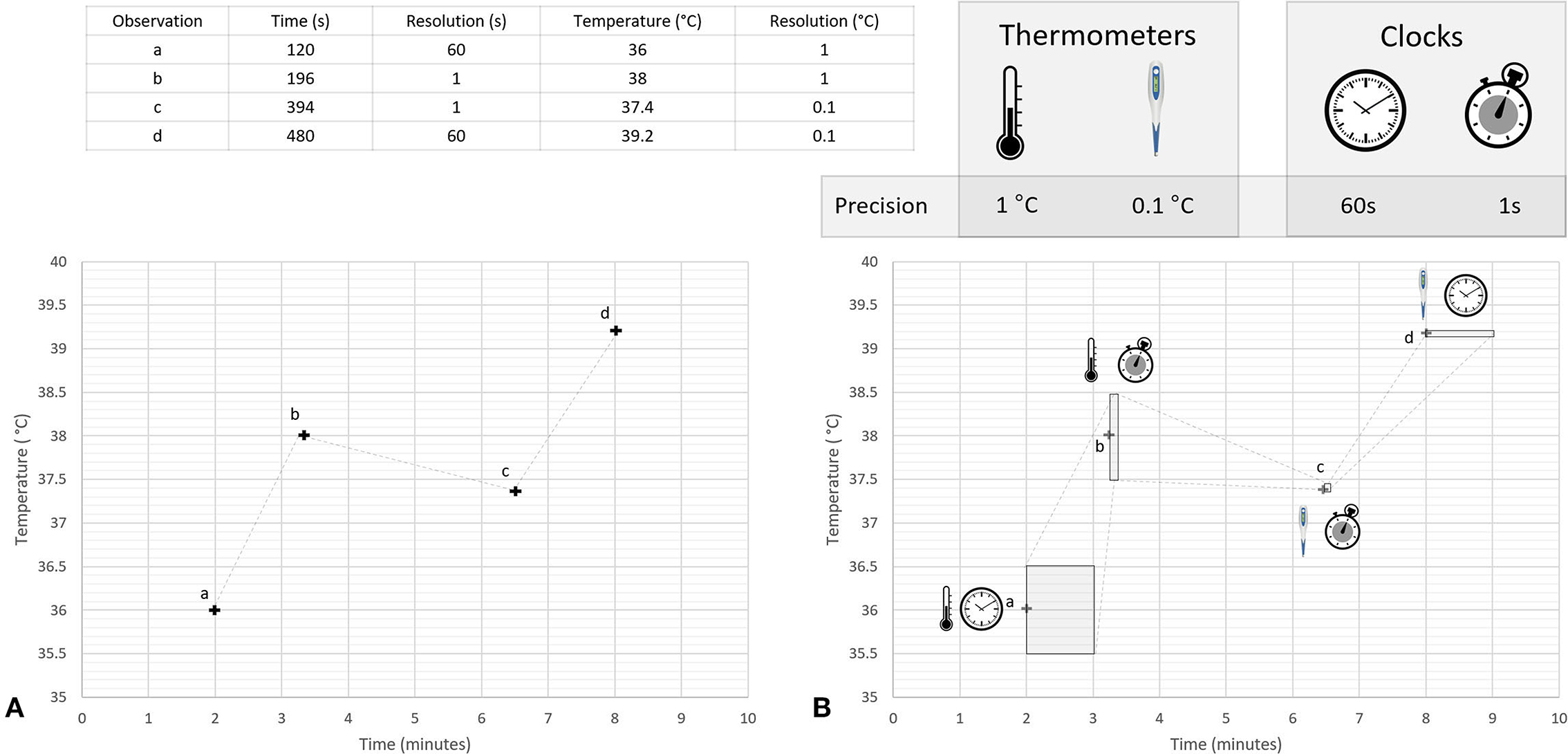
Figure 3. Conceptual illustration of heteroscedastic uncertainties associated with a time series of temperature measurements. This figure illustrates concepts discussed in the literature cited in Sections 4.3, 7.1, and 7.2. Two different thermometers were used to measure temperatures during a hypothetical experiment, a mercury thermometer with a resolution of 1°C and a digital thermometer with a resolution of 0.1°C; times for each temperature were recorded using two different timepieces, a wall clock with a temporal resolution of 1 min and a wristwatch with temporal resolution of 1 s. Four observations (labeled a, b, c, and d) are made using different combinations of these clocks and thermometers. Panel (A) shows a plot of the numerical values displayed on the instruments when making the observation, while Panel (B) uses shaded regions to represent the range of possible true values that could have resulted in these values. The shape of the shaded regions in Panel (B) are determined by the temporal and thermal resolution of the instruments used to make each individual observation. For simplicity, other sources of uncertainty are not considered in this figure.
4.2. Human perception of elapsed time
Human perception of time is fallible (125), and accurate recollection of elapsed time may be impacted by exposure to stressful situations (126–130). The expectation that bedside providers deliver both direct care and simultaneously record the details of that care creates a need to chart interventions retrospectively (131, 132), potentially requiring recall to determine exactly what time they occurred (133, 134). This problem is exacerbated by the fact that the number and complexity of patient care related tasks increases with patient acuity (104, 135).
4.3. Rounding of times
Times may be arbitrarily or systematically rounded to a nearby integer value during the recording or transcription process (136). In one study, 7% of intubations after cardiac arrest were found to have been erroneously recorded as having occurred after 0 min had elapsed since the arrest (137). The authors later explained that all time intervals had been rounded down to the nearest minute, thereby reducing their duration by up to 60 s (138).
Times may also be rounded to simplify a decision-making process, either as part of a formal rule-based model (139), or as a mental shortcut used to streamline the calculation of probabilities when assessing risk (135, 140). The act of rounding a timestamp decreases its precision, which in turn increases its aleatoric uncertainty. Modeling uncertainty due to imposed precision is discussed in more detail in Section 7.1.
4.4. Digit preferencing
Spoken and recorded times may be rounded to multiples of 5, 10, 15, 30, or 60 min in a process that is often referred to as digit preferencing (141). Rounding to larger multiples of minutes may be done deliberately to convey an increasing sense of imprecision to a human listener, but this connotation is lost once the information is recorded into a database. The prevalence of digit preferencing may increase when event times are retrospectively estimated, or when the nominal time of an event is recorded (142).
Locker et al. observed a wide variety of digit preference patterns in admission and discharge times from 137 emergency departments in England and Wales (143). Unsurprisingly the study concluded that rounded times were more prevalent in departments where manual systems of recording were used. This phenomenon has also been explored by several other groups in relation to emergency department admission and discharge times (144, 145), anesthesia start and end times (146, 147), and during the documentation of cardiac arrests (148).
Digit preferencing is similar to rounding in the sense that quantization of the minute component of the timestamp decreases its temporal resolution. When manually rounding to the nearest 5 min then, at least conceptually, the effect is the same as if the time had been accurately read from a clock that has a resolution of 5 min. In cases involving a mixture of different rounding options (i.e., a combination of rounding to the nearest 5, 10, 15, 30 min etc.) the resulting mix of resolutions is effectively dependent on a series of random decisions made during the data collection process (149). Datasets that contain a mixture of different temporal resolutions are discussed in more detail in Section 7.2.
4.5. Transcription errors
Timing errors can be introduced if text is misread or mistyped while it is being transcribed from one location to another (64, 150, 151). These errors, known as transcription errors, are surprisingly common and can result in the introduction of random errors or corruption of timestamps (152). Transcription errors may occur more frequently during periods when large numbers of events are recorded over a short period of time, or when observations are made in the heat of the moment (153, 154).
5. Impact of software, networks, and systems
A complex clinical environment, such as an intensive care unit, can contain a myriad of different devices and systems (155). These systems may function in a way that delays, shifts, or otherwise alters the timestamps associated with the data. In this section, we describe how the operation (and inter-operation) of these systems can impact the accuracy and precision of temporal measurements. Note that these kinds of errors can be difficult to model as they are often the result of random processes.
5.1. Device integration systems and streaming data
Medical devices and other clinical systems will often re-sample or buffer digital signals before releasing them to downstream devices (156, 157). For example, Burmeister et al. measured a buffer-related delay of 30 ms between capture of video and subsequent timestamping inside a video camera system while attempting to synchronize biosignals in their experimental setup (158). Delays of up to 5 s in ECG and 8 s in PPG waveforms were reported by Potera, who also noted that the magnitude of the delay varied with the amount of wireless interference, network load, and server processing time (159, 160).
Medical devices and data integration middleware may also introduce undisclosed latencies (161) or frequent minor adjustments of timestamps to reconcile the differences between the sensor's nominal and true sample rate (90). For example, Charlton found that physiological waveform data acquired using BedMaster software (Excel Medical Electronics, Jupiter, Florida) was sometimes incorrectly timestamped, and suggested some post processing techniques that might be applied to correct the problem (162).
5.2. Time shifting and data anonymization
Clinical data will often need to be anonymized before they can be used for research purposes (163). A common method of anonymization involves introduction of random temporal shifts on a per patient basis (164, 165). This technique has been applied to timestamps in the MIMIC-III database for example, where dates have been shifted into the future by a random offset for each individual patient. Although the magnitude of the time shifts applied to the MIMIC database were random, they were performed in a manner that preserved the time of day, day of the week, and approximate seasonality of the original data (166).
Despite the common use of such anonymization approaches, a tension exists between maintaining temporal consistency and preserving privacy (167, 168) as time shifting may remove temporal relationships between signals or disconnect the data from important contextual information (18, 168, 169). Shifting each patient's data by a different random amount may also hinder the ability to perform some kinds of analysis, such as examining the impact of bottlenecks of patients waiting for care on a busy day (170).
5.3. Time zones and daylight saving
Time zone settings must be correctly configured in databases to ensure that numerical timestamps are correctly converted into human readable dates and times (171). Incorrectly configured time zone information may also affect the functionality of some clinical algorithms. For example, basal and bolus dosing on insulin pumps have been shown to be impacted by issues relating to daylight saving (172) and when these devices are carried across time zones (173).
Clocks may need to be manually changed at daylight saving changeovers, a process that can take some time to execute (64). The exact time that each clock was changed may be unknown, leading to uncertainty around times recorded during the hours that follow the start or end of daylight saving. Additionally, the schedule of daylight saving transitions may be altered, with changes announced too late to allow software updates to be developed and deployed (174–176).
5.4. Lack of standardized definitions
Variability in standards and definitions can lead to inconsistencies in the documentation of clinical events. For example, the definitions of patient length of stay (177, 178), ventilator free days (179, 180) or time of onset of sepsis (181) may vary between different hospitals and jurisdictions. This variability can lead to later confusion about which definition was used for a particular event, making it difficult to compare results across different studies (182).
5.5. Software bugs
A wide variety of bugs and formatting issues can arise in relation to management of time in digital systems. For instance, missing times may be represented with a zero, which may in turn be interpreted as midnight by some algorithms (183). Software bugs may introduce random errors that may be detected using temporal conformance checks as discussed in Section 6.5.
6. Improving timing accuracy and precision
In this section, we discuss some of the approaches that can be used to reduce timing errors and minimize temporal uncertainties in a clinical environment. A summary of the solutions discussed in this review is presented in Table 1.
Table 1. Sources of timing errors and solutions.
6.1. Choosing a common source of truth for time
Ideally all clinical systems should refer to a master clock as a common source of time (184). This master clock should be both accurate and precise, and should also have the ability to provide timestamps programmatically to other systems on a network. If such a time source is unavailable or impractical to use, such as while taking handwritten notes during a resuscitation for example, then a single source of time should be selected and agreed upon by all participants (153).
All other clocks will need to be regularly synchronized with the master clock, either manually or via automated synchronization using the Network Time Protocol (NTP) (185–187). NTP can, in principle, be used to synchronize clocks and other medical devices on a network with microsecond precision (188, 189). In practice however, many medical devices lack this capability (62).
Computer clocks are generally well-synchronized and have relatively low drift rates, rendering them suitable as a source of truth in many situations (190, 191). However, care must be taken when using clocks on virtual servers since their drift rates may be higher than hardware based clocks (192–194). While smartphones and wristwatches are ubiquitous and relatively accurate sources of time (195) they can also act as a source of infection, so their use for timing purposes may be discouraged in some clinical situations (196–198).
The process of synchronization may cause a clock to “jump” forward or backward in time, creating the appearance of discontinuity in any signal that uses timestamps assigned by that clock (199). Across such a jump a signal will be continuously sampled, but when plotted against the time supplied by the sensor it will appear to have a discontinuity (200). A conceptual example of this phenomenon is illustrated in Figure 4, which shows the reference time of a signal jumping by around 900 μs each time the clock resynchronizes.
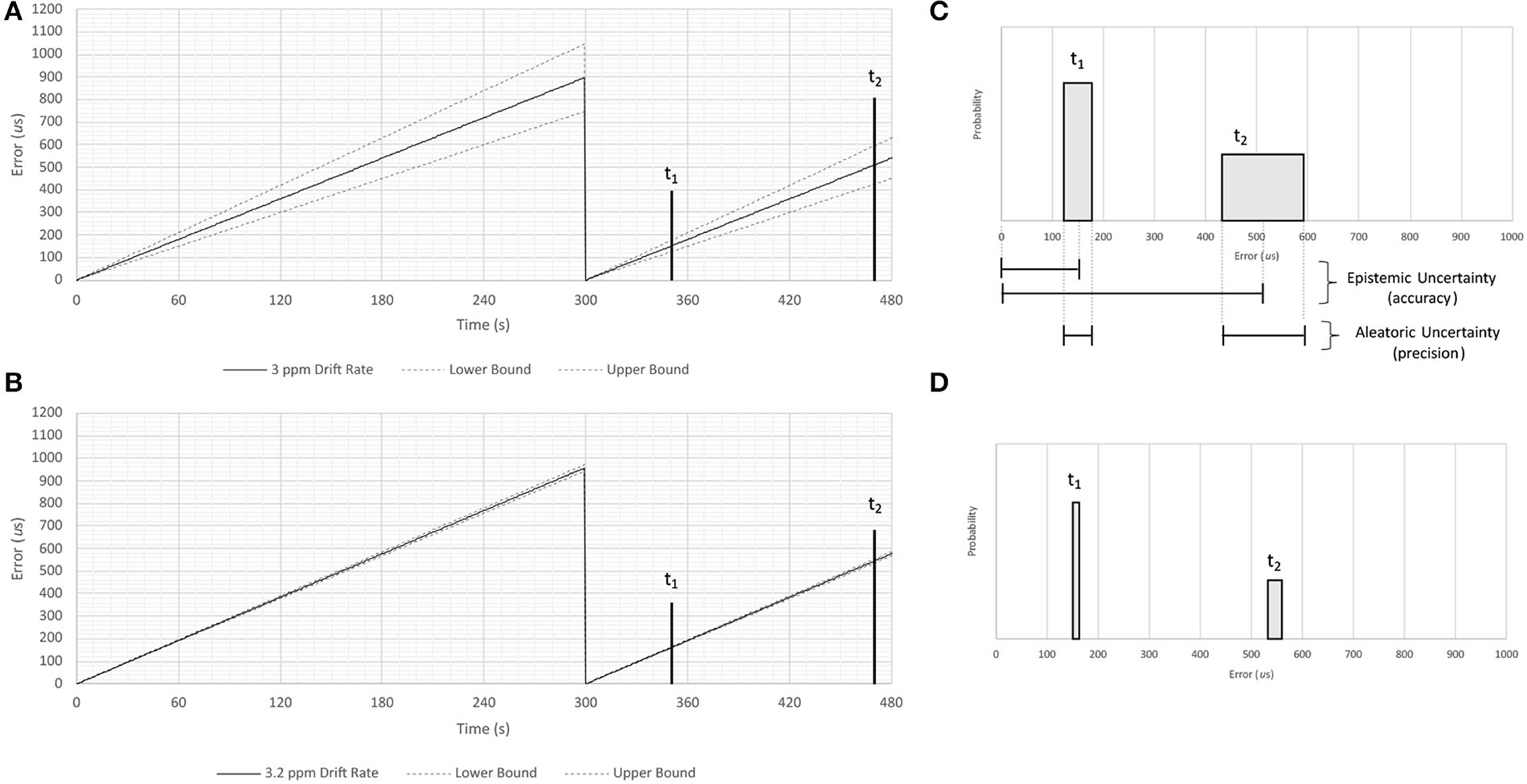
Figure 4. Conceptual illustration of epistemic and aleatoric uncertainties resulting from clock drift. This figure illustrates concepts discussed in the literature cited in Sections 2.2 and 7.1. A series of measurements of time are made using a hypothetical clock that is synchronized with a more accurate timepiece once every 300 seconds. Panel (A) shows timing errors caused by a drift rate measured to one significant figure (3 ppm), while panel (B) shows timing errors caused by a drift rate measured to two significant figures (3.2 ppm). Shaded regions in Panels (C,D) show the accuracy and precision of temporal measurements assuming these two drift rates 50 and 170 s after synchronization (labeled t1 and t2, respectively). Note that imprecisely specified drift rates result in aleatoric uncertainties that increase as a function of time, and that the magnitude of the uncertainty is inversely proportional to the number of significant figures used to specify the drift rate.
6.2. Signal synchronization
Precise signal synchronization is required when generating high-fidelity inter-signal correlations (187, 201, 202). Although this capability has been commonplace in other industries for decades (86, 203), bespoke solutions may be required in a clinical environment due to the presence of independent and proprietary timekeeping systems (199).
Physiological signals from different devices may be synchronized via simultaneous assignment of timestamps using a highly accurate and independent clock, however this multiplexing approach requires that both signals are routed through a third-party system, a process which may be affected by network jitter and other random effects (204). These variable network delays, and other confounding factors, can be overcome through the use of software such as Lab Streaming Layer (LSL) (205), OpenSynch (206), or corrected retrospectively using algorithmic approaches such as Deep Canonical Correlation Alignment (202). For example, LSL was used by Wang et al. to assess the quality of timing in medical and consumer grade EEG systems (207), and by Siddharth et al. to time align multiple bio-signals including PPG, EEG, eye-gaze headset data, body motion capture, and galvanic skin response (208).
Artifacts or other information common to both signals can be identified and retrospectively aligned in situations where system constraints preclude real-time synchronization. This process may rely upon artifacts that are introduced into the data streams while they are being recorded (201, 209–211), or may utilize features such as heart beats that are naturally present and accessible in a wide range of high frequency physiological signals (212–216). This method of synchronization requires artifacts or features from multiple time points throughout the signals to ensure that clock drift is properly accounted for (85). Another interesting approach to signal synchronization involves simultaneous introduction of white noise to both signals while they are being recorded (217). White noise has rich frequency characteristics that facilitate signal alignment yet is also random enough that it doesn't interfere with the information content of the signals.
Retrospective approaches that rely on common information will only be able align two signals relative to each other, i.e., neither signal will necessarily be mapped to UTC time. This may be acceptable in situations where high resolution inter-signal correlation is required but accuracy of the timestamps associated with the derived features is unimportant.
6.3. Digitization of data recording systems
Computerized systems can improve timekeeping by eliminating some sources of error such as transcription errors and digit preferencing (146). Deployment of a computerized system will mark the beginning of a new epoch of reduced temporal uncertainty, as both accuracy and precision of recorded times may change after its introduction (218).
Examples of digital timekeeping systems that can be deployed in a clinical setting include computerized EMRs (143, 218), tablet-based applications (219), bar-code systems (220), Radio Frequency Identification (RFID) technology (221), and audio recordings (222).
6.4. Algorithmic determination of event times
In some situations, it may be possible to algorithmically determine the times of clinically relevant events via the analysis of high frequency physiological data streams. For example, Cao et al. utilized a wide range of signal types to retrospectively determine ventilation times in the MIMIC-II database (223), and Nagaraj et al. determined the times that blood samples were drawn from patients' arterial lines via automated detection of associated artifacts in the ABP waveform (224). Information obtained in this manner can be used to augment an incomplete dataset or to improve the temporal accuracy of manually recorded observations.
6.5. Temporal conformance checks and auditing
The presence of transcription errors may be revealed via implementation of temporal conformance checks (225, 226). These checks will apply logic to search for implausible dates and times in a database. For instance, one study in an Australian drug and alcohol service ran checks on their database and found that 834 out of 9,379 admissions (8.9%) had recorded a start time that was after the end time (227). Other examples of temporal conformance checks include ensuring that timestamps from a particular patient encounter fall between the admission and discharge dates (227, 228) and checking that patient age is equal to date of admission minus the date of birth (229). Erroneous timestamps may be flagged and optionally removed before analysis in order to improve the overall temporal accuracy of a dataset, and uncertainties associated with random errors may also be estimated via audits designed to assess the integrity of timekeeping activities (230, 231).
6.6. Use of appropriate temporal data types
Although it is tempting to use floating point values to represent “continuous” time, these data types can become problematic (91, 232, 233). Not only are such values ultimately quantized in some way (234) but the resolution of floating point data types is dependent on the magnitude of the value being represented (235). Additionally, both floating point and integer data types are unable to exactly represent some frequencies (91, 236). These properties of floating point data types can create problems during numerical analysis, and may result in models that are not reproducible (237). Rounding errors associated with floating point representations of time will accumulate, sometimes with devastating effects (238).
An ideal digital representation of time would be time zone agnostic, contain sufficiently fine resolution to accommodate any analytical technique for which it may be used, and have a range that is large enough to accommodate the timescale being recorded or modeled (239). The smallest unit of time that can be represented in a digital data type will determine its temporal resolution. This smallest unit, referred to as a chronon (240), should have a resolution that remains constant throughout the full range of possible values. Longer intervals of time (milliseconds, seconds, hours, etc.) can then be represented by aggregating chronons (241).
7. Modeling temporal uncertainty
Quantification of uncertainty plays a pivotal role in the application and optimization of machine learning techniques (242). The reproducibility of analytical approaches can be improved by explicitly considering sources of uncertainty in the input data (243), and numerical methods can be applied that provide more faithful representations of uncertainty than those provided by classical error bounds (244). Despite the existence of such techniques, many clinical models fail to adopt a strict approach toward handling and propagation of uncertainty, perhaps due to a general misconception that the use of very large training datasets will lead to exact results (38, 245, 246).
In Sections 2–5, we described numerous mechanisms that can lead to times being measured erroneously, yet timestamps are typically incorporated into clinical models without any consideration for measurement errors or temporal uncertainty. In this section we outline some methods that can be used to quantify temporal uncertainty, and we give a brief overview of techniques that can be employed these results to be incorporated into downstream analyses (247).
7.1. Resolution of times and frequencies
The resolution of a recorded time is determined by the timepiece used to make the observation. For example, a clock that displays only minutes (i.e., a clock with resolution of 1 min) is unable to provide information about what second an event occurred (248). Measurements made using such a clock can be represented as a uniform probability density function which spans the 60 s after the recorded minute, providing a probabilistic representation of the fact that the displayed time is equally likely to represent any moment during the following 60 s. This approach is illustrated in Figure 3B which shows the uncertainties associated with measurements made using two timepieces, each having a different native resolution.
A similar approach can be used when quantifying uncertainty associated with the resolution of a sample frequency. “Resolution” in this case relates to how precisely the sample rate has been defined, i.e., how many significant figures have been used to describe the sample frequency (40). If a medical device manufacturer reports that a signal's sample frequency is 500 Hz then the associated analysis must account for the fact that the fourth significant digit is unknown, and that the true sample frequency could be anywhere between 499.5 Hz and 500.5 Hz (36). This range of possible sample frequencies (given the specified sample frequency and number of known significant figures) can also be represented using a uniform probability distribution.
An illustrative example of the relationship between sample frequency resolution and its impact on uncertainty is shown in Figure 4. Note that the aleatoric uncertainty grows with time after the moment of synchronization, and that the range of the uncertainty is inversely proportional to the number of significant figures to which the sample rate is known. This uncertainty will hinder one's ability to model and correct any clock drift that might occur when timestamps are inferred by a signal's sample rate.
7.2. Heteroscedastic temporal uncertainty
Clinical information can be collected using a wide variety of different systems and devices. This mix of different systems can result in divergent representation of clinical information across different sites (249). One hospital may use an automated system to record admission times for example, while another may use a paper-based system that is potentially subject to rounding and transcription errors (143). Combining these two databases for use in a multi-site research project would generate a single dataset containing timestamps with a mix of temporal accuracies and precisions (i.e., the dataset would contain heteroscedastic temporal uncertainties). Data collected from a single site may also contain heteroscedastic temporal uncertainties, due to a change in temporal accuracy and resolution after the introduction of a new software system for example (167, 219, 250).
A visual representation of heteroscedastic temporal uncertainties is illustrated in Figure 3. This figure shows a hypothetical time series of temperature readings collected using a variety of clocks and thermometers, each with different temporal and thermal resolutions. Shaded regions in Panel B represent the range of true temperatures and times that could have resulted in the quantized information that was recorded in the database. The shape of these shaded regions is different for each measurement, ie, the dataset contains heteroscedastic uncertainties. For simplicity only uncertainties caused by instrument precision are shown in this figure. It is important to note that while heteroscedastic uncertainty is often modeled as being a function of the magnitude of the measurand, this is unlikely to be the cause when considering temporal measurements.
A dataset that has been subject to digit preferencing will also contain timestamps with a mix of different uncertainties. This concept was introduced in Section 4.4 where we demonstrated that times rounded to larger values will have lower resolution, and therefore larger aleatoric uncertainty. Although it is impossible to retrospectively determine which individual observations had been subject to rounding it is still possible to draw some inferences (251). For example, if the timestamps have potentially been rounded to a mix of 1, 5, 10, and 15 min, then a time ending in :17 cannot have been rounded to a multiple of 5, 10, or 15. Similarly, a time ending in 5 could not have been rounded to a multiple of 10. Rietveld developed an approach that could de-convolve the characteristic heaped distribution of minutes that results from digit preferencing and calculate the uncertainty associated with each individual recorded time (as a function of the minute component of the recorded time) (149).
7.3. Monte Carlo simulations
Probability density functions representing temporal uncertainty can be used as input into stochastic methods like Monte Carlo models (252–255). These techniques allow uncertainty to be numerically propagated through models and algorithms. Pretty et al. used this approach in their glucose insulin model to propagate uncertainty resulting from timestamps that had been recorded by hand and rounded to the nearest hour (256), and Ward used a Monte Carlo simulation to model the impact of transcription errors on emergency department performance metrics (257).
At a smaller time scale, algorithms that calculate Heart Rate Variability (HRV) are sensitive to the time of the fiducial point of the R-peak. However, uncertainties associated with these times are rarely considered (258). To overcome this problem, the finite resolution of an R-peak can be represented as a uniform probability density function as discussed in Section 7.1. Monte Carlo simulations can then be used to model the impact of R-R intervals with uncertain durations (259, 260). Temporal uncertainty can be propagated through the calculations, generating a distribution of HRV values that may have been possible given the resolution of the times of the R-peaks. The same approach can be used with other features derived from ECG such as example Q-T intervals (261). These techniques may allow more direct comparison of HRV and other features derived from ECG signals that have been acquired using different clinical devices (262).
7.4. Biases resulting from measurement errors
Measurement errors in one or more variables can introduce a bias into both linear and non-linear regression techniques (263, 264). Counterintuitively, the bias introduced by the measurement errors does not reduce to zero as the number of observations approaches infinity. The problem can be resolved by using maximum likelihood estimation, but this requires knowledge of the (relative) variance of the errors on X and Y (265).
Errors in Variables (EIV) models have been used in clinical research to account for measurement errors in general (266–268) and in some situations to account for uncertainty in timestamps in particular. For example, several researchers have used EIV models to account for uncertainty in self-reported meal times while modeling blood glucose trajectories (269, 270) and to account for the difference between the scheduled and actual time of drug administration when modeling pharmokinetics (142).
8. Discussion
In this review we have examined sources of errors and uncertainty in relation to recorded times in clinical databases. We have described how multiple sources of error may be associated with a single measurement, with contributions from human, system, and device related factors. These sources of timing error are not mutually exclusive, and their collective impacts are additive. We have also described sources of heteroscedastic temporal uncertainty, where the amount of uncertainty associated with different timestamps within a single time series may be variable. It is evident that timekeeping errors are distressingly common in clinical databases, and it is our opinion that clinical modeling outcomes will be improved if temporal uncertainty is considered when analyzing time series data (133).
Although, in principle, most timing errors can be reduced or eliminated through system improvements, solutions to some clinical timekeeping errors remain elusive. Medical device manufacturers continue to use proprietary time synchronization systems or publish imprecisely defined sample rates in documentation and marketing material. These practices make it difficult to reduce epistemic uncertainties, hindering one's ability to synchronize signals from disparate devices.
When taking physiological measurements, one must accept that poor repeatability is a result of the high variance that is inherent in biological systems (36). Clocks and time in general however are not part of the biological system, and therefore should not be given a free pass when it comes to acceptance of variability in measurement between systems. Indeed, a more metrologic approach to all aspects of physiological measurement may be key to generating reproducible analytical results (271–274).
The healthcare industry is undergoing a transformation from closed system medical devices to a fully interconnected digital ecosystem (275). Throughout this process, the demand for “off-label” use of high frequency physiological data streams may result in information from clinical monitors being used in ways that were not envisaged by the manufacturer (276). Seemingly inconsequential differences in hardware and software used to capture data can result in datasets with divergent temporal characteristics. Failure to explicitly account for this variability may hamper development and adoption of generalizable of machine learning models (277–279).
We suggest that the following actions be considered when planning improvements to timekeeping systems in a clinical environment:
• Establish a highly accurate and precise master clock as a reference time source
• Synchronize clocks to the master clock using NTP wherever possible
• Introduce data quality initiatives focusing on human factors, such as raising awareness of the impact of rounding practices
• Adopt computer-based documentation approaches during critical events such as resuscitations
• Note the temporal resolution of all timepieces
• Develop an understanding of the strengths and limitations of data types used for storage of dates and times
• Accurately measure the sample rate of all signals, especially where other systems rely on this sample rate to infer time
• Quantify delays due to software and systems
• Model and correct systemic timing errors
• Critically assess timing systems in new medical devices
• Audit databases to reveal the presence of transcription errors
• Identify and characterize sources of heteroscedastic temporal uncertainty
• Note the beginning and end of different “epochs” of temporal uncertainty
• Adopt a data quality framework that facilitate the quantification and storage of temporal uncertainty
• Employ techniques that incorporate temporal uncertainty into analysis.
The issues discussed in this narrative review highlight an increasing need to understand temporal aspects of signal collection and pre-processing in medical devices (280, 281). Our goal in describing these findings has been to spur discussion and to advocate for consensus means by which the medical research community may approach vulnerabilities around time management. We believe that a more standardized approach to time management would provide substantial benefits to the research community, allowing high precision correlation of signals from disparate devices. Standardization of algorithms used in medical devices is essential (282), and, in the end, it may be the users of medical technologies that demand improved interoperability (283).
9. Conclusion
Errors in recorded times may have multiple causes and are disturbingly common in clinical environments. These errors can create uncertainty around the temporal sequence of events, confounding analysis and hindering development of generalizable machine learning models. Datasets collected at different hospitals can exhibit divergent temporal characteristics due to the wide range of medical devices, pre-processing methods, and storage systems that may be in use between sites. To mitigate these issues one should identify, quantify, and correct biases in recorded times, and characterize any residual temporal uncertainty so that it can be incorporated into downstream analysis.
Author contributions
AG: original concept and scoping, wrote the majority of manuscript, generated the figures, sourcing and reading external references, and formatting. DE: paragraphs on clinical relevance, proofreading, and editing. WD: technical support for computer science related sections, support for sections focusing on algorithms, and data types. SG: proofreading, guidance on initial structure and direction, and contributions to sections about algorithms. ZD: proofreading, contribution to digit preferencing section, and suggestions with clinical relevance of the work. RG: technical support, contributions to sections related to systems, and medical devices. AM: proofreading and scoping and technical direction on hardware related paragraphs. PL: initial problem statement, material support, and proofreading. MT: proofreading. AA: proofreading and clinical relevance. MM: writing contributions to initial draft of manuscript, proofreading, guidance on scope and direction, and contributions to discussion around clinical relevance and applications. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer BRC declared a shared affiliation with the author PL to the handling editor at the time of review.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Moskovitch R, Shahar Y, Wang F, Hripcsak G. Temporal biomedical data analytics. J Biomed Inform. (2019) 90:103092. doi: 10.1016/j.jbi.2018.12.006
2. Augusto JC. Temporal reasoning for decision support in medicine. Artif Intell Med. (2005) 33:1–24. doi: 10.1016/j.artmed.2004.07.006
3. Barro S, Marin R, Otero R, Ruiz R, Mira J. On the handling of time in intelligent monitoring of CCU patients. In: 1992 14th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Paris: IEEE (1992). p. 871–3. doi: 10.1109/IEMBS.1992.594627
4. Ornato JP, Doctor ML, Harbour LF, Peberdy MA, Overton J, Racht EM, et al. Synchronization of timepieces to the atomic clock in an urban emergency medical services system. Ann Emerg Med. (1998) 31:483–7. doi: 10.1016/S0196-0644(98)70258-6
5. Combi C, Keravnou-Papailiou E, Shahar Y. Temporal Information Systems in Medicine. Springer Science & Business Media (2010). doi: 10.1007/978-1-4419-6543-1
6. Shahar Y. Dimension of time in illness: an objective view. Ann Internal Med. (2000) 132:45–53. doi: 10.7326/0003-4819-132-1-200001040-00008
7. McCartney PR. Synchronizing with standard time and atomic clocks. MCN Am J Maternal Child Nurs. (2003) 28:51. doi: 10.1097/00005721-200301000-00014
8. Miksch S, Horn W, Popow C, Paky F. Time-oriented analysis of high-frequency data in ICU monitoring. In: Intelligent Data Analysis in Medicine and Pharmacology. Springer (1997). p. 17–36. doi: 10.1007/978-1-4615-6059-3_2
9. Maslove DM, Lamontagne F, Marshall JC, Heyland DK. A path to precision in the ICU. Crit Care. (2017) 21:1–9. doi: 10.1186/s13054-017-1653-x
10. Park Y, Park I, You J, Hong D, Lee K, Chung S. Accuracy of web-based recording program for in-hospital resuscitation: laboratory study. Emerg Med J. (2008) 25:506–09. doi: 10.1136/emj.2007.054569
11. Holder AL, Clermont G. Using what you get: dynamic physiologic signatures of critical illness. Crit Care Clin. (2015) 31:133–64. doi: 10.1016/j.ccc.2014.08.007
12. Marini JJ. Time-sensitive therapeutics. Crit Care. (2017) 21:55–61. doi: 10.1186/s13054-017-1911-y
13. Kusunoki DS, Sarcevic A. Designing for temporal awareness: The role of temporality in time-critical medical teamwork. In: Proceedings of the 18th ACM Conference on Computer Supported Cooperative Work & Social Computing. Vancouver, BC: ACM (2015). p. 1465–76. doi: 10.1145/2675133.2675279
14. Rush B, Celi LA, Stone DJ. Applying machine learning to continuously monitored physiological data. J Clin Monitor Comput. (2019) 33:887–93. doi: 10.1007/s10877-018-0219-z
15. Antonelli M, Levy M, Andrews PJ, Chastre J, Hudson LD, Manthous C, et al. Hemodynamic monitoring in shock and implications for management. Intens Care Med. (2007) 33:575–90. doi: 10.1007/s00134-007-0531-4
16. Karter AJ, Parker MM, Moffet HH, Spence MM, Chan J, Ettner SL, et al. Longitudinal study of new and prevalent use of self-monitoring of blood glucose. Diabetes Care. (2006) 29:1757–63. doi: 10.2337/dc06-2073
17. Fu LH, Knaplund C, Cato K, Perotte A, Kang MJ, Dykes PC, et al. Utilizing timestamps of longitudinal electronic health record data to classify clinical deterioration events. J Am Med Inform Assoc. (2021) 28:1955–63. doi: 10.1093/jamia/ocab111
18. Agniel D, Kohane IS, Weber GM. Biases in electronic health record data due to processes within the healthcare system: retrospective observational study. BMJ. (2018) 361:k1479. doi: 10.1136/bmj.k1479
19. Hripcsak G, Albers DJ. High-fidelity phenotyping: richness and freedom from bias. J Am Med Inform Assoc. (2018) 25:289–94. doi: 10.1093/jamia/ocx110
20. Cruz-Correira RJ, Rodrigues PP, Frietas A, Almeida FC, Chen R, Costa-Pereira A. Data quality and integration issues in electronic health records. In: Information Discovery on Electronic Health Records. New York, NY: Chapman and Hall; CRC Press (2009). p. 73–114. doi: 10.1201/9781420090413-9
21. Zaleski J. Semantic Data Alignment of Medical Devices Supports Improved Interoperability. (2016). Available online at: https://esmed.org/MRA/mra/article/download/591/450/
22. Ferguson EA, Bayer CR, Fronzeo S, Tuckerman C, Hutchins L, Roberts K, et al. Time out! Is timepiece variability a factor in critical care? Am J Crit Care. (2005) 14:113–20. doi: 10.4037/ajcc2005.14.2.113
23. Zhang Y. Real-Time Analysis of Physiological Data and Development of Alarm Algorithms for Patient Monitoring in the Intensive Care Unit. Massachusetts Institute of Technology (2003).
24. Gschwandtner T, Gartner J, Aigner W, Miaksch S. A taxonomy of dirty time-oriented data. In: International Conference on Availability, Reliability, and Security. Berlin; Heidelberg: Springer (2012). p. 58–72. doi: 10.1007/978-3-642-32498-7_5
25. Kilkenny MF, Robinson KM. Data Quality: “Garbage In-Garbage Out”. London: SAGE Publications (2018). doi: 10.1177/1833358318774357
26. Dussenberry MW, Tran D, Choi E, Kemp J, Nixon J, Jerfel G, et al. Analyzing the role of model uncertainty for electronic health records. In: Proceedings of the ACM Conference on Health, Inference, and Learning. Toronto, ON: ACM (2020). p. 204–13. doi: 10.1145/3368555.3384457
27. Kirkup L, Frenkel RB. Introduction to Uncertainty in Measurement: Using the GUM (Guide to the Expression of Uncertainty in Measurement). Cambridge: Cambridge University Press.
28. Loken E, Gelman A. Measurement error and the replication crisis. Science. (2017) 355:584–5. doi: 10.1126/science.aal3618
29. Jiang T, Gradus JL, Lash TL, Fox MP. Addressing measurement error in random forests using quantitative bias analysis. Am J Epidemiol. (2021) 190:1830–40. doi: 10.1093/aje/kwab010
30. Gawlikowski J, Tassi CRN, Ali M, Lee J, Humt M, Feng J, et al. A survey of uncertainty in deep neural networks. arXiv[Preprint].arXiv:210703342. (2021). doi: 10.48550/arXiv.2107.03342
31. Groenwold RH, Dekkers OM. Measurement error in clinical research, yes it matters. Eur J Endocrinol. (2020) 183:E3–5. doi: 10.1530/EJE-20-0550
32. Roy CJ, Oberkampf WL. A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing. Comput Methods Appl Mech Eng. (2011) 200:2131–44. doi: 10.1016/j.cma.2011.03.016
33. Ghanem R, Higdon D, Owhadi H. Handbook of Uncertainty Quantification, Vol. 6. Cham: Springer (2017). doi: 10.1007/978-3-319-12385-1_1
34. White GH. Basics of estimating measurement uncertainty. Clin Biochem Rev. (2008) 29(Suppl 1):S53.
35. Rabinovich SG. Measurement Errors and Uncertainties: Theory and Practice. New York, NY: Springer (2006).
36. Koumoundouros E. Clinical engineering and uncertainty in clinical measurements. Austral Phys Eng Sci Med. (2014) 37:467–70. doi: 10.1007/s13246-014-0288-3
37. Brakenhoff TB, Mitroiu M, Keogh RH, Moons KG, Groenwold RH, van Smeden M. Measurement error is often neglected in medical literature: a systematic review. J Clin Epidemiol. (2018) 98:89–97. doi: 10.1016/j.jclinepi.2018.02.023
38. Mencatini A, Salmeri M, Lordi A, Casti P, Ferrero, Salicone S, et al. A study on a novel scoring system for the evaluation of expected mortality in ICU-patients. In: 2011 IEEE International Symposium on Medical Measurements and Applications. Bari: IEEE (2011). p. 482–7. doi: 10.1109/MeMeA.2011.5966743
39. Kompa B, Snoek J, Beam AL. Second opinion needed: communicating uncertainty in medical machine learning. NPJ Digit Med. (2021) 4:1–6. doi: 10.1038/s41746-020-00367-3
40. Levine J. Introduction to time and frequency metrology. Rev Sci Instrum. (1999) 70:2567–96. doi: 10.1063/1.1149844
41. Karaböce B. Challenges for medical metrology. IEEE Instrument Meas Mag. (2020) 23:48–55. doi: 10.1109/MIM.2020.9126071
42. Squara P, Imhoff M, Cecconi M. Metrology in medicine: from measurements to decision, with specific reference to anesthesia and intensive care. Anesthesia Analgesia. (2015) 120:66. doi: 10.1213/ANE.0000000000000477
43. Arney D, Mattegunta P, King A, Lee I, Park S, Mullen-Fortino M, et al. Device time, data logging, and virtual medical devices. J Med Dev. (2012) 6. doi: 10.1115/1.4026774
44. Capobianco E. Imprecise data and their impact on translational research in medicine. Front Med. (2020) 7:82. doi: 10.3389/fmed.2020.00082
45. Campos M, Palma J, Llamas B, Gonzalez A, Mwnarguez M, Marin R. Temporal data management and knowledge acquisition issues in medical decision support systems. In: International Conference on Computer Aided Systems Theory. Berlin; Heidelberg: Springer (2003). p. 208–19. doi: 10.1007/978-3-540-45210-2_20
46. Begoli E, Bhattacharya T, Kusnezov D. The need for uncertainty quantification in machine-assisted medical decision making. Nat Mach Intell. (2019) 1:20–3. doi: 10.1038/s42256-018-0004-1
47. Goodwin A, Eytan D, Greer R, Mazwi M, Thommandram A, Goodfellow SD, et al. A practical approach to storage and retrieval of high frequency physiological signals. Physiol Meas. (2020) 41. doi: 10.1088/1361-6579/ab7cb5
48. Hripcsak G. Physics of the medical record: handling time in health record studies. In: Conference on Artificial Intelligence in Medicine in Europe. Cham: Springer International Publishing Switzerland (2015). p. 3–6. doi: 10.1007/978-3-319-19551-3_1
49. Karaboce B, Durmucs HO, Cetin E. The importance of metrology in medicine. In: International Conference on Medical and Biological Engineering. Cham: Springer Nature (2019). p. 443–50. doi: 10.1007/978-3-030-17971-7_67
50. Baillie M, le Cessie S, Schmidt CO, Lusa L, Huebner M, Topic Group “Initial Data Analysis” of the STRATOS Initiative. Ten simple rules for initial data analysis. PLoS Comput Biol. (2022) 18:e1009819. doi: 10.1371/journal.pcbi.1009819
51. Goodwin A, Mazwi M, Eytan D, Greer R, Goodfellow S, Assadi A, et al. Abstract P-428: high fidelity physiological modelling-it's about time. Pediatr. Crit Care Med. (2018) 19:179. doi: 10.1097/01.pcc.0000537885.23241.6a
52. Faux DA, Godolphin J. Manual timing in physics experiments: error and uncertainty. Am J Phys. (2019) 87:110–15. doi: 10.1119/1.5085437
53. Keogh RH, Shaw PA, Gustafson P, Carroll RJ, Deffner V, Dodd KW, et al. STRATOS guidance document on measurement error and misclassification of variables in observational epidemiology: Part 1–basic theory and simple methods of adjustment. Stat Med. (2020) 39:2197–231. doi: 10.1002/sim.8532
54. Panfilo G, Arias F. The Coordinated Universal Time (UTC). Metrologia. (2019) 56:042001. doi: 10.1088/1681-7575/ab1e68
55. Arias E, Guinot B. Coordinated universal time UTC: historical background and perspectives. In: 2004 Journees systemes de reference spatio-temporels. Paris (2004). p. 254–9.
56. Seidelmann PK, Seago JH. Time scales, their users, and leap seconds. Metrologia. (2011) 48:S186. doi: 10.1088/0026-1394/48/4/S09
57. Winchester S. Exactly: How Precision Engineers Created the Modern World. London: William Collins.
58. Der Kiureghian A, Ditlevsen O. Aleatory or epistemic? Does it matter? Struct Saf. (2009) 31:105–12. doi: 10.1016/j.strusafe.2008.06.020
59. Hüllermeier E, Waegeman W. Aleatoric and epistemic uncertainty in machine learning: an introduction to concepts and methods. Mach Learn. (2021) 110:457–506. doi: 10.1007/s10994-021-05946-3
60. Kendall A, Gal Y. What uncertainties do we need in Bayesian deep learning for computer vision? arXiv[Preprint].arXiv:170304977. (2017).
61. Chan PS, Nichol G, Krumholz HM, Spertus JA, Nallamothu BK. Hospital variation in time to defibrillation after in-hospital cardiac arrest. Arch Internal Med. (2009) 169:1265–73. doi: 10.1001/archinternmed.2009.196
62. Frisch AN, Dailey MW, Heeren D, Stern M. Precision of time devices used by prehospital providers. Prehospital Emerg Care. (2009) 13:247–50. doi: 10.1080/10903120802706062
63. Halpern NA. Innovative designs for the smart ICU: Part 3: advanced ICU informatics. Chest. (2014) 145:903–12. doi: 10.1378/chest.13-0005
64. Goldman JM. Medical Device Interoperability Ecosystem Updates: Device Clock Time, Value Proposion, the FDA Regulatory Pathway. (2012). Available online at: https://rtg.cis.upenn.edu/MDCPS/SiteVisit/MDCPS
65. Castrén M, Kurola J, Nurmi J, Martikainen M, Vuori A, Silfvast T. Time matters; what is the time in your defibrillator?: An observational study in 30 emergency medical service systems. Resuscitation. (2005) 64:293–5. doi: 10.1016/j.resuscitation.2004.08.017
66. Gordon BD, Flottemesch TJ, Asplin BR. Accuracy of staff-initiated emergency department tracking system timestamps in identifying actual event times. Ann Emerg Med. (2008) 52:504–11. doi: 10.1016/j.annemergmed.2007.11.036
67. Wiles M, Moppett I. Accuracy of hospital clocks. Anaesthesia. (2008) 63:786–7. doi: 10.1111/j.1365-2044.2008.05598.x
68. Newland J, Gilbert S, Rohlandt D, Haslam A. The clocks of Malta: accuracy of clocks in the Women's Assessment Unit and Delivery Suite at Waikato Hospital. N Z Med J. (2012) 125:87–9. Available online at: https://assets-global.website-files.com/5e332a62c703f653182faf47/5e332a62c703f6b06c2fdcad_newland.pdf
69. Cordell WH, Olinger ML, Kozak PA, Nyhuis AW. Does anybody really know what time it is? Does anybody really care? Ann Emerg Med. (1994) 23:1032–6. doi: 10.1016/S0196-0644(94)70099-0
70. Watts J, Ni K, Rose A. Accuracy of hospital clocks. Anaesthesia. (2009) 64:1028–1028. doi: 10.1111/j.1365-2044.2009.06044.x
71. Davies J, Bishai A. Watch out! where's the time gone? Anaesthesia. (2008) 63:787–7. doi: 10.1111/j.1365-2044.2008.05599.x
72. Russell I. Labour ward clocks. Anaesthesia. (2003) 58:930–1. doi: 10.1046/j.1365-2044.2003.03362_27.x
73. Topping A, Laird R. The accuracy of clocks and monitors in clinical areas throughout a district general hospital-an audit. Anaesthesia. (2010) 65:101. doi: 10.1111/j.1365-2044.2009.06184_10.x
74. Hyde E, Brighton A. Accuracy and synchronisation of clocks between delivery suite and operating theatre. N Z Med J. (2012) 125:31–35.
75. Brabrand M, Hosbond S, Petersen DB, Skovhede A, Folkestad L. Time telling devices used in Danish health care are not synchronized. Dan Med J. (2012) 59:A4512.
76. Srour FJ, Badr NG. Time synchronization in emergency response time measurement. In: Healthinf. Porto (2017). p. 199-204. doi: 10.5220/0006096001990204
77. Sparnon E, Authority PPS. Potential Hazards of Clock Synchronization Errors. Pennsylvania Patient Safety Advisory Prepublication (2012).
78. Stoker MR. Common errors in clinical measurement. Anaesthesia Intensive Care Med. (2008) 9:553–8. doi: 10.1016/j.mpaic.2008.09.016
79. Singh H, Kusuda S, McAdams RM, Gupta S, Kalra J, Kaur R, et al. Machine learning-based automatic classification of video recorded neonatal manipulations and associated physiological parameters: a feasibility study. Children. (2021) 8:1. doi: 10.3390/children8010001
80. Van Beek J, Puers R. A review of MEMS oscillators for frequency reference and timing applications. J Micromech Microeng. (2011) 22:013001. doi: 10.1088/0960-1317/22/1/013001
81. Zhou H, Nicholls C, Kunz T, Schwartz H. Frequency Accuracy & Stability Dependencies of Crystal Oscillators. Carleton University, Systems and Computer Engineering, Technical Report SCE-08-12 (2008).
82. Becker D. Timestamp Synchronization of Concurrent Events, Vol. 4. Julich: Forschungszentrum Julich (2010).
83. Vilhar A, Depolli M. Synchronization of time in wireless ECG measurement. In: 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO). IEEE (2017). p. 292–6. doi: 10.23919/MIPRO.2017.7973437
84. Vilhar A, Depolli M. Time synchronization problem in a multiple wireless ECG sensor measurement. In: 2018 14th Annual Conference on Wireless On-demand Network Systems and Services (WONS). IEEE (2018). p. 83–6. doi: 10.23919/WONS.2018.8311666
85. Artoni F, Barsotti A, Guanziroli E, Micera S, Landi A, Molteni F. Effective synchronization of EEG and EMG for mobile brain/body imaging in clinical settings. Front Hum Neurosci. (2018) 11:652. doi: 10.3389/fnhum.2017.00652
86. Melvin H, Shannon J, Stanton K. Time, frequency and phase synchronisation for multimedia-basics, issues, developments and opportunities. In: MediaSync. Springer (2018). p. 105–46. doi: 10.1007/978-3-319-65840-7_4
87. Vollmer M, Blasing D, Kaderali L. Alignment of multi-sensored data: adjustment of sampling frequencies and time shifts. In: 2019 Computing in Cardiology. Singapore: IEEE (2019). doi: 10.22489/CinC.2019.031
88. Monitor IP. MP20/30, MP40/50. MP60/70/80/90, Release G. 0 with Software Revision G. 0x. xx (PHILIPS). (2008).
89. Shimmer. Shimmer3 GSR+ Unit. (2022). Available online at: https://shimmersensing.com/product/shimmer3-gsr-unit/
90. Jarchi D, Casson AJ. Description of a database containing wrist PPG signals recorded during physical exercise with both accelerometer and gyroscope measures of motion. Data. (2016) 2:1. doi: 10.3390/data2010001
91. Vicino D, Dalle O, Wainer G. An advanced data type with irrational numbers to implement time in DEVS simulators. In: 2016 Symposium on Theory of Modeling and Simulation (TMS-DEVS). IEEE (2016). p. 1–8.
92. Goldberger AL, Amaral LA, Glass L, Hausdorff JM, Ivanov PC, Mark RG, et al. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation. (2000) 101:e215–20. doi: 10.1161/01.CIR.101.23.e215
93. Moody GB. WFDB Programmer's Guide. (2019). Available online at: https://physionet.org/physiotools/wpg/wpg.pdf
94. Laird P, Wertz A, Welter G, Maslove D, Hamilton A, Yoon JH, et al. The critical care data exchange format: a proposed flexible data standard for combining clinical and high-frequency physiologic data in critical care. Physiol Meas. (2021) 42. doi: 10.1088/1361-6579/abfc9b
95. CCDEF Group. CCDEF - Timestamp Storage. (2020). Available online at: https://conduitlab.github.io/ccdef/format.html#timestamp-storage
96. Bors C, Bernard J, Bögl M, Gschwandtner T, Kohlhammer J, Miksch S. Quantifying uncertainty in multivariate time series pre-processing. (2019).
97. Teh HY, Kempa-Liehr AW, Kevin I, Wang K. Sensor data quality: a systematic review. J Big Data. (2020) 7:1–49. doi: 10.1186/s40537-020-0285-1
98. Squara P, Scheeren TW, Aya HD, Bakker J, Cecconi M, Einav S, et al. Metrology part 2: Procedures for the validation of major measurement quality criteria and measuring instrument properties. J Clin Monitor Comput. (2020) 35:27–37. doi: 10.1007/s10877-020-00495-x
99. Sun C, Hong S, Song M, Li H. A review of deep learning methods for irregularly sampled medical time series data. arXiv[Preprint].arXiv:201012493. (2020). doi: 10.48550/arXiv.2010.12493
100. Shukla SN, Marlin BM. Modeling irregularly sampled clinical time series. arXiv[Preprint].arXiv:181200531. (2018). doi: 10.48550/arXiv.1812.00531
101. Moskovitch R. Multivariate temporal data analysis - a review. Wiley Interdiscipl Rev Data Mining Knowledge Discovery. (2022) 12:e1430. doi: 10.1002/widm.1430
103. Nabian M, Yin Y, Wormwood J, Quigley KS, Barrett LF, Ostadabbas S. An open-source feature extraction tool for the analysis of peripheral physiological data. IEEE J Transl Eng Health Med. (2018) 6:1–11. doi: 10.1109/JTEHM.2018.2878000
104. Hripcsak G, Albers DJ, Perotte A. Parameterizing time in electronic health record studies. J Am Med Inform Assoc. (2015) 22:794–804. doi: 10.1093/jamia/ocu051
106. Amsterdam PNV. Philips-Electronics 2008 IntelliVue X2, Multi-Measurement Module. (2008). Available online at: https://medaval.ie/docs/manuals/Philips-M3002A-Manual.pdf
107. Ahmed SJM, Rich W, Finer NN. The effect of averaging time on oximetry values in the premature infant. Pediatrics. (2010) 125:e115–21. doi: 10.1542/peds.2008-1749
108. Vagedes J, Poets CF, Dietz K. Averaging time, desaturation level, duration and extent. Arch Dis Childhood Fetal Neonatal Ed. (2013) 98:F265–6. doi: 10.1136/archdischild-2012-302543
109. Bent B, Goldstein BA, Kibbe WA, Dunn JP. Investigating sources of inaccuracy in wearable optical heart rate sensors. NPJ Digit Med. (2020) 3:1–9. doi: 10.1038/s41746-020-0226-6
110. Clifford GD, Scott DJ, Villarroel M. User Guide and Documentation for the MIMIC II Database. MIMIC-II Database Version. Cambridge, MA (2009).
111. Sukiennik P, Białasiewicz JT. Cross-correlation of bio-signals using continuous wavelet transform and genetic algorithm. J Neurosci Methods. (2015) 247:13–22. doi: 10.1016/j.jneumeth.2015.03.002
112. Bracco D, Backman SB. Philips monitors: catch the wave! Can J Anesthesia. (2012) 59:325–6. doi: 10.1007/s12630-011-9645-9
113. Foo JYA, Wilson SJ, Dakin C, Williams G, Harris MA, Cooper D. Variability in time delay between two models of pulse oximeters for deriving the photoplethysmographic signals. Physiol Meas. (2005) 26:531. doi: 10.1088/0967-3334/26/4/017
114. Lin YT, Lo YL, Lin CY, Frasch MG, Wu HT. Unexpected sawtooth artifact in beat-to-beat pulse transit time measured from patient monitor data. PLoS ONE. (2019) 14:e0221319. doi: 10.1371/journal.pone.0221319
115. Bennis FC, van Pul C, van den Bogaart JJ, Andriessen P, Kramer BW, Delhaas T. Artifacts in pulse transit time measurements using standard patient monitoring equipment. PLoS ONE. (2019) 14:e0218784. doi: 10.1371/journal.pone.0218784
116. Supratak A, Wu C, Dong H, Sun K, Guo Y. Survey on feature extraction and applications of biosignals. In: Machine Learning for Health Informatics. Springer (2016). p. 161–82. doi: 10.1007/978-3-319-50478-0_8
117. Pan J, Tompkins WJ. A real-time QRS detection algorithm. IEEE Trans Biomed Eng. (1985) 3:230–6. doi: 10.1109/TBME.1985.325532
118. Esper SA, Pinsky MR. Arterial waveform analysis. Best Pract Res Clin Anaesthesiol. (2014) 28:363–80. doi: 10.1016/j.bpa.2014.08.002
119. Sinex JE. Pulse oximetry: principles and limitations. Am J Emerg Med. (1999) 17:59–66. doi: 10.1016/S0735-6757(99)90019-0
120. Manal K, Rose W. A general solution for the time delay introduced by a low-pass Butterworth digital filter: an application to musculoskeletal modeling. J Biomech. (2007) 40:678–81. doi: 10.1016/j.jbiomech.2006.02.001
121. Sörnmo L. Time-varying digital filtering of ECG baseline wander. Med Biol Eng Comput. (1993) 31:503–8. doi: 10.1007/BF02441986
122. Sowan AK, Vera A, Malshe A, Reed C. Transcription errors of blood glucose values and insulin errors in an intensive care unit: secondary data analysis toward electronic medical Record-Glucometer Interoperability. JMIR Med Inform. (2019) 7:e11873. doi: 10.2196/11873
123. Hong S, Zhou Y, Shang J, Xiao C, Sun J. Opportunities and challenges in deep learning methods on electrocardiogram data: a systematic review. arXiv[Preprint].arXiv:200101550. (2019). doi: 10.1016/j.compbiomed.2020.103801
124. Sehgal A, Bamber J. Different clocks, different times. Anaesthesia. (2003) 58:398. doi: 10.1046/j.1365-2044.2003.03095_19.x
125. Nasin bin M, Ismail M, Seow VK. Measured time and perceived time: crucial data in reducing and managing the time spent at the emergency department. J Patient Saf Qual Improvement. (2019) 7:9–12.
126. Brabrand M, Folkestad L, Hosbond S. Perception of time by professional health care workers during simulated cardiac arrest. Am J Emerg Med. (2011) 29:124–6. doi: 10.1016/j.ajem.2010.08.013
127. Callaham M. Manually recorded time. Ann Emerg Med. (1994) 24:990. doi: 10.1016/S0196-0644(94)70222-5
128. Karaduman C, Meslec N, Oerlemans L. Time judgment during a crisis. In: Academy of Management Proceedings. Briarcliff Manor, NY: Academy of Management (2020). p. 21055. doi: 10.5465/AMBPP.2020.21055abstract
129. Hancock PA, Weaver J. On time distortion under stress. Theoret Issues Ergon Sci. (2005) 6:193–211. doi: 10.1080/14639220512331325747
130. Hosbond S, Folkestad L, Brabrand M. Does cardio-pulmonary resuscitation influence perception of time? Scand J Trauma Resuscit Emerg Med. (2009) 17:1–1. doi: 10.1186/1757-7241-17-S2-P8
131. Jagannath S, Sarcevic A, Young V, Myers S. Temporal rhythms and patterns of electronic documentation in time-critical medical work. In: Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems. (2019). p. 1–13. doi: 10.1145/3290605.3300564
132. Isaacs E, Callaham ML. Ability of laypersons to estimate short time intervals in cardiac arrest. Ann Emerg Med. (2000) 35:147–54. doi: 10.1016/S0196-0644(00)70134-X
133. Frisch A, Reynolds JC, Condle J, Gruen D, Callaway CW. Documentation discrepancies of time-dependent critical events in out of hospital cardiac arrest. Resuscitation. (2014) 85:1111–4. doi: 10.1016/j.resuscitation.2014.05.002
134. Wong C, Stenson B, Laing I. As time goes by. Scot Med J. (2002) 47:138–9. doi: 10.1177/003693300204700606
135. Coussens S. Behaving discretely: heuristic thinking in the emergency department. SSRN J. (2018). doi: 10.2139/ssrn.3743423 [Epub ahead of print].
136. Huttenlocher J, Hedges LV, Bradburn NM. Reports of elapsed time: bounding and rounding processes in estimation. J Exp Psychol Learn Mem Cogn. (1990) 16:196. doi: 10.1037/0278-7393.16.2.196
137. Andersen LW, Raymond TT, Berg RA, Nadkarni VM, Grossestreuer AV, Kurth T, et al. Association between tracheal intubation during pediatric in-hospital cardiac arrest and survival. JAMA. (2016) 316:1786–97. doi: 10.1001/jama.2016.14486
138. Stewart JA. Time-interval data in a pediatric in-hospital resuscitation study. JAMA. (2017) 317:973–973. doi: 10.1001/jama.2016.21138
139. Holmberg MJ, Granfeldt A, Moskowitz A, Andersen LW, American Heart Association's Get With The Guidelines-Resuscitation Investigators, et al. Age-related cognitive bias in in-hospital cardiac arrest. Resuscitation. (2021) 162:43–6. doi: 10.1016/j.resuscitation.2021.01.016
140. Olenski AR, Zimerman A, Coussens S, Jena AB. Behavioral heuristics in coronary-artery bypass graft surgery. N Engl J Med. (2020) 382:778–9. doi: 10.1056/NEJMc1911289
141. Camarda CG, Eilers PH, Gampe J. Modelling general patterns of digit preference. Stat Modell. (2008) 8:385–401. doi: 10.1177/1471082X0800800404
142. Bennett J, Wakefield J. Errors-in-variables in joint population pharmacokinetic/pharmacodynamic modeling. Biometrics. (2001) 57:803–12. doi: 10.1111/j.0006-341X.2001.00803.x
143. Locker TE, Mason SM. Digit preference bias in the recording of emergency department times. Eur J Emerg Med. (2006) 13:99–101. doi: 10.1097/01.mej.0000195677.23780.fa
144. Endo T, Johnston T. Digit Preference Bias in the Recording of Times in Emergency Department Data in Queensland. Health Statistics Unit, Queensland Health (2013).
145. Mullins L. Patterns Within Emergency Department Timestamps. (2011). Available online at: https://www.health.qld.gov.au/__data/assets/pdf_file/0025/361438/statbite41.pdf
146. Phelps M, Latif A, Thomsen R, Slodzinski M, Raghavan R, Paul SL, et al. Comparison of minute distribution frequency for anesthesia start and end times from an anesthesia information management system and paper records. J Clin Monitor Comput. (2017) 31:845–50. doi: 10.1007/s10877-016-9893-x
147. Deal LG, Nyland ME, Gravenstein N, Tighe P. Are anesthesia start and end times randomly distributed? The influence of electronic records. J Clin Anesthesia. (2014) 26:264–70. doi: 10.1016/j.jclinane.2013.10.016
148. Lapostolle F, Schneider E, Agostinucci JM, Nadiras P, Martineau L, Metzger J, et al. Digit preference and biased conclusions in cardiac arrest studies. (2021). doi: 10.21203/rs.3.rs-292881/v1
149. Rietveld P. Rounding of arrival and departure times in travel surveys: an interpretation in terms of scheduled activities. J Transport Stat. (2002) 5:71–82.
150. Tuble SC. Perfusion Downunder Collaboration Database–data quality assurance: Towards a high quality clinical database. J Extra Corporeal Technol. (2011) 43:P44.
151. Fontaine P, Mendenhall TJ, Peterson K, Speedie SM. The Measuring Outcomes of Clinical Connectivity" (MOCC) trial: investigating data entry errors in the electronic Primary Care Research Network (ePCRN). J Am Board Fam Med. (2007) 20:151–9. doi: 10.3122/jabfm.2007.02.060069
152. Fahimi F, Abbasi NM, Abrishami R, Sistanizad M, Mazidi T, Faghihi T, et al. Transcription errors observed in a teaching hospital. Arch Iran Med. (2009) 12:173–5.
153. Kaye W, Mancini ME, Truitt TL. When minutes count–the fallacy of accurate time documentation during in-hospital resuscitation. Resuscitation. (2005) 65:285–90. doi: 10.1016/j.resuscitation.2004.12.020
154. Skyttberg N, Vicente J, Chen R, Blomqvist H, Koch S. How to improve vital sign data quality for use in clinical decision support systems? A qualitative study in nine Swedish emergency departments. BMC Med Inform Decis Mak. (2016) 16:61. doi: 10.1186/s12911-016-0305-4
155. Jacono FJ, De Georgia MA, Wilson CG, Dick TE, Loparo KA. Data acquisition and complex systems analysis in critical care: developing the intensive care unit of the future. J Healthcare Eng. (2010) 1:337–55. doi: 10.1260/2040-2295.1.3.337
156. von Dincklage F, Jurth C, Schneider G, Garcia PS, Kreuzer M. Technical considerations when using the EEG export of the SEDLine Root device. J Clin Monitor Comput. (2020) 1–8. doi: 10.1007/s10877-020-00578-9
157. Turakhia MP, Estes III NM, Drew BJ, Granger CB, Wang PJ, Knight BP, et al. Latency of ECG displays of hospital telemetry systems: a science advisory from the American Heart Association. Circulation. (2012) 126:1665–9. doi: 10.1161/CIR.0b013e31826ae459
158. Burmeister O, Litza M, Nitschke M, Hofmann U. Synchronous stereo-video and biosignal recording-a basic setup for Human-Computer-Interface applications. In: Conference Proceedings. 2nd International IEEE EMBS Conference on Neural Engineering. IEEE (2005). p. 501–5.
159. Potera C. Delays in cardiac rhythm display in wireless telemetry systems. Am J Nurs. (2012) 112:13. doi: 10.1097/01.NAJ.0000423487.06113.16
160. Arney D, Goldman JM, Bhargav-Spantzel A, Basu A, Taborn M, Pappas G, et al. Simulation of medical device network performance and requirements for an integrated clinical environment. Biomed Instrument Technol. (2012) 46:308–15. doi: 10.2345/0899-8205-46.4.308
161. Orlov K, Shevtsova K, Zavyalova Y. Blood pressure calculation based on data received from cardiac monitor jointly with PPG sensor. In: Conference of Open Innovations Association, FRUCT 22. Jyvaskyla: FRUCT Oy (2018). p. 373–7.
162. Charlton P. Monitoring Physiological Trajectories. Transfer of status report. King's College London (2014).
163. Kushida CA, Nichols DA, Jadrnicek R, Miller R, Walsh JK, Griffin K. Strategies for de-identification and anonymization of electronic health record data for use in multicenter research studies. Med Care. (2012) 50:S82. doi: 10.1097/MLR.0b013e3182585355
164. Lo B. Sharing clinical trial data: maximizing benefits, minimizing risk. JAMA. (2015) 313:793–794. doi: 10.1001/jama.2015.292
165. El Emam K, Malin B. Appendix B: Concepts and Methods for De-identifying Clinical Trial Data. Committee on Strategies for Responsible Sharing of Clinical Trial Data; Board on Health Sciences Policy. (2015). p. 1–290.
166. Johnson AE, Pollard TJ, Shen L, Li-Wei HL, Feng M, Ghassemi M, et al. MIMIC-III, a freely accessible critical care database. Sci Data. (2016) 3:1–9. doi: 10.1038/sdata.2016.35
167. Nestor B, McDermott MB, Boag W, Berner G, Naumann T, Hughes MC, et al. Feature robustness in non-stationary health records: caveats to deployable model performance in common clinical machine learning tasks. In: Machine Learning for Healthcare Conference. PMLR (2019). p. 381–405.
168. Hripcsak G, Mirhaji P, Low AF, Malin BA. Preserving temporal relations in clinical data while maintaining privacy. J Am Med Inform Assoc. (2016) 23:1040–5. doi: 10.1093/jamia/ocw001
169. Black N. Is hospital mortality higher at weekends? If so, why? Lancet. (2016) 388:108–11. doi: 10.1016/S0140-6736(16)30505-0
170. Kurniati AP, Rojas E, Hogg D, Hall G, Johnson OA. The assessment of data quality issues for process mining in healthcare using Medical Information Mart for Intensive Care III, a freely available e-health record database. Health Inform J. (2019) 25:1878–93. doi: 10.1177/1460458218810760
171. Cruz-Correia R, Ferreira D, Bacelar G, Marques P, Maranhao P. Personalised medicine challenges: quality of data. Int J Data Sci Anal. (2018) 6:251–9. doi: 10.1007/s41060-018-0127-9
172. Lunt H. Incorrect AM/PM insulin pump clock settings can result in an unstable insulin dosing feedback loop. J Diabetes Sci Technol. (2017) 11:842–3. doi: 10.1177/1932296816678633
173. Aldasouqi SA, Reed AJ. Pitfalls of insulin pump clocks: technical glitches that may potentially affect medical care in patients with diabetes. J Diabetes Sci Technol. (2014) 8:1215–20. doi: 10.1177/1932296814541811
174. Ehlers A, Dyson RL, Hodgson CK, Davis SR, Krasowski MD. Impact of daylight saving time on the clinical laboratory. Acad Pathol. (2018) 5. doi: 10.1177/2374289518784222
175. Dowing M. Spring Forward: The Annual Madness of Daylight Saving Time. Berkely, CA: Counterpoint Press (2006).
176. Lyon AW, Delayen K, Reddekopp R. No lab tests when you are born in the twilight zone: a clinical informatics case report. J Appl Lab Med. (2020) 5:1395–400. doi: 10.1093/jalm/jfaa080
177. Harhay MO, Ratcliffe SJ, Small DS, Suttner LH, Crowther MJ, Halpern SD. Measuring and analyzing length of stay in critical care trials. Med Care. (2019) 57:e53. doi: 10.1097/MLR.0000000000001059
178. Harhay MO, Ratcliffe SJ, Halpern SD. Measurement error due to patient flow in estimates of intensive care unit length of stay. Am J Epidemiol. (2017) 186:1389–95. doi: 10.1093/aje/kwx222
179. Contentin L, Ehrmann S, Giraudeau B. Heterogeneity in the definition of mechanical ventilation duration and ventilator-free days. Am J Resp Crit Care Med. (2014) 189:998–1002. doi: 10.1164/rccm.201308-1499LE
180. Colantuoni E, Koneru M, Akhlaghi N, Li X, Hashem MD, Dinglas VD, et al. Heterogeneity in design and analysis of ICU delirium randomized trials: a systematic. Trials. (2021) 22:354. doi: 10.1186/s13063-021-05299-1
181. Barnes J, Hunter J, Harris S, Shankar-Hari M, Diouf E, Jammer I, et al. Systematic review and consensus definitions for the Standardised Endpoints in Perioperative Medicine (StEP) initiative: infection and sepsis. Brit J Anaesthesia. (2019) 122:500–8. doi: 10.1016/j.bja.2019.01.009
182. Centner FS, Schoettler JJ, Fairley AM, Lindner HA, Schneider-Lindner V, Weiss C, et al. Impact of different consensus definition criteria on sepsis diagnosis in a cohort of critically ill patients–insights from a new mathematical probabilistic approach to mortality-based validation of sepsis criteria. PLoS ONE. (2020) 15:e0238548. doi: 10.1371/journal.pone.0238548
183. Perimal-Lewis L, Teubner D, Hakendorf P, Horwood C. Application of process mining to assess the data quality of routinely collected time-based performance data sourced from electronic health records by validating process conformance. Health Inform J. (2016) 22:1017–29. doi: 10.1177/1460458215604348
184. De Georgia M, Kaffashi F, Jacono FJ, Loparo K. Information technology in critical care. In: Neurocritical Care Informatics. Springer (2020). p. 1–12. doi: 10.1007/978-3-662-59307-3_1
185. Mills D. Computer network time synchronization: the network time protocol on earth and in space.
186. Zhang Z, Guo C, Fu Z, Ren S, Venkatasubramanian N. Prevent potential hazards caused by medical device time differences in integrated clinical environments. In: 2019 IEEE International Conference on Embedded Software and Systems (ICESS). Las Vegas, NV: IEEE (2019). p. 1–4. doi: 10.1109/ICESS.2019.8782486
187. Zaleski JR. Medical device interoperability and data integration to clinical information systems: medical device data alignment. Biomed Instrument Technol. (2012) 46:65–70. doi: 10.2345/0899-8205-46.s2.65
188. Mills D. A brief history of NTP time: memoirs of an Internet timekeeper. ACM SIGCOMM Comput Commun Rev. (2003) 33:9–21. doi: 10.1145/956981.956983
189. Jones PG, Miles JL. Overcoming barriers to in-hospital cardiac arrest documentation. Resuscitation. (2008) 76:369–75. doi: 10.1016/j.resuscitation.2007.08.021
190. Marouani H, Dagenais M. Internal clock drift estimation in computer clusters. J Comput Syst Netw Commun. (2008) 2008:9. doi: 10.1155/2008/583162
191. Laner M, Caban S, Svoboda P, Rupp M. Time synchronization performance of desktop computers. In: 2011 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication. Munich: IEEE (2011). p. 75–80. doi: 10.1109/ISPCS.2011.6070154
192. Broomhead T, Cremean L, Rodoux J, Veitch D. Virtualize everything but time. In: Proceedings of the 9th USENIX conference on Operating systems design and implementation. Vancouver, BC (2010). p. 451–64.
193. Lampe U, Kieselmann M, Miede A, Zoller S, Steinmetz R. A tale of millis and nanos: Time measurements in virtual and physical machines. In: European Conference on Service-Oriented and Cloud Computing. Mailaga: Springer (2013). p. 172–79. doi: 10.1007/978-3-642-40651-5_14
194. Chauhan J, Makaroff D, Arkles A. VM clock synchronization measurements. In: 30th IEEE International Performance Computing and Communications Conference. Orlando, FL: IEEE (2011). p. 1–2. doi: 10.1109/PCCC.2011.6108101
195. Sandha SS, Noor J, Anwar FM, Srivastava M. Exploiting smartphone peripherals for precise time synchronization. In: 2019 IEEE Global Conference on Signal and Information Processing. Ottawa, ON: IEEE (2019). p. 1–6. doi: 10.1109/GlobalSIP45357.2019.8969519
196. Ulger F, Esen S, Dilek A, Yanik K, Gunaydin M, Leblebicioglu H. Are we aware how contaminated our mobile phones with nosocomial pathogens? Ann Clin Microbiol Antimicrob. (2009) 8:1–4. doi: 10.1186/1476-0711-8-7
197. Velvizhi G, Anupriya G, Sucilathangam G, Ashihabegum M, Jeyamuruga T, Palaniappan N. Wristwatches as the potential sources of hospital-acquired infections. J Clinical Diagnost Res. (2012) 6:807–810.
198. Jeans A, Moore J, Nicol C, Bates C, Read R. Wristwatch use and hospital-acquired infection. J Hospital Infect. (2010) 74:16–21. doi: 10.1016/j.jhin.2009.06.032
199. Schutz N, Botros AA, Knobel SEJ, Saner H, Buluschek P, Nef T. Real-world consumer-grade sensor signal alignment procedure applied to high-noise ECG to BCG signal synchronization. In: 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society. Montreal, QC: IEEE (2020). p. 5858–962.
200. Ryu M, Park J, Hong S. Timing constraint remapping to avoid time discontinuities in distributed real-time systems. In: Proceedings of the Fifth IEEE Real-Time Technology and Applications Symposium. IEEE (1999). p. 89–98.
201. Sivanathan A, Lim T, Louchart S, Ritchie J. Temporal multimodal data synchronisation for the analysis of a game driving task using EEG. Entertainment Comput. (2014) 5:323–34. doi: 10.1016/j.entcom.2014.03.004
202. Schütz N, Botros A, Single M, Naef AC, Buluschek P, Nef T. Deep canonical correlation alignment for sensor signals. arXiv[Preprint].arXiv:210603637. (2021).
203. Huang Z, Nahrstedt K, Steinmetz R. Evolution of temporal multimedia synchronization principles: a historical viewpoint. ACM Trans Multimedia Comput Commun Appl. (2013) 9:1–23. doi: 10.1145/2490821
204. Oliver A. EEG Synchronization With Other Biosensors (EEG, ECG, EMG, eye Tracking, etc.), and Software. (2020). Available online at: https://www.bitbrain.com/blog/eeg-synchronization
205. Kothe C. Lab Streaming Layer (LSL). (2014). Available online at: https://github.com/sccn/labstreaminglayer
206. Razavi M, Janfaza V, Yamauchi T, Leontyev A, Longmire-Monford S, Orr J. OpenSync: An opensource platform for synchronizing multiple measures in neuroscience experiments. arXiv[Preprint].arXiv:210714367. (2021). doi: 10.1016/j.jneumeth.2021.109458
207. Wang Y, Markham C, Deegan C. Assessing the time synchronisation of EEG systems. In: Proceedings of the Fifth IEEE Real-Time Technology and Applications Symposium. Vancouver, BC: IEEE (1999). p. 89–98. doi: 10.1109/ISSC.2019.8904947
208. Siddharth, Patel AN, Jung TP, Sejnowski TJ. A wearable multi-modal bio-sensing system towards real-world applications. IEEE Trans Biomed Eng. (2019) 66:1137–47. doi: 10.1109/TBME.2018.2868759
209. Muhammed N, Lim TH. Dynamic time division scheduling protocol for medical application using frog synchronization algorithm. In: International Conference on IoT Technologies for HealthCare. Viana do Castello: Springer (2020). p. 148–61. doi: 10.1007/978-3-030-69963-5_11
210. Xue J, Quan C, Li C, Yue J, Zhang C. A crucial temporal accuracy test of combining EEG and Tobii eye tracker. Medicine. (2017) 96. doi: 10.1097/MD.0000000000006444 [Epub ahead of print].
211. O'Connor JM, Pretorius PH, Johnson K, King MA. A method to synchronize signals from multiple patient monitoring devices through a single input channel for inclusion in list-mode acquisitions. Med Phys. (2013) 40:122502. doi: 10.1118/1.4828844
212. Siems A, Tomaino E, Watson A, Spaeder MC, Su L. Improving quality in measuring time to initiation of CPR during in-hospital resuscitation. Resuscitation. (2017) 118:15–20. doi: 10.1016/j.resuscitation.2017.06.018
213. Maier C, Rodler V, Wenz H, Dickhaus H. ECG fingerprints of obstructed breathing in sleep apnea patients. IEEE Eng Med Biol Mag. (2009) 28:41–8. doi: 10.1109/MEMB.2009.934907
214. Benarrouch R, Moin A, Solt F, Frappe A, Cathelin I, Kaiser A, et al. Heartbeat-based synchronization scheme for the human intranet: Modeling and analysis. In: 2020 IEEE International Symposium on Circuits and Systems. Seville: IEEE (2020). p. 1–5. doi: 10.1109/ISCAS45731.2020.9180427
215. Li H, Tan J. Heartbeat-driven medium-access control for body sensor networks. IEEE Trans Inform Technol Biomed. (2009) 14:44–51. doi: 10.1109/TITB.2009.2028136
216. Wolling F, Van Laerhoven K, Siirtola P, Ronong J. PulSync: The heart rate variability as a unique fingerprint for the alignment of sensor data across multiple wearable devices. In: 2021 IEEE International Conference on Pervasive Computing and Communications Workshops and other Affiliated Events. Kassel: IEEE (2021). p. 188–193. doi: 10.1109/PerComWorkshops51409.2021.9431015
217. Vaz P, Almeida V, Ferreira L, Correia C, Cardoso J. Signal (Stream) synchronization with White noise sources, in biomedical applications. Biomed Signal Process Control. (2015) 18:394–400. doi: 10.1016/j.bspc.2015.02.015
218. Ward MJ, Froehle CM, Hart KW, Lindsell CJ. Operational data integrity during electronic health record implementation in the ED. Am J Emerg Med. (2013) 31:1029–33. doi: 10.1016/j.ajem.2013.03.027
219. Grundgeiger T, Albert M, Reinhardt D, Happel O, Steinisch A, Wurmb T. Real-time tablet-based resuscitation documentation by the team leader: evaluating documentation quality and clinical performance. Scand J Trauma Resuscitation Emerg Med. (2016) 24:51. doi: 10.1186/s13049-016-0242-3
220. Stewart JA, Short FA. Time accuracy of a barcode system for recording resuscitation events: laboratory trials. Resuscitation. (1999) 42:235–40. doi: 10.1016/S0300-9572(99)00104-5
221. Martin N. Using indoor location system data to enhance the quality of healthcare event logs: opportunities and challenges. In: International Conference on Business Process Management. Sydney, NSW: Springer (2018). p. 226–38. doi: 10.1007/978-3-030-11641-5_18
222. Gröschel J, Philipp F, Skonetzki S, Genzwürker H, Wetter T, Ellinger K. Automated speech recognition for time recording in out-of-hospital emergency medicine an experimental approach. Resuscitation. (2004) 60:205–12. doi: 10.1016/j.resuscitation.2003.10.006
223. Cao H, Lee KP, Ennett CM, Eshelman L, Nielsen L, Saeed M, et al. Heuristics to determine ventilation times of ICU patients from the MIMIC-II database. In: 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology. Buenos Aires: IEEE (2010). p. 5213–6. doi: 10.1109/IEMBS.2010.5626286
224. Nagaraj S, Goodwin A, Goodfellow SD, Greer B, Eytan D, Goldenberg A, et al. A novel approach to machine learning-based automated vascular catheter access detection in a pediatric critical care setting. In: Joint Paediatric Critical Care International Meeting. London (2019).
225. Wang Z, Talburt JR, Wu N, Dagtas S, Zozus MN. A rule-based data quality assessment system for electronic health record data. Appl Clin Inform. (2020) 11:622–34. doi: 10.1055/s-0040-1715567
226. Pegoraro M, Uysal MS, van der Aalst WM. Conformance checking over uncertain event data. Inform Syst. (2021) 2021:101810. doi: 10.1016/j.is.2021.101810
227. Qian S, Munyisia E, Yu P, Hailey DM, Reid D. Precision of EMR data: the case for a drug and alcohol service. Stud Health Technol Inform. (2017).
228. Verma AA, Pasricha SV, Jung HY, Kushnir V, Mak DY, Koppula R, et al. Assessing the quality of clinical and administrative data extracted from hospitals: the General Medicine Inpatient Initiative (GEMINI) experience. J Am Med Inform Assoc. (2021) 28:578–87. doi: 10.1093/jamia/ocaa225
229. Perren A, Cerutti B, Kaufmann M, Rothen HU, Swiss Society of Intensive Care Medicine. A novel method to assess data quality in large medical registries and databases. Int J Qual Health Care. (2019) 31:1–7. doi: 10.1093/intqhc/mzy249
230. Su L, Waller M, Kaplan S, Watson A, Jones M, Wessel DL. Cardiac resuscitation events: one eyewitness is not enough. Pediatr Crit Care Med. (2015) 16:335–42. doi: 10.1097/PCC.0000000000000355
231. Park HS, Jung SK, Kim HC. Accuracy of the cardiopulmonary resuscitation registry in an emergency department. Emerg Med J. (2012) 29:287–9. doi: 10.1136/emj.2011.112151
232. Faux D, Godolphin J. The floating point: rounding error in timing devices. Am J Phys. (2021) 89:815–6. doi: 10.1119/10.0003919
233. Faux DA, Godolphin J. The floating point: tales of the unexpected. Am J Phys. (2021) 89:806–14. doi: 10.1119/10.0003915
234. Goldberg D. What every computer scientist should know about floating-point arithmetic. ACM Comput Surv. (1991) 23:5–48. doi: 10.1145/103162.103163
235. Gustafson JL, Yonemoto IT. Beating floating point at its own game: posit arithmetic. Supercomput Front Innovat. (2017) 4:71–86. doi: 10.14529/jsfi170206
236. Faux DA, Godolphin J. The floating point: tales of the unexpected. Am J Phys. (2021) 89:806–14.
237. Polhill JG, Izquierdo LR, Gotts NM. The ghost in the model (and other effects of floating point arithmetic). J Artif Soc Soc Simul. (2005) 8:1–5.
238. Marshall E. Fatal error: how patriot overlooked a Scud. Science. (1992) 255:1347–8. doi: 10.1126/science.255.5050.1347
239. Vicino D, Wainer GA, Trabes GG. Investigation of versatile datatypes for representing time in discrete event simulation. In: 2019 Winter Simulation Conference (WSC). National Harbor, MD: IEEE (2019). p. 2701–12. doi: 10.1109/WSC40007.2019.9004689
240. Jensen CS, Dyreson CE, Bohlen M, Clifford J, Elmasri R, Gadia SK, et al. “The consensus glossary of temporal database concepts - February 1998 version,” in Temporal Databases: Research and Practice. Berlin; Heidelberg: Springer (1998). p. 367–405. doi: 10.1007/BFb0053710
241. Goldstein R, Khan A, Dalle O, Wainer G. Multiscale representation of simulated time. Simulation. (2018) 94:519–58. doi: 10.1177/0037549717726868
242. Abdar M, Pourpanah F, Hussain S, Rezazadegan D, Liu L, Ghavamzadeh M, et al. A review of uncertainty quantification in deep learning: techniques, applications and challenges. Information Fusion. (2021). doi: 10.1016/j.inffus.2021.05.008
243. Plant AL, Becker CA, Hanisch RJ, Boisvert RF, Possolo AM, Elliott JT. How measurement science can improve confidence in research results. PLoS Biol. (2018) 16:e2004299. doi: 10.1371/journal.pbio.2004299
244. Briol FX, Girolami M. Bayesian numerical methods as a case study for statistical data science. Stat Data Sci. (2018) 99–110. doi: 10.1142/9781786345400_0006
245. van Smeden M, Lash TL, Groenwold RH. Reflection on modern methods: five myths about measurement error in epidemiological research. Int J Epidemiol. (2020) 49:338–347. doi: 10.1093/ije/dyz251
246. Friedrich S, Antes G, Behr S, Binder H, Brannath W, Dumpert F, et al. Is there a role for statistics in artificial intelligence? Adv Data Anal Class. (2021) 1–24. doi: 10.1007/s11634-021-00455-6
247. Billiet C, De Tré G. The role of computational intelligence in temporal information retrieval: a survey of imperfect time in information systems. In: Andreasen T, Christiansen H, Kacprzyk J, Larsen H, Pasi G, Pivert O, De Tré, G, Vila MA, Yazici A, and Zadrożny, S, editors. Flexible Query Answering Systems. Cham: Springer (2016). p. 41–56. doi: 10.1007/978-3-319-26154-6_4
248. Henderson J, McCracken S. Clinical value of a wristwatch. BMJ. (2008) 336:10. doi: 10.1136/bmj.39423.586331.1F
249. Moore JH, Boland MR, Camara PG, Chervitz H, Gonzalez G, Himes BE, et al. Preparing next-generation scientists for biomedical big data: artificial intelligence approaches. Pers Med. (2019) 16:247–57. doi: 10.2217/pme-2018-0145
250. Looten V, Chang LKW, Neuraz A, Landau-Loriot MA, Vedie B, Paul JL, et al. What can millions of laboratory test results tell us about the temporal aspect of data quality? Study of data spanning 17 years in a clinical data warehouse. Comput Methods Prog Biomed. (2019) 181:104825. doi: 10.1016/j.cmpb.2018.12.030
251. Sato Y, Maruyama T. Modeling the rounding of departure times in travel surveys: comparing the effect of trip purposes and travel modes. Transport Res Rec. (2020) 2674:628–37. doi: 10.1177/0361198120935435
252. Wübbeler G, Krystek M, Elster C. Evaluation of measurement uncertainty and its numerical calculation by a Monte Carlo method. Meas Sci Technol. (2008) 19:084009. doi: 10.1088/0957-0233/19/8/084009
253. Couto PG, Damasceno JC. Monte Carlo simulations applied to uncertainty in measurement. In: Theory and Applications of Monte Carlo Simulations. (2013). p. 27–51.
254. Hennig P, Osborne MA, Girolami M. Probabilistic numerics and uncertainty in computations. Proc R Soc A Math Phys Eng Sci. (2015) 471:20150142. doi: 10.1098/rspa.2015.0142
255. Allen JF. Time and time again: the many ways to represent time. Int J Intell Syst. (1991) 6:341–55. doi: 10.1002/int.4550060403
256. Pretty CG, Signal M, Fisk L, Penning S, Le Compte A, Shaw GM, et al. Impact of sensor and measurement timing errors on model-based insulin sensitivity. Comput Methods Prog Biomed. (2014) 114:e79–86. doi: 10.1016/j.cmpb.2013.08.007
257. Ward MJ, Self WH, Froehle CM. Effects of common data errors in electronic health records on emergency department operational performance metrics: a Monte Carlo simulation. Acad Emerg Med. (2015) 22:1085–92. doi: 10.1111/acem.12743
258. Garcia-Gonzalez M, Fernandez-Chimeno M, Ramos-Castro J. Bias and uncertainty in heart rate variability spectral indices due to the finite ECG sampling frequency. Physiol Meas. (2004) 25:489. doi: 10.1088/0967-3334/25/2/008
259. Napoli NJ, Demas MW, Mendu S, Stephens CL, Kennedy KD, Harrivel AR, et al. Uncertainty in heart rate complexity metrics caused by R-peak perturbations. Comput Biol Med. (2018) 103:198–207. doi: 10.1016/j.compbiomed.2018.10.009
260. Ellis RJ, Zhu B, Koenig J, Thayer JF, Wang Y. A careful look at ECG sampling frequency and R-peak interpolation on short-term measures of heart rate variability. Physiol Meas. (2015) 36:1827. doi: 10.1088/0967-3334/36/9/1827
261. Baumert M, Schmidt M, Zaunseder S, Porta A. Effects of ECG sampling rate on QT interval variability measurement. Biomed Signal Process Control. (2016) 25:159–64. doi: 10.1016/j.bspc.2015.11.011
262. Govindan RB, Massaro AN, Kota S, Grabowski RC, Wilson JD, du Plessis A. Effect of EKG sampling rate on heart rate variability analysis. In: 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Paris: IEEE (2019). p. 6780–3. doi: 10.1109/EMBC.2019.8857754
263. Meijer E, Oczkowski E, Wansbeek T. How measurement error affects inference in linear regression. Empirical Econ. (2021) 60:131–55. doi: 10.1007/s00181-020-01942-z
264. Hutcheon JA, Chiolero A, Hanley JA. Random measurement error and regression dilution bias. BMJ. (2010) 340. doi: 10.1136/bmj.c2289 [Epub ahead of print].
265. Söderström T. Errors-in-variables methods in system identification. Automatica. (2007) 43:939–58. doi: 10.1016/j.automatica.2006.11.025
266. Gilchrist S. Clinical Applications of Errors-In-Variables Methodology. University of Wales College of Medicine (2005).
267. Wang N, Davidian M. A note on covariate measurement error in nonlinear mixed effects models. Biometrika. (1996) 83:801–12. doi: 10.1093/biomet/83.4.801
268. Kulathinal S, Kuulasmaa K, Gasbarra D. Estimation of an errors-in-variables regression model when the variances of the measurement errors vary between the observations. Stat Med. (2002) 21:1089–101. doi: 10.1002/sim.1062
269. Zhang G, Ashrafi RA, Juuti A, Pietiläinen K, Marttinen P. Errors-in-variables modeling of personalized treatment-response trajectories. IEEE J Biomed Health Inform. (2020) 25:201–8. doi: 10.1109/JBHI.2020.2987323
270. Ashrafi RA, Ahola AJ, Rosengård-Bärlund M, Saarinen T, Heinonen S, Juuti A, et al. Computational modelling of self-reported dietary carbohydrate intake on glucose concentrations in patients undergoing Roux-en-Y gastric bypass versus one-anastomosis gastric bypass. Ann Med. (2021) 53:1885–95. doi: 10.1080/07853890.2021.1964035
271. Plant RR, Quinlan PT. Could millisecond timing errors in commonly used equipment be a cause of replication failure in some neuroscience studies? Cogn Affect Behav Neurosci. (2013) 13:598–614. doi: 10.3758/s13415-013-0166-6
272. Smith NA, Sinden D, Thomas SA, Romanchikova M, Talbott JE, Adeogun M. Building confidence in digital health through metrology. Brit J Radiol. (2020) 93:20190574. doi: 10.1259/bjr.20190574
273. Sené M, Gilmore I, Janssen JT. Metrology is key to reproducing results. Nature News. (2017) 547:397. doi: 10.1038/547397a
274. Plant AL, Hanisch RJ. Reproducibility in Science: A Metrology Perspective. Cambridge, MA: MIT Press. doi: 10.1162/99608f92.eb6ddee4
275. O'Neil M. System engineering enabling transformational change: Engineering a new healthcare ecosystem. In: INCOSE International Symposium, Vol. 23. Philadelphia, PA: Wiley (2013). p. 1324-9. doi: 10.1002/j.2334-5837.2013.tb03090.x
276. Shelley K, Cannesson M. 'Off-label' use of clinical monitors: what happens when new physiologic understanding meets state-of-the-art technology. LWW. (2014) 119:1241–1242. doi: 10.1213/ANE.0000000000000479
277. Futoma J, Simons M, Panch T, Doshi-Velez F, Celi LA. The myth of generalisability in clinical research and machine learning in health care. Lancet Digit Health. (2020) 2:e489–92. doi: 10.1016/S2589-7500(20)30186-2
278. Weininger S, Jaffe MB, Goldman JM. The need to apply medical device informatics in developing standards for safe interoperable medical systems. Anesthesia Analgesia. (2017) 124:127. doi: 10.1213/ANE.0000000000001386
279. Hemphill JC, Barton CW, Morabito D, Manley GT. Influence of data resolution and interpolation method on assessment of secondary brain insults in neurocritical care. Physiol Meas. (2005) 26:373. doi: 10.1088/0967-3334/26/4/004
280. Feldman JM. Can clinical monitors be used as scientific instruments? LWW. (2006) 103:1071–1072 doi: 10.1213/01.ane.0000247882.20257.b6
281. Feldman JM, Kuck K, Hemmerling T. Black box, gray box, clear box? How well must we understand monitoring devices? Anesthesia Analgesia. (2021) 132:1777–80. doi: 10.1213/ANE.0000000000005500
282. Landsverk SA, Hoiseth LO, Kirkeboen KA. Oscillations in the plethysmographic waveform amplitude: phenomenon hides behind artifacts. J Am Soc Anesthesiol. (2009) 111:207–8. doi: 10.1097/ALN.0b013e3181a96055
Keywords: time, clocks, uncertainty, clinical, ICU, medicine, errors, metrology
Citation: Goodwin AJ, Eytan D, Dixon W, Goodfellow SD, Doherty Z, Greer RW, McEwan A, Tracy M, Laussen PC, Assadi A and Mazwi M (2022) Timing errors and temporal uncertainty in clinical databases—A narrative review. Front. Digit. Health 4:932599. doi: 10.3389/fdgth.2022.932599
Received: 30 April 2022; Accepted: 11 July 2022;
Published: 18 August 2022.
Edited by:
Vangelis Sakkalis, Foundation for Research and Technology Hellas (FORTH), GreeceReviewed by:
Bhaskara Rao Chintada, Massachusetts General Hospital and Harvard Medical School, United StatesYael Bensoussan, University of Southern California, United States
Copyright © 2022 Goodwin, Eytan, Dixon, Goodfellow, Doherty, Greer, McEwan, Tracy, Laussen, Assadi and Mazwi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrew J. Goodwin, YW5kcmV3Lmdvb2R3aW4mI3gwMDA0MDtzaWNra2lkcy5jYQ==