- 1Department of Physics and Astronomy, University of Catania, Catania, Italy
- 2Department of Clinical and Experimental Medicine, University of Catania, Catania, Italy
Temporal networks are graphs where each edge is linked with a timestamp, denoting when an interaction between two nodes happens. According to the most recently proposed definitions of the problem, motif search in temporal networks consists in finding and counting all connected temporal graphs Q (called motifs) occurring in a larger temporal network T, such that matched target edges follow the same chronological order imposed by edges in Q. In the last few years, several algorithms have been proposed to solve motif search, but most of them are limited to very small or specific motifs due to the computational complexity of the problem. In this paper, we present MODIT (MOtif DIscovery in Temporal Networks), an algorithm for counting motifs of any size in temporal networks, inspired by a very recent algorithm for subgraph isomorphism in temporal networks, called TemporalRI. Experiments show that for big motifs (more than 3 nodes and 3 edges) MODIT can efficiently retrieve them in reasonable time (up to few hours) in many networks of medium and large size and outperforms state-of-the art algorithms.
1. Introduction and Related Works
Networks (also named graphs) are tools for the description and analysis of entities, called nodes, that interact with each other by means of edges. There are many types of data that can be represented by graphs, including computer networks, social networks, communication networks, biological networks, and so on. A wide range of domains can be modeled and studied with static networks but many complex systems are fully dynamic, indeed interactions between entities change over time. Systems of this type can be modeled as temporal networks, in which edges between nodes are associated with temporal information such as, for example, the duration of the interaction and the instant in which the interaction begins. Annotations of edges with temporal data is important to understand the formation and the evolution of such systems.
In literature, several definitions of temporal networks have been proposed (Holme and Saramaki, 2012; Masuda and Lambiotte, 2020). In few works, these are also referenced as dynamic (Carley et al., 2007), evolutionary (Aggarwal and Subbian, 2014) or time-varying (Casteigts et al., 2011) networks. In this paper, we define temporal network as a multigraph (i.e a graph where two nodes may interact multiple times). Each edge is associated with an integer, called timestamp, which denotes when two nodes interact.
In the last few years, there has been a growing interest in analyzing temporal networks and studying their properties. Analysis of temporal networks includes network centrality (Lv et al., 2019; Tsalouchidou et al., 2020), network clustering (Crawford and Milenkovic, 2018), community detection (Rossetti and Cazabet, 2018), link prediction (Divakaran and Mohan, 2020), graph mining (Sun et al., 2019), graph embedding (Torricelli et al., 2020), network sampling (Rocha et al., 2017), random models (Petit et al., 2018; Hiraoka et al., 2020; Singh and Cherifi, 2020), and epidemic spreading (Tizzani et al., 2018; Williams et al., 2019; Masuda and Holme, 2020). Extensive reviews of temporal networks and their main features can be found in Holme and Saramaki (2012, 2019), Masuda and Lambiotte (2020).
In this work, we focus on motif search in temporal networks. Different definitions of temporal motifs have been proposed so far (Kovanen et al., 2011; Hulovatyy et al., 2015; Paranjape et al., 2017). Here, we follow the most recent definition proposed by Paranjape et al. (2017), which is becoming the most accepted one. A temporal motif is a temporal network where edges denote a succession of events. In addition to the original definition proposed by Paranjape et al. (2017), simultaneous events, represented by edges with equal timestamps, are allowed, provided that such edges do not link the same pair of nodes. Temporal graphs Q1 and Q2 of Figure 1 are two examples of motifs. Applications of Temporal Motif Search include the creation of evolution rules that govern the way the network changes over time (Berlingerio et al., 2009; Ugander et al., 2013) allowing also to identify all the time an edge participates to particular pattern in a time window. A second application consists in the identification of motifs in temporal network at different time resolution to identify patterns at different time scale. Another application consists in temporal network classification using a feature representation based on the temporal motifs distribution (Tu et al., 2018).
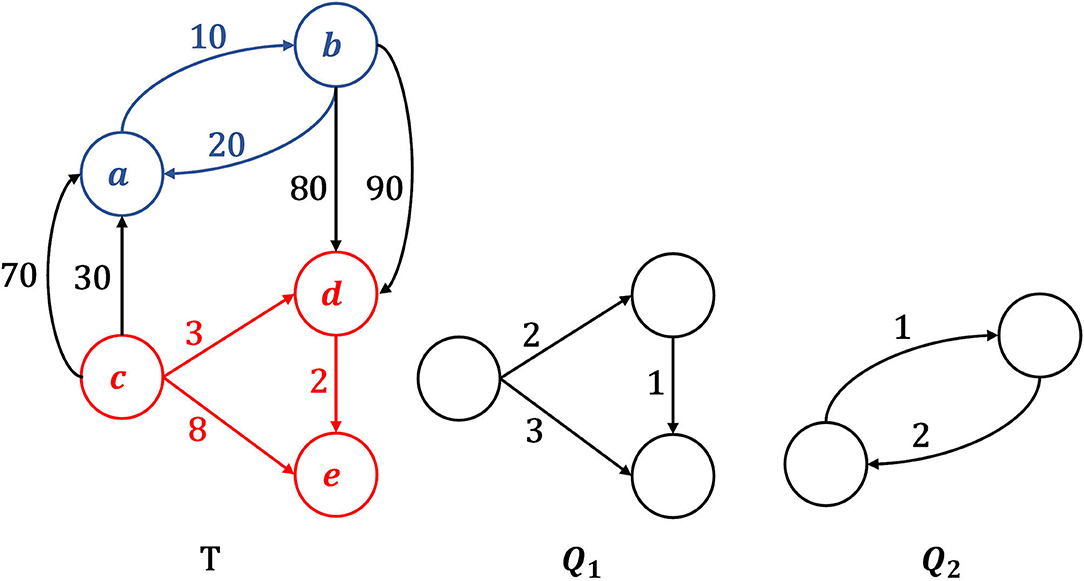
Figure 1. Example of motif Δ-occurrence in a temporal graph T, given Δ = 6. Motif Q1 has exactly one Δ-occurrence in T, which is the subgraph formed by nodes and edges colored in red. Motif Q2, instead, does not Δ-occur in T. In fact, the subgraph with blue nodes and blue edges is isomorphic to Q2 and respects the chronological order imposed by Q2's edges, but its edges are not observed within the time window Δ.
Given a time interval Δ, we say that a motif Q Δ-occurs in T, iff: (i) Q is isomorphic (i.e., structurally equivalent) to a subgraph S of T (called an occurrence of Q in T), (ii) edges in S follow the same chronological order imposed by corresponding matched edges in Q, (iii) all interactions in S are observed in a time interval less than or equal to Δ (i.e., they are likely to be related each other). In Figure 1, motif Q1 Δ-occurs (Δ = 6 in the example) in T, while Q2 does not.
For a given temporal graph T and time interval Δ, motif search aims at retrieving all motifs that Δ-occurs in T. In addition, for each such motif Q, we also count the number of occurrences of Q in T. It has been shown that Temporal Motif Search (TMS) problem is NP-complete, even for star topologies (Liu et al., 2019). For this reason, motif search is usually restricted to motifs with up to a certain number of nodes and edges. Given Δ = 10, Figure 2 shows all temporal motifs with up to 3 nodes and 3 edges that Δ-occur in a toy temporal graph, together with the corresponding number of occurrences.
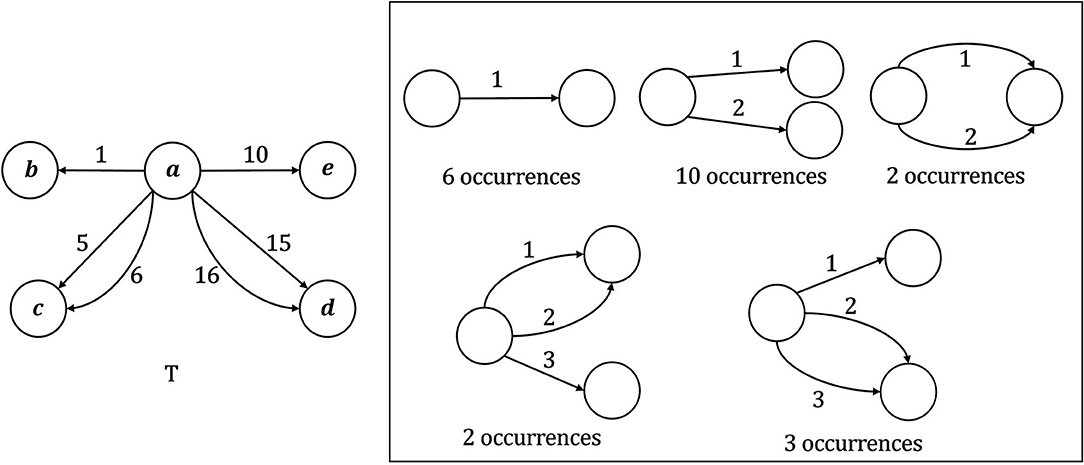
Figure 2. Example of application of the Temporal Motif Search (TMS) problem for a temporal graph T, given Δ = 10, k = 3, and l = 3. For each motif, the relative number of Δ-occurrences in T is reported.
Recently, several TMS algorithms have been introduced (Kovanen et al., 2011; Hulovatyy et al., 2015; Paranjape et al., 2017; Liu et al., 2019). However, the proposed solutions are limited to very small motifs or specific topologies.
Temporal motifs have been introduced for the first time by Kovanen et al. (2011). Authors define a motif as an ordered set of edges such that: (i) the difference between the timestamps of two consecutive edges must be less than or equal to a certain threshold Δ and (ii) if a node is part of a motif, then all its adjacent edges have to be consecutive (consecutive edge restriction).
In Hulovatyy et al. (2015) the consecutive edge restriction was relaxed and the authors considered only induced subgraphs, called graphlets, in order to reduce the computational complexity while obtaining approximate results.
Paranjape et al. (2017) describes a temporal motif as a sequence of edges ordered by increasing timestamps. More precisely, the authors define a k-node, l-edge, Δ-temporal motif as a sequence of l edges, M = (u1, v1, t1), (u2, v2, t2), …, (ul, vl, tl) that are time-ordered within a Δ duration, i.e., t1 < t2 ⋯ < tl and tl − t1 ≤ Δ, such that the static graph induced by the edges is connected and has k nodes. The authors present an algorithm to efficiently calculate the frequencies of all possible directed temporal motifs with 3 edges. For bigger motifs they use a naive algorithm that first computes static matches, then filters out occurrences which do not match the temporal constraints.
To tackle with the NP-completeness of TMS, approximate solutions have been proposed too. Liu et al. (2019) propose a general sampling framework to estimate motif counts. It consists in partitioning time into intervals, finding exact counts of motifs in each interval and weighting counts to get the final estimate, using importance sampling.
In this paper, we present a new motif search algorithm, called MODIT (MOtif DIscovery in Temporal networks). The method is inspired by the temporal subgraph matching algorithm TemporalRI (Locicero et al., 2021; Micale et al., 2021). Our algorithm overcomes many of the limitations imposed by other motif search methods. In fact, MODIT is general and can search for motifs of any size. It has no consecutive edge restriction and allows edges with equal timestamps, provided that they do not link the same pair of nodes.
The rest of the paper is organized as follows. In section 2, we give preliminary definitions about temporal networks and temporal motif search, then we illustrate MODIT and evaluate its computational complexity. In section 3, we assess the performance of MODIT on a dataset of real networks and compare it with the algorithm presented in Paranjape et al. (2017). Finally, section 4 ends the paper.
2. Methods
2.1. Preliminary Definitions
In this section, we formally define the concepts of temporal graph and temporal motif, then we introduce the temporal motif search problem.
2.1.1. Temporal Graph
A temporal graph (or network) G is a pair of sets (V, E), where V is the set of nodes and E ⊆ V × V × ℝ is the set of edges. Each edge is a triple (s, d, t) where s is the source node, d is the destination node and t is the timestamp, denoting the moment or the time interval in which the two nodes interact.
By definition, a temporal graph is a multigraph, because there can be multiple edges between two nodes. However, triplets in E are distinct, therefore such edges need to have different timestamps. With e.source, e.dest, and e.time we denote the source, the destination and the timestamp of edge e, respectively. A temporal graph G = (V, E) is undirected if ∀(s, d, t) ∈ E(G) we have (d, s, t) ∈ E(G), otherwise it is directed. With Inc(v) we denote the set of all edges that are incident to node v, i.e., having v as source or destination.
2.1.2. Temporal Motif
Let Q = (V, E) a connected temporal graph with l edges and (t1, t2, …, tl) the sequence of Q's edges timestamps in ascending order. Q is a temporal motif iff: (i) t1 = 1, (ii) ti+1 − ti ≤ 1∀1 ≤ i ≤ l − 1.
In other words, a temporal motif Q can be considered a sort of standardized temporal graph, in which edge timestamps denote an order in which events happen starting from the initial event (i.e., event 1). Edges with equal timestamps (if any) in Q represent simultaneous event. Examples of temporal motifs are the graphs Q1 and Q2 depicted in Figure 1.
To establish if a temporal graph contains a temporal motif, we need to introduce the concept of Temporal Subgraph Isomorphism. We follow the definition reported in Micale et al. (2021).
2.1.3. Temporal Subgraph Isomorphism
Given two temporal graphs Q = (VQ, EQ) and T = (VT, ET), called, respectively, query and target, and an integer Δ, the Temporal Subgraph Isomorphism (TSI) problem consists in finding an injective function f:VQ → VT, called node mapping, and an injective function g:EQ → ET, called edge mapping, such that the following conditions hold:
1. ∀eQ = (u, v, tQ) ∈ EQ ∃ eT ∈ ET s.t. eT = g(eQ) = (f(u), f(v), tT);
2. s.t. ;
3. .
The first condition ensures that the edge mapping is consistent with the node mapping. The second condition requires that the chronological order between query edges is respected in the target network. The third condition imposes that all matching target edges are observed within a fixed time interval Δ.
The TSI problem can have one or more solutions. In this case, we say that Q Δ-occurs in T. Given an edge mapping g between Q and T, a Δ-occurrence of Q in T is a temporal graph S formed by edges g(q1), g(q2), …, g(qk) and all nodes that are sources or destinations of at least one of these edges.
In Figure 1, given Δ = 6, query Q1 Δ-occurs in target T and the corresponding occurrence is the subgraph of T highlighted in red. Query Q2, instead, has no Δ-occurrences in T. Indeed, there is only one subgraph of T (highlighted in blue) that is isomorphic to Q2 but violates the Δ constraint on edge timestamps.
Finally, we define the temporal motif search problem.
2.1.4. Temporal Motif Search
Given a temporal graph T = (VT, ET) and three integers k, l and Δ, the Temporal Motif Search (TMS) problem consists in: (i) retrieving all temporal motifs that Δ-occurs in T and have at most k nodes and l edges, (ii) counting the number of Δ-occurrences of such motifs.
An example of application of the TMS problem is shown in Figure 2 where k = 3, l = 3 and Δ = 10.
2.2. The MODIT Algorithm
In what follows we introduce a new algorithm for solving the TMS problem, called MODIT (MOtif DIscovery in Temporal networks).
Given three parameters k, l, and Δ, MODIT scans a temporal graph T to retrieve all temporal motifs with at most k nodes and l edges which Δ-occur in T and counts the number of Δ-occurrences of each motif in T.
For each newly identified occurrence, the algorithm performs the following steps:
1. Standardization of edge timestamps;
2. Construction of the canonical form and identification of the corresponding temporal motif;
3. Update of the count of the number of motif occurrences.
The search starts from the smallest motif occurrences formed by single edges. We call these edges seeds. Each of these occurrences is then recursively extended by adding one edge at the time until the specified maximum number of nodes and edges is reached.
MODIT can work on both undirected and directed graphs. For ease of presentation, we illustrate the functioning of the algorithm for undirected networks. However, all the procedures presented here can be easily adapted to directed networks.
The pseudocode of MODIT is reported in Algorithm 1. All motifs retrieved by the algorithm, together with the number of their occurrences, are stored in a hash map motifMap, empty at the beginning (line 1). Each motif in the map is uniquely represented by a string, called canonical form. In addition, since the same occurrence of a motif may be examined multiple times, we also need to store all the distinct retrieved subgraph occurrences in a hash set minedSubgraphs (line 2). For each edge e = (u, v, t) of the target graph, MODIT performs the following steps. First, e and its nodes are embedded in a new occurrence graph S, which is added to the set minedSubgraphs (lines 4–7). The timestamp of the seed edge e is stored in a variable minTime, which will be used throughout the search to avoid scanning some subgraphs of T multiple times (line 8). Each edge that will be added to the subgraph must have a timestamp greater than or equal to minTime. To ensure that each subgraph obtained by expanding S does not violate the Δ temporal constrain, MODIT also uses three auxiliary variables: timestampSet, maxTime, and λ (lines 9–12). Variable timestampSet is a multi-set containing the timestamps of the currently examined subgraph S (at the beginning just t). maxTime will store at each step the maximum timestamp of edges in S. λ represents how much we can extend the time window covered by edges in S (i.e., the difference between the maximum and the minimum timestamps), without exceeding Δ. maxTime and λ are initialized and kept updated during the search using Algorithm 2 (line 13).
Next, the timestamps of the current subgraph S are standardized, i.e they are modified in order to transform S into a temporal motif M, in compliance with the definition provided in section 2.1 (line 14). Standardization of timestamps aims at identifying the motif M of which S is an occurrence and works as follows. First, the list of edge timestamps in S (without duplicates) is sorted in ascending order. Then, each edge of S is assigned the rank of the corresponding timestamp in the sorted list.
Standardization alone may produce distinct motifs that are actually structurally equivalent and in which equivalent edges have the same timestamps. To avoid this, a canonical form C is extracted from M (line 15). The canonical form is a string that uniquely represents a motif, so that two motifs that are equivalent have exactly the same canonical forms. C is obtained by concatenating motif edges based on a given order of motif nodes. Nodes are first ordered according to their degree. Possible ties are solved comparing their sorted adjacency lists, in which edges are ordered by timestamp and, in case of ties, by destination node. Following the calculated node ordering, sorted adjacency lists of nodes are concatenated to yield the canonical form. Figure 3 shows an example of computation of canonical form. In the depicted motif, node a is the first node in the ordering, since it has the maximum degree (2). Nodes b and c have both degree 1. If the adjacency lists of b and c are sorted by timestamps, b comes before c because the first edge in the sorted adjacency list of b has timestamp 1, while the first edge in the sorted adjacency list of c has timestamp 2. Following the node ordering {a, b, c}, sorted adjacency lists of a, b and c are appended to yield the final canonical form of the motif, i.e., the string C = {(a, 1, b), (a, 2, c), (b, 1, a), (c, 2, a)}.
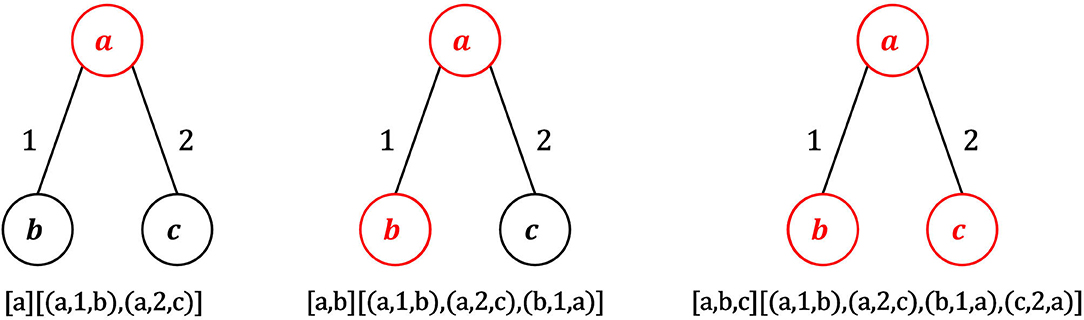
Figure 3. Example of construction of the canonical form. Node a has the highest degree (2), so a is the first node of the ordering. Nodes b and c have the same degree, so we need to examine the adjacency lists of b and c sorted by timestamp and destination node. The first edge in the sorted list of b has timestamp 1, while the first edge in the sorted list of c has timestamp 2, so the second node of the ordering is b and the third one is c. Following such node ordering, the canonical form of the graph in the figure is {(a, 1, b), (a, 2, c), (b, 1, a), (c, 2, a)}.
After constructing the canonical form, the number of occurrences of M is incremented in motifMap (line 17).
Next, MODIT continues the search of new occurrences by extending S edge by edge, starting from an anchor node. This is done using the recursive procedure RECURSIVESEARCH described in Algorithm 3 (lines 17-18). The first two calls to the procedure will extend the seed using both endpoints as anchors. In general, S will be extended by adding an edge which is not already present in S and is incident to an anchor node already present in S.
The structure of RECURSIVESEARCH procedure is very similar to Algorithm 1. First, we check if the currently examined subgraph has reached the maximum allowed number of edges (lines 1-2). If so, the recursive algorithm stops, otherwise the search goes on, considering all possible edges e = (u, a, t) not already present in S and incident to the anchor node a (line 3). For each such edge, MODIT ensures that by adding e to S, the Δ temporal constrain is not violated (line 4). Based on the current values of minTime, maxTime and λ, we can add e to S without violating the Δ constraint iff minTime ≤ t ≤ maxTime + λ. We impose that t is no lower than minTime, i.e., the timestamp of the seed edge, to reduce the number of redundant candidates generated.
If e does not violate the Δ constraint, before adding it to S (line 11), we do the following steps. First, we check if e does not connect two nodes already present in S (line 5). If so, we verify if the currently examined subgraph has not reached the maximum allowed number of nodes (line 6). In this case, node u is added to S (line 7). Otherwise, we proceed with the next edge (line 10).
Boolean conditions expressed in line 4 does not prevent examining some subgraphs multiple times. Therefore, before going on with the search, we need to check if S has not been already examined before (line 12). This is done by simply comparing the list of edge ids of S and each subgraph of the minedSubgraphs set.
If S is new, we follow the same steps performed in Algorithm 1. First, we include t in timestampSet and add S to minedSubgraph (lines 13–14). We update temporal auxiliary variables minTime, maxTime and λ (line 15). Then, edge timestamps are standardized to obtain a temporal motif M (line 16). From M we extract the canonical form C (line 17) and increase the number of its occurrences (line 18).
Next, Algorithm 3 is called recursively twice using the endpoints of u as anchor nodes (lines 19–20). After returning from the recursive calls, backtracking is performed (lines 21–26). Backtracking implies: (i) removing from S the last added edge e, (ii) removing from S the last added node, (iii) removing the timestamp of e from timestampSet, (iv) updating auxiliary variables maxTime and λ.
2.3. MODIT Complexity Analysis
In this subsection, we analyze the complexity of MODIT. The search starts from the smallest motif occurrences formed by single edges. Therefore, the for-loop in Algorithm 1 is performed |E(G)| times, where G is the target graph. Inside the loop, MODIT tries to expand each occurrence as long as possible. Lines 4–7 of Algorithm 3 require constant time because they are applied to a subgraph formed by only one edge.
Now let's analyze the complexity of Algorithm 3. Let dmax the maximum node degree of G. The for-loop in Algorithm 3 is performed, in the worst case, dmax times. Assuming Δ = ∞, all dmax edges are candidates to extend the motif. Lines 4–14 of Algorithm 3 require a constant time. The complexity of Algorithm 2 depends on the number of distinct timestamps of the current motif. In the worst case there are l edges and all timestamps are different. Identifying the minimum and maximum requires an ordering of timestamps that has linear complexity. The rest of the operations can be done in constant time. So, the complexity of Algorithm 2 is O(l). However, in practice, these operations are done faster because MODIT stores timestamps in a data structure that is self-sorted as elements are inserted/removed. Standardization of timestamps requires linear time with respect to the number of edges. Since a motif can have at most l edges, the complexity is O(l). The time required to build the canonical form depends on the number of nodes and the number of edges of the motif. Sorting the adjacency list of a node requires, in the worst case, l operations. Since a motif can have at most k nodes, sorting their adjacency lists requires at most k · l operations. The ordering of nodes has linear complexity with respect to the number of nodes, thus performs in the worst case, k operations. Therefore, the number of operations required to calculate the canonical form is at most k · l + k. Updating the number of occurrences of a motif is done using a hash map, so it takes constant time.
To derive the final complexity of Algorithm 3, we need to evaluate the maximum depth of the recursion. Each call to Algorithm 3 adds one edge at the time, so the maximum recursion depth is l. Assuming no early backtracking, this implies that the complexity of the recursive procedure is . So overall, the complexity of MODIT is .
3. Results
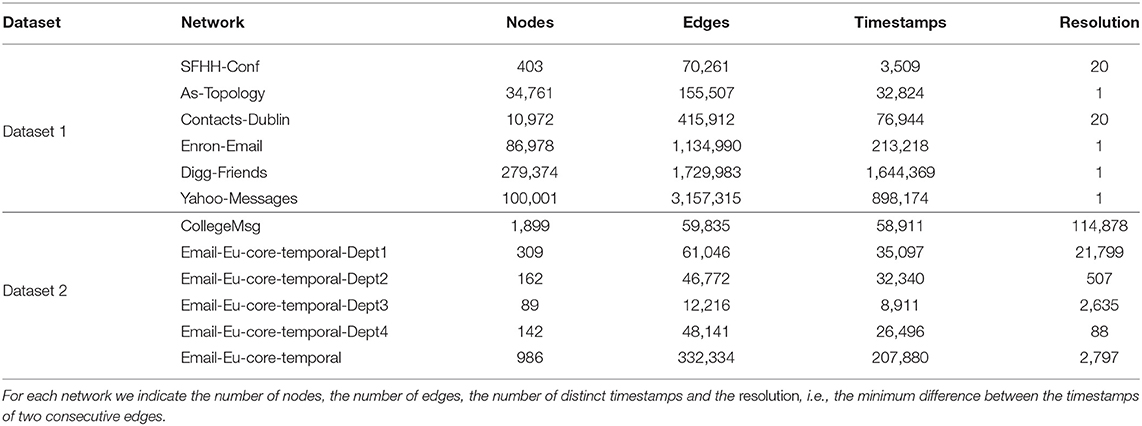
MODIT has been implemented in Java and tested on two datasets of real temporal networks of different sizes, denoted as Dataset 1 and Dataset 2, respectively. Table 1 lists the main features of the networks of the two datasets. For each graph we report the number of nodes, the number of edges, the number of distinct timestamps and the resolution, i.e., the minimum difference between consecutive timestamps.
Dataset 1 is formed by six networks: SFHH-CONF, AS-TOPOLOGY, CONTACTS-DUBLIN, ENRON-EMAIL, DIGG-FRIENDS, and YAHOO-MESSAGES.
SFHH-CONF is a network that describes the interactions between the 405 participants of the SFHH conference in Nice, France (Génois and Barrat, 2018). AS-TOPOLOGY is a peer-to-peer communication network between autonomous systems, with data collected between February and March of 2010. CONTACTS-DUBLIN is a contact network of attendees at the Infectious SocioPatterns event held in the Science Gallery in Dublin, Ireland (Isella et al., 2011). ENRON-EMAIL is a network of e-mail exchanges of Enron corporation employees between 1999 and 2003 (Keila and Skillicorn, 2005). DIGG-FRIENDS describes friendly bonds between users of Digg, a web news aggregator used in America (Hogg and Lerman, 2012). It is based on data collected in 1 month of 2009. YAHOO-MESSAGES represents the exchange of e-mails between users of Yahoo-Mail in 1 month of 2010.
Dataset 2 includes 6 temporal networks taken from the SNAP dataset1. COLLEGEMSG consists of private messages sent on an online social network at the University of California, Irvine (Panzarasa et al., 2009). The network EMAIL-EU-CORE-TEMPORAL was generated using email data from a large European research institution. Only emails exchanged between institution members were taken into account. EMAIL-EU-CORE-TEMPORAL-DEPT1, EMAIL-EU-CORE-TEMPORAL-DEPT2, EMAIL-EU-CORE-TEMPORAL-DEPT3 and EMAIL-EU-CORE-TEMPORAL-DEPT4 are four sub-networks including communications between members of four different departments of the institution (Paranjape et al., 2017).
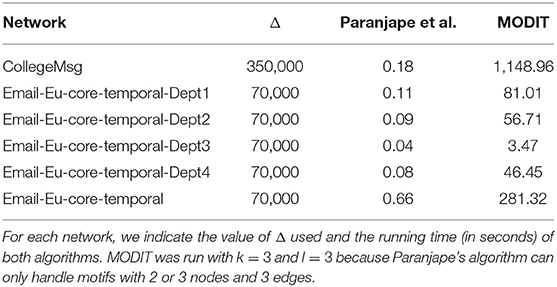
We first ran MODIT on each network of Dataset 1 for different combinations of values of Δ, k (maximum number of motif nodes) and l (maximum number of motif edges). Then, we compared MODIT to the algorithm proposed by Paranjape et al. (2017), which is included in the SNAP platform for network analysis and uses the same definition of temporal motif. All other methods were discarded because they use different definitions of temporal motifs. This comparison was done on the networks of Dataset 2.
All experiments were performed on an Intel Core i5-7500 processor with 16GB of RAM, 10 of which were used for the Java Virtual Machine.
3.1. Experiments on Dataset 1
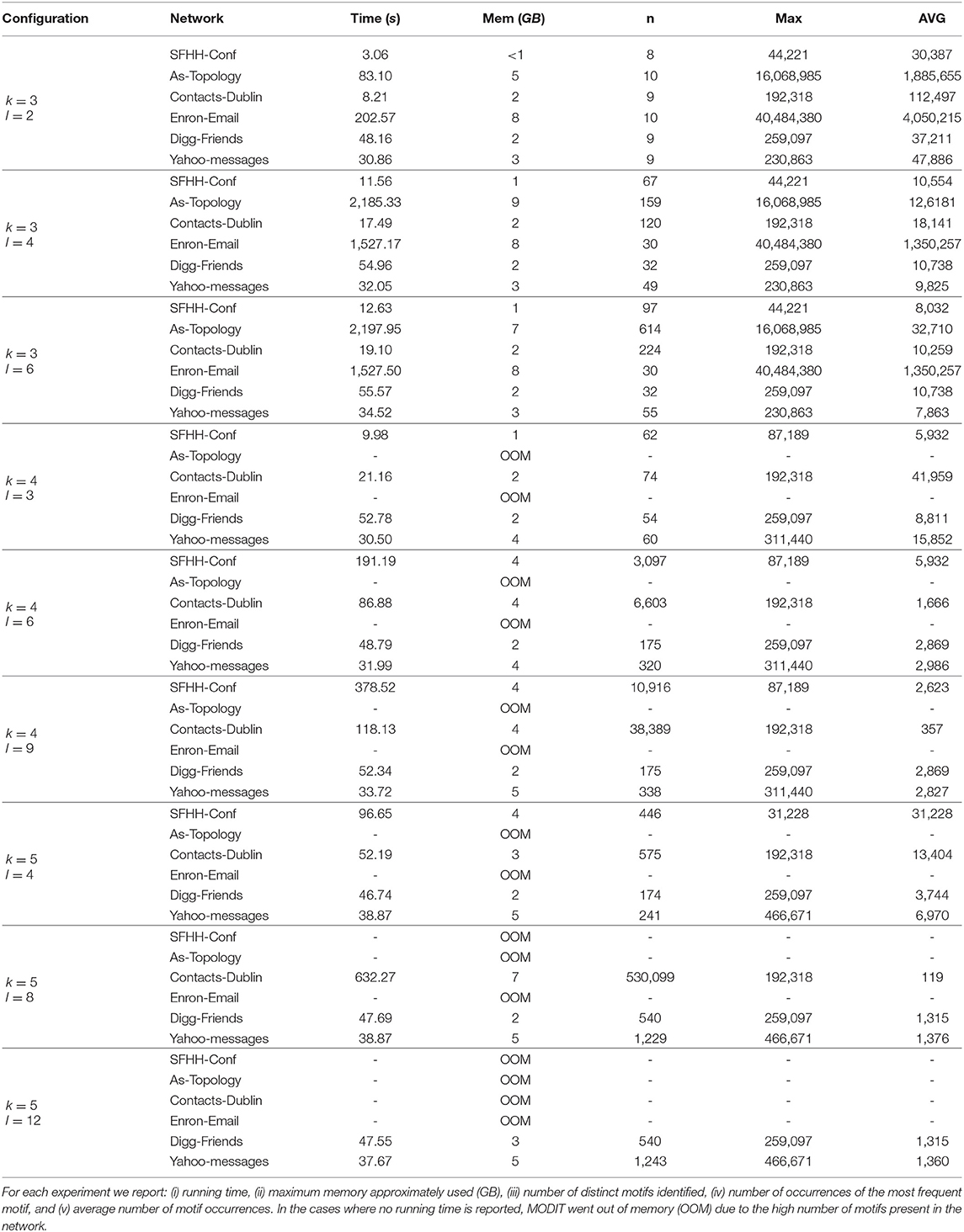
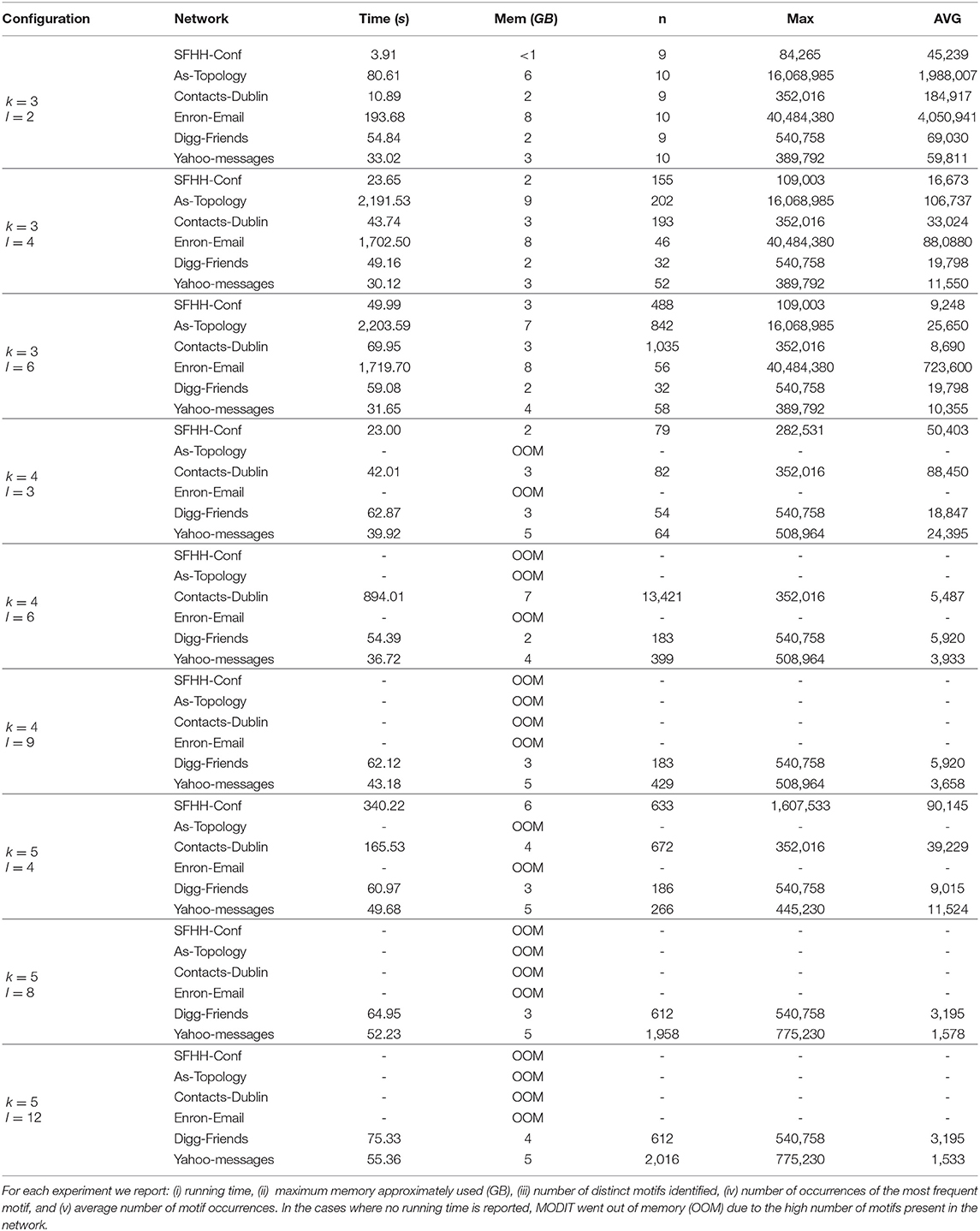
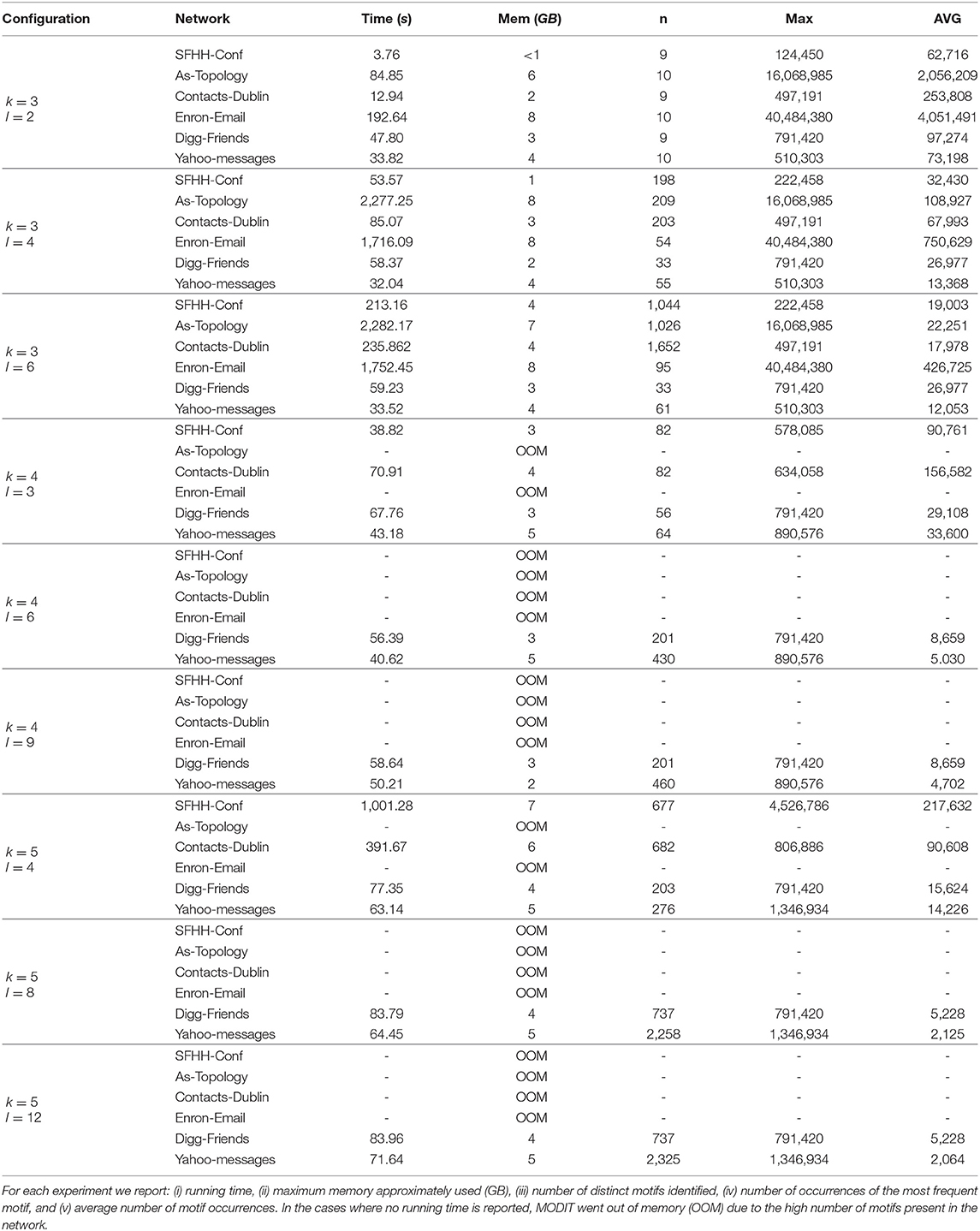
In this section, we illustrate the results of the experiments on Dataset 1. We report in Tables 2–4 the results in terms of (i) execution times, (ii) number of distinct motifs identified, (iii) number of occurrences of the most frequent motif, and (iv) average number of motif occurrences. The experiments were performed for different combinations of values of Δ, k and l. Δ was set to r, 2r, and 3r, where r is the resolution of the temporal network. For k we used values 3, 4, and 5. l was varied as a function of k and set to values k − 1, 2 · (k − 1) and 3 · (k − 1). In some networks (in particular, in AS-TOPOLOGY and ENRON-EMAIL) and for some configurations of the parameters, MODIT went out of memory and was unable to finish the execution. In these cases we did not report any running time. This is due to the large number of distinct motifs present in the networks, which leads to an excessive growth of the map of motif counts, together with a large number of occurrences causing many recursive calls of Algorithm 3. In fact, as k and l increase, the number of motif topologies and the number of combinations of standardized timestamps increases exponentially [e.g., SFHH-CONF network in the following configurations: (Δ = 3r, k = 3, l = 2), (Δ = 3r, k = 3, l = 4) and (Δ = 3r, k = 3, l = 6)]. This is confirmed by the high values of the number of occurrences of the most frequent motif and the average number of motif occurrences found for small values of k and l.
Interestingly, in some networks (e.g., ENRON-EMAIL, DIGG-FRIENDS) we observe that keeping Δ and k fixed and varying l, the number of distinct motifs, the number of occurrences of the most frequent motif and average number of occurrences remain the same.
3.2. Comparison With Paranjape's Algorithm
Finally we compared MODIT with the algorithm proposed by Paranjape et al. (2017) on the networks of Dataset 2.
For the comparison, we set k = 3 and l = 3 because Paranjape's algorithm can handle only motifs with 2 or 3 nodes and 3 edges.
Results are reported in Table 5 and show that Paranjape's algorithm is much faster than MODIT. This gap is mainly due to the fact that Paranjape's method uses a series of efficient dynamic programming algorithms, which are specifically designed to count specific classes of motifs, i.e., motifs with 3 edges. On the other hand, MODIT is general and designed to find motifs of any size and any type. Furthermore, Paranjape's algorithm searches only motifs having exactly the specified number of nodes and edges. On the other hand, MODIT looks for all motifs having at most the number of nodes and edges specified by the user.
4. Conclusions
In this paper, we presented MODIT (MOtif DIscovery in Temporal Networks), an algorithm for counting motifs of any size in temporal networks, inspired by a very recent algorithm for subgraph isomorphism in temporal networks, called TemporalRI. Given the three parameters k, l, and Δ, MODIT scans the whole temporal graph to search for all subgraphs having at most k nodes and l edges and in which the difference between the maximum and the minimum timestamp is no greater than Δ. We ran MODIT on a dataset of real temporal networks of medium and large size by varying Δ, the maximum number of nodes and edges. We also compared MODIT with the algorithm proposed by Paranjape et al. (2017) using a different dataset of temporal networks downloaded from SNAP.
For the future, we plan to:
1. Introduce measures of statistical significance of motifs similar to the ones already devised for static graphs (i.e., the z-score);
2. Make MODIT iterative, in order to reduce the overhead introduced by recursion, and optimize the search strategy;
3. Implement MODIT on a SPARK framework, to manage very large networks.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s. The source code of MODIT can be found at the following URL: https://github.com/RobertoGrasso96/MODIT.
Author Contributions
AP and GM coordinated the project. GM and RG developed the algorithm. RG performed the experiments. RG, GM, AF, and AP wrote the manuscript. All authors conceived the project, read, and approved the final manuscript.
Funding
AP and AF have been partially supported by the following research projects: MIUR PON BILIGeCT Liquid Biopsies for Cancer Clinical Management (CUP B96G18000590005); PO-FESR Sicilia 2014-2020 DiOncoGen: Innovative diagnostics (CUP G89J18000700007).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
References
Aggarwal, C., and Subbian, K. (2014). Evolutionary network analysis: a survey. ACM Comput. Surv. 47:10. doi: 10.1145/2601412
Berlingerio, M., Bonchi, F., Bringmann, B., and Gionis, A. (2009). “Mining graph evolution rules,” in ECML/PKDD 2009 (Bled), 115–130. doi: 10.1007/978-3-642-04180-8_25
Carley, K. M., Diesner, J., Reminga, J., and Tsvetovat, M. (2007). Toward an interoperable dynamic network analysis toolkit. Decis. Support Syst. 43, 1324–1347. doi: 10.1016/j.dss.2006.04.003
Casteigts, A., Flocchini, P., Quattrociocchi, W., and Santoro, N. (2011). “Time-Varying graphs and dynamic networks,” in Ad-hoc, Mobile, and Wireless Networks, eds H. Frey, X. Li, and S. Ruehrup (Berlin: Springer), 346–359. doi: 10.1007/978-3-642-22450-8_27
Crawford, J., and Milenkovic, T. (2018). Cluenet: Clustering a temporal network based on topological similarity rather than denseness. PLoS ONE 13:e0195993. doi: 10.1371/journal.pone.0195993
Divakaran, A., and Mohan, A. (2020). Temporal link prediction: a survey. N Gen. Comput. 38, 213–258. doi: 10.1007/s00354-019-00065-z
Génois, M., and Barrat, A. (2018). Can co-location be used as a proxy for face-to-face contacts? EPJ Data Science 7:11. doi: 10.1140/epjds/s13688-018-0140-1
Hiraoka, T., Masuda, N., Li, A., and Jo, H. (2020). Modeling temporal networks with bursty activity patterns of nodes and links. Phys. Rev. Res. 2:023073. doi: 10.1103/PhysRevResearch.2.023073
Holme, P., and Saramaki, J. (2012). Temporal networks. Phys. Rep. 519, 97–125. doi: 10.1016/j.physrep.2012.03.001
Holme, P., and Saramaki, J. (2019). Temporal Network Theory. Cham: Springer International Publishing. doi: 10.1007/978-3-030-23495-9
Hulovatyy, Y., Chen, H., and Milenkovic, T. (2015). Exploring the structure and function of temporal networks with dynamic graphlets. Bioinformatics 31, i171–i180. doi: 10.1093/bioinformatics/btv227
Isella, L., Stehle, J., Barrat, A., Cattuto, C., Pinton, J. F., and Van den Broeck, W. (2011). What's in a crowd? Analysis of face-to-face behavioral networks. J. Theoret. Biol. 271, 166–180. doi: 10.1016/j.jtbi.2010.11.033
Keila, P., and Skillicorn, D. (2005). Structure in the enron email dataset. Comput. Math. Organ. Theory 11, 183–199. doi: 10.1007/s10588-005-5379-y
Kovanen, L., Karsai, M., Kaski, K., Kertész, J., and Saramaki, J. (2011). Temporal motifs in time-dependent networks. J. Stat. Mech. Theory Exp. 2011:P11005. doi: 10.1088/1742-5468/2011/11/P11005
Liu, P., Benson, A. R., and Charikar, M. (2019). “Sampling methods for counting temporal motifs,” in Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, WSDM '19 (New York, NY), 294–302. doi: 10.1145/3289600.3290988
Locicero, G., Micale, G., Pulvirenti, A., and Ferro, A. (2021). “TemporalRI: a subgraph isomorphism algorithm for temporal networks,” in Complex Networks & Their Applications IX, 675–687. doi: 10.1007/978-3-030-65351-4_54
Lv, L., Zhang, K., Zhang, T., Bardou, D., Zhang, J., and Cai, Y. (2019). Pagerank centrality for temporal networks. Phys. Lett. A 383, 1215–1222. doi: 10.1016/j.physleta.2019.01.041
Masuda, N., and Holme, P. (2020). Small inter-event times govern epidemic spreading on networks. Phys. Rev. Res. 2:023163. doi: 10.1103/PhysRevResearch.2.023163
Masuda, N., and Lambiotte, R. (2020). A Guide to Temporal Networks, 2nd Edn. World Scientific. doi: 10.1142/q0268
Micale, G., Locicero, G., Pulvirenti, A., and Ferro, A. (2021). TemporalRI: subgraph isomorphism in temporal networks with multiple contacts. Appl. Netw. Sci. 6:55. doi: 10.1007/s41109-021-00397-0
Panzarasa, P., Opsahl, T., and Carley, K. (2009). Patterns and dynamics of users' behavior and interaction: network analysis of an online community. J. Am. Soc. Inform. Sci. Technol. 60, 911–932. doi: 10.1002/asi.21015
Paranjape, A., Benson, A. R., and Leskovec, J. (2017). “Motifs in temporal networks,” in Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, WSDM '17 (New York, NY), 601–610. doi: 10.1145/3018661.3018731
Petit, J., Gueuning, M., Carletti, T., Lauwens, B., and Lambiotte, R. (2018). Random walk on temporal networks with lasting edges. Phys. Rev. E 98:052307. doi: 10.1103/PhysRevE.98.052307
Rocha, L. E. C., Masuda, N., and Holme, P. (2017). Sampling of temporal networks: methods and biases. Phys. Rev. E 96:052302. doi: 10.1103/PhysRevE.96.0523020
Rossetti, G., and Cazabet, R. (2018). Community discovery in dynamic networks: a survey. ACM Comput. Surv. 51:3172867. doi: 10.1145/3172867
Singh, E. A., and Cherifi, H. (2020). Centrality-based opinion modeling on temporal networks. IEEE Access 8, 1945–1961. doi: 10.1109/ACCESS.2019.2961936
Sun, X., Tan, Y., Wu, Q., Chen, B., and Shen, C. (2019). TM-miner: TFS-based algorithm for mining temporal motifs in large temporal network. IEEE Access 7, 49778–49789. doi: 10.1109/ACCESS.2019.2911181
Tizzani, M., Lenti, S., Ubaldi, E., Vezzani, A., Castellano, C., and Burioni, R. (2018). Epidemic spreading and aging in temporal networks with memory. Phys. Rev. E 98:062315. doi: 10.1103/PhysRevE.98.062315
Torricelli, M., Karsai, M., and Gauvin, L. (2020). weg2vec: Event embedding for temporal networks. Sci. Rep. 10:7164. doi: 10.1038/s41598-020-63221-2
Tsalouchidou, I., Baeza-Yates, R., Bonchi, F., Liao, K., and Sellis, T. (2020). Temporal betweenness centrality in dynamic graphs. Int. J. Data Sci. Anal. 9, 257–272. doi: 10.1007/s41060-019-00189-x
Tu, K., Li, J., Towsley, D., Braines, D., and Turner, L. D. (2018). Network classification in temporal networks using motifs. arXiv [Preprint]. arXiv:1807.03733.
Ugander, J., Backstrom, L., and Kleinberg, J. (2013). “Subgraph frequencies: mapping the empirical and extremal geography of large graph collections,” in WWW '13: Proceedings of the 22nd International Conference on World Wide Web (New York, NY). 1307–1318. doi: 10.1145/2488388.2488502
Keywords: temporal networks, network motifs, motif search algorithms, motif counting, network analysis, data mining
Citation: Grasso R, Micale G, Ferro A and Pulvirenti A (2022) MODIT: MOtif DIscovery in Temporal Networks. Front. Big Data 4:806014. doi: 10.3389/fdata.2021.806014
Received: 31 October 2021; Accepted: 28 December 2021;
Published: 23 February 2022.
Edited by:
Italo Zoppis, University of Milano-Bicocca, ItalyReviewed by:
Reynold Cheng, The University of Hong Kong, Hong Kong SAR, ChinaPatrick Mackey, Pacific Northwest National Laboratory (DOE), United States
Copyright © 2022 Grasso, Micale, Ferro and Pulvirenti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giovanni Micale, Z2lvdmFubmkubWljYWxlJiN4MDAwNDA7dW5pY3QuaXQ=; Alfredo Pulvirenti, YWxmcmVkby5wdWx2aXJlbnRpJiN4MDAwNDA7dW5pY3QuaXQ=
 Roberto Grasso
Roberto Grasso Giovanni Micale
Giovanni Micale Alfredo Ferro
Alfredo Ferro Alfredo Pulvirenti
Alfredo Pulvirenti