
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Big Data, 25 April 2019
Sec. Data Mining and Management
Volume 2 - 2019 | https://doi.org/10.3389/fdata.2019.00003
This article is part of the Research TopicWhen Deep Learning Meets Social NetworksView all 5 articles
Characterizing and modeling the distribution of a particular family of graphs are essential for the studying real-world networks in a broad spectrum of disciplines, ranging from market-basket analysis to biology, from social science to neuroscience. However, it is unclear how to model these complex graph organizations and learn generative models from an observed graph. The key challenges stem from the non-unique, high-dimensional nature of graphs, as well as graph community structures at different granularity levels. In this paper, we propose a multi-scale graph generative model named Misc-GAN, which models the underlying distribution of graph structures at different levels of granularity, and then “transfers” such hierarchical distribution from the graphs in the domain of interest, to a unique graph representation. The empirical results on seven real data sets demonstrate the effectiveness of the proposed framework.
A graph is a fundamental tool for depicting and modeling complex systems in various domains, ranging from market-basket analysis to biology, from social science to neuroscience. Characterizing and modeling the distribution of a particular family of graphs is essential in many real-world applications. For example, in financial fraud detection, generative models are adopted to produce synthetic financial networks, when the empirical studies need to be conducted by the third parties without divulging private information (Fich and Shivdasani, 2007); in drug discovery and development, sampling from the generic model can facilitate the discovery of new medicines which equip new configurations while preserving the property of the existing medicines (Gómez-Bombarelli et al., 2016); in social network analysis, the distributions on graphs can be used to discover new graph structures and generate evolving graphs (You et al., 2018a).
Generative models of graphs have been studied well for decades. Traditional graph generative models (Erdös and Rényi, 1959; Albert and Barabási, 2002; Leskovec et al., 2010) are usually built upon some structural premises, e.g., heavy tails for the nodes' degree distribution, small diameters, and densification in graph evolution. More recent studies on deep generative models (e.g., Kingma and Welling, 2013; Goodfellow et al., 2014), reveal a surge of research interest in modeling graphs. For example, Liu et al. (2017) proposes a deep model for learning characteristic topological features from the given graphs via generative adversarial networks (GAN); (You et al., 2018a) uses a deep autoregressive model to efficiently learn the complex joint probability of all the nodes and edges from an observed set of graphs.
However, real-world networks typically exhibit hierarchical distribution over graph communities, while the existing graph generative models are either restricted to certain structural premises (Erdös and Rényi, 1959; Albert and Barabási, 2002; Leskovec et al., 2010), or unable to capture the hierarchical community structures over the graphs (Grover et al., 2018; Li et al., 2018; Simonovsky and Komodakis, 2018). Developing graph generative models that can capture not only the low connectivity patterns at the level of individual nodes and edges, but also the higher-order connectivity patterns, i.e., the hierarchical community structures in the given graphs, will significantly improve the fidelity of graph generative models and help reveal more intriguing patterns in various domains. For instance, given an author-collaborative network, research groups of well-established and closely collaborated researchers could be identified by the existing graph clustering methods in the lower-level granularity. While, from a coarser level, we may find that these research groups constitute large-scale communities, which correspond to various research topics or subjects. Moreover, different from image data or text data, a graph with n nodes can be represented by n! equivalent adjacency matrices with node permutation, which increases the difficulty of training the generative model in the first place.
In this paper, we aim to address the following challenges: (C.1) How to capture the community structures at different levels of granularity and how to generate a unique graph representation that preserves such hierarchical graph structures. (C.2) How to alleviate the high complexity of modeling numerous representations of graphs and how to ensure the fidelity of the proposed graph generative model. To address the preceding challenges, we propose a generic generative model of graphs (Misc-GAN) to learn the underlying distribution of graph structures at different levels of granularity. In particular, our proposed framework consists of three key steps. First, it coarsens the input graph into the structured representations of different levels (i.e., granularity). Then, inspired by the success of deep generative models in image translation (Kingma and Welling, 2013; Goodfellow et al., 2014), a cycle-consistent adversarial network (CycleGAN) (Zhu et al., 2017) is adopted to learn the graph structure distribution and generate a synthetic coarse graph at each granularity level. Last, the Misc-GAN framework defines a reconstruction process, which reconstructs the graphs at each granularity level and aggregates them into a unique representation.
The main contributions of this paper can be summarized as these three aspects:
1. A novel problem setting which aims to model the complex distribution of community structures at different granularity levels in the real networks.
2. A graph generative model which is capable of modeling hierarchical topology features from a single or a set of observed graphs producing high-quality domain specific synthetic graphs.
3. Extensive experiments and case-studies on seven real-world data sets, showing the effectiveness of the proposed framework Misc-GAN.
The rest of this paper is organized as follows. We briefly review some related work in section 2, formally define the multi-scale domain adaptive graph generation problem in section 3 and present the formulation and implementation of our proposed Misc-GAN framework in section 4. The empirical studies are conducted in section 5. Finally, we conclude this paper in section 6.
In this section, we briefly review the related studies on the generative adversarial network, multi-scale analysis of graph and cycle consistency.
In Goodfellow et al. (2014), the authors propose the generative adversarial networks (GANs) to create a generative model and a discriminative model and compare them with each other in the adversarial setting. The authors denote Pz(z) to be the prior of the input noise variables z and G(z; θg) to represent a mapping to data space, where G is a differentiable function represented by a multi-layer perceptron with parameters θg. G(z) maps the noise variables to data space and it aims to generate samples as genuine as possible. The authors also define D(x; θd) to be another multi-layer perceptron or discriminator distinguishing whether the given samples are drawn from the real-world data set or from the fake data set. D(x) is the probability of x coming from the real-world data set rather than the generated data set. In this min-max game, the discriminator D aims to maximize the probability of assigning the correct label to both the real samples and the faked samples generated by the generator G, while the generator G aims to minimize the probability that the discriminator D successfully distinguishes the faked samples from the real samples. The objective of this min-max game is written as:
More recently, a surge of research interest has been observed in data mining and machine learning communities, with respect to using GANs in various real applications. For example, in Du et al. (2018), the authors proposed the adversarially learned inference model to generate shared representation by matching cross-domain joint distribution; the domain-adaptation works in Ganin et al. (2016), Zhang et al. (2017), and Tzeng et al. (2017) tried to minimize the domain-specific latent feature representations in adversarial settings; some GANs-based approaches have been proposed to minimize the distance between feature distributions, such as Ganin et al. (2016), Zhang et al. (2017), and Tzeng et al. (2017). In this paper, the generative adversarial network is the basis from which to transfer graphs from one domain to another, while the local valuable structures of graphs are preserved.
Multi-scale analysis of graphs has been studied for years in machine learning with wide applications in numerous areas, such as simplification and compression of graphs (Cour et al., 2005; Safro and Temkin, 2011), dynamics of graphs at different resolutions (Lee and Maggioni, 2011; Gao et al., 2016), graph visualization (Stolte et al., 2003), recommendation systems (Gou et al., 2011) and so on. The common assumption of multi-scale analysis is that the given data in a high dimensional space has a much lower dimensional intrinsic geometry. Take the document text as an example, the dependencies among words constrain the distribution of word frequency in a lower dimensional space. Diffusion wavelets (Coifman and Maggioni, 2006) is one common method used in multi-scale analysis which allows us to construct functions on the graph for statistical learning tasks by producing coarser and coarser graphs at different resolution levels. In this paper, we adopt the concept of multi-scale analysis to capture the local structure of graphs at different resolution levels and then reconstruct the graph while preserving these important local structures.
The concept of cycle consistency has been applied to various computer vision problems, including image matching (Huang and Guibas, 2013; Zhou et al., 2015), co-segmentation (Wang et al., 2013, 2014), style transfer (Zhu et al., 2017; Chang et al., 2018), and structure from motion (Zach et al., 2010; Wilson and Snavely, 2013). The idea of cycle consistency constrain is utilized as a regularizer in these algorithms, such as cycle consistency loss used in Zhou et al. (2016) and Godard et al. (2017) to push the mappings to be as consistent with each other as possible in the supervised convolution neural network training. Zhu et al. (2017) proposes the Cycle-Consistent generative adversarial network to learn two mappings or generators G:X → Y and F:Y → X between two domains X and Y. The authors introduce two adversarial discriminators DX and DY, where DX aims to distinguish the images x drawn from the real data set X from the fake images generated by F(Y); similarly, DY aims to distinguish the images y drawn from data set Y from the fake images generated by G(X). In this paper, we apply this concept to find the graph transfer mappings between domain X and domain Y, such that the transferred graph from domain Y to domain X is sufficiently similar to the graph in domain X.
In this section, we introduce the notation and problem definition of this paper. The main symbols and notations are summarized in Table 1. We use ordinary lowercase letters to denote scalars, boldface lowercase letters to denote vectors, and boldface uppercase letters to denote matrices and tensors. Moreover, the elements (e.g., entries, fibers and slices) in a matrix or a tensor are represented in the same way as the Matlab, e.g., M(i, j) is the element at the ith row and jth column of the matrix M, and M(i, :) is the ith row of M, etc.
The goal of this paper is to generate a synthetic target domain graph , by learning mapping functions between the source domain graph Gs and the target domain graph Gt. Without loss of generality, in this paper, we assume that a universal structure distribution pdata exists, which defines the structural role of each entity, i.e., node, edge, and subgraph, of the observed graphs. Many existing graph generative models (Bojchevski et al., 2018; You et al., 2018b) are designed to learn the structure distribution of G at a single scale, and therefore they might overlook some intriguing patterns in the underlying networks, e.g., the multi-level cluster-within-cluster structures (Ravasz and Barabási, 2003). Figure 1 presents an illustrative example of the hierarchical structures in collaboration networks. In particular, the graph exhibits four-level hierarchies including (L1) all the entities in the collaboration network, (L2) early-stage researchers, (L3) mid-career researchers and (L4) senior researchers. It is unclear how to characterize such hierarchical structures and generate domain-specific synthetic graphs. Moreover, the generative model needs to be scalable when modeling large-scale networks that have exponentially many representations. In this paper, we aim to learn a graph generative model that can automatically translate any source-domain graph into the target-domain graph while preserving the hierarchical structure distribution over the observed target graph. In real cases, the source-domain graphs are sensitive and hard to obtain, while only the target-domain graphs are available to the analysts. For example, in financial fraud detection, the source-domain graphs could be the online transaction network that contains sensitive information (e.g., bank account, personal identification information, transaction amount, etc.); the target-domain graphs that are available to the analysts could be outdated data (transaction data 100 years ago) or the simulated graphs with user-defined graph statistics (e.g., the number of nodes, the number of edges). Thus, by learning such generative model, the third-party analysts can study the data without divulging the sensitive information. With the above notations and objects, we formally define our problem as follows:
Problem 1. Multi-level Structure-Preserving Graph Generation Input: (i) a target domain graph Gt = (Vt, Et), (ii) a source domain graph Gs = (Vs, Es), (iii) the number of granularity levels L.
Output: (i) a mapping function that can translate any source-domain graphs to the corresponding target domain graphs while preserving the hierarchical structure distribution over the observed target graph Gt, (ii) a generated synthetic target domain graph .
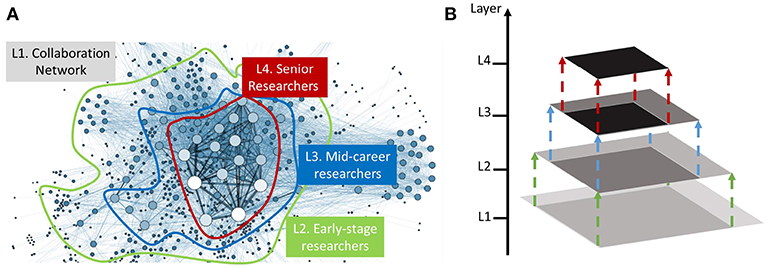
Figure 1. An illustration example. (A) Presents a visualization of the collaboration network (Grandjean, 2016). (B) Shows the hierarchical structure of the research communities, from early-stage researchers to mid-career researchers and senior researchers.
In this section, we present our multi-scale graph generative model Misc-GAN, which simultaneously characterizes and models the structural distribution of the observed graphs at multiple scales. In particular, we first formulate our framework into a generic optimization problem, and then discuss the details on three modules, i.e., multi-scale graph representation module, graph generation module, and graph reconstruction module, in our proposed framework Figure 2.
To address the proposed problem of multi-level structure-preserving graph generation, our joint learning framework should primarily focus on the following aspects. First (problem setting), the existing methods are mainly restricted to a single granularity level of graph structures, which might increase the possibility of overlooking the hierarchical community structures in the observed graphs. Thus, the graph generation model should be able to capture the community structures at multiple levels of granularity and generate a unique graph representation. Second (graph generation performance), it is unclear how to alleviate the high complexity and ensure the fidelity of the graph generation. This is crucial especially if the observed graphs are noisy and large-scale. With these objectives in mind, we propose a generic graph generation framework as an optimization problem with the following objective function:
where the objective consists of four terms. The first term Lms is the multi-scale reconstruction loss, which is designed to minimize the Kullback-Leibler (KL) divergence (Moreno et al., 2004) between the target graph Gt and the generated graph , i.e., . We generalize the conventional KL divergence to our problem setting to compare two graphs as follows
where At and Ãt are the adjacency metrics of and Gt, ϵ is a constant with a small value to avoid log(0) or division by 0. The second term learns a forward mapping function from the source graph Gs to Gt. The discriminator aims to figure out whether the given graph is a real graph from the target domain or a fake graph generated by the generator which is transferred from the source domain graph. Similar to the second term, the third term defines a backward adversarial loss, which aims to learn the mapping function from the target domain to the source domain. The fourth term is the cycle consistency loss, which is introduced to further reduce the space of possible mapping function. We argue that learning such bi-directional mapping can largely prevent the learned mapping functions from contradicting each other. At last, we also introduce three positive constants, i.e., α, β, γ, to balance the impact of these four terms in the overall objective function. Follow the min-max scheme of GAN, we aim to solve:
Here, we present our Misc-GAN framework (Figure 2). Overall, our framework can be separated into three stages (i.e., modules). In the first stage, our framework takes the input graphs Gt and explores the hierarchical structures by constructing the coarse graphs in L levels of granularity (w.r.t. L layers in Figure 2). In the second stage, our framework trains an independent graph generative model and produces the multi-scale coarse graph in each layer. In the third stage, our framework autonomously combines the outputs from the previous stage to construct the synthetic graph that preserves the hierarchical topology features of the given graphs Gt.
In this module, we explore the hierarchical cluster-within-cluster structures in order to better characterize the given graph Gt, by using the multi-scale approaches, e.g., hierarchical clustering (Johnson, 1967), algebraic multigrid (AMG) (Ruge and Stüben, 1987). The main idea of AMG-based coarsening is a process of aggregating the strongly coupled nodes with a small algebraic distance to form coarser nodes (Ron et al., 2011). Given a symmetric matrix Gt, the coarser graph at the first layer is defined as follows:
where P(1) is a coarser operator for generating . This coarser operator follows the weighted aggregation scheme used in Sharon et al. (2000) by assigning the weight to the edge connecting two coarse aggregates, where the weight of is the fraction of the ith node that will belong to the jth aggregate. Extending this idea to the lth layer, the multi-scale approaches recursively construct a multi-scale hierarchy of increasingly coarser graphs at the l-th layer as follows:
where l = 1, …, L, P(1), …, P(l−1) are the coarsening operators, and Gl is the coarse graph at the l-th layer. Based on Equation (5), we construct a set of coarse graphs with multiple scales from the target domain graph Gt. These coarse graphs will be fed into the following graph generative module in order to learn the hierarchical structures of Gt.
It is challenging to learn the underlying structure distribution pdata of the target domain graph Gt, as the graph with n nodes can be represented by n! equivalent adjacency matrices with node permutations (You et al., 2018a). Some recent works have been proposed to tackle this issue. For example, Simonovsky and Komodakis (2018) proposes an approximate graph matching scheme that requires O(n4) operations in the worst case; (You et al., 2018a) develops a tree-structure node ordering scheme, which is based on breadth-first-search (BFS) to reduce the computational complexity. However, these methods may either suffer from the intractable time complexity, or not well preserve the hierarchical structures of the given networks.
Here, we propose a multi-scale graph generation scheme, which models the complex distribution of graph structures over a pyramid of coarse graphs rather than the original graphs. The intuitions are in the following two aspects: (1) directly training from the coarse graphs facilitates the learning process of the generative model, as the coarse graphs serve as the abstractions of the original graphs; (2) this scheme provides the flexibility for the users to decide the granularity-level of the coarse graphs to be learned, which could be attractive when we need to model the large-scale networks. To be more specific, the graph generation module at each layer (shown in Figure 2) can be separated into three steps: First, we partition the graph into multiple non-overlapping subgraphs using state-of-the-art graph clustering methods (Ester et al., 1996; Schaeffer, 2007). Then, based on the detected communities, we generate a set of block diagonal matrices by shuffling community blocks over the diagonals, which are used to characterize the community-level graph structures. At last, the generated block diagonal matrices are fed into an independent graph generative model to generate the synthetic coarse graphs at each layer.
In this stage, we first adopt the multi-scale approaches to reconstruct the graph from coarse to fine. Given a coarser matrix at the second layer, the fine graph at the first layer is defined as follows:
where R(1) is a reconstruction operator mapping the coarser graph back to the fine graph . Extending this idea to multiple layers, the multi-scale approaches recursively construct a multi-scale hierarchy of increasingly refined graphs at the l-th layer as follows:
where l = 1, …, L, is the reconstructed adjacency matrix from the l-th layer, and R(1), …, R(l−1) are the reconstruction operators that maps the coarser graph to the fine graph . After that, all the reconstructed graphs at each layer are in the same scale as the target graph Gt, which could be aggregated into a unique one by a linear function, , where w(1), …, w(L) are the non-negative weights, and b is a bias. Compared with the existing graph generative models (Erdös and Rényi, 1959; Albert and Barabási, 2002; You et al., 2018a), the advantages of using such multi-scale graph reconstruction models are twofold. First, by reconstructing the graph form the multiple coarse graphs, the graph generated by Misc-GAN naturally preserves the hierarchical community structures at the different levels of granularity. Moreover, we claim that our proposed Misc-GAN framework is more scalable than most existing GAN-based graph generative models, as our model provides the flexibility of being trained from the coarse graph of input networks at a user's preferred scale. In particular, given an online transaction network with millions of nodes, the running and space complexity could be intractable for either GAN or CycleGAN to store and perform computations at the original scale of the input graph. Instead, Misc-GAN allows end users to learn from a pyramid of the coarse graphs (e.g., ten thousands of nodes) that preserves the key information of community structures but requires less memory and computational resources.
We applied the technique of cycleGAN to the transfer graph from one domain to another domain. Different from the density property of images, the adjacency matrix for a graph is much sparser. In our algorithm, two convolution layers are used to capture the hierarchical structure information of the graph. Because the adjacency matrix of a graph is sparser than the dense matrix of an image, we set the size of stride to four, the size of kernels to 4 × 4 matrices, and the number of kernels to 32 for each convolution layer. Then, k iterations of ResNet (He et al., 2016) are applied to accelerate the convergence. Finally, two deconvolution layers were used to reconstruct the adjacency matrix with similar settings used in convolution layers.
Second, following the strategy mentioned in Shrivastava et al. (2017) and Zhu et al. (2017), we updated two discriminators with the history of the generated graph in the l-th layer to reduce the vibration of the model. For all the experiments, we set the training iterations to 250. Adam solver (Kingma and Ba, 2014), with a batch size of one, is used to minimize the loss function and all networks are trained with a learning rate of 0.0002 in the tensorflow deep learning framework.
In this section, we demonstrate the performance of our proposed Misc-GAN framework on real networks. Moreover, we present a case study to illustrate the effectiveness of Misc-GAN in learning the topological features at different levels of granularity.
We evaluated our proposed algorithm on seven real-world networks from the Stanford Network Analysis Project (SNAP) (Leskovec and Krevl, 2015). The statistics of data sets are summarized in Table 2. In particular, Email is a communication network, where an edge exists if one person sends at least one email to another person; Facebook is a social network, where each edge represents a social connection between the users in Facebook; Wiki is a voting network, which is used by Wikipedia to elect administrators among the huge contributors; P2P is a file-sharing network, where each node represents a host and each edge represents a connection between hosts; GNU is another Gnutella peer-to-peer file sharing network, which is similar to P2P network; Bitcoin is a who-trusts-whom network that covers the bitcoin trading information on the Bitcoin OTC platform, where each node represents a user and each edge represents the trustfulness between two users; CA is a collaboration network from arXiv, where each node represents an author and each edge represents the collaborations between authors. For different weights in a graph, i.e., Bitcoin graph, we convert the values of edges to binary values in order to feed them to our model.
We compared Misc-GAN with two random graph models, i.e., Erdös-Rényi (E-R) model (Erdös and Rényi, 1959) and Barabási-Albert (B-A) model (Albert and Barabási, 2002), and one recent deep graph generative model, i.e., GAE (Kipf and Welling, 2016). All the graph statistics are outlined in Table 2. In our setting, the graphs in Table 2 are target domain graphs, and the source domain graphs are generated under a random normal distribution with the same numbers of nodes and edges as the target domain graphs.
All the data sets are publicly available. We will release the code of our algorithms through the authors' website after the paper is published. The experiments are performed on a Windows machine with four 3.5 GHz Intel Cores and 256 GB RAM.
The comparison results, in terms of effectiveness across a diverse set of real networks, are shown in Figure 3. In particular, we present the results regarding the following metrics: (1) AD: the average degree of all nodes in a graph; (2) LCC: the size of the largest connected component of the graph; (3) EPL: the exponent of the power law distribution of the graph; (4) GC: the Gini coefficient of the degree distribution of the graph; (5) KL: the symmetric Kullback-Leibler (KL) divergence (Moreno et al., 2004) between the local clustering coefficient distributions of the original graphs and the generated graphs; (6) Graph Kernel: the similarity between the original graph and the generated one by using the random-walk based graph kernel (Kang et al., 2012). From these figures, the x-axis of each figure represents a data set, and the y-axis is the value of metrics. From Figures 3A–D, we mainly compare various graph statistics between the original graph and the generated ones using baseline methods. If the value of the metric of the generated graph is close to that of the original graph, it means the generated graph is much more similar to the original graph. We observed that the AD of our proposed algorithm is almost identical to the AD of the original graph for all data sets; for the other three metrics, our proposed algorithm also outperformed the others in most cases. In Figures 3E,F, we present the divergence and similarity score between the original graphs and the generated graphs. Note that, for presentation purposes, all the results in Figures 3E,F are presented using a negative log function, i.e., f(x) = −log(x). In general, we observe that (1) our proposed Misc-GAN outperforms the comparison methods across most of the datasets and evaluation metrics in most cases. For example, in the Email data, Misc-GAN is 66% smaller on the clustering coefficient distribution evaluation; (2) our proposed Misc-GAN framework better preserves the local topological features (e.g., the largest connected component and local clustering coefficient) and the global features (e.g., mean degree, the power law coefficients of the degree distribution of graphs) than other deep generative models (e.g., GAE). It is because our method explores the network structures at multiple resolutions and automatically learns the weight of the importance of topological features at different levels, while the existing deep generative models may fail to model such fine-grained topological features.
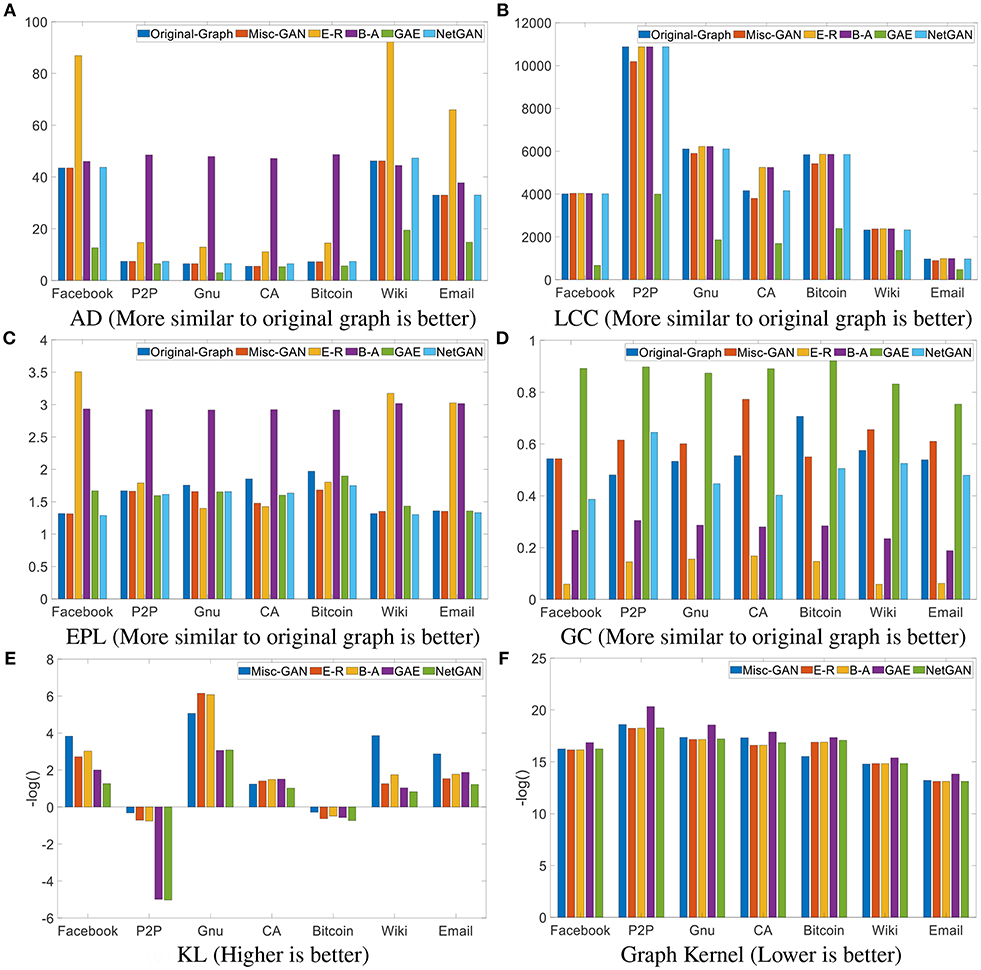
Figure 3. Effectiveness analysis. (A) AD (More similar to original graph is better). (B) LCC (More similar to original graph is better). (C) EPL (More similar to original graph is better). (D) GC (More similar to original graph is better). (E) KL (Higher is better). (F) Graph Kernel (Lower is better).
Moreover, we present the comparison results regarding running time (s) on the Email dataset in Figure 4. In particular, we show the running of Misc-GAN learning from the original graph (i.e., Misc-GAN (L1)), the Layer 2 coarsen graph with around 700 nodes (i.e., Misc-GAN (L2)), the Layer 3 coarsen graph with around 500 nodes (i.e., Misc-GAN (L3)), by comparing the two neural network based methods (i.e., GAE and NetGAN). Due to the random graph algorithms (e.g., E-R and B-A) do not have a certain training process, we do not include them in Figure 4. In general, we observed the following: (1) Misc-GAN (42s) have comparable running time with GAE (38s), and way faster than NetGAN (1092s); (2) by learning from the Layer 2 coarse graph and Layer 3 coarse graph, the running time of Misc-GAN dramatically reduced from 42 s to 26 s and 12 s, respectively.
A simple but intuitive way to evaluate the generated graphs is to visualize the network layout in a two-dimensional space. In Figure 5, we compared the multi-scale network representations of the original graph (i.e., Email) and the generated graphs. In particular, we selected the deep generative model GAE and NetGAN as our baseline methods and constructed coarse graphs at four different scales based on Equation (4). In general, we found that (1) our framework preserved the graph structures at multiple levels of granularity well; (2) NetGAN only preserved the lower-level connectivity patterns (e.g., clusters within a loop pattern) in Layer 1, but failed to capture the higher-level connectivity patterns (e.g., the cluster of super-nodes) in Layer 3, Layer 4 and Layer 5. The reason for the preceding phenomenon is that NetGAN is trained at a single level (i.e., a single granularity of nodes), which results in the coarse reconstruction of high-level network structures. GAE also has a similar problem, due to the failure of capturing higher-level connectivity patterns(i.e., in Layer 5).
We propose a multi-scale generative model named Misc-GAN for graph-structured data, which explores the network structures at multiple resolutions and automatically generates a unique graph representation that preserves such fine-grained topological features. The empirical studies show that Misc-GAN achieves significantly better performance than state-of-the-art models do on real networks. However, various challenges remain in this problem, such as how to make the deep generative model scale to massive graphs, and how to generate the domain-specific graph with complex connectivity patterns (e.g., modeling the online transaction networks with money laundering patterns).
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
This material is supported by the National Science Foundation under Grant No. IIS-1651203, IIS-1715385, IIS-1743040, and CNS-1629888, by DTRA under the grant number HDTRA1-16-0017, by the United States Air Force and DARPA under contract number FA8750-17-C-01531, by Army Research Office under the contract number W911NF-16-1-0168, and by the U.S. Department of Homeland Security under Grant Award Number 2017-ST-061-QA0001. The content of the information in this document does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation here on.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. ^Distribution Statement “A” (Approved for Public Release, Distribution Unlimited).
Albert, R., and Barabási, A. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. doi: 10.1103/RevModPhys.74.47
Bojchevski, A., Shchur, O., Zügner, D., and Günnemann, S. (2018). “Netgan: generating graphs via random walks,” in Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Sweden, July 10-15, 2018 (Stockholm), 609–618.
Chang, H., Lu, J., Yu, F., and Finkelstein, A. (2018). “Pairedcyclegan: asymmetric style transfer for applying and removing makeup,” in 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Salt Lake City, UT), 40–48. doi: 10.1109/CVPR.2018.00012
Coifman, R. R., and Maggioni, M. (2006). Diffusion wavelets. Appl. Comput. Harmonic Anal. 21, 53–94. doi: 10.1016/j.acha.2006.04.004
Cour, T., Benezit, F., and Shi, J. (2005). “Spectral segmentation with multiscale graph decomposition,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005. CVPR 2005, Vol. 2 (San Diego, CA: IEEE), 1124–1131. doi: 10.1109/CVPR.2005.332
Du, C., Du, C., Xie, X., Zhang, C., and Wang, H. (2018). “Multi-view adversarially learned inference for cross-domain joint distribution matching,” in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2018, August 19-23, 2018 (London), 1348–1357.
Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996). “A density-based algorithm for discovering clusters in large spatial databases with noise,” in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96) (Portland, OR), 226–231. Available online at: http://www.aaai.org/Library/KDD/1996/kdd96-037.php
Fich, E. M., and Shivdasani, A. (2007). Financial fraud, director reputation, and shareholder wealth. J. Finan. Econ. 86, 306–336.
Ganin, Y., Ustinova, E., Ajakan, H., Germain, P., Larochelle, H., Laviolette, F., et al. (2016). Domain-adversarial training of neural networks. J. Mach. Learn. Res. 17, 2096–2030.
Gao, Z.-K., Cai, Q., Yang, Y.-X., Dang, W.-D., and Zhang, S.-S. (2016). Multiscale limited penetrable horizontal visibility graph for analyzing nonlinear time series. Sci. Rep. 6:35622. doi: 10.1038/srep35622
Godard, C., Mac Aodha, O., and Brostow, G. J. (2017). “Unsupervised monocular depth estimation with left-right consistency,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, July 21-26, 2017 (Honolulu, HI), 6602–6611.
Gómez-Bombarelli, R., Wei, J. N., Duvenaud, D., Hernández-Lobato, J. M., Sánchez-Lengeling, B., Sheberla, D., et al. (2016). Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Sci.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative adversarial nets,” in Advances in Neural Information Processing Systems 27: Annual Conference on Neural Information Processing Systems 2014 (Montreal, QC), 2672–2680. Available online at: http://papers.nips.cc/paper/5423-generative-adversarial-nets
Gou, L., You, F., Guo, J., Wu, L., and Zhang, X. L. (2011). “Sfviz: interest-based friends exploration and recommendation in social networks,” in Proceedings of the 2011 Visual Information Communication-International Symposium (Hong Kong: ACM), 15. doi: 10.1145/2016656.2016671
Grandjean, M. (2016). How to Display Complex Network Data With Information Visualization. CC BY-SA 3.0. Available online at: https://www.interaction-design.org/literature/article/how-to-display-complex-network-data-with-information-visualization
Grover, A., Zweig, A., and Ermon, S. (2018). Graphite: iterative generative modeling of graphs. arXiv:1803.10459.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, USA, June 27-30, 2016 (Las Vegas, NV), 770–778.
Huang, Q., and Guibas, L. J. (2013). Consistent shape maps via semidefinite programming. Comput. Graph. Forum 32, 177–186. doi: 10.1111/cgf.12184
Johnson, S. C. (1967). Hierarchical clustering schemes. Psychometrika. 32, 241–254. doi: 10.1007/BF02289588
Kang, U., Tong, H., and Sun, J. (2012). “Fast random walk graph kernel,” in Proceedings of the Twelfth SIAM International Conference on Data Mining (Anaheim, CA), 828–838. doi: 10.1137/1.9781611972825.71
Lee, J. D., and Maggioni, M. (2011). “Multiscale analysis of time series of graphs,” in International Conference on Sampling Theory and Applications (SampTA) (Singapore).
Leskovec, J., Chakrabarti, D., Kleinberg, J., Faloutsos, C., and Ghahramani, Z. (2010). Kronecker graphs: an approach to modeling networks. JMLR. 11, 985–1042.
Leskovec, J., and Krevl, A. (2015). {SNAP Datasets}:{Stanford} large network dataset collection. Available online at: https://snap.stanford.edu/data/
Li, Y., Vinyals, O., Dyer, C., Pascanu, R., and Battaglia, P. (2018). Learning deep generative models of graphs. arXiv:1803.03324.
Liu, W., Cooper, H., Oh, M. H., Yeung, S., Chen, P., Suzumura, T., et al. (2017). Learning graph topological features via gan. arXiv:1709.03545.
Moreno, P. J., Ho, P. P., and Vasconcelos, N. (2004). “A kullback-leibler divergence based kernel for svm classification in multimedia applications,” in Advances in Neural Information Processing Systems 16, Neural Information Processing Systems, NIPS (Vancouver, BC; Whistler, BC).
Ravasz, E., and Barabási, A. (2003). Hierarchical organization in complex networks. Phys. Rev. E. 67:026112. doi: 10.1103/PhysRevE.67.026112
Ron, D., Safro, I., and Brandt, A. (2011). Relaxation-based coarsening and multiscale graph organization. Multiscale Model. Simulat. 9, 407–423. doi: 10.1137/100791142
Safro, I., and Temkin, B. (2011). Multiscale approach for the network compression-friendly ordering. J. Discrete Algorithms 9, 190–202. doi: 10.1016/j.jda.2010.09.007
Schaeffer, S. (2007). Graph clustering. Comput. Sci. Rev. 1, 27–64. doi: 10.1016/j.cosrev.2007.05.001
Sharon, E., Brandt, A., and Basri, R. (2000). “Fast multiscale image segmentation,” in Conference on Computer Vision and Pattern Recognition (CVPR) (Hilton Head, SC: IEEE), 1070–1077 doi: 10.1109/CVPR.2000.855801
Shrivastava, A., Pfister, T., Tuzel, O., Susskind, J., Wang, W., and Webb, R. (2017). “Learning from simulated and unsupervised images through adversarial training,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, July 21-26, 2017 (Honolulu, HI), 2242–2251.
Simonovsky, M., and Komodakis, N. (2018). Graphvae: towards generation of small graphs using variational autoencoders. arXiv:1802.03480.
Stolte, C., Tang, D., and Hanrahan, P. (2003). Multiscale visualization using data cubes. IEEE Trans. Visual. Comput. Graph. 9, 176–187. doi: 10.1109/TVCG.2003.1196005
Tzeng, E., Hoffman, J., Saenko, K., and Darrell, T. (2017). “Adversarial discriminative domain adaptation,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Honolulu, HI), 2962–2971. doi: 10.1109/CVPR.2017.316
Wang, F., Huang, Q., and Guibas, L. J. (2013). “Image co-segmentation via consistent functional maps,” in IEEE International Conference on Computer Vision, ICCV 2013, Australia, December 1-8, 2013 (Sydney, NSW), 849–856.
Wang, F., Huang, Q., Ovsjanikov, M., and Guibas, L. J. (2014). “Unsupervised multi-class joint image segmentation,” in 2014 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2014, USA, June 23-28, 2014 (Columbus, OH), 3142–3149.
Wilson, K., and Snavely, N. (2013). “Network principles for sfm: disambiguating repeated structures with local context,” in IEEE International Conference on Computer Vision, ICCV 2013, Australia, December 1-8, 2013 (Sydney, NSW), 513–520.
You, J., Ying, R., Ren, X., Hamilton, W. L., and Leskovec, J. (2018a). Graphrnn: a deep generative model for graphs. arXiv: 1802.08773.
You, J., Ying, R., Ren, X., Hamilton, W. L., and Leskovec, J. (2018b). “Graphrnn: generating realistic graphs with deep auto-regressive models,” in Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Sweden, July 10-15, 2018 (Stockholm), 5694–5703.
Zach, C., Klopschitz, M., and Pollefeys, M. (2010). “Disambiguating visual relations using loop constraints,” in The Twenty-Third IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2010, USA, 13-18 June 2010 (San Francisco, CA), 1426–1433.
Zhang, Y., Barzilay, R., and Jaakkola, T. S. (2017). Aspect-augmented adversarial networks for domain adaptation. TACL 5, 515–528. doi: 10.1162/tacl_a_00077
Zhou, T., Krähenbühl, P., Aubry, M., Huang, Q., and Efros, A. A. (2016). “Learning dense correspondence via 3d-guided cycle consistency,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, USA, June 27-30, 2016 (Las Vegas, NV), 117–126.
Zhou, T., Lee, Y. J., Yu, S. X., and Efros, A. A. (2015). “Flowweb: joint image set alignment by weaving consistent, pixel-wise correspondences,” in IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2015, USA, June 7-12, 2015 (Boston, MA), 1191–1200.
Keywords: multi-scale analysis method (MSA), graph generation, generative adversarial network, neural network, cycle consistency
Citation: Zhou D, Zheng L, Xu J and He J (2019) Misc-GAN: A Multi-scale Generative Model for Graphs. Front. Big Data 2:3. doi: 10.3389/fdata.2019.00003
Received: 01 December 2018; Accepted: 21 March 2019;
Published: 25 April 2019.
Edited by:
Yuxiao Dong, Microsoft Research, United StatesReviewed by:
Le Wu, Hefei University of Technology, ChinaCopyright © 2019 Zhou, Zheng, Xu and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dawei Zhou, ZGF2aWRjaG91emR3QGdtYWlsLmNvbQ==
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.