Lucas Spiske
Philipp N. Plessow1
Felix Studt- 1Institute of Catalysis Research and Technology, Karlsruhe Institute of Technology, Karlsruhe, Germany
- 2TotalEnergies OneTech Belgium, Feluy, Belgium
Hybrid density functional theory calculations are used to investigate different mechanisms of the isomerization of n-butane to isobutane via intermediate formation of olefins. The monomolecular mechanism for isomerization of butene and isobutene is found to be prevalent, with a Gibbs free energy barrier of 155 kJ/mol at 400°C, compared to the bimolecular mechanism (190 kJ/mol) due to less favorable entropy for the latter. Hydrogen transfer reactions that convert olefins into alkanes (and vice versa) are also included in the investigations, and show a free energy barrier of 203 kJ/mol for conversion of isobutene to isobutane. Additionally, a methyl transfer mechanism is discussed as a possible pathway for formation of C3 and C5 side products, in comparison to the bimolecular mechanism; the highest barrier of the initial methyl transfer is calculated to be 227 kJ/mol. We discuss the influence of entropy and anharmonicity on all mechanisms, stating that through the uncertainties in computational methods when calculating these systems, the calculated reaction barriers are likely to be overestimated here.
1 Introduction
In the cracking and refining of crude oil, short-chain hydrocarbons, like butane, are important products. The isomerization of n-butane to isobutane is performed on an industrial scale (Ono, 2003). The demand for isobutane is expected to further increase (Isobutane market to reach USD, 2021) since it is a feedstock, e.g., high octane fuels (Potter et al., 2020) and C4 alkylation reactions (Wulfers and Jentoft, 2015), and an important reactant in methyl-tert-butyl ether (MTBE) synthesis (Ono, 2003).
While the skeletal isomerization of long-chain olefins is rather well-understood and thought to occur via monomolecular pathways (Rey et al., 2019a; Rey et al., 2019b), mechanisms for the isomerization of n-butane are still debated, with experiments suggesting that a bimolecular mechanism might also play a dominant role (Bearez and Guisnet, 1983; Asuquo and Lercher, 1995; Houžvička and Ponec, 1997; Ono, 2003; Luzgin et al., 2005; Tuma and Sauer, 2005; Kangas et al., 2008). Although both the monomolecular and bimolecular mechanisms are widely accepted as the two possibilities for n-butane isomerization, no clear consensus has been reached yet about the extent of these pathways in product formation. While earlier research proposed the bimolecular mechanism as the main reaction pathway (Bearez and Guisnet, 1983; Asuquo and Lercher, 1995), recent research states that the monomolecular mechanism is favored (Houžvička and Ponec, 1997; Wulfers and Jentoft, 2015; He et al., 2017). The bimolecular pathway, however, is thought to be responsible for the formation of unwanted products that lead to lower product selectivity and deactivation of the catalyst (Houžvička and Ponec, 1997). In a recent article, the influence of both acid site density and support acidity/metal balance is discussed as an important factor impacting the participation ratio of the monomolecular to bimolecular mechanism (Potter et al., 2020).
Both mechanisms are thought to occur via the formation of olefinic intermediates. Recently, the effect of olefin concentration in the feed on the conversion and product distribution has been investigated, and calculation of the activation energy for isobutane formation indicates a monomolecular mechanism (Wulfers and Jentoft, 2015). However, further investigations are still needed to understand how side products with different chain lengths such as C3 and C5 are formed.
The aim of this work is to investigate the isomerization pathways catalyzed by the H-SSZ-13 zeolite (CHA structure), chosen as a model catalyst due to its computational simplicity and common use. The monomolecular isomerization pathway (He et al., 2017), the bimolecular pathway, and alkane–alkene hydrogen transfers (HT) are modeled using hierarchical cluster models and accurate hybrid-functional DFT calculations. Additional mechanisms that lead to C3 and C5 products are also investigated.
2 Computational details
The H-SSZ-13 zeolite with CHA structure has a narrow pore window size of 0.38 × 0.38 nm (Breck and Breck, 1973). A CHA unit cell containing 36 T-sites has been chosen for this work. The optimized periodic CHA structure has lattice parameters of
Geometry optimizations and energy calculations of periodic structures have been performed with the VASP program package (Kresse and Hafner, 1993; Kresse and Hafner, 1994; Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b; Kresse and Joubert, 1999) in version 5.4.1 using the atomic simulation environment (ASE) Python library as a facilitator (Hjorth Larsen et al., 2017), at the PBE-D3 level of theory (Perdew et al., 1997; Grimme et al., 2010). The projector augmented wave (PAW) method was used with standard PAW potentials, an energy cutoff of 400 eV for the wave function, an SCF energy convergence criterion of 10–8 eV, and a geometry convergence criterion of 10–2 eV/Å for atomic forces. The Brillouin zone was sampled only at the Γ-Point. Transition state optimization was performed using automated relaxed potential energy surface scans (ARPESS) (Plessow, 2018). As there are four different oxygen sites that the acid proton can occupy, it has been ensured that for all structures, the energetically most favorable structure or transition state is chosen. For the clean acid site, the hydrogen atom is bound to the crystallographic O4 position. Harmonic frequencies were computed based on a partial Hessian, where the adsorbate as well as the acid site (Al) and its four neighboring oxygen and silicon atoms are included. All stationary states were confirmed to contain the correct amount of imaginary harmonic frequencies, i.e., 0 for minima and 1 for transition states. Entropy contributions at the given temperature were calculated using the harmonic approximation, where all frequencies under a threshold of 12 cm-1 are treated as 12 cm-1 to avoid inaccuracies in the entropy for low-frequency vibrations (Brogaard et al., 2014a; Brogaard et al., 2014b).
To improve the accuracy of the computed energies at the PBE-D3 level, which widely underestimates barriers in zeolite catalysis (Goncalves et al., 2019), smaller non-periodic 46T cluster models were constructed (see Supplementary Figure S1B in the SI), as described by Goncalves et al. (2019). Single-point calculations were performed for them, using the TURBOMOLE program package (Ahlrichs et al., 1989; Von Arnim and Ahlrichs, 1998) and the hybrid M06 functional (Zhao and Truhlar, 2008), as this has been shown to provide very accurate reaction energies and barriers (Goncalves et al., 2019). Corrections were calculated according to Equation (1), where the differences between the PBE-D3 functional (Perdew et al., 1997; Perdew et al., 2008; Perdew et al., 2009) and the M06 functional (Zhao and Truhlar, 2008), both using the def2-TZVPP basis set (Weigend et al., 2003; Weigend and Ahlrichs, 2005), were calculated. The final energy E of a structure is accordingly given by
Free energies were calculated in the harmonic oscillator approximation at T = 400°C and p = 1 bar.
3 Results and discussion
3.1 Reaction overview
The H-SSZ-13 zeolite in the chabazite structure has been chosen due to its simplicity with only one possible T-site for Al substitution. A general scheme of the reaction mechanism is shown in Figure 1. It is important to note that the direct skeletal isomerization of n-butane to isobutane is kinetically hindered and does not take place at reasonable reaction conditions (Kangas et al., 2008). It is, therefore, generally assumed that this reaction involves the formation of olefins through dehydration of n-butane. We choose a temperature of 400°C for our calculations in this work, as it is representative of general reaction conditions in butane isomerization, even though it lies toward the upper end of temperatures used for this reaction (Asuquo and Lercher, 1995; Adeeva and Sachtler, 1997; Wulfers and Jentoft, 2015; He et al., 2017; Wang et al., 2018). We calculated the direct dehydrogenation barrier of n-butane to the n-butyl cation and H2 to be 247 kJ/mol at 400°C (see Supplementary Figure S2) and, therefore, disregard this reaction as a possibility for olefin production. However, as shown in Figure 1, olefins only need to be present in catalytic amounts as they can be interconverted by hydrogen transfer (HT) reactions, though each butane has to go through an olefinic state in the reaction mechanism.
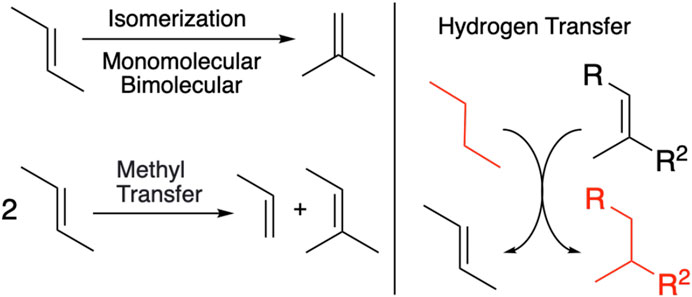
FIGURE 1. Overview of the n-butane isomerization reaction mechanism. The actual isomerization reaction is that of 2-butene to isobutene, shown in the top left. Through methyl transfer, hydrocarbons of differing carbon chain length can be obtained as well. n-Butane, together with an olefin, is catalytically converted by two successive hydrogen transfers (HTs) to the respective alkane and 2-butene, which can then again isomerize to isobutene. The main reaction of n-butane to isobutane is shown in red.
Using olefins as the reactive species, we will discuss the outcome of our calculations for the monomolecular and bimolecular isomerization reactions of 2-butene to isobutene along the lines discussed in the literature. In principle, 1-butene could also act as a reactant, as the isomerization between 1-butene and 2-butene is facile at 128 kJ/mol at 400°C (see Supplementary Figure S3), but we will specifically focus on 2-butene as the reactant in this work. Afterward, we will discuss the energetics of the two HTs that convert olefins into alkanes and vice versa. Last, we will take a look at a methyl transfer (MT) mechanism involving surface methoxy species (SMS) as a potential source for the side products propane and pentane. This reaction pathway also involves two HTs and can be seen as the reverse reaction of the methylation of olefins in the methanol-to-olefin process (Plessow and Studt, 2017). Last, we compare the results for the different mechanisms and assess their influence on the overall reaction performance.
3.2 Monomolecular mechanism
The monomolecular pathway (also called unimolecular pathway) was investigated based on the transition state geometries reported by He et al. (2017), who investigated the reactions over H-ZSM-23 and H-ZSM-48 zeolites using the combined B3LYP:UFF method ONIOM scheme. The related reaction mechanism is shown in black in Figure 2A, and the corresponding enthalpy and free energy diagrams for the pathway are shown in Figures 2B, C, respectively. Images of transition states, as well as important bond distances, are shown in Supplementary Figure S2. This reaction pathway is similar to the one proposed by He et al., albeit with the difference that we focused on 2-butene as the reactant, while He et al. started from 1-butene. As the double-bond migration in 1-butene is much faster than the skeletal isomerization reactions (Kangas et al., 2008), this does not affect the findings presented here. There is another difference in the proposed mechanisms: He et al. found that 2-butene (E2) is protonated by the acid site proton and immediately forms n-butoxide. The n-butoxide then isomerizes to isobutoxide, passing through a cyclopropyl transition state. Our calculations indicate that the 2-butyl cation (A1) that forms after the protonation is a local minimum. However, the barriers for decomposition of this cation toward 2-butene or isobutoxide are very low (6 and 3 kJ/mol, respectively), making it an unstable intermediate. The 2-butyl cation isomerizes through a structurally very similar cyclopropyl transition state to form isobutoxide (A2), see Supplementary Table S1. This is also true for the following two transition state structures, which are again very similar to those identified for H-ZSM-23 and H-ZSM-5 by He et al. (2017). In the next step, the C–O bond of the isobutoxide is broken; the proton from the adjacent carbon then shifts over to yield the stable tertiary isobutyl cation (A3). In the final step, the acid site abstracts a proton from the cation, and isobutene (P1) is formed. Isobutene can then desorb from the pore into the gas phase, leaving the empty zeolite behind (P2).
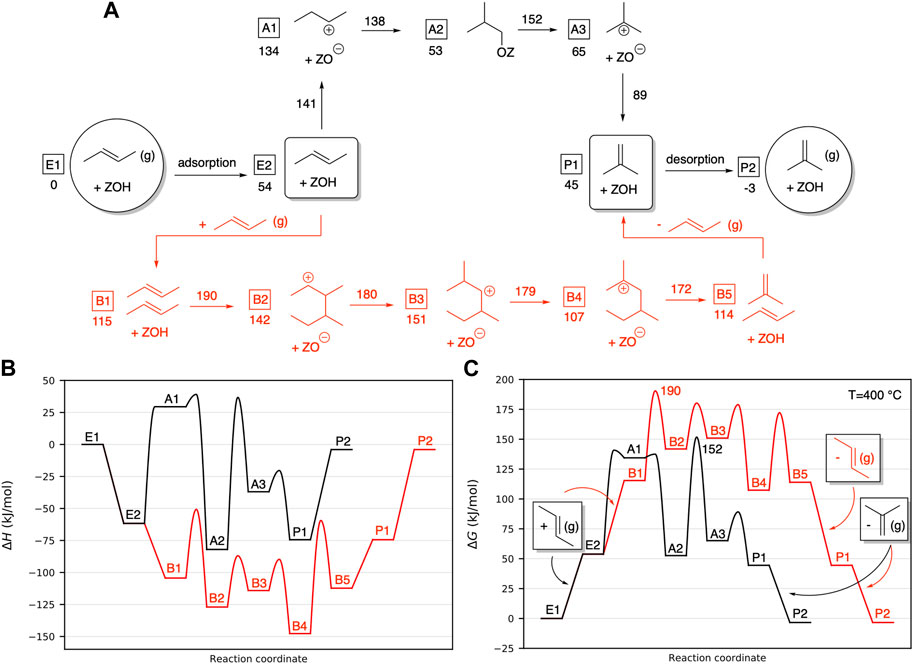
FIGURE 2. (A) Overview of the monomolecular (black) and bimolecular (red) 2-butene isomerization mechanisms, referenced to the empty H-SSZ-13 zeolite and 2-butene in the gas phase. Free energies of intermediate structures are shown next to the structures; free energies of the transition state structures are above the reaction arrows. All energies and barriers are calculated at T = 400°C. (B) Enthalpy diagram of the monomolecular and bimolecular 2-butene isomerization mechanisms. (C) Free energy diagram of the monomolecular and bimolecular 2-butene isomerization mechanisms. The highest barriers of the overall mechanisms are 190 and 152 kJ/mol, respectively. All energies are given in kJ/mol, at T = 400°C and 1 bar.
Our calculated pathway via the stable 2-butyl cation has an overall free energy barrier of 87 kJ/mol for conversion of 2-butene to isobutoxide, which is 39 kJ/mol lower than that of the previously considered mechanism over n-butoxide, which we also optimized in H-SSZ-13 (see Supplementary Figure S5 in the SI). Comparing the free energy diagram of this reaction (Figure 2C, black line) to the one in the work of He et al. (2017), we see that, with this lower isomerization barrier, the reaction from isobutoxide to the isobutyl cation now becomes the rate-determining step.
When referencing all energies and barriers to the empty H-SSZ-13 zeolite and 2-butene in the gas phase, we obtain an overall reaction barrier of only 152 kJ/mol at 400°C (see Figure 2C) for the considered monomolecular mechanism.
3.2 Bimolecular mechanism
In the bimolecular mechanism, two C4 olefins adsorb within the same zeolite pore and react with each other, forming a C8 intermediate that can undergo different hydrogen and methyl shifts. These shifts have been calculated to have very low reaction barriers (Plessow and Studt, 2020), which leads to a multitude of different C8 isomers being produced. After isomerization, the C8 intermediates can crack again to yield either different C4 species, in our case, n-butene and isobutene, or C3 and C5 olefins through uneven ß-scission. It is important to note that herein, we only considered one specific pathway for the C8 intermediate that yields the desired products, isobutene and 2-butene. We did this, as we can directly compare this to other mechanisms herein. The bimolecular mechanism investigated is shown schematically in Figure 2A in red; images of transition states and important bond distances are shown in Supplementary Figure S6.
After adsorption of two 2-butene molecules into the zeolite pore (B1), the 2-butene molecule closest to the active site is protonated, which triggers the formation of a new C–C bond between the now positively charged carbon adjacent to the protonated carbon and one of the sp2 carbons of the second 2-butene molecule, forming the 3,4-dimethylhexan-2-ylium ion (B2). This ion then first undergoes a methyl shift to a 2,4-dimethylhexan-3-ylium ion (B3) and then an HT to form the more stable tertiary 2,4-dimethylhexan-2-ylium ion (B4). Both these shifts have rather low barrier energies of 38 and 28 kJ/mol, respectively, and are, therefore, expected to happen fast once B2 has been formed. Last, the 2,4-dimethylhexan-2-ylium ion can crack into isobutene and the 2-butyl ion, which is readily deprotonated by the acid site to yield 2-butene (B5). The first and last transition states of the bimolecular pathway, olefin dimerization and cracking, mirror each other, with almost identical bond lengths in the transition states (see Supplementary Table S2). After desorption of both olefins (P1 and P2), one of the two reacting 2-butenes is isomerized to isobutene.
When comparing the calculated enthalpic (Figure 2B) and free energy pathways (Figure 2C) for the bimolecular mechanism, it is evident that there is a large difference originating from the huge entropy penalty due to the adsorption of two olefins within the pore of H-SSZ-13. While the bimolecular mechanism seems to be more favorable than the monomolecular mechanism as observed from Figure 2B, the inclusion of entropic contributions reveals that the bimolecular mechanism has higher overall free energy barriers. It should be noted that a similar effect has been observed for the concerted and stepwise mechanism of the methylation of olefins (Brogaard et al., 2014b). The most important difference between the monomolecular and bimolecular pathways is that in the latter, co-adsorption of a second olefin into the zeolite pore is necessary (E2 to B1).
This co-adsorption is unfavorable because of strong entropic effects, giving rise to a very high free energy after co-adsorption. The isomerization, on the other hand, is not very demanding: From two 2-butene molecules adsorbed in H-SSZ-13, the difference to the highest transition state is 62 kJ/mol, which is 36 kJ/mol lower than for the monomolecular pathway (98 kJ/mol). However, taking the adsorption energies and entropic penalties into account, the free energy difference between the reference molecules and the highest transition state is 190 kJ/mol for the bimolecular pathway, whereas it amounts to only 152 kJ/mol for the monomolecular pathway. This shows that when looking at the actual reaction barriers, it is essential to consider entropic effects. Doing so, we see that the bimolecular pathway has an overall free energy barrier that is 38 kJ/mol higher than that from the monomolecular pathway.
One of the reasons why the bimolecular pathway has been considered for n-butane isomerization is that through the possibility of uneven ß-scission, it can explain side product hydrocarbons with chain lengths other than 4. A barrier for the cracking of 2,3,4-trimethylpent-2-ene into C3 and iso-C5 has been calculated in earlier work (Plessow and Studt, 2018) and is shown to be 168 kJ/mol; 57 kJ/mol higher than that of the even scission of a similar C8 intermediate (E−3,4,4-trimethylpent-2-ene into C4 and iso-C4). Other uneven ß-scission reactions are calculated to exhibit even higher barriers. This shows that the even cracking toward two C4 species is favored for C8 cracking, likely because of the ability to form the stable t-butyl cation intermediate.
For the adsorption of alkanes in zeolites, investigations have been carried out assuming a loss of 1/3 of the molecule´s translational entropy upon adsorption, as the adsorbed species are still able to retain some translational modes inside the zeolite pore (Janda et al., 2016; Dauenhauer and Abdelrahman, 2018). We used this approximation herein (see Supplementary Figure S9 in the SI) and found free energy barriers of 95 kJ/mol for the monomolecular and 80 kJ/mol for the bimolecular pathway. This should be seen as a lower bound, as we would expect that a significantly higher fraction of translational entropy is lost when considering the tightly bound transition states (see Supplementary Figures S4C, S6A). However, this analysis nicely highlights that a different treatment of entropic contribution would decrease the overall barriers for the bimolecular pathway by twice the amount, hence decreasing their free energy differences.
3.3 Intermolecular hydrogen transfer mechanism
Until this point, we have only discussed the isomerization reaction of 2-butene to isobutene. A reaction mechanism for HTs between olefins and hydrocarbons is illustrated in Figure 3 for two C4 molecules as reactants. Images of the two transition states and important bond distances are shown for the reaction of n-butane with isobutene in Supplementary Figure S7. The free energies and barriers for propene, iso-butene, and 2-methyl-2-butene as the reactants are shown in Table 1.
FIGURE 3. Mechanistic scheme of the HT reactions to convert selected alkenes into the respective saturated alkanes. Shown here in blue is the mechanism for converting isobutene into isobutane; the same mechanism is used for converting propene into propane and 2-methylbut-2-ene into 2-methylbutane. Structure H2 needs to rotate 180° in the cavity before the second HT can take place. Intermediate energies and reaction barriers for this mechanism are given in Table 1.
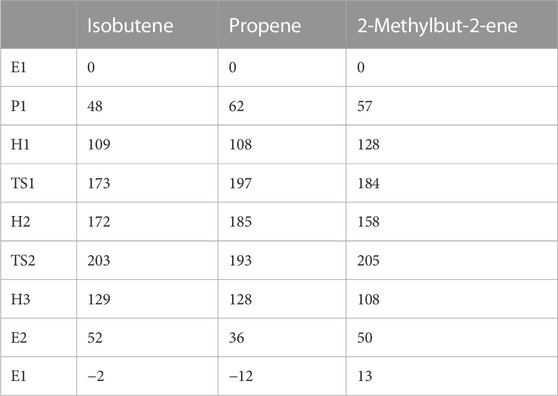
TABLE 1. Free energies and barriers for the HT mechanism presented in Figure 4, between n-butane and isobutene, propene, and 2-methylbut-2-ene as possible reactants (shown in blue). All energies and barriers calculated at T = 400°C and given in kJ/mol.
The reaction mechanisms are similar for all reactants: After co-adsorption of the olefin and n-butane within the zeolite pore (H1), protonation of the olefin with the proton from the acid site (TS1) yields the tert-butyl cation, co-adsorbed with n-butane (H2). The next reaction requires a rotation of the two co-adsorbed hydrocarbons by 180°. We assume the associated rotational barriers to be negligible based on previous work (Fecik et al., 2018). After rotation, n-butane now faces the acid site. Subsequently, a concerted reaction takes place as n-butane gets deprotonated by the acid site, while simultaneously a hydride is transferred from n-butane toward the isobutyl cation to form isobutane and 2-butene (H3).
As in the case of the bimolecular mechanism, two hydrocarbons have to co-adsorb within the zeolite pore, which is entropically unfavorable. Using isobutene and n-butane in the gas phase as the reference, the highest barrier would be deprotonation to yield 2-butene and isobutane, being 203 kJ/mol. This barrier is even higher than that of the bimolecular mechanism by 13 kJ/mol and is somewhat too high for the reaction to take place at reasonable rates at reaction conditions typically employed.
3.4 Methyl transfer mechanism
As discussed previously, C3 and C5 hydrocarbons are by-products formed during n-butane isomerization, which is typically attributed to the bimolecular mechanism. An alternative possibility for their formation that we investigate here is the transfer of a methyl group (methyl transfer, MT) from an olefin to the acid site, forming a surface methoxy species (SMS), while reducing the olefin length by one CH2 unit. For example, 2-butene is first protonated by the acid site, forming the 2-butyl cation, from which a CH3 group can then transfer back to the acid site, forming propene and an SMS. A detailed free energy diagram for the MT reactions is shown in Figure 4. Here, 2-butene adsorbed in H-SSZ-13 (E2) can undergo the aforesaid reaction to yield propene and an SMS (M1). The propene molecule can then desorb, leaving the SMS behind (M2). Now, a second 2-butene molecule can adsorb at the SMS (M3) and after being methylated yields 2-methylbut-2-ene and the empty acidic zeolite (M4). The 2-methylbut-2-ene molecule can desorb afterward and partake in the next reaction.
FIGURE 4. Free energy diagram of the formation of an SMS species and propene from 2-butene and successive methyl transfer (MT) to form 2-methylbut-2-ene. The rate-determining step is indicated to have a barrier of 227 kJ/mol at T = 400°C, referenced to the empty zeolite and 2-butene in the gas phase.
As evident from Figure 4, the reaction between n-butene and an acid site yielding an SMS is accompanied by a free energy barrier of 227 kJ/mol. After this first step, successive reactions that ultimately yield C3 and C5 alkanes all have somewhat lower barriers: 205 kJ/mol for the C5 pathway and 197 kJ/mol for the C3 pathway. The highest free energy barrier of the MT mechanism is 37 kJ/mol higher than the highest barrier within the bimolecular mechanism, rendering C3 and C5 formation unlikely through this pathway in comparison. It is important to note, however, that the comparison between the two reaction pathways also greatly depends on the partial pressures and temperature since the MT reaction is monomolecular. This indicates that, in general, side product formation may happen more easily through one or the other of the mechanisms, depending on the reaction conditions.
4 Conclusion and discussion
Mono- and bimolecular isomerization mechanisms from 2-butene to isobutene, as well as HTs to form isobutane, have been studied in the H-SSZ-13 (CHA) zeolite structure using periodic DFT calculations with high-level hybrid-functional (M06) corrections on cluster models. A slightly modified monomolecular mechanism via a 2-butyl cation is proposed for this zeolite. Additionally, an alternative mechanism to produce non-C4 side products has been investigated, called methyl transfer mechanism, encompassing methyl transfers to and from the acid site of the catalyst.
The main results from our calculations are that the overall free energy barriers increase from the monomolecular (152 kJ/mol) to the bimolecular (190 kJ/mol) to the methyl transfer reaction mechanism (227 kJ/mol) when referenced to olefins in the gas phase at 400°C. Importantly, only the latter two can form C3 and C5 species that are observed experimentally. The reason for the high free energy barriers required for the bimolecular pathway lies in the large entropy penalty for the adsorption of two olefins within one pore of the zeolite, which is particularly important for the high temperatures (400°C) considered herein. Lower temperatures will hence eventually favor the bimolecular mechanism. It is important to note here that we only model the co-catalyst species as 2-butene. It could, in principle, also be any other unsaturated hydrocarbon, aliphatic or aromatic, like, e.g., cyclic hydrocarbons, which might be produced during the reaction through coking of the catalyst (Wei et al., 2022). In such a case, because bulky hydrocarbons cannot leave the CHA cavity, an adsorbed olefin would be the correct energy reference state, thus lowering the overall free energy barrier.
Comparing our findings to those of recent work on this topic in the literature, Wulfers and Jentoft (2015) found that on H-mordenite at temperatures of 534–583 K, reaction orders of 1.0–1.2 point toward a predominantly monomolecular isomerization. Adding small amounts of olefin to the reaction increased the formation of disproportionation products drastically, indicating that with the presence of olefinic species, the bimolecular mechanism becomes more dominant. We generally find similar qualitative trends, but point out that they used a different zeolite than the one in this study.
When discussing our theoretical results, we should highlight that while the enthalpy part of the free energy can be calculated at a reasonably high accuracy (<10 kJ/mol with M06/def2-TZVPP (Goncalves et al., 2019)), there is to date no realistic estimate to the errors originating from the harmonic oscillator approximation of entropic contributions, and therefore the calculation of accurate entropies remains a challenge (Kundu et al., 2016; Sprowl et al., 2016; Jørgensen and Grönbeck, 2017; Li et al., 2018; Amsler et al., 2021; Studt, 2021). DFT-based molecular dynamics (MD) simulations of isobutene adsorption in H-SSZ-13 have, for example, shown that the error in entropic contributions using the harmonic approximation between adsorption through the π-complex and carbenium ion is as high as 20 kJ/mol at 400°C (De Wispelaere et al., 2022). Similarly, Piccini et al. showed that the -T∆S term for the case of adsorption of ethanol in H-ZSM-5 is different by approximately 20 kJ/mol at 400 K when comparing the harmonic and anharmonic approximation (Piccini et al., 2018), which is similar to the findings of Alexopoulos et al. (2016). We thus speculate that the error of the entropic part (-T∆S) of the highest transition state of the bimolecular mechanism (B1-B2) is larger than those reported for small molecules such as ethanol. Given that the transition state of the bimolecular mechanism has two C4 fragments, while the unimolecular only contains one, the error of the bimolecular mechanism should be higher, which should lower the reaction barrier for the bimolecular mechanism more, but whether this makes it comparable to or even lower than the unimolecular mechanism is difficult to estimate and will only be possible using extensive MD simulations in conjunction with thermodynamic integration (TI) (Rey et al., 2020; Amsler et al., 2021).
A simple estimate using the approximation that two-thirds of the translational entropy is retained in species in zeolites yields free energy barriers of 95 kJ/mol for the monomolecular and 80 kJ/mol for the bimolecular mechanism. These barriers seem to be rather low, suggesting that less than two-thirds of the translational entropy is lost, as the transition states are more tightly bound than adsorbed species.
Overall, our computational results shed light on the energetics of the monomolecular and bimolecular mechanisms for butane isomerization in H-SSZ-13. Our study shows how small amounts of olefins can catalyze n-butane isomerization through the HT mechanism. We also studied an MT mechanism as a third competing mechanism, through which non-C4 hydrocarbons can also be formed. We found, however, that this mechanism is not likely to play a significant role. For an overall assessment of which reaction pathways are preferred, however, one would also need to establish kinetic models to evaluate the influences of temperature, partial pressures, and residence times and to include possible effects of diffusion limitations.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This study was conducted as part of the Consortium of Metal Nanocatalysis funded by TotalEnergies OneTech Belgium. The authors acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology. Support from TotalEnergies through Houston HPC computational resources is greatly acknowledged.
Conflict of interest
The authors declare that this study received funding from TotalEnergies OneTech Belgium. The funder had the following involvement in the study: Discussion and interpretation of data, as well as the decision to submit and support in writing the publication.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fctls.2023.1213803/full#supplementary-material
References
Adeeva, V., and Sachtler, W. M. (1997). Mechanism of butane isomerization over industrial isomerization catalysts. Appl. Catal. A 163 (1-2), 237–243. doi:10.1016/s0926-860x(97)00149-x
Ahlrichs, R., Bar, M., Haser, M., Horn, H., and Kolmel, C. (1989). Electronic-structure calculations on workstation computers - the program system Turbomole. Chem. Phys. Lett. 162 (3), 165–169. doi:10.1016/0009-2614(89)85118-8
Alexopoulos, K., Lee, M.-S., Liu, Y., Zhi, Y., Liu, Y., Reyniers, M.-F., et al. (2016). Anharmonicity and confinement in zeolites: Structure, spectroscopy, and adsorption free energy of ethanol in H-ZSM-5. J. Phys. Chem. C 120 (13), 7172–7182. doi:10.1021/acs.jpcc.6b00923
Amsler, J., Plessow, P. N., Studt, F., and Bučko, T. (2021). Anharmonic correction to adsorption free energy from DFT-based MD using thermodynamic integration. J. Chem. Theory Comput. 17 (2), 1155–1169. doi:10.1021/acs.jctc.0c01022
Breck, D. W., and Breck, D. W. (1973). Zeolite molecular sieves: Structure, chemistry, and use. Hoboken, USA: Wiley.
Brogaard, R. Y., Henry, R., Schuurman, Y., Medford, A. J., Moses, P. G., Beato, P., et al. (2014). Methanol-to-hydrocarbons conversion: The alkene methylation pathway. J. Catal. 314, 159–169. doi:10.1016/j.jcat.2014.04.006
Brogaard, R. Y., Wang, C.-M., and Studt, F. (2014). Methanol–alkene reactions in zeotype acid catalysts: Insights from a descriptor-based approach and microkinetic modeling. ACS Catal. 4 (12), 4504–4509. doi:10.1021/cs5014267
Bearez, C. F. C., and Guisnet, M. (1983). Mechanism of butane tranformation on H mordenite I, kinetic study. React. Kinet. Catal. Lett. 22, 405–409. doi:10.1007/bf02066212
Dauenhauer, P. J., and Abdelrahman, O. A. (2018). A universal descriptor for the entropy of adsorbed molecules in confined spaces. ACS Cent. Sci. 4 (9), 1235–1243. doi:10.1021/acscentsci.8b00419
De Wispelaere, K., Plessow, P. N., and Studt, F. (2022). Toward computing accurate free energies in heterogeneous catalysis: A case study for adsorbed isobutene in H-ZSM-5. ACS Phys. Chem. Au 2 (5), 399–406. doi:10.1021/acsphyschemau.2c00020
Fecik, M., Plessow, P. N., and Studt, F. (2018). Simple scheme to predict transition-state energies of dehydration reactions in zeolites with relevance to biomass conversion. J. Phys. Chem. C 122, 23062–23067. doi:10.1021/acs.jpcc.8b07659
Goncalves, T. J., Plessow, P. N., and Studt, F. (2019). On the accuracy of density functional theory in zeolite catalysis. ChemCatChem 11 (17), 4368–4376. doi:10.1002/cctc.201900791
Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132 (15), 154104. doi:10.1063/1.3382344
He, M., Zhang, J., Liu, R., Sun, X.-L., Chen, B.-H., and Wang, Y.-G. (2017). Density functional theory studies on the skeletal isomerization of 1-butene catalyzed by HZSM-23 and HZSM-48 zeolites. RSC Adv. 7 (15), 9251–9257. doi:10.1039/c6ra26894c
Hjorth Larsen, A., Jorgen Mortensen, J., Blomqvist, J., Castelli, I. E., Christensen, R., Dulak, M., et al. (2017). The atomic simulation environment-a Python library for working with atoms. J. Phys. Condens. Matter 29 (27), 273002. doi:10.1088/1361-648x/aa680e
Houžvička, J., and Ponec, V. (1997). Skeletal isomerization of butene: On the role of the bimolecular mechanism. Ind. Eng. Chem. Res. 36 (5), 1424–1430. doi:10.1021/ie960588b
Isobutane market to reach USD (2021). Isobutane market to reach USD 34.00 billion by 2026, reports and data. Available at: https://www.globenewswire.com/news-release/2019/03/21/1758764/0/en/Isobutane-Market-To-Reach-USD-34%E2%80%9300-Billion-By-2026-Reports-And-Data.html.
Janda, A., Vlaisavljevich, B., Lin, L.-C., Smit, B., and Bell, A. T. (2016). Effects of zeolite structural confinement on adsorption thermodynamics and reaction kinetics for monomolecular cracking and dehydrogenation of n-butane. J. Am. Chem. Soc. 138 (14), 4739–4756. doi:10.1021/jacs.5b11355
Jørgensen, M., and Grönbeck, H. (2017). Adsorbate entropies with complete potential energy sampling in microkinetic modeling. J. Phys. Chem. C 121 (13), 7199–7207. doi:10.1021/acs.jpcc.6b11487
Kangas, M., Kumar, N., Harlin, E., Salmi, T., and Murzin, D. Y. (2008). Skeletal isomerization of butene in fixed beds. 1. Experimental investigation and Structure−Performance effects. Ind. Eng. Chem. Res. 47 (15), 5402–5412. doi:10.1021/ie800061q
Kresse, G., and Furthmüller, J. (1996), Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6 (1), 15–50. doi:10.1016/0927-0256(96)00008-0
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab-initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169
Kresse, G., and Hafner, J. (1993). Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47 (1), 558–561. doi:10.1103/physrevb.47.558
Kresse, G., and Hafner, J. (1994). Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 49 (20), 14251–14269. doi:10.1103/physrevb.49.14251
Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758
Kundu, A., Piccini, G., Sillar, K., and Sauer, J. (2016). Ab initio prediction of adsorption isotherms for small molecules in metal-organic frameworks. J. Am. Chem. Soc. 138 (42), 14047–14056. doi:10.1021/jacs.6b08646
Li, H., Paolucci, C., and Schneider, W. F. (2018). Zeolite adsorption free energies from ab initio potentials of mean force. J. Chem. Theory Comput. 14 (2), 929–938. doi:10.1021/acs.jctc.7b00716
Luzgin, M. V., Stepanov, A. G., Arzumanov, S. S., Rogov, V. A., Parmon, V. N., Wang, W., et al. (2005). Mechanism studies of the conversion of 13C-labeled n-butane on zeolite H-ZSM-5 by using 13C magic angle spinning NMR spectroscopy and GC-MS analysis. Chemistry 12 (2), 457–465. doi:10.1002/chem.200500382
Ono, Y. (2003). A survey of the mechanism in catalytic isomerization of alkanes. Catal. Today 81, 3–16. doi:10.1016/s0920-5861(03)00097-x
Perdew, J. P., Ruzsinszky, A., Csonka, G. b. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100 (13), 136406. doi:10.1103/physrevlett.100.136406
Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized gradient approximation made simple. Phys. Rev. Lett. 78, 1396–1396. doi:10.1103/physrevlett.78.1396
Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2009). Erratum: Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 102 (3), 039902. doi:10.1103/physrevlett.102.039902
Piccini, G., Alessio, M., and Sauer, J. (2018). Ab initio study of methanol and ethanol adsorption on Brønsted sites in zeolite H-MFI. Phys. Chem. Chem. Phys. 20 (30), 19964–19970. doi:10.1039/c8cp03632b
Plessow, P. N. (2018). Efficient transition state optimization of periodic structures through automated relaxed potential energy surface scans. J. Chem. Theory Comput. 14 (2), 981–990. doi:10.1021/acs.jctc.7b01070
Plessow, P. N., and Studt, F. (2020). Correction: Olefin methylation and cracking reactions in H-SSZ-13 investigated with ab initio and DFT calculations. Catal. Sci. Technol. 10 (19), 6738–6739. doi:10.1039/d0cy90088e
Plessow, P. N., and Studt, F. (2018). Olefin methylation and cracking reactions in H-SSZ-13 investigated with ab initio and DFT calculations. Catal. Sci. Technol. 8 (17), 4420–4429. doi:10.1039/c8cy01194j
Plessow, P. N., and Studt, F. (2017). Unraveling the mechanism of the initiation reaction of the methanol to olefins process using ab initio and DFT calculations. ACS Catal. 7 (11), 7987–7994. doi:10.1021/acscatal.7b03114
Potter, M. E., Le Brocq, J. J. M., Oakley, A. E., McShane, E. B., Vandegehuchte, B. D., and Raja, R. (2020). Butane isomerization as a diagnostic tool in the rational design of solid acid catalysts. Catalysts 10 (9), 1099. doi:10.3390/catal10091099
Asuquo, R. A., and Lercher, J. A. (1995). n-Butane isomerization over acidic mordenite. J. Catal. 155, 376–382. doi:10.1006/jcat.1995.1219
Rey, J., Bignaud, C., Raybaud, P., Bucko, T., and Chizallet, C. (2020). Dynamic features of transition states for beta-scission reactions of alkenes over acid zeolites revealed by AIMD simulations. Angew. Chem. Int. Ed. Engl. 59 (43), 19100–19104. doi:10.1002/ange.202006065
Rey, J., Gomez, A., Raybaud, P., Chizallet, C., and Bucko, T. (2019). On the origin of the difference between type A and type B skeletal isomerization of alkenes catalyzed by zeolites: The crucial input of ab initio molecular dynamics. J. Catal. 373, 361–373. doi:10.1016/j.jcat.2019.04.014
Rey, J., Raybaud, P., Chizallet, C., and Bučko, T. (2019). Competition of secondary versus tertiary carbenium routes for the type B isomerization of alkenes over acid zeolites quantified by ab initio molecular dynamics simulations. ACS Catal. 9 (11), 9813–9828. doi:10.1021/acscatal.9b02856
Sprowl, L. H., Campbell, C. T., and Árnadóttir, L. (2016). Hindered translator and hindered rotor models for adsorbates: Partition functions and entropies. J. Phys. Chem. C 120 (18), 9719–9731. doi:10.1021/acs.jpcc.5b11616
Studt, F. (2021). Grand challenges in computational catalysis. Front. Catal. 1. doi:10.3389/fctls.2021.658965
Tuma, C., and Sauer, J. (2005). Protonated isobutene in zeolites: tert-butyl cation or alkoxide?. Angew. Chem. Int. Ed. Engl. 44 (30), 4769–4771. doi:10.1002/anie.200501002
Von Arnim, M., and Ahlrichs, R. (1998). Performance of parallel TURBOMOLE for density functional calculations. J. Comput. Chem. 19 (15), 1746–1757. doi:10.1002/(sici)1096-987x(19981130)19:15<1746:aid-jcc7>3.0.co;2-n
Wang, P., Zhang, W., Zhang, Q., Xu, Z., Yang, C., and Li, C. (2018). Comparative study of n-butane isomerization over SO42−/Al2O3-ZrO2 and HZSM-5 zeolites at low reaction temperatures. Appl. Catal. A 550, 98–104. doi:10.1016/j.apcata.2017.11.006
Wei, J., Zheng, M., Chen, D., Wei, C., Bai, Y., Zhao, L., et al. (2022). Insights into the reaction of 1-butene catalytic cracking in HZSM-5 from first-principles: Reaction mechanism and microkinetics research. Ind. Eng. Chem. Res. 61 (16), 5429–5441. doi:10.1021/acs.iecr.2c00045
Weigend, F., and Ahlrichs, R. (2005). Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 7 (18), 3297–3305. doi:10.1039/b508541a
Weigend, F., Furche, F., and Ahlrichs, R. (2003). Gaussian basis sets of quadruple zeta valence quality for atoms H-Kr. J. Chem. Phys. 119 (24), 12753–12762. doi:10.1063/1.1627293
Wulfers, M. J., and Jentoft, F. C. (2015). Mechanism of n-butane skeletal isomerization on H-mordenite and Pt/H-mordenite. J. Catal. 330, 507–519. doi:10.1016/j.jcat.2014.12.035
Zhao, Y., and Truhlar, D. G. (2008). The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 120 (1-3), 215–241. doi:10.1007/s00214-007-0310-x
Keywords: zeolites, isomerization, chabazite, H-SSZ-13, DFT, ab initio, hydrocarbons
Citation: Spiske L, Plessow PN, Kazmierczak K, Vandegehuchte BD and Studt F (2023) Theoretical investigation of catalytic n-butane isomerization over H-SSZ-13. Front. Catal. 3:1213803. doi: 10.3389/fctls.2023.1213803
Received: 28 April 2023; Accepted: 26 May 2023;
Published: 05 July 2023.
Edited by:
Tibor Szilvási, University of Alabama, United StatesReviewed by:
Florian Goeltl, University of Arizona, United StatesBenjamin W. J. Chen, Technology and Research (A∗STAR), Singapore
Copyright © 2023 Spiske, Plessow, Kazmierczak, Vandegehuchte and Studt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Felix Studt, Felix.studt@kit.edu