Erratum: Global versus local Lyapunov approach used in disturbance observer-based wind turbine control

An Erratum on
Global versus local Lyapunov approach used in disturbance observer-based wind turbine control

by Gauterin E, Pöschke F and Schulte H (2023). Front. Control. Eng. 3:787530. doi: 10.3389/fcteg.2022.787530

Due to a production error, the equation in section 2.2.1 Global Controller was incorrect.

$\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{w}\mathrm{a}\mathrm{s}:X:=P^{-1}\left(\Rightarrow \stackrel{10}{=}X\right)$

$\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{s}:X:=P^{-1}\left(\Rightarrow \stackrel{Eq.10}{=}X\right)$

In section 3.2 Simulation Results: Disturbance Observer Variation, Resulting System Dynamics and Mechanical Loads, at the beginning of subsection Pole locations, Figure 5 instead of Figure 4 was incorrectly referenced.

Due to a production error, the equations in section Discussion, subsection Pole Locations were incorrect.

$\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{w}\mathrm{e}\mathrm{r}\mathrm{e}{s}_{P,i}^{OL,3}\mathrm{a}\mathrm{n}\mathrm{d}{s}_{P,i}^{OL,1/2}$

$\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{a}\mathrm{r}\mathrm{e}{s}_{P,i}^{OL,1}\mathrm{a}\mathrm{n}\mathrm{d}{s}_{P,i}^{OL,2\vee 3}$

Due to a production error, the equation in section Error-feedback gains (page 16) was incorrect.

$\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{w}\mathrm{a}\mathrm{s}:\left.{\left|L_{\overline{i}\mathcal{B}}^{w,\overline{j}}\right|}_2\left(\forall w\in \left[B,D\right]\right)>{\left|L_{\overline{i}\mathcal{B}}^{w,\overline{j}}\right|}_2\left(\forall w\in \left[G,I\right]\right)\right)$

$\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{s}:{\parallel L_{\overline{i}\mathcal{B}}^{B,\overline{j}}\parallel }_2>{\parallel L_{\overline{i}\mathcal{B}}^{G,\overline{j}}\parallel }_2,{\parallel L_{\overline{i}\mathcal{B}}^{C,\overline{j}}\parallel }_2>{\parallel L_{\overline{i}\mathcal{B}}^{H,\overline{j}}\parallel }_2\mathrm{a}\mathrm{n}\mathrm{d}{\parallel L_{\overline{i}\mathcal{B}}^{D,\overline{j}}\parallel }_2>{\parallel L_{\overline{i}\mathcal{B}}^{I,\overline{j}}\parallel }_2$

Due a production error, the first paragraph in section Wind speed reconstruction and actuation signals was incorrect. You can find the correct paragraph below:

With the mitigated error-feedback gains $L_{i\mathcal{B}}^{w,j}$, the reconstructed states $\underset{\_}{\widehat{x}}$, especially the reconstructed wind speeds $\widehat{v}$, are mitigated, too (see Eq. 7¹¹): While the reconstructed wind speed ${\widehat{v}}^w\left(t_1\right)$ of a single and arbitrary time point t = t₁ decreases steadily for the wind speed observer design with a local Lyapunov approach (i.e., ${\widehat{v}}^F\left(t_1\right)\approx {\widehat{v}}^G\left(t_1\right)>{\widehat{v}}^H\left(t_1\right)>{\widehat{v}}^I\left(t_1\right)\left[>{\widehat{v}}^J\left(t_1\right)\right]$¹⁰, see left column in Figure 6), the reconstructed wind speed ${\widehat{v}}^w\left(t_1\right)$ for the wind speed observer design with a global Lyapunov approach decreases unsteadily (i.e., ${\widehat{v}}^A\left(t_1\right)>{\widehat{v}}^D\left(t_1\right)\left[>{\widehat{v}}^E\left(t_1\right)\right]>{\widehat{v}}^C\left(t_1\right)>{\widehat{v}}^B\left(t_1\right)$, corresponding to the unsteady decrease of the mean Euclidean norm of the wind error state gains ${‖L_{\overline{i}\mathcal{B}}^{w,\overline{\mathbf{3}}}‖}_2$ of the global wind speed observers (with (w [A, E], see Table 3; i.e., $‖L_{\overline{i}\mathcal{B}}^{A,\overline{3}}{\Vert }_2>‖L_{\overline{i}\mathcal{B}}^{D,\overline{3}}{\Vert }_2>‖L_{\overline{i}\mathcal{B}}^{C,\overline{3}}{\Vert }_2>‖L_{\overline{i}\mathcal{B}}^{B,\overline{3}}{\Vert }_2$)¹⁰

In the same section, footnotes 12 and 13 were assigned incorrectly, and these have been replaced with footnote 10 in the updated article.

¹⁰The global and local wind speed observers E and J are not taken into account, because of their (closed-loop) pole locations, which are moved beyond the open-loop pole locations, as explained before in the subsection Pole locations.

Footnote 12 was also incorrect, the correct version is:

¹²with two exceptions for the tower side-to-side-bending moments $S_{eq}^B\left(TwrBsMxt\right)<S_{eq}^J\left(TwrBsMxt\right)$ and $S_{eq}^C\left(TwrBsMxt\right)<S_{eq}^J\left(TwrBsMxt\right)$ (see Figure 8B and line 7 in Table A9 as well as line 7 in Table A10.

Due to a production error, section Load Mitigation, paragraph number 3, appears to be interrupted and broken into two parts. This has been corrected into one single paragraph.

In the Appendix, part of section Specification of the LMI constraints was not included in the article. The corrected entire section appears below:

To calculate the mean Euclidian norm ${\Vert L_{i\mathcal{B}}^{w,\overline{j}}\Vert }_2$ of the error-feedback gains $L_{i\mathcal{B}}^{w,j}$ [see (26)] and the average, mean Euclidian norm ${\Vert L_{\overline{i}\mathcal{B}}^{w,\overline{j}}\Vert }_2$ [see (27)] the worksheet Uebersicht_L_Matrizen_Pitchwinkel-YYYY_MM_DD.xlsx is used.

In the Appendix, the section Load Analysis was not included in the article. This has now been added to the article, you can find it below:

Load analysis

For the ultimate loads max^w and fatigue loads $S_{eq}^w$ resulting from five different wind speed observers (i.e., for the $w\in \left[A,,,E\right]$ $\text{global wind speed observers}$ and $w\in \left[A,,,E\right]$ $\text{local}\hspace{0.17em}\text{wind speed observers}$; see Figure 8), the steady increase or decrease of the loads is evaluated separately for each of the two observer approaches (see Table A9) and in comparison to each other (see Table A10).

Due to a production error, Tables A9 and A10 in the Appendix were not included in the article, and the layout of Tables A1–A8 in the Appendix was incorrect. The corrected Tables are listed below:

The font color has been corrected in the table captions and in the body of the text, throughout the article.

The publisher apologizes for this mistake. The original version of this article has been updated.

TABLE A1

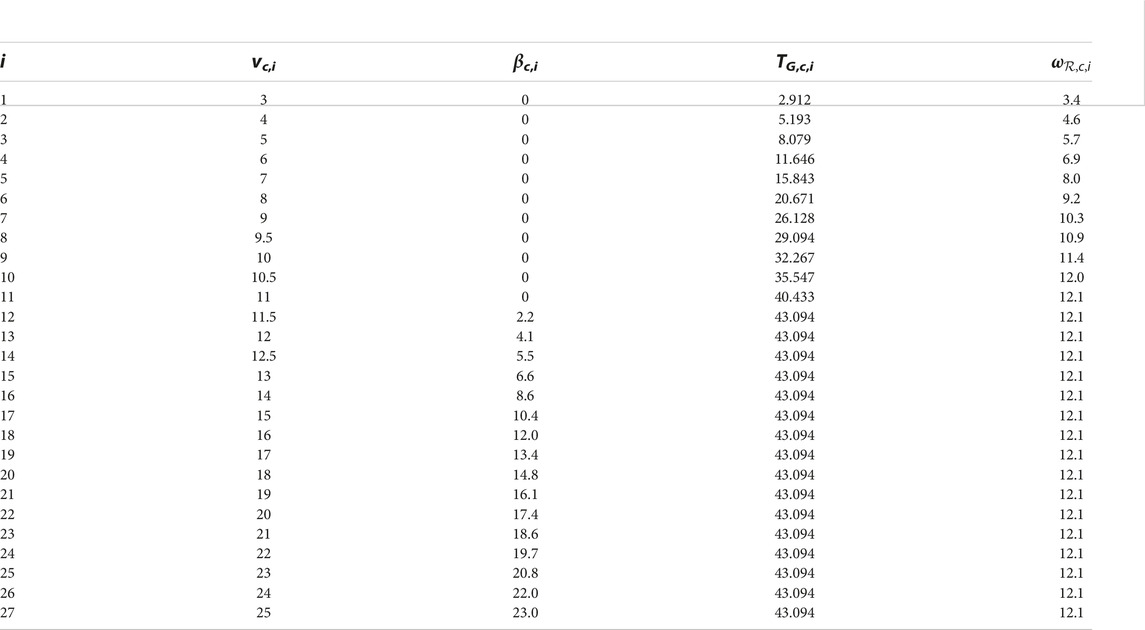
TABLE A1. States of the i steady state operations points OP_i of the NREL FAST 5MW reference wind turbine with the wind speed v_c,i, rotor rotational speed ${\omega }_{\mathcal{R},c,i}$, generator torque T_G,c,i and pitch angle β_c,i.

TABLE A2

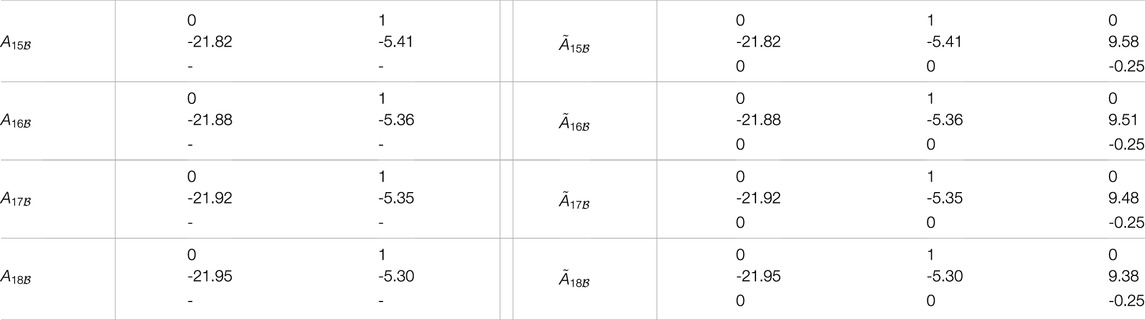
TABLE A2. State matrices $A_{i\mathcal{B}}$ and augmented state matrices ${\tilde{A}}_{i\mathcal{B}}$ of the $\mathcal{B}$lade model (for the submodels i ∈ [15,18]).

TABLE A3

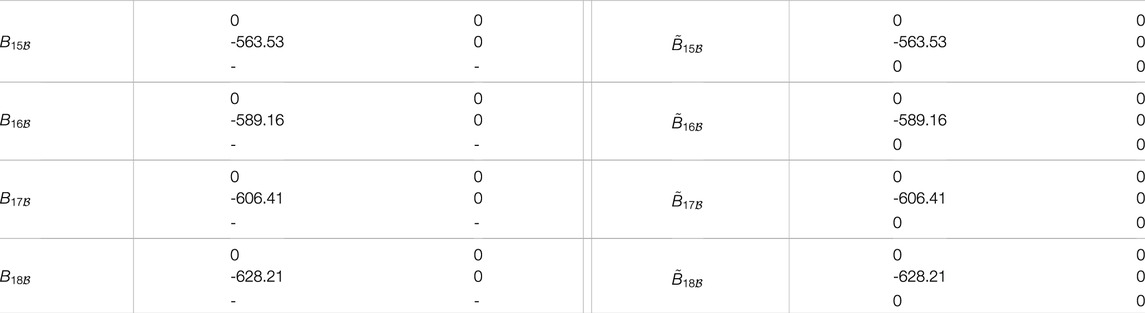
TABLE A3. Input matrices $B_{i\mathcal{B}}$ and augmented input matrices ${\tilde{B}}_{i\mathcal{B}}$ of the $\mathcal{B}$lade model (for the submodels i ∈ [15,18]).

TABLE A4

TABLE A4. Common output matrix $C_{\mathcal{B}}$ and augmented common output matrix ${\tilde{C}}_{\mathcal{B}}$ of the $\mathcal{B}$lade model (for all submodels).

TABLE A5

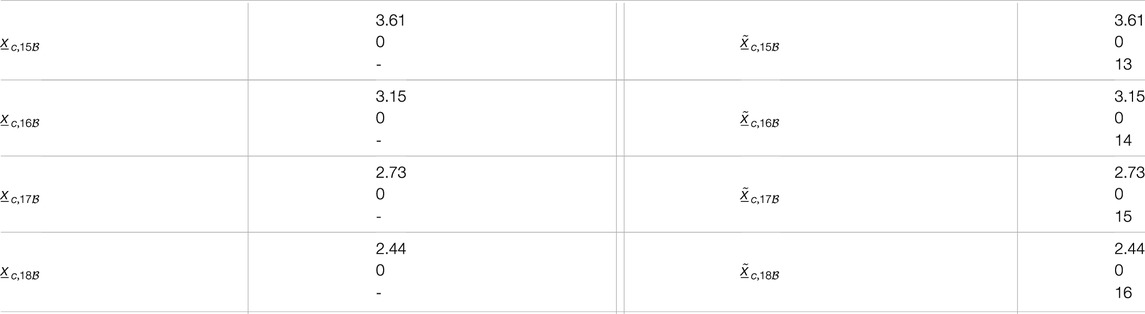
TABLE A5. Steady states ${\underline{x}}_{c,i\mathcal{B}}$ and augmented steady states ${\underline{\tilde{x}}}_{c,i\mathcal{B}}$ of the $\mathcal{B}$lade model (for the submodels i ∈ [15,18]).

TABLE A6

TABLE A6. Steady state pitch angle β_c,i and generator torque T_G,i (for the submodels i ∈ [15,18]).

TABLE A7

TABLE A7. State feedback matrices $K_{i\mathcal{R}}$ of the (rigid body) $\mathcal{R}$otion drive train model (for the submodels i ∈ [15,18]).

TABLE A8

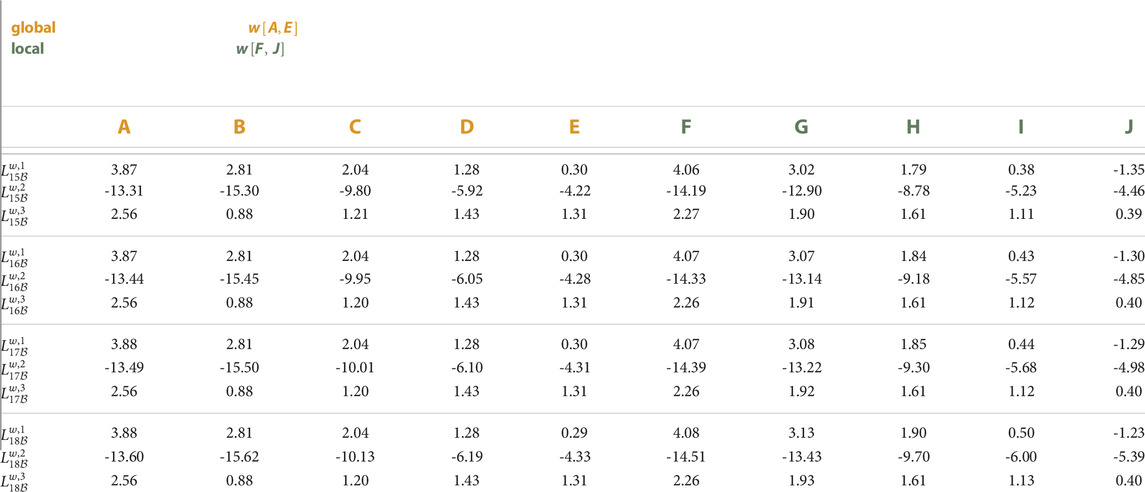
TABLE A8. Error state feedback gain matrices $L_{i\mathcal{B}}^{w,j}$ of the blade model based wind speed observers $\mathcal{B}$ for:- $\text{global}$ Lyapunov approach with $w\in \left[A,,,E\right]$- $\text{local}$ Lyapunov approach with $w\in \left[F,,,J\right]$- submodels i ∈ [15,18]- matrix elements j ∈ [1,3].

TABLE A9

TABLE A9. Analysis of the ultimate loads max^w and fatigue loads $S_{eq}^w$ resulting from five different wind speed observers regarding the steady increase or decrease of the loads (evaluated separately for each of the two Lyapunov approaches with $w\in \left[A,,,E\right]$ for the $\text{global wind speed observers}$ and with $w\in \left[F,,,J\right]$ for the $\text{local wind speed observers;}$ based on the loads depicted in Figure 8).

TABLE A10

TABLE A10. Analysis of the ultimate loads max^w and fatigue loads $S_{eq}^w$ resulting from five different wind speed observers regarding the steady increase or decrease of the loads (comparing both Lyapunov approaches with each other with $w\in \left[A,,,E\right]$ for the $\text{global wind speed observers}$ and with $w\in \left[F,,,J\right]$ for the $\text{local wind speed observers;}$ based on the loads depicted in Figure 8).