A process-model-free method for model predictive control via a reference model-based proportional-integral-derivative controller with application to a thermal power plant

1 Introduction

Model predictive control (MPC), originally known as model predictive heuristic control (MPHC), was first proposed by Richalet et al. (1976) and has been widely applied to industrial process control because of its ability to handle multivariable processes and constraints of inputs and states (Dughman and Rossiter, 2020). It is designed based on three elements: model prediction, receding horizon optimization and feedback control. Late last century, the embryonic forms of MPC appeared in industrial process control, including model algorithm control (MAC) (Richalet et al., 1978), dynamic matrix control (DMC) (Cutler and Ramaker, 1980), quadratic DMC (QDMC) (García and Morshedi, 1986), shell multivariable optimizing control (SMOC) (Marquis and Broustail, 1988), and so forth. However, these original MPCs has large amount of computation, which brings challenges to the industrial control systems. To reduce the computation of the predictive control, some advanced MPCs, such as generalized predictive control (GPC) (Clarke et al., 1987a, 1987b; Forouz et al., 2021), non-linear MPC (NMPC) (Ellis et al., 2014; Mazaeda et al., 2019) and economic MPC (EMPC) (Zhang Q. et al., 2018; Bürger et al., 2021), were developed to handle with the non-linearity in practical processes and obtain optimal performance in industrial process control. As is known to all, MPC can achieve satisfactory tracking performance because it utilizes the accurate process model to predict the future response of a plant (Qin and Badgwell, 2003), which means that its control performance is tied to the accuracy of the established process model (Ji et al., 2013).

It has been pointed out by the researcher from Cambridge University that it is rarely possible to find process models which are 100% accurate in large-scale industrial systems (Kähm, 2019). In terms of the modeling of the process, parameters within the model can be uncertain (Sirohi and Choi, 1996; Kalmuk et al., 2017) or the model might have wrong structure which is usually called model mismatch (Badwe et al., 2010). Uncertainty in the process model can have significant effects on the control performance of the MPC. The thermal power plant is one of the typical large-scale industrial systems (Wu et al., 2021). Processes of large-scale thermal power plants are difficult to model accurately (Sun and You, 2021), which limits the application of MPC to coal-fired units. Because of the continuously increasing power demand and penetration of renewable energy in the electricity market, the unit is usually under the deep peak-shaving operation, which means that its working condition is changing frequently in a wide range (Qu and Lyu, 2020). As a result, the mathematical descriptions of thermal processes are usually varying, which brings uncertainties to the control system. For example, superheated steam temperature (SST) (Shi et al., 2020), regarded as a vital parameter in the daily operation for a power plant, is difficult to model accurately for the reason that.

1. Its dynamic characteristics are significantly changing with the operating condition of the unit (Fan et al., 1997).

2. It is difficult to model mechanistically (Zhang et al., 2005).

3. Its accuracy of system identification is unable to be guaranteed (Wu et al., 2019).

To handle with the uncertainties of the process model of the thermal power plant, the robust MPC (Campo and Morari, 1987; Kothare et al., 1996) was proposed. However, its algorithm is complex which is difficult to implement on the distributed control system (DCS) widely used in thermal power plants. Therefore, the MPC is usually combined with the PI or PID controllers (Khan et al., 2017; Zhu et al., 2021; Zhang et al., 2022) to eliminate the dependency on the process model for possible application of MPC to the thermal power plant. The MPC-PID hierarchical control strategy were applied to several subsystems in the thermal power plant, such as the turbine-generator power system (Chen et al., 2020), the selective catalytic reduction system (Zhang K. et al., 2018), the distillation system (Zhu and Butoyi, 2002), and so forth. However, the closed-loop identification of the PID controller is time-consuming and costs large amount of computations (Somefun et al., 2021). Besides, processes in thermal power plants are affected by various disturbances so that the test data contain the information of the disturbance and measurement noise, which may deteriorate the accuracy of the identification (Wu et al., 2022a). As a result, an extended state observer (ESO)-based MPC strategy was proposed to avoid the closed-loop identification and handle with uncertain disturbances (Chen et al., 2016; Ren et al., 2021; Suhail et al., 2021). Nevertheless, when the coal-fired unit is running, it is impractical to test whether the plant has been modified as an integral process by the ESO (Sun et al., 2018).

A reference model (RM)-based PID controller—desired dynamic equational (DDE)-PID, proposed by authors previously (Shi et al., 2022a; Wang et al., 2008), can be considered as a viable alternative of traditional PID and ESO in the MPC-based hierarchical structure. Its core idea is that parameters of DDE-PID are evaluated based on the coefficients of the desired dynamic equation. If the DDE-PI or PID is tuned appropriately, the closed-loop output can accurately track the response of the typical first- or second-order system. Up to now, the advantages of DDE-PI or PID, such as fast and moderate reference tracking performance, strong disturbance rejection ability, and simple tuning procedure, have been validated by both simulations (Wang et al., 2009; Hu et al., 2010; Xue et al., 2010; Zhang et al., 2010; Makeximu et al., 2015; Wang et al., 2018) and field tests on the coal-fired power plant (Shi et al., 2022b; Shi et al., 2022c).

Aiming at aforementioned problems and keeping simplicity into account, this paper develops a hierarchical control strategy based on MPC and DDE-PID (abbreviated as MPC-DDE). DDE-PID provides its desired dynamic equation as a design model for the MPC without using accurate process-model and identification. The followings are the main contributions of this paper.

1. A hierarchical control strategy MPC-DDE is designed to implement the design of MPC without using the accurate process-model and identification.

2. Superiorities of the proposed MPC-DDE controller are verified by both simulation examples and the non-linear model of a fluidized-bed combustor (FBC) unit under variable working condition.

3. The proposed hierarchical control strategy is applied to the flow control of the secondary air in a 330 MW coal-fired power plant.

The rest of this article is organized as follows: Combined with the problem formulations in Section 2, the principles of MPC-DDE are detailed in Section 3. In Section 4, its practical tuning procedure is presented. Then, in Section 5, the control performance of MPC-DDE is demonstrated by several typical thermal process models and a non-linear FBC unit model. In Section 6, a field test on a coal-fired power plant is carried out to further demonstrate the superiorities of the proposed synthetic controller. Finally, concluding remarks are presented in the last section.

2 The current MPC-Based hierarchical control strategies

MPC has good control performance, especially in reference tracking, but it requires high accuracy of the established process model. If the process model and the established model are mismatched, the control quality of MPC will be sharply deteriorated (Zhu et al., 2021). However, thermal processes have strong non-linearities and various uncertain disturbances, which makes it difficult to model accurately. Moreover, basic controllers which are currently applied to the control system of the coal-fired power plant, such as PID and active disturbance rejection controller (ADRC) (Han, 2009; Wu et al., 2021), are unable to optimize the control signal according to the operating condition of the unit. As a result, their response speeds are limited.

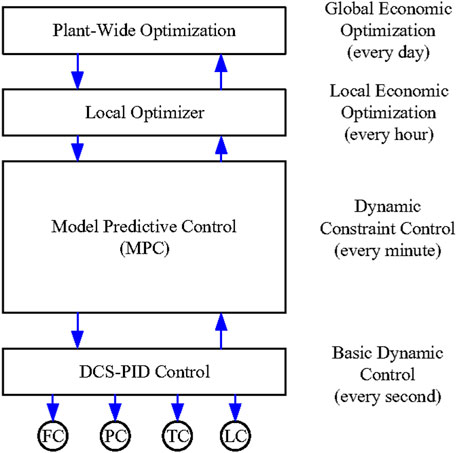
Thermal MPC control strategies are usually designed based on the hierarchical structure as shown in Figure 1 (Qin and Badgwell, 2003). Using this structure, MPC will be no longer designed based on the process model. Moreover, the basic controller will obtain the ability to optimize the control signal according to the working condition of the large-scale thermal equipment. In Figure 1, FC, PC, TC, and LC are denoted as the flow control, the pressure control, the temperature control and the level control, respectively.

FIGURE 1

FIGURE 1. MPC-based hierarchical control structure.

According to Reference (Qin and Badgwell, 2003), it can be learnt about this structure as follows. At the top of the structure, a plant-wide optimizer determines optimal steady-state settings for each unit in the plant, which may be sent to local optimizers at each unit. The local optimizers compute optimal economic steady states and pass them to the MPC for implementation. The MPC must move the plant from one constrained steady state to another while minimizing constraint violations along the way by using a PID controller.

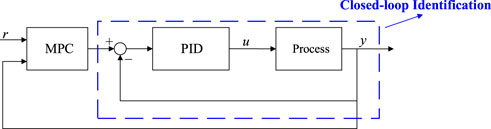
In the hierarchical structure illustrated in Figure 1, MPC is designed based on the identified closed-loop model with the PID control. The MPC-PID hierarchical structure can be simplified as illustrated in Figure 2. If the PID controller is well-tuned, the identified model of the closed-loop PID-based system can be used as the design model of the MPC without using the process-model. Nevertheless, the closed-loop identification is not only complex but also time-consuming.

FIGURE 2

FIGURE 2. The structure of MPC-PID hierarchical control strategy.

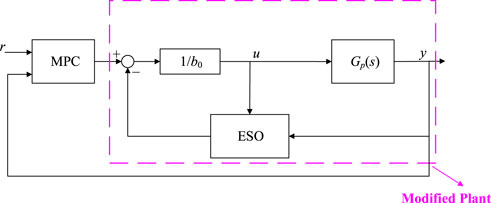
In Figure 2, r, u, and y are denoted as the set point, the control signal and the output respectively. To eliminate the dependency on the identification, an MPC-ESO hierarchical control strategy was proposed in Reference (Chen et al., 2016; Ren et al., 2021), which is shown as Figure 3.

FIGURE 3

FIGURE 3. The structure of MPC-ESO hierarchical control strategy.

The ESO can compensate the process as a modified plant whose transfer function model can be approximated as,

$G_{MP}\left(s\right)\approx \frac{1}{s^2}(1)$

where G_MP(s) refers to the transfer function model of the modified plant. As a result, the MPC-ESO can avoid the closed-loop identification. However, according to Eq. 1, the modified plant is an open-loop unstable system. When the thermal unit is running, it is difficult to test whether the plant has been full-compensated by ESO because the modified process model is an integral system which is open-loop unstable.

Therefore, this paper proposes the MPC-DDE control strategy in order to solve the aforementioned problems and implement the field application of MPC to the in-service thermal power plant.

3 MPC-DDE

3.1 The core idea of MPC-DDE

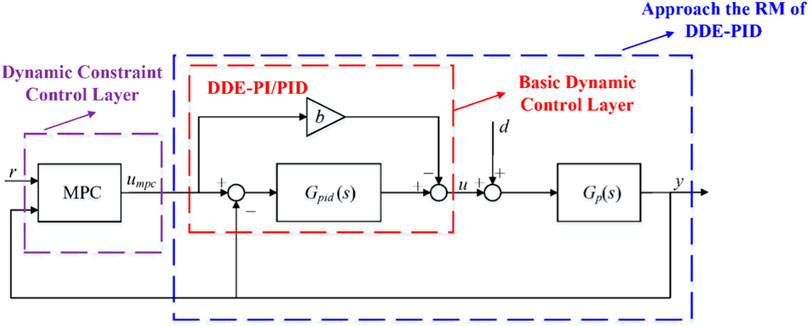
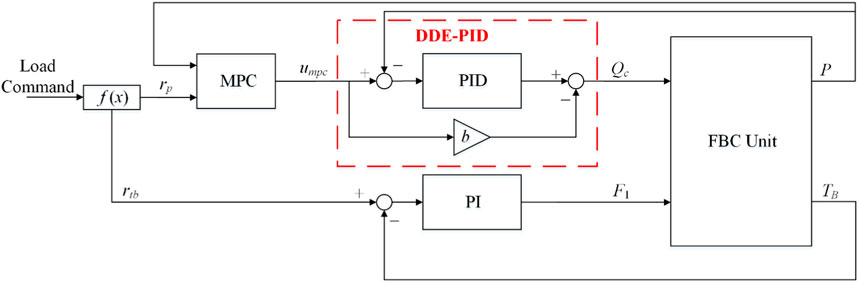
The structure of MPC-DDE is illustrated in Figure 4, where u_mpc, d and b are denoted as the output of MPC, the disturbances, and the feedforward coefficient of DDE-PID, respectively. Besides, G_pid(s) and G_p(s) are defined as the transfer functions of the PID controller and the process, respectively. Note that the output of the MPC, u_mpc, can be regarded as the set point of DDE-PID as well.

FIGURE 4

FIGURE 4. The structure of MPC-DDE.

From Figure 4, it is obvious that the proposed MPC-DDE has two layers: the dynamic constraint control layer (upper layer) and the basic dynamic control layer (lower layer). The former one contains MPC while the latter one contains DDE-PID.

First, we concern the function of DDE-PID in the hierarchical control structure. According to Reference (Shi et al., 2022c), if parameters of DDE-PID are tuned appropriately, the closed-loop output can accurately track the response of the RM which is depicted as,

$H_{RM}\left(s\right)=\frac{{{\omega }_d}^2}{{\left(s+{\omega }_d\right)}^2}(2)$

where ω_d represents the desired closed-loop bandwidth and H_RM(s) is denoted as the transfer function of the RM. If the process has the pure time delay, H_RM(s) should be chosen as Eq. 3 since the delay is unavoidable (Luo et al., 2015).

$H_{RM}\left(s\right)=\frac{{{\omega }_d}^2}{{\left(s+{\omega }_d\right)}^2}{e}^{-\tau s}(3)$

where τ is denoted as the delay time. When DDE-PID is well-tuned, it becomes

$\frac{Y\left(s\right)}{U_{MPC}\left(s\right)}\approx H_{RM}\left(s\right)(4)$

where Y(s) and U_MPC(s) are denoted as transfer functions of the closed-loop system output and u_mpc, respectively. From Eqs 2–4, it is easy to learn that the desired dynamic equation is a strong assumption. When the closed-loop system output of the DDE-PID tracks the response of Eq. 2 or Eq. 3, this assumption is reasonable. According to Reference (Shi et al., 2022c), if the following criteria are satisfied, the closed-loop output of the DDE-PID tracks the desired dynamic response accurately.

1) The error of the integral absolute error (IAE) between the closed-loop system output and the desired dynamic response is no larger than 10%;

2) The overshoot of the closed-loop output should be lower than 1%;

3) The closed-loop output has no obvious oscillation;

4) The actuator should be unsaturated.

Therefore, MPC can be designed based on the RM without using accurate process model or closed-loop identification. Besides, DDE-PID originates from a non-linear robust controller with a disturbance observer—Tornambè controller (TC) (Tornambè and Valigi, 1994). Thus, the DDE-PID can assist MPC to reject unmeasured external disturbances in thermal processes, and provide strong robustness.

Above all, the design intent of MPC-DDE is summarized as that the DDE-PID provides a design model for MPC when the accurate process model is unknown or difficult to obtain and enhances the ability of MPC to reject unmeasured disturbances in thermal processes.

3.2 The design principles of MPC-DDE

In this subsection, the design principles of MPC-DDE are presented. First, DDE-PID in the lower layer is designed. Consider a thermal process whose transfer function model is generally depicted as,

$G_p\left(s\right)=H\frac{a_0+a_{1}s+\cdots +a_{m-n-1}{s}^{m-n-1}+s^{m-n}}{b_0+b_{1}s+\cdots +b_{m-1}{s}^{m-1}+s^m}{e}^{-\tau s}(5)$

where m, n and H are respectively denoted as the order of the denominator, the relative degree and the unknown high-frequency gain. Moreover, a_i (i = 0, 1, ⋯, m—n–1) and b_j (j = 0, 1, ⋯, m − 1) are defined as coefficients of the numerator and the denominator, respectively, which are usually unknown. In terms of the general thermal processes, following assumptions are proposed.

1. Its relative degree n is known;

2. It is a minimum-phase process;

3. Its sign of the high-frequency gain H is known;

4. Its denominator and the numerator are relatively prime, and the uncontrollable and unobservable modes are asymptotically stable.

Then, the general thermal process can be written in normalized state-space form as,

$\left\{\begin{array}{l}{\dot{x}}_i=x_{i+1},\left(i=1,\cdots ,n-1\right)\\ {\dot{x}}_n=-{\sum }_{i=0}^{n-1}{\lambda }_i{x}_{i+1}-{\sum }_{i=0}^{m-n-1}{\zeta }_i{x}_{i+1}+Hu\\ {\dot{w}}_i=w_{i+1},\left(i=1,\cdots ,m-n-1\right)\\ y=x_1\end{array}\right.(6)$

where λ_i (i = 0, 1, ⋯, n − 1) and ζ_i (i = 0, 1, ⋯, m − n − 1) are unknwon parameters while x_i (i = 1, 2, ⋯, n − 1) and w_i (i = 1, 2, ⋯, m − n − 1) are state variables and uncertainties, respectively. Define an extended state f as,

$f\left(x,w,u\right)=-{\sum }_{i=0}^{n-1}{\lambda }_i{x}_{i+1}-{\sum }_{i=0}^{m-n-1}{\zeta }_i{x}_{i+1}+\left(H-l\right)u(7)$

where l is the estimated value of H. Then, in Eq. 6, ${\dot{x}}_n$ can be rewritten as,

${\dot{x}}_n=f+lu(8)$

If n = 2, which means that the process can be considered as a general second-order system, the state-space expression of the process is depicted as,

$\left\{\begin{array}{c}{\dot{x}}_1=x_2\\ {\dot{x}}_2=f+lu\\ y=x_1\end{array}\right.(9)$

Correspondingly, to approach the closed-loop desired dynamic equation depicted as,

$\ddot{y}+2{\omega }_d\dot{y}+{{\omega }_d}^{2}y={{\omega }_d}^2{u}_{mpc}(10)$

the control law should be designed. According to Eq. 9, $\ddot{y}=f+lu$, $\dot{y}={\dot{x}}_1=x_2$ and $y=x_1$, therefore the desired dynamic equation can be rewritten as,

$f+lu+2{\omega }_d{x}_2+{{\omega }_d}^2{x}_1={{\omega }_d}^2{u}_{mpc}(11)$

Therefore, the control law can be derived as,

$u=\frac{{{\omega }_d}^2\left(u_{mpc}-x_1\right)-2{\omega }_d{x}_2-f}{l}(12)$

However, f is usually uncertain in practical processes. As a result, the control law should be rewritten as,

$u=\frac{{{\omega }_d}^2\left(u_{mpc}-x_1\right)-2{\omega }_d{x}_2-\widehat{f}}{l}(13)$

where $\widehat{f}$ represents the estimation of f which can be estimated by following disturbance observer algorithm,

$\left\{\begin{array}{c}\dot{\xi }=-k\xi -k^2{x}_2-klu\\ \widehat{f}=\xi +k{x}_2\end{array}\right.(14)$

where k and ξ are defined as the gain and the intermediate variable of the disturbance observer, respectively. According to the disturbance observer algorithm, it is easy to derived that,

$\widehat{f}=\frac{k}{s+k}f(15)$

Therefore, when k → ∞, $\widehat{f}$ → f. In this case, the closed-loop desired dynamic equation is approached.

Combined with Eq. 13, the control law can be rewritten as,

$u=-\frac{\xi +k{x}_2}{l}-\frac{{{\omega }_d}^2\left(u_{mpc}-x_1\right)+2{\omega }_d{x}_2}{l}(16)$

Based on Eq. 14 and Eq. 16, the derivative of ξ can be derived as,

$\dot{\xi }=k\left[{{\omega }_d}^2\left(u_{mpc}-x_1\right)+2{\omega }_d{x}_2\right](17)$

By integrating both sides of Eq. 17, it is evident that,

$\xi =k\left[{{\omega }_d}^2\int \left(x_1-u_{mpc}\right)dt+2{\omega }_d{x}_1\right](18)$

Combined with Eq. 13, the control law is derived as,

$\begin{array}{c}u=\frac{{{\omega }_d}^2+2k{\omega }_d}{l}e+\frac{{{k\omega }_d}^2}{l}\int edt+\frac{k+2{\omega }_d}{l}\dot{e}-\frac{2k{\omega }_d}{l}\\ u_{mpc}=k_{p}e+k_i\int edt+k_d\dot{e}-b{u}_{mpc}\end{array}(19)$

where e = u_mpc—x₁ while k_p, k_i and k_d are denoted as the proportional, integral and derivative gains, respectively. From Eq. 19, it is easy to learn that DDE-PID is a type of two-degree-of-freedom (TDOF) PID controller.

Second, MPC in the upper layer is designed. The simplest MPC controller—linear MPC is designed since only simple controllers can be implemented on the current DCS of the coal-fired power plant in China. This brings the limitation that the MPC of the proposed MPC-DDE can only be the simplest one for the possible application of the proposed hierarchical control strategy to the thermal power plant. The design model of the MPC is known as the RM of DDE-PID which can be described in the following state-space form,

$\left\{\begin{array}{c}\dot{\mathbf{x}}={\mathbf{A}}_{\mathbf{s}}\mathbf{x}+{\mathbf{B}}_{\mathbf{s}}{u}_{mpc}\\ y=\mathbf{C}\mathbf{x}\end{array}\right.(20)$

where,

${\mathbf{A}}_{\mathbf{s}}=\left[\begin{array}{cc}0& 1\\ -{{\omega }_d}^2& -2{\omega }_d\end{array}\right](21)$

${\mathbf{B}}_{\mathbf{s}}={\left[\begin{array}{cc}0& {{\omega }_d}^2\end{array}\right]}^{\mathrm{T}}(22)$

$\mathbf{C}=\left[\begin{array}{cc}1& 0\end{array}\right](23)$

Discretize Eq. 20, we have,

$\left\{\begin{array}{c}\mathbf{x}\left(\kappa +1\right)=\mathbf{A}\mathbf{x}\left(\kappa \right)+\mathbf{B}{u}_{mpc}\left(\kappa \right)\\ y\left(\kappa \right)=\mathbf{C}\mathbf{x}\left(\kappa \right)\end{array}\right.(24)$

where κ represents the current moment. Moreover, A = I + A_sΔT and B = B_sΔT where ΔT refers to the sample time of the industrial control platform. Define p and m_p as the prediction horizon and the control horizon of the MPC, respectively. Then, the MPC is designed to optimize the following quadratic problem depicted as,

$\begin{array}{c}J\left(\kappa \right)={\displaystyle \sum _{i=1}^p}{‖y\left(\kappa +i|\kappa \right)-r\left(\kappa +1\right)‖}_{{\mathbf{Q}}_{\mathbf{0}}}^2+{\displaystyle \sum _{i=1}^m}{‖\Delta u_{mpc}\left(\kappa +i-1\right)‖}_{{\mathbf{R}}_{\mathbf{0}}}^2\\ \mathrm{s}.\mathrm{t}.\mathbf{x}\left(\kappa +1\right)=\mathbf{A}\mathbf{x}\left(\kappa \right)+\mathbf{B}{u}_{mpc}\left(\kappa \right)\\ \begin{array}{c}y\left(\kappa \right)=\mathbf{C}\mathbf{x}\left(\kappa \right)\\ r_{\mathit{min}}\le u_{mpc}\le r_{\mathit{max}}\\ \begin{array}{c}{\Delta r}_{\mathit{min}}\le \Delta u_{mpc}\le {\Delta r}_{\mathit{max}}\\ y_{\mathit{min}}\le y\le y_{\mathit{max}}\end{array}\end{array}\end{array}(25)$

Another aspect should be addressed that although DDE-PID is proposed in continuous time domain, its implementation on DCS is discretized. The sample time of the discrete DDE-PID is the same as that of the DCS. As a result, in this paper, the sample time of the MPC is set the same as that of the DCS in order to guarantee the simultaneous control actions of DDE-PID and MPC.

4 Tuning procedure

In this section, the tuning procedure of the proposed MPC-DDE is summarized. Since disturbances in thermal processes of the coal-fired power plant are usually unmeasured, MPC is unable to handle with them. As a result, DDE-PID determines the disturbance rejection performance while MPC determines the reference tracking performance.

First, the tuning procedure of DDE-PID has been previously proposed by Shi et al. (2022c), and its effectiveness has been validated by a field test on a high-pressure heater of a 600 MW thermal unit. Therefore, it will not be detailed in this paper. Moreover, it was suggested that k = 10ω_d to obtain better control performance and avoid the noise amplification (Dorf and Bishop, 2017; Shi et al., 2022c). Note that the tuning of DDE-PID in the proposed hierarchical control structure of MPC-DDE is based on the previously proposed method, and that the actuator constraint is considered when DDE-PID is being tuned (Shi et al., 2022c).

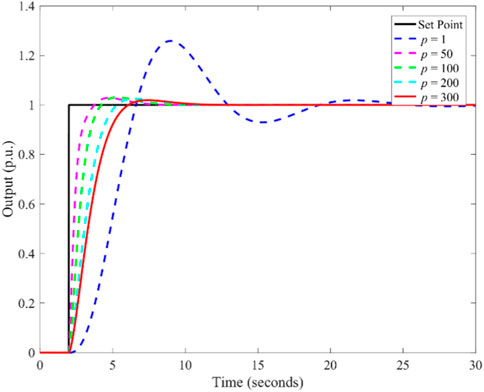
Second, the tuning of MPC is analyzed. In terms of the coal-fired unit, its safe and stable operation is cardinal. To avoid the non-convergence of the closed-loop system, let m_p = 1 in this paper (Maurath et al., 1988; Zhang and Qian, 2007), which can also simplify the tuning of MPC. Hence only the prediction horizon p is the tunable parameter of MPC. The simulation of a simple example is carried out to illustrate the influence of the prediction horizon on the control performance of MPC-DDE. Consider a simple plant whose transfer function model is depicted as,

$G_{p1}\left(s\right)=\frac{1}{\left(s+1\right)\left(0.2s+1\right)}(26)$

Parameters of DDE-PID are set as ω_d = 1, k = 10, and l = 1, and MPC is designed based on the RM of DDE-PID. Figure 5 shows the influence of p on the control performance of MPC-DDE.

FIGURE 5

FIGURE 5. The influence of the prediction horizon on the control performance of MPC-DDE.

From Figure 5, with the augment of p, tracking performance will be more moderate, the overshoot will be smaller and the response speed will be slower. This is because a larger prediction horizon means wider predictive range and higher computations. As a result, there should be a compromise between the response speed and the overshoot.

Above all, referring to (Shi et al., 2022c), the step-by-step tuning procedure of MPC-DDE is summarized as follows.

Step 1:. Select a small ω_d;

Step 2:. Let k = 10ω_d and l = l₀. Note that l₀ is denoted as the initial value of l whose evaluation has been mentioned in (Shi et al., 2022c);

Step 3:. Judge whether the closed-loop output of DDE-PID tracks the response of the RM accurately. If tracks, proceed to Step 4. If not, reduce l and continue the judgement;

Step 4:. Judge whether the requirements of disturbance rejection are satisfied. If satisfied, proceed to the next step. If not, augment ω_d and go back to Step 2;

Step 5:. Connect the DDE-PID with MPC and set the design model of MPC as the RM of DDE-PID.

Step 6:. Let p = m_p = 1;

Step 7:. Judge whether the requirements of tracking performance are satisfied. If satisfied, terminate the tuning procedure. If not, augment p and continue the judgement.Based on Steps 1–7, the tuning procedure of MPC-DDE can be intuitively summarized as a flow chart illustrated in Supplementary Image S1.

5 Numerical simulations

To validate its effectiveness, the proposed MPC-DDE is designed for six typical transfer function models and a classical non-linear model of the FBC unit in this section. In this paper, two widely-recognized PID applied in thermal process control, Skogestad internal model control (SIMC)-PID (Skogestad, 2003) and approximated maximum-sensitivity integral gain optimization (AMIGO)-PID (Åström and Hägglund, 2006), are selected as comparative controllers. Moreover, MPC-DDE has the same p and m_p as MPC on the one hand, and on the other hand it has the same k, l and ω_d as DDE-PID.

5.1 Application of MPC-DDE on linear transfer function models

In this subsection, six typical transfer functions which are depicted as Eqs. 26–31 are regarded as the controlled plants. These transfer function models can describe most types of thermal processes in coal-fired units. For example, the simple process (G_p1), the high-order process (G_p2, G_p3), the time-delay process (G_p4), and the integral process (G_p5) exist in the subsystems of the low-pressure heater, the SST, the high-pressure heater and the drum, respectively (Wu et al., 2021).

$G_{p2}\left(s\right)=\frac{2\left(15s+1\right)}{\left(20s+1\right)\left(s+1\right){\left(0.1s+1\right)}^2}(27)$

$G_{p3}\left(s\right)=\frac{1}{\left(s+1\right)\left(0.2s+1\right)\left(0.04s+1\right)\left(0.008s+1\right)}(28)$

$G_{p4}\left(s\right)=\frac{e^{-s}}{\left(20s+1\right)\left(2s+1\right)}(29)$

$G_{p5}\left(s\right)=\frac{{\left(0.17s+1\right)}^2}{s{\left(s+1\right)}^2\left(0.028s+1\right)}(30)$

$G_{p6}\left(s\right)=\frac{4}{\left(4s-1\right)\left(s+1\right)}(31)$

Based on Eqs. 26–31, Table 1 lists parameters of different controllers. In Table 1, T_i and T_d are denoted respectively as the integral time and the derivative time, which means that the PID controllers of SIMC-PID and AMIGO-PID have the form of,

$G_{pid}\left(s\right)=k_p\left(1+\frac{1}{T_{i}s}+T_{d}s\right)(32)$

TABLE 1

TABLE 1. Parameters of different controllers.

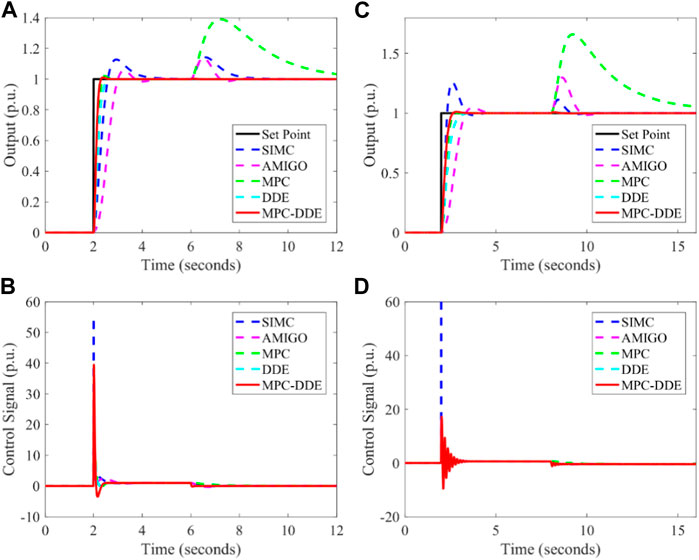
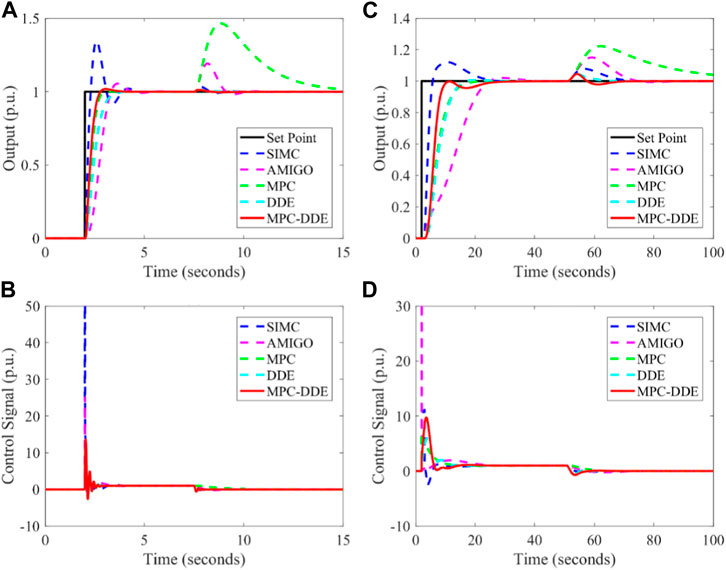
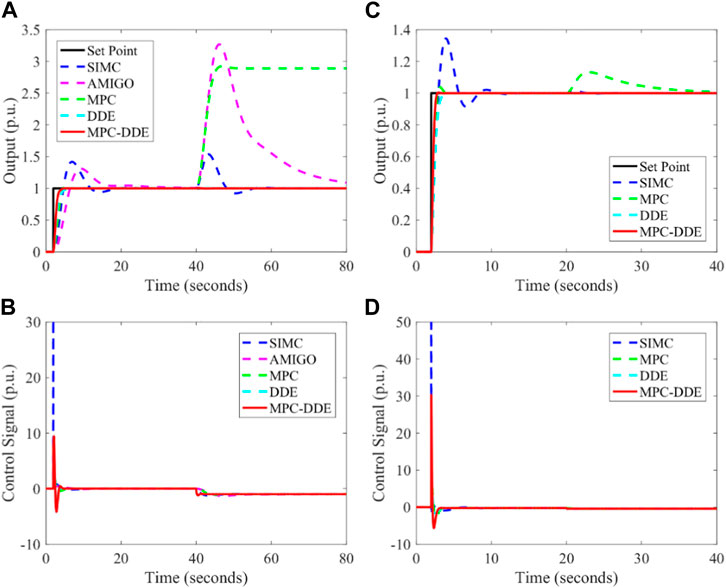
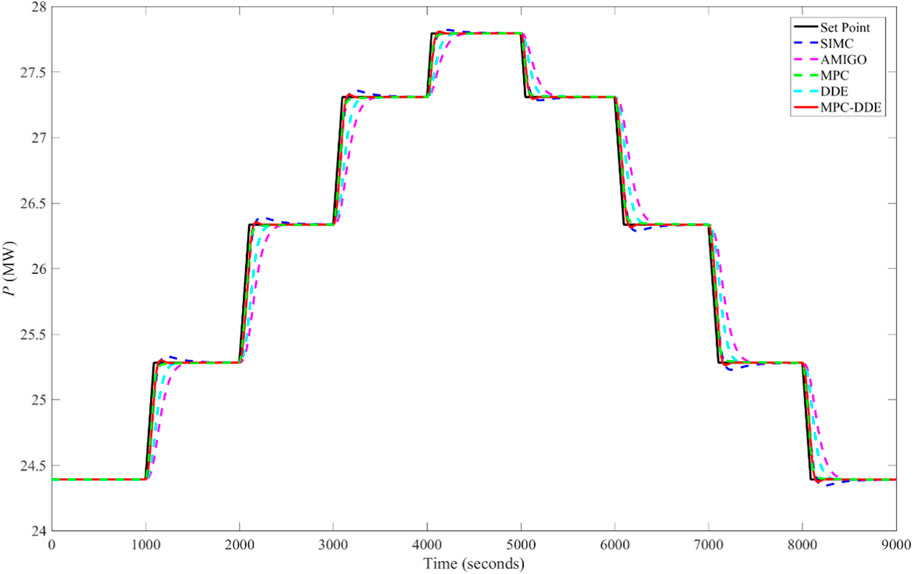
Based on Table 1 and Figures 6–8 illustrate the control performance of different controllers. Note that the set point has a unit change at 2s and a step disturbance is added when the output is stable.

FIGURE 6

FIGURE 6. Control performance of different controllers: (A,B) G_p1; (C,D) G_p2.

FIGURE 7

FIGURE 7. Control performance of different controllers: (A,B) G_p3; (C,D) G_p4.

FIGURE 8

FIGURE 8. Control performance of different controllers: (A,B) G_p5; (C,D) G_p6.

From Figures 6–8, it is clear that.

1. Compared with SIMC-PID and AMIGO-PID, the proposed hierarchical controller has more moderate reference tracking performance and better disturbance rejection performance. This is because the MPC can provide an optimal set-point for DDE-PID at every moment. Therefore, the DDE-PID in MPC-DDE can regulate the control signal actively.

2. In contrast to normal MPC, MPC-DDE has stronger ability of disturbance rejection. Particularly, MPC is unable to reject the disturbance for the process with an integrator. During the simulation, the step disturbance is considered as unmeasurable disturbance. MPC has no ability to reject the unmeasurable disturbances while DDE-PID can handle with these disturbances because it has the ability of the disturbance observer designed as Eq. 14.

3. The reference tracking performance of DDE-PID will be improved by adding an MPC because the MPC can update the set point of the DDE-PID according to the operating condition.

Another aspect should be addressed that the premise of the design of the proposed MPC-DDE is that the output of the DDE-PID can track the desired dynamic response accurately. However, the results in Figures 6–8 is unable to demonstrate that DDE-PID and MPC-DDE are suitable for all processes. According to Reference (Wang, 2010), if the process has large relative delay (the ratio between time delay and time constant), it is difficult to let the output of the DDE-PID track the desired dynamic response accurately. As a result, MPC-DDE is not suitable for the processes with large relative delay.

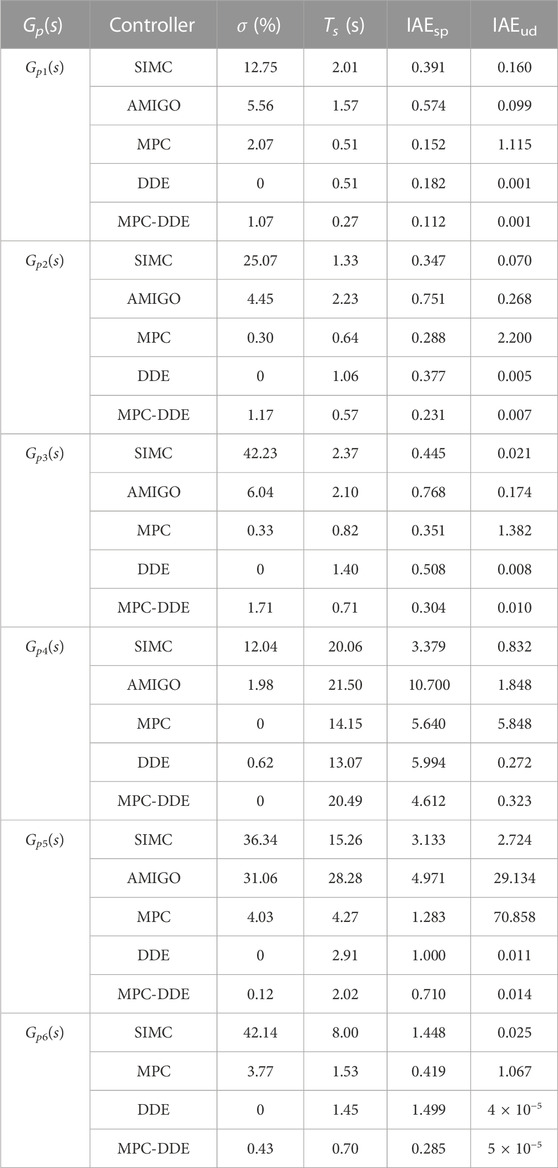
To evaluate the control performance of different controllers quantitatively, dynamic indices such as the overshoot σ, the settling time T_s and the integral absolute error (IAE) between the set point and output are calculated. Table 2 lists dynamic indices of different controllers for all processes. In this paper, IAE_sp represents IAE of reference tracking while IAE_ud represents that of disturbance rejection.

TABLE 2

TABLE 2. Dynamic indices of different controllers for all transfer function models.

From Table 2, in terms of most transfer function models, compared with SIMC-PID, AMIGO-PID, MPC, and DDE-PID, the proposed hierarchical control strategy has the shortest settling time, smallest IAE_sp and IAE_ud, which means that MPC-DDE has advantages in both reference tracking and disturbance rejection. Besides, the overshoot of MPC-DDE is acceptable although it is usually larger than that of DDE-PID.

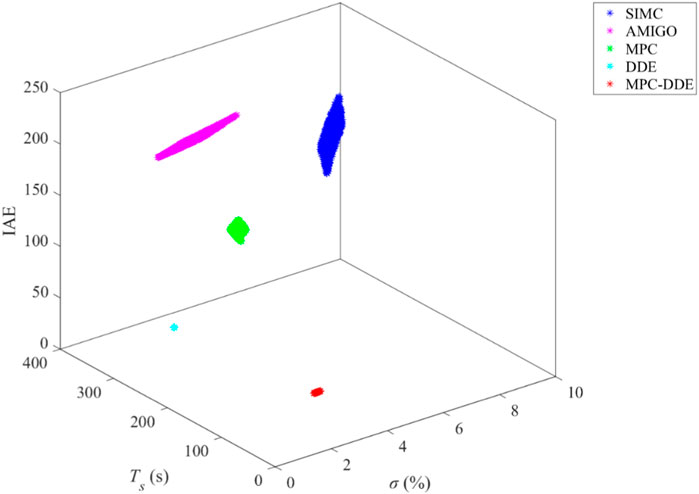
Robustness tests are important for validation of controllers. When the coal-fired unit is under variable working condition operation, the controllers must be robust enough to handle with uncertainties caused by the characteristics of the thermal processes. To test the robustness of a controller, Monte Carlo simulation is an effective method because it can intuitively indicate that the closed-loop system with which controller will obtain stronger robustness and better dynamic performance (Ray and Stengel, 1993). In this subsection, Monte Carlo trials are carried out 1000 times for each transfer function model to test the robustness of different controllers. Note that coefficients of Eqs. 26–31 are perturbed within a range of ±10%. Figure 9 shows results of Monte Carlo trials.

FIGURE 9

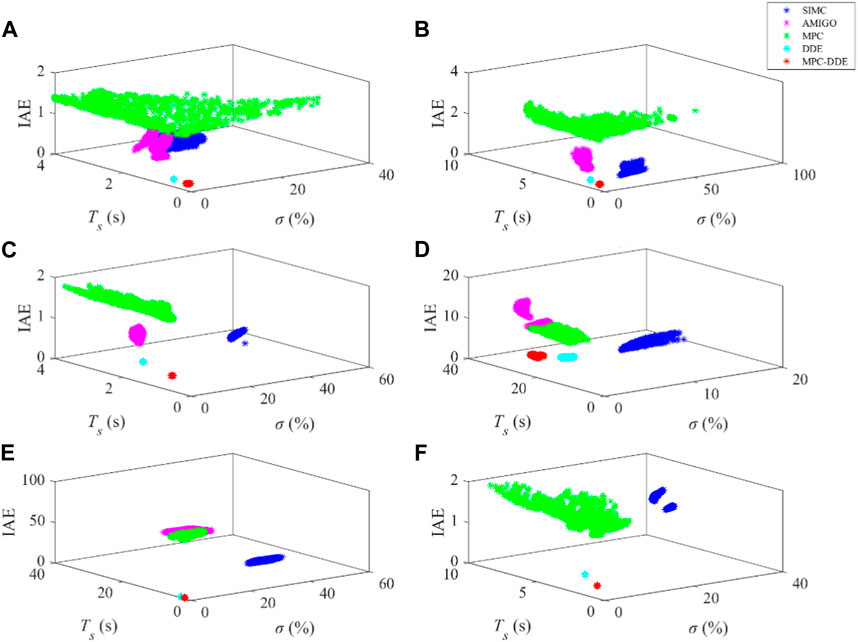
FIGURE 9. Results of Monte Carlo trials of all perturbed systems with different controllers: (A) G_p1; (B) G_p2; (C) G_p3; (D) G_p4; (E) G_p5; (F) G_p6.

Note that IAE refers to the sum of IAE_sp and IAE_ud. In terms of the results of Monte Carlo trails, if the scatters of the controller are more intensive, the controller has stronger ability to handle with the perturbation of the coefficients of the plant-model, which means that it has stronger robustness; if the scatters of the controller are closer to the origin, the controller has smaller overshoot, shorter settling time and smaller IAE, which means that it has better dynamic performance.

From Figure 9, it is easy to learn that.

1. Compared with those of MPC, SIMC-PID and AMIGO-PID, scatters of MPC-DDE are more intensive and nearer to the origin, which means that the proposed controller can achieve better control performance with stronger robustness.

2. For most processes, DDE-PID has stronger robustness than MPC-DDE. However, its dynamic performance is worse than that of the proposed synthesis controller.

According to aforementioned phenomena, following comments are summarized to explain them.

1. According to Eq. 13 and Eq. 14, the DDE-PID can be equivalent to the control structure with the state feedback and the disturbance observer. Therefore, it has stronger ability to handle with model uncertainties and stronger robustness than SIMC-PID and AMIGO-PID.

2. Since the DDE-PID has strong ability to handle with perturbations of plant-models, the design model of the MPC in MPC-DDE has little variations. As a result, the proposed MPC-DDE has stronger robustness than the traditional MPC.

Based on all these simulations, generally speaking, MPC-DDE can not only obtain satisfactory tracking and disturbance rejection performance but also has strong robustness.

5.2 Application of MPC-DDE on linear transfer function models

The FBC unit has been widely applied to modern coal-fired power plants because of its low pollutant emission, strong fuel adaptability, strong load regulation and high combustion efficiency. Nevertheless, requirements of economy and safety are usually strict when the large-scale unit is operating under variable working condition, which bring challenges to the controller design of the FBC unit. To enhance the performance of FBC unit under the deep peak-regulating operation, the proposed hierarchical controller is designed for the power loop of an FBC unit in this section.

As for the real FBC unit, it is a complex system which contains subsystems of primary air, secondary air, SST, etc. In this paper, the MPC-DDE is designed for the non-linear model of an FBC unit which was built based on several dynamic equations (Ikonen and Najim, 2001). This model has been widely recognized (Sun et al., 2015; Wu et al., 2020) and its expression is depicted as follows:

$\left\{\begin{array}{c}\frac{\mathrm{d}{W}_c\left(t\right)}{\mathrm{d}t}=\left(1-V\right)k_c{Q}_c\left(t\right)-Q_B\left(t\right)\\ \frac{\mathrm{d}{C}_B\left(t\right)}{\mathrm{d}t}=\frac{1}{V_B}\left[C_1{F}_1\left(t\right)-Q_B\left(t\right)X_C-C_B\left(t\right)F_1\left(t\right)\right]\\ \frac{\mathrm{d}{T}_B\left(t\right)}{\mathrm{d}t}=\frac{1}{c_I{W}_I}\left\{H_C{Q}_B\left(t\right)+c_1{F}_1\left(t\right)T_1-{\alpha }_{Bt}{A}_{Bt}\left[T_B\left(t\right)-T_{Bt}\right]-c_F{F}_1\left(t\right)T_B\left(t\right)\right\}\\ \frac{\mathrm{d}{C}_F\left(t\right)}{\mathrm{d}t}=\frac{1}{V_F}\left\{C_B\left(t\right)F_1\left(t\right)+C_2\left(t\right)F_2\left(t\right)T_1-V{Q}_c\left(t\right)X_V-C_F\left(t\right)\left[F_1\left(t\right)+F_2\left(t\right)\right]\right\}\\ \frac{\mathrm{d}{T}_F\left(t\right)}{\mathrm{d}t}=\frac{1}{c_F{W}_F}=\left\{\begin{array}{c}{H}_{V}V{Q}_c\left(t\right)+c_F{F}_1\left(t\right)T_B\left(t\right)+c_2{F}_2\left(t\right)T_2\left(t\right)-{\alpha }_{Ft}{A}_{Ft}\left[T_F\left(t\right)-T_{Ft}\right]\\ +c_1\left[F_1\left(t\right)+F_2\left(t\right)\right]T_F\left(t\right)\end{array}\right\}\\ \frac{\mathrm{d}P\left(t\right)}{\mathrm{d}t}=\frac{1}{{\tau }_{mix}}\left[P_c\left(t\right)-P\left(t\right)\right]\\ Q_B\left(t\right)=\frac{W_c\left(t\right)C_B\left(t\right)}{t_c{C}_1}\\ P_c\left(t\right)=H_c\left(t\right)Q_B\left(t\right)+H_{V}V{Q}_c\left(t\right)\end{array}\right.(33)$

Note that definitions and values of all parameters in (33) are presented in the appendix of (Ikonen and Najim, 2001). Supplementary Table S1 lists five different steady-state operating conditions of the FBC unit, which are denoted as Operating Condition A, B, C, D, and E.

In Supplementary Table S1, Q_c, F₁, P, and T_B are defined as the fuel feed, the primary air flow, the output power and the bed temperature, respectively.

5.2.1 Control Difficulties

Components of the FBC unit are connected by pipes, which would form strong non-linearities. As a result, the dynamic characteristics of FBC unit has significant change at different operating points. Supplementary Image S2 illustrates open-loop responses of the FBC unit under different steady-state working conditions.

From Supplementary Image S2, it is obvious that the open-loop response of the FBC unit varies significantly at different steady-state operating points. Therefore, its dynamic characteristic is changing when the FBC unit is operating under variable working condition.

Based on Supplementary Table S1 and Supplementary Image S2, the FBC unit can be simplified as a two-input-two-output (TITO) system which is depicted as,

$\left[\begin{array}{c}P\\ T_B\end{array}\right]=\left[\begin{array}{cc}{G}_{11}\left(s\right)& G_{12}\left(s\right)\\ G_{22}\left(s\right)& G_{22}\left(s\right)\end{array}\right]\left[\begin{array}{c}{Q}_c\\ F_1\end{array}\right](34)$

where G₁₁(s), G₁₂(s), G₂₁(s), and G₂₂(s) are denoted as transfer functions of the TITO system. Vinnicombe gap, defined as v_g, is usually calculated to evaluate the non-linearity of the FBC unit quantitatively (Tan et al., 2005). It is known as a measurement of the distance between two linear-time-invariant (LTI) systems (Yuan et al., 2019), which is defined as,

$v_g\left(G_1,G_2\right)=\max \left[{\overrightarrow{v}}_g\left(G_1,G_2\right),{\overrightarrow{v}}_g\left(G_2,G_1\right)\right](35)$

where G₁ and G₂ are denoted as transfer functions linearized around two different working conditions. Besides, ${\overrightarrow{v}}_g$ is defined as the direct gap which is depicted as,

${\overrightarrow{v}}_g\left(G_1,G_2\right)=\underset{\mathbf{\Lambda }\in {\mathrm{H}}_{\infty }}{\inf }‖\left[\begin{array}{c}{P}_1\\ Q_1\end{array}\right]-\left[\begin{array}{c}{P}_2\\ Q_2\end{array}\right]\mathbf{\Lambda }‖(36)$

where G₁ = Q₁P₁⁻¹ and G₂ = Q₂P₂⁻¹ and Λ is a matrix parameter which has H_∞ norm. Note that the direct gap is constrained in the range of (0, 1). In this section, G₁ is considered as the nominal transfer function matrix of the FBC unit which is linearized around the operating condition A. Note that all transfer function matrices are identified using the System Identification Toolbox of MATLAB. Supplementary Image S3 illustrates the gap measurement of different operating points.

Higher value of gap means stronger non-linearity and vice versa. From Supplementary Image S3, it is evident that the gap is large when the load is high. Therefore, we can learn that the dynamic characteristics of the FBC unit will change significantly when the load is regulated frequently in a large scale.

Since the FBC unit is a TITO system, couplings may exist between its control loops. The frequency-dependent relative gain array (RGA) is a tool to measure the coupling degree between different loops of the multiple-input-multiple-output (MIMO) system. Supplementary Image S4 shows the frequency-dependent RGA of the FBC unit under all operating conditions.

According to Supplementary Image S4, it is obvious that the FBC unit is diagonally dominant, which results in that decentralized controllers can be designed to control this TITO system.

5.2.2 MPC-DDE design for the power loop of the FBC unit

As mentioned in Section 5.2.1, since the coupling degree is weak between two loops of the FBC unit, decentralized controllers can be designed to control this TITO system. In this subsection, we only focus on the MPC-DDE design for the power loop of the FBC unit. In addition, the proportional-integral controller with fixed parameters (Wu et al., 2020) is designed for the bed temperature loop. Figure 10 shows the control structure of FBC unit with MPC-DDE.

FIGURE 10

FIGURE 10. Control structure of FBC unit with MPC-DDE.

In Figure 10, r_p and r_tb are denoted as set points of P and T_B. Moreover, f(x) refers to the functional relationship between r_p and r_tb. Note that the PI controller is designed as −0.01 (1 + 0.001/s) in (Wu et al., 2020).

In this paper, the operating condition A, whose steady-state power is 24.39 MW, is chosen as the nominal working condition. According to Reference (Wu et al., 2020), its G₁₁(s) is identified as,

$G_{11A}\left(s\right)=\frac{7.2725}{\left(393.9242s+1\right)\left(0.04837s+1\right)}{e}^{-20.5025s}(37)$

Based on Supplementary Image S2, we can learn that the identified transfer function depicted as Eq. 34 can be used for preliminary simulation. Similarly with Section 5.1, SIMC-PID, AMIGO-PID, MPC, and DDE-PID are selected as comparative controllers as well. Supplementary Table S2 lists parameters of different controllers for the power loop of the FBC unit.

Using parameters listed in Supplementary Table S2, Figure 11 illustrates the control performance of the power loop of the FBC unit with different controllers under the nominal operating condition. During the simulation, the set point has a unit change at 100s while a unit step disturbance is added at 1000s.

FIGURE 11

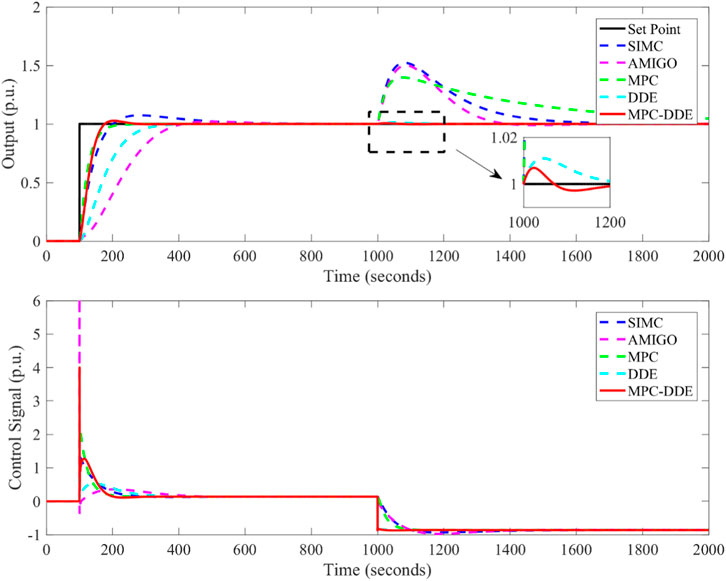
FIGURE 11. Control performance of the power loop of the FBC unit with different controllers under the operating condition A.

According to Figure 11, in terms of reference tracking, the proposed MPC-DDE is better than SIMC-PID, AMIGO-PID, and DDE-PID; as for disturbance rejection, the MPC-DDE has better control performance than other comparative controllers. Although MPC has more moderate tracking performance than DDE-PID, its dynamic deviation caused by the disturbance is larger.

To quantitatively evaluate the control performance of different controllers, dynamic indices are calculated in Supplementary Table S3.

Compared with SIMC-PID, AMIGO-PID and DDE-PID, the MPC-DDE has better tracking and disturbance rejection performance. Moreover, MPC shows its superiority in reference tracking, but its ability to reject disturbance is weak.

To test robustness of different controllers, Monte Carlo trails are carried out 1000 times and coefficients of Eq. 37 are perturbed within a range of ±10%. Figure 12 illustrates results of Monte Carlo trials.

FIGURE 12

FIGURE 12. Records of σ, T_s and IAE of different controllers for the perturbed power loop.

From Figure 12, evidently, scatter points of MPC-DDE are more intensive than those of SIMC-PID, AMIGO-PID and MPC, which means that the robustness of the proposed hierarchical control strategy is stronger than these controllers. Although DDE-PID has stronger robustness, its dynamic performance is worse than that of MPC-DDE. Based on results of Monte Carlo trials, it can be concluded that MPC-DDE may achieve better control performance than other comparative controllers when the FBC unit is under variable working condition operation.

5.2.3 Simulation results

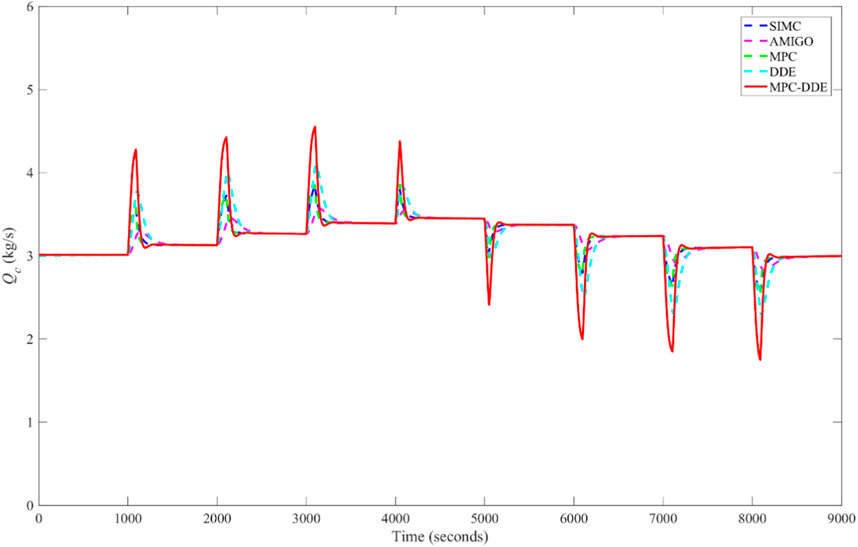
First, it is assumed that the working condition of the FBC unit is changing frequently between the operating condition A and the operating condition E. Therefore, the set point of power is varying with the load command as well. Figure 13 shows the variation of power when the FBC unit is operating under variable working condition. Note that the set point of power is changing with a rate limit of ±0.01 MW/s. Additionally, the variation of the fuel feed Q_c is illustrated in Figure 14.

FIGURE 13

FIGURE 13. Variations of the output power when the FBC unit is under variable working condition.

FIGURE 14

FIGURE 14. Variations of the fuel feed when the FBC unit is under variable working condition.

From Figure 13, it can be concluded that the reference tracking performance of MPC-DDE is better than that of SIMC-PID, AMIGO-PID and DDE-PID. Although MPC can track the set point with no overshoot, it needs longer time to track the set point than the proposed hierarchical controller.

To evaluate the tracking performance of different controllers under the variable working condition, IAE_sp is evaluated from 0s to 30000s for each controller in Table 3. According to Table 3, it is obvious that MPC-DDE has the second smallest IAE_sp, which shows its superiority in reference tracking when the FBC unit is under variable working condition operation.

TABLE 3

TABLE 3. IAE_sp of different controllers under variable working condition operation.

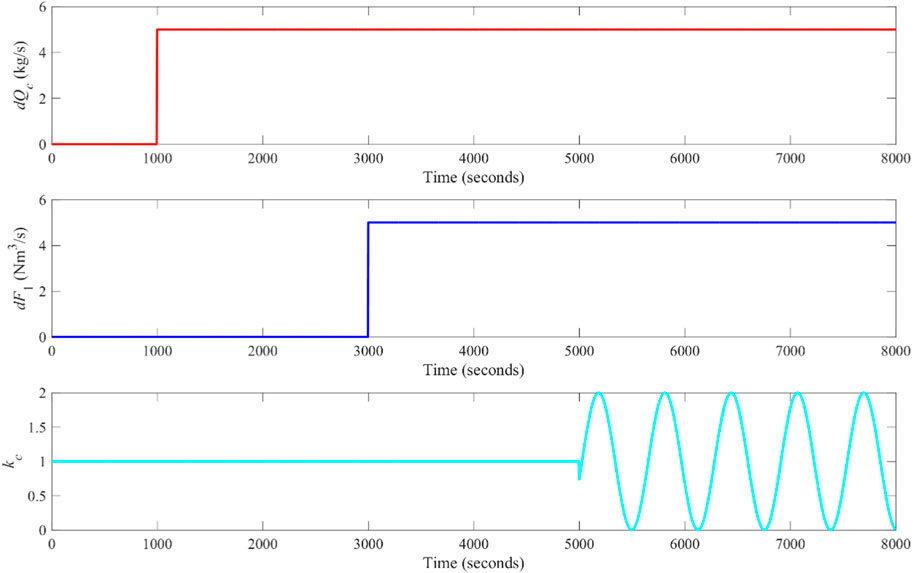
Second, to test the ability of different controllers to reject disturbances, three external disturbances are added when the FBC unit is working under the operating condition A. Figure 15 shows disturbances caused by the fuel feed, the primary air flow and the coal quality.

FIGURE 15

FIGURE 15. External disturbances in the FBC unit.

In Figure 15, dQ_c and dF₁ are denoted as disturbances caused by the fuel feed and the primary air. In addition, k_c refers to the coefficient of coal quality and its nominal value is 1. Figure 16 illustrates the disturbance rejection performance of different controllers when the FBC unit is operating under the nominal working condition.

FIGURE 16

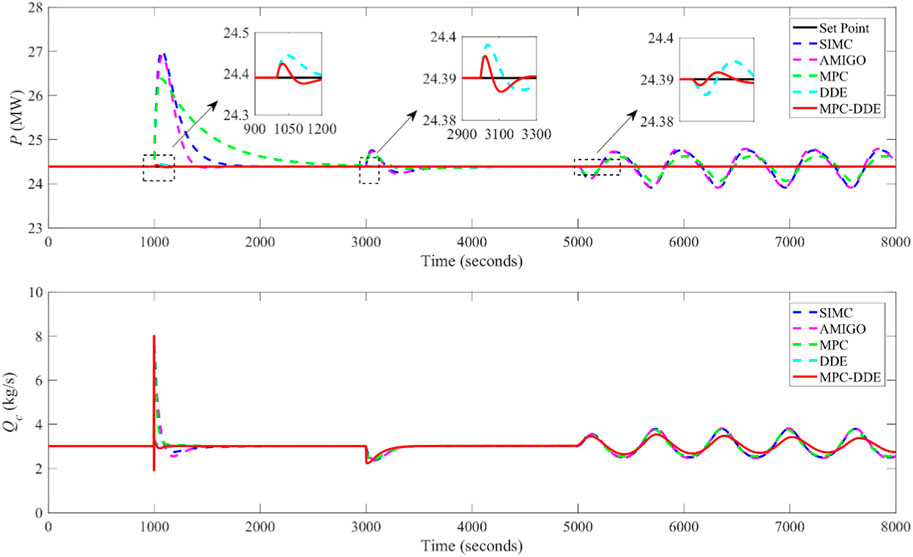
FIGURE 16. Disturbance rejection performance of different controllers when the FBC unit is operating under the nominal working condition.

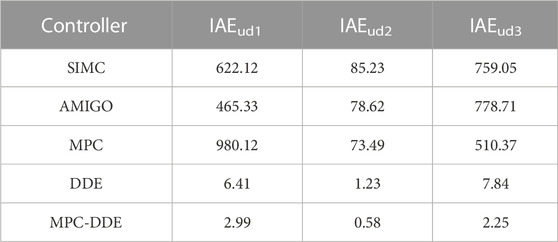
According to Figure 16, compared with other comparative controllers, the proposed MPC-DDE can reject external disturbances caused by Q_c, F₁ and k_c effectively, which shows its advantages in external disturbance rejection. Besides, the IAE_ud of different controllers is evaluated in Table 4. Particularly, IAE_ud1, IAE_ud2 and IAE_ud3 are recorded to evaluate dynamic deviations of different controllers caused by disturbances of Q_c, F₁ and k_c, respectively.

TABLE 4

TABLE 4. IAE_ud of different controllers.

Based on Table 4, we can learn that the proposed synthesis controller has smallest IAE_ud1, IAE_ud2, and IAE_ud3. Therefore, MPC-DDE has strong ability to reject external disturbances caused by the fuel feed, the primary air flow and the coal quality. Based on Table 4, it is easy to learn that the proposed control strategy has the smallest IAE_ud1, IAE_ud2, and IAE_ud3. Therefore, MPC-DDE has strong ability to reject external disturbances caused by the fuel feed, the primary air flow and the coal quality.

Based on Table 4, it is easy to learn that the proposed control strategy has the smallest IAE_ud1, IAE_ud2, and IAE_ud3. Therefore, MPC-DDE has strong ability to reject external disturbances caused by the fuel feed, the primary air flow and the coal quality.

Third, another aspect should be addressed is that the measurement noise usually exists in practical thermal systems, which may lead to the oscillation of control signal. Hence it is necessary to test whether control signals of controllers are sensitive to the measurement noise. Supplementary Image S5 and Supplementary Image S6 show the output power and control signals, respectively, of different controllers with the measurement noise.

From Supplementary Image S6, it is obvious that the control signal of MPC-DDE is less sensitive to the measurement noise than those of MPC, SIMC-PID, AMIGO-PID and DDE-PID. Besides, to further demonstrate the superiority of the proposed hierarchical controller when the measurement noise exists, root mean square (RMS) values of control signals of different controllers are calculated in Supplementary Table S4.

Supplementary Image S6 Variations of fuel feed of different controllers with the measurement noise.

According to Supplementary Table S4, the proposed MPC-DDE has the smallest RMS value. As a result, MPC-DDE can guarantee the safety and longevity of the actuator.

6 Field application on the secondary air system of a thermal power plant

Motivated by encouraging results of simulations, a field test is carried out based on the proposed MPC-DDE as described in this section. Note that the MPC-DDE is applied to the secondary air system in a 330 MW in-service unit of Shenxi Power Plant, which is located in Shenyang, Liaoning Province, China.

6.1 Process description

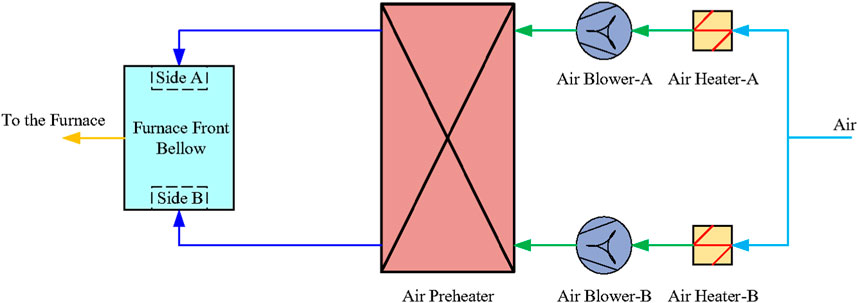
The secondary air system is one of the most important components of the coal-fired unit, which determines the combustion efficiency of the furnace and the pollutant of the NOx of the unit (Wu et al., 2018). In terms of a real unit, the secondary air is controlled by regulating the blade position of the blower, and it influences the oxygen for the combustion. The command of the secondary air is real-time computed by the load, the main steam pressure and the fuel feed of the unit in order to reach the highest combustion efficiency (Ding et al., 2016). As a result, the secondary air should track its command as accurate as possible.

The structure of the secondary air system is illustrated in Figure 17, which shows that the air flow is controlled by two blowers. For the design of the control system, only one controller is used to control the blowers of the both sides (Wu et al., 2022b). In this section, MPC-DDE is designed based on the aforementioned control strategy as well.

FIGURE 17

FIGURE 17. The structure of the secondary air system.

6.2 Results of the field tests

The field test was carried out on 11 August 2022. During the tests, the load of the unit was varying in the range from 140 to 175 MW. Note that the original controller is the PI controller, which is tuned by the experienced thermal engineers. It is denoted as PI_f in this section. Moreover, as for MPC-DDE, DDE-PI was designed. Considering the safe operation of the unit, the open-loop step tests are not allowed. Consequently, the MPC is unable to be designed based on the identified process model. Table 5 lists parameters of different controllers for the field tests.

TABLE 5

TABLE 5. Parameters of different controllers for the field tests.

Based on parameters listed in Table 5 and Figures 18–20 illustrate the field test result of different controllers. Note that the result of PI_f was obtained by searching the historical running data of the unit. Besides, the air blower-A and the air blower-B are denoted as “MV1” and “MV2”, respectively.

FIGURE 18

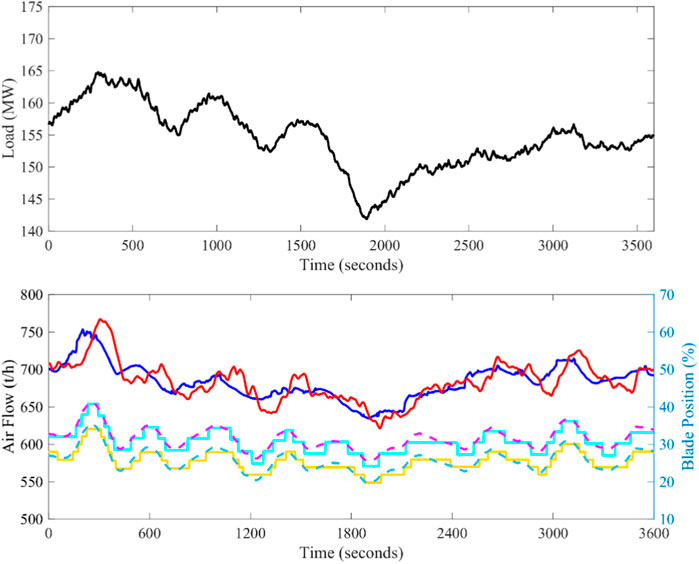
FIGURE 18. Field test results of PI_f (Date: July 10-11, 2022; Time span: 11:21:39 p.m. to 0:21:39 a.m.; Legend:

the command of the secondary air,

the feedback of the secondary air,

the feedback of MV1,

the command of MV1,

the feedback of MV2,

the command of MV2).

FIGURE 19

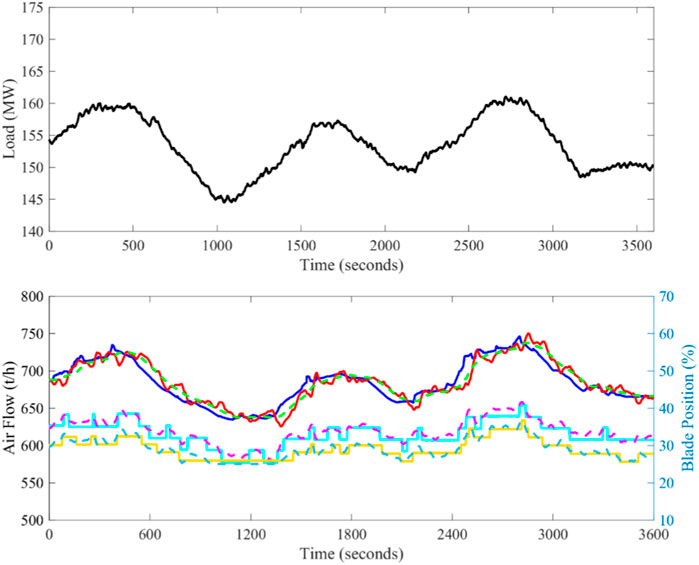
FIGURE 19. Field test results of DDE-PI (Date: August 11, 2022; Time span: 10:01:38 a.m. to 11:01:38 a.m.; Legend:

the command of the secondary air,

the feedback of the secondary air,

the feedback of MV1,

the command of MV1,

the feedback of MV2,

the command of MV2).

FIGURE 20

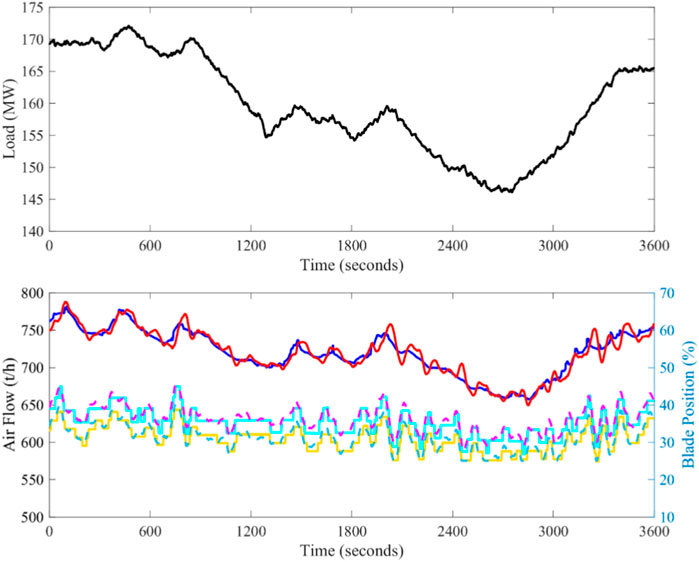
FIGURE 20. Field test results of MPC-DDE (Date: August 11, 2022; Time span: 2:23:45 p.m. to 3:23:45 p.m.; Legend:

the command of the secondary air,

the feedback of the secondary air,

the feedback of MV1,

the command of MV1,

the feedback of MV2,

the command of MV2).

From results of the field tests, it is obvious that the blade positions of the blowers have the significant dead zone with an amplitude of 3%. That is, because of the under-developed field measurement devices of the blade position, which is unavoidable. When the actions of the blade are frequent and large, the feedbacks of MV1 and MV2 are able to be approximately linearized. According to Figure 19, it is easy to learn the secondary air of DDE-PI can track its desired dynamic response. Therefore, MPC can be designed on the RM of DDE-PI. From Figures 18–20, it is evident that the reference tracking performance is large improved when MPC-DDE comes into service. However, control signals of MPC-DDE changes frequently.

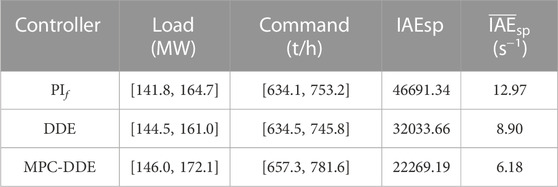
To evaluate the control performance of different controllers quantitatively, dynamic indices are calculated. Since the command of the secondary air is changing with the working condition, the overshoot and the settling time are inappropriate to evaluate the control performance. Based on the suggestion in (Wu et al., 2022b), IAE_sp and the average IAE_sp are calculated in Table 6.

TABLE 6

TABLE 6. Parameters of different controllers for the field tests.

Denote ${\overline{\mathrm{I}\mathrm{A}\mathrm{E}}}_{\mathrm{s}\mathrm{p}}$ as the average IAE_sp. From Table 6, it can be concluded that MPC-DDE experienced wider load range and command range than PI_f and DDE-PI. Moreover, dynamic indices of MPC-DDE are smaller than those of PI_f and DDE-PI, which shows its superiorities in reference tracking

7 Conclusion

This paper proposed a hierarchical controller—MPC-DDE to provide a process-model-free method for MPC to implement its application to the thermal power plant. According to the design, simulations and field tests, some concluding remarks about MPC-DDE are summarized as follows.

1. Based on the numerical simulation results, the proposed MPC-DDE has better disturbance rejection performance than the traditional MPC and faster reference tracking speed than the conventional DDE-PID.

2. If the DDE-PID is well-tuned, the MPC can be designed based on the RM of the DDE-PID without using the accurate process model and identifications; besides, DDE-PID can assist MPC to handle with unmeasured disturbances in thermal processes;

3. According to the field test results in Section 6.2, the average IAE_sp of the secondary air of the thermal power plant decreases from 12.97 to 6.18, which means that the deviation between the secondary air and its set point can be largely reduced by the proposed control strategy. This successful application of MPC-DDE to the secondary air system of a coal-fired unit indicates its promising prospect in the future thermal power industry with the increasing demand to integrate more renewables into the grid.

Our future work will focus on.

1. The development of an auto-tuning toolbox for MPC-DDE based on the proposed tuning procedure;

2. MPC-DDE design for multi-input-multi-output (MIMO) systems;

3. The hierarchical control design of DDE-PID combined with other model-based control strategies, such as H_∞ controller, linear quadratic regulator (LQR), and so forth because the DDE-PID provides its RM as their design model;

4. The hierarchical control design of MPC combined with other RM-based controllers, such as TC and linear ADRC (LADRC).

5. The practical implementation of the MPC with implicit solution on the DCS.

6. The relationship between the constraints of the MPC of the proposed MPC-DDE and the actuator constraints.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

GS, MM, DL, and KL contributed to conception and design of the study. GS carried out the simulations and field tests on the practical coal-fired power plant. GS wrote the first draft if the manuscript. GS, MM, DL, YD, and KL wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The second author would like to thank the financial support from National Nature Science Foundation of China No. 61873091.

Acknowledgments

Special thanks go to Shenxi Thermal Power Plant of CHN Energy Liaoning Power Co. Ltd. and Guoneng Zhishen Control Technology Co. Ltd. for the support of the field test. The first author, the corresponding author and the fourth author would like to thank the financial support provided by State Key Lab of Power Systems in the Department of Energy and Power Engineering at Tsinghua University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcteg.2023.1185502/full#supplementary-material

References

Åström, K. J., and Hägglund, T. (2006). Advanced PID control. Research Triangle Park, North Carolina: ISA-The Instrumentation, Systems, and Automation Society.

Google Scholar

Badwe, A. S., Patwardhan, R. S., Shah, S. L., Patwardhan, S. C., and Gudi, R. D. (2010). Quantifying the impact of model-plant mismatch on controller performance. J. Process Control 20 (4), 408–425. doi:10.1016/j.jprocont.2009.12.006

CrossRef Full Text | Google Scholar

Bürger, A., Bull, D., Sawant, P., Bohlayer, M., Klotz, A., Beschütz, D., et al. (2021). Experimental operation of a solar-driven climate system with thermal energy storages using mixed-integer nonlinear model predictive control. Optim. Control Appl. Meth. 42 (5), 1293–1319. doi:10.1002/oca.2728

CrossRef Full Text | Google Scholar

Campo, P. J., and Morari, M. (1987). “Robust model predictive control,” in Paper presented at the the 1987 American Control Conference, 1021–1026.

Google Scholar

Chen, Z., Li, Y., Sun, M., Zhang, Q., Sun, Q., and Xiang, Y. (2016). Retention and molecular evolution of lipoxygenase genes in modern rosid plants. J. Harbin Inst. Technol. 48 (9), 176–180. doi:10.3389/fgene.2016.00176

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, M., Zhao, J., Xu, Z., Liu, Y., Zhu, Y., and Shao, Z. (2020). Cooperative distributed model predictive control based on topological hierarchy decomposition. Control Eng. Pract. 103, 104578. doi:10.1016/j.conengprac.2020.104578

CrossRef Full Text | Google Scholar

Clarke, D. W., Mohatadi, C., and Tuffs, P. S. (1987a). Generalized predictive control—Part I: The basic algorithm. Automatica 23 (2), 137–148. doi:10.1016/0005-1098(87)90087-2

CrossRef Full Text | Google Scholar

Clarke, D. W., Mohatadi, C., and Tuffs, P. S. (1987b). Generalized predictive control—Part II: Extensions and interpretations. Automatica 23 (2), 149–160. doi:10.1016/0005-1098(87)90088-4

CrossRef Full Text | Google Scholar

Cutler, C. R., and Ramaker, B. L. (1980). “Dynamic matrix control—a computer control algorithm,” in Paper presented at the the Joint Automatic Control Conference.

Google Scholar

Ding, C., Guo, S., Shi, W., and Wang, J. (2016). The optimizing control of the secondary air control system of power plant. Electr. Autom. 38 (4), 106–109. doi:10.3969/j.issn.1000-3886.2016.04.033

CrossRef Full Text | Google Scholar

Dorf, R. C., and Bishop, R. H. (2017). Modern control systems. 13th ed. New York: Pearson Education, Inc.

Google Scholar

Dughman, S. S., and Rossiter, J. A. (2020). Systematic and effective embedding of feedforward of target information into MPC. Int. J. Control 93 (1), 98–112. doi:10.1080/00207179.2017.1281439

CrossRef Full Text | Google Scholar

Ellis, M., H, H. D., and Christofides, P. D. (2014). A tutorial review of economic model predictive control methods. J. Process Control 24 (8), 1156–1178. doi:10.1016/j.jprocont.2014.03.010

CrossRef Full Text | Google Scholar

Fan, Y., Xu, Z., and Chen, L. (1997). Study of adaptive fuzzy control of boiler superheated steam temperature based on dynamic mechanism analysis. Proc. CSEE 17 (1), 23–28.

Google Scholar

Forouz, B. S., Manzar, M. N., and Khaki-Sedigh, A. (2021). Multiple model unfalsified adaptive generalized predictive control based on the quadratic inverse optimal control concept. Optim. Control Appl. Meth. 42 (3), 769–785. doi:10.1002/oca.2700

CrossRef Full Text | Google Scholar

García, C. E., and Morshedi, A. M. (1986). Quadratic programming solution of dynamic matrix control (QDMC). Chem. Eng. Commun. 46, 73–87. doi:10.1080/00986448608911397

CrossRef Full Text | Google Scholar

Han, J. (2009). From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 56 (3), 900–906. doi:10.1109/tie.2008.2011621

CrossRef Full Text | Google Scholar

Hu, Z., Li, D., Jiang, X., and Wang, J. (2010). “Desired-dynamics-based design of control strategy for multivariable system with time delays,” in 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), 191–196.

Google Scholar

Ikonen, E., and Najim, K. (2001). Advanced process identification and control. Florida: CRC Press.

Google Scholar

Ji, G., Huang, J., Zhang, K., Zhu, Y., Lin, W., Ji, T., et al. (2013). Identification and predictive control for a circulation fluidized bed boiler. Knowledge-Based Syst. 45, 62–75. doi:10.1016/j.knosys.2013.02.006

CrossRef Full Text | Google Scholar

Kähm, W. (2019). Thermal stability criteria embedded in advanced control systems for batch process intensification. Ph. D. Cambridge: Cambridge Univeristy.

Google Scholar

Kalmuk, A., Tyushev, K., Granichin, O., and Yuchi, M. (2017). “Online parameter estimation for MPC model uncertainties based on LSCR approach,” in Paper presented at the 1st Annual IEEE Conference on Control Technology and Applications, 1256–1261.

CrossRef Full Text | Google Scholar

Khan, M., Tahiyat, M., Imtiaz, S., Choudhury, M. A. A. S., and Khan, F. (2017). Experimental evaluation of control performance of MPC as a regulatory controller. ISA Trans. 70, 512–520. doi:10.1016/j.isatra.2017.04.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Kothare, M. V., Balakrishnan, V., and Morari, M. (1996). Robust constrained model predictive control using linear matrix inequalities. Automatica 32 (10), 1361–1379. doi:10.1016/0005-1098(96)00063-5

CrossRef Full Text | Google Scholar

Luo, J., Zhang, X., Li, D., and Hu, Y. (2015). Tuning of PID controller for unstable plant systems. J. Xi’an Univ. Technol. 31, 475–481.

Google Scholar

Makeximu, , Li, D., Zhu, M., and Sun, L. (2015). Desired dynamic equation based PID control for combustion vibration. J. Low. Freq. Noise Vib. Act. Control 34 (2), 107–117. doi:10.1260/0263-0923.34.2.107

CrossRef Full Text | Google Scholar

Marquis, P., and Broustail, J. P. (1988). “SMOC, a bridge between state space and model predictive controllers: Application to the automation of a hydrotreating unit,” in Paper presented at the the 1988 IFAC Workshop on Model based Process Control, 37–43.

CrossRef Full Text | Google Scholar

Maurath, P. R., Mellichamp, D. A., and Seborg, D. E. (1988). Predictive controller design for single-input/single-output (SISO) systems. Ind. Eng. Chem. Res. 27 (6), 956–963. doi:10.1021/ie00078a011

CrossRef Full Text | Google Scholar

Mazaeda, R., Cristea, S. P., and Prada, C. d. (2019). Hierarchically coordinated economic MPC plantwide control of mixed continuous-batch units in process industries with application to a beet sugar plant. Optim. Control Appl. Meth. 41 (1), 190–214. doi:10.1002/oca.2535

CrossRef Full Text | Google Scholar

Qin, S. J., and Badgwell, T. A. (2003). A survey of industrial model predictive control technology. Control Eng. Pract. 11, 733–764. doi:10.1016/s0967-0661(02)00186-7

CrossRef Full Text | Google Scholar

Qu, X., and Lyu, J. (2020). Reheat steam temperature prediction and control based on iterative learning algorithm for ultra-supercritical units under deep peak shaving. J. Chin. Soc. Power Eng. 40 (8), 614–620.

Google Scholar

Ray, L. R., and Stengel, R. F. (1993). A Monte Carlo approach to the analysis of control system robustness. Automatica 29 (1), 229–236. doi:10.1016/0005-1098(93)90187-x

CrossRef Full Text | Google Scholar

Ren, J., Chen, Z., Sun, M., and Sun, Q. (2021). Frequency performance analysis of proportional integral-type active disturbance rejection generalized predictive control for time delay systems. Optim. Control Appl. Meth. 10, 1–14. doi:10.1080/21642583.2021.2020182

CrossRef Full Text | Google Scholar

Richalet, J., Rault, A., Testud, J., and Papon, J. (1976). “Algorithmic control of industrial processes,” in Paper presented at the the 4th IFAC Symposium on Identification and System Parameter Estimation, 1119–1167.

Google Scholar

Richalet, J., Rault, A., Testud, J., and Papon, J. (1978). Model predictive heuristic control: Applications to industrial processes. Automatica 14, 413–428. doi:10.1016/0005-1098(78)90001-8

CrossRef Full Text | Google Scholar

Shi, G., Wu, Z., Guo, J., Li, D., and Ding, Y. (2020). Superheated steam temperature control based on a hybrid active disturbance rejection control. Energies 13 (7), 1757. doi:10.3390/en13071757

CrossRef Full Text | Google Scholar

Shi, G., Li, D., Ding, Y., and Chen, Y. (2022a). Desired dynamic equational proportional-integral-derivative controller design based on probabilistic robustness. Int. J. Robust Nonlinear Control 32 (18), 9556–9592. doi:10.1002/rnc.5667

CrossRef Full Text | Google Scholar

Shi, G., Liu, S., Li, D., Ding, Y., and Chen, Y. (2022b). A controller synthesis method to achieve independent reference tracking performance and disturbance rejection performance. ACS Omega 7 (18), 16164–16186. doi:10.1021/acsomega.2c01524

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, G., Wu, Z., Liu, S., Li, D., Ding, Y., and Liu, S. M. (2022c). Research on the desired dynamic selection of a reference model-based PID controller: A case study on a high-pressure heater in a 600 MW power plant. Processes 10, 1059. doi:10.3390/pr10061059

CrossRef Full Text | Google Scholar

Sirohi, A., and Choi, K. Y. (1996). On-line parameter estimation in a continuous polymerization process. Ind. Eng. Chem. Res. 35, 1332–1343. doi:10.1021/ie950487y

CrossRef Full Text | Google Scholar

Skogestad, S. (2003). Simple analytic rules for model reduction and PID controller tuning. J. Process Control 13 (4), 291–309. doi:10.1016/s0959-1524(02)00062-8

CrossRef Full Text | Google Scholar

Somefun, O. A., Akingbade, K., and Dahunsi, F. (2021). The dilemma of PID tuning. Annu. Rev. Control 52, 65–74. doi:10.1016/j.arcontrol.2021.05.002

CrossRef Full Text | Google Scholar

Suhail, S. A., Bazaz, M. A., and Hussain, S. (2021). MPC based active disturbance rejection control for automated steering control. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 235 (12), 3199–3206. doi:10.1177/09544070211004506

CrossRef Full Text | Google Scholar

Sun, L., and You, F. (2021). Machine learning and data-driven techniques for the control of smart power generation systems: An uncertainty handling perspective. Engineering 7 (9), 1239–1247. doi:10.1016/j.eng.2021.04.020

CrossRef Full Text | Google Scholar

Sun, L., Li, D., and Lee, K. Y. (2015). Enhanced decentralized PI control for fluidized bed combustor via advanced disturbance observer. Control Eng. Pract. 42, 128–139. doi:10.1016/j.conengprac.2015.05.014

CrossRef Full Text | Google Scholar

Sun, L., Shen, J., Hua, Q., and Lee, K. Y. (2018). Data-driven oxygen excess ratio control for proton exchange membrane fuel cell. Appl. Energy 231, 866–875. doi:10.1016/j.apenergy.2018.09.036

CrossRef Full Text | Google Scholar

Tan, W., Marquez, H. J., Chen, T., and Liu, J. Z. (2005). Analysis and control of a nonlinear boiler-turbine unit. J. Process Control 15 (8), 883–891. doi:10.1016/j.jprocont.2005.03.007

CrossRef Full Text | Google Scholar

Tornambè, A., and Valigi, P. (1994). A decentralized controller for the robust stabilization of a class of MIMO dynamical systems. J. Dyn. Syst. Meas. Control 116, 293–304. doi:10.1115/1.2899223

CrossRef Full Text | Google Scholar

Wang, W., Li, D., Gao, Q., and Wang, C. (2008). A two-degree-of-freedom PID controller tuning method. J. Tsinghua Univ. 48 (11), 1962–1966.

Google Scholar

Wang, W., Li, D., and Xue, Y. (2009). “Decentralized two degree of freedom PID tuning method for MIMO processes,” in Paper presented at the the IEEE International Symposium on Industrial Electronics, 143–148.

Google Scholar

Wang, X., Yan, X., Li, D., and Sun, L. (2018). An approach for setting parameters for two-degree-of-freedom PID controllers. Algorithm 11, 48. doi:10.3390/a11040048

CrossRef Full Text | Google Scholar

Wang, W. (2010). Research on PID tuning rule and its applications in control of thermal plant. Master. Beijing: Tsinghua University.

Google Scholar

Wu, Z., He, T., Sun, L., Li, D., and Xue, Y. (2018). The facilitation of a sustainable power system: A practice from data-driven enhanced boiler control. Sustainability 10 (4), 1112. doi:10.3390/su10041112

CrossRef Full Text | Google Scholar

Wu, Z., He, T., Li, D., Xue, Y., Sun, L., and Sun, L. M. (2019). Superheated steam temperature control based on modified active disturbance rejection control. Control Eng. Pract. 83, 83–97. doi:10.1016/j.conengprac.2018.09.027

CrossRef Full Text | Google Scholar

Wu, Z., Li, D., Xue, Y., Sun, L. M., He, T., and Zheng, S. (2020). Modified active disturbance rejection control for fluidized bed combustor. ISA Trans. 102, 135–153. doi:10.1016/j.isatra.2020.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Z., Gao, Z., Li, D., Chen, Y., and Liu, Y. (2021). On transitioning from PID to ADRC in thermal power plants. Control Theory Technol. 19, 3–18. doi:10.1007/s11768-021-00032-4

CrossRef Full Text | Google Scholar

Wu, Z., Liu, Y., Sun, L., Pan, F., Yuan, J., Li, D., et al. (2022a). Control optimization via a practical closed-loop identification method for a low-pressure heater in power plant. IFAC-PapersOnLine 55 (9), 519–524. doi:10.1016/j.ifacol.2022.07.090

CrossRef Full Text | Google Scholar

Wu, Z., Makeximu, , Yuan, J., Liu, Y., Li, D., and Chen, Y. (2022b). A synthesis method for first-order active disturbance rejection controllers: Procedures and field tests. Control Eng. Pract. 127, 105286. doi:10.1016/j.conengprac.2022.105286

CrossRef Full Text | Google Scholar

Xue, Y., Li, D., and Liu, J. (2010). “DDE-based PI controller and its application to gasifier temperature control,” in Paper presented at the the International Conference on Control, Automation and Systems, 2194–2197.

CrossRef Full Text | Google Scholar

Yuan, J., Wu, Z., S, S. F., and Chen, Y. (2019). Hybrid model-based feedforward and fractional-order feedback control design for the benchmark refrigeration system. Ind. Eng. Chem. Res. 58 (38), 17885–17897. doi:10.1021/acs.iecr.9b01854

CrossRef Full Text | Google Scholar

Zhang, L., and Qian, J. (2007). Design and parameter tuning of multivariable model predictive controller. Mach. Tools Hydraul. 35 (9), 31–34. doi:10.3969/j.issn.1001-3881.2007.09.011

CrossRef Full Text | Google Scholar

Zhang, X., Ni, W., Li, Z., and Zheng, S. (2005). Dynamic modeling study of superheater steam temperature based on principal component analysis method and online data. Proc. CSEE 25 (5), 131–135.

Google Scholar

Zhang, M., Wang, J., and Li, D. (2010). “Simulation analysis of PID control system based on desired dynamic equation,” in Paper presented at the the 8th World Congress on Intelligent Control and Automation, 3638–3644.

Google Scholar

Zhang, W., Ma, C., Li, H., Xuan, L., and An, A. (2022). DMC-PID cascade control for MEA-based post-combustion CO2 capture process. Chem. Eng. Res. Des. 182, 701–713. doi:10.1016/j.cherd.2022.04.030

CrossRef Full Text | Google Scholar

Zhang, K., Zhao, J., and Zhu, Y. (2018). MPC case study on a selective catalytic reduction in a power plant. J. Process Control 62, 1–10. doi:10.1016/j.jprocont.2017.11.010

CrossRef Full Text | Google Scholar

Zhang, Q., Turton, R., and Bhattacharyya, D. (2018). Nonlinear model predictive control and H∞ robust control for a post-combustion CO2 capture process. Int. J. Greenh. Gas. Control 70, 105–116. doi:10.1016/j.ijggc.2018.01.015

CrossRef Full Text | Google Scholar

Zhu, Y., and Butoyi, F. (2002). Case studies on closed-loop identification for MPC. Control Eng. Pract. 10, 403–417. doi:10.1016/s0967-0661(02)00007-2

CrossRef Full Text | Google Scholar

Zhu, Y., Yan, W., and Zhu, Y. C. (2021). MPC closed-loop identification without excitation. J. Process Control 106, 122–129. doi:10.1016/j.jprocont.2021.08.018

CrossRef Full Text | Google Scholar