
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Control Eng. , 13 January 2023
Sec. Networked Control
Volume 4 - 2023 | https://doi.org/10.3389/fcteg.2023.1104745
This article is part of the Research Topic Cooperative Control and Team Behaviors in Adversarial Environments View all 5 articles
In this work, we study the problem of decentralized multi-agent perimeter defense that asks for computing actions for defenders with local perceptions and communications to maximize the capture of intruders. One major challenge for practical implementations is to make perimeter defense strategies scalable for large-scale problem instances. To this end, we leverage graph neural networks (GNNs) to develop an imitation learning framework that learns a mapping from defenders’ local perceptions and their communication graph to their actions. The proposed GNN-based learning network is trained by imitating a centralized expert algorithm such that the learned actions are close to that generated by the expert algorithm. We demonstrate that our proposed network performs closer to the expert algorithm and is superior to other baseline algorithms by capturing more intruders. Our GNN-based network is trained at a small scale and can be generalized to large-scale cases. We run perimeter defense games in scenarios with different team sizes and configurations to demonstrate the performance of the learned network.
The problem of perimeter defense games considers a scenario where the defenders are constrained to move along a perimeter and try to capture the intruders while the intruders aim to reach the perimeter without being captured by the defenders (Shishika and Kumar, 2020). A number of previous works have solved this problem with engagements on a planar game space (Shishika and Kumar, 2018; Chen et al., 2021). However, in the real world, the perimeter may be represented by a three-dimensional shape as the players (e.g., defenders and intruders) may have the ability to perform three-dimensional motions. For example, a perimeter of a building that defenders aim to protect can be enclosed by a hemisphere. As a result, the defender robots should be able to move in three-dimensional space. For example, aerial robots have been well studied in various settings (Lee et al., 2016; Lee et al., 2020a; Nguyen et al., 2019; Chen et al., 2020), and all these settings can be real-world use-cases for perimeter defense. For instance, intruders try to attack a military base in the forest and defenders aim to capture the intruders.
In this work, we tackle the perimeter defense problem in a domain where multiple agents collaborate to accomplish a task. Multi-agent collaboration has been explored in many areas including environmental mapping (Thrun et al., 2000; Liu et al., 2022), search and rescue (Baxter et al., 2007; Miller et al., 2020), target tracking (Lee et al., 2022b; Ge et al., 2022), on-demand wireless infrastructure (Mox et al., 2020), transportation (Ng et al., 2022; Xu et al., 2022), and multi-agent learning (Kim et al., 2021). Our approach employs a team of robots that work collectively towards a common goal of defending a perimeter. We focus on developing decentralized strategies for a team of defenders for various reasons: i) the teammates can be dynamically added or removed without disrupting explicit hierarchy; ii) the centralized system may fail to cope with the high dimensionality of a team’s joint state space; and iii) the defenders have a limited communication range and can only communicate locally.
To this end, we aim to develop a framework where a team of defenders collaborates to defend the perimeter using decentralized strategies based on local perceptions and communications. Specifically, we explore learning-based approaches to learn policies by imitating expert algorithms such as the maximum matching algorithm (Chen et al., 2014). Maximum matching algorithm that runs the exhaustive search to find the best policy is very computationally intensive at large scales since this approach is combinatorial in nature and assumes global information. We utilize GNN as the learning paradigm and demonstrate that the trained network can perform close to the expert algorithm. GNNs have decentralized communication architecture that capture the neighboring interactions and transferability that allows for generalization to previously unseen scenarios (Ruiz et al., 2021). We demonstrate that our proposed GNN-based network can be generalized to large scales in solving multi-robot perimeter defense games.
With this insight, we make the following primary contributions in this paper:
Framework for decentralized perimeter defense using graph neural networks. We propose a novel learning framework that utilizes a graph-based representation for the perimeter defense game. To the best of our knowledge, we are the first to solve the decentralized hemisphere perimeter defense problem by learning decentralized strategies via graph neural networks.
Robust perimeter defense performance with scalability. We demonstrate that our methods perform close to an expert policy (i.e., maximum matching algorithm Chen et al. (2014)) and are superior to other baseline algorithms. Our proposed networks are trained at a small scale and can be generalized to large scales.
In a perimeter defense game, defenders aim to capture intruders by moving along a perimeter while intruders try to reach the perimeter without being captured by the defenders. We refer to (Shishika and Kumar, 2020) for a detailed survey. Many previous works dealt with engagements on a planar game space (Shishika and Kumar, 2018; Macharet et al., 2020; Bajaj et al., 2021; Chen et al., 2021; Hsu et al., 2022). For example, a cooperative multiplayer perimeter-defense game was solved on a planar game space in (Shishika and Kumar, 2018). In addition, an adaptive partitioning strategy based on intruder arrival estimation was proposed in (Macharet et al., 2020). Later, a formulation of the perimeter defense problem as an instance of the flow networks was proposed in (Chen et al., 2021). Further, an engagement on a conical environment was discussed in (Bajaj et al., 2021), and a model with heterogeneous teams was addressed in (Hsu et al., 2022).
High-dimensional extensions of the perimeter defense problem have been recently explored in (Lee et al., 2020b; Lee et al., 2021; Lee et al., 2022a; Lee and Bakolas, 2021; Yan et al., 2022). For example, Lee and Bakolas (2021) analyzed the two-player differential game of guarding a closed convex target set from an attacker in high-dimensional Euclidean spaces. Yan et al. (2022) studied a 3D multiplayer reach-avoid game where multiple pursuers defend a goal region against multiple evaders. Lee et al. (2020b); Lee et al., 2021; Lee et al., 2022a) considered a game played between aerial defender and ground intruder.
All of the aforementioned works focus on solving centralized perimeter defense problems, which assume that players have global knowledge of other players’ states. However, decentralized control becomes a necessity as we reach a large number of players. To remedy this problem, Velhal et al. (2022) formulated the perimeter defense game into a decentralized multi-robot spatio-temporal multitask assignment problem on the perimeter of a convex shape. Paulos et al. (2019) proposed neural network architecture for training decentralized agent policies on the perimeter of a unit circle, where defenders have simple binary action spaces. Different from the aforementioned works, we focus on the high-dimensional perimeter, specialized to a hemisphere, with continuous action space. We solve multi-agent perimeter defense problems by learning decentralized strategies with graph neural networks.
We leverage graph neural networks as the learning paradigm because of their desirable properties of decentralized architecture that captures the interactions between neighboring agents and transferability that allows for generalization to previously unseen cases (Gama et al., 2019; Ruiz et al., 2021). In addition, GNNs have shown great success in various multi-robot problems such as formation control (Tolstaya et al., 2019), path planning (Li et al., 2021), task allocation (Wang and Gombolay, 2020), and multi-target tracking (Zhou et al., 2021; Sharma et al., 2022). Particularly, Tolstaya et al. (2019) utilized a GNN to learn a decentralized flocking behavior for a swarm of mobile robots by imitating a centralized flocking controller with global information. Later, Li et al. (2021) implemented GNNs to find collision-free paths for multiple robots from start positions to goal positions in obstacle-rich environments. They demonstrated that their decentralized path planner achieves a near-expert performance with local observations and neighboring communication only, which can also be generalized to larger networks of robots. The GNN-based approach was also employed to learn solutions to the combinatorial optimization problems in a multi-robot task scheduling scenario (Wang and Gombolay, 2020) and multi-target tracking scenario (Zhou et al., 2021; Sharma et al., 2022).
Perimeter defense is a relatively new field of research that has been explored recently. One particular challenge is that the high-dimensional perimeters add spatial and algorithmic complexities for defenders to execute their optimal strategies. Although many previous works considered engagements on a planar game space and derived optimal strategies in 2D motions, the extension towards high-dimensional spaces is unavoidable for practical applications of perimeter defense games in real-world scenarios. For instance, a perimeter of a building that defenders aim to protect can be enclosed by a generic shape, such as a hemisphere. Since defenders cannot pass through the building and are assumed to be close to the building at any time, they are employed to move along the surface of the dome, which leads to the “hemisphere perimeter defense game.” The intruder is moving on the base plane of the hemisphere, which implies a constant altitude during moving. The movement of the intruder is constrained to 2D since it is assumed that intruders may want to stay low in altitude to hide from the defenders in the real world.
It is worth noting that the hemisphere defense problem is more challenging to solve than a problem where both agents are allowed to freely move in a 3D space. There were previous works in which both defenders and intruders could move in 3-dimensional spaces (Yan et al., 2022; Yan et al., 2019; Yan et al., 2020). In all cases, the authors were able to explicitly derive the optimal solutions even in multi-robot scenarios. Although our problem limits the dynamics of the defenders to the surface of the hemisphere, these constraints make the finding of an optimal solution intractable and challenging.
We consider a hemispherical dome with radius of R as perimeter. The hemisphere constraint is for the defender to safely move around the perimeter (e.g., building). In this game, consider two sets of players:
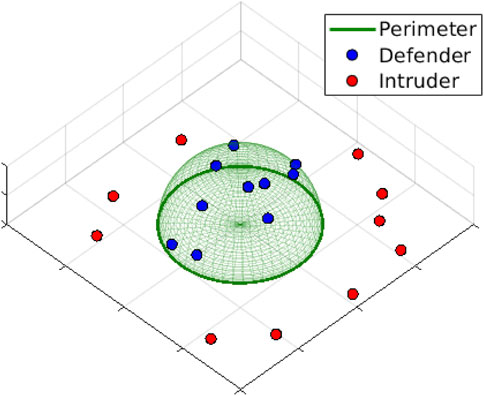
FIGURE 1. Instance of 10 vs. 10 perimeter defense. Defenders are constrained to move on the surface of the dome while intruders are constrained to move on the ground plan.
Given zD, zA, we call breachingpoint as a point on the perimeter at which the intruder tries to reach the target, as shown B in Figure 2. We call the azimuth angle that forms the breaching point as breaching angle, denoted by θ, and call the angle between (zA−zB) and the tangent line at B as approach angle, denoted by β. It is proved in (Lee et al., 2020b) that given the current positions of defender zD and intruder zA as point particles, there exists a unique breaching point such that the optimal strategy for both defender and intruder is to move towards it, known as optimal breaching point. The breaching angle and approach angle corresponding to the optimal breaching point are known as optimal breaching angle, denoted by θ*, and optimal approach angle, denoted by β*. As stated in (Lee et al., 2020b), although there exists no closed-form solution for θ* and β*, they can be computed at any time by solving two governing equations:
and
We call the target time as the time to reach B and define τD(zD, zB) as the defender target time, τA(zA, zB) as the intruder target time, and the following as payoff function:
The defender reaches B faster if p < 0 and the intruder reaches B faster if p > 0. Thus, the defender aims to minimize p while the intruder aims to maximize it.
It is proven in (Lee et al., 2020b) that the optimal strategies for both defender and intruder are to move towards the optimal breaching point at their maximum speed at any time. Let Ω and Γ be the continuous vD and vA that lead to B so that τD(zD, Ω) ≜ τD(zD, zB) and τA(zA, Γ) ≜ τA(zA, zB), and let Ω* and Γ* be the optimal strategies that minimize τD(zD, Ω) and τA(zA, Γ), respectively, then the optimality in the game is given as a Nash equilibrium:
To maximize the number of captures during N vs. N defense, we first recall the dynamics of a 1 vs. 1 perimeter defense game. It is proven in (Lee et al., 2020b) that the best action for the defender in one-on-one game is to move towards the optimal breaching point (defined in Section 3.3). The defender reaches the optimal breaching point faster than the intruder does if payoff p (defined in Section 3.4) is negative, and the intruder reaches faster if p > 0. From this, we infer that maximizing the number of captures in N vs. N defense is the same as finding a matching between the defenders and intruders so that the number of the negative payoff of assigned pairs is maximized. In an optimal matching, the number of negative payoffs stays the same throughout the overall game since the optimality in each game of defender-intruder pairs is given as a Nash equilibrium (see Section 3.5).
The expert assignment policy is a maximum matching (Chen et al., 2014; Shishika and Kumar, 2018). To execute this algorithm, we generate a bipartite graph with D and A as two sets of nodes (i.e.,
where
Problem 1 (Decentralized Perimeter Defense with Graph Neural Networks). Design a GNN-based learning framework to learn a mapping
We describe in detail our learning architecture for solving Problem 1 in the following section.
In this paper, we learn decentralized strategies for perimeter defense using graph neural networks. Inference of our approach is in real-time, which is scalable to a large number of agents. We use an expert assignment policy to train a team of defenders who share information through communication channels. In Section 4.1, we introduce the perception module for processing the features that are input to GNN. Learning the decentralized algorithm through GNN and planning the candidate matching for the defenders are discussed in Section 4.2. The control of the defender team is explained in Section 4.3, and the training procedure is detailed in Section 4.4. The overall framework is shown in Figure 3. For the choice of architecture, we decouple the control module from the learning framework since directly learning the actions is unnecessary. Learning an assignment between agents is sufficient, and the best actions can be computed by the optimal strategies (Section 3.5).
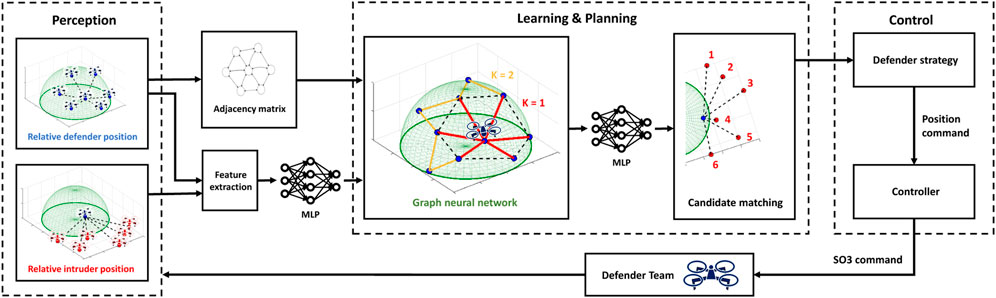
FIGURE 3. Overall framework. Perception module collects local information. Learning & Planning module processes the collected information using GNN through K-hop neighboring communications. Control module computes the optimal strategies and executes the controller to close the loop.
In this section, we assume N aerial defenders and N ground intruders. Each defender Di is equipped with a sensor and faces outwards the perimeter with a field of view FOV. The defenders’ horizontal field of view FOV is chosen as π assuming a fisheye-type camera.
For each i, a defender observes the set of intruders Aj, and the relative positions in spherical coordinates between Di and Aj are represented by
To make the system scalable, we build communication with a fixed number of closest defenders. Each defender Di communicates with nearby defenders Dj within its communication range rc. For each i, the relative positions between Di and Dj are represented by
Feature extraction is performed by concatenating the relative positions of observed intruders and communicated defenders, forming the local perceptions
We employ graph neural networks with K-hop communications. Defenders communicate their perceived features with neighboring robots. The communication graph
We consider each defender
where
Here, the adjacency matrix S is called the Graph Shift Operator (GSO) (Gama et al., 2019).
With the shift operation, we define the graph convolution by a linear combination of the shifted features on graph
where
Applying a point-wise non-linearity
Then, we define a GNN module by cascading L layers of graph perceptions (Eq. 9):
where the output feature of the previous layer ℓ−1,
The output of the GNN, which represents the fused information from the K-hop communications, is then processed with another MLP to provide a candidate matching for each defender. Figure 3 shows a candidate matching instance if
It is worth noting that our proposed GNN-based learning approach is scalable due to permutation equivalence. This means that given a decentralized defender, it should be able to decide the action based on local perceptions that consist of an arbitrary number of unnumbered intruders. An instance of a perimeter defense game is illustrated to show this property in Figure 4. The plots focus on a single defender and intruders are gradually approaching the perimeter as time passes by. The same intruders are colored in the same color across different time stamps. Notice that a new light-blue intruder enters into the field of view of the defender at t = 2, and a purple intruder begins to appear at t = 3. Although an arbitrary number of intruders are detected at each time, our system gives IDs to intruders shown as blue numbers in Figure 4. We number them clockwise but could have done differently in any permutation (e.g., counterclockwise) because graph neural networks perform label-independent processing. The reason for the numbering is to specify which intruders would be matched with which defenders from the network outputs. Without loss of generality, we assign the IDs clockwise but we note that these IDs are arbitrary since the IDs can change at different stamps. For instance, the yellow intruder ID is 2 at t = 1 but becomes 3 at t = 2, 3. Similarly, the red intruder ID is 3 at t = 1 but changes to 4 at t = 2 and 5 at t = 3. In this way, we accommodate an arbitrary amount of intruders and thus our system is permutation equivalent.
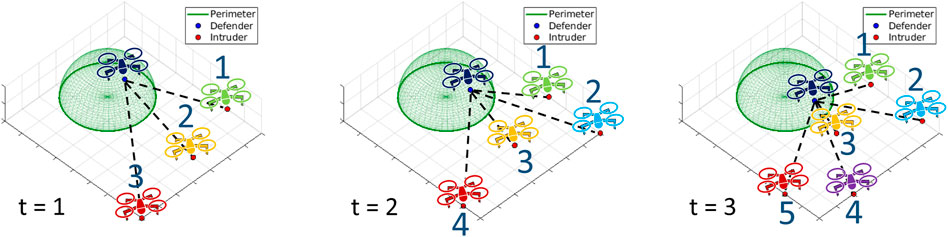
FIGURE 4. Instance of perimeter defense game at different time stamps. The plots focus on a single defender and its local perceptions.
The output from the Section 4.2 is inputted to the defender strategy module in Figure 3. This module handles all the matched pairs (Di, Aj) and computes the optimal breaching points for each of the one-on-one hemisphere perimeter defense games (see Section 3.3). The defender strategy module collectively outputs the position commands, which are towards the direction of the optimal breaching points. The SO(3) command (Mellinger and Kumar, 2011) that consists of thrust and moment to control the robot at a low level is then passed to the defender team D for control. The state dynamics for the defender-intruder pair is detailed in (Lee et al., 2020b). The defenders move based on the commands to close the perception-action loop. Notably, the expert assignment likelihood
To train our proposed networks, we use imitation learning to mimic an expert policy given by maximum matching (explained in Section 3), which provides the optimal assignment likelihood
Our model architecture consists of a 2-layer MLP with 16 and 8 hidden layers to generate the post-processed feature vector xi, a 2-layer GNN with 32 and 128 hidden layers to exchange the collected information from defenders, and a single-layer MLP to produce an assignment likelihood
In implementing graph neural networks, we construct a 1-hop connectivity graph by connecting defenders within communication range rc = 1. Given that the default radius is R = 1, we foresee that three neighboring agents within 1-hop would provide a wide sensing region for the defenders. Accordingly, we assume that communications occur in real-time with
The experiments are conducted using a 12-core 3.50 GHz i9-9920X CPU and an Nvidia GeForce RTX 2080 Ti GPU. We implement the proposed networks using PyTorch v1.10.1 (Paszke et al., 2019) accelerated with Cuda v10.2 APIs. We use the Adam optimizer with a momentum of 0.5. The learning rate is scheduled to decay from 5 × 10–3 to 10–6 within 1500 epochs with batch size 64, using cosine annealing. We choose these hyperparameters for the best performance.
We evaluate our decentralized networks using imitation learning where the expert assignment policy is the maximum matching. The perimeter is a hemisphere with a radius R, which is defined by
We are mainly interested in the percentage of intruders caught (i.e., number of captures/total number of intruders). At small scales (e.g., N ≤ 10), an expert policy (i.e., the maximum matching) can be run and a direct comparison between the expert policy and our policy is available. At large scales (e.g., N > 10), the maximum matching is too expensive to run. Thus we compare our algorithm with other baseline approaches: greedy, random, and mlp, which will be explained in Section 5.3. To observe the scalability on small and large scales, we run a total of five different algorithms for each scale: expert, gnn, greedy, random, and mlp. In all cases, we compute the absolute accuracy, which is defined by the number of captures divided by the team size, to verify if our network can be generalized to any team size. Furthermore, we also calculate the comparative accuracy, defined as the ratio of the number of captures by gnn to the number of captures by another algorithm, to observe comparative results.
In baseline algorithms, defenders do not communicate their “intentions” of which intruders would be captured by which neighboring defenders for a fair comparison since GNN does not share such information either. For the GNN framework, each defender perceives nearby intruders, and the relative positions of perceived intruders, not the “intentions,” are shared by GNN through communications. The power of the GNNs is to learn these “intentions” implicitly via K-hop communications. That way, the decentralized decision-making (i.e., for both GNN and baselines) may allow multiple defenders to aim to capture the same intruder while the centralized planner knows the “intentions” of all the defenders and would avoid such a scenario.
The greedy algorithm can be run in polynomial time and thus becomes a good candidate algorithm to be compared with our approach using GNN. For a fair comparison, we run a decentralized greedy algorithm based on local perception
The random algorithm is similar to the greedy algorithm in that the K-hop neighboring communications are enabled for the expanded perception. Among sensible intruders, a defender Di randomly picks an intruder to determine the assignment.
For the MLP algorithm, we only train the current MLP of our proposed framework in isolation by excluding the GNN module. By comparing our GNN framework to this algorithm, we can observe if the GNN gives any improvement.
We run the perimeter defense game in various scenarios with different team sizes and initial configurations to evaluate the performance of the learned networks. In particular, we conduct the experiments at small (N ≤ 10) and large (N > 10) scales. The snapshots of the simulated perimeter defense game in top view with our proposed networks for different team sizes are shown in Figure 5. The perimeter, defender state, intruder state, and breaching point are marked in green, blue, red, and yellow, respectively. We observe that intruders try to reach the perimeter. Given the defender-intruder matches, the intruders execute their respective optimal strategies to move towards the optimal breaching points (see Section 3.5). If an intruder successfully reaches it without being captured by any defender, the intruder is consumed and leaves a marker called “Intrusion”. If an intruder fails and is intercepted by a defender, both agents are consumed and leave a marker called “Capture”. The points on the perimeter aimed by intruders are marked as “Breaching point”. In all runs, the game ends at terminal time Tf when all the intruders are consumed. See the supplemental video for more results.
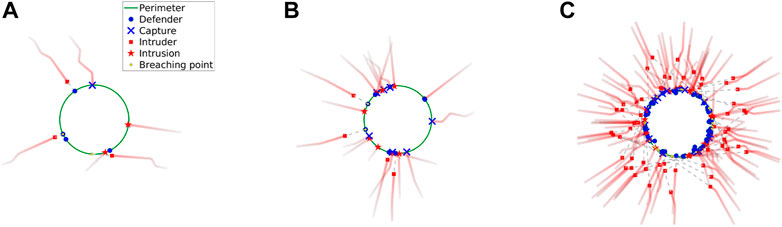
FIGURE 5. (A–C) Snapshots of simulated perimeter defense in top view using the proposed method gnn for three different team sizes.
As mentioned in Section 5.1, we run the five algorithms expert, gnn, greedy, random, and mlp at small scales, and run gnn, greedy, random, and mlp in large scales. As an instance, the snapshots of simulated 20 vs. 20 perimeter defense game in top view at terminal time Tf using the four algorithms are displayed in Figure 6. The four subfigures (a)-(d) show that these algorithms exhibit different performance although the game begins with the same initial configuration in all cases. The number of captures by these algorithms gnn, greedy, random, and mlp are 12, 11, 10, 7, respectively.
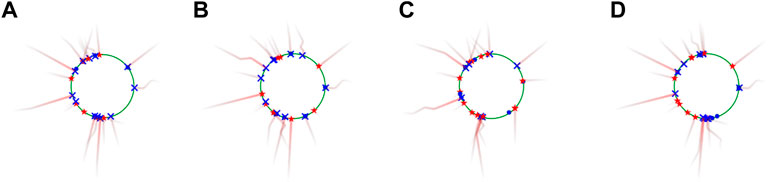
FIGURE 6. (A–D) Snapshots of simulated 20 vs. 20 perimeter defense game in top view at terminal time Tf using the four algorithms gnn, greedy, random, and mlp. The number of captures using these algorithms are 12, 11, 10, and 7, respectively.
The overall results of the percentage of intruders caught by each of these methods are depicted in Figure 7. It is observed that gnn outperforms other baselines in all cases, and performs close to expert at the small scales. In particular, given that our default team size Ndef is 10, the performance of our proposed algorithm stays competitive with that of the expert policy near N = 10.
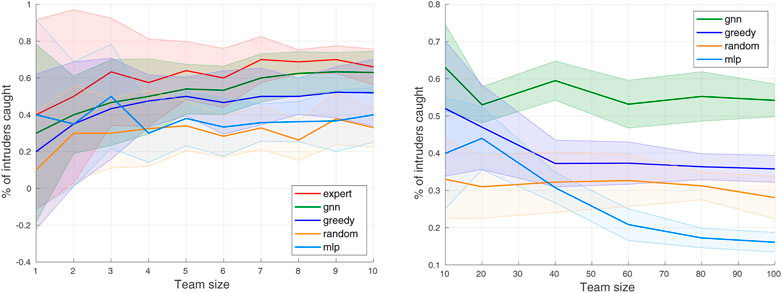
FIGURE 7. Percentage of intruders caught (average and standard deviation over 10 trials) by different algorithms on small (N ≤ 10) and large (N > 10) scales.
At large scales, the percentage of captures by gnn stays constant, which indicates that the trained network can be well generalized to the large scales even if the training has been performed at the small scale. The percentage of captures by greedy also seems constant but performs much worse than gnn as the team size gets large. At small scales, only a few combinations are available in matching defender-intruder pairs and thus the greedy algorithm would perform similarly to the expert algorithm. As the number of agents increases, the number of possible matching increases exponentially so the greedy algorithm performs worse since the problem complexity gets much higher. The random approach performs worse than all other algorithms at small scales, but the mlp begins to perform worse than the random when the team size increases over 40. This tendency tells that the policy trained only with MLP cannot be scalable at large scales. Since the training is done with 10 agents, it is optimal near N = 10, but the mlp cannot work at larger scales and even performs worse than the random algorithm. It is confirmed that the GNN added to the MLP significantly improves the performance. Overall, compared to other algorithms, gnn performs better at large scales than at small scales, which validates that GNN helps the network become scalable.
To quantitatively evaluate the proposed method, we report the absolute accuracy and comparative accuracy (defined in Section 5.2) in Table 2 and Table 3. As expected, the absolute accuracy reaches the maximum when team size approaches N = 10. The overall values of the absolute accuracy are fairly consistent except when N = 2. We conjecture that there may not be much information shared by the two defenders and there could be no sensible intruders at all based on initial configurations.
The comparative accuracy between gnn and expert shows that our trained policy gets much closer to the expert policy as N approaches 10, and we expect the performance of gnn to be close to that of expert even at the large scales. The comparative accuracy between gnn and other baselines shows that our trained networks perform much better than baseline algorithms at the large scales (N ≥ 40) with an average of 1.5 times more captures. The comparative accuracy between gnn and random is somewhat noisy throughout the team size due to the nature of randomness, but we observe that our policy can outperform random policy with an average of 1.8 times more captures at small and large scales. We observe that mlp performs much worse than other algorithms at large scales.
Based on the comparisons, we demonstrate that our proposed networks, which are trained at a small scale, can generalize to large scales. Intuitively, one may think that greedy would perform the best in a decentralized setting since each defender does its best to minimize the value of the game (defined in Eq. 5). However, we can infer that greedy does not know the intentions of nearby defenders (e.g., which intruders to capture) so it cannot achieve the performance close to the centralized expert algorithm. Our method implements graph neural networks to exchange the information of nearby defenders, which perceive their local features, to plan the final actions of the defender team; therefore, implicit information of where the nearby defenders are likely to move is transmitted to each neighboring defender. Since the centralized expert policy knows all the intentions of defenders, our GNN-based policy learns the intention through communication channels. The collaboration among the defender team is the key for our gnn to outperform greedy approach. These results validate that the implemented GNNs are ideal for our problem with the properties of the decentralized communication that captures the neighboring interactions and transferability that allows for generalization to unseen scenarios.
To analyze the algorithm performance, we have trained our GNN-based architecture with a different number of expert demonstrations (e.g., 10 million, 1 million, 100 k, and 10 k). The percentage of intruders caught (average and standard deviation over 10 trials) on team size 10 ≤ N ≤ 50 are shown in Figure 8. The plot validates that our proposed network learns better with more demonstrations.
We have tested the GNN-based proposed method with different perimeter radii. Intuitively, given the fixed number of agents, increasing the radius may lead to a failure in the defense system. We set the default team size of defenders as 40 and increase the perimeter radius until the percentage of intruders caught converges to zero. As shown in Figure 9, the percentage decreases as the radius changes from 100 m to 800 m, converging to zero.
The performance of our GNN-based approach with different numbers of intruder (e.g.,
As perimeter defense is a relatively new field of research, this work has underlying limiting assumptions. In the problem formulation, we assume the robots are point particles. Accordingly, we assume optimal trajectories obey first-order assumptions. There is a preliminary work (Lee et al., 2021) to bridge the gap between the point particle assumptions and three-dimensional robots for one-on-one hemisphere perimeter defense, and we hope to extend the idea of this work to our multi-agent perimeter defense problem in the future. Another limitation is that there is no available expert policy, which can be compared with our proposed method, at large scales. Running the maximum matching algorithm is very expensive at large scales, so we compare our GNN-based algorithm with other baseline methods. Although the consistent performances of tested algorithms along different scales confirm that our trained networks can be generalized to large scales, we hope to explore another algorithm that can be used as an expert policy at large scales to replace the maximum matching. One consideration is utilizing reinforcement learning since the algorithm performance at large scales will be available.
This paper proposes a novel framework that employs graph neural networks to solve the decentralized multi-agent perimeter defense problem. Our learning framework takes the defenders’ local perceptions and the communication graph as inputs and returns actions to maximize the number of captures for the defender team. We train deep networks supervised by an expert policy based on the maximum matching algorithm. To validate the proposed method, we run the perimeter defense game in different team sizes using five different algorithms: expert, gnn, greedy, random, and mlp. We demonstrate that our GNN-based policy stays closer to the expert policy at small scales and the trained networks can generalize to large scales.
One future work is to implement vision-based local sensing for the perception module, which would relax the assumptions of perfect state estimation. Realizing multi-agent perimeter defense with vision-based perception and communication within the defenders will be an end goal. Another future research direction is to find a centralized expert policy in multi-robot systems by utilizing reinforcement learning.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
EL, LZ, and VK contributed to conception and design of the study. EL and AR performed the statistical analysis. EL wrote the first draft of the manuscript. All authors contributed to manuscript revision, read and approved the submitted version.
We gratefully acknowledge the support from ARL DCIST CRA under Grant W911NF-17-2-0181, NSF under Grants CCR-2112665, CNS-1446592, and EEC-1941529, ONR under Grants N00014-20-1-2822 and N00014-20-S-B001, Qualcomm Research, NVIDIA, Lockheed Martin, and C-BRIC, a Semiconductor Research Corporation Joint University Microelectronics Program cosponsored by DARPA.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bajaj, S., Torng, E., Bopardikar, S. D., Von Moll, A., Weintraub, I., Garcia, E., et al. (2021). Competitive perimeter defense of conical environments. arXiv preprint arXiv:2110.04667.
Baxter, J. L., Burke, E., Garibaldi, J. M., and Norman, M. (2007). “Multi-robot search and rescue: A potential field based approach,” in Autonomous robots and agents (Springer), 9–16.
Chen, A. K., Macharet, D. G., Shishika, D., Pappas, G. J., and Kumar, V. (2021). “Optimal multi-robot perimeter defense using flow networks,” in International symposium distributed autonomous robotic systems (Springer), 282–293.
Chen, M., Zhou, Z., and Tomlin, C. J. (2014). “Multiplayer reach-avoid games via low dimensional solutions and maximum matching,” in 2014 American control conference (IEEE), 1444–1449.
Chen, S. W., Nardari, G. V., Lee, E. S., Qu, C., Liu, X., Romero, R. A. F., et al. (2020). Sloam: Semantic lidar odometry and mapping for forest inventory. IEEE Robotics Automation Lett. 5, 612–619. doi:10.1109/lra.2019.2963823
Gama, F., Marques, G., Leus, G., and Ribeiro, A. (2019). Convolutional neural network architectures for signals supported on graphs. IEEE Trans. Signal Process. 67, 1034–1049. doi:10.1109/tsp.2018.2887403
Ge, R., Lee, M., Radhakrishnan, V., Zhou, Y., Li, G., and Loianno, G. (2022). Vision-based relative detection and tracking for teams of micro aerial vehicles. arXiv preprint arXiv:2207.08301.
Hsu, C. D., Haile, M. A., and Chaudhari, P. (2022). A model for perimeter-defense problems with heterogeneous teams. arXiv preprint arXiv:2208.01430.
Kim, D. K., Liu, M., Riemer, M. D., Sun, C., Abdulhai, M., Habibi, G., et al. (2021). “A policy gradient algorithm for learning to learn in multiagent reinforcement learning,” in International Conference on Machine Learning (PMLR), 5541–5550.
Lee, E. S., Loianno, G., Jayaraman, D., and Kumar, V. (2022a). Vision-based perimeter defense via multiview pose estimation. arXiv preprint arXiv:2209.12136.
Lee, E. S., Loianno, G., Thakur, D., and Kumar, V. (2020a). Experimental evaluation and characterization of radioactive source effects on robot visual localization and mapping. IEEE Robotics Automation Lett. 5, 3259–3266. doi:10.1109/lra.2020.2975723
Lee, E. S., Shishika, D., and Kumar, V. (2020b). “Perimeter-defense game between aerial defender and ground intruder,” in 2020 59th IEEE Conference on Decision and Control (CDC) (IEEE), 1530–1536.
Lee, E. S., Shishika, D., Loianno, G., and Kumar, V. (2021). “Defending a perimeter from a ground intruder using an aerial defender: Theory and practice,” in 2021 IEEE international symposium on safety, security, and rescue robotics (SSRR) (IEEE), 184–189.
Lee, E. S., Zhou, L., Ribeiro, A., and Kumar, V. (2022b). Learning decentralized strategies for a perimeter defense game with graph neural networks. arXiv preprint arXiv:2211.01757.
Lee, S., Har, D., and Kum, D. (2016). “Drone-assisted disaster management: Finding victims via infrared camera and lidar sensor fusion,” in 2016 3rd asia-pacific world congress on computer science and engineering (APWC on CSE) (IEEE), 84–89.
Lee, Y., and Bakolas, E. (2021). Guarding a convex target set from an attacker in Euclidean spaces. IEEE Control Syst. Lett. 6, 1706–1711. doi:10.1109/lcsys.2021.3132083
Li, Q., Gama, F., Ribeiro, A., and Prorok, A. (2020). “Graph neural networks for decentralized multi-robot path planning,” in 2020 IEEE/RSJ Intl Conference on Intelligent Robots and Systems (IROS) (IEEE).
Li, Q., Lin, W., Liu, Z., and Prorok, A. (2021). Message-aware graph attention networks for large-scale multi-robot path planning. IEEE Robotics Automation Lett. 6, 5533–5540. doi:10.1109/lra.2021.3077863
Liu, X., Prabhu, A., Cladera, F., Miller, I. D., Zhou, L., Taylor, C. J., et al. (2022). Active metric-semantic mapping by multiple aerial robots. arXiv preprint arXiv:2209.08465.
Macharet, D. G., Chen, A. K., Shishika, D., Pappas, G. J., and Kumar, V. (2020). “Adaptive partitioning for coordinated multi-agent perimeter defense,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).
Mellinger, D., and Kumar, V. (2011). “Minimum snap trajectory generation and control for quadrotors,” in 2011 IEEE international conference on robotics and automation (IEEE), 2520–2525.
Miller, I. D., Cladera, F., Cowley, A., Shivakumar, S. S., Lee, E. S., Jarin-Lipschitz, L., et al. (2020). Mine tunnel exploration using multiple quadrupedal robots. IEEE Robotics Automation Lett. 5, 2840–2847. doi:10.1109/lra.2020.2972872
Mox, D., Calvo-Fullana, M., Gerasimenko, M., Fink, J., Kumar, V., and Ribeiro, A. (2020). “Mobile wireless network infrastructure on demand,” in 2020 IEEE International Conference on Robotics and Automation (ICRA) (IEEE), 7726–7732.
Ng, E., Liu, Z., and Kennedy, M. (2022). It takes two: Learning to plan for human-robot cooperative carrying. arXiv preprint arXiv:2209.12890.
Nguyen, T., Shivakumar, S. S., Miller, I. D., Keller, J., Lee, E. S., Zhou, A., et al. (2019). Mavnet: An effective semantic segmentation micro-network for mav-based tasks. IEEE Robotics Automation Lett. 4, 3908–3915. doi:10.1109/lra.2019.2928734
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). Pytorch: An imperative style, high-performance deep learning library. Adv. neural Inf. Process. Syst. 32.
Paulos, J., Chen, S. W., Shishika, D., and Kumar, V. (2019). “Decentralization of multiagent policies by learning what to communicate,” in 2019 International Conference on Robotics and Automation (ICRA) (IEEE), 7990–7996.
Ruiz, L., Gama, F., and Ribeiro, A. (2021). Graph neural networks: Architectures, stability, and transferability. Proc. IEEE 109, 660–682. doi:10.1109/jproc.2021.3055400
Sharma, V. D., Zhou, L., and Tokekar, P. (2022). D2coplan: A differentiable decentralized planner for multi-robot coverage. arXiv preprint arXiv:2209.09292.
Shishika, D., and Kumar, V. (2020). “A review of multi agent perimeter defense games,” in International Conference on Decision and Game Theory for Security (Springer), 472–485.
Shishika, D., and Kumar, V. (2018). “Local-game decomposition for multiplayer perimeter-defense problem,” in In 2018 IEEE Conference on Decision and Control (CDC) (IEEE), 2093–2100.
Thrun, S., Burgard, W., and Fox, D. (2000). “A real-time algorithm for mobile robot mapping with applications to multi-robot and 3d mapping,” in Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (IEEE), 321–328. (Cat. No. 00CH37065).
Tolstaya, E., Gama, F., Paulos, J., Pappas, G., Kumar, V., and Ribeiro, A. (2019). “Learning decentralized controllers for robot swarms with graph neural networks,” in Conference Robot Learning 2019 (Osaka, Japan: Int. Found. Robotics Res.).
Velhal, S., Sundaram, S., and Sundararajan, N. (2022). A decentralized multirobot spatiotemporal multitask assignment approach for perimeter defense. IEEE Trans. Robotics 38, 3085–3096. doi:10.1109/tro.2022.3158198
Wang, Z., and Gombolay, M. (2020). Learning scheduling policies for multi-robot coordination with graph attention networks. IEEE Robotics Automation Lett. 5, 4509–4516. doi:10.1109/lra.2020.3002198
Xu, J., D’Antonio, D. S., and Saldaña, D. (2022). Modular multi-rotors: From quadrotors to fully-actuated aerial vehicles. arXiv preprint arXiv:2202.00788.
Yan, R., Duan, X., Shi, Z., Zhong, Y., and Bullo, F. (2022). Matching-based capture strategies for 3d heterogeneous multiplayer reach-avoid differential games. Automatica 140, 110207. doi:10.1016/j.automatica.2022.110207
Yan, R., Shi, Z., and Zhong, Y. (2019). “Construction of the barrier for reach-avoid differential games in three-dimensional space with four equal-speed players,” in 2019 IEEE 58th Conference on Decision and Control (CDC) (IEEE), 4067–4072.
Yan, R., Shi, Z., and Zhong, Y. (2020). Guarding a subspace in high-dimensional space with two defenders and one attacker. IEEE Trans. Cybern. 52, 3998–4011. doi:10.1109/tcyb.2020.3015031
Keywords: graph neural networks, perimeter defense, multi-agent systems, perception-action-communication loops, imitation learning
Citation: Lee ES, Zhou L, Ribeiro A and Kumar V (2023) Graph neural networks for decentralized multi-agent perimeter defense. Front. Control. Eng. 4:1104745. doi: 10.3389/fcteg.2023.1104745
Received: 22 November 2022; Accepted: 03 January 2023;
Published: 13 January 2023.
Edited by:
Douglas Guimarães Macharet, Federal University of Minas Gerais, BrazilReviewed by:
Ziyang Meng, Tsinghua University, ChinaCopyright © 2023 Lee, Zhou, Ribeiro and Kumar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elijah S. Lee, ZWxzbGVlQHNlYXMudXBlbm4uZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.