Automatic generation and updating of process industrial digital twins for estimation and control - A review

This review aims at assessing the opportunities and challenges of creating and using digital twins for process industrial systems over their life-cycle in the context of estimation and control. The scope is, therefore, to provide a survey on mechanisms to generate models for process industrial systems using machine learning (purely data-driven) and automated equation-based modeling. In particular, we consider learning, validation, and updating of large-scale (i.e., plant-wide or plant-stage but not component-wide) equation-based process models. These aspects are discussed in relation to typical application cases for the digital twins creating value for users both on the operational and planning level for process industrial systems. These application cases are also connected to the needed technologies and the maturity of those as given by the state of the art. Combining all aspects, a way forward to enable the automatic generation and updating of digital twins is proposed, outlining the required research and development activities. The paper is the outcome of the research project AutoTwin-PRE funded by Strategic Innovation Program PiiA within the Swedish Innovation Agency VINNOVA and the academic version of an industry report prior published by PiiA.

1 Introduction

Digital twins have gained widespread adoption as a tool for representing physical assets from many industrial domains in a computer environment (Wright and Davidson, 2020). However, the definition of a digital twin is not unique and may vary from application to application. For example, a digital twin may be a 3D CAD model of a factory floor (Minos-Stensrud et al., 2018), a mechatronic model of an assembly line (Oppelt et al., 2014; Rosen et al., 2019), a model of an aircraft (Liu et al., 2018), or a simulation model for plant monitoring, control, and optimization (Santillán Martínez et al., 2018a; Sierla et al., 2020). Boschert and Rosen, (2016) refer to the vision of a digital twin as “[…] a comprehensive physical and functional description of a component, product or system, which includes more or less all information which could be useful in all—the current and subsequent—lifecycle phases […]” and point out the value of the simulation aspect of digital twins (Boschert and Rosen, 2016).

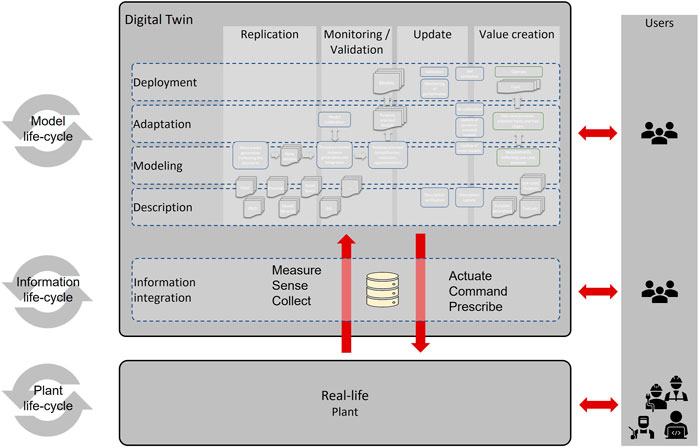
In order to reflect the real-life asset, the digital twin needs to contain a model of the asset as an integral part. The digital twin’s simulation aspect relates to the model’s execution with the help of data from the asset, such as online, synthetic, or historic data. Further, the digital twin should create value by providing the user with actionable insights or taking action by itself. The insights or actions are generated by algorithms making use of the embedded models in the digital twin, representing some form of intelligence providing answers to questions. These questions could be predefined ones (reflecting a use-case) or, in a more flexible scenario, open questions. In the latter case, the digital twin needs to comprise learning and execution seamlessly integrated in the digital twin to provide meaningful answers. In Figure 1, this principle architecture is shown. From an estimation and control perspective, the embedded models in a digital twin enable model-based approaches, while it often remains unclear if these models are feasible for use.

FIGURE 1

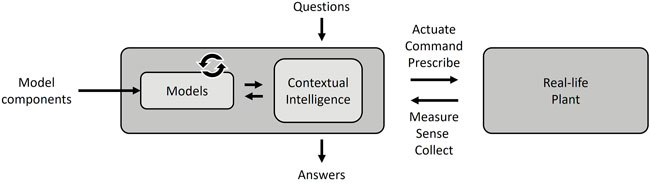
FIGURE 1. Illustration of a generic digital twin that takes asset data and user questions as inputs to provide answers about the asset.

Consequently, a digital twin needs to be connected to its real-life counterpart and adapt itself to track the life-cycle phases of its counterpart. Figure 1 also shows that models need to be generated, updated, and operate within the digital twin, where the digital twin not only is a model, but also hosts several technologies. These are needed for its description, like a blue print, for the modeling of the physical asset, for the adaptation of the models, and for the deployment of it to online operation. In addition, an integration layer is needed that combines the needed technologies to connect the digital twin with its real-life counter-part.

This review focuses on digital twins in the form of an eco-system of large-scale purpose-oriented dynamic models for process industrial applications. A purpose-oriented dynamic model is used for a specific purpose in the context of the operation and maintenance of the plant. Examples are production planning, service, and maintenance, or education and training. The general requirements for such a model are that it captures the underlying physical process sufficiently well, ensures observability of the variables of interest, and can be run sufficiently fast in relation to the required timescale (Wright and Davidson, 2020). Furthermore, one should be able to generate the model from a combination of static plant information such as pumping and instrumentation diagrams (P&IDs) or component descriptions, and historical and current process measurement data (Sierla et al., 2020).

The contribution of this work is twofold: First, we summarize the state-of-the-art of automatic model generation, calibration, monitoring, and update for such scenarios, with a focus on the current modeling and machine learning literature. Second, we identify the research directions of interest in order to build a fully autonomous toolkit for the automatic generation, calibration, and updating of the resulting purpose-oriented digital twins. Note that this also raises questions about interoperability, communication, data management, and information access. These issues are clearly very important for such a concept to work, and it is assumed that such a system is in place. An industry-oriented version of this study was formerly handed in to the funding body and is also available at their site (Birk et al., 2021).

The remainder of the article is organized as follows. The technologies, asset information, and tools required to implement such digital twins successfully are discussed in Section 2. The specific use-cases and requirements are discussed in Section 3, and the state-of-the-art survey is provided in Section 4. Finally, Section 5 discusses the identified promising research directions with respect to the above aims.

2 Technologies, information, and tools

The engineering of digital twins has certain similarities to the engineering of the plant that the digital twin is replicating. While the digital twin is foreseen to facilitate the planning, operation, maintenance, and engineering of the plant over its life-cycle, the engineering might still be worthwhile. An improved scenario is that the engineering of the digital twin is guided and automated to a large degree, as well as the ability to keep itself up to date with the real-life counterpart. Thereby, it is possible to create more value with the digital twin.

Figure 2 envisions a framework for digital twins of process industrial plants. There, the verticals relate to the actions that are taken by the digital twin, which is the replication of the physical asset, the monitoring/validation of the embedded models, the update of the models during the life-cycle phases of the real-life counterpart and the value creation, occurring during the live operation of the digital twin.

FIGURE 2

FIGURE 2. A framework for digital twins considering the life-cycle phases of the physical asset.

Figure 3 now provides a more detailed view of the different technologies that are needed. It illustrates how such a purpose-oriented model is generated. In particular, the description layer consists of a set of static plant descriptions, ranging from P&IDs to GIS plant data and model libraries (e.g., Modelica). This static information is the input to the modeling layer, where large-scale models are automatically generated from the plant data. These models are too general to be used in practice, and thus, the models have to be simplified and pruned for a particular purpose, yielding the purpose-oriented model. This model may be further approximated, taking the added uncertainty into account, before it can be calibrated (and validated) using actual plant data. At this point, the model is ready to be used for the specific purpose defined by the use-case, and the model maintenance phase begins. During this phase, the model parameters must be kept up to date to account for environmental factors or equipment wear (re-calibration) and constantly be monitored to detect model inaccuracies, or when the model is not valid anymore. This also includes aspects such as the detection of operating points not covered by models.

FIGURE 3

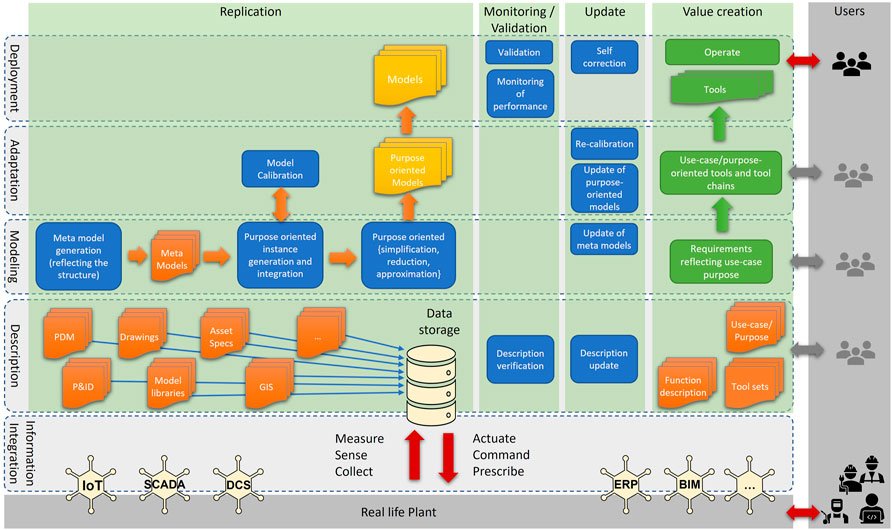
FIGURE 3. Technologies (blue) and information (orange/yellow) embedded in a digital twin along with the tools (green) needed to create value during operation.

As stated earlier, the primary usage of DTs is for the value creation using automated tools, as exemplified by the green boxes in Figure 3. These tools include several mechanisms that help the DT users to take decisions in the operation of the process. In this case, these tools are directly connected to the application case that the users are interested in. For example, for planning a maintenance operation, the users will be interested in using the DT in a long-term plant simulation and analyzing the wear and tear of the critical plant components. Thus, the DT will incorporate the remaining useful life model calculating/estimating the remaining useful life of components. Also, to initialize the model with proper information from historical data will be required to estimate the current status of the designated components. Here, an appropriate definition of the required tools, models, and simulation scenarios is needed.

In Figure 3 technologies, pieces of information, and tools that are needed to generate and operate the digital twin connected to the real-life counterpart are depicted. The plant and process information (orange boxes) needs to be available through a plant information system that the digital twin can access, either based on a local database or remotely through an application programming interface (API). In the latter case, the plant description system will be a front-end for the user or the digital twin to interface to the complete plant information. Thus the plant information system is a required technology that needs to be in place for the generation, update, and operation of digital twins. Furthermore, since the plant information system requires input from a variety of different data sources, interoperability between the different underlying systems becomes a key requirement. Moreover, in Figure 3, there are two technologies indicated for the plant information system which is the description verification and the description update. Such technologies are essential for a plant information system but are assumed to be an integral part and will not be further discussed within this review.

The needed technologies to generate, update and operate digital twins are given in Table 1. The order of the technologies can also be seen as a workflow for implementing a systematic and potentially automated approach for deploying and maintaining of estimation and control solutions in process industrial systems.

TABLE 1

TABLE 1. Required technologies.

Clearly, the purpose of a digital twin is to create value within a specific use-case. Depending on the use-case, there is more or less interaction with the user. In the case of simulation, the user monitors the simulation and also interprets the outcome, while a soft sensor use-case means that the digital twin operates fully autonomously. In the latter, the purpose oriented models need to be complemented by tools. An example of that case is the well-known Kalman filter that estimates a process’s internal states using a purpose-oriented model.

3 Potential application cases and prerequisites

A model-oriented way of working means that models become a central representation of the process industrial plant that is operated, maintained, and managed over its life-cycle and needs to stay up to date all the time. This alignment of the virtual representation and the real-life counterpart enables the use of more advanced and high performing methods to operate, optimize, control, monitor, maintain, and predict on all levels of the industrial plant. It not only enables new application cases to be realized, but also to become more efficient in terms of resource usage.

The digital twin is a natural extension of a model where, besides replicating the real-life system in terms of a model, user value creating functionalities along with mechanisms to monitor and update the models are realized. The digital twin further exhibits the ability to operate in parallel with the real life system and in an offline setting. The latter enables typical what-if analyses or investigations relating to different scenarios that may have rare occurrences.

3.1 Relationship between application cases and purposes

Generally, the models are an abstract description of a system with a wide area of application. An application case can be supported by models but will put requirements on the models used. Essentially, there is a purpose for the model, and there can be several purposes for models within an application case.

As an example, consider model-based control of the concentrate quality in a flotation process as depicted in Figure 4. The application case would then involve the estimation of the concentrate quality and the subsequent control using actuators like agitator speed, feed, and air supply. Measurements on foam properties bubbling intensity as feed properties could then serve to provide the estimates. Clearly, the model for estimating the concentrate quality has a very different purpose compared to the model for controlling the quality.

FIGURE 4

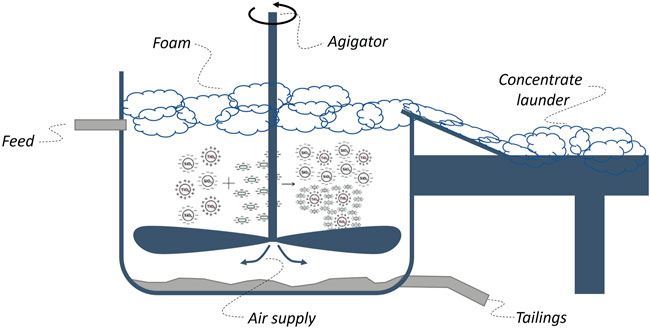
FIGURE 4. Principle sketch of a flotation process as discussed in Krivoshapkina et al. (2019).

In classic textbook examples, the suggested models would often serve both purposes, which is often not realistic or the model will have different levels of fidelity for the two purposes. Thus, using several models with a dedicated purpose for the different parts of the application cases seems to be the right way forward. As such, the purpose might directly overlap with the application cases but generally, there could be multiple purposes associated with an application case. A purpose-oriented model is then a model tailored for a specific part of a application case, which implies that a model for a certain purpose may be worthless for another.

3.2 Identified application cases

We will now summarize identified application cases where estimation and control play an important role. Thus, digital twins reflecting the dynamic behavior of a process industrial system are targeted, aiding in understanding planning, operation and maintenance of the system. The application cases are organized in the following five categories:

1) Process and production development,

2) process and production control,

3) production planning,

4) service and maintenance, and

5) education and training.

Each of these categories contains several application cases impacting the efficiency and efficacy of the production system. Each of the application cases, in turn, imposes requirements on the needed models, their properties, and purpose. An individual use-case might require several models with different characteristics.

3.2.1 Process and production development

Process and production development aims at the steps resulting in a process or production and usually have no real-life counterpart in place. Thus, the digital twin is not used in live operation or online in this case, representing the first life-cycle phase of a process. Potential process and production development applications are:

• Process or site design. A process or site is designed for a purpose. A DT can be used for analysis during the design phase enabling better design choices, consensus, and understanding within the team or organization. The DT will also reduce subjectivity and decisions made on the basis of personal opinion or preference.

• Bottleneck analysis. The DT can be used to assess different operational scenarios and thereby identify and aid in investigating bottlenecks. A fully developed DT can be used to monitor bottlenecks and also to identify them faster, which could become a monitoring tool in real-life operation. This is related to what-if analysis.

• Investment decision making. Investment decisions depend on correct insights with regards to processes and production. A DT can lower the investment risk since the outcome could be quantified beforehand. Insights are usually derived by performing different studies for the investment and those studies can be performed in a shorter time and at a lower cost.

• Developing control strategies. Control strategies should be developed using models representing a process, which is rarely available during design. A better performing strategy reduces start-up times and enables well performing processes right from the start. The DT enables the development of control strategies with high confidence on their performance. Tests and trials are immensely reduced. This can be used for a running plant as well.

3.2.2 Process and production control

Process and production control aims to keep a process efficient over its life-cycle and production according to targets. Here, the digital twin is supposed to operate in parallel with the process and provide actionable insights. Typical process and production control applications are:

• Monitoring and diagnostics. Here, the aim is to monitor the process and its operation continuously. Deviations in the process can be detected and related to adverse operating modes or faulty equipment. Deviating process performance can be detected and extended periods with sub-optimal performance can be avoided. The performance can be monitored and related to the theoretical optimum. High level control loop monitoring enables controller adaptation to avoid sub-optimal settings. Monitoring can also be used as a soft sensor providing new data for control purposes.Anomalies from unknown circumstances or events can trigger process development and improved risk management.Monitoring can also target quality from an objective perspective.

• Prediction. The aim of the DT is to predict the production in real-time and one can test how different courses of action will affect the predicted outcome (production). This enables better choices for actions that relate to production efficiency and efficacy.

• Control. The real-time engagement of the DT enables the development of data-driven (machine-learning-based) and self-learning control strategies. The focus is on resource efficiency and renders increased utilization of raw material and generates more income per time unit.

• Real time decision support for process optimization. This application case focus is on the operators and to guide them in their decision making. When the DT is sufficiently validated and guides to the correct actions, autonomous decision making can be started. Thus the DT takes its own decision independently. The application case enables a better decision making in complex situations and the operators can focus their attention on more important tasks.

• Quality and safety. A DT will limit the influence of personal opinions and subjective decision making in production. The DT is also able to perform repeatable in accordance with the best possible line of action.

3.2.3 Production planning

Production planning aims at a plant- or company-wide planning of the production such that an economic optimum is achieved, taking possible constraints into account. A solution can start out from a process or process section to then scale up to the whole plant and company levels. The digital twin should then reflect the product in accordance with the scale and comprise models feasible for economic optimization or plant wide production planning. In particular, specific applications are:

• Holistic optimization. Production is planned such that an economic optimum is achieved on the chosen scale, and thereby limiting sub-optimal production plans.

• Overall equipment efficiency analysis. Overall equipment efficiency (OEE) depends not only on the performance of the plant while it is producing but also when unit processes are loosing uptime. The weakest link is usually the limiting process and reducing OEE. A digital twin than can predict the OEE given different scenarios and unit process availability can provide the needed insights to prioritize the actions/improvements that matter most.

• Optimize maintenance from an overall perspective. Related to OEE but more focusing on maintenance actions. When and where to put effort on a plant-wide scale. The digital twin needs to understand process degradation and from that, predict degraded states to determine an effective maintenance plan. In the long term multiple sites could be considered and their interrelation, but that requires multi-site models for the production system.

3.2.4 Service and maintenance

Service and maintenance aims at efficient and in-time maintenance actions and providing the engineers with information and support on the spot. The specific application cases are:

• Predictive maintenance. Condition-based maintenance where the degraded system condition is foreseen with confidence enables the planning of maintenance actions such that downtime of the asset is minimized and aligned with planned maintenance windows or non-sensitive production. It also facilitates a balanced maintenance approach prolonging process life-cycle while considering cost. On the basis of the both operational and degradation related models in the DT, it is possible to state an optimization problem that is continuously solved by the DT and providing decision support for the engineers and operators.

• Virtual expert assistance. A DT with a descriptive model of the asset can reflect the current state of condition with potential failure or degraded states. Combining virtual or augmented reality technologies, a remote expert (from a supplier or similar) can support the maintenance or corrective action by supervising local personnel.

3.2.5 Education and training

Education and training is essential for operators and engineers to understand the strategies of planning, operation, and maintenance of a process, plant or site. Simulator-based training using a digital twin enables not only the simulation, but also the assessment of the trainees’ performance. Moreover, decided practices can be conveyed in a more realistic manner reducing misunderstandings and limiting decision making on the basis of personal opinion or preference. An up to date DT for a specific site will enable site specific training and the training will remain relevant. Actionable knowledge can thereby be gained in a safe and secure way.

3.3 A mock-up for assessment and readiness

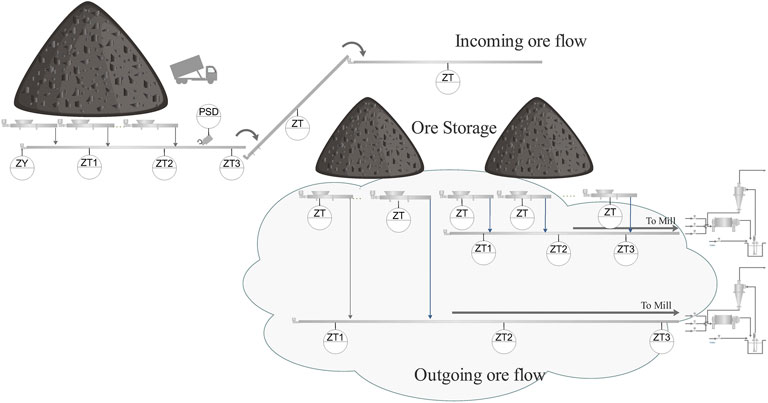
As a specific example, we consider the material transportation to the refining stage including the ore storage at Boliden’s Aitik mine. The ore storage is illustrated in Figure 5. The purpose of a mock-up is to have a specific case to test our assumptions and concepts against. This limited scale pilot plant is used to explore and characterize the pre-requisites and requirements.

FIGURE 5

FIGURE 5. Illustration of the ore storage (Courtesy of Boliden AB).

While this plant can appear relatively simple, the use-case determines the complexity that is encountered when it comes to models and availability of data. Below, two application cases, how they would be supported by an automatically generated digital twin, and their requirements are discussed: Soft sensing with material tracking, and predictive maintenance. The application cases are chosen to reflect two different operations and maintenance aspects.

1) Soft sensing of the material amount and the composition in the ore storage could be treated as a local unit process problem, which is not highly interacting with the prior and later process stages. Moreover, soft sensing is broad and rather unspecified as such and a clear requirement set would be needed. Depending on the physical property that needs to be estimated by the soft sensor, there is either an abundance of models and data available or none at all (see, for example, Lin et al. (2007); Zhang S. et al. (2019)). This variability creates a problem in the automatic model generation part of the digital twin, as there might be model prototypes available or not for the model instantiation.

If no model prototypes are available, then, the automatic generation might fail, as data-driven model generation is the only viable approach depending on labeled data sets and a large amount of historic data. Even the historic data might be fragmented as soft sensing usually targets an issue which has been observed but has not yet been targeted for a solution. An obvious hinder here is the lack of plant information and problem related to data, information, and domain knowledge which is usually represented in the plant information system.

Nevertheless, before fully automated model generation can be realized, a guided approach would be the first step. It would support the user creation of the models rendering prototypes for later similar problems. These models could then be both data-driven or physics-based.

2) Predictive maintenance of the mockup targets an increased availability of the transport and storage system reducing the amount and time of unplanned stops. The models needed to understand the degradation and condition of the assets involved in the transport can be both data-driven models and physics-based models. A good example with the mockup process is the BT2030 conveyor belt system which could be modelled purely on the basis of data that reflects the operation, breakdown characteristics of components and exogenous data. From such data and annotated maintenance information a degradation model could be learned that predicts component condition and remaining useful life.

On the other hand, physics-based degradation models for drums, rollers, the belt, and the drive system could be established on the basis of the mechanical stresses that occur. These models could then be complemented by condition data that is acquired, for example from vibration sensors, and operational data such as bulk feeding, belt speeds, mass distribution, or belt tension. The calibrated models could then be used to estimate the remaining useful life and condition of the assets in the system.

The issue here is the complexity in the derivation of the models and the availability of the needed information that would allow an automated modeling approach. Again, guided modeling could be a first step.

Both cases are affected by similar challenges, while the involved models are very different. The joint challenge for a framework that supports the automated generation is the diversity of the application cases and how to support various modeling approaches with a variety of hyper-parameters. When models are in place and validated for the targeted purpose, then the monitoring and update is somewhat more straightforward. Nevertheless, the automation of that step is still depending on high quality data and a decision making which is not negatively affected by the involved uncertainties, like unmodelled disturbances and the question if the plant has changed or is temporarily affected by faults.

To conclude, the assessment shows that the readiness level is generally low for the needed technologies, both from an organizational as well as from an information perspective.

4 State of the art review

The main focus of this state of the art review is automated DT generation, monitoring, and update in accordance with the building blocks illustrated in Figure 3. Hence, this section first briefly touches upon interoperability as an enabling technology, which is followed by the review of the main components, namely:

• Model generation and approximation,

• model calibration and validation, and

• model monitoring and update.

4.1 Interoperability

Interoperability can be defined as the ability of (IT) systems to interact and collaborate. Hence, when systems are required to work together, interoperability is central. Without standardized interoperability, the solutions are at risk of continuously loosing functionality and requiring continuous updates due to changing interfaces.

International standardization in interoperability has been ongoing for several decades. The oil and gas industry, led by Norway and the USA, has done pioneering standardization work in the area of industrial interoperability. This has lead to the International Standardisation Organisation (ISO) standard ISO 15926 managed by the ISO technical committee (TC) ISO/TC 184/SC 4 (“Industrial data”) (International Standardisation Organisation, 2018a). Currently, ISO 15926 includes the following parts of relevance to this study:

• Part 2: Data Model;

• Part 4: Reference Data;

• Part 7: Templates;

• Part 8: Implementation in RDF;

• Part 9: Triple Store (under development);

• Part 10: Conformance Testing (under development).

One of the core parts in ISO 15926 is Part 4, reference data. It defines the common ground for the information exchange between the different systems and their interoperability based on reference data libraries, with a reference data service hosted by the POSC Caesar Association (POSC Caesar Association, 2021).

In addition to ISO 15926, which defines interoperability of asset data (plant data), the standard ISO 10303 (International Standardisation Organisation, 2014) defines interoperability standards for product data. Furthermore, a combined standard to define the structure is given by the joint International Electrotechnical Commission (IEC)–ISO standard IEC/ISO 81346 (International Standardisation Organisation, 2018b).

Furthermore, the ISO/TS 18101 describes how to integrate a set of existing standards to achieve systems-of-systems interoperability in the oil and gas, petrochemical, power generation, public utilities, and other asset-intensive industries. It incorporates the use of a standardized connectivity architecture and a use-case architecture to describe a supplier-neutral, open industrial digital ecosystem and the interoperability requirements of standardized industry use-cases (International Standardisation Organisation, 2019). The Open Industrial Interoperability Ecosystem (OIIE) provides an example of the proposed, supplier-neutral industrial digital ecosystem. Key inter-enterprise relationships for the process industry digital ecosystem have been modeled in standard use-cases as illustrated in Figure 6 (OpenO and M, 2021).

FIGURE 6

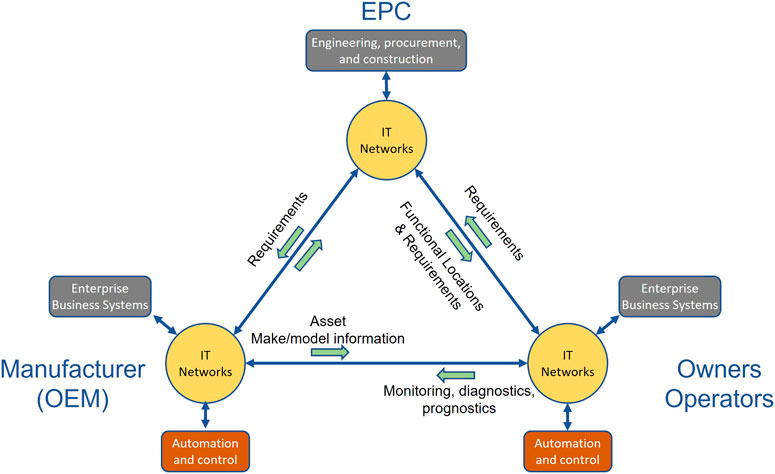
FIGURE 6. OIIE inter-enterprise interoperability architecture OpenO and M, (2021)

In summary, to solve the problem of industry information exchange, standards and reference data are required. In particular, international standards need to be adopted and integrated in our systems, instead of re-inventing new solutions to the same problem.

4.2 Model generation and approximation

The first step in automatically generating a purpose-oriented DT is to generate a (large-scale) process model from several sources of plant description. Such sources include static plant structure information, P&IDs, and component models. The latter may be based on anything ranging from first-principles (white-box) models, hybrid (grey-box) models, or purely machine learning (e.g., deep learning) models. This typically results in a very detailed process model. In fact, the resulting model may be unnecessarily complex for the considered purpose. For example, the model could include a component that depends on an infinite-dimensional partial differential equation model (e.g., from fluid dynamics), which makes the model computationally demanding, even though that component does not contribute significantly to the overall model. Hence, the automatically generated models can be reduced in order to approximate the model to fit the particular purpose of the DT. Naturally, this model approximation step includes the trade-off between simplifying the model structure and keeping the right amount of detail.

The field of automatic model generation and approximation from process and plant information is not new. Significant progress has been made in the past and this is already used in industry to some extent. Below follows a brief overview of these fields. Note that traditional learning of individual component models (e.g., using machine learning or system identification) is not part of model generation in the sense outline here and thus not discussed at this point.

4.2.1 Model generation

The idea of automatic model generation is not new. However, it has only recently gained a significant interest in industry. This trend is probably due to the increased use of model-based design technologies and the emergence of DTs as a transformative technology (Shafto et al., 2012). In the vision of DT, automatic model generation means that models are maintained over the entire life-cycle of the plant in a cost-efficient way (Oppelt et al., 2014). Methods for automatic modeling include the model generation from computer-aided design (CAD) diagrams using, for example, Matlab and Simulink (Hermansson et al., 2018), using information mapping algorithms for automatic generation of models from 3D plant diagrams and equipment information (Santillán Martínez et al., 2018a; Santillán Martínez et al., 2018b), or generation of Modelica models from P&IDs (Cavron et al., 2017).

The abstract structure, behavior, properties, and requirements of a DT model can be defined using a meta-model. Such meta-models can be developed using meta languages such as SysML, which is widely used in various domains (Nikolaidou et al., 2016). Additionally, SysML has recently received many efforts for automatic generation of models. In AutoTwin, meta-models are exploited for automatic model generation by leveraging results of previous projects such as AutoMod-PRE (funded by the Swedish Agency for Innovation Systems; VINNOVA), OPTi (funded by Horizon 2020), and Arrowhead (funded by Horizon 2020).

4.2.2 Model reduction and approximation

A limitation of most traditional analysis, control, and optimization techniques is that they require the availability of certain classes of models such as linear models with low order. This implies that models generated dynamically cannot be directly exploited by such techniques due to their large complexity or model order. Therefore, model reduction must precede the application of the aforementioned techniques. These approximations have to achieve a desired accuracy with a minimum degree of complexity.

In the literature, there are two approaches to decrease the complexity of the models: model simplification and model approximation (Upreti, 2017). In model simplification the following strategies are typically used (Surovtsova et al., 2012; Upreti, 2017): Linearization of non-linear models around operating conditions, scaling analysis to identify and resolve numerical weaknesses, and separation of time scales.

On the other hand, model approximation strategies include:

• Dimensional analysis for reducing the number of variables through representations based of dimensionless numbers such as Mach and Reynolds (Szirtes, 2007),

• parameter number reduction using model fitting methods such as the MIMO ARX–Laguerre model for large-scale processes (Bouzrara et al., 2013),

• model order reduction such as interpolation-based methods (Antoulas et al., 2010) and H₂ optimal model approximation,

• multi-model approaches to replace unique nonlinear representations by a piece-wise combination of linearized models around operating conditions (Elfelly et al., 2012), and

• distillation of knowledge by training a set of machine learning models and compressing them in a single model, such as neural networks (Hinton et al., 2015).

4.3 Model calibration and validation

4.3.1 Background

The parameters of automatically generated digital twin models need to be calibrated for the model to reflect the processes’ operational state and operating point. This is achieved by using an estimation or learning algorithm (Kay, 1993; Van Trees et al., 2013; Gelman et al., 2015), and thus, the problem can be considered a parameter estimation problem. In the context of dynamic systems and control systems, this is also part of system identification (Söderström and Stoica, 1989; Ljung, 1997; Pintelon and Schoukens, 2001). Note, however, that system identification typically also includes design of input and output signals for model identification and model identification itself, and not only estimation of the model parameters.

In particular, a digital twin model is typically parametrized by a set of parameters θ. Then, to calibrate the model, we have to determine the parameters θ given a set of process input-output data ${\{u_n,y_n\}}_{n=1}^N$ to enable purpose-oriented prediction for new input data u_⋆. In general, we can distinguish two approaches for estimating the parameters θ and making predictions for new inputs u_⋆:

1) Approaches that yield a point estimate of the parameters. This is typically the case when using approaches from frequentist statistics such as the least squares or maximum likelihood methods, but also when using parameter regularization, which can be seen as a Bayesian approach. Point estimates are typically easy to implement and computationally efficient but provide no or only limited information about parameter uncertainty. Thus, parameter uncertainty is not taken into account when using the point estimates for prediction. Point estimates are obtained when using optimization-based approaches.

2) Approaches that yield a posterior distribution over the possible parameter values. This is the case when using a fully Bayesian approach and provides richer information about the parameter values themselves, but also takes the parameter uncertainty into account when predicting new outputs. This is at the expense of computational complexity.

4.3.2 Optimization-based calibration

Methods that yield point estimates typically minimize a cost function J(u_1:N, y_1:N; θ) of the data parametrized by the parameters θ, that is,

$\theta =\arg \underset{\theta }{\min }J\left(u_{1:N},y_{1:N};\theta \right).$

Closed form solutions to this type of minimization problems can only be found for a very limited number of models (e.g., linear models). Instead, this often results in a numerical optimization problem, which can be solved using traditional optimization methods such as gradient descent (Gustafsson, 2013), the Gauss–Newton algorithm (Gustafsson, 2013), the Levenberg–Marquart algorithm (Levenberg, 1944; Marquardt, 1963; Nocedal and Wright, 2006), or interior-point methods (Boyd and Vandenberghe, 2004). However, some of these methods require the analytical expressions for the Hessian matrix, which may be difficult to obtain. Instead, so-called quasi-Newton methods such as the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method, may be used (Nocedal and Wright, 2006). Quasi-Newton methods use the gradient evaluations of subsequent iterations to numerically estimate the Hessian, which yields second-order optimization algorithms that only require the gradient. However, either type of optimization approach can be implemented using automatic differentiation (Brücker et al., 2006; Baydin et al., 2018), which does not require manual derivation of the gradient and Hessian matrix.

One particularly important issue when using numerical optimization methods to obtain point estimates of the parameters is the problem of this kind of methods finding local minima of the cost function. However, more recently, stochastic optimization methods have shown that they avoid getting stuck in local minima (Bottou et al., 2018). The basic idea of stochastic optimization methods is to exploit that the cost function J(u_1:N, y_1:N; θ) in many cases can be written as an average of K terms, that is,

$J\left(u_{1:N},y_{1:N};\theta \right)=\frac{1}{K}\sum _{k=1}^K{J}_k\left(u_k,y_k;\theta \right).$

Here, u_k and y_k denote subsets of size M of the whole input-output dataset u_1:N and y_1:K. (Note that if M = 1, we have that K = N and each input-output pair contributes to the cost function independently.) Then, instead of solving one large optimization problem, K smaller optimization problems are solved sequentially, where the parameters θ^(k) at the kth iteration are a function of the current term J_k(u_k, y_k; θ) as well as the previous’ iterations parameters, that is, θ^(k−1).

One of the most prominent stochastic optimization approaches is stochastic gradient descent (SGD), which is the stochastic variant of the ordinary gradient descent method. SGD has successfully been applied to many large-scale parameter estimation problems, for example in training of deep artificial neural networks (Bottou, 2010; Bottou and Bousquet, 2011; Goodfellow et al., 2016). Successful SGD-based methods are, for example, ADAM (Kingma and Ba, 2014) or AdaGrad (McMahan and Streeter, 2010; Duchi et al., 2011).

The sequential nature of the parameter updating strategy of SGD-based methods implies two things. First, the iterative procedure can be interpreted as the solution of an ordinary differential equation (Barrett and Bherin, 2020). This means that this kind of methods could possibly benefit of recent developments in probabilistic differential equation solvers, for example, Bosch et al. (2020); Tronarp et al. (2021). Second, such algorithms can actually be interpreted as a (Kalman) filtering problem (Chen et al., 2020). This implies that this approach can be extended to other approaches of Kalman filtering for nonlinear systems such as unscented or cubature Kalman filtering (Julier and Uhlmann, 2004; Arasaratnam and Haykin, 2009), or more general statistical linear regression approaches (Arasaratnam et al., 2007; García-Fernández et al., 2015). These methods are based on so-called sigma-points, which do not require the analytical expression of the gradient of the cost function, but use numerical integration instead (quadrature). This potentially yields more accurate SGD-type of methods, at the expense of slightly increased computational complexity (which can be alleviated by exploiting model structure, though; Hostettler and Särkkä, (2019)).

From an automated model generation and calibration point of view, stochastic optimization methods are the most promising. This mainly due to the fact that they are more robust towards local minima and the fact that they already have shown great success in calibrating large-scale models in the form of deep artificial neural networks.

Prediction is done by simply using the estimated parameter values in the predictive model. This neglects possible uncertainty in the calibrated parameters and only takes uncertainty of the prediction model into account.

4.3.3 Fully bayesian calibration

A simple form of obtaining Bayesian estimates of the parameters, that is, parameter estimates that are not only based on the data itself but also on any (possibly vague) prior knowledge about the parameters, is by using point estimate methods (i.e., optimization methods) together with cost functions that include a regularizing term (see, e.g., Calvetti and Somersalo, (2018)). This yields the maximum posteriori (MAP) parameter estimate (Kay, 1993). While conceptually simple and easy to implement (the only thing that changes is the cost function, which can be used together with a standard optimization method), this does not leverage the full power of Bayesian methods.

Instead, the full power of Bayesian methods lies in their ability to estimate the posterior distribution of the parameters, that is,

$p\left(\theta \mid y_{1:N}\right)=\frac{p\left(y_{1:N}\mid \theta \right)p\left(\theta \right)}{p\left(y_{1:N}\right)},$

where p(θ) is the parameters prior distribution, p(y_1:N∣θ) the likelihood (measurement model), and p(y_1:N) the marginal likelihood (or evidence) (Gelman et al., 2015). Estimating the posterior distribution rather than a point estimate not only gives the most likely parameter values, but also the uncertainty about the parameters. While conceptually simple, the posterior distribution can not be calculated for most models. Instead, one often has to resort to either assumed density methods or Monte-Carlo-based methods (simulation methods), see Gelman et al. (2015).

Assumed density methods are based on the assumption that the posterior density follows a certain distribution, for example a Gaussian distribution or a Student’s t distribution. This assumption may be valid or not, and entirely depends on the data model. Inference then amounts to estimating the parameters of the posterior distribution. Typical inference methods include the Laplace approximation and integrated nested Laplace approximations (INLA; Rue et al. (2017)), expectation propagation (Minka, 2001), or posterior linearization based on statistical linear regression (Arasaratnam and Haykin, 2009; García-Fernández et al., 2015), mainly for Gaussian assumed density methods (Gaussian densities are particularly interesting because they admit closed-form solutions when the prior is Gaussian and the likelihood is linearized.) Furthermore, variational inference is used in cases when the posterior is assumed to factorize over the different parameters (Blei et al., 2017; Zhang C. et al., 2019), that is,

$p\left(\theta \mid y_{1:N}\right)=\prod _{m=1}^{M}p\left({\theta }_m\mid y_{1:N}\right).$

This is particularly useful when the different parameters have different characteristics and need to be described by different (assumed) posterior distributions.

Monte Carlo methods on the other hand approximate the posterior density not analytically, but by simulation. That is, instead of imposing an assumed posterior density onto the model, the posterior density is approximated by generating (weighted) samples that are (approximately) distributed according to the posterior distribution (Andrieu et al., 2003; Geyer, 2011). This can be achieved by using relatively simple methods such as rejection or importance sampling, or more advanced methods such as Gibbs sampling or the Metropolis–Hastings algorithm (Geyer, 2011; Gelman et al., 2015). Of these, the Metropolis–Hastings algorithm can be widely employed, but great care has to be taken in the choice of the algorithms parameters.

All these approaches can be applied to the problem of high-dimensional models for digital twins. From a practical perspective, assumed density methods are the most practical ones. They might also be sufficient in capturing the problem’s associated uncertainty.

Prediction based on a Bayesian posterior estimate is achieved by marginalizing with respect to the parameters. This yields a prediction which also takes the uncertainty of the parameter estimate, that is, the uncertainty of the calibration into account. This in turn gives a better estimate of the uncertainty of the prediction, compared to point-estimation methods.

4.3.4 Re-calibration

The system’s parameters will inevitably change over time, for example due to varying external conditions or component wear, which requires re-calibration of the parameters. Re-calibration can be achieved in several ways. First, current parameter estimates can be discarded entirely, and a new calibration can be done using one of the approaches discussed above. This is mainly useful in scenarios where large and significant parameter variations can be expected. Otherwise, useful information form the previous calibration is discarded, which increases the uncertainty of the calibration.

Second, the current (outdated) parameter (or posterior) estimate can be used as a regularizing term for the updated parameters. This approach can be developed further such as to actually model the dynamics of the parameters at a relatively slow time-scale, for example as a random walk. Then, sequential Bayesian estimation methods such as filters can be used, which yields an efficient system (Särkkä, 2013). For large-scale systems, assumed density methods (e.g., Gaussian filters) are most directly applicable. From a research perspective, research in high-dimensional sequential Monte Carlo methods is of interest in this context, see, for example, (Septier and Peters, 2015; Septier and Peters, 2016; Naesseth et al., 2019).

4.3.5 Validation

To quantify how well a model is calibrated, the calibration has to be validated. Formally, the basic idea of validation is to analyze the posterior predictive power of a model, that is, to check the capability of a calibrated model to make predictions about other input data. This is achieved by using a dataset that is different from the calibration (or training) data set. The validation dataset may be an entirely different dataset, or a subset of the whole calibration data (cross-validation) (Hastie et al., 2017; Gelman et al., 2015). The former approach ensures a clear separation between calibration and validation, but gives only limited insight into the actual quality of the calibration quality as the validation is only performed on a single validation dataset, which does not provide any uncertainty information about the calibration.

Cross-validation can be divided into two approaches (Hastie et al., 2017; Gelman et al., 2015): Leave-p-out cross-validation and k-fold cross-validation. Leave-p-out cross-validation uses all permutations of the dataset where p datapoints are used for validation and the remaining datapoints for calibration. This is computationally expensive as there are a large number of ways to partition the dataset. A somewhat simplified version (leave-one-out cross-validation; LOO cross-validation) uses p = 1, that is, one datapoint is used for validation and the remaining for calibration. k-fold cross-validation on the other hand divides the dataset into k equally sized subsets. Then, k − 1 subsets are used for calibration and 1 subset is used for validation. This is repeated for all combinations of calibration and validation subsets (i.e., k times) and the results are averaged over the individual runs to obtain the average validation performance and uncertainty. These methods are well-established. However, recent research related to the large-scale digital twin models considered in this project includes the particularities of cross-validation for large data (Magnusson et al., 2019; Magnusson et al., 2020) or uncertainty quantification in model comparison (Sivula et al., 2020).

In the context of large-scale DTs, a major problem lies in the validation objective: A model validated using these validation approaches might yield poor validation performance but still be useful in practice. Hence, the challenge here is to formulate proper requirements and validation criteria to ensure that the model is fit for the particular purpose. This is not straight-forward and should be investigated.

4.4 Model monitoring and update

To ensure the safety and reliability of the systems, prognostic and health management (PHM) is essential. The aims of PHM are as follows (Booyse et al., 2020):

• Detection of anomalous or faulty behavior of the system based on its intrinsic degradation mechanism and operating data,

• diagnostics as differentiating various types of anomalous events or failure modes, and

• prognostics, that is, providing a measure of system health.

Early detection and diagnosis of process faults can help to avoid progressing abnormal events and can reduce productivity loss. In general, the process faults comprise sensor faults, actuator faults, and the faults that can occur in the components or parameters of the plant dynamics. Parameter failures arise when a disturbance enters the process through one or more exogenous variables, for example, a change in the concentration of the reactant from its normal or steady state value in a reactor feed (Venkatasubramanian et al., 2003). Sensor faults (e.g., offset faults and drift faults) typically manifest as additive faults, while actuator faults (e.g., clogging faults and constant gain deviations) manifest as multiplicative faults (He et al., 2019). The PHM system should detect and diagnose faulty events quickly. This characteristic can make it sensitive to high frequency influences and noise. This system should be robust to various noise and uncertainties. Then, there is a trade-off between robustness and performance. PHM strategies have to distinguish between different failures and faults and identify their source. Furthermore, the ability to identify multiple faults is an important but difficult requirement due to the interacting nature of most faults (Venkatasubramanian et al., 2003). The application of DTs in PHM technology consists mainly of condition monitoring, fault diagnosis and prognosis, and remaining useful life prediction (Yu et al., 2021).

Methods for monitoring and fault diagnosis and prognosis can be classified into data-driven, physics-based, and hybrid methods. Data-driven methods rely on statistical models and are including various approaches, such as Bayasian network (Yu et al., 2021), generalized likelihood ratio (GLR) (He et al., 2019), principal component analysis (PCA), partial least squares (PLS) (Ding et al., 2011; Yin et al., 2012), fisher discriminant analysis (FDA) and support vector machine (SVM) (Severson et al., 2016), general soft sensor technologies (Kadlec et al., 2009) and machine learning methods (Zhang and Zhao, 2017; Lu et al., 2018; Pan et al., 2019; Xu et al., 2019; Booyse et al., 2020). Physics-based methods rely on the understanding of the system and the degradation mechanisms and may offer a greater degree of interpretability, reliability, and predictive capability (Magargle et al., 2017; Aivaliotis et al., 2019; Johansen and Nejad, 2019). Considering uncertainty, incompleteness of data and different data distribution in data-driven methods as well as high computational complexity of physics-based approaches in large-scale systems, hybrid methods formed by the combination of the data-driven and physics-based approaches can obtain a more robust health assessment of the system and provide more robust predictions and deal with computational issues (Cubillo et al., 2016).

To ensure that the DT can accurately track the state of the physical system in real-time, it is important to update the DT. Model updating can be studied from various perspectives such as soft sensor adaptation (Kadlec et al., 2011), concept drift adaptation (Gama et al., 2014), state estimation (Maasoumy et al., 2013), adaptive control (Dougherty and Cooper, 2003), and disturbance model adaptation (Wang et al., 2012).

In AutoTwin, DTs need to reflect the state of the asset with the required application accuracy throughout their life-cycle. Thus, it is essential to continuously update the DT to meet the changing needs and improve performance in terms of efficiency, flexibility, and reliability. DT updates can be done manually by a user (e.g., by replacing altered components with updated ones) or automatically. The automatic approach has the advantage that the validity of the DT is not dependent on the user’s knowledge of the process, but on the ability of the DT for self-adaptation (see Tomforde et al. (2014)).

Automatic DT updates can be triggered by several events such as physical component wear, change of components, process reconfiguration, or as a response to extrinsic parameters. Changes in the plant can be identified by the monitoring concept. Monitoring enables the identification of these changes by continuously comparing the output data of DT with those of the real plant and allows to validate that the plant in its actual status still meets all requirements (Zipper et al., 2018). Furthermore, periodic model validation is an essential part of any automatic DT updating scheme in order to validate whether the DT still captures process behaviour accurately (runtime verification; Bu et al. (2011)).

Successful automatic DT updates rely upon the following key aspects: Scope of the update, type of update, and computational paradigm. With respect to the scope of the update, updates can be performed on several layers of the DT, such as component and model parameter updates, or a top-level update in DT structure (Musil et al., 2017). Excessive use of model updates may result in insignificant performance changes (Lee, 2015). With respect to the type of the update, self-adaptation triggered by an external factor such as wear or component change is reactive in nature (Ditzler et al., 2015; Moreno et al., 2015). In contrast, passive adaptation does not require the detection of triggering events. Instead, passive adaptation continuously updates the DT models based on the observed inputs (e.g., sensory data) using methods such as online parameter estimation for component models (Haykin, 2013; Kokkala et al., 2015). Furthermore, the DT update methodology should also consider a horizon of validity of the DT in order to be usable for predictions.

Finally, with respect to the computational paradigm, there is a strong dependency on the use case. Some use cases (e.g., simulation or what-if analysis) require a centralized DT. In such a scenario, all the components of the DT are centrally managed. This also implies that updates of the DT should be managed and performed centrally, with access to all of the DT’s components, models, and data. For other use cases (e.g., monitoring and fault detection or predictive maintenance), however, the DT might be decentralized with its components and models being managed in a distributed manner (e.g., by subsystems). In this case, even the DT update can be performed decentralized (e.g., using edge computing) and the updated components can immediately be used by the corresponding tool chains (see, e.g., McMahan et al. (2017); Stankovic et al. (2011)).

Technical solutions, platforms, and software, in particular, should enable the continuous adaption and evolution of DTs over the long term. There are several methods for updating DTs. The approach applied to update the model depends on the size of the data used for updating and the number of parameters that should be updated. Some of the most common approaches applied to update the models are based on machine learning algorithms, such as optimal trees (Kapteyn et al., 2020b), probabilistic learning on manifolds (Ghanem et al., 2020), or Gaussian processes (Chakraborty and Adhikari, 2021). Due to the modeling ability of artificial neural networks (ANN), they have served as a basic tool for various applications in the process industry. In the context of DTs, adaptive ANNs are used to design the DTs and adapt them over time through continuous learning (Reed et al., 2021). Moreover, Bayesian networks can be employed to create and update the DTs. In these networks, the parameters are updated in some ways, for example, the prior known parameters can be updated in real-time by a Gaussian particle filter, while Dirichlet process mixture models can be applied to update the unknown parameters, making the model have the ability to self-updating the structure (Yu et al., 2021).

Bayesian algorithms are also used for online adaption of DTs and soft sensors through an automatic mechanism of bias updating based on continuous monitoring of the mean and standard deviation of the prediction error (Sangoi et al., 2021). A combination of Bayesian state estimation and a library of component-based models can be applied to create and update data-driven physics-based digital twins (Kapteyn et al., 2020a). The component-based models scale to large and complex assets, while the construction of a model library enables flexible and expressive model adaptation via parametric modification and component replacement.

Furthermore, updating the DTs can be regarded as a solution to an optimization problem that minimizes the difference between the outputs of the DT and the physical system. The optimization algorithms face great challenges to meet the real-time requirements in such cases. If the number of parameters is small, then some optimization approaches such as methods based on parameter sensitivity analysis (Wang et al., 2019) and differential evolution for parameter estimation in a sliding window (Ohenoja et al., 2018; Nikula et al., 2020) may be appropriate. When a system contains high-dimensional variables, large computational overheads and memory issues could lead to inefficient results. In these situations, suitable approaches include decomposing the plant into meaningful blocks associated with a physical unit and using adaptive identification methods for every block (He et al., 2019), model order reduction (Chinesta et al., 2011; Quarteroni and Rozza, 2014; Kapteyn et al., 2020b; Chinesta et al., 2020), or using surrogate models or meta models (Yang et al., 2016; Nikula et al., 2020; Chakraborty et al., 2021).

5 Suggested research activities

On the basis of the use-cases, the needed technologies, and the state of the art, a way forward to achieve automated generation and update of digital twins can be sketched out. The way forward looks at the needed technologies from the perspective of technology readiness and what research and development is still required together with the complexity of the task ahead.

Note that, as already pointed out before, access to complete data and plant information are essential for any of the modeling approaches that are targeted by AutoTwin. The information does not need to be stored in a centralized way, but needs to be accessible for the technologies. This requires solutions for information storage, exchange and sharing between the different tools (see, for example, Mogos et al. (2019)). During the mock-up study it was confirmed that complete plant information is a challenge onward and also a limiting factor to achieve automated modeling for digital twins. The development, deployment, and usage of a plant information system is complex, both from a technical and organizational perspective, and also hard to foresee when it is in place. There are also commercial solutions available which at least partly provide the needed features. Hence, this aspect is out of the scope of this paper and it is therefore assumed that a plant information system is available and that the developed technologies are setting up requirements for such a plant information system.

There are also numerous ongoing research, development, and standardization activities that focus on plant information systems and interoperability, and will thus not be focused on here.

5.1 Activities

From the gap analysis following the state-of-the-art analysis and the insights created by the mock-up study, the research and development activities in Table 2 should be prioritized. Each of the activities by itself aims at methods and tool capable of rendering a certain degree of autonomy for a DT. This means the degree of supervision needed by the user or the guidance that the user receives in the engineering task differs. In order to achieve full autonomy, gaining the trust of the user is essential and depends largely on the achieved performance of the methods or tools during the validation or testing.

TABLE 2

TABLE 2. Proposed research and development activities.

5.2 Roadmap

The research activities themselves do not provide insights on how the vision of the framework depicted in Figure 2 can be achieved. The technologies view in Figure 3 provides a decomposition where the individual components can be realized by manual, guided and automated engineering efforts and a combination of those, enabling a development roadmap focusing on continuous value creation. For each of the technologies, three levels of autonomy are therefore foreseen:

• Manual means that the engineering efforts are conducted in a manual fashion. For online technologies it means that manual monitoring, decision making, and updating are realized,

• Guided means that the engineering efforts are supported by tools that perform analysis and provide insights that guide the engineer in their efforts to achieve good results. For online technologies it means that the monitoring is automated to some degree and that decision support is provided.

• Autonomous means that the engineering efforts are fully automated and eventual decision making is done by the technologies themselves. Both offline and online technologies should exhibit the same behavior with no need for user interaction.

Thus, activities 1 and 2 can be performed independently of 3–5 as the latter could be operated on manually engineered digital twins and their embedded models, minimizing risks for long research activities with little industrial benefits. Further, the basic idea of the roadmap is a bottom-up approach, meaning the technologies needed for the online operation of DTs over a longer time period need to be addressed first and need to achieve autonomy first.

The outset for the roadmap is now the availability of a plant information system and manual engineering efforts representing the needed technologies and extends from there as follows.

1) Guided Monitoring and Validation. Systematic description of validation criteria for models on the basis of use-case requirements will enable automated assessment of models where the user is guided in the selection of data and interpretation of the outcomes. The remaining technologies will be conducted in manual engineering mode for both online and offline.

2) Autonomous Monitoring and Self-Correction. The monitoring will then be further matured to allow for an autonomous approach that will also capture the ability to update the local models while in operation. The initial DT is manually engineered such that the models are possible to be used in self-correction. The requirements on the models to enable autonomous self-correction will be investigated and established. This step also includes the validation of purpose oriented models.

3) Guided Calibration and Update. The monitoring will generate triggers for update mechanisms not possible to accommodate by the self-correction. The algorithms used in the self-correction will serve as a foundation to create update and calibration algorithms that guide the user. There will be numerous hyper-parameters that need to be set and data selection for the update and calibration need to be performed. The experience from the engineering in setting these parameters will enable the development of autonomous versions of these algorithms. The prerequisites for methodologies feasible for both, a guided or autonomous operation, will be investigated and established. The applicable methodologies might set up requirements on the modeling paradigms that are used. The scope will be on purpose-oriented models and it needs to be investigated to what degree the approach can become generic.

4) Autonomous Calibration and Update. The algorithms will be further developed to allow for autonomy of the calibration and update for purpose oriented models. Autonomy might only be achieved for certain purpose oriented models which need to be investigated and clarified. This step requires the involvement of the user to understand the requirements for autonomy and to build trust in the technology.

5) Guided Model Instantiation. The technology relates to activity 2 and can be developed in parallel with the prior steps. Purpose-oriented model generation depends on the use case and the requirements on the models. Similarly, the model instantiation depends on the plant information system and the availability of modeling information. The user will be provided with guidance on which information is needed for the model generation and instantiation and will be guided through the process of hyper-parameter selection. The resulting models need to be compatible with the calibration and validation. The objectives for the calibration and validation are also prepared here and the user is guided. It need to be investigated which model types and paradigms can be used in the model instantiation and generation.

6) Guided Meta Model Generation. Similar to the model instantiation a guided approach for the model generation is a first step, where the user interacts with the technology and in part performs the engineering efforts manually. The base of the development is on available technologies which solve the problem in part or for specific case studies. The resulting learnings on requirements and scope aid in the further development to autonomy. In the guided approach the user will be provided with choices to generate the meta model of a process of varying size and complexity. The principles to engineer the requirements for the model generation will be investigated and established.

7) Autonomous meta model generation and model instantiation. The requirements engineering step will be further developed to result in requirements feasible for the meta model generation. The requirements remain a manual engineering effort as those are essential along the complete technology chain. The guided algorithms will be further developed to achieve autonomy where the setting of the hyper-parameters for the algorithms is no longer needed. Again, the trust of the user in the technology and its explainability need to be thoroughly investigated.

8) Integrated technologies. While the requirements are the key to the interoperability of the technologies, the integration might impose additional requirements on the information that is generated within the technologies and exchanged between. The integrated framework need to be benchmarked and validated, although the individual technologies have been validated already.

During all steps of the roadmap, benchmarking and validation of the resulting technologies need to accompany the research and development activities. Pilot studies should specifically focus on the value creation of the technologies and the quantification of the increase in availability of digital twins. Life-cycle aspects are essential to be investigated.

6 Conclusion

The aim of this study was to understand the research and development challenges when it comes to the use of digital twins for estimation and control of process industrial systems. The paper first unveiled the complex nature of a digital twin which is sometimes merely understood as a simulation model with visualization capabilities for engineered systems of any kind, especially when the digital twin should remain relevant over the life cycle of a process industrial system. The key result of the assessment is the introduction of a framework that comprises interacting technologies that need to be in place to enable digital twins for process industrial systems.

One of the most important aspects of digital twins is the generation and update of them. While they can be engineer similar to the process industrial system itself, the automation of these steps is crucial to not only make them available in the first place but also to keep them relevant as tedious manual labor is not an option for large scale systems. The value creation that becomes possible when they are available with up-to-date embedded models of the real-life counter part is immense as virtually all model-based methodologies in process automation and control become applicable. The most relevant use-cases for such digital twins have then been discussed and also highlight the direction for the gap analysis and state of the art review.

For the needed technologies the state of the art is reviewed where several gaps are identified hindering an efficient use of digital twins for estimation and control. Subsequently, suggested research activities or topics are summarized and organized in a roadmap towards the automated model generation and update of process industrial digital twins. It can be in general concluded that manual model generation and update is possible given the available methodologies, while guided and automated approaches still require substantial research to be conducted.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors are grateful for the financial support provided for the AutoTwin-PRE project funded by VINNOVA within the PiiA Program under grant number 2020-02816.

Acknowledgments

Further, the authors want to thank our industry partners Johannes Sikström, and David Degerfeldt from Boliden AB, Göran Tuomas from LKAB, Erik Molin from SEIIA, Johannes Hölmström from Calejo Industrial Intelligence AB, Peter Lingman from Optimation AB for their insights and contributions to the project. We are also grateful to Petter Kyösti and Pär-Erik Martinsson from ProcessIT Innovations at Luleå University of Technology for hosting the project.

Conflict of interest

Author WB was employed by company Predge AB. Author RT was employed by Boliden Mines Technology.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aivaliotis, P., Georgoulias, K., and Chryssolouris, G. (2019). The use of Digital Twin for predictive maintenance in manufacturing. Int. J. Comput. Integr. Manuf. 32 (11), 1067–1080. doi:10.1080/0951192x.2019.1686173

CrossRef Full Text | Google Scholar

Andrieu, C., de Freitas, N., Doucet, A., and Jordan, M. I. (2003). An introduction to MCMC for machine learning. Mach. Learn. 50, 5–43. doi:10.1023/a:1020281327116

CrossRef Full Text | Google Scholar

Antoulas, A. C., Beattie, C. A., and Gugercin, S. (2010). “Interpolatory model reduction of large-scale dynamical systems,” in Efficient modeling and control of large-scale systems (Springer).

CrossRef Full Text | Google Scholar

Arasaratnam, I., and Haykin, S. (2009). Cubature kalman filters. IEEE Trans. Autom. Contr. 54 (6), 1254–1269. doi:10.1109/tac.2009.2019800

CrossRef Full Text | Google Scholar

Arasaratnam, I., Haykin, S., and Elliott, R. J. (2007). Discrete-time nonlinear filtering algorithms using Gauss–Hermite quadrature. Proc. IEEE 95 (5), 953–977. doi:10.1109/jproc.2007.894705

CrossRef Full Text | Google Scholar

Barrett, D. G. T., and Bherin, B. (2020). Implicit gradient regularization. arXiv. doi:10.48550/ARXIV.2009.11162

CrossRef Full Text | Google Scholar

Baydin, A. G., Pearlmutter, B. A., Andreyevich Radul, A., and Siskind, J. M. (2018). Automatic differentiation in machine learning: A survey. J. Mach. Learn. Reasearch 18, 1–43.

Google Scholar

Birk, W., Hostettler, R., Razi, M., and Atta, K. (2021). Automatic generation and updating of purpose-oriented process industrial digital twins - A roadmap. Available at: https://sip-piia.se/om-piia/piia-insight/(accessed 05 27, 2022).

Google Scholar

Blei, D. M., Kucukelbir, A., and McAuliffe, J. D. (2017). Variational inference: A review for statisticians. J. Am. Stat. Assoc. 112 (518), 859–877. doi:10.1080/01621459.2017.1285773

CrossRef Full Text | Google Scholar

Booyse, W., Wilke, D. N., and Heyns, S. (2020). Deep digital twins for detection, diagnostics and prognostics. Mech. Syst. Signal Process. 140, 106612. doi:10.1016/j.ymssp.2019.106612

CrossRef Full Text | Google Scholar

Bosch, N., Henning, P., and Tronarp, F. (2020). Calibrated adaptive probabilistic ODE solvers. arXiv. doi:10.48550/ARXIV.2012.08202

CrossRef Full Text | Google Scholar

Boschert, S., and Rosen, R. (2016). “Digital twin — the simulation aspect,” in Mechatronic futures. Editors P. Hehenberger, and D. Bradley (Cham, Switzerland: Springer).

Google Scholar

Bottou, L., and Bousquet, O. (2011). “The tradeoffs of large scale learning,” in Optimization for machine learning. Editors S. Sra, S. Nowozin, and S. J. Wright (MIT Press), 351–368.

Google Scholar

Bottou, L., Curtis, F. E., and Nocedal, J. (2018). Optimization methods for large-scale machine learning. SIAM Rev. Soc. Ind. Appl. Math. 60 (2), 223–311. doi:10.1137/16m1080173

CrossRef Full Text | Google Scholar

Bottou, L. (2010). “Large-scale machine learning with stochastic gradient descent,” in International conference on computational statistics (COMPSTAT). Editors Y. Lechevallier, and G. Saporta.

CrossRef Full Text | Google Scholar

Bouzrara, K., Garna, T., Ragot, J., and Messaoud, H. (2013). Online identification of the ARX model expansion on Laguerre orthonormal bases with filters on model input and output. Int. J. Control 86, 369–385. doi:10.1080/00207179.2012.732710

CrossRef Full Text | Google Scholar

Boyd, S., and Vandenberghe, L. (2004). Convex optimization. Cambridge, UK: Cambridge University Press.

Google Scholar

Brücker, H. M., Corliss, G., Hovland, P., Naumann, U., and Norris, B. (2006). Automatic differentiation: Applications, theory, and impelementations 50. Heidelberg, Germany: Springer.

Google Scholar

Bu, L., Wang, Q., Chen, X., Wang, L., Zhang, T., Zhao, J., et al. (2011). Toward online hybrid systems model checking of cyber-physical systems’ time-bounded short-run behavior. SIGBED Rev. 8, 7–10. doi:10.1145/2000367.2000368

CrossRef Full Text | Google Scholar

Calvetti, D., and Somersalo, E. (2018). Inverse problems: From regularization to Bayesian inference. WIREs Comp. Stat. 10, e1427. doi:10.1002/wics.1427

CrossRef Full Text | Google Scholar

Cavron, J., Rauffet, P., Kesraoui, D., Berruet, P., Bignon, A., and Prat, S. (2017). “An automated generation approach of simulation models for checking control/monitoring system,” in 20th IFAC world congress, 6202–6207.

CrossRef Full Text | Google Scholar

Chakraborty, S., Adhikari, S., and Ganguli, R. (2021). The role of surrogate models in the development of digital twins of dynamic systems. Appl. Math. Model. 90, 662–681. doi:10.1016/j.apm.2020.09.037

CrossRef Full Text | Google Scholar

Chakraborty, S., and Adhikari, S. (2021). Machine learning based digital twin for dynamical systems with multiple time-scales. Comput. Struct. 243, 106410. doi:10.1016/j.compstruc.2020.106410

CrossRef Full Text | Google Scholar

Chen, R. T. Q., Choi, D., Balles, L., Duvenaud, D., and Henning, P. (2020). Self-tuning stochastic optimization with curvature-aware gradient filtering. arXiv. doi:10.48550/ARXIV.2011.04803

CrossRef Full Text | Google Scholar

Chinesta, F., Cueto, E., Abisset-Chavanne, E., Duval, J. L., and El Khaldi, F. (2020). Virtual, digital and hybrid twins: A new paradigm in data-based engineering and engineered data. Arch. Comput. Methods Eng. 27, 105–134. doi:10.1007/s11831-018-9301-4

CrossRef Full Text | Google Scholar

Chinesta, P., Ladeveze, P., and Cueto, E. (2011). A short review on model order reduction based on Proper Generalized Decomposition. Arch. Comput. Methods Eng. 18, 395–404. doi:10.1007/s11831-011-9064-7

CrossRef Full Text | Google Scholar

Cubillo, A., Perinpanayagam, S., Rodriguez, M., Collantes, I., and Vermeulen, J. (2016). “Prognostics health management system based on hybrid model to predict failures of a planetary gear transmission,” in Machine learning for cyber physical systems. Editors O. Niggemann, and J. Beyerer (Berlin, Heidelberg, Germany: Springer), 33–44.

CrossRef Full Text | Google Scholar

Ding, S. X., Zhang, P., Jeinsch, T., Ding, E. L., Engel, P., and Gui, W. (2011). “A survey of the application of basic data-driven and model-based methods in process monitoring and fault diagnosis,” in The 18th IFAC world congress (Milano, Italy, 12380–12388.

CrossRef Full Text | Google Scholar

Ditzler, G., Roveri, M., Alippi, C., and Polikar, R. (2015). Learning in nonstationary environments: A survey. IEEE Comput. Intell. Mag. 10, 12–25. doi:10.1109/mci.2015.2471196

CrossRef Full Text | Google Scholar

Dougherty, D., and Cooper, D. (2003). A practical multiple model adaptive strategy for single loop MPC. Control Eng. Pract. 11 (2), 141–159. doi:10.1016/s0967-0661(02)00106-5

CrossRef Full Text | Google Scholar

Duchi, J., Hazan, E., and Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 12 (61), 2121–2159.

Google Scholar

Elfelly, N., Dieulot, J. Y., Benrejeb, M., and Borne, P. (2012). A multimodel approach for complex systems modeling based on classification algorithms. Int. J. Comput. Commun. Control 7, 645. doi:10.15837/ijccc.2012.4.1364

CrossRef Full Text | Google Scholar

Gama, J., Žliobaitė, I., Bifet, A., Pechenizkiy, M., and Bouchachia, A. (2014). A survey on concept drift adaptation. ACM Comput. Surv. 46 (4), 1–37. doi:10.1145/2523813

CrossRef Full Text | Google Scholar

García-Fernández, A. F., Svensson, L., Morelande, M. R., and Särkkä, S. (2015). Posterior linearization filter: Principles and implementation using sigma points. IEEE Trans. Signal Process. 63 (20), 5561–5573. doi:10.1109/tsp.2015.2454485

CrossRef Full Text | Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2015). Bayesian data analysis. New York, NY: Chapmen, and Hall/CRC Press.

Google Scholar

Geyer, C. J. (2011). “Introduction to Markov chain Monte Carlo,” in Handbook of Markov chain Monte Carlo. Editors S. Brooks, A. Gelman, G. L. Jones, and X.-L. Meng (Chapman and Hall/CRC).

CrossRef Full Text | Google Scholar

Ghanem, R., Soize, C., Mehrez, L., and Aitharaju, V. (2020). Probabilistic learning and updating of a digital twin for composite material systems. Int. J. Numer. Methods Eng. 123, 3004–3020. doi:10.1002/nme.6430

CrossRef Full Text | Google Scholar

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep learning. Cambridge, Massachusetts: MIT Press.

Google Scholar

Gustafsson, F. (2013). Statistical sensor fusion. 2 edition. Lund, Sweden: Studentlitteratur AB.

Google Scholar

Hastie, T., Tibshirani, R., and Friedman, J. (2017). The elements of statistical learning: Data mining, inference, and prediction. New York, NY: Springer.

Google Scholar

Haykin, S. O. (2013). Adaptive filter theory. Pearson Education, Essex, England: Pearson.

Google Scholar

He, R., Chen, G., Dong, C., Sun, S., and Shen, X. (2019). Data-driven digital twin technology for optimized control in process systems. ISA Trans. 95, 221–234. doi:10.1016/j.isatra.2019.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Hermansson, K., Kos, C., Starfelt, F., Kyprianidis, K., Lindberg, C. F., Zimmerman, N., et al. (2018). An automated approach to building and simulating dynamic district heating networks. IFAC-PapersOnLine 51, 855–860. doi:10.1016/j.ifacol.2018.04.021

CrossRef Full Text | Google Scholar

Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling the knowledge in a neural network. arXiv preprint. doi:10.48550/ARXIV.1503.02531

CrossRef Full Text | Google Scholar

Hostettler, R., and Särkkä, S. (2019). Rao–blackwellized Gaussian smoothing. IEEE Trans. Autom. Contr. 64 (1), 305–312. doi:10.1109/tac.2018.2828087

CrossRef Full Text | Google Scholar

International Standardisation Organisation (2014). ISO 10303: Industrial automation systems and integration — product data representation and exchange. Geneva, Switzerland: ISO Standard.

Google Scholar

International Standardisation Organisation (2018a). ISO 15926: Industrial automation systems and integration — integration of life-cycle data for process plants including oil and gas production facilities. Geneva, Switzerland: ISO Standard.

Google Scholar

International Standardisation Organisation (2018b). ISO 81346: Industrial systems, installations and equipment and industrial products — structuring principles and reference designations. Geneva, Switzerland: ISO Standard.

Google Scholar

International Standardisation Organisation (2019). ISO 18101: Automation systems and integration — oil and gas interoperability. Geneva, Switzerland: ISO Standard.

Google Scholar

Johansen, S. S., and Nejad, A. R. (2019). “On digital twin condition monitoring approach for drivetrains in marine applications,” in ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2019) Glasgow, Scotland, UK.

CrossRef Full Text | Google Scholar

Julier, S. J., and Uhlmann, J. K. (2004). Unscented filtering and nonlinear estimation. Proc. IEEE 92 (3), 401–422. doi:10.1109/jproc.2003.823141

CrossRef Full Text | Google Scholar

Kadlec, P., Gabrys, B., and Strandt, S. (2009). Data-driven soft sensors in the process industry. Comput. Chem. Eng. 33 (4), 795–814. doi:10.1016/j.compchemeng.2008.12.012

CrossRef Full Text | Google Scholar

Kadlec, P., Grbić, R., and Gabrys, B. (2011). Review of adaptation mechanisms for data-driven soft sensors. Comput. Chem. Eng. 35 (1), 1–24. doi:10.1016/j.compchemeng.2010.07.034

CrossRef Full Text | Google Scholar

Kapteyn, M., Knezevic, D., Huynh, D., Tran, M., and Willcox, K. (2020a). Data-driven physics-based digital twins via a library of component-based reduced-order models. Int. J. Numer. Methods Eng. 123, 2986–3003. doi:10.1002/nme.6423

CrossRef Full Text | Google Scholar

Kapteyn, M., Knezevic, D., and Willcox, K. (2020b). Toward predictive digital twins via component-based reduced-order models and interpretable machine learning in 2020 AIAA SciTech Forum and Exhibition Orlando, FL.

Kay, S. M. (1993). Fundamentals of statistical signal processing: Estimation theory. Upper Saddle River, NJ, USA: Prentice-Hall.

Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: A method for stochastic optimization. arXiv. doi:10.48550/ARXIV.1412.6980

CrossRef Full Text | Google Scholar

Kokkala, J., Solin, A., and Särkkä, S. (2015). Sigma-point filtering and smoothing based parameter estimation in nonlinear dynamic systems. J. Adv. Inf. Fusion 11, 15–30. doi:10.48550/ARXIV.1504.06173

CrossRef Full Text | Google Scholar

Krivoshapkina, E. F., Mikhaylov, V. I., Perovskiy, I. A., Torlopov, M., Ryabkov, Y. I., Krivoshapkin, P. V., et al. (2019). The effect of cellulose nanocrystals and pH value on the flotation process for extraction of minerals. J. Solgel. Sci. Technol. 92 (2), 319–326. doi:10.1007/s10971-019-04983-8

CrossRef Full Text | Google Scholar

Lee, E. A. (2015). The past, present and future of cyber-physical systems: A focus on models. Sensors 15, 4837–4869. doi:10.3390/s150304837

PubMed Abstract | CrossRef Full Text | Google Scholar

Levenberg, K. (1944). A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 2 (2), 164–168. doi:10.1090/qam/10666

CrossRef Full Text | Google Scholar

Lin, B., Recke, B., Knudsen, J. K., and Jørgensen, S. B. (2007). A systematic approach for soft sensor development. Comput. Chem. Eng. 31 (5), 419–425. doi:10.1016/j.compchemeng.2006.05.030

CrossRef Full Text | Google Scholar

Liu, Z., Meyendorf, N., and Mrad, N. (2018). The role of data fusion in predictive maintenance using digital twin. AIP Conf. Proc. 1949, 020023. doi:10.1063/1.5031520

CrossRef Full Text | Google Scholar

Ljung, L. (1997). System identification: Theory for the user. Upper Saddle River, NJ, USA: Prentice-Hall.

Google Scholar

Lu, W., Li, Y., Cheng, Y., Meng, D., Liang, B., Zhou, P., et al. (2018). Early fault detection approach with deep architectures. IEEE Trans. Instrum. Meas. 67 (7), 1679–1689. doi:10.1109/tim.2018.2800978

CrossRef Full Text | Google Scholar

Maasoumy, M., Moridian, B., Razmara, M., Shahbakhti, M., and Sangiovanni-Vincentelli, A. (2013). “Online simultaneous state estimation and parameter adaptation for building predictive control,” in ASME 2013 Dynamic Systems and Control Conference Palo Alto, USA.

CrossRef Full Text | Google Scholar

Magargle, R., Johnson, L., Mandloi, P., Davoudabadi, P., Kesarkar, O., Krishnaswamy, S., et al. (2017). “A simulation-based digital twin for model-driven health monitoring and predictive maintenance of an automotive braking system,” in the 12th International Modelica Conference Prague, Czech Republic, 35–46.

CrossRef Full Text | Google Scholar

Magnusson, M., Andersen, M., Jonasson, J., and Vehtari, A. (2019). “Bayesian leave-one-out cross-validation for large data,” in 36th International Conference on Machine Learning (ICML), 4244–4253.

Google Scholar

Magnusson, M., Vehtari, A., Jonasson, J., and Andersen, M. (2020). “Leave-one-out cross-validation for Bayesian model comparison in large data,” in 23rd International Conference on Artificial Intelligence and Statistics (AISTATS), 341–351.

Google Scholar

Marquardt, D. (1963). An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Industrial Appl. Math. 11 (2), 431–441. doi:10.1137/0111030

CrossRef Full Text | Google Scholar

McMahan, B., Moore, E., Ramage, D., Hampson, S., and Agüera y Arcas, B. (2017). “Communication-efficient learning of deep networks from decentralized data,” in 20th International Conference on Artificial Intelligence and Statistics, 1273–1282.54

Google Scholar

McMahan, H. B., and Streeter, M. (2010). Adaptive bound optimization for online convex optimization. arXiv. doi:10.48550/ARXIV.1002.4908

CrossRef Full Text | Google Scholar

Minka, T. P. (2001). “Expectation propagation for approximate Bayesian inference,” in 17th Conference on Uncertainty in Artificial Intelligence (UAI), 362–369.

Google Scholar

Minos-Stensrud, M., Haakstad, O. H., Sakseid, O., Westby, B., and Alcocer, A. (2018). “Towards automated 3D reconstruction in SME factories and digital twin model generation,” in 18th International Conference on Control (Automation and Systems ICCAS), 1777–1781.

Google Scholar

Mogos, M. F., Eleftheriadis, R. J., and Myklebust, O. (2019). Enablers and inhibitors of industry 4.0: Results from a survey of industrial companies in Norway. Procedia CIRP 81, 624–629. doi:10.1016/j.procir.2019.03.166

CrossRef Full Text | Google Scholar

Moreno, G. A., Cámara, J., Garlan, D., and Schmerl, B. (2015). “Proactive self-adaptation under uncertainty: A probabilistic model checking approach,” in 10th Joint Meeting on Foundations of Software Engineering, 1–12.

CrossRef Full Text | Google Scholar

Musil, A., Musil, J., Weyns, D., Bures, T., Muccini, H., and Sharaf, M. (2017). “Patterns for self-adaptation in cyber-physical systems,” in Multi-Disciplinary Engineering for Cyber-Physical Production Systems. Editors S. Biffl, A. Lüder, and D. Gerhard (Springer), 331–368.

CrossRef Full Text | Google Scholar

Naesseth, C. A., Lindsten, F., and Schön, T. B. (2019). High-dimensional filtering using nested sequential Monte Carlo. IEEE Trans. Signal Process. 67 (16), 4177–4188. doi:10.1109/tsp.2019.2926035

CrossRef Full Text | Google Scholar

Nikolaidou, M., Kapos, G.-D., Tsadimas, A., Dalakas, V., and Anagnostopoulos, D. (2016). Challenges in SysML model simulation. Adv. Comput. Sci. Int. J. 5 (4), 49–56.

Google Scholar

Nikula, R.-P., Paavola, M., Ruusunen, M., and Joni, K.-R. (2020). Towards online adaptation of digital twins. Open Eng. 10 (1), 776–783. doi:10.1515/eng-2020-0088

CrossRef Full Text | Google Scholar

Nocedal, J., and Wright, S. J. (2006). Numerical optimization. New York, NY: Springer.

Google Scholar

Ohenoja, M., Ruusunen, M., Koistinen, A., Kaartinen, J., Paaso, J., Isokangas, A., et al. (2018). Towards mineral beneficiation process chain intensification. IFAC-PapersOnLine 51 (21), 201–206. doi:10.1016/j.ifacol.2018.09.418

CrossRef Full Text | Google Scholar

OpenO and M (2021). Open industrial interoperability ecosystem (OIIE) specification. Available at: http://openoandm.org/standards (accessed 05 27, 2021).

Google Scholar

Oppelt, M., Wolf, G., Drumm, O., Lutz, B., Stöß, M., Urbas, L., et al. (2014). Automatic model generation for virtual commissioning based on plant engineering data. In 19th IFAC Proceedings, 11635–11640. doi:10.3182/20140824-6-za-1003.01512

CrossRef Full Text | Google Scholar

Pan, Z., Li, J., Chen, Y., Hariri, S., Pacheco, J., and Song, X. (2019). Digital twin for fault detection based on hybrid neural networks. Int. J. Inf. Technol. 25 (2), 1–16.

Google Scholar

Pintelon, R., and Schoukens, J. (2001). System identification: A frequency domain approach. Piscataway, NJ, USA: Wiley-IEEE Press.

Google Scholar

POSC Caesar Association (2021). Reference data services. Available at: https://www.posccaesar.org/wiki/Rds (accessed 05 27, 2021).

Google Scholar

Quarteroni, A., and Rozza, G. (2014). Reduced order methods for modeling and computational reduction. Springer Switzerland: Springer.

Google Scholar

Reed, S., Löfstrand, M., and Andrews, J. (2021). Modelling stochastic behaviour in simulation digital twins through neural nets. J. Simul., 1–14. doi:10.1080/17477778.2021.1874844

CrossRef Full Text | Google Scholar

Rosen, R., Fischer, J., and Boschert, S. (2019). “Next generation digital twin: An ecosystem for mechatronic systems?,” in 8th IFAC Symposium on Mechatronic Systems (MECHATRONICS), 265–270.52

CrossRef Full Text | Google Scholar

Rue, H., Riebler, A., Sørbye, S. H., Illian, J. B., Simpson, D. P., Lindgren, F. K., et al. (2017). Bayesian computing with INLA: A review. Annu. Rev. Stat. Appl. 4 (1), 395–421. doi:10.1146/annurev-statistics-060116-054045

CrossRef Full Text | Google Scholar

Sangoi, E., Sanseverinatti, C. I., Clementi, L. A., and Vega, J. R. (2021). A Bayesian bias updating procedure for automatic adaptation of soft sensors. Comput. Chem. Eng. 147, 107250. doi:10.1016/j.compchemeng.2021.107250

CrossRef Full Text | Google Scholar

Santillán Martínez, G., Sierla, S., Karhela, T., and Vyatkin, V. (2018a). “Automatic generation of a simulation-based digital twin of an industrial process plant,” in 44th Annual Conference of the IEEE Industrial Electronics Society (IECON), 3084–3089.

Google Scholar

Santillán Martínez, G., Sierla, S. A., Karhela, T. A., Lappalainen, J., and Vyatkin, V. (2018b). Automatic generation of a high-fidelity dynamic thermal-hydraulic process simulation model from a 3D plant model. IEEE Access 6, 45217–45232. doi:10.1109/access.2018.2865206

CrossRef Full Text | Google Scholar

Särkkä, S. (2013). Bayesian filtering and smoothing. Cambridge, UK: Cambridge University Press.

Google Scholar

Septier, F., and Peters, G. W. (2015). “An overview of recent advances in Monte-Carlo methods for Bayesian filtering in high-dimensional spaces,” in Theoretical aspects of spatial-temporal modeling. Editors G. W. Peters, and T. Matsui (Tokyo: Springer Japan), 31–61.

CrossRef Full Text | Google Scholar

Septier, F., and Peters, G. W. (2016). Langevin and Hamiltonian based sequential MCMC for efficient Bayesian filtering in high-dimensional spaces. IEEE J. Sel. Top. Signal Process. 10 (2), 312–327. doi:10.1109/jstsp.2015.2497211

CrossRef Full Text | Google Scholar

Severson, K., Chaiwatanodom, P., and Braatz, R. D. (2016). Perspectives on process monitoring of industrial systems. Annu. Rev. Control 42, 190–200. doi:10.1016/j.arcontrol.2016.09.001

CrossRef Full Text | Google Scholar

Shafto, M., Conroy, M., Doyle, R., Glaessgen, E., Kemp, C., LeMoigne, J., et al. (2012). Modeling, simulation, information technology and processing roadmap. Washington, DC: National Aeronautics and Space Administration NASA Headquarters.

Google Scholar

Sierla, S., Sorsamäki, L., Azangoo, M., Villberg, A., Hytönen, E., Vyatkin, V., et al. (2020). Towards semi-automatic generation of a steady state digital twin of a brownfield process plant. Appl. Sci. 10, 6959. doi:10.3390/app10196959(19)

CrossRef Full Text | Google Scholar

Sivula, T., Magnusson, M., Matamoros, A., and Vehtari, A. (2020). Uncertainty in bayesian leave-one-out cross-validation based model comparison. arXiv. doi:10.48550/ARXIV.2008.10296

CrossRef Full Text | Google Scholar

Söderström, T., and Stoica, P. (1989). System identification. Upper Saddle River, NJ: Prentice–Hall International.

Google Scholar

Stankovic, S. S., Stankovic, M. S., and Stipanovic, D. M. (2011). Decentralized parameter estimation by consensus based stochastic approximation. IEEE Trans. Autom. Contr. 56, 531–543. doi:10.1109/tac.2010.2076530

CrossRef Full Text | Google Scholar

Surovtsova, I., Simus, N., Hübner, K., Sahle, S., and Kummer, U. (2012). Simplification of biochemical models: A general approach based on the analysis of the impact of individual species and reactions on the systems dynamics. BMC Syst. Biol. 6, 14. doi:10.1186/1752-0509-6-14

PubMed Abstract | CrossRef Full Text | Google Scholar

Szirtes, T. (2007). Applied dimensional analysis and modelling. 2 edition. Burlington, MA: Butterworth-Heinemann.

Google Scholar

Tomforde, S., Hähner, J., von Mammen, S., Gruhl, C., Sick, B., and Geihs, K. (2014). “Know thyself - Computational self-reflection in intelligent technical systems,” in 8th IEEE International Conference on Self-Adaptive and Self-Organizing Systems Workshops, 150–159.

Google Scholar

Tronarp, F., Särkkä, S., and Henning, P. (2021). Bayesian ODE solvers: The maximum a posteriori estimate. Statistics Comput.. 31 (3), 23. doi:10.1007/s11222-021-09993-7

CrossRef Full Text | Google Scholar

Upreti, S. (2017). Process modeling and simulation for chemical engineers: Theory and practice. Chichester, West Sussex: John Wiley and Sons.

Google Scholar

Van Trees, H. L., Bell, K. L., and Tian, Z. (2013). Detection, estimation, and modulation theory: Part 1: Detection, estimation, and filtering theory. 2 edition. Hoboken, NJ, USA: John Wiley and Sons.

Google Scholar

Venkatasubramanian, V., Rengaswamy, R., Yin, K., and Kavuri, S. N. (2003). A review of process fault detection and diagnosis: Part I: Quantitative model-based methods. Comput. Chem. Eng. 27 (3), 293–311. doi:10.1016/s0098-1354(02)00160-6

CrossRef Full Text | Google Scholar

Wang, J., Ye, L., Gao, R. X., Li, C., and Zhang, L. (2019). Digital twin for rotating machinery fault diagnosis in smart manufacturing. Int. J. Prod. Res. 57 (12), 3920–3934. doi:10.1080/00207543.2018.1552032

CrossRef Full Text | Google Scholar

Wang, W., Zhao, J., and Xu, Z. (2012). “On parameter design for predictive control with adaptive disturbance model,” in the 31st Chinese Control Conference (China: Hefei), 4160–4165.

Google Scholar

Wright, L., and Davidson, S. (2020). How to tell the difference between a model and a digital twin. Adv. Model. Simul. Eng. Sci. 7, 13. doi:10.1186/s40323-020-00147-4

CrossRef Full Text | Google Scholar

Xu, Y., Sun, Y., Liu, X., and Zheng, Y. (2019). A digital-twin-assisted fault diagnosis using deep transfer learning. IEEE Access 7, 19990–19999. doi:10.1109/access.2018.2890566

CrossRef Full Text | Google Scholar

Yang, Z., Eddy, D., Krishnamurty, S., Grosse, I., Denno, P., and Lopez, F. (2016). “Investigating predictive metamodeling for additive manufacturing,” in ASME 2016 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE 2016), Charlotte North Carolina, USA.

CrossRef Full Text | Google Scholar

Yin, S., Ding, S. X., Haghani, A., Hao, H., and Zhang, P. (2012). A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 22 (9), 1567–1581. doi:10.1016/j.jprocont.2012.06.009

CrossRef Full Text | Google Scholar

Yu, J., Song, Y., Tang, D., and Dai, J. (2021). A Digital Twin approach based on nonparametric Bayesian network for complex system health monitoring. J. Manuf. Syst. 58, 293–304. doi:10.1016/j.jmsy.2020.07.005

CrossRef Full Text | Google Scholar

Zhang, C., Bütepage, J., Kjellström, H., and Mandt, S. (2019). Advances in variational inference. IEEE Trans. Pattern Anal. Mach. Intell. 41 (8), 2008–2026. doi:10.1109/tpami.2018.2889774

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Chu, F., Deng, G., and Wang, F. (2019). Soft sensor model development for cobalt oxalate synthesis process based on adaptive Gaussian mixture regression. IEEE Access 7, 118749–118763. doi:10.1109/access.2019.2936542

CrossRef Full Text | Google Scholar

Zhang, Z., and Zhao, J. (2017). A deep belief network based fault diagnosis model for complex chemical processes. Comput. Chem. Eng. 107, 395–407. doi:10.1016/j.compchemeng.2017.02.041

CrossRef Full Text | Google Scholar

Zipper, H., Auris, F., Strahilov, A., and Paul, M. (2018). “Keeping the digital twin up-to-date — Process monitoring to identify changes in a plant,” in IEEE International Conference on Industrial Technology (ICIT), 1592–1597.

Google Scholar