
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Control Eng. , 10 January 2023
Sec. Control and Automation Systems
Volume 3 - 2022 | https://doi.org/10.3389/fcteg.2022.1083419
This article is part of the Research Topic Advances in the Control of Dead-time processes and applications View all 4 articles
Proportional–integral–derivative (PID) control is a durable control technology that has been widely applied in the process control industry. However, PID controllers cannot achieve satisfactory performance for oscillatory systems with long time delays; thus, high-order controllers like the proportional–integral–double derivative (
Proportional–integral–derivative (PID) control is a durable control technology that has been widely applied in the process control industry (Kim and Lee, 2021). The principal reason is its relatively simple structure, which can be easily implemented, understood, and maintained in practical industry production processes. PID is so wildly used in process control system applications, and it is one of the important factors in the development of the industry (Borase et al., 2021). Hence, most studies in the field of process control have only focused on PID control, which includes intelligent PID (Chan et al., 2007; Gundes and Ozguler, 2007), fuzzy PID (Tzafestas and Papanikolopoulos, 1990; Jin et al., 2017), optimal PID (Halikias and Zolotas, 1999; Chao et al., 2019; Memon and Shao, 2020; Memon and Shao, 2021), adaptive PID control (Radke and Isermannt, 1987; Pan et al., 2007), and fractional-order PID (Zhao et al., 2005; Chevalier et al., 2019).
It is well-known that the oscillatory dynamics of the process have various features, and parameter tuning is complicated and difficult. To facilitate research, the oscillatory dynamics of the process can be modeled as the standard second-order process with a dead-time (SOPDT) model. Up to now, research on the tuning of the SOPDT system has been mostly restricted to PID. Weng et al. (1997) derived the tuning formula of the PID controller based on the gain and phase margin for the underdamped oscillatory system. The user-specified gain and phase margins can be adaptively achieved, but the trade-off optimization between stability and tracking performance is not designed. Wang et al. (1999) proposed a PID controller parameter tuning method based on the closed-loop pole assignment strategy of the root locus for the oscillatory system; the parameter design process is more complicated. Huang et al. (2000) proposed an inverse-based synthesis PID controller for the oscillatory system and analyzed its robustness by the gain and phase margins. However, the effect of noise was not considered. Basilio and Matos (2002) designed the PID controller for the underdamping system, but the controlled plant did not account for dead time. Oliveira and Vrančić (2012) addressed the problem of decreasing the overshoot by switching controllers for underdamped second-order systems, which is not convenient for practical engineering applications. Kurokawa et al. (2020) proposed an optimal trade-off PID control system for a SOPDT system, which does not consider the impact of measurement noise. The aforementioned literature reports are devoted to the study of the controller from the perspective of the frequency domain. Although some research has been carried out on PID controllers, it is still unclear whether or not PID can effectively handle oscillatory process uncertainties like disturbance and measurement noise. Furthermore, it may be necessary to manually adjust the PID controller for the step response of the oscillatory process through trial and error, which may inevitably result in inaccuracies. More importantly, it is difficult for the conventional PID controller to guarantee the stability of the oscillatory process with a time delay. The scenario is quite different from the step response of the non-oscillatory plant, where numerous well-known formulas exist (Lee et al., 1998; Skogestad and Grimholt, 2012; Garpinger et al., 2014). Therefore, it would be desirable if there are tuning criteria for the oscillatory plant with time delays to improve the performance of systems.
As an example, consider the following oscillatory system with a time delay (
The dynamic response of SOPDT under the conventional PID (Huang et al., 2000) is shown in Figure 1 when a unit step reference signal (the amplitude is 1) is inserted at
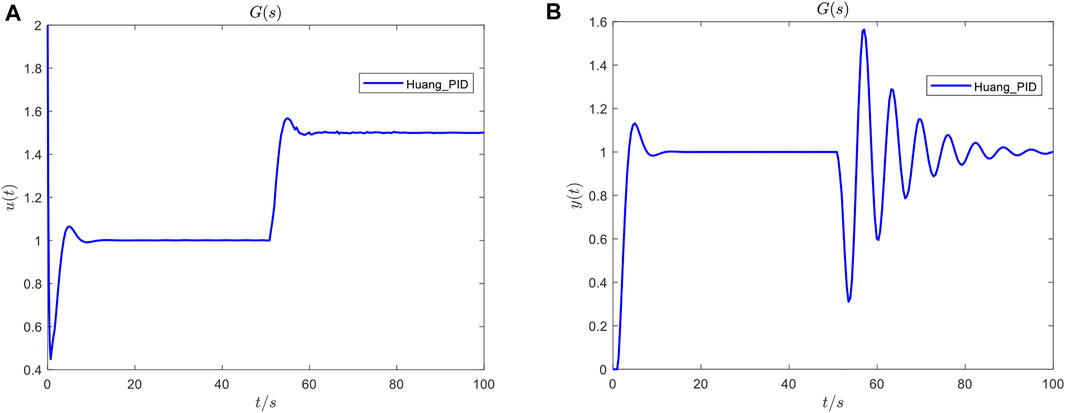
FIGURE 1. Dynamic response of the SOPDT model under PID: (A) controller output responses and (B) system output responses.
To improve the performance of conventional PID, a new conventional controller named the proportional−integral−double derivative (
For practical implementation issues, we will investigate a state-space
The rest of the paper consists of four parts. In Section 2,
A PID controller has been frequently utilized in the industry due to its simplicity and efficiency. The
where
Here,
The state vector is as follows:
The state-feedback gain is as follows:
The state vector
Let
Then, Eq. 7 can be written in the following state-space form:
where
Thus, the following Luenberger observer can be used to estimate
where
If
By combining Eq. 11 and Eq. 13, we have an estimation of the state vector of Eq. 5 with the following observer:
where
When
Hence, the third-order state-space PID is the implementation of
So the feedback controller from
Figure 2 shows the structural block diagram of the third-order state-space PID (SS-
The dynamics of the oscillatory SOPDT system is relatively complicated, and the controller parameter design process faces severe challenges. In general, the low-order controller often neglects the higher-order dynamics of oscillatory systems. Thus, the result of the control effect is not accurate (Wang et al., 2021). The well-known internal model control has the advantage of using one or two tuning parameters to achieve good control performance to model inaccuracies (Shamsuzzoha and Lee, 2007, p.). Therefore, in this section, we will discuss in detail how the parameters of the SS-
Figure 3 shows the structural block diagram of the two-degree-of-freedom IMC (TDF-IMC) controller.
We can divide the design process of the TDF-IMC controller into the following steps (Tan and Fu, 2015):
1) Factor the plant model
where
2) Design the set-point tracking controller
where
Here,
3) The disturbance rejection controller
where
The corresponding transfer function of the IMC controller is as follows:
By designing the IMC controller, we can get the controller gain of SS-
The controllers
Here, the order of the disturbance rejection filter
From the aforementioned derivation, the final form of Eq. 25 is given as follows:
From the aforementioned analysis, we can cancel the roots of
Then, the simplified form of Eq. 29 becomes
where the expression of
This subsection focuses on how to attain the parameters of SS-
According to the aforementioned Eq. 19, the transfer function form of SS-
where
To make the SS-
where
Thus, the controller gain of SS-
The final parameters of SS-
The performance of the IMC controller is decided by the parameters
In the process of calculating the parameters of SS-
To describe the detailed derivation process of the tuning formula, suppose
where
The corresponding function expressions are given in Eq. 42:
So we can rewrite Eq. 42 as follows:
When
where
The corresponding function expressions are given in Eq. 45:
Similar to Eq. 44, we can obtain the following:
When
In practice, the relationship between
As a result, combining Eqs 43−47, we can obtain the following tuning formula of SS-
Similarly, using the same process, we can obtain the tuning formula when
This section demonstrates the tuning formula for several examples. In every simulation example, a different control effect has been analyzed and compared with existing methods.
Simple second-order oscillatory plants with damping ratios
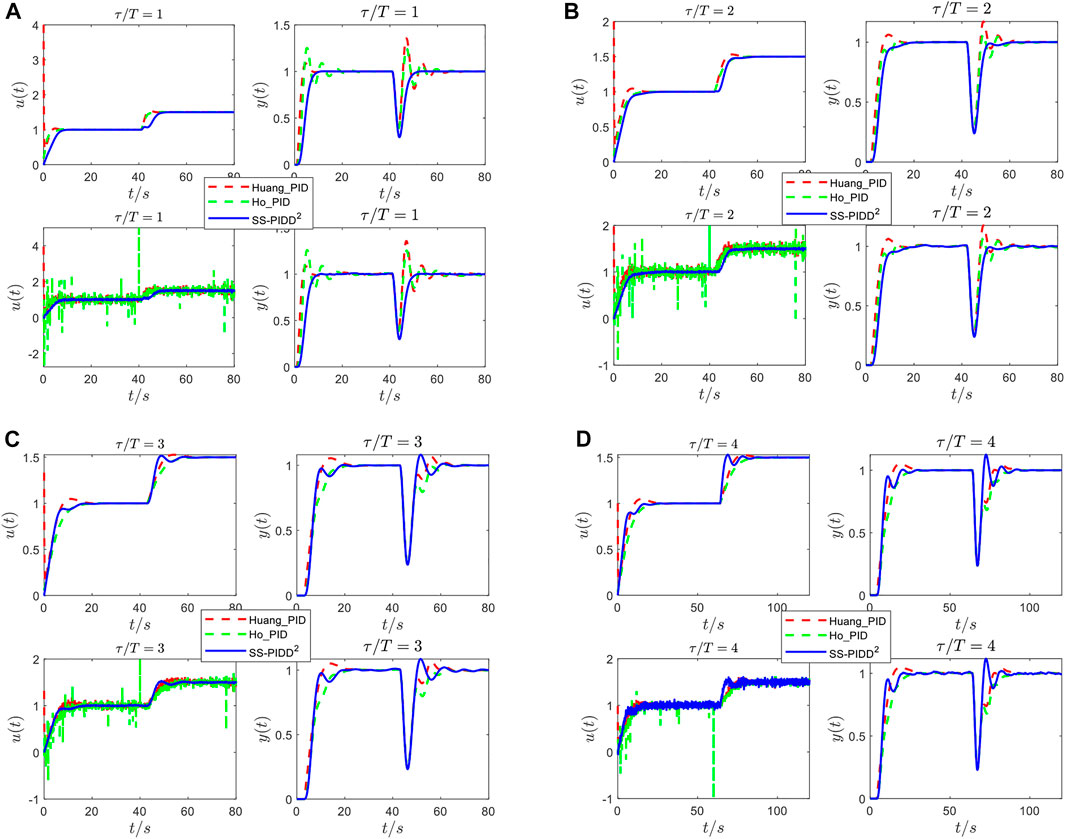
FIGURE 9. Responses of the SOPDT system with ξ = .2 under different controllers: controller output responses without noise [the top left of (A–D)]; system output responses without noise [the top right of (A–D)]; controller output responses with noise [the bottom left of (A–D)]; (B) system output responses with noise [the bottom right of (A–D)].
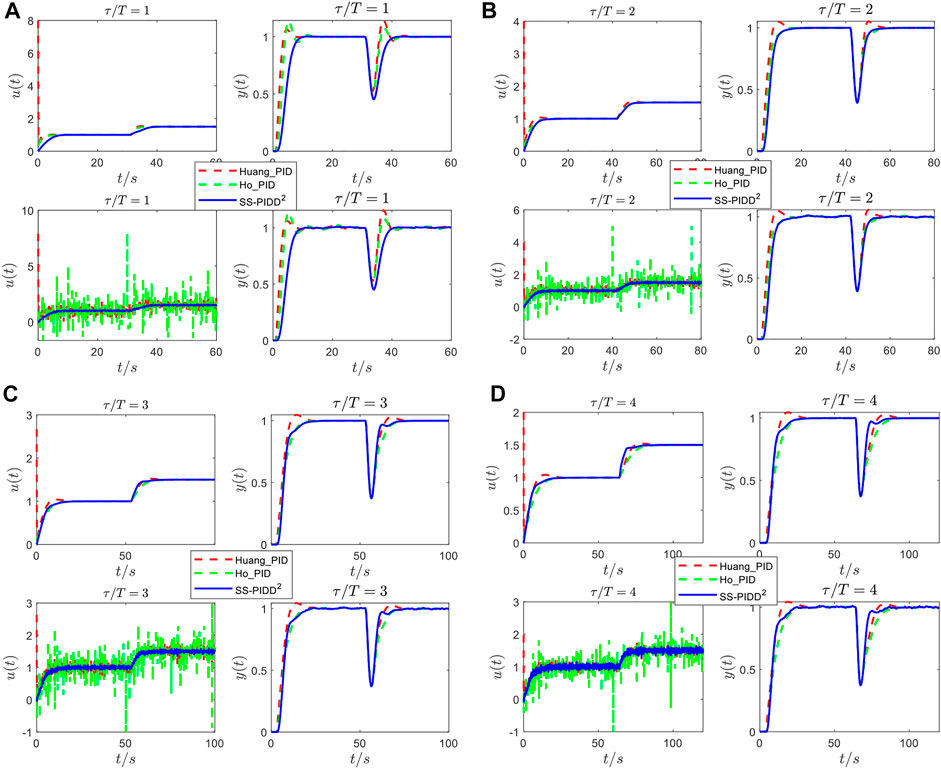
FIGURE 10. Responses of the SOPDT system with ξ = 0.4 under different controllers: controller output responses without noise [the top left of (A–D)]; system output responses without noise [the top right of (A–D)]; controller output responses with noise [the bottom left of (A–D)]; (B) system output responses with noise [the bottom right of (A–D)].
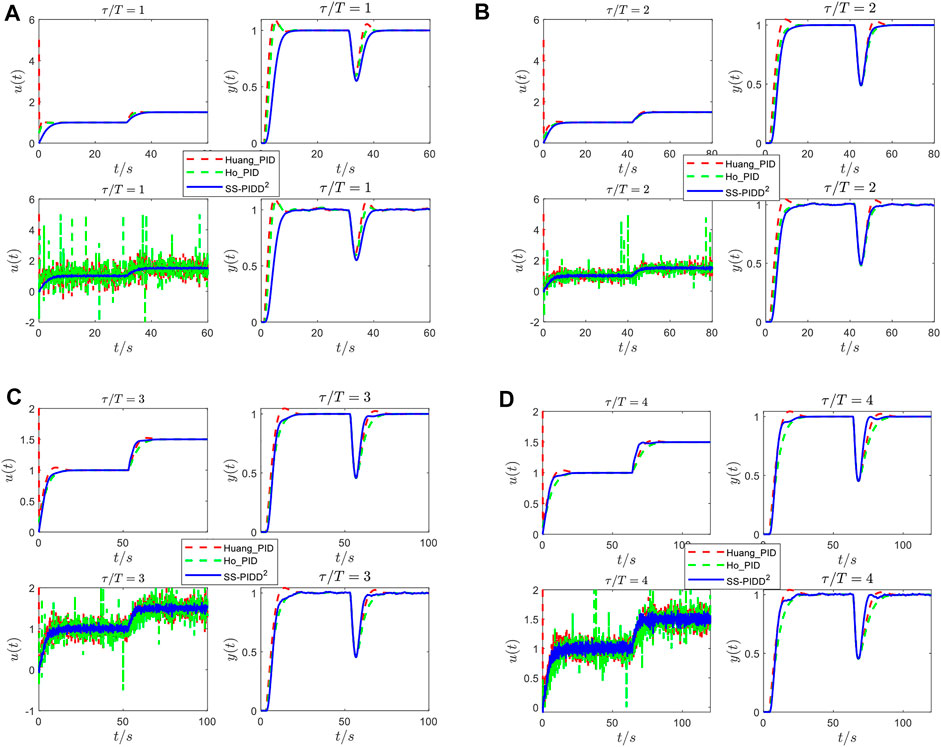
FIGURE 11. Responses of the SOPDT system with ξ = 0.6 under different controllers: controller output responses without noise [the top left of (A–D)]; system output responses without noise [the top right of (A–D)]; controller output responses with noise [the bottom left of (A–D)]; (B) system output responses with noise [the bottom right of (A–D)].
Remark: 1) Robustness is the property that a control system maintains for some other performance under certain (structure and size) parameter perturbations.
where
2) ITSE is the integral of the time squared error.
3) TV is the total variation in the output of the controller.
In this subsection, we use three relatively complex oscillatory plants (
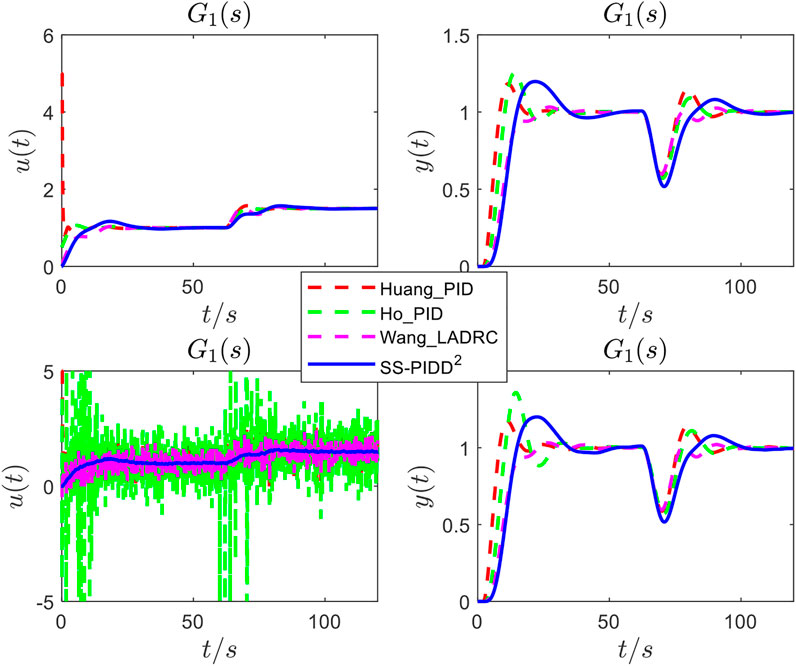
FIGURE 12. Responses of
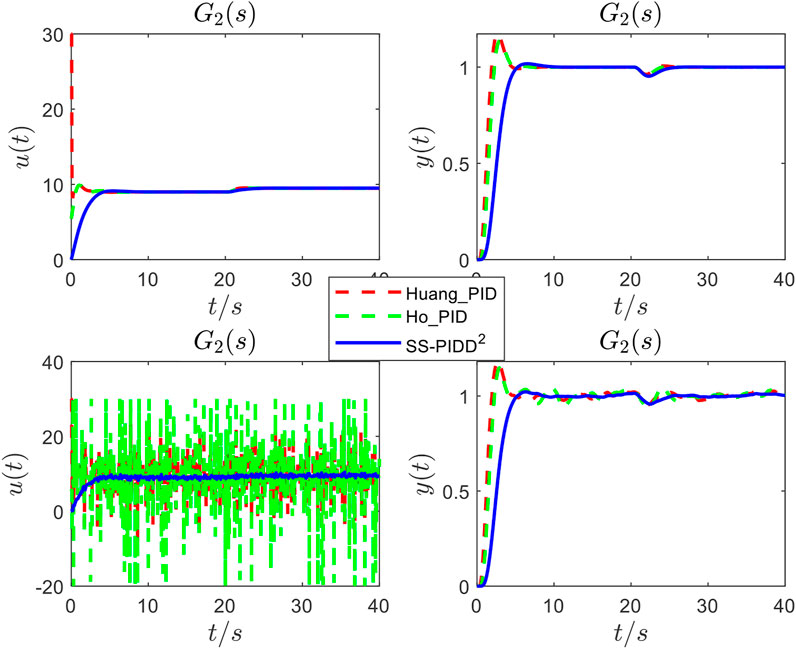
FIGURE 13. Responses of
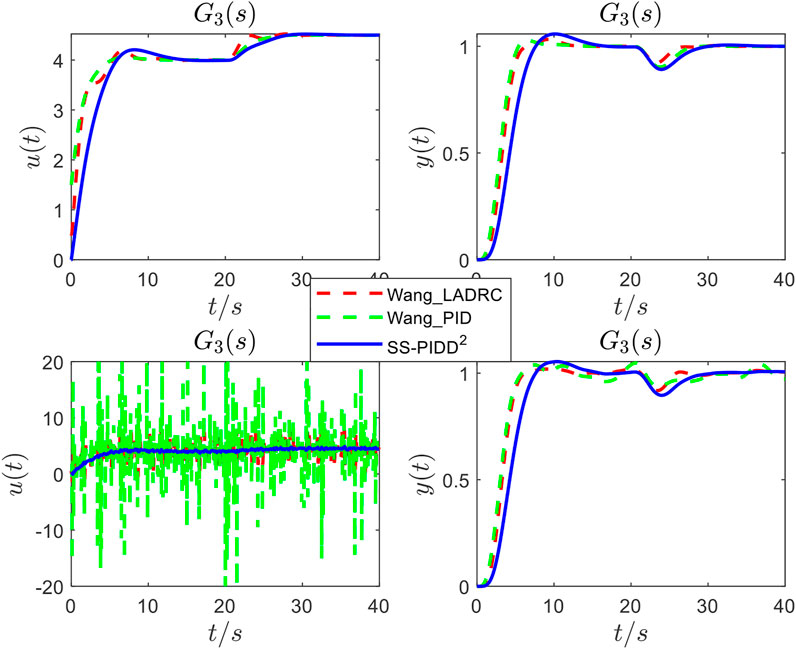
FIGURE 14. Responses of
Consider the load frequency control system as a typical oscillatory SOPDT system. Additionally, the system’s uncertainty and control complexity will rise due to communication delays. Therefore, the proposed SS-
To illustrate the issue, we take the one-area non-reheat system as an example (Fu and Tan, 2018). The transfer function model of the LFC system is shown in Figure 15. The transfer function of each part is as follows:
and
The system parameters are as follows (Fu and Tan, 2018):
Suppose there is a disturbance of
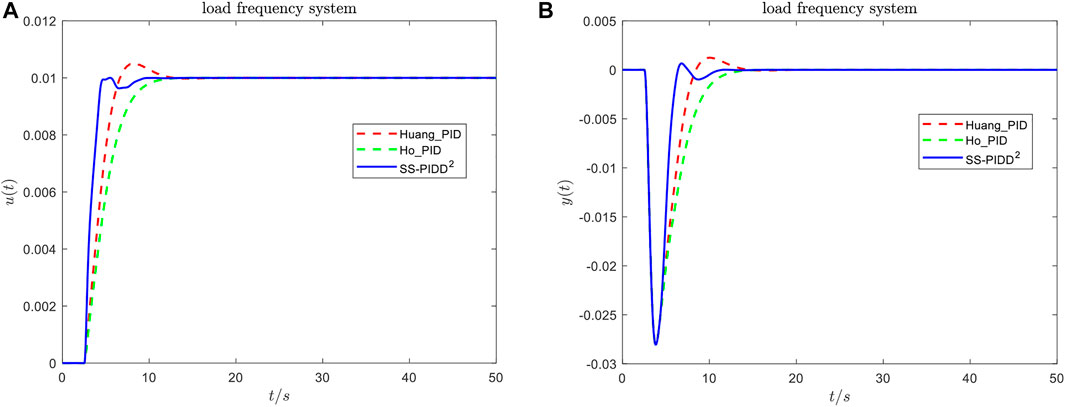
FIGURE 16. System responses under different controllers: (A) controller output responses and (B) system output responses.
The purpose of this paper was to provide a tuning formula of the
The empirical findings in this study provide a new understanding of
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
HX, HG, and TW contributed to the conceptualization and methodology. HX wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Basilio, J. C., and Matos, S. (2002). Design of PI and PID controllers with transient performance specification. IEEE Trans. Educ. 45, 364–370. doi:10.1109/te.2002.804399
Borase, R. P., Maghade, D. K., Sondkar, S. Y., and Pawar, S. N. (2021). A review of PID control, tuning methods and applications. Int. J. Dynam. Control 9, 818–827. doi:10.1007/s40435-020-00665-4
Chan, Y. F., Moallem, M., and Wang, W. (2007). Design and implementation of modular FPGA-based PID controllers. IEEE Trans. Ind. Electron. 54, 1898–1906. doi:10.1109/tie.2007.898283
Chao, C.-T., Sutarna, N., Chiou, J.-S., and Wang, C.-J. (2019). An optimal fuzzy PID controller design based on conventional PID control and nonlinear factors. Appl. Sci. 9, 1224. doi:10.3390/app9061224
Chatterjee, S., Dalel, M. A., and Palavalasa, M., 2019. “Design of PID plus second order derivative controller for automatic voltage regulator using whale optimizatio algorithm,” in 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), NOIDA, India, 10-11 October 2019 (IEEE), 574–579.Presented at the 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE).
Chevalier, A., Francis, C., Copot, C., Ionescu, C. M., and De Keyser, R. (2019). Fractional-order PID design: Towards transition from state-of-art to state-of-use. ISA Trans. 84, 178–186. doi:10.1016/j.isatra.2018.09.017
Farooq, Z., Rahman, A., and Lone, S. A. (2021). “Fuzzy and MBO optimized load frequency control of hybrid power system,” in 2021 IEEE 18th India Council International Conference (INDICON). Presented at the 2021 IEEE 18th India Council International Conference (INDICON), Guwahati, India, 19-21 December 2021 (IEEE), 1–6.
Fu, C., and Tan, W. (2018). Decentralised load frequency control for power systems with communication delays via active disturbance rejection. IET Generation, Transm. Distribution 12, 1397–1403. doi:10.1049/iet-gtd.2017.0852
Gao, Z. (2003). “Scaling and bandwidth-parameterization based controller tuning,” in Proceedings of the 2003 American Control Conference, 2003, Denver, CO, USA, 04-06 June 2003 (IEEE), 4989–4996. Presented at the 2003 American Control Conference.
Garpinger, O., Hägglund, T., and Åström, K. J. (2014). Performance and robustness trade-offs in PID control. J. Process Control 24, 568–577. doi:10.1016/j.jprocont.2014.02.020
Gundes, A. N., and Ozguler, A. B. (2007). PID stabilization of MIMO plants. IEEE Trans. Autom. Contr. 52, 1502–1508. doi:10.1109/tac.2007.902763
Halikias, G. D., and Zolotas, A. C. (1999). Optimal design of PID controllers using the QFT method. IEE Proc. - Control Theory Appl. 146, 585–589. doi:10.1049/ip-cta:19990746
Horn, I. G., Arulandu, J. R., Gombas, C. J., VanAntwerp, J. G., and Braatz, R. D. (1996). Improved filter design in internal model control. Ind. Eng. Chem. Res. 35, 3437–3441. doi:10.1021/ie9602872
Huang, H.-P., Jeng, J.-C., and Luo, K.-Y. (2005). Auto-tune system using single-run relay feedback test and model-based controller design. J. Process Control 15, 713–727. doi:10.1016/j.jprocont.2004.11.004
Huang, H.-P., Lee, M.-W., and Chen, C.-L. (2000). Inverse-based design for a modified PID controller. J. Chin. Inst. Chem. Eng. 31, 225–236.
Jin, Z., Chen, J., Sheng, Y., and Liu, X. (2017). Neural network based adaptive fuzzy PID-type sliding mode attitude control for a reentry vehicle. Int. J. Control Autom. Syst. 15, 404–415. doi:10.1007/s12555-015-0181-1
kalyan, C. N. S., and Suresh, C. V. (2021). “PIDD controller for AGC of nonlinear system with PEV integration and AC-DC links,” in 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 21-23 January 2021 (IEEE), 1–6. Presented at the 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET).
Kalyan, C. N. S. (2021). “UPFC and SMES based coordinated control strategy for simultaneous frequency and voltage stability of an interconnected power system,” in 2021 1st International Conference on Power Electronics and Energy (ICPEE), Bhubaneswar, India, 02-03 January 2021 (IEEE), 1–6. Presented at the 2021 1st International Conference on Power Electronics and Energy (ICPEE).
Kim, M., and Lee, S.-U. (2021). PID with a switching action controller for nonlinear systems of second-order controller canonical form. Int. J. Control Autom. Syst. 19, 2343–2356. doi:10.1007/s12555-020-0346-4
Koley, I., Sarkar, B., Datta, A., and Panda, G. K. (2020). “Load frequency control of a wind energy integrated multiarea power system with CSA tuned PIDD controller,” in 2020 IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 25-26 September 2020 (IEEE), 1–6. Presented at the 2020 IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC).
Kurokawa, R., Sato, T., Vilanova, R., and Konishi, Y. (2020). Design of optimal PID control with a sensitivity function for resonance phenomenon-involved second-order plus dead-time system. J. Frankl. Inst. 357, 4187–4211. doi:10.1016/j.jfranklin.2020.03.015
Lee, Y., Park, S., Lee, M., and Brosilow, C. (1998). PID controller tuning for desired closed-loop responses for SI/SO systems. AIChE J. 44, 106–115. doi:10.1002/aic.690440112
Memon, F., and Shao, C. (2020). An optimal approach to online tuning method for PID type iterative learning control. Int. J. Control Autom. Syst. 18, 1926–1935. doi:10.1007/s12555-018-0840-0
Memon, F., and Shao, C. (2021). Robust optimal PID type ILC for linear batch process. Int. J. Control Autom. Syst. 19, 777–787. doi:10.1007/s12555-019-1033-1
Mohanty, B. (2020). Hybrid flower pollination and pattern search algorithm optimized sliding mode controller for deregulated AGC system. J. Ambient. Intell. Hum. Comput. 11, 763–776. doi:10.1007/s12652-019-01348-5
Mohanty, B. (2018). Performance analysis of moth flame optimization algorithm for AGC system. Int. J. Model. Simul. 39 (1), 1–15. 16. doi:10.1080/02286203.2018.1476799
Mokeddem, D., and Mirjalili, S. (2020). Improved Whale Optimization Algorithm applied to design PID plus second-order derivative controller for automatic voltage regulator system. J. Chin. Inst. Eng. 43, 541–552. doi:10.1080/02533839.2020.1771205
Oliveira, P. B. M., and Vrančić, D. (2012). Underdamped second-order systems overshoot control. IFAC Proc. Vol. 45, 518–523. doi:10.3182/20120328-3-it-3014.00088
Pan, T., Li, S., and Cai, W.-J. (2007). Lazy learning-based online identification and adaptive PID control: A case study for cstr process. Ind. Eng. Chem. Res. 46, 472–480. doi:10.1021/ie0608713
Radke, F., and Isermannt, R. (1987). A parameter-adaptive PID-controller with stepwise parameter optimization 9. Elsevier.
Shamsuzzoha, M., and Lee, M. (2008). Analytical design of enhanced PID filter controller for integrating and first order unstable processes with time delayfilter controller for integrating and first order unstable processes with time delay. Chem. Eng. Sci. 15, 2717–2731. doi:10.1016/j.ces.2008.02.028
Shamsuzzoha, M., and Lee, M. (2007). IMC−PID controller design for improved disturbance rejection of time-delayed processes. Ind. Eng. Chem. Res. 46, 2077–2091. doi:10.1021/ie0612360
Simanenkov, A. L., Rozhkov, S. A., and Borisova, V. A. (2017). “An algorithm of optimal settings for PIDD 2 D 3 -controllers in ship power plant,” in 2017 IEEE 37th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine (IEEE), 152–155. Presented at the 2017 IEEE 37th International Conference on Electronics and Nanotechnology (ELNANO).
Skogestad, S., and Grimholt, C. (2012). “The SIMC method for smooth PID controller tuning,” in PID control in the third millennium, advances in industrial control. Editors R. Vilanova,, and A. Visioli (London: Springer London), 147–175.
Sonkar, P., and Rahi, O. P. (2016). “Unified tuning of PID-derivative filter load frequency controller for two area interconnected system including wind power plant,” in 2016 IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON), Varanasi, India, 09-11 December 2016 (IEEE), 388–393. Presented at the 2016 IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON).
Tan, W., and Fu, C. (2015). Linear active disturbance rejection control: Analysis and tuning via IMC. IEEE Trans. Ind. Electron. 63, 2350–2359. doi:10.1109/tie.2015.2505668
Tzafestas, S., and Papanikolopoulos, N. P. (1990). Incremental fuzzy expert PID control. IEEE Trans. Ind. Electron. 37, 365–371. doi:10.1109/41.103431
Wang, Q-G., Lee, T-H., Fung, H-W., Bi, Q., and Zhang, Y. (1999). PID tuning for improved performance. IEEE Trans. Contr. Syst. Technol. 7, 457–465. doi:10.1109/87.772161
Wang, Y., Tan, W., Cui, W., Han, W., and Guo, Q. (2021). Linear active disturbance rejection control for oscillatory systems with large time-delays. J. Frankl. Inst. 358, 6240–6260. doi:10.1016/j.jfranklin.2021.06.016
Weng, K. H., Chang, C. H., and Zhou, J. (1997). Self-tuning PID control of a plant with under-damped response with specifications on gain and phase margins. IEEE Trans. Contr. Syst. Technol. 5, 446–452. doi:10.1109/87.595926
Zhang, B., Tan, W., and Li, J. (2019). Tuning of linear active disturbance rejection controller with robustness specification. ISA Trans. 10, 237–246. doi:10.1016/j.isatra.2018.10.018
Zhao, C., Xue, D., and Chen, Y. Q. (2005). “A fractional order PID tuning algorithm for a class of fractional order plants,” in IEEE International Conference Mechatronics and Automation, 2005, Niagara Falls, ON, Canada (IEEE), 216–221. Presented at the 2005 IEEE International Conference on Mechatronics and Automation.
Keywords: oscillatory systems, internal model control, parameter tuning, robustness, time domain performance, measurement noise, PID plus second-order controller
Citation: Xingqi H, Guolian H and Wen T (2023) Tuning of
Received: 29 October 2022; Accepted: 12 December 2022;
Published: 10 January 2023.
Edited by:
Tito Luís Maia Santos, Federal University of Bahia, BrazilReviewed by:
Andrzej Pawlowski, University of Brescia, ItalyCopyright © 2023 Xingqi, Guolian and Wen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hu Xingqi, MTg2MDEyNjA2NTFAMTYzLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.