ORIGINAL RESEARCH article

Front. Control Eng., 25 April 2022

Sec. Networked Control

Volume 2 - 2021 | https://doi.org/10.3389/fcteg.2021.797362

Distributed Control of Discrete-Time Linear Multi-Agent Systems With Optimal Energy Performance

  • School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an, China

Abstract

This paper investigates the leader-based distributed optimal control problem of discrete-time linear multi-agent systems (MASs) on directed communication topologies. In particular, the communication topology under consideration consists of only one directed spanning tree. A distributed consensus control protocol depending on the information between agents and their neighbors is designed to guarantee the consensus of MASs. In addition, the optimization of energy cost performance can be obtained using the proposed protocol. Subsequently, a numerical example is provided to demonstrate the effectiveness of the presented protocol.

1 Introduction

Inspired by biological motion in nature, the cooperative motion of multi-agent systems (MASs) has been studied extensively in the past decade (Wang et al., 2017, 2019; Wang and Sun, 2018; Wang et al., 2020b; Koru et al., 2021; Wang and Sun, 2021). Compared to a single agent, networked MASs have the advantages of fast command response and robustness. Due to the distributed network computing system having the characteristics of strong scalability and fast computing speed, the study of distributed cooperative control problems for multi-agent systems has attracted increasing attention of control scientists and robotics engineers by virtue of its extensive applications in many cases, such as mobile robots (Mu et al., 2017; Zhao et al., 2019), autonomous underwater vehicles (AUVs) (Zuo et al., 2016; Li et al., 2019), and spacecrafts (Zhang et al., 2018; 2021a). A classical framework for the cooperative control of MASs with switching topologies is discussed in the study by Olfati-Saber and Murray (2004). Ren and Beard (2005) have further relaxed the conditions given by Olfati-Saber and Murray (2004), which present some new results with regard to the consensus of linear MASs.

In practice, it is necessary to investigate the control problem of multi-agent systems in discrete time with most computer systems being discrete structures. In the study by Liang et al. (2017), the cooperative containment control problem of a nonuniform discrete-time linear multi-agent is studied, and a novel internal mode compensator is designed to deal with the uncertain part of system dynamics. A solution method of the discrete-time MAS decentralized consensus problem based on linear matrix inequality (LMI) is given in the study by Liang et al. (2018). The problem of multi-agent consensus control based on the terminal iterative learning framework is discussed by Lv et al. (2018) where an adaptive control method based on time-varying control input is proposed to improve the control performance of the system. Su et al. (2019) proposed a distributed control algorithm based on the low-gain feedback method and the modified algebraic Riccati equation to achieve a semi-global consensus of discrete-time MASs under input saturation conditions. A multi-agent consensus framework based on the distributed model predictive controller is proposed by Li and Li (2020), while the self-triggering mechanism is adopted to reduce communication cost and solve the problem of asynchronous discrete-time information exchange. Liu et al. (2020) proposed a distributed state feedback control algorithm based on the Markov state compensator to solve the problem, that is, some followers cannot directly obtain the leader’s own state information. For MASs with unknown system parameters, a distributed adaptive control protocol containing local information was designed by Li et al. (2020) to ensure the inclusiveness of the system. In the study by Li et al. (2021), a class of discrete-time MASs adaptive fault-tolerant tracking problem based on reinforcement learning is studied, in which an adaptive auxiliary signal variable is designed to compensate the effect of actuator faults on the control system.

In practical applications, the energy cost performance of the designed protocols should be considered carefully, especially for the systems with low loadability, for example, autonomous underwater vehicles and spacecrafts. In the study by Zhang et al. (2017), the discrete-time MAS optimal consensus problem is discussed, and a data-driven adaptive dynamic programming method is proposed to solve the problem, that is, it is difficult to obtain an accurate mathematical model of the system. Wen et al. (2018) constructed a reinforced learning framework based on fuzzy logic system (FLS) approximators for the identifier–actor–critic system to achieve optimal tracking control of MASs. An optimal signal generator is presented in the study by Tang et al. (2018), where an embedded control scheme by embedding the generator in the feedback loop is adopted to realize the optimal output consensus of multi-agent networks. Tan (2020) transformed the distributed H∞ optimal tracking problem of a class of physically interconnected large-scale systems with a strict feedback form and saturated actuators into the equivalent control problem of MASs; meanwhile, a feedback control algorithm is designed to learn the optimal control input of the system. In the study by Wang et al. (2020a), the optimal consensus problem of MASs is decomposed into three sub-problems: input optimization, consensus state optimization, and dual optimization, and a distributed control algorithm is proposed to achieve the optimal consensus of the system. The nonuniform MAS distributed optimal steady-state regulation is investigated in the study by Tang (2020), and the results are extended to the case where the system only has real-time gradient information using high gain control techniques. The single-agent goal representation heuristic dynamic programming (GrHDP) technique is extended to the multi-agent consensus control problem in by Zhong and He (2020), and an iterative learning algorithm based on GrHDP is designed to make the local performance indexes of the system converge to the optimal value. In the study by Xu et al. (2021), the optimal control problem with piecewise-constant controller gain in a random environment is solved, and an improved Hamilton–Jacobi –Bellman (HJB) partial differential equation is obtained by the splitting method and Feynman-KAC formula.

However, to the authors’ best knowledge, there are very few studies focusing on the optimal control of discrete-time MASs only containing a directed spanning tree. In this study, the leader-based distributed optimal control problem of discrete-time linear MASs on directed communication topologies is investigated. A distributed discrete-time consensus protocol based on the directed graph is designed, and it is proved that the optimization of energy cost performance can be satisfied with the presented consensus protocol. Furthermore, the optimal solution can be obtained by solving the algebraic Riccati equation (ARE), and the design of the protocol presented in this study does not require global communication topology information and relies on only the agent dynamics and relative states of neighboring agents, which means that every agent manages its protocol in a fully distributed way.

Notation. stands for the Euclidean space with N-dimension; In is an identity matrix of n-order; 1N is a N-dimensional vector with all elements equaling 1, and 0m×n denotes a zero matrix of order m × n; ‖x‖ stands for the Euclidean norm of the vector x; A ⊗ B denotes the Kronecker product between the matrices A and B; P > 0 represents the positive definiteness of the matrix P, and P ≥ 0 represents the positive semi-definiteness of P; P−1 and PT are the inverse matrix and transpose matrix of P, respectively.

2 Preliminaries

2.1 Algebraic Graph Theory

A digraph is used to describe the communication topology of MASs, where denotes the set of nodes. An edge (νj, νi) is included in the set if the relative information can be transfered from νi to νj. A path from νi to νj is made up of a set of edges (νi, νl1), … (νln, νj). A graph is supposed to be connected if a path from νi to νj for all pairs of (νi, νj) existed. An adjacency matrix is used to describe the digraph , where aii = 0, and aij = 1, i ≠ j, if , but 0 otherwise. Let denote the Laplacian matrix of such that lij = −aij for i ≠ j and .

2.2 Problem Formulation

Considering a group of N agents with the discrete-time system presented by the following equation.where denotes the state variable and denotes the control input; A and B are constant matrices with suitable dimensions. The purpose of this study is to design a protocol that guarantees the states of N agents in Eq. 1 to achieve an asymptotic consensus. i.e., and optimizes the cost function (which will be defined later).

Assumption 1the leader agent’s index is defined as 0, and the leader agent’s and the follower agent’s index are defined as 1, … , N,. The digraph contains a directed spanning tree with the leader as the root node.

Lemma 1(Matrix Inversion Lemma (Horn and Johnson, 1996)): For any nonsingular matrices E ∈ CN×N, G ∈ CN×M and the general matrices F ∈ CN×N, H ∈ CN×M holds. Then, the inverse of the matrix(E + FGH) is as follows.

3 Main Results

In this section, a distributed optimal controller is designed to solve the consensus of the system in Eq. 1, and the optimization of cost function is achieved with the presented protocol.

Since Assumption 1 holds, the Laplacian matrix can be regraded as (Zhang and Lewis, 2012)where is a nonsingular matrix.

Let , then we havewhere = , and ; it implies that the leader-following consensus of the system in Eq. 1 can be achieved i.e., and can be achieved if and only if .

A distributed optimal controller is developed as follows.where c represents the coupling strength, and K denotes the control gain matrix.

The error system can be obtained by taking the difference of Eq. 3 as follows.where .

Inspired by reference given by Zhang et al. (2021b), the cost function is chosen to bewhere the matrices and denote the appropriate weighting matrices. In addition, the energy-cost function constraint performance for the system in Eq. 5 is considered as follows.

In Eq. 7, represents the process cost and represents the control cost. Therefore, J can be considered the goal of comprehensive optimization of control energy and error quantity. Furthermore, a Hamiltonian equation is utilized to optimize the cost function L(k) aswhere λT (k + 1) represents the costate variable and .

Next, the protocol presented in Eq. 4 is proved to guarantee the optimization of the energy cost performance and stability of system in Eq. 5.

Theorem 1

For the given matrices Q = QT > 0 and R = RT > 0, the cost function L(k) is optimized and the stability of system in Eq. 5 can be achieved if and only if the following ARE holds:where P is the positive definite solution of Eq. 9, and the control gain matrix is ; c is a constant value satisfying the condition c > 1.

Proof

i) Optimization of Cost Function

  • (i–i) Necessity

The optimal control input can be solved from the equation as follows.Let λ(k) = −(IN ⊗ P)ξ(k), then the optimal controller can be obtained in Eq. 10 as follows.Let , where R = RT > 0. Since Eq. 11 holds true, Eq. 5 can be rewritten asAccording to Lemma 1, it indicates that the expression of U* can be rewritten aswhere is the control gain of the optimal controller in Eq. 4, which can guarantee the optimization of the cost function L(k).Considering the costate variable λ(k) = −(IN ⊗ P)ξ(k), it can be obtained by the following equation.which indicates thatLet be a positive definite matrix, and Q = QT > 0 holds true, then we havewhich is identical to the ARE presented in Eq. 9.

It is to be noted that if

c

≥ 1, we have

, which implies that

. Then, the positive definiteness of

is achieved by

c

> 1.

  • (i–ii) Sufficiency

Considering the following equation:Based on and , the abovementioned Eq. 17 can be rewritten asSince Eq. 5 and Eq. 15 hold true, we haveAccording to the following conditional equationThen, Eq. 19 can be regarded asLet denote the Lyapunov function, then, substituting Eq. 21 into Eq. 18, we haveLet , that is ϕ = 0 holds true if and only if U(k) = U*(k) holds, and the cost function L(k) can be rewritten asThen, the cost function can be optimized, that is, L*(k) = −ΔV(k) with the controller .

Hence, it indicates that the optimal performance index

J

* is derived as follows.

where

V

(0) represents the initial value of

V

(

k

).

  • (ii) The Stability of System

Based on the expressions of U*(k), we haveIt is inferred from Eq. 25 that − limk→∞V(k) = 0. Then, the optimal performance index J* can be rewritten asAs a consequence, the conditions in Theorem 1 are all satisfied, which completes the proof.

Remark 1Based on Theorem 1, it is obvious that the value of the control gain matrix K mainly depends on the matrix P and the coupling strength c, where the value of P is directly solved by Eq. 9, and c is a constant value satisfying the condition c > 1. Therefore, the design of the control protocol ui(k) in Eq. 4 does not require global communication topology information and relies only on the agent dynamics and relative states of neighboring agents, that is, every agent manages its control protocol ui(k) in a fully distributed way.

Remark 2The topology considered in this study is a structure containing only one directed spanning tree, which means that the agent can only obtain the information of a single neighbor, and we prove the effectiveness of the proposed distributed optimal controller under the abovementioned conditions. In fact, the proposed controller is also suitable for the case with the general case, such as reference given by Wang et al. (2017), Wang et al. (2019).

4 Numerical Example

In this section, a numerical example is provided to demonstrate the effectiveness of the proposed controller.

Considering a network with seven agents, the communication topology is described by Figure 1. Moreover, the system parameters of each agent are given as follows (Xi et al., 2020).

FIGURE 1

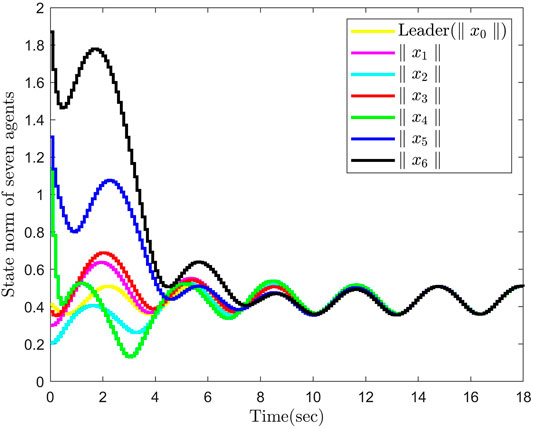
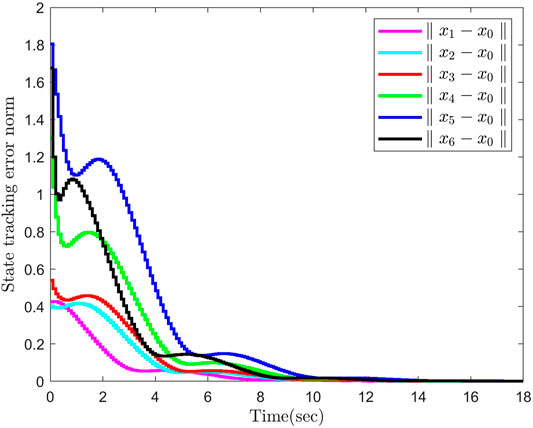
Let R = 10, Q = 10*I3, and the coupling strength c = 2, then the matrix P and the control gain K can be calculated by Theorem 1. The initial conditions are given by x0 (0) = [0.2–0.2 0.3]T, x1 (0) = [0.1 0.2 0.2]T, x2 (0) = [−0.15–0.1 0.1]T, x3 (0) = [0.3 0.2 0.1]T, x4 (0) = [−0.2 0.2–1.1]T, x5 (0) = [1.3 0.1–0.1]T, and x6 (0) = [1.0 0.5 1.5]T. Then, the trajectories of the state norm and tracking error norm are shown in Figures 2, 3.

FIGURE 2

FIGURE 3

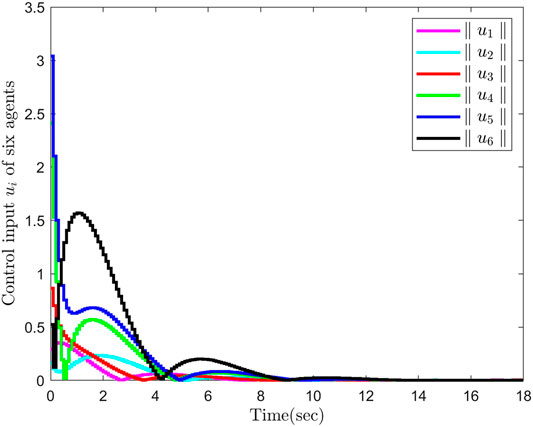
It can be seen from Figures 2, 3 that six followers can track the leader successfully within about 11 s by using the proposed optimal controller, and the steady-state tracking error is less than 2.0. In addition, it is shown in Figure 4 that the control input of six agents will nearly reach zero at about 13 s.

FIGURE 4

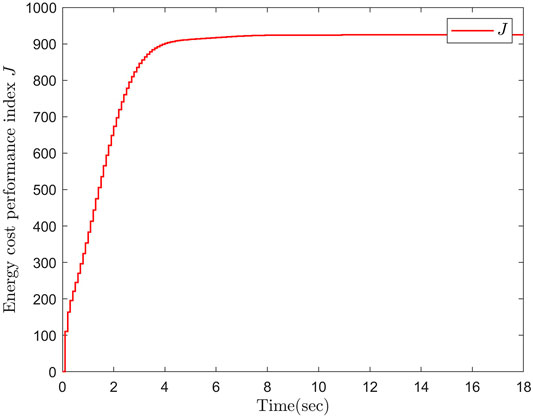
Moreover, the trajectories of energy cost performance J are displayed in Figure 5, which shows that the optimal performance of J equals 924. It can be acquired from Theorem 1 that the theoretical value of the optimal performance is . Consequently, the simulated value of J* is consistent with its theoretical value, which proves that the controller proposed in this study satisfies the optimality requirements.

FIGURE 5

5 Conclusion

In this study, the leader-based distributed optimal control of discrete-time linear MASs only containing a directed spanning tree has been investigated. A distributed optimal consensus control protocol is presented to guarantee that multiple followers can successfully track the leader. It can be proved that the proposed protocol can ensure the optimization of the energy performance index with the optimal gain parameters which can be realized by solving the ARE. Moreover, the design of the protocol presented in this study is independent with the global information of topologies, which indicates that every agent manages its protocol in a fully distributed way. Finally, a numerical example which illustrates the effectiveness of the designed protocol is reported.

Statements

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

GH is responsible for the simulation and the writing of this manuscript. ZZ is responsible for the design idea of this study. WY is responsible for the revision of this manuscript.

Funding

This study was supported in part by the National Key R&D Program of China 2019YFB1310303, in part by the Key R&D program of Shaanxi Province, 2021GY-289, in part by the National Natural Science Foundation of China under Grant U21B2047, Grant U1813225, Grant 61733014, and Grant 51979228.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

  • 1

    HornR.JohnsonC. (1996). Matrix Analysis. Berlin: Springer.

  • 2

    KoruA. T.SarslmazS. B.YucelenT.JohnsonE. N. (2021). Cooperative Output Regulation of Heterogeneous Multiagent Systems: A Global Distributed Control Synthesis Approach. IEEE Trans. Automat. Contr.66, 4289–4296. 10.1109/TAC.2020.3032496

  • 3

    LiH.LiX. (2020). Distributed Model Predictive Consensus of Heterogeneous Time-Varying Multi-Agent Systems: With and without Self-Triggered Mechanism. IEEE Trans. Circuits Syst.67, 5358–5368. 10.1109/TCSI.2020.3008528

  • 4

    LiH.WuY.ChenM. (2021). Adaptive Fault-Tolerant Tracking Control for Discrete-Time Multiagent Systems via Reinforcement Learning Algorithm. IEEE Trans. Cybern.51, 1163–1174. 10.1109/TCYB.2020.2982168

  • 5

    LiJ.DuJ.ChangW.-J. (2019). Robust Time-Varying Formation Control for Underactuated Autonomous Underwater Vehicles with Disturbances under Input Saturation. Ocean Eng.179, 180–188. 10.1016/j.oceaneng.2019.03.017

  • 6

    LiN.FeiQ.MaH. (2020). Distributed Adaptive Containment Control for a Class of Discrete-Time Nonlinear Multi-Agent Systems with Unknown Parameters and Control Gains. J. Franklin Inst.357, 8566–8590. 10.1016/j.jfranklin.2020.06.009

  • 7

    LiangH.LiH.YuZ.LiP.WangW. (2017). Cooperative Robust Containment Control for General Discrete‐time Multi‐agent Systems with External Disturbance. IET Control. Theor. Appl.11, 1928–1937. 10.1049/iet-cta.2016.1475

  • 8

    LiuZ.YanW.LiH.ZhangS. (2020). Cooperative Output Regulation Problem of Discrete-Time Linear Multi-Agent Systems with Markov Switching Topologies. J. Franklin Inst.357, 4795–4816. 10.1016/j.jfranklin.2020.02.020

  • 9

    LvY.ChiR.FengY. (2018). Adaptive Estimation‐based TILC for the Finite‐time Consensus Control of Non‐linear Discrete‐time MASs under Directed Graph. IET Control. Theor. Appl.12, 2516–2525. 10.1049/iet-cta.2018.5602

  • 10

    MahmoudM. S.KhanG. D.YuZ.LiP.WangW. (2018). Lmi Consensus Condition for Discrete-Time Multi-Agent Systems. Ieee/caa J. Autom. Sinica5, 509–513. 10.1109/JAS.2016.7510016

  • 11

    MuB.ChenJ.ShiY.ChangY. (2017). Design and Implementation of Nonuniform Sampling Cooperative Control on a Group of Two-Wheeled mobile Robots. IEEE Trans. Ind. Electron.64, 5035–5044. 10.1109/tie.2016.2638398

  • 12

    Olfati-SaberR.MurrayR. M. (2004). Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Automat. Contr.49, 1520–1533. 10.1109/TAC.2004.834113

  • 13

    SuH.YeY.QiuY.CaoY.ChenM. Z. Q. (2019). Semi-global Output Consensus for Discrete-Time Switching Networked Systems Subject to Input Saturation and External Disturbances. IEEE Trans. Cybern.49, 3934–3945. 10.1109/TCYB.2018.2859436

  • 14

    TanL. N. (2020). Distributed H∞ Optimal Tracking Control for Strict-Feedback Nonlinear Large-Scale Systems with Disturbances and Saturating Actuators. IEEE Trans. Syst. Man. Cybern, Syst.50, 4719–4731. 10.1109/TSMC.2018.2861470

  • 15

    TangY.DengZ.HongY. (2019). Optimal Output Consensus of High-Order Multiagent Systems with Embedded Technique. IEEE Trans. Cybern.49, 1768–1779. 10.1109/TCYB.2018.2813431

  • 16

    TangY. (2020). Distributed Optimal Steady-State Regulation for High-Order Multiagent Systems with External Disturbances. IEEE Trans. Syst. Man. Cybern, Syst.50, 4828–4835. 10.1109/TSMC.2018.2866902

  • 17

    WangB.ChenW.ZhangB. (2019). Semi-global Robust Tracking Consensus for Multi-Agent Uncertain Systems with Input Saturation via Metamorphic Low-Gain Feedback. Automatica103, 363–373. 10.1016/j.automatica.2019.02.002

  • 18

    WangB.WangJ.ZhangB.LiX. (2017). Global Cooperative Control Framework for Multiagent Systems Subject to Actuator Saturation with Industrial Applications. IEEE Trans. Syst. Man. Cybern, Syst.47, 1270–1283. 10.1109/TSMC.2016.2573584

  • 19

    WangQ.DuanZ.WangJ. (2020a). Distributed Optimal Consensus Control Algorithm for Continuous-Time Multi-Agent Systems. IEEE Trans. Circuits Syst.67, 102–106. 10.1109/TCSII.2019.2900758

  • 20

    WangQ.PsillakisH. E.SunC. (2020b). Adaptive Cooperative Control with Guaranteed Convergence in Time-Varying Networks of Nonlinear Dynamical Systems. IEEE Trans. Cybern.50, 5035–5046. 10.1109/TCYB.2019.2916563

  • 21

    WangQ.SunC. (2018). Adaptive Consensus of Multiagent Systems with Unknown High-Frequency Gain Signs under Directed Graphs. IEEE Trans. Syst. Man, Cybernetics: Syst.50, 2181–2186. 10.1109/TSMC.2018.2810089

  • 22

    WangQ.SunC. (2021). Distributed Asymptotic Consensus in Directed Networks of Nonaffine Systems with Nonvanishing Disturbance. Ieee/caa J. Autom. Sinica8, 1133–1140. 10.1109/JAS.2021.1004021

  • 23

    Wei RenW.BeardR. W. (2005). Consensus Seeking in Multiagent Systems under Dynamically Changing Interaction Topologies. IEEE Trans. Automat. Contr.50, 655–661. 10.1109/TAC.2005.846556

  • 24

    WenG.ChenC. L. P.FengJ.ZhouN. (2018). Optimized Multi-Agent Formation Control Based on an Identifier-Actor-Critic Reinforcement Learning Algorithm. IEEE Trans. Fuzzy Syst.26, 2719–2731. 10.1109/TFUZZ.2017.2787561

  • 25

    XiJ.WangL.ZhengJ.YangX. (2020). Energy-constraint Formation for Multiagent Systems with Switching Interaction Topologies. IEEE Trans. Circuits Syst.67, 2442–2454. 10.1109/tcsi.2020.2975383

  • 26

    XuS.CaoJ.LiuQ.RutkowskiL. (2021). Optimal Control on Finite-Time Consensus of the Leader-Following Stochastic Multiagent System with Heuristic Method. IEEE Trans. Syst. Man. Cybern, Syst.51, 3617–3628. 10.1109/TSMC.2019.2930760

  • 27

    ZhangH.JiangH.LuoY.XiaoG. (2017). Data-driven Optimal Consensus Control for Discrete-Time Multi-Agent Systems with Unknown Dynamics Using Reinforcement Learning Method. IEEE Trans. Ind. Electron.64, 4091–4100. 10.1109/TIE.2016.2542134

  • 28

    ZhangH.LewisF. L. (2012). Adaptive Cooperative Tracking Control of Higher-Order Nonlinear Systems with Unknown Dynamics. Automatica48, 1432–1439. 10.1016/j.automatica.2012.05.008

  • 29

    ZhangZ.ShiY.YanW. (2021a). A Novel Attitude-Tracking Control for Spacecraft Networks with Input Delays. IEEE Trans. Contr. Syst. Technol.29, 1035–1047. 10.1109/TCST.2020.2990532

  • 30

    ZhangZ.ShiY.ZhangZ.ZhangH.BiS. (2018). Modified Order-Reduction Method for Distributed Control of Multi-Spacecraft Networks with Time-Varying Delays. IEEE Trans. Control. Netw. Syst.5, 79–92. 10.1109/TCNS.2016.2578046

  • 31

    ZhangZ.YanW.LiH. (2021b). Distributed Optimal Control for Linear Multiagent Systems on General Digraphs. IEEE Trans. Automat. Contr.66, 322–328. 10.1109/TAC.2020.2974424

  • 32

    ZhaoS.LiZ.DingZ. (2019). Bearing-Only Formation Tracking Control of Multiagent Systems. IEEE Trans. Automat. Contr.64, 4541–4554. 10.1109/TAC.2019.2903290

  • 33

    ZhongX.HeH. (2020). Grhdp Solution for Optimal Consensus Control of Multiagent Discrete-Time Systems. IEEE Trans. Syst. Man. Cybern, Syst.50, 2362–2374. 10.1109/TSMC.2018.2814018

  • 34

    ZuoL.YanW.CuiR.GaoJ. (2016). A Coverage Algorithm for Multiple Autonomous Surface Vehicles in Flowing Environments. Int. J. Control. Autom. Syst.14, 540–548. 10.1007/s12555-014-0454-0

Summary

Keywords

leader-based, distributed optimal control, discrete-time, multi-agent systems, directed communication topologies

Citation

Huang G, Zhang Z and Yan W (2022) Distributed Control of Discrete-Time Linear Multi-Agent Systems With Optimal Energy Performance. Front. Control. Eng. 2:797362. doi: 10.3389/fcteg.2021.797362

Received

18 October 2021

Accepted

29 December 2021

Published

25 April 2022

Volume

2 - 2021

Edited by

Chao Shen, Carleton University, Canada

Reviewed by

Bohui Wang, Nanyang Technological University, Singapore

Qingling Wang, Southeast University, China

Updates

Copyright

© 2022 Huang, Zhang and Yan.

This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Zhuo Zhang,

This article was submitted to Networked Control, a section of the journal Frontiers in Control Engineering

Disclaimer

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Outline

Figures

Cite article

Copy to clipboard


Export citation file


Share article

Share on WeChat

Scan with WeChat to share this article

Article metrics