- School of Automation and Key Laboratory of Measurement and Control of Complex Systems of Engineering, Ministry of Education, Southeast University, Nanjing, China
The applications of the deep reinforcement learning method to achieve the arcs welding by multi-robot systems are presented, where the states and the actions of each robot are continuous and obstacles are considered in the welding environment. In order to adapt to the time-varying welding task and local information available to each robot in the welding environment, the so-called multi-agent deep deterministic policy gradient (MADDPG) algorithm is designed with a new set of rewards. Based on the idea of the distributed execution and centralized training, the proposed MADDPG algorithm is distributed. Simulation results demonstrate the effectiveness of the proposed method.
1 Introduction
Welding control is an important technology in industrial manufacturing due to the fact that its performance can determine the product quality (Shan et al., 2017). With the development of information technology, coordinated welding control, using multiple arc-welding robots to achieve a complex welding task, has increasingly received attention. Some details can be found in Hvilshøj et al., 2012; Feng et al., 2020; Zhao and Wu, 2020). The key of coordinated welding control is to optimize collaborative welding path without collision.
The classical method in this line of research is trajectory planning. In Cao et al. (2006), an artificial potential field algorithm is presented. However, such method just achieves the local optimization. In Enayattabar et al. (2019), a greedy method called the Dijkstra algorithm is designed only for the graphs with positively weighted edges. The so-called
Recently, reinforcement learning methods stand out in various competitions, for example, Go game (Silver et al., 2016) and StarCraft (Vinyals et al., 2019; Sutton and Barto, 2018). Such methods using the reward values and the information of the environment to update an intelligent algorithm give lights in coordinated trajectory planning. In Tang et al. (2019), the idea of a multi-agent reinforcement learning method is introduced in the case of trajectory planning. With knowledge of the whole environmental information, a rule-based shallow trial reinforcement learning algorithm is given. In Qie et al. (2019), a reinforcement learning method for the continuous state and action space is given based on the Actor-Critic (AC) framework. In Lowe et al. (2017), a MADDPG algorithm is designed based on the structure of the distributed execution and the centralized training. As we all know, the reinforcement learning method has not been used in the coordinated welding control problem.
This paper deals with the coordinated welding control problem of multi-robot systems. To achieve the time-varying welding task, the optimization of robot trajectory, and collision avoidance, a MADDPG algorithm with a new set of rewards is designed based on local information available to each robot in the welding environment. This is the first result of the application of using the deep reinforcement learning method in the coordinated welding control problem.
The remainder of the paper is structured as follows: Section 2 presents the problem formulation of coordinated welding. Section 3 provides the MADDPG with a new set of rewards. Section 4 gives the validation of the algorithm by simulations. Conclusions are given in Section 5.
2 Problem Formulation
Since two or three mechanical arms are generally used in the actual ship welding, let us consider that
where
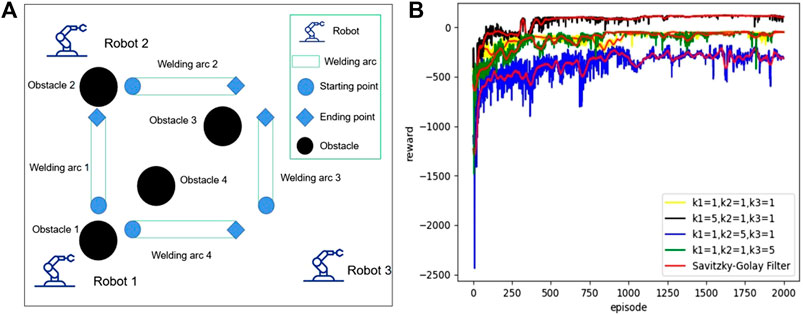
FIGURE 1. The environment of assumed welding and the reward of the robots with different weight coefficients.
The objectives of this paper are to optimally accomplish all the welding arcs without any collision. In this paper, the following assumptions are required: 1) a welding arc can be welded by a robot with a constant speed; 2) once a welding arc is accomplished, it can not be welded again; 3) the states of welding arcs are accessible to all robots but only the neighbors’ states and obstacle status with local measurements are known to each robot; 4) without loss of generality, the shapes of all robots and all obstacles are round and the shapes of all welding arcs are straight lines.
3 MADDPG Algorithm
In this section, the main designing process will be given by referring to MADDPG (Lowe et al., 2017). The environment consists of agents model, action space, and state space, where the model of each agent moving the 2D environment, and the states
In our algorithm, there are actor network, critic network, and two target networks used for each robot. Specifically, there are two Muti-Layer Perception (MLP) layers of 256 and 128 neurons with Rectified Linear Unit (RELU) activation and softmax action selection on the output layer in the actor network. In the critic network for each robot, there are three MLP layers of 256, 128, and 64 neurons with RELU activation and softmax action selection on the output layer. The structures of two target networks are the same as the actor network and the critic network, respectively, but their update times are not synchronized for satisfying the independence and the distribution of the sampled data. In the execution, the actor network outputs the action of each robot for the exploration based on the states obtained by itself. Then, the environment outputs the rewards and the states at the next moment according to the actions. In the training, the critic network evaluates the action chosen by each actor network to improve the performance of the actor network by constructing a loss function. The in-batch data of tuples is sampled uniformly from the replay buffer D composed of the states and the actions of all robots at the current moment, and the reward and the state of all robots at the next moment, which is the input of each critic network. Episodes are used for learning such that it is terminated when all welds are executed or the number of steps reaches the maximum.
The total reward
consists of three terms, where
This forces the robots to find the welding arcs that are not welded. In Equation 2, the distance-based reward
Here,
Here,
Let
1: for episode = 1 to Max-episode do 2: Initialize a random process P for action exploration. 3: Receive the initial states 4: for 5: For robot i select action 6: Execute the actions 7: by interacting with the environment based on Equation 1. 8: Store 9: 10: for agent 11: Sample a random minibatch of S samples 12: Set 13: Update critic by minimizing the loss by 14: Update actor using the sampled policy gradient: 15: 16: end for 17: Update target network parameters by 18: end for 19: end for
4 Simulation Results and Analysis
The simulation environment is under Pytorch, which includes three welding robots and four welding arcs. The radiuses of the robots are 0.01 m, and the radiuses of the obstacles are 0.08 m. The hyperparameters of the neural network in training are set as follows. The size of the replay buffer D is set to
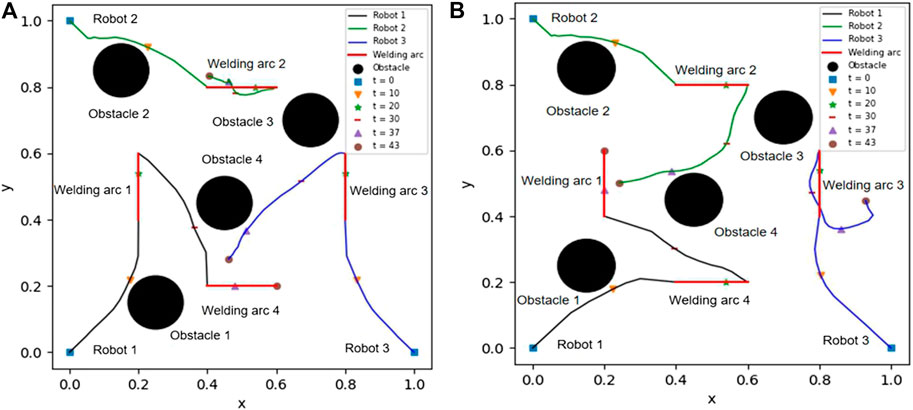
Figure 1B shows that the cumulative rewards in different weight coefficients increase gradually and finally reach some stable values, which implies that a good policy is learned in each case. From Figure 1B, one can also obviously see that the selection of the coefficients does not significantly affect the learning results; in other words, the differences of the parameters do not change the convergence speed too much. Figures 2A,B present the trajectories of the robots in two situations with the different positions of obstacles. From Figure 2A, it is shown that the robots 1, 2, and 3 first figure out the nearest welding arcs 1, 2, and 3 and then robot 1 continuously accomplishes the welding arc 4 after finishing arc 1. Similar precedence is shown in Figure 2B when the positions of obstacles are changed. From the above figures, we conclude that all the trajectories for the robots are almost shortest and there is no collision between the robots and obstacles.
5 Conclusion and Future Work
A MADDPG algorithm with a new set of rewards is designed for the coordinated welding of multiple arc-welding robots. The proposed MADDPG algorithm is distributed, and only local information is available to each arc-welding robot. In the ongoing work, we will devote ourselves to the coordinated welding control problem in the three-dimensional space and the situation that one welding arc is operated by multiple robots.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author Contributions
L-XX is responsible for the simulation and the writing of this paper. Y-YC is responsible for the design idea and the revision of this paper.
Funding
This work has been partially supported by the National Natural Science Foundation of China under Grant No. 61673106.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Cao, Q., Huang, Y., and Zhou, J. (2006). “An evolutionary artificial potential field algorithm for dynamic path planning of mobile robot,” in 2006 IEEE/RSJ international conference on intelligent robots and systems, Beijing (IEEE), 3331–3336.
Chen, Y.-Y., Wang, Z.-Z., Zhang, Y., Liu, C.-L., and Wang, Q. (2017). A geometric extension design for spherical formation tracking control of second-order agents in unknown spatiotemporal flowfields. Nonlinear Dynam. 88, 1173–1186. doi:10.1007/s11071-016-3303-2
Chen, Y.-Y., Yu, R., Zhang, Y., and Liu, C.-L. (2019). Circular formation flight control for unmanned aerial vehicles with directed network and external disturbance. IEEE/CAA J. Automat. Sinica. 7, 505–516. doi:10.1109/JAS.2019.1911669
Enayattabar, M., Ebrahimnejad, A., and Motameni, H. (2019). Dijkstra algorithm for shortest path problem under interval-valued pythagorean fuzzy environment. Complex Intell. Syst. 5, 93–100. doi:10.1007/s40747-018-0083-y
Feng, Z., Hu, G., Sun, Y., and Soon, J. (2020). An overview of collaborative robotic manipulation in multi-robot systems. Annu. Rev. Contr. 49, 113–127. doi:10.1016/j.arcontrol.2020.02.002
Hu, Y., and Yang, S. (2004). “A knowledge based genetic algorithm for path planning of a mobile robot,” in IEEE international conference on robotics and automation, 2004. roceedings, New Orleans, LA, United States ICRA’04. 2004 (IEEE), Vol. 5, 4350–4355.
Hvilshøj, M., Bøgh, S., Nielsen, O. S., and Madsen, O. (2012). Autonomous industrial mobile manipulation (AIMM): past, present and future. Ind. Robot: Int. J. 39, 120–135. doi:10.1108/01439911211201582
Karaboga, D., and Akay, B. (2009). A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 214, 108–132. doi:10.1016/j.amc.2009.03.090
Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in Proceedings of ICNN’95-international conference on neural networks, Perth, WA, Australia (IEEE), Vol. 4, 1942–1948.
Lowe, R., Wu, Y., Tamar, A., Harb, J., Abbeel, O. P., and Mordatch, I. (2017). Multi-agent actor-critic for mixed cooperative-competitive environments. In advances in neural information processing systems, Ithaca, New York: arXiv, Cornell University, 6379–6390.
Luo, C., and Yang, S. X. (2008). A bioinspired neural network for real-time concurrent map building and complete coverage robot navigation in unknown environments. IEEE Trans. Neural Network. 19, 1279–1298. doi:10.1109/tnn.2008.2000394
Luo, M., Hou, X., and Yang, S. X. (2019). A multi-scale map method based on bioinspired neural network algorithm for robot path planning. IEEE Access. 7, 142682–142691. doi:10.1109/access.2019.2943009
Mohammed, A. J., Ghathwan, K. I., and Yusof, Y. (2020). Optimal robot path planning using enhanced particle swarm optimization algorithm. Iraqi J. Sci. 61, 178–184. doi:10.24996/ijs.2020.61.1.20
Nazarahari, M., Khanmirza, E., and Doostie, S. (2019). Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 115, 106–120. doi:10.1016/j.eswa.2018.08.008
Pu, X., Xiong, C., Ji, L., and Zhao, L. (2020). 3d path planning for a robot based on improved ant colony algorithm. Evol. Intell. 1–11.
Qie, H., Shi, D., Shen, T., Xu, X., Li, Y., and Wang, L. (2019). Joint optimization of multi-uav target assignment and path planning based on multi-agent reinforcement learning. IEEE Access. 7, 146264–146272. doi:10.1109/access.2019.2943253
Shan, Z., Xu, X., Tao, Y., and Xiong, H. (2017). “A trajectory planning and simulation method for welding robot,” in 2017 IEEE 7th annual international conference on CYBER technology in automation, control, and intelligent systems (CYBER), Honolulu, HI (IEEE), 510–515.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G. G., et al. (2016). Mastering the game of go with deep neural networks and tree search. Nature 529, 484–489. doi:10.1038/nature16961 |
Song, R., Liu, Y., and Bucknall, R. (2019). Smoothed A* algorithm for practical unmanned surface vehicle path planning. Appl. Ocean Res. 83, 9–20. doi:10.1016/j.apor.2018.12.001
Sutton, R. S., and Barto, A. G. (2018). Reinforcement learning: an introduction ( Cambridge: MIT press)
Tang, K., Fu, H., Jiang, H., Liu, C., and Wang, L. (2019). “Reinforcement learning for robots path planning with rule-based shallow-trial,” in 2019 IEEE 16th international conference on networking, sensing and control (ICNSC) (IEEE), 340–345.
Vinyals, O., Babuschkin, I., Czarnecki, W. M., Mathieu, M., Dudzik, A., Chung, J. J., et al. (2019). Grandmaster level in starcraft ii using multi-agent reinforcement learning. Nature 575, 350–354. doi:10.1038/s41586-019-1724-z |
Keywords: deep reinforcement learning, multiple arc-welding robots, local information, distribution, MADDPG
Citation: Xu L-X and Chen Y-Y (2021) Deep Reinforcement Learning Algorithms for Multiple Arc-Welding Robots. Front. Control. Eng. 2:632417. doi: 10.3389/fcteg.2021.632417
Received: 23 November 2020; Accepted: 18 January 2021;
Published: 22 February 2021.
Edited by:
Kim-Doang Nguyen, South Dakota State University, United StatesReviewed by:
Praneel Acharya, South Dakota State University, United StatesElHussein Shata, South Dakota State University, United States
Bo Chen, Zhejiang University of Technology, China
Copyright © 2021 Xu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang-Yang Chen, eXljaGVuQHNldS5lZHUuY24=
 Lei-Xin Xu
Lei-Xin Xu Yang-Yang Chen
Yang-Yang Chen