Cooperation and the social brain hypothesis in primate social networks

The social brain hypothesis posits that species with larger brains tend to have greater social complexity. Various lines of empirical evidence have supported the social brain hypothesis, including evidence from the structure of social networks. Cooperation is a key component of group living, particularly among primates, and theoretical research has shown that particular structures of social networks foster cooperation more easily than others. Therefore, we hypothesized that species with a relatively large brain size tend to form social networks that better enable cooperation. In the present study, we combine data on brain size and social networks with theory on the evolution of cooperation on networks to test this hypothesis in non-human primates. We have found a positive effect of brain size on cooperation in social networks even after controlling for the effect of other structural properties of networks that are known to promote cooperation.

1 Introduction

The social brain hypothesis states that, among primates, brain size is positively associated with social complexity (Dunbar, 1998). Group size, in terms of the number of individuals, is one aspect of social complexity (Kappeler et al., 2019). Studies have found a positive association between brain size and the typical sizes of defined social units (Dunbar, 1992; Dunbar, 1998) as well as more focused subgroups, such as the number of regular social contacts an individual maintains (Kudo and Dunbar, 2001; Bickart et al., 2011; Lewis et al., 2011; Kanai et al., 2012). However, some studies have found stronger relationships between brain size and other behaviors, such as diet (DeCasien et al., 2017), or found the relationship between brain size and group size to be relatively weak (Street et al., 2017) or inconsistent across data sets (Powell et al., 2017).

Although group size is the most studied potential correlate of brain size in the social brain hypothesis literature, it is not the only one (Dunbar and Shultz, 2017). Patterns of behavior between individuals in differentiated pairwise interactions can also be thought of as an important component of social complexity (Dunbar and Shultz, 2017; Kappeler et al., 2019; Shultz and Dunbar, 2022). Such pairwise interactions can be represented as social networks. Network science is a common tool for studying complex systems, and researchers have investigated several network indices in relation to the social brain hypothesis. Examples include the number of connections an individual maintains (also known as the node’s degree) (Kudo and Dunbar, 2001; Bickart et al., 2011; Kanai et al., 2012), the number of different types of connections (Bickart et al., 2011), the number of individuals in a subgroup who can connect to each other by a sequence of edges (i.e., the size of strongly connected components) (Kudo and Dunbar, 2001), the number of observed connections normalized by the number of possible connections (called the network density) (Lehmann and Dunbar, 2009), and more sophisticated measures of network structure (Lehmann and Dunbar, 2009; Pasquaretta et al., 2014). The results of all of these network-based studies are largely consistent with the social brain hypothesis.

Social networks have both benefits and costs that make them relevant to the evolution of sociality. The structure of animal social networks has been suggested to affect, for example, the speed of diffusion of information, mating behavior, predator avoidance, communication efficiency, and group movement (Pasquaretta et al., 2014; Pinter-Wollman et al., 2014; Kruase et al., 2015; Brask et al., 2021). On the other hand, network structure determines disease transmission potential and epidemic outcomes in populations, because a pathogen can only spread if the relevant form of contact exists between two individuals. Networks with high degree heterogeneity (i.e., high variation in the number of contacts among individuals) have increased transmission potential due to the presence of superspreaders which cause rapid, explosive outbreaks of disease in a population (Bansal et al., 2007). Animal social networks that we observe today may therefore be a result of evolutionary processes in which more advantageous network structures have proliferated at the expense of less advantageous structures under restrictions imposed by the environment and trade-offs between different objectives.

One function for which social networks are particularly relevant is cooperation. Individuals of various animal species cooperate with each other, even cooperating with non-kin and in social dilemma situations in which non-cooperation is more lucrative than cooperation (Smith, 1982; Kappeler and Van Schaik, 2006; Noë, 2006; Cheney, 2011; Croft et al., 2015; McAuliffe and Thornton, 2015; Gokcekus et al., 2021) (but see Clutton-Brock (2009), Cheney et al. (2010), and Cheney (2011), which point out that empirical evidence of cooperation in animal groups remains relatively scarce). Although cooperation under social dilemmas is an evolutionary puzzle, theoretical research has suggested various mechanisms enabling cooperation, such as direct reciprocity (i.e., repeated interaction) and indirect reciprocity (specifically, reputation-based mechanisms) (Fudenberg and Levine, 1998; Nowak, 2006a). Signaling, including symbolic communication, has been proposed as another mechanism that can enable cooperation (Smith, 2010), and recent theory has suggested that structured populations may facilitate the spread of cooperation in the presence of symbolic communication when compared to well-mixed populations (Salahshour, 2020). The structure of social networks is itself one mechanism that may promote cooperation, a concept known as network reciprocity (Nowak, 2006a; Szabó and Fáth, 2007; Perc et al., 2013; Perc et al., 2017; Takács et al., 2021). Specifically, a relatively small node degree (i.e., the number of neighboring individuals per individual) (Ohtsuki et al., 2006; Allen et al., 2017) and heterogeneity among individuals in the network in terms of the degree (Santos and Pacheco, 2005; Santos et al., 2006) can both promote cooperation compared to well-mixed populations depending on the assumptions underlying the evolutionary process models. In addition, it has long been known that clustering of the network (i.e., abundance of short cycles such as triangles and squares) promotes cooperation, which is often referred to as spatial reciprocity (Nowak and May, 1992; Hauert, 2001; Nowak, 2006a).

The purpose of the present study is to investigate the link between the social brain hypothesis and cooperation in social networks. While cooperation occurs in various animal taxa (Noë, 2006; Croft et al., 2015), here we focus on non-human primates because both brain size and social network data are available for many primate species. Recently developed mathematical theory enables us to quantify the extent to which a network itself supports the spread of cooperation (Allen et al., 2017). We use this theory and test whether species with larger brains form social networks that foster cooperation to a greater extent than networks for other species.

Specifically, using game theory and the properties of random walks on networks, Allen et al. (2017) derived an expression which predicts, for an arbitrary weighted and undirected network, how much larger the benefit b of cooperating must be, when compared to its cost c, in order to favor the spread of cooperation. The theory by Allen and colleagues relies on a death-birth process which, given an invading cooperator and assuming no mutation, leads to fixation of either cooperation or defection (Figure 1; see Section 2 for details). For a given network, cooperation fixates with a higher probability when b/c is larger in general. In particular, cooperation fixates with a probability larger than a baseline probability when b/c is larger than a threshold value, denoted (b/c)*, and the (b/c)* value depends on the network structure (see Section 2 for mathematical details). Because a small (b/c)* value implies that cooperation fixates relatively easily for a relatively small value of b/c, networks with a small (b/c)* value favor the spread of cooperation. Our hypothesis is that nonhuman primate species with larger neocortex ratios are associated with social networks that have lower (b/c)* values.

FIGURE 1

FIGURE 1. A single round of the death-birth process with selection on birth. (A) Each player gains an averaged payoff by interacting with all its neighbors. We denote cooperator and defector by C and D, respectively. (B) We select a node to be updated uniformly at random. In our example we choose the node denoted by i. Then, one of i’s neighbors, denoted by j, whose payoff value is shown, will replace i. We select as j each neighbor of i with probability proportional to its expected payoff; the probability to select this j is given by [1 + η(b/2 − c)]/[1 + η(−c) + 1 + η(b/2) + 1 + η(b/3) + 1 + η(b/4 − c) + 1 + η(b/2 − c)] = [12 + 6η(b − 2c)]/[60 + η(19b − 36c)], where η ≪ 1 denotes the selection strength, b denotes the benefit from cooperating, and c denotes the cost of cooperating. (C) In this example, j is a cooperator and replaces the defector on the ith node.

2 Materials and methods

2.1 Evolutionary game dynamics and the derivation of (b/c)*

In this section, we explain the derivation of (b/c)* for any given network under the weak selection limit, following Allen et al. (2017).

2.1.1 Networks and discrete-time random walk

We assume connected and undirected networks with N nodes. For each pair of nodes i, j ∈ {1, …, N}, we denote the edge weight by w_ij ≥ 0. We set w_ij = 0 if there is no edge (i, j). We allow self-loops, i.e., the case of w_ii > 0 (Allen et al., 2017). The weighted degree of node i, also referred to as node strength, is given by $s_i={\sum }_{j=1}^N$w_ij.

We start with explaining discrete-time random walks on networks because they are necessary for describing both the evolutionary game dynamics and the derivation of (b/c)*. By definition, a discrete-time random walk on the network is simple if the walker located on the ith node moves to any jth node in a single time step with probability proportional to w_ij, i.e., with probability p_ij = w_ij/s_i. The transition probability matrix P = (p_ij) of the simple random walk is given by P = D⁻¹W, where D = diag(s₁, …, s_N), i.e., the diagonal matrix whose diagonal entries are equal to s₁, s₂, …, s_N, and W = (w_ij) with i, j ∈ {1, …, N} is the weighted adjacency matrix. Let π = (π₁, …, π_N) be the stationary probability vector of the random walk with transition probability matrix P. Vector π is the solution of πP = π satisfying ${\sum }_{i=1}^N{\pi }_i=N$. The following Eq. 1 holds true for undirected networks that (Aldous and Fill, 2002; Masuda et al., 2017):

${\pi }_i=\frac{s_i}{{\sum }_{\ell =1}^N{s}_{\ell }},i\in \left\{1,\dots ,N\right\}.(1)$

2.1.2 Gift-giving game and evolutionary dynamics under the death-birth updating rule

We use the gift-giving game, also called the donation game, which is a subtype of the prisoner’s dilemma game. In the gift-giving game, which is a two-player game, one player, called the donor, decides whether or not to pay a cost c (>0). If the donor pays c, which we refer to as cooperation, then the other player, called the recipient, receives benefit b, which we assume to be larger than c. If the donor decides not to pay c, which we refer to as defection, then the donor does not lose anything, and the recipient does not gain anything. We assume that each player plays the game with each neighbor once as donor and another time as recipient in a single round of evolutionary dynamics. Then, the payoff matrix of the gift-giving game between a pair of players is given by the following Eq. 2:

$\underset{\begin{array}{c}\mathrm{C}\\ \mathrm{D}\end{array}\left(\begin{array}{ccc}b-c& & -c\\ b& & 0\end{array}\right)}{\mathrm{C}\mathrm{D}}(2)$

where C and D represent cooperation and defection, respectively, and the payoff values represent those for the row player.

We set x_i = 0 or x_i = 1 when the ith player is defector or cooperator, respectively. Then, the state of the entire network is specified by a binary vector x = (x₁, …, x_N) ∈ {0,1}^N. The payoff of the ith node averaged over all its neighbors is given by the following Eq. 3:

$f_i\left(\mathit{x}\right)=-c{x}_i+b{\displaystyle \sum _{j=1}^N}{p}_{ij}{x}_j.(3)$

We set the reproductive rate of node i in state x by the following Eq. 4:

$R_i\left(\mathit{x}\right)=1+\eta f_i\left(\mathit{x}\right),(4)$

where η (≥0) represents the strength of natural selection. When η → 0, the payoff, f_i(x) only weakly impacts the selection, which is called the weak selection regime. A justification of weak selection is that, in reality, many different factors may contribute to the overall fitness of an individual, and the prisoner’s dilemma game may be just one such contributor (Ohtsuki et al., 2006; Allen et al., 2017).

We assume evolutionary dynamics of the gift-giving game driven by the death-birth process with selection on birth (Ohtsuki et al., 2006; Allen et al., 2017). By definition, we first select a node to be updated (i.e., die), denoted by i, uniformly at random. Second, we select one of the neighbors of the ith node, denoted by j, for reproduction (i.e., give birth), with the probability proportional to w_ijR_j(x). Third, i copies the type (i.e., defection or cooperation) of j. These three steps constitute a single round of the evolutionary dynamics; see Figure 1 for a schematic.

2.1.3 Fixation probability for cooperation and the expression of (b/c)*

Because we omitted mutation, the death-birth process in any finite network eventually terminates in the state in which all individuals are uniformly cooperators or defectors. We call these final states fixation of cooperation or defection. According to a standard convention, we assume that the initial state contains one cooperator node and N − 1 defector nodes and that each node is the unique initial cooperator with the equal probability 1/N. We denote by ρ_C the probability that cooperation fixates. Defection fixates with probability 1 − ρ_C. We say that natural selection favors cooperation if ρ_C > 1/N (Nowak et al., 2004; Nowak, 2006b; Ohtsuki et al., 2006; Allen et al., 2017).

Allen et al. showed that (Allen et al., 2017)

${\rho }_{\text{C}}=\frac{1}{N}+\frac{\eta }{2N}\left[-c{\tau }_2+b\left({\tau }_3-{\tau }_1\right)\right]+O\left({\eta }^2\right),(5)$

where

${\tau }_k={\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}{\pi }_i{p}_{ij}^{\left(k\right)}{t}_{ij},(6)$

$p_{ij}^{(k)}$ is the (i, j)th entry of matrix P^k, which implies that $p_{ij}^{(1)}=p_{ij}$, and

$t_{ij}=\left\{\begin{array}{cc}0\hfill & \mathrm{i}\mathrm{f}i=j,\hfill \\ 1+\frac{1}{2}{\sum }_{k=1}^N\left(p_{ik}{t}_{jk}+p_{jk}{t}_{ik}\right)\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.(7)$

Eq. 7 implies that t_ij = t_ji is the mean coalescence time of two random walkers when one walker is initially located at the ith node and the other walker is initially located at the jth node. Note that $p_{ij}^{(k)}$ is the k-step transition probability of the random walk from the ith to the jth node. Therefore, τ_k, given by Eq. 6, is the expected value of t_ij when j is the node at which the random walker arrives after k steps starting at the ith node under the stationary distribution (Allen et al., 2017). Eq. 5 implies that the natural selection favors cooperation (i.e., ρ_C > 1/N) under weak selection if and only if

$\left(\frac{b}{c}\right)>{\left(\frac{b}{c}\right)}^{*}\equiv \frac{{\tau }_2}{{\tau }_3-{\tau }_1}.(8)$

It should be noted that the right-hand side of Eq. 8 only depends on the adjacency matrix of the network, W. Therefore, the network structure determines whether and how much natural selection favors cooperation in the present model. Note that (b/c)* is a threshold value: cooperation is predicted to fixate with a probability larger than 1/N when the ratio of benefit b to cost c of a particular cooperative behavior is larger than (b/c)*. Thus, cooperation spreads more easily on networks with lower (b/c)*.

We calculated (b/c)* for each network using our in-house code in Python 3.10, which implements the procedures described in (Allen et al., 2017); the code is available at https://github.com/ngmaclaren/cooperation-threshold.

2.2 Data

The data for this study come from the Animal Social Network Repository (ASNR) (Sah et al., 2019; Collier et al., 2021). The ASNR contains 770 non-human social networks from eight animal classes and 69 species. For each network in this data set, nodes represent an individual animal. Edges represent a specific type of contact between two animals, such as grooming in primates and trophallaxis in ants, as well as more general contact such as group membership and spatial proximity.

There are 114 non-human primate social networks in the ASNR, including 60 grooming networks, 31 spatial proximity networks, 10 mating networks, and 13 networks with other contact types. Most sampled populations are free-ranging (84), with some captive (18) and some semi-freeranging (7) populations, as well as five populations for which the type was not recorded. There are 99 catarrhine primate networks, 13 platyrrhine networks, and 2 strepsirrhine networks. Sampling of the different contrasts represented in the ASNR is thus somewhat unbalanced but reflects the sampling effort present in the literature.

To test our hypothesis we require that, to the best extent possible, the edges represent prosocial contacts between individuals. Other contact types, such as dominance or mating, may reflect motives that are not relevant to the spread of cooperative behaviors, and proximity-based networks may reflect individuals who are co-located by chance or interest in a common resource rather than for social interaction. We therefore used the ASNR networks with the interaction types labeled “grooming,” “physical contact,” and “overall mix”; the “overall mix” category captures one additional network that recorded grooming behavior. We thus obtained 67 possible networks, which we regarded as undirected weighted networks.

Thirteen out of the 67 networks yielded negative (b/c)* values, which imply that spiteful behavior evolves instead of cooperation (Allen et al., 2017; Su et al., 2022). We discarded these networks because we are interested in cooperation under social dilemma situations, and because the qualitatively different interpretation of a unit change for (b/c)* values above and below zero (i.e., a unit change in the positive direction below zero means that spite evolves more easily, whereas a similar change above zero means that cooperation evolves less easily) violates regression modeling assumptions. Additionally, we discarded one network that was composed of two disconnected dyads and used the remaining 53 connected networks for our analysis. Most species had a single network in the repository. The exceptions were Papio cynocephalus (which had 23 networks), Macaca fascicularis (2), M. fuscata (4), M. mulatta (9), and M. radiata (2). For these species we computed the median of the (b/c)* and network-based explanatory variable (explained in Section 2.3) values; we used these values in further analysis to prevent a few species, such as P. cynocephalus and M. mulatta, from dominating the set of networks to be analyzed. In this manner, we reduced the 53 networks to observations on 17 species for further analysis (Table 1).

TABLE 1

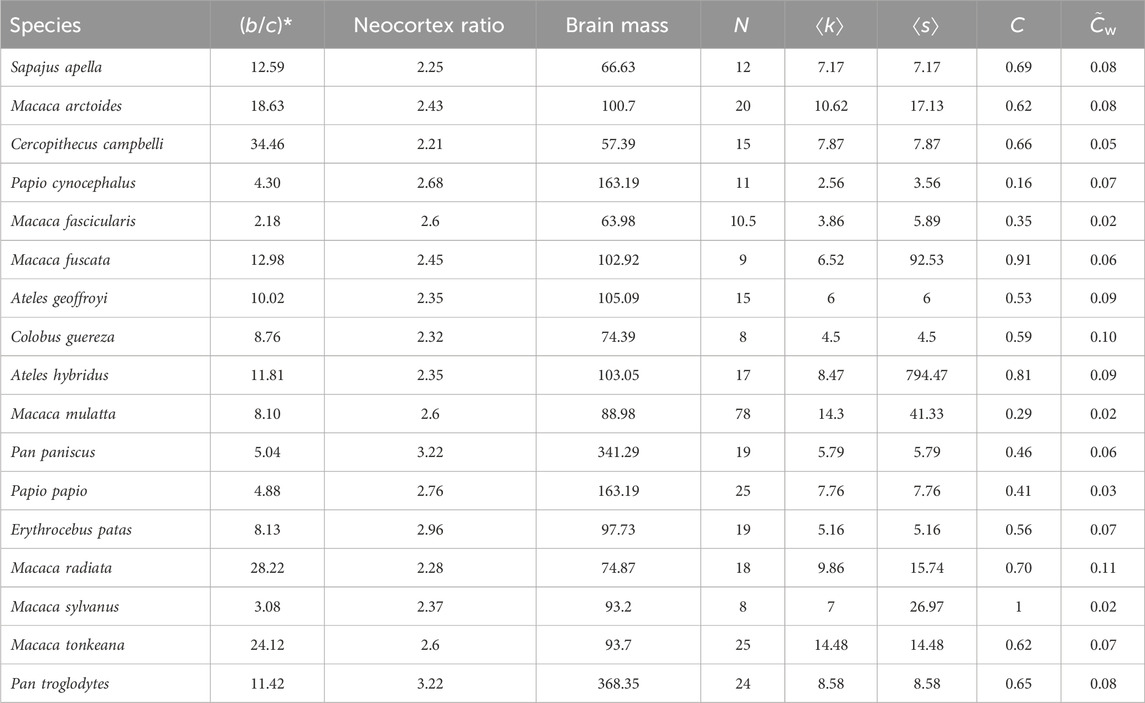
TABLE 1. Properties of primate social networks returned by our selection procedures, sorted by (b/c)*. Values are medians of all the networks for Papio cynocephalus, Macaca fasicularis, M. fuscata, M. mulatta, and M. radiata. NCR: neocortex ratio, N: number of nodes, ⟨k⟩: average node degree, ⟨s⟩: average node strength, C: clustering coefficient, ${\tilde{C}}_{\text{w}}$: weighted clustering coefficient.

We used the species-level neocortex ratio (NCR) estimate from Kudo and Dunbar (2001) for all but one species, Colobus guereza; a species-level NCR estimate was not available in Kudo and Dunbar (2001), so we used the genus-level NCR estimate from Dunbar (1992). Additionally, we used the brain mass data from Smaers et al. (2021) for all species except Papio papio, for which the data is not present. For Papio papio, we used the data of the closely related species P. cynocephalus (Newman et al., 2004). Because the size of several regions of the brain may correlate with social complexity (Bickart et al., 2011; Lewis et al., 2011; Kanai et al., 2012), we included overall brain mass as a relatively simple measure, when compared to the NCR, of species’ neurological complexity (DeCasien et al., 2017) that may also correlate with sociality (Smaers et al., 2019). These two measures (i.e., brain mass and NCR) are highly correlated with each other (see Section 3). Given the unbalanced sampling mentioned above, we did not include controls for phylogeny, social system, foraging behavior, whether the group was free-ranging or captive, or type of behavior captured by the network. See Section 4 for further discussion of this limitation.

2.3 Analysis

Data analysis was conducted in R (R Core Team, 2022); the code is available at https://github.com/ngmaclaren/cooperation-threshold. We used the “MuMIn” package (Bartoń, 2022) to implement the model selection procedure described below.

We fitted generalized linear models (GLMs) to test whether NCR and other variables were associated with the difficulty of cooperation, (b/c)*, which we used as the dependent variable. We considered seven explanatory variables: NCR, brain mass in grams, and five network indices. The five network indices are the number of nodes in the network, denoted by N, the average degree over the N nodes, ⟨k⟩, the average node strength (i.e., the average of the weighted degree over the N nodes), ⟨s⟩, the clustering coefficient, C, and the weighted clustering coefficient, ${\tilde{C}}_{\text{w}}$. The clustering coefficient is the average over all nodes of the local clustering coefficient; the local clustering coefficient for the ith node is the number of triangles (i.e., (i, i′), (i, i″), and (i′, i″) are edges of the network) divided by the number of possible triangles involving the ith node (i.e., k_i(k_i − 1)/2, where k_i is the node i’s degree) (Wasserman and Faust, 1994; Newman, 2018). The weighted clustering coefficient is calculated similarly to the unweighted version except that it uses the geometric mean of the edge weights instead of a count of edges (Fagiolo, 2007). We include these network indices because each of these indices can affect (b/c)* regardless of the potential relationship between brain size and (b/c)* (Allen et al., 2017). Because brain mass, body mass, ⟨s⟩, and ${\tilde{C}}_{\text{w}}$ are positive and obey right-skewed distributions, we used the natural logarithm transform of each of these variables.

We began our modeling process from a position of relative ignorance, including these seven explanatory variables as predictors. By design, our outcome variable, (b/c)*, is positive and continuous, suggesting a model with gamma-distributed errors. To test our choice, we built five different models, each with all seven explanatory variables, with different error models and link functions (i.e., gamma and Gaussian distributions with both inverse and log links, and a quasi-Poisson model) and calculated the deviances of each (Faraway, 2016). As expected, the gamma models fit well (χ² test with d.f. = 8; p = 0.968 and 0.991 for the inverse and log links, respectively), whereas the other models did not (p ≤ 0.001 for each). The residual deviances associated with both gamma-based models are small (inverse link: 2.90, log link: 2.01) relative to the remaining models (quasi-Poisson: 27.61, Gaussian inverse link: 236.09, Gaussian log link: 374.50), further suggesting good fit (Faraway, 2016). Because the model with gamma-distributed errors and the log link had the minimum residual deviance, we used that model for further analysis (Faraway, 2016).

The number of explanatory variables (i.e., seven) is relatively large given the number of observations (i.e., 17). Therefore, we ran an AIC-based model selection, as follows. First, we evaluated all possible models—excluding any model with both brain mass and NCR as predictor variables—and calculated the AICc for each model. AICc is a modification of the Akaike Information Criterion (AIC) that is preferred for model selection when data sets are relatively small (Burnham and Anderson, 2002). Specifically, AICc is defined as AIC+(2k² + 2k)/(n − k − 1), where k is the degrees of freedom of the model and n is the number of observations. When n is small, AICc values increase more with each additional model parameter than the traditional AIC does; the difference between the two metrics becomes small when n is large. Model selection based on AICc thus tends to support fewer model parameters at small n than traditional AIC. A recommended rule is to use AICc when n/k < 40 (Burnham and Anderson, 2002); for a model in this study with three predictor variables, an intercept, and an error parameter, we obtain n/k = 17/5 = 3.4 ≪ 40. We sorted all evaluated models by AICc: the models with minimal AICc values realize the best fit to the data with the fewest variables.

3 Results

We show the sorted AICc values for all 96 models which met our initial selection criteria in Figure 2. Figure 2 shows that the best and second-best models are fairly similar in terms of AICc, but the third-best model has somewhat poorer AICc. Setting a cutoff at ΔAICc = 3, where ΔAICc means the absolute difference in the AICc value relative to the smallest value, allows us to focus on two models that are similar in terms of AICc but clearly better than any other alternatives. We summarize these two models in Table 2. These two models are superior to the full model in terms of AICc (full model AICc: 132.39, Model 1: 106.91, Model 2: 108.01) and collinearity (maximum variance inflation factor for the full model: 5.08, Model 1: 1.03, Model 2: 1.02) without a substantial reduction in variance explained (full model McFadden’s pseudo-R²: 0.77, Model 1: 0.73, Model 2: 0.72).

FIGURE 2

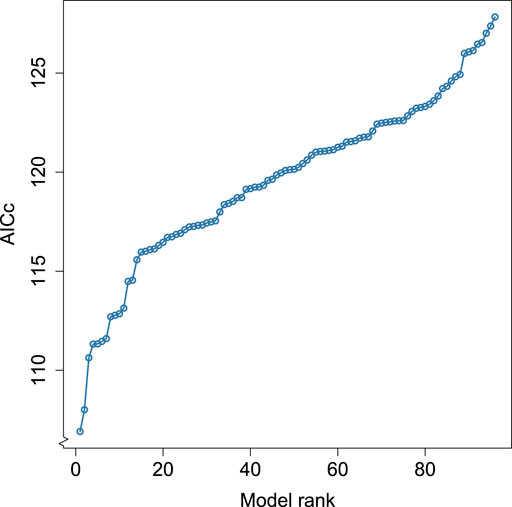
FIGURE 2. Akaike Information Criterion adjusted for small samples (AICc) for all possible models. Possible models are generalized linear models with gamma-distributed errors, a natural logarithm link function, and zero or more of the following explanatory variables: neocortex ratio, brain size, number of nodes, average node degree, average node strength, clustering coefficient, and weighted clustering coefficient.

TABLE 2

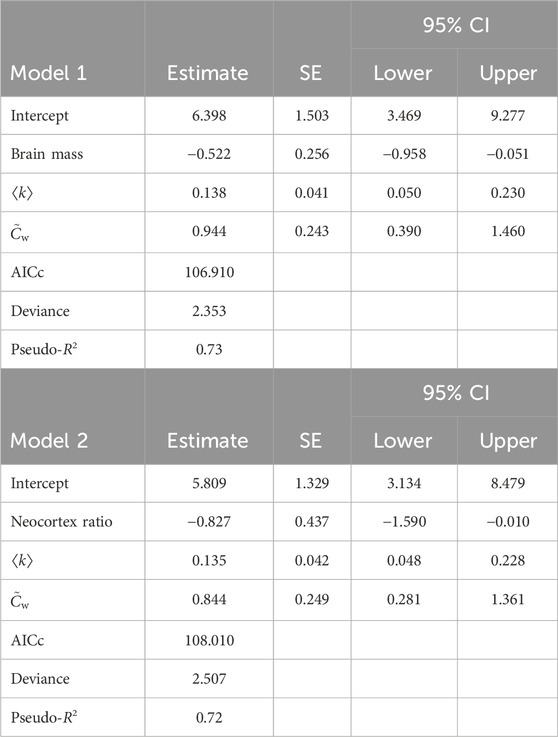
TABLE 2. The best two models, i.e., the models with ΔAICc $<3$. The dependent variable is (b/c)*. All models are generalized linear models with gamma-distributed errors and a natural logarithm link. A negative coefficient indicates that a larger value of the predictor is associated with a smaller value of (b/c)*, suggesting that cooperation spreads more easily on a network. SE stands for the standard error; CI stands for confidence interval; ⟨k⟩ and ${\tilde{C}}_{\text{w}}$ represent average degree and the weighted clustering coefficient, respectively.

The two best models both include a measure of brain size—overall brain mass in Model 1 and NCR in Model 2—and two network features: average node degree ⟨k⟩ and the weighted clustering coefficient ${\tilde{C}}_{\text{w}}$ (Table 2). As is expected given the correlation between brain mass and NCR in this data (r = 0.843, mentioned above), coefficient estimates for the two models are similar: the coefficients on both brain size variables are both negative, whereas the coefficients on average node degree and weighted clustering are positive. Thus, we find that, when average degree and weighted clustering are held constant, brain size is inversely associated with (b/c)* in this data: primates with larger brains are associated with social networks that favor the spread of cooperation. We visualize the association between NCR and (b/c)*, controlling for average degree and weighted clustering, in Figure 3.

FIGURE 3

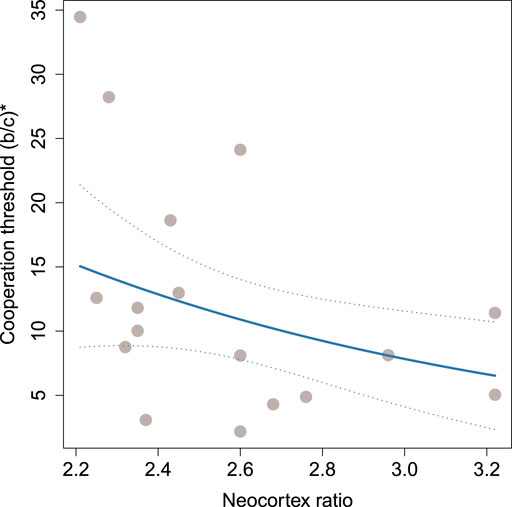
FIGURE 3. Threshold for cooperation, (b/c)*, as a function of the neocortex ratio. Each circle represents a primate species. The solid line represents the predicted (b/c)* given median values for average degree and weighted clustering coefficient. The dotted lines indicate twice the standard error of prediction.

Although overall trends in the data support the social brain hypothesis, there is substantial uncertainty in the coefficient estimates (see Table 2). We visualize this uncertainty in Figure 4, which shows the point estimate for each coefficient (open markers) in both models (indicated by color and marker shape) along with the profile likelihood 95% confidence intervals (horizontal lines). The confidence intervals are all relatively wide compared with the magnitude of the coefficient, suggesting that the size and noisiness of our data inhibit our ability to make precise estimates of the relationship between brain size and (b/c)*.

FIGURE 4

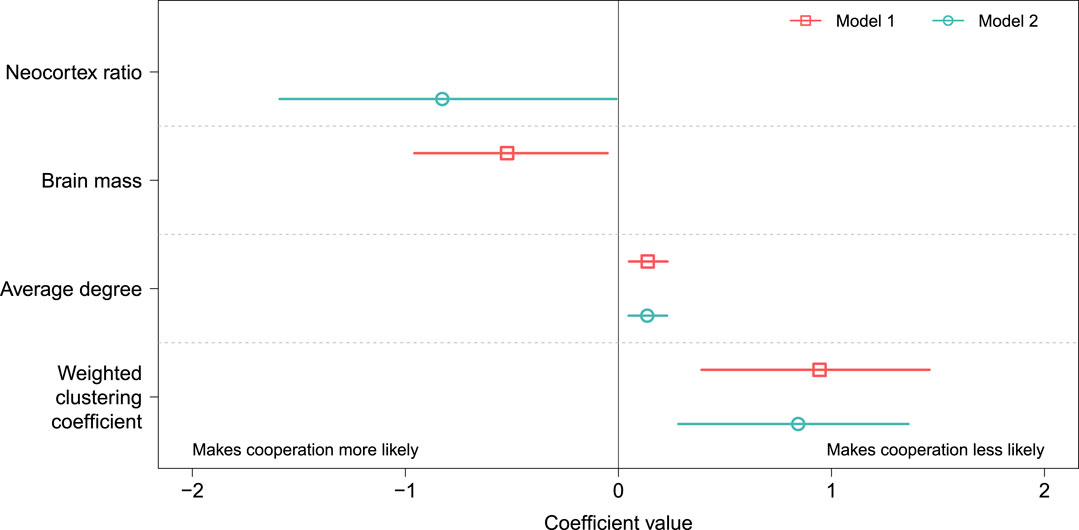
FIGURE 4. Coefficient estimates for the two models with ΔAICc $<3$. Both models are generalized linear models with gamma-distributed errors and a natural logarithm link function and express the association beteween three explanatory variables and (b/c)*. Each model is represented by a different color and type of marker. The markers represent the coefficient values. The lines represent the profile likelihood 95% confidence intervals.

Finally, we note that neither of the best two models has more than three explanatory variables, suggesting that adding more explanatory variables would not be useful in better explaining (b/c)* across the different networks. This observation indicates that our data do not support differentiating between the effects of brain mass and neocortex ratio by, for example, including one as a control on the other in a regression model. The failure of group size N to appear in the best models is also notable, which we discuss in Section 4. This finding suggests that the relationship between brain size and the spread of cooperative behavior may be independent of group size. Finally, neither the average weighted degree ⟨s⟩ nor the unweighted clustering coefficient C appeared in the five best models.

4 Discussion

Our findings suggest that primate species with larger brains tend to form networks which, based on results from game theory (Allen et al., 2017), support the spread of cooperative behaviors. Thus, our primary results are consistent with the social brain hypothesis. Our results are also consistent with previous findings on the effect of network structure on cooperation in primates (Voelkl and Kasper, 2009).

Group size and NCR are only weakly correlated with each other in our data (r = 0.203). This result is only marginally consistent with previous studies, which showed a strong association between group size, which has been used as a proxy for social complexity (Dunbar and Shultz, 2017), and NCR; this association is a central result supporting the social brain hypothesis (Dunbar and Shultz, 2021). A weak association between group size and NCR in our data may be due to different definitions of the group size used in our study and the previous ones. The group size used in this study is the observed number of individuals in a single group. That group was captive in some studies, and there may be other constraints on the observed group size in a particular study that may make the group size value different from what may be typical in wild populations. This difference may have depressed the relationship between group size and the NCR, and also the relationship between group size and cooperation in the present study. Alternatively, we note that primate groups may form for a variety of reasons, such as protection from predators, which neither relate specifically to cooperation nor necessarily indicate an increased cognitive demand on group members. By including group size as a potential predictor of the cooperation threshold, we hypothesized that groups with larger size will have consistent differences in their cooperation threshold from groups of smaller size. We found that this is not the case within the limits of our analysis. Thus, our present findings are orthogonal to previous tests of the social brain hypothesis.

Our data indicate a notable level of uncertainty in the observed trends. An important reason for this uncertainty is the relatively small sample size of our final data set. Additionally, as we described in Section 2, our models do not control for a variety of factors, such as phylogeny and study design. Omitting these variables might account for some of our reported error variance. However, these factors are represented in a very uneven way in the primate networks available in the ASNR, limiting our ability to control for them in our models in a meaningful way. For example, of the 17 species in our final data set, 11 are cercopithecine primates and of those, seven are macaques. No lemur or other strepsirrhine species are represented at all. The situation is even more extreme in the data set prior to aggregation to the species level, in which 44 of the 53 networks came from two cercopithecine genera: Papio (23) and Macaca (21). Thus, although the phylogenetic signal in group size and related variables has been previously shown to be relatively weak (Kamilar and Cooper, 2013), we are limited in our ability to control for phylogenetic effects that may be present in our model. We face a similar situation in attempting to control for study design, which can affect the structure of observed networks (Collier et al., 2022): in our data, most groups were sampled according to social group membership, none were sampled according to a geographic area, and the only captive groups were 10 of the 21 macaque networks. Finally, some uncertainty in our estimates may be due to the brain mass and NCR measurements themselves, which are difficult to obtain and thus not based on large samples of individuals nor available for all species (Stephan et al., 1981). Because of these conditions, we have chosen to simplify our model to accommodate a small sample (Matuschek et al., 2017), rather than take a maximal approach, with which we would include as many theoretically important variables in the model as possible (Barr et al., 2013; McElreath, 2016). We recognize that our decisions reduce both the sample size and the potential generalizability of our study (Yarkoni, 2022). Additional data from species more evenly spread across primate taxa will help address these concerns, as well as support mediation analysis to better test between competing causal hypotheses.

From a theoretical perspective, our work is also limited by the assumptions made by Allen et al.’s theory (Allen et al., 2017). Specifically, their theory assumes fixed, undirected networks and binary strategies (i.e., cooperation or defection). Such assumptions do not realistically represent primate social networks, which may be dynamic, have asymmetric ties (i.e., individual A grooms individual B more than the reverse), and be characterized by complex behavioral strategies. This lack of an explicit connection between models and reality has been recognized as a major challenge in evolutionary game theory (Jusup et al., 2022). The strength of Allen et al.’s results and others is in providing insight into the general mechanisms of the evolution of cooperation (Akçay, 2020). Our study addresses this gap by showing that predictions from the social brain hypothesis, based on observations, are in line with those from evolutionary game theory.

Despite these caveats, the present results allow us to make several additional observations. For example, we observe that cooperation spreads less easily on networks in which individuals tend to have many social partners (i.e., large average degree) or tend to form clusters (i.e., connected triangles). While the former observation agrees with the literature (Ohtsuki et al., 2006; Allen et al., 2017), the latter is apparently inconsistent with the concept of spatial reciprocity, which states that high clustering in networks promotes cooperation (Nowak and May, 1992; Hauert, 2001; Nowak, 2006a). In fact, results supporting spatial reciprocity have been derived for the fraction of cooperators in the quasi-stationary state of evolutionary dynamics in relatively large networks rather than the fixation probability for the cooperator strategy; we examined the latter quantity in this study. The effect of clustering on the fixation probability for cooperation is not systematically known. For example, some numerical simulations suggest that clustering, which is present in most empirical networks, does not facilitate the fixation of cooperation (Ohtsuki et al., 2006; Wu et al., 2014). Therefore, our results are in fact not contradictory to the known results for spatial reciprocity, and fixation of cooperation in clustered networks remains to be investigated.

Cooperative group living is often advantageous in the animal kingdom because it can provide protection from predators and increase the efficiency of foraging tactics (Alexander, 1974; Kappeler and Van Schaik, 2006). However, one of the most commonly cited disadvantages to cooperative group living is the increase in disease transmission potential (Alexander, 1974; Freeland, 1976). In fact, previous work suggests that the average degree is the most important aspect of network structure in determining the transmission potential for pathogens on a network (Collier et al., 2022). Our results show that average degree is negatively associated with the evolution of cooperation, a finding supported by previous theoretical work (Ohtsuki et al., 2006). Given that small average degrees are beneficial for both enhancing cooperation and reducing pathogen transmission opportunity, cooperation and protection against disease transmission potential might have coevolved through a decrease in the average degree of social networks. Maintaining contacts is also costly for individuals. However, a large average degree helps robustness of networks against node and edge failures (Cohen and Havlin, 2010; Brask et al., 2021). We may be able to further discussion of the evolution of network structure and social brain hypotheses by simultaneously taking into account multiple functions of animal society such as cooperation, protection against infection, robustness, and communication efficiency.

The present work also opens avenues for further work to explore the intersection between the social brain hypothesis, networks, and cooperation. For example, most of the social networks in our sample are grooming networks. However, network structure may vary according to the type of prosocial contact even for the same species of animals (Collier et al., 2022). It is not currently known if differences in network structure associated with different behaviors also reflect differences in the spread of cooperation or other indices of social complexity. Furthermore, the spread of spite on ostensibly prosocial networks is an important possibility, but insufficiently characterized. Although further comparative work along these lines is currently limited by available data (Sah et al., 2019), various technological and algorithmic developments of automatic data collection (Krause et al., 2013; Brask et al., 2021) are expected to allow us to access more data and explore these topics in the near future.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/bansallab/asnr.

Author contributions

NeM: Investigation, Visualization, Writing–original draft, Writing–review and editing. LM: Investigation, Writing–review and editing. MC: Data curation, Writing–review and editing. NaM: Conceptualization, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. NaM acknowledges support from AFOSR European Office (under Grant No. FA9550-19-1-7024), the Japan Science and Technology Agency (JST) Moonshot R & D (under Grant No. JPMJMS 2021), the National Science Foundation (under Grant Nos 2052720 and 2204936), and JSPS KAKENHI (under Grant Nos JP 21H04595 and 23H03414). MC acknowledges funding from the Morris Animal Foundation (under Grant No. D22ZO-059).

Acknowledgments

We thank Shweta Bansal for her thoughtful comments on this work. We thank Pratha Sah, Jose Mendez, Grant Rosensteel, Elly Meng, and Sania Ali for their contributions to the development and growth of the Animal Social Network Repository.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akçay, E. (2020). Deconstructing evolutionary game theory: coevolution of social behaviors with their evolutionary setting. Am. Nat. 195 (2), 315–330. doi:10.1086/706811

PubMed Abstract | CrossRef Full Text | Google Scholar

Aldous, D., and Fill, J. A. (2002). Reversible Markov chains and random walks on graphs. Unfinished monograph, recompiled 2014. Available at: https://www.stat.berkeley.edu/users/aldous/RWG/book.html (Accessed on August 6, 2022).

Google Scholar

Alexander, R. D. (1974). The evolution of social behavior. Annu. Rev. Ecol. Syst. 5, 325–383. doi:10.1146/annurev.es.05.110174.001545

CrossRef Full Text | Google Scholar

Allen, B., Lippner, G., Chen, Y.-T., Fotouhi, B., Momeni, N., Yau, S.-T., et al. (2017). Evolutionary dynamics on any population structure. Nature 544 (7649), 227–230. doi:10.1038/nature21723

PubMed Abstract | CrossRef Full Text | Google Scholar

Bansal, S., Grenfell, B. T., and Meyers, L. A. (2007). When individual behaviour matters: homogeneous and network models in epidemiology. J. R. Soc. Interface 4 (16), 879–891. doi:10.1098/rsif.2007.1100

PubMed Abstract | CrossRef Full Text | Google Scholar

Barr, D. J., Levy, R., Scheepers, C., and Tily, H. J. (2013). Random effects structure for confirmatory hypothesis testing: keep it maximal. J. Mem. Lang. 68 (3), 255–278. doi:10.1016/j.jml.2012.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartoń, K. (2022). MuMIn: multi-model inference. Available at: https://cran.r-project.org/package=MuMIn.

Google Scholar

Bickart, K. C., Wright, C. I., Dautoff, R. J., Dickerson, B. C., and Barrett, L. F. (2011). Amygdala volume and social network size in humans. Nat. Neurosci. 14 (2), 163–164. doi:10.1038/nn.2724

PubMed Abstract | CrossRef Full Text | Google Scholar

Brask, J. B., Ellis, S., and Croft, D. P. (2021). Animal social networks: an introduction for complex systems scientists. J. Complex Netw. 9 (2), cnab001. doi:10.1093/comnet/cnab001

CrossRef Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2002). Model selection and multi-model inference. 2nd edition. New York, NY: Springer-Verlag.

Google Scholar

Cheney, D. L. (2011). Extent and limits of cooperation in animals. Proc. Natl. Acad. Sci. 108 (2), 10902–10909. doi:10.1073/pnas.1100291108

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheney, D. L., Moscovice, L. R., Heesen, M., Mundry, R., and Seyfarth, R. M. (2010). Contingent cooperation between wild female baboons. Proc. Natl. Acad. Sci. 107 (21), 9562–9566. doi:10.1073/pnas.1001862107

PubMed Abstract | CrossRef Full Text | Google Scholar

Clutton-Brock, T. (2009). Cooperation between non-kin in animal societies. Nature 462 (7269), 51–57. doi:10.1038/nature08366

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, R., and Havlin, S. (2010). Complex networks: structure, robustness and function. Cambridge, UK: Cambridge University Press.

Google Scholar

Collier, M., Albery, G. F., McDonald, G. C., and Bansal, S. (2022). Pathogen transmission modes determine contact network structure, altering other pathogen characteristics. Proc. Biol. Sci. 289 (1989), 20221389. doi:10.1098/rspb.2022.1389

PubMed Abstract | CrossRef Full Text | Google Scholar

Collier, M., Ali, S., and Bansal, S. (2021). Animal social network repository. Zenodo. doi:10.5281/zenodo.7595404

CrossRef Full Text | Google Scholar

Croft, D. P., Edenbrow, M., and Darden, S. K. (2015). “Assortment in social networks and the evolution of cooperation,” in Animal social networks (Oxford, UK: Oxford University Press), 13–23.

PubMed Abstract | Google Scholar

DeCasien, A. R., Williams, S. A., and Higham, J. P. (2017). Primate brain size is predicted by diet but not sociality. Nat. Ecol. Evol. 1 (5), 0112. doi:10.1038/s41559-017-0112

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunbar, R. I. M. (1992). Neocortex size as a constraint on group size in primates. J. Hum. Evol. 22 (6), 469–493. doi:10.1016/0047-2484(92)90081-j

CrossRef Full Text | Google Scholar

Dunbar, R. I. M. (1998). The social brain hypothesis. Evol. Anthropol. Issues, News, Rev. 6 (5), 178–190. doi:10.1002/(sici)1520-6505(1998)6:5<178::aid-evan5>3.3.co;2-p

CrossRef Full Text | Google Scholar

Dunbar, R. I. M., and Shultz, S. (2017). Why are there so many explanations for primate brain evolution? Philosophical Trans. R. Soc. B Biol. Sci. 372 (1727), 20160244. doi:10.1098/rstb.2016.0244

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunbar, R. I. M., and Shultz, S. (2021). Social complexity and the fractal structure of group size in primate social evolution. Biol. Rev. 96 (5), 1889–1906. doi:10.1111/brv.12730

PubMed Abstract | CrossRef Full Text | Google Scholar

Fagiolo, G. (2007). Clustering in complex directed networks. Phys. Rev. E 76 (2), 026107. doi:10.1103/physreve.76.026107

PubMed Abstract | CrossRef Full Text | Google Scholar

Faraway, J. J. (2016). Extending the linear model with R: generalized linear, mixed effects and nonparametric regression models. 2nd edition. Boca Raton, FL: Chapman and Hall/CRC.

Google Scholar

Freeland, W. J. (1976). Pathogens and the evolution of primate sociality. Biotropica 8 (1), 12–24. doi:10.2307/2387816

CrossRef Full Text | Google Scholar

Fudenberg, D., and Levine, D. K. (1998). The theory of learning in games. Cambridge, MA: MIT Press.

Google Scholar

Gokcekus, S., Cole, E. F., Sheldon, B. C., and Firth, J. A. (2021). Exploring the causes and consequences of cooperative behaviour in wild animal populations using a social network approach. Biol. Rev. 96 (5), 2355–2372. doi:10.1111/brv.12757

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauert, Ch. (2001). Fundamental clusters in spatial 2×2 games. Proc. R. Soc. Lond. Ser. B Biol. Sci. 268 (1468), 761–769. doi:10.1098/rspb.2000.1424

PubMed Abstract | CrossRef Full Text | Google Scholar

Jusup, M., Holme, P., Kanazawa, K., Takayasu, M., Romić, I., Wang, Z., et al. (2022). Social physics. Phys. Rep. 948, 1–148. doi:10.1016/j.physrep.2021.10.005

CrossRef Full Text | Google Scholar

Kamilar, J. M., and Cooper, N. (2013). Phylogenetic signal in primate behaviour, ecology and life history. Philosophical Trans. R. Soc. B Biol. Sci. 368 (1618), 20120341. doi:10.1098/rstb.2012.0341

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanai, R., Bahrami, B., Roylance, R., and Rees, G. (2012). Online social network size is reflected in human brain structure. Proc. R. Soc. B Biol. Sci. 279 (1732), 1327–1334. doi:10.1098/rspb.2011.1959

PubMed Abstract | CrossRef Full Text | Google Scholar

Kappeler, P. M., Clutton-Brock, T., Shultz, S., and Lukas, D. (2019). Social complexity: patterns, processes, and evolution. Behav. Ecol. Sociobiol. 73 (5), 5. doi:10.1007/s00265-018-2613-4

CrossRef Full Text | Google Scholar

Kappeler, P. M., and Van Schaik, C. P. (2006). Cooperation in primates and humans. Berlin, Germany: Springer.

Google Scholar

Krause, J., Krause, S., Arlinghaus, R., Psorakis, I., Roberts, S., and Rutz, C. (2013). Reality mining of animal social systems. Trends Ecol. Evol. 28 (9), 541–551. doi:10.1016/j.tree.2013.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Kruase, J., James, R., Franks, D. W., and Croft, D. P. (Editors) (2015). Animal social networks. Oxford, UK: Oxford University Press.

Google Scholar

Kudo, H., and Dunbar, R. I. M. (2001). Neocortex size and social network size in primates. Anim. Behav. 62 (4), 711–722. doi:10.1006/anbe.2001.1808

CrossRef Full Text | Google Scholar

Lehmann, J., and Dunbar, R. I. M. (2009). Network cohesion, group size and neocortex size in female-bonded old world primates. Proc. R. Soc. B Biol. Sci. 276 (1677), 4417–4422. doi:10.1098/rspb.2009.1409

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewis, P. A., Rezaie, R., Brown, R., Roberts, N., and Dunbar, R. I. M. (2011). Ventromedial prefrontal volume predicts understanding of others and social network size. NeuroImage 57 (4), 1624–1629. doi:10.1016/j.neuroimage.2011.05.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Masuda, N., Porter, M. A., and Lambiotte, R. (2017). Random walks and diffusion on networks. Phys. Rep. 716-717, 1–58. doi:10.1016/j.physrep.2017.07.007

CrossRef Full Text | Google Scholar

Matuschek, H., Kliegl, R., Vasishth, S., Baayen, H., and Bates, D. (2017). Balancing Type I error and power in linear mixed models. J. Mem. Lang. 94, 305–315. doi:10.1016/j.jml.2017.01.001

CrossRef Full Text | Google Scholar

McAuliffe, K., and Thornton, A. (2015). The psychology of cooperation in animals: an ecological approach. J. Zoology 295 (1), 23–35. doi:10.1111/jzo.12204

CrossRef Full Text | Google Scholar

McElreath, R. (2016). A Bayesian course with examples in R and Stan. Boca Raton, Fla: Chapman and Hall/CRC.

Google Scholar

Newman, M. (2018). Networks. 2nd edition. Oxford, UK: Oxford University Press.

Google Scholar

Newman, T. K., Jolly, C. J., and Rogers, J. (2004). Mitochondrial phylogeny and systematics of baboons (Papio). Am. J. Phys. Anthropol. 124 (1), 17–27. doi:10.1002/ajpa.10340

PubMed Abstract | CrossRef Full Text | Google Scholar

Noë, R. (2006). Cooperation experiments: coordination through communication versus acting apart together. Anim. Behav. 71 (1), 1–18. doi:10.1016/j.anbehav.2005.03.037

CrossRef Full Text | Google Scholar

Nowak, M. A. (2006a). Five rules for the evolution of cooperation. Science 314, 1560–1563. doi:10.1126/science.1133755

PubMed Abstract | CrossRef Full Text | Google Scholar

Nowak, M. A. (2006b). Evolutionary dynamics. Cambridge, MA: Belknap Press of Harvard University Press.

Google Scholar

Nowak, M. A., and May, R. M. (1992). Evolutionary games and spatial chaos. Nature 359 (6398), 826–829. doi:10.1038/359826a0

CrossRef Full Text | Google Scholar

Nowak, M. A., Sasaki, A., Taylor, C., and Fudenberg, D. (2004). Emergence of cooperation and evolutionary stability in finite populations. Nature 428 (6983), 646–650. doi:10.1038/nature02414

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohtsuki, H., Hauert, Ch., Lieberman, E., and Nowak, M. A. (2006). A simple rule for the evolution of cooperation on graphs and social networks. Nature 441 (7092), 502–505. doi:10.1038/nature04605

PubMed Abstract | CrossRef Full Text | Google Scholar

Pasquaretta, C., Levé, M., Claidiere, N., Van de Waal, E., Whiten, A., MacIntosh, A. J. J., et al. (2014). Social networks in primates: smart and tolerant species have more efficient networks. Sci. Rep. 4 (1), 7600. doi:10.1038/srep07600

PubMed Abstract | CrossRef Full Text | Google Scholar

Perc, M., Gómez-Gardeñes, J., Szolnoki, A., Floría, L. M., and Moreno, Y. (2013). Evolutionary dynamics of group interactions on structured populations: a review. J. R. Soc. Interface 10 (80), 20120997. doi:10.1098/rsif.2012.0997

PubMed Abstract | CrossRef Full Text | Google Scholar

Perc, M., Jordan, J. J., Rand, D. G., Wang, Z., Boccaletti, S., and Szolnoki, A. (2017). Statistical physics of human cooperation. Phys. Rep. 687, 1–51. doi:10.1016/j.physrep.2017.05.004

CrossRef Full Text | Google Scholar

Pinter-Wollman, N., Hobson, E. A., Smith, J. E., Edelman, A. J., Shizuka, D., De Silva, S., et al. (2014). The dynamics of animal social networks: analytical, conceptual, and theoretical advances. Behav. Ecol. 25 (2), 242–255. doi:10.1093/beheco/art047

CrossRef Full Text | Google Scholar

Powell, L. E., Isler, K., and Barton, R. A. (2017). Re-evaluating the link between brain size and behavioural ecology in primates. Proc. R. Soc. B Biol. Sci. 284 (1865), 20171765. doi:10.1098/rspb.2017.1765

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2022). R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing.

Google Scholar

Sah, P., Méndez, J. D., and Bansal, S. (2019). A multi-species repository of social networks. Sci. Data 6, 44. doi:10.1038/s41597-019-0056-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Salahshour, M. (2020). Coevolution of cooperation and language. Phys. Rev. E 102 (4), 042409. doi:10.1103/physreve.102.042409

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, F. C., and Pacheco, J. M. (2005). Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 95 (9), 098104. doi:10.1103/physrevlett.95.098104

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, F. C., Pacheco, J. M., and Lenaerts, T. (2006). Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. 103 (9), 3490–3494. doi:10.1073/pnas.0508201103

PubMed Abstract | CrossRef Full Text | Google Scholar

Shultz, S., and Dunbar, R. I. M. (2022). Socioecological complexity in primate groups and its cognitive correlates. Philosophical Trans. R. Soc. Lond. Ser. B, Biol. Sci. 377 (1860), 20210296. doi:10.1098/rstb.2021.0296

CrossRef Full Text | Google Scholar

Smaers, J. B., Mongle, C. S., Safi, K., and Dechmann, D. K. N. (2019). Allometry, evolution and development of neocortex size in mammals. Prog. Brain Res. 250, 83–107. doi:10.1016/bs.pbr.2019.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Smaers, J. B., Rothman, R. S., Hudson, D. R., Balanoff, A. M., Beatty, B., Dechmann, D. K. N., et al. (2021). The evolution of mammalian brain size. Sci. Adv. 7 (18), eabe2101. doi:10.1126/sciadv.abe2101

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, E. A. (2010). Communication and collective action: language and the evolution of human cooperation. Evol. Hum. Behav. 31 (4), 231–245. doi:10.1016/j.evolhumbehav.2010.03.001

CrossRef Full Text | Google Scholar

Smith, J. M. (1982). Evolution and the theory of games. Cambridge: Cambridge University Press.

Google Scholar

Stephan, H., Frahm, H., and Baron, G. (1981). New and revised data on volumes of brain structures in insectivores and primates. Folia Primatol. 35 (1), 1–29. doi:10.1159/000155963

PubMed Abstract | CrossRef Full Text | Google Scholar

Street, S. E., Navarrete, A. F., Reader, S. M., and Laland, K. N. (2017). Coevolution of cultural intelligence, extended life history, sociality, and brain size in primates. Proc. Natl. Acad. Sci. 114 (30), 7908–7914. doi:10.1073/pnas.1620734114

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, Q., McAvoy, A., and Plotkin, J. B. (2022). Evolution of cooperation with contextualized behavior. Sci. Adv. 8 (6), eabm6066. doi:10.1126/sciadv.abm6066

PubMed Abstract | CrossRef Full Text | Google Scholar

Szabó, G., and Fáth, G. (2007). Evolutionary games on graphs. Phys. Rep. 446, 97–216. doi:10.1016/j.physrep.2007.04.004

CrossRef Full Text | Google Scholar

Takács, K., Gross, J., Testori, M., Letina, S., Kenny, A. R., Power, E. A., et al. (2021). Networks of reliable reputations and cooperation: a review. Philosophical Trans. R. Soc. Lond. Ser. B, Biol. Sci. 376 (1838), 20200297. doi:10.1098/rstb.2020.0297

CrossRef Full Text | Google Scholar

Voelkl, B., and Kasper, C. (2009). Social structure of primate interaction networks facilitates the emergence of cooperation. Biol. Lett. 5 (4), 462–464. doi:10.1098/rsbl.2009.0204

PubMed Abstract | CrossRef Full Text | Google Scholar

Wasserman, S., and Faust, K. (1994). Social network analysis: methods and applications. New York, NY: Cambridge University Press.

Google Scholar

Wu, Z.-X., Rong, Z., and Yang, H.-X. (2014). Community structure benefits the fixation of cooperation under strong selection. Available at: https://arxiv.org/abs/1408.3267.

Google Scholar

Yarkoni, T. (2022). The generalizability crisis. Behav. Brain Sci. 45, 1–78. doi:10.1017/s0140525x20001685

CrossRef Full Text | Google Scholar