Habitat management decisions for conservation: a conceptual framework

Nichols, James D.; Breininger, David R.; Armstrong, Doug P.; Lacy, Robert C.

doi:10.3389/fcosc.2024.1450000

METHODS article

Front. Conserv. Sci., 28 October 2024

Sec. Animal Conservation

Volume 5 - 2024 | https://doi.org/10.3389/fcosc.2024.1450000

This article is part of the Research Topic Linking Habitat Quality to Population Dynamics for Conservation Decision Making View all 8 articles

Habitat management decisions for conservation: a conceptual framework

¹Department of Wildlife Ecology and Conservation, University of Florida, Gainesville, FL, United States
²Department of Biology, University of Central Florida, Orlando, FL, United States
³Wildlife Ecology Group, Massey University, Palmerston North, New Zealand
⁴Independent Researcher, Jonesboro, ME, United States

The focus of this selection of papers is the linkage of habitat and population dynamics for the purpose of conservation. We thus provide a general framework for making conservation decisions, emphasizing how knowledge of habitat–population linkages fits into this framework. We begin by describing structured decision-making (SDM) as a general approach to making conservation decisions. SDM requires the development of the following elements: objectives, actions, model(s), monitoring, and decision algorithm. We then describe adaptive resource management (ARM), a specific type of SDM developed for recurrent decisions characterized by potentially resolvable uncertainty. Many different classes of actions can be used to influence animal population dynamics, and modification of habitat is one class of action that is frequently used. Habitat management requires models for predicting responses of the managed system to management actions, and these models are based on our knowledge of habitat–population linkages. Frequently, these models are decomposed into two submodels: one used to predict habitat changes expected to result from management actions and another used to predict population responses to habitat changes. This latter modeling focuses generally on the influence of habitat change on vital rates governing the dynamics of population state variables (variables such as population size or density that describe the status or health of a population). Specific recommendations depend on 1) the vital rates and state variable(s) being considered, 2) the relative spatial scales of animal movement and habitat measurement, and 3) the relative temporal scales of habitat change and vital rate estimation. Finally, we present an example of an ARM program for habitat management, highlighting the role of habitat-linked population modeling in this effort.

Introduction

Conservation of wildlife populations requires taking actions intended to meet specified objectives. One specific class of action widely used to influence wildlife populations is habitat management. Specifically, habitat quality influences populations by influencing the vital rates that determine population dynamics. Vital rates that define the dynamics of single populations are rates of survival, recruitment, immigration, and emigration. For metapopulations, the rates of local extinction and colonization are the vital rates often used to describe dynamics. Here, we describe structured decision-making (SDM) as a general approach to selecting management actions. We then describe adaptive resource management (ARM), a subset of SDM developed for recurrent decision processes that are characterized by uncertainty. Many habitat management programs are candidates for the use of ARM.

One element of SDM and ARM processes is one or more models that can be used to predict the consequences of different management actions. In the case of habitat management, such modeling frequently includes two sequential submodels: one concerning the influence of management actions on habitat and the other concerning the influence of habitat changes on wildlife population dynamics. This latter submodel is the focal topic for this collection of papers.

Our aim in this paper is to show how models linking habitat to wildlife population dynamics fit into larger conservation programs. We first describe SDM, which provides a general framework for all decisions in conservation. We then describe ARM as a special case of SDM developed for recurrent decision processes that are characterized by uncertainty. These descriptions of SDM and ARM are intentionally general, as we seek to emphasize their applicability to a wide range of decision problems.

Manipulating habitat is one class of management action used in conservation decision problems and is the focus of this set of papers. Habitat management using SDM or ARM requires models to predict the effects of these actions on system responses and “returns” (benefits, as defined by objectives). These predictions are used to make smart, even optimal, decisions within SDM and ARM programs. We thus provide a conceptual framework for using models linking habitat management to wildlife population dynamics in conservation decision processes. We provide some general observations about developing such models and using them to learn, and we describe an example of an ARM process of habitat management, highlighting the role of models in this process.

Structured decision-making

Selecting a management action represents a decision, and structured decision-making (see Martin et al., 2009; Gregory et al., 2012; Hemming et al., 2021) provides a means of making logical and transparent decisions. SDM breaks a decision process into key elements, focusing on each element separately, and then combining them to make a decision.

The SDM process should begin with an effort to define and frame the decision problem (Runge et al., 2020; Hemming et al., 2021). Problem definition identifies the issue that the decision process is intended to resolve. Framing requires identifying the decision-maker, the geographic and temporal scales of the problem, relevant laws and regulatory constraints, likely stakeholders, and key uncertainties. Attention to problem definition and framing prevents unnecessary expenditure of time and effort on vaguely defined problems.

The major elements of SDM are objectives, potential actions, model(s) of system response to actions, a monitoring program, and a decision algorithm. Objectives are simply statements of what the decision-maker and relevant stakeholders would like to achieve. Allocating adequate time and effort to the development of objectives is essential, as objectives drive the entire process, strongly influencing all of the other elements of the SDM process. Objectives may appear to be obvious, yet it is surprising how frequently like-minded stakeholders differ in their ideas about what they would like to achieve. Failure to explicitly define objectives is a common reason for the breakdown of decision processes.

Potential actions represent the set of management alternatives to be considered. The decision process is designed to select one of the potential actions for implementation, and this selection represents the decision. In some problems, the set of potential actions is clear, but this is not always the case. As with all other SDM elements, the development of potential actions should be guided by the objectives.

Models are abstractions of the managed system designed to provide specific predictions used to help the decision-maker select the best action with respect to objectives. The abstractions are frequently mathematical although this is not necessary. Indeed, models may be encoded in a computer program, the mind of the manager, or on a sheet of paper. Models useful for decision-making must make predictions about how the system responds to the different management actions. For each action in the set, the model must predict the returns and, for recurrent decisions, the subsequent state of the system. Some managers view models as interesting to academics, but not useful for people who make real-world decisions. However, if there is no way to predict the consequences of management actions, then there is no basis for selecting one option over another. Management requires predictions, so models are not optional for informed management.

Monitoring programs provide information that serves multiple needs for SDM. An estimate of a system state (e.g., abundance for single-population management) is needed for making state-dependent decisions. For example, if the population size is too small relative to our objectives, we would likely select a very different action than if the population size is too large. Monitoring also permits the manager to gauge the success of the management action. Monitoring data are frequently used to develop and improve the models required for management. In the case of recurrent decisions (see below), monitoring data can be used to learn about system responses to management.

A decision algorithm requires input from all of the other elements of the SDM process and combines these to determine which action is predicted to be best, based on expected returns. In some cases, determination of the best action to take is straightforward, but when this is not the case, optimization algorithms can be used (e.g., Puterman, 1994; Williams et al., 2002).

SDM provides a very general approach to decision-making. SDM can be used for one-time decisions (e.g., conservation land acquisition), as well as recurrent decisions, and it can be used for problems regardless of whether they are characterized by uncertainty. A key point with respect to the topic of this paper is that SDM requires models in order to predict the consequences of management actions.

Adaptive resource management

Recurrent decision processes

Recurrent decisions are made periodically, usually for the same system (Figure 1). At each decision point in Figure 1, an “action” is selected and imposed on the system. “State” refers to the general condition of the system, often assessed by the values of one or more state variables (e.g., population size, habitat type, species richness). The action generates two responses: 1) it produces returns, and 2) it drives the system to a new state (Figure 1). “Returns” are benefits, as defined by the objectives. For example, in harvest management, returns are usually defined in terms of the number of animals harvested (e.g., Johnson et al., 1997). In many other types of conservation problems, the objectives are defined in terms of the state variables that characterize the resource system. For example, returns associated with a conservation action might include change in population size (e.g., Eaton et al., 2021) or change in the probability of a population going extinct.

Figure 1

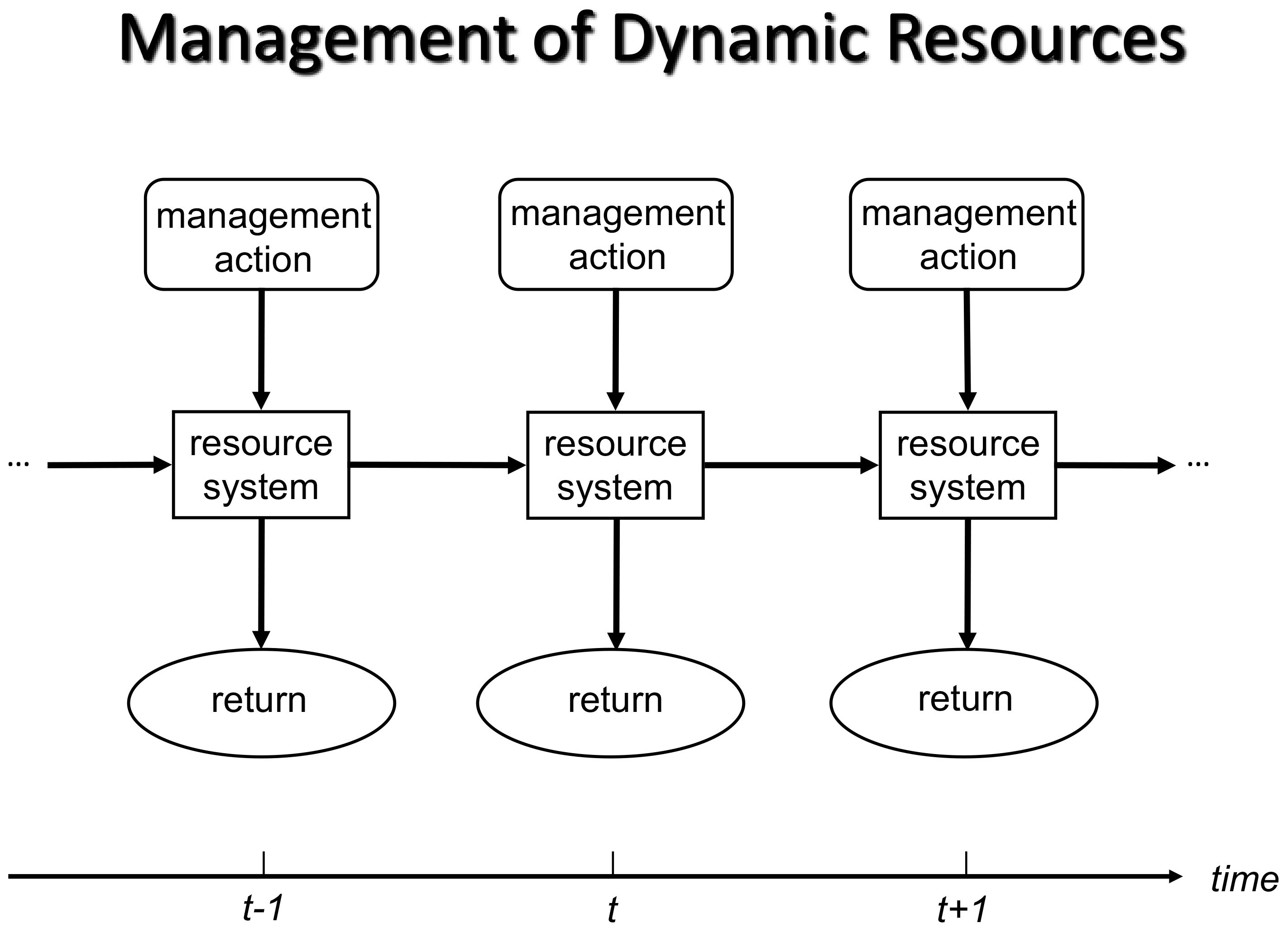
Figure 1. Diagram of a generalized recurrent decision process. A management action is selected and taken at each decision point (time step, t). The action leads to the production of returns (variables that are components of management objectives) and potential changes in the resource system itself. Note that objectives (and thus returns) may include functions of state variables that characterize the resource system (modified from Nichols and Williams, 2013).

Recurrent decision processes impose additional complexity for decision algorithms because current decisions affect system dynamics and thus future decisions. For example, we cannot just maximize returns for the immediate time step. Instead, we must also consider the predicted state for the next time step, as objectives are typically based on the entire time horizon of the process. Recurrent decisions also admit the possibility of learning as management proceeds. Adaptive resource management is a subset of SDM developed for making recurrent decisions in the face of uncertainty about the effects of different management actions. ARM incorporates a scientific step (the comparison of observations against model-based predictions for the purpose of learning) within the larger decision process in order to reduce uncertainty and learn (Walters, 1986; Williams et al., 2007). Here, we revisit the elements of SDM from the perspective of a recurrent decision process and ARM.

ARM elements

As with SDM, objectives retain their primacy in ARM and all the other decision process elements derive from them. Objectives for recurrent decisions typically include the accrual of benefits and costs over time. Often, this is quantified by simply summing returns over the time horizon of the process. Time may also be incorporated by defining the objective in terms of a specific time interval, for example, when our objective is to minimize the probability of a local population going extinct over a specified time horizon (e.g., the next 50 years), as computed via population viability analysis (Beissinger and McCullough, 2002).

The set of potential actions for recurrent decisions may remain fixed for the entire process or it may evolve. Recurrent decisions admit the possibility of modifying the set of actions, either adapting them to a changing system or else considering new alternatives (see Double-loop learning).

The role of models in decision processes is to project the consequences of management actions. Models for one-time decisions may only need to predict immediate returns, but models used for recurrent decision processes must predict immediate and subsequent returns, as well as system state for the next, and subsequent, decision points (Figure 1). For habitat management, models may need to predict both the effects of management actions on habitat and the effects of habitat change on the managed wildlife population or community.

Decision processes are frequently characterized by many sources of uncertainty. Four of these are often highlighted and should be incorporated into modeling when possible: environmental variation, partial controllability, partial observability, and structural uncertainty. Although the primary focus of SDM and ARM modeling is on the effects of management actions, environmental variables external to management actions may also influence system dynamics. If certain environmental variables are identified as important system drivers, they may be incorporated individually into models. Variation associated with environmental variables that are not explicitly modeled simply adds variation to model predictions.

Partial controllability refers to variation in the implementation of management actions. For example, habitat management actions such as prescribed burning may be based on very precise and specific instructions, but the actual habitat effects that these actions produce can exhibit substantial variation, depending on such factors such as wind, recent weather (vegetation dry or wet), extent of bare ground, and fuel load (e.g., Breininger et al., 2010).

Partial observability refers to the ubiquitous problem in studying wildlife populations and communities that we can hardly ever count individuals perfectly. Instead, our counts nearly always “miss” individuals present on surveyed sample units, such that we require estimation methods to deal with non-detection (e.g., Seber, 1982; Williams et al., 2002; Kery and Royle, 2015; Seber and Schofield, 2019). For many problems in conservation, focal populations and communities inhabit areas so large that they cannot be surveyed completely. These situations require spatial sampling, which also adds variation to estimates of state variables (e.g., Lancia et al., 1994, 2005; Thompson, 2002; Williams et al., 2002). Such variation naturally adds to the variance of predictions and should be accounted for when possible.

Structural uncertainty refers to imperfect knowledge of the manner in which systems respond to management actions. This uncertainty is sometimes expressed in the form of different discrete models of system behavior. Define a discrete model set as the models (usually small in number) considered to provide plausible descriptions of the dynamics of the managed system. Each model in the set is characterized by a model weight, reflecting the predictive ability of that model expressed relative to the other models in the set. Model weights sum to one for all the models in the set. We have more confidence in models with higher weights, believing them to be more likely to represent reasonable abstractions of the modeled processes. The weight of each model at a decision point determines its relative influence on the optimal decision. As the ARM process proceeds, weight should increase for model(s) that predict well and decrease for those that predict poorly (see Learning).

Another way to express structural uncertainty is by using parameters in a general model that permit a range of model behaviors. Such models are general with respect to the system response to management actions, such that different values of the parameters produce substantial differences in system response. As the ARM process proceeds and more observations are obtained, the estimated parameters should become more accurate (decreased bias and increased precision).

Monitoring in an ARM program serves the same three purposes listed above for any general SDM program. Monitoring 1) provides estimates of system state for making state-dependent decisions, 2) permits the manager to gauge the success of management, and 3) provides data used to develop and update management models. In ARM, monitoring is also 4) critical to learning, providing estimates to be compared against model predictions.

Decision algorithms provide a means of determining the “best” action based on the other process elements, where “best” is determined by the objectives. Decision algorithms can range from the thought processes of a manager to dynamic optimization programs. As noted above, recurrent decisions require consideration not only of expected returns for the current time step but also for all remaining steps in the decision process time horizon. Such decision problems can be solved using dynamic optimization approaches such as stochastic dynamic programming (SDP) (Bellman, 1957; Puterman, 1994). SDP deals with environmental variation and partial controllability, but not directly with the other two sources of uncertainty: partial observability and structural uncertainty.

An extension of SDP known as adaptive stochastic dynamic programming (ASDP) (Williams, 1996) projects both system and learning dynamics through time in order to determine optimal decisions for processes with structural uncertainty. Partially observable Markov decision process (POMDP) optimization was developed to deal with dynamic systems for which system state variables cannot be directly observed but must be estimated (Chades et al., 2021; Williams and Brown, 2022). The theoretical framework for dynamic optimization that can deal with all four sources of uncertainty has been developed (Williams, 2011; Fackler and Pacifici, 2014). SDP and ASDP have been used for most of the ARM programs implemented over the last 25–30 years in North America (Johnson et al., 1997; Martin et al., 2011; McGowan et al., 2015; Eaton et al., 2021; U.S. Fish and Wildlife Service, 2021).

ARM: deliberative phase

The deliberative or set-up phase of adaptive management entails the initial development of the above elements (Table 1). The establishment of objectives is a critical first step and requires attention to legal and regulatory considerations, as well as input from all relevant stakeholders for the managed system. Objectives are based on human values, and different stakeholder groups frequently differ in how they value any system. Workshops are sometimes held to obtain stakeholder input and to accomplish the difficult task of developing compromise objectives to which all stakeholders can agree. Scientists may be stakeholders, but their perspectives carry no extra weight in identifying objectives.

Table 1

Table 1. Operational steps in adaptive management include the development of ARM elements in the deliberative or set-up phase and the iterative process of making and implementing decisions.

Deciding on a set of potential actions also requires substantial stakeholder input, as some actions (e.g., predator control) may be deemed unacceptable for social or political reasons. Scientists may have a more substantial role than other stakeholders in developing a set of potential actions, as scientists sometimes have specific insights about the relative effectiveness of different actions.

Development of the other three elements—models, monitoring program, and decision algorithm—is typically carried out primarily by scientists and managers. Other stakeholders may be asked to contribute, but the technical aspects of these elements usually require specialized expertise. Technical experts are often organized into ARM working groups, which then report back periodically to the full stakeholder group. Models, monitoring, and the decision algorithm should be tailored to the specified objectives and actions. Examples of deliberative phase efforts for different ARM programs are provided by Johnson et al. (1997), Nichols (2000); McGowan et al. (2015), and Eaton et al. (2021).

ARM: iterative phase

The initial step of the iterative phase entails selecting a management action at the first decision point (Figure 1) using the decision algorithm with all the elements developed in the deliberative phase (Table 1). The selected action is then applied to the system, producing returns and driving the system to a new state.

The new system state is estimated before the next decision point via the monitoring program. The estimated state is compared against model-based predictions in order to update model weights or model parameters (see Learning). At the next decision point, a management action is selected using the decision algorithm and based on the objectives, actions, and models, all of which typically remain the same as in the first step, together with the new estimate of the system state and the updated model weights. The new action is applied, returns are accrued, and the system again moves to a new state. The iterative process proceeds in this manner (Table 1).

The iterative phase thus entails selecting actions that are good or optimal with respect to the specified objectives while simultaneously reducing uncertainty by learning which model(s) represents the best approximation to the processes governing system responses to management actions. This combination of wise decision-making and simultaneous learning distinguishes adaptive management from other forms of management.

Learning

Learning in ARM occurs via the incorporation into the decision process of a scientific step, entailing the comparison of model-based predictions against observations. When structural uncertainty is expressed as a set of discrete models, learning occurs via the updating of model weights via Bayes’ theorem (e.g., Williams et al., 2002; Link and Barker, 2010). The updating is based on two sources of information for each model. The first source is the current (prior) weight, reflecting the relative predictive ability of each model based on past observations accrued up until the decision point. The second source of information is the probability of observing the current value of the system’s state variable (as estimated via monitoring) under each model. The updating entails computing a new model weight (posterior) based on both the old weight and how well each model predicts the new data on the system state. If the model set includes a good approximating model, then the weight for that model should evolve to approach 1, whereas the weights of models that predict more poorly should eventually approach 0.

Model uncertainty can also be expressed using a very general model with one or more focal parameters, the values of which can produce models with very different behaviors. For example, we might have a model parameter for a habitat effect that can take any value between 0 and 1, with 1 indicating a maximal effect of the habitat manipulation and 0 indicating no effect. Such a model can be viewed as providing a continuous model set, and we reduce uncertainty by increasing the accuracy of the estimate of this parameter and its distribution. The updating of the distribution(s) of the parameter(s) again follows Bayes’ theorem and includes the information about the distributions based on all data collected through time t (the prior distributions), as well as the new data (time t+1). The estimated distributions of these parameters are expected to become more and more accurate through time.

Learning in adaptive management is thus accomplished by this updating of either model weights or focal model parameters that specify structural uncertainty. Sometimes, a distinction is made between active and passive adaptive management. Under passive ARM, learning is an anticipated, but untargeted, by-product of management. In passive ARM, the dynamic decision algorithm uses the current state of knowledge to represent knowledge in all future points in the time horizon (Nichols and Williams, 2013). In active ARM, learning is anticipated and targeted, such that the management decision is based not only on the system state (e.g., abundance) and projections of it into the future but also on the current state of knowledge (e.g., model weights or parameter estimates) and projections of its future evolution. Active adaptive management thus addresses the “dual control” problem of balancing short-term benefits (immediate returns) with the long-term benefits that result from learning. Both approaches incorporate learning and then use what is learned to manage, essential features of adaptive management.

Double-loop learning phase

We have emphasized the importance of the deliberative phase in carefully establishing the various elements of the ARM process. However, the adoption of ARM does not mean that these elements cannot be modified at some later time in the process. Double-loop learning is the term used to indicate a phase of ARM at which one or more of the decision process elements are revisited and possibly revised (Williams et al., 2007; Williams and Brown, 2018).

Double-loop learning can be initiated for a variety of different reasons. For example, experience with the ARM process could produce changes in perspective that would lead to reconsideration and possible modification of objectives. New ideas may arise for additional actions that might be effective. If none of the models in the model set seems to predict well, then modifications or new models may be considered. Monitoring programs may be modified in efforts to produce more accurate estimates.

The temporal scale of double-loop learning is typically longer than that of the iterative phase of ARM. For example, the iterative phase may entail decision points every year. However, double-loop learning interventions often occur irregularly, for example, after 5 or 10 years of experience with the ARM process, if reconsideration of one or more of the process elements seems warranted.

ARM and habitat–population linkages

It is common in grant proposals and introductions to ecological papers to claim conservation utility for the proposed and reported work. It is true that any information about an ecological system has the potential to be somewhat relevant to conservation decisions for the managed system. However, it is also true that different kinds of information about a system can vary greatly in their utility to conservation. Our primary motivation for describing SDM and ARM is to provide a shared understanding of these processes and how they work in general. Using this framework, we next specify exactly how information about habitat–population linkages fits into these formal decision processes (see Habitat management). Specifically, when actions for an SDM or ARM process include habitat manipulations, models predicting the consequences of such actions for the managed system are required for informed decision-making. Such models will typically include submodels for predicting 1) the effects of actions on habitat and 2) the effects of habitat changes on the focal population (habitat–population linkages). It is our hope that knowledge of this use of habitat–population linkages will provide greater focus for those wishing to contribute to conservation via habitat management. A secondary motivation for this description of SDM and ARM is to create greater awareness of these formal approaches to conservation decisions, leading to good decisions now and to learning (reducing uncertainty) that allows even better decisions in the future.

Habitat management

A frequent objective in conservation biology and wildlife management is to increase or maintain the population size of a focal species. The management actions that can be used to achieve such an objective are usually very limited and frequently entail efforts to modify habitat, in a broad sense. For the purposes of this set of papers, we operationally define “habitat” as “the resources and conditions present in an area that produce occupancy - including survival and reproduction - by a given organism” (Hall et al., 1997).

Models for habitat management: general

SDM (including ARM) approaches to management require models to project responses of the focal population to the different management actions (Figure 1). Habitat management models developed for this purpose are frequently comprised of two submodels. First, we attempt to project the consequences of management actions on habitat itself. Second, we try to project the consequences of changed habitat for the focal population(s)—the topic of this special issue. This decomposition usually leads to models that include at least two state variables: one characterizing habitat and the other the focal population.

Models used for habitat management do not require the decomposition of focal processes as described above. We could model focal population responses to habitat management actions directly, but this less mechanistic approach may not be as useful in some respects. For example, if direct modeling of population response to habitat management provides poor predictions, then it may be more difficult to diagnose the reasons for the problem than if the two processes had been modeled separately. The poor performance could be attributed to the failure of the management action to affect habitat in the predicted way, the failure of the habitat change to affect the focal population as predicted, or a combination of both issues.

Models for habitat management: habitat responses to management

Models of habitat dynamics are used for projecting the consequences of management actions on the habitat state variable(s), where such variables are defined based on their relevance to the focal wildlife population(s). Such habitat models can focus on the processes governing habitat change, frequently parameterized as habitat state transition probabilities. For example, we might have one set of transition probabilities that govern changes in habitat state in situations with no habitat management (e.g., arising from natural successional processes) and another set of transition probabilities associated with the application of a management action to habitats of each specific state.

As a specific example, we consider management of Florida scrub and flatwoods habitat for the Florida scrub-jay, Aphelocoma coerulescens. Scrub-jay habitat can be classified by structural height into four classes: short (Sh), optimal (Op, the best habitat state for scrub-jays), tall-mix (Tm), and tall (Ta; see Breininger and Carter, 2003; Breininger and Oddy, 2004). For the purposes of scrub-jay management, habitat within a managed area can be subdivided into a grid of 10-ha cells (the approximate size of a scrub-jay territory). We define $n_{t}^{r}$ as the number of patches (cells) in habitat class r at time t and transition probability $ψ_{t}^{r s}$ as the probability that a habitat patch in state r in year t is in habitat state s in year t+1. Habitat dynamics can be modeled as a first-order Markov process governed by a matrix of transition probabilities:

\begin{array}{l} [\begin{matrix} n_{t + 1}^{S h} \\ n_{t + 1}^{O p} \\ n_{t + 1}^{T m} \\ n_{t + 1}^{T a} \end{matrix}] = [\begin{matrix} ψ_{t}^{S h S h} & ψ_{t}^{O p S h} & ψ_{t}^{T m S h} & ψ_{t}^{T a S h} \\ ψ_{t}^{S h O p} & ψ_{t}^{O p O p} & ψ_{t}^{T m O p} & ψ_{t}^{T a O p} \\ ψ_{t}^{S h T m} & ψ_{t}^{O p T m} & ψ_{t}^{T m T m} & ψ_{t}^{T a T m} \\ ψ_{t}^{S h T a} & ψ_{t}^{O p T a} & ψ_{t}^{T m T a} & ψ_{t}^{T a T a} \end{matrix}] [\begin{matrix} n_{t}^{S h} \\ n_{t}^{O p} \\ n_{t}^{T m} \\ n_{t}^{T a} \end{matrix}] . & (1) \end{array}

We expect such transition matrices to differ for different habitat management actions. The probabilistic nature of habitat transitions reflects, among other things, the partial controllability of habitat management.

Inferences about habitat state transition probabilities are readily obtained from data on habitat classification of patches over time. Each habitat patch forms a row in a data matrix with columns identifying the different times (e.g., year 1, 2,…) they were visited. Habitat classes are the matrix entries specifying the habitat class of the patch at each sampling occasion during the study. Any of several software packages can then be used to estimate the $ψ_{t}^{r s}$ and associated variances from such data. For example, if no patches become non-habitat and all patches can be located by investigators each time step (year), then multistate capture–recapture software (e.g., White and Burnham, 1999; Choquet et al., 2009) can be used to estimate transition parameters by setting survival and detection parameters equal to one. Loss of sites and non-detection can be dealt with as well. If habitat classification is based on remote sensing data, then misclassification may be an issue but can be handled if a subset of ground truth patches is available (Veran et al., 2012). Figure 2 provides a schematic diagram for a multistate model analysis of habitat dynamics in Florida scrub and flatwoods systems (Breininger et al., 2010).

Figure 2

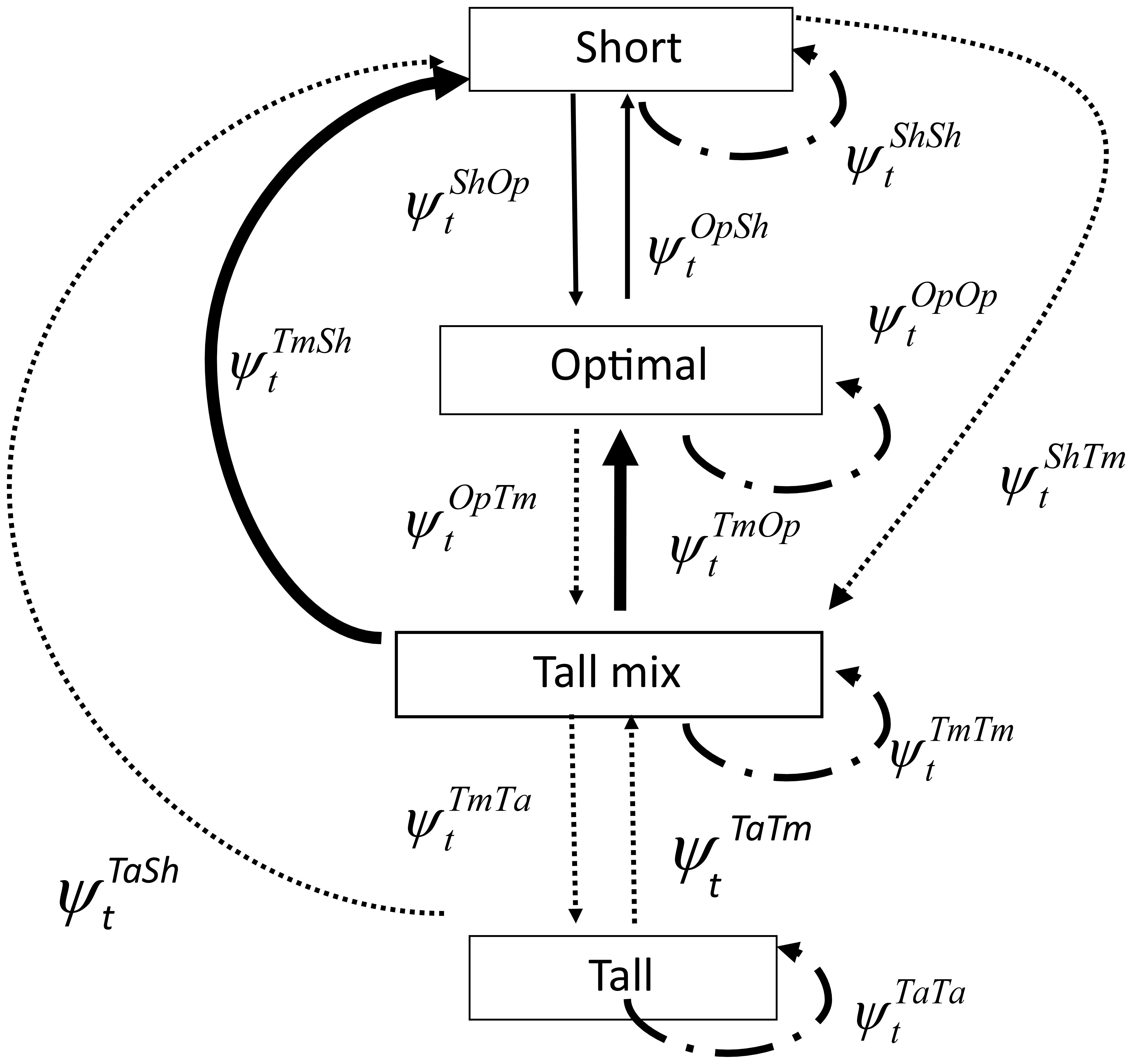
Figure 2. Transitions and associated probabilities estimated using a multistate model of scrub and flatwoods at Kennedy Space Center, Florida, 1994–2004 (Breininger et al., 2010). $ψ_{t}^{r s}$ = probability that a patch in habitat state r at time t is in state s at time t+1, where Sh = short; Op = optimal; Tm = tall mix; and Ta = tall. Transitions depicted by heavy solid lines had adequate sample sizes for models including all covariates. Transitions depicted by thin sold lines occurred infrequently and were modeled using fewer covariates. Transitions with dotted lines had few occurrences and were modeled using only the covariate oak. Transitions from short to tall, optimal to tall, and tall to optimal never occurred and were constrained to zero. Transition probabilities for states that remained the same were estimated by subtraction (modified from Breininger et al., 2010).

In addition to the estimation of transition probabilities, analytic methods such as multistate capture–recapture and occupancy modeling also permit direct inferences about the potential influence of covariates on habitat transitions. For decision problems, these covariates can include management actions such as burning and mechanical cutting, leading to different transition matrices for different management actions. Examples of such analyses for Florida scrub and flatwoods systems are found in Breininger et al. (2009, 2010), Johnson et al. (2011), and Eaton et al. (2021), with the latter two references describing the incorporation of such modeling into decision processes.

In some situations, the classification of habitat into a small number of discrete states may not be feasible or as useful as simply focusing on a single habitat variable. In the case of Florida scrub-jay habitat, an important habitat variable for defining habitat quality is simply vegetation height (Breininger and Carter, 2003; Breininger et al., 2010). Thus, another approach to modeling would be to treat average vegetation height as a continuous variable, with different management actions (e.g., burning, mechanical cutting) predicted to decrease average height by different amounts. Scrub-jay survival and reproduction would then be predicted to be greater at intermediate heights and lower at shorter and taller heights.

Models for habitat management: population responses to management

The objectives of most programs of animal conservation and wildlife management focus on animal populations, and efforts to modify habitat provide one means of achieving such objectives. Although models of habitat change as a function of management actions are required by ARM, additional modeling is needed to specify focal population responses to changes in habitat, the focus of papers comprising this special topic. State variables frequently used in population management models include abundance, density, and occupancy. One way to draw inferences about population responses to habitat management is by observing static patterns of species abundance, density, or presence–absence in different locations characterized by different sets of habitat variables. However, such associations may not be good predictors of changes in abundance associated with habitat changes (e.g., Van Horne, 1983; Yackulic et al., 2015; MacKenzie et al., 2017). A more reliable approach is to address the effects of habitat on the vital rates governing population change (see Tyre et al., 2001; Yackulic et al., 2015).

Models most useful for management are also based on the effects of management actions on the vital rates governing state variable dynamics (Nichols, 2021). For example, assume that we are able to estimate abundance of a focal species in two different habitats within a system. If the system is in approximate equilibrium, then the estimated difference in abundance can be viewed as a measure of habitat effect. However, if we take a management action that converts a patch of one habitat type into the other, then we would not necessarily expect to predict the new abundance on that patch using the habitat effect. Instead, we would expect a period of transient dynamics as abundances changed in the direction predicted by the effect. When systems are not in equilibrium, the difference between abundances in patches of the different habitat types would not necessarily be useful in predicting abundance response to habitat changes either. However, when habitat effects on vital rates are estimated, then these effects can be used, together with estimates of current abundance, to directly predict abundance responses to habitat changes. In general, vital rates are used to predict time-specific changes in abundance resulting from any management action, absent any assumptions about equilibrium.

The selection of data used to estimate system responses to changes in habitat depends on the system state variable(s) being modeled and on the methods chosen to estimate the variable(s) and associated vital rates. For example, there are many ways to estimate abundance, density, and vital rates (survival, recruitment, movement) that govern population dynamics (e.g., Seber, 1982; Williams et al., 2002; Royle et al., 2013; Kery and Royle, 2015, 2021; Seber and Schofeld, 2019). Many of the approaches for estimating abundance and density only require data from relatively short periods of time. Inferences about vital rates require multiple detections from individually marked individuals over longer time periods or, sometimes, temporal sequences of simple counts at multiple sampling locations (Dail and Madsen, 2011; Kery and Royle, 2021).

The occupancy state variable focuses on the presence or absence of a species in each of a set of specified sample units, and inference methods based on species-level detection–non-detection data are well-developed (MacKenzie et al., 2002, 2017). Similarly, methods are available for estimating the rates of local extinction and colonization from temporal sequences of detection–non-detection data across multiple sample units (MacKenzie et al., 2003, 2017).

Selection of analytic methods for estimating the effects of habitat on vital rates of animal populations is dictated by 1) the types of vital rates (hence, state variable) being considered, 2) the relative spatial scales of animal movement and habitat measurement, and 3) the relative temporal scales of habitat change and vital rate estimation. The relevance of identifying the appropriate vital rates stems from the need for reasonable samples of marked individuals for estimation of survival, recruitment, and movement using capture–recapture methods (e.g., Williams et al., 2002; Seber and Schofeld, 2019; Kery and Royle, 2021). If the scale of habitat assessment is relatively coarse, and if spatial sample units are large relative to the scale of animal movement, and if habitat change is very slow relative to study duration, then it may be reasonable to assume that animals remain associated with specific habitats for the duration of a study. In such cases, sample units may be grouped by habitat type, or habitat covariates can be measured for each unit, and tests for a habitat effect can be conducted using standard capture–recapture models for open populations (Pradel, 1996; Schwarz and Arnason, 1996). For example, Conway et al. (1995) used capture–recapture modeling to test for differences in overwintering survival between neotropical migrant birds in successional habitat vs. mature tropical forest in Belize but found survival to be very similar for the two habitat types. In addition to capture–recapture, inferences about survival and recruitment can also be drawn from raw counts of individuals in multiple sample units (Dail and Madsen, 2011; Kery and Royle, 2021) although this approach requires greater dependence on the selected model and its underlying assumptions.

If habitat remains relatively constant, but individuals move from one habitat type to another between sampling occasions, then capture history records of animals that are known to have moved can be manipulated and used with standard open-population capture–recapture models to draw inferences about associations between vital rates and habitat type (Franklin et al., 2000). However, multistate capture–recapture models were developed specifically for this situation of individual animal movement between sampling occasions (Arnason, 1972; Brownie et al., 1993; Schwarz et al., 1993; Lebreton et al., 2009) and are a natural choice. For example, Senar et al. (2002) used multistate models with capture–recapture data on the citril finch (Serinus citrinella) in a metapopulation containing one high-quality and one low-quality habitat in southern Spain. Birds in the high-quality habitat had higher survival rates, and movement from low- to high-quality habitat was greater than that in the reverse direction. While most studies focus on the habitat of patches inhabited by the focal species, multistate models can also be used to draw inferences about the effects of matrix habitat (occurring between patches) on rates of between-patch movement (Skvarla et al., 2004).

If habitat remains relatively constant over the period of study, but the scale of habitat assessment is very fine-grained such that animals are likely to move among multiple habitat classes frequently during a study, then near-continuous radio telemetry data may be required to properly estimate habitat-specific survival (Conroy, 1993; Conroy et al., 1996). In a radio-telemetry study of wintering American woodcock (Scolopax minor) in coastal Virginia, Conroy et al. (1996) used a proportional hazards approach (Cox, 1972, 1975) and found no apparent difference in daily survival rates between pine and hardwood habitats.

Data requirements for estimating probabilities of local extinction and colonization within an occupancy framework are generally less stringent than for estimation of survival and recruitment. Periodic surveys are used to collect species-level detection–non-detection data for the focal species on multiple sample units, and if habitat change is slow relative to study duration, units may be grouped by habitat type or characterized by a continuous habitat covariate. In an early application of this approach, Ferraz et al. (2007) investigated habitat fragmentation effects experimentally for 55 Amazon bird species in Brazil, finding strong evidence of a negative effect of patch size on local extinction probabilities.

Two general approaches can be used to investigate habitat–population relationships when habitat and the focal population exhibit dynamics operating at approximately the same time scale during a study. One approach is similar to that used for relatively static habitat, in the sense that habitat for each sample unit at each sampling occasion in the study is recorded and inserted as a standard covariate, absent any effort to model habitat dynamics. Multistate capture–recapture models can be used with changes of state induced by either animals moving or animals remaining in a sample unit, but habitat changing.

The other approach is to model habitat and population dynamics jointly. Breininger et al. (2009) used multistate capture–recapture models to estimate survival rates of Florida scrub-jays on breeding territories, with habitat state defined at each sampling occasion as short, optimal, tall-mix, or tall (see above). Survival was greatest for birds in territories with optimal habitat, as predicted. Territory habitat dynamics were modeled separately and used to conclude that most changes of habitat state experienced by birds resulted not from birds moving, but from birds remaining in territories that changed habitat state via natural succession or management action (e.g., burning). So, both habitat and population dynamics were modeled, and the next step would be to directly link the two models using a joint likelihood. The advantages of a joint likelihood include the ability to deal with potential misclassification of habitat (or missing values) in certain sampling occasions. In addition, joint likelihoods admit reciprocal relationships in which wildlife populations can also influence habitat dynamics (as with some grazing systems), and provide a natural approach for the direct estimation of variances associated with habitat–population relationships.

Joint likelihoods can also be developed for the occupancy state variable, permitting simultaneous modeling of population and habitat dynamics (MacKenzie et al., 2011). As an example, MacKenzie et al. (2011) surveyed seasonal pools for spotted salamander (Ambystoma maculatum) egg masses in Canaan Valley National Wildlife Refuge (NWR), West Virginia, for the purpose of investigating the potential effects of pool size (based on the surface area of water) as a habitat variable. The probability that a pool with no egg masses (no breeding) in breeding season t was colonized and had egg masses in t+1 was greater for pools that were larger in t+1. The probability that a pool with egg masses in year t again had egg masses in year t+1 was also greater for pools that were larger in year t+1.

Investigations may also include multiple habitat variables that differ with respect to the temporal scale of their dynamics. Miller et al. (2012) investigated the occupancy of the arroyo toad (Anaxyrus californicus) in southwestern California focusing on the effects of two habitat variables: watershed class and water availability. Watershed class referred to areas populated by mostly ephemeral or mostly perennial streams, and this classification did not vary during the study. Sample units were stream segments within watersheds and were classified as unsuitable (dry) or suitable (containing water) each breeding season. This aspect of habitat suitability was highly dynamic throughout the study and modeled as a first order Markov process that was linked with toad occupancy dynamics. Inferences were available about the effects of both habitat variables on local extinction and colonization of toads.

In summary, there are multiple analytic approaches for investigating the relationships between habitat variables and population dynamics. Such relationships underlie any attempt to manage populations by managing their habitat and must be incorporated into models used in decision processes such as SDM and ARM. Models of habitat effects on population vital rates are expected to be more useful to management than models describing the relationships between habitat and static state variables. Multiple approaches are available for drawing inferences about these habitat–population relationships, and selection of the most appropriate approach for a study depends on the selected state variables and vital rates, the rate of habitat change relative to study duration, and the rate of animal movement relative to study duration and habitat change.

ARM for habitat management: an example

We describe a program of adaptive habitat management for the Florida scrub-jay inhabiting scrub and flatwoods habitat in coastal Florida. As described above, habitat in this system can be divided into classes based on vegetation height and value to scrub-jays. For the purposes of the scrub-jay ARM program, habitat of optimal height in previous classifications was further classified as either optimal-open (containing numerous patches of open sand) or optimal-closed (sand patches grown over by encroaching vegetation), producing five overall habitat classes: short, optimal-open, optimal-closed, tall-mix, and tall. These five habitat classes can be located on soils characteristic of either scrub or flatwoods, providing one other habitat variable relevant to transitions of both habitat class and scrub-jays.

Scrub-jay population growth is greatest in the optimal-open habitat class (Breininger and Carter, 2003; Eaton et al., 2021), which represents a transitional stage of natural vegetative succession in this system. Alterations in the natural fire regime caused by human land-use changes over the last half-century in Florida’s Atlantic coast have resulted in significant losses of open scrub and flatwoods habitats with a transition to taller scrub and fire-resistant forests (Duncan et al., 1999; Duncan and Schmalzer, 2004). The management problem is thus one of maintaining enough optimal habitat to permit the maintenance and growth of Florida scrub-jay populations. However, habitat management actions (burning and mechanical cutting) do not usually lead directly to optimal habitat. Instead, these actions can increase the probabilities that tall-mix and tall habitat transition to short habitat, which can then transition to optimal-open habitat in subsequent years. So, despite the availability of potentially useful management actions, the problem of creating and maintaining enough optimal-open habitat to promote scrub-jay population growth is a difficult one.

The 1990s and early 2000s were characterized by a general concern for the loss of good scrub and flatwoods habitat in coastal Florida and the consequent problems for scrub-jay populations. An adaptive habitat management program for Florida scrub-jays was developed for Merritt Island National Wildlife Refuge and the Kennedy Space Center (Johnson et al., 2011). This ARM program was not fully implemented, but aspects of it were viewed as successful, and it provided a blueprint for subsequent efforts.

In the early-mid 2000s, Brevard County community leaders, land managers, and local biologists expressed interest in developing an ARM program for the mainland ecosystem. Potential stakeholders were identified and invited to two workshops in 2006 to discuss the idea of developing an ARM program for scrub and flatwoods habitat directed at Florida scrub-jays (Eaton et al., 2021). The positive response to these initial workshops led to a decision to develop an ARM program in Brevard and Indian River counties. As part of the deliberative phase of ARM, subsequent workshops proceeded with program development, focusing on eliciting management objectives, identifying alternative actions, developing preliminary hypotheses and associated models, and establishing a monitoring program. The iterative phase of the ARM program was implemented in 2012, with results through 2018 summarized by Eaton et al. (2021).

The overall objective of this scrub-jay ARM program was to maximize the number of 10-ha grid cells (the approximate size of a scrub-jay territory) within managed land units that were occupied by scrub-jays. The larger management units were areas administered by different agencies or land ownership groups. The four potential management actions were identified as follows:

1. Burn (BRN): the use of prescribed burning with high-intensity fires generally applied when vegetation is low enough to carry fire, often during the growing season;

2. Light mechanical cutting, followed by burn (LMB): the targeted spot-cutting of taller, less flammable vegetation, followed by a prescribed burn within 3 months;

3. Heavy mechanical cutting, followed by burn (HMB): a more intensive mechanical treatment than LMB in sites where vegetation is beyond the height to perform a fire;

4. No action (NONE): no management action.

The ARM process entailed selecting one of these actions for each 10-ha cell each year.

The modeling for this ARM program included one submodel for habitat responses to management actions and another submodel for scrub-jay responses to habitat. Both submodels were developed at the 10-ha cell level. For habitat state, there were 5 × 5 transition probability matrices for each soil type (scrub, flatwoods) and each management action, producing 8 matrices and 200 transition probabilities. These transition probabilities provided a natural way to incorporate the partial controllability of scrub-jay habitat management. During the deliberative phase, managers and knowledgeable stakeholders were asked to provide their estimates for each of these 200 transition probabilities, and elicited estimates were used to develop pseudo-observations that provided the prior distributions for these initial transition matrices (Eaton et al., 2021). Subsequent values for these transition matrices were obtained by updating based on new monitoring data each year.

A dynamic occupancy model (MacKenzie et al., 2003, 2017) was developed to model scrub-jay dynamics. Cell-level probabilities of local extinction and colonization were modeled as functions of habitat state, neighborhood cell occupancy (an autologistic effect; Augustin et al., 1996; Yackulic et al., 2012; Eaton et al., 2014), and overall system occupancy. The neighborhood and overall occupancy levels (proportions of cells occupied by scrub-jays) were included because of their potential influence on probabilities of cell-level colonization (sources of colonists) and extinction (via the rescue effect; Brown and Kodric-Brown, 1977). Initial occupancy levels were estimated directly from monitoring data, and the habitat effect parameters were initially estimated based on expert elicitation from the group of managers and then updated with monitoring data as the program proceeded.

Many of the land managers participating in the program were already doing some level of habitat and scrub-jay monitoring prior to the program. A monitoring protocol for ARM was developed to ensure that the needed information was being collected each year. In cases where the land managers were unable to monitor, other program biologists carried out these tasks.

Optimal state-dependent decisions were obtained beginning in 2014 using modified stochastic dynamic programming approaches (Miranda and Fackler, 2002; Fackler, 2012). A passive adaptive management approach was used, such that the optimization was based on anticipated system responses to management and not on anticipated learning. Efforts were made to share the recommended actions with the set of land managers, but carrying out these recommendations was difficult and inconsistent. These difficulties resulted from several factors, including 1) the numerous different land managers involved and their different levels of resources to devote to management, 2) the fact that most land managers had multiple management cells with different actions recommended for different cells, and 3) some recommended actions (e.g., those that included fire) could not always be applied because of the absence of suitable weather conditions during the appropriate time periods. Thus, the recommended optimal actions were not applied at all times and to all sites. However, this did not preclude learning, as an action (recall that the action set included “none”) was taken at every cell in every year, responses of habitat and scrub-jays were estimated via monitoring every year, and these data were used with model predictions for annual parameter updating.

The deliberative phase of this ARM program was quite long, extending from approximately 2006 to 2012–2014. We believe that the main reason for this was the increased difficulty in bringing the stakeholder group together and eliciting objectives, actions, values of parameters for prior distributions, etc., from such a diverse group, as opposed to a more streamlined situation with a single agency and decision-maker. Indeed, this is the first ARM program that we know of to have been developed successfully by a consortium of public and private landowners and stakeholders.

The iterative phase of ARM then proceeded as described in general above. Management actions were carried out at sites, resulting habitat and scrub-jay changes were identified by the monitoring program, and transition parameter estimates for both habitat and scrub-jays were updated each year using this new information. Precision of habitat and scrub-jay transition probability estimates increased through the years of the ARM program, and the dissimilarity of the sets of annual estimates decreased with time as well. Both of these trends provide evidence of learning about these key management parameters during the ARM program. Learning was also consistent with a-priori hypotheses, with greater probabilities of scrub-jay colonization and occupancy and lower probabilities of extinction, associated with optimal habitat and with greater system-wide occupancy. Scrub-jay colonization probabilities were higher for cells with more occupied neighbors as well. The general consistency of new results for scrub-jays with predictions was expected because of the substantial research previously conducted on this species. Some predictions about action-specific habitat transitions were supported, whereas others were not, emphasizing the importance of dealing with uncertainty even for well-studied systems.

With respect to management of the system, the number of optimal-open cells increased modestly over the course of the program, and the number of tall-mix and tall habitat cells decreased, reflecting success in habitat management. The proportion of cells occupied by scrub-jays did not increase over the 2013–2018 period, emphasizing the difficulty associated with managing this species using this type of habitat management. Specifically, the habitat management actions for suboptimal tall and tall-mix states increased transitions of patches to the short state (also suboptimal), and short state patches eventually grew to the optimal state. However, the time spent by patches in suboptimal states, even post-management, presents a substantial difficulty. Recognition of this difficulty is an important result, in this case leading to consideration of new potential management actions. More generally, the results of this ARM program emphasize the importance of recognizing the limits of some management actions and directly assessing via monitoring, rather than assuming, the effects of management (e.g., Nichols, 2012).

Summary and conclusions

SDM provides a general framework for virtually any decision process. ARM is a special case of SDM developed for recurrent decisions characterized by potentially resolvable uncertainty. In the iterative phase of ARM, periodic decisions are made based on objectives, potential actions, models of system response to actions, system monitoring, and a decision algorithm. Models, such as those linking habitat quality to population dynamics, are important in providing predictions about which action will be “best” at achieving objectives. Model uncertainty impedes decision-making but is the focus of ARM and is addressed by incorporating a scientific step directly within the overall management process.

Linking habitat quality to population dynamics for conservation decision-making, the theme of this group of papers, primarily concerns the development of models to predict population responses to habitat management. A logical way to think about this modeling entails two steps: 1) linking management actions to habitat dynamics and 2) linking habitat dynamics to population dynamics. We describe one way to model habitat dynamics using matrices of habitat state transition probabilities, with different matrices associated with different management actions. We argue that the linkage of habitat dynamics to population dynamics is best accomplished by linking habitat and habitat change to population vital rates. We further argue that the selection of methods used to estimate the effects of habitat on population vital rates should be based on 1) the types of vital rates (and state variable) being considered, 2) the relative spatial scales of animal movement and habitat measurement, and 3) the relative temporal scales of habitat change and vital rate estimation. We outline modeling approaches appropriate for different scenarios.

In order to illustrate how this modeling is incorporated within a management program, we describe an example program of habitat management focusing on the Florida scrub-jay, a species that relies on a transitional stage of natural habitat succession. Decreases in natural disturbance (fire) over the last half-century have produced decreases in the amount of habitat in this transitional stage, motivating habitat management efforts. An ARM program was developed to make good decisions for this recurrent decision problem and to simultaneously reduce uncertainties that impeded good decision-making. Models were developed to predict habitat transitions as a function of management actions and scrub-jay population dynamics as a function of habitat state. These predictions informed annual decision-making. In addition, a monitoring program provided information on both habitat and population dynamics, permitting the updating of key model parameter estimates (i.e., learning) and the use of the updated models to make subsequent decisions.

It is very common for studies of habitat to claim a conservation motivation. However, conservation requires the selection of actions that will increase the likelihood of attaining program objectives, and explanations of exactly how habitat study results will be used to make those decisions are rare. We believe that SDM and ARM provide frameworks that should be useful in making decisions about habitat management. In particular, these frameworks specify exactly how models linking management to habitat, and habitat to population dynamics, are incorporated into the decision process. We believe that models that are developed in the context of these frameworks, and with explicit knowledge of their uses within these frameworks, are most likely to be useful in developing decisions about habitat management.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

JN: Writing – original draft, Writing – review & editing. DB: Writing – original draft, Writing – review & editing. DA: Writing – original draft, Writing – review & editing. RL: Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arnason A. N. (1972). Parameter estimates from mark-recapture experiments on two populations subject to migration and death. Res. Pop. Ecol. 13, 97–113. doi: 10.1007/BF02521971