Meaning and Measures: Interpreting and Evaluating Complexity Metrics

Ehret, Katharina; Blumenthal-Dramé, Alice; Bentz, Christian; Berdicevskis, Aleksandrs

doi:10.3389/fcomm.2021.640510

ORIGINAL RESEARCH article

Front. Commun., 24 May 2021

Sec. Psychology of Language

Volume 6 - 2021 | https://doi.org/10.3389/fcomm.2021.640510

This article is part of the Research Topic Motivations for Research on Linguistic Complexity: Methodology, Theory and Ideology View all 11 articles

Meaning and Measures: Interpreting and Evaluating Complexity Metrics

$\nKatharina Ehret,$ Katharina Ehret^1,2^*

Alice Blumenthal-Dramé¹^†

Christian Bentz³^†

Aleksandrs Berdicevskis⁴^†

¹Department of English, University of Freiburg, Freiburg, Germany
²Discourse Processing Lab, Department of Linguistics, Simon Fraser University, Burnaby, BC, Canada
³Department of Linguistics, University of Tübingen, Tübingen, Germany
⁴Språkbanken, Department of Swedish, University of Gothenburg, Gothenburg, Sweden

Research on language complexity has been abundant and manifold in the past two decades. Within typology, it has to a very large extent been motivated by the question of whether all languages are equally complex, and if not, which language-external factors affect the distribution of complexity across languages. To address this and other questions, a plethora of different metrics and approaches has been put forward to measure the complexity of languages and language varieties. Against this backdrop we address three major gaps in the literature by discussing statistical, theoretical, and methodological problems related to the interpretation of complexity measures. First, we explore core statistical concepts to assess the meaningfulness of measured differences and distributions in complexity based on two case studies. In other words, we assess whether observed measurements are neither random nor negligible. Second, we discuss the common mismatch between measures and their intended meaning, namely, the fact that absolute complexity measures are often used to address hypotheses on relative complexity. Third, in the absence of a gold standard for complexity metrics, we suggest that existing measures be evaluated by drawing on cognitive methods and relating them to real-world cognitive phenomena. We conclude by highlighting the theoretical and methodological implications for future complexity research.

1. Introduction

This paper is situated at the intersection of corpus linguistics, language typology, and cognitive linguistics research. We specifically contribute to the sociolinguistic-typological complexity debate which originally centered around the question of whether all languages are equally complex and, if not, which factors affect the distribution of complexity across languages (e.g., McWhorter, 2001a; Kusters, 2003). Against this backdrop, we discuss how existing complexity metrics and the results of the studies that employ them can be interpreted from an empirical-statistical, theoretical, and cognitive perspective.

Language complexity has been a popular and hotly-debated topic for a while (e.g., Dahl, 2004; Sampson et al., 2009; Baerman et al., 2015; Baechler and Seiler, 2016; Mufwene et al., 2017). Thus, in the past two decades, a plethora of different complexity measures has been proposed to assess the complexity of languages and language varieties at various linguistic levels such as morphology, syntax, or phonology (Nichols, 2009; Szmrecsanyi and Kortmann, 2009), and, in some cases, at the overall structural level (Juola, 2008; Ehret and Szmrecsanyi, 2016). To date, there is no consensus on how to best measure language complexity, however, there is plenty of empirical evidence for the fact that languages vary in the amount of complexity they exhibit at individual linguistic levels (e.g., morphology) (Bentz and Winter, 2013; Koplenig, 2019)¹. In explaining the measured differences in complexity, researchers have proposed a range of language-external factors such as language contact (McWhorter, 2001b) and isolation (Nichols, 2013), population size (Lupyan and Dale, 2010; Koplenig, 2019), or a combination of factors (Sinnemäki and Di Garbo, 2018) as determinants of language complexity. Such theories, in our view, are extremely important since they make complexity more than a parameter of cross-linguistic variation: It becomes a meaningful parameter involved in explanatory theories. These theories, if they are correct (which we currently consider an open question), contribute to our understanding of why languages are shaped the way they are, how language change is influenced by social interaction, and how language is organized and functions in the brain (Berdicevskis and Semenuks, 2020).

In this spirit, the paper addresses three major gaps in the current literature which are of important empirical and theoretical implication. First, previous research has established differences in complexity between languages, yet, it is often unclear how meaningful these differences are. In this context, we define complexity differences as meaningful if they are systematic and predictable rather than the outcome of chance. In this vein, we address the question of how these differences can be statistically assessed. Second, in much of previous research absolute complexity metrics, i.e., metrics which assess system-inherent properties, are employed to address research questions on relative complexity, i.e., complexity related to a language user. In other words, the metrics do not match the research questions. This is a common methodological issue potentially leading to misinterpretations, yet, as we show, one that can be addressed. Third, there is no gold-standard or real-world benchmark against which complexity measurements could be evaluated. In the absence of such a benchmark, then, we explore the meaningfulness of complexity measures and propose how they could be related to real-world cognitive phenomena by drawing on methods common in psycholinguistics and neuroscience (such as, for instance, online processing experiments).

This paper is structured as follows. Section 2 sketches, in broad strokes, common measures and factors discussed in the sociolinguistic-typological complexity debate. In section 3 complexity differences are statistically assessed. In section 4 we discuss the mismatch between measures and their intended meaning, and suggest how to address it. Section 5 proposes how to benchmark complexity measures against cognitive phenomena. Section 6 offers a brief summary and some concluding remarks.

2. Background

Theoretical research on language complexity has produced an abundance of different complexity measures and approaches to measuring language complexity². Although there is no consensus on how to best measure language complexity, a general distinction is made between relative and absolute measures of complexity (Miestamo, 2008, see also Housen et al. 2019). Absolute measures usually assess system-inherent, abstract properties or the structural complexity of a language, for instance, by counting the number of rules in a grammar (McWhorter, 2012), or the number of irregular markers in a linguistic system (Trudgill, 1999), or applying information-theoretic measures (Ackerman and Malouf, 2013). Sometimes, absolute complexity is measured in terms of information-theory as the length of the shortest possible description of a naturalistic text sample (Juola, 1998; Ehret, 2018). Relative measures, in contrast, assess language complexity in relation to a language user, for instance, by counting the number of markers in a linguistic system which are difficult to acquire for second language (L2) learners (Kusters, 2008), or in terms of processing efficiency (Hawkins, 2009). As a matter of fact, relative complexity is often (either implicitly or explicitly) equated with “cost and difficulty” (Dahl, 2004), or with second language acquisition difficulty. It goes without saying that this list is by no means exhaustive. More detailed reviews of absolute and relative metrics can be found in, for example, Ehret (2017, p.11–42) which includes a tabular overview, Kortmann and Szmrecsanyi (2012), or Kortmann and Schröter (2020).

Despite the fact that this theoretical distinction is generally accepted among complexity researchers, it is, in many cases, difficult to make a clear-cut distinction between absolute and relative measures. This is often the case for redundancy-based and transparency-based metrics which basically measure system-inherent properties. However, these properties are then considered redundant or transparent relative to a language user. In other words, absolute measures are sometimes applied and interpreted in terms of relative complexity notions without experimentally testing this assumption. This absolute-relative mismatch is addressed in section 4.

Be that as it may, most approaches, both absolute and relative, measure complexity at a local level, i.e., in a linguistic subsystem such as morphology or phonology, although some approaches (for instance, information-theoretic ones) also measure complexity at a global, or overall level.

Observed differences in language complexity have been attributed to language-external, sociolinguistic, historical, geographic, or demographic parameters. In this context, contact and isolation, as well as associated communicative and cognitive constraints in the cultural transmission of language, feature prominently in theories explaining complexity differences. Essentially, three types of contact situation have been proposed in the literature to influence complexification and simplification. (1) In low-contact situations, i.e., languages are spoken by isolated and usually small speech communities with close social networks, complexity tends to be retained or to increase. (2) In high-contact situations with L2-acquisition, i.e., languages are spoken by communities with high rates of (adult) second language acquisition, complexity tends to decrease (Trudgill, 2011). (3) In high-contact situations with high rates of child bilingualism complexity tends to increase (Nichols, 1992). Inspired by Wray and Grace (2007) and Lupyan and Dale (2010) propose a similar framework distinguishing between esoteric and exoteric languages, i.e., languages with smaller and larger speaker communities, respectively. Esoteric speaker communities could be said to correspond to the low-contact situations described in (1) above, while exoteric speaker communities would roughly correspond to the high-contact scenario described in (2).

3. Assessing the Meaning of Complexity Differences

Researchers have employed a panoply of measures to establish differences in the complexity of languages, be it in a particular subsystem like morphology or syntax, or at an overall level³. Such measures are often applied to different languages (e.g., represented by texts or grammars) to obtain one complexity value per language, and, to compare them, ranked according to the value of the respective measure. For instance, Nichols (2009) provides a “total complexity” score for 68 languages. In a laborious and careful analysis of grammatical descriptions, she weighs in aspects of phonology, the lexicon, morphology, and syntax. In her ranking, Basque has the lowest score (13.0) and Ingush (27.9) the highest. In the middle ground we find, for instance, Kayardild and Chukchi with values of 18.0 and 18.1 respectively. Intuitively, we might conclude that the difference between Basque and Ingush is rather large, i.e., “meaningful,” while the difference between Kayardild and Chukchi is rather negligible, i.e., “meaningless.” However, there are several theoretical problems with this intuition.

1. What if several other linguists use further grammatical descriptions of Basque and assign total complexity scores ranging from 5 to 50 to it? – This would suggest that there is considerable discrepancy in the measurement procedure, and call into question the “meaningfulness” of an alleged complexity difference.

2. What if across all 7,000 or so languages of the world the respective total complexity values turn out to range between 1 and 1,000? – This would make the difference between Basque and Ingush look rather small on a global scale.

3. What if it turned out that Basque and Ingush are closely related languages? Should we be surprised or not by their relative distance on our complexity scale?

The first point relates to the statistical concept of variance, the second point relates to the concept of effect size, and the third point relates to the problem of relatedness and, hence, (potentially) statistical non-independence. In the following, we will discuss basic considerations for assessing and interpreting complexity differences in light of these core statistical concepts. For illustration, we furnish two case studies: Firstly, a Brownian motion simulation of pseudo-complexity values along a simplified phylogeny of eight Indo-European languages. This illustrates the workings of a “random walk.” Secondly, a meta-analysis of values derived from an empirical study of ten different languages (including the eight Indo-European ones of the simulation). These case studies aim to disentangle the effects of purely random changes from genuine – and hence “meaningful” – shifts in complexity values. All statistics, data and related code reported in this section are available at GitHub⁴.

3.1. Two Case Studies

In our first case study, a simulation with Brownian motion on a phylogeny is conducted in order to illustrate some basic statistical implications of relatedness – and what relatedness does not imply. Natural languages are linked via family (and areal) relationships. If two languages A and B are related, i.e., two descendants of the same proto-language, then any measurements taken from these languages are likely non-independent (i.e., correlated). One of the most basic models of trait value evolution (here pseudo-complexity) is Brownian motion along a phylogeny (Harmon, 2019). Brownian motion is another term for what is more commonly referred to as “random walk.” In the simplest version, this model consists of two parameters: the mean trait value in the origin (i.e., at time t = 0), which is denoted here as μ(0); and the variance ( $σ_{r}^{2}$ ) or “evolutionary rate” of the diffusion process (Harmon, 2019, p. 40). The changes in trait values at any point in time t are then drawn from a normal distribution with mean 0 and the variance calculated as the product of the variance of the diffusion process and the evolutionary time ( $σ_{r}^{2} t$ ). For the mean trait value μ after time t we thus have

\begin{array}{l} μ (t) ~ N (0, σ_{r}^{2} t) . & (1) \end{array}

How does the relatedness of languages come into the picture? Let us assume that two languages A and B sprung from a common ancestor at time t₁, and subsequently evolved independently from one another for time t₂ and time t₃, respectively. These evolutionary relationships could be captured on a tree with a single split, and branch lengths t₁, t₂, and t₃. This pattern of relatedness in conjunction with a Brownian motion model would predict the following values of language A and B on the tips of the tree (Harmon, 2019, p. 52):

\begin{array}{l} μ_{A} ~ N (0, σ_{r}^{2} (t_{1} + t_{2})), & (2) \end{array}

\begin{array}{l} μ_{B} ~ N (0, σ_{r}^{2} (t_{1} + t_{3})) . & (3) \end{array}

In order to calculate mean tip values for real languages under Brownian motion – and compare them to our empirical measurements – we need a phylogeny (including branch lengths) of the respective languages. Therefore, we here posit a pruned phylogeny for eight Indo-European languages – which are selected to match the sample for which we have empirical measurements in the second case study. The original phylogeny is part of a collection of family trees in Bentz et al. (2018). It is built by calculating distances between word lists from the ASJP database (Wichmann et al., 2020). For details on this procedure see Jäger (2018). A schematic plot of the underlying Newick tree is provided in Figure 1. Note that this tree (roughly) reflects actual historical relationships. For instance, the deepest split is between Romance and Germanic languages. Spanish, Italian, and French are more closely related than either of them is to Romanian⁵.

FIGURE 1

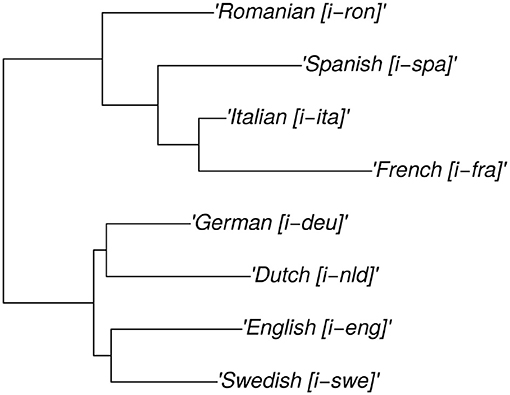
Figure 1. Phylogenetic tree for the eight Indo-European languages represented in the complexity sample.

Imagine that while these languages have diversified in terms of their core vocabulary, their complexities have changed purely randomly. Is this a realistic assumption? – Probably not. Against the backdrop of a corpus based study on frequency distributions of words Kilgarriff (2005) points out that “language is never ever ever random.” However, using a Brownian motion model as a baseline is still valid and important for two main reasons: (a) It is a precise mathematical formulation of the rather vague idea that “historical accidents” might have led to differences in languages; (b) even if this simple model is unlikely to perfectly capture the patterns in the empirical data, it is necessary to evaluate how close it gets.

To simulate the “random walk” scenario, we let 20 pseudo-complexity values⁶ for each language evolve along the branches of the family tree by Brownian motion (with μ = 0 in the origin, and $σ_{r}^{2} = 2$ as the variance of the diffusion process)⁷. See Appendix 2 in Supplementary Material for further details and R code. We then contrast the outcome of this Brownian motion model with the actual complexity measurements obtained from empirical data.

As a second case study we present a meta-analysis of Kolmogorov-based morphological complexity. The data is drawn from a study by Ehret and Szmrecsanyi (2016) which harnessed parallel texts of Alice's Adventures in Wonderland by Lewis Caroll in ten languages. In this study, Kolmogorov-based language complexity was measured at three different linguistic levels: at the overall, morphological, and syntactic level. We refer to the original article for further explanations of the methodology. From the original data set 20 morphological Kolmogorov complexity measurements per language, i.e., chunks of parallel texts, are chosen⁸. Needless to say, we do not claim that this is the only valid measure of morphological complexity across languages. Rather, it is utilized as one possible set of empirical data for illustrating the workings of statistical hypothesis testing.

3.2. Statistics

Assessing the complexity of a given language is not straightforward as there is no agreement on a single complexity measure nor a single representation of a language (e.g., a corpus). On the contrary, there is a multitude of different approaches which makes it necessary to assess whether measured differences in complexity are “meaningful.” Whenever the complexity of a language is measured there are at least two types of variance that need to be addressed: (a) the variance in the chosen measures, (b) the variance in the data. These inevitably translate into variance in the measurements.

On a methodological plane, we thus apply standard frequentist statistics to assess whether distributions of complexity (and pseudo-complexity) values significantly differ between the respective languages. Although these methods are well researched and described in the literature, there is sometimes contradictory advise on how to exactly proceed with hypothesis testing, for instance, in the case of normally vs. non-normally distributed data. We generally adhere to the following steps according to the references in parentheses:

• Center and scale the data⁹.

• Check for normality of the distributions via quantile-quantile plots (Crawley, 2007; Baayen, 2008; McDonald, 2014; Rasch et al., 2020).

• Choose an appropriate test, i.e., t-test vs. Wilcoxon test in our setup (Crawley, 2007; Baayen, 2008; Cahusac, 2021).

• Adjust p-values for multiple testing (McDonald, 2014).

• Calculate effect sizes (Patil, 2020; Cahusac, 2021).

In this spirit, we utilize t-tests for the roughly normally distributed data of the simulation study and the empirical data set (see Appendices 2, 3 in Supplementary Material for details). Note that across the languages of each data set the same “measurement procedure” was applied. The resulting vectors of complexity measurements are hence “paired.” A more general term is “related samples” (Cahusac, 2021, p. 56). We thus use paired t-tests. The null hypothesis for the t-test is that the difference in means between two complexity value distributions is 0. Due to the fact that multiple pairwise tests for each data set are performed, the p-values need to be adjusted accordingly. For this purpose, we draw on the Holm-Bonferroni method as it is less conservative than the Bonferroni method, and therefore more appropriate for the present analysis in which tests are not independent (each language is compared to other languages multiple times) (cf. McDonald, 2014, p. 254–260).

Statistical significance, however, is only one part of the story. A measured difference might be statistically significant, yet so small that it is negligible for any further theorizing. See also Kilgarriff (2005) as well as Gries (2005) for a discussion of this issue in corpus linguistics. A common effect size measure in conjunction with the t-test is Cohen's d. An effect is typically considered “small” when d < 0.2, “medium” when 0.2 < d < 0.8, and “large” when d > 0.8. Sometimes “very large” is attributed to d > 1.3 (Cahusac, 2021, p. 14).

For a worked example and literature references on the respective methods see Appendix 1 in Supplementary Material. Further details on the Brownian motion simulation and the meta analysis can be found in Appendices 2, 3 in Supplementary Material. All code and data is also available on our GitHub repository (see Footnote 4).

3.3. Results

First, we report descriptive statistics, i.e., the location parameters (mean, median, standard deviation) of the complexity distributions in the two case studies (see Table 1). In the Brownian motion simulation, the mean and median values are all close to 0 irrespective of the language and its relationship to the other languages on the family tree (see Figure 2). A detailed discussion of the meaning of this result is given in section 3.4. In terms of the Kolmogorov-based morphological complexity Finnish and Hungarian exhibit the highest median complexities (0.93), while English and German have the lowest complexity values (–0.8 and –0.98). French, Italian, and Spanish cluster together in the middle range with medians of 0.02, 0.06, –0.03 respectively (see also Figure 3). We thus have a complexity ranking of languages like in the example with Basque and Ingush introduced above, yet, with one important difference: in the present analysis we have multiple measurements rather than a single value. This allows us to assess whether the respective differences in the location statistics are significant.

TABLE 1

Table 1. Descriptive statistics of pseudo-complexity and empirical complexity distributions.

FIGURE 2

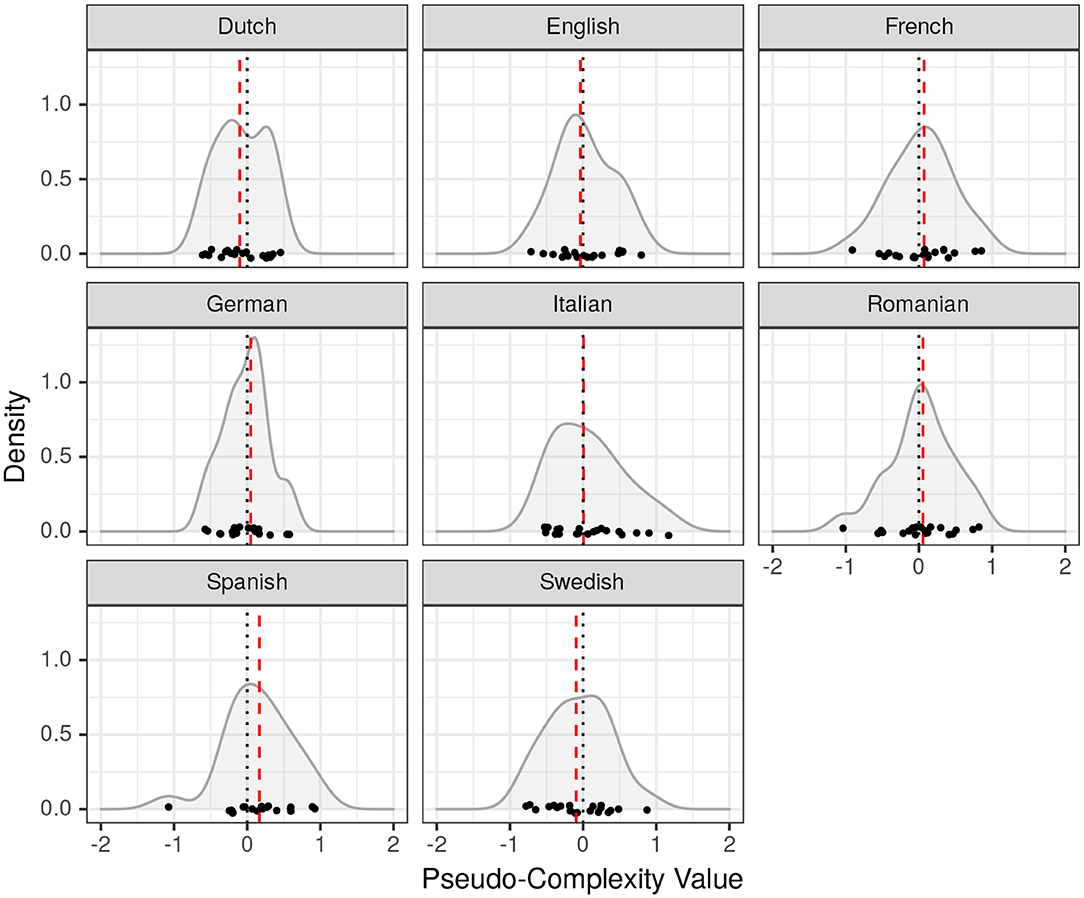
Figure 2. Densities of pseudo-complexity values generated by Brownian motion along the Indo-European phylogeny in Figure 1. Red dashed lines indicate median values.

FIGURE 3

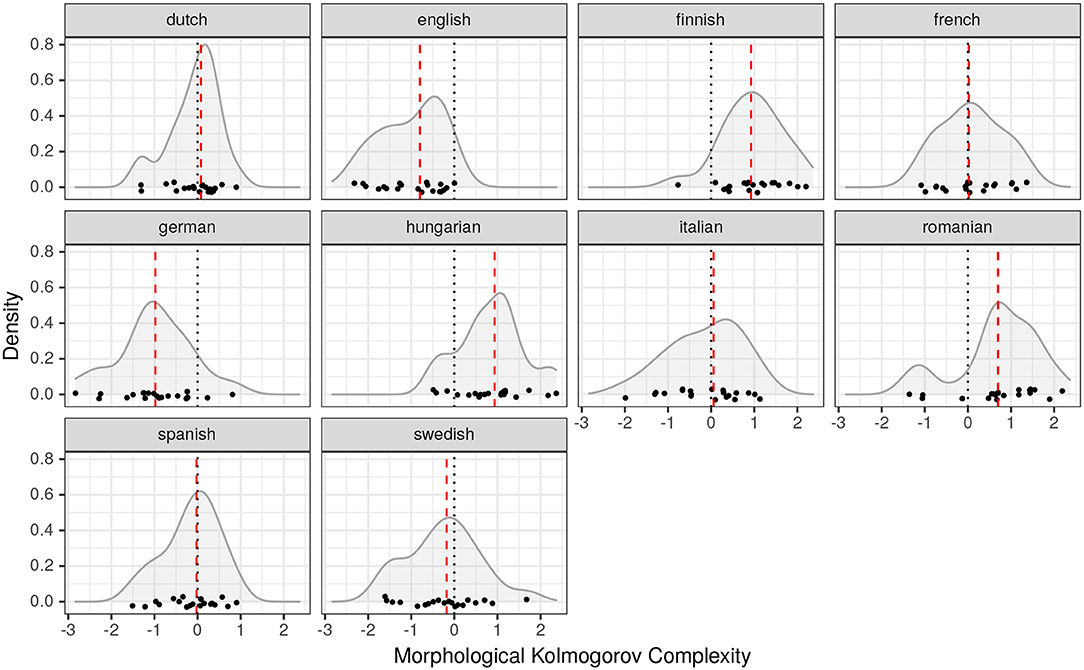
Figure 3. Densities of Kolmogorov-based morphological complexity for 10 languages. Each dot corresponds to a measurement applied to one of 20 chunks of text. Red dashed lines indicate median values.

The results of the statistical significance tests are given in Table 2. In the Brownian motion simulation, there is no significant difference whatsoever. In contrast, the empirical study with 10 languages paints a more variegated picture: The null hypothesis needs to be mostly rejected, i.e., for most pairs of languages we observe a significant location shift in the Kolmogorov-based morphological complexity distributions. That said, for some pairs of languages (e.g., Spanish and French, German and English, Hungarian and Romanian), we do not find a significant location shift. To illustrate, the paired t-test is non-significant for Spanish and French, while it is significant for Spanish and English, and for French and English (see Appendix 3 in Supplementary Material for the full results of all pairs of languages).

TABLE 2

Table 2. Results of statistical significance tests (for three selected languages).

Let us now turn to effect size. The effect size metrics for the three case studies are visualized in Figures 4, 5. In the case of Brownian motion, the effects in complexity differences are mostly negligible or small. The meta-analysis of real languages, again, shows a variegated picture: While for many pairwise comparisons the effect size is large, e.g., English and Finnish, it is rather medium for some languages (e.g., Swedish and German), and virtually negligible for others (e.g., Italian and Spanish, English and German).

FIGURE 4

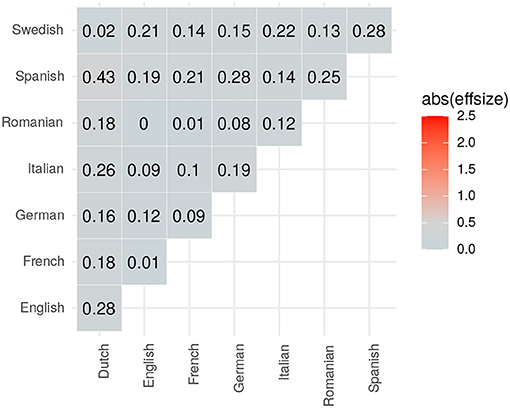
Figure 4. Effect size estimations (Cohen's d) for the pseudo-complexity differences in the Brownian Motion simulation.

FIGURE 5

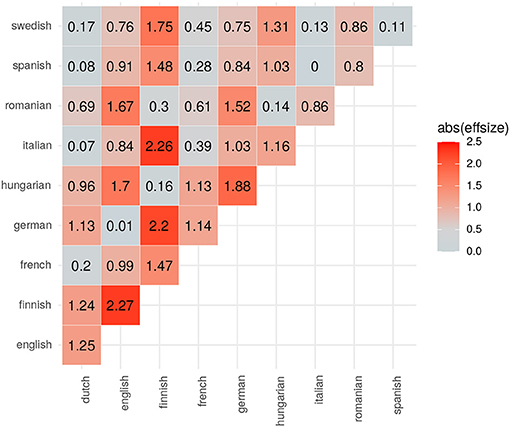
Figure 5. Effect size estimations (Cohen's d) for the complexity differences in the meta-analysis of 10 languages.

3.4. Interpreting Complexity Differences

Based on the results of our two case studies, we now turn to discuss how complexity differences can be interpreted with regard to the core statistical concepts of variance, effect size, and relatedness (non-independence).

Given variance in the measurements, the question of whether there actually is a systematic difference between complexity distributions of different languages needs to be addressed. Our meta-analysis of ten languages shows that, at the level of morphology, Finnish is more complex than Spanish and French, and these are in turn more complex than English. These findings are hard to deny. Likewise, it is hard to deny that French and Spanish are virtually equivalent in their measured complexity. However, these conclusions hinge, of course, on the choice of complexity measure(s) and data. In order to reach a more forceful conclusion, we could include various measures and corpora to cover more of the diversity of viewpoints. In fact, it is an interesting empirical question to address in further research if this would yield clearer results, or would – on the contrary – inflate the variance, and render the observed differences non-significant.

Statistical hypothesis testing is a means to assess if the differences we measure are potentially the outcome of random noise. Once the null-hypothesis can be rejected, the natural next step is to ask whether the differences are worth mentioning. In other words, how large, and hence meaningful, are the effect sizes? In the case of the comparison between Finnish and the other languages in our sample (except Hungarian and Romanian) the effect sizes are certainly meaningful. The same holds for the differences between English and Spanish, as well as English and French. The contrast between French and Spanish, on the other hand, is rather small (0.28)¹⁰. Such observations raise the question of why there are large differences in the complexity between certain languages but not in others, i.e., are these differences mere “historical accidents” or rather systematic?

The results discussed above might not seem surprising after all, since French and Spanish are closely related Romance languages, while English is a more distant sister in the Germanic branch of the Indo-European family. Finnish is a Uralic language not related to Indo-European languages at all (as far as we know). Our intuition tells us that related languages are likely to “behave similarly” – be it with regards to typological features in general or complexity more specifically. However, the Brownian motion simulation we presented illustrates that this intuition is not necessarily warranted. To be more precise, we found no significant differences in average pseudo-complexity values between any of the eight Indo-European languages, despite some languages being clearly more closely related to one another than to others. In fact, this result directly follows from one of the core properties of Brownian motion (Harmon, 2019, p. 41), namely that

\begin{array}{l} E [μ (t)] = μ (0), & (4) \end{array}

where μ(t) is the mean trait value at time t and μ(0) is the mean trait value in the origin. In other words, given a Brownian motion process along the branches of a tree we do not expect a shift in the mean trait values on the tips¹¹. In order to model a significant difference in trait value distributions – as found for English and French/Spanish in terms of Kolmogorov-based morphological complexity – we would have to go beyond the most basic Brownian motion model and incorporate evolutionary processes with variation in rates of change, directional selection, etc. (Harmon, 2019, p. 87). This is an interesting avenue for further experiments.

The bottom line of our current analyses is: if we want to understand the diachronic processes which led to significant complexity differences in languages like English and French/Spanish, it is not enough to point at their (un)relatedness. Two unrelated languages can share statistically indistinguishable complexity values, while two closely related languages can display significantly differing values. Such patterns are apparently not just the outcome of “historical accidents,” rather, the complexity distributions of languages must have been kept together or driven apart by systematic pressures.

Although frequentist statistical approaches – such as the ones applied here – are a very common choice across disciplines, we acknowledge that there are also alternative statistical frameworks such as Bayesian statistics and “evidence-based” statistics (Cahusac, 2021, p. 7). For example, a Bayesian alternative to the t-test has been proposed in Kruschke (2013). However, Cahusac (2021, p. 8) states that: “If the collected data are not strongly influenced by prior considerations, it is somewhat reassuring that the three approaches usually reach the same conclusion.” Given the controlled setting of our analyses, we expect the general results to extrapolate across different frameworks. Finally, we do not claim that statistical significance and effect size are sufficient conditions for the “meaningfulness” of complexity differences. Rather, we consider them necessary conditions. Bare any statistically detectable effects, it is possible that the differences we measure are just noise. Against this backdrop, we discuss more generally the methodological issue of choosing appropriate complexity measures, as well as the link between measured complexity and cognitive complexity in the following sections.

4. Matching Measures and Their Meaning

This section focuses on the choice of complexity measures and their intended meaning. Specifically, we address an important methodological mismatch that is often observed in studies on language complexity: absolute complexity measures are utilized to address research questions on relative complexity (see section 2 for definitions of absolute and relative complexity). We do not claim that this discrepancy necessarily makes the measurements invalid, but we argue that it deserves attention. At the very least, the mismatch should be made explicit and, if possible, evidence should be provided showing that the absolute measure is a reasonable approximation to the relative research question. In this section, we define the mismatch between complexity measures and their meaning (henceforth called absolute-relative mismatch), and explain why we consider it problematic. To highlight its relevance we conduct a systematic literature review, and offer suggestions on how complexity measures can be evaluated despite this mismatch.

4.1. The Absolute-Relative Mismatch

Language complexity is usually not measured for its own sake. The purpose of measuring complexity is usually to learn something about language, society, the brain or other real-world phenomena, in other words, to use language complexity as an explanatory variable for addressing fundamental research questions. Due to the existence of such questions and theories, complexity measures have a purpose, yet not necessarily a meaning. Complexity measures become meaningful only if they are valid, i.e., if they do indeed gauge the linguistic properties that are meant to be assessed by the researcher. For this reason, measures should ideally be evaluated against a benchmark, i.e., a gold standard, a set of ground-truth values. However, such benchmarks are not always available for complexity metrics.

The type of questions that feature prominently in sociolinguistic-typological and evolutionary complexity research, and, to some extent, in comparative and cognitive research are (i) whether all languages are equally complex, (ii) which factors potentially affect the distribution of complexity across languages (complexity as an explanandum), and (iii) which consequences complexity differences between languages entail (complexity as an explanans).

Most explanatory theories which aim to address these and similar questions are interested in some type of relative complexity, usually either acquisition difficulty, production effort or processing cost. For example, the researcher might be interested in how difficult it is to acquire a certain construction in a given language for an adult learner, or for a child; how much articulatory effort it takes to utter the construction, or how much cognitive effort is required to produce and perceive it. Notwithstanding this fact, many such studies measure some type of absolute complexity. For instance, they measure some abstract quantifiable property of a written text such as the frequency of a specific construction, the predictability of its choice in a certain context, or the compressibility of a given text. In other words, these studies address relative research questions with absolute measures.

This mismatch is important for the following two reasons: First, as we claim above, complexity measures should be evaluated against a benchmark in order to be valid. However, absolute measures, by their very nature, cannot be benchmarked directly because they do not correspond to any real-world phenomena, and thus there is no ground truth to establish (see sections 4.3 and 5).

Second, misinterpretations are likely to emerge. An illustrative example can be found in Muthukrishna and Henrich (2016). The authors claim that Lupyan and Dale (2010) show that “languages with more speakers have an inflectional morphology more easily learned by adults” (Muthukrishna and Henrich, 2016, p. 8). Crucially, this is not what Lupyan and Dale show, nor do they claim to have shown that. In contrast, they show that languages spoken in larger populations have a simpler inflectional morphology. Morphology is measured in terms of absolute complexity. Based on these absolute measurements, they hypothesize indeed that simpler morphology is also easier for adults to learn, and that large languages tend to have more adult learners, which is the reason for the observed effect. This hypothesis seems plausible. Still, it does not warrant conclusions regarding the learnability of morphologies in large languages. Such conclusions would have to be based on empirically established findings showing that simpler morphologies are indeed easier to learn for adults. This could be done, for instance, through psycholinguistic experiments or any other method (see sections 4.3 and 5) that directly assesses relative complexity. It can be tempting to skip this step, assuming instead that simpler morphologies are easier to learn because Lupyan and Dale show that they occur more often in larger languages. That, however, leads to a circular argument: assuming that languages become simpler because that makes them easier to learn, and then assuming that they are easier to learn because they are simpler. This is one of the dangers of the absolute-relative mismatch.

To reiterate, we do not claim that the absolute-relative mismatch makes a study invalid. On the contrary, measuring absolute complexity may be extremely valuable and actually necessary to address the relative hypotheses but it is important to understand that such approaches cannot provide definitive evidence and have to be complemented by relative measures.

Similarly, Koplenig (2019) shows, inter alia, that population size correlates with morphological complexity, but that proportion of L2 learners does not. His results are in keeping with the absolute measurements of Lupyan and Dale (2010), yet not with their theoretical explanation which is based on relative complexity. Assuming Koplenig's results are correct, they imply that Lupyan and Dale successfully identified an existing phenomenon (i.e., the correlation between population size and relative complexity). However, their explanation of the phenomenon would need to be revised. This is another illustration of the importance of the absolute-relative mismatch: even if the absolute complexity measurements per se are correct, it does not necessarily mean that they can be used as the basis for making hypotheses about relative complexity.

4.2. Systematic Literature Review

To estimate how common the absolute-relative mismatch actually is we conduct a systematic review of the literature. For this purpose, we tap The Causal Hypotheses in Evolutionary Linguistics Database¹² (CHIELD) (Roberts et al., 2020) which lists studies containing explicit hypotheses about the role of various factors in language change and evolution. These hypotheses are represented as causal graphs. We extract all database entries (documents) where at least one variable contains either the sequence complex or the sequence simpl (sic), to account for words like complex, complexity, complexification, simple, simplicity, simplification etc. On 2020-10-16, this search yielded 76 documents. Then we manually remove all documents that do not conform to the following criteria:

1. The study is published as an article, a chapter or a conference paper (not as a conference abstract, a book, or a thesis). If a smaller study has later been reproduced in a larger one (e.g., a conference paper developed into a journal article), we exclude the earlier one;

2. The study is empirical (not a review);

3. The study makes explicit hypotheses about the complexity of human language. Some studies are borderline cases with respect to this criterion. This usually happens when the authors of the studies do not use the label “complexity” (or related ones) to name the properties being measured, but the researchers who added the study to CHIELD and coded the variables do. In most cases, we included such documents;

4. These hypotheses are being tested by measuring complexity (or are put forward to explain an effect observed while measuring). We include ordinal measurements (ranks).

For each of the 21 studies which satisfy these criteria we note (i) which hypotheses about complexity are being put forward, (ii) whether these hypotheses are about relative or absolute complexity, (iii) how complexity is measured, (iv) the type of measure (absolute or relative), (v) the type of study. This information is summarized in Supplementary Table 1. Note that (Ehret, 2017, p. 26–29) conducts a somewhat similar review. The main differences are that here, we focus on the absolute-relative mismatch, and do not include studies without explanatory hypotheses. We also attempt to make the review more systematic by drawing the sample from CHIELD.

Some of the reviewed publications consist of several studies. As a rule of thumb, we list all hypothesis-measurement pairs within one study separately (since that is what we are interested in) but lump together everything else. For brevity's sake we list only the main hypothesis-measurement pairs, omitting fine-grained versions of the same major hypothesis and additional measurements.

The coding was not at all straightforward and involved making numerous decisions on borderline cases¹³. It is particularly important to highlight that “hypothesis,” in this context, is defined as a hypothesis about a causal mechanism. Many hypotheses on a surface level are formulated as if they address absolute complexity (e.g., “larger languages will have less grammatical rules…”) but the assumed mechanism involves, in fact, a relative explanation (e.g., “…because they are difficult to learn for L2 speakers”).

Our review reveals that 24 out of 36 hypothesis-measurement pairs contain a hypothesis about relative complexity and an absolute measurement, similarly to Lupyan and Dale (2010)‘s study above.

In only six hypothesis-measurement pairs, there is a direct match: In two cases, both the hypothesis and the measurement address absolute complexity, and in four cases both are relative. One of the absolute-absolute studies is the hypothesis that the complexity of kinship systems depends primarily on social practices of the respective group (Rácz et al., 2019). In another case (Baechler, 2014), the hypothesis is, simply put, that socio-geographic isolation facilitates complexification. Since the main assumed mechanism is the accumulation of random mutations, it can be said that complexification here means “increase in absolute complexity.”

The relative-relative studies are different. In one of them, the hypothesis is that larger group size and a larger amount of shared knowledge facilitate more transparent linguistic conventions, while the measurement of transparency is performed by asking naive observers to interpret the conventions that emerged during a communication game and gauging their performance (Atkinson et al., 2018a). Somewhat similarly, in a study by Lewis and Frank (2016), the complexity of a concept is measured by means of either giving an implicit task to human subjects or asking them to perform an implicit task. In both studies, the relative complexity is actually measured directly. Another case is the agent-based model by Reali et al. (2018) where every “convention” is predefined as either easy or hard to learn by the agents.

Finally, six studies are particularly difficult to fit into the binary relative vs. absolute distinction. In one case, Koplenig (2019) tries to reproduce Lupyan and Dale (2010)'s results without making any assumptions about the potential mechanism, which means that the complexity type cannot be established. Likewise, Nichols and Bentz (2018) do not propose any specific mechanism when they hypothesize that morphological complexity may increase in high-altitude societies due to isolation¹⁴. Atkinson et al. (2018b) apply an absolute measurement of signal complexity but show very convincingly that it is likely to affect how easily the signals are interpreted. In a similar vein, the simple absolute measurements of Reilly and Kean (2007) are backed up by psycholinguistic literature. In both cases, we judge that absolute measurements can be considered as proxies to relative complexity. Related attempts are actually made in several other studies although it is often difficult to estimate whether the absolute-relative link is sufficiently validated. Two more studies that we list as “difficult to classify” are those by Kusters (2008) and Szmrecsanyi and Kortmann (2009). Both studies point out that their absolute measures should be correlated with relative complexity, which is in line with our suggestions in this section. Dammel and Kürschner (2008) also explicitly make the same claim (the study is not included in the review since it does not put forward any explicit hypotheses). Yet another attempt of linking absolute and relative measures can be found in the Appendix S12 in Lupyan and Dale (2010) about child language acquisition (not included in the review, since it is not discussed in the main article). In all these cases, however, the absolute-relative link is rather speculative. It is based to a large extent on limited evidence from earlier acquisitional studies that do not perform rigorous quantitative analyses. There is often not enough evidence to know whether the particular measure assesses the relative complexity reasonably well. The authors acknowledge this discrepancy and claim that further empirical work in this direction is needed. We fully support this claim.

4.3. Benchmarking Despite the Mismatch

As shown in the previous subsection, absolute complexity measures are very often used as approximations to relative complexity (either explicitly or implicitly). Although relative complexity can, in principle, be measured directly via e.g., human experiments or brain studies, such approaches are usually much more costly than corpus-based or grammar-based absolute measurements. Nonetheless, we argue that benchmarking of absolute measures can be performed, and propose the following general procedure.

1. An absolute measure is defined and applied to a certain data set.

2. A relative property that it is devised to address is explicitly specified and operationalized.

3. This property is measured by a direct method (see below for examples).

4. The correlation between the measure in question and the direct measurement is estimated and used to evaluate the measure.

5. If there is a robust correlation and there are reasons to expect that it will hold for other data sets, the measure can be used for approximate quantification of the property in question. Some of its strength and weaknesses may become obvious in the course of such analyses and should be kept in mind.

Below, we list some of the methods which we consider most promising for directly (or almost directly) measuring relative complexity. In section 5, we provide a more detailed discussion of cognitive methods in neuroscience and psycholinguistics.

• Experiments on human subjects that directly measure learnability (Semenuks and Berdicevskis, 2018), structural systematicity (Raviv et al., 2019), or interpretability (Street and Dąbrowska, 2010) of languages/features/units.

• Corpus-based analyses of errors/imperfections/variation in linguistic production (Schepens et al., 2020).

• Using machine-learning as a proxy for human learning (Berdicevskis and Eckhoff, 2016; Çöltekin and Rama, 2018; Cotterell et al., 2019). It has to be shown then, however, that the proxy is valid.

• Using psycho- and neurolinguistic methods to tap directly into cognitive processes in the human brain.

5. Complexity Metrics and Cognitive Research

A driving assumption of corpus-based cognitive linguistics has been that frequencies and statistical distributions in the language input critically modulate language users' mental representation and online processing of language (Blumenthal-Dramé, 2012; Divjak and Gries, 2012; Bybee, 2013; Behrens and Pfänder, 2016; Schmid, 2016). This usage-based view has been bolstered by various studies attesting to principled correlations between distributional statistics over corpora and language processing at different levels of language such as morphology, lexicon, or syntax (Ellis, 2017). Such findings are in line with the so-called corpus-cognition postulate, namely, the idea that statistics over distributions in “big data” can serve as a shortcut to language cognition (Bod, 2015; Milin et al., 2016; Sayood, 2018; Lupyan and Goldstone, 2019). It should be noted that research in this spirit has typically focused on correlations between corpus data and comprehension (rather than production) processes, for the following reason: By their very nature, statistics across large corpora aggregate over individual differences. As such (and provided that the corpora under consideration are sufficiently representative), they are necessarily closer to the input that an idealized average language user receives than to their output, which depends on individual choices in highly specific situations and, furthermore, might be influenced by the motivation to be particularly expressive or informative by deviating from established patterns. Exploring the extent to which wide-scope statistical generalizations pertaining to idealized language users correlate with comprehension processes in actual individuals is part of the empirical challenge outlined in this section. The link between corpora and production processes is much more elusive and will therefore not take center stage.

Some of the relevant research has explicitly aimed at achieving an optimal calibration between distributional metrics and language cognition. Typically, this has been done by testing competing metrics against a cognitive benchmark assessing processing cost. For example Blumenthal-Dramé et al. (2017) conducted a behavioral and functional magnetic resonance imaging (fMRI) study comparing competing corpus-extracted distributional metrics against lexical decision times to bimorphemic words (e.g., government, kissable). In the behavioral study, (log-transformed) transition probability between morphemes (e.g., govern-, -ment) outperformed competing metrics in predicting lexical decision latencies. The fMRI analysis showed this measure to significantly modulate blood oxygenation level dependent (BOLD) activation in the brain, in regions that have been related to morphological analysis or task performance difficulty. In a similar vein, McConnell and Blumenthal-Dramé (2019) assessed the predictive power of competing collocation metrics by pitting the self-paced reading times for modifier-noun sequences like vast majority against nine widely used association scores. Their study identified (log-transformed) backwards transition probability and bigram frequency as the cognitively most predictive metrics.

This and similar research (for a review see Blumenthal-Dramé, 2016) has shown that corpus-derived metrics can be tested against processing cost at different levels of language description, from orthography up to syntax. This makes it possible to adjudicate between competing metrics so as to identify the cognitively most pertinent and thus meaningful metrics for a given language. However, this strand of monolingual “relative complexity” research gauging the power of competing complexity metrics within a given language has largely evolved independently from strands of cross-linguistic “absolute complexity” research.

We suggest that it is time to bridge this gap via cross-linguistic research establishing a link between corpora and cognition. This would allow us to explore the extent to which statements pertaining to absolute complexity differences between languages can be taken to be cognitively meaningful. This can be illustrated based on the cross-linguistic comparison of morphological complexity conducted in section 3. Among other things, this comparison showed that Finnish and English exhibit statistically significant differences in morphological complexity, with Finnish being more complex than English in terms of Kolmogorov-based morphological complexity. If this difference in absolute complexity goes along with significant processing differences in cognitive experiments, this information-theoretic comparison can be taken to be cognitively meaningful (above and beyond being statistically meaningful). In other words, if the above morphological complexity estimations are cognitively realistic, then morphological processing in Finnish and English should be significantly different in their respective L1 speakers. This prediction could be easily tested, and possibly falsified, in morphological processing experiments such as the one mentioned above.

However, it is important to point out that in this endeavor, a number of intuitively appealing, but epistemologically naive assumptions should be avoided. In the following, we introduce some of these assumptions, explain why they are problematic and sketch possible ways of avoiding them. The first unwarranted expectation is that higher values on absolute complexity metrics necessarily translate into higher cognitive complexity values. For example, one could assume that a larger number of syntactic rules and thus a higher degree of absolute syntactic complexity, as, for example, measured in terms of Kolmogorov-based syntactic complexity (e.g., Ehret and Szmrecsanyi, 2016; Ehret, 2018) leads to increased cognitive processing complexity. This, however, is a problematic assumption to make, since a higher number of syntactic rules is related to a tighter fit form and meaning, or, in other words, to a higher degree of explicitness and specificity (Hawkins, 2019). On the side of the language comprehender, greater explicitness is likely to facilitate bottom-up decoding effort and to decrease reliance on inferential processing (based on context, world knowledge, etc.). By contrast, in languages with fewer syntactic rules, the sensory signal will be more ambiguous. As a result, comprehenders will arguably rely less on the signal and draw more on inferential (or: top-down) processing (Blumenthal-Dramé, 2021). Whether bottom-down, signal-driven processing is overall easier than inference-driven processing is not clear.

This example highlights that deriving directed cognitive hypotheses from absolute complexity differences between languages would be overly simplistic. By contrast, a prediction that can be safely drawn from such research is that the native speakers of different languages are likely to draw on different default comprehension strategies (e.g., more or less reliance on the explicit signal; more or less pragmatic inferencing). Also important to highlight is the fact that predictions for language comprehension and language production need not align: As far as language production is concerned, greater absolute syntactic complexity (i.e., a larger number of rules) might well be related to greater processing effort, since the encoder has to select from a larger number of options.

In a similar vein, the number of irregular markers in morphology (e.g., McWhorter, 2012) need not positively correlate with processing effort. Irregularity is widely assumed to be related to holistic memory storage and retrieval, whereas regularity is arguably related to online concatenation of morphemes on the basis of stored rules (Blumenthal-Dramé, 2012). Which of those processing strategies is more difficult for language producers and comprehenders is hard to say (and might depend on confounding factors such as the degree of generality and number of rules), but again, a prediction that can be made is that the processing styles of users of different languages should differ if morphological complexity measures yield significantly different values.

On a more general note, it is worth emphasizing that holistic processing is likely to be much more ubiquitous than traditionally assumed. Thus, different lines of theoretical and empirical research converge to suggest that the phenomenon of holistic processing extends well-beyond the level of irregular morphology. Rather, even grammatically decomposable multi-word sequences which are semantically fully transparent (like “I don't know”) tend to be processed as unitary chunks, if they occur with sufficient frequency in language use. This insight, which has received increasing support from corpus linguistics, construction grammar, aphasiology, neurolinguistics, and psycholinguistics (Bruns et al., 2019; Buerki, 2020; Sidtis, 2020), highlights the fact that the building blocks of descriptive linguistics need not be coextensive with the cognitive building blocks drawn on in actual language processing. In the long term, findings such as those should feed back into absolute complexity research so as to achieve a better alignment with cognitive findings.

Thus, our suggestion is that while complexity metrics do not grant directed hypotheses as to processing complexity, they allow us to come up with falsifiable predictions as to differences in processing strategies. To what extent different processing strategies are cognitively more or less taxing is a separate question. Moreover, in conducting processing experiments, it is important to keep in mind that there might be huge differences between the members of a given language community. Some of this variance will be random noise, but some of it will be systematic (i.e., related to individual variables like age, idiosyncratic differences in working memory and executive functions, differential language exposure, multilingualism) (Kidd et al., 2018; Andringa and Dąbrowska, 2019; Dąbrowska, 2019). Likewise, it is important to acknowledge that the processing strategies adopted by individuals might vary as a function of task, interlocutor, and communicative situation, among other things (McConnell and Blumenthal-Dramé, 2019). To arrive at (necessarily coarse, but) generalizable comparisons, it is important to closely match experimental subjects and situations on a maximum of dimensions known to correlate with language processing.

A further important challenge is the fact that cognitive research has typically relied on metrics predicting the processing cost for a specific processing unit in a precise sentential context (e.g., in the sentence John gave a present to …, how difficult is it to process the word to?). By contrast, absolute complexity research has typically quantified the complexity of some specific descriptive level as a whole (i.e., how complex is the morphological system of a language?). On the one hand, such aggregate metrics, by their very nature, do not have the potential to provide highly specific insights into online processing, which unfolds in time, with crests and troughs in complexity. On the other hand, aggregate metrics seem cognitively highly promising (and so far unduly neglected in the relevant community), because they offer the possibility to provide insights into the overall processing style deployed by the users of different languages. We suggest that the online processing cost for a specific segment in the language stream has to be interpreted against language-specific processing biases, which depend on the make-up of a language as a whole (Granlund et al., 2019; Günther et al., 2019; Mousikou et al., 2020; Blumenthal-Dramé, 2021).

For this reason, we call for a tighter integration between the metrics and methods used in the different “complexity” communities. In our view, the absolute and relative strands of complexity research are complementary: Cognitive research can provide a benchmark to assess and fine-tune the cognitive realism of absolute complexity metrics, or, in other words, to examine the extent to which absolute complexity metrics have a real-world cognitive correlate and to select increasingly realistic ones. At the same time, absolute complexity research can contribute to refining cognitive hypotheses as to how languages are processed. While this endeavor might seem ambitious, we believe it can be achieved on the basis of cross-linguistic cognitive studies gauging the predictive value of competing complexity metrics in experiments involving maximally matched participant samples, experimental situations, and texts (in terms of genre and contents).

6. Conclusion

In this paper, we raised three issues relating to the interpretation and evaluation of complexity metrics. As such, our paper contributes to research on language complexity in general, and the sociolinguistic-typological complexity debate in particular. Specifically, we offer three perspectives on the meaning of complexity metrics:

First, taking a statistical perspective we demonstrate in two case studies how the meaningfulness of measured differences in complexity can be assessed. For this purpose we discuss the core statistical concepts of variance (in our case variance in observed complexity measurements), effect size, and non-independence. Based on our results we argue that both statistical significance and sufficiently large effect size are necessary conditions for being able to consider measured differences to be meaningful, rather than the outcome of chance. In our view, it is therefore important to statistically assess the meaningfulness of complexity differences before drawing conclusions from – and formulating theories based on – such measurements. Furthermore, we find that relatedness of languages does not necessarily imply similarity of their complexity distributions. Understanding systematic shifts in complexity distributions in diachrony hence requires more elaborate models which incorporate evolutionary scenarios such as variable rates of change and selection pressures.

Second, we highlight an important methodological mismatch, i.e., the absolute-relative mismatch, and illustrate how it can lead to misinterpretations and unfounded hypotheses about language complexity and explanatory factors. We suggest that this issue can be addressed by making it explicit. If possible, direct methods (e.g., psycholinguistic experiments) should be used to evaluate whether absolute measures are a robust approximation of the relative complexity intended to be measured. We further suggest some methods for measuring relative complexity directly.

Third, from a cognitive perspective, we discuss how absolute complexity metrics can be evaluated by drawing on methods from psycholinguistics and neuroscience. Cognitive processing experiments, for instance, can be used to assess the cognitive realism of absolute corpus-derived metrics and thus help us pinpoint metrics which are cognitively meaningful. At the same time, we caution against drawing hasty conclusions from such experiments. For instance, it is not to be taken for granted that the same predictions in terms of processing complexity equally apply to different types of languages, to native and non-native speakers, or to language production and comprehension. Nevertheless, the integration of cognitive methods in typological complexity research would greatly contribute to benchmarking absolute complexity.

In sum, this paper aims at raising awareness of the theoretical and methodological challenges involved in complexity research and making a first step toward fruitful cross-talk and exchange beyond the field of linguistics.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

Following the CRediT system¹⁵. KE: administration, conceptualization, validation, writing - original draft sections Introduction, Background, and Conclusion, and writing - review & editing. AB-D: conceptualization, validation, writing - original draft section Complexity metrics and cognitive research, and writing - review & editing. CB: conceptualization, validation, statistical analysis, writing - original draft section Assessing the meaning of complexity differences, and writing - review & editing. AB: conceptualization, validation, literature review, writing - original draft section Matching measures and their meaning, and writing - review & editing. All authors contributed to the article and approved the submitted version.

Funding

AB acknowledges funding by Nationella Språkbanken – jointly funded by its 10 partner institutions and the Swedish Research Council (2018–2024; dnr 2017-00626). The article processing charge was funded by the Baden-Württemberg Ministry of Science, Research and Art and the University of Freiburg in the funding programme Open Access Publishing. CB was funded by SNF grant #176305. Non-randomness in morphological diversity: A Computational Approach Based on Multilingual Corpora.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomm.2021.640510/full#supplementary-material

Footnotes

1. ^In this paper, we remain agnostic about whether such observed differences hint at an overall equi-complexity of languages or not. For the (un)feasibility of measuring overall complexity see Fenk-Oczlon and Fenk (2014) and Deutscher (2009).

2. ^Second language acquisition research (SLA) has produced an equally abundant amount of approaches to complexity. Yet, a discussion of SLA approaches is outside the scope of this paper.

3. ^In fact, whether the measure relates to “complexity,” “diversity,” or any other concept, is secondary for this discussion as long as the concept can be measured in numbers.

4. ^https://github.com/IWMLC/complexityMeaning.

5. ^German, English, and Dutch would be expected to form a clade, while English is here put closer to Swedish. Also, Spanish is normally considered closer to French than Italian.

6. ^Cahusac (2021, p. 55) remarks that a sample size of >15 should be sufficient to generally assume “normality of the means,” which is a precondition for using the t-distribution in standard statistical tests. On the other hand, Bland and Altman (2009) discuss an example with n = 20 for which the t-test is clearly not appropriate due to skew in the data. We thus assume that n = 20 is a sample size where the question of normal or non-normal data is still relevant. We discuss the issue of choosing statistical tests further in the Appendices in Supplementary Material.

7. ^The choice of μ and $σ_{r}^{2}$ is somewhat arbitrary here. But note that the core results we report are independent of this choice. This can be tested by changing the values of these parameters in our code and re-running the analyses.

8. ^The measure was originally applied 1,000 times to randomly sampled sentences of the respective texts. The present analysis instead uses 20 chunks of 80 sentences per language in order to match the number of “measurements” in the simulated data.

9. ^This is only relevant for the empirical complexity values in the second case study.

10. ^As one reviewer points out, we should not generally equate the size of an effect with its “meaningfulness.” Baayen (2008, p. 125), for instance, points out: “Even though effects might be tiny, if they consistently replicate across experiments and laboratories, they may nevertheless be informative [...].” So even small differences in the complexities of languages might be considered meaningful if they replicate across different measurements.

11. ^We do, however, expect to find covariance and hence a correlation in trait values between the more closely related languages. Appendix 2 in Supplementary Material shows that this is indeed the case in our simulation.

12. ^https://chield.excd.org/.

13. ^We are solely responsible for this coding. It is in no way endorsed by the authors of the original studies.

14. ^Note that Nichols and Bentz (2018) also make hypotheses about simplification but assume that L2 difficulty, i.e., relative complexity, is the main factor.

15. ^https://casrai.org/credit/.

References

Ackerman, F., and Malouf, R. (2013). Morphological organization: the low conditional entropy conjecture. Language 89, 429–464. doi: 10.1353/lan.2013.0054

CrossRef Full Text | Google Scholar

Andringa, S., and Dąbrowska, E. (2019). Individual differences in first and second language ultimate attainment and their causes: individual differences in ultimate attainment. Lang. Learn. 69, 5–12. doi: 10.1111/lang.12328

CrossRef Full Text | Google Scholar

Atkinson, M., Mills, G. J., and Smith, K. (2018a). Social group effects on the emergence of communicative conventions and language complexity. J. Lang. Evol. 4, 1–18. doi: 10.1093/jole/lzy010

CrossRef Full Text | Google Scholar

Atkinson, M., Smith, K., and Kirby, S. (2018b). Adult learning and language simplification. Cogn. Sci. 42, 2818–2854. doi: 10.1111/cogs.12686

CrossRef Full Text | Google Scholar

Baayen, R. H. (2008). Analyzing Linguistic Data: A Practical Introduction to Statistics Using R. Cambridge: Cambridge University Press.