Dendritic plateau potentials can process spike sequences across multiple time-scales

The brain constantly processes information encoded in temporal sequences of spiking activity. This sequential activity emerges from sensory inputs as well as from the brain's own recurrent connectivity and spans multiple dynamically changing timescales. Decoding the temporal order of spiking activity across these varying timescales is a critical function of the brain, but we do not yet understand its neural implementation. The problem is, that the passive dynamics of neural membrane potentials occur on a short millisecond timescale, whereas many cognitive tasks require the integration of information across much slower behavioral timescales. However, actively generated dendritic plateau potentials do occur on such longer timescales, and their essential role for many aspects of cognition has been firmly established by recent experiments. Here, we build on these discoveries and propose a new model of neural computation that emerges from the interaction of localized plateau potentials across a functionally compartmentalized dendritic tree. We show how this interaction offers a robust solution to the timing invariant detection and processing of sequential spike patterns in single neurons. Stochastic synaptic transmission complements the deterministic all-or-none plateau process and improves information transmission by allowing ensembles of neurons to produce graded responses to continuous combinations of features. We found that networks of such neurons can solve highly complex sequence detection tasks by breaking down long inputs into sequences of shorter, random features that can be classified reliably. These results suggest that active dendritic processes are fundamental to neural computation.

Introduction

The ability to recognize patterns of spiking activity across multiple timescales is a remarkable and crucial function of the brain. For example, consider a rodent searching for food. The receptive fields of its place and grid cells tile a spatial map of the environment and encode its current position by their respective population activities (O'Keefe and Dostrovsky, 1971; Hafting et al., 2005). To navigate successfully, the animal needs to know not only its present location, but also the path it took to get there. This path is encoded in the sequential firing of place and grid cells on behavioral timescales that can span hundreds of milliseconds or more (Eichenbaum, 2017). While the exact timing of these spikes depends on the speed of the animal, the chosen path through a space is encoded in the sequential order in which these cells are activated. As another perhaps more familiar modality, consider natural language: We can understand the same utterances over a wide variety of speech tempos and rhythms, provided that the order of specific sounds is preserved. In auditory cortex, for example, sequences of brief phonemes encode longer syllables which can last for around 200 ms (Luo and Poeppel, 2007). Early olfactory areas represent odors as ordered sequences on a similar timescale (Broome et al., 2006; Bathellier et al., 2008). And visual cortex can learn to reproduce sequential activation patterns on cue, but on a compressed timescale (Xu S. et al., 2012; Lu et al., 2021). The sum of these and other findings suggest that sequential patterns of spiking activity, the precise timing of which can vary across timescales of up to several hundred milliseconds, are a ubiquitous occurrence in the brain. Therefore, the ability to detect and decode such sequences of neural activity is likely crucial for complex behavior in humans and animals alike (Lashley, 1951). But how neural circuits implement this is currently unknown.

Point-neurons such as leaky integrate-and-fire models operate on the fixed timescale of passive membrane potential dynamics, which is typically on the order of tens of milliseconds or less (Melamed et al., 2004). Since this is at least one order of magnitude shorter than the behavioral timescales we are interested in here, there must be additional working memory to bridge the silent periods between successive bouts of neural activity in longer sequences. Often, this longer memory is attributed to network-level effects such as slow recurrent dynamics (Sandamirskaya and Schöner, 2010) or fast synaptic plasticity (Mongillo et al., 2008). However, computational properties of neural systems are also dependent on the structure and dynamics in the neural dendrites of single neurons (London and Häusser, 2005), which make up the vast majority of neural tissue (Braitenberg and Schüz, 2013). Early modeling work on the dynamics of dendritic membrane potentials showed that sequences of synaptic activation can elicit higher somatic voltages when they activate different locations of the dendrite in order, starting from the peripheral dendrite of a neuron and continuing toward the soma (Rall, 1964). This selectivity was first attributed to dendritic conductance delays in the dendritic cable model. More recent experiments suggest that besides these linear effects, the nonlinear amplification by NMDA channels is crucial for sequence detection (Branco et al., 2010). In combination with a pronounced impedance gradient along the dendrite (i.e., thin distal tips have higher impedance than thick proximal dendrite segments) and voltage-gated ion channels, this can lead to supra-linear summation in the centripetal direction (Branco et al., 2010). Here, we are particularly interested in the longer lasting dendritic plateau potentials (Milojkovic et al., 2004), a localized all-or-none response mediated by the very same NMDA channels in dendrites of pyramidal neurons. Because plateaus are triggered by synchronous volleys of presynaptic spikes (Gasparini et al., 2004) they can decode spatial patterns as single elements of sequences. Because the resulting elevated membrane potentials are actively maintained for up to hundreds of milliseconds (Milojkovic et al., 2004; Major et al., 2008) after their initiation, they can decouple the timescale of sequence recognition from the timescale of passive membrane potential dynamics. Importantly, plateau potentials are ubiquitous throughout the brain (Antic et al., 2010; Oikonomou et al., 2014), and recent in-vivo experiments link the prolonged high internal Ca²⁺ concentrations caused by dendritic plateaus to various cognitive tasks (Jia et al., 2010; Xu N.-L. et al., 2012; Takahashi et al., 2016; Kerlin et al., 2019). As previously suggested (Antic et al., 2010; Hawkins and Ahmad, 2016), this implies that dendritic plateau potentials may be the key missing ingredient in current models of sequence processing in the brain, but their precise role is still debated.

Our main idea is that dendritic plateaus provide the long-lasting memory traces needed for sequence processing: By generating a plateau potential, the dendrite quickly reacts to the detection of a stimulus, i.e., coherent synaptic input, and retains a long-lasting memory trace of this event in the local membrane potential. The key mechanism for detecting sequences of such stimuli on behavioral timescales is the interaction of plateau potentials across nearby segments, i.e., the depolarizing effect they exert on neighboring segments (Figure 1A). We propose that localized dendritic plateaus thus turn the complex dendritic trees of single neurons into reliable sequence processors with long temporospatial, yet timing-invariant receptive fields.

FIGURE 1

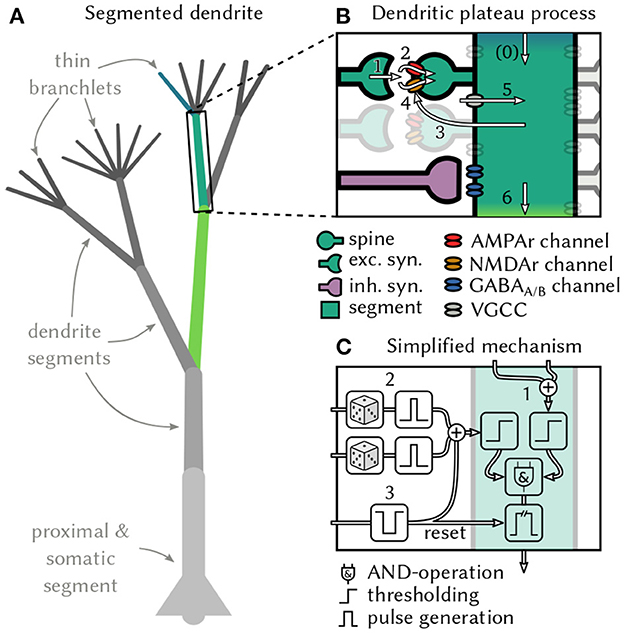
Figure 1. Generation and interaction of dendritic plateau potentials. (A) A stylized neuron with dendritic arbor. (B) Summary of the biological processes involved. A spike (1) releases glutamate, which opens AMPAr-gated ion-channels that depolarize the post-synaptic spine and cause an EPSP (2). If sufficiently many EPSPs coincide with up-stream dendritic input (0), the local membrane potential rises (3) and NMDAr-gated ion-channels activate, causing a further localized depolarization (4). Additional voltage-gated calcium channels can amplify and prolong this process (5) and cause a plateau potential, which can in turn moderately depolarize the parent segment (6 & 0). (C) An algorithmic approximation of a dendrite segment in our model. If a dendrite segment is depolarized by sufficiently strong input from its child segments (1) and receives sufficiently strong excitatory input from its stochastic synapses (2), a local plateau potential is initiated. If the plateau is not interrupted by shunting inhibitory input (3), it depolarizes the parent segment for an extended period of time. The root segment comprising proximal dendrite and soma lacks the ability to generate plateau potentials – instead, it generates somatic action potentials in response to super-threshold excitation.

In the following, we first derive from recent biological observations a conceptual model of dendritic computation that is built on this interaction of plateau potentials. Then we demonstrate how this mode of computation allows single neurons and networks to recognize complex sequences across various timescales and modalities.

Stochastic generation and inhibition of localized dendritic plateau potentials

Most of a cortical pyramidal neuron's excitatory synaptic inputs terminate on dendritic spines (Beaulieu and Colonnier, 1985), where they activate both AMPAr and NMDAr gated ion channels via glutamate-carrying vesicles. The AMPAr channel opens immediately, which leads to a brief depolarization in the corresponding spine referred to as the excitatory post-synaptic potential (EPSP) (Watkins and Evans, 1981). The NMDAr channel, however, is blocked by an Mg⁺ ion that must first be displaced by sufficient depolarization of the postsynaptic membrane to become conductive (Monyer et al., 1994; Götz et al., 1997). This requires the cumulative effect of coincident EPSPs in multiple nearby spines (Losonczy and Magee, 2006). Experimental as well as simulation studies report that a volley of 4–20 or even up to 50 spikes within a window of 1 ms to 4 ms is needed to provide sufficient depolarization, depending on the location along the dendritic tree (Gasparini et al., 2004; Gasparini and Magee, 2006; Losonczy and Magee, 2006; Bono and Clopath, 2017). The opening of NMDAr channels triggers a massive influx of different ionic currents that lead to a full depolarization of the local dendritic membrane potential. Although the isolated NMDAr response itself is reported to only last on the order of around 25 ms (Rhodes, 2006), in vivo recordings reveal that voltage-gated channels in the dendritic membrane (Spruston, 2008) prolong this effect, resulting in an actively maintained depolarization that can last from tens to hundreds of milliseconds (Major et al., 2013). This prolonged depolarization is called a dendritic plateau potential (Figure 1B).

Two further aspects of the interaction between dendritic plateaus and synapses are noteworthy. Firstly, spikes in presynaptic neurons only lead to the required glutamate release some of the time with a synapse specific probability (del Castillo and Katz, 1954; Stevens, 1993). In hippocampal synapses for example, the median release probability is only 0.22 (Branco et al., 2008). Secondly, the activation of inhibitory GABA_A and GABA_B synapses can strongly interfere with the dendritic plateau process and outright stop or prevent plateau generation (Kim et al., 1995; Doron et al., 2017; Du et al., 2017). The importance of inhibitory synapses is further emphasized by their locations, which are often in critical positions to control dendritic excitability (Gidon and Segev, 2012) and gate specific dendritic activity from reaching the soma (Muñoz et al., 2017).

Functional compartmentalization of dendritic trees

Plateau potentials remain localized to specific sites in the dendritic tree because their generation and maintenance requires the binding of external glutamate to NMDAr channels (Silver et al., 2016). Therefore, the structure of dendritic arbors, which has long been conjectured to play an important role for neural computation, is crucial for plateau computation. For example, functional subunits emerge in the dendrites of various types of retinal ganglion cells due to impedance mismatches at branching points in the dendritic tree (Koch et al., 1982). These are regions of roughly equal local membrane potentials throughout, but they are only weakly coupled to neighboring regions. Other experiments in rats confirmed that thin dendrites in neocortical pyramidal neurons can act as independent computational subunits and provide neurons with additional non-linear integration sites (Polsky et al., 2004). This behavior is not limited to pyramidal neurons, but rather appears to be a general principle that can be found in various forms across different cell types. For example, Purkinje cells in the cerebellum also generate localized Ca²⁺ events in response to coincident input on individual dendrite segments (Ekerot and Oscarsson, 1981; Zang et al., 2018), and thalamo-cortical neurons respond to strong synaptic input with localized plateaus in distal dendritic branches (Augustinaite et al., 2014). In some neurons, functional subunits can be identified with individual dendritic branches (Branco and Häusser, 2010). More generally, these subunits can also stretch across multiple nearby branches if they are sufficiently strongly coupled so that coherent synaptic input across the branches can trigger local, regenerative events such as plateau potentials (Wybo et al., 2019). We view dendrites as complex structures composed of functional subunits in the latter sense and will refer to them as dendrite segments¹.

Neural cable theory predicts an asymmetric passive propagation of membrane potentials throughout the dendrite (Rall, 1962; Goldstein and Rall, 1974). In the anterograde direction, the signal attenuation is generally so strong that synaptic input onto thin apical dendrites has little measurable effect of the membrane potential at the soma (Stuart and Spruston, 1998; Spruston, 2008). On the one hand, this may suggest that superlinear NMDAr responses along the dendrite serve to boost distal input signals (Magee and Cook, 2000; Häusser, 2001). On the other hand, plateau potentials are also subject to attenuation along the dendritic cable and thus only have a moderately depolarizing effect on their immediate neighborhood (Larkum et al., 2009). This can effectively raise the local resting potential of a neighboring segment closer to the soma and thus lower the amount of coinciding spikes in presynaptic terminals required to initiate a plateau potential in it (Major et al., 2008).

From dendritic nonlinearity to dendritic computation

Neither stochastically generated active dendritic processes nor the structure of the dendritic tree are considered in most computational models of spiking neurons, although there is lively debate about the appropriate level of abstraction (Herz et al., 2006). Some authors argue that the dendritic integration of spikes can be largely explained by a linear stochastic model with one additional non-linear term (Ujfalussy et al., 2018). Others contend that the computational function of the dendritic tree is best captured by a non-linear hidden layer in a neural network model (Poirazi et al., 2003), whereas modeling the temporal dynamics of the membrane potential would require significantly more complex temporally convolutional deep neural networks (Beniaguev et al., 2020). But the long-lasting all-or-none response characteristic of dendritic plateaus is not captured by either of these model classes. We therefore take a different approach and focus entirely on dendritic plateaus and their interactions in the dendrite. Since only nearby synapses cooperate to trigger plateau potentials, correlated synaptic inputs have to arrive at the same dendrite segment at the same time to effectively drive plateau generation (Gasparini and Magee, 2006). This has been confirmed in experiments (Larkum and Nevian, 2008), suggesting that some information in the brain is conveyed by highly synchronized spike volleys that target individual dendrite segments (Takahashi et al., 2012) and trigger dendritic plateaus there. We avoid complex non-linear membrane dynamics in our model and instead conceive of dendritic computation as fast, local coincidence detection driving the interaction of long plateau potentials (see the next section). At the expense of some quantitative accuracy, this simplification affords a clearer qualitative explanation of the computational mechanism that may underlie sequence detection in single neurons.

A computational model for dendritic plateau computation

From the biological observations outlined above, we derive a simple, qualitative model of active dendrites. At the core of the model lies the interaction of two types of events on distinct timescales—short, spike-triggered EPSPs and long, actively generated dendritic plateau potentials—in a tree structure of dendrite segments. We define a segment as a minimal functional subunit of the dendritic tree, a single physical branch or multiple branches that have the following properties: Firstly, synaptic inputs to a segment can cooperatively generate a plateau potential. Secondly, the plateau potential is actively maintained locally within a segment and spreads passively to neighboring segments in the dendritic tree. The passive spread of plateau potentials is attenuated along the dendritic cable in centripetal direction, in particular at branching points with mismatched impedances. The dendrite segments form a tree structure with proximal dendrites and the soma at its root and thin, distal branchlets as leaves.

First, consider the function of one individual dendrite segment i in more detail (see Figure 1C for a schematic). We distinguish excitatory and inhibitory synapses, which, respectively, produce excitatory (EPSPs) and inhibitory (IPSPs) postsynaptic potentials. An excitatory synapse from neuron k to segment i only successfully transmits each presynaptic spike with probability p_{i, k}. A successfully transmitted presynaptic spike induces EPSPs κ_E(t) with duration τ_E and magnitude w_{i, k} where w_{i, k} depends on the synaptic efficacy. At inhibitory synapses, the duration τ_I of the IPSP was set to be slightly longer than the τ_E EPSP. We model the shape of the post-synaptic potentials by rectangular pulses:

$k_E(t)=\{\begin{array}{ll}1\hfill & \text{if }0\le t\le {\tau }_{\text{E}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array},{\kappa }_I(t)=\{\begin{array}{ll}1\hfill & \text{if }0\le t\le {\tau }_{\text{I}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$

We use exc_i and inh_i to represent the set of excitatory and inhibitory neurons targeting segment i, we denote the time of the m^th spike by neuron k with $t_k^m$, and introduce the i.i.d. random variables ${\xi }_{i,k}^m~\text{Bernoulli}(p_{i,k})$ to simplify notation. We can then define the combined effect of excitatory as well as inhibitory input for segment.i²

$\begin{array}{lll}EPS{P}_i(t)& ={\displaystyle \sum _{k\in \text{ex}{\text{c}}_i}}{\displaystyle \sum _{m|t_k^m\le t}}{\xi }_{i,k}^m{w}_{i,k}{\kappa }_E(t-t_k^m)& (1)\end{array}$

$\begin{array}{lll}IPS{P}_i(t)& ={\displaystyle \sum _{k\in \text{in}{\text{h}}_i}}{\displaystyle \sum _{m|t_k^m\le t}}{\xi }_{i,k}^m{w}_{i,k}{\kappa }_I(t-t_k^m)& (2)\end{array}$

$\begin{array}{lll}PS{P}_i(t)& =\text{EPS}{\text{P}}_i(t)-\text{IPS}{\text{P}}_i(t)& (3)\end{array}$

One of the necessary preconditions for generating a dendritic plateau potential is a sufficiently strong net depolarization of the dendrite by synaptic input. This means that the coincidence of multiple synchronous spikes caused depolarization larger than a segment-specific synaptic threshold TS_i. In thin dendrite branchlets, which are the leaf nodes of our tree structure, this is sufficient to trigger a plateau potential. But in the general case, additional depolarizing input from dendritic child branches is required. Here, we are only interested in the large depolarizing effects that actively generated plateau potentials have on directly adjacent segments, and we ignore the much weaker passive propagation of sub-threshold voltages along the dendrite. We define a segment's dendritic input to be the sum of the strongly attenuated, passively spreading depolarization from plateau potentials in child segments. We therefore introduce additional notation: parent_i denotes the parent segment of i (if any), child_i denotes the set of the direct children of segment i (if any), and O_k(t), k∈child_i is the effect that the child segment k exerts on i at time t. Just like we did for the post-synaptic potentials, we can then define the total dendritic input D_i(t) into segment i:

$\begin{array}{ll}{D}_i(t)={\displaystyle \sum _{k\in \text{chil}{\text{d}}_i}}{\text{O}}_k(t)& (4)\end{array}$

The segment-specific dendritic threshold TD_i determines how much dendritic input is required in addition to synaptic input to trigger a plateau potential in segment i. For leaf nodes of the dendritic tree we set TD_i = 0. When both conditions become satisfied, i.e., there is sufficient synaptic and dendritic input, then a plateau potential is initiated. We use $T_i^m$ to denote the starting-time of the m^th plateau potential in segment i:

$\begin{array}{ll}\begin{array}{ll}\hfill & T_i^m=\min t\ge T_i^{m-1}\hfill \\ \text{\hspace{1em}such that \hspace{1em}}\hfill & {\text{PSP}}_i(t)\ge {\text{TS}}_i\wedge {\text{D}}_i(t)\ge {\text{TD}}_i\hfill \end{array}& (5)\end{array}$

The plateau potential then typically ends at time ${\tilde{T}}_i^m=T_i^m+{\tau }_P$ after a duration τ_P. The plateau duration is a constant in our model, but shunting inhibition may interrupt plateaus and thus cut their duration short. We formalize this special case as follows: The first inhibitory spike, if any, from neuron k∈inh_i at time $t_k^l\in \left[T_i^m;T_i^m+{\tau }_P\right]$ can end the plateau which means ${\tilde{T}}_i^m=t_k^l$ in that case.

We can now define the output of segment i as a sequence of binary pulses, the plateau potentials:

$\begin{array}{ll}{\text{O}}_i(t)=\{\begin{array}{ll}1\hfill & \text{ if }\exists m:t\in [T_i^m;{\tilde{T}}_i^m]\hfill \\ 0\hfill & \text{ otherwise}\hfill \end{array}& (6)\end{array}$

Since the plateau potential is an all-or-none response in our model, we classify the segments' membrane potentials into three functionally distinct states V_i(t)∈{low, elevated, high}: If the dendrite segment receives no depolarizing input from its upstream neighbors, it is approximately at resting potential and localized synaptic input alone is unlikely to trigger a plateau potential—the dendrite is in the low state. If plateau potential(s) further upstream from the segment elevate its local voltage, it becomes excitable by synaptic input—the segment is in the elevated state. If either the segment itself maintains a plateau or its parent segment is currently in a high voltage state, the membrane potential in the segment is fully depolarized, and additional synaptic input has little effect – the segment is in the high state. This can be expressed as follows:

$\begin{array}{ll}{\text{V}}_i(t)=\{\begin{array}{ll}\text{high}\hfill & {\text{ if V}}_{{\text{parent}}_i}(t)=\text{high or }{O}_i(t)=1\hfill \\ \text{elevated}\hfill & \text{ if }{D}_i(t)\ge T{D}_i\hfill \\ \text{low}\hfill & \text{ otherwise}\hfill \end{array}& (7)\end{array}$

This formalism can be iteratively applied to all dendrite segments of a neuron³. The root segment of the dendritic tree consists of the proximal dendrite and soma, which do not generate plateau potentials themselves. Nevertheless, we use the same formalism as for other dendrite segments: An action potential, instead of a plateau, is generated at the soma when sufficient synaptic input coincides with sufficient dendritic input. The dendritic input from plateau potentials in child segments causes prolonged depolarization of the somatic membrane potential also referred to as a neural UP-state (Milojkovic et al., 2004).

Each action potential is followed by a refractory period τ_refrac during which no further spikes can be generated. Since the somatic UP-state can persist for the entire plateau duration, which is much longer than the neuron's refractory period, multiple spikes or bursts of spikes might be generated during this period.

Conceptually, each segment in our model acts first and foremost as a coincidence detector for a volley of synchronized spikes on the fast timescale of EPSPs. On the second, slower timescale of dendritic plateaus each segment is gated by its children in the dendritic tree. Thus, the main computation performed by the neuron is to detect a sequence of activations of its segments by spike volleys in the correct order. Each consecutive plateau event extends the memory available for sequence detection by another plateau duration. Shunting inhibition can interrupt this cascade of sequential activations by deactivating a plateau potential before the next sequence element is detected.

To efficiently simulate this model for the upcoming experiments, we implemented a fast, event-based software simulator in the Julia programming language (see Section Materials and methods).

Results

Dendrites can recognize movement trajectories from place cell activity on multiple timescales

To illustrate how dendritic plateau computation can be used in a close-to-real-world example, consider again the sequential patterns emitted by place cell populations. The location of an animal in its environment is represented by place-cells (O'Keefe and Dostrovsky, 1971; Hafting et al., 2005), each of which has a receptive field centered at a specific location. Navigation naturally produces sequential activation patterns as different locations are visited. The timescale of these patterns can be long and is variable because it is directly linked to the movement speed of the animal (Eichenbaum, 2017). This variability in timing is exacerbated during sleep-replay, where the same patterns can be replayed at significantly compressed timescales (Lee and Wilson, 2002). This makes reliable detection of these sequential place-cell patterns particularly difficult. Active dendritic processes likely play an important role in this sequence detection task, since they frequently occur in cortical pyramidal neurons of freely moving rats (Moore et al., 2017) and have been shown to be selective for specific sequences of synaptic inputs (Branco et al., 2010). Plateau computation can allow single neurons to solve this detection problem across varying movement speeds and during replay.

We numerically simulate a rat moving through a small, 2-dimensional environment by generating stochastic paths at varying movement speed (more details in Section Materials and methods). The environment is tiled by the receptive fields of place cell populations, each 20 neurons strong. These populations emit spike volleys, the magnitude of which increases as the animal gets closer to the center of the respective receptive field (Figure 2A). This encoding could arise from increased firing rates, increased correlation of the spike timings, or both (Pipa et al., 2013). The task is to recognize whether the animal followed a specific path leading through the receptive fields of three place cell populations in the correct order: from the bottom left (A, in yellow) through the center (B, in blue) to the top right (C, in purple). A neuron composed of two sequential dendrite segments and the soma can solve this task reliably if each of the segments receives synaptic input from one of the place cell populations (Figure 2A). In this example, a plateau potential is triggered in segment A if TS_i = 13 or more of the 20 neurons in the associated place cell population fire a synchronous spike volley, which implies that the animal crossed through the corresponding receptive field (Figures 2B, C). This detection is memorized in the elevated membrane potential of segment A for the duration of the plateau (Figure 2E). This also raises the resting potential of segment B (Figure 2D) and enables it to respond to a spike volley from its corresponding place cell population with a plateau of its own. Likewise for the soma, which can finally fire a spike in response to a spike volley from place cell population C. Since each of the successive detections depends on the preceding plateau potential, the neuron only responds if the three stimuli A→B→C occur in the correct order. In the reverse direction (Figures 2F–I), segment C cannot respond to the spike volleys received early on in the trial, as the child segment B is not yet in a plateau state. Therefore, the neuron does not spike when the rodent traverses the C location. Therefore, the neuron is highly selective to the correct order of inputs.

FIGURE 2

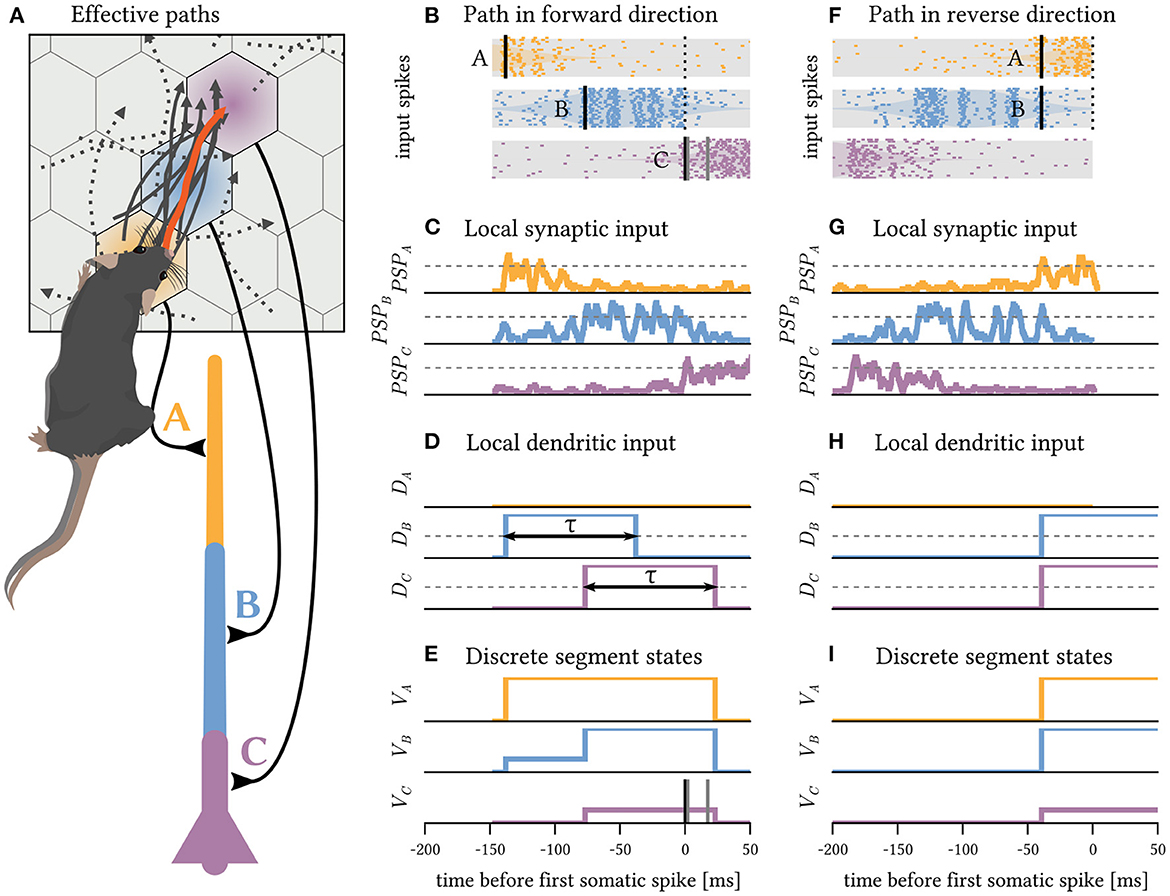
Figure 2. A simple neuron with three segments as shown below (A) can detect directed paths on a timescale of hundreds of milliseconds. (A) The receptive fields of place cell populations tile the environment into a hexagonal grid. The populations A,B and C are each connected to a different segment of the neuron (color coded). Random trajectories are generated through a stochastic process with randomized initial positions, velocities and angular heading to simulate the animal's movements. A random sample of 10 trajectories that elicit a neural response are shown as solid gray lines; all of them follow the same direction through receptive fields A→B→C. A few randomly sampled paths that did not elicit a spike are shown as dotted lines. (B) As the animal follows the highlighted path, it passes through receptive fields, and the place cell populations emit spike volleys. (C) The PSPs induced by these spikes sum up and locally depolarize the dendrite. (D) Additionally, child segments provide depolarizing for a duration τ input to their parents while in a plateau state. (E) The dendritic input can elevate the local membrane potential of the segment. If there is sufficient synaptic and dendritic input to a segment (thresholds shown in gray), a plateau potential (or somatic spike) is triggered there. Toward the end of the path, the neuron fires a somatic spike; all times are aligned to this first spike time. As the soma stays depolarized after the spike until the plateaus have subsided, further spikes may be triggered. (F–I) If the same path is followed in reverse order, no somatic spike is generated, because while the soma receives strong input from population C early during the trial, no plateaus have (yet) been triggered in segments A and B.

However, because each plateau enables the subsequent segment for a fixed, prolonged duration, the exact timing of the next sequence element within this time interval is irrelevant (Figure 3). The model neuron is invariant to faster movement along the path A→B→C (Figure 3A) and can even accommodate orders of magnitude faster replay of the pattern, as can be observed during hippocampal sleep replay (Figure 3B). Sequence detection via dendritic plateaus thus combines two distinct timescales: the fast estimation of the current location through coincident spike volleys and the slower integration of these events through interacting plateau potentials. The spatiotemporal receptive field of the neuron can thus be very sensitive and responsive to changes in location, but largely invariant to the speed at which the animal travels along the path on a much slower timescale (see Supplementary material 1).

FIGURE 3

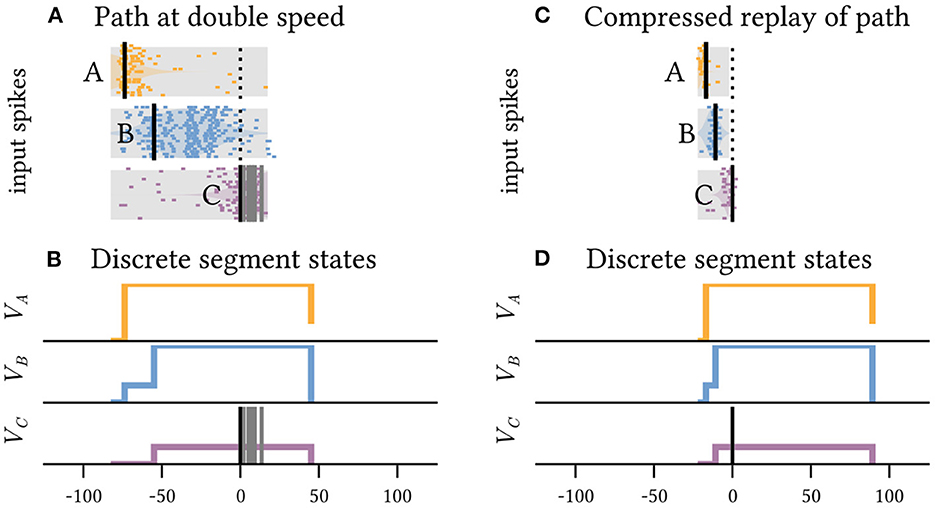
Figure 3. The neuron shown in Figure 2 is invariant to the precise timing of spike volleys as long as their order is preserved. It can detect the same path across timescales that differ by orders of magnitude. (A) Shows the inputs received when the same highlighted path in Figure 2 is traversed at twice the speed, and (C) shows a tenfold faster pattern, which can for example occur during compressed sleep replay. In both cases, a somatic spike is triggered and the path is detected. (B, D) Show the respective internal states of the segments.

Because compressed re- and preplay mechanisms are implicated in planning and skill learning (Ólafsdóttir et al., 2018), we expect that the robustness of dendritic sequence processing to compressed pattern representation is critical for theses tasks. However, this timing invariance also implies that techniques to identify spatiotemporal receptive fields via temporal averaging, such as the spike-triggered average (Simoncelli et al., 2004), are inadequate for neurons with active dendrites. Instead, new techniques are required that identify individual receptive fields of dendrite segments and compare the relative timings of the generated plateau potentials (see Supplementary material 2).

Shunting inhibition can prevent false positives

The mechanism outlined above only relies on excitatory synapses and is able to identify specifically ordered sequential patterns of spike volleys on varying timescales. However, if the same stimuli are frequently repeated in incorrect order, the likelihood of errors increases. To illustrate this, consider the sequence A→B→C and its reverse C→B→A, i.e., the same path but traveled in the opposite direction (Figure 4). During sleep replay, or while running in a circle, this reverse sequence may be presented multiple times in quick succession. Naturally, the sequence C→B→A→C→B→A→C→B→A also contains the sub-sequence A→B→C (highlighted) which would trigger the neuron. Because the additional excitatory spike volleys cannot prevent the neuron from firing, the repeated presentation of the reverse sequence will therefore lead to a false detection (Figure 4A). Anti-patterns such as this are an inevitable side-effect of the desirable timing-invariance of sequence detection.

FIGURE 4

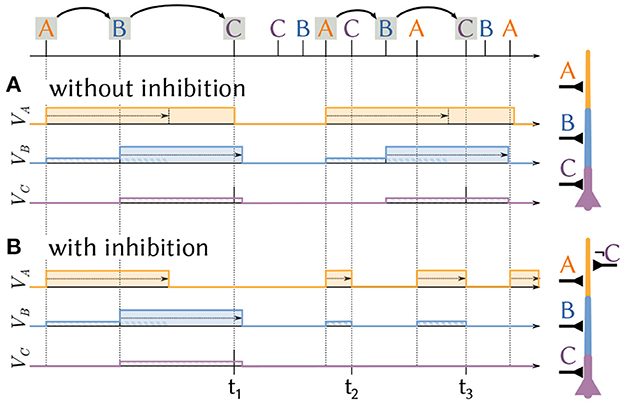
Figure 4. Shunting inhibition can prevent false detections. A neuron receives a sequence of spike volleys from three populations A, B and C. The internal state of the three segments is shown. (A) A neuron with a chain of dendrite segments A and B and soma C fires whenever they are activated in the correct order A→B→C, for example at time t₁. This also results in a false detection at t₃ if the desired sequence A→B→C is contained in fast repetitions of the undesired sequence C→B→A. (B) By adding shunting inhibition, input for segment C also stops the plateau at the first segment A at t₂ and t₃ which prevents the false detection.

Shunting inhibition can prevent such false positives and restore the neuron's high selectivity to sequence order in these situations (Figure 4B). Consider the same situation as before, but now additional inhibitory synapses from population C can disrupt plateaus in the neuron's first segment. If a spike volley from C immediately follows a volley from A, the previously generated plateau in the first segment is stopped and sequence detection has to start anew with a novel detection of a spike volley from population A. However, if populations A, B and C all fire in order the neuron will fire a spike before the inhibition of the first segment takes effect. Inhibition therefore acts as an important complementary mechanism for dendritic plateau computation and can “veto” anti-patterns from erroneously activating sequence detecting neurons.

Unlike excitatory spikes, which need to be synchronized into spike volleys to efficiently drive plateau generation, shunting inhibition can disrupt a plateau potential at any point.

Probabilistic and graded plateau responses increase information content

In the previous example, each place cell population codes for a single location. The magnitude of the spike volley encodes the proximity to the receptive field center, or, in other words, the evidence for the fact that the animal was close to the specified location. If the spike volley is transmitted deterministically (p = 1.0), the receiving dendrite segment detects it if and only if it exceeds a hard threshold at which a plateau is generated (Figure 5A). If the spike volley is instead transmitted stochastically (p < 1.0), the probability of generating a plateau is directly proportional to the spike volley magnitude (see Section Materials and methods). The response of an individual dendrite segment to one spike volley is of course binary in both cases, but if we assume that many segments respond to the same spike volley with stochastic synapses, then the expected number of emitted plateau potentials becomes a smooth sigmoidal function of the volley's magnitude (Figure 5B). In an ensemble of neurons with dendrite segments that respond to the same input probabilistically and independently due to unreliable synaptic transmission, the number of active plateau potentials can therefore encode the magnitude of the received spike volleys.

FIGURE 5

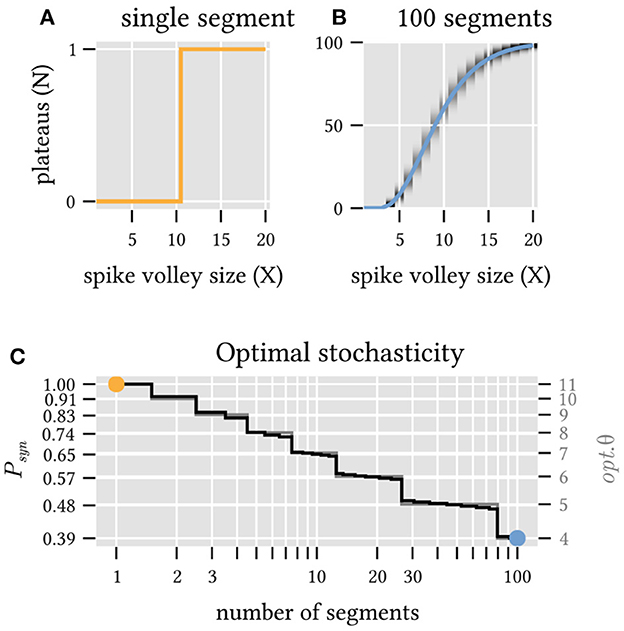
Figure 5. Unreliable synapses can improve information transmission for ensembles of dendrite segments. (A) A single dendrite segment with 20 inputs and deterministic synapses (transmission probability P_syn = 1.0 and threshold θ = 11) provides a binary classification (1 bit) of the magnitude X of the incoming spike volley. (B) The expected number N of plateaus (solid line) in an ensemble of 100 segments with stochastic synapses (P_syn = 0.39 and θ = 4) is a continuous function of the volley magnitude X and thus conveys more than 1 bit of information. Gray shading indicates the probability distribution around this mean value. (C) Combinations of θ and P_syn that maximize the mutual information between the magnitude of the incoming spike volleys and the number of generated plateau potentials for a varying number of independent segments. Note that increased stochasticity is beneficial as the ensemble size increases.

How well this encoding works can be quantified by the mutual information between spike volley magnitude and number of triggered plateaus. While there is clearly no benefit to synaptic stochasticity if only a single segment receives the spike volley, multiple dendrite segments can in fact benefit significantly from stochastic synaptic transmission. For example, a synaptic transmission probability as low as p = 0.39 maximizes information transmission for an ensemble of 100 dendrite segments that receive spike volleys from a population of 20 neurons. In this case, unreliable synapses allow an ensemble of otherwise identical deterministic neurons to exceed the information capacity of any individual neuron (Figure 5C and Section Materials and methods).

In our model, consecutive segments gate consecutive plateaus. In the path-detection example above, three consecutive spike volleys in a sequence must all be detected for the neuron to fire a spike. The probability of the spike response is therefore the product of all three plateau probabilities and thus directly proportional to the combined evidence for all sequence elements as encoded by the corresponding spike volleys. This affords another interpretation of the neuron's behavior: the probability to fire a spike encodes how closely the animal passed each of the receptive field centers along the path. An ensemble of neurons is therefore able to report not only if the animal followed some desired path, but also how closely its chosen path came to the three receptive field centers.

In the context of sequence detection, the stochasticity of synaptic spike transmission serves one other important purpose. Since plateau potentials endow the neuron with a long lasting internal state, any neuron that is already engaged in the detection of a sequence is not ready to detect another until its plateau potentials have subsided. Consider, for example, that we stimulate a neuron that normally detects A→B→C with the sequence A→B→A→B→C instead where subsequent input volleys are each half a plateau duration apart. On the first two inputs A and B, the neuron will advance its internal state and then wait for C until the plateau triggered by B has expired (or has been interrupted by inhibition). Within that time frame, the third and fourth inputs A and B arrive, but since the corresponding dendrite segments are already fully depolarized, they have no effect on the neuron in our model. Then, the plateau triggered by B expires before the final volley C arrives, which thus fails to trigger a somatic spike. Therefore, although this sequence contains the desired sub-sequence A→B→C at the end, the model neuron would fail to fire. The neuron is only able to begin the detection of a new sequence after it has returned to its initial state, i.e., all plateau potentials have expired or been reset by inhibition. In biology, reduced excitability of dendrite segments after a plateau potential seems to be related to the high Ca²⁺ concentration at the initiation site which can outlast the plateau depolarization (Milojkovic et al., 2007). The refractory period of dendritc computation we describe here may thus extend even beyond the plateau duration. This imposes a strict limit on the maximum rate at which any sequence could be detected by our model neurons: the inverse of the plateau duration, which is independent of the actual length of the sequence. With deterministic synapses, this limitation also applies to an ensemble of such neurons, because all neurons, given the same initial condition and synaptic connections, will operate in lockstep and detect or fail to detect the same instances of the target sequence. Synaptic stochasticity can help in this situation because it decorrelates individual detectors such that only some of the neurons will respond to the misleading initial sequence A→B and thus fail to detect the later valid sequence A→B→C. The remaining neurons failed to respond to the first two inputs and are hence ready to detect the final sub-sequence A→B→C. While the response of the ensemble is therefore reduced in magnitude due to the initial misleading input, it is crucially still able to detect the sequence in question.

Stochastic spike volleys can encode events in multi-dimensional feature space

So far, we only considered sequences of discrete events, such as an animal traversing specific receptive fields in order. In many situations, however, the individual sequence elements may not be as simple and binary as that. For example, the sequential activation of dense and overlapping representations of individual odorants in mitral cell populations gives rise to odor codes (Bathellier et al., 2008). Unlike place cells, no single population exclusively codes for one odorant in the sequence. Instead, the odorant is encoded by a weighted combination of different sub-populations each of which represents one feature of the odorant, e.g., the response of a particular receptor protein (Malnic et al., 1999). Similarly in vision, where many complex shapes can be represented by different combinations of the same simpler features, e.g., oriented edges. It is therefore important to note that our model of sequence detection, which we framed in terms of spike volleys and coincidence detection, is also able to detect sequences of specific linear combinations of simpler features. This is enabled by stochastic synaptic transmission, which provides a simple way for each dendrite segment to only detect a specific multi-dimensional combination of different features.

In the following, we identify each input feature with a spike-volley from a specific randomly selected subset of a much larger neuron population. These subsets can overlap for different features, but the expected overlap is small for sufficiently sparse subsets. By stochastically co-activating different fractions p_i of neurons from each of these sub-populations i, a single spike volley can thus encode various combinations of features. This approach is closely related to hyper-dimensional computing (Kanerva, 2009); see Section Materials and methods for a formal derivation.

Suppose we are interested in combinations $(p_1^j,p_2^j,p_3^j)$ of three arbitrary features P₁, P₂ and P₃. These could, for example, represent three different populations of olfactory receptors. For simplicity, ${(p_1^j)}^2+{(p_2^j)}^2+{(p_3^j)}^2=1$ is normed. The possible feature combinations thus span a continuous two-dimensional manifold, a sector of the surface of the unit sphere, embedded into the high-dimensional space of the neuron population's spiking output. Figure 6A shows an approximately distance-preserving projection of this manifold.

FIGURE 6

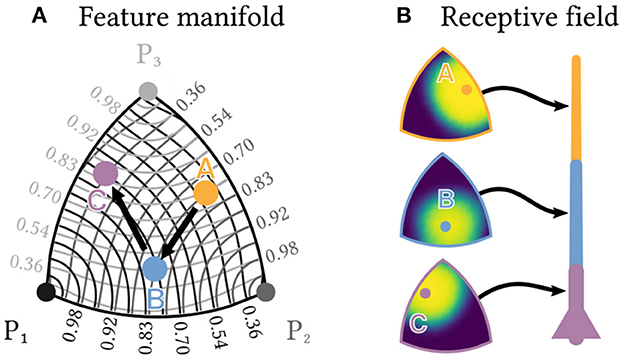
Figure 6. Individual neurons can detect sequences of feature combinations. Consider a sequence of the three elements A, B and C, each of which is a different normed combination of the three basis features P₁,P₂ and P₃ and therefore lies in a two-dimensional manifold. (A) shows an approximately distance preserving projection of that manifold. Contour lines show the similarity of each point to the three basis features. (B) Each of a neuron's segments can be tuned to respond only to a specific combination of basis features by a corresponding choice of synaptic transmission probabilities. Heatmaps show the resulting receptive fields for a neuron designed to detect the sequence A→B→C.

Within this manifold, we want to detect a specific sequence A→B→C, e.g., a sequence of three specific odorants, each of which is a different combination $(p_1^A,p_2^A,p_3^A)$, $(p_1^B,p_2^B,p_3^B)$ or $(p_1^C,p_2^C,p_3^C)$ of the three basic features. The same kind of neuron as described above can solve this task, if the transmission probability of each synapse is tuned to the desired strength $p_i^j$ of the corresponding feature. Each dendrite segment can then selectively respond with a plateau potential to only one specific combination of features (see Figure 6B), which allows the neuron to detect the sequence A→B→C. Note that instead of changing the magnitude of EPSPs for different synapses, this approach works entirely by tuning synaptic transmission probabilities.

Populations of plateau computing neurons improve sequence detection

The sequence detection capabilities of individual neurons can be extended to networks. As a sequence of interest gets longer and comprises more elements, it seems increasingly unlikely that the brain would rely on a single highly complex and specific neuron, or an ensemble of such neurons, to detect it. It is much more likely that multiple neurons code for different, shorter sequences—features—that occur in different combinations as parts of longer sequences. In analogy to the original Perceptron model (Rosenblatt, 1958), these features can be task-independent and chosen at random. To detect a specific long sequence of interest, a neuron would then only need to detect the right combination of a few of these features in correct order. A concrete example is the 10 element sequence D→B→C→A→F→E→D→H→B→F. It contains an enormous number of possible features such as (D→B→C), (C→A→E), (D→C→E) and so on, each of which might be detected by one random sequence detection neuron with just three segments (see Figures 7F–H). If many of these short features are present in the stimulus in the correct order, which can be recognized by a specialized sequence detection neuron, this provides strong evidence for the long sequence.

FIGURE 7

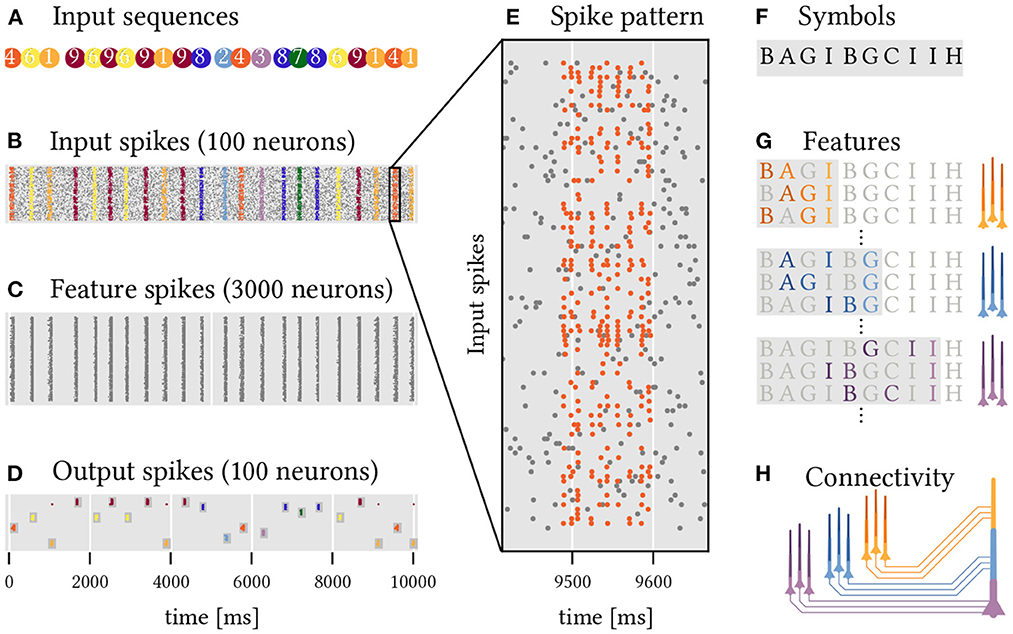
Figure 7. A two layer network of sequence detecting neurons with dendritic plateaus recognizes complex, overlapping, and long sequential patterns. Ten random sequences (1 through 10) of 10 random code-words (A through J) have to be detected. (A) The different target sequences are presented in random order (color coded). (B) Each of these instances results in a temporal pattern of spikes across 100 input neurons. Noise is modeled by additional spikes (gray dots). See also (E) for a close-up of sequence 5, which is composed of the symbols shown in (F). (C) 3, 000 neurons in a first layer each detect a random sequence of three symbols from the input spikes. (D) 100 Neurons in the output layer detect specific sequences of spike volleys from the hidden layer, i.e., sequences of sequences of symbols. This leads to a rather reliable detection of the 10 different target sequences by the corresponding output neurons. (G) Sub-populations of neurons in the hidden layer that code for different sequences ending in the same symbol fire synchronized spike volleys. (H) Neurons in the output layer can detect specific sequences of these spike volleys that are characteristic of the respective target sequence.

We set up a simple experiment to demonstrate how effective this strategy can be. The task is to classify 10 different sequences of spike volleys (labeled 1 to 10, see Figure 7A) that are generated by a population of 100 input neurons. Each of these sequences is a series of 10 randomly selected symbols with randomized timing. There are 10 symbols (labeled A to J) in total and each is represented by a spike volley from a randomly selected subset of 30 input neurons. The same symbols may appear multiple times within a sequence and are shared across the different sequences which makes classification challenging. In addition to these stimuli, the input neurons also generate spikes at random to emulate a backdrop of noise. Figure 7B shows the resulting spikes from the input population, and Figure 7E zooms in on a single example of such a sequence.

To solve this task, we construct a network of simple sequence detection neurons arranged into two layers. All of the neurons comprise just three segments in series, just like in the examples above, and are therefore able to detect sequences of up to three elements. In the first hidden layer of the network, 3, 000 neurons each detect a random sequence, or feature, composed of three symbols (Figure 7C). These features are drawn entirely at random from the set of all possible symbols⁴. Each segment receives input from the 30 input neurons that represent the associated symbol. A second layer of 100 output neurons (ten for each target sequence, see Figure 7D) uses the spikes coming from the hidden layer to classify the 10 different target sequences. To achieve this, each output neuron needs to detect a sequence of feature-combinations that is characteristic for the target sequence of interest. Each segment and soma of an output neuron thus detects a combination of relevant features, all of which terminate in the same symbol and thus produce a synchronized spike volley once that symbol appears in the target sequence. Here, we use a simple algorithm to select these feature combinations (see Section Materials and methods), but the same might be realized through a combination of structural and homeostatic plasticity in the brain. Now, whenever the target sequence is presented, the corresponding feature detectors in the hidden layer fire in order, which successively activates the dendrite segments of the output neurons, ultimately leading to spikes that signal a detection. Despite noisy inputs and timing variability in the spike patterns, the results are remarkably robust and each target sequence is reliably detected. Because the feature detectors in the hidden layer are agnostic to the target sequences, this scheme can be extended to another target sequence by adding just one additional output neuron to detect the right sequence of feature combinations.

Discussion

Mounting biological evidence suggests that dendritic function is critical to neural computation. We therefore constructed a new model of dendritic computation that relies primarily on the generation and interaction of dendritic plateau potentials. It explains conceptually how individual neurons with segmented dendritic trees can robustly detect long sequences of spike volleys in a particular order—even if they are presented across vastly different timescales. We also showed that stochastic synapses can turn the all-or-none response of plateau potentials into a more informative graded response. This allows individual neurons to detect complex sequences of stimuli that are themselves combinations of multiple features. Stacking such sequence detection neurons as features into a larger population further expands their ability to detect very long sequential patterns—even when based on generic, randomly generated feature detectors.

Early theoretical work already predicted that the dendritic tree would play a crucial role for sequence detection (Rall, 1964), albeit based on conductance delays that are too short to account for behaviorally relevant timescales. More recent work confirms that neurons indeed preferentially respond to sequential activation of dendritic spines in the centripetal direction along a single dendrite, but attributes this effect to the voltage-gating of NMDA channels in combination with a strong impedance gradient along the dendrite (Branco et al., 2010). Further experimental work has revealed the important role that NMDA channels play for the generation of plateau potentials and neural UP states, which endow the neuron with a much longer timescale (Milojkovic et al., 2004, 2005; Antic et al., 2010). The interaction of active dendrites and neural UP states was used in the hierarchical temporal memory model of neural computation (George and Hawkins, 2009) to explain how networks of neurons can process sequences (Hawkins and Ahmad, 2016). In contrast, our model takes advantage of the interaction of plateau potentials across distinct dendrite segments which provides a robust mechanism for sequence detection in single neurons. In our model, coincident spikes on neighboring synapses represent spatial patterns on a fast timescale, whereas plateau potentials act as long-lasting local memory traces of these short events and thus decouple the timescale of sequence detection from the timescale of membrane dynamics. Further, each detected sequence element initiates a new plateau and therefore extends the memory of the currently ongoing sequence by another plateau duration. This allows individual neurons to recognize long sequences with significant timing variability. The degree of the timing invariance is determined by the length of plateau potentials, which in turn has been found to be a function of the amount of presynaptic glutamate released (Milojkovic et al., 2005). This parameter, which corresponds to the spike volley magnitude in our model, is likely functionally significant and warrants further investigation, since it relates the duration of the plateau memory trace to the amount of evidence for the stored sequence element. In addition, the structure of the neural dendrite, its functional compartmentalization, and the location of synapses determine the neuron's ability to detect specific sequences in our model. This provides a different perspective on the functional relevance of the observed diversity of dendrite morphologies and their potential ability to adapt compartmentalization in cortex (Wybo et al., 2019).

We limited our discussion to simple examples of dendrites composed of a single chain of segments, but more intricate branching patterns can enable individual neurons to detect more complex sequential patterns such as “A or B and then C” (see Supplementary material 3). The relevance of such more complex patterns for neural computation should be investigated in future work. Since plateau generation requires highly correlated synaptic input, we also rely on spike volleys as the primary unit of information transmission. Although new statistical techniques are being developed to detect such volleys in-vivo, there are competing ideas about the mechanisms that could cause this synchronization. A particularly interesting prospect is the emergence of stimulus-dependent synchronization from recurrent activity (Korndörfer et al., 2017).

Here, we focused entirely on the role of dendritic plateaus for computation. Our hypothesis that plateau potentials are an integral part of neural computation is supported by a growing number of recent studies that show long-lasting calcium signals in dendrites to be associated with task relevant information in a variety of experiments (Takahashi et al., 2016, 2020; Kerlin et al., 2019). Future work should also address their implications for learning. For example, it is still unclear how dendrites can learn to detect specific sequences based on local plasticity mechanisms alone. One recent approach uses both the somatic and the local dendritic membrane potential in a two-compartment neuron model to learn temporal patterns via synaptic plasticity (Brea et al., 2016) but does not yet include non-linear amplification in active dendrites. However, experimental result show that localized plateau potentials and the resulting long-lasting high Ca²⁺ concentrations appear to be the primary drivers of synaptic plasticity (Hardie and Spruston, 2009). This is at odds with most current learning algorithms for spiking neurons, which instead rely on short somatic feedback signal such as backpropagating action potential (Song et al., 2000).

Other forms of plasticity also become more relevant in the context of our proposed model. For example, since the location of a synapse on the dendrite matters, structural plasticitity (Knoblauch and Sommer, 2016) is decisive for the neuron's function. The localized coincidence detection requires homeostatic processes to adjust synaptic transmission probabilities (Turrigiano, 2012; Leugering and Pipa, 2018) in order to appropriately balance the excitability threshold and synaptic input. And lastly, a recently proposed mechanisms for tuning transmission delays through controlled (de-)myelinization (Fields, 2015) might allow neuron populations to synchronize their spike volleys more precisely.

Beyond its role as a candidate mechanism for sequence processing in the brain, dendritic plateau computation may also have applications outside of neuroscience. In particular, the simplicity of our proposed mechanism lends itself to a hardware implementation that uses asynchronous communication and complex dendrite structures, rather than larger networks, to boost computational efficiency. The prospect of energy efficient dendritic computation has also motivated others to research potential implementations in neuromorphic hardware. For example, Intel's Loihi chip (Davies et al., 2018) and the DYNAPSE architecture (Moradi et al., 2018) already support some forms of active non-linear processing in functionally isolated dendrite segments. Our model provides a new perspective on how these existing capabilities could be utilized for computation and extended in future neuromorphic technologies.

Materials and methods

Simulation framework for dendritic plateau computation

All simulations are implemented in a custom package developed in the Julia programming language (Bezanson et al., 2017), publicly available via the code repository hosted at https://github.com/jleugeri/DPC.jl. The simulator implements the neuron model outlined in this paper using a fast and extensible event-based formalism. All experiments and configuration files can be found in the examples subfolder of the repository. Further documentation of the simulator, its interfaces, and implementation details can be found there as well.

Implementation of the navigation experiment

To simulate the stochastic movements of an animal in a two-dimensional environment, random paths are generated with time-varying location l(t) = (X(t), Y(t))∈ℝ² as solutions of the following system of stochastic differential equations:

$\begin{array}{ll}\begin{array}{ll}\text{d}X\hfill & =\cos (2\pi A)V\text{d}t\hfill \\ \text{d}Y\hfill & =\sin (2\pi A)V\text{d}t\hfill \\ \text{d}A\hfill & =0.25\text{d}{W}_A\hfill \\ \text{d}V\hfill & =10.0(0.25-V)\text{d}t+0.1\text{d}{W}_V\hfill \\ \hfill & \hfill \end{array}& (8)\end{array}$

A represents the angular heading of the animal, V represents its velocity in ms⁻¹ and W_A, W_V represent independent standard Brownian motion processes. Each path is generated with a randomized initial position within a rectangular domain of 10 cm × 9.5 cm, a random angular heading and a random velocity according to the marginal stationary distribution of V in the equation above, and is simulated for a fixed duration of 200 ms. Three populations of place cells, each 20 neurons strong, are centered on a hexagonal grid with center-to-center distance of r ≈ 2.9 cm. Each population randomly emits spike volleys following a homogeneous Poisson process with rate λ = 250Hz. The magnitude of each spike volley is determined by the population's mean activity at the time which depends on the animal's location within the environment through a receptive field tuning curve. The tuning curves model the probability of each individual neuron within the population to participate in a given spike volley by the bell-curves $f_i(x)=exp(-\frac{x-{\mu }_i}{2{\sigma }^2})$ with coefficient σ = 9.7mm, centered on the tiles of the hexagonal grid. The total number of spikes emitted during a volley from population i at time t is therefore a random variable distributed according to a Binomial distribution with population size n = 20 and probability p = f_i(l(t)). Additionally, each neuron in the population emits random spikes at a rate of 10 Hz to emulate background activity.

Each of the simulated neuron's dendrite segments receives spiking input from the 20 neurons of one place cell population and requires 13 coincident spikes to trigger a plateau potential. The three segments are connected in a chain that requires sequential activation by spike volleys from the input populations in correct order to fire a spike. A random path is considered to be accepted by the neuron if the neuron responds with a spike at any point in time during the corresponding simulation run.

Implementation of the stochastic plateau generation experiment

For a single dendrite segment with K = 20 stochastic synapse, each with transmission probability P_syn, the total number of transmitted spikes for an incoming volley of X spikes is a conditional random variable S|X~Binomial(X, P_syn). Whether the segment fires a plateau in response to the volley (Z = 1) or not (Z = 0) is another conditional random variable Z|X~Bernoulli(P_Z|X), where P_Z|X = P(S≥θ) = 1−F_S|X(θ−1) is the probability to exceed a fixed threshold θ. In an ensemble of M i.i.d. segments that receive the same spike volley as input, the number of triggered plateaus is then again a conditional random variable N|X~Binomial(M, P_Z|X). If the magnitude of the spike volleys X~P_X is chosen at random from some distribution P_X (here a discrete uniform distribution on [1, 20]), the amount of information conveyed by the number of triggered plateaus can be computed as

$I(N;X)={\displaystyle \sum _{N=1}^M}{\displaystyle \sum _{X=1}^K}p(X)p(N|X)log\frac{p(N|X)}{{\displaystyle \sum _X}p(X)p(N|X)}.$

For different numbers of segments M from 1 to 100, we perform a grid search over the parameters P_syn and θ and identify the optimal parameter combination that maximizes the mutual information. The two parameters are almost perfectly correlated (see Figure 5C), with an optimal synaptic transmission probability of 1 (i.e., deterministic synapses) and a threshold of 11 for M = 1, and a transmission probability of only 0.39 (i.e., highly stochastic synapses) with a correspondingly lowered threshold of 4 for M = 100 segments. For these two extreme cases (see Figures 5A, B), we vary X from 0 to 20 and plot the expected number of plateaus (solid lines) as well as the conditional probability P(N|X) (gray heatmap).

Implementation of the multi-dimensional feature space experiment

For a neuron population of N neurons (here N = 1, 000), we can collect the indices of the neurons associated with a particular feature i in a sparsely populated binary vector $v_i\in {\left\{0,1\right\}}^N$. The degree to which feature i matches the current stimulus j can be encoded by the probability $p_i^j$ that an input neuron coding for feature i would actually participate in a spike volley for j. Since the same input neuron k can be associated with multiple (here M = 3) features i∈{1, 2, 3}, its total probability to fire a spike for stimulus j with coefficients $p_i^j$ is

${\omega }_k^j=1-{\displaystyle \prod _{i=1}^M}(1-p_i^j{(v_i)}_k)={\displaystyle \sum _{i=1}^3}{p}_i^j{(v_i)}_k-{O}(p^2).$

For small p_i, the expected input vector ω^j thus approximates a weighted linear combination of the basis vectors v_i with coefficients ${\nu }^j=(p_1^j,p_2^j,p_3^j)$. We require that ||ν^j|| = 1. Using the same equation, we can fix a set of target coefficients $\widehat{\nu }$ with $\left|\right|\widehat{\nu }\left|\right|=1$ and compute the optimal weight vector $\widehat{\omega }$. The total number X of spikes received for stimulus j by a dendrite segment with synaptic transmission probabilities $\widehat{\omega }$ is then a random variable with expected value $E\left[X\right]=\langle {\omega }^j,\widehat{\omega }\rangle$. The expected value is maximized for ${\omega }^j=\widehat{\omega }$, i.e., when input and weight vector are perfectly aligned. Since both ω^j and $\widehat{\omega }$ are normalized, they lie on a two-dimensional manifold (the positive sector of the surface of a unit sphere). The probability that X exceeds a segment's threshold θ for a stimulus j and thus causes a plateau is a radially symmetric function on this manifold. Figure 6B shows an approximately distance preserving projection of this probability distribution for three different weight-vectors, the coefficients of which correspond to the coefficients ν^A, ν^B and ν^C of the three sequence elements A, B and C, respectively. See Supplementary material for details on the used projection method.

Implementation of the network experiment

There are 3, 000 neurons in the hidden layer, each of which codes for a different random sub-sequence (three elements long) of any of the 10 target sequences (ten elements long). The synaptic transmission probability is 0.5, and 8 coincident spikes are needed to trigger a plateau (or somatic spike) in the hidden layer. Of the 100 output neurons, each segment (and the soma) receives synaptic input from a different subset of the hidden layer's neurons. Since our model relies on synchronized spike volleys, these inputs are chosen according to a simple heuristic algorithm: Each segment i (and the soma) of an output neuron is associated with a specific index X_i of the neuron's target sequence in appropriate order, i.e., 1 ≤ X_i<X_j ≤ 10 for i<j. Now consider only the slice of the neuron's target sequence that includes the first X_i elements. Any neuron in the hidden layer is connected to segment (or soma) i, if it codes for a feature that occurs as a sub-sequence of this slice and ends with the symbol at index X_i. All neurons connected to the same segment thus code for features ending in the same final symbol. Therefore, they form a population that fires a spike volley when triggered by this final symbol. The magnitude of the resulting volley depends on the number of features that were detected by the population for the current stimulus. Since the size of each of these input populations is random, the synaptic threshold for plateau or spike generation in a segment or soma is dynamically set to 40% of the number of synapses.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JL and PN conceived of the model, designed the experiments and the simulation software, and wrote the article. GP participated in discussions, supervised the work, and revised the final text.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcogn.2023.1044216/full#supplementary-material

Footnotes

1. ^We avoid the term “compartment” to prevent confusion with the concept of multi-compartment neuron models, which are commonly used as a spatially discretized solution to partial differential equation models of neurons.

2. ^We assume that spike arrival times $t_{i,k}^m$ are at least τ_E apart.

3. ^In addition to the forward-propagation of membrane potentials that we focused on so far (i.e., from child branches to the parent), the reverse direction typically has an even stronger effect—strong enough for the parent segment to depolarize its child segments by itself. To capture this effect, we recursively defined a segment k's membrane potential to also be high whenever its parent's membrane potential is high. However, we focus on the forward-propagation of plateau potentials and their role for dendritic computation here.

4. ^We discard sequences that are not a sub-sequence of any target sequence. We call a sequence X a sub-sequence of another sequence T if all elements from X also occur in T in the same order.

References

Antic, S. D., Zhou, W.-L., Moore, A. R., Short, S. M., Ikonomu, K. D. (2010). The decade of the dendritic NMDA spike. J. Neurosci. Res. 88, 2991–3001. doi: 10.1002/jnr.22444

PubMed Abstract | CrossRef Full Text | Google Scholar

Augustinaite, S., Kuhn, B., Helm, P. J., Heggelund, P. (2014). NMDA spike/plateau potentials in dendrites of thalamocortical neurons. J. Neurosci. 34, 10892–10905. doi: 10.1523/JNEUROSCI.1205-13.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

Bathellier, B., Buhl, D. L., Accolla, R., Carleton, A. (2008). Dynamic ensemble odor coding in the mammalian olfactory bulb: sensory information at different timescales. Neuron 57, 586–598. doi: 10.1016/j.neuron.2008.02.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Beaulieu, C., Colonnier, M. (1985). A laminar analysis of the number of round-asymmetrical and flat-symmetrical synapses on spines, dendritic trunks, and cell bodies in area 17 of the cat. J. Comp. Neurol. 231, 180–189. doi: 10.1002/cne.902310206

PubMed Abstract | CrossRef Full Text | Google Scholar

Beniaguev, D., Segev, I., London, M. (2020). “Single cortical neurons as deep artificial neural networks,” in Cold Spring Harbor Laboratory, 613141.

PubMed Abstract | Google Scholar

Bezanson, J., Edelman, A., Karpinski, S., Shah, V. B. (2017). Julia: a fresh approach to numerical computing. SIAM Rev. 59, 65–98. doi: 10.1137/141000671

CrossRef Full Text | Google Scholar

Bono, J., Clopath, C. (2017). Modeling somatic and dendritic spike mediated plasticity at the single neuron and network level. Nat. Commun. 8, 706. doi: 10.1038/s41467-017-00740-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Braitenberg, V., Schüz, A. (2013). Cortex: Statistics and Geometry of Neuronal Connectivity. Springer Science &Business Media.

PubMed Abstract | Google Scholar

Branco, T., Clark, B. A., Häusser, M. (2010). Dendritic discrimination of temporal input sequences in cortical neurons. Science 329, 1671–1675. doi: 10.1126/science.1189664

PubMed Abstract | CrossRef Full Text | Google Scholar

Branco, T., Häusser, M. (2010). The single dendritic branch as a fundamental functional unit in the nervous system. Curr. Opin. Neurobiol. 20, 494–502. doi: 10.1016/j.conb.2010.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Branco, T., Staras, K., Darcy, K. J., Goda, Y. (2008). Local dendritic activity sets release probability at hippocampal synapses. Neuron 59, 475–485. doi: 10.1016/j.neuron.2008.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Brea, J., Gaál, A. T., Urbanczik, R., Senn, W. (2016). Prospective coding by spiking neurons. PLoS Comput. Biol. 12, e1005003. doi: 10.1371/journal.pcbi.1005003

PubMed Abstract | CrossRef Full Text | Google Scholar

Broome, B. M., Jayaraman, V., Laurent, G. (2006). Encoding and decoding of overlapping odor sequences. Neuron 51, 467–482. doi: 10.1016/j.neuron.2006.07.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Davies, M., Srinivasa, N., Lin, T.-H., Chinya, G., Cao, Y., Choday, S. H., et al. (2018). Loihi: a neuromorphic manycore processor with On-Chip learning. IEEE Micro 38, 82–99. doi: 10.1109/MM.2018.112130359

CrossRef Full Text | Google Scholar

del Castillo, J., Katz, B. (1954). Quantal components of the end-plate potential. J. Physiol. 124, 560–573. doi: 10.1113/jphysiol.1954.sp005129

PubMed Abstract | CrossRef Full Text | Google Scholar

Doron, M., Chindemi, G., Muller, E., Markram, H., Segev, I. (2017). Timed synaptic inhibition shapes NMDA spikes, influencing local dendritic processing and global I/O properties of cortical neurons. Cell Rep. 21, 1550–1561. doi: 10.1016/j.celrep.2017.10.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, K., Wu, Y. W., Lindroos, R., Liu, Y. others (2017). Cell-type-specific inhibition of the dendritic plateau potential in striatal spiny projection neurons. Proc. Natl. Acad. Sci. U.S.A. 114, E7612-E7621. doi: 10.1073/pnas.1704893114

PubMed Abstract | CrossRef Full Text | Google Scholar

Eichenbaum, H. (2017). On the integration of space, time, and memory. Neuron 95, 1007–1018. doi: 10.1016/j.neuron.2017.06.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Ekerot, C., Oscarsson, O. (1981). Prolonged depolarization elicited in purkinje cell dendrites by climbing fibre impulses in the cat. J. Physiol. 318, 207–221. doi: 10.1113/jphysiol.1981.sp013859

PubMed Abstract | CrossRef Full Text | Google Scholar

Fields, R. D. (2015). A new mechanism of nervous system plasticity: activity-dependent myelination. Nat. Rev. Neurosci. 16, 756–767. doi: 10.1038/nrn4023

PubMed Abstract | CrossRef Full Text | Google Scholar

Gasparini, S., Magee, J. C. (2006). State-dependent dendritic computation in hippocampal CA1 pyramidal neurons. J. Neurosci. 26, 2088–2100. doi: 10.1523/JNEUROSCI.4428-05.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Gasparini, S., Migliore, M., Magee, J. C. (2004). On the initiation and propagation of dendritic spikes in CA1 pyramidal neurons. J. Neurosci. 24, 11046–11056. doi: 10.1523/JNEUROSCI.2520-04.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

George, D., Hawkins, J. (2009). Towards a mathematical theory of cortical micro-circuits. PLoS Comput. Biol. 5, e1000532. doi: 10.1371/journal.pcbi.1000532

PubMed Abstract | CrossRef Full Text | Google Scholar

Gidon, A., Segev, I. (2012). Principles governing the operation of synaptic inhibition in dendrites. Neuron 75, 330–341. doi: 10.1016/j.neuron.2012.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldstein, S. S., Rall, W. (1974). Changes of action potential shape and velocity for changing core conductor geometry. Biophys. J. 14, 731–757. doi: 10.1016/S0006-3495(74)85947-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Götz, T., Kraushaar, U., Geiger, J., Lübke, J., Berger, T., Jonas, P. (1997). Functional properties of AMPA and NMDA receptors expressed in identified types of basal ganglia neurons. J. Neurosci. 17, 204–215. doi: 10.1523/JNEUROSCI.17-01-00204.1997

PubMed Abstract | CrossRef Full Text | Google Scholar

Hafting, T., Fyhn, M., Molden, S., Moser, M.-B., Moser, E. I. (2005). Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806. doi: 10.1038/nature03721

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardie, J., Spruston, N. (2009). Synaptic depolarization is more effective than back-propagating action potentials during induction of associative long-term potentiation in hippocampal pyramidal neurons. J. Neurosci. 29, 3233–3241. doi: 10.1523/JNEUROSCI.6000-08.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Häusser, M. (2001). Synaptic function: dendritic democracy. Curr. Biol. 11, R10-R12. doi: 10.1016/S0960-9822(00)00034-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hawkins, J., Ahmad, S. (2016). Why neurons have thousands of synapses, a theory of sequence memory in neocortex. Front. Neural Circ. 10, 23. doi: 10.3389/fncir.2016.00023

PubMed Abstract | CrossRef Full Text | Google Scholar

Herz, A. V. M., Gollisch, T., Machens, C. K., Jaeger, D. (2006). Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science 314, 80–85. doi: 10.1126/science.1127240

PubMed Abstract | CrossRef Full Text | Google Scholar

Jia, H., Rochefort, N. L., Chen, X., Konnerth, A. (2010). Dendritic organization of sensory input to cortical neurons in vivo. Nature 464, 1307–1312. doi: 10.1038/nature08947

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanerva, P. (2009). Hyperdimensional computing: an introduction to computing in distributed representation with high-dimensional random vectors. Cognit. Comput. 1, 139–159. doi: 10.1007/s12559-009-9009-8

CrossRef Full Text | Google Scholar

Kerlin, A., Boaz, M., Flickinger, D., MacLennan, B. J., Dean, M. B., Davis, C., et al. (2019). Functional clustering of dendritic activity during decision-making. Elife 8, e46966. doi: 10.7554/eLife.46966

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, H. G., Beierlein, M., Connors, B. W. (1995). Inhibitory control of excitable dendrites in neocortex. J. Neurophysiol. 74, 1810–1814. doi: 10.1152/jn.1995.74.4.1810

PubMed Abstract | CrossRef Full Text | Google Scholar

Knoblauch, A., Sommer, F. T. (2016). Structural plasticity, effectual connectivity, and memory in cortex. Front. Neuroanat. 10, 63. doi: 10.3389/fnana.2016.00063

PubMed Abstract | CrossRef Full Text | Google Scholar

Koch, C., Poggio, T., Torre, V. (1982). Retinal ganglion cells: a functional interpretation of dendritic morphology. Philos. Trans. R. Soc. Lond. B Biol. Sci. 298, 227–263. doi: 10.1098/rstb.1982.0084

PubMed Abstract | CrossRef Full Text | Google Scholar

Korndörfer, C., Ullner, E., García-Ojalvo, J., Pipa, G. (2017). Cortical spike synchrony as a measure of input familiarity. Neural Comput. 29, 2491–2510. doi: 10.1162/neco_a_00987

PubMed Abstract | CrossRef Full Text | Google Scholar

Larkum, M. E., Nevian, T. (2008). Synaptic clustering by dendritic signalling mechanisms. Curr. Opin. Neurobiol. 18, 321–331. doi: 10.1016/j.conb.2008.08.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Larkum, M. E., Nevian, T., Sandler, M., Polsky, A., Schiller, J. (2009). Synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science 325, 756–760. doi: 10.1126/science.1171958

PubMed Abstract | CrossRef Full Text | Google Scholar

Lashley, K. S. (1951). The Problem of Serial Order in Behavior, Vol. 21. Bobbs-Merrill.

Google Scholar

Lee, A. K., Wilson, M. A. (2002). Memory of sequential experience in the hippocampus during slow wave sleep. Neuron 36, 1183–1194. doi: 10.1016/S0896-6273(02)01096-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Leugering, J., Pipa, G. (2018). A unifying framework of synaptic and intrinsic plasticity in neural populations. Neural Comput. 30, 945–986. doi: 10.1162/neco_a_01057

PubMed Abstract | CrossRef Full Text | Google Scholar

London, M., Häusser, M. (2005). Dendritic computation. Annu. Rev. Neurosci. 28, 503–532. doi: 10.1146/annurev.neuro.28.061604.135703

PubMed Abstract | CrossRef Full Text | Google Scholar

Losonczy, A., Magee, J. C. (2006). Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron 50, 291–307. doi: 10.1016/j.neuron.2006.03.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, J., Luo, L., Wang, Q., Fang, F., Chen, N. (2021). Cue-triggered activity replay in human early visual cortex. Sci. China Life Sci. 64, 144–151. doi: 10.1007/s11427-020-1726-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, H., Poeppel, D. (2007). Phase patterns of neuronal responses reliably discriminate speech in human auditory cortex. Neuron 54, 1001–1010. doi: 10.1016/j.neuron.2007.06.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Magee, J. C., Cook, E. P. (2000). Somatic epsp amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat. Neurosci. 3, 895–903. doi: 10.1038/78800

PubMed Abstract | CrossRef Full Text | Google Scholar

Major, G., Larkum, M. E., Schiller, J. (2013). Active properties of neocortical pyramidal neuron dendrites. Annu. Rev. Neurosci. 36, 1–24. doi: 10.1146/annurev-neuro-062111-150343

PubMed Abstract | CrossRef Full Text | Google Scholar

Major, G., Polsky, A., Denk, W., Schiller, J., Tank, D. W. (2008). Spatiotemporally graded NMDA spike/plateau potentials in basal dendrites of neocortical pyramidal neurons. J. Neurophysiol. 99, 2584–2601. doi: 10.1152/jn.00011.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Malnic, B., Hirono, J., Sato, T., Buck, L. B. (1999). Combinatorial receptor codes for odors. Cell 96, 713–723. doi: 10.1016/S0092-8674(00)80581-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Melamed, O., Gerstner, W., Maass, W., Tsodyks, M., Markram, H. (2004). Coding and learning of behavioral sequences. Trends Neurosci. 27 11–4; discussion 14-5. doi: 10.1016/j.tins.2003.10.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Milojkovic, B. A., Radojicic, M. S., Antic, S. D. (2005). A strict correlation between dendritic and somatic plateau depolarizations in the rat prefrontal cortex pyramidal neurons. J. Neurosci. 25, 3940–3951. doi: 10.1523/JNEUROSCI.5314-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Milojkovic, B. A., Radojicic, M. S., Goldman-Rakic, P. S., Antic, S. D. (2004). Burst generation in rat pyramidal neurones by regenerative potentials elicited in a restricted part of the basilar dendritic tree. J. Physiol. 558, 193–211. doi: 10.1113/jphysiol.2004.061416

PubMed Abstract | CrossRef Full Text | Google Scholar

Milojkovic, B. A., Zhou, W.-L., Antic, S. D. (2007). Voltage and calcium transients in basal dendrites of the rat prefrontal cortex. J. Physiol. 585, 447–468. doi: 10.1113/jphysiol.2007.142315

PubMed Abstract | CrossRef Full Text | Google Scholar

Mongillo, G., Barak, O., Tsodyks, M. (2008). Synaptic theory of working memory. Science 319, 1543–1546. doi: 10.1126/science.1150769

PubMed Abstract | CrossRef Full Text | Google Scholar

Monyer, H., Burnashev, N., Laurie, D. J., Sakmann, B., Seeburg, P. H. (1994). Developmental and regional expression in the rat brain and functional properties of four NMDA receptors. Neuron 12, 529–540. doi: 10.1016/0896-6273(94)90210-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, J. J., Ravassard, P. M., Ho, D., Acharya, L., Kees, A. L., Vuong, C., et al. (2017). Dynamics of cortical dendritic membrane potential and spikes in freely behaving rats. Science 355, 6331. doi: 10.1126/science.aaj1497

PubMed Abstract | CrossRef Full Text | Google Scholar

Moradi, S., Qiao, N., Stefanini, F., Indiveri, G. (2018). A scalable multicore architecture with heterogeneous memory structures for dynamic neuromorphic asynchronous processors (DYNAPs). IEEE Trans. Biomed. Circ. Syst. 12, 106–122. doi: 10.1109/TBCAS.2017.2759700

PubMed Abstract | CrossRef Full Text | Google Scholar

Muñoz, W., Tremblay, R., Levenstein, D., Rudy, B. (2017). Layer-specific modulation of neocortical dendritic inhibition during active wakefulness. Science 355, 954–959. doi: 10.1126/science.aag2599

PubMed Abstract | CrossRef Full Text | Google Scholar

Oikonomou, K. D., Singh, M. B., Sterjanaj, E. V., Antic, S. D. (2014). Spiny neurons of amygdala, striatum, and cortex use dendritic plateau potentials to detect network UP states. Front. Cell. Neurosci. 8, 292. doi: 10.3389/fncel.2014.00292

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Keefe, J., Dostrovsky, J. (1971). The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 34, 171–175. doi: 10.1016/0006-8993(71)90358-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ólafsdóttir, H. F., Bush, D., Barry, C. (2018). The role of hippocampal replay in memory and planning. Curr. Biol. 28, R37-R50. doi: 10.1016/j.cub.2017.10.073

PubMed Abstract | CrossRef Full Text | Google Scholar

Pipa, G., Grün, S., Van Vreeswijk, C. (2013). Impact of spike train autostructure on probability distribution of joint spike events. Neural Comput. 25, 1123–1163. doi: 10.1162/NECO_a_00432

PubMed Abstract | CrossRef Full Text | Google Scholar

Poirazi, P., Brannon, T., Mel, B. W. (2003). Pyramidal neuron as two-layer neural network. Neuron 37, 989–999. doi: 10.1016/S0896-6273(03)00149-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Polsky, A., Mel, B. W., Schiller, J. (2004). Computational subunits in thin dendrites of pyramidal cells. Nat. Neurosci. 7, 621–627. doi: 10.1038/nn1253

PubMed Abstract | CrossRef Full Text | Google Scholar

Rall, W. (1962). Electrophysiology of a dendritic neuron model. Biophys. J. 2(2 Pt 2), 145–167. doi: 10.1016/S0006-3495(62)86953-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Rall, W. (1964). “Theoretical significance of dendritic trees for neuronal input-output relations,” in Neural Theory and Modelling, ed. R. F. Reiss (Stanford University Press).

Google Scholar

Rhodes, P. (2006). The properties and implications of NMDA spikes in neocortical pyramidal cells. J. Neurosci. 26, 6704–6715. doi: 10.1523/JNEUROSCI.3791-05.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386. doi: 10.1037/h0042519

PubMed Abstract | CrossRef Full Text | Google Scholar

Sandamirskaya, Y., Schöner, G. (2010). An embodied account of serial order: how instabilities drive sequence generation. Neural Netw. 23, 1164–1179. doi: 10.1016/j.neunet.2010.07.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Silver, R. A., MacAskill, A. F., Farrant, M. (2016). “Neurotransmitter-gated ion channels in dendritesm” in Dendrites, 3rd Edn (New York, NY: Oxford University Press), 217–257.

Google Scholar

Simoncelli, E. P., Paninski, L., Pillow, J., Schwartz, O. (2004). Characterization of neural responses with stochastic stimuli. Cogn. Neurosci. 3, 1–20. Available online at: https://www.cns.nyu.edu/pub/lcv/simoncelli03c-preprint.pdf

PubMed Abstract | Google Scholar

Song, S., Miller, K. D., Abbott, L. F. (2000). Competitive hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926. doi: 10.1038/78829

PubMed Abstract | CrossRef Full Text | Google Scholar

Spruston, N. (2008). Pyramidal neurons: dendritic structure and synaptic integration. Nat. Rev. Neurosci. 9, 206–221. doi: 10.1038/nrn2286

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevens, C. F. (1993). Quantal release of neurotransmitter and long-term potentiation. Cell 72(Suppl.), 55–63. doi: 10.1016/S0092-8674(05)80028-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Stuart, G., Spruston, N. (1998). Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J. Neurosci. 18, 3501–3510. doi: 10.1523/JNEUROSCI.18-10-03501.1998

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, N., Ebner, C., Sigl-Glöckner, J., Moberg, S., Nierwetberg, S., Larkum, M. E. (2020). Active dendritic currents gate descending cortical outputs in perception. Nat. Neurosci. 23, 1277–1285. doi: 10.1038/s41593-020-0677-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, N., Kitamura, K., Matsuo, N., Mayford, M., Kano, M., Matsuki, N., et al. (2012). Locally synchronized synaptic inputs. Science 335, 353–356. doi: 10.1126/science.1210362

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, N., Oertner, T. G., Hegemann, P., Larkum, M. E. (2016). Active cortical dendrites modulate perception. Science 354, 1587–1590. doi: 10.1126/science.aah6066

PubMed Abstract | CrossRef Full Text | Google Scholar

Turrigiano, G. (2012). Homeostatic synaptic plasticity: local and global mechanisms for stabilizing neuronal function. Cold Spring Harb. Perspect. Biol. 4, a005736. doi: 10.1101/cshperspect.a005736

PubMed Abstract | CrossRef Full Text | Google Scholar

Ujfalussy, B. B., Makara, J. K., Lengyel, M., Branco, T. (2018). Global and multiplexed dendritic computations under in vivo-like conditions. Neuron 100, 579.e5–592.e5. doi: 10.1016/j.neuron.2018.08.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Watkins, J., Evans, R. (1981). Excitatory amino acid transmitters. Annu. Rev. Pharmacol. Toxicol. 21, 165–204. doi: 10.1146/annurev.pa.21.040181.001121

PubMed Abstract | CrossRef Full Text | Google Scholar

Wybo, W. A. M., Torben-Nielsen, B., Nevian, T., Gewaltig, M.-O. (2019). Electrical compartmentalization in neurons. Cell Rep. 26, 1759.e7–1773.e7. doi: 10.1016/j.celrep.2019.01.074

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, N.-L., Harnett, M. T., Williams, S. R., Huber, D., O'Connor, D. H., Svoboda, K., et al. (2012). Nonlinear dendritic integration of sensory and motor input during an active sensing task. Nature 492, 247–251. doi: 10.1038/nature11601

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S., Jiang, W., Poo, M.-M., Dan, Y. (2012). Activity recall in a visual cortical ensemble. Nat. Neurosci. 15, 449–455, S1–2. doi: 10.1038/nn.3036

PubMed Abstract | CrossRef Full Text | Google Scholar

Zang, Y., Dieudonné, S., De Schutter, E. (2018). Voltage- and Branch-Specific climbing fiber responses in purkinje cells. Cell Rep. 24, 1536–1549. doi: 10.1016/j.celrep.2018.07.011

PubMed Abstract | CrossRef Full Text | Google Scholar