Spike-based statistical learning explains human performance in non-adjacent dependency learning tasks

Grammar acquisition is of significant importance for mastering human language. As the language signal is sequential in its nature, it poses the challenging task to extract its structure during online processing. This modeling study shows how spike-timing dependent plasticity (STDP) successfully enables sequence learning of artificial grammars that include non-adjacent dependencies (NADs) and nested NADs. Spike-based statistical learning leads to synaptic representations that comply with human acquisition performances under various distributional stimulus conditions. STDP, therefore, represents a practicable neural mechanism underlying human statistical grammar learning. These findings highlight that initial stages of the language acquisition process are possibly based on associative learning strategies. Moreover, the applicability of STDP demonstrates that the non-human brain possesses potential precursor abilities that support the acquisition of linguistic structure.

Introduction

The understanding of the neural mechanisms underlying our ability to learn the grammatical structure from sequential input is of core interest to cognitive science. While language remains a human-specific capacity, the last few years have brought forth enormous advancements in the understanding of its putative precursor abilities in early infancy and non-human animals (Mueller et al., 2018). Here, we focus on the important ability to compute dependencies between non-adjacent elements in sequential input, a capacity that develops early in human infants (Mueller et al., 2012; Kabdebon et al., 2015; Winkler et al., 2018) and is shared with other animals, including primates and songbirds (Abe and Watanabe, 2011; Watson et al., 2020). The computation of non-adjacent dependencies (NADs) is important for understanding sentences, such as, “The scientists who revealed the brain's secrets won the Nobel Prize.” where the verb “won” has to be linked to “the scientists” and not to “secrets” although the latter word is adjacent. An important tool to assess the acquisition of NADs is artificial grammar. While they do not scale up to the full complexity of human language (Beckers et al., 2012; Chen et al., 2021; Rawski et al., 2021) artificial grammars can, nonetheless, be used to test important aspects of human grammar in isolation. Studies using artificial grammar have yielded a large body of impressive findings on humans' and animals' skills when faced with the task to extract NADs from auditory (Abe and Watanabe, 2011; Mueller et al., 2012; Kabdebon et al., 2015; Winkler et al., 2018; Watson et al., 2020) or visual (Bahlmann et al., 2009) sequences. Nonetheless, learning such complex patterns is by no means a simple task and is influenced by many different input factors relating to both statistical (distributional and conditional) and perceptual stimulus properties (Gómez, 2002; Peña et al., 2002; Newport and Aslin, 2004; Gómez and Maye, 2005; Onnis et al., 2005; Lany and Gómez, 2008; Pacton and Perruchet, 2008; Mueller et al., 2010; de Diego-Balaguer et al., 2016; Grama et al., 2016). Despite this rich body of evidence, our knowledge of potential underlying learning mechanisms at the neural level remains limited.

The present study aims at revealing to which degree statistical learning, as instantiated by spike-timing dependent plasticity (STDP) (Markram et al., 1997; Bi and Poo, 1998; Dan and Poo, 2006; Morrison et al., 2008), has the power to explain various findings from human experiments on the learning of artificial NADs. Specifically, we focus on grammar properties that are known to facilitate their acquisition (Wilson et al., 2018). These include a large variability of intervening material (Gómez, 2002; Gómez and Maye, 2005), short intervening chunks (Lany and Gómez, 2008), pauses between grammar samples (Peña et al., 2002; Mueller et al., 2010), and additional cues that emphasize the grammar such as perceptual similarities (Newport and Aslin, 2004), phonological (Onnis et al., 2005), and prosodic cues (Mueller et al., 2010; Grama et al., 2016), or the triggering of directed attention (Pacton and Perruchet, 2008; de Diego-Balaguer et al., 2016). By doing this, we aim to explore the possibility of a unitary learning mechanism for core processes in the domain of grammar acquisition that plausibly accounts for learning in both human and non-human animals. A major motivation for testing the applicability of STDP for NAD acquisition was to find a potential link between low-level neural mechanisms and high-level cognitive skills. While STDP is considered a central statistical learning mechanism of the biological brain (Dan and Poo, 2006; Markram et al., 2011), statistical learning is also hypothesized to underlie human language learning especially in early acquisition phases (Erickson and Thiessen, 2015; Mueller et al., 2018; Saffran and Kirkham, 2018). This remarkable commonality of essential learning types in both neurobiology and language might therefore represent a potential link for bridging the gap between these fields (Poeppel and Embick, 2005). In detail, STDP implements sensitivity to distributional cues that are important for learning structure from sequences such as (i) the order in which stimulus elements succeed, (ii) the temporal proximity within which transitions happen, (iii) the overall occurrence frequency of elements and transitions, and (iv) the stimulus elements' strengths. It therefore provides a bandwidth of sensitivities that we hypothesized to be essential for learning NADs from the sequential language signal.

Statistical learning models already explain linguistic operations such as the extraction of meaningful chunks (Perruchet and Vinter, 1998), the acquisition of phonemic categories, and also the learning of non-adjacent relations (Thiessen and Pavlik, 2013). Trained on large language corpora, statistical machine learning models even produce human-like text (Floridi and Chiriatti, 2020). While these approaches advance our understanding of the power of statistical learning, the question of its neural realization remains, however, largely unaddressed. Vector-based and machine-learning models rely on symbolic stimulus representations and global, algebraic-like learning mechanisms that contrast with both the distributed stimulus encoding and local online-learning routines of neural networks. In this context, reservoir computing neural networks were already applied successfully for modeling the acquisition of artificial grammars (Duarte et al., 2014) and also NADs (Fitz, 2011). Overall, distributed, i.e., binary or spiking, neural network models are ideal candidates for the achievement of a linkage between neural and cognitive processes that support sequence learning (Lazar et al., 2009; Klampfl and Maass, 2013; Tully et al., 2016; Klos et al., 2018) and language acquisition (Garagnani et al., 2017; Tomasello et al., 2018). In this study, we introduced a spiking recurrent neural network (RNN) for fully unsupervised artificial NAD learning (Figure 1). The network consisted of excitatory (E) and inhibitory (I) leaky integrate-and-fire (LIF) neurons that emitted so-called “spikes” whenever their membrane voltages crossed an activation threshold (i.e., modeling the time point of neuronal action potential generation). On the one hand, these time points of spike emission represented the network activity, but also triggered local changes of continuously evolving network variables that were responsible for learning. Statistical learning by STDP was implemented locally in the excitatory recurrent connections of neurons, also called “synapses,” and further combined with a short- to long-term memory transition (SLMT). Both were grounded in a spike-triggered initialization and readout of memory traces at synapses, defining the degree of induced potentiation and depression of synaptic weights (w) and weight time constants (τ_w). Grammars were AXB-type isolated or nested NADs that comprised grammatical A and B element pairs defined by their nesting level (NL), transition (i.e., λ: A → B), and non-grammatical intervening X elements. While the acquisition of isolated NADs requires learning grammatical dependencies across the intervening material, the acquisition of nested NADs additionally requires differentiating grammatical from non-grammatical A and B pairings of a sample (i.e., ¬λ: A → B) across even larger temporal gaps. Grammatical A and B pairings of nested NADs are therefore more difficult to learn and are viewed as a critical prerequisite for mastering linguistic embedding (Winkler et al., 2018). In the experiments, training sequences of spiking grammar samples were successively presented to the RNN and incorporated varying distributional properties. The learning performance was measured by synaptic weights of the stimulus elements and transition encoding assemblies reached during training. Learning was successful when grammatical assemblies (Λ) were stronger than non-grammatical assemblies (¬Λ) as indicated by separability ratios larger than one. Overall, the grammar learning experiments mimicked passive listening procedures as frequently used in infant artificial grammar learning tasks or tasks in which adults learn by mere exposure. While only correct exemplars were presented to the RNN, the setup still allowed the comparison of grammatical and non-grammatical transitions as the stimulus sequences contained both transitions that were relevant as well as irrelevant with respect to the grammatical structure.

FIGURE 1

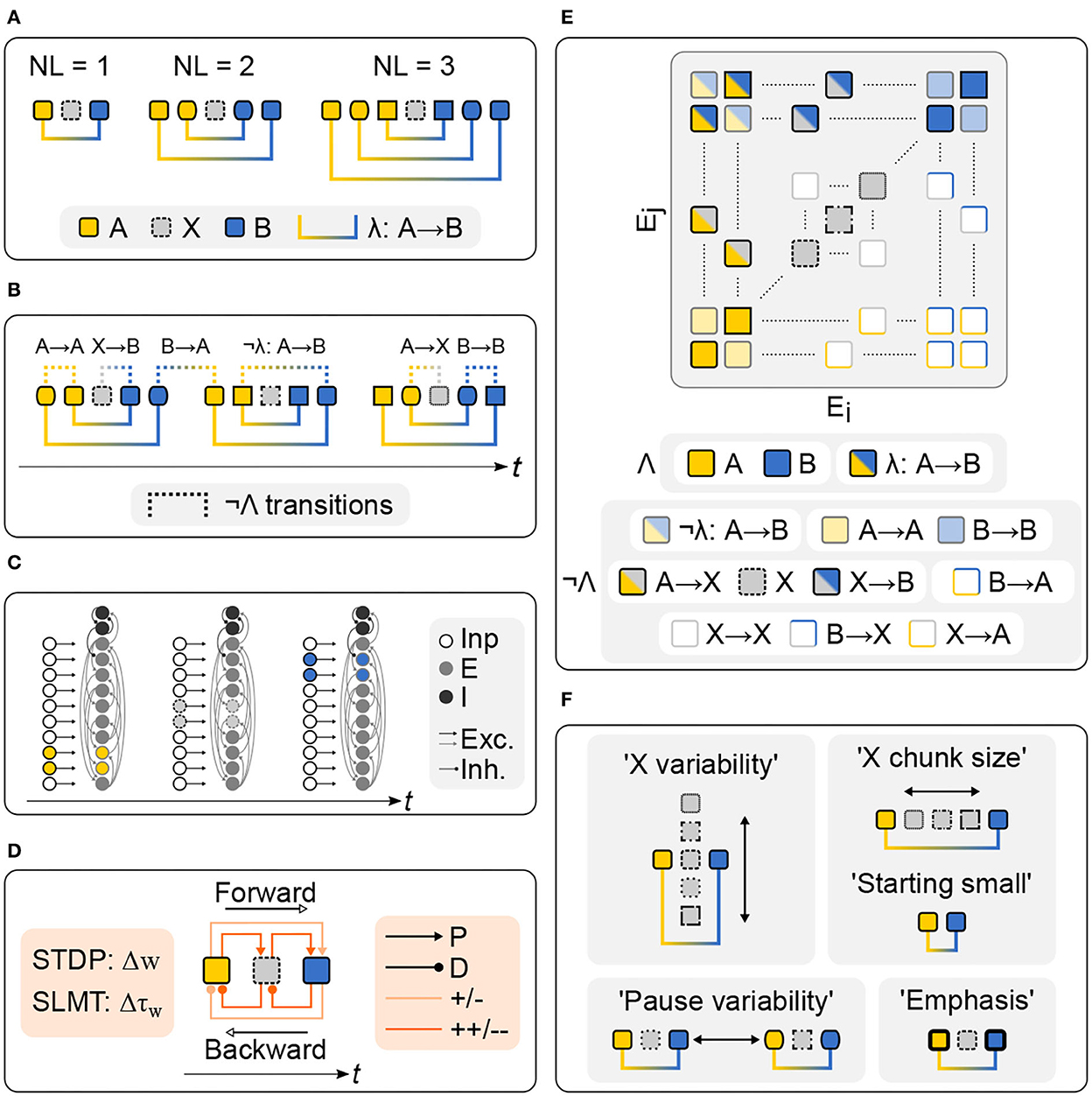
Figure 1. Statistical learning of isolated and nested non-adjacent dependencies in a spiking RNN. (A) AXB-type grammars; NL = nesting level; NL = 1: isolated NAD, NL = 2 and NL = 3: nested NADs. (B) Stimulus stream with non-grammatical transitions (¬Λ) next to grammars. (C) Stimulation of a RNN of excitatory (E) and inhibitory (I) neurons; subgroups in the input population (Inp) successively coded for A, X, and B elements. (D) Statistical learning by spike-timing dependent plasticity (STDP: Δw) and short-to long-term memory transition (SLMT: Δτ_w); strengthening/potentiation (P) of forward-transitions, weakening/depression (D) of backward-transitions and ad-hoc stronger changes for adjacent (++/−−) over non-adjacent (+/−) transitions. (E) Excitatory-to-excitatory synapses (E_i = source/pre, E_j = target/post) and stimulus encoding grammatical (Λ) and non-grammatical (¬Λ) assemblies. (F) Grammar learning experiments: “X variability” (i.e., varying number of available X elements), “X chunk size” (i.e., varying number of X elements per grammar sample) and “Starting small” (i.e., AB grammar samples), “Pause variability” (i.e., varying pause durations between grammar samples) and “Emphasis” (i.e., increased stimulus firing rate of A and B elements, representatively studying the effect of additional cues); compare Figure 3 in Wilson et al. (2018).

Results

Spike-timing dependent plasticity gave rise to distributions of synaptic weights that complied with performance patterns in human NAD acquisition (Figure 2). It led to a better acquisition of isolated NADs than of nested NADs (Figure 2A) and benefited from a high X variability (Figure 2B). Here, only during learning with one X element, separability measures were below the critical mark of one. STDP benefited from small X chunk sizes whereby the “Starting small” condition was optimal (Figure 2C). Long stimulus pauses were beneficial whereby the learning of isolated NADs benefited the most (Figure 2D). Finally, emphasis made a functional difference by pushing the separability from X elements clearly above the critical mark of one (Figure 2E).

FIGURE 2

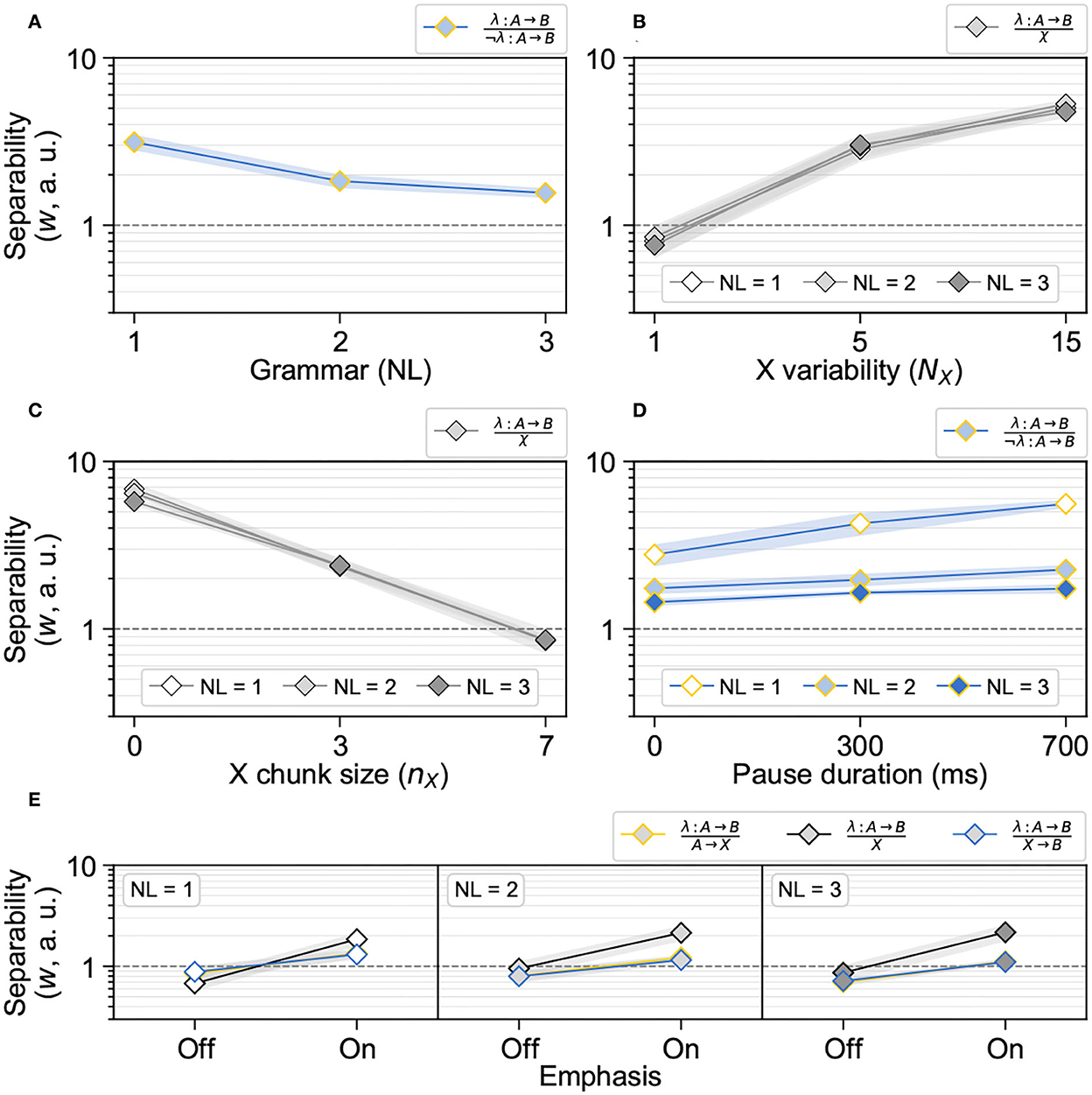
Figure 2. Statistical learning leads to synaptic representations that comply with human NAD learning performance patterns. Each individual data point (= n) indicates mean ± standard deviation (SD) of separability measures (synaptic weight w) across the RNNs (N = 10); each panel shows those separability measures with a main effect in response to the experimental stimulus modification. (A) Statistical learning leads to a better acquisition of isolated NADs (NL = 1) than nested NADs (NL = 2 and NL = 3), as demonstrated by the separability of λ: A → B from ¬λ: A → B; data pooled across the N_X parameter range of experiment “X variability” (n = 30). (B) Statistical learning benefited from a high X variability (n = 30), as demonstrated by the separability of λ: A → B from χ. (C) Statistical learning benefited from small X chunk sizes (n = 30), as demonstrated by the separability of λ: A → B from χ. (D) Statistical learning benefited from long stimulus pauses (n = 10), as demonstrated by the separability of λ: A → B from ¬λ: A → B. (E) Emphasis on grammar elements made a functional difference, as demonstrated by the separability of λ: A → B from χ; “Off”-data taken from experiment “X variability” in the N_X = 1 condition (n = 10).

Separability measure dynamics were explained by underlying synapse assembly weights (Figure 3). The best acquisition of isolated NADs arose by weakest ¬λ: A → B in this grammar (Figure 3A). The different strength levels across grammars were explained by their structural composition. In isolated NADs, only individual A and B pairs existed per grammar sample. Thus, ¬λ: A → B could only grow due to cross-sample interference of potentiation traces. Nested NADs, however, consisted of several sequentially occurring A and B pairs so that already within individual samples ¬λ: A → B existed. They therefore occurred comparably more often, with a greater temporal proximity and consequently grew comparably stronger. A high X variability was beneficial because it led to a decrease of χ while λ: A → B remained constant (Figure 3B). The strength consistency of λ: A → B was explained by its independence from the X variability. The decrease of χ was explained by reduced occurrence frequencies of X elements under high variabilities. However, during training with one X element, χ was stronger than λ: A → B. This was explained by an increased relative occurrence frequency of X vs. A and B elements. The beneficial effect of short X chunk sizes was explained by both a decrease of λ: A → B and an increase of χ (Figure 3C). The decrease of λ: A → B was explained by increasing within-sample temporal gaps between A and B elements. With long X chunks, the potentiation traces of A elements decayed more strongly until the onset of grammatical B elements by what the growth of λ: A → B was impaired. Here, the “Starting small” condition represented an optimal structural composition for the induction of strong potentiation in λ: A → B given that AB samples had no temporal gap. The increase of χ was explained by the elevated occurrence frequency of individual X elements. This frequency effect additionally contributed to an optimal separability in the “Starting small” condition. Here, X elements did not occur so that λ: A → B was compared against χ that remained at the baseline level. The beneficial effect of long stimulus pauses was mainly based on a moderate increase of λ: A → B (Figure 3D). In isolated NADs, ¬λ: A → B additionally consistently decreased. These dynamics were explained by a reduced amount of cross-sample interference as prolonged pauses introduced extended decay periods of memory traces. While the increase of λ: A → B was explained by decreased cross-sample depression, underlying to the decrease of ¬λ: A → B in isolated NADs was a reduced amount of cross-sample potentiation. The effect of pauses on ¬λ: A → B was the strongest in isolated NADs because here, they could only grow due to cross-sample potentiation. In nested NADs, however, the growth of ¬λ: A → B was mainly driven by within-sample potentiation and therefore only marginally affected. The beneficial effect of emphasis on the separability from X elements was based on an increase of λ: A → B (Figure 3E). This was explained by the elevated stimulus firing rate assigned to A and B elements that led to an increased spiking activity and consequently to more maximization and readout events of potentiation traces in λ: A → B. While X elements were independent from emphasis, the increase of A → X was explained by elevated potentiation traces of A elements and the increase of X → B by more readout events of X element potentiation traces during higher frequent B element activity.

FIGURE 3

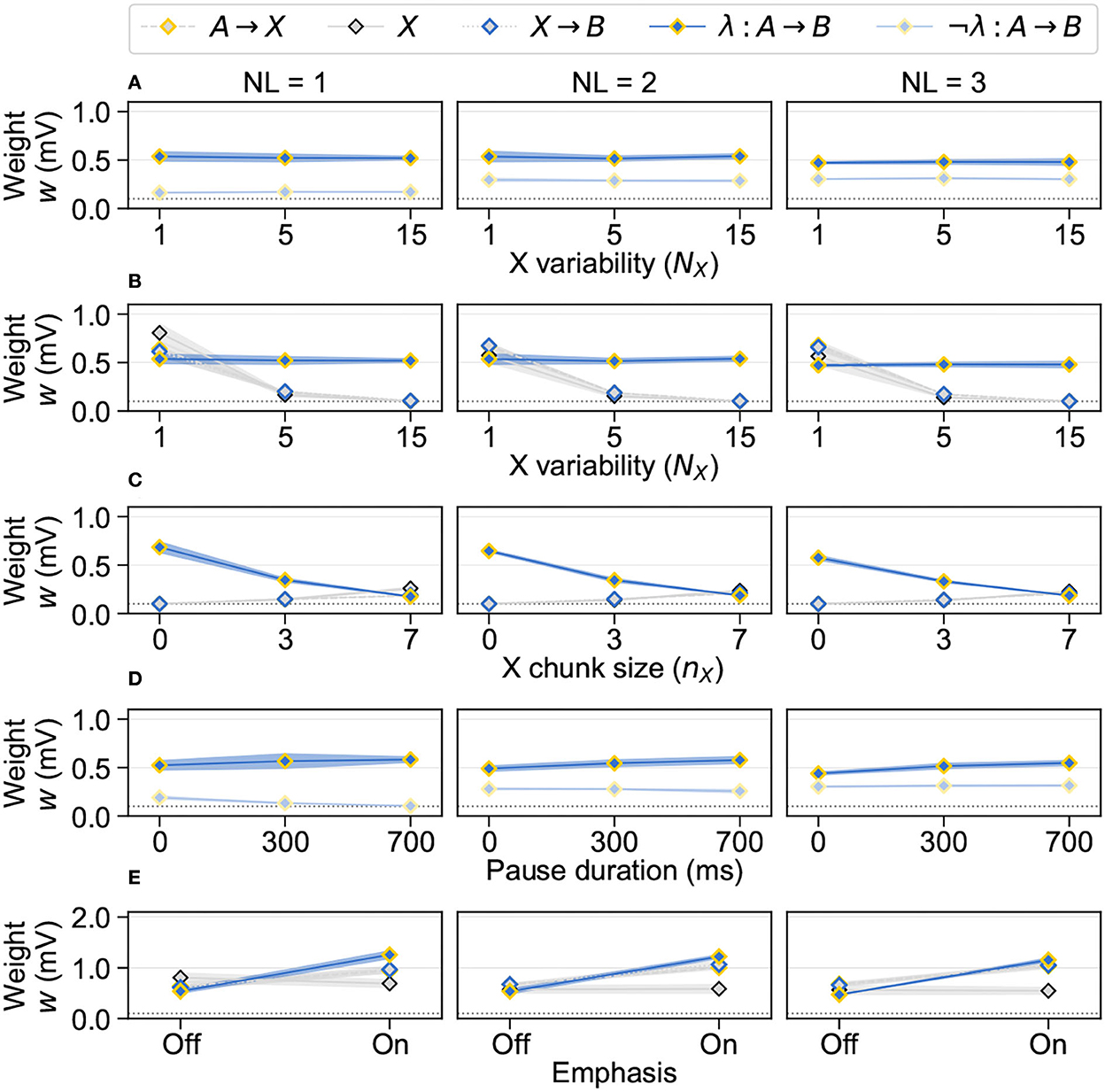
Figure 3. Synapse assembly weights encode the accumulated stimulus sequence statistics. Each individual data point (= n) indicates mean ± standard deviation (SD) of assembly medians (synaptic weight w) across the RNNs (N = 10); columns indicate grammar (NL); each row shows the selection of assemblies that respectively underlie the separability measures (see Figure 2). (A) Weights underlying to better acquisition of isolated NADs than nested NADs, i.e., λ: A → B and ¬λ: A → B (n = 10). (B) Weights underlying to beneficial effect of large X variabilities, i.e., λ: A → B and χ: {A → X, X, X → B} (n = 10). (C) Weights underlying to beneficial effect of short X chunk sizes, i.e., λ: A → B and χ:{A → X, X, X → B} (n = 10). (D) Weights underlying to beneficial effect of long stimulus pauses, i.e., λ: A → B and ¬λ: A → B (n = 10). (E) Weights underlying to beneficial effect of emphasis on grammatical A and B elements, i.e., λ: A → B and χ: {A → X, X, X → B} (n = 10).

Discussion

In this study, we showed that a variety of human performance patterns in artificial NAD learning (Wilson et al., 2018) was modeled by a cortical, spike-based statistical plasticity mechanism (Dan and Poo, 2006; Morrison et al., 2008). The finding that a biologically founded neural algorithm accounts for non-adjacent dependency acquisition exemplifies how unsupervised, domain-general learning can account for complex, high-order cognition that forms a basic prerequisite for human language processing. Particularly, STDP comprises a powerful combination of mechanisms for the unsupervised online-learning of sequential structure. Recently, the integration of forgetting gained increased importance as a decisive memory feature for STDP and other statistical models (Thiessen and Pavlik, 2013; Panda and Roy, 2017; Panda et al., 2018; Endress and Johnson, 2021). Here, we presented a new and fully symmetric implementation of decay adaptivity into pair-based STDP. While STDP was the mechanism responsible for synaptic weight changes (Δw), i.e., the synaptic representation and storage of learned stimulus statistics, SLMT implemented synaptic weight time constant changes (Δτ_w), i.e., the conceptual realization of memory on adaptive time scales. Notably, the time scales of memory traces applied in this model (i.e., τ_P = 700 ms and τ_D = 100 ms) exceeded those measured experimentally (Markram et al., 1997; Bi and Poo, 1998). For the model, the extension of plasticity windows was essential for a successful acquisition of NADs. The rationale behind this deviance from the biological evidence was to explore if the core STDP algorithm was applicable to learning problems taking place on larger time scales (Testa-Silva et al., 2010). Moreover, as the evidence of temporal STDP windows in humans is scarce (Koch et al., 2013), testing parameter spaces “fitted” to the learning task of interest remained a practicable solution.

STDP and SLMT enabled the acquisition of NADs in the following way. At the start of training, w and τ_w were at their baseline levels. Thus, weights were in a naive state and additionally very volatile, i.e., decaying quickly to their baseline level when increased. During training first, the temporal order of stimulus element successions defined whether synapses were strengthened or weakened. While forward-transitions, i.e., pre-post activations at synapses, generally induced potentiation, backward-transitions, i.e., post-pre activations, induced depression. For instance, during the processing of an AXB grammar sample, synapses experiencing the forward-transitions between the A and X element (i.e., A → X), the A and B element (i.e., λ: A → B) and the X and B element (i.e., X → B) were strengthened, while synapses experiencing the respective backward-transitions (i.e., X → A, B → A and B → X) were weakened. Due to the recurrent connectivity of excitatory synapses, both assemblies experiencing the forward- and backward-transitions during the processing of an A → X → B succession existed concurrently. Second, the temporal proximity of successive stimulus elements defined the degree of induced potentiation and depression. The extent of w and τ_w changes depended on the values of exponentially decaying memory traces so that changes were larger for temporally close successions than for temporally distant transitions. As a consequence, the learning mechanism promoted an ad-hoc stronger learning of non-grammatical adjacent dependencies (i.e., A → X and X → B) over grammatical non-adjacent dependencies (i.e., λ: A → B). Notably, the learning of adjacent and non-adjacent transitions happened concurrently, i.e., by the same underlying mechanism. Third, the overall occurrence frequency of stimulus elements and transitions defined the final strength of their assemblies. The more often an element or a transition occurred, the more often spike-triggered plasticity changes were induced. Due to combining STDP with SLMT, the growth of w was consistently impaired by the decay. During the course of training, i.e., under a repeated activation by the above described principles, τ_w grew and enabled the assemblies' transition from quickly fading to temporally more persistent representations. This subsequently also supported the continuous growth of the assemblies' weights. Therefore, consistent distributional cues in the input (i.e., λ: A → B) were finally encoded by durable and strong assemblies whereas less consistent distributional cues (i.e., ¬λ: A → B and χ) had comparably quicker fading and weaker representations. Fourth, spike-triggered plasticity changes were positively correlated to the firing rate of excitatory neurons. High firing rates resulted in an increased amount of maximization and readout events of memory traces. The more often memory traces were maximized, the higher their values were at the onset of any following stimulus element. Additionally, the more often memory traces were read out, the more plasticity changes happened. Even though emphasis on the A and B elements had as well an enhancing effect on non-grammatical transitions (i.e., A → X and X → B), successful NAD learning was not negatively affected as only in λ: A → B both, increased amounts of maximization and readouts, were combined. As a final learning dynamic, exponentially decaying memory traces led to cross-sample interference when they did not fully decay during stimulus pauses. Consequently, cross-sample learning of non-grammatical transitions additionally happened. However, given that λ: A → B remained the most consistent structure in the input, cross-sample interference did not impair successful NAD learning.

The observation that a statistical algorithm of the non-human cortex benefited from the same NAD variations as human learners highlights the importance of low-level neural mechanisms for high-level cognition. Apparently, the acquisition of potential precursors to linguistic grammars can be explained by the learning of pair associations, a fairly low-level computation. Importantly, its combination with sensitivity to sequential order, temporal proximity, occurrence frequency and stimulus strength explained the wide applicability across distributional stimulus features. Notably, experimental NAD learning patterns in humans (Wilson et al., 2018) are thought to be grounded in statistical mechanisms that are comparable to those implemented by STDP. For example, isolated NADs are considered less complex than nested NADs and thus, potentially also easier to learn (Winkler et al., 2018). In the model, this was demonstrated by an optimal learning of isolated NADs (Figure 2A) that was explained by a strong contrast of grammatical A to B transitions (i.e., λ: A → B) from non-grammatical A to B transitions (i.e., ¬λ: A → B). Further, a high variability of the intervening material is considered beneficial for NAD learning as it facilitates a detection of the statistically more persistent, invariant non-adjacent grammars (Gómez, 2002; Gómez and Maye, 2005). But also in general, highly frequent linguistic structures or words seem to be valuable cues for learning and efficient processing (Mintz, 2003; Brysbaert et al., 2018). In the model, this effect became visible during training with high X variabilities (Figure 2B) that allowed for an increased separability of comparably higher-frequent NADs (i.e., λ: A → B) from lower-frequent X elements and X element-related transitions (i.e., χ). Further, training procedures with an incremental transition from adjacent to non-adjacent dependencies are considered beneficial (Lany and Gómez, 2008). In this context, learning grammatical dependencies of short length is generally thought to be easier because less intervening material has to be processed (van den Bos and Poletiek, 2008). In the model, this effect was demonstrated during training with short X chunks (Figure 2C) that allowed for an optimal separability of NADs (i.e., λ: A → B) from X elements and X element related transitions (i.e., χ). Next, pauses between grammar exemplars are considered beneficial as they introduce segmental cues that facilitate their detection (Peña et al., 2002; Mueller et al., 2010; de Diego-Balaguer et al., 2015). But also in natural language, pauses are valuable cues for the detection of phrase boundaries (Männel and Friederici, 2009). In the model, prolonged stimulus pauses were also beneficial (Figure 2D) as they reduced the amount of cross-sample interference of memory traces which led to a better acquisition of the actual grammars (i.e., λ: A → B). Potentially, such reduced amounts of interference might also support linguistic segmentation performances. Finally, grammar learning can be enhanced by emphasis on NADs introduced via perceptual similarities, phonological or prosodic cues, as well as directed attention (Newport and Aslin, 2004; Onnis et al., 2005; Pacton and Perruchet, 2008; Mueller et al., 2010; de Diego-Balaguer et al., 2016; Grama et al., 2016). In the model, emphasis was implemented in a simplistic fashion by increased stimulus firing rates of the grammatical A and B elements. As learning by STDP is positively correlated to frequency, emphasis led to increased separabilities of NADs (i.e., λ: A → B) from X elements that were not emphasized (Figure 2E). On the one hand, these findings further support statistical learning as a central language acquisition framework (Erickson and Thiessen, 2015; Saffran and Kirkham, 2018). Beyond, STDP is remarkably compatible with the associative language learning hypothesis (Thompson-Schill et al., 2009; Mueller et al., 2018). Especially during passive listening, associative learning is considered an automatic process for the extraction of statistical structure without the need to rely on actively controlled reasoning or attention. While a large body of evidence highlights the importance of statistical learning (Saffran et al., 1996; Aslin et al., 1998; Pelucchi et al., 2009; Kidd, 2012; Christiansen and Chater, 2016; Yang and Piantadosi, 2022), associative mechanisms are still considered insufficient for explaining the mastery of complex language hierarchies (Chen et al., 2021; Rawski et al., 2021). Nonetheless, we argue that despite missing the full complexity of language structure, it is nothing but parsimonious to assume that simple statistical processing mechanisms also substantially contribute to higher level linguistic operations. Here, we possibly described an early phase in the language acquisition process where a previously naive neural network acquires initial knowledge about the structures of a language. Potentially, low-level representations shape the outcome of subsequent analyzes with the information representing a biasing signal for subsequent processing steps. For example, discrimination processes might rely on the acquired representations of grammatical standards for differentiating them from deviants. Future model extensions could therefore test the applicability of assembly-based knowledge representations for grammaticality judgments. Given that the low-level synapse representations in this study already complied with high-level human learning outcomes, they certainly contain essential information for such linguistic computations.

Conclusion

Taken together, we argue in favor of views on language acquisition that assign statistical processes an important role, either as sole, unitary mechanisms or as important contributors in concert with other cognitive strategies (Marcus et al., 1999; Endress and Bonatti, 2007; Thiessen et al., 2013; Christiansen and Chater, 2016; Yang and Piantadosi, 2022). The availability of these is not necessarily limited to human infants (Kabdebon et al., 2015). While aspects of human grammar are explained by general purpose associative learning as evidenced in non-human animals (Markram et al., 1997; Bi and Poo, 1998), it becomes increasingly apparent that humans share potential precursor abilities of language with other species (Abe and Watanabe, 2011; Watson et al., 2020).

Materials and methods

Simulation environment

Simulations were conducted in Python using the “Brian 2” spiking neural network simulator (Stimberg et al., 2014, 2019).

Network architecture

The RNN was based on the self-organizing neural network SORN (Lazar et al., 2009) and the leaky integrate-and-fire LIF-SORN (Miner and Triesch, 2016). It had an input (N_Inp = 500), an excitatory (N_E = 500), and an inhibitory (N_I = 100) population with input-to-excitatory (InpE), excitatory-to-excitatory (EE), excitatory-to-inhibitory (EI), inhibitory-to-excitatory (IE), and inhibitory-to-inhibitory (II) synapses. Inp projected with a one-to-one connectivity onto E so that each excitatory neuron had one dedicated input neuron. The connections of E and I were established randomly (p_EE = 0.1, p_EI = 0.1, p_IE = 0.1, p_II = 0.5). Connections had a transmission delay (Δt_EE = 1.5 ms, Δt_EI = 0.5 ms, Δt_IE = 1.0 ms, Δt_II = 1.0 ms), a weight (w_InpE = 2.0 mV, w_EE = 0.1 mV*, w_EI = 1.5 mV, w_IE = –1.5 mV, w_II = –1.5 mV), and plastic EE synapses had a weight time constant (τ_wEE = 0.1 s*). Throughout, initialization values are indicated by *.

Leaky integrate-and-fire neurons with intrinsic plasticity

E and I were modeled as leaky integrate-and-fire (LIF) neurons:

$\begin{array}{ll}\frac{d{V}_m}{dt}=\frac{-(V_m(t)-V_{\hookrightarrow })}{{\tau }_{V_m}},& (\mathrm{1a})\end{array}$

with the membrane voltage (V_m), the resting voltage (V_↪ = –60 mV), and the membrane voltage time constant (τ_Vm = 20 ms). The emission of a spike was defined by the time point of spiking (t_θ) when V_m crossed the threshold voltage (V_θ = –55 mV*):

$\begin{array}{ll}{t}_{\theta }:V_m(t)>V_{\theta }.& (\mathrm{1b})\end{array}$

After t_θ, V_m was set to the reset voltage (V_⊥, for E = –70 mV and I = –60 mV):

$\begin{array}{ll}t>t_{\theta }:V_m(t)\leftarrow V_{\perp }.& (\mathrm{1c})\end{array}$

LIF neurons had an intrinsic plasticity (IP) of V_θ derived from Stimberg et al. (2014):

$\begin{array}{ll}\frac{d{V}_{\theta }}{dt}=\frac{-(V_{\theta }(t)-V_{{\theta }_{\hookrightarrow }})}{{\tau }_{V_{\theta }}},& (\mathrm{2a})\end{array}$

with the threshold resting voltage (V_θ↪ = –56 mV) and the threshold voltage time constant (τ_Vθ = 60 s). After t_θ, V_θ was increased by a constant value (V_θΔ = 0.1 mV):

$\begin{array}{ll}t>t_{\theta }:V_{\theta }=V_{\theta }(t)+V_{{\theta }_{\text{Δ}}}.& (\mathrm{2b})\end{array}$

Synaptic transmission

The emission of a spike in a presynaptic neuron i caused an increase of the V_ms of all postsynaptic neurons js, defined by the respective synaptic weights w_ijs:

$\begin{array}{ll}t>t_i+\text{Δ}{t}_{ij}:V_{m_j}=V_{m_j}(t)+w_{ij},& (3)\end{array}$

with the time point of a presynaptic spike (t_i), the synaptic transmission delay (Δt_ij), and the membrane voltage of a postsynaptic neuron V_mj.

Spike-timing dependent plasticity with short- to long-term memory transition

Plasticity changes of w and τ_w in EE were based on synaptic memory traces:

$\begin{array}{ll}\begin{array}{c}\frac{d{D}_{ij}}{dt}=\frac{-D_{ij}(t)}{{\tau }_D},\\ \frac{d{P}_{ij}}{dt}=\frac{-P_{ij}(t)}{{\tau }_P},\end{array}& (\mathrm{4a})\end{array}$

with the depression trace (D_ij), its time constant (τ_D = 100 ms), the potentiation trace (P_ij), and its time constant (τ_P = 700 ms). After a presynaptic spike (t_i) and the synaptic transmission delay, P_ij and w_ij were updated:

$\begin{array}{l}t>t_i+\text{Δ}{t}_{ij}:P_{ij}(t)=T_{\top },\\ w_{ij}=w_{ij}(t)+D_{\perp w}·D_{ij}(t).& (\mathrm{4b})\end{array}$

P_ij was increased to the trace maximum (T_⊤ = 1) and w_ij was decreased by the scaled w depression maximum (D_⊥w = –0.125 mV). After a postsynaptic spike (t_j), D_ij and the w_ij were updated:

$\begin{array}{l}t>t_j:D_{ij}(t)=T_{\top },\\ w_{ij}=w_{ij}(t)+P_{\top w}·P_{ij}(t).& (\mathrm{4c})\end{array}$

D_ij was increased to the trace maximum and w_ij was increased by the scaled w potentiation maximum (P_⊤w = 0.25 mV). Throughout, w changes were only allowed within lower and upper boundaries (w_⊥ = 0.1 mV and w_⊤ = 5 mV). Similar to Panda and Roy (2017) and Panda et al. (2018), the implementation of SLMT included a decay of EE weights:

$\begin{array}{ll}\frac{d{w}_{ij}}{dt}=\frac{-(w_{ij}(t)-w_{\perp })}{{\tau }_{w_{ij}}},& (\mathrm{5a})\end{array}$

with the resting weight (w_⊥ = 0.1 mV) and the adaptive weight time constant (τ_wij = 0.1 s*). The plasticity of τ_w followed the same principles as the plasticity of w. After t_i and the synaptic transmission delay, τ_wij was depressed:

$\begin{array}{ll}t>t_i+\text{Δ}{t}_{ij}:{\tau }_{w_{ij}}={\tau }_{w_{ij}}(t)+D_{\perp {\tau }_w}·D_{ij}(t),& (\mathrm{5b})\end{array}$

by the scaled τ_w depression maximum (D_⊥τw = –5 s). After t_j, τ_wij was potentiated:

$\begin{array}{ll}t>t_j:{\tau }_{w_{ij}}={\tau }_{w_{ij}}(t)+P_{\top {\tau }_w}·P_{ij}(t),& (\mathrm{5c})\end{array}$

by the scaled τ_w potentiation maximum (P_⊤τw = 10 s). Throughout, τ_w changes were only allowed within lower and upper boundaries (τ_w⊥ = 0.1 s and τ_w⊤ = 1,000 s), whereby the upper limit was set to an arbitrarily high value.

Grammatical stimuli

Training stimuli comprised sequences (S) of grammatical A and B pairs (λ). For isolated NADs (NL = 1), two λs as in Mueller et al. (2012) were used, generating two sequences (S: {a₁, X, b₁} and {a₂, X, b₂}). For nested NADs with two nesting levels (NL = 2), three λs and six sequences were generated (S: {a₂, a₁, X, b₁, b₂}, {a₁, a₂, X, b₂, b₁}, {a₁, a₃, X, b₃, b₁}, {a₃, a₁, X, b₁, b₃}, {a₂, a₃, X, b₃, b₂} and {a₃, a₂, X, b₂, b₃}). For nested NADs with three nesting levels (NL = 3), four λs and eight standard sequences existed (S: {a₂, a₁, a₃, X, b₃, b₁, b₂}, {a₁, a₂, a₃, X, b₃, b₂, b₁}, {a₁, a₂, a₄, X, b₄, b₂, b₁}, {a₂, a₁, a₄, X, b₄, b₁, b₂}, {a₃, a₄, a₂, X, b₂, b₄, b₃}, {a₄, a₃, a₂, X, b₂, b₃, b₄}, {a₄, a₃, a₁, X, b₁, b₃, b₄}, {a₃, a₄, a₁, X, b₁, b₄, b₃}). Sets of nested NADs were derived from Winkler et al. (2018) by changing the identity relation into λs. Throughout, λs were equally often presented at all NLs and equally often combined with the other λs. Thus, even though λs of nested NADs were partly presented at the innermost NL, i.e., like in isolated NADs, they comparably often also occurred at the outer NLs and therefore, were separated by larger temporal gaps. Grammar samples were random combinations of sequences and intervening X elements. Training sequences were random concatenations of samples with pauses in between.

Spiking training sequences

Inp encoded the training sequence by its spiking activity at a Poisson firing rate (FR) of 40 Hz. Subgroups in Inp were assigned to the stimulus elements and sequentially activated according to the order defined by the training sequence. They had a size of 15 neurons and were individually activated for a stimulus duration of 100 ms.

Grammar learning experiments

Experiments applied variations of the following stimulus parameters: N_X = number of available X elements, n_X = number of X elements per grammar sample, ∪_Δ = pause duration between grammar samples and FR = Poisson stimulus firing rate of grammatical (Λ) and non-grammatical (¬Λ) subgroups. In experiment “X variability,” the number of available X elements varied (N_X range = {1, 5, 15}, ∪_Δ = 100 ms, n_X = 1, FR_Λ = FR_¬Λ = 40 Hz). In experiment “X chunk size” and “Starting small,” the number of X elements per grammar sample varied (N_X = 15, ∪_Δ = 100 ms, n_X range = {0, 3, 7}, FR_Λ = FR_¬Λ = 40 Hz). Individual X elements were allowed to occur only once per grammar sample. In experiment “Pause variability,” the duration of pauses varied (N_X = 15, ∪_Δ range = {0 ms, 300 ms, 700 ms}, n_X = 1, FR_Λ = FR_¬Λ = 40 Hz). In experiment “Emphasis,” the stimulus firing rate of grammatical subgroups was elevated by 10 Hz (N_X = 1, ∪_Δ = 100 ms, n_X = 1, FR_Λ = 50 Hz, FR_¬Λ = 40 Hz). In total, 10 RNNs were tested that varied with regard to their randomized connectivities. For each experiment condition and RNN, a new training sequence with 300 grammar samples was generated (see Supplementary Figure S1 for stimulus element counts). After full presentation of a training sequence and storage of EE weights, RNNs were reset to their initialization status before presenting a new training sequence.

Separability measures

The measure of successful learning was defined as the separability of grammatical (Λ) from non-grammatical (¬Λ) synapse assemblies, calculated as their ratio ($\frac{\text{Λ}}{\neg \text{Λ}}$). Learning was successful for ratios larger than one (i.e., Λ > ¬Λ) and not successful for ratios equal to or below one (i.e., Λ ≤ ¬Λ). Grammatical assemblies were defined as the set Λ = {{A, B}, {λ: A → B}} and non-grammatical assemblies as ¬Λ = {{¬λ: A → B}, {χ:{A → X, X, X → B}}, {χ′:{X → X, B → X, X → A}}, {B → A}, $\widehat{AA}\widehat{BB}$: {A → A, B → B}}. The analysis was focused on the separability measures $\frac{\lambda :A\to B}{\neg \lambda :A\to B}$ and $\frac{\lambda :A\to B}{\chi }$. Synaptic weights were grouped by assembly types (i.e., A:{a₁, a₂, ...}, A → X:{a₁ → x₁, a₂ → x₁, ...}, etc.) and the medians of these collections (see Supplementary Figures S2–S5 for w of all assembly types) were used to calculate the $\frac{\text{Λ}}{\neg \text{Λ}}$ ratios. Ratios were pooled across the RNNs and, if applicable, grouped into the assembly sets. Finally, the mean values and standard deviations (SD) of these collections were calculated. Throughout, stimulus element encoding assemblies (i.e., A, X and B) comprised those synapses with identical pre- and postsynaptic neuron indices (i.e., E_i = E_j, see assemblies along the diagonal of the excitatory-to-excitatory synapse matrix in Figure 1E). Element transition encoding assemblies (i.e., λ: A → B, ¬λ: A → B, χ, χ′, B → A and $\widehat{AA}\widehat{BB}$) comprised those synapses with different pre- and postsynaptic neuron indices (i.e., E_i ≠ E_j, see remaining assemblies in the excitatory-to-excitatory synapse matrix in Figure 1E).

Data availability statement

The original contributions presented in the study are publicly available. This data and the code can be found here: https://osf.io/6bhea/.

Author contributions

SL, JM, and GP designed the research. SL performed the research, analyzed the data, and wrote the manuscript. JM contributed to the writing. JM and GP supervised the project and guided the writing process. All authors contributed to the article and approved the submitted version.

Funding

The project was financed by the funds of the research training group Computational Cognition (GRK2340) provided by the Deutsche Forschungsgemeinschaft (DFG), Germany.

Acknowledgments

We kindly acknowledge the support of the Deutsche Forschungsgemeinschaft (DFG), Germany.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcogn.2022.1026819/full#supplementary-material

Abbreviations

NAD, Non-adjacent dependency; AXB, NAD with grammatical A and B elements separated by a non-grammatical X element; NL, Nesting level; N_X, Number of available X elements; n_X, Number of X elements per grammar sample; ∪_Δ, Pause duration between grammar samples; FR, Poisson stimulus firing rate; Λ, Grammatical assemblies; A, Grammatical A element assemblies; B, Grammatical B element assemblies; λ: A → B, Grammatical A to B transition assemblies; ¬Λ, Non-grammatical assemblies; ¬λ: A → B, Non-grammatical A to B transition assemblies; χ, First set of X element related assemblies; A → X, Non-grammatical A to X transition assemblies; X, Non-grammatical X element assemblies; X → B, Non-grammatical X to B transition assemblies; χ′, Second set of X element related assemblies; X → X, Non-grammatical X to X transition assemblies; B → X, Non-grammatical B to X transition assemblies; X → A, Non-grammatical X to A transition assemblies; B → A, Non-grammatical B to A transition assemblies; $\widehat{AA}\widehat{BB}$, Set of A to A and B to B transition assemblies; A → A, Non-grammatical A to A transition assemblies; B → B, Non-grammatical B to B transition assemblies; RNN, Recurrent neural network; Inp, Input neurons; E, Excitatory neurons; I, Inhibitory neurons; LIF, Leaky integrate-and-fire; w, Synaptic weight; τ_w, Synaptic weight time constant; STDP, Spike-timing dependent plasticity; SLMT, Short- to long-term memory transition; IP, Intrinsic plasticity.

References

Abe, K., Watanabe, D. (2011). Songbirds possess the spontaneous ability to discriminate syntactic rules. Nat. Neurosci. 14, 1067–1074. doi: 10.1038/nn.2869

PubMed Abstract | CrossRef Full Text | Google Scholar

Aslin, R. N., Saffran, J. R., Newport, E. L. (1998). Computation of conditional probability statistics by 8-month-old infants. Psychol. Sci. 9, 321–324. doi: 10.1111/1467-9280.00063

PubMed Abstract | CrossRef Full Text | Google Scholar

Bahlmann, J., Schubotz, R. I., Mueller, J. L., Koester, D., Friederici, A. D. (2009). Neural circuits of hierarchical visuo-spatial sequence processing. Brain Res. 1298, 161–170. doi: 10.1016/j.brainres.2009.08.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Beckers, G. J. L., Bolhuis, J. J., Okanoya, K., Berwick, R. C. (2012). Birdsong neurolinguistics: songbird context-free grammar claim is premature. Neuroreport 23, 139–145. doi: 10.1097/WNR.0b013e32834f1765

PubMed Abstract | CrossRef Full Text | Google Scholar

Bi, G.-Q., Poo, M.-M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998

PubMed Abstract | CrossRef Full Text | Google Scholar

Brysbaert, M., Mandera, P., Keuleers, E. (2018). The word frequency effect in word processing: an updated review. Curr. Direct. Psychol. Sci. 27, 45–50. doi: 10.1177/0963721417727521

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Goucha, T., Männel, C., Friederici, A. D., Zaccarella, E. (2021). Hierarchical syntactic processing is beyond mere associating: functional magnetic resonance imaging evidence from a novel artificial grammar. Hum. Brain Mapp. 42, 3253–3268. doi: 10.1002/hbm.25432

PubMed Abstract | CrossRef Full Text | Google Scholar

Christiansen, M. H., Chater, N. (2016). The now-or-never bottleneck: a fundamental constraint on language. Behav. Brain Sci. 39, e62. doi: 10.1017/S0140525X1500031X

PubMed Abstract | CrossRef Full Text | Google Scholar

Dan, Y., Poo, M.-M. (2006). Spike timing-dependent plasticity: from synapse to perception. Physiol. Rev. 86, 1033–1048. doi: 10.1152/physrev.00030.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

de Diego-Balaguer, R., Martinez-Alvarez, A., Pons, F. (2016). Temporal attention as a scaffold for language development. Front. Psychol. 7, 44. doi: 10.3389/fpsyg.2016.00044

PubMed Abstract | CrossRef Full Text | Google Scholar

de Diego-Balaguer, R., Rodríguez-Fornells, A., Bachoud-Lévi, A.-C. (2015). Prosodic cues enhance rule learning by changing speech segmentation mechanisms. Front. Psychol. 6, 1478. doi: 10.3389/fpsyg.2015.01478

PubMed Abstract | CrossRef Full Text | Google Scholar

Duarte, R., Seriès, P., Morrison, A. (2014). Self-organized artificial grammar learning in spiking neural networks. Proc. Ann. Meet. Cogn. Sci. Soc. 36, 427–432. Available online at: https://escholarship.org/uc/item/75j1b2t0

Google Scholar

Endress, A. D., Bonatti, L. L. (2007). Rapid learning of syllable classes from a perceptually continuous speech stream. Cognition 105, 247–299. doi: 10.1016/j.cognition.2006.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Endress, A. D., Johnson, S. P. (2021). When forgetting fosters learning: a neural network model for statistical learning. Cognition 213, 104621. doi: 10.1016/j.cognition.2021.104621

PubMed Abstract | CrossRef Full Text | Google Scholar

Erickson, L. C., Thiessen, E. D. (2015). Statistical learning of language: theory, validity, and predictions of a statistical learning account of language acquisition. Dev. Rev. 37, 66–108. doi: 10.1016/j.dr.2015.05.002

CrossRef Full Text | Google Scholar

Fitz, H. (2011). A liquid-state model of variability effects in learning nonadjacent dependencies. Proc. Ann. Meet. Cogn. Sci. Soc. 33, 897–902. Available online at: https://escholarship.org/uc/item/0rt2d1b4

Google Scholar

Floridi, L., Chiriatti, M. (2020). Gpt-3: its nature, scope, limits, and consequences. Minds Mach. 30, 681–694. doi: 10.1007/s11023-020-09548-1

CrossRef Full Text | Google Scholar

Garagnani, M., Lucchese, G., Tomasello, R., Wennekers, T., Pulvermüller, F. (2017). A spiking neurocomputational model of high-frequency oscillatory brain responses to words and pseudowords. Front. Comput. Neurosci. 10, 145. doi: 10.3389/fncom.2016.00145

PubMed Abstract | CrossRef Full Text | Google Scholar

Gómez, R., Maye, J. (2005). The developmental trajectory of nonadjacent dependency learning. Infancy 7, 183–206. doi: 10.1207/s15327078in0702_4

PubMed Abstract | CrossRef Full Text | Google Scholar

Gómez, R. L. (2002). Variability and detection of invariant structure. Psychol. Sci. 13, 431–436. doi: 10.1111/1467-9280.00476

PubMed Abstract | CrossRef Full Text | Google Scholar

Grama, I. C., Kerkhoff, A., Wijnen, F. (2016). Gleaning structure from sound: the role of prosodic contrast in learning non-adjacent dependencies. J. Psycholinguist Res. 45, 1427–1449. doi: 10.1007/s10936-016-9412-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Kabdebon, C., Pena, M., Buiatti, M., Dehaene-Lambertz, G. (2015). Electrophysiological evidence of statistical learning of long-distance dependencies in 8-month-old preterm and full-term infants. Brain Lang. 148, 25–36. doi: 10.1016/j.bandl.2015.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Kidd, E. (2012). Implicit statistical learning is directly associated with the acquisition of syntax. Dev. Psychol. 48, 171–184. doi: 10.1037/a0025405

PubMed Abstract | CrossRef Full Text | Google Scholar

Klampfl, S., Maass, W. (2013). Emergence of dynamic memory traces in cortical microcircuit models through stdp. J. Neurosci. 33, 11515–11529. doi: 10.1523/JNEUROSCI.5044-12.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Klos, C., Miner, D., Triesch, J. (2018). Bridging structure and function: a model of sequence learning and prediction in primary visual cortex. PLoS Comput. Biol. 14, e1006187. doi: 10.1371/journal.pcbi.1006187

PubMed Abstract | CrossRef Full Text | Google Scholar

Koch, G., Ponzo, V., Di Lorenzo, F., Caltagirone, C., Veniero, D. (2013). Hebbian and anti-hebbian spike-timing-dependent plasticity of human cortico-cortical connections. J. Neurosci. 33, 9725–9733. doi: 10.1523/JNEUROSCI.4988-12.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Lany, J., Gómez, R. L. (2008). Twelve-month-old infants benefit from prior experience in statistical learning. Psychol. Sci. 19, 1247–1252. doi: 10.1111/j.1467-9280.2008.02233.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazar, A., Pipa, G., Triesch, J. (2009). Sorn: a self-organizing recurrent neural network. Front. Comput. Neurosci. 3, 2009. doi: 10.3389/neuro.10.023.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Männel, C., Friederici, A. D. (2009). Pauses and intonational phrasing: Erp studies in 5-month-old german infants and adults. J. Cogn. Neurosci. 21, 1988–2006. doi: 10.1162/jocn.2009.21221

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcus, G. F., Vijayan, S., Bandi Rao, S., Vishton, P. M. (1999). Rule learning by seven-month-old infants. Science 283, 77–80. doi: 10.1126/science.283.5398.77

PubMed Abstract | CrossRef Full Text | Google Scholar

Markram, H., Gerstner, W., Sjöström, P. J. (2011). A history of spike-timing-dependent plasticity. Front. Synaptic Neurosci. 3, 4. doi: 10.3389/fnsyn.2011.00004

PubMed Abstract | CrossRef Full Text | Google Scholar

Markram, H., Lübke, J., Frotscher, M., Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps. Science 275, 213–215. doi: 10.1126/science.275.5297.213

PubMed Abstract | CrossRef Full Text | Google Scholar

Miner, D., Triesch, J. (2016). Plasticity-driven self-organization under topological constraints accounts for non-random features of cortical synaptic wiring. PLoS Comput. Biol. 12, e1004759. doi: 10.1371/journal.pcbi.1004759

PubMed Abstract | CrossRef Full Text | Google Scholar

Mintz, T. H. (2003). Frequent frames as a cue for grammatical categories in child directed speech. Cognition 90, 91–117. doi: 10.1016/S0010-0277(03)00140-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrison, A., Diesmann, M., Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybern. 98, 459–478. doi: 10.1007/s00422-008-0233-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mueller, J. L., Bahlmann, J., Friederici, A. D. (2010). Learnability of embedded syntactic structures depends on prosodic cues. Cogn. Sci. 34, 338–349. doi: 10.1111/j.1551-6709.2009.01093.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mueller, J. L., Friederici, A. D., Männel, C. (2012). Auditory perception at the root of language learning. Proc. Natl. Acad. Sci. U.S.A. 109, 15953–15958. doi: 10.1073/pnas.1204319109

PubMed Abstract | CrossRef Full Text | Google Scholar

Mueller, J. L., Milne, A., Männel, C. (2018). Non-adjacent auditory sequence learning across development and primate species. Curr. Opin. Behav. Sci. 21, 112–119. doi: 10.1016/j.cobeha.2018.04.002

CrossRef Full Text | Google Scholar

Newport, E. L., Aslin, R. N. (2004). Learning at a distance i. statistical learning of non-adjacent dependencies. Cogn. Psychol. 48, 127–162. doi: 10.1016/S0010-0285(03)00128-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Onnis, L., Monaghan, P., Richmond, K., Chater, N. (2005). Phonology impacts segmentation in online speech processing. J. Mem. Lang. 53, 225–237. doi: 10.1016/j.jml.2005.02.011

CrossRef Full Text | Google Scholar

Pacton, S., Perruchet, P. (2008). An attention-based associative account of adjacent and nonadjacent dependency learning. J. Exp. Psychol. Learn. Mem. Cogn. 34, 80–96. doi: 10.1037/0278-7393.34.1.80

PubMed Abstract | CrossRef Full Text | Google Scholar

Panda, P., Allred, J. M., Ramanathan, S., Roy, K. (2018). Asp: learning to forget with adaptive synaptic plasticity in spiking neural networks. IEEE J. Emerg. Select. Top. Circ. Syst. 8, 51–64. doi: 10.1109/JETCAS.2017.2769684

CrossRef Full Text | Google Scholar

Panda, P., Roy, K. (2017). Learning to generate sequences with combination of hebbian and non-hebbian plasticity in recurrent spiking neural networks. Front. Neurosci. 11, 693. doi: 10.3389/fnins.2017.00693

PubMed Abstract | CrossRef Full Text | Google Scholar

Pelucchi, B., Hay, J. F., Saffran, J. R. (2009). Statistical learning in a natural language by 8-month-old infants. Child Dev. 80, 674–685. doi: 10.1111/j.1467-8624.2009.01290.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Peña, M., Bonatti, L. L., Nespor, M., Mehler, J. (2002). Signal-driven computations in speech processing. Science 298, 604–607. doi: 10.1126/science.1072901

PubMed Abstract | CrossRef Full Text | Google Scholar

Perruchet, P., Vinter, A. (1998). Parser: a model for word segmentation. J. Mem. Lang. 39, 246–263. doi: 10.1006/jmla.1998.2576

CrossRef Full Text | Google Scholar

Poeppel, D., Embick, D. (2005). “Defining the relation between linguistics and neuroscience,” in Twenty-First Century Psycholinguistics: Four Cornerstones: Four Cornerstones, 1st edn., ed A. Cutler (Routledge), 103–118. doi: 10.4324/9781315084503

CrossRef Full Text | Google Scholar

Rawski, J., Idsardi, W., Heinz, J. (2021). Comment on “nonadjacent dependency processing in monkeys, apes, and humans”. Sci. Adv. 7, eabg0455. doi: 10.1126/sciadv.abg0455

PubMed Abstract | CrossRef Full Text | Google Scholar

Saffran, J. R., Kirkham, N. Z. (2018). Infant statistical learning. Annu. Rev. Psychol. 69, 181–203. doi: 10.1146/annurev-psych-122216-011805

PubMed Abstract | CrossRef Full Text | Google Scholar

Saffran, J. R., Newport, E. L., Aslin, R. N. (1996). Word segmentation: the role of distributional cues. J. Mem. Lang. 35, 606–621. doi: 10.1006/jmla.1996.0032

CrossRef Full Text | Google Scholar

Stimberg, M., Brette, R., Goodman, D. F. M. (2019). Brian 2, an intuitive and efficient neural simulator. Elife 8, e47314. doi: 10.7554/eLife.47314

PubMed Abstract | CrossRef Full Text | Google Scholar

Stimberg, M., Goodman, D. F. M., Benichoux, V., Brette, R. (2014). Equation-oriented specification of neural models for simulations. Front. Neuroinform. 8, 6. doi: 10.3389/fninf.2014.00006

PubMed Abstract | CrossRef Full Text | Google Scholar

Testa-Silva, G., Verhoog, M. B., Goriounova, N. A., Loebel, A., Hjorth, J. J. J., Baayen, J. C., et al. (2010). Human synapses show a wide temporal window for spike-timing-dependent plasticity. Front. Synaptic. Neurosci. 2, 12. doi: 10.3389/fnsyn.2010.00012

PubMed Abstract | CrossRef Full Text | Google Scholar

Thiessen, E. D., Kronstein, A. T., Hufnagle, D. G. (2013). The extraction and integration framework: a two-process account of statistical learning. Psychol. Bull. 139, 792–814. doi: 10.1037/a0030801

PubMed Abstract | CrossRef Full Text | Google Scholar

Thiessen, E. D., Pavlik Jr, P. I. (2013). iminerva: a mathematical model of distributional statistical learning. Cogn. Sci. 37, 310–343. doi: 10.1111/cogs.12011

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson-Schill, S. L., Ramscar, M., Chrysikou, E. G. (2009). Cognition without control: when a little frontal lobe goes a long way. Curr. Dir. Psychol. Sci. 18, 259–263. doi: 10.1111/j.1467-8721.2009.01648.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomasello, R., Garagnani, M., Wennekers, T., Pulvermüller, F. (2018). A neurobiologically constrained cortex model of semantic grounding with spiking neurons and brain-like connectivity. Front. Comput. Neurosci. 12, 88. doi: 10.3389/fncom.2018.00088

PubMed Abstract | CrossRef Full Text | Google Scholar

Tully, P. J., Lindén, H., Hennig, M. H., Lansner, A. (2016). Spike-based bayesian-hebbian learning of temporal sequences. PLoS Comput. Biol. 12, e1004954. doi: 10.1371/journal.pcbi.1004954

PubMed Abstract | CrossRef Full Text | Google Scholar

van den Bos, E., Poletiek, F. H. (2008). Effects of grammar complexity on artificial grammar learning. Mem. Cogn. 36, 1122–1131. doi: 10.3758/MC.36.6.1122

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, S. K., Burkart, J. M., Schapiro, S. J., Lambeth, S. P., Mueller, J. L., Townsend, S. W. (2020). Nonadjacent dependency processing in monkeys, apes, and humans. Sci. Adv. 6, eabb0725. doi: 10.1126/sciadv.abb0725

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, B., Spierings, M., Ravignani, A., Mueller, J. L., Mintz, T. H., Wijnen, F., et al. (2018). Non-adjacent dependency learning in humans and other animals. Top. Cogn. Sci. 12, 843–858. doi: 10.1111/tops.12381

PubMed Abstract | CrossRef Full Text | Google Scholar

Winkler, M., Mueller, J. L., Friederici, A. D., Männel, C. (2018). Infant cognition includes the potentially human-unique ability to encode embedding. Sci. Adv. 4, eaar8334. doi: 10.1126/sciadv.aar8334

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Piantadosi, S. T. (2022). One model for the learning of language. Proc. Natl. Acad. Sci. U.S.A. 119, e2021865119. doi: 10.1073/pnas.2021865119

PubMed Abstract | CrossRef Full Text | Google Scholar