Comparing extremes indices in recent observational and reanalysis products

1. Introduction

For a number of reasons (e.g., computational constraints, restrictions on data exchange), information on extremes is often represented in index form such as the number of days above or below a fixed threshold. These “extremes indices” have been collated for a long time, but over the last couple of decades in particular, the 27 indices defined by the former World Meteorological Organization (WMO)/World Climate Research Programme (WCRP)/Joint WMO-IOC (UNESCO's [United Nations Educational, Scientific, and Cultural Organization] Intergovernmental Oceanographic Commission [IOC]) Technical Commission for Oceanography and Marine Meteorology (JCOMM) Expert Team on Climate Change Detection and Indices (ETCCDI) have enhanced our understanding of past temperature and precipitation extremes over the land surface as well as our ability to project future changes in extremes (Zhang et al., 2011). Alongside the definitions of these indices, computer software for their calculation together with workshops to gather data from around the world have enabled the creation of globally consistent datasets and the investigation of changes in these extremes over time. The HadEX family of datasets (Alexander et al., 2006; Donat et al., 2013b; Dunn et al., 2020a) use both publicly available archives of daily observations and data collected from the aforementioned regional workshops and other contacts providing regional data. Despite these efforts, ongoing issues around the open sharing of meteorological data (Thorne et al., 2017) result in gaps in spatial coverage, which increase toward early periods even in the most recent dataset version. The impact of this lack of information can be assessed using a complete global data product (especially in the early part of a record; Brohan et al., 2006; Dunn et al., 2020a), which indicates that reasonable estimates of the global average anomalies can be obtained even from coverage restricted to North America and Eurasia, particularly for the temperature indices (Dunn et al., 2020a).

First developed during the 1990s (Kalnay et al., 1996), meteorological reanalysis products are created by assimilating observational data into physically derived numerical models, often very similar to operational numerical weather-forecasting systems. The result of this approach is fields of climate variables which are complete in both space and time over the period of the reanalysis and also physically consistent across different variable fields. Their completeness and physical consistency is a major advantage over datasets derived purely from observational data which have no or limited infilling. Reanalyses are operationally maintained and so are also very useful for (near)-real time climate monitoring. Delays in the availability of in situ observations result in a slower update cycle for datasets derived therefrom, though these delays can also affect real-time updates on reanalysis products.

Although based on observational (in situ and satellite) data, reanalyses are not completely free from artifacts. Over the most recent few decades a range of issues have been reported (Dee et al., 2011), inhomogeneities are naturally introduced by changes in the data assimilated, with the beginning of the satellite era in the late 1970s being a clear example (Kistler et al., 2001).

With the recent release of the HadEX3 dataset, we expand on earlier work by Donat et al. (2014) to compare this product against a selection of current-generation reanalyses over a recent period. The Donat et al. (2014) comparison of HadEX2 against the previous generation of reanalyses showed good agreement for the temperature indices, and reasonable agreement for the precipitation indices. To assess the agreement over the entire twentieth century, HadEX2 was separately compared to another two reanalyses which have similarly long periods of coverage (Donat et al., 2016). Unsurprisingly, during the early part of last century there were some large differences between the products, a result of the much lower number of observations available to constrain both HadEX2 and the reanalyses. In this assessment we focus on the most recent period (since 1980) where the greatest number of the current set of reanalysis products have data.

Although the results of this study could be used to conclude whether one (type of) product is better than another, this is not our intention. Rather, these investigations should be used to help users in deciding which product to choose depending on their application of the ETCCDI indices. For example regional monitoring, detection and attribution, or impacts studies are all likely to need datasets with different properties and characteristics.

We describe the observational and reanalyses products in Section 2. The results for temperature and precipitation extremes are contrasted in Sections 3 and 4. We discuss these two assessments in Section 5.

2. Data and methods

2.1. Indices

The ETCCDI indices (Table 1) were designed to enable robust intercomparison of temperature and precipitation extremes across the globe (Zhang et al., 2011), especially in the context of Detection and Attribution analyses, as well as to improve data exchange. While many of these extremes are moderate, in the sense that they occur every year, these indices have been in widespread use over the last two decades for the study of past and future changes in global climate extremes. In a subset of these indices, exceedence thresholds are calculated from percentile values which have been determined over a reference period. For example, TX90p counts the number of days where the maximum temperature exceeded a seasonally varying 90th percentile, which was determined over a specified reference period, which in HadEX3 is referenced to both 1961–1990 and 1981–2010.

TABLE 1

Table 1. Details of the ETCCDI indices used in this analysis.

The ETCCDI initially defined 27 indices, though all the HadEX datasets included three additional ones (ETR, R95pTOT, R99pTOT), but left out Rnnmm (which uses user defined thresholds of daily precipitation amounts, and so is not as easily combined across data sources). In this work we select some representative indices for clarity, with the figures for all 29 indices available in the Supplementary material. Although some of the indices are available on a monthly basis, this analysis focusses on indices derived on an annual timescale. For a full description of the indices and their definitions, see Table 1. The temperature indices cluster together into several families: the frequency (number of days) when the percentile thresholds are exceeded (TX90p, TN90p, TX10p, TN10p); the most extreme values in a temporal (annual) block (TXx, TXn, TNx, TNn); the count of days exceeding specific, fixed thresholds (SU, TR, FD, ID); the durations of threshold exceedances (WSDI, CSDI, GSL); and the ranges (DTR, ETR). The precipitation indices also cluster but into smaller families: block extremes of intense accumulations (Rx1day, Rx5day); the count of days exceeding specific, set accumulation thresholds (R10mm, R20mm); duration (CWD, CDD); the accumulation on days where a high percentile threshold is exceeded (R95p, R99p); and the fraction of total annual precipitation falling in extreme events set by the high percentile thresholds (R95pTOT, R99pTOT). We note that although PRCPTOT and SDII (total precipitation and the specific daily intensity index) are part of the family of ETCCDI indices, they are not a measure of extremes in the same way as the other indices.

2.2. Observations

The primary observational dataset in this assessment is the HadEX3 product (Dunn et al., 2020a). This is an update to the HadEX family of datasets, with increased spatio-temporal coverage and spatial resolution over previous versions. We use the most recent update (version 3.0.4), which is on a 1.875 × 1.25° grid and covers 1901–2018 inclusive. For comparison, we also include GHCNDEX (Donat et al., 2013a) in our comparisons; this is regularly updated albeit with a lower spatial coverage in the most recent years (Dunn et al., 2020a,b, 2022; Perkins-Kirkpatrick et al., 2021).

Both these datasets are based on observations of daily maximum and minimum temperatures as well as daily precipitation accumulation at individual meteorological stations. Index values are calculated at station locations and then interpolated onto a regular grid using the Angular Distance Weighting (ADW) method (Shepard, 1968) which utilizes a decorrelation length scale (DLS) to determine which stations contribute to a grid box. For full details of the construction of these datasets, please see the aforementioned papers. The main differences are that the spatial resolution is higher in HadEX3 (1.25 × 1.875°) than in GHCNDEX (2.5 × 2.5°), and GHCNDEX is regularly updated from a single data source whereas HadEX3 uses many contributing data sources and has a static temporal coverage.

As most of the reanalysis products start in the late 1970s (at the time of writing), we use the version of HadEX3 which takes 1981–2010 as a reference period (Dunn et al., 2020a) when comparing indices that require a reference period in their construction.

2.3. Reanalyses

There are a wide range of dynamical reanalysis products available and most of them are updated regularly. We have chosen to analyse six products which are commonly used in climate monitoring, using the most recent variant of the dataset in each case. All are updated in near-real-time and so are available beyond the end of the HadEX3 record (2018). The one exception to this is the twentieth Century Reanalysis (20CR version 3, Slivinski et al., 2019) which ends in 2015 and so has been less used for monitoring in recent years. However, by solely assimilating in situ pressure data this product has a different set of biases and inhomogeneities than the other reanalysis datasets and hence is an important inclusion here.

For those reanalyses where the daily maximum (Tmax) and minimum (Tmin) temperatures are available (see Table 2) no further processing was necessary. For CFSR, the Tmax and Tmin values were available as 6-hourly fields which were appropriately combined to obtain daily values. Where only instantaneous 2-m temperature fields were available, then we take the maximum and minimum for each 24 h period to obtain Tmax and Tmin fields. Precipitation accumulations are aggregated to daily values, and if necessary converted from rates to accumulation. Extremes indices are then calculated from these gridded daily fields.

TABLE 2

Table 2. Details of the reanalyses used in this study.

When calculating the Tmax and Tmin fields, or accumulating the sub-daily precipitation values we use a 24 h period defined from 0000-2359UTC and make no adjustment for the longitude of the grid box. For the reanalyses where this is performed (as opposed to those where daily fields are provided) this approach is different to the observational datasets, where the daily values for the local time zone will have been provided. It is possible that for some parts of the world that this could result in double counting of, e.g., afternoon Tmax or morning Tmin values. However, as we assess the annual indices in this study, these effects are likely to be small in comparison to other differences between the reanalyses and observational datasets. Any timezone adjustment combined with the varied fixed temporal resolution of some of the reanalyses (see Table 2), would result in longitudinal discontinuities. Furthermore, adjusting the reanalyses purely by longitude would still be different to HadEX3/GHCNDEX as the timezone adjustments in these are nation or region specific (and not necessarily consistent across longitudes), and are in any case then smoothed during the gridding process.

This method is in contrast to that employed in the observational datasets and represents a difference in the order of operation (index-then-grid vs. grid-then-index). This order of operation effect has been investigated for observational data by, e.g., Donat et al. (2014), Avila et al. (2015), and Contractor et al. (2015) and was shown to substantially influence the gridded values when using the ADW method. Donat et al. (2014) used both GHCNDEX (index-then-grid), and indices calculated from the HadGHCND (grid-then-index) gridded temperature dataset (Caesar et al., 2006) to investigate this order of operation as both these datasets are based on largely the same input stations. They showed that indices are less extreme when calculated from HadGHCND compared to GHCNDEX as local extreme values of temperature and precipitation are smoothed when averaging to daily data to grids.

We note that recently ERA5 has been extended back in time to 1950 (Bell et al., 2021). However, as at the time of writing this is still preliminary, we do not include this pre-1979 data in our analysis.

2.4. Data preparation

Although the ETCCDI indices were calculated for the reanalyses at their native resolution, for the comparison to HadEX3, they are interpolated to the HadEX3 grid (1.875 × 1.25°) using a linear interpolation scheme using the Python3 (Van Rossum and Drake, 2009) Iris (Met Office, 2022) library, with no extrapolation. The spatial coverage of HadEX3 varies over the period of study, so to ensure a consistent comparison we match the spatial coverage of the reanalysis products to that of HadEX3, although we do also show some results using the complete land coverage. For our spatial analyses, we additionally impose the restriction that: (i) a grid box has to contain valid data for at least 66% of the time (≥25 years in 1980–2018), and (ii) that the final year is 2010 or later, which are the same criteria used in Dunn et al. (2020a) (albeit over a longer period). We compare the reanalyses over their common periods with HadEX3 (1980–2018 except 20CR, which is shown for 1980–2015).

2.5. Comparison methods

2.5.1. Global time series analyses

We start with a simple comparison of the annual, globally-averaged time series for the indices (using cosine weighting of the grid box latitude to account for the varying grid box sizes over the globe, e.g., Jones and Moberg, 2003). Together with HadEX3 we show time series from the six reanalyses. As HadEX3 does not have complete global land coverage, the solid lines in the time series plots show the reanalyses which have had their spatio-temporal coverage matched to that of HadEX3. We also show as dashed lines, the global averages of the reanalyses using the complete land coverage. We expect these time series of the absolute values to have a spread across the different products, because of the underlying differences in the temperature and precipitation fields. And for the two observationally based products these have different spatio-temporal coverage. Therefore, we also show time series derived from anomalies from the 1981 to 2010 average. To reduce the effect of varying spatio-temporal coverage on these time series, global averages are only calculated from grid boxes which have 90% temporal completeness (>35 years in 1980–2018), the same criterion as in Dunn et al. (2020a). We note that this is different to the 66% criterion used for the maps, but is consistent with the approach in Dunn et al. (2020a) and Donat et al. (2013b).

To evaluate the agreement of the spatial fields, we also calculate the pattern correlation for each year, using the HadEX3 dataset as the reference. Following Donat et al. (2014), the Spearman rank correlation coefficient is determined using the anomalies relative to the 1981–2010 mean at each grid box rather than absolute values, and uses the coverage-matched reanalysis grids. This is to ensure that the statistic measures local rather than global agreement, by removing the obvious global-scale distributions of temperature and precipitation indices. The Spearman rank correlation is the equivalent to the Pearson correlation coefficient of the ranks of the yearly values, and we explicitly exclude the empty grid boxes from this assessment.

Finally, we show a Taylor diagram (Taylor, 2001) which graphically represents how well two time series match (one acting as a reference). These are polar plots showing a sector, with the x and y axes are the standard deviation of the time series, and the reference dataset (HadEX3) plotted on the x-axis. The polar axis represents the correlation between the datasets, from zero at 0° to one at 90°, as calculated over the entire period. The Taylor diagram also shows the root-mean-square difference (d_RMS) as semi-circles centered on the reference dataset (we note that root-mean-square error is more commonly used, but as our reference dataset, HadEX3, also contains errors, only the difference can be measured). Hence the closer points appear to the reference dataset, the better the agreement between the two. We use the global average anomaly time series to construct these diagrams.

2.5.2. Geospatial analyses

We use two measures to assess the spatial comparison of the reanalyses against HadEX3. To indicate how well the reanalyses capture these extremes indices we plot a simple correlation map of the temporal correlation at each grid box. We again use the Spearman rank correlation coefficient. For indices with a large change over the period (e.g., many of the temperature indices), this will be the main determinant of the correlation coefficient. However, for regions or indices which have little long-term change over the period, the year-to-year variation will be the main aspect summarized by these plots.

The second measure is the integrated quadratic distance (IQD, Figure 5), which was introduced by Thorarinsdottir et al. (2013) and used for assessing the differences between extremes indices datasets, reanalyses, and historical climate model runs by Thorarinsdottir et al. (2020). This quantity measures the differences between the cumulative distribution functions for each grid box between each reanalysis and HadEX3. The construction ensures that changes in both shape and location of the distribution are captured, with a greater value of the IQD indicating worse agreement between the two products. As this quantity compares the cumulative distributions, the values obtained will depend not only on the agreement of the distributions, but also the range and units of the index being assessed. Hence, high IQD values may be a few degrees or tens of millimeters, and therefore we do not recommend that numerical comparisons are done between all indices without thought. However, comparisons can be made between the IQD distributions for the different reanalysis products for single indices, or within families of similar indices (e.g., TXx, TXn, TNx, and TNn as one family or Rx1day and Rx5day as another).

3. Temperature extremes

3.1. Global time series analyses

Starting with the time series for the annual maxima and minima, examples shown in Figure 1, and in the Supplementary Figure 13 [TXx], Supplementary Figure 16 [TXn], Supplementary Figure 19 [TNx], Supplementary Figure 22 [TNn], demonstrate that each of the datasets have different absolute values for the global averages and are offset from each other. However, in the time series derived from the anomalies relative to 1981–2010 (Figures 1B,D), both the year-to-year and long period changes agree very well in most cases up to around 2010. Focusing on the reanalyses masked to the observational coverage in the absolute time series (solid lines in Figures 1A,C), for TXn, HadEX3 is the warmest. Whereas, for TNx, HadEX3 is located more toward the middle of the range. The complete global land averages for the reanalyses are relatively similar to the masked versions for TXn (except MERRA-2), but are 2 − 3°C lower for TNx. Each index in HadEX3 has a different spatial coverage. Depending on which regions are missing and whether these are climatologically warmer or colder than the global average, these gaps in the spatial coverage can introduce systematic differences when comparing to the complete land-coverage available from the reanalyses. For example, Antarctica is nearly almost always missing from HadEX3, and often large parts of central Africa are too, and how these balance against each other will result in systematic differences for, e.g., TXx, TNn.

FIGURE 1

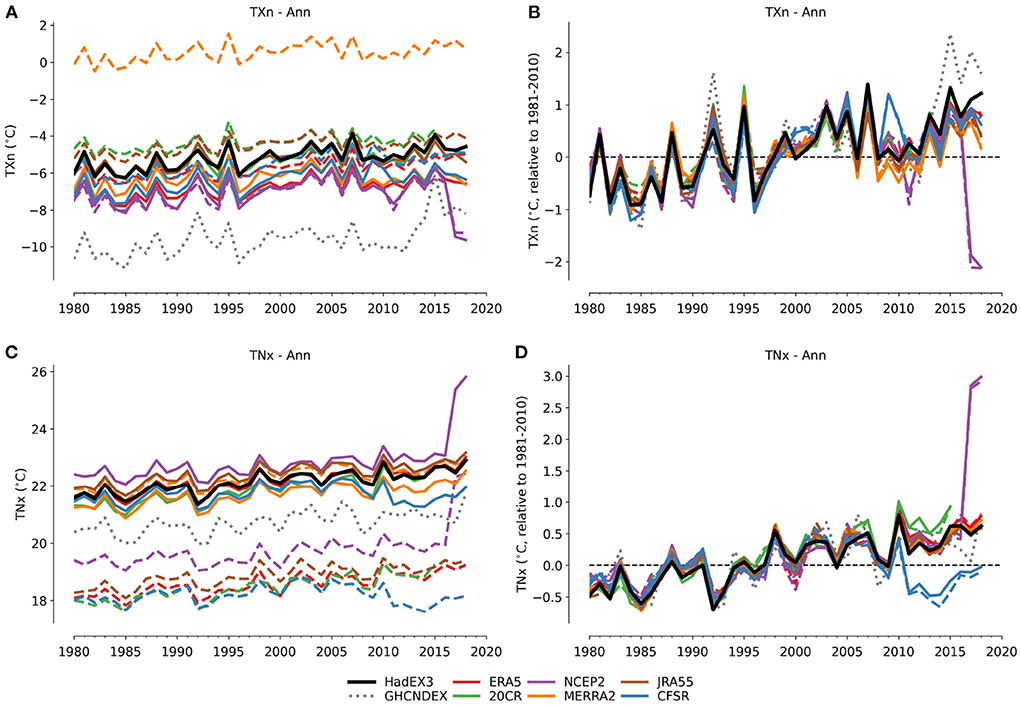
Figure 1. Time series of absolute values (A,C) and anomalies (relative to 1981–2010), (B,D) of TXn (minimum Tmax) and TNx (maximum Tmin). The dashed lines are for reanalyses using complete global land coverage, the solid ones are matched to the spatio-temporal coverage of HadEX3.

In Figure 1, the behavior of both NCEP2 and CFSR is clearly different in the last few years of the time series, particularly in the anomalies (Figures 1B,D). For the last 2 years of the NCEP2 record the values are around 3° C cooler in TXn than the preceding few years and also in the other reanalyses, and warmer by a similar amount in the TNx time series. On further investigation, we noted a discontinuity of a similar magnitude in the NCEP2 fields of maximum and minimum temperatures (tmax.2m and tmin.2m) from 2017 onwards, which we show in Figure A1 (Appendix) which appears to be the cause of this strong jump in the index values.

In the anomaly time series (Figure 1D), values for TNx from CFSR are cooler by around 0.75° C after 2011, as they also are in TXx (Figure A2). There is close agreement between all reanalyses in the anomaly time series before this date. The date of the start of this feature corresponds to the time point where the upgrade to version 2 of the operational Climate Forecast System occurred (Saha et al., 2010, 2014). There was a change in the spatial resolution of CFSR on the change to version 2, but the data available via the NCAR RDA were all on a 0.5 × 0.5° grid which we have used for all the pre-processing. However, no such divergence from the other datasets is seen in the anomaly time series for TXn and TNn (Supplementary Figure 22, though 2009 and 2010 stand out as warmer than other reanalyses in TNn), suggesting that the annual minimum values are not as affected as the annual maximum values and that it is not an issue with our processing of CFSR.

In the indices quantifying the exceedence of percentile thresholds calculated for a specific 30-year reference period (e.g., TX90p, Supplementary Figure 1 [TX90p], Supplementary Figure 4 [TX10p], Supplementary Figure 7 [TN90p], Supplementary Figure 10 [TN10p]), as well as WSDI and CSDI (Supplementary Figures 25, 28), the time series of global averages show good agreement. This also holds for the absolute values due to the use of dataset-specific thresholds which side-steps relative biases between data sets. The use of these relative thresholds reduces the variation of the global average values between datasets. The agreement is better during the reference period (1981–2010), but the spread between datasets increases a little in the last years of the comparison period.

The counts of fixed-threshold exceedences (e.g., SU, Supplementary Figure 31 [SU], Supplementary Figure 34 [TR], Supplementary Figure 37 [FD], Supplementary Figure 40 [ID]) also show different actual values for the global averages, but on the whole good agreement for both long-term trends and inter-annual variability between the datasets when using anomalies. FD and ID in GHCNDEX show departures from the remaining datasets toward the end of their records, with lower than expected counts for these indices. This is most likely the result of the declining spatial coverage in the last years of GHCNDEX in regions which experience temperatures below freezing. ETR (Supplementary Figure 46, not a core ETCCDI index, but often included in this family) shows good agreement on both long and short timescales, which is unsurprising as it is derived from the values of TXx and TNn. And GSL (Supplementary Figure 49) exhibits a large range in absolute values, but reasonable agreement in both the long-term trends and inter-annual variability. However, for DTR (Supplementary Figure 43) the agreement is poor, with datasets presenting DTR of anywhere between 8°C (JRA55) and 12°C (GHCNDEX). The drop in values of DTR for NCEP2 arising from the inhomogeneity noted above is also very clear. There is no clear long term change for this index, and little agreement on the short-term variations between the datasets.

A few things stand out across the indices. Firstly, comparing the datasets against HadEX3 as a reference, GHCNDEX can show larger differences in the average absolute values than the majority of the reanalyses, especially toward the end of its period of record. This is very likely due to the different spatial coverage of GHCNDEX compared to HadEX3, as it has not been coverage matched.

Secondly, we show time series from the absolute global average, and also those calculated from anomalies. The use of anomalies removes the spread in absolute values, and so makes the agreement (or lack thereof) between the datasets on both the long term and year-to-year behavior clearer. The spread in values for the average absolute indices derived from the reanalyses shows how different datasets are warmer or cooler compared to others.

The average absolute values calculated using the complete land coverage obviously include parts of the world where HadEX3 does not have data for those indices. In all cases this adds values from Antarctica to the global average, but for some indices Greenland and large parts of Africa are also included, as only indices with a large DLS will cover these regions with sparse station networks. Depending on which regions are included, and which index is being assessed, this changes the global average values, but seems to have very little effect on the year to year behavior. For example, in TXx (Supplementary Figure 13), the addition of Antarctic values unsurprisingly reduces the global values, whereas for FD (Supplementary Figure 37), contributions from Antarctica and Africa result in no dramatic change.

GSL (Supplementary Figure 49) is a special case. As the growing season length for the southern hemisphere spans two calendar years, the value for the final year of the data series will be incomplete for this region. Hence the global average will be strongly affected in this final year, as can be seen in 20CR.

The spatial rank correlation (Figure 2) shows the yearly pattern correlation between each reanalysis and HadEX3, and for the two indices shown there is good agreement between the results for all the reanalysis datasets except for the last year studied (TNx), both on the absolute level as well as the year-to-year variations. However, the overall correlations for the daily minimum temperature index are lower than for the index derived from the daily maximum.

FIGURE 2

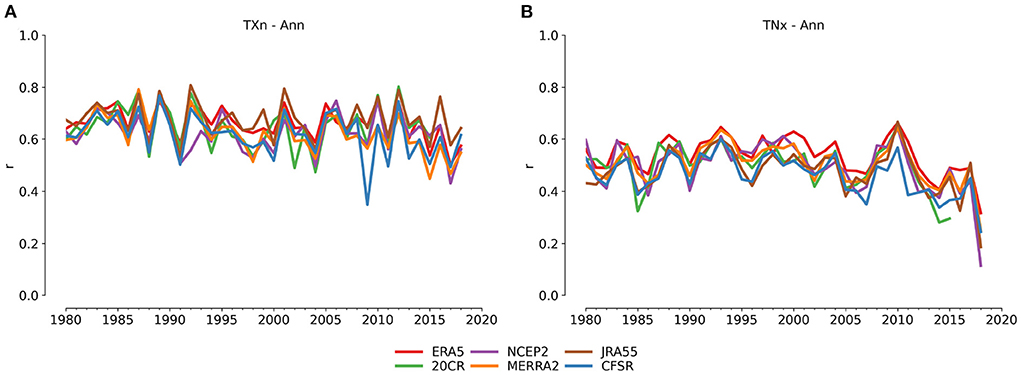
Figure 2. Spatial rank correlation of the coverage-matched reanalyses datasets against HadEX3 for (A) TXn and (B) TNx annual indices.

The spatial rank correlations for the indices using percentile-based thresholds are similar to those for the block maxima (e.g., TNx), and again the pattern agreement of the maximum temperature indices is higher (0.6–0.8) than for the minimum temperature indices (0.4–0.7) (Supplementary Figure 1 [TX90p], Supplementary Figure 4 [TX10p], Supplementary Figure 7 [TN90p], Supplementary Figure 10 [TN10p]). The counts of fixed threshold indices all have pattern correlation values around 0.5–07, except TR which is lower at (0.2–0.6) (Supplementary Figure 31 [SU], Supplementary Figure 34 [TR], Supplementary Figure 37 [FD], Supplementary Figure 40 [ID]). In fact, across most of the temperature indices, those derived from daily minimum temperatures have lower spatial correlations than their counterparts calculated from the daily maximum temperatures. This may be an effect, not of the temperature measurement itself, but of the details of the search radius used in the HadEX3 gridding algorithm. In the Angular Distance Weighting routine, this search radius (the decorrelation length scale, DLS) is used to determine which stations contribute to the value for the grid box (see also Figure 1 in Dunn et al., 2020a). The DLS is determined from the e-folding distance of decay of the correlation coefficients between the index time series as the separation between station pairs increase. This DLS is on average larger for the minimum temperature derived indices than those from maximum temperatures, as on average the correlations between station pairs is higher for minimum temperature derived indices. A larger DLS means a greater search radius, and hence data from a greater number of stations contributing toward the weighted mean when calculating the grid cell value. For a fixed spatial distribution of stations, these additional stations are all at larger distances from the grid box for the minimum temperature indices compared to the maximum temperature ones. This has two effects.

Firstly, even using distance weighting, an increased search radius includes more stations from a greater distance, which will on average be less representative of those closer to the grid box, and so dilute the contribution of nearby stations. This may result in the grid box value being less representative when using a larger DLS than when compared to when using a smaller one. Secondly, a larger DLS means more interpolation can occur into regions with few or no stations. Although the correlation structure from the DLS (which is calculated in latitudinal bands) suggests this action is reasonable, it is possible that for large DLS values (which can be >1,000 km) changes in land use, climate zones and other differences reduce the accuracy of the interpolated values relative to values from a reanalysis. Both these effects would reduce the spatial correlations of the minimum temperature indices when compared to those derived from maximum temperatures.

The ADW is comparatively simple but was shown to be an appropriate method for irregularly spaced data (New et al., 2000). However, it does not take other co-variates, for example (station) altitude, into account when interpolating grid box values which have large separations from stations. Other gridding routines have been applied to these indices on smaller scales for these indices (Avila et al., 2015) or in other variables (Contractor et al., 2015) but not on a global basis as yet.

The spatial correlations with the reanalyses for the block extremes (e.g., TXx) are lower than those for the previous generation of datasets assessed in Donat et al. (2014). As noted above, the ADW method applied in HadEX3 does not account for any co-variates, and also can blend stations from large distances. This results in smooth fields which do not capture the variations over orography, especially for these absolute indices. This could lead to larger differences with the reanalyses, which do account for geophysical features, and hence the observed lower correlations (see Section 3.2). There is also less variation between the spatial correlations of the different reanalysis datasets compared to the previous generation, suggesting that for these temperature indices, the reanalyses are more similar to each other than they are to the observational dataset. A reduction in grid box size (as was done for HadEX3) means that the impacts from orographic features could be more clearly resolved. However, the effective resolution is set by the search radius (the DLS in the ADW method) rather than the grid box size. Therefore, by reducing the grid box size, this has not changed the effective resolution of HadEX3, but has increased the resolution of the matched reanalyses meaning differences over orographic features stand out more in HadEX3 than they did in the comparison to HadEX2 (Donat et al., 2014).

Furthermore, the slight decrease in the spatial correlation values over time may be the result of the decreases in spatial coverage of HadEX3 toward the end of its record period (see plots in Dunn et al., 2020a), roughly from 2010 onwards. In the case of TXn and TNx, large parts of Africa have no coverage after 2010, and there is also a reduction in the coverage of the Canadian Arctic in 2018. There may also be a contribution from increases in the numbers of observations ingested by the reanalyses over time. This may have led to an increase in the general detail available in these products over the entire record, and hence a worsening agreement with HadEX3 over time.

The helpful summary provided by the Taylor Diagrams (Taylor, 2001; see also Section 2.5.1) in Figure 3 show that many of the reanalysis datasets are very similar in comparison to HadEX3, with a cluster around r = 0.9 with similar or slightly lower standard deviations for TXn. The root-mean-square difference (RMSD) of these datasets is around 0.2 for these two indices. CFSR and NCEP2 appear as outliers due to the inhomogeneities outlined earlier. GHCNDEX has poorer agreement for both indices, and again this is the result of the severe drop in spatial coverage for the most recent years when compared to HadEX3. What is also clear is that most of the reanalyses cluster close together suggesting that their representation of these indices is more similar across different reanalyses than to HadEX3.

FIGURE 3

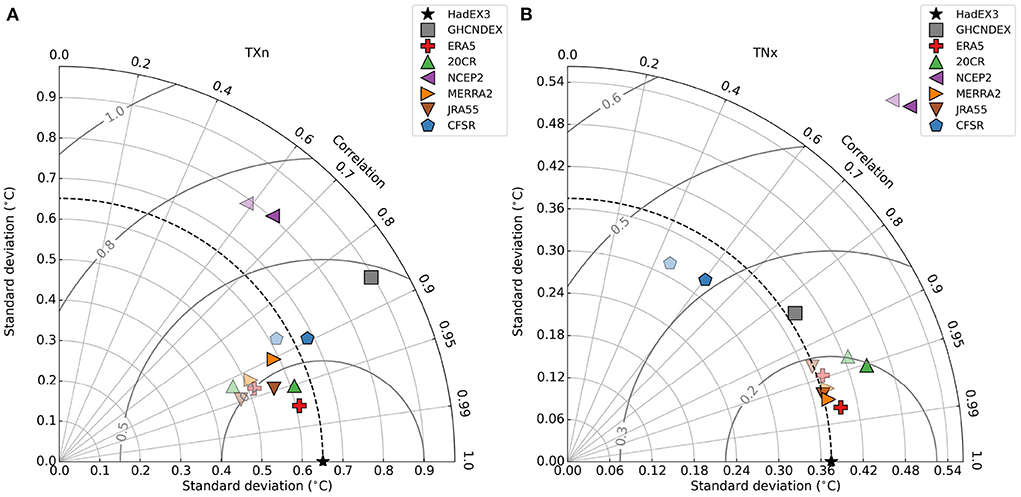
Figure 3. Taylor diagram for (A) TXn and (B) TNx. The x and y axes on this polar plot show the standard deviation of the time series for each dataset, with the polar axis showing the correlation with the reference dataset, HadEX3. The semi-circles centered on HadEX3 show values of the root-mean-square difference. The fainter symbols are for reanalyses using complete global land coverage, the darker ones are matched to the spatio-temporal coverage of HadEX3. These use the anomaly time series shown in Figures 1B,D.

The percentile-based indices show relatively good matches across all datasets (Supplementary Figure 1, [TX90p] Supplementary Figure 4 [TX10p], Supplementary Figure 7 [TN90p], Supplementary Figure 10 [TN10p]), with both the reanalyses and observational datasets showing relatively similar correlation values, but with a greater spread in the standard deviations. Again NCEP stands out (and for TX10p and TN90p in fact falls outside of the plot area). There is less clustering of the reanalyses, suggesting that for these indices they are as similar to each other as they are to HadEX3. The fixed threshold indices are more scattered, with correlation being similar between the reanalyses, but with a spread of standard deviations (Supplementary Figure 31 [SU], Supplementary Figure 34 [TR], Supplementary Figure 37 [FD], Supplementary Figure 40 [ID]). We also show the reanalyses datasets when using the complete land coverage, and as expected from the time series, these tend to have greater RMSD relative to HadEX3 than their coverage matched counterparts, but only in very few cases do these fall outside of the cluster of points from the matched datasets.

3.2. Geospatial analyses

For each index, we show the map of linear trends from HadEX3 as context for the spatial analyses. In the Supplementary material, we also include a map showing the length of the HadEX3 record in each grid box (over the analysis period 1980–2018 used in this study), as this can give context to the other maps as some features can align with regions with shorter records than their neighbors. Linear trends are calculated using the median of pairwise slopes estimator (Thiel, 1950; Sen, 1968; Lanzante, 1996). As the trend period is different (and hence also the completeness criterion), these trend maps differ from those shown in Dunn et al. (2020a) and on the dataset website.

By plotting the Spearman correlation for the anomalies at each grid box we can see more easily where the reanalyses and HadEX3 differ. Overall, for the reanalyses and indices shown in Figure 4, many regions show correlations higher than r = 0.6, but some have low or even negative correlations. Again, as noted in the temporal analysis, the correlations are better for the maximum temperature index than the minimum temperature index.

FIGURE 4

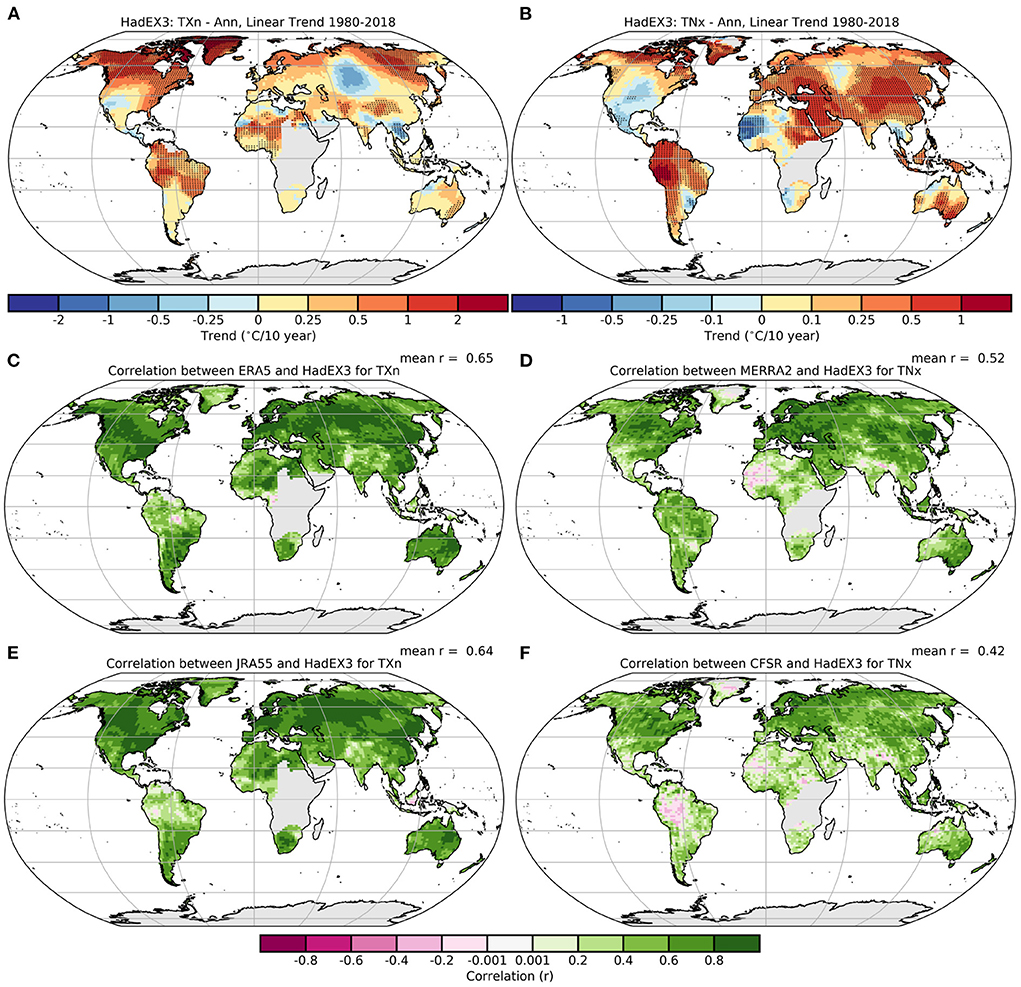
Figure 4. (A,B) Linear trends in TXn and TNx in HadEX3 (°C/decade). Correlation maps for (C,E) TXn, and (D,F) TNx (anomalies relative to 1981–2010) with a selection of reanalyses (ERA5, MERRA-2, JRA-55, and CFSR).

There are a number of reasons why certain regions can have lower correlations (northern South America, India for TXn, Supplementary Figure 17, South America more widely, northern Africa [especially the west] for TNx, Supplementary Figure 20). For example, the decorrelation length scales used in the ADW scheme for these indices are comparatively high (see Section 3.1, around 1,000 km for TNx in the 30 to 60 N band), which means that relatively distant stations can contribute to a grid box value. Not all stations have records which cover the complete HadEX3 period, resulting in the decline in spatial coverage seen in HadEX3 toward the end of its period (see Dunn et al., 2020a). In some cases, this change in the station network can result in more distant stations with longer records contributing more strongly to the grid box average. In South America, a collection of stations at altitude in the Andes finishes in 2015, after which this region has a greater contribution from lower-lying, hence warmer stations. And in western Africa, most stations end in 2010, after which only stations on the Canary Islands have data, which suppresses temperatures over Morocco and the coastal parts of Mauritania because of their maritime contribution. Hence changes in the station network used in HadEX3 can result in inhomogeneities in the grid box time series, and also hence low or negative correlations.

Away from the coast of West Africa, the correlations for TNx are still low/negative (e.g., Mali, southern Algeria). There are few stations located in this region (the Sahara and Sahel), but there are many further south, in more tropical locations, and a few on the Mediterranean coast. Interpolation in HadEX3 by the ADW routine from these wetter regions is unlikely to accurately reproduce the behavior of the desert interior, resulting in lower values for this index. TXn has a much smaller decorrelation length scale (around 700 km) in this region, therefore less interpolation across climate zones can occur, and hence correlations with the reanalyses are better in these regions.

HadEX3 is dependent on the underlying station network, however reanalyses can assimilate other information. Data with complete global coverage, especially from satellites, along with physical models in principle allow them to better represent the temperature behavior in these sparsely observed regions. The reanalyses have warmer values for TNx over the Sahara desert than HadEX3, and also clearly capture the colder temperatures over high elevation areas.

For the percentile-based indices (Supplementary Figure 2 [TX90p], Supplementary Figure 5 [TX10p], Supplementary Figure 8 [TN90p], Supplementary Figure 11 [TN10p]) the correlations are generally higher, up to around r = 0.8, except with NCEP2 and more generally over South America. The use of a threshold determined from the percentiles of the distribution means these indices are more easily compared across regions than those based on actual values (which vary due to, e.g., altitude). This results in longer correlation lengths, and also smoother fields in HadEX3 than other indices. There is almost no effect when using the anomalies to calculate the time series as the use of percentiles has already standardized these curves over the 1981–2010 reference period. Despite also being derived using percentile-determined thresholds, WSDI and CDSI (Supplementary Figures 26, 29) have lower overall correlations (r = 0.6–0.7), with tropical areas (which have less variable temperatures) standing out in CSDI.

The fixed threshold indices (Supplementary Figure 32 [SU], Supplementary Figure 35 [TR], Supplementary Figure 38 [FD], Supplementary Figure 41 [ID]) can show missing areas in the correlation maps, despite both HadEX3 and the reanalyses having data over these regions. These are locations where these indices equal zero for almost the entire record (e.g., tropical areas in ID where the maximum temperatures never fall below 0° C) for either dataset. In these regions, the correlation calculation is meaningless, and hence are missing in the figures. Overall, these indices do have slightly lower correlations than the block extremes (e.g., TXx), of around r = 0.6.

Using the integrated quadratic distance (IQD, Thorarinsdottir et al., 2013, 2020) as shown in Figure 5 highlights regions where there is a mismatch between the distributions of the reanalysis and HadEX3. Given the differing units and values of the underlying distributions assessed by the IQD, numerical comparisons between different indices should be done with care. However, the spatial patterns of relatively high or low IQD show where there is good or poor agreement between the cumulative probability distributions of the reanalyses and HadEX3. The areas which immediately stand out are mountainous regions, e.g., the Himalayas and Andes. Even the European Alps and parts of the North American Rockies show greater IQD values than their immediate surroundings. In these mountainous regions, the blending of the ADW scheme used in HadEX3 is unlikely to fully capture the values of these block extremes indices (e.g., TXx), as it is more likely that stations are based alongside settlements in the lower valley floors. Whereas, the reanalyses can potentially capture the temperature variation with altitude more accurately. The other regions with clear differences are Greenland and northern latitudes (TXn). As the only stations in Greenland are coastal, HadEX3 cannot represent the high-altitude interior well, leading to the larger IQD values.

FIGURE 5

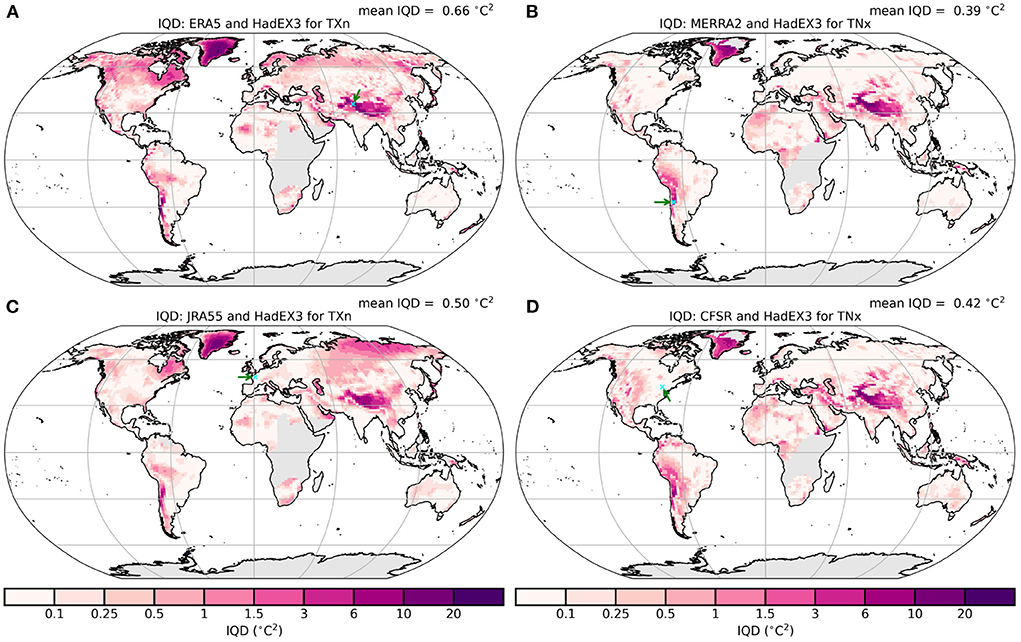
Figure 5. Integrated quadratic distance (IQD) map between HadEX3 and (A) ERA5 and (C) JRA55 for TXn and (B) MERRA-2 and (D) CFSR for TNx. Small (so as not to distract from the underlying values) blue crosses mark the locations of grid boxes presented in Figure A2, which are also indicated by a green arrow [(A) northern Indian subcontinent, (B) western South America, (C) France, (D) north-eastern USA].

In Figure A2, we show the cumulative distribution plots from which the IQD is calculated for one grid box from each of the four panels in Figure 5, two from regions of low IQD and two from high IQD. In regions of low IQD (JRA55: France, CFSR: north-eastern USA), the cumulative difference curves are very close, whereas for the regions of high IQD (ERA5: Himalaya, MERRA2: Andes), the curves are well separated, with HadEX3 at higher temperatures than the reanalyses. In these regions HadEX3 has not captured the lower temperatures found at these high-altitude regions.

For the percentile-based indices (Supplementary Figure 3 [TX90p], Supplementary Figure 6 [TX10p], Supplementary Figure 9 [TN90p], Supplementary Figure 12 [TN10p]) the IQD values show less variation across the globe, except for NCEP2 in TX10p (Supplementary Figure 6). Parts of Africa and South America do stand out for some reanalysis and index combinations, and usually toward the edges of the regions with coverage. This suggests that interpolation by the ADW scheme is leading to the difference between the reanalyses and HadEX3 in these regions.

Again, the smaller variations in IQD values are because the use of data-specific thresholds calculated over the reference period removes some of the relative biases. Whereas, for the fixed threshold indices (Supplementary Figure 33 [SU], Supplementary Figure 36 [TR], Supplementary Figure 39 [FD], Supplementary Figure 42 [ID]) some very large differences are demonstrated which are mainly in regions where the thresholds for these indices are almost always or almost never exceeded (in high-latitude, high-altitude, or tropical regions) and arise because of the offset in the actual temperatures in different reanalyses (see SU, TR, FD).

4. Precipitation extremes

4.1. Global time series analysis

As is clear from the anomaly plots in Figure 6 and in the Supplementary material, the agreement between the different datasets for precipitation indices is on average less good than for the temperature indices. Unlike changes in the temperature extremes, which are responding to the rise in temperatures globally and so show strong trends, changes in precipitation are spatially much more heterogeneous (see below). Therefore, on the global average the magnitude of any long term change is smaller and hence the short timescale variability more prominent. These larger differences in the representation of precipitation indices are also in line with the uncertainty across different observational datasets (and reanalyses) discussed in Alexander et al. (2020).

FIGURE 6

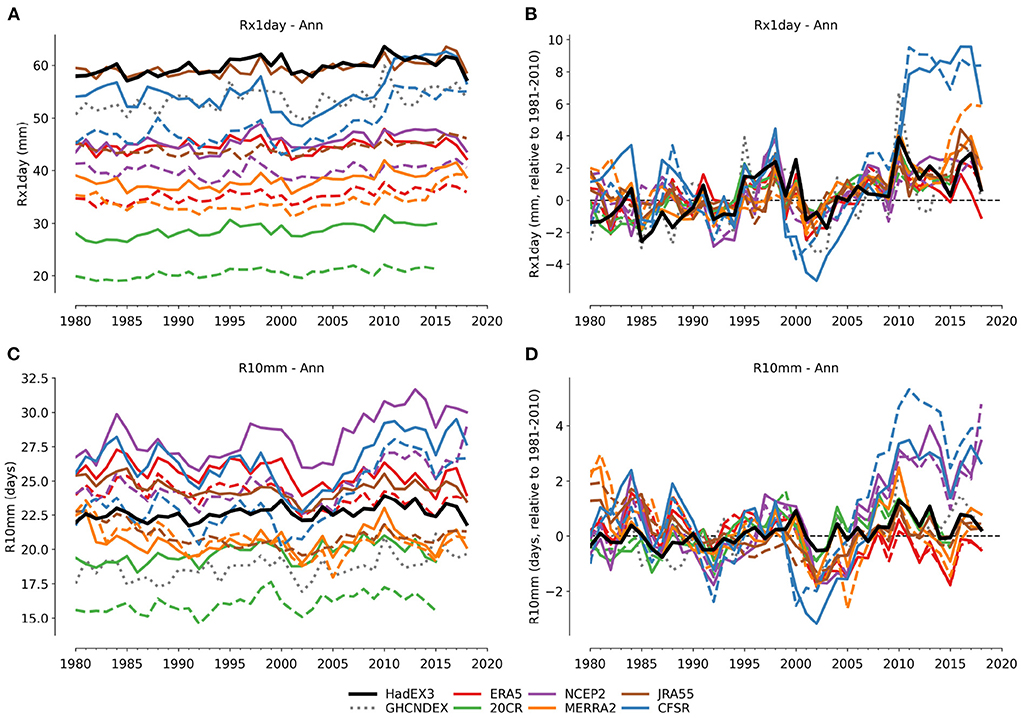
Figure 6. Time series from absolute values (A,C) and anomalies (B,D) for Rx1day and R10mm. The dashed lines are for reanalyses using complete global land coverage, the solid ones are matched to the spatio-temporal coverage of HadEX3.

As seen in the temperature indices, the time series derived from absolute values have different values between datasets, but there is no precipitation index where there is good agreement in the absolute values. Larger differences remain than for temperature, even when calculating the average global time series using the anomalies. However, there are some short-term similarities in the year-to-year changes in the anomaly time series for parts of the record. For example in R10mm, the year-to-year variation between 2010 and 2018 in HadEX3 is similar to ERA5, 20CR and JRA55 though the absolute values are offset. Earlier in the record, however, there are fewer similarities in the inter-annual variation of the global average time series.

Clearly in Figure 6, both CFSR (Rx1day and R10mm) and NCEP2 (R10mm) show large differences in the temporal behavior compared to the other products. For CFSR in Rx1day, it is almost as if the temporal behavior is more exaggerated, with larger anomalies arising from inter-annual variations than, e.g., HadEX3. Though, as for the temperature indices, there is a stronger departure by CFSR2 after 2010, suggesting some inhomogeneity at this point for the wettest days rainfall values. In R10mm, both CFSR and NCEP2 show similar strong positive anomalies over the last years of the period of study, and although CFSR also maybe has greater interannual variation in this index, it is not clear that NCEP2 has the same interannual variation. Similar behavior is seen in PRCPTOT, but with no clear distinction at 2010, which suggests that precipitation in these two reanalyses is generally greater than other products, and especially in recent years. For CFSR some other indices are not as affected (e.g., CDD, CWD, SDII), but R95p(TOT) and R99p(TOT) also show these large comparative differences after 2010.

Two indices which have relatively good agreement over longer timescales are R95pTOT and R99pTOT (Supplementary Figures 82, 85). In contrast CWD (Supplementary Figure 64) demonstrates much lower levels of short term variability in HadEX3 then in many of the reanalyses. For this index the map of HadEX3 trends shows few areas with clear trends, and a roughly equal distribution of positive and negative trends over the globe.

As noted in Donat et al. (2014) for Rx5day, the observational datasets have higher average absolute values in Rx1day than most of the reanalyses. They conclude that this is likely the result of the different order of operation between the observational and reanalysis datasets. As outlined in Section 2.3, the observational datasets interpolate extremes calculated at each station. Whereas in the reanalyses the extremes have been derived from daily grid box average values and hence influenced by smoothing effects resulting from the gridding of information from the reanalyses.

In a recent comparison of annual precipitation indices and extremes, (Alexander et al., 2020) found that CFSR and MERRA-2 were the wettest datasets across a range of reanalyses, satellite and in situ precipitation datasets over the full land surface. They also noted that the reanalyses had a wider spread across the datasets than the other dataset types they studied. We also find CFSR more often than not among the wettest datasets across the indices, but MERRA-2 is more variable in its comparative position.

In terms of long-term changes, using the full time coverage of HadEX3 (1901–2018), Dunn et al. (2020a) found increases in many of the extreme precipitation indices. Using a shorter time period, Alexander et al. (2020) also found significant trends over 1988–2013 for many indices across the reanalyses they studied using the complete land coverage over 50°N to 50°S. However, in this analysis where reanalyses coverage is restricted to that of HadEX3 we find results in time series that are much noisier than in Alexander et al. (2020). Hence increases in extreme precipitation are not as clear from this assessment alone.

Unsurprisingly the spatial correlation values for all reanalyses compared with HadEX3 are on average lower for the precipitation indices than for the temperature indices (Figure 7), as precipitation fields are generally less homogeneous than temperature fields. In the examples in Figure 7, R10mm has generally higher correlations than Rx1day as the latter index is more likely to measure extremes dominated by localized heavy convective events, rather than accumulations dominated by large-scale, dynamic patterns of rainfall. Across all the indices the spatial correlations range between around 0.2 and 0.4, with only a few reaching up to 0.6 (e.g., PRCPTOT, R10mm).

FIGURE 7

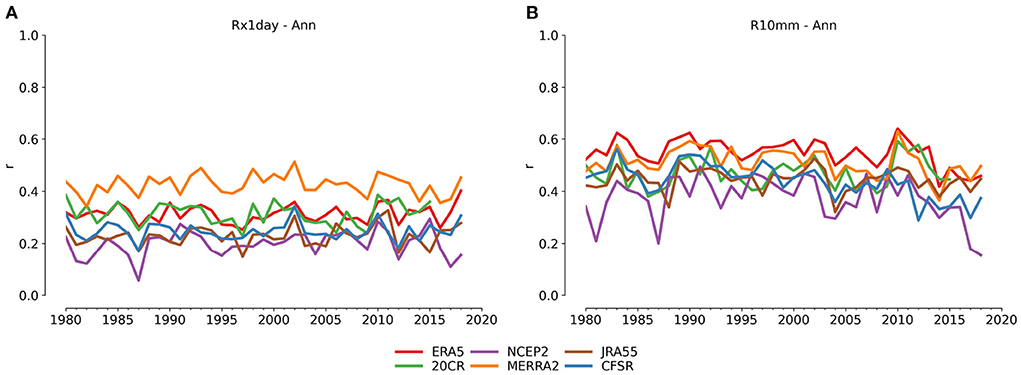
Figure 7. Spatial rank correlation of the coverage-matched reanalyses datasets against HadEX3 for (A) Rx1day and (B) R10mm annual indices.

The Taylor diagrams in Figure 8 confirm the generally lower correlations for the precipitation indices, and a much greater range in standard deviation. Even the other observational datasets have a much greater spread across this diagram than they do for the temperature indices. Despite the higher spatial correlation of the reanalyses for R10mm than Rx1day, the Taylor diagrams show better agreement for the global average time series for Rx1day than R10mm, consistent with Figure 6D.

FIGURE 8

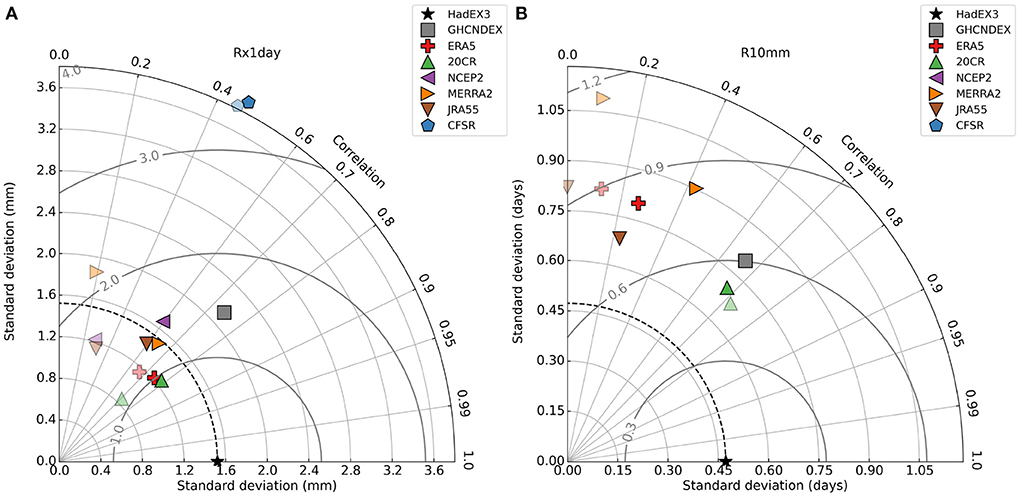
Figure 8. Taylor diagram for (A) Rx1day and (B) R10mm. The fainter symbols are for reanalyses using complete global land coverage, the darker ones are matched to the spatio-temporal coverage of HadEX3.

4.2. Geospatial analysis

Immediately apparent in Figures 9, 10 is the much smaller fraction of land area covered by these indices than the temperature indices. Although this varies, the precipitation indices tend to have smaller coverage, despite an often larger number of contributing stations. The reason behind this is the shorter correlation length scale for these indices, which is used in the ADW algorithm when selecting stations to contribute toward a grid box value. For some indices with particularly small decorrelation length scales (e.g., R99pTOT), there is little interpolation, with data in HadEX3 only available where the grid boxes themselves contain sufficient stations.

FIGURE 9

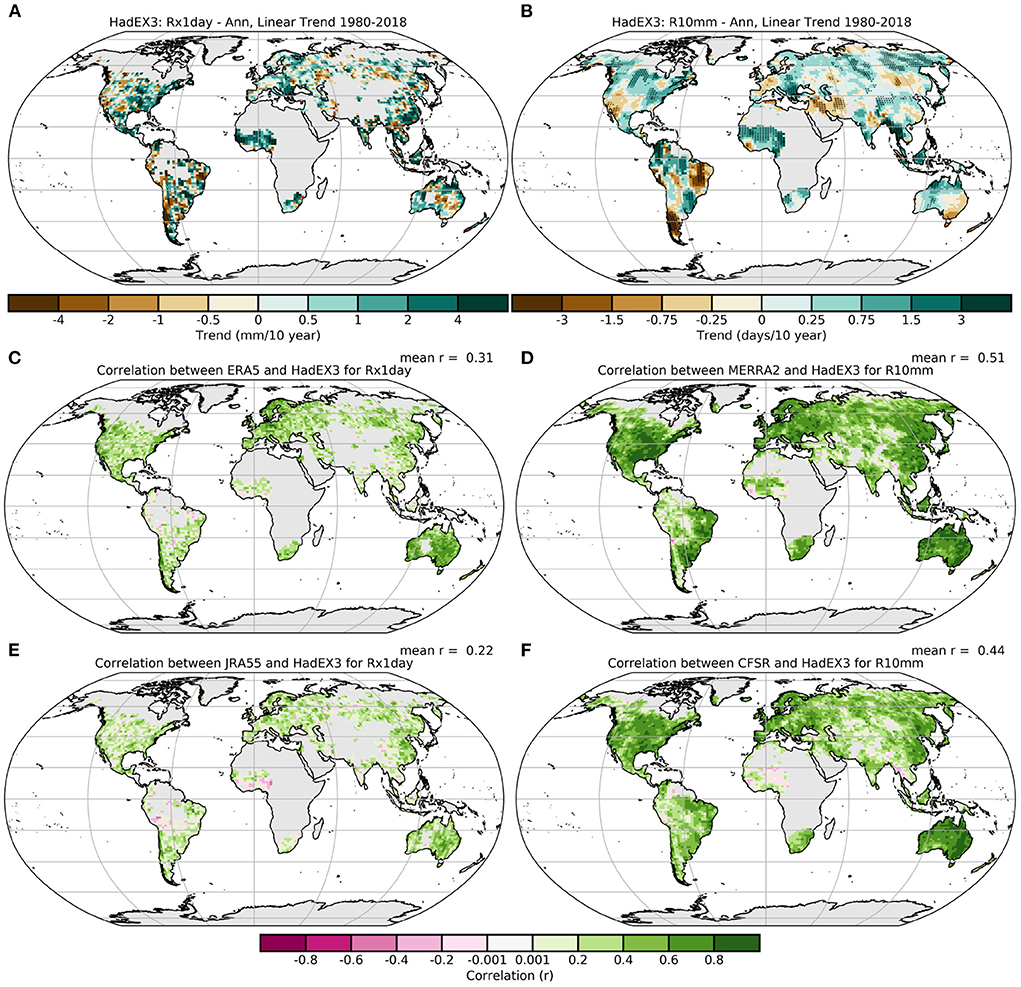
Figure 9. (A,B) Linear trends in Rx1day (mm/decade) and R10mm (days/decade) in HadEX3. Correlation maps for (C,E) Rx1day, and (D,F) R10mm (anomalies relative to 1981–2010) with a selection of reanalyses (ERA5, MERRA-2, JRA-55, and CFSR).

FIGURE 10

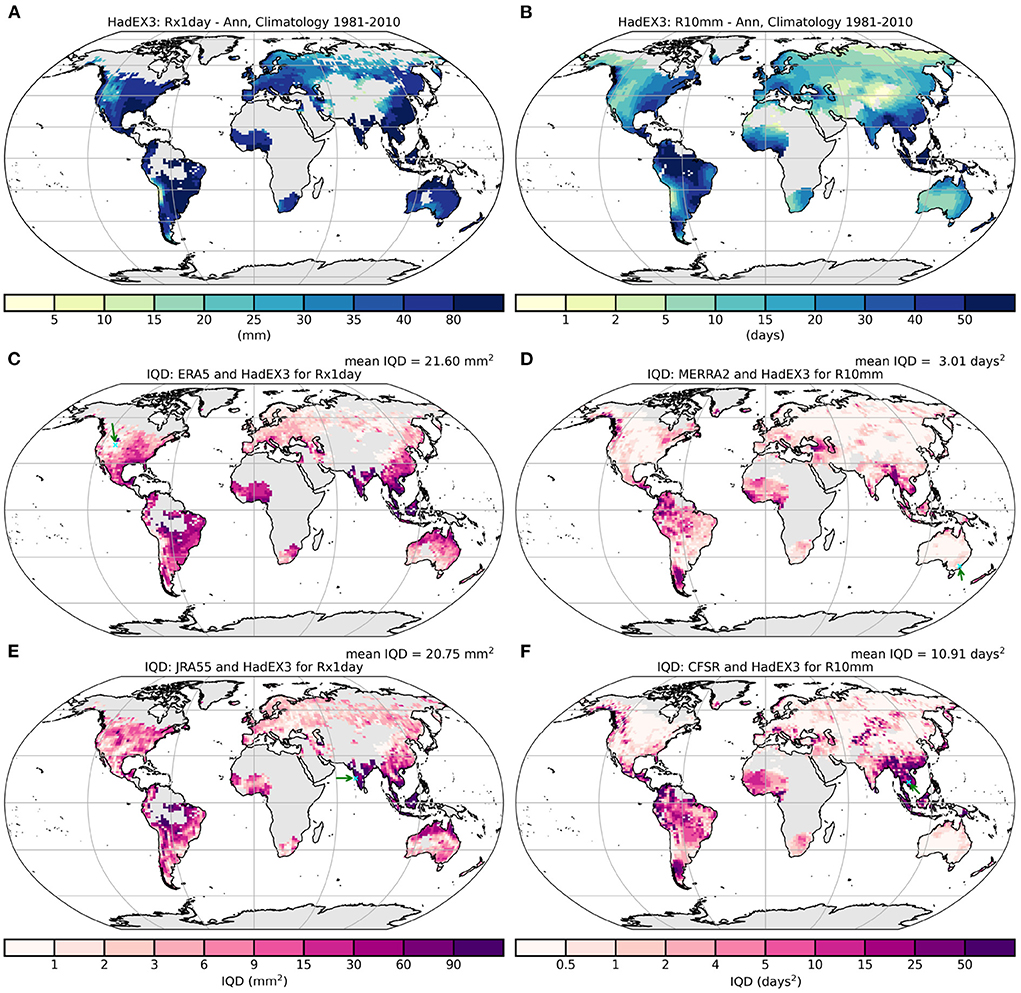
Figure 10. The 1981–2010 climatology maps for (A) Rx1day, and (B) R10mm, using the same selection criteria for the maps of trends and IQDs. The IQD maps for Rx1day with (C) ERA5, and (E) JRA-55, and R10mm with (D) MERRA-2, and (F) CFSR. Small (so as not to distract from the underlying values) blue crosses mark the locations of grid boxes presented in Figure A2, which are also indicated by a green arrow [(C) North America, (D) south-eastern Australia, (E) western India, (F) south-eastern Asia].

Overall, the correlations between HadEX3 and the reanalyses are higher for indicators of more moderate extremes, such as R10mm than for annual maxima (Rx1day), also with a greater spatial coverage. In both these indices, similar regions stand out as having higher than the average correlation for the index, but with the addition of eastern South America in R10mm. But Mountainous regions, e.g., the Andes, central Asia and parts of the Rocky Mountains do appear to have lower correlations. The spatial distribution of the trends for Rx1day in HadEX3 is more heterogeneous than in R10mm, which shows relatively large regions of contiguous increasing or decreasing tendencies compared to the noisier Rx1day. The DLS is larger for R10mm than for Rx1day, which results in smoother fields for R10mm along with greater spatial coverage in HadEX3. However, the reanalyses also show similar differences in the spatial distribution of trends, with Rx1day being on average more heterogeneous than R10mm. Hence the correlation maps reflect the relative heterogeneity of the fields of these two indices.

As expected from the prior discussion, the correlations are on the whole lower for the precipitation indices and also more spatially heterogeneous than those exhibited for the temperature indices (compare Figure 9 with Figure 4). But in the overwhelming majority of grid boxes for Rx1day, and other precipitation indices, the correlations between HadEX3 and the reanalyses are positive. Higher correlations are found for Australia, North America, Europe, and eastern Asia, which also correspond to regions with large numbers of stations that were included in HadEX3.

Locations with lower correlations often correspond to regions with few stations in HadEX3, suggesting that these are not as well represented. Also, if only few stations contribute to the grid box value, then this weighted average is more susceptible to changes in the station network, potentially leading to interpolated values from more distant stations dominating the signal (see Section 3.2). The station distribution in HadEX3 reflects the more general availability of station data (Thorne et al., 2017), which also impacts the representation of these regions in the reanalyses. The effect of the density of the underlying observation network was noted in Donat et al. (2014), Donat et al. (2016), and Alexander et al. (2020), where the agreement, even between different reanalysis datasets, is lower in regions where observations are sparser.

A number of the indices have very similar definitions and can be grouped into pairs of different threshold values (e.g., R10mm and R20mm). In many cases the indices measuring less extreme events (lower percentiles or thresholds) show higher correlations between the reanalyses and HadEX3 than the indices of the more extreme events, e.g., R95p, R95pTOT, and R10mm all have higher correlations than R99p, R99pTOT, and R20mm, respectively (Supplementary Figures 56, 59, 77, 80, 83, 86). This suggests that the agreement between HadEX3 and the reanalyses is on average better for the moderate extreme precipitation characteristics than the more extreme indices. For the extreme rainfall amounts, Rx5day shows on average higher correlations than Rx1day, suggesting longer term events agree better than those from single days (Supplementary Figures 71, 74). Finally, CDD has higher correlations than CWD, again suggesting that the reanalyses and HadEX3 agree better for dry spells than wet ones (Supplementary Figures 62, 65).

For these indices, we show a map of the climatology along with the integrated quadratic distance (IQD) in Figure 10 as this can help understand the distribution of differences. There can be large range of index values across the globe, unlike for some of the temperature indices. Any mismatches between the HadEX3 and reanalysis distributions in regions with high index values are likely to result in larger IQD values than those in regions with low index values. Hence although the absolute difference in the distributions is larger, the relative difference may not be. However, we have not added any normalization to these plots using, e.g., the climatology. It is also therefore important to remember that although spatial patterns of IQD variation can be compared between indices, numerical values should only be compared within index (families).

For this reason, regions with large values for the indices have a tendency for a larger IQD, but this is not always the case. For R10mm, the eastern part of North America has higher values for R10mm than the west, but this region does not stand out in the IQD especially when contrasted to similar values for R10mm in South America. Similarly over the Indian subcontinent, the IQD values are smaller there than in neighboring south-east Asia but both have similar R10mm values. In the Rx1day panel, the IQD values are comparatively lower around the Mediterranean than they are in eastern North America for similar values of Rx1day.

In Figure A2, we show the cumulative distribution plots from which the IQD is calculated for one grid box from each of the four panels in Figure 10, two from regions of low IQD and two from high IQD. In regions of low IQD (ERA5: north-western USA, MERRA2: south-eastern Australia), the cumulative difference curves are close, though ERA5 has consistently lower Rx1day values than HadEX3, whereas MERRA2 is a very close match to HadEX3 for R10mm. In the regions of high IQD (JRA55: south-western India, CFSR: Cambodia), the curves are well separated. JRA55 also has lower Rx1day values than HadEX3, but by between 50 and 200 mm, rather than the 5 mm that ERA5 is lower, with the highest HadEX3 values being much higher than JRA55 compared to the lowest values. This is similar for CFSR in R10mm, but in this case CFSR has more of these very wet days, and this difference increases as the number of wet days increases.

The regional variation shown by exceedences of set accumulation thresholds (R10mm, R20mm, Supplementary Figures 57, 60) is greater in the tropics, with lower values at mid and high latitudes. A similar pattern is seen for the percentile exceedences (R95p, R99p, Supplementary Figures 78, 81) and the intense accumulations (Rx1day, Rx5day, Supplementary Figures 72, 75), but with less of a decrease toward higher latitudes. For R95pTOT and R99pTOT, the normalizing effect of PRCPTOT in the construction of these indices results in the IQD being relatively uniform across the globe (Supplementary Figures 84, 87).

In each pair of similar indices the regional variation is similar, but the indices measuring more extreme events had on average a lower IQD, with, e.g., R99pTOT, R99p and R20mm all having lower values than R95pTOT, R95p, and R10mm, respectively. This arises naturally from the construction of the indices, where those measuring more extreme characteristics result in smaller quantities, and hence the difference between these distributions is also smaller. However, the IQD values for Rx1day and Rx5day are relatively similar. The duration indices show very different behavior, with CWD showing high IQD in the tropics, especially in those regions with monsoonal rains, likely because these are not well represented in HadEX3, as noted earlier for the temperature indices (Supplementary Figures 63, 66).

5. Discussion

Overall, both the year-to-year and long-term changes match very well between the different reanalysis and observational datasets for the globally-averaged timeseries of the temperature indices (Figure 1). As there are differences in the average absolute values between the datasets, this agreement is clearer in the anomalies. Deviations between datasets are most commonly seen toward the end of the record of the observational datasets, as their spatial coverage reduces (Dunn et al., 2020a). Changes in the spatial coverage can result in contiguous regions no longer contributing to the global average, which for some indices can lead to a deviation, especially for those using fixed thresholds.

The relative offsets in absolute values for the global averages of the temperature indices means that some datasets are “warmer” and others are “cooler” when comparing to one another. However, given the much closer agreement when using anomalies, any single dataset is good at capturing both the year-to-year variation and long term change of these indices, apart from those where we identify issues, in particular with cold-tail indices toward the end of the data period (CFSR and NCEP2). Hence when using absolute values of these indices in the reanalyses, we recommend that more than one product is used so that the range in values can be captured.

The precipitation indices do not show such close agreement in the reanalyses, either with the observational datasets or with each other. These indices show on average a much larger range in absolute average values between the different datasets. Even when using anomalies, both long and short term variations do not align as well in many indices, though for many precipitation indices there is no strong long-term trend over the time period used herein. On a regional basis, the correlations of these indices are average lower than the temperature indices in many locations.

High IQD values are often found in regions which also have high values for the precipitation indices, but this is not always the case. Where low IQD values are found in regions with high index values, then there is very good agreement between the cumulative probability distributions. In some cases these regions are those which have sparser station networks, which affects both the ability of HadEX3 to capture the detail of the precipitation properties, and the quantity of observations available for assimilation by reanalyses (where performed).

As noted in Section 2.3, there is an order-of-operation difference between the observation-based datasets (index-then-grid) compared to the reanalyses (grid-then-index). For Rx1day, for the two example grid boxes shown in Figure A2, HadEX3 shows higher values than the two reanalyses. This suggests that the maximum one day precipitation amounts in the reanalyses are not as extreme as in the observation based HadEX3, perhaps the consequence of the grid-box-average nature of the precipitation values (with more muted extremes) in the reanalyses.

Alexander et al. (2020) compared a number of reanalysis datasets with in situ and space-based datasets on a common grid. The HadEX family of datasets were not included in that study, but many of the reanalysis datasets included here were. They found substantial differences even in the climatological values for different datasets (as we do here), with reanalyses tending to fall into “wet” or “dry” groups, and variation across all data sources depending on the index.

The maps shown in earlier sections for selected indices (and also in the Supplementary material) are useful in highlighting which regions in each reanalysis have low or high correlations or IQD values against HadEX3 across the globe. We summarize these by showing global average values for each index in Figure 11. The spatial fields of correlation or IQD for each reanalysis (as shown in, e.g., Figures 4, 10) are averaged across the globe using cosine latitude weighting.

FIGURE 11

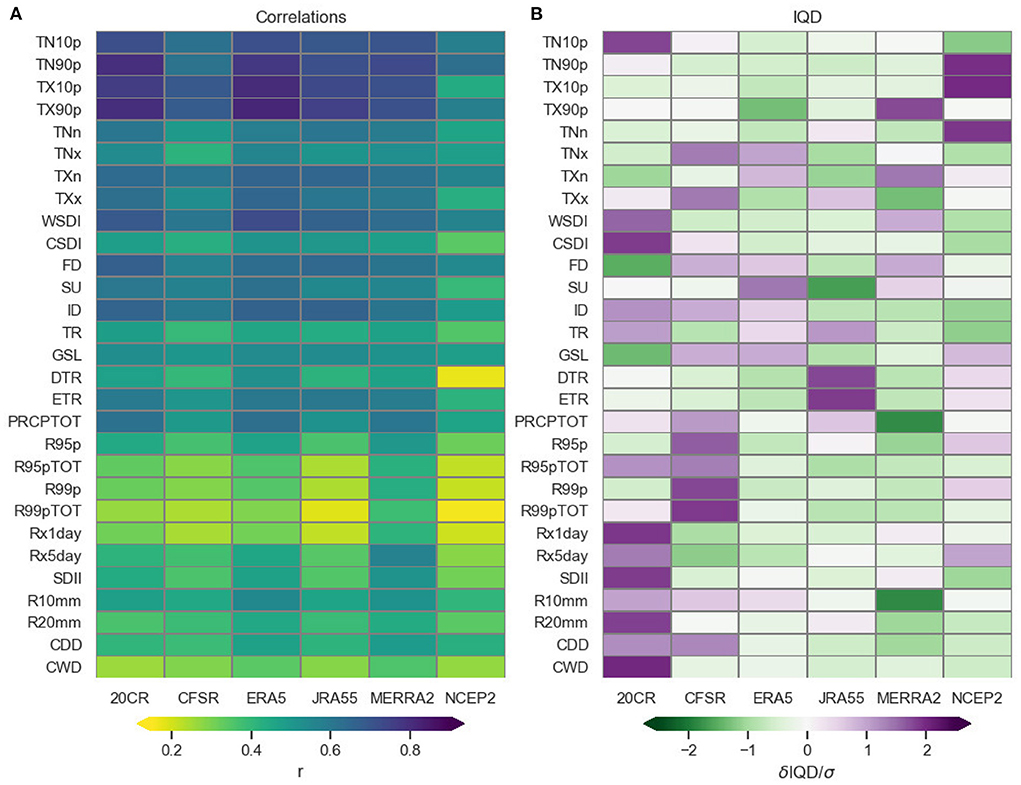
Figure 11. Summary heatmaps for (A) the globally averaged (cosine-weighted) correlation and (B) normalized IQD values (difference of the IQD from the average across all reanalyses per index, normalized by the standard deviation) calculated against HadEX3. Note the change in color scale used for the correlation panel compared to the maps in other figures. The updated colors were chosen for clarity over the range shown.

Starting with the correlations, the split between temperature and precipitation indices is clear, as are the families of the different index types. The highest correlations for temperature are in the indices counting the exceedence of percentile thresholds (TX90p etc.) whereas for precipitation PRCPTOT shows highest correlations, followed by R10mm. The lowest correlations are for the indices counting the (fraction of) annual precipitation amounts from days above the 99th percentile (R99p, R99pTOT) and the maximum one day accumulation (Rx1day). Across all indices, 20CR, ERA5, MERRA-2 have the best correlations with HadEX3, with NCEP-2 showing clearly lower correlations across almost all indices.

The range of IQD values shown for each index has a large range, with TXn in the range of tens of °C, but PRCPTOT measured in hundreds of mm. Hence comparing global average values for each index is not trivial. Nonetheless, it would be useful to be able to see how different reanalyses and index families compare. In order to show these comparisons on a single diagram we show the difference of the IQD from the average across all reanalyses for each index and then normalized by dividing by the standard deviation of the distribution of values of the each index for the reanalyses. Hence this panel in Figure 11 shows the standard deviation of a particular reanalysis from the average, with lower values showing that a reanalysis has a smaller IQD from HadEX3 than the average for the reanalyses for that index.

The IQD, measuring differences between the cumulative distributions at each grid box, will also depend on the absolute magnitudes of the values forming these distributions. For example, in desert regions distributions of PRCPTOT will be formed from values of low numbers of mm/year, whereas in regions with high annual rainfall, values could be in the 1,000 s mm/year. Hence, for this index, and others which show large variation in absolute values across the globe, a global average may be dominated by specific regions which have large IQDs because of their climate. However, within a single index, these effects should balance out and so enable the reanalyses to be compared. But, as noted in Section 4, it will also be valuable to refer to the maps of the IQD to obtain the more detailed picture of where the cumulative distributions of HadEX3 and the reanalyses differ.

For many of the precipitation indices, 20CR has greater than average IQD values, whereas NCEP2 shows high IQD values for some of the temperature indices, probably related to the large drop in temperature toward the end of the time series. In contrast, MERRA2 shows lower than average IQDs for R10mm and PRCPTOT, and ERA5 is close to the average across almost all indices.

Considering both panels in Figure 11, the correlation measures how well the reanalyses track HadEX3, and the IQD whether this tracking is offset, or under/over-estimates the changes. So, for example, 20CR has good correlation for many of the indices but the cumulative distributions differ for many of the precipitation ones. As examples, in many of the regions of high IQD for Rx1day, this is because the values in 20CR are less extreme than in HadEX3 (similar to JRA55 in Figure A2), whereas for R10mm the offset varies across the globe as to whether HadEX3 has greater or fewer wet days. What is clear is that ERA5 and MERRA-2 show both high correlations and average or below-average IQDs for the majority of the indices. But JRA-55 also compares well to HadEX3 except for the two temperature range indices (DTR, ETR) which stand out in the IQD.

Other recent studies have used one or other of these reanalyses in comparisons with in situ and other datasets. In comparisons to the CHIRTS dataset (Funk et al., 2019), they found MERRA-2 did not track a recent increase in annual T_max values observed therein and also in CRU-TS 4.01 (Harris et al., 2014), with the long term trend being of lower magnitude. Also using CHIRTS along with station and forcing based datasets, Verdin et al. (2020) found ERA5 the “coolest” in a metric of days over 40.6°C, and both the trend and short term variability in this metric in ERA5 were smaller than in other datasets. This is consistent with what we find in TXx, with only JRA55 and 20CRv3 being cooler than ERA5 in the un-anomalized comparison (Supplementary Figure 13), and MERRA-2 showing a smaller trend in TXx than in HadEX3 (not shown). There is no ETCCDI index closely corresponding to the metric in Verdin et al. (2020), but for SU (count of when Tx>25°C) ERA5 very closely follows HadEX3 (Supplementary Figure 31).

5.1. Effects of the angular distance weighting scheme

Several of the analyses in this comparison between HadEX3 and reanalyses have referred to the HadEX3 gridding scheme and its decorrelation length scale. Firstly, the spatial correlations for the indices based on daily minimum temperatures are lower than for their counterpart indices based on daily maximum temperatures (Figure 2). The DLS is longer for the indices based on minimum temperatures, which results in both more stations contributing to a grid box average and also more interpolation into regions which only have stations at their edges. This reduces how representative the grid boxes are of the underlying “true” extremes, and also increases the chances of interpolating into regions where the climate is different from those where there are data. Both of these have the effect of smoothing the spatial fields in indices with larger DLS values, and so the minimum temperature indices are more strongly affected. The smoother spatial fields result in greater differences between HadEX3 and the reanalyses and hence smaller spatial correlations.

The effect of interpolating into regions with few stations is seen in the correlation maps (Figure 4). For example, coverage over the western parts of the Sahara has been interpolated from stations to the north and south which have very different climates. By using a wide variety of global data (e.g., satellite measurements) and a physically motivated model, the reanalyses are more likely than HadEX3 to accurately capture the values of the indices in this region. This difference of course will lead to low (or even negative) correlations. A change to the network can also lead to a similar effect. If the record of a large number of stations in a region stops earlier than others, then contributions from more distant stations within the DLS may result in a step-change. In the construction of HadEX3, the effect of this was minimized by selecting only stations which ended after 2009. This date was chosen as a balance between retaining sufficient stations while reducing this network change effect.

Secondly, these spatial rank correlations are lower than in a similar comparison for HadEX2 and the previous generation of datasets analyzed in Donat et al. (2014) despite an increase in the number of stations and spatial coverage over the previous dataset (Figure 2). This may be a consequence of using the ADW gridding scheme on a finer spatial grid for HadEX3. This scheme was used for consistency with the previous versions (HadEX and HadEX2), though the grid box area in HadEX3 is a factor of four smaller. Studies have shown that, although ADW is helpful in the case of sparse station networks (New et al., 2000), when applied at high spatial resolution (e.g., in smaller study regions) it results in very smooth fields (Avila et al., 2015; Contractor et al., 2015).

Thirdly, for the temperature indices capturing absolute values (e.g., TXn, TNx), the inability of ADW to easily include co-variates like altitude means that in topographically complex regions, even with the smaller grid boxes, the ADW gridding routine smooths out the effects related to complex orography. Additionally, with smaller grid boxes, the reanalyses (which natively have an even higher spatial resolution) are able to more closely follow the effects of the topography these indices. Hence the cumulative distributions at each grid box differ between HadEX3 and the reanalyses over these regions (Figure 5, Figure A2).

Finally, there is also a further effect of where stations in mountainous regions are likely to be located, more often than not, in settlements in the valleys. The reanalyses on the other hand include orographic information including altitude and so can better represent the mountainous regions. Hence, for any future update of the HadEX datasets it will be necessary to carefully consider the gridding method used.

On the whole, the precipitation indices have much shorter DLS values as the spatial scales of rain- and snow-fall are shorter, and so are not as strongly affected by the issues mentioned above as the temperature indices. Smaller DLS values means less interpolation occurs into regions with no observations. Also, a shorter DLS results in fewer stations contributing to the grid box average compared to the case of a longer DLS (for a fixed station network). These fewer stations will be more representative of the local climate, compared to the case where stations at great distance from the grid box form part of the weighted average.

Fewer stations results also in less smoothing, but in turn makes the values more dependent on each of the contributing stations, and so more variable, both over time and space (compare Rx1day and R10mm in Figure 9). Despite a larger number of precipitation stations than temperature stations being used in HadEX3, the smaller DLS does mean the spatial coverage is much reduced.

Lastly, this method does not appear to cope well when changes in the station network result in sudden interpolation over large distances, despite efforts to use a stable network over time. Future work will look into alternative gridding schemes for these ETCCDI indices to create global datasets, as these datasets will still be needed to link other datasets (reanalyses and historical model simulations) to an observational reference, as well as for other applications.

6. Summary

We have compared the latest version of a dataset of observation-based, gridded temperature and precipitation extremes indices (HadEX3), to indices calculated from six of the latest dynamical reanalysis datasets. In this work we showed results of temporal and spatial comparisons from a subset of these indices, with results for all indices available in the Supplementary material.

The temporal agreement between many of the reanalysis datasets and HadEX3 across almost all temperature indices is very good for the coverage-matched global averages. Both the inter-annual variation and long-term changes seen in the time series of HadEX3 are clearly captured in these reanalyses. However, there is a spread in the range of absolute values for most of the indices, and hence conclusions drawn from a single product may over- or underestimate the magnitude of the extreme events captured. Both NCEP and CFSR show inhomogeneities at the end of their record in the temperature indices, of around 3°C for 2017–2018 for NCEP and 0.75°C for 2011–2018 for CFSR.

There is also good agreement demonstrated for many of the ETCCDI indices by a spatial rank correlation and clustering of the datasets around HadEX3 in a Taylor diagram. Spatial agreement is assessed using maps of correlation and integrated quadratic distance (IQD) between the cumulative distributions, on a grid box level. For the temperature indices, the temporal correlations are high overall (r>0.8), but regions of lower correlations can be seen in regions with low station densities. The IQD also highlights regions with low station densities and locations where the spatial interpolation in HadEX3 has not been able to account for regional features in the underlying climate (e.g., in high altitude regions).

A lower level of temporal agreement is found for the precipitation indices, which on the whole show stronger year-to-year variability than large long-term changes, which is unsurprising as the spatial pattern of trends is inhomogeneous compared to those from the temperature indices. However there are indications that the short-timescale variability in the global averages is captured by some of the reanalyses in some cases. Again, many indices show a spread in their absolute values, and the use of multiple products will help in demonstrating the spread in the underlying precipitation values for regional and global assessments.

The high spatial variation in the long-term trends leads to lower correlations for some indices (e.g., Rx1day), but in others there are large, contiguous regions of high correlation values (e.g., R10mm). Interpreting the IQD for the precipitation indices is made more complex because of the large range in values of these indices.

Regions which show poorer agreement are sometimes areas with relatively few or no stations, next to or in between areas with a dense station network, especially for the temperature indices. The HadEX3 infilling routine, especially for the temperature indices where a long decorrelation length scale is used, interpolates from the high station density region to regions of low density. If the low density region has a very different climate (e.g., deserts, high altitude regions), the infilling routine is unable to capture this change accurately.

HadEX3 and its predecessors were always intended for the monitoring of extremes on a global or continental scale. The use of the extremes indices allowed the sharing of information on temperature and precipitation extremes at a time when studies were limited by data availability. As can be seen in the global time series for the temperature indices, the agreement of HadEX3 and many of the reanalyses in year-to-year and long term changes suggests that both types of datasets are useful for this kind of assessment. Furthermore, the close agreement between the coverage-matched and full reanalysis fields shows that even with data gaps, HadEX3 provides a good estimate of the global changes for these indices. This supports with the coverage uncertainty presented in Dunn et al. (2020a) which is not large in comparison to the magnitude of the long-term global trend in the temperature indices.

As we have shown in this study, both HadEX3 and the reanalysis datasets are useful when investigating the behavior of the ETCCDI extremes indices. For the temperature indices, almost all of the datasets agree with each other in most areas, but we have also identified issues with some of the modern reanalyses. Reanalyses have the advantage that they have complete global coverage, but HadEX3 has a longer record and is more closely linked to the observations. For the precipitation indices it depends on the index, with those assessing more moderate extremes or for longer accumulation periods agreeing better.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found at: https://www.metoffice.gov.uk/hadobs/hadex3; https://www.climdex.org/learn/datasets; https://psl.noaa.gov/data/gridded/data.20thC_ReanV3.monolevel.html; https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form; https://jra.kishou.go.jp/JRA-55/index_en.html; https://psl.noaa.gov/data/gridded/data.ncep.reanalysis2.gaussian.html; https://doi.org/10.5065/D69K487J; https://doi.org/10.5065/D61C1TXF.

Author contributions

RD developed the code and performed the analyses and wrote the initial draft of the manuscript. MD and LA suggested extensions for the analyses and guided the analyses. All authors contributed to the final version of the article.

Funding

RD was supported by the Hadley Centre Climate Programme funded by BEIS and the UK-China Research & Innovation Partnership Fund through the Met Office Climate Science for Service Partnership (CSSP) China as part of the Newton Fund. LA was supported by the Australian Research Council (ARC) Centre of Excellence for Climate Extremes (CE170100023).

Acknowledgments

We thank Nick Rayner, Lizzie Good, and John Kennedy for helpful comments on earlier drafts of this manuscript. The Python code for the Taylor diagrams was adapted from Yannick Copin's code at: https://gist.github.com/ycopin/3342888, doi:10.5281/zenodo.5548061.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2022.989505/full#supplementary-material

References

Alexander, L. V., Bador, M., Roca, R., Contractor, S., Donat, M. G., and Nguyen, P. L. (2020). Intercomparison of annual precipitation indices and extremes over global land areas from in situ, space-based and reanalysis products. Environ. Res. Lett. 15:055002. doi: 10.1088/1748-9326/ab79e2

CrossRef Full Text | Google Scholar

Alexander, L. V., Zhang, X., Peterson, T. C., Caesar, J., Gleason, B., Klein Tank, A. M. G., et al. (2006). Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 111. doi: 10.1029/2005JD006290

CrossRef Full Text | Google Scholar

Avila, F. B., Dong, S., Menang, K. P., Rajczak, J., Renom, M., Donat, M. G., et al. (2015). Systematic investigation of gridding-related scaling effects on annual statistics of daily temperature and precipitation maxima: a case study for south-east Australia. Weath. Clim. Extremes 9, 6–16. doi: 10.1016/j.wace.2015.06.003

CrossRef Full Text | Google Scholar

Bell, B., Hersbach, H., Simmons, A., Berrisford, P., Dahlgren, P., Horányi, A., et al. (2021). The ERA5 global reanalysis: Preliminary extension to 1950. Q. J. R. Meteorol. Soc. 147, 4186–4227. doi: 10.1002/qj.4174

CrossRef Full Text | Google Scholar

Brohan, P., Kennedy, J. J., Harris, I., Tett, S. F., and Jones, P. D. (2006). Uncertainty estimates in regional and global observed temperature changes: a new data set from 1850. J. Geophys. Res. 111. doi: 10.1029/2005JD006548

CrossRef Full Text | Google Scholar

Caesar, J., Alexander, L., and Vose, R. (2006). Large-scale changes in observed daily maximum and minimum temperatures: creation and analysis of a new gridded data set. J. Geophys. Res. 111:D05101. doi: 10.1029/2005JD006280

CrossRef Full Text | Google Scholar

Contractor, S., Alexander, L. V., Donat, M. G., and Herold, N. (2015). How well do gridded datasets of observed daily precipitation compare over Australia? Adv. Meteorol. 2015:325718. doi: 10.1155/2015/325718

CrossRef Full Text | Google Scholar

Dee, D. P., Källén, E., Simmons, A. J., and Haimberger, L. (01 Jan. 2011). Comments on “reanalyses suitable for characterizing long-term trends”. Bull. Am. Meteorol. Soc. 92, 65–70. doi: 10.1175/2010BAMS3070.1

CrossRef Full Text | Google Scholar

Donat, M. G., Alexander, L. V., Herold, N., and Dittus, A. J. (2016). Temperature and precipitation extremes in century-long gridded observations, reanalyses, and atmospheric model simulations. J. Geophys. Res. 121, 11,174–11,189. doi: 10.1002/2016JD025480

CrossRef Full Text | Google Scholar

Donat, M. G., Alexander, L. V., Yang, H., Durre, I., Vose, R., and Caesar, J. (2013a). Global land-based datasets for monitoring climatic extremes. Bull. Am. Meteorol. Soc. 94, 997–1006. doi: 10.1175/BAMS-D-12-00109.1

CrossRef Full Text | Google Scholar

Donat, M. G., Alexander, L. V., Yang, H., Durre, I., Vose, R., Dunn, R. J. H., et al. (2013b). Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: the hadex2 dataset. J. Geophys. Res. 118, 2098–2118. doi: 10.1002/jgrd.50150

CrossRef Full Text | Google Scholar

Donat, M. G., Sillmann, J., Wild, S., Alexander, L. V., Lippmann, T., and Zwiers, F. W. (2014). Consistency of temperature and precipitation extremes across various global gridded in situ and reanalysis datasets. J. Clim. 27, 5019–5035. doi: 10.1175/JCLI-D-13-00405.1

CrossRef Full Text | Google Scholar

Dunn, R. J. H., Alexander, L. V., Donat, M. G., Zhang, X., Bador, M., Herold, N., et al. (2020a). Development of an updated global land in situ-based data set of temperature and precipitation extremes: Hadex3. J. Geophys. Res. 125:e2019JD032263. doi: 10.1029/2019JD032263

CrossRef Full Text | Google Scholar

Dunn, R. J. H., Perkins-Kirkpatrick, S., Schlegel, R. W., and Donat, M. G. (2020b). Temperature extremes in [“state of the climate in 2019”]. Bull. Am. Meteorol. Soc. 101, S28—S30. doi: 10.1175/BAMS-D-20-0104.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunn, R. J. H., Schlegel, R. W., Donat, M. G., and Perkins-Kirkpatrick, S. (2022). Temperature extremes in [“state of the climate in 2021”]. Bull. Am. Meteorol. Soc. 103, S23–S26. doi: 10.1175/BAMS-D-22-0092.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Funk, C., Peterson, P., Peterson, S., Shukla, S., Davenport, F., Michaelsen, J., et al. (2019). A high-resolution 1983-2016 t max climate data record based on infrared temperatures and stations by the climate hazard center. J. Clim. 32, 5639–5658. doi: 10.1175/JCLI-D-18-0698.1

CrossRef Full Text | Google Scholar

Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., et al. (2017). The modern-Era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 30, 5419–5454. doi: 10.1175/JCLI-D-16-0758.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, I., Jones, P. D., Osborn, T. J., and Lister, D. H. (2014). Updated high-resolution grids of monthly climatic observations-the CRU TS3. 10 dataset. Int. J. Climatol. 34, 623–642. doi: 10.1002/joc.3711

CrossRef Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Horányi, A., Sabater, J., Nicolas, J., et al. (2019). Global reanalysis: goodbye era-interim, hello Era5. ECMWF Newsl. 159, 17–24.

Google Scholar

Jones, P. D., and Moberg, A. (2003). Hemispheric and large-scale surface air temperature variations: an extensive revision and an update to 2001. J. Clim. 16, 206–223. doi: 10.1175/1520-0442(2003)016<0206:HALSSA>2.0.CO;2

CrossRef Full Text | Google Scholar

Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., et al. (1996). The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–472. doi: 10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2

CrossRef Full Text | Google Scholar

Kanamitsu, M., Ebisuzaki, W., Woollen, J., Yang, S.-K., Hnilo, J., Fiorino, M., et al. (2002). NCEP-DOE AMIP-II reanalysis (R-2). Bull. Am. Meteorol. Soc. 83, 1631–1644. doi: 10.1175/BAMS-83-11-1631

CrossRef Full Text | Google Scholar

Kistler, R., Kalnay, E., Collins, W., Saha, S., White, G., Woollen, J., et al. (2001). The NCEP-NCAR 50-year reanalysis: monthly means CD-ROM and documentation. Bull. Am. Meteorol. Soc. 82, 247–268. doi: 10.1175/1520-0477(2001)082<0247:TNNYRM>2.3.CO;2

CrossRef Full Text | Google Scholar

Kobayashi, S., Ota, Y., Harada, Y., Ebita, A., Moriya, M., Onoda, H., et al. (2015). The JRA-55 reanalysis: general specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 93, 5–48. doi: 10.2151/jmsj.2015-001

CrossRef Full Text | Google Scholar

Lanzante, J. R. (1996). Resistant, robust and non-parametric techniques for the analysis of climate data: theory and examples, including applications to historical radiosonde station data. Int. J. Climatol. 16, 1197–1226. doi: 10.1002/(SICI)1097-0088(199611)16:11<1197::AID-JOC89>3.0.CO;2-L

CrossRef Full Text | Google Scholar

Met Office (2010–2022). Iris: A Python Library for Analysing and Visualising Meteorological and Oceanographic Data Sets. Exeter: Met Office.

Google Scholar

New, M., Hulme, M., and Jones, P. (2000). Representing twentieth-century space-time climate variability. Part ii: Development of 1901-96 monthly grids of terrestrial surface climate. J. Clim. 13, 2217–2238. doi: 10.1175/1520-0442(2000)013<2217:RTCSTC>2.0.CO;2

CrossRef Full Text | Google Scholar

Perkins-Kirkpatrick, S., Dunn, R. J. H., Donat, M. G., Schlegel, R. W., and Bosilovich, M. G. (2021). Temperature extremes in [“state of the climate in 2020”]. Bull. Am. Meteorol. Soc. 102, S31–S34. doi: 10.1175/BAMS-D-21-0098.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Saha, S., Moorthi, S., Pan, H.-L., Wu, X., Wang, J., Nadiga, S., et al. (2010). The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 91, 1015–1058. doi: 10.1175/2010BAMS3001.1

CrossRef Full Text | Google Scholar

Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., et al. (2014). The NCEP climate forecast system version 2. J. Clim. 27, 2185–2208. doi: 10.1175/JCLI-D-12-00823.1

CrossRef Full Text | Google Scholar

Sen, P. K. (1968). Estimates of the regression coefficient based on Kendall's tau. J. Am. Stat. Assoc. 63, 1379–1389. doi: 10.1080/01621459.1968.10480934s

PubMed Abstract | CrossRef Full Text | Google Scholar

Shepard, D. (1968). “A two-dimensional interpolation function for irregularly-spaced data,” in Proceedings of the 1968 23rd ACM National Conference, 517–524. doi: 10.1145/800186.810616

CrossRef Full Text | Google Scholar

Slivinski, L. C., Compo, G. P., Whitaker, J. S., Sardeshmukh, P. D., Giese, B. S., McColl, C., et al. (2019). Towards a more reliable historical reanalysis: Improvements for version 3 of the twentieth century reanalysis system. Q. J. R. Meteorol. Soc. 145, 2876–2908. doi: 10.1002/qj.3598

CrossRef Full Text | Google Scholar

Taylor, K. E. (2001). Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 106, 7183–7192. doi: 10.1029/2000JD900719

CrossRef Full Text | Google Scholar

Thiel, H. (1950). “A rank-invariant method of linear and polynomial regression analysis, parts 1-3,” in Proceedings of Koninalijke Nederlandse Akademie van Weinenschatpen A, Vol. 53 (Amsterdam) 386–392, 521–525, 1397–1412.

Google Scholar

Thorarinsdottir, T. L., Gneiting, T., and Gissibl, N. (2013). Using proper divergence functions to evaluate climate models. SIAM/ASA J. Uncertain. Quant. 1, 522–534. doi: 10.1137/130907550

CrossRef Full Text | Google Scholar

Thorarinsdottir, T. L., Sillmann, J., Haugen, M., Gissibl, N., and Sandstad, M. (2020). Evaluation of CMIP5 and CMIP6 simulations of historical surface air temperature extremes using proper evaluation methods. Environ. Res. Lett. 15:124041. doi: 10.1088/1748-9326/abc778

CrossRef Full Text | Google Scholar

Thorne, P. W., Allan, R. J., Ashcroft, L., Brohan, P., Dunn, R. J. H., Menne, M. J., et al. (2017). Toward an integrated set of surface meteorological observations for climate science and applications. Bull. Am. Meteorol. Soc. 98, 2689–2702. doi: 10.1175/BAMS-D-16-0165.1

CrossRef Full Text | Google Scholar

Van Rossum, G., and Drake, F. L. (2009). Python 3 Reference Manual. Scotts Valley, CA: CreateSpace.

Google Scholar

Verdin, A., Funk, C., Peterson, P., Landsfeld, M., Tuholske, C., and Grace, K. (2020). Development and validation of the CHIRTS-daily quasi-global high-resolution daily temperature data set. Sci. Data 7, 1–14. doi: 10.1038/s41597-020-00643-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Alexander, L., Hegerl, G. C., Jones, P., Tank, A. K., Peterson, T. C., et al. (2011). Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. 2, 851–870. doi: 10.1002/wcc.147

CrossRef Full Text | Google Scholar

Appendix

Figure A1 shows the globally averaged time series of the maximum and minimum temperature from NCEP2, with the inhomogeneity in the last few years clearly visible.

FIGURE A1

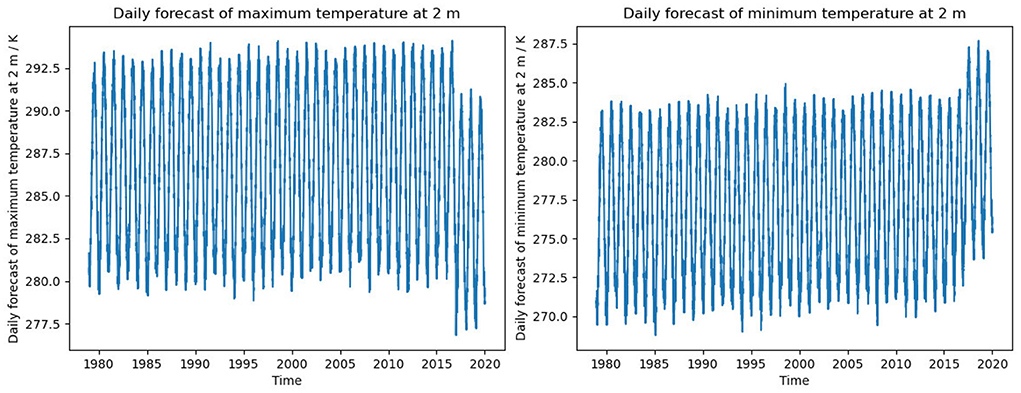
Figure A1. Globally averaged land-surface time series of maximum and minimum temperature from NCEP2.

In Figure A2, we show plots of the cumulative probability distribution of HadEX3 and selected reanalyses for selected individual grid boxes. The selected reanalyses and layout matches Figures 5, 10, respectively. The locations of the grid boxes are stated on the panels, and also marked with a small blue cross in Figures 5, 10.

FIGURE A2

Figure A2. Cumulative probability distributions for HadEX3 and four selected reanalyses for selected individual grid boxes, showing the area defined by the IQD measure. The rows show TXn, TNx, Rx1day, and R10mm, respectively.