Enhanced weathering potentials—the role of in situ CO2 and grain size distribution

The application of rock powder on agricultural land to ameliorate soils and remove carbon dioxide (CO₂) from the air by chemical weathering is still subject to many uncertainties. To elucidate the effects of grain size distribution and soil partial pressure of carbon dioxide (pCO₂) levels on CO₂ uptake rates, two simple column experiments were designed and filled nearly daily with an amount of water that simulates humid tropical conditions, which prevail in areas known for being hotspots of weathering. Multiple materials (dunite, basanite, agricultural oxisol, a combination of the latter two, and loess) were compared under ambient and 100% CO₂ atmosphere. In a second series, single material columns (dunite) were filled with three different grain size distributions. Total alkalinity, pH, major ions, and dissolved silica were determined in the outflow water of the columns for about 300 days. Under ambient atmospheric conditions, the CO₂ consumption was the lowest in the oxisol column, with 100 t CO₂ km⁻² year⁻¹, while dunite and basanite showed similar consumption rates (around 220 t CO₂ km⁻² year⁻¹). The values are comparable to high literature values for ultramafic lithologies. Interestingly, the mixture of basanite and oxisol has a much higher consumption rate (around 430 t CO₂ km⁻² year⁻¹) than the basanite alone. The weathering fluxes under saturated CO₂ conditions are about four times higher in all columns, except the dunite column, where fluxes are increased by a factor of more than eleven. Grain size distribution differences also play a role, with the highest grain surface area normalized weathering rates observed in the columns with coarser grains, which at first seems counterintuitive. Our findings point to some important issues to be considered in future experiments and a potential rollout of EW as a carbon dioxide removal method. Only in theory do small grain sizes of the spread-material yield higher CO₂ drawdown potentials than coarser material. The hydrologic conditions, which determine the residence times in the pore space, i.e., the time available for weathering reactions, can be more important than small grain size. Saturated-CO₂ column results provide an upper limit for weathering rates under elevated CO₂.

Introduction

Chemical weathering of silicate rocks exposed to meteoric water is a process that removes carbon dioxide (CO₂) from the atmosphere (Ebelmen, 1845). To counteract rising CO₂ levels by removal of CO₂ from the atmosphere, the use of rock products was briefly proposed by Seifritz (1990) and made popular in the climate science community as Enhanced Weathering (EW) by Schuiling and Krijgsman (2006). Since then, assessing the realistic potential of EW as a tool for carbon dioxide removal (CDR) has become the focus of literature reviews (Hartmann et al., 2013) and modeling studies (e.g., Hartmann and Kempe, 2008; Hartmann et al., 2013; Taylor et al., 2015; Beerling et al., 2018; Strefler et al., 2018a). However, these studies have relied on several assumptions for the parameterization of the weathering process. Moreover, robust experimental data are still missing, aside from a few laboratories (Renforth et al., 2015), mesocosm (ten Berge et al., 2012; Dietzen et al., 2018; Amann et al., 2020; Kelland et al., 2020; Vienne et al., 2022), and field trials (Haque et al., 2020).

In addition to CDR, the application of rock products has also been thought to improve soil conditions (via fertilization and physical amelioration effects), thereby increasing agricultural production (Julius, 1894; Leonardos et al., 1987; van Straaten, 2002). The resulting increase in biomass growth leads to additional CO₂ uptake and storage as organic carbon, thereby augmenting the overall CDR potential of EW.

The sensitivity of weathering reactions to CO₂ concentrations in a system, i.e., the magnitude of chemical weathering effects from CO₂ concentration changes, has implications for estimates of weathering rates of EW applications, and therefore CO₂ removal. The parameterization of Earth system models targeting long time scales relies on, for example, realistic assumptions of the CO₂ and related climate sensitivity (e.g., Royer et al., 2007). In general, the sensitivity of weathering rates to CO₂ levels also has consequences for the evolution of the atmospheres on other planets and is important for, e.g., habitability assessments for early Mars (Teitler et al., 2014; Cockell et al., 2016; Foley and Smye, 2018).

Small grain sizes (i.e., with high surface areas) are favorable for fast reaction rates in the system, but the comminution of rock to fine grain sizes implies energy costs that may render EW less attractive. Thus, an ideal grain size range that balances these two constraint needs must be defined for different types of source material and soil targets. This energy constraint may not be relevant if side products from the mining process, often deposited as fines, are used.

To address these issues, column experiments were set up to better understand the effects of the grain size distribution (also referred to as particle size distribution) and partial pressure of CO₂ in soils with respect to CO₂ uptake rates, these being important controls on weathering rates in the field, and thus the overall CDR potential. One of the objectives of this study was therefore to test realistic upper limits of weathering rates and CDR potential considering CO₂ levels as the primary driver of weathering rates.

To explore the CO₂ effect, different materials were treated under humid tropical conditions, typical for weathering hotspots, with two soil CO₂ conditions, ambient (0.046%) and saturated (100%) CO₂, where the latter is an upper limit for this parameter, which is of course not realized in soils. Four rock types were used: dunite, basanite, laterite, and loess. Olivine-rich dunite was selected as a chemically simple model rock type that is primarily composed of olivine, while basaltoids (like the basanite used here) were proposed as a more suitable rock type for EW (Hartmann et al., 2013; Amann and Hartmann, 2019) that is widely available (Börker, 2019). Laterite or oxisol was included as a representative of typically abundant soil types associated with weathering hotspots in humid tropical regions. As a commonly proposed EW substrate, this laterite was used in pure form and as a laterite-basanite mixture. The last material type is loess sediment from aeolian deposits—these can be considered a natural analog for EW. The effect of grain sizes and their distribution was tested using the dunite with three different grain size distributions under fixed ambient CO₂ conditions.

Methods

Material origin and characterization

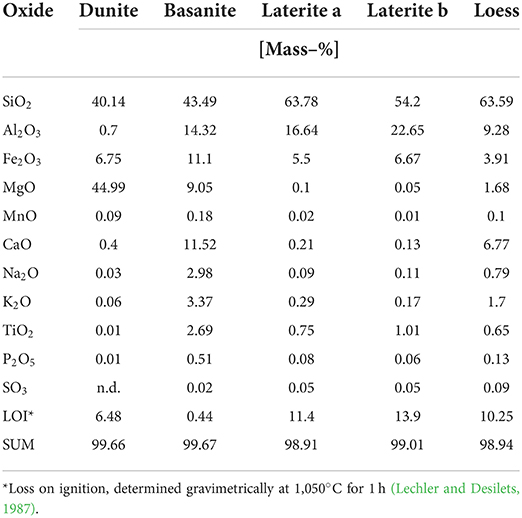
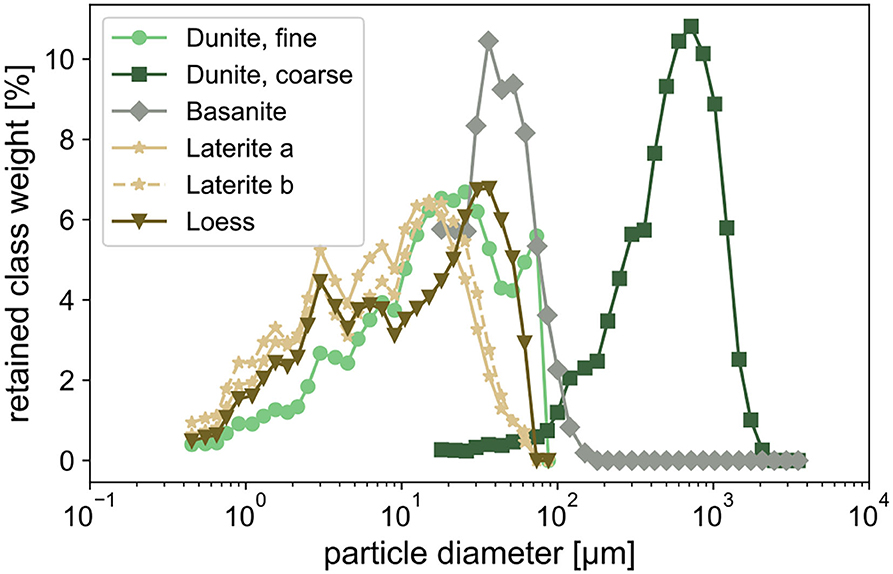
Materials used in the experiments were dunite, basanite, laterite, a basanite-laterite mix, and loess. The bulk chemical composition of all materials (Table 1) was determined by Panalytical Magix Pro wavelength dispersive X-ray fluorescence (XRF) analysis. Specific surface areas (Table 2) were measured by BET analyses using Kr adsorption (Brunauer et al., 1938) with a Quantachrome autosorb iQ. Particle size characteristics (Table 2, Figure 1) were determined using Sympatec Helos KFMagic laser granulometry coupled to a Quixel wet dispersing unit, covering a range of 0.5/18–3,200 μm.

TABLE 1

Table 1. Geochemical analysis of the source material.

TABLE 2

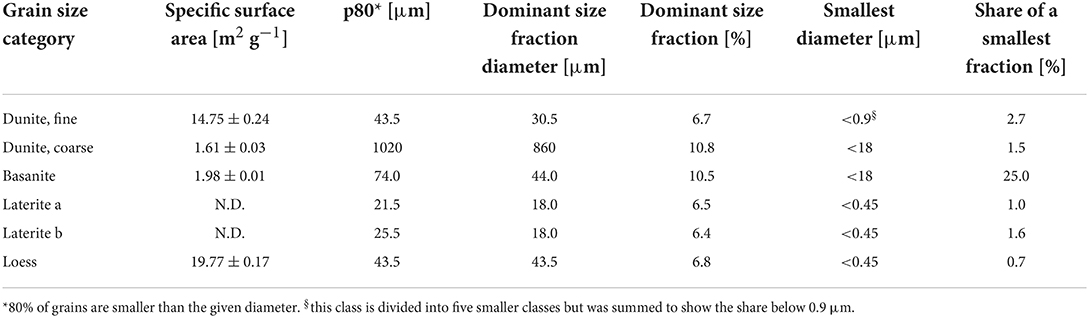
Table 2. Specific surface areas of the source material, derived by BET analyses, as well as grain size distribution characteristics.

FIGURE 1

Figure 1. Grain size distribution of the applied material.

Dunite

The dunite rock used here, also deployed in Amann et al. (2020), contains ~93% forsterite (Mg-endmember olivine, Mg₂SiO₄). The other 7% are comprised of lizardite (Mg-rich serpentine), Cr-bearing chlorite (including chromite or chrome-spinel inclusions), and traces of chabazite (zeolite group) and Mg-hornblende (amphibole). The mineralogical composition was determined by energy-dispersive X-ray spectroscopy (Zeiss LEO 1455 VP coupled with an Oxford Instruments EDX detector). The sample originates from the Almklovdalen peridotite complex (Åheim mineral deposit mined by the North Cape Minerals Company, Norway). More information on the geochemistry of the material can be found in Beyer (2006); Hövelmann et al. (2012) describes the geological setting. The material was provided in two-grain sizes, a fine and a coarse fraction (Figure 1).

Basanite (basaltoid)

The material used is a commercially available rock powder called Eifelgold, produced by Lava Union GmbH (https://www.rpbl.de) and sourced from the Eifel, a low mountain range in western Germany with notable volcanic rock occurrences. It was used in an “as delivered” condition with a grain size similar to the fine dunite, with 44 μm as the dominant grain size fraction (Figure 1). Based on the geochemical composition the calculated normative mineralogy (based on the CIPW norm by Cross et al. (1902) is diopside (32%), plagioclase (16%), leucite (15%), olivine (14%), nepheline (14%), and others (10%). Based on the modal mineralogical QAPF classification of volcanic rocks (Streckeisen, 1980) or the TAS classification (Le Bas et al., 1986), this nepheline-rich material is of basaltic composition, and more specifically, it is classified as basanite.

Laterite (oxisol/ultisol)

This material, received from coffee farmers through private contact, originates from the area of Conceição de Ipanema, Minas Gerais, Brazil. According to the USDA soil taxonomy (Soil Survey Staff, 1999), it can be considered to be oxisol or ultisol, yet a more detailed soil description is not available. We use the more generic term laterite here and chose this material based on its cation-depleted character and high iron and aluminum content. As this soil material comes from an actively used agricultural plot, it is known that some fertilizer had been applied to the soil, but more precise information on the fertilizer type and quantities used is not known. There are two types of laterite (Table 1), which were sampled at different locations of the same plot. One type was used for the pure laterite column experiments, and due to insufficient material, the second type was used for the basanite-laterite mix.

Loess

The loess material was freshly collected from a well-described Upper Pleistocene loess occurrence in Remagen, western Germany (50.5611°N, 7.2435°E; Klasen et al., 2015) during a field trip in 2017. It was dried at 40°C to remove moisture. The average CaCO₃ content is reported as 17–19%, depending on the formation (Schirmer, 2011).

Experimental setup

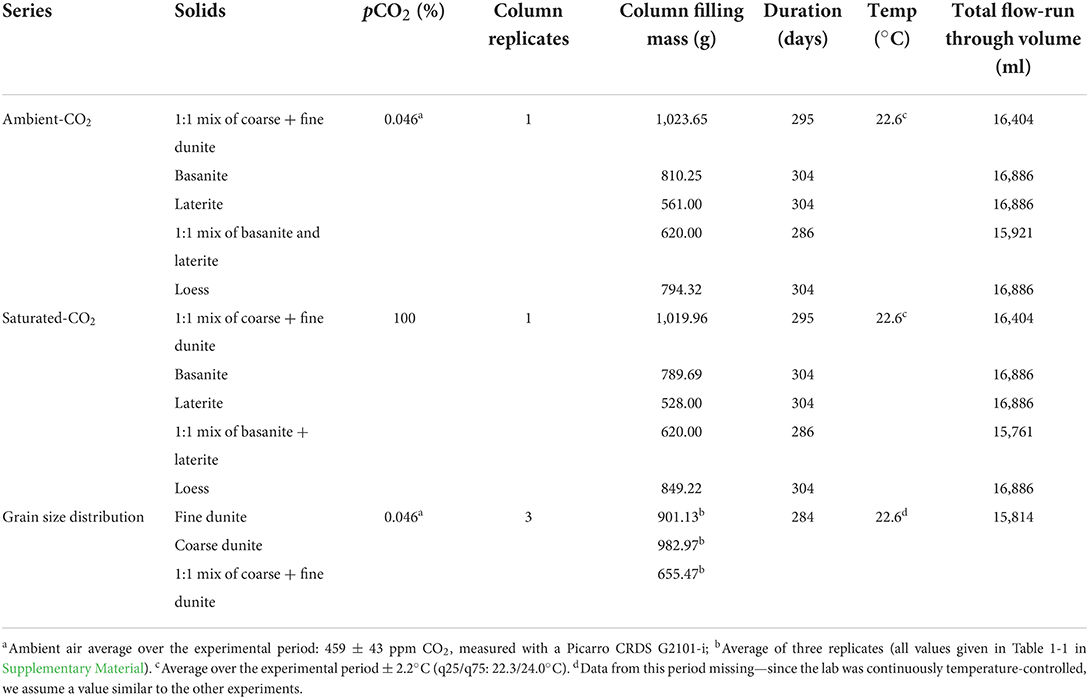
Acrylic cylindrical tubes (outer-ø/inner-ø/length: 60/56/250 mm) were filled with the untreated materials (Table 3) to a height of 20 cm while tapping the cylinder to gently settle the powder. All cylinders were fixed vertically using clamps and clamp stands (Figure 2). The top/inlet was covered to decrease water loss by evaporation. A 20-μm nylon mesh was fixed at the bottom of each column to allow water to pass through while retaining the fill material. The experiments were carried out in a temperature-regulated room at about 23°C (Table 3 for details) during the duration of each run. In total, 75 ml of deionized water was added (all at once) to each cylinder every morning, 5 days a week. This amounts to about 8,000 mm a⁻¹ (= 8 m³ m⁻² a⁻¹), to simulate intensive tropical rainfall (e.g., up to 10,000 mm a⁻¹ on La Réunion (Strasberg et al., 2005) or Hawai'i (Giambelluca et al., 2013). In contrast to these natural settings where a variable, but significant amount of water is surface runoff, water is forced through the column material in the experiments.

TABLE 3

Table 3. Experimental series and parameters.

FIGURE 2

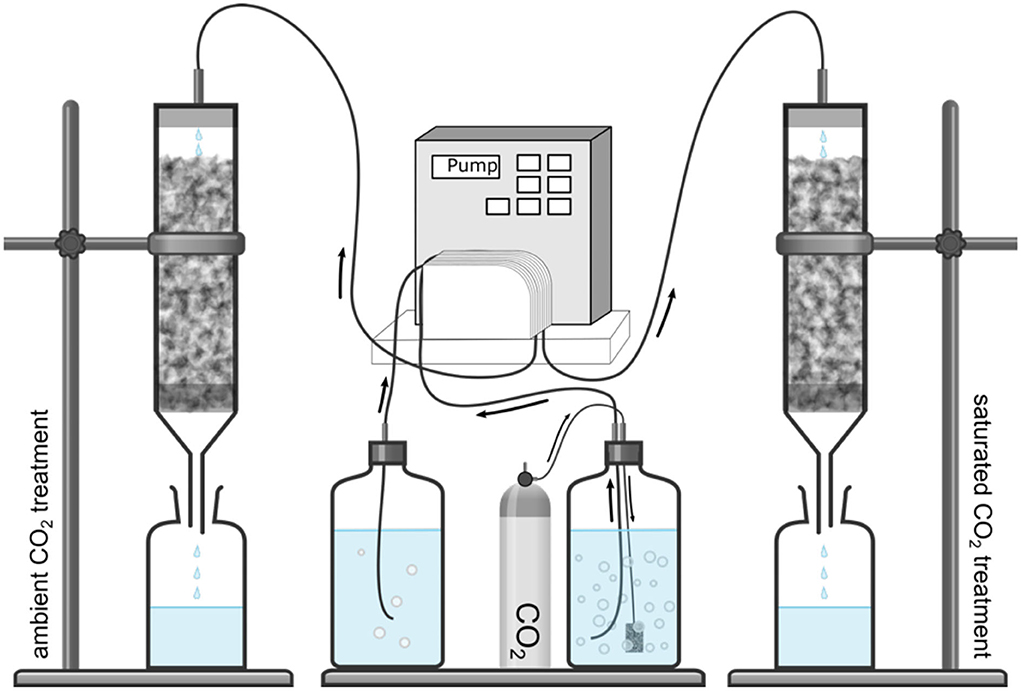
Figure 2. Experimental setup showing the semi-automated watering system for the CO₂ column experiment.

The effluent solution was collected in polyethylene (PE) bottles, and initially, collected and measured daily. The sampling frequency was then decreased in the later stages of the experiment when the fluid composition showed decreasing variability. The experiments ran for about 10 months (Table 3). Samples were not pooled over multiple watering events. It should be noted that each daily-collected fluid only represents the water that flowed through the column starting from the day before. The samples were stored in a cool and dark environment until analyses.

CO₂ experiment

One series of columns was treated with deionized water in equilibrium with ambient air. The saturated-CO₂ series used deionized water that was sparged with a pure CO₂ stream for 15 min before application. These columns were capped with a gas-tight cover.

Stock solutions had an average pH of 5.34 (5.58; note that all values in parentheses were calculated with PhreeqC) and an average electrical conductivity (EC) of 0.9 ± 0.6 μS cm⁻¹ (1.0) when in equilibrium with the ambient lab atmosphere. Under CO₂-saturated conditions, the average pH was 3.93 (3.91) and the average EC was 43.9 ± 5.6 μS cm⁻¹ (48.0).

Grain size experiment

This experiment was run with dunite (Table 3). Three replicates of three-grain size distributions were prepared: a coarse fraction, a fine fraction, and a 1:1 mix by mass of the two-grain size fractions. The mass of the dunite powder in each cylinder was subsequently measured.

Fluid composition analysis

The fluid effluent samples were measured for pH, alkalinity, dissolved silica, and major ion composition. Alkalinity was measured by automated titration to pH 4.3, using a Metrohm Titrando. The titration method determines total alkalinity (TA), defined by Dickson (1981) as:

$\begin{array}{l}TA=\left[HC{O}_3^{-}\right]+2\left[C{O}_3^{2-}\right]+\left[B{(OH)}_4^{-}\right]+\left[O{H}^{-}\right]\\ +\left[HP{O}_4^{2-}\right]+2\left[P{O}_4^{3-}\right]+\left[SiO{(OH)}_3^{-}\right]+\left[H{S}^{-}\right]\\ +2\left[S^{2-}\right]+\left[N{H}_3\right]-\left[H^{+}\right]-\left[HS{O}_4^{+}\right]-\left[HF\right]-\left[H_{3}P{O}_4\right]& (1)\end{array}$

Measurements were calibrated with certified references by A. Dickson (recovery ≥ 99%). Dissolved silica was measured using the molybdate blue colorimetric method (after Hansen and Koroleff, 1999). The average and standard deviation of the coefficients of variation from multiple measurements were 0.6 ± 0.8% for all measured samples. The major cations, Na⁺, K⁺, Ca²⁺, and Mg²⁺, were determined by ion chromatography (Metrohm 881 Compact IC Pro system). Measurements were considered valid when the standard recovery (done every ten samples) was ≥ 95%. The pH was measured using a WTW handheld pH meter calibrated with 3 buffer standards. The effluent solution was routinely sampled before new water was added, implying that the solution was in equilibrium with the atmosphere (time for equilibration was generally ~24 h).

Cation release

To estimate the total cation loss from the column material, data gaps in the obtained time series were approximated by linear interpolations between measured values. In the next step, daily fluxes of each major cation were summed over the entire experimental period. To derive the percentage loss of cations relative to the amount present in the initial fresh material, the following expression was employed:

$\begin{array}{ll}Cationloss(\%)=(1-\frac{n_{cat}-{\displaystyle {\sum }_{t=1}^{t_{max}}}Q(t)\times c_{cat}(t)}{n_{cat}})\times 100& (2)\end{array}$

here Q [L] is the solution outflux volume from the column per time step t [day] and c [mol L⁻¹] is the concentration of the considered cation. The moles of a given cation are initially present, n_cat [mol], can be calculated using this expression:

$\begin{array}{ll}{n}_{cat}=\frac{\left(m_{Ca{t}_{x}O}\times \frac{M_{Cat}}{\left(M_{Cat}+M_O\right)}\right)}{M_{Cat}}& (3)\end{array}$

where M_Cat and M_O are the molar mass of the given cation and oxygen, m_CatχO is the column-specific available mass [g] of the considered cation oxide (Cat_x%), as derived by XRF and found in Table 1:

$\begin{array}{ll}{m}_{Ca{t}_{x}O}=\frac{Ca{t}_x\%}{100}\times m_c& (4)\end{array}$

with m_c [g] being the initial mass of the solid material in the column.

Weathering rate calculations

TA release rate

To calculate the “average” instantaneous release rate of TA from a particular material, we used the following equation:

$\begin{array}{ll}{R}_{TA}=\frac{Q(t)\times c_{TA}(t)}{A_{TSA}\times \tau }& (5)\end{array}$

As is commonly the case, weathering or elemental release rates are typically reported in terms of moles per unit area of solid reactant per unit time (mol m⁻² s⁻¹). In the above equation, Q [L] is the solution outflux volume from the column per time step t, c [mol L⁻¹] is the concentration of total alkalinity (TA) at timestep t, A_TSA [m²] is the initial total surface area of the column material (which changes over time but is approximated here as being constant), and τ [s] is the residence time of the solution occupying the pore space of the material.

The total surface area is given by:

$\begin{array}{ll}{A}_{TSA}=m_c\times A_{SSA}& (6)\end{array}$

where m_c [g] is the material mass and A_SSA [m² g⁻¹] is the specific surface area.

The residence time is calculated by:

$\begin{array}{ll}\tau =\frac{V_p}{V_o(t)}\times t& (7)\end{array}$

with V_p as the calculated porespace within the column and V_o(t) is the volume of outflowing water per timestep t, with t being the length of each time step (sampling interval).

The pore space is derived from the density differences as:

$\begin{array}{ll}{V}_p=V_c-\frac{m_c}{{\rho }_s}& (8)\end{array}$

where ρ_s is the material-specific density [g m⁻³] and V_c [m³] is the volume of the empty column. Column mass and material density data are given in Supplementary Material 1.

Equation 5 is equivalent to the standard equation used to calculate mineral dissolution rates using mixed-flow reactors (e.g., Equation 2 in Hellmann, 1994). Nonetheless, the release rates based on Equation 5 provide what can be considered to be a ‘column-averaged' elemental release rate, which in all cases would be less than the corresponding rate based on the dissolution of the same amount of material in an MFR. The reason for this is that as the solution flows from top to bottom in a column, non-linear chemical gradients will develop along the column axis, such that the rate of dissolution of material at the top of the reactor will be higher than that at the bottom. For the purposes of this study, the use of an “average rate” should be an acceptable proxy.

Land surface-based CO₂ consumption rate (R_land)

Based on the weathering reactions for two common silicate minerals, forsterite:

$\begin{array}{l}\stackrel{Forsterite}{\overbrace{M{g}_{2}Si{O}_4}}+4C{O}_2+4H_{2}O\to 2M{g}^{2+}+4HC{O}_3^{-}+H_{4}Si{O}_4\\ \to 2MgC{O}_3\downarrow +Si{O}_2\downarrow +2C{O}_2\uparrow +4H_{2}O& (9)\end{array}$

or albite:

$\begin{array}{l}2\stackrel{Albite}{\overbrace{NaAlS{i}_3{O}_8}}+2C{O}_2+11H_{2}O\to 2N{a}^{+}+2HC{O}_3^{-}\\ +{4H}_{4}Si{O}_4+\stackrel{Kaolinite}{\overbrace{A{l}_{2}S{i}_2{O}_5{(OH)}_4}}\downarrow \to 2N{a}^{+}+2HC{O}_3^{-}\\ +4Si{O}_2\downarrow +8H_{2}O& (10)\end{array}$

we assume a 1:1 conversion of CO₂ into alkalinity in the second step of the reaction, which represents the initial weathering product, while the second steps in Equations 9 and 10 represent the long-term final stages of the reaction.

Based on this conversion, we use the TA concentrations together with outflow volumes to calculate a first-order estimate of land surface-based weathering rates, which are equal to the CO₂ consumption rates.

The annual CO₂ consumption is estimated based on average TA fluxes during the final stages of the experiments, based on the assumption that dynamic near-equilibrium conditions are representative of long-term fluxes. The values used were t > 225 days for dunite, t > 268 days for basanite-laterite, and t > 289 days for basanite, laterite, and loess experiments.

Individual, daily TA fluxes were calculated according to

$\begin{array}{ll}{F}_d=Q(t)\times c_{TA}(t)& (11)\end{array}$

based on the measured data for outfluxes Q(t) [L d⁻¹] and TA concentrations c_TA(t) [mol L⁻¹] from the aforementioned experiments and corresponding periods.

With these individual fluxes, an average annual CO₂ consumption (in t km⁻² a⁻¹) was calculated by

$\begin{array}{ll}{R}_{land}=\frac{\frac{1}{n}{\displaystyle {\sum }_{d=1}^n}{F}_d}{A_c}\times M_{C{O}_2}\times 365& (12)\end{array}$

where n is the number of available flux values, A_c is the cross-sectional surface area of the column, M_CO2 is the molar mass of CO₂, and the factor of 365 serves to convert daily to annual CO₂ uptake.

To evaluate the additional CO₂ uptake over the first year, which is characterized by non-equilibrium fluxes, a simplified approach was chosen. Since TA concentrations were not determined every day due to economic and time constraints, the available data were fitted to a non-linear function in order to derive an estimate of the TA fluxes over the course of the experiments (curve fits shown in Supplementary Material 2). Based on the fitting parameters, modeled daily TA concentrations were summed over 1 year:

$\begin{array}{ll}{R_{land}}_{year1}=\frac{{\displaystyle {\sum }_{d=1}^{365}}{F}_d}{A_c}\times M_{C{O}_2}& (13)\end{array}$

The additional CO₂ consumption in the first year is then simply calculated by

$\begin{array}{ll}{R}_{lan{d}_{add}}={{R_{land}}_{year1}-R}_{land}& (14)\end{array}$

Saturation indices

All saturation indices were calculated using the Python package PhreeqPython (Vitens, 2021), which is based on PhreeqC (Parkhurst and Appelo, 2013). Thermodynamic input was taken from the WATEQ4F database (Ball and Nordstrom, 1991). Calculations consider the major cation concentrations, dissolved silica, phosphate, alkalinity, pH, and temperature as input variables.

Results

CO₂ experiment

Total alkalinity and pH

All experiments show an immediate effect of watering after the start of each experiment, for both ambient CO₂ and saturated CO₂ conditions (Figure 3). There is an initial phase in which all materials show an immediate spike in TA concentration, followed by a slow exponential decrease, and then the attainment of a roughly linear relation characterized by slowly decreasing concentrations (Figures 3A,B). The weak linear (downward) trends remain, even during the final stages of each experiment, indicating that true steady-state conditions were not yet fully reached.

FIGURE 3

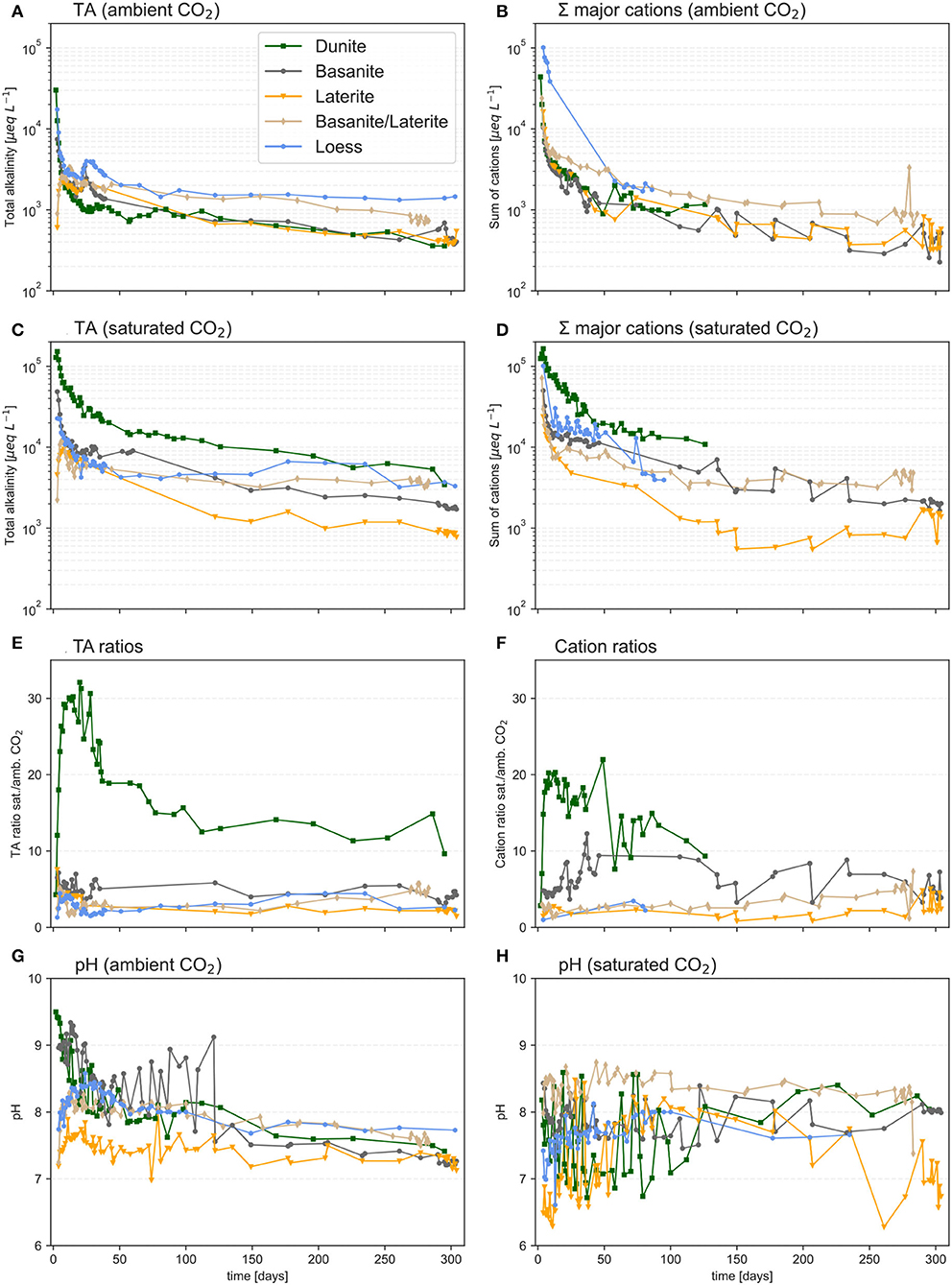
Figure 3. Development of TA, the sum of cation equivalent concentrations, and pH in the columns treated under ambient (A,B,G) and saturated (C,D,H) CO₂ conditions. The ratios of TA and total cations (CO_{2 saturated}/CO_{2 ambient}) are shown in (E,F). pH is given in (G,H), note the starting pH for water under ambient CO₂ was on average 5.34, while the starting pH under 100% CO₂ was on average 3.93.

Except for the first week, the highest TA concentrations under ambient CO₂ were observed for basanite, with values around 2,000 μmol L⁻¹ (Figure 3A), whereas under CO₂-saturated conditions, dunite showed the highest concentrations, with values starting >100,000 μmol L⁻¹, and then leveling out further on to around 10,000 μmol L⁻¹ (Figure 3C).

The strongest effect of CO₂ saturation on TA was observed for dunite, as evidenced by a TA ratio (CO₂-saturated/CO₂-ambient) equalling 15–30. The effect was less pronounced for the other materials, but all columns showed higher TA concentrations under saturated conditions (Figure 3E).

The pH measurements in the effluent solutions are quite scattered, but nonetheless, there is an overall trend of decreasing pH with time for CO₂-ambient conditions, which does not seem to be the case in saturated-CO₂ conditions. In general, it appears that higher pH values occurred during the first half of all experiments for CO₂-ambient conditions, but during the second half, the output pH values were slightly higher at saturated-CO₂ conditions (Figures 3G,H). The effluent pH values reflect in large part the significant differences in the starting pH values of the input solutions.

Cation release

The sum of cation equivalents released follows trends similar to those for TA (Figures 3B,D,F), in particular the sharp initial spike followed by an exponential decrease and then the attainment of a weak but negative linear relation (Figures 3B,D).

The relative loss of cations after the experimental period was generally higher under CO₂-saturated conditions in all materials (Table 4). The ratio between the losses at ambient and saturated CO₂ varies, depending on the cation and source material. On average, the loss ratio is 3.7 ± 3.8. The loss ratio of Mg is highest in the dunite column, where the presence of high CO₂ concentrations leads to a nearly 16× higher flux than under ambient-CO₂ conditions (Table 4). While the ratio is highest for Mg, it stands out that major cation losses from the dunite are dominated by monovalent K and Na. Also, basanite and basanite/laterite released relatively higher Na and K contents than Mg under saturated-CO₂ conditions (Table 4). Losses from the laterite are markedly high for Mg, Ca, and K. The loess column lost predominantly divalent cations.

TABLE 4

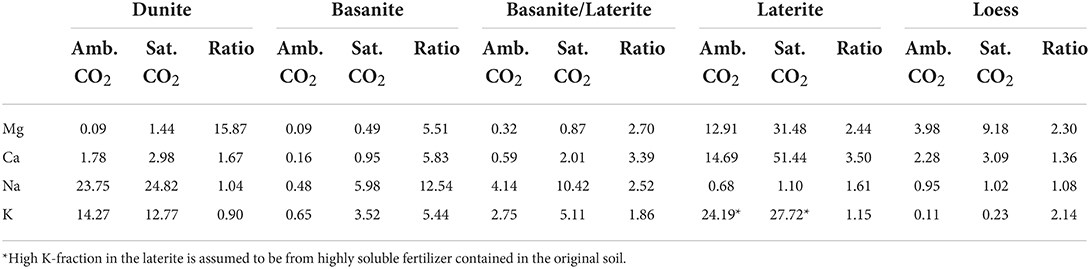
Table 4. Fraction of major cations (mole %) relative to the cation content of the fresh/unreacted column material released during the experiment phase. The resulting ratios between saturated and ambient CO₂ treatment can be interpreted as the maximum achievable ratios in the field since watering volumes were chosen to simulate tropical humid high precipitation rates with enhanced complete drainage.

The relative release of elements is not proportional to their content in the untreated substrates (Figure 4). The major cation release of dunite is dominated by Na and K, even though their abundance is only 1% in the dunite. The basanite columns predominantly show Mg release under saturated CO₂ conditions, but Ca, Na, and K contribute 35% under atmospheric conditions (Figure 4). Compared to the original material, laterite shows a pronounced release of K at ambient CO₂ and of Ca at saturated CO₂. The cation release from loess is proportionally larger for Mg at both CO₂ concentrations, while Na and K releases are very low compared to the original composition.

FIGURE 4

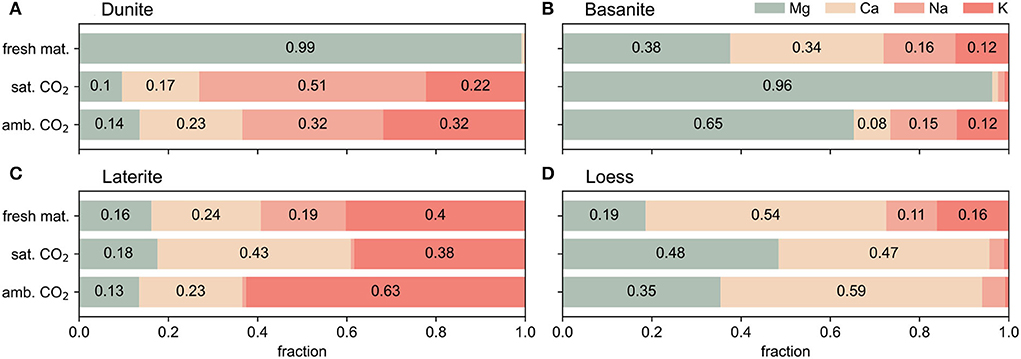
Figure 4. Relative fractions of major cations [from left to right: Mg (green), Ca (light orange), Na (light red), K (red)] in the original, unreacted material (see XRF analyses, Table 1) and the relative cumulative fractions of each cation released over the 300-day reaction time under ambient and saturated-CO₂ conditions. (A) Dunite, (B) Basanite, (C) Laterite, (D) Loess.

Grain size

This series of experiments was designed to shed light on the effects of grain sizes (their distribution and specific surface area) on weathering rates and ion fluxes using dunite. Columns with smaller grain sizes resulted in higher Mg, TA, and effluent pH (Figure 5). The mixed granulometry results approximated those of the fine grain size rather than the coarse grains. Results for Mg (Figure 5B) and TA concentrations (Figure 5C) show similar trends, as was the case for dunite under ambient CO₂ in the CO₂ experimental series (Figures 3A,C). The effluent pH trends are very similar to TA and show a sharp initial spike, and then an exponential decrease to values of ~8 (Figure 5D). Si concentrations do not follow the generally observed trends of TA, Mg, and pH (Figure 5A). Dissolved silica concentrations are very low (<90 μmol L⁻¹, Figure 5A) in comparison to the released magnesium (>1,500 μmol L⁻¹). Moreover, Si release showed very similar trends for the three-grain sizes, with the mixed case showing three anomalous concentration excursions of unknown origin (Figure 5B). Si values generally fluctuate between 5 and 20 μmol L⁻¹, with four outliers.

FIGURE 5

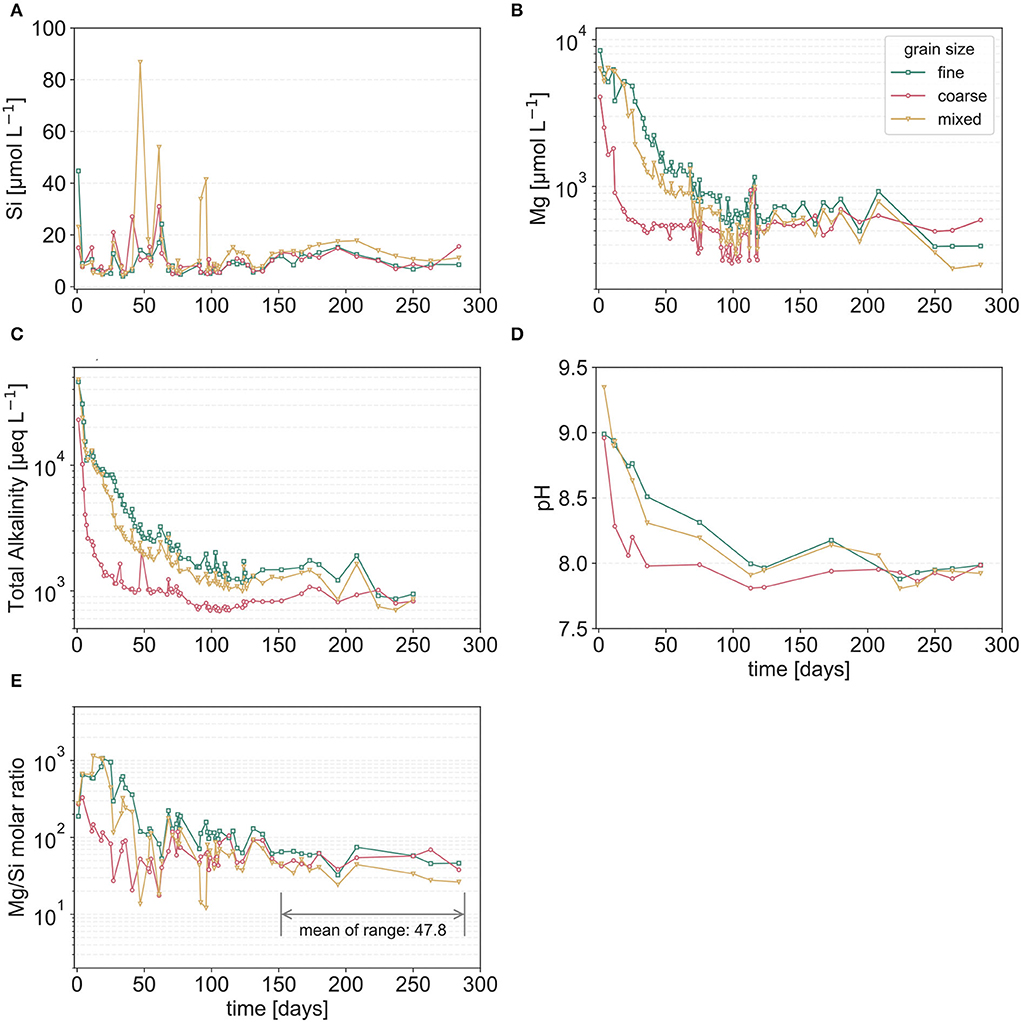
Figure 5. Temporal evolution of averaged dissolved silica [Si, (A)], magnesium [Mg, (B)], total alkalinity [TA, (C)] concentrations, and pH (D) in the outflow of the columns filled with dunite of different grain size distributions under ambient CO₂ conditions. (E) Evolution of the Mg/Si molar ratio; here the y-axis minimum was chosen to represent the nominal ratio of Mg/Si in olivine, i.e., congruent dissolution (Mg₂SiO₄ → 2:1), Note that during the final period, values are far higher than 2, indicating a non-stoichiometric alteration process. All the data are differentiated by fine (green squares), coarse (red circles), and mixed (yellow triangles) grain sizes.

The Mg/Si molar ratios are always well above the theoretical value of 2 (Figure 5E), with values >100 at the beginning and an average long-term average of 47.8. The mechanism responsible for this non-stoichiometry can (in theory) result from either preferential Mg release, or preferential Si retention, and can only be elucidated with nanometer-scale solid-state surface analyses (e.g., Hellmann et al., 2012, 2021; Zandanel et al., 2022).

Annual CO₂ sequestration based on TA fluxes

The initial period spanning the first few weeks showed substantially elevated TA concentrations (Figures 3, 5), which in turn corresponded to initially higher land surface-based release rates. Over significantly longer time periods (up to 1 year) the TA concentrations, and consequently the CO₂ removal rates, decreased until a baseline characterized by a more constant behavior was reached, which can be considered to be representative of the first year (Figure 6). These lower, but constant weathering rates show that, under ambient-CO₂ conditions, CO₂ consumption is highest in the loess column and lowest in the laterite column, with 730 and 100 t CO₂ km⁻² a⁻¹, respectively (Figure 6A). Dunite (all-grain sizes under ambient CO₂) and basanite have similar consumption rates (around 220 t CO₂ km⁻² a⁻¹). These values are comparable to the plotted literature values for ultramafic lithologies (Figure 6A). The mix of basanite and laterite has a much higher consumption rate (around 430 t CO₂ km⁻² a⁻¹) compared to the basanite alone. If the initial intensive weathering period is considered representative of the first year, CO₂ consumption rates are significantly higher in all ambient-CO₂ experiments (by 20–250%). The CO₂-saturated experiments show higher CO₂ consumption rates (Figure 6B), compared to the ambient CO₂ treatment by roughly a factor of four for the basanite, laterite, and basanite/laterite, but around 11 for the dunite column, excluding the initial flushing phase (Figure 6C).

FIGURE 6

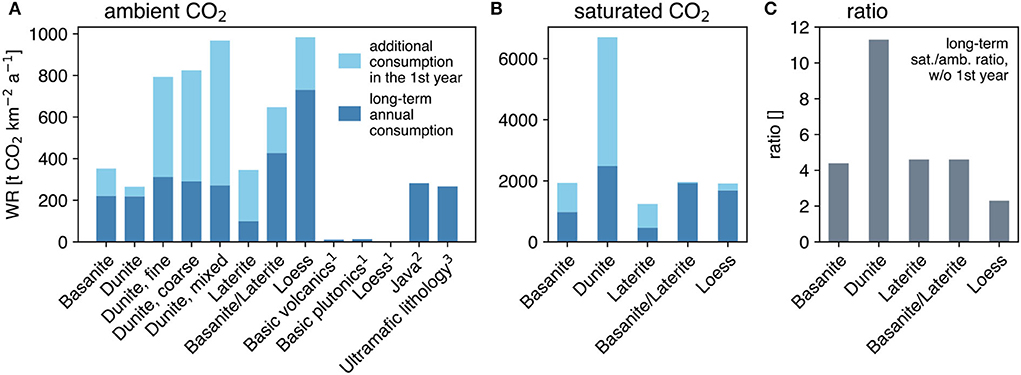
Figure 6. The long-term annual CO₂ consumption normalized to land surface area in t CO₂ km⁻² a⁻¹ under ambient-CO₂ (A) and saturated-CO₂ conditions (B). The light blue bars indicate the additional CO₂ consumption during the first year, as rates steeply increase during the first weeks of deployment. (C) The ratio between rates of saturated over ambient CO₂ conditions is based on the expected annual consumption without the initial flushing phase. ¹from Table 1 in Hartmann et al. (2009): 11.77, 13.97, and 2.05 t CO₂ km⁻² a⁻¹, respectively; ²from Table 1 in Dessert et al. (2003); ³from Table 6 in Schopka et al. (2011).

Mineral saturation states

As a simplified indicator for potential secondary mineral precipitation, saturation indices (SI) were calculated. It should be kept in mind that these are thermodynamic calculations, and therefore may not correctly predict precipitation, given that kinetics may in fact be rate-controlling. The SI of calcite and amorphous silica throughout the experiments was calculated using the composition of the outflow solution from all columns (Figure 7). Under ambient conditions, the saturation indices of the effluent solutions suggest that the precipitation of carbonate minerals (e.g., calcite, Figures 7A–D) was thermodynamically favorable only for a short period at the beginning of the experiment. Beyond this initial period, the solutions were undersaturated with respect to all considered carbonate species (Supplementary Material 3). Under CO₂-saturated conditions, water draining the columns was, after equilibration with the atmosphere, most of the time oversaturated or near saturation with respect to calcite for the basanite and basanite-laterite columns (Figures 7A,B). These SI indices change if it is assumed that the effluent water remained 100% CO₂-saturated; in this scenario, the solutions were then consistently undersaturated with respect to calcite. When the dunite columns were considered with the same scenario (100% CO₂-saturated effluent solution), calcite was also undersaturated, except over the first few weeks. Similar results were calculated for aragonite and dolomite (Supplementary Material 3-1). The hydrous magnesium mineral nesquehonite was always undersaturated, even in the dunite experiment (Supplementary Material 3-2). Magnesite may have precipitated throughout the experiment if equilibration with the atmosphere occurred.

FIGURE 7

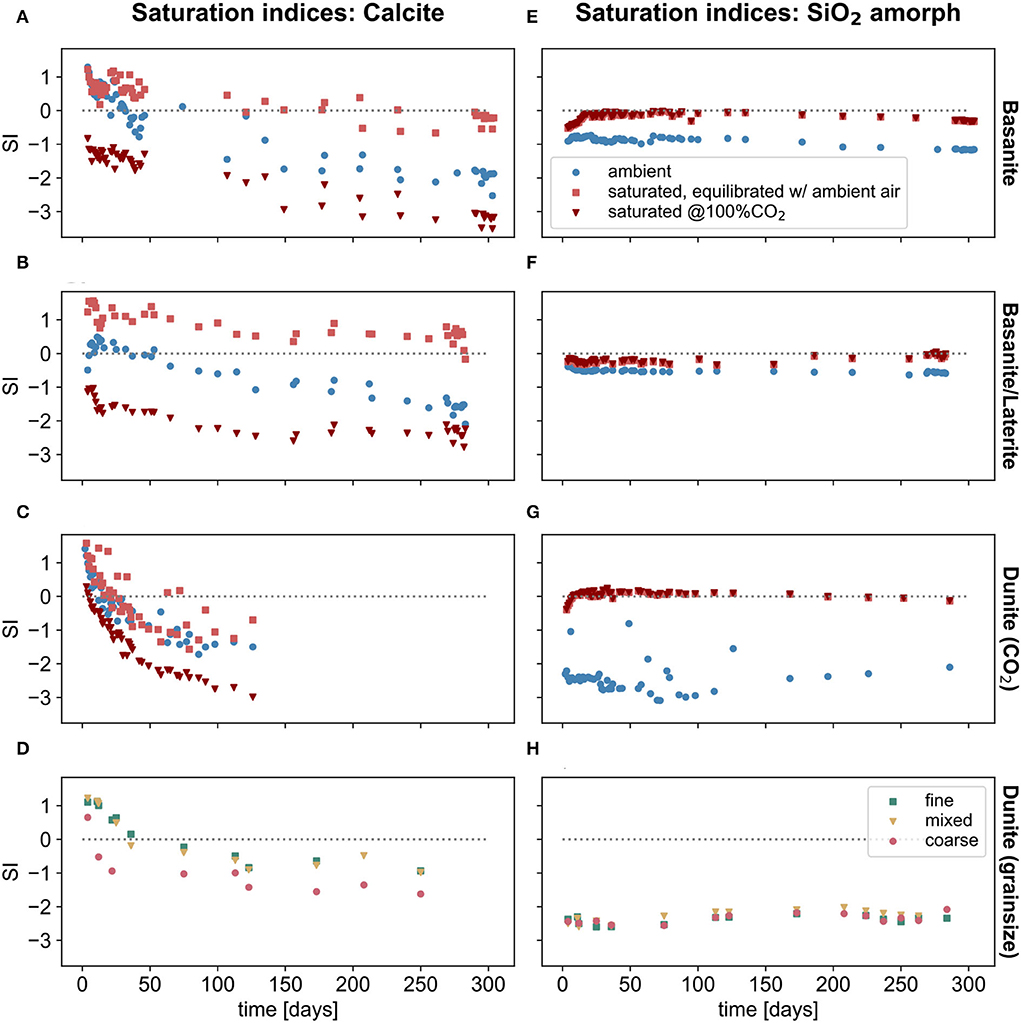
Figure 7. Calculated saturation indices for calcite (A–D) and amorphous silica (E–H) based on the composition of the outflow solution of the column experiments. Values were calculated using PhreeqC. Ambient and saturated values in (A–C,E,F) are calculated based on the outflow solution, which was equilibrated for 24 h or longer with the laboratory atmosphere. In addition, saturation indices were calculated assuming the effluent solutions remained CO₂-saturated.

All solutions were generally below saturation with respect to amorphous SiO₂ under ambient-CO₂ conditions, while at saturated-CO₂ conditions values fluctuated around zero, indicating that precipitation could have occurred (Figures 7E,F).

Discussion

Land surface-based CO₂ consumption

The CO₂ consumption rates shown in Figure 6 were calculated with a straightforward approach based on TA fluxes from the columns. Two perspectives on achievable CO₂ sequestration rates can be drawn from our results. When scaled to 1 year, total CO₂ uptake of nearly 1,000 t CO₂ km² a⁻¹ was calculated for loess and dunite. However, this estimate is only valid for the first year of application, which includes a very elevated weathering signal contribution from the first 3 weeks. Further on in time, the systems approach an approximate dynamic steady-state state that leads to markedly lower overall CO₂ uptake rates. The possible explanations for the decline in rates are discussed in Section 4.2. The dynamic steady-state in the later stages of the experiments yields significantly lower CO₂ uptake rates, which for dunite and basanite are comparable to the highest reported literature values of catchments found for tropical areas with volcanic rocks. This order of magnitude equivalence in CO₂ removal validates the applied environmental parameters in this study (temperature and precipitation simulating tropical conditions). Applying the observed rates to the globally available tropical agricultural areas [5.1 × 10⁶ km², Strefler et al. (2018a), yields a total annual CO₂ uptake of 1.1 Gt CO₂ a⁻¹]. This is about 14% of the annual minimum required CDR to attain the 1.5° target estimate, stipulated in the Paris Agreement (United Nations, 2015; Strefler et al., 2018b), and indicates that inorganic carbon uptake by EW based on atmospheric CO₂ levels in soils might contribute significantly to a portfolio of CDR methods. Moreover, in situ soil pCO₂ is normally considerably higher than ambient atmospheric values, where estimates of up to 70,000 ppm in tropical soils are not unusual (Brook et al., 1983; Davidson and Trumbore, 2017; Hashimoto et al., 2017; Romero-Mujalli et al., 2018). Higher CO₂ levels increase CO₂ drawdown rates, by a factor of more than four under a scenario of 100% CO₂-saturated conditions compared to ambient levels, as demonstrated in this study. Counterintuitively, the land surface-normalized CO₂ sequestration rate of dunite is roughly equal to that of basanite under ambient-CO₂ conditions (Figure 6A), and yet the ratio of CO₂-saturated to ambient-CO₂ uptake in the dunite columns is more than two times higher than for all other materials (11.3 vs. ~4.5). We hypothesize that the weathering reaction in the dunite column under ambient-CO₂ conditions was limited by the available CO₂.

To put into perspective the weathering rates that we present, it needs to be re-iterated that the experiments in this study were designed to simulate plausible maximum weathering rates, under specific conditions of (very) humid tropics, and an (unlikely) 100% drainage of water within the columns (water flowing through a bed of rock powder). Although the investigated effects of saturated-CO₂ conditions are not realistic for natural soils, the results likely represent the upper limit for inorganic weathering, without considering the potential contributions of plants, microbes, and bioturbation. The CO₂-enhancement factor for elevated realistic CO₂ levels in soils compared to ambient conditions remains to be determined and might not be linear (c.f. discussion Section The CO₂ effect and feedback constraints in Earth system model parameterizations).

Decrease of weathering rates with time

The surface area normalized weathering rates, here represented by TA (Figure 8), are in general lower than far-from-equilibrium rates using mixed-flow or batch reactors (cf., Palandri and Kharaka, 2004). Dissolution experiments using the latter types of reactors are generally characterized by very low solid to solution ratios, pre-treatment of grains to remove fines, uniform grain sizes, and run times commonly on the order of hundreds of hours to several tens of days. In contrast, our column experiments, which have a high rock-to-water volume ratio, provide rates that have maximum values below (ambient) or in the lower range of one standard deviation of fitted reported literature values [basanite columns, Figures 8C,D, comparison with fitted data from Bandstra and Brantley (2008)]. Moreover, in column experiments rates can decrease by up to two orders of magnitude within the first year (Figures 8E,F).

FIGURE 8

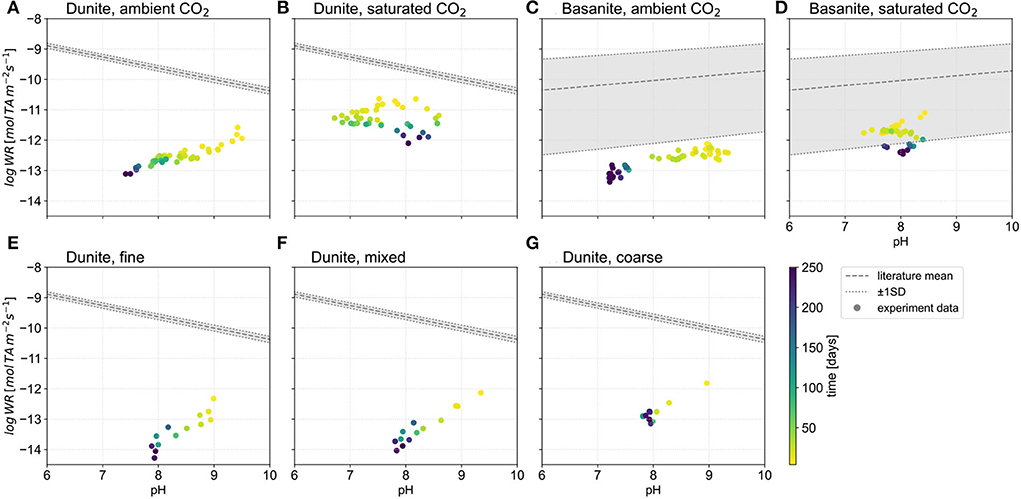
Figure 8. TA based weathering rates plotted against pH. Fitted data for literature weathering rates (gray area and dashed lines) from Bandstra and Brantley (2008); rate values were recalculated with a stoichiometric factor to get TA to release rates. Four moles TA are produced from one mole forsterite (Equation 9). Rates for basalt are reported as mol Si m-2 s-1; here, the conversion to TA release rates is based on a generalized basalt composition (from Navarre-Sitchler and Brantley, 2007), where the equivalent of one mole Si yields 2.5 moles TA. Gradient colors indicate elapsed time of the experiment. Note that in configurations e.g., there are more rate values available, yet no corresponding pH values were recorded. (A) Dunite, ambient CO₂, (B) Dunite, saturated CO₂, (C) Basanite, ambient CO₂, (D) Basanite, saturated CO₂, (E) Dunite, fine, (F) Dunite, mixed, (G) Dunite, coarse.

The decrease in reaction rates with time can be attributed to several processes. Initially, sample preparation conditions can lead to hardly quantifiable decreases in observed dissolution rates (Eggleston et al., 1989). Furthermore, a natural continuous decrease of available material may also influence the observed rate to a minor extent.

More importantly, dissolution rate declines may be attributed to the very rapid dissolution of fine particles, and/or surface sites having high surface energies (Holdren and Berner, 1979; Brantley, 2008). The crushed materials used in this study contain fines (no effort was made to remove them, e.g., see SEM images of dunite in Supplementary Material 4 and Table 2, column “share of smallest class”), and most likely also grain surfaces with sites of high energy density that were created during comminution.

Reaction rates reported in the literature based on mixed-flow and batch reactors, typically with agitators stirring a few grams of the minerals in a fluid medium, mitigate against transport-limited conditions of mineral dissolution and rather favor surface-controlled reactions (Awad et al., 2000; Martinez et al., 2014).

In a column reactor, the somewhat fast and preferential flow of water through channels, canals, or pore interconnections will be similar and also surface reaction controlled. Water with dissolved CO₂ is moving through the pore system, and not all pores will exchange water at the same rate. We observed slight compaction of the material during the experimental runs, decreasing the pore space and the surface area available for solid-fluid contact, which also could have contributed to the reduction of dissolution rates.

In addition, the material will be in contact with stagnant fluids trapped within very tiny fluid pore spaces where it is unlikely that the reactions are transport controlled.

Past experiments on forsterite dissolution have observed non-stochiometric release of Mg/Si in the initial phase of dissolution, becoming stoichiometric after a few 100 h of reaction (Pokrovsky and Schott, 2000b). This was attributed to the formation of an amorphous silica-rich layer (ASL) on the mineral surface and has been reported for many other silicate minerals including albite, labradorite, diopside, wollastonite, and garnet (Wogelius and Walther, 1992; Pokrovsky and Schott, 2000b; Hellmann et al., 2012). At steady-state, the layer thickness varies and depends on the mineral, as well as the fluid dynamics, solution chemistry and pH, and temperature. Reported thicknesses range from <1 nm for laboratory altered forsterite [Zandanel et al., 2022; see also evidence for slightly thicker layers in Pokrovsky and Schott (2000a)] to 50 nm on naturally weathered K-feldspars and 200 nm on serpentine (Hellmann et al., 2012). The high Mg/Si ratio at the end of the dunite experiment (Figure 5E) suggests that Si is actively precipitating, even after 250 days. These results indicate that the system was still far from the steady-state, unlike in experiments with low mineral to water ratios, where steady-state and stoichiometric dissolution were often observed within a few 100 h (Wogelius and Walther, 1992; Pokrovsky and Schott, 2000b; Hellmann et al., 2012).

If it is assumed that the formation of the ASL is governed by a coupled interfacial dissolution-reprecipitation (CIDR) mechanism (Hellmann et al., 2003, 2012, 2021), and the ASL is porous, it should not impede dissolution of the silicates (Putnis and Putnis, 2007). However, if the ASL is non-porous and impermeable to fluid exchange between the dissolving silicate surface and the surrounding bulk fluid, the dissolution reaction may become kinetically hindered, or in a worst-case scenario, the reaction rate would evolve to such low values so as to be unmeasurable (Putnis and Putnis, 2007). Even if the ASL is porous and permeable, the distance between the exterior bulk fluid and the reacting silicate surface might result in a decline in rates over the course of the reaction (Pedrosa et al., 2016), at least for low pressure and temperature conditions (Pedrosa et al., 2017). Moreover, recent studies suggest that ASLs are heterogeneous and can structurally evolve with time, e.g., an increase in density. As a consequence, dissolution rates may decline further over time (Daval et al., 2011, 2017; Maher et al., 2016). Considering all of our experiments, after 1 year of reaction there was no evidence that the dissolution of the minerals stopped, even if some of the release curves are noisy and do not display clear trends (Figure 3).

Si can also precipitate with different morphologies. In an experiment by Lazaro et al. (2012), it was found that amorphous silica precipitated during intense olivine dissolution as nano-silica colloids, with a high SSA of 100–300 m²g⁻¹. The observed nano-silica has primary particles of 10–25 nm that were agglomerated in clusters with an average pore size of ~20 nm. An increase in mesopores could (further) increase the water holding capacity of the soil (Schaller et al., 2020). This probably important aspect in the context of drought conditions needs further research to assess application consequences from the evolution of amorphous silica in quality and quantity, depending on the applied amount of silicate minerals, their grain sizes, and shapes.

Comparing pH-controlled dissolution experiments from the literature and the column-derived data from this study is difficult as the experiment conditions are different, yet they can provide a reference for the discussion. In the ambient-CO₂ column experiments, dunite rates increase with pH (Figure 8) with values >7, as opposed to the trends shown by literature data fits (from Bandstra and Brantley, 2008). While in the literature, rates are measured at fixed pH in a system far from equilibrium, the column experiment is a system that reacts dynamically with water and CO₂ input by proton production or consumption. Under ambient conditions, the capacity to consume protons declines toward the end of the experiment, indicated by lower pH and decreased weathering rates. Under CO₂-saturated conditions, rates also decline with time, but the pH range is greater and not directly correlated with alkalinity production (Figures 8B,D). Weathering rates are still higher at the end of the experiment compared to rates under ambient conditions.

Effect of grain size (distribution)

It is often assumed that finer rock material grain sizes purposed for enhanced weathering would yield higher CO₂ capture rates (e.g., Strefler et al., 2018a), simply due to the higher surface area available for reaction. This hypothesis is not supported by our experiment results for EW.

The experimental series designed to evaluate the effect of different grain sizes using the same dunite material shows higher TA fluxes from the fine grain size column, especially over the first 100 days. However, when normalized to the total grain surface areas, this result changes: while the total grain surface area of the fine column material is on average 8.4 ± 0.2 times higher than the surface area of the material in the coarse columns, the CO₂ consumption of the fine material is only ~7% higher. Although the porosity is much higher in the fine grain size column (Table 1-3 in Supplementary Material), which would indicate a larger potential contact area for rock-water interaction, it is assumed that the characteristics of this larger pore space do not allow for rate-stimulating effects. The pore sizes may be much smaller, reflected in decreased hydraulic conductivity, qualitatively observed by longer residence times of the supernatant water (which percolated more slowly through the column). Moreover, significantly smaller pores likely did not contribute much to the transport of water through the column, which was more likely characterized by preferential fluid channels. In contrast, fluid flow through the coarse material with larger and inter-connected pores likely enabled a greater material-water contact area, leading to enhanced dissolution.

A comparable effect may explain the higher weathering fluxes of the laterite/basanite mix, compared to basanite alone, although the mix is only comprised of 50% basanite. The plain tropical soil, laterite, naturally dominated by very small grains (p80 < 30 μm) showed little hydraulic conductivity and long retention times of the supernatant water. Mixing with the coarse basanite yielded a grain size distribution more suitable for enhanced weathering, so the effect of hydrology, an increase of hydraulic conductivity, and enhanced grain-water contact time may lead to the enhanced observed weathering fluxes.

Both observed effects underline the importance of the hydrologic conditions within the material, which are controlled by the grain size distribution (as also hypothesized in Amann et al., 2020; c.f., modeled hydrological effects from EW in de Oliveira Garcia et al., 2020) and the nature of grain packing, which in the experiment was also influenced by manually filling the columns. Preferential flow along the column walls, or clogging and missing pore interconnections (as could be visually observed in the columns) may decrease apparent weathering rates, while a grain size distribution optimized for water residence times, with a balance between sufficient reaction time and oversaturation, can maximize the weathering effect and thus the CO₂ uptake efficiency (de Oliveira Garcia et al., 2020).

For a real-world application, simply testing the rock flour material alone, without considering the soils it is applied to, will not be an effective strategy. Besides testing material mixed with the target soil, it seems imperative that hydrological effects should also be considered. Moreover, the effects of bioturbation, plant roots, or uptake of elements by plants (Akter and Akagi, 2010; Taylor et al., 2015; Krahl, 2020; Verbruggen et al., 2021) affect the transferability of the column experiment results to real-world soil-plant systems. Such effects on EW must be studied in more detail to enable enhanced predictions by models in the future, backed up of course, by experimental data.

Cation release

Studies of major cation leaching are relevant for the assessment of different rock types to act as potential CO₂ sinks via weathering. Our results (Table 4) suggest that the total dissolution of any of the evaluated materials under the conditions in this study would take about a century or longer under atmospheric pCO₂ while being accelerated in the CO₂-saturated environment. It is relevant for a CDR application scenario to understand the cation release rate and alkalinity production as a function of CO₂ levels in the amended soils.

The relative release of major cations from the substrate diverges from its relative content in the parent mineral (Figure 4). Cation release is largely determined by the dissolution kinetics of dominant minerals. Mg dominates the cation flux from the dunite column, which is expected, as forsterite (Mg₂SiO₄) dominates the source rock. In the dunite experiment, notable amounts of K were released, which might be unexpected, given the general composition of the material. This behavior may be traced back to the occurrence of chabazite (Supplementary Material 5), a mineral from the zeolite group, which can contain K and has rather rapid weathering rates (Schofield et al., 2015; Moravec et al., 2021). K is relevant for achieving additional carbon sequestration via EW through biological processes (Goll et al., 2021), as K is an important nutrient to most plants. The release of Na and K from the basanite columns could be explained by the abundance of nepheline [(Na,K)AlSiO₄], a feldspathoid mineral that commonly occurs in the silica-depleted magmas of the Eifel (Mertes and Schmincke, 1985). The dissolution rate of nepheline is significantly higher than other Na-dominated rock-forming minerals, i.e., albite (Lasaga et al., 1994; Franke, 2009). The high dissolution rate indicates that rocks rich in this mineral may be a preferable source for EW, even if a monovalent ion is associated with ~50% less CO₂ drawdown compared to a divalent cation.

Target materials for EW application should be tested for available water (rainfall) and CO₂ concentration gradients in the soil, as these two external parameters predominantly govern CO₂ uptake. However, since K, but also Mg and Ca, are taken up by plants, their removal from the soil-water system is likely to decrease the instantaneous CO₂ sequestration rate because plant uptake of cations is counterbalanced by the release of protons (Britto and Kronzucker, 2008), and cation concentrations in the water phase leaving the system should be lower due to their temporal storage in plants. The quantity of these elements that remain in agricultural fields after crop/tree harvest will affect the final long-term field-based CO₂ removal rate. At the same time, given sufficient time, the leftover organic matter could re-release cations. These processes call for further investigations to provide a better picture of full inorganic CO₂ sequestration through EW. To assess the full EW potential, inorganic and organic CO₂ sequestration should be studied in parallel, focusing additionally on the effects of P release, an important micro-nutrient for plants that are commonly used in fertilizers, and which is abundant in the basanite (Table 1) but was not the focus of this study.

Riverine cation elemental ratios in watersheds (e.g., Ca/Na) can be used to distinguish between carbonate and silicate weathering (Gaillardet et al., 1999). Results here suggest that EW application with high amounts of nepheline might change Ca/Na ratios due to the non-stoichiometry of the alteration process, which potentially affects the interpretation of weathering sources, and also can alter the geochemical baselines of rivers (Hartmann et al., 2007). Under a large-scale EW deployment scenario, the influence of altered geochemical fluxes in natural systems on scientific interpretations has to be considered as a side effect not addressed so far.

The CO₂ effect and feedback constraints in earth system model parameterizations

The CO₂ feedback on weathering rates and CO₂ consumption in Earth system or planetary models is often represented by the factor $\alpha ={\left(p_{C{O}_2}/preind.p_{C{O}_2}\right)}^n$ (Walker et al., 1981). In an abiotic world, as in our column experiments, this feedback would represent the direct effect of CO₂ dissolution and consumption in water, in addition to hydrological feedback, as the weathering flux is largely controlled by water throughflow, given a fixed lithological composition. In general, it is not possible to distinguish the proportions each of these effects contribute to the feedback. The exponent n is often modulated to fit an assumed feedback-strength range (Uchikawa and Zeebe, 2008; Lehmer et al., 2020). We can compare our results with the resulting feedback strength for n = 0.1 to n = 0.5 using a p_CO2 of 400 ppm as a baseline, instead of the pre-industrial value. This comparison would only consider the CO₂ effect and no further hydrological feedback due to elevated CO₂ in the atmosphere. Solving the above equation for n with α = 4.5, representative of the results in this experiment (Figure 6C) leads to n = 0.2, a value that matches the assumed default conditions in the simulations of Uchikawa and Zeebe (2008). This value might be representative of conditions on Mars or other planets with a high pCO₂ atmosphere. With n = 0.3 the feedback is comparable to results from the dunite column, where it must be assumed that observed weathering fluxes are diffusion-limited (see above). The case of n = 0.5 would result in an even higher CO₂-enhancement factor of 50. This would imply that in a basalt-dominated world, the additional hydrological effect would be stronger by a factor of 10. As the early, primitive surfaces of Earth or Mars were more likely to be comparable to a basaltic than to an olivine-dominated surface, this comparison invites a discussion about the combined effects of CO₂ and hydrology in a planetary system, and how they can be best represented. If the CO₂ feedback effect due to EW is modeled at the planetary scale, one should distinguish CO₂ effects on mineral weathering and on hydrology separately.

Results suggest that n values in the lower range of values considered are more realistic. As only two CO₂ conditions were tested, a simple scaling law would suggest that for humid tropical areas a doubling to tripling in weathering rates can be assumed for elevated (>70,000 ppm) CO₂ conditions compared to ambient CO₂ conditions (Table 5).

TABLE 5

Table 5. Weathering rate factor $\alpha ={\left(p_{C{O}_2}/p_{C{O}_{2-baseline}}\right)}^n$, normalized to the baseline condition of 400 ppm CO₂ as applied in common Earth system models to simulate weathering rate changes with increased p_CO2, depending on the choice of exponent n.

Enhancement of weathering by rhizosphere processes

As the column experiment was primarily abiotic, the influence of biological processes on weathering rates was not explicitly considered, although microbial components may have exerted a minor influence on the columns filled with soils, as these were not sterilized. Processes in the rhizosphere can speed up dissolution processes and therefore increase EW potentials (Krahl, 2020; Verbruggen et al., 2021). Beerling et al. (2020) deduced a biotic weathering enhancement factor normalized to net primary productivity in the range of 1–7 (from work of Akter and Akagi, 2005, 2010; Quirk et al., 2012, 2014). This factor incorporates the effects of rhizosphere biologically accelerated weathering. Given the overall scarcity of data, but the relevant influence of plants and the rhizosphere, these processes need to be considered to determine realistic constraints on the boundaries of EW for diverse environmental settings in the future.

Precipitation of carbonates

The secondary precipitation of carbonates as the final long-term step in the weathering process can release half of the captured CO₂ counterbalanced by Ca and to some proportion of Mg. Thus, carbonate precipitation should be monitored to evaluate the overall carbon sequestration potential of an agricultural system. However, carbonate mineral saturation indices indicate that carbonate formation only occurred during the initial phases of our experiments, since long-term oversaturation was not observed. Consequently, the precipitation of carbonates may not be expected in agricultural soils under long-term treatment with rock material, given the humid, tropical conditions. Precipitation downstream of the application area might occur after water is re-equilibrating with the atmosphere (Figure 7). See further discussion on efficacy of enhancing carbonate weathering for carbon dioxide sequestration in Knapp and Tipper (2022).

Conclusion

Our counter-intuitive finding that the smallest grain sizes may not lead to the fastest CO₂ uptake (Figure 6) calls for a more detailed investigation of the influence of grain size distributions and packing density of soils in individual application cases. Larger target grain sizes will decrease the energy requirements for comminution. This will lower costs and the potential CO₂ penalty from fossil energy use.

The pronounced alkalinity production during the initial phases of the experiments suggests that a modified application scheme might be considered: rock flour replenishment at shorter intervals (e.g., annually) may be preferable over a one-time application of a larger amount of material to achieve higher CO₂ drawdown rates. This, however, needs to be tested with further experiments, as biological processes were not simulated in this study.

We have also shown that the individual mineral compositions making up applied rock material is important for the evaluation of CO₂ uptake speeds and side effects. A site-specific material selection process, going further than a simple search for local “basalt,” can optimize dissolution rates (and thus CO₂ uptake potential), as well as plant nutrient potential. Looking beyond basaltic material, loess can sustain rather high dissolution rates over millennia (Börker et al., 2020), which also showed high dissolution rates in the experiments. As such, it may even be a well-suited material to produce alkalinity—and remove CO₂–in the context of CDR as it is often regionally available, easily extractable, and fertile. Material-specific aging processes and the formation of secondary precipitates will be issues that also need to be understood in more detail.

Overall, future models and projections for EW-related CDR should consider the dissolution rates obtained from column experiments under 100% CO₂, as they will represent an upper boundary in an inorganic system. Further studies should assess the soil pCO₂ gradients, simulating conditions in soils of different climates and environments with up to more than 100,000 ppm. Biologic processes should further accelerate the observed rates, which demands tailored experiments, distinguishing biological and inorganic geochemical processes, to improve EW-CDR-potential assessments.

A further observation from the experiments, the promising utilization of electrical conductivity as a predictor for TA production, a proxy for the CO₂ sequestration effect, is discussed in a complementary publication (Amann and Hartmann, 2022).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JH, TA, and AM designed the study. AM ran the first experiment comparing grain sizes and contributed to the discussion. TA wrote the manuscript with input from JH, RH, EP, and AM. EP contributed to the discussion. RH provided input throughout the manuscript and especially to section decrease of weathering rates with time. All authors approved the submitted version.

Funding

This work was funded by Germany's Excellence Strategy—EXC 2037 Climate, Climatic Change, and Society—project number 390683824, contribution to the Center for Earth System Research and Sustainability (CEN) of the Universität Hamburg.

Acknowledgments

We acknowledge the help of Tom Jäppinen, Peggy Bartsch, Rhiannon Breider, Mark Brosell, Marvin Keitzel, Eric Marques, and Walid Karimi for valuable contributions from the wet lab, and Sebastian Lindhorst for providing granulometric analyses (all from the Institute for Geology, Universität Hamburg). We thank Stephan Jung and Joachim Ludwig (from the Institute for Mineralogy and Petrography, Universität Hamburg) for contributing to the XRF and XRD analyses. Discussions were further stimulated by work with the Carbon Drawdown Initiative (Project Carbdown).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2022.929268/full#supplementary-material

References

Akter, M., and Akagi, T. (2005). Effect of fine root contact on plant-induced weathering of basalt. Soil Sci. Plant Nutr. 51, 861–871. doi: 10.1111/j.1747-0765.2005.tb00121.x

CrossRef Full Text | Google Scholar

Akter, M., and Akagi, T. (2010). Dependence of plant-induced weathering of basalt and andesite on nutrient conditions. Geochem. J. 44, 137–150. doi: 10.2343/geochemj.1.0052

CrossRef Full Text | Google Scholar

Amann, T., and Hartmann, J. (2019). Ideas and perspectives: synergies from co-deployment of negative emission technologies. Biogeosciences 16, 2949–2960. doi: 10.5194/bg-16-2949-2019

CrossRef Full Text | Google Scholar

Amann, T., and Hartmann, J. (2022). Carbon accounting for enhanced weathering. Front. Clim. 4, 849948. doi: 10.3389/fclim.2022.849948

CrossRef Full Text | Google Scholar

Amann, T., Hartmann, J., Struyf, E., de Oliveira Garcia, W., Fischer, E. K., Janssens, I., et al. (2020). Enhanced weathering and related element fluxes – a cropland mesocosm approach. Biogeosciences 17, 103–119. doi: 10.5194/bg-17-103-2020

CrossRef Full Text | Google Scholar

Awad, A., Koster van Groos, A. F., and Guggenheim, S. (2000). Forsteritic olivine: effect of crystallographic direction on dissolution kinetics. Geochim. Cosmochim. Acta 64, 1765–1772. doi: 10.1016/S0016-7037(99)00442-1

CrossRef Full Text | Google Scholar

Ball, J. W., and Nordstrom, D. K. (1991). “User's manual for WATEQ4F, with revised thermodynamic data base and text cases for calculating speciation of major, trace, and redox elements in natural waters,” in Open-File Report. Version 2.0 (Menlo Park, CA). doi: 10.3133/ofr91183

CrossRef Full Text | Google Scholar

Bandstra, J. Z., and Brantley, S. L. (2008). “Data fitting techniques with applications to mineral dissolution kinetics,” in Kinetics of Water-Rock Interaction, eds S. L. Brantley, J. D. Kubicki, and A. F. White (New York, NY: Springer), 211–257. doi: 10.1007/978-0-387-73563-4_6

CrossRef Full Text | Google Scholar

Beerling, D. J., Kantzas, E. P., Lomas, M. R., Wade, P., Eufrasio, R. M., Renforth, P., et al. (2020). Potential for large-scale CO2 removal via enhanced rock weathering with croplands. Nature 583, 242–248. doi: 10.1038/s41586-020-2448-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Beerling, D. J., Leake, J. R., Long, S. P., Scholes, J. D., Ton, J., Nelson, P. N., et al. (2018). Farming with crops and rocks to address global climate, food and soil security. Nat. Plants 4, 138–147. doi: 10.1038/s41477-018-0108-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Beyer, E. E. (2006). Transformation of archaean lithospheric mantle by refertilization: evidence from exposed peridotites in the western Gneiss Region, Norway. J. Petrol. 47, 1611–1636. doi: 10.1093/petrology/egl022

CrossRef Full Text | Google Scholar

Börker, J. (2019). Quantifications of Global Chemical Weathering Fluxes Applying New Lithological Maps and New Parameterizations. Hamburg: Staats- und Universitätsbibliothek Hamburg.

Börker, J., Hartmann, J., Amann, T., Romero-Mujalli, G., Moosdorf, N., and Jenkins, C. (2020). Chemical weathering of loess and its contribution to global alkalinity fluxes to the coastal zone during the last glacial maximum, mid-holocene, and present. Geochem. Geophys. Geosyst. 21, e2020GC008922. doi: 10.1029/2020GC008922

CrossRef Full Text | Google Scholar

Brantley, S. L. (2008). “Kinetics of mineral dissolution,” in Kinetics of Water-Rock Interaction, eds S. L. Brantley, J. D. Kubicki, and A. F. White (New York, NY: Springer), 151–210. doi: 10.1007/978-0-387-73563-4_5

CrossRef Full Text | Google Scholar

Britto, D. T., and Kronzucker, H. J. (2008). Cellular mechanisms of potassium transport in plants. Physiol. Plant. 133, 637–650. doi: 10.1111/j.1399-3054.2008.01067.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Brook, G. A., Folkoff, M. E., and Box, E. O. (1983). A world model of soil carbon dioxide. Earth Surf. Proc. Landf. 8, 79–88. doi: 10.1002/esp.3290080108

CrossRef Full Text | Google Scholar

Brunauer, S., Emmett, P. H., and Teller, E. (1938). Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 60, 309–319. doi: 10.1021/ja01269a023

PubMed Abstract | CrossRef Full Text | Google Scholar

Cockell, C. S., Bush, T., Bryce, C., Direito, S., Fox-Powell, M., Harrison, J. P., et al. (2016). Habitability: a review. Astrobiology 16, 89–117. doi: 10.1089/ast.2015.1295

PubMed Abstract | CrossRef Full Text | Google Scholar

Cross, W. I., Joseph, P., Pirsson, L. V., and Washington, H. S. (1902). A quantitative chemico-mineralogical classification and nomenclature of igneous rocks. J. Geol. 10, 555–690. doi: 10.1086/621030

CrossRef Full Text | Google Scholar

Daval, D., Bernard, S., Rémusat, L., Wild, B., Guyot, F., Micha, J. S., et al. (2017). Dynamics of altered surface layer formation on dissolving silicates. Geochim. Cosmochim. Acta 209, 51–69. doi: 10.1016/j.gca.2017.04.010

CrossRef Full Text | Google Scholar

Daval, D., Sissmann, O., Menguy, N., Saldi, G. D., Guyot, F., Martinez, I., et al. (2011). Influence of amorphous silica layer formation on the dissolution rate of olivine at 90 °C and elevated pCO2. Chem. Geol. 284, 193–209. doi: 10.1016/j.chemgeo.2011.02.021

CrossRef Full Text | Google Scholar

Davidson, E. A., and Trumbore, S. E. (2017). Gas diffusivity and production of CO2in deep soils of the eastern Amazon. Tellus B Chem. Phys. Meteorol. 47, 550–565. doi: 10.3402/tellusb.v47i5.16071

CrossRef Full Text | Google Scholar

de Oliveira Garcia, W., Amann, T., Hartmann, J., Karstens, K., Popp, A., Boysen, L. R., et al. (2020). Impacts of enhanced weathering on biomass production for negative emission technologies and soil hydrology. Biogeosciences 17, 2107–2133. doi: 10.5194/bg-17-2107-2020

CrossRef Full Text | Google Scholar

Dessert, C., Dupré, B., Gaillardet, J., François, L. M., and Allègre, C. J. (2003). Basalt weathering laws and the impact of basalt weathering on the global carbon cycle. Chem. Geol. 202, 257–273. doi: 10.1016/j.chemgeo.2002.10.001

CrossRef Full Text | Google Scholar

Dickson, A. G. (1981). An exact definition of total alkalinity and a procedure for the estimation of alkalinity and total inorganic carbon from titration data. Deep Sea Res. Part A Oceanogr. Res. Pap. 28, 609–623. doi: 10.1016/0198-0149(81)90121-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietzen, C., Harrison, R., and Michelsen-Correa, S. (2018). Effectiveness of enhanced mineral weathering as a carbon sequestration tool and alternative to agricultural lime: an incubation experiment. Int. J. Greenh. Gas Con. 74, 251–258. doi: 10.1016/j.ijggc.2018.05.007

CrossRef Full Text | Google Scholar

Ebelmen, J. J. (1845). Sur les Produits de la Décomposition des Espèces Minérales de la Famille des Silicates. Paris: Carilian-G.ury et Vor Dalmont, Libraires des Corps Royaux des Ponts et Chausees et dus Mines.

Eggleston, C. M., Hochella, M. F., and George, P. A. (1989). Sample preparation and aging effects on the dissolution rate and surface composition of diopside. Geochim. Cosmochim. Acta 53, 797–804. doi: 10.1016/0016-7037(89)90026-4

CrossRef Full Text | Google Scholar

Foley, B. J., and Smye, A. J. (2018). Carbon cycling and habitability of earth-sized stagnant lid planets. Astrobiology 18, 873–896. doi: 10.1089/ast.2017.1695

PubMed Abstract | CrossRef Full Text | Google Scholar

Franke, W. A. (2009). The durability of rocks–Developing a test of rock resistance to chemical weathering. Am. J. Sci. 309, 711–730. doi: 10.2475/08.2009.04

CrossRef Full Text | Google Scholar

Gaillardet, J., Dupré, B., Louvat, P., and Allègre, C. J. (1999). Global silicate weathering and CO2 consumption rates deduced from the chemistry of large rivers. Chem. Geol. 159, 3–30. doi: 10.1016/S0009-2541(99)00031-5

CrossRef Full Text | Google Scholar

Giambelluca, T. W., Chen, Q., Frazier, A. G., Price, J. P., Chen, Y.-L., Chu, P.-S., et al. (2013). Online rainfall atlas of Hawai‘i. Bull. Am. Meteorol. Soc. 94, 313–316. doi: 10.1175/BAMS-D-11-00228.1

CrossRef Full Text | Google Scholar

Goll, D. S., Ciais, P., Amann, T., Buermann, W., Chang, J., Eker, S., et al. (2021). Potential CO2 removal from enhanced weathering by ecosystem responses to powdered rock. Nat. Geosci. 14, 545–549. doi: 10.1038/s41561-021-00798-x

CrossRef Full Text | Google Scholar

Hansen, H. P., and Koroleff, F. (1999). “Determination of nutrents,” in Methods of Seawater Analysis. doi: 10.1002/9783527613984.ch10

CrossRef Full Text | Google Scholar

Haque, F., Santos, R. M., and Chiang, Y. W. (2020). CO2 sequestration by wollastonite-amended agricultural soils – an Ontario field study. Int. J. Greenh. Gas Con. 97, 103017. doi: 10.1016/j.ijggc.2020.103017

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann, J., Jansen, N., Dürr, H. H., Kempe, S., and Köhler, P. (2009). Global CO₂-consumption by chemical weathering: what is the contribution of highly active weathering regions? Glob. Planet. Change 69, 185–194. doi: 10.1016/j.gloplacha.2009.07.007

CrossRef Full Text | Google Scholar

Hartmann, J., Jansen, N., Kempe, S., and Dürr, H. (2007). Geochemistry of the river rhine and the upper danube: recent trends and lithological influence on baselines. J. Environ. Sci. Sustain. Soc. 1, 39–46. doi: 10.3107/jesss.1.39

CrossRef Full Text | Google Scholar

Hartmann, J., and Kempe, S. (2008). What is the maximum potential for CO(2) sequestration by “stimulated” weathering on the global scale? Naturwissenschaften 95, 1159–1164. doi: 10.1007/s00114-008-0434-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann, J., West, A. J., Renforth, P., Köhler, P., De La Rocha, C. L., Wolf-Gladrow, D. A., et al. (2013). Enhanced chemical weathering as a geoengineering strategy to reduce atmospheric carbon dioxide, supply nutrients, and mitigate ocean acidification. Rev. Geophys. 51, 113–149. doi: 10.1002/rog.20004

CrossRef Full Text | Google Scholar

Hashimoto, S., Tanaka, N., Suzuki, M., Inoue, A., Takizawa, H., Kosaka, I., et al. (2017). Soil respiration and soil CO2 concentration in a tropical forest, Thailand. J. For. Res. 9, 75–79. doi: 10.1007/s10310-003-0046-y

CrossRef Full Text | Google Scholar

Hellmann, R. (1994). The albite-water system: part I. The kinetics of dissolution as a function of pH at 100, 200 and 300°C. Geochim. Cosmochim. Acta 58, 595–611. doi: 10.1016/0016-7037(94)90491-X

CrossRef Full Text | Google Scholar

Hellmann, R., Penisson, J. M., Hervig, R. L., Thomassin, J. H., and Abrioux, M. F. (2003). An EFTEM/HRTEM high-resolution study of the near surface of labradorite feldspar altered at acid pH: evidence for interfacial dissolution-reprecipitation. Phys. Chem. Min. 30, 192–197. doi: 10.1007/s00269-003-0308-4

CrossRef Full Text | Google Scholar

Hellmann, R., Wirth, R., Daval, D., Barnes, J.-P., Penisson, J.-M., Tisserand, D., et al. (2012). Unifying natural and laboratory chemical weathering with interfacial dissolution–reprecipitation: a study based on the nanometer-scale chemistry of fluid–silicate interfaces. Chem. Geol. 294–295, 203–216. doi: 10.1016/j.chemgeo.2011.12.002

CrossRef Full Text | Google Scholar

Hellmann, R., Zhai, Y., Robin, E., Findling, N., Mayanna, S., Wirth, R., et al. (2021). The hydrothermal alkaline alteration of potassium feldspar: a nanometer-scale investigation of the orthoclase interface. Chem. Geol. 569. doi: 10.1016/j.chemgeo.2021.120133

CrossRef Full Text | Google Scholar

Holdren, G. R., and Berner, R. A. (1979). Mechanism of feldspar weathering—I. Experimental studies. Geochim. Cosmochim. Acta 43, 1161–1171. doi: 10.1016/0016-7037(79)90109-1

CrossRef Full Text | Google Scholar

Hövelmann, J., Austrheim, H., and Jamtveit, B. (2012). Microstructure and porosity evolution during experimental carbonation of a natural peridotite. Chem. Geol. 334, 254–265. doi: 10.1016/j.chemgeo.2012.10.025

CrossRef Full Text | Google Scholar

Julius, H. (1894). Bread from Stones - A New and Rational System of Land Fertilization and Physical Regeneration (Translated From the German), ed A. J. Tafel. Philadelphia, PA.

Kelland, M. E., Wade, P. W., Lewis, A. L., Taylor, L. L., Sarkar, B., Andrews, M. G., et al. (2020). Increased yield and CO2 sequestration potential with the C4 cereal Sorghum bicolor cultivated in basaltic rock dust-amended agricultural soil. Glob. Chang. Biol. 26, 3658–3676. doi: 10.1111/gcb.15089

PubMed Abstract | CrossRef Full Text | Google Scholar

Klasen, N., Fischer, P., Lehmkuhl, F., and Hilgers, A. (2015). Luminescence dating of loess deposits from the Remagen-Schwalbenberg site, Western Germany. Geochronometria 42. doi: 10.1515/geochr-2015-0008

CrossRef Full Text | Google Scholar

Knapp, W., and Tipper, E. (2022). The efficacy of enhancing carbonate weathering for carbon dioxide sequestration. Front. Clim. doi: 10.17863/CAM.85785

CrossRef Full Text | Google Scholar

Krahl, L. L. (2020). Mineral Formation and Element Release From Aluminosilicate Rocks Promoted by Maize Rhizosphere (Ph.D). Available online at: https://repositorio.unb.br/bitstream/10482/38678/1/2020_LuiseLotticiKrahl.pdf

Lasaga, A. C., Soler, J. M., Ganor, J., Burch, T. E., and Nagy, K. L. (1994). Chemical weathering rate laws and global geochemical cycles. Geochim. Cosmochim. Acta 58, 2361–2386. doi: 10.1016/0016-7037(94)90016-7

CrossRef Full Text | Google Scholar

Lazaro, A., Brouwers, H. J. H., Quercia, G., and Geus, J. W. (2012). The properties of amorphous nano-silica synthesized by the dissolution of olivine. Chem. Eng. J. 211–212, 112–121. doi: 10.1016/j.cej.2012.09.042

CrossRef Full Text | Google Scholar

Le Bas, M. J., Maitre, R. W. L., Streckeisen, A., and Zanettin, B. (1986). A chemical classification of volcanic rocks based on the total alkali-silica diagram. J. Petrol. 27, 745–750. doi: 10.1093/petrology/27.3.745

PubMed Abstract | CrossRef Full Text | Google Scholar

Lechler, P. J., and Desilets, M. O. (1987). A review of the use of loss on ignition as a measurement of total volatiles in whole-rock analysis. Chem. Geol. 63, 341–344. doi: 10.1016/0009-2541(87)90171-9

CrossRef Full Text | Google Scholar

Lehmer, O. R., Catling, D. C., and Krissansen-Totton, J. (2020). Carbonate-silicate cycle predictions of earth-like planetary climates and testing the habitable zone concept. Nat. Commun. 11, 6153. doi: 10.1038/s41467-020-19896-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Leonardos, O. H., Fyfe, W. S., and Kronberg, B. I. (1987). The use of ground rocks in laterite systems: an improvement to the use of conventional soluble fertilizers? Chem. Geol. 60, 361–370. doi: 10.1016/0009-2541(87)90143-4

CrossRef Full Text | Google Scholar

Maher, K., Johnson, N. C., Jackson, A., Lammers, L. N., Torchinsky, A. B., Weaver, K. L., et al. (2016). A spatially resolved surface kinetic model for forsterite dissolution. Geochim. Cosmochim. Acta 174, 313–334. doi: 10.1016/j.gca.2015.11.019

CrossRef Full Text | Google Scholar

Martinez, R. E., Weber, S., and Bucher, K. (2014). Quantifying the kinetics of olivine dissolution in partially closed and closed batch reactor systems. Chem. Geol. 367, 1–12. doi: 10.1016/j.chemgeo.2013.12.017

CrossRef Full Text | Google Scholar

Mertes, H., and Schmincke, H. U. (1985). Mafic potassic lavas of the quaternary west eifel volcanic field.1. Major and trace-elements. Contribut. Mineral. Petrol. 89, 330–345. doi: 10.1007/BF00381555

CrossRef Full Text | Google Scholar

Moravec, B. G., Keifer, V., Root, R. A., White, A. M., Wang, Y., Olshansky, Y., et al. (2021). Experimental weathering of a volcaniclastic critical zone profile: Key role of colloidal constituents in aqueous geochemical response. Chem. Geol. 559, 119886. doi: 10.1016/j.chemgeo.2020.119886

CrossRef Full Text | Google Scholar

Navarre-Sitchler, A., and Brantley, S. (2007). Basalt weathering across scales. Earth Planet. Sci. Lett. 261, 321–334. doi: 10.1016/j.epsl.2007.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Palandri, J. L., and Kharaka, Y. K. (2004). A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling. Menlo Park, CA: U.S. Geological Survey. doi: 10.3133/ofr20041068

CrossRef Full Text | Google Scholar

Parkhurst, D. L., and Appelo, C. A. J. (2013). “Description of input and examples for PHREEQC version 3—a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations,” in U.S. Geological Survey Techniques and Methods (Denver, CO). doi: 10.3133/tm6A43

CrossRef Full Text | Google Scholar

Pedrosa, E. T., Boeck, L., Putnis, C. V., and Putnis, A. (2017). The replacement of a carbonate rock by fluorite: kinetics and microstructure. Am. Min. 102, 126–134. doi: 10.2138/am-2017-5725

CrossRef Full Text | Google Scholar

Pedrosa, E. T., Putnis, C. V., Renard, F., Burgos-Cara, A., Laurich, B., and Putnis, A. (2016). Porosity generated during the fluid-mediated replacement of calcite by fluorite. Cryst. Eng. Comm. 18, 6867–6874. doi: 10.1039/C6CE01150K

CrossRef Full Text | Google Scholar

Pokrovsky, O. S., and Schott, J. (2000a). Forsterite surface composition in aqueous solutions: a combined potentiometric, electrokinetic, and spectroscopic approach. Geochim. Cosmochim. Acta 64, 3299–3312. doi: 10.1016/S0016-7037(00)00435-X

CrossRef Full Text | Google Scholar

Pokrovsky, O. S., and Schott, J. (2000b). Kinetics and mechanism of forsterite dissolution at 25°C and pH from 1 to 12. Geochim. Cosmochim. Acta 64, 3313–3325. doi: 10.1016/S0016-7037(00)00434-8

CrossRef Full Text | Google Scholar

Putnis, A., and Putnis, C. V. (2007). The mechanism of reequilibration of solids in the presence of a fluid phase. J. Solid State Chem. 180, 1783–1786. doi: 10.1016/j.jssc.2007.03.023

CrossRef Full Text | Google Scholar

Quirk, J., Andrews, M. Y., Leake, J. R., Banwart, S. A., and Beerling, D. J. (2014). Ectomycorrhizal fungi and past high CO2 atmospheres enhance mineral weathering through increased below-ground carbon-energy fluxes. Biol. Lett. 10, 20140375. doi: 10.1098/rsbl.2014.0375

PubMed Abstract | CrossRef Full Text | Google Scholar

Quirk, J., Beerling, D. J., Banwart, S. A., Kakonyi, G., Romero-Gonzalez, M. E., and Leake, J. R. (2012). Evolution of trees and mycorrhizal fungi intensifies silicate mineral weathering. Biol. Lett. 8, 1006–1011. doi: 10.1098/rsbl.2012.0503

PubMed Abstract | CrossRef Full Text | Google Scholar

Renforth, P., Pogge von Strandmann, P. A. E., and Henderson, G. M. (2015). The dissolution of olivine added to soil: implications for enhanced weathering. Appl. Geochem. 61, 109–118. doi: 10.1016/j.apgeochem.2015.05.016

CrossRef Full Text | Google Scholar

Romero-Mujalli, G., Hartmann, J., Börker, J., Gaillardet, J., and Calmels, D. (2018). Ecosystem controlled soil-rock pCO2 and carbonate weathering – constraints by temperature and soil water content. Chem. Geol. 527, 118634. doi: 10.1016/j.chemgeo.2018.01.030

CrossRef Full Text | Google Scholar

Royer, D. L., Berner, R. A., and Park, J. (2007). Climate sensitivity constrained by CO2 concentrations over the past 420 million years. Nature 446, 530–532. doi: 10.1038/nature05699

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaller, J., Cramer, A., Carminati, A., and Zarebanadkouki, M. (2020). Biogenic amorphous silica as main driver for plant available water in soils. Sci. Rep. 10, 2424. doi: 10.1038/s41598-020-59437-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Schirmer, W. (2011). Rhine loess at Schwalbenberg II — MIS 4 and 3. E&G Q. Sci. J. 61, 32–47. doi: 10.3285/eg.61.1.03

CrossRef Full Text | Google Scholar

Schofield, R. E., Hausrath, E. M., and Gainey, S. R. (2015). “Zeolite weathering in laboratory and natural settings, and implications for mars,” in 46th Lunar and Planetary Science Conference (The Woodlands, TX).

Schopka, H. H., Derry, L. A., and Arcilla, C. A. (2011). Chemical weathering, river geochemistry and atmospheric carbon fluxes from volcanic and ultramafic regions on Luzon Island, the Philippines. Geochim. Cosmochim. Acta 75, 978–1002. doi: 10.1016/j.gca.2010.11.014

CrossRef Full Text | Google Scholar

Schuiling, R. D., and Krijgsman, P. (2006). Enhanced weathering: an effective and cheap tool to sequester CO2. Clim. Change 74, 349–354. doi: 10.1007/s10584-005-3485-y

CrossRef Full Text | Google Scholar

Seifritz, W. (1990). CO2 disposal by means of silicates. Nature 345, 486–486. doi: 10.1038/345486b0

PubMed Abstract | CrossRef Full Text | Google Scholar

Soil Survey Staff (1999). “Soil taxonomy: a basic system of soil classification for making and interpreting soil surveys,” in Natural Resources Conservation Service. U.S. Department of Agriculture Handbook 436, 2nd edn (Soil Survey Staff). Available online at: https://www.nrcs.usda.gov/wps/portal/nrcs/main/soils/survey/class/taxonomy/

Strasberg, D., Rouget, M., Richardson, D. M., Baret, S., Dupont, J., and Cowling, R. M. (2005). An Assessment of habitat diversity and transformation on la réunion island (Mascarene Islands, Indian Ocean) as a basis for identifying broad-scale conservation priorities. Biodivers. Conserv. 14, 3015–3032. doi: 10.1007/s10531-004-0258-2

CrossRef Full Text | Google Scholar

Streckeisen, A. (1980). Classification and nomenclature of volcanic rocks, lamprophyres, carbonatites and melilitic rocks IUGS Subcommission on the systematics of igneous rocks. Geol. Rundschau 69, 194–207. doi: 10.1007/BF01869032

CrossRef Full Text | Google Scholar

Strefler, J., Amann, T., Bauer, N., Kriegler, E., and Hartmann, J. (2018a). Potential and costs of carbon dioxide removal by enhanced weathering of rocks. Environ. Res. Lett. 13, 034010. doi: 10.1088/1748-9326/aaa9c4

CrossRef Full Text | Google Scholar

Strefler, J., Bauer, N., Kriegler, E., Popp, A., Giannousakis, A., and Edenhofer, O. (2018b). Between scylla and charybdis: delayed mitigation narrows the passage between large-scale CDR and high costs. Environ. Res. Lett. 13, 044015. doi: 10.1088/1748-9326/aab2ba

CrossRef Full Text | Google Scholar

Taylor, L. L., Quirk, J., Thorley, R. M. S., Kharecha, P. A., Hansen, J., Ridgwell, A., et al. (2015). Enhanced weathering strategies for stabilizing climate and averting ocean acidification. Nat. Clim. Chang. 6, 402–406. doi: 10.1038/nclimate2882

CrossRef Full Text | Google Scholar

Teitler, Y., Le Hir, G., Fluteau, F., Philippot, P., and Donnadieu, Y. (2014). Investigating the Paleoproterozoic glaciations with 3-D climate modeling. Earth Planet. Sci. Lett. 395, 71–80. doi: 10.1016/j.epsl.2014.03.044

CrossRef Full Text | Google Scholar

ten Berge, H. F. M., van der Meer, H. G., Steenhuizen, J. W., Goedhart, P. W., Knops, P., and Verhagen, J. (2012). Olivine weathering in soil, and its effects on growth and nutrient uptake in ryegrass Lolium perenne L.: a pot experiment. PLoS ONE 7, e42098. doi: 10.1371/journal.pone.0042098

PubMed Abstract | CrossRef Full Text | Google Scholar

Uchikawa, J., and Zeebe, R. E. (2008). Influence of terrestrial weathering on ocean acidification and the next glacial inception. Geophys. Res. Lett. 35, L23608. doi: 10.1029/2008GL035963

CrossRef Full Text | Google Scholar

United Nations (2015). Chapter XXVII Environment, 7.d Paris Agreement. New York, NY: United Nations.

van Straaten, P. (2002). Rocks for Crops: Agrominerals of Sub-Saharan Africa. Nairobi: ICRAF. doi: 10.1046/j.1465-5101.2001.132.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Verbruggen, E., Struyf, E., and Vicca, S. (2021). Can arbuscular mycorrhizal fungi speed up carbon sequestration by enhanced weathering? Plants People Planet 3, 445–453. doi: 10.1002/ppp3.10179

CrossRef Full Text | Google Scholar

Vienne, A., Ibanez, S. P., Portillo-Estrada, M., Hartmann, J., Ijiehon, S., Wade, P., et al. (2022). Enhanced weathering using basalt rock powder: carbon sequestration, co-benefits and risks in a mesocosm study with Solanum tuberosum. Front. Clim. 4, 869456. doi: 10.3389/fclim.2022.869456

CrossRef Full Text | Google Scholar

Vitens (2021). PhreeqPython. Vitens. Available online at: https://github.com/Vitens/phreeqpython).

Walker, J. C. G., Hays, P. B., and Kasting, J. F. (1981). A negative feedback mechanism for the long-term stabilization of earth's surface temperature. J. Geophys. Res. 86, 9776–9782. doi: 10.1029/JC086iC10p09776

CrossRef Full Text | Google Scholar

Wogelius, R. A., and Walther, J. V. (1992). Olivine dissolution kinetics at near-surface conditions. Chem. Geol. 97, 101–112. doi: 10.1016/0009-2541(92)90138-U

CrossRef Full Text | Google Scholar

Zandanel, A., Hellmann, R., Truche, L., Roddatis, V., Mermoux, M., Choblet, G., et al. (2022). Geologically rapid aqueous mineral alteration at subfreezing temperatures in icy worlds. Nat. Astron. 6, 554–559. doi: 10.1038/s41550-022-01613-2

CrossRef Full Text | Google Scholar