Can signal-to-noise ratio indicate prediction skill? Based on skill assessment of 1-month lead prediction of monthly temperature anomaly over Japan

Doi, Takeshi; Nonaka, Masami; Behera, Swadhin

doi:10.3389/fclim.2022.887782

ORIGINAL RESEARCH article

Front. Clim., 23 September 2022

Sec. Predictions and Projections

Volume 4 - 2022 | https://doi.org/10.3389/fclim.2022.887782

This article is part of the Research Topic Progresses in Indo-Pacific Climate Predictions View all 7 articles

Can signal-to-noise ratio indicate prediction skill? Based on skill assessment of 1-month lead prediction of monthly temperature anomaly over Japan

$\nTakeshi Doi &#x;$ Takeshi Doi^*^†

Masami Nonaka

Swadhin Behera

Application Laboratory (APL), Research Institute for Value-Added-Information Generation (VAiG), Japan Agency for Marine-Earth Science and Technology (JAMSTEC), Yokohama, Japan

We present a skill assessment of 1-month lead deterministic predictions of monthly surface air temperature anomalies over most part of Japan based on a large-ensemble climate model, SINTEX-F. We found that September is the most predictable and the only month in which the prediction skill beats the persistence. Interestingly, however, prediction of December becomes skillful (correlation skill: 0.67) when we select only years in which the signal-to-noise ratio of the predictions is relatively high. This means that the signal-to-noise ratio can partly indicate the prediction skill. The inter-member co-variability suggests that a combination of the tropical Pacific and western Indian Ocean surface temperature is the key for the prediction. Although seasonal climate prediction in the mid-latitude regions, such as Japan, is still challenging in general, providing the signal-to-noise ratio and the inter-member co-variability in addition to the real-time prediction might be useful for stakeholders to know how confident the individual prediction is, as well as its potential sources of predictability. Such information can be helpful to take necessary mitigation measures to reduce socio-economic losses associated with extreme climate.

Introduction

Monthly surface air temperature exhibits substantial year-to-year variability leading to large socioeconomic impacts. In particular, cold surges in winter and heat waves in summer affect the socio-economy of a region via issues in agriculture, health, water resources, electrical energy demand, etc., (e.g., Hill and Mjelde, 2002; Meza et al., 2008; Akihiko et al., 2014; Cawthorne et al., 2021). Therefore, skillful predictions of surface air temperature a few months ahead would be helpful for stakeholders to prepare in advance for such abnormal monthly climate events (e.g., Charles et al., 2012).

The seasonal predictability of rainfall and temperature in some regions is often linked to climate phenomena. For example, El Niño/Southern Oscillation (ENSO) modulates the East Asian climate and thus could work as the main potential source of its seasonal predictability (e.g., Wang et al., 2000). Besides ENSO, the Indian Ocean Dipole (IOD) (Saji et al., 1999) could influence the East Asian climate as suggested by several studies (Behera and Yamagata, 2003; Guan and Yamagata, 2003; Saji and Yamagata, 2003; Yamagata et al., 2004). Furthermore, teleconnection patterns in the western North Pacific provide crucial links of high seasonal predictability from the tropics to East Asia in summer (Kosaka et al., 2013; Xie et al., 2016). Molteni et al. (2015) discussed such a teleconnection from the central Pacific to East Asia, the maritime continents, and the western Indian Ocean. Recently, Doi et al. (2020c) also showed the western tropical Indian Ocean as one of the major potential sources of predictability for the East Asian winter climate.

The prediction skill scores (Kumar, 2007, 2009) form an important component of real-time seasonal predictions while developing decision making tools. As conducted in this study, the skills can be generally estimated by the reforecast experiments for the past cases generally available for 20–40 years. In addition, a priori skill of an individual prediction could be estimated by the ensemble spread as in case of numerical weather prediction systems (e.g., Buizza and Palmer, 1998; Whitaker and Louche, 1998). However, in seasonal climate prediction systems, relationships between the ensemble spread and the actual prediction skill are still limited (Kumar et al., 2000; Tang et al., 2008a, 2014). However, there are some tools available to access the skills of seasonal climate predictions. For example, the signal-to-noise ratio (SNR) has been widely regarded as a good measure for quantifying potential seasonal predictability (Rowell, 1998; Scaife and Smith, 2018). Tang et al. (2008b) showed that the SNR as well as the ensemble signal square are useful measures of the prediction skills of the ENSO and the Arctic Oscillation (AO).

In this study, we explored the potential of SNR in determining the prediction skill for the 1-month lead monthly temperature over Japan. We examined the prediction skill based on the reforecast experiments using the large-ensemble dynamical seasonal prediction system known as Scale Interaction Experiment–Frontier Research Center for Global Change (FRCGC) model “SINTEX-F” (Doi et al., 2019). We note that the large ensemble of the SINTEX-F system will help extract predictable signals and increase the chances of capturing potential teleconnection patterns from the tropics to the mid-latitude climate because the SNR is generally low in the mid-latitudes. We briefly described the prediction system and presented how we assessed the prediction skill in section 2. In section 3, we examined seasonality of the prediction skill. Then, we explored possible processes with large-scale circulations that work as potential sources of the predictability based on co-variability of the inter-member anomalies defined as deviations from the ensemble mean. Finally, we presented discussions and conclusions in sections 4 and 5, respectively.

Methods

The 108-member ensemble seasonal prediction system

The dynamical seasonal prediction system is based on an fully coupled global ocean–atmosphere circulation model (CGCM) called SINTEX-F ver. 2 developed under the EU–Japan collaborative framework (Masson et al., 2012; Sasaki et al., 2013), which has a dynamical sea-ice model, together with a higher-resolution relative to its previous version (Luo et al., 2003, 2005; Masson et al., 2005). This system adopts a relatively simple initialization scheme based only on the nudging of the SST data (Doi et al., 2016) and a three-dimensional variational ocean data assimilation (3DVAR) method by taking three-dimensional observed ocean temperature and salinity data into account (Doi et al., 2017). In consideration of the uncertainties of both initial conditions and model physics, the original system had 12 members for the predictions initiated on the first day of each month. The 12-member system has recently been upgraded to a bigger ensemble system of 108 members using the Lagged Average Forecasting (LAF) method (Doi et al., 2019, 2020b). Based on this new system, we conducted the reforecast experiments from the nine initialized dates (1st−9th) in every month of 1983–2020. The prediction anomalies were determined by removing the model climatology at each lead-time and ensemble member using the reforecast outputs over the period 1983–2015.

Skill assessment

To evaluate the prediction results, we used the NCEP/NCAR reanalysis data (Kalnay et al., 1996) and the NOAA Interpolated Outgoing Longwave Radiation (OLR), for atmospheric variables. The monthly climatologies of these datasets were calculated by averaging the monthly data from 1983 to 2015, and then the anomalies were derived through deviations from those climatologies. The linear trends were removed for all of the analyses.

In this study, the correlation coefficient and root-mean-square error (RMSE) between the anomaly of prediction and the verification value based on the observation/reanalysis datasets were adopted as the deterministic prediction skill scores. The p-value was calculated based on a paired t-test. We also assessed the potential predictability by dividing the predicted variability into signal (S) and unpredictable noise (N) components. S is the common feature among the ensemble members, and could be the predictable component of variability mainly due to tropical SST forcing, which was estimated as the ensemble mean of the 108 members. N was estimated as the ensemble spread that provided a measure of uncertainties among the predictions arising from the random effects of chaotic atmosphere-ocean variability. By calculating the SNR, we measured robustness of the prediction of the signal as well as the potential predictability. When the ensemble mean is small relative to the ensemble spread, the prediction is potentially difficult due to the large uncertainty.

Analysis of inter-member co-variability

Anomalies among the ensemble members (defined as deviations from the ensemble mean) and their co-variability in the ensemble space may provide useful insights into possible precursors and teleconnection patterns related to a climate event (Ma et al., 2017; Ogata et al., 2019; Doi et al., 2020a,b,c). Here, we calculated an inter-ensemble correlation among the 108-member ensemble predictions in target months. The Pearson correlation measures how two continuous timeseries co-vary over time and indicate the linear relationship as a number between – 1 and 1. In contrast, inter-ensemble correlation measures how two predictions co-vary over ensemble members by adding the ensemble phase space to the conventional time dimension. Here, we calculated it as

\begin{array}{l} R (x, y) = \frac{\frac{1}{n t^{*} n e} \sum_{e = 1}^{n e} \sum_{t = 1}^{n t} (X (t, e) - \bar{X}) (Y (x, y, t, e) - \bar{Y (x, y)})}{\sqrt{\frac{1}{n t^{*} n e} \sum_{e = 1}^{n e} \sum_{t = 1}^{n t} {(X (t, e) - \bar{X})}^{2}} \sqrt{\frac{1}{n t^{*} n e} \sum_{e = 1}^{n e} \sum_{t = 1}^{n t} {(Y (x, y, t, e) - \bar{Y (x, y)})}^{2}}} \end{array}

Here nt is the number of target years, ne is the ensemble size (108), X(t, e) is predictions of the target index [area-averaged anomalous temperature, e.g., monthly surface air temperature regionally averaged over most part of Japan (129°-141°E, 30°N−37°N) for Figures 3, 5; Niño3.4 index (SST anomaly averaged in 170°W−120°W, 5°S−5°N) for Figure 4] and a function of time (t) and ensemble member (e), $\bar{X}$ is the average of X(t, e) over target years and all ensemble members, Y(x, y, t, e) is predictions of the target variables (anomalous temperature, OLR, geopotential height (GH) at 200 hPa, and velocity potential at 200 hPa) and a function of two-dimensional horizontal (x, y), time (t) and ensemble member (e), $\bar{Y (x, y)}$ is the average of Y(x, y, t, e) over target years and all ensemble members, respectively.

Results

Which month is predictable?

Figure 1 shows seasonality of skills of 1-month lead prediction (e.g., prediction of December issued on 1st−9th of November) of monthly surface air temperature regionally averaged over most part of Japan (129°-141°E, 30°N−37°N). Based on the correlation skill, temperature in September is the most predictable (the skill: ~0.7), then, that in May and October are the second (the skill: ~0.5) and the third most predictable (the skill: ~0.4), respectively (Figure 1A). September is the only month in which the model prediction skill beats the persistence. The correlation skills for the other months are not statistically significant beyond the 95% confidence levels on the paired t-test.

FIGURE 1

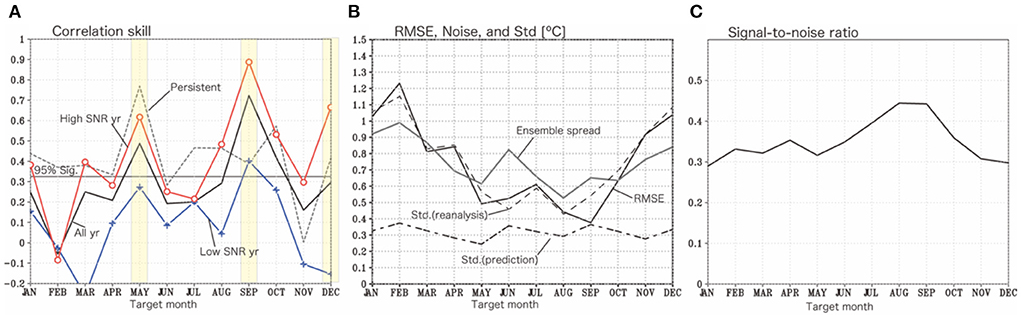
Figure 1. (A) Correlation skills for 1-month lead prediction (e.g., prediction of December issued on 1st−9th of November) of monthly temperature regionally averaged over most part of Japan (129°E−141°E, 30°N−37°N) for each calendar month. Correlation skills for all years of 1983–2020 (black), for years when the SNR is larger than its 1983–2020 mean (red), and for the other years (blue) are shown. Persistent skills (e.g., lag auto-correlation of December with previous November) are shown by a gray line. (B) RMSE (black line), ensemble spread (grey line), standard deviations of the reanalysis (dashed line) and the ensemble mean prediction (long and short dashed line) for each calendar month (°C). (C) 1983–2020 mean of SNR for each calendar month.

The reanalysis data shows the seasonality of the standard deviations of the averaged air temperature; large in wintertime and small in summertime (Figure 1B). It is not captured well by the ensemble mean prediction. Because atmospheric intrinsic variability included in the observation is largely removed in the ensemble mean, this suggests that the model is not skillful at predicting the amplitude. Interestingly, the ensemble spread shows a strong seasonality, large in wintertime and small in summertime, similar to what is seen in the standard deviation of the reanalysis data. The large standard deviation in the reanalysis data and the large ensemble spread in the predictions for wintertime can be partly due to strong atmospheric internal variability such as blocking events (e.g., Takaya and Nakamura, 2005). Note that a relatively large ensemble spread is also seen in June (Figure 1B), when the Baiu season onsets (e.g., Tomita et al., 2011). For other summer months, the ensemble spread is relatively small, in particular for August (~0.5°C), which is almost half of that in wintertime. In August, the Bonin High is formed around Japan, which is relatively stationary, as a separate system from the Tibetan and North Pacific anticyclones (Neyama, 1968; Enomoto et al., 2003). The Bonin High is also stable in some years, keeping aside the interannual variations, associated with limited propagations of stationary Rossby waves along the Asian jet (Enomoto, 2004). Those features may explain the small ensemble spread in August. Figure 1B also shows the relationship between the RMSE and the ensemble spread. The differences among the ensemble members are larger than the difference between the ensemble mean prediction and the observed value in September. In other words, the uncertainty of the prediction is overestimated (Fortin et al., 2014). In wintertime prediction, the opposite occurs, where the model underestimates the sources of error. The problem is common to most dynamical seasonal prediction systems based on GCMs (Scaife and Smith, 2018). Those errors in the prediction of the amplitude can be corrected by a postprocessing step that would amplify the predictable signal based on the correlation skills (Eade et al., 2014).

The SNRs are low in all calendar months (0.3–0.4) except for those in August and September (< 0.4) (Figure 1C), when the correlation skill and the RMSE are also relatively high. This suggests that the SNR can partly indicate the seasonality of the prediction skill.

Interestingly, we found the correlation skill of December becomes high and beats the persistence when we selected years in which the SNR is larger than the 1983–2020 mean of the SNR (Figure 1A). Therefore, we will focus on December as well as the most predictable September hereafter. Note that the SINTEX-F prediction system is not skillful in the 2-month lead prediction for all months.

September prediction

At a first glance, the model seems to be skillful in predicting most of the significant events from the timeseries for September (Figure 2A). The correlation skill is 0.72. Figure 2A shows that the SNR has substantial interannual variability (0.1–1.4), although the ensemble spread is almost constant. In high SNR years when SNR is higher than its 1983–2020 mean, the correlation skill is higher (~0.9) compared to the values considered with all the years (~0.7) (Figure 2B). Even for the low-SNR years, when SNR is lower than its 1983–2020 mean, the correlation skill is still about 0.4, which is comparable to that of the persistent skill.

FIGURE 2

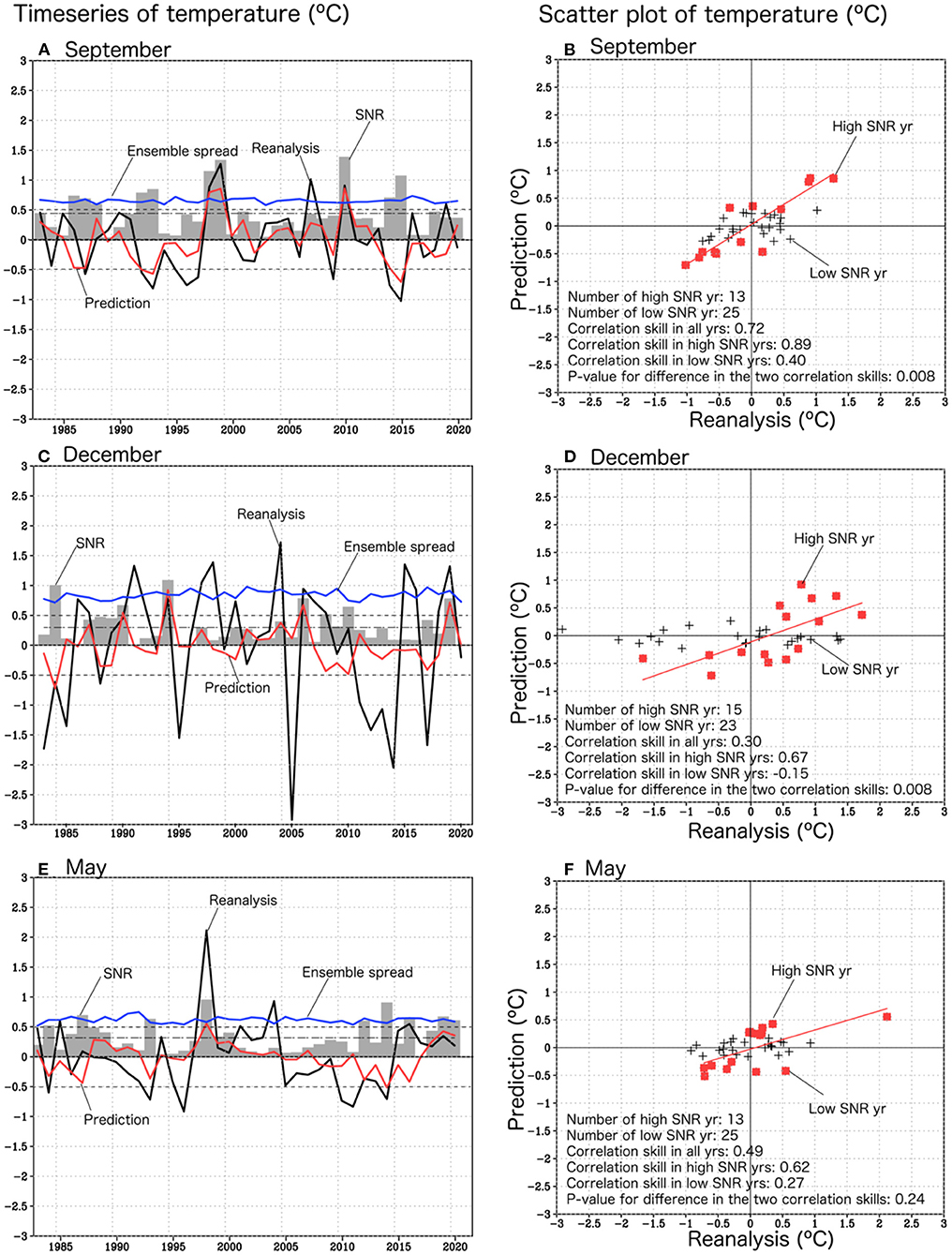
Figure 2. (A) Interannual time series of September temperature regionally averaged over most part of Japan (129°E−141°E, 30°N−37°N) for 1983–2020 by the reanalysis (black line), the ensemble mean predictions issued on 1st−9th of August (red line). Interannual variations of the ensemble spread (blue curve), the SNR (grey bars), and the 1983–2020 averaged SNR (chain line) are also shown. (B) Scatter plot of September temperature regionally averaged over most part of Japan (129°E−141°E, 30°N−37°N) for 1983–2020 by the reanalysis (x-direction) and the ensemble mean predictions issued on 1st−9th of August (y-direction). The plots in years when the SNR are larger than the 1983–2020 mean (high SNR yr) are shown by red square, the plot in the other years (low SNR yr) are shown by black cross. Linear regression lines are also shown for high SNR yr (red). The numbers of sample years in high/low SNR yr, the correlation skills in high/low SNR yr, and p-value for the difference in the correlation skills between high and low SNR years are shown on lower-left corner. (C,D) Same as (A,B), but for December (predictions issued on 1st−9th of November). (E,F) Same as (A,B), but for May (predictions issued on 1st−9th of April).

We selected warm years when the anomaly in the reanalysis data was above +0.5°C (1998, 1999, 2007, 2010, and 2019) and cold years when the anomaly in the reanalysis data was below – 0.5°C (1987, 1992, 1993, 1996, 1997, 2009, 2014, and 2015), then analyzed the inter-ensemble correlations. For the warm years, ensemble members that predicted a La Niña Modoki-like state (Ashok et al., 2007) mostly tend to predict an intensely warmer-than-normal condition over Japan (Figure 3A). They also tend to predict an enhanced convection (Figure 3C) and a positive SST anomaly (Figure 3A) over the Philippine Sea around 20°N and a positive GH200 anomaly over Japan (Figure 3E). Note that for Figure 3C, negative correlation (blue color) means that ensemble members that predicted an intense warmer-than-normal condition over Japan mostly tend to predict enhanced convection. The ensemble co-variability may suggest the teleconnection from the Philippine Sea into Japan via the enhanced local Hadley circulation associated with the La Niña-Modoki-like state. The suppressed (enhanced) convective activity over the western/central equatorial Pacific (tropical Indian Ocean) (Figure 3C), and the positive (negative) velocity potential anomaly at 200 hPa over the western Pacific and the tropical Indian Ocean (the eastern Pacific) (Figure 3G) suggest an enhancement of the Walker circulation in the Indo-Pacific basin, which also may contribute to the positive temperature and GH200 anomaly over Japan. The inter-ensemble correlations suggest that the La Niña Modoki could work as a potential source of the 1-month predictability of temperature over Japan. This may be partly consistent with the La Niña Modoki developing in autumn (Zhang et al., 2011). Note that the negative GH anomalies at 200 hpa associated with the cold SST anomaly are also seen in the central and western tropical Pacific (Figures 3A,E), which are similar to a typical La Niña Modoki state. However, they are not simply linked with the velocity potential at 200 hPa (Figure 3G), which looks similar to the canonical La Niña-like state. The ensemble co-variability may suggest a pattern resembling a mixture of a La Niña Modoki-type and a canonical-type (Karnauskas, 2013).

FIGURE 3

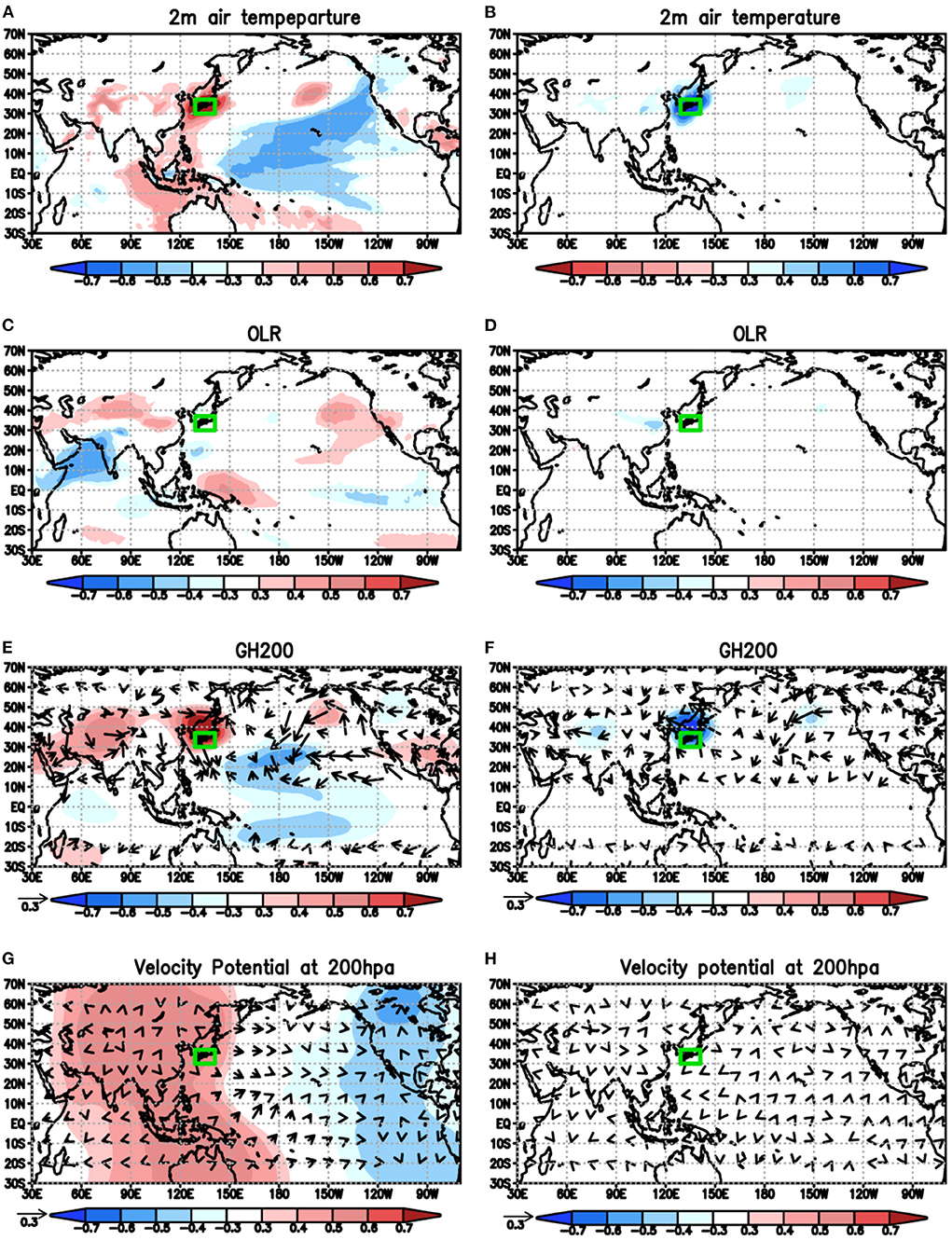
Figure 3. (A) A horizontal map of inter-ensemble correlations between 2m-air temperature anomaly averaged in 129°E−141°E, 30°N−37°N (shown by the green box) and a horizontal map of 2m-air temperature anomaly in 108-member ensemble predictions for September of the 5 warm years (1998, 1999, 2007, 2010, and 2019) issued on 1st−9th of August [sample size: 540, 12 (ensemble members) × 9 (initialized dates, 1st−9th) × 5 (warm years)]. Considering that the degree of freedom is based on the sample size, a correlation beyond 0.3 is statistically significant at the 95% confidence level (using the two-tailed Student's t-test) and are shaded. (C,E,G) Same as (A), but for (C) OLR, (E) GH (shaded) and the wave activity flux (Takaya and Nakamura, 2001) (vector) at 200 hPa, and (G) velocity potential (shaded) and divergent/convergent flows (vector) at 200 hPa. For (C), negative correlation (blue color) means that ensemble members that predicted an intense warmer-than-normal condition over Japan mostly tend to predict enhanced convection. (B,D,F,H) Same as (A,C,E,G), but for 8 cold years (1987, 1992, 1993, 1996, 1997, 2009, 2014, and 2015) (sample size: 108 member × 8 year = 864).

Interestingly, we could not find the ensemble co-variability between prediction of the tropical Pacific condition and prediction of atmospheric variables over Japan for the cold years (Figures 3B,D,F,H). The cold years include the super El Niño years: 1997 and 2015, then we also focused on those 2 years (Figure 4). As similar to Figures 3B,D,F,H, we could not find the ensemble co-variability between prediction of the super El Niño and prediction of atmospheric variables over Japan, although it suggested a weakening of the Walker circulation in the tropical Pacific (Figures 4G,H). Since the El Niño-Modoki and its impacts on East Asian summer are different from those of ENSO (Weng et al., 2007), further studies are necessary for deeper understanding of the uncertainty in their predictions.

FIGURE 4

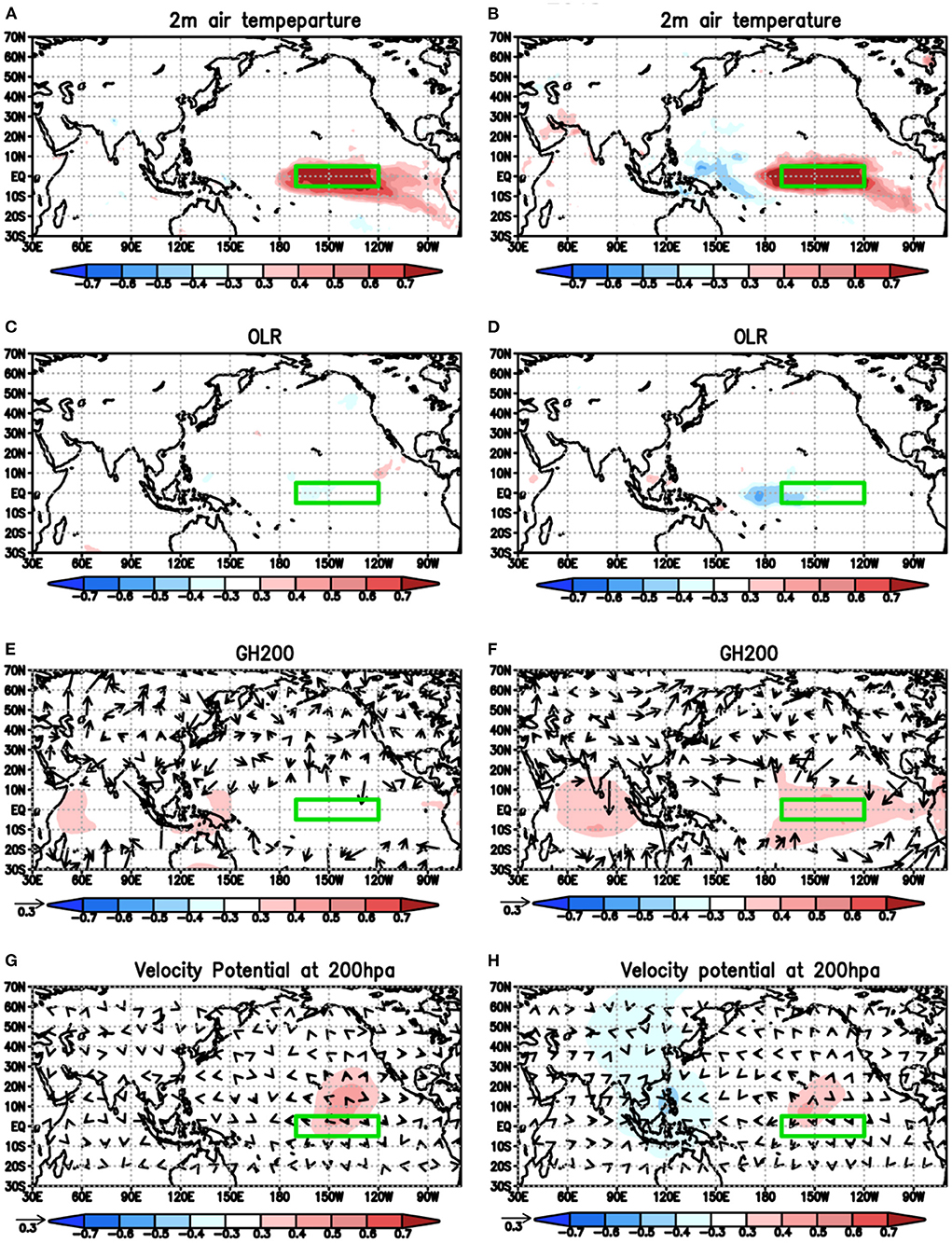
Figure 4. (A,C,E,G) Same as (Figures 3A,C,E,G), but for co-variability with prediction of Niño3.4 index (SST anomaly averaged in 170°W−120°W, 5°S−5°N) in 1997 (sample size: 108 member). (B,D,F,H) Same as (A,C,E,G), but for 2015.

December prediction

In stark contrast to September, the model seems to be not skillful in predicting most of significant events in December at a first glance (Figure 2C). However, when we selected 15 years in which the SNR is higher than the 1983–2020 mean of the SNR (1984, 1987, 1988, 1989, 1990, 1994, 1997, 2000, 2004, 2006, 2008, 2009, 2010, 2017, 2019), the correlation skill becomes 0.67, while that in the other 23 years it is – 0.15 (Figure 2D). The difference is statistically significant beyond the 99% confidence levels based on the t-test.

For the warm years, ENSO-Modoki contributions are also found as was seen in September, but with the opposite sign; warmer-than-normal conditions over Japan are linked with the El Niño-Modoki like condition in the tropical Pacific (Figure 5A). Ensemble members that predicted an El Niño Modoki-like state mostly tend to predict a suppressed convection (Figure 5C), a negative SST anomaly (Figure 5A) and a negative velocity potential anomaly (Figure 5G) over the Philippine Sea and the Maritime Continent, and a positive GH200 anomaly over Japan (Figure 5E). It may suggest the weakened local Hadley circulation in the western Pacific associated with the El Niño Modoki. The ensemble co-variability are also consistent with a possible teleconnection pattern from suppressed convection over the western Pacific associated with El Niño/El Niño Modoki into warm winters in Japan via an emanation of the Rossby wave train in the upper troposphere as discussed by previous works (Sakai and Kawamura, 2009; Ueda et al., 2015; Kuramochi et al., 2021).

FIGURE 5

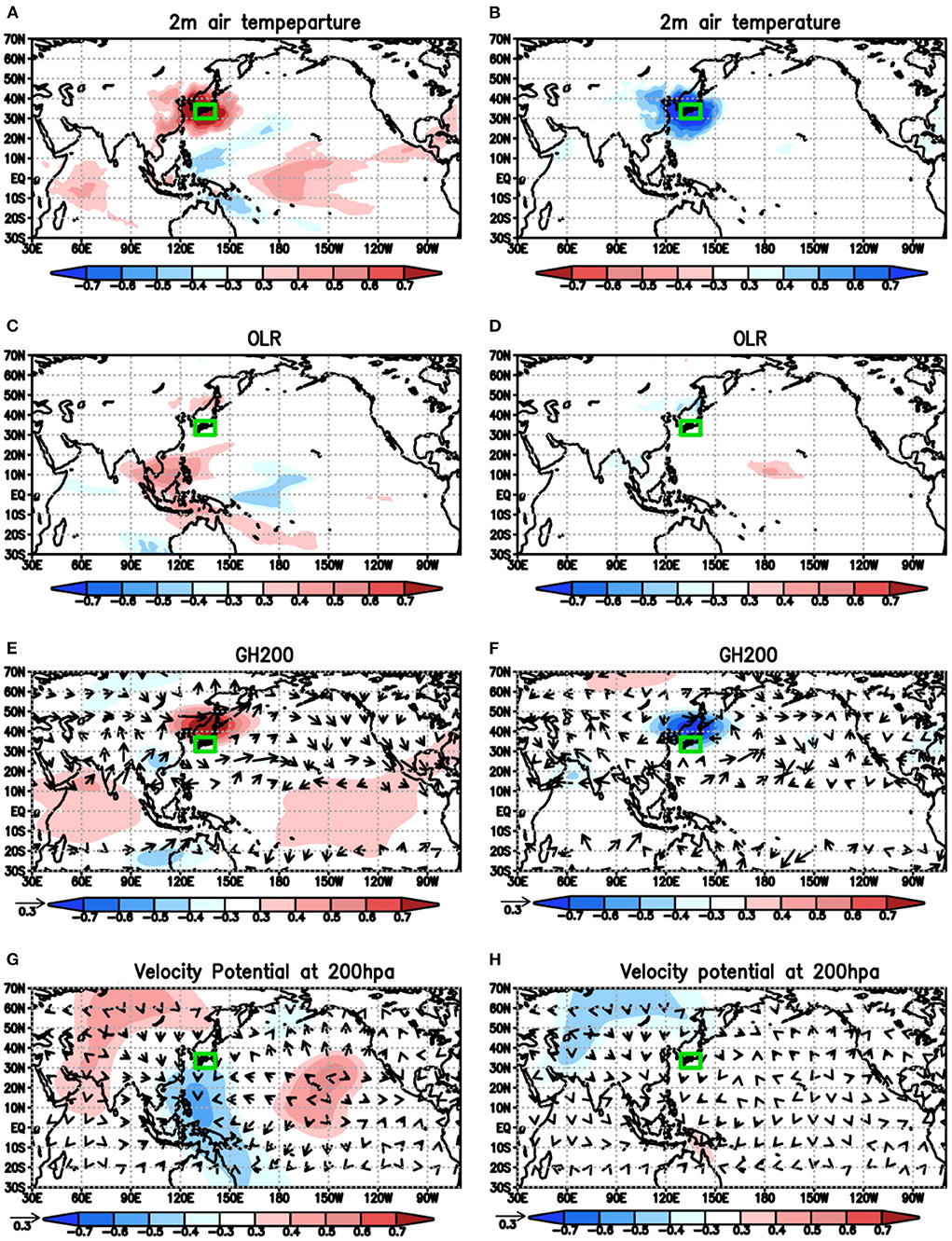
Figure 5. Same as Figure 3, but for December (prediction issued on issued on 1st−9th of November) for 10 warm years (1987, 1990, 1994, 1997, 2000, 2004, 2006, 2008, 2010, 2019) and 5 cold years (1984, 1988, 1989, 2009, 2017).

In addition, ensemble members that predicted warmer conditions in the western tropical Indian Ocean tend to predict warm temperature around Japan (Figure 5A). They also tend to predict an enhanced convection in the western tropical Indian Ocean (Figure 5C), a negative GH anomaly over southern China and a positive GH anomaly in the upper troposphere over Japan (Figure 5E). The ensemble co-variability suggests a possible teleconnection from the western tropical Indian Ocean via stationary Rossby waves along the subtropical jet. Although this is partly seen by the wave activity fluxes at 200 hPa (Takaya and Nakamura, 2001; Morioka et al., 2014) for the warm years (Figure 5E), we could not find the significant ensemble correlations between prediction of the temperature around Japan and prediction of the wave activity flux along the subtropical jet. Doi et al. (2020b) demonstrated the propagation pathways of stationary Rossby waves from the western tropical Indian Ocean to Japan for the record-breaking warm winter case over Japan in 2019/2020 by the SINTEX-F, when the positive SST anomaly in the western tropical Indian Ocean was observed after the super Indian Ocean Dipole (IOD) (Doi et al., 2020a). As a result, the southern penetration of cold air masses into Japan from high latitudes was weakened, causing warmer winter.

Interestingly, we could not find the ensemble co-variability between prediction of the tropical Pacific and Indian Ocean condition and prediction of atmospheric variables over Japan for the cold years (Figures 5B,D,F,H). Further studies are necessary for deeper understanding of such asymmetries.

Discussion

In this study, we found some cases that the SNR can partly indicate the prediction skill. Since the year-to-year variations of the noise are small, the SNR variations are large mainly due to the variations of the signal and the ensemble mean. It is partly consistent with Tang et al. (2008b), who showed that the SNR are useful measures of the prediction skills, but not as good as the ensemble mean square for predictions of ENSO and AO. We have confirmed the similar features for 1-month lead prediction of monthly temperature anomaly over Japan based on the large-ensemble prediction system. However, we tried not to generalize the relationship between SNR and prediction skills based on the results of this study. Rather, we picked the months when we found the skills are better than persistence to discuss here. Further extensive modeling and careful analyses are certainly necessary to recognize other factors affecting the predictability and reach a general conclusion.

We found September is the most predictable in the SINTEX-F prediction system but could not reach a definite conclusion why it is so and why other months are not so well-predicted in the SINTEX-F prediction system. ENSO/ENSO-Modoki phenomena should be the key factors explaining the seasonality in the prediction skill although the mechanism appears not to be so simple (e.g., asymmetry of their influences). They generally have the seasonal-phase locking nature; for example, they develop from the early summer through autumn, mature in winter, and decay in spring. For winter, although the ENSO amplitude is relatively large, the atmospheric internal variability is also large over the East Asia including Japan. For spring and summer, the amplitude is relatively small for both ENSO and ENSO Modoki. As a result, teleconnections of ENSO/ENSO-Modoki to the East Asia cannot work as main potential sources of the seasonal predictability in these seasons. This might be one of possible reasons.

The correlation skill of prediction of May, is relatively high (~0.5), although it is less than that of the persistence. Though the correlation skill became higher (0.62) (Figure 2F) when we selected years with the SNR higher than its 1983–2020 mean, it still could not beat the persistence (Figure 1A). It could be due to the presence of other signals in the time series. For example, as seen in the time series (Figure 2E), decadal signals are apparent in May. While it would be interesting to remove the decadal signal, that can affect the prediction skill, when a high-passed filter is applied, a certain part of the original information may be somehow perturbed because it is difficult to clearly separate the interannual variations from the decadal and longer timescale variations mainly owing to the limited sample size. Considering the possible interactions between interannual and decadal variability, we may need to develop skillful seamless prediction abilities from seasonal-to-decadal (S2D) timescale in the future.

A lot of previous studies demonstrated that East Asian climate is influenced by the AO (e.g., He et al., 2017) and the Madden-Julian Oscillation (MJO) (Jeong et al., 2005), and those could be additional potential sources of seasonal predictability of East Asian climate. However, predictions of those phenomena on a seasonal time scale by dynamical models, including SINTEX-F, are still challenging (Kumar and Chen, 2018; Lim et al., 2018) relative to predictions of the tropical climate variations such as ENSO and the IOD. Further studies and developments of dynamical prediction systems are necessary. In addition, a machine learning technique and a hybrid statistic-dynamical approach become powerful tools for seasonal prediction. Such a research stream is also helpful for understanding predictability as well as improvement of prediction skill (e.g., Ratnam et al., 2019, 2021a,b).

Having said that the errors in the prediction of the amplitude can be corrected in the postprocessing step, the errors should be reduced for more successful prediction by the model. Further studies are necessary, for example, to improve the model itself as well as the generation method of ensemble members.

Conclusions

We presented a skill assessment of 1-month lead predictions of monthly surface air temperature anomalies averaged in the region that covers most part of Japan based on the reforecast experiments with the large-ensemble SINTEX-F seasonal prediction system. While remarkable progresses are made for the prediction of tropical climate variations on longer lead time (6–12 months), the predictions of subtropical and mid-latitude climate even on 1-month lead is still a challenge. Comparing all the monthly predictions, we found that prediction of September temperature is the most predictable largely due to its association with the La Niña-Modoki-like state in the tropical Pacific. In other months, the SINTEX-F model could not provide useful prediction of temperature over Japan 1-month ahead. Through the skill assessment, however, we found that prediction of December temperature interestingly becomes skillful when we select years in which the SNR of the predictions is relatively high. It suggests that the SNR partly can indicate skill of deterministic prediction a priori as well as its potential predictability. It encouraged us to develop a practical method for estimating how confident the real-time prediction is in an individual year. For example, when the SNR is relatively high for deterministic prediction of a coming event, we could say that the prediction is relatively reliable. This information is intrinsically different from probability prediction.

The ensemble co-variability analysis might also be useful for stakeholders to know the potential sources of individual seasonal predictability; for example, we showed that prediction of December temperature over most of Japan could be due to a combination of the tropical Pacific and the western Indian Ocean surface temperature, at least as the SINTEX-F model.

Although prediction of wintertime temperature over Japan is still challenging, additional information of the SNR and the ensemble co-variability together with the real-time seasonal prediction can lead to a better understanding of an individual prediction. This will help stakeholders interpret the limits of the prediction as well as the potential for relevant applications, and take necessary mitigation measures to reduce the associated socio-economic losses.

Since the number of high SNR years is limited, the skill assessment in this study may be influenced by sampling errors. Besides, our results are based only on a single system. In a next step, the skills will be tested further by including results of multi-model prediction systems.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TD, MN, and SB contributed to designing the research, interpreting results and writing the paper. TD performed the seasonal prediction system on a basis of the ocean-atmosphere coupled model and analyzed the observation data and model prediction outputs. All authors contributed to the article and approved the submitted version.

Acknowledgments

The SINTEX-F seasonal climate prediction system was run by the Earth Simulator at JAMSTEC (see http://www.jamstec.go.jp/es/en/index.html, for the system overview). We are grateful to Drs. Wataru Sasaki, Jing-Jia Luo, Sebastian Masson, Antonio Navarra, and Toshio Yamagata and our European colleagues of INGV/CMCC, L'OCEAN, and MPI for their valuable contributions in developing the prototypes of the systems. We would also like to thank Drs. J. V. Ratnam, Yushi Morioka, and Pascal Oettli for his helpful comments and suggestions. The GrADS software was used to create the figures and maps. This research was supported by JSPS KAKENHI Grants 20K04074 and 19H05701. The NCEP Reanalysis data and the NOAA Interpolated OLR data were provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their web sites at https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.derived.surfaceflux.html, https://psl.noaa.gov/data/gridded/data.interp_OLR.html, respectively.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akihiko, T., Morioka, Y., and Behera, S. K. (2014). Role of climate variability in the heatstroke death rates of Kanto region in Japan. Sci. Rep. 4, 5655. doi: 10.1038/srep05655

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashok, K., Behera, S. K., Rao, S. A., Weng, H., and Yamagata, T. (2007). El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean. 112, 1–27. doi: 10.1029/2006JC003798