Adapting Technology Learning Curves for Prospective Techno-Economic and Life Cycle Assessments of Emerging Carbon Capture and Utilization Pathways

Introduction

Carbon capture, utilization, and storage (CCUS) can serve as an important tool in emissions mitigation. Various sources indicate that billions of metric tons of CO₂ will ultimately be utilized or sequestered every year [CO₂ Sciences Global CO₂ Initiative, 2016; Hepburn et al., 2019; International Energy Agency (IEA), 2019]. Carbon capture and storage (CCS) has high mitigation potential due to the large number of CO₂-emitting plants where it can be applied (Mac Dowell et al., 2017; Hepburn et al., 2019). Carbon capture and utilization (CCU) is attractive because of its ability to substitute conventional carbon-intensive production routes and offset high capture costs (Mac Dowell et al., 2017). The production of building materials such as concrete, cement, and aggregates offers particularly significant utilization potential ranging from one to five billion metric tons of CO₂ per year by 2050 (CO₂ Sciences Global CO₂ Initiative, 2016).

Despite CCU's significant potential, one of the most significant barriers to its large-scale deployment is the current low technology readiness level (TRL) of most CCU technologies (Hepburn et al., 2019). Due to the lack of available data and high uncertainty at low TRLs, identifying promising CCU pathways that scale well remains a challenge (Roh et al., 2020; Zimmermann et al., 2022). Moreover, a lack of a common analysis method that includes technological, economic, environmental, and social aspects makes comparisons of different CCU technologies difficult (Zimmermann and Schomäcker, 2017).

Identifying the best available technologies and developing appropriate policy support is complex and requires advanced assessment tools. As the goal of CCU development is to displace carbon-intensive products in an economically and environmentally viable manner (Mac Dowell et al., 2017), a harmonized approach for evaluating CCU technologies through the means of techno-economic assessment (TEA) and life cycle assessment (LCA) is necessary. To support this effort, the Global CO₂ Initiative (GCI) has published guidelines for conducting such assessments (Zimmermann et al., 2020) along with guidance on how to commission, understand and derive decisions for CCU processes for practitioners, decision-makers, and research commissioners (Cremonese et al., 2020). There are a couple of other guidance documents covering LCA and cost estimation for CCUS technologies as well (Skone et al., 2019; Roussanaly et al., 2021). This study seeks to expand on this previous work by offering a framework for improving the robustness of impact forecasting for emerging CCU technologies.

New technologies such as CCU are often at a disadvantage compared to incumbent technologies that have generally already gone through a significant level of iteration and optimization. Novel technologies and pilot plants do not have a high degree of technological learning or experience. Some methods for incorporating learning effects into economic and environmental assessment have previously been proposed (Thomassen et al., 2020; Roussanaly et al., 2021), and many involve assessing data for similar technologies that have already been optimized. Given data gaps and methodological limitations, current TEA and LCA assessments offer limited value for informing projections about the viability of CCU in climate mitigation pathways. Not considering technological learning or using unfounded assumptions associated with scaling and future research and development (R&D) will likely lead to misleading predictions. As CCU technologies generally include several process units with different maturity levels and scalability challenges, there is a need to develop granular technology learning curves (TLCs) to improve assessments and subsequent projections and planning. Furthermore, current learning curves are mostly limited to projecting cost changes, and there has been little work on forecasting greenhouse gas (GHG) emission performance. Thus, there is a need to develop TLC approaches that can be implemented with existing TEAs and LCA approaches using consistent and harmonized methodologies.

To this end, this study evaluates the state of the art of learning curve assessment in order to develop a harmonized framework and high-level roadmap for CCU technology assessments. After a short introduction to learning curves and learning rates, we review the application of these principles to relevant fields such as energy generation and storage. With sufficient background information, we then integrate established methodologies with the more nascent field of CCU to enable fair comparison across TRLs. Finally, a case study on a CCU mineralization pathway is implemented to demonstrate the proposed methodology.

Learning Curves: Brief Literature Review

Current Approaches

The concept of technological learning curves has been used since at least 1899, when they were applied to telegraph operation (William and Harter, 1899). More famously, learning curves received their first significant quantitative treatment in 1936 when they were applied by Theodore Paul Wright (the namesake of Wright's law; unrelated to the Wright brothers) in the aircraft industry to quantify the observation that labor time decreased by 20% for every doubling of aircraft production (Wright, 1936). Since then, they have been applied to a wide range of technologies and have guided companies and policy-makers for strategic purposes. Simply put, learning curves refer to an increase in performance per unit of a specific technology as the cumulative production volume of that technology increases (Zauner et al., 2019). Cost per unit and even other metrics that derive from performance, such as energy use and emissions per unit, can be used in place of performance. Cost will be used throughout this section to demonstrate the concept of technology learning, although it should be noted that changes in cost derive from increased performance due to learning. Thus, performance metrics for a given technology could be used in place of cost variables in the formulas featured here. In its simplest form, the relationship between cost and production is often represented by a power law as shown in Equation (1).

$\begin{array}{ll}{c}_t=c_0{\left(\frac{P_t}{P_0}\right)}^{- \alpha }& (1)\end{array}$

Here, the unit cost (c_t) and cumulative production (P_t) at time t are related to the unit cost (c₀) and cumulative production (P₀) at some initial time through the learning index exponent, α. When plotted on a log–log scale, this learning index is represented linearly and usually with a negative slope to indicate decreasing costs over time (Rivera-Tinoco et al., 2012). Often, a learning rate, LR, that represents the percentage cost reduction with each doubling of cumulative production is derived using Equation (2).

$\begin{array}{ll}LR=1-2^{-\alpha }& (2)\end{array}$

Learning rates are often calculated for various industries or technologies for comparison or projection purposes. For example, the learning rate for solar PV is often cited at around 20% (McDonald and Schrattenholzer, 2001; Görig and Breyer, 2016) and the rate for aerospace industry generally has been cited at 15% (Thomassen et al., 2020). Ultimately, learning rates for different technologies arise from numerous factors including labor efficiency, standardized manufacturing, optimization of product design, and shared utilization of resources within the company—all factors that lead to increased efficiencies in the overall process (Zauner et al., 2019). Using the formulas provided above, all of the factors contributing to technology learning are aggregated into one factor, and therefore this process can be referred to as a one-factor learning curve (OFLC) (Wiesenthal et al., 2012). OFLCs benefit from leveraging easily accessible data such as investment costs and production volumes and, as a result, tend to be widely used when deriving learning curves (Rubin et al., 2015). While relatively simple, convenient, and resistant to overfitting, OFLCs have been criticized for not accurately representing the dynamics of cost reductions from learning (Yeh and Rubin, 2012; Rubin et al., 2015). Moreover, OFLCs are only able to represent technology that has reached a degree of actual commercialization, as cost data are generally either non-existent or confidential at early TRLs (Elia et al., 2020).

Two-factor learning curves (TFLCs) were developed in order to disaggregate some of the different learning factors (Kouvaritakis et al., 2000). Specifically, the TFLC separates learning into learning-by-searching (LBS, which is also sometimes referred to as learning-by-researching) and learning-by-doing (LBD). LBS describes cost reductions in the technology as a result of research activities, while LBD refers to cost reductions in the technology as a result of experience gained during production (Elia et al., 2020). Explicitly integrating a research variable can help with modeling early-stage technologies. The formula for the TFLC is shown below, where α is the LBD index, KS is the knowledge stock from R&D activities (potentially measured in R&D expenditures), and β is the LBS index as shown in Equation (3).

$\begin{array}{ll}{c}_t=c_0{\left(\frac{P_t}{P_0}\right)}^{-\alpha }\ast {\left(KS\right)}^{-\beta }& (3)\end{array}$

Multi-factor learning curves (MFLCs) expand on TFLCs. In MFLCs, LBD is just one component of learning-by-deployment and is accompanied by learning-by-using (LBU), which models cost reductions arising from user feedback, and learning-by-interacting (LBI), which models cost reductions from knowledge exchange through the supply chain (Elia et al., 2020). Each factor seeks to delineate the effect of individual learning areas but increases the complexity of the learning curve.

Previous studies have highlighted the importance of public R&D in technological learning and correspondingly advocate for the use of a TFLC (Wene, 2008; Wiesenthal et al., 2012). Furthermore, studies have delineated the relative importance of learning at various stages of the innovation process, with learning being relatively high during the R&D stage, likely as a result of LBS (Elia et al., 2020). Learning was found to be highest during the pilot stage due to the combined effect of LBS and LBD, after which additional effects such as economies of scale and automation became the dominant factors in subsequent cost reductions (Elia et al., 2020). Fluctuations in markets—often leading to different costs for feedstocks, energy, or labor—also frequently play an important role in changing costs over time (Elia et al., 2020). It is important to acknowledge the difference between endogenous and exogenous factors that affect costs. Endogenous factors include technological learning, whereas exogenous factors arise from market factors such as materials and labor costs that are unrelated to the fundamental technology. Exogenous factors can also be referred to as “spillovers” from other industries. It can be challenging for statistical models to separate endogenous and exogenous factors, which can lead to biased estimates of learning when analyzing past data (Nordhaus, 2014).

This article offers a framework for applying OFLCs to carbon capture and utilization technologies to model how capital costs and greenhouse gas emissions could change with increased deployment. The OFLC approach focusing only on deployment was chosen due to the lack of data on both cumulative production and R&D funding. Therefore, the approach offered in this study is only the first step in constructing defensible projections of the total cost for carbon capture and utilization technologies. A more comprehensive approach would include other learning effects—such as LBS, LBI, and LBU—coupled with economy-of-scale effects and projections for important market costs like feedstocks, labor, and even carbon taxes, which can complement learning effects through market-pull mechanisms that accelerate innovation (Jordaan et al., 2017). Expected changes in emissions of feedstocks and energy sources should naturally be integrated into projections of environmental impact. Importantly, projections should also account for disconnects between R&D-level designs and large-scale, commercial processes, as doing otherwise risks neglecting design gaps that hinder scalability (Huang et al., 2018). For high-level and rapid projections, general learning rates that have been shown to cluster around 20% (Wene, 2008) could be applied to CCU, although this study details approaches that can allow for more precise calculations. Ultimately, creating granular and fully-informed projection models for various low carbon technologies will help identify gaps and therefore opportunities for accelerating the mitigation of climate change.

Learning Curves for Relevant Technologies

Calculation of learning rates is widely performed in literature, often for energy generation and storage (Jamasb, 2007; Rubin et al., 2015; Schmidt et al., 2017; Elia et al., 2020; Thomassen et al., 2020) but more recently for CCS (Rubin, 2019; Zauner et al., 2019) and hydrogen technologies (Schoots et al., 2008; Saba et al., 2018). We reviewed the state-of-the-art approaches for different technologies such as batteries, energy generation systems (e.g., solar PV, wind), fuel cells (solid oxide fuel cells in particular), electrolysis, methanation, and CCS to understand the challenges and benefits that come with these different approaches.

Assessing methods used to calculate learning for CCS is particularly relevant for CCU as both of these technology classes involve a capture component. Capture costs can vary from tens of dollars per metric ton of CO₂ to hundreds of dollars per ton depending on the source and the plant (House et al., 2011; Budinis et al., 2018), although learning will likely occur for each individual capture technology. As CO₂ capture can significantly increase operating costs, future studies should be standardized to include this component. Rubin et al. looked at the use of learning curves to estimate costs and learning rates of seven technologies relevant to power plants with CO₂ capture (Rubin et al., 2015). These learning rates are then combined according to the required processes for four power plant types with capture technologies: natural gas combined cycle, pulverized coal, integrated gasification combined cycle, and oxyfuel. Our approach incorporates an approach similar to Rubin et al. (2015) to include these costs and consequent learning rates.

A report from the National Energy Technology Laboratory (NETL) analyzed learning rates for estimating costs between first-of-a-kind (FOAK) and n^th-of-a-kind (NOAK) plants (2013). The report provides a comprehensive list of suggested learning rates for different processes in various energy systems derived from a literature search. Notably, the report notes that Fischer–Tropsch synthesis has a suggested learning rate of 5%, CO₂ capture, recovery, and compression has a suggested learning rate of 3%, and CO₂ transport and sequestration has a suggested learning rate of 5% (National Energy Technology Laboratory, 2013).

Findings and Limitations

A 2020 review by Thomassen et al. provides an overview of learning effects in new technology assessment and offers five recommendations (Thomassen et al., 2020). These include: (a) analyzing technologies using both component-level and end product-level learning rates to understand drivers of learning; (b) using technical, economic, and environmental learning rates to develop a comprehensive learning model; (c) combining projections from experts with extrapolated performance metrics generated with learning curves; (d) considering LBS effects using patent and experimental data when possible; and (e) prioritizing the use of historical data and literature values (over rates from similar technologies or derivations from current projections) when calculating learning rates (Thomassen et al., 2020). The authors also provide an extensive list of learning rates—including rule-of-thumb rates—from literature in their work (Thomassen et al., 2020). When rule-of-thumb values are used, it is recommended that the underlying uncertainty of these values be fully acknowledged to properly characterize the learning curve of the technology under consideration. As a final comment, the authors discuss the importance of harmonizing data before calculating a learning rate, which includes adjusting for inflation and scale.

Further review of existing literature on TLCs yielded the following insights that complemented those from Thomassen et al. (2020) during the development of our methodology.

• There is significant uncertainty when estimating learning rates due to a lack of high-quality data, resulting in diverse estimates across studies. Due to this variation, sensitivity analysis and alternative model formulations are recommended (Yeh and Rubin, 2012).

• If operational expenditures are included in cost projections, the use of a cost or price floor is recommended to avoid excessively low-cost estimates (Gross et al., 2014).

• The overall learning rate for a technological system is typically larger than the learning rates of the system's components (Jamasb, 2007; Rubin et al., 2015).

• Learning occurs more slowly for mature technologies that have already had a significant degree of deployment and subsequent optimization and LBD (Jamasb, 2007).

• For simplicity, it is essential to determine the factors most responsible for the cost reductions. Disaggregating cost drivers for CCU technologies may help provide more informed predictions of cost decreases moving forward (Rivera-Tinoco et al., 2012; Elia et al., 2020).

• The influence of cost drivers such as learning (both by doing and by researching, among others), economies of scale, and markets (encapsulating feedstock, labor, and energy costs) are often different at different stages of development (i.e., research and development, demonstration, market formation, and full commercialization). In the early stages of technological development, learning, particularly LBS, is generally more important, while at later stages market demand and economies of scale take over (Rivera-Tinoco et al., 2012; Elia et al., 2020).

• Generating learning curves for components rather than entire technology systems can provide more precise predictions (Krishnan et al., 2020).

• Data availability is a concern for TFLC models, as R&D investment is often not reported or not transparent. As a result, LBS is often only used to qualitatively discuss the effects of further research on technological progress (Rubin et al., 2015).

• For learning rates in general, the modeling approach is an important consideration when projecting costs. Modeling considerations include the choice of learning rate but also the initial cost and experience level, shape of the learning curve, consideration of a cost floor, correct measure of experience, geographical limitations, and individual components of the overall technology (Rubin et al., 2015).

• Uncertainty analysis is critical for generalizable models (Rubin et al., 2015; Elia et al., 2020).

The authors of the aforementioned NETL report note that there are limitations when using learning curves because they cannot account for cost increases that may occur during the early stages of plant development (2013). They also argue that an S-shaped learning curve should be used, although this has policy implications as the forecasted price reductions vary widely from standard learning curves. Overall, the report summarizes the methodology provided in the IEAGHG report (Antes et al., 2005). This methodology includes the following steps: (a) break each plant design into major technology sub-sections; (b) estimate current plant costs and contributions of each sub-section; (c) select an appropriate learning rate for each sub-section/component; (d) estimate the current capacity of major plant components; (e) set the start of learning (FOAK) and ending (NOAK) period; and (f) perform a sensitivity analysis (National Energy Technology Laboratory, 2013). These steps informed the development of the methodology featured in this study.

In recent studies by Roussanaly et al. and Rubin, the authors propose a hybrid bottom-up/engineering-economic and top-down/learning curve approach for cost estimation (Rubin, 2019; Roussanaly et al., 2021). That is, the FOAK plant is estimated using a comprehensive bottom-up approach that models the costs of each component of the plant while the NOAK plant cost is generated using learning curves applied to the calculated FOAK cost (Rubin, 2019; Roussanaly et al., 2021). FOAK plants are designed with over-sized and redundant equipment to reduce risk of failure during operation. These designs tend to be optimized in mature technologies. The study further discusses several other uncertainties and contingencies typically found in FOAK plant designs. The authors also emphasize that NOAK plant costs should not be derived using a bottom-up costing approach as it is not really possible to predict the exact costs of future plants, so it is only possible to model high-level cost behaviors deriving from original FOAK costs (Rubin, 2019; Roussanaly et al., 2021). For nascent CCU technologies, an approach such as the one defined here can also allow practitioners to bypass uncertainty in future bottom-up cost estimates.

There is little literature on learning rates for CCU technology in particular, as most CCU technologies are still at low TRLs. One study created a framework for evaluating CCU technologies at low TRLs (TRL 2–4) (Roh et al., 2020). Another discusses how “apples-to-apples,” early-stage evaluation of CCU technologies can help guide R&D investment (Zimmermann et al., 2021), which could increase the rate of LBS. The following section details this study's approach to synthesizing these insights from past literature on early-stage CCU technologies and on TLCs to ultimately apply them in a consistent and harmonized manner to CCU technology assessment.

Proposed Tlc Methodology

To derive TLCs for CCU, we first investigate which method can be applied depending on the data available. As CCU systems generally involve multiple subsystems or components composing the overall process, the hybrid method proposed by Rubin et al. is applicable (Rubin et al., 2013). Here, the one-factor learning rate is employed first, where LR is the learning rate and α is the learning index. α can be derived from Equation (2) using Equation (4).

$\begin{array}{ll}-\alpha =\frac{log(1-LR)}{log(2)}& (4)\end{array}$

Either a historical learning rate for a given CCU pathway or a rate for the same or a similar technology from literature should be chosen and justified, based on their tier method from Thomassen et al. (2020). The learning index can then be calculated for use in the projection.

As learning generally occurs with equipment rather than operational inputs such as materials or energy, learning rates are most often applied to capital expenditures (CapEx) rather than both CapEx and operating expenditures (OpEx). For example, learning for solar PV technologies is often expressed in terms of the change in dollars per kilowatt over time (de La Tour et al., 2013; Görig and Breyer, 2016; Kavlak et al., 2018), with dollars per kilowatt being a common metric when discussing the capital expenditures associated with solar energy generation. Here, CapEx are calculated using a series of steps to reach “total plant costs.” First, the total direct cost (TDC) of the plant and the factor for the indirect cost (f_indirect) must be calculated or estimated from literature in order to calculate the engineering, procurement, and construction (EPC) cost of the plant using Equation (5).

$\begin{array}{ll}EPC=TD{C}^{*}(1+f_{indirect})& (5)\end{array}$

Factors for process contingency (f_process) and project contingency (f_project) must then be used with the EPC cost in Equation (6) to estimate the total plant costs (TPC) for a FOAK plant. TPC is used synonymously with CapEx in the rest of this study.

$\begin{array}{ll}TP{C}_{FOAK}=EP{C}^{*}(1+f_{process}+f_{project})& (6)\end{array}$

Next, the previously-calculated learning index α and N, the number of plants necessary to reach the desired NOAK plant, can be applied to TPC_FOAK using Equation (7) to calculate total plant costs for the NOAK plant (TPC_NOAK) (Rubin et al., 2013).

$\begin{array}{ll}TP{C}_{NOAK}=TP{C}_{FOAK}*N^{-\alpha }& (7)\end{array}$

In addition to the whole-system approach, a more granular approach for estimating cost learning is presented where in the first step the learning rate is estimated for each system element individually [similar to what is recommended by Roussanaly et al. (2021) and Rubin (2019)] and in the second step a composite learning rate (LR_composite) is derived for the overall system as shown in Equation (8).

$\begin{array}{ll}L{R}_{composite}={\displaystyle \sum _i}\left[L{R}_{systemelementi}*\frac{TD{C}_{systemelementi}*(1+f_{indirect})*(1+f_{process}+f_{project})}{TP{C}_{overallsystem}}\right]& (8)\end{array}$

This composite learning rate may be higher or lower than the whole-system learning rate depending on the learning rates of the system elements and the indirect and contingency factors for each system element. Once the composite rate is calculated, a learning index can be derived and applied to FOAK metrics using the same method shown in this section.

For projecting GHG emissions, a similar approach is followed. Emissions for the FOAK plant (GHG_FOAK) must be estimated and a separate learning rate and learning index for emissions specifically may need to be calculated as well. Environmental learning rates could be estimated based on historical data or using CapEx learning rates as proxies. While emissions for a system could technically go to zero if every part of the system were fully decarbonized, in this approach there is a limit on emissions decreases that can arise from learning alone. This methodology's projections of environmental learning are inclusive of factors traditionally considered as OpEx, and this poses stoichiometric and energetic limits on how efficient the process can be. Thus, the minimum level of emissions of the foreground system—which could be based on factors such as a 100% reaction rate or 100% heat recovery—is represented in Equation (9) as GHG_min.

$\begin{array}{ll}GH{G}_{NOAK}=MAX\left\{GH{G}_{FOAK}*N^{-\alpha },GH{G}_{min}\right\}& (9)\end{array}$

Any further progress after reaching GHG_min would need to come from factors exogenous to the system under consideration (i.e., from the background system), such as less emissions-intensive electricity or feedstock materials. The CapEx learning approach proposed here excludes any considerations of OpEx as learning is traditionally only applied to capital expenditures, but if OpEx were to be considered, then a similar principle would apply. Costs for variable raw material and energy needs, which would be considered as operating expenditures, would set a cost floor, and from that point only exogenous changes to the costs of these inputs could lower costs of the system further. This methodology does not explicitly consider such changes so as to focus on technological learning of the foreground system alone.

The learning curve formulas above require an estimate of N, which is the number of plants that need to be built to reach NOAK. This number might be determined differently depending on the overarching research question. Methods for finding a suitable N could include: (a) calculating the cumulative capacity that would need to be installed for a plant to break even (Rubin et al., 2013); (b) finding the cumulative capacity where the learning curve flattens out (Larson et al., 2020); (c) using a number of plants that would translate into a pre-defined market share; or (d) using a number of plants that corresponds to those that would receive external subsidies.

Case Study: Direct Aqueous Mineralization

Introduction

As one of the largest emitters of anthropogenic CO₂ accounting for ~7% of global emissions, the cement industry in particular needs solutions to move toward a sustainable future [International Energy Agency (IEA), 2018; le Quéré et al., 2018]. Around 50% of these emissions are direct process emissions released from limestone during the calcination to produce clinker (Hoenig and Schneider, 2002). Given that these emissions will occur as long as limestone is used as a feedstock for cement production, they cannot be mitigated by increasing energy efficiency or switching to alternative fuels. Hence, many believe that solutions such as CCUS will play a significant role in decarbonizing the cement industry. The general idea is to not emit CO₂ directly but rather to store or use produced CO₂ as a feedstock for products. One technological concept that has been developed in this area is so-called “CO₂ carbonation” also often referred to as “CO₂ mineralization.” With this technology, CO₂ reacts with activated minerals or industrial waste to form carbonates (Gerdemann et al., 2007; Sanna et al., 2014; Eikeland et al., 2015; Ostovari et al., 2020), which store CO₂ permanently. The obtained carbonates can be used as cementitious materials for various purposes, such as for fillers, cement additives, or clinker substitutes (Sanna et al., 2014; Romanov et al., 2015; Kremer et al., 2019). Cement is a competitive commodity market, and major hurdles for implementing CCU technologies in the cement industry are their costs and economic viability (Zimmermann and Schomäcker, 2017). Analyzing the effects of technological learning is crucial for identifying the cost reduction or environmental improvement that can be realized when transitioning from a new technology (a FOAK plant) to a widely used technology (a NOAK plant).

Process Description

Multiple processes for CO₂ carbonation have been proposed, and they can be categorized into direct and indirect processes. Direct processes react minerals in a pressurized autoclave using an aqueous slurry with additives in one step (Sanna et al., 2014). In contrast, indirect processes extract alkaline earth metal oxides and treat them in a first step and then react them with CO₂ to form carbonates in a second step. Due to its simplicity in design, we used data for a direct process based on a publication by Ostovari et al. and Strunge et al. in this case study (2020, 2021). For direct processes, multiple minerals feedstocks such as olivine- or serpentine-bearing rocks have been proposed in the literature (Geerlings and Zevenhoven, 2013; Sanna et al., 2014; Romanov et al., 2015). Both mineral feedstocks require a pre-treatment step; olivine-bearing rocks must first be crushed and ground for activation whereas serpentines require an additional calcination step for activation (Gerdemann et al., 2007; Sanna et al., 2014; Stopic et al., 2018; Kremer et al., 2019). The CO₂ necessary for the carbonation reaction comes from flue gas or ambient air and must first be captured and compressed. Post-treatment steps such as separation might have to be added to reach commercial specifications for supplementary cementitious materials (Sanna et al., 2014; Kremer et al., 2019; Ostovari et al., 2020; Strunge et al., 2022). Some of the separated material will then have to be landfilled. The general process is shown in Figure 1.

FIGURE 1

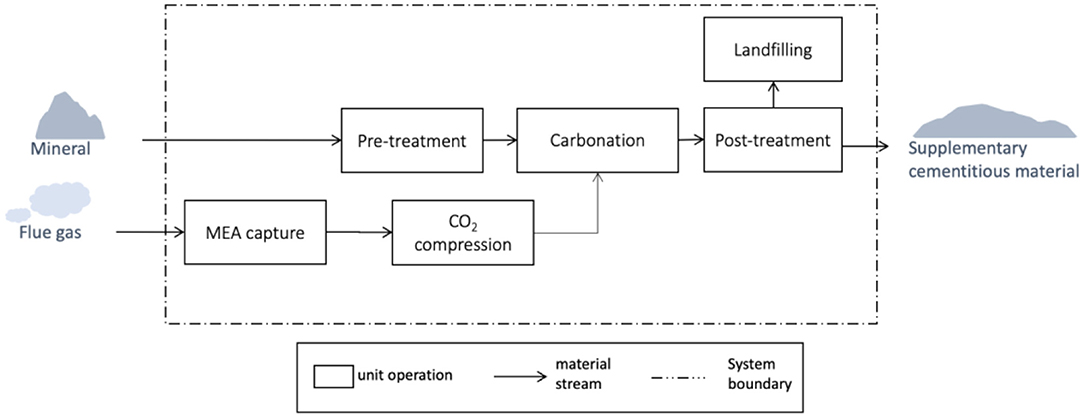
Figure 1. Direct aqueous carbonation unit operations and system adapted from Strunge (2022).

Following previous work in Strunge et al. (2022), the case study uses the process described by Eikeland et al. (2015) where Mg-silicate rich minerals (i.e., olivine-bearing rocks) are ground to 10 μm in diameter and are reacted with captured CO₂ in an aqueous solution using the additives NaCl and NaHCO₃ under increased temperature and pressure (T = 185°C, p = 100 bar). An overall product yield of 75–100% can be achieved (Eikeland et al., 2015).

System Data

To begin estimating the technological learning of the process, we first identify the TRL for each system element. These are located in Table 1.

TABLE 1

Table 1. TRL definitions of the relevant system elements.

The simplest method to estimate the capital expenditure for NOAK (CapEx_NOAK) is finding applicable existing learning rates and applying them to the corresponding parts of the system. Assumptions for the whole-system learning rate are based on the estimations by Rubin et al. (2015) for energy generation using coal-fired power plants with CCS (i.e., integrated gasification combined cycle and pulverized coal combustion, both equipped with post-combustion capture). The unit operations of both of these processes feature similar equipment that allows for grinding, gravity separation, post-combustion capture, and CO₂ compression, for example. Assumptions including process contingencies are shown in Table 2.

TABLE 2

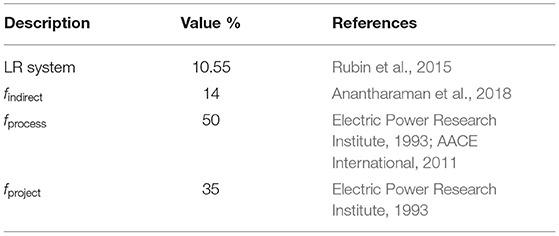
Table 2. Assumed indirect costs, contingencies, and learning rates for system (guidelines for deriving project and process contingencies are shown in Tables 3, Table 4).

Guidelines for deriving process and project contingencies are provided in Tables 3, 4.

TABLE 3

Table 3. Guidelines for deriving process contingency (Electric Power Research Institute, 1993; AACE International, 2011; Rubin et al., 2015).

TABLE 4

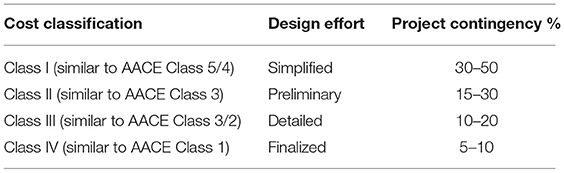
Table 4. Guidelines for deriving project contingency (Electric Power Research Institute, 1993; AACE International, 2011; Rubin et al., 2015).

The system element assumptions are shown in Table 5. Using solely the system elements for a bottom-up economic analysis is useful if an overall learning rate for the whole system is unavailable or if the technology learning is applied at a higher level of detail (Rubin et al., 2013).

TABLE 5

Table 5. Assumed indirect costs, contingencies, and learning rates for system elements (guidelines for deriving process and project contingencies are shown in Tables 3, 4).

For the techno-economic part of the case study, capacity and CapEx data for the FOAK plant were adapted from Anantharaman et al. (2018) and Strunge et al. (2022), leading to a TDC_FOAK of around $150 per metric ton of mineral product. This derivation assumes a constant plant capacity of 500,000 metric tons of product per year or 160,000 tons of CO₂ stored each year. Data from Ostovari et al. (2020) on emissions from electricity and thermal energy consumption along with material use and transportation data were used to calculate GHG_FOAK for the process, which was ultimately around 330 kg CO₂-eq per metric ton of the mineral product. Full calculations can be viewed in the file in the Supplementary Material.

Results

For the case study featured here, we assume that up to 5% of the 193 cement plants in Western Europe¹ will receive public subsidies, translating to about 10 plants at the NOAK level. This is only one way to estimate the number of NOAK plants, but it can help determine whether a given CCU process will be economically viable when external funding ceases. For the whole-system approach, CapEx_FOAK are around $320 per metric ton of mineral product per year and the estimated learning rate is 10.6%, resulting in CapEx_NOAK of ~$220/t for the tenth plant. The system element approach has CapEx_FOAK of around $290 per metric ton of mineral product per year (which is lower than the FOAK cost in the whole-system approach due to lower process contingencies for constituent processes) and estimates a slightly lower composite learning rate of 10.5%. These estimates result in CapEx_NOAK of approximately $200/t when using the system element approach as shown in Figure 2. Results represent projected gains from technological learning alone and do not account for changes in the cost of factors external to the analysis, such as changes in raw materials and energy costs, which will also likely have significant effects on system costs. However, it can be quite difficult if not impossible to fully separate the effects of exogenous and endogenous factors on cost (Nordhaus, 2014).

FIGURE 2

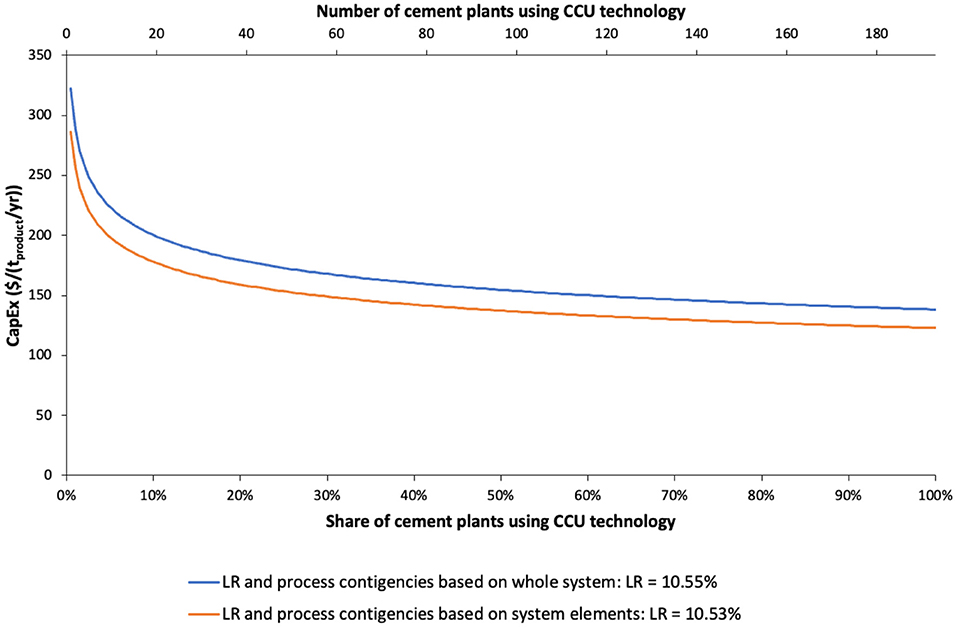
Figure 2. Technology learning curve for mineralization capital costs. FOAK costs differ due to differences in how process contingencies are calculated. Total number of cement plants in Western Europe is 193 (100%) (see text footnote 1).

Generally, technology learning is applied to capital expenditures. However, as technology learning affects the entire plant, it also influences other criteria and indicators. Here, we apply the concept of technology learning to the GHG emissions environmental indicator using the methodology proposed in a previous section.

Greenhouse gas emissions in kilograms of carbon dioxide equivalent were first calculated on a per metric ton of product basis for the FOAK plant. An emissions floor was then calculated using two proxy factors: recycling of additives and process yield. The use of these proxy factors allows the results to account for theoretical limits, as the recycling of additives and process yield cannot exceed 100%. The GHG emissions for the core processes in the foreground system cannot be further improved if an ideal yield and additive recycling rate have been reached, although emissions for the overall process can decrease further due to changes in exogenous variables in the background system, however, as discussed below. The general approach for modeling the effects of learning on emissions can be used with any life cycle inventory parameters of interest across CCU systems.

An environmental learning rate of 4.35% was assumed based on the average learning rate for operating and maintenance costs for post-combustion CO₂ capture facilities from Rubin et al. (2007). This rate was used as a proxy due to the correlation between energy consumption, energy-related operations costs, and GHG emissions. Figure 3 shows the results of the analysis. GHG emissions of the process alone (which exclude credits from the mineral storage of the captured CO₂) would be reduced from ~330 kg CO₂-eq per ton of the mineral product for the FOAK plant to 285 kg CO₂-eq/t for the tenth plant. Storage credits were excluded from these calculations to focus exclusively on emissions arising from the core processes in the foreground system; if these credits were included, the mineralization process itself could be carbon negative depending on the system boundary. The technological limit of additive recycling and process yield is reached after building about 30 plants, and no further improvement of GHG emissions from the core processes in the foreground system will likely occur. However, there may be improvements in GHG emissions due to factors in the background system, such as the de-carbonization of heat and electricity as well as electrified transportation of raw materials. It is important to emphasize that the technology learning curves in this study apply to the core processes in the foreground system rather than these external factors in the background system, which would need to be modeled separately.

FIGURE 3

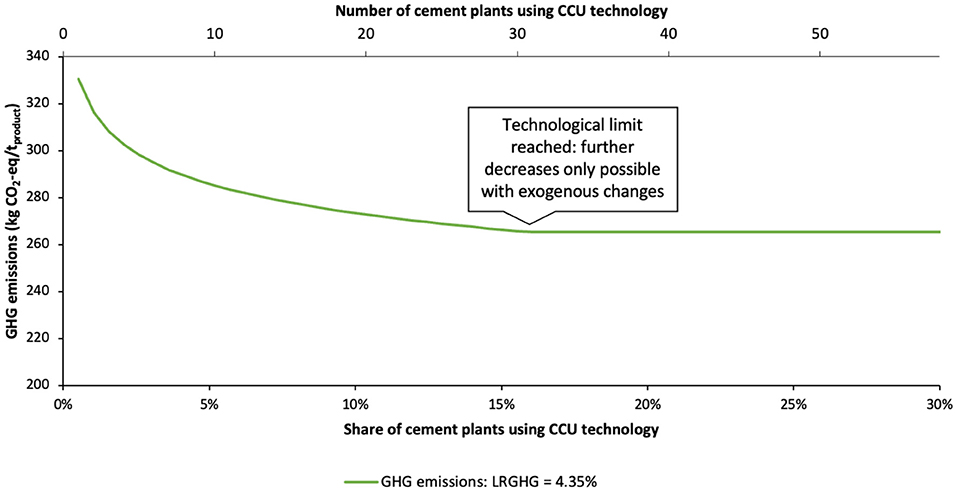
Figure 3. Technology learning curve for mineralization system emissions. Technological limit occurs when additive recycling and process yield are 100%; further improvements to environmental performance would have to arise from improvements in the environmental performance of exogenous factors, such as feedstocks or energy supplies. Total number of cement plants in Western Europe is 193 (100%) (see text footnote 1). Only process emissions are shown in the figure; overall emissions per ton of product would be negative when accounting for the mineralization credit.

Sensitivity Analysis

Sensitivity analysis can help demonstrate how sensitive final results for CapEx and GHG emissions are to various inputs. Such analysis can help identify what would have to be true in order to meet certain targets, including economic and environmental viability relative to the status quo. A simple, one-way sensitivity analysis (i.e., where only one input parameter is altered at a time) was conducted using the results in the previous section. The results are shown in Figure 4. Two input parameters for TLCs were altered: the learning rate and number of plants required to reach NOAK relative to the base values. The results demonstrate that the selection of the learning rate has a significantly higher impact on the outcomes relative to the estimated number of plants to reach NOAK. As the sensitivity of the GHG emission calculations is lower than for the CapEx, it also shows that the impact of changing the learning rate decreases when the overall learning rate is lower.

FIGURE 4

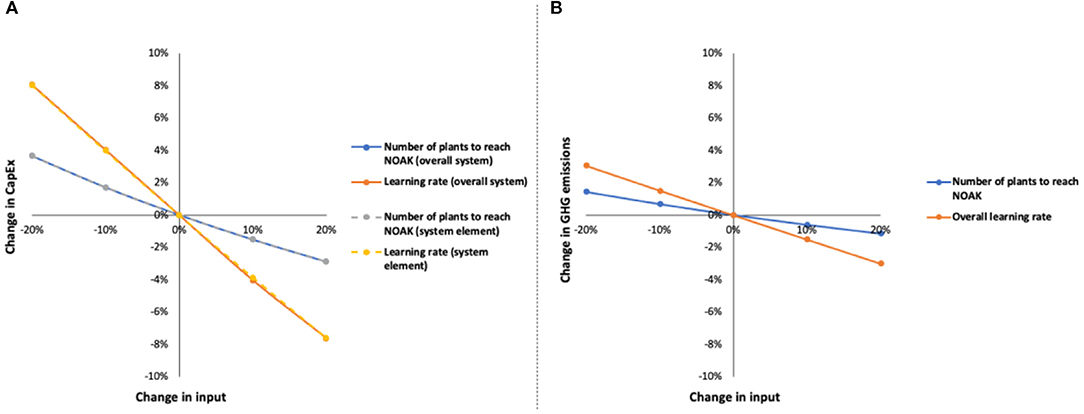
Figure 4. One-way, local sensitivity analysis calculating (A) CapEx and (B) GHG emissions altering the assumed number of plants and learning rates around their base values. Base value for the number of plants is 10, and the base values for the learning rates for CapEx are 10.55% (overall system), 10.53% (system element), and 4.35% for GHG emissions.

Case Study Conclusions

Being a significant emitter of greenhouse gases, the cement industry has developed a series of new technologies for the capture and utilization of carbon dioxide including mineral carbonation, producing cementitious materials with lower emission footprints. The economic and environmental characteristics of these technologies can improve when transitioning from a new technology (FOAK) to a mature technology (NOAK) due to technological learning. The methodology proposed in this study, if paired with sampling of estimated baseline trajectories, can help determine the scale of deployment necessary to meet target CapEx and greenhouse gas emissions per unit of mineral product. Understanding this necessary scale can assist with determining proper incentive structures and making comparisons between different climate mitigation pathways.

Discussion and Conclusion

In this study, we present how the concept of technology learning can be applied to the estimation of capital expenditure and greenhouse gas emissions for various CCU technologies. We show the approaches for applying learning rates to CapEx based on whole systems, to CapEx based on system elements, and to GHG emissions based on proxy factors. As expected, CapEx and GHG emissions decrease with deployment when accounting for technology learning. Learning could be further applied to additional criteria and indicators, such as operational expenditure and costs of goods sold or even other technology performance metrics. Furthermore, this analysis can help determine the scale at which cost or emissions goals can be met, which can in turn aid in the process of determining necessary levels of government incentives or even carbon taxes to enable proliferation of the technology in the marketplace.

The magnitude of technology learning is essential information, potentially changing outcomes in economic, environmental, or social criteria and leading to more informed decision-making in technology research, development and deployment. These considerations and modeling techniques will help industry, policymakers, and academics alike identify and accelerate economically viable pathways toward a sustainable future. For example, policymakers can use learning curves to help conduct cost–benefit analysis on particular policies and determine the returns to society from subsidizing certain technologies (Duke and Kammen, 1999).

However, the robustness of this forecast is limited due to significant data gaps and general uncertainty. To improve the quality of emerging CCU pathways assessments a more coordinated effort in generating and building data inventories at different scales and maturity levels is critical. Practitioners of life cycle and techno-economic assessment of CCU technologies should focus on transparently and accurately reporting relevant data and indicators to enable more informed quantification of TLCs over time. Previous comparative studies (Nagy et al., 2013; Farmer and Lafond, 2016; Lafond et al., 2018) of technological learning have relied heavily upon corresponding product-level data recorded over several years, with much of it recorded in the Santa Fe Institute Performance Curve Database.² A similar database devoted to CCU technologies that is also inclusive of emissions performance over time would be extremely useful in the development of increasingly accurate learning curves, particularly as many TLC estimation studies rely on hindcasting to develop relatively high-resolution models. This is especially the case as measuring improvements in emissions performance over time is becoming increasingly important and there is currently very little data on environmental learning rates.

Over time, updated TLCs for CCU technologies will enable a more accurate understanding of cost and emissions trajectories, ultimately enabling better decisions regarding further investments of time and resources. When integrated with theoretical minimum emissions and costs as determined by LCA and TEA, respectively, TLCs will assist with determining if and when a particular CCU pathway will be environmentally and economically viable. Such information will help better inform private investors about the potential impact and profitability of their investments. More importantly, it will also inform governments about further subsidies, taxes, regulations, or R&D funding that may be required to increase the viability of CCU technologies. CCU companies could also use these results to understand whether further innovations, increased scale, more favorable policies, or a combination are required for them to succeed.

With a limited number of years to completely decarbonize society to reach the global goal of limiting warming to 1.5°C, understanding the progress and development of climate technologies is more important than ever. Scholars, technology developers, investors, and governments need as much information as possible to compare all possible portfolios of climate solutions and mitigate potential innovation bottlenecks. Modeling technological learning curves for carbon capture and utilization technologies will help these stakeholders understand the potential promise and pitfalls in CCU, allowing for more informed and higher-impact decisions.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

TL and FB: conceptualization. AR: investigation. GF, AR, TS, TL, AZ, SM, and LT: writing—original draft. GF, AR, TL, MH, and SM: writing—review and editing. GF, AR, MH, FB, and SM: methodology. GF and TS: visualization. TS, AZ, and LT: case study conceptualization and analysis. FB, SM, and LT: supervision. All authors contributed to the article and approved the submitted version.

Funding

GF: Global CO₂ Initiative. AR: National Research Council of Canada. TS: Global CO₂ Initiative. TL: EIT Climate-KIC (Co-funded by the European Union). AZ: Netzero.Partners, Berlin. MH: Dutch Research Foundation (NWO), Project: ‘Global environmental trade-offs of renewable energy technologies' (016.Vici.170.190). FB: National Research Council of Canada. SM: U.S. Department of Energy National Energy Technology Laboratory (NETL) Contract Number DE-FE0025912. LT: National Renewable Energy Laboratory.

Author Disclaimer

This project was funded by the United States Department of Energy, National Energy Technology Laboratory, in part, through a site support contract. Neither the United States Government nor any agency thereof, nor any of their employees, nor the support contractor, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge the support and feedback from the entire International CCU Assessment Harmonization Group, which includes representatives from the National Energy Technology Laboratory, the National Renewable Energy Laboratory, Argonne National Laboratory, the National Research Council of Canada, IASS Potsdam, TU Berlin, RWTH Aachen, The University of Sheffield, the Global CO₂ Initiative at the University of Michigan, and EIT Climate-KIC. Volker Sick and Tim Skone offered expert oversight of this project along with all the other teams in the group.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2022.820261/full#supplementary-material

Abbreviations

CCU, carbon capture and utilization (or use); TEA, techno-economic assessment; LCA, life cycle assessment; CCUS, carbon capture, utilization (or use), and storage (or sequestration); CCS, carbon capture and storage (or sequestration); IEA, International Energy Agency; CO₂, carbon dioxide; TRL, technology readiness level; GCI, Global CO₂ Initiative; R&D, research and development; TLC, technology learning curve; GHG, greenhouse gas; OFLC, one-factor learning curve; TFLC, two-factor learning curve; LBS, learning-by-searching; LBD, learning-by-doing; MFLC, multi-factor learning curve; LBU, learning-by-using; LBI, learning-by-interacting; NETL, National Energy Technology Laboratory; FOAK, first-of-a-kind; NOAK, n^th-of-a-kind; IEAGHG, International Energy Agency Greenhouse Gas R&D Programme; CapEx, capital expenditures; OpEx, operating expenditures; LR, learning rate; MEA, monoethanolamine.

Footnotes

1. ^https://www.cemnet.com/global-cement-report/

2. ^http://pcdb.santafe.edu/

References

AACE International (2011). Cost Estimate Classification System – as Applied in Engineering, Procurement, and Construction for the Process Industries.

Google Scholar

Anantharaman, R., Berstad, D., Cinti, G., De Lena, E., Gatti, M., Hoppe, H., et al. (2018). CEMCAP framework for comparative techno-economic analysis of CO2 capture from cement plants - D3.2 (Revision 2). Zenodo. doi: 10.5281/zenodo.1257112

CrossRef Full Text | Google Scholar

Antes, M., Yeh, S., and Berkenpas, M. (2005). Estimating Future Trends in the Cost of CO2 Capture Technologies. Final Report to IEA GHG RandD Program.

Google Scholar

Budinis, S., Krevor, S., Dowell, N., mac Brandon, N., and Hawkes, A. (2018). An assessment of CCS costs, barriers and potential. Energy Strategy Rev. 22, 61–81. doi: 10.1016/j.esr.2018.08.003

CrossRef Full Text | Google Scholar

CO2 Sciences and Global CO2 Initiative (2016). Global Roadmap for Implementing CO₂ Utilization.

Google Scholar

Cremonese, L., Olfe-Kräutlein, B., Strunge, T., Naims, H., Zimmermann, A., Langhorst, T., et al. (2020). Making Sense of Techno-Economic Assessment and Life Cycle Assessment Studies for CO₂ Utilization: a Guide on How to Commission, Understand, and Derive Decisions From TEA and LCA Studies. Global CO₂ Initiative. doi: 10.3998/2027.42/156039

CrossRef Full Text | Google Scholar

de La Tour, A., Glachant, M., and Ménière, Y. (2013). Predicting the costs of photovoltaic solar modules in 2020 using experience curve models. Energy 62, 341–348. doi: 10.1016/j.energy.2013.09.037

CrossRef Full Text | Google Scholar

Duke, R., and Kammen, D. M. (1999). The economics of energy market transformation programs. Energy J. 20. doi: 10.5547/ISSN0195-6574-EJ-Vol20-No4-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Eikeland, E., Blichfeld, A. B., Tyrsted, C., Jensen, A., and Iversen, B. B. (2015). Optimized carbonation of magnesium silicate mineral for CO2 storage. ACS Appl. Mater. Interfaces 7, 5258–5264. doi: 10.1021/am508432w

PubMed Abstract | CrossRef Full Text | Google Scholar

Electric Power Research Institute (1993). Technical Assessment Guide Volume 1: Electricity Supply (1993). TR-102276-V1R1.

Google Scholar

Elia, A., Kamidelivand, M., Rogan, F., and Gallachóir, B. Ó. (2020). Impacts of innovation on renewable energy technology cost reductions. Renew. Sustain. Energy Rev. 138:110488. doi: 10.1016/j.rser.2020.110488

CrossRef Full Text | Google Scholar

Farmer, J. D., and Lafond, F. (2016). How predictable is technological progress? Res. Policy 45, 647–665. doi: 10.1016/j.respol.2015.11.001

CrossRef Full Text | Google Scholar

Geerlings, H., and Zevenhoven, R. (2013). CO₂ mineralization—bridge between storage and utilization of CO2. Annu. Rev. Chem. Biomol. Eng. 4, 103–117. doi: 10.1146/annurev-chembioeng-062011-080951

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerdemann, S. J., O'Connor, W. K., Dahlin, D. C., Penner, L. R., and Rush, H. (2007). Ex situ aqueous mineral carbonation. Environ. Sci. Technol. 41, 2587–2593. doi: 10.1021/es0619253

PubMed Abstract | CrossRef Full Text | Google Scholar

Görig, M., and Breyer, C. (2016). Energy learning curves of PV systems. Environ. Prog. Sustain. Energy 35, 914–923. doi: 10.1002/ep.12340

CrossRef Full Text | Google Scholar

Gross, R., Heptonstall, P., Greenacre, P., Candelise, C., Jones, F., and Castillo Castillo, A. (2014). Presenting the Future: An Assessment of Future Cost Estimation Methodologies in the Electricity Sector. UK Energy Research Center.

Google Scholar

Hepburn, C., Adlen, E., Beddington, J., Carter, E. A., Fuss, S., mac Dowell, N., et al. (2019). The technological and economic prospects for CO₂ utilization and removal. Nature 575, 87–97. doi: 10.1038/s41586-019-1681-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoenig, V., and Schneider, M. (2002). CO₂ Reduction in the Cement Industry. VDZ Congress.

Google Scholar

House, K. Z., Baclig, A. C., Ranjan, M., van Nierop, E. A., Wilcox, J., and Herzog, H. J. (2011). Economic and energetic analysis of capturing CO₂ from ambient air. Proc. Nat. Acad. Sci. U.S.A. 108, 20428–20433. doi: 10.1073/pnas.1012253108

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, K. J., Li, L., and Olivetti, E. A. (2018). Designing for manufacturing scalability in clean energy research. Joule 2, 1642–1647. doi: 10.1016/j.joule.2018.07.020

CrossRef Full Text | Google Scholar

International Energy Agency (IEA) (2018). Technology Roadmap: Low-Carbon Transition in the Cement Industry.

Google Scholar

International Energy Agency (IEA) (2019). Putting CO₂ to Use. Available online at: https://www.iea.org/reports/putting-co2-to-use

Google Scholar

Jamasb, T.. (2007). Technical change theory and learning curves: patterns of progress in electricity generation technologies. Energy J. 28. doi: 10.5547/ISSN0195-6574-EJ-Vol28-No3-4

CrossRef Full Text | Google Scholar

Jordaan, S. M., Romo-Rabago, E., McLeary, R., Reidy, L., Nazari, J., and Herremans, I. M. (2017). The role of energy technology innovation in reducing greenhouse gas emissions: a case study of Canada. Renew. Sustain. Energy Rev. 78, 1397–1409. doi: 10.1016/j.rser.2017.05.162

CrossRef Full Text | Google Scholar

Kavlak, G., McNerney, J., and Trancik, J. E. (2018). Evaluating the causes of cost reduction in photovoltaic modules. Energy Policy 123, 700–710. doi: 10.1016/j.enpol.2018.08.015

CrossRef Full Text | Google Scholar

Kouvaritakis, N., Soria, A., and Isoard, S. (2000). Modelling energy technology dynamics: methodology for adaptive expectations models with learning by doing and learning by searching. Int. J. Glob. Energy 14, 104–115. doi: 10.1504/IJGEI.2000.004384

CrossRef Full Text | Google Scholar

Kremer, D., Etzold, S., Boldt, J., Blaum, P., Hahn, K. M., Wotruba, H., et al. (2019). Geological mapping and characterization of possible primary input materials for the mineral sequestration of carbon dioxide in Europe. Minerals 9:485. doi: 10.3390/min9080485

CrossRef Full Text | Google Scholar

Krishnan, S., Fairlie, M., Andres, P., de Groot, T., and Kramer, G. J. (2020). “Power to gas (H2): alkaline electrolysis,” in Technological Learning in the Transition to a Low-Carbon Energy System (Elsevier), 165–187. doi: 10.1016/B978-0-12-818762-3.00010-8

CrossRef Full Text | Google Scholar

Lafond, F., Bailey, A. G., Bakker, J. D., Rebois, D., Zadourian, R., McSharry, P., et al. (2018). How well do experience curves predict technological progress? A method for making distributional forecasts. Technol. Forecast. Soc. Change 128, 104–117. doi: 10.1016/j.techfore.2017.11.001

CrossRef Full Text | Google Scholar

Larson, E. D., Kreutz, T. G., Greig, C., Williams, R. H., Rooney, T., Gray, E., et al. (2020). Design and analysis of a low-carbon lignite/biomass-to-jet fuel demonstration project. Appl. Energy 260:114209. doi: 10.1016/j.apenergy.2019.114209

CrossRef Full Text | Google Scholar

le Quéré, C., Andrew, R. M., Friedlingstein, P., Sitch, S., Hauck, J., Pongratz, J., et al. (2018). Global carbon budget 2018. Earth Syst. Sci. Data 10, 2141–2194. doi: 10.5194/essd-10-2141-2018

CrossRef Full Text | Google Scholar

Mac Dowell, N., Fennell, P. S., Shah, N., and Maitland, G. C. (2017). The role of CO2 capture and utilization in mitigating climate change. Nat. Clim. Change 7, 243–249. doi: 10.1038/nclimate3231

CrossRef Full Text | Google Scholar

McDonald, A., and Schrattenholzer, L. (2001). Learning rates for energy technologies. Energy Policy 29, 255–261. doi: 10.1016/S0301-4215(00)00122-1

CrossRef Full Text | Google Scholar

Nagy, B., Farmer, J. D., Bui, Q. M., and Trancik, J. E. (2013). Statistical basis for predicting technological progress. PLoS ONE 8:e52669. doi: 10.1371/journal.pone.0052669

PubMed Abstract | CrossRef Full Text | Google Scholar

National Energy Technology Laboratory (2013). Technology Learning Curve (FOAK to NOAK).

Google Scholar

Nordhaus, W. D.. (2014). The perils of the learning model for modeling endogenous technological change. Energy J. 35, 1–13. doi: 10.5547/01956574.35.1.1

CrossRef Full Text | Google Scholar

Ostovari, H., Sternberg, A., and Bardow, A. (2020). Rock ‘n'use of CO₂: carbon footprint of carbon capture and utilization by mineralization. Sustain. Energy Fuels 4, 4482–4496. doi: 10.1039/D0SE00190B

CrossRef Full Text | Google Scholar

Rivera-Tinoco, R., Schoots, K., and van der Zwaan, B. (2012). Learning curves for solid oxide fuel cells. Energy Conv. Manag. 57, 86–96. doi: 10.1016/j.enconman.2011.11.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Roh, K., Bardow, A., Bardow, A., Bardow, A., Bardow, A., Bongartz, D., et al. (2020). Early-stage evaluation of emerging CO₂ utilization technologies at low technology readiness levels. Green Chem. 22, 3842–3859. doi: 10.1039/C9GC04440J

CrossRef Full Text | Google Scholar

Romanov, V., Soong, Y., Carney, C., Rush, G. E., Nielsen, B., and O'Connor, W. (2015). Mineralization of carbon dioxide: a literature review. ChemBioEng Rev. 2, 231–256. doi: 10.1002/cben.201500002

CrossRef Full Text | Google Scholar

Roussanaly, S., Rubin, E. S., van der Spek, M., Booras, G., Berghout, N., Fout, T., et al. (2021). Towards improved guidelines for cost evaluation of carbon capture and storage. doi: 10.2172/1779820

CrossRef Full Text | Google Scholar

Rubin, E. S.. (2019). Improving cost estimates for advanced low-carbon power plants. Int. J. Greenhouse Gas Control 88, 1–9. doi: 10.1016/j.ijggc.2019.05.019

CrossRef Full Text | Google Scholar

Rubin, E. S., Azevedo, I. M. L., Jaramillo, P., and Yeh, S. (2015). A review of learning rates for electricity supply technologies. Energy Policy 86, 198–218. doi: 10.1016/j.enpol.2015.06.011

CrossRef Full Text | Google Scholar

Rubin, E. S., Short, C., Booras, G., Davison, J., Ekstrom, C., Matuszewski, M., et al. (2013). A proposed methodology for CO₂ capture and storage cost estimates. Int. J. Greenhouse Gas Control 17, 488–503. doi: 10.1016/j.ijggc.2013.06.004

CrossRef Full Text | Google Scholar

Rubin, E. S., Yeh, S., Antes, M., Berkenpas, M., and Davison, J. (2007). Use of experience curves to estimate the future cost of power plants with CO₂ capture. Int. J. Greenhouse Gas Control 1, 188–197. doi: 10.1016/S1750-5836(07)00016-3

CrossRef Full Text | Google Scholar

Saba, S. M., Müller, M., Robinius, M., and Stolten, D. (2018). The investment costs of electrolysis–A comparison of cost studies from the past 30 years. Int. J. Hydrogen Energy 43, 1209–1223. doi: 10.1016/j.ijhydene.2017.11.115

CrossRef Full Text | Google Scholar

Sanna, A., Uibu, M., Caramanna, G., Kuusik, R., and Maroto-Valer, M. M. (2014). A review of mineral carbonation technologies to sequester CO 2. Chem. Soc. Rev. 43, 8049–8080. doi: 10.1039/C4CS00035H

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, O., Hawkes, A., Gambhir, A., and Staffell, I. (2017). The future cost of electrical energy storage based on experience rates. Nat. Energy 2:17110. doi: 10.1038/nenergy.2017.110

CrossRef Full Text | Google Scholar

Schoots, K., Ferioli, F., Kramer, G. J., and van der Zwaan, B. C. C. (2008). Learning curves for hydrogen production technology: an assessment of observed cost reductions. Int. J. Hydrogen Energy 33, 2630–2645. doi: 10.1016/j.ijhydene.2008.03.011

CrossRef Full Text | Google Scholar

Skone, T. J., Mutchek, M., Krynock, M., Cooney, G., Pegallapati, A., Rai, S., et al. (2019). Carbon Dioxide Utilization Life Cycle Analysis Guidance. Available online at: https://netl.doe.gov/projects/files/NETLCO2ULCAGuidanceDocument_092019.pdf

PubMed Abstract | Google Scholar

Stopic, S., Dertmann, C., Modolo, G., Kegler, P., Neumeier, S., Kremer, D., et al. (2018). Synthesis of magnesium carbonate via carbonation under high pressure in an autoclave. Metals 8:993. doi: 10.3390/met8120993

CrossRef Full Text | Google Scholar

Strunge, T.. (2022). The Costs of CO₂ Carbonation in the Cement Industry. Available online at: https://www.nature.com/articles/s43247-022-00390-0

Google Scholar

Strunge, T., Renforth, P., and van der Spek, M. (2022). Towards a business case for CO2 mineralisation in the cement industry. Commun. Earth Environ. 3. doi: 10.21203/rs.3.rs-478558/v1

CrossRef Full Text | Google Scholar

Thomassen, G., van Passel, S., and Dewulf, J. (2020). A review on learning effects in prospective technology assessment. Renew. Sustain. Energy Rev. 130:109937. doi: 10.1016/j.rser.2020.109937

CrossRef Full Text | Google Scholar

Wene, C.-O.. (2008). Energy technology learning through deployment in competitive markets. Eng. Econ. 53, 340–364. doi: 10.1080/00137910802482287

CrossRef Full Text | Google Scholar

Wiesenthal, T., Dowling, P., Morbee, J., Thiel, C., Schade, B., Russ, P., et al. (2012). Technology learning curves for energy policy support. JRC Sci. Policy Rep. 332. doi: 10.2790/59351

CrossRef Full Text | Google Scholar

William, L. B., and Harter, N. (1899). Studies on the telegraphic language: the acquisition of a hierarchy of habits. Psychol. Rev. 6, 345–375. doi: 10.1037/h0073117

CrossRef Full Text | Google Scholar

Wright, T. P.. (1936). Factors affecting the cost of airplanes. J. Aeronaut. Sci. 3, 122–128. doi: 10.2514/8.155

CrossRef Full Text | Google Scholar

Yeh, S., and Rubin, E. S. (2012). A review of uncertainties in technology experience curves. Energy Econ. 34, 762–771. doi: 10.1016/j.eneco.2011.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Zauner, A., Böhm, H., Rosenfeld, D. C., and Tichler, R. (2019). Innovative Large-Scale Energy Storage Technologies and Power-to-Gas Concepts After Optimization. D7. 7. Analysis on Future Technology Options and on Techno-Economic Optimization. Report Ares 4315303.

Google Scholar

Zimmermann, A., Buchner, G. A., and Schomäcker, R. (2021). Apples and apples: a shortcut assessment framework for early-stage carbon capture and utilization technologies based on efficiency, feasibility, and risk. Energy Technol. 9. doi: 10.1002/ente.202000691

CrossRef Full Text | Google Scholar

Zimmermann, A., Langhorst, T., Moni, S., Schaidle, J., Bensebaa, F., and Bardow, A. (2022). Early-Stage Assessment of Carbon Capture and Utilization Technologies – Current Challenges and Best Practices for Technology Readiness Level Identification and Methodology Adaptation. Frontiers in Climate.

Google Scholar

Zimmermann, A., and Schomäcker, R. (2017). Assessing early-stage CO₂ utilization Technologies—Comparing apples and oranges? Energy Technol. 5, 850–860. doi: 10.1002/ente.201600805

CrossRef Full Text | Google Scholar

Zimmermann, A., Wang, Y., Wunderlich, J., Buchner, G. A., Schomäcker, R., Müller, L. J., et al. (2020). Techno-Economic Assessment and Life Cycle Assessment Guidelines for CO₂ Utilization (Version 1.1).

Google Scholar