Sub-seasonal to seasonal drivers of dry extreme rainfall events over Northeast Thailand

The interannual El Niño-Southern Oscillation (ENSO) and the Boreal Summer Intraseasonal Oscillation (BSISO) strongly modulate sub-seasonal to seasonal rainfall variability, leading to dry extreme rainfall events (DEREs) over Northeast (NE) Thailand. In this study, the ability of climate models to simulate the ENSO-BSISO-induced DEREs and associated synoptic features are evaluated using self-organizing maps. Observed DEREs occur most frequently during ENSO Neutral and La Niña conditions, when enhanced convection is located over central India and the Bay of Bengal. The intensity of observed DEREs are strengthened during El Niño when enhanced convection is observed over the western Pacific region. The climate models exhibit a diverse frequency of DEREs during ENSO phases, with some models showing better skill than others. On intraseasonal time scales, observed DEREs are favored when enhanced BSISO convection in phases 3–5 is located over the Bay of Bengal and the western Pacific region. Five models out of the 19 examined capture the observed pattern during BSISO phases 4 and 5, while only three models capture the BSISO phase 3 behavior. Composite maps of observed DEREs during the combined BSISO and ENSO conditions indicate that BSISO convection increases (decreases) DERE frequency during El Niño and Neutral (La Niña) phase(s). Climate models can simulate the occurrence of dry events associated with the combined BSISO and ENSO phases, but they do so in different BSISO phases.

1. Introduction

Dry extreme rainfall events (DEREs), including decreases in frequency and intensity of rainfall and prolonged drought episodes, are a natural phenomenon, but their impact is dangerous to physiological wellbeing (Vicente-Serrano et al., 2010; Abatan et al., 2017; Abiodun et al., 2019). From time immemorial, DEREs has been a threat to humanity and impacts can be measured in economic terms. Furthermore, the devastating impact of DEREs has been manifested in terms of losses of environment and socioeconomic activities including vegetation and peatlands due to extreme fire outbreaks, depletion of air quality, water resources diminution, agricultural production, and health risk of lives—humans and wildlife (Prapertchop et al., 2007; Page and Hooijer, 2016). In more recent times, several vulnerable countries in Southeast Asia (SEA) including Thailand have been inundated by DEREs (Mongkolsawat et al., 2001; Danny, 2011; Pavelic et al., 2012), with water resources management and agriculture being the worst hit. The Ministry of Agriculture and Cooperative of Thailand estimated that the 2012 drought over Northeast (NE)—a region where farming of cassava, rice, and livestock rearing amongst others is a major occupation—affected about 0.1 million hectares of land of which 0.08 million hectares were rice fields (Faisal et al., 2014; and references therein). The 2015 severe drought left unprecedented hardship in its wake. The agricultural damage, valued at 3.6 billion USD (119 billion Thai baht), ominously reduced Thailand's economic growth rate by about 0.85% [Center for Economic and Business Forecasting (CEBF), 2016]. This El Niño-Southern Oscillation-induced drought also forbade the local inhabitants to celebrate the traditional and famous Songkran water festival. Variability of the DEREs over Thailand is no doubt associated with perturbation of the climate through the global-scale modes of climate variability and by climate change. Danny (2011) indicated that “the impacts of climate change on Thailand are already serious and will likely create or exacerbate a number of additional problems during the next few decades.” Therefore researchers, policy decision-makers, and the government need to have an improved understanding of how to adapt and mitigate the impact of climatic mode and climate change-related extremes over this region.

Dry extreme rainfall events over SEA are modulated by several atmospheric phenomena at various temporal scales ranging from intraseasonal to interannual. In particular, the El Niño-Southern Oscillation (ENSO) and the Boreal Summer Intraseasonal Oscillation (hereafter; BSISO), the focus of this study, are two of the major atmospheric climate modes that influence sub-seasonal to seasonal rainfall variability over the region (Räsänen and Kummu, 2013; Muangsong et al., 2014; Xavier et al., 2014). ENSO is an atmospheric-oceanic mode of variability on interannual time scales that is known to play a dominant role in controlling the climate variability of tropical and subtropical areas, with significant weather impacts (Todd et al., 2018; Roy et al., 2019; Pillai et al., 2021). The BSISO, which is characterized by 10–20-day and 30–60-day time scales, is known to play an important role in determining the intraseasonal variability of the Asian summer monsoon system (Li et al., 2015; Hsu et al., 2016; Lee et al., 2017; Yang et al., 2020; Abatan et al., 2021).

These two climate modes individually affect the climate variability at different temporal scales over several regions of the Asia continent, leading to changes in the characteristics (intensity and frequency) of extreme rainfall-induced droughts and floods (Juneng and Tangang, 2005; Villafuerte II and Matsumoto, 2015; Hao et al., 2018; Supari et al., 2018). Meanwhile, the impact may vary from one country to another depending on the ENSO—El Niño, La Niña, and Neutral—and BSISO phases. Several studies have been conducted to examine the relationship between ENSO and climate over Thailand (e.g., Muangsong et al., 2014; Limsakul and Singhruck, 2016; Sriwicha et al., 2016; Bridhikitti, 2019). Focusing on the Mekong River Basin and using multiple statistical methods, Räsänen and Kummu (2013) showed that the hydrology of the Mekong is significantly influenced by ENSO. A strong link between annual precipitation variations and the decay of an ENSO phase is observed. Limsakul and Singhruck (2016) noted that total and extreme precipitation in Thailand are remotely influenced by the large-scale climate phenomena in the Pacific Ocean. During the period from 1955 to 2015, the region experienced downward trends in consecutive wet days, which is consistent with a drying pattern in consecutive dry days (CDD). The study showed that the annual number of days with CDD is shorter than normal during La Niña years and the cool phase of the Pacific Decadal Oscillation, and vice versa during El Niño years. This is consistent with other studies such as Singhrattna et al. (2005) and Buckley et al. (2007) who showed that drought in Thailand is associated with El Niño events. However, it is noted that the impact of ENSO on rainfall variability is more diverse and complex, in particular, when it co-exists with other modes of climate variability (Peralta-Hernández et al., 2009; Prasanna et al., 2020). In a study of ENSO diversity and observed rainfall over southern peninsular India during the Northeast monsoon, Prasanna et al. (2020) noted that the rainfall anomalies over the region do not always produce above-normal (below-normal) rainfall in all cases of pure El Niño (La Niña) events. Whereas, in the case when El Niño (La Niña) events co-occurred with positive (negative) Indian Ocean Dipole, positive rainfall anomalies are observed. Shimizu et al. (2017) showed that precipitation anomaly associated with ENSO events can be weakened or strengthened when MJO and ENSO co-occur. Their study shows that the frequency of dry extreme precipitation is higher during only-neutral events. However, the higher number of extreme events did not result in more intense extremes. On the other hand, they showed that the intensity of dry precipitation extremes during El Niño years is affected by the MJO. These studies indicate that rainfall variability exhibits diversity in ENSO activity. There are other climatic oscillations such as Interdecadal Pacific Oscillation that co-occur with ENSO to modulate rainfall variability (Power et al., 1999; Salinger et al., 2001; Weir et al., 2021); though not a focus of this study.

Previous studies have highlighted the connections of BSISO with rainfall extremes over Asia. Wet precipitation extremes are associated with the BSISO phase and amplitude (e.g., Hsu et al., 2016; Lee et al., 2017). Lee et al. (2017) examine the connection between BSISO modes and extreme rainfall over Asia concluding that, over some land regions, increases in the probability of extreme precipitation exceeding the 90th percentile are strongly modulated by BSISO activity (phase and amplitude). Consistently, Ren et al. (2018) showed that the probability of extreme rainfall events greater than the 90th percentile during summer over southeastern China is strongly dependent on BSISO phases, with the probability distribution function skewed toward higher values during BSISO phases 4 and 8 in southern China. The active BSISO phases promote high rainfall extremes through the intensification of moisture convergence and upward moisture transport (Hsu et al., 2016). These studies demonstrate the linkage between BSISO and rainfall extremes.

Most of the studies highlighted above have focused on the influence of the individual climate modes on rainfall variability. There is still a knowledge gap on the combined influence of the two dominant modes on dry extremes. Also, the response of DEREs over Thailand to BSISO is not known. Understanding the combined impacts of ENSO and BSISO on extremes is critical to providing information on planning, adaptation, and mitigating the risk of extremes when they occur. However, adaptation information on climate change hinges on consistent information that is often obtained from the state-of-the-art general circulation models (GCMs) simulation (Abiodun et al., 2019). Hence, our study will gather information on BSISO- and ENSO-induced DEREs over NE Thailand (Figure 1) from the Coupled Model Intercomparison Project Phase 6 (CMIP6; Eyring et al., 2016).

FIGURE 1

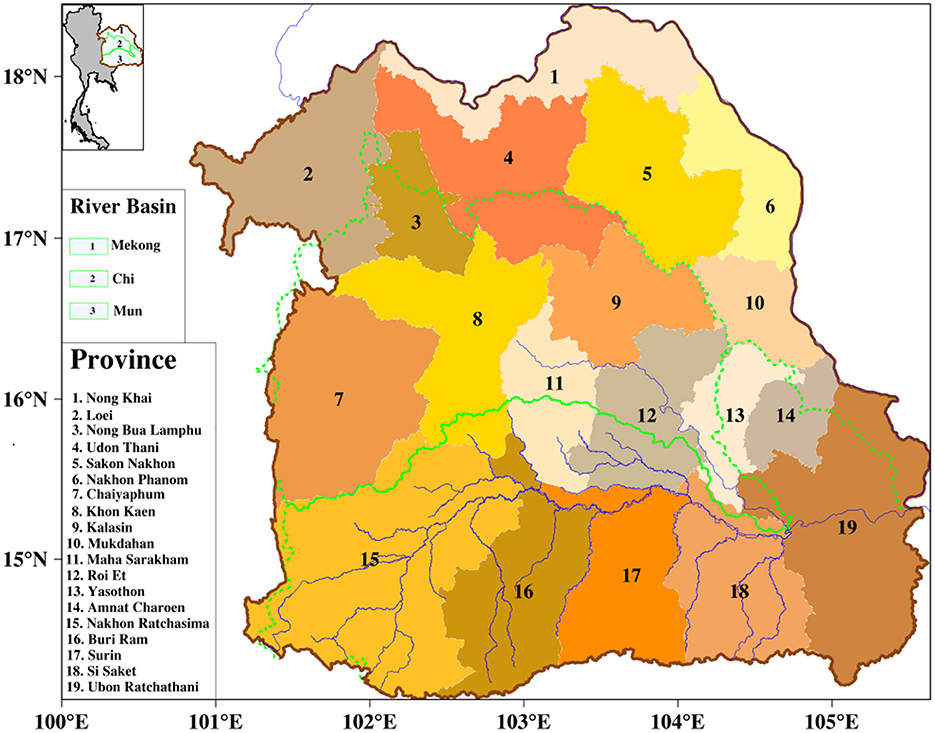
Figure 1. Map of Northeast Thailand detailing the outline of the provinces, the river basin, and its location relative to Thailand on the inset map (top left corner).

The analysis of the compound effect of ENSO and large-scale climate modes has been reported elsewhere (Cherchi and Navarra, 2013; Singh et al., 2021). For example, the influence of the Madden-Julian Oscillation on the characteristics of summer extreme precipitation events over northern South America during the ENSO episodes was the focus of the study by Shimizu et al. (2017). However, the current study aims to examine the differential role as well as the combined influence of BSISO and ENSO phases on DEREs during summer over NE Thailand. To do this, we analyze the observed and simulated rainfall and large-scale variable datasets. Details of the datasets and methodology are presented in Section 2, results of the analysis are presented in Section 3, and conclusions are presented in Section 4.

2. Data and method of analysis

2.1. Rainfall and large-scale fields: Reanalysis and simulations

This study uses a rainfall dataset from the gauge-based products (hereafter; observation or observed) and simulation output, while the dynamic variables are from the reanalysis product and simulation output. The gauge-based rainfall dataset is from the Global Precipitation Climatology Project (GPCP) version 1.3 Huffman et al., 2001. This global scale daily resolution rainfall product is available from 1997 to 2014 at a spatial resolution of 1.0°. The GPCP is a blend of rain-gauge observations and satellite infrared measurements. The second rainfall observation dataset is from the Asian Precipitation Highly Resolved Observational Data Integration Towards Evaluation of Water Resources (APHRODITE). APHRODITE provides high high-resolution precipitation datasets that are created primarily by collecting and analyzing rain-gauge observation data across Asia (Yatagai et al., 2012). The dataset has been developed by the Research Institute for Humanity and Nature (RIHM) and the Meteorological Research Institute of Japan Meteorological Agency (MRI/JMA) and is available for all land areas in Asia from 1951 to 2015 at a spatial resolution of 0.25°. The credibility of these datasets to represent rainfall characteristics over Asia has been documented in previous studies (e.g., He et al., 2019; Kim I. et al., 2019; Kim K. et al., 2019; Abatan et al., 2021; Khadka et al., 2022).

The reanalysis large scale fields used for the composite of physical dynamics associated with observed extreme rainfall events comes from the European Centre for Medium-Range Weather Forecasts Reanalysis v5 (ERA5; Hersbach et al., 2020). ERA5 is available on 37 pressure levels from 1979 to date and on a spatial resolution grid of 0.25° × 0.25°. The atmospheric datasets consider here are, zonal (U) and meridional (V) winds at 850- and 250-hPa levels, and outgoing longwave radiation (OLR) at the top of the atmosphere.

This study uses 19 GCMs from the CMIP6 historical experiments to characterize the combined impact of ENSO and BSISO on dry extreme rainfall events over NE Thailand. The daily data from the first ensemble member of each of the 19 CMIP6 models are considered based on the accessibility of the required variables needed for this study. The models' native grid resolution and the institute names are listed in Table 1. To facilitate a comparison of analysis among all the models, observation, and reanalysis, all the variables are interpolated to a 1° × 1° horizontal resolution using the bilinear interpolation method. This study analyses data for the period of May–October 1997–2014.

TABLE 1

Table 1. Nineteen selected CMIP6 climate models used for the analysis in this study.

2.2. Methods

2.2.1. Oceanic Niño index computation

The Oceanic Niño index (ONI), which is used as a measure of ENSO variability, is computed following the procedures described below. Since the ONI is based on monthly data, the monthly SST and monthly long-term mean are first computed from the daily values. From these two datasets, the monthly SST anomaly is computed. Next, we define the ONI following the NOAA's operational definition. The definition, which characterizes the El Niño, La Niña, and Neutral years, is based on the 3-month running mean of SST anomaly spatially averaged over the east-central tropical Pacific (Niño 3.4 region; 120°-170°W and 5°S−5°N). Finally, we define El Niño (La Niña) year when the ONI is greater (less) than +0.5 (−0.5) for at least three consecutive overlapping months. Otherwise, the year is defined as a neutral year.

2.2.2. BSISO index computation

The computation of the BSISO index is as follows. The intraseasonal signal is first isolated from the daily OLR and U850 by subtracting the daily climatological cycle. Next, we apply Lanczos bandpass filtered weights to obtain the 30–60-day OLR and U850 anomalies. These anomalies are thereafter normalized by their respective area-averaged standard deviation over the Asian summer monsoon region (10°S−40°N, 40°E−160°E) during boreal summer (May to October) for the period 1997 to 2014. Finally, the two anomaly datasets are combined to form a single series in readiness for the BSISO index computation. The combined empirical orthogonal function (CEOF), a multivariate statistical tool that is often used for research analysis in many fields to characterize the dominant modes of climate variability at both spatial and temporal (principal component; PC) scales, is then applied to the daily averaged 30–60-day filtered OLR and U850 anomalies to compute the multivariate BSISO index. Here, the first two leading modes of CEOFs (hereafter; PC1 and PC2) are considered to represent the spatio-temporal evolution of the BSISO; consistent with Abhik et al. (2016). The BSISO index is characterized by both amplitude and phase. These features are computed, respectively, from the PCs as: amplitude = (PC1² + PC2²)^1/2 and phase = arctan (PC1/PC2). The BSISO life cycle can be categorized into two groups; inactive (amplitude < 1.0) and active (amplitude > 1.0), with the inactive group dominated by phase 0 while the active group can further be categorized into eight phases of equal angular extent. Further information on data processing and BSISO index calculation can be found in the literature (for instance; NCAR Climate Data Guide website¹; North et al., 1982; Lee et al., 2013; Li and Mao, 2019; Yang et al., 2019).

2.2.3. Dry extreme rainfall events index computation

To facilitate the analysis of dry extreme rainfall events, we define a rainfall index conditioned on daily rainfall anomaly over NE Thailand (Figure 1; 13°N−20°E, 100°E−106°E). To do this, we first compute the daily anomalies by subtracting the long term daily mean from the daily value, using 1997–2014 as the base period. For example, the anomaly for September 1 is obtained as the difference between the data for September 1 and the long term mean for September 1. Then, we compute the daily time series of spatially averaged rainfall anomalies over the region. This rainfall index is ordered in ascending order and we determine the 10th percentile threshold. Dry extreme rainfall days are classified when the daily rainfall index is lower than the selected threshold. The composite analyses for anomalous dry rainfall days and associated atmospheric fields are shown in Figure 2. It is expected that there would be a large inter-model spread of the frequency of extremes, thus we assess the degree of model agreement. First, we compute the model ensemble mean. Then we define the ensemble mean to be robust when more than 80% of the models individually agree on the sign of the change of the ensemble mean. We choose this threshold for consistency with literature (e.g., Nikulin et al., 2018; Abiodun et al., 2019; Akinyemi and Abiodun, 2019).

FIGURE 2

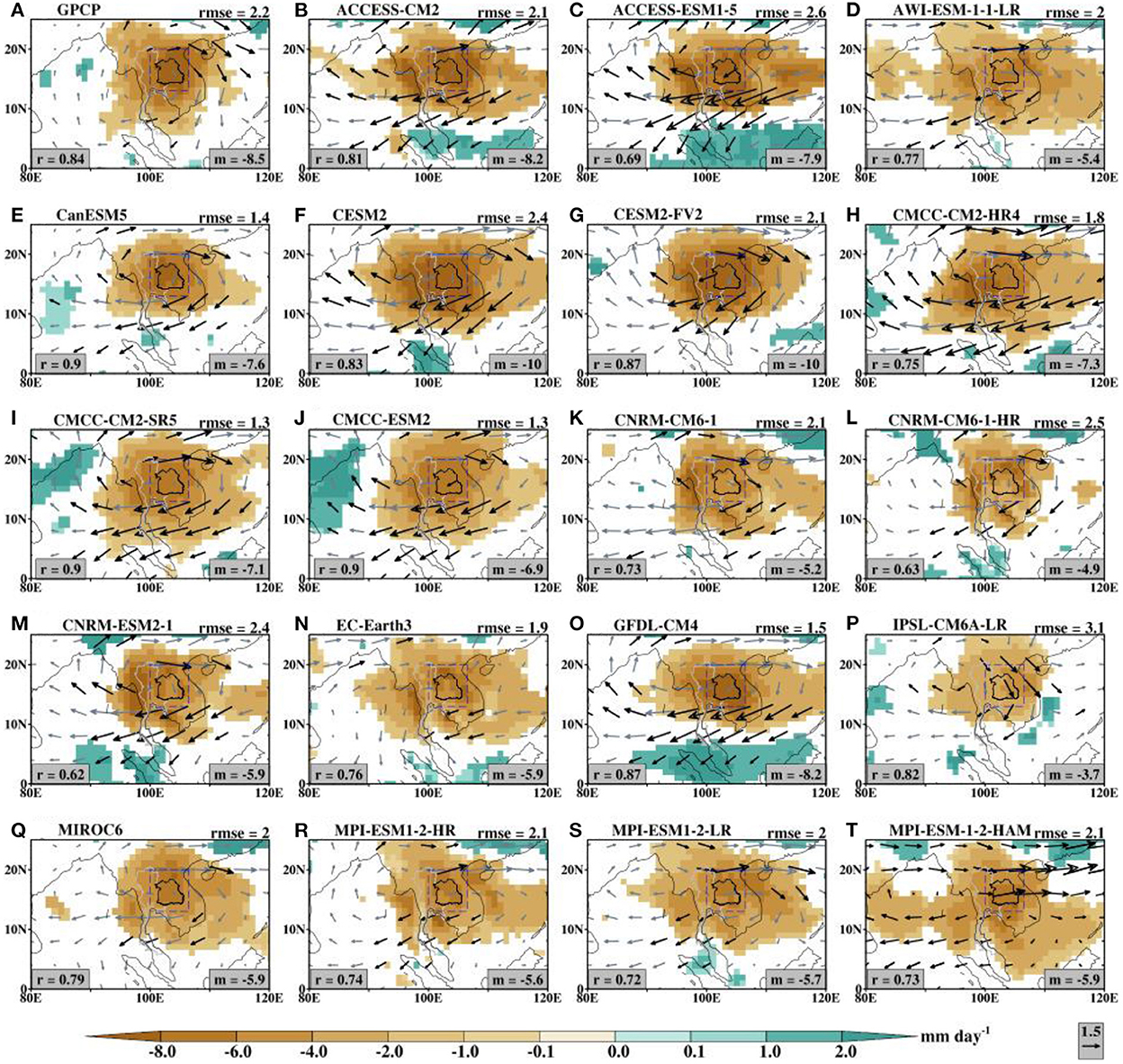
Figure 2. Dry spells composite anomalies of (A) observed and (B–T) simulated rainfall (shaded) and associated wind field at 850 mb level (vectors) for the May–October season during the period 1997–2014. The wind field overlaid on (A) is from ERA5 reanalysis. The value of the Root-Mean-Square-Error (rmse; top right corner) and Spearman correlation [(R); bottom left corner] of rainfall anomaly are obtained against GPCP as the reference observation. The median value (m) of the rainfall anomaly over the study domain is indicated at the bottom right corner. The values on (A) are for GPCP vs. Aphrodite. Only statistically significant rainfall composites are shown. The black arrows are statistically significant at the 95% level while the slategrey arrows are not.

2.2.4. Self-organizing maps

This study also uses a self-organizing map (SOM) analysis to evaluate the simulated DEREs. SOM is a clustering methodology tool based on a non-linear artificial neural network that is widely employed in climate and synoptic climatology studies (Hewitson and Crane, 2002; Sheridan and Lee, 2011) for pattern classification based on their similarities (Cavazos, 1999; Guèye et al., 2011; Wolski et al., 2018). Hence, it reduces the dimensionality of a large dataset into nodes that represent the major patterns of the data. In the literature, SOM has been applied to meteorological parameters and climate variables to map and analyze their spatial distribution (e.g., Cavazos, 2000; Gutowski et al., 2004; Guèye et al., 2011; Omar and Abiodun, 2021). A detail review of some of the fundamental aspects of SOMs and their applications appears in Sheridan and Lee (2011). The SOM algorithm can be found in Kohonen (1995; 2001; software available at http://www.cis.hut.fi/research/som_lvq_pak.shtml), while detailed SOM documentation can be found in Kohonen (1995) and Johnson et al. (2008). The SOM_PAK 3.2 software is available at the Helsinki University of Technology website (http://www.cis.hut.fi/research/som_pak). In this study, we separately use four different anomalous dry extreme event rainfall datasets as input data into the SOM_PAK 3.2 software. All the observed and simulations for the dry events make up the first datasets. The second and third dry extreme event rainfall datasets consist of observed and simulations associated with only-ENSO and only-BSISO, respectively. The last group of datasets consists of observed and simulations associated with the combined ENSO and BSISO phases.

A common feature in SOM analysis is the number of SOM nodes. However, there is no restriction on the number of nodes to retain in SOM. The decision on the number of nodes to use for the pattern classification lies with the user. For instance, Leloup et al. (2007) use 10 × 10 SOM arrays to examine decadal changes in ENSO. Abiodun et al. (2016) use a 3 × 4 SOM to evaluate the simulations of widespread extreme rainfall events in the Western Cape, South Africa. Cavazos (1999) stated that using a few SOM patterns results in the identification of only the primary and dominant modes of the atmosphere, hence the loss of the continuity of the atmospheric events. Similarly, Gutowski et al. (2004) states that small arrays of maps (e.g., 2 × 4) may allow rapid SOM generation but results in the poor discretization of the pattern space spanned by the input fields. In their study, they note that a 4 × 6 SOM depicts the primary patterns of observed precipitation. Hence, for this study, we use a 2 × 3, 3 × 3, and 3 × 3 SOM array of maps for the first, second, and third datasets, respectively. Using pattern correlation and root-mean-square-error (RMSE) statistics, we classify some of the SOM nodes that exhibit similar spatial patterns, as indicated by their high correlation and low RMSE values.

3. Results

3.1. Climatology of DEREs and associated atmospheric large-scale features

The spatial patterns of the observed and simulated DEREs and the associated large-scale features are examined and compared using various statistics including correlation coefficient (r), median (m), and root-mean-square-error (rmse). The composite anomalies of observed boreal summer DEREs, consisting of all ENSO and BSISO phases, for the period 1997–2014 show an intense and significant widespread dry condition (Figure 2A). This pattern is supported by a significant wet condition over the Bay of Bengal (BoB). The whole region of Southeast Asia and the adjacent oceanic areas are characterized by reduced rainfall anomalies, with the maximum negative rainfall intensity over Northeast Thailand. A similar anomalous rainfall characteristic pattern is depicted by the land-only Aphrodite rainfall data with a correlation of 0.87 and a rmse of 1.6 mm day⁻¹ (figure not shown; Table 2). The median value of anomalous rainfall over the study domain is −8.5 mm day⁻¹ (GPCP) and −3.9 mm day⁻¹ (Aphrodite), respectively. Although the correlation between the two observations is high, the intensity of the Aphrodite rainfall anomaly is slightly weaker than that of the GPCP rainfall anomaly as indicated by the rmse value and the median statistic. This error metric indicates the existence of uncertainty in the observational datasets, which may be due to the differences in their calibration.

TABLE 2

Table 2. Statistics of observed and simulated rainfall anomalies over the study domain.

In comparison with the GPCP dataset, the CMIP6 models can reproduce the spatial distribution of the significant negative rainfall anomalies, but with variations in magnitude and spatial extent (Figures 2B–T). This is evident by the statistics with the correlation that ranges from 0.62 to 0.90, the median value that ranges from −3.7 to −10.0, and rmse that ranges from 1.3 to 2.6 mm day⁻¹, respectively. IPSL-CM6A-LR and CNRM-CM6-1-HR have the lowest median value, as well as the size of the significant cluster in contrast to other models.

To identify the models that reproduce the features of the anomalous rainfall which are as close to GPCP as possible, we subject all the datasets in Figure 2 to a 2 × 3 SOMs nodes analysis. The SOMs group the rainfall patterns into different nodes (Figure 3 and Table 3). Based on their similarities, these nodes can further be categorized into three main patterns. The first pattern consists of nodes 1, 4, and 5 (red band), the second pattern consists of nodes 2 and 3 (blue band), and the third pattern consists of only node 6 (brown band). It is noted that the corner nodes can sometimes have similar patterns (Abiodun et al., 2020) as indicated in the case of nodes 1 and 4.

FIGURE 3

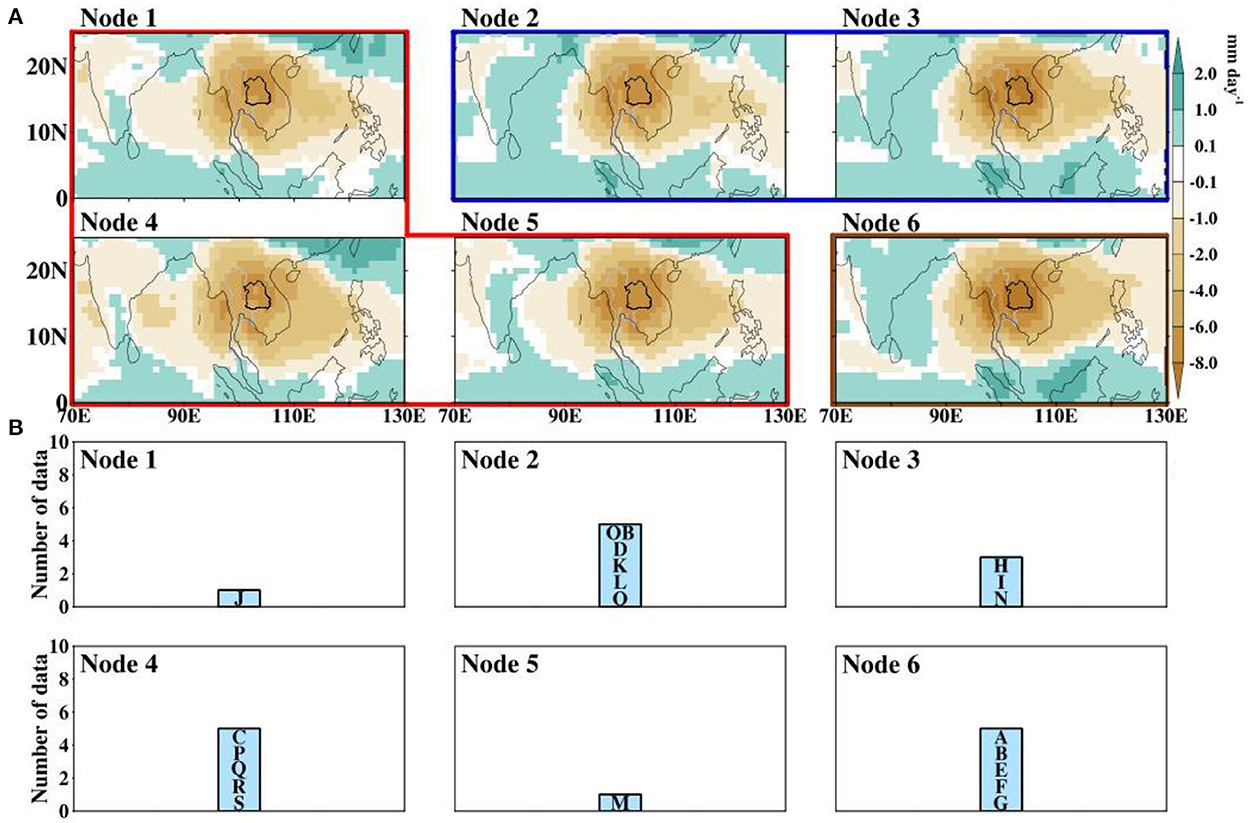
Figure 3. SOMS maps of Figure 2 for dry spells composite anomalies of (A) observed and (B–T) simulated rainfall. The top panels (A) show the classification of the rainfall patterns while the bottom panels (B) show the number of data that contribute to the rainfall patterns in the nodes in the top panels. The alphabet tag in the bar represents the code of the models that make up the bar (Table 1).

TABLE 3

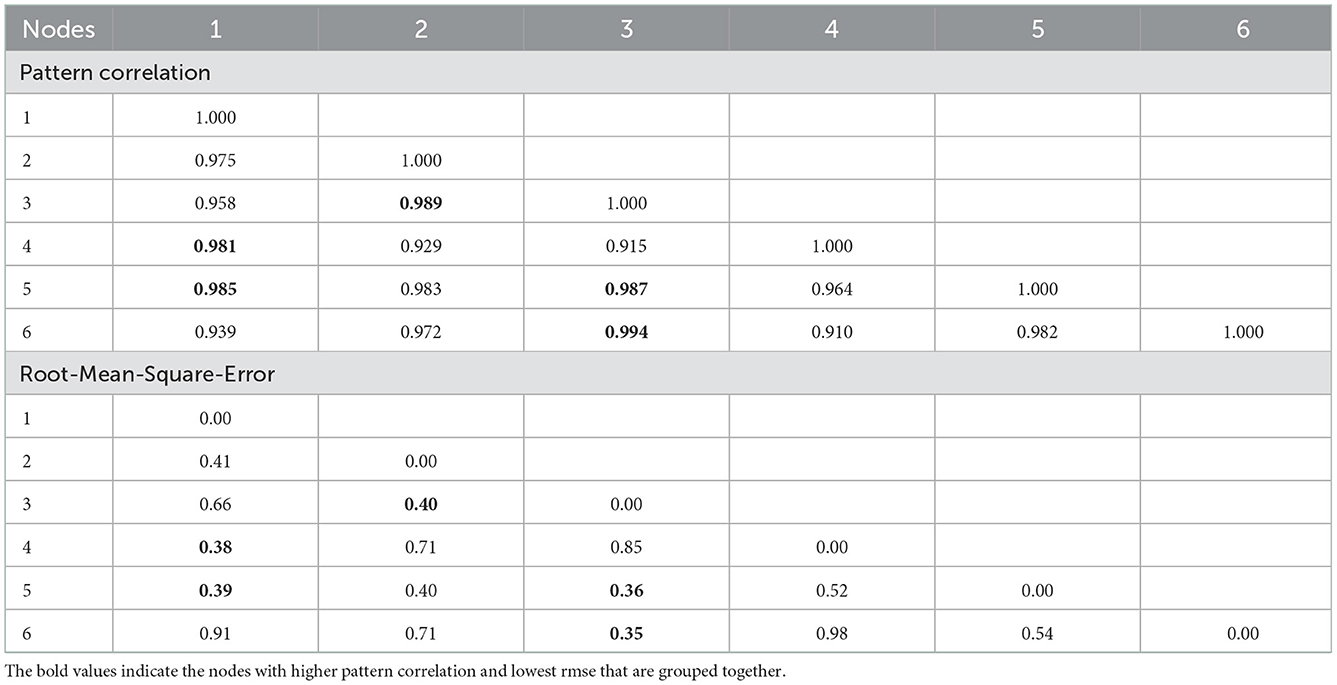
Table 3. Pattern correlation (top) and root-mean-square-error (bottom) between SOMs nodes of the composite of rainfall anomalies in Figure 3A.

The first pattern is characterized by a northwest-southeast (zonally) oriented negative rainfall anomaly over the northern part of India and the BoB (Southeast Asia and the Pacific Ocean), respectively. A positive rainfall anomaly is found over the equatorial ocean with a slight northward extension over the Indian Ocean. These rainfall patterns consist of rainfall distributions from seven CMIP6 models (Figure 3B; AWI-ESM1-1-LR, CNRM-CM6-1, EC-Earth3, MIROC6, MPI-ESM1-2-LR, MPI-ESM1-2-HR, MPI-ESM-1-2-HAM). The second pattern, unlike the first pattern, is characterized by a dipole rainfall pattern. Here, a large part of India, BoB, and the equatorial Indian Ocean are dominated by positive rainfall anomalies while negative rainfall anomalies dominate the other regions. These rainfall patterns consist of the rainfall distribution from the GPCP and seven other CMIP6 models (Figure 3B; CanESM5, CMCC-CM2-SR5, CMCC-ESM2, CNRM-CM6-1-HR, CNRM-ESM2-1, GFDL-CM4, and IPSL-CM6A-LR) with the lowest error values (rmse = 1.3–2.5) and high correlation (r = 0.62–0.90). The third rainfall pattern is similar to the second pattern, except for the appearance of a strip of negative rainfall anomalies along 5°N, separating the positive anomalies over India and those in the equatorial region. These nodes belong to ACCESS-CM2, ACCESS-ESM1-5, CESM2, CESM2-FV2, and CMCC-CM2-HR4 (Figure 3B), with rmse and correlation that ranges from 1.8 to 2.6 and 0.69 to 0.87, respectively. From the foregoing, all models capture the significantly reduced rainfall anomaly (Figure 2), and some of them have features that are highly correlated with GPCP. The similarities between the observed and simulated rainfall features suggest that the models can reproduce the large-scale features inducing extremes over NE Thailand.

In support of the above, we analyze the composite anomaly of the low- and upper-level winds and OLR during the DEREs (Figure 4). Figure 4A indicates that the negative rainfall anomalies (Figure 2) are associated with strongly suppressed convection (positive), with the maximum anomalous center over the study region; an indication of the subsidence of the air column over Thailand and an ascending motion elsewhere. This assertion is supported by the strong low-level anticyclonic circulation (Figure 2A) and the upper-level cyclonic circulation (Figure 4A) centers over Thailand. Consistent with the ERA5 reanalysis, the strong suppression of convection and the accompanied circulations are also simulated by the models (Figures 4B–T) but with some biases. The variability in correlation and rmse results between ERA5 and simulated OLR can attest to the models' good performance (r = 0.50–0.93, rmse = 3.5–14.3). All the models capture the low-level anticyclonic circulation (Figure 2) and the upper-level convergence associated with the suppressed OLR (Figure 4). Despite this, slight differences among the models are apparent. There is also a modest spread in the median OLR, with median values that range from 25.1 to 41.6 W m⁻². Nevertheless, CMIP6 models in this study perform very well at simulating the basic features of the anomalous OLR and associated circulation features inducing dry extreme rainfall events over NE Thailand.

FIGURE 4

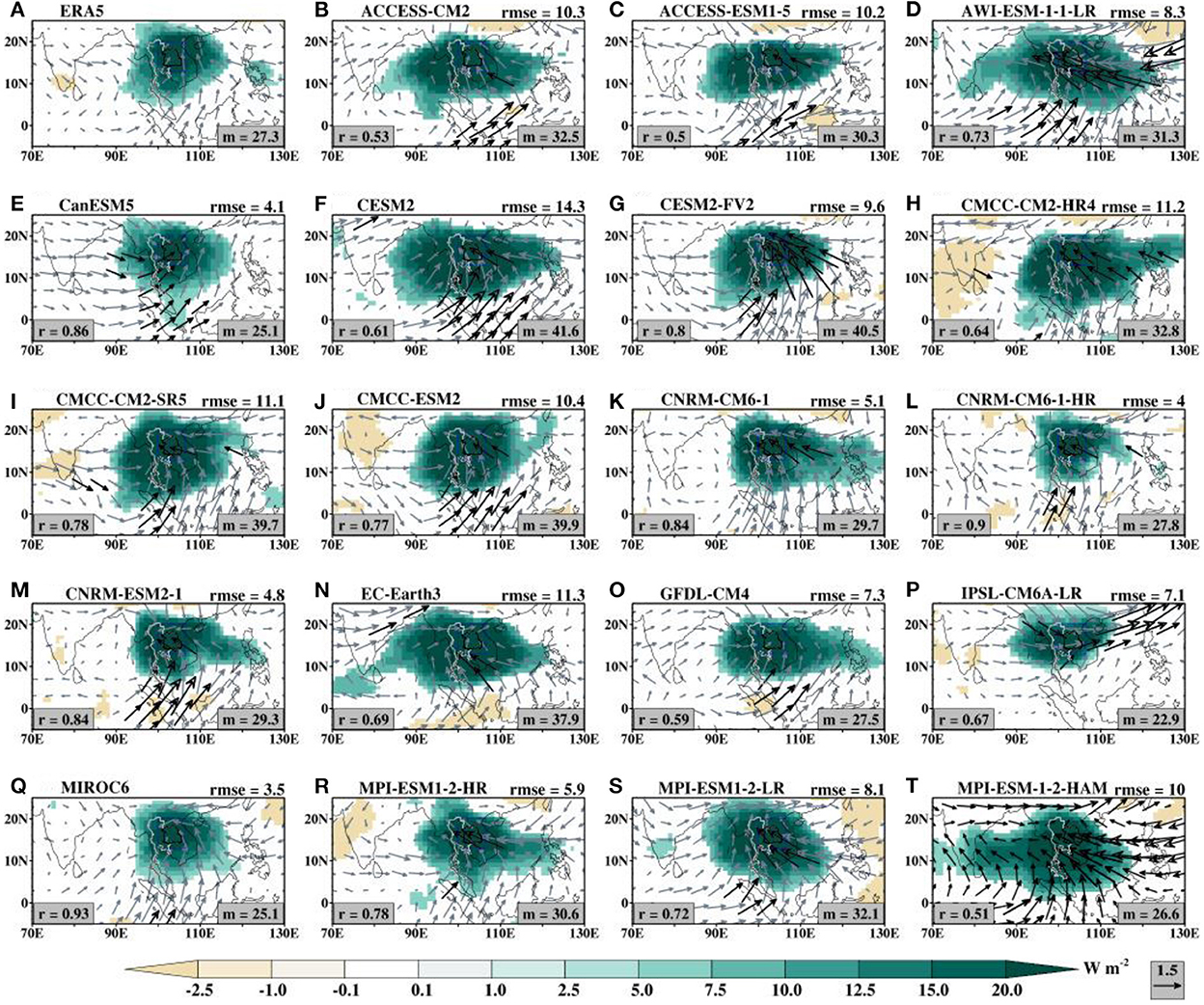
Figure 4. As in Figure 2, but for (A) ERA5 and (B–T) simulated OLR (shaded) and associated wind fields at 250 mb level.

3.2. Frequency distribution of DEREs associated with ENSO and BSISO

The bar chart of the number of days of DEREs is constructed to highlight the frequency of extreme events for each category of ENSO and BSISO phases (Figures 5–7). For the only-ENSO (Figure 5), the Neutral years associated with inactive BSISO (phase 0) appear to favor the frequency of observed DEREs over NE Thailand. Of the 144 event days, the Neutral phase of ENSO accounts for 75 events (52%). This is followed by the La Niña phase with 54 events (38%) while the El Niño phase has the least events 14 (10%). There is a large variability in the simulated frequency distribution of DEREs, with the values ranging from 9 to 55 during El Niño, 11 to 75 during La Niña, and 22 to 139 during Neutral years, respectively. During ENSO-Neutral conditions, about 58% (11 of 19) of the models agree with the observation that the frequency of DEREs is higher during this ENSO phase than in other ENSO phases. Whereas only 1 of the 19 models (5%) has the same order as observed frequency. For the frequency of observed DEREs during active BSISO, there are 176 events distributed among the 8 BSISO phases (Figure 6). The highest number of events occur during BSISO phase 4 (34) and the least during BSISO phase 2 (14). The simulated frequency of DEREs ranges from 130 to 260. The frequency distribution of DEREs over NE Thailand during the combined influence of ENSO and active BSISO phases are presented in Figure 7. The observed frequency ranges from 1 to 19, with the highest number of events during BSISO phases 4 and 8 of the Neutral year (Figures 7D, H). The CMIP6 models show considerable inter-model variability of the frequency of the DEREs. The composite analysis of these events will be presented in the following sections.

FIGURE 5

Figure 5. Number of days of dry extreme rainfall events for ENSO phases during inactive BSISO.

FIGURE 6

Figure 6. Number of days of dry extreme rainfall events for active BSISO phases.

FIGURE 7

Figure 7. (A–H) Number of days of dry extreme rainfall events for ENSO and active BSISO phases.

3.3. Composite anomalies of DEREs associated with only ENSO conditions

Figures 8A–C (top panel) shows the composite anomalies of observed rainfall, OLR, and 850 mb wind vectors associated with ENSO phases—namely only-El Niño, only-La Niña, and only-Neutral—and inactive BSISO during the dry extremes over Northeast Thailand. Statistically significant reduced rainfall composites over NE Thailand during the three phases of ENSO are linked with strong suppressed convection and subsidence–induced anticyclonic circulation. For the only-La Niña and only-Neutral events, statistically significant positive rainfall anomalies over central India and BoB associated with enhanced convection coexist with the reduced rainfall over NE Thailand. However, the dry extreme rainfall composite for the only-El Niño case is characterized by weak non-widespread convection over India and BoB. These features suggest that extreme dry events over NE Thailand can be maintained by enhanced convection over India and BoB during only-La Niña and only-Neutral events, while it can be maintained by enhanced convection over the western Pacific Ocean during the only-El Niño phase. The ensemble composites of simulated rainfall anomalies are presented in the bottom panel of Figures 8D–F. The CMIP6 models show the ability to simulate the observed ENSO-induced rainfall anomalies, but the magnitudes are weaker. There is a strong agreement among the simulations over Thailand, where at least 80% of the models agree on the sign of the negative rainfall anomalies than elsewhere. The models did not show agreement on the weak positive rainfall anomalies over India and the BoB.

FIGURE 8

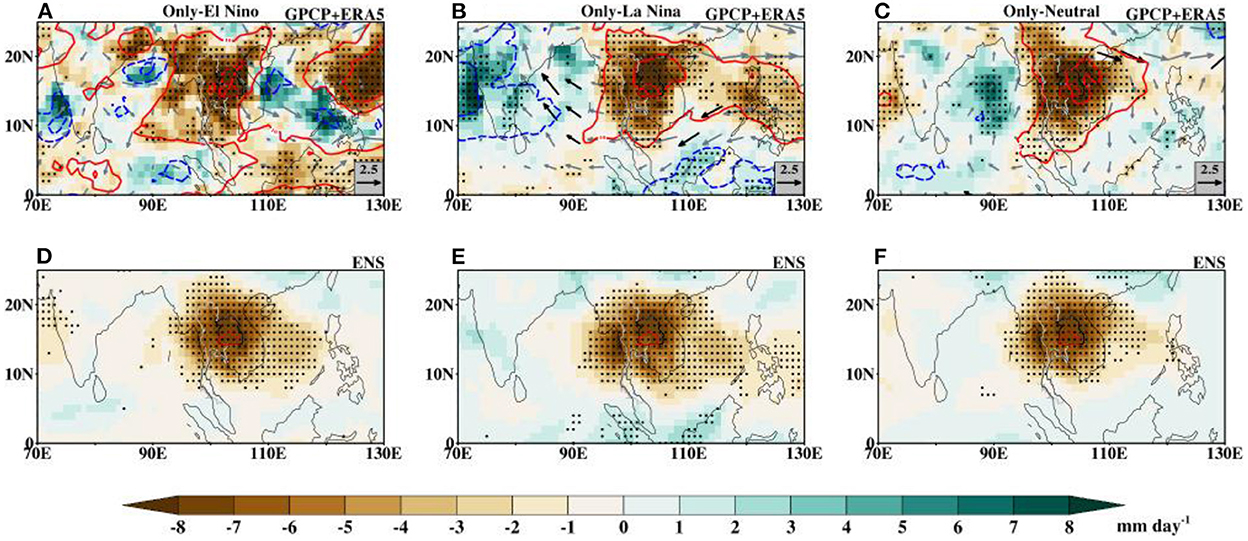
Figure 8. (A–F) Dry spells composite anomalies of observed rainfall (shaded), OLR (contours), and wind fields at 850 mb level (vectors) for ENSO phases and inactive BSISO for the May–October season during the period 1997–2014. The dotted areas signify statistically significant rainfall composites. The black arrows are statistically significant at the 95% level while the slategrey arrows are not. The bottom three panels is the ensemble mean of simulated rainfall anomalies. The dotted areas show where at least 80% of the models agree on the sign of change of the ensemble mean.

To further examine the fidelity of the models to depict the characteristic features of anomalous rainfall for the only ENSO conditions, we analyze the dry extreme rainfall composites using 3 × 3 SOMs nodes (Figure 9). As expected of the SOM grouping, nodes 1, 3, 7, and 9 depict different rainfall patterns, while the other nodes depict a similar rainfall pattern to either of these four edge nodes. Through pattern correlation and rmse statistics (Supplementary Table S1), this 3 × 3 SOMs nodes can be grouped into 4 rainfall clusters, red, blue, green, and brown bands, respectively.

FIGURE 9

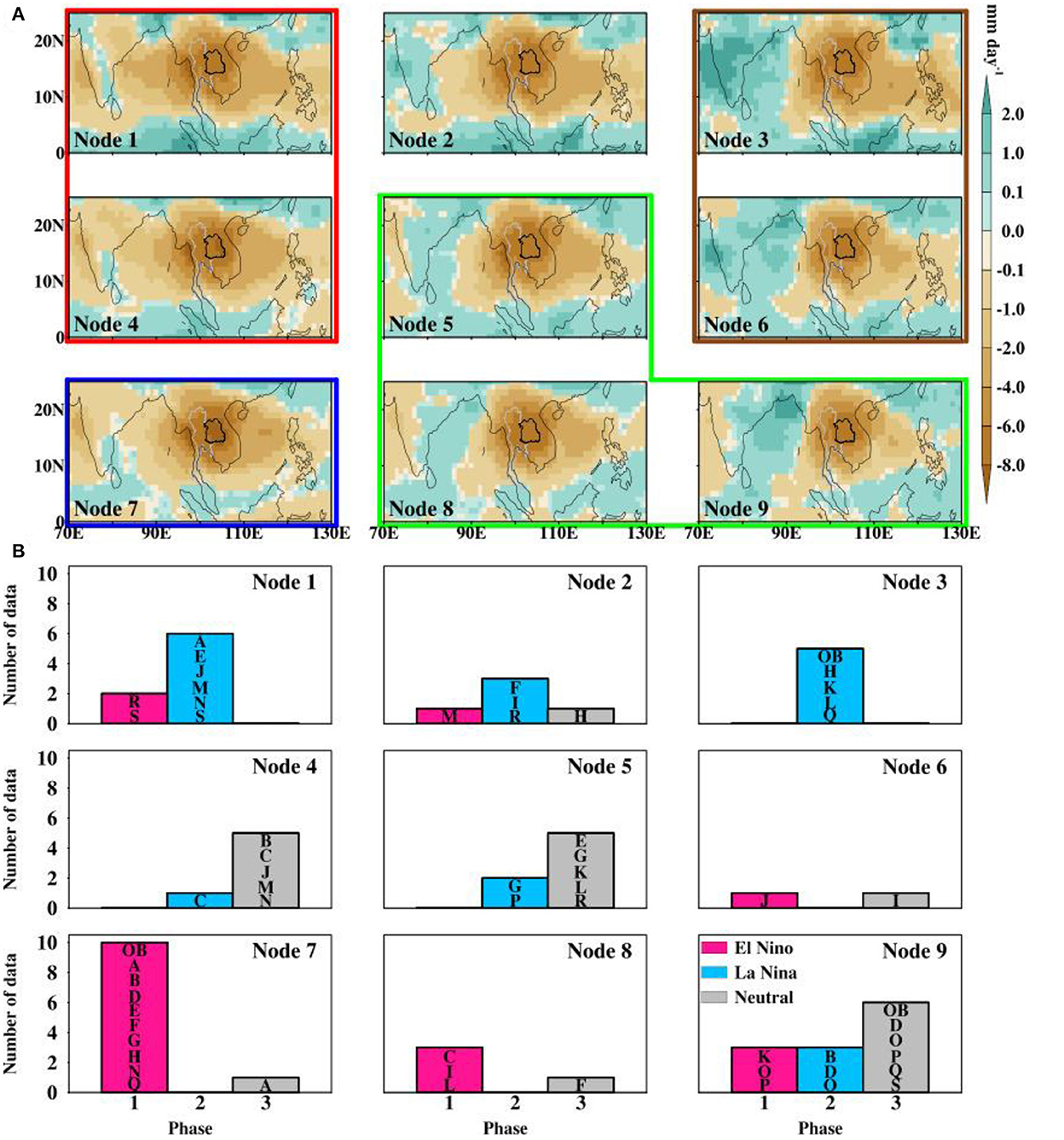
Figure 9. (A) The 3 × 3 SOMs distribution of dry spells composite rainfall anomalies over NE Thailand in the ENSO condition during inactive BSISO phase [top panels; (A)], and the frequency distribution of data for each ENSO phase in the SOMs nodes [bottom panels; (B)]. The alphabet tag in each ENSO bar represents the code of the models that make up the bar (Table 1).

The first pattern (red band) consists mainly of anomalous rainfall dominated by only-La Niña (Figure 9A; node 1) and only-Neutral composites (Figure 9A; node 4). These nodes are characterized by a zonally elongated negative rainfall anomaly centered along latitude 15°N, with the exception of the equatorial Indian Ocean. The second pattern (blue band) is dominated by mainly only-El Niño composites as shown in the bottom panel (nodes 7). The frequency distribution indicates that 9 CMIP6 models capture the features of the observed anomalous rainfall pattern for the only-El Niño composite. The third pattern (green band; nodes 5, 8, and 9) features a tri-pole rainfall pattern with a vertical strip of positive rainfall anomalies separating the negative rainfall pattern to the western part of India and the one centered over Thailand. This group is a mix of all the ENSO phases, but with ENSO Neutral rainfall dominating nodes 5 and 9. The fourth group (brown band; nodes 3 and 6) is, to some extent similar to the third pattern, but with a dipole rainfall pattern. This group is mainly dominated by only-La Niña composites with the largest extreme frequency in node 3, where 4 simulations show the ability to capture the observed rainfall pattern quite well. These patterns are consistent with Figure 3 (nodes 2 and 3). The last node in Figure 9 is node 2. The spatial distribution of rainfall anomaly in this node is a bit different from the neighboring and other nodes. Here, the positive rainfall pattern is constrained over mainland India. Of the three ENSO conditions, the rainfall pattern in this node is largely contributed by the only-La Niña composites. In general, Figure 9 confirms that DEREs over NE Thailand that is associated with both only-La Niña and only-Neutral conditions are induced by enhanced convection over India and BoB, while those associated with only-El Niño condition is teleconnected to enhanced convection in other regions.

3.4. Composite anomalies of DEREs associated with active BSISO phases

To shed light on our understanding of the modulation of BSISO on DEREs over NE Thailand, Figure 10 presents the spatial distributions of observed rainfall anomalies associated with only-BSISO phases. During phase 1, significant positive rainfall anomalies associated with enhanced convection exist over central India and parts of the equatorial Indian Ocean (EIO), while significant negative rainfall anomalies and suppressed convection dominate the Southeast Asia region with an eastward extension over the western Pacific Ocean (WP). The convection weakens over both central India and the equatorial Indian Ocean as the suppressed rainfall progress eastward in phase 2. At this point, a weak positive rainfall anomaly appears over the western part of the BoB, in conjunction with a southwesterly circulation. At phase 3, a drastic change in convection is observed. The convection over the EIO and the Maritime Continent is replaced by significantly weak suppressed convection, while the convection over the western part of the BOB significantly intensity and expands eastward covering the whole basin. At the same time, a sickle shape-like enhanced convection appears over the WP Ocean replacing the earlier suppressed convection. The processes going on over these oceanic regions lead to the maintenance of the suppressed convection residing over Thailand. During phase 4 of the BSISO, the positive convective areas weakens and gives way to large areas of significantly reduced rainfall anomalies. In a comparison of this phase with phase 5, a slight difference in their evolution is observed. For example, in phase 5 the convection over the BoB and the WP Ocean re-appear with an intensification over WP Ocean and the magnitude of the anomalous rainfall also decreases. Also, the positive convection over Southeast Asia assumes a clear Northeast-southwest tilt. During phase 6, the enhanced convection over the WP Ocean rapidly decays and the northern part of the suppressed convection and the core of the significant negative rainfall over the equatorial region begins their zonally northward propagation. The northward propagation continues progressively during phase 7 with the appearance of a very weak positive rainfall over EIO and strong positive convection over Thailand. As BSISO propagates to phase 8, the EIO and the Maritime Continent's enhanced convection rapidly intensifies significantly. This leads to further northward propagation and the reduction in the areas of the suppressed convection. At this phase, the rainfall feature is very similar to that of phase 1. The spatial evolution of rainfall during active BSISO suggests that DEREs over NE Thailand are strongly favored when the BoB and the Pacific region are characterized by enhanced convection leading to strong subsidence over NE Thailand during phases 3–5. Consistent with Figure 8, the evolution of the simulated ensemble mean of anomalies of DEREs during the BSISO phases is depicted in Supplementary Figure S1. The ensemble mean shows the characteristic anomalous suppressed convection centered over Thailand, where at least 80% of the CMIP6 models in this study show a strong model agreement in the simulations of extreme rainfall events associated with BSISO phases. The mean rainfall value averaged over the study domain, NE Thailand, ranges from −7.0 to −7.34, with the least intensity during phases 3 and 5. There are also differences in the magnitude and spatial spread of anomalous positive rainfall from one phase to another.

FIGURE 10

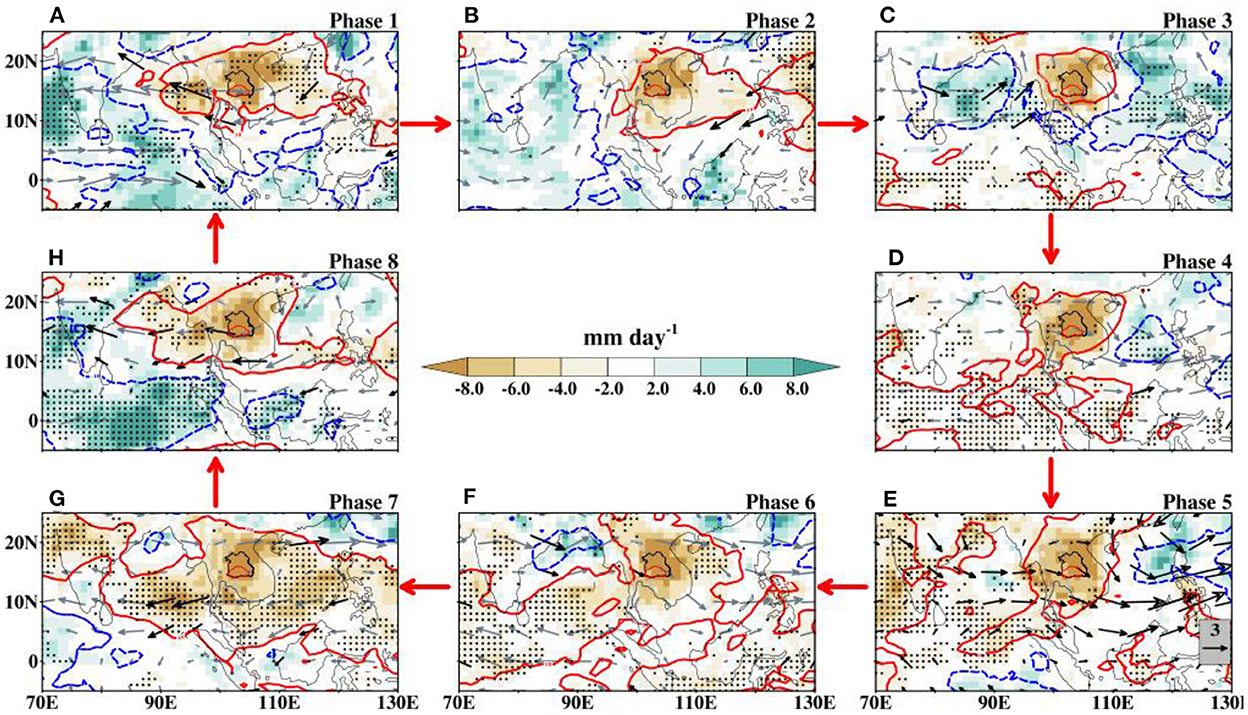
Figure 10. (A–H) Composite evolution of anomalies of observed dry extreme rainfall events (shaded), OLR (blue and red contours; W m⁻²), and 850 hPa wind (gray vectors, m s⁻¹) for the May-October season during the period 1997–2014 during active BSISO phases. The OLR contour starts at ±10 W m⁻² at an interval of 10 W m⁻². Only the significant vector anomalies are shown with solid black arrows while the statistically significant rainfall anomalies are indicated with dots. The significance statistic is at the 95% confidence level.

The individual simulated rainfall anomalies associated with only-BSISO phases are evaluated through a 3 × 3 SOMs distribution (Figure 11). Based on their spatial similarities, the rainfall patterns are grouped in the SOMs algorithm and the composites can be categorized into 5 patterns using statistics (Supplementary Table S2). Observed rainfall anomalies during phases 1 and 2 are grouped in the same node (Node 7) and banded together with some simulated rainfall patterns (blue band). No simulation closely matches the observed rainfall anomaly during phase 1, but 3 simulations give a good representation of the observed rainfall pattern during phase 12. The patterns of observed anomalous rainfall during the DEREs associated with only-BSISO phases 3, 4, and 5 are located in Nodes 1 and 2. These nodes are all ordered into one main pattern (red band). Of all the simulations in this group, 3, 2, and 3 CMIP6 models, respectively, accurately capture the observed rainfall pattern during phases 3, 4, and 5 (see Table 1). As indicated in Figure 10, there is a clear difference in the observed rainfall pattern between phases 6 and 7 and phase 8. This is also indicated in the SOMs space where the anomalous rainfall patterns associated with phases 6 and 7 are located in the same node (Node 3), while that associated with phase 8 is located in Node 8, respectively. From Node 3, we find that 7 CMIP6 models can perfectly simulate the observed rainfall pattern during phase 7, while only one model can reproduce the observed pattern during phases 6 (Node 3) and 8 (Node 8).

FIGURE 11

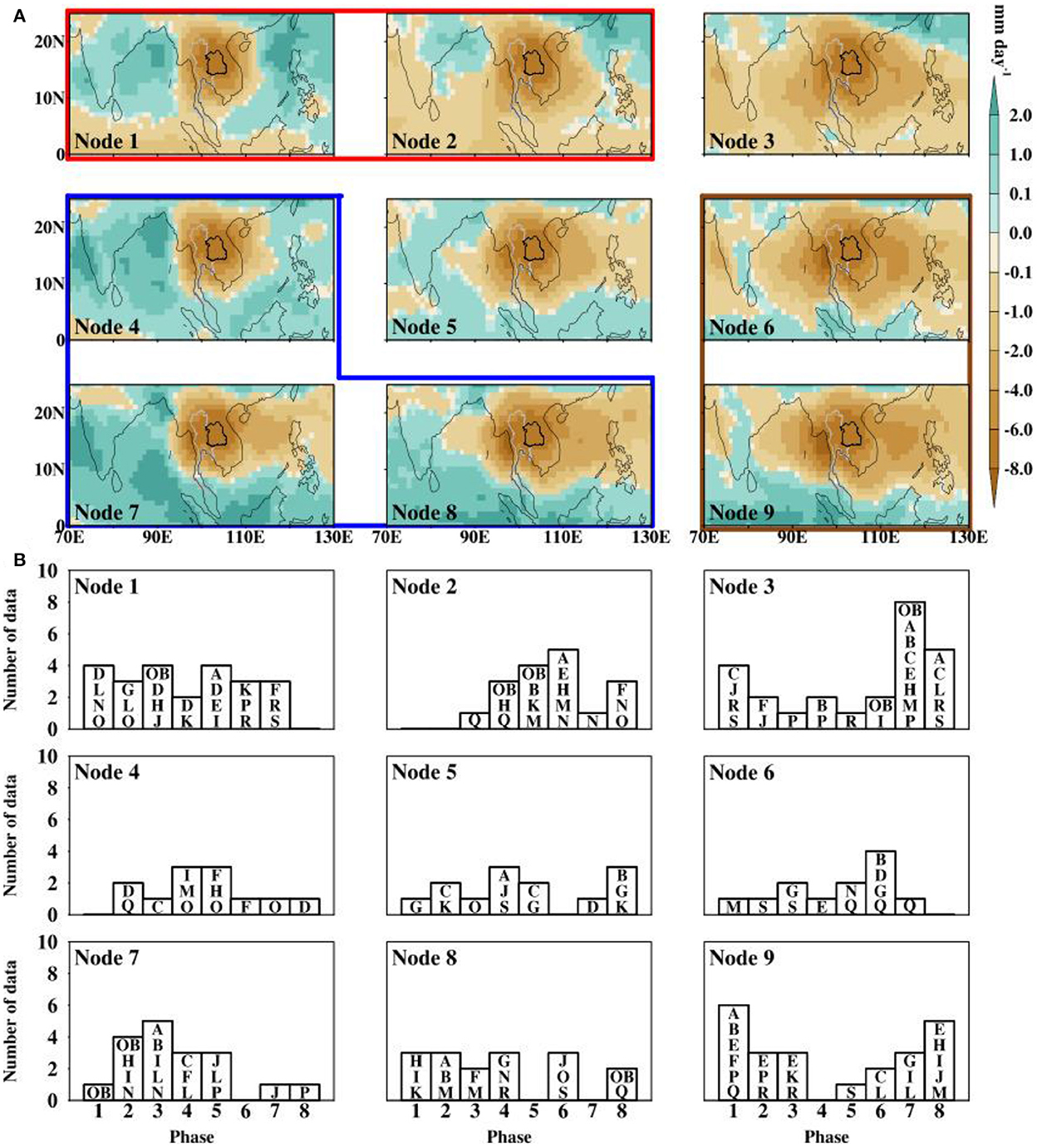
Figure 11. (A) The 3 × 3 SOMs distribution of evolution of rainfall anomalies over NE Thailand during the active BSISO phase [top panels; (A)], and the frequency distribution of data for each phase in the SOMs nodes [bottom panels; (B)]. The alphabet tag in each bar represents the code of the models that make up the bar (Table 1).

3.5. Composite anomalies of rainfall associated with the combined influence of BSISO and ENSO

The distributions of rainfall anomalies in response to the mutual effect of active BSISO and ENSO phases (combined composites) are presented in Figures 12–14. We employ correlation and rmse statistics to determine the relationships between these patterns and those of Figures 8A–C, 10. In the selection, we give high priority to the patterns with low rmse and high correlation values for both the rainfall and OLR anomalies (Table 4). Depending on the BSISO phase, the summer intraseasonal oscillation can increase or reduce the intensity of dry extreme rainfall anomalies over NE Thailand. Hence, we present the percentage change of mean rainfall between composites of only-BSISO and only-ENSO and the combined composites in Table 5. This table will give insight into the impact of BSISO on the intensity of the extreme rainfall over the region.

FIGURE 12

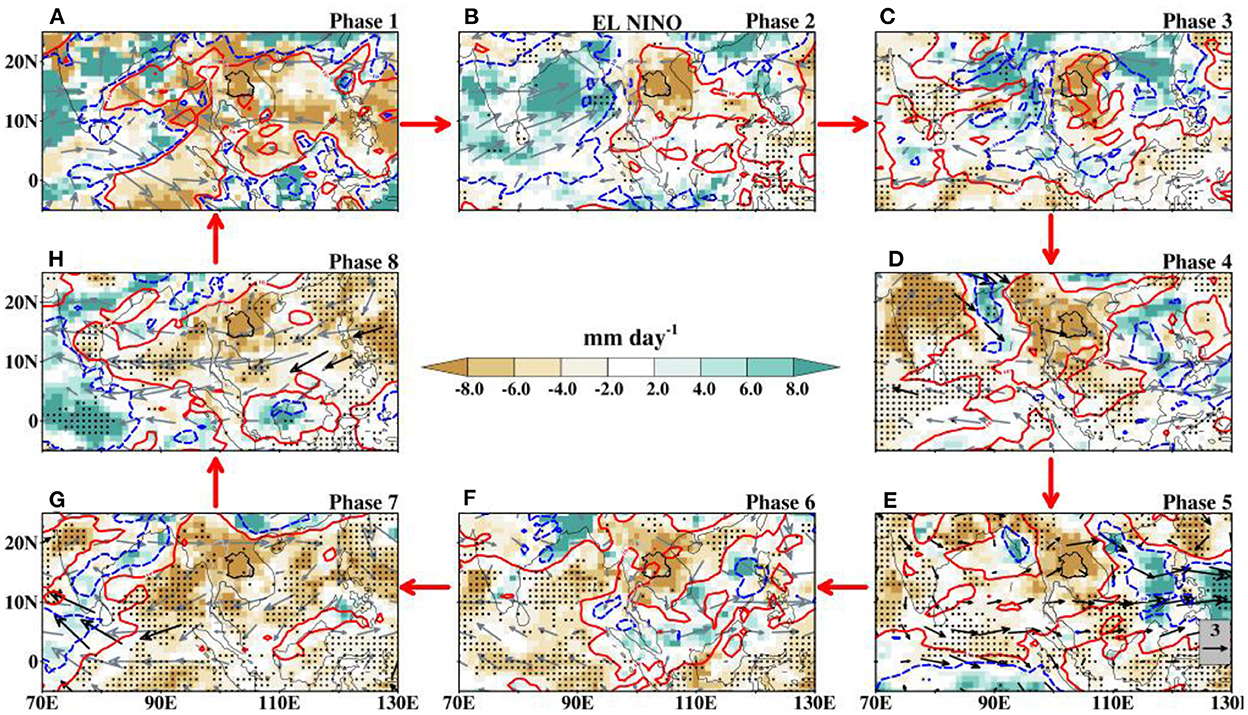
Figure 12. (A–H) Composite evolution of anomalies of observed dry extreme rainfall events (shaded), OLR (blue and red contours; W m⁻²), and 850 hPa wind (gray vectors, m s⁻¹) for the May–October season during the period 1997–2014 for El Niño and active BSISO phases. The OLR contour starts at ±10 W m⁻² at an interval of 10 W m⁻². Only the significant vector anomalies are shown with solid black arrows while the statistically significant rainfall anomalies are indicated with dots. The significance statistic is at the 95% confidence level.

FIGURE 13

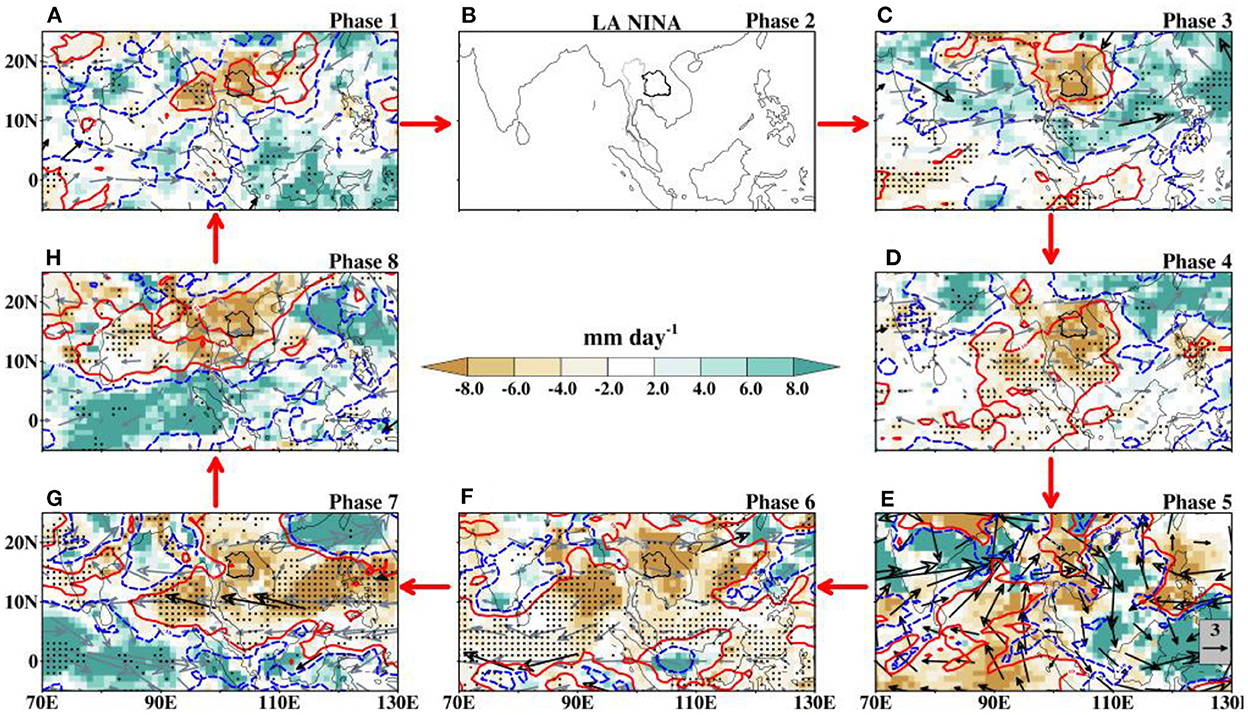
Figure 13. (A–H) Same as Figure 12 but for La Niña and active BSISO phases.

FIGURE 14

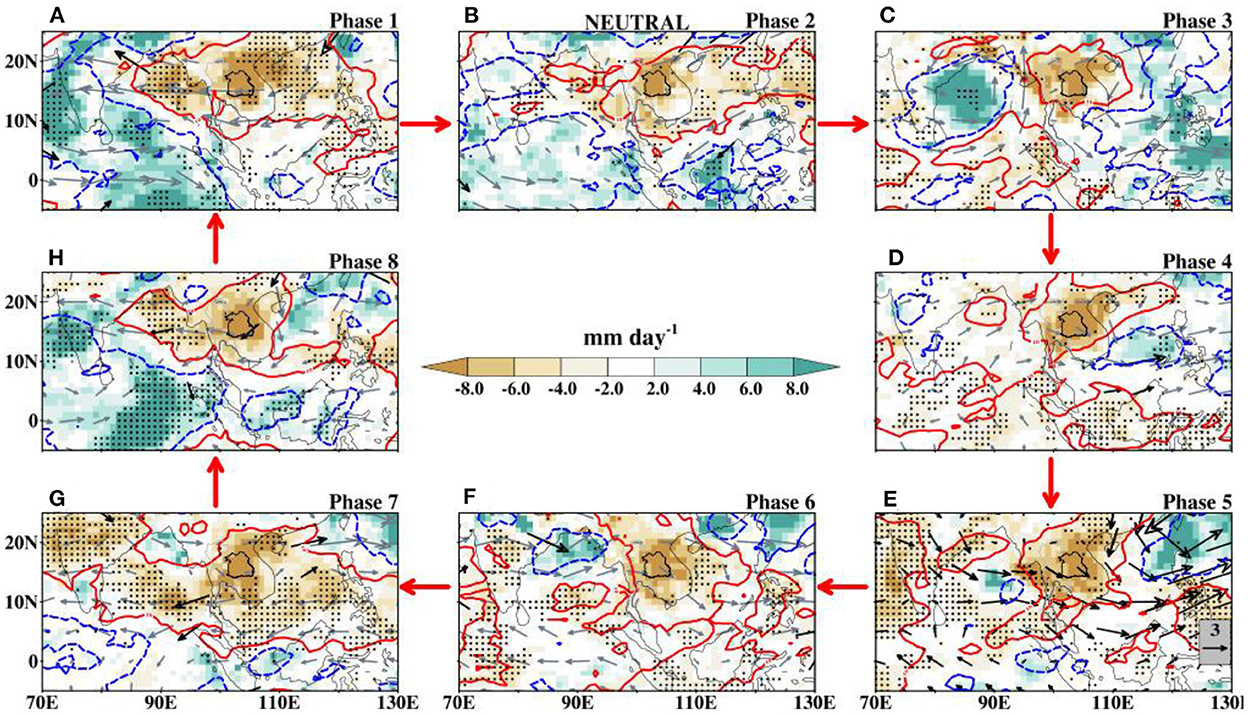
Figure 14. (A–H) Same as Figure 12 but for Neutral and active BSISO phases.

TABLE 4

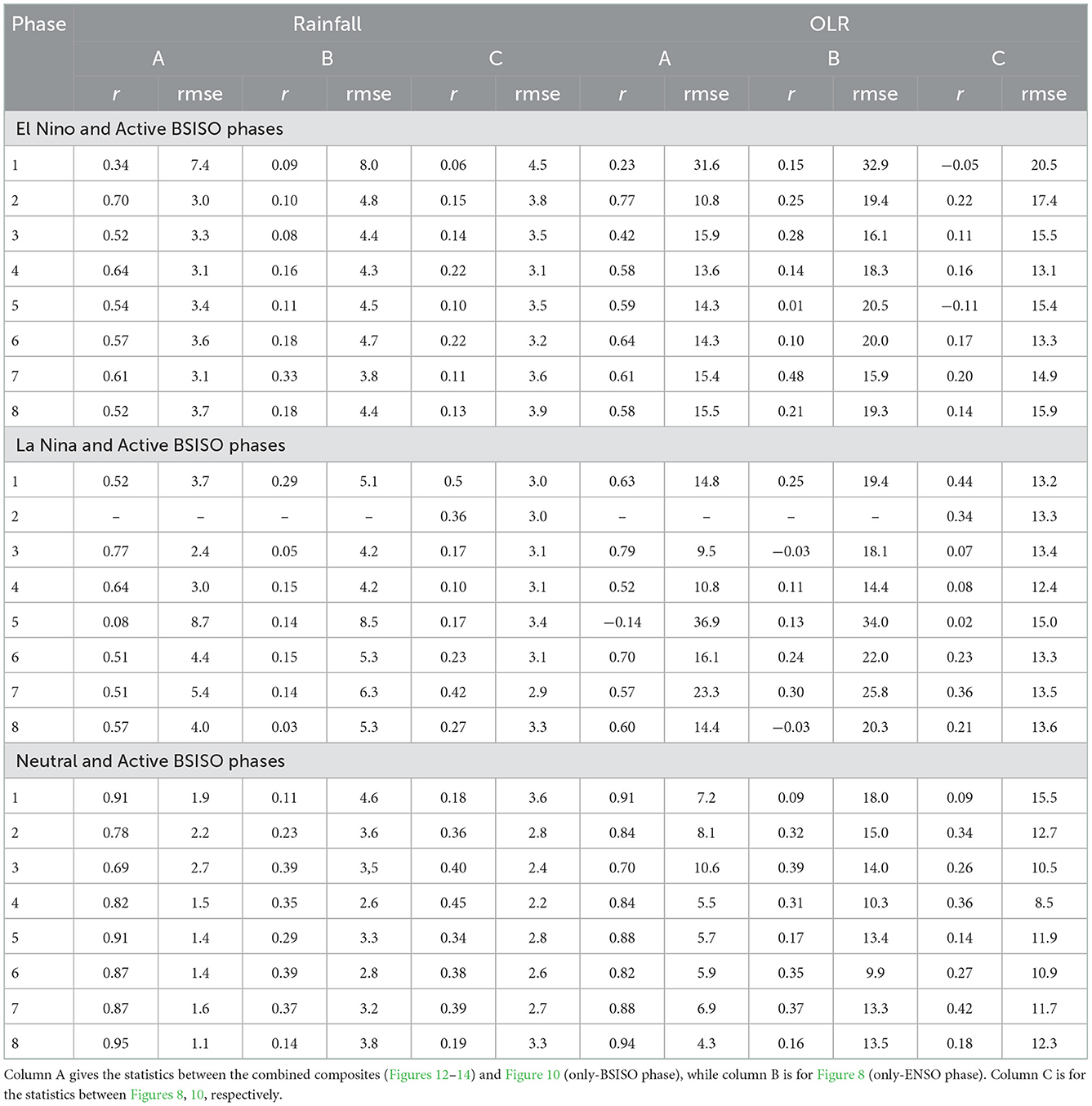
Table 4. Pattern correlation and root-mean-square error between observed rainfall anomalies in response to the compound effect of ENSO-BSISO and those of only-BSISO and only-ENSO phases.

TABLE 5

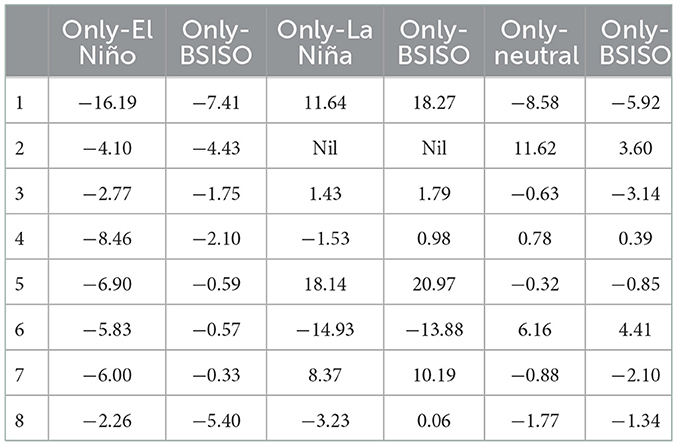
Table 5. Percent changes in mean rainfall anomalies between composites of only-BSISO and only-ENSO and the combined composites over NE Thailand.

Comparison of the composite of only-BSISO phases (Figure 10) with those of the combined composites (Figures 12–14) indicates that anomalous rainfall, OLR, and circulation patterns linked with DEREs over NE Thailand during neutral years and active BSISO phases (Figure 14) exhibit close resemblance to that of only-BSISO phases (Figure 10), with the highest correlation and least rmse values (Table 4). The mean correlation values for rainfall are 0.56, 0.51, and 0.85 for the El Niño, La Niña, and Neutral phases, respectively. On the first hand, this similarity in patterns may suggest the response of extreme events to the dominance of BSISO over the Neutral ENSO phase. However, as noted from the statistics (Table 4), the similarities in the patterns of the rainfall and convection anomalies between the only-Neutral composite (Figure 8C) and the combined composite (Figure 14C; Neutral years and active BSISO phase 4), as well as with only-BSISO phase 4 (Figure 10C), confirm that the frequency of occurrence of DEREs over NE Thailand during Neutral years of the ENSO conditions is indeed modulated by BSISO activity.

The combined composites echo the frequency distribution results that active BSISO acts to increase the number of dry extreme events; from 75 events during the only-Neutral years (Figure 5) to 104 events during the combined period of Neutral and active BSISO (Figure 7), with the highest event during BSISO phases 4 and 8 (Figures 7D, H). Despite the similarity in patterns and an increase in frequency of events, Table 5 shows, on average, that the impact of BSISO is to weaken the intensity of extreme rainfall during the Neutral phase of ENSO.

For La Niña years, there are similarities in patterns for rainfall and convection anomalies between only-BSISO composites (Figure 10) and the combined composites (Figure 13; phase 3; RMSE = 2.4), suggesting the control of BSISO over La Niña during this phase. There are other phases also with RMSE values < 4.0. The correlation between only-La Niña composite (Figure 8B) and the combined composites (Figure 13) is very weak (maximum value = 0.29) affirming the control of BSISO on this ENSO phase. The influence of BSISO during La Niña years is to decrease the frequency of DEREs from 54 events during the only-La Niña years (Figure 5) to 32 events during the combined period of La Niña and active BSISO (Figure 7). The BSISO convection anomalies appear to contribute to a decrease in the frequency of extreme events and an increase of the intensity of extremes (Table 5).

As for the only-El Niño, the frequency of extreme events increases from 14 during only-El Niño to 40 in response to the combined influence of active BSISO and El Niño. Despite the increase in extreme events, the similarities between Figures 8A, 10, 12 are not easily discernible. Here, the influence of BSISO convection results in an increase in the number of dry extremes, but with a decrease in their intensity (Table 5; phases 1, 3, 4, 5, 6, and 7) and stronger intensity (phases 2 and 8). This result indicates that the impact of El Niño on dry extremes does not depend on BSISO phases. This result is consistent with other studies over Thailand that showed that El Niño events promote dry conditions over the region (e.g., Singhrattna et al., 2005; Limsakul and Singhruck, 2016).

The composites of the CMIP6 ensemble mean of dry extreme rainfall anomalies during the combined ENSO-BSISO phases are presented in Supplementary Figures S2–S4. The ensemble mean displays variability in the spatial patterns of anomalous rainfall and their mean intensity averaged over NE Thailand. For the El Niño-BSISO composites, the mean rainfall anomalies range from −7.47 to −6.68, with the highest intensity during phase 3. In comparison with phase 3 of Supplementary Figure S1, where we find the least extreme intensity, the ensemble mean suggests that BSISO convection only acts during this ENSO phase to weaken the extreme intensity. This shows the ability of the simulations to capture the independence of El Niño extreme occurrences on BSISO phases. It is noteworthy that the models show agreement in the simulations of extreme rainfall events in all the phases, with the exception of phase 3. The simulated ensemble mean of dry extremes during La Niña years shows no model agreement during phases 3 and 5. All the other phases show variations in model agreement in the simulations of extreme rainfall over Thailand. The ensemble mean rainfall ranges from −7.85 to −6.96, with the highest intensity during phase 7 where the ensemble mean is characterized by an anomalous rainfall dipole. The ensemble dry events for the Neutral ENSO conditions (Supplementary Figure S4) show that intense dry extreme events can be sustained when BSISO convection resides over a large expanse of BoB and India.

4. Conclusion

To understand the combined impact of two atmospheric-oceanic climate modes on drought over NE Thailand, this study examines the composite maps of DEREs associated with individual and combined BSISO and ENSO phases. For these analyses, daily rainfall datasets from 19 CMIP6 coupled general circulation model simulations are used and evaluated with GPCP to examine the performance of the models over NE Thailand. The evaluation procedure includes the use of statistics (rms error and pattern correlation) and the SOMs. The large-scale circulation patterns associated with the simulated DEREs are also evaluated with the ERA5 atmospheric variables. The results are summarized as follows:

• The statistically significant dry spell composite anomalies during boreal summer over NE Thailand co-exists with the significant wet condition over BoB. The importance of large-scale atmospheric features to extremes is demonstrated where DEREs over the region is favored when suppressed convection (positive OLR) is associated with subsidence-induced anomalous circulations. The statistics and SOM classification establish that some CMIP6 models can capture the features of anomalous rainfall and large-scale patterns, but with some biases. In particular, seven models (CanESM5, CMCC-CM2-SR5, CMCC-ESM2, CNRM-CM6-1-HR, CNRM-ESM2-1, GFDL-CM4, and GFDL-CM4) reproduce the observed composite of anomalous dry extreme rainfall well, as indicated by the lowest error and high correlation values and SOMs classification.

• Considering the only-ENSO composites, our study shows that DEREs are favored when enhanced convection is located over central India and BoB during only-La Niña and only-Neutral events, whereas it is over the western Pacific region during only-El Niño. Some groups of models have the ability to capture the observed rainfall pattern in the ENSO phases more than others. The CMCC and CNRM-CERFACS capture the observed DERE during only-La Niña, while NCAR and CNRM-CERFACS capture the observed DERE during only-Neutral events.

• DEREs over NE Thailand is mostly maintained during BSISO phases 3–5 when enhanced convective activities are located over BoB and the western Pacific region. These regions act as the source of the ascending motions promoting the drought-induced subsidence motion over Thailand. The intensity of mean rainfall over NE Thailand is smallest during BSISO phase 3. The CMIP6 ensemble mean also captures this behavior during BSISO phase 3 and also phase 5. The SOMs classification of DEREs related to only-BSISO phases indicates that only a few of the models reproduce the observed rainfall patterns well during BSISO phases 3, 4, and 5.

• The results of our analysis suggest that DEREs during ENSO-Neutral years are modulated by enhanced BSISO convection over BoB and the western Pacific Ocean. The influence of BSISO convection is to increase the frequency of occurrence of the extreme event, not the intensity. For the La Niña phase, the BSISO convection acts to decrease the number of extreme events and enhance the extreme intensity. The occurrence of DEREs over NE Thailand during El Niño years appears not to depend on the BSISO convection, as there is no clear similarity between the composite of anomalous rainfall during only-El Niño and only-BSISO, and the combined composites. However, when BSISO convection co-exists with El Niño conditions, it acts to weaken the intensity of extreme events.

These results offer insight into the impact of the combined boreal summer intraseasonal oscillation and ENSO on the dry extreme rainfall events over NE Thailand. It is demonstrated that different phases of ENSO in conjunction with certain phases of BSISO convection over BoB and the western Pacific Ocean maintain extreme rainfall events. This study provides information on the combined stressors of climate extremes and the current state-of-the-art climate models that are useful for adaptation measures for droughts management to improve future water management by the stakeholders.

Code availability

The study used codes written by AA and some functions from NCAR Command Language (https://www.ncl.ucar.edu/).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AA, MC, MB, DK, and YD contributed to the conception and design of the paper. AA performed the analysis and writing of the paper. All authors contributed to the paper revision and approved the final revision for publication.

Funding

This ENRICH project (Enhancing Resilient to future Hydrometeorological extremes in the Mun river basin in Northeast Thailand) was supported by the UK. Natural Environment Research Council/Newton Fund under NE/S002901/1 and by the Thailand Science Research and Innovation/National Research Council of Thailand under RDG6130025.

Acknowledgments

We acknowledge the computational resources and data storage facility provided by the UK JASMIN team. Also, our appreciation goes to the reviewers for their helpful comments. In addition, we acknowledge the climate modeling group for the availability of their model output and the World Climate Research Programme's Working Group on Coupled Modelling that facilitates access to CMIP model output.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2022.1031226/full#supplementary-material

Footnotes

1. ^https://climatedataguide.ucar.edu/climate-data-tools-and-analysis/empirical-orthogonal-function-eof-analysis-and-rotated-eof-analysis

References

Abatan, A. A., Collins, M., Babel, M. S., Khadka, D., and De Silva, Y. K. (2021). Assessment of the ability of CMIP6 GCMS to simulate the Boreal Summer Intraseasonal Oscillation over Southeast Asia. Front. Clim. 3, 716129. doi: 10.3389/fclim.2021.716129

CrossRef Full Text | Google Scholar

Abatan, A. A., Gutowski, W. J. Jr., Ammann, C. M., Kaatz, L., Brown, B. G., Buja, L., et al. (2017). Multi-year droughts and pluvials over upper Colorado River basin and associated circulations. J. Hydrometeor. 18, 799–818. doi: 10.1175/JHM-D-16-0125.1

CrossRef Full Text | Google Scholar

Abhik, S., Mukhopadhyay, P., Krishna, R. P. M., Salunke, K. D., Dhakate, A. R., and Rao, S. A. (2016). Diagnosis of boreal summer intraseasonal oscillation in high resolution NCEP climate forecast system. Clim. Dyn. 46, 3287–3303. doi: 10.1007/s00382-015-2769-9

CrossRef Full Text | Google Scholar

Abiodun, B. J., Makhanya, N., Petja, B., Abatan, A. A., and Oguntunde, P. G. (2019). Future projection of droughts over major river basins in Southern Africa at specific global warming levels. Theor. Appl. Climatol. 137, 1785–1799. doi: 10.1007/s00704-018-2693-0

CrossRef Full Text | Google Scholar

Abiodun, B. J., Mogebisa, T. O., Petja, B., Abatan, A. A., and Roland, T. R. (2020). Potential impacts of specific global warming levels on extreme rainfall events over southern Africa in CORDEX and NEX-GDDP ensembles. Int. J. Climatol. 40, 3118–3141. doi: 10.1002/joc.6386

CrossRef Full Text | Google Scholar

Abiodun, B. J., Omar, S. A., Lennard, C., and Jack, C. (2016). Using regional climate models to simulate extreme rainfall events in the Western Cape, South Africa. Int. J. Climatol. 36, 689–705. doi: 10.1002/joc.4376

CrossRef Full Text | Google Scholar

Akinyemi, F. O., and Abiodun, B. J. (2019). Potential impacts of global warming levels 1.5°C and above on climate extremes in Botswana. Clim. Change 154, 387–400. doi: 10.1007/s10584-019-02446-1

CrossRef Full Text | Google Scholar

Bridhikitti, A. (2019). Connections of ENSO/IOD and aerosols with Thai rainfall anomalies and associated implications for local rainfall forecasts. Int. J. Climatol. 33, 2836–2845. doi: 10.1002/joc.3630

CrossRef Full Text | Google Scholar

Buckley, B., Palakit, K., Duangsathaporn, K., Sanguantham, P., and Prasomsin, P. (2007). Decadal scale droughts over northwestern Thailand over the past 448 years: links to the tropical Pacific and Indian Ocean sectors. Clim. Dyn. 29, 63–71. doi: 10.1007/s00382-007-0225-1

CrossRef Full Text | Google Scholar

Cavazos, T. (1999). Large-scale circulation anomalies conducive to extreme precipitation events and derivation of daily rainfall in northeastern Mexico and southeastern Texas. J. Clim. 12, 1506–1523. doi: 10.1175/1520-0442(1999)012<1506:LSCACT>2.0.CO;2

CrossRef Full Text | Google Scholar

Cavazos, T. (2000). Using self-organizing maps to investigate extreme climate events: an application to wintertime precipitation in the Balkans. J. Clim. 13, 1718–1732. doi: 10.1175/1520-0442(2000)013<1718:USOMTI>2.0.CO;2

CrossRef Full Text | Google Scholar

Center for Economic and Business Forecasting (CEBF) (2016). Surveyed Report of Drought Situation in Thailand: Year 2016 (in Thai). Bangkok.

Cherchi, A., and Navarra, A. (2013). Influence of ENSO and of the Indian Ocean Dipole on the Indian summer monsoon variability. Clim. Dyn. 41, 81–103. doi: 10.1007/s00382-012-1602-y

CrossRef Full Text | Google Scholar

Danny, M. (2011). Climate change and Thailand: impact and response. Contemporary Southeast Asia. J. Int. Strateg. Affairs. 33, 229–258. doi: 10.1355/cs33-2d

CrossRef Full Text | Google Scholar

Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model. Dev. 9, 1937–1958. doi: 10.5194/gmd-9-1937-2016

CrossRef Full Text | Google Scholar

Faisal, A. H., Polthanee, A., and Promkhambut, A. (2014). Farmers' perceptive of drought and its impact on a community livelihood in rural Northeastern Thailand. Khon. Kaen. Agr. J. 42, 427–442.

Guèye, A. K., Janicot, S., Niang, A., Sawadogo, S., Sultan, B., Diongue-Niang, A., et al. (2011). Weather regimes over Senegal during the summer monsoon season using self-organizing maps and hierarchical ascendant classification. Part I: Synoptic time scale. Clim. Dyn. 36, 1–18. doi: 10.1007/s00382-010-0782-6

CrossRef Full Text | Google Scholar

Gutowski, W. J., Otieno, F. O., Arritt, R. W., Takle, E. S., and Pan, Z. (2004). Diagnosis and attribution of a seasonal precipitation deficit in a USA regional climate simulation. J. Hydrometeor. 5, 230–243. doi: 10.1175/1525-7541(2004)005<0230:DAAOAS>2.0.CO;2

CrossRef Full Text | Google Scholar

Hao, Z., Hao, F., Singh, V. P., and Zhang, X. (2018). Quantifying the relationship between compound dry and hot events and El Niño-southern Oscillation (ENSO) at the global scale. J. Hydrol. 567, 332–338. doi: 10.1016/j.jhydrol.2018.10.022

CrossRef Full Text | Google Scholar

He, S., Yang, J., Bao, Q., Wang, L., and Wang, B. (2019). Fidelity of the observational/reanalysis datasets and global climate models in representation of extreme precipitation in East China. J. Clim. 32, 195–212. doi: 10.1175/JCLI-D-18-0104.1

CrossRef Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Quart. J. Roy. Meteor. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

CrossRef Full Text | Google Scholar

Hewitson, B. C., and Crane, R. G. (2002). Self-organizing maps: applications to synoptic climatology. Clim. Res. 22, 13–26. doi: 10.3354/cr022013

CrossRef Full Text | Google Scholar

Hsu, P.-C., Lee, J.-Y., and Ha, K.-J. (2016). Influence of boreal summer intraseasonal oscillation on rainfall extremes in southern China. Int. J. Climatol. 36, 1403–1412. doi: 10.1002/joc.4433

CrossRef Full Text | Google Scholar

Huffman, G. J., Adler, R. F., Morrissey, M. M., Bolvin, D. T., Curtis, S., Joyce, R., et al. (2001). Global precipitation at one degree daily resolution from multisatellite observations. J. Hydrometeor. 2, 36–50. doi: 10.1175/1525-7541(2001)002<0036:GPAODD>2.0.CO;2

CrossRef Full Text | Google Scholar

Johnson, N. C., Feldstein, S. B., and Tremblay, B. (2008). The continuum of Northern Hemisphere teleconnection patterns and a description of the NAO shift with the use of self-organizing maps. J. Clim. 21, 6354–6371. doi: 10.1175/2008JCLI2380.1

CrossRef Full Text | Google Scholar

Juneng, L., and Tangang, F. T. (2005). Evolution of ENSO-related rainfall anomalies in Southeast Asia region and its relationship with atmosphere-ocean variations in the Indo-Pacific sector. Clim. Dyn. 25, 337–350. doi: 10.1007/s00382-005-0031-6

CrossRef Full Text | Google Scholar

Khadka, D., Babel, M. S., Abatan, A. A., and Collins, M. (2022). An evaluation of CMIP5 and CMIP6 climate models in simulating summer rainfall in the Southeast Asian monsoon domain. Int. J. Climatol. 42, 1181–1202. doi: 10.1002/joc.7296

CrossRef Full Text | Google Scholar

Kim, I., Oh, J., Woo, S., and Kripalani, R. H. (2019). Evaluation of precipitation extremes over the Asian domain: observation and modelling studies. Clim. Dyn. 52, 1317–1342. doi: 10.1007/s00382-018-4193-4

CrossRef Full Text | Google Scholar

Kim, K., Kim, J., Boo, K., Shim, S., and Kim, Y. (2019). Intercomparison of precipitation datasets for summer precipitation characteristics over East Asia. Clim. Dyn. 52, 3005–3022. doi: 10.1007/s00382-018-4303-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohonen, T. (1995). “Self-organizing Maps. Vol. 30,” in Springer Series in Information Sciences. Berlin: Springer-Verlag. doi: 10.1007/978-3-642-97610-0

CrossRef Full Text | Google Scholar

Kohonen, T. (2001). Self-organizing Maps. New York, NY: Springer. doi: 10.1007/978-3-642-56927-2

CrossRef Full Text | Google Scholar

Lee, J. Y., Wang, B., Wheeler, M. C., Fu, X. H., Waliser, D. E., and Kang, I. S. (2013). Real-time multivariate indices for the boreal summer intraseasonal oscillation over the Asian summer monsoon region. Clim. Dyn. 40, 493–509. doi: 10.1007/s00382-012-1544-4

CrossRef Full Text | Google Scholar

Lee, S.-S., Moon, J.-Y., Wang, B., and Kim, H.-J. (2017). Subseasonal prediction of extreme precipitation over Asia: boreal summer intraseasonal oscillation perspective. J. Clim. 30, 2849–2865. doi: 10.1175/JCLI-D-16-0206.1

CrossRef Full Text | Google Scholar

Leloup, J. A., Lachkar, Z., Boulanger, J.-P., and Thiria, S. (2007). Detecting decadal changes in ENSO using neutral networks. Clim. Dyn. 28, 147–162. doi: 10.1007/s00382-006-0173-1

CrossRef Full Text | Google Scholar

Li, J., and Mao, J. (2019). Factors controlling the interannual variation of 30–60-day boreal summer intraseasonal oscillation over the Asian summer monsoon region. Clim. Dyn. 52, 1651–1672. doi: 10.1007/s00382-018-4216-1

CrossRef Full Text | Google Scholar

Li, J., Mao, J., and Wu, G. (2015). A case study of the impact of boreal summer intraseasonal oscillations on Yangtze rainfall. Clim. Dyn. 44, 2683–2702. doi: 10.1007/s00382-014-2425-9

CrossRef Full Text | Google Scholar

Limsakul, A., and Singhruck, P. (2016). Long-term trends and variability of total and extreme precipitation in Thailand. Atmos. Res. 169, 301–317. doi: 10.1016/j.atmosres.2015.10.015

CrossRef Full Text | Google Scholar

Mongkolsawat, C., Thirangoon, P., Suwanwerakamtorn, R., Karladee, N., Paiboonsak, S., and Champathet, P. (2001). An evaluation of drought risk area in Northeast Thailand using remotely sensed data and GIS. Asian J. Geoinform. 1, 33–43.

Muangsong, C., Cai, B., Pumijumnong, N., Hu, C., and Cheng, H. (2014). An annually laminated stalagmite record of the changes in Thailand monsoon rainfall over the past 387 years and its relationship to IOD and ENSO. Quat. Int. 349, 90–97. doi: 10.1016/j.quaint.2014.08.037

CrossRef Full Text | Google Scholar

Nikulin, G., Lennard, C., Dosio, A., Kjellstroem, E., Chen, Y., Haensler, A., et al. (2018). The effects of 1.5 and 2 degrees of global warming on Africa in the CORDEX ensemble. Environ. Res. Lett. 13, 065003. doi: 10.1088/1748-9326/aab1b1

PubMed Abstract | CrossRef Full Text | Google Scholar

North, G. R., Bell, T. L., Cahalan, R. F., and Moeng, F. J. (1982). Sampling errors in the estimation of empirical orthogonal functions. Mon. Wea. Rev. 110, 699–706. doi: 10.1175/1520-0493(1982)110<0699:SEITEO>2.0.CO;2

CrossRef Full Text | Google Scholar

Omar, S. A., and Abiodun, B. J. (2021). Simulating the characteristics of cut-off low rainfall over the Western Cape using WRF. Clim. Dyn. 56, 1265–1283. doi: 10.1007/s00382-020-05532-8

CrossRef Full Text | Google Scholar

Page, S. E., and Hooijer, A. (2016). In the line of fire: the peatlands of Southeast Asia. Philos. Trans. R. Soc. B 371, 20150176. doi: 10.1098/rstb.2015.0176

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavelic, P., Srisuk, K., Saraphirom, P., Nadee, S., Pholkern, K., Chusanathas, S., et al. (2012). Balancing-out floods and droughts: opportunities to utilize floodwater harvesting and groundwater storage for agricultural development in Thailand. J. Hydrol. 470–471, 55–64. doi: 10.1016/j.jhydrol.2012.08.007

CrossRef Full Text | Google Scholar

Peralta-Hernández, A. R., Balling Jr, R. C., and Barba-Martínez, L. R. (2009). Comparative analysis of indices of extreme rainfall events: variations and trends from southern México. Atmosfera 22, 219–228.

Pillai, P. A., Ramu, D. A., and Nair, R. C. (2021). Recent changes in the major modes of Asian summer monsoon rainfall: influence of ENSO-IOD relationship. Theor. Appl. Climatol. 143, 869–881. doi: 10.1007/s00704-020-03454-3

CrossRef Full Text | Google Scholar

Power, S., Casey, T., Folland, C., Colman, A., and Mehta, V. (1999). Inter-decadal modulation of the impact of ENSO on Australia. Clim. Dyn 15, 319–324. doi: 10.1007/s003820050284

CrossRef Full Text | Google Scholar

Prapertchop, P., Bhandari, H., and Pandey, S. (2007). “Economic cost of drought and rice farmers' coping mechanism in northeast Thailand,” in Economic Cost of Drought and Rice Farmers' Coping Mechanisms: A Cross Country Comparative Analysis, eds S. Pandey, H. Bhandari, B. Hardy (Los Banos: International Rice Research Institute), 116–148.

Prasanna, K., Chowdary, J. S., Naidu, C. V., Gnanaseelan, C., and Parekh, A. (2020). Diversity in ENSO remote connection to northeast monsoon rainfall in observations and CMIP5 (models). Theor. Appl. Climatol. 141, 827–839. doi: 10.1007/s00704-020-03208-1

CrossRef Full Text | Google Scholar

Räsänen, T., and Kummu, M. (2013). Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River basin. J. Hydrol. 476, 154–168. doi: 10.1016/j.jhydrol.2012.10.028

CrossRef Full Text | Google Scholar

Ren, P., Ren, H. -L., Fu, J. -X., Wu, J., and Du, L. (2018). Impact of boreal summer intraseasonal oscillation on rainfall extremes in Southeastern China and its predictability in CFSv2. J. Geophys Res: Atmos. 123, 4423–4442. doi: 10.1029/2017JD028043

CrossRef Full Text | Google Scholar

Roy, I., Tedeschi, R. G., and Collins, M. (2019). ENSO teleconnections to the Indian summer monsoon under changing climate. Int. J. Climatol. 39, 3031–3042. doi: 10.1002/joc.5999

CrossRef Full Text | Google Scholar

Salinger, M. J., Renwick, J. A., and Mullan, A. B. (2001). Interdecadal Pacific oscillation and South Pacific climate. Int. J. Climatol. 21, 1705–1721. doi: 10.1002/joc.691

CrossRef Full Text | Google Scholar

Sheridan, S. C., and Lee, C. C. (2011). The self-organizing map in synoptic climatological research. Prog. Phys. Geogr. 35, 109–119. doi: 10.1177/0309133310397582

CrossRef Full Text | Google Scholar

Shimizu, M. H., Ambrizzi, T., and Liebmann, B. (2017). Extreme precipitation events and their relationship with ENSO and MJO phases over northern South America. Int. J. Climatol. 37, 2977–2989. doi: 10.1002/joc.4893

CrossRef Full Text | Google Scholar

Singh, J., Ashfaq, M., Skinner, C. B., Anderson, W. B., and Singh, D. (2021). Amplified risk of spatially compounding droughts during co-occurrences of modes of natural ocean variability. Clim. Atmos. Sci. 4, 7. doi: 10.1038/s41612-021-00161-2

CrossRef Full Text | Google Scholar

Singhrattna, N., Rajagopalan, B., Kumar, K. K., and Clark, M. (2005). Interannual and interdecadal variability of Thailand summer monsoon season. J. Clim. 18, 1697–1708. doi: 10.1175/JCLI3364.1

CrossRef Full Text | Google Scholar

Sriwicha, S., Busababodhin, P., and Kumphon, B. (2016). The impact of ENSO on rainfall in the Northeast of Thailand. Burapha Sci. J. 31, 190–202.

PubMed Abstract | Google Scholar

Supari, T. F., Salimun, E., Aldrian, E., Sopaheluwakan, A., and Juneng, L. (2018). ENSO modulation of seasonal rainfall and extremes in Indonesia. Clim. Dyn. 51, 2559–2580. doi: 10.1007/s00382-017-4028-8

CrossRef Full Text | Google Scholar

Todd, A., Collins, M., and Lambert, F. H. (2018). Diagnosing ENSO and global warming tropical precipitation shifts using surface relative humidity and temperature. J. Clim. 31, 1413–1433. doi: 10.1175/JCLI-D-17-0354.1

CrossRef Full Text | Google Scholar

Vicente-Serrano, S. M., Beguería, S., and López-Moreno, J. I. (2010). A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 23, 1696–1718. doi: 10.1175/2009JCLI2909.1

CrossRef Full Text | Google Scholar

Villafuerte II, M. Q., and Matsumoto, J. (2015). Significant influences of global mean temperature and ENSO on extreme rainfall in Southeast Asia. J. Clim. 28, 1905–1919. doi: 10.1175/JCLI-D-14-00531.1

CrossRef Full Text | Google Scholar

Weir, T., Kumar, R., and Ngari, A. (2021). Interdecadal modulation of the effect of ENSO on rainfall in the southwestern Pacific. J. Southern Hemisphere Earth Syst. Sci. 71, 53–65. doi: 10.1071/ES19053

CrossRef Full Text | Google Scholar

Wolski, P., Jack, C., Tadross, M., van Aardenne, L., and Lennard, C. (2018). Interannual rainfall variability and SOM-based circulation classification. Clim. Dyn. 50, 479–492. doi: 10.1007/s00382-017-3621-1

CrossRef Full Text | Google Scholar

Xavier, P., Rahmar, R., Cheong, W. K., and Wallace, E. (2014). Influence of Madden-Julian Oscillation on Southeast Asia rainfall extremes: observations and predictability. Geophys. Res. Lett. 41, 4406–4412. doi: 10.1002/2014GL060241

CrossRef Full Text | Google Scholar

Yang, Y.-M., Lee, J.-Y., and Wang, B. (2020). Dominant process for northward propagation of boreal summer Intraseasonal oscillation over the Western North Pacific. Geophys. Res. Lett. 47, e2020GL089808. doi: 10.1029/2020GL089808

CrossRef Full Text | Google Scholar

Yang, Y.-M., Wang, B., and Lee, J.-Y. (2019). Mechanisms of northward propagation of boreal summer intraseasonal oscillation revealed by climate model experiments. Geophys. Res. Lett. 46, 3417–3425. doi: 10.1029/2018GL081612

CrossRef Full Text | Google Scholar

Yatagai, A., Kamiguchi, K., Arakawa, O., Hamada, A., Yasutomi, N., and Kitoh, A. (2012). APHRODITE: constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteor. Soc. 93, 1401–1415. doi: 10.1175/BAMS-D-11-00122.1

CrossRef Full Text | Google Scholar