The Impact of Socio-Economic Inertia and Restrictions on Net-Negative Emissions on Cost-Effective Carbon Price Pathways

Introduction

The increased international concern about climate change has led to ambitious climate targets in the Paris Agreement: countries have agreed to limit global mean temperature change to well below 2°C and pursue efforts to limit it to 1.5°C. Achieving these targets requires strong policy interventions. Carbon pricing is regarded as one of the main policy instruments available to reduce greenhouse gas emissions. According to the UNFCCC¹, two-thirds of all submitted Nationally Determined Contributions (NDCs) consider the use of carbon pricing. Currently, 21.5% of all greenhouse gas emissions are already subject to carbon pricing (World Bank, 2021), compared to 12% in 2015 (Kossoy et al., 2015). In 2021, a total of 64 carbon pricing instruments have been implemented. However, the level of the carbon prices implemented differs considerably, from <1 to more than 100 USD/tCO₂eq. This raises the question of the appropriate carbon price level, or, in other words, which carbon price level is consistent with meeting the targets of the Paris Agreement. This strongly depends on the timing of mitigation action, which has been an important topic of research for many years (Nordhaus, 1982; Ulph and Ulph, 1994; Hourcade and Robinson, 1996; Peck and Wan, 1996; Wigley et al., 1996; Grubler and Messner, 1998; Goulder and Mathai, 2000; Lemoine and Rudik, 2017) and is of key importance for defining least-cost policy response strategies under the Paris Agreement.

Different approaches have been used to derive timing profiles of emission reductions, ranging from rather stylized mathematical rules to more refined economic methods. Most commonly, model-based approaches apply some form of cost-minimization over time, sometimes in combination with specific constraints representing policy. One key element in the discussion of least-cost emission profiles is the so-called Hotelling rule. The Hotelling rule states that for exhaustible resources, equalizing the marginal productivity of capital with the growth rate of the resource's marginal productivity leads to an optimal shift rate (Hotelling, 1931). In other words, the growth rate of the resource's price must equal the interest rate. For climate change, the CO₂ holding capacity of the atmosphere can be viewed as the exhaustible resource (Lemoine and Rudik, 2017), especially as the climate problem can be viewed as limiting cumulative emissions to a certain level (Allen et al., 2009; Meinshausen et al., 2009). In this view, the price (or tax) of carbon has to increase at the same rate as the interest rate according to the Hotelling rule. Indeed, many models show that least-cost carbon prices increase exponentially over time (see Supplementary Material). Some recursive dynamic integrated assessment models even use the Hotelling rule to approximate intertemporal optimization (Capellán-Pérez et al., 2014; Bauer et al., 2015).

An important distinction in the discussion on the optimal carbon price trajectory is between cost-effectiveness and cost-benefit studies. Cost-effectiveness studies focus on the least-cost trajectory to achieve predefined carbon budgets or temperature targets. Cost-benefit studies optimize the mitigation costs and benefits over time. Contrary to cost-effectiveness studies, cost-benefit studies also take the (avoided) damages of climate change into account in determining the optimal carbon price pathway. A pioneering study by Goulder and Mathai (2000) showed that the Hotelling rule does not apply in a cost-benefit setting: higher initial carbon prices than resulting from the Hotelling rule lead to additional benefits, as it reduces damage from climate change. Other studies have confirmed this result under a range of different settings regarding initial oil stocks (Van Der Ploeg and Withagen, 2014), carbon capture and storage (Lontzek and Rickels, 2008), and discount rates and climate damages.

Cost-effectiveness studies, in contrast, focus on the least-cost pathway in achieving exogenously set climate targets. Such targets can, for instance, be based on the Paris Agreement, which states the objective to limit global temperature change to well below 2°C and pursue efforts to limit it to 1.5°C. The Goulder and Mathai paper mentioned above concluded that Hotelling applies for cost-effectiveness studies even if induced technological change by either research and development (R&D) and learning by doing is taken into account. Later studies stressed that if technologies are represented in more detail in the framework analysis, a Hotelling carbon tax, combined with other policies, such as subsidizing clean technologies (either directly or through R&D in renewables) is still optimal (Van Der Zwaan et al., 2002; Kverndokk and Rosendahl, 2007; Fischer and Newell, 2008; Gerlagh et al., 2009; Acemoglu et al., 2012; Kalkuhl et al., 2012, 2013; Mattauch et al., 2015; Prices, 2017). Some of these studies conclude that if subsidizing R&D is not available or feasible as a policy instrument, the second-best policy is to apply a higher carbon tax, but still increasing over time according to the Hotelling rule (Gerlagh et al., 2009; Acemoglu et al., 2012; Mattauch et al., 2015).

However, all of the above studies do not consider how real-world socio-economic and political barriers could affect the shape of the carbon price pathway. Important economic barriers include unstable macroeconomic conditions, missing markets, distorted prices, and financial market imperfections (Sathaye et al., 2001). Besides these economic barriers, political, institutional, social, cultural, and psychological factors also can slow the diffusion of new energy technologies and thereby the speed by which emissions can be reduced. The speed by which a complete transition to electric vehicles can take place, for instance, depends on available infrastructure and how easy certain habits can be changed. As already shown by Ha-Duong et al. (1997) and Schwoon and Tol (2006), inertia in changing the energy system, in combination with, respectively, learning by doing and uncertainty in the climate target, may impact the optimal emission abatement trajectory—but both did not analyse its effect on the optimal carbon price pathway.

Moreover, socio-economic barriers can also influence the level of net-negative emissions that can be achieved. Net-negative emissions are possible by carbon dioxide removal (CDR) technologies. While there are several promising CDR technologies, such as enhanced weathering of rocks (Strefler et al., 2018) and Direct Air Capture (DAC), the most important ones currently included in long-term scenarios are bioenergy combined with carbon capture and storage (BECCS) and large-scale reforestation (Clarke et al., 2014), both requiring substantial amounts of land. There is a heavy debate about these CDR technologies, largely due to their possible impact on biodiversity and food security (Anderson and Peters, 2016; Smith et al., 2016; Van Vuuren et al., 2017; Fridahl and Lehtveer, 2018; Fuss et al., 2018). Because of these risks, recent scenario analyses have focused more on how the climate objectives of the Paris Agreement can be achieved without (large-scale) use of CDR technologies (Grubler et al., 2018; Van Vuuren et al., 2018; Rogelj et al., 2019).

This paper introduces a simple and transparent model to analyse how learning by doing and socio-economic barriers, causing inertia in reducing emissions and restrictions on the achievable levels of net-negative emissions, influence the optimal carbon price pathway in a cost-effectiveness setting. We limit cumulative CO₂ emissions to a certain level, given the almost linear relationship between cumulative CO₂ emissions and mean global temperature change (Allen et al., 2009; Meinshausen et al., 2009; Dietz and Venmans, 2019). As discussed above, this setting is generally associated with a Hotelling carbon price pathway, making it a good analysis framework for analyzing the hypothesis that the Hotelling path is optimal.

Materials and Methods

Below, we first provide a general overview of the set-up of the experiments, followed by an explanation of the experiments and optimization procedure.

General Settings

We use intuitive numerical experiments calibrated to ranges found in the literature to show the impact of learning by doing and socio-economic restrictions on least-cost carbon price and emission trajectories. In these experiments, we vary the way in which technology costs develop over time and impose different restrictions on emissions abatement. In all the experiments, we assume a quadratic marginal abatement cost (MAC) curve, where a is the relative abatement level:

$\begin{array}{ll}{\text{MAC}}_{\text{default}}(a)=\text{learning factor}·\gamma ·{\text{a}}^{\beta }.& (1)\end{array}$

Here, the learning factor is a factor between 0 and 1 used to model technological progress and depends on either time or cumulative abatement, depending on the experiment. The parameter γ is used to calibrate the size of the MAC to match medium values of the IPCC mitigation cost range (based on Figure 6.23 of Clarke et al., 2014), and β is equal to 2 in our experiments to yield a quadratic MAC.

We assume that a carbon price is the only instrument that is applied, as climate change is the only externality considered here (this is in line with most Integrated Assessment models used to develop mitigation scenarios). The optimal carbon price pathway is defined as the price path which minimizes total discounted abatement costs between 2020 and 2100 to limit total cumulative CO₂ emissions (or carbon budget) to a predefined level. The assumed carbon budget is set at cumulative CO₂ emissions of the RCP2.6 emission pathway (van Vuuren et al., 2011), equal to 25% of baseline cumulative CO₂ emissions, and consistent with a 67% probability to achieve the 2°C climate target. Our sensitivity analysis also looks at the impact of reducing the carbon budget to cumulative emissions of the RCP1.9 emission pathway (Rogelj et al., 2018), equal to about 10% of baseline cumulative CO₂ emissions and consistent with restricting median global warming to below 1.5°C. Baseline emissions follow a slightly concave, quadratic path that leads to a doubling of CO₂ emissions by the end of the century relative to 2020. This pathway strongly resembles the pathway of the SSP2 marker scenario (Riahi et al., 2017).

Experiments

Learning Over Time

As a reference, an experiment is conducted in which technical change depends on autonomous trends and no restrictions on the speed and level of emission reductions are assumed. In this experiment, the costs of abatement technologies decrease only as a function of time. The learning factor is given by:

$\begin{array}{ll}{\text{learning factor}}_{\text{LoT}}(t)=\frac{1}{{(1+\text{rate})}^{t-t_0}}.& (2)\end{array}$

The default learning rate is set at 1.5%/year, based on typical rates of autonomous energy efficiency improvement assumed in macroeconomic environmental models (Grubb et al., 2002). The value of the MAC is reduced by this factor:

$\begin{array}{ll}{\text{MAC}}_{\text{default}}(a;t)=\text{MAC}(a)·\text{learning factor}(t).& (3)\end{array}$

Learning by Doing

In the second experiment, learning by doing, the MAC curve decreases as a function of relative cumulative abatement RCA(t) (equal to cumulative baseline emissions minus cumulative emissions of the mitigation pathway, as fraction of cumulative baseline emissions until 2100) to account for endogenous technological growth. Again, no restrictions on the speed and level of emission reductions are assumed. The learning factor in this experiment is given by

$\begin{array}{ll}\text{learning }{\text{factor}}_{\text{LBD}}\text{=}{\left(\alpha \cdot \text{RCA}\left(t\right)\text{+1}\right)}^{{\log }_2\left(\text{ρ}\right)}.& (4)\end{array}$

The value for the progress ratio ρ (i.e., the reduction in costs for doubling cumulative capacity) is taken from van Vuuren (2006). It represents empirical studies of endogenous technological learning. This value amounts to ρ = 0.82.

The value of the calibration factor α is calibrated such that the same level of learning is achieved in 2100 as in the learning over time experiment. As shown in Equation (4), the learning factor in 2100 in the learning by doing experiment only depends on the carbon budget. By setting learning factor for learning by doing (Equation 4) in 2100 equal to the learning factor from learning over time in 2100, i.e., $\frac{1}{{(1+\mathrm{\text{rate}})}^{2100-2020}}={(1+\mathrm{\text{rate}})}^{-80}$, we obtain the following expression for the calibration factor α:

$\begin{array}{ll}\text{α}=\frac{{\left(\text{1+LoT rate}\right)}^{-80/{\text{log}}_{\text{2}}\left(\text{ρ}\right)}-1}{\text{RCA}\left(\text{80}\right)}.& (5)\end{array}$

With the learning over time rate of 1.5%/year, the default progress ratio of ρ = 0.82 and a RCA of 75% for a carbon budget of 25% of baseline emissions, we obtain α = 84.1.

In the sensitivity analysis, we capture the uncertainty range in the learning factors. We use the range from van Vuuren (2006) for the progress ratio: from ρ = 0.65 for high learning to ρ = 0.95 for low technological learning. Using Equations (1) and (3), we obtain the corresponding learning-over-time rates: 3.3%/year and 0.4%/year for the high and low learning cases, respectively.

Socio-Economic Inertia

The socio-economic inertia experiment reflects that energy and infrastructure systems need some time to change and adapt. Consequently, emissions cannot be reduced at an unlimited speed. Based on maximum reduction speeds of the scenarios in the scenario explorer for 1.5°C pathways underpinning the IPCC Special Report on Global Warming of 1.5°C (https://data.ene.iiasa.ac.at/iamc-1.5c-explorer), we assumed that when annual reductions approach 5.5% of the 2015 emission level, abatement costs increase sharply by adding an extra term to the MAC curve (in the sensitivity runs, we also analyzed annual reduction thresholds of 3 and 8% of the 2015 emissions level).

This is modeled as follows. We first determine an abatement limit caused by inertia. We define inertia as a limit on the change in emissions between two consecutive timesteps:

$\begin{array}{ll}{E}_t\ge E_{(t-\Delta t)}-\Delta t·\text{inertia rate}.& (6)\end{array}$

Since the emissions at time t depend on baseline emissions B(t) and the relative abatement a_t:

$\begin{array}{ll}{E}_t=B_t·(1-a_t),& (7)\end{array}$

we find a relative abatement limit a_t* of:

$\begin{array}{ll}{a}_t^{*}=1-(E_{(t-\Delta t)}-\Delta t·\text{inertia rate})/B(t)& (8)\end{array}$

As mentioned above, the inertia rate is set at 5.5% of the 2015 emission level. Given the abatement limit $a_t^{*}$, the total MAC becomes:

$\begin{array}{ll}{\text{MAC}}_{\text{total}}(\text{a})={\text{MAC}}_{\text{default}}(\text{a})+\frac{1}{2}\gamma ·{\eta }^{(\text{a}-{\text{a}}_t^{*})/ϵ},& (9)\end{array}$

where the scaling parameters η and ϵ determine the steepness of the additional costs. By default, we use η = 1.025 and ϵ = 0.0003. These values are chosen so that the marginal costs begin to slightly increase when the rate of emission change approach half the inertia rate, after which it increases more strongly toward four times the marginal costs at the abatement limit (see left panel of Figure 1 for an example how the inertia constraint influences the MAC curve). This follows a similar methodology as Schwoon and Tol (2006). The main difference is that we use an exponential term instead of a quadratic term, allowing us to let inertia really have an effect at the abatement limit a_t*. We also include learning over time in this experiment to compare abatement costs. The annual learning rate is set at the same level as in the learning over time experiment.

FIGURE 1

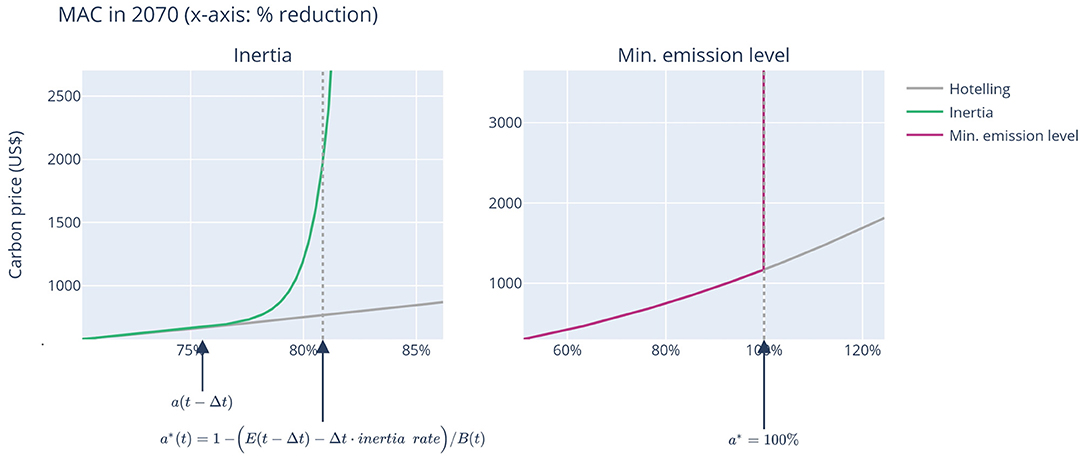
Figure 1. Example of the MAC curve of the socio-economic inertia and minimum emission level experiments.

Minimum Emission Level

The minimum emission level experiment reflects the difficulties associated with CDR technologies. Like in the socio-economic inertia experiment, these difficulties can be of economic (e.g., land becoming increasingly scarce or increased dependence on very expensive storage sites) and socio-political (concerns about biodiversity and food security) nature. We assumed that net-negative emissions are not allowed in the default setting, resulting in a MAC curve as depicted in the right panel of Figure 1 (i.e., net emissions cannot go below zero). Again, we include an annual learning rate of 1.5% in this experiment. In the sensitivity runs, we also analyse the effect of allowing some level of net-negative emissions based on the minimum level of annual emissions of scenarios in the same IPCC 1.5°C degrees database as used for the socio-economic inertia experiment, yielding values of 10 GtCO₂ and 20 GtCO₂ annually.

Solving the Optimal Control Problem

In all experiments, total discounted abatement costs are minimized under the restriction that total cumulative CO₂ emissions in the period 2020–2100 are limited to a predefined level globally. This automatically means that overshoot of the budget (and thus temperature) is temporarily allowed, but it is restricted in the minimum emission level experiment. Emission reductions are modeled by choosing a carbon price p(t). Depending on the experiment, the MAC curve depends on either time or cumulative abatement. Since we impose a constraint on the total CO₂ emissions through a carbon budget CB, we consider the cumulative emissions CE(t) as state variable in our minimization process. Every time step, the cumulative emissions are increased by the instantaneous emission level E(t) (equal to the baseline emission level B(t) minus the abatement level):

$\begin{array}{l}d\text{CE}(t)/dt=E(t)\\ :=B(t)(1-{\text{MAC}}^{-1}(p(t))),\text{ CE}(T)\le \text{CB}.& (10)\end{array}$

The optimal price path is calculated by minimizing the total discounted abatement costs. For every time step, the abatement costs are defined as the area under the MAC. Therefore, the following function is minimized:

$\begin{array}{ll}{\displaystyle \underset{p(t)}{\text{minimize}}}{\displaystyle {\int }_0^T}{e}^{-rt}\text{AC}(t)dt,& (11)\end{array}$

where r is the discount rate (for which we use a value of 5%) and the abatement costs AC(t) are defined as the area under the MAC from 0 to the abatement level a_t:

$\begin{array}{ll}\text{AC}(t)=B(t)\left({\displaystyle {\int }_0^{a_t}}\text{MAC}(a)\text{d}a\right).& (12)\end{array}$

The abatement level a_t is determined by the carbon price p_t and is equal to the inverse of the MAC:

$\begin{array}{ll}{a}_t={\text{MAC}}^{-1}(p(t)).& (13)\end{array}$

The final optimal control problem is given by Equation (9), subject to Equation (8). This can be solved analytically for the experiments learning over time and learning by doing using Pontryagin's Maximum Principle (see Supplementary Material). The other experiments are too complex to obtain closed-form analytical results. These are solved numerically using the open-source Python optimization modeling framework Pyomo (Hart et al., 2011, 2017). The dynamical optimal control formulations were programmed with Pyomo.DAE (Differential-Algebraic Equations; Nicholson et al., 2018). The model is solved using the Ipopt solver (Wächter and Biegler, 2006), widely used for large-scale non-linear optimization. The full model code is available at https://mybinder.org/v2/gh/kvanderwijst/Hotelling/HEAD?filepath=Calculations.ipynb.

Results

Figure 2 shows the optimal carbon price paths, and resulting emission pathways and abatement costs for all experiments and Figure 3 shows the carbon price pathways and abatement costs relative to the learning over time experiment, which makes it easier to see the differences with the Hotelling carbon price pathway. The results of the sensitivity analysis of the parameter settings and carbon budget are given in section Sensitivity Analysis.

FIGURE 2

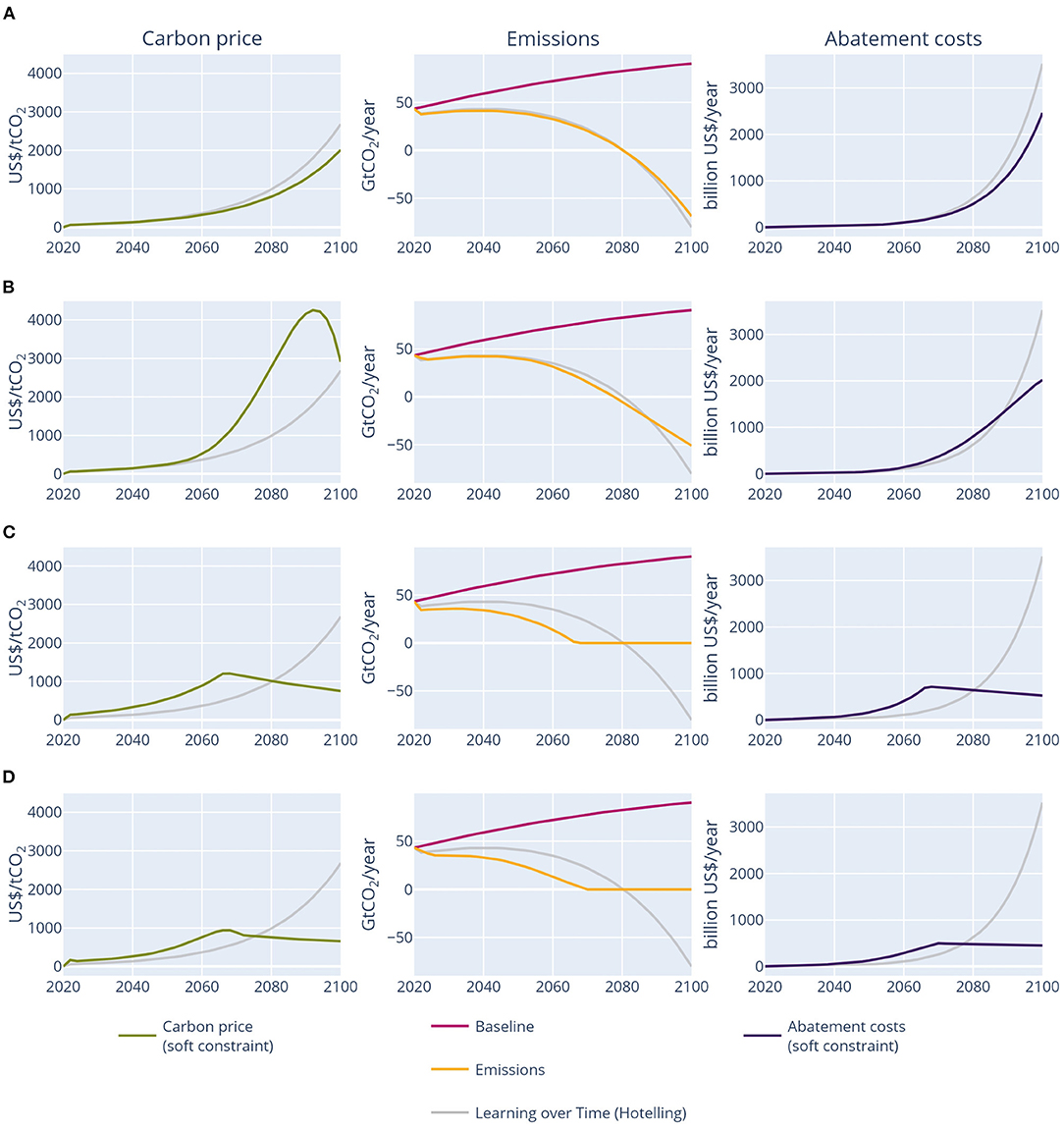
Figure 2. Carbon price, emission, and abatement costs over time for different constraints and learning assumptions. (A) Learning by doing, (B) socio-economic inertia, (C) minimum emission level, and (D) combination.

FIGURE 3

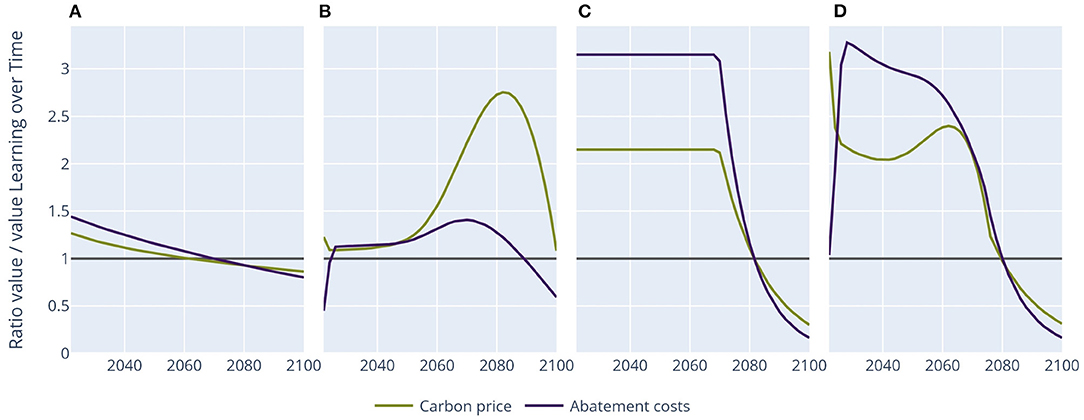
Figure 3. Carbon price pathways and abatement costs relative to the learning over time pathway. (A) Learning by doing, (B) socio-economic inertia, (C) minimum emission level, and (D) combination.

Impact of Different Learning Assumptions

Consistent with earlier studies, the reference scenario learning over time results in a hoteling carbon price pathway, as proven in the Supplementary Material.

In the learning by doing experiment, the initial optimal carbon tax is about 25% higher than in the learning over time experiment, after which it increases less strongly (this is shown analytically as well in the Supplementary Material). The carbon price is lower than the learning over time pathway from about mid-century onwards. Carbon neutrality is achieved by 2080 in this experiment, after which emissions decrease strongly to large net-negative values. As a consequence, abatement costs increase sharply from 2080 as well. However, the increase in abatement costs is lower than for learning over time, even though the same level of learning is achieved in both cases. This is because learning over time shifts abatement to the present, and therefore less abatement is needed by 2100.

This experiment shows that, with our simple model calibrated to literature values for costs and carbon budgets, no restrictions at all on net-negative emissions technologies or the reduction speed lead to cost-optimal carbon price pathways with large net-negative emissions and high abatement costs late in the century. Learning by doing leads to only slightly less net-negative emissions and lower abatement costs.

Interestingly, these results contradict the findings of Goulder and Mathai (2000), who found that even with learning by doing, the optimal carbon price follows the Hotelling rule. The reason is that in the model of Goulder and Mathai, learning by doing did not directly affect abatement costs but only indirectly via the accumulation of knowledge, as explained in more detail in the Supplementary Material. In this formulation, the accumulation of knowledge does not affect the shape of the carbon price trajectory. With our representation, learning by doing directly impacts costs and therefore does have an impact on the carbon price pathway.

Impact of Constraints on the Speed and Level of Emission Reductions

The socio-economic inertia experiment shows the development of carbon prices and abatement costs of socio-economic inertia. Socio-economic inertia requires a higher carbon price throughout the century, given the additional constraint. Until about mid-century, the carbon price pathway closely follows a Hotelling path. Around mid-century, however, the emission reduction speed approaches the maximum possible level. This leads to a steeply increasing carbon price, after which it decreases just before the end of the century. This decrease is due to slightly lower reduction speeds at the end of the century, for which the carbon price is strongly sensitive. The annual abatement costs are slightly higher than without inertia until 2085. After 2085, abatement costs are lower than without inertia, as emissions decline less rapidly. This experiment shows that inertia strongly influences the carbon price pathway, with strong increases during the century and a leveling off and even decreasing prices late in the century.

If net-negative emissions are not allowed, the carbon price pathway exactly follows a Hotelling path until emissions reach net zero. The only difference with no restrictions is that the carbon price is about twice as high, which is required to achieve the same carbon budget with less abatement potential. This higher carbon price leads to much higher abatement costs (about a factor 3). After net-zero emissions are achieved around 2065, emissions stay on this level, leading to declining carbon prices and abatement costs due to technological learning.

Combining Restrictions

The carbon price pathway becomes irregular when combining learning by doing, socio-economic inertia, and restrictions on net-negative emissions. Initially, the carbon price is two to three times as high as in the learning over time experiment without constraints, as both learning by doing and the two constraints lead to higher initial carbon prices. By 2070, the carbon price shortly decreases as net-zero emissions are reached.

Sensitivity Analysis

Figure 4 shows the results of the sensitivity of learning by doing, socio-economic inertia, and the minimum emission level on the optimal carbon price pathway and abatement costs relative to the learning over time experiment. Stronger learning and socio-economic inertia lead to carbon price pathways that deviate more strongly from Hotelling and vice versa. The carbon price pathway is especially sensitive to assumptions on the maximum reduction speed of emissions: if this is restricted to 3% of the 2015 emission level, the carbon price strongly increases to a factor of more than four times the level we found without restrictions by 2070.

FIGURE 4

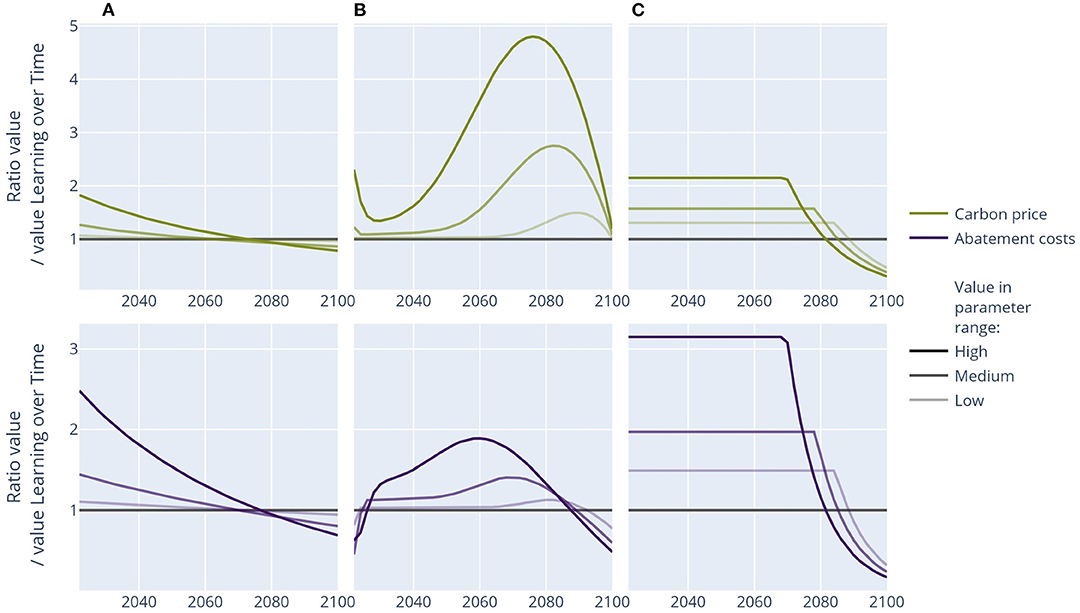
Figure 4. Carbon price pathways and abatement costs of the parameter sensitivity runs relative to the learning over time pathway. Parameter values: (A) Learning by doing: rho = 0.65, 0.82, and 0.95. (B) Socio-economic inertia: 3, 5.5, and 8% of 2015 emissions. (C) Minimum emission level: 0, −10, and −20 GtCO₂.

If the hard assumption of disallowing net-negative emissions is loosened, the carbon price is substantially lower. However, for a maximum annual level of 20 GtCO₂ net-negative emissions, the carbon price is still 50% higher than the case with no restrictions on net-negative emissions at all.

All the above experiments were based on a carbon budget consistent with a 67% probability to achieve the 2°C climate target. The impact of the restrictions on the speed and minimum level of emissions is higher for more ambitious targets, such as a carbon budget consistent with a 50% probability of achieving the 1.5°C target. This is shown in Figure 5. Learning by doing does not significantly affect the carbon price pathway under this more restrictive carbon budget, but socio-economic inertia and especially not allowing for net negative emissions does. Under a 1.5°C carbon budget, not allowing for net-negative emissions leads to a five times higher carbon price until 2050, when net-zero emissions are achieved. If combined with realistic assumptions on the maximum speed of emission reductions, the initial carbon price is even a factor 10 higher than without these restrictions.

FIGURE 5

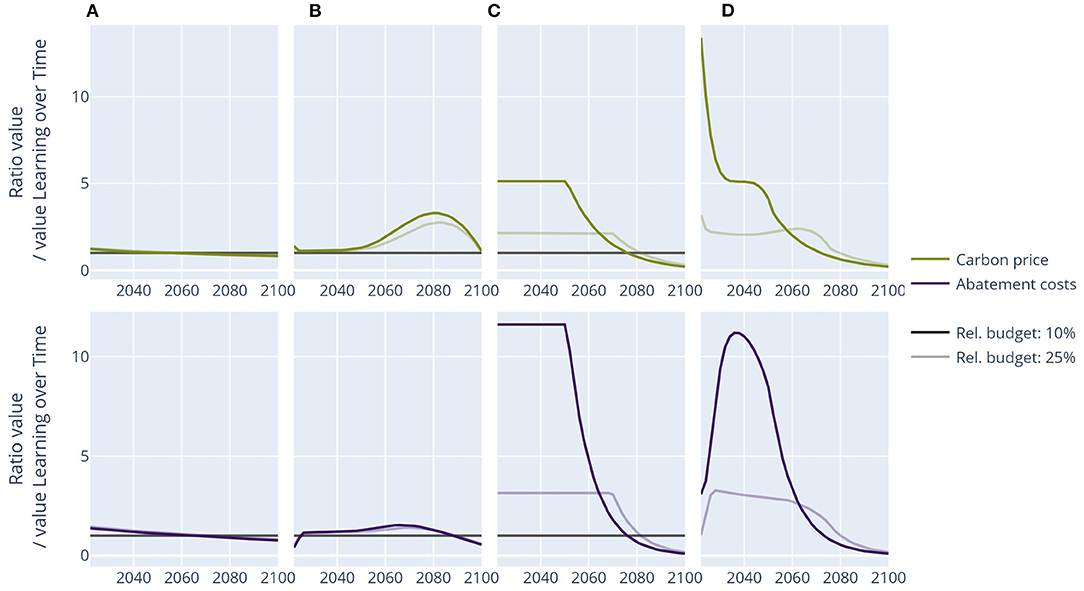
Figure 5. Carbon price pathways and abatement costs relative to the learning over time pathway: 1.5°C budget (25% of cumulative baseline emissions) compared with 2°C budget (10% of cumulative baseline emissions). (A) Learning by doing, (B) socio-economic inertia, (C) minimum emission level, and (D) combination.

Discussion

Our analysis has shown that the cost-effective carbon price pathway is strongly influenced by realistic restrictions on the speed by which emissions can be reduced. Not allowing for net-negative emissions does not lead to changes in the pathway in the short to medium term, but it does increase the initial carbon price by a factor 2 for a 2°C climate target to a factor 5 for a 1.5°C climate target.

This leads to the conclusion that an exponentially increasing carbon tax (as suggested by the Hotelling rule) is not necessarily the cost-effective outcome. In several situations, especially with more stringent climate targets, a higher carbon tax early in the century is cost-effective. Putting it in different words, with ambitious climate targets, the carbon price depends more and more on real-world restrictions, which affect the maximum speed and level of emission reductions. This can explain why some integrated assessment models, especially ones in which the speed of emission reductions and the level of net-negative emissions is implicitly or explicitly constrained, show carbon price trajectories that do not follow the Hotelling rule.

Therefore, we argue that minimization of mitigation costs by setting only the initial carbon price and letting the pathway be determined based on the Hotelling rule is too simplistic. Real-world dynamics related to inertia, learning, and restrictions on net-negative emissions, especially with the ambitious climate targets agreed upon in the Paris Agreement, have a strong impact on the carbon price pathway. While full inter-temporal optimization may for many models not be an alternative to Hotelling, given the complexity of most integrated assessment models, a possible alternative could be to approximate a cost-effective pathway based on an iterative procedure in which the carbon price pathway is slightly adjusted each time. Compared to applying Hotelling, this will likely lead to carbon prices which are higher in the short term and which increase less rapidly.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://mybinder.org/v2/gh/kvanderwijst/Hotelling/HEAD?filepath=Calculations.ipynb.

Author Contributions

AH supervised the work and developed the original idea. All authors were involved in designing the study, the experiments, the analysis of the data, and contributed to writing the paper. K-IvdW performed the experiments and provided the analytical solutions of optimal pathways. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Comments from Reyer Gerlagh are gratefully acknowledged. The sole responsibility for the analysis results is borne by the authors.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2021.785577/full#supplementary-material

Footnotes

1. ^https://unfccc.int/about-us/regional-collaboration-centres/the-ci-aca-initiative/about-carbon-pricing#eq-6

References

Acemoglu, D., Aghion, P., Bursztyn, L., and Hemous, D. (2012). The environment and directed technical change. Am. Econ. Rev. 102, 131–166. doi: 10.1257/aer.102.1.131

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, M. R., Frame, D. J., Huntingford, C., Jones, C. D., Lowe, J. A., Meinshausen, M., et al. (2009). Warming caused by cumulative carbon emissions towards the trillionth tonne. Nature 458, 1163–1166. doi: 10.1038/nature08019

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, K., and Peters, G. (2016). The trouble with negative emissions. Science 354, 182–183. doi: 10.1126/science.aah4567

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauer, N., Bosetti, V., Hamdi-Cherif, M., Kitous, A., McCollum, D., Méjean, A., et al. (2015). CO₂ emission mitigation and fossil fuel markets: dynamic and international aspects of climate policies. Technol. Forecast. Soc. Change 90, 243–256. doi: 10.1016/j.techfore.2013.09.009

CrossRef Full Text | Google Scholar

Capellán-Pérez, I., González-Eguino, M., Arto, I., Ansuategi, A., Dhavala, K., Patel, P., et al. (2014). New Climate Scenario Framework Implementation in the GCAM Integrated Assessment Model. BC3 Working Paper Series 2014–04.

Google Scholar

Clarke, L., Jiang, K., Akimoto, K., Babiker, M., Blanford, G., Fisher-Vanden, K., et al. (2014). “Assessing transformation pathways,” in Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds O. Edenhofer, R. Pichs-Madruga, Y. Sokona, E. Farahani, S. Kadner, K. Seyboth, A. Adler, I. Baum, S. Brunner, P. Eickemeier, B. Kriemann, J. Savolainen, S. Schlömer, C. V. Stechow, T. Zwickel, and J. C. Minx (Cambridge, UK; New York, NY: Cambridge University Press) 416–510.

Google Scholar

Dietz, S., and Venmans, F. (2019). Cumulative carbon emissions and economic policy: in search of general principles. J. Environ. Econ. Manage. 96, 108–129. doi: 10.1016/j.jeem.2019.04.003

CrossRef Full Text | Google Scholar

Fischer, C., and Newell, R. G. (2008). Environmental and technology policies for climate mitigation. J. Environ. Econ. Manage. 55, 142–162. doi: 10.1016/j.jeem.2007.11.001

CrossRef Full Text | Google Scholar

Fridahl, M., and Lehtveer, M. (2018). Bioenergy with carbon capture and storage (BECCS): global potential, investment preferences, and deployment barriers. Energy Res. Soc. Sci. 42, 155–165. doi: 10.1016/j.erss.2018.03.019

CrossRef Full Text | Google Scholar

Fuss, S., Lamb, W. F., Callaghan, M. W., Hilaire, J., Creutzig, F., Amann, T., et al. (2018). Negative emissions—part 2: costs, potentials and side effects. Envrion. Res. Lett. 13, 063002. doi: 10.1088/1748-9326/aabf9f

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerlagh, R., Kverndokk, S., and Rosendahl, K. E. (2009). Optimal timing of climate change policy: interaction between carbon taxes and innovation externalities. Environ. Resour. Econ. 43, 369–390. doi: 10.1007/s10640-009-9271-y

CrossRef Full Text | Google Scholar

Goulder, L. H., and Mathai, K. (2000). Optimal CO₂ abatement in the presence of induced technological change. J. Environ. Econ. Manage. 39, 1–38. doi: 10.1006/jeem.1999.1089

CrossRef Full Text | Google Scholar

Grubb, M., Köhler, J., and Anderson, D. (2002). Induced technical change in energy and environmental modeling: analytic approaches and policy implications. Annu. Rev. Energy Environ. 27, 271–308. doi: 10.1146/annurev.energy.27.122001.083408

CrossRef Full Text | Google Scholar

Grubler, A., and Messner, S. (1998). Technological change and the timing of mitigation measures. Energy Econ. 20, 495–512.

Google Scholar

Grubler, A., Wilson, C., Bento, N., Boza-Kiss, B., Krey, V., McCollum, D. L., et al. (2018). A low energy demand scenario for meeting the 1.5 °C target and sustainable development goals without negative emission technologies. Nat. Energy 3, 515–527. doi: 10.1038/s41560-018-0172-6

CrossRef Full Text | Google Scholar

Ha-Duong, M., Grubb, M. J., and Hourcade, J. C. (1997). Influence of socioeconomic inertia and uncertainty on optimal CO₂-emission abatement. Nature 390, 270–273.

Google Scholar

Hart, W. E., Laird, C. D., Watson, J.-P., Woodruff, D. L., Hackebeil, G. A., Nicholson, B. L., et al. (2017). Optimization Modeling in Python, 2nd Edn., Vol. 67. Cham: Springer.

Google Scholar

Hart, W. E., Watson, J.-P., and Woodruff, D. L. (2011). Pyomo: modeling and solving mathematical programs in Python. Math. Prog. Comp. 3, 219. doi: 10.1007/s12532-011-0026-8

CrossRef Full Text | Google Scholar

Hotelling, H. (1931). The economics of exhaustible resources. J. Polit. Econ. 39, 137–175. doi: 10.1086/254195

CrossRef Full Text | Google Scholar

Hourcade, J.-C., and Robinson, J. (1996). Mitigating factors: assessing the costs of reducing GHG emissions. Energy Policy 24, 863–873. doi: 10.1016/S0301-4215(96)00071-7

CrossRef Full Text | Google Scholar

Kalkuhl, M., Edenhofer, O., and Lessmann, K. (2012). Learning or lock-in: optimal technology policies to support mitigation. Resour. Eng. Econ. 34, 1–23. doi: 10.1016/j.reseneeco.2011.08.001

CrossRef Full Text | Google Scholar

Kalkuhl, M., Edenhofer, O., and Lessmann, K. (2013). Renewable energy subsidies: second-best policy or fatal aberration for mitigation? Resour. Eng. Econ. 35, 217–234. doi: 10.1016/j.reseneeco.2013.01.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Kossoy, A., Peszko, G., Oppermann, K., Prytz, N., Klein, N., Blok, K., et al. (2015). State and Trends of Carbon Pricing. Washington, DC: World Bank.

Google Scholar

Kverndokk, S., and Rosendahl, K. E. (2007). Climate policies and learning by doing: impacts and timing of technology subsidies. Resour. Eng. Econ. 29, 58–82. doi: 10.1016/j.reseneeco.2006.02.007

CrossRef Full Text | Google Scholar

Lemoine, D., and Rudik, I. (2017). Steering the climate system: using inertia to lower the cost of policy. Am. Econ. Rev. 107, 2947–2957. doi: 10.1257/aer.20150986

CrossRef Full Text | Google Scholar

Lontzek, T. S., and Rickels, W. (2008). Carbon Capture and Storage and the Optimal Path of the Carbon Tax. Kiel Working Papers 1475.

Google Scholar

Mattauch, L., Creutzig, F., and Edenhofer, O. (2015). Avoiding carbon lock-in: policy options for advancing structural change. Econ. Model. 50, 49–63. doi: 10.1016/j.econmod.2015.06.002

CrossRef Full Text | Google Scholar

Meinshausen, M., Meinshausen, N., Hare, W., Raper, S. C. B., Frieler, K., Knutti, R., et al. (2009). Greenhouse-gas emission targets for limiting global warming to 2°C. Nature 458, 1158–1162. doi: 10.1038/nature08017

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicholson, B., Siirola, J. D., Watson, J.-P., Zavala, V. M., and Biegler, L. T. (2018). pyomo.dae: a modeling and automatic discretization framework for optimization with differential and algebraic equations. Math. Progr. Comput. 10, 187–223. doi: 10.1007/s12532-017-0127-0

CrossRef Full Text | Google Scholar

Nordhaus, W. (1982). How fast should we graze the global commons. Am. Econ. Rev. 72, 242–246.

Google Scholar

Peck, S. C., and Wan, Y. S. (1996). “Analytic solutions of simple optimal greenhouse gas emission models,” in Economics of Atmospheric Pollution. NATO ASI Series (2. Environment), Vol. 14, eds E. C. van Ierland and K. Görka (Berlin; Heidelberg: Springer), 113–121.

Google Scholar

Prices, H.-L. (2017). Report of the High-Level Commission on Carbon Prices. License: Creative Commons Attribution CC BY 3.0 IGO. Washington, DC: World Bank.

Google Scholar

Riahi, K., van Vuuren, D. P., Kriegler, E., Edmonds, J., O'Neill, B. C., Fujimori, S., et al. (2017). the shared socioeconomic pathways and their energy, land use, and greenhouse gas emissions implications: an overview. Glob. Environ. Change 42, 153–168. doi: 10.1093/oep/46.Supplement_1.857

CrossRef Full Text | Google Scholar

Rogelj, J., Huppmann, D., Krey, V., Riahi, K., Clarke, L., Gidden, M., et al. (2019). A new scenario logic for the Paris Agreement long-term temperature goal. Nature 573, 357–363. doi: 10.1038/s41586-019-1541-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogelj, J., Popp, A., Calvin, K. V., Luderer, G., Emmerling, J., Gernaat, D., et al. (2018). Scenarios towards limiting global mean temperature increase below 1.5 °C. Nature Clim Change 8, 325–332. doi: 10.1038/s41558-018-0091-3

CrossRef Full Text | Google Scholar

Sathaye, J., Bouille, D., Biswas, D., Crabbe, P., Geng, L., Hall, D., et al. (2001). “Barriers, opportunities, and market potential of technologies and practices,” in Climate Change 2001: Mitigation. Contribution of Working Group III to the Third Assessment Report of the Intergovernmental Panel on Climate Change, eds B. Metz, O. Davidson, R. Swart, and J. Pan (Cambridge, UK; New York, NY: Cambridge University Press), 346–398.

Google Scholar

Schwoon, M., and Tol, R. S. J. (2006). Optimal CO₂-abatement with socio-economic inertia and induced technological change. Energy J. 27, 25–59. doi: 10.5547/ISSN0195-6574-EJ-Vol27-No4-2

CrossRef Full Text | Google Scholar

Smith, P., Davis, S. J., Creutzig, F., Fuss, S., Minx, J., Gabrielle, B., et al. (2016). Biophysical and economic limits to negative CO₂ emissions. Nat. Clim. Change 6, 42–50. doi: 10.1038/nclimate2870

CrossRef Full Text | Google Scholar

Strefler, J., Amann, T., Bauer, N., Kriegler, E., and Hartmann, J. (2018). Potential and costs of carbon dioxide removal by enhanced weathering of rocks. Envrion. Res. Lett. 13, 034010. doi: 10.1088/1748-9326/aaa9c4

CrossRef Full Text | Google Scholar

Ulph and Ulph (1994). The optimal time path of a carbon tax. Oxf. Econ. Pap. 46, 857–868.

Google Scholar

Van Der Ploeg, F., and Withagen, C. (2014). Growth, renewables, and the optimal carbon tax. Int. Econ. Rev. 55, 283–311. doi: 10.1111/iere.12049

CrossRef Full Text | Google Scholar

Van Der Zwaan, B. C. C., Gerlagh, R., Klaassen, G., and Schrattenholzer, L. (2002). Endogenous technological change in climate change modelling. Energy Econ. 24, 1–19. doi: 10.1016/S0140-9883(01)00073-1

PubMed Abstract | CrossRef Full Text | Google Scholar

van Vuuren, D. P. (2006). Energy Systems and Climate Policy - Long-Term Scenarios for an Uncertain Future. Dissertation, Department of Science, Technology and Society, Faculty of Science, Utrecht University. Available online at: http://dspace.library.uu.nl/handle/1874/21449

Google Scholar

Van Vuuren, D. P., Hof, A. F., Van Sluisveld, M. A. E., and Riahi, K. (2017). Open discussion of negative emissions is urgently needed. Nat. Energy 2, 902–904. doi: 10.1038/s41560-017-0055-2

CrossRef Full Text | Google Scholar

van Vuuren, D. P., Stehfest, E., den Elzen, M. G. J., Kram, T., van Vliet, J., Deetman, S., et al. (2011). RCP2.6: exploring the possibility to keep global mean temperature increase below 2°C. Clim. Change 109, 95–116. doi: 10.1007/s10584-011-0152-3

CrossRef Full Text | Google Scholar

Van Vuuren, D. P., Stehfest, E., Gernaat, D. E. H. J., Van Den Berg, M., Bijl, D. L., De Boer, H. S., et al. (2018). Alternative pathways to the 1.5 °C target reduce the need for negative emission technologies. Nat. Clim. Change 8, 391–397. doi: 10.1038/s41558-018-0119-8

CrossRef Full Text | Google Scholar

Wächter, A., and Biegler, L. T. (2006). On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Progr. 106, 25–57. doi: 10.1007/s10107-004-0559-y

CrossRef Full Text | Google Scholar

Wigley, T. M. L., Richels, R., and Edmonds, J. A. (1996). Economic and environmental choices in the stabilisation of CO₂ concentrations. Nature 379, 240–243. doi: 10.1038/379240a0

CrossRef Full Text | Google Scholar

World Bank (2021). State and Trends of Carbon Pricing. License: CC BY 3.0. Washington, DC: IGO. Available online at: https://openknowledge.worldbank.org/handle/10986/35620

Google Scholar