Sensitivity Analysis of Geomechanical Constraints in CO2 Storage to Screen Potential Sites in Deep Saline Aquifers

In order to tackle the exponential rise in global CO₂ emissions, the Intergovernmental Panel on Climate Change (IPCC) proposed a carbon budget of 2,900 Gt to limit the rise in global temperature levels to 2°C above the pre-industrial level. Apart from curbing our emissions, carbon sequestration can play a significant role in meeting these ambitious goals. More than 500 Gt of CO₂ will need to be stored underground by the end of this century to make a meaningful impact. Global capacity for CO₂ storage far exceeds this requirement, the majority of which resides in unexplored deep aquifers. To identify potential storage sites and quantify their storage capacities, prospective aquifers or reservoirs need to be screened based on properties that affect the retention of CO₂ in porous rocks. Apart from the total volume of a reservoir, the storage potential is largely constrained by an increase in pore pressure during the early years of injection and by migration of the CO₂ plume in the long term. The reservoir properties affect both the pressure buildup and the plume front below the caprock. However, not many studies have quantified these effects. The current analysis computes the effect of rock properties (porosity, permeability, permeability anisotropy, pore compressibility, and formation water salinity) and injection rate on both these parameters by simulating CO₂ injection at the bottom of a 2D mesh grid with hydrostatic boundary conditions. The study found that the most significant property in the sensitivity analysis was permeability. Porosity too affected the CO₂ plume migration substantially, with higher porosities considerably delaying horizontal and vertical migration. Injection rate impacted both the pressure rise and plume migration consistently. Thus, in screening potential storage sites, we can infer that permeability is the dominant criterion when the pore pressure is closer to the minimum principal stress in the rocks, due to which injection rate needs to be managed with greater caution. Porosity is more significant when the lateral extents of the reservoir limit the storage potential.

Introduction

Anthropogenic carbon dioxide levels in the atmosphere have been rising continuously at an alarming rate for the past few decades. We have already seen an increase of more than 1°C in the global average temperature ever since the industrial age started more than a century ago. In order to limit the global temperature rise to 2°C above pre-industrial levels, the Intergovernmental Panel on Climate Change (IPCC) proposed a carbon budget of 2,900 Gt (Metz et al., 2005; IPCC, 2013), providing an upper bound on the net global CO₂ emissions. Based on current levels of anthropogenic CO₂ emissions, only 500 Gt of the carbon budget is left for crossing the temperature threshold (Le Quéré et al., 2018; IPCC, 2021). According to Wei et al. (2021), large-scale carbon capture and storage can significantly reduce our CO₂ emissions and is indispensable for limiting global warming to below 2°C. An estimated 510 Gt of CO₂ will be needed to be stored in the ground worldwide by 2100 (Luderer et al., 2018) for the technology to make a meaningful impact on reversing climate change. However, currently, only 300 Mt (~0.006%) has been stored worldwide, with a capacity of around 40 Mt/yr (Global CCS Institute, 2018, 2020; Loria and Bright, 2021). In order to fill the large gap between requirement and current capacity, new sites need to be located for long-term CO₂ storage. Additionally, reservoir responses under different conditions must be studied in detail to select and evaluate suitable formations.

Deep saline aquifers represent large storage potential for carbon dioxide. Kearns et al. (2017) estimate the global capacity at approximately between 8,000 Gt and 55,000 Gt. Saline formations usually run quite deep, are unused, and contain non-potable water reserves; therefore, they are perfect for storing CO₂ safely without affecting near-surface groundwater. The biggest limitation in the utilization of such saline formations is the lack of in-depth geological understanding about them because they hold no economic value for exploitation and are largely unexplored territories. Fortunately, due to their similarity with oil and gas fields, the technology used for exploring and exploiting hydrocarbon resources can be easily adapted for such formations (Shukla et al., 2010). However, a lot of resources still need to be devoted to the accurate mapping of the storage capacities that are present in these reservoirs. Despite the constraints, large storage projects have been undertaken worldwide: more than 24 and 6.5 Mt of CO₂ have been stored in the Sleipner and Snøhvit projects in the North Sea, respectively (Furre et al., 2017; Ringrose, 2020; Ringrose and Sæther, 2020), 4.7 Mt in the Cranfield project (NETL, 2017), 5 Mt in the Quest project in Alberta since 2015, more than 2 Mt in the Illinois Industrial CCS project in the USA, 1 Mt in the Gorgon carbon dioxide injection facility in Western Australia (Orr, 2018; Global CCS Institute, 2020), 100 Kt in Aquistore project in Canada (White et al., 2017), and 3.8 Mt of CO₂ was injected in In Salah in Algeria between 2004 and 2013 (Bissell et al., 2011; Rutqvist, 2012; Verdon et al., 2015).

Apart from saline formations, depleted oil and gas fields have also been extensively used for CO₂ storage in various projects worldwide due to the benefit of existing infrastructure and in-depth subsurface knowledge (Bachu, 2016). Close to 40 Mt of CO₂ has been utilized in the Weyburn-Midale field for enhanced oil recovery (EOR) (Brown et al., 2017; Global CCS Institute, 2019), and the Petrobras Santos Basin CCS facility has stored more than 14 Mt of CO₂ in the subsurface (Eide et al., 2019; Global CCS Institute, 2020). However, the enormous global storage potential of deep saline formations makes them a more promising prospect for future CO₂ storage. They are also generally superior in thickness and have a much larger areal cover than hydrocarbon reservoirs, which are often a subset of these formations. Subsequently, there is also a higher probability of finding CO₂ sources closer to potential saline formation storage sites, leading to reduced transportation costs (NETL, 2017).

Carbon dioxide storage essentially involves injecting CO₂ at high pressures into porous formations that are conducive for long-term storage over periods of the order 10⁴ years. The CO₂ is compressed before injecting such that it forms a supercritical fluid. CO₂ is a gas at atmospheric conditions, but when it encounters pressure above 7.39 MPa, and temperature beyond 31.1°C, also known as its critical point, it becomes a supercritical fluid (Doughty and Pruess, 2004). It then displays characteristics of both liquids and gases and becomes conducive for storage in the subsurface. Its density becomes comparable to that of liquids allowing more CO₂ to be stored in the limited pore spaces of the rocks, while its viscosity remains similar to that of gases, permitting it to flow easily through rocks (Metz et al., 2005). Typical reservoirs usually lie at depths >1 km, are 10–500 m in thickness, and can stretch several hundred kilometers laterally (Szulczewski, 2013). These reservoir depths allow the injected CO₂ to remain in a supercritical state. In this state, it is lighter (~700 kg/m³) than brine, oil, or other fluids that might be present in situ, which push it to the top of the reservoir because of buoyancy forces. Most reservoirs consist of cemented sediments overlain by a low-permeability layer known as seal or caprock. The CO₂ stops rising until it encounters the caprock, which helps in trapping it underground. This mechanism of storage is known as structural or stratigraphic trapping, and is the dominant storage mechanism in the initial stage of injection (IEAGHG, 2009). Another form of trapping is residual gas trapping, where CO₂ gets trapped in the pores of the rocks due to surface tension. Solubility or dissolution trapping becomes the dominant mechanism in the long term when the migration of CO₂ slows down, and CO₂ gets dissolved in the formation brine through diffusion, convection, and dispersion. In the longer term (~10³ years), mineral trapping starts playing a major role where CO₂ precipitates in the form of carbonates due to geochemical interaction with the formation fluids and rock matrix (De Silva and Ranjith, 2012).

Typically the CO₂ trapping after injection follows the above trend. However, the reservoir conditions and rock properties can affect the dominant storage mechanism, and consequentially the storage effectiveness. The suitability of the reservoir depends on a multitude of factors: the depth of the reservoir; the pressure gradient; its state of stress and faulting; reservoir and seal integrity; the salinity of the reservoir fluids; and most significantly, the total storage capacity based on the porosity and the lateral and vertical extents of the formation (Rodosta et al., 2011; Bachu, 2016; NETL, 2017). These factors chiefly deal with the initial reservoir conditions, and they provide screening criteria for a preliminary analysis. The next step involves comprehension of the specific reservoir response to fluid injection in the short and long terms and the mitigation of the challenges that are introduced by CO₂ sequestration.

A 99% retention rate of stored CO₂ after 100 years is generally considered a requirement for effective CO₂ storage (Hepple and Benson, 2005; Metz et al., 2005; Alcalde et al., 2018). Until now, the longest-running CO₂ storage project has been operating at the Sleipner field in Norway since 1996 and has injected more than 24 Mt of CO₂ underground (Ringrose and Sæther, 2020). Unlike CO₂ injection for EOR, where injection in intervals or huff-n-puff method leads to better recovery and economic benefit, CO₂ storage projects usually employ constant injection rates through multiple wells depending on the reservoir permeability and optimum injectivity (Michael et al., 2010). Continuous CO₂ injection at high rates (~1 Mt/yr) for long periods (>10 years), as is typical of commercial CO₂ storage projects (Michael et al., 2010; Furre et al., 2017; Greenberg et al., 2017; Global CCS Institute, 2020), can substantially increase pore pressures near the injection site, which can permeate throughout the reservoir. This brings geomechanical issues to the forefront (Zoback and Gorelick, 2012). Changes in the subsurface stress regime are dependent on the net volume of the fluid injected, the injection and extraction rates, the total storage capacity, and the ease of fluid flow in the reservoir. Possible geomechanical concerns include the activation of pre-existing faults, which can act as preferential leakage pathways for CO₂ to escape to shallow potable aquifers or, in certain conditions, even to the surface (Ferronato et al., 2010; Heidari and Hassanzadeh, 2018). There is a greater risk of maximum magnitude events in CO₂ storage projects that involve a large volume of fluids being injected over long periods (Ellsworth, 2013; Pan et al., 2016). The potential magnitude of a seismic event correlates strongly with the fault rupture area, which, in turn, relates to the magnitude of the pore pressure change and the rock volume in which it exists (Verdon, 2011). The induced seismicity can severely affect reservoir integrity and cause conditions that could lead to caprock failure along with a risk of the generation of new faults (Shukla et al., 2010; Vilarrasa et al., 2019). Thus, the practical storage capacity of the reservoir is not only limited by the empty volume in the rocks but also by the maximum sustainable pressure buildup. Szulczewski et al. (2011) showed that the pressure constraint is the principal limiting factor in CO₂ storage in the short term, while space-limited capacity dominates in the long term.

The initial pressure buildup in the reservoir depends mainly on the rock properties such as porosity, permeability, permeability anisotropy, pore compressibility, and the like, and the planned injection rate (Sarkarfarshi et al., 2014). These parameters are reservoir-dependent and cannot be controlled, but they can aid in the evaluating of reservoirs for CO₂ storage (Zhou et al., 2008). Once the site is selected, formulating an optimal CO₂ injection rate is essential to ensure that the pressure rise does not create unwanted geomechanical complications while optimizing for maximum long-term storage (Yang et al., 2015).

Sensitivity analyses to study the geomechanical effects of CO₂ sequestration have been conducted only in a limited number of studies in the past. Kopp et al. (2007) used the extended Morris method (Morris, 1991; Campolongo et al., 2005) in a sensitivity analysis to study the effects of various parameters on CO₂ migration, free-phase CO₂, the ratio of free-phase CO₂ and dissolved CO₂, and the maximum pressure below the caprock in a dipping aquifer. They qualitatively ranked parameters and found that the model results were most sensitive to the permeability, reservoir volume, injection interval, and geothermal gradient. In contrast, the CO₂ injection temperature, porosity, sorting factor (the exponent in the Brooks and Corey relationship) (Brooks and Corey, 1964), and brine salinity were the least sensitive parameters. The study covered a comprehensive range of variables that affect CO₂ storage; however, it avoided quantifying parameter-specific effects. Deng et al. (2012) studied the effects of porosity and permeability distributions on the total storage capacity of a section of Rock Springs Uplift, Wyoming, by constraining the injection pressure to 75% of the lithostatic load. They also found that the evolution of the CO₂ plume depended not only on buoyant forces and injection rates but also on pressure gradients in the reservoir. Thus, the two primary considerations in estimating the storage capacity of a site—CO₂ migration and pressure buildup in the reservoir—are implicitly linked.

This study intends to compare and contrast the effects of CO₂ storage constraints with injection rate in order to identify pivotal parameters in the large-scale screening of reservoirs. It also intends to enable the planning of injection scenarios that are sustainable for the project as well as the environment. In order to develop valid estimates of CO₂ storage capacities and to assess potential sites, major decision factors must be identified and screening workflows must be designed for quick assessment of viable reservoirs. This study aims to aid in such scenarios to identify suitable CO₂ storage sites at a regional and global scale.

Methodology

At the reservoir scale, numerical modeling provides (with a high degree of realism) a suitable pathway to predict and visualize the processes that occur in the subsurface. It helps us to understand how fluids interact with underground rocks and gives us insights into how small changes in our base parameters can bring about significantly different outcomes. Every numerical model has certain assumptions built into it, and so, the level of accuracy varies with each study. The ultimate goal is to minimize the assumptions in order to make the study as close to the real-world scenario as possible. However, the innumerable factors involved make it physically impossible to model each particle. Therefore, physicists rely on assumptions to make the studies practical while also providing a realistic picture of the subsurface, which yields enough useful information on which to base our decisions.

Reservoir simulation provides an effective way to study the effects of constraints and to plan injection parameters. Modeling the flow and retention of carbon dioxide is beset by uncertainties. These relate to the physical structure of the reservoirs, such as permeability and stratal geometries (Cappa and Rutqvist, 2012); the problems that are inherent in modeling multiphase flow (Settari and Mourits, 1998); the behavior of sealing strata that is in contact with CO₂-rich fluids (Vilarrasa et al., 2013); the possibility of reactions between CO₂ and minerals in the reservoir (Johnson et al., 2004); and the rate of the progressive dissolution of CO₂ in the saline fluid that fills the reservoirs (Huppert and Neufeld, 2013). These uncertainties must be accommodated in the model to accurately predict the interaction between fluids and the reservoir and to study various parameters' effects.

Governing Equations

To model the flow of CO₂, the TOUGH code (Moridis and Freeman, 2014) has been employed, which has been extensively tested and utilized in studying CO₂ injection for storage and EOR processes (Rutqvist, 2011; De Lucia et al., 2016; Rinaldi et al., 2017).

The mass and energy balance equations that are used in the modeling are of the form:

$\begin{array}{ll}\frac{d}{dt}{\displaystyle {\int }_{V_n}{M}^{\kappa }}dV={\displaystyle {\int }_{{\Gamma }_n}{F}^{\kappa }·ndA+}{\displaystyle {\int }_{V_n}{q}^{\kappa }dV}& (1)\end{array}$

where V, V_n represent the total volume and volume of the subdomain n, M^κ is the mass accumulation term of the component κ, A represents the surface area and Γ_n is the surface area of the subdomain n, F^κ is the Darcy flux vector of component κ, n is the inward unit normal vector, q^κ is the source/sink term of component κ, and t is time.

The term for mass accumulation, M^k is defined as

$\begin{array}{l}{M}^k={{\displaystyle \sum }}_{\beta \equiv A,G,H}\varphi S_{\beta }{\rho }_{\beta }{X^{\kappa }}_{\beta }+{\delta }_{\Psi }^i(1-\varphi ){\rho }_R{\text{Ψ}}^i,\\ \kappa \equiv w,g^i,s;i=1,...,N_G& (2)\end{array}$

where φ represents porosity, ρ_β is the density of phase β, S_β is the saturation of phase β, ${\text{X}}_{\beta }^{\kappa }$ is the mass fraction of component κ in phase β, Ψⁱ represents the mass of sorbed component gⁱ per unit mass of rock, and ${\delta }_{\text{Ψ}}^i$ is equal to 1 only in gas-sorbing species onto a given medium, and otherwise zero. The components κ refer to w (water), gⁱ (various gaseous components making up the gas mixture), and s (salt). The absence or presence of salt dictates the possible number of phases, β: A (aqueous), G (gaseous), and H (solid: precipitated halite). N_G refers to the total number of gaseous components.

The water, gas mixture, and the halite contribute to the mass fluxes, given by the equation:

$\begin{array}{ll}{F}^{\kappa }={{\displaystyle \sum }}_{\beta \equiv A,G}{F}_{\beta }^{\kappa },\kappa \equiv w,g^{i}i=1,\dots ,N_g& (3)\end{array}$

The solid phase is not involved in the fluid fluxes because it is immobile.

The mass flux, F^k, of a component includes contributions from all mobile phases in the model and can be described by several equations, the most common of which is the Darcy's law:

$\begin{array}{ll}{F}_{\beta }=-k\frac{k_{r\beta }{\rho }_{\beta }}{{\mu }_{\beta }}\left({\nabla P}_{\beta }-{\rho }_{\beta }g\right)& (4)\end{array}$

Where k represents the intrinsic permeability, k_rβ, μ_β, and P_β represent the relative permeability, the viscosity, and the pressure of the β phase, respectively, and g is the gravitational acceleration vector.

The injection of fluids is described using the source term, which allows for multiple phases, including contributions from multiple phases:

$\begin{array}{ll}{q}^{\kappa }={{\displaystyle \sum }}_{\beta \equiv A,G}{X}_{\beta }^{\kappa }{q}_{\beta },\kappa \equiv w,g^i,s;i=1,\dots ,N_g& (5)\end{array}$

Where q_β is the injection rate of the phase β.

The continuum equation (Equation 1) is discretized in space using the integral finite difference method (IFD) in the following way:

$\begin{array}{ll}{\displaystyle {\int }_{V_n}}MdV={V_{n}M}_n& (6)\end{array}$

Where M is volume-normalized quantity, and M_n is the average value of M over the volume V_n. The surface integrals are discretized using a sum of averages over surface sections A_nm:

$\begin{array}{ll}{\displaystyle {\int }_{{\Gamma }_n}{F}^{\kappa }·nd\Gamma }={\displaystyle {{\displaystyle \sum }}_m{A}_{nm}}{F}_{nm}& (7)\end{array}$

where F_nm is the inward normal component of F over the surface segment A_nm between volume elements Vn and Vm.

Substituting the discretizations into Equation (1), we get a first-order differential equation,

$\begin{array}{ll}\frac{d{M}_n^k}{dt}=\frac{1}{V_n}{\displaystyle \sum }{A}_{nm}{F}_{nm}^k+q_n^k& (8)\end{array}$

The time discretization of the differential equation by using the Newton-Raphson iteration method results in the following set of coupled non-linear, algebraic equations

$\begin{array}{ll}{R}_n^{\kappa ,k+1}=M_n^{\kappa ,k+1}-M_n^{\kappa ,k}-\frac{\Delta t}{V_n}\left({{\displaystyle \sum }}_m{A}_{nm}{F}_{nm}^{\kappa ,k+1}+V_n{q}_n^{\kappa ,k+1}\right)=0& (9)\end{array}$

For each volume element (grid block), Vn, there are “m” equations, so that a system that is discretized into “n” grid blocks, representing a total of “m × n” coupled non-linear equations. The continuum equations are discretized in space and are solved in every subdomain using the integral finite difference method.

Assumptions

The current modeling study is carried out in isothermal conditions at 60°C in the storage formation. The temperature was calculated by assuming a surface temperature of 10°C and a geothermal gradient of 33°C/km. Dirichlet boundary conditions are chosen at the edges. The fixed-state conditions at the boundaries essentially make it an infinite-acting reservoir that simulates large laterally extended saline aquifers (Vilarrasa et al., 2013). The flow at the boundaries allows for greater relaxation of the pressure that is induced by a constant CO₂ influx at the bottom center of the reservoir. The code employed assumes a linear porosity-permeability relation with pressure, and the rock compressibility is assumed to be zero in the base case.

Model Setup

A 2D numerical simulation of CO₂ injection at a constant rate was conducted with a Dirichlet boundary condition of no flow at the top and bottom of the reservoir and constant pressure at the lateral boundaries, far from the injection site. The model was validated by comparing the CO₂ plume migration with values obtained by Vilarrasa et al. (2013). The pressure perturbation was studied in order to understand the geomechanical effects of fluid injection.

The size of the reservoir is 15 km by 50 m for the x (sub-horizontal) and z (sub-vertical) directions, respectively. The cell dimension in the x-direction is 25 m, while that in the y- and z-direction is 5 m. The y-direction is not discretized, essentially making it a 2D simulation. The average depth of the reservoir is 1.5 km, and its initial temperature and pressure conditions are 60°C and 14.7 MPa. Water pressure is assumed hydrostatic, and partial pressure of CO₂ is assumed to be 0.01 MPa, which leads to an initial concentration of dissolved CO₂ at 2.44 × 10⁻⁵ kg/kg of water (Vilarrasa et al., 2016). The simulation is carried out in isothermal conditions. A well injects CO₂ at the bottom of the reservoir, and the rate of injection for the base case is 0.05 kg/s. Extrapolating the injection rate for a horizontal well of 2 km, the annual injection rate would equal 0.63 Mt/yr. This value is close to the real injection rates (0.5–1 Mt/yr) at the In Salah CO₂ storage (Rutqvist et al., 2010). In the base case, the injection is carried out for a year. The parameters used in the base case are listed in Table 1.

TABLE 1

Table 1. List of input parameters used in the base case simulation.

Mesh Convergence

A mesh convergence study was undertaken to select appropriate discretization of the reservoir in the horizontal (x) and vertical (z) directions. The primary objective was to optimize between accuracy in evaluating the pressure rise in the model and the computational times. Horizontal discretization was tested with 100, 200, 300, 400, 500, 600, 750, and 1,000 uniformly-sized cells. As can be seen in Figure 1A, there was no appreciable difference in the pressure buildup for more than 600 cells in the horizontal direction. Correspondingly, in the vertical direction, discretization of 5, 10, 15, 20, and 25 cells was analyzed, and a sampling of 10 cells was chosen for the study because higher discretization did not provide greater precision in the results, as shown in Figure 1B.

FIGURE 1

Figure 1. Mesh convergence for (A) horizontal and (B) vertical discretization.

Sensitivity Analysis

Sensitivity analysis is an essential tool for validation, what-if analysis, and optimization of complex simulation models. The purpose of the current analysis is to evaluate the individual effect of the variation of geomechanical parameters on the long-term stability of the reservoir under CO₂ injection. Two critical factors have been identified to characterize the stability and the CO₂ storage capacity: pressure buildup and CO₂ migration (Szulczewski et al., 2011). The rise in pore pressure in the reservoir directly upsets the natural stress regime and increases the risk of fracturing and faulting of the reservoir and the caprock; critically stressed faults are more sensitive to the changes (Mazzoldi et al., 2012). CO₂ also needs to be confined to the reservoir extents to minimize the risk of leakage through gaps in the form of faults in the caprock or abandoned wells (Heidari and Hassanzadeh, 2018). Consequently, reduced CO₂ migration would enhance confidence in the long-term stability of the storage project. Therefore, studying the reservoir response to these factors should enable a reasonable evaluation of the reservoir for CO₂ storage.

Five critical rock properties (porosity, permeability, permeability anisotropy, pore compressibility, and formation water salinity) along with CO₂ injection rate are selected as the parameters to be investigated in the sensitivity analysis. The Morris one-factor-at-a-time global sensitivity analysis method (Morris, 1991) is chosen for the analysis. It allows the isolating of the influence of parameters on pressure changes by varying a single parameter while keeping the rest of the model as is. Nevertheless, more than one factor may be interlinked. Therefore, to maintain the result as the effect of a single parameter, suitable adjustments have been made after careful consideration, which are detailed when discussing the respective parameters. The range of values for the selected parameters is detailed in Table 2. The results of the simulation for the base case are presented in Figure 2. Figure 2A shows the evolution of CO₂ plume in the reservoir at the end of 3, 6, 9, and 12 months. Figure 2B represents the pressure buildup in the reservoir at the end of 1 year.

TABLE 2

Table 2. Range of parameters used for sensitivity analysis.

FIGURE 2

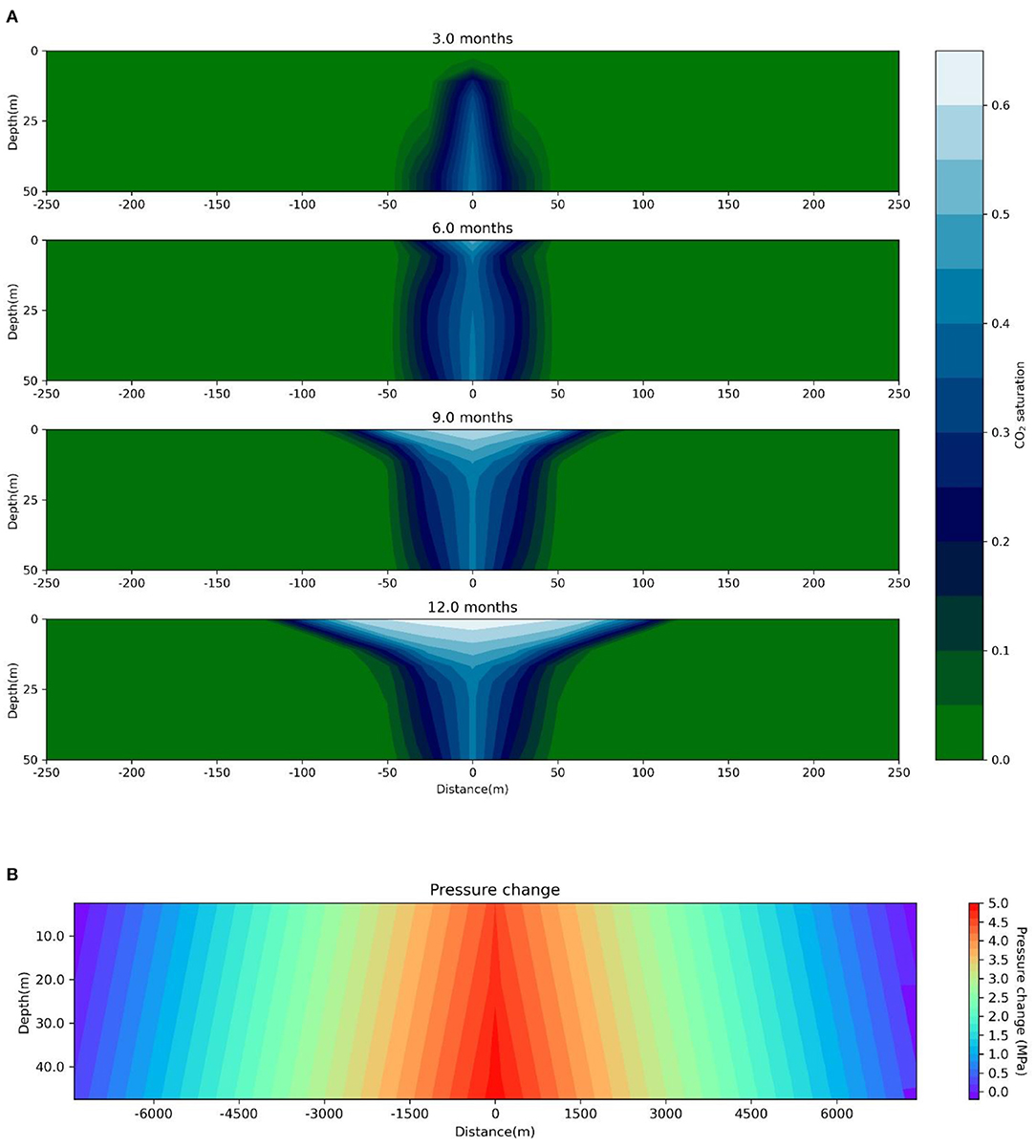
Figure 2. (A) CO₂ plume evolution in the reservoir at the end of 3, 6, 9, and 12 months. (B) Pressure evolution at the end of 1 year of injection (base case).

Results

Porosity

Porosity is one of the major parameters that govern the poromechanical behavior of the reservoir during CO₂ injection. It determines the amount of total space that is available for CO₂ storage within the confines of a reservoir. Consequently, it also affects the total pressure buildup, which influences the propensity for rock failure following Biot's effective stress law (Biot, 1941). In this study, the values of porosity ranged from 10 to 35% (in steps of 5%); the base value was 23% (Förster et al., 2006). The selection of porosity values is based on the wide span of values observed in different CO₂ storage sites worldwide (Michael et al., 2010; Eiken et al., 2011). Figure 3A shows the variation of pressure with time due to changes in the porosity at the top of the reservoir (below the caprock) directly above the injection point. A negative linear trend was observed between the pressure rise and the porosity at the end of 1 year of injection, as is shown in Figure 3B. Although the pressure change declines almost linearly with an increase in porosity—as expected with the increase in pore space, which allows more CO₂ to be injected to reach the same pressure—the pressure difference between the minimum and maximum porosity case is less than anticipated. A 250% increase in porosity from 10 to 35% leads to a difference of only about 8% in pressure change.

FIGURE 3

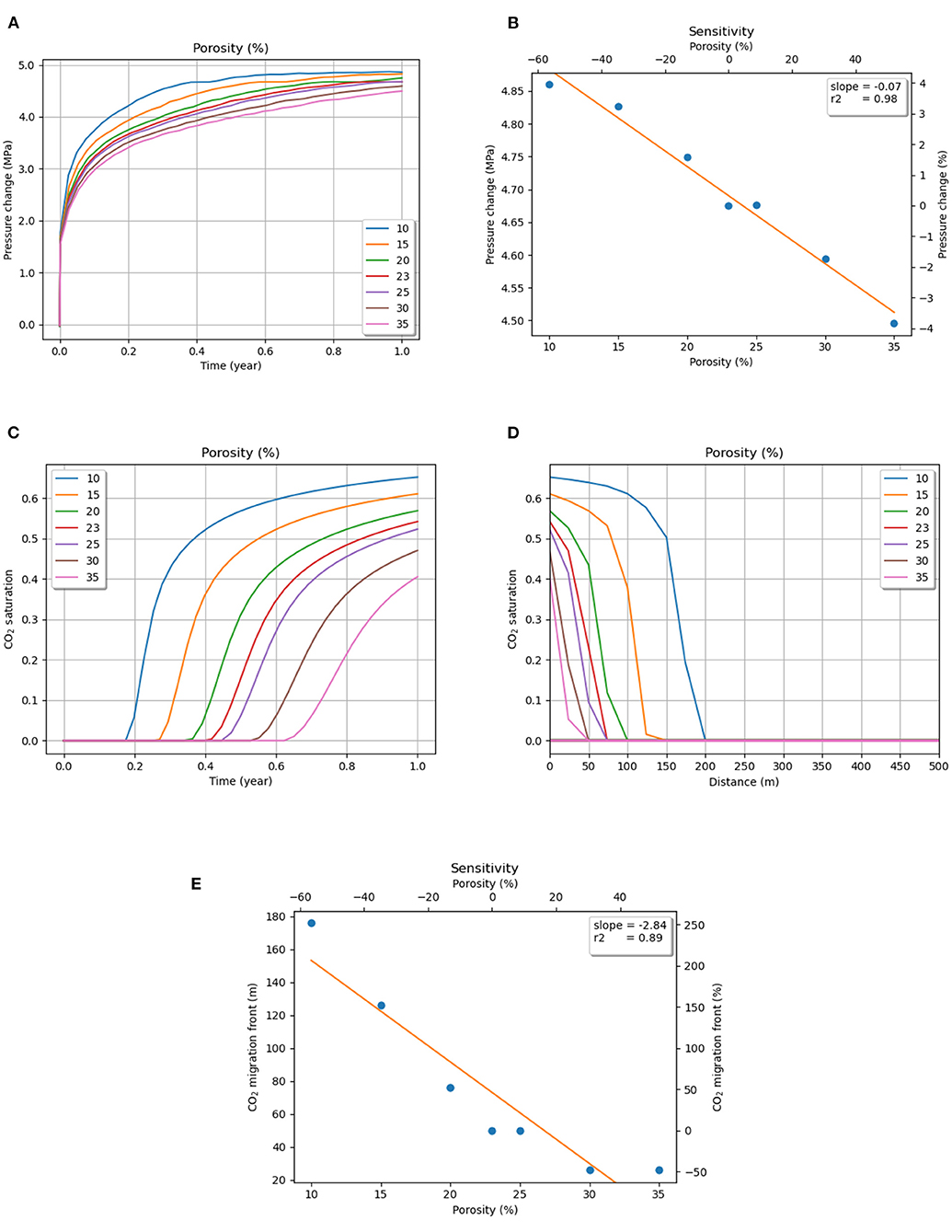
Figure 3. (A) Pressure evolution with injection time (at the top of the reservoir), and (B) sensitivity of pressure to porosity. CO₂ saturation change (at the top of the reservoir) with (C) injection time and (D) distance from injection point for different porosities. (E) Sensitivity of the CO₂ migration front to porosities.

On the other hand, porosity has a significant effect on the CO₂ migration front as well as on the maximum CO₂ saturation at the top of the reservoir. A lower porosity leads to an early increase in the CO₂ saturation below the caprock; this causes a rapid horizontal spread of CO₂. Inversely, the extra amount of pore space that is available with higher porosities extends the travel time of CO₂ to the caprock and delays its horizontal migration, as shown in Figures 3C,D. Figure 3E shows an increase in porosity (from 10 to 30%) by three times, which reduces the migration front by seven times (175–25 m). We infer that porosity affects the migration of the CO₂ wavefront substantially more than the pressure increase and that the latter might be more sensitive to other parameters.

Permeability

Permeability affects the reservoir's ability to dissipate pore pressure through fluid flow from one connected region to another. Any sudden local changes in the pore pressure, such as CO₂ injection, would disrupt the equilibrium of the reservoir; permeability acts as the limiting factor in determining how quickly the equilibrium is restored. Permeability can vary significantly in different reservoirs based on the rock type. Tight sandstones may have permeabilities as low as 40 mD (Vilarrasa et al., 2016), whereas good, oil-producing reservoirs have been shown to have permeabilities of more than 1,000 mD (Ganguli et al., 2016). Thus, the sensitivity analysis for permeability was carried out for the range of 40–1,000 mD in this study, with 100 mD being the base permeability.

As evidenced from Figure 4A, low permeability, acting as a barrier to fluid flow, causes a large increase in the local pressure, which permeates the reservoir. The pressure at the injection site is the highest, and it decreases linearly as we move away from it. In the sensitivity study, a logarithmic trend was observed between permeability values and pressure change (Figure 4B). A sharp decrease in pressure change at the top of the reservoir is observed in the lower range (40–200 mD) of permeability cases: pressure buildup decreases by a factor of four from more than 8 MPa to nearly 2 MPa by increasing the permeability from 40 to 200 mD. In the higher permeability range (200–1,000 mD), pressure buildup decreases nearly by a factor of five for a similar increase in permeability by five times from 200 to 1,000 mD. The observation implies that permeability plays a critical role in pressure perturbation throughout the wide range. To compare and rank permeability with other parameters, we chose to run our sensitivity analysis on the logarithm of the permeability, defining the modified parameter as log₁₀(k), where k represents permeability. Pressure shows relatively high sensitivity to our modified parameter with a slope of −2.47. As shown in Figure 4C, an overall difference of 70% in log₁₀(k) results in a difference of almost 200% in pressure rise. An interesting observation from Figure 4A is that in the case of permeabilities of 200 mD or more, the pressure increases non-linearly to a maximum value and then stabilizes at a value that is lower than or equal to it. In the cases of 150 mD and below, the pressure keeps on increasing at a rate that is dependent on the value of permeability: the lower the permeability, the higher the rate. Thus, it can be deduced that at a specific limiting permeability (in this case, 200 mD,) the reservoir is able to stabilize the influx of pressure through fluid injection, depending on the different reservoir conditions and injection parameters (assuming that the reservoir is large enough to be approximated as “infinite-acting”).

FIGURE 4

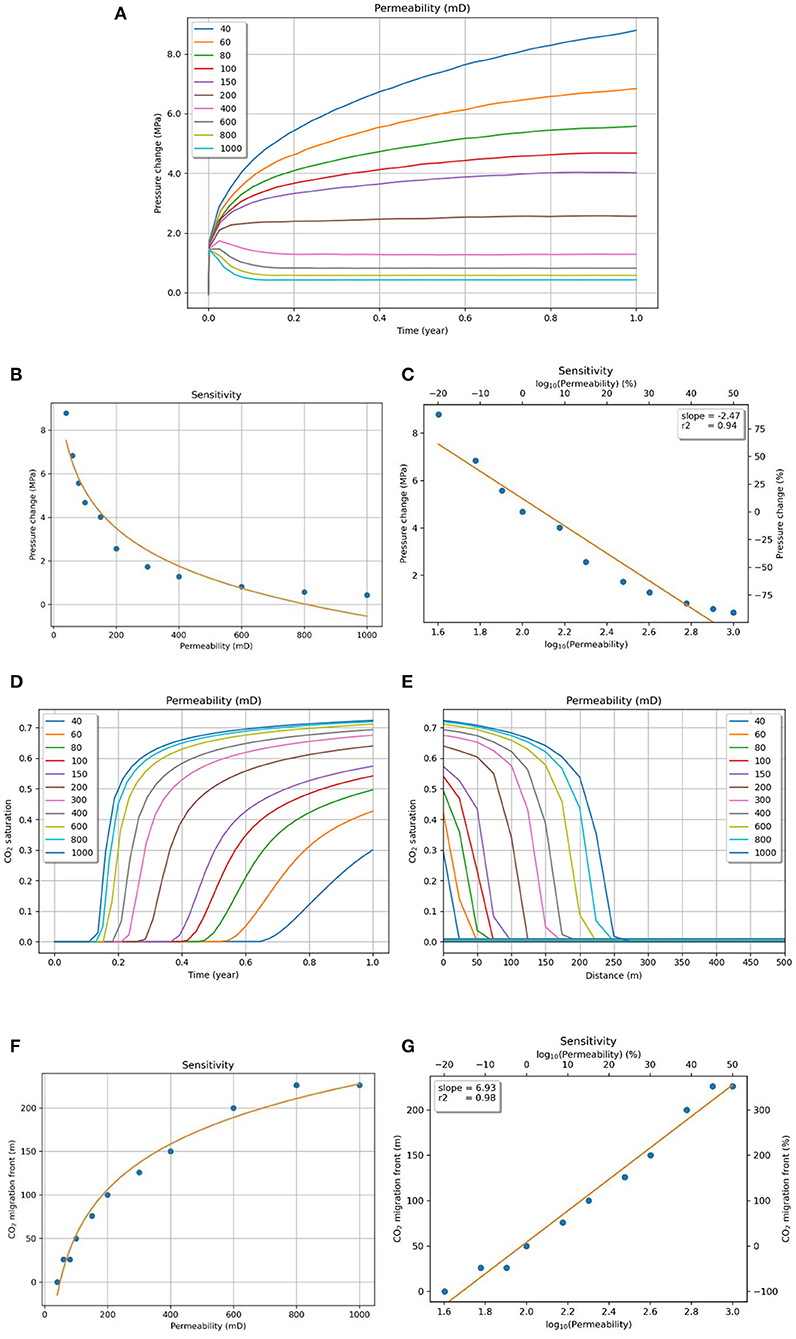
Figure 4. (A) Pressure evolution (at the top of the reservoir) with injection time for different permeabilities. Sensitivity of pressure to (B) permeability and (C) the modified parameter log₁₀(k). CO₂ saturation change at the top of the reservoir with (D) injection time and (E) distance from injection point for different permeabilities. Sensitivity of the CO₂ migration front to (F) permeability and (G) the modified parameter log₁₀(k).

Higher permeabilities allow CO₂ to travel at a faster rate to the top of the reservoir and subsequently migrate farther horizontally. Lower permeabilities are less sensitive to gravity override effects and show more horizontal migration in the lower half of the reservoir than near the caprock. The migration front displays a nearly 1:1 correlation with permeability in the lower range, but the curve flattens out with higher permeabilities (Figure 4F). The saturation changes at the top of the reservoir also show a similar trend at higher permeabilities, as shown in Figures 4D,E. This shows that the sensitivity plateaus at higher permeability values for saturation. Similar to pressure sensitivity, the values fit a logarithmic trend reasonably well. Thus, the modified parameter log₁₀(k) was used again for the analysis, and it displayed a substantially high sensitivity to CO₂ migration with a slope of almost 7 (Figure 4G). A 70% increase in log₁₀(k) from 1.6 (40 mD) to 3.0 (1,000 mD) led to a 400% increase in the CO₂ migration front in the reservoir.

Permeability Anisotropy

Permeability anisotropy is defined here as the ratio of vertical to horizontal permeability (k_v/k_h). Vertical permeability in sedimentary formations is often observed to be much less than horizontal permeability due to intermixing layers of shale and sand in the reservoir. Due to lower vertical permeability, CO₂ tends to migrate much more laterally from the injection point, and vertical migration in the reservoir is reduced (Zhao et al., 2010).

Here we have taken the minimum vertical permeability as one-hundredth (1 mD) of the base horizontal permeability (100 mD) and maximum as equal to the base permeability (Kopp et al., 2007). The sensitivity analysis was conducted for anisotropy values of 0.01, 0.05, 0.1, 0.5, and 1. As shown in Figure 5A, the change in vertical permeability does not affect the pressure buildup significantly. Lower values of permeability anisotropy are associated with lower pressure buildup; however, a decrease in vertical permeability by a factor of 100 only reduces the pressure change by 5% below the caprock (Figure 5B). Nevertheless, there was a clear logarithmic trend observed between permeability anisotropy and pressure change. In order to compare and rank the parameter with other parameters, we chose to run our sensitivity analysis on the logarithm of the permeability anisotropy, defining the modified parameter as log₁₀(k_v/k_h). As Figure 5C shows, the slope of the graph is quite low (0.02), making the parameter almost insignificant to pressure sensitivity.

FIGURE 5

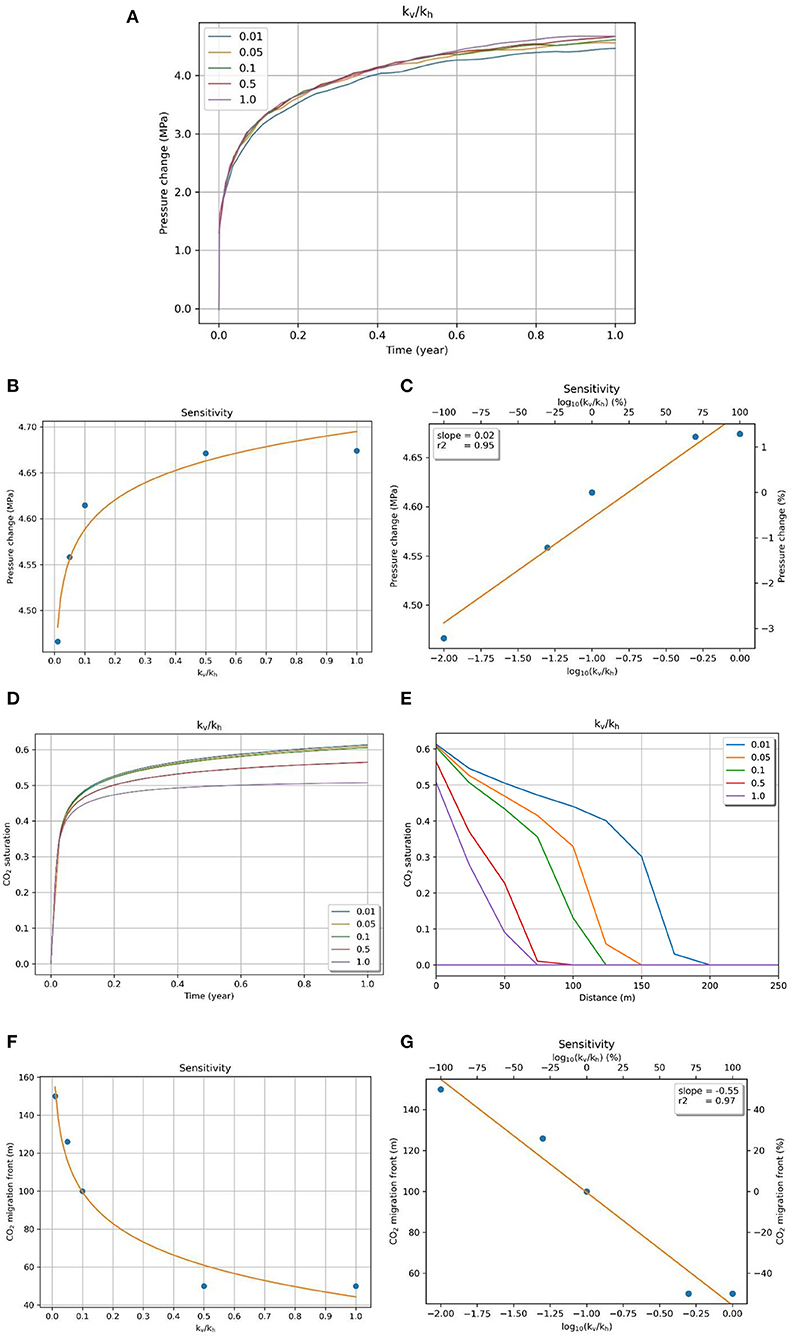
Figure 5. (A) Pressure evolution (at the top of the reservoir) with injection time for different permeabilities. Sensitivity of pressure to (B) permeability anisotropy (C) the modified parameter log₁₀(k_v/k_h). CO₂ saturation change (at the bottom of the reservoir) with (D) injection time and (E) distance from injection point for different permeability anisotropies. Sensitivity of the CO₂ migration front to (F) permeability anisotropy and (G) the modified parameter log₁₀(k_v/k_h).

Reduced vertical permeability delays the vertical migration of CO₂ considerably and promotes horizontal migration. In the lowest anisotropy case, the CO₂ could not even reach the caprock in the simulation time. Therefore, we selected the values of CO₂ saturation at the bottom of the reservoir for Figure 5. The CO₂ saturation increases rapidly for all the cases up to 0.4 (Figure 5D). It then flattens at different slopes for different anisotropy values—lower values leading to higher saturation. The CO₂ saturation decreases almost linearly with horizontal distance from the injection point for most cases, as shown in Figure 5E. A significant decrease in CO₂ plume front was observed with an increase in vertical permeability, forming a clear decreasing logarithmic trend (Figure 5F). Similar to sensitivity analysis for pressure change, we used the modified parameter log₁₀(k_v/k_h) for measuring sensitivity to the migration front. As indicated by Figure 5G, CO₂ migration was quite sensitive to the parameter, affecting it negatively. Overall, a 200% increase in log₁₀(k_v/k_h) led to a nearly 100% decrease in CO₂ migration front.

Compressibility

Pore compressibility defines the amount of deformation that the rock will undergo per unit change in pressure. Thus, it directly affects the rocks' mechanical properties such as porosity and permeability. Generally, sandstones show compressibility to the order of 10⁻¹⁰ Pa⁻¹ (Birkholzer et al., 2009). A sensitivity analysis was carried out for the range of 0 to 10⁻⁹ Pa⁻¹ in increments of 10⁻¹⁰ Pa⁻¹ in this study, based on a wide range of values for consolidated sandstones (Newman, 1973; Domenico and Schwartz, 1998; Hart, 2000). By default, the numerical code assumes the compressibility to be zero, so that is assumed the base case.

The results indicate that compressibility has a significantly negative linear effect on the pressure buildup in the reservoir (Figure 6B). An increase in compressibility provides much relief to the flow of fluid without affecting the porosity much. Overall, a 1,000% increase in compressibility from 1 to 10 (10⁻¹⁰) Pa⁻¹ causes the maximum pressure change to decrease by 30%. The results indicate that lower compressibility, or higher rigidity, leads to a substantial increase in the permeation of pressure through the rocks. Increased compressibility allows the rocks to compress in response to the higher pressure, which absorbs the impact of the increased volume of the fluid that is injected into the system. Figure 6A shows the pressure buildup with time for different injection rates.

FIGURE 6

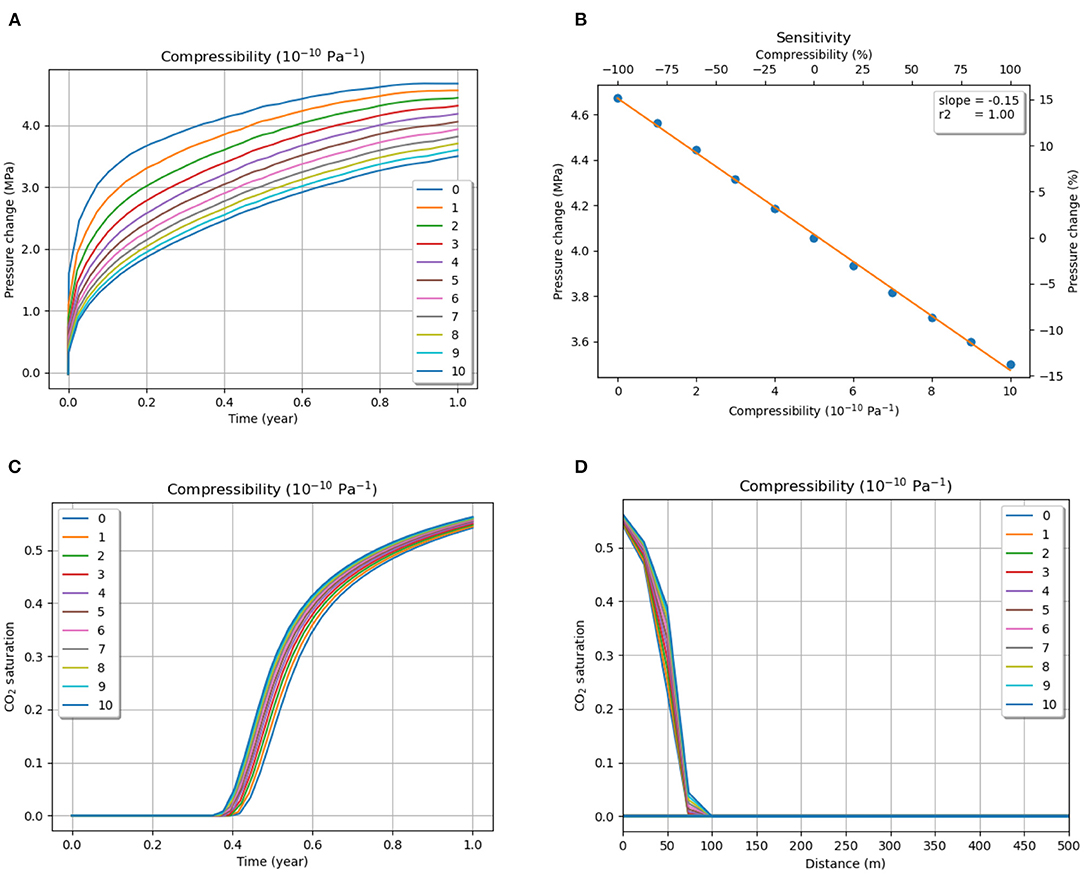
Figure 6. (A) Pressure evolution (at the top of the reservoir) with injection time for different values of compressibility and (B) Sensitivity of pressure change to compressibility. CO₂ saturation change (at the top of the reservoir) with (C) injection time and (D) distance from injection point for different values of compressibility.

It was observed that compressibility affected neither the horizontal migration of CO₂ significantly nor the vertical rise of CO₂ to the top of the reservoir. The result must be interpreted cautiously because the numerical code does not account for large mechanical property changes due to changes in compressibility. Thus, porosity and permeability are not significantly affected, leading to a very minor increase in plume migration due to the increase in compressibility. Figures 6C,D show the CO₂ saturation change with time and distance from the injection point in the reservoir.

Salinity

Salinity refers to the amount of salt mass dissolved per unit mass of brine in the reservoir. Higher salinity decreases the dissolution of CO₂ in the water, resulting in less effective solubility trapping (Zhao et al., 2010). This can lead to free phase CO₂ migrating to more considerable distances and might increase risks of leakage through fractures in the caprock far away from the injection point. In such a case, structural or stratigraphic trapping will play a higher role in the containment of CO₂ in the reservoir. In previous studies (Kopp et al., 2007), salinity has been shown to have a low effect on pressure and CO₂ migration. Nevertheless, we have added the parameter in our study for completeness.

US DOE defines the minimum cutoff of water salinity for saline aquifers as 10,000 mg/L (0.01 kg/kg) (CSLF, 2008). Usually, the salinity of typical reservoirs ranges from 0.05–0.3 kg/kg (Brennan, 2014). In our study, sensitivity analysis was carried out for the range of 0.05 to 0.25 kg/kg in increments of 0.05 kg/kg. The results show that salinity has a moderate positive linear effect on the pressure buildup in the reservoir (Figure 7B). An interesting observation is that the initial pressure buildup is lower in cases with higher salinity, but the rate of increase in pressure is higher. The pressure buildup from lower salinity flattens off, but higher salinity leads to a sustained increase in pressure for a more extended period (Figure 7A). Overall, a 250% increase in salinity from 0 to 0.25 kg/kg of water increases the pressure buildup by 30%.

FIGURE 7

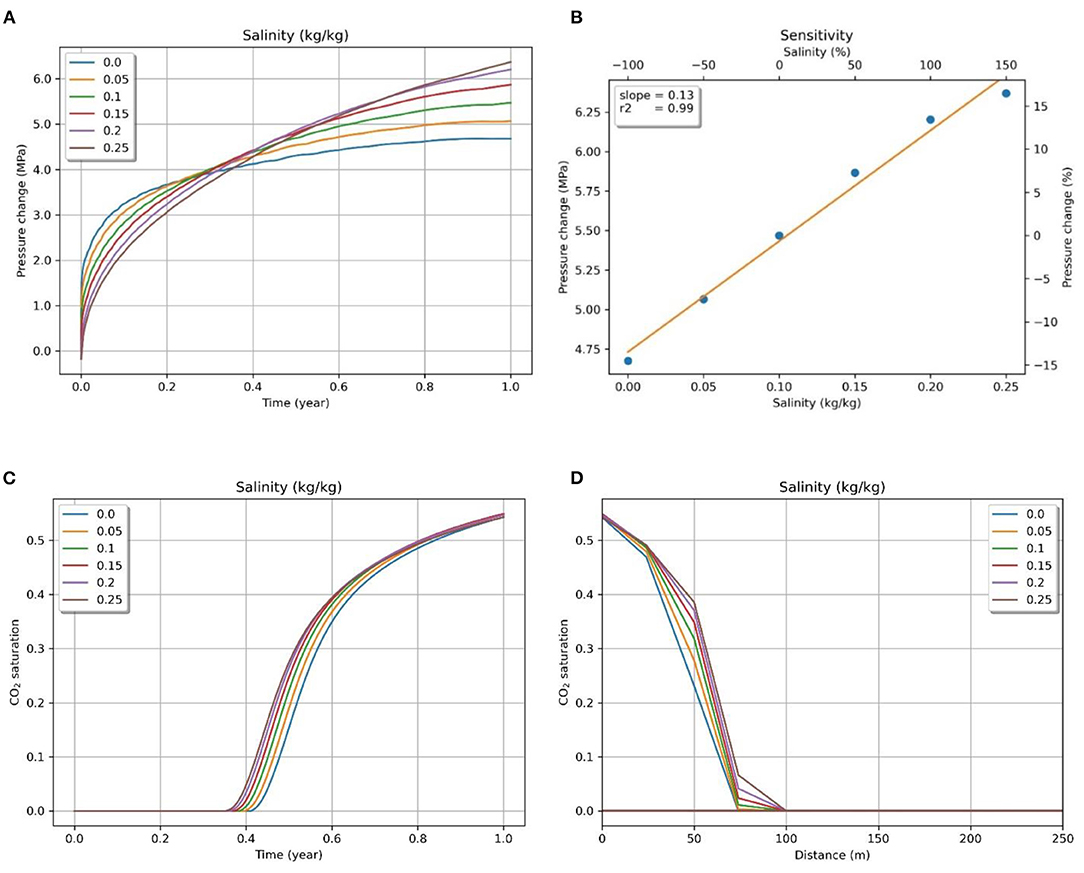
Figure 7. (A) Pressure evolution (at the top of the reservoir) with injection time for different values of salinity and (B) sensitivity of pressure change to salinity. CO₂ saturation change (at the top of the reservoir) with (C) injection time and (D) distance from injection point for different values of salinity.

In the case of CO₂ plume, contrary to expectation, salinity had an almost negligible effect on both the horizontal migration of CO₂ and the vertical rise of CO₂ to the top of the reservoir. We observed a slight difference in the time taken in each case for CO₂ to reach the top of the reservoir, but CO₂ saturation converged to nearly the same value for all of the cases (Figure 7C). Similarly, CO₂ saturation decreased in an identical manner for each of the salinity cases, causing very minor variations in the migration front (Figure 7D).

Injection Rate

Injection rate is the key parameter in planning CO₂ storage. The rate and amount of fluid that is injected affect the pressure increase in the reservoir locally as well as in the far-field. The base case for the rate of injection was set at 0.05 kg/s, and the parameter varied between 0.01 and 0.1 kg/s in steps of 0.01 kg/s. The relationship between injection rate and pressure is clearly a direct correlation: the increase in the rate of injection, and consequently the total amount of fluid injected, causes a linear increase in pressure (Figure 8B). However, both the rate of injection and the total amount of injected fluid are implicit factors in the result. In order to isolate the effect of the rate of injection, the amount of injected fluid was kept constant by varying the injection time by a factor of the ratio of parameter and the base case. The sensitivity analysis of this normalized injection rate still shows a direct correlation, but the trend plateaus with higher rates (Figure 8C). Specifically, a 175% increase in the injection rate (normalized) leads to an increase in pressure change by 140% over the range of parameters. Figure 8A shows the pressure buildup with time for different injection rates.

FIGURE 8

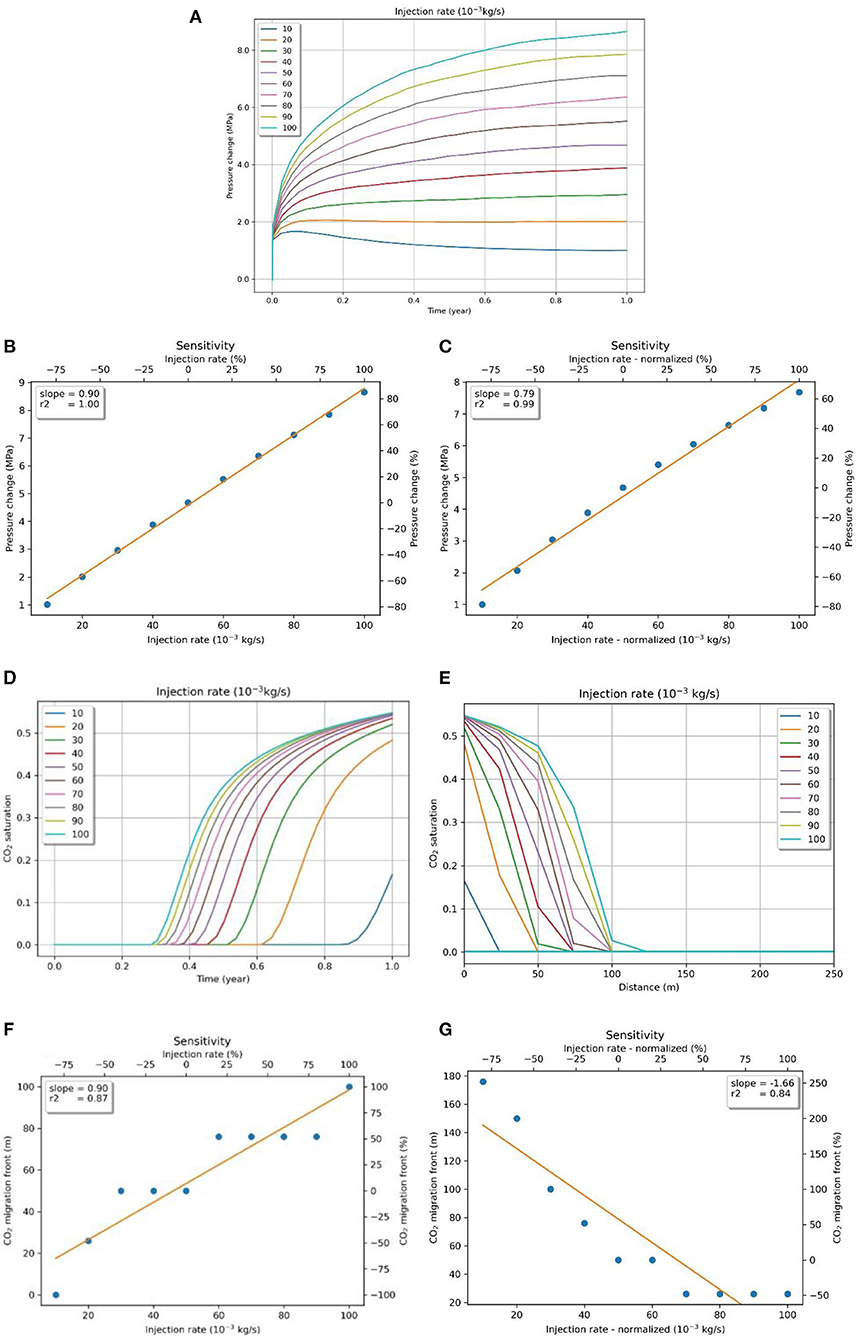
Figure 8. (A) Pressure evolution (at the top of the reservoir) with injection time for different injection rates. Sensitivity of pressure to (B) injection rate and (C) injection rate normalized by the amount of injected fluid. CO₂ saturation change (at the top of the reservoir) with (D) injection time and (E) distance from injection point for different injection rates. Sensitivity of the CO₂ migration front to injection rate with (F) the same injection time and (G) the injection time normalized for the same amount of CO₂ influx.

The injection rate also positively affects the horizontal migration of CO₂, especially in the lower portion of the reservoir. With a low injection rate, CO₂ quickly rises to the top of the reservoir through buoyancy effects and then spreads horizontally. Higher injection rates cause substantially more CO₂ trapping, and the plume spreads horizontally from the injection point itself, causing the horizontal migration front to be much more uniform throughout the thickness of the reservoir, as shown in Supplementary Figure 1. Figures 8D,E show the CO₂ saturation change with time and distance from the injection point in the reservoir. In the case of the same injection time of a year, higher injection rates still show farther CO₂ migration due to a much larger amount of total CO₂ injection. However, the trends are reversed when the injection time is corrected to equalize the amount of total CO₂ injection in the reservoir. This is contrary to the observation in pressure sensitivity because normalization only decreased the pressure, while the trend remained the same. In the case of non-normalization, the migration front increases by 200% for an increase of 175% (0.01–0.1 kg/s) in the injection rate (Figure 8F). Conversely, the migration front decreases by 300% in the case of normalized injection rate over the range of parameters (Figure 8G). This is an interesting observation because it becomes a critical factor in planning CO₂ injection to maximize stability, depending on whether the primary objective is to curb CO₂ migration or keep maximum overpressure to the minimum.

Long-Term CO₂ Injection

Another important factor in CO₂ storage projects is the long-term integrity of the storage system. In order to study the effects of CO₂ injection in a reservoir for long periods, a 50-year injection scenario was analyzed using the base case parameters. In our initial model, free flow boundary conditions were assumed at the lateral extents. However, in the case of injection for 50 years, the CO₂ plume would be affected by the lateral boundaries, and the assumption of an infinite-acting reservoir will not be valid. Thus, we have assumed no-flow conditions at all the boundaries. Accordingly, the size of the reservoir was increased in the x (sub-horizontal) direction to 100 km to accommodate the increased influx of CO₂ and the subsequent pressure buildup and make it resemble a real saline formation. The size in the z (sub-vertical) direction was maintained at 50 m. The cell dimension in the x-direction is 200 m, while that in the y- and z-direction is 25 and 5 m, respectively. The rest of the base case parameters are chosen to be the same, except salinity is assumed to be 0.1 kg/kg. This is because dissolution trapping becomes the dominant mechanism in the long term, and it is directly affected by the salinity of the formation water. The results of the simulation are presented in Figure 9. Figure 9A shows the evolution of CO₂ plume in the reservoir at the end of 10, 20, 35, and 50 years. Figure 9B shows the pressure buildup in the reservoir at the end of 50 years.

FIGURE 9

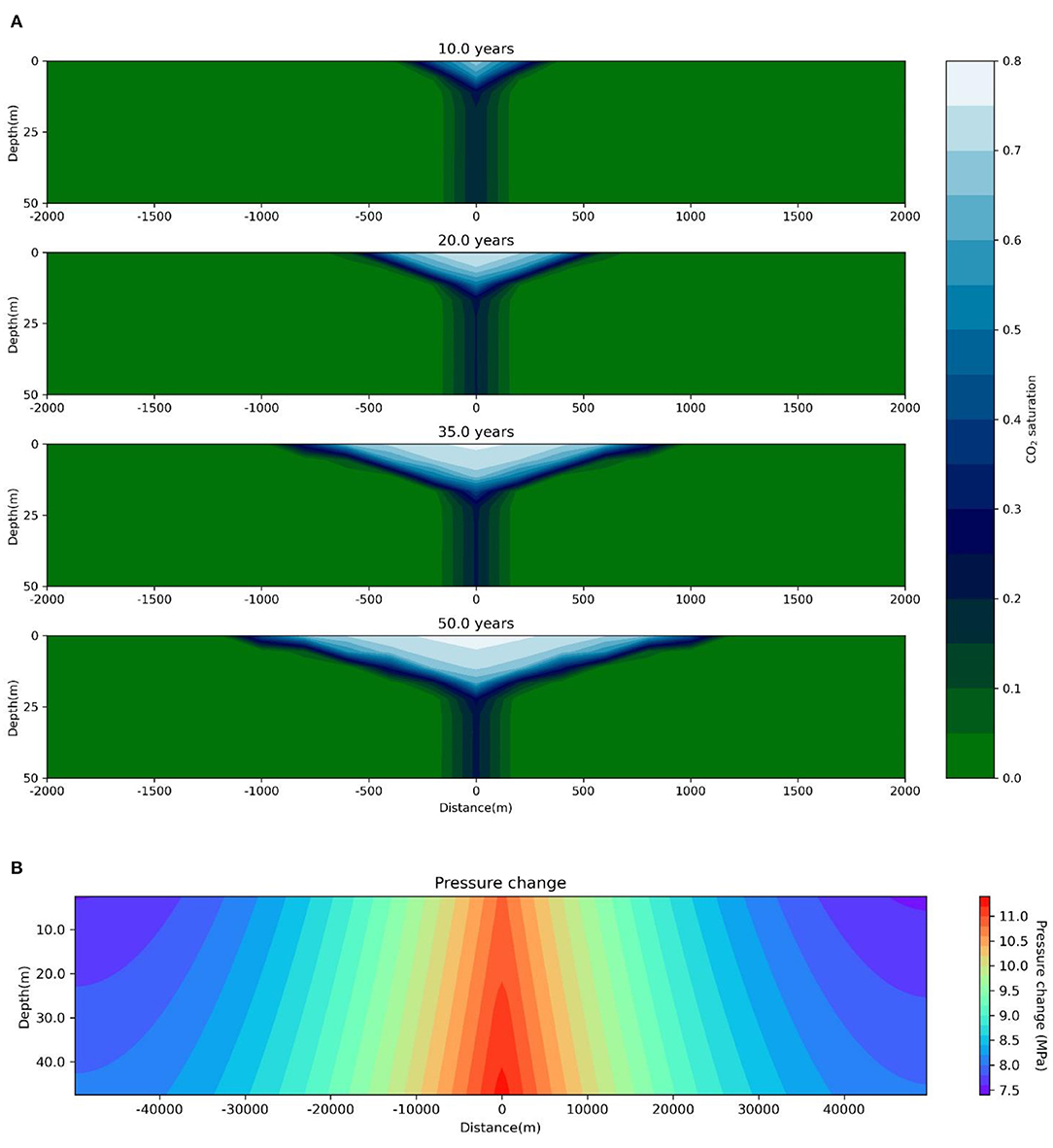
Figure 9. (A) CO₂ plume evolution in the reservoir at the end of 10, 20, 35, and 50 years. (B) Pressure evolution in the reservoir at the end of 50 years.

Figure 10A shows the pressure buildup with time for the 50-year injection case. An almost linear rise in pressure with injection time is observed, which shows that the risks associated with pore pressure buildup in the formation continuously increase as long as the injection continues. Figures 10B,C show the CO₂ saturation change with time and distance from the injection point in the reservoir. The saturation at the top of the reservoir reaches a saturation point (~0.75) and decreases rapidly after a certain distance from the injection point.

FIGURE 10

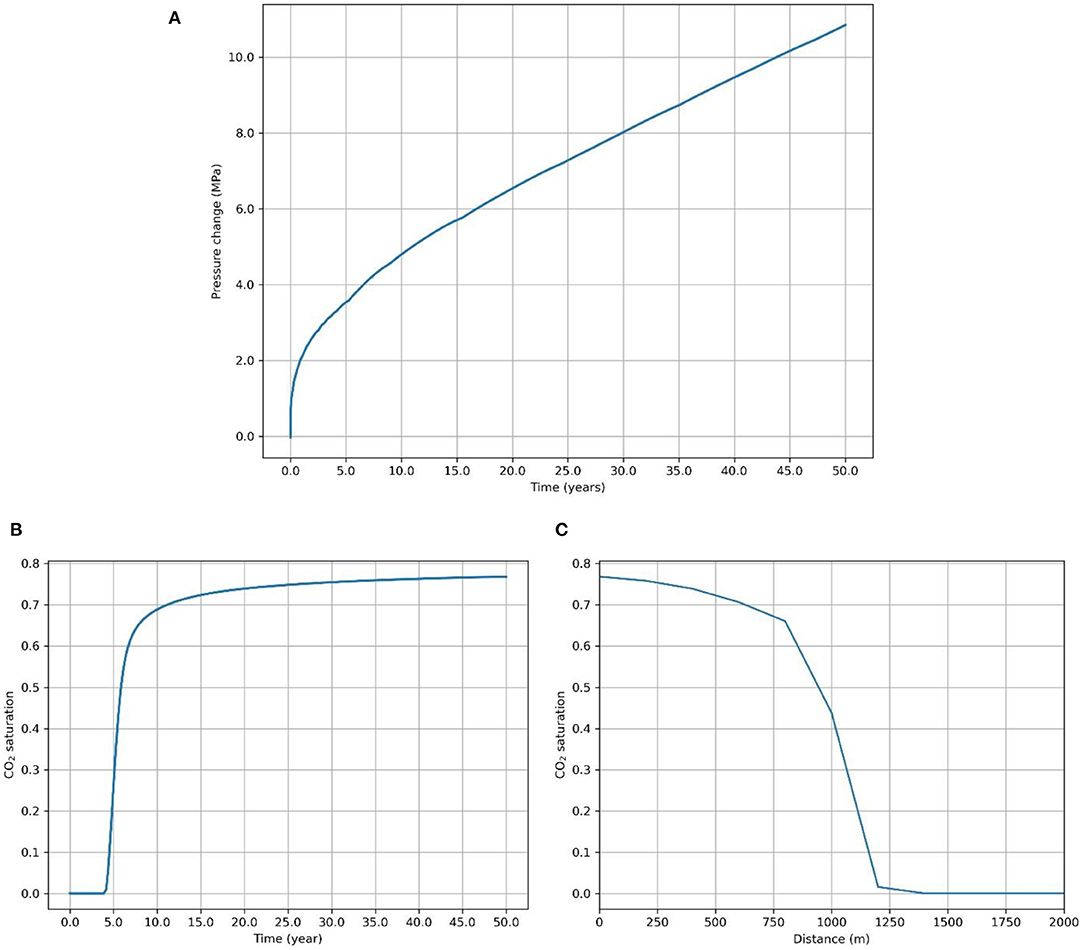
Figure 10. (A) Pressure evolution (at the top of the reservoir) with injection time for 50 years. CO₂ saturation change (at the top of the reservoir) with (B) time and (C) horizontal distance from the injection point.

Discussion

The results of the parametric analysis indicate a negative correlation of pore pressure buildup with porosity, permeability, and compressibility. They also show a strong positive correlation with injection rate, even after normalizing the injection time to correct for the total amount of fluid injected. Salinity and permeability anisotropy also affected pressure buildup positively but very mildly. The ranking of the parameters on sensitivity to pore pressure change and CO₂ migration front is shown in Table 3. Pressure buildup in the reservoir is the most sensitive to permeability (log₁₀(k)), while least sensitive to permeability anisotropy. Similar to pressure buildup, the modified permeability parameter ranks the highest in sensitivity in the case of CO₂ plume migration, too, while salinity ranks the lowest. Porosity, permeability anisotropy (log₁₀(k_v/k_h)), and normalized injection rate have a strong negative correlation with plume migration, while the rest of the parameters correlate positively.

TABLE 3

Table 3. Ranking of parameters based on sensitivity to pressure build-up and CO₂ migration.

However, the effects of porosity and permeability display a significant contrast. Porosity controls the amount of CO₂ storage that is available in the reservoir, which leads to the assumption that the pore pressure increase should be significantly lower in the case of high porosity. However, the results indicate that increasing the porosity by 3.5 times from 10 to 35% only reduces the pressure rise at the caprock by 10%. A similar trend is also observed by Sarkarfarshi et al. (2014). In the case of permeability, the decrease in pressure is significant (about 200%) over the whole range of permeability values. The analysis clearly reveals that permeability plays a much more substantial role in regulating the pressures in a reservoir, even in a considerably wider range, which is in agreement with similar studies by Yang et al. (2015) and Zhao et al. (2010). Permeability anisotropy, however, had an almost negligible effect on regulating pressure buildup in the reservoir. Lower values of permeability anisotropy parameter (log₁₀(k_v/k_h)) led to delayed vertical migration and increased horizontal migration of the CO₂ plume in the lower half of the reservoir. Salinity had a mild effect on both pressure change and CO₂ migration and is ranked toward the bottom in both parameters. This result is in agreement with the salinity's effect observed by Kopp et al. (2007).

There has been some research on pore compressibility as a factor in CO₂ injection (Yang et al., 2015). However, the observations from our study show higher effects of compressibility on the maximum pressure buildup, compared to Yang et al. (2015), even though it is already ranked low on sensitivity. Conversely, compressibility showed a negligible effect on the migration of the CO₂ plume. This leads to the conclusion that the effects on pressure were due to the increased ability of the rock matrix to absorb the fluid injection-induced stress rather than an increase in pore space. In our simulation, pore compressibility is also interlinked with other rock properties such as porosity and permeability. However, in our study, we observed an insignificant change in the porosity and permeability values (<1%) at the end of injection due to the rise in pressure for different compressibility values. So, the assumption of zero compressibility in the base case did not significantly impact the base results. Thus, compressibility in the base case could safely be assumed to be zero. This essentially makes the rocks stiffer and increases the overall stress due to CO₂ injection, making it a worst-case scenario. Moreover, it implies that the individual parameters could be considered to be independent in the scope of this study.

Due to our focus on the geomechanical properties, one parameter that we did not consider in the scope of this study was the height of the reservoir. The base height of the reservoir was chosen to be 50 m based on previous modeling studies and field data from various parts of the world (Birkholzer et al., 2009; Zhao et al., 2010; Rutqvist et al., 2015; Vilarrasa et al., 2016). Variations in the height of the reservoir mainly affect the total pore volume in the reservoir. Thus, it can be correlated with changes in porosity, as both the parameters essentially modify the total available pore space available for CO₂ in the reservoir. As shown in previous studies (Kopp, 2009), increasing the height will lead to a lower pressure buildup and reduced plume migration, which is analogous to the response to porosity. However, the specific sensitivity to reservoir height could be a potential topic for future studies.

A unique conclusion from the observations is that permeability and injection rate affect the reservoir in an analogous but opposite manner, even though the effect of injection rate is more significant. The injection rate, especially at lower rates, shows an almost 1:1 correlation with the pressure rise, but the slope decreases with higher rates. The decline in slope can be explained by this mechanism: higher local pressures due to greater injection rates accelerate fluid flow away from the injection point, and the reservoir, in a certain manner, adapts to the increasing influx of fluid in the system. These results support the idea that the rate of fluid flow rather than the total storage space for fluid is the driving factor in minimizing pressure buildup through CO₂ injection in the reservoir. This should be a major deciding factor in screening a reservoir instead of relying on only the theoretical capacity for CO₂ storage. The lower the pressure buildup at the caprock, the more the caprock stability and, consequently, the more confidence in the reservoir for storage of carbon dioxide.

Vilarrasa et al. (2019) studied the stress states in different CO₂ storage sites and concluded that all the sites were far from being critically stressed. Thus, they could sustain a fair amount of pressure buildup due to fluid injection. Usually, faulting of the caprock takes place when the pore pressure exceeds the rock's minimum principal stress. The difference between the minimum principal stress and the pore pressure at different sites ranges from around 50% in Weyburn and Snøhvit (White and Johnson, 2009; Chiaramonte et al., 2015) to 250% in Otway, Australia (Nelson et al., 2006). Previous studies (Birkholzer et al., 2009; Yang et al., 2015) have considered a 50% increase from the initial pore pressure to be the limit for the fracturing of the rocks. Moreover, reservoir rocks are usually stiffer than caprocks, and thus, caprocks can sustain larger stress variations (Vilarrasa and Makhnenko, 2017). Nevertheless, to avoid unaccounted risk, a rise in pore pressure of 25–30% could be considered safe in terms of caprock integrity depending on the initial stress state and the existing faulting regime (normal/reverse/strike-slip). Given that the initial pore pressure in our reservoir model is 14.7 MPa, a pressure rise restricted to 4–5 MPa could avoid unwanted geomechanical deformations in the caprock, including faulting. Essentially, in our study, any pressure change greater than the base case could be considered a risk. In the case of the long-term injection scenario of 50 years, maximum pressure change was observed to be more than 11 MPa—a 75% increase from the initial pore pressure of 14.7 MPa. Such a substantial pressure buildup could induce significant seismicity and lead to pore pressure exceeding the minimum principal stress, based on stress data by Vilarrasa et al. (2019). Thus, CO₂ injection needs to be carefully planned depending on the initial reservoir conditions and duration of the storage project.

Based on the rankings of the chosen parameters for our sensitivity analysis, it would seem that permeability remains the most critical parameter in assessing a formation for CO₂ storage. However, it should be noted that our parameter refers to the logarithm of permeability instead of permeability itself. Therefore, minor changes in the modified parameter correspond to substantial differences in actual permeability, and the resulting slope can inflate its actual sensitivity. Nevertheless, given the much higher sensitivity values for log₁₀(k) to both pressure buildup (2.47) and CO₂ migration (6.93) compared to other parameters, permeability should still play a vital role in screening potential sites. Among other intrinsic parameters, porosity is the next most significant factor for site selection. A high porosity would provide ideal conditions for storage, given it reduces both pressure rise and CO₂ migration (both vertical and horizontal). Porosity would especially be a critical factor in formations where the distance between the injection point and leakage pathways (faults, fractures, and abandoned wells) is a concern (Kopp et al., 2010). Permeability anisotropy (log₁₀(k_v/k_h)) and salinity have shown to be less effective in perturbing both storage constraints. Regardless, lower salinity values would support more dissolution trapping, which becomes the dominant storage mechanism in the long term, and consequently higher storage efficiencies (Brennan, 2014). Similarly, a lower ratio of vertical and horizontal permeability would be favorable as it would delay the vertical migration of CO₂, reducing leakage risks through caprock.

Some CO₂ storage capacity assessments have considered minimum cutoffs for intrinsic reservoir properties for screening storage sites (Heidug, 2013). The Queensland CO₂ storage atlas (Bradshaw et al., 2011) set minimum porosity requirement at 10% and minimum permeability at 5 mD, while the UK CO₂ storage appraisal project (Gammer et al., 2011) and Independent storage assessment by TNO (Neele et al., 2011) considered site-specific conditions and simulations to define reservoir property criteria. Based on our results, it would be highly ambitious to define limits of reservoir properties to reject sites. Instead, we can define different cases where certain combinations of reservoir properties would be more advantageous. For example, in stress conditions where the pore pressure is close to the minimum principal stress, operators should look for formations with lower salinity but higher permeability and pore compressibility, as both correlate negatively with pressure buildup. In cases of highly fractured formations where the distance between the injection point and leakage pathways is critical, lower permeability, compressibility, and salinity, along with higher permeability anisotropy value would aid in better storage containment. Higher porosity values would always be a plus point for selecting storage units, as it correlates negatively with both pressure and CO₂ migration. The rate of injection affects both storage constraints positively and thus would have to be carefully managed depending on the combination of the intrinsic reservoir properties. Ultimately, a thorough field-specific risk assessment using laboratory experiments and reservoir simulation, including best and worst case injection strategies, would be needed to select a site for CO₂ storage.

Conclusions

A parametric sensitivity analysis was carried out for CO₂ injection in an infinitely acting reservoir for screening potential sites based on storage constraints. Initially, the selection of mesh cell sizes was carried out through a mesh convergence study for optimal accuracy and simulation run-times. Subsequently, parameters such as porosity, permeability, permeability anisotropy, compressibility, salinity, and injection rate, with and without injection times normalized to correct for the total amount of fluid injected in the reservoir, were selected for the sensitivity analysis. Permeability (log₁₀(k)) was the most sensitive parameter in case of pressure change: an increase in permeability significantly reduced the pressure buildup locally as well as throughout the reservoir. The injection rate, even after correcting for the amount of fluid injected by adjusting the injection times, was ranked second, and showed a positive correlation with the reservoir pressure buildup. Compressibility showed a marginal influence in causing changes in pressure from the base scenario. Porosity was even less effective, and large variations in porosity resulted in comparatively minor divergence in the maximum pore pressure reached, and it was ranked second to last.

In the case of CO₂ migration, the permeability (log₁₀(k)) was ranked again the highest in sensitivity and showed a consistently positive effect throughout the entire range (40–1,000 mD), similar to the effect on pressure buildup. Porosity was ranked second and affected migration strongly with a negative trend. Higher porosities from the base case significantly delayed the migration of the CO₂ vertically as well as horizontally due to the extra space available in the rocks. Injection rate, when normalized for equal CO₂ influx, was the next most sensitive property. Compressibility had an almost negligible effect on the migration of the plume.

The injection rate displayed a two-pronged behavior. When equal injection times were used, the horizontal migration exhibited a positive trend with increasing injection rates, as expected. However, when injection times were normalized for an equal CO₂ influx, the trend was reversed. The lowest injection rate led to almost double the migration distance when compared with the highest injection rate in the former case. We conclude that along with injection rate, the injection time also impacts the CO₂ front to a great extent, and is certainly a prominent injection planning parameter if the amount of CO₂ that is to be stored is pre-decided for a project.

The results lead to the implication that the ease of fluid flow has a prominent influence on the buildup of pore pressure in the reservoir. Since pore pressure is the critical constraint in CO₂ storage during the initial stage of the project, we argue that the rate of fluid flow and not merely reservoir capacity should be a key element in determining the stability of the storage. Consequently, rock properties that affect fluid movement, such as tortuosity, fracture roughness, and the like, should be analyzed to measure their impact on pressure accumulation. In the case of formations where reservoir capacity is constrained either through the limited dimensions of the reservoir or the presence of leakage pathways, porosity plays a dominant role in restricting CO₂ migration and increasing confidence in storage. We believe these findings can augment the decision-making process of stakeholders in selecting appropriate reservoirs for long-term CO₂ storage.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YV: conceptualization, methodology, software, visualization, formal analysis, investigation, data curation, and writing—original draft. VV: conceptualization, methodology, validation, resources, writing—review and editing, supervision, project administration, and funding acquisition. PR: writing—review and editing and supervision. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge the support received under the Mission Innovation scheme of the Department of Science & Technology, Government of India, New Delhi [DST/TM/EWO/MI/CCUS/24].

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2021.720959/full#supplementary-material

References

Alcalde, J., Flude, S., Wilkinson, M., Johnson, G., Edlmann, K., Bond, C. E., et al. (2018). Estimating geological CO₂ storage security to deliver on climate mitigation. Nat. Commun. 9:2201. doi: 10.1038/s41467-018-04423-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bachu, S. (2016). Identification of oil reservoirs suitable for CO₂-EOR and CO₂ storage (CCUS) using reserves databases, with application to Alberta, Canada. Int. J. Greenh. Gas Control 44, 152–165. doi: 10.1016/j.ijggc.2015.11.013

CrossRef Full Text | Google Scholar

Biot, M. A. (1941). General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164. doi: 10.1063/1.1712886

CrossRef Full Text | Google Scholar

Birkholzer, J. T., Zhou, Q., and Tsang, C. F. (2009). Large-scale impact of CO₂ storage in deep saline aquifers: a sensitivity study on pressure response in stratified systems. Int. J. Greenh. Gas Control 3, 181–194. doi: 10.1016/j.ijggc.2008.08.002

CrossRef Full Text | Google Scholar

Bissell, R. C., Vasco, D. W., Atbi, M., Hamdani, M., Okwelegbe, M., and Goldwater, M. H. (2011). Energy procedia a full field simulation of the in salah gas production and CO₂ storage project using a coupled geo-mechanical and thermal. Energy Procedia 4, 3290–3297. doi: 10.1016/j.egypro.2011.02.249

CrossRef Full Text | Google Scholar

Bradshaw, B. E., Spencer, L. K., Lahtinen, A. L., Khider, K., Ryan, D. J., Colwell, J. B., et al. (2011). An assessment of Queensland's CO₂ geological storage prospectivity - The Queensland CO₂ geological storage atlas. Energy Procedia 4, 4583–4590. doi: 10.1016/j.egypro.2011.02.417

CrossRef Full Text | Google Scholar

Brennan, S. T. (2014). The U. S. Geological survey carbon dioxide storage efficiency value methodology: results and observations. Energy Procedia 63, 5123–5129. doi: 10.1016/j.egypro.2014.11.542

CrossRef Full Text | Google Scholar

Brooks, R., and Corey, T. (1964). Hydraulic properties of porous media. Hydrol. Pap. Color. State Univ. 24:37.

Google Scholar

Brown, K., Whittaker, S., Wilson, M., Srisang, W., Smithson, H., and Tontiwachwuthikul, P. (2017). The history and development of the IEA GHG weyburn-midale CO₂ monitoring and storage project in Saskatchewan, Canada (the world largest CO₂ for EOR and CCS program). Petroleum 3, 3–9. doi: 10.1016/j.petlm.2016.12.002

CrossRef Full Text | Google Scholar

Campolongo, F., Cariboni, J., Saltelli, A., and Schoutens, W. (2005). “Enhancing the Morris method,” in Sensitivity Analysis of Model Output. Proceedings of the 4th International Conference on Sensitivity Analysis of Model Output (SAMO 2004) (Los Alamos: Los Alamos National Laboratory),369–379.

Google Scholar

Cappa, F., and Rutqvist, J. (2012). Seismic rupture and ground accelerations induced by CO₂ injection in the shallow crust. Geophys. J. Int. 190, 1784–1789. doi: 10.1111/j.1365-246X.2012.05606.x

CrossRef Full Text | Google Scholar

Chiaramonte, L., White, J., a, and Trainor-Guitton, W. (2015). Probabilistic geomechanical analysis of compartmentalization at the Snøhvit CO₂ sequestration project. J. Geophys. Res. Solid Earth 120, 1195–1209. doi: 10.1002/2014JB011376

CrossRef Full Text | Google Scholar

CSLF (2008). Comparison Between Methodologies Recommended for Estimation of CO₂ Storage Capacity in Geological Media. Available online at: http://www.cslforum.org/publications/documents/PhaseIIIReportStorageCapacityEstimationTaskForc%0Ae0408.pdf

Google Scholar

De Lucia, M., Kempka, T., Afanasyev, A., Melnik, O., and Kühn, M. (2016). Coupling of geochemical and multiphase flow processes for validation of the MUFITS reservoir simulator against TOUGH. Energy Procedia 97, 502–508. doi: 10.1016/j.egypro.2016.10.060

CrossRef Full Text | Google Scholar

De Silva, P. N. K., and Ranjith, P. G. (2012). A study of methodologies for CO₂ storage capacity estimation of saline aquifers. Fuel 93, 13–27. doi: 10.1016/j.fuel.2011.07.004

CrossRef Full Text | Google Scholar

Deng, H., Stauffer, P. H., Dai, Z., Jiao, Z., and Surdam, R. C. (2012). Simulation of industrial-scale CO₂ storage: multi-scale heterogeneity and its impacts on storage capacity, injectivity and leakage. Int. J. Greenh. Gas Control 10, 397–418. doi: 10.1016/j.ijggc.2012.07.003

CrossRef Full Text | Google Scholar

Domenico, P. A., and Schwartz, F. W. (1998). Physical and Chemical Hydrogeology, Vol. 1. New York, NY: Wiley.

Google Scholar

Doughty, C., and Pruess, K. (2004). Modeling supercritical carbon dioxide injection in heterogeneous porous media. Vadose Zo. J. 3, 837–847. doi: 10.2113/3.3.837

CrossRef Full Text | Google Scholar

Eide, L. I., Batum, M., Dixon, T., Elamin, Z., Graue, A., Hagen, S., et al. (2019). Enabling large-scale carbon capture, utilisation, and storage (CCUS) using offshore carbon dioxide (CO₂) infrastructure developments — a review. Energies 12, 1–21. doi: 10.3390/en12101945

CrossRef Full Text | Google Scholar

Eiken, O., Ringrose, P., Hermanrud, C., Nazarian, B., Torp, T. A., and Høier, L. (2011). Lessons learned from 14 years of CCS operations: sleipner, In Salah and Snøhvit. Energy Procedia 4, 5541–5548. doi: 10.1016/j.egypro.2011.02.541

CrossRef Full Text | Google Scholar

Ellsworth, W. L. (2013). Injection-induced earthquakes. Science 341:1225942. doi: 10.1126/science.1225942

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferronato, M., Gambolati, G., Janna, C., and Teatini, P. (2010). Geomechanical issues of anthropogenic CO₂ sequestration in exploited gas fields. Energy Convers. Manag. 51, 1918–1928. doi: 10.1016/j.enconman.2010.02.024

CrossRef Full Text | Google Scholar

Förster, A., Norden, B., Zinck-Jørgensen, K., Frykman, P., Kulenkampff, J., Spangenberg, E., et al. (2006). Baseline characterization of the CO₂SINK geological storage site at Ketzin, Germany. Environ. Geosci. 13, 145–161. doi: 10.1306/eg.02080605016

CrossRef Full Text | Google Scholar

Furre, A. K., Eiken, O., Alnes, H., Vevatne, J. N., and Kiær, A. F. (2017). 20 Years of Monitoring CO₂-injection at Sleipner. Energy Procedia 114, 3916–3926. doi: 10.1016/j.egypro.2017.03.1523

CrossRef Full Text | Google Scholar

Gammer, D., Green, A., Holloway, S., and Smith, G. (2011). “The Energy Technologies Institute's UK CO₂ Storage Appraisal Project (UKSAP),” in SPE Offshore Europe Oil and Gas Conference Aberdeen (SPE 148426) (Aberdeen). Available online at: http://onepetro.org/SPEOE/proceedings-pdf/11OE/All-11OE/SPE-148426-MS/1706339/spe-148426-ms.pdf/1

Google Scholar

Ganguli, S. S., Vedanti, N., Akervoll, I., and Dimri, V. P. (2016). Assessing the feasibility of CO₂-enhanced oil recovery and storage in mature oil field: a case study from Cambay basin. J. Geol. Soc. India 88, 273–280. doi: 10.1007/s12594-016-0490-x

CrossRef Full Text | Google Scholar

Global CCS Institute (2018). The Global Status of CCS 2018, 84. Available online at: www.globalccsinstitute.com

Google Scholar

Global CCS Institute (2019). Global Status of CCS. Available online at: https://www.globalccsinstitute.com/resources/global-status-report/

Google Scholar

Global CCS Institute (2020). Global Status of CCS 2020. Melbourne. Available online at: https://www.globalccsinstitute.com/resources/global-status-report/

Google Scholar

Greenberg, S. E., Bauer, R., Will, R., Locke, R., Carney, M., Leetaru, H., et al. (2017). Geologic carbon storage at a one million tonne demonstration project: lessons learned from the Illinois Basin - Decatur Project. Energy Procedia 114, 5529–5539. doi: 10.1016/j.egypro.2017.03.1913

CrossRef Full Text | Google Scholar

Hart, D. J. (2000). Laboratory measurements of poroelastic constants and flow parameters and some associated phenomena (ProQuest Diss. Theses). Available online at: https://www.proquest.com/dissertations-theses/laboratory-measurements-poroelastic-constants/docview/304637159/

Google Scholar

Heidari, P., and Hassanzadeh, H. (2018). Modeling of carbon dioxide leakage from storage aquifers. Fluids 3:80. doi: 10.3390/fluids3040080

CrossRef Full Text | Google Scholar

Heidug, W. (2013). Methods to Assess Geologic CO₂ Storage Capacity: Status and Best Practice. Paris: International Energy Agency.

Google Scholar

Hepple, R. P., and Benson, S. M. (2005). Geologic storage of carbon dioxide as a climate change mitigation strategy: performance requirements and the implications of surface seepage. Environ. Geol. 47, 576–585. doi: 10.1007/s00254-004-1181-2

CrossRef Full Text | Google Scholar

Huppert, H. E., and Neufeld, J. A. (2013). The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272. doi: 10.1146/annurev-fluid-011212-140627

CrossRef Full Text | Google Scholar

IEAGHG (2009). Development of Storage Coefficients for Carbon Dioxide Storage in Deep Saline Formations. Available online at: https://www.globalccsinstitute.com/archive/hub/publications/96126/development-storage-coefficients-co2-storage-deep-saline-formations-technical-study.pdf

Google Scholar

IPCC (2013). Intergovernmental Panel on Climate Change Working Group I. Climate Change 2013: The Physical Science Basis. Long-Term Climate Change: Projections, Commitments and Irreversibility. New York, NY: Cambridge University Press.

Google Scholar

IPCC (2021). “Climate change 2021: the physical science basis,” in Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, eds V. Masson-Delmotte, P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Berger, et al. (Geneva: Cambridge University Press), 3919. Available online at: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_Full_Report.pdf

Google Scholar

Johnson, J. W., Nitao, J. J., and Morris, J. P. (2004). Reactive Transport Modeling of Cap Rock Integrity During Natural and Engineered CO₂ Storage. Available online at: https://www.osti.gov/servlets/purl/15015132

Google Scholar

Kearns, J., Teletzke, G., Palmer, J., Thomann, H., Kheshgi, H., Chen, Y. H. H., et al. (2017). Developing a consistent database for regional geologic CO₂ storage capacity worldwide. Energy Procedia 114, 4697–4709. doi: 10.1016/j.egypro.2017.03.1603

CrossRef Full Text | Google Scholar

Kopp, A. (2009). Evaluation of CO₂ injection processes in geological formations for site screening (Thesis). University of Stuttgart. doi: 10.18419/opus-312

CrossRef Full Text | Google Scholar

Kopp, A., Binning, P. J., Johannsen, K., Helmig, R., and Class, H. (2010). A contribution to risk analysis for leakage through abandoned wells in geological CO₂ storage. Adv. Water Resour. 33, 867–879. doi: 10.1016/j.advwatres.2010.05.001

CrossRef Full Text | Google Scholar

Kopp, A., Class, H., and Helmig, R. (2007). Sensitivity analysis of CO₂ injection processes in brine aquifers. Presentation given European Geosciences Union General Assembly (Vienna).

Google Scholar

Le Quéré, C., Andrew, R., Friedlingstein, P., Sitch, S., Hauck, J., Pongratz, J., et al. (2018). Global carbon budget 2018. Earth Syst. Sci. Data 10, 2141–2194. doi: 10.5194/essd-10-2141-2018

CrossRef Full Text | Google Scholar

Loria, P., and Bright, M. B. H. (2021). Lessons captured from 50 years of CCS projects. Electr. J. 34:106998. doi: 10.1016/j.tej.2021.106998

CrossRef Full Text | Google Scholar

Luderer, G., Vrontisi, Z., Bertram, C., Edelenbosch, O. Y., Pietzcker, R. C., Rogelj, J., et al. (2018). Residual fossil CO₂ emissions in 1.5-2°C pathways. Nat. Clim. Chang. 8, 626–633. doi: 10.1038/s41558-018-0198-6

CrossRef Full Text | Google Scholar

Mazzoldi, A., Rinaldi, A. P., Borgia, A., and Rutqvist, J. (2012). Induced seismicity within geological carbon sequestration projects: maximum earthquake magnitude and leakage potential from undetected faults. Int. J. Greenh. Gas Control 10, 434–442. doi: 10.1016/j.ijggc.2012.07.012

CrossRef Full Text | Google Scholar

Metz, B., Davidson, O., de Coninck, H., Loos, M., and Meyer, L. (2005). IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge; New York, NY.

Google Scholar

Michael, K., Golab, A., Shulakova, V., Ennis-King, J., Allinson, G., Sharma, S., et al. (2010). Geological storage of CO₂ in saline aquifers-a review of the experience from existing storage operations. Int. J. Greenh. Gas Control 4, 659–667. doi: 10.1016/j.ijggc.2009.12.011

CrossRef Full Text | Google Scholar

Moridis, G. J., and Freeman, C. M. (2014). The RealGas and RealGasH₂O options of the TOUGH+ code for the simulation of coupled fluid and heat flow in tight/shale gas systems. Comput. Geosci. 65, 56–71. doi: 10.1016/j.cageo.2013.09.010

CrossRef Full Text | Google Scholar

Morris, M. D. (1991). Factorial sampling plans for preliminary computational experiments. Technometrics 33, 161–174. doi: 10.1080/00401706.1991.10484804

CrossRef Full Text | Google Scholar

Neele, F., Nepveu, M., Hofstee, C., and Meindertsma, W. (2011). CO₂ storage capacity assessment methodology. TNO Report, Geological Survey of Netherlands, Utrecht, Netherlands.

Google Scholar

Nelson, E., Hillis, R., Sandiford, M., Reynolds, S., and Mildren, S. (2006). Present-day state-of-stress of southeast Australia. APPEA J. 46:283. doi: 10.1071/AJ05016

CrossRef Full Text | Google Scholar

NETL (2017). BEST PRACTICES: Site Screening, Site Selection, and Site Characterization for Geologic Storage Projects. Available online at: https://netl.doe.gov/node/5829

Google Scholar

Newman, G. H. (1973). Pore-volume compressibility of consolidated, friable, and unconsolidated reservoir rocks under hydrostatic loading. J. Pet. Technol. 25, 129–134. doi: 10.2118/3835-PA

CrossRef Full Text | Google Scholar

Orr, F. M. (2018). Carbon Capture, Utilization, and Storage (CCUS) - An Update. Spe. Available online at: http://tv.theiet.org/technology/power/15777.cfm

Google Scholar

Pan, P., Wu, Z., Feng, X., and Yan, F. (2016). Geomechanical modeling of CO₂ geological storage: a review. J. Rock Mech. Geotech. Eng. 8, 936–947. doi: 10.1016/j.jrmge.2016.10.002

CrossRef Full Text | Google Scholar

Rinaldi, A. P., Rutqvist, J., Finsterle, S., and Liu, H. H. (2017). Inverse modeling of ground surface uplift and pressure with iTOUGH-PEST and TOUGH-FLAC: the case of CO₂ injection at In Salah, Algeria. Comput. Geosci. 108, 98–109. doi: 10.1016/j.cageo.2016.10.009

CrossRef Full Text | Google Scholar

Ringrose, P. (2020). How to Store CO₂ Underground: Insights From Early-Mover CCS Projects. Available online at: http://link.springer.com/10.1007/978-3-030-33113-9. doi: 10.1007/978-3-030-33113-9

CrossRef Full Text | Google Scholar

Ringrose, P., and Sæther, Ø. (2020). CO₂ injection operations: Insights from Sleipner and Snøhvit” in SPE CCUS Conference (Aberdeen), 1–14. Available online at: https://www.spe-aberdeen.org/wp-content/uploads/2020/11/Mon_Equinor_SPE-CCUS-Insights-from-Sleipner-and-Snchvit-26Oct2020.pdf

Google Scholar

Rodosta, T. D., Litynski, J. T., Plasynski, S. I., Hickman, S., Frailey, S., and Myer, L. (2011). U.S. Department of Energy's site screening, site selection, and initial characterization for storage of CO₂ in deep geological formations. Energy Procedia 4, 4664–4671. doi: 10.1016/j.egypro.2011.02.427

CrossRef Full Text | Google Scholar

Rutqvist, J. (2011). Status of the TOUGH-FLAC simulator and recent applications related to coupled fluid flow and crustal deformations. Comput. Geosci. 37, 739–750. doi: 10.1016/j.cageo.2010.08.006

CrossRef Full Text | Google Scholar

Rutqvist, J. (2012). The geomechanics of CO₂ storage in deep sedimentary formations. Geotech. Geol. Eng. 30, 525–551. doi: 10.1007/s10706-011-9491-0

CrossRef Full Text | Google Scholar

Rutqvist, J., Cappa, F., Rinaldi, A. P., and Godano, M. (2014). Dynamic modeling of injection-induced fault reactivation and ground motion and impact on surface structures and human perception. Energy Procedia 63, 3379–3389. doi: 10.1016/j.egypro.2014.11.367

CrossRef Full Text | Google Scholar

Rutqvist, J., Rinaldi, A. P., Cappa, F., and Moridis, G. J. (2015). Modeling of fault activation and seismicity by injection directly into a fault zone associated with hydraulic fracturing of shale-gas reservoirs. J. Pet. Sci. Eng. 127, 377–386. doi: 10.1016/j.petrol.2015.01.019

CrossRef Full Text | Google Scholar

Rutqvist, J., Vasco, D. W., and Myer, L. (2010). Coupled reservoir-geomechanical analysis of CO₂ injection and ground deformations at In Salah, Algeria. Int. J. Greenh. Gas Control 4, 225–230. doi: 10.1016/j.ijggc.2009.10.017

CrossRef Full Text | Google Scholar

Sarkarfarshi, M., Malekzadeh, F. A., Gracie, R., and Dusseault, M. B. (2014). Parametric sensitivity analysis for CO₂ geosequestration. Int. J. Greenh. Gas Control 23, 61–71. doi: 10.1016/j.ijggc.2014.02.003

CrossRef Full Text | Google Scholar

Settari, A., and Mourits, F. M. (1998). A coupled reservoir and geomechanical simulation system. SPE J. 3, 219–226. doi: 10.2118/50939-PA

CrossRef Full Text | Google Scholar

Shukla, R., Ranjith, P., Haque, A., and Choi, X. (2010). A review of studies on CO₂ sequestration and caprock integrity. Fuel 89, 2651–2664. doi: 10.1016/j.fuel.2010.05.012

CrossRef Full Text | Google Scholar

Szulczewski, M. L. (2013). The subsurface fluid mechanics of geologic carbon dioxide storage (PhD Dissertation). Massachusetts Institute of Technology. Available online at: https://dspace.mit.edu/handle/1721.1/82834

Google Scholar

Szulczewski, M. L., MacMinn, C. W., and Juanes, R. (2011). How pressure buildup and CO₂ migration can both constrain storage capacity in deep saline aquifers. Energy Procedia 4, 4889–4896. doi: 10.1016/j.egypro.2011.02.457

CrossRef Full Text | Google Scholar

Verdon, J. (2011). Microseismic monitoring and geomechanical modeling of CO₂ storage in subsurface reservoirs. Geophysics 76, Z102–Z103. doi: 10.1190/2011-0926-GEODIS.6

CrossRef Full Text | Google Scholar

Verdon, J. P., Stork, A. L., Bissell, R. C., Bond, C. E., and Werner, M. J. (2015). Simulation of seismic events induced by CO₂ injection at In Salah, Algeria. Earth Planet. Sci. Lett. 426, 118–129. doi: 10.1016/j.epsl.2015.06.029

CrossRef Full Text | Google Scholar

Vilarrasa, V., Carrera, J., Olivella, S., Rutqvist, J., and Laloui, L. (2019). Induced seismicity in geologic carbon storage. Solid Earth 10, 871–892. doi: 10.5194/se-10-871-2019

CrossRef Full Text | Google Scholar

Vilarrasa, V., Makhnenko, R., and Gheibi, S. (2016). Geomechanical analysis of the influence of CO₂ injection location on fault stability. J. Rock Mech. Geotech. Eng. 8, 805–818. doi: 10.1016/j.jrmge.2016.06.006

CrossRef Full Text | Google Scholar

Vilarrasa, V., and Makhnenko, R. Y. (2017). Caprock Integrity and Induced Seismicity from Laboratory and Numerical Experiments. Energy Procedia 125, 494–503. doi: 10.1016/j.egypro.2017.08.172

CrossRef Full Text | Google Scholar

Vilarrasa, V., Silva, O., Carrera, J., and Olivella, S. (2013). Liquid CO₂ injection for geological storage in deep saline aquifers. Int. J. Greenh. Gas Control 14, 84–96. doi: 10.1016/j.ijggc.2013.01.015

CrossRef Full Text | Google Scholar

Wei, Y. M., Kang, J. N., Liu, L. C., Li, Q., Wang, P. T., Hou, J. J., et al. (2021). A proposed global layout of carbon capture and storage in line with a 2°C climate target. Nat. Clim. Chang. 11, 112–118. doi: 10.1038/s41558-020-00960-0

CrossRef Full Text | Google Scholar

White, D., Harris, K., Roach, L., Roberts, B., Worth, K., Stork, A., et al. (2017). Monitoring results after 36 ktonnes of deep CO₂ injection at the aquistore CO₂ Storage Site, Saskatchewan, Canada. Energy Procedia 114, 4056–4061. doi: 10.1016/j.egypro.2017.03.1546

CrossRef Full Text | Google Scholar

White, D. J., and Johnson, J. W. (2009). Integrated geophysical and geochemical research programs of the IEA GHG Weyburn-Midale CO₂ monitoring and storage project. Energy Procedia 1, 2349–2356. doi: 10.1016/j.egypro.2009.01.305

CrossRef Full Text | Google Scholar

Yang, Z., Niemi, A., Tian, L., Joodaki, S., and Erlström, M. (2015). Modeling of pressure build-up and estimation of maximum injection rate for geological CO₂ storage at the South Scania site, Sweden. Greenh. Gases Sci. Technol. 5, 277–290. doi: 10.1002/ghg.1466

CrossRef Full Text | Google Scholar

Zhao, H., Liao, X., Chen, Y., and Zhao, X. (2010). Sensitivity analysis of CO₂ sequestration in saline aquifers. Pet. Sci. 7, 372–378. doi: 10.1007/s12182-010-0080-2

CrossRef Full Text | Google Scholar

Zhou, Q., Birkholzer, J. T., Tsang, C. F., and Rutqvist, J. (2008). A method for quick assessment of CO₂ storage capacity in closed and semi-closed saline formations. Int. J. Greenh. Gas Control 2, 626–639. doi: 10.1016/j.ijggc.2008.02.004

CrossRef Full Text | Google Scholar

Zoback, M. D., and Gorelick, S. M. (2012). Earthquake triggering and large-scale geologic storage of carbon dioxide. Proc. Natl. Acad. Sci. U.S.A. 109, 10164–10168. doi: 10.1073/pnas.1202473109

PubMed Abstract | CrossRef Full Text | Google Scholar