Toward Consistent Observational Constraints in Climate Predictions and Projections

Observations facilitate model evaluation and provide constraints that are relevant to future predictions and projections. Constraints for uninitialized projections are generally based on model performance in simulating climatology and climate change. For initialized predictions, skill scores over the hindcast period provide insight into the relative performance of models, and the value of initialization as compared to projections. Predictions and projections combined can, in principle, provide seamless decadal to multi-decadal climate information. For that, though, the role of observations in skill estimates and constraints needs to be understood in order to use both consistently across the prediction and projection time horizons. This paper discusses the challenges in doing so, illustrated by examples of state-of-the-art methods for predicting and projecting changes in European climate. It discusses constraints across prediction and projection methods, their interpretation, and the metrics that drive them such as process accuracy, accurate trends or high signal-to-noise ratio. We also discuss the potential to combine constraints to arrive at more reliable climate prediction systems from years to decades. To illustrate constraints on projections, we discuss their use in the UK's climate prediction system UKCP18, the case of model performance weights obtained from the Climate model Weighting by Independence and Performance (ClimWIP) method, and the estimated magnitude of the forced signal in observations from detection and attribution. For initialized predictions, skill scores are used to evaluate which models perform well, what might contribute to this performance, and how skill may vary over time. Skill estimates also vary with different phases of climate variability and climatic conditions, and are influenced by the presence of external forcing. This complicates the systematic use of observational constraints. Furthermore, we illustrate that sub-selecting simulations from large ensembles based on reproduction of the observed evolution of climate variations is a good testbed for combining projections and predictions. Finally, the methods described in this paper potentially add value to projections and predictions for users, but must be used with caution.

Introduction

Information about future climate relies on climate model simulations. Given the uncertainty in the future climate's response to external forcings and climate models' persistent biases, there is a need for coordinated multi-model experiments. This need is addressed by the Coupled Model Intercomparison Project (CMIP), proposing a uniform protocol to evaluate the future climate. Currently, this protocol proposes to explore two future timescales separately: firstly the evolution of the climate toward the end of the century, and secondly the evolution of the climate within the first decade ahead (Eyring et al., 2016). Climate variations on the longer timescale are primarily driven by the climate responses to different scenarios of socio-economic development and resulting anthropogenic emissions of greenhouse gases and aerosols (Gidden et al., 2019; see also Forster et al., 2020). At decadal timescales on the other hand, the internal variability of the climate system is an important source of uncertainty, and part of the associated skill comes from successfully initializing models with the observed state of the climate. The two timescales are thus subject to different challenges and are therefore addressed by distinct experimental setups. In both cases, coordinated multi-model approaches are necessary to estimate uncertainty from model simulations.

To account for internal variability, the size of individual climate model ensembles has increased, so that there is a growing need to extract the maximum information from these ensembles and to grasp the opportunities associated with large ensembles (e.g., Kay et al., 2015). In particular, treating each model as equally likely (the so-called one-model-one-vote approach) may not provide the best information for climate decision making; This demonstrates the need for a well-informed decision on choice and processing of models for projections, while large ensembles may overcome, at least in part, concerns about signal-to-noise ratios in weighted ensembles (Weigel et al., 2010).

Furthermore, there is also a desire to provide decision makers with seamless information on the time-scale from a season to decades ahead. This involves the even more complex step of combining ensembles from initialized predictions started from observed conditions of near present-day with those from projections, the latter of which are typically started from conditions a century or more earlier. This paper discusses available methods using observations to evaluate and constrain ensemble predictions and projections, supporting the long-term goal of a consistent framework for their use in seamless predictions from years to decades.

Multiple techniques are available to constrain future projections drawing on different lines of evidence and considering different sources of uncertainty (e.g., Giorgi and Mearns, 2002; Knutti, 2010; Knutti et al., 2017; Sanderson et al., 2017; Lorenz et al., 2018; Brunner et al., 2020a,b; Ribes et al., 2021). Models that explore the full uncertainty in parameter space provide very wide uncertainty ranges (Stainforth, 2005), motivating the need to use observational constraints. Usually observational constraints are based on the assumption that there is a reliable link between model performance compared to observations over the historical era with future model behavior. This link is expressed using emergent constraints, weights, or other statistical approaches. For instance, this could mean excluding or downweighting models which are less successful in reproducing the climatological mean state or seasonal cycle. The constraint can also be based on the variability, representation of mechanisms or relationships between different variables, or changes in multi-model assessments of future changes (e.g., Hall and Qu, 2006; Sippel et al., 2017; Donat et al., 2018), which includes evaluation of the climate change magnitude in detection and attribution approaches (e.g., Stott and Kettleborough, 2002; Tokarska et al., 2020b). In a similar manner, the risk of experiencing an abrupt change in the subpolar North Atlantic gyre has been constrained by the capability of CMIP5 climate models to reproduce stratification in this region, which plays a key role in the dynamical behavior of the ocean (Sgubin et al., 2017). This is based on the fundamental idea that certain physical mechanisms of climate need to be appropriately simulated for the model to be “fit for purpose,” and consistent with this thought, the Intergovernmental Panel on Climate Change (IPCC) reports have consistently dedicated a chapter to climate model evaluations. The IPCC has also drawn on observational constraints from attribution to arrive at uncertainty estimates in predictions both in assessment reports four (AR4) (Knutti et al., 2008) and AR5 (Collins et al., 2013).

Many methods constraining projections have been evaluated using model-as-truth approaches and several of them have been part of a recent method intercomparison based on a consistent framework (Brunner et al., 2020a). The authors found that there is a substantial diversity in the methods' underlying assumptions, uncertainties covered, and lines of evidence used. Therefore, it is maybe not surprising that the results of their application are not always consistent, and that they tend to be more consistent for the central estimate than the quantification of uncertainty. The latter is important, as reliable uncertainty ranges are often key to actionable climate information.

Emergent constraints is another highly visible research area that makes use of relationships between present day observable climate and projected future changes. Emergent constraints rely on statistical relationships between present day, observable, climate properties and the magnitude of future change. There is currently effort within this community to discriminate between those that are purely statistical from those where there is further confirmational evidence to support their usage (e.g., Caldwell et al., 2018, Hall et al., 2019). Efforts to identify consensus or consolidate constraints from multiple, often conflicting, emergent constraints have started to take place within the climate sensitivity context (Bretherton and Caldwell, 2020, Sherwood et al., 2020). However, these frameworks do not yet account for common model structural errors that will likely lead such assessments to an overly confident constraint (Sanderson et al., 2021). The reliability of emergent constraints for general climate projections is even less clear at this time (e.g., Brient, 2020), and therefore, we do not discuss such constraints further here as it is not clear how complete and reliable such constraints are.

For initialized predictions (Pohlmann et al., 2005; Meehl et al., 2009, 2021; Yeager and Robson, 2017; Merryfield et al., 2020; Smith et al., 2020), skill scores assess the model system's performance in hindcasts compared to observations, allowing for a routine evaluation of the prediction system that is unavailable to projections. Multi-model studies on predictions have, however, only recently started to emerge as more sets of initialized decadal prediction simulations have become available as part of the CMIP6 Decadal Prediction Project (DCPP; Boer et al., 2016). Some studies merged CMIP5 and CMIP6 decadal prediction systems to maximize ensemble size for optimal filtering of the noise (e.g., Smith et al., 2020), or contrasted the multi-model means of CMIP5 and CMIP6 to pinpoint specific improvements in prediction skill from one CMIP iteration to the other (Borchert et al., 2021). Attempts to explicitly contrast and explain the decadal prediction skill of different model systems are yet very rare (Menary and Hermanson, 2018). There are therefore no methods of constraining or weighting multi-model ensembles of decadal prediction simulations in the literature which we could rely upon.

For these reasons, we provide in this paper a first exploration of discriminant features of multi-model decadal prediction ensembles with the aim of providing an indication which inherent model features benefit, and which degrade skill. We also discuss the contribution of forcing and internal variability to decadal prediction skill over time, and show how times of low and high skill (windows of opportunity; Mariotti et al., 2020) can be used to constrain sources of skill in space and time. We consider the cross-cutting relevance of observational constraints and reflect on their consistency across prediction and projection timescales and approaches. We also pilot opportunities for building upon multiple methods and investigate how observational constraints may be used in uncertainty characterization in a seamless prediction. Finally, we discuss the challenges in applying observational constraints to predictions, where skill varies over time and may therefore not be consistent across prediction timelines.

This paper examines the potential for observational constraints in the three European SREX regions Northern Europe (NEU), Central Europe (CEU) and Mediterranean (MED) [see, e.g., Brunner et al. (2020a)]. Many of our results will be transferable to other regions, although the signal-to-noise ratio as well as the skill of initialized predictions might be different for larger regions or lower latitude regions, with the potential for observational constraints being more powerful in some regions as a consequence. Hence our European example can be seen as a stress test for observational constraints in use.

We first illustrate examples of observational constraints for projections, identify contributing factors to model skill metrics, and explore the potential to use multiple constraints in sequence. We then illustrate, on the interface from projections to predictions, that the performance of a prediction system can be emulated by constraining a large ensemble to follow observational constraints on modes of sea surface temperature (SST). Lastly, the origin of skill and observational constraints in initialized predictions is illustrated across different models, different timelines and different regions as a first step toward consistently constraining predictions and projections for future merging applications. We draw lessons and recommendations for the use of observational constraints in the final section.

Constraining Projections

Lessons Learned From the Use of Observational Constraints in Climate Projections in UKCP18

Observational constraints have played an important role in the latest generation of the UK climate projections (UKCP18; Murphy et al., 2018). UKCP18 includes sets of 28 global model simulations (~60 km resolution), 12 regional (12 km resolution), and 12 local (2.2 km resolution) realizations of 21st century climate consisting of raw climate model data, for use in detailed analysis of climate impacts (Murphy et al., 2018; Kendon et al., 2019). Also provided is a set of probabilistic projections, the role of which is to provide more comprehensive estimates of uncertainty for use in risk assessments in their own right, and also as context for the realizations. The probabilistic climate projections are derived from a larger set of 360 model simulations, based on a combination of perturbed parameter ensembles with a single model, combined with simulations with different CMIP5 models. These have been combined to make probability density functions representing uncertainties due to internal variability and climate response, using a Bayesian framework that includes the formal application of observational constraints. The UKCP18 probabilistic approach is one of the methods covered in Brunner et al. (2020a). Key aspects include: (a) use of emulators to quantify parametric model uncertainties, by estimating results for parts of parameter space not directly sampled by a climate model simulation; (b) use of CMIP5 earth system models to estimate the additional contribution of structural model uncertainties (termed “discrepancy” in this framework) to the pdfs; (c) sampling of carbon cycle uncertainties alongside those due to physical climate feedbacks. The method, described in Murphy et al. (2018), is updated from earlier work by Sexton et al. (2012), Harris et al. (2013), Sexton and Harris (2015), and Booth et al. (2017). The climatological constraints are derived from seasonal spatial fields for 12 variables. These include latitude-longitude fields of surface temperature, precipitation, sea-level pressure, total cloud cover and energy exchanges at the surface and at the top of the atmosphere, plus the latitude-height distribution of relative humidity (denoted HIST in Figure 1). This amounts to 175,000 observables, reduced in dimensionality to six through eigenvector analysis (Sexton et al., 2012). Constraints from historical surface air temperature (SAT) change include the global average, plus three indices representing large-scale patterns (Braganza et al., 2003). The ocean heat content metric (OHC) is the global average in the top 700 m. The CO₂ constraint arises because the UKCP18 projections include results from earth system model simulations that predict the historical and future response of CO₂ concentration to carbon emissions, thus including uncertainties due to both carbon cycle and physical climate feedbacks. The observed trend in CO₂ concentration is therefore combined with the other metrics in the weighting methodology, to provide a multivariate set of constraints used to update joint prior probability distributions for a set of historical and future prediction variables (further details in Murphy et al., 2018).

FIGURE 1

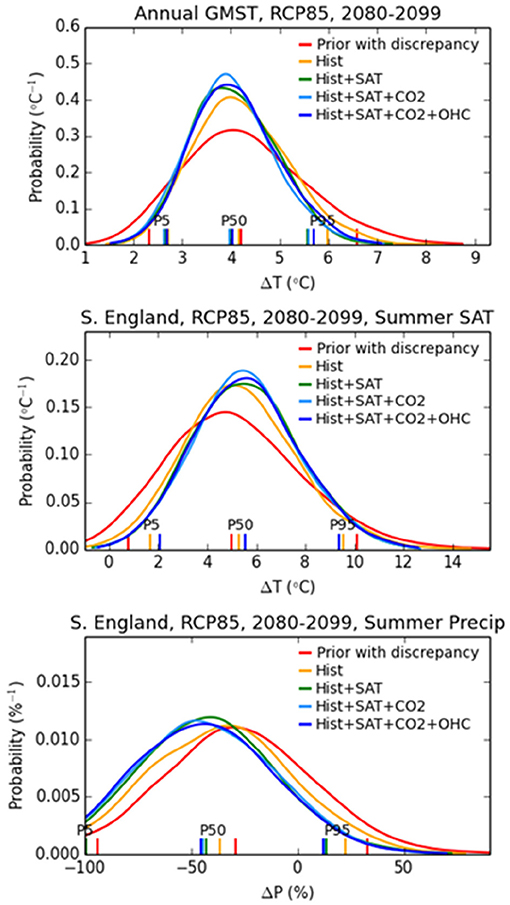
Figure 1. Examples of the impact of constraints derived from historical climatology (Hist), added historical global surface air temperature trends (Hist+SAT), added historical trends in atmospheric CO₂ concentration (Hist+SAT+CO2), and added upper ocean heat content (Hist+SAT+CO2+OHC), in modifying the prior distribution to form the posterior. The 5th, 50th (median), and 95th percentiles are plotted, along with the pdfs. Results prior to the application of observational constraints (Prior with discrepancy) are also shown. Reproduced from Murphy et al. (2018).

Figure 1 illustrates the impact of observational constraints on the UKCP18 pdfs for global mean temperature, and summer temperature and precipitation for Southern England; 2080–2099 relative to 1981–2000, under RCP8.5. Results show that as well as narrowing the range, specific constraints can also weight different parts of the pdf up or down, compared to the prior distribution. As an example, the chance of a summer drying is upweighted in the posterior, by the application of both the climatology and historical temperature trend constraints. Experiences with use of observational constraints in UKCP18 illustrate that considering multiple constraints can be powerful. This is shown in Figure 1 by a sensitivity test, in which each pdf is modified by adding individual constraints in sequence. However, the impact of specific constraints can depend on the order in which they are applied. Here, e.g., the effect of historic changes in ocean heat content might appear larger, if applied as the first step in this illustration. This illustrates that there is plenty of scope to refine such constraint methods in the future. For example, metrics of climate variability are not yet considered in the set of historical climatology constraints.

Examples of Methods for Observational Constraints on Projections

Performance Weighting Methods (ClimWIP)

Methods using performance weighting evaluate if models are fit for purpose and weight them accordingly (see also UKCP18 Example discussed above). The fundamental idea is that projected climate change can only be realistic if the model simulates processes determining present day climate realistically as discussed e.g., in Knutti et al. (2017) for the case of Arctic sea ice. An updated version of the same method (termed Climate model Weighting by Independence and Performance—ClimWIP) was recently applied by Brunner et al. (2020b) to the case of global mean temperature change. Each model's weight is based on a range of performance predictors establishing its ability to reproduce observed climatology, variability and trend fields. These predictors are selected to be physically relevant and correlated to the target of prediction. Other approaches, such as emergent constraints, often use a single highly correlated metric, while ClimWIP draws on several such metrics. This can avoid giving heavy weight to a model which fits the observations well in one metric but is very far away in several others. In addition to that, they also include information about model dependencies within the multi-model ensemble (see Knutti et al., 2013), effectively downweighting model pairs which are similar to each other.

We show results from two applications of ClimWIP here: Figure 2 illustrates the effect of ClimWIP, alongside other methods, compared to using unconstrained predictions from a set of CMIP5 models, illustrating that ClimWIP reduces spread in some seasons and regions, and also shifts the central tendency somewhat, depending on the case (Brunner et al., 2019), and in a similar manner as illustrated above for UKCP18. The CMIP6 weights used in the later part of the study are based on the latest version of ClimWIP described in Brunner et al. (2020b) and based on earlier work by Merrifield et al. (2020), Brunner et al. (2019), Lorenz et al. (2018), and Knutti et al. (2017). We used performance weights based on each model's generalized distance to reanalysis products (ERA5; Hersbach et al., 2020, and MERRA2, Gelaro et al., 2017) in five diagnostics evaluated from 1980 to 2014: global, spatially resolved fields of climatology and variability of near-surface air temperature and sea level pressure, as well as global, spatially resolved fields of near-surface air temperature trend (Brunner et al., 2020b). The weights were retrieved from the same setup as used in Brunner et al. (2020b) and it is important to note that they are optimized to constrain global mean temperature change in the second half of the 21st century for the full CMIP6 ensemble. Here we use them only to show the general applicability combining ClimWIP with the ASK approach (outlined next), which illustrates common inputs across constraints on projections and their relation to each other. We apply them to a subset of nine models for which Detection and Attribution Model Intercomparison Project (DAMIP simulations; Gillett et al., 2016) are available, and then focus on projections for Europe. For applications beyond the illustrative approach shown here, it is critical to retune the method for the chosen target and model subset.

FIGURE 2

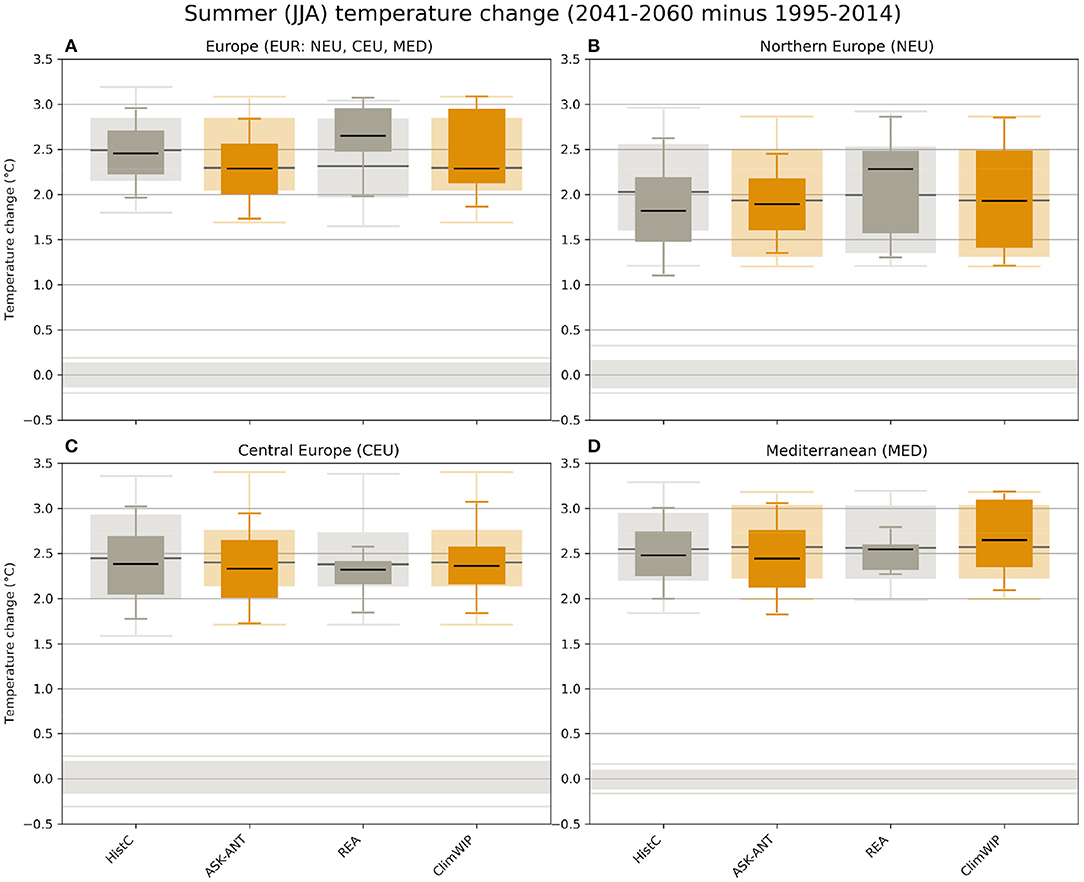
Figure 2. Projected summer (June–August) temperature change 2041–2060 relative to 1995–2014 for (A) the combined European region as well as (B–D) the three European SREX regions (Northern Europe, Central Europe, and the Mediterranean) using RCP8.5. The lighter boxes give the unconstrained distributions originating from model simulations; the darker boxes give the observationally constrained distributions. Shown are median, 50% (bars) and 80% (whiskers) range. The gray box and lines centered around zero show the same percentiles of 20-years internal variability based on observations. Methods ASK-ANT and ClimWIP used in this paper are colored, additional methods HistC and REA shown in Brunner et al. (2020a), but not used in this paper, are in gray. After Figure 6 in Brunner et al. (2020a).

Trend and Attribution Based Methods (ASK Method)

Another widely used method for constraining projections focuses on the amplitude of forced changes (here referred to as “trend,” although the constrained time-space pattern may be more complex than a simple trend). This method focuses on the performance of climate models in simulating externally forced climate change, with the idea that a model that responds too strongly or too weakly over the historical period may also do so in the future. Trend performance is included in ClimWIP, as its full implementation accounts for trends, and also in UKCP18, as illustrated above.

Trend based methods need to consider that the observed period is not only driven by greenhouse gas increases, but also influenced by aerosol forcing, natural forcings (e.g., Bindoff et al., 2013) as well as internal variability¹, all of which impact on the magnitude of the observed climate change Since the future may show different combinations of external forcing than the past, including reducing aerosol forcing with increased pollution control, and different phases of natural forcing, non-discriminant use of trends may introduce errors. Two approaches have been used to circumvent this problem: one method is to use a period of globally flat aerosol forcing and argue that the largest contributor to trends is greenhouse gases over such periods, and then use trends as emergent constraints (Tokarska et al., 2020a). An alternative, the so-called Allen Stott Kettleborough “ASK method,” introduced in the early 2000s (Allen et al., 2000; Stott and Kettleborough, 2002; Shiogama et al., 2016) uses results from detection and attribution of observed climate change to constrain projections. These methods seek to disentangle the role of different external forcings and internal variability in observed trends, and result in an estimate of the contribution by natural forcings, greenhouse gases, and other anthropogenic factors to recent warming. This allows us to estimate the observed greenhouse gas signal, and use it to constrain projections. This can be done by selecting climate models within the observed range of greenhouse gas response (Tokarska et al., 2020b) or by using the uncertainty range of greenhouse warming that is consistent with observations as an uncertainty range in future projections around the multi-model mean fingerprint (Kettleborough et al., 2007). The latter method has been included in assessed uncertainty ranges in projections in IPCC (see Knutti et al., 2008; Collins et al., 2013).

Here we illustrate the use of attribution based observational constraints. This method assumes that the true observed climate response, y_obs, to historical forcing is a linear combination of one or more (n) individual forcing fingerprints, X_j, scaled by adjustable scaling factors, β_j, to observations. We use the gridded observations E-OBS v19.0e dataset (Haylock et al., 2008), with monthly values computed from the daily data. Scaling factors are determined that optimize the fit to observations. Hence this method uses the response in observations to estimate the amplitude of a model-estimated space time pattern of response, with the rationale that uncertain feedbacks may lead to a larger or smaller response than anticipated in climate models (e.g., Hegerl and Zwiers, 2011). We use a total-least-squares (TLS) method to estimate the scaling factors, which accounts for noise in both the observations ε_obs, and in the modeled response to each of the forcings ε_j(see e.g., Schurer et al., 2018),

$\begin{array}{ll}{y}_{obs}={\displaystyle \sum _{j=1}^n}{\beta }_j(X_j-{\epsilon }_j)+{\epsilon }_{obs}& (1)\end{array}$

where the n fingerprints chosen may include the response to greenhouse gases only (GHG), natural forcings only (NAT), other anthropogenic forcings (OTH) or combinations thereof (ANT = GHG+OTH). A confidence interval for each of the scaling factors describes the range of magnitudes of the model response that are consistent with the observed signal. A forced model response is detected if the range of scaling factors are significantly >0, and can be described as being consistent with observations if the range of values contains the magnitude of one (=1). The uncertainty due to internal climate variability is here estimated by adding samples from the preindustrial Control simulations (of the same length) to the noise-reduced fingerprints and observations, and recomputing the TLS regression (10,000 times) in order to build a distribution of scaling factors, from which the 5th−95th percentile range can be computed. We have also explored confidence intervals based on bootstrapping (DelSole et al., 2019), and while there are slight differences in the spread, the two measures generally provide consistent and robust agreement.

CMIP6 model simulations (Eyring et al., 2016) run with historical forcings, and Detection and Attribution MIP (DAMIP) single-forcing simulations (Gillett et al., 2016) are used over the same period as E-OBS (1950–2014) to determine the fingerprints. Our analysis uses a set of nine models with 33 total ensemble members (Table 1), that were available in the Center for Environmental Data Analysis (CEDA) curated archive (retrieved in September 2020), common to the required set of simulations. For application of the ASK method, single forcing experiments are needed. Monthly surface air temperature fields from the observations and each of the CMIP6 model ensemble members were spatially regridded to a regular 2.5° × 2.5° latitude-longitude grid, with only the grid boxes over land (with no missing data throughout time) being retained in the analysis. The resulting masked fields (from observations and all individual model ensemble members) were spatially averaged over a European domain (EUR) and three sub-domains (NEU, CEU, and MED; as described in Brunner et al., 2020a). Fingerprints for each forcing are based on an unweighted, and in the example below (section Contrasting and Combining Constraints From Different Methodologies), weighted, average of each model's ensemble mean response to individual forcings. The total least squares approach requires an estimate of the signal-to-noise ratio of the fingerprint. This is calculated considering the noise reduction by averaging individual model ensemble averages, and assuming that the resulting variance adds in quadrature when averaging across ensembles. When weights are used, these are included in the calculation. Results from ASK are illustrated in Figure 2, again illustrating that the method reduces spread in some cases, and influences central tendency as well.

TABLE 1

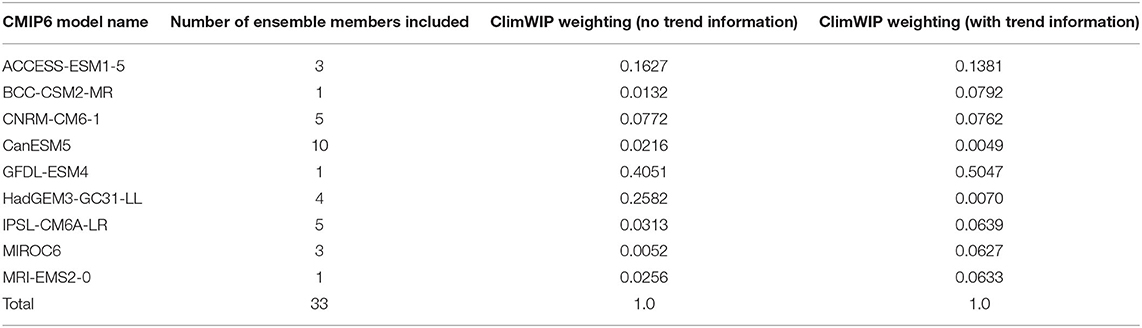
Table 1. List of the CMIP6 models used in the ASK-ClimWIP constraining intercomparison pilot study (restricting to models with individual forcing simulations available and normalizing weights to sum to unity for these relative to those shown in Figure 3).

Whether this reduction in spread improves the reliability of projections is still uncertain, although some recent analysis supports these approaches: Gillett et al. (2021) applied an (im-) perfect model approach to estimate the attributable warming to CMIP6 models, and Schurer et al. (2018) an approach to estimate the transient climate sensitivity from individual simulations with withheld climate models for CMIP5. Gillett et al. (2021) found high reliability of the estimate of attributable warming, which increases confidence in its use for projections. Schurer et al. (2018) found that the method was somewhat overconfident for future warming if using the multi-model mean fingerprint, but conservative if accounting fully for model uncertainty in a Bayesian approach, or if inflating residual variability.

Contrasting and Combining Constraints From Different Methodologies

Eight different methods to arrive at weighted or constrained climate projections were recently compared for European regions in Brunner et al. (2020a). The study identified a lack of coordination across methods as a main obstacle for comparison since even studies which look at the same region in general might report results for slightly different domains, seasons, time periods or model subsets hindering a consistent comparison. Therefore, a common framework was developed to allow such a comparison between the different methods, including a set of European sub-regions. The results in Brunner et al. (2020a) focus on temperature and precipitation changes between 1995–2014 and 2041–2060 under RCP8.5 (i.e., using CMIP5) in the three European SREX regions. In addition, reasons for agreements and disagreements across these methods were also discussed.

Figure 2 shows some results of the comparison illustrated in that review (for a detailed discussion of the results and the underlying methods see Brunner et al., 2020a). While all methods clearly show the anthropogenic warming signal, the comparison reveals different levels of agreement based on the region considered and the metric of interest (e.g., median vs. 80% range). In general, methods tend to agree better on the central estimate while uncertainty ranges can be fairly different, particularly for the more extreme percentiles (see, e.g., Figure 2D). However, for some regions also the median values can differ across methods and in isolated cases methods even disagree on the direction of the shift from the unconstrained distributions. Methods also constrain projections to different extents, with some methods leading to stronger constraints and others to weaker constraints. This can be due to using observations more or less completely and efficiently, but can also reflect differences in the underlying assumptions of the methods such as the statistical paradigm used. Some methods assume the models are exchangeable realization of the true observed response, while others assume that the models converge, as a sample, toward the truth, ranking models close to the model average as more likely to be correct.

For cases with such substantial differences, Brunner et al. (2020a) recommend careful evaluation of constraints projecting the future change in a withheld model based on each method. Full application of such withheld model approaches requires withholding a large number of simulations to ensure robust statistics, and is computationally expensive. Such work is ongoing in the community and will help resolve uncertainty across performance metrics. Brunner et al., also suggest attempting to merge methods, either based on their lines of evidence (before applying them) or based on their results (after applying them).

Here we pilot an example of combining two observational constraint methods. We do this to both illustrate what aspects of observed climate change influence performance metrics, and in order to test if a combined approach might harness the strengths of each paradigm. Results also illustrate the challenges and limitations involved in such an endeavor.

In order to do so, we limit the constraint used in ClimWIP to climatology and variance-based performance weights only. These can then be used to construct a weighted fingerprint (mentioned above) of the forced climate change that could be, arguably, more credible as a best estimate of the expected change than the simple one-model-one vote fingerprint generally used. It is also conceivable to combine both differently, e.g., by using the ASK constraint relative to a model's raw projection as weight in a ClimWIP weighted prediction. We chose the weighted ASK method for its ability to project changes outside the model range in cases where models over- or underestimate the actual climate change signal, but different choices are possible.

We use two different combinations of diagnostics to calculate the ClimWIP performance weights for this combination of constraints: one including temperature trends, and one without temperature trends (i.e., using only climatology and variability of temperature and sea level pressure). This is done to avoid accounting for trends twice when applying the constraints subsequently (Table 1), since the ASK method is strongly driven by temperature trends (while using also spatial information and the shape of the time series particularly to distinguish between the effects of different forcing and variability). Note that this modification of ClimWIP will most likely reduce its performance as a constraint on its own.

The weights assigned to each of the 33 CMIP6 models (and the nine DAMIP models used in the ASK method) are shown in Figure 3, both when using all five diagnostics, and when not using the temperature trend. Results show that the performance weights from trends show a substantial influence on ClimWIP weights compared to the variant without trends, with largest differences for models with unusually strong trends, such as HadGEM3, which is almost disregarded in trend-based weighting but performs well on climatology. In contrast, trend information enhances the perceived value of a group of other models in the bottom left corner of the diagram, with very small weights in climatology-only cases compared to slightly larger ones in trend including cases. However, for many other models both metrics correlate (although their correlation is largely driven by a few highly weighted models). This illustrates that different information used can pull observational constraints in different directions.

FIGURE 3

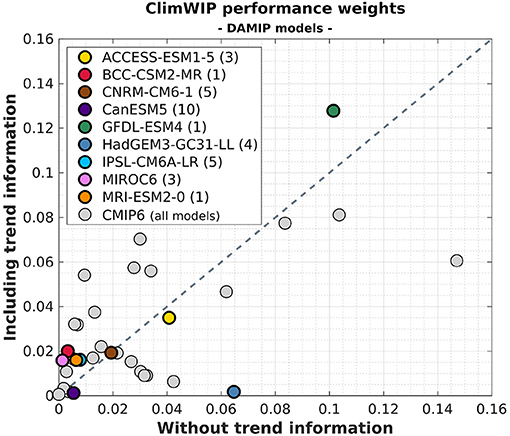
Figure 3. Role of temperature trends in model performance weights, illustrating the relationship between the model-specific relative weights assigned by ClimWIP, computed using global fields excluding temperature trend information (along the x-axis), and including a temperature trend metric (along the y-axis). Climate models across CMIP6 are shown in gray; those also available in the DAMIP simulations (used in the ASK method) have been colored, with the number of ensemble members (n) shown in the legend.

There are suggestions that the role of trends in downweighting projections of higher end warming in both ClimWIP and ASK may be common across the wider set of projection methodologies. Historical trends in the UKCP18 methodology (Figure 1, labeled SAT) tend to reduce the upper tails of projected changes. Similarly, the HistC methodology (Brunner et al., 2020a section) is largely based on trend information, which also consistently downweights high end projected changes (Ribes et al., 2021), in response to too large change in such models over parts of the historical period.

We now use model performance weighting in constructing each of the multi-model mean fingerprints (Figure 4) that are subsequently used in the detection and attribution constraint. Thus, two sets of multi-model mean fingerprints are computed. Firstly, an equal-weighted set of multi-model fingerprints and, for comparison, a second set of multi-model fingerprints are computed as weighted average of each model's individual fingerprint in response to forcings. When combining the constraints in this way, we use the ClimWIP performance weights that were derived without temperature trend information (Table 1).

FIGURE 4

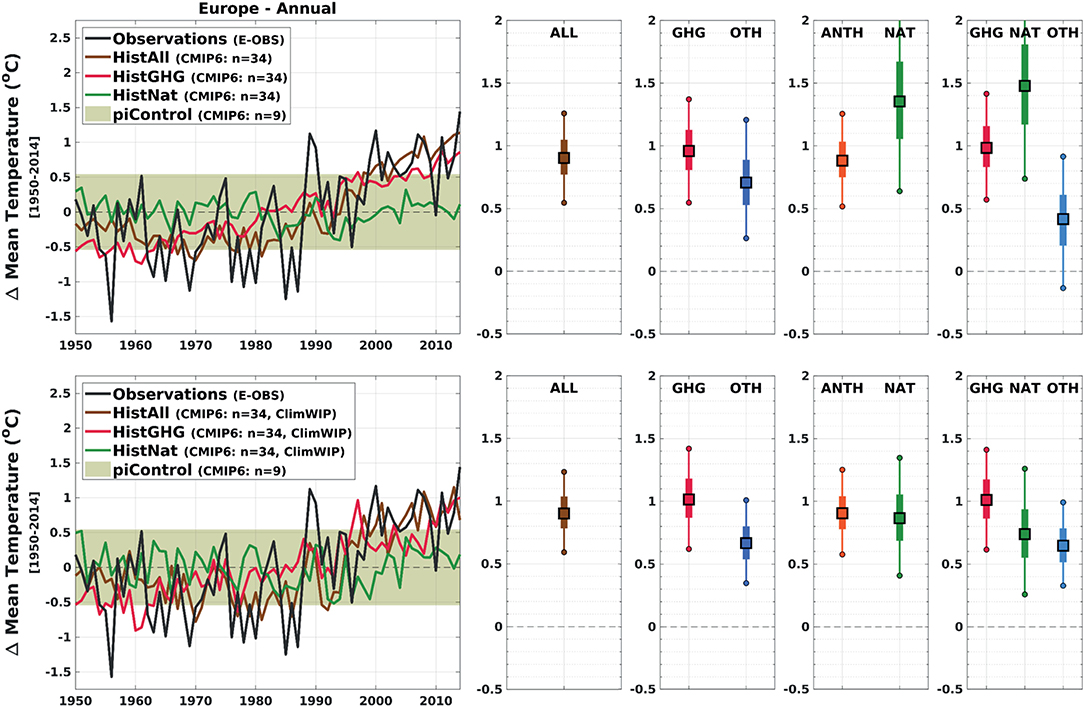
Figure 4. Annual time series (left panels) of European surface air temperature anomalies (relative to 1950–2014) from observations (E-OBS v19, black line) and CMIP6 historical simulations (all forcings, brown line; GHG-only forcing, red line; and NAT-only forcing, green line). We display the multi-model mean of ensemble means from nine models, with the shaded region denoting the multi-model mean variability (±1 standard deviation) of the associated preindustrial Control simulations. The scaling factors (right panels) are derived by regression of the CMIP6 model fingerprints on the observations and indicate to what extent the multi-model mean fingerprint needs to be scaled to best match observations. Results show the 1-signal (ALL), two-signal (GHG & OTH; ANTH & NAT), and three-signal (GHG, NAT & OTH) scaling factors. The upper panels display the time-series fingerprints and associated scaling factors using an equal-weighted multi-model mean; the lower panels use ClimWIP performance weighting to weight the multi-model mean fingerprints for deriving the scaling factors. Confidence intervals show the 5th−95th (thin bars) and 25th−75th (thicker bars) percentile ranges of the resulting scaling factors.

Annual surface temperature anomalies from 1950 to 2014 averaged over nine models (33 runs) are displayed in Figure 4 with the upper left panel showing the equal-weighted time series, and the lower left panel showing the time series after applying the ClimWIP weights (without trend). The same observed annual time series (E-OBS, black line) has been plotted in each panel, along with the CMIP6 multi-model mean (of ensemble means) of the all-forcing historical simulations (brown line), the greenhouse gas single-forcing historical simulations (red line), and the natural single-forcing historical simulations (green line). A measure of the internal variability of the CMIP6 models is estimated by averaging the standard deviation (65-years samples) of the associated piControl simulations, and is indicated by the background shaded region.

The scaling factors were derived through a total least squares regression of the multi-model mean fingerprints onto the observations, estimating the amplitude of a single-fingerprint all forcing signal (“ALL”), and determining the separate amplitudes for combinations of fingerprints (for more details, see Brunner et al., 2020a; Ballinger et al., pers. com.; GHG, OTH, ANT, NAT). The scaling factors shown in Figure 4 were derived using fingerprints comprising the conjoined annual time series of the three spatially-averaged European subregions (NEU, CEU, and MED; 3 × 65 = 195 years), each having first been normalized by a measure of that subregion's internal variability (using the standard deviation of equivalent piControl simulations). Hence the fingerprint used captures an element of the spatial signal in the three regions, and of their temporal evolution. The analysis was also performed using a single European average fingerprint, and separate single-subregion fingerprints (NEU/CEU/MED; not shown). As expected, the three-region fingerprint generally provides a tighter constraint because of the additional (spatial) information included, which strengthens the signal to noise ratio. However, the qualitative differences of using an equal-weighted or ClimWIP-weighted fingerprint, are found to be fairly robust irrespective of the particular fingerprint formulation.

Figure 4 shows an overall narrowing of the uncertainty range in the scaling factors (providing a slightly tighter constraint) when using the ClimWIP-weighted model fingerprints, particularly for NAT, suggesting that at least in this case, the weighted fingerprints are more successful in identifying and separating responses to greenhouse gases from those to other forcings. The best-estimate magnitudes of the leading signal (ALL, GHG, ANTH) scaling factors remain reasonably robust. Results suggest that the weighted multi-model mean response to aerosols is larger than that in the observations, significantly so in the weighted case. Overall, the illustrated sensitivity of the estimated amplitude of natural and aerosol response probably reflects model differences in emphasis between ClimWIP weighted and unweighted cases.

We have further explored the robustness of results over different seasons (not shown). Results again suggest that the use of ClimWIP weights in the multi-model mean fingerprint yields stronger constraints when separating out the greenhouse gas signal (which is particularly useful for constraints). Also, the contribution by natural forcing, other anthropogenic and greenhouse gas forcing to winter temperature change is far less degenerate in the ClimWIP constrained case, although it needs to be better understood why this is the case. This illustrates some promise in combining constraints.

However, in order to evaluate if these narrowed uncertainty estimates reliably translate into better prediction skill, careful “perfect” and “imperfect” model studies will need to be performed, where single model simulations are withheld to predict their future evolution as a performance test, calculating performance weights relative to each withheld model (see e.g., Bo and Terray, 2015; Schurer et al., 2018; Brunner et al., 2020b). When doing so, it would be useful to consider forecast evaluation terminology used in predictions and to assess reliability (i.e., if model simulations that are synthetically predicted are within the uncertainty range of the prediction, given the statistical expectation; Schurer et al., 2018; Gillett et al., 2021), and if they show improved sharpness, i.e., their RMS error is smaller in order to avoid penalizing more confident methods unnecessarily). Another avenue is to draw perfect models from a different generation as explored, e.g., by Brunner et al. (2020b) where the skill of weighting CMIP6 was explored based on models from CMIP5 in order to provide an out-of-sample test to the extent that CMIP6 can be considered independent of CMIP5. A first pilot study using CMIP6 simulations to hindcast single CMIP5 simulations showed mixed results and no consistent preference for the ClimWIP vs. ASK vs. combined method in either metric (not shown; Ballinger et al., pers. com.).

In summary, there is an indication that the use of model weighting can potentially provide improved constraints on projections, fundamentally due to using fingerprints that rely strongly on the most successful models. Europe as a target of reconstruction might be particularly tricky given high variability over a small continent, rendering more noisy fingerprints from weighted averages compared to straight multi-model averages, which can reduce the benefit in weighting approaches (Weigel et al., 2010).

However, climate variability can be considered as more than just “noise” in near term predictions, and hence the next method focuses on constraints for variability.

Toward Seamless Predictions: Constraining Large Projection Ensembles to Match Recent Observed Variability

Above, observations were employed to evaluate projections in terms of processes, trends and climatology. Climate variability is considered in those previous analyses a random uncertainty that is separate from projections and adds uncertainty. This is in sharp contrast to initialized predictions, where one of the goals is to predict modes of variability. The forced signal is included in predictions, but skill initially originates largely from the initial condition and phasing in modes of climate variability. Observations are employed both to initialize the prediction and then to evaluate the hindcast.

In this section we illustrate the use of observations to align climate model projections with observed variability. The aim is to obtain improved information for predicting the climate of the following seasons and years, and to evaluate how such selected projections merge with the full ensemble as a case example for merging predictions and projections, as recommended in Befort et al. (2020). Sub-selecting ensemble members from a large ensemble that more closely resemble the observed climate state (e.g., Ding et al., 2018; Shin et al., 2020), is an attempt to try to align the internal climate variability of the sub-selected ensemble with the observed climate variability, similar to initialized climate prediction. We therefore also refer to these constraints relative to the observed anomalies as “pseudo-initialisation.”

We use the Community Earth System Model (CESM) Large Ensemble (LENS; Kay et al., 2015) of historical climate simulations, extended with the RCP8.5 scenario after 2005. For each year (from 1961 to 2008) we select 10 ensemble members that most closely resemble the observed state of global SST anomaly patterns, as measured by pattern correlations. We then evaluate the skill of the sub-selected constrained ensembles in predicting the observed climate in the following months, years and decade, using anomaly correlation coefficient (ACC; Jolliffe and Stephenson, 2003). We also compare the skill of “un-initialised” (LENS40, the ensemble of all 40 LENS simulations) and “pseudo-initialised” (LENS10, the ensemble of the best 10 ensemble members identified in each year) simulations against “initialised” decadal predictions with the CESM Decadal Prediction Large Ensemble consisting of 40 initialized ensemble members (DPLE40; Yeager et al., 2018). The ocean and sea-ice initial conditions for DPLE40 are taken from an ocean/sea ice reconstruction forced by observation-based atmospheric fields from the Coordinated Ocean-Ice Reference Experiment forcing data, and the atmospheric initial conditions taken from LENS simulations. The anomalies are calculated based on lead-time dependent climatologies.

In this explorational study, the best 10 members of the LENS simulations are selected based on their pattern correlation of global SST anomalies with observed anomalies obtained from the Met Office Hadley Center's sea ice and sea surface temperature data (HadISST; Rayner et al., 2003). These pattern correlations are calculated using the average anomalies of the 5 months prior to 1st November of each year, for consistency of the ‘pseudo-initialisation' with the initialized predictions (i.e., DPLE40), which are also initialized on 1st November of each year. We also tested ensemble selection based on the pattern correlation of different time periods (up to 10 years) prior to the 1st November initialization date, to better phase in low-frequency variability, but these tests did not provide clearly improved skill over the 5-months selection.

Figure 5 compares the skill of different SST indices for the constrained pseudo-initialized ensemble (i.e., LENS10), the full LENS40, and the initialized prediction system. All three ensembles show very high skill (R > 0.9) in predicting global mean SSTs on inter-annual to decadal time-scales, primarily due to capturing the warming trend. For the first few months after initialization the constrained LENS10 ensemble shows skill that is comparable to the DPLE40 for global mean SSTs. Larger differences in the prediction skill between the three ensembles are apparent for indices of Pacific (El Nino Southern Oscillation, ENSO, and Interdecadal Pacific Oscillation, IPO) and Atlantic SST variability (Atlantic Multidecadal Variability, AMV). The constrained LENS10 ensemble shows significant skill in predicting the ENSO and IPO indices in the first ~6–7 months after initialization, with correlations only about ~0.1 lower compared to the initialized DPLE40 ensemble. LENS10 further shows improved skill over LENS40 during the first 2 forecast years for ENSO and IPO. For the AMV index, LENS10 shows increased skill over LENS40 for up to seven forecast years, while DPLE40 shows high skill (R > 0.7) for all forecast times up to one decade.

FIGURE 5

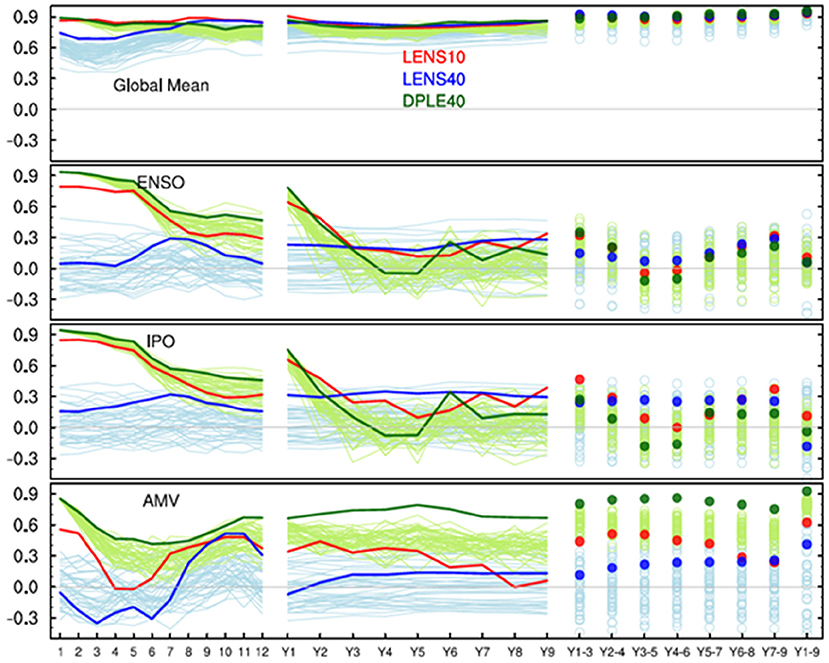
Figure 5. Correlation skill for different forecast times: left lines represent skill for first 12 forecast months; center lines represent skill for first nine forecast years; dots represent skill for multi-annual mean forecasts. IPO is calculated as a tripole index (Henley et al., 2015) from SST anomalies, ENSO is based on area-weighted mean of SST anomalies at Nino3.4 region (i.e., 5°S−5°N, 170°W−120°W), and AMV is calculated as a weighted area average SST anomalies for 0–60°N of the North Atlantic ocean with global mean (60°S−60°N) SST removed.

Figure 6 shows that the spatial distribution of forecast skill of the LENS10 ensemble is often comparable to that of the DPLE40 for seasonal and annual mean forecasts. The skill of LENS40 is relatively lower than both the pseudo-initialized and the initialized predictions at least for the first few forecast months and the first forecast year. On longer time scales, LENS10 has some added skill in the North Atlantic, but decreased skill in other regions such as parts of the Pacific.

FIGURE 6

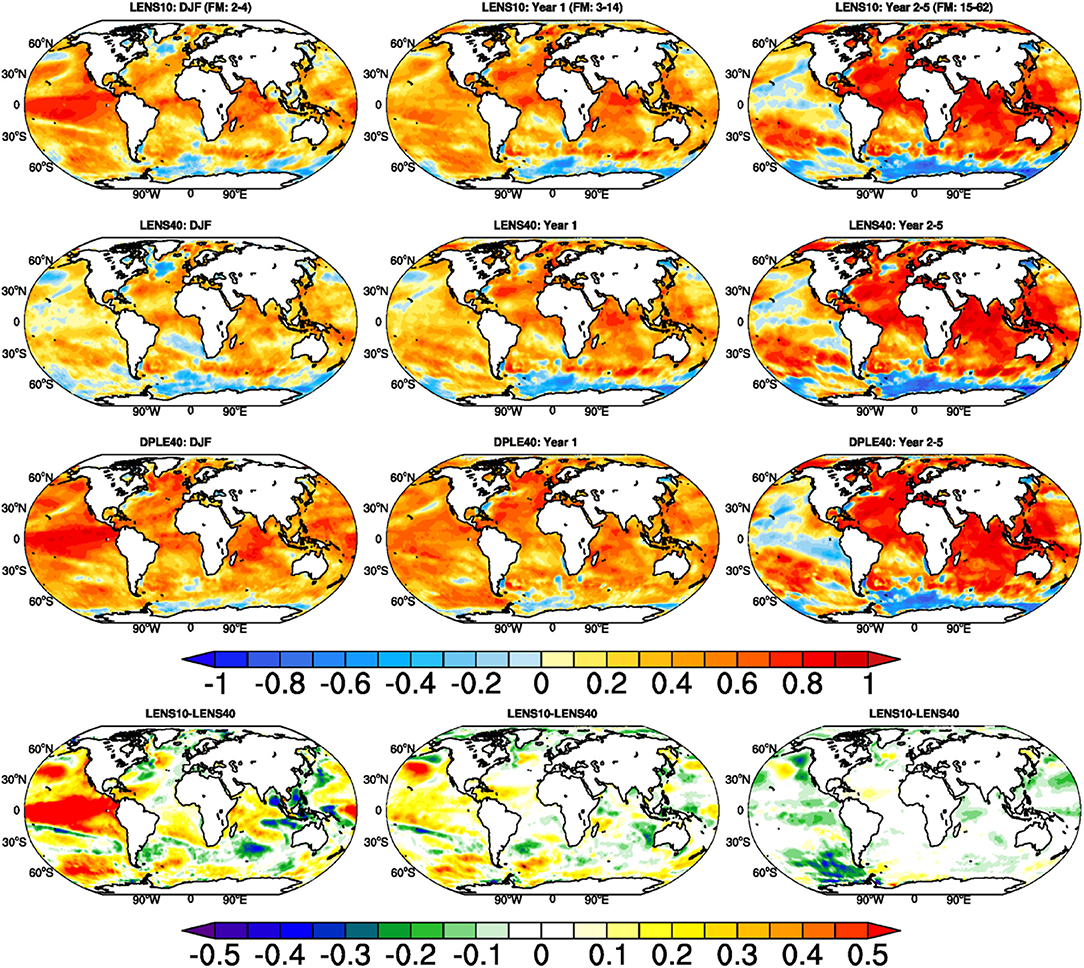
Figure 6. Forecast skill, measured as anomaly correlation against HadISST, for LENS10 (top row), LENS40 (second row), DPLE40 (third row), and skill difference between LENS10 and LENS40 (bottom row). Left, center and right columns represent forecast skill of the mean of forecast months 2–4, forecast months 3–14, and forecast months 15–62, respectively.

These analyses demonstrate the value of constraining large ensembles of climate simulations according to the phases of observed variability for predictions of the real-world climate. We find added value in comparison to the large (un-constrained) ensemble for up to 7 years in the Atlantic, and up to 2 years in indices of Pacific variability. It illustrates that using observational constraints by targeting modes of climate variability can produce skill that can approach that from initialization in some cases for large scale variability. Figure 6 also illustrates that this skill is most pronounced in the first season in tropical regions and the Pacific, while added skill in near-term projections over the North Atlantic is more modest which could be related to weaker-than-observed variability in simulating North Atlantic Oscillation in LENS simulations (Kim et al., 2018). This work bridges between un-initialized and initialized predictions and their evaluation with observations, and illustrates how observational constraints can be used within a large ensemble of a single model to improve performance nearterm. The latter is the goal of initialized predictions, which we focus on in the subsequent sections.

Observational Constraints on Initialized Predictions

In this section, several examples of observational constraints in initialized decadal climate prediction simulations are presented and tested for their potential. These examples include: identifying the level of agreement between model simulations and observations (predictive skill) that arises from the initialization process as well as different forcings of the climate system over time; identifying the predictive skill found in different initialized model systems using the models' inherent characteristics; and identifying the change of predictive skill over time, illustrated using predictions of North Atlantic sea surface temperature (SST). As with observational constraints for projections, we explore if there is potential to improve predictions by weighting or selecting prediction systems and chosen time horizons with the goal to improve performance.

We thus test decadal prediction experiments for observational constraints on the time dimension (exploring the changing importance of various forcings and internal variability over time) and the model dimension (a first step toward weighing initialized climate prediction ensembles). These analyses are both closely related to the approaches used for climate projections discussed above, and they will offer an indication about the degree to which the observational constraints that are applied to projections (see above) represent observed climatic variability. All of these explorational investigations will also pave the way toward eventually combining initialized and non-initialized climate predictions in order to tailor near-term climate prediction to individual users' needs.

The analyses we present rely on the following methods: We consider sea surface temperature (SST) and surface air temperature (SAT) for the period 1960–2014 in our analyses, based on simulations from the CMIP6 archive. We analyze initialized decadal hindcasts from the DCPP project (HC; Boer et al., 2016), as well as non-initialized historical simulations that are driven with reconstructed external forcing (HIST; Eyring et al., 2016). For comparison and to constrain predictions, SST from HadISST (Rayner et al., 2003) and SAT from the HadCRUTv4 gridded observational data set (Morice et al., 2012) are used. Agreement between model simulations and observations (prediction or hindcast skill) is quantified here as Pearson correlation between ensemble mean simulations and observations (Anomaly Correlation Coefficient, ACC) and mean squared skill score (MSSS; Smith et al., 2020). ACC tests whether a linear relationship exists between prediction and observation and quantifies the standardized variance explained by it (in its square), whereas MSSS quantifies the absolute difference between simulations and observations. Both ACC and MSSS indicate perfect agreement between prediction and observation at a value of 1 and decreasing agreement at decreasing values. Note that we do not compare these skill scores against a baseline (e.g., the uninitialized historical simulations); this was done and discussed extensively in Borchert et al. (2021). Instead much of our analysis focuses on detrended data to reduce the influence of anthropogenic forcing.

In all cases, anomalies against the mean state over the period 1970–2005 of the respective data set are formed; this equates to a lead time dependent mean bias correction in initialized hindcasts. We also subtract the linear trend from all time series prior to skill calculation to avoid the impact of linear trends on the results. When focusing on the example of temperature in the subpolar gyre (SPG), we analyze area-weighted average SST in the region 45–60°N, 10–50°W. Surface temperature over Europe is represented by land grid-points in the NEU, CEU and MED SREX regions defined above. We examine summer (JJA) temperature over Europe. We also analyze how prediction skill changes over time (so-called windows of opportunity; Borchert et al., 2019; Christensen et al., 2020; Mariotti et al., 2020) to attribute changes in skill to specific climatic phases.

Sources of Decadal Prediction Skill for North Atlantic SST

A recent paper detailed the influence of external forcing and internal variability on North Atlantic subpolar gyre region (SPG) SST variations and predictions (Borchert et al., 2021). The authors found North Atlantic SST to be significantly better predicted by CMIP6 models than by CMIP5 models, both in non-initialized historical simulations and initialized hindcasts. These findings indicated a larger role for forcing in influencing predictions of North Atlantic SST than previously thought. This work further showed that at times of strong forcing, predictions and projections of North Atlantic SST with CMIP6 multi-model averages exhibit high skill for predicting North Atlantic SST. Natural forcing, particularly major volcanic eruptions (Swingedouw et al., 2013; Hermanson et al., 2020; Borchert et al., 2021), plays a prominent role in influencing skill during the historical period, notably due to their impact on decadal variations of the oceanic circulation (e.g., Swingedouw et al., 2015). In the absence of strong forcing trends, initialization is needed to generate skill in decadal predictions of North Atlantic SST (Borchert et al., 2021; their Figure 2). Analyzing the contributions of forcing and internal variability to climate variations and their prediction is therefore an important step toward understanding observational constraints on initialized climate predictions. By examining the dominant factors governing the skill of predictions in the past, conclusions may be drawn for predictions of the future as well. This also illustrates that metrics for initialized model performance based on evaluating hindcasts are influenced not only by how well the method reproduces observed variability, but also by the response to forcing. Hence sources of skill in predictions (initialization) and projections (forcing) overlap, which is important to consider when comparing the role of observational constraints in both. This also needs to be considered when aiming to merge predictions and projections, which are driven by forcing only, and generally do not include volcanic forcing.

Toward Performance Based Weighting for Initialized Predictions

Approaches discussed above, which identify the origin of skill among different external forcings and variability, could be seen as an observational constraint on predictions (section Sources of Decadal Prediction Skill for North Atlantic SST), constraining them based on the emerging importance of forcing and internal variability over time. This makes that technique similar to that used in ASK constraints (which, however, focuses on a different timescale). We now consider an approach similar to model-related weights used in the ClimWIP method. Instead of multi-model means, we here assess the seven individual CMIP6 DCPP decadal prediction systems (Table 2) with the aim of linking the skill in model systems to their inherent properties. We focus this analysis on North Atlantic subpolar gyre SST due to its high predictability (e.g., Marotzke et al., 2016; Brune and Baehr, 2020; Borchert et al., 2021) as well as its previously demonstrated ties to European summer SAT (Gastineau and Frankignoul, 2015; Mecking et al., 2019).

TABLE 2

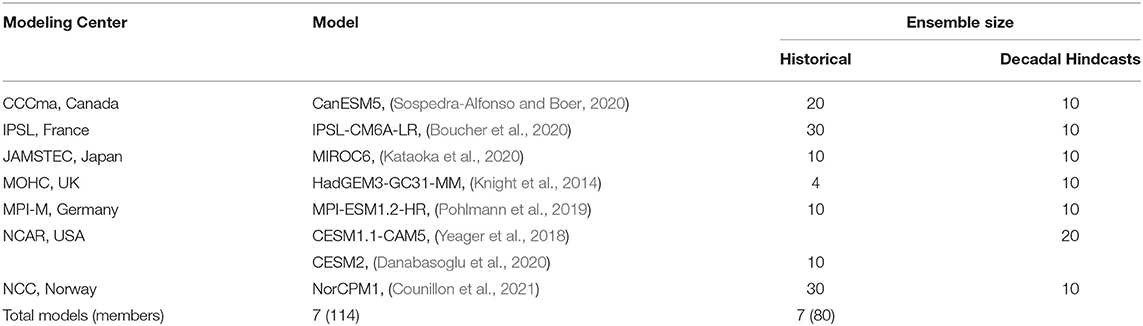
Table 2. Models used in the analysis presented in Section Observational Constraints on Initialized Predictions, based on availability at the time of analysis.

Initialized predictions from CMIP6 show broad agreement on ACC skill for SPG SST, with high initial skill and skill degradation over time (Figure 7A). The only prominent outlier to this is the CanESM5 model, which displays a strong initialization shock until approximately lead year 7 due to issues in the North Atlantic region with the direct initialization from the ORAS5 ocean reanalysis (Sospedra-Alfonso and Boer, 2020; Tietsche et al., 2020). For this reason, we will discuss CanESM5 as a special case whenever appropriate. The other six models generally agree on high skill in the initial years, which degrades over lead time (Figure 7), showing some degree of spread in ACC that could be linked to model or prediction system properties. This spread is found for both ACC (Figure 7A) and MSSS (Figure 7B), indicating the robustness of this result. Forming multi-model means results in comparatively high skill compared to individual models, evident in placement of the multi-model mean (black) at the upper half of ACC and MSSS skills. This is likely related to an improved filtering of the predictable signal from the noise (e.g., Smith et al., 2020), and the compensation of model errors between the systems; suggesting potential for further increased skill if using a weighted rather than simple average multimodel means. Skill degradation occurs at different rates in the different model systems, representing a possible angle at which to try and explain the skill differences.

FIGURE 7

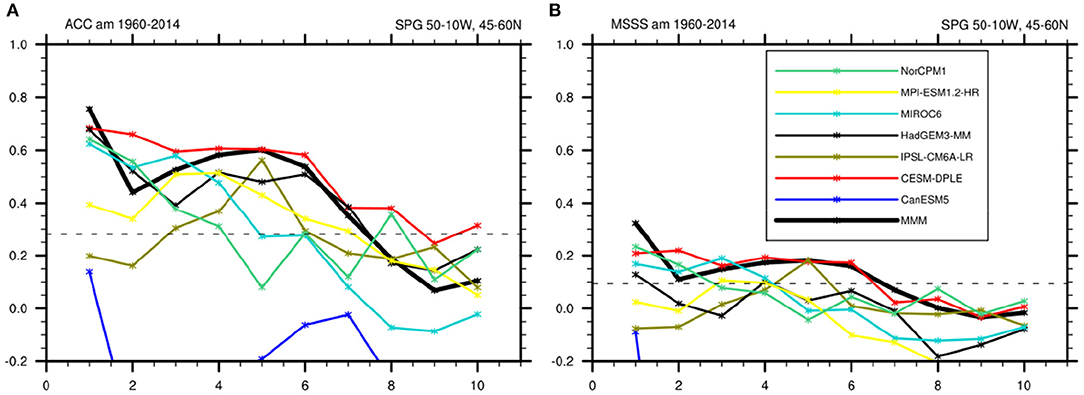
Figure 7. (A) Anomaly correlation coefficient (ACC) for SPG SST in seven initialized CMIP6 model systems (y-axis) against lead time in years (x-axis). (B) as (A), but showing mean squared skill score (MSSS) on the y-axis. Colors indicate the individual models, the thick black line the multi-model mean. The horizontal dashed line indicates the 95% confidence level compared to climatology based on a two-sided t-test.

Constraint Based on SPG Stratification

Sgubin et al. (2017) showed that the representation of stratification over the recent period in the upper 2,000 m of the North Atlantic subpolar gyre in different models is a promising constraint on climate projections, impacting among other things the likelihood with which a sudden AMOC collapse is projected to happen in the future. Ocean stratification impacts North Atlantic climate variability not only on multidecadal time scales, but also locally on the (sub-)decadal time scale. It appears therefore appropriate to explore stratification as an observational constraint on the model dimension in predictions, and test whether models that show comparatively realistic SPG stratification also show higher SPG SST prediction skill and vice versa. To this end, we calculate a stratification indicator as in Sgubin et al. (2017) by integrating SPG density from the surface to 2,000 m depth for the period 1985–2014 in the different CMIP6 HIST models and EN4 reanalysis (Ingleby and Huddleston, 2007). We then calculate the root-mean square difference between modeled and observed stratification (as in²). This index is then examined for a possible linear relationship to SPG SST prediction skill. Note that comparing stratification in the historical simulations to initialized predictions is not necessarily straight-forward as initialization may change the stratification.

For short lead times of up to 5 years, we find a strong, negative and linear relationship between SPG SST prediction skill in terms of ACC and MSSS in the seven prediction systems analyzed here, and mean SPG stratification bias in the corresponding historical simulation (Figures 8A–C). Models that simulate a more realistic SPG stratification show higher SST prediction skill than those that simulate less realistic stratification. At lead times longer than 6 years, this linear relationship is not as strong (Figure 8C), which also diminishes the skill-stratification relationship for the full 1–10 years lead time range (Figure 8A). Note that due to the initialization issue in CanESM5 discussed above, that model does not behave in line with the other models at short lead times.

FIGURE 8

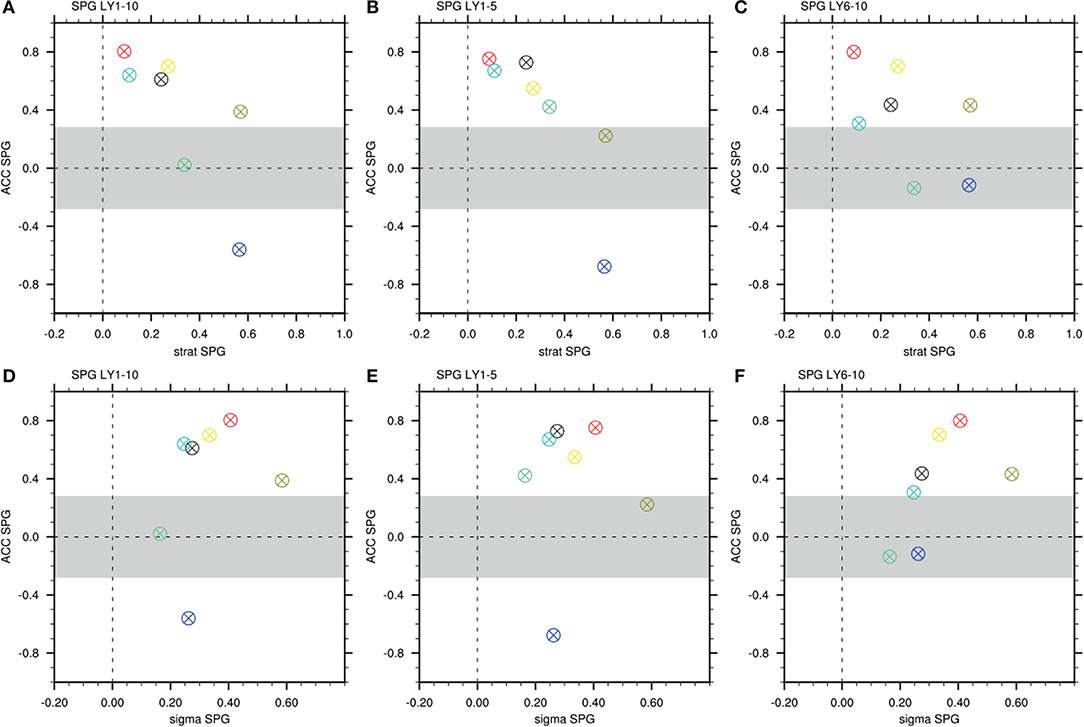
Figure 8. ACC for SPG SST in seven initialized CMIP6 model systems at lead years (A) 1–10, (B) 1–5, and (C) 6–10 against RMSE between observed (vertical dashed line) and simulated SPG stratification in the period 1960–2014 from the corresponding historical simulations (x-axis). (D–F) as (A–C), but showing the standard deviation of SPG SST in the first 500 years of the respective model's piControl simulation on the x-axis. Colors indicate the individual models: blue = CanESM5, red = CESM-DPLE, brown = IPSL-CM6A-LR, black = HadGEM3-GC31-MM, cyan = MIROC6, yellow = MPI-ESM1.2-HR, green = NorCPM1. The gray area indicates insignificant prediction skill at the 5% significance level based on 1,000 bootstraps.

These findings show that models that simulate a more realistic SPG stratification tend to predict SPG surface temperature for up to 5 years into the future more skillfully than models with a less realistic SPG stratification. The fact that mean stratification in the historical simulation seems to have an influence on the skill of initialized predictions at short lead time (although initialization has modified mean stratification) suggests that the modification of stratification through initialization is weak. Moreover, this finding hints at a reduced initialization-related shock in some models: models that simulate realistic SPG stratification without initialization experience less shock through initialization, while the shock itself may hamper the skill at long lead time. The role of physical realism of climatology vs. initialization shock should be explored further when analyzing performance of and constraints on prediction systems. While inspiring hope that SPG mean stratification state might be an accurate indicator of SPG SST hindcast skill, this result is based on a regression over 6 data points and therefore lacks robustness.

Constraint Based on Internal Climate Variability

The amount of climate variability inherently produced by the models might also relate to the skill of prediction systems. The assumption is that models that produce pronounced SPG SST variability by themselves reproduce strong observed decadal SPG SST changes more accurately than those that do not. This is a reasonable assumption since previous studies have shown that North Atlantic SST variability appears to be underestimated in climate models (Murphy et al., 2017; Kim et al., 2018). We represent this variability by standard deviation of SPG SST over 500 years in the pre-industrial control (piC) simulations of the seven different CMIP6 models (sigma SPG). Decadal SPG SST hindcast skill shows some increase with sigma SPG in the respective control simulations (Figures 8D–F), particularly at long lead time (Figure 8F). A possible cause for increased skill in models with higher sigma is a linear relationship of sigma SPG to the time lag at which autocorrelation becomes insignificant in the piControl simulations (not shown): higher variability implies longer decorrelation time scales which might indeed lead to longer predictability. Another hypothesis could be more robust variability produced by models with higher sigma, less perturbed by noise, associated with higher levels of variability. More work is needed to decipher the exact cause of this effect. The linear correlation between sigma SPG and SPG hindcast skill, however, is not robust across lead times. At long lead time of 6–10 years, the CanESM and IPSL models are outliers that potentially inhibit significant linear regression, due to the known initialization issue in CanESM (see above) and possible effect of the weak initialization in IPSL-CM6A (Estella-Perez et al., 2020). Again, this analysis is limited by the small number of models for which decadal hindcast simulations are currently available. Adding more models to this analysis could point toward other conclusions, or strengthen the results presented here. Additionally, extending this analysis to other regions in the piControl simulations (as in Menary and Hermanson, 2018) would provide valuable insights into the way that the representation of underlying dynamics in different models preconditions their skill for prediction of the SPG SST.

Other possible discriminant factors for decadal SPG SST prediction skill, such as equilibrium climate sensitivity (ECS), model initialization strategy (e.g., Smith et al., 2013) and resolution of the ocean model in the respective model have been investigated, but with no firm conclusions at this point.

Multi-Model Exploration of Windows of Opportunity

Analyses presented above analyze prediction skill for the period 1960–2014 as a whole, i.e., operate under the assumption that predictive skill is constant over time. In the North Atlantic region, however, the skill of decadal predictions was previously shown to change over time, forming windows of opportunity, with possible implications for the constraints discussed above. Here, we examine the model-dependency of windows of opportunity for decadal SPG SST prediction skill as a call for caution when applying observational constraints to predictions and projections.

Windows of opportunity for annual mean North Atlantic SPG SST across all models are presented for a lead time average over years 1–10 in Figure 9. These lead time averages bring out more skill due to temporal filtering of the time series, which is achieved by averaging all 10 predicted years that are predicted from a certain start year. The analysis of windows of opportunity enables an identification of model differences of prediction skill across time.

FIGURE 9

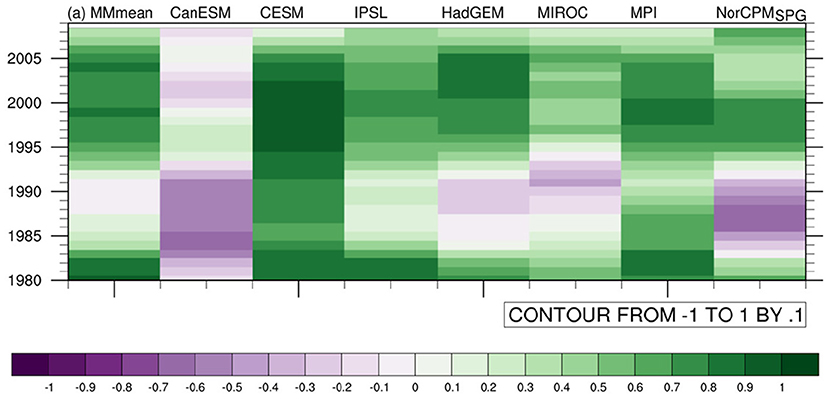
Figure 9. Decadal ACC hindcast skill for detrended annual mean North Atlantic subpolar gyre SST for a sliding 20-years long window (the end year of which is shown on the y-axis) across multi-model mean and individual model means (x-axis). Colors indicate ACC (low to high = purple to green).

We find that there is general agreement among models on the approximate timing of windows of opportunity for SPG skill, where the general level of skill depends on the models' mean performance (Figures 7, 8). Skill is high early and late in the analyzed time horizon, with a “skill hole” around the 1970s and 80s. These windows have been noted in earlier studies (e.g., Christensen et al., 2020), and interpreted by Borchert et al. (2018) to result from changes in oceanic heat transport. Since all examined models agree on this timing, it could be argued that windows of opportunity arise from the predictability of the climate system rather than the performance of individual climate models over time. This limits the applicability of observational constraints at times of low skill. Windows of opportunity should therefore be taken into account in observational constraints. While times of low skill appear to coincide with times of low trends for North Atlantic SST (e.g., Borchert et al., 2019; 2021), they are possibly caused by modes of climate variability that are mis-represented in the models, or times of small forced trends. As windows of opportunity found here are generally in line with those found for uninitialized historical simulations in Borchert et al. (2021), they appear to be at least partly a result of changes in forcing, e.g., natural forcing. This conclusion likely holds for observational constraints in predictions and projections alike.

While this assessment remains mainly qualitative, it highlights the potential for better estimating sources of prediction skill when combining observation-based skill metrics in time as well as between models. The presented analysis should thus be extended to include more models, and studying the underlying physics at work in-depth to produce actionable predictions for society.

Potential for Constraining Decadal Prediction Skill of European Summer Temperature

Finally, we examine prediction skill for European surface air temperature, which is known to be difficult to predict due to small signal-to-noise ratio (e.g., Hanlon et al., 2013; Wu et al., 2019; Smith et al., 2020), yet one of our ultimate goals in terms of prediction. We contrast the skill of the different prediction systems currently available, and its change depending on time horizon, as a first step toward model weighing or selection. As in Section Constraining Projections, we use the SREX regions as a first step of homogenizing analysis methods between prediction and projection research.

We analyze the decadal prediction skill for SAT in SREX regions in CMIP6 models during summer (JJA) (Figure 10) after subtracting the linear trend. Summer temperature in SREX regions shows generally low hindcast skill for individual lead years. We find some differences between the different regions, with a tendency for higher skill toward the South. Forming the multi-model mean as a simple first step toward improving skill due to improved filtering of the signal from the noise (see above) does in fact lead to comparatively higher skill, but does not consistently elevate SREX summer temperature skill to significance at the 95% level (Figure 10). Because SPG SST was shown to impact European surface temperature during boreal summer (e.g., Gastineau and Frankignoul, 2015; Mecking et al., 2019) and hindcast skill for SREX SAT shows similar inter-model spread as for SPG SST, attempts to connect hindcast skill in individual models to inherent properties of the model (as above) is promising. The generally low (and mostly insignificant) level of skill for all models in the SREX regions indicates, however, that discriminatory features of skill between models would not enable the identification of skillful models without further treatment. Hence, further efforts such as an analysis of windows of opportunity (see Multi-Model Exploration of Windows of Opportunity) might reveal times of high prediction skill in the SREX regions in the future, indicating boundary conditions that benefit prediction skill.

FIGURE 10

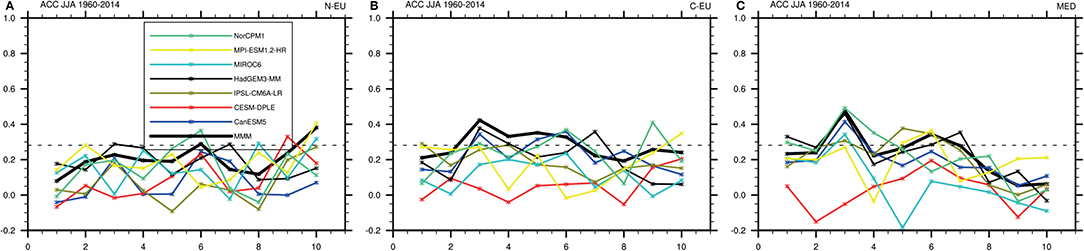
Figure 10. ACC of detrended summer (JJA) SAT in the SREX regions (A) Northern Europe, (B) Central Europe, and (C) Mediterranean (y-axis) against lead time in years (x-axis). The horizontal dashed line represents the 95% confidence level compared to climatological prediction based on a two-sided t-test.

SPG Prediction Skill as Model Weights for Projections Over Europe

Finally, we experimented with using lead-year correlations from Subpolar gyre predictions, instead of the ClimWIP performance weights, for constructing weighted multi-model mean fingerprints of the response to external forcing, and estimating their contribution to observed change using the ASK method (Section Contrasting and Combining Constraints From Different Methodologies). While the estimate of the GHG signal against other forcings remained fairly robust, we found that when using those skill weighted fingerprints, the ASK method's ability to distinguish between contributions to JJA change from different forcings degenerated sharply compared to what is shown in Figure 4, top row (not shown). This is not very surprising as it is not clear that a model's prediction skill over the SPG would necessarily relate to its skill in simulating the response to forcing over European land, but an approach like this might prove more promising in other regions and seasons.

When considering combinations of performance-based weights derived from initialized model skill and long-term projection skill, different properties of models might come into play. For example, a model that shows strong response to forcings will show a higher signal-to-noise ratio in the response, which can drive up ACC skills influenced by forcing (although, potentially, at a cost of lower MSSS). Such a model may also show higher signal-to-noise ratio in fingerprints used for attribution which also improves the constraint from the forced response. On the other hand, a model that shows too strong trends (which may improve signal-to-noise ratios) would get penalized by ClimWIP for over-simulating trends, and hence rightly be identified as less reliable for predictions. Moreover, the skill of initialized predictions is heavily dependent on lead time and time-averaging windows, which requires careful consideration when applied as a weighting scheme to climate projections. This illustrates that different approaches to use observational constraints can pull a prediction system into different directions. It would be interesting to investigate links between the reliability of projections and the skill of predictions. Presently, the limited overlap between models providing individually forced simulations necessary for ASK, and being used in initialized predictions makes it difficult to pursue this further.

Conclusions and Lessons Learnt

Observational constraints for projections may both originate from weighting schemes that weight according to performance (Knutti et al., 2017; Sanderson et al., 2017; Lorenz et al., 2018; Brunner et al., 2020b), as well as from a binary decision which models are within an observational constraint and which outside (model selection methods; see e.g., discussion in Tokarska et al., 2020b; drawing on the ASK method; and Nijsse et al., 2020). Constraining projections based on the agreement with the observed climate state can phase in modes of climate variability and add skill, similar to initialization in decadal predictions. Retrospective initialized predictions (hindcasts) are evaluated against observations using skill scores that may also provide input for performance-based model weighting. This study illustrates that the prediction skill may vary strongly with lead time, climate model, in space, with climate state and over time (Borchert et al., 2019; Christensen et al., 2020; Yeager, 2020), suggesting a careful selection of cases to choose. Similarly, performance weighting varies depending on whether trends are included in the analysis (i.e., if weights include evaluation of the forced response), or whetherthe weights are limited to performance in simulating mean climate. Constraints on future projections from attributed greenhouse warming (ASK, see Section Constraining Projections) show smaller uncertainties for targets of predictions where the signal-to-noise ratio is high compared to noisier variables, and correct implicitly for too strong or too weak a forced response compared to observations. In our view, these factors that control the skill of initialized predictions as well as the strength of observational constraints on projections need to be accounted for in upcoming attempts to combine projections and predictions, and this might complicate the seamless application of observational constraints in predictions and projections.

Overall, observational constraints on projections show substantial promise to correct for biases in the model ensemble of opportunity as illustrated from the UKCP18 example (Figure 1) as well as for other methods (Figure 2). However, several questions arise: If applied to similar model data, will different metrics for model performance favor similar traits and hence similar models? This is important when attempting to merge predictions and projections: If the choice of timescale strongly influences the model weights, or leads to selection of different models, the merged predictions might be inconsistent over time: in cases where the climate sensitivity deviates between up-weighted or selected models for projections and predictions, the merged predictions may have a discontinuous underlying climate change signal. Where high performance models show, possibly by chance, different variability dependends on choice of weights from projections or predictions, the merged predictions may also show different variability over time. It remains to be explored how detrimental a signal-strength discontinuity might be, as the signal during the initialized time horizon is still small compared to noise on all but global scales (Smith et al., 2020).

Finally, we found that observational constraints show promise and should be included in predictions and projections. This is a lesson also learned from UKCP18, where observational constraints have been used successfully in a major climate projections product, and thus influence planning and adaptation decisions based on the application. Figures 1, 2 both illustrate observational constraints and show potential to correct for model biases, such as too strong (or weak) response to forcing. However, we need to address the question to what extent observational constraints are reliable, even if they are intuitively well-justified (Weisheimer and Palmer, 2014). This is more straightforward for predictions than projections. For projections, such a ‘perfect' or ‘imperfect' model evaluation is not a trivial task, as it requires retuning the observational constraint for every model whose future performance is predicted in order to arrive at robust statistics. However, it provides powerful evaluation of observational constraints (see e.g., Schurer et al., 2018 or Brunner et al., 2020b among other recent examples).

Our analysis of initialized prediction simulations indicates that there are several dimensions (such as the change of skill over time) that add complexity when aiming to use observational constraints on climate projections combined with predictions. For an optimized constraining of merged, seamless climate prediction for the next 40 years, these dimensions need to be considered. Furthermore, initialization can introduce shocks that lead the initialized climate simulations into a different climate state to the uninitialised simulations (Bilbao et al., 2021), which can hamper attempts to merge predictions and projections, or to apply common constraints.

Questions that need to be considered when evaluating observational constraints and use them across prediction and projection timescales include:

• Is there potential to improve performance of prediction and projection systems by combining observed constraints? First results indicate that improvements may be possible, at least over projection timescales, particularly if combining climatological constraints and those based on the forced signal. This is unsurprising given that the one-model-one-vote system may well be suboptimal. However, any possible improvements need to be carefully evaluated, including in a perfect model setting. And the prediction-projection merging still requires some work.

• To what extent do weighting or model selection criteria used across projections and predictions favor similar model traits and to what extent are they uncorrelated or pull in different directions? Particularly:

• do any of the weighting schemes preferentially select or highly weight models with stronger or weaker response to forcing? This can arise if correlation skills, e.g., are influenced by response to external forcing, such as volcanism (Borchert et al., 2021). Are there any other factors where different weighting schemes select differently?

• relatedly, do any of the schemes which also draw on variability reward or penalize climate models with high or low internal climate variability, i.e., with low or high signal-to-noise ratio for external forcing or predictable signals? High variability may degrade the performance of the ASK system, but on the other hand appears to favor good performance over the subpolar gyre (Figure 8).

• which dimensions beyond the model dimension show promise in the application of observational constraints? Is there a role for lead-time dependent skill, or skill depending on climatological conditions (see Section Observational Constraints on Initialized Predictions)?

Overall, we recommend that:

• Assumptions and mechanisms behind constraining methods need to be clear and transparent (this point was also made in Brunner et al., 2020a, but only for projections).

• It needs to be clear what main model characteristics explain a constraint. Skill/high model accuracy can originate from different model properties, e.g., from strong climatological performance of models, from the representation of physical mechanisms in specific models, from realistic representation of internal climate variability or from response to external forcing, or combinations of all.

• This is particularly important when considering observational constraints across the prediction/projection boundary. Furthermore, it needs to be considered that skill may vary over time, and short hindcast periods can be misleading. On the other hand, we can increase performance by drawing on more lines of evidence but need to be wary of over fitting

• When evaluating/combining methods (for projections and across projections and predictions) we need a common and consistent test protocol for skill and reliance to ensure performance. This test protocol needs to consider all dimensions on which the skill of climate simulations varies. Combining different observational constraints may increase performance by drawing on more lines of evidence, but need to be wary of over fitting.

• It is important that consistent model versions and releases are used across the prediction/projection timeline to enable physically consistent merging for seamless prediction across the next 40 years. Carefully-designed simulations are thus required, using the same model versions for predictions and projections. Longer prediction lead times would be helpful to improve on some of the above robustness issues for bringing predictions and predictions closer together.

Last, but not least, it is important to also consider what our findings mean for users of climate information. Firstly, they illustrate that there may be a much greater information content in model prediction and projection ensembles than is first apparent when considering the raw ensemble alone to look at the spread in future conditions. Indeed, without applying constraints users may get a rather skewed view of the spread of future climate simulations. Secondly, the results show that whilst there are methods to extract this extra information they are currently affected by multiple choices around choice of constraint and how they are applied. It is recommended that studies include more focus on showing the effect of applying particular constraints, for instance using out of sample testing or the effect of windows of opportunity on constraining projections. This will help users avoid selecting approaches that provide over-confidence. Thirdly, although at an earlier stage in development, there is the growing potential for merging predictions and projections over their respective time-scales. Consideration of observational constraints is a vital part of this merging.

Data Availability Statement

The datasets analyzed for this study can be found in the CEDA archive, with derived products available on request.

Author Contributions

JMM and GRH drafted the first subsection of the section on constraints for projections, the next two sections are the result of a collaboration with LB, APB, and GCH, while the final subsection toward seamless predictions was drafted by RM, MGD, and FJD-R. LFB, JM, and DS drafted the section on initialized decadal predictions. GCH led the storyline across the manuscript and drafted the conclusions. All authors contributed to writing, and provided figures and text.

Funding

All authors were supported by the EUCP project funded by the European Commission's Horizon 2020 programme, Grant Agreement number 776613. JM was also supported by the french ANR MOPGA project ARCHANGE and by the EU-H2020 Blue Action (GA 727852) and 4C projects (GA 821003). MGD also received funding by the Spanish Ministry for the Economy, Industry and Competitiveness grant reference RYC-2017-22964.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling Editor declared a past co-authorship with several of the authors GCH, BBBB, GRH, JL, JMM, DS.

Footnotes

1. ^Bonnet R., Swingedouw D., Gastineau G., Boucher O., Deshayes J., Hourdin F., et al. (2021). Increased risk of near term global warming level due to a recent AMOC weakening. Nat. Commun. (in review).

2. ^Swingedouw, D., Bily, A., Esquerdo, C., Borchert, L. F., Sgubin, G., Mignot, M., et al. On the risk of abrupt changes in the North Atlantic subpolar gyre in CMIP6 models. Ann. NY Acad. Sci. (in review).

References

Allen, M. R., Stott, P. A., Mitchell, J. F., Schnur, R., and Delworth, T. L. (2000). Quantifying the uncertainty in forecasts of anthropogenic climate change. Nature 407, 617–620. doi: 10.1038/35036559

PubMed Abstract | CrossRef Full Text | Google Scholar

Befort, D. J., O'Reilly, C. H., and Weisheimer, A. (2020). Constraining projections using decadal predictions. Geophys. Res. Lett. 47:e2020GL087900. doi: 10.1029/2020GL087900

CrossRef Full Text | Google Scholar

Bilbao, R., Wild, S., Ortega, P., Acosta-Navarro, J., Arsouze, T., Bretonnière, A. P., et al. (2021). Assessment of a full-field initialized decadal climate prediction system with the CMIP6 version of EC-Earth, Earth System Dynamics. 12, 173–196. doi: 10.5194/esd-12-173-2021

CrossRef Full Text | Google Scholar

Bindoff, N. L., Stott, P. A., AchutaRao, K. M., Allen, M. R., Gillett, N., Gutzler, D., et al. (2013). Chapter 10 - Detection and attribution of climate change: From global to regional. In: Climate Change 2013: The Physical Science Basis. IPCC Working Group I Contribution to AR5. Cambridge: Cambridge University Press.

Google Scholar

Bo,é, J., and Terray, L. (2015). Can metric-based approaches really improve multi-model climate projections? The case of summer temperature change in France. Climate Dynamics, 45(7–8), pp.1913–1928. doi: 10.1007/s00382-014-2445-5

CrossRef Full Text | Google Scholar

Boer, G. J., Smith, D. M., Cassou, C., Doblas-Reyes, F., Danabasoglu, G., Kirtman, B., et al. (2016). The Decadal Climate Prediction Project (DCPP) contribution to CMIP6. Geosci. Model Dev. 9, 3751–3777. doi: 10.5194/gmd-9-3751-2016

CrossRef Full Text | Google Scholar

Booth, B. B. B., Harris, G. R., Murphy, J. M., House, J. I., Jones, C. D., Sexton, D. M. H., et al. (2017). Narrowing the range of future climate projections using historical observations of atmospheric CO₂. J. Clim. 30, 3039–3053. doi: 10.1175/jcli-d-16-0178.1

CrossRef Full Text | Google Scholar

Borchert, L. F., Düsterhus, A., Brune, S., Müller, W. A., and Baehr, J. (2019). Forecast-oriented assessment of decadal hindcast skill for North Atlantic SST. Geophys. Res. Lett. 46, 11444–11454. doi: 10.1029/2019GL084758

CrossRef Full Text | Google Scholar

Borchert, L. F., Menary, M. B., Swingedouw, D., Sgubin, G., Hermanson, L., and Mignot, J. (2021). Improved decadal predictions of North Atlantic subpolar gyre SST in CMIP6. Geophys. Res. Lett. 48:e2020GL091307. doi: 10.1029/2020GL091307

CrossRef Full Text | Google Scholar

Borchert, L. F., Müller, W. A, and Baehr, J. (2018). Atlantic ocean heat transport influences interannual-to-decadal surface temperature predictability in the north atlantic region. Climate J. 31, 6763–6782. doi: 10.1175/JCLI-D-17-0734.1

CrossRef Full Text | Google Scholar

Boucher, O., Servonnat, J., Albright, A. L., Aumont, O., Balkanski, Y., Bastrikov, V., et al. (2020). Presentation and evaluation of the IPSL-CM6A-LR climate model. J. Adv. Model. Earth Syst. 12:e2019MS002010. doi: 10.1029/2019MS002010

CrossRef Full Text | Google Scholar

Braganza, K., Karoly, D. J., Hirst, A. C., Mann, M. E., Stott, P., Stouffer, R. J., et al. (2003). Simple indices of global climate variability and change: part I — variability and correlation structure. Clim. Dyn. 20, 491–502. doi: 10.1007/s00382-002-0286-0

CrossRef Full Text | Google Scholar

Bretherton, C. S., and Caldwell, P. M. (2020). Combining Emergent Constraints for Climate Sensitivity, Journal of Climate. 33, 7413–7430.

Google Scholar

Brient, F. (2020). Reducing uncertainties in climate projections with emergent constraints: concepts, examples and prospects. Adv. Atmos. Sci. 37, 1–15. doi: 10.1007/s00376-019-9140-8

CrossRef Full Text | Google Scholar

Brune, S., and Baehr, J. (2020). Preserving the coupled atmosphere–ocean feedback in initializations of decadal climate predictions. WIREs Clim Change. 11:e637. doi: 10.1002/wcc.637

CrossRef Full Text | Google Scholar

Brunner, L., Lorenz, R., Zumwald, M., and Knutti, R. (2019). Quantifying uncertainty in European climate projections using combined performance-independence weighting. Environ. Res. Lett. 14:124010. doi: 10.1088/1748-9326/ab492f

CrossRef Full Text | Google Scholar

Brunner, L., McSweeney, C., Ballinger, A. P., Befort, D. J., Benassi, M., Booth, B., et al. (2020a). Comparing methods to constrain future european climate projections using a consistent framework. J. Climate. 33, 8671–8692. doi: 10.1175/jcli-d-19-0953.1

CrossRef Full Text | Google Scholar

Brunner, L., Pendergrass, A. G., Lehner, F., Merrifield, A. L., Lorenz, R., and Knutti, R. (2020b). Reduced global warming from CMIP6 projections when weighting models by performance and independence. Earth Syst. Dynam. Discuss. 11, 995–1012. doi: 10.5194/esd-2020-23

CrossRef Full Text | Google Scholar

Caldwell, P. M., Zelinka, M. D., and Klein, S. A. (2018). Evaluating emergent constraints on equilibrium climate sensitivity. J. Climate 31, 3921–3942. doi: 10.1175/JCLI-D-17-0631.1

CrossRef Full Text | Google Scholar

Christensen, H. M., Berner, J., and Yeager, S. (2020). The value of initialization on decadal timescales: state-dependent predictability in the CESM decadal prediction large ensemble. Climate J. 33, 7353–7370. doi: 10.1175/JCLI-D-19-0571.1

CrossRef Full Text | Google Scholar

Collins, M., Knutti, R., Arblaster, J., Dufresne, J.-L., Fichefet, T., Friedlingstein, P., et al. (2013). “Long-term climate change: projections, commitments and irreversibility,” in Climate Change: 2013 Physical Science Basis, ed T. Stocker et al. (Cambridge: Cambridge University Press), 1029–1136. doi: 10.1017/CBO9781107415324.024

CrossRef Full Text | Google Scholar

Counillon, F., Keenlyside, N., Toniazzo, T., Koseki, S., Demissie, T., Bethke, I., et al. (2021). Relating model bias and prediction skill in the equatorial Atlantic. Clim. Dyn. 56, 2617–2630. doi: 10.1007/s00382-020-05605-8

CrossRef Full Text | Google Scholar

Danabasoglu, G., Lamarque, J.-F., Bacmeister, J., Bailey, D. A., DuVivier, A. K., Edwards, J., et al. (2020). The community earth system model version 2 (CESM2). J. Adv. Model. Earth Syst. 12:e2019MS001916. doi: 10.1029/2019MS001916

CrossRef Full Text | Google Scholar

DelSole, T., Trenary, L., Yan, X., et al. (2019). Confidence intervals in optimal fingerprinting. Clim. Dyn. 52, 4111–4126. doi: 10.1007/s00382-018-4356-3

CrossRef Full Text | Google Scholar

Ding, H., Newman, M., Alexander, M. A., and Wittenberg, A. T. (2018). Skillful climate forecasts of the tropical Indo-Pacific Ocean using model-analogs. J. Climate. 31, 5437–5459. doi: 10.1175/JCLI-D-17-0661.1

CrossRef Full Text | Google Scholar

Donat, M., Pitman, A. J., and Angélil, O. (2018). Understanding and reducing future uncertainty in midlatitude daily heat extremes via land surface feedback constraints. Geophys. Res. Lett. 45, 10627–10636. doi: 10.1029/2018GL079128

CrossRef Full Text | Google Scholar

Estella-Perez, V., Mignot, J., Guilyardi, E., Swingedouw, D., and Reverdin, G. (2020). Advances in reconstructing the AMOC using sea surface observations of salinity. Clim. Dyn. 55, 975–992. doi: 10.1007/s00382-020-05304-4

CrossRef Full Text | Google Scholar

Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958. doi: 10.5194/gmd-9-1937-2016

CrossRef Full Text | Google Scholar

Forster, P. M., Maycock, A. C., McKenna, C. M., and Smith, C. J. (2020). Latest climate models confirm need for urgent mitigation. Nat. Clim. Change 10, 7–10. doi: 10.1038/s41558-019-0660-0

CrossRef Full Text | Google Scholar

Gastineau, G., and Frankignoul, C. (2015). Influence of the north atlantic sst variability on the atmospheric circulation during the twentieth century. Clim. J. 28, 1396–1416. doi: 10.1175/JCLI-D-14-00424.1

CrossRef Full Text | Google Scholar

Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., et al. (2017). The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). Clim. J. 30, 5419–5454. doi: 10.1175/JCLI-D-16- 0758.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Gidden, M., Riahi, K., Smith, S., Fujimori, S., Luderer, G., Kriegler, E., et al. (2019). Global emissions pathways under different socioeconomic scenarios for use in CMIP6: a dataset of harmonized emissions trajectories through the end of the century. Geosci. Model Dev. Discus. 12, 1443–1475. doi: 10.5194/gmd-2018-266

CrossRef Full Text | Google Scholar

Gillett, N. P., Kirchmeier-Young, M., Ribes, A., Shiogama, H., Hegerl, G. C., Knutti, R., et al. (2021). Constraining human contributions to observed warming since the pre-industrial period. Nat. Clim. Chang. 11, 207–212. doi: 10.1038/s41558-020-00965-9

CrossRef Full Text | Google Scholar

Gillett, N. P., Shiogama, H., Funke, B., Hegerl, G., Knutti, R., Matthes, K., et al. (2016). The detection and attribution model intercomparison project (DAMIP v1.0) contribution to CMIP6. Geosci. Model Dev. 9, 3685–3697. doi: 10.5194/gmd-9-3685-2016

CrossRef Full Text | Google Scholar

Giorgi, F., and Mearns, L. O. (2002). Calculation of average, uncertainty range, and reliability of regional climate changes from AOGCM simulations via the “Reliability Ensemble Averaging” (REA) method. J. Climate. 15, 1141–1158.

Google Scholar

Hall, A., Cox, P., Huntingford, C., and Klein, S. (2019). Progressing emergent constraints on future climate change. Nat. Clim. Change. 9, 269–278. doi: 10.1038/s41558-019-0436-6

CrossRef Full Text | Google Scholar

Hall, A., and Qu, X. (2006). Using the current seasonal cycle to constrain snow albedo feedback in figure climate change. Geophys. Res. Lett. 33:L03502. doi: 10.1029/2005GL025127

CrossRef Full Text | Google Scholar

Hanlon, H. M., Morak, S., and Hegerl, G. C. (2013). Detection and prediction of mean and extreme European summer temperatures with a multimodel ensemble. J. Geophys. Res. Atmos. 118, 9631–9641. doi: 10.1002/jgrd.50703

CrossRef Full Text | Google Scholar

Harris, G. R., Sexton, D. M. H., Booth, B. B. B., Collins, M., and Murphy, J. M. (2013). Probabilistic projections of transient climate change. Clim. Dyn. 40:2937. doi: 10.1007/s00382-012-1647-y

CrossRef Full Text | Google Scholar

Haylock, M., Hofstra, N., Klein Tank, A. M. G., and Klok, E. J. (2008). A European daily high-resolution gridded dataset of surface temperature, precipitation and sea-level pressure. J. Geophys. Res. 113:D20119. doi: 10.1029/2008JD010201

CrossRef Full Text | Google Scholar

Hegerl, G., and Zwiers, F. (2011). Use of models in detection and attribution of climate change. Wiley Interdisc. Rev. Clim. Change. 2, 570–591. doi: 10.1002/wcc.121

CrossRef Full Text | Google Scholar

Henley, B. J., Gergis, J., Karoly, D. J., Power, S., Kennedy, J., and Folland, C. K. (2015). Tripole index for the interdecadal pacific oscillation. Clim. Dyn. 45, 3077–3090. doi: 10.1007/s00382-015-2525-1

CrossRef Full Text | Google Scholar

Hermanson, L., Bilbao, R., Dunstone, N., Ménégoz, M., Ortega, P., Pohlmann, H., et al. (2020). Robust multiyear climate impacts of volcanic eruptions in decadal prediction systems. J. Geophys. Res. Atmosph. 125:e2019JD031739. doi: 10.1029/2019JD031739

CrossRef Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muãoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

CrossRef Full Text | Google Scholar

Ingleby, B., and Huddleston, M. (2007). Quality control of ocean temperature and salinity profiles - historical and realtime data. J. Mar. Syst. 65, 158–175. doi: 10.1016/j.jmarsys.2005.11.019

CrossRef Full Text | Google Scholar

Jolliffe, I. T., and Stephenson, D. B. (2003). Forecast Verification. A Practitioner's Guide in Atmospheric Science. Hoboken: John Wiley & Sons Ltd., 240.

Google Scholar

Kataoka, T., Tatebe, H., Koyama, H., Mochizuki, T., Ogochi, K., Naoe, H., et al. (2020). Seasonal to decadal predictions with MIROC6: description and basic evaluation. J. Adv. Model. Earth Syst. 12:e2019MS002035. doi: 10.1029/2019MS002035

CrossRef Full Text | Google Scholar

Kay, J. E., Deser, C., Phillips, A., Mai, A., Hannay, C., Strand, G., et al. (2015). The Community Earth System Model (CESM) Large Ensemble project: a community resource for studying climate change in the presence of internal climate variability. Bull. Amer. Meteor. Soc. 96, 1333–1349. doi: 10.1175/BAMS-D-13-00255.1

CrossRef Full Text | Google Scholar

Kendon, M., McCarthy, M., Jevrejeva, S., Matthews, A., and Legg, T. (2019). State of the UK climate 2018. Int J Climatol. 39 (Suppl. 1), 1–55. doi: 10.1002/joc.6213

CrossRef Full Text | Google Scholar

Kettleborough, J. A., Booth, B. B, Stott, P. A., and Allen, M. R. (2007). Estimates of uncertainty in predictions of global mean surface temperature. Clim. J. 20, 843–855. doi: 10.1175/JCLI4012.1

CrossRef Full Text | Google Scholar

Kim, W. M., Yeager, S., Chang, P., and Danabasoglu, G. (2018). Low-frequency north atlantic climate variability in the community earth system model large ensemble. J. Clim. 31, 787–813. doi: 10.1175/JCLI-D-17-0193.1

CrossRef Full Text | Google Scholar

Knight, J. R., Andrews, M. B., Smith, D. M., Arribas, A., Colman, A. W., Dunstone, N. J., et al. (2014). Predictions of climate several years ahead using an improved decadal prediction system. J. Clim. 27, 7550–7567. doi: 10.1175/JCLI-D-14-00069.1

CrossRef Full Text | Google Scholar

Knutti, R. (2010). The end of model democracy? Clim. Change 102, 395–404. doi: 10.1007/s10584-010-9800-2

CrossRef Full Text | Google Scholar

Knutti, R., Allen, M. R., Friedlingstein, P., Gregory, J. M., Hegerl, G. C., Meehl, G. A., et al. (2008). A review of uncertainties in global temperature projections over the twenty-first century. J. Clim. 21, 2651–2663. doi: 10.1175/2007JCLI2119.1

CrossRef Full Text | Google Scholar

Knutti, R., Masson, D., and Gettelman, A. (2013). Climate model genealogy: CMIP5 and how we got there. GRL 40, 1194–1199. doi: 10.1002/grl.50256

CrossRef Full Text | Google Scholar

Knutti, R., Sedláček, J., Sanderson, B. M., Lorenz, R., Fischer, E. M., and Eyring, V. (2017). A climate model projection weighting scheme accounting for performance and interdependence. Geophys. Res. Lett. 44, 1909–1918. doi: 10.1002/2016GL072012

CrossRef Full Text | Google Scholar

Lorenz, R., Herger, N., Sedláček, J., Eyring, V., Fischer, E. M., and Knutti, R. (2018). Prospects and caveats of weighting climate models for summer maximum temperature projections over north america. J. Geophys. Res. Atmosph. 123, 4509–4526. doi: 10.1029/2017JD027992

CrossRef Full Text | Google Scholar

Mariotti, A., Baggett, C., Barnes, E. A., Becker, E., Butler, A., Collins, D. C., et al. (2020). Windows of opportunity for skillful forecasts subseasonal to seasonal and beyond. Bull. Amer. Meteor. Soc. 101, E608–E625. doi: 10.1175/BAMS-D-18-0326.1

CrossRef Full Text | Google Scholar

Marotzke, J., Müller, W. A., Vamborg, F. S. E., Becker, P., Cubasch, U., et al. (2016). MiKlip: a national research project on decadal climate prediction. Bull. Am. Meteorol. Soc. 97, 2379–2394. doi: 10.1175/BAMS-D-15-00184.1

CrossRef Full Text | Google Scholar

Mecking, J. V., Drijfhout, S. S. J. J.-M, and Hirschi Blaker, A. T. (2019). Ocean and atmosphere influence on the 2015 European heatwave. Environ. Res. Lett. 14:114035. doi: 10.1088/1748-9326/ab4d33

CrossRef Full Text | Google Scholar

Meehl, G. A., Goddard, L., Murphy, J., Stouffer, R. J., Boer, G., Danabasoglu, G., et al. (2009). Decadal prediction: can it be skillful? BAMS 2009, 1467–1486. doi: 10.1175/2009BAMS2778.1

CrossRef Full Text | Google Scholar

Meehl, G. A., Richter, J. H., Teng, H., Capotondi, A, Cobb, k., Doblas-Reyes, F., et al. (2021). Initialized Earth System prediction from subseasonal to decadal timescales. Nat. Rev. Earth Environ. 2, 340–357. doi: 10.1038/s43017-021-00155-x

CrossRef Full Text | Google Scholar

Menary, M. B., and Hermanson, L. (2018). Limits on determining the skill of north atlantic ocean decadal predictions. Nat. Commun. 9:1694. doi: 10.1038/s41467-018-04043-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Merrifield, A. L., Brunner, L., Lorenz, R., Medhaug, I., and Knutti, R. (2020). An investigation of weighting schemes suitable for incorporating large ensembles into multi-model ensembles. Earth System Dyn. 11, 807–834. doi: 10.5194/esd-11-807-2020

CrossRef Full Text | Google Scholar

Merryfield, W. J., Baehr, J., Batté, L., Becker, E. J., Butler, A. H., Coelho, C. A., et al. (2020). Current and emerging developments in subseasonal to decadal prediction. Bull. Am. Meteorol. Soc. 101, E869–E896. doi: 10.1175/BAMS-D-19-0037.1

CrossRef Full Text | Google Scholar

Morice, C. P., Kennedy, J. J., Rayner, N. A., and Jones, P. D. (2012). Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. J. Geophys. Res. 117:D08101. doi: 10.1029/2011JD017187

CrossRef Full Text | Google Scholar

Murphy, J. M., Harris, G. R., Sexton, D. M. H., Kendon, E. J., Bett, P. E., Clark, R. T., et al (2018). UKCP18 Land Projections: Science Report. Exeter: Met Office Hadley Centre. Available online at: https://www.metoffice.gov.uk/pub/data/weather/uk/ukcp18/science-reports/UKCP18-Land-report.pdf

Google Scholar

Murphy, L. N., Bellomo, K., Cane, M., and Clement, A. (2017). The role of historical forcings in simulating the observed Atlantic multidecadal oscillation. Geophys. Res. Lett. 44, 2472–2480. doi: 10.1002/2016GL071337

CrossRef Full Text | Google Scholar

Nijsse, F., Cox, P., and Williamson, M. (2020). An emergent constraint on Transient Climate Response from simulated historical warming in CMIP6 models. Earth Syst. Dynamics 1–14. doi: 10.5194/esd-2019-86

CrossRef Full Text | Google Scholar

Pohlmann, H., Botzet, M., Latif, M., Roesch, A., Wild, M., and Tschuck, P. (2005). Estimating the decadal predictability of a coupled AOGCM. J. Climate. 17, 4463–4472. doi: 10.1175/3209.1

CrossRef Full Text | Google Scholar

Pohlmann, H., Müller, W. A., Bittner, M., Hettrich, S., Modali, K., Pankatz, K., et al. (2019). Realistic quasi-biennial oscillation variability in historical and decadal hindcast simulations using CMIP6 forcing. Geophys. Res. Lett. 46, 14118–14125. doi: 10.1029/2019GL084878

CrossRef Full Text | Google Scholar

Rayner, N. A., Parker, D. E., Horton, E. B., Folland, C. K., Alexander, L. V., Rowell, D. P., et al. (2003). Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 108, 4407. doi: 10.1029/2002JD002670,D14

CrossRef Full Text | Google Scholar

Ribes, A., Qasmi, S., and Gillett, N. P. (2021). Making climate projections conditional on historical observations. Sci. Adv. 7:eabc0671. doi: 10.1126/sciadv.abc0671

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanderson, B. M., Pendergrass, A., Koven, C. D., Brient, F., Booth, B. B. B., Fisher, R. A., et al. (2021). On structural errors in emergent constraints. Earth Syst. Dynamics (in review). doi: 10.5194/esd-2020-85

CrossRef Full Text | Google Scholar

Sanderson, B. M., Wehner, M., and Knutti, R. (2017). Skill and independence weighting for multi-model assessments. Geo. Sci. RModel Dev. 10, 2379–2395. doi: 10.5194/gmd-10-2379-2017

CrossRef Full Text | Google Scholar

Schurer, A., Hegerl, G., Ribes, A., Polson, D., Morice, C., and Tett, S. (2018). Estimating the transient climate response from observed warming. J. Clim. 31, 8645–8663. doi: 10.1175/JCLI-D-17-0717.1

CrossRef Full Text | Google Scholar

Sexton, D. M., and Harris, G. R. (2015). The importance of including variability in climate change projections used for adaptation. Nat. Clim. Change. 5, 931–936. doi: 10.1038/nclimate2705

CrossRef Full Text | Google Scholar

Sexton, D. M. H., Murphy, J. M., Collins, M., and Webb, M. J. (2012). Multivariate probabilistic projections using imperfect climate models, Part I: outline of methodology. Clim. Dyn. 38:2513. doi: 10.1007/s0038201112089

CrossRef Full Text | Google Scholar

Sgubin, G., Swingedouw, D., Drijfhout, S., Mary, Y., and Bennabi, A. (2017). Abrupt cooling over the North Atlantic in modern climate models. Nat. Commun. 8:14375. doi: 10.1038/ncomms14375

PubMed Abstract | CrossRef Full Text | Google Scholar

Sherwood, S. C., Webb, M. J., Annan, J. D., Armour, K. C., Forster, P. M., Hargreaves, J. C., et al. (2020). An assessment of Earth's climate sensitivity using multiple lines of evidence. Rev. Geophys. 58:e2019RG000678. doi: 10.1029/2019RG000678

PubMed Abstract | CrossRef Full Text | Google Scholar

Shin, J., Park, S., Shin, S.-I., Newman, M., and Alexander, M. (2020). Enhancing ENSO prediction skill by combining model analog and linear inverse models (MA-LIM). Geophys. Res. Lett. 47:e2019GL085914. doi: 10.1029/2019GL085914

CrossRef Full Text | Google Scholar

Shiogama, H., Stone, D., Emori, S., et al. (2016). Predicting future uncertainty constraints on global warming projections. Sci. Rep. 6, 18903. doi: 10.1038/srep18903

PubMed Abstract | CrossRef Full Text | Google Scholar

Sippel, S., Zscheischler, J., Mahecha, M. D, Orth, R, Reichstein, M., Vogel, M., et al. (2017). Refining multi-model projections of temperature extremes by evaluation against land–atmosphere coupling diagnostics. Earth Syst. Dynam. 8, 387–403. doi: 10.5194/esd-8-387-2017

CrossRef Full Text | Google Scholar

Smith, D., Eade, R., and Pohlmann, H. (2013). A comparison of full-field and anomaly initialization for seasonal to decadal climate prediction. Clim. Dyn. 41, 3325–3338.

Google Scholar

Smith, D. M., Scaife, A. A., Eade, R., Athanasiadis, P., Bellucci, A., Bethke, I., et al. (2020). North Atlantic climate far more predictable than models imply. Nature 583, 796–800. doi: 10.1038/s41586-020-2525-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sospedra-Alfonso, R., and Boer, G. J. (2020). Assessing the impact of initialization on decadal prediction skill. Geophys. Res. Lett. 47:e2019GL086361. doi: 10.1029/2019GL086361

CrossRef Full Text | Google Scholar

Stainforth, D. A. (2005). Uncertainty in predictions of the climate response to rising levels of greenhouse gases. Nature 433, 403–406. doi: 10.1038/nature03301

PubMed Abstract | CrossRef Full Text | Google Scholar

Stott, P. A., and Kettleborough, J. A. (2002). Origins and estimates of uncertainty in predictions of twenty-first century temperature rise. Nature, 416, 723–726. doi: 10.1038/416723a

PubMed Abstract | CrossRef Full Text | Google Scholar

Swingedouw, D., Mignot, J., Labetoule, S., Guilyardi, E., and Madec, G. (2013). Initialisation and predictability of the AMOC over the last 50 years in a climate model. Clim. Dyn. 40, 2381–2399. doi: 10.1007/s00382-012-1516-8

CrossRef Full Text | Google Scholar

Swingedouw, D., Ortega, P., Mignot, J., Guilyardi, E., Masson-Delmotte, V., Butler, P., et al. (2015). Bidecadal North Atlantic ocean circulation variability controlled by timing of volcanic eruptions. Nat. Commun. 6:6545. doi: 10.1038/ncomms7545

PubMed Abstract | CrossRef Full Text | Google Scholar

Tietsche, S., Balmaseda, M., Zuo, H., Roberts, C., Mayer, M., and Ferranti, L. (2020). The importance of North Atlantic Ocean transports for seasonal forecasts. Clim. Dyn. 55, 1995–2011. doi: 10.1007/s00382-020-05364-6

CrossRef Full Text | Google Scholar

Tokarska, K., Hegerl, G. C., Schurer, A. P., Forster, P., and Marvel, K. (2020b). Observational Constraints on the effective climate sensitivity from the historical record. Environ. Res. Lett. 15:034043. doi: 10.1088/1748-9326/ab738f/pdf

CrossRef Full Text | Google Scholar

Tokarska, K. B., Stolpe, M. B., Sippel, S., Fischer, E. M., Smith, C. J., Lehner, F., et al. (2020a). Past warming trend constrains future warming in CMIP6 models. Sci. Adv. 6:eaaz9549. doi: 10.1126/sciadv.aaz9549

PubMed Abstract | CrossRef Full Text | Google Scholar

Weigel, A. A. P., Knutti, R., Liniger, M. A., and Appenzeller, C. (2010). Risks of model weighting in multimodel climate projections. J. Clim. 23, 4175–4191. doi: 10.1175/2010jcli3594.1

CrossRef Full Text | Google Scholar

Weisheimer, A., and Palmer, T. N. (2014). On the Reliability of Seasonal Climate Forecasts. J. R. Soc. Interface. 11:9620131162. doi: 10.1098/rsif.2013.1162

CrossRef Full Text | Google Scholar

Wu, B., Zhou, T., Li, C., Müller, W. A., and Lin, J. (2019). Improved decadal prediction of Northern-Hemisphere summer land temperature. Clim. Dyn. 53, 1–13. doi: 10.1007/s00382-019-04658-8

CrossRef Full Text | Google Scholar

Yeager, S. (2020). The abyssal origins of North Atlantic decadal predictability. Clim. Dyn. 55, 2253–2271. doi: 10.1007/s00382-020-05382-4

CrossRef Full Text | Google Scholar

Yeager, S. G., Danabasoglu, G., Rosenbloom, N.A, Strand, W., Bates, S. C., Meehl, G. A., et al. (2018). A large ensemble of initialized decadal prediction simulations using the community earth system model. Bull. Amer. Meteor. Soc. 99, 1867–1886. doi: 10.1175/BAMS-D-17-0098.2

CrossRef Full Text | Google Scholar

Yeager, S. G., and Robson, J. I. (2017). Recent progress in understanding and predicting atlantic decadal climate variability. Curr. Clim. Change Rep. 3, 112–127. doi: 10.1007/s40641-017-0064-z

PubMed Abstract | CrossRef Full Text | Google Scholar